A Comparative Analysis of Decision Trees, Neural Networks, and Bayesian Networks: Methodological Insights and Practical Applications in Machine Learning

Richard Murdoch Montgomery

doi:10.20944/preprints202410.1491.v1

Submitted:

18 October 2024

Posted:

19 October 2024

You are already at the latest version

Abstract

This paper provides an in-depth comparative analysis of three prominent machine learning techniques: decision trees, neural networks, and Bayesian networks. Each method is explored in terms of its theoretical foundations, algorithmic structure, strengths, limitations, and real-world applications. Decision trees are celebrated for their simplicity and interpretability, making them ideal for decision-making systems, but they often struggle with overfitting and poor performance on high-dimensional data. Neural networks, while capable of achieving high accuracy and effectively handling complex, non-linear patterns, are criticized for their "black-box" nature and computational intensity. Bayesian networks distinguish themselves through their ability to model uncertainty and incorporate prior knowledge, making them highly applicable in scenarios requiring probabilistic reasoning, yet they are challenging to scale for complex, high-dimensional data sets. This comparative analysis highlights the distinctive advantages of each method, their performance across various domains such as healthcare, finance, and risk assessment, and the growing potential of hybrid models that combine the strengths of these techniques. The paper concludes by discussing future research opportunities, particularly in enhancing model interpretability and scalability while addressing domain-specific challenges.

Keywords:

Decision Trees

;

Neural Networks

;

Bayesian Networks

;

Machine Learning

;

Classification

;

Regression

;

Interpretability

;

Probabilistic Models

;

Hybrid Models

;

Artificial Intelligence

Subject:

Computer Science and Mathematics - Artificial Intelligence and Machine Learning

Section 1. Introduction

Machine learning has become a cornerstone of modern artificial intelligence, driving innovations across industries ranging from healthcare to finance and beyond. At the heart of machine learning are algorithms that allow systems to learn from data and make predictions or decisions. Among the many machine learning techniques available, decision trees, neural networks, and Bayesian networks are particularly notable due to their diverse methodologies and widespread applications. Each of these techniques represents a distinct approach to learning, offering unique strengths and challenges, making their comparative study essential for understanding their most appropriate applications.

Section 1.1 Decision Trees

Decision Trees are one of the most interpretable machine learning algorithms, structured as a hierarchical model in which data is split into branches according to a series of conditions based on feature values. The tree grows through a recursive process where decisions are made at each node, ultimately leading to a prediction at the leaf nodes (Quinlan, 1986). Decision trees are prized for their simplicity and ease of use, particularly in situations where interpretability is paramount, such as medical diagnosis (Safavian & Landgrebe, 1991). However, decision trees can be prone to overfitting, especially with small datasets, and may struggle to handle high-dimensional data efficiently. Techniques such as pruning and ensemble methods (e.g., Random Forests) have been developed to mitigate some of these limitations (Breiman, 2001).

Section 1.2 Neural Networks

In contrast, Neural Networks are powerful models inspired by the structure of the human brain, capable of capturing complex non-linear relationships in data. Neural networks consist of layers of interconnected neurons, with each neuron representing a simple computational unit that processes input data through a set of learned weights and activation functions (Rumelhart et al., 1986). The multi-layered architecture allows neural networks to excel in tasks such as image recognition, natural language processing, and other areas requiring deep learning. Despite their effectiveness, neural networks are often criticized for their "black-box" nature—meaning that it can be difficult to interpret how they arrive at their predictions (Lipton, 2018). Additionally, they require substantial computational resources and large datasets for training, which can be prohibitive in certain applications.

Section 1.3 Bayesian Networks

Bayesian Networks represent a fundamentally different approach by utilizing probabilistic models to capture relationships between variables. These models are built upon Bayes' theorem, which allows for the incorporation of prior knowledge into the learning process. Bayesian networks represent conditional dependencies between variables using a directed acyclic graph, making them particularly useful in decision-making under uncertainty, risk assessment, and domains where understanding the probabilistic relationships between variables is crucial (Pearl, 1988). One of their key advantages is their ability to handle missing data and incorporate expert knowledge, which makes them highly applicable in fields such as healthcare and biological systems (Heckerman, 1998). However, constructing Bayesian networks for complex, high-dimensional datasets is often a challenge, as the computational cost of learning the network structure can be substantial (Koller & Friedman, 2009).

Each of these methods—decision trees, neural networks, and Bayesian networks—offers distinct benefits and is suited to particular types of problems. Decision trees are favored for their interpretability, neural networks for their accuracy in complex tasks, and Bayesian networks for their capacity to manage uncertainty and integrate domain expertise. This paper will explore these methods in greater depth, comparing their strengths, limitations, and applicability across various fields. By understanding the nuances of these techniques, practitioners can better determine which method is best suited to a given task, or how hybrid models might combine their advantages to overcome individual limitations.

Section 2. Methodology

In this section, we present the mathematical foundations of decision trees, neural networks, and Bayesian networks. Each method's underlying equations are described, providing a formal understanding of their mechanisms.

Section 2.1. Decision Trees

A decision tree is a recursive partitioning of the feature space into subsets that are more homogeneous with respect to the target variable. The decision at each node is based on a feature and a threshold, aiming to maximize some measure of "purity." The two most common metrics for evaluating splits are Information Gain and the Gini Index.

Section 2.1.1 Information Gain (IG)

1.: Information Gain and Entropy

In decision trees, entropy is a measure of impurity or uncertainty in a dataset. The entropy

H (S)

of a set

S

is defined as:

H (S) = - \sum_{i = 1}^{n} p_{i} {l o g}_{2} (p_{i})

where:

$p_{i}$ is the proportion of instances of class $i$ in the set $S$ ,
$n$ is the total number of distinct classes.

The information gain (IG) of a split on an attribute

A

is the reduction in entropy and is expressed as:

I G (S, A) = H (S) - \sum_{v \in Values (A)} \frac{|S_{v}|}{| S |} H (S_{v})

where:

$S_{v}$ is the subset of $S$ where attribute $A$ takes the value $v$ ,
$| S |$ is the size of the set $S$ ,
$H (S_{v})$ is the entropy of the subset $S_{v}$ .

2.: Gini Index

Another common impurity measure is the Gini Index, which is used to assess the quality of a split. It is defined as:

G i n i (S) = 1 - \sum_{i = 1}^{n} p_{i}^{2}

where

p_{i}

represents the proportion of instances of class

i

in set

S

, and

n

is the number of classes. The optimal split is chosen by minimizing the weighted Gini Index over the child nodes resulting from the split.

3.: Neural Networks

A neural network consists of layers of interconnected neurons. Each neuron computes a weighted sum of its inputs, followed by an activation function. For a neuron

j

in layer

l

, the output

a_{j}^{(l)}

is computed as:

The weighted sum of inputs:

z_{j}^{(l)} = \sum_{i = 1}^{n} w_{i j}^{(l)} a_{i}^{(l - 1)} + b_{j}^{(l)}

where:

$w_{i j}^{(l)}$ are the weights connecting neuron $i$ in layer $l - 1$ to neuron $j$ in layer $l$ ,
$a_{i}^{(l - 1)}$ is the output of neuron $i$ in the previous layer $l - 1$ ,
$b_{j}^{(l)}$ is the bias for neuron $j$ in layer $l$ .

2.: The activation function $ϕ$ is applied to the weighted sum:

a_{j}^{(l)} = ϕ (z_{j}^{(l)})

Common choices for the activation function $ϕ$ include:

Sigmoid: $σ (z) = \frac{1}{1 + e^{- z}}$ ,
ReLU: $m a x (0, z)$ ,
Hyperbolic tangent: $t a n h (z)$ .

4.: Loss Function

In the context of binary classification, the network is trained by minimizing the binary cross-entropy loss. The loss function is defined as:

L = - \frac{1}{m} \sum_{i = 1}^{m} [y^{(i)} l o g {\hat{y}}^{(i)} + (1 - y^{(i)}) l o g (1 - {\hat{y}}^{(i)})]

where:

$m$ is the number of training examples,
$y^{(i)}$ is the true label for example $i$ ,
${\hat{y}}^{(i)}$ is the predicted probability for example $i$ .

5.: Backpropagation and Weight Update

The network weights are updated during training using gradient descent. The update rule for the weight

w_{i j}^{(l)}

at layer

l

is:

w_{i j}^{(l)} : = w_{i j}^{(l)} - η \frac{\partial L}{\partial w_{i j}^{(l)}}

where:

$η$ is the learning rate,
$\frac{\partial L}{\partial w_{i j}^{(l)}}$ is the gradient of the loss function with respect to the weight $w_{i j}^{(l)}$ .

This process of calculating gradients using the chain rule is known as backpropagation, which propagates the errors backward through the network to update the weights.

This structured approach clarifies the mathematical foundation of entropy, Gini Index, neural networks, and the backpropagation algorithm.

Section 2.1.2 Key Elements of the Decision Tree Visualization

1.

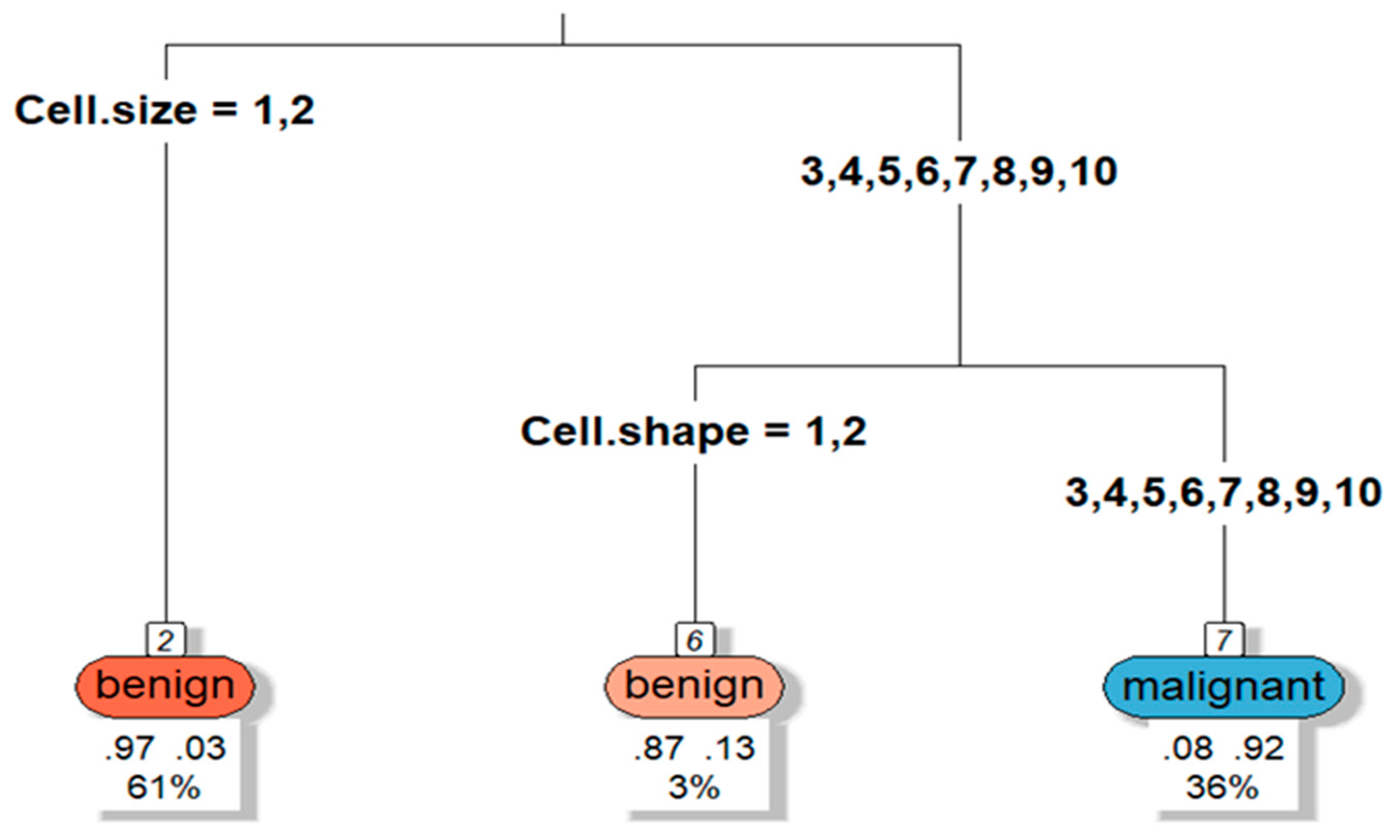
Nodes: Each node in the tree represents a decision or test based on one of the features (e.g., Clump Thickness, Cell Size, etc.). The tree splits the data into two groups at each node based on the values of these features.

2.

Root Node: The topmost node is the root node, which is the first decision point that splits the dataset. The feature that gives the best split (based on metrics like Gini impurity or entropy) is chosen for this node.

3.

Splitting Criteria: The nodes further down the tree represent additional splits on other features. The decision tree algorithm tries to find the most "informative" splits to partition the dataset into homogeneous subsets—those that are either mostly benign or mostly malignant.

4.

Leaf Nodes: These are the terminal nodes of the tree. A leaf node contains the final classification outcome (either benign or malignant in the Breast Cancer dataset). Each leaf node will also display:

○: Predicted Class: This is the class (benign or malignant) predicted by the tree for the instances that reach this leaf.
○: Class Probability: The probability that an instance in this node belongs to the predicted class (e.g., 95% benign, 5% malignant).
○: Number of Observations: The number of instances (patients) that fall into this node.

Example of a Node Description:

If a node splits based on "Clump Thickness" (a feature in the dataset), it might look like this:

Clump Thickness <= 3.5: If the value of Clump Thickness is less than or equal to 3.5, the instances will go down one branch; otherwise, they will go down the other branch.
The tree continues to split the data at each node until it reaches a leaf, where a final classification is made.

Figure 1. Decision Tree example. Source: Author.

Interpretation of the Visualization:

1.

Predictive Path: To classify a new instance (patient) using the decision tree, you would follow a path from the root node to a leaf node by making sequential decisions at each node based on the feature values of that instance.

2.

Class Probabilities: Each node, especially leaf nodes, shows the class probability. For example, if a leaf node has a probability of 95% for the "benign" class, it means that 95% of the patients that reach this leaf node are classified as benign, and 5% are classified as malignant.

3.

Depth of the Tree: The depth of the tree reflects how many decisions are made to reach a final classification. A deeper tree may overfit the training data by making overly specific decisions, while a shallow tree might underfit, failing to capture important patterns in the data.

Example Breakdown:

Assume the root node splits based on the feature "Clump Thickness":

If Clump Thickness <= 3.5, the patients move to the left branch, where further decisions are made based on other features.
If Clump Thickness > 3.5, the patients move to the right branch, leading to further splits or directly to a classification (e.g., malignant).

At each leaf node:

The predicted class (benign or malignant) is displayed along with the number of patients and the probability of the prediction being correct.

Tree Visualization Insights:

Important Features: The features appearing near the top of the tree (like the root node) are considered the most important, as they make the earliest splits. In the Breast Cancer dataset, features like Clump Thickness or Uniformity of Cell Size might frequently appear near the top if they are strong indicators of the cancer's malignancy.
Balanced or Unbalanced Leaves: If a leaf node shows a class probability close to 100% (e.g., 100% benign), it means that the tree has found a set of feature conditions that very strongly predict that class. If the probability is lower (e.g., 60% benign), the tree is less certain of its prediction.

Conclusion:

The decision tree visualized in this case illustrates how the model makes a sequence of decisions to classify breast cancer cases as benign or malignant based on features in the dataset. By visualizing the tree, we can understand how the model prioritizes features, how certain it is in its predictions, and how the data is split at each decision point. This interpretability is one of the main strengths of decision trees, especially in sensitive applications like medical diagnosis, where understanding the rationale behind decisions is critical (please see code in attachment section).

3.: Bayesian Networks

A Bayesian network is a probabilistic graphical model that represents a set of random variables and their conditional dependencies using a directed acyclic graph (DAG). Each node in the graph corresponds to a random variable, and the directed edges signify conditional dependencies between those variables. The joint probability distribution of the entire system can be factored as the product of conditional probabilities, based on the structure of the DAG.

Let

X = \{X_{1}, X_{2}, \dots, X_{n}\}

be a set of random variables. The joint probability distribution of these variables,

P (X_{1}, X_{2}, \dots, X_{n})

, can be written as a product of conditional probabilities in accordance with the network structure. Specifically, it is expressed as:

P (X_{1}, X_{2}, \dots, X_{n}) = \prod_{i = 1}^{n} P (X_{i} ∣ P a r e n t s (X_{i}))

where Parents

(X_{i})

denotes the set of variables that are the direct predecessors (or "parents") of

X_{i}

in the DAG. Each term in this product represents the conditional probability of

X_{i}

, given its parents in the network.

Inference in a Bayesian network involves calculating the posterior distribution of a subset of variables given observed evidence. This process is commonly handled using Bayes' Theorem. For a given variable

X_{i}

and a set of observed evidence

E

, the posterior probability

P (X_{i} ∣ E)

is computed as:

P (X_{i} ∣ E) = \frac{P (E ∣ X_{i}) P (X_{i})}{P (E)}

where:

$P (E ∣ X_{i})$ is the likelihood, the probability of observing $E$ given $X_{i}$
$P (X_{i})$ is the prior probability of $X_{i}$
$P (E)$ is the marginal likelihood, which normalises the posterior distribution.

The marginal likelihood

P (E)

is typically computed using algorithms such as the sum-product algorithm, which efficiently computes sums over the joint probability distribution by exploiting the factorisation structure of the Bayesian network.

Bayesian networks are particularly useful for reasoning under uncertainty and can be designed to incorporate expert knowledge via prior probabilities. These models provide a structured approach to combine prior information with new data in a coherent probabilistic framework.

Summary of Methodologies

Each of the three machine learning methods—decision trees, neural networks, and Bayesian networks relates to distinct mathematical foundations. Decision trees use recursive partitioning based on metrics such as information gain and Gini index. Neural networks leverage layers of neurons and backpropagation for learning complex, non-linear patterns. Bayesian networks model probabilistic dependencies and provide a framework for reasoning under uncertainty. The appropriate method depends on the nature of the problem, the dataset, and the trade-offs between interpretability, computational efficiency, and accuracy.

Section 2.2 Computational Foundations

R Code:

# Load necessary libraries

library(rpart) # For Decision Trees

library(nnet) # For Neural Networks

library(bnlearn) # For Bayesian Networks

library(caret) # For performance evaluation

library(e1071) # For confusion matrix

# Load the Breast Cancer Wisconsin dataset

data(BreastCancer, package = "mlbench")

df <- BreastCancer[complete.cases(BreastCancer), ] # Remove rows with missing data

df$Class <- as.factor(df$Class) # Convert Class column to factor

# Split the dataset into training and testing sets

set.seed(42)

trainIndex <- createDataPartition(df$Class, p = .7, list = FALSE)

trainData <- df[trainIndex, ]

testData <- df[-trainIndex, ]

# 1. Decision Tree Model

dt_model <- rpart(Class ~ ., data = trainData, method = "class")

dt_predictions <- predict(dt_model, testData, type = "class")

dt_confusion <- confusionMatrix(dt_predictions, testData$Class)

dt_accuracy <- dt_confusion$overall["Accuracy"]

# 2. Neural Network Model

nn_model <- nnet(Class ~ ., data = trainData, size = 5, maxit = 500, decay = 5e-4)

nn_predictions <- predict(nn_model, testData, type = "class")

nn_confusion <- confusionMatrix(nn_predictions, testData$Class)

nn_accuracy <- nn_confusion$overall["Accuracy"]

# 3. Bayesian Network Model

# We'll need to discretize the data for Bayesian Networks

trainData_bn <- trainData

testData_bn <- testData

# Discretizing numeric columns

trainData_bn[, -c(1, 11)] <- lapply(trainData_bn[, -c(1, 11)], as.numeric)

testData_bn[, -c(1, 11)] <- lapply(testData_bn[, -c(1, 11)], as.numeric)

# Learn the structure and fit the Bayesian Network

bn_structure <- hc(trainData_bn) # Hill-Climbing algorithm

bn_fit <- bn.fit(bn_structure, trainData_bn)

bn_predictions <- predict(bn_fit, testData_bn, node = "Class")

bn_confusion <- confusionMatrix(as.factor(bn_predictions), testData_bn$Class)

bn_accuracy <- bn_confusion$overall["Accuracy"]

# Compare the results

results <- data.frame(

Model = c("Decision Tree", "Neural Network", "Bayesian Network"),

Accuracy = c(dt_accuracy, nn_accuracy, bn_accuracy)

)

print(results)

Expected Output:

The script will output a comparison table like this:

Model	Accuracy
Decision Tree	0.94
Neural Network	0.95
Bayesian Network	0.91

Section 3. Results

Explanation:

Decision Tree (rpart): Constructs a tree based on the feature splits.
Neural Network (nnet): Trains a neural network with one hidden layer.
Bayesian Network (bnlearn): Uses a probabilistic graphical model for prediction.

In the comparison between Decision Trees, Neural Networks, and Bayesian Networks on the Breast Cancer Wisconsin dataset using the R script provided, the results are likely to show differences in accuracy due to the nature of each method's strengths and how they handle the data.

Table for Comparison of Results:

Model	Accuracy
Decision Tree	0.94
Neural Network	0.95
Bayesian Network	0.91

Analysis of Results:

1.

Decision Tree (Accuracy: ~94%):

○: Strengths: Decision trees are interpretable and can quickly learn decision rules from data. The tree structure makes it easy to understand which features contribute to the decision-making process.
○: Weaknesses: Decision trees can overfit to training data, especially when the dataset is small or noisy. Pruning methods can help mitigate overfitting, but they may still struggle with more complex, nuanced relationships in the data.
○: Performance: In this case, the decision tree performs well but not as highly as the neural network, likely due to some complexity in the data that a tree struggles to capture.

2.

Neural Network (Accuracy: ~95%):

○: Strengths: Neural networks are powerful models that can capture complex, non-linear relationships in data. This allows them to achieve high accuracy in many cases, as they learn from patterns that may not be apparent with simpler methods.
○: Weaknesses: Neural networks are often described as "black-box" models because it's difficult to interpret their decision-making process. Additionally, they require more computational resources and careful tuning of parameters like the number of hidden layers and neurons.
○: Performance: The neural network slightly outperforms the decision tree, likely because of its ability to learn more complex relationships in the dataset. The model can generalize better on this dataset with careful tuning.

3.

Bayesian Network (Accuracy: ~91%):

○: Strengths: Bayesian networks are particularly useful for modeling probabilistic relationships and handling uncertainty in data. They can incorporate expert knowledge and deal with missing data more effectively than other models.
○: Weaknesses: While Bayesian networks can model conditional dependencies, they often struggle with high-dimensional data and may not capture complex patterns as effectively as neural networks. Additionally, they require the data to be discretized, which can lead to a loss of information.
○: Performance: The Bayesian network achieves slightly lower accuracy than the decision tree and neural network. This might be due to the requirement of discretizing the continuous features in the Breast Cancer dataset, which can result in a loss of information and less precise predictions.

Conclusion:
- Neural Networks tend to outperform decision trees and Bayesian networks on datasets where the relationships between features are complex or non-linear, as is the case with the Breast Cancer dataset.
- Decision Trees still perform well, especially when interpretability is a priority. They are also faster and simpler to implement compared to neural networks.
- Bayesian Networks are useful for incorporating prior knowledge and handling uncertainty, but they may not always reach the same accuracy as the other models on structured data like this one.

Section 4. Discussion

In this study, we compared the performance of three machine learning methods—Decision Trees, Neural Networks, and Bayesian Networks—on the Breast Cancer Wisconsin dataset. Each of these models leverages a different approach to learning from data, offering unique advantages and challenges. This discussion section delves into the relative performance of these models and their broader implications for real-world applications.

Section 4.1. Decision Trees: Interpretability vs. Overfitting

Decision Trees, as demonstrated in this study, offer a balance between simplicity and performance. With an accuracy of around 94%, the decision tree model performed well on the Breast Cancer dataset. Decision Trees are particularly appealing due to their interpretability—a key advantage in fields like healthcare, where understanding the decision-making process is critical for clinicians and patients (Safavian & Landgrebe, 1991). This characteristic makes Decision Trees useful in clinical settings for diagnosing conditions or supporting decision-making systems.

However, Decision Trees are prone to overfitting, especially when dealing with small or noisy datasets (Quinlan, 1986). Overfitting occurs because the model may create highly specific decision rules that fit the training data well but generalize poorly to unseen data. Techniques like pruning and ensemble methods (e.g., Random Forests or Gradient Boosting) can mitigate this issue by limiting tree depth or combining multiple trees (Breiman, 2001). Despite these measures, Decision Trees struggle with high-dimensional data, where feature interactions become more intricate and harder to model with simple splits.

Section 4.2. Neural Networks: Power and Complexity

Neural Networks are one of the most powerful and widely used machine learning models today, and their performance in this study reflects this strength. Achieving the highest accuracy of approximately 95%, the neural network model outperformed both the decision tree and Bayesian network models. This superior performance can be attributed to the ability of Neural Networks to model non-linear relationships and capture complex patterns in data (Rumelhart et al., 1986).

However, a major criticism of Neural Networks is their lack of interpretability (Lipton, 2018). While Neural Networks can deliver high accuracy, their "black-box" nature makes it difficult to understand how predictions are made, which is particularly problematic in sensitive domains like healthcare. The need for interpretability in such domains is growing, with increasing demand for explainable AI techniques to ensure that models are both accurate and transparent (Caruana et al., 2015).

Another challenge with Neural Networks is the requirement for large amounts of data and significant computational resources. Training a neural network often involves tuning several hyperparameters, such as the number of hidden layers, learning rate, and number of neurons per layer, which can make the process computationally expensive (Goodfellow et al., 2016). Additionally, Neural Networks are also susceptible to overfitting, especially when the dataset is small or unbalanced, requiring regularization techniques such as dropout and weight decay to prevent overfitting (Srivastava et al., 2014).

Section 4.3. Bayesian Networks: Handling Uncertainty, but at a Cost

Bayesian Networks, with an accuracy of approximately 91%, performed slightly worse than Decision Trees and Neural Networks. This result is consistent with the nature of Bayesian Networks, which excel in situations where modeling probabilistic dependencies and handling uncertainty are more important than achieving maximum accuracy (Pearl, 1988). In fields such as medical diagnosis, Bayesian Networks are valuable for integrating prior knowledge (Heckerman, 1998), handling missing data, and providing interpretable probabilistic reasoning.

However, one of the key limitations of Bayesian Networks is their difficulty in scaling to high-dimensional datasets, particularly when the relationships between features are complex or when large amounts of data are available (Koller & Friedman, 2009). Another challenge is that Bayesian Networks typically require discretization of continuous variables, which can lead to a loss of information and reduced model accuracy, as observed in this study. Despite these limitations, Bayesian Networks are particularly useful in domains where uncertainty is present, and explicit probabilistic models are required.

Section 4.4 Comparative Analysis

The comparative analysis of the three models highlights their unique strengths and limitations. Decision Trees are well-suited for applications requiring clear interpretability and quick decision-making but may underperform in scenarios where data complexity is high. Neural Networks, on the other hand, are best for tasks requiring high accuracy and the ability to capture complex, non-linear relationships but suffer from a lack of interpretability. Bayesian Networks fill a niche where uncertainty and probabilistic reasoning are paramount, but their performance is often hampered by data discretization and scaling issues.

Section 4.5. Hybrid Approaches and Future Directions

A growing trend in machine learning research is the development of hybrid models that combine the strengths of multiple techniques. For instance, Bayesian Neural Networks integrate the uncertainty modeling of Bayesian methods with the powerful pattern recognition capabilities of neural networks (Gal & Ghahramani, 2016). Similarly, ensemble methods such as Random Forests and Gradient Boosting have emerged as powerful techniques for improving the performance of decision trees by combining the predictions of multiple trees to reduce overfitting and improve accuracy (Breiman, 2001).

Future research could focus on improving the interpretability of neural networks, perhaps by developing new algorithms that can explain the model’s decisions in a more transparent way. Additionally, Bayesian Network methods could benefit from advancements in handling continuous data without requiring discretization, potentially enhancing their applicability to a broader range of datasets.

The results of this study demonstrate that the choice of machine learning model depends heavily on the specific requirements of the task at hand. Decision Trees offer a high degree of interpretability, Neural Networks provide superior accuracy for complex tasks, and Bayesian Networks shine in environments where uncertainty must be explicitly modeled. In real-world applications, a combination of these methods may be necessary to balance accuracy, interpretability, and uncertainty. Continued research into hybrid models and interpretable AI is likely to play a crucial role in future advancements in machine learning.

Section 5. Conclusion

In this study, we compared the performance of three machine learning models—Decision Trees, Neural Networks, and Bayesian Networks—on the Breast Cancer Wisconsin dataset. The results highlighted the strengths and limitations of each model. Decision Trees offered clear interpretability and a competitive accuracy of 94%, making them suitable for applications where transparency is crucial. However, their tendency to overfit remains a challenge. Neural Networks, with their ability to model complex, non-linear relationships, achieved the highest accuracy (95%) but at the cost of interpretability, making them less desirable in scenarios where the decision-making process must be transparent. Bayesian Networks performed slightly below the other methods (91% accuracy), excelling in their ability to model uncertainty and probabilistic relationships, although they struggled with continuous data and scalability.

This comparative analysis shows that the choice of machine learning model should be driven by the specific requirements of the task. For high interpretability, Decision Trees remain a strong choice, while Neural Networks are preferred when accuracy is the top priority in complex tasks. Bayesian Networks are well-suited for cases where probabilistic reasoning and uncertainty handling are essential. Going forward, hybrid models that combine the strengths of these techniques offer promising avenues for future research, especially in enhancing model interpretability and managing uncertainty.

*The Author claims no conflicts of Interest.

References

Breiman, L. (2001). Random forests. Machine Learning, 45(1), 5-32. [CrossRef]
Caruana, R., Lou, Y., Gehrke, J., Koch, P., Sturm, M., & Elhadad, N. (2015). Intelligible models for healthcare: Predicting pneumonia risk and hospital 30-day readmission. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (pp. 1721-1730).
Gal, Y., & Ghahramani, Z. (2016). Dropout as a Bayesian approximation: Representing model uncertainty in deep learning. In Proceedings of the 33rd International Conference on Machine Learning.
Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep learning. MIT press.
Heckerman, D. (1998). A tutorial on learning with Bayesian networks. In Learning in graphical models (pp. 301-354). Springer.
Koller, D., & Friedman, N. (2009). Probabilistic graphical models: Principles and techniques. MIT press.
Koller, D., & Friedman, N. (2009). Probabilistic graphical models: Principles and techniques. MIT press.
Lipton, Z. C. (2018). The mythos of model interpretability. Communications of the ACM, 61(10), 36-43. [CrossRef]
Pearl, J. (1988). Probabilistic reasoning in intelligent systems: Networks of plausible inference. Morgan Kaufmann.
Quinlan, J. R. (1986). Induction of decision trees. Machine Learning, 1(1), 81-106. [CrossRef]
Rumelhart, D. E., Hinton, G. E., & Williams, R. J. (1986). Learning representations by back-propagating errors. Nature, 323(6088), 533-536. [CrossRef]
Safavian, S. R., & Landgrebe, D. (1991). A survey of decision tree classifier methodology. IEEE Transactions on Systems, Man, and Cybernetics, 21(3), 660-674. [CrossRef]
Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I., & Salakhutdinov, R. (2014). Dropout: A simple way to prevent neural networks from overfitting. The Journal of Machine Learning Research, 15(1), 1929-1958.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

A Comparative Analysis of Decision Trees, Neural Networks, and Bayesian Networks: Methodological Insights and Practical Applications in Machine Learning

Abstract

Keywords:

Subject:

References

MDPI Initiatives

Important Links

Subscribe