1. Introduction
Approximation theory is fast becoming a key instrument not only in classical approximation theory but also in other fields of mathematics such as differential equations, orthogonal polynomials and geometric design. Since Korovkin’s famous theorem was first published in 1950, the issue of approximation by linear positive operators has became increasingly important area as part of approximation theory. A considerable amount of literature has been published on that [
1,
2,
10,
12,
14,
15,
23,
24].
In the past two decades, the applications of
calculus in approximation theory have been studied extensively. Firstly, the Bernstein polynomials based on
integers was done by Lupaş [
6]. As approximation of
Bernstein polynomials studied by Lupaş is better than classical one under convenient choice of
q, many authors introduced
q-generalization of many operators and examined several approximation properties. Several studies have revealed that [
3,
7,
8,
13].
In recent years, Mursaleen et al. have focused on
-calculus in approximate by linear positive operator and proposed
analogue of Bernstein operators [
20,
21]. They computed uniform convergence of the operators and rate of convergence. For some recent study directed to
-operators, we can refer the readers to [
17,
18,
19,
26,
27].
The main motivation in this paper, to the best of authors knowledge, no study about approximate two variable operator has been found so far using calculus. In the present study, we define the two dimensional Chlodovsky type Bernstein operators based on integer. We examine approximation properties of our new operator by the help of Korovkin-type theorem. In addition, we present the local approximation properties and establish the rates of convergence by means of the modulus of continuity and the Lipschitz type maximal function. Also, we give a Voronovskaja type theorem for this operators. Another important aim of this study is to examine weighted approximation properties of these our operators on . In order to get these results, we will apply the weighted Korovkin type theorem.
Let us recall some definitions and notations regarding the concept of
calculus. The
integer of the number
n is defined by
The
factorial
and the
binomial coefficients are defined as :
and
Further, the
binomial expansions are given as
and
Further information related to
calculus can be found in [
25,
28].
2. Construction of the Operators
Recently, Ansari and Karaisa [
16] have defined and studied
analogue of Chlodovsky operators as follows:
where
For
, we define Chlodovsky type two dimensional Bernstein operator based on
integers as follows:
for all
,
with
and
. Here
and
be increasing unbounded sequences of positive real numbers such that
Also, the basis elements are
Now, we need following lemmas for proving our main results.
From Lemma 1, we have following:
Lemma 2.
Using Lemma 2 and by linearity of , we have
Theorem 1.
Let , , , such that . If
the sequence convergence uniformly to , on for each , where be reel numbers such that , and be the space of all real valued continuous function on with the norm
Proof. Assume that the equities (
7),(
3) and (4) are holds. Then, we have
as
. From Lemma 2, we obtain
uniformly on
, where
are the test functions. By Korovkin’s theorem for functions of two variables was presented by Volkov [
29], it follows that
, uniformly on
, for each
. □
3. Rate of Convergence
In this section, we compute the rates of convergence of operators to by means of the modulus of continuity. Proceeding further, we provide a summary of the notations and definitions of the modulus of continuity and the Peetre’s functional for bivariate real valued functions.
For
, the complete modulus of continuity for a bivariate case is defined as follows:
for every
. Further, partial moduli of continuity with respect to
x and
y are defined as
It is obvious that they satisfy the properties of the usual modulus of continuity [
11].
For
, the Peetre-K functional [
22] is given by
where
is the space of functions of
f such that
f,
and
in
. The norm
on the space
is defined by
Now, we give an estimate of the rate of convergence of operators .
Theorem 2.
Let . For all , we have
where
Proof. By definition the complete modulus of continuity of
and linearity and positivity our operator, we can write
Using Cauchy-Scwartz inequality, from (
5) and (6), one can write following
Choosing
, for all
, we get desired the result.
□
Theorem 3.
Let , then the following inequalities satisfy
where
Proof. By definition partial moduli of continuity of
and applying Cauchy-Scwartz inequality, we have
Consider (
5), (6) and choosing
we reach the result. □
For
and
, we define the Lipschitz class
for the bivariate case as follows:
Theorem 4.
Let . Then, for all , we have
where and defined in (8) and (9), respectively.
Proof. As
, it follows
For
and
applying the Hölder’s inequality, we get
Hence, we get desired the result. □
Theorem 5.
Let and . Then, we have
Proof. For
, we obtain
Applying our operator on both sides above equation, we deduce
As
we have
Using the Cauchy-Schwarz inequality, we can write following
Form (
5) and (6), we get desired the result. □
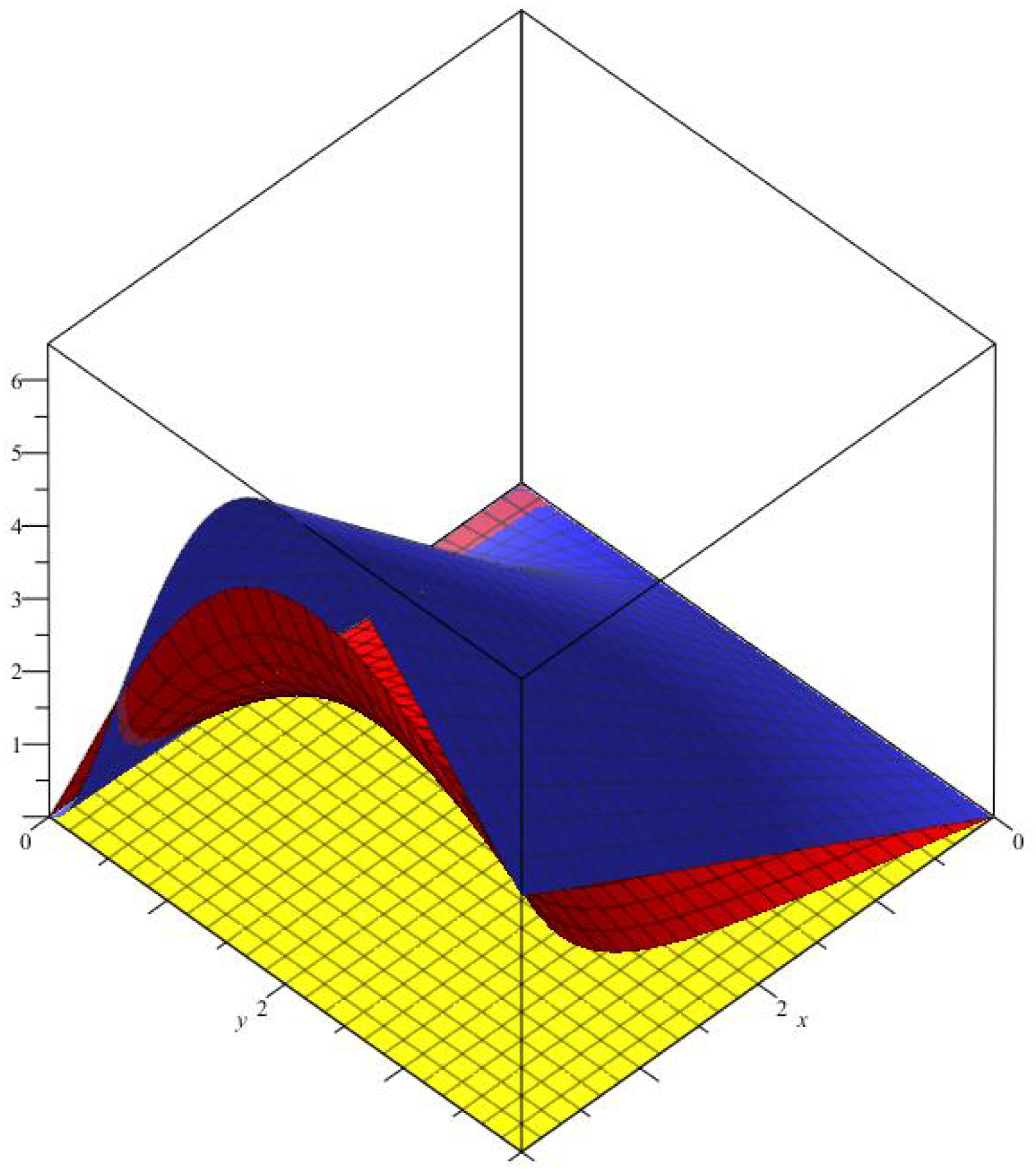
By means of Maple, illustrative graphics show the rate of convergence of
operators to certain functions:
Figure 1.
The comparison convergence of (red), (yellow) with , and (blue)
Figure 1.
The comparison convergence of (red), (yellow) with , and (blue)
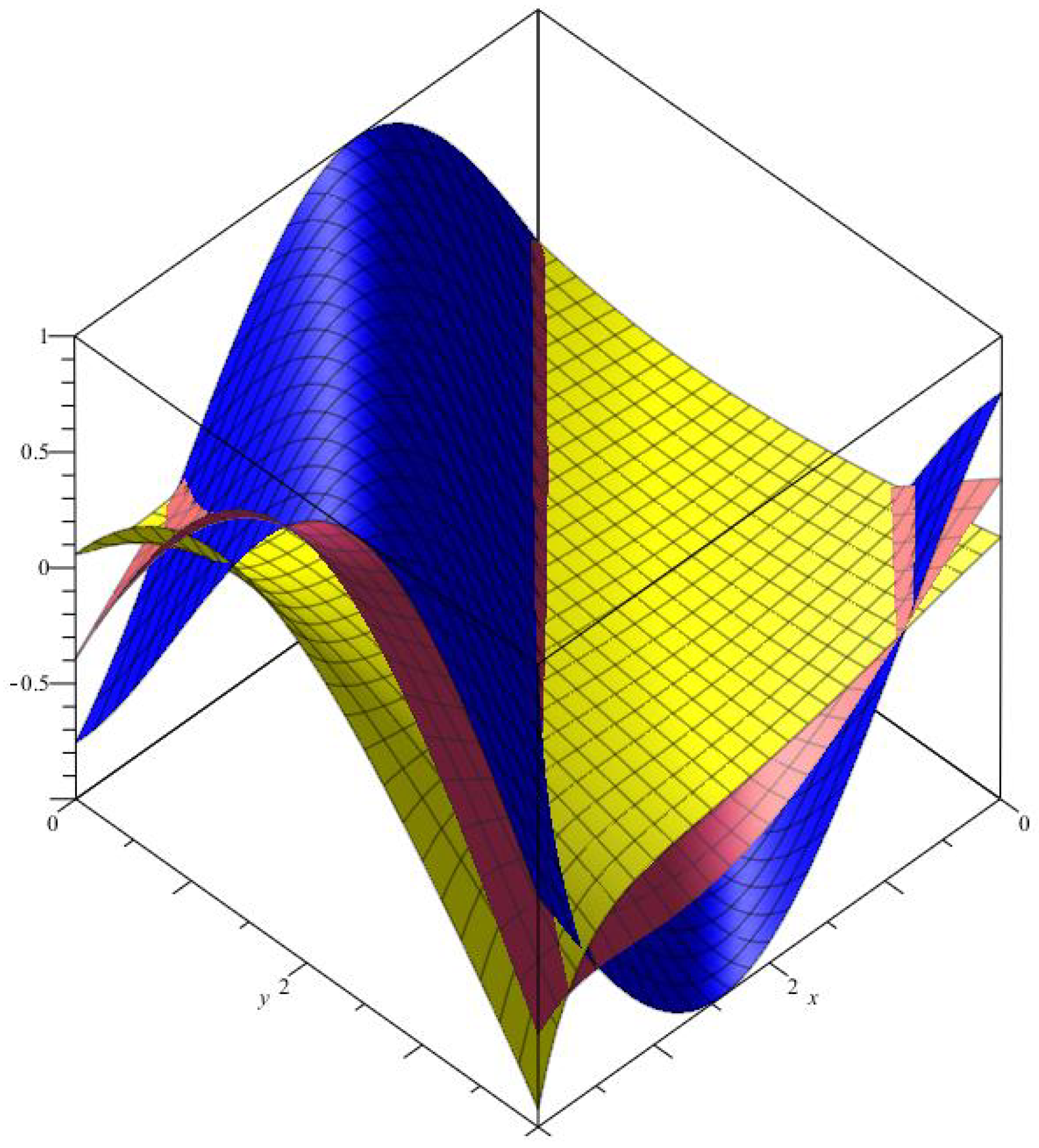
Figure 2.
The comparison convergence of (red), (yellow) with , and (blue).
Figure 2.
The comparison convergence of (red), (yellow) with , and (blue).
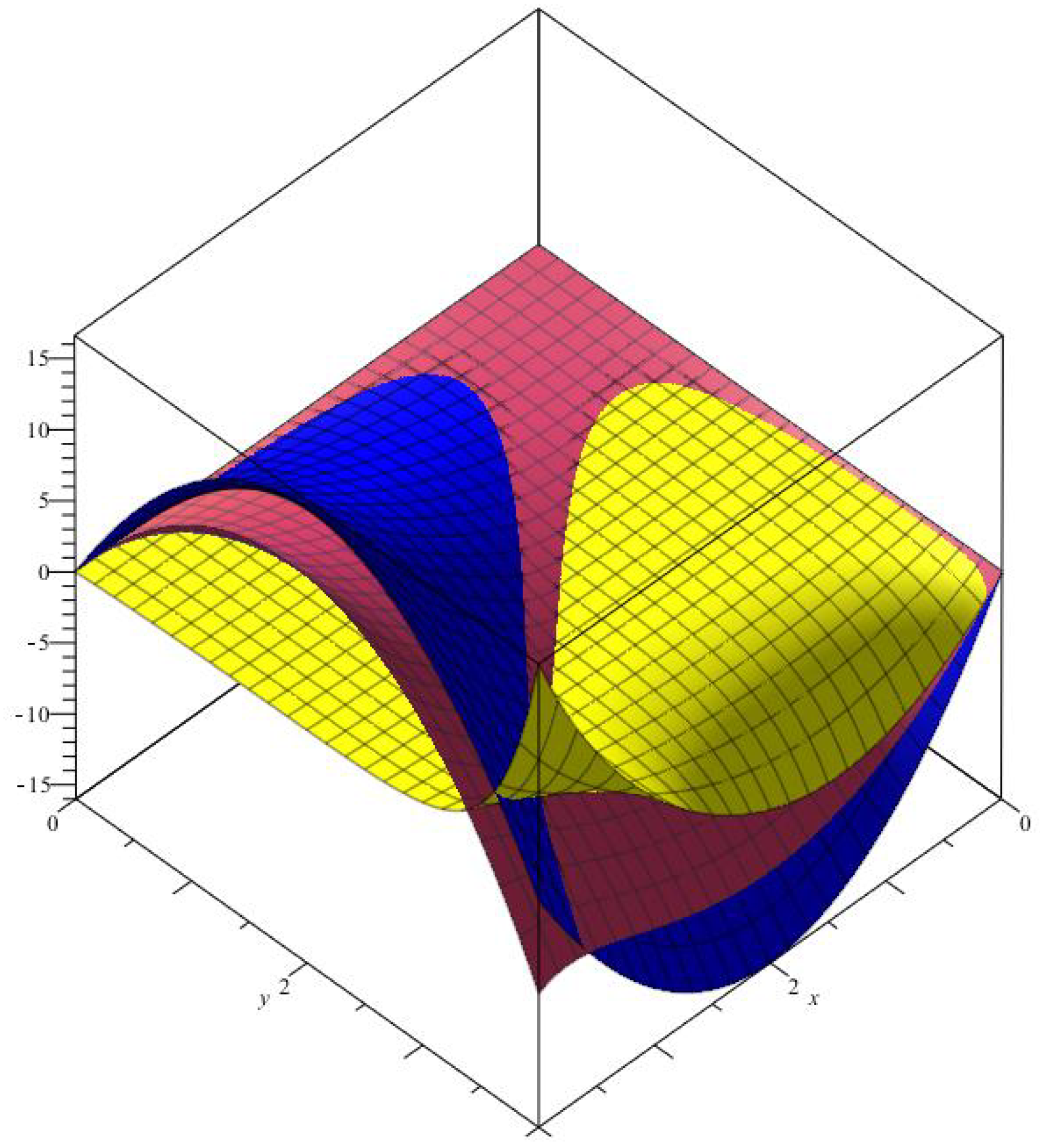
Figure 3.
The comparison convergence of (red), (yellow) with , and (blue).
Figure 3.
The comparison convergence of (red), (yellow) with , and (blue).
Theorem 6.
Let , then we have
Proof. Let
. By the Taylor’s formula, we get
Applying
to the both sides of the above equation, we obtain
As
and
, one can write following
By (
5), (6), we deduce,
By the linearity
, we obtain
By (
10) and (
11), one can see that
This step completes the proof. □
First, we need the auxiliary result contained in the following lemma.
Lemma 3. Let be sequences such that and as . Then, we have the following limits:
- (i)
- (ii)
.
Proof. (i) Using Lemma 1, we have
Then, we get
Let us take the limit of both sides of the above equality as
, then we can write
(ii) By Lemma 1 and by the linearity of the operators
, we have
where
Taking the limit of both sides of
, we get
Similarly, we can show that;
By combining (
14)-(
16), we reach the desired the result. □
Now, we ready present a Voronovskaja type theorem for .
Theorem 7.
Let . Then, we have
Proof. Let
. Then, write Taylor’s formula of
f as follows:
where
and
as
.
If we apply the operator
on (
17), we obtain
Applying the limit of both sides of the above equality, we get
, □
By Cauchy-Schwartz inequality, we can write the following
As
and from Lemma 3(ii)
is finite, then we have
Hence, we deduce
This step completes the proof.
4. Weighted Approximation Properties of Two Variable
Function
In this section, the convergence of the sequence of linear positive operator to a functions of two variables which defined on weighted space and compute rate of convergence via weighted modulus continuity.
Let
and
be the space of all functions
f defined on the real axis provide with
where
is a positive constant depending only on
f. Let
be the subspace of
of all continuous functions with the norm:
Let
denote the subspace of all functions
such that
exists finitely. For all
the weighted modulus of continuity is defined by
Lemma 4.
The operators defined (2) act from to if and only if the inequality
holds for some positive constant c.
Theorem 8.
Let be sequence of linear positive operators defined (2), then for each and for all , we have
Proof.
Again by Lemma 2, we can write following
Taking the limit of both sides of above inequality as
with by (
3) and (4), we get
Applying weighted Korovkin theorem for two variable which presented by Gadzhiev [
4,
5], we get desired the results. □
For estimate rate of convergence we need the following lemma.
Lemma 5.
For all , by (5), (6) and (13), one can write the following
and
Now, compute rate of convergence the operator in weighted spaces .
Theorem 9.
If then we have
, where is a constant independent of and , .
Proof. Taking into account the following inequality given in [
9], we deduce
Applying
both side above inequality and using Cauchy-Schwarz inequality, one can write following
By (
19)-(22), we obtain
Taking
, one write the following:
where
is a constant independent of
Since
for sufficiently large
we get
This step completes the proof. □
Author Contributions
Conceptualization, Ü.K.; validation, A.K.; formal analysis, A.K.; and writing, A.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Acknowledgments
We thank the referees for their careful reading of the original manuscript and for the valuable comments.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| MDPI |
Multidisciplinary Digital Publishing Institute |
| DOAJ |
Directory of open access journals |
| TLA |
Three letter acronym |
| LD |
Linear dichroism |
References
- A. Karaisa, Approximation by Durrmeyer type Jakimoski–Leviatan operators, Math Methods Appl Sci In Press(2015), 1–12. [CrossRef]
- Karaisa and F.Karakoc, Stancu type generalization of Dunkl analogue of Szàsz operators, Adv Appl, 1–14. [CrossRef]
- A. Karaisa, DT. Tollu and Y. Asar, Stancu type generalization of q-Favard-Szàsz operators, Appl Math Comput.(2015), 264: 249–257. [CrossRef]
- A D. Gadjiev, Linear positive operators in weighted space of functions of several variables, Izvestiya Acad of Sciences of Azerbaijan(1980), 1: 32-37.
- AD. Gadjiev, H. Hacýsalihoglu, On convergence of the sequences of linear positive operators, Ph. D. thesis, Ankara University, 1995, in Turkish.
- A. Lupaş, q-analogue of the Bernstein operator, Seminar on Numerical and Statistical Calculus, University of Cluj-Napoca(1987), 9: 85-92.
- AM. Acu and CV. Muraru, Approximation Properties of bivariate extension of q- Bernstein-Schurer-Kantorovich operators, Result Math.(2015), 67: 265–279. [CrossRef]
- A. Aral, V. Gupta and RP. Agarwal, Applications of q- calculus in operator theory, Berlin: Springer, 2013. [CrossRef]
- C. Atakut and N. Ispir, Approximation by modified Szász-Mirakjan operators on weighted spaces, Proc Indian Acad Sci Math.(2002), 112: 571-578. [CrossRef]
- D. Barbosu, Some Generalized Bivariate Bernstein Operators, Mathematical Notes Miskolc.(2000), 1: 3–10. [CrossRef]
- GA. Anastassiou and SG. Gal, Approximation theory: moduli of continuity and global smoothness preservation, Birkha¨user: Boston, 2000.
- H. Karsli, A Voronovskaya type theory for the second derivative of the Bernstein-Chlodovsky polynomials, Proc Est Acad Sci.(2012),61: 9–19. [CrossRef]
- I. Büyükyazıcı, On the approximation properties of two-dimensional q-Bernstein-Chlodowsky polynomials, Math Commun.(2009), 14: 255–269.
- I. Büyükyazıcı and H. Sharma Approximation properties of two-dimensional q-Bernstein–Chlodowsky–Durrmeyer operators, Numer Funct Anal Optim.(2012), 33:1351–1371. [CrossRef]
- I. Büyükyazıcı, Approximation by Stancu–Chlodowsky polynomials, Comput Math Appl., 2010; 59: 274–282. [CrossRef]
- KJ. Ansari and A. Karaisa, Chlodovsky type generalization of Bernstein operators based on (p,q) integer, under the cominication.
- M. Mursaleen, MD. Nasiuzzaman and A. Nurgali, Some approximation results on Bernstein–Schurer operators defined by (p,q)-integers, Jour Ineq Appl.(2015),249: 1–15. [CrossRef]
- M. Mursaleen, KJ. Ansari and A. Khan, Some approximation results by (p,q)-analogue of Bernstein–Stancu operators, Appl Math Comput.(2015),64: 392–402. [CrossRef]
- M. Mursaleen, MD. Nasiruzzaman, A. Khan and KJ. Ansari, Some approximation results on Bleimann-Butzer–Hahn operators defined by (p,q)-integers, 2015. [CrossRef]
- M. Mursaleen, KJ. Ansari and A. Khan, On (p,q)-analogue of Bernstein operators, Appl Math Comput.(2015). [CrossRef]
- M. Mursaleen, KJ. Ansari and A. Khan, Erratum to on (p,q)- analogue of Bernstein Operators, [Appl. Math. Comput. 266 (2015) 874-882] Appl. Math. Comput.(2016); 278: 70-71. [CrossRef]
- PL. Butzer and H. Berens, Semi-groups of operators and approximation, Springer, New York, 1967.
- PL. Butzer and H.Karsli, Voronovskaya-type theorems for derivatives of the Bernstein-Chlodovsky polynomials and the Szá sz–Mirakyan operator, Comment Math.(2009), 49: 33–58.
- PN. Agrawal and N. Ispir, Degree of Approximation for Bivariate Chlodowsky–Szász-Charlier Type Operator, Results Math.(2015). [CrossRef]
- Sadjang, On the fundamental theorem of (p,q)-calculus and some (p,q)-Taylor formulas, 2015; [math.QA]. [CrossRef]
- T. Acar, A. Aral and SA. Mohiuddine, Approximation by bivariate (p,q)-Bernstein–Kantorovich operator(2016), [math.CA]. [CrossRef]
- V. Gupta, (p,q)-Szàsz-Mirakyan-Baskakov operators, Complex Anal Oper Theory(2015), 1–9. [CrossRef]
- V. Sahai and S. Yadav Representations of two parameter quantum algebras and p,q-special functions, J Math Anal Appl.(2007), 335: 268-279. [CrossRef]
- VJ. Volkov, On the convergence of linear positive operators in the space of continuous functions of two variables, (Russian). Doklakad Nauk SSSR, (1957)115: 17-19.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).