Ramsey Approach to Quantum Mechanics

Preprint

Article

Ramsey Approach to Quantum Mechanics

Altmetrics

Downloads

Views

Comments

This version is not peer-reviewed

Submitted:

10 October 2024

Posted:

11 October 2024

You are already at the latest version

Alerts

Abstract

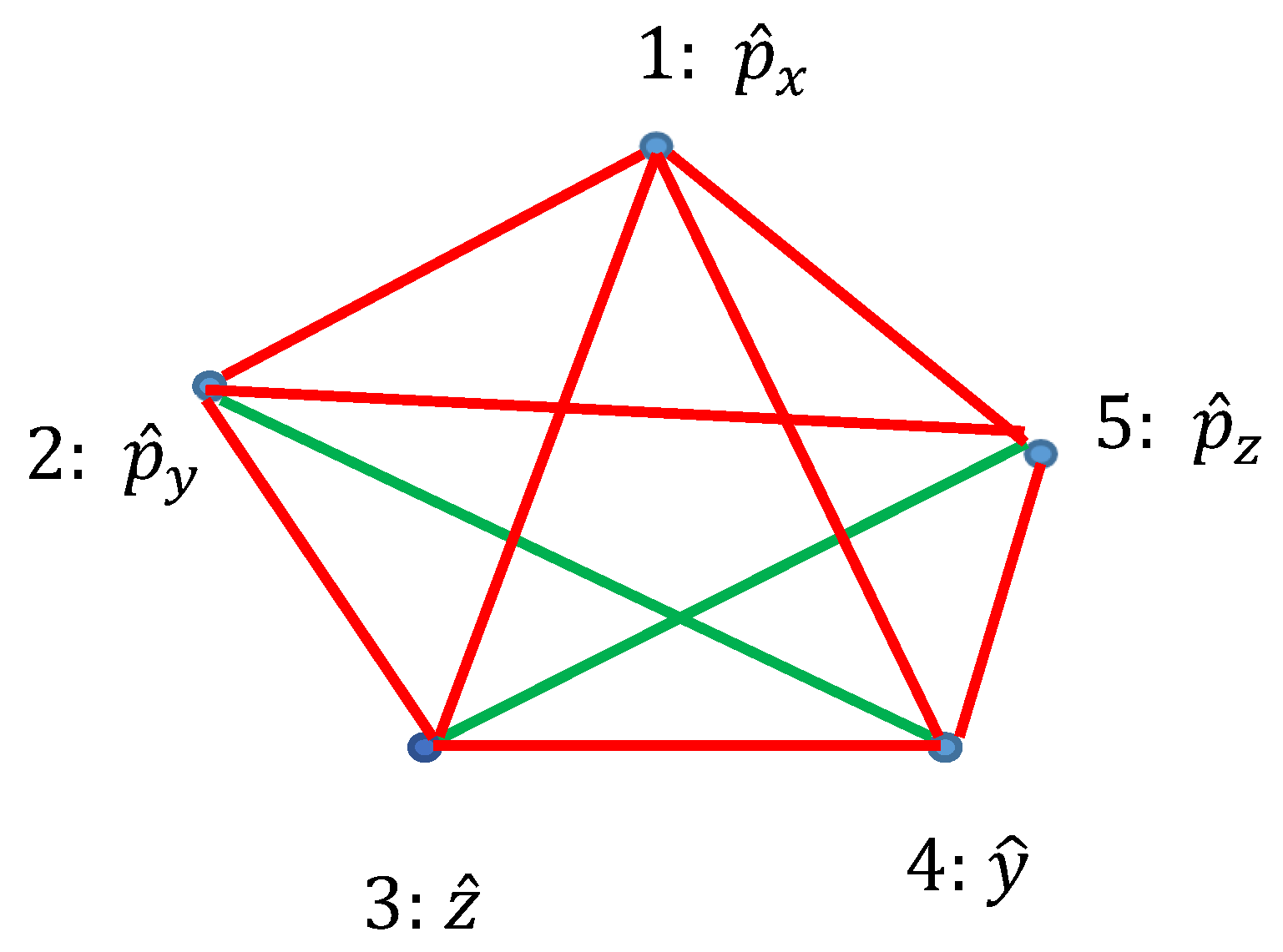
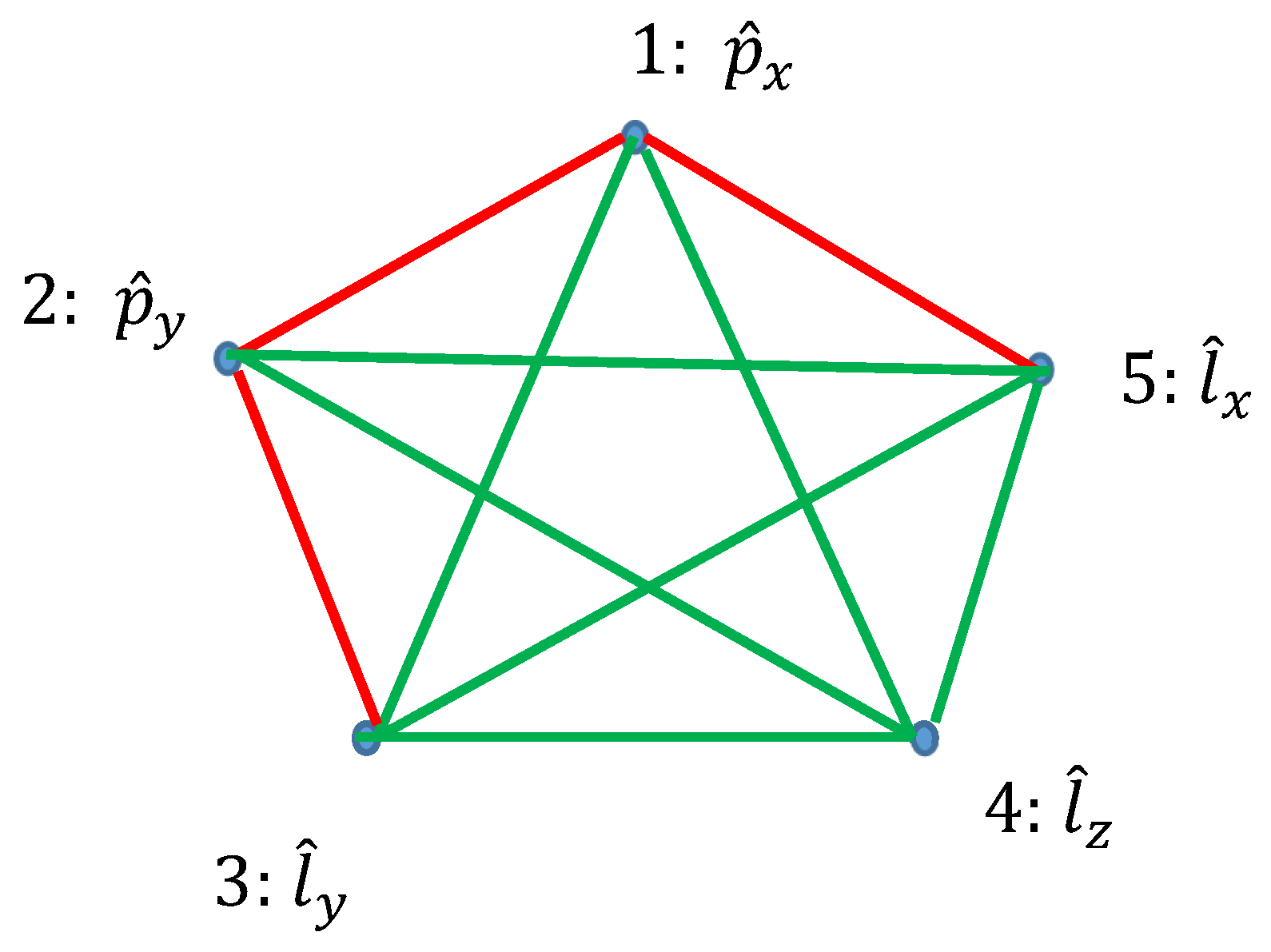
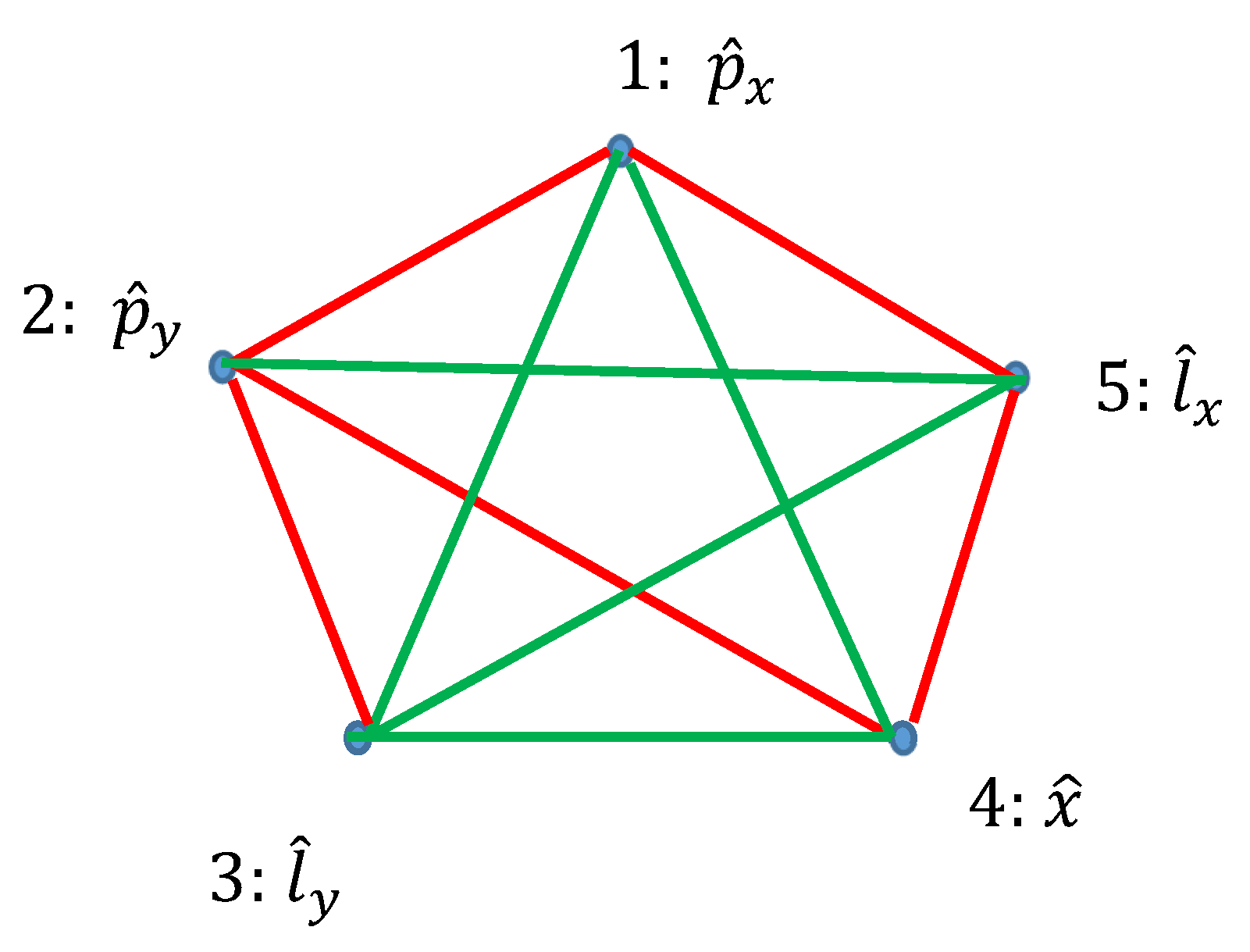
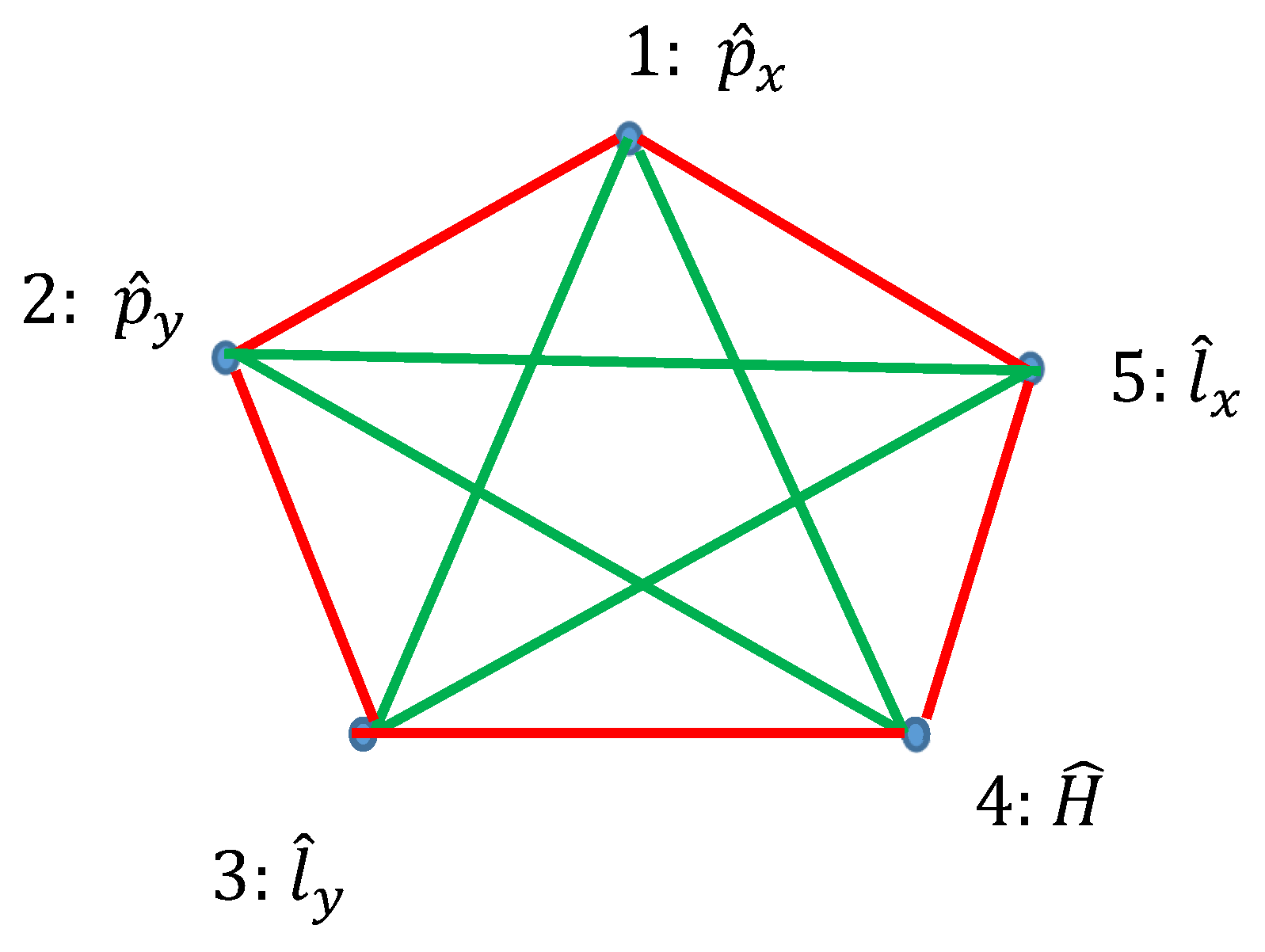
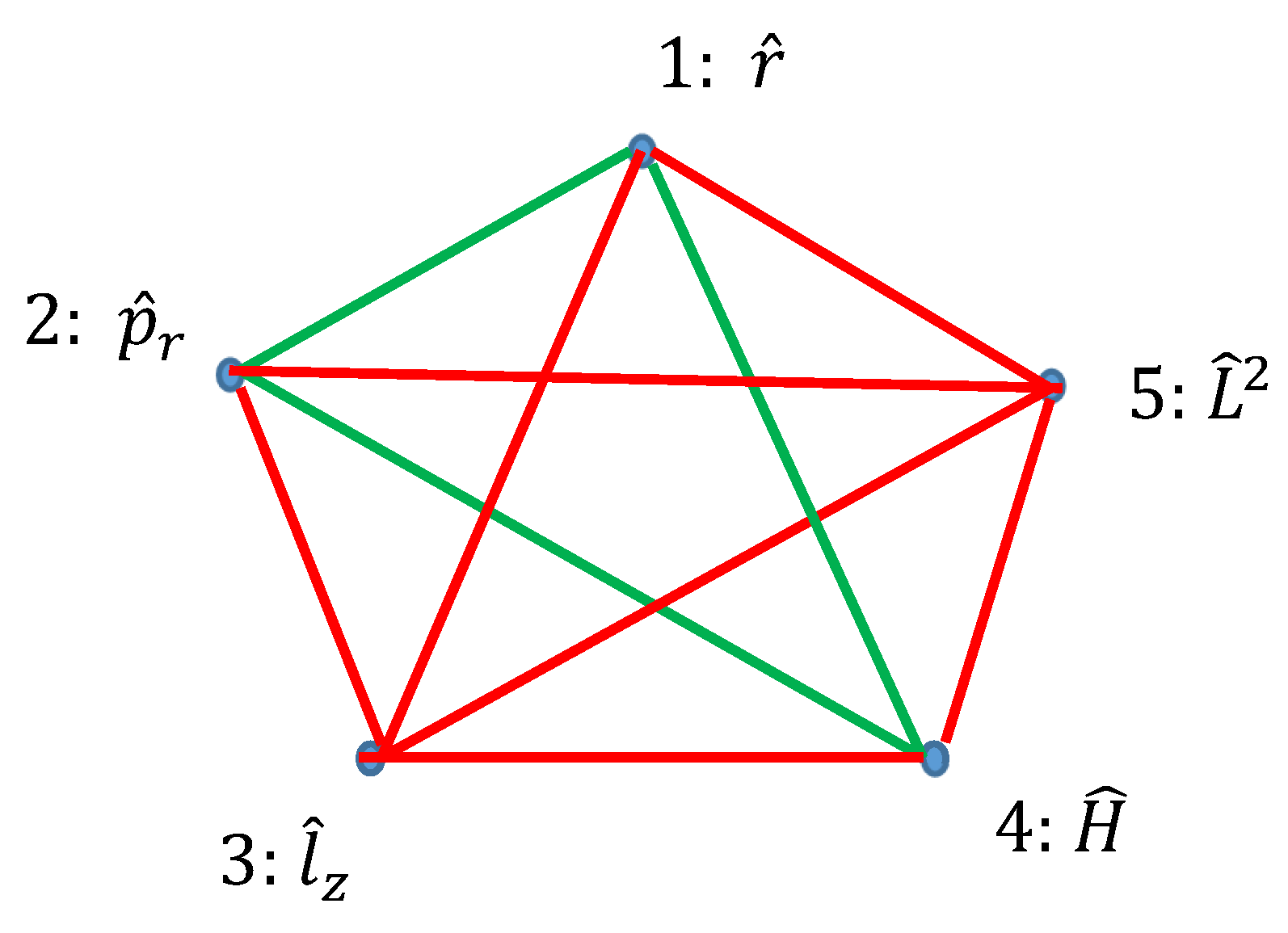
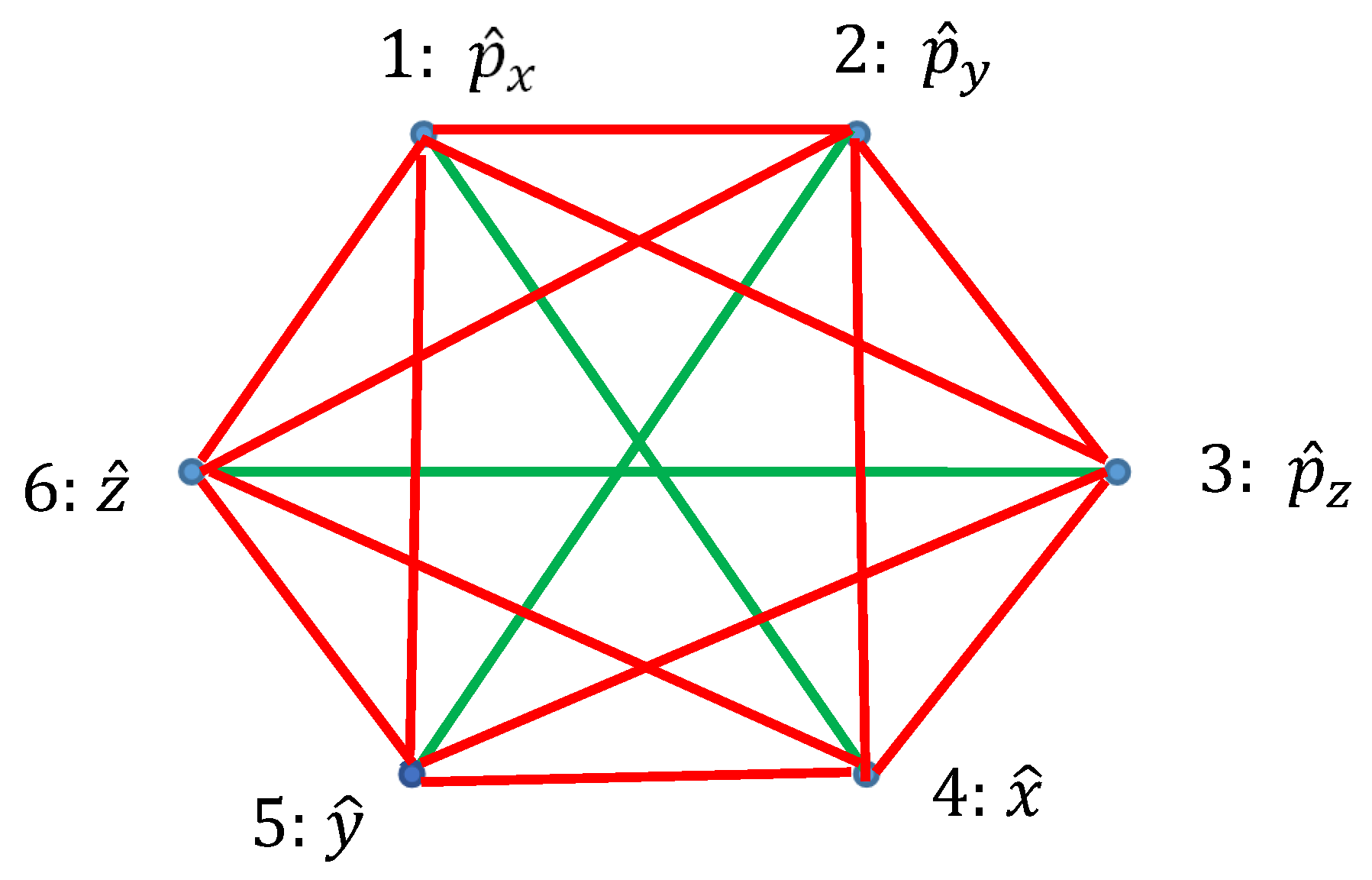
Ramsey theory enables re-shaping of the basic ideas of the quantum mechanics. Quantum observables, represented by linear Hermitian operators are seen as the vertices of the graph. Relation of commutation define coloring of the edges linking the vertices: if the operators commute, they are connected with the red link; if they do not commute they are connected with the green link. Thus, a bi-colored, complete, Ramsey graph emerges. According to the Ramsey theorem, complete, bi-colored graph built of six vertices, will inevitably contain at least one monochromatic triangle; in other words, the Ramsey number R(3,3)=6. In our interpretation, this triangle represents the triad of observables, which could or, alternatively, could not be established simultaneously in a given quantum system. The Ramsey approach to the quantum mechanics is illustrated with the numerous examples, including the motion of a particle in a centrally symmetrical field.

Keywords:

Subject: Physical Sciences - Quantum Science and Technology

1. Introduction

In this paper, we introduce the Ramsey approach for the analysis of the fundamental quantum mechanics problems. We implement the theory of graphs for the analysis of foundations of quantum mechanics. In particular, we demonstrate that the Ramsey theory enables re-shaping of the basic principles of quantum mechanics, when operators/observables are seen as the vertices of the complete, bi-colored graph and their commutative properties represent the relations between the vertices of the graph. In its very general meaning, the Ramsey theory refers to any mathematical problem which states that a structure of a given kind is guaranteed to contain a prescribed substructure. The classical problem in Ramsey theory is the so-called seminal “party problem”, which asks the minimum number of guests (each of whom is either a “friend” or a “stranger” to the others) denoted

R (m, n)

that must be invited so that at least m will know each other, or at least n will not know each other [1,2,3,4,5,6,7,8,9,10,11]). When Ramsey theory is re-shaped in the notions of the graph theory, it states that any structure will necessarily contain an interconnected substructure [3,6]. The Ramsey theorem, in its graph-theoretic form, states that one will find monochromatic cliques in any edge color labelling of a sufficiently large complete graph [3,6]. Applications of the Ramsey theory to physics remain scarce [12,13,14]. In our paper, we address the Ramsey graphs emerging from Hermitian operators, representing the quantum mechanics observables [15,16,17,18].

2. Results and Discussion

2.1. Observables, Operators and Graphs

In quantum mechanics, an observable is a linear operator, denoted in the text

\hat{l}

[15,16,17,18]. Observables manifest as Hermitian, self-adjoint operators on a separable complex Hilbert space representing the quantum state space, which possess a complete orthogonal set of eigenfunctions [15,16,17,18]. For every physical quantity in quantum mechanics, there is a definite corresponding linear operator. All Hermitian operators do not possess a complete orthogonal set of eigenfunctions; however the Hermitian operators capable of representing physical quantities possess such a set. To prove that a specific Hermitian operator is an observable is, often, a very difficult physical problem [15]. The proof has already been given for simple cases, such as coordinate, momentum and angular momentum [15]. Two operators

\hat{f}

and

\hat{g}

say to commute with each other if Equation (1) takes place:

\hat{f} \hat{g} - \hat{g} \hat{f} = 0

(1)

If a particle can be in a definite state for two observables, then the two operators associated with those observables will commute [15,16,17,18]. The converse is therefore also true; if two operators do not commute, then it is not possible for a quantum state to have a definite value of the corresponding two observables at the same time [15,16,17,18]. The operator of momentum is defined as:

\hat{p} = - j ℏ \nabla

j = \sqrt{- 1}

, or in components:

{\hat{p}}_{x} = - j ℏ \frac{\partial}{\partial x}, {\hat{p}}_{y} = - j ℏ \frac{\partial}{\partial y}, {\hat{p}}_{z} = - j ℏ \frac{\partial}{\partial z}

(2)

The operator corresponding to coordinate q is simply multiplication by q [15,16,17,18]. The spectrum of this operator is continuous. The commutation rules for

\hat{p}

and x are given by Equation (3):

{\hat{p}}_{i} x_{k} - x_{k} {\hat{p}}_{i} = - j ℏ δ_{i k}

(3)

where

δ_{i k}

is a Kronecker delta. Equation (3) demonstrates that the coordinate of the particle along one of the axes can have a definite value at the same time as the components of the momentum along the other two axes; contrastingly the coordinate and the momentum component along the same axis, cannot be established simultaneously [15,16,17,18]. For the angular momentum component operators of a particle, denoted

{\hat{l}}_{i}, i = 1 . . 3,

we have, in turn [15,16,17,18]:

ℏ {\hat{l}}_{x} = y {\hat{p}}_{z} - z {\hat{p}}_{y}; ℏ {\hat{l}}_{y} = z {\hat{p}}_{x} - x {\hat{p}}_{z}; ℏ {\hat{l}}_{z} = x {\hat{p}}_{y} - y {\hat{p}}_{x},

(4)

The rules for commutation of the angular momentum operators with the operators of coordinates and linear momenta are given by Equations (5) and (6):

\{{\hat{l}}_{i}, x_{k}\} = j e_{i k l} x_{l},

(5)

\{{\hat{l}}_{i}, p_{k}\} = j e_{i k l} p_{l},

(6)

where

e_{i k l}

is the antisymmetric unit tensor of rank three, and summation is implied over those indices, which appear twice,

e_{123} = 1

[16]. The rules of commutation for the operator of angular momentum are given by Equation (7):

\{{\hat{l}}_{i}, {\hat{l}}_{k}\} = j e_{i k l} {\hat{l}}_{l}

(7)

For the commutation rules established for the total angular momentum of the system, denoted

\hat{L}

, see ref. 16. It should be emphasized that the commutation relations given by Equations (3)–(7) are non-transitive. The transitive Ramsey numbers are different from the non-transitive ones [19].

2.2. Graph Approach to the Observables: Converting Observables into Graph

We start from the motion of a single quantum particle m. Following mathematical procedure enabling converting of the observables into graph is suggested: observables themselves are represented by the vertices of the graph. The relation between observables/vertices/operators are established by the commutation rules, namely: if the observables/vertices commute, they are linked with the red edge (they are “friends” within the terminology of the Ramsey theory). And, when the observables/vertices do not commute (thus, they are “strangers”), they are connected with the green link, as shown in Figure 1.

Let us illustrate the idea with the graphs depicted on Figure 2. The commutating relations are given by Equation (6). The vertices/observables in inset A are

{\hat{p}}_{x}, {\hat{p}}_{y} a n d {\hat{l}}_{x}

. The emerging graph is bi-colored.

The vertices/observables shown in inset B are

{\hat{l}}_{x}, {\hat{l}}_{y} a n d {\hat{l}}_{z}

. The commutating relations between observables are given in this case by Equation (7). The emerging graph is mono-colored/green. This means that three components of the angular momentum could not be measured simultaneously [15,16,17,18].

Now address the graph built of four vertices, depicted in Figure 3. No monochromatic/mono-colored triangle is recognized in the graph. This means that no triad of the addressed observables may be measured simultaneously. The graph shown in Figure 3 is complete, i.e., it is a graph in which every pair of distinct vertices is connected by a unique edge [6].

Now consider the graph emerging from five vertices/observables presented in Figure 4. The bi-colored, complete Ramsye graph shown in Figure 4, emerges from the vertices/observables

{\hat{p}}_{x}, {\hat{p}}_{y}, {\hat{p}}_{z}, \hat{z}

and

\hat{y}

. This graph contains the monochromatic triangles, numbered “123”, “125”; “134” and “144”. This means that the triads of observables

{(\hat{p}}_{x}, {\hat{p}}_{y}, \hat{z})

;

({\hat{p}}_{x}, {\hat{p}}_{y}, {\hat{p}}_{z}); {(\hat{p}}_{x}, \hat{z}, \hat{y})

and

{(\hat{p}}_{x}, {\hat{p}}_{z}, \hat{y})

may be measured simultaneously. Moreover, it contains the monochromatic pentagon “12345”. Analysis of this pentagon leads to the paradoxical; however, true conclusion: the pairs of observables

({\hat{p}}_{x}, {\hat{p}}_{z})

; (

{\hat{p}}_{z}, \hat{y}); (\hat{y}, \hat{z}); \hat{(z}, {\hat{p}}_{y})

and (

{\hat{p}}_{y}, {\hat{p}}_{x})

may be measured simultaneously. However, it does not mean that all of five observables may be established at the same time; indeed, this is forbidden for the pairs of observables

({\hat{p}}_{y}, \hat{y})

and (

{\hat{p}}_{z}, \hat{z}) .

Only if the complete graph/subgraph is totally built of monochromatic red links, the entire set of observables may be established simultaneously. Or, alternatively, all of observables could not be measured at the same time, if the links are all monochromatic green (see Figure 2B).

We conclude that the analysis of the complete graph built according to the suggested coloring procedure leads to important conclusions, which may be verified experimentally.

Now consider the bi-colored, complete graph emerging from the five observables

{\hat{p}}_{x}, {\hat{p}}_{y}, {\hat{p}}_{z}, {\hat{l}}_{y}

and

{\hat{l}}_{z}

, depicted in Figure 5. Triangle “125” is monochromatic red, and triangle “134” is monochromatic green one. This means that the triads of observables (

{\hat{p}}_{x}, {\hat{p}}_{y}, {\hat{p}}_{z})

may be measured simultaneously; whereas, observables

({\hat{p}}_{x}, {\hat{l}}_{y}, {\hat{l}}_{z})

could not be established at the same time.

Now we address the graph arising from the observables

{\hat{p}}_{x}, {\hat{p}}_{y}, {\hat{l}}_{x}, {\hat{l}}_{y}

and

{\hat{l}}_{z}

, shown in Figure 6. No red triangle is recognized. This means that the triad of the observables, which may be simultaneously established, does not exist in this case. Triangles “134” and “345” are monochromatic green. This means that the triads of observables

({\hat{p}}_{x}, {\hat{l}}_{y},

{\hat{l}}_{z}

) and (

{\hat{l}}_{x}, {\hat{l}}_{y},

{\hat{l}}_{z})

could not be fixed at the same time.

Figure 7 presents the bi-colored, complete, Ramsey graph containing five vertices, namely

{\hat{p}}_{x}, {\hat{p}}_{y}, {\hat{l}}_{x}, {\hat{l}}_{y}

and

\hat{x}

. Triangle “134” is a monochromatic green one. This means that the observables

{\hat{p}}_{x}, {\hat{l}}_{y}

and

\hat{x}

could not be established simultaneously. We recognize the monochromatic quadrangle “1245” in the graph, shown in Figure 7. However, it does not mean, that the observables

{\hat{p}}_{x}, {\hat{p}}_{y}, {\hat{l}}_{x},

\hat{x}

may be established in the same time, as discussed above. Indeed, the pairs of observables

({\hat{p}}_{x}, x)

and

({\hat{p}}_{y}, {\hat{l}}_{x})

could not be measured simultaneously.

Graphs depicted in Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7 contain mono-colored triangles. However, it is possible to build bi-colored, complete graph which will not contain any mono-colored triangle, and this is due to the fact that the Ramsey number

R (3,3) = 6 .

Such a graph is shown in Figure 8.

Graph depicted in Figure 8 emerges from five vertices/observables, namely

{\hat{p}}_{x}, {\hat{p}}_{y}, {\hat{l}}_{x}, {\hat{l}}_{y}

and

\hat{H},

where

\hat{H}

is the Hamiltonian of the particle. We also assume that the Hamiltonian

\hat{H}

depends explicitly on the coordinates of the particle. In this situation is does not commute with operators

{\hat{p}}_{x}, {\hat{p}}_{y}, {\hat{l}}_{x}, {\hat{l}}_{y} [15 - 18]

Thus, the graph shown in Figure 8 arises. The graph does not contain any mono-chromatic triangle, thus illustrating the Ramsey theorem (

R (3,3) = 6)

In order to illustrate, how all this works we consider the motion of the particle in the centrally symmetric field U(r) [15,16,17,18]. In this case, we already have the motion of two particles

m_{1}

and

m_{2},

which, however, may be represented by the wave function

ψ ({\vec{r}}_{1}, {\vec{r}}_{2}) = φ (\vec{R}) ψ (\vec{r})

, where the function

φ (\vec{R})

describes the motion of the center of mass (seen as a free particle

m_{1} + m_{2}

) and

ψ (\vec{r})

describes the relative motion of the particles, as a particle of effective mass

m = \frac{m_{1} m_{2}}{m_{1} + m_{2}}

moving in the centrally symmetric field U(r) [15,16,17,18].

The Shrodinger equation for the motion of the particle m in the centrally symmetric field U(r) is:

Δ ψ + \frac{2 m}{ℏ^{2}} [E - U (r)] ψ = 0

(8)

where E is the energy of the particle. So, the problem is reduced to the problem of the motion of a single particle m in the centrally symmetric field U(r) [15,16,17,18]. The graph arising from operators

\hat{r}, {\hat{p}}_{r}, {\hat{l}}_{x}, \hat{H}

and

{\hat{L}}^{2}

;

{\hat{L}}^{2} = {\hat{l}}_{x}^{2} + {\hat{l}}_{y}^{2} + {\hat{l}}_{z}^{2}

is shown in Figure 9. For the commutation rules see refs. 15-18.

We recognize that the triangle “235” in Figure 9 is monochromatic red and the triangle “124” is a monochromatic green one. This means that the triad of observables

({\hat{p}}_{r}, {\hat{l}}_{z},

{\hat{L}}^{2})

may be established simultaneously; whereas, the triad of observables

(\hat{r}, {\hat{p}}_{r}, \hat{H})

could not be established at the same time. The triangle “135” is also monochromatic red. This means that the triad of observables

(\hat{r}, {\hat{L}}^{2}, {\hat{l}}_{z})

may be established experimentally at the same time.

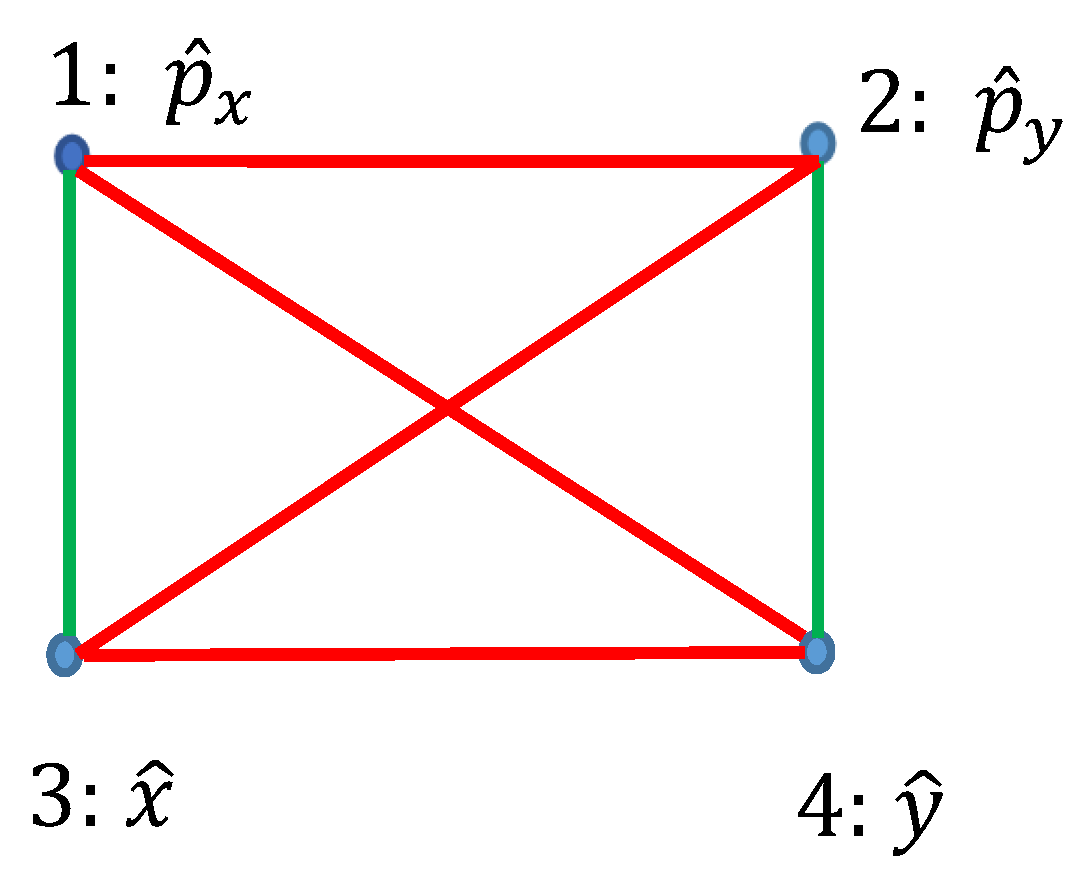
2.3. Graphs Possessing Six Vertices Emerging from Quantum Observables and the Ramsey Theorem

Now address complete, bi-colored graph possessing six vertices emerging from six quantum observables/Hermitian operators, depicted in Figure 10. This graph reflects the 3D motion of a quantum particle. The observables are

{\hat{p}}_{x}, {\hat{p}}_{y}, {\hat{p}}_{y}

\hat{x}, \hat{y}

and

\hat{z .}

Triangles “123”, “234”, “345”, “456”, “156”, “246” and “135” are monochromatic red ones. This means that the triads of observables: (

{\hat{p}}_{x}, {\hat{p}}_{y}, {\hat{p}}_{z}); ({\hat{p}}_{y}, {\hat{p}}_{z}

\hat{x});

({\hat{p}}_{z}

\hat{x}, \hat{y);}

{\hat{(p}}_{z}

\hat{x}, \hat{y)}

;

({\hat{p}}_{x}, \hat{y}

\hat{z})

and (

\hat{x}, \hat{y}

\hat{z})

may be established simultaneously. No green monochromatic triangle is recognized in the graph. This means, in turn, that there is no a triad of observables, which may be established at the same time.

The reported result is far from to be trivial. Indeed, any graph built of six vertices/observables/Hermitian operators will contain at least one monochromatic triangle, whatever are the observables. This conclusion arises from the Ramsey analysis of observables itself. It is noteworthy, that the vertices of the graph may represent the complete set of commuting observables (CSCO) [15,16,17,18]. What do we have if the number of vertices of the graph is large? We know, the restricted quantity of Ramsey numbers, and there is no algorithm for their calculation [2,3]. The problem of calculation of Ramsey numbers remains open [2,3].

3. Discussion

We demonstrate that the Ramsey theory enables re-shaping of the classical quantum theory with the tools of the graph theory, when the observables/Hermitian operators appear as the vertices of the graph, and the commutation relations define the coloring of the edges linking the vertices. Thus, the complete, bi-colored Ramsey graph emerges [2,3,4,5,6,7,8,9,10]. If this graph possesses six vertices, it inevitably contains at least one monochromatic triangle (

R (3,3) = 6)

. Regrettably, the Ramsey theory does not establish the exact color of the mono-colored triangle to be necessarily present in the graph. Analysis of the specific graphs enables identification of the triads of the observables, which could or could not be established simultaneously. We foresee the following directions of future investigations:

i): Generalization of the reported approach for the systems of quantum particles.
ii): Involving infinite Ramsey theory for the analysis of the problems of quantum mechanics and quantum electrodynamics.

4. Conclusions

We applied the Ramsey approach to the analysis of the basic problems of the quantum mechanics. The Ramsey theory is seen today as a field of combinatorics, or alternatively as a field of the graph theory [2,3,4,5,6,7,8]. Applications of the Ramsey theory to the analysis of physical systems are scarce until now [12,13,14,20,21,22]. We introduce the mathematical procedure enabling converting of quantum observables into a complete, bi-colored graph. Within this procedure, the observables/Hermitian operators are seen as the vertices of the graph. The commutation rules establish the color of the links, connecting the vertices/observables: if the operators commute, they are connected with a red link (they are “friends” in the terms of the Ramsey theory). When the operators do not commute, they are connected with a green link (they are, in turn, “strangers). Thus, the complete, bi-colored, Ramsey graph emerges. It should be emphasized, that the commutation relations of quantum mechanics are non-transitive [19,22]. Thus, the use of conventional Ramsey numbers becomes possible [2,3,4,5,6,7,8]. The complete, bi-colored, Ramsey graph built of six vertices/observables/Hermitian operators will inevitably contain at least one monochromatic triangle (

R (3,3) = 6

). Thus, a triad of observables, which could or could not be measured simultaneously, will be necessarily present in the graph containing six vertices/observables/Hermitian operators. Regrettably, the Ramsey theory does not predict the exact color of the monochromatic triangle to be present in the graph [2,3,4,5,6,7,8,9,10]. This is the weakest point of the Ramsey theory [2,3,4,5,6,7,8].

The procedure of converting of the quantum observables/Hermitian operators into the complete, bi-colored, Ramsey graph is illustrated with numerous examples. The examples include the motion of the quantum particle in the centrally symmetrical field. Triads of the observables, which could and could not be measured simultaneously in this case, are revealed with the analysis of the corresponding complete, bi-colored graph. Thus, we conclude that the Ramsey theory enables re-shaping of interrelations between quantum observables.

Author Contributions

Conceptualization, E.B. and N.S.; methodology, E.B; formal analysis, E. B. and N.S.; investigation, E.B. and N.S.; writing—original draft preparation, E.B. and N.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The data are contained within the article.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Ramsey, F. P. On a Problem of Formal Logic. In: Gessel, I., Rota, GC. (eds) Classic Papers in Combinatorics. Modern Birkhäuser Classics. Birkhäuser Boston, 2009, pp. 264-286.
Chartrand, G.; Zhang, P. New directions in Ramsey theory. Discrete Math. Lett. 2021, 6, 84–96. [Google Scholar]
Graham, R. L.; Rothschild, B.L.; Spencer, J, H. Ramsey theory, 2nd ed., Wiley-Interscience Series in Discrete Mathematics and Optimization, John Wiley & Sons, Inc., New York, A Wiley-Interscience Publication, 1990, pp. 10-110.
Graham, R.; Butler, S. Rudiments of Ramsey Theory (2nd ed.). American Mathematical Society: Providence, Rhode Island, USA, 2015; pp. 7–46.
Landman, B. M.; Robertson, A. Ramsey Theory on the Integers, Student Mathematical Library, vol. 24, Providence, RI: AMS, 2004.
Li, Y.; Lin, Q. Elementary methods of the graph theory, Applied Mathematical Sciences. Springer, pp. 3-44, Cham, Switzerland, 2020.
Di Nasso, M.; Goldbring, I.; Lupini M., Nonstandard Methods in Combinatorial Number Theory, Lecture Notes in Mathematics, vol. 2239, Springer-Verlag, Berlin, 2019.
Katz, M.; Reimann, J. Introduction to Ramsey Theory: Fast Functions, Infinity, and Metamathematics, Student Mathemati-cal Library Volume: 87; 2018; pp. 1-34.
Erdős, P. , Gyárfás, A. A variant of the classical Ramsey problem. Combinatorica 1997, 17, 459–467. [Google Scholar] [CrossRef]
Erdős, P. Solved and unsolved problems in combinatorics and combinatorial number theory. Congressus Numerantium 1981, 32, 49–62. [Google Scholar]
Conlon, J.; Fox, B. Sudakov, Recent developments in graph Ramsey theory. Surveys in Combinatorics, 2015, 424, 49–118. [Google Scholar]
Gaitan, F.; Clark, L. Ramsey Numbers and Adiabatic Quantum Computing. Phys. Rev. Lett. 2012, 108, 010501. [Google Scholar] [CrossRef] [PubMed]
Bian, Z.; Chudak, F.; Macready, W. G.; Clark, L.; Gaitan, F. Experimental Determination of Ramsey Numbers. Phys. Rev. Lett. 2013, 111, 130505. [Google Scholar] [CrossRef] [PubMed]
Wouters, J.; Giotis, A.; Kang, R.; Schuricht, D.; Fritz, L. Lower bounds for Ramsey numbers as a statistical physics problem. J. Stat. Mech. 2022, 2022, 0332. [Google Scholar] [CrossRef]
Messiah, A. Quantum Mechanics, Dover Books on Physics, Dover Publications, Mineola, NY, 2014.
Landau L. D.; Lifshitz, E. M. Quantum mechanics. Non-Relativistic Theory, Volume 3 of Course of Theoretical Physics, 3rd Ed., Pergamon Press, Oxford, 1965.
Zettili, N. Quantum Mechanics. Concepts and Applications. 2nd Ed., John Wiley & Sons Ltd., The Atrium, Southern Gate, Chichester, West Sussex, PO19 8SQ, United Kingdom, 2009.
Bohm, D. Quantum Theory, Dover Publications, New York, NY, USA, 1989.
Choudum, S. A.; Ponnusamy, B. Ramsey numbers for transitive tournaments. Discrete Mathematics 1999, 206, 119–129. [Google Scholar] [CrossRef]
Shvalb, N.; Frenkel, M.; Shoval, Sh.; Bormashenko, Ed. Dynamic Ramsey Theory of Mechanical Systems Forming a Complete Graph and Vibrations of Cyclic Compounds. Dynamics 2023, 3, 272–281. [Google Scholar] [CrossRef]
Frenkel, M.; Shoval, Sh.; Bormashenko, Ed. Fermat Principle, Ramsey Theory and Metamaterials. Materials 2023, 16, 7571. [Google Scholar] [CrossRef] [PubMed]
Bormashenko, E. Universe as a Graph (Ramsey Approach to Analysis of Physical Systems). World Jour. of Physics 2023, 1, 1–24. [Google Scholar]

Figure 1. Mathematical procedure enabling converting of observables into graph is depicted. A. Vertex 1 represents observable

{\hat{p}}_{x} = - j ℏ \frac{\partial}{\partial x}

; Vertex 2 represents observable

{\hat{p}}_{y} = - j ℏ \frac{\partial}{\partial y}

; the observables commute, therefore are connected with the red link. B. Vertex 1 represents observable

{\hat{p}}_{x} = - j ℏ \frac{\partial}{\partial x}

; Vertex 2 represents observable

\hat{x}

; the observables do not commute, hence they are connected with the green link.

Figure 1. Mathematical procedure enabling converting of observables into graph is depicted. A. Vertex 1 represents observable

{\hat{p}}_{x} = - j ℏ \frac{\partial}{\partial x}

; Vertex 2 represents observable

{\hat{p}}_{y} = - j ℏ \frac{\partial}{\partial y}

; the observables commute, therefore are connected with the red link. B. Vertex 1 represents observable

{\hat{p}}_{x} = - j ℏ \frac{\partial}{\partial x}

; Vertex 2 represents observable

\hat{x}

; the observables do not commute, hence they are connected with the green link.

Figure 2. Graphs possessing three vertices, representing observables are depicted. A. The observables are:

{\hat{p}}_{x}, {\hat{p}}_{y} a n d {\hat{l}}_{x}

. The graph is bi-colored. B. The observables are

{\hat{l}}_{x}, {\hat{l}}_{y} a n d {\hat{l}}_{z}

. The graph is mono-colored/green.

Figure 2. Graphs possessing three vertices, representing observables are depicted. A. The observables are:

{\hat{p}}_{x}, {\hat{p}}_{y} a n d {\hat{l}}_{x}

. The graph is bi-colored. B. The observables are

{\hat{l}}_{x}, {\hat{l}}_{y} a n d {\hat{l}}_{z}

. The graph is mono-colored/green.

Figure 3. Complete bi-colored graph arising from four observables

{\hat{p}}_{x}, {\hat{p}}_{y}, \hat{x} a n d \hat{y}

is depicted. No monochromatic triangle is recognized.

Figure 3. Complete bi-colored graph arising from four observables

{\hat{p}}_{x}, {\hat{p}}_{y}, \hat{x} a n d \hat{y}

is depicted. No monochromatic triangle is recognized.

Figure 4. Bi-color graph emerging form the observables:

{\hat{p}}_{x}, {\hat{p}}_{y}, {\hat{p}}_{z}, \hat{z}

and

\hat{y} .

Triangles “123”, “125”, “134” and “145” monochromatic red.

Figure 4. Bi-color graph emerging form the observables:

{\hat{p}}_{x}, {\hat{p}}_{y}, {\hat{p}}_{z}, \hat{z}

and

\hat{y} .

Triangles “123”, “125”, “134” and “145” monochromatic red.

Figure 5. Bi-colored, complete graph emerging form the observables:

{\hat{p}}_{x}, {\hat{p}}_{y}, {\hat{p}}_{z}, {\hat{l}}_{y}

and

{\hat{l}}_{z} .

Triangle “125” is monochromatic red, and triangle “134” is monochromatic green.

Figure 5. Bi-colored, complete graph emerging form the observables:

{\hat{p}}_{x}, {\hat{p}}_{y}, {\hat{p}}_{z}, {\hat{l}}_{y}

and

{\hat{l}}_{z} .

Triangle “125” is monochromatic red, and triangle “134” is monochromatic green.

Figure 6. The graph arising from the observables

{\hat{p}}_{x}, {\hat{p}}_{y}, {\hat{l}}_{x}, {\hat{l}}_{y}

and

{\hat{l}}_{z}

. Triangles “134” and “345” are monochromatic green.

Figure 6. The graph arising from the observables

{\hat{p}}_{x}, {\hat{p}}_{y}, {\hat{l}}_{x}, {\hat{l}}_{y}

and

{\hat{l}}_{z}

. Triangles “134” and “345” are monochromatic green.

Figure 7. Graph containing five vertices, namely

{\hat{p}}_{x}, {\hat{p}}_{y}, {\hat{l}}_{x}, {\hat{l}}_{y}

and

\hat{x}

. Triangle “134” is monochromatic green.

Figure 7. Graph containing five vertices, namely

{\hat{p}}_{x}, {\hat{p}}_{y}, {\hat{l}}_{x}, {\hat{l}}_{y}

and

\hat{x}

. Triangle “134” is monochromatic green.

Figure 8. Complete, bi-colored graph containing five vertices, namely

{\hat{p}}_{x}, {\hat{p}}_{y}, {\hat{l}}_{x}, {\hat{l}}_{y}

and

\hat{H} .

The graph does not contain any mono-chromatic triangle.

Figure 8. Complete, bi-colored graph containing five vertices, namely

{\hat{p}}_{x}, {\hat{p}}_{y}, {\hat{l}}_{x}, {\hat{l}}_{y}

and

\hat{H} .

The graph does not contain any mono-chromatic triangle.

Figure 9. Bi-colored, complete graph, arising from the operators

\hat{r}, {\hat{p}}_{r}, {\hat{l}}_{z}, \hat{H}

and

{\hat{L}}^{2}

{\hat{L}}^{2} = {\hat{l}}_{x}^{2} + {\hat{l}}_{y}^{2} + {\hat{l}}_{z}^{2}

. Triangles “135” and “235” is monochromatic red and triangle “124” is a monochromatic green.

Figure 9. Bi-colored, complete graph, arising from the operators

\hat{r}, {\hat{p}}_{r}, {\hat{l}}_{z}, \hat{H}

and

{\hat{L}}^{2}

{\hat{L}}^{2} = {\hat{l}}_{x}^{2} + {\hat{l}}_{y}^{2} + {\hat{l}}_{z}^{2}

. Triangles “135” and “235” is monochromatic red and triangle “124” is a monochromatic green.

Figure 10. Complete bi-colored graph emerging from quantum observables

{\hat{p}}_{x}, {\hat{p}}_{y}, {\hat{p}}_{z}

\hat{x}, \hat{y}

and

\hat{z .}

. Triangles “123”, “234”, “345”, “456”, “156”, “246” and “135” are monochromatic red ones. No monochromatic green triangle is recognized.

Figure 10. Complete bi-colored graph emerging from quantum observables

{\hat{p}}_{x}, {\hat{p}}_{y}, {\hat{p}}_{z}

\hat{x}, \hat{y}

and

\hat{z .}

. Triangles “123”, “234”, “345”, “456”, “156”, “246” and “135” are monochromatic red ones. No monochromatic green triangle is recognized.

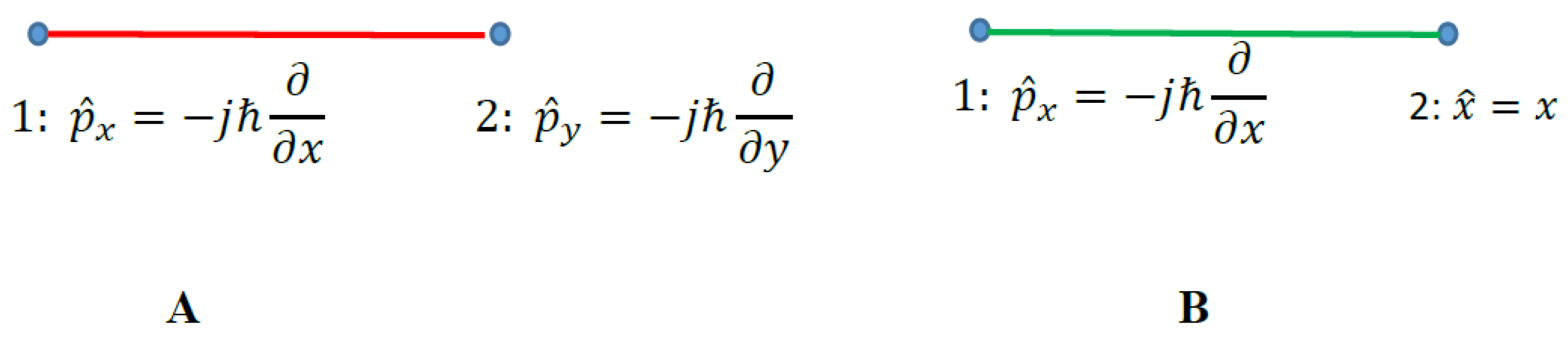
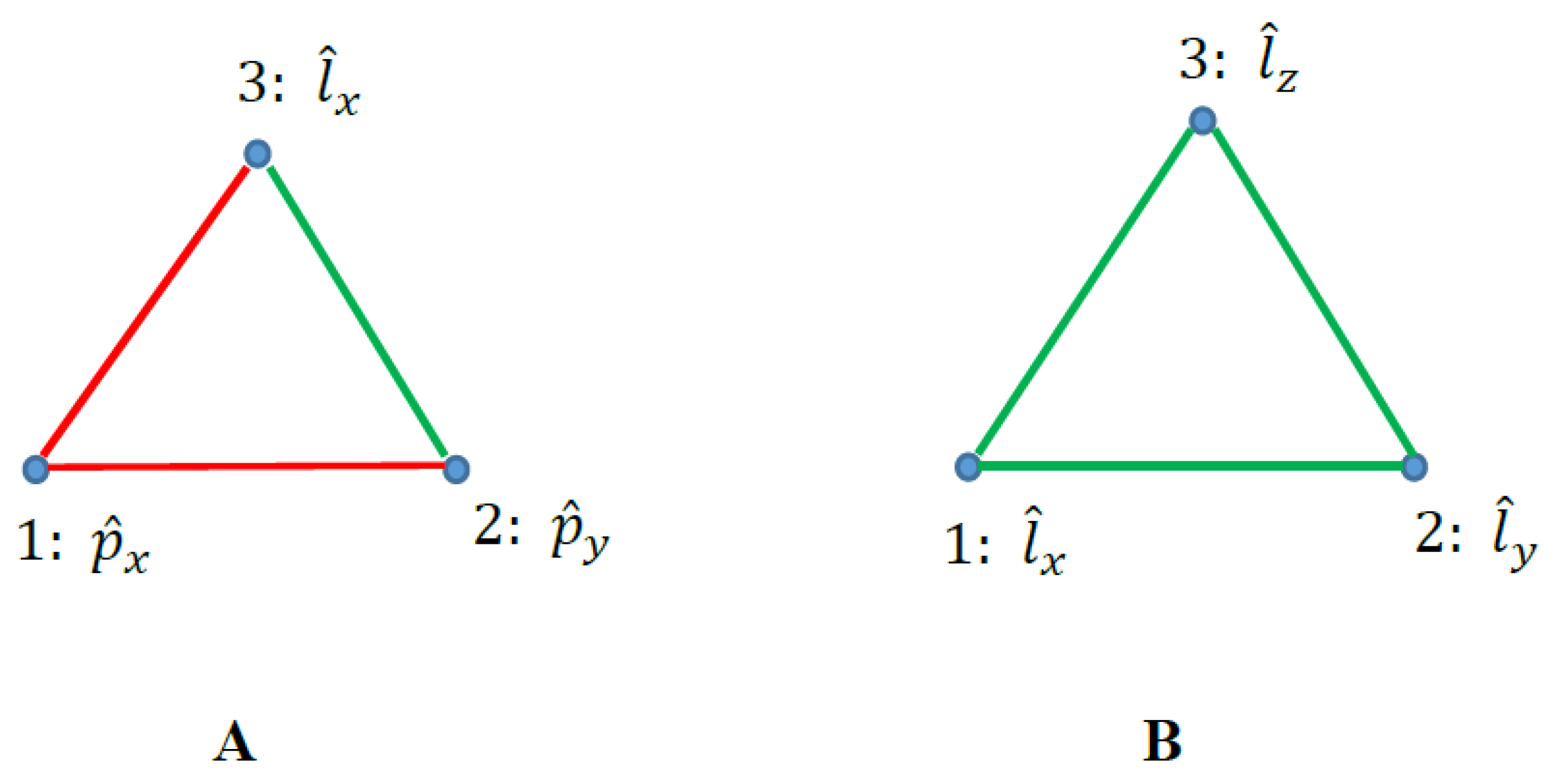
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Ramsey Approach to Quantum Mechanics

Abstract

1. Introduction

2. Results and Discussion

2.1. Observables, Operators and Graphs

2.2. Graph Approach to the Observables: Converting Observables into Graph

2.3. Graphs Possessing Six Vertices Emerging from Quantum Observables and the Ramsey Theorem

3. Discussion

4. Conclusions

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe