Submitted:
09 October 2024
Posted:
11 October 2024
Read the latest preprint version here
Abstract
Keywords:
1. Introduction
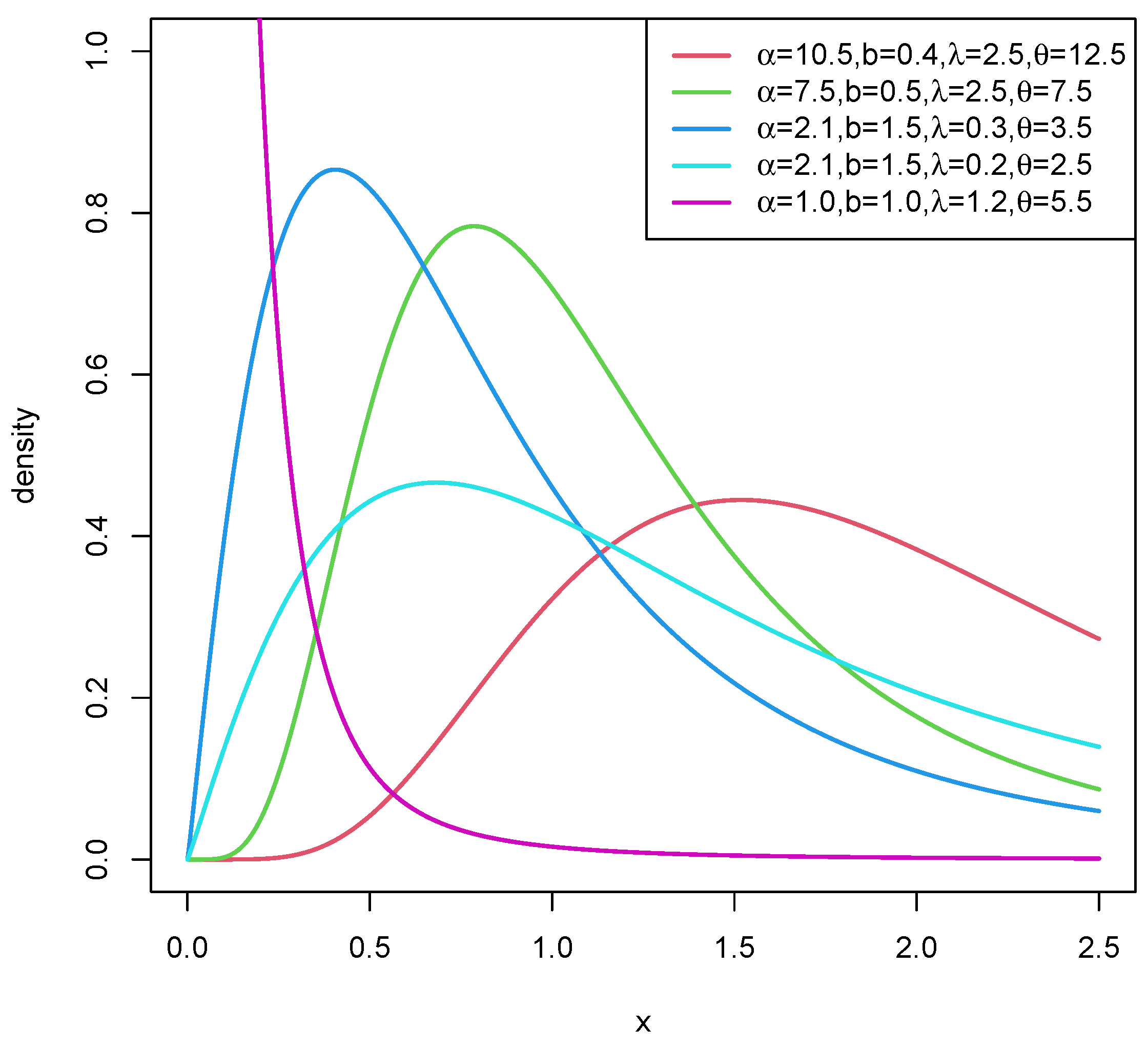
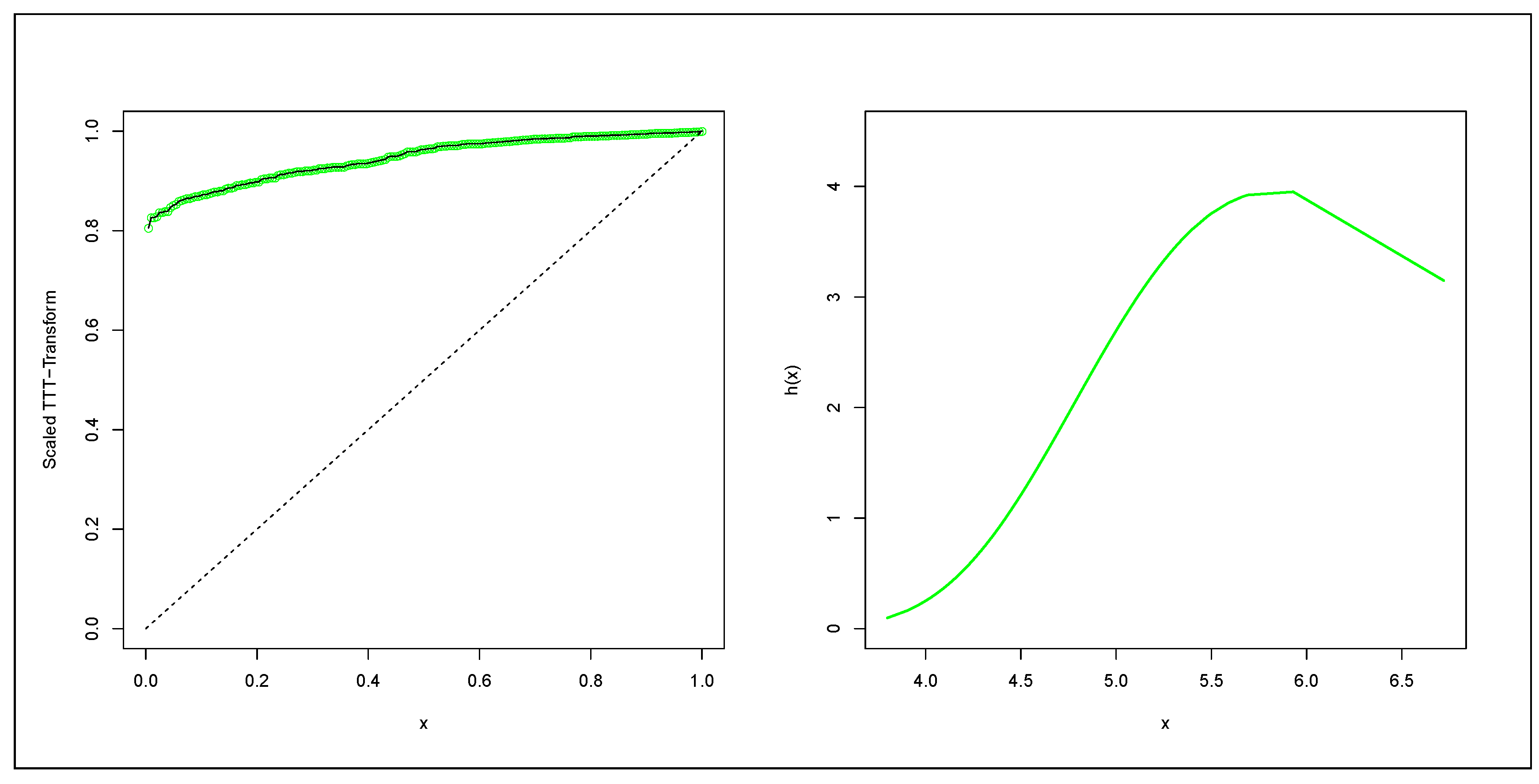
2. The Model
3. Some Statistical Properties
3.1. Quantile Function
3.2. Moments and Moment Generating Function
3.3. Distribution of Order Statistics
3.4. Rényi Entropy
4. Estimation
5. Simulations
6. Inference
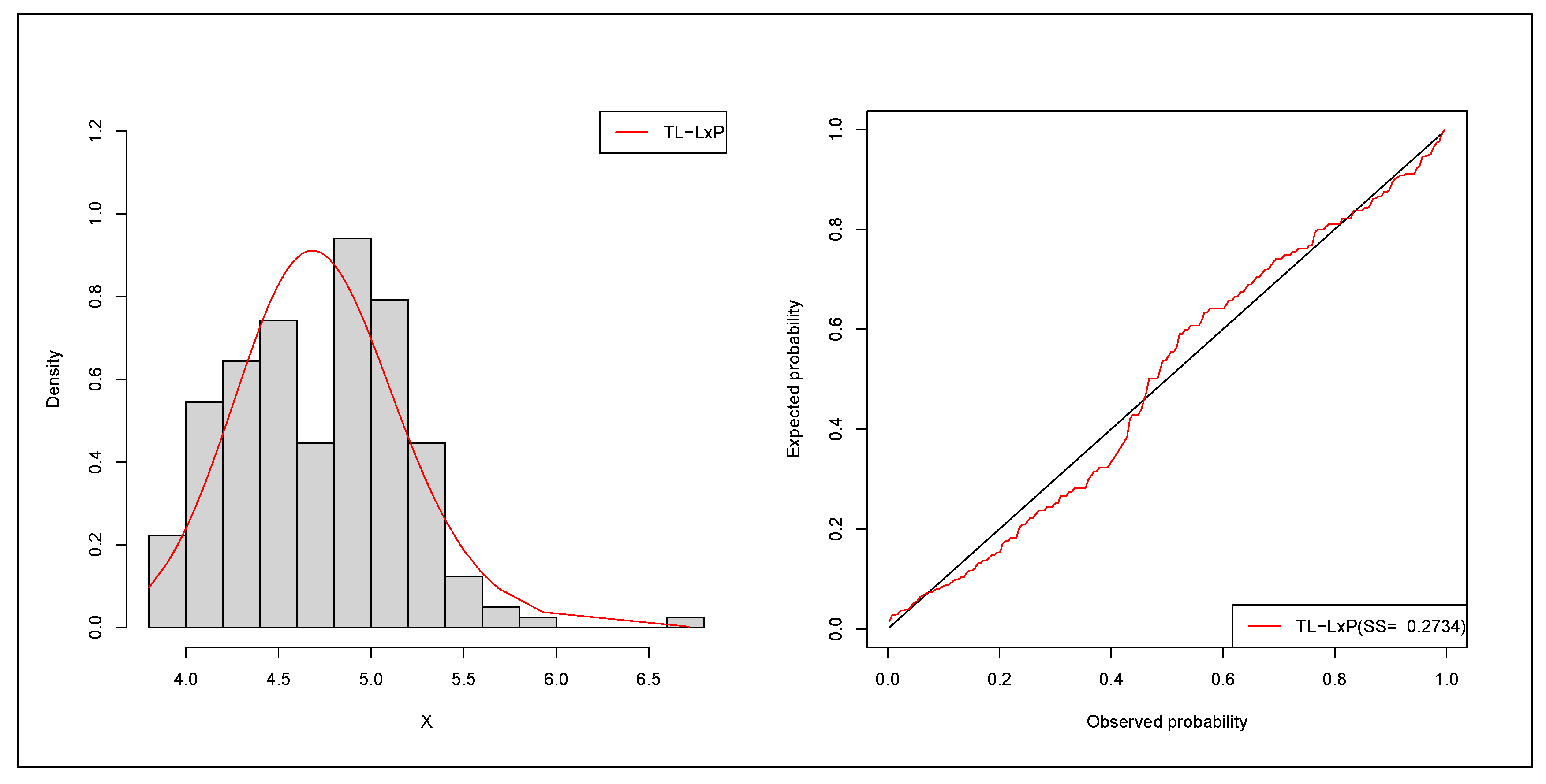
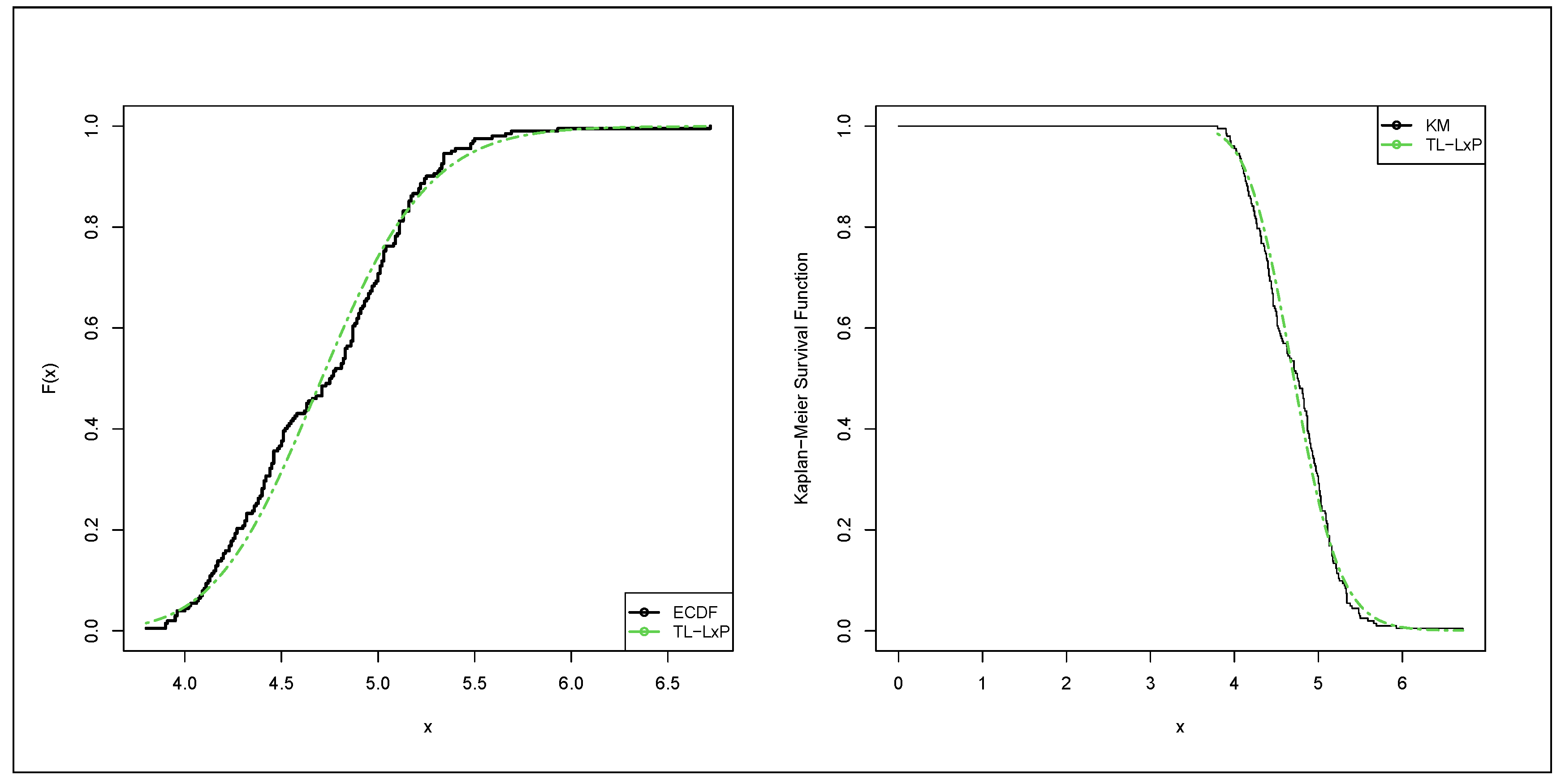
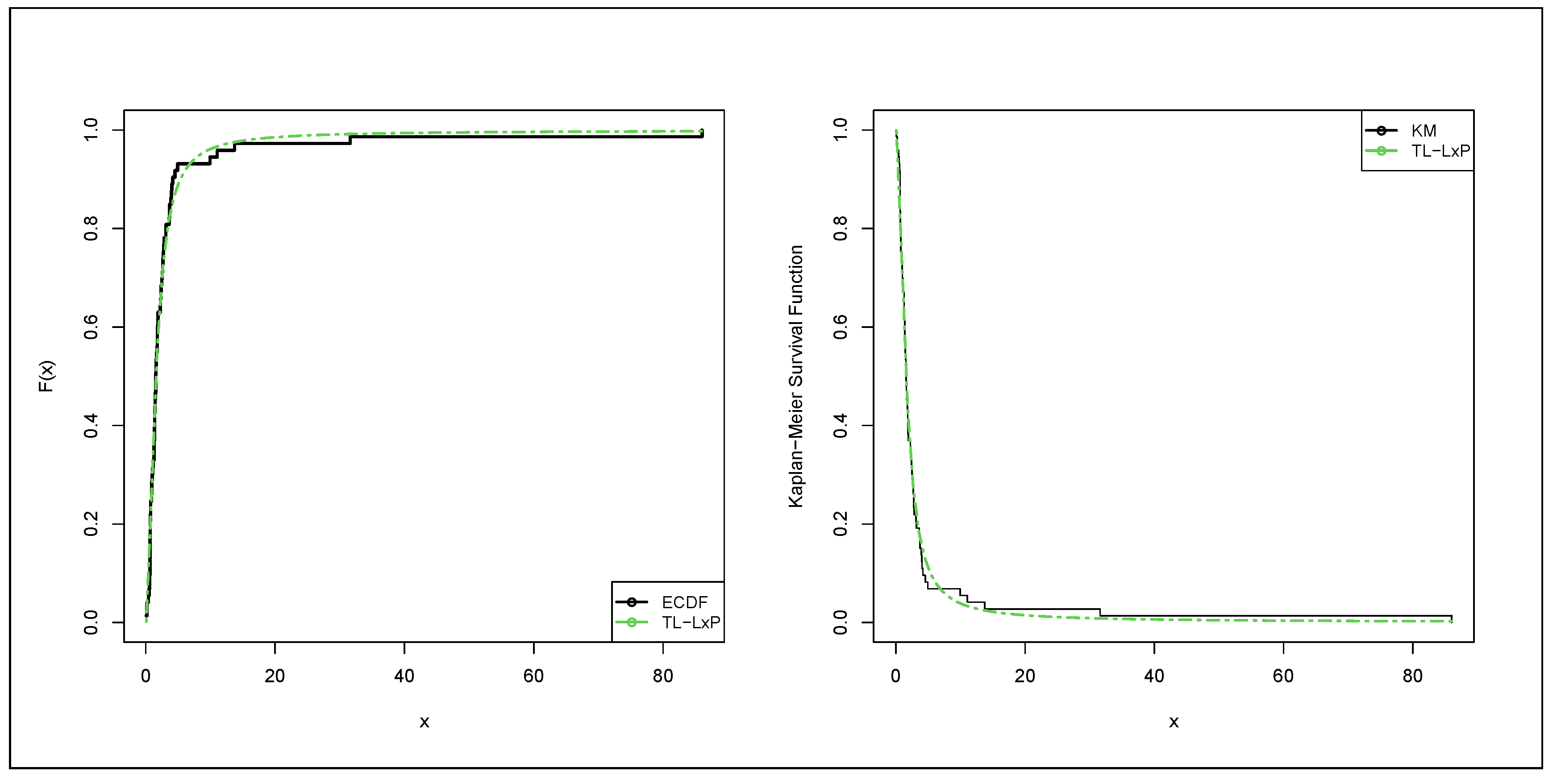
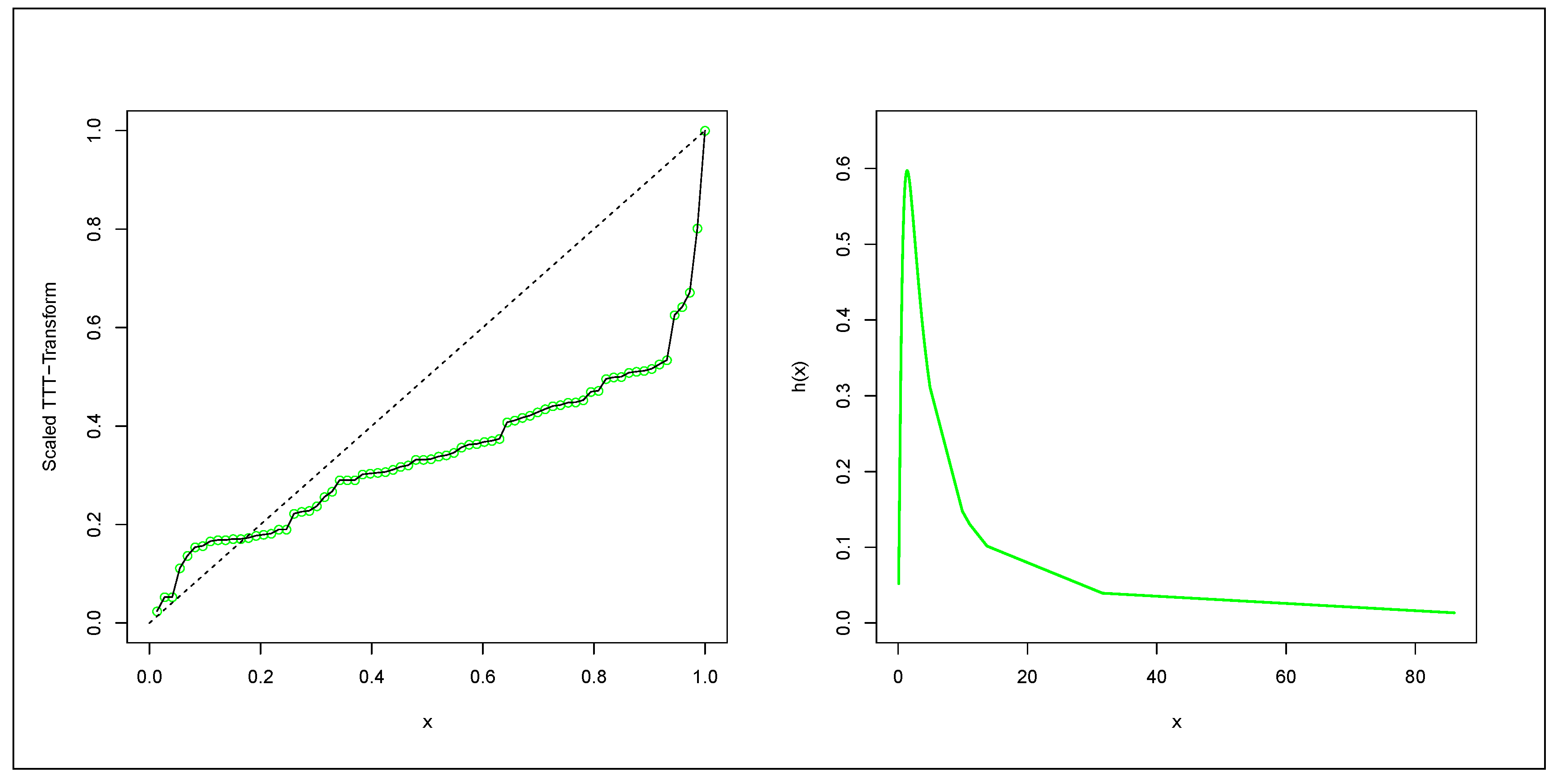
6.1. Failure Times Data
6.2. Red Cells Data
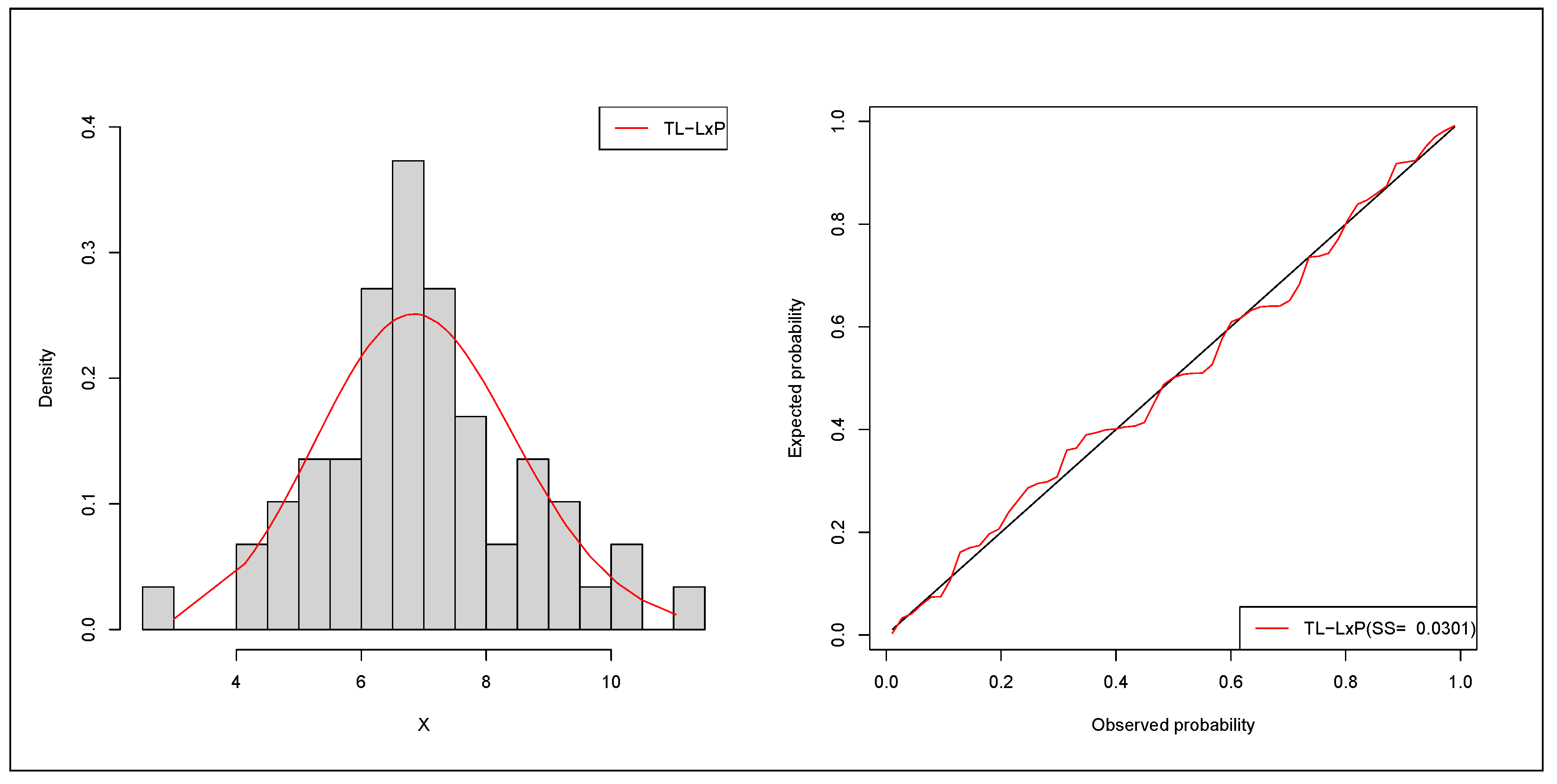
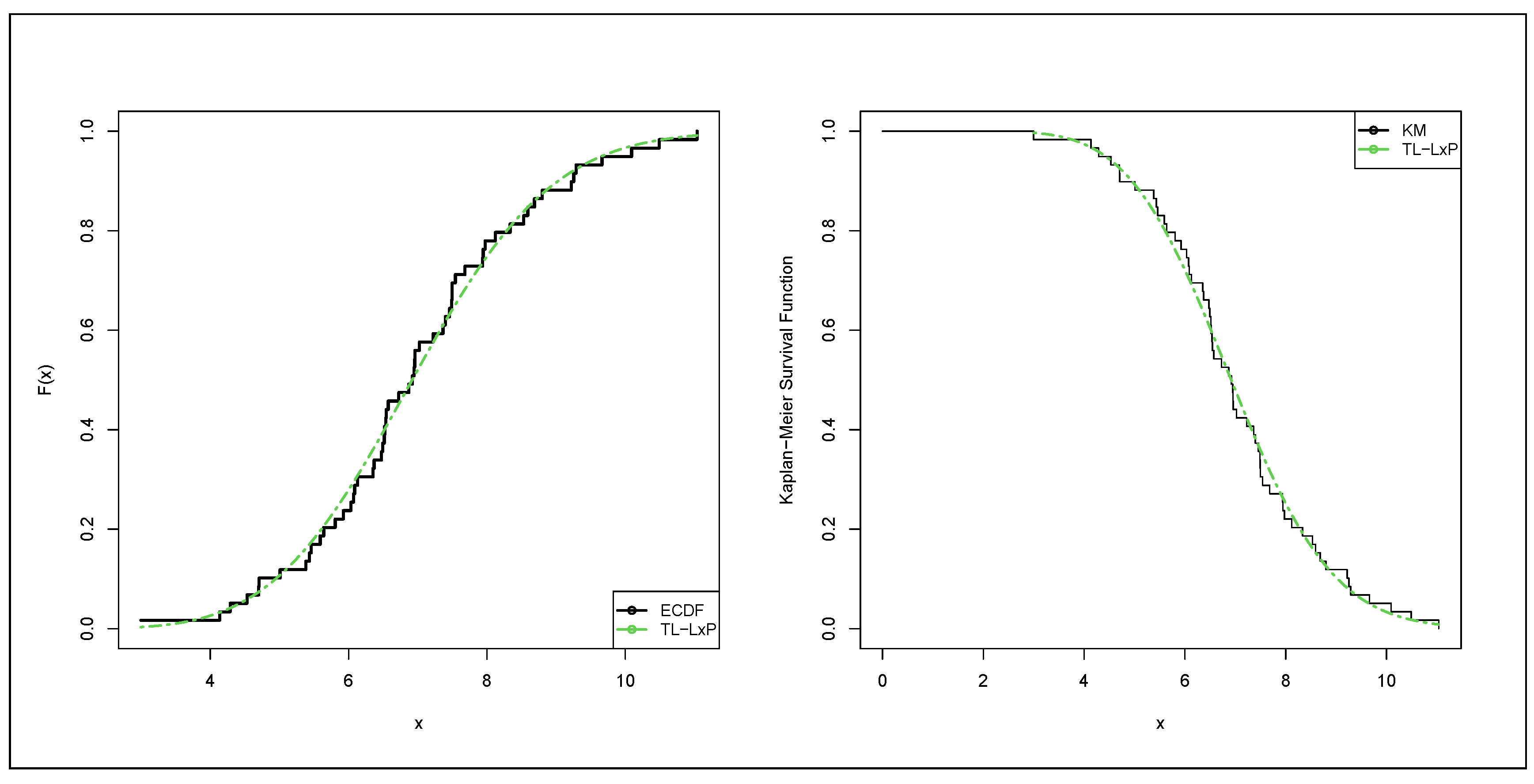
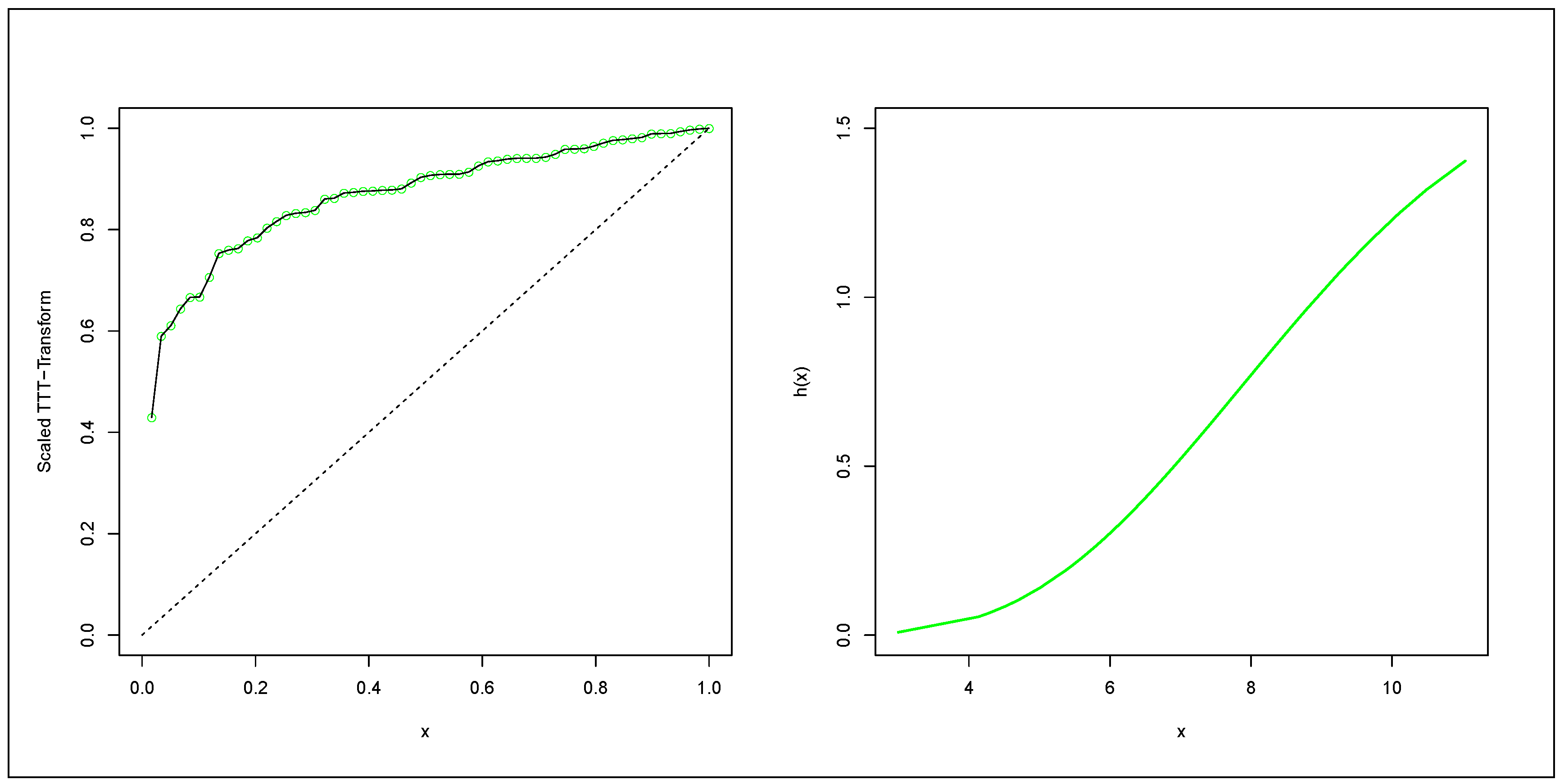
6.3. Acute Bone Cancer Data
7. Concluding Remarks
References
- Aarset, M. V. (1987). How to Identify Bathtub Hazard Rate. IEEE Transaction of Reliability, 36(1), 106-108.
- Abdul-Moniem, I. B. and Abdel-Hameed, H. F. (2012). On Eponentiated Lomax Distribution. International Journal of Mathematical Archive, 3(5), 1-7.
- Al-Shomrani, A., Arif, O., Shawky, A., Hanif, S., Shahbaz, M.Q. (2016). The Topp-Leone Family of Distributions: Some Properties and Application. Pakistan Journal of Statistics and Operation Research, 12(3), 443-451.
- Alzaatreh, A., Lee, C. and Famoye, F. (2013). A New Method for Generating Families of Continuous Distributions. Metron, 71(1), 63-79.
- Bassiouny, A. H., Abdo, N. F., and Shahen, H. S. (2015). Exponential Lomax Distribution. Journal of Computer Applications, 121(13), 24-29.
- Chipepa, F. and Oluyede, B. (2021). The Topp-Leone Odd Exponential Half Logistic-G Family of Distributions with Applications. Pakistan Journal of Statistics, 37(3), 253–277.
- Cordeiro, G. M., Alizadeh, M., Ortega, E. M., (2014). The Exponentiated Half-Logistic Family of Distributions: Properties and Applications. Hindawi Publishing Corporation Journal of Probability and Statistics Volume 2014, Article ID 864396, 21 pages. [CrossRef]
- Johnson, N. L., Kotz, S., and Balakrishnan, N. (1994). Continuous Distributions, Volume 1, John Wiley & Sons, New York, NY.
- Lomax, K.S. (1954). Business Failures: Another example of the Analysis of Failure Data. Journal of the American Statistical Association 49, 847-852.
- Mansour, M., Yousof, H.M., Shehata, W.A., and Ibrahim, M.( 2020). A New two Parameter Burr XII Distribution: Properties, Copula, Different Estimation Methods and Modeling Acute Bone Cancer Data. Journal of Nonlinear Science and Applications, 13, 223-238.
- Moakofi, T., Oluyede, B. and Gabanakgosi, M. (2022). The Topp-Leone Odd Burr III-G Family of Distributions: Model, Properties and Applications. Statistics Optimization and Information Computing, 1, 1–27.
- Oluyede, B., Dingalo, N. and Chipepa, F. (2023). The Topp-Leone-Harris-G Family of Distributions with Applications. International Journal Mathematics in Operational Research, 24(4), 554-582.
- Oguntunde, P. E., Khaleel, M. A., Okbue, H. I., and Odetunmibi, O. A. (2019). The Topp-Leone Lomax Distribution with Applications to Airborne Communication Transceiver Dataset. Wireless Personal Communications, 109, 349-360.
- Rényi, A. (1960). On Measures of Entropy and Information. Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, 1, 547 - 561.
- Ristić, M. M. and Balakrisihnan, N. (2012). The Gamma Exponentiated Exponential Distribution. Journal of Computation and Simulation, 82, 1191-1206.
- Shannon, C. E. (1951). Prediction and Entropy of Printed English, The Bell System Technical Journal, 30, 50-64.
- Tahir, M. H., Cordeiro, G. M., Mansoor, M., and Zubair, M. (2015). The Weibull-Lomax Distribution: Properties and Applications. Hacettepe Journal of Mathematics and Statistics, 44(2), 455-474.
- Torabi, H. and Montazari, H. N. (2012). The Gamma-Uniform Distribution and its Applications. Kybernetika, 48(1), 16–30.
- Weibull W. A. (1951). Statistical Distribution Function of Wide Applicability. Journal of Applied Mechanics, 18, 293-296.
- Zografos, K. and Balakrishnan, N. (2009). On Families of Beta- and Generalized Gamma Generated Distributions and Associated Inference. Statistical Methodology, 6, 344-362.

| u | (1.5,1.5,0.1,1.5) | (0.5,1,0.5,0.9) | (1.5,0.5,0.3,1.5) | (0.5,1.5,0.9,0.5) | (1.1,1.1,0.3,0.6) |
|---|---|---|---|---|---|
| 0.1 | 0.5267 | 0.00461 | 0.5549 | 0.0024 | 0.1585 |
| 0.2 | 0.9252 | 0.0200 | 1.0134 | 0.0101 | 0.3278 |
| 0.3 | 1.3448 | 0.04923 | 1.5337 | 0.0244 | 0.5264 |
| 0.4 | 1.8225 | 0.0973 | 2.1748 | 0.0472 | 0.7693 |
| 0.5 | 2.3994 | 0.1731 | 3.0212 | 0.0818 | 1.0792 |
| 0.6 | 3.1417 | 0.2929 | 4.2321 | 0.1344 | 1.4967 |
| 0.7 | 4.1807 | 0.4918 | 6.1721 | 0.2176 | 2.1059 |
| 0.8 | 5.8442 | 0.8624 | 9.9251 | 0.3628 | 3.1224 |
| 0.9 | 9.3687 | 1.7807 | 20.8868 | 0.6879 | 5.3899 |
| (1.5,1.5,0.1,1.5) | (0.5,1,0.5,0.9) | (1.1,0.5,0.8,1.5) | (1.5,1.5,0.9,0.5) | (1.1,0.9,0.3,0.6) | |
|---|---|---|---|---|---|
| 0.1208 | 0.1736 | 0.2224 | 0.2903 | 0.1827 | |
| 0.0823 | 0.0873 | 0.1277 | 0.1540 | 0.1139 | |
| 0.0622 | 0.0569 | 0.0878 | 0.1002 | 0.0820 | |
| 0.0498 | 0.0419 | 0.0664 | 0.0730 | 0.0638 | |
| 0.0415 | 0.0331 | 0.0532 | 0.0570 | 0.0521 | |
| SD | 0.2603 | 0.2390 | 0.2797 | 0.2641 | 0.2838 |
| CV | 2.1555 | 1.3770 | 1.2579 | 0.9096 | 1.5535 |
| CS | 2.0333 | 1.6097 | 1.1231 | 0.8146 | 1.3891 |
| CK | 5.7439 | 4.7457 | 3.0822 | 2.7208 | 3.6022 |
| (1, 1, 0.4, 1) | (1.0, 1.1, 0.4, 1.1) | ||||||
| n | Mean | RMSE | Bias | Mean | RMSE | Bias | |
| 40 | 1.1187 | 0.4721 | 0.1187 | 1.1094 | 0.3637 | 0.1094 | |
| 80 | 1.0418 | 0.2124 | 0.0418 | 1.0438 | 0.2134 | 0.0438 | |
| 100 | 1.0287 | 0.1808 | 0.0287 | 1.0268 | 0.1863 | 0.0268 | |
| 200 | 1.0141 | 0.1252 | 0.0141 | 1.0101 | 0.1200 | 0.0101 | |
| 400 | 1.0003 | 0.0886 | 0.0003 | 1.0008 | 0.0886 | 0.0008 | |
| 40 | 3.0728 | 4.6544 | 2.0728 | 3.4046 | 5.1203 | 2.3046 | |
| 80 | 2.1885 | 3.0581 | 1.1885 | 2.5260 | 3.6024 | 1.4260 | |
| b | 100 | 1.8541 | 2.4040 | 0.8541 | 2.2194 | 2.9517 | 1.1194 |
| 200 | 1.3472 | 1.2323 | 0.3472 | 1.6549 | 1.8163 | 0.5549 | |
| 400 | 1.1522 | 0.5702 | 0.1522 | 1.3192 | 0.7852 | 0.2192 | |
| 40 | 0.5926 | 3.1108 | 0.1926 | 0.4847 | 0.6640 | 0.0847 | |
| 80 | 0.3932 | 0.3985 | -0.0068 | 0.4118 | 0.4269 | 0.0118 | |
| 100 | 0.3985 | 0.3761 | -0.0015 | 0.4036 | 0.4167 | 0.0036 | |
| 200 | 0.3823 | 0.2763 | -0.0177 | 0.3832 | 0.2979 | -0.0168 | |
| 400 | 0.3670 | 0.2154 | -0.0330 | 0.3746 | 0.2305 | -0.0254 | |
| 40 | 1.7883 | 1.3726 | 0.7883 | 1.8600 | 1.3326 | 0.7600 | |
| 80 | 1.6869 | 1.2467 | 0.6869 | 1.7232 | 1.2241 | 0.6232 | |
| 100 | 1.6333 | 1.1739 | 0.6333 | 1.7066 | 1.1771 | 0.6066 | |
| 200 | 1.5767 | 1.1279 | 0.5767 | 1.6617 | 1.1304 | 0.5617 | |
| 400 | 1.4849 | 1.0079 | 0.4849 | 1.5532 | 1.0065 | 0.4532 | |
| (1, 1.1, 0.4, 0.9) | (1.0, 1,0, 1.1, 1.1) | ||||||
| n | Mean | RMSE | Bias | Mean | RMSE | Bias | |
| 40 | 1.1179 | 0.4445 | 0.1179 | 1.1161 | 0.4619 | 0.1161 | |
| 80 | 1.0481 | 0.2139 | 0.0481 | 1.0401 | 0.2156 | 0.0401 | |
| 100 | 1.0297 | 0.1878 | 0.0297 | 1.0280 | 0.1891 | 0.0280 | |
| 200 | 1.0156 | 0.1221 | 0.0156 | 1.0100 | 0.1204 | 0.0100 | |
| 400 | 1.0010 | 0.0878 | 0.0010 | 1.0014 | 0.0876 | 0.0014 | |
| 40 | 3.3695 | 4.9285 | 2.2695 | 4.7556 | 8.7554 | 3.7556 | |
| 80 | 2.4850 | 3.3800 | 1.3850 | 3.3262 | 6.3080 | 2.3262 | |
| b | 100 | 2.2942 | 2.9945 | 1.1942 | 2.5351 | 4.6243 | 1.5351 |
| 200 | 1.6291 | 1.6175 | 0.5291 | 1.4946 | 2.0599 | 0.4946 | |
| 400 | 1.3773 | 0.8805 | 0.2773 | 1.1591 | 0.7450 | 0.1591 | |
| 40 | 0.4667 | 0.7443 | 0.0667 | 2.2409 | 19.8829 | 1.1409 | |
| 80 | 0.3895 | 0.4034 | -0.0105 | 1.0952 | 1.1146 | -0.0048 | |
| 100 | 0.3831 | 0.3863 | -0.0169 | 1.1261 | 1.1634 | 0.0261 | |
| 200 | 0.3640 | 0.2778 | -0.0360 | 1.0627 | 0.7570 | -0.0373 | |
| 400 | 0.3461 | 0.2167 | -0.0539 | 1.0402 | 0.6162 | -0.0598 | |
| 40 | 1.7507 | 1.3448 | 0.8507 | 1.9460 | 1.7794 | 0.8460 | |
| 80 | 1.6485 | 1.2425 | 0.7485 | 1.8051 | 1.3196 | 0.7051 | |
| 100 | 1.5747 | 1.1319 | 0.6747 | 1.7437 | 1.2722 | 0.6437 | |
| 200 | 1.5370 | 1.0988 | 0.6370 | 1.6684 | 1.1725 | 0.5684 | |
| 400 | 1.4525 | 0.9974 | 0.5525 | 1.5819 | 1.1029 | 0.4819 |
| Estimates | Statistics | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Model | b | |||||||||
| TL-LxP | 10.6068 | 3.2757 | 0.0291 | 30.7911 | 222.65 | 230.65 | 231.40 | 238.96 | 0.0354 | 0.2003 |
| (1.5962) | (1.0727) | (0.0075) | (0.2066) | |||||||
| TL-Lx | 53.9590 | 154.2200 | 0.0021 | - | 230.05 | 236.05 | 236.49 | 242.28 | 0.1061 | 0.6512 |
| (6.9886 ) | (9.9495 ) | (7.2301 ) | - | |||||||
| Exp-Lx | 53.2240 | - | 0.0015 | 424.1200 | 230.01 | 236.01 | 236.44 | 242.24 | 0.1053 | 0.6467 |
| (3.7181 ) | - | (5.2423 ) | (1.8960 ) | |||||||
| E-Lx | 101.2300 | 155.7100 | 0.0071 | - | 234.90 | 240.90 | 241.34 | 247.13 | 0.2237 | 1.2920 |
| (3.5910 ) | (2.2705 ) | (0.0009) | - | |||||||
| a | b | - | ||||||||
| W-Lx | 9.5584 | 0.2642 | 1.6864 | - | 224.02 | 230.02 | 230.46 | 236.28 | 0.0669 | 0.3739 |
| (9.7424) | (0.3376) | 6.0967 | - | |||||||
| Estimates | Statistics | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Model | b | |||||||||
| TL-LxP | 275.1900 | 18.0300 | 0.0287 | 12.1300 | 252.25 | 260.25 | 260.45 | 273.48 | 0.2756 | 1.4905 |
| (4.6929 ) | (3.2923 ) | (1.9392 ) | (3.9722 ) | |||||||
| TL-Lx | 2.3999 | 7.0413 | 1.5861 | - | 262.89 | 268.89 | 269.01 | 278.82 | 0.4186 | 2.3022 |
| (7.6362 ) | (2.5623 ) | (1.1394 ) | - | |||||||
| Exp-Lx | 2.7839 | - | 3.6145 | 6.2847 | 261.95 | 267.95 | 268.07 | 277.87 | 0.422 | 2.3240 |
| (3.3390 ) | - | (2.5735 ) | (1.4804 ) | |||||||
| E-Lx | 79.4110 | 46.9440 | 3.7495 | - | 343.91 | 349.91 | 359.71 | 353.81 | 0.2664 | 2.1860 |
| (1.0190 ) | (1.6366 ) | (2.6382 ) | - | |||||||
| a | b | - | ||||||||
| W-Lx | 14.1610 | 0.4390 | 0.7813 | - | 293.41 | 299.41 | 299.54 | 309.34 | 0.2224 | 1.8017 |
| (1.1162) | (0.0465) | (0.1648) | - | |||||||
| Estimates | Statistics | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Model | b | |||||||||
| TL-LxP | 2.5917 | 0.5558 | 0.5351 | 4.1833 | 278.29 | 286.29 | 286.88 | 295.45 | 0.0568 | 0.4391 |
| (0.7412) | (0.3128) | (0.4295) | (2.0482) | |||||||
| TL-Lx | 3.3768 | 0.9318 | 0.9169 | - | 281.67 | 287.67 | 288.02 | 294.54 | 0.0919 | 0.6886 |
| (1.1532) | (0.2168) | (0.9169) | - | |||||||
| Exp-Lx | 3.3768 | - | 0.9169 | 1.8637 | 281.67 | 287.67 | 288.02 | 294.54 | 0.0919 | 0.6886 |
| (1.1532) | - | (0.5215) | (0.4337) | |||||||
| E-Lx | 0.7659 | 2.6643 | 1.3793 | - | 322.81 | 328.81 | 329.15 | 335.68 | 0.6017 | 3.6470 |
| (9.2412 ) | (3.3325 ) | (1.3220 ) | - | |||||||
| a | b | - | ||||||||
| W-Lx | 1.7750 | 0.2582 | 5.0702 | - | 300.52 | 306.52 | 306.87 | 313.87 | 0.3067 | 1.9958 |
| (0.4286) | (0.0759) | (4.3144) | - | |||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





