Differential Quadrature Free Vibration Analysis of Sandwich Plates with Curvilinear Fiber Variable Stiffness Composite Face Sheets

1. Introduction

The cost and weight of sandwich materials are lower than that of single materials, and they have better mechanical properties and process properties, which are gradually being widely used. Typically, a sandwich construction has three sections: a top, middle, and bottom segment with a core located in the center and skins at the top and bottom, where the skins have the same material and thickness while the core can be made of almost any material or architecture.[1] The face sheets require high strength and the core requires light weight.[2] Because of their extraordinarily high stiffness-to-weight and strength-to-weight ratios,[3,4] sandwich plates are very often utilized in engineering settings like aerospace and automotive applications, naval vessels, ships, bridge construction and wind turbines.[5–7] Sandwich structures have many benefits, including the need for high-strength, lightweight materials and the ongoing discovery of new materials, which has led to their continual usage in structural design.[8] The conventional skins of constant stiffness composite laminates (CSCL) consist of straight fibers whose stiffness, such as elasticity and flexibility, remains uniform or constant in all directions in the plane of the material. While VSCL are typically made by carefully designing and arranging layers of different materials or by altering the path of reinforcing fibers (curvilinear fiber) in the construction.[9] It is obvious that a more flexible method of increasing a plate's rigidity can be achieved by using VSCL.[10] Researchers have recently used theoretical analysis, empirical and semi-empirical modelling, numerical simulations, and experimental testing to examine the mechanical properties of sandwich constructions. [11] Experimental data is typically used to verify the modelling,[12] while numerical simulations are preferred for their computational efficiency and rapid turnaround time.[13]

The foundation for VSCL has been laid by numerous academics using the statics analysis of CSCL sandwich plates. Kant et al.[14] have analyzed the fundamental frequency of CSCL laminates and sandwich plates and the solution method used is finite element. They used a higher–order refined theory as the basis for their modelling and as parametric inputs, they systematically changed the plate thickness, the ratio of core to skin thickness, and the boundary conditions. Furthermore, their investigation included a rigorous comparative analysis with established methods to demonstrate the precision and robustness of their chosen theory. Yuan et al.[15] looked at the vibration properties of conventional sandwich plates that are rectangular in shape, including the natural frequencies and modes, using the spline finite strip method and it was concluded that the techniques of single-plate analysis were not applicable to the structural analysis of most plat constructions. To lower the computational cost in the fundamental frequency prediction of sandwich plates and composite laminates, Mantari et al.[16] presented a simplified FSDT. Reducing the amount of unknowns in the modeling computations allows for the reduction of the number of degrees of freedom. Comparing the computational results with those of other computational models serves as verification of the method's accuracy.

The advent of advanced technologies ushered in a new era of VSCL plates and revolutionized the design landscape of composite plates. By manipulating the fiber orientation, VSCL plates offer improved mechanical properties by altering the stiffness distribution. Gürdal et al.[17] used a numerical model to solve static problems such as displacement field and overall stiffness of VSCL symmetric laminates. They pointed out that by choosing an appropriate starting and ending angle, the given loading conditions can be better considered and a certain stiffness can be achieved or possibly the buckling behavior can be improved. Lopes et al.[18] predicted various failure modes of VSCL plates in compression and simulated the first layer failure in post-buckling. Finite element modelling was used to predict the physical failure criteria for different modes of failure of the VSCL plates. Khani et al.[19] applied a new solution to incorporate the failure criteria for strength into the parameter space of the laminates. The numerical results showed an increase in strength compared with the quasi–isotropic construction. Akhavan et al.[20] analyzed the law of variation of fundamental frequencies and mode shapes with fiber orientation angles for VSCL laminates, third-order shear deformation theory (TSDT) was the modelling technique applied, and p-version finite elements were employed in the solution. Through data comparison, they explored some connections that exist between fiber orientation angles and fundamental frequencies.

Existing research on VSCL plates focuses on statics and has only investigated their dynamics to a limited extent, which warrants further research into their dynamics in future studies. Houmat[21] and Hachemi[22,23] are among the few scholars who have performed free vibration analysis of VSCL sandwich plates. Houmat’s modelling theory is three-dimensional elasticity theory, while Hachemi’s analysis is grounded in both layer-wise theory and HSDT. They both chose p-version finite elements as the solution method. By adjusting factors including fiber orientation angles, boundary conditions, and skin-to-core thickness ratios, the variation patterns of fundamental frequencies as well as other dynamic responses were examined, highlighting the benefits of VSCL sandwich plates in structural investigations.

Systems of partial differential equations that typically have difficult-to-find closed-form solutions characterize engineering challenges.[24] Consequently, engineers and researchers frequently turn to approximative numerical techniques to solve such systems. These methods include the finite element, the p-version finite element, the Rayleigh–Ritz methods, the finite volume method and so on. Bellman et al.[25] developed the differential quadrature technique (DQM) for solving partial differential equations. DQM has the advantage of having a smaller number of discrete points with higher computational accuracy. Liu[26] utilized Mindlin plate theory as the modelling theory and applied DQM to the investigation of rectangular plate buckling. Liew et al.[27] used DQM to conduct a static study of a rectangular plate on Winkler’s basis, utilizing FSDT as the modelling theory. This is the first successful application of DQM to thick–plate problems. Based on previous work, Liew et al. [28] applied the moving least squares differential quadrature (MLSDQ) to calculate and study the fundamental frequency of symmetric laminates of medium thickness and the modelling theory is FSDT. The free vibration problem of sandwich plates with functional grades on an elastic foundation was investigated by Fu et al.[29]. They employed DQM, and the modelling theory is NSDT. To the best of our knowledge, no studies have yet applied the DQM to the free vibration analysis of VSCL sandwich plates modelling by FSDT.

This work proposes an FSDT-based DQM approach to give a reasonably accurate and computationally cheap computer model for the free vibration analysis of VSCL sandwich structures. The plate consists of two VSCL skins and an isotropic core. Based on the FSDT, the governing equations were derived using the von Kármán strain–displacement relationship and Hamilton's principle. By applying the DQM, the fundamental frequencies of the sandwich plates were determined numerically, and the impacts of several parameters on the plate's vibration behaviour were examined.

This is how the remainder of the paper is structured. The modelling procedure and analytical method employed are stated in the second section. In the third section, numerical applications and discussion, encompassing both CSCL and VSCL sandwich plates, are presented. The last section summarizes the conclusions.

2. Theoretical Formulation

2.1. Geometric Description

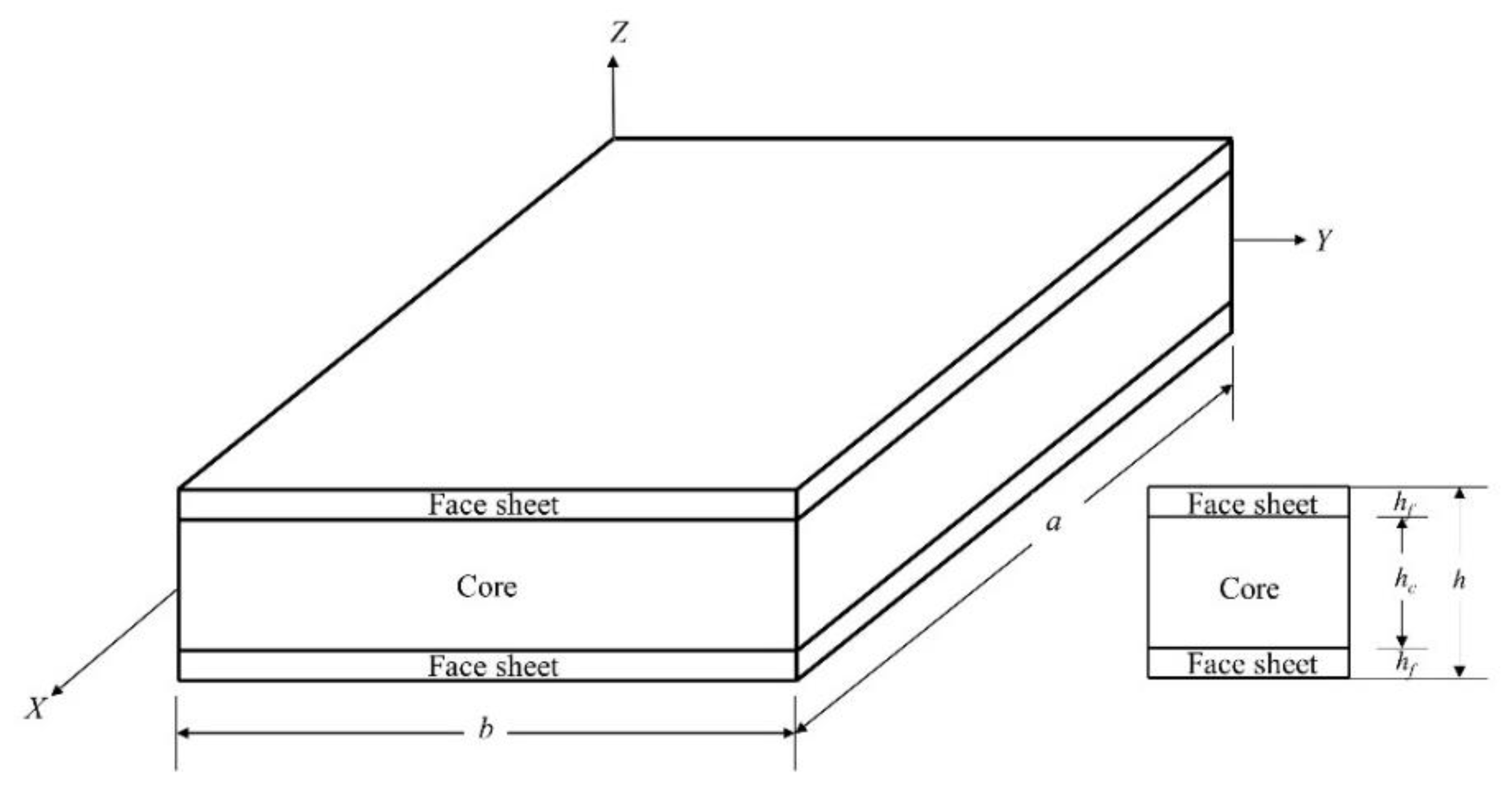
The geometrical design and parameterization of a sandwich plate with variable stiffness skins are displayed in Figure 1. The upper and lower composite skins, every stratum of the skin consisting of single or laminated composite layers with curvilinear fibers, with a soft core in the centre, make up the entire plate. Assume that the dimensions of the plate are a, b, and h, respectively, for length, breadth, and thickness. The total thickness h can be decomposed into upper and lower skins $h_f$ and intermediate core $h_c$. It is considered that every interface on the board is flawlessly integrated. Given that the entire plate consists of N layers, the thickness of each single layer of the face sheet is $h_{layer}=2h_s/\left(N-1\right)$. The entire plate's Cartesian coordinate system is specified as $0\le X\le a，0\le Y\le b,-h/2\le Z\le h/2$.

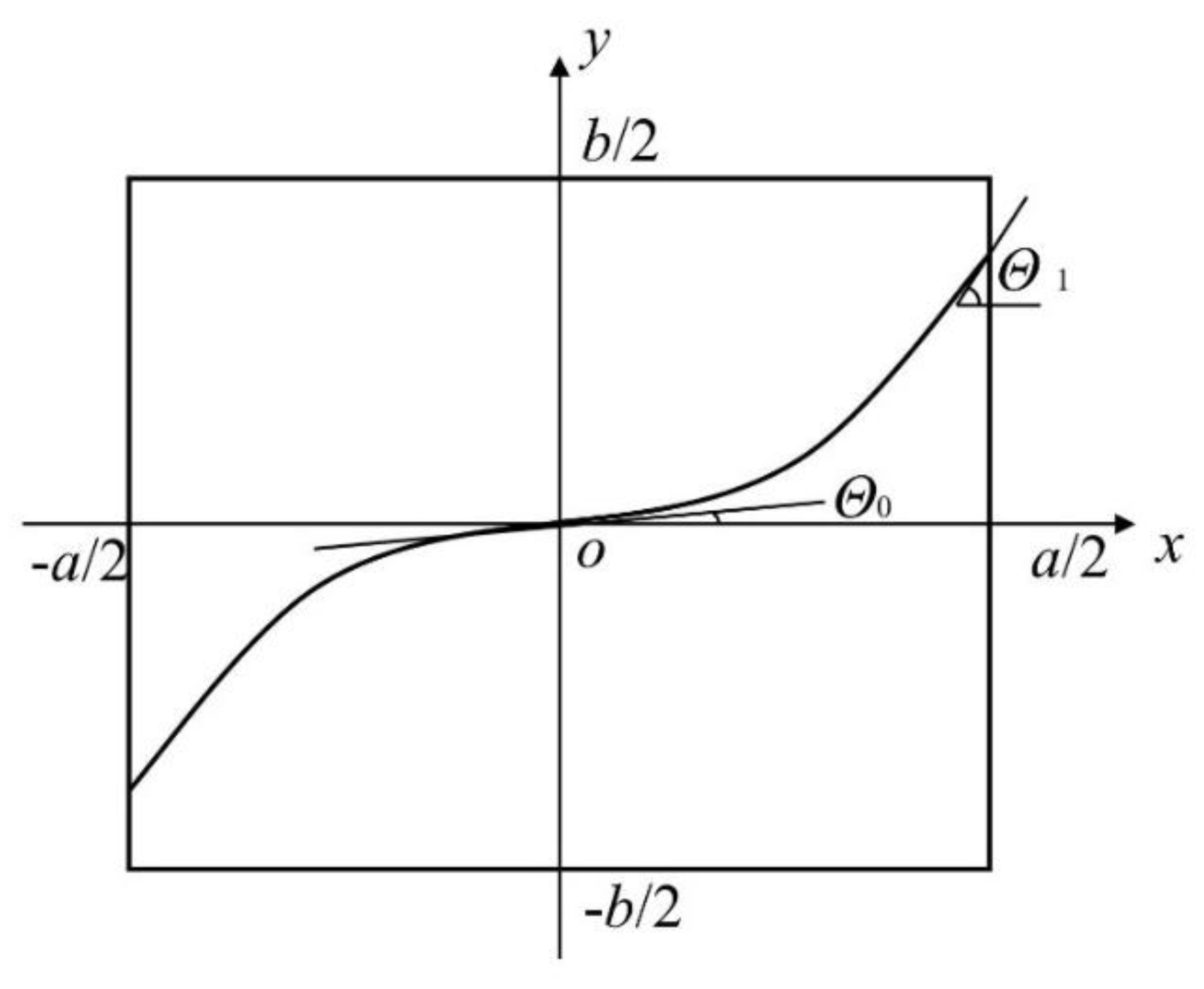
To simplify the definition, the point of central symmetry of the reference path is typically specified to be at the center of each individual layer of the skin, as illustrated in Figure 2, and the Cartesian coordinate system is defined as $-a/2\le x\le a/2,-b/2\le x\le b/2,-h_{layer}/2\le z\le h_{layer}/2$. Assuming that the angle of the fiber direction varies linearly along the x–direction, it is expressed mathematically as follows:[20]

$$\left\{\begin{array}{c}\theta \left(x\right)={\displaystyle \frac{2\left({\Theta }_1-{\Theta }_0\right)}{a}}\left|x\right|+{\Theta }_0\\ y^{\prime }={\displaystyle \frac{\mathrm{d}y}{\mathrm{d}x}}=\tan \theta \left(x\right)\end{array}\right.$$

(1)

where, ${\Theta }_0$ is the starting angle of the fiber, characterizing the angle between the tangent of the fiber curve at the center point and the x–axis of the relative horizontal line, the fiber’s ending angle, or ${\Theta }_1$, is the angle formed by the tangent of the fiber curve and the x-axis of the relative horizontal line at the location where the layer's outer boundary is $a/2$, and $a$ is the plate length.

Integrating the above equation gives the reference path for the curvilinear fiber placement as follows:

$$y\left(x\right)=\left\{\begin{array}{cc}{\displaystyle \frac{a}{2\left({\Theta }_1-{\Theta }_0\right)}}\left\{\ln \left(\cos {\Theta }_0\right)-\ln \left[\cos \left({\displaystyle \frac{2\left({\Theta }_1-{\Theta }_0\right)}{a}}x+{\Theta }_0\right)\right]\right\}& \left(0\le x\le {\displaystyle \frac{a}{2}}\right)\\ {\displaystyle \frac{a}{2\left({\Theta }_0-{\Theta }_1\right)}}\left\{\ln \left(\cos {\Theta }_0\right)-\ln \left[\cos \left({\displaystyle \frac{2\left({\Theta }_0-{\Theta }_1\right)}{a}}x+{\Theta }_0\right)\right]\right\}& \left(-{\displaystyle \frac{a}{2}}\le x\le 0\right)\end{array}\right.$$

(2)

2.2. Modelling Theory

Between the skin and core materials of sandwich plates, there are significant differences in stiffness and material properties, making the performance analysis of the sandwich structure quite intricate. As a result, the calculation model selected has a significant impact on how accurately the sandwich structure is calculated.[30] Transverse shear deformation is not taken into account by the classical laminated plate theory (CLPT), which is predicated on Kirchhoff's assumptions. Therefore, for plates of moderate thickness, CLPT's estimates on both static and dynamic analysis are biased.[31–34] For the purpose of this study's free vibration analysis of sandwich plates, the author employed the FSDT modelling theory,[35] which accounts for the impact of shear deformation.

Based on Kirchhoff’s first two assumptions, the third assumption was not considered. In case a symmetric sandwich plate is used, the vibrations in the transverse and in-plane directions are separated by the symmetry in the z direction, and the in-plane deformation at$z=0$can be ignored. The displacement field has the following expression.[36]

$$\begin{array}{l}u\left(x,y,z,t\right)=u_0\left(x,y,t\right)+z{\phi }_x\left(x,y,t\right)\\ v\left(x,y,z,t\right)=v_0\left(x,y,t\right)+z{\phi }_y\left(x,y,t\right)\\ w\left(x,y,z,t\right)=w_0\left(x,y,t\right)\end{array}$$

(3)

where the displacements along the three coordinate axes are denoted by u, v, and w, and the midplane of the plate rotates about the x and y axes at angles ${\phi }_x$ and ${\phi }_y$, respectively.

According to the von Kármán strain–displacement relationship, the components of the linear strains can be expressed as follows:

$$\left\{\begin{array}{c}{\epsilon }_x\\ {\epsilon }_y\\ {\gamma }_{yz}\\ {\gamma }_{xz}\\ {\gamma }_{xy}\end{array}\right\}=\left\{\begin{array}{c}{\displaystyle \frac{\partial u_0}{\partial x}}+{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{\partial w_0}{\partial x}}\right)}^2\\ {\displaystyle \frac{\partial v_0}{\partial y}}+{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{\partial v_0}{\partial y}}\right)}^2\\ {\displaystyle \frac{\partial w_0}{\partial y}}+{\phi }^y\\ {\displaystyle \frac{\partial w_0}{\partial x}}+{\phi }^x\\ {\displaystyle \frac{\partial u_0}{\partial y}}+{\displaystyle \frac{\partial v_0}{\partial x}}+{\displaystyle \frac{\partial w_0}{\partial x}}{\displaystyle \frac{\partial w_0}{\partial y}}\end{array}\right\}+z\left\{\begin{array}{c}{\displaystyle \frac{\partial {\phi }^x}{\partial x}}\\ {\displaystyle \frac{\partial {\phi }^y}{\partial y}}\\ 0\\ 0\\ {\displaystyle \frac{\partial {\phi }^x}{\partial y}}+{\displaystyle \frac{\partial {\phi }^y}{\partial x}}\end{array}\right\}$$

(4)

Applying Hooke’s law and assuming plane stress, the stress components of the plate areas are obtained in the following way:

$$\left\{\begin{array}{c}\begin{array}{c}\begin{array}{c}{\sigma }_x\\ {\sigma }_y\end{array}\\ {\tau }_{xy}\\ {\tau }_{xz}\end{array}\\ {\tau }_{yz}\end{array}\right\}=\left[\begin{array}{ccccc}{\overline{Q}}_{11}& {\overline{Q}}_{12}& {\overline{Q}}_{16}& 0& 0\\ {\overline{Q}}_{12}& {\overline{Q}}_{22}& {\overline{Q}}_{62}& 0& 0\\ {\overline{Q}}_{61}& {\overline{Q}}_{26}& {\overline{Q}}_{66}& 0& 0\\ 0& 0& 0& {\overline{Q}}_{55}& {\overline{Q}}_{54}\\ 0& 0& 0& {\overline{Q}}_{45}& {\overline{Q}}_{44}\end{array}\right]\left\{\begin{array}{c}\begin{array}{c}\begin{array}{c}{\epsilon }_x\\ {\epsilon }_y\end{array}\\ {\gamma }_{xy}\\ {\gamma }_{xz}\end{array}\\ {\gamma }_{yz}\end{array}\right\}$$

(5)

where ${\overline{Q}}_{ij}$ are given in the following way:

$$\begin{array}{l}\left[\overline{\mathrm{Q}}\right]=\left[\begin{array}{ccc}{\overline{Q}}_{11}& {\overline{Q}}_{12}& {\overline{Q}}_{16}\\ {\overline{Q}}_{21}& {\overline{Q}}_{22}& {\overline{Q}}_{62}\\ {\overline{Q}}_{61}& {\overline{Q}}_{26}& {\overline{Q}}_{66}\end{array}\right]=\left[{\mathrm{T}}_{\sigma }\right]\left[\begin{array}{ccc}{Q}_{11}& Q_{12}& 0\\ Q_{21}& Q_{22}& 0\\ 0& 0& Q_{66}\end{array}\right]{\left[{\mathrm{T}}_{\sigma }\right]}^T\\ \left[{\overline{\mathrm{Q}}}_s\right]=\left[\begin{array}{cc}{\overline{Q}}_{55}& {\overline{Q}}_{54}\\ {\overline{Q}}_{45}& {\overline{Q}}_{44}\end{array}\right]=\left[{\mathrm{T}}_s\right]\left[\begin{array}{cc}{Q}_{55}& 0\\ 0& Q_{44}\end{array}\right]{\left[{\mathrm{T}}_s\right]}^T\\ \left[{\mathrm{T}}_{\sigma }\right]=\left[\begin{array}{ccc}{\cos }^2\theta & {\sin }^2\theta & -2\sin \theta \cos \theta \\ {\sin }^2\theta & {\cos }^2\theta & 2\sin \theta \cos \theta \\ \sin \theta \cos \theta & -\sin \theta \cos \theta & {\cos }^2\theta -{\sin }^2\theta \end{array}\right]\\ \left[{\mathrm{T}}_s\right]=\left[\begin{array}{cc}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right]\end{array}$$

(6)

Where

$$\begin{array}{l}{Q}_{11}={\displaystyle \frac{E_1}{1-{\nu }_{12}{\nu }_{21}}},Q_{22}={\displaystyle \frac{E_2}{1-{\nu }_{12}{\nu }_{21}}},Q_{12}={\displaystyle \frac{{\nu }_{21}{E}_1}{1-{\nu }_{12}{\nu }_{21}}},\\ Q_{66}=G_{12},Q_{55}=k{G}_{13},Q_{44}=k{G}_{23}\end{array}$$

(7)

where $E_i$, $G_{ij}$, and ${\nu }_{ij}$ are the mechanical properties and k = 5/6 is the shear correction factor used in this study. [37]

Hamilton's principle can be used to generate the moving equations in the following way:[35]

$${\displaystyle {\int }_{t_1}^{t_2}\delta \left(U-T\right)}\mathrm{d}t=0$$

(8)

where U is the strain form and T is the kinetic form of energy, respectively.

The strain energy can be shown in the following way:

$$U={\displaystyle \underset{V}{\iiint }\frac{1}{2}\left({\sigma }_x{\epsilon }_x+{\sigma }_y{\epsilon }_y+{\sigma }_z{\epsilon }_z+{\tau }_{xy}{\gamma }_{xy}+{\sigma }_{yz}{\gamma }_{yz}+{\tau }_{xz}{\gamma }_{xz}\right)}\mathrm{d}V$$

(9)

The kinetic energy can be shown in the following way:

$$T={\displaystyle \underset{V}{\iiint }\frac{1}{2}\rho \left(z\right)\left[{\left(\frac{\partial u}{\partial t}\right)}^2+{\left(\frac{\partial v}{\partial t}\right)}^2+{\left(\frac{\partial w}{\partial t}\right)}^2\right]}\mathrm{d}V$$

(10)

The moving equations for the sandwich plate's free vibration may be acquired by substituting equations (4)–(7), (9) and (10) into equation (8):

$$\left\{\begin{array}{c}{\displaystyle \frac{\partial Q_x}{\partial x}}+{\displaystyle \frac{\partial Q_y}{\partial y}}=I_0{\displaystyle \frac{{\partial }^{2}w}{\partial t^2}}\\ {\displaystyle \frac{\partial M_x}{\partial x}}+{\displaystyle \frac{\partial M_{xy}}{\partial y}}-Q_x=I_2{\displaystyle \frac{{\partial }^2{\phi }_x}{\partial t^2}}\\ {\displaystyle \frac{\partial M_y}{\partial y}}+{\displaystyle \frac{\partial M_{xy}}{\partial x}}-Q_y=I_2{\displaystyle \frac{{\partial }^2{\phi }_y}{\partial t^2}}\end{array},\right.$$

(11)

where $I_i={\displaystyle {\int }_{-\frac{h}{2}}^{\frac{h}{2}}\rho z^i\mathrm{d}z},i=0,2$.

2.3 Equation of Motion

The stress resultants M_ij and transverse shear force Q_ij can be determined by integrating the stresses in each single layer along the direction of thickness.

$$\begin{array}{l}\left\{\begin{array}{c}{M}_x\\ M_y\\ M_{xy}\end{array}\right\}={\displaystyle {\int }_{-\frac{h}{2}}^{\frac{h}{2}}z}\left\{\begin{array}{c}{\sigma }_x\\ {\sigma }_y\\ {\tau }_{xy}\end{array}\right\}\mathrm{d}z=\left[\begin{array}{ccc}{D}_{11}& D_{12}& D_{16}\\ D_{12}& D_{22}& D_{26}\\ D_{16}& D_{26}& D_{66}\end{array}\right]\left\{\begin{array}{c}{\displaystyle \frac{\partial {\phi }_x}{\partial x}}\\ {\displaystyle \frac{\partial {\phi }_y}{\partial y}}\\ {\displaystyle \frac{\partial {\phi }_x}{\partial y}}+{\displaystyle \frac{\partial {\phi }_y}{\partial x}}\end{array}\right\},\\ \left\{\begin{array}{c}{Q}_y\\ Q_x\end{array}\right\}={\displaystyle {\int }_{-\frac{h}{2}}^{\frac{h}{2}}\left\{\begin{array}{c}{\tau }_{yz}\\ {\tau }_{xz}\end{array}\right\}}\mathrm{d}z=\left[\begin{array}{cc}{A}_{44}& A_{45}\\ A_{45}& A_{55}\end{array}\right]\left\{\begin{array}{c}{\phi }_y+{\displaystyle \frac{\partial w}{\partial y}}\\ {\phi }_x+{\displaystyle \frac{\partial w}{\partial x}}\end{array}\right\},\end{array}$$

(12)

Equation (11) can be substituted with equation (12) to assemble the following formulations for the governing equations of the sandwich plate's free vibration.

$$A_{55}\left({\displaystyle \frac{\partial {\phi }_x}{\partial x}}+{\displaystyle \frac{{\partial }^{2}w}{\partial x^2}}\right)+A_{45}\left({\displaystyle \frac{\partial {\phi }_y}{\partial x}}+{\displaystyle \frac{\partial {\phi }_x}{\partial y}}+2{\displaystyle \frac{{\partial }^{2}w}{\partial x\partial y}}\right)+A_{44}\left({\displaystyle \frac{\partial {\phi }_y}{\partial y}}+{\displaystyle \frac{{\partial }^{2}w}{\partial y^2}}\right)=I_0{\displaystyle \frac{{\partial }^{2}w}{\partial t^2}},$$

(13)

$$\begin{array}{l}{D}_{11}{\displaystyle \frac{{\partial }^2{\phi }_x}{\partial x^2}}+D_{12}{\displaystyle \frac{{\partial }^2{\phi }_y}{\partial x\partial y}}+D_{16}\left(2{\displaystyle \frac{{\partial }^2{\phi }_x}{\partial x\partial y}}+{\displaystyle \frac{{\partial }^2{\phi }_y}{\partial x^2}}\right)+D_{26}{\displaystyle \frac{{\partial }^2{\phi }_y}{\partial y^2}}+D_{66}\left({\displaystyle \frac{{\partial }^2{\phi }_x}{\partial y^2}}+{\displaystyle \frac{{\partial }^2{\phi }_y}{\partial x\partial y}}\right)\\ -A_{55}\left({\phi }_x+{\displaystyle \frac{\partial w}{\partial x}}\right)-A_{45}\left({\phi }_y+{\displaystyle \frac{\partial w}{\partial y}}\right)=I_2{\displaystyle \frac{{\partial }^2{\phi }_x}{\partial t^2}},\end{array}$$

(14)

$$\begin{array}{l}{D}_{16}{\displaystyle \frac{{\partial }^2{\phi }_x}{\partial x^2}}+D_{66}\left({\displaystyle \frac{{\partial }^2{\phi }_x}{\partial x\partial y}}+{\displaystyle \frac{{\partial }^2{\phi }_y}{\partial x^2}}\right)+D_{12}{\displaystyle \frac{{\partial }^2{\phi }_x}{\partial x\partial y}}+D_{22}{\displaystyle \frac{{\partial }^2{\phi }_y}{\partial y^2}}+D_{26}\left({\displaystyle \frac{{\partial }^2{\phi }_x}{\partial y^2}}+2{\displaystyle \frac{{\partial }^2{\phi }_y}{\partial x\partial y}}\right)\\ -A_{45}\left({\phi }_x+{\displaystyle \frac{\partial w}{\partial x}}\right)-A_{44}\left({\phi }_y+{\displaystyle \frac{\partial w}{\partial y}}\right)=I_2{\displaystyle \frac{{\partial }^2{\phi }_y}{\partial t^2}}\end{array}$$

(15)

where A_ij and D_ij are the stretching and bending stiffnesses, respectively.

2.4. Differential Quadrature Method

DQM is essentially a differential equation in the function at each node of the derivative with the calculation of the region of all nodes at the function value of the weighted sum to replace.[25] The required differential equation's numerical solution can be found in the resultant system of equations. This is how DQM transforms the differential equation solution problem into the linear equation system solving problem.[38–40] Appendix I provides the specific implementation of this technique.

To simplify the calculation, for the DQM discretization of the moving equations, the expressions for the weighting coefficients were obtained:

$${\overline{A}}_{ij}^{\left(1\right)}={\displaystyle \frac{A_{ij}^{\left(1\right)}}{a}},{\overline{B}}_{ij}^{\left(1\right)}={\displaystyle \frac{B_{ij}^{\left(1\right)}}{b}},{\overline{A}}_{ij}^{\left(2\right)}={\displaystyle \frac{A_{ij}^{\left(2\right)}}{a^2}},{\overline{B}}_{ij}^{\left(2\right)}={\displaystyle \frac{B_{ij}^{\left(2\right)}}{b^2}}$$

(16)

The separating variables for the displacement terms (w, ${\phi }^x$, and ${\phi }^y$) can be written in the following way:

$$w\left(x,y,t\right)=W\left(x,y\right)e^{i\omega t},{\phi }_x\left(x,y,t\right)={\psi }_y\left(x,y\right)e^{i\omega t},{\phi }_y\left(x,y,t\right)={\psi }_y\left(x,y\right)e^{i\omega t}$$

(17)

where $W\left(x,y\right)$ is the vibration mode function, ${\phi }_x$ and ${\phi }_y$ are the rotational angles functions and $\omega$ is the fundamental frequency of the sandwich plate.

To facilitate subsequent calculations and comparisons, the data are dimensionless as follows:

$$\xi ={\displaystyle \frac{x}{a}},\eta ={\displaystyle \frac{y}{b}},D_{ij}\left(\xi \right)={\displaystyle \frac{\left[D\right]}{D_{110}}},A_{ij}\left(\xi \right)={\displaystyle \frac{\left[A\right]}{A_{440}}},\overline{\omega }={\displaystyle \frac{\omega b^2}{h}}{\sqrt{\left({\displaystyle \frac{\rho }{E_2}}\right)}}_f$$

(18)

where $D_{110}$ represents $D_{11}\left(x\right)$ at x = 0 and $A_{440}$ represents $A_{44}\left(x\right)$ at x = 0.

Substituting equations (16)–(18) into equations (13)–(15) and performing a DQM discretization, the governing equations can be shown as follows:

$$\begin{array}{l}{A}_{55}\left({\xi }_i\right){\displaystyle \sum _{m=1}^{N_x}{\overline{A}}_{im}^{\left(2\right)}}{W}_{mj}+A_{44}\left({\xi }_i\right){\displaystyle \sum _{n=1}^{N_y}{\overline{B}}_{jn}^{\left(2\right)}}{W}_{in}+2A_{45}\left({\xi }_i\right){\displaystyle \sum _{m=1}^{N_x}{\overline{A}}_{im}^{\left(1\right)}}{\displaystyle \sum _{n=1}^{N_y}{\overline{B}}_{jn}^{\left(1\right)}}{W}_{mn}\\ +A_{55}\left({\xi }_i\right){\displaystyle \sum _{m=1}^{N_x}{\overline{A}}_{im}^{\left(1\right)}}{\psi }_{x,mj}+A_{45}\left({\xi }_i\right){\displaystyle \sum _{n=1}^{N_y}{\overline{B}}_{jn}^{\left(1\right)}}{\psi }_{x,in}+A_{45}\left({\xi }_i\right){\displaystyle \sum _{m=1}^{N_x}{\overline{A}}_{im}^{\left(1\right)}}{\psi }_{y,mj}\\ +A_{44}\left({\xi }_i\right){\displaystyle \sum _{n=1}^{N_y}{\overline{B}}_{jn}^{\left(1\right)}}{\psi }_{y,in}=-I_0{\overline{\omega }}^2{W}_{ij}\end{array}$$

(19)

$$\begin{array}{l}-A_{55}\left({\xi }_i\right){\displaystyle \sum _{m=1}^{N_x}{\overline{A}}_{im}^{\left(1\right)}}{W}_{mj}-A_{45}\left({\xi }_i\right){\displaystyle \sum _{m=1}^{N_x}{\overline{B}}_{jn}^{\left(1\right)}}{W}_{in}-A_{55}\left({\xi }_i\right){\psi }_{x,mn}\\ +D_{11}\left({\xi }_i\right){\displaystyle \sum _{m=1}^{N_x}{\overline{A}}_{im}^{\left(2\right)}}{\psi }_{x,mj}+2D_{16}\left({\xi }_i\right){\displaystyle \sum _{m=1}^{N_x}{\overline{A}}_{im}^{\left(1\right)}}{\displaystyle \sum _{n=1}^{N_y}{\overline{B}}_{jn}^{\left(1\right)}}{\psi }_{x,mn}+D_{66}\left({\xi }_i\right){\displaystyle \sum _{n=1}^{N_y}{\overline{B}}_{jn}^{\left(2\right)}}{\psi }_{x,in}\\ -A_{45}\left({\xi }_i\right){\psi }_{y,mn}+D_{16}\left({\xi }_i\right){\displaystyle \sum _{m=1}^{N_x}{\overline{A}}_{im}^{\left(2\right)}}{\psi }_{y,mj}+D_{26}\left({\xi }_i\right){\displaystyle \sum _{n=1}^{N_y}{\overline{B}}_{jn}^{\left(2\right)}}{\psi }_{y,in}\\ +\left(D_{12}\left({\xi }_i\right)+D_{66}\left({\xi }_i\right)\right){\displaystyle \sum _{m=1}^{N_x}{\overline{A}}_{im}^{\left(1\right)}}{\displaystyle \sum _{n=1}^{N_y}{\overline{B}}_{jn}^{\left(1\right)}}{\psi }_{y,mn}=-I_2{\overline{\omega }}^2{\psi }_{x,ij}\end{array}$$

(20)

$$\begin{array}{l}-A_{45}\left({\xi }_i\right){\displaystyle \sum _{m=1}^{N_x}{\overline{A}}_{im}^{\left(1\right)}}{W}_{mj}-A_{44}\left({\xi }_i\right){\displaystyle \sum _{m=1}^{N_x}{\overline{B}}_{jn}^{\left(1\right)}}{W}_{in}\\ -A_{45}\left({\xi }_i\right){\psi }_{x,mn}+D_{16}\left({\xi }_i\right){\displaystyle \sum _{m=1}^{N_x}{\overline{A}}_{im}^{\left(2\right)}}{\psi }_{x,mj}+D_{26}\left({\xi }_i\right){\displaystyle \sum _{n=1}^{N_y}{\overline{B}}_{jn}^{\left(2\right)}}{\psi }_{x,in}\\ +\left(D_{66}\left({\xi }_i\right)+D_{12}\left({\xi }_i\right)\right){\displaystyle \sum _{m=1}^{N_x}{\overline{A}}_{im}^{\left(1\right)}}{\displaystyle \sum _{n=1}^{N_y}{\overline{B}}_{jn}^{\left(1\right)}}{\psi }_{x,mn}\\ -A_{44}\left({\xi }_i\right){\psi }_{y,mn}+D_{66}\left({\xi }_i\right){\displaystyle \sum _{m=1}^{N_x}{\overline{A}}_{im}^{\left(2\right)}}{\psi }_{y,mj}+D_{22}\left({\xi }_i\right){\displaystyle \sum _{n=1}^{N_y}{\overline{B}}_{jn}^{\left(2\right)}}{\psi }_{y,in}\\ +2D_{26}\left({\xi }_i\right){\displaystyle \sum _{m=1}^{N_x}{\overline{A}}_{im}^{\left(1\right)}}{\displaystyle \sum _{n=1}^{N_y}{\overline{B}}_{jn}^{\left(1\right)}}{\psi }_{y,mn}=-I_2{\overline{\omega }}^2{\psi }_{y,ij}\end{array}$$

(21)

where

$$W_{ij}=W\left({\xi }_i,{\eta }_j\right),{\psi }_{x,ij}={\psi }_x\left({\xi }_i,{\eta }_j\right),{\psi }_{y,ij}={\psi }_y\left({\xi }_i,{\eta }_j\right)$$

(22)

To simplify the calculation, equations (19)–(21) can be stated more succinctly in the following way:

$$\left[\begin{array}{ccc}{K}_{1,W}& K_{1,{\psi }^x}& K_{1,{\psi }^y}\\ K_{2,W}& K_{2,{\psi }^x}& K_{2,{\psi }^y}\\ K_{3,W}& K_{3,{\psi }^x}& K_{3,{\psi }^y}\end{array}\right]\left\{\begin{array}{c}W\\ {\psi }^x\\ {\psi }^y\end{array}\right\}=-{\overline{\omega }}^2\left[\begin{array}{ccc}{I}_0& 0& 0\\ 0& I_2& 0\\ 0& 0& I_2\end{array}\right]\left\{\begin{array}{c}W\\ {\psi }^x\\ {\psi }^y\end{array}\right\}$$

(23)

Or

$$\left[K\right]\left\{R\right\}=-{\overline{\omega }}^2\left[I\right]\left\{R\right\},\left\{R\right\}={\left\{{\left\{W\right\}}^T{\left\{{\psi }^x\right\}}^T{\left\{{\psi }^y\right\}}^T\right\}}^T$$

(24)

Similarly, the boundary conditions can be derived by discretization using the DQM

$$\left\{T\right\}\left\{R\right\}=\left\{0\right\}$$

(25)

The solution of the specific matrix $\left\{T\right\}$ is given in the next section.

To find the basic frequencies, or eigenvalues, and the accompanying eigenvectors, all mesh points were divided into two groups: internal domain points and boundary points. The boundary points, indicated by {b} in vector form, are situated at the plate's four edges. The domain points are the set of all remaining interior points and are denoted by {d}. After substituting the boundary conditions into the governing equations, the following equation is obtained by dividing and rearranging the matrix according to the above division:

$$\left[\begin{array}{cc}{K}_{bb}& K_{bd}\\ K_{db}& K_{dd}\end{array}\right]\left\{\begin{array}{c}{R}_b\\ R_d\end{array}\right\}=-{\overline{\omega }}^2\left\{\begin{array}{c}0\\ R_d\end{array}\right\}$$

(26)

By eliminating the non–zero element $\left\{R_b\right\}$, equation (26) can be shown in the following way:

$$\left(\overline{K}-{\overline{\omega }}^2\right)\left\{R_d\right\}=0$$

(27)

where $\overline{K}=K_{dd}-K_{db}{K_{bb}}^{-1}{K}_{bd}$. The fundamental frequencies and amplitudes of the plate can be determined by solving equation (27) using the standard eigenvalue matrix.

2.5 Boundary Conditions

For the four edges—clamped, simply supported, and free—CCCC, SSSS, and FFFF can be utilized as the boundary conditions. Hybrid boundary conditions such as CSCS, CFCF, and CFFF were also used in this study. The following are the boundary condition phrases for each edge:

(a) Clamped

$$w={\phi }^x={\phi }^y=0,x=0\mathrm{or}x=1(y=0\mathrm{or}y=1),$$

(28)

(b) Simply supported

$$\begin{array}{l}w={\phi }_y={\displaystyle \frac{\partial {\phi }_x}{x}}=0,x=0\mathrm{or}x=1,\\ w={\phi }_x={\displaystyle \frac{\partial {\phi }_y}{y}}=0,y=0ory=1,\end{array}$$

(29)

(c) Free

$$\begin{array}{l}{Q}_x=M_x=M_{xy}=0,x=0,orx=1,\\ Q_x=M_y=M_{xy}=0,y=0,ory=1,\end{array}$$

(30)

Substituting equation (12) into equation (30), gives the following:

$$\begin{array}{l}{A}_{45}\left({\phi }^y+{\displaystyle \frac{\partial w}{\partial y}}\right)+A_{55}\left({\phi }^x+{\displaystyle \frac{\partial w}{\partial x}}\right)=0,\\ D_{11}{\displaystyle \frac{\partial {\phi }_x}{\partial x}}+D_{12}{\displaystyle \frac{\partial {\phi }_y}{\partial y}}+D_{16}\left({\displaystyle \frac{\partial {\phi }_x}{\partial y}}+{\displaystyle \frac{\partial {\phi }_y}{\partial x}}\right)=0,\\ D_{16}{\displaystyle \frac{\partial {\phi }_x}{\partial x}}+D_{22}{\displaystyle \frac{\partial {\phi }_y}{\partial y}}+D_{66}\left({\displaystyle \frac{\partial {\phi }_x}{\partial y}}+{\displaystyle \frac{\partial {\phi }_y}{\partial x}}\right)=0,x=0\mathrm{or}x=1,\\ A_{44}\left({\phi }_y+{\displaystyle \frac{\partial w}{\partial y}}\right)+A_{45}\left({\phi }_x+{\displaystyle \frac{\partial w}{\partial x}}\right)=0,\\ D_{12}{\displaystyle \frac{\partial {\phi }_x}{\partial x}}+D_{22}{\displaystyle \frac{\partial {\phi }_y}{\partial y}}+D_{26}\left({\displaystyle \frac{\partial {\phi }_x}{\partial y}}+{\displaystyle \frac{\partial {\phi }_y}{\partial x}}\right)=0,\\ D_{16}{\displaystyle \frac{\partial {\phi }_x}{\partial x}}+D_{22}{\displaystyle \frac{\partial {\phi }_y}{\partial y}}+D_{66}\left({\displaystyle \frac{\partial {\phi }_x}{\partial y}}+{\displaystyle \frac{\partial {\phi }_y}{\partial x}}\right)=0,y=0ory=1,\end{array}$$

(31)

Equations (28)–(30) can be combined to express the boundary conditions for a sandwich plate with hybrid boundary conditions.

After applying the DQM to discretize the above equations, the following equations can be got:

(a) Clamped

$$\begin{array}{l}W\left({\xi }_1,{\eta }_j\right)=W\left({\xi }_{N_x},{\eta }_j\right)=W\left({\xi }_i,{\eta }_1\right)=W\left({\xi }_i,{\eta }_{N_y}\right)=0,\\ {\psi }_x\left({\xi }_1,{\eta }_j\right)={\psi }_x\left({\xi }_{N_x},{\eta }_j\right)={\psi }_x\left({\xi }_i,{\eta }_1\right)={\psi }_x\left({\xi }_i,{\eta }_{N_y}\right)=0,\\ {\psi }_y\left({\xi }_1,{\eta }_j\right)={\psi }_y\left({\xi }_{N_x},{\eta }_j\right)={\psi }_y\left({\xi }_i,{\eta }_1\right)={\psi }_y\left({\xi }_i,{\eta }_{N_y}\right)=0,\xi =0,1or\eta =0,1\end{array}$$

(32)

(b) Simply supported

$$\begin{array}{l}W\left({\xi }_1,{\eta }_j\right)=W\left({\xi }_{N_x},{\eta }_j\right)=0,\\ {\psi }_y\left({\xi }_1,{\eta }_j\right)={\psi }_y\left({\xi }_{N_x},{\eta }_j\right)=0,\\ {\displaystyle \sum _{m=1}^{N_x}{A}_{im}}{\psi }_x\left({\xi }_m,{\eta }_j\right)=0,\xi =0,1,\\ W\left({\xi }_i,{\eta }_1\right)=W\left({\xi }_i,{\eta }_{N_y}\right)=0,\\ {\psi }_x\left({\xi }_i,{\eta }_1\right)={\psi }_x\left({\xi }_i,{\eta }_{N_y}\right)=0,\\ {\displaystyle \sum _{n=1}^{N_y}{B}_{jn}}{\psi }_y\left({\xi }_i,{\eta }_n\right)=0,\eta =0,1\end{array}$$

(33)

(c) Free

$$\begin{array}{l}{A}_{45}\left({\xi }_i\right)\left({\psi }_{y,mn}+{\displaystyle \sum _{n=1}^{N_y}{\overline{B}}_{jn}^{\left(1\right)}}{W}_{in}\right)+A_{55}\left({\xi }_i\right)\left({\psi }_{x,mn}+{\displaystyle \sum _{m=1}^{N_x}{\overline{A}}_{im}^{\left(1\right)}}{W}_{mj}\right)=0,\\ D_{11}\left({\xi }_i\right){\displaystyle \sum _{m=1}^{N_x}{\overline{A}}_{im}^{\left(1\right)}}{\psi }_{x,mj}+D_{12}\left({\xi }_i\right){\displaystyle \sum _{n=1}^{N_y}{\overline{B}}_{jn}^{\left(1\right)}}{\psi }_{y,in}+D_{16}\left({\xi }_i\right)\left({\displaystyle \sum _{n=1}^{N_y}{\overline{B}}_{jn}^{\left(1\right)}}{\psi }_{x,in}+{\displaystyle \sum _{m=1}^{N_x}{\overline{A}}_{im}^{\left(1\right)}}{\psi }_{y,mj}\right)=0,\\ D_{16}\left({\xi }_i\right){\displaystyle \sum _{m=1}^{N_x}{\overline{A}}_{im}^{\left(1\right)}}{\psi }_{x,mj}+D_{26}\left({\xi }_i\right){\displaystyle \sum _{n=1}^{N_y}{\overline{B}}_{jn}^{\left(1\right)}}{\psi }_{y,in}+D_{66}\left({\xi }_i\right)\left({\displaystyle \sum _{n=1}^{N_y}{\overline{B}}_{jn}^{\left(1\right)}}{\psi }_{x,in}+{\displaystyle \sum _{m=1}^{N_x}{\overline{A}}_{im}^{\left(1\right)}}{\psi }_{y,mj}\right)=0,\\ \xi =0,or\xi =1,\\ A_{44}\left({\xi }_i\right)\left({\psi }_{y,mn}+{\displaystyle \sum _{n=1}^{N_y}{\overline{B}}_{jn}^{\left(1\right)}}{W}_{in}\right)+A_{45}\left({\xi }_i\right)\left({\psi }_{x,mn}+{\displaystyle \sum _{m=1}^{N_x}{\overline{A}}_{im}^{\left(1\right)}}{W}_{mj}\right)=0,\\ D_{12}\left({\xi }_i\right){\displaystyle \sum _{m=1}^{N_x}{\overline{A}}_{im}^{\left(1\right)}}{\psi }_{x,mj}+D_{22}\left({\xi }_i\right){\displaystyle \sum _{n=1}^{N_y}{\overline{B}}_{jn}^{\left(1\right)}}{\psi }_{y,in}+D_{26}\left({\xi }_i\right)\left({\displaystyle \sum _{n=1}^{N_y}{\overline{B}}_{jn}^{\left(1\right)}}{\psi }_{x,in}+{\displaystyle \sum _{m=1}^{N_x}{\overline{A}}_{im}^{\left(1\right)}}{\psi }_{y,mj}\right)=0,\\ D_{16}\left({\xi }_i\right){\displaystyle \sum _{m=1}^{N_x}{\overline{A}}_{im}^{\left(1\right)}}{\psi }_{x,mj}+D_{26}\left({\xi }_i\right){\displaystyle \sum _{n=1}^{N_y}{\overline{B}}_{jn}^{\left(1\right)}}{\psi }_{y,in}+D_{66}\left({\xi }_i\right)\left({\displaystyle \sum _{n=1}^{N_y}{\overline{B}}_{jn}^{\left(1\right)}}{\psi }_{x,in}+{\displaystyle \sum _{m=1}^{N_x}{\overline{A}}_{im}^{\left(1\right)}}{\psi }_{y,mj}\right)=0,\\ \eta =0,or\eta =1,\end{array}$$

(34)

In this way, the specific matrix $\left\{T\right\}$ in equation (25) can be calculated.

3. Results and Discussion

3.1. Validation and Convergence Studies

The validation and convergence investigations of the free vibration for VSCL sandwich plates using the DQM solution method are provided in this part. By comparing the results with other FSDT-based numerical solution solutions for currently available CSCL sandwich plates, the quantity of DQM grid points was ascertained. In the study, material I and material III in Table 1. were used as the skins and the core, respectively.

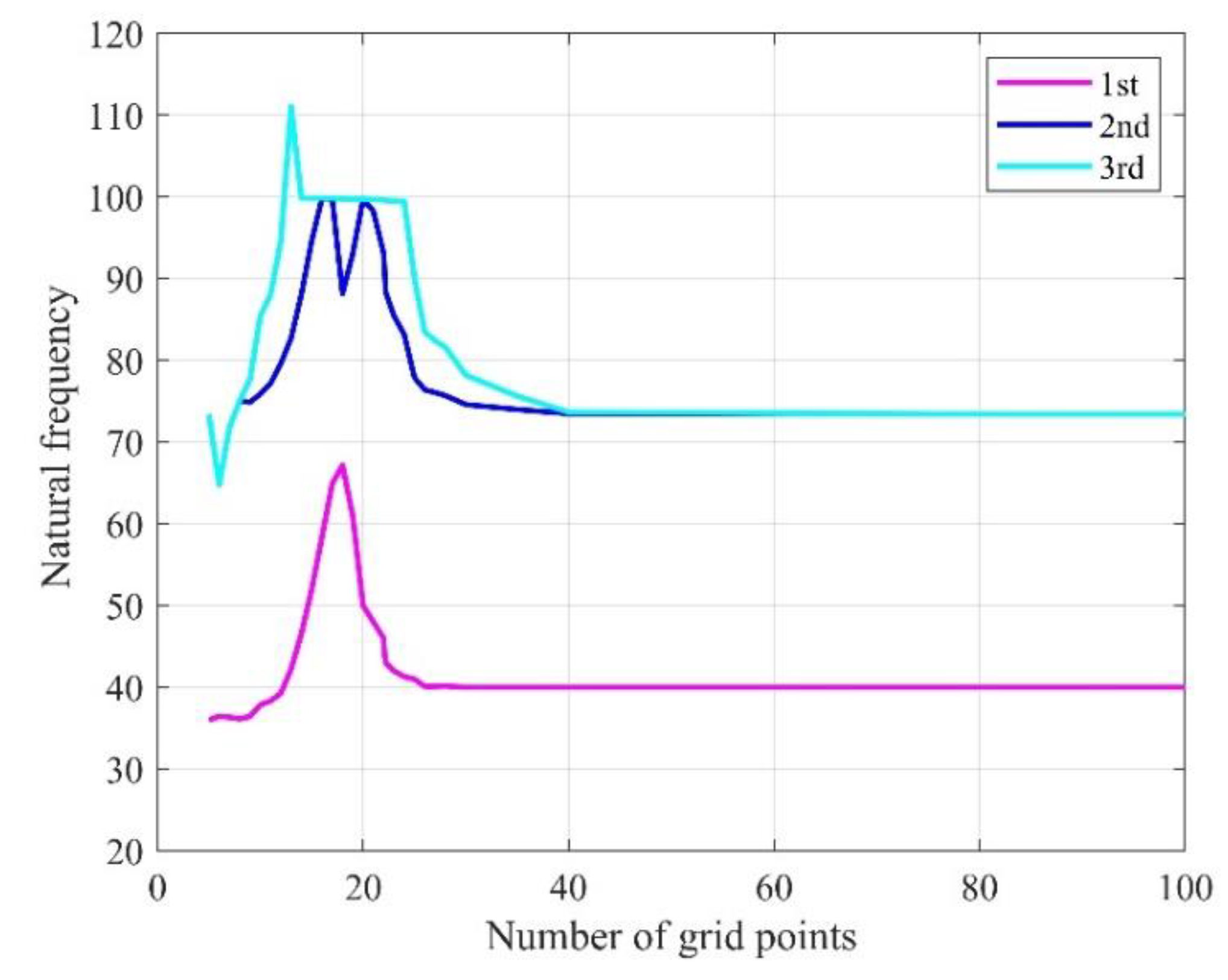
First, the quantity of grid points at which the natural frequency generated by this method might be stabilized is determined by selecting an anti–symmetric sandwich plate of [0/90/core/0/90] with the geometric parameters a/b = 0.5, a/h = 10, and t_c/t_f = 10. With an increasing number of grid points, Figure 3. displays the pattern of the sandwich plate's first three orders of natural frequency. It is evident that when the quantity of grid points rises, the frequency values' computation results typically yield steady results. It shows that the application of DQM to the problem in this study can provide convergent results.

The quantity of grid points in this investigation was selected as $N_x=N_y=38$ when DQM was used. For comparison, various aspect ratios ($a/h$) and ($a/b$) were chosen, as shown in Table 2 and Table 3.

As is evident from Tables 2–3, the results of the DQM used in this study to calculate the composite sandwich plates are only slightly different from those of the references, indicating that the mechanical model and calculation method used in this study are correct. At the same time, only 38 × 38 grid points are used in this study, which enables high accuracy of the results. Regarding computation effectiveness, the current paper's approach is better.

3.2. Parameter Study

A parameter research of the free vibrations was carried out to enhance the vibratory behavior of the VSCL sandwich plates. The fundamental frequency of the sandwich plate was examined in relation to the fiber orientation angles, boundary conditions, number of layers, and core/skin thickness.

3.2.1. Fiber Orientation Angles

First, the effect of changes in the start and termination angles was investigated. In this section, a VSCL sandwich plate with four symmetric skins $\left[\pm {〈{\Theta }_0|{\Theta }_1〉}_s/core/\pm {〈{\Theta }_0|{\Theta }_1〉}_s\right]$ is chosen as the object of investigation. Materials II in Table 1. were used as the face sheets and materials IV and VI in Table 1. were used as the two kinds of core, respectively. Among the two selected core materials, material VI is an aluminum honeycomb core.[42] The plate thickness h = 0.1a, the core thickness $h_c={\displaystyle \frac{4h}{5}}$, and each single layer were taken as $h_{layer}={\displaystyle \frac{h}{40}}$. For comparison, the first and second dimensionless natural frequencies $\overline{\omega }={\displaystyle \frac{\omega b^2}{h}}{\sqrt{\left({\displaystyle \frac{\rho }{E_2}}\right)}}_f$were chosen. The fiber orientation angles ${\Theta }_0$ and ${\Theta }_1$ are both varied from 0° to 90°. Both CCCC and SSSS boundary conditions were considered, and the results are listed in Table 4, Table 5, Table 6 and Table 7, respectively.

Tables 4–7 reveal that the majority of fundamental frequencies typically rise with the increase of fiber orientation angle. A corresponding decrease in the natural frequency was observed when the fiber orientation angle reached the maximum value. Therefore, sandwich plates can be made stiffer by using curvilinear fibers with low curvatures. In certain instances, industry designers must alter the fundamental frequency to a greater or lesser value for the purpose of preventing resonance. This can be accomplished by using VSCL sandwich plates without having to change the size of the plate or constituent materials. The reason for this is that the natural frequency is sensitive to changes in fiber orientation in each layer.

3.2.2. Boundary Conditions

In order to investigate the first two fundamental frequencies at various fiber orientation angles, five boundary conditions were taken into consideration in this section. A comparative study between the CSCL and VSCL sandwich plates was also conducted. In this section, sandwich plates with single-ply skins $\left[〈{\Theta }_0|{\Theta }_1〉/core/〈{\Theta }_0|{\Theta }_1〉\right]$ are chosen, and the fiber orientation angles ${\Theta }_0$ and ${\Theta }_1$ are varied from 0° to 70°. Materials II and V from Table 1. were used as the skins and the core, respectively. The plate thickness $h=0.1a$, core thickness$h_c={\displaystyle \frac{8h}{9}}$, and each single layer were taken as $h_{layer}={\displaystyle \frac{h}{18}}$. Table 8, Table 9, Table 10, Table 11 and Table 12 present the results with five boundary conditions: CCCC, SSSS, CSCS, CFCF, and CFFF. The natural frequencies of the CSCL sandwich plates are bolded in these tables.

Tables 8–12 demonstrate that for the SSSS, CSCS, CFCF, and CFFF boundary conditions, the VSCL sandwich plate's natural frequency tends to grow when the ending angle ${\Theta }_1$ increases, the situation is reversed for the CCCC. For CFCF and CFFF, the VSCL sandwich plate's fundamental frequency increased by 15.175% and 32.708%, respectively, when the ending angle ${\Theta }_1$ was increased from 0° to 70°. Nonetheless, under SSSS and CSCS boundary circumstances, the VSCL sandwich plate's fundamental frequency dropped by 2.228% and 1.128%, respectively, when the endings angle ${\Theta }_1$ is increased from 50° to 70°. According to the findings, the fundamental frequencies of the VSCL sandwich plates are affected by the fiber orientation angle as the curvilinear fiber’s curvature increases.

3.2.3. Number of Layers

This section looks into how the amount of layers affects sandwich plate’s fundamental frequency. Based on sandwich plates with single-ply skins $\left[〈{\Theta }_0|{\Theta }_1〉/core/〈{\Theta }_0|{\Theta }_1〉\right]$, the quantity of layers was raised, and sandwich plates with two-layer anti-symmetric skins $\left[\pm 〈{\Theta }_0|{\Theta }_1〉/core/\pm 〈{\Theta }_0|{\Theta }_1〉\right]$ were selected. The thicknesses and mechanical properties were selected to match those mentioned in the preceding section. The results with five boundary conditions are listed in Table 12, Table 13, Table 14, Table 15, Table 16 and Table 17.

From Tables 13–17, it is clear that when ${\Theta }_1$ increases, the fundamental frequency shifts. In the CCCC boundary condition, when ${\Theta }_1$ rises from 0° to 10° and from 10° to 90°, the natural frequency falls and increases, respectively. Under the SSSS and CSCS boundary conditions, the natural frequency increases when ${\Theta }_1$ increases from 0° to 60° and decreases from 60° to 90°. When the number of layers grows, the fundamental frequency for sandwich plates with anti-symmetric two-layer skins often rises as well.

When CCCC and CSCS were met, the fundamental frequencies of the VSCL sandwich plates were found to be greater than those of the CSCL sandwich plates. This was determined by comparing the fundamental frequencies of the two sandwich plates. Sandwich plate vibration properties can be considerably altered by the application of curvilinear fiber. For instance, when comparing ${\Theta }_0={\Theta }_1={40}^{\circ }$ to ${\Theta }_0={\Theta }_1={50}^{\circ }$ under the boundary conditions of SSSS and CCCC, the fundamental frequency of CSCL plates is zero, but the fundamental frequencies of VSCL plates are changed when ${\Theta }_1$ increases from 40° to 50°.

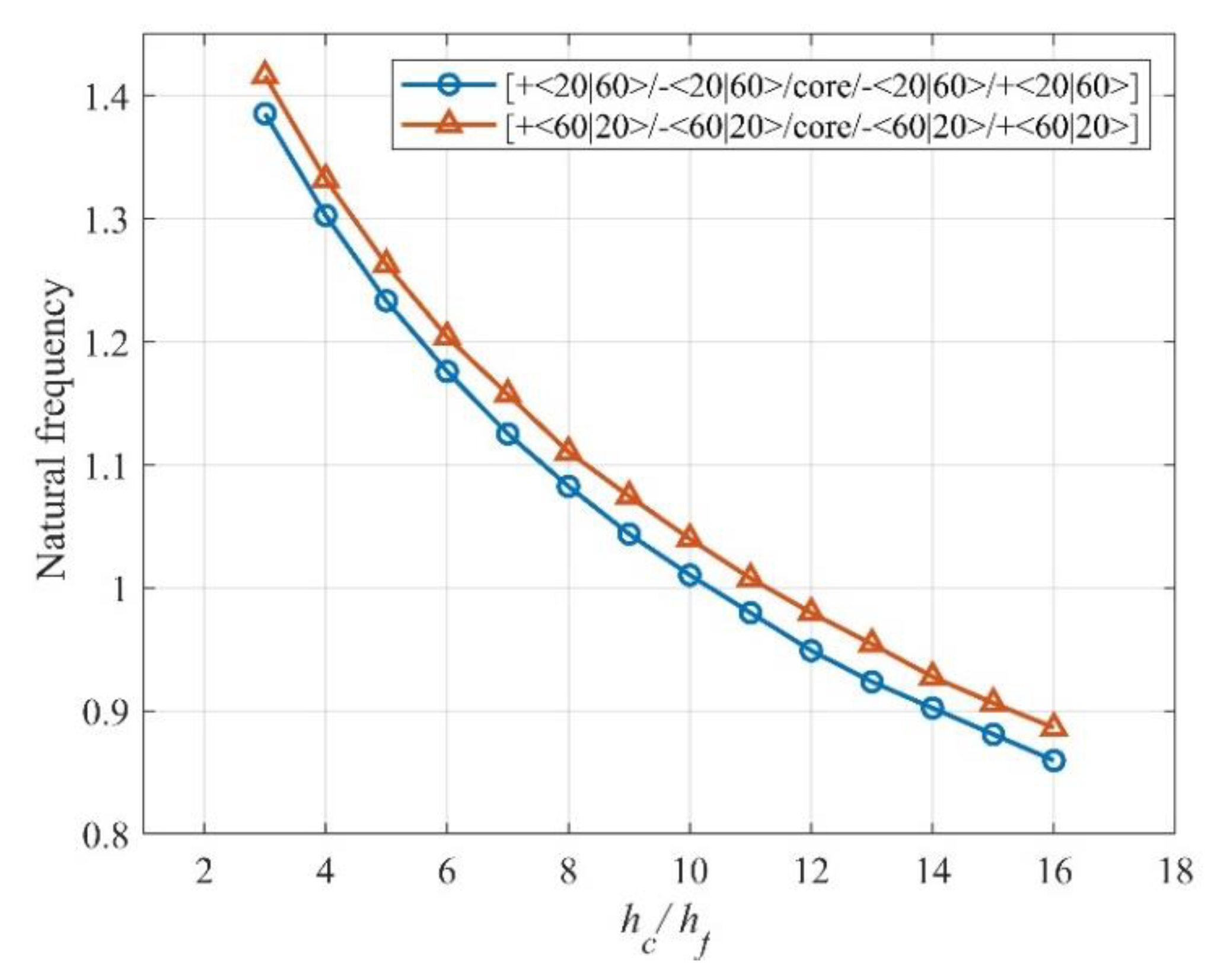
3.2.4. Core/Skin Thickness

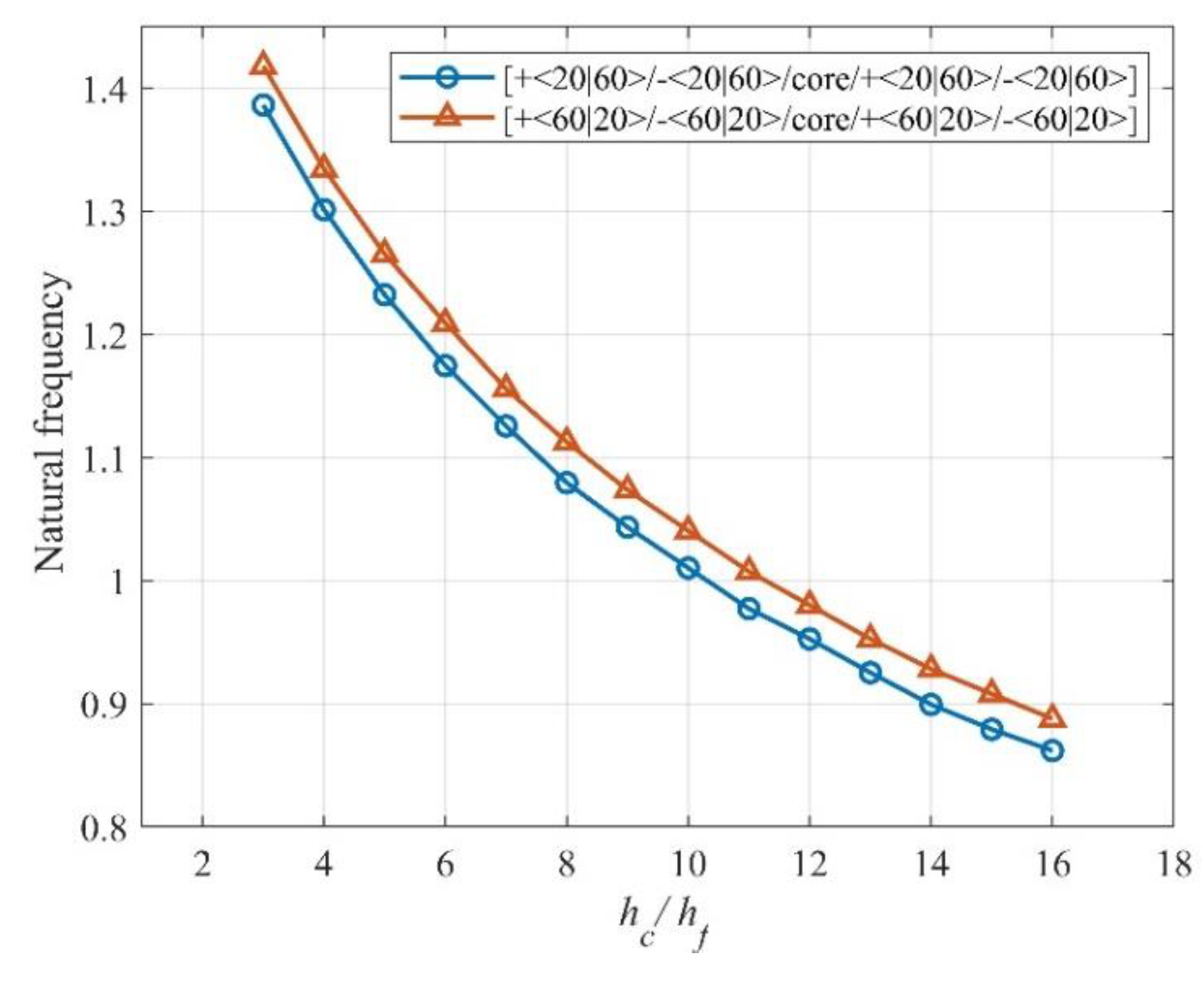
Sandwich plates that are symmetric and anti-symmetric are used in this part to examine the connection between the fundamental frequency and the ratio of the core to skin. The skins and core were selected with the same thickness and mechanical characteristics as those in the preceding section, except for the plate thickness $h=0.01a$. The core thickness/face sheet thickness, h_c / h_f, varied from 3 to 16 as variation parameters. The fundamental frequencies of $\left[\pm 〈{\Theta }_0|{\Theta }_1〉/core/\mp 〈{\Theta }_0|{\Theta }_1〉\right]$ and $\left[\pm 〈{\Theta }_0|{\Theta }_1〉/core/\pm 〈{\Theta }_0|{\Theta }_1〉\right]$ are chosen to study the variation rule and CSCS boundary condition is chosen. Changes in fundamental frequency with core/skin thickness ratio $h_c/h_f$ are shown in Figure 4 and Figure 5.

As shown in Figures 4 and 5, the VSCL sandwich plates exhibit the highest natural frequency at the lowest core/skin thickness ratio. The average decline in fundamental frequency from the greatest to the lowest point was 67%.

The findings of the aforementioned parametric study suggest that VSCL sandwich plates hold promise for aircraft panel design applications. By manipulating the starting and ending angles along with the curvature of the fiber reference path, these plates can potentially exhibit reduced lateral deformation, increased stiffness, and higher natural frequencies. Moreover, lower structural mass can be achieved under certain mechanical and environmental loading circumstances by using VSCL sandwich plates.

4. Conclusions

This study used FSDT in conjunction with DQM to examine the free vibration of sandwich plates with curvilinear fiber variable stiffness skins. In this study, the x-coordinate was supposed to fluctuate linearly with the fiber orientation angle. Compared with other numerical solution methods, the DQM is computationally inexpensive, converges quickly, and it is capable of precisely forecasting sandwich plate fundamental frequencies. The reduction or increase in the natural frequency when using VSCL face sheets was investigated and compared with that of CSCL face sheets. The impacts of fiber orientation angles, boundary conditions, number of layers, and core/skin thickness were investigated parametrically. Notably, the integration of higher-order theory and layer theory can enhance the accuracy of sandwich plate analysis, particularly when investigating thick plates. The computations used in this study allow for the following deductions.

1. In the vast majority of cases, as the fiber orientation angle increases, the fundamental frequency rises as well. The use of curvilinear fibers leads to VSCL sandwich plates with lower lateral deformations and higher natural frequencies.

2. The sandwich plate's natural frequency was impacted by the fiber orientation angle as the curvilinear fibers' curvature grew. The larger the angle of the center fiber was, the more rigid the curvilinear fiber became. The plate's rigidity can be raised by using low-curvature curvilinear fibers.

3. With an increase in layers came a rise in the sandwich plate's fundamental frequency. This also indicates that the fundamental frequency increases with rising plate thickness.

4. The VSCL sandwich plates exhibited greater natural frequencies in comparison to the CSCL sandwich plates when subjected to the CCCC and CSCS boundary conditions. As boundary restrictions get tighter, the frequency rises. Due to their increased ability to adapt to complex boundary circumstances, curvilinear fibers have higher fundamental frequencies than parallel fibers.

5. The frequency response was strongly impacted by the ratio of skin to core thickness. The natural frequency of the sandwich plate reached its maximum value at the lowest core–to-skin thickness ratio. The effect of adding more layers was in line with this trend.

The precise insights obtained from this study guide researchers seeking viable solutions and can serve as a foundation for further exploration into panel flutter in VSCL sandwich plates.