Submitted:
07 February 2025
Posted:
13 February 2025
You are already at the latest version
Abstract
Insurance companies need to calculate solvency capital requirements in order to ensure that they can meet their future obligations to policyholders and beneficiaries. The solvency capital requirement is a risk management tool essential for, when extreme catastrophic events occur, resulting in a high number of possibly interdependent claims. This paper studies the problem of aggregating the risks coming from several insurance business lines and analyses the effect of reinsurance in the level of risk. Our starting point is to use a Hierarchical Risk Aggregation method, which was initially based on 2-dimensional elliptical copulas. We then propose the use of copulas from the Archimedean family and a mixture of different copulas. Our results show that a mixture of copulas can provide a better fit to the data than an individual copula and consequently avoid over or underestimating of the capital requirement of an insurance company. We also investigate the significance of reinsurance in reducing the insurance company’s business risk and its effect on diversification. The results show that reinsurance does not always reduce the level of risk, but can also reduce the effect of diversification for insurance companies with multiple business lines.
Keywords:
1. Introduction
2. Copula-Based Hierarchical Aggregation Model
2.1. The Definition of Copula
2.2. Hierarchical Aggregation Copula Models
- Each leaf node in the rooted tree is associated with the loss of business line i, represented by a random variable .
- Each branching node is associated with the sum of the business lines mapped to that node’s children.
- a rooted tree structure ,
- univariate cdf’s for all leaf nodes i in , and
- bivariate copula functions for the two children of each branching node j in .
2.2.1. Existence and Uniqueness of a Joint Distribution
2.2.2. Simulation of Joint Distributions
Sample Reordering Numerical Approximation Algorithm
- Define the number of simulations .
- Simulate N independent samples from the univariate random variables () associated with d leaf nodes: for and , where is the pre-determined univariate cdf for .
- Simulate N independent samples from the bivariate copula () associated with each of the branching nodes: for and .
- Following a bottom-up approach, beginning at the branching nodes closer to the leaf nodes and ending at the root nodes define the approximation for the cdf of each branching node asrecursively, where is the indicator function2, and are (simulated) sample values of the random variables associated with the two nodes children of the branching node j, is the weight given to variable , is the (componentwise) rank of , and , are the ordered sample.
2.3. Risk Estimation of the Aggregate Loss
2.4. The Data
2.4.1. Loss Ratios
3. Estimation of the Hierarchical Aggregation Copula Model
3.1. Tree Structure of the Hierarchical Copula Model
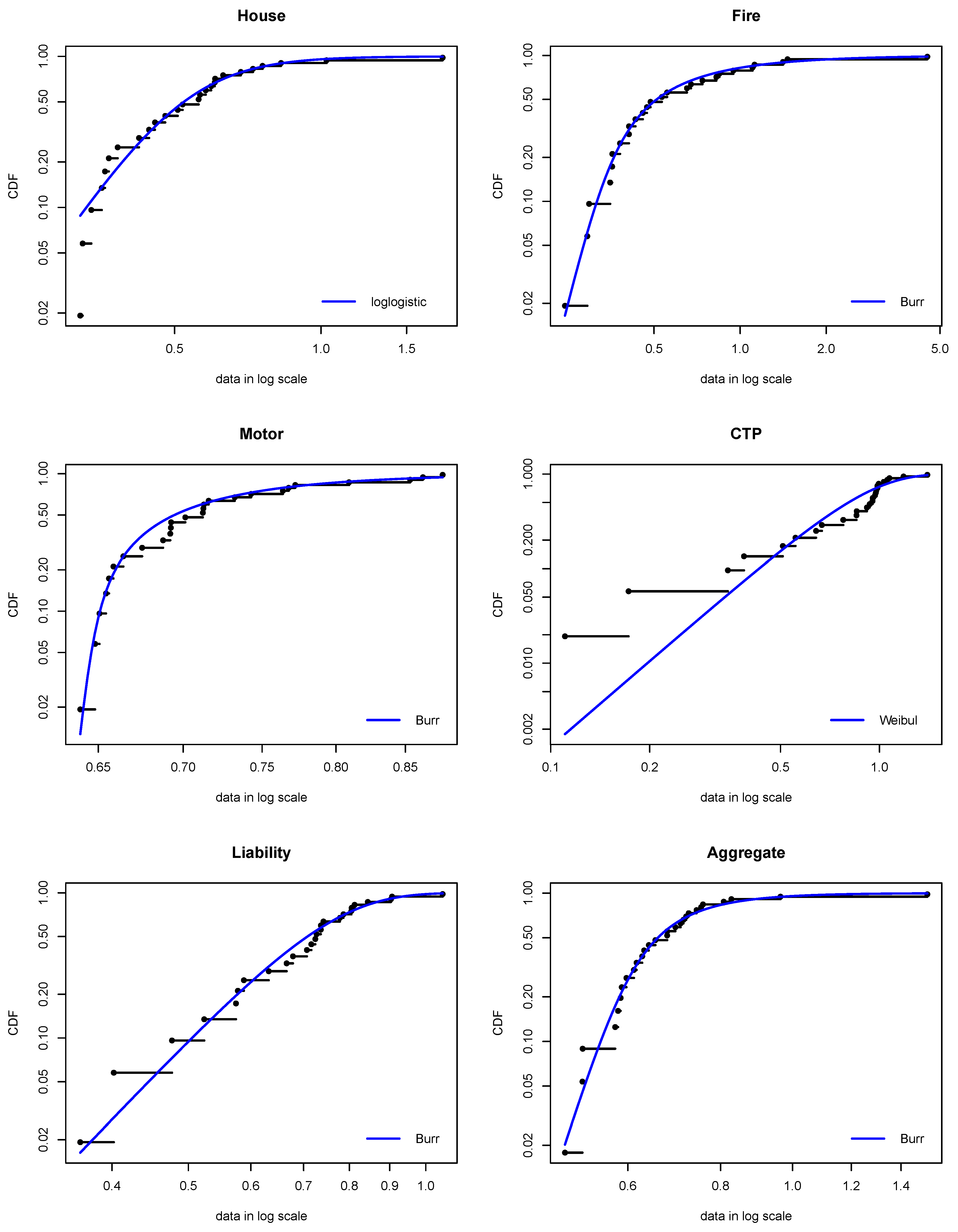
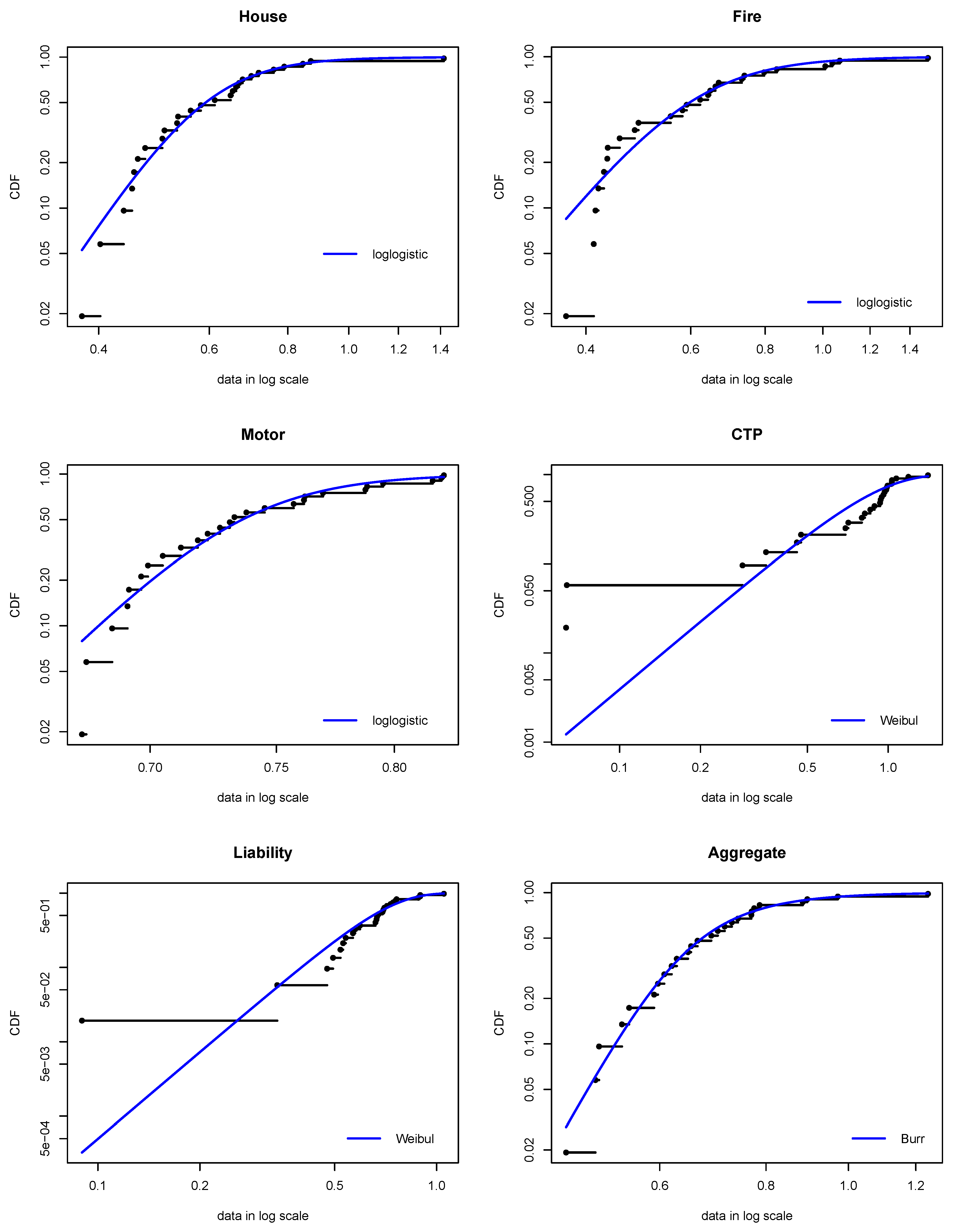
3.2. Fitting the Univariate Probability Distributions
3.3. Determining Joint Distribution Through Copulas
3.4. Simulation of the Aggregate Loss Ratios
3.4.1. Analysis of the Results
4. The Effect of Reinsurance
4.1. Reinsurance and Weighted Premiums Diversification
4.2. Reinsurance and Source of Risk Diversification
5. Conclusion
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aas, K., Czado, C., Frigessi, A. and Bakken, H. 2009, `Pair-copula constructions of multiple dependence’, Insurance: Mathematics and Economics 44(2), 182 – 198.http://www.sciencedirect.com/science/article/pii/S0167668707000194. [CrossRef]
- Acerbi, C., Nordio, C. and Sirtori, C. 2001, `Expected shortfall as a tool for financial risk management’, arXiv preprint cond-mat/0102304.
- Acerbi, C. and Tasche, D. 2002, `On the coherence of expected shortfall’, Journal of Banking & Finance 26(7), 1487 – 1503.http://www.sciencedirect.com/science/article/pii/S0378426602002832.
- Adam, A., Houkari, M. and Laurent, J.-P. 2008, `Spectral risk measures and portfolio selection’, Journal of Banking & Finance 32(9), 1870 – 1882.http://www.sciencedirect.com/science/article/pii/S0378426608000101.
- Anderson, T. W. and Darling, D. A. 1954, `A test of goodness of fit’, Journal of the American Statistical Association 49(268), 765–769.
- Arbenz, P., Hummel, C. and Mainik, G. 2012, `Copula based hierarchical risk aggregation through sample reordering’, Insurance: Mathematics and Economics 51(1), 122–133.
- Bargès, M., Cossette, H. and Marceau, E. 2009, `Tvar-based capital allocation with copulas’, Insurance: Mathematics and Economics 45(3), 348–361.
- Baur, P., Breutel-O’Donoghue, A. and Hess, T. 2004, Understanding reinsurance: How reinsurers create value and manage risk, Swiss Re, Swiss Reinsurance Company.
- Becker, B., Opp, M. M. and Saidi, F. 2022, `Regulatory forbearance in the us insurance industry: The effects of removing capital requirements for an asset class’, The Review of Financial Studies 35(12), 5438–5482.
- Brechmann, E. C. 2014, `Hierarchical Kendall copulas: Properties and inference’, The Canadian Journal of Statistics 42(1), 78–108.
- Bürgi, R., Dacorogna, M. M. and Iles, R. 2008, `Risk aggregation, dependence structure and diversification benefit’, Stress Testing for Financial Institutions. [CrossRef]
- Chaoubi, I., Cossette, H., Marceau, E. and Robert, C. Y. 2021, `Hierarchical copulas with archimedean blocks and asymmetric between-block pairs’, Computational Statistics & Data Analysis 154, 107071.https://www.sciencedirect.com/science/article/pii/S0167947320301626.
- Choueifaty, Y. and Coignard, Y. 2008, `Toward maximum diversification’, Journal of Portfolio Management 35(1), 4051.
- Cipra, T. 2010, Financial and Insurance Formulas, Physica-Verlag.
- Clemente, G. P., Savelli, N. and Zappa, D. 2015, `The impact of reinsurance strategies on capital requirements for premium risk in insurance’, Risks 3(2), 164–182.
- Cossette, H., Gadoury, S.-P., Marceau, É. and Mtalai, I. 2017, `Hierarchical archimedean copulas through multivariate compound distributions’, Insurance: Mathematics and Economics 76(Supplement C), 1 – 13.http://www.sciencedirect.com/science/article/pii/S0167668716304553. [CrossRef]
- Côté, M.-P. and Genest, C. 2015, `A copula-based risk aggregation model’, The Canadian Journal of Statistics 43(1), 60–81.
- Cummins, J. D., Dionne, G., Gagné, R. and Nouira, A. 2008, `The costs and benefits of reinsurance’. Available at SSRN: https://ssrn.com/abstract=1142954.
- Czado, C. 2019, Analyzing Dependent Data with Vine Copulas: a practical guide with R, Lecture Notes in Statistics, 222, Springer.
- DeMiguel, V., Garlappi, L. and Uppal, R. 2009, `Optimal versus naive diversification: How inefficient is the 1/n portfolio strategy?’, The Review of Financial Studies 22(5), 1915–1953.
- Diestel, R. 2017, Graph Theory, 5th edn, Springer, Heidelberg.
- Embrechts, P., Lindskog, F. and McNeil, A. 2003, Modelling dependence with copulas and application to risk management, in S. Rachev, ed., `Handbook of Heavy Tailed Distributions in Finance’, Elsevier, chapter 8, pp. 329–384.
- Engmann, S. and Cousineau, D. 2011, `Comparing distributions: the two-sample Anderson-Darling test as an alternative to the Kolmogorov-Smirnoff test’, Journal of Applied Quantitative Methods 6(3), 1–17.
- Floreani, A. 2013, `Risk measures and capital requirements: a critique of the solvency ii approach’, The Geneva Papers on Risk and Insurance Issues and Practice 38(2), 189–212.
- Genest, C. and Nešlehová, J. 2012, `Copulas and copula models’, In:Encyclopedia of Environmetrics, 2nd ed., vol. 2, A.H. El-Shaarawi and W.W. Piegorsch, editors. Wiley, Chichester pp. 541–553. [CrossRef]
- Genest, C., Rémillard, B. and Beaudoin, D. 2009, `Goodness-of-fit tests for copulas: A review and a power study’, Insurance: Mathematics and economics 44(2), 199–214.
- Giuzio, M., Krušec, D., Levels, A., Melo, A. S., Mikkonen, K. and Radulova, P. 2019, `Climate change and financial stability’, Financial Stability Review 1.
- Haff, I. H., Aas, K. and Frigessi, A. 2010, `On the simplified pair-copula construction—simply useful or too simplistic?’, Journal of Multivariate Analysis 101(5), 1296–1310.
- Iman, R. and Conover, W. 1982, `A distribution-free approach to including rank correlation among input variables’, Communications in Statistics - Simulation and Computation 11(3), 311–334.
- Joe, H. 1996, `Families of m-variate distributions with given margins and m(m-1)/2 bivariate dependence parameters’, Lecture Notes-Monograph Series 28, 120–141.http://www.jstor.org/stable/4355888.
- Kolmogorov, A. 1933, `Sulla determinazione empirica di una lgge di distribuzione’, Inst. Ital. Attuari, Giorn. 4, 83–91.
- Kurowicka, D. and Joe, H. 2010, Dependence Modeling. Vine Copula Handbook, World Scientific, Singapore.
- Li, P. and Yin, C. 2024, `The tail mean–variance optimal capital allocation under the extended skew-elliptical distribution’, Journal of Computational and Applied Mathematics 448, 115965.
- Mai, J.-F. and Scherer, M. 2012, `H-extendible copulas’, Journal of Multivariate Analysis 110(Supplement C), 151 – 160. Special Issue on Copula Modeling and Dependence.http://www.sciencedirect.com/science/article/pii/S0047259X12000802. [CrossRef]
- McNeil, A. J., Frey, R. and Embrechts, P. 2015, Quantitative Risk Management: Concepts, Techniques and Tools, second edn, Princeton University Press, Princeton, NJ.
- MunichRe 2010, `A basic guide to facultative and treaty reinsurance.’, Munich Reinsurance America.
- Nanthakumar, A. 2022, `A comparison of vine and hierarchical copulas as discriminants’, International Journal of Statistics and Probability 11(4), 13–24.
- Nelsen, R. B. 2006, An Introduction to Copulas, second edn, Springer-Verlag, New York.
- Nguyen, T., Molinari, R. D. et al. 2011, `Risk aggregation by using copulas in internal models’, Journal of Mathematical Finance 1(03), 50.
- OECD 2017, `International comparisons.’, OECD Insurance Statistics 2016, OECD Publishing, Paris. pp. 45–79.
- Schmid, F. and Schmidt, R. 2007, `Multivariate conditional versions of spearman’s rho and related measures of tail dependence’, Journal of Multivariate Analysis 98, 1123–1140.
- Shannon, C. 1948, `A mathematical theory of communication’, The Bell System Technical Journal 27(3), 379–423.
- Sibuya, M. 1960, `Bivariate extreme statistics’, Annals of the Institute of Statistical Mathematics 11(3), 195–210.
- Sklar, A. 1959, `Fonctions de répartition à n dimensions et leurs marges’, Publ. Inst. Statist. Univ. Paris 8, 229–31.
- Smirnov, N. 1948, `Table for estimating the goodness of fit of empirical distributions’, Annals of Mathematical Statistics 19, 279–281.
- Tang, A. and Valdez, E. A. 2006, `Economic capital and the aggregation of risks using copulas’, Proceedings of the 28th International Congress of Actuaries, Paris, France. Available at:http://www.ica2006.com/282.html.
- Taylor, J. M. 1997, Claim Reserving Manual, 1997 rev. edn, Faculty and Institute of Actuaries, Great Britain.
- Torri, G., Radi, D. and Dvořáčková, H. 2022, `Catastrophic and systemic risk in the non-life insurance sector: A micro-structural contagion approach’, Finance Research Letters 47, 102718. [CrossRef]
- Wang, S. 1998, Aggregation of correlated risk portfolios: models and algorithms, in `Proceedings of the Casualty Actuarial society’, Vol. 85, pp. 848–939.
| 1 | The symbol ′ denote the transpose of vector. |
| 2 | |
| 3 | ISR stands for Industrial Special Risk |
| 4 | To simplify notations, we will use X for the LR, unless otherwise stated |
| 5 |
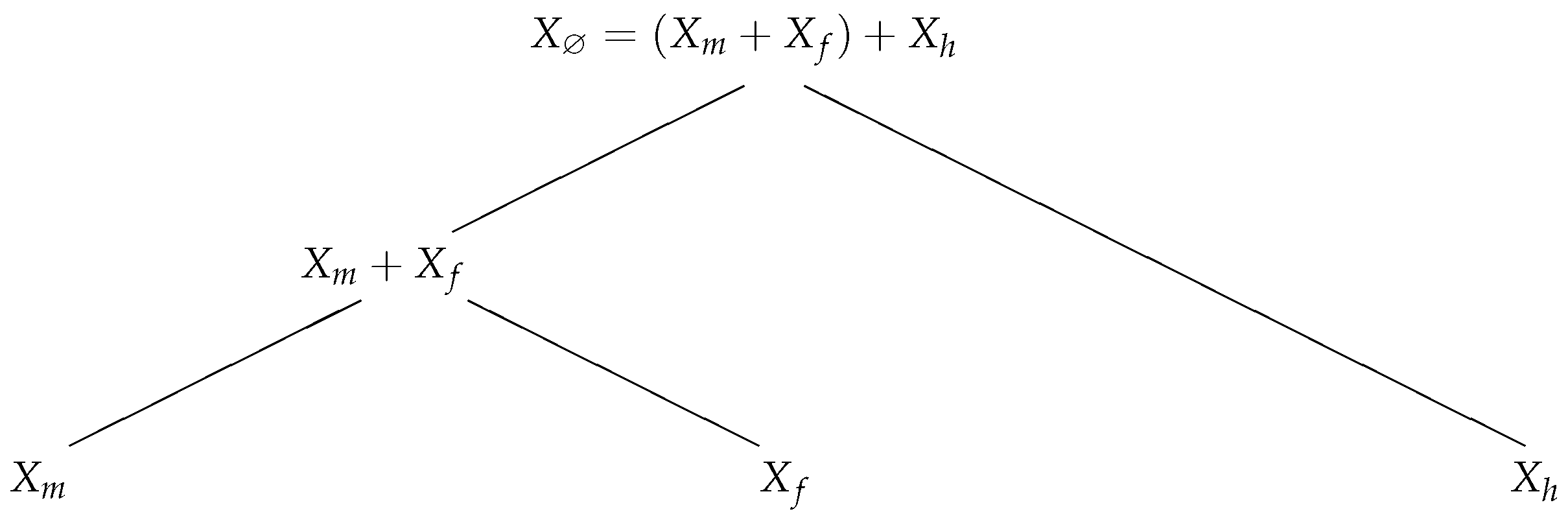
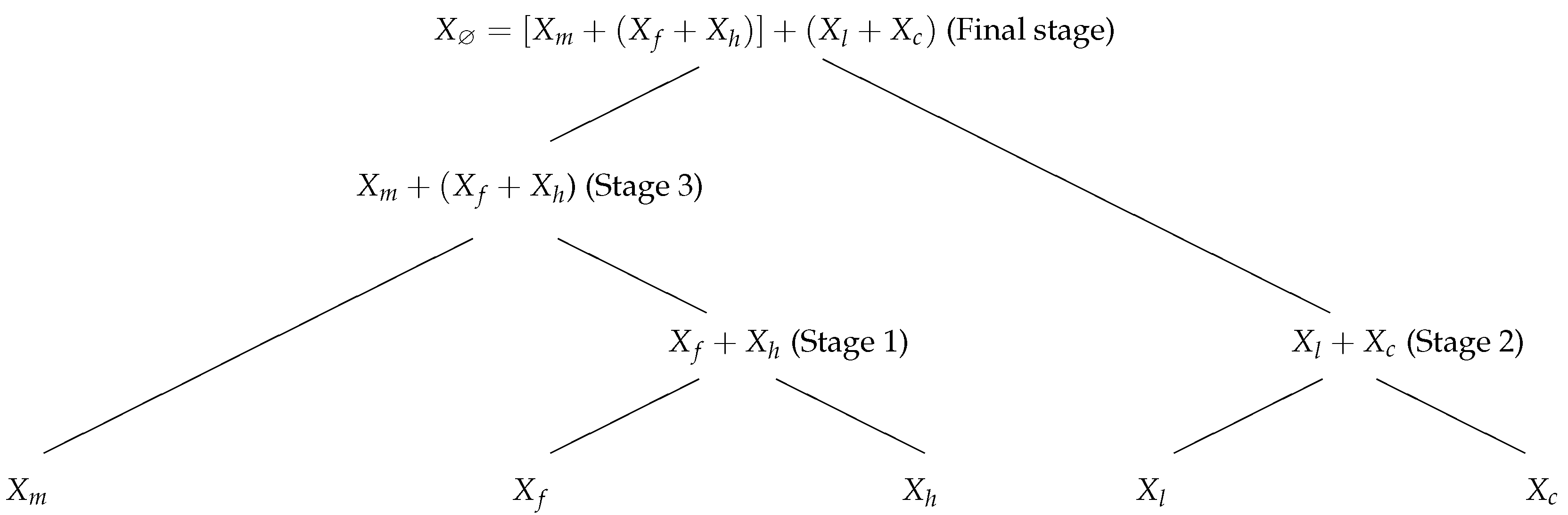
| House | Fire | Motor | CTP | Liability | Aggregate loss | |
| Gross loss ratios | ||||||
| Mean | 0.5849 | 0.7820 | 0.7211 | 0.8172 | 0.7024 | 0.7005 |
| Standard deviation | 0.2981 | 0.8334 | 0.0682 | 0.3100 | 0.1566 | 0.1971 |
| Skewness | 2.6290 | 3.6449 | 0.9729 | -0.7432 | -0.2392 | 2.8759 |
| Excess kurtosis | 8.0694 | 13.819 | 0.0075 | 0.0036 | 0.0671 | 9.6254 |
| Average weight, | 0.25 | 0.14 | 0.33 | 0.11 | 0.18 | 1 |
| Weight at June 2017, | 0.26 | 0.12 | 0.33 | 0.13 | 0.16 | 1 |
| Net loss ratios | ||||||
| Mean | 0.6272 | 0.6549 | 0.7394 | 0.8051 | 0.6499 | 0.7018 |
| Standard deviation | 0.2105 | 0.2639 | 0.0454 | 0.3333 | 0.1907 | 0.1659 |
| Skewness | 2.0440 | 1.4870 | 0.3835 | -0.8458 | -0.6556 | 1.3425 |
| Excess kurtosis | 5.6319 | 2.2074 | -0.9542 | 0.0960 | 1.5980 | 2.4629 |
| Average weight, | 0.22 | 0.10 | 0.36 | 0.13 | 0.18 | 1 |
| Weight at June 2017, | 0.24 | 0.09 | 0.36 | 0.13 | 0.17 | 1 |
| Stage 1 | ||||
| House | Fire | Motor | CTP | |
| Fire | 0.5262 | 1 | – | – |
| Motor | 0.4338 | 0.2308 | 1 | – |
| CTP | 0.0154 | -0.0523 | -0.1815 | 1 |
| Liability | 0.0585 | -0.1323 | 0.1446 | 0.3662 |
| Stage 2 | ||||
| House + Fire | Motor | CTP | ||
| Motor | 0.3169 | 1 | – | |
| CTP | -0.0400 | -0.1815 | 1 | |
| Liability | -0.0338 | 0.1446 | 0.3662 | |
| Stage 3 | ||||
| House + Fire | Motor | |||
| Motor | 0.3169 | 1 | ||
| CTP+Liability | 0.0154 | -0.0523 | ||
| Stage 1 | ||||
| House | Fire | Motor | CTP | |
| Fire | 0.5446 | 1 | – | – |
| Motor | 0.4338 | 0.2492 | 1 | – |
| CTP | -0.0154 | -0.0031 | -0.2369 | 1 |
| Liability | 0.0092 | -0.0646 | -0.0523 | 0.4954 |
| Stage 2 | ||||
| House + Fire | Motor | CTP | ||
| Motor | 0.3969 | 1 | – | |
| CTP | -0.0400 | -0.2369 | 1 | |
| Liability | -0.0523 | -0.0523 | 0.4954 | |
| Stage 3 | ||||
| House + Fire | Motor | |||
| Motor | 0.3969 | 1 | ||
| CTP+Liability | -0.0523 | -0.2123 | ||
| House | Fire | Motor | CTP | Liability | Aggregate loss | |
| Gross loss ratios | ||||||
| Distribution | Log-logistic | Burr | Burr | Weibull | Burr | Burr |
| Shape 1 | 4.76266 | 0.19159 | 0.04799 | 3.00527 | 7.70166 | 0.3732 |
| (s.e.) | (0.776) | (0.122) | (0.042) | (0.505) | (22.63) | (0.199) |
| Shape 2 | – | 8.11427 | 189.928 | – | 5.64960 | 15.8580 |
| (s.e.) | – | (4.012) | (155.0) | – | (1.555) | (5.441) |
| Scale* | 0.52243 | 3.04747 | 1.55319 | 0.90936 | 0.92955 | 1.70254 |
| (s.e.) | (0.037) | (0.415) | (0.014) | (0.061) | (0.604) | (0.095) |
| A-D statistic | 0.294 | 0.147 | 0.335 | 1.417 | 0.270 | 0.230 |
| A-D p-value | 0.942 | 0.998 | 0.909 | 0.197 | 0.958 | 0.979 |
| Net loss ratios | ||||||
| Distribution | Log-logistic | Log-logistic | Log-logistic | Weibull | Weibull | Burr |
| Shape 1 | 6.37499 | 4.96750 | 27.9840 | 2.53352 | 3.87399 | 0.50244 |
| (s.e.) | (1.031) | (0.801) | (4.469) | (0.439) | (0.599) | (0.269) |
| Shape 2 | – | – | – | – | – | 18.4406 |
| (s.e.) | – | – | – | – | – | (5.898) |
| Scale* | 0.59180 | 0.59840 | 0.73616 | 0.89199 | 0.71298 | 1.55857 |
| (s.e.) | (0.031) | (0.041) | (0.009) | (0.071) | (0.037) | (0.073) |
| A-D statistic | 0.246 | 0.455 | 0.371 | 1.962 | 0.602 | 0.197 |
| A-D p-value | 0.971 | 0.791 | 0.875 | 0.097 | 0.643 | 0.991 |
| Copula | p-value | |||||
| (s.e.) | (s.e.) | |||||
| Gross loss ratios | ||||||
| 0.5218 | 0.5694 | 0.4 Clayton + 0.6 SurvClayton | 0.4640 | 4.886 | 2.148 | |
| (4.161) | (1.966) | |||||
| 0.1496 | 0.2742 | 0.25 Clayton + 0.75 SurvClayton | 0.5410 | 1.022 | 1.482 | |
| (3.194) | (1.596) | |||||
| 0.2772 | 0.4383 | 0.1 Clayton + 0.9 SurvClayton | 0.8986 | 1.160 | 1.029 | |
| (5.796) | (0.548) | |||||
| 0.0000 | 0.0000 | Gaussian | 0.9815 | 0.013036 | ||
| (0.285) | ||||||
| Net loss ratios | ||||||
| 0.5390 | 0.5401 | 0.6 Gumbel + 0.4 SurvGumbel | 0.7298 | 2.126 | 2.801 | |
| (1.265) | (2.083) | |||||
| 0.2772 | 0.1070 | Student-t | 0.5549 | 0.7376 | 1.2910 | |
| (0.115) | (0.593) | |||||
| 0.3977 | 0.4038 | 0.7 SurvGumbel + 0.3 SurvClayton | 0.7607 | 1.750 | 1.047 | |
| (0.954) | (2.884) | |||||
| 0.0143 | 0.1531 | Rotated Gumbel | 0.5569 | 1.0865 | ||
| (0.186) | ||||||
| House | Fire | Motor | CTP | Liability | Weighted Sum of risk measures | Risk measure of aggregate loss, | |
| Gross loss ratios | |||||||
| VaR | 0.8284 | 1.4422 | 0.8283 | 1.1991 | 0.8915 | 0.9603 | 0.8806 |
| [0.800,0.856] | [1.301,1.60] | [0.814,0.843] | [1.172,1.225] | [0.879,0.903] | [0.940,0.981] | [0.859,0.902] | |
| VaR | 0.9693 | 2.2516 | 0.8931 | 1.3088 | 0.9417 | 1.1377 | 1.0184 |
| [0.925,1.024] | [1.959,2.593] | [0.872,0.916] | [1.278,1.341] | [0.926,0.957] | [1.099,1.182] | [0.979,1.064] | |
| VaR | 1.365 | 6.2017 | 1.0602 | 1.5049 | 1.0346 | 1.8101 | 1.5937 |
| [1.227,1.534] | [4.463,8.642] | [1.008,1.122] | [1.451,1.56] | [1.008,1.061] | [1.603,2.095] | [1.385,1.891] | |
| TVaR | 1.063 | 4.1271 | 0.9299 | 1.3413 | 0.9576 | 1.4060 | 1.2644 |
| [1.007,1.128] | [2.873,6.202] | [0.906,0.957] | [1.313,1.37] | [0.944,0.972] | [1.256,1.652] | [1.118,1.518] | |
| TVaR | 1.2353 | 6.4776 | 1.0026 | 1.4322 | 1.0003 | 1.7755 | 1.5895 |
| [1.144,1.341] | [4.096,10.578] | [0.966,1.042] | [1.397,1.466] | [0.983,1.019] | [1.488,2.276] | [1.304,2.094] | |
| TVaR | 1.7244 | 18.4861 | 1.1898 | 1.6042 | 1.0836 | 3.4412 | 3.1437 |
| [1.459,2.074] | [8.037,37.647] | [1.1,1.299] | [1.54,1.669] | [1.051,1.118] | [2.178,5.761] | [1.897,5.461] | |
| Net loss ratios | |||||||
| VaR | 0.835 | 0.9313 | 0.7961 | 1.2386 | 0.8843 | 0.8821 | 0.801 |
| [0.813,0.857] | [0.9,0.965] | [0.791,0.801] | [1.207,1.273] | [0.869,0.899] | [0.874,0.89] | [0.792,0.81] | |
| VaR | 0.9383 | 1.0821 | 0.8177 | 1.3737 | 0.9462 | 0.9563 | 0.844 |
| [0.904,0.973] | [1.033,1.134] | [0.811,0.825] | [1.334,1.414] | [0.927,0.965] | [0.945,0.967] | [0.832,0.857] | |
| VaR | 1.2087 | 1.4985 | 0.8662 | 1.6234 | 1.0549 | 1.1271 | 0.9443 |
| [1.124,1.311] | [1.366,1.668] | [0.851,0.883] | [1.56,1.693] | [1.026,1.083] | [1.101,1.156] | [0.916,0.976] | |
| TVaR | 0.9987 | 1.1803 | 0.8273 | 1.4158 | 0.9638 | 0.9916 | 0.8651 |
| [0.959,1.04] | [1.121,1.246] | [0.821,0.835] | [1.379,1.453] | [0.948,0.981] | [0.979,1.004] | [0.853,0.878] | |
| TVaR | 1.1164 | 1.3622 | 0.8487 | 1.5303 | 1.0144 | 1.0674 | 0.9098 |
| [1.055,1.183] | [1.266,1.468] | [0.839,0.859] | [1.483,1.579] | [0.995,1.034] | [1.049,1.087] | [0.891,0.93] | |
| TVaR | 1.4311 | 1.8778 | 0.8983 | 1.7503 | 1.1077 | 1.2516 | 1.021 |
| [1.27,1.636] | [1.605,2.216] | [0.876,0.924] | [1.664,1.837] | [1.074,1.146] | [1.201,1.312] | [0.976,1.075] | |
| House | Fire | Motor | CTP | Liability | Shannon’s entropy | |
| Gross loss ratio weights | 0.26 | 0.12 | 0.33 | 0.13 | 0.16 | 1.52 |
| Net loss ratio weights | 0.24 | 0.09 | 0.36 | 0.13 | 0.17 | 1.49 |
| Weighted Sum of risk measures | Risk measure of aggregate loss, | |||
| Gross loss ratios | ||||
| 0.2654 | 0.1956 | 1.35 | ||
| VaR | 0.9603 | 0.8806 | 1.09 | |
| VaR | 1.1377 | 1.0184 | 1.12 | |
| VaR | 1.8101 | 1.5937 | 1.14 | |
| TVaR | 1.4060 | 1.2644 | 1.11 | |
| TVaR | 1.7755 | 1.5895 | 1.12 | |
| TVaR | 3.4412 | 3.1437 | 1.09 | |
| Net loss ratios | ||||
| 0.1752 | 0.1040 | 1.68 | ||
| VaR | 0.8821 | 0.8010 | 1.10 | |
| VaR | 0.9563 | 0.8440 | 1.13 | |
| VaR | 1.1271 | 0.9443 | 1.19 | |
| TVaR | 0.9916 | 0.8651 | 1.15 | |
| TVaR | 1.0674 | 0.9098 | 1.17 | |
| TVaR | 1.2516 | 1.0210 | 1.23 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





