Ramsey Approach to Dynamics: Ramsey Theory and Conservation Laws

1. Introduction

In this communication, we expand the Ramsey Theory to the analysis of dynamic systems, built of point masses. In its most general meaning Ramsey Theory refers to any set of objects interrelated by different kinds of distinguishable connections/interrelations [1,2,3,4,5,6,7,8,9,10,11,12]. The Ramsey theory was introduced by the British mathematician, logician and thinker Frank Plumpton Ramsey [1]. Today, it is seen as a field of combinatorics/graph theory, which deals with the specific kind of mathematical structures, namely: complete graphs [3,4,5,6]. A graph is a mathematical structure comprising a set of objects in which pairs of the objects are in some sense "related" [3,4,5,6]. A complete graph, in turn, is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge [2,3]. In our communication, we propose the procedure enabling treatment of dynamics problem with the tools of the graph theory.

The much progress in the field of the Ramsey Theory was achieved by Paul Erdős [7,8]. The Ramsey Theorem states that a structure of a given kind is guaranteed to contain a well-defined substructure. The classical problem in Ramsey theory is the so-called “party problem”, which asks the minimum number of guests denoted R(m,n) that must be invited so that at least m will know each other, or at least n will not know each other (i.e., there exists an independent set of order n [1,2,3,4,5,6,7,8,9,10,11,12]). R(m,n) is called the Ramsey number. When Ramsey theory is reshaped in the notions of the graph theory, it states that any structure will necessarily contain an interconnected substructure [2,3,4,5,6]. The Ramsey theorem, in its graph-theoretic forms, states that one will find monochromatic cliques in any edge color labelling of a sufficiently large complete graph [2,3,4,5,6]. In the discrete problems of physics, we deal with objects/particles interacting via various forces. Thus, it seems, that the Ramsey Theory is well suited for physical problems. However, the papers addressing the Ramsey analysis of physical systems are still scarce [13,14,15].

3. Results

3.1. Isolated System of Point Masses and Its Analysis with the Ramsey Theory

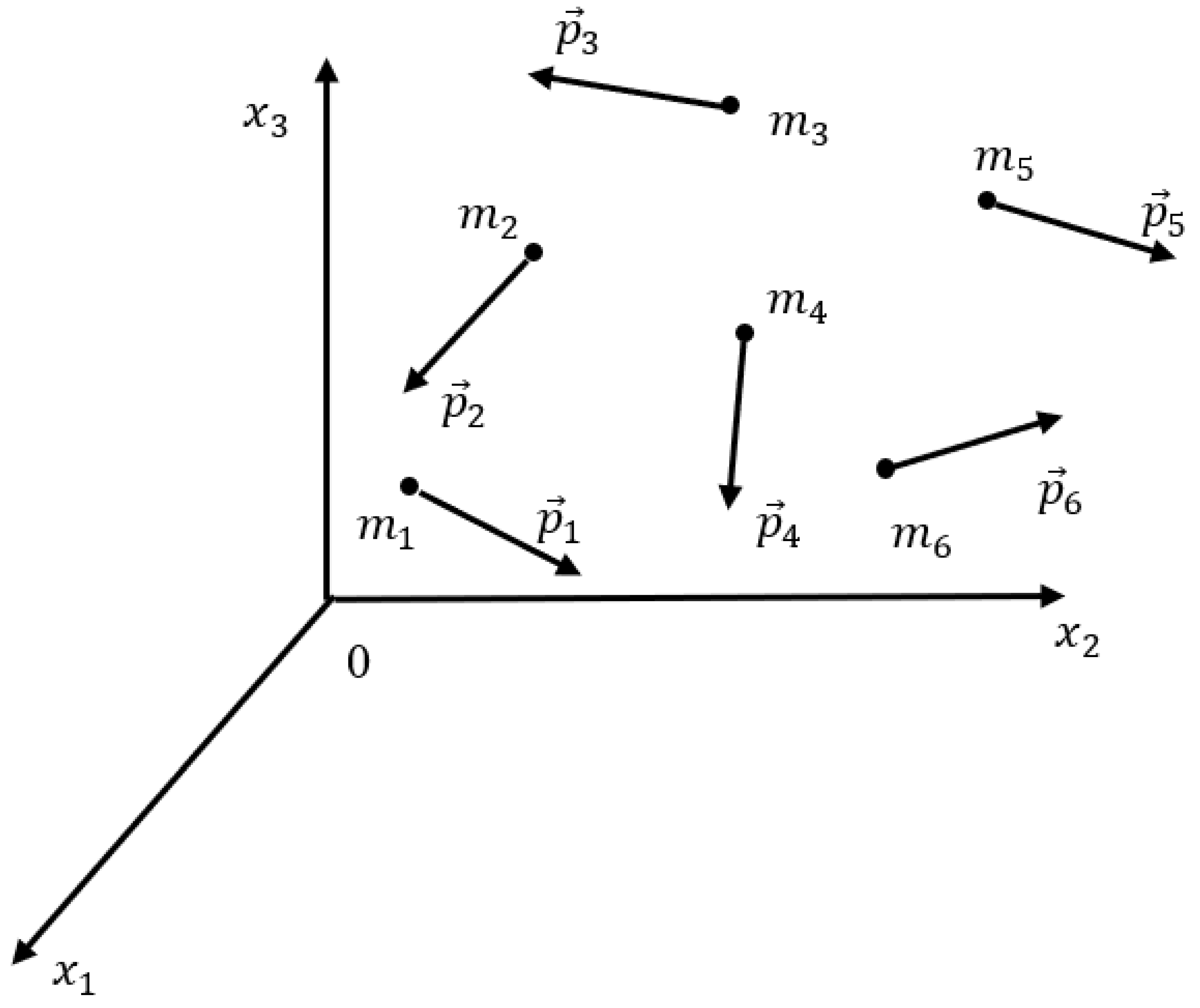
Consider the isolated system built of six interacting non-relativistic point masses $m_i,i=1,\dots ,6$ , depicted in Figure 1. The momenta of the particles are ${\overrightarrow{p}}_i\left(t\right)=m_i{\overrightarrow{v}}_i\left(t\right)$.

The system is isolated; thus, the conservation of the total momentum of the system, denoted ${\overrightarrow{P}}_{tot}$ expressed with Eq. (1) takes place:

$${\sum }_{i=1}^6{\overrightarrow{p}}_i={\overrightarrow{P}}_{tot}=const.$$

(1)

There exists the frame in which the total momentum is zero, and this is a frame related to the center of masses of the system, which moves with the velocity${\overrightarrow{v}}_{cm}$ [16]:

$${\overrightarrow{v}}_{cm}={\displaystyle \frac{\sum _{i=1}^6{\overrightarrow{p}}_i}{\sum _{i=1}^6{m}_i}}$$

(2)

It is convenient to consider the motion of the particles in the frame related to the center of masses of the system (the center mass system). Momenta of the particles in this system we denote ${\overrightarrow{p}}_{cmi}$. The total momentum of the set of the interacting particles in the center mass system is zero; $\sum _{i=1}^6{\overrightarrow{p}}_i={\overrightarrow{P}}_{tot}=0.$ Now we develop the Ramsey approach to the motion of the system. We define the set of momenta ${\overrightarrow{p}}_{cmi}\left(t\right),i=(1,\dots ,6)$ as the set of vectors generating the complete bi-colored graph. Vectors ${\overrightarrow{p}}_{cmi},i=(1,\dots ,6)$ we consider as the “generators” of the Ramsey graph. In other words, vectors ${\overrightarrow{p}}_{cmi},i=(1\dots 6)$ serve as the vertices of the graph. The graph is built according to the following procedure. Vertices numbered i and j are connected with the red link, when Eq. (3) takes place:

$${(\overrightarrow{p}}_{cmi}\left(t\right)·{\overrightarrow{p}}_{cmj}\left(t\right))=e_{ij}\ge 0$$

(3)

Parenthesis denote the scalar product of the vectors. And, correspondingly, the vertices numbered i and j are connected with the green link, when Eq. (4) occurs:

$${(\overrightarrow{p}}_{cmi}\left(t\right)·{\overrightarrow{p}}_{cmj}\left(t\right))=e_{ij}(t)<0;i,j=1,\dots ,6$$

(4)

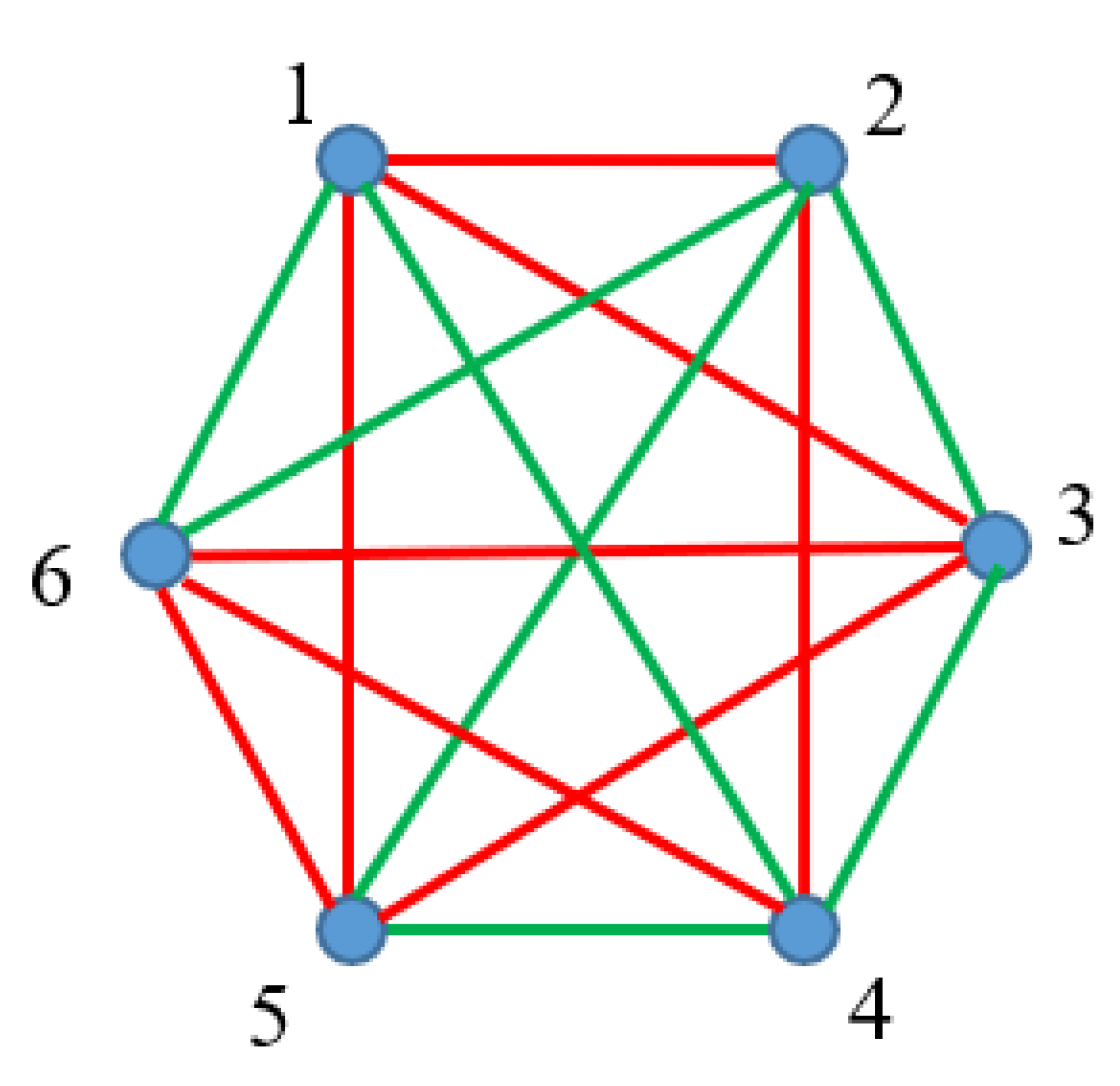
Within the terms of the Ramsey Theory (recall the “party problem” addressed in the Introduction Section) the momenta of the particles are “acquainted” each with another and they are connected with the red link, when Eq. (3) takes place, and vectors are “not acquainted” each with another, and they are connected with the green link, when Eq. (4) is true. Figure 2 exemplifies the suggested coloring procedure. Thus, typical Ramsey problem arises, and the Ramsey numbers may be introduced [2,3,4,5,6].

According to the Ramsey theorem, we recognized two monochromatic triangles (namely triangles “135” and “356 in the graph, shown in Figure 2. Indeed, R(3,3)=6; this means, that at least one mono-colored triangle should inevitably appear in the bi-colored, complete graph built of six vertices. Regrettably, the Ramsey Theorem says nothing about what kind of monochromic triangles will be necessarily present in the graph.

$e_{12},e_{13,}{e}_{15},e_{24},e_{35},e_{36},e_{46},e_{56}\ge 0;e_{14},e_{16},e_{23},e_{25},e_{26},e_{34},e_{45}<0.$ Triangles “135” and “356” are the monochromatic ones.

Now, consider that we built the graph, emerging from the momenta of the particles established in the frame of the center of mass. The scalar product of momenta defined by Eqs. 3-4, being time dependent, is invariant relatively to the rotations and translations of frames. Thus, introduced coloring procedure at a given time is invariant relatively to the aforementioned transformations of frames. However, coloring is sensitive to Galilean/Lorenz transformations. Indeed, the sign of the scalar products defined by Eqs. (3-4) is sensitive to the Galilean/Lorenz transformations). It is noteworthy, that it remains the same for the slow motions of system of frames ${\mathit{S}}^{\prime }$ relatively the frame related to the center of masses, denoted S. Consider the system of frames ${\mathit{S}}^{\prime }$ moving with the velocity $\overrightarrow{\mathit{u}}$ relatively to S (we restrict our treatment by the Galilean transformations). The scalar product of momenta in ${\mathit{S}}^{\prime }$ is given by:

$$\left({\overrightarrow{\mathit{p}}}_{\mathit{i}}^{\prime }·{\overrightarrow{\mathit{p}}}_{\mathit{j}}^{\prime }\right)={\mathit{m}}_{\mathit{i}}{\mathit{m}}_{\mathit{j}}\left({\overrightarrow{\mathit{v}}}_{\mathit{c}\mathit{m}\mathit{i}}-\overrightarrow{\mathit{u}}\right)·\left({\overrightarrow{\mathit{v}}}_{\mathit{c}\mathit{m}\mathit{j}}-\overrightarrow{\mathit{u}}\right).$$

(5)

Neglecting terms of the second order of smallness in speed u we obtain

$$\left({\overrightarrow{\mathit{p}}}_{\mathit{i}}^{\prime }·{\overrightarrow{\mathit{p}}}_{\mathit{j}}^{\prime }\right)\cong \left({\overrightarrow{\mathit{p}}}_{\mathit{c}\mathit{m}\mathit{i}}·{\overrightarrow{\mathit{p}}}_{\mathit{c}\mathit{m}\mathit{j}}\right)-{\mathit{m}}_{\mathit{i}}{\mathit{m}}_{\mathit{j}}\overrightarrow{\mathit{u}}\left({\overrightarrow{\mathit{v}}}_{\mathit{c}\mathit{m}\mathit{i}}+{\overrightarrow{\mathit{v}}}_{\mathit{c}\mathit{m}\mathit{j}}\right).$$

(6)

The scalar product $\left({\overrightarrow{\mathit{p}}}_{\mathit{i}}^{\prime }·{\overrightarrow{\mathit{p}}}_{\mathit{j}}^{\prime }\right)$ will be close to the scalar product$\left({\overrightarrow{\mathit{p}}}_{\mathit{c}\mathit{m}\mathit{i}}·{\overrightarrow{\mathit{p}}}_{\mathit{c}\mathit{m}\mathit{j}}\right)$ when Eq. 7 takes place:

$$\left(\overrightarrow{\mathit{u}}·\left({\overrightarrow{\mathit{v}}}_{\mathit{c}\mathit{m}\mathit{i}}+{\overrightarrow{\mathit{v}}}_{\mathit{c}\mathit{m}\mathit{j}}\right)\right)\ll \left({\overrightarrow{\mathit{v}}}_{\mathit{c}\mathit{m}\mathit{i}}·{\overrightarrow{\mathit{v}}}_{\mathit{c}\mathit{m}\mathit{j}}\right).$$

(7)

Eq. 7 defines when the motion of the frames may be considered as “slow”. Thus, we come to a very important and general conclusion: the mono-colored triangles appearing in the frame of the center of mass will remain mono-colored under rotations and translations of frames and it will remain monochromatic in any slowly moving inertial frame, when Eq. (7) is true. It again should be emphasized, that coloring of the graph changes with time. Thus, we discovered somewhat surprising invariant: the monochromatic triangles, emerging from the coloring procedure defined by Eqs. (3-4) will remain monochromatic when aforementioned conditions take place.

3.2. The Ring-like System of Momenta and Its Properties

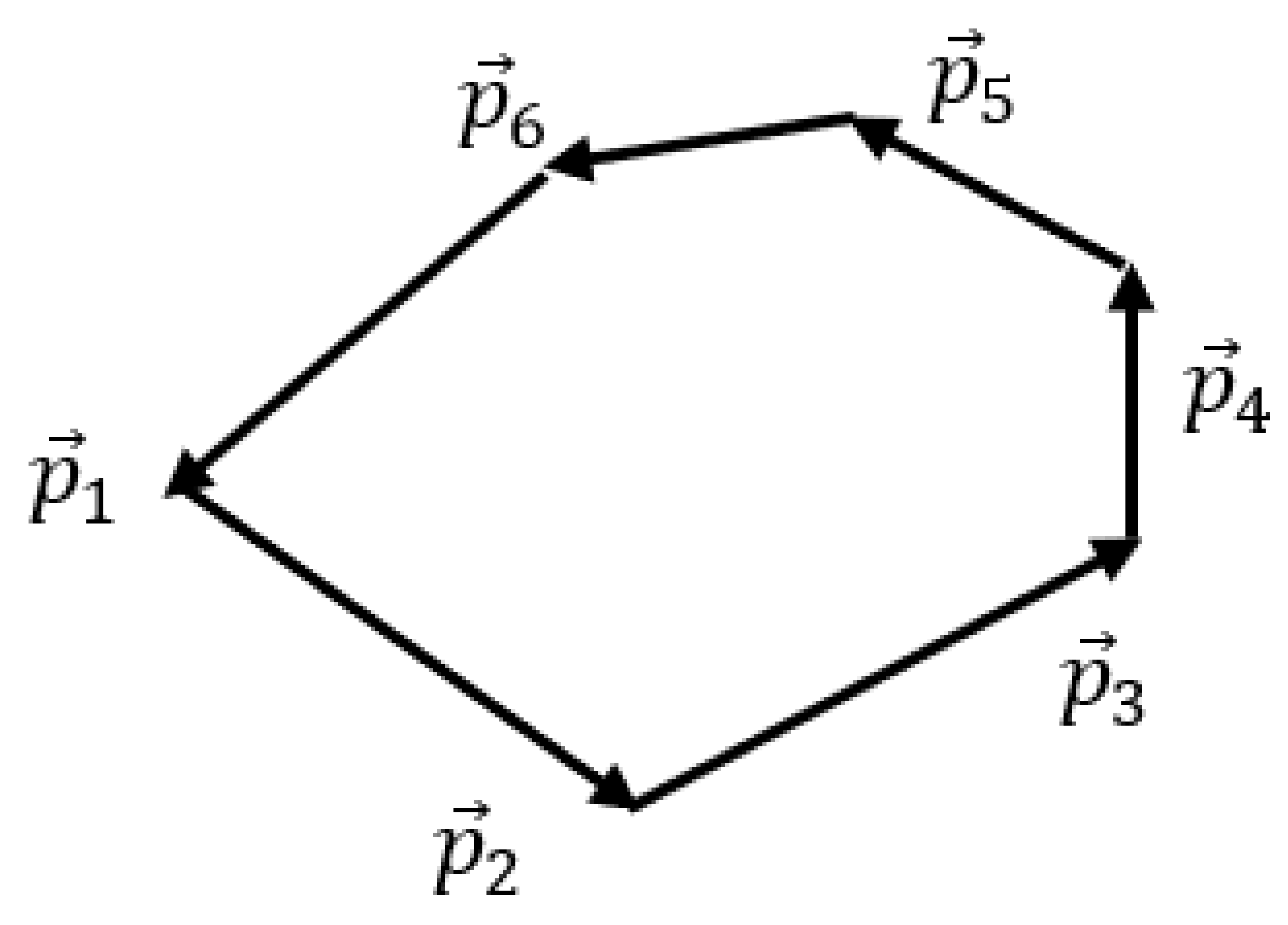
The introduced Ramsey approach enables elegant geometric interpretation in the frame of the center of mass, in which $\sum _{\mathit{i}=1}^6{\overrightarrow{\mathit{p}}}_{\mathit{i}}={\overrightarrow{\mathit{P}}}_{\mathit{t}\mathit{o}\mathit{t}}=0$ is true. The conservation of momentum may be interpreted as follows: the momenta of particles form the ring-like system of vectors, such as that, depicted in Figure 3. Of course, this is true only in the frame of the center of mass. In general, the ring-like system of vectors shown in Figure 3 is a 3D one.

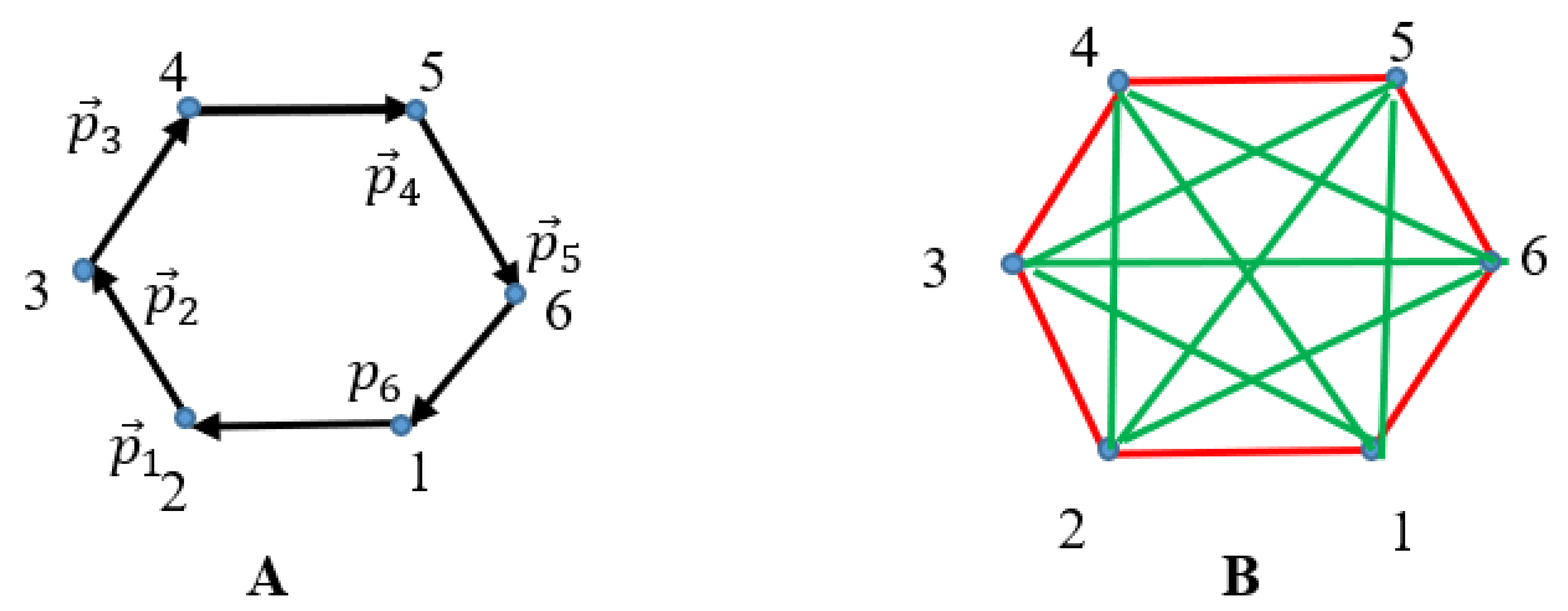
This set of momenta will give rise to the bi-colored, complete graph, built according to the procedure described by Eqs. (3-4). It will be instructive to build the graph for the system of particles in which $\left|{\overrightarrow{\mathit{p}}}_{\mathit{i}}\right|=\mathit{c}\mathit{o}\mathit{n}\mathit{s}\mathit{t}$ takes place, i.e. the moduli of the momenta remain constant. We adopt that vectors ${\overrightarrow{\mathit{p}}}_{\mathit{i}}$ form hexagon (in principle, the hexagon may rotate), shown in Figure 4A.

The bi-colored, 2D complete Ramsey graph generated by the vectors of momenta ${\overrightarrow{p}}_i,i=1\dots 6$ ($\left|{\overrightarrow{p}}_i\right|=const$) according to Eqs. (3-4), is shown in Figure 4B. According to the Ramsey theorem $R\left(\mathrm{3,3}\right)=6;$ this guarantees presence of at least one mono-colored triangle in the graph, shown in Figure 4B. Indeed, triangles “135” and “246” appearing in Figure 4B are green ones. It should again be stressed, that the suggested coloring of the Ramsey graph will remain untouched under rotations/translations of frames. And now ($\left|{\overrightarrow{p}}_i\right|=const$) the coloring will not evolve with time. The suggested coloring procedure, given by Eqs. (3-4), is easily generalized for any arbitrary number of the momenta vectors. However, calculation of the large Ramsey numbers remains an unsolved problem [2,3,4]. Now consider the graph emerging from the five generating momenta vectors ${\overrightarrow{p}}_i,i=1\dots 5$, $\left|{\overrightarrow{p}}_i\right|=const$, forming pentagon.

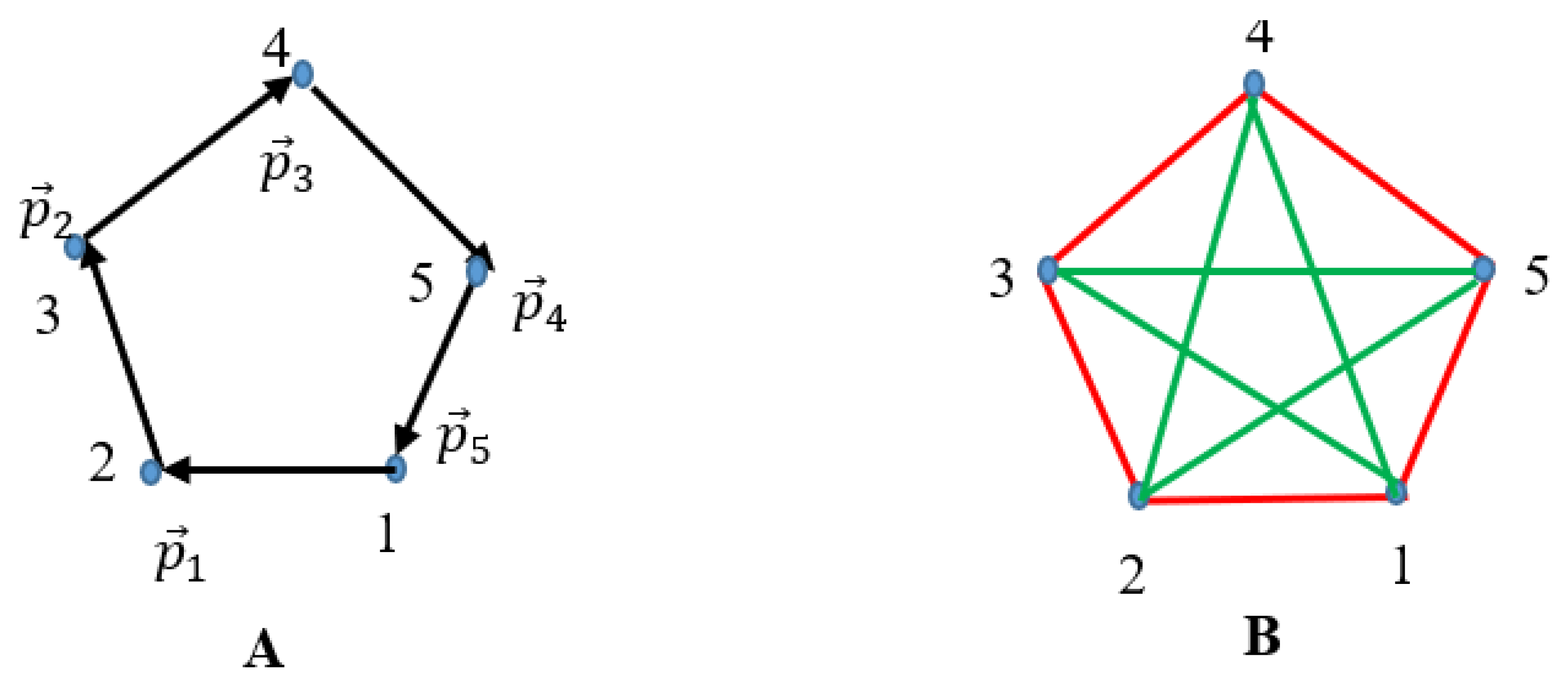
In this specific case, the conservation of momentum is also assumed: $\sum _{i=1}^5{\overrightarrow{p}}_i=0$ (the system is isolated, the frame of the center of mass is considered). The 2D ring-like system of the momenta vectors is shown in Figure 5A. The bi-colored graph generated by the momenta vectors ${\overrightarrow{p}}_i,i=1,\dots ,5,$ defined by Eqs. 3-4, is shown in Figure 5B. The coloring of the graph follows constituting Equations 3-4. Five momenta vectors ${\overrightarrow{p}}_i,i=1,\dots ,5$ serve now as the vertices of the Ramsey complete graph, shown in Figure 5B.

Complete bi-colored graph, shown in Figure 5B, does not contain any mono-colored triangle. Indeed, the Ramsey number $R\left(\mathrm{3,3}\right)=6.$ Moreover, we state that any graph emerging from the vectors ${\overrightarrow{p}}_i,i=1,\dots ,5$, $\left|{\overrightarrow{p}}_i\right|=const$ forming pentagon shown in Figure 5A will not contain the monochromatic triangle in any frame obtained from the center of mass frame by rotations or translations.

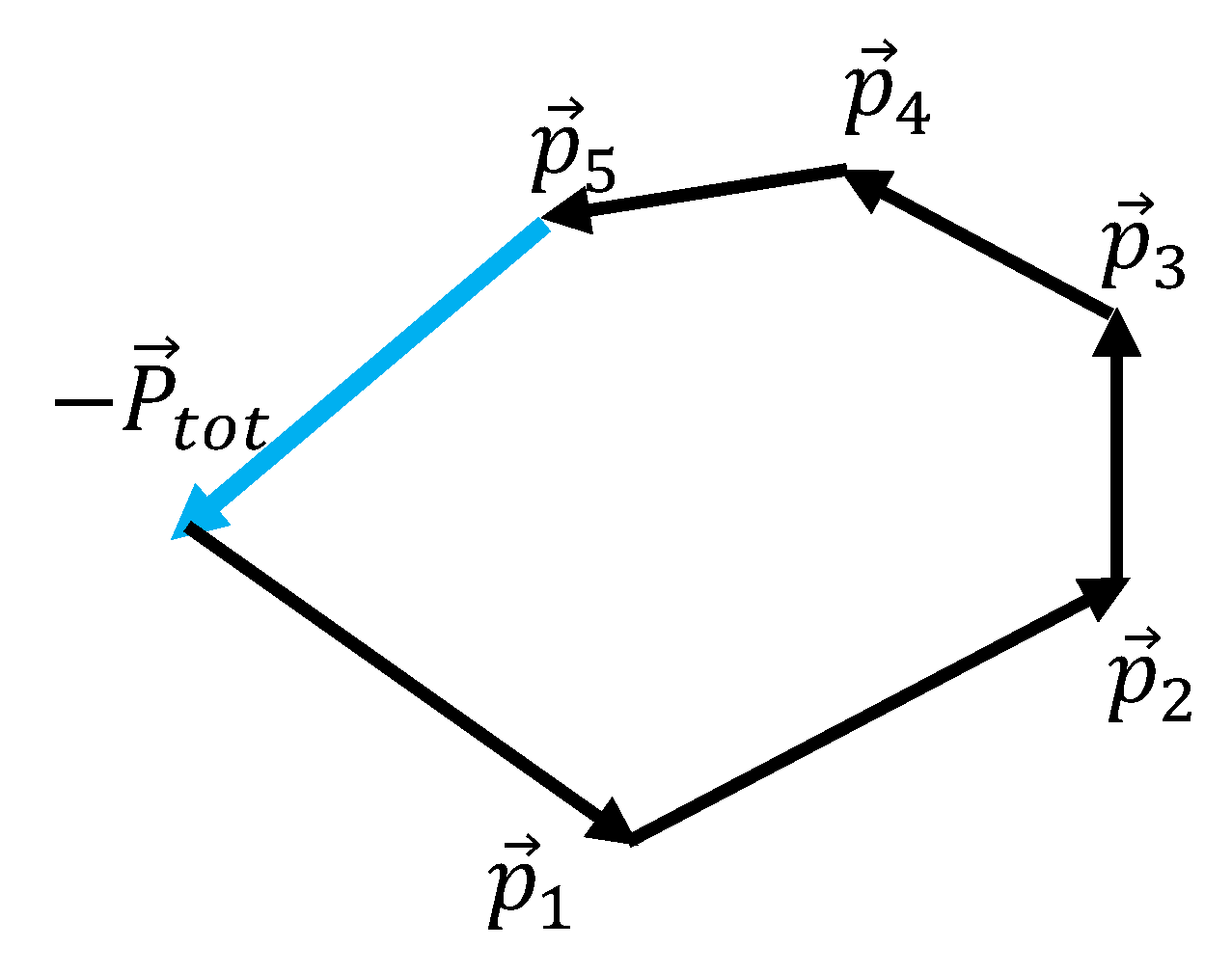
What do we have when the total moment of the system is not equal to zero? Consider the system containing five particles, for which $\sum _{i=1}^5{\overrightarrow{p}}_i={\overrightarrow{P}}_{tot}\ne 0$ takes place. In this case we have the open chain of momenta such as shown in Figure 6. The chain may be easily closed by vector $-{\overrightarrow{P}}_{tot}$ as depicted in Figure 6.

The further Ramsey graph treatment is trivially reduced to the aforementioned mathematical procedure, when $-{\overrightarrow{P}}_{tot}$ is included into the set of generating vectors.

3.3. Extension of the Suggested Analysis for the Angular Momenta of the Particles

The suggested Ramsey approach is easily extended to the angular momenta of particles, denoted ${\overrightarrow{L}}_i$. Consider the isolated system built of N interacting point masses $m_i,i=1,\dots ,N$. For a sake of simplicity assume that the total initial angular moment of the system is zero. Thy system is isolated, thus, the total angular moment of the system is conserved. Now we define the set of angular momenta ${\overrightarrow{L}}_i\left(t\right),i=(1,\dots ,N)$ as the set of vectors generating the complete bi-colored graph. Vectors${\overrightarrow{L}}_i\left(t\right),i=(1,\dots ,N)$ serve now as the vertices of the graph. The graph is built according to the following procedure. Vertices numbered i and j are connected with the red link, when Eq. (8) takes place:

$${(\overrightarrow{L}}_i(t)·{\overrightarrow{L}}_j(t))\ge 0,i,j=1,...,N.$$

(8)

Parenthesis denote the scalar product of the vectors. And, correspondingly, the vertices numbered i and j are connected with the green link, when Eq. (9) is true:

$${(\overrightarrow{L}}_i(t)·{\overrightarrow{L}}_j(t))<0$$

(9)

The further reasoning is similar to that discussed in Section 3.1 and Section 3.2. Bi-colored graphs arising from the coloring procedure defined by Eqs. (8-9) are analyzed within the Ramsey theory. The number of mono-colored substructures remains invariant in all of the frames emerging from the original frame under its translations or rotations.

It is noteworthy, that there exist a particular case when coloring of momenta graph coincides with that of angular momenta. Angular momentum is defined according to Eq. (10):

$$\left({\overrightarrow{\mathit{L}}}_{\mathit{i}}·{\overrightarrow{\mathit{L}}}_{\mathit{j}}\right)=$$

(10)

Considering the equation $\left(\overrightarrow{\mathit{a}}\times \overrightarrow{\mathit{b}}·\overrightarrow{\mathit{c}}\times \overrightarrow{\mathit{d}}\right)=\left(\overrightarrow{\mathit{a}}·\overrightarrow{\mathit{c}}\right)\left(\overrightarrow{\mathit{b}}·\overrightarrow{\mathit{d}}\right)-\left(\overrightarrow{\mathit{a}}·\overrightarrow{\mathit{d}}\right)\left(\overrightarrow{\mathit{b}}·\overrightarrow{\mathit{c}}\right)$ and Eq. 10 yields:

$$\left({\overrightarrow{\mathit{L}}}_{\mathit{i}}·{\overrightarrow{\mathit{L}}}_{\mathit{j}}\right)={\mathit{r}}^2\left({\overrightarrow{\mathit{p}}}_{\mathit{i}}·{\overrightarrow{\mathit{p}}}_{\mathit{j}}\right)-\left(\overrightarrow{\mathit{r}}·{\overrightarrow{\mathit{p}}}_{\mathit{i}}\right)\left(\overrightarrow{\mathit{r}}·{\overrightarrow{\mathit{p}}}_{\mathit{j}}\right)$$

(11)

We conclude from Eq. (11) that when $\left(\overrightarrow{\mathit{r}}·{\overrightarrow{\mathit{p}}}_{\mathit{i}}\right)=0,\mathit{i}=1,\dots ,\mathit{N}$, the signs of the scalar products $\left({\overrightarrow{\mathit{L}}}_{\mathit{i}}·{\overrightarrow{\mathit{L}}}_{\mathit{j}}\right)$ and $\left({\overrightarrow{\mathit{p}}}_{\mathit{i}}·{\overrightarrow{\mathit{p}}}_{\mathit{j}}\right)$ coincide. This takes place when the rotational motion of the point masses occurs. In this case, coloring of the momenta graph coincides with that of the angular momenta graph.

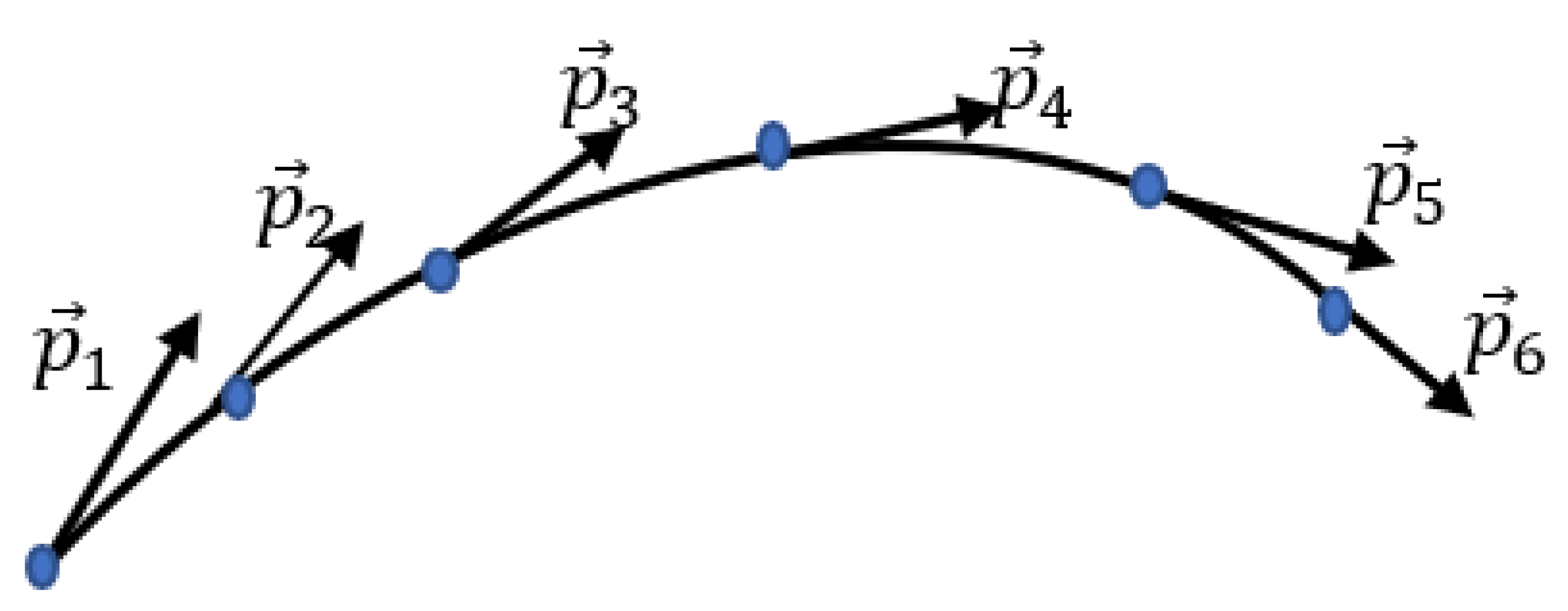
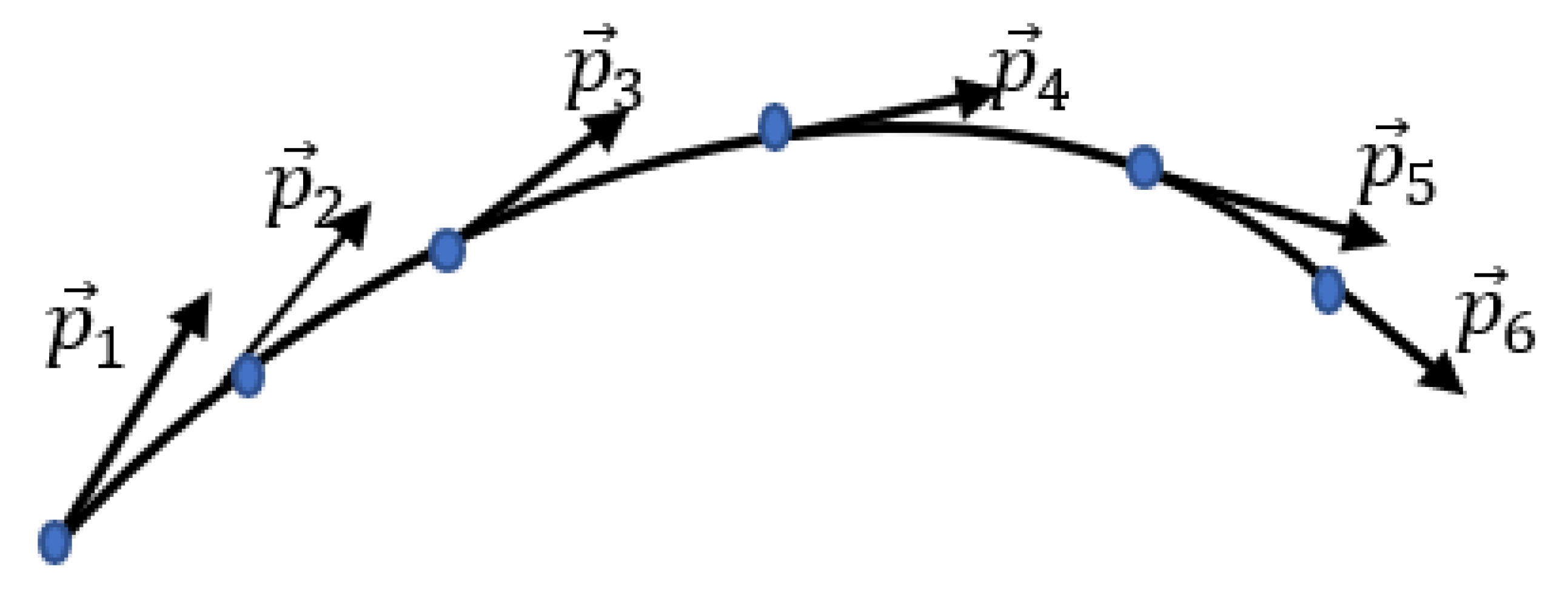
3.4. Graph Representation of the Motion of the Single Point Mass

The suggested approach is easily extended to the motion of the single point mass shown in Figure 7.

The motion of the particle is seen in the momentum space, which is used broadly for the solution of physical problems [17,18]. Time sequence of six momenta of the point mass performing the curvilinear movement ${\overrightarrow{\mathit{p}}}_{\mathit{i}}$ is presented in Figure 7. The graph representing the motion and its coloring is carried out as discussed in detail in Section 3.1.The coloring procedure is defined with Eqs. (3-4). The emerging bi-colored graph according to the Ramsey theorem will inevitably contain at least one monocromatic triangle.

Consider one possible application of the suggested approach. We address the system called dynamical billiard, in which a particle moves along a straight line and is reflected from the boundaries. Billiards are Hamiltonian idealizations of the known billiard game, in which the boundaries have a general geometric shape (rather than a rectangular shape). In Figure 8, a point particle m alternates between free motion (presupposed to be a straight line,) and specular reflections from an elliptic boundary. This class of systems is called a dynamical billiard [19,20,21]. Dynamical billiards are described by mathematical models that appear in a broad diversity of physical phenomena [19,20,21]. The dynamical properties of such models are determined by the shape of the walls of the container, and they may vary from completely regular (integrable) to fully chaotic [19,20,21]. Thus, consider the simplest system in which the particles move in a 2D elliptic container and collide with its walls/boundary, as shown in Figure 8. The reflection points are marked as circles. Consider the set of six reflections from the boundary; momenta after the reflections are denoted ${\overrightarrow{\mathit{p}}}_{\mathit{i}},\mathit{i}=1,\dots ,\mathbf{6}.$

The reflections may be elastic or non-elastic. The motion of the particle may be regular or chaotic. The graph generated by momenta and its coloring is performed as discussed in Section 3.1.The coloring procedure is defined with Eqs. (3-4). The emerging bi-colored, complete graph according to the Ramsey theorem will inevitably contain at least one monocromatic triangle, whatever is the motion of the particle m.

4. Discussion

We introduced the procedure enabling the Ramsey analysis of the isolated mechanical systems. Vectors of momenta or angular momenta of the particles are taken as the vertices of the graph. Vertices are connected with colored links. The coloring procedure is defined by Eqs. (3-4) and Eqs. (8-9). It should be stressed that the coloring defined by Eqs. (3-4) and Eqs. (8-9) is non-transitive [22,23]. The transitive Ramsey numbers are different from non-transitive ones [22,23]. The aforementioned coloring of the graphs, being time-dependent, is insensitive to the translations/rotations of frames. However, it is sensitive to the Galilean/Lorenz transformations. Isolated system containing six interacting particles will contain at least one mono-colored triangle.

In our future investigations we plan:

(i)

to investigate Hamiltonian interpretation of the introduced graphs, emerging from the Hamiltonian of a given mechanical system.

(ii)

to study the relativistic generalization of the introduced graphs.

5. Conclusions

The paper introduces the Ramsey theory based analysis of the mechanical systems. The Ramsey theory is a field of discrete mathematics which refers to any set of objects interrelated by different kinds of connections. Today it is seen, as a field of graph theory [24]. We propose to consider the vectors of momenta labeled ${\overrightarrow{\mathit{p}}}_{\mathit{i}}$ and angular momenta of the interacting point masses, denoted ${\overrightarrow{\mathit{L}}}_{\mathit{i}}$, constituting the isolated physical system as the vertices of the graph [24]. We start from the analysis of the Ramsey dynamics of the isolated system from the establishment of the momenta of the point masses in the frames of the center of masses, denoted ${\overrightarrow{\mathit{p}}}_{\mathit{c}\mathit{m}\mathit{i}}$. The coloring of the links/edges of the graph is performed as follows: If ${(\overrightarrow{\mathit{p}}}_{\mathit{c}\mathit{m}\mathit{i}}(\mathit{t})·{\overrightarrow{\mathit{p}}}_{\mathit{c}\mathit{m}\mathit{j}}(\mathit{t}))\ge \mathbf{0}$ is true, vectors of momenta of the particles are connected with the red link; if ${(\overrightarrow{\mathit{p}}}_{\mathit{c}\mathit{m}\mathit{i}}(\mathit{t})·{\overrightarrow{\mathit{p}}}_{\mathit{c}\mathit{m}\mathit{j}}(\mathit{t}))<\mathbf{0}$ takes place, the vectors of momenta are connected with the green link. Thus, the complete bi-colored Ramsey graph emerges. If the mechanical system contains six point masses, the emerging graph contains at least one monochromatic triangle (which is totally red or green). The coloring of the graph may evolve with time; however, it is independent on the rotations/translations of the frames. Thus, the number of monochromatic triangles will be the same in all of frames obtained by rotation/translation of original frame at a given time. However, the coloring procedure is sensitive to the Galilean transformations. On the other hand, the Ramsey theory predicts that the isolated physical system built of five interacting point masses may be represented by the bi-colored momenta graph, which does not contain monochromatic triangles (if the coloring procedure remains untouched). In the isolated systems, the total momentum is conserved. The conservation of momentum may be geometrically interpreted as follows: the momenta of particles form the 3D ring-like system of vectors. Bi-colored, complete graphs emerging from the 2D ring-like sets of momentum vectors are treated. Systems of particles in which $\left|{\overrightarrow{\mathit{p}}}_{\mathit{i}}\right|=\mathit{c}\mathit{o}\mathit{n}\mathit{s}\mathit{t}$ takes place, i.e. the moduli of the momenta remain constant are addressed. Ramsey graphs, illustrating the Ramsey theorem and demonstrating the Ramsey numbers, built for these systems are supplied. The presented approach is easily extended for the bi-colored complete graphs emerging from the angular momenta of interacting particles. Extension of the suggested approach to the system in which momentum is not conserved is suggested. Generalization of the approach to the motion of a single particle seen in the momenta space is introduced.