SAT in Polynomial Time: A Proof of P = NP

1. Introduction

The P versus NP problem is a fundamental question in computer science that asks whether problems whose solutions can be easily checked can also be easily solved [1]. “Easily” here means solvable in polynomial time, where the computation time grows proportionally to the input size [1,2]. Problems solvable in polynomial time belong to the class P, while NP includes problems whose solutions can be verified efficiently given a suitable “certificate” [1,2]. Alternatively, P and NP can be defined in terms of deterministic and non-deterministic Turing machines with polynomial-time complexity [1,2].

The central question is whether P and NP are the same. Most researchers believe that P is a strict subset of NP, meaning that some problems are inherently harder to solve than to verify. Resolving this problem has profound implications for fields like cryptography and artificial intelligence [3,4]. The P versus NP problem is widely considered one of the most challenging open questions in computer science. Techniques like relativization and natural proofs have yielded inconclusive results, suggesting the problem’s difficulty [5,6]. Similar problems, such as the VP versus VNP problem in algebraic complexity, remain unsolved [7].

The P versus NP problem is often described as a “holy grail” of computer science. A positive resolution could revolutionize our understanding of computation and potentially lead to groundbreaking algorithms for critical problems. The problem is listed among the Millennium Prize Problems. While recent years have seen progress in related areas, such as finding efficient solutions to specific instances of NP-complete problems, the core question of P versus NP remains unanswered [3]. A polynomial-time algorithm for any NP-complete problem would directly imply P equals NP [8]. Our work focuses on presenting such an algorithm for a well-known NP-complete problem.

2. Background and ancillary results

NP-complete problems are the Everest of computational challenges. Despite the ease of verifying proposed solutions with a succinct certificate, finding these solutions efficiently remains an elusive goal. A problem is classified as NP-complete if it satisfies two stringent criteria within computational complexity theory:

• Efficient Verifiability: Solutions can be quickly checked using a concise proof [8].
• Universal Hardness: Every problem in the class NP can be reduced to this problem without significant computational overhead [8].

The implications of finding an efficient algorithm for a single NP-complete problem are profound. Such a breakthrough would serve as a master key, unlocking efficient solutions for all problems in NP, with transformative consequences for fields like cryptography, artificial intelligence, and planning [3,4].

Illustrative examples of NP-complete problems include:

• Boolean Satisfiability (SAT) Problem: Given a logical expression in conjunctive normal form, determine if there exists an assignment of truth values to its variables that makes the entire expression true [9].
• Boolean 3-Satisfiability (3SAT) Problem: Given a Boolean formula in conjunctive normal form with exactly three literals per clause, determine if there exists a truth assignment to its variables that makes the formula evaluate to true [9].
• Not-All-Equal 3-Satisfiability (NAE-3SAT) Problem: Given a Boolean formula in conjunctive normal form with exactly three literals per clause, decide if there exists a satisfying truth assignment such that each clause has at least one true variable and at least one false variable [9].
• Exact K-Coloring Problem: Given a graph G and a positive integer k, determine if there exists a valid coloring of G such that exactly k vertices have the same color and no adjacent vertices have the same color. This problem is equivalent to finding an independent set of size k, an NP-complete problem [9].

The provided examples represent a small subset of the extensively studied NP-complete problems relevant to our current work. An independent set $V^{\prime }$ is a subset of vertices in a graph G where no two vertices in the set are connected by an edge. In addition, a vertex cover (sometimes called a node cover) of a graph G is a subset of its vertices, denoted by $V^{\prime }$, such that every edge in G has at least one endpoint in $V^{\prime }$. A bipartite graph, denoted as $B=(U,V,E)$, is an undirected graph characterized by the existence of two node sets $U,V$ and edges in E that only connect nodes from opposite sets. The following problems can be solved in polynomial time:

 Definition 1. 

Exact Independent Vertex Cover (XIVC) Problem

INSTANCE: An undirected graph $G=(V,E)$ and a positive integer k.

QUESTION: Is there set $V^{\prime }$ of exactly k vertices such that $V^{\prime }$ is both a vertex cover and an independent set in G?

REMARKS: The XIVC problem is reducible to the problem of finding a 2-coloring of a bipartite graph with a specified color class size of k. Given the polynomial-time solvability of the 2-coloring problem for bipartite graphs, the XIVC problem can also be solved in polynomial time.

 Definition 2. 

Exact 2-Cover By Sets (X2SC) Problem

INSTANCE: A universe set U, a collection of n sets $C=S_1,S_2,\dots ,S_n$ with $S_i\subseteq U$ and a positive integer $k\le n$, where each element in U appears exactly twice in C.

QUESTION: Is there a partition of exactly k sets $S_1^{\prime },\dots ,S_k^{\prime }$ such that $S_i^{\prime }\cap S_j^{\prime }=\varnothing$ for $1\le i\ne j\le k$ and $S_1^{\prime }\cup \dots \cup S_k^{\prime }=U$?

Formally, a Boolean formula $\varphi$ is composed of:

• Boolean variables: $x_1,x_2,\dots ,x_n$;
• Boolean connectives: Any Boolean function with one or two inputs and one output, such as ∧(AND), ∨(OR), ¬(NOT), ⇒(IMPLICATION), ⇔(IF AND ONLY IF);
• and parentheses.

A truth assignment for a Boolean formula $\varphi$ is a mapping from the variables of $\varphi$ to the Boolean values $\{\mathit{true},\mathit{false}\}$. A truth assignment is satisfying if it makes $\varphi$ evaluate to true. A Boolean formula is satisfiable if it has at least one satisfying truth assignment. A literal is a Boolean variable or its negation. A Boolean formula is in Conjunctive Normal Form ($CNF$) if it is a conjunction (AND) of clauses, where each clause is a disjunction (OR) of one or more literals [8]. The SAT problem asks whether a given Boolean formula in $CNF$ is satisfiable [9]. A $3CNF$ formula is a $CNF$ formula in which each clause contains exactly three distinct literals [8]. For example, the following formula is in $3CNF$:

$$(x_1\vee \neg x_2\vee x_3)\wedge (\neg x_1\vee x_3\vee x_2)\wedge (\neg x_1\vee \neg x_3\vee x_2).$$

The first clause, $(x_1\vee \neg x_2\vee x_3)$, contains the three literals $x_1$, $\neg x_2$ and $x_3$. The version of SAT where formulas are in $3CNF$ is called 3SAT [8]. In addition, a $2CNF$ formula is a Boolean formula in conjunctive normal form with exactly two distinct literals per clause. We formally define the following NP-complete problems:

 Definition 3. 

Monotone Not-All-Equal 3-Satisfiability (NAE-3MSAT) Problem

INSTANCE: A Boolean formula in $3CNF$ with monotone clauses (meaning the variables are never negated).

QUESTION: Is there exists a satisfying truth assignment such that each clause has at least one true variable and at least one false variable?

REMARKS: This problem is complete for NP [10]. Here, the certificate is a valid satisfying truth assignment, meaning it satisfies the NAE-3MSAT condition for each clause.

 Definition 4. 

Exact Monotone XOR 2-Satisfiability (X2MXSAT) Problem

INSTANCE: A Boolean formula in $2CNF$ with monotone clauses (meaning the variables are never negated) using XOR logic operators ⊕ (instead of using the operator ∨) and a positive integer k.

QUESTION: Is there exists a satisfying truth assignment in which exactly k of the variables are true?

By presenting the NP-completeness and a polynomial-time solution to SAT, we would establish a proof that P equals NP.

3. Main Result

Even though the following reductions are widely known, we will rely on them as supporting results in our analysis [9].

 Theorem 1. 

The problem SAT can be reduced to 3SAT in polynomial time.

 Proof. 

We will not delve into the specific steps of this reduction, as it is a standard technique in computer science [8]. To reduce a general SAT instance to a 3SAT formula, we can follow these steps:

• Expand Clauses with Few Literals: To ensure that all clauses contain exactly three literals, we introduce two new variables and expand clauses with at most two literals into clauses with three literals by considering all possible combinations of the new variables, both negated and positive. For instance, consider the two new variables A and B. A single-literal clause $\left(x\right)$ can be equivalently expressed as:

  $$(x\vee A\vee B)\wedge (x\vee \neg A\vee \neg B)\wedge (x\vee A\vee \neg B)\wedge (x\vee \neg A\vee B).$$
  Similarly, a two-literal clause $(x\vee y)$ is equivalent to:

  $$(x\vee y\vee A)\wedge (x\vee y\vee \neg A)\wedge (x\vee y\vee B)\wedge (x\vee y\vee \neg B).$$
  Note that the same variables A and B are used in both cases.
• Identify Long Clauses: Find all clauses with more than three literals.
• Introduce New Variables: For a clause with n literals (where $n>3$), introduce $n-3$ new variables.
• Create New Clauses: Create a chain of clauses with three literals each, using the original literals and the new variables. Ensure that the satisfiability of the original clause is preserved in this chain of new clauses. To exemplify, consider a clause containing four literals, $(x\vee y\vee z\vee w)$. By introducing a single additional variable, D, this clause can be logically represented as the conjunction of the following two clauses:

  $$(x\vee y\vee \neg D)\wedge (D\vee z\vee w).$$

By systematically applying this reduction to each clause, we can transform any SAT instance into an equivalent 3SAT formula. This reduction demonstrates that 3SAT is at least as hard as the general SAT problem, and thus, it is an NP-complete problem. □

 Theorem 2. 

The problem 3SAT can be reduced to NAE-3SAT in polynomial time.

 Proof. 

Any 3SAT formula $\varphi$ can be reduced to an equivalent NAE-3SAT instance. We assume that no clause contains a literal and its negation. Such tautological clauses can be removed. We also remove clauses containing literals whose negations do not appear in the 3SAT instance. This reduction involves the following steps:

• Variable Introduction:
  • Global Variable: Introduce a new variable w that does not appear in $\varphi$.
  • Clause Variables: For each clause $c_i=(x\vee y\vee z)$ in $\varphi$, introduce a new variable $a_i$.
• Clause Construction:
  • -Clause Reduction: For each clause $c_i=(x\vee y\vee z)$, construct two NAE-3SAT clauses:
    • $\ast (x\vee y\vee a_i)\wedge (z\vee \neg a_i\vee w)$.

By construction, a satisfying truth assignment for $\varphi$ corresponds to a valid satisfying truth assignment for the NAE-3SAT instance when w is assigned the value false, and vice versa. When w is true, we can obtain a satisfying truth assignment for $\varphi$ by negating all the values in a valid satisfying truth assignment for the NAE-3SAT instance. This reduction demonstrates that NAE-3SAT is NP-complete. □

 Theorem 3. 

The problem NAE-3SAT can be reduced to NAE-3MSAT in polynomial time.

 Proof. 

It is well-known that any Boolean formula $\varphi$ in NAE-3SAT can be reduced to an equivalent NAE-3MSAT instance. This reduction involves the following steps:

• Variable Introduction:
  • Literal Variables: For each variable x in $\varphi$, introduce two variables: $x_{+}$ representing the positive literal x and $x_{-}$ representing the negative literal $\neg x$. Additionally, we introduce three new variables $a_x$, $b_x$, and $c_x$ for each variable x in $\varphi$.
• Clause Construction:
  • Clause Reduction: For each clause $c_i=(x\vee y\vee z)$, construct one NAE-3MSAT clause:
    • $-(x_{s_x}\vee y_{s_y}\vee z_{s_z})$, where $s_v$ is + if literal $v\in \{x,y,z\}$ is positive and − otherwise.
  • Variable Consistency: For each variable x in $\varphi$, construct four NAE-3MSAT clauses:
    • $-(x_{+}\vee x_{-}\vee a_x)$, $(x_{+}\vee x_{-}\vee b_x)$, $(x_{+}\vee x_{-}\vee c_x)$, and $(a_x\vee b_x\vee c_x)$. These clauses ensure that exactly one of $x_{+}$ and $x_{-}$ is true.

By construction, a valid satisfying truth assignment for $\varphi$ corresponds to a valid satisfying truth assignment for the NAE-3MSAT instance, and vice versa. Thus, this reduction proves that NAE-3MSAT is NP-complete. □

These are key findings.

 Theorem 4. 

$XIVC\in P$.

 Proof. 

Given the efficient solvability of the 2-coloring problem in bipartite graphs, we claim that the XIVC problem can be accomplished within polynomial time. This is a straightforward dynamic programming algorithm similar to solve subset sum: Let $(A_1,B_1),(A_2,B_2)\dots ,(A_p,B_p)$ be the sides of partitions $A_i$ and $B_i$ in a connected component i of the bipartite graph $B=(U,V,E)$, such that every vertex in a single partition has the same color.

Now, we create a dynamic programming table $DP[i,t]$ that stores whether it is possible to have a bipartite graph with exactly t vertices on one color using the i first components. The bi-dimensional boolean array $DP$, having dimensions $(p+1)$ by $(k+1)$ and zero-based indexing. All elements are assigned the value $\mathit{false}$, with the exception of the element at index $(0,0)$ which is assigned the value $\mathit{true}$ (i.e., $DP[0,0]=\mathit{true}$). Using the recurrence

$$DP[i,t]=DP[i-1,t-\mid A_i\mid ]\vee DP[i-1,t-\mid B_i\mid ],$$

we correctly decide whether there exists an entire partitioning of exactly k vertices with the same color after by examining $DP[p,k]$, where $\mid \dots \mid$ is the cardinality set function. The recurrence evaluates $DP[i,t]$ as false for any i and t that do not satisfy $0\le i\le p$ and $0\le t\le k$. This is a polynomial time algorithm since the running time is bounded by $O(\mid U\mid +\mid V\mid +\mid E\mid +p·(k+1\left)\right)$. Identifying 2-color partitions takes $O(\mid U\mid +\mid V\mid +\mid E\mid )$ time using breadth-first search algorithm (BFS), while finding k vertices of the same color requires $O(p·(k+1\left)\right)$ iterations. We can easily determine if a graph is two-colorable by performing a breadth-first search and assigning alternating colors to the nodes. Every connected component is partitioned into two sets using two colors. For isolated vertices, one of the sets is empty. Similarly, the dynamic programming algorithm to solve subset sum (in this specific variation) can be solved by systematically checking all possible values from 0 to k using each pair of partitions for every connected component. □

 Theorem 5. 

$X2MXSAT\in P$.

 Proof. 

There is a connection between finding a satisfying truth assignment in X2MXSAT with exactly k true variables and finding a set of k vertices that is both a vertex cover and an independent set in a specific graph construction.

Here’s a breakdown of the equivalence:

• Graph Construction:
  • Each vertex in the new graph represents a variable in the X2MXSAT formula.
  • Edges are created between variables based on the structure of the $2CNF$ clauses: If two variables appear in a clause (e.g., $(x\oplus y)$), then an edge is drawn between the corresponding vertices in the graph.
• X2MXSAT and the Graph:
  • A satisfying truth assignment in X2MXSAT where exactly k variables are true directly translates to a set of k vertices in the constructed graph where true variables correspond to the vertices included in the set.
  • The properties of X2MXSAT clauses ensure that:
    • -Vertex Cover: The chosen vertices cover all the edges (due to the structure of the clauses and the way edges are formed). This satisfies the vertex cover condition.
    • -Independent Set: The chosen vertices don’t have any edges connecting them (because the variables are connected in the graph, and only one variable from each clause can be true). This satisfies the independent set condition.

Therefore, finding a satisfying truth assignment with exactly k true variables in X2MXSAT is indeed equivalent to finding a set of k vertices that fulfills both vertex cover and independent set requirements in the corresponding graph. However, we know the problem of finding a set of k vertices that is both a vertex cover and an independent set can be solved in polynomial time. Consequently, the instances of the problem X2MXSAT can be solved in polynomial time as well. □

 Theorem 6. 

The problem X2SC can be reduced to X2MXSAT in polynomial time.

 Proof. 

Given an instance of X2SC defined by a universe $U=\{u_1,u_2,\dots ,u_m\}$ and a collection $C=S_1,S_2,\dots ,S_n$ of sets $S_i\subseteq U$, where each element in U appears exactly twice in C, and the goal is to select exactly k mutually disjoint sets from C that cover U, we construct an equivalent instance of X2MXSAT as follows:

• Formula Construction:
  • Variables: For each element $u_k\in U$, we introduce variables $u_{(k,1)}$ and $u_{(k,2)}$. For each set $S_i$ in C, we create a corresponding variable $s_i$.
  • Clauses: For every pair of sets $S_i,S_j\in C$ that share a common element $u_k\in U$, create the following element-formula:

    $$F_k=(s_i\oplus u_{(k,1)})\wedge (s_j\oplus u_{(k,2)})\wedge (u_{(k,1)}\oplus u_{(k,2)}).$$
  • Formula: The complete X2MXSAT instance is the conjunction of all element-formulas $F_k$:

    $$\varphi =\underset{i=1}{\overset{m}{\bigwedge }}{F}_i=F_1\wedge F_2\wedge F_3\wedge \dots \wedge F_{m-1}\wedge F_m,$$

    where m is the number of elements in U.
  Mapping between X2SC solutions and X2MXSAT assignments:
  • A satisfying truth assignment in the $X2MXSAT$ formula corresponds to a partition of k sets covering U if:
    • -Set variables $s_i$ assigned true represent the sets inside of the partition.
    • -Set variables $s_j$ assigned false represent the sets outside of the partition.
    • -The satisfiability of clause $(u_{(k,1)}\oplus u_{(k,2)})$ indicates that the corresponding element $u_k$ has been covered.
• Equivalence of Solutions:
  • A solution to the X2SC instance, consisting of k mutually disjoint sets that cover U, directly corresponds to a satisfying truth assignment to the X2MXSAT instance where $k+m$ variables are true.
  • Conversely, a satisfying truth assignment to the X2MXSAT instance with $k+m$ true variables corresponds to a selection of k sets in C that are mutually disjoint and cover U.
  To see why, consider the following:
  • Covering the Universe: The element-formula structure ensures that every element in U is covered by exactly one selected set. If an element $u_k$ is not covered, then the corresponding element-formula $F_k$ would be unsatisfied.
  • Mutual Disjointness: The element-formula structure enforces mutual disjointness between pairs of intersecting sets. If two sets with a common element $u_k$ are both selected, the corresponding element-formula $F_k$ would be unsatisfied.

Therefore, the X2SC problem and the X2MXSAT problem are equivalent, and a solution to one can be efficiently transformed into a solution to the other. □

This is a Main Insight.

 Theorem 7. 

The problem NAE-3MSAT can be reduced to X2SC in polynomial time.

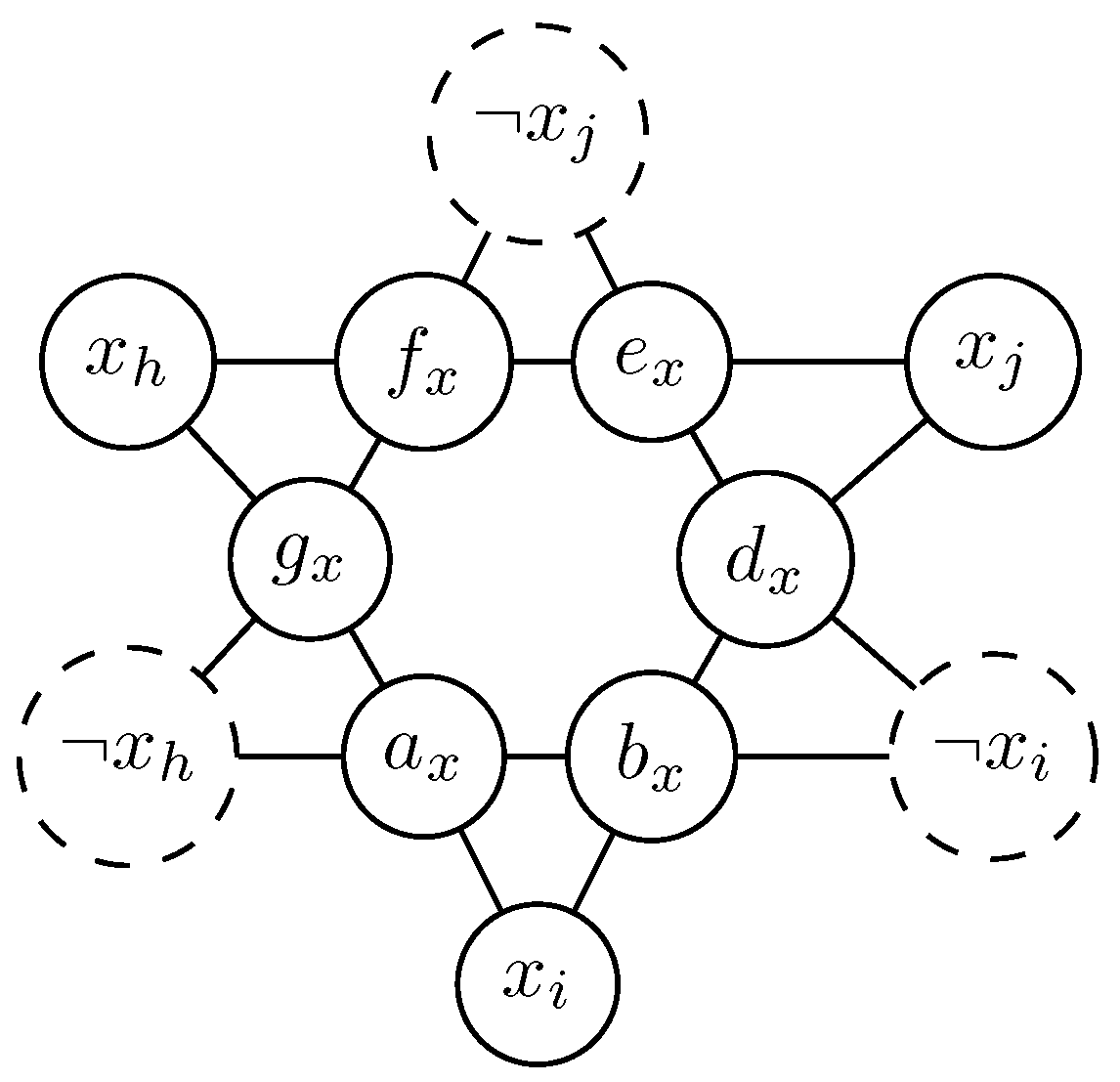
 Proof. 

To better visualize this polynomial-time reduction, we will use a graphical representation of the sets involved. To represent a NAE-3MSAT formula $\varphi$ as a collection of set C over a universe U, we introduce a gadget for each variable x in $\varphi$. This gadget consists of $2·t$ triangles, where t is the larger of the number of occurrences of x in $\varphi$. Each triangle in the gadget corresponds to a possible truth assignment for the variable x. The apexes of the triangles are labeled with $x_i$ or $\neg x_i$ to denote the truth assignment required for clause $c_i$ in $\varphi$.

The topology of the gadget ensures consistency. The construction (e.g., Figure 1) guarantees that if any positive vertex is matched with some vertices outside of the gadget then all negative vertices can only be matched by the triangles inside this gadget, and vice versa. Thus, the "availability" of a vertex to be matched by an outside vertex corresponds to the truth assignment. For instance, in Figure 1, these sets would be:

$$\begin{array}{cc}\hfill & \{x_i,a_x,b_x\},\{\neg x_i,b_x,d_x\},\hfill \\ \hfill & \{x_j,d_x,e_x\},\{\neg x_j,e_x,f_x\},\hfill \\ \hfill & \{x_h,f_x,g_x\},\{\neg x_h,g_x,a_x\},\hfill \end{array}$$

where dashed vertices correspond to the literals of x that are absent from clauses $c_i,c_j,c_h$ in $\varphi$.

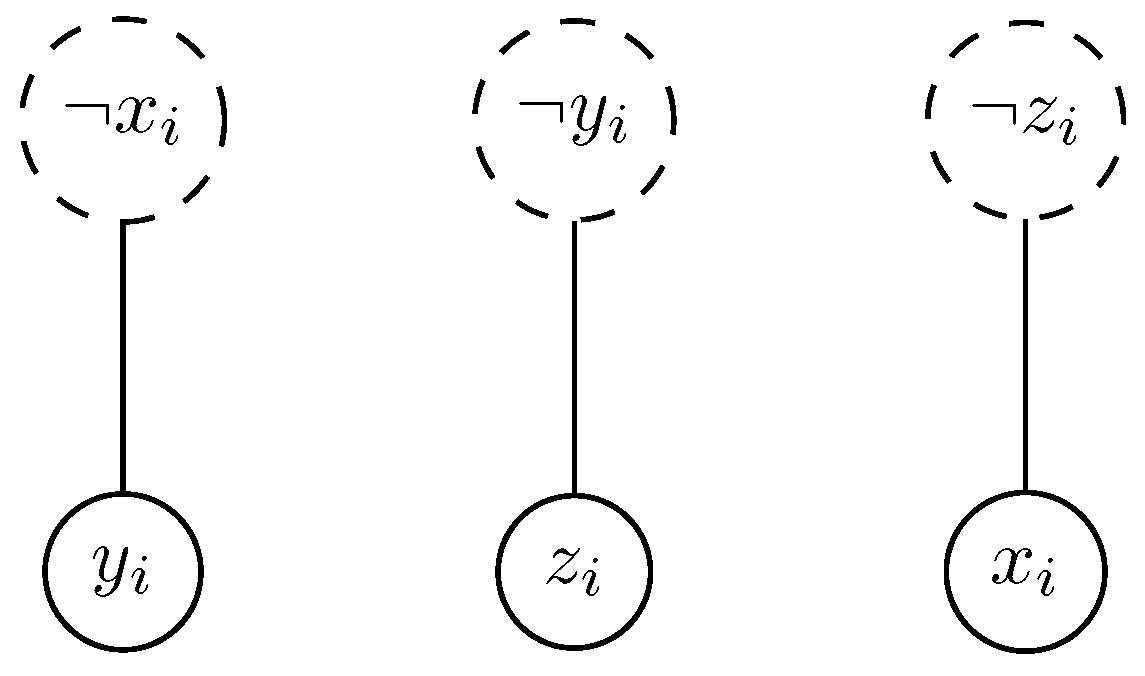
To represent each clause $c_i=(x\vee y\vee z)$ in $\varphi$, we employ a gadget consisting of three sets:

$$\{\neg x_i,y_i\},\{\neg y_i,z_i\},\{\neg z_i,x_i\}.$$

This gadget, illustrated in Figure 2, is used to encode each clause within the overall construction, where dashed vertices correspond to the literals that are absent in $c_i$. By ensuring that exactly one of these sets is chosen, we satisfy the NAE-3MSAT condition for clause $c_i$. If all variables in $c_i$ have the same truth assignment, none of these sets can be selected. Conversely, if $c_i$ is satisfied under the NAE-3MSAT condition, then exactly one of these sets can be covered.

A Boolean formula $\varphi$ satisfies the NAE-3MSAT constraints if and only if its corresponding collection of sets C can be partitioned into exactly $4·m$ disjoint sets, where m is the number of clauses in $\varphi$. This equivalence follows directly from the construction of C, which is designed to faithfully represent the logical structure of $\varphi$ over the universe U. The collection of sets C incorporates two types of set:

• Variable Sets: The construction depicted in Figure 1 enables the selection of exactly one set for each variable occurrence within a clause of $\varphi$. Since each clause comprises three distinct variables, there are precisely $3·m$ such sets.
• Clause Sets: The final step in Figure 2 ensures the NAE-3MSAT condition by requiring each clause in $\varphi$ to choose exactly one set. This guarantees the existence of precisely m clause sets that induce a valid satisfying truth assignment for $\varphi$.

Hence, a valid satisfying truth assignment for $\varphi$ directly corresponds to a partition of C into exactly $4·m$ disjoint sets: $3·m$ variable sets and m clause sets. Conversely, any such partition of C can be interpreted as a valid satisfying truth assignment for $\varphi$. This one-to-one correspondence establishes the equivalence between the valid satisfiability of $\varphi$ and the existence of $4·m$ disjoint sets in C covering U, where each element in U belongs to exactly two sets in C. □

This is the Main Theorem.

 Theorem 8. 

$SAT\in P$.

 Proof. 

This follows directly from Theorems 1, 2, 3, 4, 5, 6, and 7. □

This is the definitive result.

 Theorem 9. 

$P=NP$.

 Proof. 

Cook’s Theorem states that every NP problem can be reduced to SAT in polynomial time [9]. Given that SAT is an NP-complete problem, a polynomial-time solution for it, as presented here, would directly imply P equals NP. □

4. Conclusion

A definitive proof that P equals NP would fundamentally reshape our computational landscape. The implications of such a discovery are profound and far-reaching:

• Algorithmic Revolution.
  • -The most immediate impact would be a dramatic acceleration of problem-solving capabilities. Complex challenges currently deemed intractable, such as protein folding, logistics optimization, and certain cryptographic problems, could become efficiently solvable [3,4]. This breakthrough would revolutionize fields from medicine to cybersecurity. Moreover, everyday optimization tasks, from scheduling to financial modeling, would benefit from exponentially faster algorithms, leading to improved efficiency and decision-making across industries [3,4].
• Scientific Advancements.
  • -Scientific research would undergo a paradigm shift. Complex simulations in fields like physics, chemistry, and biology could be executed at unprecedented speeds, accelerating discoveries in materials science, drug development, and climate modeling [3,4]. The ability to efficiently analyze massive datasets would provide unparalleled insights in social sciences, economics, and healthcare, unlocking hidden patterns and correlations [3,4].
• Technological Transformation.
  • -Artificial intelligence would be profoundly impacted. The development of more powerful AI algorithms would be significantly accelerated, leading to breakthroughs in machine learning, natural language processing, and robotics [3,4]. While the cryptographic landscape would face challenges, it would also present opportunities to develop new, provably secure encryption methods [3,4].
• Economic and Societal Benefits.
  • -The broader economic and societal implications are equally significant. A surge in innovation across various sectors would be fueled by the ability to efficiently solve complex problems. Resource optimization, from energy to transportation, would become more feasible, contributing to a sustainable future [3,4].

In conclusion, a proof of $P=NP$ would usher in a new era of computational power with transformative effects on science, technology, and society. While challenges and uncertainties exist, the potential benefits are immense, making this a compelling area of continued research.