Extreme Rainfall Anomalies Based on IMERG Remote Sensing Data in CONUS: A Multi-Decade Case Study via the IPE Web Application

1. Introduction

With the rise in extreme precipitation driven by global climate change [1,2], precipitation-induced floods have increasingly overwhelmed flood retention infrastructures such as dams, culverts, levees, and bridges, leading to widespread destruction of farmlands, buildings, urban flooding, waterborne diseases, groundwater pollution, and loss of life [3,4,5,6,7,8,9,10]. The Intergovernmental Panel on Climate Change (IPCC) has reported that climate patterns are shifting, with many regions experiencing wetter conditions and an increasing trend in the median of annual maximum daily precipitation [11,12]. Although extreme precipitation is increasing globally, regional trends deviate significantly, raising questions about the magnitude of anomalies in extreme rainfall [11,13,14,15].

In the United States, earlier studies have documented an increase in both the intensity and frequency of precipitation extremes [1,11,16], prompting concerns about the relevance of the National Oceanic and Atmospheric Administration (NOAA) Atlas-14 precipitation estimates (PE) for modeling and planning extreme events. The NOAA Atlas-14 PE is widely used for planning across the conterminous United States (CONUS), excluding some northwestern states (Idaho, Montana, Oregon, Washington, and Wyoming) [17,18,19,20]. However, Atlas-14 primarily incorporates historical observations, without accounting for projected future extremes, making it less suitable for planning in a changing climate where extreme precipitation events are becoming more frequent in the CONUS region [21,22]. The lacking credibility on the Atlas-14 PFE has called for a shift to try alternative sources such as the use of satellite precipitation products for rainfall analyses.

To quantify rainfall changes over time, various indices have been developed, such as the Palmer Drought Severity Index (PDSI) [23], the Standardized Precipitation Evapotranspiration Index (SPEI) [24], and the Standardized Precipitation Index (SPI) [25]. However, these indices primarily focus on drought and do not capture the extreme rainfall anomalies necessary for flood-related decision-making in the CONUS [26]. Consequently, the Rainfall Anomaly Index (RAI), developed by Van Rooy in 1965 [27], has remained a cornerstone for studying both drought and extreme rainfall globally [27,28,29]. In this study, we adopted the RAI to model rainfall anomalies based on annual maximum daily precipitation from thousands of stations across the CONUS, spanning two decades (2001 to 2022). The method is particularly suitable due to its ability to capture significant changes over short periods (≥10 years) [26,27].

Previous research has linked large-scale ocean-atmosphere conditions to local and regional manifestations of climate change, resulting in severe rainfall anomalies. The most frequently studied phenomena in the CONUS include the El Niño Southern Oscillation (ENSO), Pacific Decadal Oscillation (PDO), North Atlantic Oscillation (NAO), and Atlantic Multidecadal Oscillation (AMO) [11,30,31]. These climatic cycles influence the intensity and frequency of extreme precipitation events across the CONUS, though they fall outside the scope of this study. Rainfall observations are typically conducted at weather stations [32] or within gauged watersheds [33]. However, station data is often sparse, especially in ungauged areas, necessitating the interpolation of data where stations are lacking [17,34]. Moreover, the reliability and validity of station-based observations are frequently questioned [28,33,35,36,37,38,39,40,41]. To address these limitations, remote sensing products have become increasingly important, filling observational gaps where station data is uncertain, extending beyond the CONUS [43,44,45,46,47], and offering broad availability [38,39,48,49].

The Integrated Multi-Satellite Retrievals for Global Precipitation Measurement (IMERG), like other satellite precipitation products (SPPs), has been used to measure precipitation at local, regional, and global scales, providing critical insights for flood risk assessment [50,51,52,53]. Previous studies have shown that IMERG estimates are comparable to station-based observations [51,54,55,56,57,58,59,60,61,62]. IMERG is recognized as a next-generation SPP, covering a global latitude range of 0-65° N/S, with a spatial resolution of 0.1° and a temporal resolution of half-hourly intervals [51,63,64,65,66]. It has become a sophisticated tool for advanced hydrological applications, combining data from optical and radar sensors as well as existing SPPs like the Global Precipitation Measurement (GPM) mission and the Tropical Rainfall Measuring Mission (TRMM). Additionally, it is calibrated using data from over 80,000 Global Precipitation Climatology Centre (GPCC) gauge networks [46,51,54].

Numerous studies have assessed anomalies in extreme precipitation, both in the United States and globally, focusing on various aspects. For example, [11] examined the temporal anomalies of extreme precipitation across 1,041 stations in the U.S. and their association with different climatic modes using a quartile perturbation approach. The study identified drier conditions in the mid-20th century and wetter conditions in recent decades. In another study, [67] evaluated the impact of seasonal rainfall anomalies on catchment-scale water balance components using the Soil and Water Assessment Tool (SWAT) in southern Italy, identifying regression equations linking water yield and dryness during the wet season. Meanwhile, [68] used Global Historical Climate Network (GHCN) data to identify extreme precipitation days in the U.S. from 1979 to 2019. In another related study, [69] demonstrated the predictive power of climate-driven changes in seasonal precipitation through sea surface temperature patterns. Other studies have explored the role of large-scale circulation anomalies in influencing extreme precipitation frequencies in the U.S. [15], revealing multidecadal variations in the North American Monsoon System (NAMS) between 1948 and 2009 [30], as well as the influence of El Niño on precipitation anomalies in South America [12].

While these studies are valuable, a gap remains in the application of recent datasets, such as IMERG, which can provide more accurate insights into contemporary rainfall anomalies, offering optimal accuracy compared to gauge observations [60,63,70,71]. Furthermore, earlier research has faced challenges related to data centralization, making it difficult for non-experts to access the relevant data. To address these gaps, we adopted IMERG (Final) data and developed the IMERG Precipitation Extractor (IPE), an intuitive, self-updating web application that facilitates time series data extraction, storm tracking, real-time anomaly calculations, visualization, and data downloads. The IPE is a global web application that ensures rapid IMERG data retrieval beyond CONUS. For this study, raw IMERG data were extracted, and daily annual maximum values were computed from 2001 to 2022. RAI values were derived for each year and compared with NOAA station-based RAI to evaluate the validity of IMERG-derived RAI.

The objectives of this study are as follows: (1) to demonstrate the capability of the IPE web application for time series extraction, storm tracking, anomaly calculation, visualization, and data download; (2) to model RAI from IMERG data and compare it with NOAA station-based RAI from 2,360 stations at temporal, regional, and CONUS scales; and (3) to derive insights from IMERG RAI observations regarding recent extreme rainfall and the impacts of climate change. The remainder of this paper is structured as follows: Section 2 describes the study area and data, Section 3 outlines the methodology, Section 4 presents and discusses the results, and Section 5 offers conclusions.

2. Study Area and Data

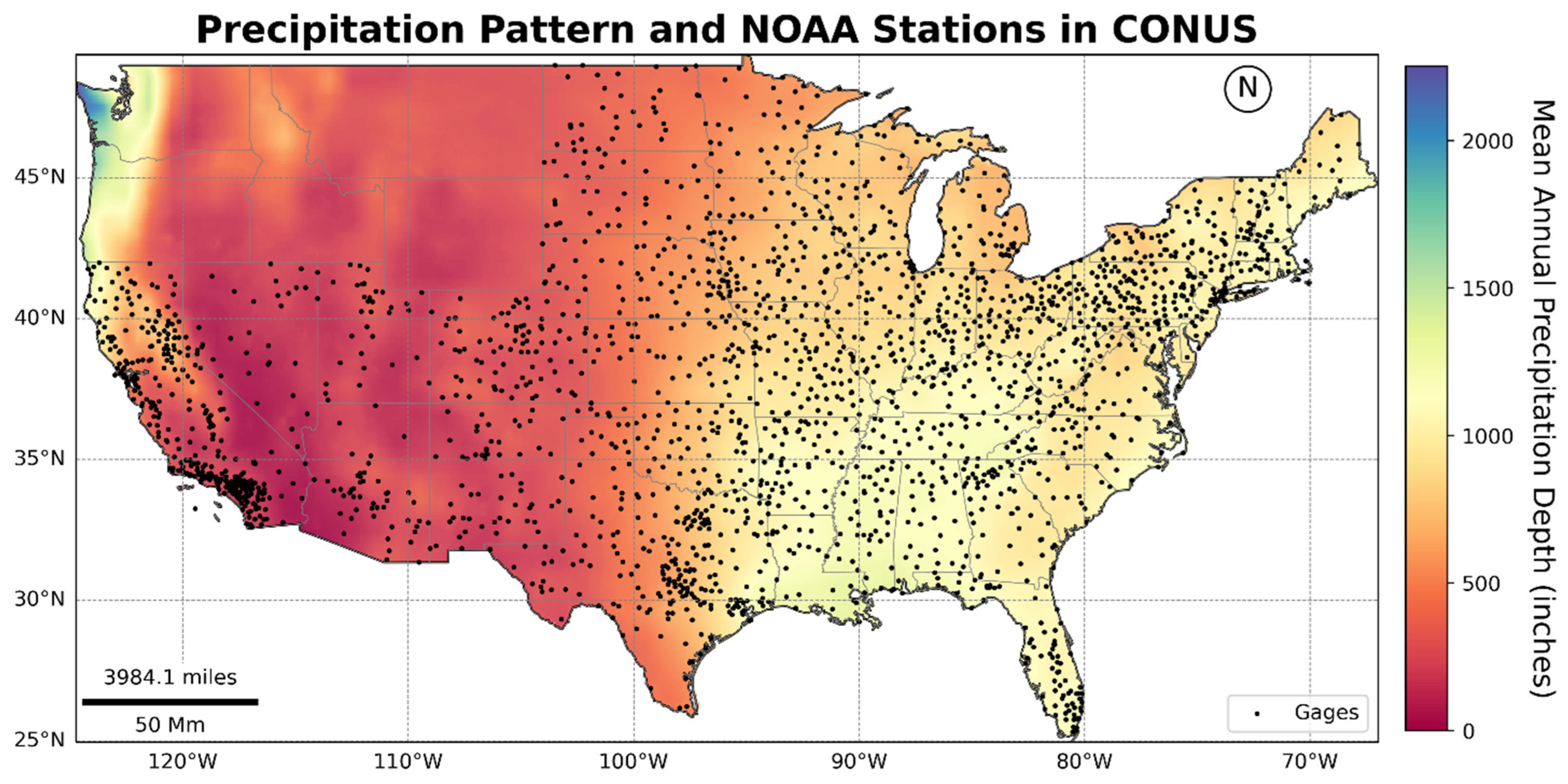
2.1. Study Area

This study covers the entire conterminous United States (CONUS), excluding five northwestern states (Idaho, Montana, Oregon, Washington, and Wyoming), where station data are unavailable. CONUS spans an estimated area of 3,119,885 square miles (8,080,464 km²), with approximately 83.65% of this area consisting of land. The region experiences a broad range of mean annual precipitation, varying from as little as 2.5 inches in the arid west to over 2,000 inches in the humid east, generally following a west-to-east increasing precipitation gradient (Figure 1).

To minimize uncertainties associated with limited gauge data, we selected 2,360 stations from the National Oceanic and Atmospheric Administration (NOAA) database [18,22,72], each with 22 years of data (2001–2022). These stations correspond to 2,360 unique pixels within the IMERG dataset, from which precipitation estimates were extracted for comparative analysis. At the time of this study, NOAA station data for the northwestern part of CONUS were not yet available, though efforts were underway to extend coverage to those areas [19,21,72,73]. Consequently, the evaluation is restricted to regions within CONUS that have sufficient NOAA station coverage.

2.2. IMERG Precipitation Data

The IMERG dataset integrates inputs from various algorithms, including the Global Precipitation Measurement Profiling Algorithm (GPROF), the Precipitation Retrievals and Profiling Scheme (PRPS), the PERSIANN-Cloud Classification System (PERSIANN-CCS), the Combined Radar-Radiometer Algorithm (CORRA), and the Global Precipitation Climatology Project’s monthly satellite-gage (PCP-SG) [51,74]. IMERG provides three distinct products: “Early,” “Late,” and “Final.” These products are generated in several stages. Initially, the “Early-run” offers preliminary estimates approximately 4 hours after observation time (AOT). The “Late-run” follows, released roughly 12 hours AOT. Finally, the “Final-run” is made available after 2.5–3 months AOT, incorporating gage calibration [62,75].

Both the Early and Late-run IMERG products include climatological corrections, while the Final-run is calibrated using data from over 80,000 Global Precipitation Climate Center (GPCC) stations worldwide [45,46,74,76]. IMERG provides data at a half-hourly temporal resolution and a spatial resolution of 0.1° × 0.1°, which may vary depending on proximity to the equator. For this study, the IMERG-Final product Version 06 was employed, as Version 07 is still under development and not yet available for research purposes. IMERG data span from 2000 to the present and include three key precipitation fields: the calibrated “PrecipitationCal,” the uncalibrated “PrecipitationUncal,” and the microwave-based “HQprecipitation.” The PrecipitationUncal represents the raw multi-satellite precipitation estimate, while HQprecipitation is derived from merged microwave data. In this study, PrecipitationCal was used, which integrates both PrecipitationUncal and HQprecipitation and is calibrated using GPCC gages [51].

2.3. NOAA Station Data

The NOAA station database [19] serves as the reference for precipitation data in this study. The dataset consists of Annual Maximum Series (AMS) spanning durations from 5 minutes to 60 days, with records extending from the 1950s to the present [21,22]. While the NOAA station database includes over 16,000 stations across the conterminous United States (CONUS), only 2,360 stations with a complete 22-year record (2001–2022) were selected for validating the IMERG-derived Rainfall Anomaly Index (RAI). The NOAA station datasets are recognized as the authoritative AMS dataset and are widely recommended for meeting national standards [22,77]. Table 1 provides a comparison between the NOAA station data and the satellite-based IMERG data.

3. Methods

3.1. Computing Annual Maximum Series (AMS) from IMERG Data

The AMS for NOAA data is provided as daily annual maximum estimates [17,22]. In contrast, IMERG data is recorded in half-hour increments [65,70]. To compute the daily annual maximums from IMERG, 30-minute rainfall data was accumulated over 24-hour periods. The accumulation period spans from January 1 at 00:00 UTC to December 31 at 23:30 UTC for each year. The dataset covers the years 2000 to 2023, though the year 2000 was excluded due to incomplete records, as IMERG data is only available starting from June 3, 2000. The accumulated daily annual maximum for each year (2001 to 2022) was computed for all 2,360 stations. Figure 2 provides a visual representation of the methodology used to develop the AMS and model the RAI for both the estimated IMERG data and the NOAA station observations.

3.2. Calculating Rainfall Anomaly Index from both IMERG and NOAA Datasets

The Rainfall Anomaly Index (RAI), developed by Van Rooy in 1965, is a rank-based index used to measure drought by assigning magnitudes to negative (deficit) and positive (surplus) precipitation anomalies [27]. This index categorizes rainfall anomalies on a scale ranging from -3 (extremely dry) to +3 (extremely wet), with values assessed against a nine-classification scheme, as presented in Table 2. The mathematical formulation of the RAI is given in Equation 1:

$$RAI=\left\{\begin{array}{c}3\left({\displaystyle \frac{P_n-\overline{P}}{\overline{M}-\overline{P}}}\right) \mathrm{if} P>\overline{P}, \\ -3\left({\displaystyle \frac{P_n-\overline{P}}{\overline{L}-\overline{P}}}\right) \mathrm{if} P<\overline{P} \end{array}\right.,$$

(1)

In this equation, $P_n$ represents the daily maximum precipitation for year n (2001 to 2022), $\overline{P}$ is the mean precipitation from the series of daily maximums, $\overline{M}$ is the average of the 10 highest values in the series, and $\overline{L}$ is the average of the 10 lowest values. ±3 is a standardization factor that limits the anomalies within the range of -3 to +3 through a unity-based scaling, ensuring an asymmetrical distribution. If the difference $P_n-\overline{P}$ is positive, the index is multiplied by +3, and if negative, it is multiplied by -3.

The selection of the 10 lowest and 10 highest values to compute $\overline{L}$ and $\overline{M}$ is an arbitrary standard that has persisted for decades, though it remains unproven. While this work does not seek to explore this choice further, it identifies it as an area for potential method development in future research. Using Equation 1, the RAI was calculated for both IMERG and NOAA datasets across 2,360 stations, covering a 22-year period. Figure 2 provides a detailed summary of the workflow used in this study.

3.3. Evaluation Metrics

To evaluate the performance of the modeled IMERG RAI index against the RAI index derived from NOAA stations across the 2,360 stations in CONUS, six statistical metrics were applied: Pearson correlation coefficient (CC), percentage relative bias (PRB), root mean squared error (RMSE), Mean Bias Ratio (MBR), Nash-Sutcliffe Efficiency (NSE), and Kling-Gupta Efficiency (KGE) (refer to Table 3). Among these, PRB is particularly critical as it indicates the level of agreement between the IMERG and NOAA station RAI indices, specifically regarding the potential overestimation or underestimation of the IMERG RAI index. A bias close to zero signifies strong agreement, while a positive bias suggests overestimation, and a negative bias indicates underestimation. The mathematical expressions and units for each evaluation metric are presented in Table 3, where O denotes the observed RAI index values from NOAA stations over the years 2001 to 2022, and P represents the modeled IMERG RAI index.

4. Results and Discussions

4.1. Comparing Time Variability between IMERG and NOAA Station RAI Index

We compared the median temporal variability between the IMERG and NOAA station RAI indices across the 2,360 stations and presented the average median time using a boxplot (Figure 3). Overall, the IMERG RAI index aligned well with the NOAA RAI index, with a few exceptions in certain years. Specifically, in 2004, 2008, 2010, and 2021, the IMERG RAI index recorded a median value above 0, while the NOAA RAI index was below 0 for the same years. However, in 2022, both IMERG and NOAA RAI indices were above the 0 mark. These results indicate that IMERG demonstrates a notable capability in estimating extreme rainfall anomalies when compared to NOAA across the years considered. The pattern in Figure 3 also reveals an increasing trend in anomaly values from 2012 to 2022, when the values consistently rose above 0, in line with earlier studies conducted in North America.

In a previous study, [67] assessed the impact of seasonal rainfall and demonstrated that due to changing climate conditions, rainfall frequency and intensity increased between 2010 and 2018 across Europe, particularly in Italy [67]. A similar pattern is observed in Figure 3, where the anomalies suggest increasing rainfall depth in CONUS, particularly from 2010 through 2022. A related study by [68] highlighted how the warming global climate is driving changes in large-scale extreme precipitation in the mid-Atlantic and northern United States. That study linked extreme precipitation days to frequent tropical cyclones, strengthened high-pressure systems over the Atlantic, and atmospheric rivers. These findings, along with other related studies [2,12,30,78], support our observation that increasing rainfall depth and frequency are contributing to positively skewed anomalies across CONUS.

To further validate IMERG, we conducted a direct statistical comparison between the IMERG RAI index and NOAA station RAI index across the years 2001 to 2022 for all 2,360 stations (Table 4). The results showed an average CC of 0.94, an average PRB of -22.32%, an average RMSE of 0.96, an average MBR of 0.74, an average NSE of 0.80, and an average KGE of 0.52. These statistical outcomes suggest that IMERG demonstrates a strong potential in estimating extreme rainfall across the 2,360 stations in CONUS. The capability of IMERG to estimate extreme rainfall has been examined in earlier research [56,60,65,79]. For instance, Guo et al. (2023) evaluated various satellite precipitation products in southern China across short to long duration precipitation intervals and found that IMERG exhibited the least error and bias compared to station observations. Similarly, [80] assessed IMERG in China and concluded that the product reliably compared with authoritative station data.

The strong agreement between IMERG and NOAA stations in estimating extreme daily rainfall is not unexpected, as IMERG is calibrated using over 8,000 GPCC gaging stations contributed by member nations of the World Meteorological Organization [74,76,81]. This calibration enhances the suitability of IMERG satellite data for extreme rainfall studies, making it a viable alternative to station data.

4.2. Relationship between Rainfall Anomaly and Maximum Depth

The comparison between estimated rainfall anomalies from both IMERG and NOAA with station-based precipitation depth is essential to understand their relationships. Figure 4 presents the scatterplot illustrating the relationship between the RAI index estimates and daily rainfall depth (in mm). The correlation coefficient (CC) between the NOAA RAI index and station daily maximum rainfall depth is labeled R1, while the CC between the IMERG RAI index and station daily maximum rainfall depth is labeled R2. By aggregating values from 2,360 stations and comparing the two index products from IMERG and NOAA across the years 2001 to 2022, we can effectively assess these relationships over time. A moderately strong correlation is observed between the RAI index of NOAA (average CC ~0.40) and IMERG (average CC ~0.42) with station daily maximum rainfall depth. Both R1 and R2 show increasing trends from 2001 to 2022, indicating that the RAI index tends to rise in a positive direction as rainfall depth increases due to extreme rainfall events. This finding suggests that the RAI index may serve as a valuable indicator for precipitation-driven climate change studies, as supported by previous research [14,82,83].

In an earlier effort to assess the relationship between the RAI index and observed rainfall depth, [26] found that different rainfall anomaly indices behave similarly, skewing positively as rainfall depth increases but reversing as depth decreases. A similar pattern is observed with the RAI index in this study. Additionally, Figure 4 reveals that the scatterplot between the NOAA RAI index and station daily maximum rainfall depth displays more noise across the years compared to the IMERG RAI index. The relatively lower noise in the IMERG RAI index’s relationship with daily maximums could be attributed to the intensive calibration and sensor averaging applied to IMERG data. In contrast, NOAA weather stations, which are highly sensitive to local environmental factors—such as wind, elevation, and obstacles like trees or buildings—may introduce noise into their readings [51].

By further analyzing Figure 4, we substantiate earlier claims that the IMERG-derived RAI index could provide significant benefits for ungaged locations beyond CONUS. It could serve as a useful tool for farmers in predicting crop yield performance in response to fluctuating rainfall intensities and frequencies. Additionally, engineers can use it to better plan for future flood impacts [34,84,85,86], while city and town planners can leverage it for informed community development strategies [4,87,88,89].

4.3. Regional Attribution of IMERG Precipitation Anomalies

Assessing the performance of the IMERG RAI index in very dry and very wet climate regions in CONUS is a key objective of this study. Previous research [11,16] identified Nevada and Louisiana as the states with the lowest and highest average annual rainfall depths in CONUS, respectively. To evaluate IMERG’s capability to model the RAI index in these precipitation-contrasting states, 20 stations were selected from each state, and the RAI index was calculated using daily annual precipitation maxima from 2001 to 2022. The following subsections present detailed results and discuss their significance in terms of climate extremes and regional variability.

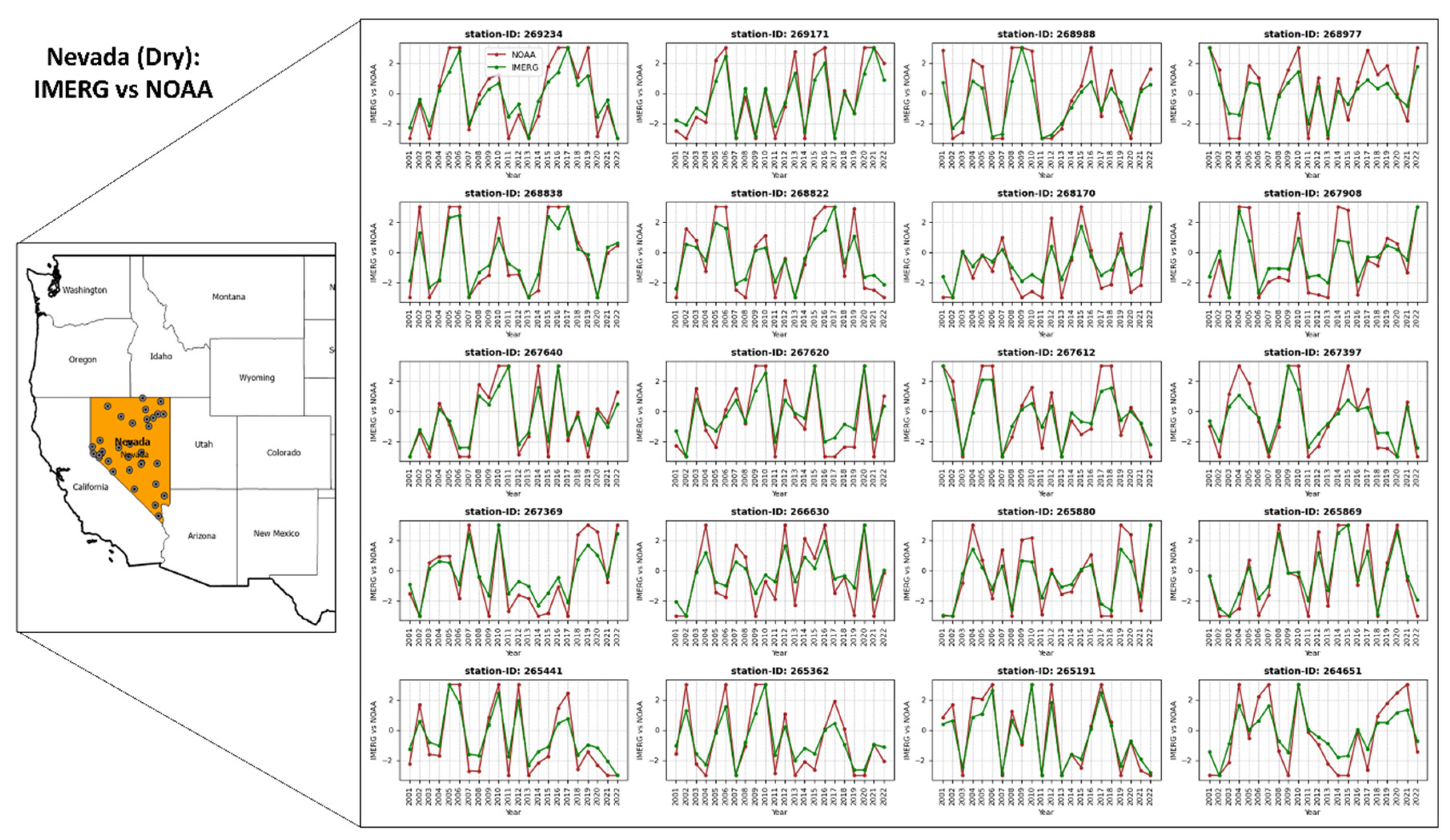
4.3.1. IMERG RAI Index Assessment in Nevada (Dry western CONUS)

Nevada is considered the driest state in CONUS, receiving the least average precipitation in terms of frequency, intensity, and humidity [90,91]. A previous study [90] investigating the effects of climate change on Nevada used a high-resolution Weather Forecasting Model with dynamic scaling and found that Nevada experiences low precipitation for most of the year. As such, Nevada was chosen to assess the IMERG RAI index. Figure 5 illustrates a strong relationship between the IMERG RAI index (in green) and the NOAA station RAI index (in red) across 20 selected stations. The IMERG RAI index performed exceptionally well, demonstrating consistency across the stations.

The statistical results presented in Table 5 show an average correlation coefficient (CC) of 0.95, an average percentage relative bias (PRB) of 20.71, an average root mean squared error (RMSE) of 0.91, an average mean bias ratio (MBR) of 0.82, an average Nash-Sutcliffe Efficiency (NSE) of 0.83, and an average Kling-Gupta Efficiency (KGE) of 0.29. The high CC indicates a strong correlation between the IMERG and NOAA RAI indices, while the MBR suggests a slight overall difference of 0.18 (18%) between the two datasets. Although the average KGE, which incorporates biases and variance, is relatively low due to the variability between the IMERG and NOAA RAI indices, the overall NSE suggests good performance of the IMERG RAI index.

Nevada experienced unusually high precipitation in 2010 [92], including an event where 8.05 inches of rain fell over several days before Christmas, leading to flooding and debris accumulation on roads [91,93,94,95]. Most stations in Nevada showed a positively skewed RAI index for both IMERG and NOAA station data (Figure 5), with other positively skewed indices occurring in different years depending on station location and the precipitation characteristics of those years. This assessment reinforces earlier research findings that satellite precipitation products have the capability to quantify rainfall anomalies at a broader spatial scale.

With increasing concerns about climate change, IMERG satellite precipitation data can provide critical insights for researchers and policymakers to effectively monitor and assess drought severity. By comparing current rainfall data to historical averages, early warning systems can be developed to support informed decision-making on water management strategies in drought-prone regions such as Nevada and Arizona. Furthermore, this approach can be extended beyond CONUS for drought monitoring in other parts of the world [24,59,97].

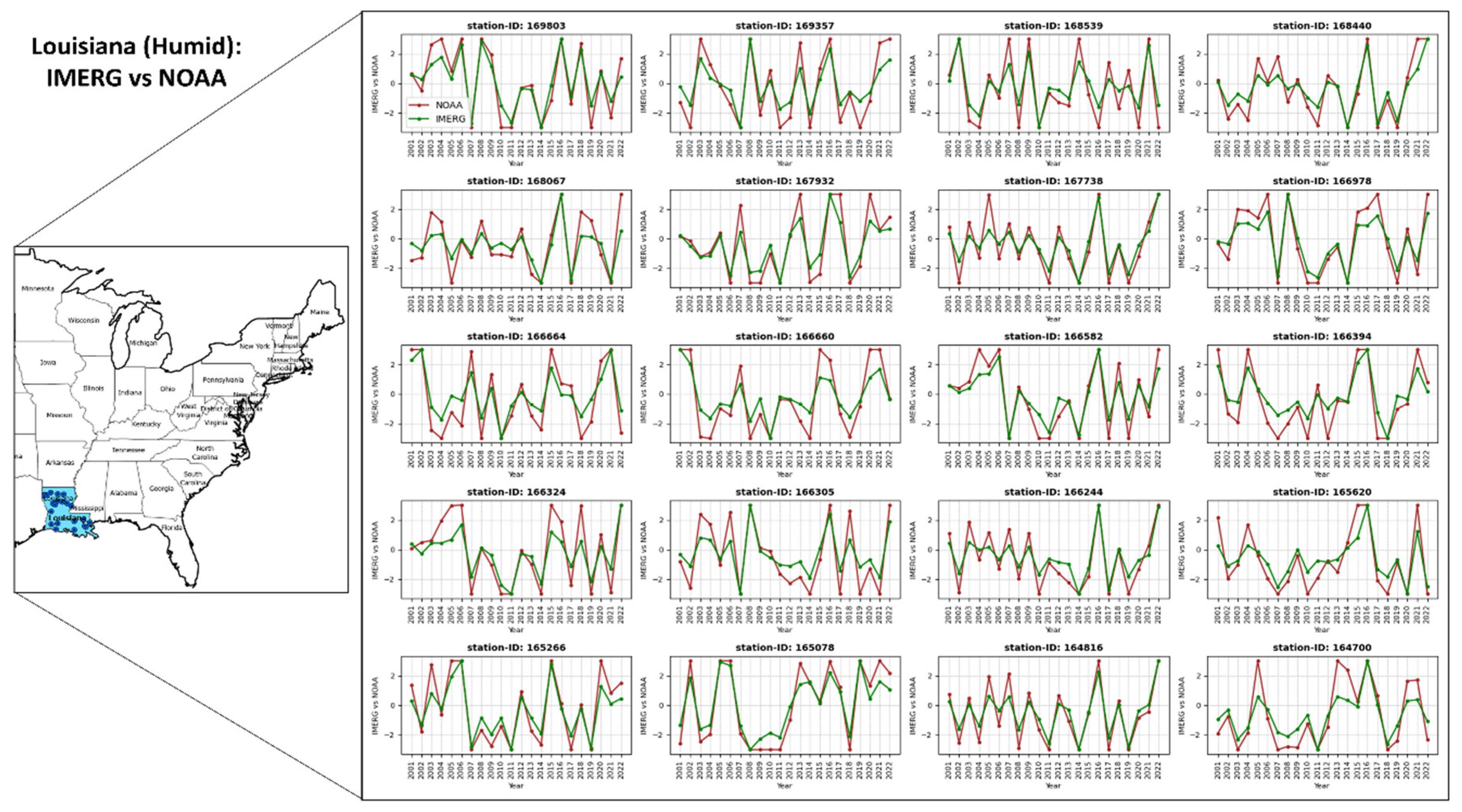
4.3.2. Evaluation of IMERG RAI Index in the High-Rainfall Region of Louisiana

Louisiana is renowned as one of the wettest states in CONUS, attributed to several climatic factors. The state’s subtropical climate features hot, long, and humid summers, and short winters. Located between the Gulf of Mexico and the flat plains of North America, Louisiana benefits from warm, moist air from the Gulf, which moderates the climate in its southern regions. Additionally, the presence of the Mississippi River, susceptibility to tropical cyclones [98], and two prominent rainy seasons—spring and fall—contribute to its high average annual rainfall depth of 57.05 inches, although this varies across the state [99,100]. Consequently, evaluating the IMERG RAI index in Louisiana is crucial for understanding the potential and limitations of IMERG precipitation data for extreme precipitation studies.

Figure 6 presents a comparison of the IMERG RAI index with the NOAA RAI index across 20 selected stations in Louisiana. The results indicate a strong agreement between IMERG and NOAA RAI indices across the years from 2001 to 2022 at each station. The average profiles of both indices are slightly above the zero mark. Statistical results, detailed in Table 6, show a mean correlation coefficient (CC) of 0.93, a mean percentage relative bias (PRB) of 24.82, a mean root mean squared error (RMSE) of 0.96, a mean bias ratio (MBR) of 0.79, a mean Nash-Sutcliffe Efficiency (NSE) of 0.80, and a mean Kling-Gupta Efficiency (KGE) of 0.18. These statistics suggest that IMERG performed well in modeling anomalies in the rainfall-rich state of Louisiana, consistent with previous studies demonstrating the potential of remote sensing precipitation capabilities to model extreme rainfall events [31,100].

The capability of IMERG to model extreme rainfall has been explored extensively in other parts of the world, revealing its potential for assessing precipitation-induced flood risks for infrastructure development [42,59,101,102,103]. However, there has been limited application of IMERG data to model extreme rainfall anomalies using dense gauge networks, such as the 2,360 stations across CONUS. Our assessment across varied climatic regions in CONUS demonstrates IMERG’s potential to detect extreme rainfall anomalies on a continental scale and beyond. We hope that this research will inspire further studies on extreme rainfall events using IMERG data, particularly in ungauged regions.

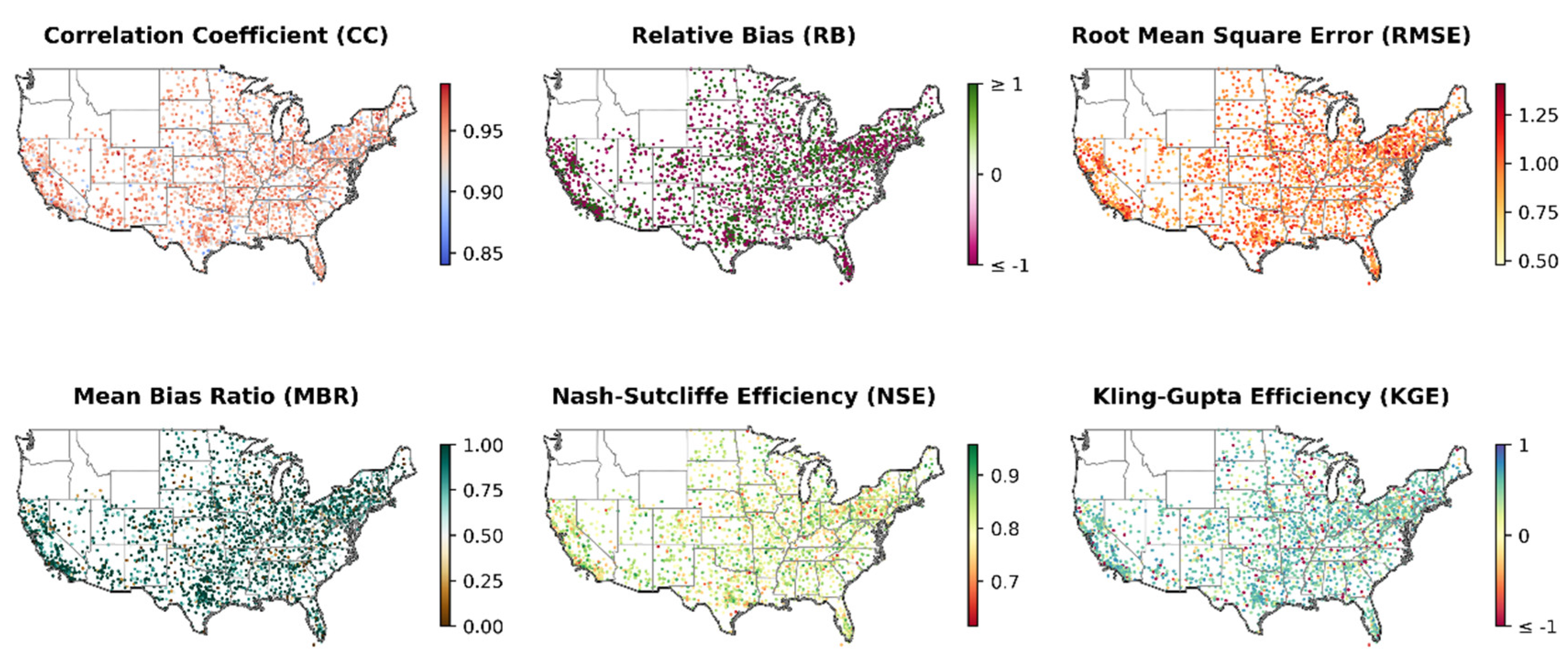
4.4. Spatial Evaluation and Hydrological Utility of IMERG RAI Index

The Rainfall Anomaly Index (RAI) derived from IMERG data for all 2,360 stations over a 22-year period was evaluated against the NOAA station-based RAI index. The statistical results for each station were mapped spatially to elucidate the spatial relationship between IMERG and NOAA RAI indices. Figure 7 presents the spatial statistics, which reveal a high correlation coefficient (CC) with an average value of ≥ 0.85. Although there is no distinct spatial trend in the distribution of CC, localized effects are observed at individual stations. The percentage relative bias (PRB) varies between -100% and 100% and does not exhibit a specific spatial pattern across CONUS. The root mean squared error (RMSE) is notably higher in the wetter eastern part of CONUS and the arid western regions, particularly in the desert areas of Nevada, Arizona, and parts of California. This finding is consistent with previous studies, which have shown that IMERG tends to underestimate observations in dry regions and overestimate in wet regions [34,56,65].

Earlier research by [56] assessed IMERG’s performance over the Tianshi region of China by comparing IMERG data with TRMM observations. This study found that IMERG not only outperformed TRMM but also had a tendency to underestimate rainfall in areas with scarce precipitation compared to regions with above-average rainfall [56]. Similarly, [80] observed that IMERG records lower bias during the winter season with low precipitation compared to the rainy seasons. Our findings align with these observations, revealing a similar pattern where biases from CC, PRB, RMSE, and MBR are lower in the dry western CONUS compared to the eastern part. It is noteworthy that precipitation increases from west to east across CONUS, with the west experiencing drier conditions and the east receiving more rainfall.

The examination of the hydrological utility of IMERG based on anomaly estimation, as presented in Figure 7, shows high Nash-Sutcliffe Efficiency (NSE) values (≥0.7) and average Kling-Gupta Efficiency (KGE) values (≥0). These high NSE and KGE estimates suggest that IMERG provides rainfall data comparable to station observations for modeling purposes. Therefore, IMERG can serve as a valuable precipitation source for regions lacking adequate rain gauge data, extending beyond CONUS. Previous studies have also affirmed the hydrological utility of IMERG. For instance, [60] evaluated IMERG satellite precipitation products in the Yellow River source region of China and found that IMERG data could drive hydrological models effectively, yielding an NSE value of 0.807 when compared with station model outputs. This is consistent with our findings, where the NSE range for IMERG RAI index compared to NOAA station RAI index falls between 0.7 and 0.9 in CONUS. Thus, IMERG can be considered a reliable data source for rainfall anomaly studies in CONUS and holds potential for application in regions beyond CONUS.

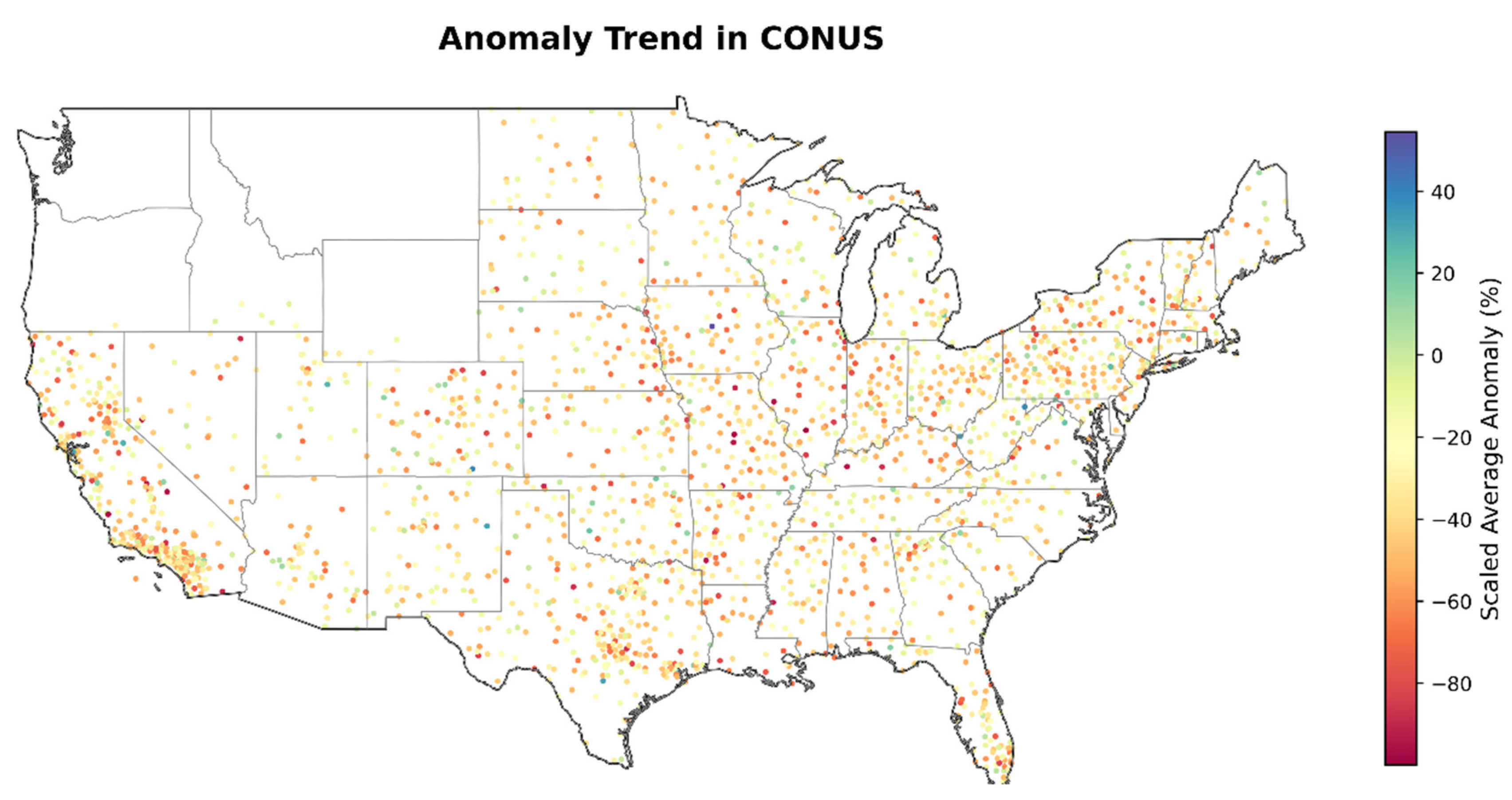
4.5. Trend in Rainfall Anomaly in CONUS and Climate Change Implications

The average Rainfall Anomaly Index (RAI) values, scaled to percentages, for all 2,360 stations across CONUS were calculated for visual examination and are presented in Figure 8. The average anomaly index does not reveal any significant patterns, as the averaging at each station tends to smooth out any spikes from the 22 years of anomaly estimates. However, a localized effect is observed, with stations in central CONUS showing average anomalies below the 0-percentage mark, while a few stations exhibit average anomalies above this threshold. The eastern part of CONUS, particularly the northeast, is prone to increased precipitation, whereas the southwest generally experiences drier conditions [11]. Consequently, the anomaly index is not uniformly positively skewed, except in instances of intense precipitation events, such as the floods of 2007 and 2019 in the Midwest [104,105]. However, in dry regions, the anomaly index can spike positively in response to unexpectedly intense precipitation.

Regarding climate change and its impact on anomalous rainfall throughout CONUS, [104] employed five rainfall projection models to demonstrate that future rainfall is expected to increase in both frequency and intensity, exhibiting positively skewed variability in total annual precipitation. Specifically, the rainfall intensity in the eastern part of CONUS is projected to increase progressively more than in the western CONUS, where projections indicate the opposite trend [104]. Given the growing number of models, IMERG could prove valuable for future studies aiming to model projected rainfall for probabilistic flood event scenarios across CONUS and beyond. This work aims to inspire further research into utilizing IMERG data for projecting or probabilistic extreme precipitation events, similar to past studies [34,106].

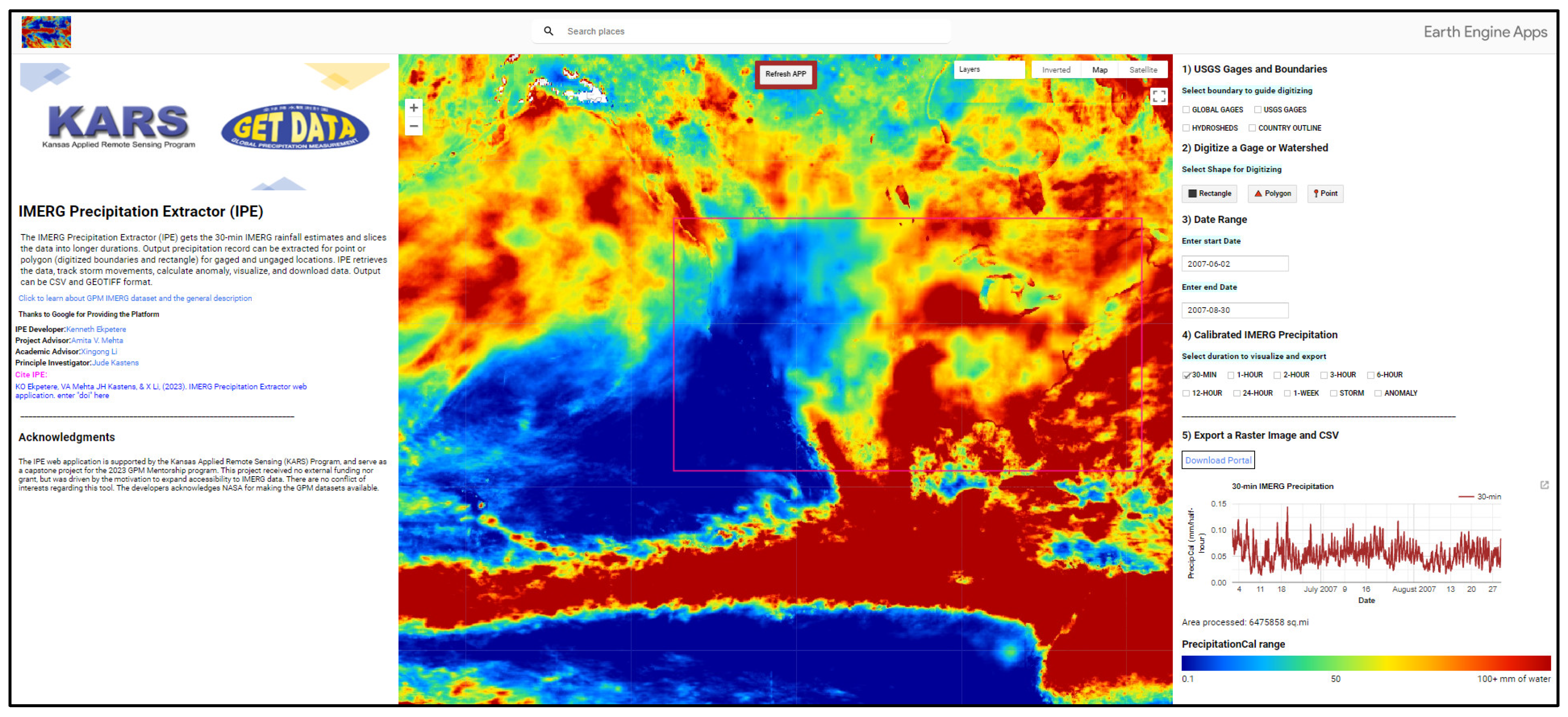
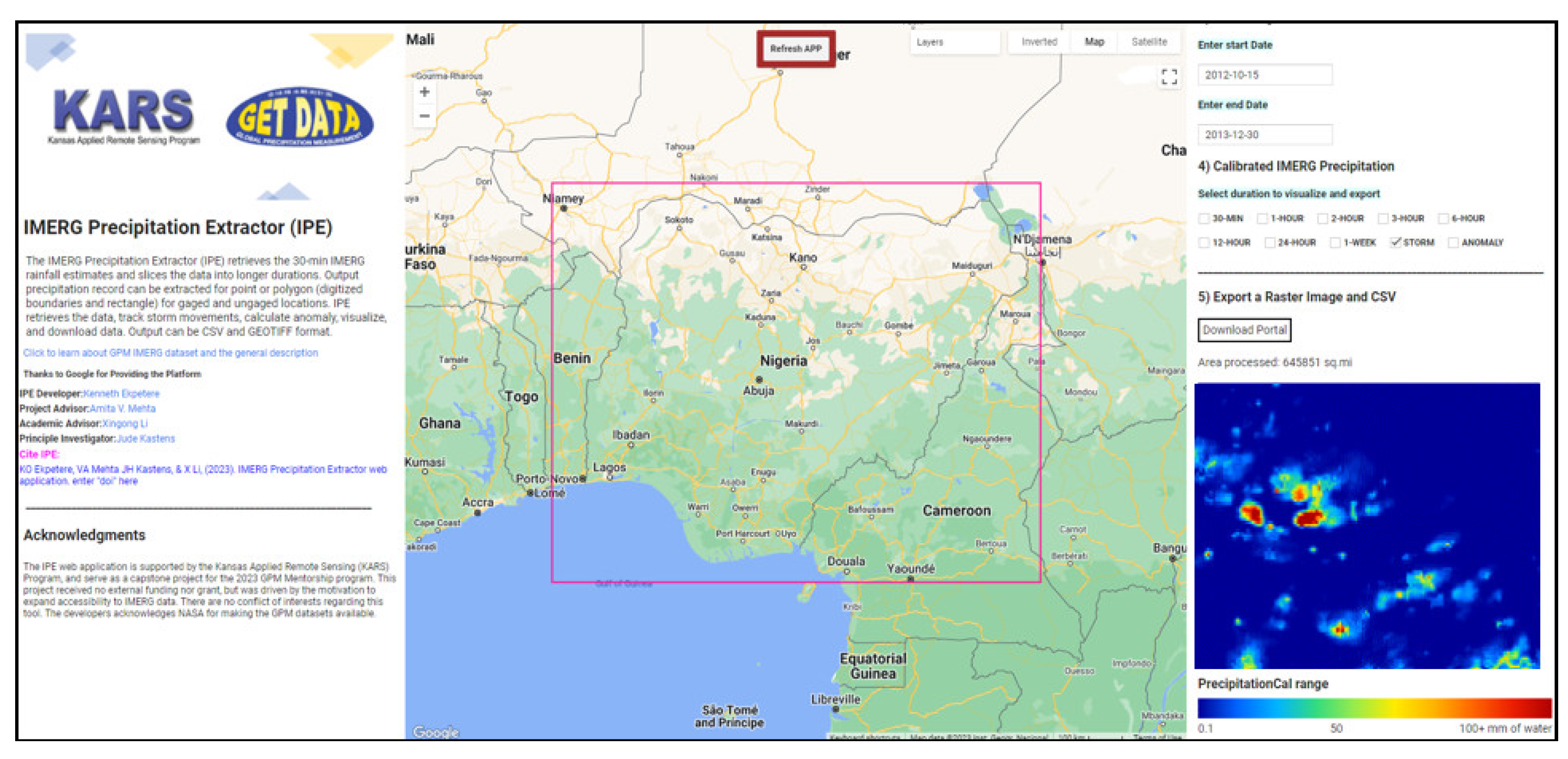
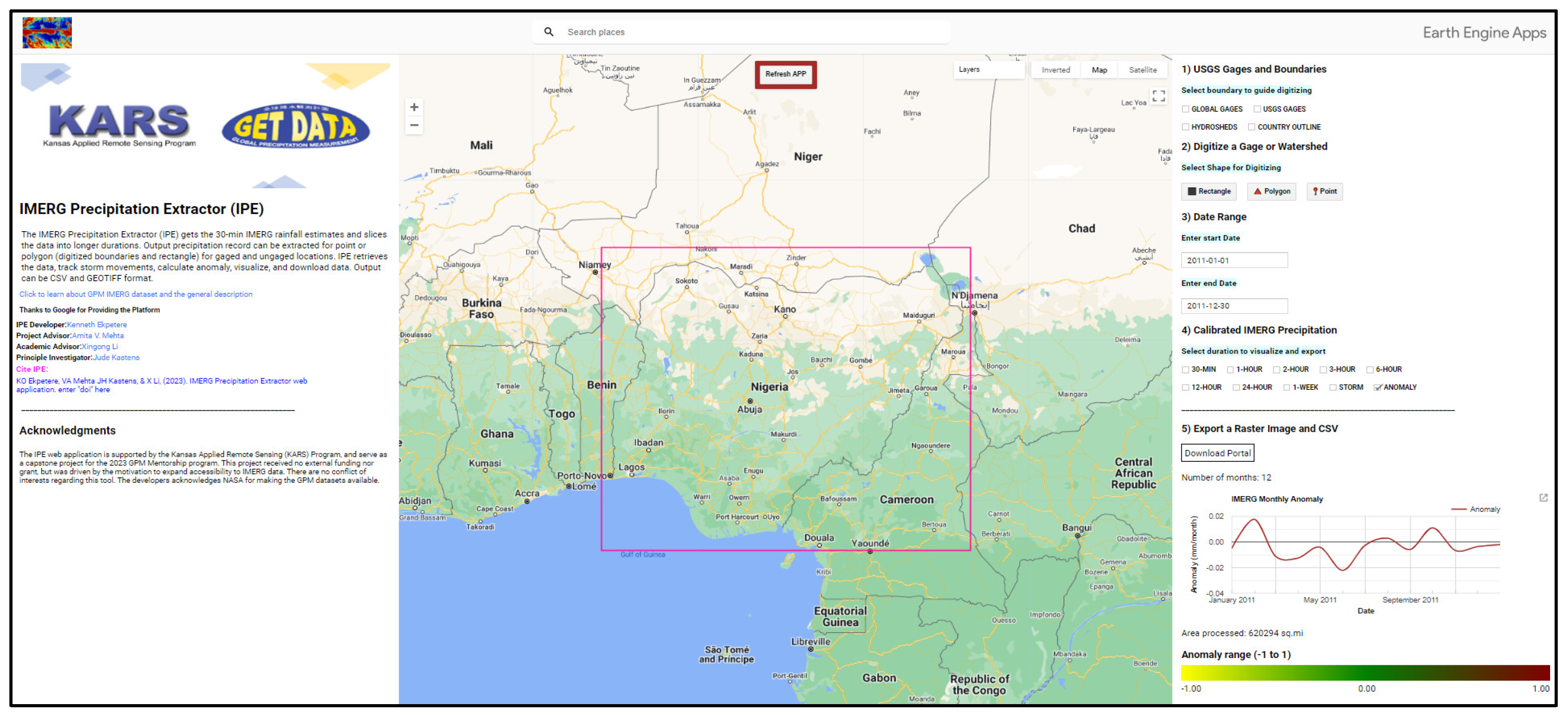
4.6. IMERG Precipitation Extractor (IPE) and Uncertainties in IMERG Data

This section introduces the IMERG Precipitation Extractor (IPE), a web application developed to facilitate the extraction and analysis of precipitation data from IMERG. This is necessary to guide users of IPE and help first term users of IMERG data get acquitted with the web application and the data and create awareness regarding uncertainties in IMERG data.

4.6.1. IMERG Precipitation Extractor (IPE): History, Potentials, and Use Cases

The IMERG precipitation extractor (IPE) was developed by Dr. Keneth Ekpetere, under the supervision of Dr. Amita V. Mahta during the 2023 NASA-GPM mentorship program. The development of IPE responded to a growing demand among researchers and academic communities for a user-friendly, efficient web tool to download precipitation data. Initially intended for visualizing and downloading time-series precipitation data for specific points and areas, the tool was later enhanced to include functionalities for computing the Rainfall Anomaly Index (RAI) and tracking storms, thus addressing broader climate change monitoring needs.

The IPE offers numerous functionalities that are particularly noteworthy. It provides global coverage, extending beyond CONUS, and allows users to filter time-series precipitation data at both point and polygon/area levels. Users can specify a date range for data extraction, visualize the data as either a time-series plot or a map (derived from the time-series average), and download the data in CSV format or as a TIFF file for GIS applications. Figure 9 illustrates the IPE interface, demonstrating its use to visualize precipitation in Nigeria during the rainy season from June 2, 2007, to August 30, 2007.

Additional features of the IPE include on-the-fly conversion of half-hourly data into various longer durations (1-hour, 2-hour, 3-hour, 6-hour, 12-hour, 24-hour, and 1-week), providing users with flexible temporal resolution options. Users can digitize points or polygons for data extraction or use built-in gauges from USGS (for CONUS) or the Global Historical Climatology Network (GHCN) from NOAA. The application also integrates fine-resolution watershed boundaries from HYDROSHARE, facilitating watershed-specific precipitation extraction and allowing downloads at the country scale.

For climate change monitoring, the IPE includes functions for visualizing and tracking storm events through their stages of initiation, formation, movement, and dissipation. Storm movement can be exported as a Graphics Interchange Format (GIF) file for playback or further analysis. Figure 10 demonstrates the IPE’s application in tracking storms that caused significant flooding in Nigeria during 2012–2013 [107]. The monthly rainfall anomaly index for this area, computed using the IPE’s built-in anomaly index calculator, is presented in Figure 11.

We encourage further testing of the IPE beyond the scope of this study, aiming to advance research in precipitation extremes, climate change anomaly studies, and storm behavior analysis. The IPE is publicly accessible at https://cartoviews.users.earthengine.app/view/ipe, and we hope it will be a valuable resource for the scientific community.

4.6.2. Possibilities, Limitations, and Uncertainties in IMERG Data

The IMERG data offers significant opportunities for advancing precipitation research. Its most notable advantage is its global coverage [74], which enables researchers to conduct comprehensive regional to global precipitation analyses. The extensive IMERG datasets support critical observations and findings with broad implications. Since its introduction, IMERG has alleviated issues related to data scarcity that were prevalent before the early 2000s [37,38]. Additionally, IMERG integrates multiple satellite precipitation products and is highly calibrated with global gauge networks, making it a valuable resource for rainfall studies [46,108,109]. Furthermore, IMERG is freely accessible, removing financial barriers that could otherwise hinder research.

However, IMERG data also presents certain limitations. One significant drawback is its relatively short record length, with just over 20 years of data. This constraint poses challenges for researchers requiring extended precipitation records for multi-decade global analysis [110,111]. Although IMERG began in February 2014, it incorporated data from TRMM starting in 2020, resulting in a continuous record extending from 2000 to the present. Nonetheless, the integration of earlier TRMM data into IMERG has been a point of contention among researchers [76,103].

Like other satellite precipitation products, IMERG is subject to uncertainties. Its spatial resolution of 0.1° x 0.1° (~11 km near the tropics) can be inadequate for modeling precipitation over small areas, where a few pixels may encompass the entire region. Additionally, the half-hourly temporal resolution may not capture short-duration, high-intensity rainfall events effectively. The reliance on multiple satellite sources with varying resolutions also raises concerns, particularly for users unfamiliar with the data fusion algorithms [45,59,62,112]. Despite these challenges, IMERG has demonstrated itself as a reliable tool for advanced precipitation research [51,103].

5. Summary and Conclusions

This research significantly advances the field by developing the IMERG Precipitation Extractor (IPE), a web application designed for querying, visualizing, and downloading time series remote sensing precipitation data. The IPE supports various temporal resolutions (0.5-hour, 1-hour, 2-hour, 3-hour, 6-hour, 12-hour, 24-hour, and 1-week) and offers functionality for points, watersheds, country extents, and user-defined areas on a global scale. Users can track storms through their stages—initiation, formation, mobility, and dissipation—and download storm videos in Graphics Interchange Format (GIF) for further analysis. Additionally, the IPE facilitates the calculation of rainfall anomalies, with the results available for download as CSV files.

A second major contribution of this research is the evaluation of the IMERG-derived Rainfall Anomaly Index (RAI) against the NOAA station RAI index using data from 2,360 dense gauge networks in the conterminous United States. This study is the first to utilize such a large number of stations for a nationwide analysis, thereby enhancing validity and reducing uncertainties associated with sparse station networks. The assessment involved comparing IMERG RAI indices across various regions, specifically contrasting 20 stations from Nevada (a dry region) and 20 from Louisiana (a wet region), as well as examining the performance of the IMERG RAI index annually from 2001 to 2022.

The study also compared the spatial trends of the computed RAI indices from IMERG data with climate change studies focused on precipitation anomalies in CONUS. Several key findings emerged:

(1)

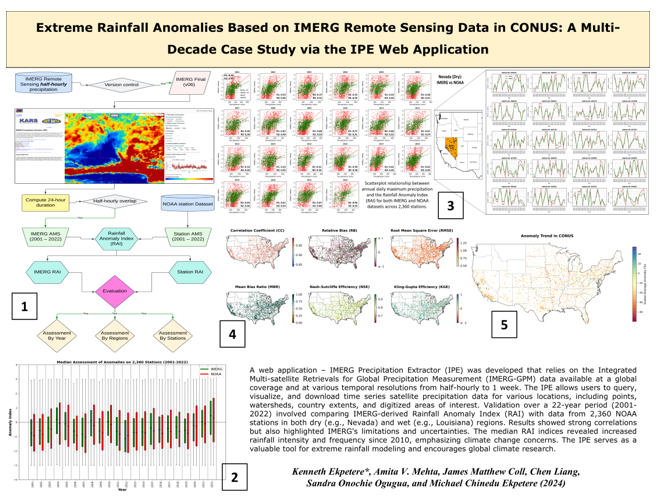
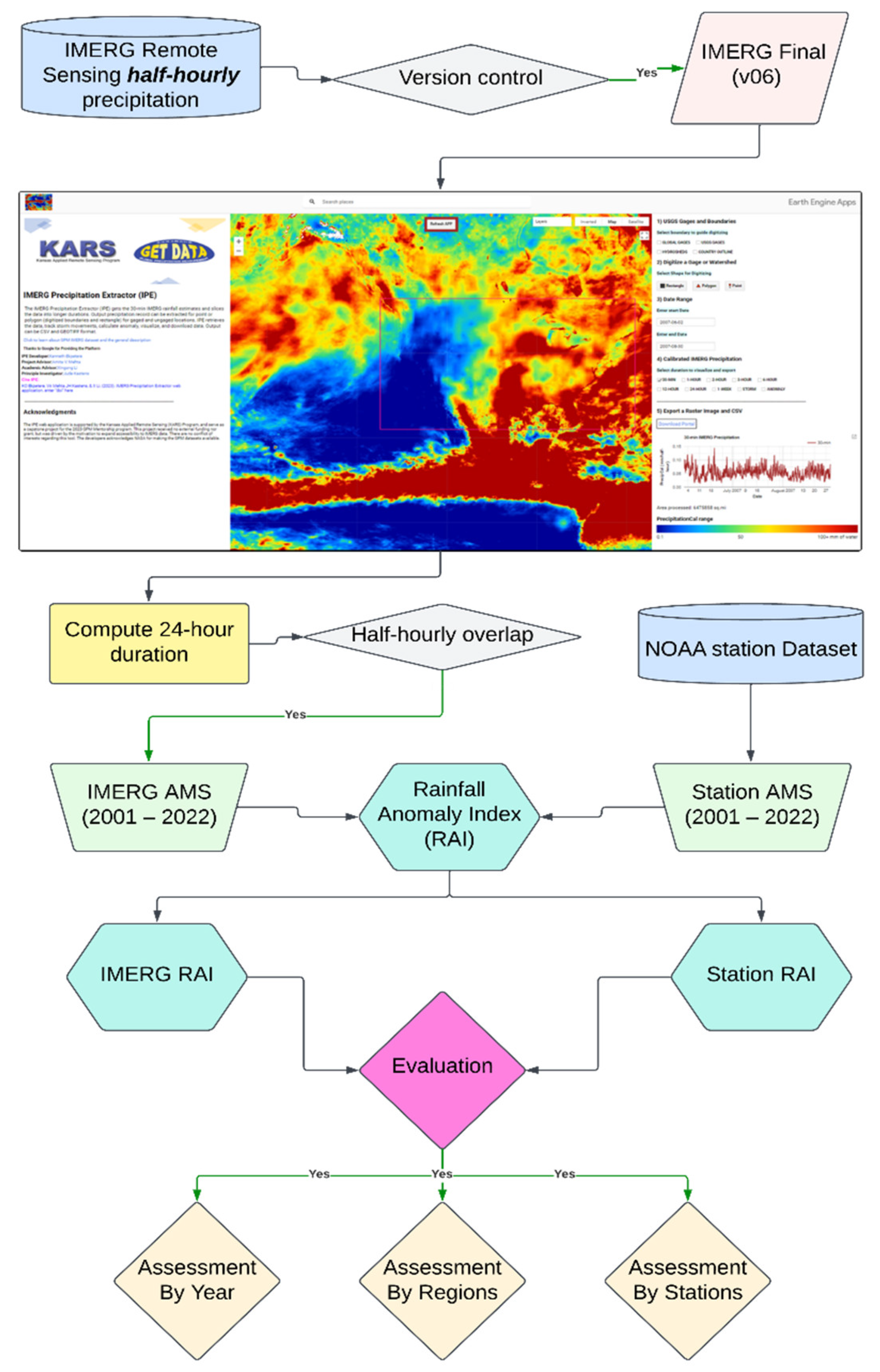
The IPE web application proves to be an effective tool for rapid precipitation data extraction, visualization, and download at multiple durations globally. It offers functionality for tracking and downloading storm signatures and calculating and downloading anomaly data for specific areas of interest.

(2)

The IMERG RAI index demonstrates strong agreement with the NOAA station RAI index. Analysis of data from 2,360 stations reveals an average correlation coefficient (CC) of 0.94, a percent residual bias (PRB) of -22.32%, a root mean square error (RMSE) of 0.96, a mean bias ratio (MBR) of 0.74, a Nash-Sutcliffe efficiency (NSE) of 0.80, and a Kling-Gupta efficiency (KGE) of 0.52. Furthermore, the IMERG RAI index shows a positive correlation with daily annual maximum precipitation depths, with an average CC of 0.42 across the years.

(3)

Regional assessments indicate that the IMERG RAI index shows an average CC of 0.95, PRB of 20.71%, RMSE of 0.91, MBR of 0.82, NSE of 0.83, and KGE of 0.29 in the arid western CONUS (Nevada). In contrast, in Louisiana, the wettest state, the statistics are similar with a mean CC of 0.93, PRB of 24.82%, RMSE of 0.96, MBR of 0.79, NSE of 0.80, and KGE of 0.18.

(4)

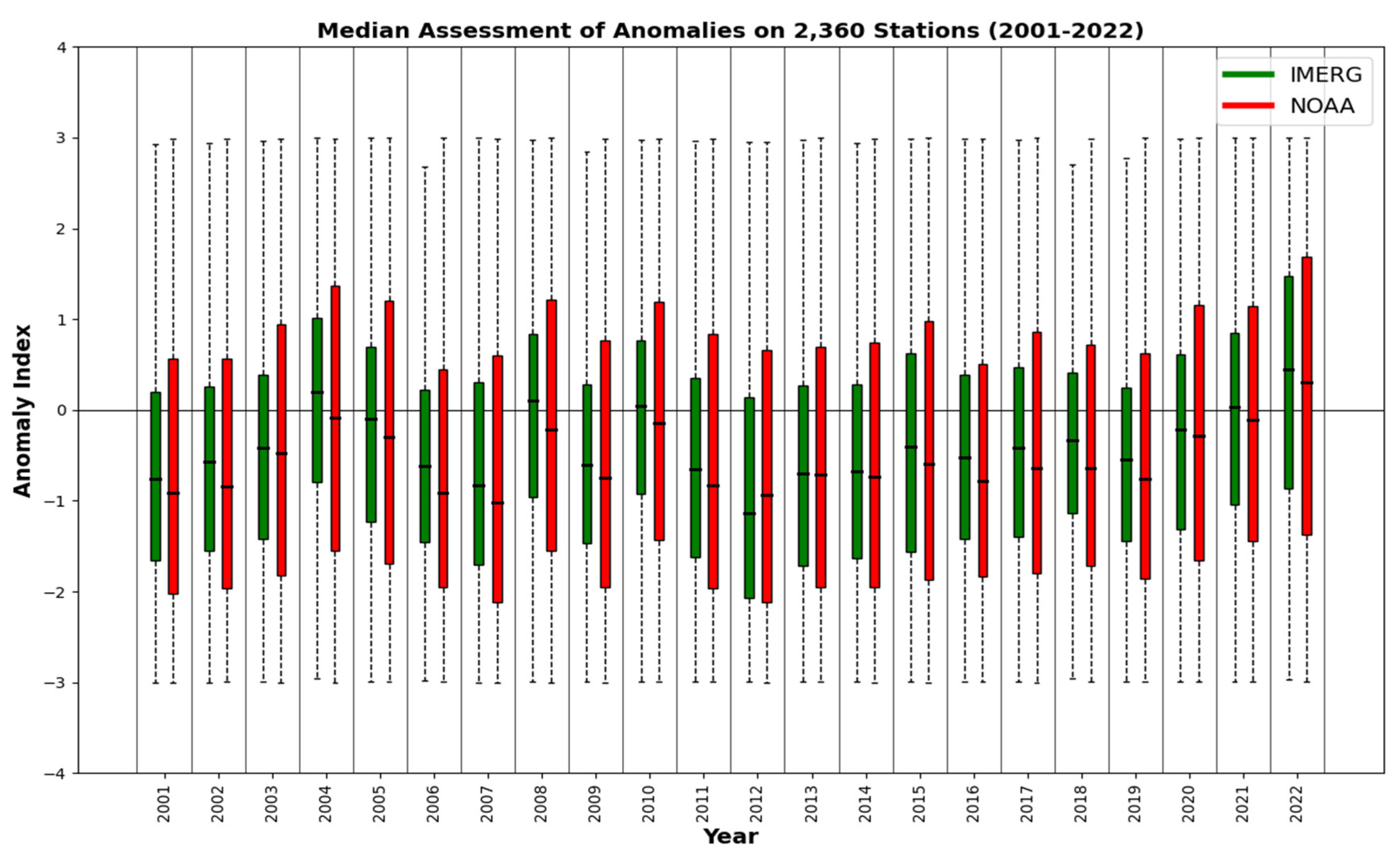
Across CONUS, from west to east, the IMERG RAI index shows good agreement with the station RAI index. Additionally, median RAI indices from both IMERG and NOAA reveal increasing rainfall intensity and frequency since 2010, highlighting climate change issues that have garnered attention in recent years.

This study thoroughly evaluates the performance of IMERG remote sensing precipitation data in modeling rainfall anomalies, underscoring its potential as a valuable resource for climate change research and investigations. While IMERG shows strong agreement with station observations across CONUS, attributed to its high gauge-based calibration, users should remain cautious and perform regional evaluations to identify potential biases. Previous studies, including those discussed here, indicate that IMERG may underestimate precipitation in low-rainfall regions and overestimate it in high-rainfall areas. It is anticipated that the IPE web application will benefit a wide range of users, including hydrologists, engineers, scientists, researchers, universities, government agencies, and private individuals, by providing valuable insights into precipitation anomalies and climate change.