Submitted:
19 September 2024
Posted:
23 September 2024
You are already at the latest version
Abstract
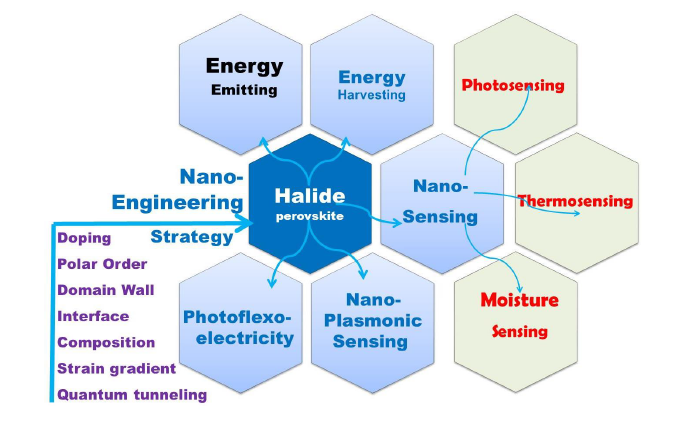
Keywords:
Broader context
1. Background
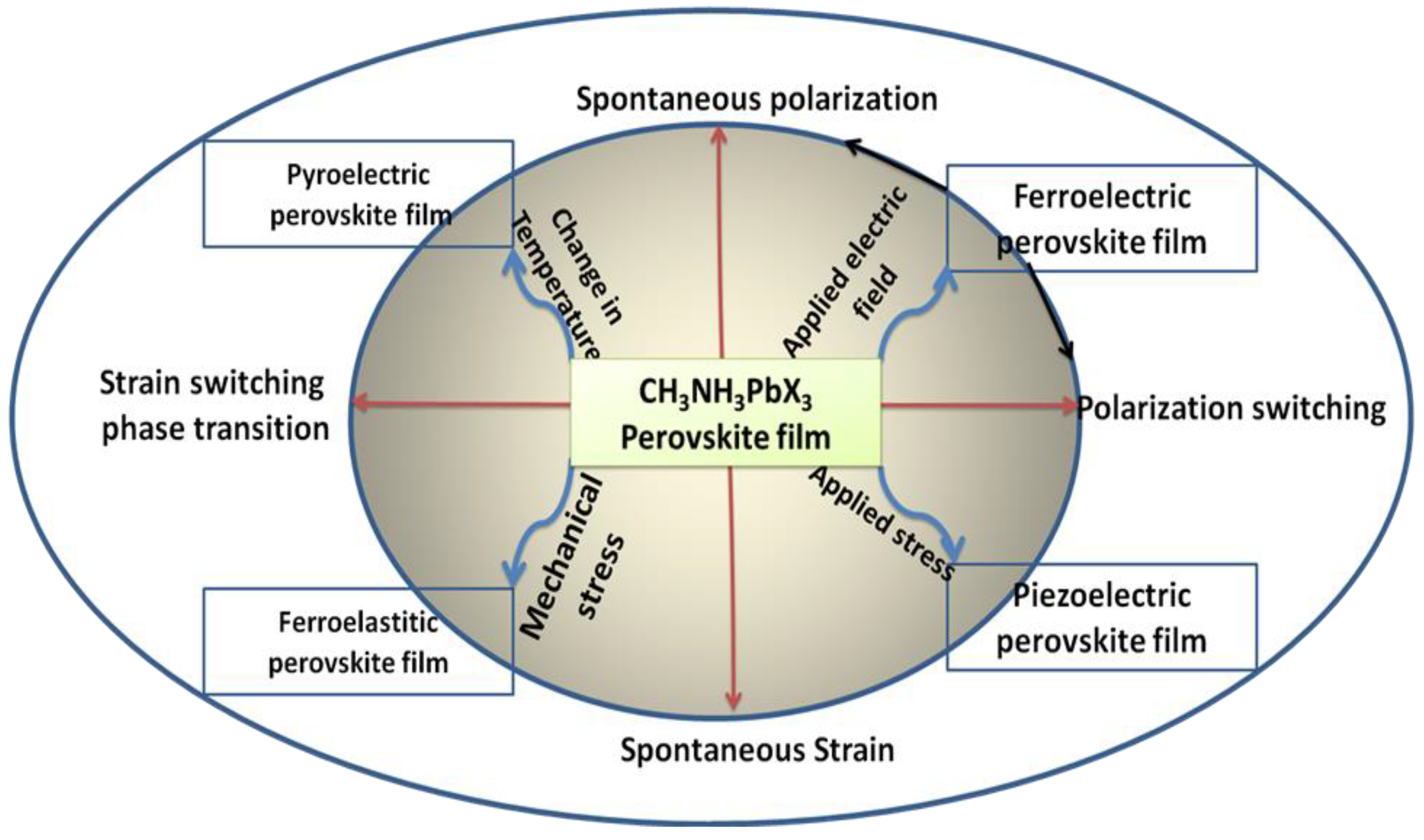
2. Nano-Engineering Strategy of Designing New Property
Can Nano-Engineering Make Halide Perovskite Revolutionize New Application Paradigm Shift?
2.1. Strain and Doping Engineering Approach
2.1.1. Strain Engineering
2.1.2. Doping Engineering
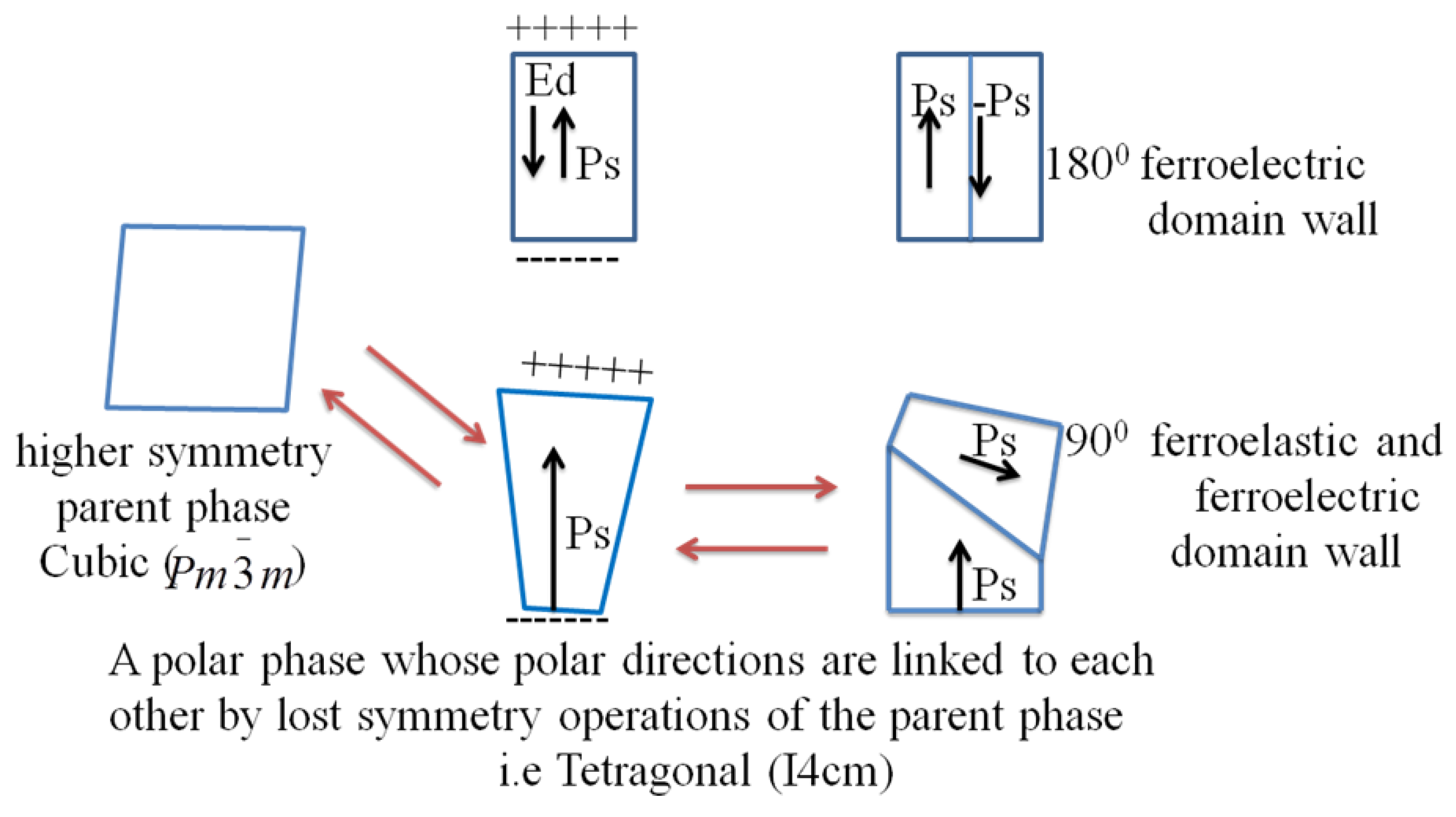
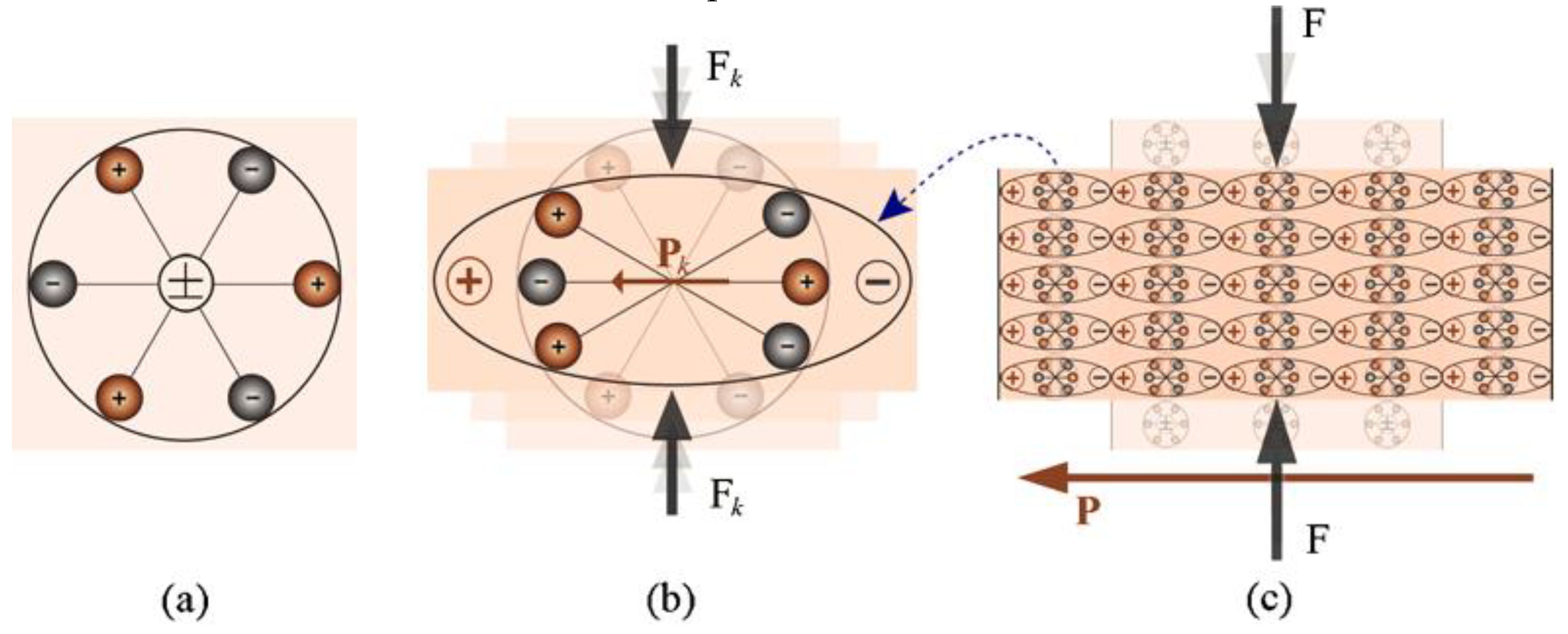
2.2. Polar Order and Domain Wall Engineering Approach
2.2.1. Polar Order Engineering
2.2.2. Interface and Domain Order Engineering
2.3. Composition Engineering Strategy
3. Microscopic Mechanisms and Origins of New Property
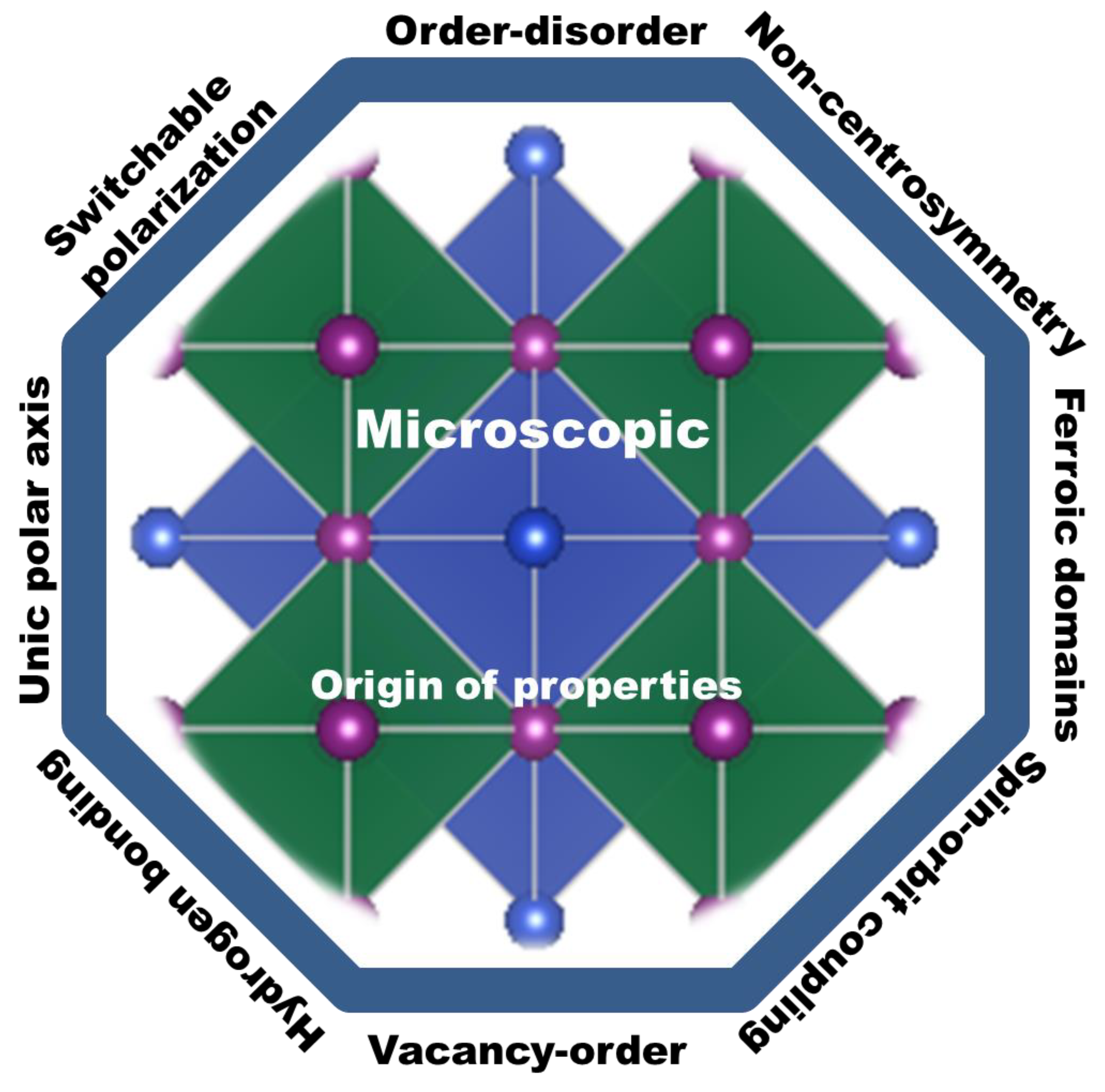
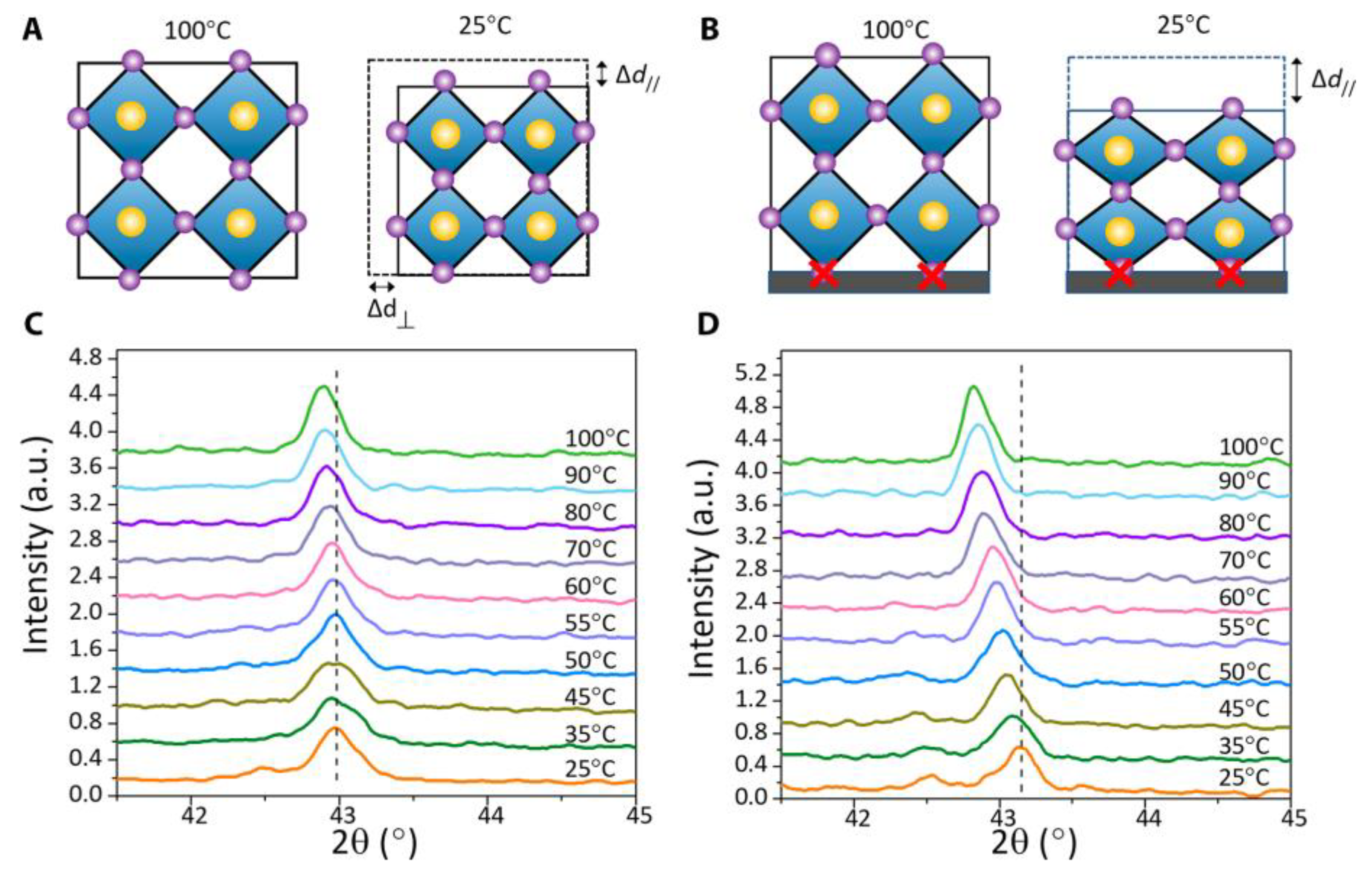
3.1. Order-Disorder Property
3.2. Hydrogen Bonding and Emerging van der Waals
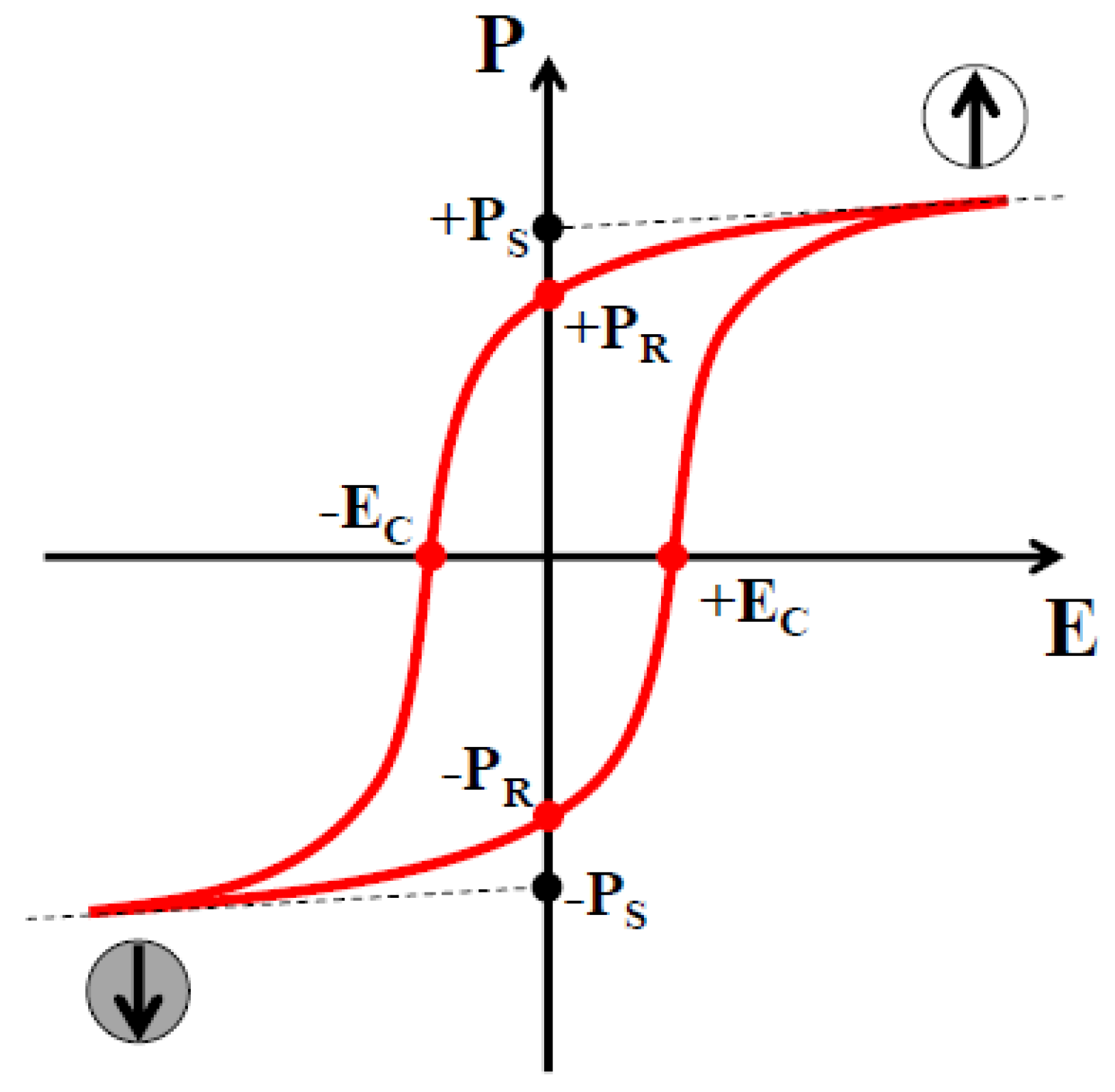
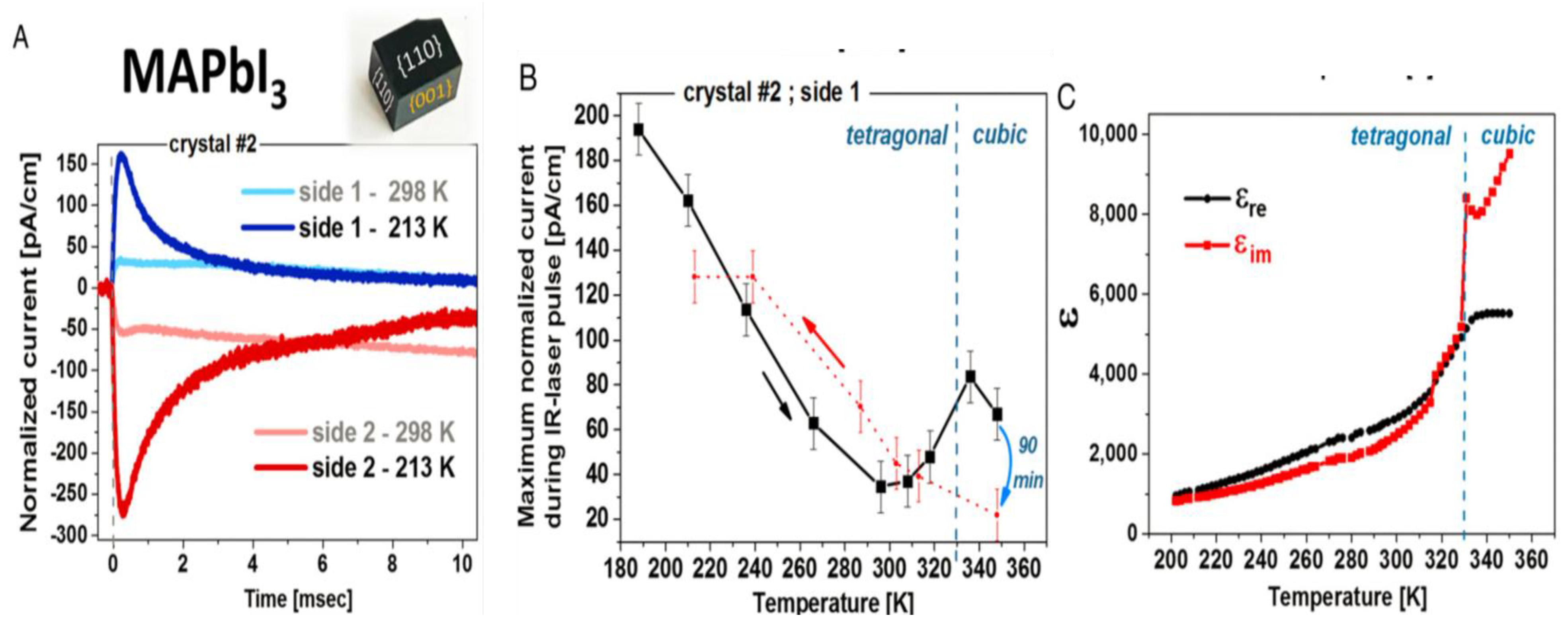
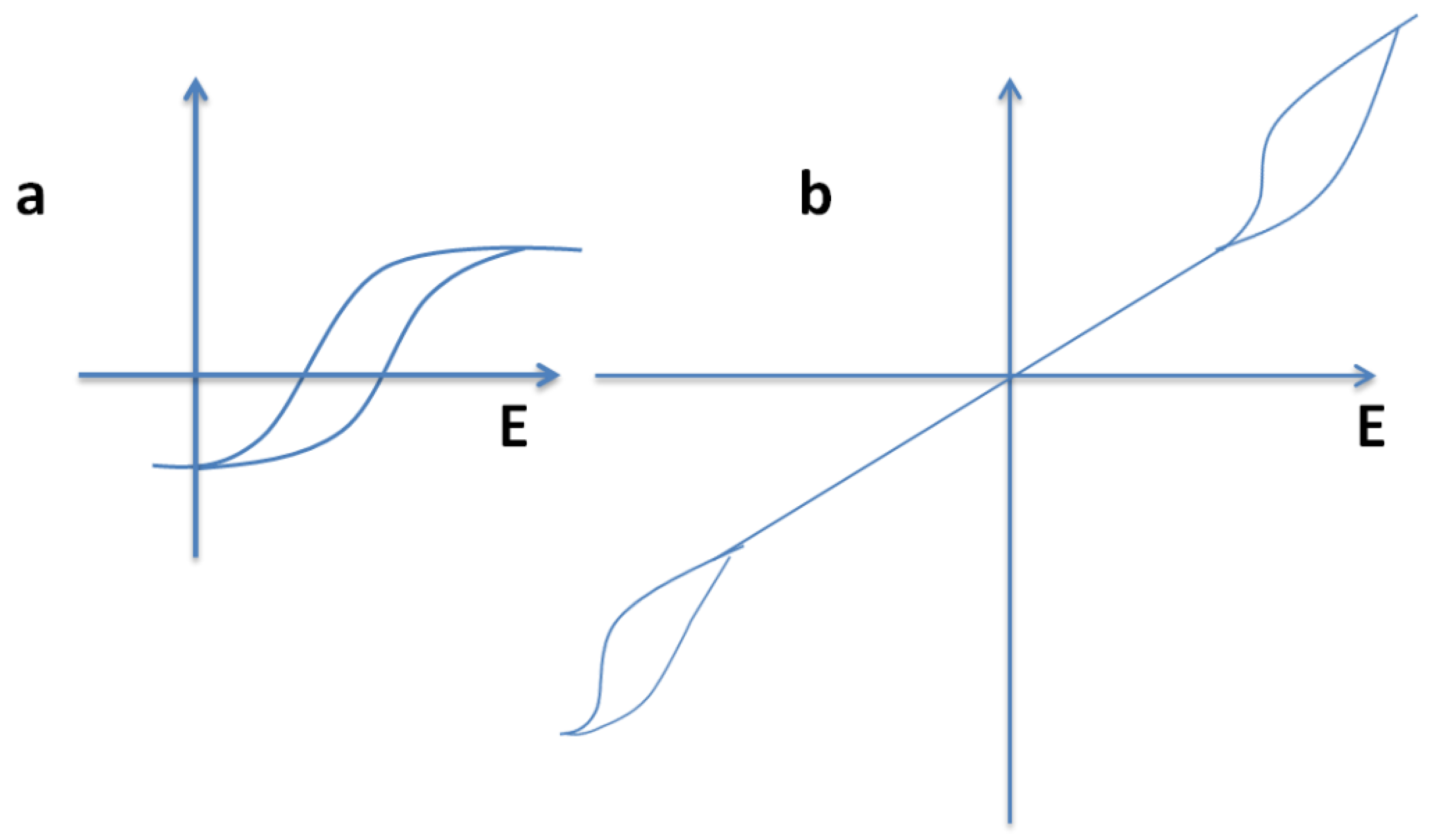
3.3. Switchable Polarization Property
3.4. Unique Polar Axis
3.5. Local Non-Centrosymmetry Property
3.6. Ferroic Domains
3.7. Rashba and Dresselhaus Effects
3.8. Vacancy Ordered-Provskites
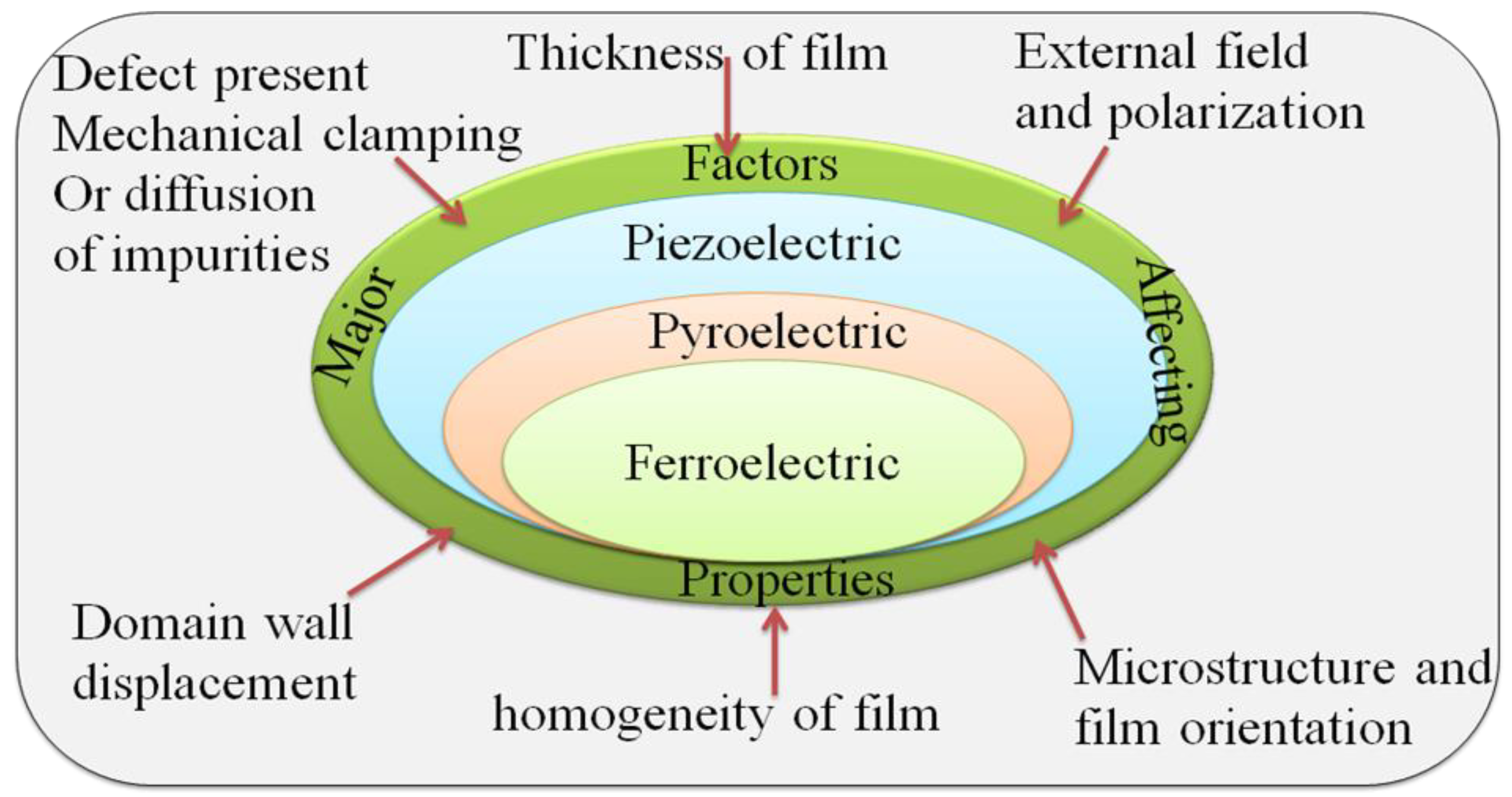
4. Multifunctional Properties beyond Ferroelectrics
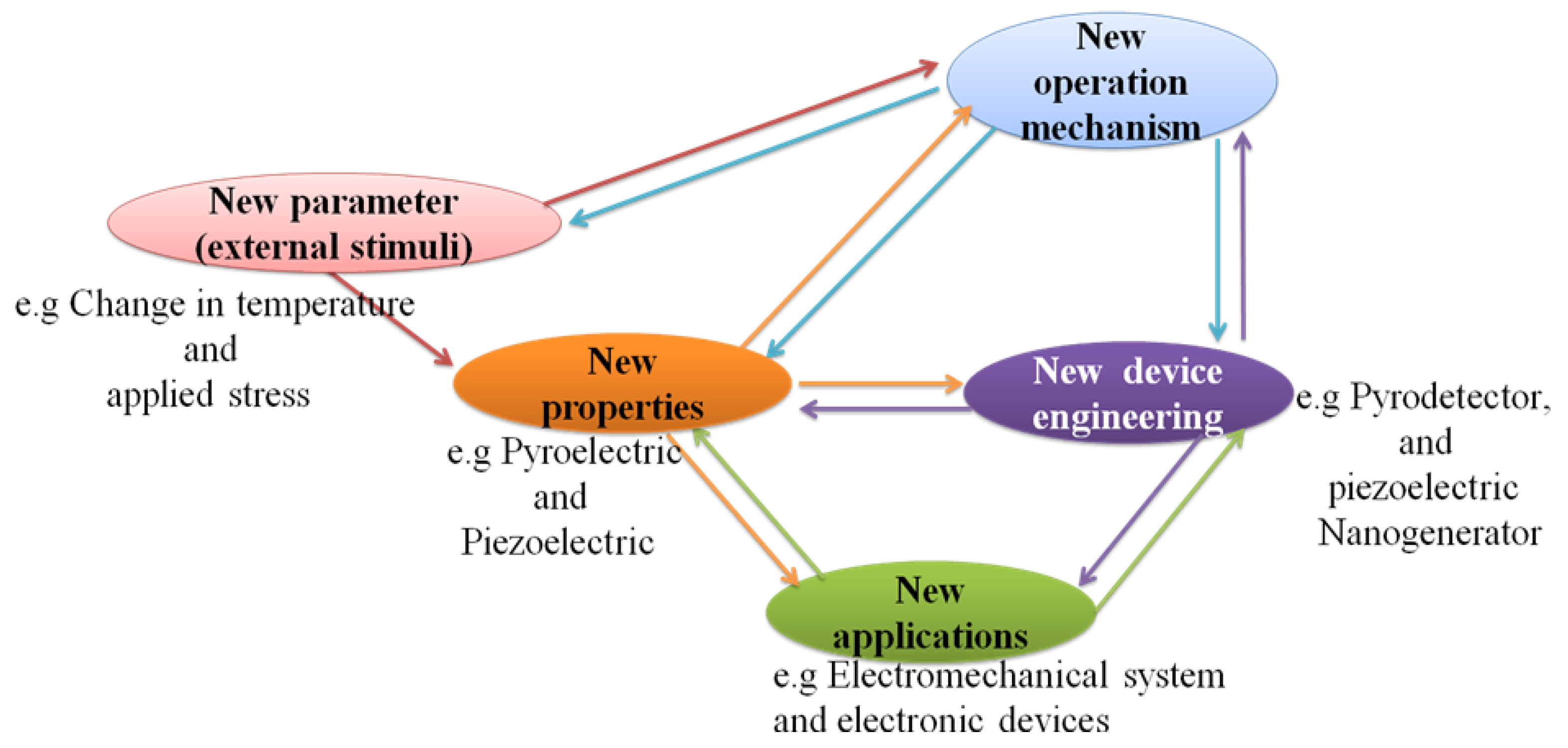
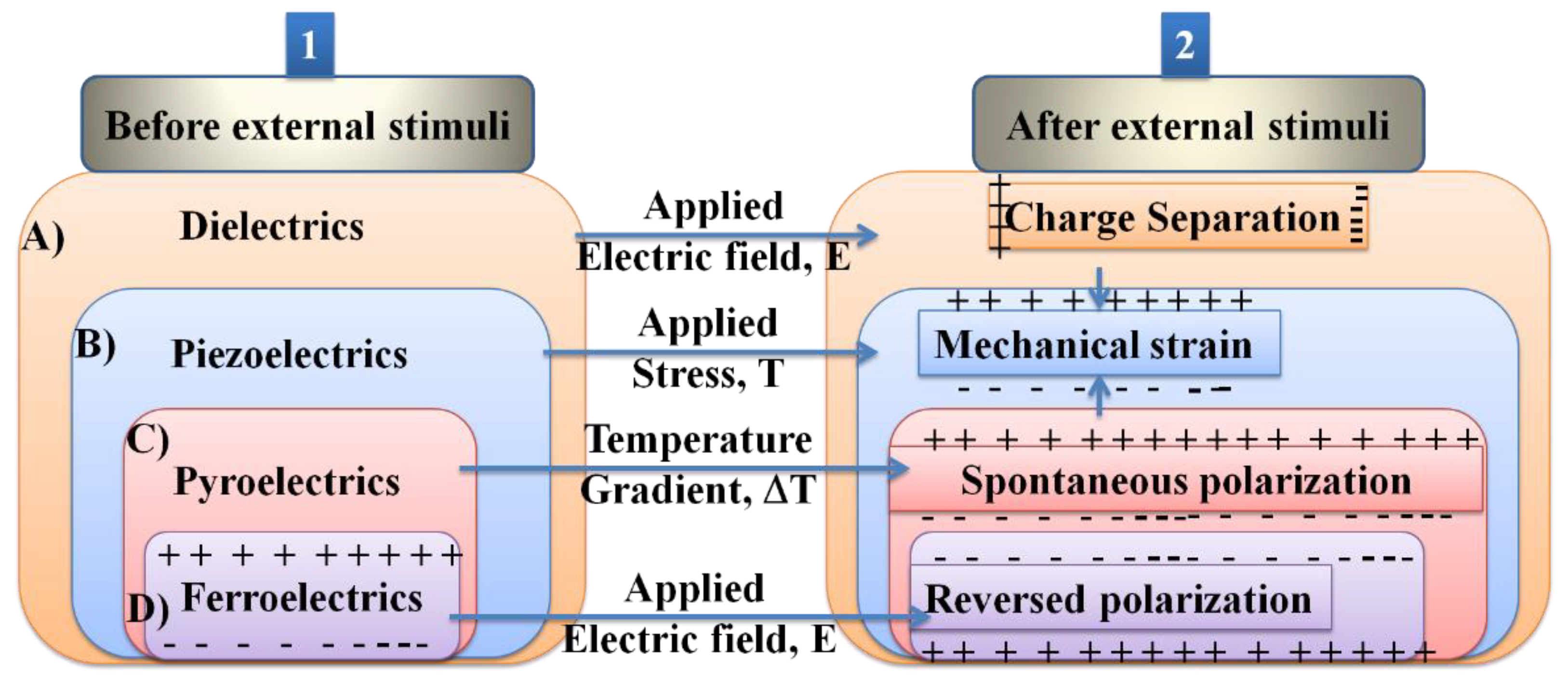
4.1. Tunable Material Composition
4.2. Ferroelastic New Properties
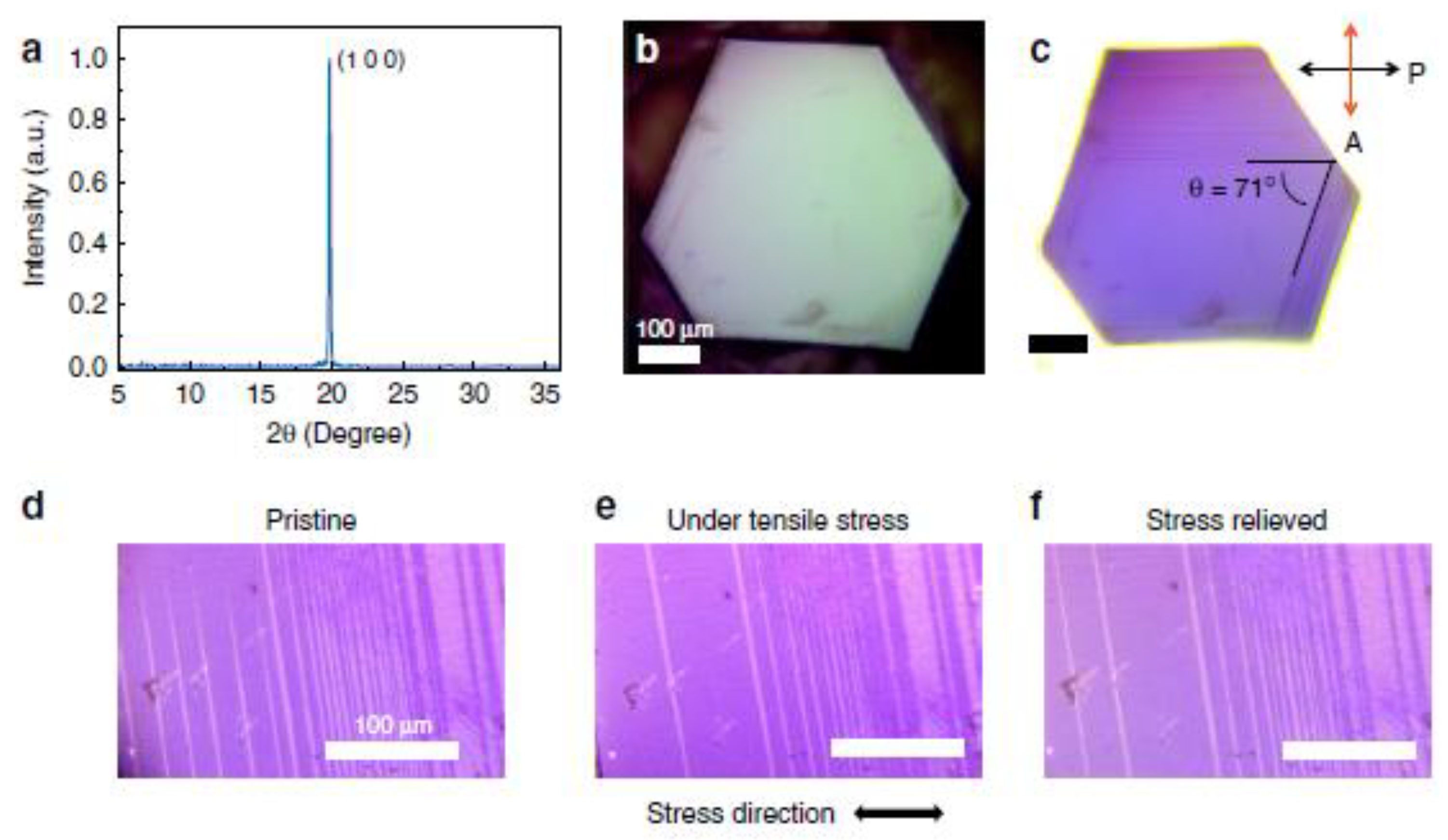
4.2.1. Stiffness and Elastic Compliance
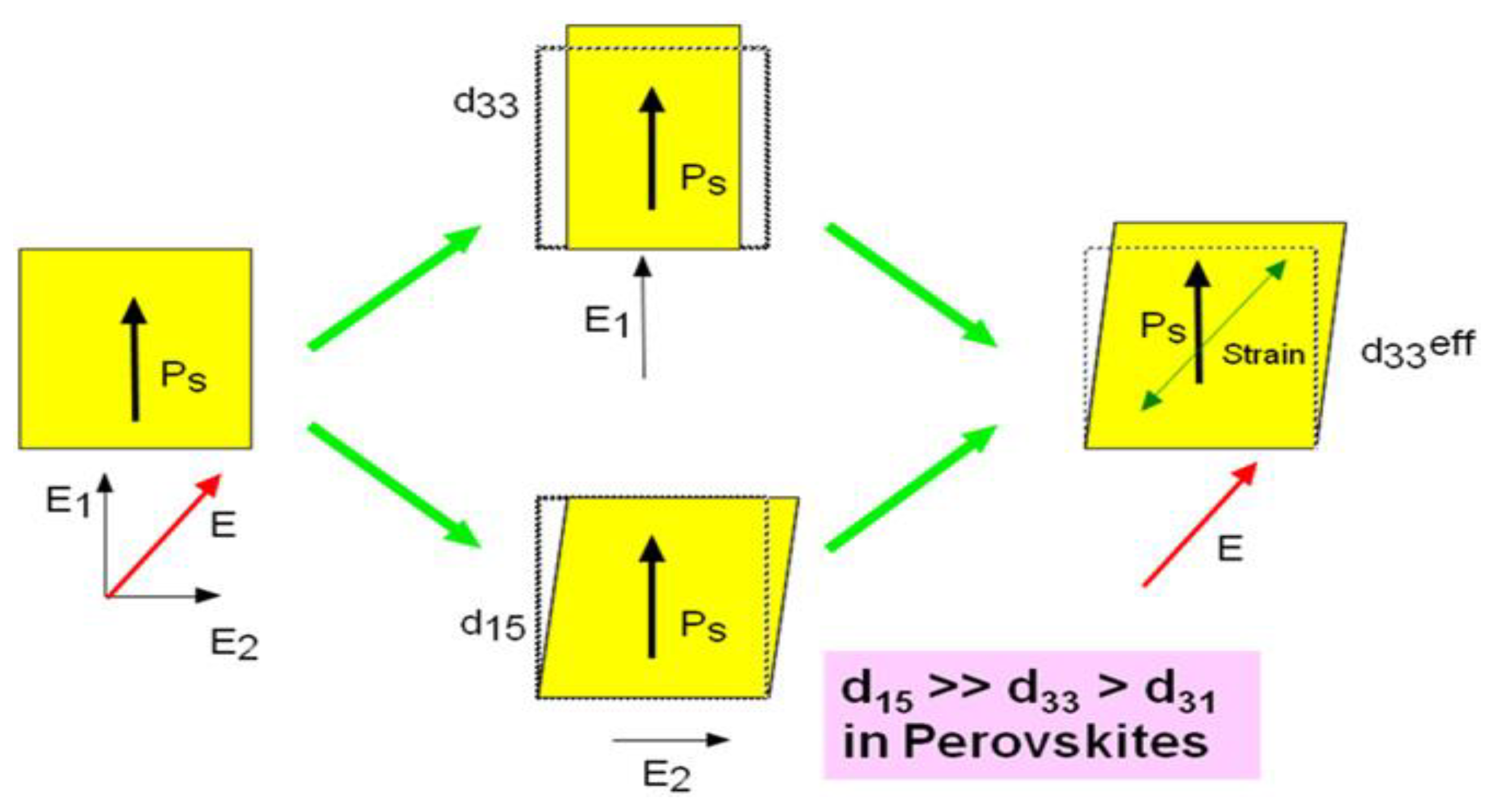
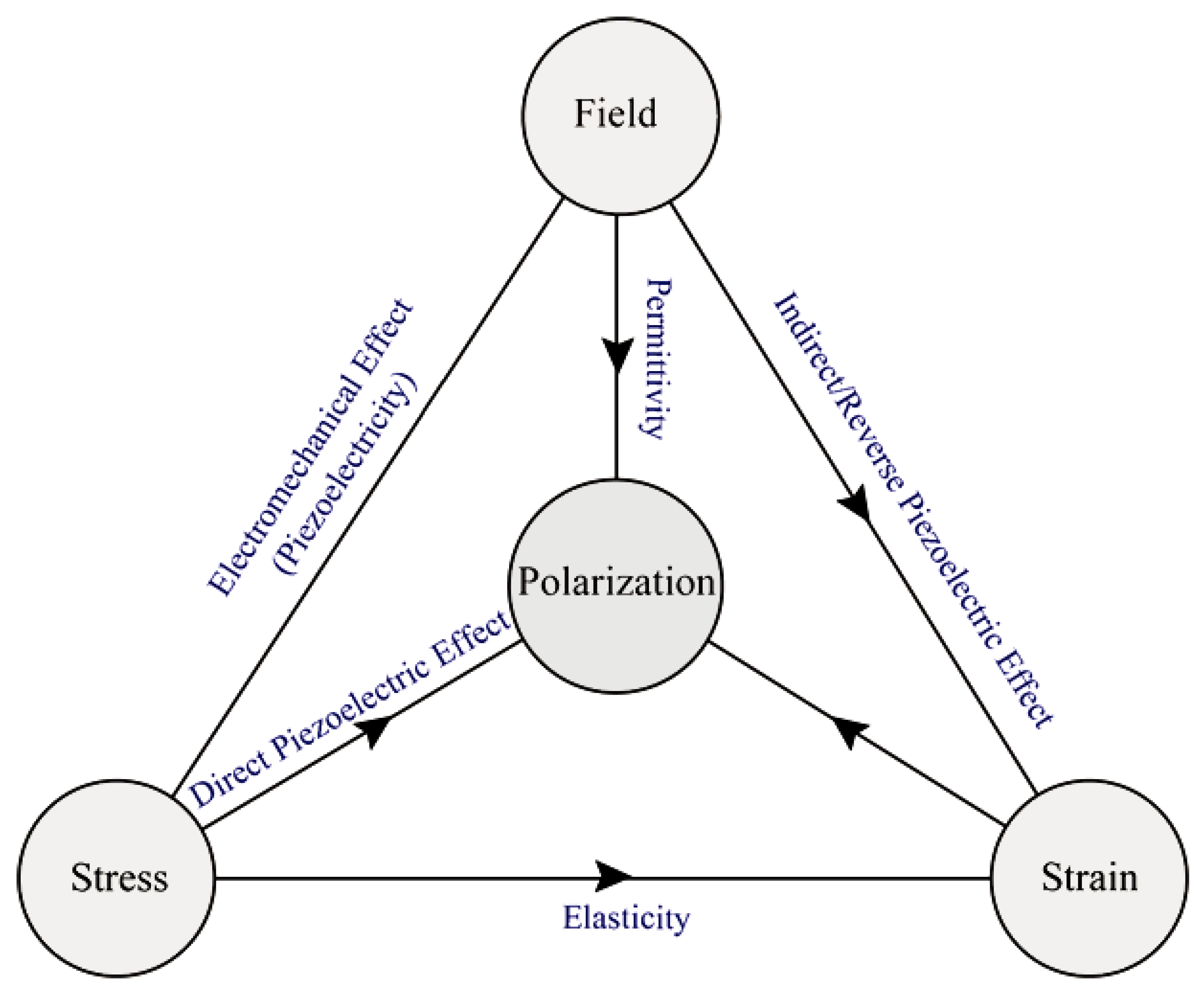
4.3. Piezoelectric New Properties
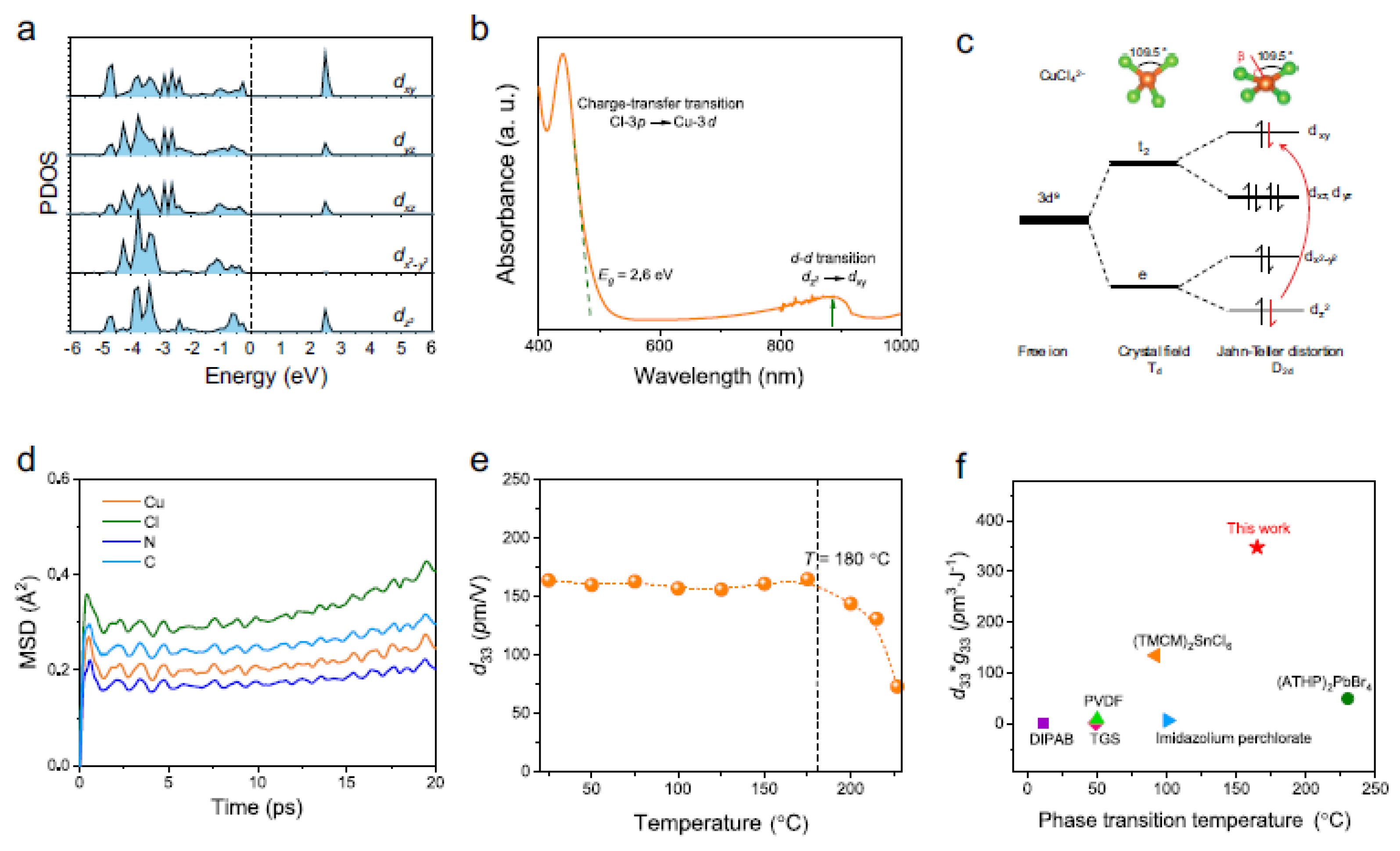
4.3.1. Origin of Piezoelectricity
4.3.2. Enhancing Halide Perovskite Piezoelectricity
4.3.3. Constructing Low Loss Halide Perovskite Piezoelectric
4.3.4. Essential Issues during Studying Piezoelectric Properties
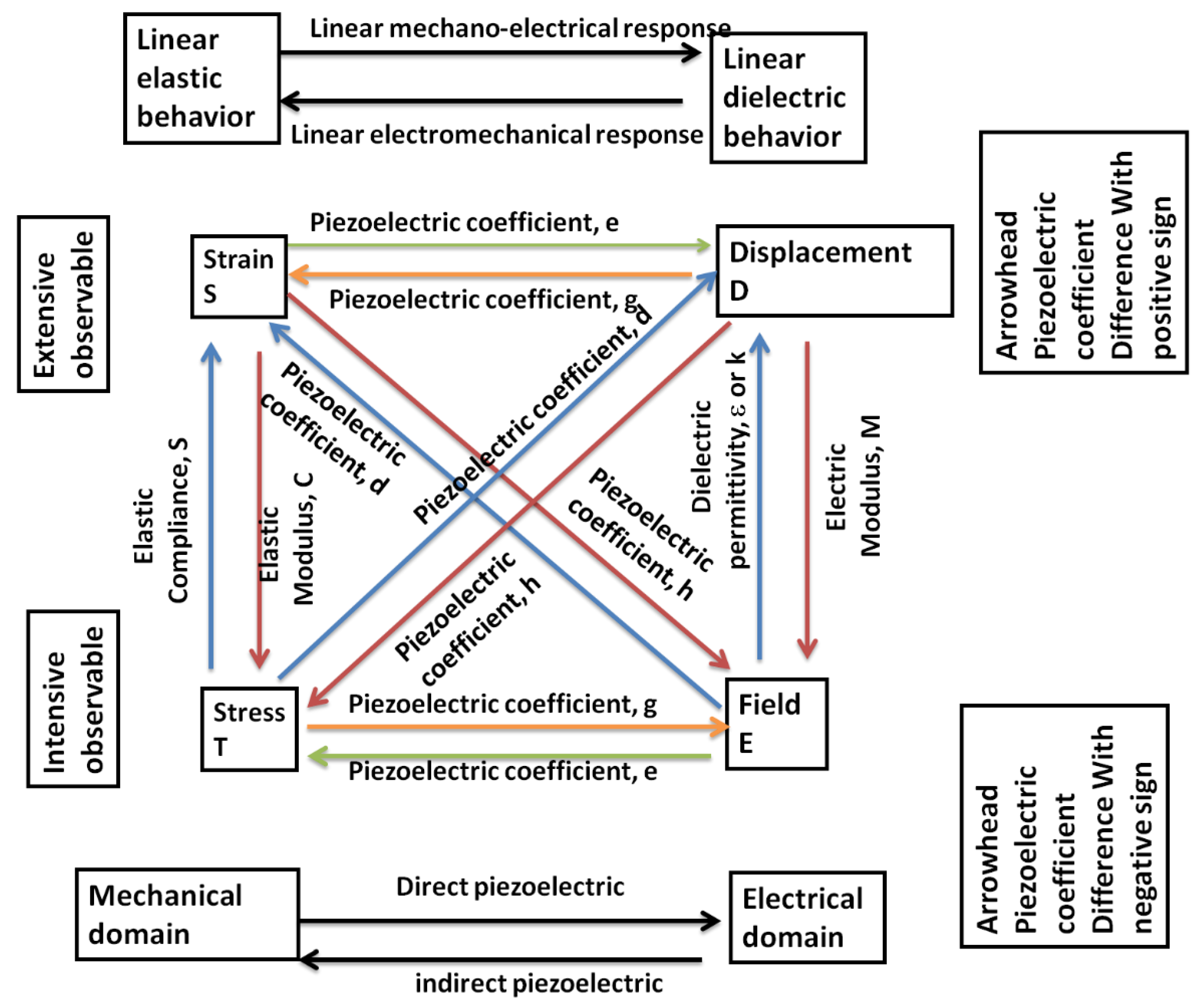
4.3.5. Measurement of Piezoelectric Coefficients
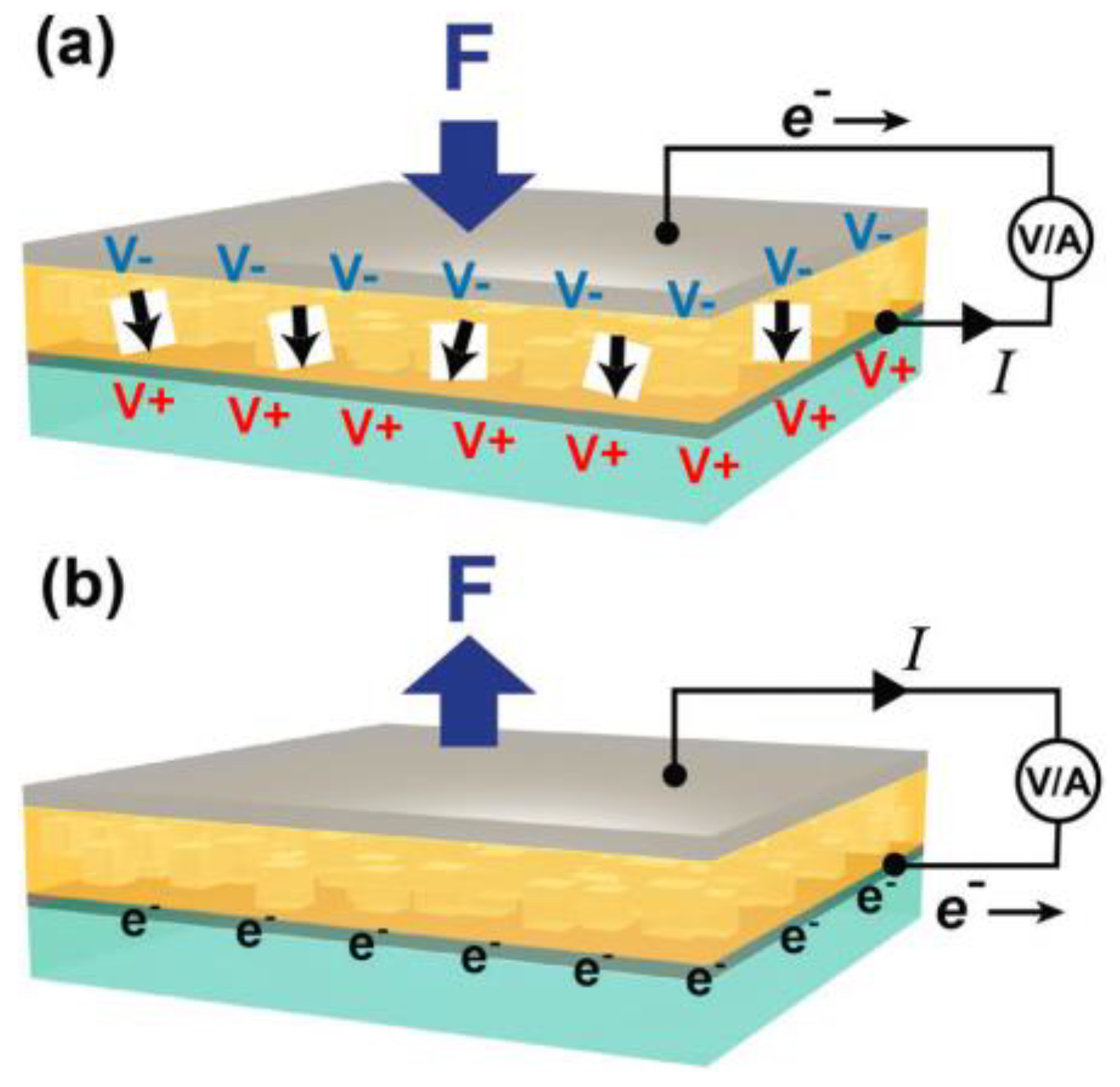
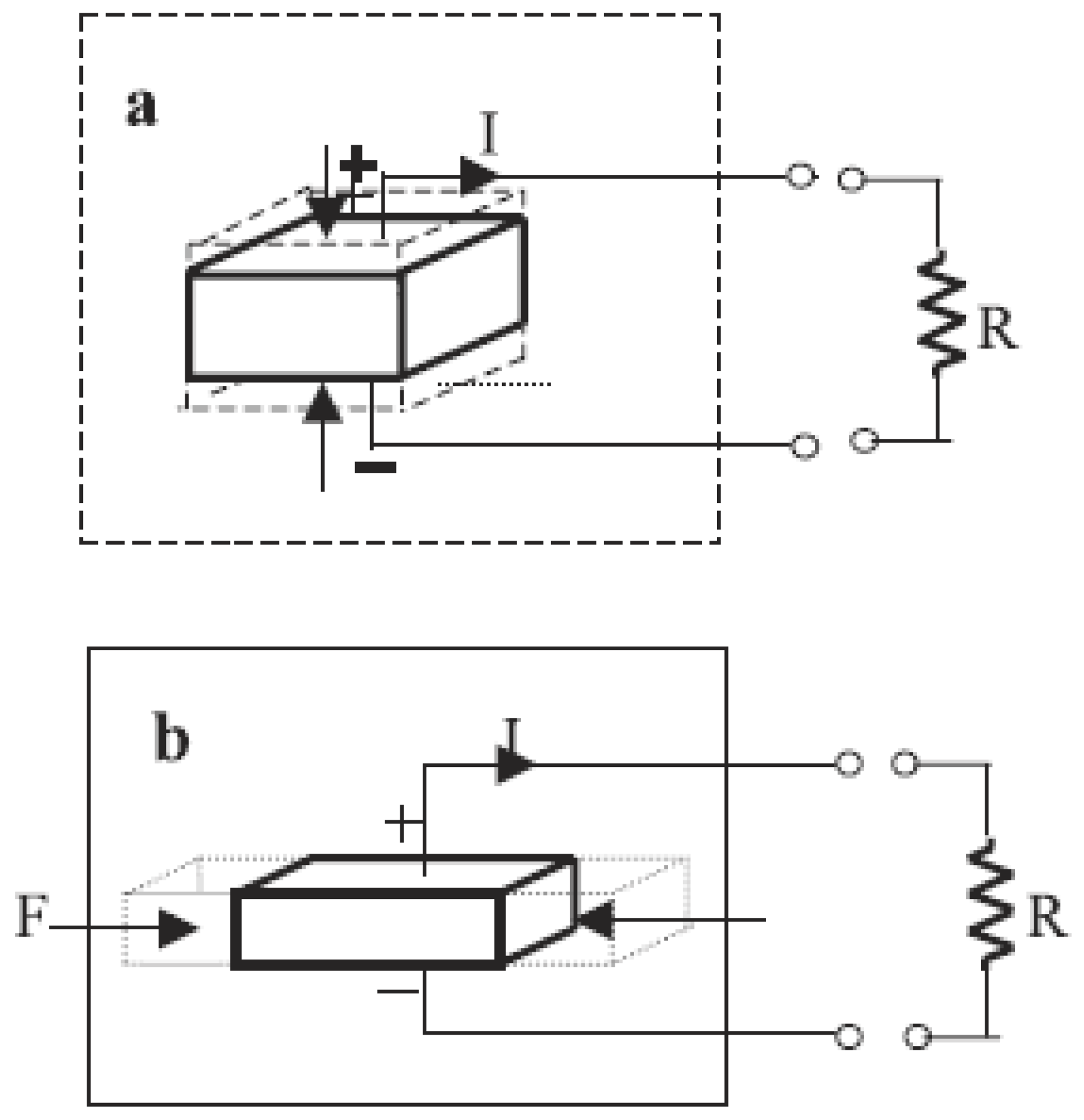
4.3.6. Piezoelectric Effects
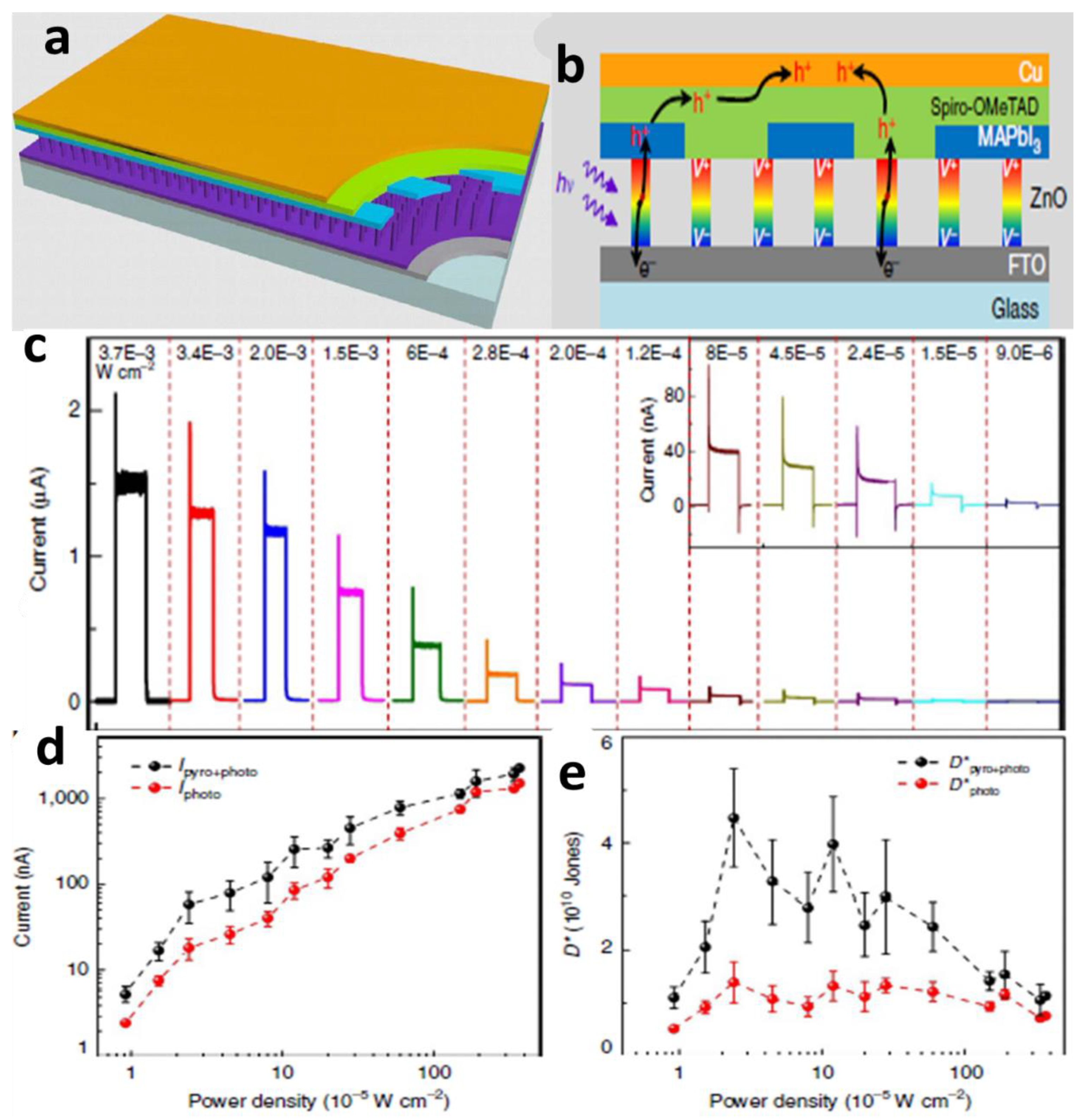
4.4. Pyroelectric New Properties
4.4.1. Pyroelectric Effect
4.4.2. Non-Centrosymmetry and Spontaneous Polarization
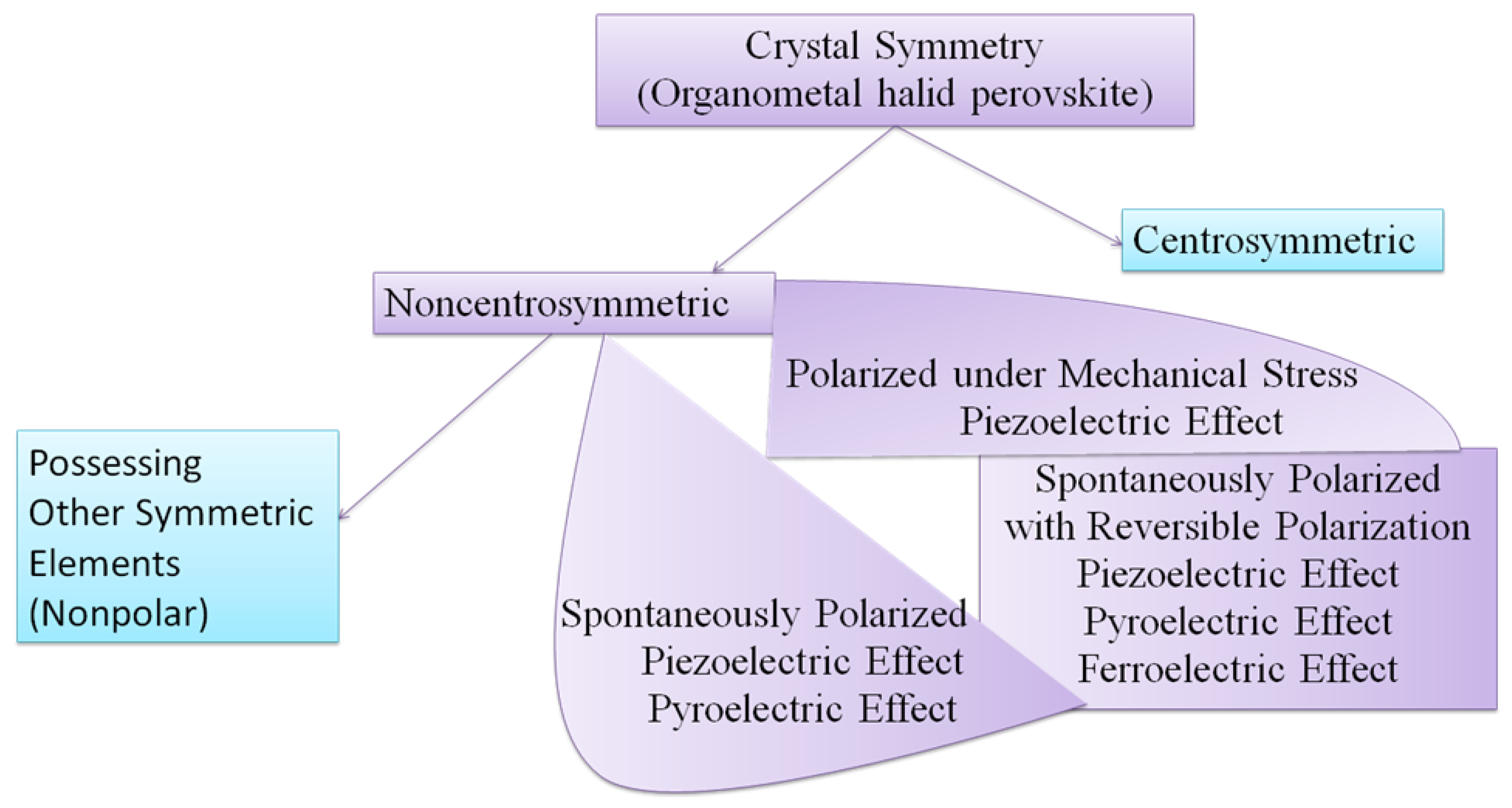
4.4.3. Strain Properties
4.5. Thermoelectric Properties
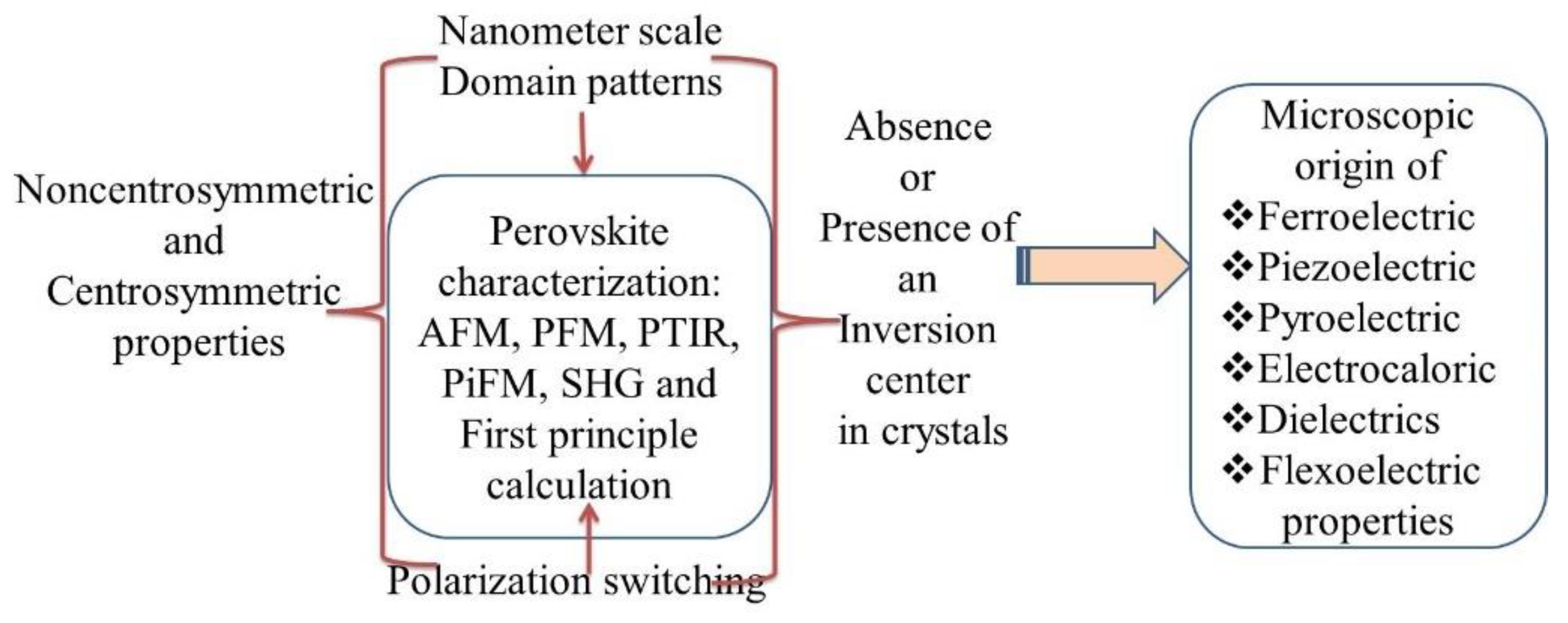
5. Nanometer Scale Domain Characterization
5.1. First-Principles Calculations
5.2. Atomic force Microscopy
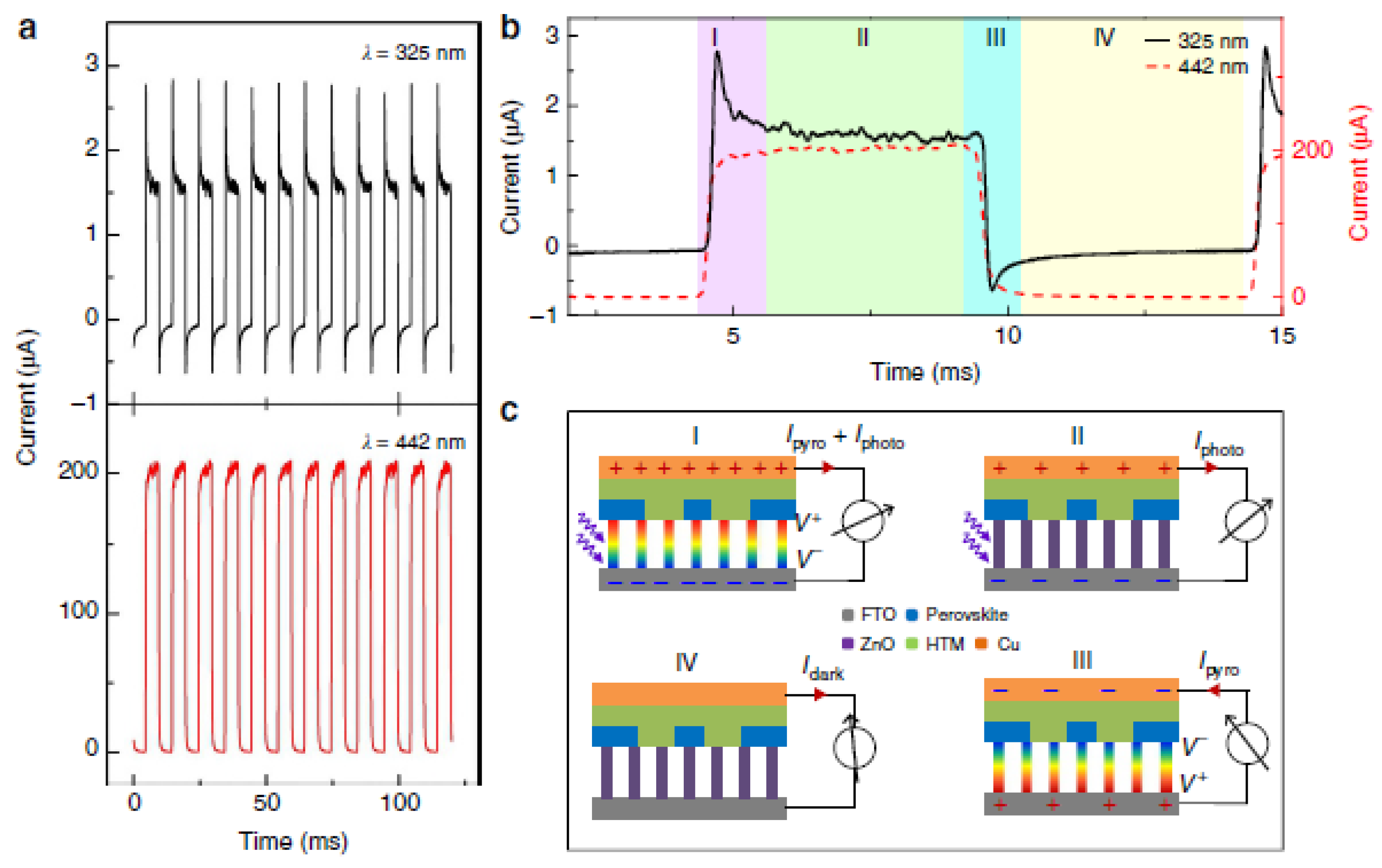
5.3. Photo Induced Force Microscope
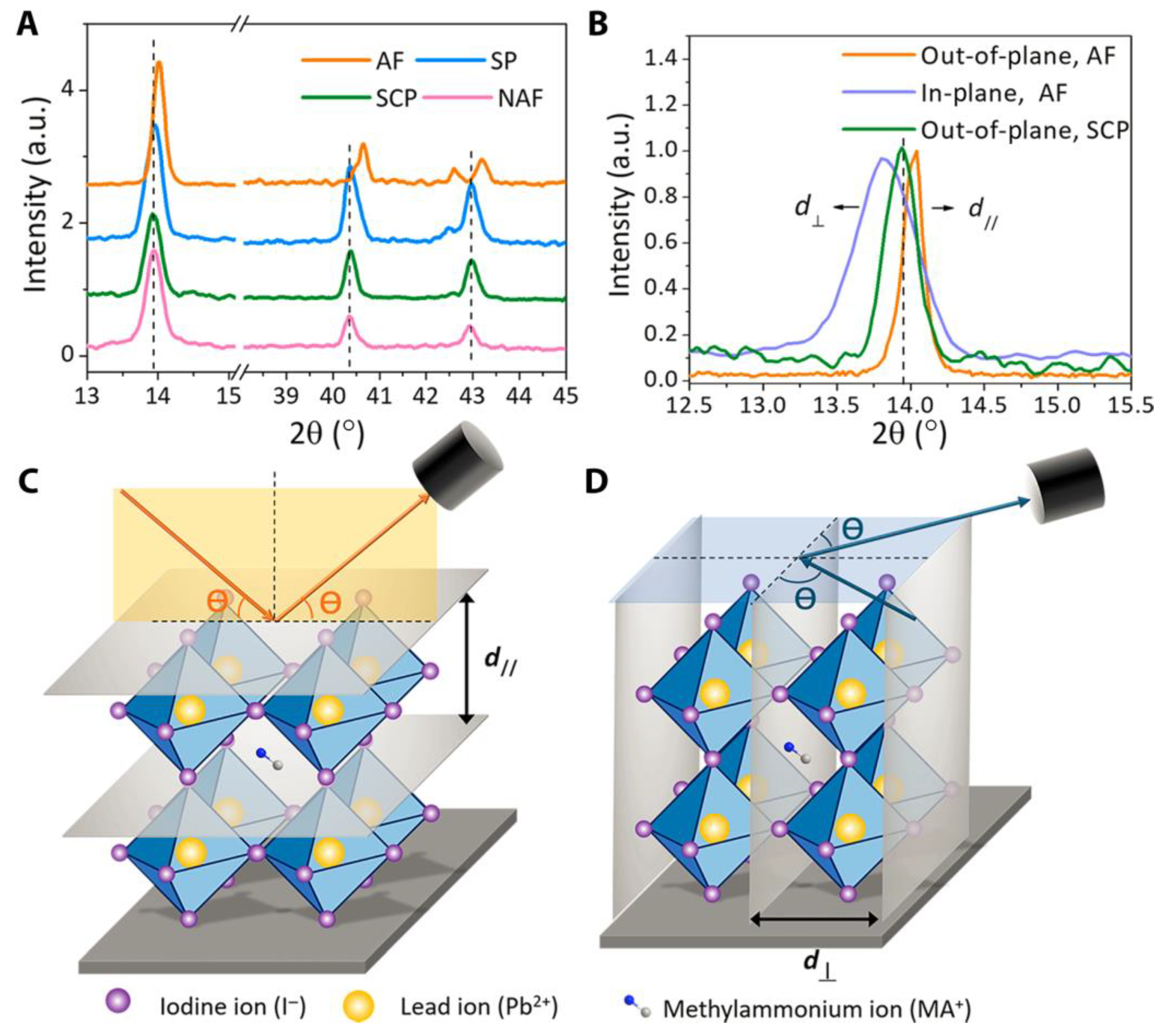
5.4. Visualizing Nanometer-Scale Domain Patterns
5.5. Photothermal Induced Resonance
5.6. Differentiating Noncentrosymmetric and Centrosymmetric Crystals
5.7. Identification of Inversion Center and Non-Centrosymmetry
5.8. Identification of the Polar Crystallographic Orientation
6. New Application Trends beyond Photovoltaic
6.1. Electrical Properties and Corresponding Applications
6.2. Structure Preference of Halide Perovskite Nanogenerators
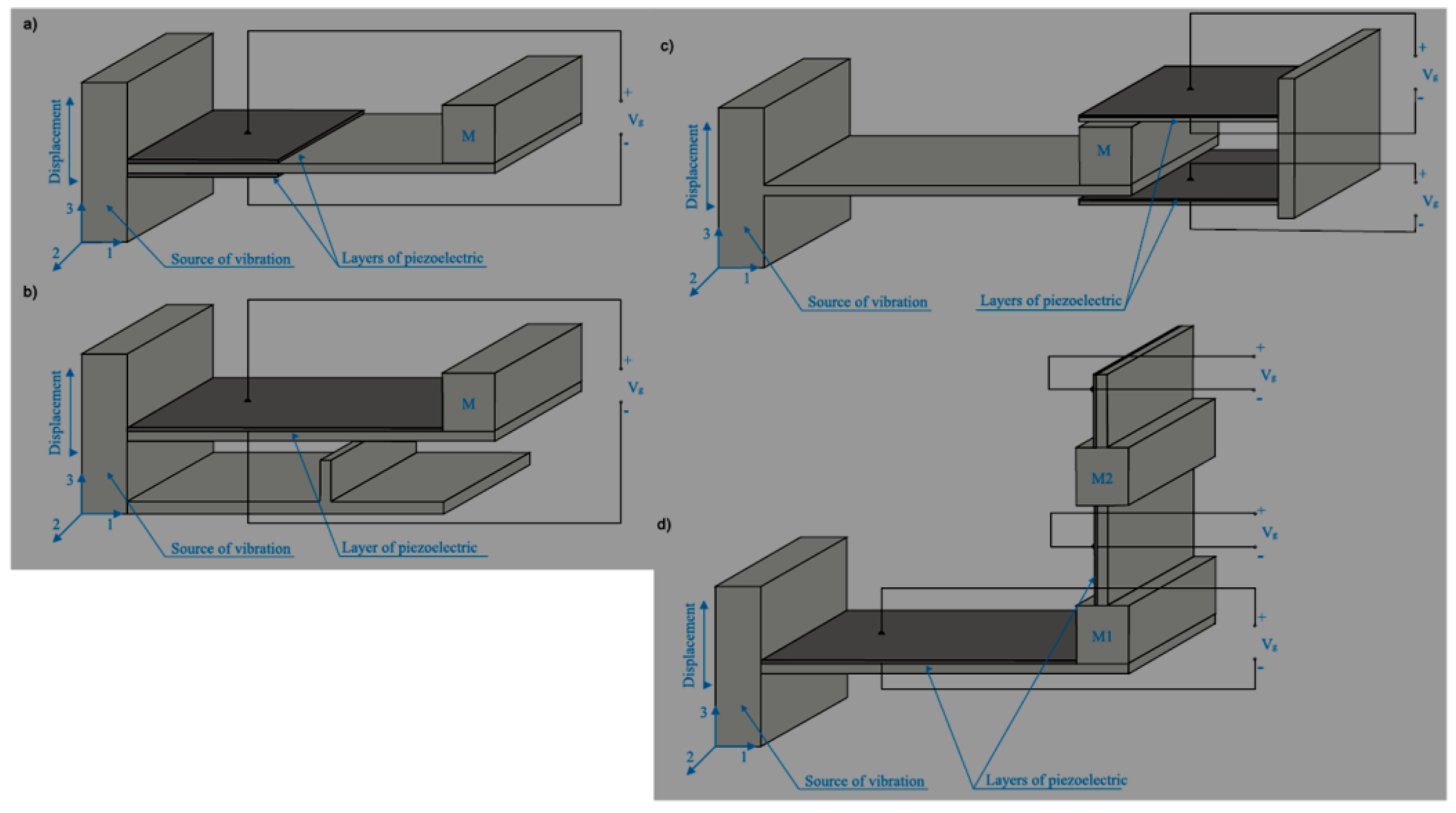
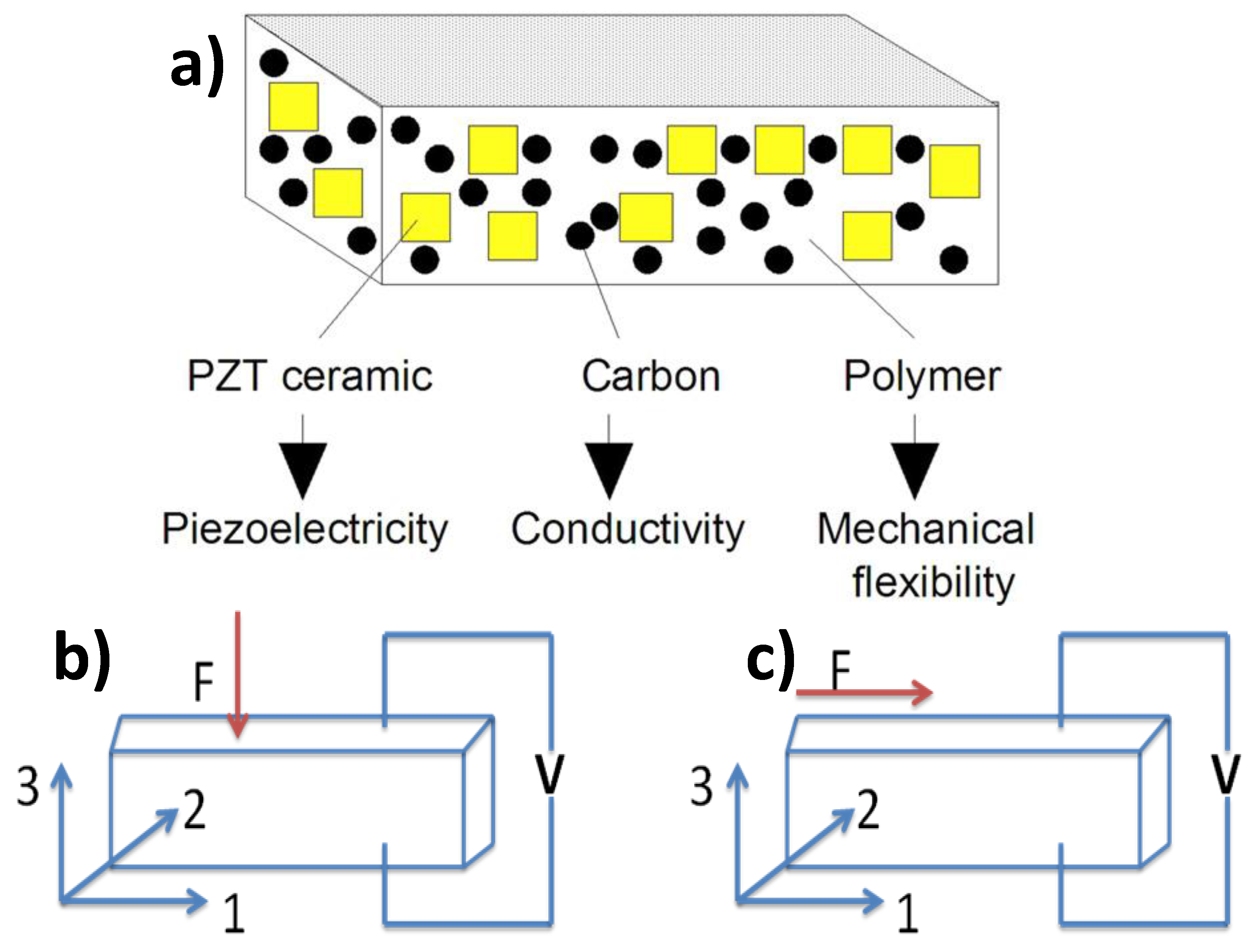
- beam made of the base material, with no piezoelectric properties, on which there is one (unimorph) or two piezoelectric material layers (bimorph). Generator with two plates of PZT ceramics (bimorph) is presented in Figure 17a,
- beam with an additional element influencing the increase of stresses in the piezoelectric material layers. An example of generator with one piezoelectric layer and an additional element is presented in Figure 17b,
- beam without piezoelectric material layers with the additional setup containing a piezoelectric material. An example of a generator of this type is presented in Figure 17c,
6.3. Expected Piezoelectric Energy Conversion from Perovskite Materials
6.4. Constructing Halide Perovskite Piezoelectric Dampers
6.5. Constructing Halide Perovskite Piezoelectric Energy Harvesters
6.6. A Self-Charging Power Unit and Wireless Electronic Applications
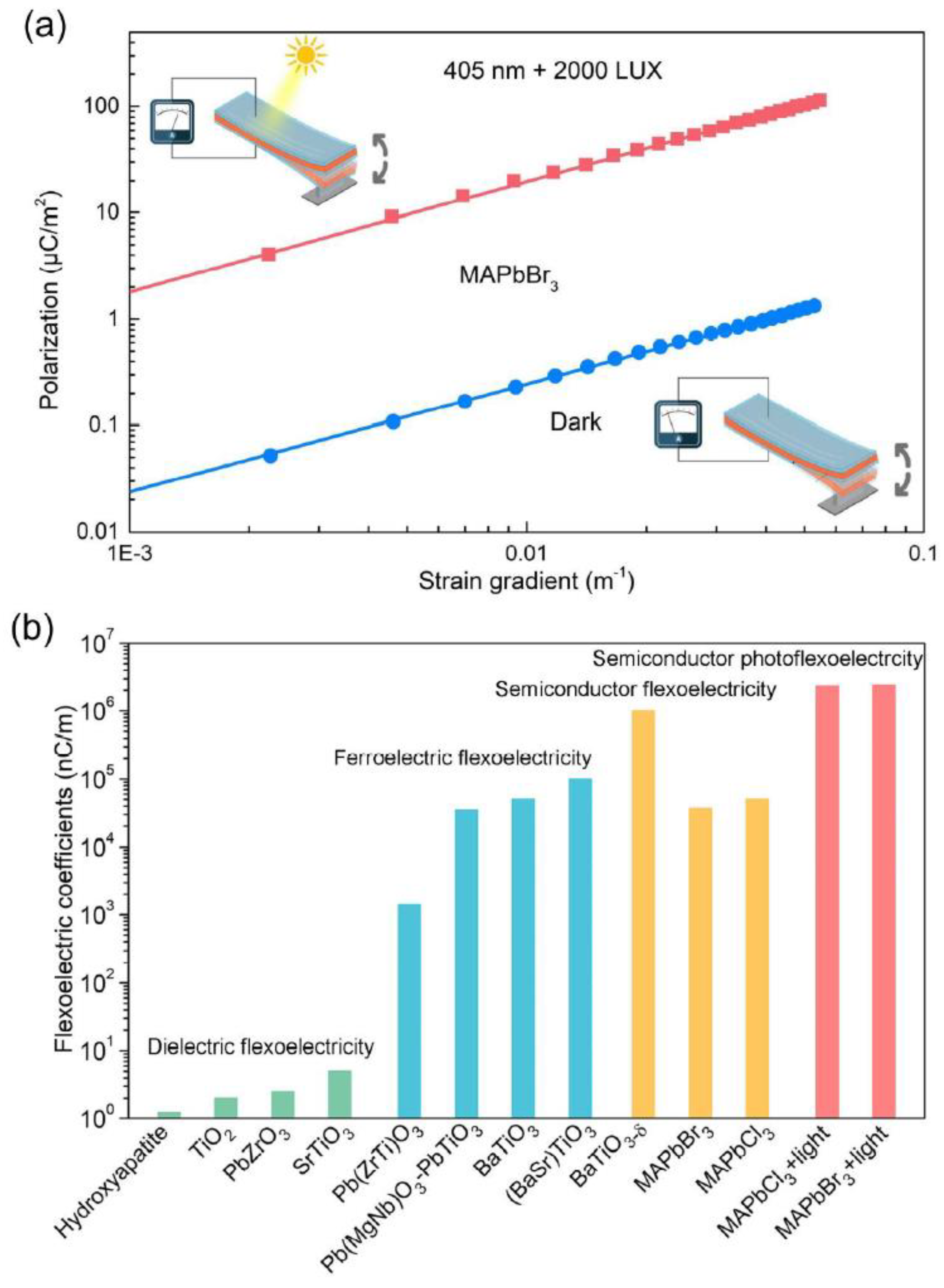
6.7. Nano-Plasmonic Sensing and Photoflexoelectric Effect
7. Big Challenges for Halide Perovskite Functionalization
7.1. Lattice Instability and Subtle Steadiness between the Short-Range Repulsions
7.2. The Influence of Nanoscale Defects
7.3. Surface and Bulk Effect
7.4. Materials Degradation Effect
8. Concluding Remark
Contributions
Data availability
Acknowledgement
Competing Interests
References
- A. Al-Ashouri, E. Köhnen, B. Li, A. Magomedov, H. Hempel, P. Caprioglio, J. A. Márquez, A. B. Morales Vilches, E. Kasparavicius, J. A. Smith, N. Phung, D. Menzel, M. Grischek, L. Kegelmann, D. Skroblin, C. Gollwitzer, T. Malinauskas, M. Jošt, G. Matič, B. Rech, R. Schlatmann, M. Topič, L. Korte, A. Abate, B. Stannowski, D. Neher, M. Stolterfoht, T. Unold, V. Getautis and S. Albrecht, Science, 2020, 370, 1300-1309.
- Y. Y. a. S. Y. e. a. Xiao Z, Nat Mater, 2015, 14, 193–198.
- A. Richter, M. Hermle and S. W. Glunz, IEEE Journal of Photovoltaics, 2013, 3, 1184-1191.
- L. Jonathan, L. J. Diguna, O. Samy, M. Muqoyyanah, S. Abu Bakar, M. D. Birowosuto and A. El Moutaouakil, Polymers, 2022, 14, 1059.
- J. H. S. DeWolf, S.-J. Moon, P. Löper, B. Niesen, M. Ledinsky, F.-J. Haug, J.-H. Yum, and C. Ballif,, J. Phys. Chem. Lett., 2014, 5, 1035.
- Y. Y. Y. Yang, M. Yang, S. Choi, K. Zhu, J. M. Luther, and M. C. Beard, , Nat. Commun., 2015, 6, 7961.
- A. M. A. Miyata, P. Plochocka, O. Portugall, J. T.-W.Wang, S. D. Stranks, H. J. Snaith, and R. J. Nicholas, , Nat. Phys., 2015, 11, 582.
- G. E. E. C. Wehrenfennig, M. B. Johnston, H. J. Snaith, and L. M. Herz, , Adv. Mater., 2014, 26, 1584.
- K. T. B. J. M. Frost, F. Brivio, C. H. Hendon, M. van Schilfgaarde, and A. Walsh, , Nano Letters, 2014, 14, 2584.
- F. Z. S. Liu, I. Grinberg, and A. M. Rappe, , Journal of Physical Chemistry Letters 2016, 7, 1460.
- A. G. M. Coll, E. M. Marza, O. Almora, G. G. Belmonte, M. C. Quiles, J. Bisquert, , J. Phys. Chem. Lett., 2015, 6, 1408.
- G. S. H. D. Seol, C. Bae, H. Shin, H. S. Jung, and Y. Kim, , Journal of Materials Chemistry A, 2015, 3, 20352.
- J. F. S. Q. F. Dong, Y. J. Fang, Y. C. Shao, S. Ducharme, and J. S. Huang, , Advanced Materials,, 2016, 28, 2816.
- H. L. R. Ding, X. Zhang, J. Xiao, R. Kishor, H. Sun, B. Zhu, G. Chen, F. Gao, X. Feng, J. Chen, X. Chen, X. Sun, and Y. Zheng, , Advanced Functional Materials, 2016, 26, 7708.
- T.-V. D. Y.-J. Kim, H.-J. Choi, B.-J. Park, J.-H. Eom, H.-A. Song, D. Seol, Y. Kim, S.-H. Shin, J. Nah, and S.-G. Yoon,, Journal of Materials Chemistry A 2016, 4, 756.
- Q. D. E. Strelcov, T. Li, J. Chae, Y. Shao, Y. Deng, A. Gruveman, J. Huang, and A. Centrone, , , Sci. Adv. accepted, 2016.
- B. Huang, Z. Liu, C. Wu, Y. Zhang, J. Zhao, X. Wang and J. Li, National Science Review, 2021, 8.
- L. Y. Y. Zhou, S. W. Wang, Z. L. Ku, H. J. Fan, D. Schmidt, A. Rusydi, L. Chang, L. Wang, P. Ren, L. F. Chen, G. L. Yuan, L. Chen, and J. L. Wang, , Nat Commun, 2016, 7.
- K. T. B. J. M. Frost, A. Walsh,, APL Mater., 2014, 2, 081506.
- F. Z. S. Liu, N. Z. Koocher, H. Takenaka, F. Wang, and A. M. Rappe,, J. Phys. Chem. Lett., 2015, 6, 693.
- D. A. E. T. M. Brenner, L. Kronik, G. Hodes, and D. Cahen, , Nat. Rev. Mater., 2016, 1, 15007.
- D. Li, H. Wu, H. C. Cheng, G. Wang, Y. Huang and X. Duan, ACS Nano, 2016, 10, 6933-6941.
- R. Singh and M. Parashar, in Soft-Matter Thin Film Solar Cells: Physical Processes and Device Simulation, eds. J. Ren and Z. Kan, AIP Publishing LLC, p. 0. [CrossRef]
- K.-G. L. Hobeom Kim† , Tae-Woo Lee*, Energy Environ. Sci., 2015, 00, 1-3.
- D. H. S. Jin Hyuck Heo , Hye Ji Han , Seong Yeon Kim , Jun Ho Kim , Dasom Kim , Hee Won Shin , Tae Kyu Ahn , Christoph Wolf , Tae-Woo Lee , and Sang Hyuk Im* Adv. Mater. , 2015.
- S. I. Ryotaro Inoue, Ryota Imura, Yuuki Kitanaka, Takeshi Oguchi, Yuji Noguchi & Masaru Miyayama, Scientific RepoRts, 2015, 5, 14741.
- a. D. K. Hyeon Han, a Sangmin Chae,b Jucheol Park,c Sang Yeol Nam,c,d Mingi Choi,e Kijung Yong,e Hyo Jung Kim,b Junwoo Son,*a and Hyun Myung Jang*a, Nanoscale, 2018.
- F. Z. Lu You1*, Liang Fang3*, Yang Zhou1, Liang Z. Tan2, Zeyu Zhang4, Guohong Ma4, Daniel Schmidt5‡, Andrivo Rusydi5, Le Wang1§, Lei Chang1, Andrew M. Rappe2¶, Junling Wang1¶, Sci. Adv., 2018, 4.
- a. J. S. Bo Chen, b Xiaojia Zheng,*a Yuan Zhou,a Kai Zhu,c Shashank Priya*a, J. Mater. Chem. A, 2015. [CrossRef]
- X. S. Jingjiao Zhang1, Mingrong Shen1, Zhihua Dai1, Lingjun Zhang1, Xiyun He2, Wenxiu Cheng2, Mengyu Cao1 & Guifu Zou1, Scientific Reports, 3, 2109.
- I. B. W. Padinhare Cholakkal Harikesh, Biplab Ghosh, Rohit Abraham John, Stener Lie, Krishnamoorthy Thirumal, Lydia Helena Wong, Tze Chien Sum, Subodh Mhaisalkar, and Nripan Mathews*, Adv. Mater., 2018, 1802080.
- C. R. V. Fridkin, 2001, 46, 654-658.
- V. 18 L. Pintilie, G. Le Rhun and M. Alexe, , J. Appl. Phys., , 2007, 101, 064109.
- J. Oh, Yuan, H. C. & Branz, H. M. , Nat. Nanotechnol., 2012, 7, 743-748.
- B. G. t. O’Regan, M. , Nature , , 1991, 353, 737-740.
- S. R. Wenham, Green, M. A., Watt, M. E. & Corkish, R. , Earthscan Ltd, , 2006.
- D. G. McGehee, Nature Photonics, 2009, 3, 250-252.
- H. S. Nalwa, American Scientific Publishers, 2008.
- a. J. S. Bo Chen, b Xiaojia Zheng,*a Yuan Zhou,a Kai Zhu,c Shashank Priya*a, J. Mater. Chem. A 2012, 00, 1-3.
- B. Chen, J. Shi, X. Zheng, Y. Zhou, K. Zhu and S. Priya, Journal of Materials Chemistry A, 2015, 3, 7699-7705.
- S. M. Young, F. Zheng and A. M. Rappe, Phys. Rev. Lett., 2012, 109, 236601.
- F. Z. S. M. Young, A. M. Rappe, , Phys. Rev. Lett., 2012, 109, 236601.
- V. D. L. A. M. Glass, T. J. Negran, Appl. Phys. Lett., 1974, 25, 233.
- J. S. S. Y. Yang, S. J. Byrnes, P. Shafer, C.-H. Yang, M. D. Rossell, P. Yu, Y.-H. Chu, J. F. Scott, J. W. Ager III, L. W. Martin, R. Ramesh, , Nat. Nanotechnol., 2010, 5, 143-147.
- A. R. C. A. Bhatnagar, Y. H. Kim, D. Hesse, M. Alexe, , Nat. Commun., 2013, 4, 2835.
- H. Y. L. Ye, W. Q.; Hu, C. L.; Zhang, Y.; You, Y. M.; Mao, J. G.; Li, P. F.; Xiong, R. G. , Adv. Mater. , 2016, 28 (13), 2579−2586.
- H.-Y. W. Zhang, Z.; Li, P.-F.; Tang, Y.-Y.; Liao, W.-Q.; Ye, H.-Y.; Cai, H.; Xiong, R.-G. , Angew. Chem., Int. Ed. , 2018 57 (2), 526−530.
- W. T. a. H. B. e. a. Ahmadi M, AdvMater 2017, 29, 1605242.
- Evgheni Strelcov, 2* Qingfeng Dong,3* Tao Li,4* Jungseok Chae,1,2*†‡ Yuchuan Shao,3,4 Yehao Deng,3,4 Alexei Gruverman,4§ Jinsong Huang,3§ Andrea Centrone1§ Sci. Adv., 2017, 3, e1602165.
- G. R. Gou, J. M. , Adv. Mater. Interfaces, 2014, 1, 1400042.
- M. B. Yuheng Li, Joseph Wong, and Kesong Yang, J. Phys. Chem. C,, 2017.
- Y. Chen, Y. Lei, Y. Li, Y. Yu, J. Cai, M.-H. Chiu, R. Rao, Y. Gu, C. Wang, W. Choi, H. Hu, C. Wang, Y. Li, J. Song, J. Zhang, B. Qi, M. Lin, Z. Zhang, A. E. Islam, B. Maruyama, S. Dayeh, L.-J. Li, K. Yang, Y.-H. Lo and S. Xu, Nature, 2020, 577, 209-215.
- R. A. Surmenev and M. A. Surmeneva, Materials Today, 2023, 67, 256-298.
- B. Yang, D. Bogachuk, J. Suo, L. Wagner, H. Kim, J. Lim, A. Hinsch, G. Boschloo, M. Nazeeruddin and A. Hagfeldt, Chemical Society Reviews, 2022. [CrossRef]
- S. B. Nazir, M.; Yang, K. , Appl. Phys. Lett., 2014, 105, 141602-141605.
- K. S. Yang, W.; Wang, S.; Nardelli, M. B.; Curtarolo, S. , Nat. Mater., 2012, 11, 614-619.
- M.-J. Choi, J. W. Lee and H. Jang, Advanced materials (Deerfield Beach, Fla.), 2023, e2308827. [CrossRef]
- Y. D. Jingjing Zhao, 1 Haotong Wei,1 Xiaopeng Zheng,1 Zhenhua Yu,1 Yuchuan Shao,1 Jeffrey E. Shield,1 Jinsong Huang1,2*, Sci. Adv. , 2017, 3, eaao5616.
- D. B. Kim, J. Y. Kim, J. Han and Y. S. Cho, Nano Energy, 2024, 125, 109551.
- N. Muralidharan, R. Carter, L. Oakes, A. P. Cohn and C. L. Pint, Scientific Reports, 2016, 6, 27542.
- S. S. Won, H. Seo, M. Kawahara, S. Glinsek, J. Lee, Y. Kim, C. K. Jeong, A. I. Kingon and S.-H. Kim, Nano Energy, 2019, 55, 182-192.
- M.-J. Choi, J.-W. Lee and H. W. Jang, Advanced Materials, 2024, 36, 2308827.
- D. Liu, D. Luo, A. N. Iqbal, K. W. P. Orr, T. A. S. Doherty, Z.-H. Lu, S. D. Stranks and W. Zhang, Nature Materials, 2021, 20, 1337-1346.
- W. Meng, K. Zhang, A. Osvet, J. Zhang, W. Gruber, K. Forberich, B. Meyer, W. Heiss, T. Unruh, N. Li and C. J. Brabec, Joule, 2022, 6, 458-475.
- J. Liu, M. P. Garman, J. Dong, B. van der Zee, L. Qiu, G. Portale, J. C. Hummelen and L. J. A. Koster, ACS Applied Energy Materials, 2019, 2, 6664-6671.
- X. Yu, Y. Hou, M. Zheng, J. Yan, W. Jia and M. Zhu, Journal of the American Ceramic Society, 2019, 102, 275-284.
- Y. Zhong, Y.-E. Huang, T. Deng, Y.-T. Lin, X.-Y. Huang, Z.-H. Deng and K.-Z. Du, Inorg. Chem., 2021, 60, 17357-17363.
- E. Arkan, A. Karabiber, M. A. Topçu, Z. Kinas, A. Sarilmaz, S. S. Ozel and F. Ozel, Surfaces and Interfaces, 2023, 37, 102683.
- M. Martín-González, O. Caballero-Calero and P. Díaz-Chao, Renewable and Sustainable Energy Reviews, 2013, 24, 288-305.
- X. Yu, L. Zhu, X. Li, J. Zhao, T. Wu, W. Yu and W. Li, Materials, 2023, 16, 1778.
- W. Yao, L. Shen, P. Liu, C. Liu, J. Xu, Q. Jiang, G. Liu, G. Nie and F. Jiang, Materials Chemistry Frontiers, 2020, 4, 597-604.
- N. K. Sinha, P. Roy, D. S. Ghosh and A. Khare, Materials Today: Proceedings, 2023, 83, 6-13.
- S. Jiang, M. Liu, D. Zhao, Y. Guo, J. Fu, Y. Lei, Y. Zhang and Z. Zheng, Physical Chemistry Chemical Physics, 2024, 26, 4794-4811.
- C. He, J. Qiu, Z. Mu and X. Liu, CCS Chemistry, 2023, 5, 1961-1972.
- Y. Lin, Y. Zhong, Y. Lin, J. Lin, L. Pang, Z. Zhang, Y. Zhao, X.-Y. Huang and K.-Z. Du, Frontiers of Optoelectronics, 2024, 17, 6.
- T. J. C.-B. Jacobsson, J.-P.; Pazoki, M.; Saliba, M.; Schenk, K.; Gratzel, M.; Hagfeldt, A. , Energy Environ. Sci., 2016, 9, 1706-1724.
- W.-L. L. Yan, G.-H.; Liu, F. , J. Phys. Chem. C , , , 2016, 120, 17972-17977.
- L. V. Atourki, E.; Mar , B.; Mollar, M.; Ahsaine, H. A.; Bouabid, K.; Ihlal, A. , Appl. Sur. Sci., 2016, 371.
- D. S. D. a. B. P. e. a. Stroppa A, Nat Commun 2014, 5 5900.
- J. P. a. B. P. e. a. Stroppa A, Angew Chem, 2011, 123, 5969–5972.
- B. P. a. J. P. e. a. Stroppa A, Adv Mater 2013, 25, 2284–2290.
- S. A. a. J. P. e. a. Di Sante D, J Am Chem Soc 2013, 135, 18126–18130.
- S. Bhatti, C. Ma, X. Liu and S. N. Piramanayagam, IEEE Transactions on Magnetics, 2019, PP.
- S. Pruvost, A. Hajjaji, L. Lebrun, D. Guyomar and Y. Boughaleb, The Journal of Physical Chemistry C, 2010, 114, 20629-20635.
- A. R. Balakrishna and J. E. Huber, Smart Materials and Structures, 2016, 25, 104001.
- S. K. b. Wei-Jian Xu a, Andrei Kholkin b,c,⇑, João Rocha a, Coordination Chemistry Reviews, 2019, 387, 398–414.
- K. S. a. K. A. e. a. Xu WJ, Coord Chem Rev 2019, 387 398–414.
- T. R. S. S.-E. Park, J. Appl. Phys., 1997, 82, 1804-1811.
- D. G. S. J. Mannhart, Science, 2010, 327, 1607-1611.
- Y. I. H. Y. Hwang, M. Kawasaki, B. Keimer, N. Nagaosa, Y. Tokura, , Nat. Mater., 2012, 11, 103-113.
- C. M. B. J. A. Mundy, M. E. Holtz, J. A. Moyer, H. Das, A. F. Rébola, J. T. Heron, J. D. Clarkson, S. M. Disseler, Z. Liu, A. Farhan, R. Held, R. Hovden, E. Padgett, Q. Mao, H. Paik, R. Misra, L. F. Kourkoutis, E. Arenholz, A. Scholl, J. A. Borchers, W. D. and R. R. Ratcliff, C. J. Fennie, P. Schiffer, D. A. Muller, D. G. Schlom, Nature, 2016, 537, 523-527.
- J.-M. L. S. Dong, S.-W. Cheong, Z. Ren, , Adv. Phys., 2015, 64, 519-626.
- D. V. M. Stengel, N. A. Spaldin, Nat. Mater., 2009, 8, 392-397.
- M. D. E. Bousquet, N. Stucki, C. Lichtensteiger, P. Hermet, S. Gariglio, J. M. Triscone, P. Ghosez, Nature, 2008, 452, 732-736.
- Y. L. Z. Y. L. Tang, X. L. Ma, A. Y. Borisevich, A. N. Morozovska, E. A. Eliseev, W. Y. Wang, Y. J. Wang, Y. B. Xu, Z. D. Zhang, S. J. Pennycook, , Science 2015, 348, 547-551.
- Y. Y. Kutes, L.; Zhou, Y.; Pang, S.; Huey, B. D.; Padture, N. P, J. Phys. Chem. Lett., 2014, 5, 3335−3339.
- F. Z. Shi Liu, Nathan Z. Koocher, Hiroyuki Takenaka, Fenggong Wang, and Andrew M. Rappe*, J. Phys. Chem. Lett. , 2015, 6, 693−699.
- Z. C. Deyang Chen, Qian He, James D. Clarkson, Claudy R. Serrao, Ajay K. Yadav, Mark E Nowakowski, Zhen Fan, Long You, Xingsen Gao, Dechang Zeng, Lang Chen, Albina Y. Borisevich, Sayeef Salahuddin, Jun-Ming Liu, and Jeffrey Bokor, Nano Lett., 2016.
- G. Arlt, J. Mat. Sci. , 1990, 25, 2655--2666.
- R. E. Newnham, Springer-Verlag, Berlin, 1975.
- W. R. Cook, J. Am. Ceram. Soc., 1956, 39, 17-19.
- Y. e. a. Kutes, J. Phys. Chem. Lett., 2014, 5, 3335−3339.
- R. Pandey, G. Sb, S. Grover, S. K. Singh, A. Kadam, S. Ogale, U. V. Waghmare, V. R. Rao and D. Kabra, ACS Energy Lett, 2019, 4, 1004-1011.
- S. Ippili, J. H. Kim, V. Jella, S. Behera, V.-H. Vuong, J.-S. Jung, Y. Cho, J. Ahn, I.-D. Kim, Y. H. Chang, H.-S. Kim and S.-G. Yoon, Nano Energy, 2023, 107, 108148.
- M. M. Rana, A. A. Khan, W. Zhu, M. F. A. Fattah, S. Kokilathasan, S. Rassel, R. Bernard, S. Ababou-Girard, P. Turban, S. Xu, C. Wang and D. Ban, Nano Energy, 2022, 101, 107631.
- Tie Zhang1, †, Ke Xu1,†, Jie Li1, Lei He 1, Da-Wei Fu2,∗, Qiong Ye1,∗ and Ren-Gen Xiong 1,∗, Natl Sci Rev 2023,, 10, nwac240.
- Z. H. a. C. X. e. a. Liu HY, J Am Chem Soc 2020, 142, 15205–15218.
- V. Jella, S. Ippili and S.-G. Yoon, ACS Applied Electronic Materials, 2020, 2, 2579-2590.
- L. F. a. B. S. e. a. Breternitz J, AngewChem Int Ed 2020, 59 424–428.
- Peng Gao1, Heng-Jui Liu3, Yen-Lin Huang3, Ying-Hao Chu3,4, Ryo Ishikawa5, Bin Feng5, Ying Jiang2,6, Naoya Shibata5, En-Ge Wang2,6 & Yuichi Ikuhara5,7,8, Nat. Commun., 2016, 7, 11318.
- L. K. a. L. Z. G. e. a. An LC, Small, 2021, 17.
- T. Y. a. L. P. e. a. Liao WQ, J Am Chem Soc 2018, 140, 3975–3980.
- M. S. Bokdam, T.; Stroppa, A.; Picozzi, S.; Sarma, D. D.; Franchini, C.; Kresse, G., , Sci. Rep., 2016, 6, 28618.
- Jia-Bin Li1, 3,7, Zhi-Kang Jiang1,2,7, Rui Wang 4,5,6, Jin-Zhu Zhao 1,2,6✉ and Ruiqiang Wang1,2✉, npj Computational Materials 2023, 9, 62.
- J. H. N. N.J. Jeon, W.S. Yang, Y.C. Kim, S. Ryu, J. Seo, S.I. Seok, , Nature, 2015, 517, 476-480.
- F. Igbari, R. Wang, Z.-K. Wang, X.-J. Ma, Q. Wang, K.-L. Wang, Y. Zhang, L.-S. Liao and Y. Yang, Nano Letters, 2019, 19, 2066-2073.
- J. Zhou, Z. Xia, M. S. Molokeev, X. Zhang, D. Peng and Q. Liu, Journal of Materials Chemistry A, 2017, 5, 15031-15037.
- K. A. Bush, K. Frohna, R. Prasanna, R. E. Beal, T. Leijtens, S. A. Swifter and M. D. McGehee, ACS Energy Lett, 2018, 3, 428-435.
- E. T. M. Matthew R. Linaburg, Jackson D. Majher, and Patrick M. Woodward*, Chem. Mater., 2017, 29, 3507−3514.
- M. B. Gray, E. T. McClure and P. M. Woodward, Journal of Materials Chemistry C, 2019, 7, 9686-9689.
- Y. e. a. Liu, Nat. Mater. , 2018, 17, 1013–1019.
- S. H. B. D. Lee, T. H. Kim, J.-G. Yoon, C. M. Folkman, C. B. Eom, T. W. Noh, , Phys. Rev., 2011, B 84, 125305.
- G. L. a. G. a. Chen C, Nat Commun 2019, 10.
- T. K. a. M. H. e. a. Huang PJ, J Am Chem Soc 2019, 141, 14520–14523.
- J. P. Even, L.; Jancu, J.-M.; Katan, C.,, J. Phys. Chem. Lett., 2013, 4, 2999-3005.
- E. T. B. Fedwa El-Mellouhi1, Asma Marzouk1, Sergey N Rashkeev1, Sabre Kais1,2,3 and Fahhad H Alharbi1,2, npj Computational Materials 2016, 16035.
- G. K. a. P. M. Woodward*, J. Mater. Chem., 2010, 20, 5785-5796.
- G. P. a. B. P. Uberuaga, JOURNAL OF APPLIED PHYSICS , , 2015, 117, 114103.
- A. M. Amat, E.; Ronca, E.; Quarti, C.; Umari, P.;Nazeeruddin, M. K.; Grätzel, M.; De Angelis, F. , Nano Lett., 2014, 14, 3608−3616.
- H. K. Jongseob Kim1, Mahesh Chandran3, Seung-Cheol Lee3,a), Sang Hyuk Im4, and Ki-Ha Hong5,b), APL Materials, 2018, 6, 084903.
- F. D. a. S. N. e. a. Passarelli JV, J Am Chem Soc 2018, 140, 7313–7323.
- B. S. Chen, J.; Zheng, X.; Zhou, Y.; Zhu, K.; Priya, S., , J. Mater. Chem. A, 2015, 3, 7699-7705.
- M. N. a. E. J. Katan C, Chem Rev 2019, 119, 3140–3192.
- S. X. a. Z. Z. e. a. Chen XG, J Am Chem Soc 2020 142, 10212–10218.
- M. G. Mączka, A.; Ptak, M.; Paraguassu, W.; da Silva, T. A.; Sieradzki, A.; Pikul, A. , Chem. Mater., 2017, 29 (5), 2264−2275.
- M. P. Mączka, M.; Gągor, A.; Stefańska, D.; Sieradzki, A. , Chem. Mater., 2019, 31 (20), 8563−8575.
- W. Q. Z. Liao, D. W.; Tang, Y. Y.; Zhang, Y.; Li, P. F.; Shi, P. P.; Chen, X. G.; You, Y. M.; Xiong, R. G. , Science 2019, 363 (6432),, 1206−1210.
- e. a. Rakita Y, Proc Natl Acad Sci USA, 2017, 114, E5504-E5512.
- J. M. Frost, K. T. Butler, F. Brivio, C. H. Hendon, M. van Schilfgaarde and A. Walsh, Nano Letters, 2014, 14, 2584-2590.
- C. D. a. J. H. Berlincourt DA, Physical Acoustics: Principles and Methods 1964, 1(Part A), 202–204.
- Z.-R. Gao, X.-F. Sun, Y.-Y. Wu, Y.-Z. Wu, H.-L. Cai and X. S. Wu, The Journal of Physical Chemistry Letters, 2019, 10, 2522-2527.
- B. Liu, M. Long, M.-Q. Cai, X. Hao and J. Yang, The Journal of Physical Chemistry C, 2018, 122, 17820-17824.
- F. Ke, J. Yan, S. Niu, J. Wen, K. Yin, H. Yang, N. R. Wolf, Y.-K. Tzeng, H. I. Karunadasa, Y. S. Lee, W. L. Mao and Y. Lin, Nature Communications, 2022, 13, 7067.
- S. Colella, E. Mosconi, P. Fedeli, A. Listorti, F. Gazza, F. Orlandi, P. Ferro, T. Besagni, A. Rizzo, G. Calestani, G. Gigli, F. De Angelis and R. Mosca, Chemistry of Materials, 2013, 25, 4613-4618.
- L. X. a. H. S. e. a. Guo W, Angew Chem Int Ed ;, 2020, 59, 13879–13884.
- T. Y. a. L. P. e. a. Zhang WY, J Am Chem Soc;, 2017, 139, 10897–10902.
- C. X. a. Z. Z. e. a. Zhang HY, Adv Mater 2020 32, 2005213.
- L. Z. a. T. Y. e. a. Pan Q, J Am Chem Soc 2017, 139, 3954–3957.
- Z. Z. M. G. Ehrenreich, S. Burger, M. R. Warren, M. W. Gaultois, J.-C. Tan, G. Kieslich, Chem. Commun., 2019, 55, 3911–3914.
- J. Xiao, J. Chang, B. Li, F. H. Isikgor, D. Wang, Z. Fan, Z. Lin, J. Ouyang, K. Zeng and J. Chen, Journal of Materials Chemistry A, 2018, 6, 9665-9676.
- A. Iefanova, N. Adhikari, A. Dubey, D. Khatiwada and Q. Qiao, AIP Advances, 2016, 6.
- H. Wei, Yang, Y. L., Chen, S. Y. & Xiang, H. J. , Nat. Commun. , 2021, 12, 1–8.
- C. C. M. Stoumpos, C. D.; Kanatzidis, M. G., Inorg. Chem., 2013, 52, 9019−9038.
- M. Caputo, N. Cefarin, A. Radivo, N. Demitri, L. Gigli, J. R. Plaisier, M. Panighel, G. Di Santo, S. Moretti, A. Giglia, M. Polentarutti, F. De Angelis, E. Mosconi, P. Umari, M. Tormen and A. Goldoni, Scientific Reports, 2019, 9, 15159.
- T. Zhang, K. Xu, J. Li, L. He, D. W. Fu, Q. Ye and R. G. Xiong, Natl Sci Rev, 2023, 10, nwac240.
- A. a. D. Sagdeo, Shankar and Rambadey, Omkar V. and Sagdeo, Pankaj R., , SSRN: https://ssrn.com/abstract=4198120 or http://dx.doi.org/10.2139/ssrn.4198120, 2022.
- S. Dutt, O. V. Rambadey, P. R. Sagdeo and A. Sagdeo, Materials Chemistry and Physics, 2023, 295, 127169.
- M. Bari, A. A. Bokov and Z.-G. Ye, Journal of Materials Chemistry C, 2020, 8, 9625-9631.
- T.-V. D. Y.-J. Kim, H.-J. Choi, B.-J. Park, J.-H. Eom, H.-A. Song, D. Seol, Y. Kim, S.-H. Shin, J. Nah, S.-G. Yoon, , J. Mater.Chem. , 2016, A 4, 756–763.
- T. A. Berhe, W.-N. Su, C.-H. Chen, C.-J. Pan, J.-H. Cheng, H.-M. Chen, M.-C. Tsai, L.-Y. Chen, A. A. Dubale and B.-J. Hwang, Energy & Environmental Science, 2016, 9, 323-356.
- J. Fan, B. Jia and M. Gu, Photon. Res., 2014, 2, 111-120.
- C. He and X. Liu, Light: Science & Applications, 2023, 12, 15.
- G. E. E. T. Leijtens, S. Pathak, A. Abate, M.M. Lee, and H.J. Snaith:, Nat. Commun., 2013, 4, 2885.
- Peng Gao 1, Abd Rashid Bin Mohd Yusoff 2,3 & Mohammad Khaja Nazeeruddin 2, NATURE COMMUNICATIONS 2018, 9, 5028.
- P. Wannasut, P. Jaiban, P. Jaita, M. Promsawat, O. Khamman and A. Watcharapasorn, Journal of Asian Ceramic Societies, 2023, 11, 88-97.
- T. Leijtens, E. Hoke, G. Grancini, D. Slotcavage, G. Eperon, J. Ball, M. De Bastiani, A. Bowring, N. Martino, K. Wojciechowski, M. McGehee, H. Snaith and A. Petrozza, Advanced Energy Materials, 2015, 5.
- C. Zhang, D. Sun, X. Liu, C.-X. Sheng and Z. V. Vardeny, The Journal of Physical Chemistry Letters, 2017, 8, 1429-1435.
- G. A. Sewvandi, K. Kodera, H. Ma, S. Nakanishi and Q. Feng, Scientific Reports, 2016, 6, 30680.
- M. E. Kiziroglou and E. M. Yeatman, in Functional Materials for Sustainable Energy Applications, eds. J. A. Kilner, S. J. Skinner, S. J. C. Irvine and P. P. Edwards, Woodhead Publishing, 2012, pp. 541-572. [CrossRef]
- H. Wang and A. Jasim, in Eco-Efficient Pavement Construction Materials, eds. F. Pacheco-Torgal, S. Amirkhanian, H. Wang and E. Schlangen, Woodhead Publishing, 2020, pp. 367-382. [CrossRef]
- T. L. Holger Röhm, Alexander D. Schulz, Susanne Wagner, Michael J. Hoffmann, and Alexander Colsmann*, Adv. Mater., 2019, 1806661.
- H. G. Shunbo Hu, Yuting Qi, Yongxue Tao, Yongle Li, Jeffrey R. Reimers, Menno Bokdam, Cesare Franchini, Domenico Di Sante, Alessandro Stroppa, and Wei Ren J. Phys. Chem. C, , 2017. [CrossRef]
- G. J, Springer Theses (Springer International Publishing, Basel, Switzerland), , 2014, pp 7-24.
- Y. L. a. X. B. e. a. Hu YZ, Nat Mater, 2021, 20, 612–617.
- H. Röhm, Leonhard, T., Hoffmann, M. J. & Colsmann, A. , Energy Environ. Sci. , 2017, 10, 950–955.
- A. Puhan, B. Bhushan, A. K. Nayak and D. Rout, in Fundamentals and Properties of Multifunctional Nanomaterials, eds. S. Thomas, N. Kalarikkal and A. R. Abraham, Elsevier, 2021, pp. 275-293. [CrossRef]
- R. F. Mueller, in Mineralogy, Springer US, Boston, MA, 1983, pp. 344-348. [CrossRef]
- K. Fykouras, J. Lahnsteiner, N. Leupold, P. Tinnemans, R. Moos, F. Panzer, G. A. de Wijs, M. Bokdam, H. Grüninger and A. P. M. Kentgens, Journal of materials chemistry. A, 2023, 11, 4587-4597.
- O. Yaffe, Y. Guo, T. Hull, C. Stoumpos, L. Tan, D. Egger, F. Zheng, G. Szpak, O. Semonin, A. Beecher, T. Heinz, L. Kronik, A. Rappe, M. Kanatzidis, J. Owen, M. Pimenta and L. Brus, 2016.
- C. Gehrmann and D. A. Egger, Nature Communications, 2019, 10, 3141.
- N. J. Weadock, T. C. Sterling, J. A. Vigil, A. Gold-Parker, I. C. Smith, B. Ahammed, M. J. Krogstad, F. Ye, D. Voneshen, P. M. Gehring, A. M. Rappe, H.-G. Steinrück, E. Ertekin, H. I. Karunadasa, D. Reznik and M. F. Toney, Joule, 2023, 7, 1051-1066.
- F. L. Huilin Lia, Zhitao Shena, Su-Ting Hand, Junwei Chenb, Chao Dongb, Chong Chena,⁎,1, Ye Zhouc,⁎,2, Mingtai Wangb,⁎,3, Nano Today 2021, 37 101062.
- C. Ning, Q. Ji, Y. Wu, J. Wang and M.-G. Ju, The Journal of Physical Chemistry Letters, 2023, 14, 8034-8042.
- A. Garrote-Márquez, L. Lodeiro, R. Suresh, N. Cruz Hernández, R. Grau-Crespo and E. Menéndez-Proupin, The Journal of Physical Chemistry C, 2023, 127, 15901-15910.
- J. Ibaceta-Jaña, M. Chugh, A. S. Novikov, H. Mirhosseini, T. D. Kühne, B. Szyszka, M. R. Wagner and R. Muydinov, The Journal of Physical Chemistry C, 2022, 126, 16215-16226.
- J. H. Lee, J.-H. Lee, E.-H. Kong and H. M. Jang, Scientific Reports, 2016, 6, 21687.
- P. R. Varadwaj, A. Varadwaj, H. M. Marques and K. Yamashita, Scientific Reports, 2019, 9, 50.
- R. Laref, F. Massuyeau and R. Gautier, Small, 2024, 20, e2306481.
- G. Saleh, G. Biffi, F. Di Stasio, B. Martín-García, A. L. Abdelhady, L. Manna, R. Krahne and S. Artyukhin, Chemistry of Materials, 2021, 33, 8524-8533.
- L. Tao, X. Du, J. Hu, S. Wang, C. Lin, Q. Wei, Y. Xia, G. Xing and Y. Chen, Science China Chemistry, 2022, 65, 1650-1660.
- A. V. Varadwaj, Pradeep R. Marques, Helder M. Yamashita, Koichi, Materials Today Chemistry, 2018, 9, 1-16.
- F. Xue, J.-H. He and X. Zhang, Applied Physics Reviews, 2021, 8.
- A. A. Zhumekenov, M. I. Saidaminov, O. F. Mohammed and O. M. Bakr, Joule, 2021, 5, 2027-2046.
- M. Coll, A. Gomez, E. Mas-Marza, O. Almora, G. Garcia-Belmonte, M. Campoy-Quiles and J. Bisquert, The Journal of Physical Chemistry Letters, 2015, 6, 1408-1413.
- A. Y. Grishko, M. A. Komkova, E. I. Marchenko, A. V. Chumakova, A. B. Tarasov, E. A. Goodilin and A. A. Eliseev, Nano Research, 2023, 16, 9435-9442.
- B. Chen, X. Zheng, M. Yang, Y. Zhou, S. Kundu, J. Shi, K. Zhu and S. Priya, Nano Energy, 2015, 13, 582-591.
- J. C. Frederick, Graduate Theses and Dissertations, 2010, 11636.
- E. J. S. Juarez-Perez, R. S.; Badia, L.; Garcia-Belmonte, G.; Kang, Y. S.; Mora-Sero, I.; Bisquert, J., J. Phys. Chem. Lett. , 2014, 5, 2390-2394.
- F. W. Linkai Li, Xiaojing Wu, Hui Yu, Shuang Zhou, and Ni Zhao, J. Phys. Chem. C, 2016. [CrossRef]
- S. L. Ruijuan Xu1, Ilya Grinberg2, J. Karthik1, Anoop R. Damodaran1, Andrew M. Rappe2 and LaneW. Martin1,3*, Nat mater, 2015, 14.
- K. Muzaffar Iqbal and U. Trilok Chandra, in Multifunctional Ferroelectric Materials, ed. S. Dipti Ranjan, IntechOpen, Rijeka, 2021, p. Ch. 2. [CrossRef]
- R. Chakraborty, P. K. Rajput, G. M. Anilkumar, S. Maqbool, R. Das, A. Rahman, P. Mandal and A. Nag, Journal of the American Chemical Society, 2023, 145, 1378-1388.
- M. Yang, H. Cheng, Y. Xu, M. Li and Y. Ai, Chinese Chemical Letters, 2022, 33, 2143-2146.
- R. Pandey, G. Vats, J. S. Yun, C. Bowen, A. Ho-Baillie, J. Seidel, K. Butler and S. I. Seok, Advanced Materials, 2019, 31, 1807376.
- M. M. a. M. Clarissa Coccia, Molecules, 2023, 28.
- J. Ravez, Comptes Rendus de l'Académie des Sciences - Series IIC - Chemistry, 2000, 3, 267-283.
- V. W. W. Bergmann, S. A. L.; Javier Ramos, F.; Nazeeruddin, M. K.; Grätzel, M.; Li, D.; Domanski, A. L.; Lieberwirth, I.; Ahmad, S.; Berger, R., , Nat. Commun., 2014, 5.
- R. D. Berger, A. L.; Weber, S. A. L., , Eur. Polym. J. , 2013, 49, 1907-1915.
- E. Soergel, J. Phys. D: Appl. Phys., 2011, 44, 464003.
- S. V. R. Kalinin, B. J.; Kholkin, A. L.,, In Encyclopedia of Nanotechnology, Bhushan, B., Ed. Springer Netherlands, 2012, pp 2117-2125.
- Y. Y. Kutes, L.; Zhou, Y.; Pang, S.; Huey, B. D.; Padture, N. P., J. Phys. Chem. Lett., 2014, 3335-3339.
- B. Z. Chen, X.; Yang, M.; Zhou, Y.; Kundu, S.; Shi, J.; Zhu, K.; Priya, S., , Nano Energy, 2015, 13, 582-591.
- H.-S. K. Kim, S. K.; Kim, B. J.; Shin, K.-S.; Gupta, M. K.; Jung, H. S.; Kim, S.-W.; Park, N.-G., J. Phys. Chem. Lett., 2015, 1729-1735.
- P. X. Zhao, J.; Ma, C.; Ren, W.; Wang, L.; Bian, L.; Chang, A., , Scr. Mater., 2015, 102, 51-54.
- Z. Y. Xiao, Y.; Shao, Y.; Wang, Q.; Dong, Q.; Bi, C.; Sharma, P.; Gruverman, A.; Huang, J., Nat. Mater., 2015, 14, 193−198.
- M. G. Coll, A.; Mas-Marza, E.; Almora, O.; Garcia-Belmonte, G.; Campoy-Quiles, M.; Bisquert, J., , J. Phys. Chem. Lett., 2015, 6, 1408-1413.
- Z. X. Fan, J.; Sun, K.; Chen, L.; Hu, Y.; Ouyang, J.; Ong, K. P.; Zeng, K.; Wang, J.,, J. Phys. Chem. Lett., 2015, 6, 1155-1161.
- R. P. A. Dazzi, E. Glotin, J. M. Ortega, , Opt. Lett., 2005, 30, 2388-2390.
- A. Centrone, Annu. Rev. Anal. Chem., 2015, 8, 101-126.
- J. C. A. M. Katzenmeyer, G. Holland, D. Farrusseng, A. Centrone,, Angew. Chem. Int. Ed., 2014, 53, 2852-2856.
- J. C. Y. Yuan, Y. Shao, Q. Wang, Z. Xiao, A. Centrone, J. Huang, , Adv. Energy Mater., 2015, 5, 1500615.
- V. A. A. M. Katzenmeyer, A. Centrone,, Anal. Chem., 2013, 85, 1972-1979.
- P. B. F. Tang, Z. Su, , Anal. Chem. , 2016, 88, 4926-4930.
- M. L. C. Marcott, K. Kjoller, C. Prater, I. Noda, , Appl. Spectrosc., 2011, 65, 1145-1150.
- G. L. F. S. Ruggeri, S. Faggiano, E. Lipiec, A. Pastore, G. Dietler, , Nat. Commun., 2015, 6, 7831.
- D. B. C. L. Gong, I. Noda, J. Liu, D. C. Martin, C. Ni, J. F. Rabolt,, Macromolecules, 2015, 48, 6197-6205.
- A. Manchon and A. Belabbes, in Solid State Physics, eds. R. E. Camley and R. L. Stamps, Academic Press, 2017, vol. 68, pp. 1-89.
- J. Wang et al., Nat. Commun, 2019, 10, 129–133.
- D. Giovanni et al., Nano Lett., 2015, 15, 1553–1558.
- C. Z. e. al., Nat. Phys., 2015, 11, 427–434.
- P. O. e. al., Nat. Phys., 2017, 13, 894–899.
- H. W. S. Chen, N.; Ikegami, M.; Miyasaka, T., , J. Phys. Chem. Lett. , 2015, 6, 164-169.
- J. Z. Wei, Y.; Li, H.; Li, G.; Pan, J.; Xu, D.; Zhao, Q.; Yu, D., , J. Phys. Chem. Lett., 2014, 5, 3937-3945.
- A. García-Fernández, et al., , Inorganic chemistry, 2017.
- T. M. E. Brenner, D. A.; Rappe, A. M.; Kronik, L.; Hodes, G.; Cahen, D., , The Journal of Physical Chemistry Letters 2015, 6, 4754-4757.
- Y. Zhai et al., Sci. Adv., 2017, 3.
- S. Picozzi, Frontiers in Physics, 2014, 2.
- W. Q. Ren, Z.; Wang, J.; Sun, Q.; Guo, H.,, Phys. Rev. Lett 2006, 97, 066603.
- Z. R. Qiao, W.; Wang, J.; Guo, H., , Phys. Rev. Lett . 2007, 98, 196402.
- P. M. Azarhoosh, S.; Frost, J. M.; Walsh, A.; van Schilfgaarde, M., , APL Materials,, 2016, 4, 091501.
- M. R. Kepenekian, R.; Katan, C.; Sapori, D.; Pedesseau, L.; Even, J., , ACS Nano 2015, 9, 11557-11567.
- T. M. Etienne, E.; De Angelis, F.,, J. Phys. Chem. Lett. , 2016, 7, 1638-1645.
- T. M. E. Brenner, D. A.; Rappe, A. M.; Kronik, L.; Hodes, G.; Cahen, D., , The Journal of Physical Chemistry Letters, 2015, 6, 4754-4757.
- J. E. Moser, Nat. Mater., 2016, 16, 4-6.
- J. P. Jankowska, O. V.,, J. Phys. Chem. Lett. , 2017, 8, 812-818.
- P. M. Azarhoosh, S.; Frost, J. M.; Walsh, A.; van Schilfgaarde, M., , APL Materials, 2016, 4, 091501.
- J. M. B. Frost, K. T.; Brivio, F.; Hendon, C. H.; van Schilfgaarde, M.; Walsh, A., Nano Lett., 2014, 14, 2584−2590.
- W. Q. Ren, Z.; Wang, J.; Sun, Q.; Guo, H., , Phys. Rev. Lett 2006, 97, 066603.
- Z. R. Qiao, W.; Wang, J.; Guo, H., , Phys. Rev. Lett., 2007, 98, 196402.
- A. B. R. Yu, E. I., , Journal of Physics C: Solid State Physics, 1984, 17, 6039.
- A. A. Y. Mostofi, J. R.; Pizzi, G.; Lee, Y.-S.; Souza, I.; Vanderbilt, D.; Marzari, N., , Computer Physics Communications 2014, 185, 2309-2310.
- L. X. a. K. T. e. a. Sun ZH, Angew Chem Int Ed 2016, 55, 6545–6550.
- K. Frohna, T. Deshpande, J. Harter, W. Peng, B. A. Barker, J. B. Neaton, S. G. Louie, O. M. Bakr, D. Hsieh and M. Bernardi, Nature Communications, 2018, 9, 1829.
- J. Even, L. Pedesseau, J.-M. Jancu and C. Katan, The Journal of Physical Chemistry Letters, 2013, 4, 2999-3005.
- A. Gómez, Q. Wang, A. R. Goñi, M. Campoy-Quiles and A. Abate, Energy & Environmental Science, 2019, 12, 2537-2547.
- a. b. J. C. Juanxiu Xiao†, b,c Bichen Li,b Furkan Halis Isikgor, b Dong Wang, a Zhen Fan, d Zhenhua Lin, c Jianyong Ouyang*, b Kaiyang Zeng*e and Jingsheng Chen*b, J. Name., 2012, 00, 1-3.
- G. Huang, A. A. Khan, M. M. Rana, C. Xu, S. Xu, R. Saritas, S. Zhang, E. Abdel-Rahmand, P. Turban, S. Ababou-Girard, C. Wang and D. Ban, ACS Energy Lett, 2021, 6, 16-23.
- H. Z. A. Liu, Y. Reo, M.-G. Kim, H.Y. Chu, J.H. Lim, H.-J.; Kim, W. Ning, S.; Bai, Y.-Y. Noh, Cell Rep. Phys. Sci. , 2022, 3.
- Y.Z. a. a. K. Zhu*b, Chem. Soc. Rev., 2016, 45.
- Joseph S. Manser, ‡ Jeffrey A. Christians,† and Prashant V. Kamat*,†,‡,§, Chem. Rev. , 2016, 116, 12956−13008.
- B. R. S. a. E. H. Sargent*, Nature photonics, 2016, 10.
- b. Qi Chena, Nicholas De Marcoa,b, Yang (Michael) Yanga,Tze-Bin Songa,b, Chun-Chao Chena, Hongxiang Zhaoa,b,Ziruo Honga, Huanping Zhoua,b, Yang Yanga,b,∗, Nano Today, 2015, 49.
- a. S. S. n. Kun Chen, b Seulki Songb and Harun Tu¨ysu¨z *b, Chem. Soc. Rev., 2018. [CrossRef]
- A. S. Prashant Jain1, 3, Dmitrii Nabok4, Antigone Marino5, Andrea Rubano5, Domenico Paparo5, Masakazu Matsubara6,7, Heinz Nakotte8, Manfred Fiebig6, Silvia Picozzi2, Eun Sang Choi9, Anthony K Cheetham10, Claudia Draxl4, Naresh S Dalal11 and Vivien S Zapf1, npj Quantum Materials, 2016, 1.
- Y.-S. Kim, Z. Jin, M. W. Park, H. C. Jeon and J. Y. Lim, Materials Today Physics, 2023, 35, 101109.
- F. Ambrosio, F. De Angelis and A. R. Goñi, The Journal of Physical Chemistry Letters, 2022, 13, 7731-7740.
- K. Gałkowski, 2017.
- J. N. Wilson, J. M. Frost, S. K. Wallace and A. Walsh, APL Materials, 2019, 7.
- Z. G. Yu, Scientific Reports, 2016, 6, 28576.
- E. Ouaaka, M. Aazza, A. Bouymajane and F. Cacciola, Molecules, 2023, 28, 2880.
- G. W. a. W. J. e. a. Xu H, J Am Chem Soc 2021, 143, 14379–14385.
- Z. X. a. L. D. e. a. Chen XX, ChemSci 2021, 12, 8713–8721.
- S. R. a. Z. Y. e. a. Ai Y, Chem Sci 2021, 12, 9742–9747.
- V. Keppens, nature materials, 2013, 12.
- K. A. e. a. Mosiewicz, Nature Mater., 2013, 12, 1072-1078.
- S. H. Lee, Moon, J. J. & West, J. L. , Biomaterials 2008, 29, 2962-2968.
- C.A. DeForest, Polizzotti, B. D. & Anseth, K. S., Nature Mater., 2009, 8, 659-664.
- R. E. Newham, Springer Verlag, New York, 1975.
- M. Manzo, KTH – Royal Institute of Technology, 2015.
- T. S. Wan-Jian Yin , and Yanfa Yan *, Adv. Mater. , 2014. [CrossRef]
- H. L. C. T. Z. D. Deng, Appl. Phys. Rev. , 2014, 1.
- E. K. H. Salje, Cambridge University Press: Cambridge, NY, USA, 1990.
- A. K. C. Tagantsev, L. E.; Fousek, J., Springer New York, 2010.
- Y. H. Zhou, S.-T. , Science 2020, 367 (6478), 627−628.
- J. I. Long, M. S.; Khomchenko, V. A.; Mamontova, E.; Thibaud, J.-M.; Rouquette, J.; Beaudhuin, M.; Granier, D.; Ferreira, R. A. S.; Carlos, L. D.; Donnadieu, B.; Henriques, M. S. C.; Paixao, J. A.; Guari, Y.; Larionova, J. , Science 2020, 367 (6478), 671−676.
- Xun Xiao 1, Wenhao Li2,4, Yanjun Fang3,4, Ye Liu 3, Yuchuan Shao1, Shuang Yang3, Jingjing Zhao 3, Xuezeng Dai 1, Rashid Zia2 & Jinsong Huang 1,3✉, NATURE COMMUNICATIONS, 2020, 11.
- J. Nye, Oxford science publications; Clarendon Press, , 1985.
- L. M. E. a. G. A. M, (Oxford: Clarendon), 1979.
- T. I. a. N. E. Mitsui T, London: Gordon and Breach, 1976.
- D. S. D. a. S. A. e. a. Ghosh S, J Phys Chem Lett, 2015, 6, 4553–4559.
- D. S. D. a. B. P. e. a. Stroppa A, Nat Commun 2014, 5, 5900.
- B. C. Jaffe, W.; Jaffe, H. , ; Academic Press, New York, 1971.
- A. Ballato, IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 1995, 42, 916-926.
- H. Park, C. Ha and J.-H. Lee, Journal of Materials Chemistry A, 2020, 8, 24353-24367.
- S. Z. Liu, F.; Koocher, N. Z.; Takenaka, H.; Wang, F.; Rappe, A. M. , J. Phys. Chem. Lett. , 2015, 6, 693-699.
- J. W. Ma, L.-W., Nano Lett., 2015, 15, 248-253.
- Sahoo, T. Paul, N. H. Makani, S. Maiti and R. Banerjee, Sustainable Energy & Fuels, 2022, 6, 4484-4497.
- S. Wang, A. A. Khan, S. Teale, J. Xu, D. H. Parmar, R. Zhao, L. Grater, P. Serles, Y. Zou, T. Filleter, D. S. Seferos, D. Ban and E. H. Sargent, Nature Communications, 2023, 14, 1852.
- X. e. a. Yu, J. Mater. Chem. C. , 2019, 7, 3479–3485.
- Y. Bai, Jantunen, H. & Juuti, J. , Adv. Mater. , 2018, 30.
- A. Ballato, IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 1995, 42, 916-926.
- L. Bellaiche, Current Opinion in Solid State and Materials Science, 2002, 6, 19-25.
- J.-J. M. Chao Shi, Jia-Ying Jiang, Miao-Miao Hua, Qi Xu, Hui Yu, Yi Zhang,* and Heng-Yun Ye*, J. Am. Chem. Soc., 2020, 142, 9634−9641.
- Z. H. a. F. e. a. Wang ZX, J Am Chem Soc 2020, 142, 12857–12864.
- C. M. a. X. B. e. a. Li F, Science 2019, 364, 264–268.
- Shi Liu, † Fan Zheng,‡ Ilya Grinberg,‡ and Andrew M. Rappe ,‡, J. Phys. Chem. Lett., 2016.
- D. D., Rep Prog Phys 1998, 61, 1267–1324.
- K. T. Butler, J. M. Frost and A. Walsh, Energy & Environmental Science, 2015, 8, 838-848.
- N. Chelil, M. Sahnoun, Z. Benhalima, R. Larbi and S. M. Eldin, RSC Advances, 2023, 13, 1955-1963.
- Y. L. Yan Zhang , and Zhong Lin Wang *, Adv. Mater. , 2011, XX, 1-10.
- Y. L. C. Y. F. Hu , P. Fei , R. L. Snyder , Z. L. Wang , , ACS Nano., 2010 4, 1234.
- Y. Z. Y. F. Hu , Y. L. Chang , R. L. Snyder , Z. L. Wang , , ACS Nano, 2010, 4 4220.
- C. L. H. J. H. He , J. Liu , L. J. Chen , Z. L. Wang , , Adv. Mater., 2007 19, 781.
- J. Z. X. D. Wang , J. H. Song , J. Liu , N. S. Xu , Z. L. Wang , , Nano Lett. , 2006, 6, 2768.
- Q. K. C. S. Lao , Z. L. Wang , M. C. Park , Y. L. Deng , , Appl. Phys. Lett., 2007, 90, 262107.
- J. H. S. Z. L. Wang Science 2006, 312, 242.
- J. H. S. X. D. Wang , J. Liu , Z. L. Wang , , Science, 2007, 316, 102.
- X. D. W. ] Y. Qin , Z. L. Wang , . Nature, 2008, 451, 809.
- Z. D. Weber, Naturforsch., 1978, 33, 1443.
- D. W. A. Poglitsch, J. Chem. Phys., 1987, 87, 6373.
- K. T. B. J. M. Frost, F. Brivio, C. H. Hendon, M. van Schilfgaarde, A. Walsh, , Nano Lett., 2014, 14, 2584.
- F. Z. S. Liu, N. Z. Koocher, H. Takenaka, F. Wang, A. M. Rappe, , J. Phys. Chem. Lett., 2015, 6, 693.
- T. V. D. Y. J. Kim, H. J. Choi, B. J. Park, J. H. Eom, H. A. Song, D. Seol, Y. Kim, S. H. Shin, H. Nah, S. G. Yoon, , J. Mater. Chem. A 2016, 4, 756.
- S. Shahrokhi, W. Gao, Y. Wang, P. R. Anandan, M. Z. Rahaman, S. Singh, D. Wang, C. Cazorla, G. Yuan, J.-M. Liu and T. Wu, Small Methods, 2020, 4, 2000149.
- H. L. Ran Ding, Xiaoli Zhang,* Juanxiu Xiao, Rahul Kishor, Huaxi Sun, Bowen Zhu, Geng Chen, Fei Gao, Xiaohua Feng, Jingsheng Chen, Xiaodong Chen, Xiaowei Sun,* and Yuanjin Zheng*, Adv. Funct. Mater., 2016.
- K. Uchino, Sci Technol Adv Mater, 2015, 16, 046001.
- B. U. a. U. K. Du X H, Jpn. J. Appl. Phys. , 1997, 36 5580-5587.
- J. F. S. Q. F. Dong, Y. J. Fang, Y. C. Shao, S. Ducharme, and J. S. Huang, , Adv. Mater. (Weinheim, Ger.), 2016, 28, 2816.
- a. F. Y. S. Zhang, Journal of the American Ceramic Society 2011, 94, 3153.
- G. H. Haertling, Journal of the American Ceramic Society,, 1999, 82, 797.
- Z. L. W. M. H. Zhao, and S. X. Mao, , Nano Letters, 2004, 4, 587.
- A. G. M. Coll, E. Mas-Marza, O. Almora, G. Garcia-Belmonte, M. , Journal of Physical Chemistry Letters, 2015, 6, 1408.
- Z. X. Jingfeng Song1, Bo Chen2, Spencer Prockish1, Xuegang Chen1, Jinsong Huang2,3 and Xia Hong1,3*, University of Nebraska-Lincoln, 2017.
- Q. Zhang, Bharti, V, Kavarnos, G, Schwartz, M , , Encyclopedia of smart materials, Wiley, New York, , 2002, Vols 1-2,, pp 807-825.
- C. Lee, Joo, J, Han, S and Koh, SK , , Appl. Phys. Lett,, 2004, 85 1841-1843.
- C. Lee, Joo, J, Han, S, Lee, JH and Koh, SK ,, Proc. Int. Conf. on Science and Technology of Synthetic Metals, , 2005, vol. 152, , pp 49-52.
- U. S. O. Zhuang Y, Tuncdemir S, Amin A and Uchino K Jpn. J. Appl. Phys. , 2010 49, 021503.
- Z. Y. a. U. S. O. Uchino K, J. Adv. Dielectrics 2011 1, 17-31.
- J. H. Z. K. UCHINO, Y. H. CHEN, X. H. DU, J. RYU, Y. GAO, S. URAL, S. PRIYA, JOURNAL OF MATERIALS SCIENCE, 2006, 41 217-228.
- K. Uchino, Sci. Technol. Adv. Mater., 2015, 16, 046001 (046016pp).
- H. L. Xin Pan, Uyen Huynh, and Z. Valy Vardeny J. Chem. Phys., 2020, 152.
- D. Damjanovic, Rep. Prog. Phys. , 1998, 61, 1267-1324.
- K. D. Lefki, G. J. M. , J. Appl. Phys., 1994, 76, 1764.
- K. L. a. G. J. M. Dormans, J. Appl. Phys., 1994, 76, 1764.
- R. Dahiya and M. Valle, 2008. [CrossRef]
- e. a. G S, J Phys Chem Lett., 2016, 7, 2412-2419.
- O. B.-E. Yevgeny Rakitaa, Elena Meirzadeha, Hadar Kaslasia, Yagel Pelega, Gary Hodesa, Igor Lubomirskya, Dan Oronb, David Ehrea,1, and David Cahena,1, PNAS Early Edition, 2017.
- S. B, Available at https://www.tcm.phy.cam.ac.uk/∼bds10/phase.html. Accessed May 24, 2017., 1997.
- Z. J. Liu ST, Long D, Ferroelectrics, 1975, 9, 39-43.
- e. a. Sewvandi GA, Phys Rev Appl, 2016, 6, 024007.
- D. D. (), Rep Prog Phys, 1998, 61, 1267.
- T. M, Eur J Phys, 2000, 21, 459.
- e. a. Rakita Y, APL Mater . 2016, 4, 051101.
- J. K. Harada, Y.; Takahashi, Y.; Uemura, Y.; Hasegawa, T.; Taniguchi, H.; Maruyama, K. , J. Am. Chem. Soc., 2019, 141.
- Y. Ma, W. Li, Y. Liu, W. Guo, H. Xu, S. Han, L. Tang, Q. Fan, J. Luo and Z. Sun, ACS Central Science, 2023, 9, 2350-2357.
- T. Choi, S. Lee, Y. J. Choi, V. Kiryukhin and S. W. Cheong, Science, 2009, 324, 63-66.
- I .Grinberg, D. V. West, M. Torres, G. Gou, D. M. Stein, L. Wu, G. Chen, E. M. Gallo, A. R. Akbashev, P. K. Davies, J. E. Spanier and A. M. Rappe, Nature, 2013, 503, 509-512.
- Z. Wang, R. Yu, C. Pan, Z. Li, J. Yang, F. Yi and Z. L. Wang, Nature Communications, 2015, 6, 8401.
- Xi Zeng 1, Yi Liu1,2, WenWeng 1,2, Lina Hua1, Liwei Tang1, Wuqian Guo1,2, Yaoyao Chen1, Tian Yang1, Haojie Xu1,2, Junhua Luo 1,2,3 & Zhihua Sun 1,2,3, Natur comm., 2023, 14.
- C. Zhu, X. Niu, Y. Fu, N. Li, C. Hu, Y. Chen, X. He, G. Na, P. Liu, H. Zai, Y. Ge, Y. Lu, X. Ke, Y. Bai, S. Yang, P. Chen, Y. Li, M. Sui, L. Zhang, H. Zhou and Q. Chen, Nature Communications, 2019, 10, 815.
- T. A. Berhe, ‡a Ju-Hsiang Cheng, ‡b Wei-Nien Su, *a Chun-Jern Pan, b Meng-Che Tsai, b Hung-Ming Chen,b Zhenyu Yang,c Hairen Tan, c Ching-Hsiang Chen,b Min-Hsin Yeh,b Andebet Gedamu Tamirat,b Shin-Fu Huang,b Liang-Yih Chen, b Jyh-Fu Lee,d Yen-Fa Liao,d Edward H. Sargent,*c Hongjie Daie and Bing-Joe Hwang *bd, Journal of Materials Chemistry A, 2017, 5, 21002.
- L. e. a. Liao, ACS Nano 2009, 3, 700-706.
- V. B. Garcia, M. , Nature, 2012, 483, 279-281.
- A. K. Jamil, T. S. , IEEE Transact. Ultrason. Ferr., 2007, 54, 222-226.
- T. e. a. Choi, Science, 2009, 324, 63-66.
- V. e. a. Garcia, Science 2010, 327, 1106-1110.
- Y. Zhang, Q. Yao, J. Qian, X. Zhao, D. Li and Q. Mi, Chemical Physics Letters, 2020, 754, 137637.
- K. Yamamoto, G. Narita, J. Yamasaki and S. Iikubo, Journal of Physics and Chemistry of Solids, 2020, 140, 109372.
- Y. Zhou, J. Wang, D. Luo, D. Hu, Y. Min and Q. Xue, Nano Energy, 2022, 94, 106949.
- U.-G. Jong, C.-J. Yu, Y.-H. Kye, S.-N. Hong and H.-G. Kim, Physical Review Materials, 2020, 4, 075403.
- S. Hu, Z. Ren, A. B. Djurišić and A. L. Rogach, ACS Energy Lett, 2021, 6, 3882-3905.
- M. A. Haque, S. Kee, D. R. Villalva, W.-L. Ong and D. Baran, Advanced Science, 2020, 7, 1903389.
- L. Yan, L. Zhao, G. Yang, S. Liu, Y. Liu and S. Lin, Frontiers in Energy, 2022, 16, 581-594.
- S. N. Hsu, W. Zhao, Y. Gao, Akriti, M. Segovia, X. Xu, B. W. Boudouris and L. Dou, Nano Lett., 2021, 21, 7839-7844.
- A. K. Baranwal, S. Hayase, K. Miyazaki, S. Saini and T. Yabuki, MRS Advances, 2019, 4, 1719-1725.
- H. Xie, S. Hao, J. Bao, T. J. Slade, G. J. Snyder, C. Wolverton and M. G. Kanatzidis, Journal of the American Chemical Society, 2020, 142, 9553-9563.
- R. Chen, L. Chen and Z. Liang, Advanced Functional Materials, 2023, 33, 2303774.
- T. Liu, X. Zhao, J. Li, Z. Liu, F. Liscio, S. Milita, B. C. Schroeder and O. Fenwick, Nature Communications, 2019, 10, 5750.
- P. Wu, Y. Xiong, L. Sun, G. Xie and L. Xu, Organic Electronics, 2018, 55, 90-96.
- Y.-K. Jung, I. T. Han, Y. C. Kim and A. Walsh, npj Computational Materials, 2021, 7, 51.
- S. A. a. U. V. W. Koushik Pal, J. Mater. Chem. C, 2015. [CrossRef]
- B. B. I. J. Snyder, K. Borup, E. Mueller, J. de Boor, L. Chen, X. Shi, F. Gascoin, H. Wang and M. Fedorov, , Energy Environ. Sci, 2014. [CrossRef]
- L. M. E. a. G. A. M, (Oxford: Clarendon), 1979.
- R. L. E, (London: Edward Arnold), 1980.
- R. Newnham, Properties of Materials: Anisotropy, Symmetry, StructureAnisotropy, Symmetry, Structure, 2004.
- Y. L. Wei Liu 1, Ju Wang 1, Cuncun Wu 1, Congyue Liu 1, Lixin Xiao 1, Zhijian Chen 1, Shufeng Wang 1,2,* ID and Qihuang Gong 1,2, Crystals 2018, 8, 216.
- J. C. Slater, Phys. Rev., 1950, 78(6), p. 748-761.
- H. a. R. E. C. Fu, Nature,, 2000, 403, p. 281-283.
- B. P. Burton, E. Cockayne, and U.V. Waghmare, , Phys. Rev. B, 2005, 72(6), p. 064113.
- S. Tinte, et al., , Phys. Rev. Lett., 2006, 97(13), p. 137601-137604.
- Z. a. R. E. C. Wu, Phys. Rev. Lett.,, 2005, 95, p. 037601.
- I. A. Kornev, et al., , Phys. Rev. Lett., 2005, 95(19), p. 196804.
- Z. X. Fan, J.; Sun, K.; Chen, L.; Hu, Y.; Ouyang, J.; Ong, K. P.; Zeng, K.; Wang, J. , J. Phys. Chem. Lett., 2015, 6, 1155-1161.
- F. T. Zheng, H.; Wang, F.; Koocher, N. Z.; Rappe, A. M. , J. Phys. Chem. Lett. , ,, 2015, 6, 31−37.
- A. Q. Stroppa, C.; De Angelis, F.; Picozzi, S. , J. Phys. Chem. Lett. , 2015, 6, 2223-2231.
- J. M. B. Frost, K. T.; Brivio, F.; Hendon, C. H.; van Schilfgaarde, M.; Walsh, A. , Nano Lett., 2014, 14, 2584−2590.
- J. M. B. Frost, K. T.; Brivio, F.; Hendon, C. H.; Van Schilfgaarde, M.; Walsh, A., Nano Lett., 2014, 14, 2584-2590.
- F. T. Zheng, H.; Wang, F.; Koocher, N. Z.; Rappe, A. M. , J. Phys. Chem. Lett., 2014, 6, 31-37.
- V. W. W. Bergmann, S. A. L.; Javier Ramos, F.; Nazeeruddin, M. K.; Grätzel, M.; Li, D.; Domanski, A. L.; Lieberwirth, I.; Ahmad, S.; Berger, R., , Nat. Commun., 2014, 5.
- E. Soergel, J. Phys. D: Appl. Phys., 2011, 44, 464003.
- S. V. R. Kalinin, B. J.; Kholkin, A. L.,, Bhushan, B., Ed. Springer Netherlands:, 2012, pp 2117-2125.
- R. P. B. J. Rodriguez, P. Maksymovych and S. V. Kalinin:, Weinheim, Wiley-VCH Verlag GmbH & Co. KGaA., 2012, 539-614.
- C. Q. G. Binnig, F. Calvin and C. Gerber, Phys. Rev. Lett., 1986, 56, 930.
- H. J. H. a. R. B. E. Meyer, Berlin, Springer., 2004.
- D. A. Bonnell:, Weinheim, Wiley-VCH., 2001.
- S. V. K. a. A. Gruverman:, Berlin, Springer., 2007, 1.
- L. Gross:, Nat. Chem.,, 2011, 3, 273.
- Y. M. a. H. K.Wickramasinghe:, Appl. Phys. Lett.,, 1987, 50, 1455.
- M. P. O. B. a. H. K. W. 20. M. Nonnenmacher, Appl. Phys. Lett., 1991, 58, 2921.
- C. D. F. A. Noy, L. F. Rozsnyaiand, M. S. Wrighton and C. M. Lieber: , J. Am. Chem. Soc., 1995, 117, 7943.
- S. A. a. C. Y. e. a. Tian Y, Phys Status SolidiRRL, 2015, 9, 62–67.
- P. M. Saurabh, S. , J. Chem. Phys., 2014, 140, 161107.
- J. B. Jahng, J.; Fishman, D. A.; Huang, F.; Li, X.; Tamma, V. A.; Wickramasinghe, H. K.; Potma, E. O. , Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 155417.
- D. A. F. Junghoon Jahng, ‡ Sung Park,∥ Derek B. Nowak,∥ Will A. Morrison,∥H. Kumar Wickramasinghe,§ and Eric O. Potma*,‡, Acc. Chem. Res., 2015. [CrossRef]
- L. Y. Y. Kutes, Y. Zhou, S. Pang, B. D. Huey, N. P. Padture,, J. Phys. Chem. Lett., 2014, 5, 3335.
- J. X. Z. Fan, K. Sun, L. Chen, Y. Hu, J. Ouyang, K. P. Ong, K. Zeng, J. Wang, , J. Phys. Chem. Lett., 2015, 6, 1155.
- T.-V. D. Y.-J. Kim, H.-J. Choi, B.-J. Park, J.-H. Eom, H.-A. Song, D. Seol, Y. Kim, S.-H. Shin, J. Nah, S.-G. Yoon, , J. Mater. Chem. A, 2016, 4, 756.
- S. K. K. H.-S. Kim, B. J. Kim, K.-S. Shin, M. K. Gupta, H. S. Jung, S.-W. Kim, N.-G. Park, , J. Phys. Chem. Lett., 2015, 6, 1729.
- W.-Q. L. H.-Y. Ye, C.-L. Hu, Y. Zhang, Y.-M. You, J.-G. Mao, P.-F. Li, R.-G. Xiong,, Adv. Mater., 2016, 28, 2579.
- Y. Z. W.-Q. Liao, C.-L. Hu, J.-G. Mao, H.-Y. Ye, P.-F. Li, S. D. Huang, R.-G. Xiong, , Nat. Commun., 2015, 6, 7338.
- , !!! INVALID CITATION !!!
- L. J. Li J, Yu Q, Chen QN, Xie S. , Journal of Materiomics, 2015, 1, 3-21.
- S. J. S. V. Kalinin, A. Tselev, A. P. Baddorf, N. Balke, , ACS Nano, 2011, 5, 5683.
- F. C. A. Kumar, A. N. Morozovska, S. V. Kalinin, S. Jesse, , Nat. Chem., 2011, 3, 707.
- A. K. T. M. Arruda, S. V. Kalinin, S. Jesse,, Nano Lett.,, 2011, 11, 4161.
- N. B. S. Kalinin, S. Jesse, A. Tselev, A. Kumar, T. M. Arruda, S. L. Guo, R. Proksch, , Mater. Today, 2011, 14, 548.
- B. J. R. J. Shin, A. P. Baddorf, T. Thundat, E. Karapetian, M. Kachanov, A. Gruverman, S. V. Kalinin, , J. Vac. Sci. Technol., B, 2005, 23, 2102.
- S. G. S. Jesse, A. Kumar, B. J. Rodriguez, R. Proksch, S. V. Kalinin, , Nanotechnology, 2010, 21, 405703.
- S. A. B. I. M. Hermes, V. W. Bergmann, D. Li, A. Klasen, J. Mars, W. Tremel, F. Laquai, H.-J. Butt, M. Mezger, R. Berger, B. J. Rodriguez, S. A. L. Weber, , J. Phys. Chem. C, 2016, 120, 5724.
- M. K. M. Shirayama, T. Miyadera, T. Sugita, T. Fujiseki, S. Hara, H. Kadowaki, D. Murata, M. Chikamatsu, H. Fujiwara, , J. Appl. Phys., 2016, 119, 115501.
- X. G. G. Niu, L. Wang, J. Mater. , Chem. A, 2015, 3, 8970.
- A. Dazzi, Prazeres, R., Glotin, F. & Ortega, J.M. , Opt. Lett., 2005, 30, 2388-2390.
- A. Centrone, Annual Review of Analytical Chemistry, 2015, 8, 101-126.
- A. M. Katzenmeyer, Holland, G., Kjoller, K. & Centrone, A. , Analytical Chemistry ,, 2015, 87, 3154-3159.
- B. Lahiri, Holland, G. & Centrone, A. , Small, 2013, 9, 439-445.
- J. Chae, Dong, Q., Huang, J. & Centrone, A. , Nano Letters, 2015, 15, 8114-8121.
- F. S. e. a. Ruggeri, Nat Commun, 2015, 6.
- B. Lahiri, Holland, G., Aksyuk, V. & Centrone, A. , Nano Letters, 2013, 13, 3218-3224.
- S. e. a. Ghosh, Nat Mater, 2015, 14, 505-511.
- A. M. Katzenmeyer, Canivet, J., Holland, G., Farrusseng, D. & Centrone, A. , Angewandte Chemie International Edition,, 2014, 53, 2852-2856.
- Y. e. a. Yuan, Advanced Energy Materials, 2015, 5, n/a-n/a.
- C. L. Marcott, M.; Kjoller, K.; Prater, C.; Noda,, I. Appl. Spectrosc., 2011, 65, 1145−1150.
- K. F. Kjoller, J. R.; Cook, D.; Prater, C. B.; King, W. P. , Nanotechnology, 2010, 21, 185705.
- V. A. Aaron M. Katzenmeyer, † and Andrea Centrone*,†,‡, Anal. Chem., 2013, 85, 1972−1979.
- P. M. S. G, B. P. Kore, S. Mukherjee, M. S. Pavan, C. De, S. Ghara, A. Sundaresan, A. Pandey, T. N. Guru Row, D. D. Sarma, , J. Phys. Chem. Lett., 2016, 7, 2412.
- F. C. C. Stoumpos, D. J. Clark, Y. S. Kim, S. H. Rhim, A. J. Freeman, J. B. Ketterson, J. I. Jang, M. G. Kanatzidis,, J. Am. Chem. Soc. , 2015, 137, 6804.
- R. Kanis, Ratner, M.A., and Marks, T.J., Chem. Rev., 1994, 94, 195-242.
- J. Zyss, and Ledoux, I., Chem. Rev., 1994, 94, 77-105.
- T. J. Marks, and Ratner, M.A., Angew. Chem. Int. Ed., 1995, 34, 155-173.
- S. R. Marder, Gorman, C.B., Meyers, F., Perry, J.W., Bourhill, G., Bre´ das, J.L., and Pierce, B.M., Science, 1994, 265, 632-635.
- G. Bourhill, Bredas, J.L., Cheng, L.T., Marder, S.R., Meyers, F., Perry, J.W., and Tiemann, B.G., J. Am. Chem. Soc., 1994, 116, 2619-2620.
- S. K. Kurtz, and Perry, T.T., J. Appl. Phys., 1968, 39, 3798-3813.
- C. C. a. A. Gontean, Sensors, 2020,, 20.
- Y.-J. Kim, T.-V. Dang, H.-J. Choi, B.-J. Park, J.-H. Eom, H.-A. Song, D. Seol, Y. Kim, S.-H. Shin, J. Nah and S.-G. Yoon, Journal of Materials Chemistry A, 2016, 4, 756-763.
- T.-V. D. Yun-Jeong Kim, 1 Hyung-Jin Choi,1 Byeong-Ju Park,1 Ji-Ho Eom,1 Hyun-A Song,2 Daehee Seol,3 Yunseok Kim,3 Sung-Ho Shin,4 Junghyo Nah,4,* and Soon-Gil Yoon1,*, J. Mater. Chem. A, , 2015.
- X. Yu, Y. Wang, J. Zhang, J. Duan, X. Yang, L. Liu and Q. Tang, Journal of Materials Chemistry A, 2020, 8, 14299-14307.
- H. Wu, J. Pi, Q. Liu, Q. Liang, J. Qiu, J. Guo, Z. Long, D. Zhou and Q. Wang, The Journal of Physical Chemistry Letters, 2021, 12, 4125-4129.
- H.-R. Xia, W.-T. Sun and L.-M. Peng, Chemical Communications, 2015, 51, 13787-13790.
- N. Vicente and G. Garcia-Belmonte, J Phys Chem Lett, 2017, 8, 1371-1374.
- T. Gao, J. Liao, J. Wang, Y. Qiu, Q. Yang, M. Zhang, Y. Zhao, L. Qin, H. Xue, Z. Xiong, L. Chen and Q.-m. Wang, Journal of Materials Chemistry A, 2015, 3, 9965-9971.
- S. Chen, Y. Xin, Y. Zhou, Y. Ma, H. Zhou and L. Qi, Energy & Environmental Science, 2014, 7, 1924-1930.
- O. S. Auciello, J. F.; Ramesh, R. , Phys. Today, 1998, 51, 22.
- N. A. Hill, J. Phys. Chem. B, 2000, 104, 6694.
- S. I. Tao, J. T. S. , Nat. Mater., 2003, 2, 320.
- A. G. M. Schrott, J. A.; Nagarajan, V.; Ramesh, R. , Appl. Phys. Lett., 2003, 82, 4770.
- material matters, aldrich material science, 2010, 5.
- S.-Y. K. Chung, I.-D.; Kang, S.-J. L. , Nat. Mater. , 2004, 3, 774.
- R. L. Ding, H.; Zhang, X.; Xiao, J.; Kishor, R.; Sun, H.; Zhu, B.; Chen, G.; Gao, F.; Feng, X.; Chen, J.; Chen, X.; Sun, X.; Zheng, Y., Adv. Funct. Mater., 2016, 26, 7708−7716.
- V. I. Jella, S.; Eom, J. H.; Pammi, S. V. N.; Jung, J. S.; Tran, V. D.; Nguyen, V. H.; Kirakosyan, A.; Yun, S.; Kim, D.; Sihn, M. R.; Choi, J.; Kim, Y. J.; Kim, H. J.; Yoon, S. G. A Nano Energy, 2019, 57, 74−93.
- V. Jella, S. Ippili, J.-H. Eom, S. V. N. Pammi, J.-S. Jung, V.-D. Tran, V. H. Nguyen, A. Kirakosyan, S. Yun, D. Kim, M. R. Sihn, J. Choi, Y.-J. Kim, H.-J. Kim and S.-G. Yoon, Nano Energy, 2019, 57, 74-93.
- R. J. Erturk A., Inman D., and 529–544., “Journal of Intelligent Material Systems and Structures”, 2009, 20.
- D. Grzybek, Pomiary Automatyka Robotyka nr, 2013, 10.
- S. Roundy, Journal of Intelligent Material Systems and Structures., 2005, 16, 809-823.
- W. P. Goldschmidtboeing F., “Journal of Micromechanics and Microengineering”, 2008, 18.
- A. M. Defosseux M., Basrour S., , . Proceedings of PowerMEMS 2010.
- Z. J, (Amsterdam: Elsevier), 1986.
- R. M. J. a. C. W, Proc. SPIE 2001, 4332, 429-438.
- H. L. a. S. P. L. F Lu, Smart Mater. Struct. , 2004, 13, 57-63.
- Y. T. C. H. J. Song, N. M. Wereley, A. Purekar, , Journal of Intelligent Material Systems and Structures., 2014, 25, 1825-1837.
- http://www.smart-material.com.
- S.-S. Jung-Hoon Lim, Na-RiKima, Seong-KyuCheona, Myong-HoKimb, Tae-Gone Park, , Ceramics International., 2013, 39, 641-645.
- P. K. W. S. Roundy, Smart Materials and Structures 2004, 13, 1131-1142.
- S.-W. K. M. K. Gupta, B. Kumar, , ACS Appl. Mater. Interfaces 2016, 8, 1766.
- V. H. T. C. Chang, J. Wang, Y.-K. Fuh, L. Lin, , Nano Lett., 2010, 10, 726.
- B. K. K. Y. Lee, J.-S. Seo, K.-H. Kim, J. I. Sohn, S. N. Cha, D. Choi, Z. L. Wang, S.-W. Kim, , Nano Lett., 2012, 12, 1959.
- Y. Q. R. Yang, L Dai, Z. L. Wang,, Nat. Nanotechnol., 2009, 4, 34.
- D. K. K. Y. Lee, J.-H. Lee, T. Y. Kim, M. K. Gupta, S.-W. Kim, , Adv. Funct. Mater., 2014, 24, 37.
- M. L. J. H. Jung, J.-I. Hong, Y. Ding, C.-Y. Chen, L.-J. Chou, Z. L. Wang, , ACS Nano 2011, 5, 10041.
- Y. K. P. B. K. Yun, M. Lee, N. Lee, W. Jo, S. Lee, J. H. Jung, , Nanoscale Res. Lett. , 2014, 9, 4.
- Y. Y. Z. H. Lin, J. M. Wu, Y. Liu, F. Z. Zhang, L. Wang, , Phys. Chem. Lett. , 2012, 3, 3599.
- Y.-W. Y. S. Xu, G. Poirier, M. C. Mcalpine, R. A. Register, N. Yao, . Nano Lett. , 2013, 13, 2393.
- U. K. a. I. T, J. Ceram. Soc. Jpn. , 1988, 96, 863.
- U. K. Suzuki Y, Gouda H, Sumita M, Newnham R E and Ramachandran A R J. Ceram. Soc. Jpn. Int. Edn 1991 99, 1096.
- D. E. M. Chan, J. Y. Fourniols ` et al., ” Artificial Intelligence in Medicine 2012, 56(3), 137-156.
- C. O. V. Lesser, and M. Tambe, , Springer Science & Business Media, 2012.
- M. J. T. S. P. Beeby, and N. M. White, , Measurement Science and Technology, 2006, R175 17(12).
- 4 S. R. Anton and H. A. Sodano, Smart Materials and Structures 2007, 16(3), 2003-2006.
- S. G. 5 P. Li, and H. Cai, , Microsystem Technologies, 2015, 21(2), 401-414.
- S. Saadon and O. Sidek, Energy Conversion and Management, 2011, 52(1), 500-504.
- C. L. H. Liu, T. Kobayashi et al., , Smart Materials and Structures, 2012, 21(3), 035005.
- M. H. Q. Zhu, and C. H.Wu, , Applied Mathematical Modelling, 2009, 33(5), 2207-2217.
- D. J. I. H. A. Sodano, and G. Park, , Journal of Intelligent Material Systems and Structures 2005, 16(1), 67-75.
- G. P. H. A. Sodano, and D. J. Inman, , Strain J. Brit. Soc. Strain Measurement, 2004, 40(2), 49-58.
- Mohd Javaid a, Abid Haleem a, Ravi Pratap Singh b, Shanay Rab a, Rajiv Suman c, Sensors International 2021, 2.
- M. S. a. K. W. S. *, Chemosensors 2020, 8.
- F. M. I. G. W. S. E. Scavetta1, Microchimica Acta 2022, 189.
- Hyo-Seung Park1, Jongkil Park1, Joon Young Kwak1, Gyu-Weon Hwang1, Doo-Seok Jeong2 & Kyeong-Seok Lee1*, Scientific Reports, 2021, 11.
- H. Yu, Y. Peng, Y. Yang and Z.-Y. Li, npj Computational Materials, 2019, 5, 45.
- Z. S. Zhu, Q.; Zhang, Z.; Dai, J.; Xing, G.; Li, S.; Huang, X.; Huang, W. , J. Mater. Chem. C, 2018, 6, 10121–10137.
- J. U. Shamsi, A.S.; Imran, M.; De Trizio, L.; Manna, L. , Chem. Rev. , 2019, 119.
- Q. D. M. Chen, N.; Yang, Y.; Song, T.-B.; Chen, C.-C.; Zhao, H.; Hong, Z.; Zhou, H.; Yang, Y. , Nano Today, 2015, 10, 355–396.
- S. Carretero-Palacios, A. Jiménez-Solano and H. Míguez, ACS Energy Lett, 2016, 1, 323-331.
- F. Rajab, Nanoplasmonic Sensing of CH3NH3PbI3 Perovskite Formation in Mimic of Solar Cell Photoelectrodes, 2018.
- C. Huang, W. Sun, Y. Fan, Y. Wang, Y. Gao, N. Zhang, K. Wang, S. Liu, S. Wang, S. Xiao and Q. Song, ACS Nano, 2018, 12, 3865-3874.
- S. Carretero-Palacios, M. E. Calvo and H. Míguez, The Journal of Physical Chemistry C, 2015, 119, 18635-18640.
- A. N. Koya, X. Zhu, N. Ohannesian, A. A. Yanik, A. Alabastri, R. Proietti Zaccaria, R. Krahne, W.-C. Shih and D. Garoli, ACS Nano, 2021, 15, 6038-6060.
- K. S. Shu L., Fei L., Huang W., Wang Z., Gong J., Jiang X., Wang L., Li F., Lei S., Rao Z., Zhou Y., Zheng R.-K., Yao X., Wang Y., Stengel M., Catalan G.. , Nature Materials, 2020. [CrossRef]
- A. G. Petrov, M. Spassova and J. H. Fendler, Thin Solid Films, 1996, 284-285, 845-848.
- D. Yan, J. Wang, J. Xiang, Y. Xing and L.-H. Shao, Science Advances, 2023, 9, eadc8845.
- S. Das, B. Wang, T. R. Paudel, S. M. Park, E. Y. Tsymbal, L.-Q. Chen, D. Lee and T. W. Noh, Nature Communications, 2019, 10, 537.
- D. Tian, D.-Y. Jeong, Z. Fu and B. Chu, Actuators, 2023, 12, 114.
- F. Yu, J. Tian, F. Jiang, Y. Liu, C. Li, C. Wang, Z. Wang and K. Ren, Nano Research, 2023, 16, 11914-11924.
- Y. Zhang, J. Huang, M. Zhu, Z. Zhang, K. Nie, Z. Wang, X. Liao, L. Shu, T. Tian, Z. Wang, Y. Lu and L. Fei, Chemical Science, 2024, 15, 1782-1788.
- Yoon Hee Jang, ‡,⊥ Yu Jin Jang,†,⊥ Seokhyoung Kim,†,§ Li Na Quan,†,∥ Kyungwha Chung,† and Dong Ha Kim*,†, Chem. Rev. , 2016, 116, 14982−15034.
- X. L. Chen, D.; Pan, G.; Zhou, D.; Xu, W.; Zhu, J.; Wang, H.; Chen, C.; Song, H. , Nanoscale, 2018, 10, 10505–10513.
- L. G. Tan, M.; Tan, J.; Geng, Y.; Huang, S.; Tang, Y.; Su, C.; Lin, C.; Liang, Y. , Sens. Actuators B 2019, 291, 226–234.
- X. S. Zhang, Y.; Fan, Y.; Liu, Z.; Zeng, Z.; Zhao, H.; Wang, X.; Xu, J. E, J. Mater. Sci. Mater. Electron. , 2019, 30, 20624–20637.
- a. S. J. Xianwei Fu, a Ning Dong,a Gang Lian, *a Tianyu Zhao,a Song Lv,a Qilong Wangb and Deliang Cui *a, RSC Adv., 2018, 8.
- L. P. Rohit Saraf, and Vivek Maheshwari*, Adv. Mater. , 2018.
- E. G. George Kakavelakis, Konstantinos Petridis, Valia Petromichelaki, Vassilis Binas, George Kiriakidis, and Emmanuel Kymakis, ACS Sens. [CrossRef]
- F. Z. Yuwei Niu , Zelong Bai , Yuping Dong , Jian Yang , Ruibin Liu , Bingsuo Zou , Jingbo Li , and Haizheng Zhong*, Adv. Optical Mater. [CrossRef]
- a. X. T. Yongfeng Liu, a Tao Zhu,*a Ming Deng,a Iroegbu Paul Ikechukwu,b Wei Huang,a Guolu Yin,a Yongzhong Bai,c Dingrong Qu,c Xianbin Huangc and Feng Qiuc, J. Mater. Chem. C 2018.
- C. S. Xinfeng Chena, Yang Liua, Long Yua, Kui Zhangb,⁎, Abdullah M. Asiric, Hadi M. Marwanic, Hua Tand, Yuejie Aia, Xiangke Wanga, Suhua Wanga,⁎, Chemical Engineering Journal, 2020, 379.
- Y. L. Xuexi Sheng, Yu Wang, Yafei Li, Xun Wang,* Xinping Wang, Zhihui Dai, Jianchun Bao,* and Xiangxing Xu*, Adv. Mater., 2017.
- a. H. H. Xiao Chen, ‡ab Zhaoming Xia,a Wei Gao, a Wangyan Gou, a Yongquan Qua and Yuanyuan Ma *a, J. Mater. Chem. C, 2016. [CrossRef]
- M. H. Hui Huang, Yilong Song, Song Dang, Xiaoting Liu, and Qingfeng Dong*, Small 2020.
- D. Z. Nan Ding, † Gencai Pan,† Wen Xu,*,† Xu Chen,† Dongyu Li,† Xiaohui Zhang,‡ Jinyang Zhu,‡ Yanan Ji,† and Hongwei Song*,†, ACS Sustainable Chem. Eng. , 2019, 7, 8397−8404.
- A. K. R. Avisek Maity1, 2 & Barnali Ghosh 1,2, Scientific Reports, 2019, 9.
- W. Y. Yue Zhuang, Liu Qian, Shan Chen and Gaoquan Shi*, Phys. Chem. Chem. Phys., 2017. [CrossRef]
- b. Ruimin Zhua, Yingze Zhanga, Hao Zhonga, Xinlong Wanga, Hao Xiaoa, Yanli Chena, Xiyou Lia,∗, Journal of Physics and Chemistry of Solids, 2019, 129, 270–276.
- a. Bing Zhang, b,c Shijie Zhou b, Lei Tongb, Yinjie Liaob, Juxia Yib , Yao Qib and Jianxi Yaoa,b,c, Phys. Chem. Chem. Phys., 2019. [CrossRef]
- a. E. G. K. Brintakis, ‡ab A. Kostopoulou, *a V. Faka,abc A. Argyrou,ac V. Binas, abd G. Kiriakidisab and E. Stratakis *ab, Nanoscale Adv., 2019, 1.
- M.-Y. M. Authors: Li-Qiang Lu, Tian Tan, Xi-Ke Tian, Zhao-Xin Zhou, Chao Yang, Yong Li, Sensors and Actuators B: Chemical 2018. [CrossRef]
- M. G. Marc-Antoine Stoeckel, Sara Bonacchi, Fabiola Liscio, Laura Ferlauto, Emanuele Orgiu,* and Paolo Samorì*, Adv. Mater., 2017.
- E Gagaoudakis1, 7 ,APanagiotopoulos3,4,7, T Maksudov3,4,7,MMoschogiannaki2,3,DKaterinopoulou1,2, GKakavelakis3,5,GKiriakidis1,2,VBinas1,2, E Kymakis4 andKPetridis6, J. Phys.: Mater. , 2020, 3.
- Chaoqun Chen, †,‡ Qing Cai,#,† Fang Luo,*,‡,§ Nuo Dong,*,† Longhua Guo,‡ Bin Qiu,‡ and Zhenyu Lin*,‡, Anal. Chem. , 2019, 91, 15915−15921.
- M. Z. Hongjun Chen, Renheng Bo, Chog Barugkin, Jianghui Zheng, Qingshan Ma, Shujuan Huang, Anita W. Y. Ho-Baillie, Kylie R. Catchpole, and Antonio Tricoli*, Small 2017.
- V. V. Arif D. Sheikh, Amarja Katware, Krishna Pawar, and Pramod S. Patil, Adv. Mater. Technol. , 2019.
- O. N. N. Gupta, R. Grover, K. Saxena, Org. Electron., 2018, 58.
- A. K. R. A. Maity, B. Ghosh, , Sci. Rep. , 2019, 9.
- S. G. Huang, M.; Tan, J.; Geng, Y.; Wu, J.; Tang, Y.; Su, C.; Lin, C.C.; Liang, Y. , ACS Appl. Mater. Interfaces, 2018, 10, 39056–39063.
- Q. W. Li, H.; Yue, X.; Du, J. , Talanta, 2020, 211.
- B. P. a. J. P. e. a. Stroppa A, Adv Mater 2013, 25, 2284–2290.
- M. Almalki, K. Anagnostou, K. Rogdakis, F. T. Eickemeyer, M. Othman, M. M. Stylianakis, D. Tsikritzis, A. Q. Alanazi, N. Tzoganakis, L. Pfeifer, R. Therisod, X. Mo, C. M. Wolff, A. Hessler-Wyser, S. M. Zakeeruddin, H. Zhang, E. Kymakis and M. Grätzel, Journal of Energy Chemistry, 2024. [CrossRef]
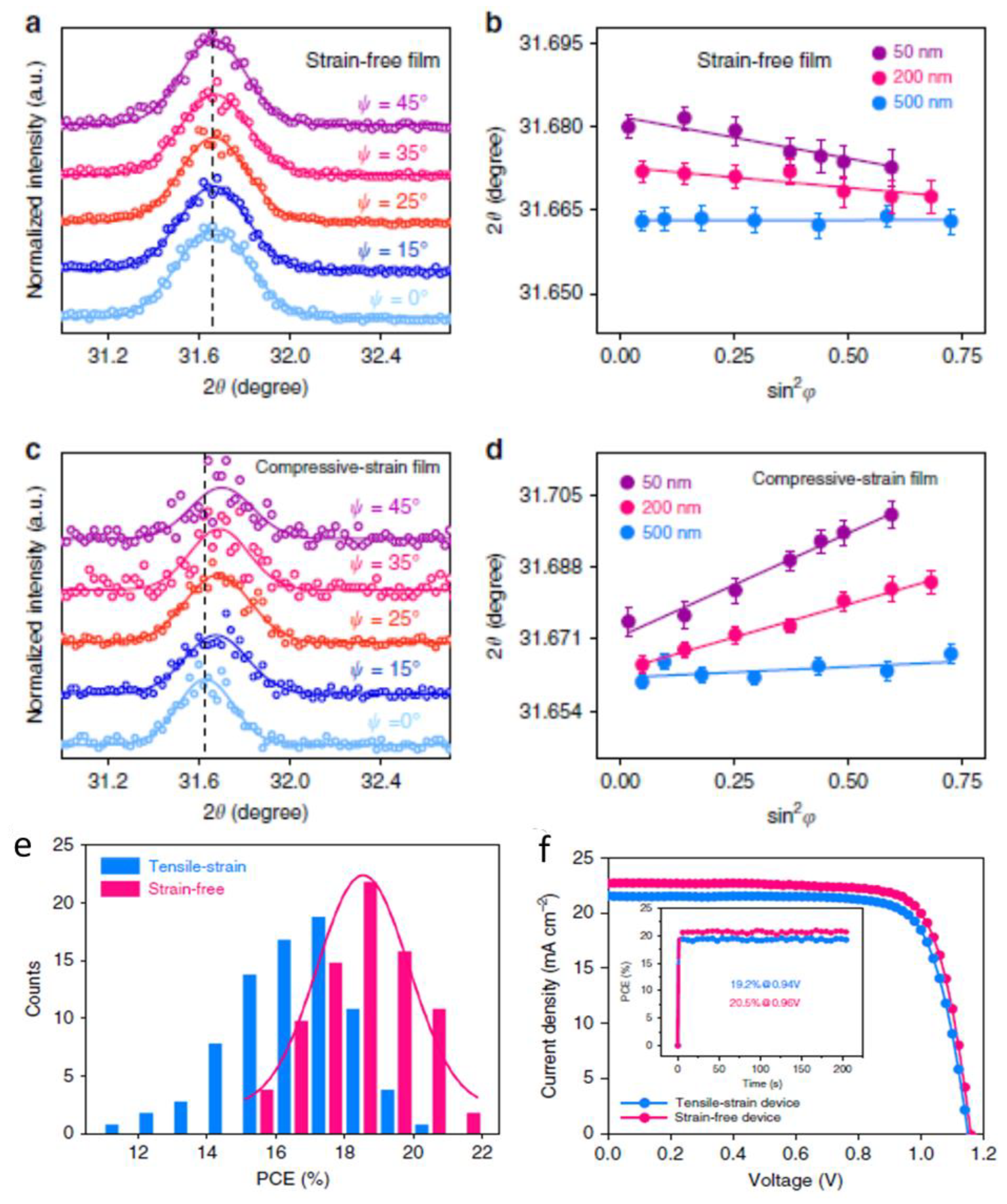
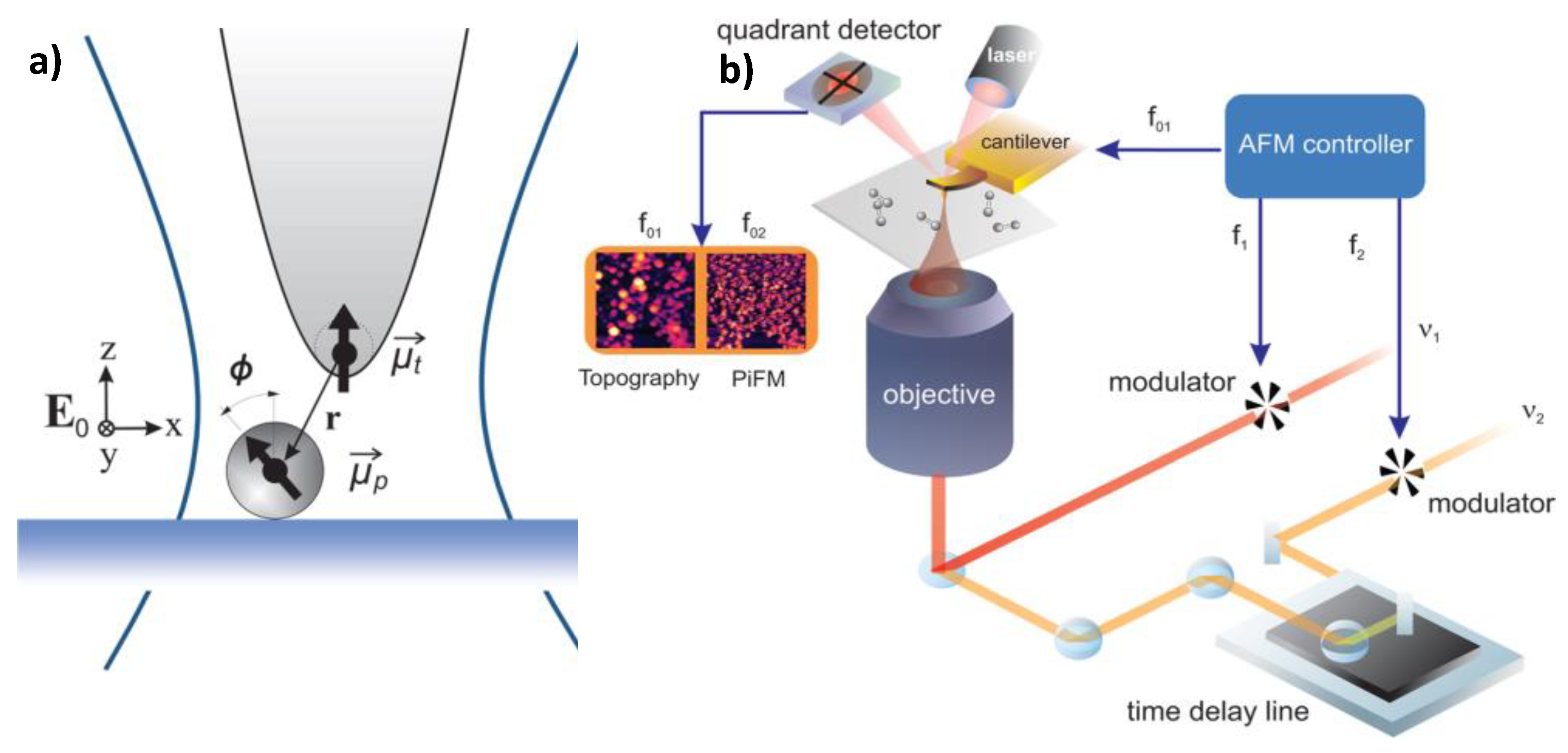
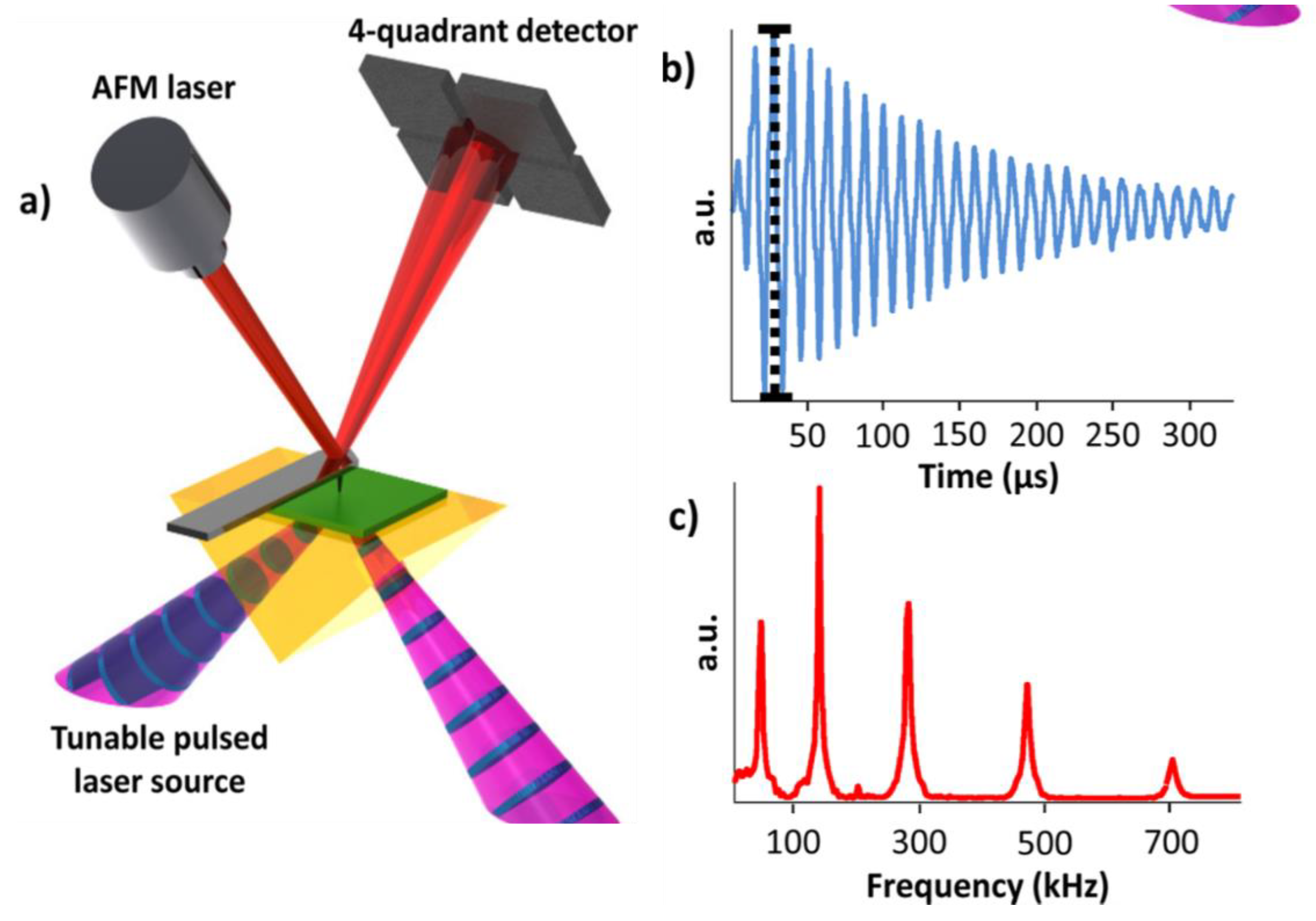
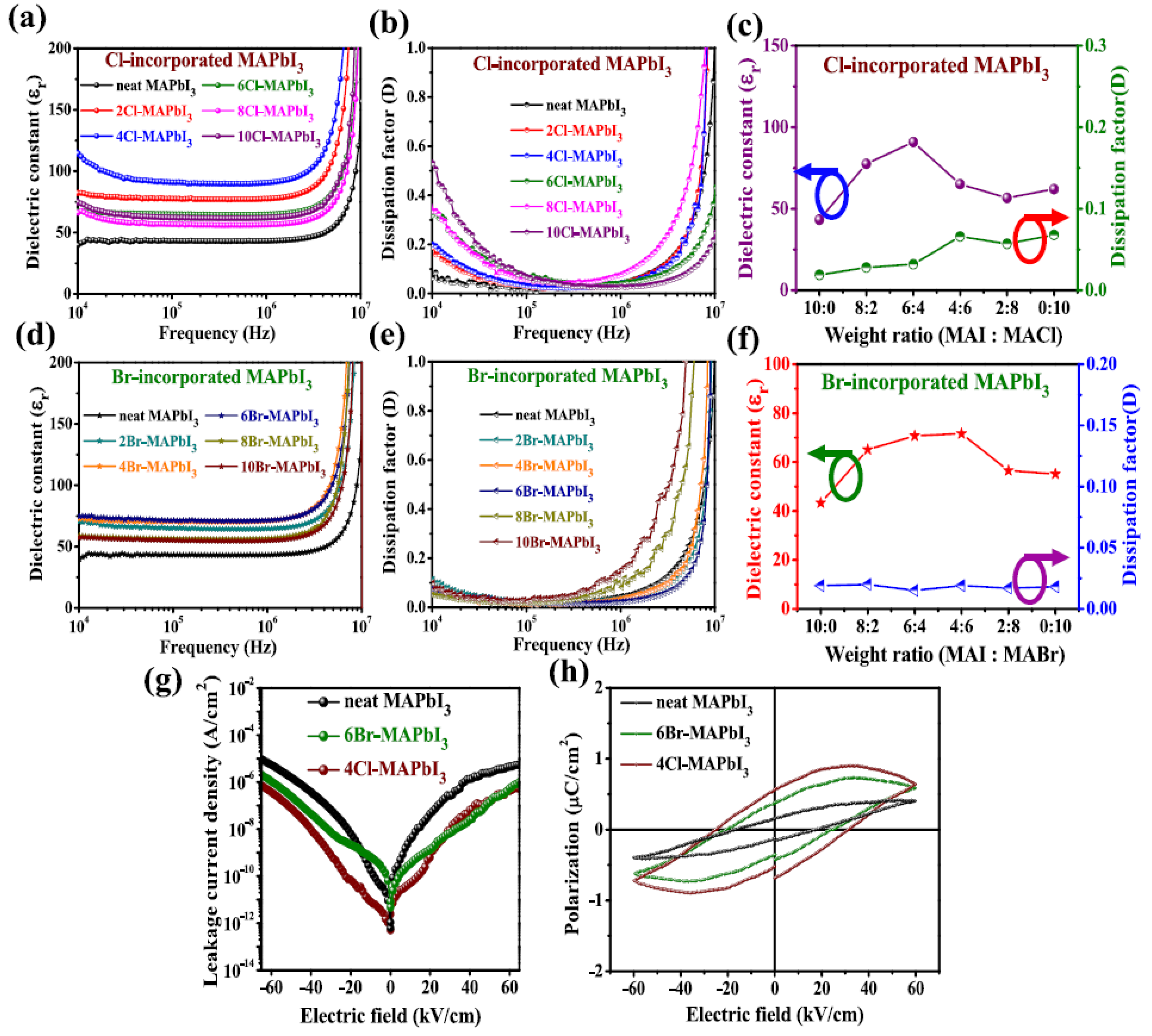
| Material | Eg/ eV | d33 /pCN−1 |
Ps / μC cm−2 |
TC /K | Young’s modulus/GPa | Symmetry change |
|---|---|---|---|---|---|---|
| (TMFM)x(TMCM)1–xCdCl3[137] | - | 1540 | - | 366.8 | - | - |
| MAPbI3[138,139] | 1.56 | - | 7.2 to~8 but 38 is expected | 330 | E[100] =10.4 | I4cm to Pmm |
| BaTiO3[140] | - | 190 | 26 | 393 | - | - |
| Tetragonal to orthorhombic MAPbBr3[141] | 2.2 | - | ∼0.35 to ∼0.4 | - | - | Pna21 to I4cm |
| CsPbI3[142,143] | 1.73 | - | - | - | 186 | Pnma to Pmn21 |
| MAPbI3-xClx[144] | 1.57 to 1.63 | - | - | - | - | - |
| NH4PbI3[114] | 1.76 | - | 5.4 | - | ||
| (ChPy)4AgBiBr8[145] | - | - | 3.2 | 305 | - | - |
| (MDABCO)RbI3[146] | 14 | 22 | 448 | R3 to P432 | ||
| MPSnBr3[147] | 2.62 | - | 4.5 | 357 | - | Pna21 to Pm¯3m |
| 3-APRbBr3[148] | - | - | - | 440 | Pm¯3m to Ia | |
| MDABCONH4X3 (X=Cl−, Br− and I−)[111,149] | 119, 248 and 178 | - | 14.7, -,- | - | ||
| MHy2PbBr4[145] | - | - | 5.8 | 351 | - | Pmn21 to Pmnm |
| MAPb(I1-xBrx)3[150] | - | - | - | - | - | |
| CH3NH3SnI3[151] | 1.30 | - | - | - | - | - |
| N(CH3)4SnI3[152] | 2.12 | - | 16.13 | - | - | R3m |
| FAPbI3[153] | 1.47 | - | - | E[100] = 11.8 | P3m1↔P63mc | |
| MAPbCl3[154,155,156,157,158] | 2.9 | - | - | - | E[100] =19.8 | - |
| TMIM-PbI3[159] | - | - | 0.67 | 312 | - | C2↔C2/m |
| Energy harvesting materials | Output voltage/V | Output current density/ | Current | specific capacity | d33 | Reference |
|---|---|---|---|---|---|---|
| 4Cl-MAPbI3 PENG | 5.9 | ∼0.61 μA/cm2 | [108] | |||
| CsPbCl3 | 257 | 3.04 Wm-2 | 27.87 μA | [456] | ||
| FASnI3:PVDF | 23 | 35.05 mWcm–2 | 73 pm/V | [103] | ||
| FASnBr3 | 94.594.5 Vp-p | 18.95 μW/cm2 | 19.1 μAp-p | 5050 pm/V | [105] | |
| MA2SnCl6 | 7.33μW cm-2 | 589.98 mAh g-1. | [104] | |||
| Cs2NaBiCl6 | Stable 300 mAh g–1 | [457] | ||||
| TMCM2SnCl6 | 81 | 0.6 kV/cm | 2 μA | 137 pC/N | [257] | |
| CH3NH3PbBr3 | 175.5 mAh g–1 | [458] | ||||
| CH3NH3PbI3 | 2.7 | 140 nAcm_2 | 43.6 mAh g–1 | 5.12 pm/V | [458] | |
| CH3NH3PbBr3:3Li+ | 200 mAhg−1 | [459] | ||||
| CsPb2Br5 | 200 | 45 mW | 2.8 | 72 pmV_1 | [460] | |
| Poled CH3NH3PbI3 | 2.7 | 140 nAcm_2 | [454] | |||
| Li4Ti5O12 | 175.5 mAhg−1 | [461] | ||||
| BaTiO3 | 6.5 | 70 nAcm-2 | [460] | |||
| EDABCO-CuCl4@PVDF | 63 | 43 µW/cm2 | 2.1 μA/cm2 | 165 pm/V | [298] |
| Materials | Properties | Applications |
|---|---|---|
| (Ba,Sr)TiO3 | pyroelectric | pyrodetector |
| BaTiO3 | dielectric | capacitor, sensor |
| PbTiO3 | piezoelectric pyroelectric | acoustic transducer pyrodetector, |
| Pb(Zr,Ti)O3 |
pyroelectric piezoelectric dielectric electro-optic |
pyrodetector surface acoustic wave device, substrate nonvolatile memory, waveguide device |
| (Pb,La)(Zr,Ti)O3 | electro-optic pyroelectric | waveguide device, optical memory display pyrodetector |
| (LiNbO3/Ti) | electro-optic |
waveguide device, second harmonic generation, optical modulator |
| LiNbO3 | piezoelectric | pyrodetector, surface acoustic wave device |
| K(Ta,Nb)O3 |
electro-optic pyroelectric | waveguide device, frequency doubler pyrodetector |
| Pb(Mg1/3Nb2/3)O3 | dielectric | memory, capacitor |
| FAPbBr3 | Piezoelectric pyroelectric electro-optica |
Piezoelectric nanogenerator Acoustic transducera, pyrodetectora Waveguide devicea, second harmonic generation?, optical modulators? |
| MAPbI3 | Piezoelectric, Pyroelectric, Electro-opticsa |
Piezoelectric energy harvesting devices, Acoustic transducera, pyrodetectora Waveguide devicea, second harmonic generationa, optical modulatorsa |
| CsPbX3 | Piezoelectrica Pyroelectrica Electro-opticsa |
Piezoelectric energy harvesting devicesa, Acoustic transducera, pyrodetectora Waveguide devicea, second harmonic generationa, optical modulatorsa |
| Structure of piezoelectric generator |
Piezoelectric material |
Dimension of piezoelectric material [mm] |
Dimension of generator [mm] |
Frequency of source vibration [Hz] |
Generated Power [mW] |
|---|---|---|---|---|---|
| Cantilever beam | PZT | 4 × patches: 25,4×50,8×0,254 |
14,3×50,8×1,27 | 29,5 | 1.4 |
| Cantilever beam | MFC | 2 × patches: 85×28×0,3 |
114,3×50,8×1,27 | 29,7 | 1.7 |
| Connected four cantilever beams |
PZT | 4 × patches: 30×10×0,5 |
200×200×0,2 | 35,5 | 8.0 |
| M-shaped beam | PZT | 2 × patches: 25×25,4 |
220×25,4×0,254 | 14.5 | 2.6 |
| Cantilever | FAPbBr3 | - | 1×3 | - | 32.3 x 10-3 |
| Nanogenerator | Output voltage [V] |
Output current | Efficiency |
|---|---|---|---|
| NaNbO3/PDMS | 3.20 | 16 nA cm−2 | - |
| LiNbO3/PDMS | 0.46 | 9.11 nA | - |
| BaTiO3/PDMS | 5.50 | 350 nA | - |
| ZnSnO3/PDMS | 9.70 | 0.9 μA cm−2 | - |
| PMN-PT/PDMS | 7.80 | 2.29 μA | - |
| FAPbBr3/PDMS | 8.50 | 3.4 μA cm−2 | 0.44% |
| MAPbX3/PDMS | ? | ? | ? |
| CsPbX3/PDMS | ? | ? | ? |
| Nano-sensing devices | Sensitivity %/kPa−1 | LOD | Ref. |
|---|---|---|---|
| CsPbBr1.5I1.5 /TiO2 | 0.012 μM | [525] | |
| NIPs@ CsPbBr3 QDs | 1.45 ng/mL. | [526] | |
| HC(NH2)2SnI3/SnO2/Pt-NPs nano-composite | 65 ppb | [527] | |
| MAPbI3_x(SCN)x | 3 | [528] | |
| ZnO nano-sheets/MAPbI3 | 0.57 | 0.5 | [529] |
| CH3NH3PbI3−xClx based ozone sensor | 9.69 | [530] | |
| (RNH3)2 PbI4 | 1.3 | [531] | |
| CsPbX3 quantum dot with Oleic acid ligand | 0.1 nM | [532] | |
| CsPbX3 (Br/I) Quantum dots/picric acid | 0.8 nM | [533] | |
| CsPbBr3 QDs/Cu2+ and Yb3+ ions | 2 × 10-5 m | [534] | |
| CsPb(Br/Cl)3 nanocrystals | 5 ppm | [535] | |
| CsPbBr3 QDs film | 8.85 ppm | [536] | |
| Cs3Bi2Br9:Eu3+ PeQDs | 10 nM | [537] | |
| CH3NH3PbI3 based NH3 gas sensor | 55 | 10 ppb | [538] |
| CH3NH3PbI3−x(SCN)x for NO2 detection | 5.3 × 10−1 ppm−1 | 200 ppb | [539] |
| MAPbBr3 room-temperature NO2 sensors | 0.1 ppm | [540] | |
| (MA)2Pb(SCN)2I2 for O3 detection | 5 ppb | [541] | |
| CsPbBr3 nanocubes | 54% | 187 ppb | [542] |
| Dual ligands capped CH3NH3PbBr3 QDs | 3.2 μM | [543] | |
| MAPbI3 thin films on SiO2 | 70 ppm | [544] | |
| CH3NH3PbI3−xClx hydrogen sensing | 10 ppm | [545] | |
| CsPbBr3 QDs for H2S detection | 0.18 μM | [546] | |
| Porous CsPbBr3 network | 1 ppm | [547] | |
| MAPbI3 pellet sensor | 200 % | [548] | |
| Ethylenediamine lead iodide chloride (EDPIC) perovskite thin film |
65% | [549] | |
| Paper coated with MAPbI3 | 55% | [550] | |
| (APTES)-capped CsPbBr3 QDs | 18.8 ng/mL | [551] | |
| AuN@(CsPbBr3NCs@BaSO4)@ melamine | 0.42 nmol/L | [552] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





