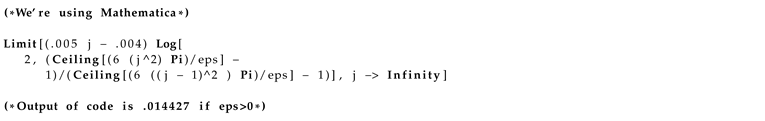1. Intro
Let . Suppose is Borel, where:
In addition, is the Hausdorff dimension and is the Hausdorff measure in its dimension on the Borel -algebra.
1.1. First Special Case of A
Suppose the n-dimensional box is B. We want an explicitA, such that:
- (1)
for all B
- (2)
for all B.
This case of A is called .
1.1.1. Potential Answer
If
, using this reddit post [
1], define
A such that:
Find some set , where for every interval I.
Hence, construct a subset of with this property (then copy and paste this set to get the desired set ):
We do this by constructing a strange map from
. Take a real number
, expand that number in binary as
and map the value to the series
. It’s possible using Khintchine’s inequality [
2] to show the sum converges for a.e.
. Thus, our desired set
will just consist of those
x for which the sum is positive.
The fact this set works is a little bit annoying to prove, but relies on Khintchine’s inequality [
2 p.187-205] and the divergence of the Harmonic series. Essentially, we want to show that for any initial seqeuence
of digits there is a positive probability that the final sum is positive and a positive probability that the final sum is negative.
Note, in case there is a research paper which can average into a finite number, consider the next example.
1.2. Second Special Case of A
Suppose the n-dimensional box is B. Is there an explicit A, such that:
- 1.
for all B
- 2.
for all B
- 3.
-
For all n-d boxes :
- (a)
- (b)
- (c)
?
If explicit A exists, what is an example? If not, how does one modify , so that it exists?
If such a set exists, this case of A is called . (We have yet to prove or disprove exists.)
1.3. Attempting to Analyze/Average A
The expected value of
A, w.r.t the Hausdorff measure in its dimension, is:
Nevertheless, we have the following problems:
Notation 1 (Problem 1). When 1.1), is undefined.
1.3.1. Explanation of Problem 1
When
, using
Section 1.1 and
Section 1.1.1, since
for all
B, notice
and
. This makes
undefined due to division by infinity. Similarly, the most obvious extension of
or
is also undefined; i.e., given the absolute value is
, then the following is false since
for all
B:
Notation 2 (Problem 2). Suppose is the set of all unbounded Borel subsets of and is the n-d Euclidean norm. If is the set of all , where is finite and the cardinality is , then (i.e., is “measure zero" in )
1.3.2. Explanation of Problem 2
All unbounded
A have means with a finite
n-d norm when the symmetry lines of
A intersect at one point. Thus, for any sequence of bounded sets
whose set-theoretic limit (
Section 1.3.3) is
A, such that the lines of symmetry of
A intersect at one point,
in the following statement (
is the absolute value):
always exists and has the same value.
Since the cardinality of the set of all unbounded sets with one or more symmetry lines is , the cardinality of all unbounded sets whose lines of symmetry intersect at one point is less than or equal to . Hence, since the cardinality of the collection of all unbounded subsets of is , and . Thus, we conclude , which shows problem 2 is correct.
Therefore, suppose:
1.3.3. Set Theoretic Limit of a Sequence of Sets
The set-theoretic limit of a sequence of sets of bounded set
is
A when:
where:
which we represent with the notation:
Now, consider an approach to solving problems and :
1.3.4. Approach
Suppose
is the set of all unbounded Borel subsets of
and is the set of all bounded Borel subsets of
, where
is an arbitrary set. In addition, suppose
is the
n-d Euclidean norm. If
is the set of all
, where for all
and
, such that
(
Section 1.3.3),
is unique,
is satisfying (
Section 3), and
is finite:
- 1.
(i.e., is “almost everywhere" in )
- 2.
If (1) isn’t true, then
1.3.5. Explanation of Approach
If
(
Section 1.3.3) where we apply
(
Section 1.3.2 Equation (
2), depending on the
chosen,
could be one of many values. Here is an example:
Example 1. Suppose . We define the bounded sequences of sets and , where 1.3.3). Note, the center of , for all , is and the center of , for all , is . Thus, and . Furthermore, depending on the chosen, can be any point in (when it exists).
Therefore, we ask the following:
1.4. Question
Is there a unique way to define “satisfying" in the approach of , which solves problems 1 and 2 with applications?
2. Extending the Expected Value of A w.r.t the Hausdorff Measure
The following are two methods to finding the most
generalized,
satisfying extension of
in Equation (
1) which we later use to answer the question in
:
One way is defining a generalized, satisfying extension of the Hausdorff measure, on all
A with positive & finite measure which takes positive, finite values for all Borel
A. This can theoretically be done in the paper “A Multi-Fractal Formalism for New General Fractal Measures"[
3], where in Equation
1 we replace the Hausdorff measure with the extended Hausdorff measure.
Another way is finding
generalized,
satisfying average of all
A in the fractal setting. This can be done with the papers “Analogues of the Lebesgue Density Theorem for Fractal Sets of Reals and Integers" [
4] and “Ratio Geometry, Rigidity and the Scenery Process for Hyperbolic Cantor Sets" [
5] where we take the expected value of
A w.r.t the densities in [
4,
5].
Note, neither approach answers
Section 1.4, since the
n-d norms of the averages in the approach are not unique for unbounded sets (ex. 1). Therefore, we ask a leading question that uses
to guide readers to an interesting solution to
Section 1.4.
3. Attempt to Define “Unique and Satisfying" in The Approach of Section 1.3
3.1. Leading Question
To define
satisfying inside the approach of
Section 1.3.4, we take the expected value of a sequence of bounded sets chosen by a choice function. To find the choice function, we ask the
leading question...
Suppose is the set of all bounded Borel subsets of , where there exists an arbitrary set , such that for all :
- (A)
- (B)
- (C)
□ is the logical symbol for “it’s necessary"
- (D)
Define C to be chosen center point of (e.g., the origin)
- (E)
Define E to be the fixed, expected rate of expansion of w.r.t center point C (e.g., )
- (F)
Define to be actual rate of expansion of w.r.t center point C ( 5.5)
Does there exist a unique choice function which chooses an unique set
, where for all
, every
is equivalent (
Section 5.3, def. 1) to
, such that:
- 1.
- 2.
For all
and
, where
(
Section 1.3.3), the “measure" (
Section 5.4.1,
Section 5.4.2) of
must increase at rate linear or superlinear to that of
- 3.
If
is the
n-d Euclidean norm,
is unique and
is finite (
Section 5.2).
- 4.
-
For some satisfying (1), (2), and (3), where for all , given , , and in (1), (2), and (3), s.t., note that for all , where satisfies (1), (2), and (3):
If is the n-d Euclidean distance between , then
-
If
, for any linear
, where
and the Big-O notation is
, there exists a function
, where the absolute value is
and (
Section 3.1.E-F):
In simpler terms, “the rate of divergence" of
(
Section 3.1.E-F) is
less than or equal to “the rate of divergence" of
(
Section 3.1.E-F).
- 5.
-
If is the set of all unbounded Borel subsets of and is the set of all , where satisfies (1), (2), (3) and (4), then:
(i.e., is “almost everywhere" in )
When , replace the Hausdorff measure in of criteria (3) with the generalized measures and densities in , where we want
When neither are possible, then
- 6.
Out of all choice functions which satisfy (1), (2), (3), (4), and (5) we choose the one with the simplest form, meaning for each choice function fully expanded, we take the one with the fewest variables/numbers?
I’m convinced
, where all
(
Section 3.1) which answers the
leading question isn’t
unique nor
satisfying enough to answer
Section 1.3.4. Still, adjustments are possible by changing the criteria or by adding new criteria to
3.1.
4. Question Regarding My Work
Most don’t have time to address everything in my research, hence I ask the following:
Is there a research paper which already solves the ideas I’m working on? (Non-published papers, such as mine [6], don’t count.)
Let
be an unbounded, Borel set. Suppose
be the Hausdorff dimension and
be the Hausdorff measure
in its dimension on the Borel
-algebra. See
Section 3.1, once reading this section, and consider the following:
Is there a simpler version of the definitions below?
5.1. Set Theoretic Limit of a Sequence of Bounded Sets
Note, the set-theoretic limit of a sequence of sets of bounded set
is
A when:
where:
which we denote
Example 2. When , we define sequences of sets and , such that . We aren’t sure how to prove this, but assume readers should be able to verify.
5.2. Expected Value of Bounded Sequences of Sets
If
is a sequence of bounded sets, where
(
Section 5.1) and the absolute value is
, the expected value of
A w.r.t
(when it exists) is a real number
which satisfies the following:
Note,
can be extended using
Section 2.
5.2.1. Example 1
Using example 2, suppose
,
, and
. Hence:
Since Equation (12) is true,
5.2.2. Example 2
Using example 2, suppose
,
, and
. Hence:
Since Equation (24) is true, .
5.3. Defining Equivelant and Non-Equivelant Sequences of Bounded Functions
Definition 1 (
Equivelant Sequences of Bounded Sets).
The sequences of sets and are equivalent, if there exists , where for all , there exists , such that:
and for all , there exists , such that:
5.3.1. Explanation
Suppose
is the set of all subsets of
. Hence,
and
are equivalent, when for all sets
, where
(
Section 5.1)
and or
exist, the following is true:
Thus, consider:
Theorem 1.
If and are equivalent, then for all , where :
Hence, consider the following:
5.3.2. Example of Equivalent Sequences of Bounded Sets
Now, suppose . Thus, using def. 1, we prove:
- 1.
-
For all
, there exists a
, where:
which is proven with the following:
In Equation (
25), since
is a 1-d interval,
. Hence,
- 2.
-
For all
, there exists a
, where:
which is proven with the following:
In Equation (
31), since
:
Since crit. and (2) is true, using definition 1, we have shown and are equivalent.
Note, there is no , where (), such that .
Definition 2 (
Non-Equivalent Sequences of Bounded Sets).
The sequences of sets and are non-equivalent, if there exists , where for all , there is either , such that:
or for all , there exists , such that:
5.3.3. Explanation
Suppose,
is the set of all subsets of
. Hence,
and
are non-equivalent, when there exists a set
, where
(
Section 5.1)
and or
exist, s.t.the following is true:
Therefore, consider the following:
5.3.4. Example of Non-Equivalent Sequences of Bounded Sets
Now, suppose . Thus, using def. 2, we prove:
- 1.
-
For all
, there exists a
, where:
which is proven using the following:
Since
is a 1-d interval,
. Therefore:
Since crit. (1) is true, using definition 2, we have shown and are non-equivalent.
5.3.5. Question
How do we find
, where
(
Section 5.1), such that
(
5.2)?
5.4. Defining the “Measure"
5.4.1. Preliminaries
We define the “measure" of in . To understand this “measure", keep reading. (If the following steps are unclear, see Section 8 for examples.)
- 1.
For every
, “over-cover"
with minimal, pairwise disjoint sets of equal
measure. (We denote the equal measures
, where the former sentence is defined
: i.e.,
enumerates all collections of these sets covering
. In case this step is unclear, see
Appendix 8.1.)
- 2.
For every
,
r and
, take a sample point from each set in
. The set of these points is “the sample" which we define
: i.e.,
enumerates all possible samples of
. (In the case this is unclear, see
Sestion 8.2.)
- 3.
-
For every , r, and ,
- (a)
Take a “pathway” of line segments: we start with a line segment from arbitrary point
of
to the sample point with smallest
n-dimensional Euclidean distance to
(i.e., when more than one sample point has smallest
n-dimensional Euclidean distance to
, take either of those points). Next, repeat this process until the “pathway” intersects with every sample point once. (If this is unclear, see
Section 8.3.1.)
- (b)
Take the set of the length of all segments in (3a), except for lengths that are outliers [
7] (i.e., for any constant
, the outliers are more than
C times the interquartile range of the length of all line segments as
). Define this
. (In case this is unclear, see
Appendix 8.3.2.)
- (c)
Multiply remaining lengths in the pathway by a constant so they add up to one (i.e., a probability distribution). This will be denoted
. (In case this step is unclear, see
Section 8.3.3.)
- (d)
Take the shannon entropy [
8, p.61-95] of step (3c). We define this:
which will be
shortened to
. (In case this is unclear, see
Section 8.3.4)
- (e)
Maximize the entropy w.r.t all "pathways". This we will denote:
- 4.
Therefore, the
maximum entropy of
w.r.t
, using (1) and (2) is:
5.4.2. What Am I Measuring?
Suppose we define two sequences of bounded sets that have a set theoretic limit of A: e.g., and , where for constant and cardinality
- (a)
Using (2) and (33e) of
Section 5.4.1, suppose:
then (using
) we get:
- (b)
Also, using (2) and (33e) of
Section 5.4.1, suppose:
then (using
) we also get:
- 1.
If using
and
we have:
then
what I’m measuring from increases at a rate
superlinear to that of
.
- 2.
If using equations
and
(where we swap
and
, in
and
, with
and
) we get:
then
what I’m measuring from increases at a rate
sublinear to that of
.
- 3.
-
If using equations , , , and , we both have:
- (a)
or are equal to zero, one or
- (b)
or are equal to zero, one or
then what I’m measuring from increases at a rate linear to that of .
Now consider the following examples:
5.4.3. Example of the “measure" of converging super-linearly to that of
Notation 3. Recall, if :
When is the cardinality, for all and ,
-
For all and , the largest can be is
Now consider:
where:
Notation 4. The area of and are:
Hence, we maximize by doing the following:
Notation 5 (Procedure to Maximize ). Consider the procedure below:
- 1.
Cover the circle, with the same or larger-sized circle, which can be divided into minimum t “pie-slices" of equal area . Notice, .
- 2.
Take the centroid of each slice
- 3.
Out of all centroids in step 2, take the centroid with the largest x-coordinate: i.e., denote this point which is the start-point of the pathway of line segments in the resulting step
- 4.
Take the distances between all pairs of consecutive centroids, starting with , rotating counter-clockwise or clockwise. Either-way, the end result should change by only a negligible amount.
- 5.
Multiply the distances by a constant so they add up to 1 (i.e., a probability distribution)
- 6.
Take the shannon entropy of the distribution using log base 2 in (33d)-(33e). (Note, since the “pie-slices" of step 1 are congruent and the distances of step 4 are equal, the entropy of the distribution is the largest possible amount (i.e., note 3 crit. 2 & note 4 crit. 1):
Repeat, steps 1-6 with , where the circle is an ellipse (i.e., with this case the “pie-slices" of step 1 are non-congruent and the distances of step 4 are non-equivelant). Hence, we use programming:
Note, the output of
ratiotable in code 5 can be written as:
and is the same as:
Hence, with:
we solve for
:
since:
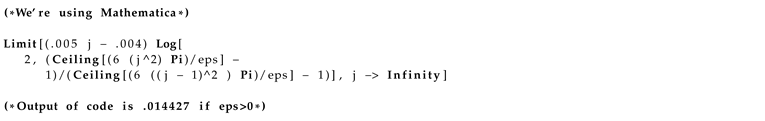
Note, using
Section 5.4.2 (0a) and
Section 5.4.2 (1), take
and use note 3 crit. ii to compute the following:
where:
-
For every , we find a , where , but the absolute value of is minimized. In other words,
for every
, we want
where:
Finally, since
, we wish to prove
within
Section 5.4.2 crit. 1:
where using mathematica, we get the limit is greater than one:
Also, using
Section 5.4.2 (0b) and
Section 5.4.2 (1), take
to compute the following:
where:
For every
, we find a
, where
, but the absolute value of
is minimized. In other words, for every
, we want
where:
Finally, since
, we wish to prove
within
Section 5.4.2 crit. 1:
where using mathematica, we get the limit is greater than one:
Hence, since the limits in Equation (
61) and Equation (
70) are greater than one and less than
: i.e.,
we have proven
what we’re measuring from increases at a rate
superlinear to that of
(i.e.,
Section 5.4.2 crit. 1).
5.4.4. Example of The “Measure" from Increasing at a Rate Sub-Linear to that of
Using our previous example, we can use the following theorem:
Theorem 2.
If what we’re measuring from increases at a rate superlinear to that of , then what we’re measuring from increases at a ratesublinearto that of
Hence, in our definition of super-linear (
Section 5.4.2 crit. 1), swap
and
for
and
within
and
(i.e.,
and
). Notice, thm. 2 is true when:
5.4.5. Example of the “measure" of converging linearly to that of
Notation 6. Recall, if :
When is the cardinality, for all and ,
-
For all and , the largest can be is
Now consider:
where:
Notation 7. The area of and is:
Notice, since
is a square, using note 6 crit. 2 and note 7 crit. 1, it’s simple to see:
Note, since
is also a square, for all
and
Thus, using Equations (
73) and (
74):
For every
, we find a
, where
, but the absolute value of
is minimized. In other words, for every
, we want
where:
which gives:
where using note 6 crit. 1:
, we wish to prove
Section 5.4.2 crit. 33a:
Note, since
is a square, using note 6 crit. 2 and note 7 crit. 2, it’s simple to see:
Thus, using
Section 5.4.2 0a and note 6 crit. 2, swap
with
and with
, such that:
Note, since
is also a square, for all
and
Therefore, using Equations (
84) and (
85):
For every
, we find a
, where
, but the absolute value of
is minimized. In other words, for every
, we want a
, where:
Hence:
and, using note 6 crit. 1 and note 6 crit. 1 with equation
92:
. Thus, we wish to prove
Section 5.4.2 crit. 33a using Equation(
93):
where
Section 5.4.2 crit. 33b is true.
Therefore, since
Section 5.4.2 crit. 3 is correct in this case, “the measure" of
increases at a rate linear to that of
5.5. Defining The Actual Rate of Expansion of Sequence of Bounded Sets From C
In the next section, we will define the actual rate of expansion of sequence of bounded sets from C and give an example.
5.5.1. Definition of Actual Rate of Expansion of Sequence of Bounded Sets
Suppose
is a bounded sequence of subsets of
, and
is the Euclidean distance between points
. Therefore, using the “chosen" center point
, when:
the
actual rate of expansion is:
Note, there are cases of when isn’t fixed and (i.e., the fixed, expected rate of expansion).
5.5.2. Example
Suppose
,
, and
. One can clearly see
is the point on
that is farthest from
. Hence,
and the actual rate of expansion is:
6. My Attempt At Answering The Approach of Section 1.3
6.1. Choice Function
Suppose is the set of all bounded Borel subsets of . We then define the following:
If is an arbitrary set, then for all , satisfies (1), (2), (3), (4), and (5) of the leading question in 3.1
For all ,
6.2. Approach
We manipulate the definitions of
Section 5.4.2 (0a), (0b) and
Section 5.4.2 (ii) to solve
3.1 (1)-(5) of the
leading question.
6.3. Potential Answer
6.3.1. Preliminaries (Definition of T)
Suppose:
then define an explicit injective , where , such that:
If , then
If , then
If , then
6.3.2. Question
Does T exist? If so, how do we define it?
Thus, using
,
,
,
E,
(
Section 5.5), and
with the absolute value function
, ceiling function
, and nearest integer function
, we define:
the choice function, which answers the
leading question in
, could be the following, s.t.we explain the reason behind choosing the choice function in
Section 6.4:
Theorem 3.
where for , we define to be equivalent to when swapping “" with “" (for Equations (109) and (110)) and sets with (for Equation (109)–(116)), then for constant and variable , if:
then for all ( crit. ii), if:
where is the ceiling function, E is the fixed rate of expansion, Γ is the gamma function, n is the dimension of , is the Hausdorff dimension of set , and is area of the smallest n-dimensional box that contains , then
such that ( 6 crit. 2) must satisfy Equations (121) and (122). (Note, we want , , and to answer the leading question of ) where the answer to problems 1 and 2 & the approach of is (when it exists).
6.4. Explaining The Choice Function and Evidence The Choice Function Is Credible
Notice, before reading the programming in code , without the “
c"-terms in Equation
121 and Equation 122:
The choice function in Equation (
121) and Equation (122) is zero, when
what I’m measuring from
(
Section 5.4.2 criteria 1) increases at a rate superlinear to that of
, where
.
The choice function in Equation (
121) and Equation (122) is zero, when for a given
and
there doesn’t exist
c where Equation
119 is satisfied or
.
-
When
c does exist, suppose:
- (a)
When
, then:
- (b)
When
, then:
Hence, for each sub-criteria under crit. (3), if we subtract one of their limits by their limit value, then Equation
121 and Equation (122) is zero. (We do this by using the “
c"-term in Equations (
121) and (122)). However, when the exponents of the “
c"-terms aren’t equal to
, the limits of Equation
121 and 122 aren’t equal to zero. We, infact, want this when we swap
with
. Moreover, we define function
(i.e., Equation (
120)), where:
- i.
When
, then Equation
121 and 122 without the “c"-terms are zero. (The “c"-terms approach zero and still allow Equations (
121) and (122) to equal zero.)
- ii.
When
then
is zero, which makes Equation
121 and equal zero.
- iii.
-
Here are some examples of the numerator of
(Equation (
120)):
- A.
When , , and , the numerator of is
- B.
When , , and , the numerator of is
- C.
When
,
, and
, the numerator of
is ceiling of constant
times the volume of an
n-dimensional ball with finite radius: i.e.,
- D.
When
,
, and
, the numerator of
is ceiling of the volume of the
n-dimensional ball: i.e.,
Notation 8. Now, consider the code for Equation (121) and Equation (122). (Note, the set theoretic limit is set A. In this example, and:
We leave it to mathematicians to figure LengthS1, LengthS2, Entropy1 and for different A, , and .
7. Questions
Does answer the in
If is the n-d Euclidean norm, using and thm. 3, where , is unique and finite?
If is the n-d Euclidean norm, using and thm. 3, where , is is unique and finite?
If there’s no time to check questions 1, 2, and 3, see .
8. Appendix of Section 5.4.1
Suppose
- 1.
- 2.
Then one example of
, using
Section 5.4.1 step 1, (where
) is:
Note, the area of each of the rectangles is
, where the borders could be approximated as:
and we’ll illustrate this as purple rectangles covering
(i.e., the red square).
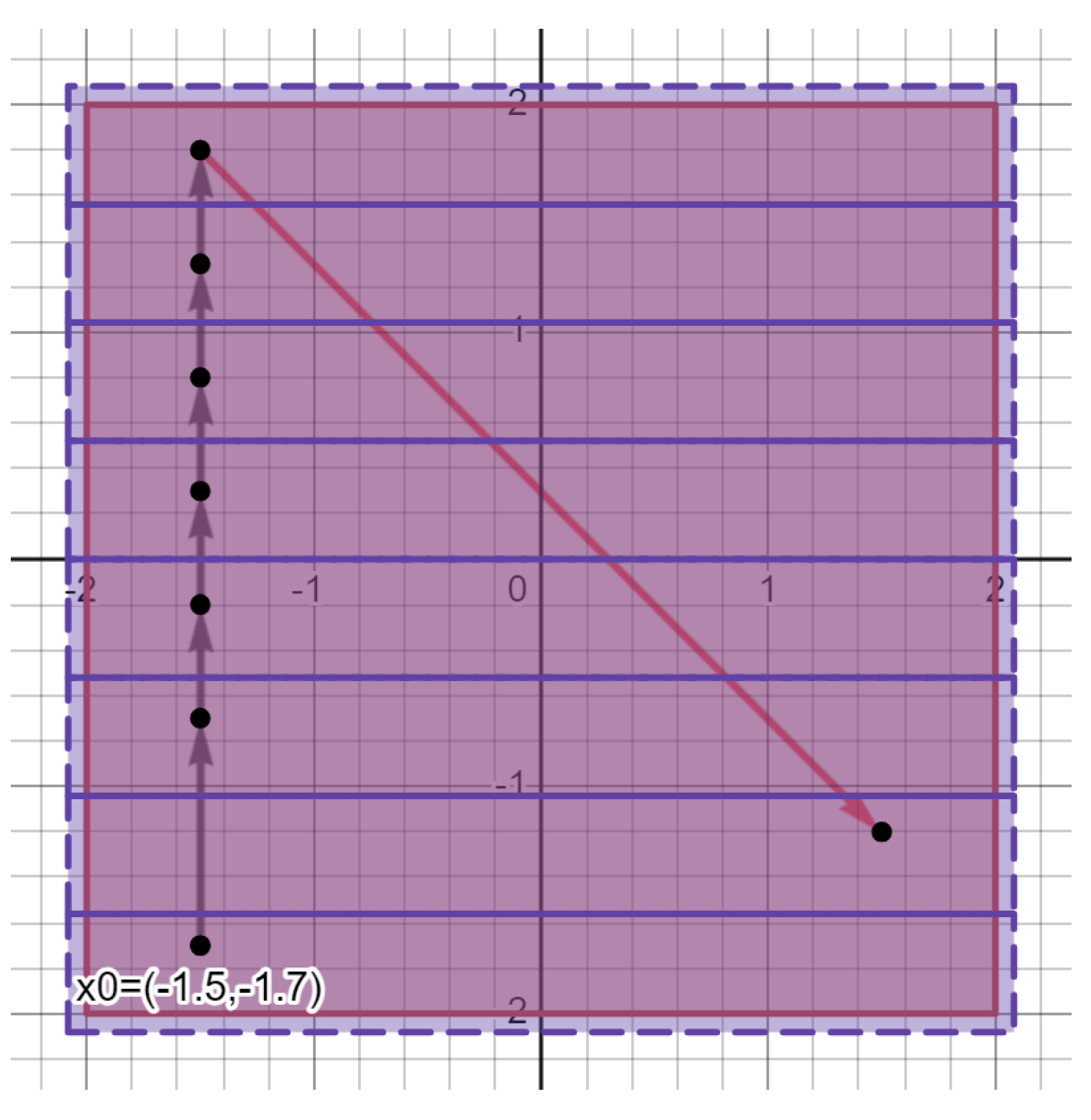
Figure 1.
Purple rectangles are the “covers" and the red square is . (Ignore the boundaries)
Figure 1.
Purple rectangles are the “covers" and the red square is . (Ignore the boundaries)
(Note, the purple rectangles in fig.
Figure 1, satisfy step (1) of
Section 5.4.1, since the Hausdorff measures
in its dimension of the rectangles is
and there is a minimum 8 covers over-covering
: i.e.,
Definition 3 (Minimum Covers of Measure
covering
).
We can compute the minimum covers , using the formula:
where )
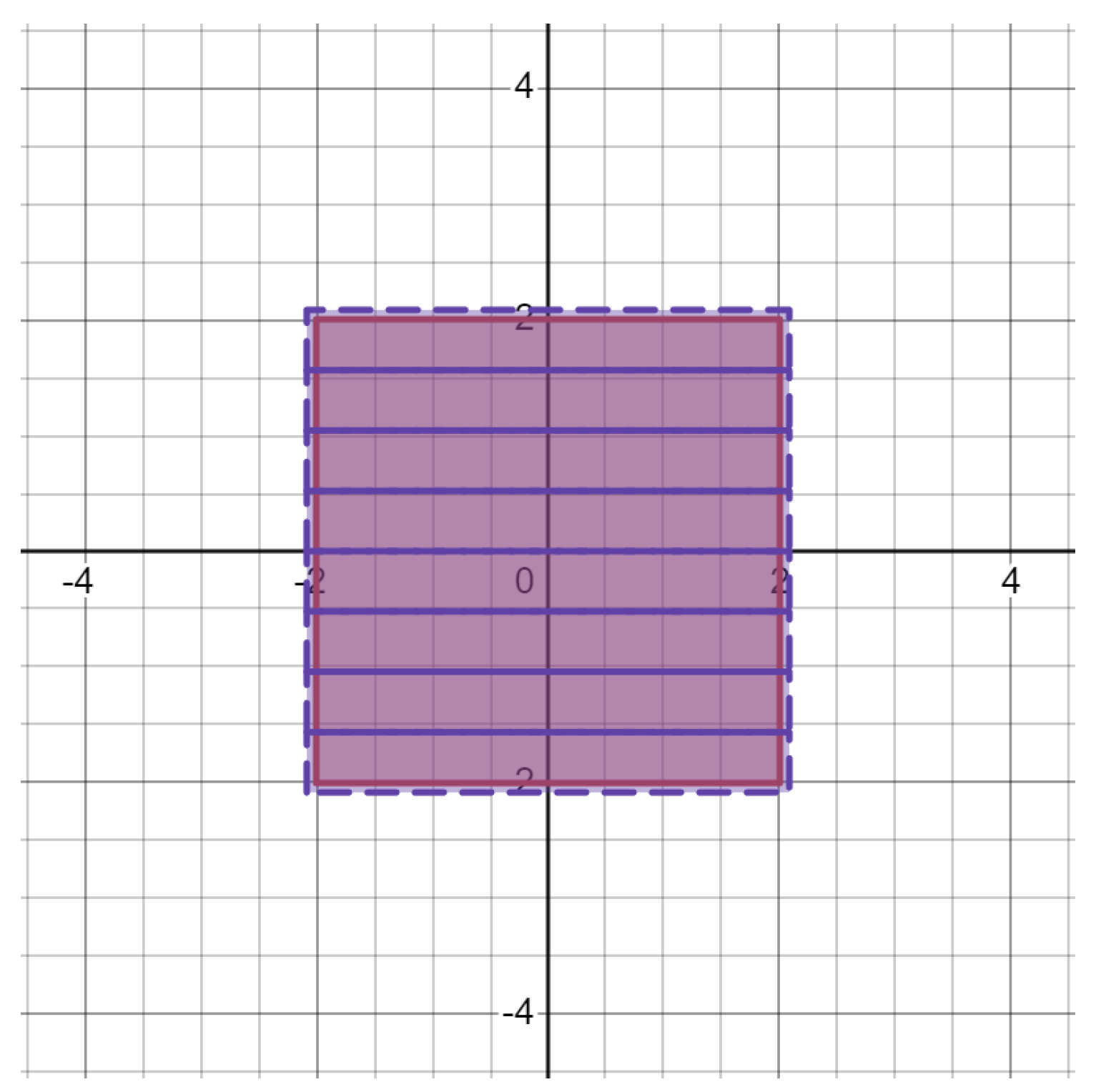
Note the covers in need not be rectangles. In fact, they could be any set as long as the “area" of those sets is , and is over-covered by the smallest number of sets possible. Here is an example:
Figure 2.
The eight purple sets are the “covers" and the red square is . (Ignore the boundaries)
Figure 2.
The eight purple sets are the “covers" and the red square is . (Ignore the boundaries)
To define this cover, start off with:
Then, for each
in
, we define:
except
where:
such that an example of
is:
In the case of , there are uncountably many of different shapes and sizes which we can use. However, these examples were the ones taken.
Suppose
- 1.
- 2.
- 3.
- 4.
, using Equation (
129) and
Figure 1, is
Then, an example of
is:
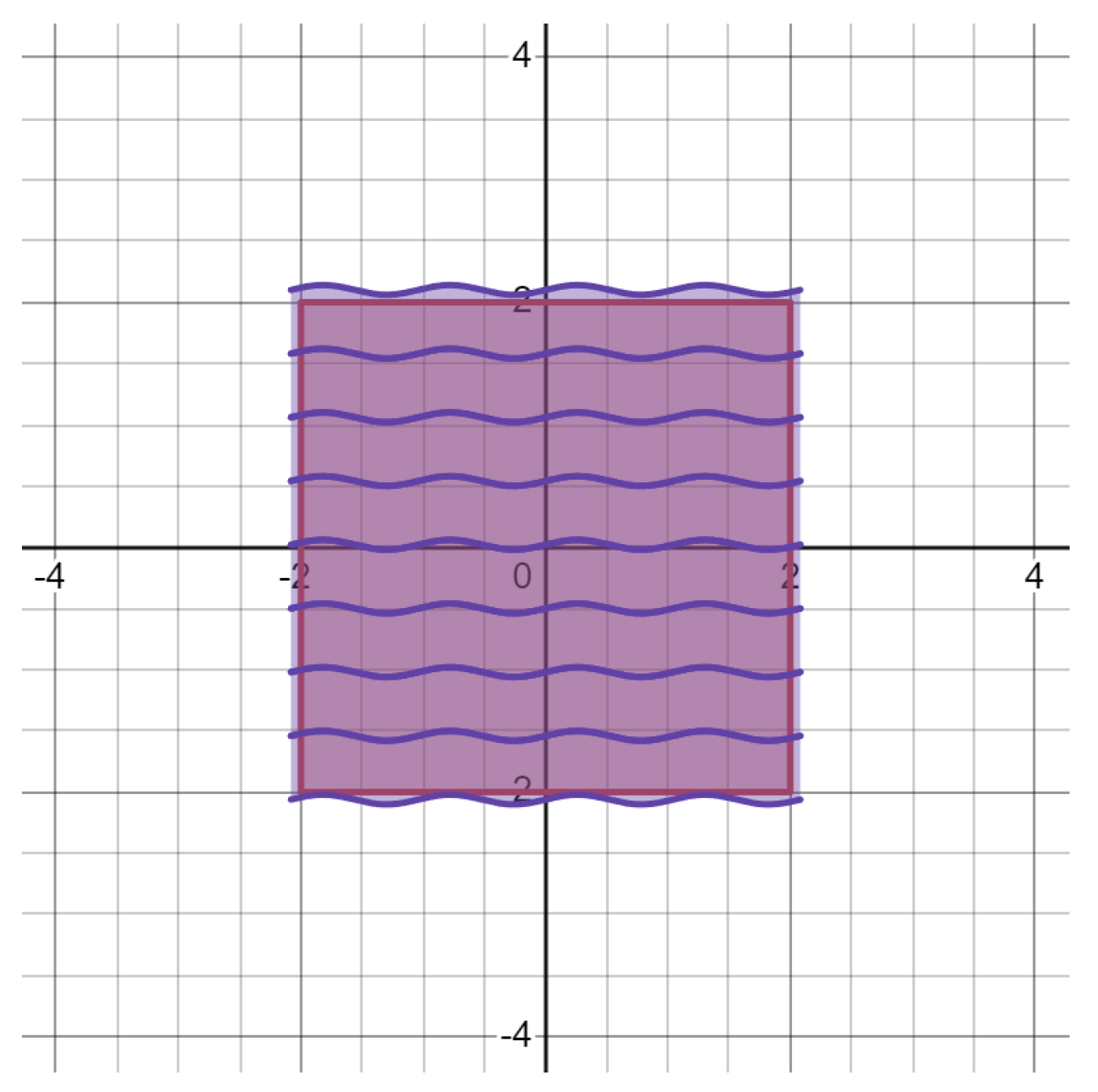
Below, is an illustration of the sample: i.e., the set of all black points in each purple rectangle of covering :
Figure 3.
The black points are the “sample points", the eight purple rectangles are the “covers", and the red square is . (Ignore the boundaries)
Figure 3.
The black points are the “sample points", the eight purple rectangles are the “covers", and the red square is . (Ignore the boundaries)
Note there are multiple samples we can take, as long as one sample point is taken from each cover in .
Suppose
- 1.
- 2.
- 3.
- 4.
, using Equation (
129) and
Figure 1, is
- 5.
, using Equation
142, is:
Therefore, consider the following process:
8.3.1. Step 33a
If
is:
suppose
. Note, the following:
is the next point in the “pathway" since it’s a point in with the smallest 2-d Euclidean distance to instead of .
is the third point since it’s a point in with the smallest 2-d Euclidean distance to instead of and .
is the fourth point since it’s a point in with the smallest 2-d Euclidean distance to instead of , , and .
we continue this process, where the “pathway" of is:
Notation 9.
If more than one point has the minimum 2-d Euclidean distance from , , , etc. take all potential pathways: e.g., using the sample in Equation (144), if , then since and have the smallest Euclidean distance from , and for point , since and have the smallest Euclidean distance from , we takethreepathways:
8.3.2. Step 33b
Take the length of all line segments in the pathway. In other words, suppose
is the
n-th dim.Euclidean distance between points
. Using the pathway of Equation (
145), we want:
Whose distances can be approximated as:
As we can see, the outlier is
(i.e., note these outliers become more prominent for
). Therefore, remove
from the set of distances:
which we can illustrate with:
Figure 4.
is the start point in the pathway. The black line segments in the “pathway" have lengths which aren’t outliers. The length of the red line segment is an outlier.
Figure 4.
is the start point in the pathway. The black line segments in the “pathway" have lengths which aren’t outliers. The length of the red line segment is an outlier.
Hence, when
, using
Section 5.4.1 step 33b & Equation (
144), we note:
8.3.3. Step 33c
To convert the set of distances in Equation (
148) into a probability distribution, we take:
Then divide each element in
by 3.5
which gives us the probability distribution:
8.3.4. Step 33d
Take the shannon entropy of Equation (
150):
We shorten
to
, giving us:
8.3.5. Step 33e
Take the entropy w.r.t all pathways of:
In other words, we’ll compute:
We do this by repeating
Section 8.3.1-
Section 8.3.4 for different
(i.e., in the equations with multiple values, see note 9)
Hence, since the largest value out of Equations (
152)–(159) is 2.52164:
References
- a.k.a u/Xixkdjfk, B.K. a.k.a u/Xixkdjfk, B.K. Is there a set with positive Lebesgue measure in any rectangle of the 2-d plane which is extremely non-uniform? https://www.reddit.com/r/mathematics/comments/1eedqbx/comment/lfdf9zb/?context=3.
- Garling, D.J.H. , Inequalities: A Journey into Linear Analysis; Cambridge University Press, 2007; p. 187–205.
- Achour, R.; Li, Z.; Selmi, B.; Wang, T. A multifractal formalism for new general fractal measures. Chaos, Solitons & Fractals 2024, 181, 114655, https://www.sciencedirect.com/science/article/abs/pii/S0960077924002066. [Google Scholar]
- Bedford, T.; Fisher, A.M. Analogues of the Lebesgue density theorem for fractal sets of reals and integers. Proceedings of the London Mathematical Society 1992, 3, 95–124, https://www.ime.usp.br/~afisher/ps/Analogues.pdf.. [Google Scholar]
- Bedford, T.; Fisher, A.M. Ratio geometry, rigidity and the scenery process for hyperbolic Cantor sets. Ergodic Theory and Dynamical Systems 1997, 17, 531–564, https://arxiv.org/pdf/math/9405217. [Google Scholar]
- Krishnan, B. Bharath Krishnan’s ResearchGate Profile. https://www.researchgate.net/profile/Bharath-Krishnan-4.
- John, R. Outlier. https://en.m.wikipedia.org/wiki/Outlier.
- M., G. M., G. Entropy and Information Theory, /: Springer New York: New York [America];, 2011; pp. 61–95., https://ee.stanford.edu/~gray/it.pdf,https://doi.org/https://doi.org/10.1007/978-1-4419-7970-4. [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).