Set Duplicability and Schröder-Bernstein Theorem

1. Introduction

In a search for a simple proof of a well-known result about infinite sets I drew a diagram (see Figure 1), which immediately suggested a striking analogy with the picture of an egg, a sort of contradiction of the logical principle: “The part cannot be equal to the whole”. The egg is a part of an organism containing information about the whole organism. This reflexivity is a sort of Dedekind’s infinity (a set bijective with a proper part of itself, Galileo Galilei was the first who noticed this property of natural numbers). Set reflexivity and infinity are strictly related to duplicability, the basis of potentially infinite reproductive lines. What is the essence of this analogy? Cells are finite multisets of molecules, how can they exhibit a characteristic typical of infinity? It is not easy to answer, but It is worthwhile to remark that even if cells are finite, they are dynamic and open structures (objects inside them change in time and can continuously enter from or exit the environment).

The infinite is the essence of mathematics and the various forms of mathematical infinities (ordinal and cardinal numbers, infinitesimals, real and hyperreal numbers, and asymptotic orders) are the fields where the power of mathematical imagination reaches the highest level of creativity with paradoxes opening windows that shock our common sense. Mathematics tells us that reality is not only what we think to be, but a wider unimaginable painting of which we can reconstruct some pieces. However, contrarily to their apparent unpractical interest, infinite processes are driving forces of important applications of mathematics. As Gregory Chaitin claimed in many papers and conferences [1], also computers are conceptually a product of Cantor’s Paradise (an expression used by Hilbert in a famous paper of 1926), because the Turing machine was invented for generating computable real numbers. Turing’s discovery of the recursive enumerable set K is a version of Cantor’s diagonal argument.

In this note, the relationship of set duplicability is linked to a famous result in set theory enunciated, without proof, by Georg Cantor in 1887.

2. Set Duplicability

In 1878, Cantor proved two instances of $A\leftrightarrow (A\times A)$, where ↔ denotes a 1-1 (bijective) function, that is, $\left|A\right|=|A\times A|$, where $\left|A\right|$ is the cardinality of the set A, such that $A\leftrightarrow \left|A\right|$, and $\left|A\right|$ is a kind of ordinal number called cardinal number. In the first instance of Cantor’s proofs $A=\mathbb{N}$, while in the second instance $A=\mathbb{R}$ (the naturals and the reals respectively). These results about cardinal numbers were a shock. In a letter to Richard Dedekind Cantor wrote: I see it, but I cannot believe it, as reported in Abraham Fränkel’s book [9].

According to Cantor, a set is infinite if it includes a subset that is equipotent (1-to-1), with the set $\mathbb{N}$ of natural numbers. An infinite set is reflexive if it includes a proper subset 1-to-1 with itself ($\mathbb{N}$ is 1-to-1 with the set $2\mathbb{N}$ of even numbers). According to Dedekind, a set A is infinite when it is reflexive, that is, when $A_{\subset }\to A$, where the inclusion arrow denotes an injective function that is not surjective.

If a set is finite, it cannot be Dedekind infinite. Therefore, when a set is Dedekind infinite, it has to be infinite. However, non-necessarily, Cantor infinity coincides with Dedekind infinity, or D-infinity, because there exist models of ZF with (Cantor) infinite sets that are not Dedekind infinite, called iDf (infinite Dedekind finite).

The bijection $A\leftrightarrow (A\times A)$ means that the set A is Cartesian Duplicable. The general proof that, for every infinite set A, $(A\times A)\leftrightarrow A$ requires the Axion of Choice AC [9]. Moreover, Tarski showed in 1924 [12] that “$A\leftrightarrow (A\times A)$ for any infinite A” is equivalent to the Axiom of Choice AC.

Informally, the axiom of choice says that for any collection of nonempty sets, it is possible to construct a new set by choosing one element from each set (even if the collection is infinite). An equivalent formulation says that the Cartesian product of a collection of non-empty sets is non-empty. Many important results in set theory need AC to be proved. Axiomatic set theories, such as ZF (Zermelo Fränkel) [3,4,5,6], establish axioms expressing the essence of sets, but avoiding the paradoxes arising when a naive notion of class is assumed, such as Russell’s paradox reported in 1902 [10]. The theory ZFC is the ZF theory with the Axiom of Choice.

A set is (sum) Duplicable if $A\times \{0,1\}\leftrightarrow A$, that is, if $A\leftrightarrow A_0\oplus A_1$ with $A_0,A_1$ both bijective with A. Dedekind Infinity implies Cantor’s infinity. If AC is assumed, set infinity is equivalent to Dedekind infinity. [5,6,8,12,13]. It was proved that set duplicability is weaker than AC [8].

Lemma 1 (Cartesian Duplicability implies Duplicability)

If A is a Cartesian duplicable set, it is a sum duplicable set.

Proof. If A is Cartesian duplicable, then:

$$(A\times A)\leftrightarrow A$$

(1)

and the following chain of bijective functions holds:

$$A^{\prime }\leftrightarrow A\leftrightarrow A\times A\leftrightarrow A^{\prime }\times A.$$

(2)

where $a_0\in A$ and $A^{\prime }=A-\left\{a_0\right\}$ (A includes a set bijective to $\mathbb{N}$ and $a_0$ can be set as the element of this set corresponding to 0), then: $(A^{\prime }\times A)=(A-\left\{a_0\right\})\times A=(A\times A)-(\left\{a_0\right\}\times A)$. if $A^{\prime \prime }=\left\{a_0\right\}\times A$ then $A\times A^{\prime }=(A\times A)-A^{\prime \prime }$ that is: $A\times A=(A^{\prime }\times A)\oplus A^{\prime \prime }.$ Therefore, by (2) the thesis follows. □

According to John von Neumann [5,6], an ordinal number is the set of numbers preceding it. Therefore, the first ordinal number is ∅, the second one is $\{\varnothing \}$, the third is $\{\varnothing ,\{\varnothing \left\}\right\}$, and in general the successor of an ordinal $\gamma$ is $\gamma \cup \left\{\gamma \right\}$. The union of all finite ordinals is $\omega$, the first infinite ordinal, also the first limit ordinal (which is not the successor of an ordinal). Then, the successor of $\omega$ is $\omega \cup \left\{\omega \right\}$, therefore, the usual counting process of numbers can be extended to all transfinite numbers. Surprisingly, Cantor’s transfinite counting is strongly related to Archimedes’ counting process based on orders and periods [7].

If we consider the set of all ordinal numbers $\gamma$ equipotent to an infinite ordinal number, then the ordinal ${\bigcup }_{\gamma \le \alpha }\gamma$ is not equipotent to $\alpha$ and is called also an initial ordinal or a cardinal number. The cardinality $\left|A\right|$ of a set A corresponds to the first cardinal number that is equipotent with A. Cardinal numbers are denoted by the symbol ℵ with an index $i\in \mathbb{N}$, where ${\aleph }_0=\left|\mathbb{N}\right|=\omega$. Cantors’s Continuum Hypothesis CH claims that ${\aleph }_{i+1}=2^{{\aleph }_i}$, and a crucial result of the last century, solving the 23^o Hilbert Problem presented in 1900, shows that there are models of ZF where CH holds and models where CH does not hold (and analogously ZF models where AC holds and ZF models where AC does not hold) [2].

As we have already noticed, (sum) set duplicability is weaker than the choice axiom AC. Hence, it is interesting to prove Schröder-Bernstein theorem by assuming that any Cantor infinite set is duplicable. However, we want to investigate the relationship between infinity and duplicability further.

CD hypothesis means that any (Cantor) infinite set is D-infinite. This hypothesis is weaker than AC and even than CC (the Countable Choice axiom). The next lemma will prove that D-infinity, or set reflexivity, implies the (sum) set duplicability, so CD implies the set duplicability.

Lemma 2 (D-Infinity implies Set Duplicability)

Any reflexive set A is duplicable, that is, it is equipotent to the union of two disjoint sets both equipotent to A.

Proof. If A is reflexive, there exists a proper subset $A_0$ of A that is 1-to-1 with A, therefore $A=A_0\oplus (A-A_0)$. Hence $A_0$ is infinite too, and we can apply to $A_0$ the same kind of partition $A_0=A_1\oplus (A_0-A_1)$. Then by iterating this process, we get, for $i\ge 0$:

$$A_i=A_{i+1}\oplus (A_i-A_{i+1})$$

where $A_i\leftrightarrow A$. Let us define:

$$A_{\omega }=\bigcap _{i\ge 0}{A}_i$$

then $A_{\omega }\leftrightarrow A$. At the same time, the proper inclusion chain of the sets $A_i$ defined above implies that for any $a\in A$, there exists some j such that $a\notin A_j$. This means that $a\notin A_{\omega }$, whence $A\leftrightarrow (A-A_{\omega })$. In conclusion, we have that:

$$A=A_{\omega }\oplus (A-A_{\omega })$$

where $A\leftrightarrow A_{\omega }$ and $A\leftrightarrow (A-A_{\omega })$, that is, A is duplicable. □

Lemma 3 (Set Duplicability implies Set Infinity)

A duplicable set is infinite.

Proof. If a set is finite, it cannot be duplicable. This means, by contraposition, that a duplicable set has to be infinite. □

The following lemma and proposition assume CD hypothesis.

Lemma 4

Given two infinite sets $X\subset Y$ if $Y-X$ is 1-to-1 with a proper part of X, then $X\leftrightarrow Y$.

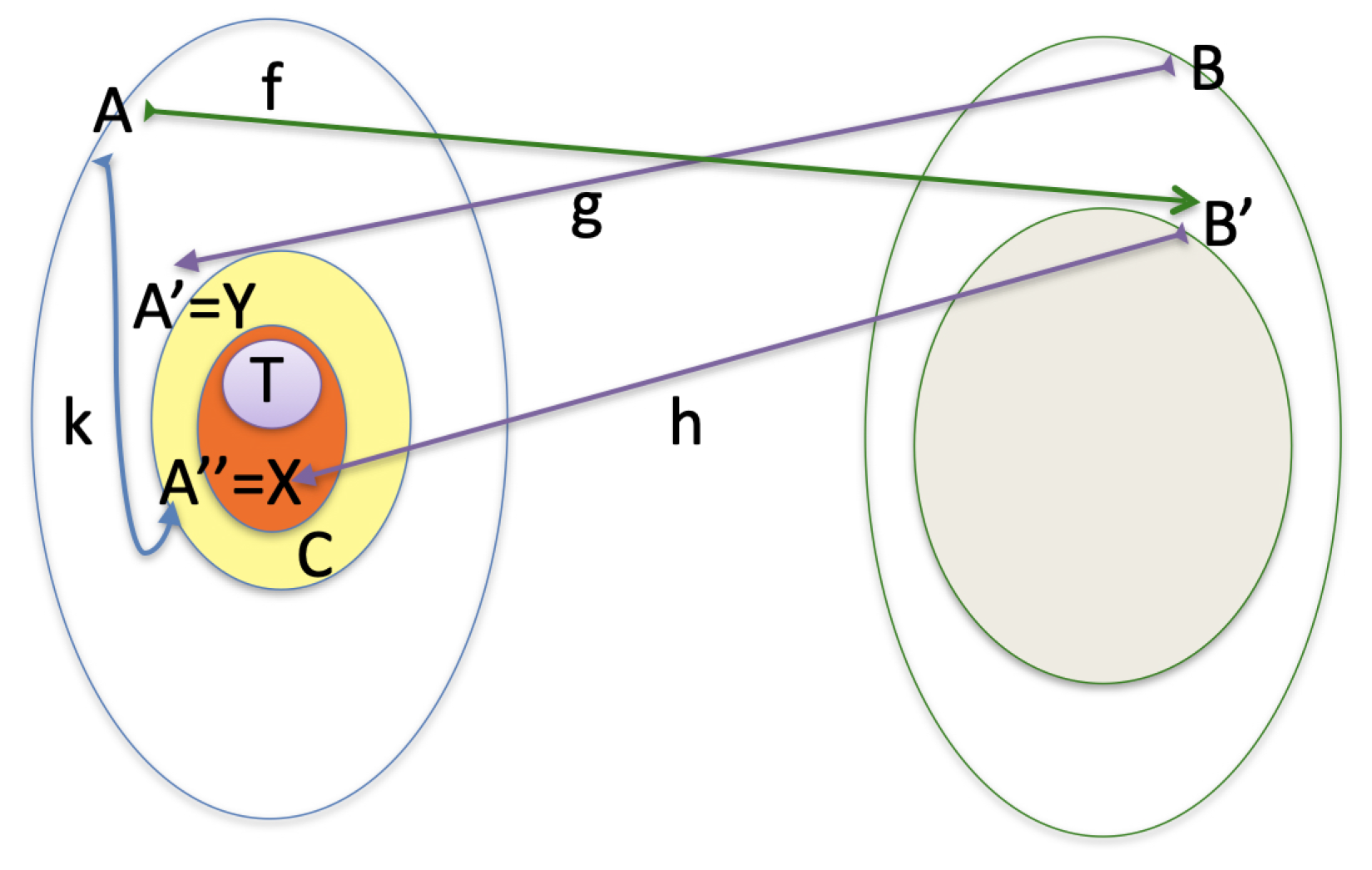
Proof. Let us denote by C the difference $Y-X$ and by T its image in X such that $C\leftrightarrow T$ (see Figure 1). At first glance, a 1-1 correspondence could be obtained by the union of the correspondence $C\leftrightarrow T$ plus the identical correspondence $X-T\leftrightarrow X-T$. However, this is not the correct way to establish a correspondence $Y\leftrightarrow X$. Namely, T (and any subset of X) has to be considered twice: when it is a subset of X and when it is a subset of Y and in the previous wrong solution T as a subset of Y remains uncovered by the correspondence. For this reason, set duplicability is essential to give the right 1-to-1 correspondence between X and Y. Let us suppose that T is infinite (otherwise the proof is trivial). For a better explanation let us denote by a superscript the superset where a set is considered. Now, by the Lemma 2, the set $T^X$ is bijective with the union of two disjoint sets $T^X\leftrightarrow T_1^X\oplus T_2^X$ that are both 1-to-1 with $T^X$. Then X is 1-to-1 with Y as the union of the following three correspondences:

$T_1^X\leftrightarrow T^X\leftrightarrow C^Y$

$T_2^X\leftrightarrow T^Y$

${(X-T)}^X\leftrightarrow {(X-T)}^Y$. □

The following Proposition will prove Schröder-Bernstein Theorem, shortly SBT, from the duplicability of sets. A classical proof of SBT can be found in [4], and historical accounts of SBT are given in [11,14]. Given two sets A and B, then $\left|A\right|\le \left|B\right|$ means $A_{\subset }\to B$ while $\left|A\right|=\left|B\right|$ means that $A\leftrightarrow B$.

Proposition 5 (Cantor-Schröder-Bernstein Theorem)

If $\left|A\right|\le \left|B\right|$ and $\left|B\right|\le \left|A\right|$, then $\left|A\right|=\left|B\right|$.

Proof. The following bijections derive from the hypotheses, as visualized in Figure 1, where $A^{\prime \prime }\subset A^{\prime }\subset A$:

1) $f:A\leftrightarrow B^{\prime }\subset B$

2) $g:B\leftrightarrow A^{\prime }\subset A$

3) $h:B^{\prime }\leftrightarrow A^{\prime \prime }$

4) $k=f\circ h:A\leftrightarrow A^{\prime \prime }$.

From 4) it follows that $C=A^{\prime }-A^{\prime \prime }$ has to be bijective (in the correspondence k) with some subset T of $A^{\prime \prime }$. Therefore, we can apply Lemma 4 where $Y=A^{\prime }$ and $X=A^{\prime \prime }$, from which the following correspondences follows:

5) $A^{\prime }\leftrightarrow A^{\prime \prime }\leftrightarrow A$. Then, from 2) and 5) we get the conclusion $A\leftrightarrow B$. □

The first proof of SBT was given in 1887 by Dedekind [14], who did not publish it. This proof and a second proof given by Dedekind in 1897 do not use AC, but both use the Dedekind Lemma [11]: $A\subseteq B\subseteq C$ and $\left|A\right|=\left|C\right|$ implies |$A|=|B|$. This Lemma easily follows from Lemma 4 given above.