Prerpints.org logo
Preprint
Article

Modelling Living Processes with Nonlinear Dynamics

Altmetrics

Downloads

38

Views

25

Comments

0

This version is not peer-reviewed

Submitted:

01 September 2024

Posted:

04 September 2024

You are already at the latest version

Alerts
Abstract
Living processes are integral to open systems for multiple reasons. From a thermodynamic perspective, they reduce local entropy at the cost of increasing environmental entropy. Furthermore, these processes are inherently nonlinear owing to their feedback interactions with the environment. Nonlinear systems exhibit diverse behaviours: some stabilize at a constant value, whereas others display bifurcations and chaotic dynamics. This study introduces a model that describes living processes as the dynamics of nonlinear single-value diverging maps, whereas chaotic evolution is associated with the increasing entropy environment. This model enables us to describe the lifetime of different species simply by varying the model parameters. This model also simplifies explaining the transition from life to death.
Keywords: 
Subject: Biology and Life Sciences  -   Life Sciences

Introduction

Life processes have been acknowledged as being spontaneous and adhering to the second law of thermodynamics [? ]. From this perspective, living processes cause a decrease in local entropy. However, owing to the interaction between the system and the environment, disorder within the environment increases. Consequently, an overall increase in total entropy is observed [1,2,3]. The dynamic relationship between a living system and its environment is characterized by feedback loops, which are essential for the sustainability of life processes [4]. Such systems demonstrate nonlinear dynamics, which implies that life processes inherently display nonlinear behavior [5,6,7]. Nonlinear systems typically exhibit universal behaviors. In certain regions, a system may converge toward a single stable value. In contrast, bifurcations may emerge in other regions, whereas under different conditions, the system may exhibit chaotic behaviors [8,9]. Several properties that characterize nonlinear systems render them suitable for describing living processes. First, the tendency of regular systems to strive for a constant value is ideal for describing living processes that maintain a stable parameter, including the temperature of homeotherms (birds and mammals) [10,11,12]. However, nonlinear systems for certain parameters become mathematically indeterminate. For instance, in the logistic map x n + 1 = R x n 1 − x n , for R > 4 , the system becomes indeterminate. This study associates the lack of definition of the mapping with death.
The proposed model correlates living processes with single-valued maps and associates chaotic dynamics with environmental interactions. If the living process is considered as a map with a constant final value, then this value can be linked to a parameter that must remain stable to sustain life, such as that occurring in homeotherms. As chaotic dynamics are intrinsically tied to an increase in entropy [13,14,15,16,17]; they can be considered as the environment.
The proposed mathematical model focuses on two main issues:
  • Similar processes in different animal species exhibit a typical lifetime. The last five years have seen publications on various factors, including Genetic Factors [18], Metabolic Rate and Energy Expenditure [19], Evolutionary Pressures [20,21], Reproductive Strategies [22] and Comparative Biology and Genetic Models [23].
    In our model, the same type of map characterized by parameters describes various processes. Lifetime is determined by setting the parameter values.
  • The transition between life and death. In biology, death is a process through which biological systems transform from one state to another [24? ]. This transition is characterized by critical points at which the systems move from order to disorder, akin to phase changes in physical systems. However, there are several problems with this approach [25]: First, biological systems are inherently complex, which renders the application of the simplified models used in physical systems challenging. Second, the interactions within biological systems are often nonlinear and involve multiple feedback loops. Consequently, the identification of phase transitions becomes a complicated task. The last difficulty offers an advantage to our approach, which already implements non-linearity. In our model, instead of implementing the complicated phase transition scenario, the transition from life to death occurs when the mapping ceases to be mathematically defined, which is prevalent in nonlinear dynamics, such as in a logistic map, inverse sine map, square root map, reciprocal map, and exponential map with logarithm [26,27,28,29,30].
Beyond the phenomenological aspect of describing life processes with a mathematical model, another research platform may be facilitated. A researcher can implement all the justifications for the different lifetimes of life processes to study their effect on the parameters of the mathematical model.

1. Terminology

For clarity, the following terminologies are presented:
  • Thermodynamics [31,32]:
    (a)
    System: A specific part (generally small) of the universe under consideration.
    (b)
    Surroundings (or Environment): All external elements that can interact with the system.
    (c)
    Universe: The total combination of the system and its surroundings.
  • Biology [33]
    (a)
    Animate processes: Processes that emphasize mobility, behavior, and sensory responses.
    (b)
    Living processes: Processes that emphasize fundamental life functions and biochemical activities.
As our theory is more closely related to systems that reduce entropy, the term “living process” is more appropriate [34,35]

2. Logistic Map

The logistic map is x n + 1 = R x n 1 − x n where R is a parameter determining the nature of the map, regular or chaotic [36,37]. In our approach, living processes are characterized by a system that converges for a predetermined fixed value, denoted as C. For that reason, we express the logistic map as follows:
x n + 1 = x n 1 − x n 1 − C
We are interested in a model with at least two adjustable parameters to define diverse life and animate processes. A single parameter characterizes the logistic model and is, therefore, inappropriate. In the next section, we present a new, more adjustable model.

3. Nonlinear Recursive Model

In the system-environment interaction cycle, two processes co-occur through a regular interaction, thereby producing the map striving for a single value (type 1) and a process that drives the system into chaos (type 2). We associated inanimate systems with convergence toward a chaotic state, whereas living processes were characterized by stabilization at a constant value. The nonlinear recursive relation was designed such that the constant value could be predicted as far in advance as possible.

3.1. Regular process-living process

We formulate the following recursive relation describing a type 1-interaction:
x n + 1 = C p − R x n C − x n p 1 p
where x is the term life parameter, with x = C indicating that the life parameter is in the best possible life status. Further, n is the time (e.g., to years), and p is another parameter that enables better control in adjusting the parameters to different biological phenomena, such as adjusting the lifetime characteristics of varying living species. In the simulations conducted in this study, we used the simplest model; that is, p = 1 .
If, during the iteration, x = C , the system stabilizes at that predefined value. Thus, the system is designed to reach the best life parameter value. The parameter R defines the map type, characterizing the process type. Numerical calculations, illustrated in Figure 1 and Figure 2, demonstrate that the final value, once achieved, remained as expected regardless of the initial condition.

3.2. System with both interactions

The second type of interaction involves the following modifications:
  • We hypothesize a gradual increase in R. This adjustment facilitates two primary effects:
    (a)
    The system progresses toward chaotic behavior. Associating this increase in chaos with increasing entropy suggests that the increased R aligns with the second law of thermodynamics.
    (b)
    Beyond a certain threshold of R, the map becomes mathematically undefined (as observed in other maps, such as logistic maps, where for R > 4 , the map becomes mathematically undefined [36,37]). We interpret this critical condition as indicative of the process of death.
  • The influence of the environment is modeled by introducing slight randomness in x and C.
A plot of x during the years is referred as to life plot, as shown in Figure 3 with the parameters R 0 = 2.5 and R n + 1 − R n = 0.002 . C = 1.5 ± 0.0075 uniformly distributed, p = 1.2 and x 0 = 0.55 . We identify four distinct phases:
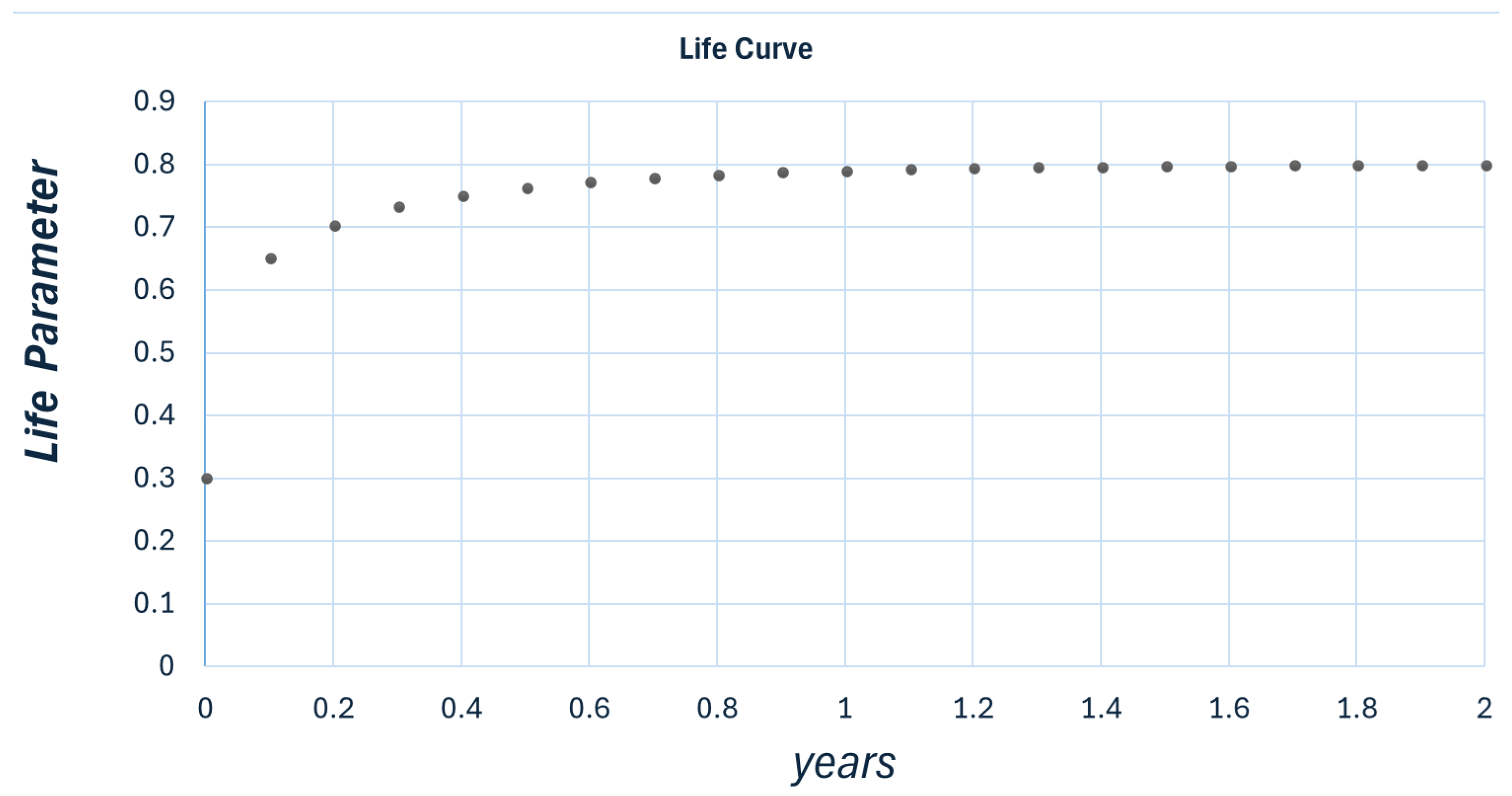
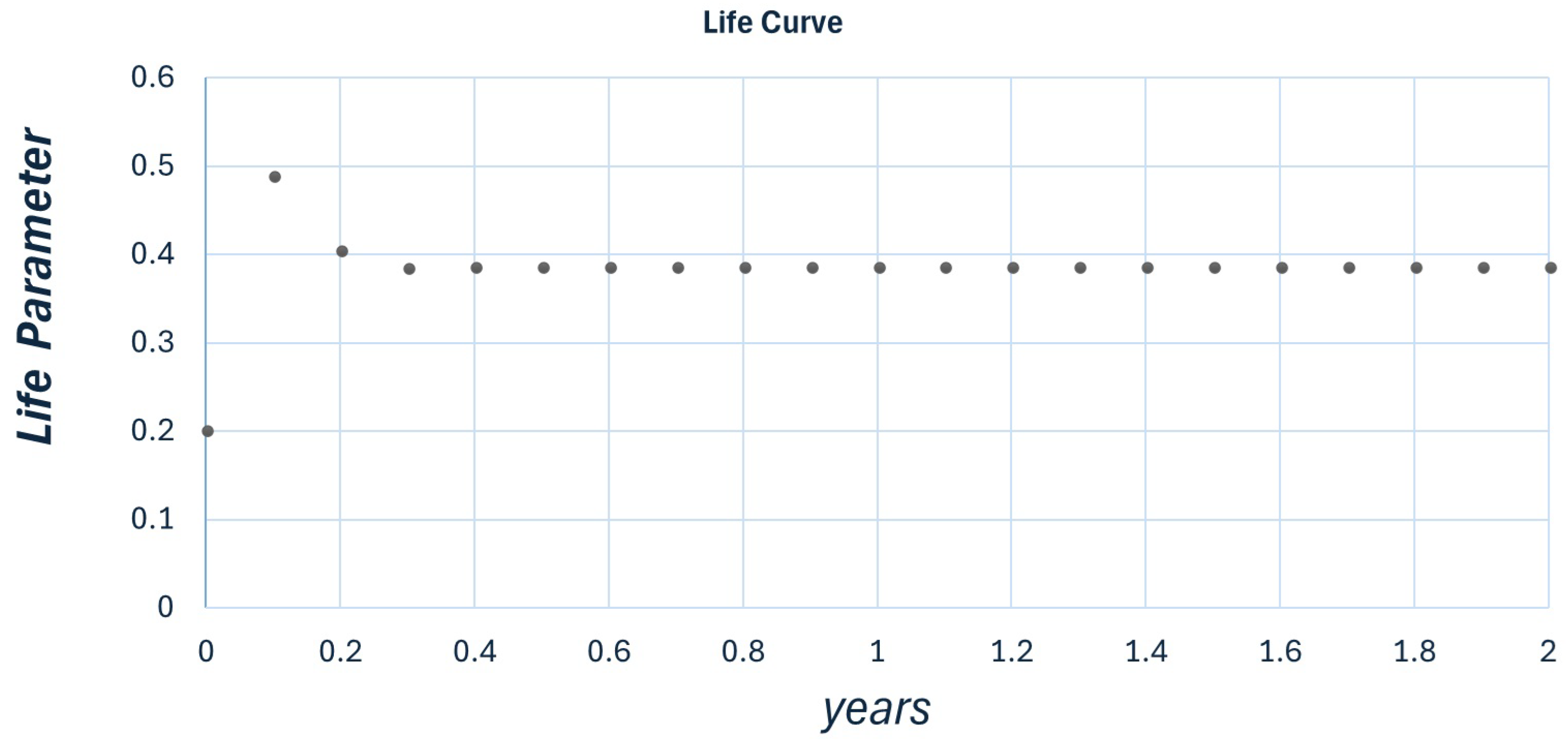
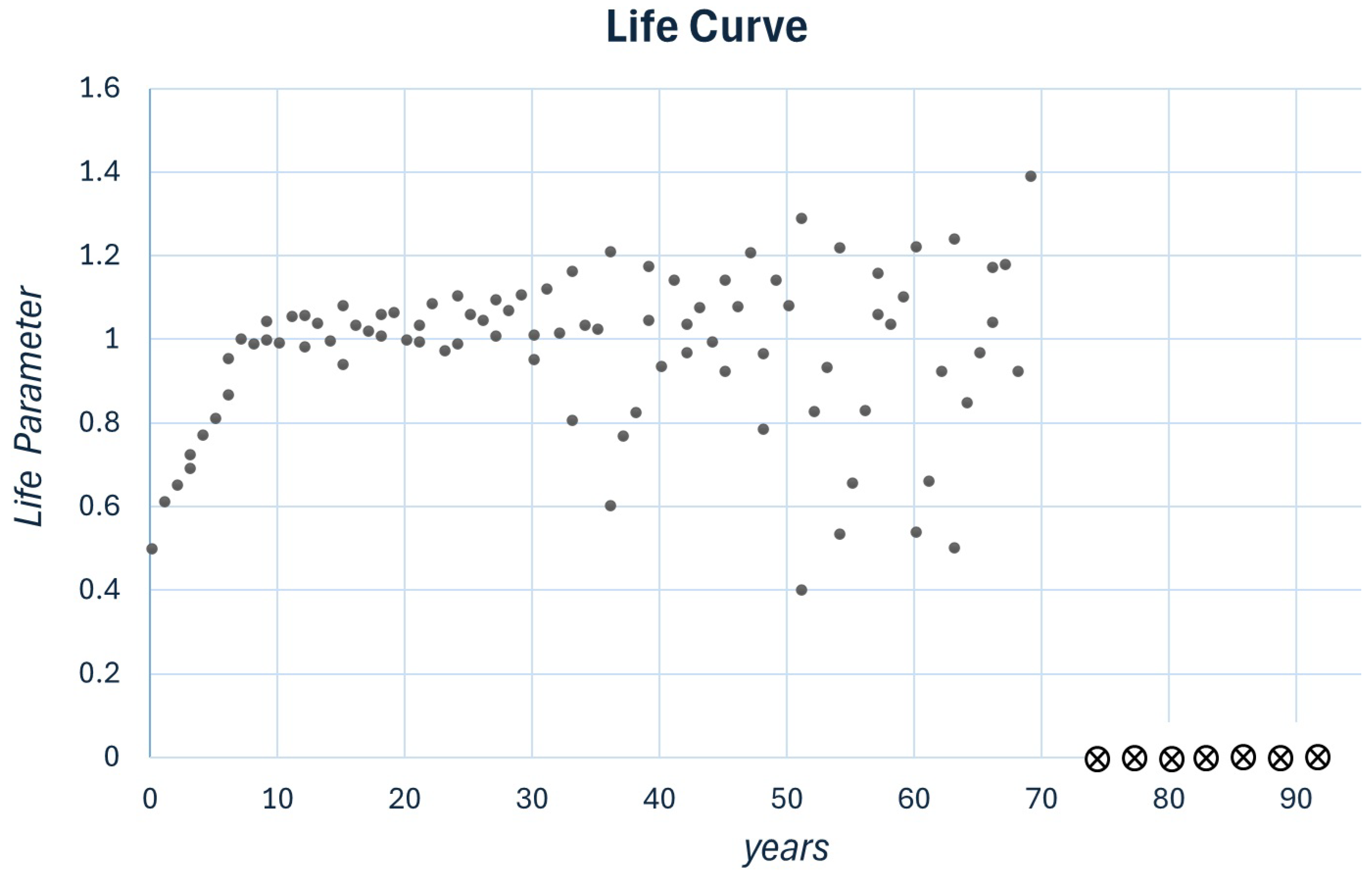
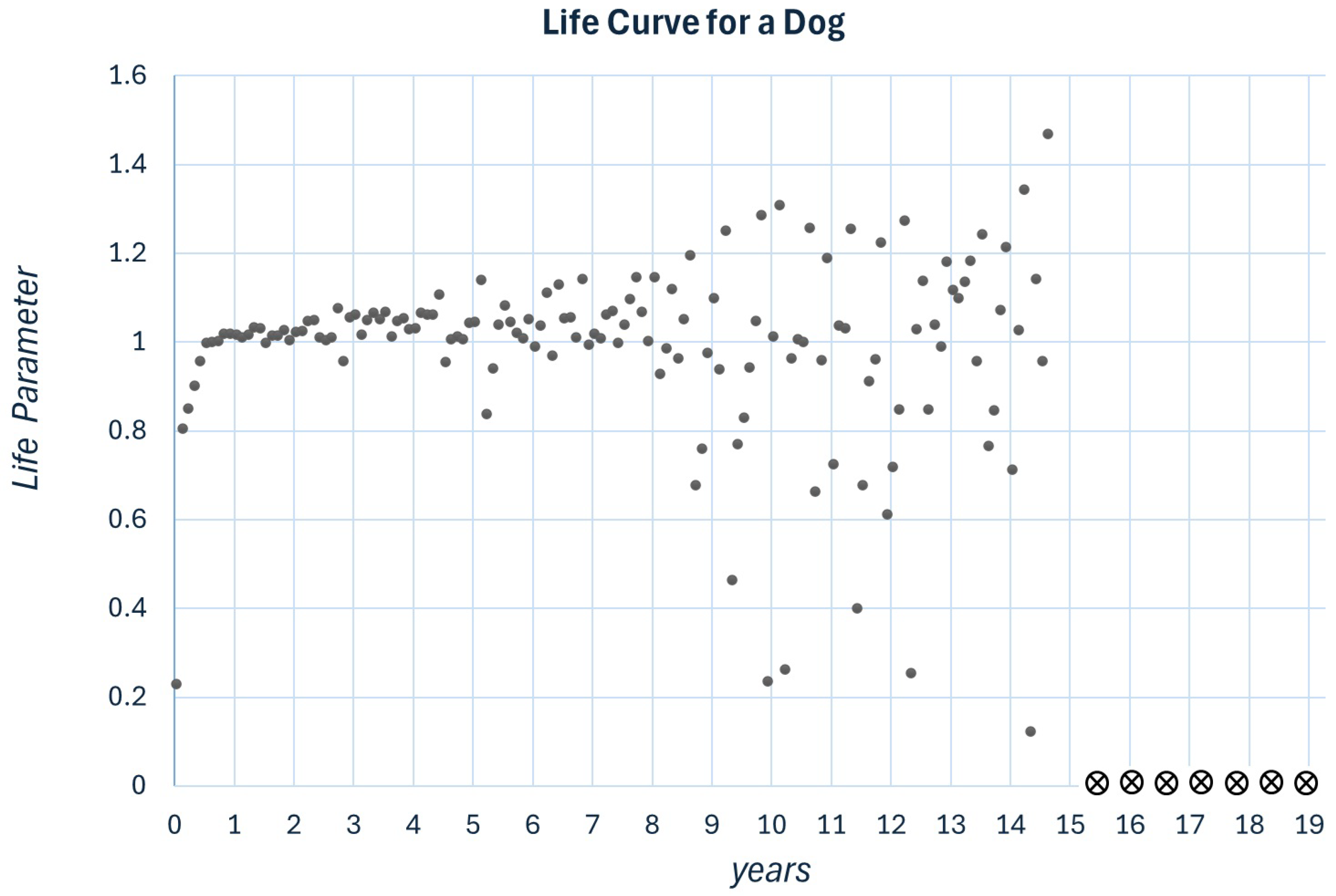
  • Evolving section:
    For n = 0 − 8 , x approaches the constant value c = 1 ± 0.0075 .
  • Sustainable zone:
    For n = 8 − 25 x is oscillating randomly around c = 1 ± 0.0075 .
  • Aging:
    For n = 30 − 60 , x represents a process wherein any disorder increases.
  • Death:
    For n > 70 the system becomes mathematically undefined. If the progression of x toward a constant value signifies a living process, the absence of a definable evolution of x, whether decreasing, increasing, or stable, indicates that this living process has ceased to exist.

4. Example for Adjusting Parameters to Describe Life Process Type

In this study, we proposed a nonlinear map characterized by the parameters R and C. To each of them, we added a random component describing the influence of the environment. We considered it more appropriate to use the current formalism to describe living processes rather than combining all processes describing the animal itself. However, to simplify the example, we describe the life curve of a dog. In Figure 3, we demonstrated a life curve that fits the description of a human who has lived for approximately 70 years. The parameters to describe different animal species could be adjusted. For example, considering a specific dog with a life expectancy of 14.5 years, we adjusted the parameters as R = 2.5 and C = 1 , as presented in Figure 4.

5. Summary

This study formulated a nonlinear recursion equation based on established characteristics of living processes; specifically, their capacity to reduce entropy locally while interacting with the environment, thus upholding the second law of thermodynamics. This equation facilitates the depiction of a living system that operates in compliance with physical laws as a spontaneous process. The proposed mathematical model offers several advantages for the scientific description of phenomena [38,39,40]. The benefits pertinent to our research are as follows:
  • Conceptual Understanding: The application of nonlinear dynamics to the study of living processes yields insights that are often not discernible through qualitative analysis alone.
  • Simulation: The proposed model facilitates the simulation of unobserved life forms. Although our current study neglects the bifurcation phenomenon common to nonlinear systems, the identification of living processes that exhibit this behavior could significantly contribute to the field and refine our model.
  • Theoretical framework. The model provides a robust theoretical framework that assists in hypothesis generation, experimental design, and data interpretation. In our approach, various life processes were classified according to distinct nonlinear mappings. The evolution of a system within a specific category is determined by the numerical values of the mapping parameters. In the case of our mode, this may indicate characteristics such as the lifespan of a process.

References

  1. Taylor, K. A New Physics Theory of Life. Quanta Magazine 2023.
  2. Kostic, M.M. Entropy and the Second Law of Thermodynamics: From the microscale to the macroscale (explaining the inefficiency of energy conversion) and the controversial, crucial concept of the arrow of time. Entropy 2020.
  3. Longdom. Life: A Complex Spontaneous Process Takes Place Against the Background of Nonspontaneous Processes Initiated by the Environment. Journal of Clinical Trials & Research 2020.
  4. El-Samad, H. Biological feedback control—Respect the loops. Cell Systems 2021, 12, 477–487.
  5. authors, V. Identification, visualization, statistical analysis and mathematical modeling of high-feedback loops in gene regulatory networks. BMC Bioinformatics 2017, 18, 574. [CrossRef]
  6. authors, V. Linking fast and slow positive feedback loops creates an optimal bistable switch in cell signaling. Physical Review E 2007, 76, 031924. [CrossRef]
  7. authors, V. Modulation of dynamic modes by interplay between positive and negative feedback loops in gene regulatory networks. Physical Review E 2018, 97, 042412. [CrossRef]
  8. Wolf, A. Simplicity and universality in the transition to chaos. Nature 1983, 305, 182–183. [CrossRef]
  9. Feigenbaum, M. Quantitative universality for a class of non-linear transformations. Journal of Statistical Physics 1978, 19, 25–52. [CrossRef]
  10. Campbell, N.A.; Reece, J.B.; Urry, L.A.; Cain, M.L.; Wasserman, S.A.; Minorsky, P.V.; Jackson, R.B. Biology; Pearson Education, 2017.
  11. Clarke, A.; Rothery, P.; Isaac, N.J.B. Thermoregulation in endotherms: evolutionary implications and consequences. Biological Reviews 2016, 91, 97–125.
  12. Hill, R.W.; Wyse, G.A.; Anderson, M. Animal Physiology; Sinauer Associates, Inc., 2020.
  13. Moysis, L.; Volos, C.; Jafari, S.; Munoz-Pacheco, J.M.; Kengne, J.; Rajagopal, K.; Stouboulos, I. Modification of the Logistic Map Using Fuzzy Numbers with Application to Pseudorandom Number Generation and Image Encryption. Entropy 2020, 22, 1096. [CrossRef]
  14. Wang, C.; Ding, Q. A Class of Quadratic Polynomial Chaotic Maps and Their Fixed Points Analysis. Entropy 2019, 21, 658. [CrossRef]
  15. Song, Y.; Yuan, F.; Li, Y. Coexisting Attractors and Multistability in a Simple Memristive Wien-Bridge Chaotic Circuit. Entropy 2019, 21, 678. [CrossRef]
  16. Robledo, A. Exploring transitions to chaos in complex systems. Research Outreach 2021. [CrossRef]
  17. Tolkacheva, E.G.; Grigoriev, R. Nonlinear Dynamics and Chaos in Cardiac Physics. Entropy 2023, 25. [CrossRef]
  18. Fitzgerald, J.e.a. Genetic determinants of healthy aging and longevity: a systematic review. Current Genetic Medicine Reports 2022, 10, 131–146.
  19. Grossi, V.; Forte, G.; Sanese, P.; Peserico, A.; Tezil, T.; Lepore Signorile, M. The longevity SNP rs2802292 uncovered: HSF1 activates stress-dependent expression of FOXO3 through an intronic enhancer. Nucleic Acids Research 2018, 46, 5587–600. [CrossRef]
  20. Atkins, J.; Jylhävä, J.; Pedersen, N.; Magnusson, P.; Lu, Y.; Wang, Y. A genome-wide association study of the frailty index highlights synaptic pathways in aging. medRxiv 2019.
  21. Willems, S.; Wright, D.; Day, F.; Trajanoska, K.; Joshi, P.; Morris, J. Large-scale GWAS identifies multiple loci for hand grip strength providing biological insights into muscular fitness. Nature Communications 2017, 8, 1–12. [CrossRef]
  22. Michel, J.P.; Graf, C.; Ecarnot, F. Individual healthy aging indices, measurements and scores. Aging Clinical and Experimental Research 2019, 31, 1719–1725.
  23. Rose, G.; Sørensen, M.; Dato, S. Genetic determinants of human longevity. MDPI 2019.
  24. Authors, V. Phase Transitions in Biological Systems with Many Components. ScienceDirect 2023, 100, 032414.
  25. Herron, L.; Mondal, K.; Schneekloth, J.S.; Tiwary, P. Inferring phase transitions and critical exponents from limited observations with Thermodynamic Maps. arXiv preprint arXiv:2308.14885 2023.
  26. May, R.M. Simple mathematical models with very complicated dynamics. Nature 1976, 261, 459–467. [CrossRef]
  27. Devaney, R.L. Transcendental Dynamics and Complex Exponentials. Bulletin of the American Mathematical Society 1978, 84, 1239–1255.
  28. Feigenbaum, M.J. Quantitative Universality for a Class of Nonlinear Transformations. Journal of Statistical Physics 1978, 19, 25–52. [CrossRef]
  29. Collet, P.; Eckmann, J.P. Iterated Maps on the Interval as Dynamical Systems. Progress in Physics 1980, 1, 1–248. [CrossRef]
  30. Guckenheimer, J.; Holmes, P. Structurally Stable Heteroclinic Cycles. Mathematical Proceedings of the Cambridge Philosophical Society 1979, 103, 189–192. [CrossRef]
  31. Callen, H.B. Thermodynamics and an Introduction to Thermostatistics; Wiley: New York, 1985.
  32. Atkins, P.; de Paula, J. Physical Chemistry; Oxford University Press: Oxford, 2010.
  33. Academic, O. Chapter on Animate and Inanimate Matter. Oxford Academic 2020.
  34. for Majors I, B. The Second Law of Thermodynamics. Lumen Learning 2023.
  35. MDPI. Life’s Mechanism. MDPI 2023.
  36. Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering; Westview Press: Boulder, CO, 1994.
  37. Hilborn, R.C. Chaos and Nonlinear Dynamics: An Introduction for Scientists and Engineers; Oxford University Press: Oxford, UK, 2020.
  38. Isaacson, E.; Keller, H.B. Analysis of Numerical Methods; Dover Publications: New York, 1994.
  39. Murray, J.D. Mathematical Biology: I. An Introduction; Springer: New York, 2002.
  40. Oppenheim, A.V.; Schafer, R.W. Discrete-Time Signal Processing; Pearson: Upper Saddle River, NJ, 2009.
Preprints 116942 g001
Figure 1. Plot for C = 0.8 , R = 1 , and x 0 = 0.2 . The map stabilizes at C = 0.8 , as expected.
Figure 1. Plot for C = 0.8 , R = 1 , and x 0 = 0.2 . The map stabilizes at C = 0.8 , as expected.
Preprints 116942 g001
Preprints 116942 g002
Figure 2. Plot for r C = 0.8 , x 0 = 0.2 , and R = 0.6 . The map stabilizes at c = 0.369 , contrary to the expected value of 0.8 .
Figure 2. Plot for r C = 0.8 , x 0 = 0.2 , and R = 0.6 . The map stabilizes at c = 0.369 , contrary to the expected value of 0.8 .
Preprints 116942 g002
Preprints 116942 g003
Figure 3. Plot for c = 1 , R = 2.5 ± 0.02 . , x and C are uniformly distributed in the range ± 5 × 10 − 5 . The simulation illustrates the four stages in the evolution of a living process (The symbol ⨂ indicates an undefined map).
Figure 3. Plot for c = 1 , R = 2.5 ± 0.02 . , x and C are uniformly distributed in the range ± 5 × 10 − 5 . The simulation illustrates the four stages in the evolution of a living process (The symbol ⨂ indicates an undefined map).
Preprints 116942 g003
Preprints 116942 g004
Figure 4. Plot for c = 1 and R = 2.5 ± 0.02 . . x and C are uniformly distributed in the range ± 5 × 10 − 5 . Simulation illustrating the four stages in the evolution of a living process.
Figure 4. Plot for c = 1 and R = 2.5 ± 0.02 . . x and C are uniformly distributed in the range ± 5 × 10 − 5 . Simulation illustrating the four stages in the evolution of a living process.
Preprints 116942 g004
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated