Submitted:
12 August 2024
Posted:
14 August 2024
Read the latest preprint version here
Abstract
Keywords:
1. Notations and Conventions
2. Introduction
2.1. Collatz’s Conjecture
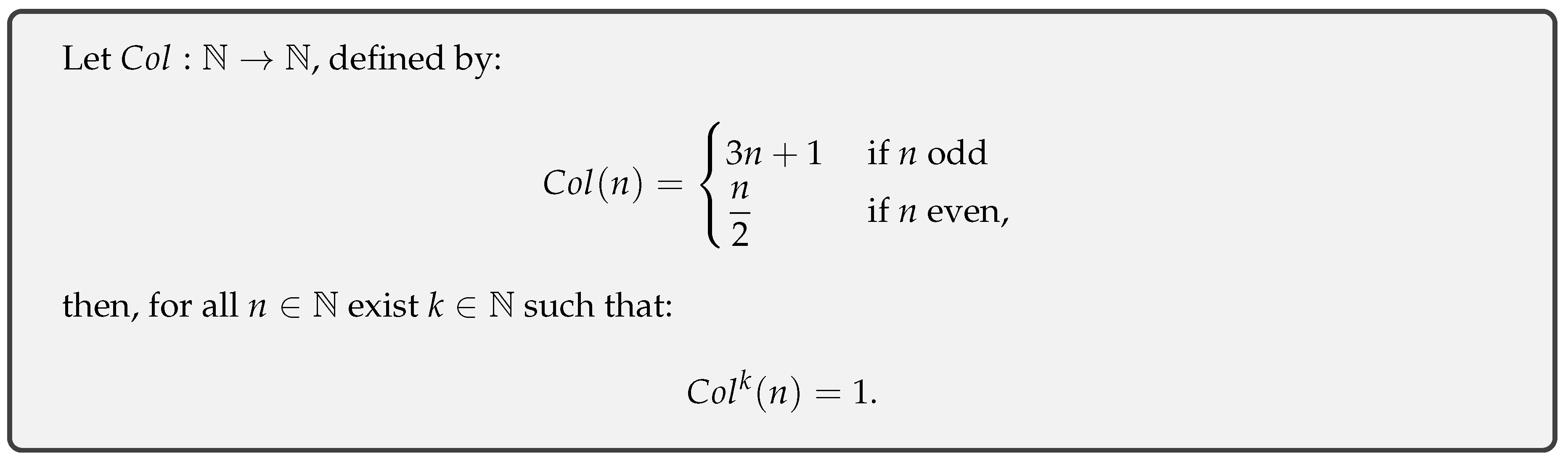
2.2. Extension of the Collatz Function



-
if p is odd, we have with , thenSince q is odd, we have independent of the simplification .
-
if with , we haveSince q is odd, we have independent of the simplification, we have .

3. Set Generate by and
3.1. Summary of Propositions in the Section
- 1
- Definition 3: Introduces the set , generated by two real linear functions and .
- 2
- Definition 4 : Defines the integer set of a function as , where are functions in the composition of S.
- 3
- Definition 5 : Defines the entire set of a function.
- 4
- Lemma 1 Monotony of Integer Set Lemma.
- 5
- Proposition 3 : Establishes a relation of monotony in the entire sets concerning the composition of functions.
- 6
- Lemma 2 Establishes a characterization of the integer sets.
- 7
- Proposition 4 : Establishes a one-to-one correspondence between functions of the same length and integer sets of the same length, and Affirms that the integer sets of functions of the same length are disjoint.
- 8
- Theorem 1: Ensures that the integer sets are the disjoint union of the integer sets of functions in with the same length.
- 9
- Proposition 5: Guarantees the existence of a unique sequence of elements for a function .
3.2. Set Generate by and
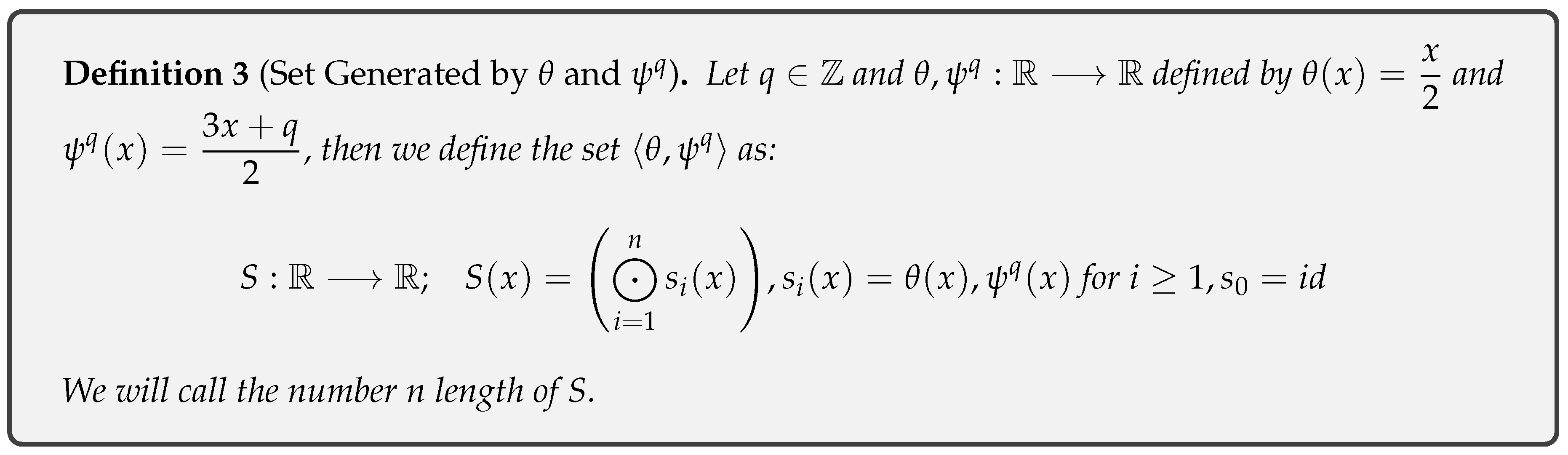

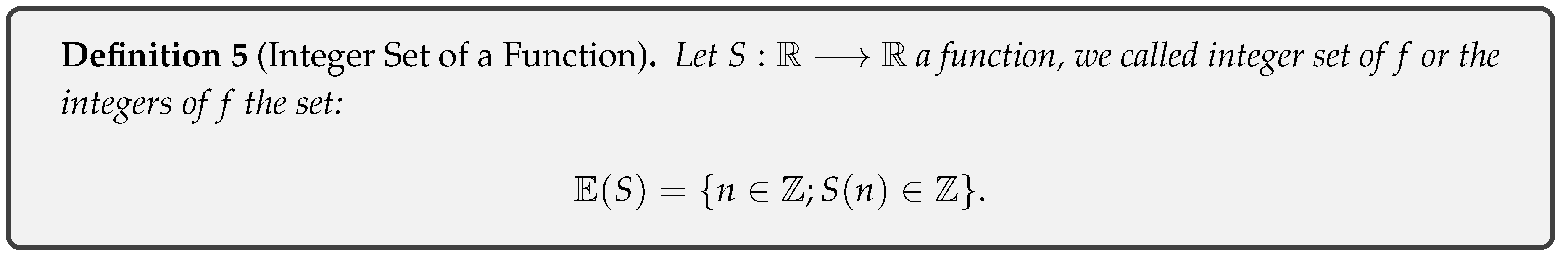
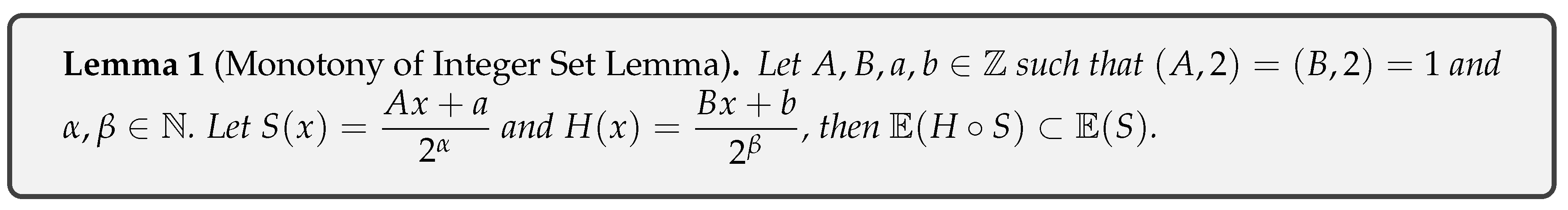
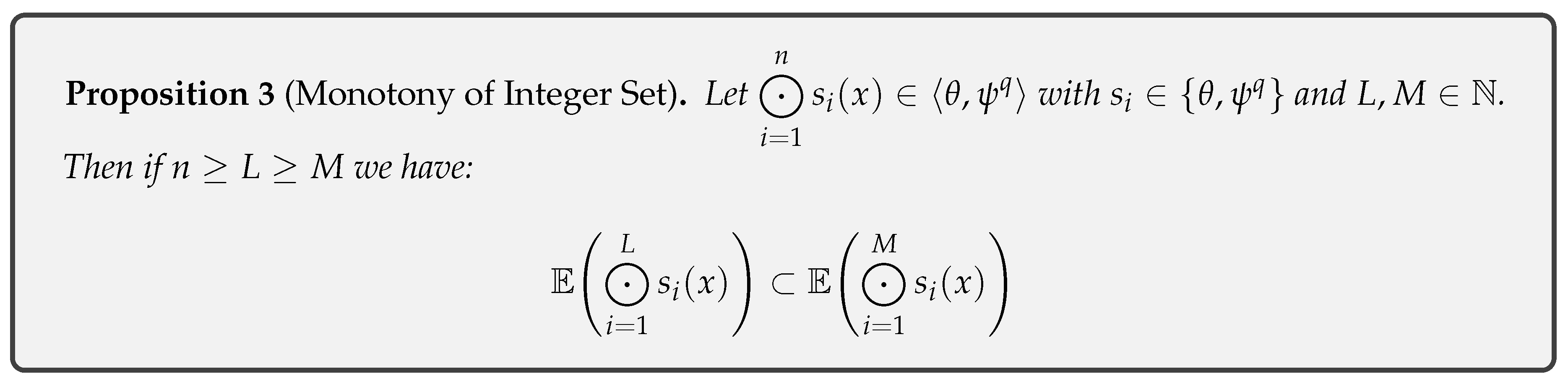




-
If . We haveby Proposition 3 we have , since and then . Since and are invertible functions, we haveFollowing the same idea up to , we haveThe latter is impossible since the slope of the resulting line is of the form with . The case is completely analogous, therefore the case where and are different is not possible.
-
If . Since the sequences are different, there must exist some such thatthen by Proposition 4 we haveHowever, this is a contradiction to the Proposition 3, because for all . Then both sequences must be identical.
4. Stability and Instability of Integer Set
4.1. Summary of Propositions in the Section
- 1
- Definition 6 : Definition of functions and .
- 2
- Proposition 6: Monotonicity of the functions and .
- 3
- Definition 7: Definition of positively (negatively) stable (unstable) sequences.
- 4
- Theorem 2: Establishes the asymptotic behavior of the integer set when we have a positively (negatively) stable (unstable) sequence.
4.2. Stability and Instability of Integer Set




5. Coding of the Orbits
5.1. Summary of Propositions in the Section
- Definition 8: Coding maps and the space of sequences 0 and 10.
- Proposition 7: General form of the elements generated by and .
- Proposition 8: Fist Cod invariance: .
- Definition 9: Definition of .
- Proposition 9: equivalence : if then .
- Proposition 10: Second Cod invariance: .
- Proposition 11: if and only if
- Proposition 12 if and only if
- Proposition 13:.
- Definition 10: The Coding set .
- Proposition 14: Monotony of the coding set .
- Proposition 15: Generating property:if then .
- Theorem 3: Uniqueness of the full coding .
5.2. Coding of the Orbits

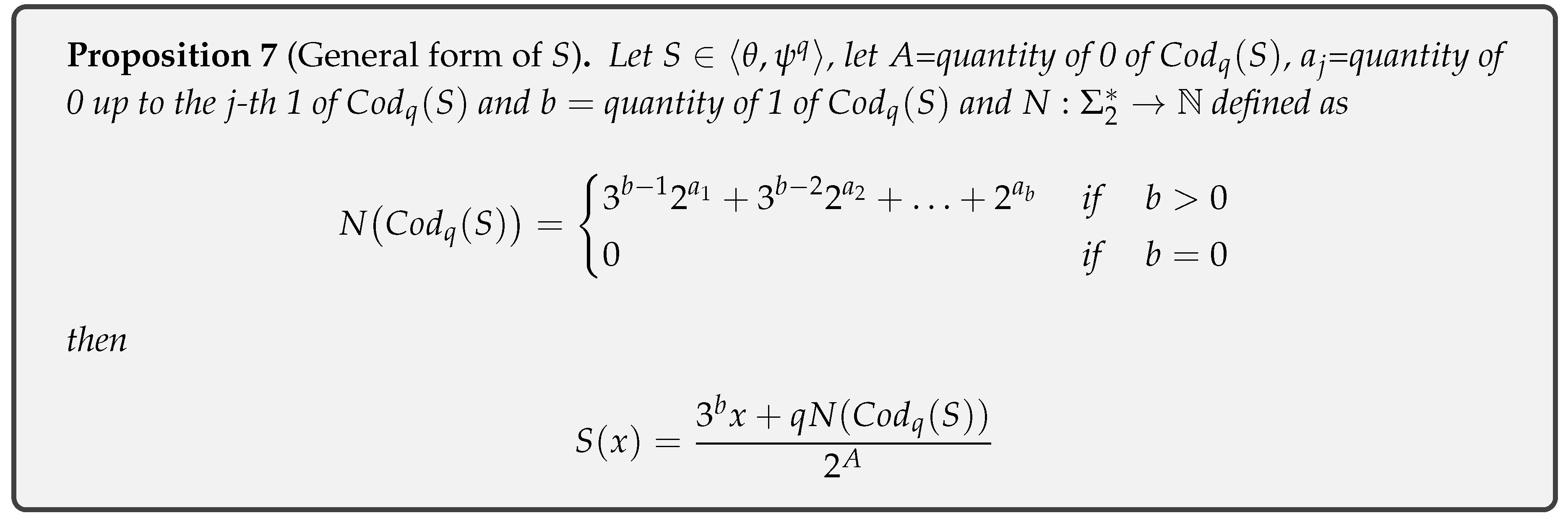
- , then, and then .
- , then, and then .
- the quantity of 1 of is
- and for and the quantity of 0 of is
- the quantity of 1 of is b.
- for
- .
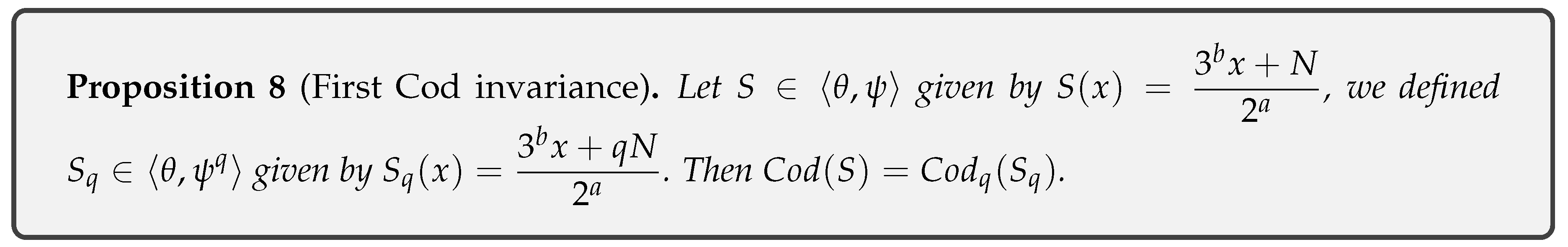
- .
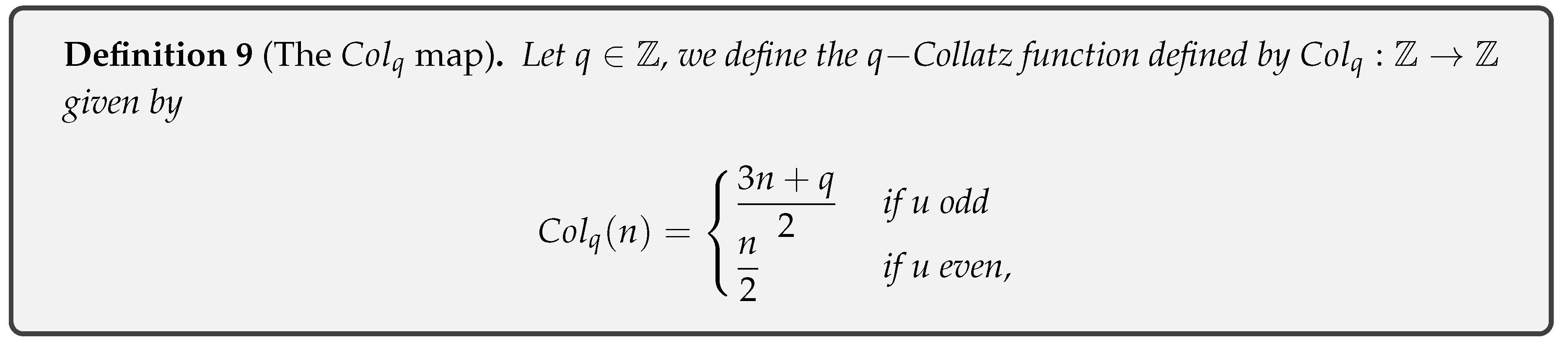
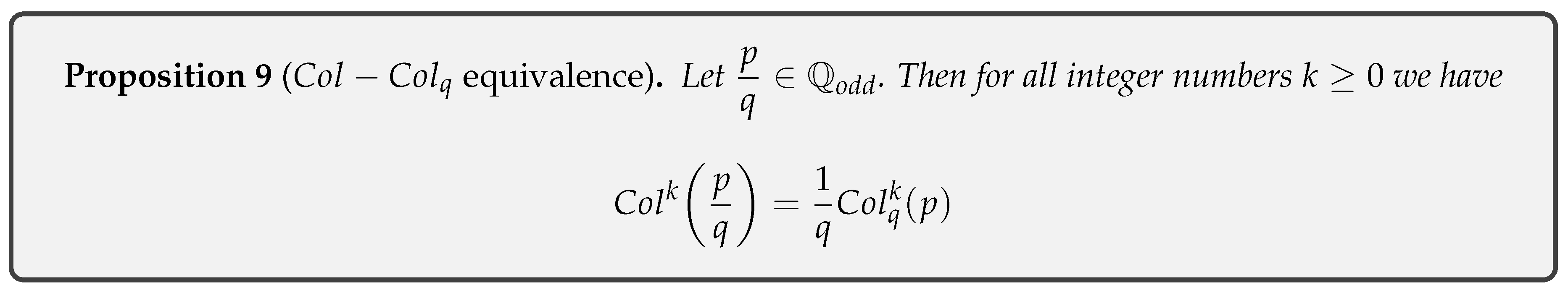
-
if it is odd. Expanding the left-hand side of the proposition,developing the right-hand side of the proposition,We conclude in this case that both parts are equal
-
if it is even. Expanding the left-hand side of the proposition,developing the right-hand side of the proposition,We conclude in this case that both parts are equal. Since in both cases it gave equality, we conclude that the proposition is true.
-
if it is odd. Expanding the left-hand side of the proposition,developing the right-hand side of the proposition,We conclude in this case that both parts are equal.
-
if it is even. Expanding the left-hand side of the proposition,developing the right-hand side of the proposition,We conclude in this case that both parts are equal. Since in both cases it gave equality, we conclude that the proposition is true.




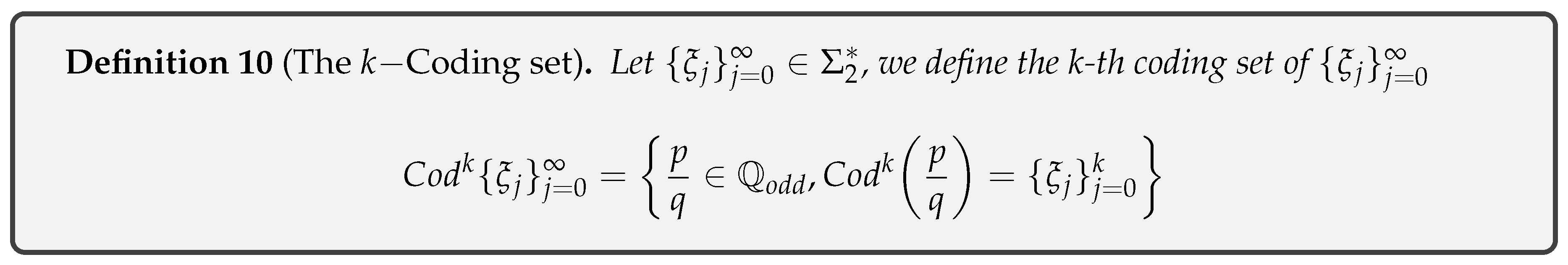
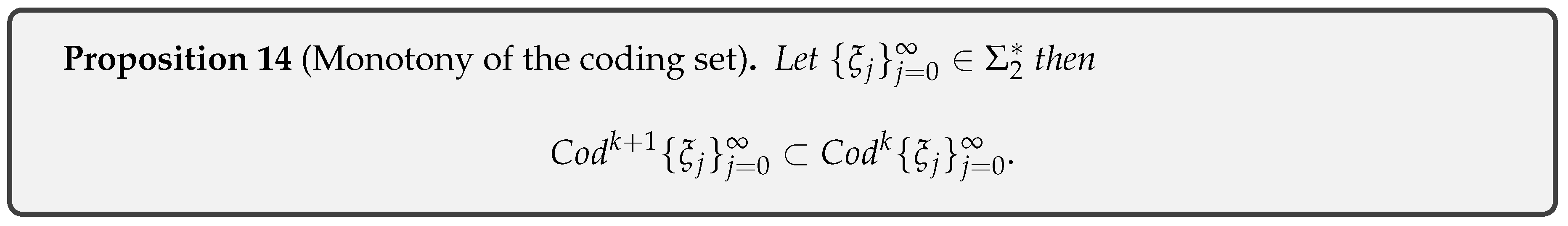
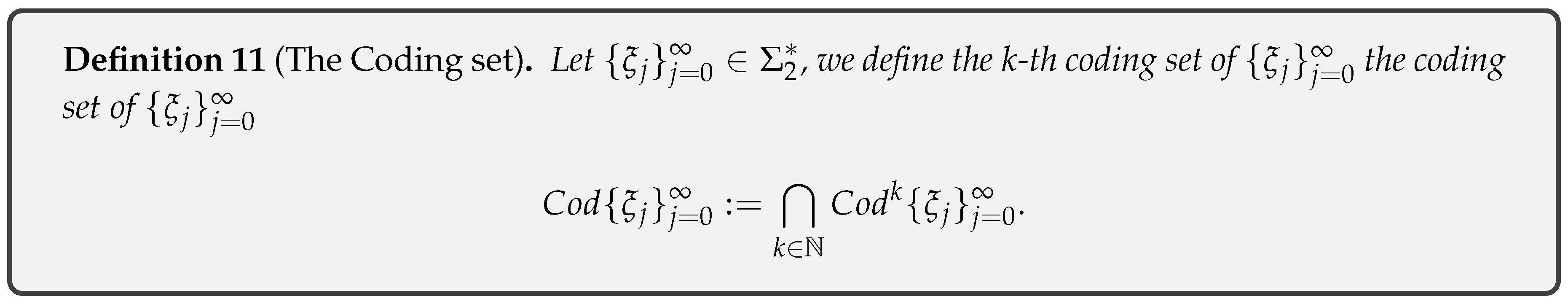
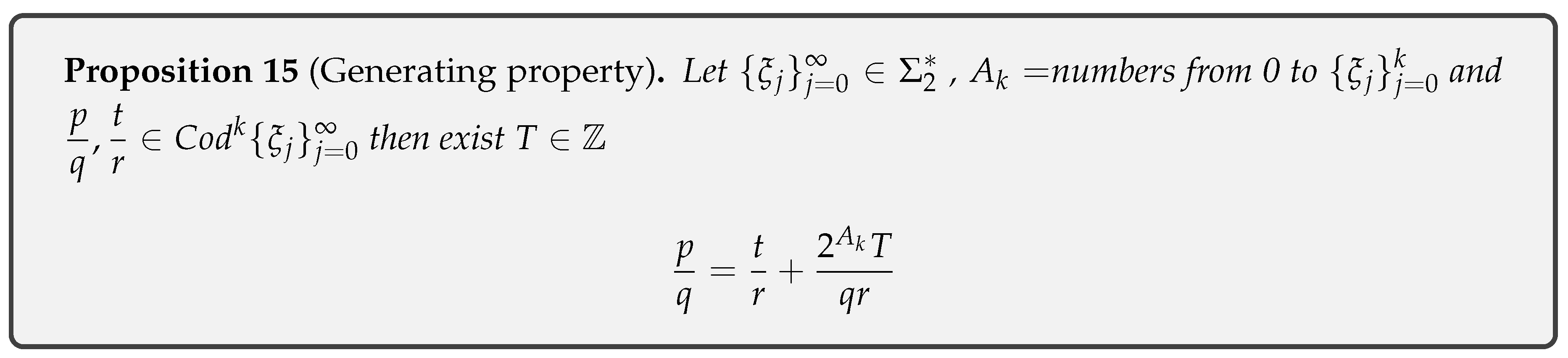

6. The and Functions
6.1. Summary of Propositions in the Section
- Definition 12: We will give the definition of the functions and .
- Definition 13: Definition of Null Tail: sequences with a finite number of 1s.
- Definition 14: Sets , and .
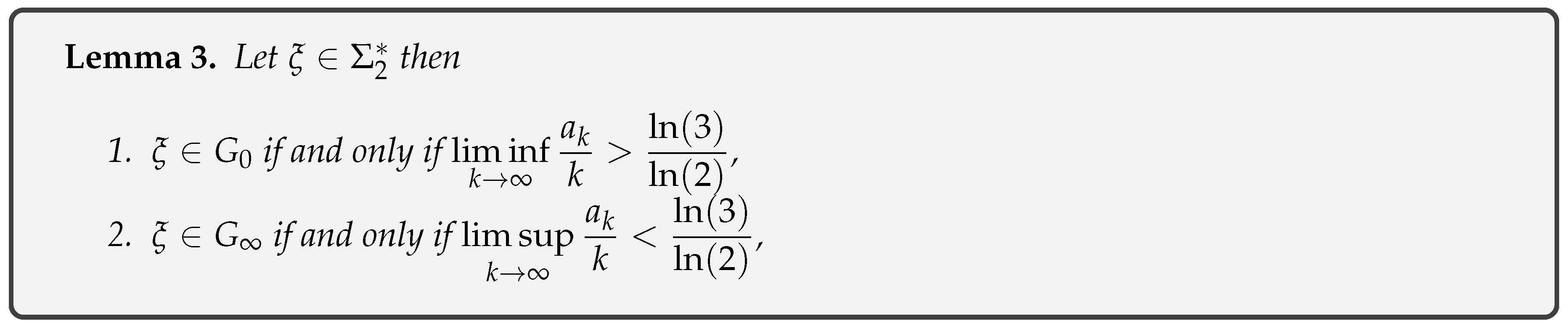
- Lemma 3 Characterization of , and through accumulation points of .
- Proposition 16 Characterization of and through functions and .
6.2. The and Functions

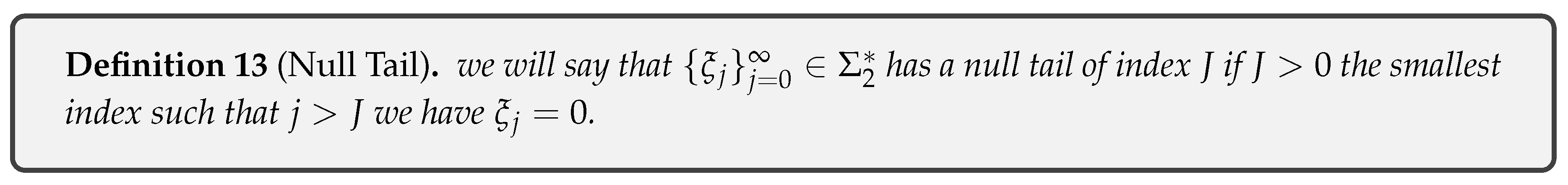
-
Let
- (a)
- .
- (b)
- for and
-
Let then we have
- (a)
- (b)
-
Let then we have
- (a)
- .
- (b)
-
Let
- (a)
- . Since, .
- (b)
-
Let then we have
- (a)
- .
- (b)
- ,, and

-
Let then as . Suppose that . Then exist such that for where , then we have,which is a contradiction with the fact that , then .Now, let’s suppose that . Then exist such that for all . Then
-
Let then as . Suppose that . Then exist such that for where , then we have,which is a contradiction with the fact that , then .Now, let’s suppose that , Then exist such that for all . Then

7. The Sigma Function
7.1. Summary of Propositions in the Section
- Definition 15: Definition of the sigma function.
- Theorem 4: Establish that and are solutions of the Diophantine equation . Additionally, is the minimum non-negative integer value.
- Corollary 1: Establishes that the minimum value grows based on the number of times the sigma function takes odd values.
- Corollary 2:
- Proposition 17: Establishes inequalities that estimate the values of the sigma function
- Proposition 18: It establishes the periods for the periodic points.
- Proposition 19: Establish algebraic properties of additivity, dependent on the parity of the addends
- Corollary 3 Establish algebraic properties’ linearity modulo
- Proposition 20 Establish that the sigma function is homogeneous modulo
- Definition 16: Extension of the sigma function on
- Definition 17: Characteristic Function
- Lemma 6: Establishes an invariance in the coding of the orbits of the sigma function.
- Proposition 21: Establishes homogeneity properties of the extension of the sigma function.
- Proposition 22 Algebraic properties of the Extension of the Sigma function.
- Definition 18: Definition of dyadic numbers.
- Proposition 23: Characterization of the dyadic representation of rational numbers.
- Definition 19: Definition of Cod-Sigma function.
- Lemma 7: Invariant coding lemma for Cod-Sigma function.
- Proposition 24: Change of basis of the Cod-Sigma function.
- Proposition 25: Let and and let such that and such that then
- Corollary 4: Let . Then .
- Proposition 26 is linear.
- Lemma 8: Rational equivalence of the Cod-Sigma function.
- Lemma 27: and
7.2. The Sigma function


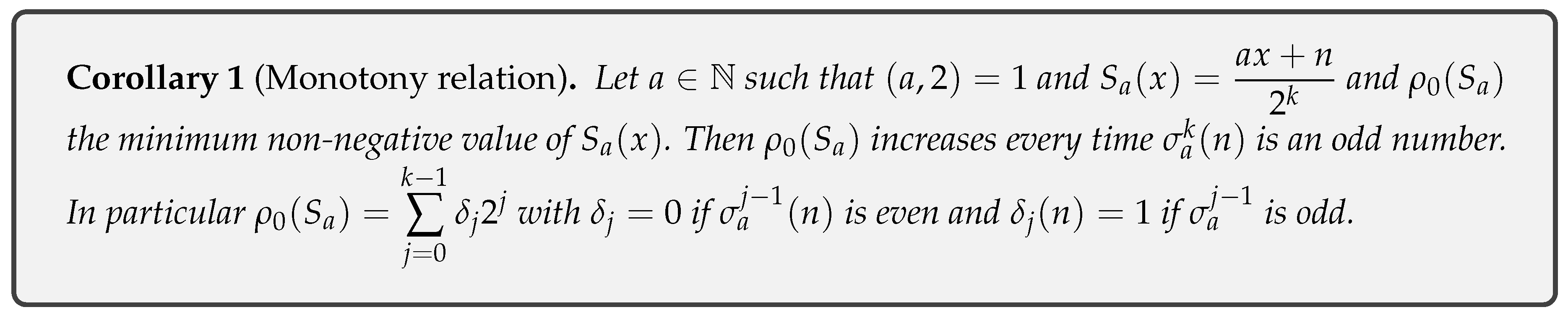
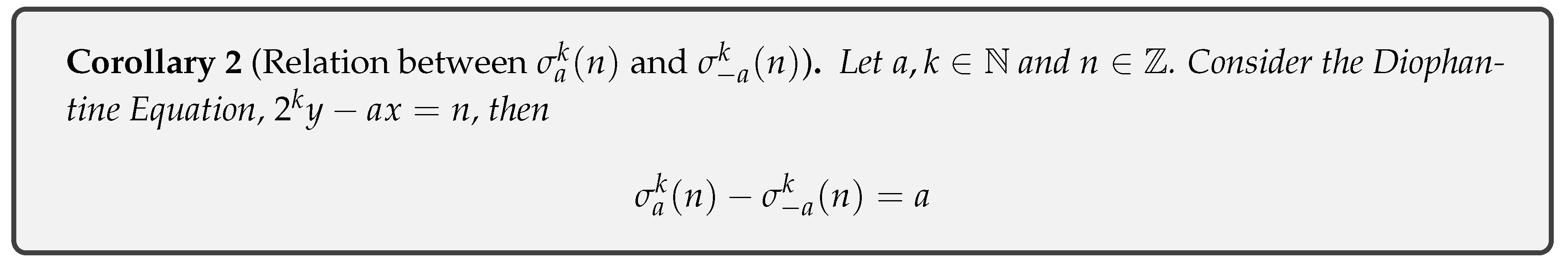

7.3. Periodicity of the Sigma Function

- Let , if u is odd, then which implies . If u is even, we have, which implies .
-
Let such that and , soThensuppose that , this implies that u is an invertible then, the equation is equivalentThe minimum value of k is given by the Carmichael function given byLet , thenas then , which is the necessary and sufficient condition for to admit decomposition in base 2 up to the power which implies that there exist such that .Now suppose that , then we divide by, dthen the development is completely analogous to the first case.In particular, when and u are co-prime with 3, then the period of the orbit of u corresponds to the Euler’s totient function, which in this case is .
7.4. Linearity of the Sigma Function Modulo a

- If are even, we have
- If m is even and n is odd, we have
- If are odd, we have
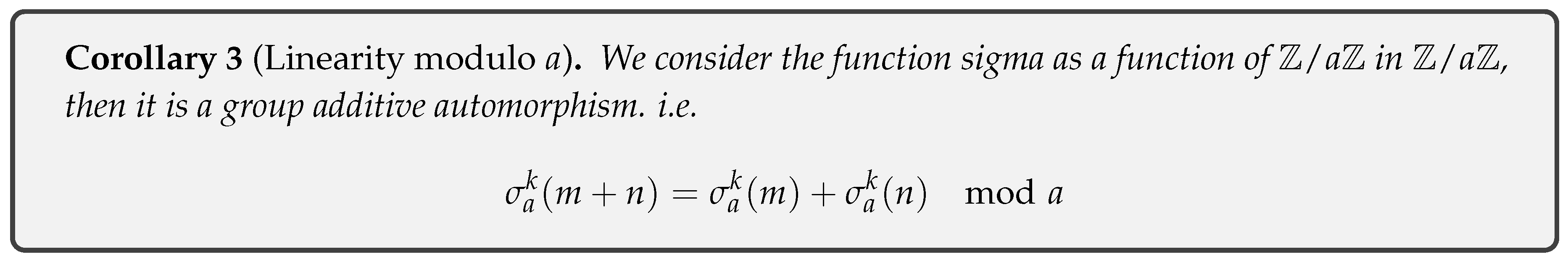
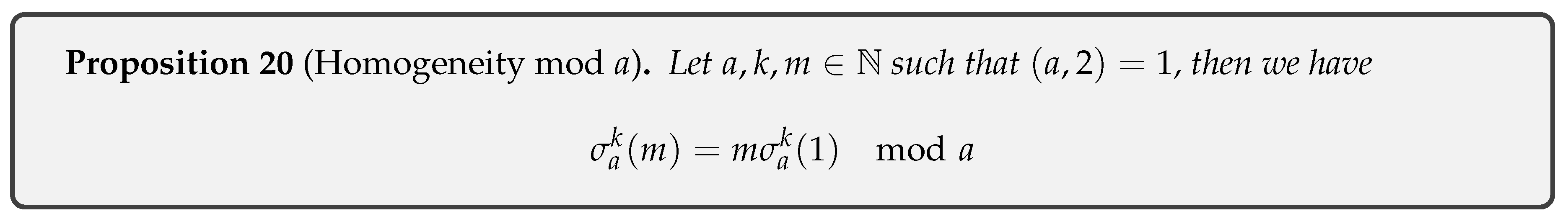
7.5. Extension on the of the Sigma Function

7.6. Properties of the Extension of the Sigma Function
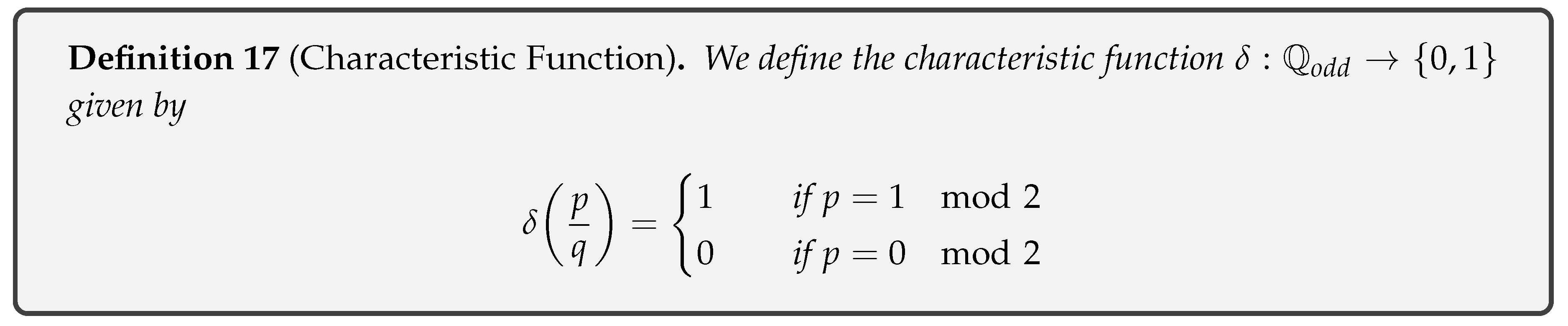

- 1
-
Let where and where . We will prove by induction thatFor , Since if v is odd (or even) then is odd (or even) thenSuppose for , then , then we haveSince u is odd, we have that and have the same parity, then
- 2
-
Let where and where . We will prove by induction thatFor , Since v is oddSuppose for , then , then we haveSince v is odd, we have that and have the same parity, then
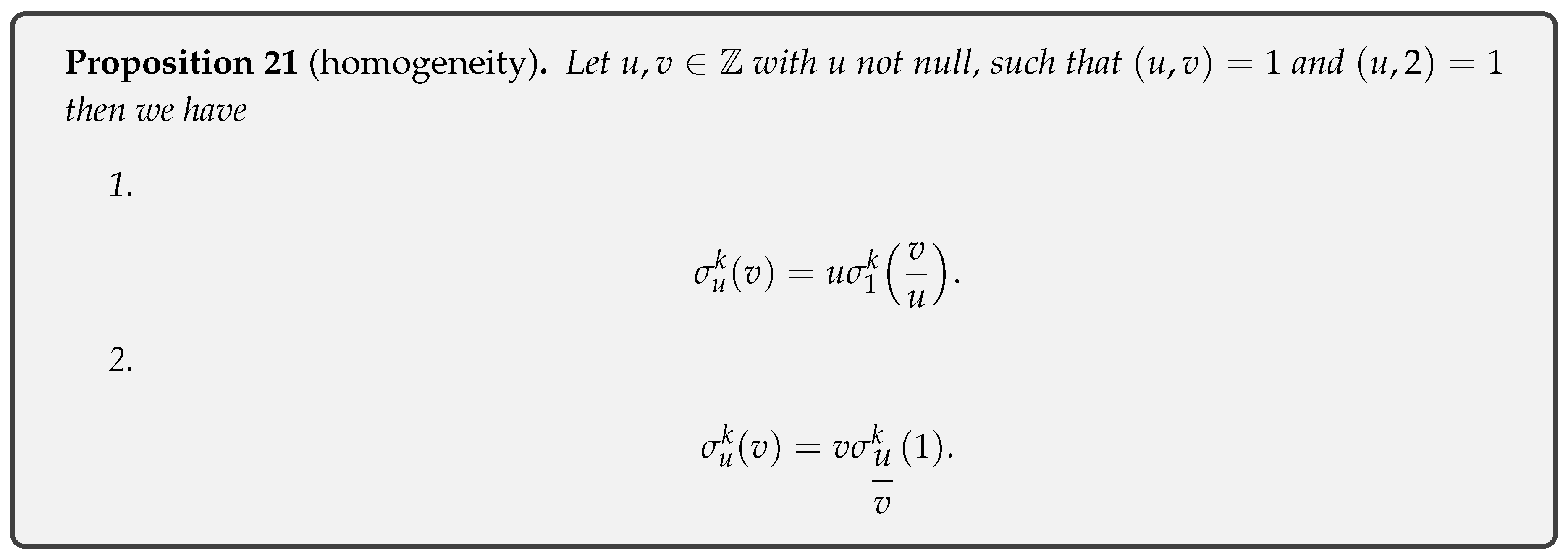
- Let where and where . Then we have
- Let where and where . Then we have

7.7. Coding of Sigma Function
7.7.1. Adic Numbers

- if then if and only if .
- Let then this is uniquely represented by convergent series ( with norm ) as
-
The adic expansion allows us to perform arithmetical operations in in way very similar to that in . Moreover, we will see that the operations in are, in fact, easier to perform than .Let and.
-
A adic number is said to be a adic integer if its canonical expansion contains only non-negative power of p. The set of adic integers is denoted by , soThis set has the property of being a complete metric subspace.
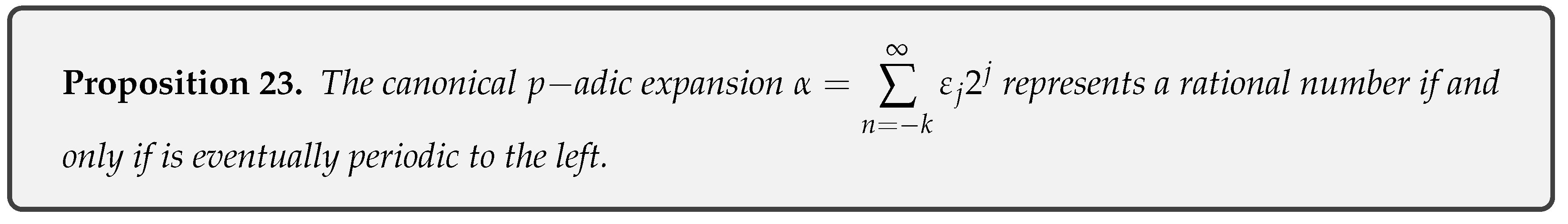
7.7.2. Coding of Sigma Function
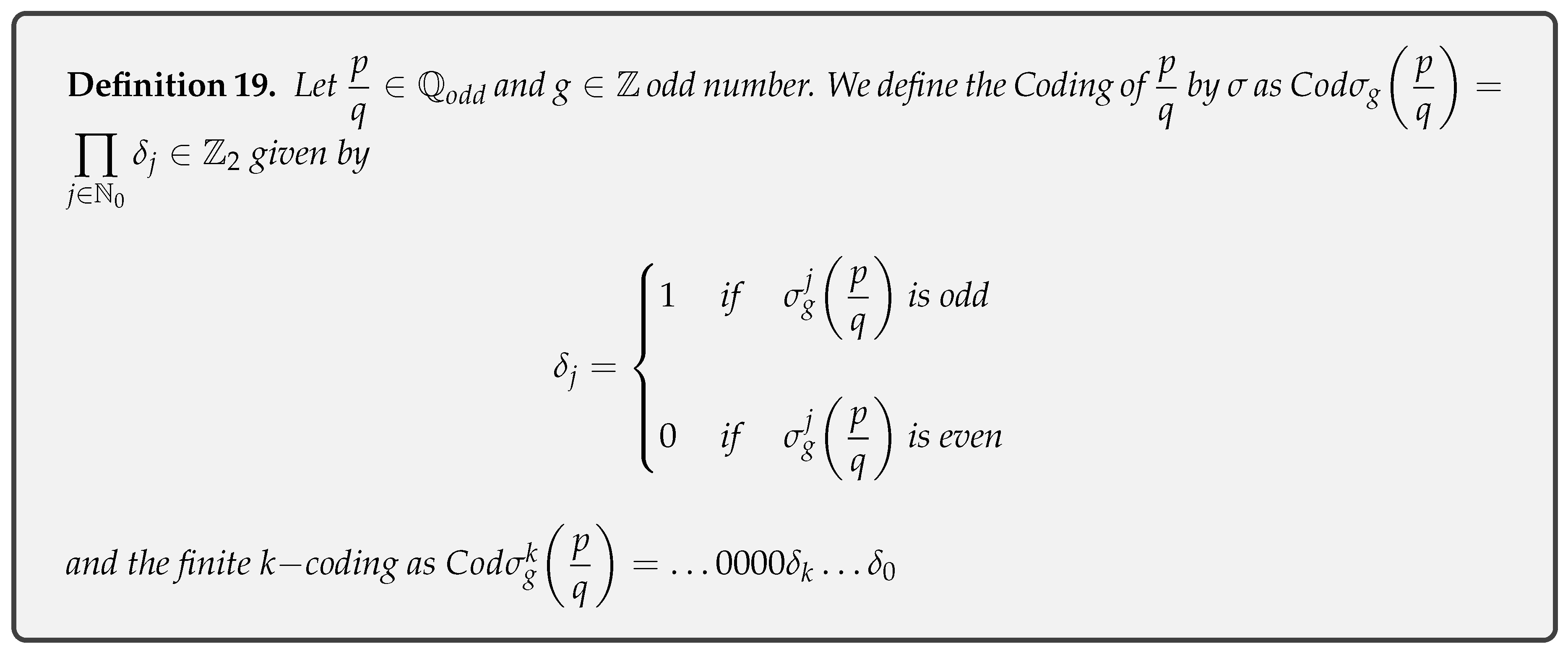


- , then . Then we have taking the coding coefficients, to base 2 we have
- , then . Then we have taking the coding coefficients, to base 2 we have
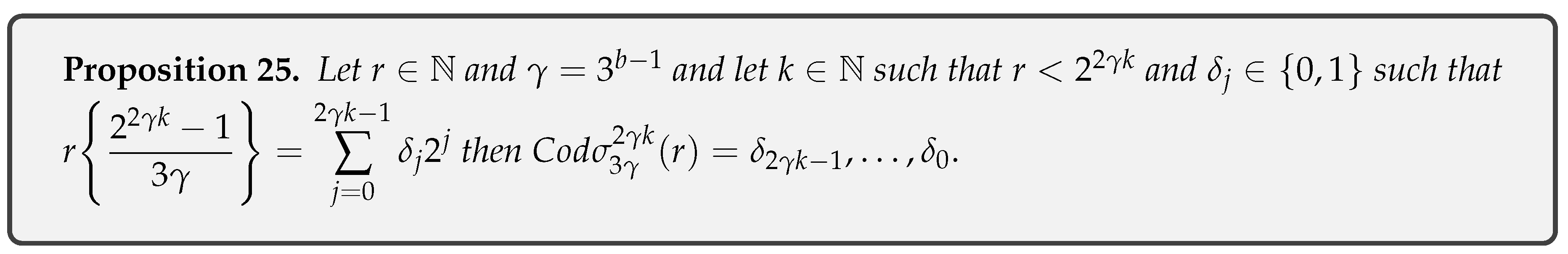
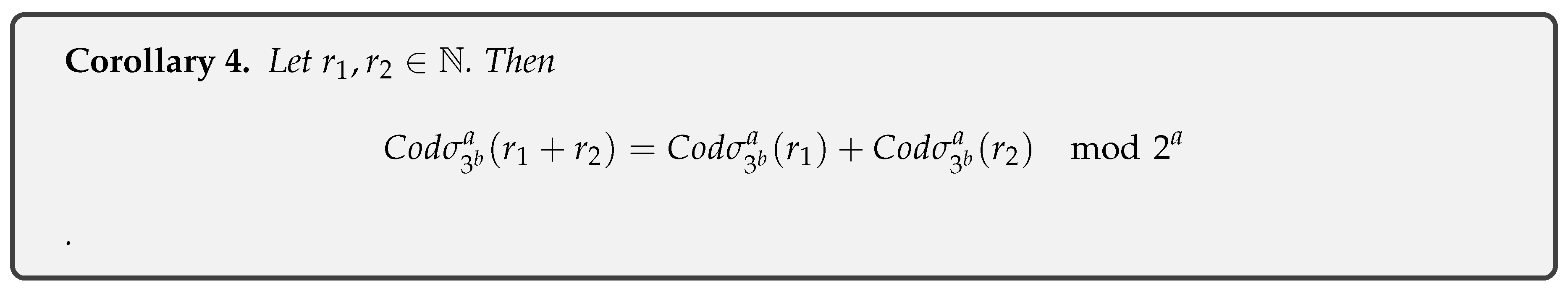
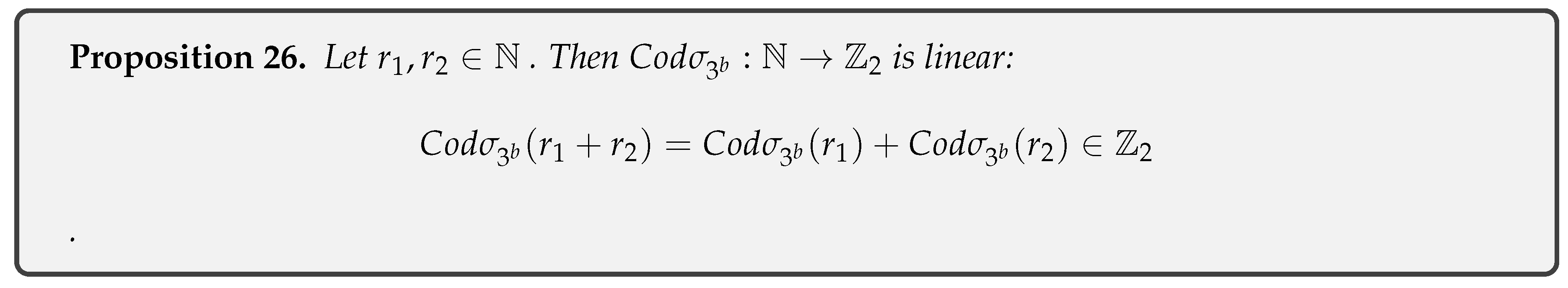
-
Let
- (a)
- then .
- (b)
- then .
then , Then we have -
Let with even. We haveThen
- (a)
- then .
- (b)
- then.
Then we haveThen we have . -
LetOn the other hand
- (a)
- then .
- (b)
- then .
Then we haveThenThat is, has a constant coding equal to 1. This is natural, since is stable.

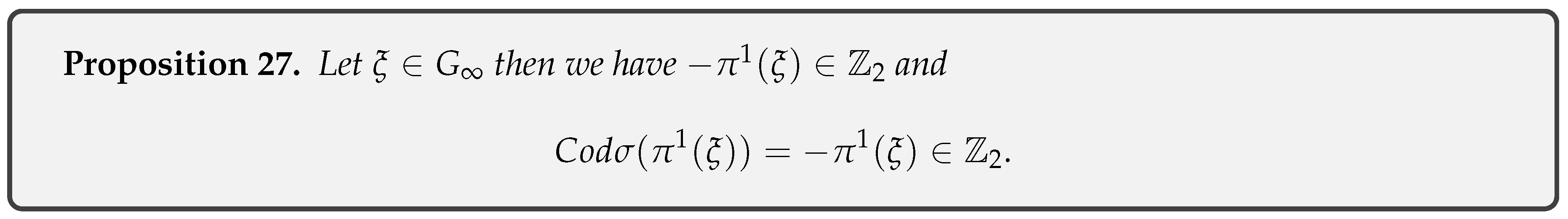
8. The Extension of Collatz Function on
8.1. Summary of Propositions in the Section
- Lemma 9: Equivalence of the parity of fractions and their dyadic representation.
- Definition 20: Extension of the Collatz function on the set of dyadic numbers and the definitions of dyadic integer set and coding set.
- Proposition 28: Characterization of the dyadic integer set.
- Proposition 29: Establishes that the Coding set and the Dyadic Integer Set are the same.
- Proposition 30: It establishes that given a coding there is a unique dyadic number with said coding.
- Theorem 5: The Collatz function on the set of dyadic numbers is topologically conjugate to the Shift function.
- Corollary 5: The periodic points of the Collatz function in are dense in .
- Proposition 31: The periodic sequences of correspond to positive periodic points of the Collatz functions and the periodic sequences of correspond to negative periodic points of the Collatz functions.
- Lemma 10:.
- Proposition 32.
- Theorem 6: The sequences in are positively and negatively unstable.
8.2. Extension of the Collatz Function on .



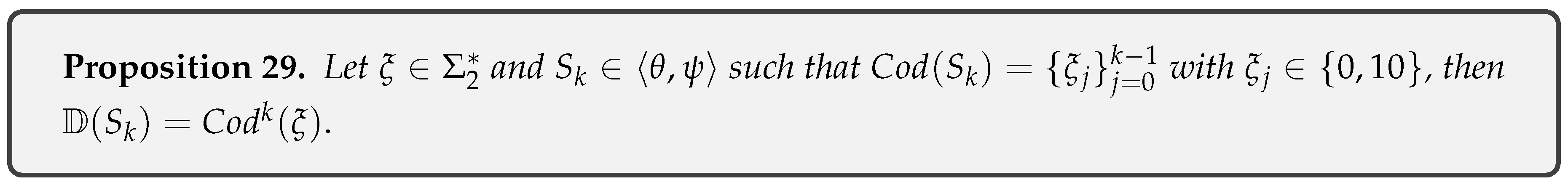
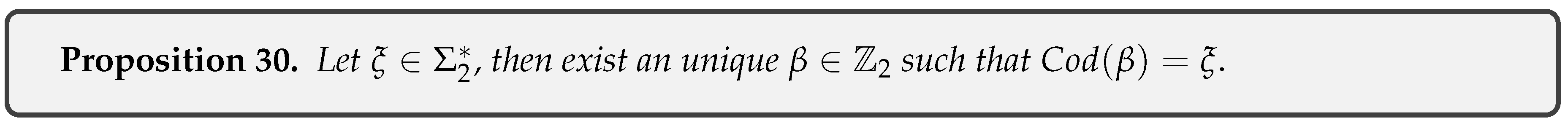
8.3. Topological Conjugation

- : By Corollary 30 we have .
- : Let and such that , so for all . On the other hand we have for all . Exists for all such that so then as Thus .




9. The Coding of
9.1. Summary of Propositions in the Section
- Lemma 11: Established that when the function then and share at least the first terms.
- Proposition 33: Established that is a complete metric space.
- Corollary 6: Established that the coding set is an open set.
- Theorem 7: Established that the full coding set is either as a singleton set or as an empty set depending on whether is rational or not.
- Proposition 34: It establishes that the parity of depends only on the first term of the series.
- Definition 21: Defines an extension of the Collatz function over all .
- Proposition 35: The Collatz functions are continuous.
- Proposition 36: The Collatz function on is topological conjugacy to Shift map on
- Corollary 7: It is stable that the periodic points of the Collatz function in are dense.
9.2. as Complete Metric Space

- If then all terms with an index less than r are null and in particular we have for . and as we already saw in the proofs above, this implies that for all .
- If . Then we have that therefore . particular we have for .

-
if and only if for all : Trivially we have that if , thenLet such thatby lemma 11 we haveIn particular, for we have .
- for all :then
- for all,then
-
Suppose that is not in , so does not converge to 0, then exist and subsequence such that for all . Since converges to . Exist such thatthen the first terms begin to equal, thenSince is a sequence in for all then as . In particular for L exist such that so this is a contradiction, then is in .
-
Let us suppose, for absurdity, that but does not converge to 0, then exist such thatIn particular, exists in such that the of both sequences are no longer equal, otherwise, we would have that for N that is large enough the distance would be less than . On the other hand, the fact that they are different implies that the terms of and must be different for , but this contradicts the fact that the sequences and come closer, since with the metric D getting closer is the same as having the first terms of the sequences become equal.
9.3. Characterization of the Full Coding Sets through the Function

- Let , then (see Example 7). Therefore .
-
Let , thenTherefore
9.4. Extension of the Collatz Function on



9.5. Topological Conjugation

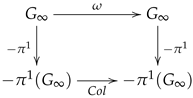
-
:Let with . Since the parity of depends only on the first term, if starts with 0 then , then is even then the first term of its coding is 0, and if starts with 1 then then is odd then the first term of coding is 10. By applying the Collatz function we obtain the same result as applying a translation of the terms of . Indeed
- (a)
-
if.
- (b)
- if
Then applying the function . Then we can repeat the same procedure and we recover . Therefore -
:Let and such that . On the other hand we have and then , applying on both sides we have .

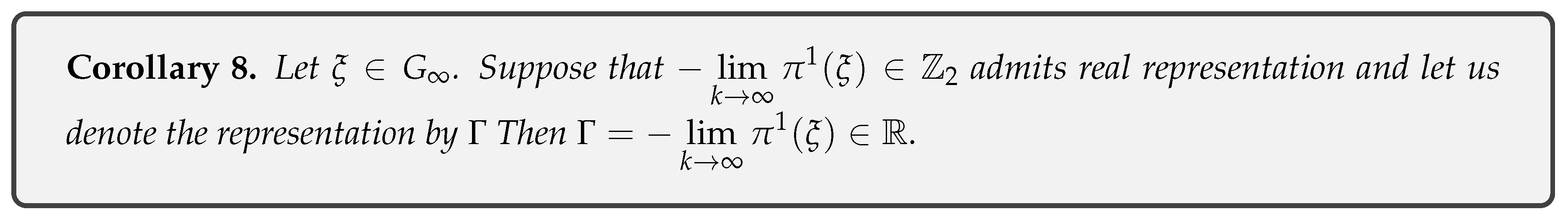
10. The Problem of Divergence
- Theorem 8: This theorem states that all sequences with a divergent slope are positively unstable, defining the sufficient condition under which a sequence becomes unstable.
- Theorem 9: This theorem shows that all orbits with codings in are bounded.
- Theorem 10: This theorem shows that all orbits with codings in are bounded.Consequently, the orbits of negative numbers necessarily fall into periodic orbits.
- Theorem 11: This theorem concludes that all natural numbers have bounded orbits, implying the non-existence of divergent orbits for natural numbers.
10.1. Summary of Propositions in the Section
- Theorem 8: It is stated that all sequences with a divergent slope are positively unstable.
- Theorem 9: It is stated that all orbits with codings in are bounded.
- Corollary 9: If exist a sub-sequence such that . Then exist such that .
- Theorem 10: Let . Then we have exits such that for all . In particular if then its orbit necessarily falls into a cycle.
- Theorem 11: It is stated that all natural numbers have bounded orbits.
10.2. The Problem of Divergence

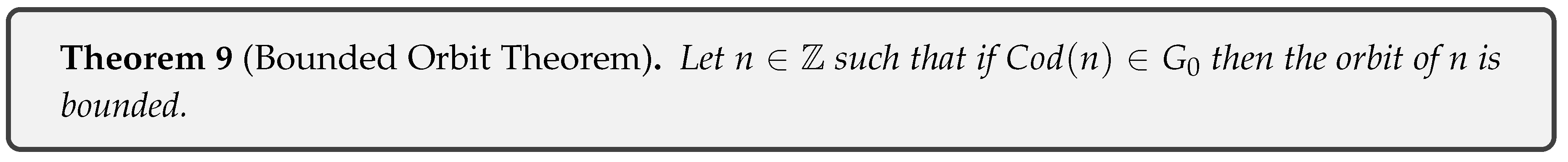

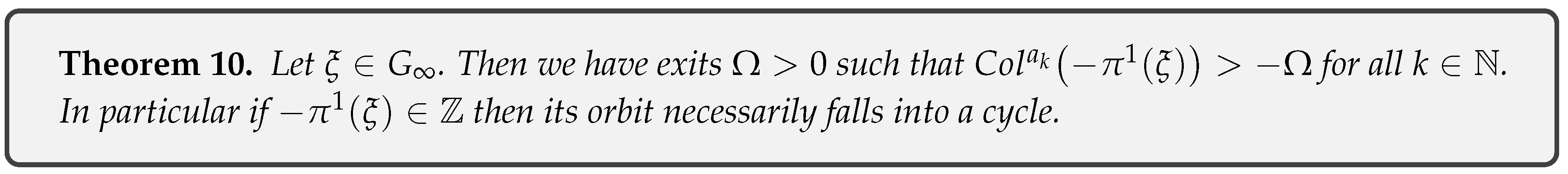

- If then by Proposition 16 we have this implies that
-
if , by Proposition 16 we have that then . Let’s show now in fact . Suppose that exist such that with , so using the estimated bound in the demonstration of the Lemma 9, we haveSince as . So then we haveSince for all , then exist such that . So we have that the orbit of n must fall into a cycle, which implies that which implies that is bounded, which contradicts the hypothesis that . Therefore . This is equivalent to as .On the other hand if by Theorem 6 we have which contradicts the hypothesis that is positively stable, so
References
- T. Tao. "Almost all orbits of the Collatz map attain almost bounded values." Forum of Mathematics, Pi. Vol. 10. Cambridge University Press, 2022. [CrossRef]
- D. Bernstein. A Non-iterative 2—adic Statement of the 3N+1 Conjecture . Proceedings of the American Mathematical Society, Q1, (1994), 405â408.
- J. Lagarias. The 3x+1 Problem and its Generalizations. American Mathematical Monthly, 92, (1985), 1â23.
- S. Eliahou. The 3x+1 Problem: New Lower Bounds on Nont’rivial Cycle Lengths. Discrete Mathematics, 118, (1993).
- J. Lagarias. The Set of Rational Cycles for the 3x+1 Problem. Acta Arithmetica, 56, (1990), 33â53.
- K. Matthews and AM. Watts. A Generalization of Hasseâs Generalization of the Syracuse Algorithm. Acta Arithmetica, 43(2), (1984), 167-175.
- S. Andrei, M. S. Andrei, M. Kudlek and RS. Niculescu. Some Results on the Collatz Problem. Acta Informatica, 31(2), (2000), 145-160.
- D. Applegate and J. Lagarias. Density Bounds for the 3x+1 Problem. I. Treeâsearch method. Mathematics of Computation 1995, 64, 411–426. [Google Scholar]
- D. Bernstein and J. Lagarias. The 3x+1 Conjugacy Map. Canadian Journal of Mathematics, Q, (1996), 1154-169.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).



