1. Introduction
Surface Plasmon Resonance (SPR) is a sensitive optical technique used for real-time, label-free analysis of molecular interactions. Its versatility spans applications in life sciences, industry, environmental monitoring, medical diagnostics, drug development, and pathogen detection. Beyond chemical and biochemical detection, SPR can measure physical parameters like magnetic fields, pressure, and temperature, enhancing its scope across various sectors. In SPR, polarized light directed through an optical fiber towards a metal-dielectric interface induces collective electron oscillations (SPR waves) on the metal surface. Key factors like the angle of incidence, light wavelength, and material dielectric functions determine resonance conditions, marked by a sharp reduction in reflected light intensity. This sensitivity to surface changes makes SPR a powerful sensing tool [
1,
2].
Since its introduction in 1983, various SPR sensor structures for chemical and biochemical detection have emerged, including Metal-Insulator-Metal (MIM) and metasurface configurations, and photonic crystal fibers (PCFs). SPR-based D-shaped fiber optic sensors (FOS) offer the advantages of optical fibers combined with SPR sensitivity. These sensors, with a polished flat surface exposing the fiber core for metal layer deposition, can detect RI changes in surrounding media or identify specific chemical or biological substances. In medicine, SPR sensors provide high sensitivity, speed, and real-time information for applications like rapid diagnosis, health monitoring, biomedical research, infection detection, and therapeutic interventions. They detect biomarkers in body fluids (blood, urine, saliva), identifying proteins, antibodies, and nucleic acids linked to diseases such as cancer and cardiovascular conditions [
3,
4].
Research into SPR sensors has focused on enhancing sensitivity and selectivity through plasmonic materials (gold, silver) and hybrid composites. Recent studies on D-shaped SPR-based FOS have explored adding coatings like graphene and metal oxides (Al
2O
3, TiO
2, SnO
2) to the plasmonic layer, improving performance by enhancing selectivity and minimizing external interferences [
5,
6].
Theoretical and numerical studies, including finite element method (FEM) and finite difference method (FDM) simulations, help optimize sensor performance by modeling the behavior of SPR sensors under various conditions. These methods enable precise, economical, and adaptable optimization of sensor design [
7]. In cancer detection, FEM simulations allow realistic modeling of the biological environment, tailoring sensor design to specific cancer types. Early detection is crucial for effective treatment, making it essential to develop biosensors capable of identifying cancer progression [
8].
This work presents a D-shaped SPR-based biosensor designed for detecting cancer cells in human organs, with FEM-based simulations optimizing sensor parameters. The sensor aims to differentiate between healthy and cancerous cells by monitoring RI changes. The study focuses on three cancer types: skin cancer (basal cell carcinoma) and two types of breast cancer (MDA-MB-231 and MCF-7). The following sections outline the D-shaped optical fiber design and numerical method (
Section 2), results and discussions (
Section 3), and conclusions (
Section 4).
3. Results and Discussions
In surface plasmon resonance (SPR)-based fiber optic biosensors (FOBs), the refractive index (RI) of the sensing medium is crucial for determining light propagation. The interaction between light and materials with varying RI is utilized to detect changes at the sensor surface, such as biomolecular interactions, DNA mutations, and tumor growth. The selectivity of the functional layer on the sensor surface allows FOBs to target specific molecules, with changes in RI providing quantitative data on analyte concentration, kinetics, and other characteristics. Designing highly sensitive FOBs to detect RI changes enhances sensitivity and response time, broadening their applications in molecular biology and environmental monitoring. Increased RI sensitivity also improves the detection selectivity and specificity for tumor tissues, enabling precise targeting of cancer cells and genetic mutations.
This study proposes a numerical analysis of a D-shaped SPR-based FOB, featuring a sensitive chip with a gold layer covered by a TiO
2 layer, aiming to optimize sensor parameters for detecting three types of cancer, including two breast cancer types (MDA-MB-231 and MCF-7) and basal cell skin cancer. The MDA-MB-231 cell line is an aggressive breast cancer model known for not overexpressing estrogen, progesterone, and HER2 receptors, making it resistant to therapies targeting these receptors. MCF-7 cells, in contrast, express hormone receptors, particularly estrogen and progesterone receptors, and are used to study hormonal regulation in breast cancer and evaluate treatments like tamoxifen. Skin cancer is one of the most common types of cancer in the world. It usually develops on areas of the skin exposed to the sun, the main type of skin cancer is basal cell carcinoma (BCC), which develops in the basal cells of the epidermis. Numerical simulations of detection tests are essential before conducting real tissue tests to optimize experimental design, minimize costs and resource use, and assess ethical and safety risks. Understanding the RI of healthy and cancerous tissues is critical for simulating light propagation in biological media, which involves various structures with distinct optical properties, like cells and proteins. These structures affect light absorption and scattering, complicating light propagation analysis. To simplify, four coefficients are often used to describe the average properties of the medium: RI, absorption coefficient, scattering coefficient, and anisotropy coefficient. The RI, a dimensionless and wavelength-dependent quantity, influences the optical path, with typical values in biological media ranging from 1.35 to 1.42. Pathological changes, such as those caused by cancer, alter tissue RI, making it a valuable diagnostic parameter. This research utilizes infrared measurement data for both healthy and cancerous cells from existing literature, as detailed in
Table 1.
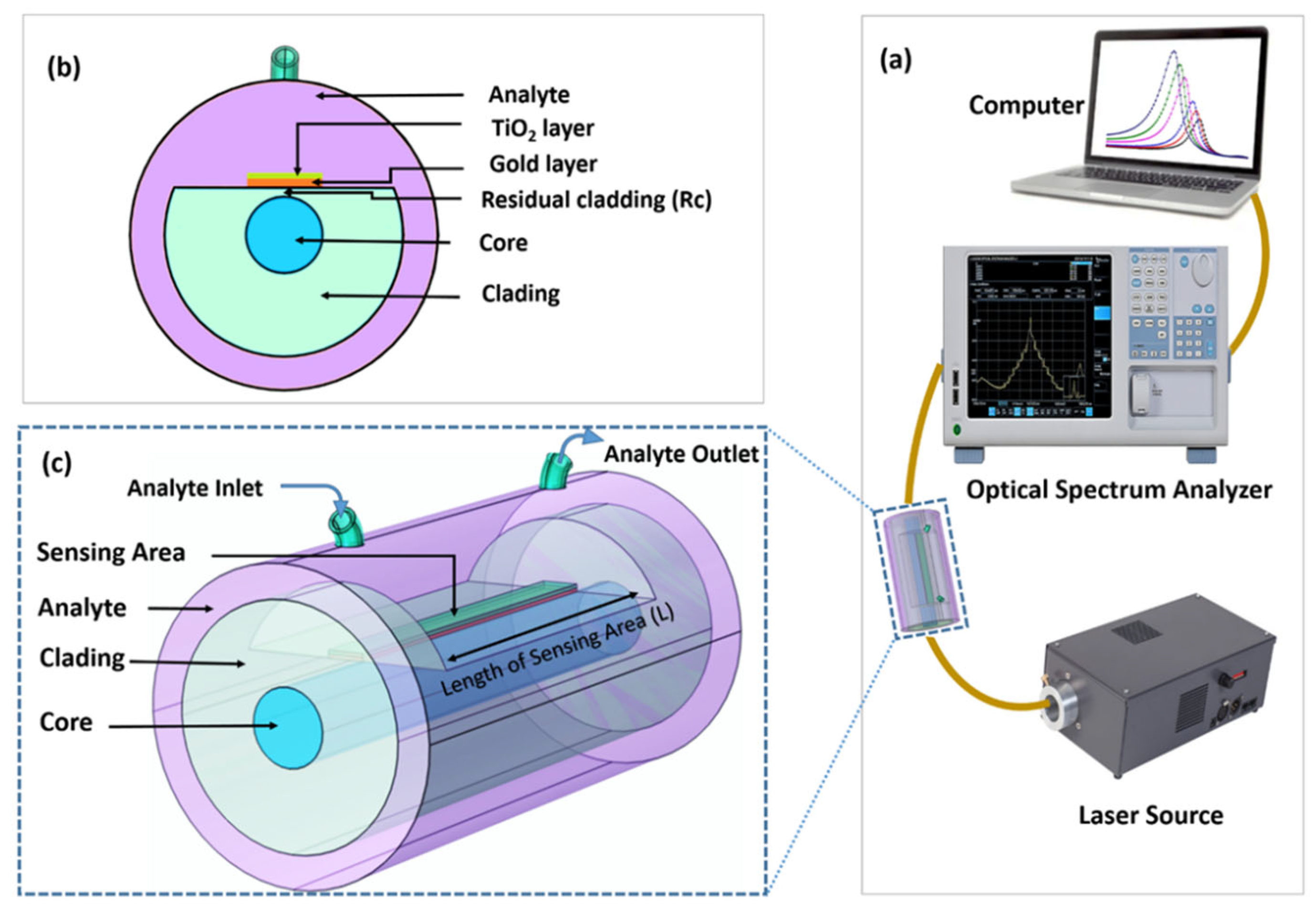
In the study of the proposed sensor, various geometric and physical parameters can influence the optical spectra obtained during the analysis of biological media. These parameters include the core and cladding composition, core and cladding diameter, and the polishing depth of the D-shaped section. The optimal configuration of a D-shaped sensor, that incorporates Au/TiO2 layers and should result in higher sensitivity in the refractive index region that is pertinent to biological tissues, has been explored. We employed the finite element technique (FEM) to simulate the sensor in order to investigate this with the following geometric parameters: The cladding diameter is , the core diameter is , and the distance between the polished surface of the sensitive zone and the end of the core is . The polished portion of the cladding was then covered by a layer of gold, with a thickness of . This layer of gold is covered by a second layer of TiO2 with thickness . The essential element of this D-shaped fiber optic SPR sensor is the evanescent TM (p-polarized) mode field that propagates through the optical fiber's core. As we are working with a single-mode OF, only one mode moves unidirectionally along the fiber because its core diameter is considerably smaller than the guided wavelength.
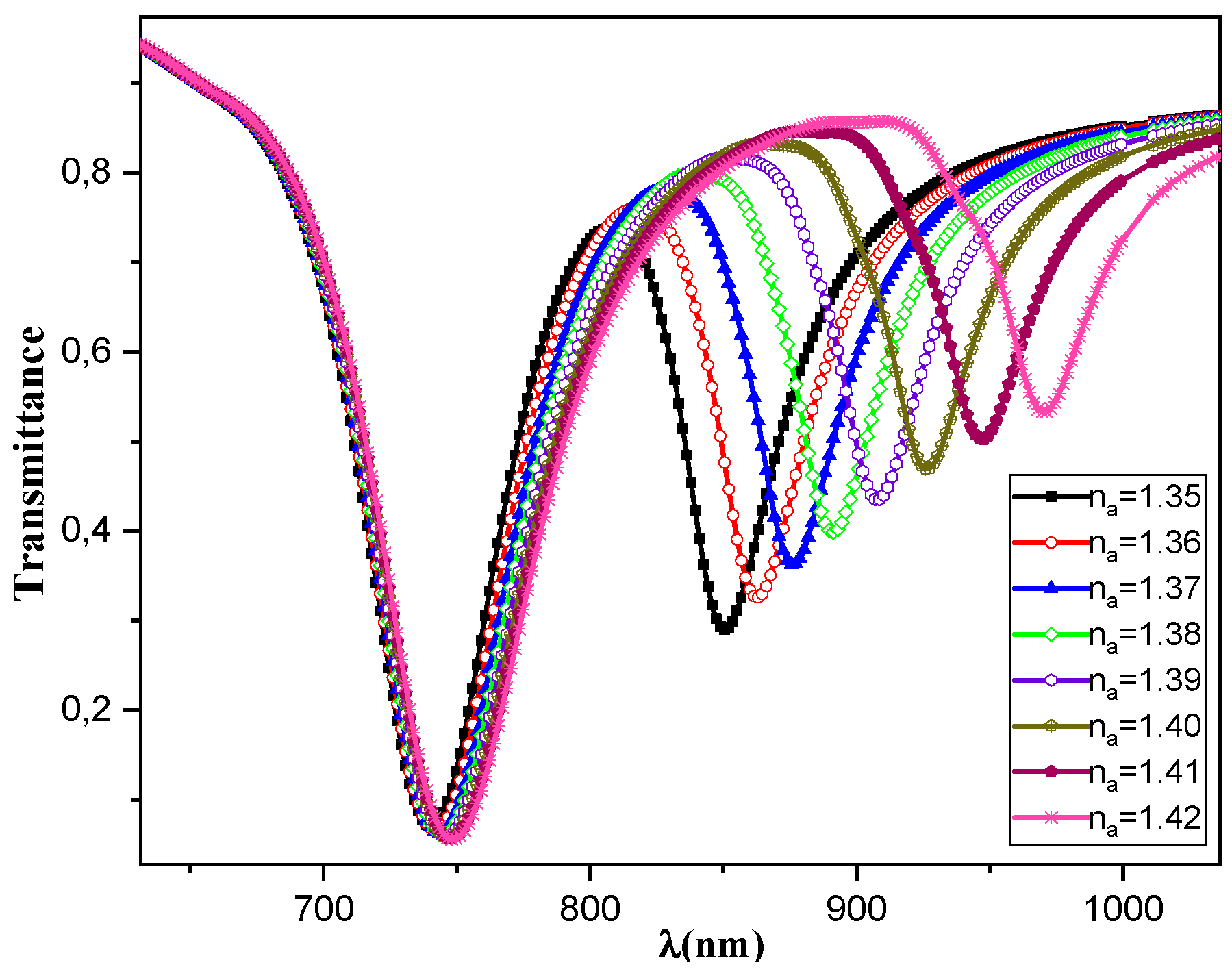
In this first study we considered the medium under study in these simulations to be biological cells, characterized by a refractive index ranging from 1.35 to 1.42. This section contains the numerical simulation results obtained to characterize the optical response of the proposed sensor. The records of light transmission as a function of wavelength for a range of external medium RI
values are shown in
Figure 2, with a step size of 0.01. The indices increase from
to
. The excitation of metal plasmons in the Vis (SPR-Vis) and NIR (SPR-NIR) bands is reflected in the two minima thus obtained in the light transmission curves through the fiber. The resonance wavelengths
and
respectively increase in concordance with the external medium's refractive index
. When the
varies from 1.35 to 1.42, the first SPR signal,
, shows a small shift from 740 nm to 748 nm, while the second signal,
, shows a large shift from 850 nm to 971 nm when the RI
varies from 1.35 to 1.42. The results highlight that the shift and amplitude of the SPR signals are more pronounced in the NIR region compared to the Vis region, making the NIR signals more suitable for detecting RI variations. The focus of the discussion will be on the NIR signal pair, as they show a significant gap in SPR signals between normal and cancerous tissues.
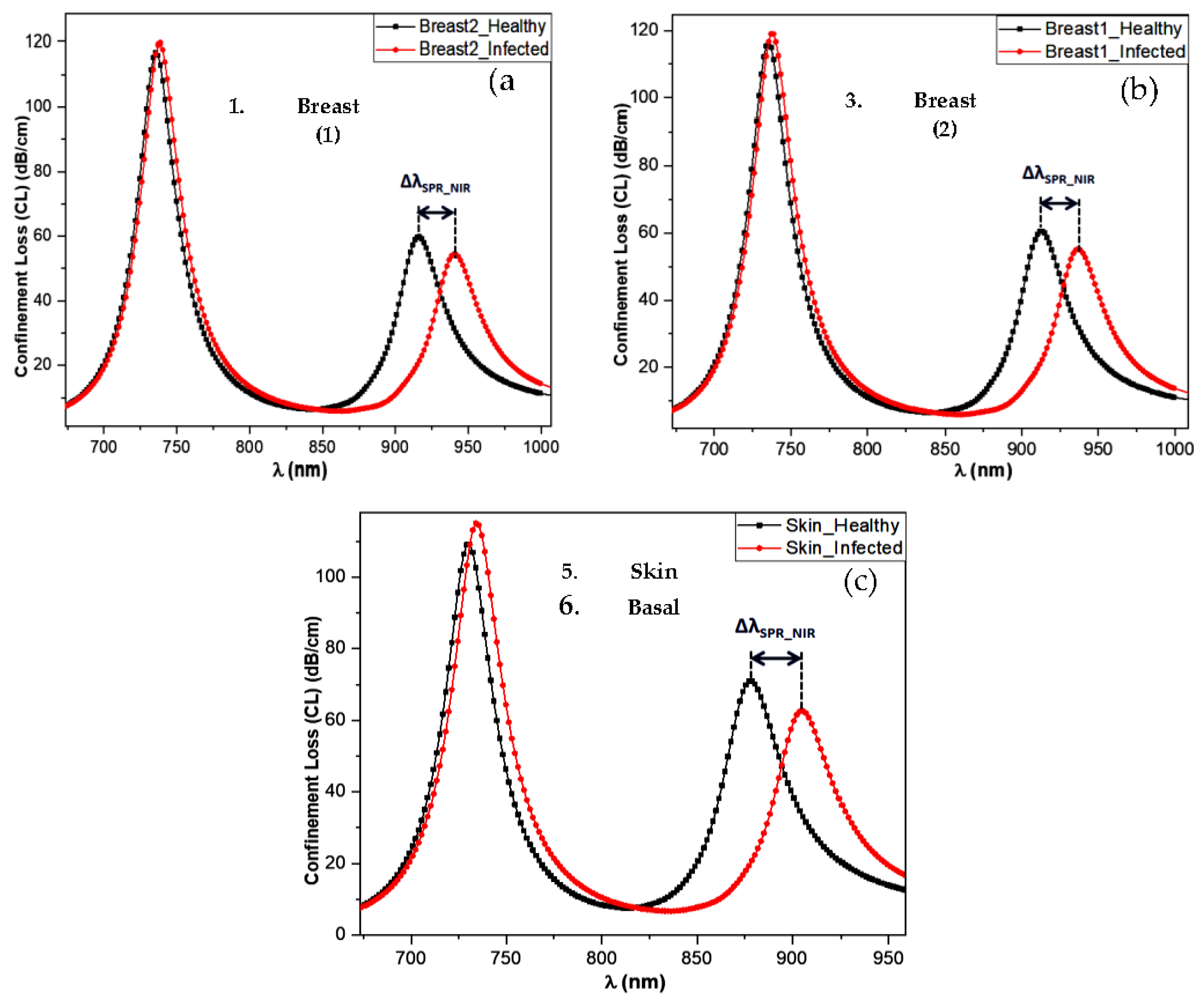
Simulation results of the proposed sensor, when used to detect MDA-MB-231 and MCF-7 breast cancers and basal cell skin cancer, are shown in
Figure 2a-c. In these figures, the pair of curves represent the cases of healthy skin tissue (black line) and infected skin (red line). The SPR signal obtained in the NIR band shows a significant shift between healthy and cancerous tissue. To achieve effective detection of the skin tumor by the sensor under study, a significant
gap must be observed between the signals corresponding to healthy and malignant tissue.
This study observes that the confinement loss signal for MDA-MB-231 and MCF-7 cancer cells shift towards longer wavelengths compared to normal cells (
Figure 1a,b), with specific shifts
in the NIR region.
Figure 2c shows that for basal cells, we obtained a resonance wavelength shift between normal and cancerous cells of
.
Figure 3.
Confinement Loss spectra obtained by the sensor as a function of wavelength for various normal and cancerous cells with and .
Figure 3.
Confinement Loss spectra obtained by the sensor as a function of wavelength for various normal and cancerous cells with and .
An important parameter impacting the assessment of detection efficiency is the resolution of the proposed sensor, which gauges its capacity to detect even minor variations in the RI of the analyte medium. Better sensor performance is indicated by a lower resolution, as determined by the following formula (9) [
21].
where the minimum value of spectral resolution
and the change in analyte RI of
are illustrated in table 1. This proposed sensor shows better RI resolution of
for Breast cells and
for Skin basal cells.