Data Obfuscation for Privacy-Preserving Machine Learning using Quantum Symmetry Properties

1. Introduction

Quantum technologies are increasingly being integrated into various disciplines, ranging from Quantum Key Distribution (QKD) [85], which enables secure key exchanges, to the advancement of quantum information processing technologies like quantum computers [87]. Furthermore, Quantum Machine Learning (QML) emerges as a promising field, leveraging quantum computational advantages to address complex problems [79]. Despite the fact that the physical realization of quantum computers and quantum circuits currently trails behind their classical counterparts, the theoretical and conceptual frameworks of quantum technologies have demonstrated promising potential across a broad spectrum of applications. Here, QML represents a frontier in computational science, blending quantum computing’s potential with classical machine learning’s algorithmic precision. The promise of QML lies in its capacity to process and analyze complex, high-dimensional data sets beyond the reach of current classical methodologies  [79]. Central to these quantum information technologies are feature maps, which are instrumental in encoding classical data onto quantum circuits or qubits. These processes rely on the algebraic principles underlying the symmetries of the SU(2) Lie group [19], and exactly these underlying algebraic structures of information encodings are the focus of this article.

Lie groups, which are continuous transformations, are instrumental in numerous physical and mathematical theories, providing a rich lexicon for describing symmetries and corresponding transformations [9,93].

This paper introduces a novel approach to data obfuscation using the exponential map of Lie group generators, tested for publicly available medical data. Similar to how quantum computing aims to harness the multidimensional and symmetrical qualities of quantum states, our method applies these same properties, specifically the symmetries found in Lie groups, to alter data within a high-dimensional space. This connection highlights our methodology’s interdisciplinary approach, effectively merging concepts from quantum mechanics, algebra, and machine learning in a novel way.

Central to our investigation is the question: Can Lie Group theory effectively obfuscate sensitive data while retaining its essential properties for successful machine learning applications, thereby preserving the accuracy and informational value of the original dataset?

Our research builds on the foundational work of Schuld et al. [11,31,44] and IBM’s Qiskit [12] in the field of Quantum Machine Learning (QML) and their exploration of feature maps for projecting data onto qubits.

Our main contributions in this article can be summarized as:

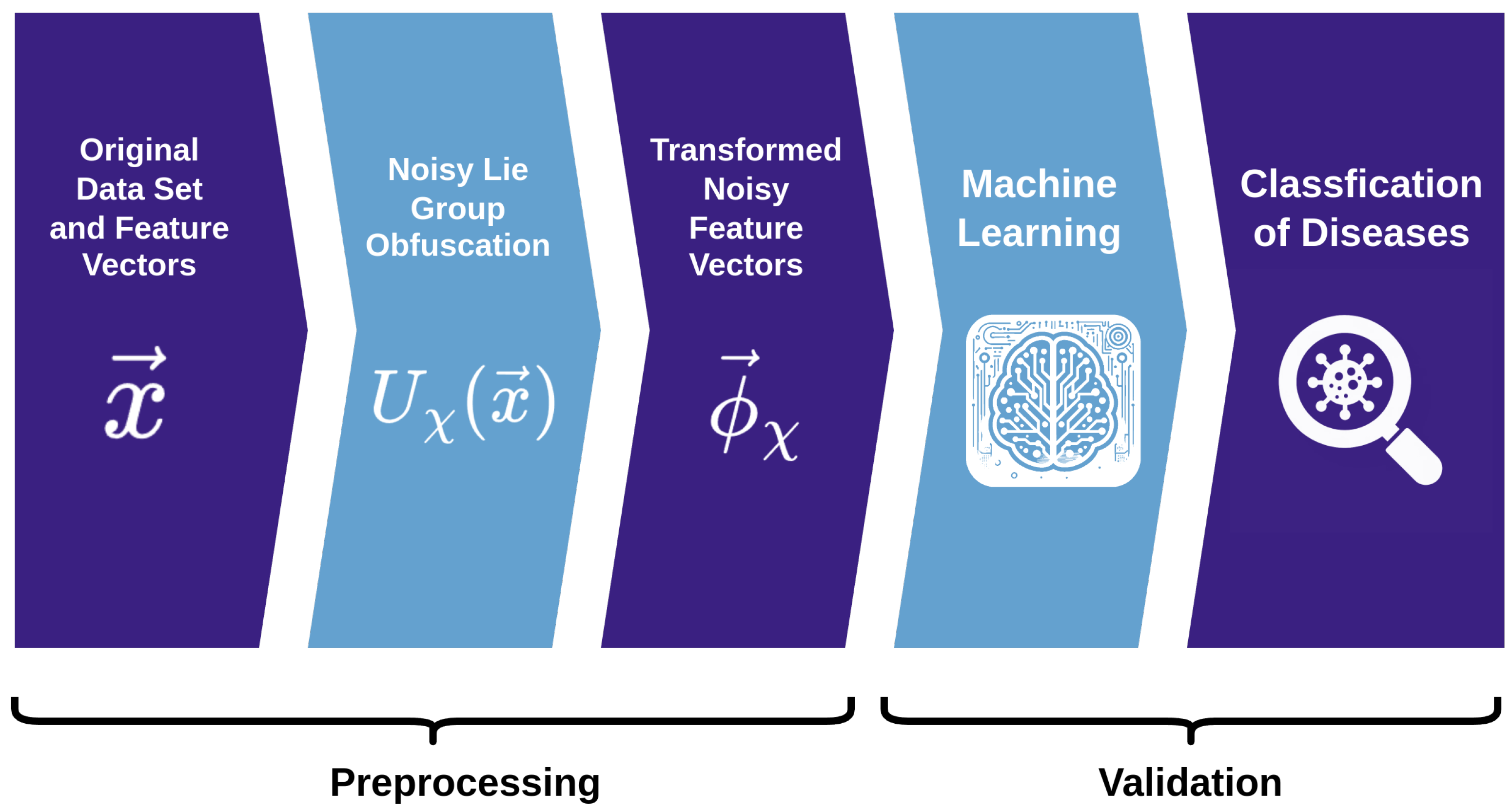
• We develop a novel data obfuscation framework using the exponential map of Lie group generators, tailored for privacy-preserving processing of medical data used in machine learning approaches.
• We show where and how the invertibility of our obfuscation technique breaks down by injecting noise into the exponential map of Lie group generators. Thus making it impossible to recover the original data.
• We demonstrate the efficacy of this approach in maintaining and occasionally surpassing the predictive accuracy of machine learning models compared to non-obfuscated datasets.
• We establish a conceptual link between the principles of quantum machine learning and our obfuscation methodology, highlighting the potential for cross-disciplinary innovation in leveraging symmetries for data privacy, thus showing the applicability of quantum mechanical concepts in this context.

The remainder of this article is organized as follows: We provide a collection of related related work in Section 2. Section 3 provides our methodology, i.e., a background on quantum feature maps, Lie groups, how to use them for data obfuscation, and where invertibility of the exponential map breaks down by injecting noise. Section 4 describes our experimental setup and the employed data sets (Section 4.1). The following Section 4.2 presents our results. The final Section 5 concludes our approach and findings, discusses the implications, and gives an outlook on future applications.

2. Related Work

The protection of patient privacy is paramount in medical data processing, making data obfuscation a critical area of research. Data obfuscation techniques aim to mask sensitive information while maintaining the utility of the data for machine learning applications. This ongoing research is vital as it addresses the dual challenge of protecting patient confidentiality and enabling the extraction of actionable insights from medical data [10].

One common approach is data anonymization, where identifiers such as names and social security numbers are removed or replaced with pseudonyms. For instance, the k-anonymity model [108] ensures that each record is indistinguishable from at least k-1 others regarding certain attributes. However, [109] highlighted the vulnerability of k-anonymity to re-identification attacks, leading to the development of more sophisticated methods. Studies by Lu et al. [111] have applied homomorphic encryption to medical datasets, enabling secure analysis without compromising patient confidentiality.

Deep learning (DL)-based algorithms for image classification have demonstrated remarkable results in improving healthcare applications’ performance and efficiency. To address privacy concerns, especially in cloud-based solutions, data obfuscation techniques like variational autoencoders (VAEs) combined with random pixel intensity mapping can be used for enabling DL model training on secured medical images while ensuring privacy [107].

Olatunji et al.’s comprehensive review [10] of healthcare data anonymization techniques underscores the delicate balance between privacy and utility in the context of modern big data and machine learning challenges, which also applies to data obfuscation.

Quantum information processing presents novel opportunities for advancing machine learning, particularly through quantum machine learning (QML). The integration of quantum computing with machine learning algorithms has the potential to revolutionize data processing, offering significant improvements in speed and efficiency.

A key concept in QML is the use of quantum feature maps, which embed classical data into high-dimensional quantum states. This process can enhance the representational capacity of machine learning models. Havlíček et al. [13] demonstrated that quantum feature maps could enable the classification of complex datasets that are challenging for classical models.

Quantum algorithms can potentially provide new methods for data privacy. For example, Lloyd et al. [112] proposed quantum algorithms for principal component analysis (PCA), which can be applied to obfuscate data while preserving essential features for machine learning tasks. Such approaches leverage the principles of quantum mechanics to enhance data security and utility simultaneously.

Synthetic data generation [113] involves creating artificial datasets that resemble real data but do not contain actual patient information. Techniques such as generative adversarial networks (GANs) have been employed to generate realistic medical data for machine learning. While synthetic data can effectively preserve privacy, ensuring the fidelity and utility of such data is an area of active investigation. For a similar purpose, but to create exemplary test classification datasets, Raubitzek et al. [81] showed that one can use Lie algebras to create synthetic and artificial data. This approach was tested using both quantum machine learning and classical machine learning algorithms.

3. Methodology

We start this section by discussing fundamentals of quantum information processing and quantum machine learning necessary to understand our ideas, which we then expand to present our novel approaches.

Quantum machine learning consists of two steps: First, the feature encoding step, and second the actual quantum computation, whereas we focus solely on the first step.

We describe a standard quantum feature encoding as:

$$|\psi \left(x\right)\rangle =U_{\Phi }\left(x\right)|0\rangle ,$$

(1)

where:

• $|\psi \left(x\right)\rangle$ denotes the quantum state obtained by applying the feature map $U_{\Phi }\left(x\right)$ to the initial state $|0\rangle$,
• $|·\rangle$ represents a state vector in the complex Hilbert space $\mathcal{H}$,
• $U_{\Phi }\left(x\right)$ is a unitary operation encoding classical data x into a quantum state, preserving total probability,
• $|0\rangle$ is the quantum system’s initial, "empty" state before encoding.

This equation captures the transformation of classical data x into a quantum state $|\psi \left(x\right)\rangle$ through a unitary feature map $U_{\Phi }\left(x\right)$.

These feature maps, i.e., unitary transformations, especially those of the Pauli class, are based on SU(2) symmetry properties, meaning that there are matrix transformations that follow certain rules to project arbitrary data on a qubit. The behavior of these Pauli-class feature maps is governed by the Pauli matrices which are three $2\times 2$ complex matrices:

$${\sigma }_x=\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right),{\sigma }_y=\left(\begin{array}{cc}0& -i\\ i& 0\end{array}\right),{\sigma }_z=\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right)$$

These matrices form a basis for the Lie algebra of the SU(2) group. SU(2) is the group of $2\times 2$ unitary matrices with determinant 1, and its Lie algebra, denoted as $\mathfrak{su}\left(2\right)$, consists of all $2\times 2$ traceless Hermitian matrices.

The Lie algebra $\mathfrak{su}\left(2\right)$ is then spanned by the Pauli matrices multiplied by ${\displaystyle \frac{1}{2}}i$:

$$\mathfrak{su}\left(2\right)=\left\{{\displaystyle \frac{1}{2}}i{\sigma }_x,{\displaystyle \frac{1}{2}}i{\sigma }_y,{\displaystyle \frac{1}{2}}i{\sigma }_z\right\}$$

(2)

However, we are expanding this concept to Lie groups SU(n) and SL(n) Lie-groups and add noise to the generators to slightly break these symmetries to obfuscate our original data, thus making the data non-reproducible. To show this, we will first discuss quantum feature maps, and here, two particular ones used in IBM’s Qiskit, [12], show where the mechanics of Lie groups are used, and expand this approach to use SU(n) and SL(n), [9,93].

Among various and custom quantum feature maps, the Z and ZZ feature maps are standard choices implemented in IBM’S Qiskit, [12]. These feature maps basically use the properties of Pauli matrices to generate rotations in a complex two-dimensional space to encode classical data into the quantum realm. The basic idea here is that similar to a standard rotation matrix, parameterized using an angle $\theta \in [0,2\pi ]$, one expands this methodology to complex rotations which are parameterized using the Pauli-matrices. This gives rise to the two following feature maps, which are variations of Equation 1, and depicted in Figure 1:

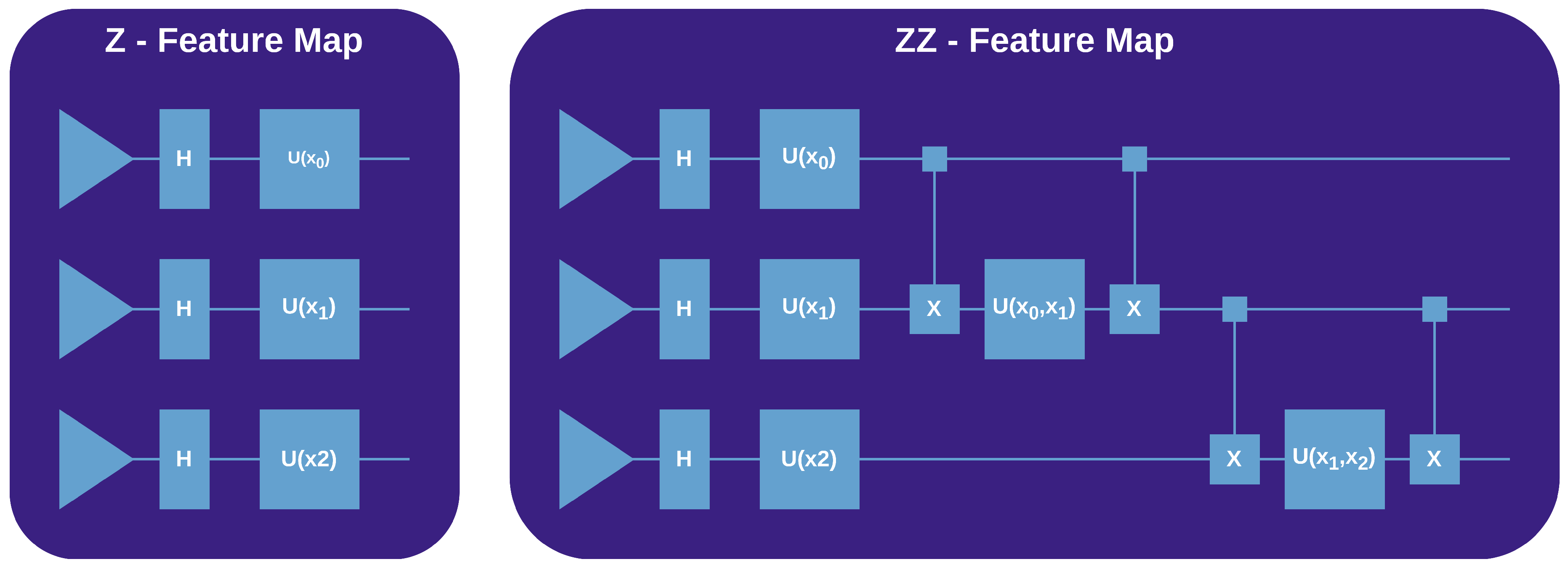
• The Z Feature Map
  The Z feature map employs the Pauli-Z operator to encode classical data into quantum states. For a given data point x, it applies a phase rotation to each qubit in a quantum register, proportional to the corresponding feature value in x. Mathematically, this operation is described by:

  $$U_{\mathrm{Z},j}\left(x\right)=exp\left(i{x}_j{Z}_j\right),$$

  (3)

  where $Z_j$ is the Pauli-Z matrix acting on the j-th qubit, and $x_j$ is the j-th component of x. This results in a rotation around the Z-axis of the Bloch sphere, effectively encoding the data within the phase of the quantum state, depicted in Figure 1.
• The ZZ Feature Map
  Building on the Z feature map, thus employing the same rotation transformations, the ZZ feature map introduces entanglement between qubits to enrich the feature space. It uses two-qubit gates controlled by the product of pairs of classical data features, depicted in Figure 1

Figure 1. Depiction of the Z- and the ZZ feature maps. Both schemes were adopted according to the implementation in IBM’s Quiskit [12]. The triangle on the left symbolizes the incoming qubit; afterward, for both feature maps, the qubit is entangled via a Hadamard gate to make the qubit more expressive. Next, the Pauli-Z-rotations are applied to the qubits.

Figure 1. Depiction of the Z- and the ZZ feature maps. Both schemes were adopted according to the implementation in IBM’s Quiskit [12]. The triangle on the left symbolizes the incoming qubit; afterward, for both feature maps, the qubit is entangled via a Hadamard gate to make the qubit more expressive. Next, the Pauli-Z-rotations are applied to the qubits.

In quantum information processing, efficient data encoding into a quantum circuit is essential. For each data feature, a corresponding manipulation is required. Our approach expands beyond standard quantum feature encoding, which uses SU(2) transformations for individual qubits. For instance, encoding 8 features requires at least 8 generators. This requirement is met, e.g., by the group SU(3), which has 8 generators, i.e., the Gell-Mann matrices. We parameterize these matrices with normalized features within the exponential map, producing a group element that is applied to a normalized vector, resulting in a complex three-component vector encoding the data sample information. This method permits the application of arbitrary Lie groups for data encoding, assuming the group’s generators are constructible. This concept and and a corresponding example are depicted in Figure 2.

In our approach, we identify a Lie group that is sufficiently large, specifically one within the families of SU(n) or SL(n), which has an adequate number of generators, i.e., more or equal. We use our normalized feature vector $\overrightarrow{x}=\left(x_0,x_1,\cdots ,x_m\right)$ to parameterize the generators, thereby obtaining the corresponding group element $U\left(\overrightarrow{x}\right)$:

$$U\left(\overrightarrow{x}\right)=exp\left(i\sum _j{x}_j{T}_j\right),$$

(4)

where $x_j$ are the individual components of the feature vector, $T_j$ are the generators of the selected symmetry group, and $U\left(\overrightarrow{x}\right)$ is a $k\times k$ matrix representing the group element. Should the number of generators exceed the number of features, we set the parameters for the excess generators to zero. This encoding transforms our data samples or vectors into a new feature space and feature vector represented by:

$$\overrightarrow{\varphi }={\displaystyle \frac{1}{\sqrt{k}}}\left(\begin{array}{c}1\\ ⋮\\ 1\end{array}\right)·U\left(\overrightarrow{x}\right),$$

(5)

For the following machine learning process, we also separate real and complex components of the so-obtained feature vector, thus obtaining $2\times k$ features.

Incorporating a noise term $\chi$ to each set of generators guarantees the data to be obfuscated. This is mathematically represented by a random uniform noise component added to each component of the summed up set of parameterized generators, if the parameterized set of generators is complex, we add both a real and a complex noise component. This results in the following expression for our noisy group elements:

$$U_{\chi }\left(\overrightarrow{x}\right)=exp\left(i\sum _j{x}_j{T}_j+\chi \right),$$

(6)

This addition of noise effectively perturbs each group element $U\left(\overrightarrow{x}\right)$ generated by the exponential map, leading to a slightly altered encoded quantum state.

This expansion of feature maps to arbitrary Lie groups enhances our ability to represent and manipulate data. By leveraging the diverse symmetries and structures of different Lie groups, we can design feature maps that are tailor-made for specific types of data or learning tasks.

Mathematically, adding a small noise vector $\chi$ ensures that the perturbed quantum state remains within a vicinity of the original state near the manifold, preserving the relative distances and geometric relationships crucial for machine learning algorithms. This proximity guarantees that while the data is obfuscated enough to protect privacy, it retains sufficient structure for effective learning.

Finally, we can apply the feature map from Equation 6 to each sample several times, every time with a different noise component, and thus use our approach not only to obfuscate data but also to increase the amount of data, i.e., synthesize additional data, thus multiplying the amount of data.

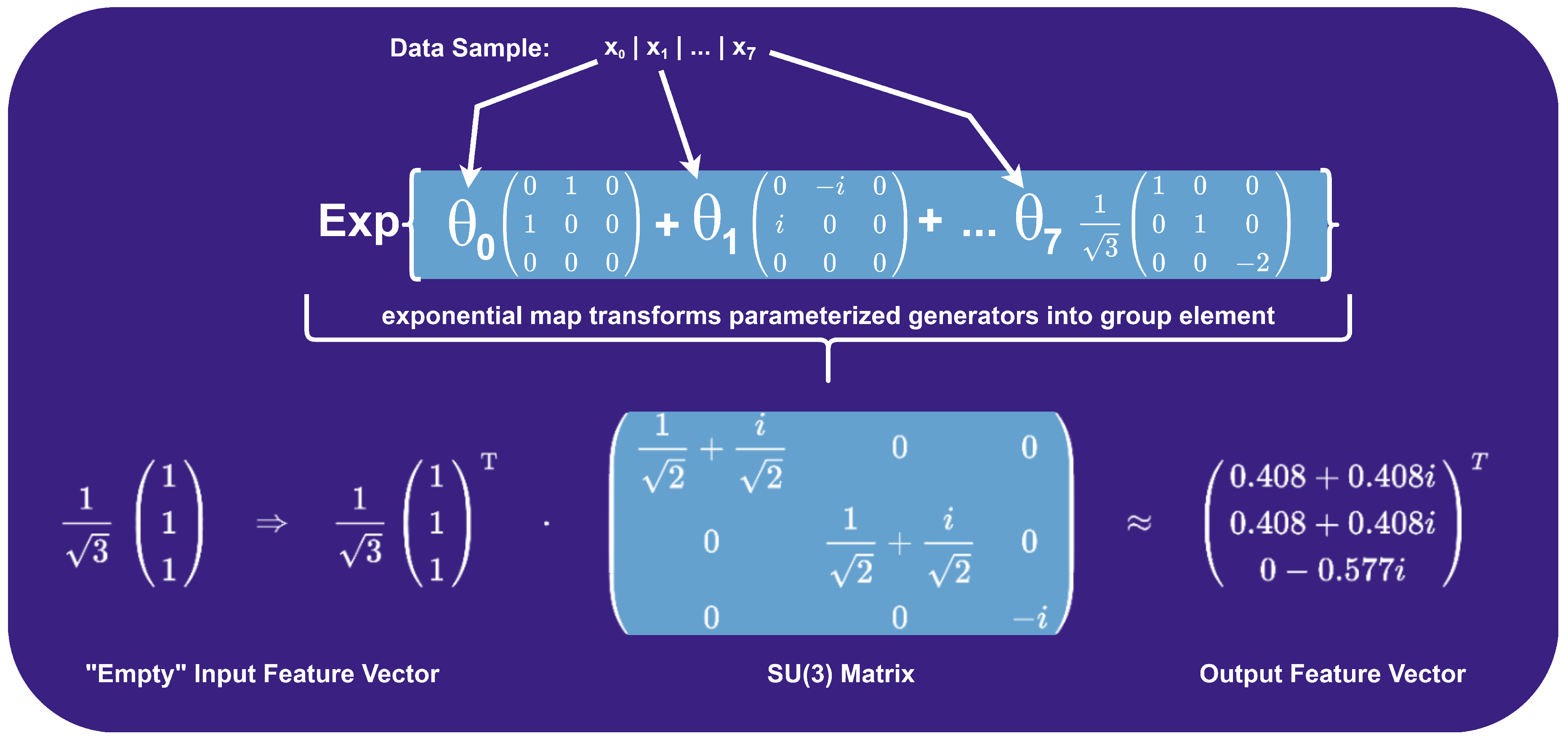
3.1. Retrieving the Original Data

Given the previously outlined discussion on constructing our data obfuscation based on the exponential map of a Lie group, we want to ensure that our original data is not retrievable, which we do using the following construction of our noise component $\chi$.

First of all, we need to make some assumptions about our discussion. We need to assume first that an attacker that wants to acquire the original data is familiar with our obfuscation approach and with Lie groups, corresponding algebras, etc. Then we need to assume an attacker knows about our base vector, as discussed in Equation 5, and finally, the attacker is capable of reproducing the transformation matrix from our transformed feature vector, i.e.

$${\overrightarrow{\varphi }}_{\chi }={\displaystyle \frac{1}{\sqrt{k}}}\left(\begin{array}{c}1\\ ⋮\\ 1\end{array}\right)·U_{\chi }\left(\overrightarrow{x}\right),$$

(7)

thus reproducing $U_{\chi }\left(\overrightarrow{x}\right)$. This starts the discussion on how to choose the noise such that one cannot retrieve the original features $\overrightarrow{x}$ from our transformation matrix $U_{\chi }\left(\overrightarrow{x}\right)$.

First, we need to discuss if and when the exponential map of a Lie group is invertible:

Local Invertibility

The exponential map, denoted as $exp:\mathfrak{g}\to G$, where $\mathfrak{g}$ is the Lie algebra of a Lie group G, is locally invertible around the identity element of G. This follows from the Inverse Function Theorem, which applies because the differential of the exponential map at the identity (zero in the Lie algebra) is the identity map, making it a local diffeomorphism at this point.

Global Invertibility

Globally, the exponential map is generally not invertible. This is because the map can be neither injective (one-to-one) nor surjective (onto):

• Injectivity: The exponential map is not injective if there exist elements $X,Y\in \mathfrak{g}$ such that $X\ne Y$ but $exp\left(X\right)=exp\left(Y\right)$. This can occur, for example, when X and Y differ by a multiple of $2\pi i$ in certain directions in $\mathfrak{g}$, particularly for compact or periodic dimensions of G.
• Surjectivity: The exponential map may not be surjective for some Lie groups, meaning not all elements of the group can be expressed as the exponential of some element in the algebra. A typical example is non-connected groups where the exponential map reaches only the connected component of the identity.

Given these arguments, we need to look at the most extreme case: Injectivity and Surjectivity are given globally for a particular Lie group, and the attacker knows which Lie group we used to encode our data and further knows the set of generators we used. Thus we construct our noise in the following way to make our original data non-retrievable:

$$U_{\chi }\left(\overrightarrow{x}\right)=exp\left(I\sum _j{x}_j{T}_j+\chi \right)$$

(8)

This noise $\chi$ can be decomposed into two components:

$$\chi ={\chi }_G+\zeta$$

(9)

where ${\chi }_G$ denotes noise that can be expressed as a linear combination of the generators of the Lie group (with a different parameterization vector $\overrightarrow{c}$), and $\zeta$ is a residual noise matrix that cannot be expressed as a linear combination of the generators. This results in the following cases: If the matrix ${\chi }_G\ne 0$ and $\zeta =0$, then the following occurs. As discussed before, given the most extreme case that one can reconstruct the generators. One can obtain a feature vector from assigning different parameterizations to these generators. However, one cannot retrieve the original feature vector exactly. The features will have a small deviation in each of its components. This means the noise injected into the exponential map slightly distorts the original features. Therefore, we construct ${\chi }_G$ such that:

$${\chi }_G=\sum _j{ϵ}_j{T}_j,\mathrm{where}\sum _j\left|{ϵ}_j\right|=ϵ.$$

(10)

Here, $ϵ$ is a controllable parameter, i.e., the level of noise that we inject into our data set. Further, we distribute $ϵ$ randomly among the coefficients ${ϵ}_j\ne 0$. Concluding again, one cannot retrieve the original feature vector except one knows precisely the random numbers/coefficients ${ϵ}_j$.

The next case we need to discuss is if our residual noise component is not zero, $\zeta \ne 0$, and assuming that ${\chi }_G=0$. In this case, the resulting matrix $U_{\chi }\left(\overrightarrow{x}\right)$ from applying the exponential map, i.e. $U_{\chi }\left(\overrightarrow{x}\right)=exp\left(I{\sum }_j{x}_j{T}_j+\chi \right)$, is not part of the regarded symmetry group, thus our initial symmetry is broken, and we leave the Lie group’s manifold. However, this means:

• Loss of Group Structure: The resulting matrix is no longer guaranteed to satisfy the properties (closure, associativity, identity, and invertibility) that define the group. Hence, it cannot be inverted within the context of the group.
• Breaking Symmetry: The exponential map is no longer mapping elements of the Lie algebra to the Lie group, breaking the symmetry and making the inverse mapping undefined.
• Non-recoverability of Original Features: Since the transformation is no longer within the group, one cannot apply the inverse of the exponential map to recover the original features. The noise $\zeta$ introduces components that do not belong to the algebra, hence the original structure and information are obfuscated beyond recoverability.

In conclusion, the introduction of residual noise $\zeta$ that cannot be expressed as a linear combination of the generators fundamentally disrupts the structure and invertibility of the exponential map, ensuring that the original feature vector cannot be reconstructed from the transformed vector. Further, the noise injected into the parameterizations of the regarded generators ensures a slight distortion of the original features, which further obfuscates the original data. Thus we conclude, the obfuscated data cannot be reconstructed.

4. Experiments

We performed experiments on four data sets to measure if the data obfuscated using our augmented noisy Lie group approach can still be classified with a machine learning approach. This means we transform all four data sets with varying amounts of noise and multipliers (i.e., synthetic data), perform a machine learning classification with 80% training data and 20% test or validation data, and note the accuracy of the machine learning prediction on the test data. We also compare this accuracy to the same machine learning approach but without obfuscating/transforming the data. This experimental design is depicted in Figure 3. In the following, we discuss details of our approach, such as the normalization, the employed machine learning algorithms, and the regarded data sets.

Normalization of Features: We normalize all features to the range [0, $\pi$] to effectively utilize the exponential map with our chosen Lie groups. Further, all categorical features were projected into a numerical space such that we give each category a distinct value between 0 and $\pi$.

Datasets and Data Augmentation: We employ four distinct datasets, each subjected to five levels of noise and data augmentation, i.e., we change the noise parameter where the noise is sampled from. Data synthetization was performed by multiplying the dataset size by factors ranging from 1 (no augmentation) up to 5, i.e., creating different noisy samples for each data point.

Bayesian Optimization and LGBM Classifier: For the classification tasks, we utilized a Light Gradient Boosting Machine (LGBM) classifier. LGBM is known for its efficiency and effectiveness in handling large datasets and high-dimensional feature spaces, making it an apt choice for our experiments [8]. Bayesian optimization with 100 iterations was employed to search through the hyperparameter space, ensuring the optimal configuration for each experimental condition.

Evaluation Strategy: The datasets were split into training and testing sets using an 80/20 ratio. The performance of the LGBM classifier, trained on the feature-mapped data, was compared against the same LGBM implementation with standard preprocessing, scaling the data to the interval [0,1] for both numerical and categorical features. We chose the standard accuracy score as our primary metric for evaluation.

4.1. Datasets

The following data sets were used to verify if our obfuscation technique can maintain a reasonable performance in classification tasks for medical use cases. All four data sets are medical data sets and are binary classifications, such that the outcome is an identified disease or not. All four data sets are publicly available and can easily be fetched from online databases, e.g., via Python scripts.

• Breast Cancer Wisconsin Dataset (scikit-learn: load_breast_cancer()): Developed by Dr. William H. Wolberg at the University of Wisconsin, this dataset focuses on breast cancer diagnosis. It includes 2 classes, with 212 malignant (M) and 357 benign (B) samples, totaling 569 instances. The dataset describes characteristics of cell nuclei present in breast mass images, with 9 numeric features and one nominal target feature indicating the prognosis (malignant or benign).
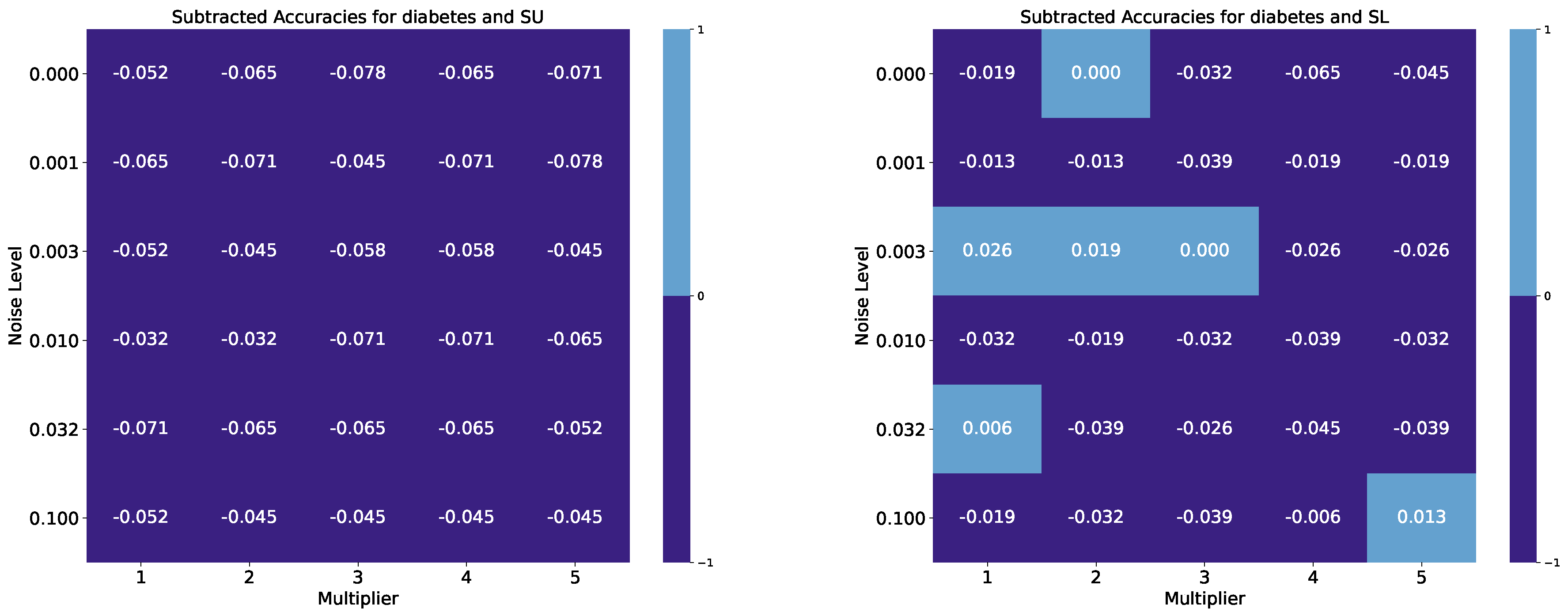
• Pima Indians Diabetes Database (OpenML: diabetes, ID: 37): Curated by Vincent Sigillito and obtained from UCI, this dataset is hosted on OpenML. It focuses on diagnosing diabetes among Pima Indian women, with 768 instances and 9 features. The features are numeric and include the number of times pregnant, plasma glucose concentration, diastolic blood pressure, triceps skinfold thickness, 2-hour serum insulin, body mass index, diabetes pedigree function, and age. The class variable is binary, indicating whether the patient tested positive or negative for diabetes (1 for positive, 0 for negative).
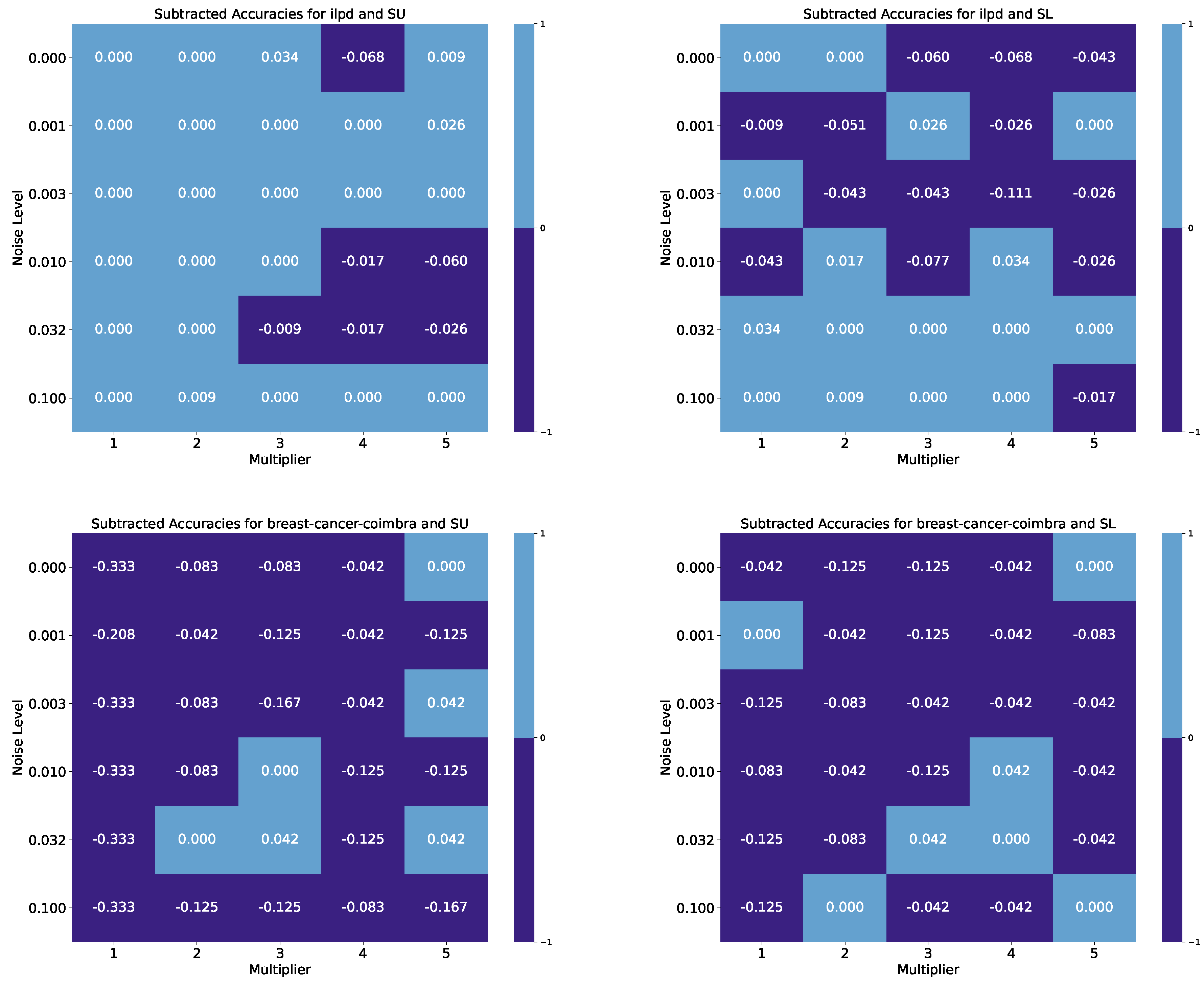
• Indian Liver Patient Dataset (OpenML: ilpd, ID: 1480): Compiled by Bendi Venkata Ramana, M. Surendra Prasad Babu, and N. B. Venkateswarlu, and sourced from UCI in 2012, this dataset is hosted on OpenML. It includes records of 583 patients, with 416 liver patient records and 167 non-liver patient records, collected from north east of Andhra Pradesh, India. The dataset contains 441 male and 142 female patient records. It features 11 attributes, including age, gender, various liver function tests (like Total Bilirubin, Direct Bilirubin, Alkaline Phosphatase, Alanine Aminotransferase, Aspartate Aminotransferase, Total Proteins, Albumin), and Albumin and Globulin Ratio. The class label divides the patients into two groups: liver patient or not.
• Breast Cancer Coimbra Dataset (OpenML: breast-cancer-coimbra, ID: 42900): Authored by Miguel Patricio et al. and sourced from UCI in 2018, focuses on breast cancer prediction. It consists of 116 instances with 10 quantitative features. These features include Age, BMI, Glucose, Insulin, HOMA, Leptin, Adiponectin, Resistin, and MCP-1, gathered from routine blood analysis and anthropometric data. The dataset has a binary dependent variable indicating the presence or absence of breast cancer, with labels for healthy controls and patients.

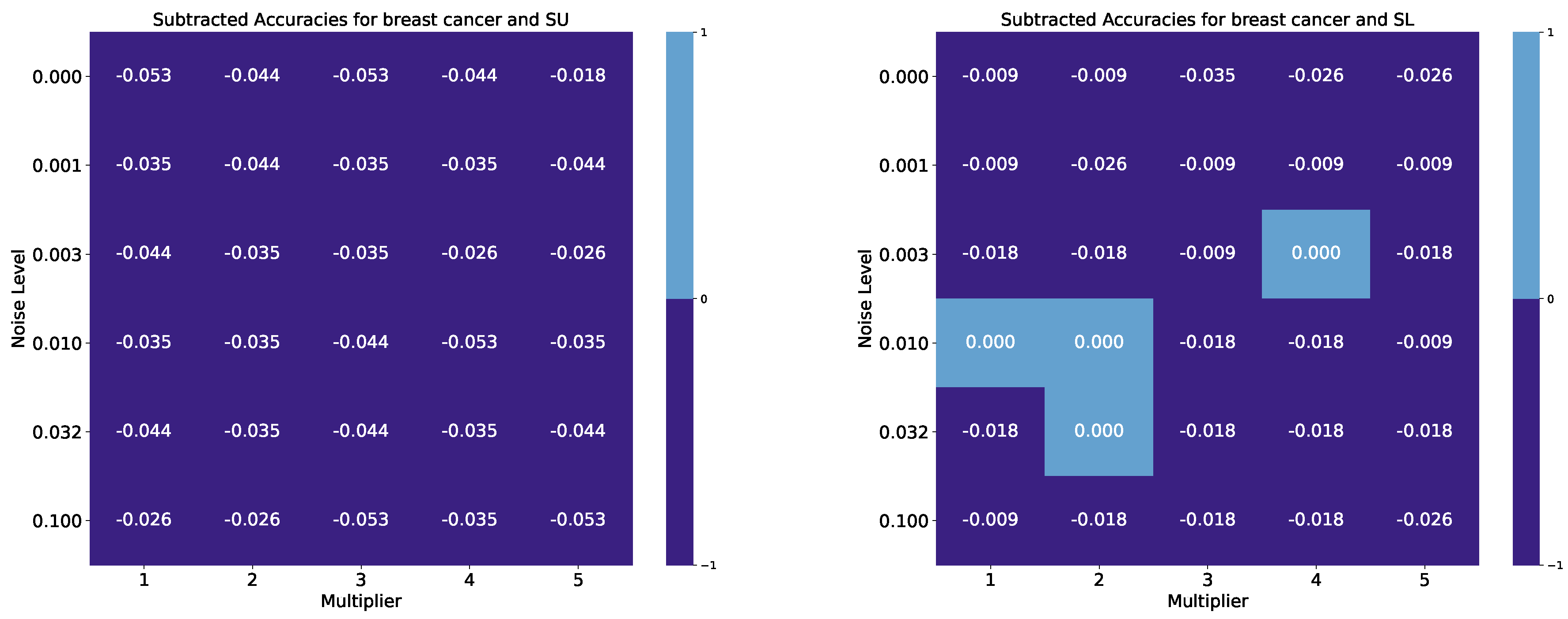
4.2. Results

The experimental results highlight the efficacy of incorporating Lie group-based feature maps with noise for data obfuscation while maintaining the utility of machine learning models. Applying Bayesian optimization and LGBM classifiers across multiple datasets and conditions provided a robust evaluation framework for our methodology.

The performance of the LGBM classifier proved resilient to the levels of noise and the degree of data obfuscation applied, as reflected by the accuracy measurements. Injecting noise into the data, with the goal of making it more private, did not undermine the model’s ability to predict correctly, suggesting that our method is practical for privacy-preserving machine learning. The accuracy figures, alongside our baseline with original features, are listed in Table 1. In Figure 4 and Figure 5, we show how our method compares with the baseline: enhancements are highlighted in light blue, and cases where the baseline is better are in purple. We also chart the differences; when there’s no change, we consider it a win for our method, as the goal is to maintain the baseline accuracy at least.

Each dataset depicts at least one instance in which our method outdid the baseline in accuracy. In fact, for some datasets, our method held up well under most test scenarios. This indicates that regardless of how much noise we added or how much we increased the dataset size—up to five times—the method was as good as, or better than, the baseline. We didn’t expect to beat the baseline in every case, as that’s not the main goal of data obfuscation, but our findings confirm that transforming the data and shifting it into a different feature space preserves enough information for machine learning models to work effectively.

5. Discussion and Conclusion

In this article, we introduced a novel approach for data obfuscation by using the mathematical framework of Lie groups and incorporating noise in the groups’ exponential map to generate obfuscated feature vectors. Our experiments, conducted using two families of Lie groups - SU(n) and SL(n) - and a Light Gradient Boosting Machine (LGBM) classifier, serve as a proof-of-concept demonstrating the viability of this methodology in enhancing data privacy while maintaining utility for machine learning tasks, as shown in Table 1, where it is apparent that the employed machine learning approach performed well on transformed data, i.e., compared to our benchmark score, by being close and sometimes outperforming the benchmark result.

Here it’s crucial to highlight the unique advantages of the developed method. This method’s utility as an obfuscation technique stems from several key factors: the unspecified group, which remains unknown to potential attackers; the obscuring of the number of original features within the parametrization of the generators; and the introduction of noise in the parametrization, which essentially creates an epsilon ball around the actual information on and off the Lie manifold and does not allow for invertibility of the exponential map to obtain the original information.

This approach, as illustrated, can effectively obfuscate medical data. While it renders the original data inaccessible, it preserves the essential information content for machine learning classification methods. For instance, consider a scenario where medical information about patients is collected, and AI-based advice is sought without sharing the patients’ data. In this case, the described technique offers a way to achieve this. When properly configured, it can provide a reliable classification of the conditions being analyzed.

We recognize that this study’s experimental setup could be expanded in several dimensions to explore the proposed method’s full potential. For instance, incorporating a wider array of Lie group families could uncover more intricate symmetries and data representations, potentially offering richer feature spaces. Similarly, evaluating the approach against a broader spectrum of machine learning algorithms could provide deeper insights into its versatility and effectiveness across different learning paradigms.

However, the primary aim of this paper was not to exhaustively test the method across all possible configurations but rather to present a novel concept grounded in symmetry and Lie group theory as a means to achieve data obfuscation in a quantum-inspired/-computing context. The scope of this article was focused on establishing a foundational understanding of this approach and illustrating its potential through a targeted set of experiments.

The presented results are significant because they demonstrate, in a proof-of-concept manner, that quantum information processing can offer a privacy-preserving method to handle data. Specifically, we focus on the implications of intentionally violated Lie group symmetries, drawing a parallel to the realm of physical quantum information processing. In quantum information systems, noise typically poses a challenge by slightly corrupting information processing. However, it is this very noise that enables privacy-preserving data processing in quantum machine learning and other quantum information processing areas that use feature maps to project data onto qubits. Our approach illustrates this by introducing noise in the generation of Lie group elements.

One might initially think that quantum information processing requires only clean channels—those that precisely preserve the structure of the transformations used and, thus, the corresponding probabilities. Yet, it’s crucial to acknowledge the extensive research on non-hermitian quantum mechanics [5,6], which could eventually integrate into various forms of quantum information processing, including quantum machine learning. Although this has not been quantitatively proven yet, the connection here can be found that the evolution of non-hermitian quantum mechanics violates the unitarity of evolution operators; similar for slightly noisy generators, we violate the unitary properties of, e.g., elements of SU(2), which govern the evolution of a qubit during a quantum circuit.

In addition to these insights, our observations align with the principles outlined by the No Free Lunch theorem, [4], which posits that there is no universally superior algorithm or parameterization for all tasks and that prior knowledge of the task at hand is necessary to find the best solution. In our experiments, we noticed that our method outperformed the baseline for certain parameter settings, such as specific choices of multipliers and noise levels. Conversely, under different settings, it did not. This variance underscores the theorem’s assertion that effectiveness heavily depends on the specific problem and dataset at hand.

In conclusion, this study is a good starting point but also highlights many areas for further research. The combination of Lie group theory, quantum computing, and machine learning is a promising area for exploration. It offers potential solutions to important challenges in data privacy and machine learning, including data synthetization, preprocessing, and data obfuscation to make data usable but not recoverable after being obscured. This field presents an opportunity for both theoretical and practical advancements in how we handle and protect data.