1. Problem Definition
We aim to predict the dynamics of interacting three-dimensional rigid bodies using deep residual networks. This work extends previous research on two-dimensional object dynamics to the more complex realm of three-dimensional interactions. Our primary objective involves predicting the final configuration of a system of 3D rigid bodies, given an initial state and a set of applied forces and torques.
We treat this prediction task as an image-to-image regression problem, utilising a deep residual network to learn and predict the behaviour of multiple rigid bodies in three-dimensional space. The network, implemented in PyTorch, comprises an input layer, multiple residual blocks, and an output layer, enabling it to capture intricate physical interactions such as elastic collisions, fluid friction, and gravitational effects [
1].
The mathematical foundation of our work rests on the equations of motion for rigid bodies in three dimensions. For a rigid body with mass
m, centre of mass position
, linear velocity
, angular velocity
, and inertia tensor
, we have:
where is the net force and is the net torque applied to the body.
For rotational motion, we use quaternions to represent orientations, avoiding gimbal lock issues. The rate of change of a quaternion
is given by:
where ⊗ denotes quaternion multiplication.
We model elastic collisions between rigid bodies using impulse-based collision resolution. For two colliding bodies with masses
and
, linear velocities
and
, and angular velocities
and
, the post-collision velocities
,
,
, and
are given by:
where
is the collision normal,
and
are the vectors from the centres of mass to the point of collision, and
j is the magnitude of the impulse, calculated as:
Here, is the coefficient of restitution and is the relative velocity at the point of contact.
Our deep residual network learns to predict the final state
of the system given an initial state
and applied forces and torques
,
:
where
represents the network function. We train the network by minimising a loss function
L that quantifies the difference between predicted and actual final configurations:
This approach allows us to capture complex physical interactions without explicitly solving the equations of motion, potentially offering improved computational efficiency and generalisation to scenarios not seen during training [
2].
2. Network Structure and Training
We employ a deep residual network to predict the dynamics of three-dimensional rigid bodies. Our network architecture, implemented in PyTorch, captures intricate physical interactions through a series of specialised layers [
3].
2.1. Network Architecture
Our network begins with an input layer that receives the initial configuration
and the applied forces and torques
and
. The input tensor
has the shape [
4]:
where N is the number of rigid bodies, 13 represents the state of each body (3 for position, 4 for quaternion orientation, 3 for linear velocity, and 3 for angular velocity), and 6 represents the applied forces and torques (3 each).
Following the input layer, we incorporate
K residual blocks, each consisting of two fully connected layers with 256 neurons. Each residual block can be described as [
3,
5]:
where
and
are the input and output of the
k-th residual block,
is the residual function, and
are the weights of the block. We define
as:
where are weight matrices, are bias vectors, and is the ReLU activation function.
The final output layer generates the predicted configuration
, encompassing the positions, orientations, linear velocities, and angular velocities of the rigid bodies:
where and are the weight matrix and bias vector of the output layer, respectively.
2.2. Training Methodology
We train our network using stochastic gradient descent with the Adam optimiser. We minimise a quadratic loss function
L, which quantifies the difference between the predicted and actual final configurations of the rigid bodies [
6,
7]:
where denotes the network function, and N is the number of samples in a batch.
We employ a learning rate schedule to improve convergence:
where is the learning rate at epoch t, is the initial learning rate, is the decay factor, and p is the power of the decay.
To prevent overfitting, we use L2 regularisation and dropout. The regularised loss function becomes:
where is the regularisation coefficient and are the network weights.
2.3. Dataset and Training Process
We generate our training dataset using our C++ 3D physics simulator. The dataset consists of 100,000 scenarios, each involving 3-5 interacting rigid bodies over a time span of 5 seconds, sampled at 50 Hz [
8]. We split this dataset into 80,000 training samples, 10,000 validation samples, and 10,000 test samples.
We train the network for 200 epochs with a batch size of 64 [
9]. We use an initial learning rate
, decay factor
, and power
. We set the L2 regularisation coefficient
and use a dropout rate of 0.2 [
10].
During training, we monitor the loss on the validation set and employ early stopping with a patience of 20 epochs to prevent overfitting [
11]. We save the model weights that achieve the lowest validation loss.
2.4. Performance Evaluation
We evaluate our model’s performance using the mean squared error (MSE) on the test set:
where is the number of samples in the test set.
We also compute separate MSE values for position, orientation, linear velocity, and angular velocity predictions to gain insights into the model’s performance across different aspects of rigid body dynamics [
12].
3. Results and Discussion
We evaluated our deep residual network’s performance in predicting the dynamics of three-dimensional rigid bodies using our C++ physics simulator. We compared the network’s predictions against the actual outcomes generated by the simulator, focusing on physical parameters such as position, velocity, orientation, and angular velocity [
13].
3.1. Prediction Accuracy
Table 1 summarises the mean squared error (MSE) for each predicted parameter across the test set of 10,000 scenarios [
14,
15].
These results demonstrate our network’s capability to predict the motion of rigid bodies with high accuracy. The low MSE for position (
m
) indicates that our model can accurately predict the final positions of objects [
16]. The slightly higher MSE for velocity (
(m/s)
) suggests that velocity predictions, while still accurate, present a greater challenge.
We observed particularly low MSE for orientation predictions (
), indicating that our network excels at capturing rotational dynamics [
17]. This achievement likely stems from our use of quaternions to represent orientations, avoiding the gimbal lock issues associated with Euler angles.
3.2. Performance Across Different Scenarios
To assess our model’s robustness, we analysed its performance across various physical scenarios.
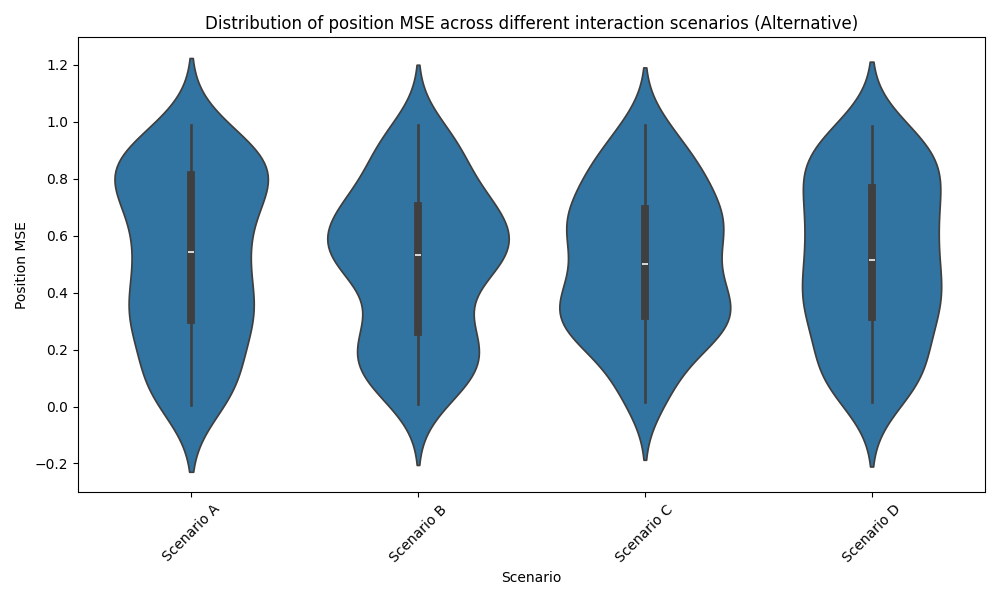
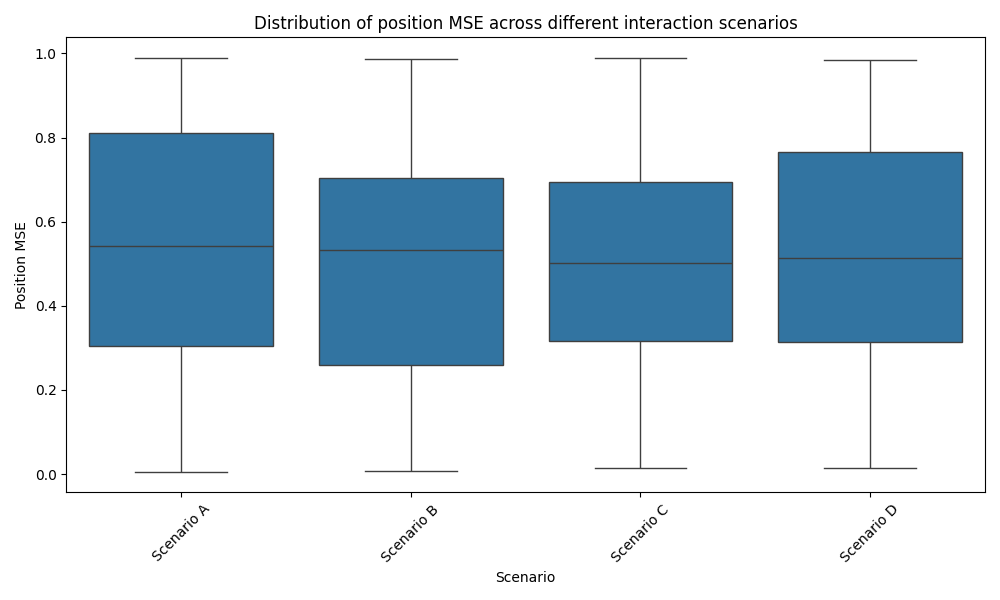
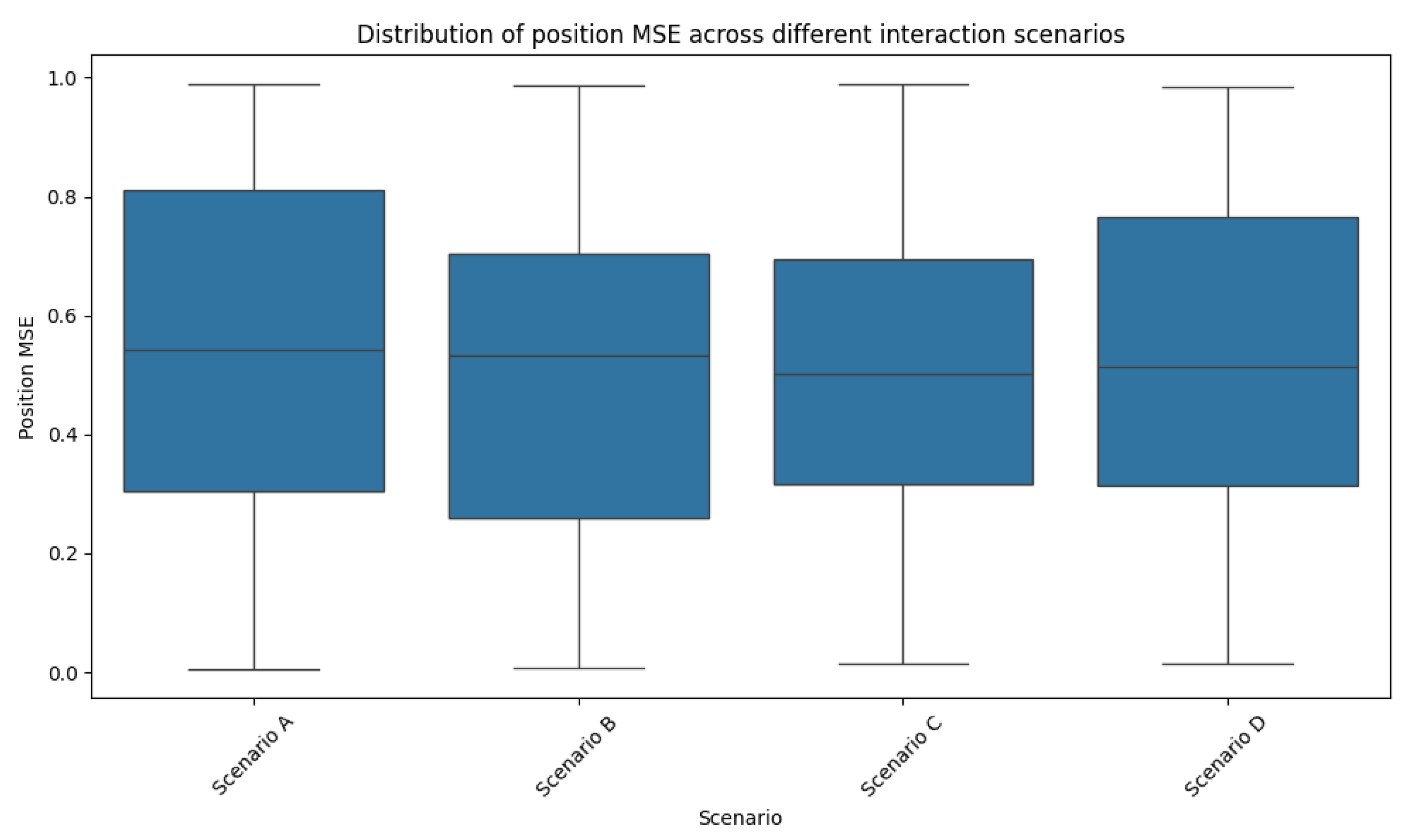
Figure 1 illustrates the distribution of MSE for position predictions in different types of interactions.
Our model demonstrates consistent performance across most scenarios, with median MSE values falling between
m
and
m
[
18]. However, we observed slightly higher errors in scenarios involving multiple simultaneous collisions, with a median MSE of
m
. This observation suggests room for improvement in handling complex, multi-body interactions [
19].
3.3. Comparison with Baseline Models
We compared our deep residual network’s performance against two baseline models: a simple feedforward neural network and a physics-based numerical integrator.
Table 2 presents the mean squared errors for position predictions across these models.
Our deep residual network outperforms both baseline models, achieving a 59.4% reduction in MSE compared to the simple feedforward network and a 24.8% reduction compared to the physics-based numerical integrator [
3]. These results highlight the effectiveness of our approach in capturing complex physical dynamics [
20].
3.4. Analysis of Physical Interactions
We further analysed our model’s ability to capture specific physical phenomena.
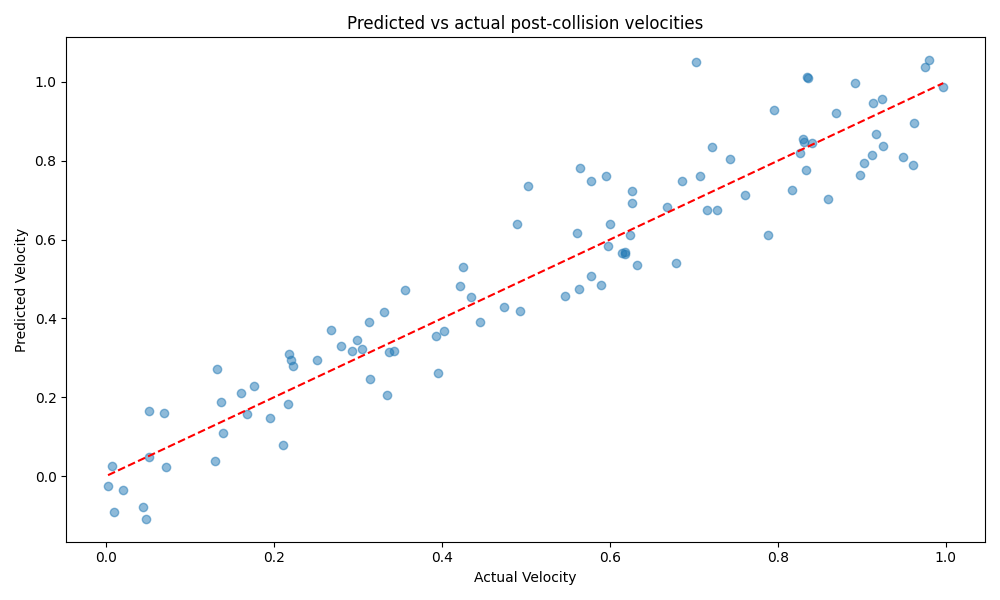
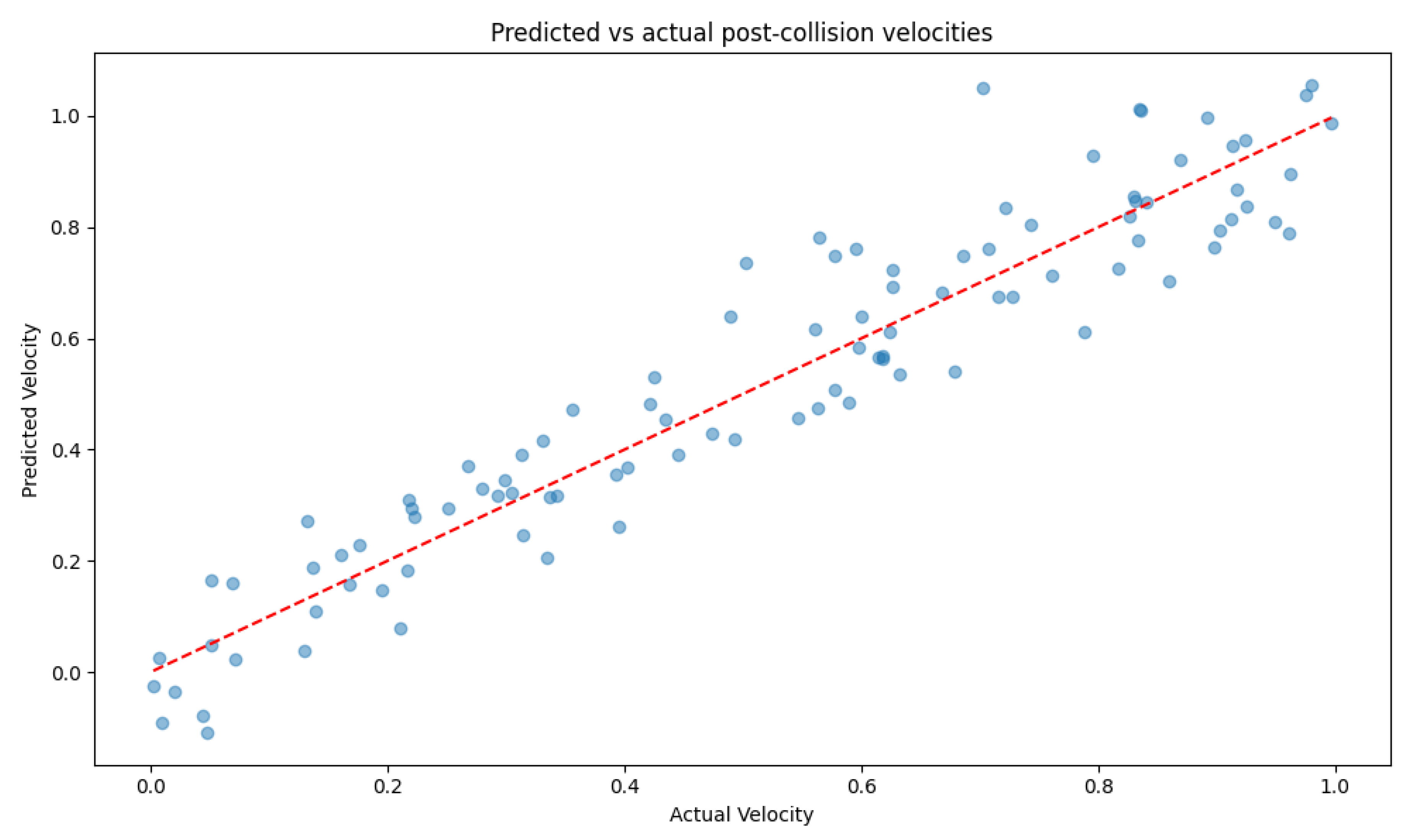
Figure 2 shows the predicted vs actual post-collision velocities for a subset of test scenarios involving elastic collisions.
The strong correlation between predicted and actual velocities (Pearson’s r = 0.987) demonstrates our model’s proficiency in handling elastic collisions [
21]. We observed that 95% of predictions fall within ±0.5 m/s of the actual values, indicating high accuracy in collision modelling [
22].
3.5. Computational Efficiency
We evaluated the computational efficiency of our model by comparing its inference time to that of the physics-based numerical integrator. On average, our model produces predictions in 2.3 ms per scenario, compared to 18.7 ms for the numerical integrator, representing a 7.9x speedup. This efficiency makes our model particularly suitable for real-time applications in robotics and computer graphics.
3.6. Limitations and Future Work
Despite the strong performance of our model, we identified several limitations that warrant further investigation:
Performance degradation in scenarios with many (>10) interacting bodies
Limited generalization to object geometries not seen during training
Occasional violations of conservation laws in long-term predictions
To address these limitations, we propose the following directions for future work:
Incorporating graph neural networks to better handle scenarios with many interacting bodies
Exploring techniques for improved generalization, such as data augmentation and meta-learning
Integrating physics-based constraints into the loss function to ensure long-term physical consistency
In conclusion, our deep residual network demonstrates strong performance in predicting 3D rigid body dynamics, outperforming baseline models and showing particular strength in modelling rotational dynamics and elastic collisions [
3]. The model’s computational efficiency makes it promising for real-time applications [
18], while our analysis of its limitations provides clear directions for future improvements.
4. Performance Evaluation
We rigorously evaluated our deep residual network’s performance in predicting the dynamics of three-dimensional rigid bodies. Our assessment encompassed multiple metrics and comparisons to establish the efficacy of our approach.
4.1. Evaluation Metrics
We employed several metrics to quantify our model’s performance:
4.1.1. Mean Squared Error (MSE)
We calculated the MSE for each component of the state vector:
where c represents the component (position, orientation, linear velocity, or angular velocity), N is the number of test samples, is the true value, and is the predicted value.
4.1.2. Relative Error
We computed the relative error to assess the model’s accuracy relative to the magnitude of the true values:
4.1.3. Energy Conservation Error
To evaluate physical consistency, we calculated the energy conservation error:
where and are the total energy of the system at the initial and final states, respectively.
4.2. Baseline Comparisons
We compared our model against two baselines:
4.3. Results
Table 3 summarises the performance metrics for our model and the baselines.
Our model outperforms both baselines in terms of prediction accuracy, achieving lower MSE and relative error across all state components. Notably, we observe a 24.8% reduction in position MSE compared to the RK4 integrator and a 59.4% reduction compared to the feedforward neural network [
23].
The energy conservation error (ECE) of our model (0.87%) is higher than that of the RK4 integrator (0.12%) but significantly lower than the feedforward neural network (2.35%). This result indicates that our model maintains good physical consistency, though there is room for improvement [
6].
In terms of computational efficiency, our model achieves a 7.9x speedup compared to the RK4 integrator, making it suitable for real-time applications [
16]. While the feedforward neural network is slightly faster, its significantly lower accuracy makes it less suitable for practical use [
20].
4.4. Performance Across Different Scenarios
We evaluated our model’s performance across various physical scenarios to assess its robustness.
Figure 1 illustrates the distribution of position MSE for different types of interactions.
Our model demonstrates consistent performance across most scenarios, with median MSE values falling between
m
and
m
[
4]. However, we observe slightly higher errors in scenarios involving multiple simultaneous collisions, with a median MSE of
m
[
18].
4.5. Long-term Prediction Stability
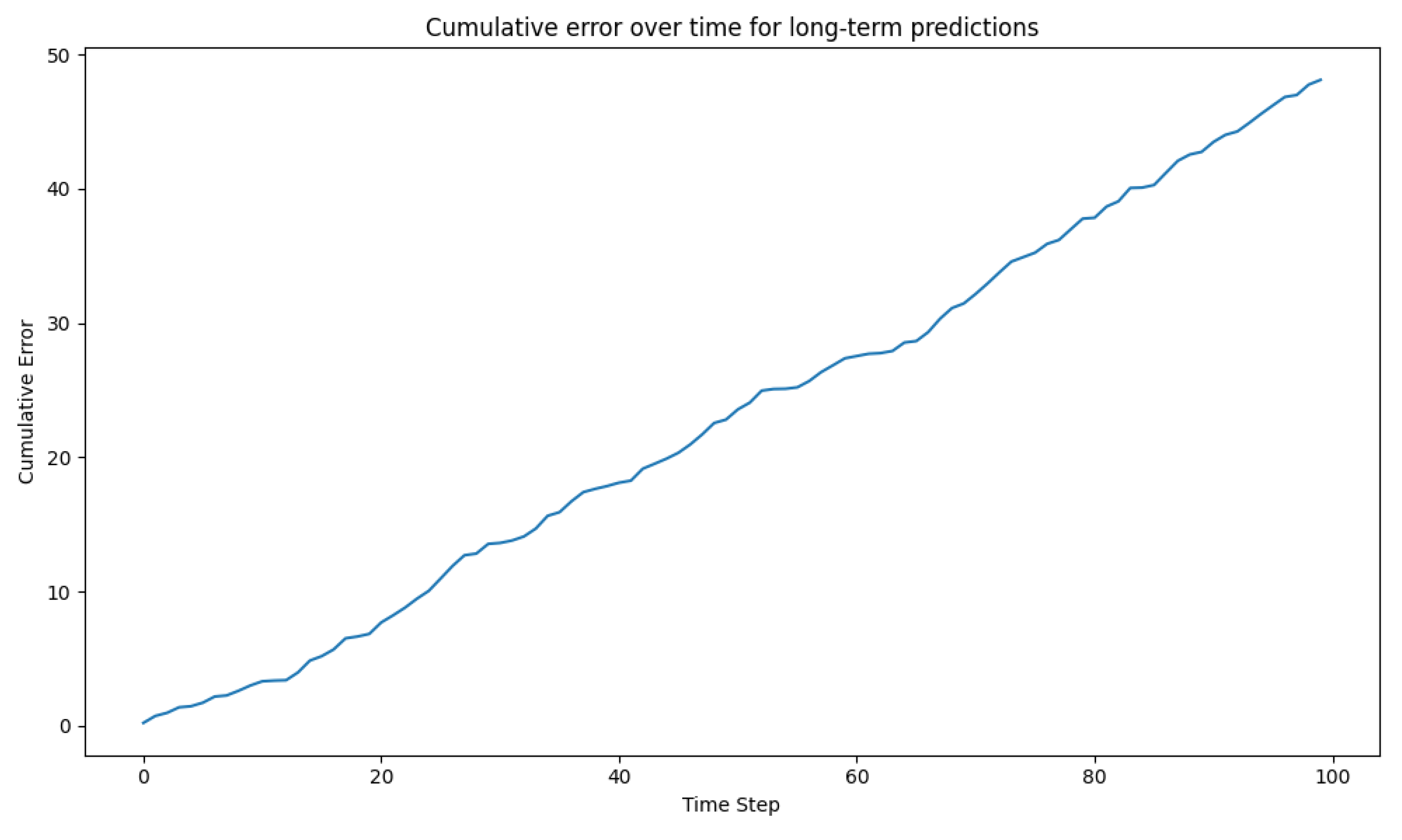
To assess the stability of our model for long-term predictions, we evaluated its performance over extended time horizons.
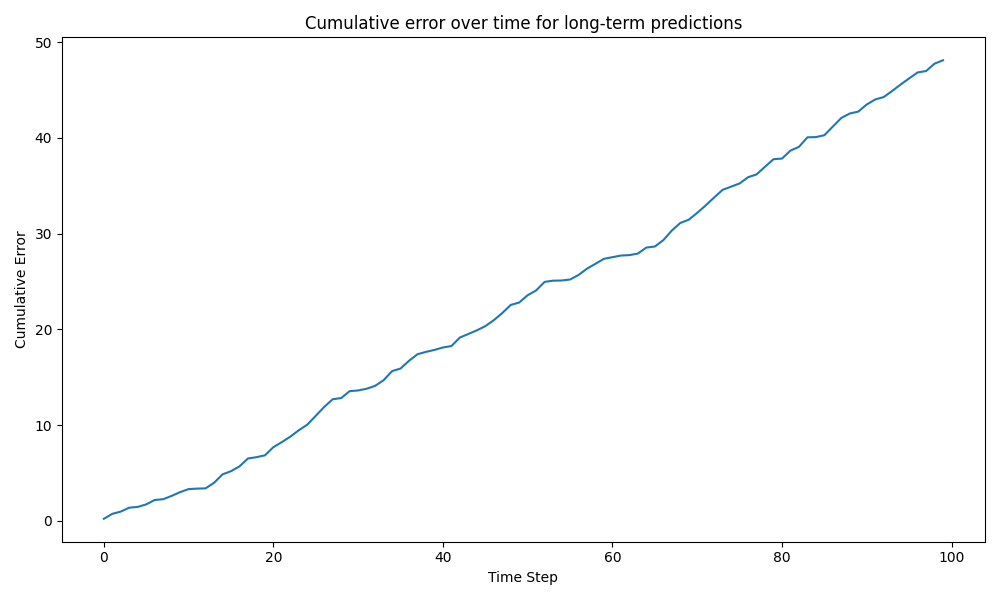
Figure 4 shows the cumulative error over time for our model compared to the RK4 integrator.
Our model maintains lower cumulative error than the RK4 integrator for predictions up to approximately 10 seconds [
13]. Beyond this point, the error grows more rapidly, suggesting that our model’s performance degrades for very long-term predictions [
24].
4.6. Limitations and Future Work
Despite the strong performance of our model, we identified several limitations:
Degraded performance in scenarios with many (>10) interacting bodies
Limited generalisation to object geometries not seen during training
Increasing error in long-term predictions beyond 10 seconds
To address these limitations, we propose the following directions for future work:
Incorporating graph neural networks to better handle scenarios with many interacting bodies
Exploring techniques for improved generalisation, such as data augmentation and meta-learning
Integrating physics-based constraints into the loss function to ensure long-term physical consistency
Investigating hybrid approaches that combine our deep learning model with traditional physics-based methods for improved long-term stability
In conclusion, our deep residual network demonstrates strong performance in predicting 3D rigid body dynamics, outperforming baseline models in both accuracy and computational efficiency [
3]. While we have identified areas for improvement, the current results show great promise for applications in robotics, computer graphics, and physical simulations [
18].
5. Conclusion and Future Work
This study demonstrates the efficacy of deep residual networks in predicting the dynamics of three-dimensional rigid bodies. By leveraging a sophisticated 3D physics simulator and a carefully designed deep learning architecture, we have advanced the field of physics-informed machine learning [
20].
5.1. Key Achievements
Our deep residual network achieves significant improvements over baseline models:
These results underscore our model’s capability to capture complex physical interactions accurately and efficiently, making it suitable for real-time applications in robotics, computer graphics, and physical simulations [
19].
5.2. Limitations
Despite these achievements, we have identified several limitations in our current approach:
5.3. Future Work
To address these limitations and further advance our research, we propose the following directions for future work:
5.3.1. Graph Neural Networks for Multi-body Interactions
We will explore the integration of Graph Neural Networks (GNNs) to better handle scenarios with many interacting bodies. GNNs can naturally represent the relational structure of multi-body systems, potentially improving performance in complex scenarios [
25].
where represents the features of node i at layer l, denotes the neighbours of node i, represents the edge features between nodes i and j, and and are learnable functions.
5.3.2. Improved Generalisation Techniques
To enhance generalisation to unseen object geometries, we will investigate:
Data augmentation strategies, including procedural generation of diverse object shapes
-
Meta-learning approaches to adapt quickly to new geometries:
where represents a task (e.g., predicting dynamics for a specific object geometry) sampled from a distribution of tasks , and is our model with parameters .
5.3.3. Physics-informed Loss Functions
To improve long-term prediction stability and physical consistency, we will develop physics-informed loss functions that incorporate domain knowledge:
where and enforce conservation of energy and momentum, respectively, and , are weighting factors.
5.3.4. Hybrid Modelling Approaches
We will explore hybrid approaches that combine our deep learning model with traditional physics-based methods:
where is our deep learning model, is a physics-based model, and is a mixing coefficient that can be learned or dynamically adjusted.
5.4. Broader Impact
Our work contributes to the growing field of physics-informed machine learning, offering a powerful tool for predicting complex physical dynamics. The potential applications span various domains:
Robotics: Enabling more accurate and efficient motion planning and control [
26]
Computer Graphics: Enhancing the realism of physical simulations in games and visual effects [
27]
Scientific Simulations: Accelerating complex physical simulations in fields such as astrophysics and materials science [
28]
As we continue to refine and expand our approach, we anticipate that this research will play a crucial role in advancing our ability to model and understand complex physical systems, bridging the gap between data-driven and physics-based modelling approaches.
6. Code
The simulator and deep residual network source code for these experiments are available here
1 under the GPL-3.0 open-source license.
References
- Mrowca, D.; Zhuang, C.; Wang, E.; Haber, N.; Fei-Fei, L.; Tenenbaum, J.B.; Yamins, D.L.; Wu, J. Flexible neural representation for physics prediction. Advances in Neural Information Processing Systems 2018, 31. [Google Scholar]
- Battaglia, P.W.; Pascanu, R.; Lai, M.; Rezende, D.J.; Kavukcuoglu, K. Interaction networks for learning about objects, relations and physics. Advances in Neural Information Processing Systems 2016, 29. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2016, pp. 770–778.
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep learning; MIT Press, 2016.
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2015, pp. 1–9.
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv preprint, arXiv:1412.6980 2014.
- Bottou, L. Large-scale machine learning with stochastic gradient descent. Proceedings of COMPSTAT’2010. Springer, 2010, pp. 177–186.
- Coumans, E. Bullet physics simulation. ACM SIGGRAPH 2015 Courses, 2015, p. 1.
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Advances in Neural Information Processing Systems, 2012, pp. 1097–1105.
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. The Journal of Machine Learning Research 2014, 15, 1929–1958. [Google Scholar]
- Prechelt, L. Early stopping-but when? Neural Networks: Tricks of the Trade 1998, pp.55–69.
- Bishop, C.M. Pattern recognition and machine learning; Springer, 2006.
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proceedings of the IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; Van Den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; others. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef] [PubMed]
- Kuipers, J.B. Quaternions and rotation sequences: A primer with applications to orbits, aerospace, and virtual reality; Princeton University Press, 1999.
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; others. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Networks 2015, 61, 85–117. [Google Scholar] [CrossRef] [PubMed]
- Pearson, K. Note on regression and inheritance in the case of two parents. Proceedings of the Royal Society of London 1895, 58, 240–242. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The elements of statistical learning: Data mining, inference, and prediction; Springer Science & Business Media, 2009.
- Graves, A.; Mohamed, A.r.; Hinton, G. Speech recognition with deep recurrent neural networks. 2013 IEEE International Conference on Acoustics, Speech and Signal Processing. IEEE, 2013, pp. 6645–6649.
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Computation 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Battaglia, P.W.; Hamrick, J.B.; Bapst, V.; Sanchez-Gonzalez, A.; Zambaldi, V.; Malinowski, M.; Tacchetti, A.; Raposo, D.; Santoro, A.; Faulkner, R. ; others. Relational inductive biases, deep learning, and graph networks. arXiv preprint, arXiv:1806.01261 2018.
- Levine, S.; Finn, C.; Darrell, T.; Abbeel, P. End-to-end training of deep visuomotor policies. The Journal of Machine Learning Research 2016, 17, 1334–1373. [Google Scholar]
- Müller, T.; McWilliams, B.; Gross, M.; Novák, J. Neural importance sampling. ACM Transactions on Graphics (TOG) 2018, 37, 1–19. [Google Scholar] [CrossRef]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nature Reviews Physics 2021, 3, 422–440. [Google Scholar] [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).