Submitted:
08 July 2024
Posted:
10 July 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Molecular Model, Systems Studied and Simulation Method
2.1 Molecular Model
2.2 Systems Studied
2.3. Simulation Method
2.4. Post-Simulation Analysis
3. Results
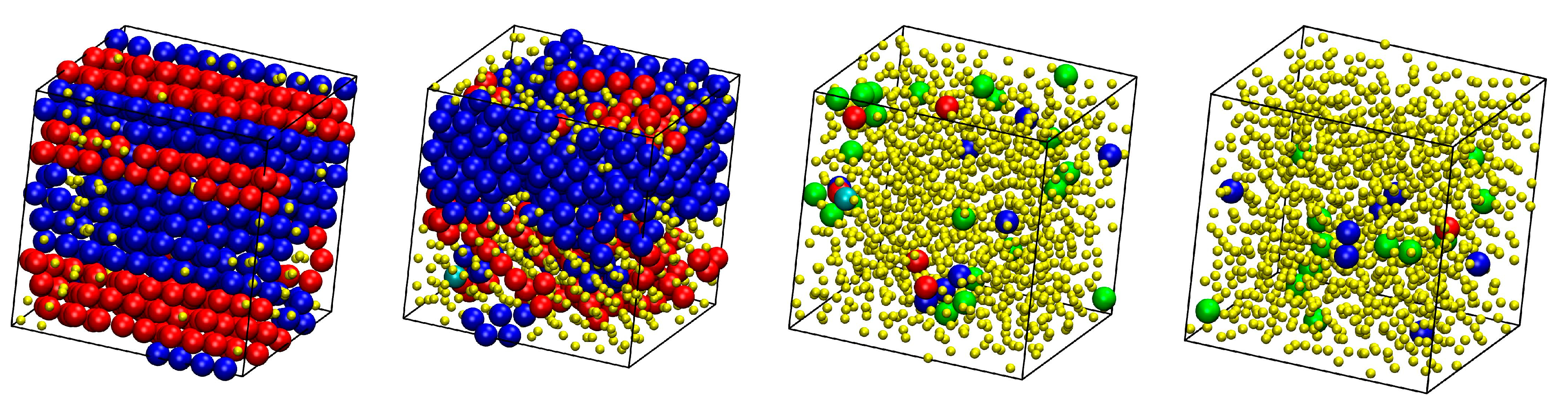
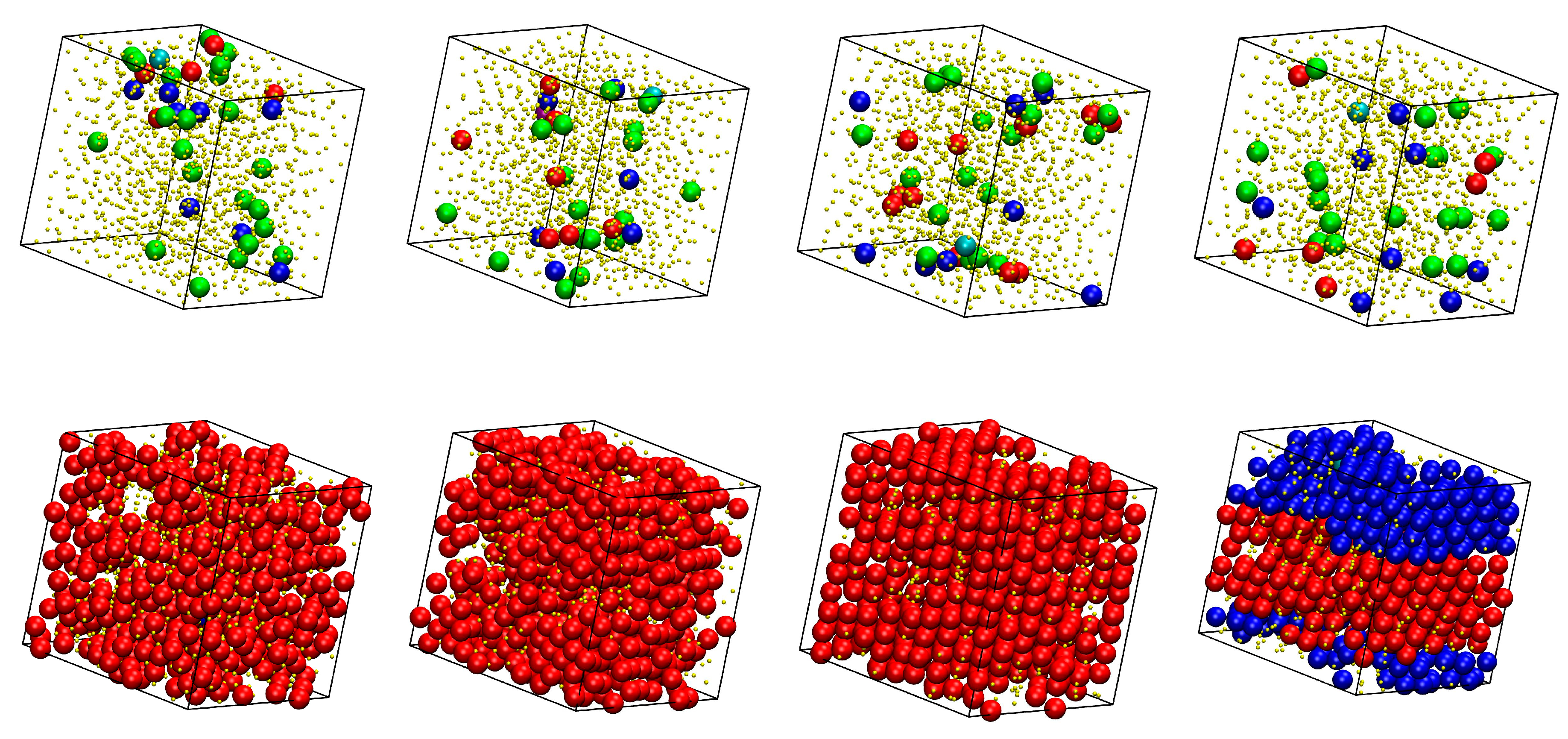
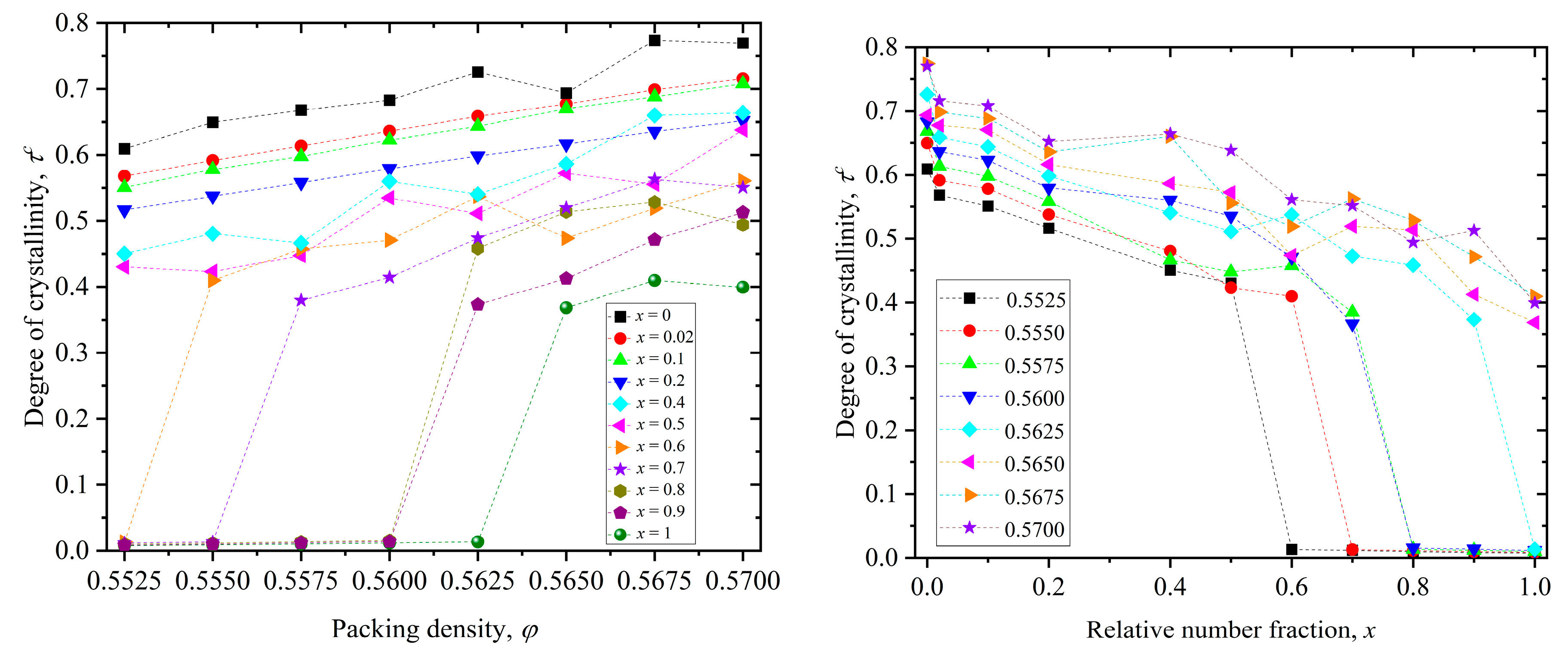
3.1. Phase Behavior
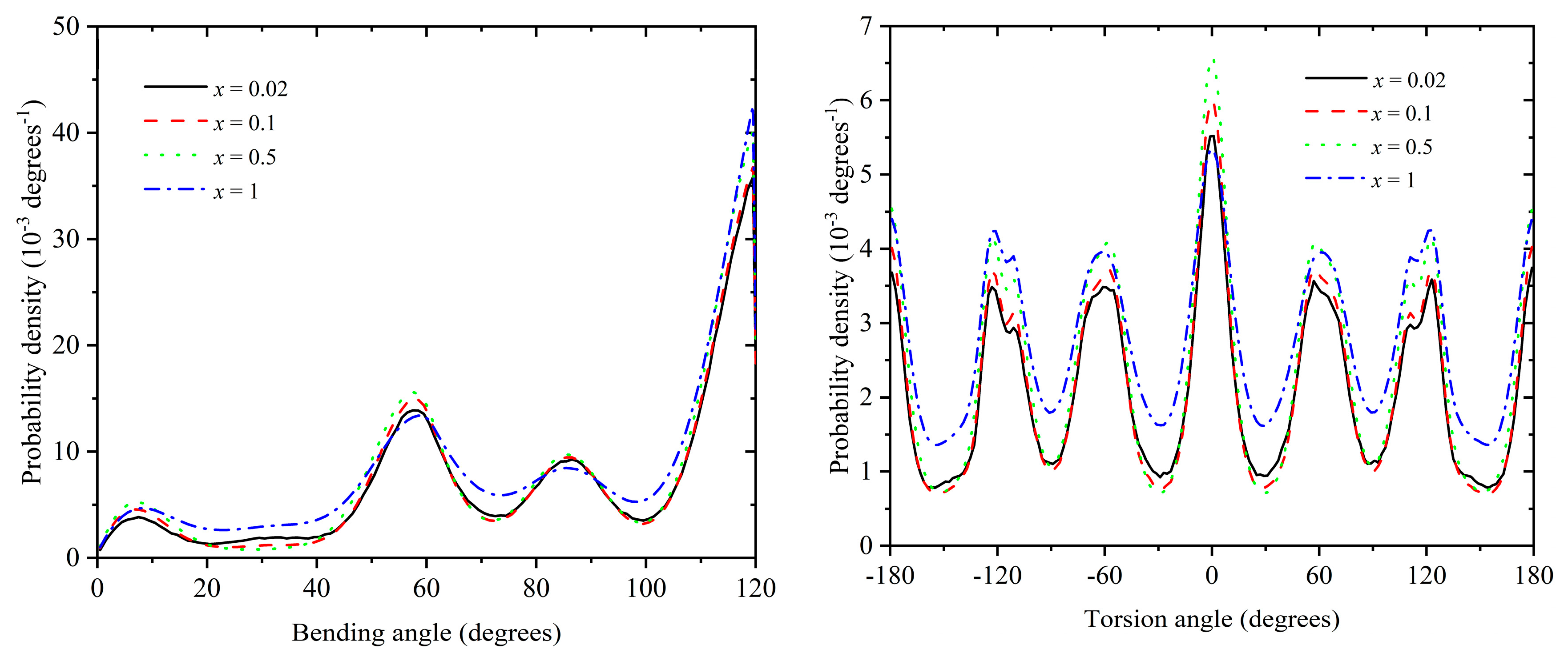
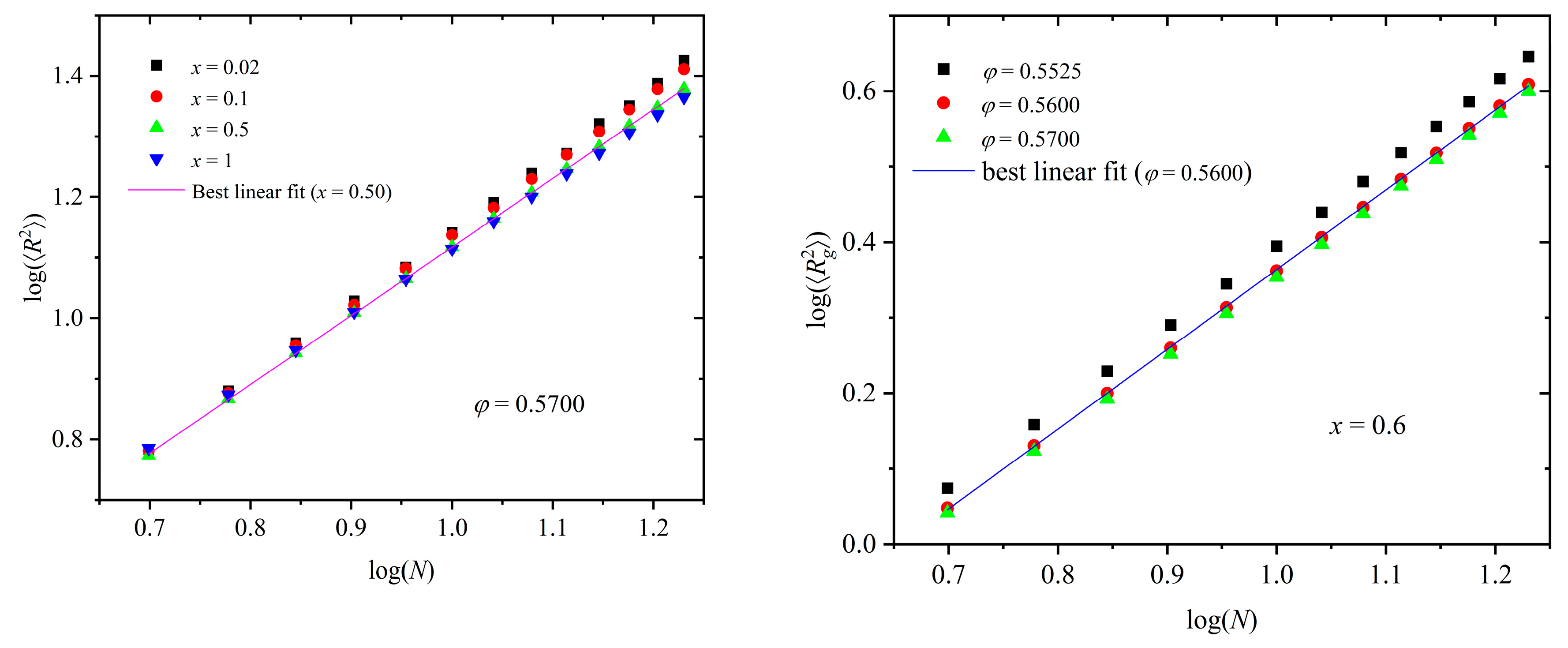
3.2. Polymer Structure
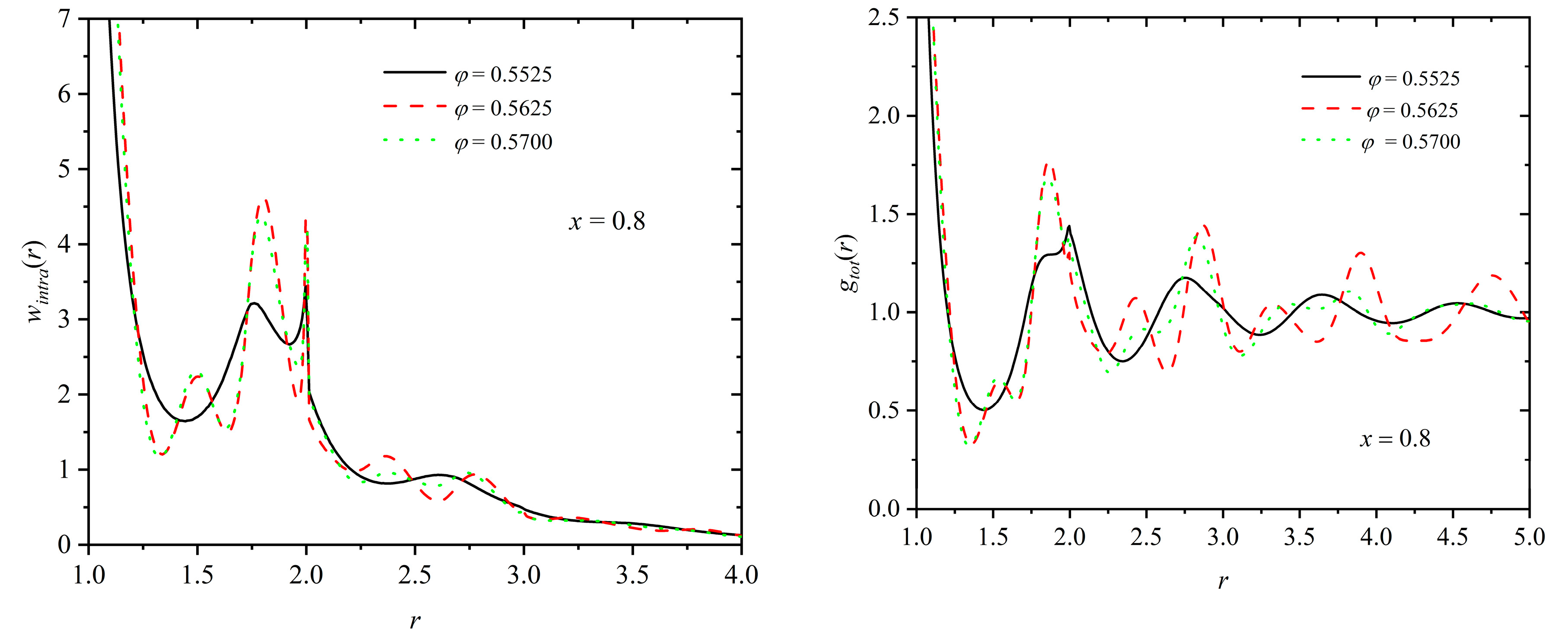
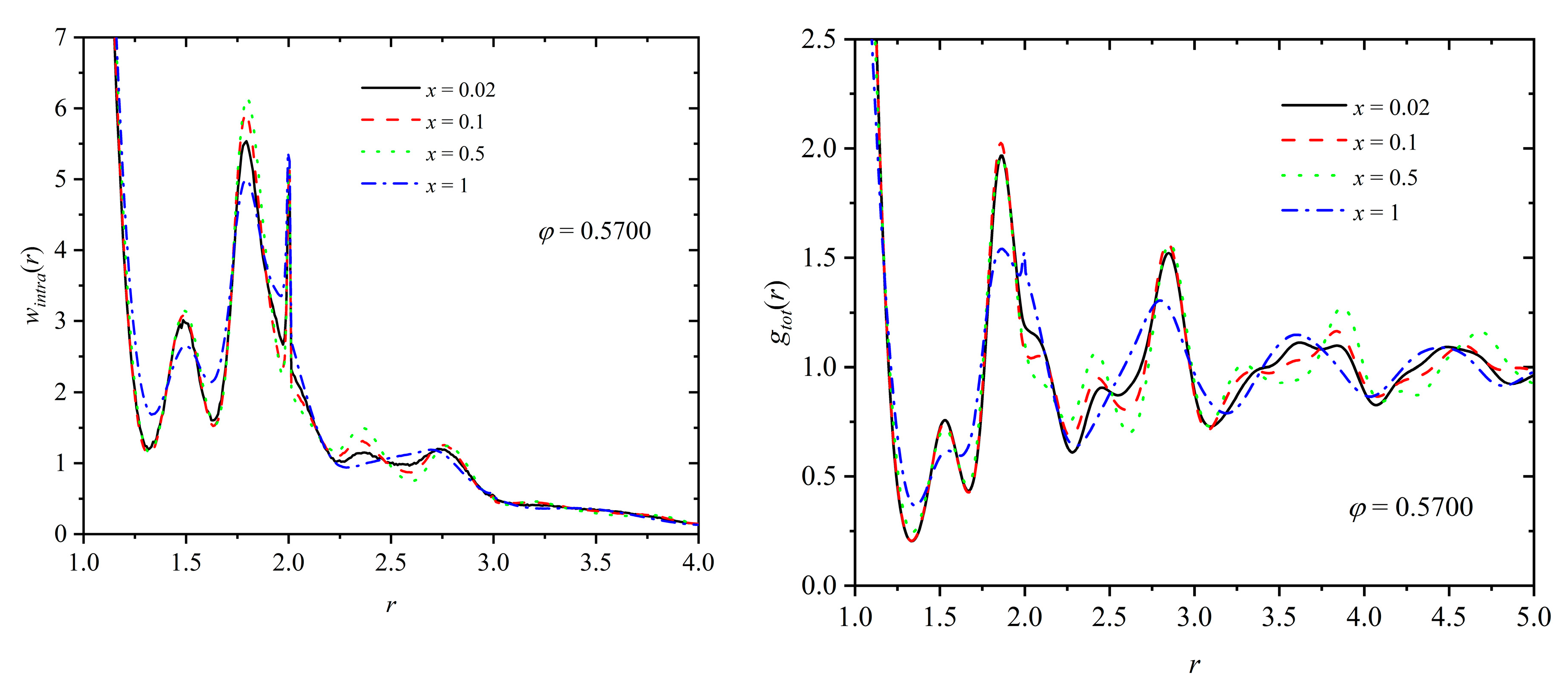
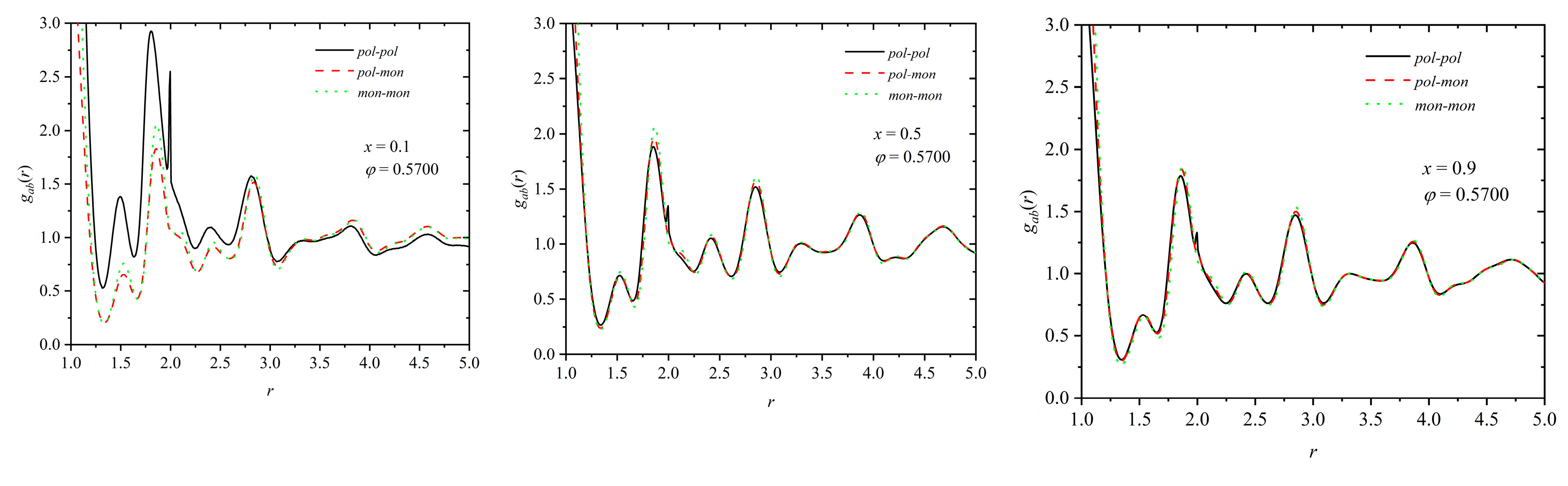
3.3. Homogeneity of the Mixture
3.3. Entropic Origins of Crystallization
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nicolis, G.; Prigogine, I. Self-organization in nonequilibrium systems: from dissipative structures to order through fluctuations; Wiley: New York, 1977. [Google Scholar]
- Self-Assembly: From Surfactants to Nanoparticles, 1st ed; Nagarajan, R., Ed. John Wiley & Sons: Hoboken, USA, 2018.
- Doi, M. Soft Matter Physics Oxford University Press: New York, 2017.
- Fultz, B. Phase Transitions in Materials; Cambridge University Press: 2020.
- Frenkel, D. Entropy-driven phase transitions. Physica A 1999, 263, 26–38. [Google Scholar] [CrossRef]
- Dijkstra, M. ENTROPY-DRIVEN PHASE TRANSITIONS IN COLLOIDS: FROM SPHERES TO ANISOTROPIC PARTICLES. In Advances in Chemical Physics, Vol 156, Rice, S.A., Dinner, A.R., Eds.; Advances in Chemical Physics; 2015; Volume 156, pp. 35-71.
- Onsager, L. THE EFFECTS OF SHAPE ON THE INTERACTION OF COLLOIDAL PARTICLES. Annals of the New York Academy of Sciences 1949, 51, 627–659. [Google Scholar] [CrossRef]
- Frenkel, D.; Lekkerkerker, H.N.W.; Stroobants, A. THERMODYNAMIC STABILITY OF A SMECTIC PHASE IN A SYSTEM OF HARD-RODS. Nature 1988, 332, 822–823. [Google Scholar] [CrossRef]
- Veerman, J.A.C.; Frenkel, D. RELATIVE STABILITY OF COLUMNAR AND CRYSTALLINE PHASES IN A SYSTEM OF PARALLEL HARD SPHEROCYLINDERS. Physical Review A 1991, 43, 4334–4343. [Google Scholar] [CrossRef]
- Bolhuis, P.; Frenkel, D. Tracing the phase boundaries of hard spherocylinders. J. Chem. Phys. 1997, 106, 666–687. [Google Scholar] [CrossRef]
- Kirkwood, J.G. Crystallization as a Cooperative Phenomenon. In Phase Transformations in Solids, Smoluchowski, R., Mayer, J.E., Weyl, W.A., Eds.; John Wiley & Sons: New York, 1951; pp. 67–76. [Google Scholar]
- Alder, B.J.; Wainwright, T.E. Phase Transition For A Hard Sphere System. J. Chem. Phys. 1957, 27, 1208–1209. [Google Scholar] [CrossRef]
- Wood, W.W.; Jacobson, J.D. PRELIMINARY RESULTS FROM A RECALCULATION OF THE MONTE CARLO EQUATION OF STATE OF HARD SPHERES. J. Chem. Phys. 1957, 27, 1207–1208. [Google Scholar] [CrossRef]
- Hoover, W.G.; Ree, F.H. Melting Transition And Communal Entropy For Hard Spheres. J. Chem. Phys. 1968, 49, 3609. [Google Scholar] [CrossRef]
- Vega, C.; Noya, E.G. Revisiting the Frenkel-Ladd method to compute the free energy of solids: The Einstein molecule approach. J. Chem. Phys. 2007, 127. [Google Scholar] [CrossRef]
- Bolhuis, P.G.; Frenkel, D.; Mau, S.C.; Huse, D.A. Entropy difference between crystal phases. Nature 1997, 388, 235–236. [Google Scholar] [CrossRef]
- Mau, S.C.; Huse, D.A. Stacking entropy of hard-sphere crystals. Phys. Rev. E 1999, 59, 4396–4401. [Google Scholar] [CrossRef]
- de Miguel, E.; Marguta, R.G.; del Rio, E.M. System-size dependence of the free energy of crystalline solids. J. Chem. Phys. 2007, 127. [Google Scholar] [CrossRef]
- Woodcock, L.V. Entropy difference between the face-centred cubic and hexagonal close-packed crystal structures. Nature 1997, 385, 141–143. [Google Scholar] [CrossRef]
- Noya, E.G.; Almarza, N.G. Entropy of hard spheres in the close-packing limit. Mol. Phys. 2015, 113, 1061–1068. [Google Scholar] [CrossRef]
- Pronk, S.; Frenkel, D. Can stacking faults in hard-sphere crystals anneal out spontaneously? J. Chem. Phys. 1999, 110, 4589–4592. [Google Scholar] [CrossRef]
- O’Malley, B.; Snook, I. Crystal nucleation in the hard sphere system. Phys. Rev. Lett. 2003, 90. [Google Scholar] [CrossRef] [PubMed]
- Medvedev, N.N.; Bezrukov, A.; Shtoyan, D. From amorphous solid to defective crystal. A study of structural peculiarities in close packings of hard spheres. J. Struct. Chem. 2004, 45, S23–S30. [Google Scholar] [CrossRef]
- Schilling, T.; Schope, H.J.; Oettel, M.; Opletal, G.; Snook, I. Precursor-Mediated Crystallization Process in Suspensions of Hard Spheres. Phys. Rev. Lett. 2010, 105. [Google Scholar] [CrossRef] [PubMed]
- O’Malley, B.; Snook, I. Structure of hard-sphere fluid and precursor structures to crystallization. J. Chem. Phys. 2005, 123. [Google Scholar] [CrossRef] [PubMed]
- Russo, J.; Tanaka, H. Crystal nucleation as the ordering of multiple order parameters. J. Chem. Phys. 2016, 145. [Google Scholar] [CrossRef] [PubMed]
- Shintani, H.; Tanaka, H. Frustration on the way to crystallization in glass. Nat. Phys. 2006, 2, 200–206. [Google Scholar] [CrossRef]
- Kawasaki, T.; Tanaka, H. Formation of a crystal nucleus from liquid. Proc. Natl. Acad. Sci. U. S. A. 2010, 107, 14036–14041. [Google Scholar] [CrossRef] [PubMed]
- Lam, M.A.; Khusid, B.; Kondic, L.; Meyer, W.V. Role of diffusion in crystallization of hard-sphere colloids. Phys. Rev. E 2021, 104. [Google Scholar] [CrossRef] [PubMed]
- Auer, S.; Frenkel, D. Prediction of absolute crystal-nucleation rate in hard-sphere colloids. Nature 2001, 409, 1020–1023. [Google Scholar] [CrossRef]
- Sanchez-Burgos, I.; Sanz, E.; Vega, C.; Espinosa, J.R. Fcc vs. hcp competition in colloidal hard-sphere nucleation: on their relative stability, interfacial free energy and nucleation rate. Physical Chemistry Chemical Physics 2021, 23, 19611–19626. [Google Scholar] [CrossRef] [PubMed]
- Espinosa, J.R.; Vega, C.; Valeriani, C.; Frenkel, D.; Sanz, E. Heterogeneous versus homogeneous crystal nucleation of hard spheres. Soft Matter 2019, 15, 9625–9631. [Google Scholar] [CrossRef] [PubMed]
- Russo, J.; Tanaka, H. The microscopic pathway to crystallization in supercooled liquids. Scientific Reports 2012, 2. [Google Scholar] [CrossRef] [PubMed]
- Leoni, F.; Russo, J. Nonclassical Nucleation Pathways in Stacking-Disordered Crystals. Physical Review X 2021, 11. [Google Scholar] [CrossRef]
- Gispen, W.; Coli, G.M.; van Damme, R.; Royall, C.P.; Dijkstra, M. Crystal Polymorph Selection Mechanism of Hard Spheres Hidden in the Fluid. ACS Nano 2023, 17, 8807–8814. [Google Scholar] [CrossRef] [PubMed]
- Richard, D.; Speck, T. Crystallization of hard spheres revisited. II. Thermodynamic modeling, nucleation work, and the surface of tension. J. Chem. Phys. 2018, 148. [Google Scholar] [CrossRef] [PubMed]
- Richard, D.; Speck, T. Crystallization of hard spheres revisited. I. Extracting kinetics and free energy landscape from forward flux sampling. J. Chem. Phys. 2018, 148. [Google Scholar] [CrossRef] [PubMed]
- Charbonneau, P.; Gish, C.M.; Hoy, R.S.; Morse, P.K. Thermodynamic stability of hard sphere crystals in dimensions 3 through 10. European Physical Journal E 2021, 44. [Google Scholar] [CrossRef] [PubMed]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. Entropy-Driven Crystallization in Dense Systems of Athermal Chain Molecules. Phys. Rev. Lett. 2009, 103. [Google Scholar] [CrossRef] [PubMed]
- Karayiannis, N.C.; Foteinopoulou, K.; Abrams, C.F.; Laso, M. Modeling of crystal nucleation and growth in athermal polymers: self-assembly of layered nano-morphologies. Soft Matter 2010, 6, 2160–2173. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. Spontaneous Crystallization in Athermal Polymer Packings. Int. J. Mol. Sci. 2013, 14, 332–358. [Google Scholar] [CrossRef] [PubMed]
- Martinez-Fernandez, D.; Herranz, M.; Foteinopoulou, K.; Karayiannis, N.C.; Laso, M. Local and Global Order in Dense Packings of Semi-Flexible Polymers of Hard Spheres. Polymers 2023, 15. [Google Scholar] [CrossRef] [PubMed]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. The role of bond tangency and bond gap in hard sphere crystallization of chains. Soft Matter 2015, 11, 1688–1700. [Google Scholar] [CrossRef] [PubMed]
- Ni, R.; Dijkstra, M. Effect of bond length fluctuations on crystal nucleation of hard bead chains. Soft Matter 2013, 9, 365–369. [Google Scholar] [CrossRef]
- Shakirov, T. Crystallisation in Melts of Short, Semi-Flexible Hard-Sphere Polymer Chains: The Role of the Non-Bonded Interaction Range. Entropy 2019, 21. [Google Scholar] [CrossRef]
- Shakirov, T.; Paul, W. Crystallization in melts of short, semiflexible hard polymer chains: An interplay of entropies and dimensions. Phys. Rev. E 2018, 97. [Google Scholar] [CrossRef] [PubMed]
- Karayiannis, N.C.; Malshe, R.; de Pablo, J.J.; Laso, M. Fivefold symmetry as an inhibitor to hard-sphere crystallization. Phys. Rev. E 2011, 83. [Google Scholar] [CrossRef] [PubMed]
- Karayiannis, N.C.; Malshe, R.; Kroger, M.; de Pablo, J.J.; Laso, M. Evolution of fivefold local symmetry during crystal nucleation and growth in dense hard-sphere packings. Soft Matter 2012, 8, 844–858. [Google Scholar] [CrossRef]
- Herranz, M.; Foteinopoulou, K.; Karayiannis, N.C.; Laso, M. Polymorphism and Perfection in Crystallization of Hard Sphere Polymers. Polymers 2022, 14. [Google Scholar] [CrossRef] [PubMed]
- Herranz, M.; Benito, J.; Foteinopoulou, K.; Karayiannis, N.C.; Laso, M. Polymorph Stability and Free Energy of Crystallization of Freely-Jointed Polymers of Hard Spheres. Polymers 2023, 15. [Google Scholar] [CrossRef] [PubMed]
- Herranz, M.; Martínez-Fernández, D.; Ramos, P.M.; Foteinopoulou, K.; Karayiannis, N.C.; Laso, M. Simu-D: A Simulator-Descriptor Suite for Polymer-Based Systems under Extreme Conditions. Int. J. Mol. Sci. 2021, 22, 12464. [Google Scholar] [CrossRef] [PubMed]
- Karayiannis, N.C.; Giannousaki, A.E.; Mavrantzas, V.G.; Theodorou, D.N. Atomistic Monte Carlo simulation of strictly monodisperse long polyethylene melts through a generalized chain bridging algorithm. J. Chem. Phys. 2002, 117, 5465–5479. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Mavrantzas, V.G.; Theodorou, D.N. A novel Monte Carlo scheme for the rapid equilibration of atomistic model polymer systems of precisely defined molecular architecture. Phys. Rev. Lett. 2002, 88. [Google Scholar] [CrossRef] [PubMed]
- Siepmann, J.I.; Frenkel, D. CONFIGURATIONAL BIAS MONTE-CARLO - A NEW SAMPLING SCHEME FOR FLEXIBLE CHAINS. Mol. Phys. 1992, 75, 59–70. [Google Scholar] [CrossRef]
- de Pablo, J.J.; Laso, M.; Suter, U.W. ESTIMATION OF THE CHEMICAL-POTENTIAL OF CHAIN MOLECULES BY SIMULATION. J. Chem. Phys. 1992, 96, 6157–6162. [Google Scholar] [CrossRef]
- Laso, M.; de Pablo, J.J.; Suter, U.W. SIMULATION OF PHASE-EQUILIBRIA FOR CHAIN MOLECULES. J. Chem. Phys. 1992, 97, 2817–2819. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Laso, M. Monte Carlo scheme for generation and relaxation of dense and nearly jammed random structures of freely jointed hard-sphere chains. Macromolecules 2008, 41, 1537–1551. [Google Scholar] [CrossRef]
- Ramos, P.M.; Karayiannis, N.C.; Laso, M. Off-lattice simulation algorithms for athermal chain molecules under extreme confinement. J. Comput. Phys. 2018, 375, 918–934. [Google Scholar] [CrossRef]
- Pant, P.V.K.; Theodorou, D.N. Variable Connectivity Method For The Atomistic Monte-Carlo Simulation Of Polydisperse Polymer Melts. Macromolecules 1995, 28, 7224–7234. [Google Scholar] [CrossRef]
- Mavrantzas, V.G.; Boone, T.D.; Zervopoulou, E.; Theodorou, D.N. End-bridging Monte Carlo: A fast algorithm for atomistic simulation of condensed phases of long polymer chains. Macromolecules 1999, 32, 5072–5096. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graphics Modell. 1996, 14, 33–38. [Google Scholar] [CrossRef] [PubMed]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. The structure of random packings of freely jointed chains of tangent hard spheres. J. Chem. Phys. 2009, 130. [Google Scholar] [CrossRef] [PubMed]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Oxford University Press: New York, 1987. [Google Scholar]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. The characteristic crystallographic element norm: A descriptor of local structure in atomistic and particulate systems. J. Chem. Phys. 2009, 130. [Google Scholar] [CrossRef] [PubMed]
- Ramos, P.M.; Herranz, M.; Foteinopoulou, K.; Karayiannis, N.C.; Laso, M. Identification of Local Structure in 2-D and 3-D Atomic Systems through Crystallographic Analysis. Crystals 2020, 10. [Google Scholar] [CrossRef]
- Giacovazzo, C.; Monaco, H.L.; Artioli, G.; Viterbo, D.; Ferraris, G.; Gilli, G.; Zanotti, G.; Gatti, M. Fundamentals of Crystallography; Oxford Science: Oxford, 2005. [Google Scholar]
- Malgrange, C.; Ricolleau, C.; Schlenker, M. Symmetry and Physical Properties of Crystals; Springer: Dordrecht, 2014. [Google Scholar]
- Nye, J.F. Physical Properties of Crystals: Their Representation by Tensors and Matrices; Oxford Science Publications: Oxford 2010.
- Herranz, M.; Pedrosa, C.; Martínez-Fernández, D.; Foteinopoulou, K.; Karayiannis, N.C.; Laso, M. Fine-tuning of colloidal polymer crystals by molecular simulation. Phys. Rev. E 2023, 107. [Google Scholar] [CrossRef] [PubMed]
- Pedrosa, C.; Martínez-Fernández, D.; Herranz, M.; Foteinopoulou, K.; Karayiannis, N.C.; Laso, M. Densest packing of flexible polymers in 2D films. J. Chem. Phys. 2023, 158. [Google Scholar] [CrossRef] [PubMed]
- Ramos, P.M.; Herranz, M.; Foteinopoulou, K.; Karayiannis, N.C.; Laso, M. Entropy-Driven Heterogeneous Crystallization of Hard-Sphere Chains under Unidimensional Confinement. Polymers 2021, 13. [Google Scholar] [CrossRef] [PubMed]
- Ramos, P.M.; Herranz, M.; Martinez-Fernandez, D.; Foteinopoulou, K.; Laso, M.; Karayiannis, N.C. Crystallization of Flexible Chains of Tangent Hard Spheres under Full Confinement. J. Phys. Chem. B 2022, 126, 5931–5947. [Google Scholar] [CrossRef] [PubMed]
- Rycroft, C.H. VORO++: A three-dimensional Voronoi cell library in C++. Chaos: An Interdisciplinary Journal of Nonlinear Science 2009, 19, 041111. [Google Scholar] [CrossRef] [PubMed]
- Flory, P.J. Principles of polymer chemistry; Cornell Univ. Press: Ithaca, 2010. [Google Scholar]
- McQuarrie, D.A. Statistical Mechanics; Viva Books: 2011.
- Jansen, J.P.; McDonald, I.R. Theory of Simple Liquids, 3rd ed.; Academic Press: 2006.
- Terban, M.W.; Billinge, S.J.L. Structural Analysis of Molecular Materials Using the Pair Distribution Function. Chem. Rev. 2022, 122, 1208–1272. [Google Scholar] [CrossRef]
- Zhu, H.; Huang, Y.L.; Ren, J.C.; Zhang, B.H.; Ke, Y.B.; Jen, A.K.Y.; Zhang, Q.; Wang, X.L.; Liu, Q. Bridging Structural Inhomogeneity to Functionality: Pair Distribution Function Methods for Functional Materials Development. Advanced Science 2021, 8. [Google Scholar] [CrossRef]
- Lábár, J.L.; Hajagos-Nagy, K.; Das, P.P.; Gomez-Perez, A.; Radnóczi, G. Simple ePDF: A Pair Distribution Function Method Based on Electron Diffraction Patterns to Reveal the Local Structure of Amorphous and Nanocrystalline Materials. Nanomaterials 2023, 13. [Google Scholar] [CrossRef] [PubMed]
- Tran, D.T.; Svensson, G.; Tai, C.W. <i>SUePDF</i>: a program to obtain quantitative pair distribution functions from electron diffraction data. J. Appl. Crystallogr. 2017, 50, 304–312. [Google Scholar] [CrossRef] [PubMed]
- Biben, T.; Hansen, J.P. PHASE-SEPARATION OF ASYMMETRIC BINARY HARD-SPHERE FLUIDS. Phys. Rev. Lett. 1991, 66, 2215–2218. [Google Scholar] [CrossRef] [PubMed]
- Lekkerkerker, H.N.W.; Stroobants, A. ON THE SPINODAL INSTABILITY OF HIGHLY ASYMMETRIC HARD-SPHERE SUSPENSIONS. Physica A 1993, 195, 387–397. [Google Scholar] [CrossRef]
- Rosenfeld, Y. PHASE-SEPARATION OF ASYMMETRIC BINARY HARD-SPHERE FLUIDS - SELF-CONSISTENT DENSITY-FUNCTIONAL THEORY. Phys. Rev. Lett. 1994, 72, 3831–3834. [Google Scholar] [CrossRef] [PubMed]
- Asakura, S.; Oosawa, F. INTERACTION BETWEEN PARTICLES SUSPENDED IN SOLUTIONS OF MACROMOLECULES. Journal of Polymer Science 1958, 33, 183–192. [Google Scholar] [CrossRef]
- Kobayashi, H.; Rohrbach, P.B.; Scheichl, R.; Wilding, N.B.; Jack, R.L. Critical point for demixing of binary hard spheres. Phys. Rev. E 2021, 104. [Google Scholar] [CrossRef] [PubMed]
- Ayadim, A.; Amokrane, S. Phase transitions in highly asymmetric binary hard-sphere fluids: Fluid-fluid binodal from a two-component mixture theory. Phys. Rev. E 2006, 74. [Google Scholar] [CrossRef] [PubMed]
- Vanduijneveldt, J.S.; Heinen, A.W.; Lekkerkerker, H.N.W. PHASE-SEPARATION IN BIMODAL DISPERSIONS OF STERICALLY STABILIZED SILICA PARTICLES. Europhys. Lett. 1993, 21, 369–374. [Google Scholar] [CrossRef]
- Miyazaki, K.; Schweizer, K.S.; Thirumalai, D.; Tuinier, R.; Zaccarelli, E. The Asakura-Oosawa theory: Entropic forces in physics, biology, and soft matter. J. Chem. Phys. 2022, 156. [Google Scholar] [CrossRef] [PubMed]
- Imhof, A.; Dhont, J.K.G. EXPERIMENTAL PHASE-DIAGRAM OF A BINARY COLLOIDAL HARD-SPHERE MIXTURE WITH A LARGE-SIZE RATIO. Phys. Rev. Lett. 1995, 75, 1662–1665. [Google Scholar] [CrossRef] [PubMed]
- Steiner, U.; Meller, A.; Stavans, J. ENTROPY-DRIVEN PHASE-SEPARATION IN BINARY EMULSIONS. Phys. Rev. Lett. 1995, 74, 4750–4753. [Google Scholar] [CrossRef] [PubMed]
- Vrij, A. POLYMERS AT INTERFACES AND INTERACTIONS IN COLLOIDAL DISPERSIONS. Pure Appl. Chem. 1976, 48, 471–483. [Google Scholar] [CrossRef]
- Lopes, J.N.C. Phase equilibra in binary Lennard-Jones mixtures: phase diagram simulation. Mol. Phys. 1999, 96, 1649–1658. [Google Scholar] [CrossRef]
- Thorneywork, A.L.; Roth, R.; Aarts, D.; Dullens, R.P.A. Communication: Radial distribution functions in a two-dimensional binary colloidal hard sphere system. J. Chem. Phys. 2014, 140. [Google Scholar] [CrossRef] [PubMed]
- Rintoul, M.D.; Torquato, S. Metastability and crystallization in hard-sphere systems. Phys. Rev. Lett. 1996, 77, 4198–4201. [Google Scholar] [CrossRef] [PubMed]
- Lin, K.H.; Crocker, J.C.; Prasad, V.; Schofield, A.; Weitz, D.A.; Lubensky, T.C.; Yodh, A.G. Entropically driven colloidal crystallization on patterned surfaces. Phys. Rev. Lett. 2000, 85, 1770–1773. [Google Scholar] [CrossRef] [PubMed]
- Pusey, P.N.; Vanmegen, W. PHASE-BEHAVIOR OF CONCENTRATED SUSPENSIONS OF NEARLY HARD COLLOIDAL SPHERES. Nature 1986, 320, 340–342. [Google Scholar] [CrossRef]
- Manoharan, V.N. Colloidal matter: Packing, geometry, and entropy. Science 2015, 349. [Google Scholar] [CrossRef] [PubMed]
- Geng, Y.N.; van Anders, G.; Dodd, P.M.; Dshemuchadse, J.; Glotzer, S.C. Engineering entropy for the inverse design of colloidal crystals from hard shapes. Science Advances 2019, 5. [Google Scholar] [CrossRef] [PubMed]

| Nch | 0 | 2 | 10 | 20 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| x | 0 | 0.02 | 0.1 | 0.2 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





