Submitted:
02 July 2024
Posted:
03 July 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Buck Converter Modeling
2.1. Lumped Parameter Model of the Standard Buck Converter
2.2. Distributed Parameter Model of the Buck Converter with Lossy Transmission Line
3. Simulation Models
3.1. Model Parameters
3.2. State-Space Model of the Standard Buck Converter
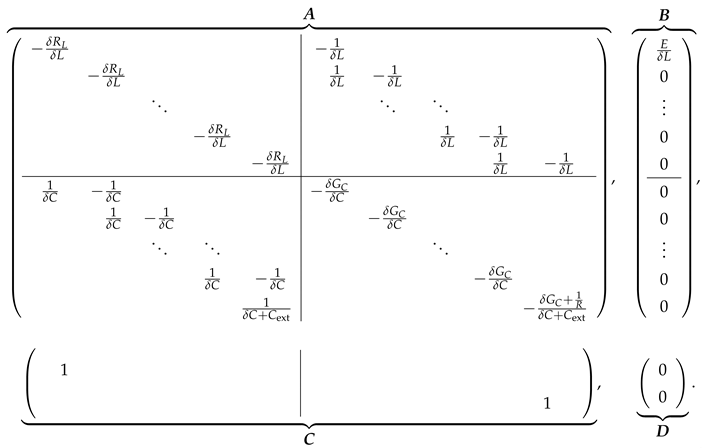
3.3. State-Space Model of the Buck Converter with Transmission Line
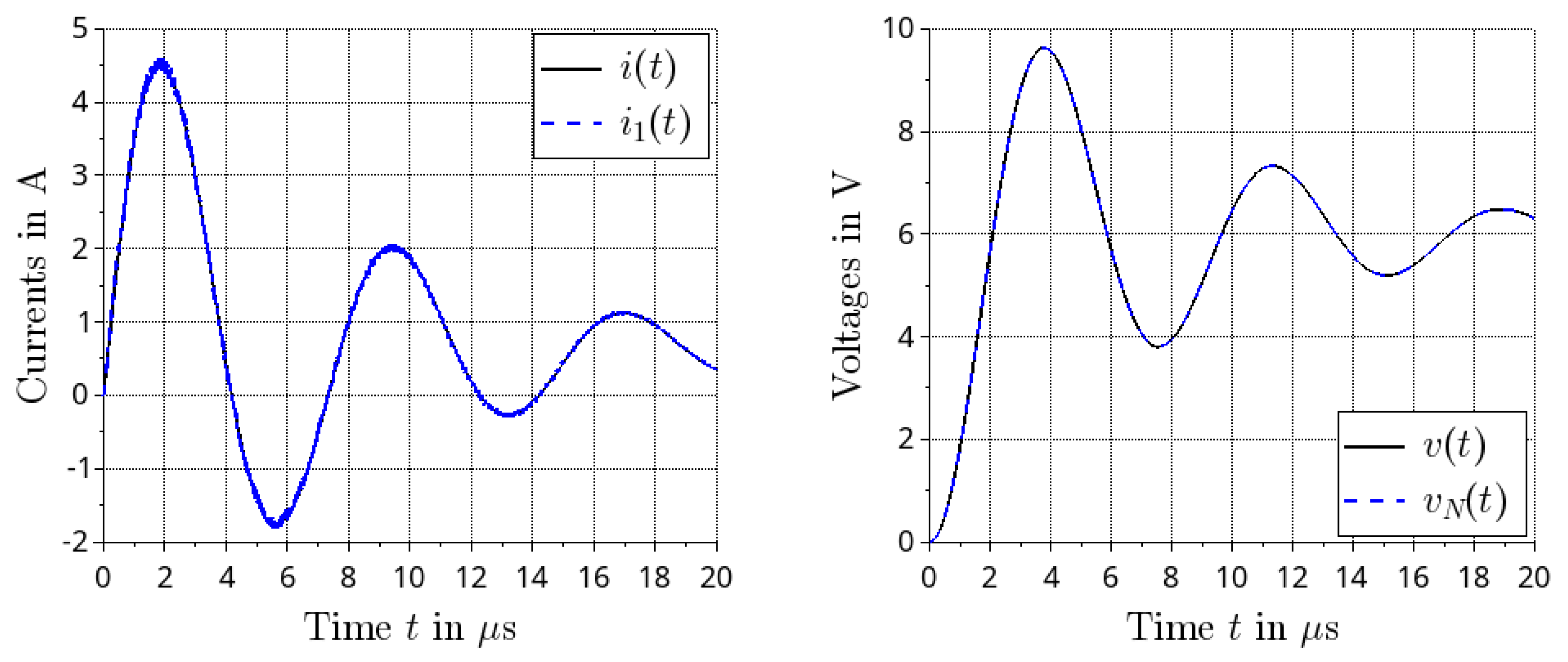
3.4. Open Loop Transient Simulation
4. Frequency Domain
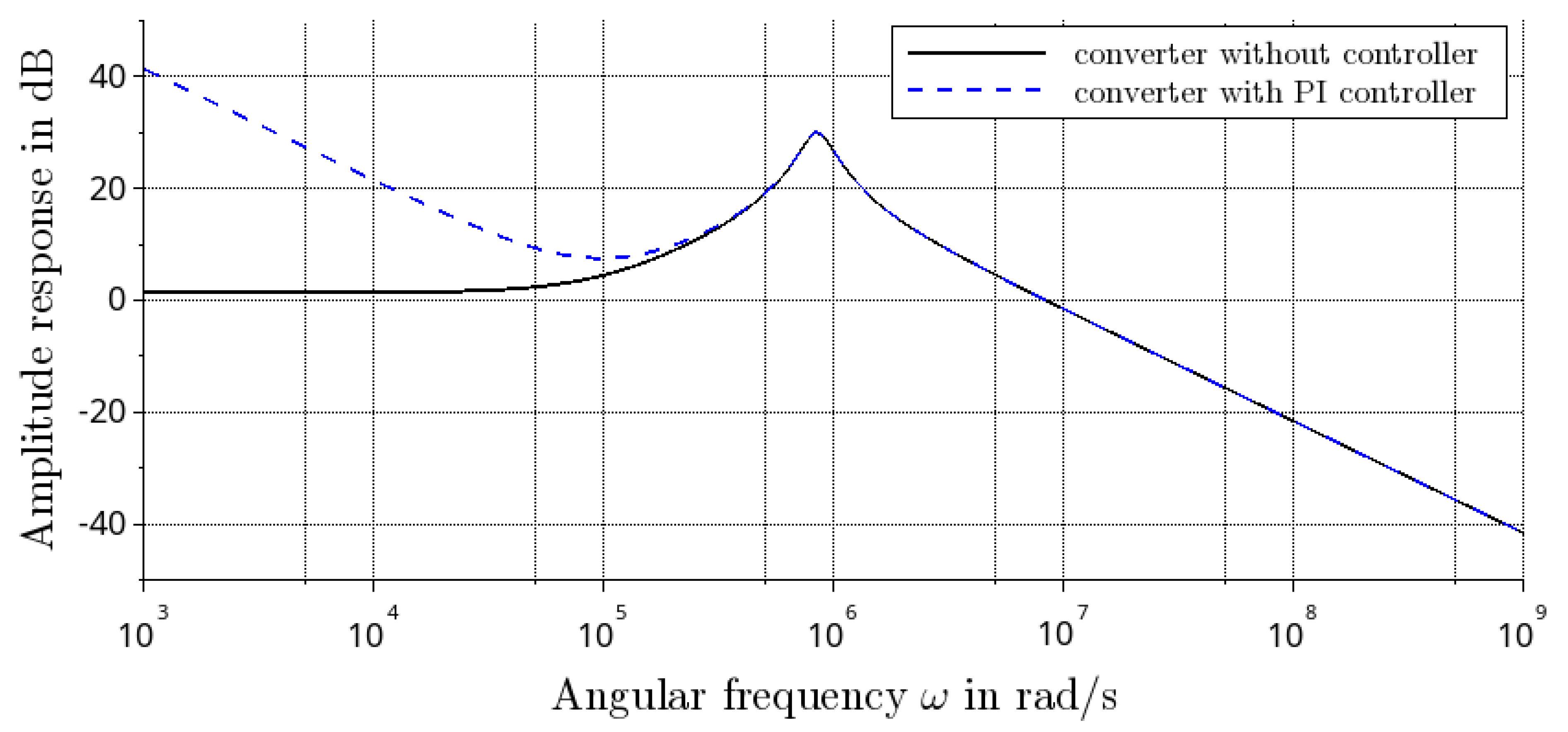
4.1. Transfer Function
4.2. Response under Sinusoidal Excitation
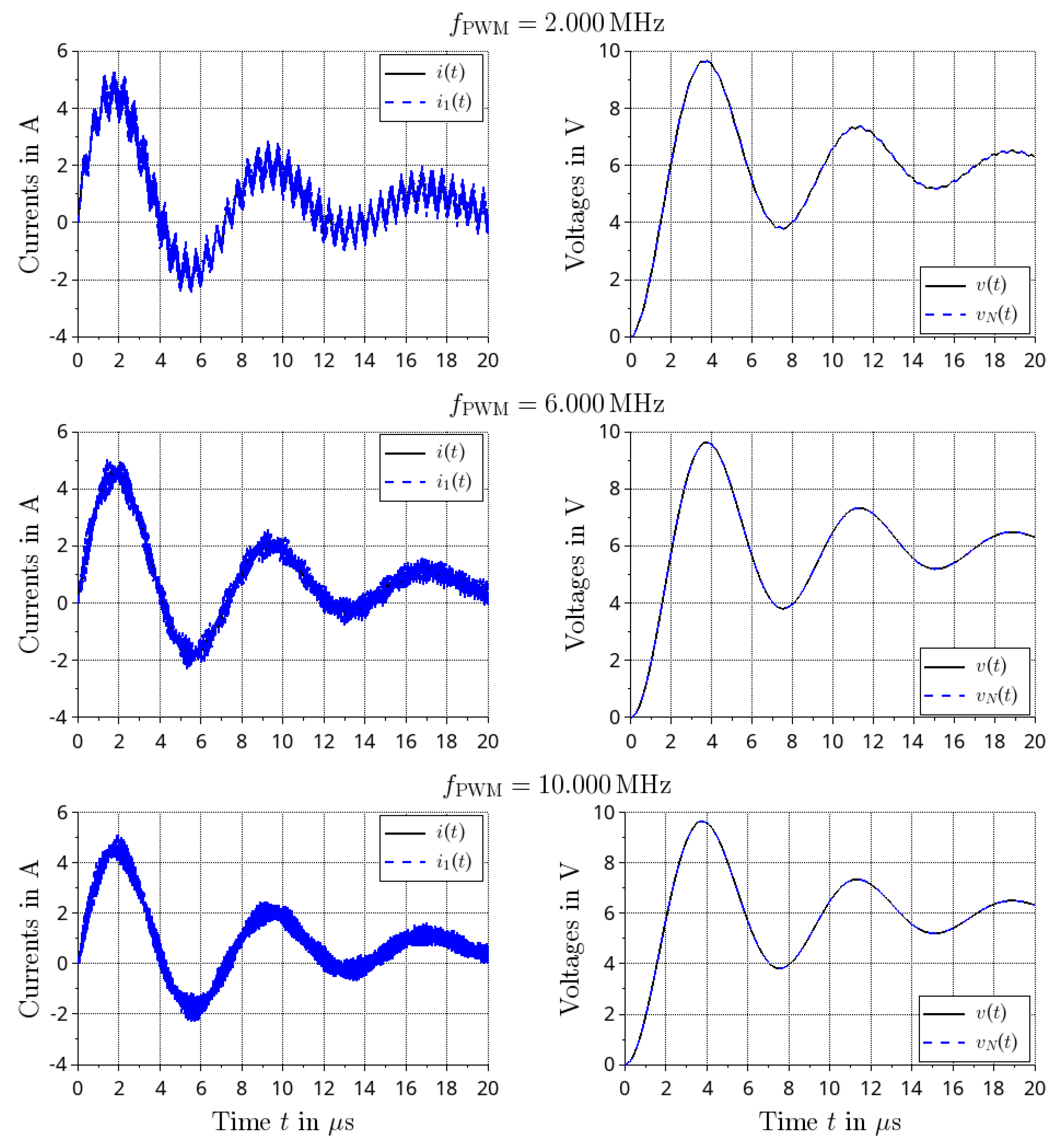
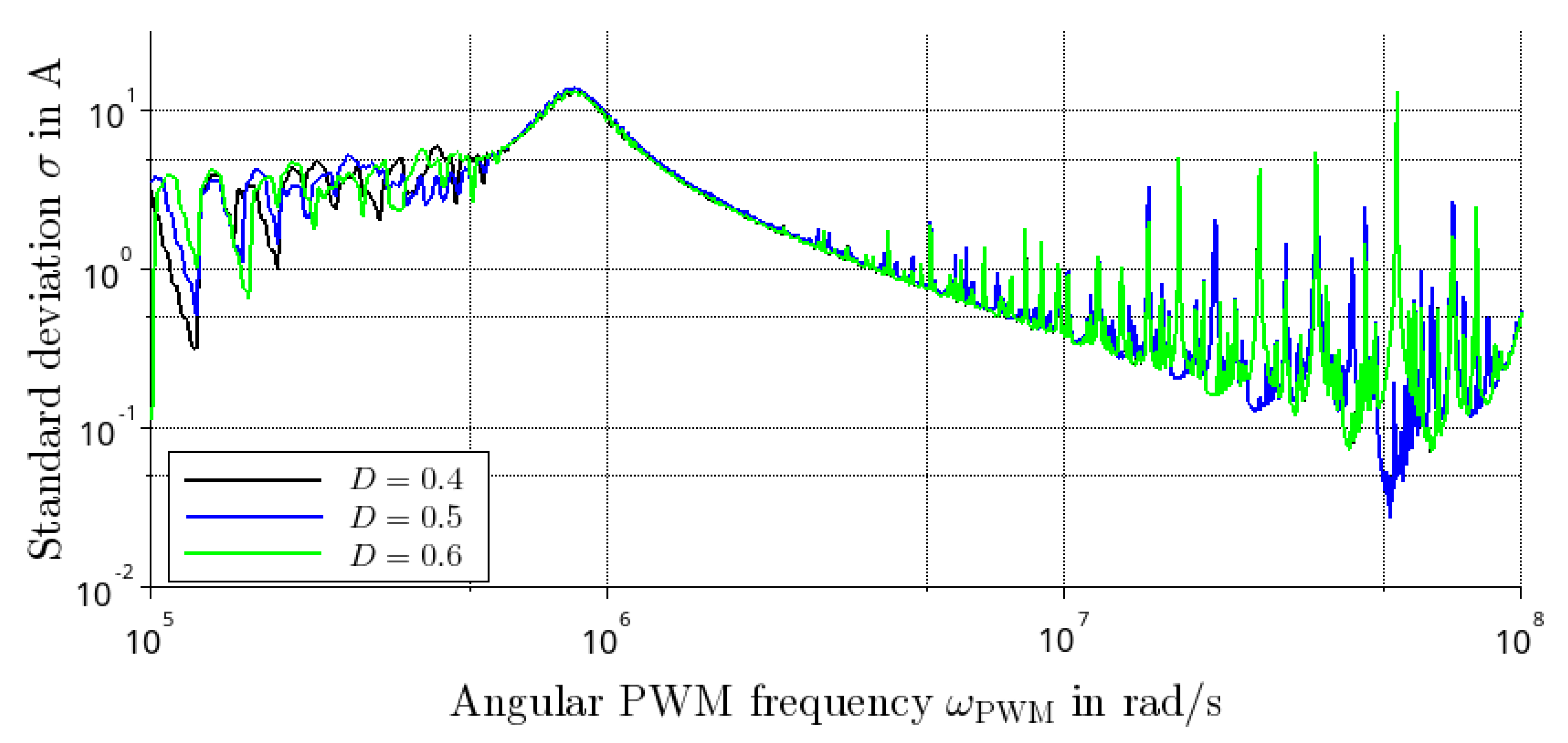
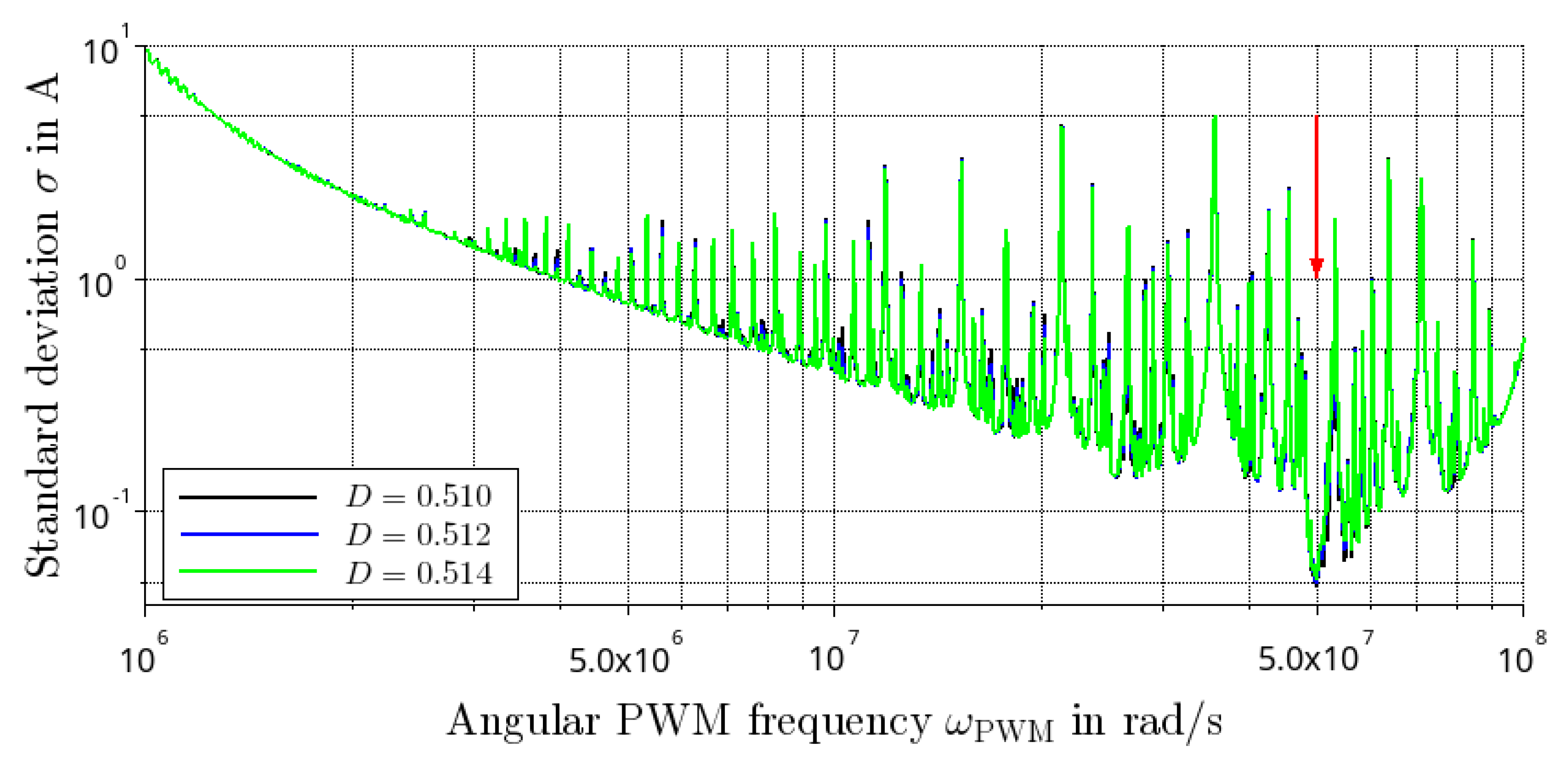
4.3. Response under PWM Excitation
5. Closed Loop Control
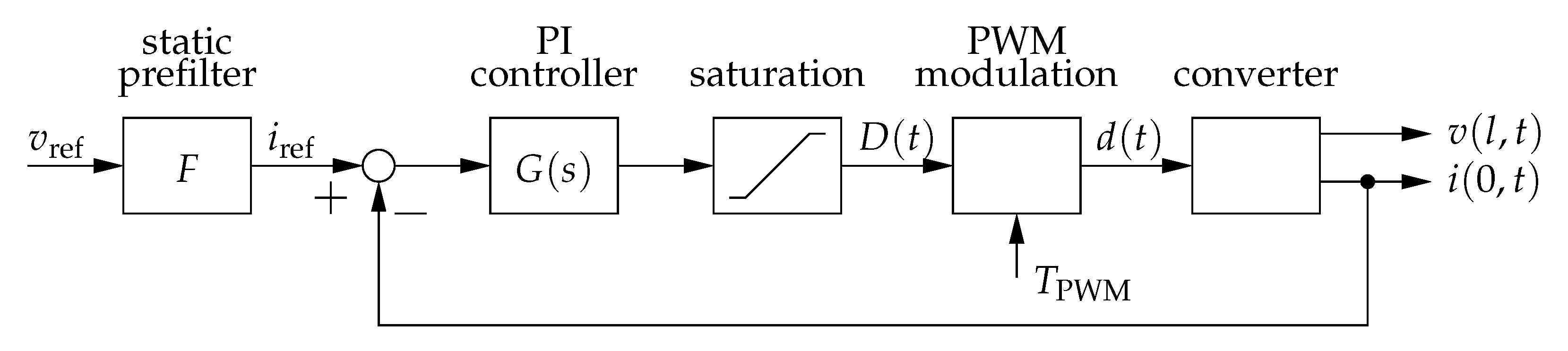
5.1. Control Structure and Static Prefilter
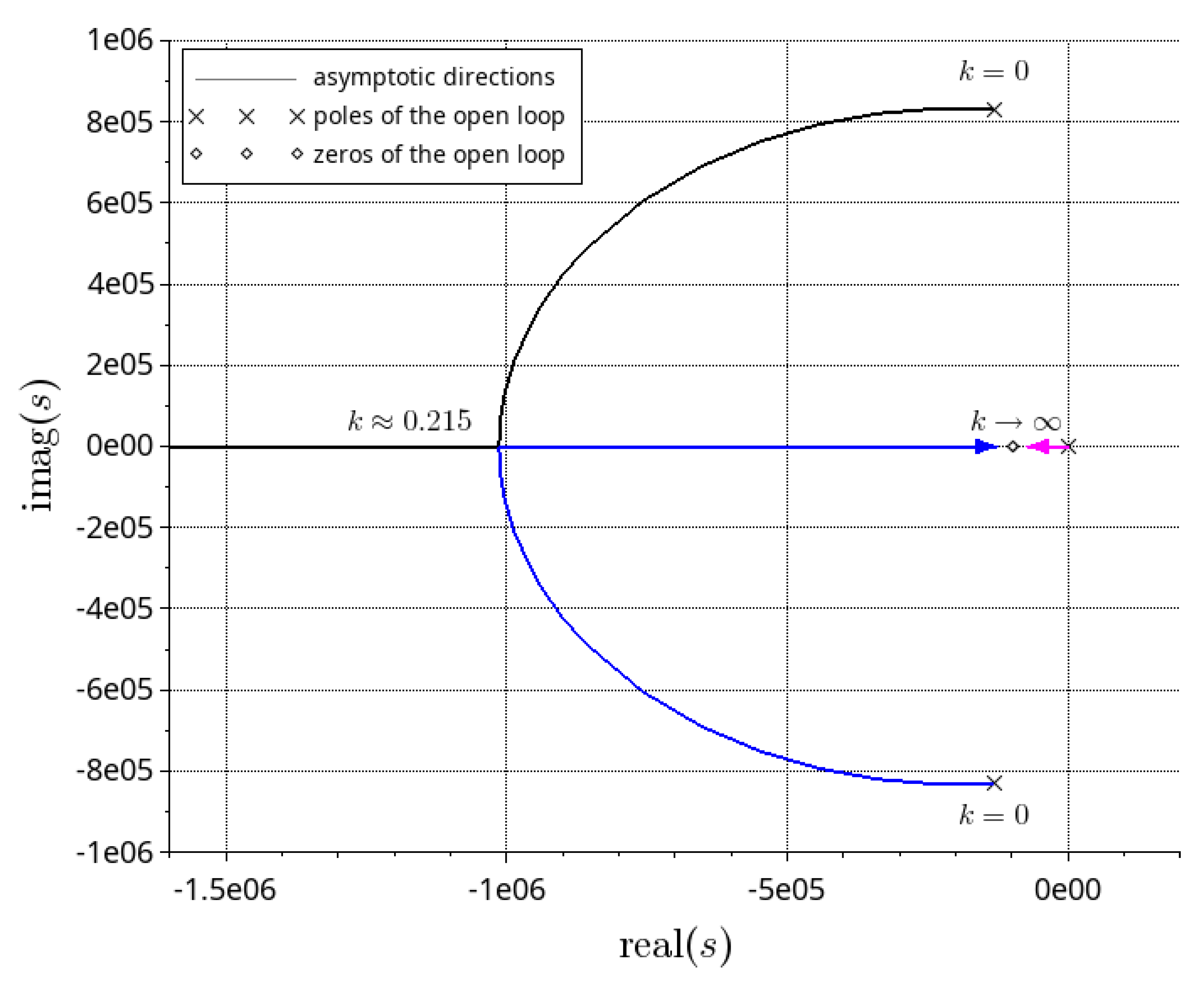
5.2. Controller Design
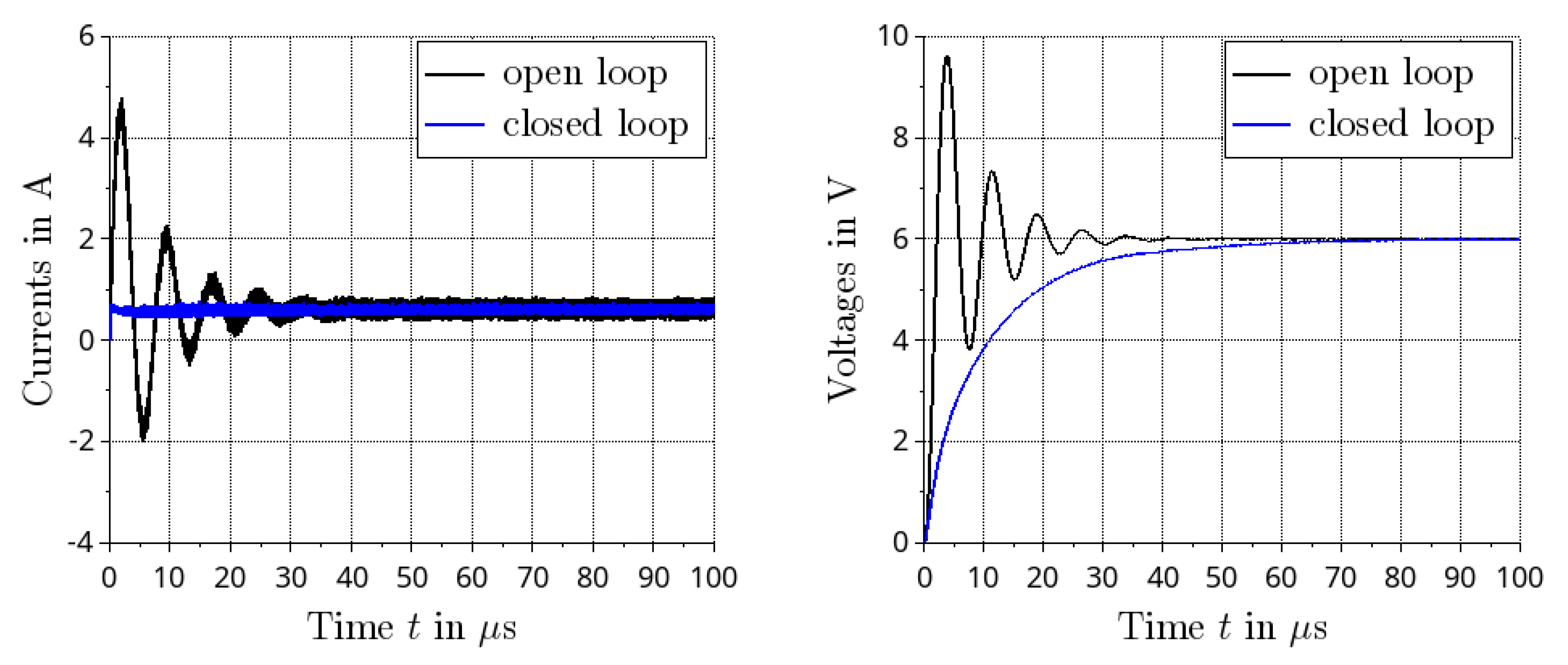
5.3. Closed Loop Transient Simulation
6. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AC | alternating current |
| DC | direct current |
| ODE | ordinary differential equation |
| PDE | partial differential equation |
References
- Bacha, S.; Munteanu, I.; Bratcu, A.I. Power Electronic Converters Modeling and Control; Springer-Verlag: London, 2014. [Google Scholar]
- Sander, S. Buck and boost converters with transmission lines. IEEE Transactions on Power Electronics 2012, 27, 4013–4020. [Google Scholar] [CrossRef]
- Sander, S.; Karvonen, A. Semiconductor component reduction in AC/DC converters with transmission lines. In Proceedings of the 15th European Conference on Power Electronics and Applications (EPE), 2013, p. 1–10.
- Röbenack, K.; Bärnklau, H. A Spatially Distributed Boost Converter – Modeling and Simulation. In Proceedings of the International Conference on System Theory, Control and Computing (ICSTCC), Timisoara, Romania; 2023; pp. 480–486. [Google Scholar] [CrossRef]
- Huang, C.; Woittennek, F.; Röbenack, K. Steady-state analysis of a distributed model of the buck converter. In Proceedings of the European Conference on Circuit Theory and Design (ECCTD); 2013; pp. 1–4. [Google Scholar] [CrossRef]
- Röbenack, K.; Herrmann, R. Analysis, Simulation and Implementation of a Distributed Buck Converter. In Proceedings of the 26th International Conference on System Theory, Control and Computing (ICSTCC), Sinaia, Romania; 2022; pp. 213–218. [Google Scholar] [CrossRef]
- Röbenack, K.; Herrmann, R. Distributed Buck Converter Realization Based on a Transmission Line. SYSTEM THEORY, CONTROL AND COMPUTING JOURNAL 2023, 3, 29–35. [Google Scholar] [CrossRef]
- Zainea, M.; van der Schaft, A.; Buisson, J. Stabilizing control for power converters connected to transmission lines. In Proceedings of the Proc. American Control Conference (ACC); 2007; pp. 3476–3481. [Google Scholar] [CrossRef]
- Daafouz, J.; Tucsnak, M.; Valein, J. Nonlinear control of a coupled PDE/ODE system modeling a switched power converter with a transmission line. Systems & Control Letters 2014, 70, 92–99. [Google Scholar] [CrossRef]
- King, W.P. Transmission Line Theory; Dover Publications, Inc., 1965.
- Mathis, W.; Reibiger, A. Küpfmüller Theoretische Elektrotechnik, 20th ed.; Springer Vieweg, 2017. [CrossRef]
- Sira-Ramírez, H. Nonlinear P-I Controller Design for Switchmode dc-to-dc power converters. IEEE Trans. on Circuits and Systems 1991, 38, 410–417. [Google Scholar] [CrossRef]
- Escobar, G.; Ortega, R.; Sira-Ramirez, H.; Vilan, J.P.; Zein, I. An experimental comparison of several non linear controllers for power converters. IEEE Control Systems 1999, 19, 66–82. [Google Scholar]
- Kugi, A.; Schlacher, K. Nonlinear H∞-Controller Design for a DC-to-DC Power Converter. IEEE Trans. on Control Systems Technology 1999, 7, 230–237. [Google Scholar] [CrossRef]
- Duong, M.Q.; Sava, G.N.; Scripcariu, M.; Mussetta, M.; et al. Design and simulation of PI-type control for the Buck Boost converter. In Proceedings of the 2017 International Conference on Energy and Environment (CIEM). IEEE; 2017; pp. 79–82. [Google Scholar] [CrossRef]
- Garg, M.M.; Hote, Y.V.; Pathak, M.K.; Behera, L. An approach for buck converter PI controller design using stability boundary locus. In Proceedings of the 2018 IEEE/PES Transmission and Distribution Conference and Exposition (T&D). IEEE, 2018, p. 1–5. [CrossRef]
- Tzafestas, S.G. Distributed parameter control systems: Theory and application; Vol. 6, International Series on Systems and Control, Pergamon Press: Oxford, UK, 2013.
- Christofides, P.D.; Daoutidis, P. Feedback control of hyperbolic PDE systems. AIChE Journal 1996, 42, 3063–3086. [Google Scholar] [CrossRef]
- Deutscher, J.; Harkort, C. A parametric approach to finite-dimensional control of linear distributed-parameter systems. International Journal of Control 2010, 83, 1674–1685. [Google Scholar] [CrossRef]
- Dimirovski, G.; Gough, N.; Barnettj, S. Categories in systems and control theory. International Journal of Systems Science 1977, 8, 1081–1090. [Google Scholar] [CrossRef]
- TimKabel. RG 58 C/U 50 Ω, Coaxial cable. http://www.tim-kabel.hr/images/stories/katalog/datasheetHRV/1502_RG58_ENG.pdf.
- LAPP. RG-58 C/U, 2020. https://e.lapp.com/apac/p/coaxial-cables/coaxial-rg-58-c-u-217000.
- Scilab. http://www.scilab.org/.
- Maxima, a Computer Algebra System. http://maxima.sourceforge.net.
- The Sage Developers. SageMath, the Sage Mathematics Software System (Version 10.2), 2024. https://www.sagemath.org.
- Marlin, T.E. Process Control, Designing Processes and Control Systems for Dynamics Performance, 2 ed.; McGraw-Hill, 2000.
- O’Dwyer, A. Handbook of PI and PID controller tuning rules; Imperial College Press: London, 2009. [Google Scholar]
- Dutoon, K.; Thompson, S.; Barraclough, B. The Art of Control Engineering; Prentice Hall, 1997.
- Hippe, P. Windup in Control: Its Effects and Their Prevention; Springer-Verlag: London, 2006. [Google Scholar]
- Röbenack, K.; Palis, S. Set-Point Control of a Spatially Distributed Buck Converter. Algorithms 2023, 16. [Google Scholar] [CrossRef]
- Economou, C.G.; Morari, M. Internal Model Contrl. 5. Extension to Nonlinear Systems. Ind. Eng. Chem. Process Des. Dev. 1986, 25, 403–411. [Google Scholar] [CrossRef]
- Henson, M.A.; Seborg, D.E. An internal model control strategy for nonlinear systems. AIChE Journal 1991, 37, 1065–1081. [Google Scholar] [CrossRef]
- Datta, A. , 1998; p. 47–58.Schemes. In Adaptive Internal Model Control; Springer: London, 1998; pp. 47–58. [Google Scholar]
- Lacoste, R. Robert Lacoste’s The Darker Side: Practical Applications for Electronic Design Concepts from Circuit Cellar; Newnes, 2009.
- Lupo, G.; Petrarca, C.; Vitelli, M.; Tucci, V. Multiconductor transmission line analysis of steep-front surges in machine windings. IEEE Transactions on Dielectrics and Electrical Insulation 2002, 9, 467–478. [Google Scholar] [CrossRef]
- Bärnklau, H.; Gensior, A.; Rudolph, J. A model-based control scheme for modular multilevel converters. IEEE Transactions on Industrial Electronics 2012, 60, 5359–5375. [Google Scholar] [CrossRef]
- Xie, Y.; Zhang, J.; Leonardi, F.; Munoz, A.R.; Degner, M.W.; Liang, F. Modeling and verification of electrical stress in inverter-driven electric machine windings. IEEE Transactions on Industry Applications 2019, 55, 5818–5829. [Google Scholar] [CrossRef]

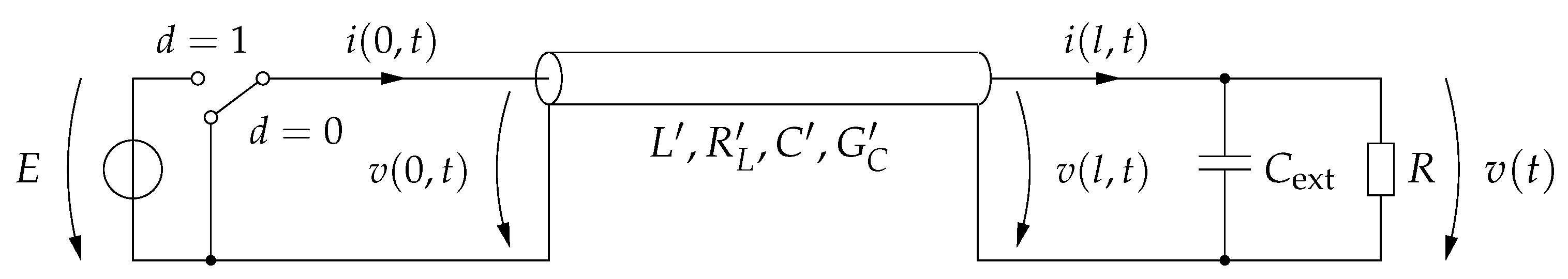
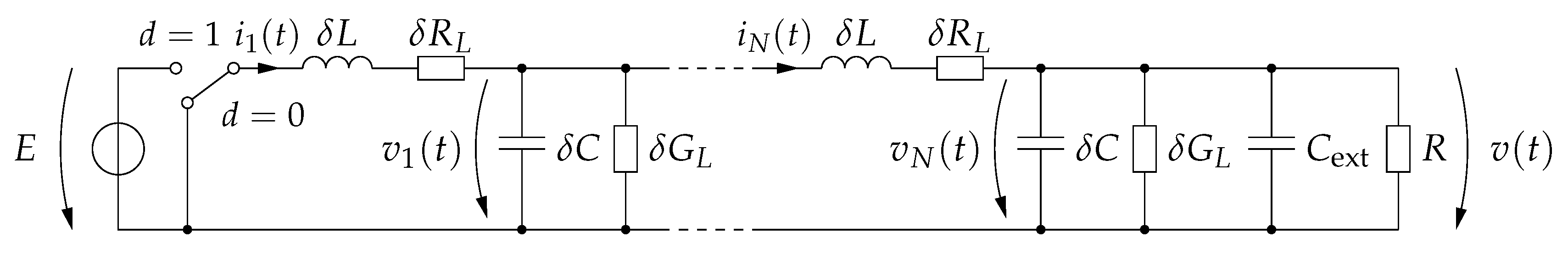
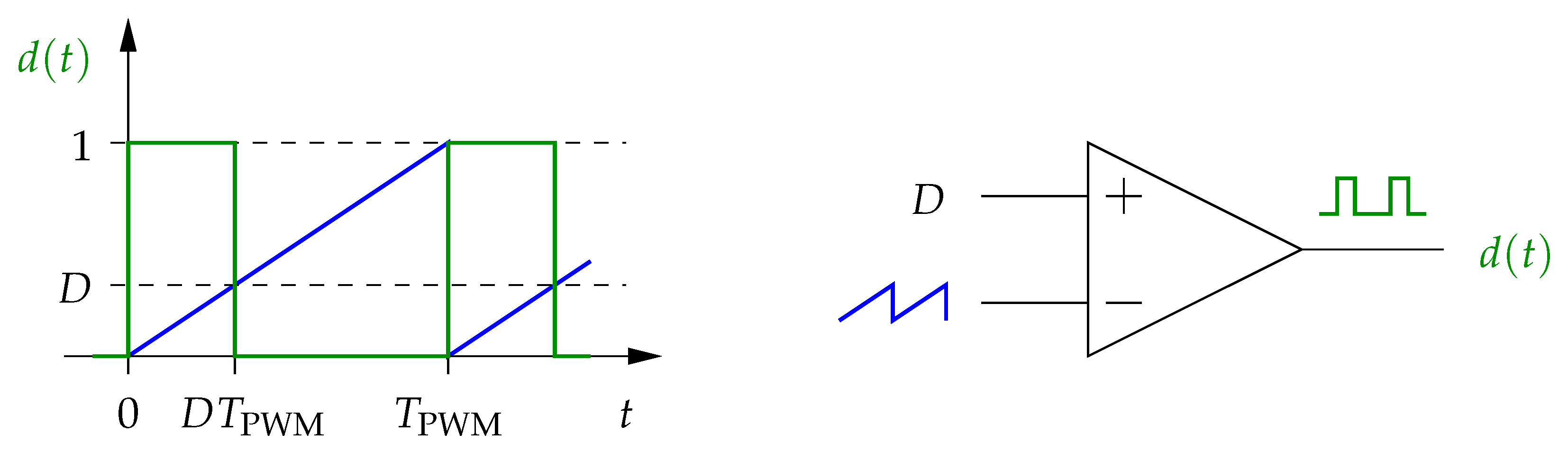

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




