Limited Time Resolution of Event Data Loggers Can Bias Intensity Measurements from Tipping-Bucket Rain Gauges

1. Introduction

Tipping bucket rain gauges (TBRGs) are probably the most widely-deployed type of rain gauge globally (Molini et al. 2005 [1] , Muñoz et al. 2016 [2] ). They provide a simple and direct physical measurement of the volume of water collected by a funnel that is made to a standard, nominated diameter (often 203 mm, or approximately 8 inches). The gauge data consist of Gregorian date- and time-stamped records of time of arrival of quantities of rain represented by fixed bucket volumes (typically about 6.5 mL, the equivalent of 0.2 mm depth over the area of the collecting funnel). These are sometimes aggregated to 5 minute or other integration times before being logged. Because the measurement is direct and has a clear physical basis, TBRGs are considered to provide the best 'ground truth' point-based rainfall data against which less direct rainfall recording methods can be calibrated. These indirect methods include for instance the monitoring of the degree of attenuation of ground-based or satellite telecommunications signals that result from the occurrence of rain falling across the signal path (Kim and Kwon 2018 [3] ).

As a result of their widespread deployment by national weather agencies and in general climatological and hydrological research, the performance of TBRGs has been extensively studied (Fankhauser 1998 [4] , Overgaard et al. 1998 [5] , Habib et al. 2001 [6] , La Barbera et al. 2002 [7] , Ciach 2003 [8] , Hodgkinson et al. 2004 [9] , Santana et al. 2018 [10] , Kochendorfer et al. 2017 [11] , Segovia-Cardozo et al. 2021 [12] , 2023 [13] ). In particular, Zhou et al. (2019) [14] evaluated the performance of a HOBO® tipping bucket rain gauge equipped with an event logger. Their analysis however was primarily on the accuracy of hourly rainfall amounts and the influence of wind and rainfall intensity on the accuracy of rainfall data. The event logger tested in the current work is of the same kind as used by Zhou et al. (2019) [14] , which log the time of each individual bucket tip. Some TBRGs log only the number of tips per clock minute. The evaluations of TBRG performance have established that there are multiple issues relating to site selection, including exposure to wind that can cause undesirable turbulence around the collecting orifice of a rain gauge, and in the correct measurement and recording of oblique, wind-driven rain. Intermittency during rain is difficult to record with TBRGs, because a bucket may remain only partly filled when rain ends, or be partially full when rain begins, such that the timing of rain onset and ending cannot reliably be judged. Various systematic errors also arise from the TBRG mechanism itself. Under-recording of rainfall amounts is a well-documented error source. This arises because inflow from the collecting funnel to a tipping-bucket during its tipping (with a duration of ~ 0.5 s, Duchon et al. 2014 [15] , Liao et al. 2020 [16] ) is unmeasured, and the associated error becomes worse at higher intensities. TBRGs also tend to over-record at low intensities, when the buckets appear to tip before they have filled with their calibrated water volume. This may be due to ripple effects in the water pooled inside the bucket, which cause premature over-balancing. In order to reduce these systematic errors, many TBRGs are equipped with a small syphon, designed to ensure a less variable rate of inflow to the bucket mechanism across a wide range of rainfall intensities. The steadier inflow makes calibration more straightforward. Many TBRGs available commercially claim that measurement inaccuracies amount to less than a few percent, at least within a restricted range of intensities. However, these specifications refer only to the TBRG mechanism itself (ignoring external sources of error such as wind or inappropriate site selection) and frequently require that careful annual re-calibration be undertaken. Furthermore, they relate to the measurement of rainfall amount (depth) over some (generally unspecified) integration time such as 1 h, and not to the assessment of short-term rainfall intensities.

Short-term rainfall intensities, for example over periods of minutes, are important in many fields. Areas of importance include urban flash-flood generation, and soil erosion processes and agrochemical wash-off. An important contemporary area of relevance is in the detection of intensification of rainfall connected with ongoing climatic variability and change. There is evidence that short-term intensities over periods of minutes are increasing more rapidly than over longer durations such as hourly rates. Secular change in annual maximum 5-minute rainfalls in Australia, as an example, was investigated by Bates et al. (2015) [17] .

Whilst short-term intensities are important, the various sources of measurement error mean that TBRGs are not ideal intensity recording devices. It is often considered that the time between successive tip events (the inter-tip time, or ITT) can be used as a measure of short-term intensity. Individual ITTs have been used to derived estimates of moment-to-moment rainfall intensities in multiple studies including Wang et al. (2008) [18] and Song et al. (2017) [19] . Additional studies were cited by Dunkerley (2024). The ITTs involved in estimating intensity in this way warrant careful consideration. For a standard collecting funnel of 203 mm (approx. 8 inches) diameter (area = 323.65 cm²), 1 mm of rain yields a water volume of 32.365 mL. The capacity of a tipping bucket designed to have a volume equivalent to 0.2 mm of rainfall would therefore need to be 20% of this, or ~ 6.47 mL. Further, during 1 hour, the rain volume collected by such a gauge at a rainfall intensity of 50 mm h^-1 would be (50 x 32.365) mL, or 1618.25 mL. Then, with a bucket capacity of 6.47 mL there would be ~ 250 tip events per h, and therefore a mean ITT of 14.4 s. This would be reduced to a mean ITT of 7.2 s at 100 mm h^-1, and to 3.6 s at 200 mm h^-1. Higher intensities (perhaps lasting only minutes, during intensity bursts) would result in even briefer ITTs, including 2.0 s at 350 mm h^-1. Gorman (2003) [20] evaluated the suitability of TBRGs for deployment by the Australian Bureau of Meteorology. Test were run to a maximum intensity of 500 mm h^-1, for which the ITT would be ~ 1.4 s.

Syphons (if fitted to a TBRG), whilst being advantageous for the measurement of cumulative rain depth, perturb short-interval intensity data because there is a delay while the syphon is filling (just as there is during the filling of a tipping-bucket) during which no rain is detected, and because syphons typically empty at a fast rate equivalent to a rainfall rate of about 260 mm h^-1 [21] . This results in more rapid tipping of the bucket mechanism than would be expected in light of the actual open-field rainfall intensity. In operation, the syphon chamber accumulates water until the syphon draining level is reached, at which point it discharges very rapidly into the tipping buckets. Only the mean ITT over a period of perhaps 15 minutes can then be taken to reflect the mean rainfall rate because of the syphon-induced alternation of long ITTs (syphon filling) and short ITTs (syphon emptying). This means that intensity cannot be estimated from individual ITTs, if the TBRG is syphon-equipped. 'Straight-through' gauges are to be preferred for the estimation of short-term intensities. Further analysis of these issues was presented by Dunkerley (2024) [21] Dunkerley (2024) [22] .

These relationship between intensity and ITT can be summarised in the relation ITT = 720 / RR, where ITT is in seconds and intensity (actually rainfall rate) RR is in mm h^-1. ITTs can be very long, as well as brief. For instance, at 5 mm h^-1, the ITT would be almost 2.5 minutes, and would exceed 12 minutes at 1 mm h^-1. Thus, during natural rainfall of fluctuating intensity, we can expect ITTs to range from perhaps a few seconds to more than several minutes, and extending to tens of minutes in very light rain. For the accurate estimation of short-term rainfall intensity, measurements of tip times with resolutions of seconds are clearly required.

1.1. Capacity of Event Data Loggers to Record Brief ITTs

If we consider how an event data logger with the specifications of the HOBO® event logger might record a series of short ITTs during intense rainfall, we encounter some difficulties which are explored next. The operation of such a logger involves recording the time of occurrence of each tip with a resolution of 1 second. Commonly, a magnet attached to the bucket tilting mechanism is used to close a reed switch mounted at a central position. The tip time that is logged corresponds with the closure of the reed switch when the buckets pass through the horizontal position, during the tipping event. This moment comes a few hundred ms after the full bucket begins to tip, but before it reaches the new inclined rest position and drains, and corresponds roughly to the mid-point of the 0.5 s tipping time.

If tip events occurred exactly at intervals that were a precise, integral number of seconds (2 s, 5 s or 10 s apart, and so on) then the event logger would be capable of faithfully recording the clock second in which each tip event occurred. However, if the tip events are not an integral number of seconds apart, then the time of occurrence of successive tip events shifts with respect to the boundaries of the clock-seconds which are the basis of the event logging process. This quantization error is illustrated in Figure 1 . Of course, natural rainfall would be expected to exhibit primarily non-integral ITTs, with the individual ITTs changing from moment to moment, as the intensity fluctuated, and Figure 1 is simply an attempt to illustrate the challenges of timing short-duration ITTs.

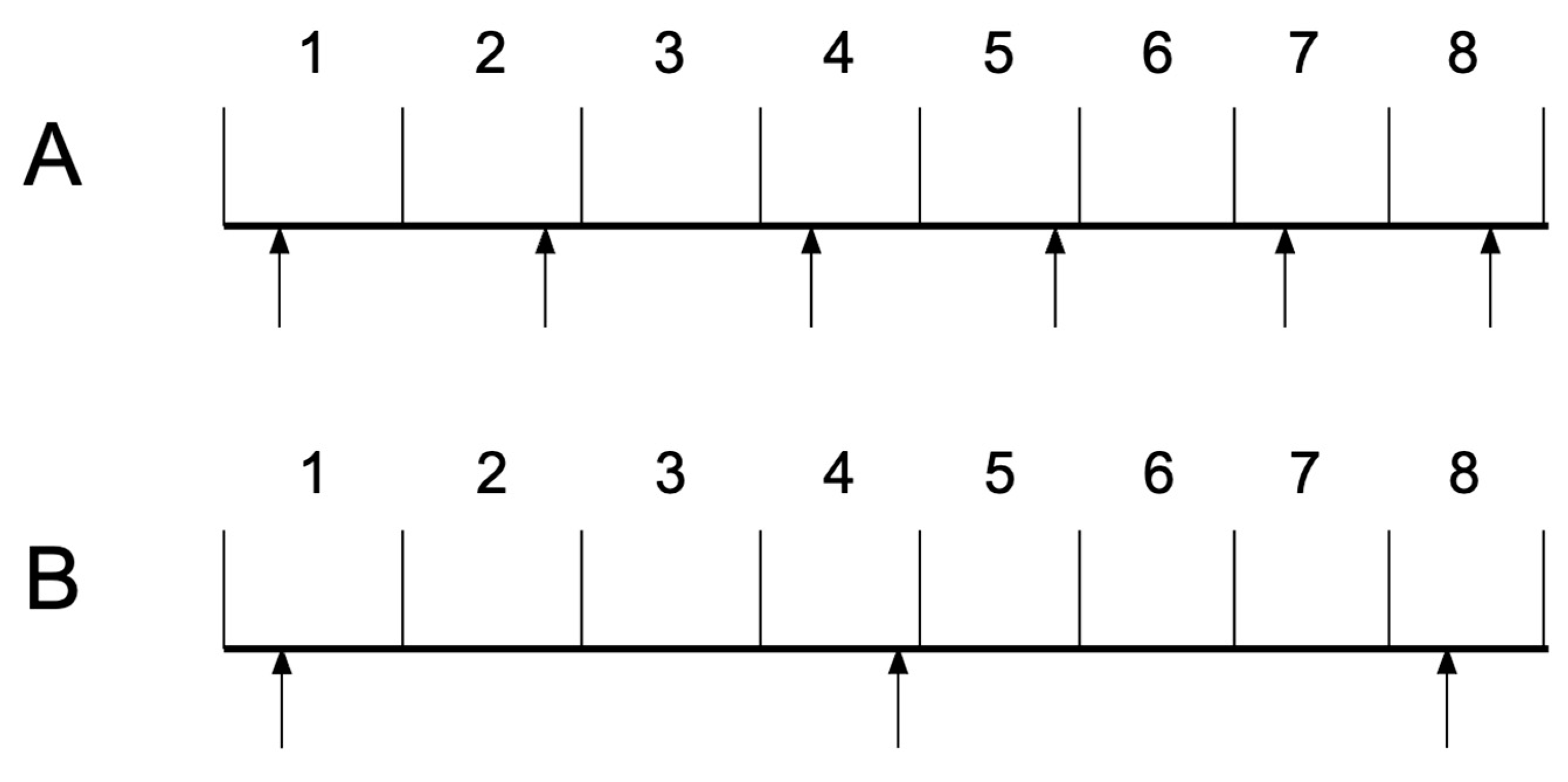
Figure 1 (A) shows a hypothetical timeline with 8 logger clock-seconds marked above the horizontal time line. Reed switch closures at fixed intervals of 1.5 s are marked by arrows below the time line. The first ITT includes seconds 1 and 2, with a resulting duration of 1 s (too short). The second ITT spans seconds 2 to 4, with a resulting duration of 2 s (too long) and this pattern then repeats. Figure 1 (B) is the same, but for reed switch closures every 3.5 s. Here the first ITT spans seconds 1 to 4, with a resulting duration of 3 s (too short) and the second ITT spans seconds 4 to 8, resulting in a duration of 4 s (too long). This sequence would also repeat. Figure 1 thus illustrates how non-integral periods between bucket tip events (reed switch closures), when recorded with an event logger that only has 1 s resolution, result in apparent ITTs that are either too brief or too long. In the case of Figure 1 (B), the erroneously short ITT of 3 s over-estimates the intensity by about 14%, and the erroneously long ITT of 4 s under-estimates the intensity by the same amount. The apparent (erroneous) spread of ITTs thus leaves an uncertainty of almost 30% in the intensity judged from a sequence of ITTs. In the case of Figure 1 (A), the error is larger, at about 33%, and hence the aggregate uncertainty in intensity estimates from a sequence of ITTs is very large, at about 66%.

It should be noted that in addition to a 1 second quantization, HOBO® event loggers have a 0.5 s lockout period, designed to eliminate recording of the contact-bounce that commonly arises in mechanical switches, including reed switches, as spurious tip events. Reed switches are described in basic electronics texts (e.g. Sinclair 2001). There can be multiple contact 'bounce' closures over several ms, and that bounce may continue for 100 ms or longer, if the magnetic field designed to trigger reed switch contact closure is weak. Given that the lock-out period is shorter than the 1 s resolution of the event logger, it does not affect the ability of the logger to record correctly the timing of tip events more than 1 s apart. However, the problem of non-integral ITTs remains. The consequences of non-integral ITTs was explored in a series of lab experiments, described next. These were intended to collect data akin to the hypothetical examples in Figure 1 , but by direct measurement using an event data logger fed with precisely-timed switch closure signals. Owing to the 0.5 s lockout period, event loggers with 1 s resolution cannot record events more closely spaced than 0.5 s.

In light of the foregoing brief account of TBRGs and of the use of ITTs to estimate short-term rainfall intensities, the objective of the work reported here was to explore the extent to which an event data logger can satisfactorily log the bucket tip events of a TBRG, especially during intense rainfall when the ITTs can be only seconds in duration. This was done through the use of accurately-timed switch closures at integral and non-integral intervals that were fed to the event data logger. Methods are outlined in detail next.

2. Materials and Methods

Controlled laboratory bench tests were devised to address the objective just set out. In-house code was prepared for an Arduino R4 Minima microcontroller (clock speed 48 MHz), to generate a succession of brief signal pulses at known intervals of time. The signal pulses (output voltages) triggered a small 5 V relay. The relay closure was equivalent to the reed switch closure in a TBRG, and the normally-open (NO) contacts of the relay were connected to the inputs of a HOBO® event data logger. This was done to see how well the event logger was able to record switch closures at non-integral intervals, such as 2.5 s, 2.75 s, 3.5 s, 4.25 s, and so on. If the interpretations contained in Figure 1 are correct, then difficulties would be expected in logging both events too closely spaced in time for the logger time resolution (1 s) and those separated by non-integral periods (e.g. 3.5 seconds).  Non-integral intervals could be expected to occur commonly in natural rainfall, though not of course at the precise values just mentioned.

The tested intervals between relay closures ranged from 0.5 s to 5.0 s in increments of 250 ms. Thus, 19 different pulse spacings were tested. For each, 25 repetitive closures were generated, and then the pulse spacing was adjusted to the next nominated interval. When data at all pulse spacings had been collected, the code halted. During the test, the details of the timing of each pulse were written to an SD memory card, including the Gregorian date and time with a precision of 1 ms - 1,000 times better than the 1 s timing resolution of the HOBO® event logger. These were then read into a spreadsheet for processing. The data logged by the HOBO® data logger were downloaded using Hoboware® software and read into a spreadsheet. The apparent ITTs between successive switch closures were compared with the known values that were electronically generated, from the SD card files written by the microcontroller. The 25 repetitive relay closures at each interval between relay closures allowed 24 intervening ITTs to be calculated for each series of relay closures.

3. Results

It was found that the event logger was able to record correctly the ITTs in all sequences of switch closures that were separated by an integral number of seconds, viz. 1 s, 2 s, 3 s, 4 s, and 5 s ( Table 1 ). However, in all cases of non-integral ITTs, the logger was unable to record the correct durations.

The results in Table 1 show that for all non-integral pulse spacings, the ITTs recorded by the event logger are a mix of ITTs that are too long and ITTs that are too short. The standard deviations of the apparent ITTs lie in the range 0.44 - 0.51 s. Only the mean ITT, calculated across all 24 ITTs, is correct. These inaccuracies result from the 1 second quantization arising from the logger clock timing.

The erroneous apparent ITTs recorded by the HOBO® event logger exhibited systematic patterns related to the changing offset between the actual ITTs and the boundaries of the clock seconds employed by the event logger. For instance, at a pulse spacing of 2.75 s, the apparent logged ITTs were arranged as three ITTs of 3 s duration, one ITT of 2 s duration, three ITTs of 3 s duration, and so on in a repeating pattern. For a pulse spacing of 2.25 s, the pattern of apparent ITTs from the event logger was three ITTs of 2 s, one ITT of 3 s, three ITTs of 2s, and so on in a repeating pattern. For a pulse spacing of 1.5 s, the sequence was alternating ITTs of 1 s and 2 s. A few examples showing the 24 recorded ITTs for non-integral intervals between switch closures are shown in Table 2.

4. Discussion

The results presented here demonstrate that event data loggers exemplified by the HOBO® event logger tested, and which are limited to 1 s resolution in the timing of reed switch closure events, have difficulty in faithfully recording ITTs that are not integral numbers of seconds. This occurs even when, as in the experiments reported here, the switch closures occur at constant, non-integral intervals longer than the minimum time of 1 s that the logger can record.

The explanation is as follows. When two switch closures are separated by more than an integral number of seconds, say 2.25 s or 4.1 s, the position of the pulse as seen on the time axis of Figure 1 progressively shifts in relation to the fixed clock-second boundaries set by the data logger clock. When the first switch closure occurs by chance close to the end of a clock second, and the next closure occurs say 1.5 s later, the entire intervening clock second is skipped. This makes the apparent ITT derived from the event logger data span 2 clock seconds, and the apparent ITT is 2 s, not the correct value of 1.5 s. This is an error of 25% in the estimated ITT. In the case of the 2.25 s pulses tested here, some ITTs calculated from the event logger data were 3 s in duration. This is an error of 44.4%, and this would translate to an error of the same size in the rainfall intensity estimated from such an erroneous ITT. Clearly, therefore, we must add event data logger timing errors to the systematic errors of tipping bucket filling and emptying, and syphon filling and emptying, discussed earlier which also affect the sequence of ITTs. Since all three error sources may act concurrently, they may introduce considerable bias in rainfall intensities estimated from unaggregated ITTs in TBRG data. Drift in the clocks of event data loggers is very small (typically no more than minutes per month). This is negligible in relation to the duration of rainfall events, and is ignored here as a further source of error. It is important to note that the errors just mentioned are only of significance in the estimation of short-term, high rainfall intensities. At low intensities, for instance less than 5 mm h^-1, ITTs grow to durations of minutes rather than seconds, and the timing errors reported here are less important. For non-integral numbers of seconds, the 1 - 2 s uncertainty described here would remain, but be of no real significance to estimates of rainfall rates. For example, a 1 s uncertainty declines to be 1% of an expected ITT of 100 s, which is the equivalent of 7.2 mm h^-1. The associated uncertainty in this case would be < 0.1 mm h^-1.

In natural rainfall, intensity fluctuates from moment to moment, and ITTs are likewise very variable. This means that it is impossible to know whether ITTs derived from TBRG records of intense rainfall reflect the actual ITT, or are perturbed by the time quantisation problem associated with limited event data logger time resolution. It seems highly likely that many ITTs during intense rainfall are indeed perturbed by such errors, with an uncertainty of about 1 s. This is precisely the same kind of problem that attends the interpretation of ITTs collected using a syphon-equipped TBRG (Dunkerley 2024), but from quite a different cause. It is worth noting that an additional potential cause of irregular ITTs is uneven calibration of the two tipping buckets. If the stop-screws of the two buckets are adjusted to slightly different positions, then even in rain of constant intensity, there would be two slightly different filling times, and two slightly different ITTs.

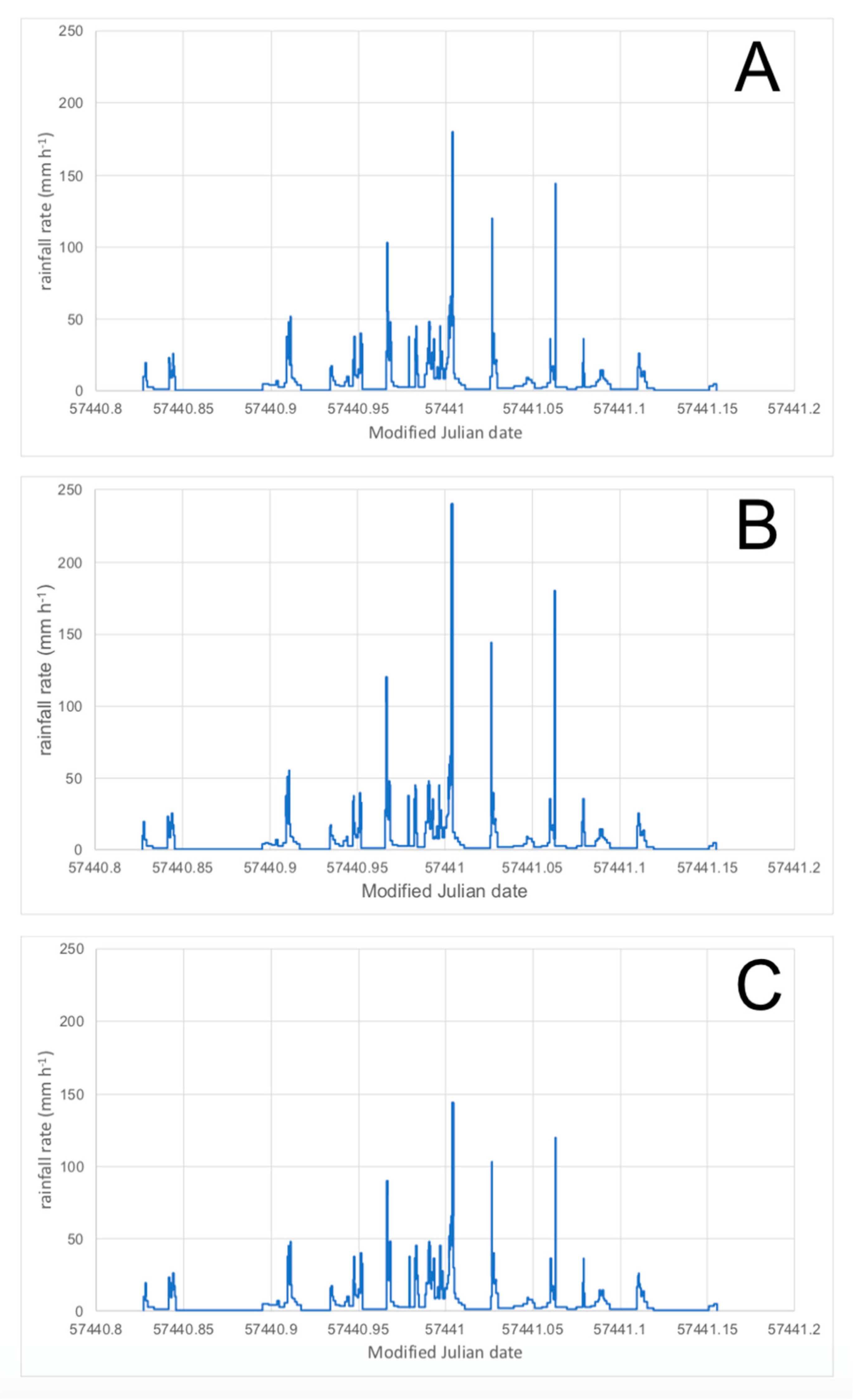
To illustrate the possible consequences of the timing resolution issue, the ITT record of a rainfall event lasting 7.8 h, recorded in northern Australia is, analysed. The observations were collected using a RIMCO 8020 TBRG with 0.2 mm sensitivity, linked to a HOBO® event data logger. The unadjusted ITTs are compared with the adjusted record in which the shortest ITTs (the most intense bursts of rain) are adjusted to show the effects of a ± 1 s uncertainty (Figure 2). The rainfall record as logged shows several intensity peaks, including four of > 100 mm h^-1, as well as several smaller peaks > 40 mm h^-1. The record illustrates well the high temporal resolution of rainfall intensity that is in principle available from unaggregated ITTs. The ITTs associated with the intensity peaks include four ITTs of 4 s duration, and others of 5 s and 6 s duration. If these ITTs are shifted in duration by ± 1 s, as might have occurred as a result of the time quantisation problem, then the intensity peaks are significantly altered (Table 3). Thus, the four ITTs of 4 s duration might in fact have been close to 3 s, or close to 5 s, and it is impossible to know the actual value. Thus, the four unadjusted intensity peaks of 180 mm h^-1 (4 s ITT) might have been as low as 144 mm h^-1 (if the ITT was in fact 5 s) or as high as 240 mm h^-1 (if the ITT was in fact 3 s). This is a range of uncertainty of ~ 100 mm h^-1. Given the importance of intensity bursts in dislodging soil particles, establishing overland flow, and other processes, this uncertainty is not helpful in documenting the intense components of a rainfall climate. For the short rainfall event in Figure 2, the mean rainfall rate of the unadjusted data is 23.9 mm h^-1. However, after adjusting only the ITTs associated with the small number of intensity peaks > 40 mm h^-1, this increases by 5.4% to 25.2 mm h^-1 if the ITTs are shortened by 1 s or falls by 3.4% to 23.1 mm h^-1 if the ITTs are lengthened by 1 s. The change in the mean rainfall rate of any particular rainfall event would clearly depend on both the number of intensity peaks during the event, and their individual intensities (ITTs).

What can be done to improve the estimation of high rainfall intensities over short time intervals, such as the 10 s ITTs equivalent to 72 mm h^-1? Even at this unexceptional intensity, a 1 s uncertainty amounts to about 10%, or ~ 7 - 8 mm h^-1. Evidently, employing an event data logger with higher timing resolution would remove some of this uncertainty. This should be readily possible if an event data logger is assembled from one of the high-clock-speed microcontrollers now available at quite low cost (e.g. < US$20). This can be exemplified by the R4 Minima used in the present experiments, for which ms timing is straightforward. There are other possible methods of avoiding the kinds of uncertainty discussed here. One method that offers better capability is the use of acoustic methods (Dunkerley 2020 [23], Wang et al. 2022 [24]) where there are no delays at all associated with bucket or syphon filling or emptying, and the acoustic signal of rain can be recorded with << 1 ms resolution if required, including even the arrival of individual drops. This is done by analysing the voltage recorded at a suitable microphone, or perhaps, with a suitable piezo-electric transducer. In common forms of audio recording, the sampling frequency is 44.1 kHz, during which the voltage at the microphone is sampled every 0.02 ms. This provides more than sufficient temporal resolution for the confident estimation of rainfall intensity.

5. Conclusions

At high rainfall intensities, the limited timing precision of event data loggers such as the HOBO® event logger results in considerable uncertainty in estimating the true time interval between bucket tip events in a TBRG. This is essentially a quantization problem. In turn, this also makes estimates of rainfall intensity that could in principle be made from unaggregated ITTs equally uncertain. It is emphasised that these issues only relate to the estimation of high rainfall intensities (i.e., short ITTs). Timing issues become negligible in rainfall of low intensity. However, intensity bursts are critical in many areas, so that the performance limitations identified here need to be borne in mind when high rainfall intensities need to be interpreted from TBRG records.