Prerpints.org logo
Preprint
Article

A Conjecture on the Possible Another Supermassive Black Hole in the Bar of Our Milky Way

This version is not peer-reviewed.

Yin Zhu  *

Submitted:

24 June 2024

Posted:

25 June 2024

Read the latest preprint version here

Abstract
In the bar of our Milky Way, there should be another supermassive black holes B which is with the mass almost 10-2--10-5 the Sgr A* and with a distance10,000--14,500 lightyears from Sgr A*. The bar is formed by the stellar orbiting around both of the black holes. In the Hill radius of B, a lots of stars orbit around B while another lots of stars orbit Sgr A*. It determines that there is a “x-shaped structure” in the bar and the shape of bar appears a peanut. As the orbits of the stars is out of the Hill radius of B, they are repulsed to a distant place by B to form the arms.
Keywords: 
galactic bar
;  
galactic spiral arms
;  
Sgr A*
;  
supermassive black hole
;  
Newtonian theory of orbit
Subject: 
Physical Sciences  -   Astronomy and Astrophysics

1. Introduction

The Milky Way is with a super gigantic scale. It only can be observed with modern technology. Therefore, the outline of the galaxy only can have been known in recent time and a long time was spent in knowing the whole image of it. First, in 1958, it was observed by Oort et al. [1] that the hydrogen clouds are in pure circular rotation about the galactic center. Second, in 1976, it was observed by Georgelin & Georgelin [2] that the galaxy is with four spiral arms. Third, it was known a line about the galactic bar by Oort & Rougoor [3,4] in 1959 and in 1960; and the bar was further confirmed by de Vaucouleurs [5] in 1964. Fourth, it was observed [6,7] that a supermassive black hole, Sgr A*, is at the center of the galaxy. Firth, it is currently thought that the radius of the Milky Way is 105 lightyears, the thicken of at the center of the galaxy is 104 lightyears; the mass of the Milky Way is almost 5.8 × 10 11 M s u n [8].
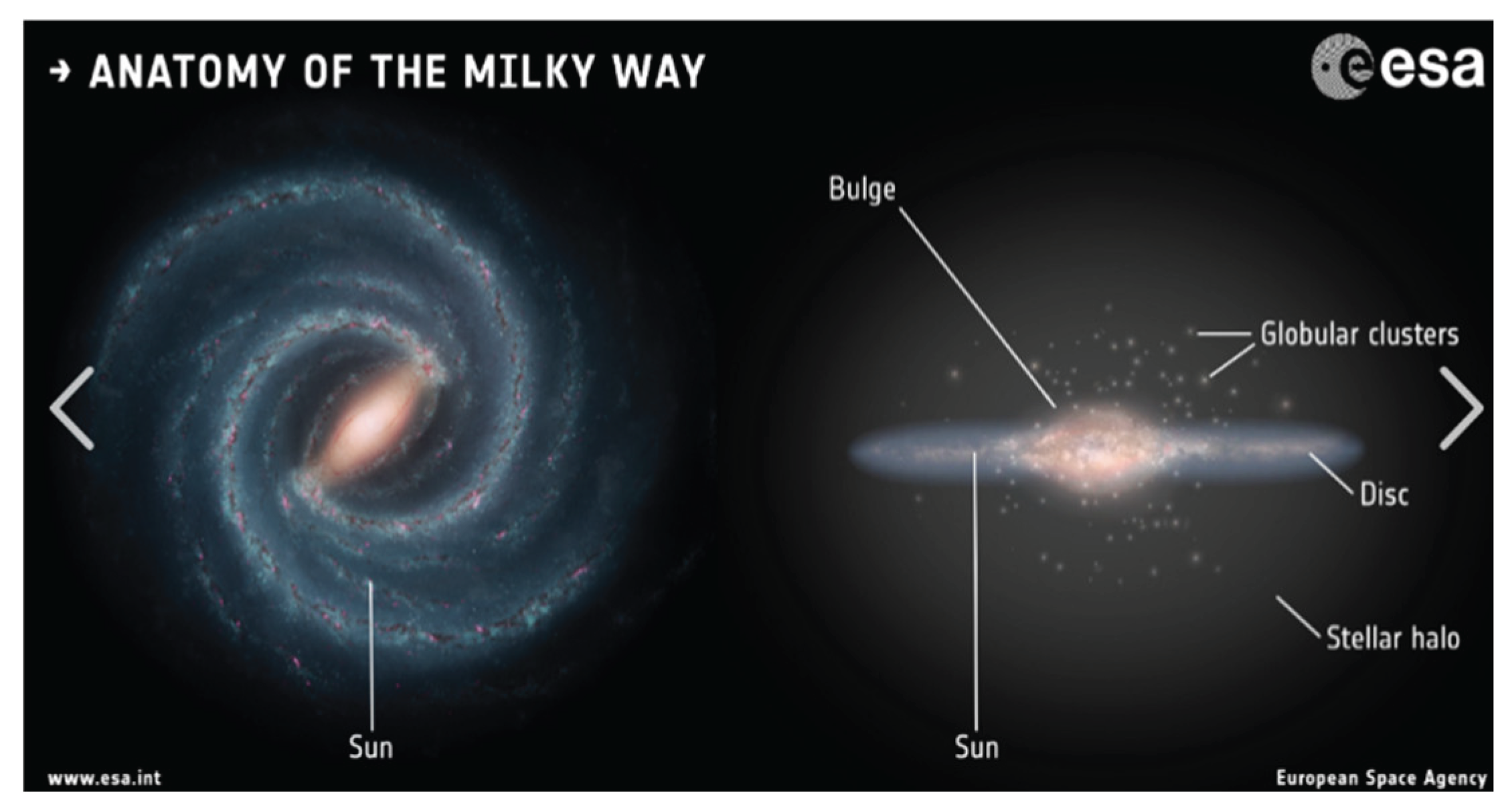
Preprints 110227 g001
Figure 1. The observed image of our Milky Way.
Figure 1. The observed image of our Milky Way.
Preprints 110227 g001

2. The “x-Shaped Structure” and Peanut Shape of the Bar: The Possible another Supermassive Black Hole

2.1. The Bar

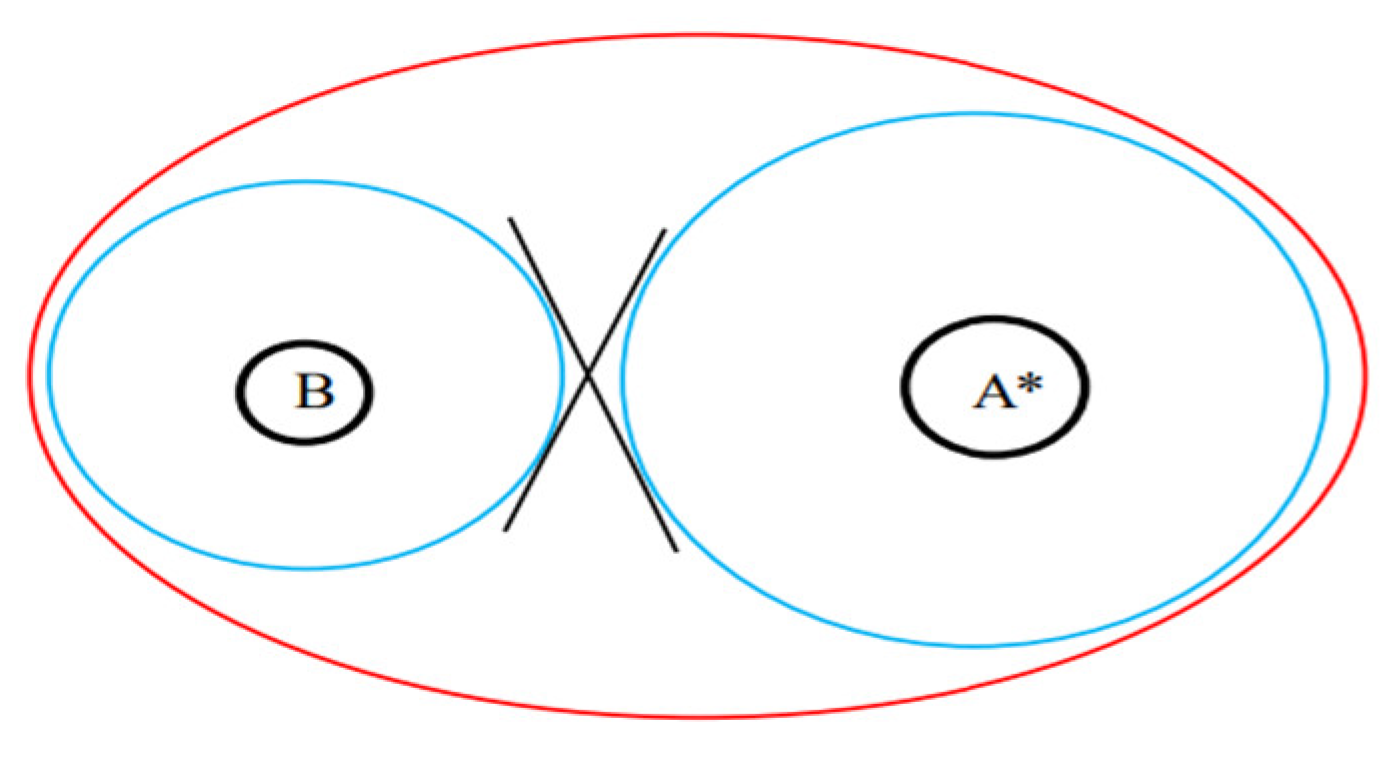
As shown in Figure 2, if there should be two supermassive black holes Sgr A* and B, there should be a lots of stars orbit around Sgr A* while another lots stars around the B. And, other a lots of stars orbit around both A* and B. It is noted that, the black hole B is orbiting around A*. But, the shape and structure of the bar cannot be changed by the orbit of B.
Bar pattern speed. Figure 2 shows that, the speed of the stars orbiting the two black holes is different and complicated. There is not a single bar pattern speed. This case was mentioned in some of observations [10,11,12]. From that the bar is with a thickness of 10,000 ly, it could be concluded that the orbits around A* and B are in a sphere and around both A* and B are in an ellipsoid, rather than in a disk. It is analogous to the orbits of the moons around the Jupiter. It results in that it is very difficult to observe the speed of the orbit around one of or both of the two black holes. But, the speed of the orbit of the black hole B around the Sgr A* could be observed. And, the mass of Sgr A* can be accurately and precisely known from this speed.
Strong and weak bar. It is observed that 44% of the spiral galaxies are with a bar with different strength [13,14]. Here, we present, the strength of a bar is determined with these factors: 1) the ratio of m B M A . There is 0 < m B M A < 1 . m B M A is larger, the bar is stronger; m B M A is less, the bar is weaker; as m B M A is very little, B shall become a satellite of A, the bar is vanished. 2) the distance d between B and A. As d is very little, no star can orbit around B. As d is very large, no star can orbit both A and B. Therefore, the necessary condition to form a bar is that the orbit of the stars is affected by both the two black holes in the same way.
Multi black holes of a bar. There should be more than two supermassive black holes in a bar and all of the black holes have a same effect on the orbit around these black holes.
There were many observations and different discussions about the galactic bar [8,13,14,15,16,17]. However, we think, as 44% of the observed 4378 disc galaxies are with a bar [13], these bars should be formed by dynamics and kinematics, rather than by accidental event, such as a collision of two galaxies.

2.2. The Arms and Hill Sphere

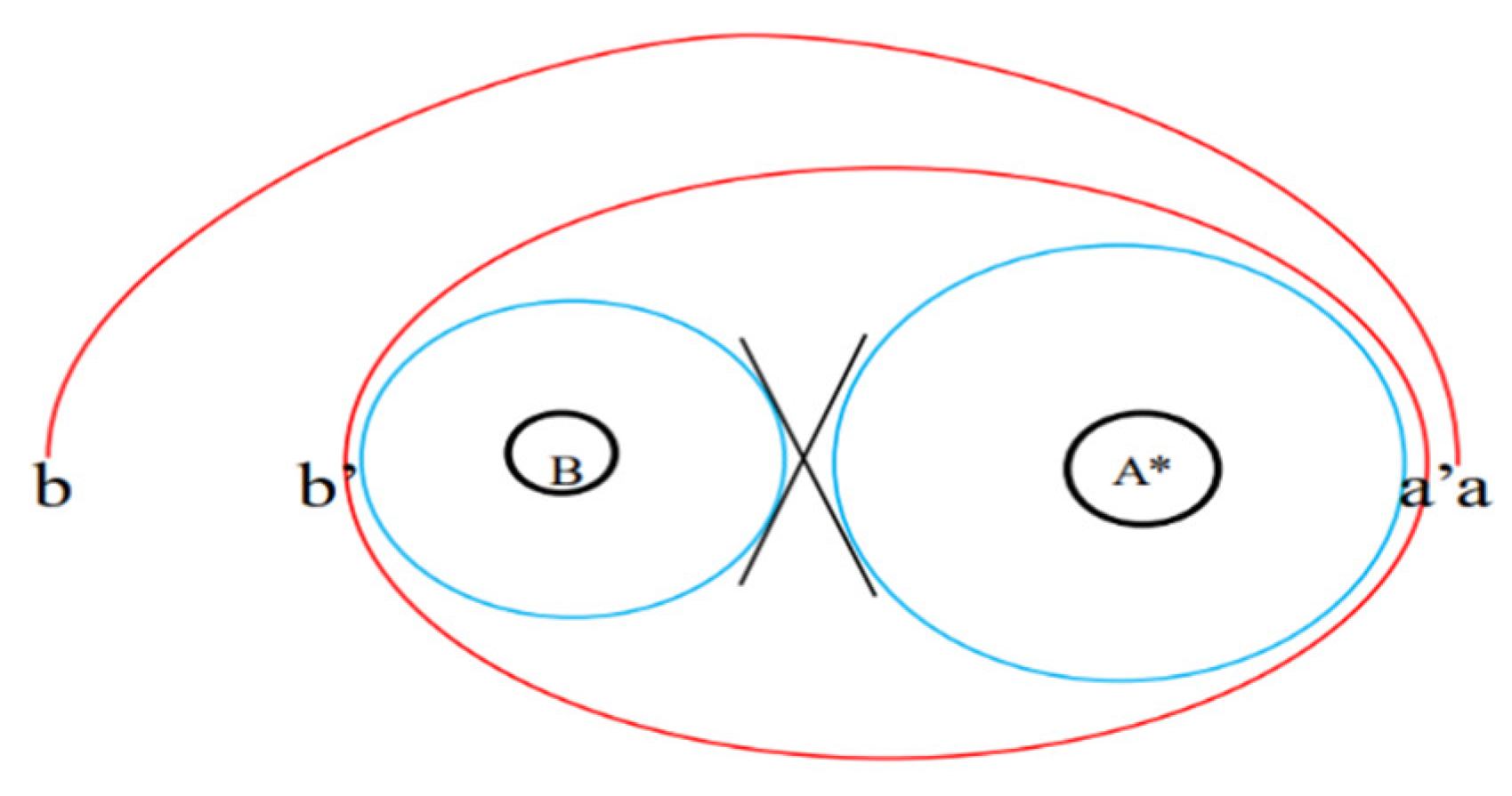
The arms could be understood with the Hill sphere. For two celestial bodies, as the body with less mass is in the Hill radius of the larger one, it can have a stable orbit around the larger one. Or, the less one can move away from the larger one. Therefore, as two stars are orbiting around the Sgr A* with orbit ab and a’b’ as shown in Figure 3, if the distance between ab and a’b’ is less than the Hill radius of the two stars, the two orbits shall merge into one single orbit. Therefore, the condition for the two orbits ab and a’b’ is that the distance between two orbits is larger than the Hill radius of the two stars.
From r = d m / 3 M 3 we know, for the same stars, the Hill radius of a star is determined with the distance d between the star and the center mass which the star is orbiting around. In the Figure 3, because the distance d for the star at point a is different from that at b, the Hill radius of the same star at point b is larger than that at point a. As the Hill radius of the star at point b is r = d m / 3 M 3 = b b ' , then, only the orbit with the distance L ≥ b b ' can be remained. It makes the spiral arm produced.
There were different understandings about the reason for the arms [8,18,19,20]. Here, we are trying to have such a reason that is accordant with celestial dynamics and kinematics. As the reason is not accordant with dynamics and kinematics, the orbit should be broken off.
It is noted that in the solar system, although the distance between the orbits of two neighboring planets is affected by the Hill sphere, the distance is much larger than the Hill radius of the planets. And, the factual distance of the neighboring orbits can be described with the Titius-Bode law. So, it could be concluded that the distance between two neighboring arms in a galaxy is much larger than that obtained from the Hill sphere.

2.3. The Mass and Position of Black Hole B

Assuming that the black hole B is orbiting around Sgr A* and that the Sgr A* is with the mass of ~ 1 × 10 11 M S u n [21]. The Hill radius of B is r = d m B / 3 M S g r A * 3 . It is known that the length of the bar of our milky way is almost 20,000 lightyears, the largest thickness is 10,000 lightyears. Under the condition that the thickness is determined with the radius of the stars orbiting around the Sgr A*, it could be concluded that the distance between Sgr A* and a’ is less than 5,000 lightyears. For the same reason, the distance between B and b’ can be observed. Here, for the convenience, we assume that Bb’=1,500 lightyears. From the Hill radius, it could be concluded that m B ~ 1 30 M S g r A * . And, the distance between B and Sgr A* should be d ~ 20,000 − 5,000 − 1,500 = 13,500 l y . If Bb’=250 ly, it could be concluded that m B ~ 1 72,000 M S g r A * . From Figure 1, it could be guessed that the radius of the orbit of the stars around B is almost 250 ~ 2,500   l y . Therefore, the mass of B should be in the range of 10 − 2 ~ 10 − 5 M S g r A * . This is only a conclusion based on the assuming condition. To accurately know the mass and position of B, the radius of the orbits around B and Sgr A* need be accurately measured.
Hill sphere was well studied and applied in the solar system and other star-planet system. But, it has not been considered in studying the galaxy. Here, we try to apply it to understand the orbit in the galaxy. And, we think, the motion and structure of a galaxy could not be understood as the Hill sphere has not been considered.

3. Discussion

The Newtonian theory of orbit is such a theory that first let human be able to well understand and describe the orbit in the solar system and to invent the artificial satellite and other spacecraft. Because of the great development of the technology for astronomical observation, now, the motion and structure of a galaxy has been completely and deeply observed as shown in Figure 1. The astronomy was developed from solar system time into galactic time. But, the Newtonian theory of gravity is misled by the Poincaré’s equation for Three-body problem and the Poisson equation. The Poincaré’s equation for Three-body problem was discussed in detailed in our previous work. For the convenience of the readers, we copy our previous sentence here [22]:
Newton established the theory of orbit in 1660s. But, Newton’s theory has not been completely understood till now. As soon as comparing Poincaré’s equation of Three-body problem with Newtonian orbital perturbation theory, we shall know what is the problem in current understanding about Newtonian theory of gravity. The Sun-Earth-Moon system is the oldest Three-Body problem. It is clear, the orbits about it was well resolved by Newton. But, there is a famous old problems: calculating with  F = G M m R 2 , the attractive force of the Sun on the Moon is almost 2.2 times that of the Earth, but the orbit of the Moon around the Earth cannot be broken off by the Sun. It is clear, as Poincaré’s equation for Three-body problem is applied on the solar system, the orbits in it should be broken off in a short time. We think, this is the crucial evidence to show that the Poincaré’s equation for Three-body problem is wrong. And, the triple star system and multiple star systems, including Six-star system, were observed. The orbit in these systems are stable and certain.
The Poincaré’s equation for Three-body problem is very strange. First, no orbit of the celestial body is chaotic. A broken orbit also is predictable. So, Poincaré’s equation cannot be related with any real orbit. Second, the orbits of the typical Three-body system, such as the Sun-Earth-Moon system and Sun-Pluto-Charon system, are stable. Poincaré’s equation is invalid to understand these orbits. Third, Poincaré’s equation is invalid to design an artificial orbit. It is very clear, the Poincaré’s equation is nonsense in understanding any real orbit. Additionally, the relationship between the Poincaré’s equation and other theory is very weak. If there was not Poincaré’s equation, the celestial dynamics could not be affected. But, very unfortunately, Poincaré’s equation is the mainstream understanding about Newtonian theory of gravity. It results in that, the current theory of orbit about the galaxy is questioned.
Here, we shall discuss the Poisson equation. 1) The Poisson equation is usually used to calculated the galactic rotation curve [23,24]. But, the new observations [10,11,12,17,21,25,26,27,28,29,30,31,32,33,34,35,36] showed that the traditional galactic rotation curve originally presented by Babcock, Oort and Rubin from 1939-1980[23,24] is questioned. And, it is shown that, in theory, the traditional galactic rotation curve cannot be obtained from the Poisson equation [37,38]. 2) No evidence showed that Poisson equation is valid to understand any celestial orbit. Just as Poincaré’s equation, as the Poisson equation is used to describe the orbits in the N-body system (such as 6-body syatem), these orbits should be chaotic. Therefore, the Poisson equation is just that the Poincaré’s equation for Three-body is applied on the N-body system. 3) It is easy to know that the Poisson equation is invalid to the orbits in N-body system. It is clear, the total mass M t o t a l = M s u n + m e a r t h is nonsense to the orbit of the Moon around the Earth. Therefore, the Newtonian theory of gravity is the only theory that is valid to understand the orbits in a galaxy. Here, by giving up the Poisson equation, we had an initial try to understand the motion and structure of our Milky Way with Newtonian theory of orbit.

4. Conclusion

The “x-shaped structure” and peanut shape of the bar very strongly implies that there should be two supermassive black holes in the bar of our Milky Way. The “x-shaped structure” is an important line to detect another black hole, i.e., the another black hole is at another side of the “x”. In addition, the another black hole could be more easily detected in the weak bar.
In the Newtonian theory of orbit, only the supermassive black holes with the larger mass is the center of a galaxy. Here, we call it the center black hole. The one with less mass is only a satellite of the center black holes, just as a general star with an orbit around the center black holes [22]. And, the Circular Velocity Curve of the Milky Way is only determined with the mass of the center black hole [21].
If the mass of Sgr A* is with the mass of ~ 4.3 × 10 6 M S u n as current thought [6], it could be concluded that B is the center black holes with the mass of ~ 1 × 10 11 M S u n [21]. And, from the Hill sphere we know, the distance between the two black holes is ~ 10,000 l y .

References

  1. Oort J. H., Kerr F. J. & Westerhout G. 1958, The galactic system as a spiral nebula (Council Note), MNRAS, 118, 379.
  2. Georgelin Y. M. & Georgelin Y. P. 1976, The spiral structure of our Galaxy determined from H II regions, A&A, 49, 57.
  3. Oort, J. H., & Rougoor, G. W. 1959, The interstellar gas in the central part of the galaxy, AJ, 64, 130.
  4. Rougoor G. W. & Oort J. H. 1960, Distribution and Motion of Interstellar Hydrogen in the Galactic System with Particular Reference to the Region Within 3 Kiloparsecs of the Center, Proceedings of the National Academy of Science, 46, 1.
  5. de Vaucouleurs G. 1964, in IAU Symposium, Vol. 20, The Galaxy and the Magellanic Clouds, ed. F. J. Kerr, 195.
  6. Genzel R., Eisenhauer F. and Gillessen S., 2010, The Galactic Center Massive Black Hole and Nuclear Star Cluster, Reviews of Modern Physics, 82.4, 3121-3195.
  7. Issaoun S., Johnson M. D., Blackburn L., Brinkerink C. D., et al., 2019, The Size, Shape, and Scattering of Sagittarius A* at 86 GHz: First VLBI with ALMA, Astrophysical Journal, 871, 1. F.
  8. Shen J. and Zheng X., 2020, The bar and spiral arms in the Milky Way: structure and kinematics, RAA, 20, 159.
  9. Busetti F., Beust H. and Harley C., 2018, Stability of planets in triple star systems, A&A619, A91.
  10. Zhou Y., et al., The Circular Velocity Curve of the Milky Way from 5–25 kpc Using Luminous Red Giant Branch Stars, ApJ, 946, 73 (2023). [CrossRef]
  11. Jiao Y., Hammer F., Wang H., Wang J., et al., 2023, Detection of the Keplerian decline in the Milky Way rotation curve, A&A678, A208.
  12. Eilers A., Hogg D. W., Rix H. and Ness M. K., 2019, The Circular Velocity Curve of the Milky Way from 5 to 25 kpc, ApJ, 871 120. [CrossRef]
  13. Yu S. and Ho L. C. 2020, The Statistical Properties of Spiral Arms in Nearby Disk Galaxies, ApJ, 900, 150. [CrossRef]
  14. Mondal D., Chattopadhyay T., 2021, Role of galactic bars in the formation of spiral arms: a study through orbital and escape dynamics—I. Celest Mech Dyn Astr 133, 43.
  15. Lindblad P. A. B. & Kristen H. 1996, Hydrodynamical simulations of the barred spiral galaxy NGC 1300. Dynamical interpretation of observations, Astronomy and Astrophysics, 313, 733-749.
  16. Yoon Y. & Lee M. I, et al. 2019, Observational evidence for bar formation in disk galaxies via cluster–cluster interaction. Nat Astron 3, 844–850.
  17. Roshan M., Ghafourian N., Kashfi T., Banik I., Haslbauer M., et al. 2021, Fast galaxy bars continue to challenge standard cosmology, Monthly Notices of the Royal Astronomical Society, 508(1) 926–939. [CrossRef]
  18. Mondal D., Chattopadhyay T. 2021, Role of galactic bars in the formation of spiral arms: a study through orbital and escape dynamics—I. Celest Mech Dyn Astr 133, 43.
  19. Davis B. L., et al., 2012, Measurement of Galactic Logarithmic Spiral Arm Pitch Angle Using Two-Dimensional Fast Fourier Transform Decomposition, ApJS, 199, 33.
  20. Dolores Mata-Chávez M., et al., 2019, On the Dynamical Relevance of Galaxy Spiral Arm Evolution. I. Arm Density Structure, ApJ, 876, 6.
  21. Zhu Y., The Mass of the Center of the Milky Way Revalued from the Fastest Orbits around the Center and the Circular Velocity Curve of the Milky Way[v3] | Preprints.org.
  22. Zhu Y., Interaction of Gravitational Field and Orbit in Sun-planet-moon system[v1] | Preprints. [CrossRef]
  23. Yoon Y., Park C., Chung H. and Zhang K. 2021, Rotation Curves of Galaxies and Their Dependence on Morphology and Stellar Mass, ApJ, 922, 249.
  24. McGaugh S. S., Lelli F. and Schombert J.M. 2016, Radial Acceleration Relation in Rotationally Supported Galaxies, Physical Review Letters, 117, 201101.
  25. Peißker F., Eckart A. and Parsa M. 2020, S62 on a 9.9 yr Orbit around SgrA*, ApJ, 889, 61.
  26. Peißker F., Eckart A., Zajaček M. and Britzen S., 2022, Observation of S4716- A star with a 4 year orbit around Sgr A*, ApJ, 933, 49.
  27. Peißker F., Eckart A., Zajaček M., Britzen S., Ali B. and Parsa M. 2020, S62 and S4711: Indications of a Population of Faint Fast-moving Stars inside the S2 Orbit—S4711 on a 7.6yr Orbit around Sgr A*, ApJ, 899, 50.
  28. Peißker F., Eckart A. and Ali B. 2021, Observation of the Apoapsis of S62 in 2019 with NIRC2 and SINFONI, APJ, 918, 25.
  29. GRAVITY Collaboration, et al., 2022, Deep images of the Galactic center with GRAVITY, A&A 657, A82.
  30. GRAVITY Collaboration, et al., 2022, Mass distribution in the Galactic Center based on interferometric astrometry of multiple stellar orbits, A&A 657, L12.
  31. Mróz P., Udalski A., Skowron D. M., Skowron J., et al., 2019, Rotation Curve of the Milky Way from Classical Cepheids, ApJL 870, L10.
  32. Wang H., ChrobákováŽ., López-Corredoira M. and Labini F. S., 2023, Mapping the Milky Way Disk with Gaia DR3: 3D Extended Kinematic Maps and Rotation Curve to ≈30 kpc, ApJ, 942, 12.
  33. Ou X., Eilers A., Necib L. and Frebel A. 2024, The dark matter profile of the Milky Way inferred from its circular velocity curve, MNRAS 528, 693–710.
  34. Fragkoudi F., Grand R. J. J., Pakmor R., Springel V., et al., 2021, Revisiting the tension between fast bars and the CDM paradigm, A&A650, L16.
  35. Corsini E. M., Aguerri J. A. L., Debattista V. P., Pizzella A., Barazza F. D. and Jerjen H. 2007, The Bar Pattern Speed of Dwarf Galaxy NGC 4431, ApJ, 659, L121.
  36. Aguerri J. A. L., Méndez-Abreu J., Falcón-Barroso J.,. Amorin A, et al., 2015, Bar pattern speeds in CALIFA galaxies I. Fast bars across the Hubble sequence, A&A,576, A102.
  37. James Q. F. and Gallo C. F. 2011, Modeling the Newtonian dynamics for rotation curve analysis of thin-disk galaxies, Res. Astron. Astrophys., 11, 1429.
  38. Hofmeister A. M. & Criss R. E., 2020, Debated Models for Galactic Rotation Curves: A Review and Mathematical Assessment, Galaxies, 8, 47.
Preprints 110227 g002
Figure 2. The bar with two black holes A* and B. The green circles are the orbits of stars around A* and B. The two obits appear a peanut. And, the “x-shaped structure” is between the two orbits. The orbits of the stars around both the two black holes is in red. This Figure is inspired by the Figure 1 in [9].
Figure 2. The bar with two black holes A* and B. The green circles are the orbits of stars around A* and B. The two obits appear a peanut. And, the “x-shaped structure” is between the two orbits. The orbits of the stars around both the two black holes is in red. This Figure is inspired by the Figure 1 in [9].
Preprints 110227 g002
Preprints 110227 g003
Figure 3. The arm produced by the orbit perturbation. The orbit ab is being perturbed by the star orbiting around both the black holes A* and B. From Hill sphere r = d m / 3 M 3 , we know, for a same star, the Hill radius of this star at point b’ is larger than that at a’ for that d b ' = b ' A * > a ' A * = d a ' , where point a’ and b’ are at the orbit around both the two black holes. It results in that the distance b b ' > a ' a .
Figure 3. The arm produced by the orbit perturbation. The orbit ab is being perturbed by the star orbiting around both the black holes A* and B. From Hill sphere r = d m / 3 M 3 , we know, for a same star, the Hill radius of this star at point b’ is larger than that at a’ for that d b ' = b ' A * > a ' A * = d a ' , where point a’ and b’ are at the orbit around both the two black holes. It results in that the distance b b ' > a ' a .
Preprints 110227 g003
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

225

Views

377

Comments

0

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

Email

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated