Submitted:
07 June 2024
Posted:
10 June 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Materials and Methods
2.1. The Construction of the Indicator System
| Primary Indicators | Secondary Indicators | Tertiary Indicators | Unit | Attribute |
|---|---|---|---|---|
| Research Inputs(A1) | Personnel(B1) | Proportion of Faculty with Doctoral Degrees(C1) | % | + |
| Number of Full Professors among Full-time Faculty(C2) | Person | + | ||
| University R&D Personnel(C3) | Person | + | ||
| Financial Resources(B2) | University R&D Funding(C4) | Ten Thousand Yuan | + | |
| Assets of Teaching and Research Instruments and Equipment(C5) | Ten Thousand Yuan | + | ||
| Time(B3) | Full-time Equivalent of University R&D Personnel(C6) | Person-Year | + | |
| Research Output(A2) | Domestic Research Output(B4) | Publication of Scientific Papers(C7) | Articles | + |
| Publication of Technological Works(C8) | Projects | + | ||
| Number of Patent Applications(C9) | Projects | + | ||
| Income from Patent Ownership Transfer and Licensing(C10) | Articles | + | ||
| Number of R&D Projects in Higher Education Institutions(C11) | Categories | + | ||
| Establishing national or industry standard figures.(C12) | Categories | + | ||
| International Research Output(B5) | Number of Scientific Papers Published Abroad(C13) | Articles | + | |
| Inclusion of Chinese Scientific Papers (SCI) in Major Foreign Indexing Tools(C14) | Articles | + | ||
| Inclusion of Chinese Scientific Papers in Major Foreign Indexing Tools (EI)(C15) | Articles | + | ||
| Inclusion of Chinese Scientific Papers in Major Foreign Indexing Tools (CPCI-S)(C16) | Articles | + |
2.2. Data
2.3. Model
2.3.1. BCC-DEA Model
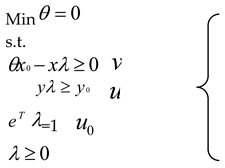

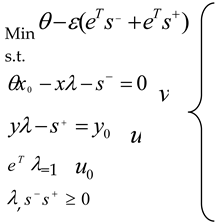
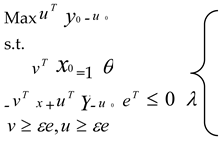
2.3.2. Malmquist-DEA Model
2.3.3. Calculation of Redundancy Ratio
3. Results
3.1. Statistical Analysis
3.2. Outcomes of BCC-DEA Model
3.2.1. The Overall Change in Research Efficiency of Universities in China from 2012 to 2022
3.2.2. Research Technical (Overall) Efficiency Values
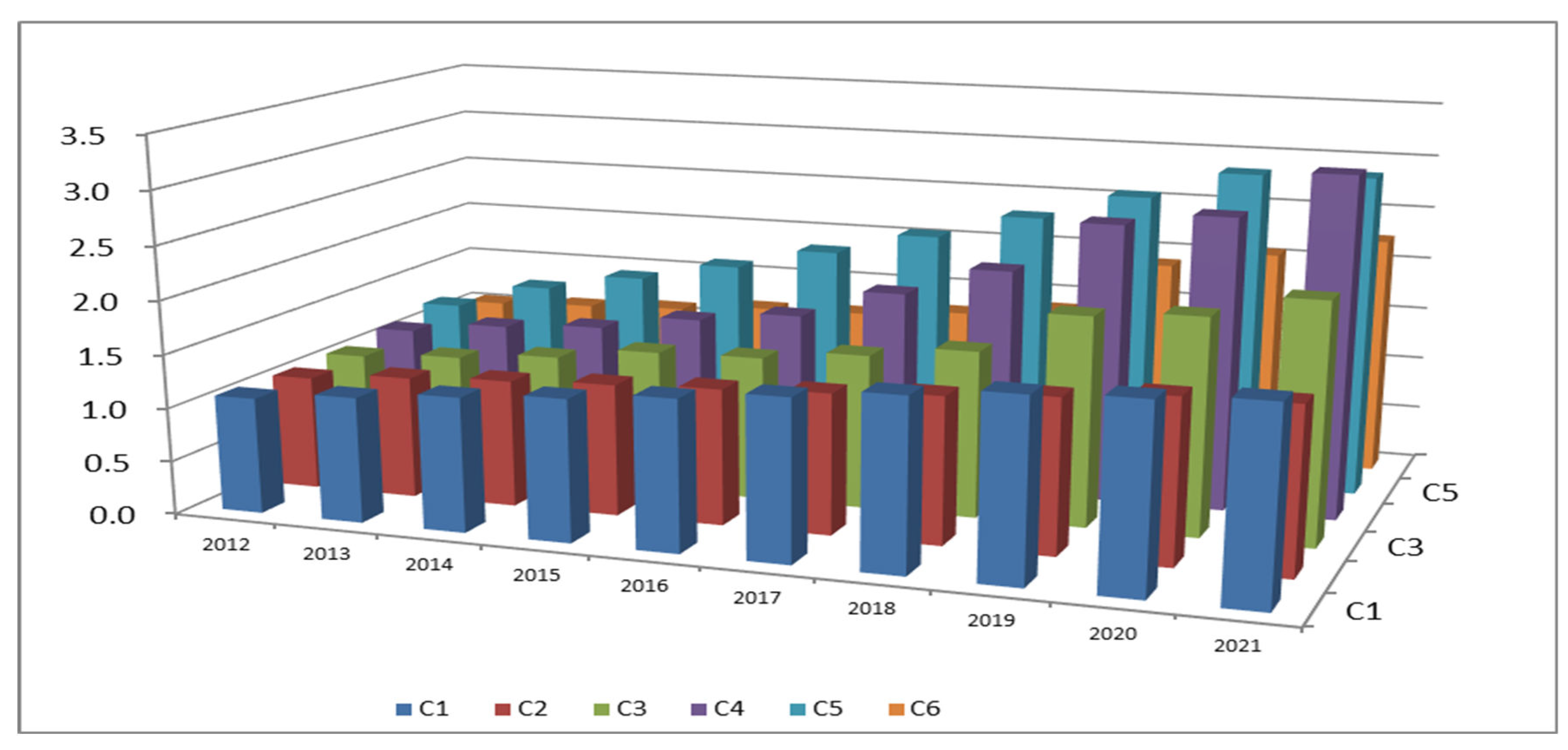
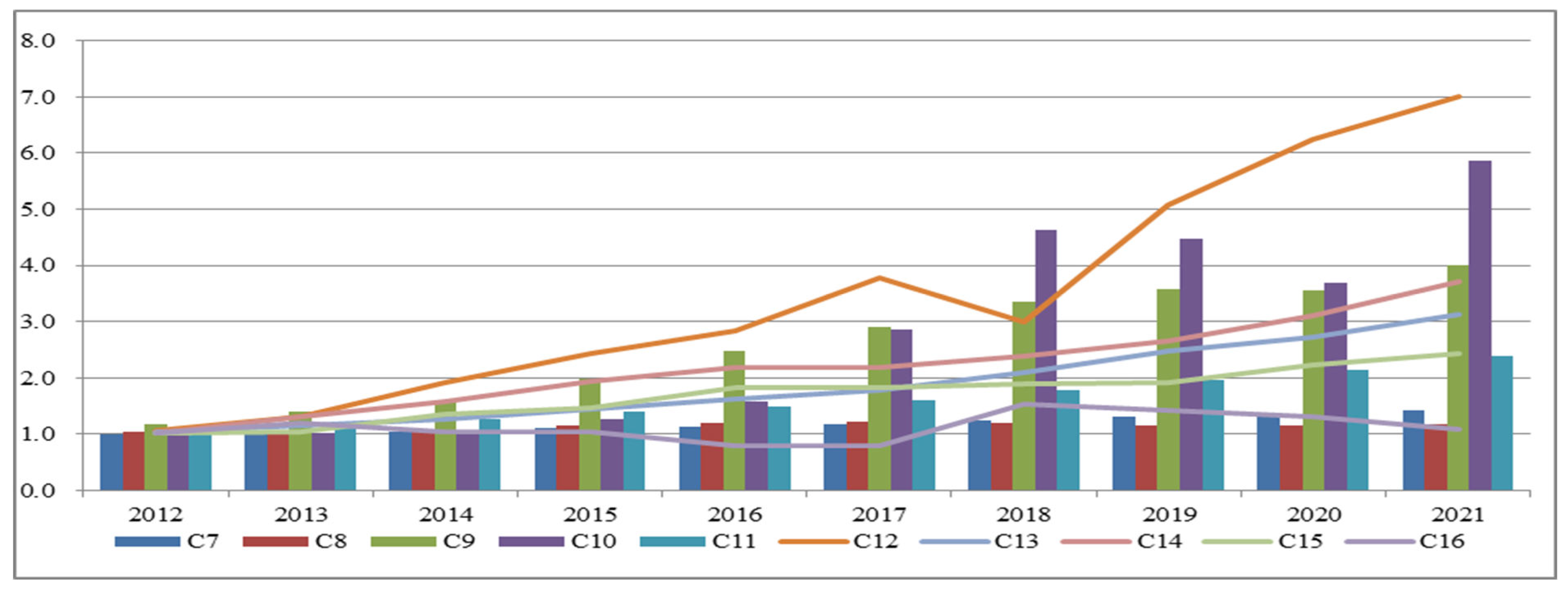
3.2.3. Each Indicators of Research Efficiency
3.3. Results of Malmquist Index
- (1)
- Overall efficiency change analysis: Table 4 and Table 5 reveal that from 2012 to 2022, the research efficiency of ordinary colleges and universities across the 31 provinces and cities of China experienced a fluctuating but upward trend. The mean value of research efficiency Malmquist productivity was 1.285, with an average annual increase of 28.5%. Moreover, the Malmquist productivity index for each year during the study period was greater than 1, indicating a steady rise in research efficiency.
4. Discussion
| provinces | C1 | C2 | C3 | C4 | C5 | C6 | C1 | C2 | C3 | C4 | C5 | C6 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Redundant investment amount | redundant investment ratio | |||||||||||
| Tianjin | 10.895 | 124.427 | 0.000 | 202130.830 | 0.000 | 2.219 | 31.459 | 2.621 | 0.000 | 43.522 | 0.000 | 0.028 |
| Hebei | 0.000 | 3599.567 | 846.539 | 11132.614 | 164086.840 | 567.348 | 0.000 | 36.071 | 8.988 | 16.008 | 11.804 | 9.041 |
| Shanxi | 0.000 | 0.000 | 2691.679 | 0.000 | 255016.610 | 1795.386 | 0.000 | 0.000 | 38.657 | 0.000 | 31.598 | 38.685 |
| Inner Mongolia | 0.272 | 426.756 | 312.241 | 0.000 | 251287.300 | 207.908 | 2.188 | 15.535 | 8.476 | 0.000 | 35.088 | 8.472 |
| Jilin | 5.294 | 346.041 | 8944.117 | 0.000 | 0.000 | 5961.572 | 22.528 | 5.448 | 50.180 | 0.000 | 0.000 | 50.186 |
| Heilongjiang | 0.000 | 613.122 | 4514.738 | 67646.649 | 0.000 | 3008.593 | 0.000 | 8.134 | 24.771 | 19.504 | 0.000 | 24.770 |
| Hubei | 0.000 | 1226.526 | 0.000 | 30252.130 | 0.000 | 0.397 | 0.000 | 11.196 | 0.000 | 6.823 | 0.000 | 0.004 |
| Ningxia | 2.198 | 621.337 | 0.371 | 0.000 | 2688.096 | 0.000 | 16.314 | 45.586 | 0.025 | 0.000 | 1.275 | 0000 |
| Mean | 2.332 | 869.722 | 2163.711 | 38895.278 | 84134.856 | 1442.928 | 9.061 | 15.574 | 16.387 | 10.732 | 9.971 | 16.398 |
| Provinces | C7 | C8 | C9 | C10 | C11 | C12 | C13 | C14 | C15 | C16 |
|---|---|---|---|---|---|---|---|---|---|---|
| Tianjin | 1900.27 | 82.93 | 265.04 | 0.00 | 0.00 | 79.87 | 1349.35 | 1068.23 | 0.00 | 0.00 |
| Hebei | 827.01 | 30.12 | 313.58 | 894.47 | 823.18 | 80.63 | 585.75 | 2820.76 | 1565.16 | 0.00 |
| Shanxi | 504.56 | 49.10 | 0.00 | 775.13 | 0.00 | 0.00 | 590.69 | 503.55 | 0.00 | 263.86 |
| Inner Mongolia | 346.02 | 2.37 | 191.60 | 24.61 | 0.00 | 0.00 | 174.50 | 169.13 | 103.30 | 0.00 |
| Jilin | 3890.13 | 287.87 | 940.01 | 1813.62 | 0.00 | 163.47 | 896.70 | 82.56 | 0.00 | 0.00 |
| Heilongjiang | 2679.90 | 105.53 | 921.35 | 1712.15 | 4727.16 | 99.37 | 1330.86 | 800.36 | 0.00 | 0.00 |
| Hubei | 4455.19 | 214.45 | 2028.98 | 2335.00 | 0.00 | 179.07 | 1380.28 | 998.62 | 2634.34 | 0.00 |
| Ningxia | 577.06 | 0.00 | 192.28 | 0.00 | 0.00 | 3.96 | 159.43 | 296.20 | 133.46 | 9.03 |
| Mean | 1897.52 | 96.55 | 606.61 | 944.37 | 693.79 | 75.80 | 808.44 | 842.43 | 554.53 | 34.11 |
5. Conclusions
| Results of the BCC-DEA Model Run | Efficiency type | provinces | ||
| Composite Efficiency | Efficient Regions | Mean = 1 | (16 provinces) Fujian, Beijing, Shanghai, Jiangsu, Zhejiang, Shandong, Hunan, Guangdong, Guangxi, Hainan, Guizhou, Yunnan, Shaanxi, Gansu, Qinghai, Xinjiang | |
| Inefficient Regions | 1>Mean >0.98 | (5 provinces) Henan, Ningxia, Anhui, Chongqing, and Hubei | ||
| Mean <0.98 | (10 provinces) Jilin, Jiangxi, Tianjin, Liaoning, Hebei, Tibet, Shanxi, Sichuan, Heilongjiang, and Inner Mongolia | |||
| Pure Technical Efficiency | Efficient Regions | Mean =1 | (2 provinces) Beijing, Liaoning、 | |
| Inefficient Regions | Mean <1 | (9 provinces) Tianjin, Shanxi, Inner Mongolia, Jilin, Heilongjiang, Hubei, Ningxia, Hebei, Chongqing | ||
| Scale Efficiency | Efficient Regions | Constant Returns to Scale | (13 provinces) Beijing, Shanghai, Jiangsu, Zhejiang, Fujian, Hunan, Guangdong, Guangxi, Hainan, Yunnan, Gansu, Qinghai, Xinjiang | |
| Inefficient Regions | Decreasing Returns to Scale | (2 provinces) Hubei, Ningxia | ||
| Increasing Returns to Scale | (16 provinces) Tianjin, Shanxi, Inner Mongolia, Jilin, Heilongjiang, Chongqing, Anhui, Jiangxi, Henan, Sichuan, Shandong, Guizhou, Shaanxi, Hebei, Liaoning, Tibet | |||
| Results of the Malmquist Model | Regions with Balanced Input-Output Ratio | (23 provinces) Beijing, Liaoning, Shanghai, Jiangsu, Zhejiang, Anhui, Fujian, Jiangxi, Shandong, Henan, Hunan, Guangdong, Guangxi, Hainan, Chongqing, Sichuan, Guizhou, Yunnan, Shaanxi, Gansu, Qinghai, Xinjiang, Tibet | ||
| Regions with Input Redundancy | (8 provinces) Tianjin, Hebei, Shanxi, Inner Mongolia, Jilin, Heilongjiang, Hubei, Ningxia | |||
| Regions with Output Shortages | (8 provinces) Tianjin, Hebei, Shanxi, Inner Mongolia, Jilin, Heilongjiang, Hubei, Ningxia | |||
| University Types/Indicators | Talent Cultivation | Scientific Research | Social Services | Cultural Heritage and Innovation | International Cooperation and Exchange | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Highlight Points | Evaluation Criteria | Highlight Points |
Evaluation Criteria | Highlight Points | Evaluation Criteria | Highlight Points |
Evaluation Criteria | Highlight Points |
Evaluation Criteria | |
| Theoretical Universities | Scientific Thinking | Reflection | Theoretical Innovation | "Fund Projects" and "Papers" | Thought Leadership | Academic Reputation | Seeking Truth |
Scientific Influence | Integration | Collaboration Depth |
| Engineering Universities | Integrated Practice | Design Implementation | Industry Leadership | "Fund Projects" and "Industry Major Projects" | Technical Support | Industry Position | Seeking Practicality | Engineering and Technological Influence | Distinctive Features | Collaboration Projects with Similar Universities |
| Applied Universities | Knowledge Application | Knowledge Mastery | Local Involvement | Lateral Funding |
Technical Services and Promotion Efforts | "Local Reputation" and "Lateral Funding" | Practicality | Popularity Among Graduates | Participation | Exchange |
| Vocational Universities | Technical Skills | Hands-on Practice | University-Enterprise Collaboration | Collaborative Funding | "Corporate Reputation" and "Student Internships" | Craftsmanship | Pursuit of Excellence | Understanding | Whether there's Mutual Learning Mode | |
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abbott, M., & Doucouliagos, C.(2003). The efficiency of Australian universities: a data envelopment analysis. Economics of Education Review, 32(1),89-97. [CrossRef]
- Adhi, I. H., Diana, S., Muhammad, A. I. M., & Kurnia, A.(2024). Efficiency of research in various fields: Evidence from Indonesia. Research Evaluation, 2024, rvae001. [CrossRef]
- Antreas, D. A., & Estelle, S.(1997). Assessing the Comparative Efficiency of Higher Education Institutions in the UK by the Means of Data Envelopment Analysis.Education Economics,5(2),117-134.
- Bhutto, A., Rashdi, P. I., Abro, Q. M.(2012).Indicators for science and technology policy in Pakistan: Entering the science, technology and innovation paradigm. Science and Public Policy,39(1):1-12. [CrossRef]
- Cai, S. F., Zhang, G. Q., &Wang, W.(2023). Evaluation of Innovation Performance of University Knowledge Economic Circles Based on Data Envelopment Analysis. Journal of Tongji University (Natural Science Edition),51(05), 682-686.
- Charnes, A., Clark, C. T. Cooper, W. W. & Golany, B. (1984)..A developmental study of data envelopment analysis in measuring the efficiency of maintenance units in the U.S. air forces. Annals of Operations Research,2(1),95-112. [CrossRef]
- Charnes, A, Cooper, W.W., Golany, B., Seiford, L., & Stutz, J.(1985). Foundations of data envelopment analysis for Pareto-Koopmans efficient empirical production functions. Journal of Econometrics, 30(1-2): 81-107. [CrossRef]
- Charnes, A., Cooper, W.W., & Rhodes, E.(1978). Measuring the efficiency of decision making units. European Journal of Operational Research,,2(6):429-444. [CrossRef]
- Dagum, C.(1997). A new approach to the decomposition of the Gini income inequality ratio. Empirical Economics, 22(4), 515-531. [CrossRef]
- Griliches, Z. (1979). Issues in Assessing the Contribution of Research and Development to Productivity Growth. The Bell Journal of Economics,1979,10(1):92-106. [CrossRef]
- Li, K., & Fan, Y. J. (2022). Evaluation of Research Efficiency of First-Class Universities under the "Double First-Class" Goal. Research Management, 43(09), 41-47. [CrossRef]
- Jiang, H., Yang, Y., & Wang, P. J. (2022). Research on Evaluation of Research Output of Universities Based on DEA and SFA Efficiency Value Method - Taking Analysis of Data from 52 "Double First-Class" Universities as an Example. Modern Education Management, (04), 40-49 . [CrossRef]
- Li, Y., & Zhang, P.(2022). Research on Efficiency of Scientific and Technological Innovation in Production, Learning and Research Based on Network DEA and Shapley Value. Research in Science and Technology Management, 42(05), 93-103.
- Liu, C. B., Dai, W., Yu, L. A., & Yang, J. A.(2022). Research on Prediction of Evaluation of University Scientific Research Platform Based on GCA-DEA-MSVC Method. Chinese Journal of Management Science, 2022,30(03): 240-247. [CrossRef]
- Liu, Z. W., & Liu, H. M.(2023). Research on Enhancing the Performance Evaluation of Regional Scientific and Technological Resources in Universities with "Double High" Construction Schools: Based on the DEA-Malmquist Model. Science and Technology Management Research, 43(09), 82-89.
- Ma, L.(2021) Promoting Differentiated Innovation in the Evaluation of Universities in the New Era. Ethnic Education Research, 32(06), 5-10. [CrossRef]
- Madria, W. F., Miguel, A. S., & Li, R. C.(2019). Quality-Oriented Network DEA Model for the Research Efficiency of Philippine Universities.International Conference on Industrial Engineering and Engineering Management, 596-600. [CrossRef]
- Nabil, A., Mehdi, R., & Norrin, H.(2020).Assessing the research efficiency of Canadian scholars in the management field: Evidence from the DEA and fsQCA. Journal of Business Research,115, 296-306. [CrossRef]
- Qi, T.(2023). Retrospective Study on the Research Efficiency of Various Types of Universities in China during the "Thirteenth Five-Year Plan" Period Based on Data Envelopment Analysis. Research in Science and Technology Management, 43(06), 114-122.
- Song, Z. Y., & Sun, B. C.(2022). Research on Input-Output Efficiency and Its Influencing Factors in Chinese Ordinary Universities: A Stochastic Frontier Analysis Based on Provincial Panel Data from 2009 to 2018. Journal of Lanzhou University (Social Sciences Edition), 50(06),128-137. [CrossRef]
- Valero, A., & Reenen, J. V.(2019). The Economic Impact of Universities: Evidence from Across the Globe.Economics of Education Review,68(1), 53-67. [CrossRef]
- Wang, X. Z., & Jiang, Z. H.(2019). Analysis of Innovation Efficiency and Environment of Universities in China: A Perspective of Value Types. Research Management,,40(10), 25-36. [CrossRef]
- Wang, Z., Lv, N. H., Wu, M. Y. (2023). Evaluation of Research Efficiency of Humanities and Social Sciences in "Double First-Class" Construction Universities Based on Three-Stage DEA. China's Higher Education of Science and Technology, Z1, 26-30. [CrossRef]
- Yang, M., Fei, X. Y., Wei, Y. Q., & Liang L. (2022).Two-Stage DEA Evaluation Method Based on Resource Sharing and Subsystem Interaction - Evaluation of Research Performance of "First-Class Universities" in China. Chinese Journal of Management Science, 30(02), 256-263. [CrossRef]
- Shi, Y. K., Wang, D. C., & Zhang, Z.M. (2022). Categorical Evaluation of Scientific Research Efficiency in Chinese Universities: Basic and Applied Research. Sustainability, 14(8), 4402. [CrossRef]
- Zhang, H. Q., & Shang, T. T.(2015). Comparative Analysis of Research and Innovation Efficiency in Universities: Based on Panel Data from 30 Provinces Nationwide. Research Management, 36(S1),181-186. [CrossRef]
- Zhang, X. M., & Zhao, G. D.(2023). Spatial-Temporal Pattern and Evolution of Efficiency in the Allocation of Graduate Education Resources in China - Supply-Side Analysis Based on Provincial Panel Data from 2003 to 2018. Journal of East China Normal University (Educational Sciences Edition),,41(06), 59-77. [CrossRef]
- Zhou, J. X., & Gao, S. H.(2022). Evaluation of Scientific and Technological Innovation Efficiency in the Construction of First-Class Universities - A Dual Perspective Based on School Types and Regional Differences. China's Higher Education of Science and Technology, (09), 8-15. [CrossRef]
| Type of Efficiency | Mean and Number of Provinces | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 | Mean |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Technical Efficiency (TE) | Mean | 0.97 | 0.97 | 0.97 | 0.98 | 0.98 | 0.99 | 0.98 | 0.98 | 0.99 | 0.99 | 0.99 | 0.98 |
| TE=1 | 24.00 | 23.00 | 26.00 | 24.00 | 23.00 | 29.00 | 27.00 | 25.00 | 28.00 | 28.00 | 28.00 | 25.91 | |
| Pure Technical Efficiency (PTE) | Mean | 0.99 | 0.98 | 1.00 | 0.99 | 0.98 | 1.00 | 1.00 | 0.98 | 1.00 | 0.99 | 1.00 | 0.99 |
| PTE=1 | 28.00 | 25.00 | 29.00 | 25.00 | 24.00 | 29.00 | 30.00 | 27.00 | 28.00 | 29.00 | 29.00 | 27.55 | |
| Scale Efficiency (SE) | Mean | 0.97 | 0.99 | 0.97 | 0.99 | 0.99 | 0.99 | 0.98 | 0.99 | 0.99 | 1.00 | 1.00 | 0.99 |
| SE=1 | 24.00 | 23.00 | 26.00 | 24.00 | 23.00 | 29.00 | 27.00 | 25.00 | 28.00 | 28.00 | 28.00 | 25.91 | |
| Scale Returns | Decreasing | 0.00 | 1.00 | 0.00 | 1.00 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.27 |
| Constant | 24.00 | 23.00 | 26.00 | 24.00 | 23.00 | 29.00 | 27.00 | 25.00 | 28.00 | 28.00 | 28.00 | 25.91 | |
| Increasing | 7.00 | 7.00 | 5.00 | 6.00 | 7.00 | 2.00 | 4.00 | 6.00 | 3.00 | 3.00 | 3.00 | 4.82 |
| Provinces | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 | Mean |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fujian | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Beijing | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Shanghai | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Jiangsu | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Zhejiang | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Shandong | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Hunan | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Guangdong | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Guangxi | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Hainan | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Guizhou | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Yunnan | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Shaanxi | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Gansu | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Qinghai | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Xinjiang | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Henan | 0.940 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.995 |
| Ningxia | 1.000 | 1.000 | 1.000 | 1.000 | 0.924 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.993 |
| Anhui | 0.953 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.988 | 0.983 | 1.000 | 0.980 | 0.941 | 0.986 |
| Chongqing | 0.952 | 0.914 | 1.000 | 0.976 | 0.997 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.985 |
| Hubei | 1.000 | 0.985 | 1.000 | 0.978 | 0.973 | 1.000 | 1.000 | 0.899 | 1.000 | 1.000 | 1.000 | 0.985 |
| Jilin | 1.000 | 0.900 | 1.000 | 0.864 | 0.957 | 1.000 | 1.000 | 0.899 | 1.000 | 1.000 | 1.000 | 0.975 |
| Jiangxi | 0.955 | 0.928 | 0.897 | 1.000 | 1.000 | 1.000 | 0.894 | 1.000 | 1.000 | 1.000 | 1.000 | 0.970 |
| Tianjin | 1.000 | 0.871 | 1.000 | 0.931 | 0.924 | 1.000 | 1.000 | 0.875 | 1.000 | 1.000 | 1.000 | 0.964 |
| Liaoning | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.859 | 0.882 | 0.876 | 0.953 | 0.961 |
| Hebei | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.818 | 0.774 | 1.000 | 1.000 | 1.000 | 0.857 | 0.950 |
| Tibet | 1.000 | 1.000 | 0.631 | 1.000 | 1.000 | 1.000 | 1.000 | 0.960 | 0.857 | 1.000 | 1.000 | 0.950 |
| Shanxi | 0.941 | 0.865 | 0.794 | 0.930 | 0.900 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.948 |
| Sichuan | 0.780 | 1.000 | 0.944 | 1.000 | 1.000 | 0.794 | 0.831 | 1.000 | 1.000 | 1.000 | 1.000 | 0.941 |
| Heilongjiang | 1.000 | 0.887 | 1.000 | 0.804 | 0.693 | 1.000 | 1.000 | 0.672 | 0.954 | 0.803 | 1.000 | 0.892 |
| Inner Mongolia | 0.457 | 0.709 | 0.834 | 0.864 | 0.926 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.890 |
| Mean | 0.967 | 0.970 | 0.971 | 0.979 | 0.977 | 0.987 | 0.983 | 0.976 | 0.990 | 0.989 | 0.992 | 0.980 |
| Type of Efficiency | 2012 | 2013 | 2014 | 2015 |
|---|---|---|---|---|
| Technical Efficiency < 1 | seven provinces: Shanxi (0.941), Inner Mongolia (0.457), Anhui (0.953), Jiangxi (0.955), Henan (0.940), Chongqing (0.952), and Sichuan (0.780). | eight provinces: Tianjin (0.871), Shanxi (0.865), Inner Mongolia (0.709), Jilin (0.901), Heilongjiang (0.887), Jiangxi (0.928), Hubei (0.985), and Chongqing (0.914). | five provinces: Inner Mongolia (0.794), Liaoning (0.834), Shandong (0.897), Guizhou (0.944), and Shaanxi (0.631). | seven provinces: Tianjin (0.931), Shanxi (0.930), Inner Mongolia (0.864), Jilin (0.864), Heilongjiang (0.804), Hubei (0.978), and Chongqing (0.976). |
| Pure Technical Efficiency < 1 | three provinces: Shanxi (0.988), Inner Mongolia (0.768), and Chongqing (0.969). | six provinces: Tianjin (0.887), Inner Mongolia (0.858), Jilin (0.906), Heilongjiang (0.894), Hubei (0.987), and Chongqing (0.929). | two provinces: Inner Mongolia (0.947) and Liaoning (0.941). | six provinces: Tianjin (0.945), Inner Mongolia (0.944), Jilin (0.879), Heilongjiang (0.835), Hubei (0.986), and Chongqing (0.999). |
| Scale Efficiency < 1 | seven provinces: Shanxi (0.953), Inner Mongolia (0.596), Anhui (0.953), Jiangxi (0.955), Henan (0.940), Chongqing (0.983), and Sichuan (0.780). | eight provinces: Tianjin (0.982), Shanxi (0.865), Inner Mongolia (0.826), Jilin (0.994), Heilongjiang (0.992), Jiangxi (0.928), Hubei (0.998), and Chongqing (0.984). | four provinces: Inner Mongolia (0.838), Liaoning (0.887), Shandong (0.897), and Guizhou (0.944). | seven provinces: Tianjin (0.985), Shanxi (0.930), Inner Mongolia (0.915), Jilin (0.983), Heilongjiang (0.963), Hubei (0.992), and Chongqing (0.977). |
| Decreasing Returns to Scale | - | one province: Hubei | - | one province: Hubei |
| Increasing Returns to Scale | Seven provinces: Shanxi, Inner Mongolia, Anhui, Jiangxi, Henan, Chongqing, Sichuan | Seven provinces: Tianjin, Shanxi, Inner Mongolia, Jilin, Heilongjiang, Jiangxi, Chongqing | five provinces: Inner Mongolia, Liaoning, Shandong, Guizhou, Shaanxi | six provinces: Tianjin, Shanxi, Inner Mongolia, Jilin, Heilongjiang, Chongqing |
| Type of Efficiency | 2016 | 2017 | 2018 | 2019 |
| Technical Efficiency < 1 | eight provinces: Tianjin (0.924), Shanxi (0.900), Inner Mongolia (0.926), Jilin (0.957), Heilongjiang (0.693), Hubei (0.973), Chongqing (0.997), and Ningxia (0.924). | Two provinces: Hebei (0.818), Sichuan (0.794) | Four provinces: Hebei (0.774), Anhui (0.988), Jiangxi (0.894), Sichuan (0.831) | Six provinces: Tianjin (0.875), Liaoning (0.859), Heilongjiang (0.672), Anhui (0.983), Hubei (0.899), Tibet (0.960) |
| Pure Technical Efficiency < 1 | Seven provinces: Tianjin (0.937), Shanxi (0.992), Inner Mongolia (0.929), Jilin (0.969), Heilongjiang (0.759), Hubei (0.978), Ningxia (0.947) | One province: Hebei (0.913) | One province: Hebei (0.913) | Four provinces: Tianjin (0.906), Liaoning (0.878), Heilongjiang (0.803), Hubei (0.930) |
| Scale Efficiency < 1 | Eight provinces: Tianjin, Shanxi, Inner Mongolia, Jilin, Heilongjiang, Hubei, Chongqing, Ningxia | Two provinces: Hebei (0.896), Sichuan (0.794) | Four provinces: Hebei (0.804), Anhui (0.988), Jiangxi (0.894), Sichuan (0.831) | Six provinces: Tianjin (0.966), Liaoning (0.978), Heilongjiang (0.837), Anhui (0.983), Hubei (0.967), Tibet (0.960) |
| Decreasing Returns to Scale | One province: Ningxia | - | - | - |
| Increasing Returns to Scale | Seven provinces: Tianjin, Shanxi, Inner Mongolia, Jilin, Heilongjiang, Hubei, Chongqing | Two provinces: Hebei, Sichuan | Four provinces: Hebei, Anhui, Jiangxi, Sichuan | Six provinces: Tianjin, Liaoning, Heilongjiang, Anhui, Hubei, Tibet |
| Type of Efficiency | 2020 | 2021 | 2022 | |
| Technical Efficiency < 1 | Three provinces: Liaoning (0.882), Heilongjiang (0.954), Tibet (0.857) | Three provinces: Liaoning (0.876), Heilongjiang (0.803), Anhui (0.980) | Three provinces: Hebei (0.857), Liaoning (0.953), Anhui (0.941) | - |
| Pure Technical Efficiency < 1 | Two provinces: Liaoning (0.924), Heilongjiang (0.969) | Two provinces: Liaoning (0.928), Heilongjiang (0.871) | Two provinces: Liaoning (0.965), Anhui (0.947) | - |
| Scale Efficiency < 1 | Three provinces: Liaoning (0.955), Heilongjiang (0.985), Tibet (0.857) | Three provinces: Liaoning (0.944), Heilongjiang (0.922), Anhui (0.980) | Three provinces: Hebei (0.857), Liaoning (0.988), Anhui (0.993) | - |
| Decreasing Returns to Scale | - | - | - | - |
| Increasing Returns to Scale | Three provinces: Liaoning, Heilongjiang, Tibet | Three provinces: Liaoning, Heilongjiang, Anhui | Three provinces: Hebei, Liaoning, Anhui | - |
| Year | Technical Efficiency | Technological Progress | Pure Technical Efficiency | Scale Efficiency | Total Factor Productivity (Malmquist Productivity Index) |
|---|---|---|---|---|---|
| 2012-2013 | 1.000 | 1.041 | 1.000 | 1.000 | 1.041 |
| 2013-2014 | 1.000 | 1.298 | 1.000 | 1.000 | 1.298 |
| 2014-2015 | 1.000 | 1.193 | 1.000 | 1.000 | 1.193 |
| 2015-2016 | 0.997 | 1.048 | 0.997 | 1.000 | 1.046 |
| 2016-2017 | 1.000 | 1.881 | 1.000 | 1.000 | 1.881 |
| 2017-2018 | 0.996 | 1.490 | 1.000 | 1.000 | 1.484 |
| 2018-2019 | 1.000 | 1.886 | 1.000 | 1.000 | 1.886 |
| 2019-2020 | 1.017 | 1.886 | 1.000 | 1.000 | 1.918 |
| 2020-2021 | 1.000 | 1.007 | 1.000 | 1.000 | 1.007 |
| 2021-2022 | 1.072 | 0.990 | 0.985 | 1.089 | 1.062 |
| Mean | 1.011 | 1.271 | 0.990 | 1.022 | 1.285 |
| 31 provinces | Technical Efficiency | Technological Progress | Pure Technical Efficiency | Scale Efficiency | Total Factor Productivity(Malmquist Productivity Index) |
|---|---|---|---|---|---|
| Beijing | 1.000 | 2.046 | 1.000 | 1.000 | 2.046 |
| Tianjin | 0.931 | 1.395 | 0.945 | 0.985 | 1.298 |
| Hebei | 1.000 | 1.457 | 1.000 | 1.000 | 1.457 |
| Shanxi | 1.171 | 1.169 | 1.056 | 1.109 | 1.369 |
| InnerMongolia | 1.035 | 1.215 | 1.003 | 1.032 | 1.258 |
| Liaoning | 1.000 | 1.230 | 1.000 | 1.000 | 1.230 |
| Jilin | 0.864 | 1.226 | 0.879 | 0.983 | 1.059 |
| Heilongjiang | 0.804 | 1.082 | 0.835 | 0.963 | 0.870 |
| Shanghai | 1.000 | 1.416 | 1.000 | 1.000 | 1.416 |
| Jiangsu | 1.000 | 1.416 | 1.000 | 1.000 | 1.416 |
| Zhejiang | 1.000 | 1.113 | 1.000 | 1.000 | 1.113 |
| Anhui | 1.000 | 1.765 | 1.000 | 1.000 | 1.765 |
| Fujian | 1.000 | 1.293 | 1.000 | 1.000 | 1.293 |
| Jiangxi | 1.115 | 1.174 | 1.000 | 1.115 | 1.309 |
| Shandong | 1.000 | 1.239 | 1.000 | 1.000 | 1.239 |
| Henan | 1.000 | 1.426 | 1.000 | 1.000 | 1.426 |
| Hubei | 0.978 | 1.500 | 0.986 | 0.992 | 1.467 |
| Hunan | 1.000 | 1.148 | 1.000 | 1.000 | 1.148 |
| Guangdong | 1.000 | 1.349 | 1.000 | 1.000 | 1.349 |
| Guangxi | 1.000 | 1.085 | 1.000 | 1.000 | 1.085 |
| Hainan | 1.000 | 0.990 | 1.000 | 1.000 | 0.990 |
| Chongqing | 0.976 | 1.038 | 0.999 | 0.977 | 1.013 |
| Sichuan | 1.059 | 1.581 | 1.000 | 1.059 | 1.675 |
| Guizhou | 1.000 | 1.111 | 1.000 | 1.000 | 1.111 |
| Yunnan | 1.000 | 1.175 | 1.000 | 1.000 | 1.175 |
| Tibet | 1.585 | 1.262 | 1.000 | 1.585 | 2.000 |
| Shaanxi | 1.000 | 1.709 | 1.000 | 1.000 | 1.709 |
| Gansu | 1.000 | 1.189 | 1.000 | 1.000 | 1.189 |
| Qinghai | 1.000 | 1.113 | 1.000 | 1.000 | 1.113 |
| Ningxia | 1.000 | 0.848 | 1.000 | 1.000 | 0.848 |
| Xinjiang | 1.000 | 1.281 | 1.000 | 1.000 | 1.281 |
| Average | 1.011 | 1.271 | 0.990 | 1.022 | 1.285 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




