Prerpints.org logo
Preprint
Article

Ramsey Theory of the Phase Transitions of the Second Order

Altmetrics

Downloads

88

Views

26

Comments

0

This version is not peer-reviewed

Submitted:

26 May 2024

Posted:

27 May 2024

You are already at the latest version

Alerts
Abstract
The Ramsey theory based approach to the phase transitions of the second order is suggested. The phase transitions of the second order are seen as switching of physical interactions/chemical bonds between the entities forming the primitive cell of the material. Such a switching is typical for a phase change materials. If the energy of the primitive cell is kept constant under the change in the spatial order of the chemical bonds, the phase transition of the second order takes place. The switching of interactions between the entities forming the primitive cell is accompanied by the breaking of the initial symmetry of the cell. The order parameter/the degree of ordering characterizing the ordering within the primitive cell is re-defined. The introduced degree of ordering quantifies ordering of links/interactions/chemical bonds between entities constituting the 2D lattice; whereas, the classical “Landau degree of order” quantifies the symmetry breaking under variation in spatial locations of these entities. The suggested approach is generalized easily for 3D primitive cells. Thermal capacity of the non-symmetrical phase is larger than that of the symmetrical phase. For the primitive cells built of six interacting entities, the Ramsey Theory predicts inevitable appearance of the unstable monochromatic triangles, when the links correspond to attraction or repulsion interactions. The situation becomes different for the primitive cells built of five interacting entities.
Keywords: 
Subject: Physical Sciences  -   Condensed Matter Physics

1. Introduction

The first classification of general types of transition between phases of matter, was suggested by Paul Ehrenfest in 1933 [1,2] It is generally accepted that the first order phase transitions occur via fluctuation mechanism accompanied by production and subsequent growth of the nuclei of the new phase [3,4,5]. Spinodal decomposition is an alternative mechanism of the first-order transitions by which a single thermodynamic phase spontaneously separates into two phases without nucleation [6]. The first order phase transitions have a nonzero latent heat [7]. On contrast, the second-order phase transformations the resultant equilibrium state can be attained by successive transitions through a series of continuous intermediate states, each of which is thermodynamically more favored than the preceding one. The latent heat in this case equals zero [7]. This indicates that there is no need for the nucleation mechanism and that there should exist another mechanism for the kinetics of the system reorganization. Second order phase transitions occur when a new state of reduced symmetry develops continuously from the disordered (high temperature) phase [8,9,10]. Typical examples of the second-order phase transitions are ferromagnetic and superconducting transitions [8,9,10]. Second order transitions in biological system were addressed [11].
We demonstrate that the second order phase transitions may be described by means of the Ramsey theory. Ramsey theory is a branch of discrete mathematics that deals with the appearance of ordered substructures within a structure of a given size. Ramsey theory states that any structure will necessarily contain an orderly substructure [11,12,13]. Thus, it is well expected. that the Ramsey theory is well-suited for the mathematical description of the phase transitions, which are accompanied by the “ordered structure”-“disordered system” transition.
Ramsey’s theorem, in one of its most popular graph-theoretic forms, states that one will find monochromatic cliques in any edge coloring of a sufficiently large complete graph [13,14,15]. Graph, in discrete mathematics is a set of vertices and edges that join pairs of vertices. A complete graph, in turn, is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge. Clique in the graph theory is a subset of vertices of an undirected graph such that every two distinct vertices in the clique are adjacent (vertices are considered as adjacent when both endpoints are connected by the same edge [13,14,15,16,17]. In the language of graph theory, the Ramsey number labeled ζ is the minimum number of vertices R m , n = ζ such that all undirected simple graphs of order   ζ (order of a graph is the number of vertices in the graph) contain a clique of order m or an independent set of order. It should be emphasized, that only restricted number of Ramsey numbers is known today; calculation of the Ramsey numbers for large graphs represents essential difficulties. Interrelation between the Ramsey theory and statistical physics was considered recently [18]. Applications of the Ramsey approach to thermodynamics was reported [19]. We implement the Ramsey approach to the analysis of the continuous phase transitions. In a somewhat paradoxical way, the discrete mathematics supplies tools for the analysis of the continuous phase transitions.

2. Results

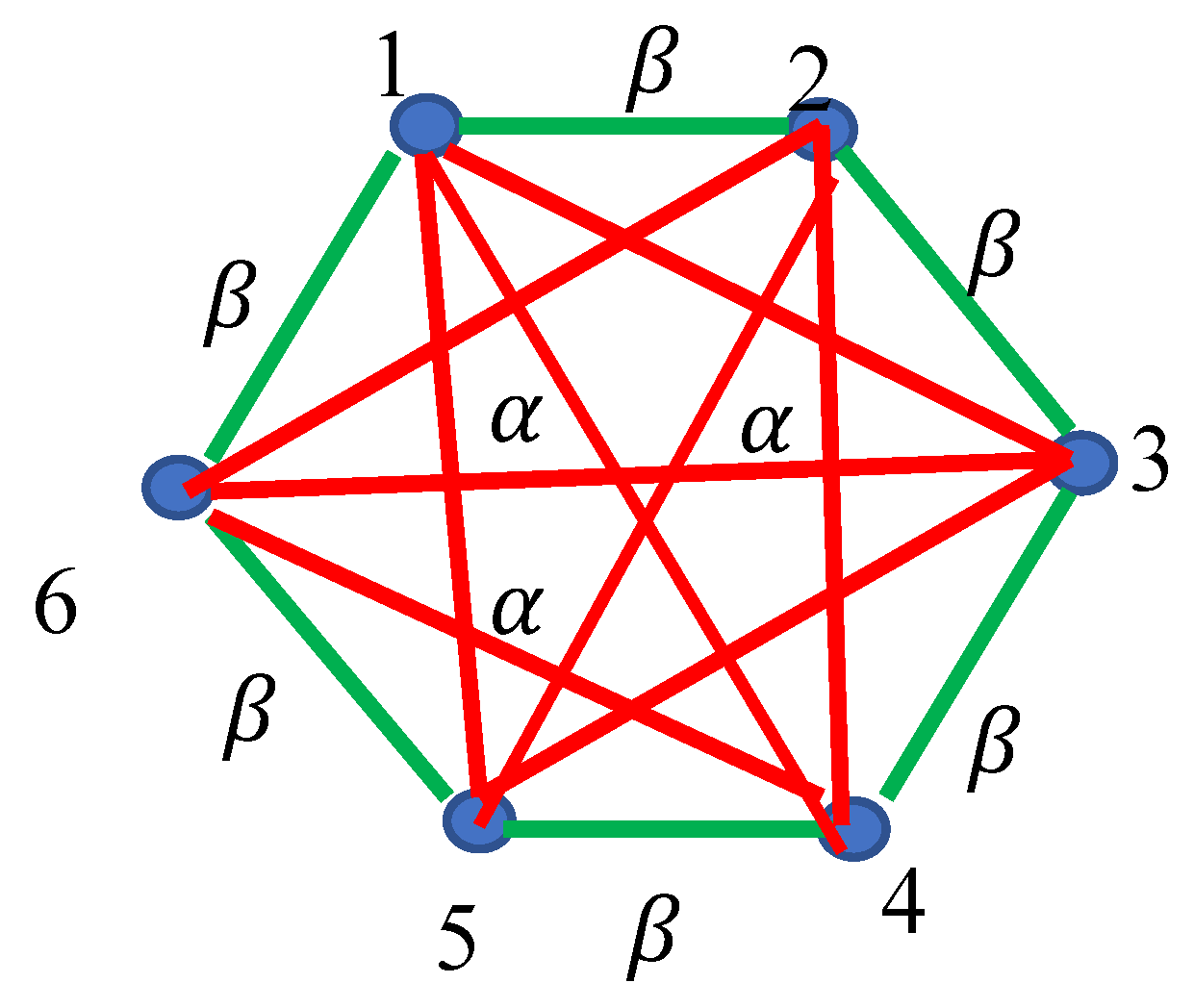
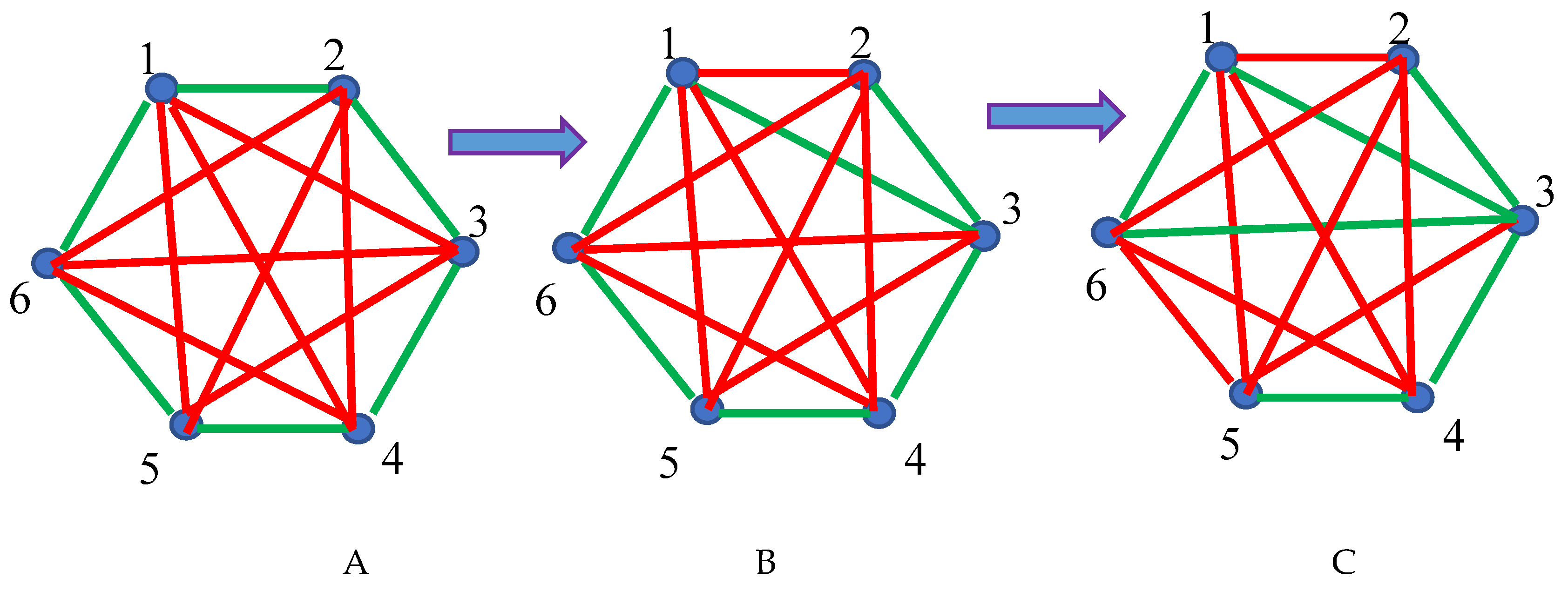
2.1. Continuous Phase Transitions in 6-Fold Symmetry Systems: The Ramsey Approach

Consider the 2D physical system built of the 6-fold symmetric planar primitive cells, such as that depicted in Figure 1. The vertices of the system may be atoms [20], molecules [21], electrical [22] or magnetic dipoles [23], colloidal particles or other interacting physical entities [22,23]. The vertices are numbered i = 1,2 … 6 in the scheme, shown in Figure 1. The edges of the cells, in turn, represent interactions/chemical bonds between atoms, molecules, dipoles or colloidal particles [22,23,24,25,26]. Now we make a suggestion enabling the use of the Ramsey approach, namely we adopt that two kinds of interactions between the vertices are possible, labeled in the text α -interactions (colored in Figure 1 with red) and β -interactions (colored in Figure 1 with green). These interactions may be repulsions (α-interactions) or attractions ( β -interactions) [26], or it is also possible that differently colored links represent various but distinct kinds of chemical interactions/bonds [27]. The Ramsey Theory is insensitive to the physical nature of the interactions; it demands the clear distinction between them only [11,12,13,14]. We also adopt the initial 6-fold rotational symmetry for the system of interacting entities, depicted in Figure 1. The interacting entities (atoms, molecules, etc.) within our approach are seen as the vertices of the graph, and interactions/chemical bonds between this entities are considered as the edges/links of the graph. We adopt, that the vertices and edges/links of system presented in Figure 1 form the complete graph. Thus, the Ramsey approach to the analysis of the graph becomes possible. Let us address the situation, when β red links represent attractions, and α   green links, in turn, – repulsion; the total energy of the system, depicted in Figure 1 is given by:
U t o t = 9 U 2 − 6 U 1
where U 1 and U 2 are the moduli of energies of the β -link and α − link correspondingly.
Two kinds of interactions act between the vertices are possible, namely β − i n t e r a c t i o n s /attractions (colored with green) and α − interactions/repulsions (colored with red). The interactions/chemical bonds are represented by the edges/links of the graph.
The Ramsey Theory states that within the complete graph built of six vertices and two-colored links, at least one monochromatic triangle should be necessarily present [11,12,13,14]. Let us take a close look at Figure 1: indeed, the triangles “236”, “136”, “356”, “346” and “246” are red-colored. This observation immediately follows from the fact that the Ramsey number R 3,3 = 6 . No monochromatic green-colored triangle is present in Figure 1. From the pure physical point of view, it is important that the monochromatic triangles representing repulsions or alternatively attractions are unstable [24].
Now let us destroy continuously the six-fold initial symmetry of the primitive cell, shown in Figure 1, under keeping the total energy of the primitive cell constant. The suggested procedure corresponds to the second-order phase transition. We re-color a pair of the links in every step, as shown in Figure 2, namely: at the first step we change the green link “12” into the red one, and simultaneously we switch red link “13” into the green one, and afterwards, we change the green link “56” into the red one, and red link “36” into the green one. The total energy of the system at every step is conserved: U t o t = 9 U 2 − 6 U 1 = c o n s t ;   indeed the number of green and red links is kept untouched at every step (the procedure may be continued). However, the six-fold symmetry of the system is already destroyed at the first step. The procedure may be continued under continuous breaking of the symmetry of the system, under conservation of its total energy. The initial 6-fold symmetry of the graph will not be restored; thus, an inverse symmetrical complete graph in which green links will be preplaced by red ones and vice versa never will be attained [28], due to the fact, that the initial numbers of red and links are not equal. Thus, the suggested procedure of re-coloring of the initial graph, leading to the continuous change in its symmetry occurs under the constant energy, and corresponds to the necessary condition of the second order phase transition (the latent heat of the transition is zero) [29,30].
When the links correspond to attraction/repulsion interactions, the Ramsey Theory predicts inevitable appearance of the unstable triangles in the complete graph and they indeed are recognized in Figure 2B,C. The green ( β − t y p e ) monochromatic triangle is already recognized in Figure 2C.
Two kinds of interactions act between the vertices, repulsions are colored with green and attractions interactions are colored with red. B. Breaking of symmetry of the system is depicted. Green link “12” is converted into the red one, and red link “13” is converted into the green one. C. The symmetry is continuously broken: the green link “56” is converted into the green one and red link “36” is converted into the green one. Arrow indicates the temporal evolution of the system.
Now let us quantify the suggested process of the symmetry breaking. It may be done with the “order parameter” (i.e., degree of ordering), introduced in the Landau theory of the second order phase transitions [29]. Let us re-define the order parameter η in a spirit of the Ramsey theory, keeping the general Landau approach untouched. Parameter η is defined now in such a way that it is zero in a disordered phase and takes various positive and negative values in patterns with various degrees of ordering.
η = P α − P β P α + P β
where P α and P β are probabilities of finding α and β links at any given location link in the 2D cell. The “order parameter” is zero in a completely disordered graph, and takes various positive or negative values in the complete graphs with various degree of ordering [29]. Parameter η defined according to Eq. 2 resembles that introduced in the classical works by Landau for quantification of the second order transitions; however, this resemblance is superficial. The degree of ordering η introduced with Eq. 1 quantifies ordering of links/interactions between entities constituting the 2D lattice; whereas, the “Landau degree of order” quantifies the symmetry breaking via variation of spatial locations of these entities. And, it seems to the authors, that the definition of the degree of ordering with Eq. 2 is more physically justified (at least for some of phase transitions, to be discussed below). Indeed, physical interactions between physical entities, rather than their spatial locations govern the phase transition. Consider the second order phase transition in the dipole-dipole system [31]. In this case, the same location of the centers of mass of interacting electrical or magnetic dipoles may correspond to both attraction and repulsion, which are switched one to another under rotation of the dipoles [32]. Thus, it looks more reasonable to attribute the second order phase transitions to the breaking of symmetry of interactions between particles and not to the spatial location of the particles themselves.
Following Landau, the thermodynamic potential/Gibbs free energy Φ may be seen as a function of the order parameter Φ = Φ P , T ,   η . The continuity of the second order phase transitions implies that the degree of ordering η takes infinitesimal values in the vicinity of the transition point [29]. According to the Landau theory, the Taylor expansion of the free energy of the system is given by Eq. 3:
G P , T , η = G 0 P , T + A P , T η 2 + ξ P , T η 4 + …
where ξ P , T > 0 , and A P , T > 0 in the symmetrical phase and A P , T < 0 in the non-symmetrical phase, ξ = ξ T c [29]. Let us emphasize that now η   is supplied by Eq.2. We adopt Eq. 4 for the thermodynamic states in the vicinity of phase transitions:
A T , P = c o n s t = δ T − T c ,   δ = c o n s t ,
where T c is the temperature of the phase transition, δ = ∂ A ∂ T T = T c = c o n s t [29]. This expansion yields for the constant pressure thermal capacity of the non-symmetrical phase:
C p = C p 0 + δ 2 T c 2 ξ
In the symmetrical phase we have C = C p 0 ; due to the fact that ξ P , T > 0 ; hence, thermal capacity grows under transition from the symmetrical phase, described by the symmetrical complete graph to the non-symmetrical, described by the complete graph in which symmetry is broken, as shown in Figure 2 [29].

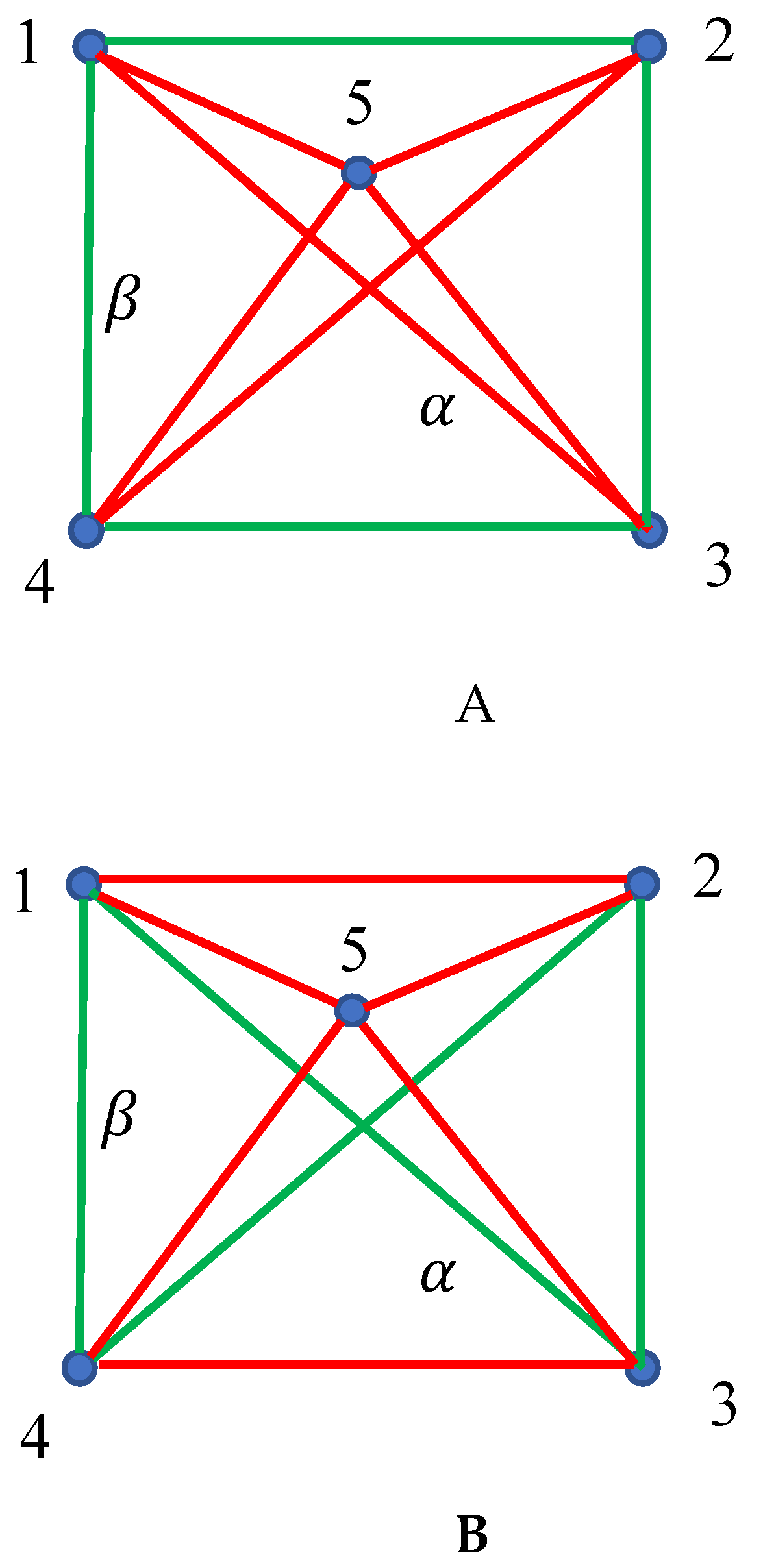
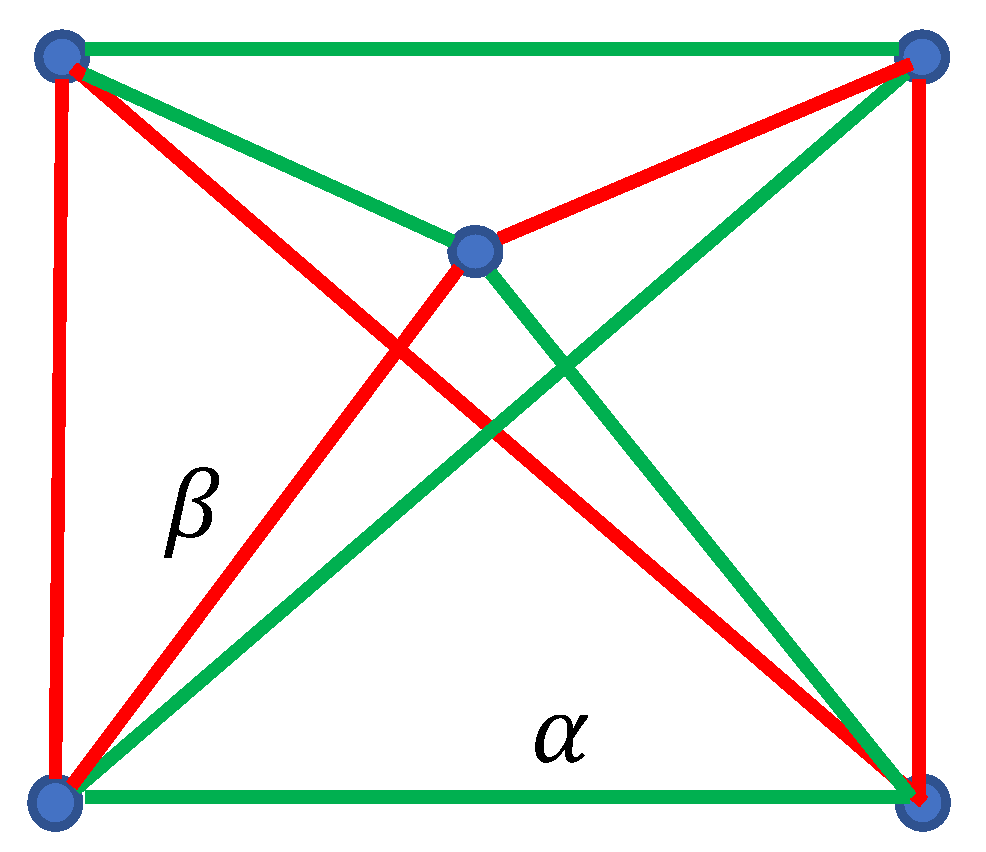
2.2. Continuous Phase Transitions in the Four-Fold Symmetry Systems: The Ramsey Approach

Consider now the second order phase transition in the system built of primitive cells comprising five interacting physical entities, as shown in Figure 4. Again, we adopt that two kinds of interactions between the vertices are possible, labeled in the text α -interactions (colored in Figure 4 with red) and β -interactions (colored in Figure 4 with green). Four-fold initial symmetry of the primitive 2D cell is adopted. Entity “5” is located in the center of the primitive cell and it is displaced in Figure 4, Figure 5 and Figure 6 from its actual position, for the purposes of clarity of the drawings. Generally, complete, bi-colored graphs containing five vertices may be colored in such a way, that no monochromatic triangle will be present in the graph. Contrastingly, it should be emphasized that the bi-coloring procedure keeping the four-fold symmetry of the graph inevitably gives rise to appearance of the mono-colored triangles; indeed, triangles “135” and “245” in inset A, and triangles “125” and “345” in inset B are monochromatic (red).
interactions); green lines depict repulsive interactions ( α − interactions) between the entities. A. Triangles “135” and “245” are monochromatic (red). B. Triangles “125” and “345” are monochromatic (red).
Breaking symmetry of the graph enables bi-coloring for which no monochromatic triangle is recognized in the graph, as shown in Figure 5.
interactions); green lines depict repulsive interactions ( α − interactions) between the bodies. Four-fold symmetry of the system is broken. No monochromatic triangle is recognized in the graph.
In this case, no monochromatic (unstable) triangle is recognized in the cell; consider R 3,3 = 6 > 5 . Perhaps, this Ramsey Theory based argument explains, prevalence of FCC crystal structures on HCP ones; indeed, for the dipole-dipole interactions (electric or magnetic) based crystals only FCC primitive cells were observed [31,32,33,34,35,36,37].
Now consider phase transitions of the second order in the system built of five interacting entities, shown in Figure 6. Initial primitive cell is symmetrical; after the transitions the cell becomes non-symmetrical, as shown in Figure 6.
Again, breaking symmetry of the links conserving the total energy of the system is suggested,
U t o t = 6 U 2 − 4 U 1 = c o n s t
and the order parameter η introduced with Eq. 2 is suggested. Now consider phase transitions of the second order in the system built of five interacting entities, shown in Figure 6. In this case, two scenarios of breaking symmetry is possible. Within the first scenario, breaking symmetry does not give rise to the formation of monochromatic interaction triangle, as shown in inset A of Figure 6. This is possible due to the fact that R 3,3 = 6 > 5 . However, breaking symmetry may give rise to the formation of monochromatic interaction triangles, as illustrated with inset B of Figure 6. Triangles “125” and “135” are monochromatic (red), unstable ones.
The jump in the thermal capacity given by Eq. 5 is foreseen, and the thermal capacity quite expectably C p   grows under transition from the symmetrical phase to non-symmetrical [29]. Thermal capacity   C p   grows under transition from the symmetrical phase, described by the initial symmetrical complete graph to the final state, which is non-symmetrical, described by the complete graph in which symmetry is broken. This is true for the both types of the final states, namely those which do not exhibit monochromatic triangles (shown in inset A of Figure 6) and those, which contain monochromatic interaction triangles (depicted in insert B of Figure 6).
The graphs, shown in Figure 4, Figure 5 and Figure 6 should not be necessarily planar they may describe 3D spatial locations of interacting physical entities. Such a 3D graph is depicted in Figure 7, in which green quadrangle “1234” is located in the plane XOY, whereas, entity “5” is located out of this plane. Four-fold symmetry is inherent for the graph, shown in Figure 7. Phase transition analogous to the aforementioned ones, illustrated with Figure 4, Figure 5 and Figure 6 are possible for the 3D structure shown in Figure 7.
interactions); green lines depict repulsive interactions ( α − interactions) between the entities.
The phase transitions, breaking the symmetry of the initial 3D graph, result in the growth of the thermal capacity in the non-symmetrical phase.

3. Discussion

The Ramsey approach to the phase transitions of the second order is presented. The phase transition of the second order is seen as a switch between interactions/chemical bonds between the entities comprising the primitive cell. The transition occurs when the symmetrical primitive cell is converted into a non-symmetrical one takes place, under switching of chemical bonds. If the energy is kept constant under such a switch we have the phase transition of the second order. Why this kind of the phase transitions, occurring under switch of the chemical bonds is important? It is important in a context of rapid development of the phase-change materials used for the optical and electronic storage of information [40,41,42,43]. The phase switching material/chalcogenide glass G e 2 S b 2 T e 5 (abbreviated GST) demonstrates phase transitions accompanied by switching of chemical bonds. Laser pulse focused onto the area corresponding to the bit size heats up the GST making it locally changing between the amorphous and the crystalline phase [43]. The different diffraction index of the two phases makes possible the optical read out [43]. Development of optical storage based on GST progressed rapidly in the last decade [41,42,43]. Ferroelectric phase transitions driven by switchable covalent bonds were reported recently [44,45]. Thus, the suggested Ramsey approach is highly relevant for the analysis of the phase transitions driven by switching of chemical bonds.

5. Conclusions

Rapid development of the phase-change materials used for the optical and electronic storage of information has drawn attention to the materials in which the phase transition occurs under switching of chemical bonds between physical entities, constituting these materials. For example, the phase switching material/chalcogenide glass G e 2 S b 2 T e 5 demonstrates phase transitions accompanied by switching of chemical bonds. Switching of chemical bonds also governs the phase transitions in silica glasses. We propose the Ramsey Theory based approach to the analysis of the phase transitions, which take place under switching of interactions between atoms/molecules/dipoles forming the materials. Ramsey theory, is a branch of the discrete mathematics, which predicts the inevitable appearance of order in a substructure given a structure of a prescribed size. It is well expected, that the Ramsey theory will be useful for the treatment of the phase transitions, resulting in the switch from the ordered to the disordered state of the matter. We propose the Ramsey theory based approach for the analysis of the phase transitions of the second order emerging from the change in the interactions between the physical entities forming the primitive cells of a given material. These entities may be atoms, molecules, electrical or magnetic dipoles. We adopt that two kinds of distnguishable interactions are possible between these entities. These interactions may be attractions or repulsions, or alternatively, they may represent two kinds of chemical bonds. Thus, the entities forming the primitive cell are seen as the vertices of the graph, and the interactions between these entities are considered as the links/edges of the graph. We assume that the vertices and the links form the bi-colored, complete graph; thus, the application of the Ramsey theory for the analysis of these graphs becomes possible. We started from the analysis of the 2D six-fold symmetrical primitive cell built of the physical entities interacting via two different kinds of physical/chemical interactions. We introduced the procedure of breaking of the initial symmetry of the initial cell, which keeps the total energy of the cell untouched. This symmetry breaking corresponds to the phase transition of the second order (the latent heat of the transition is zero). For the quantification of the transition (following Landau) we defined the order parameter/degree of ordering (denoted η ) in such a way that it is zero in a disordered phase and takes various positive and negative values in the cells/graphs with various degrees of ordering. The degree of ordering η quantifies ordering of links/interactions between entities constituting the 2D lattice. Such a definition of the degree of ordering is more physically justified for the addressed transitions, when compared to the original “Landau degree of order”, which quantifies the symmetry breaking occurring via variation of spatial locations of the atoms. Actually, physical interactions between basic entities, and not their spatial locations govern the phase transition (this is true at least for phase change materials). This also becomes clear when dipole-dipole interactions are considered. In this case, the same location of the centers of mass of interacting electrical or magnetic dipoles may correspond to both attractions and repulsions, which are switched one to another under rotation of the dipoles.
According to the Landau theory, thermal capacity of the non-symmetrical phase is larger than that of the symmetrical phase. For the primitive cells built of six interacting entities, the Ramsey Theory predicts inevitable appearance of the unstable monochromatic triangles, when the links correspond to attraction or repulsion interactions.
We also addressed the phase transitions of the second order in the system built of five interacting entities, demonstrating initial five-fold symmetry. Initial primitive cell is symmetrical; after the transitions the cell becomes non-symmetrical. Again, thermal capacity of the non-symmetrical phase is larger than that of the symmetrical phase. According to the Ramsey theorem, complete, bi-colored graphs containing five vertices may be colored in such a way, that no monochromatic triangle will be present in the graph. However, bi-coloring procedure keeping the four-fold symmetry of the graph inevitably gives rise to appearance of the mono-colored triangles. In this case, two scenarios of breaking symmetry is possible. Within the first scenario, breaking symmetry does not give rise to the formation of monochromatic interaction triangles. This is possible due to the fact that R 3,3 = 6 > 5 . However, breaking symmetry also may give rise to the formation of monochromatic interaction triangles, as demonstrated in the paper. The approach is easily generalized for 3D graphs. We conclude, that the Ramsey Theory supplies an elegant mathematical framework, enabling analysis of the phase transitions of the second order. Synthesis of the Landau and Ramsey approaches as possible. The approach demonstrates a potential for the analysis of the phase transitions in the phase-change materials and silica glasses.

Author Contributions

Conceptualization, E. B.; methodology, E.B.; formal analysis, E. B.; investigation, E.B.; writing—original draft preparation, E.B.; writing—review and editing, E. B.; visualization, X.X.;

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

No new data were created or analyzed in this study. Data sharing is not applicable to this article.

Acknowledgments

Author is thankful to Nir Shvalb and Juern Schmelzer for extremely fruitful discussions.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Ehrenfest, P. Phasenumwandlungen im ueblichen und erweiterten Sinn, classifiziert nach dem entsprechenden Singularitaeten des thermodynamischen Potentiales. Verhandlingen der Koninklijke Akademie van Wetenschappen (Amsterdam), Communications from the Physical Laboratory of the University of Leiden, 1993, Supplement No. 75b, 36, 153-157.
  2. Jaeger G. The Ehrenfest Classification of Phase Transitions: Introduction and Evolution, Archive for History of Exact Sciences 1998, 53 (1), 51-81.
  3. Schmelzer, J. W. P.; Gokhman, A. R.; Fokin, V. F. Dynamics of first-order phase transitions in multicomponent systems: a new theoretical approach. J. Colloid & Interface Sci. 2004, 272 (1), 109-133.
  4. Schmelzer, J. W. P.; Abyzov, A. S. Generalized Gibbs’ approach to the thermodynamics of heterogeneous systems and the kinetics of first-order phase transitions. J. Engin. Thermophys. 2007, 16, 119–129.
  5. Schmelzer, J. W. P.; Abyzov, A. S. Crystallization of glass-forming liquids: Thermodynamic driving force, J. Non-Crystalline Solids, 2016, 449, 41-49.
  6. Abyzov, A. S.; Schmelzer, J. W. P. Nucleation versus spinodal decomposition in confined binary solutions, J. Chem. Physics 2007, 127, 114504.
  7. Baierlein, R. Thermal Physics, Cambridge University Press, 1999, Ch. 16, pp.408-409.
  8. Lifshitz, I. M. Kinetics of Ordering during Second-Order Phase Transitions, J. Exptl. Theoret. Phys. (U.S.S.R.) 1962, 42, 1354-1359.
  9. Yukhnovskii, I. R. Phase Transitions of the Second Order. Collective Variables Method, World Scientific, Singapore, 1987.
  10. Franko, V.; Conde, A. Scaling laws for the magnetocaloric effect in second order phase transitions: From physics to applications for the characterization of materials, Int. J. Refrigeration, 2010, 33 (3), 465-473.
  11. Heffern, E. F. W.; Huelskamp, H.; Sonya, S.; Inglis, R. F. Phase transitions in biology: from bird flocks to population dynamics, Proc. R. Soc. B. 2021, 288, 1111.
  12. Ramsey, F. P. On a Problem of Formal Logic. In: Gessel, I., Rota, GC. (eds) Classic Papers in Combinatorics. Modern Birkhäuser Classics. Birkhäuser Boston 2009, pp. 264-286.
  13. Graham, R. L.; Rothschild, B. L.; Spencer, J. H. Ramsey theory, 2nd ed., Wiley-Interscience Series in Discrete Mathematics and Optimization, John Wiley & Sons, Inc., New York, A Wiley-Interscience Publication, 1990, pp. 10-110.
  14. Di Nasso, M.; Goldbring, I.; Lupini M. Nonstandard Methods in Combinatorial Number Theory, Lecture Notes in Mathematics, vol. 2239, Springer-Verlag, Berlin, 2019.
  15. Katz, M.; Reimann, J. Introduction to Ramsey Theory: Fast Functions, Infinity, and Metamathematics, Student Mathematical Library Volume: 87; 2018; pp. 1-34.
  16. Shvalb, N.; Frenkel, M.; Shoval, S.; Bormashenko, Ed. A Note on the Geometry of Closed Loops, Mathematics, 2023, 1960, 11(8).
  17. Wouters, J.; Giotis, A.; Kang, R.; Schuricht D., Fritz, L. Lower bounds for Ramsey numbers as a statistical physics problem. J. Stat. Mech. 2022, 2022, 0332.
  18. Shvalb, N.; Frenkel, M.; Shoval, Sh.; Bormashenko Ed. Ramsey theory and thermodynamics, Heliyon 2023, 9 (2), e13561.
  19. Zhang, F.; Wu, Q.; Wang, X.; Liu, N.; Yang, J.; Hu, Y.; Yu, L.; Wang, X.; Hu, Z.; Zhu, J. 6-Fold-Symmetrical AlN Hierarchical Nanostructures: Synthesis and Field-Emission Properties. J. Phys. Chem. C 2009, 113 (10), 4053–4058.
  20. Lee, C-H.; Schiros, T.; Santos, E, J.G.; Kim, B.; Yager, K. G.; Kang, S. J.; Lee, S.; Yu, J.; Watanabe, K.; Taniguchi, T.; Hone, J.; Kaxiras, E.; Nuckolls, C.; Kim, P. Epitaxial Growth of Molecular Crystals on van der Waals Substrates for High-Performance Organic Electronics, Adv. Mat. 2014, 26 (18), 2812-2817.
  21. Talapin, D. V.; Shevchenko, E.V.; Murray, C. B.; Titov, A. V.; Král, P. Dipole−Dipole Interactions in Nanoparticle Superlattices. Nano Lett. 2007, 7 (5), 1213–1219.
  22. Li, D.; Chen, Q.; Chun, J.; Fichthorn, K.; De Yoreo, J.; Zheng, H. Nanoparticle Assembly and Oriented Attachment: Correlating Controlling Factors to the Resulting Structures, Chem. Rev. 2023, 123 (6), 3127–3159.
  23. Hendley, R. S.; Zhang, L.; Bevan, M.A. Design rules for 2D field mediated assembly of different shaped colloids into diverse microstructures, Soft Matter 2022, 48, 9273–9282.
  24. Han, K. Electric and Magnetic Field-Driven Dynamic Structuring for Smart Functional Devices, Micromachines 2023, 14(3), 661.
  25. Shvalb, N.; Frenkel, M.; Shoval, Sh.; Bormashenko Ed. Universe as a Graph (Ramsey Approach to Analysis of Physical Systems), World J. Physics, 2023, 1(1), 1-24.
  26. Leko, V. K. Regularities and Peculiarities in the Crystallization Kinetics of Silica Glasses, in the: Glass: Selected Properies and Crystallization; ed. by J. W. P. Schmelzer, de Gruyter, Berlin, Ge, 2014.
  27. N. Shvalb, M. Frenkel, Sh. Shoval, Ed. Bormashenko Ed. Dynamic Ramsey Theory of Mechanical Systems Forming a Complete Graph and Vibrations of Cyclic Compounds, Dynamics 2023, 3(2), 272-281.
  28. Landau, L.D.; Lifshitz, E.M. Statistical Physics, 3rd ed.; Course of Theoretical Physics; Elsevier: Oxford, UK, 2011; Volume 5.
  29. Diamantini, M. C. Landauer Bound and Continuous Phase Transitions, Entropy, 2023, 25(7), 984.
  30. Astrakharchik, G. E.; Boronat, J.; Kurbakov, I.L.; Lozovik, Yu. E. Quantum Phase Transition in a Two-Dimensional System of Dipoles, Phys. Rev. Lett. 2007, 98, 060405.
  31. Israelachvili, J. N. Intermolecular and Surface Forces, 3rd Ed., Academic Press, Amsterdam, Netherlands, 2011.
  32. Janssen, T. The Magnetic Structure of an FCC. Spin Lattice System with Ex-change and Dipolar Interactions. Phys. kondens. Materie 1972, 15, 142-157.
  33. Siddharthan, R.; Shastry, B. S.; Ramirez, A. P.; Hayashi, A.; Cava, R. J.; Rosenkranz, S. Ising Pyrochlore Magnets: Low-Temperature Properties, “Ice Rules,” and Beyond, Phys. Rev. Lett. 1999, 83, 1854.
  34. Melko, R. G.; den Hertog, B. C.; Gingras, M. J.P. Long-Range Order at Low Temperatures in Dipolar Spin Ice. Phys. Rev. Lett. 2001, 87, 067203.
  35. Ruff, J. P.C; Melko, R. G.; Gingras, M, J, P. Finite-Temperature Transitions in Dipolar Spin Ice in a Large Magnetic Field, Phys. Rev. Lett. 2005, 95, 097202.
  36. Khan, N.; Prishchenko, D.; Skourski, Y.; Mazurenko, V. G.; Tsirlin, A. A. Cubic symmetry and magnetic frustration on the fcc spin lattice in K2IrCl6, Phys. Rev. B, 2019, 99, 144425.
  37. Axilrod, B. M. Triple-Dipole Interaction. II. Cohesion in Crystals of the Rare Gases, J. Chem. Phys. 1951, 19, 724.
  38. Singh, A. N.; Dyre, J. C.; Pedersen U. R. Solid–liquid coexistence of neon, argon, krypton, and xenon studied by simulations. J. Chem. Phys. 2021, 154, 134501.
  39. Ovshinsky, S. R. Reversible electrical switching phenomena in disordered structures, Phys. Rev. Lett. 1968, 21 (20), 1450–1453.
  40. Pirovano, A.; Lacaita, A. L.; Benvenuti, A.; Pellizzer, F.; Bez, R. Electronic Switching in Phase-Change Memories, IEEE Transact. Electron Devices, 2004, 51 (3), 452-458.
  41. Wuttig, M.; Yamada, N. Phase-change materials for rewriteable data storage, Nature Mater. 2007, 6, 824–832.
  42. Pries, J.; Cojocaru-Mirédin, O.; Wuttig, M. Phase-change materials: Empowered by an unconventional bonding Mechanism, MRS Bull. 2019, 44, 699–704.
  43. Zhang, H-Y.; Zhang, N.; Zhang, Y.; Jiang, H-H.; Zeng, Y-L.; Tang, S-Y.; Li, P-F.; Tang, Y-Y.; Xiong, R. G. Ferroelectric Phase Transition Driven by Switchable Covalent Bonds, Phys. Rev. Lett. 2023, 130, 176802.
  44. Liao, W-Q.; Zeng, Y-L.; Tang, Y-Y.; Xu, Y-Q.; Huang, X.-Y.; Lv, H-P.; Chen, X-G.; Xiong, R.-G. Dual Breaking of Molecular Orbitals and Spatial Symmetry in an Optically Controlled Ferroelectric. Adv. Mat. 2023, 35 (44), 2305471.
Preprints 107493 g001
Figure 1. 6-fold symmetrical system of interacting entities (atoms, molecules, dipoles or colloidal particles is depicted). The entities are located in the vertices of the hexagon and numbered i = 1,2 … 6 .
Figure 1. 6-fold symmetrical system of interacting entities (atoms, molecules, dipoles or colloidal particles is depicted). The entities are located in the vertices of the hexagon and numbered i = 1,2 … 6 .
Preprints 107493 g001
Preprints 107493 g002
Figure 2. A. 6-fold symmetrical system of interacting entities is depicted. The entities are located in the vertices of the hexagon and numbered i = 1,2 … 6 .
Figure 2. A. 6-fold symmetrical system of interacting entities is depicted. The entities are located in the vertices of the hexagon and numbered i = 1,2 … 6 .
Preprints 107493 g002
Preprints 107493 g003
Figure 4. Four-fold symmetrical systems of interacting physical entities, shown with blue circles; the central body is displaced from its true location in the center of the cell for the sake of clarity. Red lines depict attractive interactions ( β −
Figure 4. Four-fold symmetrical systems of interacting physical entities, shown with blue circles; the central body is displaced from its true location in the center of the cell for the sake of clarity. Red lines depict attractive interactions ( β −
Preprints 107493 g003
Preprints 107493 g004
Figure 5. System built of five interacting bodies is depicted. Red lines depict attractive interactions ( β −
Figure 5. System built of five interacting bodies is depicted. Red lines depict attractive interactions ( β −
Preprints 107493 g004
Preprints 107493 g005
Figure 6. Breaking symmetry of the elementary cell is depicted. A. No monochromatic triangle is recognized before and after the phase transition. B. Red monochromatic triangles is recognized. Triangles “125” and “135” are monochromatic (red) ones.
Figure 6. Breaking symmetry of the elementary cell is depicted. A. No monochromatic triangle is recognized before and after the phase transition. B. Red monochromatic triangles is recognized. Triangles “125” and “135” are monochromatic (red) ones.
Preprints 107493 g005
Preprints 107493 g006
Figure 7. Complete graph, depicting 3D symmetrical elementary cell containing five interacting entities is shown. Red lines depict attractive interactions ( β −
Figure 7. Complete graph, depicting 3D symmetrical elementary cell containing five interacting entities is shown. Red lines depict attractive interactions ( β −
Preprints 107493 g006
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated