Escalator Etiquette: Stand or Walk? A Systems Analysis

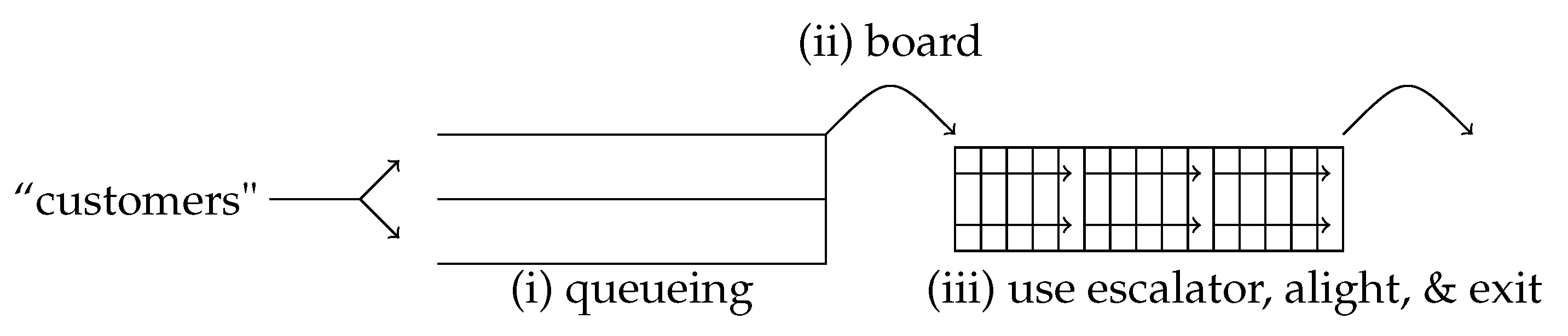
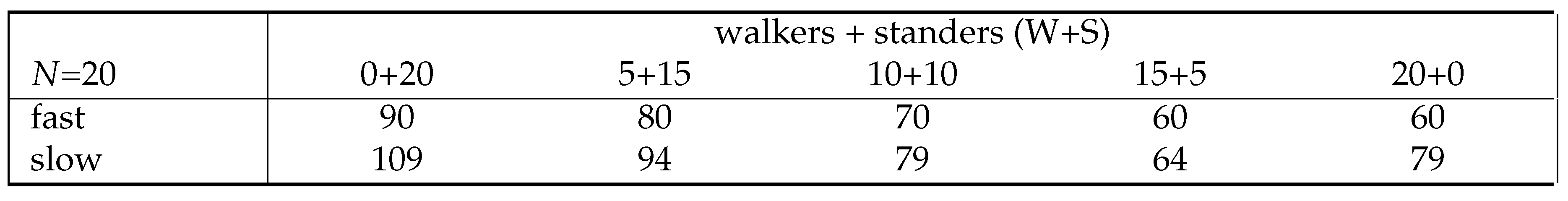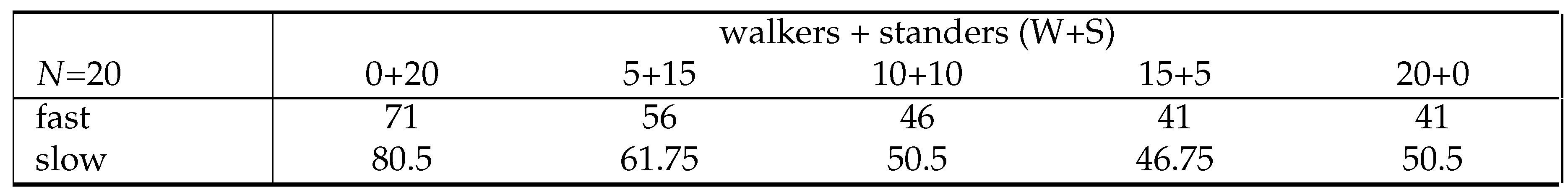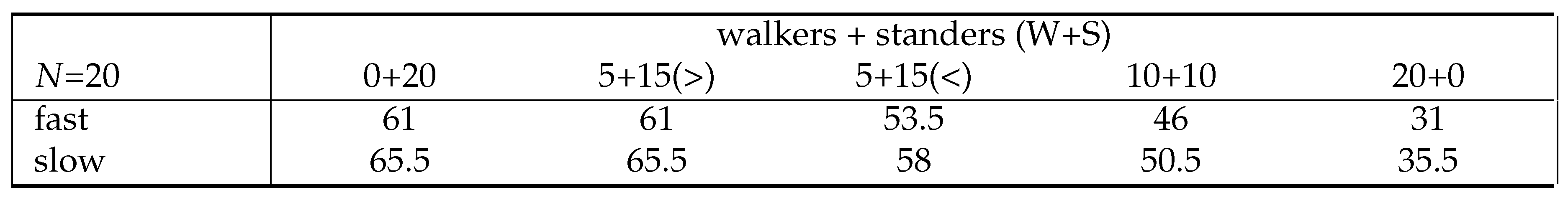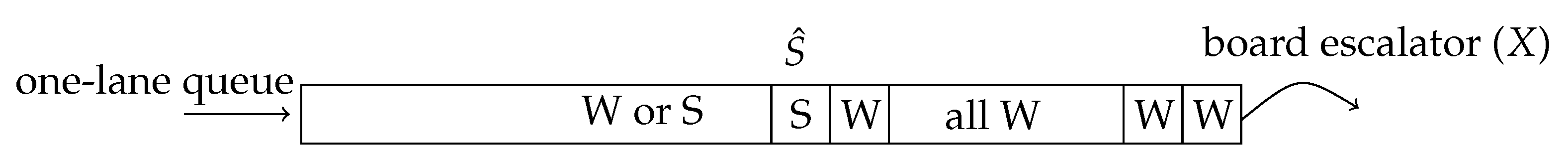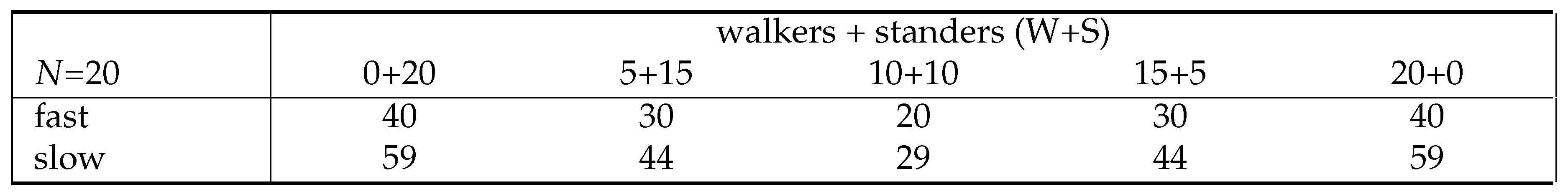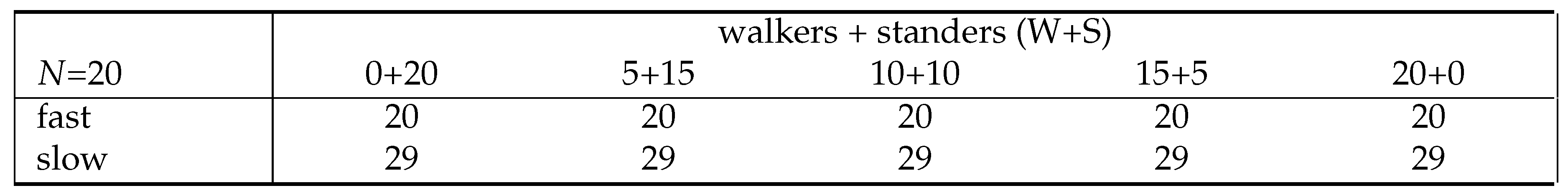1. Introduction

The Washington Metropolitan Area Transit Authority (WMATA) operates the Metrorail subway/rail (and Metrobus bus) system in the Washington, DC metropolitan area, which includes “the most elevators... and escalators (618) of any transit system in North America" [1], including “the longest single span escalators in the Western Hemisphere, taking just under three minutes to travel from top to bottom" at the Wheaton Metro station, with an escalator 230 feet (70 meters) long traveling at a speed of 90 feet (27 meters) per minute. In contrast, the longest escalator in the much larger New York City subway system is “only" 182 feet long. During morning and evening rush hours, stations such as these in Washington, D.C. and many other subway stations all over the world (e.g., London and Tokyo) experience extreme congestion at the escalators when passengers alight from a train. Most of these escalators are equipped with sufficient room (in terms of width) to accommodate two lanes of users, and standard understood practice has been to allocate one lane for those who wish to stand – referred to henceforth as “standers" – and the other for those who wish to walk – referred to henceforth as “walkers" [2]. However, many have suggested that it would be better during high-congestion periods if everyone just stood, with empirical evidence used to support this counterintuitive finding. In practice, such a policy has been notoriously difficult to implement for numerous reasons, including challenges in behavioral modification and the belief among walkers that they should have the right to walk. The goal of this work is to try and shed some light on how best to manage both the “system" and customer expectations in terms of competing objectives, using relatively simple analytical models. In other words, the overriding decision (whether made by the individual or the system) can be succinctly summarized as

Stand or walk? That is the question.

The answer of course is the same as it should be to any good question:

It depends!

In addition to the differing perspectives of system management and users (passengers), the decision is a multi-objective problem, with two main high-level commonly conflicting objectives being to maximize both safety and efficiency. Safety considerations include the following [3]:

(i)

personal hazards, i.e., the risk of individual injury – escalators were not designed for walking and are inherently more dangerous than stairs;

(ii)

operational hazards – having standers on one side and walkers on the other creates a mechanical imbalance that could cause malfunction of the escalator.

Just as flight attendants always remind you that their primary duty is ensuring safety, for the sake of the analysis in this work, we will presuppose that safety is also primary, with the further proviso that it is far more of a design issue rather than an operational issue; thus, here we focus only on efficiency and do not consider safety issues in our analyses, although clearly they are critical and should be incorporated in a more detailed long-running operational model, e.g., using simulation.

Efficiency also has many components, such as waiting time (delay) or total time spent in the system and utilization. However, for short-term analysis, such as what we will be considering, utilization is also not a major concern, because unless there is a major detour of the flow to some other option (elevator or stairs), it is not a primary goal of the escalator service system. To be specific, this work considers two main objectives:

(i) clearing a congested area, and

(ii) getting people out of the system,

under the scenario where the main bottleneck in the system is accessing the escalator, which is the case in highly congested times, such as at a high-demand subway station during rush hour, at a popular train station stop, or at the end of a sporting event in an arena or stadium. Although the two objectives are positively correlated, there is still a well-known queueing theory tradeoff between exploiting pooling at the bottleneck by dedicating both lanes to standers versus prioritizing customers with shorter “service" times by allowing walkers to exit the system much faster (optimality of shortest processing time in scheduling). Thus, the focus of this work is on modeling the congestion in accessing the escalator and approximating the total time to exit the station.

Prior to the COVID-19 pandemic, there were numerous articles touting the benefits of dedicating both lanes of a two-lane escalator to walkers during periods of high congestion, most notably in London [4,5,6]. The popular press articles highlight the congestion [7,8,9], whereas most technical models and analyses [10,11,12,13,14] focus on capacity considerations and utilization rather than honing in directly on the goal of clearing the congestion and capturing the overall time spent in the system. Simulation has been used for detailed performance analysis, but this paper proposes a simple deterministic queueing model that captures the main tradeoffs introduced above. Some of the ideas here were first proposed and presented in [15].

2. Methods

Queueing models will be used to model and analyze the system. For simplicity, I will refer to an escalator throughout, but for most of the models the resulting analysis holds for a moving walkway [16,17,18] if the corresponding model Assumptions re satisfied. Persons using the escalator will often be referred to as customers, adopting queueing theory terminology. Throughout, we assume that the escalator has exactly two lanes, so the problem becomes a classical supply/demand problem, with demand being the customers and supply being the transportation resource, in this case the escalator, which has two “servers" available (the two lanes). Assuming everything about the customers is fixed, the choice is to go with one lane each dedicated for walkers and standers, or both lanes for standers only or walkers only. In terms of queueing theory, the main tradeoff has to do with pooling versus having the availability of a faster server; in the setting of the system under consideration, this could also be alleviated by appropriate load balancing between the two servers (lanes) and two customers classes (standers and walkers). Efficiency performance measures include throughput, utilization, delay, waiting/system time, and makespan (for fixed # jobs). We focus on estimating the latter two measures in high-congestion settings, such as when there is heavy traffic trying to access subway and train station escalators, where contention for resources is of paramount concern, as opposed to low-to-moderate flow settings, such as during non-rush hours on subways or on airport station moving walkways or escalators, where accessing the escalator/walkways encounters little delay.

3. System Model and Process Flow

A model of the full system being analyzed is depicted in the process schematic shown in Figure 1 below, comprising three steps for modeling purposes, i.e., when customers enter the system (e.g., after alighting from the train), they proceed as follows:

(i)

join a queue for the escalator;

(ii)

board the escalator;

(iii)

ride the escalator, alight, and exit system.

Using standard queueing terminology, there are two primary elements in the system:

• two “classes" of customers – standers and walkers; and
• two “servers" – the two lanes in the escalator.

Depending on the objective and assumptions for the particular setting being analyzed, only a subset of the steps need to be modeled explicitly. Specifically, two objectives will be considered:

• time to clear the queues and board the escalator (i.e., the station platform), focusing on steps (i) & (ii) in Figure 1; and
• time to exit the station (includes travel time on the escalator and alighting), under the simplifying assumption that the end of the escalator constitutes the exit (almost never true in practice), covering all the process steps in Figure 1.

The first objective is the primary focus during the “rush hour" heavy traffic setting, because access to the escalator is the main bottleneck, so pooling of resources, i.e., the two lanes, would be the ideal solution, but becomes a challenge when there are two classes of customers, each of which can only be served by one of the two types of servers (dedicated lanes). Load balancing and reduction to a single class of customers (e.g., enforcing both lanes for standers only) are potential ways of addressing this challenge, and our analysis will try to assess the advantages and disadvantages of implementing this option in some form.

4. Queueing Model for Escalator Access

Due to the nature of the system, the primary contention for resources in high-congestion settings occurs in the first two steps, with the bottleneck being access to the escalator, i.e., the “boarding" process, which is assumed to take longer than normal walking; thus, for the purpose of our first simplified analysis, the other subsequent steps will be ignored initially (see Figure 2). In our model,

Time and space will be discretized.

Later, the second stage of using the escalator will be incorporated to estimate the total time spent in the station; however, a complete characterization of system behavior would employ a more detailed system model such as one utilizing stochastic simulation, whether discrete-event or agent-based.

To analyze the key trade-offs, we consider simple deterministic queueing models of the system whereby all the customers are assumed to be already queueing for the escalator, i.e., the dynamics of getting off the train to arrive at a queue for the escalator are not modeled. Access to each of the two lanes of the escalator will be modeled as a single FCFS queue, represented by a series of distinct adjacent physical “queueing spots" that can be occupied by at most one customer at a time. The boarding time is denoted by X, which for now will be assumed to be a constant across all customers and both classes, later to be differentiated between classes. To begin, we’ll introduce notions having to do with a single queue, so the superscripts will be omitted for notational brevity. Schematically, each spot in the queueing space will be represented by a square, as indicated in Figure 2 below.

As an example, Figure 3 below shows a queue with five queueing spots occupied by three customers, with one (empty) spot separating each of them:

We are interested in time to clear the queue completely, called the makespan in the production/operations scheduling literature. In the basic model, time will be measured in discrete units, which for simplicity can be thought of as seconds, and progression in the queue corresponds to these time units as formalized as follows.

Assumption 1.

It takes exactly one time unit to go from each queueing spot to the next.

For convenience, we take the time unit to be 1 second. Although Assumption 1 implicitly assumes that all customers progress at an identical rate in the queues accessing the escalator, which in a highly-congested setting is a reasonable assumption where we take a fixed number of customers at the beginning of the analysis horizon (so, for example, all runners will already be gone), we will differentiate customer queue behavior by considering two types of customer queue movements, which we call fast and slow, defined as follows.

Definition 1.

In a queue, afastcustomer moves up when (i.e., simultaneously) the customer in front is clearing their spot, whereas aslowcustomer moves only when the spot in front of them is empty. A queue is calledfast-movingif all of its customers are fast, and similarly is calledslow-movingif all of its customers are slow.

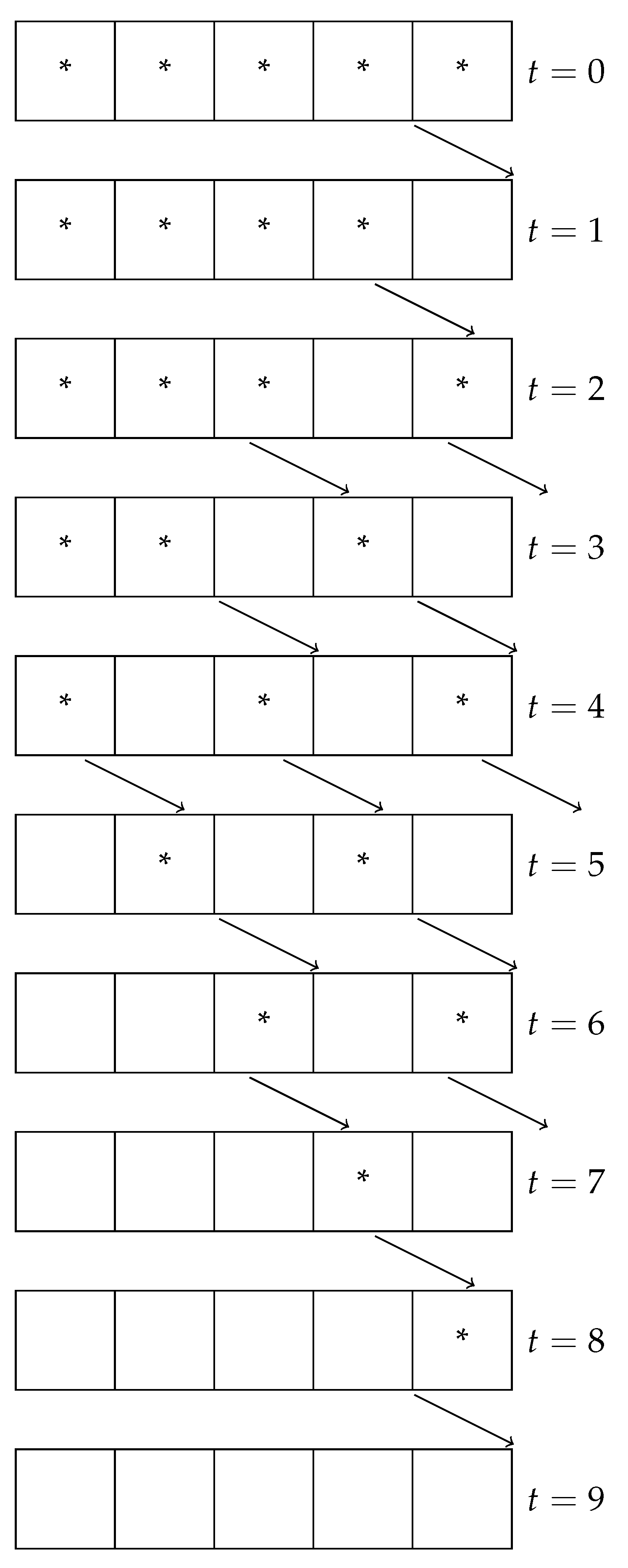
In the previous example, since the customers in queue are spaced out, the state of the queue one unit later would look as follows in both the fast-moving and slow-moving queues:

Figure 4. Queue example with three customers, one time step later after Figure 3 .

Figure 4. Queue example with three customers, one time step later after Figure 3 .

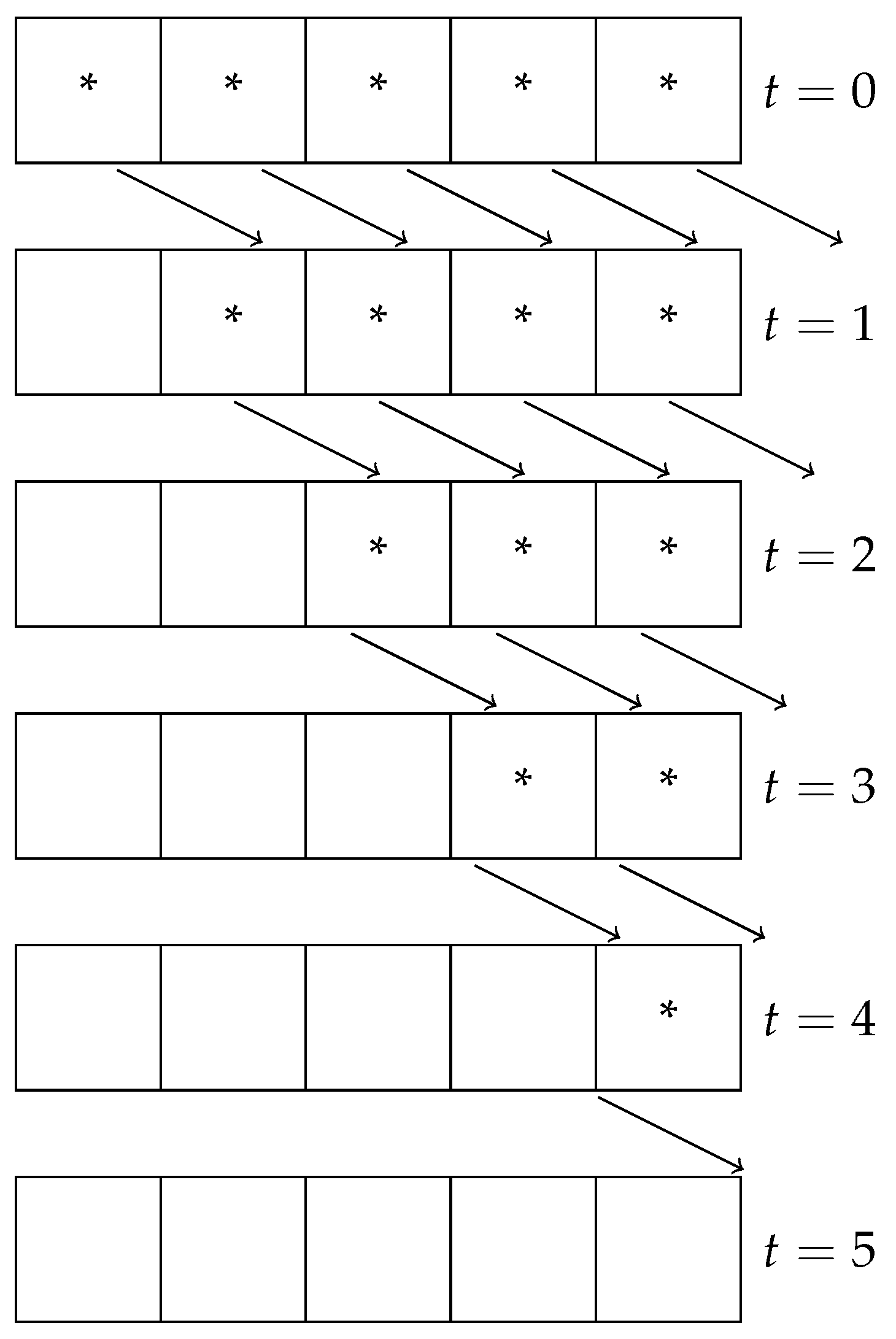
However, that would not be the case if all five spots are initially occupied, in which case the queue would progress through time as shown in Figure 5 for fast-moving customers with $X=1$, as opposed to the progression shown in Figure 6 for slow-moving customers (also with $X=1$).

Definition 2.

A queue is said to becompletely packedit it has no empty spots.

For the model of a single FCFS queue where there are no new arrivals, the time to clear the queue (also known as the makespan) is just the system time of the last customer, and we have the following result.

Proposition 1.

Under Assumption 1, the time to clear a completely packed FCFS queue that starts with N customers is given by (i) $NX$ for a fast-moving queue; and (ii) $N(X+1)-1$ for a slow-moving queue.

Proposition 1 is actually a special case of the following result.

Lemma 1.

Under Assumption 1, the time to board the escalator for the ith customer with a completely packed FCFS queue ahead of them is given by $iX$ and $i(X+1)-1$ for fast-moving and slow-moving queues, respectively.

The following notation will be used for the proofs:

$$\begin{array}{ccc}\hfill C_i& =& i\mathrm{th} \mathrm{customer},\hfill \\ \hfill D_i& =& \mathrm{delay}(“\mathrm{waiting}” \mathrm{time})\mathrm{before}{C}_i\mathrm{reaches} \mathrm{the} \mathrm{beginning} \mathrm{of} \mathrm{the} \mathrm{escalator},\hfill \\ \hfill T_i& =& \mathrm{total} \mathrm{time} \mathrm{for}{C}_i\mathrm{to} \mathrm{board} \mathrm{the} \mathrm{escalator}=D_i+X,\hfill \end{array}$$

with $D_1=0$, i.e., the first customer in queue has no delay, and $T_1=X$.

Proof of Lemma 1. 

For (i), the proof is trivial, but can be established formally by noting that $D_i=T_{i-1}$ by the definition of a fast-moving queue, and thus $T_i=T_{i-1}+X$, hence $T_i=iX$, so the result follows.

For (ii), $D_i=T_{i-1}+1$ by the definition of a slow-moving queue, so $T_i=T_{i-1}+X+1=iX+i-1$, again leading to the conclusion. □

Proof of Proposition 1. 

Since the quantity of interest is $T_N$, the proof is immediate. □

Before moving to the two-queue two-lane system, we recap the main characteristics of the escalator access queueing model:

• two classes of customers: walkers (W) and standers (S);
• two types of customer queueing behaviors: fast and slow (and correspondingly, fast-moving and slow-moving queues).

5. Two-Lane Escalator Model

We now move on to the two-lane escalator and consider two possible configurations for the two lanes (both queueing on the platform and traveling on the escalator):

• WS one lane for walkers, one lane for standers (e.g., walk left, stand right).
• S-S stand only – both lanes for standers.

We start the two-lane analysis by introducing the following assumptions.

Assumption 2.

The time to board the escalator from the front of the platform queue is given by $X\ge 1$ for both walkers and standers.

This assumption can be relaxed later to the following.

Assumption 2’The time to board the escalator from the front of the platform queue is given by $X\ge 1$ for standers and $X^{\prime }\in [1,X]$ for walkers.

Assumption 3.

There is no switching from one class (walker/stander) to the other.

Assumption 4.

There is no switching between the queues for the two lanes, i.e., no jockeying.

Under the latter two assumptions, both configurations act as two separate independent FCFS queues, whereas if Assumption 4 is relaxed (which is more realistic), the S-S configuration acts almost identically to a two-server single FCFS queue. Clearly, the S-S configuration can exploit pooling and load balancing for better performance, albeit at the cost of non-service to the walkers with no lane, so if there are customers from both classes, additional specifications are needed in our static model to take care of the walkers.

5.1. Clearing the Platform

For the WS configuration, we have the following result by applying Proposition 1 and the definition of makespan.

Proposition 2.

For the WS escalator configuration under Assumptions 1–4, the time to clear a completely packed FCFS two-lane queueing platform that starts with $N=N_W+N_S$ customers, where $N_W$ and $N_S$ denote the number of walkers and standers, respectively, is given by (i) $max\{N_W,N_S\}X$ for fast-moving queues (both lanes); and (ii) $max\{N_W,N_S\}(X+1)-1$ for slow-moving queues (both lanes).

We introduce a concrete toy example to illustrate the calculations and obtain some preliminary insights into the load balancing considerations. We take $N=20$ and $X=2$ and consider five distributions among the 20 total customers (i.e., 0, 5, 10, 15, 20 for the number of walkers or standers), performing the calculations for both fast-moving and slow-moving queues, with the results summarized in Table 1. The results highlight the fact that balancing the load between the two queues is key to achieving optimal efficiency. In the real world, one London study has shown about 75% choose to stand rather than walk [19], corresponding to the 5+15 (2nd) distribution below.

Example: WS configuration with fast-moving customers.

0+20: no walkers, last stander 40; makespan 40

5+15: last walker 10, last stander 30; makespan 30

10+10: last walker & last stander 20; makespan 20

15+5: last walker 30, last stander 10; makespan 30

20+0 last walker 40, no standers; makespan 40

Example: WS configuration with slow-moving customers.

0+20: no walkers, last stander 59; makespan 59

5+15: last walker 14, last stander 44; makespan 44

10+10: last walker & last stander 29; makespan 29

15+5: last walker 44, last stander 14; makespan 44

20+0 last walker 59, no standers; makespan 59

Carrying out analogous calculations for the S-S configuration requires some additional assumptions, because walkers would theoretically never get served in the queueing model. In practice, the simplest assumption to make is that they can still board the escalator, but would just be stymied in the next stage of riding the escalator itself, i.e., step (iii) in Figure 1. Since the primary focus of this analysis is to minimize time to clear the platform, we will make this assumption, i.e.,

Assumption 5.

Walkers will use either queue to board a stand-only (S-S-configured) escalator.

We will further consider perfect load balancing, or, equivalently, or allow jockeying between the two queues with pooled servers (lane).

Definition 3.

Two queues are said to beload balancedif they have the same number of customers. A multi-server queueing system is said to bepooledif customers in any of the queues can be served by any of the servers.

Under these this additional condition in conjunction with Assumption 5, the time to clear platform for the dedicated lane configurations would be the same, regardless of the distribution of walkers+standers; however, walkers would be “forced" to stand behind standers on the escalator itself, depending on how they were distributed in the queue. In particular, for the previous numerical example, the time to clear platform for the dedicated lane configurations would be 20 for fast-moving queues and 29 for slow-moving queues, as trivially summarized in Table 2.

Thus, in general, we have the following “negative" result, in which the makespan is independent of the distribution of the walkers and standers, as long as the queue movement behavior is the same for all customers and the queues are appropriately load balanced.

Proposition 3.

For a stand-only two-lane escalator under Assumptions 1–5, the time to clear a completely packed FCFS two-lane queueing platform that isload balanced, starting with N customers, is given by (i) $NX/2$ for fast-moving queues (both lanes); and (ii) $N(X+1)/2-1$ for slow-moving queues (both lanes), where N is assumed to be even.

Although not considered here, note that the same result holds if it were a walking-only two-lane escalator. The load-balancing condition can be dropped if jockeying is allowed, i.e., Assumption 4 is dropped, so we have the following equivalent result.

Corollary 1.

For a stand-only two-lane escalator under Assumptions 1–3 and A5, the time to clear a completely packed FCFSpooledtwo-lane queueing platform that starts with N customers is given by (i) $NX/2$ for fast-moving queues (both lanes); and (ii) $N(X+1)/2-1$ for slow-moving queues (both lanes), where N is assumed to be even.

We now introduce a concept closely related to load balancing, but it has to do with the distribution of the customers between the two classes rather than between the two queues.

Definition 4.

The distribution of customers between walkers and standers is said to beoptimally class-balancedif it minimizes the makespan time of interest.

For the time to clear the queues considered thus far, in the stand-only S-S configuration, a load-balanced queue is optimally balanced for all customer distributions, since the time to clear doesn’t depend on the customer type, whereas in the WS configuration, optimal balance occurs only when the distribution is equally split between walkers and standers.

Proposition 4.

Under Assumptions 1–5, a completely packed FCFS two-lane S-S queueing platform starting with N customers is optimally class-balanced for the time to clear the queues for all values of $N_W+N_W=N$.

Proposition 5.

Under Assumptions 1–3, a completely packed FCFS two-lane WS queueing platform starting with N customers is optimally class-balanced for the time to clear the queues if and only if $N_W=N_S=N/2$, where N is assumed to be even.

Propositions 2 through 5 can be used to reach the conclusion that for clearing the platform,

“stand-right, walk-left" is suboptimal unless optimally balanced,

more formally stated in the following result.

Corollary 2.

Under Assumptions 1–5, the time to clear a completely packed FCFS two-lane queueing platform starting with N customers for a stand-only (S-S-configured) escalator is no worse than for a “stand-right, walk-left" (WS-configured) escalator, where equality is achieved only when the platform is optimally class-balanced for the WS configuration.

In practice, it is unlikely that optimal balancing between standers and walkers will naturally occur, so for the WS configuration to come close to the performance of the stand-only configuration in terms of clearing the platform, it would be beneficial to “incentivize" customers to do so. On the other hand, in addition to the above conclusion being just for the time to clear the platform, the other assumptions underlying the conclusion have to do with customer behavior/speed, both in terms of boarding the escalator and in behavior in queue. Thus, we now extend the analysis to consider the following:

• total system time;
• unequal boarding times, i.e, two types of service times: normal (X) and quick ($X^{\prime }<X$), associated with standers and walkers, respectively;

Once total system time is considered, Proposition 4 no longer holds. Similarly, the latter extension necessitate Proposition 5 be adjusted accordingly to move the optimal balance point away from the equal distribution.

5.2. Total Time to Exit the System

The total time to exit the station requires adding the escalator time and time to walk after alighting from the escalator. For simplicity, we take the time to go from the escalator to the exit to be zero (including alighting), since any additional time can also be approximated by making the escalator longer, and assume no further delay for the walkers on the escalator itself (due to variations in different speeds of the walkers).

The following parameters will be used to estimate the total time to exit the station:

• escalator speed: 2 ft/sec, corresponding to stander speed on the escalator;
• walkers add 3 ft/sec, so their speed on the escalator is 5 ft/sec.

Thus, an escalator of 100 ft adds 50 sec for standers and 20 sec for walkers. Then the totals time to clear the entire system for the WS configuration are as follows:

Example: WS configuration with fast-moving customers.

0+20: no walkers, last stander 40 + 50 = 90; makespan 90

5+15: last walker 10 + 20 = 30, last stander 30 + 50 = 80; makespan 80

10+10: last walker 20 + 20 = 40, last stander 20 + 50 = 70; makespan 70

15+5: last walker 30 + 20 = 50, last stander 10 = 50 = 60; makespan 60

20+0 last walker 40 + 20 = 60, no standers; makespan 60

Example: WS configuration with slow-moving customers.

0+20: no walkers, last stander 59 + 50 = 109; makespan 109

5+15: last walker 14 + 20 = 34, last stander 44 + 50 = 94; makespan 94

10+10: last walker 29 + 20 = 49, last stander 29 + 50 = 79; makespan 79

15+5: last walker 44 + 20 = 64, last stander 14 + 50 = 64; makespan 64

20+0 last walker 59 + 20 = 79, no standers; makespan 79

Table 3. Total time to clear system for two-lane WS escalator for varying walkers+standers ($X=2$).

Table 3. Total time to clear system for two-lane WS escalator for varying walkers+standers ($X=2$).

However, average system time may be more relevant, calculated as follows:

Example: WS configuration with fast customers.

0+20: no walkers, standers 2*(1+2+...+20)/20 + 50 = 71

5+15: walkers 2*(1+2+3+4+5)/5 + 20 = 26, standers 2*(1+2+...+15)/15 + 50 = 66

10+10: walkers 2*(1+2+...+10)/10 + 20 = 31, standers 2*(1+2+...+10)/10 + 50 = 61

15+5: walkers 2*(1+2+...+15)/15 + 20 = 36, standers 2*(1+2+3+4+5)/5 + 50 = 56

20+0: no standers, walkers 2*(1+2+...+20)/20 + 20 = 41

Example: WS configuration with slow customers. 0+20: no walkers, standers (2+5+...56+59)/20 + 50 = 80.5

5+15: walkers (2+5+8+11+14)/5 + 20 = 28, standers (2+5+...+41+44)/15 + 50 = 73

10+10: walkers (2+5+...26+29)/10 + 20 = 35.5, standers (2+5+...26+29)/10 + 50 = 65.5

15+5: walkers (2+5+...+41+44)/15 + 20 = 43, standers (2+5+8+11+14)/5 + 50 = 58

20+0: no standers, walkers (2+5+...56+59)/20 + 20 = 50.5

Table 4. Average time to exit system for two-lane WS escalator for varying walkers+standers ($X=2$).

Table 4. Average time to exit system for two-lane WS escalator for varying walkers+standers ($X=2$).

We introduce the following notation to generalize the results:

$$\begin{array}{ccc}\hfill v_E& =& \mathrm{escalator} \mathrm{speed} (\mathrm{ft}/\sec )\hfill \\ \hfill v_W& =& \mathrm{walking} \mathrm{speed} (f/\sec )\hfill \\ \hfill p& =& \mathrm{proportion} \mathrm{of} \mathrm{customers} \mathrm{who} \mathrm{are} \mathrm{walkers}\hfill \\ \hfill N_W& =& \# \mathrm{customers} \mathrm{who} \mathrm{are} \mathrm{walkers}=pN\hfill \\ \hfill N_S& =& \# \mathrm{customers} \mathrm{who} \mathrm{are} \mathrm{standers}=(1-p)N\hfill \\ \hfill L& =& \mathrm{length} \mathrm{of} \mathrm{the} \mathrm{escalator} \left(\mathrm{ft}\right)\hfill \\ \hfill T_W& =& \mathrm{time} \mathrm{spent} \mathrm{on} \mathrm{escalator} \mathrm{for} \mathrm{walkers}=L/(v_E+v_W)\hfill \\ \hfill T_S& =& \mathrm{time} \mathrm{spent} \mathrm{on} \mathrm{escalator} \mathrm{for} \mathrm{standers}=L/v_E\hfill \end{array}$$

Proposition 6.

For the WS escalator configuration under Assumptions 1–4, the total time to clear the system starting with a completely packed FCFS queueing platform with N customers is given by

(i) $max\{N_{W}X+T_W,N_{S}X+T_S\}$ for fast-moving queues (both lanes); and

(ii) $max\{N_W(X+1)-1+T_W,N_S(X+1)-1+T_S\}$ for slow-moving queues (both lanes),

where $N_W=pN,N_S=(1-p)N,0\le p\le 1$.

The proof of Proposition 6 follows trivially from Proposition 2 and is hence omitted.

Proposition 7.

For the WS escalator configuration under Assumptions 1–4, the average time to exit the system starting with a completely packed FCFS queueing platform with N customers is given by

$$\left(i\right)\frac{X}{2N}\left[N_W(N_W+1)+N_S(N_S+1)\right]+p{T}_W+(1-p)T_{S}for fast-moving queues (both lanes);and$$

$$\left(ii\right)\frac{X+1}{2N}\left[N_W(N_W+1)+N_S(N_S+1)\right]-1+p{T}_W+(1-p)T_{S}forslow-movingqueues\left(bothlanes\right),$$

where $N_W=pN,N_S=(1-p)N,0\le p\le 1$.

Proof. 

The average total time in the system is given by

$$\frac{1}{N}\left[\sum _{i=1}^{N_W}{T}_i^{\left(W\right)}+\sum _{i=1}^{N_S}{T}_i^{\left(S\right)}\right]+p{T}_W+(1-p)T_S.$$

The summations can be found by applying Lemma 1 and ${\sum }_{i=1}^{n}i=n(n+1)/2.$

For (i), it follows directly, since Lemma 1 gives $T_i=Xi$, and for (ii), applying Lemma 1 gives $T_i=i(X+1)-1$, so

$$\sum _{i=1}^n[i(X+1)-1]=\frac{n(n+1)}{2}(X+1)-n=n\left[(n+1)(X+1)/2-1\right],$$

which substituting into the previous quantity gives

$$\frac{1}{N}\left[\frac{N_W(N_W+1)(X+1)}{2}+\frac{N_S(N_S+1)(X+1)}{2}\right]-1+p{T}_W+(1-p)T_S,$$

and trivial algebra completes the proof. □

Both Lanes Dedicated (S-S Configuration)

For the S-S configuration where both lanes are dedicated to standers but there are wannabe walkers in the mix, calculating the total time in system, whether the makespan or average, in general requires knowing both the distribution and ordering of the walkers and standers, since only walkers in the front of the queue will be able to walk on the escalators and are otherwise “forced" to stand on the escalator if even one walker is in front of them in queue. To simplify the analysis somewhat, we will now focus on the case where the queues are load-balanced, the number of walkers is no more than half the total, and all the walkers are in the left lane. This makes computing the time to clear the platform very easy, because together the assumptions imply that the right lane is full of standers and thus the bottleneck in terms of the makespan; on the other hand, the average still requires further analysis.

Assumption 6.

Walkers only occupy the left queue and only board the left escalator lane.

Adding Assumption 6, we have the following results analogous to Proposition 3 and Corollary 1.

Proposition 8.

For the stand-only (S-S) escalator configuration under Assumptions 1–6, the total time to clear the system starting with a completely packed FCFS queueing platform that is load balanced, starting with $N=N_W+N_S$ customers such that $N_W\le N_S$, is given by (i) $NX/2+T_S$ for fast-moving queues (both lanes); and (ii) $N(X+1)/2-1+T_S$ for slow-moving queues (both lanes), where N is assumed to be even.

Proof 

(Proof.). Assumption 6 combined with standers comprising at least half the customers implies that the right queue is completely packed with $N/2$ standers, from which the result follows from Proposition 1. □

The load-balancing condition can again be dropped if jockeying is allowed, i.e., dropping Assumption 4, with Assumption 6 relaxed correspondingly to the following.

Assumption 6’. Walkers only board the left escalator lane.

In this case, we have the following equivalent result.

Corollary 3.

For the stand-only (S-S) escalator configuration under Assumptions 1–3, A5, and A6’, the total time to clear the system starting with a completely packed FCFS queueing platform that allows jockeying between the two platform queues, starting with $N=N_W+N_S$ customers such that $N_W\le N_S$, is given by (i) $NX/2+T_S$ for fast-moving queues (both lanes); and (ii) $N(X+1)/2-1+T_S$ for slow-moving queues (both lanes).

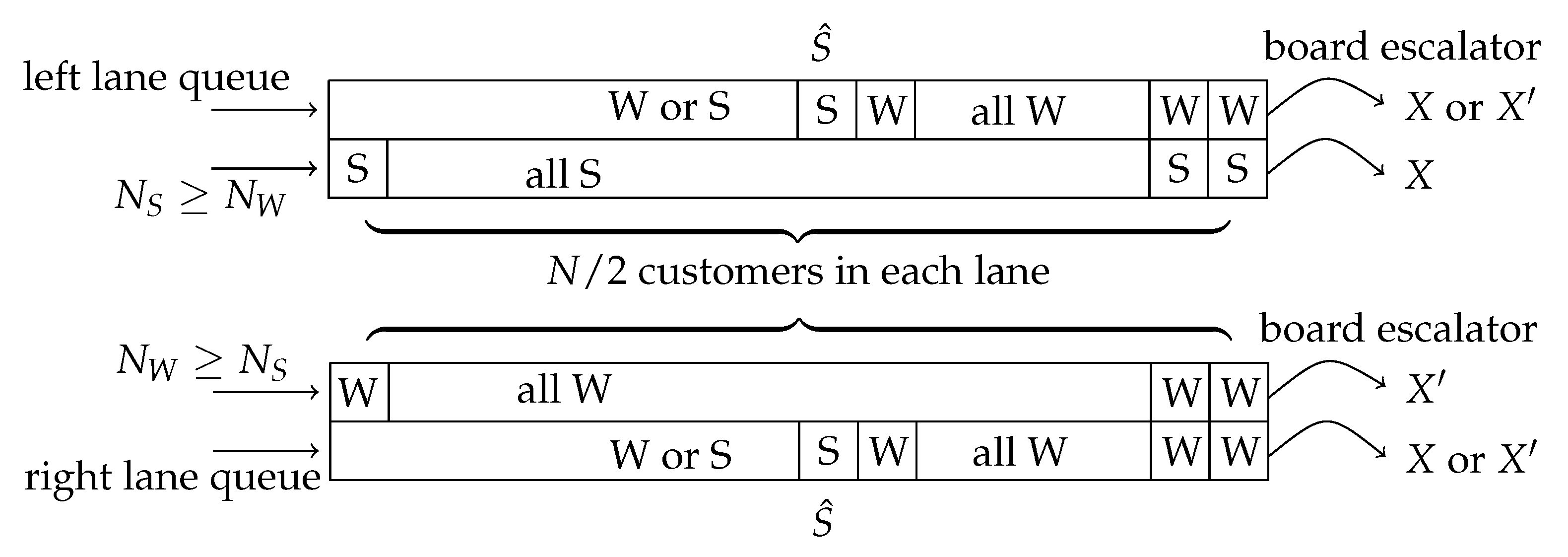
To compute average system time requires more information on the left queue. The key is to note that the system times of everyone is determined by the location of the first stander in the left lane queue, specifically, all the walkers in front of that first stander can quickly exit the system, whereas everyone else is “blocked" by that special stander; thus, if the first customer in the left queue is a stander, then everyone takes a long time to exit the system. This special stander is denoted by $\widehat{S}$, as depicted in Figure 7 for the two-queue setting.

The result is summarized by the following lemma for a single completely packed FCFS queue, which will corresponding to the left lane of the two-lane escalator system when standers are the majority and to the right lane when walkers are the majority.

Lemma 2.

Let $\widehat{S}$ denote the index of the first stander in a completely packed FCFS single queue. Under Assumptions 1 and A4, the time to exit the system for the ith customer in the queue is given by (i) $iX+T_W$ if $i<\widehat{S}$ and $iX+T_S$ if $i\ge \widehat{S}$ (for a fast-moving queue); and (ii) $i(X+1)-1+T_W$ if $i<\widehat{S}$ and $i(X+1)-1+T_S$ if $i\ge \widehat{S}$ (for a slow-moving queue).

Lemma 2 can be applied to calculate the average time to exit in the stand-only (S-S) two-lane escalator configuration.

Proposition 9.

For the stand-only (S-S) escalator configuration under Assumptions 1–6, the average time to exit the system starting with a completely packed FCFS queueing platform that is load balanced, starting with $N=N_W+N_S$ customers such that $N_W\le N_S$, is given by

$$\left(i\right)\frac{X(1+N/2)}{2}+\widehat{p}{T}_W+(1-\widehat{p})T_{S}for fast-moving queues(both lanes);and$$

$$\left(ii\right)\frac{(X+1)(1+N/2)}{2}-1+\widehat{p}{T}_W+(1-\widehat{p})T_{S}for slow-moving queues(both lanes),$$

where N is assumed to be even, $\widehat{p}=(\widehat{S}-1)/N$ for $\widehat{S}$ denoting the index of the first stander in the left lane. In the special case $N_W=N_S=N/2$, take $\widehat{p}=p=1/2$ (as $\widehat{S}$ is not defined).

Proof. 

The average total time in the system is given by

$$\frac{1}{N}\left[\sum _{i=1}^{N/2}{T}_i^{\left(l\right)}+\sum _{i=1}^{N/2}{T}_i^{\left(r\right)}\right]+\widehat{p}{T}_W+(1-\widehat{p})T_S.$$

The summations can be found by applying Lemma 1 and ${\sum }_{i=1}^{n}i=n(n+1)/2,$ where $T_i=Xi$ for (i) and $T_i=i(X+1)-1$ for (ii). Applying Lemma 2 leads to the other terms, since $\widehat{p}=(\widehat{S}-1)/N$ is the proportion of walkers who are ahead of the first stander in the left lane, hence the only customers who complete the escalator ride in $T_W$. □

An implicit assumption is that no passing is allowed on the escalator, which is enforced physically by the model having just two lanes and standers not having space to pass between them. Note that $\widehat{p}\le p$. The best-case scenario would have all wakers in front of the left lane, in which case the conclusions of Proposition 9 simply replace $\widehat{p}$ by p, and the worst-case scenario has one stander at the very front of the left queue, resulting in everyone requiring $T_S$ time on the escalator, or $\widehat{p}=0$.

We return to the numerical example used previously ($T_W=20,T_S=50)$, where the customers are split evenly between the two queues, i.e., left queue and right queue each has 10 customers, with slightly modified distributions – removing the 15-walkers case and considering the worst-case and best-case queues for the 5-walkers case (all in back and all in front, respectively). Note that we’ve kept the 20-walkers case, even though Proposition 8 doesn’t apply. For all distributions, the total time to clear system is 70 for fast; 79 for slow.

Table 5. Average time to exit system for two-lane (S-S) escalator for varying walkers+standers ($X=2$), where “>" and “<" denote all walkers at the back or in the front, respectively.

Table 5. Average time to exit system for two-lane (S-S) escalator for varying walkers+standers ($X=2$), where “>" and “<" denote all walkers at the back or in the front, respectively.

5.3. Unequal Boarding Times

For the WS escalator configuration, Propositions 2, 6, and 7 can be easily extended to the case where walkers have a quicker boarding time $X^{\prime }\le X$, where now X is the boarding time for standers. Recall that $N_W$ and $N_S$ denote the number of walkers and standers, respectively.

Proposition 10.

For the WS escalator configuration under Assumptions 1–4, $X^{\prime }\le X$, the time to clear a completely packed FCFS two-lane queueing platform that starts with $N=N_W+N_S$ customers is given by

(i) $max\{N_W{X}^{\prime },N_{S}X\}$ for fast-moving queues (both lanes); and

(ii) $max\{N_W(X^{\prime }+1),N_S(X+1)\}-1$ for slow-moving queues (both lanes).

Proposition 11.

For the WS escalator configuration under Assumptions 1–4, $X^{\prime }\le X$, the total time to clear the system starting with a completely packed FCFS queueing platform with $N=N_W+N_S$ customers, $p=N_W/N$, is given by

(i) $max\{N_W{X}^{\prime }+T_W,N_{S}X+T_S\}$ for fast-moving queues (both lanes); and

(ii) $max\{N_W(X^{\prime }+1)-1+T_W,N_S(X+1)-1+T_W\}$ for slow-moving queues (both lanes).

Proposition 12.

For the WS escalator configuration under Assumptions 1–4, $X^{\prime }\le X$, the average time to exit the system starting with a completely packed FCFS queueing platform with $N=N_W+N_S$ customers, $p=N_W/N$, is given by

$$\left(i\right)\frac{X^{\prime }{N}_W(N_W+1)+X{N}_S(N_S+1)}{2N}+p{T}_W+(1-p)T_{S}for fast-moving queues(both lanes);and$$

$$\left(ii\right)\frac{(X^{\prime }+1)N_W(N_W+1)+(X+1)N_S(N_S+1)}{2N}-1+p{T}_W+(1-p)T_S$$

for slow-moving queues (both lanes).

Recall that when the total number of walkers is less than the number of standers, then the system times of everyone in the left lane (where all the walkers are assumed to be) are determined by the location of the first stander in the left lane queue, as all the walkers in front of that first stander can quickly exit the system, whereas everyone else is “blocked" by that special stander; Figure 8 again depicts this special stander denoted by $\widehat{S}$ in the two-queue setting, this time also including the case where the number of walkers is greater than the number of standers, in which case the special stander is in the right lane.

For the stand-only (S-S) escalator system, Proposition 3 and Corollary 1 provide an upper bound when $X^{\prime }\le X$, but otherwise the result can be modified as follows.

Proposition 13.

For a stand-only two-lane escalator under Assumptions 1–5, $X^{\prime }\le X$, the time to clear a completely packed FCFS two-lane queueing platform that isload balanced, starting with $N=N_W+N_S$ customers, N assumed to be even, is given by

(i) $NX/2$ for fast-moving queues (both lanes); and

(ii) $N(X+1)/2-1$ for slow-moving queues (both lanes),

when $N_W\le N_S$ and all walkers are in the left queue; or

(i) $max\{N_{S}X,(N_W-N/2)X^{\prime }\}$ for fast-moving queues (both lanes); and

(ii) $max\{N_S(X+1),(N_W-N/2)(X^{\prime }+1)\}-1$ for slow-moving queues (both lanes),

when $N_S\le N_W$ and all standers are in the right queue.

The need to separate into two separate cases is to specify that the minority customers are all in the same lane (walkers in left queue, standers in right queue). If that is understood, then the two cases can be combined, with the following expressions for both:

(i)

$max\{min(N_S,N/2)X,{(N_W-N/2)}^{+}{X}^{\prime }\}$ for fast-moving queues (both lanes); and

(ii)

$max\{N_S(X+1),{(N_W-N/2)}^{+}(X^{\prime }+1)\}-1$ for slow-moving queues (both lanes).

Proposition 8, for the total time to clear the system, holds without any necessary changes, as long as $X^{\prime }\le X$, because the right queue is the bottleneck, and $X^{\prime }$ only speeds up the left queue, since $N_W\le N_S$ with walkers all in the left lane. For the case where walkers constitute the majority, a general result could be derived using Figure 8, but here we specialize only to the best-case scenarios where all the walkers are in the front of the right queue.

Proposition 14.

For a stand-only two-lane escalator under Assumptions 1–5, $X^{\prime }\le X$, the total time to clear the system starting with a completely packed FCFS two-lane queueing platform that isload balanced, with $N=N_W+N_S$ customers, N even, $0<N_S\le N_W$, andall walkers are in the front of the right queue, is given by

(i) $max\{min(N_S,N/2)X+T_S,{(N_W-N/2)}^{+}{X}^{\prime }+T_W\}$ for fast-moving queues; and

(ii) $max\{N_S(X+1)+T_S,{(N_W-N/2)}^{+}(X^{\prime }+1)\}-1+T_W$ for slow-moving queues.

A completely generalized version of Proposition 9 for the average time would also require more information regarding queue ordering for the lane with mixed customers; again, here we specialize only to the best-case scenarios where all the walkers are in the front of the left queue, which coincides with the WS result in Proposition 12.

Proposition 15.

For the stand-only (S-S) escalator configuration under Assumptions 1–6, the average time to exit the system starting with a completely packed FCFS queueing platform that isload balanced, starting with $N=N_W+N_S$ customers such that $N_W\le N_S$, N assumed to be even, $p=N_W/N$, andall walkers are in the front of the left queue, is given by

$$\left(i\right)\frac{X^{\prime }{N}_W(N_W+1)+X[N/2(N/2+1)+(N_S-N/2)(N_S-N/2+1)]}{2N}+p{T}_W+(1-p)T_S$$

for fast-moving queues (both lanes); and

$$\left(ii\right)\frac{(X^{\prime }+1)N_W(N_W+1)+(X+1)[N/2(N/2+1)+(N_S-N/2)(N_S-N/2+1)]}{2N}-1$$

$$+p{T}_W+(1-p)T_{S}for slow-moving queues(both lanes).$$

6. Discussion

For ease of comparison of the WS and S-S configurations, Table 6, Table 7, Table 8 and Table 9 summarize numerical results for the three metrics analyzed using the queueing model for the example: time to clear the platform; total time to clear the system; and average time to exit system (escalator times $T_W=20,T_S=50$). The color-coded entries indicate a comparison for the case where 75% of the customers are standers, the approximate proportion reported for London Tube riders, highlighting the trade-off between the two policies, depending on the objective. Although Table 6 is not really necessary, since it was already established that for the objective of clearing the platform, the stand-only policy is optimal, due to the pooling effects of using both queues to load the escalator, the numerical values provide some intuition on the relationship between the distribution of walkers and standers and the resulting performance estimates for clearing the bottleneck congestion area.

The numerical results support the conclusion that in times of congestion, it is generally better to dedicate both lanes to standers (or walkers), to take full advantage of the pooling effect of allowing quicker access to the escalators and usage of the escalators, i.e., the well-known queueing theory advantage of pooling takes precedence. However, the average time performance metrics show that there can be substantial variation between the worst-case and best-case ordering of the queues to access the escalator if the walkers are quicker to board the escalator; refer to the color-coded entries in Table 9. In other words, in terms of the overall utility of customers, the stand-only configuration may not be optimal, unless the walkers can be put at the head of the queues, so that they can exit the system more quickly. This is an example of the optimality of the shortest-processing-time queueing priority under certain conditions.

7. Conclusions and Future Research

The deterministic queueing model offers many insights for the “rush-hour" setting. First, if the overriding objective is to clear the platform during such times, then under the assumption that access to the escalator is the bottleneck (which has been demonstrated to be the case empirically), the policy of allowing everyone to access both lanes makes the most sense, just because of the pooling effect, which in this case translates to getting everyone onto the escalators as quickly as possible, regardless of their desire to walk or stand. However, taking into consideration other objectives such as the total time to exit the station requires more detailed analysis. During normal times when congestion is not an issue, it makes sense to have one lane for standers and one for walkers, as this allocation minimizes both makespan and total system time, whereas during high-congestion times, such as morning and even rush hours, it is clear that dedicating one lane for walking and one for standing is suboptimal, as has been well observed in practice. However, the solution of requiring everyone to stand during such periods has been shown to be impractical and also not always optimal either, as the main assumption is that the proportion of standers is overwhelmingly higher than walkers such as has been reported in London at 75%, but this may not hold uniformly across systems or even among different stations in the same subway network, e.g., during morning rush hour in New York City downtown Manhattan when almost everyone is in a hurry to get to work, the reverse might be true, i.e., the number of walkers could exceed the number of standers, especially for stations with relatively shorter escalators. If this is the case, the key is not to dedicate the queueing access to the two lanes a priori but to allow jockeying and load balancing to enable a pooling effect to clear the platform, and then sort out the walkers and standers over the course of the escalator. This would help improve efficiency, although there could be negative effects on safety, since it would require more movement on the escalator itself. An alternative solution would be to allow the wannabe walkers to quickly get to the head of the left lane and then after they are (mostly) cleared, convert the escalators to standing only. Signals could be used to indicate which lane is currently to be used for walkers and which lane is for standers, analogous to what is used to indicate direction of flow on some “reversible" roads and bridges, e.g., into the city in the morning rush hour, out of the city in the evening rush hour, towards the ocean beginning on a Friday afternoon, and away from the ocean starting on Sunday. Those changeovers are generally done on a fixed timing schedule, which could be followed to coincide with rush hours in a subway system, but another alternative for guiding the transition between “walk left, stand right" and standing only is to use sensors — the higher the proportion of walkers, the later the switchover would occur (analogous to the difference between fixed traffic light signaling versus sensor-based signals). If this policy were known to all the users of the system, it could also affect behavior and increase efficiency, as knowing that they would be at the head of the queue might incentivize some standers to convert to walkers.

To summarize, to best serve both the system and the riders (customers),

“stand right, walk left" (focus is on flow and “fairness/freedom")

is a sensible policy to follow the majority of the time, but during times of anticipated heavy traffic, the following behavior should be induced:

Walkers go to front of queue(s) and quickly board escalator, then switch to

“stand on both lanes" (focus on efficient clearing at the bottleneck).

Most importantly, the queues to board the escalator should be filled to take full advantage of pooling effects.

The last point may be subtle, because during normal times, there is really only a single “virtual queue" to board the escalator on the right lane, as walkers are presumably loading the left lane of the escalator at a rapid pace, so there is not really any queue forming there. Specifically, during low to medium traffic periods, boarding the escalator is not a bottleneck, so feeding a single lane does not lead to excessive congestion at that point of entry.

This work has just scratched the surface in applying a simple quantitative model to analyze the system, and numerous directions for future research include the following:

• For steady-state analysis, more sophisticated (stochastic) queueing theory could provide better analytical estimates of performance providing useful approximations for planning. In heavy traffic, fluid and diffusion approximations would be useful for deriving further analytical insights.
• Two efficiency metrics of interest were considered: the total time to clear the area leading to the escalators (makespan) and total time spent in the system (including time spent on the escalator) – both the maximum (total makespan) and the average. Other performance metrics might be of interest to operations managers, e.g., escalator capacity utilization and safety indicators.
• A critical parameter in trying to implement prescriptive solutions in real time, such as switching between one lane for walkers and standers to both lanes for standers is the proportion of each class. Practically speaking, it may not be clear how to estimate this proportion in real time, though the ubiquity of sensors may enable this, or perhaps there could be a way for passengers (customers) to indicate their preeference.
• For more accurate assessment in practice, covering all ranges of utilization, from light to medium to heavy over the entire course of a day, a detailed stochastic simulation model would be the most appropriate, which could be a discrete-event system model or an agent-based model. Such a model could incorporate safety considerations into operations by modeling the possibility of a breakdown or accident in the escalator, which as alluded to earlier should be a rare event that would only occur on a long time horizon spanning months or years.
• Building on the previous item, when Incorporating safety issues into the operational analysis, estimating safety performance metrics becomes challenging since such incidents presumably occur on a slower time scale than normal operations, so if a detailed simulation model were used, then importance sampling techniques could be investigated. Concepts from multi-fidelity modeling and multi-timescale optimization could be of interest in these settings.
• Analogous analyses may be applied to similar settings such as a highway, where there are also multiple types of customers and lanes, e.g., fast drivers and passing lanes.