Prerpints.org logo
Preprint
Technical Note

Linearized Expressions of 3D Rotational Motion

Altmetrics

Downloads

144

Views

56

Comments

0

This version is not peer-reviewed

AI and Computational Methods for Modelling, Simulations and Optimizing of Advanced Systems: Innovations in Complexity

Submitted:

11 May 2024

Posted:

14 May 2024

You are already at the latest version

Alerts
Abstract
Rotation motion in a three-dimensional physical world refers to an angular displacement of an object around a specific axis in $\mathbb{R}^3$. It is typically formulated as a non-linear and non-convex process due to the nonlinearity and nonconvexity of $\mathbb{SO}(3)$. However, this paper proposes a new perspective that the 3D rotation motion can be expressed by the linear equation without dropping any constraints and increasing any singularities. Moreover, two frequent cases, i.e., $\angle\left(\mathbf{R}\boldsymbol{x},\boldsymbol{y}\right)=0(\pi)$ and $\angle\left(\mathbf{R}\boldsymbol{x},\boldsymbol{y}\right)=\frac{\pi}{2}$, in computer vision and robotics that can be expressed linearly are deeply discussed in this paper.
Keywords: 
Subject: Computer Science and Mathematics  -   Robotics

1. Background

Rotational motion [1] in the three-dimensional physical world refers to the circular movement of an object around a fixed axis [2]. It is a basic concept and commonly used in physics, computer graphics, computer vision, robotics, aerospace, and other scientific fields [3,4,5,6]. More specifically, in many practical applications, rotational motion is not only an important means of constructing the motion of the target system [7,8] but also an important state parameter to be estimated [9,10,11]. However, rotation motion is typically formulated as a non-linear and non-convex process [11,12]. It not only makes some linear algorithms, such as Kalman filter [13,14], impossible to directly apply [15], but also makes solving the related problem more sophisticated and difficult [12,16].
In this paper, a new perspective is proposed that the rotation motion can be linearized without dropping any constraints and increasing any singularities. It is particularly worth pointing out that there are no special and advanced techniques, such as Lie groups and Lie algebras [17,18], for the methods used in this paper. Only some basic knowledge of linear algebra [19,20,21] is required to understand the ideas presented in this paper.

2. Rotation Motion

Mathematically, given a point x ∈ R 3 , if it is rotated about a fixed unit vector r ∈ S 2 through the origin and the rotated angle is θ , then the rotation motion can be formulated by multiplication of a matrix and a vector,
R x → y
where y ∈ R 3 is the rotated point by x and R is a 3 × 3 rotation matrix. There are some properties regarding the rotation motion [22],
  • Shape and Size: Rotation does not alter the shape or size of the object. More Specifically,
    • ∥ R x ∥ = ∥ R ∥ · ∥ x ∥ = ∥ x ∥ . It means the length of the point x will not be changed by rotation motion. Without loss of generality, the rotation motion in this paper is studied with unit norm vectors, i.e., x ∈ S 2 on the unit sphere surface, which represents a unit direction vector in the 3D physical world.
    • ∠ R x 1 , R x 2 = ∠ x 1 , x 2 where x 1 , x 2 ∈ S 2 are any two unit vectors. It means the angle (structure) of the object is unchanged.
  • Axis of Rotation: Rotational motion occurs around a fixed axis. Given a vector x ∈ S 2 , if R x = x , it means the after the rotation R , the vector direction x remains unchanged, and the vector x must be parallel to the rotation axis r , which is from Euler’s rotation theorem and screw theory [23,24,25,26]. In addition,
    R x = x ⇒ R − I 3 × 3 x = 0
    where I 3 × 3 is the 3 × 3 identity matrix. Algebraically, Eq.(2) means the rotation axis direction r lies in the null space of R − I 3 × 3 . Alternatively, let R x = λ x , then the rotation axis direction r is an eigenvector of R corresponding to the eigenvalue λ = 1 .
At first glance, the rotation motion is a linear process, which might be misled by the matrix representation Eq.(1). Unfortunately, R is not a regular matrix in R 3 × 3 . A rotation only has three degrees of freedom, since it can be determined by a rotation axis r ∈ S 2 and a rotation angle θ ∈ [ 0 , π ] . Formally, R ∈ SO ( 3 ) , and a rotation can be represented by a matrix and non-linear constraints,
R = r 11 r 12 r 13 r 21 r 22 r 23 r 31 r 32 r 33 , s . t . R T R = I 3 × 3 , det ( R ) = + 1
According to the famous Rodrigues’ rotation formula [27,28], given the rotation axis r = r 1 r 2 r 3 T ∈ S 2 and rotation angle θ , the matrix can be constructed by
R = exp θ [ r ] × = I 3 × 3 + sin ( θ ) [ r ] × + 1 − cos ( θ ) [ r ] × 2 , [ r ] × = 0 − r 3 r 2 r 3 0 − r 1 − r 2 r 1 0
Moreover, a rotation matrix can be represented by a quaternion vector with unit length [29,30], such that q = q 0 q 1 q 2 q 3 T ∈ S 3 . Specifically,
R = q 0 2 + q 1 2 − q 2 2 − q 3 2 2 q 1 q 2 − q 0 q 3 2 q 1 q 3 + q 0 q 2 2 q 1 q 2 + q 0 q 3 q 0 2 − q 1 2 + q 2 2 − q 3 2 2 q 2 q 3 − q 0 q 1 2 q 1 q 3 − q 0 q 2 2 q 2 q 3 + q 0 q 1 q 0 2 − q 1 2 − q 2 2 + q 3 2
It is worth noting that many different forms of parameter representation can represent the same rotation, and each form of representation has its appropriate application scenario [2,31,32,33]. For example, since a rotation can be determined by a fixed rotation axis r ∈ S 2 and a rotation angle θ ∈ 0 , π , then the rotation can be represented by axis–angle representation θ · r  [34], which geometrically is a point in a 3D ball of radius π  [28] and has been widely used in pose estimation problems [28,35,36]. Nonetheless, throughout most of this paper, quaternions are used to represent rotations [29,30] and thus to illustrate the proposed linearization theory.
Anyone who has ever used any other parametrization of the rotation group will, within hours of taking up the quaternion parametrization, lament his or her misspent youth [2,31].

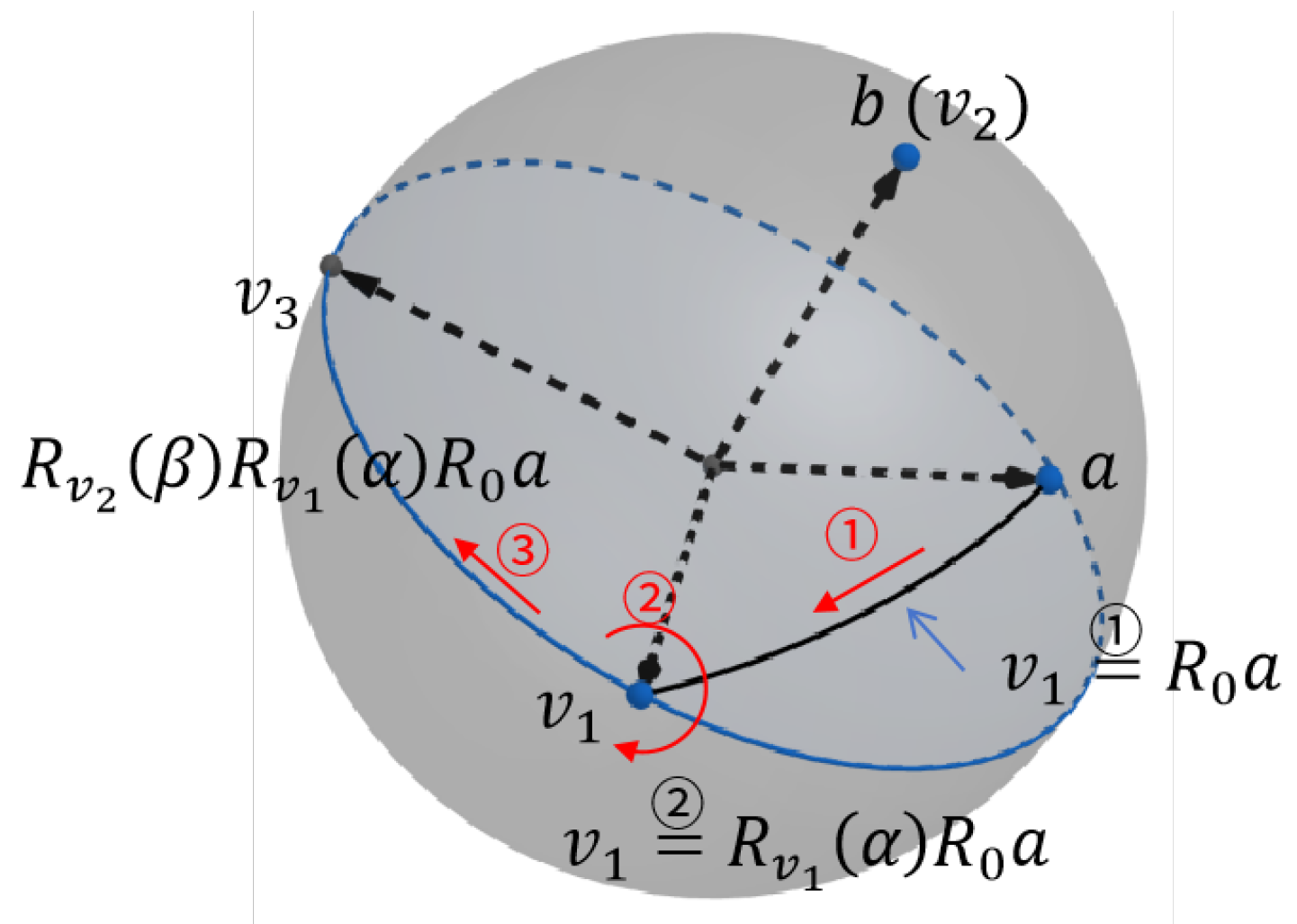
3. Linear Expressions for Rotation Motion

Given a = a 1 a 2 a 3 ∈ S 2 and a rotation R ∈ SO ( 3 ) , the rotation motion can be formulated as
R a = b ⇔ ∠ R a , b = 0 ⇔ b T R a = 1
where b = b 1 b 2 b 3 ∈ S 2 is rotated by a . This formulation is a special case of the next expression for rotational motion. Formally, given a , b ∈ S 2 and R ∈ SO ( 3 ) whose quaternion expression is q ∈ S 3 ,
∠ R a , b = τ ⇔ b T R a = cos τ ⇔ q T M q = cos τ
Here M is constructed by a and b  [29,37]. Specifically,
M = [ 0 − a 1 − a 2 − a 3 a 1 0 a 3 − a 2 a 2 − a 3 0 a 1 a 3 a 2 − a 1 0 ] T [ 0 − b 1 − b 2 − b 3 b 1 0 − b 3 b 2 b 2 b 3 0 − b 1 b 3 − b 2 b 1 0 ]
When τ = 0 , Eq.(7) degenerates back to Eq.(6).
By conducting eigendecomposition of the real symmetric matrix M = U Λ U T  [21,38], where and U = u 0 u 1 u 2 u 3 ∈ R 4 × 4 is an orthogonal matrix U U T = I 4 × 4 . Observe
det M − λ I 4 × 4 = 0 ⇒ λ 2 − 1 2 = 0
Therefore, the eigenvalue of M is
Λ = 1 0 0 0 0 1 0 0 0 0 − 1 0 0 0 0 − 1
Accordingly, q T U Λ U T q = cos τ . Let Γ = Γ 0 , Γ 1 , Γ 2 , Γ 3 T = U T q , then q = Γ 0 u 0 + Γ 1 u 1 + Γ 2 u 2 + Γ 3 u 3 . Observe
Γ T Γ = q T U U T q = Γ 0 2 + Γ 1 2 + Γ 2 2 + Γ 3 2 = 1 q T U Λ U T q = Γ T Λ Γ = Γ 0 2 + Γ 1 2 − Γ 2 2 − Γ 3 2 = cos τ ⇒ Γ 0 2 + Γ 1 2 = 1 2 1 + cos τ Γ 2 2 + Γ 3 2 = 1 2 1 − cos τ
Therefore, the possible rotation q can be reformulated linearly
q = Γ 0 u 0 + Γ 1 u 1 + Γ 2 u 2 + Γ 3 u 3
= 2 1 + cos τ 2 cos ( ϕ ) u 0 + sin ( ϕ ) u 1 + 2 1 − cos τ 2 cos ( ψ ) u 2 + sin ( ψ ) u 3
where ϕ , ψ ∈ [ − π , π ] . This result clearly shows that the rotational motion can be expressed in linear forms.
Geometrically, if ∠ R a , b = τ , then all possible rotation q that satisfy the constraint will be in a torus in S 3 . For better understanding, we draw some special cases, i.e., τ = { 0 , π 9 , 3 π 9 , 6 π 9 , 8 π 9 } via stereographic projection [39,40], as in Figure 1. It is worth noting that when τ = { 0 , π } , i.e., R a = ± b , the torus in S 3 is degenerated into a one-dimensional circle, more specifically, a great circle [41] in S 3 . Formally,
➀ : when τ = 0 ⇒ q = cos ( ϕ ) u 0 + sin ( ϕ ) u 1 ➁ : when τ = π ⇒ q = cos ( ψ ) u 2 + sin ( ψ ) u 3
In addition, when τ = π 2 , the torus is becoming to the Clifford torus in S 3  [42,43], since it has the equal diameters in cross directions. Specifically,
q = 1 2 cos ( ϕ ) u 0 + sin ( ϕ ) u 1 + 1 2 cos ( ψ ) u 2 + sin ( ψ ) u 3
These special cases will be discussed in depth in subsequent sections.

4. Special Case I: Great Circle in S 3

If τ = 0 , which means R a = b , it is one of the most common cases in practical applications. It is worth noting that there are two facts regarding R a = b ,
  • Not all rotations in SO ( 3 ) can rotate a to b .
  • There is more than one rotation that satisfies the given rotation motion.
Then according to Eq. (14) all rotations that satisfy R a = b should be in
q = cos ( ϕ ) u 0 + sin ( ϕ ) u 1
where u 0 and u 1 are the basis vectors in S 3 , and they depend on M , i.e., a and b . Geometrically speaking, q is a unit vector in R 4 , which is a linear combination of the two vectors u 0 and u 1 . In addition, q T q = 1 , which means q is on the surface of the unit quaternion sphere. Therefore, the region where all possible rotations satisfy a specific rotation motion is a great circle in S 3  [41]. Moreover, since U T U = I 4 × 4 , there will be
cos ( ϕ ) u 0 T + sin ( ϕ ) u 1 T u 2 = 0 cos ( ϕ ) u 0 T + sin ( ϕ ) u 1 T u 3 = 0 ⇒ q T u 2 = 0 q T u 3 = 0
Up until this point, the rotation motion is linearly expressed, which is closely related to U .
In addition,
M u 0 = 1 · u 0 ; M u 1 = 1 · u 1 ; M u 2 = − 1 · u 2 ; M u 3 = − 1 · u 3
It is easy to confirm [44,45],
M 0 − a − b T − a − b a + b × T = 0 − a − b T − a − b a + b × T − 1 0 0 0 0 − 1 0 0 0 0 − 1 0 0 0 0 − 1 = · − 1 · Ω −
M 0 − a + b T − a + b a − b × T = 0 − a + b T − a + b a − b × T 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 = · + 1 · Ω +
Therefore, any row of Ω − can be the eigenvector of M with eigenvalue − 1 . Similarly, any row of Ω + can be the eigenvector of M with eigenvalue 1.
Accordingly, (1) any row of Ω − is a linear combination of u 0 and u 1 . (2) any row of Ω + is a linear combination of u 2 and u 3 . Consequently, rank Ω − = rank Ω + = 2 ; Ω − and Ω + are not orthogonal matrices. Therefore, Ω − q = 0 , more specifically,
0 a 1 − b 1 a 2 − b 2 a 3 − b 3 − a 1 − b 1 0 − a 3 + b 3 a 2 + b 2 − a 2 − b 2 a 3 + b 3 0 − a 1 + b 1 − a 3 − b 3 − a 2 + b 2 a 1 + b 1 0 q 0 q 1 q 2 q 3 = 0 ⇔ 0 a − b T − a − b a + b × q 0 q 1 q 2 q 3 = 0
Now the linear expression of R a = b is constructed.
Furthermore, if more than one rotation motion constraints are given, such that
R a 1 = b 1 R a 2 = b 2 ⋯ R a N = b N → linearization Ω 1 − q = 0 Ω 2 − q = 0 ⋯ Ω N − q = 0 ⟹ Ω 1 − Ω 2 − ⋯ Ω N − q = 0
Eventually, the corresponding linear system is constructed. It must be acknowledged that there is still a constraint of length 1, i.e., q T q = 1 . However, the scale is not particularly important for homogeneous linear equations.

4.1. Alternative Way to Obtain Great Circle in S 3

In this part, a geometrical approach to obtain a great circle in S 3 is presented. Given the rotation motion R a = b , the possible rotation can be formulated as [9,34]
R = R b ( α ) R a b
where R b ( α ) is a rotation around rotated axis is b and rotated angle is α ; R a b is a rotation that can rotate a to b . To use quaternion to represent rotation [30],
R b ( α ) : = cos α 2 , sin α 2 b
R a b : = q 0 , q 1 , q 2 , q 3 T = q 0 , q 123
The formula for the multiplication of two quaternions is [29]
( r 1 , v 1 → ) ( r 2 , v 2 → ) = ( r 1 r 2 − v 1 → v 2 → , r 1 v 2 → + r 2 v 1 → + v 1 → × v 2 → )
Then,
R : = cos α 2 q 0 − sin α 2 b T q 123 , q 0 sin α 2 b + cos α 2 q 123 + sin α 2 b × q 123
Therefore,
q = q 0 q 123 cos α 2 + − b T q 123 q 0 b + b × q 123 sin α 2 = · q b 1 cos α 2 + q b 2 sin α 2
Observe
q b 1 T q b 1 = q 0 2 + q 1 2 + q 2 2 + q 3 2 = 1
q b 2 T q b 2 = b T q 123 2 + q 0 b 2 + b × q 123 2 = q 123 T q 123 cos ∠ ( b , q 123 ) 2 + q 0 2 + q 123 T q 123 sin ∠ ( b , q 123 ) 2 = q 0 2 + q 1 2 + q 2 2 + q 3 2 = 1
q b 1 T q b 2 = − q 0 b T q 123 + q 123 q 0 b + b × q 123 = 0
Therefore, q b 1 and q b 2 are two orthonormal bases in R 4 , which can be considered as u 0 and u 1 in Eq. (16). Consequently, q lies in the great circle in S 3 .

5. Special Case II: Clifford Torus in S 3

5.1. Alternative Way to Obtain Clifford Torus in S 3

In the previous text, we provide a general derivation for the connection between rotation constraint, i.e., b T R a = 0 and Clifford torus. Here we show an alternative way to obtain Clifford torus from rotation constraint.
Given a rotation constraint b T R a = 0 , the possible rotation R can be (see Figure 2)
R α , β = R v 2 β R v 1 α R 0 , α , β ∈ − π , π
where v 2 = b , v 1 T v 1 = 1 and v 1 T v 2 = 0 ; R 0 is a rotation that rotates a to v 1 ; R v 1 ( α ) = exp α [ v 1 ] × and R v 2 ( β ) = exp β [ v 2 ] × are rotations around directions b 1 and b , respectively. The rotation motion can be as follows,
v 1 = R 0 a , ⟶ v 1 = R v 1 α R 0 a , ⟶ b T R v 2 β R v 1 α R 0 a = 0 .
To use quaternion to represent rotation [30]
R v 2 β : = q v 2 ( β ) = cos β 2 v 2 T sin β 2 T
R v 1 α : = q v 1 ( α ) = cos α 2 v 1 T sin α 2 T
R 0 : = q 0 q 123 T T
The formula for the multiplication of two quaternions is [29]
( r 1 , v 1 → ) ( r 2 , v 2 → ) = ( r 1 r 2 − v 1 → v 2 → , r 1 v 2 → + r 2 v 1 → + v 1 → × v 2 → )
Define v 3 = v 1 × v 2 , then
R v 2 ( β ) R v 1 ( α ) : = cos β 2 cos α 2 v 2 T sin β 2 cos α 2 + v 1 T sin α 2 cos β 2 − v 3 T sin β 2 sin α 2 T
In addition, let w 1 = 1 2 ( α − β ) and w 2 = 1 2 ( α + β ) ,
cos β 2 cos α 2 = 1 2 cos α − β 2 + cos α + β 2 = 1 2 cos ( w 1 ) + cos ( w 2 )
sin β 2 cos α 2 = 1 2 sin α + β 2 − sin α − β 2 = 1 2 sin ( w 2 ) − sin ( w 1 )
sin α 2 cos β 2 = 1 2 sin α + β 2 + sin α − β 2 = 1 2 sin ( w 2 ) + sin ( w 1 )
sin β 2 sin α 2 = 1 2 cos α − β 2 − cos α + β 2 = 1 2 cos ( w 1 ) − cos ( w 2 )
Then,
R v 2 ( β ) R v 1 ( α ) : = 1 2 cos ( w 1 ) + cos ( w 2 ) sin ( w 1 ) v 1 T − v 2 T − cos ( w 1 ) v 3 T + sin ( w 2 ) v 1 T + v 2 T + cos ( w 2 ) v 3 T T
Therefore,
R α , β = R v 2 ( β ) R v 1 ( α ) R 0
: = 1 2 cos ( w 1 ) + cos ( w 2 ) q 0 − sin ( w 1 ) v 1 T − v 2 T − cos ( w 1 ) v 3 T + sin ( w 2 ) v 1 T + v 2 T + cos ( w 2 ) v 3 T q 123 cos ( w 1 ) + cos ( w 2 ) q 123 + sin ( w 1 ) v 1 − v 2 − cos ( w 1 ) v 3 + sin ( w 2 ) v 1 + v 2 + cos ( w 2 ) v 3 q 0 + sin ( w 1 ) v 1 − v 2 − cos ( w 1 ) v 3 + sin ( w 2 ) v 1 + v 2 + cos ( w 2 ) v 3 × q 123
 
= 1 2 k 0 k 1 k 2 k 3 cos ( w 1 ) sin ( w 1 ) cos ( w 2 ) sin ( w 2 ) , w 1 = 1 2 ( α − β ) , and , w 2 = 1 2 ( α + β )
= 1 2 k 0 cos ( w 1 ) + k 1 sin ( w 1 ) + k 2 cos ( w 2 ) + k 3 sin ( w 2 )
where
k 0 = q 0 + v 3 T q 123 q 123 − q 0 v 3 − v 3 × q 123 k 1 = − v 1 − v 2 T q 123 q 0 v 1 − v 2 + v 1 − v 2 × q 123
k 2 = q 0 − v 3 T q 123 q 123 + q 0 v 3 + v 3 × q 123 k 3 = − v 1 + v 2 T q 123 q 0 v 1 + v 2 + v 1 + v 2 × q 123
It is easy to verify
k 0 k 1 k 2 k 3 T k 0 k 1 k 2 k 3 = 2 0 0 0 0 2 0 0 0 0 2 0 0 0 0 2
Geometrically, Eq. (44) describes a Clifford torus [42,46] in S 3 .

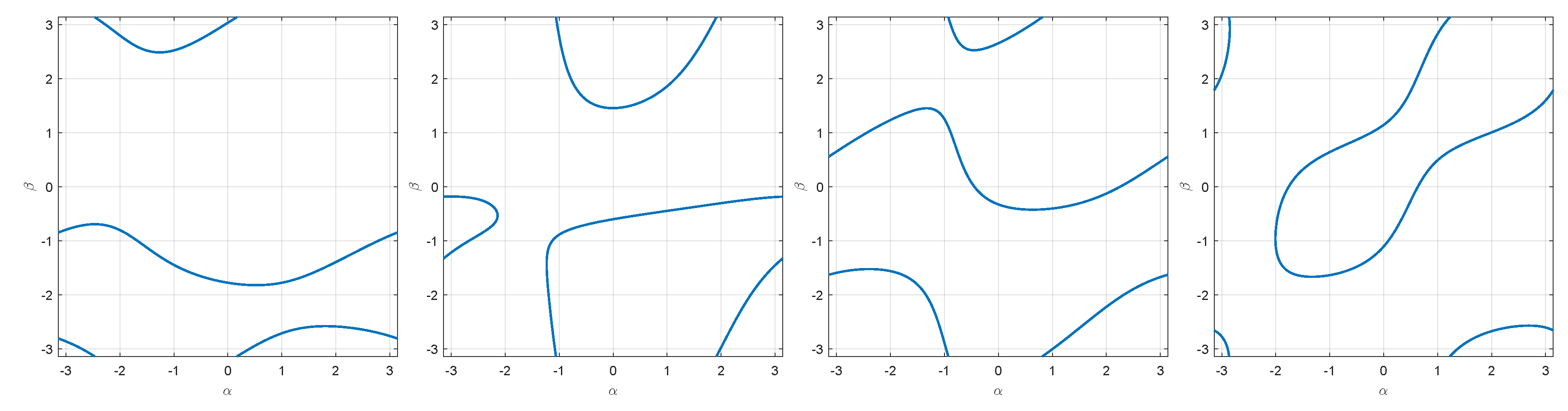
5.2. Intersections of Two Different Clifford Tori

Given two rotation constraints b 1 T R a 1 = 0 and b 2 T R a 2 = 0 , the possible rotation can be considered in the intersections of two Clifford tori (see Figure 3). Here, a solution to solve the intersection line is presented. Specifically,
b 1 T R a 1 = 0 b 2 T R a 2 = 0 ⇒ R α , β = R v 2 β R v 1 α R 0 b 2 T R a 2 = 0 ⇒ b 2 T R v 2 β R v 1 α R 0 a 2 = 0
where v 2 = b 1 and v 1 ∈ S 2 is an arbitrary vector and satisfies v 1 T v 2 = 0 ; R 0 is a specific arbitrary rotation that can rotate a to v 1 ; R v 1 ( α ) = exp α [ v 1 ] × and R v 2 ( β ) = exp β [ v 2 ] × .
According to Rodrigues’ rotation formula [3], we have
R v 1 α = exp α [ v 1 ] × = I + sin ( α ) [ v 1 ] × + 1 − cos ( α ) [ v 1 ] × 2
R v 2 β = exp β [ v 2 ] × = I + sin ( β ) [ v 2 ] × + 1 − cos ( β ) [ v 2 ] × 2
Therefore,
b 2 T I + sin ( β ) [ v 2 ] × + 1 − cos ( β ) [ v 2 ] × 2 I + sin ( α ) [ v 1 ] × + 1 − cos ( α ) [ v 1 ] × 2 R 0 a 2 = 0
Clearly, Eq.(55) shows a one-dimensional curve constructed by α and β (see Figure 4).
Specifically, given a α ∈ [ − π , π ] , β would be computed by Eq. (55). Intuitively, one should solve the following equation
sin ( β ) A + cos ( β ) B + C = 0
where A = b 2 T [ v 2 ] × R v 1 ( α ) R 0 a 2 , B = − b 2 T [ v 2 ] × 2 R v 1 ( α ) R 0 a 2 and C = b 2 T v 2 v 2 T R v 1 ( α ) R 0 a 2 . According to the tangent half-angle formula, when β ≠ ± π ,
2 tan β 2 1 + tan 2 β 2 A + 1 − tan 2 β 2 1 + tan 2 β 2 B + C = 0 → y ≜ tan β 2 2 A y + ( 1 − y 2 ) B + ( 1 + y 2 ) C = 0 ⇒ ( C − B ) y 2 + 2 A y + B + C = 0
Accordingly, β can be computed and rotation R α , β can be computed as well. Formally,
f : α ∈ [ π , π ] → β by Eq . ( ) R α , β

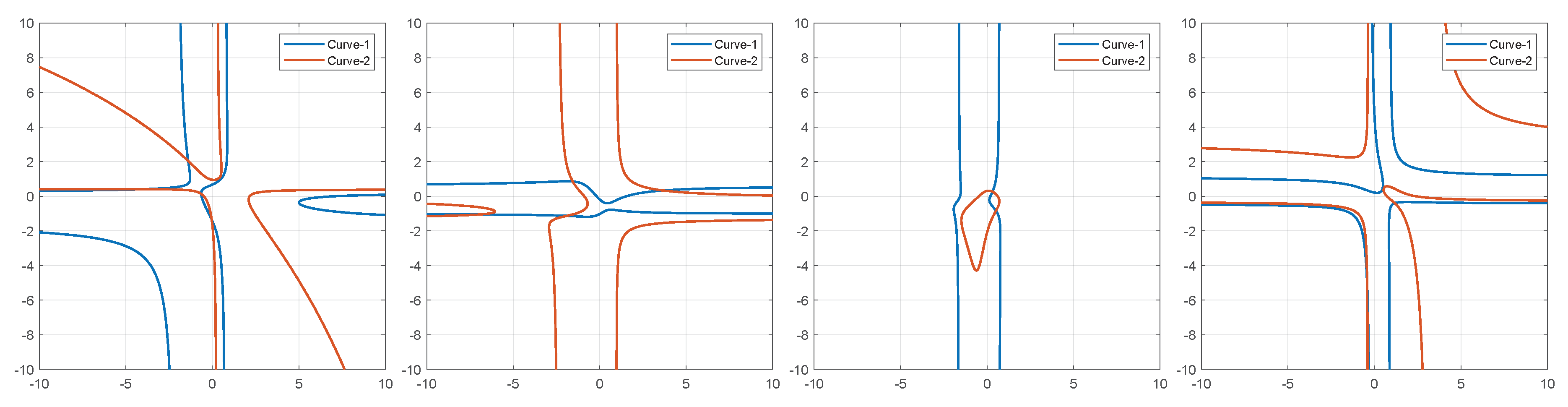
5.3. Intersections of Three Different Clifford Tori

Given three rotation constraints b 1 T R a 1 = 0 , b 2 T R a 2 = 0 and b 3 T R a 3 = 0 , the possible rotation can be considered in the intersections of three Clifford tori. Note that it belongs to the famous E3Q3 problem [47], and there are many solutions have been proposed to solve it [48,49,50,51,52]. Here this paper provides a more straight linear way. Specifically,
b 1 T R a 1 = 0 b 2 T R a 2 = 0 b 3 T R a 3 = 0 ⇒ R α , β = R v 2 β R v 1 α R 0 b 2 T R a 2 = 0 b 3 T R a 3 = 0 ⇒ b 2 T R v 2 β R v 1 α R 0 a 2 = 0 b 3 T R v 2 β R v 1 α R 0 a 3 = 0
Therefore,
b 2 T I + sin ( β ) [ v 2 ] × + 1 − cos ( β ) [ v 2 ] × 2 I + sin ( α ) [ v 1 ] × + 1 − cos ( α ) [ v 1 ] × 2 R 0 a 2 = 0
b 3 T I + sin ( β ) [ v 2 ] × + 1 − cos ( β ) [ v 2 ] × 2 I + sin ( α ) [ v 1 ] × + 1 − cos ( α ) [ v 1 ] × 2 R 0 a 3 = 0
There are two unknown variables α and β for two constraints, and the intersections can be computed.
According to tangent half-angle formula (a.k.a. Weierstrass substitution formulas),
sin ( α ) = 2 tan α 2 1 + tan 2 α 2 , cos ( α ) = 1 − tan 2 α 2 1 + tan 2 α 2 , sin ( β ) = 2 tan β 2 1 + tan 2 β 2 , cos ( β ) = 1 − tan 2 β 2 1 + tan 2 β 2
Let x = tan α 2 , and y = tan β 2 , and when α ≠ ± π , β ≠ ± π ,
b 2 T ( 1 + y 2 ) I + 2 y [ v 2 ] × + 2 y 2 [ v 2 ] × 2 ( 1 + x 2 ) I + 2 x [ v 1 ] × + 2 x 2 [ v 1 ] × 2 R 0 a 2 = 0
b 3 T ( 1 + y 2 ) I + 2 y [ v 2 ] × + 2 y 2 [ v 2 ] × 2 ( 1 + x 2 ) I + 2 x [ v 1 ] × + 2 x 2 [ v 1 ] × 2 R 0 a 3 = 0
The system of equations can be reformulated as
F ( x , y ) = y 2 y 1 A x 2 x 1 = 0 , G ( x , y ) = y 2 y 1 B x 2 x 1 = 0
where A and B ∈ R 3 × 3 , Specifically,
A = A 1 , 1 A 1 , 2 A 1 , 3 A 2 , 1 A 2 , 2 A 2 , 3 A 3 , 1 A 3 , 2 A 3 , 3 = b 2 T * [ l ] I + 2 [ v 2 ] × 2 I + 2 [ v 1 ] × 2 I + 2 [ v 2 ] × 2 2 [ v 1 ] × I + 2 [ v 2 ] × 2 2 [ v 2 ] × I + 2 [ v 1 ] × 2 2 [ v 2 ] × 2 [ v 1 ] × 2 [ v 2 ] × I + 2 [ v 1 ] × 2 2 [ v 1 ] × I * R 0 a 2
B = B 1 , 1 B 1 , 2 B 1 , 3 B 2 , 1 B 2 , 2 B 2 , 3 B 3 , 1 B 3 , 2 B 3 , 3 = b 3 T * [ l ] I + 2 [ v 2 ] × 2 I + 2 [ v 1 ] × 2 I + 2 [ v 2 ] × 2 2 [ v 1 ] × I + 2 [ v 2 ] × 2 2 [ v 2 ] × I + 2 [ v 1 ] × 2 2 [ v 2 ] × 2 [ v 1 ] × 2 [ v 2 ] × I + 2 [ v 1 ] × 2 2 [ v 1 ] × I * R 0 a 3
and * is to calculate the matrix item by item. Geometrically, if only considering real solutions, it describes the intersections of two cures computed by observations in z = 0 plane (see Figure 5).
Algebraically, it is a polynomial system containing two equations in two variables, which can be generally solved by resultant-based method [53,54,55]. We donate
y 2 y 1 A x 2 x 1 = A ( y ) x 2 x 1 = 0 , y 2 y 1 B x 2 x 1 = B ( y ) x 2 x 1 = 0
Both sides of the equations are multiplied by x,
A ( y ) x 3 x 2 x = 0 , B ( y ) x 3 x 2 x = 0
By stacking equations,
0 A ( y ) 0 B ( y ) A ( y ) 0 B ( y ) 0 x 3 x 2 x 1 = H ( y ) x 3 x 2 x 1 = 0
To solve y, it is to solve H ( y ) = 0 . This determinant is also known as a hidden-variable resultant in computer vision filed [56,57], and it is an univariate polynomial with degree 8 of the hidden variable y.
H ( y ) = a 8 y 8 + a 7 y 7 + a 6 y 6 + a 5 y 5 + a 4 y 4 + a 3 y 3 + a 2 y 2 + a 1 y + a 0 = 0
In fact, the problem is not very complex, one can directly calculate the explicit expression of each term for the resultant-based method using symbolic math. Practically, one can obtain explicit coefficients { a i } i = 0 8 by the function resultant in Matlab [55] or the function sympy.polys.polytools.resultant in SymPy1, and this paper will not list all details to avoid long-and-tedious expressions for readability. Nonetheless, the solution of y can be directly computed by solving roots of a univariate polynomial [58,59]. After solving y, it is easy to calculate x.

5.3.1. Linear Solution to Solve Intersections of Three Different Clifford Tori

Alternatively, Eq. (70) can be rewritten as a quadratic eigenvalue problem, i.e., λ 2 H 2 + λ H 1 + H 0 v = 0  [56,57,60].
H ( y ) x 3 x 2 x 1 = 0 ⇒ y 2 H 2 + y H 1 + H 0 x 3 x 2 x 1 = 0
where H 0 , H 1 and H 2 ∈ R 4 × 4 . Specifically,
H 2 = 0 A 1 , 1 A 1 , 2 A 1 , 3 0 B 1 , 1 B 1 , 2 B 1 , 3 A 1 , 1 A 1 , 2 A 1 , 3 0 B 1 , 1 B 1 , 2 B 1 , 3 0 , H 1 = 0 A 2 , 1 A 2 , 2 A 2 , 3 0 B 2 , 1 B 2 , 2 B 2 , 3 A 2 , 1 A 2 , 2 A 2 , 3 0 B 2 , 1 B 2 , 2 B 2 , 3 0 , H 0 = 0 A 3 , 1 A 3 , 2 A 3 , 3 0 B 3 , 1 B 3 , 2 B 3 , 3 A 3 , 1 A 3 , 2 A 3 , 3 0 B 3 , 1 B 3 , 2 B 3 , 3 0
Notably, there is no x and y in H 2 , H 1 and H 0 . Accordingly, it is easy to solve the system of polynomial equations by linear way [60].
Specifically, the to-be-solved eigenvector of this problem is v = x 3 x 2 x 1 T and corresponding eigenvalue is λ = y . Furthermore, the quadratic eigenvalue problem can be transformed into a generalized eigenvalue problem, i.e., A x = λ B x  [61], which has been extensively studied [57,61,62,63]. Specifically,
λ 2 H 2 + λ H 1 + H 0 v = 0 ⇒ 0 I − H 0 − H 1 v λ v = λ I 0 0 H 2 v λ v
Therefore, there will be 8 eigenvalues of this linear problem. The easiest way to solve this problem is using the Matlab function built-in polyeig2. SciPy also provides a function scipy.linalg.eig3 to solve generalized eigenvalue problems.

References

  1. Epp, R.J.; Mann, R.B.; McGrath, P.L. Rigid motion revisited: rigid quasilocal frames. Classical and Quantum Gravity 2009, 26, 035015. [Google Scholar] [CrossRef]
  2. Altmann, S.L. Rotations, quaternions, and double groups; Courier Corporation, 2005.
  3. Hartley, R.; Zisserman, A. Multiple view geometry in computer vision; Cambridge university press, 2003.
  4. Goel, R.; Gupta, P. Robotics and industry 4.0. A Roadmap to Industry 4.0: Smart Production, Sharp Business and Sustainable Development 2020, pp. 157–169.
  5. Teed, Z.; Deng, J. Raft-3d: Scene flow using rigid-motion embeddings. Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 2021, pp. 8375–8384.
  6. Kisantal, M.; Sharma, S.; Park, T.H.; Izzo, D.; Märtens, M.; D’Amico, S. Satellite pose estimation challenge: Dataset, competition design, and results. IEEE Transactions on Aerospace and Electronic Systems 2020, 56, 4083–4098. [Google Scholar] [CrossRef]
  7. Gul, F.; Rahiman, W.; Nazli Alhady, S.S. A comprehensive study for robot navigation techniques. Cogent Engineering 2019, 6, 1632046. [Google Scholar] [CrossRef]
  8. Huang, C.; Mees, O.; Zeng, A.; Burgard, W. Visual language maps for robot navigation. 2023 IEEE International Conference on Robotics and Automation (ICRA). IEEE, 2023, pp. 10608–10615.
  9. Bustos, A.P.; Chin, T.J. Guaranteed Outlier Removal for Point Cloud Registration with Correspondences. IEEE transactions on pattern analysis and machine intelligence 2018, 40, 2868–2882. [Google Scholar] [CrossRef]
  10. Eriksson, A.; Olsson, C.; Kahl, F.; Chin, T.J. Rotation averaging and strong duality. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018, pp. 127–135.
  11. Crassidis, J.L.; Markley, F.L.; Cheng, Y. Survey of nonlinear attitude estimation methods. Journal of guidance, control, and dynamics 2007, 30, 12–28. [Google Scholar] [CrossRef]
  12. Carlone, L.; others. Estimation Contracts for Outlier-Robust Geometric Perception. Foundations and Trends® in Robotics 2023, 11, 90–224. [Google Scholar] [CrossRef]
  13. Mathavaraj, S.; Butcher, E.A. SE (3)-constrained extended Kalman filtering for rigid body pose estimation. IEEE Transactions on Aerospace and Electronic Systems 2021, 58, 2482–2492. [Google Scholar] [CrossRef]
  14. Welch, G.F. Kalman filter. Computer Vision: A Reference Guide 2020, pp. 1–3.
  15. Trawny, N.; Roumeliotis, S.I. Indirect Kalman filter for 3D attitude estimation. University of Minnesota, Dept. of Comp. Sci. & Eng., Tech. Rep 2005, 2, 2005. [Google Scholar]
  16. Chin, T.J.; Suter, D. The maximum consensus problem: recent algorithmic advances; Springer Nature, 2022.
  17. Etingof, P. Lie groups and Lie algebras. arXiv arXiv:2201.09397.
  18. Dehmamy, N.; Walters, R.; Liu, Y.; Wang, D.; Yu, R. Automatic symmetry discovery with lie algebra convolutional network. Advances in Neural Information Processing Systems 2021, 34, 2503–2515. [Google Scholar]
  19. Gill, P.E.; Murray, W.; Wright, M.H. Numerical linear algebra and optimization; SIAM, 2021.
  20. Farin, G.; Hansford, D. Practical linear algebra: a geometry toolbox; Chapman and Hall/CRC, 2021.
  21. Horn, R.A.; Johnson, C.R. Matrix analysis; Cambridge university press, 2012.
  22. Taubin, G. 3D Rotations. IEEE Computer Graphics and Applications 2011, 31, 84–89. [Google Scholar] [CrossRef] [PubMed]
  23. Ball, R.S. The theory of screws: A study in the dynamics of a rigid body. Mathematische Annalen 1876, 9, 541–553. [Google Scholar] [CrossRef]
  24. Palais, B.; Palais, R. Euler’s fixed point theorem: The axis of a rotation. Journal of fixed point theory and applications 2007, 2, 215–220. [Google Scholar] [CrossRef]
  25. Kumar, V. The Theorems of Euler and Chasles. University of Pennsylvania School of Engineering and Applied Science, I-Net, USA 2000.
  26. Joseph, T. An alternative proof of Euler’s rotation theorem. The Mathematical Intelligencer 2020, 42, 44–49. [Google Scholar] [CrossRef]
  27. Fraiture, L. A history of the description of the three-dimensional finite rotation. The Journal of the Astronautical Sciences 2009, 57, 207–232. [Google Scholar] [CrossRef]
  28. Hartley, R.I.; Kahl, F. Global optimization through rotation space search. International Journal of Computer Vision 2009, 82, 64–79. [Google Scholar] [CrossRef]
  29. Jia, Y.B. Quaternions and rotations. Com S 2008, 477, 15. [Google Scholar]
  30. Quaternions and Spatial Rotation. [Online]. Available: https://en.wikipedia.org/wiki/Quaternions_and_spatial_rotation.
  31. Hartley, R.; Trumpf, J.; Dai, Y.; Li, H. Rotation averaging. International journal of computer vision 2013, 103, 267–305. [Google Scholar] [CrossRef]
  32. Kim, S.; Kim, M. Rotation representations and their conversions. IEEE Access 2023, 11, 6682–6699. [Google Scholar] [CrossRef]
  33. Shuster, M.D. A survey of attitude representation. Journal of The Astronautical Sciences 1993, 41, 439–517. [Google Scholar]
  34. Liu, Y. Globally Optimal Solutions for Unit-Norm Constrained Computer Vision Problems. PhD thesis, Technische Universität München, 2022.
  35. Liu, Y.; Dong, Y.; Song, Z.; Wang, M. 2d-3d point set registration based on global rotation search. IEEE Transactions on Image Processing 2018, 28, 2599–2613. [Google Scholar] [CrossRef] [PubMed]
  36. Yang, J.; Li, H.; Campbell, D.; Jia, Y. Go-ICP: A globally optimal solution to 3D ICP point-set registration. IEEE transactions on pattern analysis and machine intelligence 2015, 38, 2241–2254. [Google Scholar] [CrossRef]
  37. HORN, B.P. Closed-form solution of absolute orientation using unit quaternions. Journal of the Optical Society of America. A, Optics and image science 1987, 4, 629–642. [Google Scholar] [CrossRef]
  38. Peng, L.; Tsakiris, M.C.; Vidal, R. Arcs: Accurate rotation and correspondence search. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2022, pp. 11153–11163.
  39. McClintock, P. Relating plane transformations with stereographic projection. PhD thesis, 2022.
  40. Wilkins, D.R. Möbius transformations and stereographic projection, 2017.
  41. Gluck, H. Great circle fibrations and contact structures on the 3-sphere. Geometriae Dedicata 2022, 216, 72. [Google Scholar] [CrossRef]
  42. Flat torus. [Online]. Available: https://en.wikipedia.org/wiki/Torus.
  43. Ayzenberg, A. Torus action on quaternionic projective plane and related spaces. Arnold Mathematical Journal 2021, 7, 243–266. [Google Scholar] [CrossRef]
  44. Srivatsan, R.A.; Rosen, G.T.; Mohamed, D.F.N.; Choset, H. Estimating SE (3) elements using a dual quaternion based linear Kalman filter. Robotics: Science and systems, 2016.
  45. Arun Srivatsan, R.; Zevallos, N.; Vagdargi, P.; Choset, H. Registration with a small number of sparse measurements. The International Journal of Robotics Research 2019, 38, 1403–1419. [Google Scholar] [CrossRef]
  46. Andersson, O.; Bengtsson, I. Clifford tori and unbiased vectors. Reports on mathematical physics 2017, 79, 33–51. [Google Scholar] [CrossRef]
  47. Kukelova, Z.; Heller, J.; Fitzgibbon, A. Efficient intersection of three quadrics and applications in computer vision. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2016, pp. 1799–1808.
  48. Xu, C.; Zhang, L.; Cheng, L.; Koch, R. Pose estimation from line correspondences: A complete analysis and a series of solutions. IEEE transactions on pattern analysis and machine intelligence 2016, 39, 1209–1222. [Google Scholar] [CrossRef]
  49. Yu, Q.; Xu, G.; Cheng, Y. An efficient and globally optimal method for camera pose estimation using line features. Machine Vision and Applications 2020, 31, 1–11. [Google Scholar] [CrossRef]
  50. Wang, P.; Xu, G.; Cheng, Y.; Yu, Q. Camera pose estimation from lines: a fast, robust and general method. Machine Vision and Applications 2019, 30, 603–614. [Google Scholar] [CrossRef]
  51. Chan, K. A simple mathematical approach for determining intersection of quadratic surfaces. In Multiscale optimization methods and applications; Springer, 2006; pp. 271–298.
  52. Sarraga, R.F. Algebraic methods for intersections of quadric surfaces in GMSOLID. Computer Vision, Graphics, and Image Processing 1983, 22, 222–238. [Google Scholar] [CrossRef]
  53. Sturmfels, B. Introduction to resultants. Proceedings of Symposia in Applied Mathematics. American Mathematical Society, 1998, Vol. 53, pp. 25–40.
  54. Woody, H. Polynomial resultants. GNU operating system 2016. [Google Scholar]
  55. MathWorks. Resultant of two polynomials. [Online]. Available: https://www.mathworks.com/help/symbolic/sym.resultant.html.
  56. Hartley, R.; Li, H. An efficient hidden variable approach to minimal-case camera motion estimation. IEEE transactions on pattern analysis and machine intelligence 2012, 34, 2303–2314. [Google Scholar] [CrossRef] [PubMed]
  57. Kukelova, Z.; Bujnak, M.; Pajdla, T. Polynomial eigenvalue solutions to minimal problems in computer vision. IEEE Transactions on Pattern Analysis and Machine Intelligence 2011, 34, 1381–1393. [Google Scholar] [CrossRef] [PubMed]
  58. Pan, V.Y. Good News for Polynomial Root-finding. arXiv arXiv:1805.12042.
  59. Kalantari, B. Polynomial root-finding and polynomiography; World Scientific, 2008.
  60. Tisseur, F.; Meerbergen, K. The quadratic eigenvalue problem. SIAM review 2001, 43, 235–286. [Google Scholar] [CrossRef]
  61. Ghojogh, B.; Karray, F.; Crowley, M. Eigenvalue and Generalized Eigenvalue Problems: Tutorial, 2023, [arXiv:stat.ML/1903.11240].
  62. Williams, M.P. Solving polynomial equations using linear algebra. Johns Hopkins APL Technical Digest 2010, 28, 354–363. [Google Scholar]
  63. Lancaster, P.; Zaballa, I. Diagonalizable quadratic eigenvalue problems. Mechanical Systems and Signal Processing 2009, 23, 1134–1144. [Google Scholar] [CrossRef]
1
https://www.sympy.org/en/index.html
2
https://www.mathworks.com/help/matlab/ref/polyeig.html
3
https://docs.scipy.org/doc/scipy/reference/generated/scipy.linalg.eigvals.html#scipy.linalg.eigvals
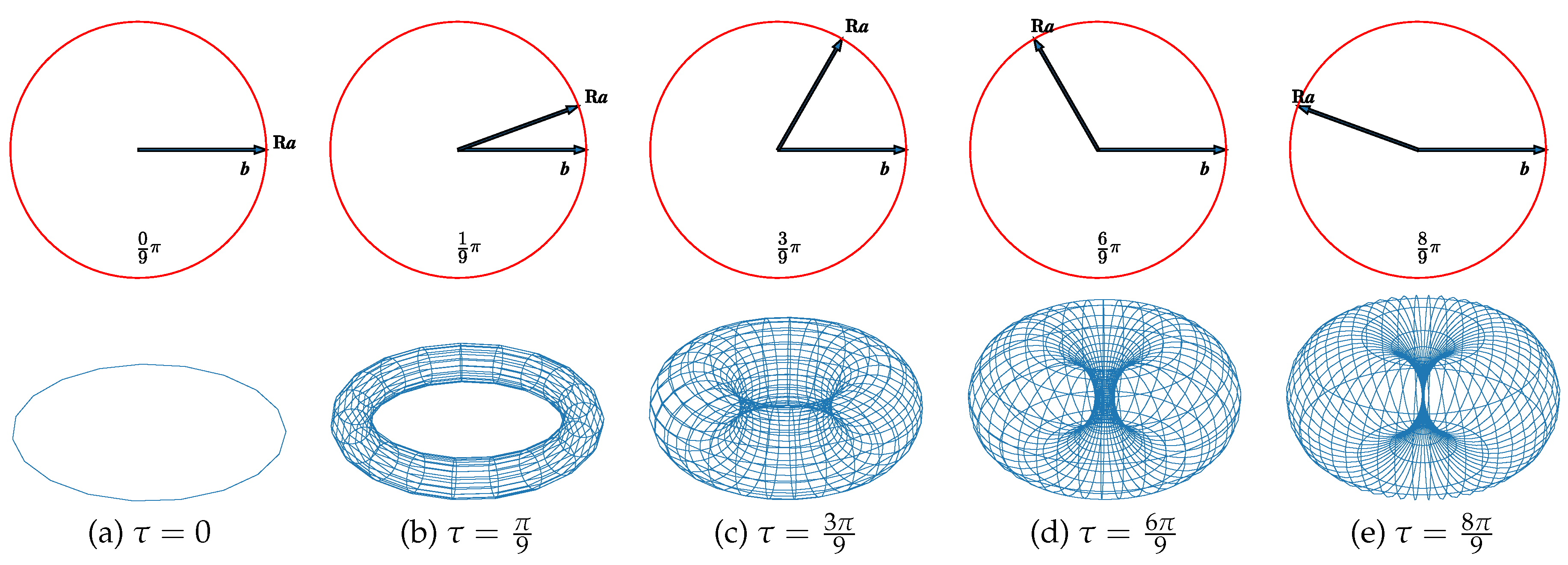
Preprints 106286 g001
Figure 1. Genera cases of rotation constraints and their corresponding tori in R 3 via stereographic projection.
Figure 1. Genera cases of rotation constraints and their corresponding tori in R 3 via stereographic projection.
Preprints 106286 g001

(a) τ = 0 (b) τ = π 9 (c) τ = 3 π 9 (d) τ = 6 π 9 (e) τ = 8 π 9
Preprints 106286 g002
Figure 2. The geometric relationship of one rotation constraint b T R a = 0 and its solution R α , β = R v 2 β R v 1 α R 0 .
Figure 2. The geometric relationship of one rotation constraint b T R a = 0 and its solution R α , β = R v 2 β R v 1 α R 0 .
Preprints 106286 g002
Preprints 106286 g003
Figure 3. The illustration for intersection curves of two Clifford tori in R 3 by stereographic projection.
Figure 3. The illustration for intersection curves of two Clifford tori in R 3 by stereographic projection.
Preprints 106286 g003
Preprints 106286 g004
Figure 4. The illustration for intersection curves of two Clifford tori in α and β space.
Figure 4. The illustration for intersection curves of two Clifford tori in α and β space.
Preprints 106286 g004
Preprints 106286 g005
Figure 5. The intersection of two curves that are constructed by rotation constraints in the 2D plane. Specifically, we can consider z = F ( x , y ) and z = G ( x , y ) as two surfaces in R 3 . Let z = 0 , it means z = 0 plane and it cuts the surfaces F ( x , y ) and G ( x , y ) . Consequently, there are two intersection lines, which can be drawn in z = 0 plane.
Figure 5. The intersection of two curves that are constructed by rotation constraints in the 2D plane. Specifically, we can consider z = F ( x , y ) and z = G ( x , y ) as two surfaces in R 3 . Let z = 0 , it means z = 0 plane and it cuts the surfaces F ( x , y ) and G ( x , y ) . Consequently, there are two intersection lines, which can be drawn in z = 0 plane.
Preprints 106286 g005
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated