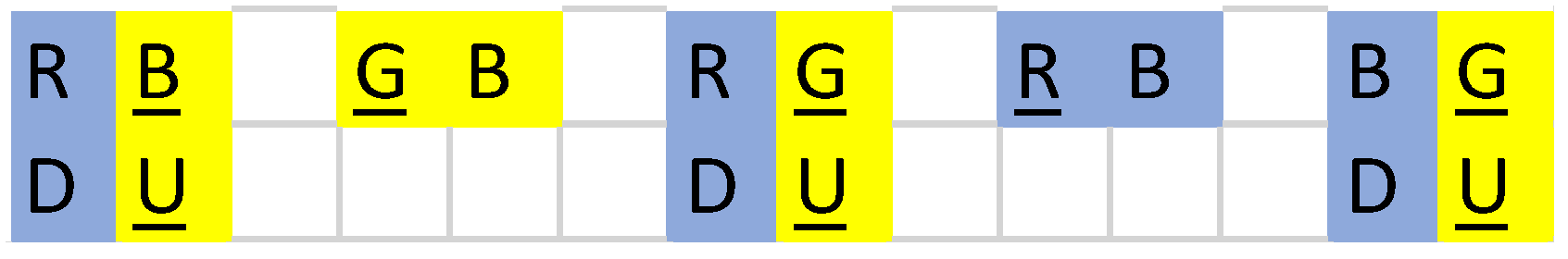1. Introduction
It is important to make clear the fundamental reason that led us to develop this model of the neutron and proton as a three-phase alternating current electric generator, which we will describe below.
At a macroscopic level, if we add the mass of 2 bodies that have 5 kg each, the sum corresponds to 10 kg, that is:
5 kg + 5 kg = 10 kg.
At a microscopic level, quark level, if we add scalarly the mass of the valence quarks inside a neutron or proton, the sum is not the mass of the proton or neutron.
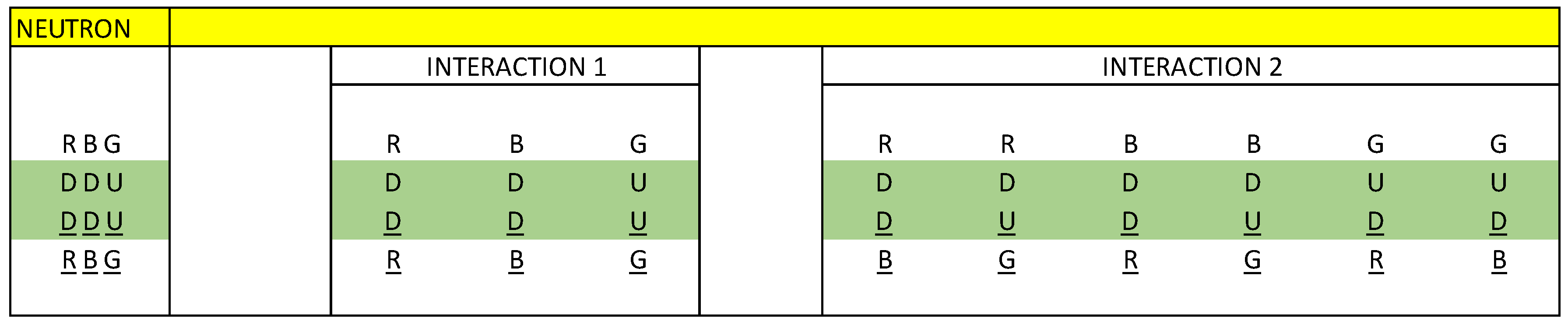
For the neutron, we have:
md + md + mu ≠ Mn
where md is the mass of the D quark, mu is the mass of the U quark and Mn is the mass of the neutron.
It is important to note that at the macroscopic level, it is true if we add the masses of the bodies scalarly, but at the microscopic level, we cannot add the masses of the bodies scalarly, especially if we are at the quark level.
This discrepancy that we have described is what motivated us to develop this paper, simply to demonstrate by means of a vector sum, using the theory of three-phase alternating current electric generators, that the following relationship is true and holds:
md + md + mu = Mn
Being the sum of md + md + mu, a vector sum.
Taking into account what has been analysed, the following question arises!!!!!
Let's analyse βˉ decay.
Neutron → Proton + e⁻ + ṽ + ∆E
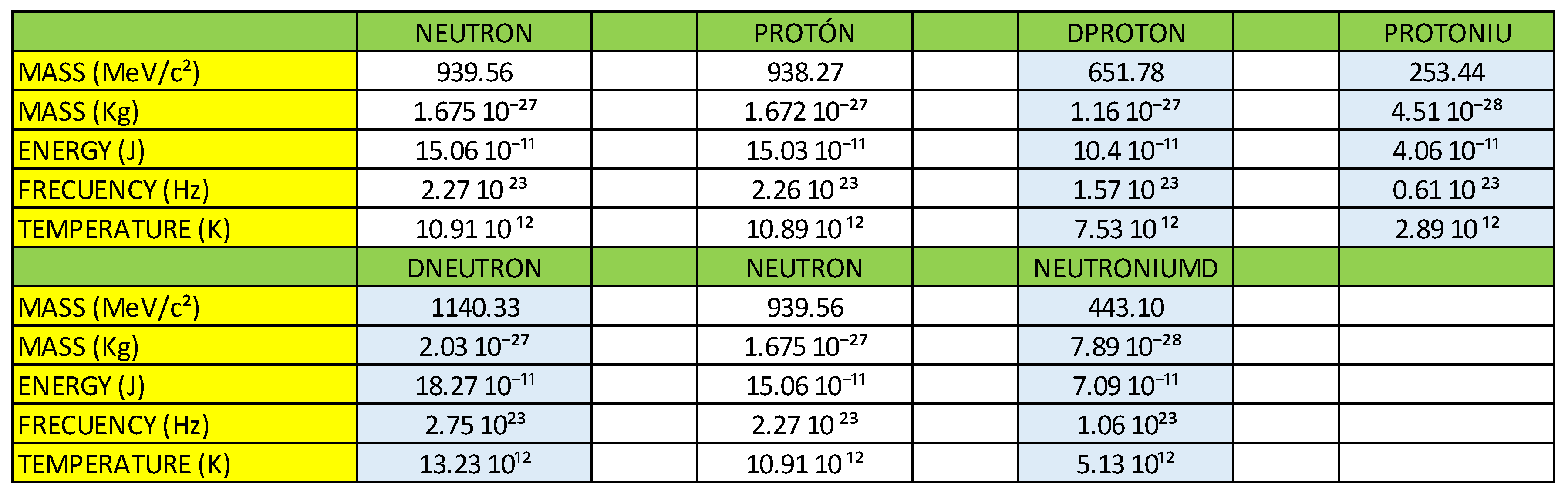
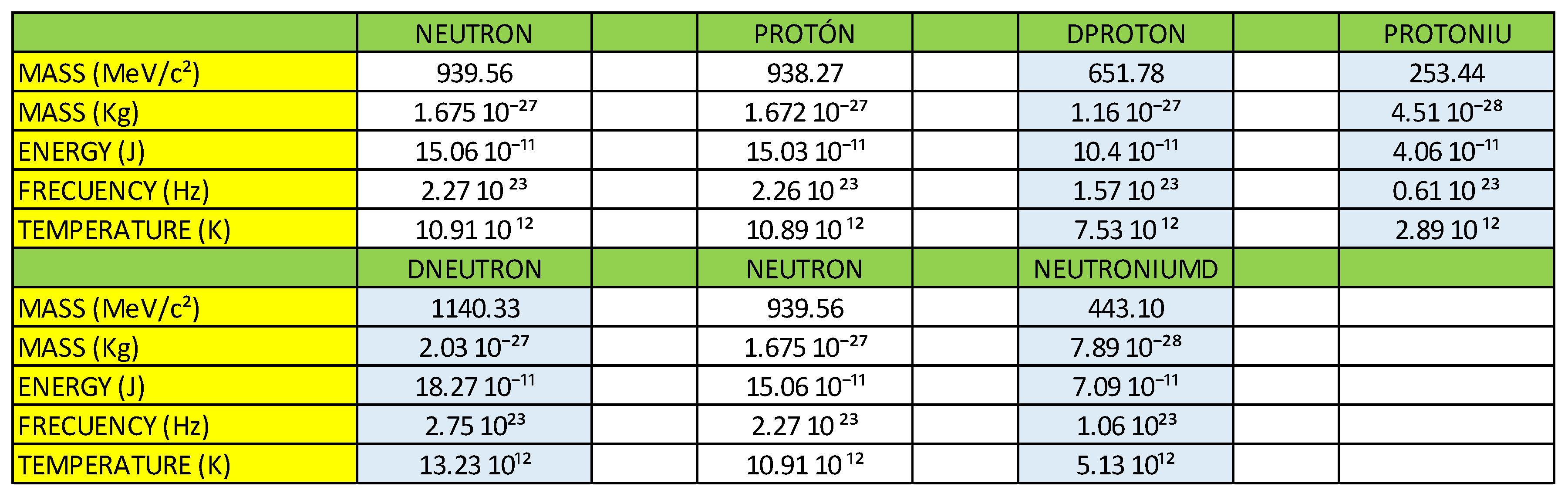
Mn = 939.56 MeV/c²
Mp = 938.27 MeV/c²
Me = 0.511 MeV/c²
∆E = 0.779 MeV/c²!!!!!!!
If we consider that at the quark level, the scalar sum of masses is not valid, then the value of ∆E is incorrect.
Taking into account the concept described, we will vector analyse proton decay and neutron reverse decay to predict new subatomic particles. We will also show that these new subatomic particles have a non-zero charge scalarly, but vectorially the net charge of these particles is zero.
Relationship between a Three-Phase Electric Generator and the Quarks-Antiquarks-Gluons Inside a Neutron and Proton
According to Max Planck, science is not only about discoveries, but also about changing the way we think, we should not be afraid of the unknown and we must feel free to follow our curiosity. Following this premise, we are going to develop this theory.
It is important to make clear that the interpretation we use of the structure of quarks does not correspond to QCD theory, it is a personal interpretation. In other words, this theory is outside the formal theory of quarks and gluons (QCD), it is totally personal.
The main idea is to try to demystify the realm in which quark-antiquark-gluon interactions dominate, presenting an alternative theory that contributes to the formal QCD theory.
Whenever we analyse scientific literature, articles, papers, that are related to collisions of subatomic particles, we see that in the collisions of subatomic particles, pairs of particles of matter and antimatter are produced, this always happens, fulfilling the principle of conservation of energy.
Taking into account what has been stated, we are going to consider matter and antimatter to develop our theory. We are going to propose the following model for the neutron and the proton.
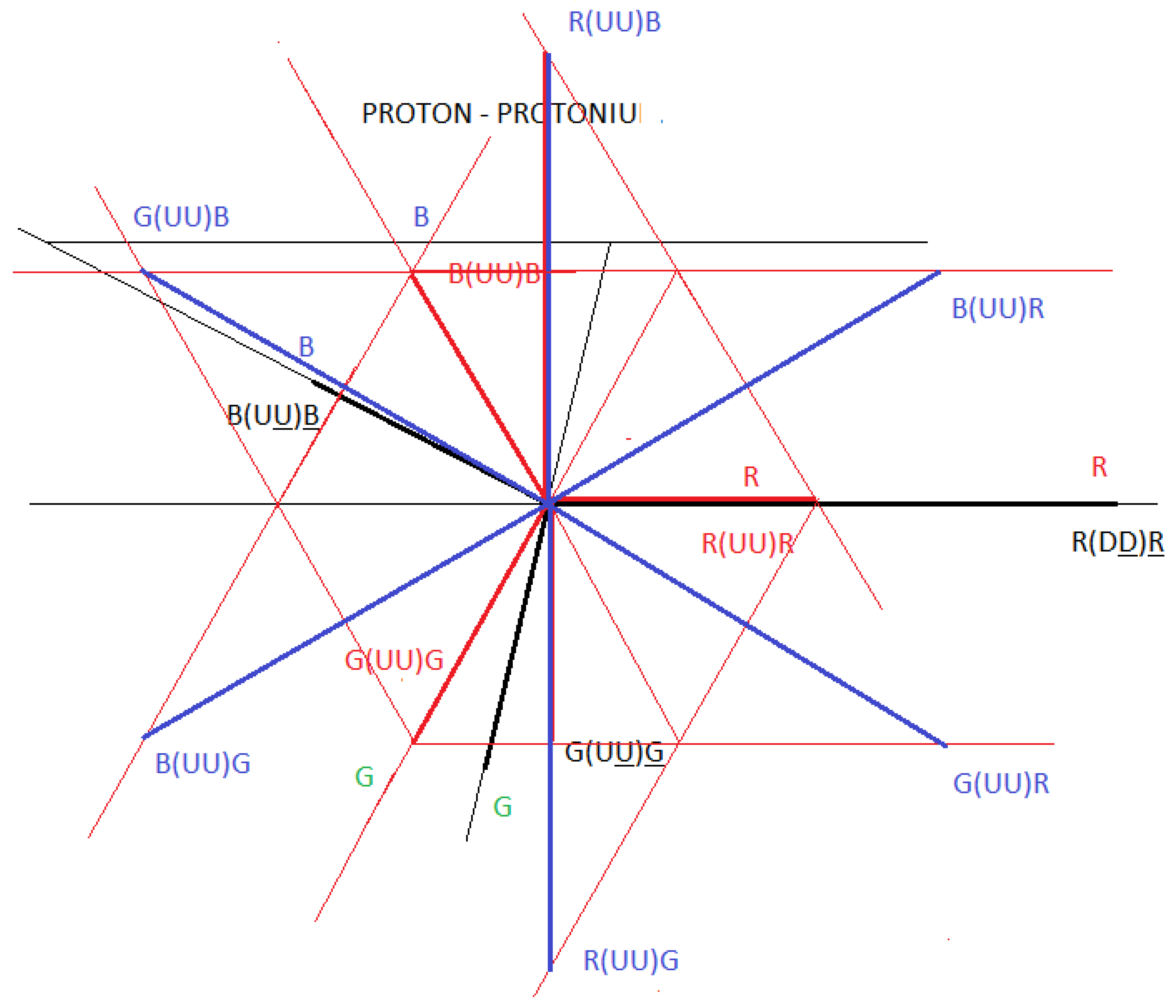
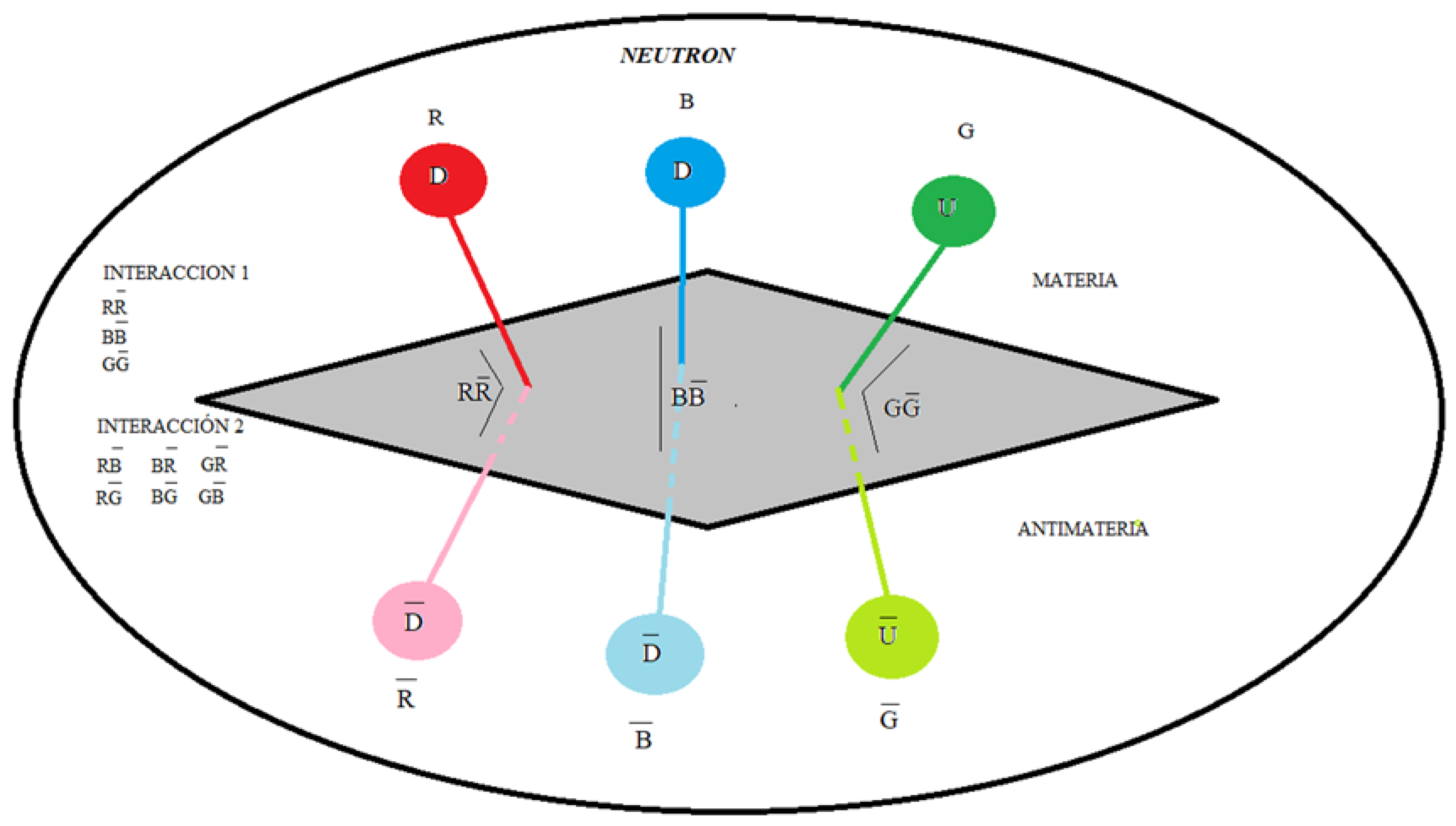
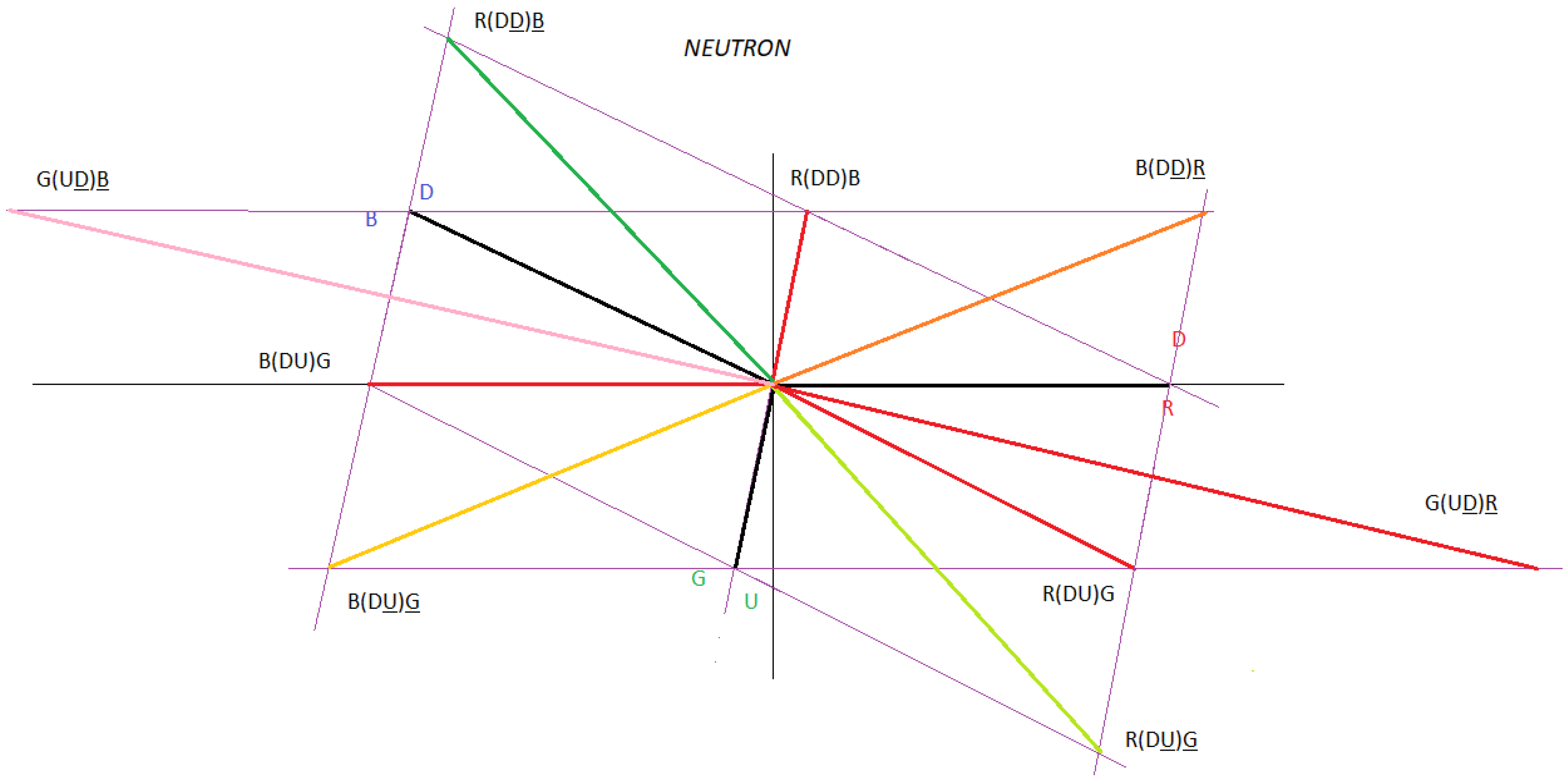
Here we put forward the hypothesis for a neutron, as a quark-antiquark-gluon interaction, and not as represented in the formal theory of QCD, as a quark-gluon interaction. See
figure 1
Where D corresponds to the D quark and D corresponds to the D antiquark.
Where U corresponds to the U quark and U corresponds to the U antiquark.
The gluon interaction is given by (R, B, G) and (R, B, G).
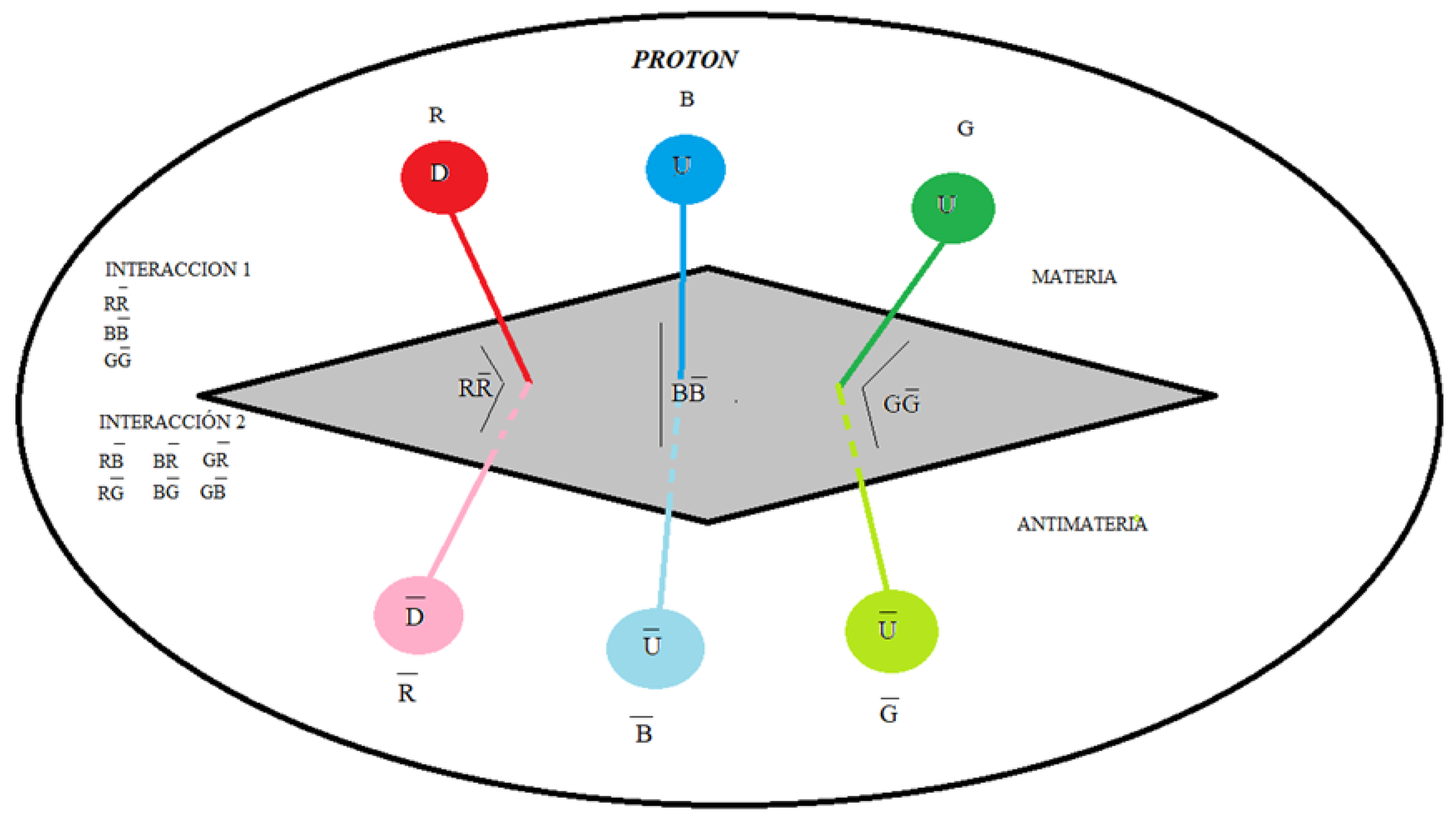
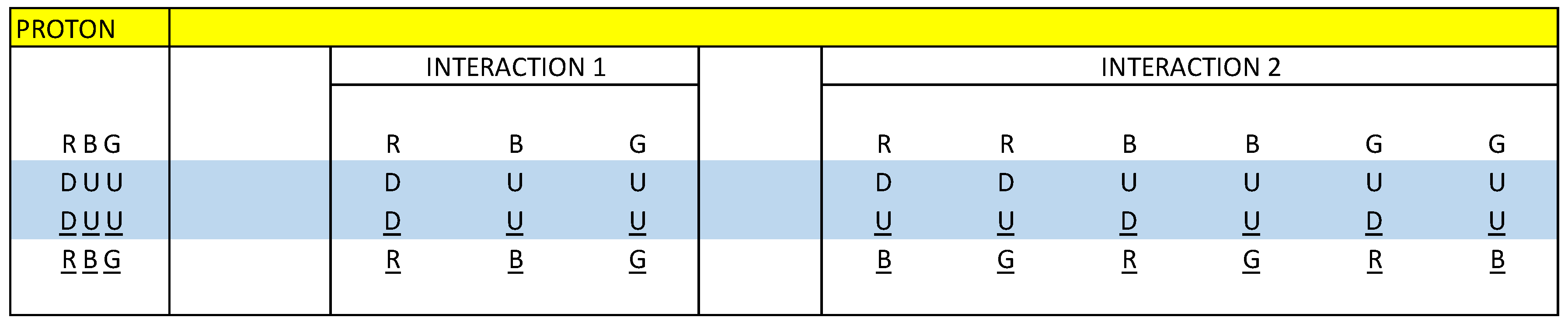
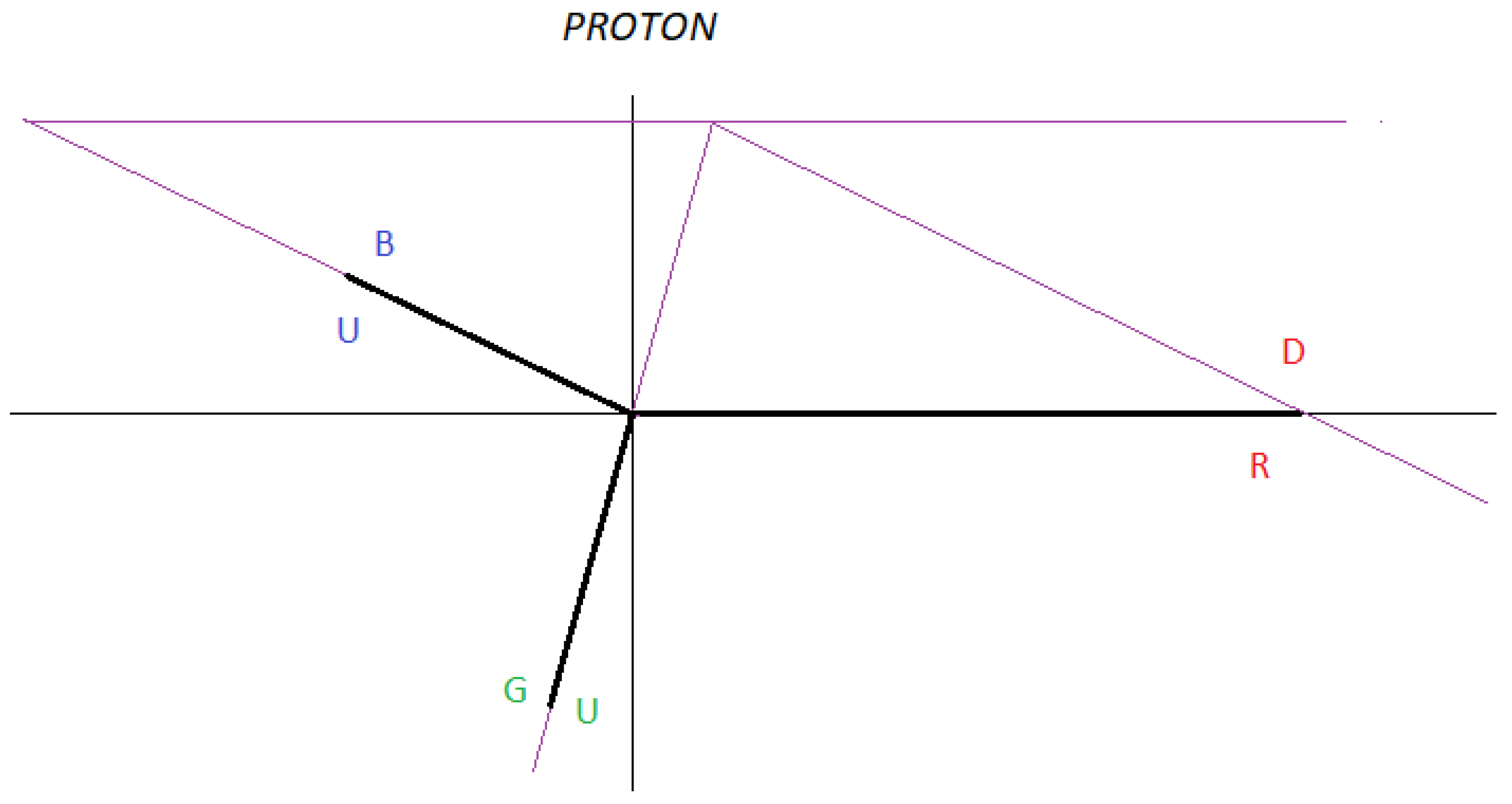
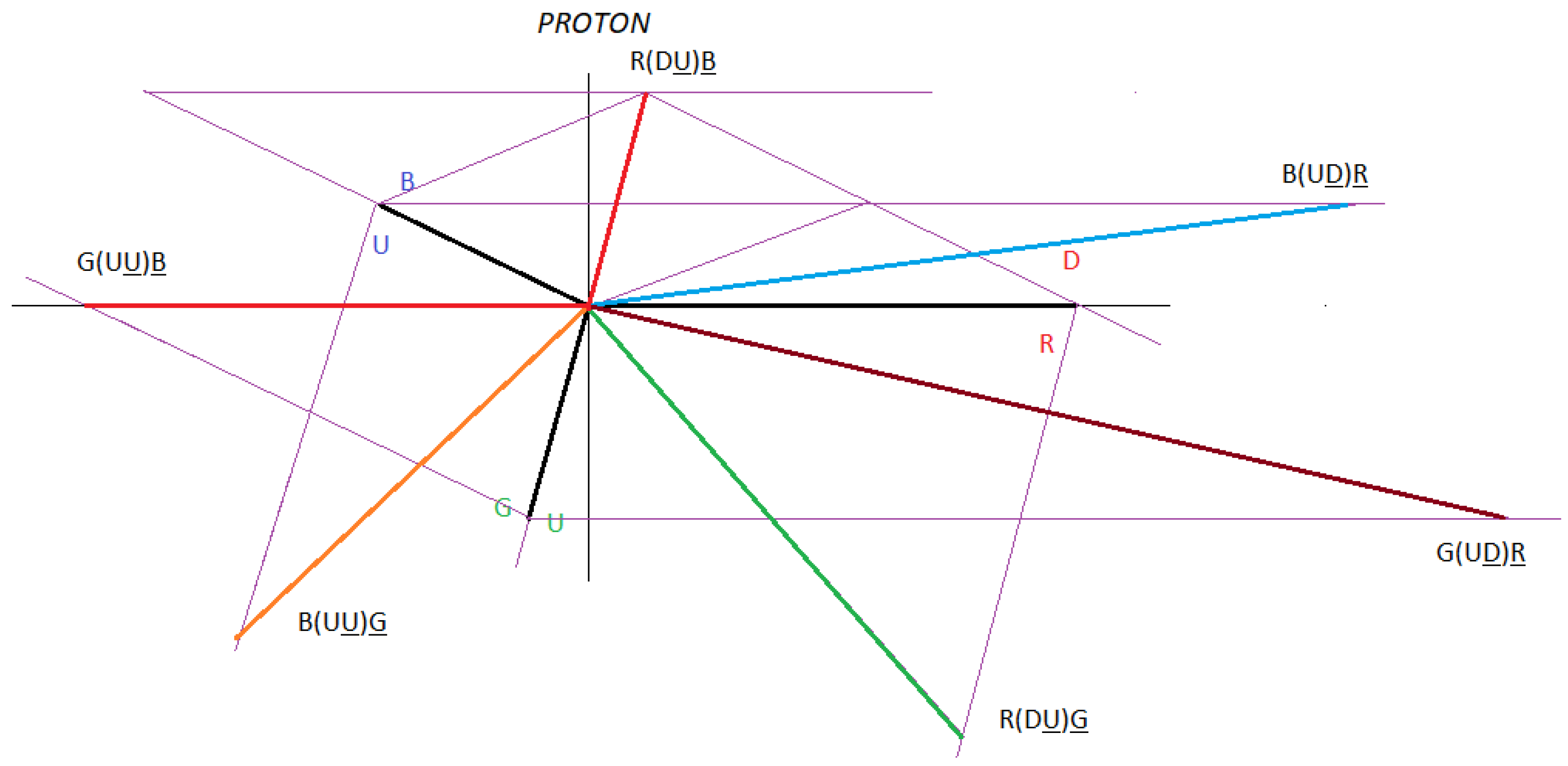
Here we put forward the hypothesis for a proton, as a quark-antiquark-gluon interaction, and not as represented in the formal theory of QCD, as a quark-gluon interaction. See
figure 2.
Before continuing, let's explain why the UU and DD dipoles do not annihilate each other.
When we developed the paper titled: Theory of the Generalization of the Boltzmann’s Constant in Curved Space-Time. Shannon-Boltzmann Gibbs Entropy Relation and the Effective Boltzmann's Constant; at the end of the paper, we show that the up quark and down quark, with a temperature of the order of 10¹⁰ K, have a space-time contraction factor of the order of 10⁶, in other words, the space-time envelope that surrounds the quark acts as a shell, like a protection, preventing the U quark and the U antiquark from annihilating each other, the same happens with the D quark and its D antiquark. , avoiding its annihilation.
This happens only at the quark level, as matter increases in complexity, this space-time protection becomes weaker, which leads to matter-antimatter annihilation.
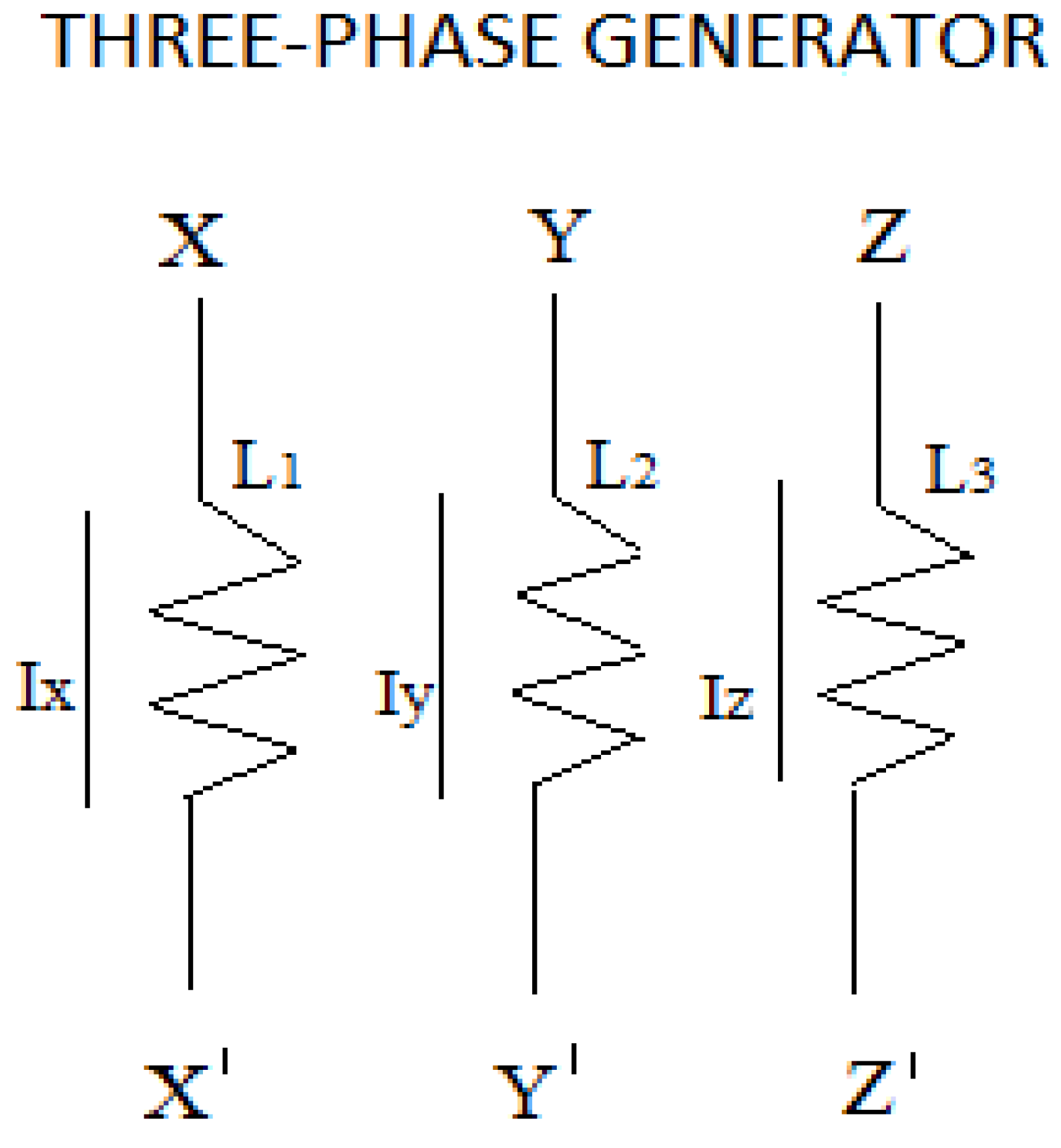
If we look at
figure 3 and
figure 4, which correspond to the electrical circuit of a three-phase generator, we see that the electrical circuit of a neutron represented in
figure 1 and the electrical circuit of a proton represented in
figure 2, have an identical diagram. Basically, the difference is the following, in a three-phase generator, the pairs, XX', YY' and ZZ' have the same frequency and in the case of a proton and neutron the D
D pairs have twice the frequency of the U
U pairs.
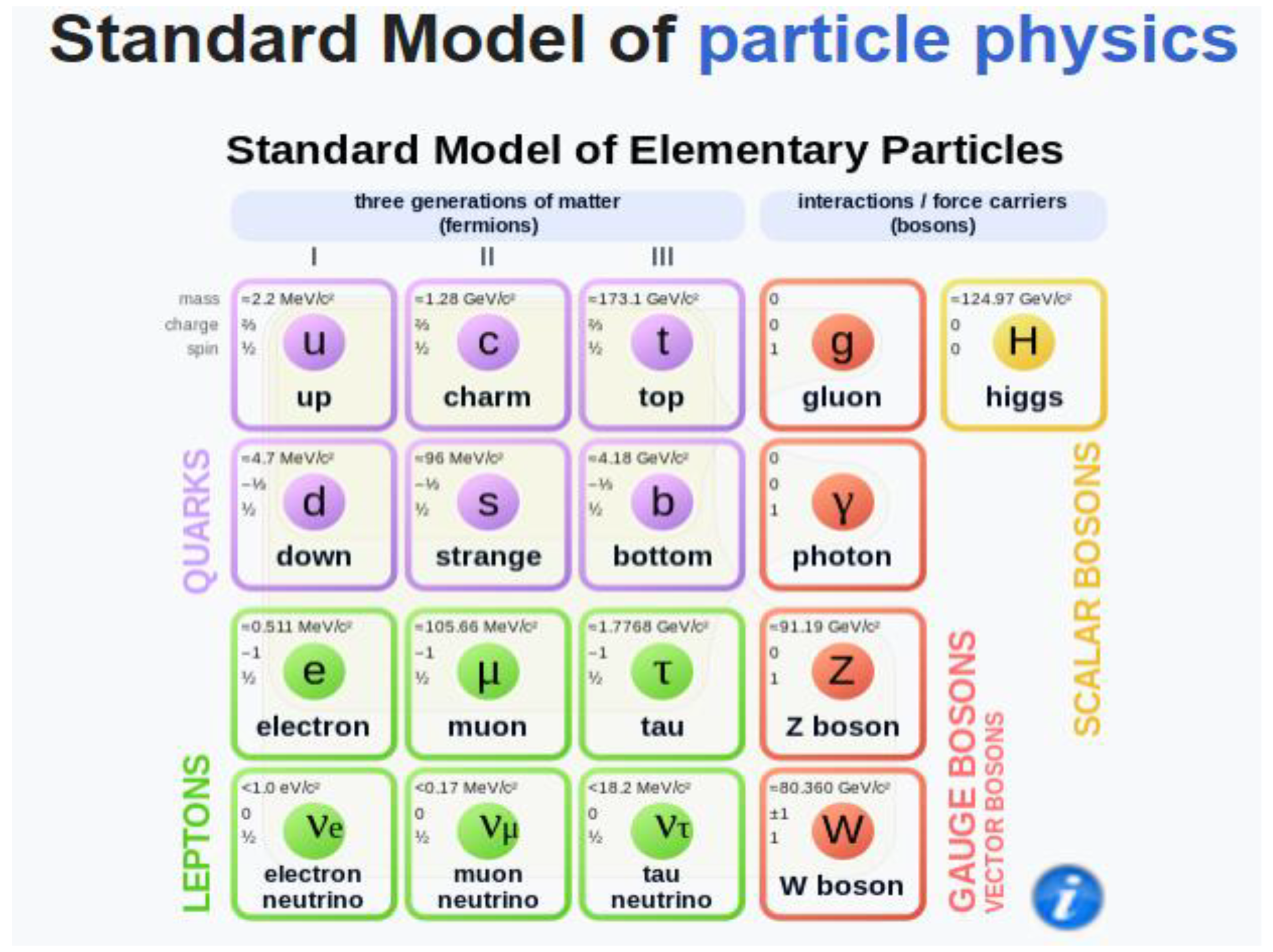
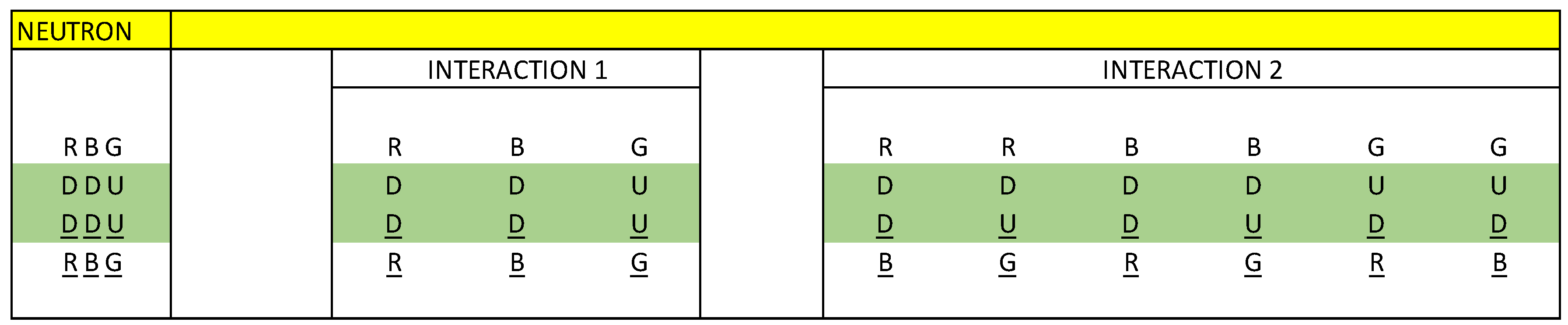
In
figure 5 we are going to represent the diagram of the standard model of particle physics.
In
figure 6, it represents the characteristics of the up and down quark, we can see that the frequency of the down quark is approximately double that of the up quark.
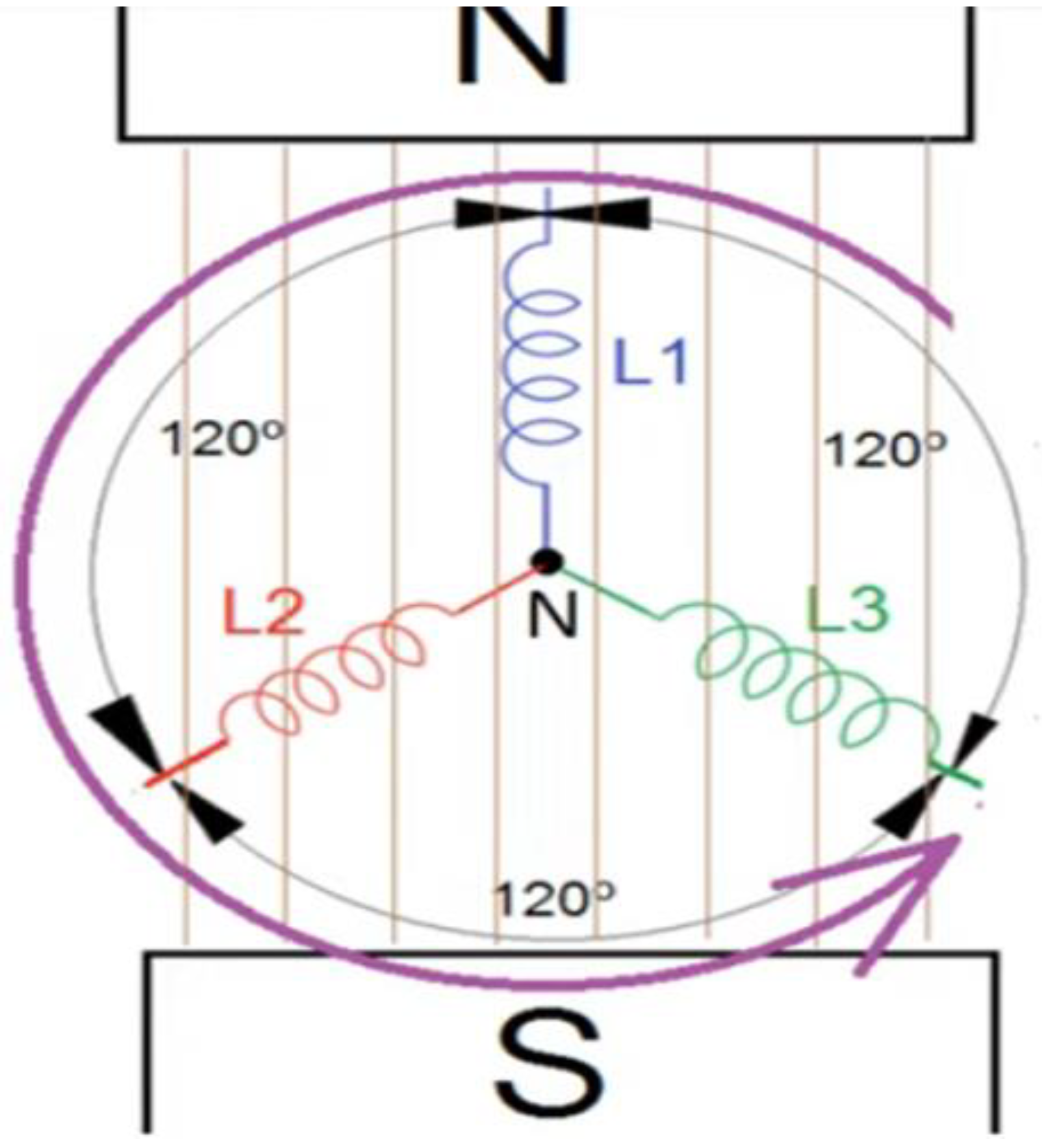
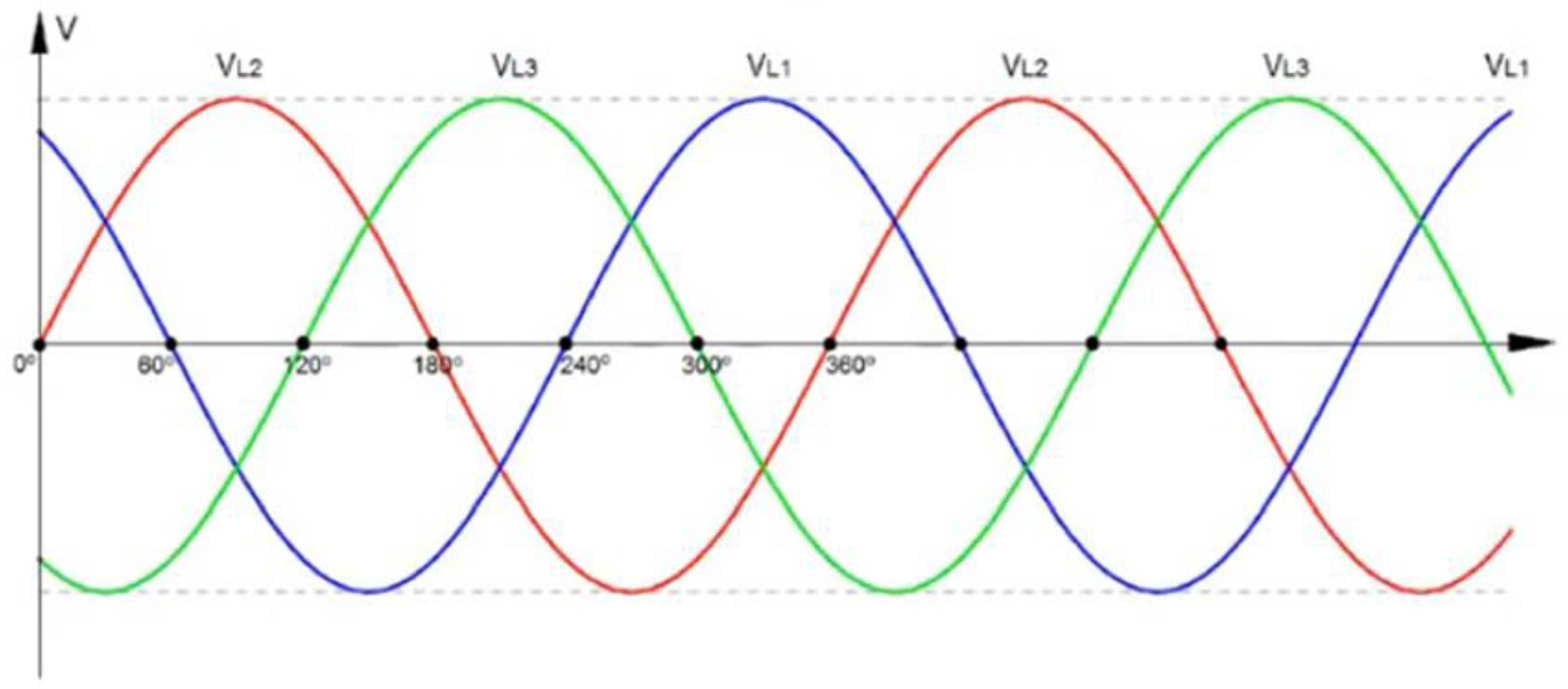
If we rotate the rotor of a generator, this induces a variable magnetic field in the stator and this generates a three-phase sinusoidal voltage, out of phase by 120 degrees, as seen in
figure 7, that is the operating principle of a generator.
In analogy to what happens in a generator, in the proton and the neutron, the DD dipoles vibrate at approximately twice the frequency of the UU dipoles. Continuing with the analogy, the dipoles, XX', YY' and ZZ' in a generator would be analogous to the dipoles DD, DD and UU in a neutron and the dipoles DD, UU and UU in a proton.
If we consider that the voltages, VL1, VL2 and VL3 are the result of rotating the rotor, which produces a variation of the magnetic field and ends up inducing and generating the voltages in the stator, continuing with the analogy, we can say that the dipoles DD, DD and UU in a neutron and the dipoles DD, UU and UU in a proton, is the result of a variable magnetic field that is generated from the interaction of quarks and anti-quarks with gluons, precisely this mechanism makes protons and neutrons generate their mass and are self-sustaining, this is the mechanism that allows the existence of hadrons.
Let us remember that Maxwell's fourth law does not say that a variable magnetic field produces a variable electric field and thus repeats itself indefinitely, precisely through this mechanism a photon is self-sustaining, we can say that a photon has infinite life, and we can confirm this with the CMB which is the result of primordial photons.
The dipoles DD, DD and UU in a neutron and the dipoles DD, UU and UU in a proton, are also out of phase with a phase angle that we are going to determine, the nomenclature of the gluons (R, B, G) and (R, B, G) serves to remind us that the Interactions between quarks and gluons are vectors.
Taking into account the statement, in
Figure 8 and
Figure 9 we are going to represent the intrinsic interactions of the neutron and the proton.
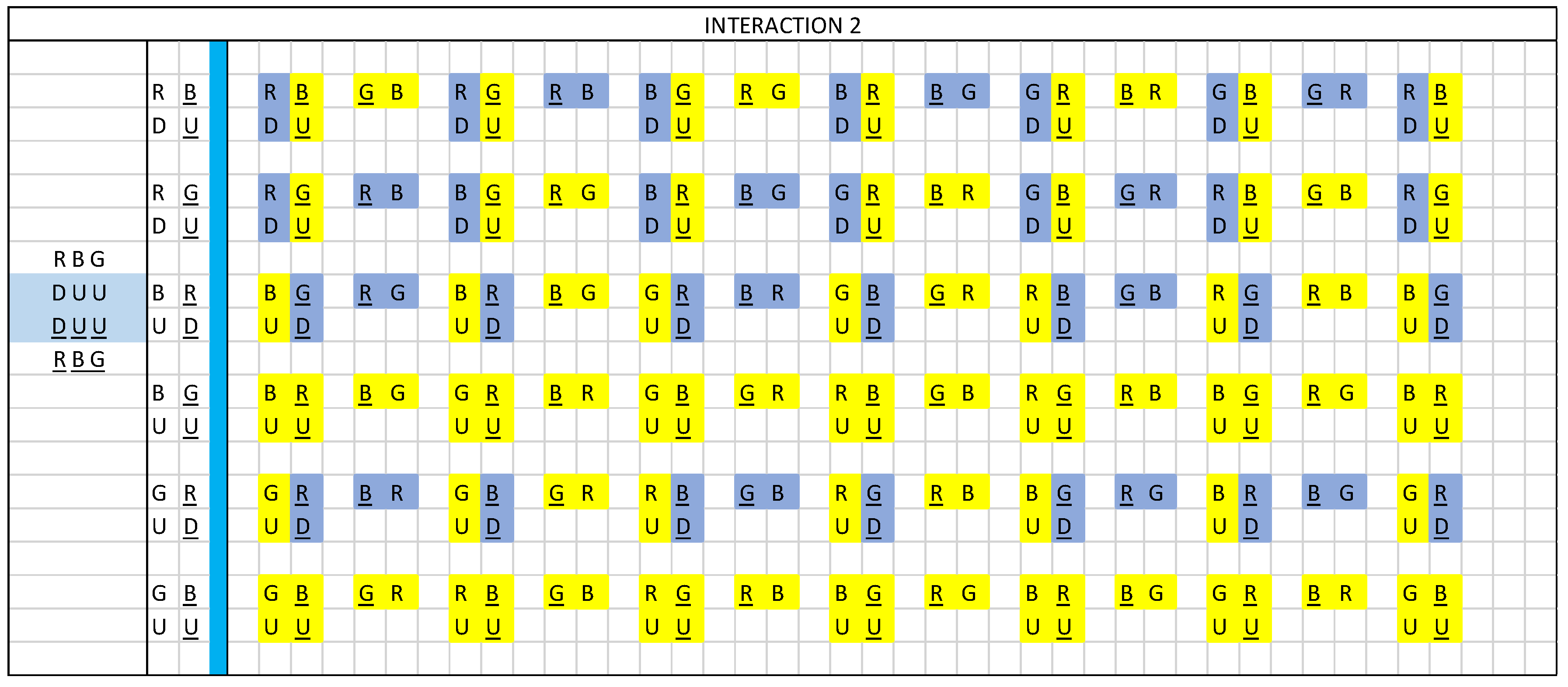
Figure 8 and
Figure 9 represent the interactions that exist in a neutron and a proton, divided into interaction 1 and interaction 2.
Interaction 1 represents direct interactions between quarks and antiquarks and interaction 2 represents cross interactions between quarks and antiquarks.
Next, we are going to analyse the frequency; We said that in a three-phase generator, the frequency is always the same, we also said that the frequency of the down quark is approximately double the frequency of the up quark. We are going to analyse precisely that difference in frequency and its interpretation.
The analysis that we are going to perform is important for the following reason, when we perform a vector or phasor operation that has the same frequency, we do not have problems, but what happens if we are going to perform a vector or phasor operation with operators that have different frequencies. In this analysis we are going to answer this question!!!!!!
If we analyse
figure 9 - proton, we observe that interaction 1 between quarks and antiquarks, direct interaction, are carried out at the same frequency.
Again, if we analyse
figure 9, proton, we observe that interaction 2 between quarks and antiquarks, cross interaction, in analogy with interaction 1, the frequency difference between quarks and antiquarks, does not represent a drawback in energy exchanges.
In
figure 10 we represent the energy exchanges between quarks and antiquarks and we see how the gluons act.
In blue we represent the quarks with the frequency of the Down quark and the associated gluon also in blue, when the energy exchange is carried out so that one quark becomes another quark.
In yellow we represent the quarks with the frequency of the up quark and the associated gluon also in yellow, when the energy exchange is carried out, so that one quark becomes another quark.
We can represent the statement in
Figure 11. We see why the exchange of gluons so that one quark becomes another quark does not represent a problem with frequency.
Quark U B transform quarks U G through gluon exchange G B, at the up-quark frequency, yellow.
Quark D R transform quarks D B through gluon exchange R B, at the down quark frequency, blue.
Taking into account what has been analysed so far, we can propose vector or phasor operations as valid, in analogy to that of a three-phase alternating current generator, which works with a single frequency.
It is the exchange of gluons, which is carried out at the appropriate frequency, allowing one quark to become another quark; it is this mechanism that allows us to perform a vector or phasor sum, as if this entire mechanism worked at a single frequency.
2. Electrical-Quantum Modelling of the Neutron as a Three-Phase Alternating Current Electrical Generator
We are going to work with
Figure 12 to create our electrical model of the neutron as a three-phase alternating current electrical generator.
The dipole DD is analogous to L1 and RR is analogous to the current flowing through L1.
The dipole DD is analogous to L2 and BB is analogous to the current flowing through L2.
The dipole UU is analogous to L3 and GG is analogous to the current flowing through L3.
We see that there are two types of interactions.
Interaction 1 or direct interaction and interaction 2 or cross interaction.
We said that down quarks have one frequency and up quarks have another frequency; Thanks to gluons, vector or phasor operations cease to be a problem, making it possible for a quark to transform into another quark, of the same frequency, thanks to the exchange of gluons. It is an amazing mechanism. We can see this mechanism in
figure 10.
In analogy to a three-phase alternating current electric generator, we are going to represent interaction 1 and interaction 2, using vectors whose resulting vector is null. In this way, we are going to simulate a neutron as a three-phase alternating current electrical generator.
In
Figure 5 of the standard model, we see that the up quark has a mass of 2.2 MeV/c² and the down quark has a mass of 4.7 MeV/c².
Taking these values as reference we are going to make our vector diagram of the neutron.
Quark Down = 4.7 MeV/c²
Quark up = 2.2 MeV/c²
It is important to make it clear that all interactions are vector, although we do not represent them as such in the figures.
Interaction 1:
If we analyse
figure 13, star connection, we see that the following vector sum is null:
R(DD)R + B(DD)B + G(UU)G = 0
If we analyse
figure 13, triangle connection, we see that the following vector sum is null:
R(DD)B + B(DU)G + R(DU)G = 0
This is telling us that the net charge in interaction 1 is zero.
Interaction 2:
If we analyse
figure 14, we observe that the following vector sum is also null:
R(DD)B + R(DU)G + B(DD)R + B(DU)G + G(UD)R + G(UD)B = 0
This is telling us that the net charge in interaction 2 is zero.
Taking into account interaction 1 and interaction 2, the total net charge of the neutron is zero, as appropriate.
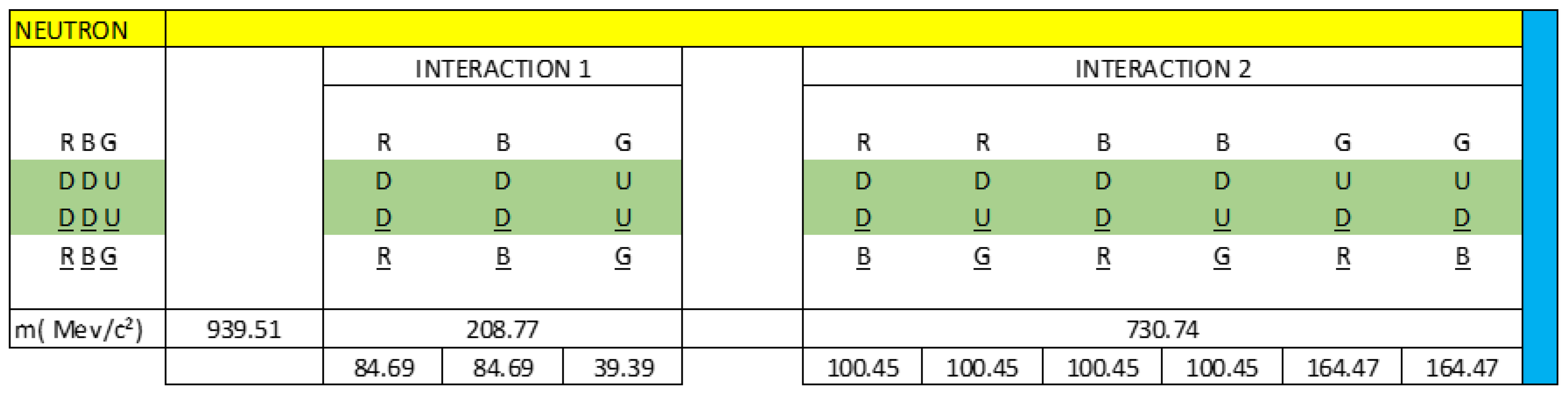
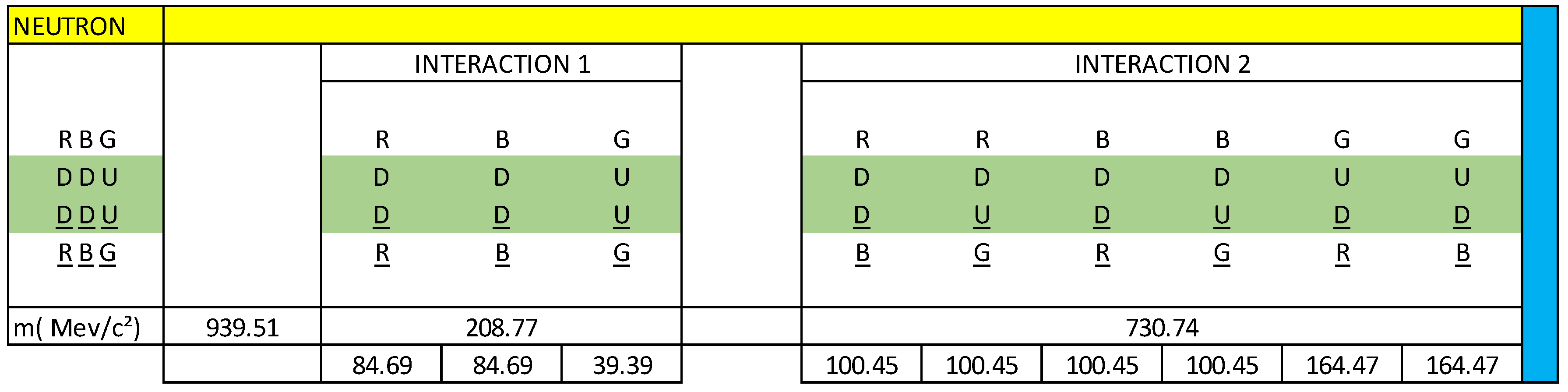
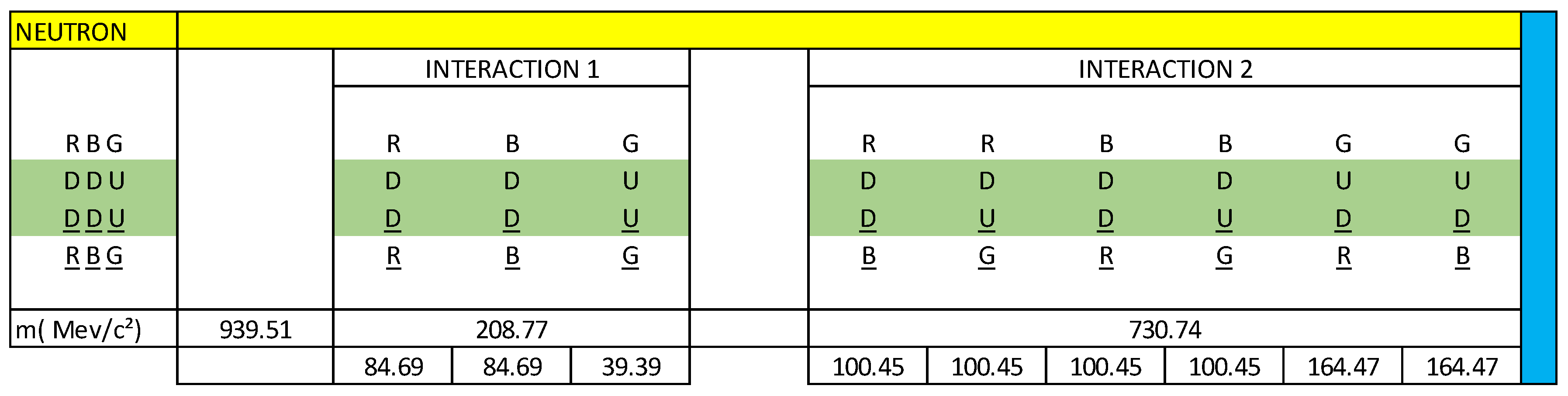
Knowing that the total mass of the neutron is 939.56 MeV/c², we are going to calculate the mass content in each interaction:
R(DD)R = 8.6 x 9.8486 = 84.69 MeV/c²
B(DD)B = 8.6 x 9.8486 = 84.60 MeV/c²
G(UU)G = 4.0 x 9.8486 = 39.39 MeV/c²
R(DD)B = 10.2 x 9.8486 = 100.45 MeV/c²
R(DU)G = 10.2 x 9.8486 = 100.45 MeV/c²
B(DD)R = 10.2 x 9.8486 = 100.45 MeV/c²
B(DU)G = 10.2 x 9.8486 = 100.45 MeV/c²
G(UD)R = 16.7 x 9.8486 = 164.47 MeV/c²
G(UD)B = 16.7 x 9.8486 = 164.47 MeV/c²
(2 x (8.6) + 4.0 + 4(10.2) + 2 x (16.7) = 95.4
NECF = Mn / 95.4 = (939.56 MeV/c²) / 95.4 = 9.8486 MeV/c², Neutron electromagnetic coupling factor. The value: 95.4, could have any type of units, for practical purposes we are going to leave it without units.
If we divide the electromagnetic coupling factor of the neutron NECF, by the energy 0.388 MeV/c², corresponding to unit binding energy per nucleon, we will have the approximate number of protons to which the neutron can be stably associated.
Qtyp = NECF / ∆Eα = (9.8486 MeV/c²) / (0.388 MeV/c²) = 25.38
where ∆Eα could be considered unit binding energy per nucleon.
Qtyp = 25 proton.
where Qtyp represents the number of protons that the neutron-proton binding energy stably supports, considering the electromagnetic coupling factor of the Neutron NECF.
Let us remember that the maximum binding energy is obtained for iron, Fe (26,30), which has 26 protons and 30 neutrons and this coincides with being the most abundant element on Earth.
According to our calculation, starting at proton number 26, the neutron-proton binding energy begins to weaken.
We are going to represent these values in
figure 15:
The electrical modelling of a neutral as a three-phase alternating current electrical generator allows us to assign a mass value to interactions 1 & 2, which we represent using a phasor diagram, as shown in
figure 14. It also allows us to verify that the sum resulting vector in interactions 1 & 2 is zero, and the scalar sum is equal to 939.56 MeV/c², as appropriate.
Analysing the vector diagrams in
Figure 13 and
Figure 14, we see that the degrees of freedom of the vectors are practically zero, there is no possibility of deviations, the hypothesis that the charge has to be zero restricts any possibility of changes in the position of the vectors, that is, the vectors have a unique configuration, given in
Figure 13 and
Figure 14.
It is important to keep in mind that the relationship between the interactions of quarks, anti-quarks and gluons is vector-type, that is, each interaction will be represented by a module and an angle.
In the neutron, if we add the phasors of interaction 1 and interaction 2 vector-wise, we see that the resulting vector is zero, in other words, the net charge is zero; but if we add the module of each vector in MeV/c² scalarly, the sum gives us 939.56 MeV/c², we represent this in
figure 14 and
figure 15, which corresponds to the neutron.
Definitely, we can assure that neutrons are true generators of energy, mass and gravity; we have verified how with three quarks that add up to approximately 10 MeV/c², we can generate a mass of 939.56 MeV/c² through the interactions of quarks, anti-quarks and gluons.
3. Electrical-Quantum Modelling of the Proton as a Three-Phase Alternating Current Electrical Generator
We are going to work with
Figure 16 to create our electrical model of the proton as a three-phase alternating current electrical generator.
The dipole DD is analogous to L1 and RR is analogous to the current flowing through L1.
The dipole UU is analogous to L2 and BB is analogous to the current flowing through L2.
The dipole UU is analogous to L3 and GG is analogous to the current flowing through L3.
We see that there are two types of interactions.
Interaction 1 or direct interaction and interaction 2 or cross interaction.
We said that down quarks have one frequency and up quarks have another frequency; Thanks to gluons, vector or phasor operations cease to be a problem, making it possible for a quark to transform into another quark, of the same frequency, thanks to the exchange of gluons. It is an amazing mechanism. We can see this mechanism in
figure 10.
In analogy to a three-phase alternating current electric generator, we are going to represent interaction 1 and interaction 2, using vectors whose resulting vector is not zero. In this way we are going to simulate a proton as a three-phase alternating current electrical generator.
In
Figure 5 of the standard model, we see that the up quark has a mass of 2.2 MeV/c² and the down quark has a mass of 4.7 MeV/c².
Taking these values as reference we are going to make our vector diagram of the neutral.
Quark Down = 4.7 MeV/c²
Quark up = 2.2 MeV/c²
It is important to make it clear that all interactions are vector, although we do not represent them as such in the figures.
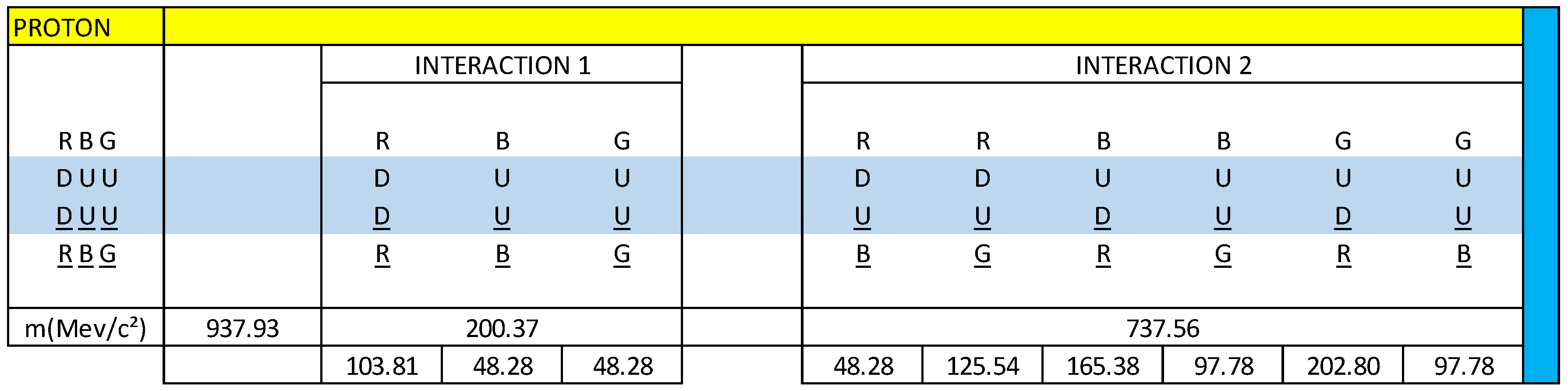
Interaction 1:
If we analyse
figure 17, star connection, we see that the following vector sum is not null:
R(DD)R + B(UU)B + G(UU)G ≠ 0
Interaction 2:
If we analyse
figure 18, we observe that the following vector sum is not null:
R(DU)B + R(DU)G + B(UD)R + B(UU)G + G(UD)R +G(UU)B ≠ 0
From a load point of view, we have:
R(DD)R + B(UU)B + G(UU)G + R(DU)B + R(DU)G + B(UD)R + B(UU)G + G(UD)R
+ G(UU)B = 1
From the mass point of view, we have:
R(DD)R + B(UU)B + G(UU)G + R(DU)B + R(DU)G + B(UD)R + B(UU)G + G(UD)R
+ G(UU)B = 938.27 MeV/c²
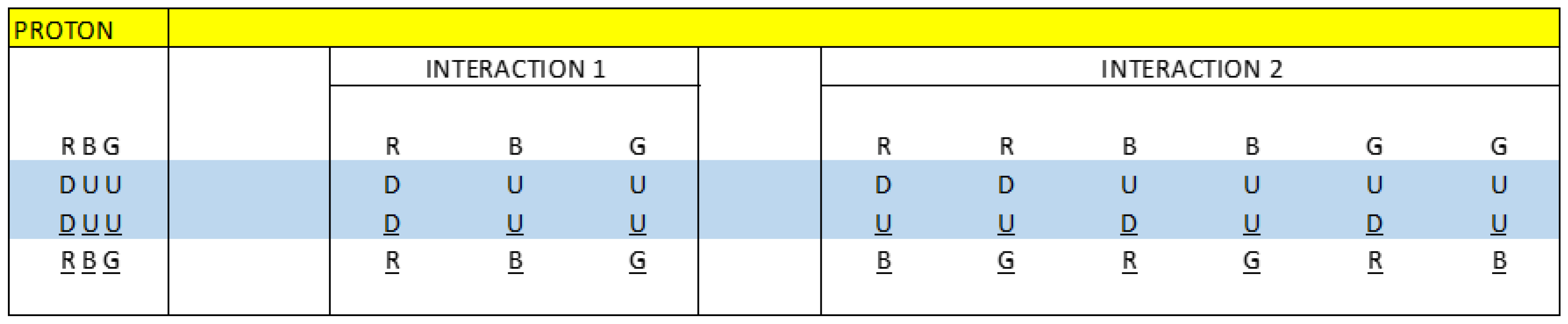
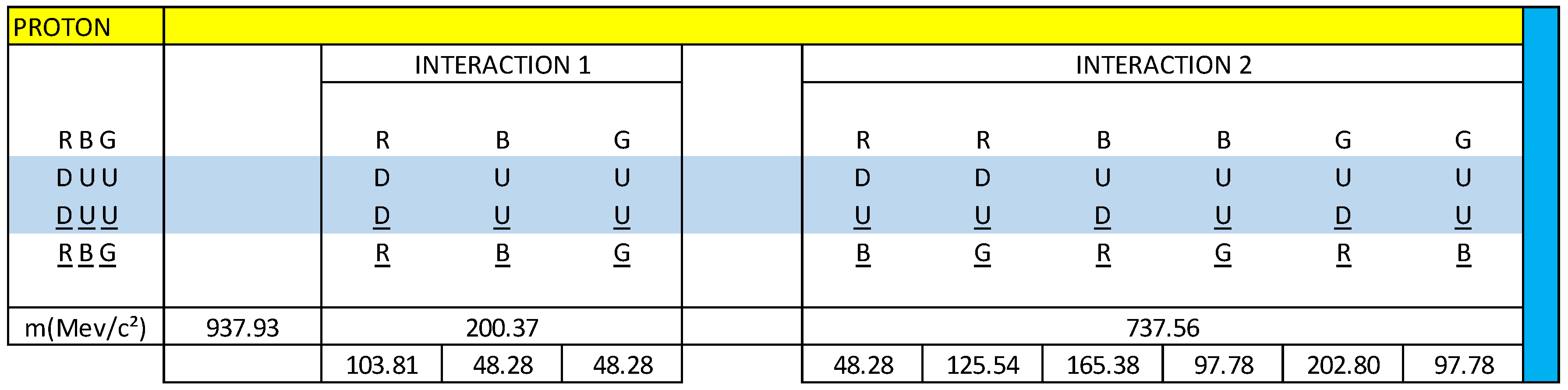
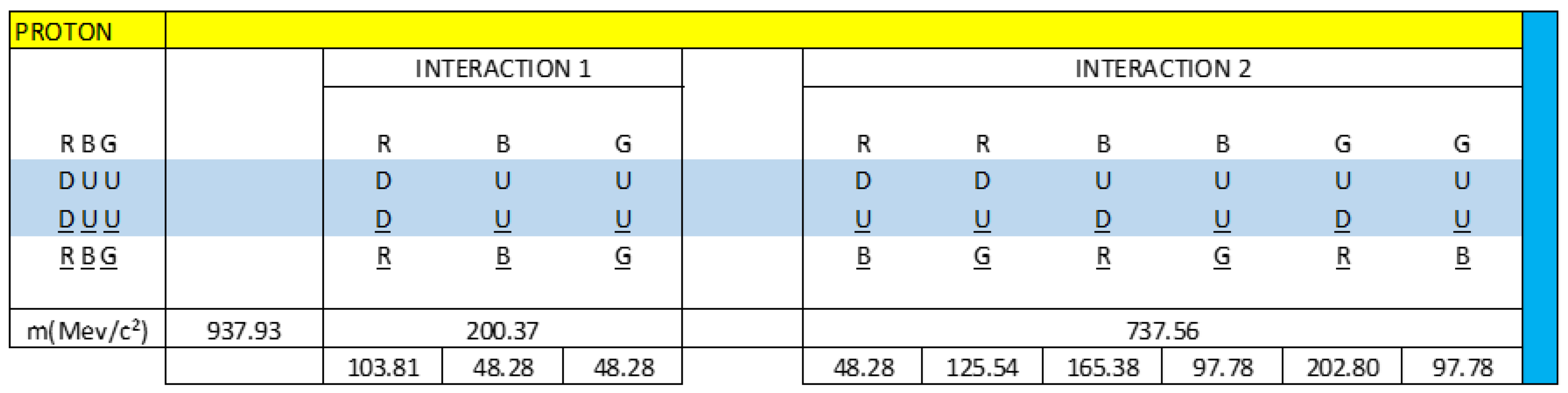
Knowing that the total mass of the proton is 938.27 MeV/c², we are going to calculate the mass content in each interaction:
R(DD)R = 8.6 x 12.0720 = 103.81 MeV/c²
B(UU)B = 4.0 x 12.0720 = 48.28 MeV/c²
G(UU)G = 4.0 x 12.0720 = 48.28 MeV/c²
R(DU)B = 4.0 x 12.0720 = 48.28 MeV/c²
R(DU)G = 10.4 x 12.0720 = 125.54 MeV/c²
B(UD)R = 13.7 x 12.0720 = 165.38 MeV/c²
B(UU)G = 8.1 x 12.0720 = 97.78 MeV/c²
G(UD)R = 16.8 x 12.0720 = 202.80 MeV/c²
G(UU)B = 8.1 x 12.0720 = 97.78 MeV/c²
8.6 + 4 x (3) + 10.4 + 13.7 + 2 x (8.1) + 16.8 = 77.7
PECF = Mp ̸ 77.7 = (938.27 MeV/c²) ̸ 77.7 = 12.0720 MeV/c², Neutron electromagnetic coupling factor. The value: 77.7, could have any type of units, for practical purposes we are going to leave it without units.
If we divide the electromagnetic coupling factor of the proton PECF, by the energy 0.388 MeV/c², corresponding to unit binding energy per nucleon, we will have the approximate number of neutrons to which the proton can be stably associated.
Qtyn = PECF / ∆Eα = (12.0720 MeV/c²) / (0.388 MeV/c²) = 31.11
where ∆Eα could be considered unit binding energy per nucleon.
Qtyn = 31 neutron.
where Qtyn represents the number of neutrons that the proton-neutron binding energy stably supports, considering the electromagnetic coupling factor of the proton PECF.
According to our calculation, starting at neutrons number 31, the proton-neutron binding energy begins to weaken.
If we consider the electromagnetic coupling factor, NECF and PECF, the maximum stability of an atomic nucleus would be achieved with a maximum number of 25 protons and a maximum number of 31 neutrons, these quantities roughly coincide with that of the iron atom Fe (26,30), a good approximation.
We are going to represent these values in
figure 19:
The electrical modelling of a proton as a three-phase alternating current electrical generator allows us to assign a mass value to interactions 1 and 2, which we represent using a vector diagram, as shown in
Figure 18 &
Figure 19.
It is important to keep in mind that the relationship between the interactions of quarks, anti-quarks and gluons is vector-type, that is, each interaction will be represented by a module and an angle.
We can assure that protons are true generators of energy, mass and gravity; We have verified how with three quarks that add up to approximately 10 MeV/c², we can generate a mass of 938.27 MeV/c² through the interactions of quarks, anti-quarks and gluons.
4. Application OF the Model and Results
4.1. Proton Decay
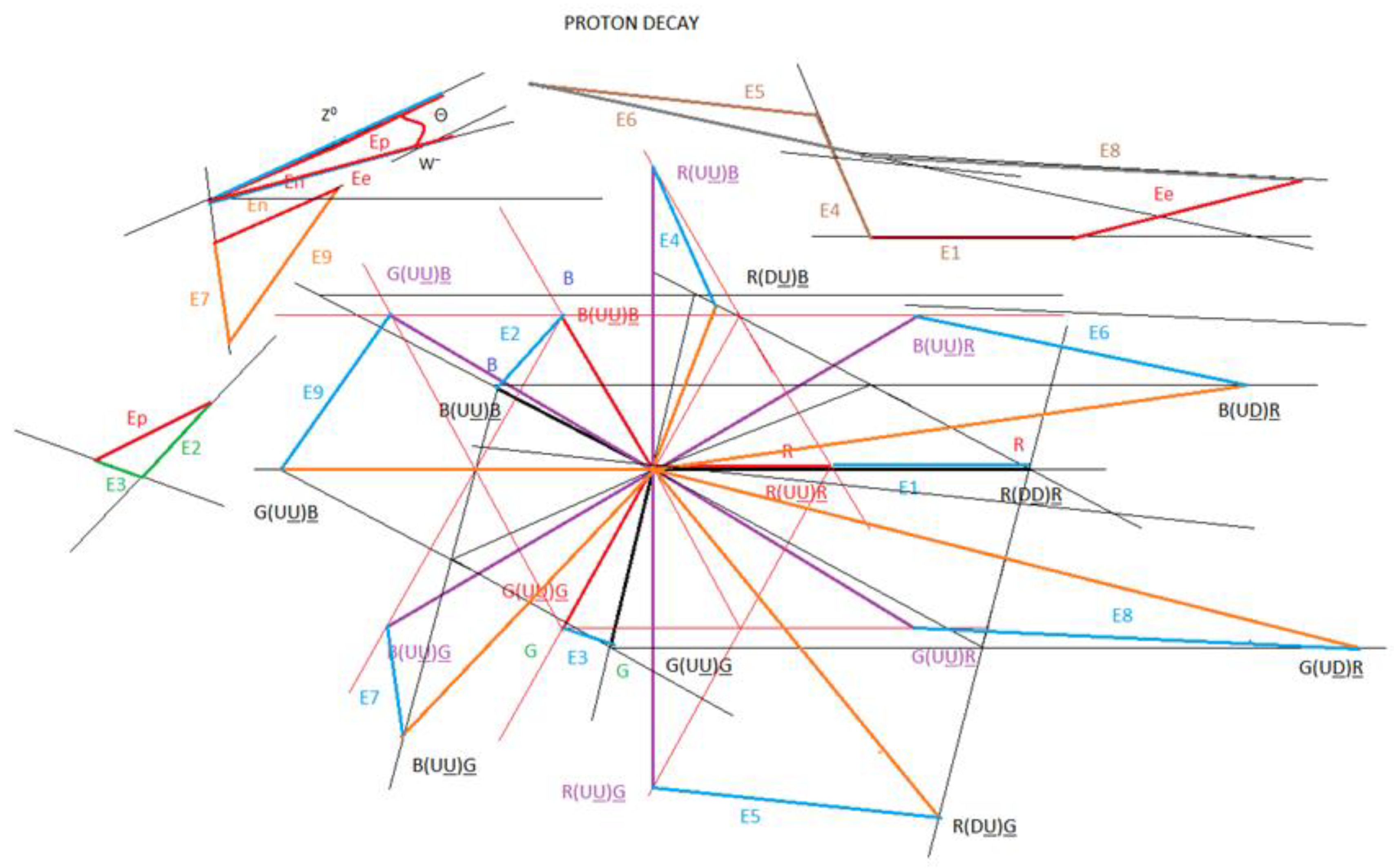
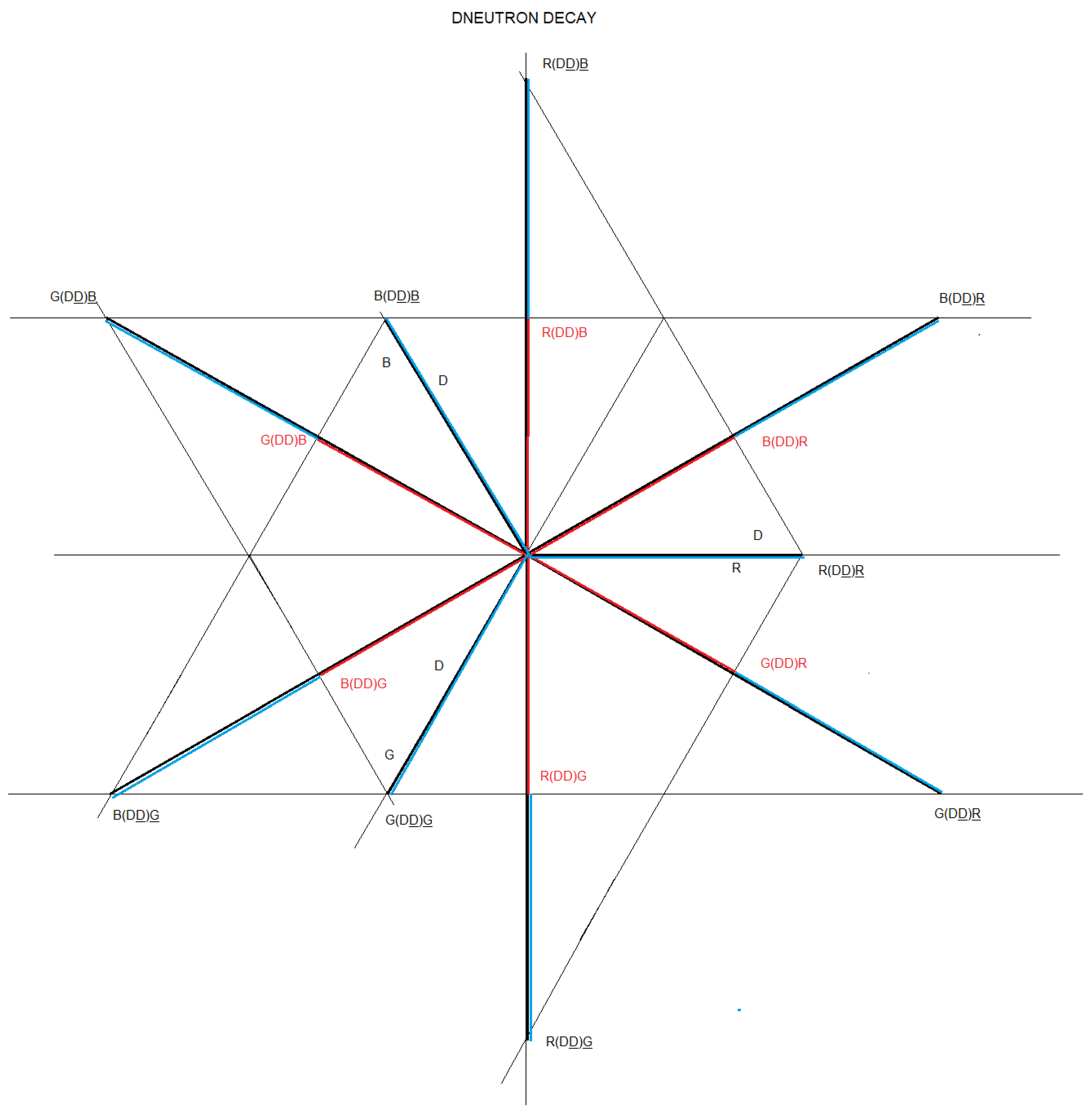
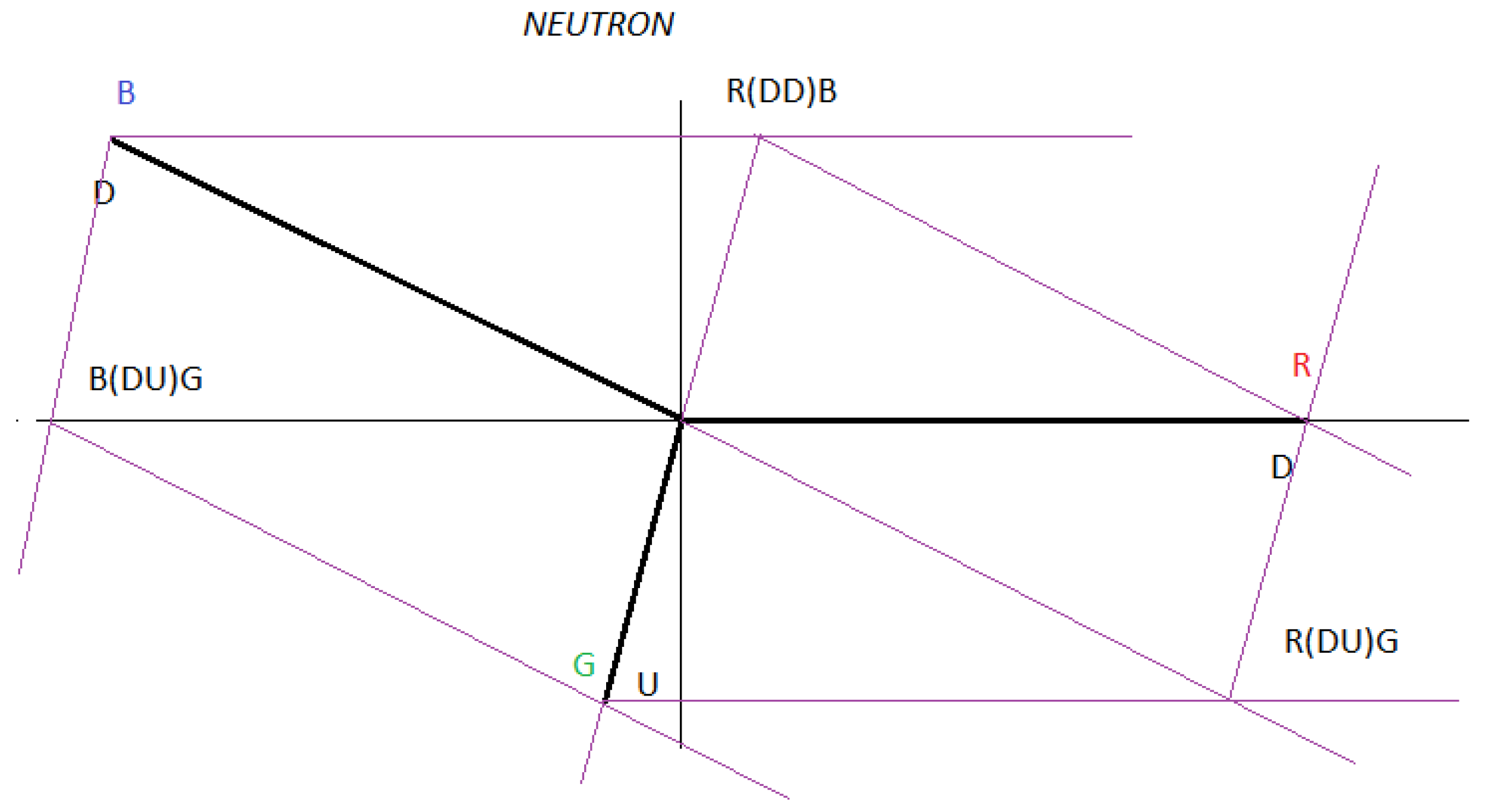
We are going to work with the following figure to represent the decay of the proton.
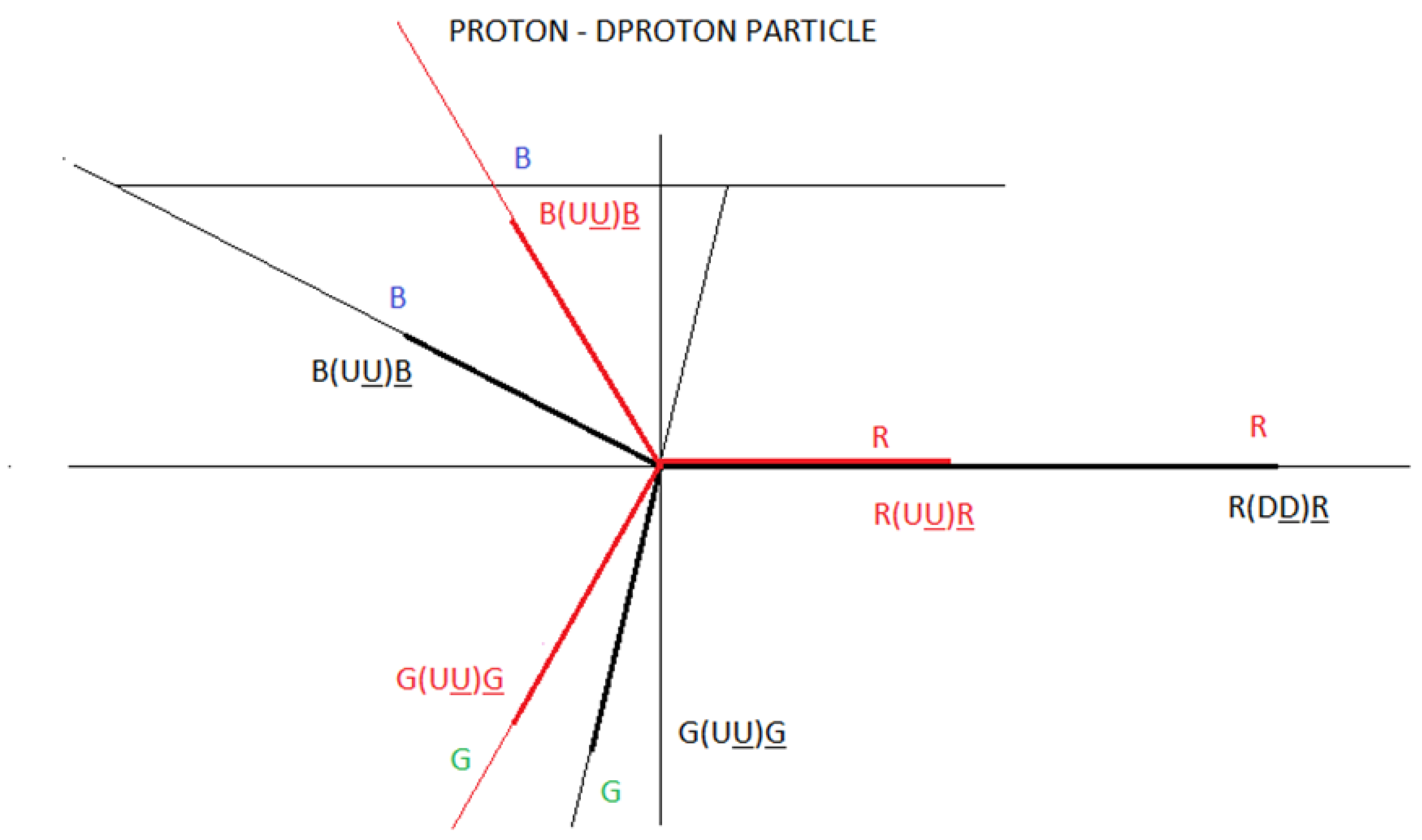
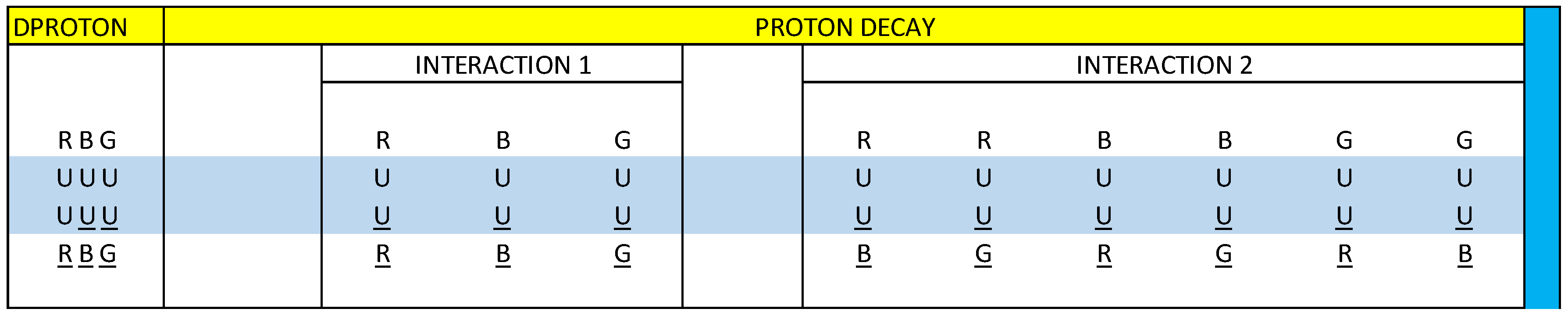
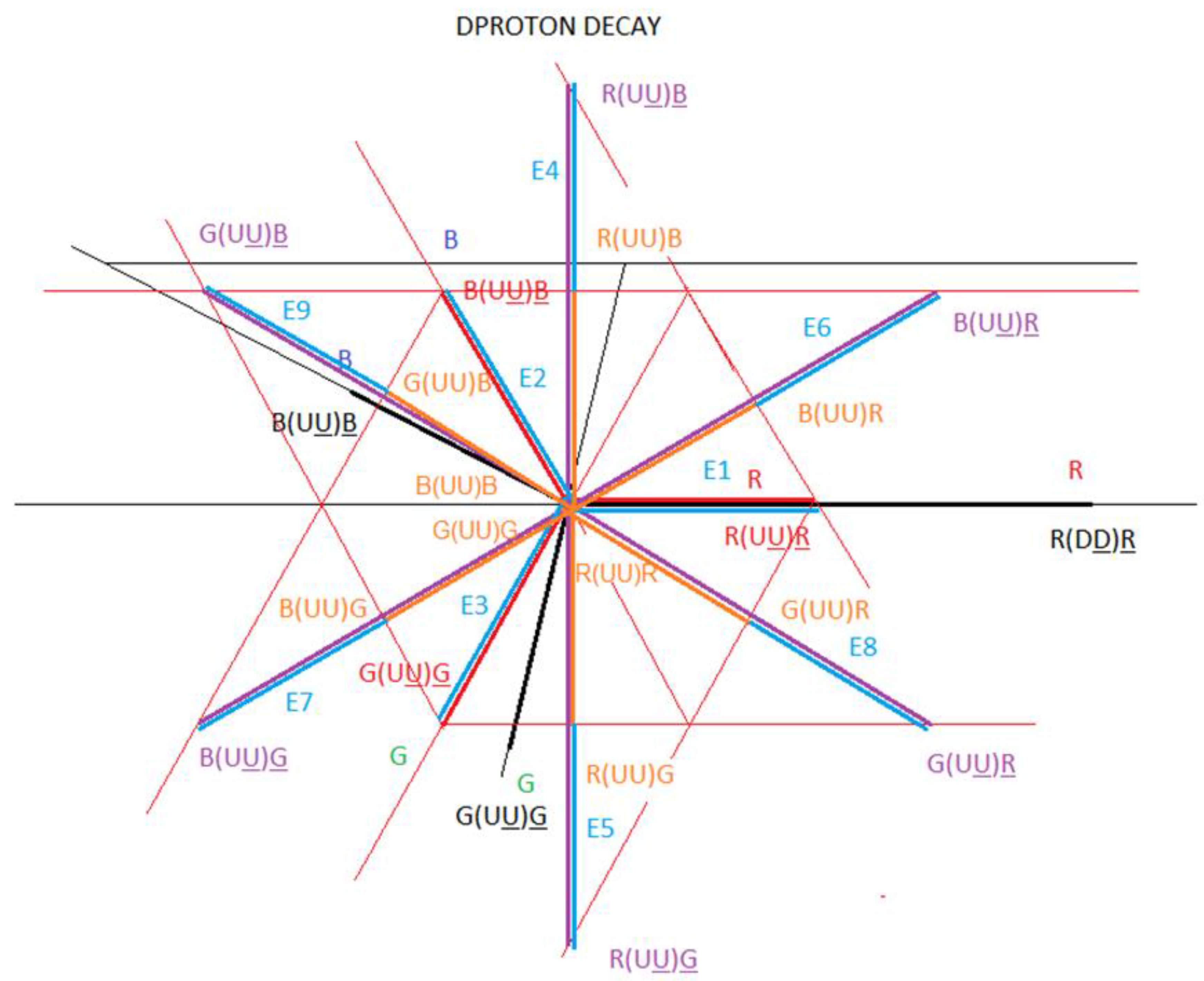
In
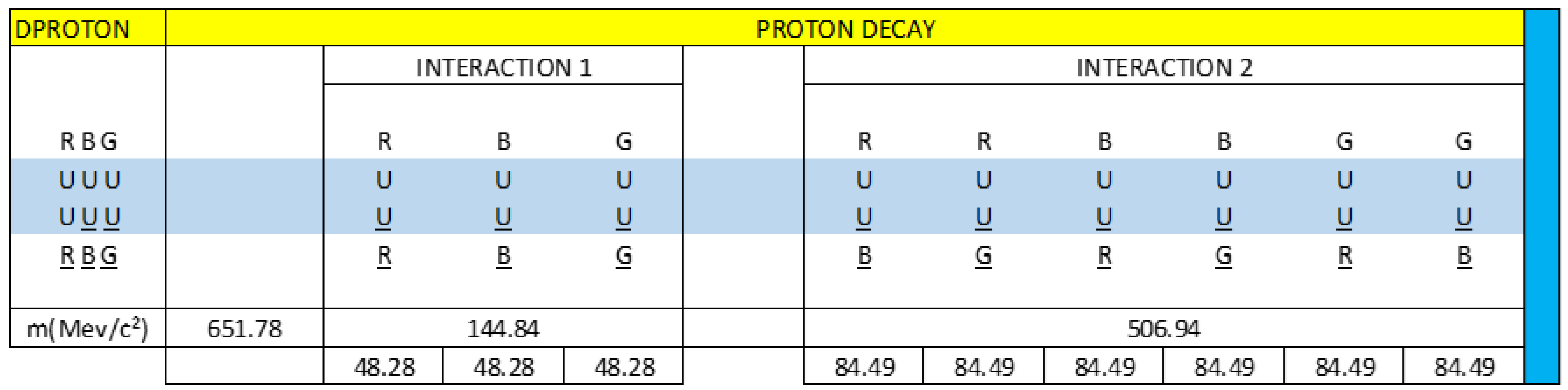
figure 21, we represent the decay of the proton, through interaction 1 and interaction 2. We call this particle Dproton. We observe that all the components are U quarks and we also observe that there are 9 U quark-antiquark dipoles, which are vector related. This proton decay configuration is represented by matter and antimatter.
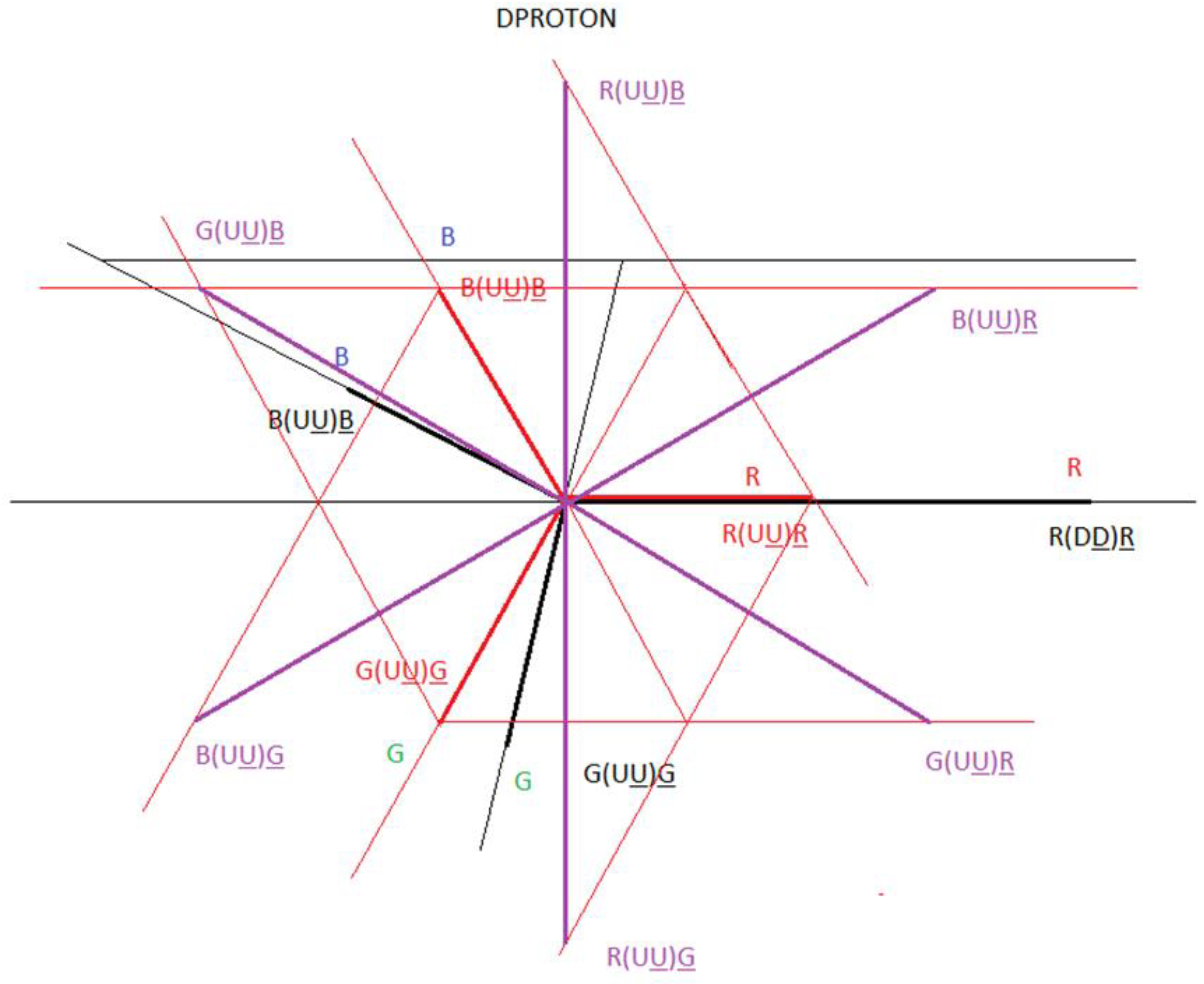
We are going to make the vector diagram of the Dproton particle, of the interaction 1 and 2:
Figure 22.
Vector diagram of the proton and Dproton particle.
Figure 22.
Vector diagram of the proton and Dproton particle.
Figure 23.
The vector diagram of the proton is represented in black. The vector diagram of Dproton particle - interaction 1 is represented in red. The vector diagram of Dproton - interaction 2 is represented in purple.
Figure 23.
The vector diagram of the proton is represented in black. The vector diagram of Dproton particle - interaction 1 is represented in red. The vector diagram of Dproton - interaction 2 is represented in purple.
At first glance, if we add the three U quarks scalarly, we can affirm that the total charge is (2/3 + 2/3 + 2/3 = 2) 2, but we have to remember that we are adding scalarly and in this situation we must consider a vector sum and this gives us a net charge of zero. We can represent the U quarks as three vectors with the same module, 120 degrees out of phase, whose vector sum is zero, in analogy to electric generators.
The Dproton particle behaves analogously to a generator, whose current, voltage and charge are perfectly balanced, in equilibrium.
The scale factor is the following:
SF = (X / 48.28) 4
SF⁻¹ = (48.28 / 4) X
This scaling factor is unique and applies to all vectors in the diagram representing the proton decay.
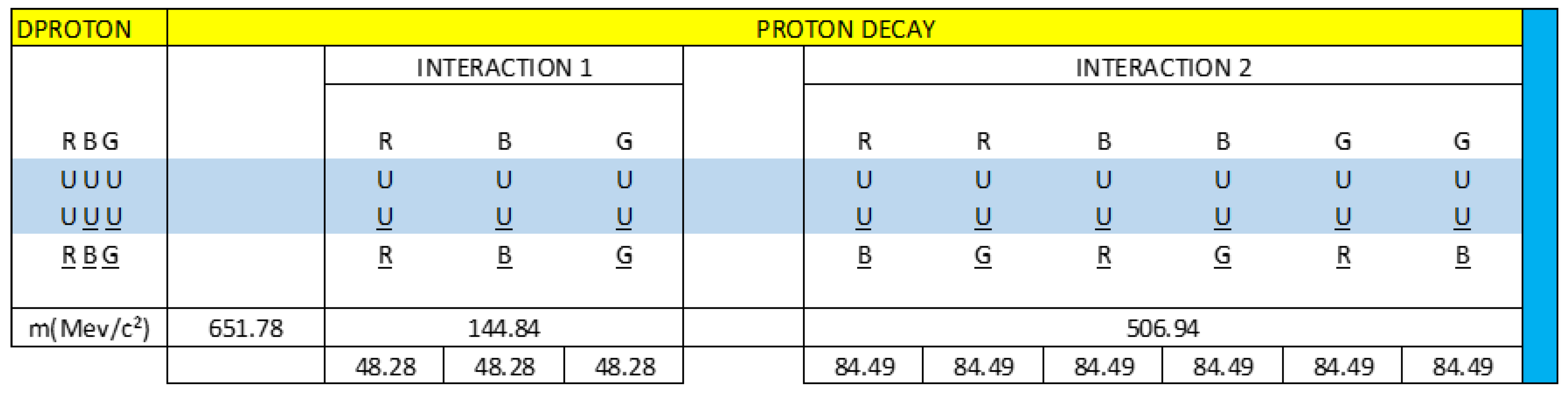
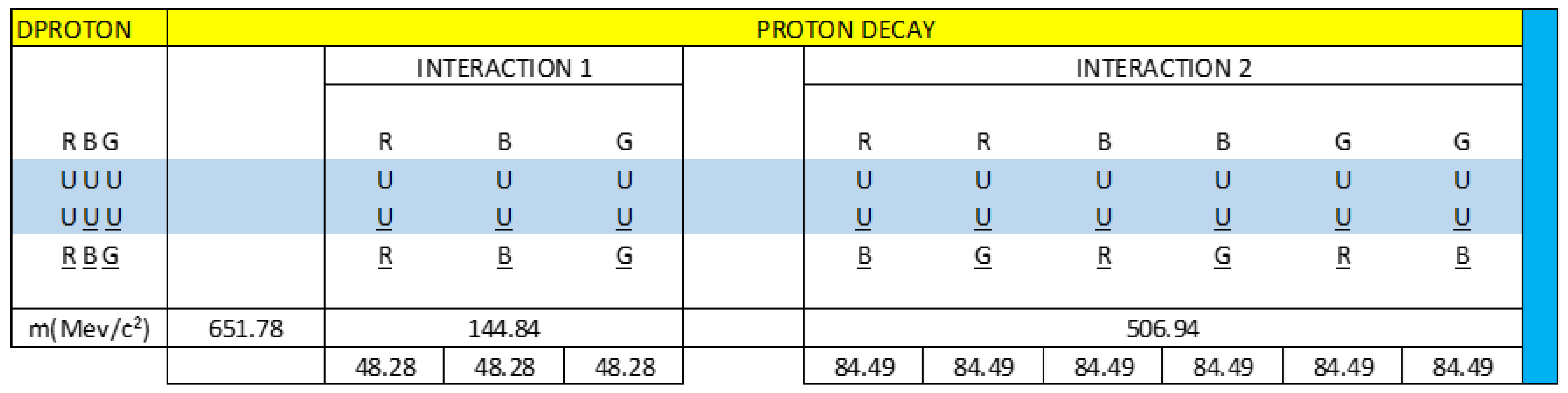
We are going to describe the mass distribution of the dipoles of interaction 1 and 2, which represent the Dproton particle.
Figure 24.
Mass distribution in the interaction 1 and 2 of the Dproton particle.
Figure 24.
Mass distribution in the interaction 1 and 2 of the Dproton particle.
According to our vector calculation, the Dproton particle has a mass of 651.78 MeV/c².
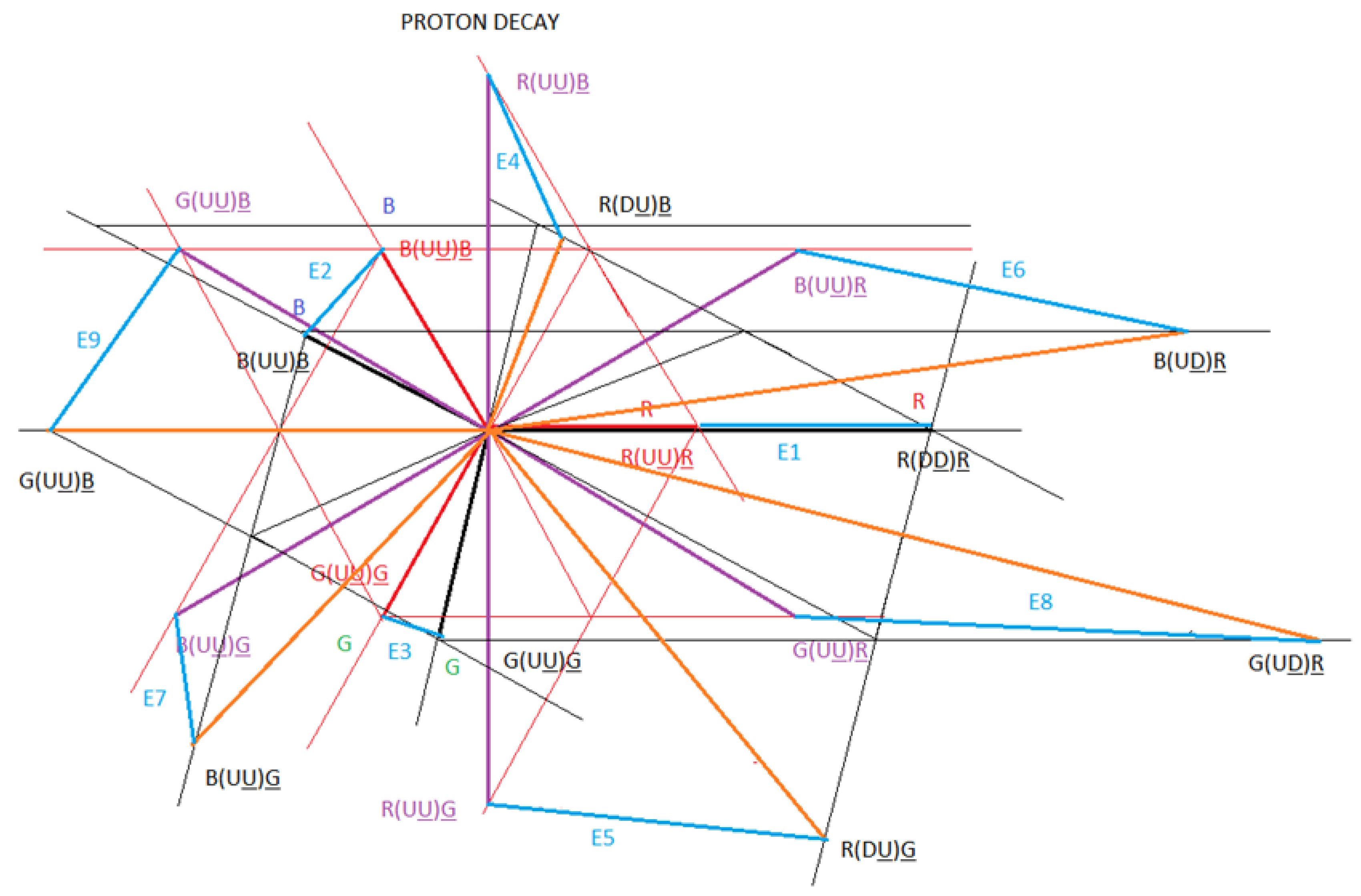
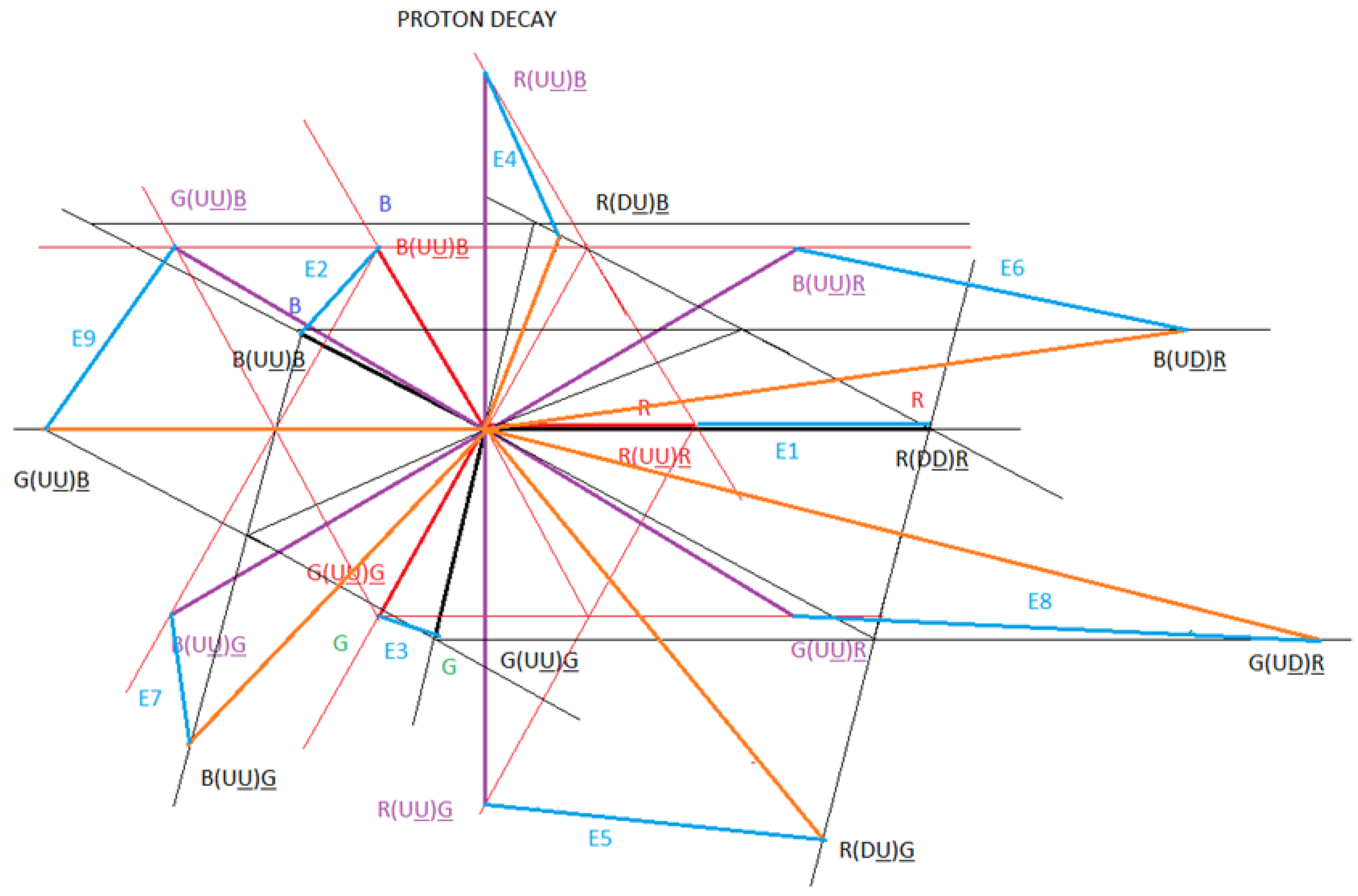
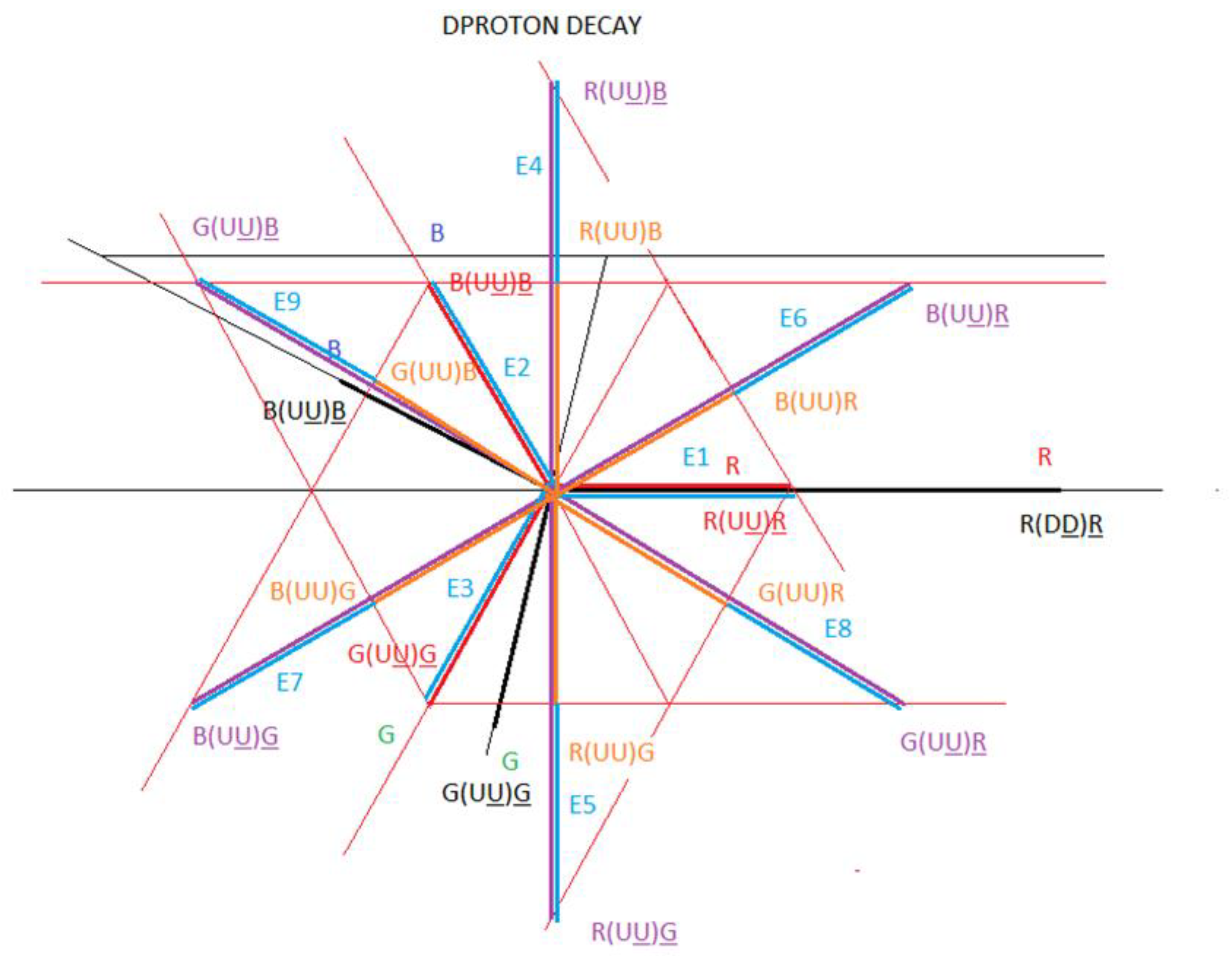
We are going to make the vector diagram of the proton decay in the Dproton particle.
The dipoles of interaction 1 of the proton are represented in black.
The dipoles of interaction 2 of the proton are represented in orange.
The dipoles of interaction 1 of the Dproton are represented in red.
The dipoles of interaction 2 of the Dproton are represented in purple.
Represented in blue are the 3 vectors of interaction 1 and the 6 vectors of interaction 2 that correspond to the decay of the proton in the Dproton particle.
Now we are going to analyse the energy (mass) changes that occur when the proton decays in the Dproton particle. These changes in energy (mass) are represented in blue in
figure 25.
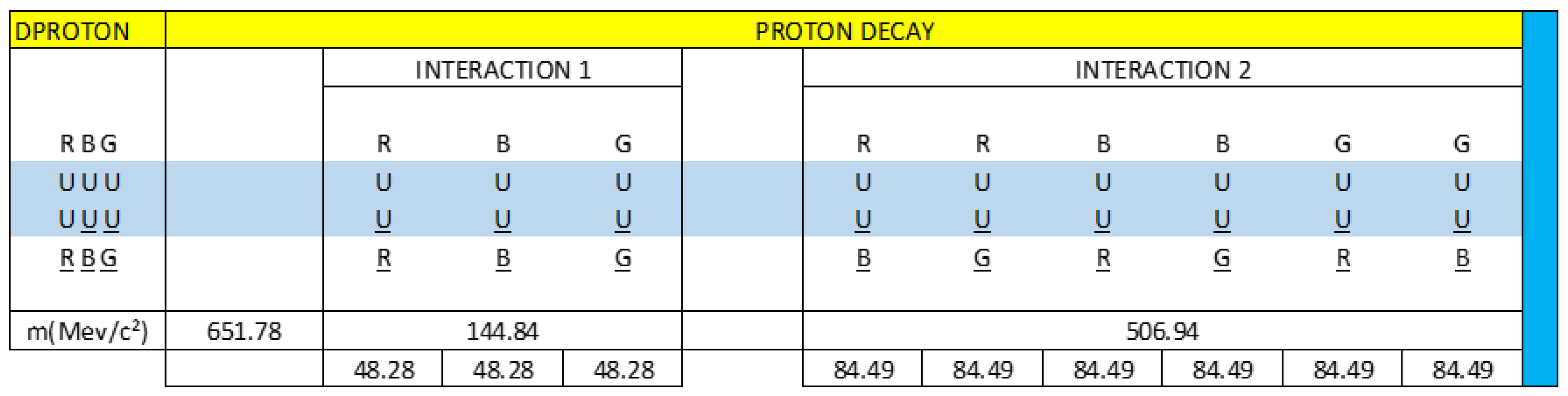
Table 1.
Calculation of the interactions in MeV/c², when the proton decays in the Dproton particle.
Table 1.
Calculation of the interactions in MeV/c², when the proton decays in the Dproton particle.
| PROTON DECAY |
| PROTON |
DPROTON |
INTERACTION |
INTERACTION (MeV/c²) |
| R(DD)R |
R(UU)R |
E1 = 4.5 |
E1 = 54.31 |
| B(UU)B |
B(UU)B |
E2 = 2.3 |
E2 = 27.76 |
| G(UU)G |
G(UU)G |
E3 = 1.1 |
E3 = 13.27 |
| R(DU)B |
R(UU)B
|
E4 = 3.5 |
E4 = 42.24 |
| R(DU)G |
R(UU)G |
E5 = 6.5 |
E5 = 78.45 |
| B(UD)R |
B(UU)R |
E6 = 7.6 |
E6 = 91.73 |
| B(UU)G |
B(UU)G
|
E7 = 2.0 |
E7 = 24.14 |
| G(UD)R
|
G(UU)R
|
E8 = 10.2 |
E8 = 123.62 |
| G(UU)B
|
G(UU)B
|
E9 = 4.4 |
E9 = 53.10 |
| TOTAL INTERACTION |
IEtI = 508.72 MeV/c² |
| (W⁻)e INTERACTION |
IEeI = W⁻ = 66.38 MeV/c² |
| (Z⁰)n INTERACTION |
IEnI = 39.83 MeV/c² |
| (Z⁰)p INTERACTION |
IEpI = 36.21 MeV/c² |
| (Z⁰) INTERACTION |
IZ⁰I = 70.00 MeV/c² |
| Θ angle, Θ = arc cos W⁻/Z⁰ |
Θ = 16⁰ |
The vectors E1 to E9 are represented in blue in
figure 25.
It is important to highlight that the decay of the proton in the Dproton particle produces a total interaction of Et = 508.72 MeV/c².
In
figure 25, we divide these vectors into three parts, which we will explain below:
En = (3.3 x 48.28) / 4 = 39.83 MeV/c²
E7 = [B(UU)G]p → [B(UU)G]Dp
E9 = [G(UU)B]p → [G(UU)B]Dp
For E7, when the decay of [B(UU)G]p of the proton to [B(UU)G]Dp of the Dproton occurs; a neutral current is produced.
For E9, when the decay of [G(UU)B]p of the proton to [G(UU)B]Dp of the Dproton occurs; a neutral current is produced.
Here, we are going to hypothesize that the En energy is what gives origin to the neutrinos. Let us note that the BG and GB gluons are of same frequencies; B and G are associated with the U quark.
When E7 + E9 interacts, it is like the BG and GB gluons cancel each other and the UU and UU quarks also cancel and, in this way, the resulting energy gives origin to the neutrinos, whose mass is neutral.
Ep = (3 x 48.28) / 4 = 36.21 MeV/c²
E2 = [B(UU)B]p → [B(UU)B]Dp
E3 = [G(UU)G]p → [G(UU)G]Dp
For E2, when the decay of [B(UU)B]p of the proton, to [B(UU)B]Dp of the Dproton, occurs; a neutral current is produced.
For E3, when the decay of [G(UU)G]p of the proton, to [G(UU)G]p of the Dproton, occurs; a neutral current is produced.
Here, we are going to hypothesize that the Ep energy is what gives origin to the photons. Here it is important to highlight that the BB and GG gluons have the same frequency; BB and GG gluons, have the frequency of the U quark.
Ee = (5.5 x 48.28) / 4 = 66.38 MeV/c²
E1 = [R(DD)R]p → [R(UU)R]Dp
E4 = [R(DU)B]p → [R(UU)B]Dp
E5 = [R(DU)G]p → [R(UU)G]Dp
E6 = [B(UD)R]p → [B(UU)R]Dp
E8 = [G(UD)R]p → [G(UU)R]Dp
For the vectors E1, E4, E5, E6 and E8, when the decay of proton to Dproton occurs, it is observed that currents with positive and negative charges are generated.
The negative net energy of the vector Ee = 66.38 MeV/c²
Here, we are going to hypothesize that the Ee energy is what gives origin to the electron.
The emission of the energy vectors En, Ep and Ee are necessary in the βˉ decay that occurs when the proton decays into the Dproton particle, so that the Dproton stabilizes and reaches its corresponding energy.
In the following vector diagram, we are going to represent the vectors En, Ep and Ee.
Figure 26.
- Calculation of En, Ep, Ee, W⁻, Z⁰ and Θ angle.
Figure 26.
- Calculation of En, Ep, Ee, W⁻, Z⁰ and Θ angle.
calculation of W ⁻ , Z ⁰ and Θ angle:
Theoretical calculations that we obtain from figure 46, proton decay diagram:
theoretical W⁻ = Ee = (5.5 x 48.28) / 4 = 66.38 MeV/c²
theoretical W⁻ = 66.38 MeV/c²
theoretical Z⁰ = (5.8 x 48.28) / 4 = 70.00 MeV/c²
theoretical Z⁰ = 70.00 MeV/c²
W⁻/ Z⁰ = cos Θ
Θ = arc cos W⁻/Z⁰ = arc cos (66.38 / 70.00) = arc cos (0.948)
Θ = 18⁰
measured Θ = 16⁰
As analysed so far, the decay of the proton in the Dproton particle also includes a βˉ decay.
4.2. Dproton Decay
We are going to work with the following figure to represent the decay of the Dproton particle.
Figure 27.
Dproton particle.
Figure 27.
Dproton particle.
Figure 28.
Protoniu particle, does not include antimatter.
Figure 28.
Protoniu particle, does not include antimatter.
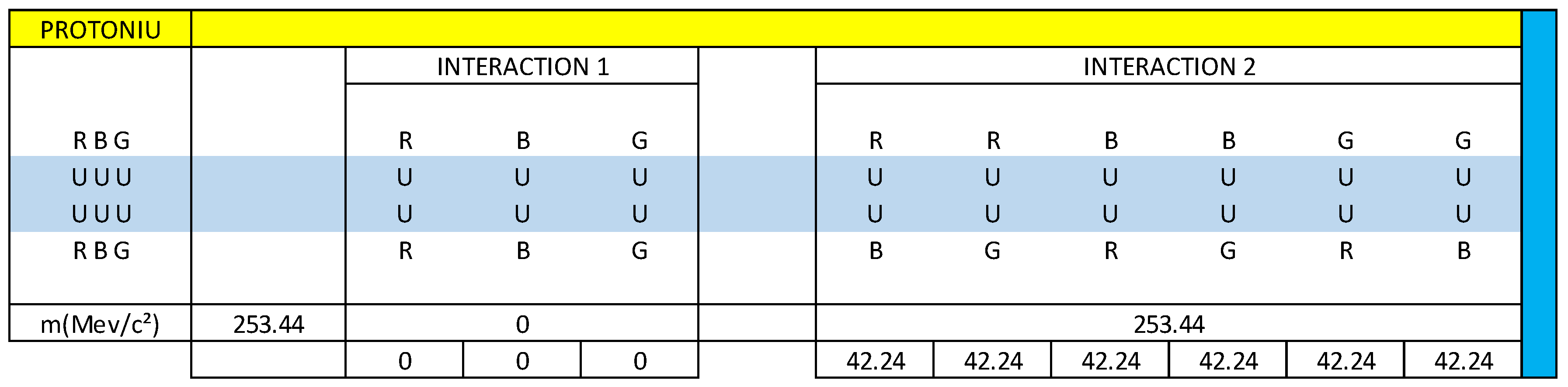
In
figure 28, we represent the protoniu particle, through interaction 1 and interaction 2. We observe that all the components are U quarks and we also observe that the 9 dipoles are U quarks, which are related vectorially. This configuration is represented only by matter, there is no antimatter in this configuration.
We are going to make the vector diagram of the Protoniu particle, of the interaction 1 and 2:
Figure 29.
Vector diagram of the proton and protoniu.
Figure 29.
Vector diagram of the proton and protoniu.
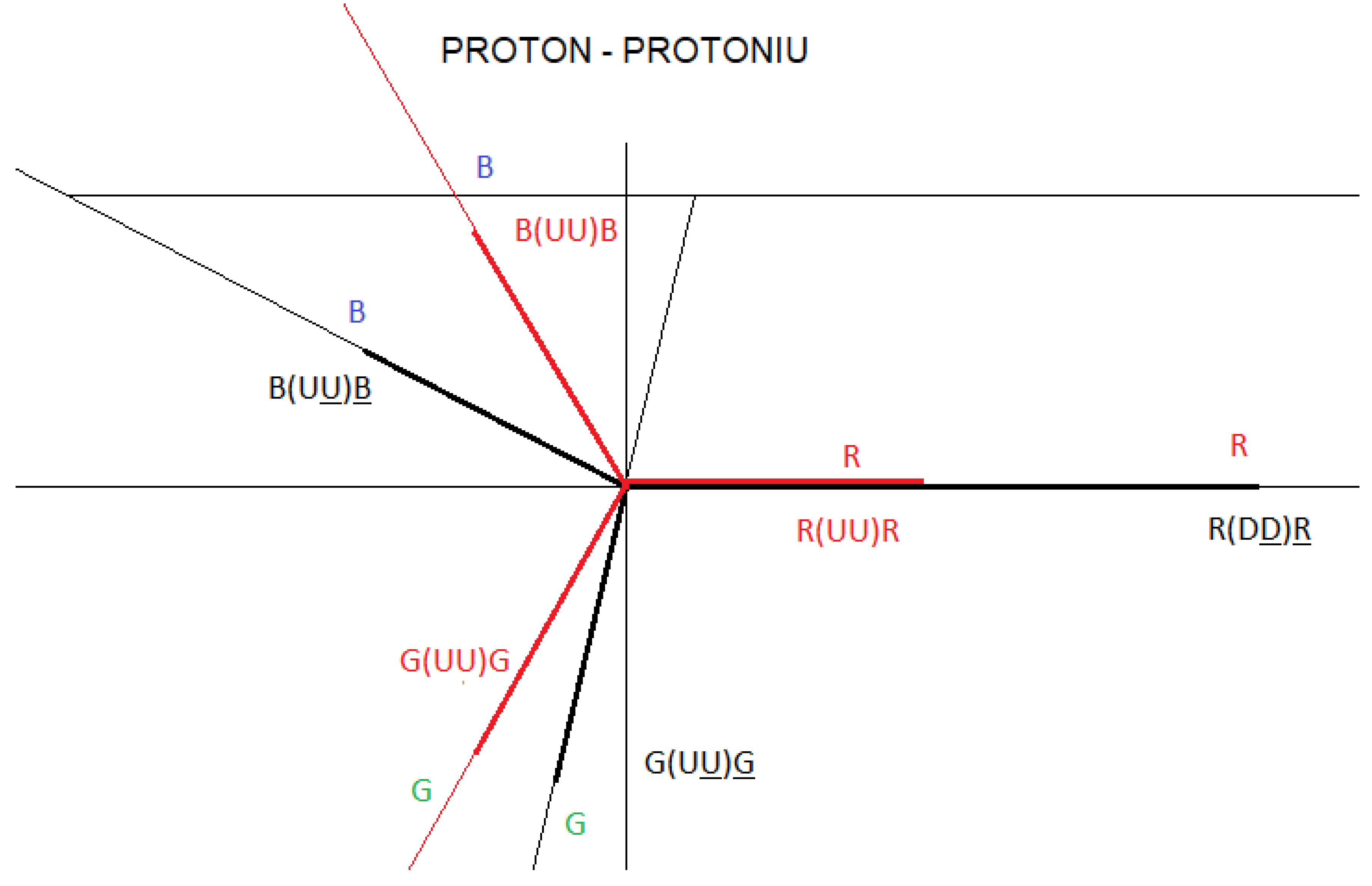
Figure 30.
The vector diagram of the proton is represented in black. The vector diagram of protonium - interaction 1 is represented in red. The vector diagram of protonium - interaction 2 is represented in blue.
Figure 30.
The vector diagram of the proton is represented in black. The vector diagram of protonium - interaction 1 is represented in red. The vector diagram of protonium - interaction 2 is represented in blue.
At first glance, if we add the three U quarks scalarly, we can affirm that the total charge is (2/3 + 2/3 + 2/3 = 2) 2, but we have to remember that we are adding scalarly and in this situation we must consider a vector sum, this gives us a net charge of zero. We can represent the U quarks as three vectors with the same module, 120 degrees out of phase, whose vector sum is zero, in analogy to electric generators.
The protoniu particle behaves analogously to a generator, whose current, voltage and charge are perfectly balanced, in equilibrium.
If we compare
figure 23 and
figure 30, the vector diagrams for interaction 1 and interaction 2 are the same, they differ in the magnitude of the vectors. In
figure 30, antimatter is not included. In
figure 23, it includes the antimatter.
The scale factor is the following:
SF = (X / 48.28) 4
SF⁻¹ = (48.28 / 4) X
This scaling factor is unique and applies to all vectors in the diagram representing the proton decay.
We are going to describe the mass distribution of the dipoles of interaction 1 and 2, which represent the Protoniu particle.
Figure 31.
Protoniu particle.
Figure 31.
Protoniu particle.
According to our vector calculation, the Protoniu particle has a mass of 253.44 MeV/c².
We are going to make the vector diagram of the Dproton decay in the Protoniu particle.
The dipoles of the interaction 1 of the proton, are represented in black.
The dipoles of the interaction 1 of the Dproton, are represented in red.
The dipoles of the interaction 2 of the Dproton, are represented in purple.
The dipoles of the interaction 1 of the protoniu correspond to the point of intersection of all the vectors.
The dipoles of the interaction 2 of the protoniu, are represented in orange.
Represented in blue are the 3 vectors of interaction 1 and the 6 vectors of interaction 2 that correspond to the decay of the Dproton in the protoniu particle.
R(UU)R = 0
B(UU)B = 0
G(UU)G = 0
This is telling us that there is no direct interaction between the quarks (U,U). In analogy with an electric generator, it is as if the pair of quarks (U,U) were at the same electric potential.
Now we are going to analyse the energy (mass) changes that occur when the Dproton decays in the Protoniu particle. These changes in energy (mass) are represented in blue in
figure 32.
Table 2.
- Calculation of the interactions in MeV/c², when the Dproton decay in the protoniu particle.
Table 2.
- Calculation of the interactions in MeV/c², when the Dproton decay in the protoniu particle.
| DPROTON DECAY |
| DPROTON |
PROTONIU |
INTERACTION |
INTERACTION (MeV/c²) |
| R(UU)R |
R(UU)R |
E1 = 4 |
E1 = 48.28 |
| B(UU)B |
B(UU)B |
E2 = 4 |
E2 = 48.28 |
| G(UU)G |
G(UU)G |
E3 = 4 |
E3 = 48.28 |
| R(UU)B
|
R(UU)B |
E4 = 3.5 |
E4 = 42.24 |
| R(UU)G |
R(UU)G |
E5 = 3.5 |
E5 = 42.24 |
| B(UU)R |
B(UU)R |
E6 = 3.5 |
E6 = 42.24 |
| B(UU)G
|
B(UU)G |
E7 = 3.5 |
E7 = 42.24 |
| G(UU)R
|
G(UU)R |
E8 = 3.5 |
E8 = 42.24 |
| G(UU)B
|
G(UU)B |
E9 = 3.5 |
E9 = 42.24 |
| TOTAL INTERACTION |
IEtI = 398.28 MeV/c² |
The vectors E1 to E9 are represented in blue in
figure 32.
It is important to highlight that the decay of the Dproton in the protoniu particle produces a total interaction of Et = 398.28 MeV/c².
In
figure 32, these vectors in blue, we will explain below:
E1 = R(UU)R → R(UU)R
E2 = B(UU)B → B(UU)B
E3 = G(UU)G → G(UU)G
E4 = R(UU)B → R(UU)B
E5 = R(UU)G → R(UU)G
E6 = B(UU)R → B(UU)R
E7 = B(UU)G → B(UU)G
E8 = G(UU)R → G(UU)R
E9 = G(UU)B → G(UU)B
When the Dproton particle decays into the protoniu particle, it is observed that matter separates from antimatter, producing energy in the form of radiation.
The particle that results from the decay of the Dproton particle, protoniu, is formed only by U quark and does not have antimatter.
The configuration of the quarks inside the protoniu particle is formed by vectors that represent the quarks, which are displaced by 120 degrees, whose vector sum makes the net charge zero.
We are going to use the following equation to represent the decay of the particle Dproton into the particle protoniu:
Dproton → protonium + ∆E
4.3. Conservation Laws:
It is important to mention the conservation laws, which indicate that there are properties that should never change.
There are three conservation laws that we have to mention when we analyse the decay of the proton and Dproton.
Electric Charge
Energy
Baryon and lepton number
Proton → Dproton + e⁻ + ṽ + ∆E
(+1) (+2) (-1)
We see that the proton has an electric charge (+1), the Dproton particle has an electric charge (+2) and the electron has an electric charge (-1); We see that the electric charge is balanced, it is conserved.
Proton → Dproton + e⁻ + ṽ + ∆E
(+1) (+1) (+1) (-1)
We see that the proton has a baryon number equal to 1 and the Dproton particle also has a baryon number equal to 1, the baryon number is conserved. We are going to analyze the lepton number, we see that the electron has a lepton number equal to (+1) and the antineutrino has a lepton number (-1), the lepton number is also conserved.
Proton → Dproton + e⁻ + ṽ + ∆E
938.27 MeV/c² 651.78 MeV/c² +…..
Considering the energy (mass), the proton has a mass of 938.27 MeV/c², the Dproton particle has a mass of 651.78 MeV/c², to this is added the mass of the electron, the neutrino and the energy of photons ∆E. Energy is also conserved.
In a simple analysis, we see that the electric charge, energy and baryon and lepton number are conserved for the decay of the proton in the Dproton particle.
Dproton → protoniu + ∆E
(+2) (+2)
We see that the Dproton has an electric charge (+2), the protonium particle has an electric charge (+2); we see that the electric charge is balanced, it is conserved.
Dproton → protoniu + ∆E
(+1) (+1)
We see that the Dproton has a baryon number equal to 1 and the protoniu particle also has a baryon number equal to 1, the baryon number is conserved.
Dproton → protoniu + ∆E
651.78 MeV/c² 253.44 MeV/c² + ……
Considering the energy (mass), the Dproton has a mass of 651.78 MeV/c², the protoniu particle has a mass of 253.44 MeV/c², to this is added the energy of photons ∆E. Energy is also conserved.
Finally, summarizing we have:
In the following graph we are going to represent some fundamental parameters that describe the following particles:
Figure 39.
Representation of characteristic parameters of the neutron, proton, Dproton and protoniu.
Figure 39.
Representation of characteristic parameters of the neutron, proton, Dproton and protoniu.
4.4. Inverse Neutron Decay
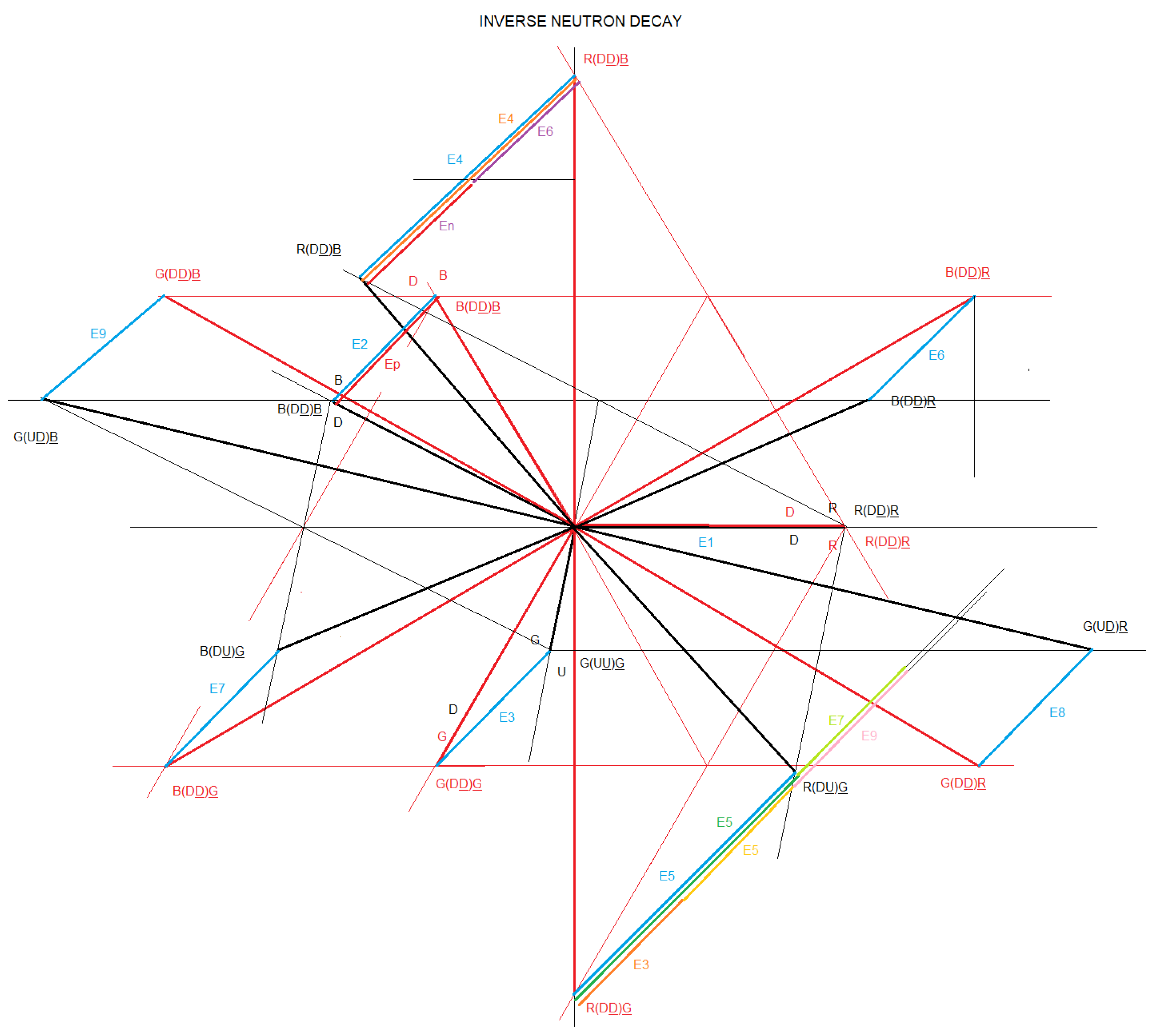
We are going to work with the following figure to represent the inverse neutron decay.
In
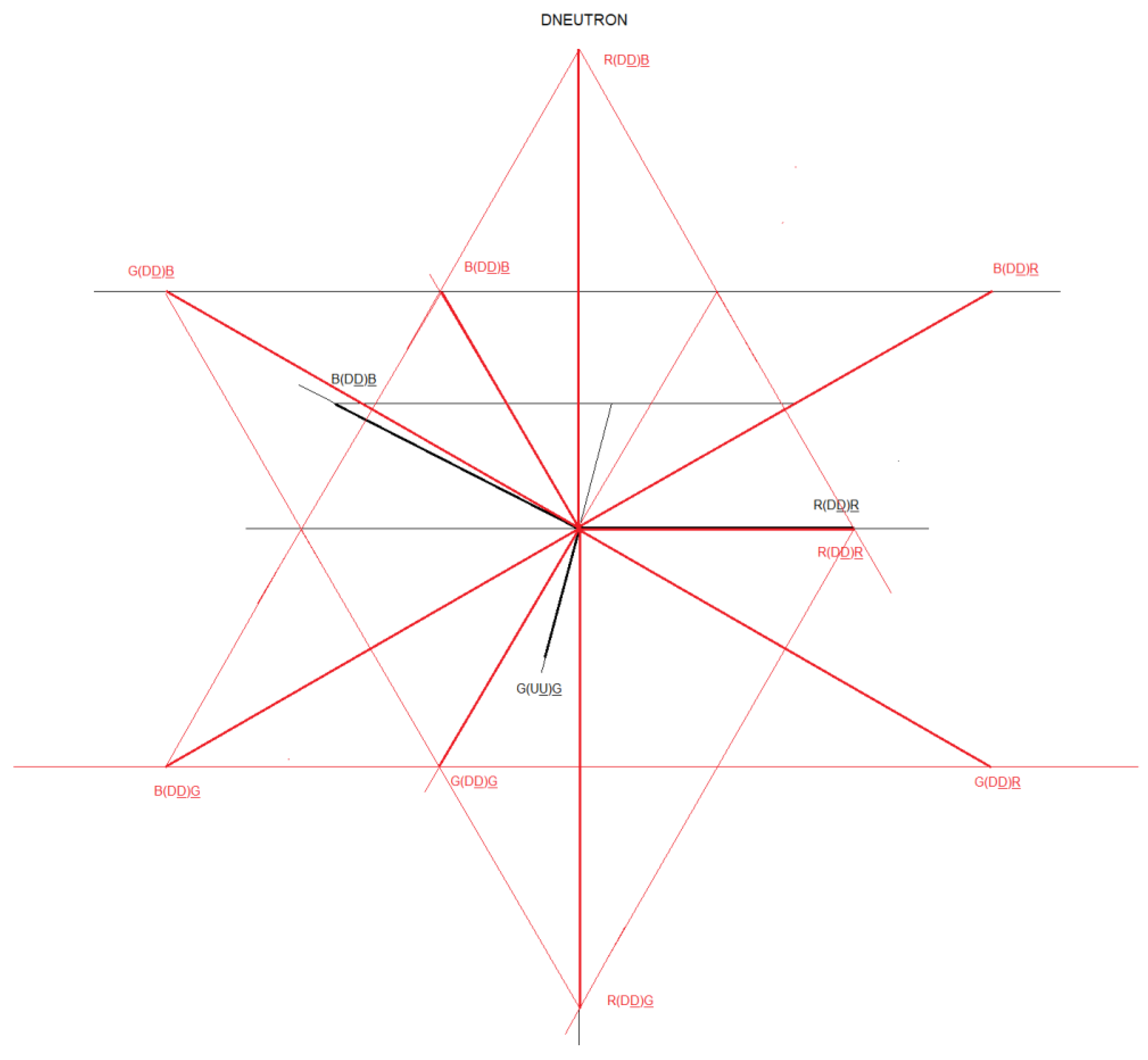
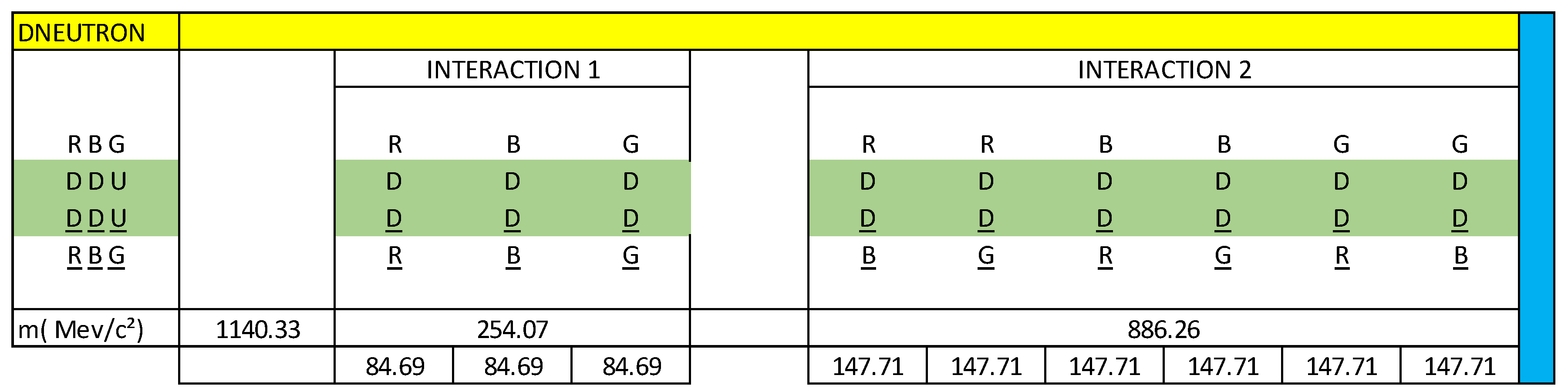
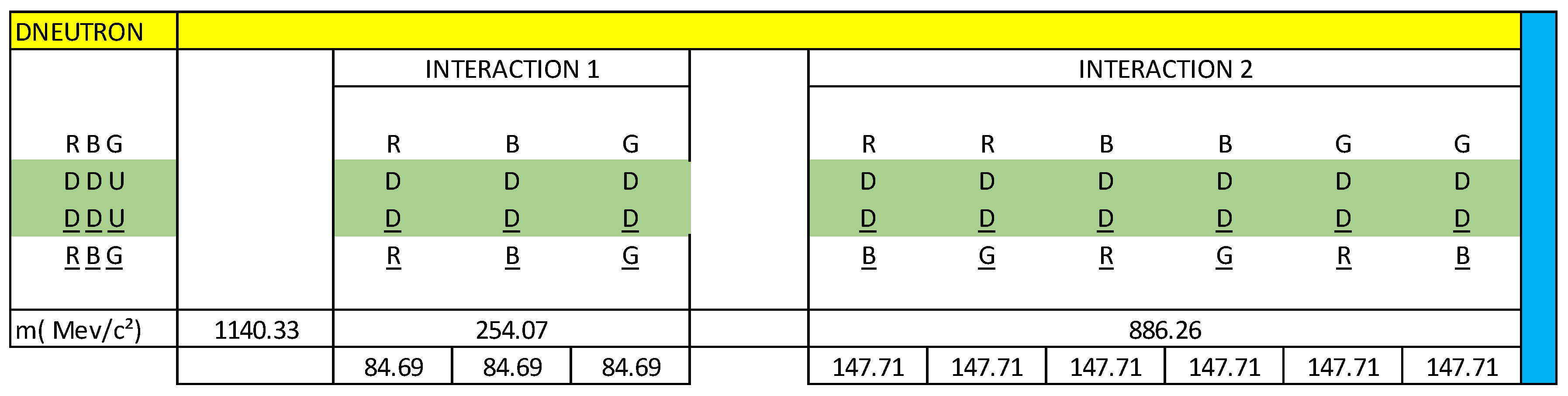
figure 41, we represent the inverse neutron decay through interaction 1 and interaction 2. We call this particle Dneutron. We observe that all the components are D quarks and we also observe that there are 9 D quark-antiquark dipoles, which are vector related. This inverse neutron decay configuration is represented by matter and antimatter.
We are going to make the vector diagram of the Dneutron particle, of the interaction 1 and 2:
Figure 42.
Vector diagram of the neutron and Dneutron particle.
Figure 42.
Vector diagram of the neutron and Dneutron particle.
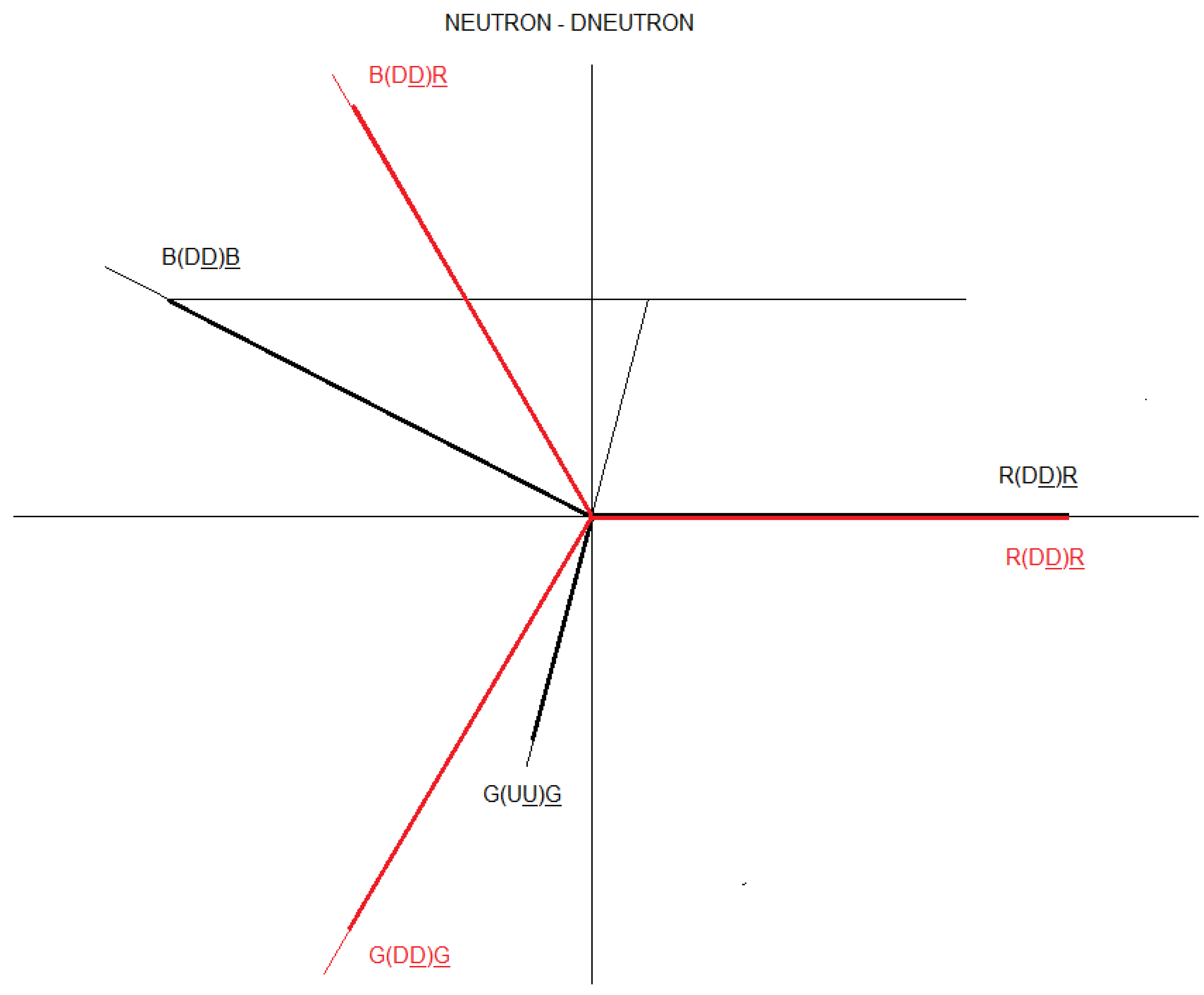
Figure 43.
The vector diagram of the neutron is represented in black. The vector diagram of Dneutron particle - interaction 1 is represented in red. The vector diagram of Dneutron - interaction 2 is represented in red.
Figure 43.
The vector diagram of the neutron is represented in black. The vector diagram of Dneutron particle - interaction 1 is represented in red. The vector diagram of Dneutron - interaction 2 is represented in red.
At first glance, if we add the three D quarks scalarly, we can affirm that the total charge is (-1/3 - 1/3 - 1/3 = -1) -1, but we have to remember that we are adding scalarly and in this situation we must consider a vector sum, and this gives us a net charge of zero. We can represent the D quarks as three vectors with the same module, 120 degrees out of phase, whose vector sum is zero, in analogy to electric generators.
The Dneutron particle behaves analogously to a generator, whose current, voltage and charge are perfectly balanced, in equilibrium.
The scale factor is the following:
SF = (X / 39.39) 4
SF⁻¹ = (39.39 / 4) X
This scaling factor is unique and applies to all vectors in the diagram representing the proton decay.
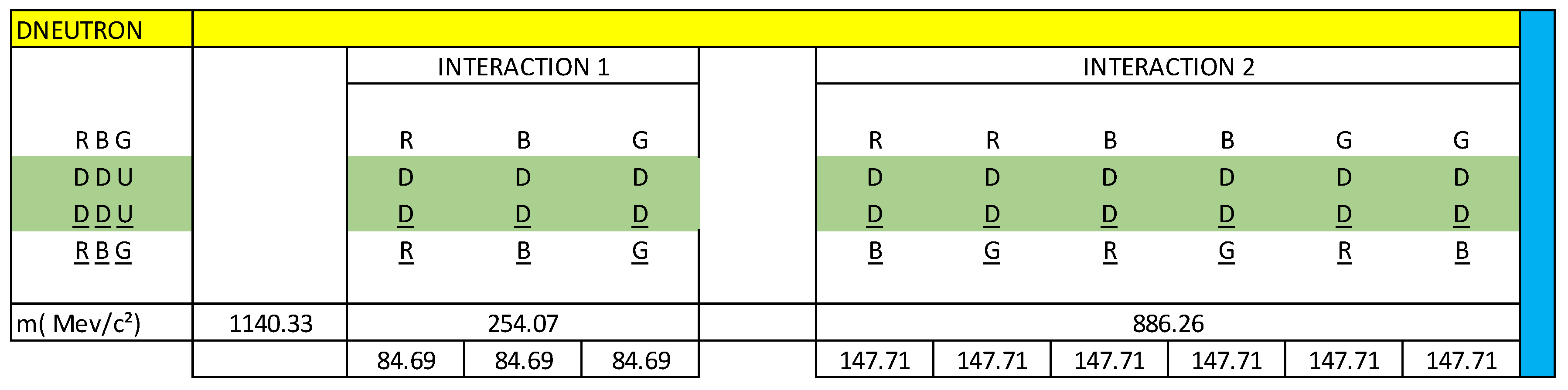
We are going to describe the mass distribution of the dipoles of interaction 1 and 2, which represent the Dneutron particle.
According to our vector calculation, the Dneutron particle has a mass of 1140.33 MeV/c².
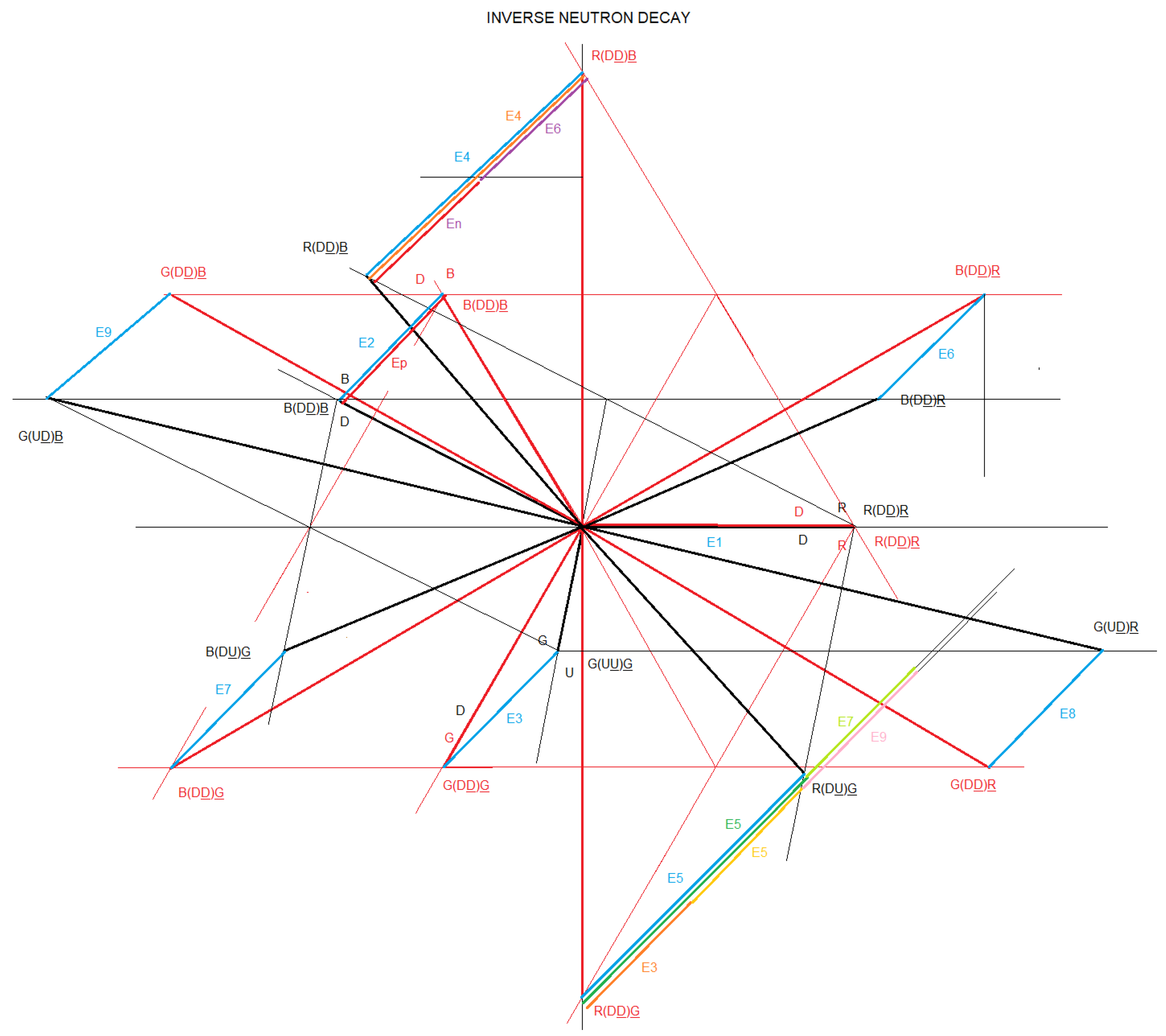
We are going to make the vector diagram of the neutron decay in the Dneutron particle.
The dipoles of the interaction 1 of the neutron, are represented in black.
The dipoles of the interaction 2 of the neutron, are represented in black.
The dipoles of the interaction 1 of the Dneutron, are represented in red.
The dipoles of the interaction 2 of the dneutron, are represented in red.
Represented in blue are the 3 vectors of interaction 1 and the 6 vectors of interaction 2 that correspond to the decay of the neutron in the Dneutron particle.
Now we are going to analyse the energy (mass) changes that occur when the inverse neutron decay in the Dneutron particle. These changes in energy (mass) are represented in blue in
figure 45.
Table 3.
Calculation of the interactions in MeV/c², when the neutron decay in the Dneutron particle.
Table 3.
Calculation of the interactions in MeV/c², when the neutron decay in the Dneutron particle.
| INVERSE NEUTRON DECAY |
| NEUTRON |
DNEUTRON |
INTERACTION |
INTERACTION (MeV/c²) |
| R(DD)R |
R(DD)R |
E1 = 0 |
E1 = 0 |
| B(DD)B |
B(DD)B |
E2 = 4.6 |
E2 = 45.29 |
| G(UU)G |
G(DD)G |
E3 = 4.6 |
E3 = 45.29 (-) |
| R(DD)B |
R(DD)B
|
E4 = 10 |
E4 = 98.47 |
| R(DU)G |
R(DD)G |
E5 = 10 |
E5 = 98.47 (+) |
| B(DD)R |
B(DD)R |
E6 = 4.7 |
E6 = 46.28 |
| B(DU)G |
B(DD)G
|
E7 = 4.7 |
E7 = 46.28 (+) |
| G(UD)R
|
G(DD)R
|
E8 = 5.0 |
E8 = 49.23 (-) |
| G(UD)B
|
G(DD)B
|
E9 = 5.0 |
E9 = 49.23 (-) |
| TOTAL INTERACTION |
IEtI = 478.54 MeV/c² |
| (W⁺)e⁺ INTERACTION |
IEeI = W⁺ = 1.00 MeV/c² |
| (Z⁰)n INTERACTION |
IEnI = 52.19 MeV/c² |
| (Z⁰)p INTERACTION |
IEpI = 45.29 MeV/c² |
| (Z⁰) INTERACTION |
IZ⁰I = 6.90 MeV/c² |
| Θ angle, Θ = arc cos W⁺/Z⁰ |
Θ = 82⁰ |
The vectors E1 to E9 are represented in blue in
figure 45.
It is important to highlight that the decay of the neutron in the Dneutron particle produces a total interaction of Et = 478.54 MeV/c².
In
figure 45, we divide these vectors into three parts, which we will explain below:
En = 98.47 – 46.28 = 52.19 MeV/c²
E4 = [R(DD)B]n → [R(DD)B]Dn
E6 = [B(DD)R]n → [B(DD)R]Dn
For E4, when the decay of [R(DD)B]n of the neutron, to [R(DD)B]Dn of the Dneutron occurs; a neutral current is produced.
For E6, when the decay of [B(DD)R]n of the neutron, to [B(DD)R]Dn of the Dneutron occurs; a neutral current is produced.
Here, we are going to hypothesize that the En energy is what gives origin to the antineutrinos. Let us note that the RB and BR gluons are of same frequencies; B and G are associated with the D quark.
When E4 + E6 interacts, it is like the RB and BR gluons cancel each other and the DD and DD quarks also cancel and, in this way, the resulting energy gives origin to the neutrinos, whose mass is neutral.
Ep = E2 = (4.6 x 39.39) / 4 = 45.29 MeV/c²
E1 = 0 MeV/c²
E1 = [R(DD)R]n → [R(DD)R]Dn
E2 = [B(DD)B]p → [B(DD)B]Dn
For E1, when the decay of [R(DD)R]n of the neutron, to [R(DD)R]Dn of the Dneutron occurs; no neutral current is produced.
For E2, when the decay of [B(DD)B]n of the neutron, to [B(DD)B]Dn of the Dneutron occurs; a neutral current is produced.
Here, we are going to hypothesize that the Ep energy is what gives origin to the photons. Here it is important to highlight that the RR and BB gluons have the same frequency; RR and BB gluons, have the frequency of the D quark.
Ee = 1 MeV/c²
E3 = [G(UU)G]n → [G(DD)G]Dn
E5 = [R(DU)G]n → [R(DD)G]Dn
E7 = [B(DU)G]n → [B(DD)G]Dn
E8 = [G(UD)R]n → [G(DD)R]Dn
E9 = [G(UD)B]n → [G(DD)B]Dn
E3 // E5 // E7 // E8 // E9
For the vectors E3, E5, E7, E8 and E9, when the decay of neutron to Dneutron occurs, it is observed that currents with positive and negative charges are generated.
The negative net energy of the vector Ee = 1 MeV/c²
Here, we are going to hypothesize that the Ee energy is what gives origin to the positron.
The emission of the energy vectors En, Ep and Ee are necessary in the β⁺ decay that occurs when the neutron decay into the Dneutron particle, so that the Dneutron stabilizes and reaches its corresponding energy.
In the following vector diagram, we are going to represent the vectors En, Ep and Ee.
It becomes difficult to graphically determine Ee, W⁺ and Θ angle.
calculation of W⁺, Z⁰ and Θ angle:
Theoretical calculations that we obtain from
figure 46, inverse neutron decay diagram:
theoretical W⁺ = Ee = E3 + E5 + E7 + E8 + E9
E3 // E5 // E7 // E8 // E9
W⁺ = Ee = (- 45.29 + 98.47 + 46.28 – 49.23 -49.23 – 49.23) MeV/c²
theoretical W⁺ = 1.00 MeV/c²
theoretical Z⁰ = En + Ep
theoretical IZ⁰I = 52.19 MeV/c² - 45.29 MeV/c²
IZ⁰I = 6.9 MeV/c²
W⁺/ Z⁰ = cos Θ
Θ = arc cos IW⁺I/IZ⁰I = arc cos (1 / 6.9) = arc cos (0.144)
Θ = 82⁰
As analysed so far, the decay of the neutron in the Dneutron particle also includes a β⁺ decay.
4.5. Dneutron Decay
We are going to work with the following figures to represent the disintegration of the Dneutron particle into the neutroniumd particle
Figure 47.
Dneutron particle.
Figure 47.
Dneutron particle.
In
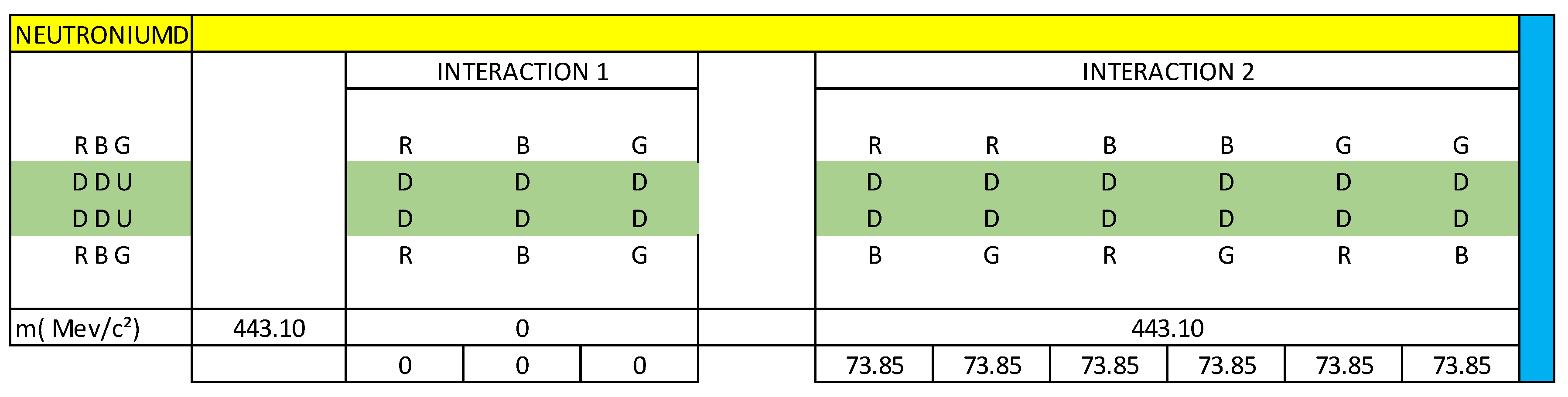
figure 48, we represent the neutroniumd particle, through interaction 1 and interaction 2. We observe that all the components are D quarks and we also observe that the 9 dipoles are quarks, which are related vectorially. This configuration is represented only by matter, there is no antimatter in this configuration.
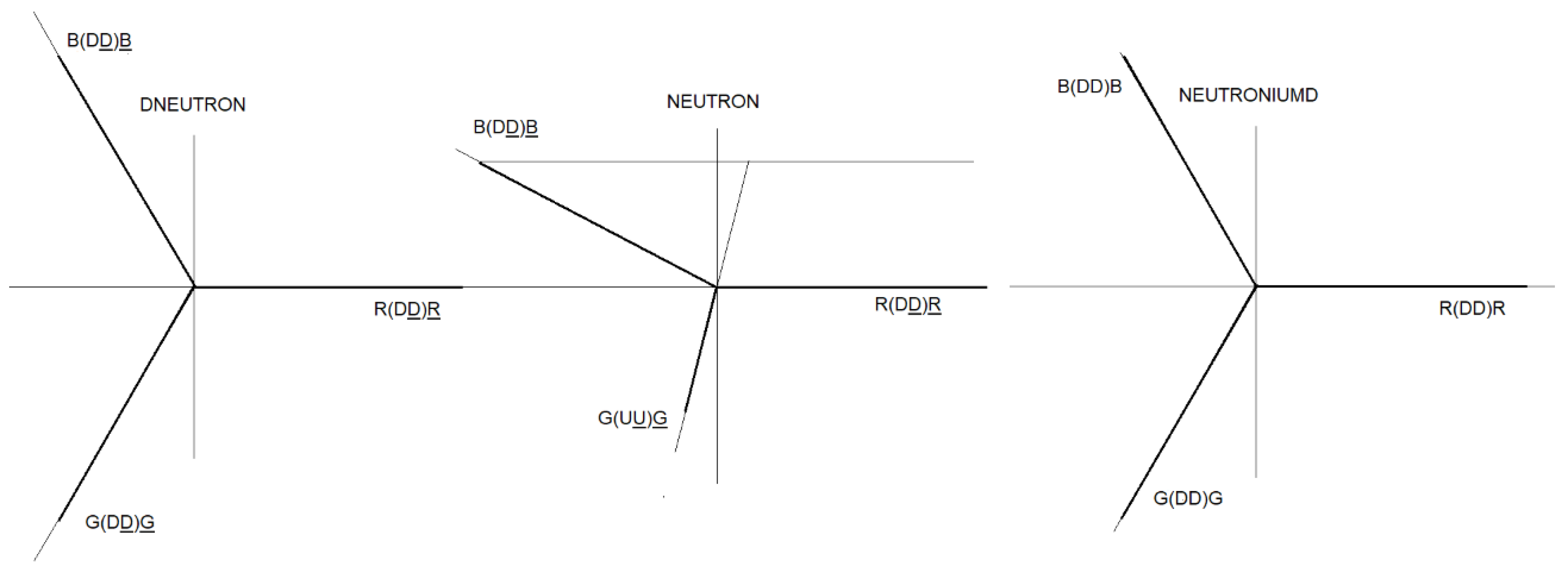
We are going to make the vector diagram of the neutroniumd particle, of the interaction 1 and 2:
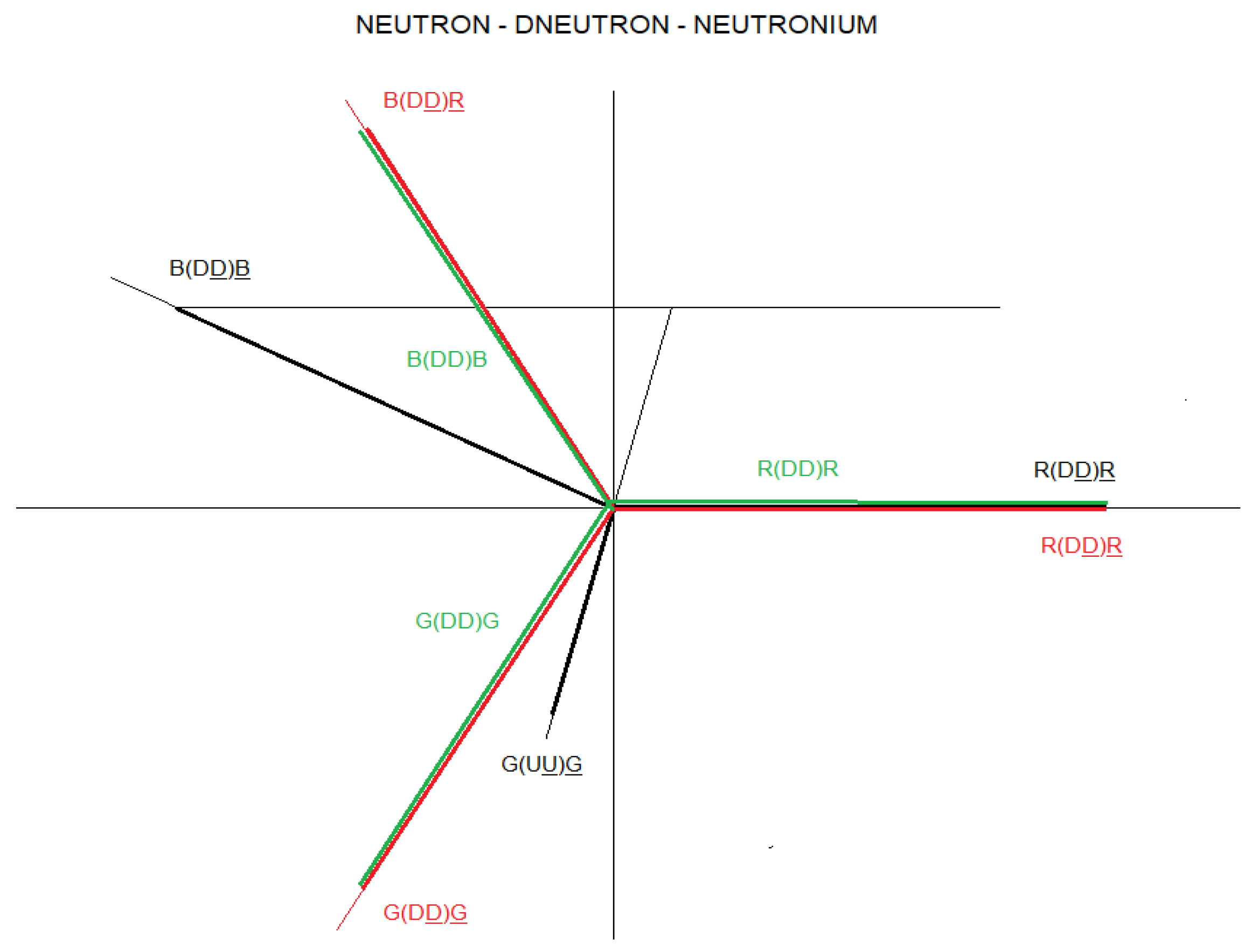
In
figure 49, the vector diagram of the neutron is represented in black.
In
figure 49, the vector diagram of the Dneutron is represented in red.
In
figure 49, the vector diagram of neutroniumd is represented in green.
The neutron and the Dneutron are particles made up of matter and antimatter.
Neutroniumd is a particle formed only by matter, it does not contain antimatter.
Figure 49.
- Diagram of neutron particles, Dneutron and Neutronium.
Figure 49.
- Diagram of neutron particles, Dneutron and Neutronium.
Figure 50.
Dneutron Decay.
Figure 50.
Dneutron Decay.
The vector diagram of the Dneutron particle, interaction 1, is represented in black.
The vector diagram of the Dneutron particle, interaction 2, is represented in black.
The vector diagram of Neutroniumd, interaction 2, is represented in red.
The vector diagram of Neutroniumd, interaction 1, is zero, there is no interaction between two D quarks of matter (DD).
Represented in blue are the 3 vectors of interaction 1 and the 6 vectors of interaction 2 that correspond to the decay of the Dneutron in the neutroniumd particle.
At first glance, if we add the three D quarks scalarly, we can affirm that the total charge is (-1/3 - 1/3 - 1/3 = -1) -1, but we have to remember that we are adding scalarly and in this situation we must consider a vector sum, this gives us a net charge of zero. We can represent the D quarks as three vectors with the same module, 120 degrees out of phase, whose vector sum is zero, in analogy to electric generators.
The neutronium particle behaves analogously to a generator, whose current, voltage and charge are perfectly balanced, in equilibrium.
The scale factor is the following:
SF = (X / 39.39) 4
SF⁻¹ = (39.39 / 4) X
This scaling factor is unique and applies to all vectors in the diagram representing the Dneutron decay.
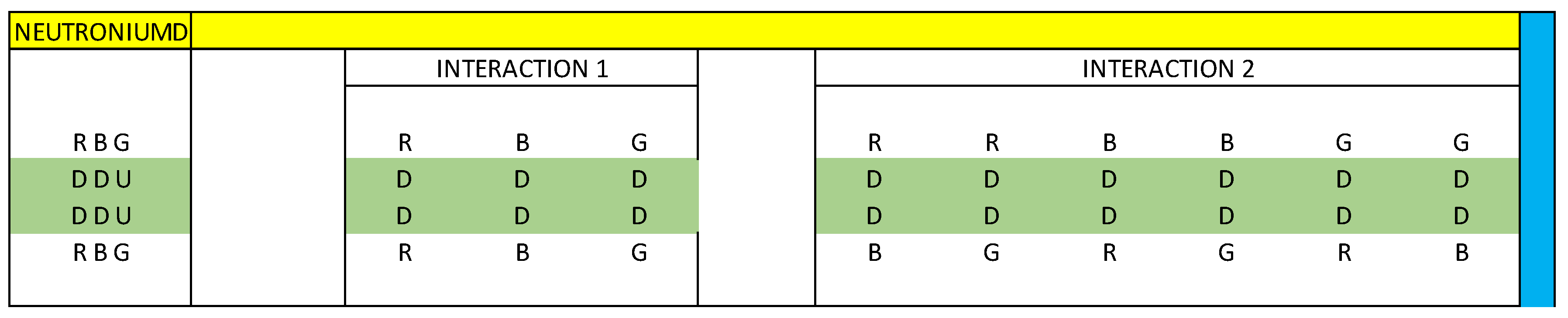
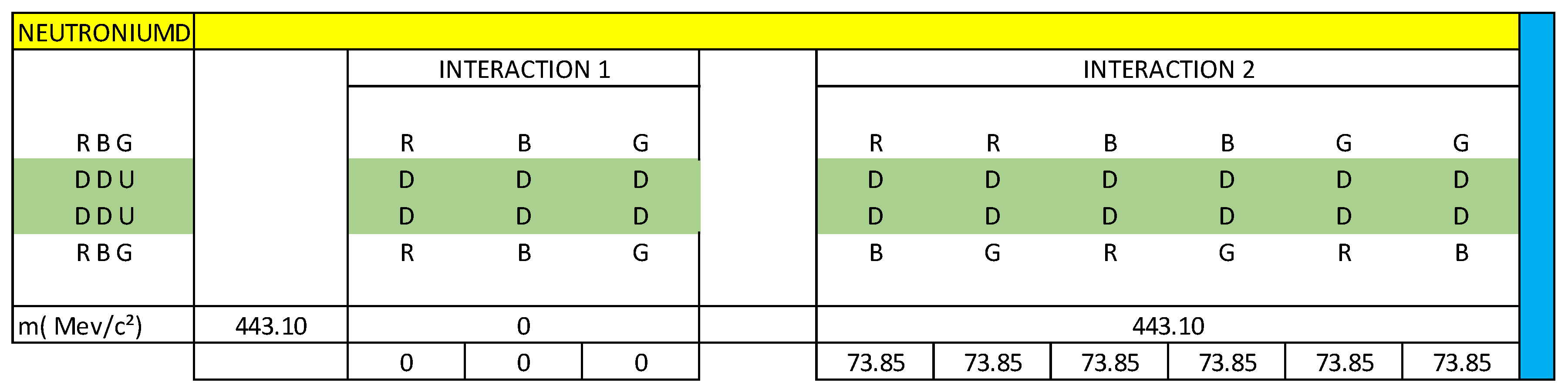
We are going to describe the mass distribution of the dipoles of interaction 1 and 2, which represent the neutroniumd particle.
According to our vector calculation, the neutroniumd particle has a mass of 443.10 MeV/c².
R(DD)R = 0
B(DD)B = 0
G(DD)G = 0
This is telling us that there is no direct interaction between the quarks (DD). In analogy with an electric generator, it is as if the pair of quarks (DD) were at the same electric potential.
Now we are going to analyse the energy (mass) changes that occur when the Dneutron decay in the neutroniumd particle. These changes in energy (mass) are represented in blue in
figure 50.
Table 4.
Calculation of the interactions in MeV/c², when the Dneutron decay in the neutroniumd particle.
Table 4.
Calculation of the interactions in MeV/c², when the Dneutron decay in the neutroniumd particle.
| DNEUTRON DECAY |
| DNEUTRON |
NEUTRONIUMD |
INTERACTION |
INTERACTION (MeV/c²) |
| R(DD)R |
R(DD)R |
E1 = 8.5 |
E1 = 84.69 |
| B(DD)B |
B(DD)B |
E2 = 8.5 |
E2 = 84.69 |
| G(DD)G |
G(DD)G |
E3 = 8.5 |
E3 = 84.69 |
| R(DD)B
|
R(DD)B |
E4 = 7.5 |
E4 = 73.85 |
| R(DD)G |
R(DD)G |
E5 = 7.5 |
E5 = 73.85 |
| B(DD)R |
B(DD)R |
E6 = 7.5 |
E6 = 73.85 |
| B(DD)G
|
B(DD)G |
E7 = 7.5 |
E7 = 73.85 |
| G(DD)R
|
G(DD)R |
E8 = 7.5 |
E8 = 73.85 |
| G(DD)B
|
G(DD)B |
E9 = 7.5 |
E9 = 73.85 |
| TOTAL INTERACTION |
IEtI = 697.17 MeV/c² |
The vectors E1 to E9 are represented in blue in
figure 50.
It is important to highlight that the decay of the Dneutron in the neutroniumd particle produces a total interaction of Et = 697.17 MeV/c².
In
figure 50, these vectors in blue, we will explain below:
E1 = R(DD)R → R(DD)R
E2 = B(DD)B → B(DD)B
E3 = G(DD)G → G(DD)G
E4 = R(DD)B → R(DD)B
E5 = R(DD)G → R(DD)G
E6 = B(DD)R → B(DD)R
E7 = B(DD)G → B(DD)G
E8 = G(DD)R → G(DD)R
E9 = G(DD)B → G(DD)B
When the Dneutron particle decay into the neutroniumd particle, it is observed that matter separates from antimatter, producing energy in the form of radiation.
The particle that results from the decay of the Dneutrom particle, neutroniumd, is formed only by D quark and does not have antimatter.
The configuration of the quarks inside the neutroniumd particle is formed by vectors that represent the quarks, which are displaced by 120 degrees, whose vector sum makes the net charge zero.
We are going to represent the decay of the Dneutron particle into neutroniumd with the following equation:
Dneutron → neutronium + ∆E
4.6. Conservation laws
It is important to mention the conservation laws, which indicate that there are properties that should never change.
There are three conservation laws that we have to mention when we analyse the decay of the neutron and Dneutron.
Electric Charge
Energy
Baryon number
We will analyse the decay of the neutron in the Dneutron particle, we will use
figure 52 and
figure 53, for our analysis:
Dneutron → neutron + e⁻ + ṽ + ∆E
(-1) (0) (-1)
We see that the neutron has an electric charge (0), the Dneutron particle has an electric charge (-1) and the electron has an electric charge (-1); We see that the electric charge is balanced, it is conserved.
Dneutron → neutron + e⁻ + ṽ + ∆E
(+1) (+1) (+1)(-1)
We see that the neutron has a baryon number equal to 1 and the Dneutron particle also has a baryon number equal to (+1), the baryon number is conserved. We are going to analyse the lepton number, we see that the electron has a lepton number equal to (+1) and the antineutrino has a lepton number (-1), the lepton number is also conserved.
Dneutron → neutron + e⁻ + ṽ + ∆E
1140.33 MeV/c² → 939.51 MeV/c² +…..
Considering the energy (mass), the Dneutron has a mass of 1140.33 MeV/c², the neutron particle has a mass of 939.51 MeV/c², to this is added the mass of the electron, the antineutrino and the energy of photons ∆E. Energy is also conserved.
In a simple analysis, we see that the electric charge, energy and baryon and lepton number are conserved for the decay of the neutron in the Dneutron particle.
We will analyse the decay of the Dneutron in the neutroniumd particle, we will use
figure 54 and
figure 55, for our analysis:
Dneutron → neutroniumd + ∆E
(-1) (-1)
We see that the Dneutron has an electric charge (-1), the neutroniumd particle has an electric charge (-1); We see that the electric charge is balanced, it is conserved.
Dneutron → neutroniumd + ∆E
(+1) (+1)
We see that the Dneutron has a baryon number equal to (+1) and the neutroniumd particle also has a baryon number equal to (+1), the baryon number is conserved.
Dneutron → neutroniumd + ∆E
1140.33 MeV/c² 443.10 MeV/c² + ……
Considering the energy (mass), the Dneutron has a mass of 1140.33 MeV/c², the neutronium particle has a mass of 443.10MeV/c², to this is added the energy of photons ∆E. Energy is also conserved.
Finally, summarizing we have:
In the following graph we are going to represent some fundamental parameters that describe the following particles:
Figure 56.
Fundamental characteristics of particles.
Figure 56.
Fundamental characteristics of particles.
Figure 57.
Proton, Dproton and Protoniu.
Figure 57.
Proton, Dproton and Protoniu.
Figure 58.
Dneutron, Neutron and Neutroniumd.
Figure 58.
Dneutron, Neutron and Neutroniumd.
5. Conclusions:
Using the theory of three-phase alternating current electric generators, analyzing vectorly the decay of the proton and the inverse decay of the neutron, we have determined the following subatomic particles:
Dproton
Protoniu
Dneutron
Neutroniumd
In the following figure we will describe some fundamental parameters that characterize these particles:
Figure 59.
Characteristic parameters of the following particles: Neutron, Proton, Dproton, Protoniu, Dneutron and Neutroniumd.
Figure 59.
Characteristic parameters of the following particles: Neutron, Proton, Dproton, Protoniu, Dneutron and Neutroniumd.
About the authors
HECTOR GERARDO FLORES (ARGENTINA, 1971). I studied Electrical Engineering with an electronic orientation at UNT (Argentina); I worked and continue to work in oil companies looking for gas and oil for more than 25 years, as a maintenance engineer for seismic equipment in companies such as Western Atlas, Baker Hughes, Schlumberger, Geokinetics, etc.
Since 2010, I study theoretical physics in a self-taught way.
In the years 2020 and 2021, during the pandemic, I participated in the course and watched all the online videos of Cosmology I and Cosmology II taught by the Federal University of Santa Catarina UFSC (graduate level).
MARIA ISABEL GONÇALVEZ DE SOUZA (Brazil, 1983). I studied professor of Portuguese language at the Federal University of Campina Grande and professor of pedagogy at UNOPAR University, later I did postgraduate, specialization. I am currently a qualified teacher and I work for the São Joao do Rio do Peixe Prefecture, Paraiba. I am Hector's wife and my studies served to collaborate in the formatting of his articles, corrections, etc; basically, help in the administrative part with a small emphasis in the technical part analyzing and sharing ideas.
HARSHIT JAIN (India ,2008) I was born on July 14, 2008, into a loving family. My father, Ajitendra Kumar Jain, and my mother, Preeti Jain, have been incredibly supportive throughout my life and education. I grew up in Lalitpur, where I attended Jawahar Navodaya Vidyalaya (JNV) for my high school education.
My passion for learning has always driven me toward subjects that explore the mysteries of the universe. I have a particular interest in physics, biology, cosmology, and mathematics. This interest led me to the Pacific Institute of Cosmology, where I am currently pursuing advanced studies in these fields.
One of the most significant influences on my academic journey has been Professor Padhi, a renowned scholar who works with several professors who hold the prestigious title of Fellow of the Royal Society (FRS). His mentorship has been invaluable, guiding me through complex concepts and encouraging me to delve deeper into research.
Throughout my studies, I've engaged in various research projects, some of which have challenged conventional thinking and opened new avenues for exploration. These experiences have not only honed my analytical skills but also strengthened my resolve to contribute meaningfully to the scientific community.
In summary, I am Harshit Jain, a young scientist with a passion for discovery. My journey is just beginning, but I'm excited about the endless possibilities that lie ahead. I owe much of my success to my supportive family, dedicated mentors, and the enriching educational environments I've been fortunate to be a part of. I look forward to continuing my research and making meaningful contributions to the fields I hold dear.