Pump System Model Parameter Identification Based on Experimental and Simulation Data

1. Theory and Modeling

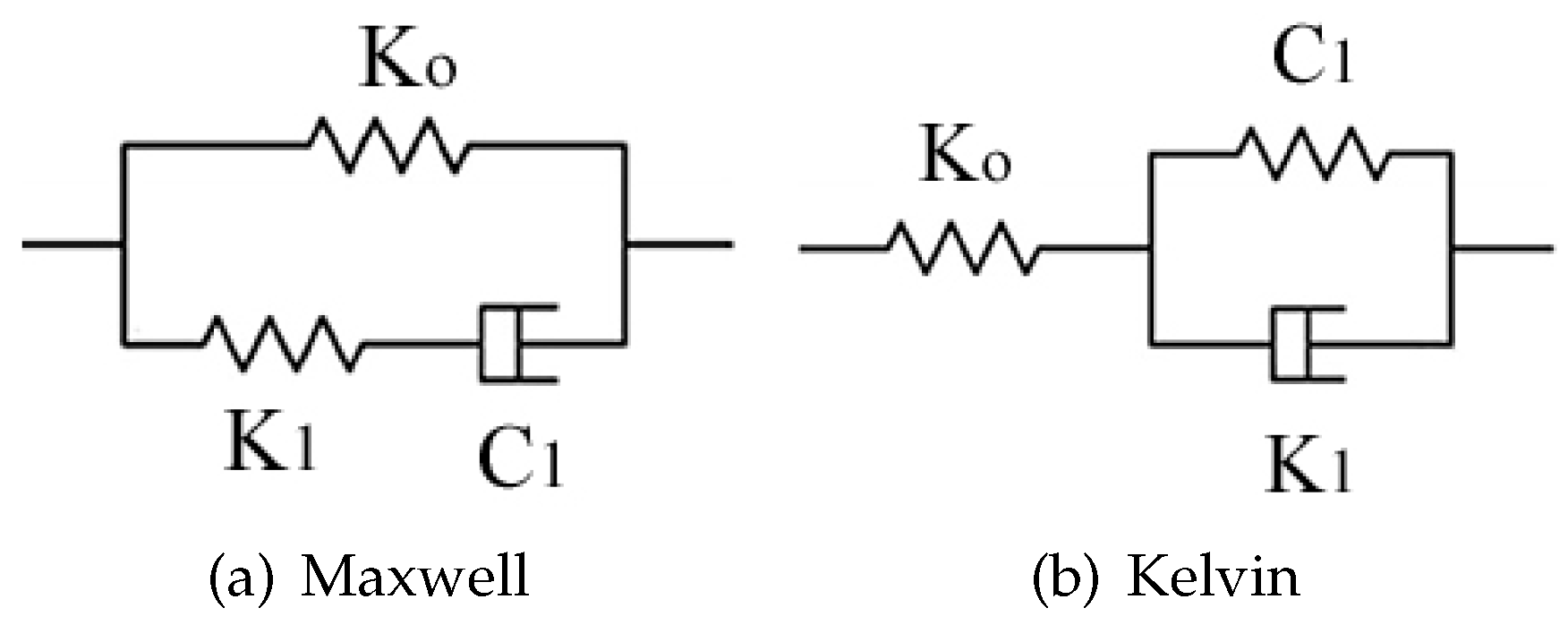
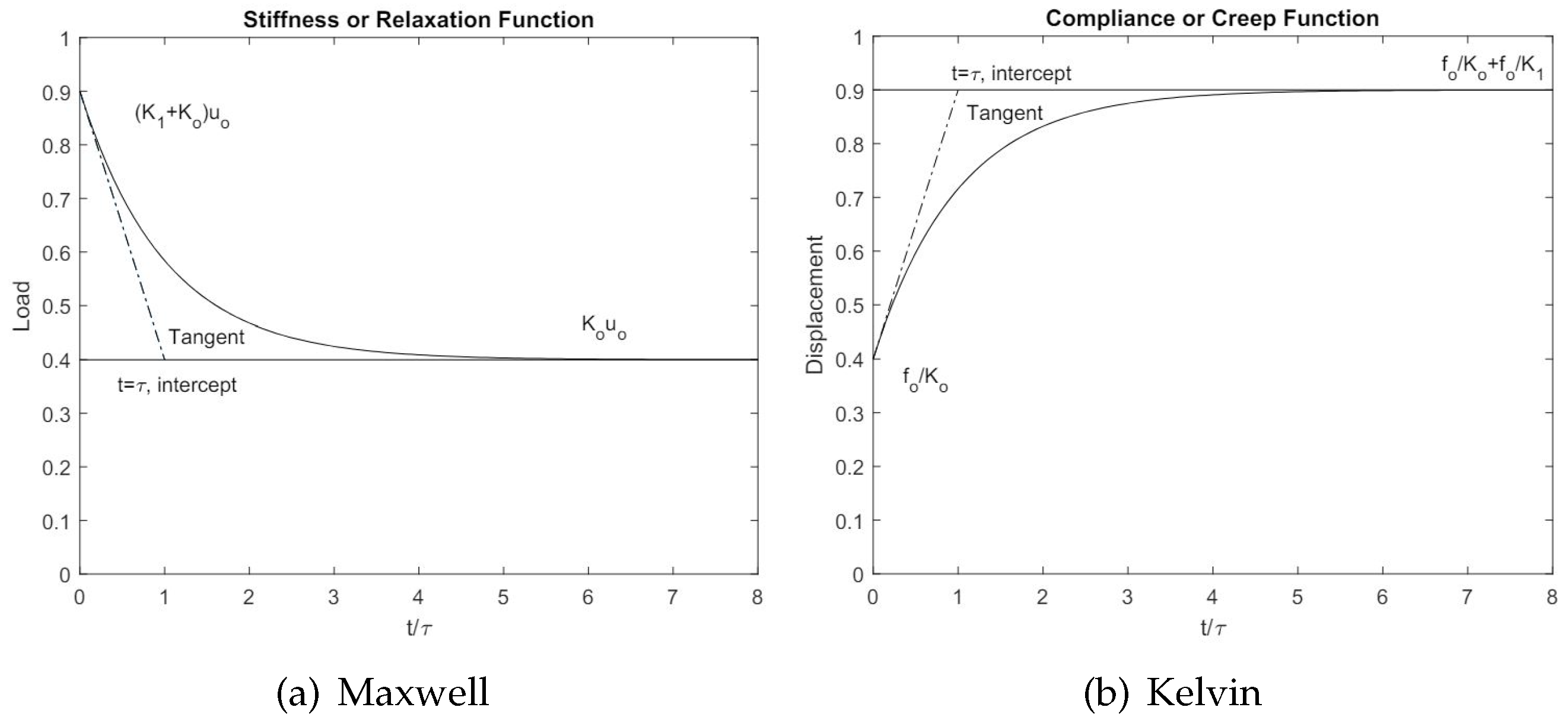
Let’s consider a lumped mass linked with either Maxwell or Kelvin models as illustrated in Figure 1. A sudden displacement is applied to the Maxwell model whereas a sudden load is introduced to the Kelvin model [28]. Consequently, the Maxwell model will yield a stiffness function or relaxation function to relate the responding force with the sudden imposed displacement $u_o$ as shown in Figure 2. Likewise, the Kelvin model will produce a compliance function or creep function to relate the resulting displacement with the suddenly imposed force $f_o$ also shown in Figure 2. For the Maxwell model, we also introduce the displacement $u\left(t\right)=u_{o}H\left(t\right)$ where $H\left(t\right)$ is the Heaviside function. The total force function $f\left(t\right)$ can be expressed as the combination of the location force $f_o\left(t\right)=K_{o}u\left(t\right)$ and $f_1\left(t\right)$ for the stiffness and dashpot couple $(K_1,C_1)$ with the relaxation time ${\tau }_1=C_1/K_1$. Furthermore, using the same force or stress for the series component and the same displacement or strain for the parallel component, we obtain the following governing equations for the Maxwell model:

$$\begin{array}{ccc}\hfill f_o& =& K_{o}u\left(t\right),\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill \dot{u}\left(t\right)& =& \frac{f_1}{C_1}+\frac{{\dot{f}}_1}{K_1}.\hfill \end{array}$$

(2)

Hence, using the concepts we have been discussing for the first-order ODE, we obtain:

$$e^{t/{\tau }_1}{f}_1\left(t\right)-0={\int }_{-\infty }^t{K}_1{e}^{t/{\tau }_1}\dot{u}\left(t\right)dt,$$

(3)

namely, by using integration by parts,

$$e^{t/{\tau }_1}{f}_1\left(t\right)=K_1{e}^{t/{\tau }_1}u\left(t\right)-{\int }_{-\infty }^t{K}_1/{\tau }_{1}u\left(t\right)e^{t/{\tau }_1}dt=K_1{e}^{t/{\tau }_1}{u}_o-{\int }_0^t{K}_1/{\tau }_1{u}_o{e}^{t/{\tau }_1}dt.$$

(4)

Finally, we have $f_1\left(t\right)=K_1{u}_o{e}^{-t/{\tau }_1}$ and the total force $f\left(t\right)=f_1\left(t\right)+f_o\left(t\right)=(K_o+K_1{e}^{-t/{\tau }_1})u_o$ for the Maxwell model. Likewise, denote the sudden load as $f\left(t\right)=f_{o}H\left(t\right)$ where $H\left(t\right)$ is a Heaviside function, the total displacement function $u\left(t\right)$ can be expressed as the combination of the location displacement $u_o\left(t\right)=f\left(t\right)/K_o$ and $u_1\left(t\right)$ for the stiffness and dashpot couple $(K_1,C_1)$ with the relaxation time ${\tau }_1=C_1/K_1$. Using the same force or stress for the series component and the same displacement or strain for the parallel component, we obtain the following governing equations for the Kelvin model:

$$\begin{array}{ccc}\hfill f\left(t\right)& =& K_o{u}_o\left(t\right),\hfill \end{array}$$

(5)

$$\begin{array}{ccc}\hfill f\left(t\right)& =& C_1{\dot{u}}_1+K_1{u}_1,1\le i\le n.\hfill \end{array}$$

(6)

Thus, using the concepts we have been discussing for the first-order ODE, we obtain:

$$e^{t/{\tau }_1}{u}_1\left(t\right)-0={\int }_{-\infty }^t{e}^{t/{\tau }_1}f/C_{1}dt={\int }_0^t{e}^{t/{\tau }_1}{f}_o/C_{1}dt.$$

(7)

Finally we have the local displacement $u_1\left(t\right)=f_o/K_1(1-e^{-t/{\tau }_1})$ and the total displacement function can be expressed as $u\left(t\right)=u_o+u_1=f_o/K_o+f_o/K_1(1-e^{-t/{\tau }_1})$ for the Kelvin model. To further the discussion with relaxation and creep functions, we can also introduce a general Kelvin viscoelastic model as elaborated in Ref. [35]. Similar approaches are also implemented for the viscoelastic vibration model with a mass m and a concentrated load $F\left(t\right)$. We introduce first the Kelvin viscoelastic model in a dynamic case as shown in Figure 9, essentially a typical Kelvin viscoelastic setup for creep test combined in series with a spring with a stiffness k and a mass m. The displacement of the parallel section of the stiffness $k_o$ and the dashpot $c_o$ share the same displacement $u_2\left(t\right)$, whereas the displacement of the stiffness k is denoted as $u_1\left(t\right)$. Since the mass m is connected with the stiffness k in series, the total displacement of the mass $u\left(t\right)$ is a combination of the two displacements $u_1\left(t\right)$ and $u_2\left(t\right)$. In general, the external load $F\left(t\right)$ is applied to the mass m. We can imagine that in the creep test, we can simply add a dead weight $W_o$ in addition to the weight of the mass $mg$.

Use the same procedure, consider each section in series and the consequent continuity of axial forces, we have

$$\begin{array}{ccc}\hfill k{u}_1\left(t\right)& =& k_o{u}_2+c_o{\dot{u}}_2,\hfill \\ \hfill k{u}_1\left(t\right)& =& F\left(t\right)-m\ddot{u}.\hfill \end{array}$$

(8)

Using the kinematic relationship $u\left(t\right)=u_1\left(t\right)+u_2\left(t\right)$, we obtain the following third-order governing equation for $u_2\left(t\right)$,

$$\frac{m{c}_o}{k}{u}_2^{\prime \prime \prime }+\frac{m}{k}(k+k_o){\ddot{u}}_2+c_o{\dot{u}}_2+k_o{u}_2=F\left(t\right).$$

(9)

In this paper, for simplicity, in the implementation of the inverse optimization approaches, Eq. (9) is directly applied with adjusted parameters k, m, $c_o$, and $k_o$. The measured force $F\left(t\right)$ is introduced to derive the closest $u_2\left(t\right)$ which matches with the measured displacement. As validated in Ref. [28], with no dashpot, namely, $c_o=0$, Eq. (8) yields

$$k_o{u}_2=k{u}_1,$$

hence

$$u=u_1+u_2=\frac{k+k_o}{k}{u}_2.$$

Finally, the governing equation (9) yields the familiar spring-mass vibration system

$$m\ddot{u}+\frac{k{k}_o}{k+k_o}u=F\left(t\right).$$

Notice the effective stiffness of two springs in series. Moreover, the infinitely stiff spring k, namely, $k\to +\infty$, consequently, $u_2\to 0$ and $u\left(t\right)=u_2\left(t\right)$. Finally, we recover the familiar spring-mass-dashpot vibration system

$$m\ddot{u}+c_o\dot{u}+k_{o}u=F\left(t\right).$$

Finally, in order to facilitate the solution, introduce the state variable $\mathbf{y}=<u_2,{\dot{u}}_2,{\ddot{u}}_2>$, we can rewrite the third-order viscoelastic vibration system with a dynamical system format,

$$\mathbf{A}=\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ -\frac{k{k}_o}{m{c}_o}& -\frac{k}{m}& -\frac{k+k_o}{c_o}\end{array}\right]\mathrm{and}\mathbf{f}=\left(\begin{array}{c}0\\ 0\\ \frac{kF}{m{c}_o}\end{array}\right).$$

Let’s consider the Maxwell viscoelastic model in a dynamic case as shown in Figure 9, essentially a typical Maxwell viscoelastic setup for relaxation test combined a mass m connecting in series with two parallel branches, one with a stiffness k and another one with a stiffness $k_o$ and a dashpot $c_o$ in series. The displacement of the parallel section shares the same displacement $u\left(t\right)$, whereas the displacement of the stiffness $k_o$ is denoted as $u_2\left(t\right)$ and the dashpot $c_o$ as $u_1\left(t\right)$. Since the displacement of the stiffness k is $u\left(t\right)$, naturally, the total displacement of the mass $u\left(t\right)$ is a combination of the two displacements $u_1\left(t\right)$ and $u_2\left(t\right)$ within one of the parallel branches. In general, the external load $F\left(t\right)$ is applied to the mass m. We can imagine that in a relaxation test, we can simply add a dead weight $W_o$ in addition to the weight of the mass $mg$. Using the same procedure, assuming the force in the dashpot and stiffness series as $F_o$, consider each section in series and the consequent continuity of axial forces, we have

$$\begin{array}{ccc}\hfill F-m\ddot{u}& =& ku+F_o,\hfill \\ \hfill \dot{u}& =& \frac{{\dot{F}}_o}{k_o}+\frac{F_o}{c_o}.\hfill \end{array}$$

(10)

Using the kinematic relationship $u\left(t\right)=u_1\left(t\right)+u_2\left(t\right)$ as well as $\dot{u}\left(t\right)={\dot{u}}_1\left(t\right)+{\dot{u}}_2\left(t\right)$, we obtain the following third-order governing equation for $u\left(t\right)$,

$$\frac{m}{k_o}{u}_2^{\prime \prime \prime }+\frac{m}{c_o}{\ddot{u}}_2+\frac{k+k_o}{k_o}{\dot{u}}_2+\frac{k}{c_o}u=\frac{\dot{F}}{k_o}+\frac{F}{c_o}.$$

(11)

Again, with no dashpot, namely, $c_o=0$. Equation (8) yields $F_o=0$, hence the governing equation (11) yields the familiar spring-mass vibration system

$$m\ddot{u}+ku=F\left(t\right).$$

Likewise, as the infinitely stiff spring $k_o$, namely, $k_o\to +\infty$, consequently, $u_2\to 0$ and $u\left(t\right)=u_1\left(t\right),$ we recover the familiar spring-mass-dashpot vibration system

$$m\ddot{u}+c_o\dot{u}+ku=F\left(t\right).$$

As presented in Ref. [28], in numerical solutions, we rewrite the third-order viscoelastic vibration system with a dynamical system format,

$$\dot{\mathbf{y}}=\mathbf{A}\mathbf{y}+\mathbf{f},$$

(12)

with the state variable $\mathbf{y}=<u_2,{\dot{u}}_2,{\ddot{u}}_2>$, and

$$\mathbf{A}=\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ -\frac{k{k}_o}{m{c}_o}& -\frac{k+k_o}{m}& -\frac{k_o}{c_o}\end{array}\right]\mathrm{and}\mathbf{f}=\left(\begin{array}{c}0\\ 0\\ \frac{\dot{F}}{m}+\frac{k_{o}F}{m{c}_o}\end{array}\right).$$

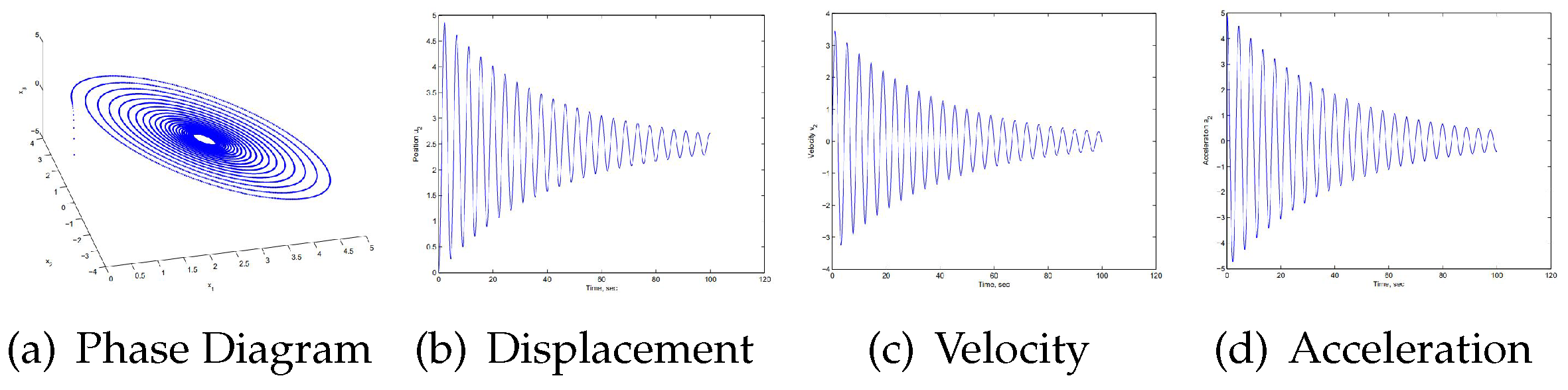
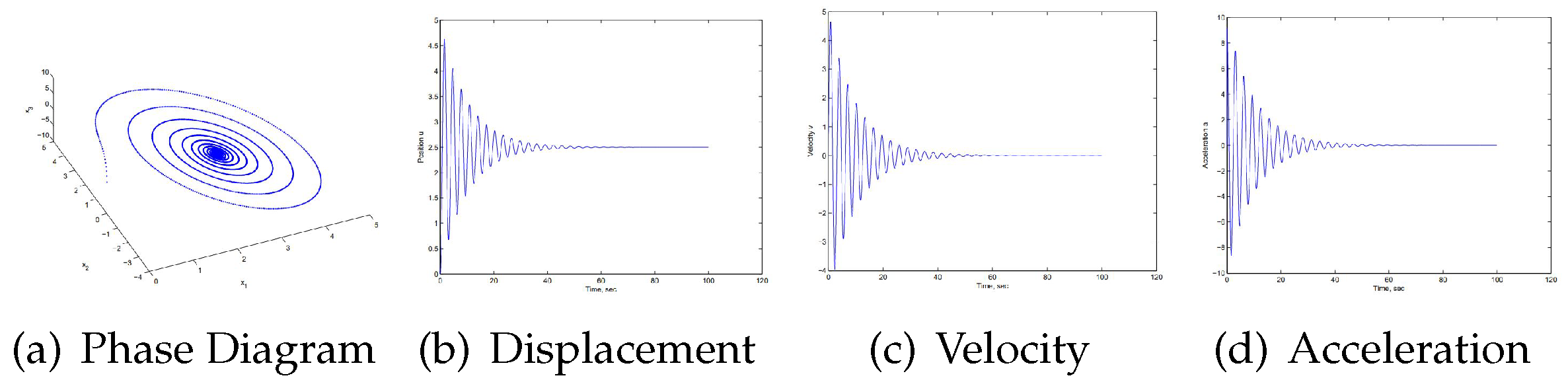
As shown in Figure 3 and Figure 4, for such a viscoelastic model representing the down-hole sucker rod system and starting from the zero position with zero velocity and zero acceleration, we employ $k=4\mathrm{N}/\mathrm{m}$, $m=1\mathrm{k}\mathrm{g}$, $c_o=0.2\mathrm{N}\mathrm{s}/\mathrm{m}$, $k_o=4\mathrm{N}/\mathrm{m}$, and $W_o=10\mathrm{N}$. The external force $F\left(t\right)$ is a deadweight $W_o$. Based on the Matlab simulation, it is clear that the vibration eventually settles down to an equilibrium position due to the dashpot damping. Of course, we will replace the deadweight with the actual dynamometer load measurements and compare the displacement solutions with the actual polish rod displacements. As shown in Figure 5, even with a very preliminary Kelvin model, we can still recreate the hysteresis loop of load and displacement for the sucker rod pump system. In the simulation, the magnification factor is 85 for both Maxwell and Kelvin models to match the actual motion of the sucker rod with the viscoelastic model in the simulation. Notice that the load $F\left(t\right)$ used in the viscoelastic model is the exact load measurement recorded in TAM software examples. In general, by reducing the parameter m, the peak of the displacement will decrease and shift to the left which corresponds to the increase of the natural frequency. In addition, the end point will also decrease accordingly. Moreover, by reducing the parameter k, the peak of the displacement will increase and the end point will also be elevated accordingly. By increasing the parameter $c_o$, the viscous damping is increased and both the displacement peak and the ending points will be increased. Finally, by increasing the stiffness parameter $k_o$, both the displacement peak and the end displacement tend to decrease. Notice that here the magnification factor C along with the parameters m, $c_o$, and $k_o$ are chosen with intuition through trial and error methods and human interventions as reported in Ref. [28]. However, in this paper, with the initial guesses of these parameters, we will implement a so-called Inversed Optimization Method to identify with iterations in the steepest decents the optimal set of parameters. With this Newton-Raphson iteration-based approach, these parameters will be searched and improved automatically. An improvement Kelvin viscoelastic vibration system with adjusted parameters m, $c_o$, and $k_o$ demonstrates a much closer displacement response with the measured force $F\left(t\right)$ as shown in Figure 5, which demonstrates the potential of inverse optimization approaches with the Newton-Raphson iterations.

2. Inverse Optimization

In engineering practice, there are many complex systems that are impossible to characterize with a simple physical and mathematical model, therefore, an implicit matrix-free iterative method is very useful in providing better guidance to the optimum operation conditions with only the availability of the input and output data. The inverse optimization based on the Newton-Raphson iterations can be used to search more strategically for the optimal system parameters. It can be used to search without knowing the true relationship between the optimal material compositions to achieve the best mechanical properties or any type of property. Of course, similar acceleration methods commonly employed in the Newton-Raphson iterations can also be available for the design of more efficient and purposeful search processes.

In inverse optimization approaches, in order to identify these intrinsic viscoelastic properties with the consideration of different physical units, we also introduce a scaling factor C. We set up an inverse engineering problem to minimize the difference measured by the following variational indicator

$$E=\sum _{n=1}^N\frac{1}{2}{(u_n-{\overline{u}}_n)}^2,$$

where N represents the number of time stations, $u_n$ is the displacement evaluated with the viscoelastic model with the stiffness k, m, $c_o$, and $k_o$, whereas ${\overline{u}}_n$ is the experimental measurement of the displacement in question at the same time intervals. For the minimized error, cost function, or variational indicator E, we have

$$\frac{\partial E}{\partial k}=0,\frac{\partial E}{\partial m}=0,\frac{\partial E}{\partial c_o}=0,\frac{\partial E}{\partial k_o}=0.$$

This estimate evaluated with finite difference schemes will be directly coupled with the system parameters, for example, k, m, $c_o$, and $k_o$,

$$\begin{array}{ccccccccc}\hfill f_1& =& \frac{\partial E}{\partial x_1}\hfill & =& \frac{\partial E}{\partial k}\hfill & =& \sum _{n=1}^N(u_n-{\overline{u}}_n)\frac{\partial u_n}{\partial k}\hfill & =& 0,\hfill \\ \hfill f_2& =& \frac{\partial E}{\partial x_2}\hfill & =& \frac{\partial E}{\partial m}\hfill & =& \sum _{n=1}^N(u_n-{\overline{u}}_n)\frac{\partial u_n}{\partial m}\hfill & =& 0,\hfill \\ \hfill f_3& =& \frac{\partial E}{\partial x_3}\hfill & =& \frac{\partial E}{\partial c_o}\hfill & =& \sum _{n=1}^N(u_n-{\overline{u}}_n)\frac{\partial u_n}{\partial c_o}\hfill & =& 0,\hfill \\ \hfill f_4& =& \frac{\partial E}{\partial x_4}\hfill & =& \frac{\partial E}{\partial k_o}\hfill & =& \sum _{n=1}^N(u_n-{\overline{u}}_n)\frac{\partial u_n}{\partial k_o}\hfill & =& 0.\hfill \end{array}$$

It is clear that we must introduce the Newton-Raphson iterative procedures to obtain the solution of the nonlinear and implicit set of equations. In general, the Newton-Raphson iterative method should be used for this type of nonlinear set of equations. The nonlinear and implicit governing equation about the unknown vector $\mathbf{x}=<k,m,c_o,k_o>$, can be rewritten as

$$\mathbf{f}\left(\mathbf{x}\right)=\mathbf{R},$$

(13)

where the given right-hand side vector $\mathbf{R}=<0,0,0,0>$.

It is very important to point out that the initial guess must be fairly close to the actual solution for the unknown $\mathbf{x}$ to ensure the convergence of the Newton-Raphson iteration scheme. In practice, we often start with a few tryouts and narrow down the true solution neighborhood. With an educated guess of the initial set of parameters ${\mathbf{x}}^o=<k^o,m^o,c_o^o,k_o^o>$, not too far from the converged solution, the Jacobian matrix can be defined and evaluated. Assume we have all the information before the $k^{th}$ iteration, namely, ${\mathbf{x}}^k$ and the corresponding $\mathbf{f}\left({\mathbf{x}}^{k-1}\right)$ as well as the so-called Jacobian matrix $\mathbf{J}\left({\mathbf{x}}^{k-1}\right)$ with all entities $J_{ij}$ defined as

$$\begin{array}{ccccc}\hfill J_{11}& =& \frac{\partial f_1}{\partial x_1}\hfill & =& \sum _{n=1}^N(u_n-{\overline{u}}_n)\frac{{\partial }^2{u}_n}{\partial k^2}+\sum _{n=1}^N\frac{\partial u_n}{\partial k}\frac{\partial u_n}{\partial k},\hfill \\ \hfill J_{22}& =& \frac{\partial f_2}{\partial x_2}\hfill & =& \sum _{n=1}^N(u_n-{\overline{u}}_n)\frac{{\partial }^2{u}_n}{\partial m^2}+\sum _{n=1}^N\frac{\partial u_n}{\partial m}\frac{\partial u_n}{\partial m},\hfill \\ \hfill J_{33}& =& \frac{\partial f_3}{\partial x_3}\hfill & =& \sum _{n=1}^N(u_n-{\overline{u}}_n)\frac{{\partial }^2{u}_n}{\partial c_o^2}+\sum _{n=1}^N\frac{\partial u_n}{\partial c_o}\frac{\partial u_n}{\partial c_o},\hfill \\ \hfill J_{44}& =& \frac{\partial f_4}{\partial x_4}\hfill & =& \sum _{n=1}^N(u_n-{\overline{u}}_n)\frac{{\partial }^2{u}_n}{\partial k_o^2}+\sum _{n=1}^N\frac{\partial u_n}{\partial k_o}\frac{\partial u_n}{\partial k_o}.\hfill \end{array}$$

Furthermore, the off-diagonal terms for the Jacobian matrix with $i\ne j$ can also be elaborated as

$$J_{ij}=\frac{\partial f_i}{\partial x_j}=\sum _{n=1}^N(u_n-{\overline{u}}_n)\frac{{\partial }^2{u}_n}{\partial x_i\partial x_j}+\sum _{n=1}^N\frac{\partial u_n}{\partial x_i}\frac{\partial u_n}{\partial x_j}.$$

It is straightforward to confirm that the Jacobian matrix is indeed symmetric. After the solution of the following incremental linear system of equations for the unknown $\Delta {\mathbf{x}}^k$

$$\mathbf{J}\left({\mathbf{x}}^{k-1}\right)\Delta {\mathbf{x}}^k=-\mathbf{f}\left({\mathbf{x}}^{k-1}\right),$$

(14)

with the following update,

$${\mathbf{x}}^k={\mathbf{x}}^{k-1}+\Delta {\mathbf{x}}^k.$$

(15)

The iteration identified in Eq. (15) will stop with the relative incremental error $ϵ$ smaller than prescribed small number ${ϵ}_o$,

$$\frac{\parallel \Delta {\mathbf{x}}^k\parallel }{\parallel {\mathbf{x}}^o\parallel }=ϵ\le {ϵ}_o.$$

(16)

In the actual implementation, since we do not the analytical expressions for $\frac{\partial u_n}{\partial x_i}$, $\frac{\partial u_n}{\partial x_i}\frac{\partial u_n}{\partial x_j}$, $\frac{{\partial }^2{u}_n}{\partial x_i^2}$, and $\frac{{\partial }^2{u}_n}{\partial x_i\partial x_j}$, a central-difference-based numerical scheme is introduced. Assume the increment $\Delta \mathbf{x}$, we will complete the numerical integration of the dynamic response of the viscoelastic model for three sets of parameters, namely, $\mathbf{x}-\Delta \mathbf{x}$, $\mathbf{x}$, $\mathbf{x}+\Delta \mathbf{x}$, and obtain the numerically the approximations as follows

$$\begin{array}{ccc}\hfill \frac{\partial u_n}{\partial x_i}& =& \frac{u_n(x_i+\Delta x_i)-u_n(x_i-\Delta x_i)}{2\Delta x_i},\hfill \\ \hfill \frac{\partial u_n}{\partial x_i}\frac{\partial u_n}{\partial x_j}& =& \frac{u_n(x_i+\Delta x_i)-u_n(x_i-\Delta x_i)}{2\Delta x_i}\frac{u_n(x_j+\Delta x_j)-u_n(x_j-\Delta x_j)}{2\Delta x_j},\hfill \\ \hfill \frac{{\partial }^2{u}_n}{\partial x_i^2}& =& \frac{u_n(x_i+\Delta x_i)-2u_n\left(x_i\right)+u_n(x_i-\Delta x_i)}{\Delta x_i^2}.\hfill \end{array}$$

(17)

As the most complicated term, the second partial derivative with respect to $x_i$ and $x_j$ with $i\ne j$, namely, $\frac{{\partial }^{2}g}{\partial x_i{x}_j}$ is evaluated as follows

$$\frac{g(x_i+\Delta x_i,x_j+\Delta x_j)+g(x_i-\Delta x_i,x_j-\Delta x_j)-g(x_i-\Delta x_i,x_j+\Delta x_j)-g(x_i+\Delta x_i,x_j-\Delta x_j)}{4\Delta x_i\Delta x_j}$$

In the implementation, we can always use a sufficiently small increment $\Delta \mathbf{x}$ for the partial derivatives of $u_n$ as a function of $\mathbf{x}$.

3. Implementation and Improvement

In order to verify this proposed inverse optimization procedure, we start with a simple first-order differential equation with one parameter, a so-called relaxation time $\tau$, expressed as

$$\frac{du}{dt}+\frac{u}{\tau }=f,$$

where $f\left(t\right)$ is a time dependent inhomogenous term.

Instead of the actual experimental measurement, in the validation process, we employ the actual analytical solution $\overline{u}$, expressed as

$$\overline{u}\left(t\right)=u_o{e}^{-t/\tau }+{\int }_0^t{e}^{-(t-s)/\tau }f\left(s\right)ds,$$

with the initial solution $u\left(0\right)=u_o$ and the convolution term with the so-called Green’s function for impulse $e^{-t/\tau }.$

Note that although we have the analytical solution as a continuous function, in engineering practice, the experimental measurements often exist in discrete form. Therefore, a proper number of time steps N must be taken before we start the inverse optimization process for the search of the system parameter which yields the solution ${\overline{u}}_n$ with $n=1,\cdots ,N.$ In the initial implementation, the maximum number of iterations is set to be 200 and the time station number is 2001. In addition, the finite difference approximation of some of the implicit terms of the Jacobian matrix is based on the $0.1\%$ perturbation of the parameter $\tau$ and the scaling factor C. The analytical solution is based on the relaxation time $\tau =5$. As shown in Table 1, the only system parameter, namely the relaxation time $\tau$, does converge to a value very close to 5 within approximately $0.1\%$ range. Moreover, the scaling factor C is also simultaneously converged to 1. The quadratic convergence rate towards the end of the iteration processes is evident in Table 1.

It is well accepted that there is no guarantee for the Newton-Raphson iteration to converge in particular when the initial guess is very far away from the desired solution. Moreover, it is often possible that different initial solutions will lead to different branches of solutions [35,36]. Different acceleration procedures have been proposed to improve the convergence behaviors of these nonlinear iterative solution procedures such as line search methods [37]. In this paper, based on the understanding of the possible solution key features, we can also start the optimization procedure from the very beginning. For example, for the first-order ordinary differential equation exponential solutions, rather than connection with the solution itself, we can choose to connect with the logarithmic of the solution. In this way, the nonlinear system can be less challenging which can fundamentally change the basin of convergence in the Newton-Raphson iterative procedures. Hence, we set up an inverse engineering problem to minimize the difference measured by the following variational indicator

$$\overline{E}=\sum _{n=1}^N\frac{1}{2}{(D+ln{u}_n-ln{\overline{u}}_n)}^2,$$

where N represents the number of time stations, $u_n$ is the displacement evaluated with the system parameter, in this case, the relaxation time $\tau$, ${\overline{u}}_n$ is the experimental measurement of the displacement in question at the same time intervals, and D stands for the new constant which is related to the initial scaling factor C with $D=lnC$.

Similarly, to the minimized error, cost function, or variational indicator E, we have

$$\frac{\partial \overline{E}}{\partial D}=0,\frac{\partial \overline{E}}{\partial \tau }=0.$$

Note that the scaling constant D still has an explicit expression, the derivative with respect to D will be evaluated directly unlike the system parameter $\tau$ which must be evaluated with finite difference schemes. This estimate of the scaling factor D will be directly coupled with the system parameter and form the unknown vector with $\mathbf{x}=<\tau ,D>$, with the nonlinear set of equations expressed as

$$\begin{array}{ccccccccc}\hfill {\overline{f}}_1& =& \frac{\partial \overline{E}}{\partial x_1}\hfill & =& \frac{\partial \overline{E}}{\partial \tau }\hfill & =& \sum _{n=1}^N(D+ln{u}_n-ln{\overline{u}}_n)\frac{\partial ln{u}_n}{\partial \tau }\hfill & =& 0,\hfill \\ \hfill {\overline{f}}_2& =& \frac{\partial \overline{E}}{\partial x_2}\hfill & =& \frac{\partial \overline{E}}{\partial D}\hfill & =& \sum _{n=1}^N(D+ln{u}_n-ln{\overline{u}}_n)=0.\hfill \end{array}$$

In order to effectively carry out the Newton-Raphson iterative procedures for the nonlinear and implicit governing equation about the unknown vector $\mathbf{x}$, the so-called Jacobian matrix $\mathbf{J}$ must be properly evaluated,

$$\begin{array}{ccccc}\hfill {\overline{J}}_{11}& =& \frac{\partial {\overline{f}}_1}{\partial x_1}\hfill & =& \sum _{n=1}^N(D+ln{u}_n-ln{\overline{u}}_n)\frac{{\partial }^{2}ln{u}_n}{\partial {\tau }^2}+\sum _{n=1}^N\frac{\partial ln{u}_n}{\partial \tau }\frac{\partial ln{u}_n}{\partial \tau },\hfill \\ \hfill {\overline{J}}_{22}& =& \frac{\partial {\overline{f}}_2}{\partial x_2}\hfill & =& \sum _{n=1}^{N}1.\hfill \end{array}$$

Furthermore, the off-diagonal terms for the Jacobian matrix can also be elaborated as

$${\overline{J}}_{12}=\frac{\partial {\overline{f}}_1}{\partial x_2}=\sum _{n=1}^N\frac{\partial ln{u}_n}{\partial \tau }=\frac{\partial {\overline{f}}_2}{\partial x_1}={\overline{J}}_{21}.$$

Again, it is straightforward to confirm that the Jacobian matrix is indeed symmetric. In the actual implementation, since we do not the analytical expressions for $\frac{\partial ln{u}_n}{\partial \tau }$, $\frac{\partial ln{u}_n}{\partial \tau }\frac{\partial ln{u}_n}{\partial \tau }$, and $\frac{{\partial }^{2}ln{u}_n}{\partial {\tau }^2}$, central difference schemes similar to Eq. (17) will be employed by replacing $u_n$ with $ln{u}_n$. It has been discovered that the range of the system parameter $\tau$ is much wide for the Newton-Raphson iteration procedures with the logarithmic modification. In Table 2, the converged solutions for the parameter $\tau =6$ and the scaling factor $D=0$ which is equivalent to $C=1$ are listed with a similar quadratic rate near the solution and $0.1\%$ system error due to the finite difference approximations with the perturbation of about $0.1\%$ of the system parameter.

The same implementation has also been extended to a more complicated second-order differential equation with three parameters, namely, the mass m, the damping c, and the stiffness k, expressed as

$$m\frac{d^{2}u}{d{t}^2}+c\frac{du}{dt}+ku=f,$$

where $f\left(t\right)$ is again a time dependent inhomogenous term.

Denote the natural frequency ${\omega }_o$ with ${\omega }_o^2=k/m$, the damping ratio $\zeta$ with $c/m=2\zeta {\omega }_o,$ and the damped natural frequency ${\omega }_d=\sqrt{1-{\zeta }^2}{\omega }_o.$ Instead of the actual experimental measurement, in the validation process, we employ the actual analytical solution $\overline{u}$, expressed as

$$\overline{u}\left(t\right)=e^{-\zeta {\omega }_{o}t}(u_{o}cos{\omega }_{d}t+\frac{v_o+\zeta {\omega }_o{u}_o}{{\omega }_d}sin{\omega }_{d}t)+{\int }_0^t{e}^{-\zeta {\omega }_o(t-s)}\frac{f\left(s\right)}{m{\omega }_d}sin{\omega }_d(t-s)ds,$$

with the initial displacement $u\left(0\right)=u_o$ and the initial velocity $v\left(0\right)=v_o$ along with the convolution term with the so-called Green’s function for impulse $e^{-\zeta \omega t}\frac{1}{m{\omega }_d}sin{\omega }_{d}t.$

In the second implementation, the maximum number of iterations is again set to be 200 and the time station number is 2001. In addition, the finite difference approximation of some of the implicit terms of the Jacobian matrix is based on the $0.1\%$ perturbation of the parameters m, c, and k along with the scaling factor C. The analytical solution is based on the set of parameters $m=9.88$, $c=4.94$, and $k=247$. As shown in Table 3, the system parameters , namely m, c, and k, do converge to the set of values very close to the true system parameters, again within approximately $0.1\%$ range. Moreover, the scaling factor C is also simultaneously converged to 1. The quadratic convergence rate towards the end of the iteration processes, when the solutions are very close to the targets, is again evident in Table 3, which also indicates proper programming and implementation of the Newton-Raphson iteration procedures.

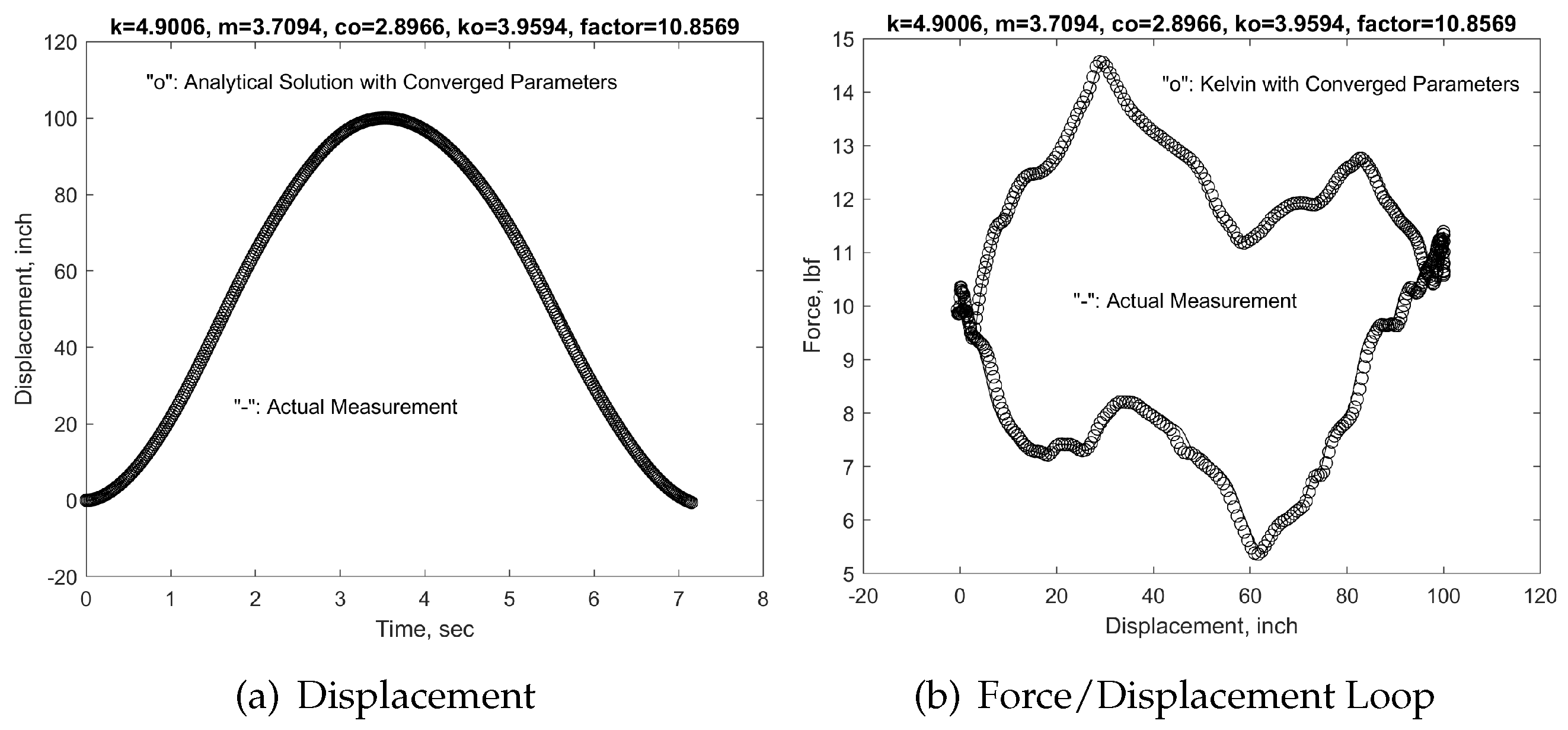
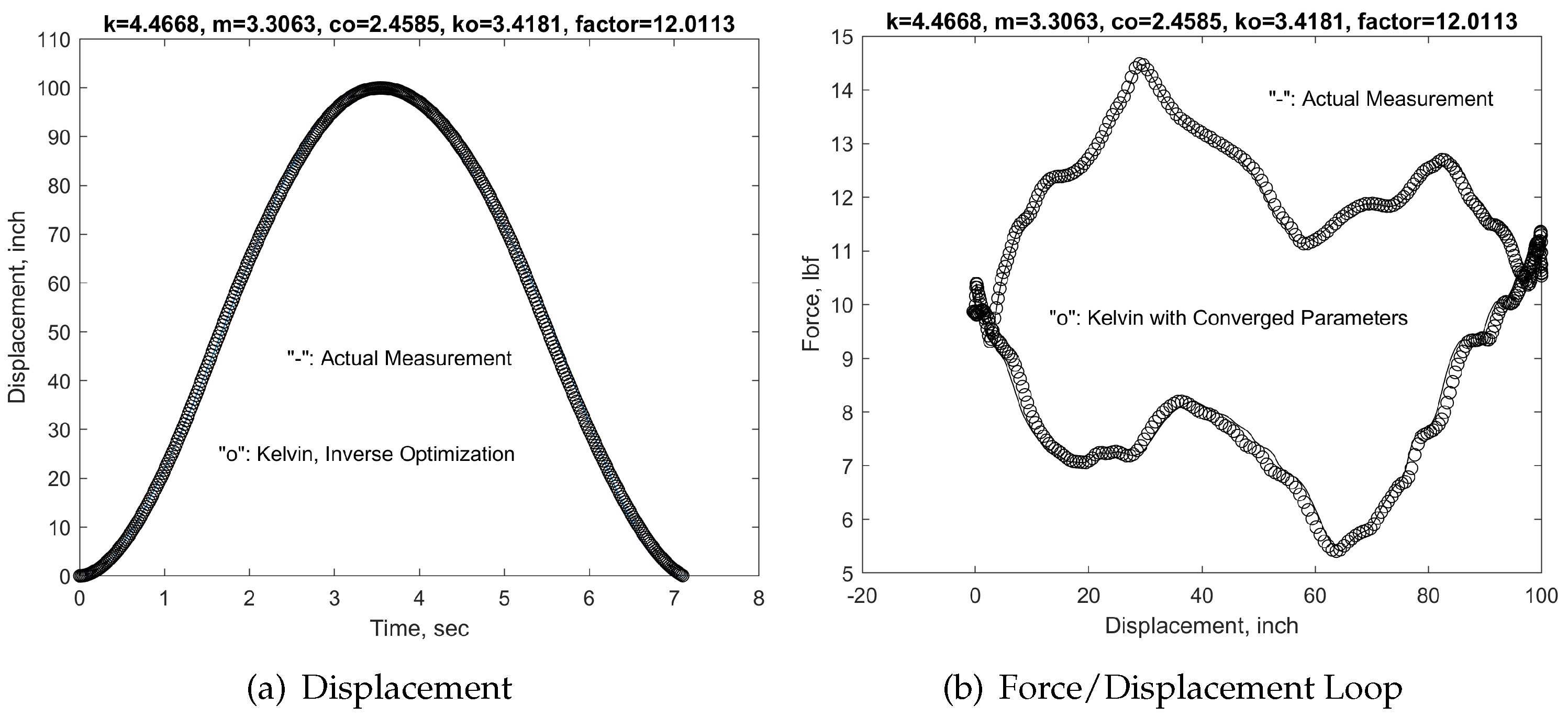
Finally, we use the experimentally measured data from V11 well documented in Echometer Co and utilized in Ref. [28] as the analytical solution of the equivalent viscoelastic vibration system modeled with the Kelvin model. With the same inverse optimization procedures, we obtain the system parameters with $k=4.4668\mathrm{l}\mathrm{b}\mathrm{f}/\mathrm{i}\mathrm{n}$, $m=3.3063\mathrm{l}\mathrm{b}\mathrm{f}·\mathrm{s}/{in}^2$, $c_o=2.4585\mathrm{l}\mathrm{b}\mathrm{f}·\mathrm{s}/in$, and $k_o=3.4181\mathrm{l}\mathrm{b}\mathrm{f}/\mathrm{i}\mathrm{n}$, and the scaling factor $C=12.0113$. The displacement and force/displacement loop match very well with the experimental data documented by Echometer Co as shown in Figure 5.

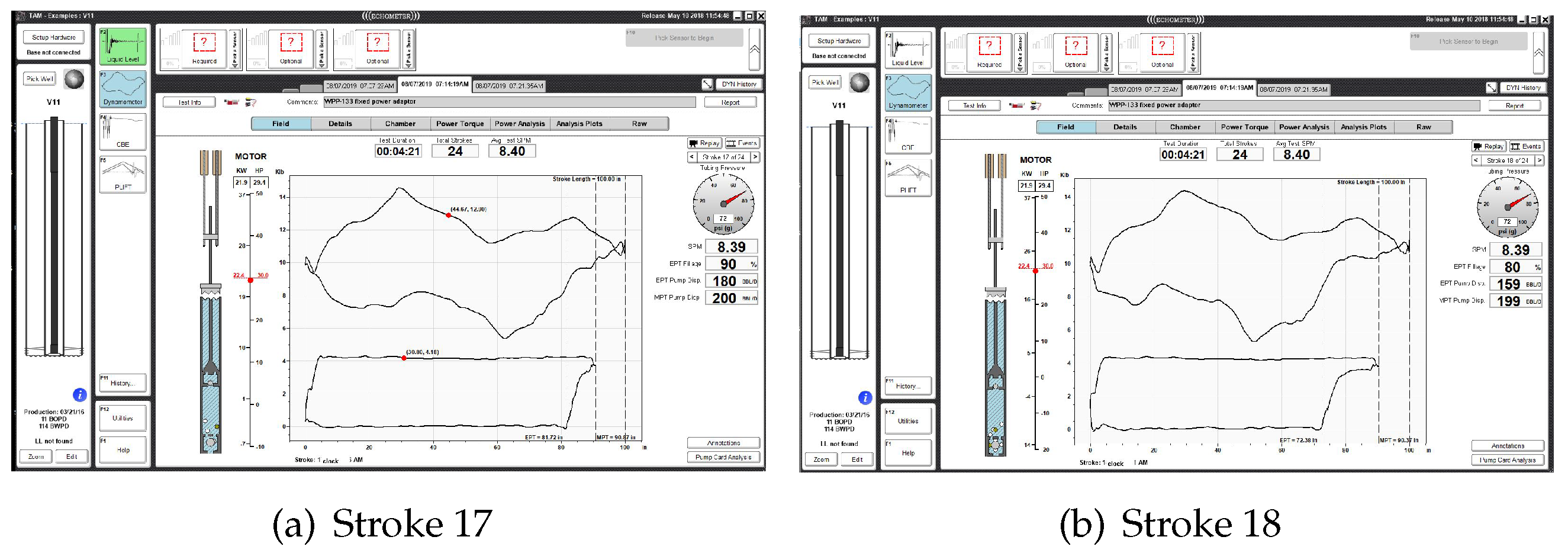
To validate the inverse optimization approach further and to test our hypothesis that the entire downhole sucker rod pump system can be approximated with the viscoelastic model, we employ the same procedures for another set of dynamometer measurements taken from the same V11 well at 7:14:19 am on August 7, 2019 Stroke 17, the exact load measurement recorded in TAM software examples, and obtain a different but similar set of system parameters with $k=4.9006\mathrm{l}\mathrm{b}\mathrm{f}/\mathrm{i}\mathrm{n}$, $m=3.7094\mathrm{l}\mathrm{b}\mathrm{f}·\mathrm{s}/{\mathrm{i}\mathrm{n}}^2$, $c_o=2.8966\mathrm{l}\mathrm{b}\mathrm{f}·\mathrm{s}/\mathrm{i}\mathrm{n}$, and $k_o=3.9594\mathrm{l}\mathrm{b}\mathrm{f}/\mathrm{i}\mathrm{n}$, and the scaling factor $C=10.8569$.

The convergence information is listed in Table 4. It is clear that the viscoelastic model does not match exactly with the sucker rod pump system. In addition, unlike the previous mathematical models from which the numerical or analytical solutions are derived, the data from the experiments are heuristic. Thus, the quadratic convergence properties of the Newton-Raphson iterative procedures are replaced with an oscillatory convergence with a rate much slower than the typical quadratic one observed for the Newton-Raphson iteration when the iterative solutions are within the neighborhood. Again, since the numerical evaluation of some of the Jacobian matrix entities has a truncation error around $O\left({10}^{-3}\right),$ the converged system parameters will hover around that relative error range.

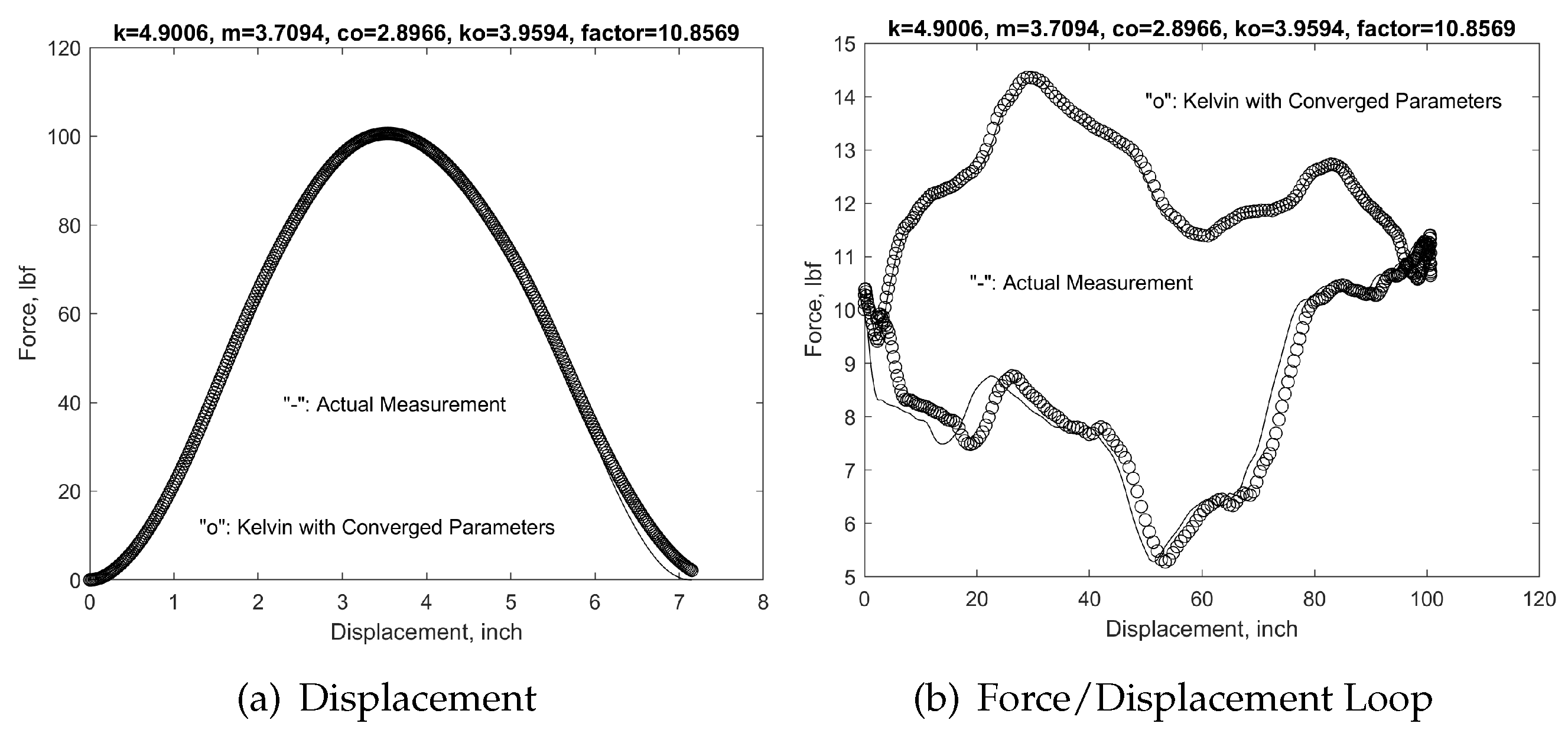
Again, the displacement and force/displacement loop match very well with the experimental data documented by Echometer Co as shown in Figure 5. Interestingly, the same system parameters have been applied to Stroke 18 and demonstrate a remarkable match with the actual experimental measurement.

Figure 6. V11 well dynamometer measurement at 7:14:19 am on August 7, 2019 Stroke 17 and 18.

Figure 6. V11 well dynamometer measurement at 7:14:19 am on August 7, 2019 Stroke 17 and 18.

Figure 7. Kelvin model analytical solutions with converged parameters in comparison with experimental measurements for Stroke 17.

Figure 7. Kelvin model analytical solutions with converged parameters in comparison with experimental measurements for Stroke 17.

Figure 8. Kelvin model analytical solutions with converged parameters in comparison with experimental measurements for Stroke 18.

Figure 8. Kelvin model analytical solutions with converged parameters in comparison with experimental measurements for Stroke 18.

4. Conclusions

In the petroleum industry, it is very difficult to quantify the dynamical behaviors of the downhole sucker rod pump systems. The proposed inverse optimization method and the viscoelastic vibration model does shed light on the understanding of the reciprocal nature of the intricate relationship between the displacement of the polish rod and the total force exerted through the pump jack. The optimal parameters of the proposed viscoelastic model for the down-hole sucker rod pump system yield almost identical results in comparison with the experimental measurements in the oil filed. With this confirmation, the same approach will be implemented for the delivery system of a very viscous non-Newtonian fluid in EV manufacturing as well as other complex engineering systems. It is promising that even one- or two- parameters can be utilized to approximate complicated relationship between the required pressure drop and the flow rate with non-Newtonian internal fluid modeled with a power law distribution and bypass full-fledge computational models which normally require a lot of resources and experiences.