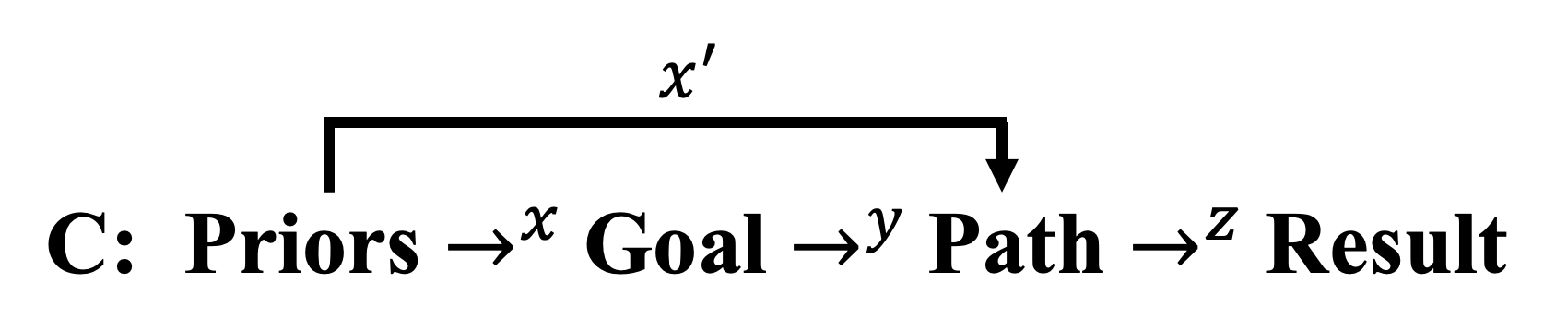A Theory of Intelligences

Michael E. Hochberg

doi:10.20944/preprints202404.0722.v2

Preprint

Article

A Theory of Intelligences

This version is not peer-reviewed.

Michael E. Hochberg^*

This version is not peer-reviewed.

Downloads

419

Views

601

Comments

Submitted:

25 May 2024

Posted:

27 May 2024

You are already at the latest version

Abstract

Intelligence is a human construct to represent the ability to achieve goals. Given this wide berth, intelligence has been defined countless times, studied in a variety of ways and represented using numerous measures. Understanding intelligence ultimately requires theory and quantification, both of which have proved elusive. I develop a framework -- the Theory of Intelligences (TIS) -- that applies across all systems from physics, to biology, humans and AI. TIS likens intelligence to a calculus, differentiating, correlating and integrating information. Intelligence operates at many levels and scales and TIS distils these into a parsimonious macroscopic framework centered on solving, planning and their optimization to accomplish goals. Notably, intelligence can be expressed in informational units or in units relative to goal difficulty, the latter defined as goal complexity relative to system (individual or benchmarked) ability. I present general equations for intelligence and its components, and a simple expression for the evolution of intelligence traits. The measures developed here could be the basis for further refinements to gauge different facets of intelligence for any step-wise transformation of information. I argue that "proxies" such as environment, technology, society and collectives are essential to a general theory of intelligence and to possible evolutionary transitions in intelligence, particularly in humans. I conclude with testable predictions of TIS and offer several speculations.

Keywords:

complexity

;

difficulty

;

encode

;

efficiency

;

evolution

;

goals

;

information

;

optimization

;

surprisal

;

uncertainty

Subject:

Biology and Life Sciences - Other

1. Introduction

The famous quote “information is the resolution of uncertainty” is often attributed to Claude Shannon. What Shannon’s seminal 1948 article “A mathematical theory of communication” and the above quote indicate is that information is a potential: unresolved order that can be perceived, filtered, deciphered and transformed. Shannon had previously equated information with the term “intelligence” in his 1939 correspondence with Vannevar Bush [1], though his observation is but one essential part of intelligence, the other being goal attainment [2]. By associating these concepts, one arrives at a simple, general description of intelligence: the resolution of uncertainty producing a result, be it reactive or an intentional goal. My objective is to unpack this statement and use this to propose a series of increasingly complete frameworks and a theory of intelligence.

Intelligent entities have one or more models of the world (e.g., [3,4,5]). Simply possessing a model however does not necessarily invoke what most humans would regard as intelligence. Thus, systems from atoms to molecules to gasses, liquids and solids are all governed by physical laws – models of a sort – but these laws are reactive: except under special circumstances, gasses, liquids and solids cannot generate structure spontaneously and they do not have the goal directedness usually associated with (human) intelligence. Nevertheless, the laws of physics and chemistry can be driven to a local reduction in entropy, that is, decreased uncertainty [6] and therefore a most bare-bones instantiation of intelligence – the reorganization or generation of information [7]. However, what is notably missing from physical intelligence that biological entities do have is alternatives to pure reaction. That is, natural physical systems do not make goals, nor can they actively choose among alternative paths or check and rectify errors towards goals. Reducing decision and prediction errors at different organizational levels is part of what differentiates thinking from non-thinking systems such as computers and AI [8,9]. Computers and artificial intelligence – even if capable of impressive feats from a human perspective – have models (e.g., software, algorithms) that are still far simpler than biological systems and humans in particular [10]. Among the features added in the huge and fuzzy steps from machine to human intelligence are dynamic environmental sensitivity and active inference [11].

These and other complexities present a major challenge to developing a theory of intelligence [12,13,14] applicable to both biological [15] and artificial [16,17] systems. Intelligence theory has largely focused on humans, identifying different milestones from simple reactions through to the more elaborate, multi-level processes involved in thought. Raymond Cattell distinguished acquired and active components of intelligence in humans, defining crystallized intelligence as the ability to accumulate and recall knowledge (much like a computer), and fluid intelligence as abilities to learn new skills and to apply knowledge to new situations (a thinking entity) [18]. Though an oversimplification of the many factors and interactions forming intelligence [19,20], this basic dichotomy is useful in differentiating the functional significance of storage/recall to familiar situations versus active decision making when faced with novel circumstances [21]. The more recent network neuroscience theory takes a mesoscopic approach in linking network structure with memory and reasoning components of intelligence [13], but is impractical for dissecting exhaustive pathways and more efficient short-cuts. Other theories of intelligence have attempted to integrate either processes, or emergent behaviors, or both (e.g., [3,22,23,24,25]). Arguably, the main shortcoming of current theory is the view that the reference for intelligence is thinking entities, thus ignoring structural features linking physics, different milestones and scales in biology and artificial systems [26], and, with notable exceptions [27,28,29,30,31,32], ignoring the roles of transmission and evolution in intelligence.

I develop the theory that intelligence is a fundamental property of all systems and is exhibited in a small number of distinct, distinguishing forms. Previous research has explained intelligence in levels or hierarchies (e.g., [3,5,33,34,35,36,37,38,39,40]) and I employ this idea to account for the variety of intelligences, including natural physical systems, biological ones and humans in particular, and artificial and designed systems. I define a “system” (also referred to as an “agent”) as an entity that uses external energy sources to lower entropy over one or more of a defined function, an object, space, or time. Generic examples include development, generating information, reproducing, and maintaining homeostasis.

The Theory of Intelligences (TIS) is developed in three parts, starting with temporal goal resolution, then recognising micro-, meso- and macroscopic abilities, and finally accounting for system-life-long changes in intelligence and transmission through time, including the evolution of intelligence traits. The key advances of TIS are (1) the partitioning of intelligence into local (“solving”) and beyond local (“planning”) strategy; (2) distinguishing challenges in the forms of goal difficulty and surprisal; (3) recognizing not only the core system, but extra-object spaces, including past sources, present proxies (i.e., any support that is not part of a system at its inception), environments, present and near-future transmission, and longer-term evolution.

As a start towards a formalization of TIS, I present mathematical expressions based on the quantifiable system features of solving and planning, difficulty, and optimal (efficient, accurate and complete) goal resolution. Goals may be imposed by necessity, such as survival imperatives, and/or be opportunistic or actively defined by the system, such as preferences, learning new skills, or goal definition itself. Solving and planning have been extensively discussed in the intelligence literature, and the advance of TIS is to mathematically formalize their contributions to intelligence and to represent how, together with optimization, they constitute a parsimonious, general theory of intelligence. The proposed partitioning of solving and planning is particularly novel since it predicts that paths to a goal not only function to achieve goals, but also may constitute experimentations leading to higher probabilities for future attainable goals and increased breadth to enter new goal spaces, and possibly serving as a generator of variations upon which future selection will act. These experimentations moreover are hypothesized to explain capacities and endeavors that do not directly affect Darwinian fitness, such as leisure, games and art. I do not discuss in any detail the many theories of intelligence nor the quantification of intelligence, the latter for which the recent overview by Hernández-Orallo [41] sets the stage for AI, but also yields insights into animal intelligence and humans. Neither do I discuss the many important, complex phenomena in thinking systems such as cognition, goal directedness and agency [42].

2. The Idea

My argument is that goals – be they outcomes or the means to obtain outcomes – are informational constructs, and because such assemblies and their component sets are potentially complex (modular, multidimensional, multi-scale), two fundamental capacities potentially contribute to optimally (efficiently, accurately and/or completely) attain resolutions. These are: (1) the ability to resolve uncertainty (`solving’) and (2) the ability to partition a complex goal into a sequence of subgoals (`planning’) (Figure 1).

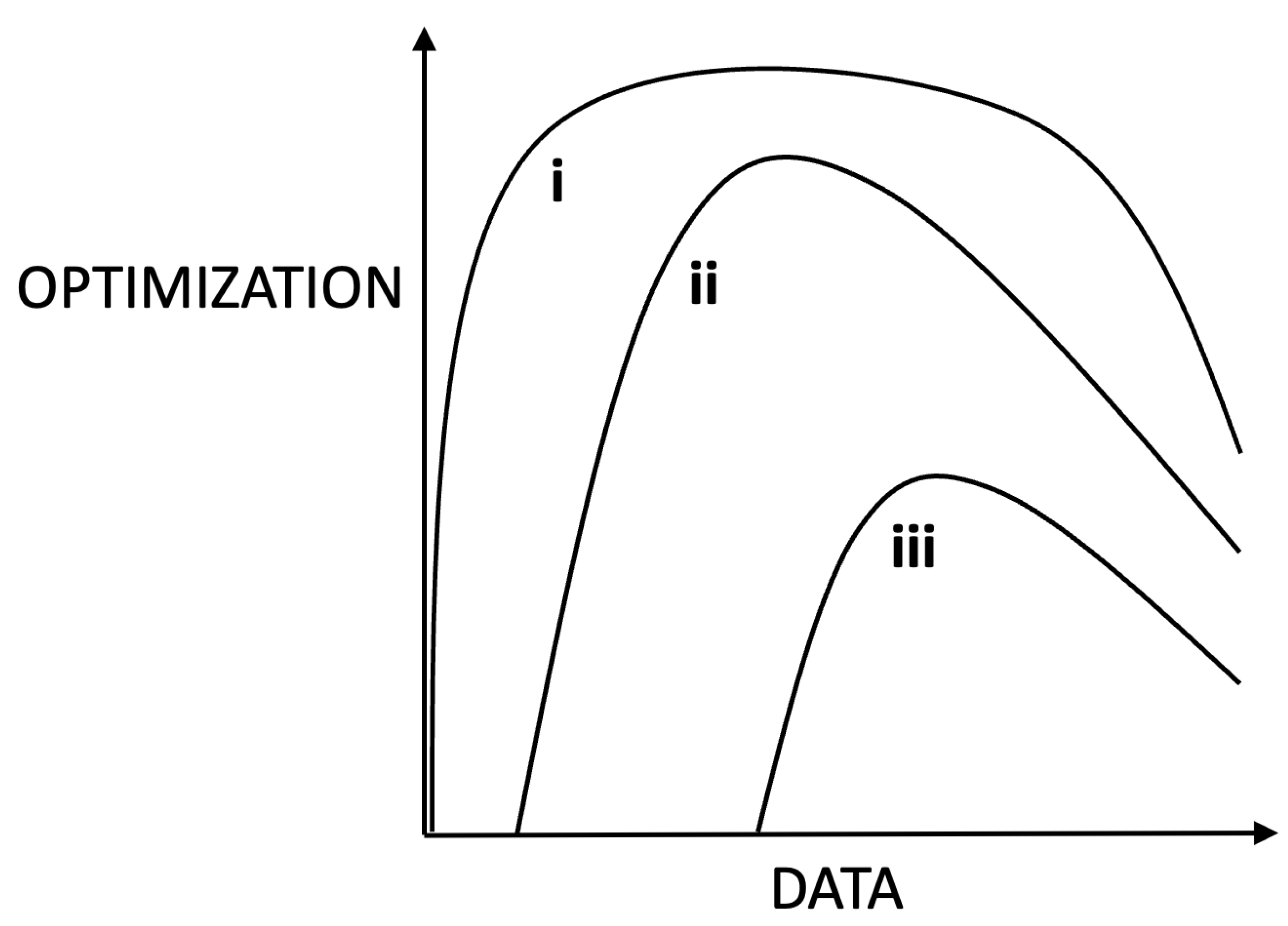
Figure 1. A – Key concepts in the Theory of Intelligences. Solving is the ability to resolve uncertainty. Planning is the ability to trace a future sequence of manageable challenges towards goal resolution. The clines refer to progressive intelligence milestones in abilities to deal with complexity. Trajectory i is gains in intelligence mostly due to solving, whereas ii is dominated by planning. Trajectory iii, which initially favors solving and gradually favors planning is the most efficient of the three examples, leading to higher marginal and overall gains in milestones. Note that the three trajectories are different rotations of the same curve. B – Time courses of path node changes for three hypothetical scenarios. Each point (node = subgoal) corresponds to a goal-related information gained in the path (represented by a continuous line). Goal resolution is indicated by an open circle. i: Monotonic decrease in path node changes leading to an intermediate resolution time (efficiency). ii: Complex trajectory in path node change, with transient information loss, subsequent discovery of a more accurate path and a consequential delay in (off graph) resolution. iii: Efficient path corresponding to a rapid resolution.

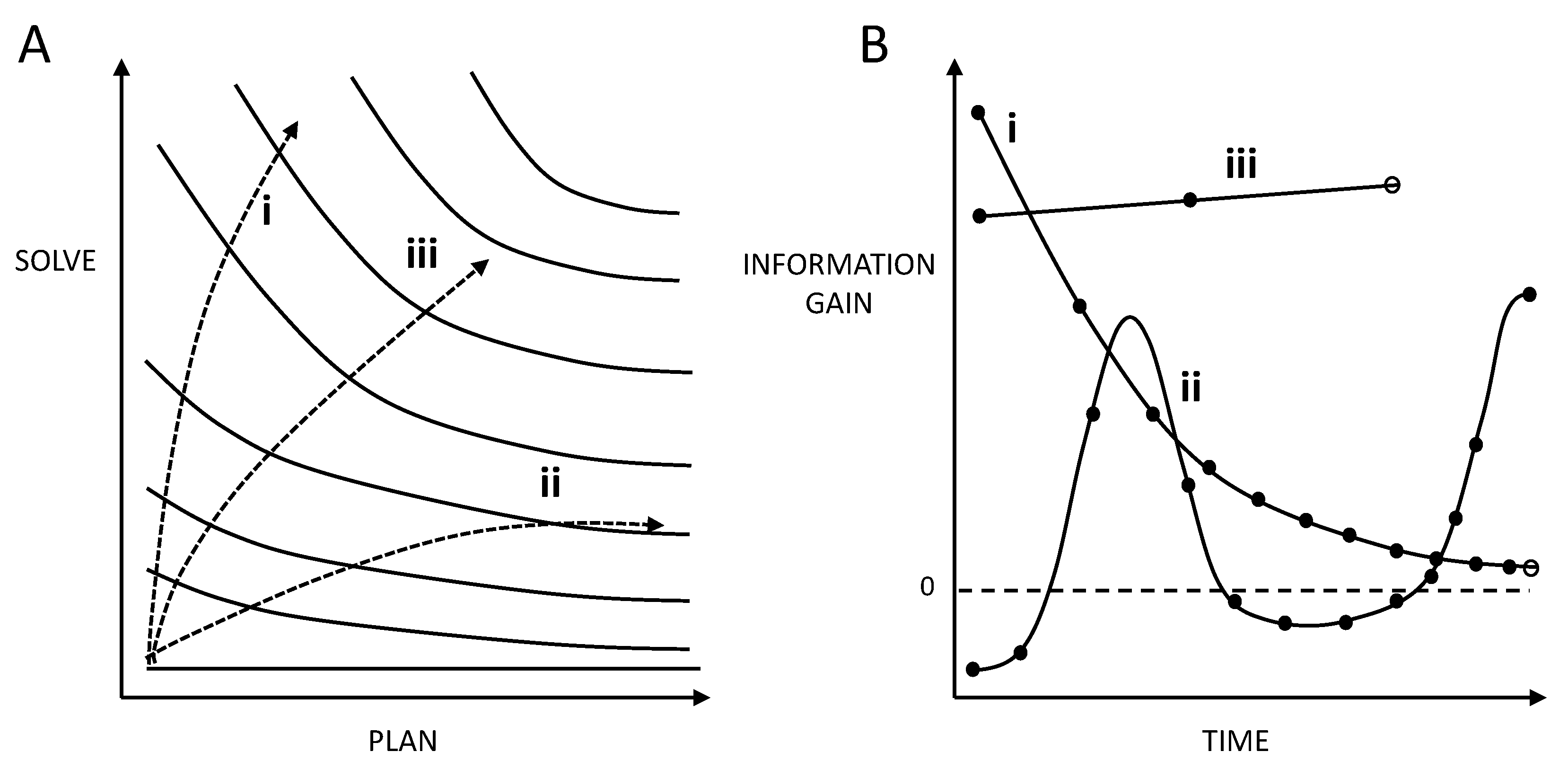
Briefly, both solving and planning harness priors, knowledge and skills to accomplish goals, but solving focuses on the myopic resolution of goal elements, whereas planning is the broader assessment of alternative steps to attain goals. Planning is a manifestation of the “adjacent possible” [43], whereby the cost of ever-future horizons is (hyper)exponentially increasing uncertainty. Not surprisingly therefore, planning is expected to require more working memory (and for hierarchical planning, causal representations of understanding) than does solving [3,12]. Planning could be influenced by a system’s ability to solve individual subgoals (including how particular choices affect future subgoals), though this does not mean that planning is necessarily harder than solving. Moreover, excellent solving ability alone could be sufficient to attain goals (i.e., solving is necessary and sometimes sufficient), whereas the capacity to identify the most promising path alone may or may not be necessary and is not sufficient to resolve a goal (Figure 1A). The value added of the latter capacity is increased accuracy, precision (hereafter precision will be lumped into the related term, accuracy), efficiency and completeness, and these become more difficult to achieve as goals become increasingly complex and therefore difficult to represent or understand (Figure 1B).

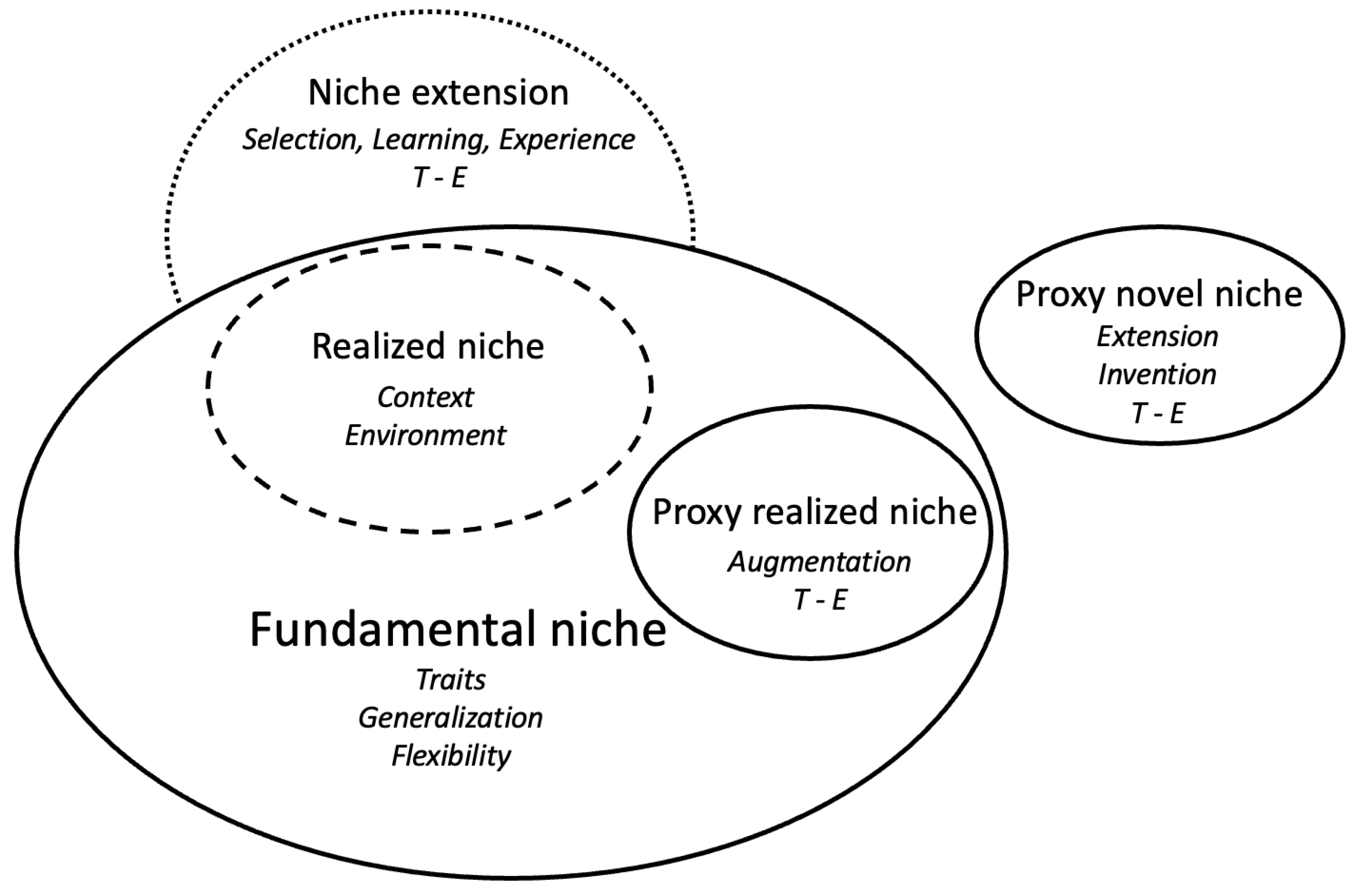
Based on the above observations, a sequence in the emergence and evolution of intelligence must begin with resolving uncertainty (solving) and thereafter possibly expand into the relevance of alternative sequential informational sequences (planning). This is the basis for evolutionary reasoning to explain differences in intelligence capacities between individual systems (trait variation, environment) and across system types (phylogeny), with physical systems at the base and a hypothetical hierarchy in complexity as one goes from artificial (and subdivisions) to biological (and subdivisions) to human. I stress that organizing systems in intelligence classes does not signify differences in performance (quality, value or superiority). Rather, it relates to how these different systems adapt to their particular spectrum of environmental conditions and goals. Differences in the amplitude and spectrum of intelligence traits are therefore hypothesized to reflect differences in the intelligence niche, that is environments, capacities and goals relevant to a system (e.g., [31,44,45]) (Figure 2).

Key to my idea is that fitness, information, complexity, entropy, uncertainty and intelligence are interrelated. There is abundant precedent for such associations, going at least back to Shannon [46], based on comparisons between subsets of the six phenomena (e.g., [47,48,49,50]). One of my objectives is to begin to explore these interrelations, recognizing that an ecological perspective could yield important and general insights. Thus, intelligence crosses ecological scales, for example, from within systems to interactions between systems and their environment, to interactions in populations of systems. Scales and the orthogonal concept of levels introduce notions of complexity, that is, heterogeneities in one or more influential factors or structures [44,51]. I hypothesize that the hierarchical nature of complexity at different scales is a manifestation of innovations in intelligence and more singular transitions in intelligence, that is, from a baseline of the resolution of local uncertainty (all systems), to sequential relations among local uncertainties (most biological systems to humans), to the ability to integrate two or more local uncertainties so as to more accurately, completely and efficiently achieve goals (higher biological cognitive systems to humans) and finally general intelligence in humans. Though largely unexplored (but see [52,53,54,55]), I suggest that the transitions from baseline uncertainty resolution to general intelligence reflect increased solving ability and for more complex goals, hierarchical planning, including its integration with basic-level solving.

That complexity and intelligence can be intertwined has important implications for explaining structure and function across systems. Insofar as systems evolve, so too do the intelligence traits employed to penetrate complexity (e.g., define and realize goals; [56]) and contribute to changes in complexity (e.g., generate novel information, structures, transitions in scales and levels), which, in turn, require greater and different forms of intelligence in order to resolve, and so on, possibly leading to a run-away process. Goal relevancy includes those actions affecting fitness (i.e., growth, survival and reproduction when faced with challenging environments, including limited resources, competitors and predators), well-being (e.g., sports, leisure, art in humans), or actions with no apparent objective at all. The goal can be within the gamut of previous experiences or an extension thereof, or be novel but realizable at least in part, despite its difficulty. To the extent that the universe of relevant, feasible goals is diverse in complexities, one expectation is that intelligence traits will not only evolve to improve fitness in existing niches (e.g., optimization), but also extend into new intelligence niches, which may or may not be more complex than existing ones (Figure 2) (for ecological niche concepts see [57]).

In sum, we need parsimonious theory that recognizes the close interconnections between uncertainty, information, complexity and intelligence, and is built on ecological and evolutionary principles.

3. A Basic Framework

The above discussion equates intelligence with a system (or a collection of systems) reacting to or engaging in a challenge or an opportunity, and to do so, perceiving, interpreting, manipulating and assembling information in its complexity, and rendering the information construct in a different, possibly more complex form. An example of a complex finality is an architecturally novel, high-level functioning business center. An example of a simple goal outcome is to win in the game of chess. Both examples may have highly challenging paths despite differences in their finalities.

Perceiving, interpreting, manipulating and assembling employ logical piece-wise associations [3,5,58] and as such at a more abstract, computational level, they differentiate, correlate and integrate raw data and existing goal-useful information (Figure 3). This involves amassing and deconstructing complex and possibly disjoint ensembles, identifying their interrelationships, and reconstructing the ensembles and existing knowledge as goal-related information, so as to infer or deduce broader implications leading to a resolution [50]. Thus, intelligence is an operator or a calculus of information.

The above coarse-grain processes emerge from more microscopic, fine-grained levels with what are often viewed as traits associated with humans such as reasoning, abstraction, generalization and imagination. Unfortunately, there is no single objective way to represent these and other microscopic features of intelligence and their interrelationships (e.g., [3,50,58,59,60,61,62,63]). Thus, to be manageable and useful, a general theory of intelligence needs to be based on higher-level macroscopic observables. To accomplish this, I begin by developing a series of increasingly complete conceptual models.

Figure 3. The hypothetical effects of data richness on the optimization (efficiency, accuracy, completeness) of a resolution to a goal. Insufficient data lowers optimality. Too much data compromises abilities to optimally parse information. Curves i – iii represent goals of increasing complexity and difficulty. Simple goals can be optimized to higher levels with less data than more complex goals. Curves i – iii can also be interpreted as decreasing intelligence profiles across individual systems.

Consider the following keyword sequence for intelligence:

A: Use Prior Information Current Data Towards Goal Path Result

Despite overlap between these descriptors, A makes plain the temporal nature of intelligence. The process requires integrating previously acquired information in the forms of priors and experience, including knowledge and skills, and the use of current data and information in a world model towards a future goal or in reaction to a challenge, producing a result. Key is the manipulation and application of raw data and more constructed information towards an objective. In what follows, I will focus on intentional goals, but the theoretical development is general to both intention and reaction. Furthermore, the descriptors and models below are simple, discrete, macroscopic representations of complex processes and behaviors, but nevertheless in being based on information, apply broadly across algorithmic and biological systems.

To integrate the above elements into a general schema we first focus on the core processing module:

B: Goal

\to^{y}

Path

\to^{z}

Result

System B is general. If B is a mere reporter such as a computer, then it simply uses input to find output from an existing list, or Goal → Result. If a system has more elaborate capacities, then

\to^{y}

may be characterized by signal processing, simulation, interpretation and eventual reformulation of the problem, followed by engagement in the decided method of resolution to

\to^{z}

, including prediction and checking for errors [58]. This more elaborate system then decides whether to go back to

\to^{y}

and possibly use what previously appeared to be useless data (or faulty computational methods), or continue on and render a result. Understanding intelligence in B thus requires we have representations of its inner workings [64,65,66].

We can further generalize B to how information is accessed, stored, processed and used towards a goal:

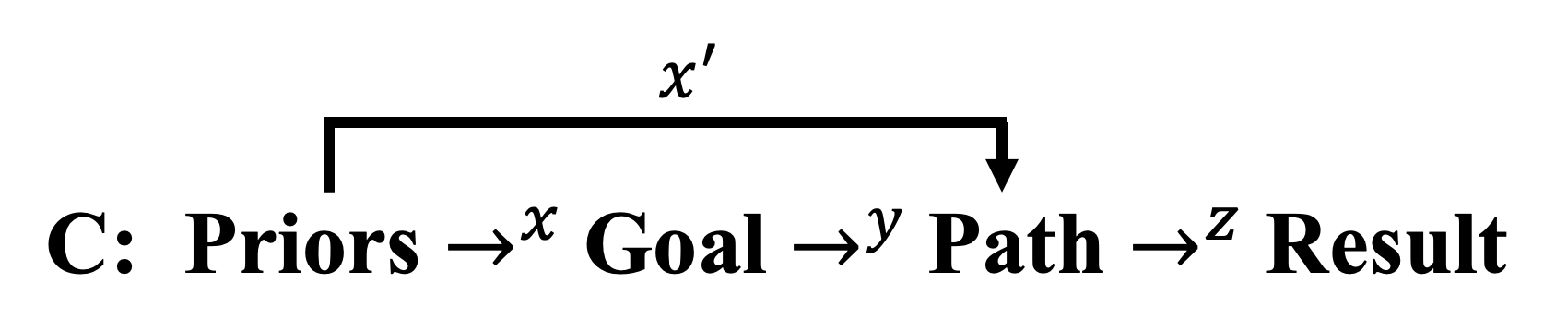
The main addition is that both

\to^{x}

and

\to^{x^{'}}

are conditional on priors, knowledge and skills. In humans, necessities such as food and shelter impose on lower-level priors (e.g., reactions to hunger and fear; notions of causality), whereas opportunities such as higher education and economic mobility require high-level priors (e.g., causal understanding, associative learning, goal directedness) [38]). The contingencies of goals and paths on information in the forms of priors, knowledge and skills highlight the temporal process nature of intelligence that is central to the Theory of Intelligences.

Temporal effects extend to the types of intelligence resources employed throughout a lifetime. Intelligence resources in humans are characterized by the growth of crystallized intelligence (knowledge, skills) into adulthood [67,68] and gains in general intelligence faculties [69] through childhood and adolescence. As individuals age, they may encounter fewer never-before seen problems and are less able, for example, to maintain working memory and processing speeds [70]. This suggests a strategy sequence in humans with a relative shift from dependence on others (parents, social), to crystallized (knowledge, skills) intelligence in youth, to fluid (thinking, creativity, flexibility) intelligence in youth and mid-life, and finally more emphasis on crystallized intelligence (possibly with more dependence on proxies, see below) into older ages. In other words, even if more nuanced [71,72], evidence points to the continual accumulation of knowledge and skills in youth enabling the ascension of novel reasoning in early and mid-life, the latter gradually being displaced by memory/recall into later life.

We can modify C to account for how feedbacks influence future intelligence resources:

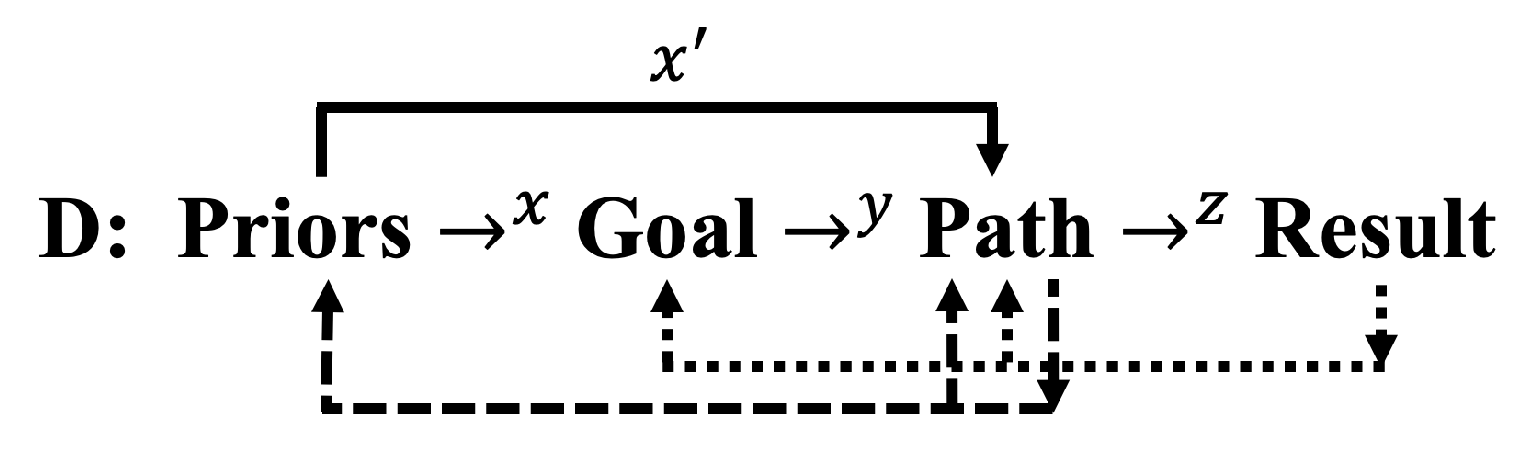
The dotted lines indicate how results can reinforce future paths and introduce novel set-points for future goals. Similarly, the dashed lines indicate how path experimentation (model flexibility, recombination of concepts) could influence future paths and knowledge and skills.

Even if more realistic than the sequences in A-C, these additions are still massive oversimplifications of the sophistication of informational dynamics in biological systems. As such, D simply makes the point that intelligence is a dynamic process with loops in the form of feedbacks (comparisons) and feedforwards (predictions) [73]. The temporal (and more generally, dimensional) nature of information change is a fundamental property of the Theory of Intelligences and as developed below, important in describing differences in information processing among system types, from physics to biology to AI.

3.1. Challenges and Abilities

The above descriptions of temporal sequences say little about system features associated with goal definition and those promoting goal attainment. Despite considerable discussion (e.g., [3,18,33,38,58,62,74,75,76]) there is no consensus on a process-based theory of intelligence, neither for biological divisions [26,53,77], nor for artificial systems [23,36,40,78]. This state of affairs stems in part from the lack of agreed first principles for candidate features and the ill-defined conceptual overlap among various traits. A way forward is a more inclusive framework based on how information is accessed and processed. I recognize that this still falls short of a readily testable, first principles framework and rather intend the developments below to stimulate discussion of next steps and refinements.

The TIS framework partitions the system into two main constructs – challenges and abilities. Challenges are further partitioned into (1) how agent capacities compare to goal complexity (difficulty) or novelty (surprisal, difficulty) [22] and (2) the capacity to arbitrate the use of stored information (exploitation) versus acquiring additional information (exploration) [79,80,81]. Although to my knowledge not previously discussed in this context, a related tradeoff is between (3) the employment of stored information (crystallized intelligence) versus higher reasoning abilities (fluid intelligence). The basis for this latter tradeoff is costs and constraints in experiencing, learning, and accurately and efficiently storing and retrieving information in the form of knowledge and skills, either alone, together with, or replaced to some degree by fluid abilities such as reasoning and creativity. Thus, for example, a computer is able to store solutions to all relevant goals and, as such, has no need for fluid abilities, but nevertheless would need to (1) inherit these solutions or have the time to sample them, (2) have the storage space and (3) have the processing abilities to recall appropriate solutions when confronted with specific challenges.

Challenges are addressed based on abilities. Previous frameworks of intelligence in humans, biology and AI have emphasized hierarchical structure in abilities (e.g., [5,33,34,35,37,38]), but the framework presented here is unique in distinguishing generic abilities from those actually applied to goals and their occurrence in different system types (Table 1). Generic abilities and goal abilities are each partitioned into multiple levels based on their hypothetical order in evolutionary appearance, that is, the necessary establishment of mechanisms on a given level for the emergence of more complex mechanisms on a “higher” level (Figure 4). For instance, planning manageable sequences of subgoals serves little purpose unless there are existing capacities to solve component tasks along a sequence. Nevertheless, solving needs references (memory, error correction) and at higher levels the ability to arbitrate or "predict" these references. Although higher accuracy and efficiency will evolve to some extent with solving and planning, an expectation based on evolutionary theory [82] is that costly optimization lags behind the inception of more grounded abilities contributing to solving and planning (e.g., reasoning, error correction, ...). Thus, the hierarchical categorizations in Table 1 are not clear-cut (and solving and planning are discussed in more detail in the next sections). Identifying component levels for various abilities is a considerable challenge, both because of the subjective nature of their definition and since abilities may articulate at more than one level.

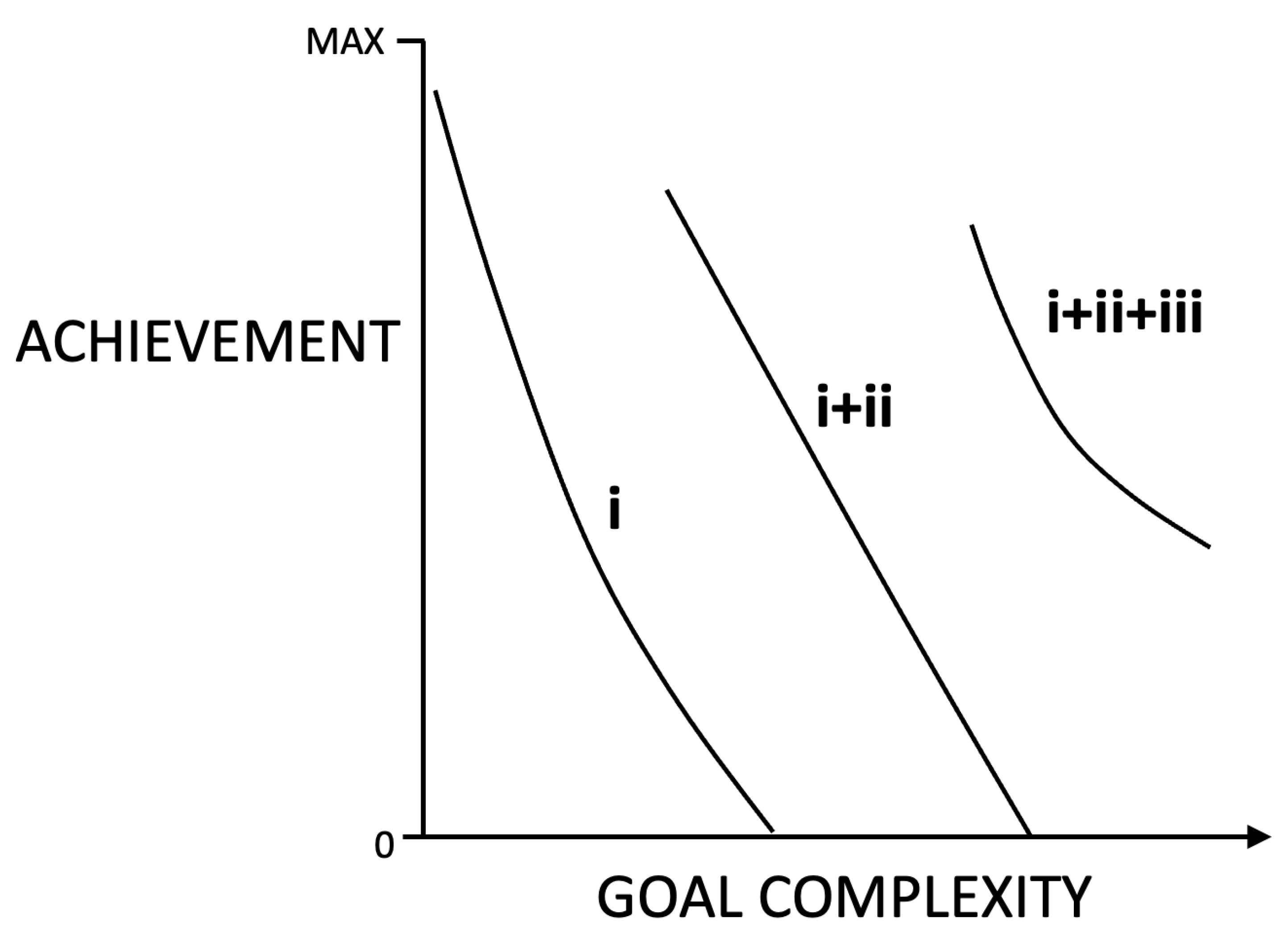
Figure 4. Hypothetical representation of how complexity in intelligence abilities respond (achievement) to complexity in goals. Curve i corresponds to solving abilities only, which are effective over a limited range of lower goal complexities. Curve i+ii corresponds to the emergence of basic-level planning together with existing solving, which increases capacities compared to solving alone. Curve i+ii+ii is higher level planning at sufficiently high goal complexity, together with basic-level planning and solving. Achievement is some combination accuracy, completeness and efficiency (e.g., eqn (3b)). Assumed is that higher levels only emerge when scaffolding already exists and evolutionary benefits of innovations exceed costs. See main text for discussion.

Table 1 also lists system types commonly associated with different abilities. Exceptions exist, notably in biology, where for example, certain avian lineages and cephalopods match or even surpass some mammals in generic and goal-associated abilities [83,84,85]. There are, nevertheless, regularities that characterize intelligence in the major system classes discussed here. Perhaps the most controversial of these are physio-chemical systems. In physio-chemical systems, events depend on the actions and influences of laws and environments. Physical systems do not have “abilities” as such, yet they do rearrange information based, in part, on the laws of thermodynamics, possibly resulting in altered information relative to initial conditions (e.g., randomly distributed minerals transforming to regular or periodic crystal lattices). Thus, at least abstractly, physical systems can reactively lower uncertainty.

4. Modelling The Theory of Intelligences

Theoretical developments to characterize intelligence are found among many disciplines and diverse systems (e.g., [3,22,23,24,86]). Explicit models have described factors such as temporal sequences from access to priors and accumulating knowledge and skills through to learning [38], and prediction error-checking and correction in achieving goals [5,58]. These and other recent advances have largely centered on AI, both because of the rapid growth in artificial intelligence and since these systems are more tractable than biological intelligence (and human intelligence in particular). The macroscopic models presented below are sufficiently flexible to apply to a range of biological or artificial intelligence systems and contexts. The models accommodate possibilities that goals can be attained with little or no insight, or that intellectual capacities do not ensure goal realization (e.g., [87]).

The framework developed so far sets the stage for theory incorporating temporal, multi-level and multi-scale factors, focusing on how intelligence is a response to uncertainty and complexity. I hypothesize that at a macroscopic level, intelligence operates across the different system types in Table 1 at local (node, subgoal) and, in a subset of those systems, at more advanced, regional or global (network, modular) levels. Building on the discussion in the previous section, local solving is addressing an arbitrarily small (manageable or imposed) unit of what might be a global objective, an example being single moves in the game of chess. As a goal becomes increasingly complex, multiple abilities might be marshalled in achieving solving, but this may be insufficient to address higher-dimension goals and particularly those where uncertainties themselves unpredictably change (e.g., an opponent in chess makes an unexpected move).

Uncertainty in achieving high-dimensional goals is reduced through planning. Planning – which appears to be a uniquely highly developed characteristic of humans [3,22], but see [28,78,88] – can involve (as does solving) depending on the system, one or more of the non-mutually exclusive capacities of computation, abstract reasoning, anticipation, prediction, mechanistic/causal understanding, and creativity (Table 1). Planning is central to optimization, that is, path efficiency and goal accuracy and completeness. Optimal path trajectories to goals become more difficult to attain as the goals themselves become more complex. Non-planned, stepwise, myopic strategies will tend to decrease the predictability of future path nodes and therefore accurate and efficient goal outcomes [43]. Thus, planning anticipates and dynamically adapts to future uncertainty [73], thereby reducing surprises and achieving more efficient resolutions [89,90]. Planning can also reduce goal difficulty by engineering the environment or altering goals themselves on-route, meaning, for example, that satisficing as opposed to optimization may emerge as the most intelligent outcome [91,92,93].

In the models below, solving and planning are each represented by a single key variable. For solving it is U_n, the useful information acquired at subgoal (node) n towards the ultimate goal or result, whereas for planning it is A_n, the accuracy, efficiency and completeness of the informational path traced to the ultimate goal. Nodes (units) form a sequence of subgoals that increasingly approach the ultimate goal if the system better solves and, for a complex goal, plans the sequence. The net change in information between start and finish of a sequence could be either positive (some degree of success) or negative (failure), yet intelligence only manifests if goal-relevant information is at least transiently gained at one or more nodes.

4.1. Modelling Solving

We assume a goal can be represented by a network of nodes, each node corresponding to an information state (subgoal) relative to the result or ultimate objective. The agent engages in the network at n=1 with stored information in the form of priors, knowledge and skills and thereafter uses this together with external data through chosen path nodes towards no, partial, or complete goal resolution at node n=N≥ 1. We assume uncertainty (information) is fixed at each node, that is, forging different paths through any given subgoal does not change the goal-related information content of that subgoal.

The solving component of intelligence

U_{y}

is the gain in information useful for goal y:

U_{y} = \frac{1}{N} \sum_{n = 1}^{N} U_{n, y} {\cdot} / {\hat{U}}_{n, y},

(1a)

where

U_{n, y}

and

{\hat{U}}_{n, y}

are, respectively, the realized gain in information (assumed equivalent to the reduction in uncertainty) at node n for goal y, and the amount of goal-related information available at node n.

U_{n, y} {\cdot}

will be a function of agent ability, and non-mutually exclusive: subgoal uncertainty, disruptive noise and surrounding environmental conditions. Disruptive noise and inhospitable environments could in principle result in information loss (time course ii in Figure 1B). Whereas

U_{n, y}

will be a complex function, the sequence of

{\hat{U}}_{n, y}

is given (i.e., there is no planning; this will be relaxed below). By definition

{\hat{U}}_{n, y}

≥

U_{n, y}

and

U_{y}

approaches 1 as

U_{n, y}

→

{\hat{U}}_{n, y}

for all n.

U_{y}

is normalized by the number of subgoals N, which does not explicitly account for solving efficiency. Efficiency could be incorporated as a first approximation by dividing

U_{n, y}

by the energy invested or time elapsed on each subgoal n. (Evidently, there will be a tradeoff: overly rapid solving will result in lower information gained). Note that Equation (1a) is a compact macroscopic form for an underlying diverse set of micro- and mesoscopic processes and although not developed here, can be related to information theory (e.g., [94]), and more specifically entropy (

{\hat{U}}_{n, y}

) and untapped information (

{\hat{U}}_{n, y}

–

U_{n, y}

Importantly, eqn (1a) makes no assumption as to whether or to what extent the goal is attained, that is, even should all visited nodes be completely resolved it is possible that the ensemble of information is goal-incomplete. Rather, (1a) only quantifies the resolution of uncertainty for chosen nodes under the implicit assumption of local, non-planned node choice.

We can modify (1a) to include the contribution

R_{n, y}

of information at node n to goal completion, with the condition

\sum_{n = 1}^{N} R_{n, y} / N \leq 1

U_{y}^{R} = \frac{1}{N} \sum_{n = 1}^{N} R_{n, y} U_{n, y} {\cdot} / {\hat{U}}_{n, y} .

(1b)

Thus,

U_{y}^{R} \to 1

as both uncertainty reduction is maximal at each node and the sum of information gained at all nodes is accurate and goal complete. Goals can be attained through some combination of solving

U_{n, y}

, insight in nodes selected

R_{n, y}

, and number of nodes visited N. Importantly,

R_{n, y}

does not assume planning, but rather reflects the quality of adjacent node choice (the lower limit of planning).

Note that the numerator in eqn (1b),

X = \sum_{n = 1}^{N} R_{n, y} U_{n, y}

is a measure of realized goal complexity.

X

can also be interpreted as a stopping condition, either an arbitrary goal-accuracy threshold (

X

W

) or a margin beyond a threshold (

X

W

>0). An example of a threshold is the game of chess where each move tends to reduce alternative games towards the ultimate goal of victory, but a brilliant move or sequence of moves does not necessarily result in victory. Examples of margins are profits in investments or points in sporting events, where there is both a victory threshold (gain vs loss, winning vs losing) and quantity beyond the threshold (profit or winning margin). We do not distinguish thresholds from maximization below, but rather highlight that goal resolution could involve one or both.

4.2. Modelling Planning

Solving does not necessarily ensure goal attainment [95]. This is because, for example, a system may either (1) correctly execute most of a complex series of computations but introduce an error that results in an inaccurate or incomplete resolution, or (2) choose nodes that, taken together, only contain a subset of the information necessary to accurately and completely attain the goal. Either or both lacuna can be diminished through planning.

We begin by modelling hierarchical planning

A_{y}

on goal y as the goal-related information contained in the actual choices

{\hat{U}}_{h, n, y}

of path nodes over node sequence n=1 to

N {h}

(the local planning horizon) relative to the optimal sequence

{\tilde{U}}_{h, g, y}

(i.e., that maximizes goal-related information) summed over g=1 to

G {h}

A_{y} = \sum_{h = 1}^{H} (\sum_{n = 1}^{N {h}} {\hat{U}}_{h, n, y} / \sum_{g = 1}^{G {h}} {\tilde{U}}_{h, g, y}),

(2a)

where the sum of the terms in parentheses is itself summed over H sequences. The capacity to plan therefore partitions the goal into two levels: local n and global h planning. In the lower limit of H=1, all planning occurs when the goal is engaged at node n=1. For H>1, planning occurs in multiple sequences (i.e., the global planning horizon). Importantly, the optimal sequence could involve a different number of nodes G≠N, but optimal information will always be greater than or equal to information in the sequence actually planned (the term in parentheses is less than or equal to 1).

Both actual (

{\hat{U}}_{h, n, y}

) and optimal (

{\tilde{U}}_{h, g, y}

) subgoals are a function of their respective local n, g planning sequences. Furthermore, the numerator of (2a) can be a function of potential information (

{\hat{U}}_{h, n, y}

) and/or acquired information (

U_{h, n, y}

) from the past (1..h-1; 1..n-1) and/or expected in the future (h+1 ...; n+1 ...). Expression (2a) – despite its complexity – does not model how node choices are actually made, nor does it account for path efficiency (i.e., number of nodes taken; spent time or energy).

Equation (2a) can be greatly simplified by assuming that planning occurs only once when the goal is engaged at n=g=1:

A_{y}^{G} = (\sum_{n = 1}^{N} {\hat{U}}_{n, y} / N) / (\sum_{g = 1}^{G} {\tilde{U}}_{g, y} / G),

(2b)

where the numerator now accounts for efficiency as the normalized sum over the N nodes and the denominator is the normalized sum over the number G of nodes potentially leading to the accurate and complete resolution of the goal. Note that one or more paths might result in having access to full goal information

{\tilde{U}}_{g, y}

and we assume for simplicity that the denominator is minimized (i.e., the most efficient, accurate and complete path).

A final index for goal attainment

A_{y}^{S}

quantifies solving based on no planning (eqn (1b)), relative to that based on optimal planning

A_{y}^{S} = U_{y}^{R} / U_{y}^{G},

(2c)

where

U_{y}^{G} = \sum_{g = 1}^{G} U_{g, y} / {\tilde{U}}_{g, y} G

and it is assumed that optimal planning is complete, i.e.,

\sum_{n = 1}^{G} R_{g, y} / G = 1

4.3. Intelligences

Any multifactorial definition of intelligence is frustrated by the arbitrariness of component weighting. In this respect, a central ambiguity is the relative importances of marshalling priors, inventing, choosing or being confronted with a goal, articulating the path to the goal, and achieving the desired result. Clearly, each phase depends to some extent those preceding it and each phase may also depend on predictions of those phases not having yet occurred. For illustration of the basic issue, consider two different algorithms available to an entity – an efficient one and an inefficient one – each yielding an answer to the same problem. There are two outcomes for each algorithm. inefficient algorithm, wrong answer (0,0); efficient algorithm, but wrong answer (1,0); efficient, correct (1,1); And yes, especially for multiple choice questions, inefficient, correct (0,1). Undoubtedly, (1,1) and (0,0) are the maximal and minimal scores respectively. But what about (1,0)’s rank compared to (0,1)? If a multiple-choice test, then one gets full points for what may be a random guess and (0,1). If the path taken is judged much more important than the answer, then an interrogator would be more impressed by (1,0) than (0,1).

In addition to possible non-accords between system design and system behavior, key abilities manifesting at both levels may or may not be highly correlated. Specifically,

U

and

A

are indicators of two complementary forms of intelligence in those systems employing both solving and planning. Although they can each serve as stand-alone assessments, they are ultimately interrelated by

{\hat{U}}_{n}

, information content at each node visited (see below). Correlations between

U

and

A

will be promoted by goal simplicity, that is either few possible nodes to accurate and complete resolution, or many nodes, but simplicity in their uncertainties and in the path to accurate and complete resolution.

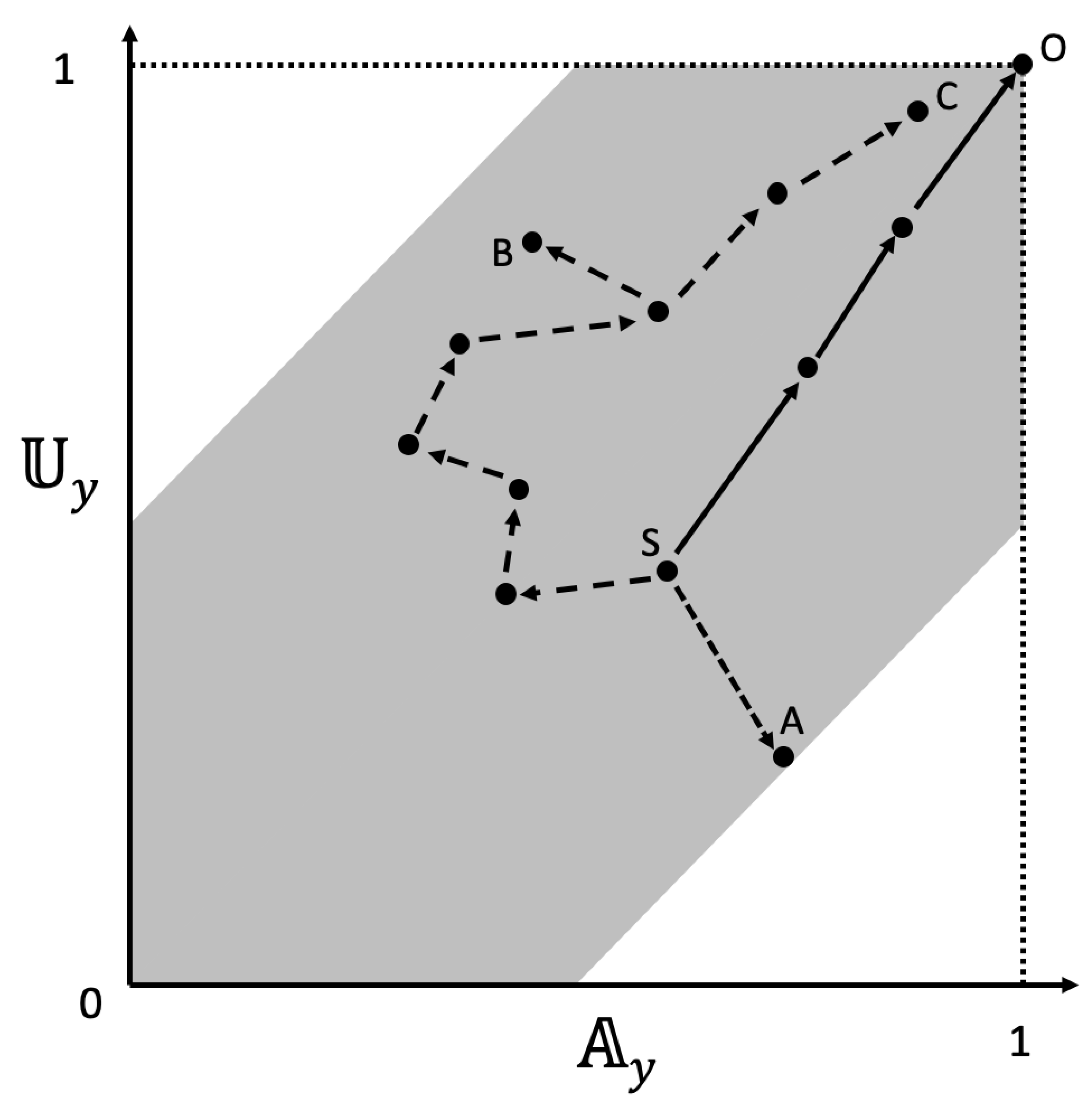
Figure 5 shows how an agent’s

A_{y}

–

U_{y}

trajectory hypothetically plots onto a space of achievements. Different nodal paths can produce a similar final outcome (S-C and S-O), and very similar paths can lead to different outcomes (S-B and S-C). Underscoring the importance of flexibility in attaining goals, one or the other of

U_{y}

and

A_{y}

might increase, decrease or remain unchanged as the agent proceeds through successive nodes. This underscores the expectation that the most efficient and accurate path to goal completion will involve the optimal allocation of (possibly competing) solving and planning abilities (cf trajectories i or ii vs iii in Figure 1A). Figure 5 also illustrates that solving and planning need not concord (e.g., path S-B in Figure 5). Nevertheless, given likely correlations among intelligence components, we predict that there will be a feasible parameter space for a given agent’s abilities (shaded area, Figure 5). We do not explicitly model these co-dependencies and rather recognize that goal complexity will tend to lower overlaps between abilities to solve and plan.

Figure 5. Hypothetical examples of sequential changes in solving

U_{y}

and planning

A_{y}

in goal resolution, based for example on equations (1b) and (2b). The maximally accurate and complete solution is denoted O. Path trajectories vary in terms of abilities to solve and plan, as reflected by the direction and length of arrows and the number of nodes from start (S) to resolution (A, B, C or O). The segments from S to O reflect an efficient, accurate and complete resolution. The single jump trajectory to a poor resolution at A (lower information, slightly greater planning accuracy) is due to low solving ability. The comparatively greater number of smaller segments from S to the sub-optimal resolution at B is due in particular to low planning ability. Finally, different nodal paths can produce a similar final outcome (S-C and S-O). These examples are oversimplifications and intended to illustrate basic principles of TIS. See main text for further explanation.

Figure 5. Hypothetical examples of sequential changes in solving

U_{y}

and planning

A_{y}

4.4. A General Equation

Expressions (1a-b) and (2a-c) provide a macroscopic basis for a theory of intelligence. They characterize two central abilities, solving and planning, but as related above, overall goal performance can (but does not necessarily) involve both capacities. I propose a more general composite index for intelligence based on the assumption that solving is necessary and planning augments solving capacities. Employing equations (1b) and (2b), we have a simple expression for the intelligence of an agent with capacities x addressing goal y

I_{x, y} = U_{x, y}^{R} {(α + β A}_{x, y}^{G}),

(3a)

where

α

and

β

a positive constants and

α

β

= 1. Planning becomes increasingly necessary to intelligence as

β \to

1. Equation (3a) is an expression of both goal attainment

U_{x, y}^{R}

and the quality of the route taken

A_{x, y}^{G}

. Substituting information terms from eqns (1b) and (2b) and dropping subscripts and summations, we have

I_{x, y} = R U (\frac{α}{\hat{U}} + \frac{β}{\tilde{U}} .

(3b)

Intelligence is the information actually gained as a fraction of the summed, weighted inverse entropies of the actual and optimal path. Note that when the agent takes the optimal path (i.e., R=1,

\hat{U}

\tilde{U}

), (3b) reduces to

I_{x, y} = U / \tilde{U},

(3c)

where U/

\tilde{U}

is now summed from 1 to G.

Although

I_{x, y}

is relative to potential information or entropy (denominators of (3b)), an additional step is necessary to relate intelligence to difficulty. Thus, intelligence defined as achievement relative to difficulty can be quantified by first proposing an expression for difficulty based on concepts developed above

D_{x, y} = C_{g, y} / Q_{x, y} .

(3d)

C_{g, y} = \sum_{g = 1}^{G} {\tilde{U}}_{g, y}

is the intrinsic complexity of goal y, that is, the minimum amount of information required to accurately and completely achieve (or describe) the goal.

Q_{x, y}

> 0 is the expected ability of the agent with expertise x to achieve goals in class y. All else being equal,

Q_{x, y}

will decrease as x and y diverge (i.e., greater surprisal). Because actual experience on a goal reduces future surprisal on similar goals,

Q_{x, y}

will be challenging if not impossible to estimate for a given agent, necessitating a subjective, interrogator-based index [64,66] or an index based on benchmarked ability [17,41].

Whereas

I_{x, y}

from equations (3a-c) is a useful measure of intelligence based on actual solving and planning, a complementary index based on the notion of difficulty is given by

{\hat{I}}_{x, y} = D_{x, y} I_{x, y} / Q_{x, y} .

(3e)

High intelligence implies a high performance on a difficult goal

C ≫ Q \approx I

, whereas

C ≪ Q ≫ I

signals lower than expected performance on an easy goal.

Equation (3e) is both general and powerful.

D, I

and

Q

are all composed of terms in units of information. By simple rearrangement of difficulty (eqn (3d)) we have an expression for the expectation of intelligence for a given level of complexity

Q / C

. The mean and variation in

I / Q

over many similar tasks is a measure of positive impacts of training (AI) or experience (biology), or negative impacts of environmental variation or noise. Moreover,

Q

could be subdivided into ability that is transmitted during a lifetime, and ability that is evolutionarily embodied in system phenotype.

4.5. Transmission and Evolution

The above mathematical developments characterize intelligence as the resolution of subgoals – and possibly the resolution of a path – culminating in a reactive result or a defined goal. The equations focus on a single system addressing a single result or goal and as such are unable to capture larger scales of intelligence, notably the transmission of capacities or traits promoting intelligence, and their evolution.

Transmission can be an important facilitator of intelligence and come from diverse sources. Examples include social interactions (e.g., collectives; [96]) and technology (e.g., tools; [97]). Social interactions are pervasive as transmitters of information and range from collective interactions at different scales within and between systems [98], to a group where individuals exchange information and act collectively towards a goal (e.g., certain microbial or animal aggregations; [99]), to a division of labor in intelligence where different functions in goal attainment are distributed among individuals (e.g., social insects [100], social mammals, human corporations). The intelligence substrates provided by these and other proxies could complement, substitute, enhance or extend an autonomous individual system’s own facilities [101]. For example, in human social learning, resolving tasks or goals is the raw material for others to observe, record and emulate, thereby contributing to the diffusion and cumulative evolution of knowledge [78,102,103]. In embodying knowledge, skills and their transmission, culture and society are at the foundation of intelligence in humans and many other animal species.

We can incorporate proxies into Equation (3e) in a simple way by assuming they reduce goal difficulty, whereby

{\hat{I}}_{P, y} = \frac{C_{g, y}}{(i P_{y} + Q_{x, y})} \frac{I_{x, y} {P_{y}}}{Q_{x, y}}

(4)

where i

P_{y}

is reduction in difficulty given the action of the proxy, and the agent’s capacity is modified (increased) as per the undefined function

I_{x, y} {P_{y}}

. Equation (4) is a compact description of how proxies influence both goal difficulty (with constant i) and realized performance

I_{x, y} {P_{y}}

. Thus, proxies decrease intelligence by decreasing difficulty, but increase intelligence by increasing performance. The balance of these two effects determine the net impact of proxies on agent intelligence as defined in eqn (4).

Two other ways in which intelligence capacities can be transmitted are genetically or culturally. To the extent that inherited traits impinging on intelligence follow the same evolutionary principles as other phenotypic traits, one should expect that some or all of genetically influenced, intelligence traits are labile and evolve, leading to alterations in existing traits or the emergence of novel traits.

Despite contentious discussion of heritable influences on intelligence in humans [104,105], the more general question of the biological evolution of intelligence continues to receive dedicated attention [24,27,28,29,31,45,106,107,108]. That intelligence traits evolve and present patterns consistent with evolutionary theory is evidenced by their influence on reproductive fitness [31] including assortative mating [109], and age-dependent (senescent) declines in fluid intelligence [110]. Nevertheless, one of the main challenges to a theory of the evolution of intelligence is identifying transmissible genetic or cultural variants that contribute to intelligence “traits”. Despite limited knowledge of actual gene functions that correlate with measures of intelligence [111,112], a reasonable hypothesis is that intelligence is manifested not only as active engagement, but also in phenotypes themselves, that is, evolution by natural selection encodes intelligence in functional entities (e.g., proteins, cells, organ systems…) at different biological levels (see also [32,94]).

The detailed development of how TIS relates to the evolution of intelligence is beyond the present study. Nevertheless, as a start, we expect that the change in the mean level of intelligence trait x in a population will be proportional to the force of selection on task y. Simplifying this process considerably we have

Δ \bar{x} \propto p_{y} {\hat{I}}_{x, y} / {\bar{I}}_{y},

(54)

where

p_{y} \leq 1

is the proportional contribution of task y to mean population fitness. The response to selection will be expressed in changes in trait x that affect benchmarked expected ability (i.e., the benchmark

Q_{x, y}

evolves) and realized performance of individuals harboring the changed trait

{\hat{I}}_{x, y}

(eqn (3b)) relative to the total population mean

{\bar{I}}_{y}

, these latter two quantities assumed to be proportional to fitness. If task y has minor fitness consequences (either y is rarely encountered and/or of little effect when encountered), then selection on trait x will be low. Note that Equation (5) can be generalized to one or more traits that impinge on one or more tasks [113]. Moreover, this simple expression implies that difficult, novel encounters have larger relative payoffs and thus, insofar as choices are made to accomplish goals of a given difficulty, fitness is proportional to the achievement level

I / Q

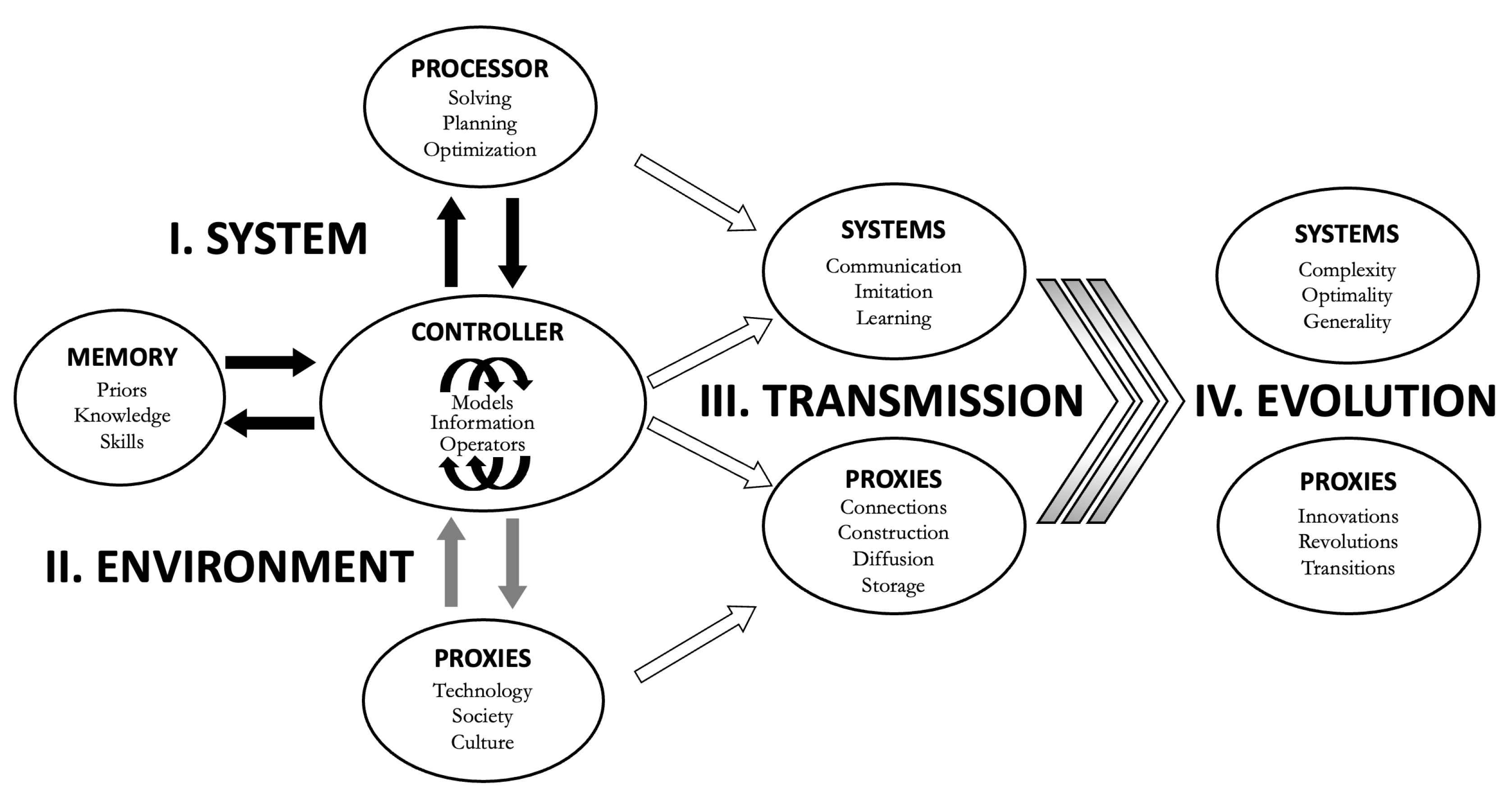
The full framework for TIS has a four-part structure (Figure 6), now including transmission within an individual system’s lifetime (information input, perception, learning) and evolution in populations (cultural, genetic). A given system’s intelligence is thus the integration of (i) the core system (controller, processor, memory), (ii) extension to proxies (niche construction, social interactions, technologies), (iii) nascent, communicated or acquired abilities (Table 1) and information (priors, knowledge, skills), and (iv) traits selected over evolutionary time. Equations (1-3) only cover point (i) and only on a macroscopic scale. Equation (4) incorporates how proxies (point (ii)) complement intrinsic system capacities, but not how they are actively used in solving and planning. Equation (5) is a start to account for evolutionary changes in intelligence traits (point (iv)).

Figure 6. Schematic diagram of TIS in the intelligence ecosystem. The SYSTEM phenotype (I) is composed of the CONTROLLER, PROCESSOR and MEMORY. The CONTROLLER generates the goal-directed information based on generic abilities (Generic Operators, Table 1), and how these abilities are instrumentalized via the PROCESSOR, which addresses challenges in their difficulty and novelty, and the arbitration of exploration and exploitation, and in so doing, solves uncertainty and plans and optimizes paths to goal resolution. The SYSTEM interacts with (II) the ENVIRONMENT both in setting and addressing GOALS. The extended phenotypes are PROXIES such as social interactions, technology and culture. Intelligence can be codified in the SYSTEM as phenotypic traits, stored MEMORY, and hard-wired or plastic behaviors. Intelligence can also be codified outside the SYSTEM in (non-mutually exclusive) PROXIES, such as collectives, society, culture, artefacts, technology and institutions. The current SYSTEM (I and II) is based on past and current TRANSMISSION and intelligence trait EVOLUTION (not shown), and develops and integrates intelligence traits over the SYSTEM’s lifetime (not shown), and influences future (III) TRANSMISSION and (IV) EVOLUTION. The intelligence niche is affected by SYSTEM EVOLUTION and possibly SYSTEM-dependent PROXY EVOLUTION and this occasionally produces intelligence innovations and, more rarely, intelligence transitions.

5. Discussion

Until relatively recently the study of intelligence focused on psychometrics in humans. With the development of AI and a greater emphasis on interdisciplinarity over the past few decades, progress has been made towards theory that spans humans and other systems, with the prospect of a general theory of intelligence based on first principles. Here, I survey recent advances towards conceptual unification of definitions of intelligence, arguing that a framework needs to incorporate dimensions (levels and scales) and be applicable to any phenomenon or system fitting the general definition of uncertainty reduction producing an intentional goal (active) or unintentional result (reactive). Levels include capacities to perceive, sort, and recombine data, the employment of higher-level reasoning, abstraction and creativity, the application of capacities in solving and planning, and optimizing accuracy and efficiency. Scales enter in diverse ways, including but not limited to how intelligence becomes evolutionarily encoded in phenotypes from cells to collective phenomena within the system and to the full system; how abilities are acquired or lost over the life of a system; and the more usual descriptor of intelligence: how capacities are actively applied to defining and achieving goals.

The theory I propose – the Theory of Intelligences (TIS) – consists of a framework (Figure 6) incorporating key levels and scales (Table 1), and mathematical models of intelligence characterizing local scale solving and larger scale planning (equations 1 – 4). TIS is parsimonious in ignoring the microscopic detail that underlies the core phenomena of solving, planning and their optimization. TIS contrasts notably with frameworks in which intelligence is partitioned into reflex/reaction and planning [5,114]. Specifically, in LeCun’s Mode 1, the system reacts to perception, perhaps minimally employing reasoning abilities. In Mode 2, the system can use higher reasoning abilities to plan, possibly in a hierarchical fashion. TIS differs from this framework by conceptualizing reflex/reaction as part of both solving and planning, and rather distinguishes subgoal phenomena from abilities to identify two or more subgoals, based on their accuracy and completeness relative to an intentional objective or unintentional result. A priority for future work is to relate how generic abilities (e.g., error correction, reasoning) map onto the goal-specific abilities of solving, planning and their optimization.

TIS is grounded in the idea that intelligence is an operator that differentiates, correlates and integrates data and information, rendering entropy into new information. Depending on the goal, an outcome of intelligence differs from the data on which it was derived and may involve any form, from random to heterogeneous, to uniformly structured, varying or unvarying in time, distributed in space, etc. Some goals, such as victory in chess resolve uncertainty in each move (solving subgoals), can anticipate future moves (planning across subgoals), and occur in huge but defined spaces leading to one of three finishes (win, draw or lose). Other endeavors such as art occur in subjective spaces and produce novel form (sculpture) or novel routes to a finality (cinema). Yet other objectives such as military or political ones may have significant degrees of uncertainty, occluded information, and unpredictable outcomes. These general examples support the idea that outcomes and the means to attain them are characteristic of different goal types. All have in common information transformation and some involve creation; that is, the differences and uncertainty in starting conditions relative to the path and/or the structure of the outcome. Interestingly, the above arguments parallel McShea’s [51] classification of types of complexity, whereby complexity can be in one or more of process, outcome and/or the levels or hierarchies in each. TIS generalizes previous theoretical treatments (e.g., [5,38,58]), fostering their interpretation in information theory and the ecological and evolutionary sciences. Nevertheless, despite the conceptual simplicity of the theory presented here, quantifying information, its transformations and goal attainment will be highly challenging, particularly in biological systems [64].

TIS posits intelligence as a universal operator of uncertainty reduction producing informational change. This has interesting implications. First, natural and artificial selection are forms of intelligence, since they reduce uncertainty and increase information (e.g., [49]). Inspired by life history theory [115,116], selection is expected to act on heritable traits that can affect accuracy and efficiency in existing intelligence niches, and those that affect flexibility, generalization and creativity in new intelligence niches. These “either/or” expectations of trait evolution will depend to some extent on contexts and tradeoffs [81]. Second, organizational change could involve some combination of assembly, disassembly, rearrangement, morphing and recombination. It is an open question as to how information dynamics via these and other modes affects complexity [94,117]. According to TIS, intelligence decreases uncertainty, but it can also transiently increase it (either due to error or counter-intuitive but viable pathways), and intelligence can either increase, decrease or leave unchanged final informational complexity. These observations do not contradict the prediction that intelligence is associated with increased information, either in the path to a goal and/or in the goal itself (see also [94]). Together with the first implication (natural selection) this is consistent with the idea that evolutionary selection encodes intelligence into (multi-scale and multi-level) structures and functions. Thus, memory – a key component of intelligence – can be stored in one or more ways: inherited as phenotypes, stored electrochemically as short- or long-term memory, or stored in proxies such as society, collectives, technology and constructed niches (Figure 6). The extent to which phenotypes and proxies are a compendium of “information past” and “intelligences past” is an open question.

5.1. Predictions

TIS makes a number of testable predictions. All are interrelated, which is both a strength and a weakness of the theory. One of the central concepts is the asymmetric interdependence between solving and planning, and how this addresses variation in complexity.

SOLVING, PLANNING AND COMPLEXITY. The interrelations between intelligence and complexity are at the foundation of TIS. Specifically, intelligence traits are expected to broadly concord with the complexity of the goals relevant to the fitness of the system, i.e., the intelligence niche (Figure 2). The intelligence niches of any two individuals of the same system type will overlap in some dimensions (e.g., musical ability), but possibly not in others (ability to play a specific musical instrument). Capacities are expected to have general characteristics across niches (e.g., visual acuity used both in foraging and avoiding predators), but also specificity in certain niches (climbing trees to escape non-climbing predators). Solving is required for goals of any complexity, whereas only as goals become sufficiently complex relative to the abilities of the system does planning (which minimally entails costs in time and energy) become useful and even necessary (Figure 4). TIS predicts goal achievement will correlate with solving and planning, correlating more strongly with capacities of the former over sufficiently low complexities, and more strongly with abilities of the latter over sufficiently high complexities (Figure 1A, Figure 4). Although I know of no evaluation of this prediction, the results of Duncan and colleagues [12] showed that proxy planning (an examiner separating complex problems into multiple parts) equalized performance among human subjects of different abilities.

PROXIES. Proxies are an underappreciated and understudied influence on intelligence and their specific roles in system intelligence remain largely unknown. One prediction of TIS is proxies such as tools, transportation and AI can function to help solve local, myopic challenges, and in augmenting the system’s own ability to solve, make planning logistically feasible. Proxies that themselves are able to plan can be important in achieving complex goals out of the reach of individual systems (e.g., human interventions à la [12]). Human social interactions have served this function for millennia and the eventual emergence of AGI could assume part of this capacity [5], possibly as proxy collectives [118]. TIS also predicts that proxies coevolve with their hosts, and insofar as the former increases the robustness of the latter’s capacities, proxies could result in system trait dependence and degeneration of costly, redundant traits [119].

SYSTEM EVOLUTION. In positing that intelligence equates with efficiency on familiar goals and reasoning and invention on novel goals, TIS provides a framework that can contribute to a greater understanding of system assembly, growth, diversification and complexity (e.g., [52,117,120,121,122]). Empirical bases for change during lifetimes and through generations include (1) on lifetime scales, intelligence is influenced by sensing and past experience (information, knowledge, skills) and influences current strategies and future goals [123,124], and (2) on multigenerational evolutionary scales, natural selection drives intelligence trait evolution in response to relative performance, needs and opportunities [31,45]. There is also theoretical support that systems can evolve or coevolve in complexity with the relevance of environmental challenges [94,123,125,126]. In contrast, excepting for humans and select animals (e.g., [127,128]), we lack evidence for how intelligence traits actually change during lifetimes given costs, benefits and tradeoffs, and suggest that life-history theory could provide testable predictions [115].

NICHE EVOLUTION. Depending on system type, different goals in the intelligence niche might vary relatively little (e.g., prokaryotes) or considerably (e.g., mammals) in complexity. This means that a system with limited capacities will – in the extreme – either need to solve each of a myopic sequence of uncertainties, or use basic n+1 planning abilities to achieve greater path manageability, efficiency, and goal accuracy and completeness. Under the reasonable assumption that systems can only persist if a sufficient number of essential (growth, survival, reproduction) goals are attainable, consistent with the “competencies in development” approach [129], TIS predicts that simple cognitive solving precedes metacognitive planning, both during the initial development of the system and in situations where systems enter new intelligence niches. Moreover, TIS predicts that due to the challenges in accepting and employing proxies, the population distribution of proxy-supported intelligence should be initially positively skewed when a new proxy (e.g., Internet) is introduced, gradually shifting towards negative skew when the majority of the population has access to, needs and adopts the innovation [130,131].

Moreover, TIS places the notions of difficulty and surprisal in a new perspective. To the extent that intelligence traits are typical of other phenotypic traits, and even if an oversimplification, selection is expected to improve existing intelligence capacities in familiar environments and diversify intelligence capacities in novel environments. Both constitute the raw material enabling successful encounters with new, more complex goals [44]. I predict that difficulty and surprisal continually decrease in current intelligence niches, but increase as systems extend existing niches or explore new niches.

TAXON EVOLUTION. The above predictions converge on the idea that solving comes before planning, but planning needs solving to be effective; that is, the latter cannot completely substitute for the former. This logic implies that solving evolution precedes the emergence of planning across phylogeny, that is, some degree of solving trait diversification would have occurred before the appearance of meta (e.g., metacognitive) abilities, and specifically planning. Nevertheless, if solving is ancestral and conserved as reactive functions or active behaviors, then transitions from B1 to B2 intelligence and from B2 to humans (see Table 1 legend for categories) would have implicated the emergence of augmented or novel solving abilities and planning capacities. For example, some cognitive adaptations in birds, mammals and cephalopods involve the development of brain regions permitting more acute perception, reaction to movement and anticipation of near future events [88]; [132]. Disentangling the selective drivers of the evolution of generic ability will be a daunting challenge.

5.2. Speculations

5.2.1. Transitions in Intelligence?

Major taxonomic groups are differentiated by their capacities to resolve their niche-relevant goals in niche-relevant environments [44]. An interesting question that emerges from TIS is whether the distribution of intelligence traits is continuous across taxa, or rather shows distinct discontinuities with the emergence of new clades, suggestive of innovations or transitions in intelligence. Although it is premature to claim the distinctions in Table 1 have a solid scientific basis, I speculate that evolutionary discontinuities in intelligence require coevolution of intelligence systems with environments. System-environment coevolution can be understood as follows. Intelligence systems are characterized by abilities at different levels (Table 1) and the system infrastructure that supports these abilities. Some, possibly all, intelligence traits are labile to change and depending on the trait and the system type, change can be due to individual experiences, associative learning, or molecular or cultural evolution. The extent to which these and other sources of change occur will depend on contexts, i.e., interactions with environments. Environments change and can “evolve” since they contain the system population itself (intraspecific interactions), other species that potentially evolve and vary in ecologies (interspecific interactions such as competition, predation and mutualism), but also changing features of the intelligence niche, including how the products of intelligence change the niche (e.g., construction and engineering; [133]). Our understanding of system-environment coevolution [94,134], system adaptation to predictive cues, and evolution to predict environments [48,135] is in its early days, but holds the potential for an assessment of the richness of intelligence traits and how intelligence ruptures and innovations may emerge.

One interesting question is whether putative discontinuities in intelligence are somehow associated with transitions in intelligence individuality. Collective intelligence can be viewed as a form of proxy to each sub-unit, suggesting that the evolution of collective intelligence might in some instances begin with individuals facultatively serving as intelligence proxies for others. Key to collective intelligence is information sharing [98] and goal alignment [136,137] and this supports the hypothesis that selection on intelligence traits when interests are aligned can favor the transition to the higher individual, including the emergence of collective intelligence traits.

Moreover, should collective intelligence emerge and the collective be sufficiently large and encounter sufficiently diverse challenges, then general theory [138] would suggest the emergence of division of labor in intelligence. Division of labor can produce faster and more efficient goal achievement and more diverse capabilities permitting more goals. Thus, the outstanding question that might lead to a theory of transitions in intelligence is whether the evolution of higher levels of individuality are accompanied (or even driven) by innovations in intelligence. Nevertheless, to the extent that a macroevolutionary theory of collective intelligence will be inspired by transitions in individuality [139] and the evolution of multicellularity [140], the theory would somehow need to incorporate division of labor in solving and planning (see [141] for information theory in social groups) and account for taxa that have not transitioned to stable collective units, notably certain mammals, birds and cephalopods [85].

5.2.2. From Crystals to Humans

CRYSTALS TO BIOLOGY. Uncertainty reduction and corresponding information gain may involve one or more of ordering, mutating, morphing and recombining code. In biological systems these transformations are usually associated with some form of activity, for example searching for resources or avoiding predators. In the absence of active behavior, intelligence minimally is information gain. Some of the simplest reactions that result in reduced uncertainty and structured regularity are the formation of inorganic crystals (e.g., [142]). Purely “physical intelligence” in inorganic crystal formation employs information (atoms or molecules) and processors (physical and chemical charges and forces) in the context of surrounding environmental conditions (pressure, temperature). To the extent that there is only a single path from disordered mineral to ordered crystal, “intelligence” is relected in the transition to order at scales beyond individual atoms. Given a single deterministic reaction sequence, there can be no surprisal since there is no memory in the system, though some crystals may be more “difficult” to form than others due to limiting environmental conditions and complex reaction sequences (e.g., [143]). These and other basic features of certain physio-chemical systems have been hypothesized to have set the stage for the emergence of biological life on Earth [144], and may comprise the scaffolding that permits certain cell behaviors, such as membrane permeability, DNA expression and replication, organelle function, protein synthesis and enzyme behavior [145].

BIOLOGY. Taxonomic comparisons of intelligence across the tree of life are largely meaningless in the absence of consideration of environments and species niches. The types, diversities and amplitudes of intelligence traits as habitat adaptations is an understudied area, with most work focusing on species with exceptional abilities from the standpoint of humans [146]. TIS posits that intelligence capacities will be influenced by environmental conditions, but gives no prediction regarding the relative fitness benefits of different traits. Rather, TIS says that difficulty is a feature of all of life, both because traits are never perfectly aligned to all goal challenges and since trait evolution always lags behind environmental change and changes in the niche [82]. Intelligence in B1 life involves the accurate sensing of the environment and decision making [147,148,149]. Behavioral alternatives in, for example, metabolic pathways and movement patterns are observed across prokaryotes and eukaryotes, although the difficulty involved is not in long-range future planning, but rather current or short-range accurate and efficient solving (rate limitations and tradeoffs among competing activities). In contrast, the notion of surprisal in B1 taxa is more nuanced, since many species can exhibit plastic responses to sufficiently infrequently encountered challenges and opportunities [150]. An interesting possibility is that plasticity is the most fundamental way to flexibly deal with uncertainty and novelty (Table 1,44]). That is, phenotypic and behavioral plasticity in B1 taxa are at the foundation of intelligence in these species and some of these traits are conserved across B2 life and in humans.

BIOLOGY TO AI. Differences between biological intelligence and artificial intelligence have been extensively discussed (e.g., [151]) the main distinctions including (1) the dependence of AI functioning on non-AI sources (memory and humans as proxies in Figure 6) and (2) limited capacities for inference in AI (controller and processor in Figure 6). Notably, since AI is a semi- or non-autonomous product of human ingenuity, AI functions as a proxy to human intelligence. TIS accounts for the evolution of designed proxies (see also [152]), that is, new functions in technology that augment or replace existing human capacities. As humans develop AI to become AGI, the latter may at some point break-away from their human hosts [153].

VOLUTION. Intelligence functions not only to achieve goals, but as experiences that promote future improvements to accuracy and efficiency and the latitude to engage in new goal spaces. Importantly, experiences are not always successful and learning from errors is well-recognized as improving performance [154,155]. As such, I speculate that in addition to successful outcomes, inefficient, erroneous or dead-end paths contribute information that can be recycled or repurposed to undertakings not necessarily affecting Darwinian fitness, such as leisure, play, sports, politics, games and art (see also [156]). If correct, then TIS is applicable to both theories of evolution (genetic, cultural, technological) and forms of goal attainment or expression not directly under natural selection.

HUMANS. A tremendous amount of research has been dedicated to the “uniqueness” of Homo sapiens with numerous hypotheses and theories on how and why humans have certain highly developed capacities that are either less developed or non-existent in other species. Empirical evidence is clear that modern humans have achieved unparalleled cognitive and communication abilities, and cumulative culture and social, technological and informational developments (e.g., [45,157,158,159]). Despite longevity [160] and environmental challenges [116] being hypothesized as key components in the evolution of human intelligence (and see similar arguments for other animals, [85]), cognitive and communication (language) capacities associated with specific regions of the human brain and vocal apparatus are the only unique body systems explaining stand-alone differences between humans and other animals [161,162]. Cumulative culture, on the other hand, could be abstractly regarded as a group proxy, that is the storage, communication and expression of cultural artefacts, including priors and knowledge, and higher-level embodiments such as social norms and institutions. Culture and brains are hypothesized to have coevolved [163], which suggests that human intelligence owes to both the slow molecular evolution (brains) and the faster evolution of information (cultures, individual and collective information). From the standpoint of an individual, culture is a gifted information proxy from the group that can increase intelligence [164], and indeed this could be a part of what distinguishes human from other-primate intelligence [165].

HUMANS AND PROXIES. As argued above, proxies are central to the scaffolding, amplification and diversification of human intelligence. This is consistent with ideas that proxies and culture coevolve [166], and that the individual can extend to proxies [167] and the emergence of a new level of individuality [168]. TIS has the ingredients to explain the generality of human intelligence, but would need to be further developed into explicit mathematical models in order to understand the contributions of individual systems and proxies such as culture. Individual brains, group culture and technology evolve on different time scales [169] and the fact that innovations such as AI are developing so rapidly is consistent with the idea that evolutionary runaways are possible [170]. Thus, a tantalizing possibly to explain the discontinuity of human intelligence with respect to other biological systems is that the coevolution of systems and their constructions in the intelligence niche is an auto-catalytic process (e.g., [171]) producing the intelligence transitions that are arguably occurring in various human-proxy systems.

Funding

This research received no external funding

Acknowledgments

I thank Steve Frank, David Krakauer, Michael Lachmann, Julien Luneau, and Melanie Mitchell for discussions.

References

Rogers, E.M. Claude Shannon’s Cryptography Research during World War II and the Mathematical Theory of Communication. Proceedings of IEEE International Carnahan Conference on Security Technology CCST-94; , 1994; pp. 1–5. [CrossRef]
Legg, S.; Hutter, M. A Collection of Definitions of Intelligence. Frontiers in Artificial Intelligence and applications 2007, 157.
Albus, J. Outline for a Theory of Intelligence. IEEE Trans. Syst., Man, Cybern. 1991, 21, 473–509. [CrossRef]
Hawkins, J. A Thousand Brains: A New Theory of Intelligence; Basic Books: New York, 2021.
LeCun, Y. A path towards autonomous machine intelligence version 0.9.2, 2022-06-27. Open Review 2022, 62.
Brillouin, L. The Negentropy Principle of Information. Journal of Applied Physics 1953, 24, 1152–1163. [CrossRef]
Landauer, R. Information Is Physical. Physics Today 1991, 44, 23–29. [CrossRef]
Tononi, G.; Koch, C. Consciousness: Here, There and Everywhere? Phil. Trans. R. Soc. B 2015, 370, 20140167. [CrossRef]
Hohwy, J. The Self-Evidencing Brain. Noûs 2016, 50, 259–285. [CrossRef]
Roitblat, H.L. Algorithms Are Not Enough: Creating General Artificial Intelligence; The MIT Press: Cambridge, Massachusetts, 2020.
Korteling, J.E.H.; Van De Boer-Visschedijk, G.C.; Blankendaal, R.A.M.; Boonekamp, R.C.; Eikelboom, A.R. Human- versus Artificial Intelligence. Front. Artif. Intell. 2021, 4, 622364. [CrossRef]
Duncan, J.; Chylinski, D.; Mitchell, D.J.; Bhandari, A. Complexity and Compositionality in Fluid Intelligence. Proc. Natl. Acad. Sci. U.S.A. 2017, 114, 5295–5299. [CrossRef]
Barbey, A.K. Network Neuroscience Theory of Human Intelligence. Trends in Cognitive Sciences 2018, 22, 8–20. [CrossRef]
Stemler, S.E.; Naples, A. Rasch Measurement v. Item Response Theory: Knowing When to Cross the Line. Practical Assessment, Research, and Evaluation 2021, 26. [CrossRef]
Epstein, R. The Empty Brain. Aeon 2016.
Carabantes, M. Black-Box Artificial Intelligence: An Epistemological and Critical Analysis. AI & Soc 2020, 35, 309–317. [CrossRef]
Bodria, F.; Giannotti, F.; Guidotti, R.; Naretto, F.; Pedreschi, D.; Rinzivillo, S. Benchmarking and survey of explanation methods for black box models. Data Mining and Knowledge Discovery 2023, 37, 1719–1778.
Cattell, R.B. Theory of Fluid and Crystallized Intelligence: A Critical Experiment. Journal of Educational Psychology 1963, 54, 1–22. [CrossRef]
McGrew, K.S.; Wendling, B.J. Cattell-Horn-Carroll Cognitive-Achievement Relations: What We Have Learned from the Past 20 Years of Research: CHC COG-ACH Relations. Psychol. Schs. 2010, 47, 651–675. [CrossRef]
Flanagan, D.P.; Dixon, S.G. The Cattell-Horn-Carroll Theory of Cognitive Abilities. In Encyclopedia of Special Education; Reynolds, C.R.; Vannest, K.J.; Fletcher-Janzen, E., Eds.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2014; p. ese0431. [CrossRef]
Parr, T.; Pezzulo, G.; Friston, K.J. Active Inference: The Free Energy Principle in Mind, Brain, and Behavior; The MIT Press, 2022. [CrossRef]
Sternberg, R.J. Toward a Triarchic Theory of Human Intelligence. Behav Brain Sci 1984, 7, 269–287. [CrossRef]
Goertzel, B. The Structure of Intelligence: A New Mathematical Model of Mind; Recent Research in Psychology, Springer-Verlag: New York, 1993.
Wang, Y. On Abstract Intelligence: Toward a Unifying Theory of Natural, Artificial, Machinable, and Computational Intelligence. International Journal of Software Science and Computational Intelligence 2009, 1, 1–17. [CrossRef]
Georgiou, G.K.; Guo, K.; Naveenkumar, N.; Vieira, A.P.A.; Das, J. PASS Theory of Intelligence and Academic Achievement: A Meta-Analytic Review. Intelligence 2020, 79, 101431. [CrossRef]
Levin, M. Technological Approach to Mind Everywhere: An Experimentally-Grounded Framework for Understanding Diverse Bodies and Minds. Front. Syst. Neurosci. 2022, 16, 768201. [CrossRef]
Flinn, M.V.; Geary, D.C.; Ward, C.V. Ecological Dominance, Social Competition, and Coalitionary Arms Races. Evolution and Human Behavior 2005, 26, 10–46. [CrossRef]
Roth, G.; Dicke, U. Evolution of the Brain and Intelligence. Trends in Cognitive Sciences 2005, 9, 250–257. [CrossRef]
Sterelny, K. Social Intelligence, Human Intelligence and Niche Construction. Phil. Trans. R. Soc. B 2007, 362, 719–730. [CrossRef]
Reader, S.M.; Hager, Y.; Laland, K.N. The Evolution of Primate General and Cultural Intelligence. Phil. Trans. R. Soc. B 2011, 366, 1017–1027. [CrossRef]
Burkart, J.M.; Schubiger, M.N.; Van Schaik, C.P. The Evolution of General Intelligence. Behav Brain Sci 2017, 40, e195. [CrossRef]
Shreesha, L.; Levin, M. Cellular Competency during Development Alters Evolutionary Dynamics in an Artificial Embryogeny Model. Entropy 2023, 25, 131. [CrossRef]
Spearman, C. "General Intelligence," Objectively Determined and Measured. The American Journal of Psychology 1904, 15, 201, [1412107]. [CrossRef]
Carroll, J.B. Human Cognitive Abilities: A Survey of Factor-Analytic Studies; Cambridge University Press, 1993. [CrossRef]
Conrad, M. Cross-Scale Information Processing in Evolution, Development and Intelligence. Biosystems 1996, 38, 97–109. [CrossRef]
Adams, S.S.; Arel, I.; Bach, J.; Coop, R.; Furlan, R.; Goertzel, B. Mapping the Landscape of Human-Level Artificial General Intelligence. AI Magazine 2012, 33, 25–41. [CrossRef]
Deary, I.J. The Stability of Intelligence From Childhood to Old Age. Curr Dir Psychol Sci 2014, 23, 239–245. [CrossRef]
Chollet, F. On the Measure of Intelligence. arXiv:1911.01547 2019.
Burgoyne, A.P.; Mashburn, C.A.; Tsukahara, J.S.; Engle, R.W. Attention Control and Process Overlap Theory: Searching for Cognitive Processes Underpinning the Positive Manifold. Intelligence 2022, 91, 101629. [CrossRef]
Friston, K.J.; Ramstead, M.J.; Kiefer, A.B.; Tschantz, A.; Buckley, C.L.; Albarracin, M. Designing Ecosystems of Intelligence from First Principles. Collective Intelligence 2024, 3, 26339137231222481. [CrossRef]
Hernández-Orallo, J. The Measure of All Minds: Evaluating Natural and Artificial Intelligence; Cambridge University Press, 2017. [CrossRef]
Babcock, G.; McShea, D.W. Goal Directedness and the Field Concept. Philos. sci. 2023, pp. 1–10; [CrossRef]
Kauffman, S.A. Investigations; Oxford University Press: New York, 2000.
Godfrey-Smith, P. Environmental Complexity and the Evolution of Cognition. In R. Sternberg, & J. Kaufman (Eds), The Evolution of Intelligence; Mahwah: Lawrence Erlbaum, 2002; pp. 233–249.
Pinker, S. The Cognitive Niche: Coevolution of Intelligence, Sociality, and Language. Proc. Natl. Acad. Sci. U.S.A. 2010, 107, 8993–8999. [CrossRef]
Shannon, C.E. A Mathematical Theory of Communication. Bell System Technical Journal 1948, 27, 379–423. [CrossRef]
Gottfredson, L.S. Why g Matters: The Complexity of Everyday Life. Intelligence 1997, 24, 79–132. [CrossRef]
Donaldson-Matasci, M.C.; Bergstrom, C.T.; Lachmann, M. The Fitness Value of Information. Oikos 2010, 119, 219–230. [CrossRef]
Frank, S.A. Natural Selection. V. How to Read the Fundamental Equations of Evolutionary Change in Terms of Information Theory. J of Evolutionary Biology 2012, 25, 2377–2396. [CrossRef]
Adami, C. The Elements of Intelligence. Artificial Life 2023, 29, 293–307. [CrossRef]
McShea, D.W. Perspective: Metazoan Complexity and Evolution: Is There a Trend? Evolution 1996, 50, 477, [2410824]. [CrossRef]
Stanley, K.O.; Miikkulainen, R. Competitive Coevolution through Evolutionary Complexification. Journal of artificial intelligence research 2004, 21, 63–100. [CrossRef]
Baluška, F.; Levin, M. On Having No Head: Cognition throughout Biological Systems. Front. Psychol. 2016, 7, 196518. [CrossRef]
Frank, A.; Grinspoon, D.; Walker, S. Intelligence as a Planetary Scale Process. International Journal of Astrobiology 2022, 21, 47–61. [CrossRef]
Fields, C.; Levin, M. Competency in Navigating Arbitrary Spaces as an Invariant for Analyzing Cognition in Diverse Embodiments. Entropy 2022, 24, 819. [CrossRef]
De Martino, B.; Cortese, A. Goals, Usefulness and Abstraction in Value-Based Choice. Trends in Cognitive Sciences 2023, 27, 65–80. [CrossRef]
Chase, J.M.; Leibold, M.A. Ecological Niches: Linking Classical and Contemporary Approaches; University of Chicago Press, 2003. [CrossRef]
LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [CrossRef]
Rosen, R. A relational theory of biological systems. The Bulletin of Mathematical Biophysics 1958, 20, 245–260. [CrossRef]
Maturana, H. The quest for the intelligence of intelligence. Journal of Social and Biological Systems 1980, 3, 135–148. [CrossRef]
McCarthy, J.; Minsky, M.; Rochester, N.; Shannon, C. A Proposal for the Dartmouth Summer Research Project on Artificial Intelligence August 31, 1955. AI Magazine 2006, 27, 12–14.
Gershman, S.J.; Horvitz, E.J.; Tenenbaum, J.B. Computational Rationality: A Converging Paradigm for Intelligence in Brains, Minds, and Machines. Science 2015, 349, 273–278. [CrossRef]
Scholkopf, B.; Locatello, F.; Bauer, S.; Ke, N.R.; Kalchbrenner, N.; Goyal, A.; Bengio, Y. Toward Causal Representation Learning. Proc. IEEE 2021, 109, 612–634. [CrossRef]
Rosen, R. On Information and Complexity. In Complexity, Language, and Life: Mathematical Approaches; Levin, S.A.; Casti, J.L.; Karlqvist, A., Eds.; Springer Berlin Heidelberg: Berlin, Heidelberg, 1986; Vol. 16, pp. 174–196. Series Title: Biomathematics, . [CrossRef]
Cronin, L.; Krasnogor, N.; Davis, B.G.; Alexander, C.; Robertson, N.; Steinke, J.H.G. The Imitation Game—a Computational Chemical Approach to Recognizing Life. Nat Biotechnol 2006, 24, 1203–1206. [CrossRef]
Hochberg, M.E. A Theory of Intelligences: Concepts, Models, Implications. arXiv:2308.12411 2023.
Horn, J.L.; Cattell, R.B. Age Differences in Fluid and Crystallized Intelligence. Acta Psychologica 1967, 26, 107–129. [CrossRef]
Nisbett, R.E.; Aronson, J.; Blair, C.; Dickens, W.; Flynn, J.; Halpern, D.F.; Turkheimer, E. Intelligence: New Findings and Theoretical Developments. American Psychologist 2012, 67, 130–159. [CrossRef]
Chai, L.R.; Khambhati, A.N.; Ciric, R.; Moore, T.M.; Gur, R.C. Evolution of Brain Network Dynamics in Neurodevelopment. Network Neuroscience 2017, 1, 14–30. [CrossRef]
Salthouse, T. Consequences of Age-Related Cognitive Declines. Annu. Rev. Psychol. 2012, 63, 201–226. [CrossRef]
Hartshorne, J.K.; Germine, L.T. When Does Cognitive Functioning Peak? The Asynchronous Rise and Fall of Different Cognitive Abilities Across the Life Span. Psychol Sci 2015, 26, 433–443. [CrossRef]
Tucker-Drob, E.M.; Brandmaier, A.M.; Lindenberger, U. Coupled Cognitive Changes in Adulthood: A Meta-Analysis. Psychological Bulletin 2019, 145, 273–301. [CrossRef]
Rosen, R. Anticipatory Systems: Philosophical, Mathematical, and Methodological Foundations; Vol. 1, IFSR International Series in Systems Science and Systems Engineering, Springer New York: New York, NY, 2012. [CrossRef]
Brooks, R.A. Intelligence without Representation. Artificial Intelligence 1991, 47, 139–159. [CrossRef]
Kabadayi, C.; Bobrowicz, K.; Osvath, M. The Detour Paradigm in Animal Cognition. Anim Cogn 2018, 21, 21–35. [CrossRef]
Wang, P. On Defining Artificial Intelligence. Journal of Artificial General Intelligence 2019, 10, 1–37. [CrossRef]
Lyon, P. Of What Is “Minimal Cognition” the Half-Baked Version? Adaptive Behavior 2020, 28, 407–424. [CrossRef]
Roli, A.; Jaeger, J.; Kauffman, S.A. How Organisms Come to Know the World: Fundamental Limits on Artificial General Intelligence. Front. Ecol. Evol. 2022, 9, 806283. [CrossRef]
Cohen, J.D.; McClure, S.M.; Yu, A.J. Should I Stay or Should I Go? How the Human Brain Manages the Trade-off between Exploitation and Exploration. Phil. Trans. R. Soc. B 2007, 362, 933–942. [CrossRef]
Mehlhorn, K.; Newell, B.R.; Todd, P.M.; Lee, M.D.; Morgan, K.; Braithwaite, V.A. Unpacking the Exploration–Exploitation Tradeoff: A Synthesis of Human and Animal Literatures. Decision 2015, 2, 191–215. [CrossRef]
Del Giudice, M.; Crespi, B.J. Basic Functional Trade-Offs in Cognition: An Integrative Framework. Cognition 2018, 179, 56–70. [CrossRef]
Maynard Smith, J. Optimization Theory in Evolution. Annu. Rev. Ecol. Syst. 1978, 9, 31–56. [CrossRef]
Emery, N.J.; Clayton, N.S. The Mentality of Crows: Convergent Evolution of Intelligence in Corvids and Apes. Science 2004, 306, 1903–1907. [CrossRef]
Edelman, D.B.; Seth, A.K. Animal Consciousness: A Synthetic Approach. Trends in Neurosciences 2009, 32, 476–484. [CrossRef]
Amodio, P.; Boeckle, M.; Schnell, A.K.; Ostojíc, L.; Fiorito, G.; Clayton, N.S. Grow Smart and Die Young: Why Did Cephalopods Evolve Intelligence? Trends in Ecology & Evolution 2019, 34, 45–56. [CrossRef]
Peraza-Vázquez, H.; Peña-Delgado, A.; Ranjan, P.; Barde, C.; Choubey, A.; Morales-Cepeda, A.B. A Bio-Inspired Method for Mathematical Optimization Inspired by Arachnida Salticidade. Mathematics 2021, 10, 102. [CrossRef]
Mashburn, C.A.; Burgoyne, A.P.; Engle, R.W. Working Memory, Intelligence, and Life Success. In Memory in Science for Society: There Is Nothing As Practical As a Good Theory; OUP, 2023; p. 149.
Smith, J.D.; Couchman, J.J.; Beran, M.J. Animal Metacognition: A Tale of Two Comparative Psychologies. Journal of Comparative Psychology 2014, 128, 115–131. [CrossRef]
Maier, H.; Guillaume, J.; Van Delden, H.; Riddell, G.; Haasnoot, M.; Kwakkel, J. An Uncertain Future, Deep Uncertainty, Scenarios, Robustness and Adaptation: How Do They Fit Together? Environmental Modelling & Software 2016, 81, 154–164. [CrossRef]
Walker, W.; Haasnoot, M.; Kwakkel, J. Adapt or Perish: A Review of Planning Approaches for Adaptation under Deep Uncertainty. Sustainability 2013, 5, 955–979. [CrossRef]
Simon, H.A. Rational Choice and the Structure of the Environment. Psychological Review 1956, 63, 129–138. [CrossRef]
Hayes-Roth, B.; Collinot, A. A Satisficing Cycle for Real-Time Reasoning in Intelligent Agents. Expert Systems with Applications 1994, 7, 31–42. [CrossRef]
Bossaerts, P.; Murawski, C. Computational Complexity and Human Decision-Making. Trends in Cognitive Sciences 2017, 21, 917–929. [CrossRef]
Adami, C. What Is Complexity? BioEssays 2002, 24, 1085–1094. [CrossRef]
Firestone, C. Performance vs. competence in human–machine comparisons. Proceedings of the National Academy of Sciences 2020, 117, 26562–26571. [CrossRef]
Krause, J.; Ruxton, G.D.; Krause, S. Swarm Intelligence in Animals and Humans. Trends in Ecology & Evolution 2010, 25, 28–34. [CrossRef]
Biro, D.; Haslam, M.; Rutz, C. Tool Use as Adaptation. Phil. Trans. R. Soc. B 2013, 368, 20120408. [CrossRef]
McMillen, P.; Levin, M. Collective intelligence: A unifying concept for integrating biology across scales and substrates. Communications Biology 2024, 7, 378. [CrossRef]
Couzin, I.D. Collective Cognition in Animal Groups. Trends in Cognitive Sciences 2009, 13, 36–43. [CrossRef]
Pacala, S.W.; Gordon, D.M.; Godfray, H.C.J. Effects of Social Group Size on Information Transfer and Task Allocation. Evol Ecol 1996, 10, 127–165. [CrossRef]
Lee, E.D.; Flack, J.C.; Krakauer, D.C. Outsourcing Memory Through Niche Construction. arXiv:2209.00476 2022. [CrossRef]
Migliano, A.B.; Vinicius, L. The Origins of Human Cumulative Culture: From the Foraging Niche to Collective Intelligence. Phil. Trans. R. Soc. B 2022, 377, 20200317. [CrossRef]
Henrich, J.; Muthukrishna, M. What Makes Us Smart? Topics in Cognitive Science, 2023. [CrossRef]
Gould, S.J. The Mismeasure of Man; Norton: New York, 1981.
Herrnstein, R.J.; Murray, C.A. The Bell Curve: Intelligence and Class Structure in American Life; Free Press: New York, 1994.
Chiappe, D.; MacDonald, K. The Evolution of Domain-General Mechanisms in Intelligence and Learning. The Journal of General Psychology 2005, 132, 5–40. [CrossRef]
Lazer, D.; Friedman, A. The Network Structure of Exploration and Exploitation. Administrative Science Quarterly 2007, 52, 667–694. [CrossRef]
Gabora, L.; Russon, A. The Evolution of Intelligence. In The Cambridge Handbook of Intelligence; Sternberg, R.J.; Kaufman, S.B., Eds.; Cambridge University Press, 2011; pp. 328–350. [CrossRef]
Plomin, R.; Deary, I.J. Genetics and Intelligence Differences: Five Special Findings. Mol Psychiatry 2015, 20, 98–108. [CrossRef]
Craik, F.I.; Bialystok, E. Cognition through the Lifespan: Mechanisms of Change. Trends in Cognitive Sciences 2006, 10, 131–138. [CrossRef]
Sabb, F.; Burggren, A.; Higier, R.; Fox, J.; He, J.; Parker, D. Challenges in Phenotype Definition in the Whole-Genome Era: Multivariate Models of Memory and Intelligence. Neuroscience 2009, 164, 88–107. [CrossRef]
Savage, J.E.; Jansen, P.R.; Stringer, S.; Watanabe, K.; Bryois, J.; De Leeuw, C.A. Genome-Wide Association Meta-Analysis in 269,867 Individuals Identifies New Genetic and Functional Links to Intelligence. Nat Genet 2018, 50, 912–919. [CrossRef]
Arnold, S.J. Morphology, Performance and Fitness. Am Zool 1983, 23, 347–361. [CrossRef]
Mattar, M.G.; Lengyel, M. Planning in the Brain. Neuron 2022, 110, 914–934. [CrossRef]
Stearns, S.C. Life History Evolution: Successes, Limitations, and Prospects. Naturwissenschaften 2000, 87, 476–486. [CrossRef]
Kaplan, H.; Hill, K.; Lancaster, J.; Hurtado, A.M. A Theory of Human Life History Evolution: Diet, Intelligence, and Longevity. Evol. Anthropol. 2000, 9, 156–185. [CrossRef]
Wong, M.L.; Cleland, C.E.; Arend, D.; Bartlett, S.; Cleaves, H.J.; Demarest, H. On the Roles of Function and Selection in Evolving Systems. Proc. Natl. Acad. Sci. U.S.A. 2023, 120, e2310223120. [CrossRef]
Duéñez-Guzmán, E.A.; Sadedin, S.; Wang, J.X.; McKee, K.R.; Leibo, J.Z. A Social Path to Human-like Artificial Intelligence. Nat Mach Intell 2023, 5, 1181–1188. [CrossRef]
Edelman, G.M.; Gally, J.A. Degeneracy and Complexity in Biological Systems. Proc. Natl. Acad. Sci. U.S.A. 2001, 98, 13763–13768. [CrossRef]
Barrett, H.C.; Kurzban, R. Modularity in Cognition: Framing the Debate. Psychological Review 2006, 113, 628–647. [CrossRef]
Tria, F.; Loreto, V.; Servedio, V.D.P.; Strogatz, S.H. The Dynamics of Correlated Novelties. Sci Rep 2014, 4, 5890. [CrossRef]
Sharma, A.; Czégel, D.; Lachmann, M.; Kempes, C.P.; Walker, S.I.; Cronin, L. Assembly Theory Explains and Quantifies Selection and Evolution. Nature 2023, 622, 321–328. [CrossRef]
Klyubin, A.; Polani, D.; Nehaniv, C. Empowerment: A Universal Agent-Centric Measure of Control. 2005 IEEE Congress on Evolutionary Computation; , 2005; pp. 128–135. [CrossRef]
Pearl, J.; Mackenzie, D. The Book of Why: The New Science of Cause and Effect; Basic Books: New York, 2018.
Frank, S.A. Natural Selection Maximizes Fisher Information. J of Evolutionary Biology 2009, 22, 231–244. [CrossRef]
Zaman, L.; Meyer, J.R.; Devangam, S.; Bryson, D.M.; Lenski, R.E.; Ofria, C. Coevolution Drives the Emergence of Complex Traits and Promotes Evolvability. PLoS Biol 2014, 12, e1002023. [CrossRef]
Li, S.C.; Lindenberger, U.; Hommel, B.; Aschersleben, G.; Prinz, W.; Baltes, P.B. Transformations in the Couplings Among Intellectual Abilities and Constituent Cognitive Processes Across the Life Span. Psychol Sci 2004, 15, 155–163. [CrossRef]
Whiten, A.; Van Schaik, C.P. The Evolution of Animal `Cultures’ and Social Intelligence. Phil. Trans. R. Soc. B 2007, 362, 603–620. [CrossRef]
Flavell, J.H. Metacognition and Cognitive Monitoring: A New Area of Cognitive–Developmental Inquiry. American Psychologist 1979, 34, 906–911. [CrossRef]
Rogers, E.M. Diffusion of Innovations, 5th Edition; Free Press, 2014.
Hochberg, M.E.; Marquet, P.A.; Boyd, R.; Wagner, A. Innovation: An Emerging Focus from Cells to Societies. Phil. Trans. R. Soc. B 2017, 372, 20160414. [CrossRef]
Schnell, A.K.; Amodio, P.; Boeckle, M.; Clayton, N.S. How Intelligent Is a Cephalopod? Lessons from Comparative Cognition. Biological Reviews 2021, 96, 162–178. [CrossRef]
Laland, K.; Matthews, B.; Feldman, M.W. An Introduction to Niche Construction Theory. Evol Ecol 2016, 30, 191–202. [CrossRef]
Brandon, R.; Antonovics, J. The Coevolution of Organism and Environment. In Concepts and Methods in Evolutionary Biology; Cambridge University Press: New York, N.Y, 1996; pp. 161–178.
Calvo, P.; Baluška, F. Conditions for Minimal Intelligence across Eukaryota: A Cognitive Science Perspective. Front. Psychol. 2015, 6, 155178. [CrossRef]
Kaufmann, R.; Gupta, P.; Taylor, J. An Active Inference Model of Collective Intelligence. Entropy 2021, 23, 830. [CrossRef]
Leonard, N.E.; Levin, S.A. Collective Intelligence as a Public Good. Collective Intelligence 2022, 1, 263391372210832. [CrossRef]
Rueffler, C.; Hermisson, J.; Wagner, G.P. Evolution of Functional Specialization and Division of Labor. Proc. Natl. Acad. Sci. U.S.A. 2012, 109, E326–E335. [CrossRef]
West, S.A.; Fisher, R.M.; Gardner, A.; Kiers, E.T. Major Evolutionary Transitions in Individuality. Proc. Natl. Acad. Sci. U.S.A. 2015, 112, 10112–10119. [CrossRef]
Hochberg, M.E.; Rankin, D.J.; Taborsky, M. The Coevolution of Cooperation and Dispersal in Social Groups and Its Implications for the Emergence of Multicellularity. BMC Evol Biol 2008, 8, 238. [CrossRef]
Gorelick, R.; Bertram, S.M.; Killeen, P.R.; Fewell, J.H. Normalized Mutual Entropy in Biology: Quantifying Division of Labor. The American Naturalist 2004, 164, 677–682. [CrossRef]
Frenkel, D. Order through Entropy. Nature Mater 2015, 14, 9–12. [CrossRef]
Gebauer, D.; Gale, J.D.; Cölfen, H. Crystal Nucleation and Growth of Inorganic Ionic Materials from Aqueous Solution: Selected Recent Developments, and Implications. Small 2022, 18, 2107735. [CrossRef]
Morowitz, H.J. The Emergence of Everything: How the World Became Complex; Oxford University Press: New York, 2002.
Smith, E.; Morowitz, H.J. The Origin and Nature of Life on Earth: The Emergence of the Fourth Geosphere; Cambridge University Press, 2016. [CrossRef]
Roth, G. Convergent Evolution of Complex Brains and High Intelligence. Phil. Trans. R. Soc. B 2015, 370, 20150049. [CrossRef]
Dussutour, A.; Ma, Q.; Sumpter, D. Phenotypic Variability Predicts Decision Accuracy in Unicellular Organisms. Proc. R. Soc. B. 2019, 286, 20182825. [CrossRef]
Calvo, P.; Gagliano, M.; Souza, G.M.; Trewavas, A. Plants Are Intelligent, Here’s How. Annals of Botany 2020, 125, 11–28. [CrossRef]
Reber, A.S.; Baluška, F.; Miller, W. The Sentient Cell: The Cellular Foundations of Consciousness; Oxford University Press: New York, 2023.
Chevin, L.M.; Hoffmann, A.A. Evolution of Phenotypic Plasticity in Extreme Environments. Phil. Trans. R. Soc. B 2017, 372, 20160138. [CrossRef]
Sinz, F.H.; Pitkow, X.; Reimer, J.; Bethge, M.; Tolias, A.S. Engineering a Less Artificial Intelligence. Neuron 2019, 103, 967–979. [CrossRef]
Lachmann, M.; Walker, S. Life ≠ Alive. Aeon 2019.
Bengio, Y.; Hinton, G.; Yao, A.; Song, D.; Abbeel, P.; Darrell, T.; Harari, Y.N.; Zhang, Y.Q.; Xue, L.; Shalev-Shwartz, S.; Hadfield, G.; Clune, J.; Maharaj, T.; Hutter, F.; Baydin, A.G.; McIlraith, S.; Gao, Q.; Acharya, A.; Krueger, D.; Dragan, A.; Torr, P.; Russell, S.; Kahneman, D.; Brauner, J.; Mindermann, S. Managing extreme AI risks amid rapid progress. Science 2024, 384, 842–845. [CrossRef]
Shadmehr, R.; Smith, M.A.; Krakauer, J.W. Error Correction, Sensory Prediction, and Adaptation in Motor Control. Annu. Rev. Neurosci. 2010, 33, 89–108. [CrossRef]
Metcalfe, J. Learning from Errors. Annu. Rev. Psychol. 2017, 68, 465–489. [CrossRef]
Chu, J.; Schulz, L.E. Play, Curiosity, and Cognition. Annu. Rev. Dev. Psychol. 2020, 2, 317–343. [CrossRef]
Gibson, K. Tools, Language and Intelligence: Evolutionary Implications. Man 1991, 26, 255, [2803831]. [CrossRef]
Tennie, C.; Call, J.; Tomasello, M. Ratcheting up the Ratchet: On the Evolution of Cumulative Culture. Phil. Trans. R. Soc. B 2009, 364, 2405–2415. [CrossRef]
Pagel, M. Adapted to Culture. Nature 2012, 482, 297–299. [CrossRef]
Kaplan, H.S.; Robson, A.J. The Emergence of Humans: The Coevolution of Intelligence and Longevity with Intergenerational Transfers. Proc. Natl. Acad. Sci. U.S.A. 2002, 99, 10221–10226. [CrossRef]
Laland, K.; Seed, A. Understanding Human Cognitive Uniqueness. Annu. Rev. Psychol. 2021, 72, 689–716. [CrossRef]
Gibson, K.R. Evolution of Human Intelligence: The Roles of Brain Size and Mental Construction. Brain Behav Evol 2002, 59, 10–20. [CrossRef]
Muthukrishna, M.; Doebeli, M.; Chudek, M.; Henrich, J. The Cultural Brain Hypothesis: How Culture Drives Brain Expansion, Sociality, and Life History. PLoS Comput Biol 2018, 14, e1006504. [CrossRef]
Sternberg, R.J. Culture and Intelligence. American Psychologist 2004, 59, 325–338. [CrossRef]
Tomasello, M. Cultural Transmission: A View from Chimpanzees and Human Infants. Journal of Cross-Cultural Psychology 2001, 32, 135–146. [CrossRef]
Brinkmann, L.; Baumann, F.; Bonnefon, J.F.; Derex, M.; Müller, T.F.; Nussberger, A.M. Machine Culture. Nat Hum Behav 2023, 7, 1855–1868. [CrossRef]
Krakauer, D.; Bertschinger, N.; Olbrich, E.; Flack, J.C.; Ay, N. The Information Theory of Individuality. Theory Biosci. 2020, 139, 209–223. [CrossRef]
Rainey, P.B. Major Evolutionary Transitions in Individuality between Humans and AI. Phil. Trans. R. Soc. B 2023, 378, 20210408. [CrossRef]
Perreault, C. The Pace of Cultural Evolution. PLoS ONE 2012, 7, e45150. [CrossRef]
Lee, E.D.; Kempes, C.P.; West, G.B. Idea Engines: Unifying Innovation & Obsolescence from Markets & Genetic Evolution to Science. Proc. Natl. Acad. Sci. U.S.A. 2024, 121, e2312468120. [CrossRef]
Cazzolla Gatti, R.; Koppl, R.; Fath, B.D.; Kauffman, S.; Hordijk, W.; Ulanowicz, R.E. On the Emergence of Ecological and Economic Niches. J Bioecon 2020, 22, 99–127. [CrossRef]

Figure 2. The intelligence niche. Shown are representations borrowed from the ecological and evolutionary sciences, whereby the fundamental niche of a system (or a species) is the set of possible conditions for which the population can persist. Conditions include contexts, environments and goal types. The realized niche is the set of conditions under which the individual or population actually operates due to limited contexts, goal types/choices, and environments experienced. The fundamental intelligence niche can be extended via some combination of transmission (learning, experience) or system evolution. Proxies can extend the realized niche, either within the fundamental niche (augmentation of existing capacities) or through the invention of new niches. New niches therefore emerge as a system innovation (e.g., cognition, language...) or extension of the individual system (e.g., social, technology...), possibly resulting in a discontinuity or transition in intelligence. T - E: transmission and evolution.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

419

Views

601

Comments

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Theory of Intelligences

Abstract

Keywords:

Subject:

1. Introduction

2. The Idea

3. A Basic Framework

3.1. Challenges and Abilities

4. Modelling The Theory of Intelligences

4.1. Modelling Solving

4.2. Modelling Planning

4.3. Intelligences

4.4. A General Equation

4.5. Transmission and Evolution

5. Discussion

5.1. Predictions

5.2. Speculations

5.2.1. Transitions in Intelligence?

5.2.2. From Crystals to Humans

Funding

Acknowledgments

References

MDPI Initiatives

Important Links

Subscribe