Improving Pitch Rate Control Performance of an F-16 Aircraft Using Fractional Order Direct-MRAC Adaptive Control Instead of Using the Classic Direct-MRAC Adaptive Control

1. Introduction

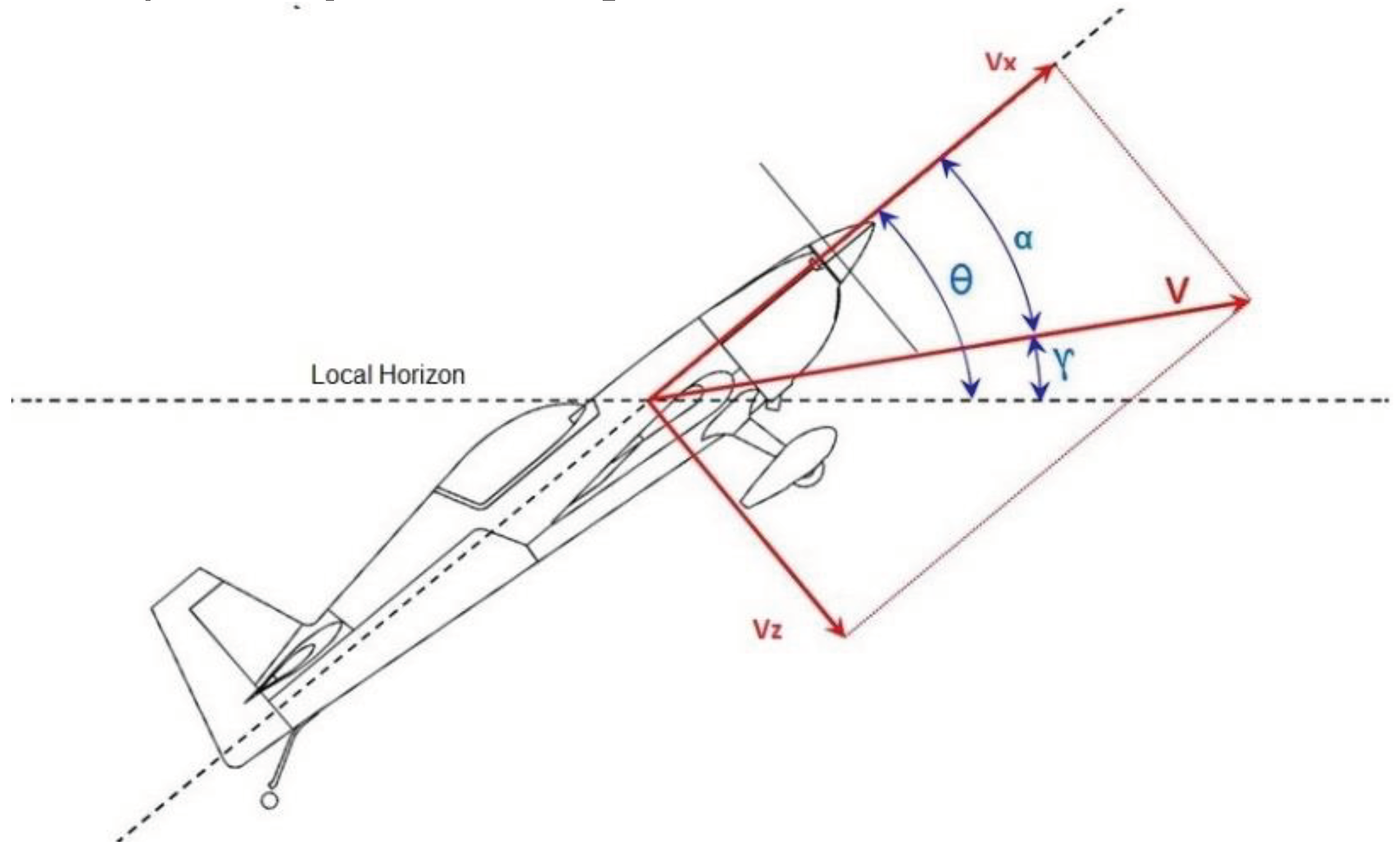
The pitch rate $q\left(t\right)=\dot{\theta }\left(t\right)$ control of an aircraft (see Figure 2.1 for angles meaning) is the main system for tracking of a target by means of a combat aircraft and landing approach [1]. In addition, the pitch rate can be useful for estimating the attitude or pitch angle of an airplane because the pitch angle is the integral of the pitch rate. Therefore, is important to design a well-suited control system. In this work, we compare the classical or integer order direct model reference adaptive control (IO-DMRAC) with its fractional order counterparts (FO-DMRAC). The mathematical F-16 longitudinal model used in this paper is a second-order one [2] which considers the short-period oscillations mode neglecting the phugoid mode (large period oscillations) because the first mode (high-frequency oscillation), is more difficult to control by the pilot. Our interest is to show the lack of oscillation during the transient period using FO-DMRAC than the classical or integer order direct model reference adaptive controller (IO-DMRAC).

Very few adaptive control attempts are made for controlling the pitch rate of an aircraft, whose adaptive laws are of FO, not to mention any.

In [2], the longitudinal control of an F-16 is analyzed using a combined MRAC control technique.

By the other hand, small planes basically use PID controllers because of the easy implementation [3,4,5,6,7,8]. The main disadvantage is that PID controllers lack adaptation capabilities in case of plant parametric variations, because of the PID control parameters are constants, but an aircraft flight dynamic is variant.

In [9] a MRAC approach for the control of the longitudinal model of an F-15 aircraft is used and the only fractional term, is a filter that approximate the plant model. Moreover, additional blocks are added doing the implementation more complex.

Finally, the paper is structured as follows. In Section 2, the F-16 aircraft model is presented for a specific flight condition (at sea level) [2]. Section 3 shows the implementation of the DMRAC control system. In Section 4, basic concepts of FO calculus are shown that will be used in this comparative analysis. Also, we make use of a lemma that relax some stability condition, which was used in the longitudinal pitch angle control of a civil airplane [10]. The simulation results are presented in Section 5. Finally, the conclusion of this work is presented in Section 6.

2. Longitudinal Model and Flight Conditions

The aircraft model considers a straight and level flight condition [2]. Figure 1 shows the main angles involved for the study of longitudinal airplane models and control.

where θ is the pitch angle, γ is the flight path angle, V is the wind speed relative to the aircraft and α is the angle of attack (AoA).

A simple model, considering the longitudinal short period can be written in matrix form as [2]

$$\left[\begin{array}{c}\dot{\alpha }\left(t\right)\\ \dot{q}\left(t\right)\end{array}\right]=\left[\begin{array}{cc}\frac{Z_{\alpha }}{V}& \frac{Z_q}{V}\\ M_{\alpha }& M_q\end{array}\right]\left[\begin{array}{c}\alpha \left(t\right)\\ q\left(t\right)\end{array}\right]+\left[\begin{array}{c}\frac{Z_{{\delta }_e}}{V}\\ M_{{\delta }_e}\end{array}\right]{\delta }_e\left(t\right)$$

(1)

where $q\left(t\right)=\dot{\theta }\left(t\right)$ is the pitch rate (output), ${\delta }_e\left(t\right)$ is the elevator deflection angle (input), V is the air trimmed speed, $\left(Z_{\alpha }, Z_q, Z_{{\delta }_e}\right)$ and $\left(M_{\alpha }, M_q, M_{{\delta }_e}\right)$ are the partial derivatives of the aerodynamic vertical force $Z$ and the pitch moment $M$ with respect to $\left(\alpha ,q,{\delta }_e\right)$ respectively. The coefficients matrix values of Equation (1) were taken from [2].

Table 1 shows the trimmed values used in this model.

Replacing the numeriacl values to Equation (1) we obtain

$$\left[\begin{array}{c}\dot{\alpha }\left(t\right)\\ \dot{q}\left(t\right)\end{array}\right]=\left[\begin{array}{cc}-\mathrm{1,0189}& \mathrm{0,9051}\\ \mathrm{0,8223}& -\mathrm{1,0774}\end{array}\right]\left[\begin{array}{c}\alpha \left(t\right)\\ q\left(t\right)\end{array}\right]+\left[\begin{array}{c}-\mathrm{0,0022}\\ -\mathrm{0,1756}\end{array}\right]{\delta }_e\left(t\right)y\left(t\right)=\left[\begin{array}{cc}0& 1\end{array}\right]\left[\begin{array}{c}\alpha \left(t\right)\\ q\left(t\right)\end{array}\right]$$

(2)

where $u\left(t\right)={\delta }_e\left(t\right)$ and $y\left(t\right)=q\left(t\right)=\acute{\theta }\left(t\right)$ are the input and output system respectively.

Then, the transfer function of interest will be

$$W_p\left(s\right)=\frac{q\left(s\right)}{{\delta }_e\left(s\right)}$$

(3)

Therefore, according to Equation (2), the transfer function $W_p\left(s\right)$, imposing null initial conditions, has the form

$$W_p\left(s\right)=C(sI-A{)}^{-1}B+D$$

(4)

where $A=\left[\begin{array}{cc}-\mathrm{1,0189}& \mathrm{0,9051}\\ \mathrm{0,8223}& -\mathrm{1,0774}\end{array}\right]$, $B=\left[\begin{array}{c}-\mathrm{0,0022}\\ -\mathrm{0,1756}\end{array}\right]$, $C=\left[\begin{array}{cc}0& 1\end{array}\right]$ and $D=0$.

Then, the transfer function, between the pitch rate $q\left(t\right)=\dot{\theta }\left(t\right)$ (the output) and ${\delta }_e\left(t\right)$ (the input), is given by

$$W_p\left(s\right)=\frac{q\left(s\right)}{{\delta }_e\left(s\right)}=C(sI-A{)}^{-1}B+D$$

(5)

$$W_p\left(s\right)=\frac{q\left(s\right)}{{\delta }_e\left(s\right)}=\frac{0.175s+0.1807}{s^2+2.096s+0.3535}$$

(6)

or equivalently,

$$W_p\left(s\right)=\frac{q\left(s\right)}{{\delta }_e\left(s\right)}=0.175\frac{s+1.0326}{s^2+2.096s+0.3535} .$$

(7)

which is a second order ($n=2$) transfer function whose relative degree is equal to 1 ($n^{*}=1$). The high frequency plant gain $k_p=0.175$. Also, $Z_p\left(s\right)=\left(s+1.0326\right)$ and $R_p\left(s\right)=s^2+2.096s+0.3535$ are the plant numerator and denominator respectively.

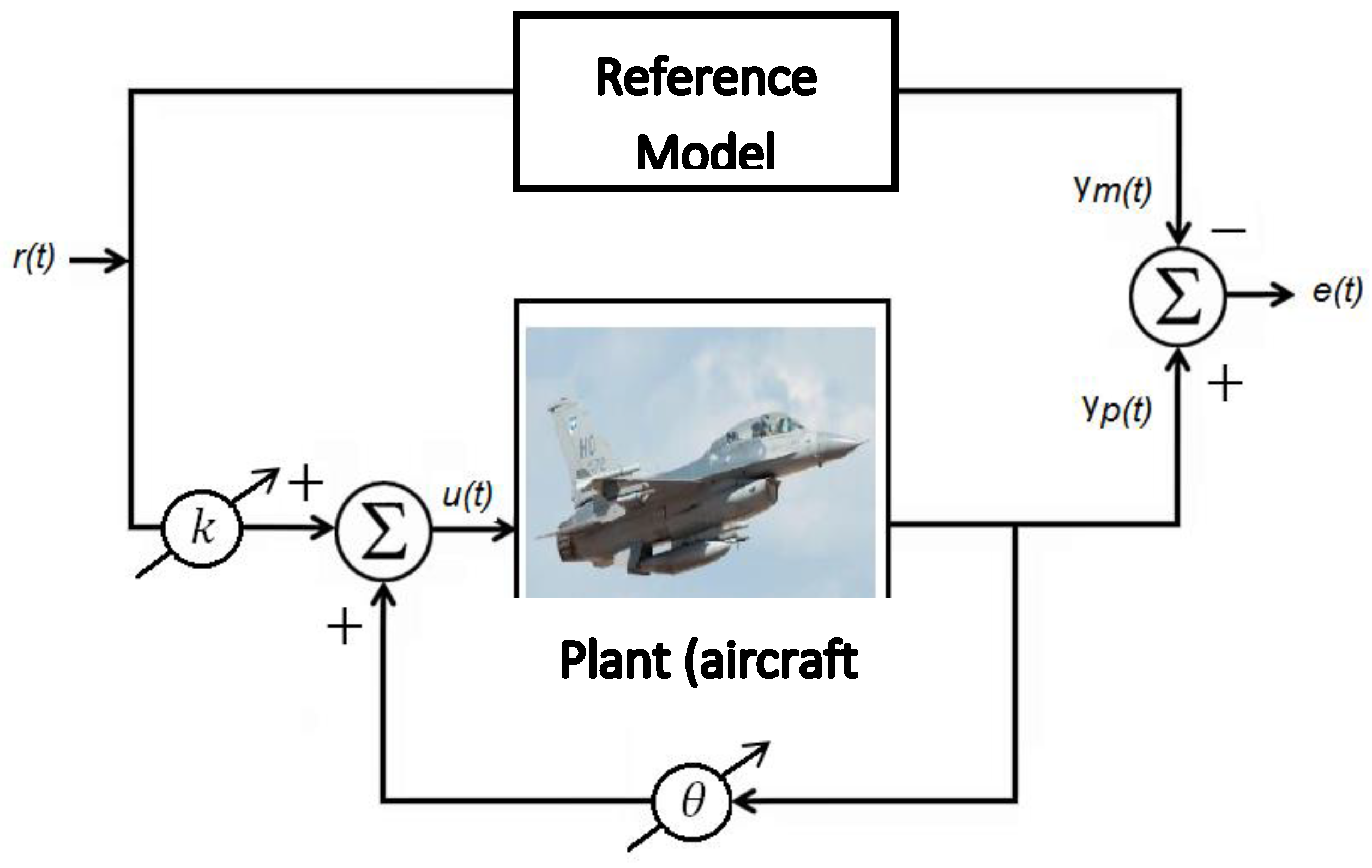
3. Control Model System

Figure 2 shows a general block diagram of the DMRAC control system, in which the control parameters and $\theta$ and $k$, are adjusted adaptively to keep the output control error $e\left(t\right)$ as small as possible.

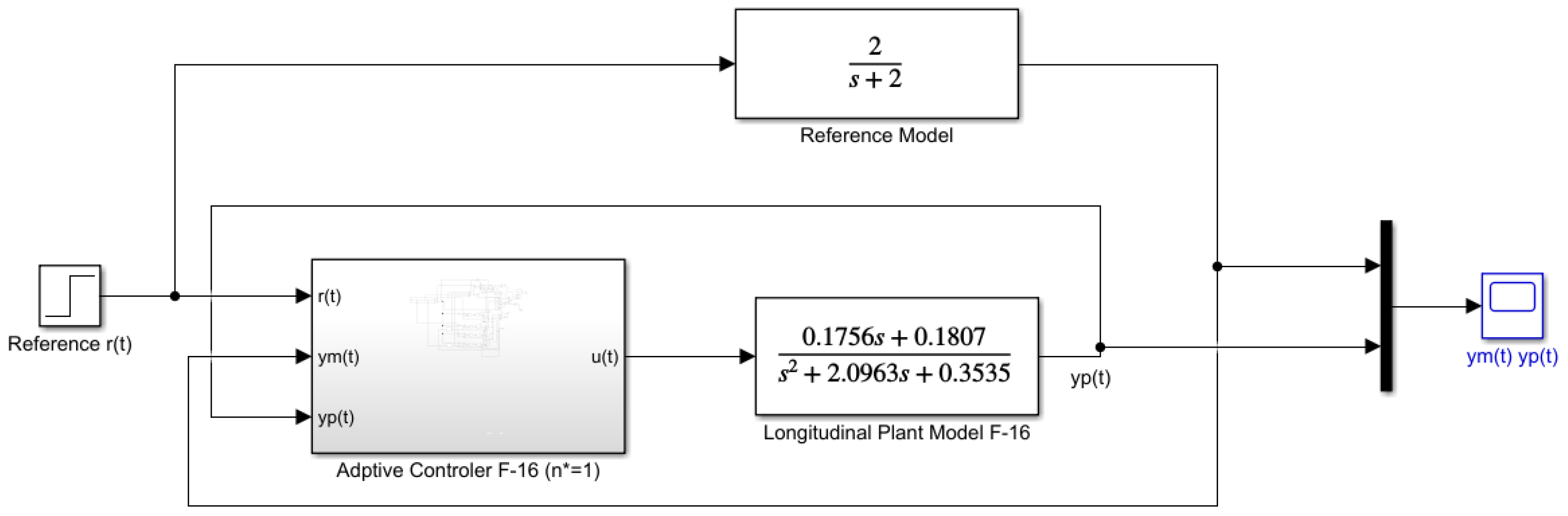
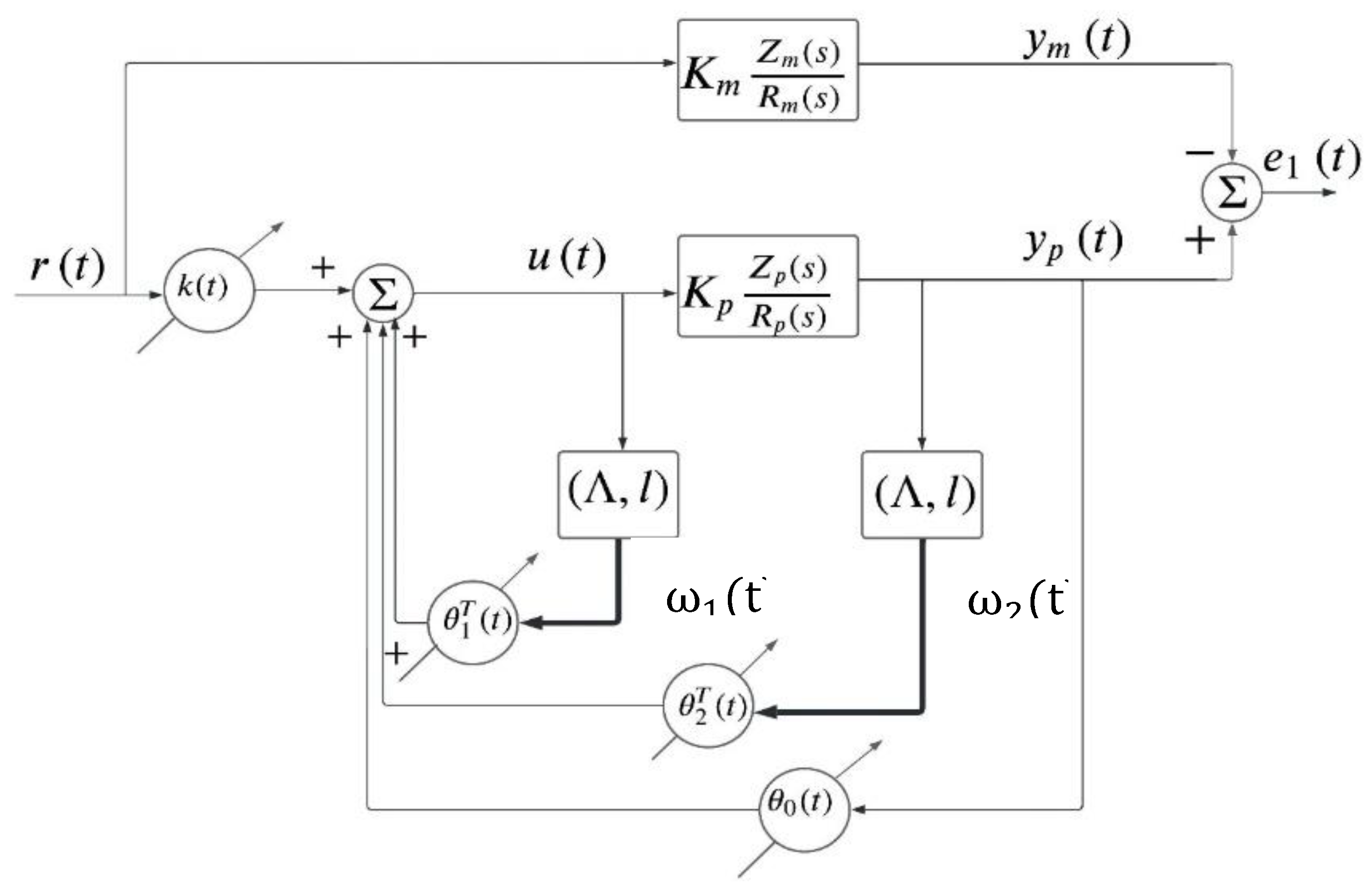
Figure 3 shows the Simulink DMRAC block diagram implemented for the simulations analysis. Also, the well-known DMRAC controller block diagram can be seen in Figure 4 [13]. The model transfer function was chosen as $W_m=\frac{2}{s+2}$. One could choose another transfer function ($W_m=\frac{1}{s+1}$ for instance), nevertheless, because we want a fast response, we used $W_m=\frac{2}{s+2}$.

4. Fractional Calculus Preliminaries

In what follows, by no means exhaustive, we present some basic definitions of the fractional order Integral and derivative respectively [14,15]

Definition 1

[14]: The Riemann-Liouville fractional integral of order $\alpha >0$ of a function $f\left(t\right)\in \mathbb{R}$ is defined by

$$I_{t_0}^{\alpha }f\left(t\right)=\frac{1}{\Gamma \left(\alpha \right)}{\int }_{t_0}^t\frac{f\left(\tau \right)}{(t-\tau {)}^{1-\alpha }}d\tau ,t>t_0 \mathrm{and}\mathcal{R}e\left(\alpha \right)>0,$$

(8)

where $\mathsf{\Gamma }\left(\alpha \right)$ is the Gamma function defined as

$$\mathsf{\Gamma }\left(\alpha \right)={\int }_0^{\infty }{t}^{\alpha -1}{e}^{-t}dt .$$

(9)

Definition 2

[14]: Let $\mathsf{\alpha }\ge 0$ and $\left[\mathbf{n}\right]=\mathsf{\alpha }$. The Caputo fractional derivative of order $\alpha$ of a function $f\left(t\right)\in \mathbb{R}$ is defined as

$${}_{t_0}{}^C{D}_t^{\alpha }f\left(t\right)=\frac{1}{\mathsf{\Gamma }\left(n-\alpha \right)}{\int }_{t_0}^t\frac{f^{\left(n\right)}\left(\tau \right)}{(t-\tau {)}^{\alpha -n+1}}d\tau ;{\mathrm{a}\mathrm{s}\mathrm{l}\mathrm{o}\mathrm{n}\mathrm{g}\mathrm{a}\mathrm{s}f}^{\left(n\right)}\in L_1\left[t_0,t\right].$$

(10)

Lemma 1

[16,17,18]: Let $\mathbf{e}\left(\mathbf{t}\right)\in {\mathbb{R}}^{\mathbf{n}}$ be a vector of differentiable functions. Then, $\forall t\ge t_0$, it is true that

$${}_{t_0}{}^C{D}_t^{\alpha }\left\{e^T\left(t\right)Pe\left(t\right)\right\}\le 2e^T\left(t\right)P{}_{t_0}{}^C{D}_t^{\alpha }e\left(t\right), \forall \alpha \in \left(\mathrm{0,1}\right],$$

where $P\in {\mathbb{R}}^{nxn}$ is a positive definite symmetric square matrix of constant coefficients. A proof of this Lemma can be found in [17].

Theorem 1:

Let the state error$e\left(t\right)$and the output error$e_1\left(t\right)$be represented by Equation (11),

$${}_{t_0}{}^C{D}_t^{\beta }e\left(t\right)=A_{mn}e\left(t\right)+b_{mn}\left[{\varphi }^T\left(t\right)\omega \left(t\right)\right], e\left(t_0\right)=e_0,e_1\left(t\right)=k_p{h}_{mn}^{T}e\left(t\right), { e}_1\left(t_0\right)=e_{10},$$

(11)

where $A_{mn}\in {\mathbb{R}}^{nxn}$ is a Hurwitz matrix and provided that $Q=Q^T>0\in {\mathbb{R}}^{nxn}$, there exists a matrix $P=P^T>0\in {\mathbb{R}}^{nxn}$ such that

$$A_{mn}^{T}P+P{A}_{mn}=-Q, P{b}_{mn}=h_{mn}{k}_p.$$

whose adaptive adjustment laws, to estimate the unknown controller parameters, are given by

$${}_{t_0}{}^C{D}_t^{\alpha }\varphi \left(t\right)={}_{t_0}{}^C{D}_t^{\alpha }\theta \left(t\right)=-\gamma sgn\left(k\right)e_1\left(t\right)\omega \left(t\right), \varphi \left(t_0\right)={\varphi }_0$$

(12)

with $\alpha <\beta$ and $\alpha \in \left(\mathrm{0,1}\right]$. Then, assuming that $e\left(t\right)$ and $\varphi \left(t\right)$ are differentiable and uniformly continuous functions, it is guaranteed that

a)

The parametric error $\varphi \left(t\right)$, the state error $e\left(t\right)$ and the output error $e_1\left(t\right)$ remain bounded for all time.

b)

Moreover, if the auxiliary signal $\omega \left(t\right)$ is bounded, then ${}_{t_0}{}^C{D}_t^{\alpha }\varphi \left(t\right)$ and ${}_{t_0}{}^C{D}_t^{\beta }e\left(t\right)$ also remain bounded.

c)

The mean value of the squared norm of the state error $\overline{{‖e\left(t\right)‖}^2}$ is $o\left(t^{\epsilon -\alpha }\right)$ $\forall \epsilon >0$,

or equivalently $\underset{t\to \infty }{\lim }\left[t^{\alpha -\epsilon }\frac{\underset{t_0}{\overset{t}{\int }}{e\left(\tau \right)}^{2}d\tau }{t}\right]=0$, $\forall \epsilon >0$ where $o\left(t^{\epsilon -\alpha }\right)$ means that the speed of converges to zero is higher than $t^{-\alpha }$. The demonstration of this theorem is available in [19].

From Theorem 1, since $e_1\left(t\right)=h_{mn}^{T}e\left(t\right)$ with $h_{mn}^T$ a constant vector, then, the control error $e_1\left(t\right)$ also will be $o\left(t^{\epsilon -\alpha }\right)$ $\forall \epsilon >0$.

If (c) holds, it must also hold for the mean value of the square norm of $e_1\left(t\right)$, since $e_1\left(t\right)=h_{mn}^{T}e\left(t\right)$ with $h_{mn}^T$ a vector whose components are constants.

The next lemma (Lemma 2), relax the hypothesis (b) imposed from Theorem 1. A proof of this lemma can be found in [10].

Lemma 2:

Let us consider an $n$ order linear system of relative degree $n^{*}=1$ whose fractional adaptive laws are given by

$${}_{t_0}{}^C{D}_t^{\alpha }\varphi \left(t\right)={}_{t_0}{}^C{D}_t^{\alpha }\theta \left(t\right)=-\gamma e_1\left(t\right)\omega \left(t\right), \varphi \left(t_0\right)=0,$$

and the error equation is given by (in this case, $\beta =1$ with $\beta >\alpha$).

$$\dot{e}\left(t\right)=A_{mn}e\left(t\right)+b_{rp}\left[\varphi \left(t\right)\omega \left(t\right)\right], e\left(t_0\right)=e_0,e_1\left(t\right)=h_{mn}^{T}e\left(t\right), { e}_1\left(t_0\right)=e_{10},$$

(13)

where all the terms of the Equations 13 are of appropriated dimensions with $A_{mn}$ Hurwitz and the reference model is of the same plant relative degree ($n^{*}=1$), then, the auxiliary signal $\omega \left(t\right)$ will also be bounded.

Furthermore, as the auxiliary signal $\omega \left(t\right)$ is bounded and because of Theorem 1 guarantees (c), then the squared norm of the output error ${\left|e_1\left(t\right)\right|}^2$, also tend to 0 as t tends to $\infty$. Therefore, the stability of the proposed FO-DMRAC is guaranteed.

4.1. FO-DMRAC Algorithm

When $n^{*}=1$, the only equation that change in the case of the FO-DMRAC algorithm, is the control parameter adaptive law (remember that the plant and the error equation are of integer order), therefore, in the classical case or IO-DMRAC, the adaptive law is given by

$$\dot{\theta }\left(t\right)=\dot{\varphi }\left(t\right)=-sgn\left(k_p\right)e_1\left(t\right)\omega \left(t\right)$$

(14)

On the other hand, for the FO-DMRAC case, the adaptive law become

$${}_{t_0}{}^C{D}_t^{\alpha }\theta \left(t\right)={}_{t_0}{}^C{D}_t^{\alpha }\varphi \left(t\right)=-sgn\left(k_p\right)e_1\left(t\right)\omega \left(t\right)$$

(15)

where $k_p=0.175$ (see Equation 7), therefore, the $sgn\left(k_p\right)=1$.

Finally, the control is given by

$$u\left(t\right)={\theta }^T\left(t\right)\omega \left(t\right)$$

(16)

5. Simulations

Simulations were performed using Matlab & Simulink [20]. Furthermore, the pitch rate initial conditions were set to zero for both cases (integer and fractional order controllers).

Table 2 shows a detailed setting of the FO-DMRAC and IO-DMRAC controllers for simulations purpose.

there ${\mathsf{\Gamma }}_i$ and ${\mathsf{\Gamma }}_j$ are diagonal matrices of adaptive gains. For the implementation of the fractional adaptive laws, the NID block based on the Oustaloup method were used [21,22].

5.1. IO-DMRAC v/s FO-DMRAC using PSO Algorithm

In this section, we compare the simulations results of using FO-DMRAC versus the classical or IO-DMRAC controller. Also, in both cases, we use the Particle Swarm Optimization (PSO) technique [23] assuring the best behavior for both cases. The numbers of particles used were 50 considering 50 iterations. Of course, any other optimization technic can be used to determine the adaptive gains $\gamma \text{'}s$ and derivative orders $\alpha \text{'}s$.

5.2. Simulation Controller Results

The most important objective is minimizing the control error, therefore, the objective function used to be optimized was defined as

$$J={\omega }_e{\int }_{t_0=0}^t{e}_1^2\left(t\right)dt$$

(17)

where $e_1\left(t\right)$ is the control error, ${\omega }_e$ is a weighted parameter and the reference input signal is the unit step.

Remark 1.

Equation 17 was chosen as the objective function (ISE index) which is a simple index but in the case of a combat aircraft, it is a good election since the most important issue is to minimize the control error as fast as possible in contrast with having minimum control effort or fuel efficiency. Nevertheless, it should not be forgotten that the objective function can be chosen by the designer.

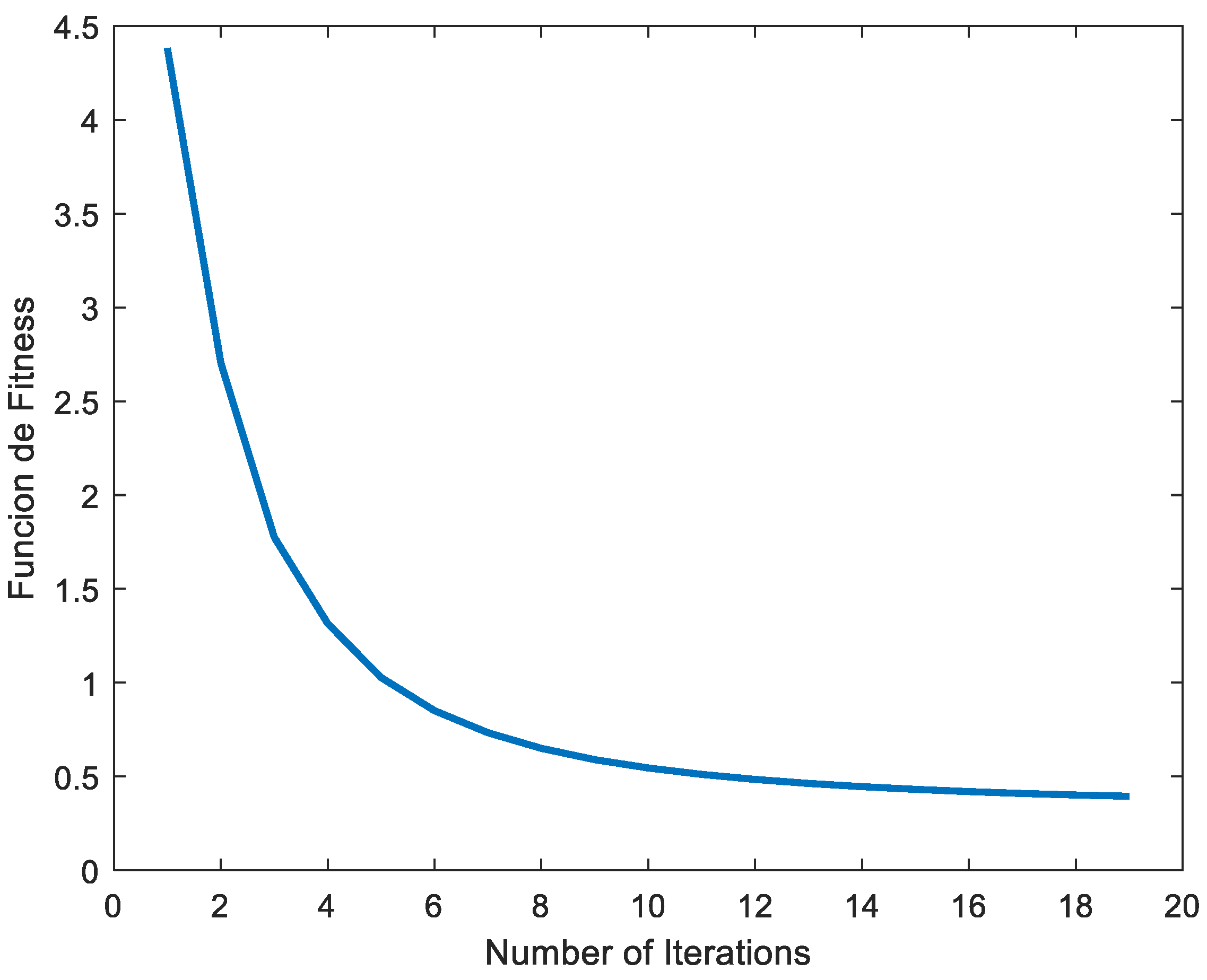
Figure 5 shows the objective function $J$ using the PSO algorithm versus the number of iterations.

The optimal parameters values obtained for the IO-DMRAC case were

$${\gamma }_k=\mathrm{605,4839}{\gamma }_1=\mathrm{248,9360}{\gamma }_0=\mathrm{60,2778}{\gamma }_2=\mathrm{301,4298}$$

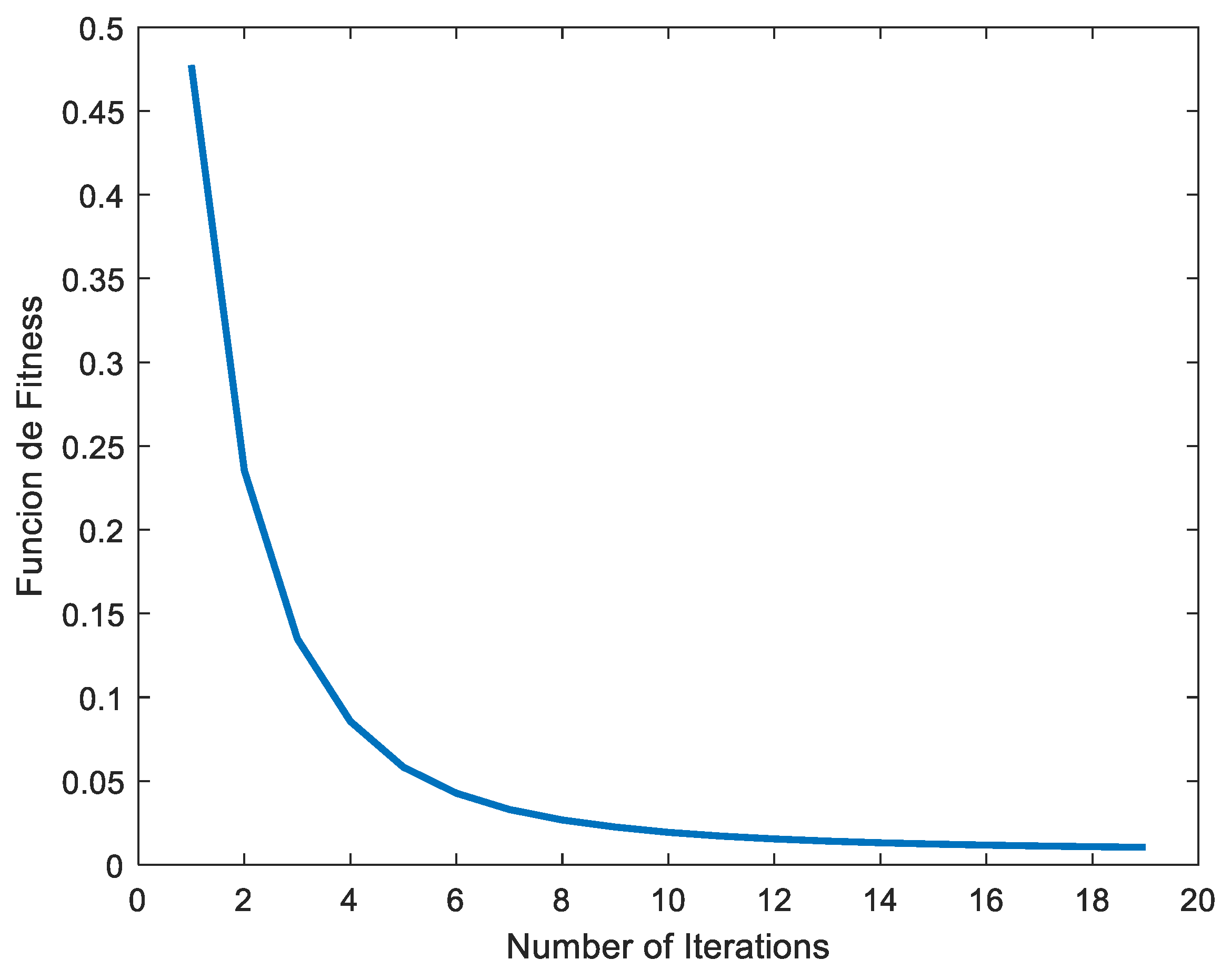
In the same way, Figure 6 shows the evolution of the objective function $J$ for the FO-DMRAC case.

Therefore, the optimal parameters obtained, for the FO-DMRAC case, were

$${\gamma }_k=\mathrm{477,3457}$$

From Figure 5 and Figure 6, it can be observed a faster convergence rate to a stable value of lower magnitude of the objective function in the FO case (Figure 6) compared to the IO one (Figure 5). Therefore, a better controller system behavior could be expected for the FO case.

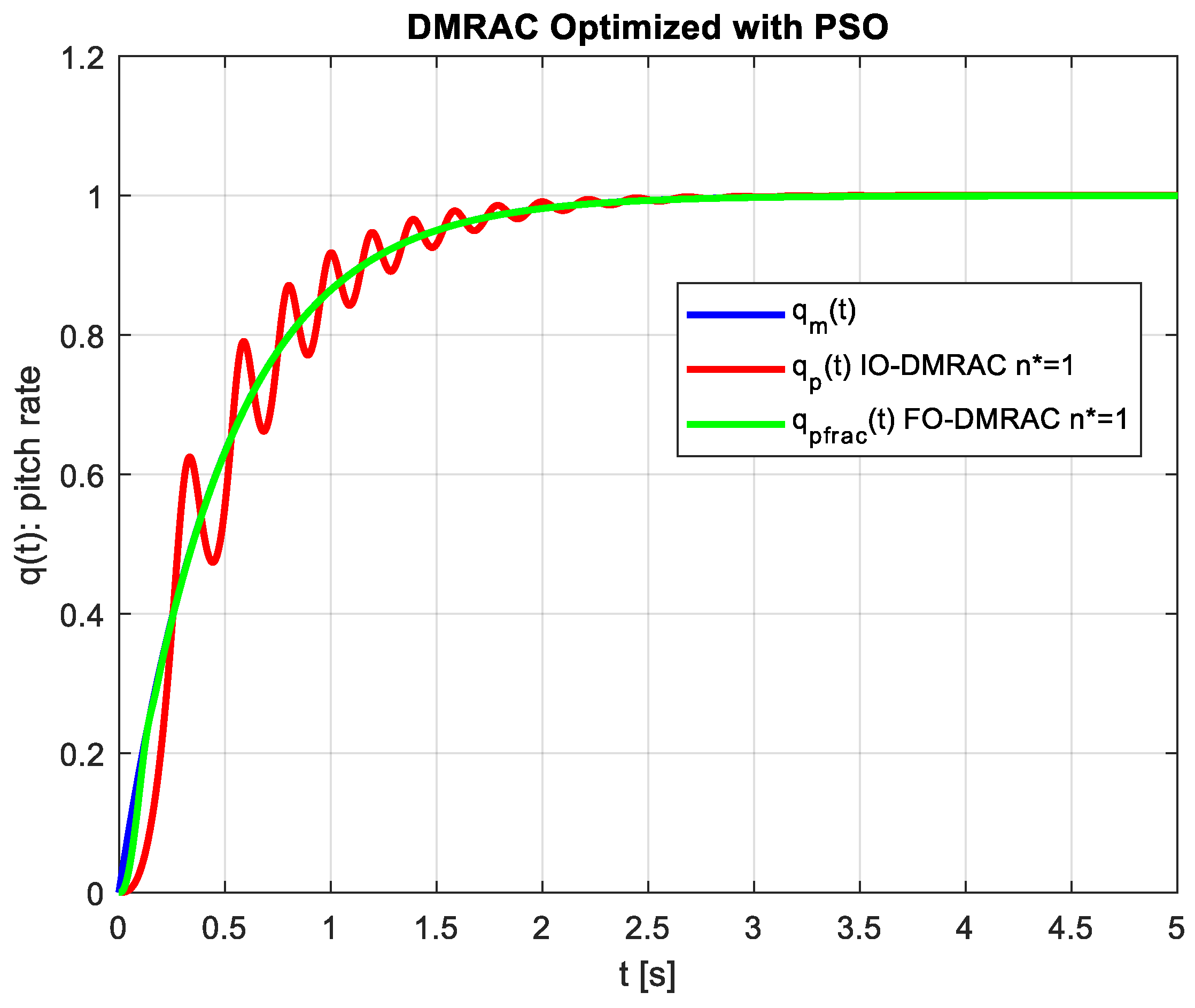
Figure 7 shows the behavior of both controllers. The reference signal (blue color) is depicted besides the outputs of the controlled systems. It is evident the better behavior of the Fractional Order controller (green color signal) which output signal is almost identical to the reference model signal without oscillations. In contrast, the Integer Order controller case (red color signal) present an evident oscillatory behavior during the transient period.

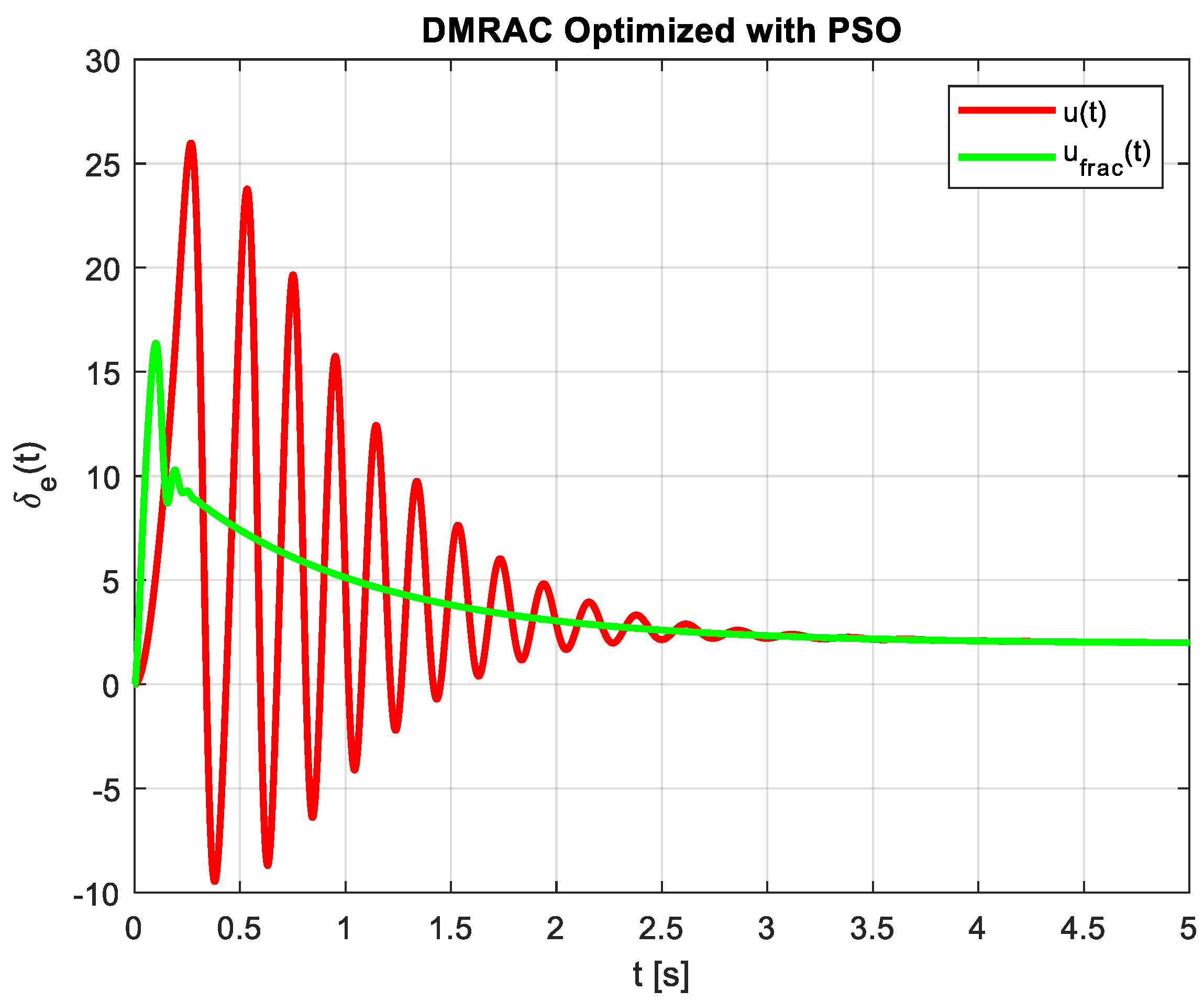
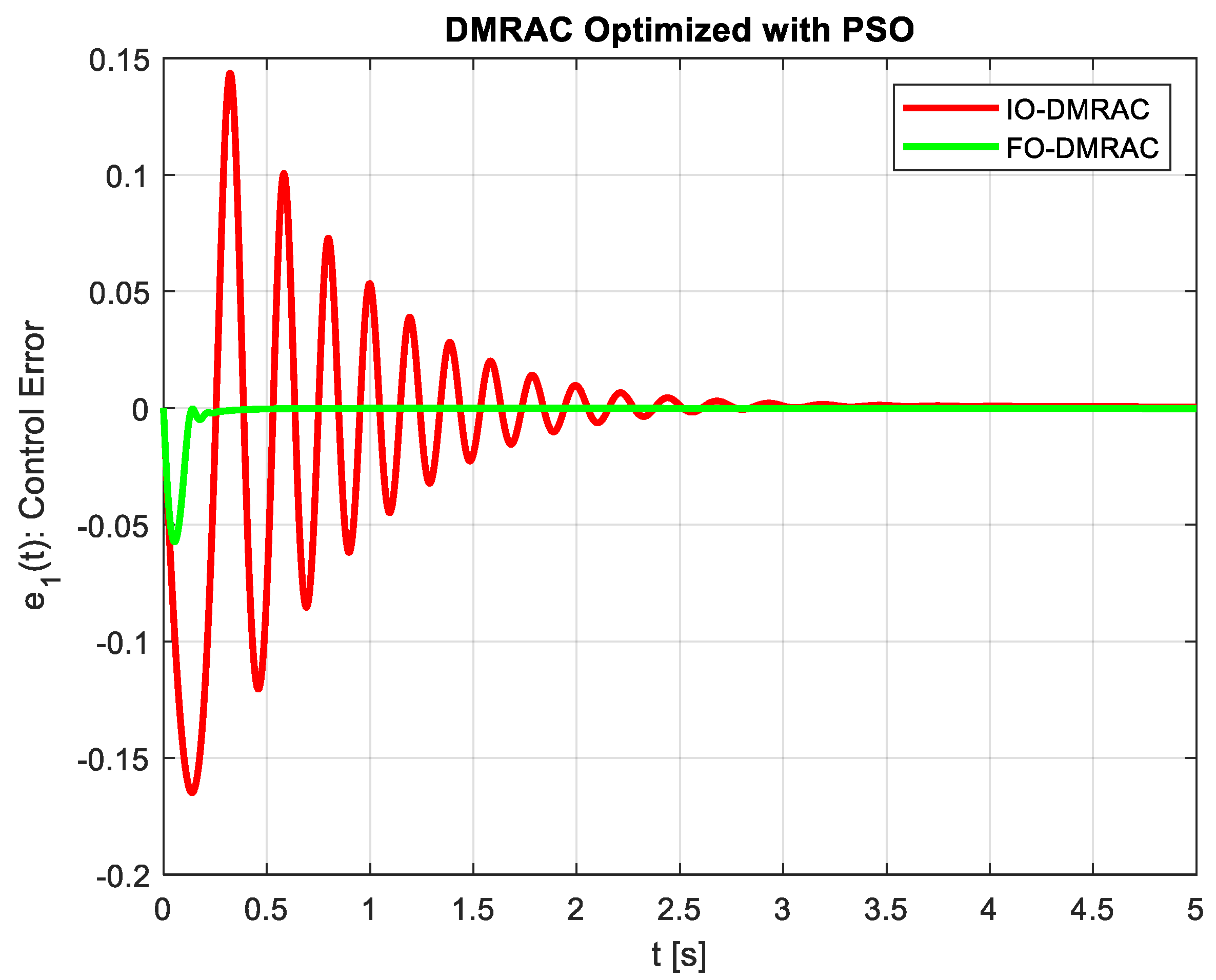
Figure 8 and Figure 9 show the control effort and control error respectively during the transient period for both cases (IO and FO controllers). As it can be seen, in the IO case, the control effort and the control output error $e_1\left(t\right)$ present an oscillatory behavior in contrast to the FO case, which is smoother.

Table 3 shows the optimal values of the objective function $J$ for both controller’s case.

Referring to Table 3, it is evident that employing FO-DMRAC results in superior performance compared to the IO-DMRAC approach, as evidenced by the smaller objective function $J$.

It is noteworthy that both controllers, the integer, and fractional ones, share the same structure, namely the classical model reference structure.

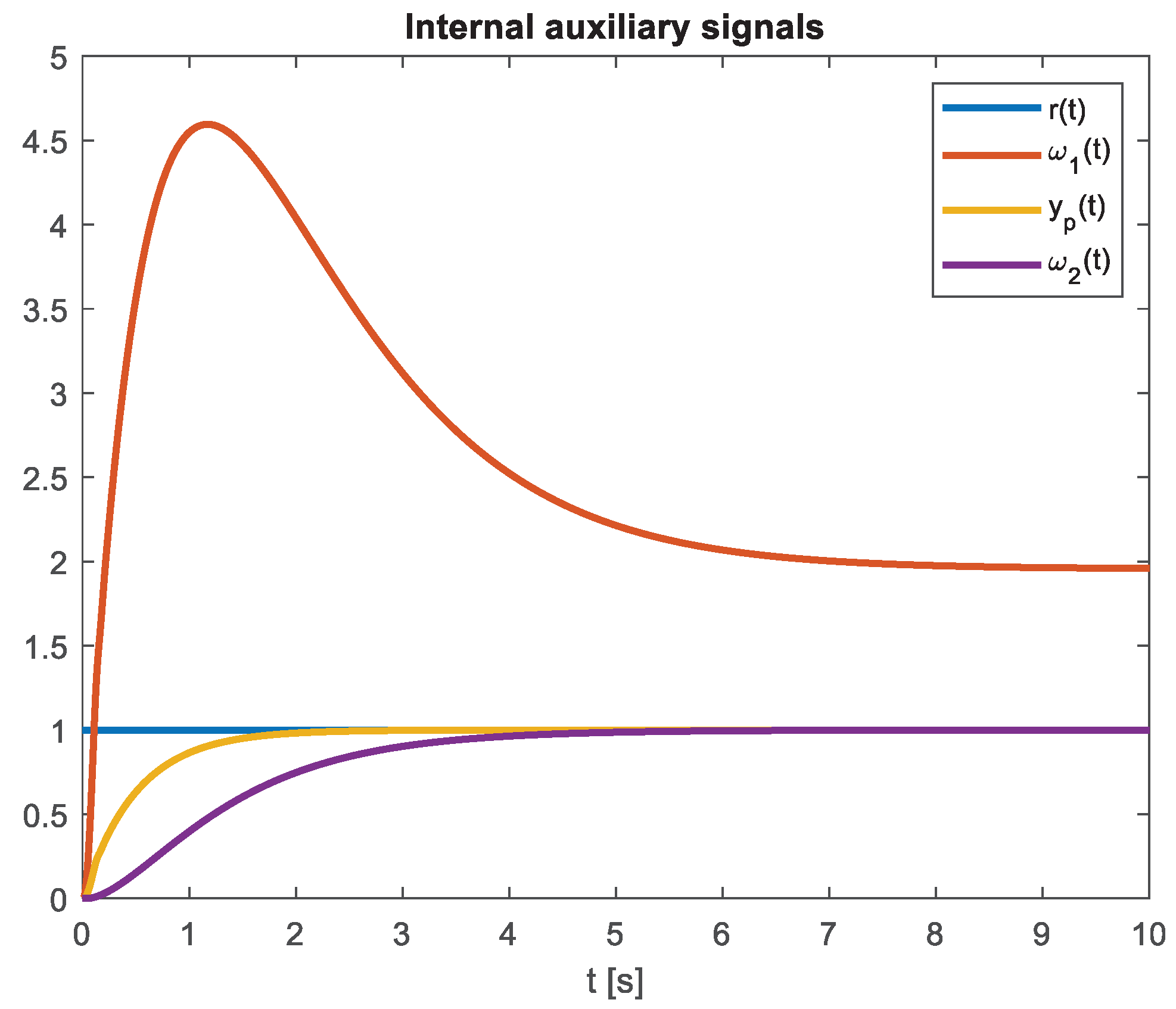
Finally, Figure 10 shows the boundedness of the auxiliary signals $\omega \left(t\right)$ using the FO-DMRAC implementation as was state by Lemma 2 [10].

6. Conclusions

The main result of this comparative study between integer order (IO-DMRAC) and fractional order (FO-DMRAC) adaptive controllers, is the better performance achieved by the FO controller in contrast with the its IO counterpart, because the oscillations during the transient period of the pitch rate output, were eliminated without sacrificing much, the rest of the controller design parameters as rise time and settling time for noun some. Moreover, the control effort in the FO controller case was lower and smoother than its IO counterpart.

Also, the simulation results allow us to verify, as assured by Lemma 2, the boundedness of all the signals, including the internal ones $\omega \left(t\right)$ in the FO-DMRAC implementation.

Further, as said before, it is the first time that a FO-DCARM pitch control is applied to an aircraft whose model is of integer order (F-16 longitudinal short-period model) and the adaptive laws are of fractional ones.

Finally, the asymptotic stability of the FO-DMRAC has been shown by means of simulations, (Figure 7), nevertheless, the theoretical proof is still a pending issue.