Another Perspective on the Relativistic Expression of Energy

Using Alfred Bucherer's electron velocity values, it is not only possible to verify the expression of                  $m=\mathrm{}\mathit{\gamma }\mathrm{}{m}_0 ,\mathit{}\mathit{ɣ}=\frac{1}{\sqrt{1-\frac{V^2}{C^2}}}$ It is also possible to deduce, by developing the binomial-$\mathit{\gamma }$, the following expression of relativistic energy: $E=E_0+K$ . (a)

By simulating Alfred Bucherer's* experiment in the Dempster mass spectrometer, it is possible to obtain, using Lienard's relativistic equation for the case of a circular orbit, a set of values of ${\mathit{E}}_{\mathit{\gamma }}$ (electromagnetic radiation anergy) that validate the general equation obtained (E). Thus, in the expression (a) there should be one more term in the equation, ${\mathit{E}}_{\mathit{\gamma }}$, which results from the variation of the constant modulus velocity vector, and which arises as consequence given that the values obtained, although not null, can be irrelevant, $\frac{E_{\gamma }}{K}\cong {10}^{-13}$ .

So, $E_{\gamma }\cong 0\mathrm{J}$, which means that this term has always been present in the relativistic equation.

This experimental result is consistent with the expression $E=E_0+K$ , by approximation, given the conditions of the experiment for the motion of the electron.

From a theoretical point of view, the equation is written as follows $E=E_0+K+E_{\gamma }$ presents greater coherence and consistency with Maxwell's theory for the accelerated motion of the electron.

In this experiment it is possible to infer, based on the conservation of energy, the following:

ΔK = - ΔEɣ, ΔE₀ = 0.

This result is in agreement with the article by Ralph Baierlein – ‘Does nature convert mass into energy?’

*If William Bertozzi's experiment and data were used for the case of linear motion, the results obtained using Lienard's relativistic equation would not be very different from Alfred Bucherer's results either- $\frac{E_{\gamma }}{K}\cong {10}^{-16}$ .

Using the Dempster mass spectrometer (Finn, Edward; Alonso M.), it is possible to simulate the experience of Alfred Bucherer. Using the electron values obtained by Alfred Bucher, which can be obtained in the Dempster mass spectrometer (using an appropriate potential difference in order to obtain the desired velocity), it is possible to conclude that the expression E = E₀ + K is just an approximation of the expression E = E₀ +K + Eγ.

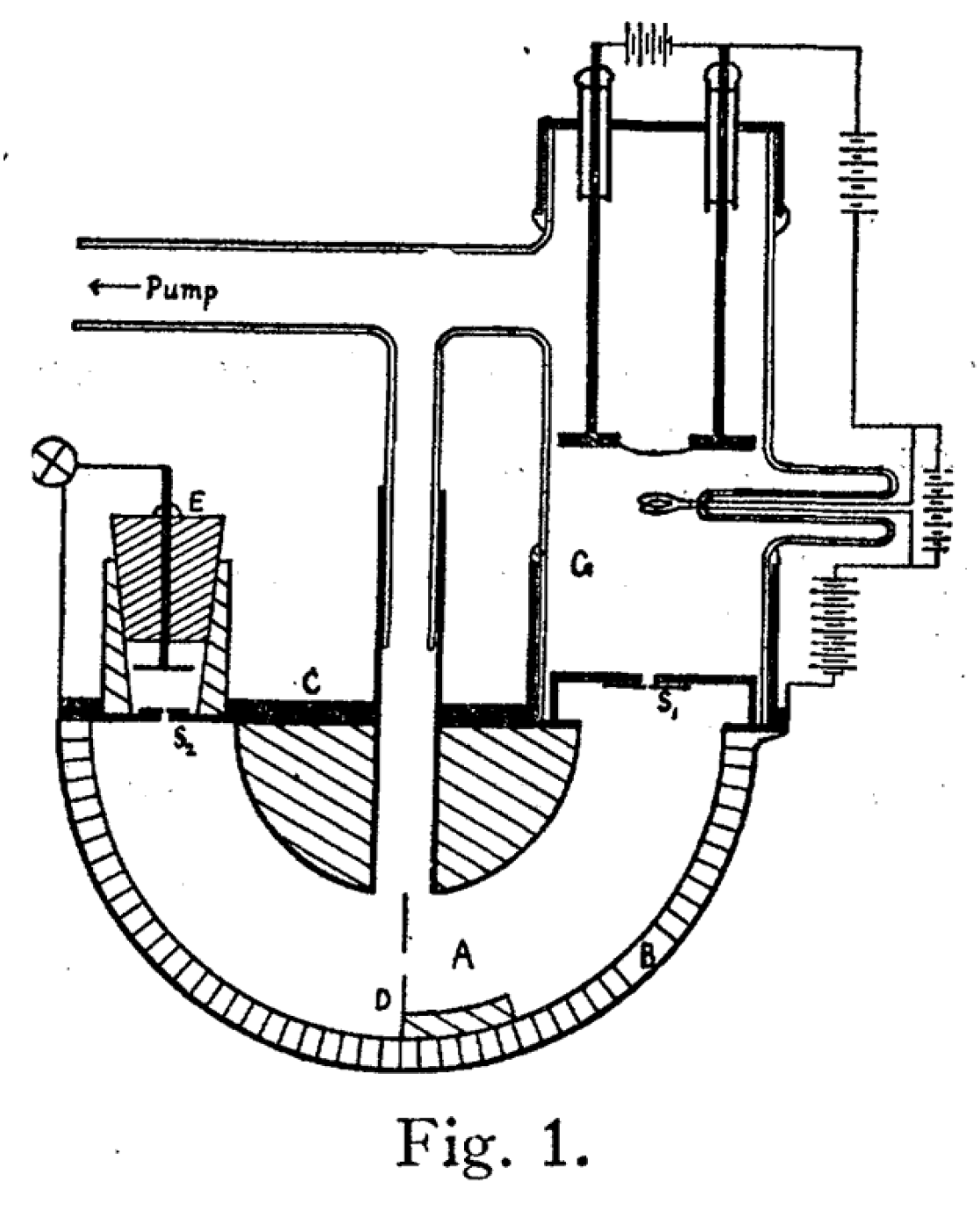
The device illustrated in Figure 1 can be used to accelerate electrons using an appropriate potential difference in order to ensure the desired velocities for the simulation of Alfred Bucherer's experiment.

Using Alfred Bucherer's data, it is possible to determine the radius of the trajectory according to the following expressions:

${\mathit{p}}_{\mathit{R}}=\frac{\sqrt{{\mathit{E}}_{\mathit{T}}^2-{\mathit{E}}_0^2}}{\mathit{C}}$ ; $\mathit{R}=\frac{p_R}{q\times B}$ ;

The following table is obtained:

According to the results in Table 1, it can be seen that using Lienard's relativistic equation and Alfred Bucherer's data, the values obtained from Eɣ are negligible and that the expression of energy predicted by Special Relativity is a more complete expression than that which is presented by high school and college physics textbooks. Although Alfred Bucherer's experiment is based on the fact that the emission of electromagnetic radiation in the context of his experiment can be irrelevant in order to ensure a circular and uniform motion for the electron, the emission of radiation is always present, and therefore the term of the associated energy of electromagnetic radiation should be included in the expression of relativistic energy.

Considering Lienard's relativistic equation for radiated power:

If acceleration is parallel to velocity, and equation (A) reduces to the following expression:$\mathit{V}\times \mathit{a}=0$

If the acceleration is perpendicular to the velocity, as in the case of a circular orbit

${\left(\mathit{V}\times \mathit{a}\right)}^2=V^2{a}^2$ the equation (A) reduces to the following expression:

Considering that the orbit under study in the Dempster mass spectrometer is circular, it is concluded that this last expression (C) is the one that should be used.

Auxiliary calculation:

Substituting in Expression (D),

Using the data in table 1 in the general expression (E), the following solutions are obtained: Eɣ-Table 2, which verify the equation (E) obtained for the case of the condition of equation (C).

Based on the results in Table 2, it can be seen that the values of Eɣ are irrelevant and that, according to the introduction, $\frac{E_{\gamma }}{K}\cong {10}^{-13}$ .

Note:

If we were to use the values obtained by William Bertozzi^#, we would have the following results:

K(Mev)#	K(J)#	dr(m)#	v(m/s)#	Eɣ(J)	Eɣ/K
0,5	8,011x10-14	8,4	2,601 x108	1,7 x10-29	2,122 x10-16
1	1,602 x10-14	8,4	2,484 x108	1,7 x10-29	1,061 x10-15
1,5	2,403 x10-13	8,4	2,766 x108	1,7 x10-29	7,074 x10-17
4,5	7,210 x10-13	8,4	2,922 x108	1,7 x10-29	2,358 x10-17

Data by William Bertozzi^# (Speed and Kinetic Energy of Relativistic Electrons) and the values obtained from the energies using Lienard's relativistic equation (condition B).

Based on the results in Table 3, it can be seen that the values of Eɣ are irrelevant and that, according to the introduction, $\frac{E_{\gamma }}{K}\cong {10}^{-16}$ .

Continuing with the study in the Dempster mass spectrometer, using the expression (F), one can deduce the expression (G) which can be analyzed through a linear regression:

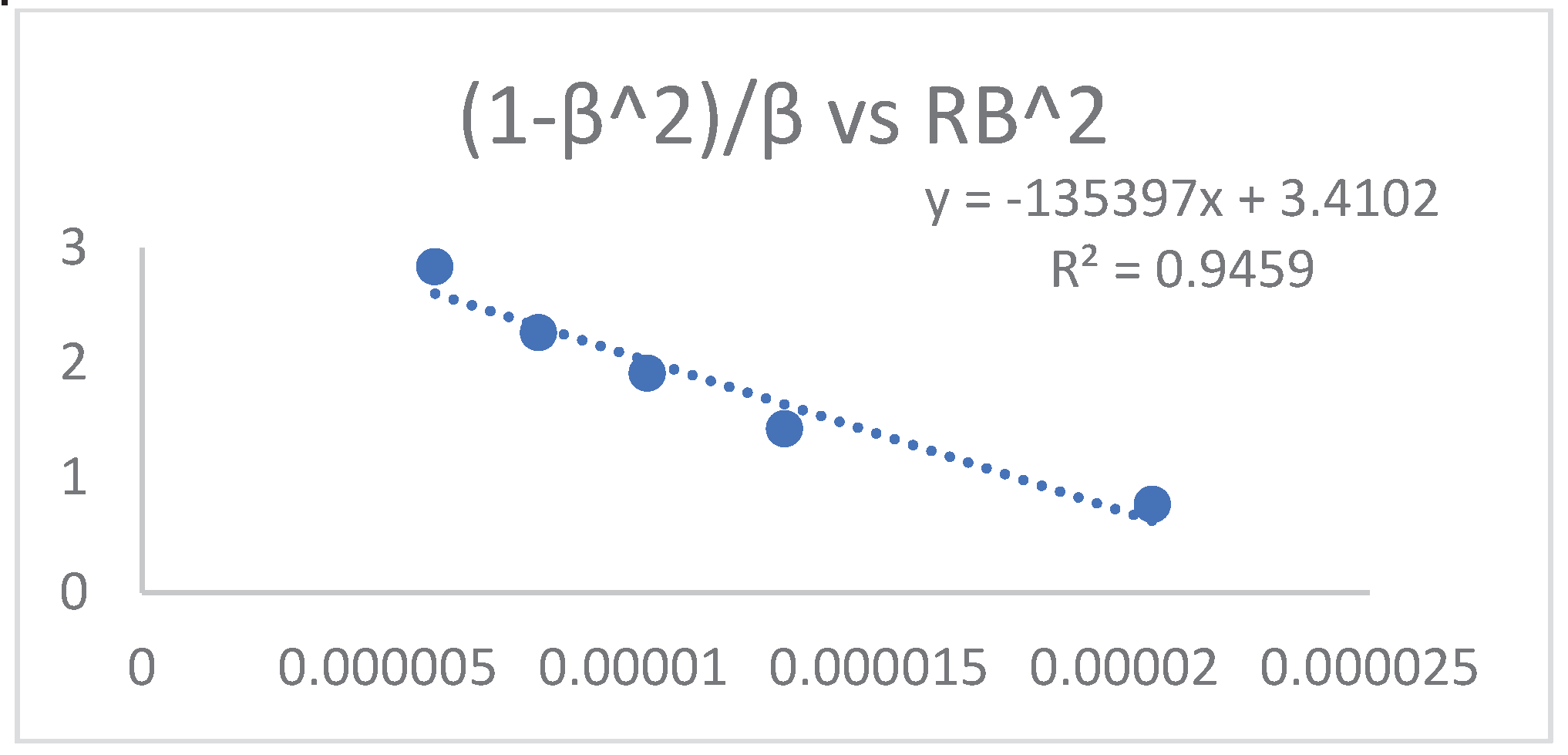
$E_{\gamma (ALfredB.)}=\mathrm{1,22}\mathrm{x}10$^-27 J

$E_{\gamma }\cong 0$ J

Note: By doing the appropriate mathematical treatment and using the data of W. Bertozzi we obtain the following value for the energy of the electromagnetic radiation:

$E_{\gamma (W.Bertozzi)}=\mathrm{1,70}\mathrm{x}10$^{- 29} J

$E_{\gamma }\cong 0$ J

Therefore, it can be seen that the expression E = E₀ + K is just an approximation of the expression E = E₀ +K + Eγ. Thus, it is concluded that this term, Eγ, has always been present in the relativistic equation of energy. And this form of energy has been absent in the expression of relativistic energy and should also be present in view of the principle of conservation of energy.

Therefore, the correct expression of relativistic energy should be written in a more general way: E = E₀ + K + Eγ. Thus, the results obtained by Alfred Bucherer and William Bertozzi through electron kinematics are in line with the model obtained by Ralph Baierlein applied to the different nuclear reactions (E = E₀ + K + Eγ). Lienard's equation was a model used to calculate the emission of electromagnetic radiation. This equation was not obtained through the development of the binomial, as mentioned in this work.

But if we accept the results of the electromagnetic radiation energy emitted by the electrons, using Lienard's relativistic equation, we find that there is a coherence between the expression of Ralph Baierlein and the experiences of Bucherer and Bertozzi.

And this expression, more general of energy, does not exist in many high school and college textbooks and should be included in order to avoid alternative conceptions regarding the learning carried out in the context of Special Relativity.

Credits the images in the following figures are from the wikimediacomons.

Figure 1. https://commons.wikimedia.org/wiki/File:Dempster_Mass_Spectrometer.gif.