Performance Analysis of Six Electro-Optical Crystals in a High-Bandwidth Traveling Wave Mach-Zehnder Light Modulator

Abtin Ataei; Paul McManamon; Andrew Sarangan

doi:10.20944/preprints202404.0179.v1

Preprint

Article

Performance Analysis of Six Electro-Optical Crystals in a High-Bandwidth Traveling Wave Mach-Zehnder Light Modulator

This version is not peer-reviewed.

Abtin Ataei^*

Paul McManamon,Andrew Sarangan

Abtin Ataei^*

Paul McManamon,Andrew Sarangan

This version is not peer-reviewed.

Downloads

110

Views

Comments

Submitted:

30 March 2024

Posted:

02 April 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract

In this study, a Traveling-Wave Mach-Zehnder intensity Modulator (TW-MZM) was designed and optimized for six different electro-optical (EO) crystals: Lithium Niobate (LNB), Potassium Niobate (KNB), Lithium Titanate (LTO), Beta Barium Borate (BBO), Cadmium Telluride (CdTe), and Indium phosphide (InP). The performance of each EO crystal, including optical and radio frequency (RF) loss, applied voltage, and modulation bandwidth, was estimated and compared. The results suggested that, in theory, KNB, LTO, BBO, and CdTe have the potential to outperform LNB. However, it should be noted that the loss associated with KNB and LTO is comparable to that of LNB. The findings demonstrated that BBO and CdTe exhibit a modulation bandwidth exceeding 100 GHz and demonstrate the lowest loss among the considered crystals based on the assumed geometry.

Keywords:

modulators

;

waveguide

;

COMSOL

;

electro-optical crystals

;

traveling wave

;

lumped elements

;

propagation constant

;

Pockels effect

;

numerical simulation

Subject:

Engineering - Electrical and Electronic Engineering

1. Introduction

The Traveling-Wave Mach-Zehnder Intensity Modulator (TW-MZM) offers high-bandwidth modulation [1]. It operates based on the electro-optic (EO) effect, enabling light intensity modulation at the output by adjusting the applied voltage to control the imposed external electric field. This modulator consists of a Mach-Zehnder interferometer with two arms through which the light signal travels and a modulator section integrated into one of the arms [2]. The modulator section is designed as a transmission line with periodically spaced electrodes, creating a radio frequency (RF) traveling-wave electric field that interacts with the optical waveguide. The RF traveling-wave electric field continuously interacts with the light signal along the transmission line, resulting in an efficient modulation of the light intensity. In contrast, other types of intensity modulators, such as the Lumped-Element Mach-Zehnder Modulator (LE-MZM), have a limited interaction length, leading to lower modulation efficiency [3,4]. The distributed interaction with the optical waveguide yields a high bandwidth and enhances the frequency response of the device, making it suitable for ultra-high-speed optical communication systems [1]. The continuous interaction between the RF electric field and the light signal, along with the distributed nature of the modulation, minimizes nonlinear effects that can degrade signal quality. Therefore, this feature can benefit applications requiring high-fidelity transmission, such as coherent optical communication systems.

The performance of a TW-MZM depends on the selected geometry, the EO medium, and other materials employed in other layers. This study aimed to investigate the effects of different EO materials on the performance of the TW-MZM after optimizing for the velocity matching between the RF and optical waves in the case of using each of those six EO mediums. This approach to optimizing the TW-MZM and evaluating the achievable bandwidth and losses was first introduced by Pascher et al. in 2003. In that research, Pascher et al. (2003) [5] assumed a structure for a TW-MZM. They optimized that structure for using InP as the EO medium to match the phase velocity of the RF wave to the group velocity of the optical wave. They reported the loss and the potential modulation bandwidth of that TW-MZM using InP as the EO medium.

In order to develop a model to design and simulate a light modulator, the type, structure, and materials should be assumed. In other words, the materials, type, and structure of the modulator will be the inputs of the model. The model’s outputs will be the optimum geometry and operating parameters, such as minimum applied voltage to modulate the light in a guiding mode, the absorption, reflection, transmission, propagation constant, and the effective index associated with the fundamental mode. By analyzing the propagation modes of the RF wave, it would be possible to adjust the silicon oxide thickness in order to match the velocity between the RF wave and optical wave and to find the bandwidth of modulation. That is because the thickness of SiO₂ does not affect the propagation constant of the optical wave and can only control the velocity of the RF wave.

This study presents a comprehensive numerical model for the design and simulation of a Mach-Zehnder intensity modulator with traveling wave electrodes. The model considers six different EO mediums: Lithium Niobate (LNB), Potassium Niobate (KNB), Lithium Titanate (LTO), Beta Barium Borate (BBO), Cadmium Telluride (CdTe), and Indium Phosphide (InP). In this investigation, a specific geometry was assumed and optimized for each EO crystal. The analysis involved estimating and comparing various parameters, including the required voltage, optical and RF losses, and modulation bandwidth.

2. Materials and Methods

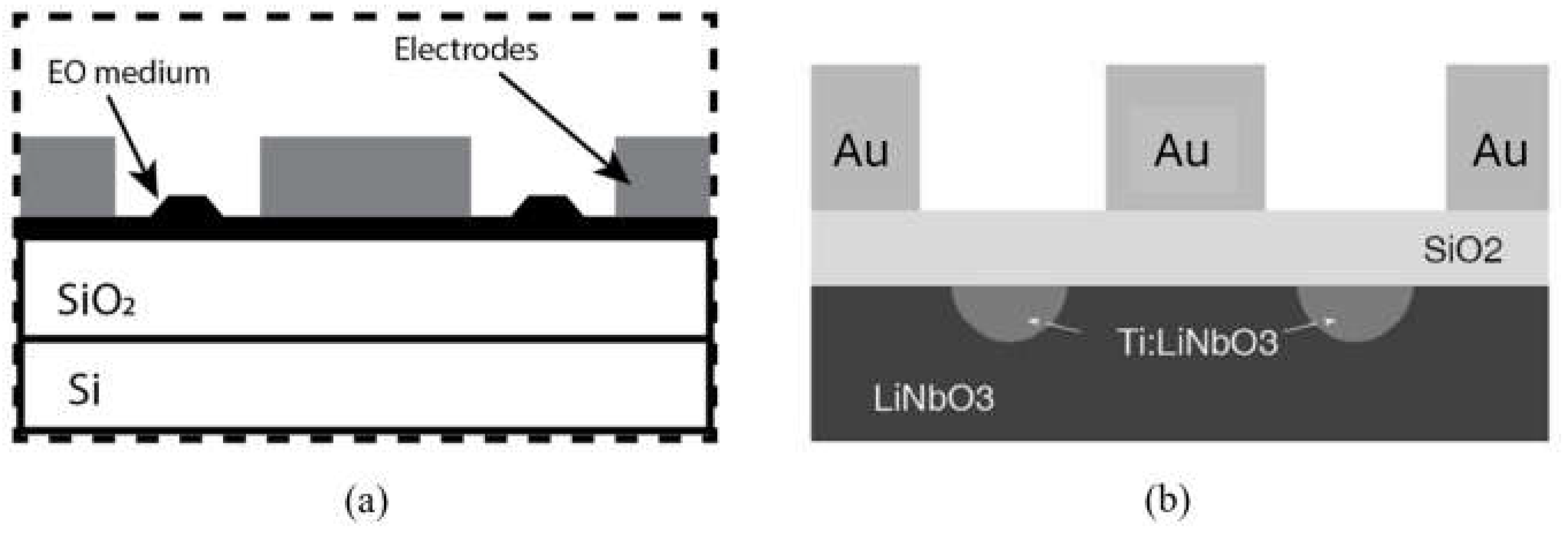
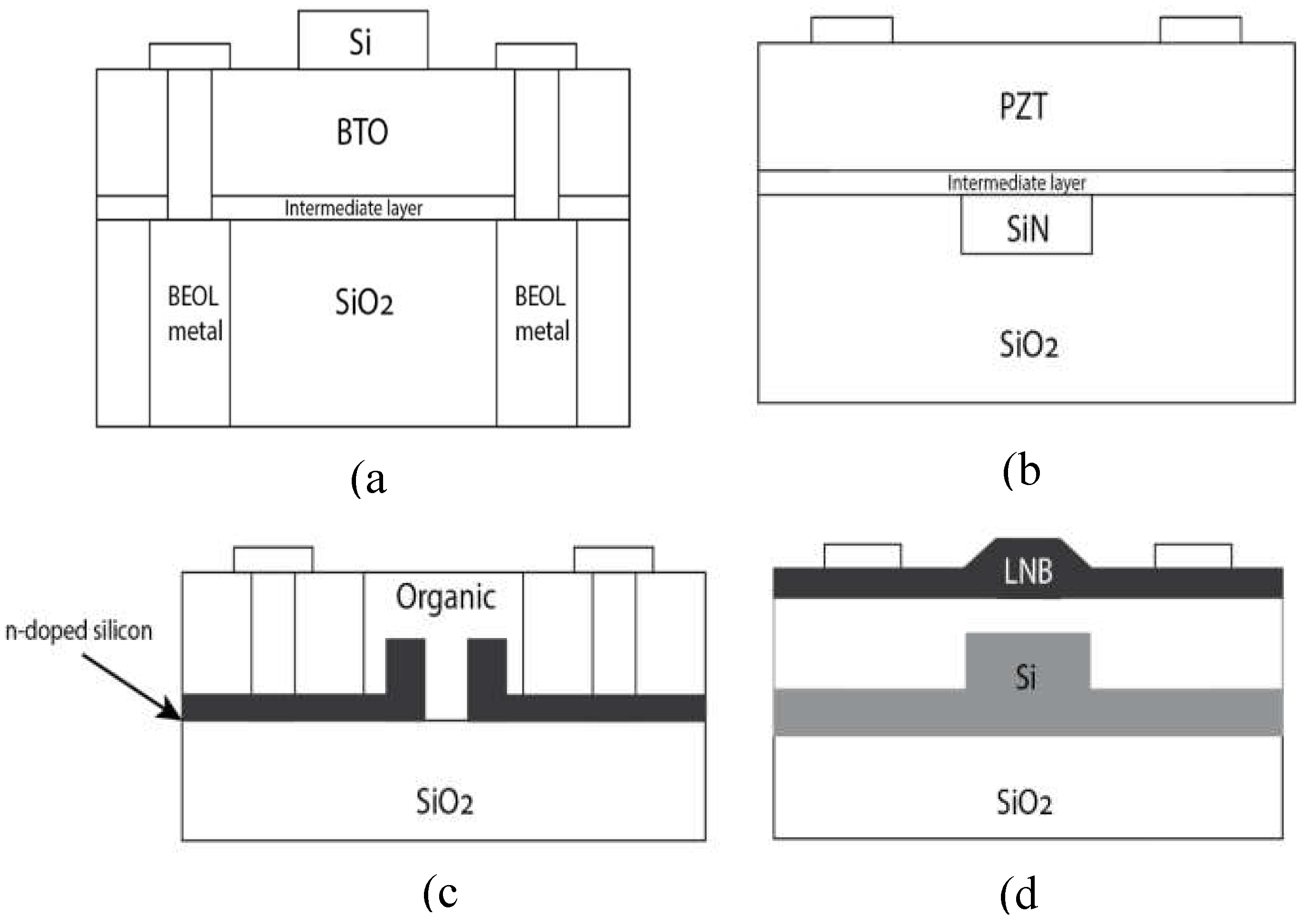
2.1. Selecting the Material and Geometry

Generally, there are two following classes of nonlinear materials to be used as the active medium under an external electric field in EO light modulators:

The traditional χ(2) materials which have low non-linearities, such as LNB, KNB, Barium Titanate (BTO), and Lead Zirconate Titanate (PZT). This class of EO materials was considered in this study, and some traditional χ(2) materials with their main properties are listed in Table 1.
The application-specific engineered quantum well-heterostructured materials which exhibit a very high χ(2) in a narrow band (Δλ≈11 nm), like organic EO molecules JRD1 in polymethylmethacrylate. The nonlinearities in this case will be 10 – 100 times higher than the traditional nonlinear materials. This class of EO materials was not considered in this study.

The optimum geometry of a MZM is varied by the selected material. For example, a model optimized for LNB is not optimized for other EO materials. No matter what geometry is selected, it must be optimized for the maximum transmission and minimum loss in the guiding mode.

Figure 1 compares the geometry of a conventional MZM with that of the MZM used in the model developed in this study. Figure 2 shows the other geometries of the light modulators based on BTO, PZT, organic EO materials, and LNB presented by other researchers [7,8].

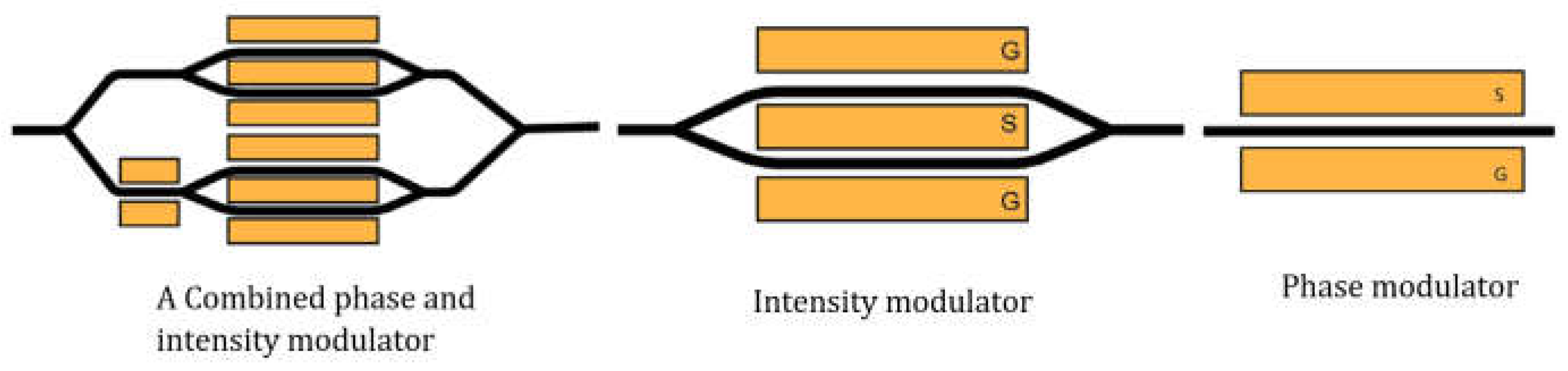
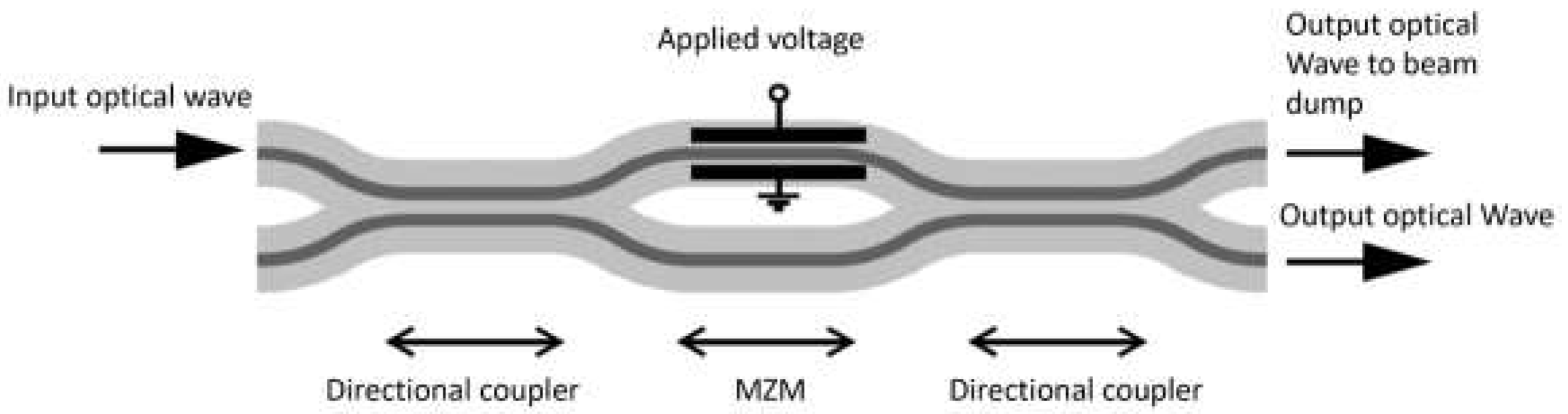
2.2. Selecting the Type and Architecture of the Modulator

Generally, the traditional light modulator has a bandwidth of around 35 GHz. In contrast, in theory, integrated CMOS-compatible light modulators can have greater than 100 GHz bandwidth, and their voltage length parameter (V.l) is between 1 to 3 V.cm depending on its type, geometry, material, and electrode type [11].

Optical modulators manipulate the output amplitude or phase of light waves as they pass through the device. Waveguide-based modulators are used in communication applications to reduce the size and required driving voltage. An EO effect, such as the Pockels effect, is utilized to control the refractive index of the waveguide with an external electric signal, where the crystal’s birefringence changes with the applied electric field. This change in the refractive index alters the phase of the wave passing through the crystal. An amplitude modulation can be achieved through interference by combining waves with different phases.

Figure 3 shows the architecture of a light phase modulator, an intensity modulator, and a combined phase and intensity modulator. The intensity modulator is more complicated because it consists of a phase modulator on one arm.

In this design and simulation model, a CMOS-compatible Mach-Zehnder intensity modulator (MZM) has been considered. Figure 4 illustrates the configuration of the MZM pursued in this study. Initially, the input optical wave is directed to a directional coupler where its intensity is evenly split between the two output waveguides. These waveguides constitute the two arms of a Mach-Zehnder interferometer. One of the arms allows for the application of an electric field, enabling the modification of the refractive index in the material and consequently altering the phase of the wave propagating through that specific arm. The two waves are subsequently merged using another 50/50 directional coupler. By adjusting the applied voltage, precise control over the amount of light exiting from the two output waveguides can be achieved.

As mentioned, six traditional χ(2) materials, including LNB, KNB, LTO, BBO, CdTe, and InP, are considered for this waveguide modulator. In the MZM, a confined mode propagates through one of those six types of EO crystal, while the cladding is comprised of a doped crystal with a lower index. The optical wavelength (λ) is considered to be 1.55 µm. In order to achieve a state where the field of confined modes exhibits zero magnitude at the exterior boundaries, it is imperative to employ a cladding radius of adequate size. As boundary conditions, it is vital to ensure a rapid decay of the electric field amplitude with respect to the cladding radius coupled with an absolute zero electric field outside the cladding region. These conditions have been implemented to maintain adherence to the prescribed theoretical framework and uphold the integrity of the system under analysis.

In a confined mode, there is no energy flow in the radial direction, making the wave evanescent in the radial direction within the cladding. This condition holds true only if the effective index (

n_{e f f}

) is greater than the index of cladding (

n_{e f f} > n_{c l a d}

). Conversely, the wave cannot be radially evanescent in the core region. Therefore, the effective index must be between the index of the core and that of the cladding (

n_{c o r e} {> n}_{e f f} > n_{c l a d}

). It is important to note that a higher effective index results in a more confined optical wave, with the fundamental mode having the highest effective index. The effective refractive index of a confined mode is calculated as Equation (1):

n_{e f f} = {β / k}_{0}

(1)

Where

k_{0}

is the vacuum wavenumber, and

β

is the propagation constant. The

n_{e f f}

is a function of the frequency. The normalized frequency of a waveguide or the V-number is calculated as Equation (2);

V = \frac{2 π a}{λ} \sqrt{n_{c o r e}^{2} - n_{c l a d}^{2}}

(2)

Where a is the radius of the core. The mode analysis is conducted on a cross-sectional plane (xy-plane) of the fiber, specifically examining the behavior of the optical wave in the z-direction. The optical wave can be characterized by the following expression:

E (x, y, z, t) = E (x, y) e^{i (w t - β z)}

(3)

Within the provided context, w is defined as 2πν, representing the frequency of the optical wave denoted by ν. To determine the eigenvalues for the electric field, the Helmholtz equation (Equation (4)) is solved, yielding the eigenvalues of (-iβ).

\nabla \times (\nabla \times E) - {k_{0}}^{2} n^{2} E = 0

(4)

To model the MZM, the interface for optical waves’ beam envelopes is formulated by assuming that the electric field can be represented as the product of a slowly varying envelope function and a rapidly varying phase function, as Equation (5).

E (r) = E_{v} e^{- i k . r}

(5)

In Equation (5), the envelope function

E_{v}

represents the electric field, where k denotes the wave vector, and r represents the position. When the wave vector k is appropriately chosen for the specific problem, the envelope function

E_{v}

exhibits spatial variation on a larger length scale compared to the wavelength. In this application, it is reasonable to assume that the wave can be accurately approximated in straight domains by utilizing the wave vector corresponding to the incident mode of β. However, in waveguide bends, assuming α is the bend angle from the x-axis and

\hat{x}

and

\hat{y}

are unit vectors in the x and y directions, the wave vector can be expressed as

β (\hat{x} c o s α + \hat{y} s i n α)

Therefore, the wave vector difference in the bent waveguide will be:

Δ β = β (\hat{x} c o s α + \hat{y} s i n α) - β \hat{x} = β \hat{x} c o s α + \hat{y} β s i n α - β \hat{x} = β ((c o s α - 1) \hat{x} + s i n α \hat{y})

(6)

The

Δ β

determines the phase variation for the envelope electric field. The splitting and recombining of light in a guiding mode inside the waveguide is the most complicated task in the model. Therefore, the first step would be to optimize the bending ratio based on the waveguide’s wavelength, core, and width to ensure the light can be split 50-50 in a guiding mode using a numerical model developed in COMSOL multiphysics [12]. That COMSOL model calculates the phase modulation from the optical path difference (OPD) resulting from the change in the index (n) of the EO medium with an appropriate EO coefficient of

r_{i j}

due to the imposition of an external electric field and the length of propagation (l) through the EO medium under the voltage (V) as Equation (7) [13].

O P D = (Δ n) l = \frac{n^{3} r_{i j} V}{2 D} l

(7)

Where D is the distance between the electrodes surrounding the EO medium. The COMSOL model defines the intensity modulation after recombining the two arms if the transmission at the outlet port drops to zero.

2.3. Selecting the Type of Electrodes

The Lumped or Traveling Wave (TW) electrodes can be used in the MZM. Lumped MZMs have a smaller length than the wavelength of the modulation field due to the low modulation frequency (f). This results in a longer modulation period (1/f) than the transit time (

τ_{t})

, which is the duration for the optical wave to propagate through the MZM.

f {< 1 / τ}_{t}

(8)

Generally, the 3-dB modulation bandwidth (

f_{3 d B}

) of an MZM depends on both transit time (

τ_{t}

) and the RC time constant (

τ_{R C}

). Since the RC time is much longer than the transit time in a lumped MZM, the modulation bandwidth is defined by the RC time constant as;

f_{3 d B} = \frac{1}{2 π τ_{R C}}

(9)

For a fixed resistance, the

τ_{R C}

gets longer by increasing the length (l) of the electrodes due to increasing the capacitance by length (

C \propto l

). Therefore,

{l f}_{3 d B} < 3 G H z . c m

. On the other hand, the optical path delay (OPD) increases by length (l) for a given index change as Eq(7). Thus, the length of the electrode would be a trade-off between the modulation bandwidth, the required OPD for phase modulation, and the voltage to impose the index change in a lumped MZM and hence the modulation bandwidth of a lumped MZM

{(f}_{3 d B})

can’t be greater than a few gigahertz.

As seen, to achieve higher bandwidth modulation, the lumped modulator’s frequency response is limited by its RC characteristics at high modulation frequencies. To overcome this limitation, a traveling wave configuration is used for the MZM. This involves matching the phase velocity of the microwave modulation field or radio frequency (RF) wave with that of the optical wave in the MZM. The MZM with traveling wave-type electrodes is called TW-MZM[14]. This type of electrode was selected for the MZM in this study.

To enable effective interaction between the microwave field and optical wave in a TW-MZM, the high-frequency modulation signal is injected and propagates in the same direction as the optical wave, terminating at the end of the electrode transmission line [15].

The modulation bandwidth

{(f}_{3 d B})

of a TW-MZM depends on the mismatch between the phase-velocity of the optical wave propagating in the waveguide and the RF wave propagating in the transmission line and also the loss of RF signal along the transmission line depending on the frequency of the RF wave. The velocity mismatch and the RF attenuation also depend on the materials and geometry of the waveguide and the transmission line[4]. Considering Z as the impedance of the transmission line (

Z = \sqrt{L / C})

, L as inductance, C as capacitance per unit of length of transmission line,

n_{R F}

as the index for the RF wave and

n_{e f f}

as the effective index of the optical wave, the phase velocity of the RF (

v_{R F}^{p}

) and the optical wave in the guided mode (

v_{o p t i c}^{p}

) can be calculated as;

v_{R F}^{p} = \frac{c}{n_{R F}} = \frac{1}{\sqrt{L C}}

(10)

v_{o p t i c}^{p} = \frac{c}{n_{e f f}}

(11)

Considering the frequency-dependent absorption coefficient of α for the RF wave in the transmission line, the voltage attenuation coefficient will be 0.5α, and therefore, the traveling voltage throughout the electrode as a function of time and space will be;

V (r, t) = V_{m a x} e^{- 0.5 α r} e^{i w (r \sqrt{L C} - t)}

(12)

Where,

V_{m a x}

is the peak of the modulation voltage, and

w

is the angular modulation frequency. That voltage variation in time and space will impose a variable change in the propagation in time and space and also frequency due to the dependence of phase velocity of RF on frequency (

Δ β (w, r, t)

). The

V_{m a x}

would impose the maximum electric field to the EO medium and achieve the maximum index change (

{Δ n}_{e f f}_{m a x}

) and therefore, the maximum change in the propagation constant (

{Δ β}_{m a x}) .

Δ β (w, r, t) = {Δ β}_{m a x} e^{- 0.5 α r} e^{i w (r \sqrt{L C} - t)}

(13)

The max change in the propagation constant results in the max phase shift (

{Δ φ}_{m a x})

as;

{Δ φ}_{m a x} = {Δ β}_{m a x} l

(14)

The optical wave entering the entrance port at the time of t will get to the point of z at

t + z / v_{o p t i c}^{p}

where the voltage at that point is

V (z, t + z / v_{o p t i c}^{p}) .

Therefore, the change in the propagation constant will be;

Δ β (w, r, t) = {Δ β}_{m a x} e^{- 0.5 α r} e^{i w (\frac{r (n_{R F} - n_{e f f})}{c} - t)}

(15)

Therefore, the phase modulation will be;

Δ φ (w, t) = \int_{0}^{l} Δ β (w, r, t) d r = \frac{{Δ φ}_{m a x}}{l} \int_{0}^{l} e^{- 0.5 α r} e^{i w (\frac{r (n_{R F} - n_{e f f})}{c} - t)} d r

(16)

In order to estimate the maximum modulation bandwidth of TW-MZM, two limitation cases can be considered: having a velocity mismatch between the RF and optical waves (

(n_{R F} - n_{e f f}) \neq 0

) but a very low loss transmission line (α≈0) as in case 1 and having minimum velocity mismatch (

n_{R F} \approx n_{e f f}

) but a lossy transmission line (

α > 0

) as in case 2.

i.: Case 1: The phase modulation in this case is;

Δ φ (w, t) = \frac{{Δ φ}_{m a x}}{l} \int_{0}^{l} e^{i w (\frac{r (n_{R F} - n_{e f f})}{c} - t)} d r

(17)

After conducting a lengthy analytical calculation, one can demonstrate that the modulation bandwidth of the TW-MZM, in this case, is calculated as follows:

f_{3 d B} = \frac{2 c}{π l (n_{R F} - n_{e f f})}

(18)

ccording to the above equation, matching the velocities of RF and optical waves in a TW-MZM with a very low-loss transmission line can yield a significantly high modulation bandwidth.

ii.: Case 2: The phase modulation in this case is;

Δ φ = \frac{{Δ φ}_{m a x}}{l} \int_{0}^{l} e^{- 0.5 α r} d r

(19)

Therefore, in this case, the modulation bandwidth of the TW-MZM will be inversely proportional to the square of the length.

f_{3 d B} \propto \frac{1}{l^{2}}

(20)

Therefore, if the phase velocity of the RF and optical waves in a TW-MZM are matched, the modulation bandwidth will be limited solely by the square of the length of the transmission line.

However, the transmission line cannot be too short due to the necessary OPD for phase modulation. To meet the OPD requirements while reducing the transmission line length, exhibiting a medium with a higher index change will be advantageous.

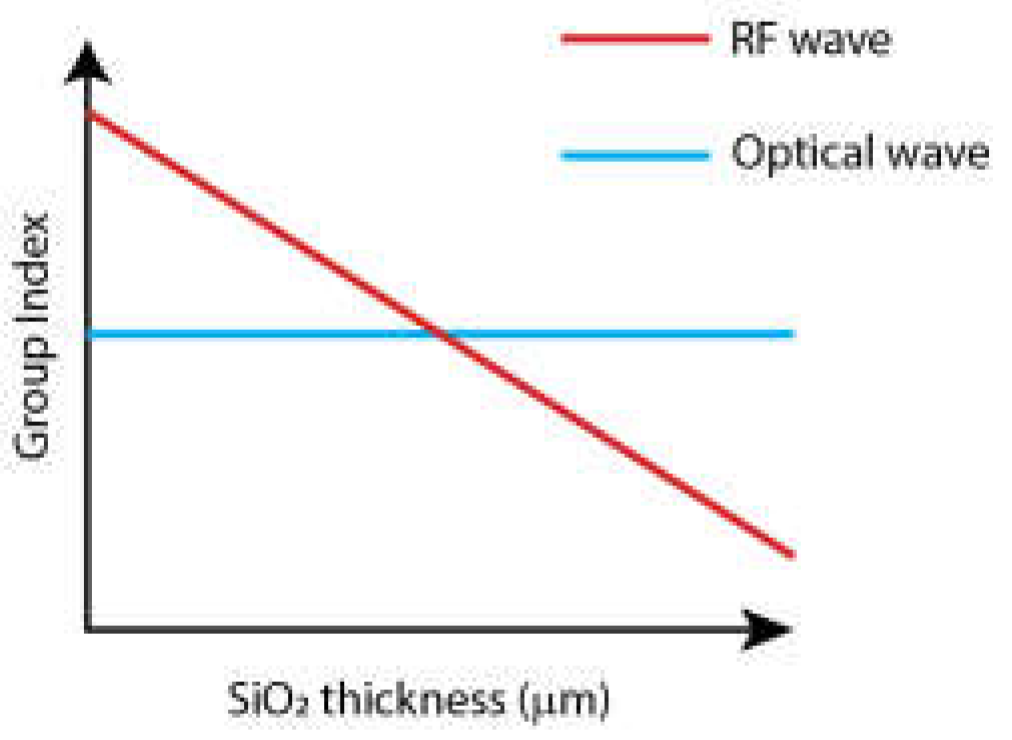
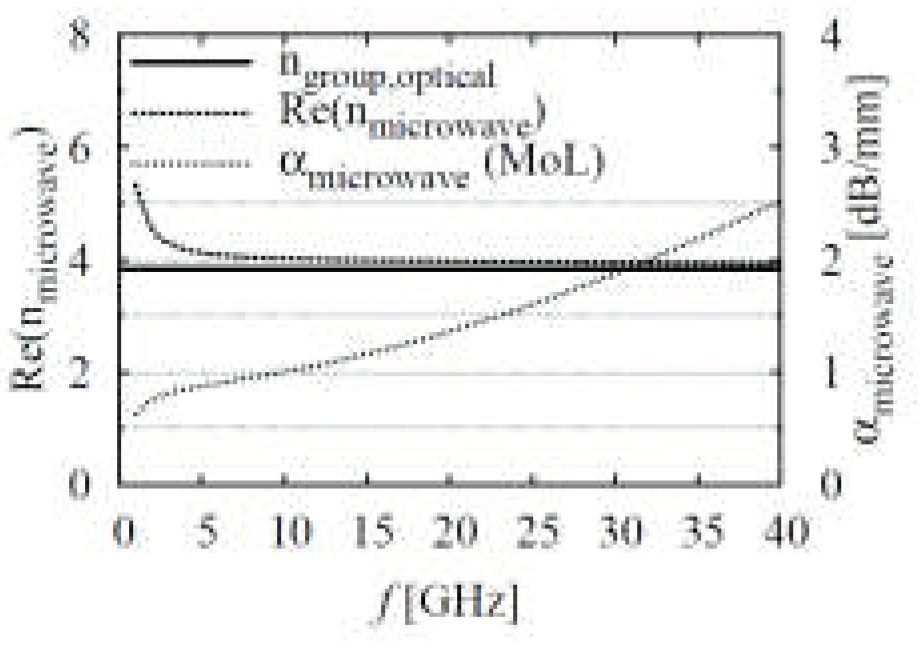
2.4. Velocity Matching between the RF and Optical Wave

As mentioned, the optical wave’s group velocity and the microwave’s phase velocity must be matched to increase the modulation bandwidth. The maximum bandwidth of the TW-MZM will be the frequency of the RF wave, which has a phase velocity matched to the group velocity of the optical wave [5].

The velocity of the optical wave is defined by the optical wave’s effective index in the waveguide, which is defined by wavelength(s), the propagation mode, the core size, and the refractive index of the core and cladding, which can be calculated independently of RF propagation. On the other hand, the RF phase velocity is a function of substrate thickness, type and size of the electrodes, cladding sizes, and refractive indices, which can be modeled after calculating the optical wave propagation. Therefore, the materials and the thickness of the SiO₂ can be controlled to get the velocity of the RF and optical waves matched together, as schematically shown in Figure 5.

The thickness of the SiO₂ layer in a TW-MZM, as depicted in Figure 1a, does not impact the optical wave’s propagation constant. However, it does affect the phase velocity of the RF wave. Adjusting the SiO₂ layer’s thickness makes it possible to achieve velocity matching between the optical and RF waves to optimize the modulation bandwidth.

As shown in Figure 1a, it is essential to note that the SiO₂ layer in the TW-MZM considered in this study is not positioned on top of the nonlinear layer, unlike conventional MZMs. Therefore, altering the SiO₂ thickness does not affect the propagation constant of the optical wave; instead, it solely controls the propagation constant of the RF wave (Figure 5).

Wang et al. (2018) and Pascher et al. (2003) [5,11] conducted similar studies where they optimized the SiO₂ layer thickness in a thin film TW-MZM to attain velocity matching between the RF and optical waves to maximize the modulation bandwidth. Wang et al. (2018) [11] focused on a TW-MZM with an assumed geometry and LNB as the EO medium, while Pascher et al. (2003) [5] explored a different geometry using InP as the EO medium.

2.5. The Loss Estimation Method for the RF and Optical Waves in the TW-MZM

In the TW-MZM depicted in Figure 4, the input optical wave, characterized by a known intensity, is introduced through one of the inlet ports. The COMSOL model can compute the intensity of the outgoing light from both outlet ports. Consequently, the optical loss can be determined as the disparity between the input and output intensities. This variation can be visually presented by plotting the optical loss along the length of the directional coupler waveguide.

Although the calculation of optical loss, as described earlier, appears straightforward, determining the loss of the radio frequency (RF) wave is more complex and requires evaluating the RF propagation constant following velocity matching. Assuming the complex RF propagation constant is

\hat{β_{R F}} = β_{R} + i β_{I} = k_{0} {(n}_{R F} + i κ)

, the RF field will be;

E (x, y, z, t) = E (x, y) e^{i \hat{{(β}_{R F}} z - ω t)} = E (x, y) e^{i {(k}_{0} {(n}_{R F} + i κ) z - ω t)} = E (x, y) e^{i (2 π {(n}_{R F} + i κ) z / λ - ω t)} = e^{- 2 π κ z / λ} E (x, y) e^{i (2 π n_{R F} z / λ - ω t)}

(21)

As the intensity of the radio frequency (RF) wave is directly proportional to the square of the field, the RF intensity follows an exponential decay per the Beer-Lambert law.

I_{R F} (z) = I_{o} e^{- 4 π κ z / λ}

(22)

Therefore, the RF absorption coefficient will be

α = \frac{4 π κ}{λ}

and is reported in terms of dB/mm.

In this model developed in COMSOL multiphysics, the loss associated with the RF wave is computed as described above for the six EO crystals under investigation. The calculations involve optimizing the shape and adjusting the thickness of the silicon dioxide layer (or the silicon layer in the case of CdTe) to achieve a velocity matching between the RF and optical waves, and the results will be compared.

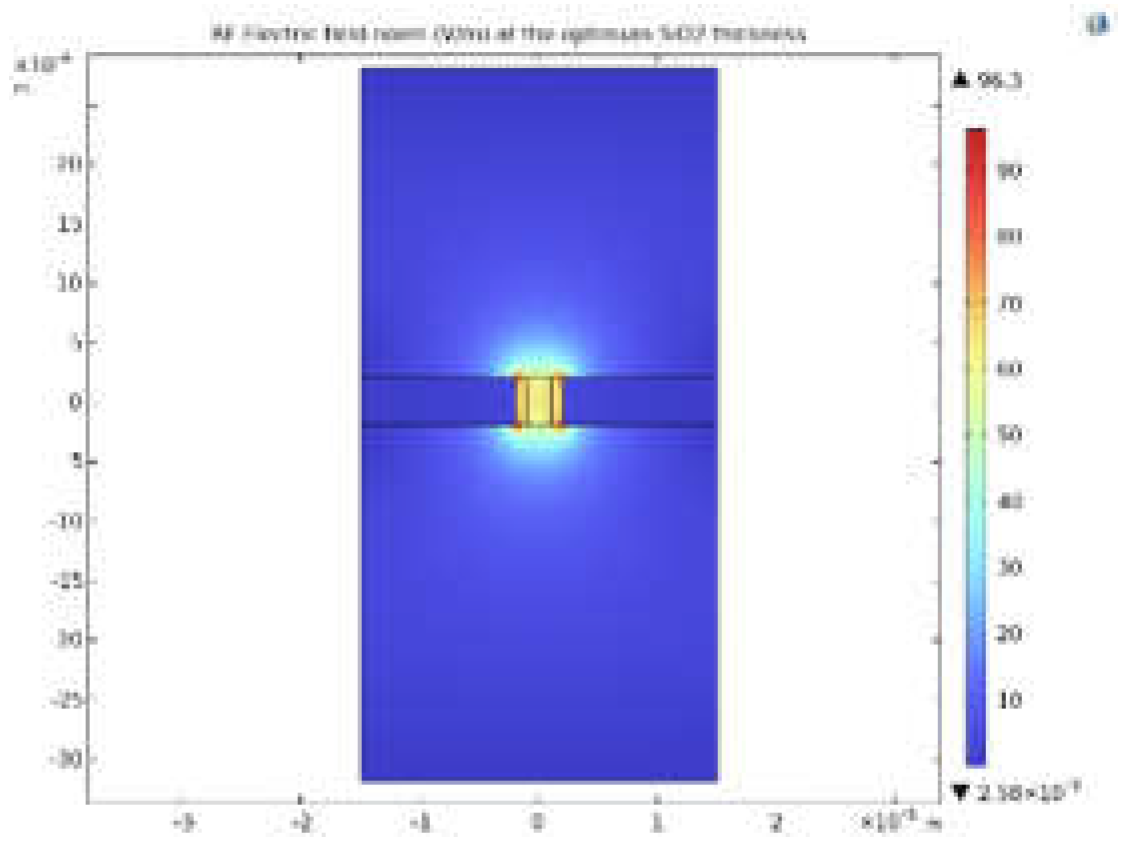
2.6. Modeling in COMSOL Multiphysics

The model developed in COMSOL multiphysics [12]defines the fundamental mode of the optical wave propagating through the TW-MZM based on the geometry, structure, and EO medium used in the waveguide. Then, the cross-section of that TW-MZM with a variable SiO2 thickness is used to adjust the propagation constant and the phase velocity of the RF wave to match the optical wave group velocity. Since the propagation constant of the RF depends on its frequency and the size and structure of the TW-MZM designed in the previous section, only the SiO2 thickness, which does not affect the propagation constant of the optical wave, is optimized for each RF frequency in order to match the velocity of RF and Optical waves. The model can find an RF frequency with the same phase velocity as the optical wave to define the maximum bandwidth of modulation associated with the EO medium selected.

2.6.1. The Inputs of the Model

As mentioned, a TW-MZM with a specific geometry is considered in this model. Figure 6 shows the top view and the section view of the TW-MZM.

As seen in the top view of the TW-MZM (Figure 6a), this TW-MZM has four ports. One port on the right side is the input, and the other is a dummy port for ease of modeling. On the left side, one port is the output, and the other one will be connected to a beam dump. As seen, the light enters the device from one port on the right side, split into two arms while one arm is under an external electric field, and the medium is electrooptically activated for phase modulation. Then, the two arms get recombined. The intensity of the light in the output part is modulated by changing the voltage applied to the electrodes. Changing the applied voltage would alter the external electric field and the refractive index of the EO material on one arm, leading to a phase delay on one arm. Recombining the phased modulated light in one arm with the light propagating in the other will cause destructive or constructive interference between the lights, resulting in intensity modulation at the output port.

The light is propagated inside the core, and an evanescent field will exist in the cladding. The RF wave, on the other hand, propagates beyond the core; therefore, the other layers and electrodes become important to calculate the propagation constant of the RF wave. Figure 6b shows the cross-section of the TW-MZM modulating arm, which is used to calculate the propagation constant of the RF wave.

The top layer in Figure 6b is made of air; the electrodes are made of gold, and the substrate is SiO2 for the EO crystals investigated in this study, except CdTe. The core is made of an EO material, and the cladding has a slightly lower index.

The list of the inputs of the model is given in Table 2. The input data in Tabe 2 uses LNB as the EO medium, just as an example.

2.6.2. The Two Steps of the Model

The design and simulation of a TW-MZM are conducted in this model through two following steps:

i.

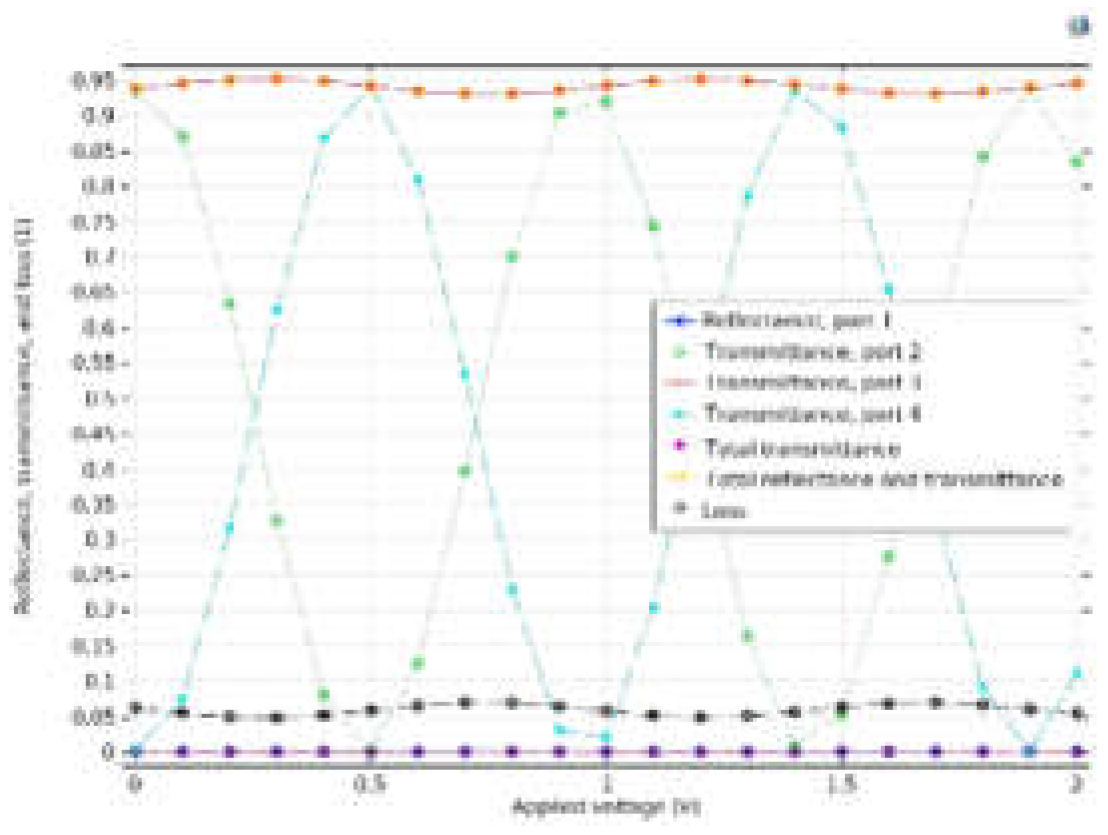
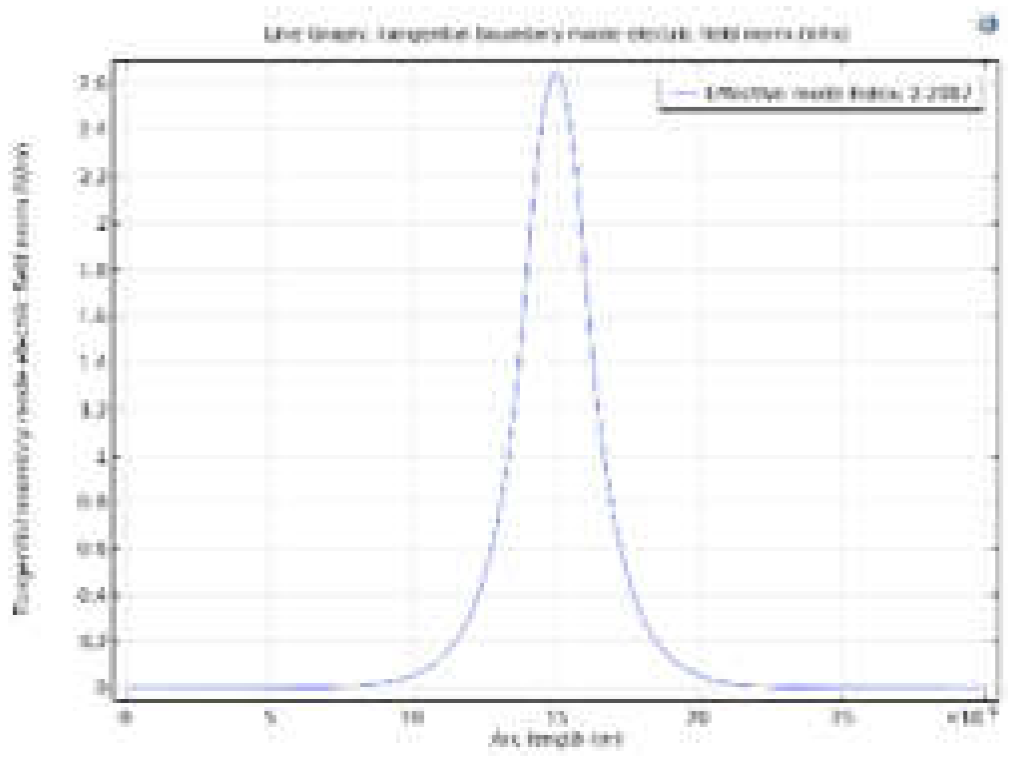
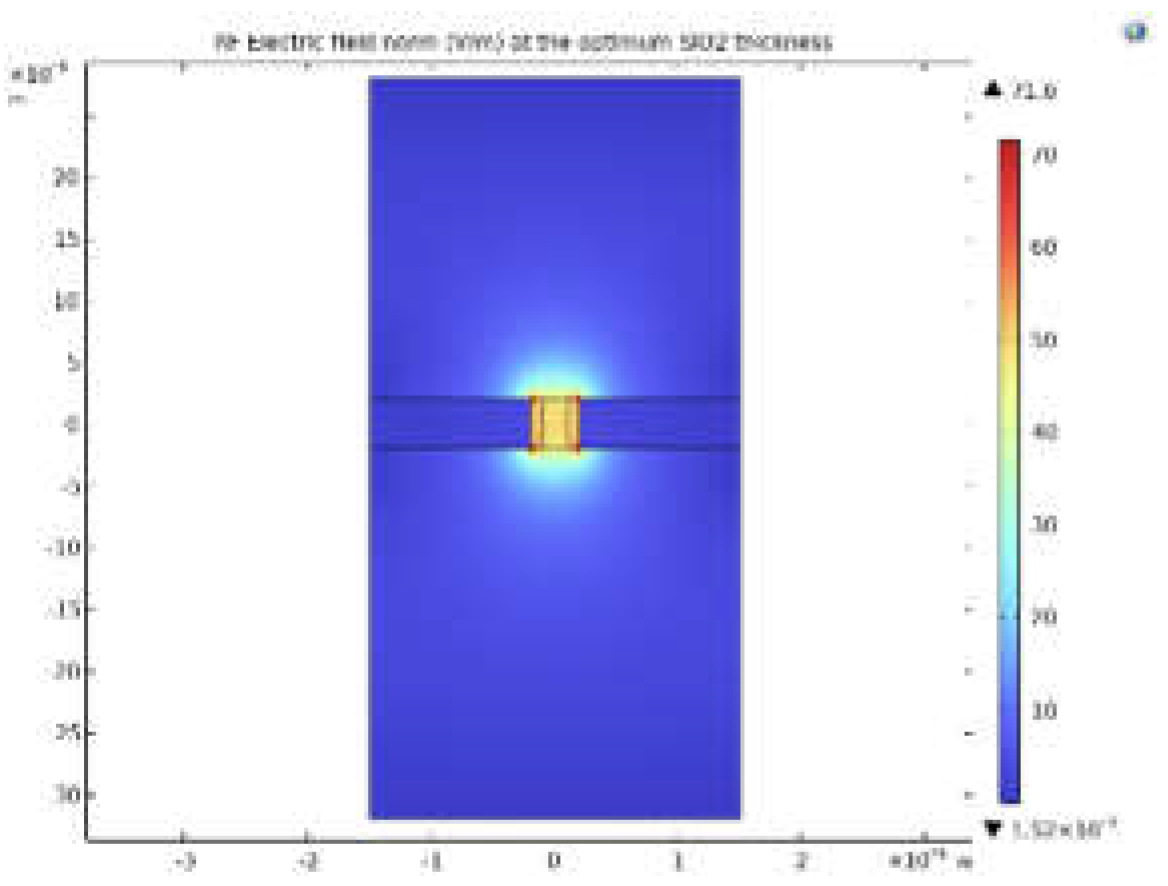
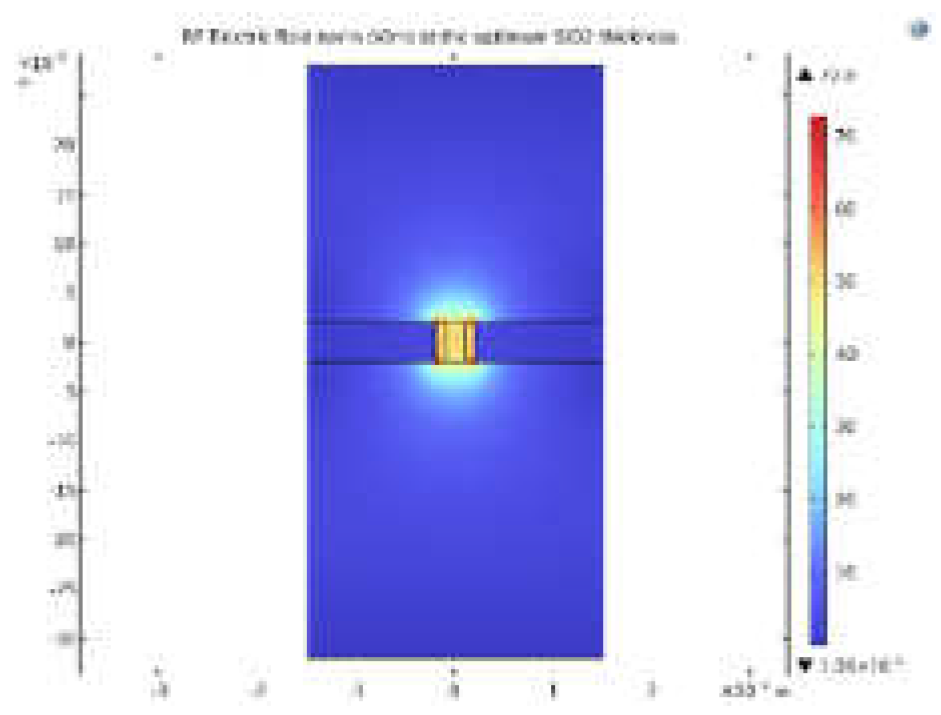
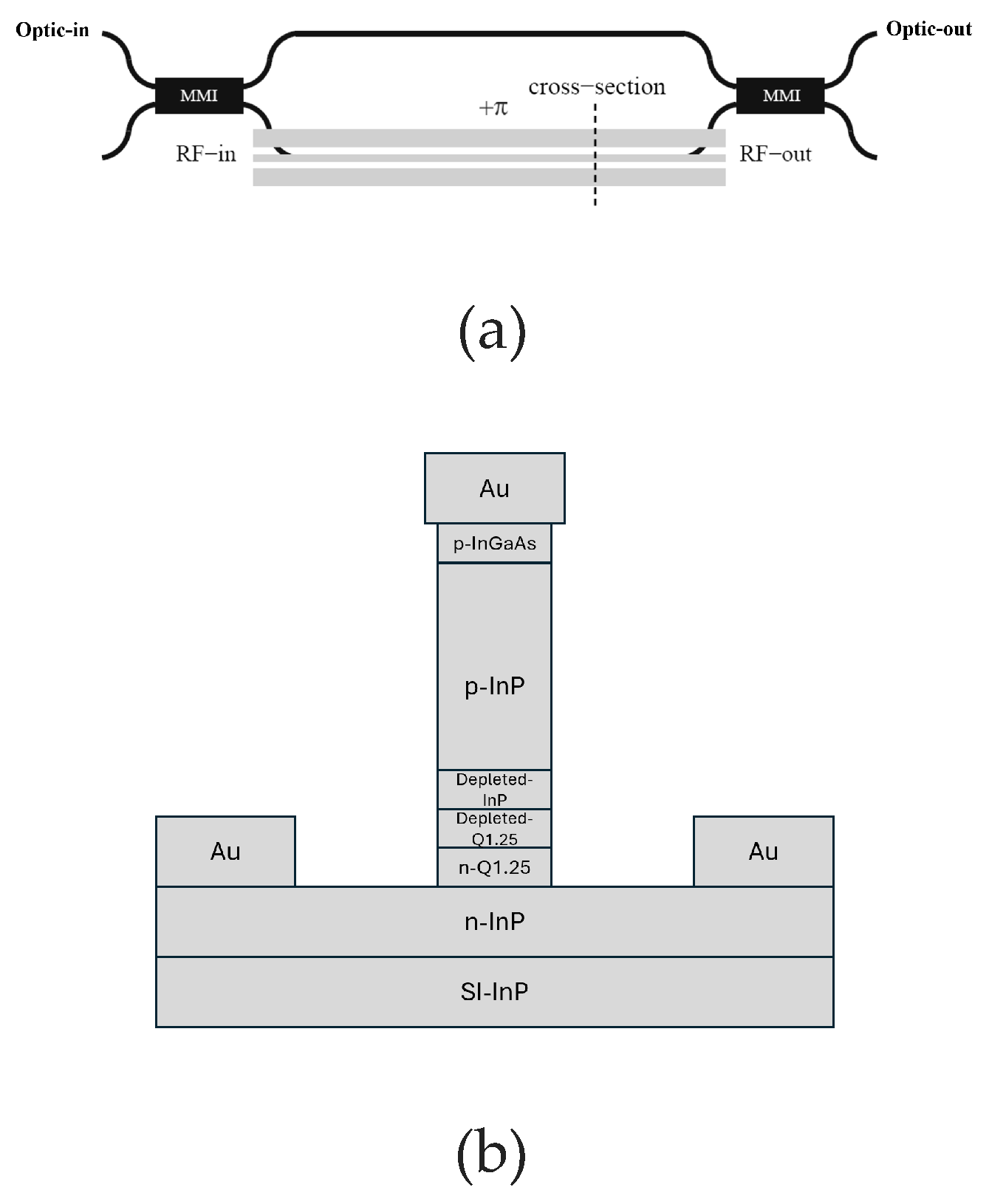
Step 1, the optical wave side: In this step, the top view of the modulator is considered (Figure 6a), and the geometry is constructed according to the inputs (Table (2)). The parameters calculated in this step are as follows;

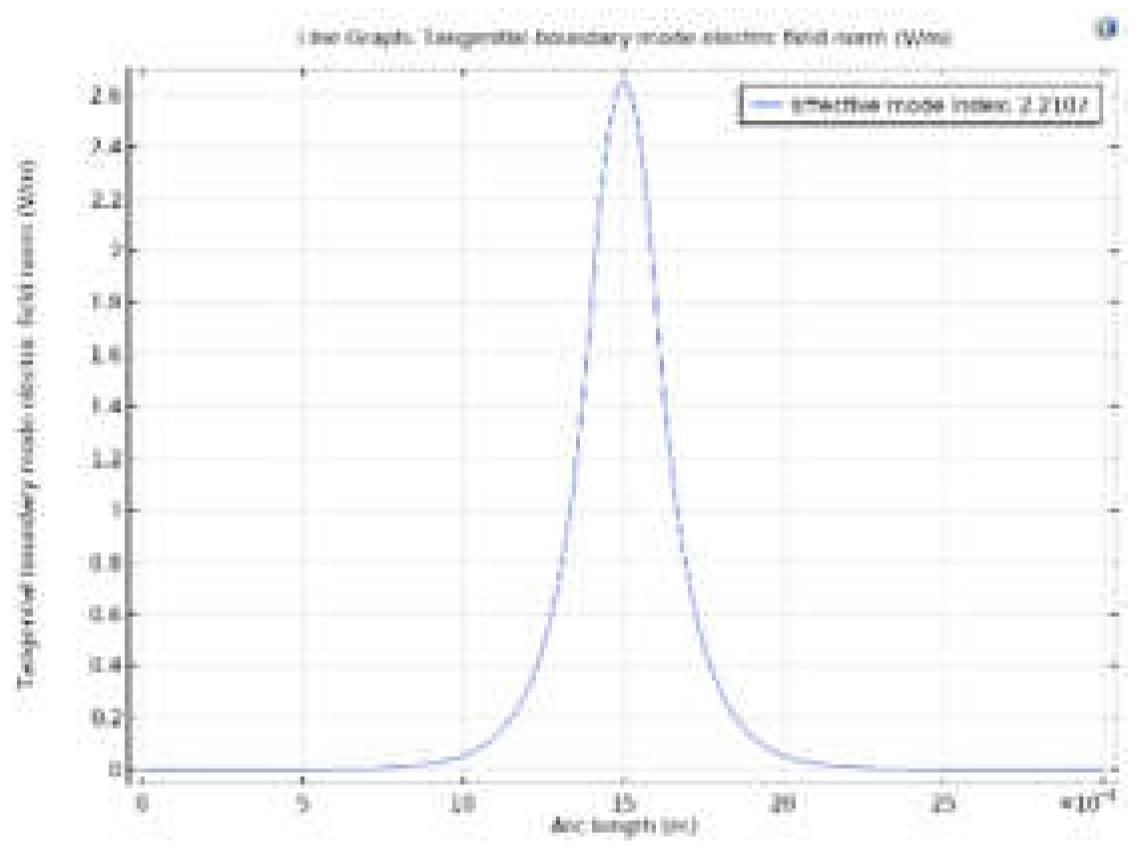
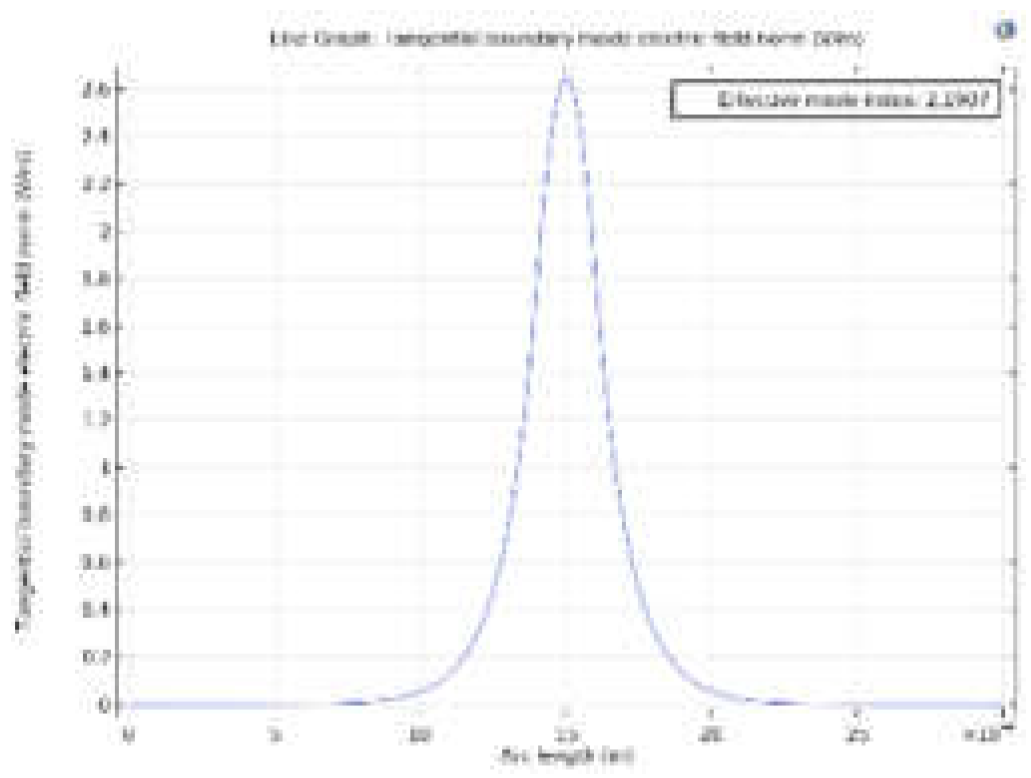
The propagation constant of the fundamental mode for the optical wave.
The effective index of the fundamental mode for the optical wave.
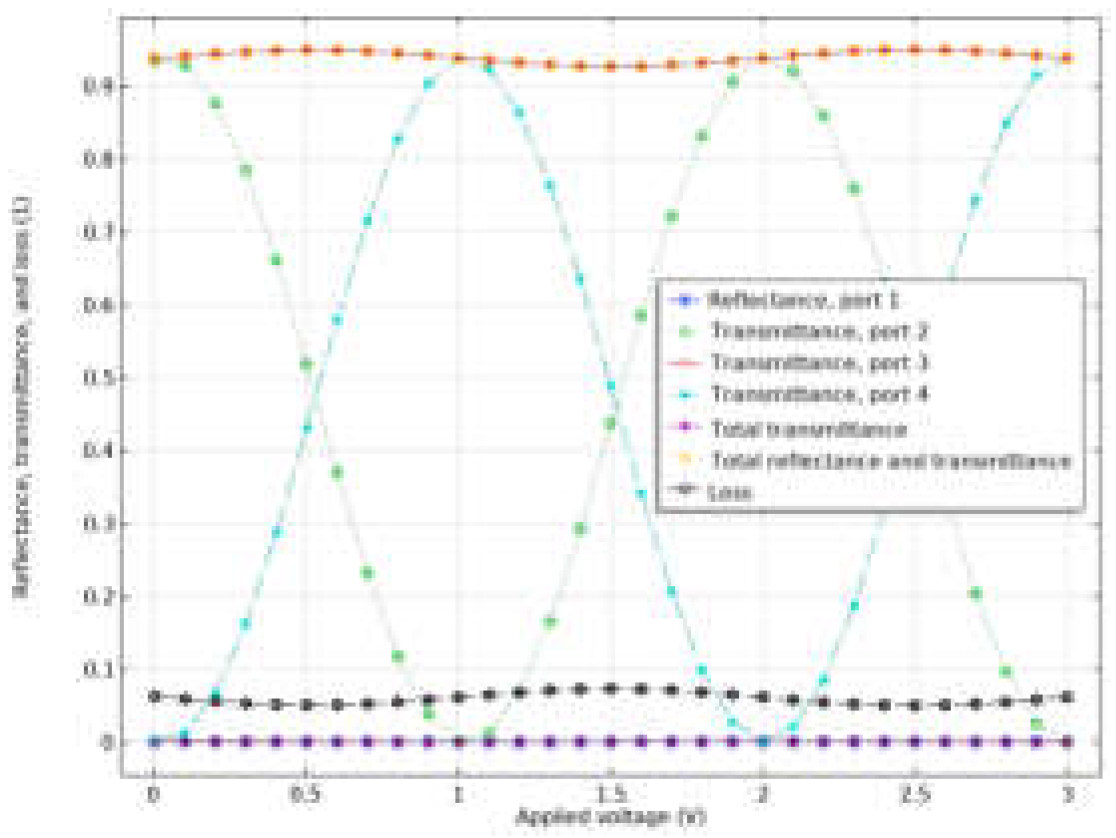
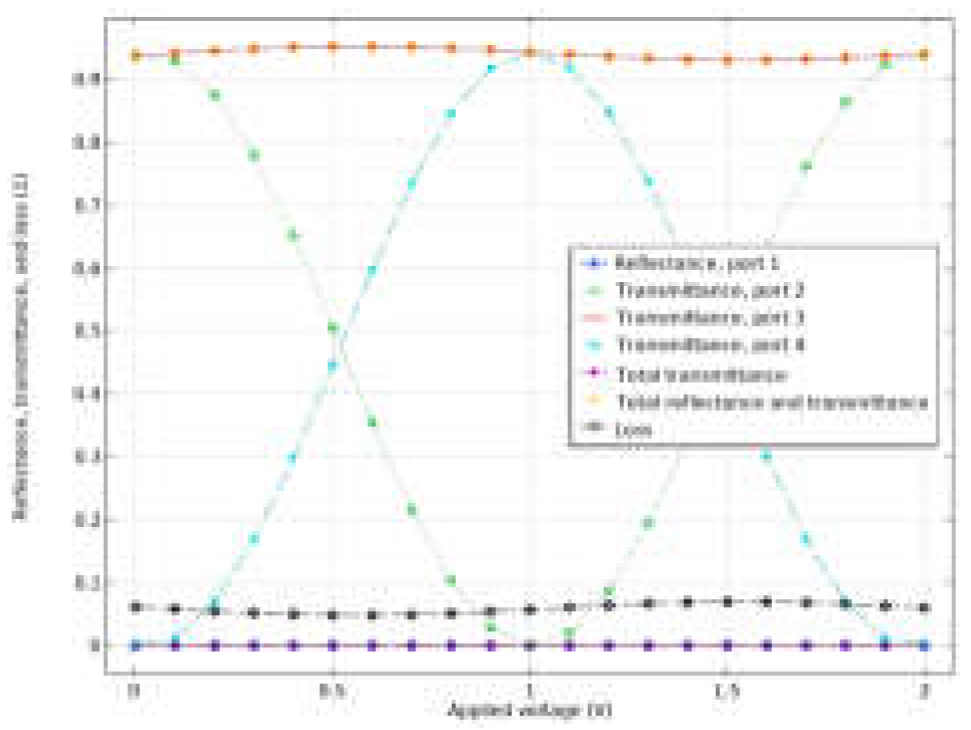
The transmission, reflectance, and loss in all ports at the given range for the applied voltage;
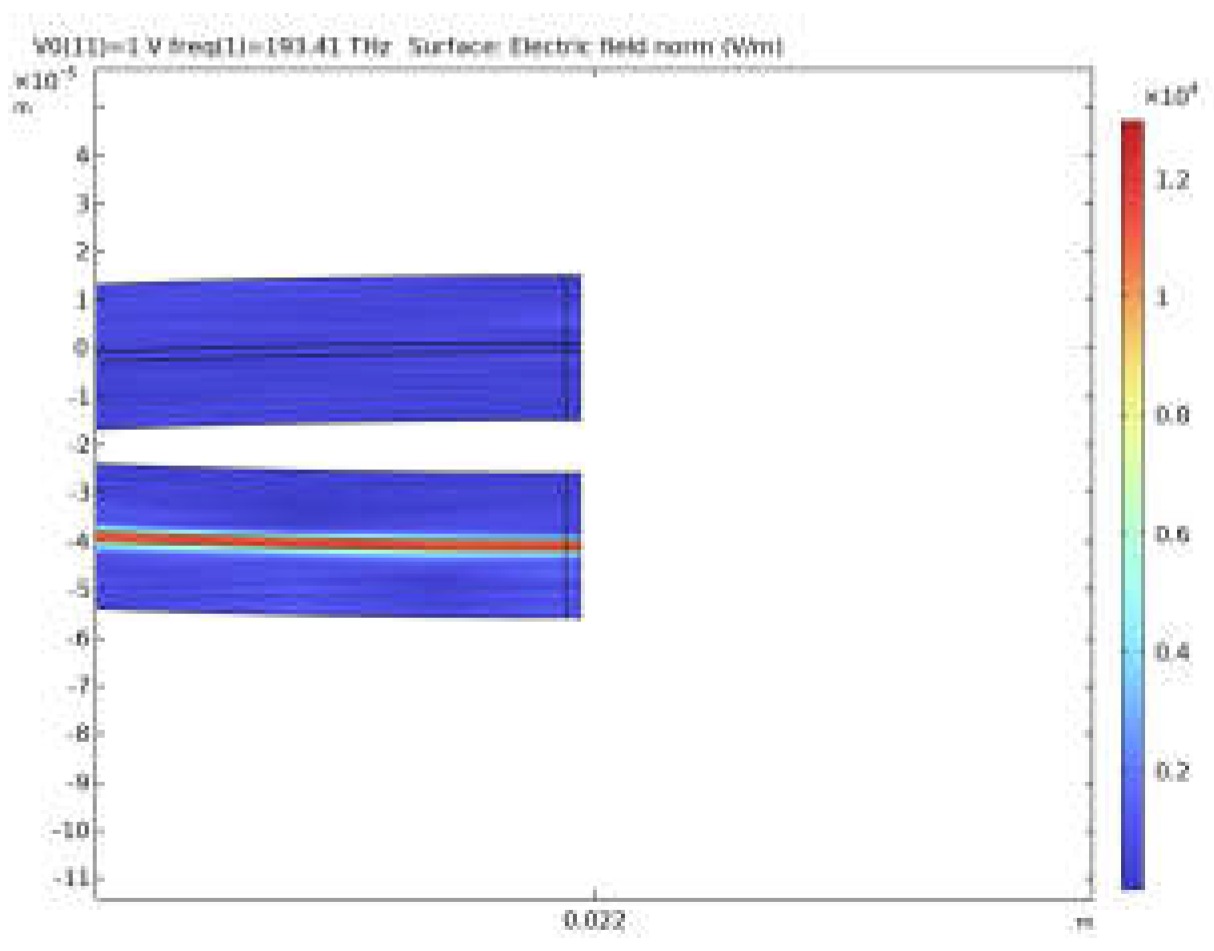
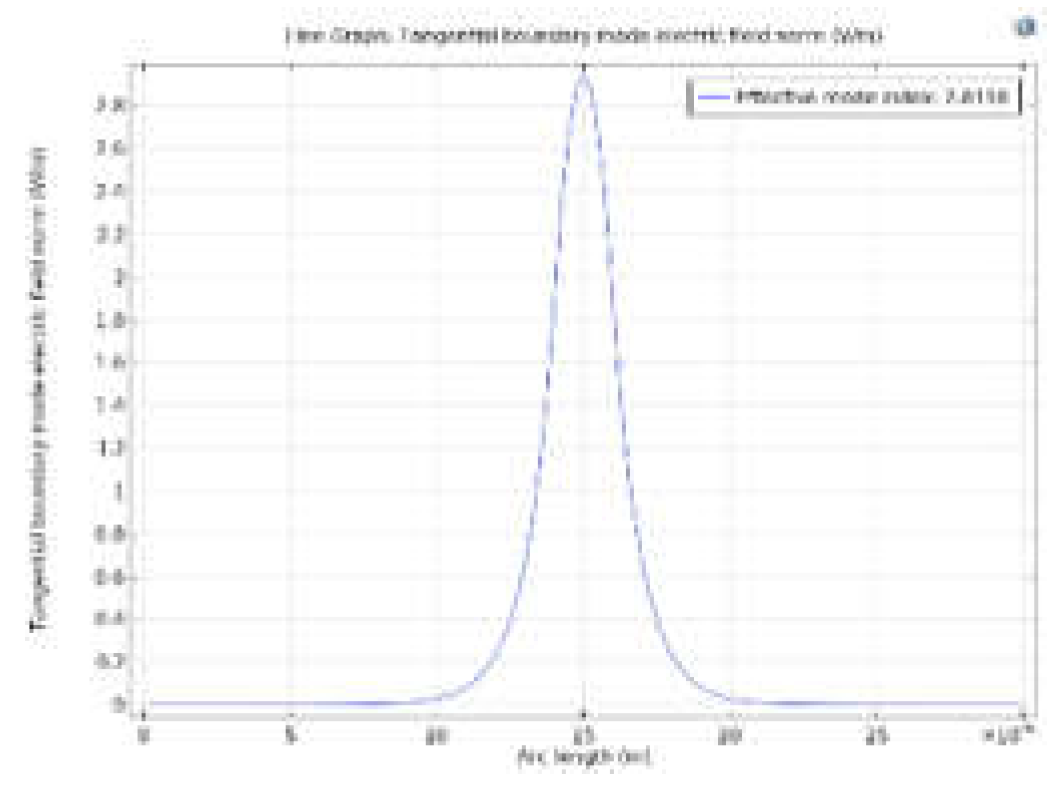
The optical guided field at all ports under different applied voltages.

Having the effective index or group velocity of the optical wave makes it possible to optimize the SiO2 layer (or Si layer in the case of CdTe) thickness of the TW-MZM to get the phase velocity of the RF wave equal to the group velocity of the optical wave. These calculations are performed in the second step as follows;

ii.

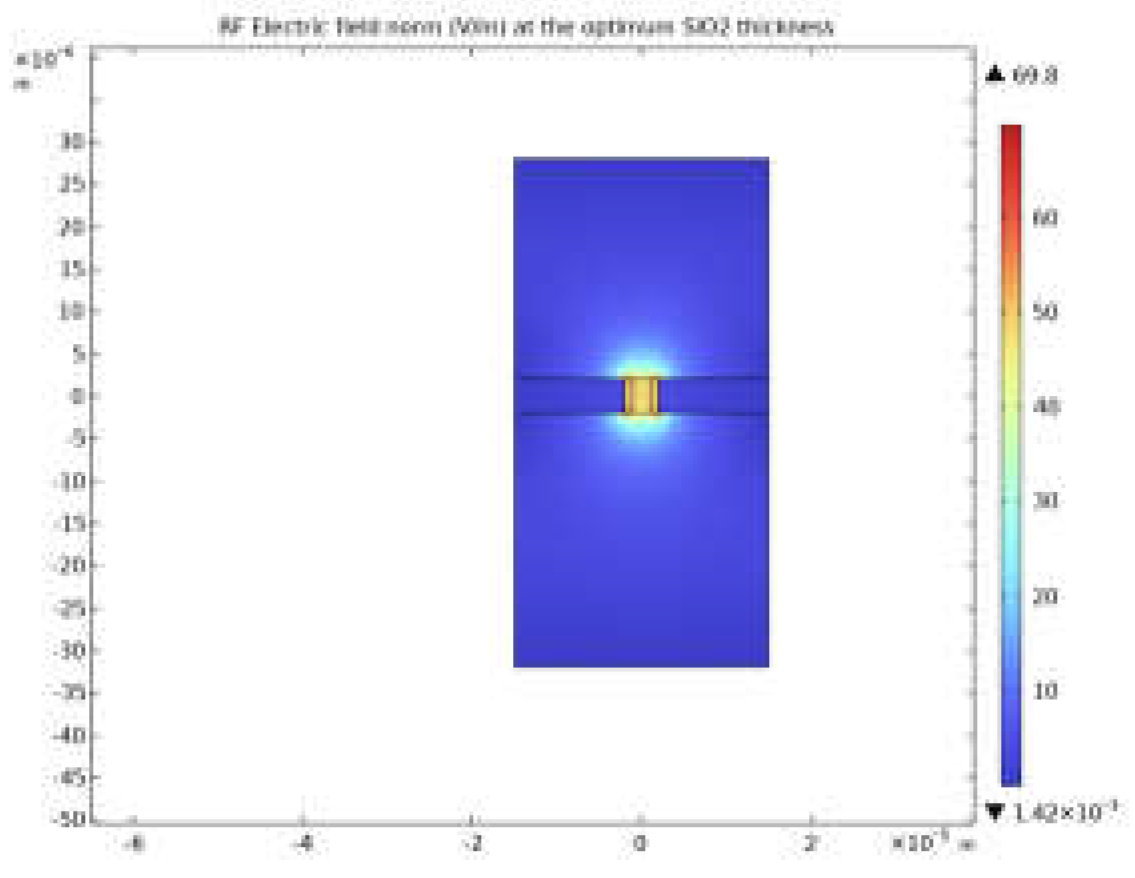
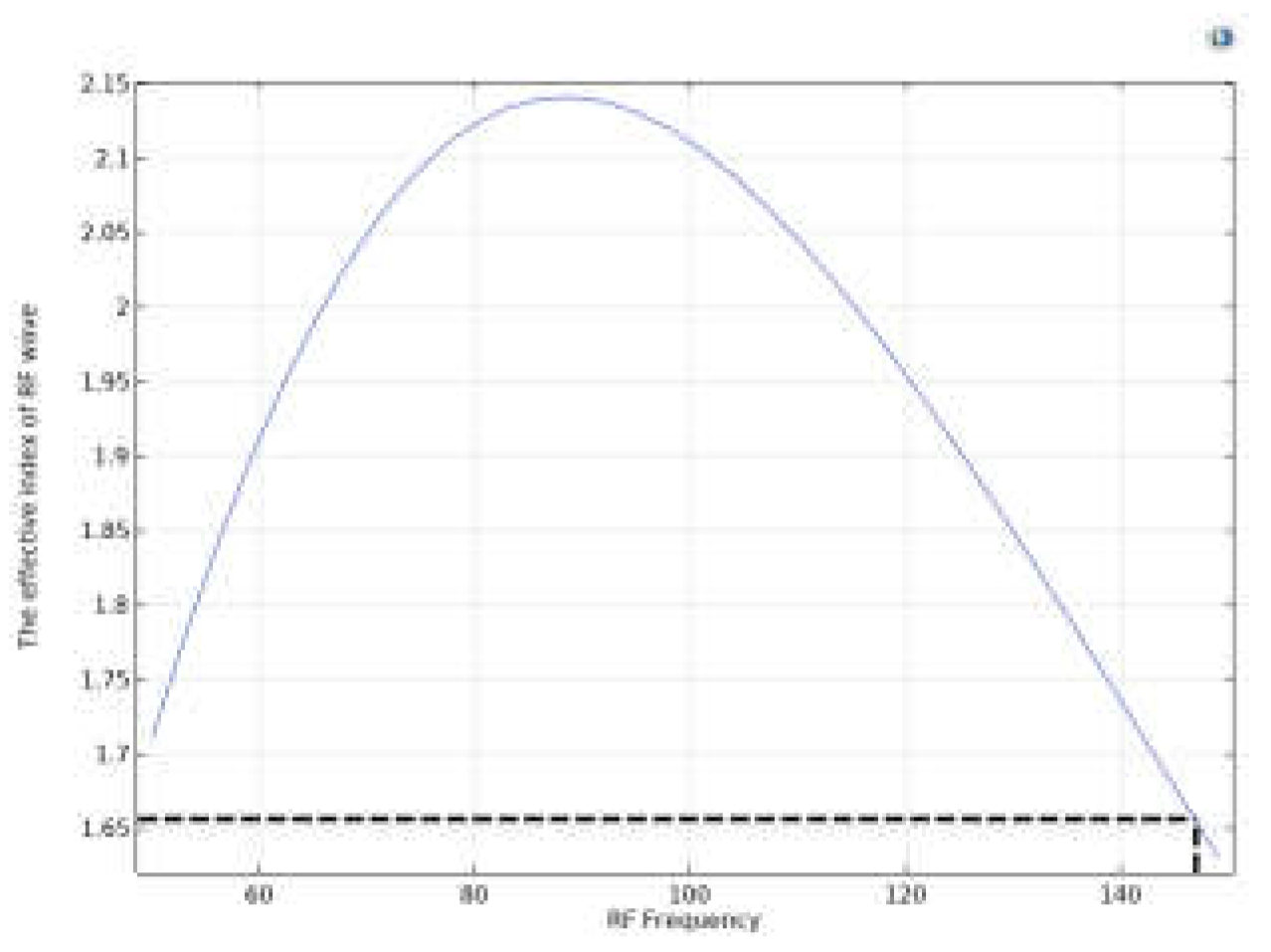
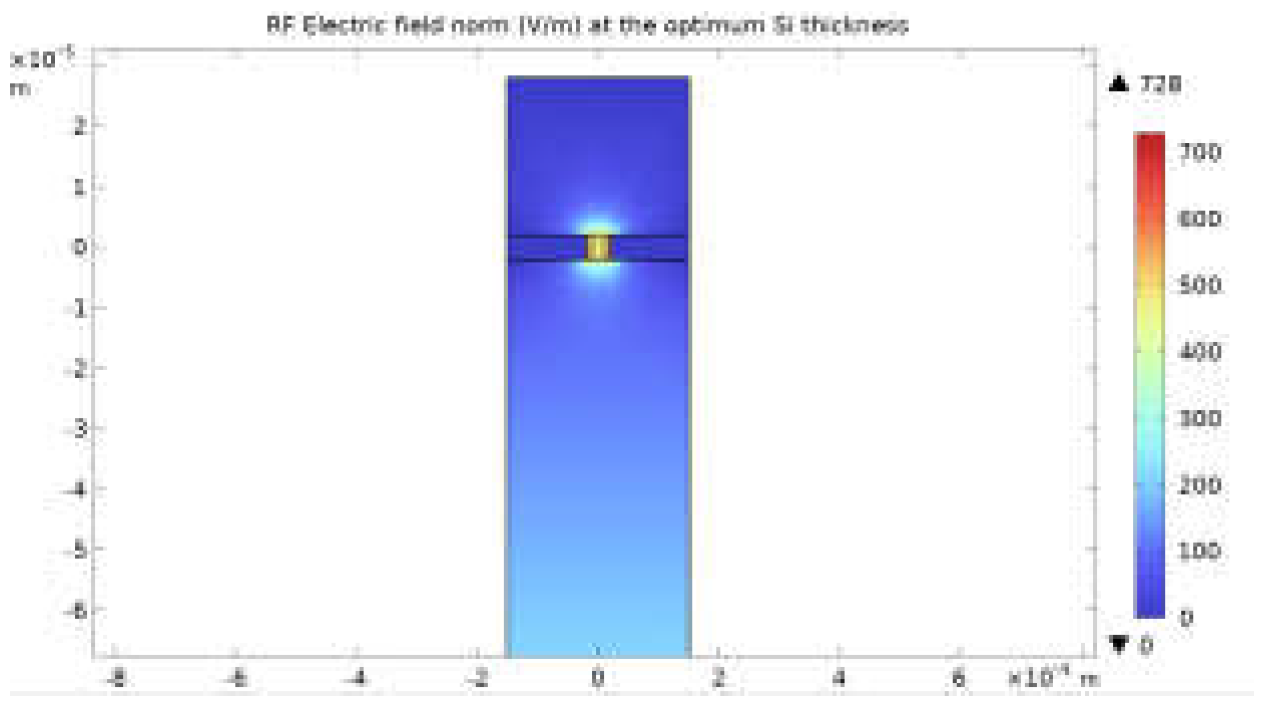
Step 2, The RF wave side: In this step, the section view of the modulator (Figure 6b) is considered, and the geometry is constructed according to the inputs. Then, the thickness of the SiO2 layer (or Si layer in the case of CdTe) is optimized for every single RF frequency in the given range to minimize the difference between the effective indices of the fundamental mode of the RF and optical waves propagating through the TW-MZM. The parameters calculated in this step are as follows;

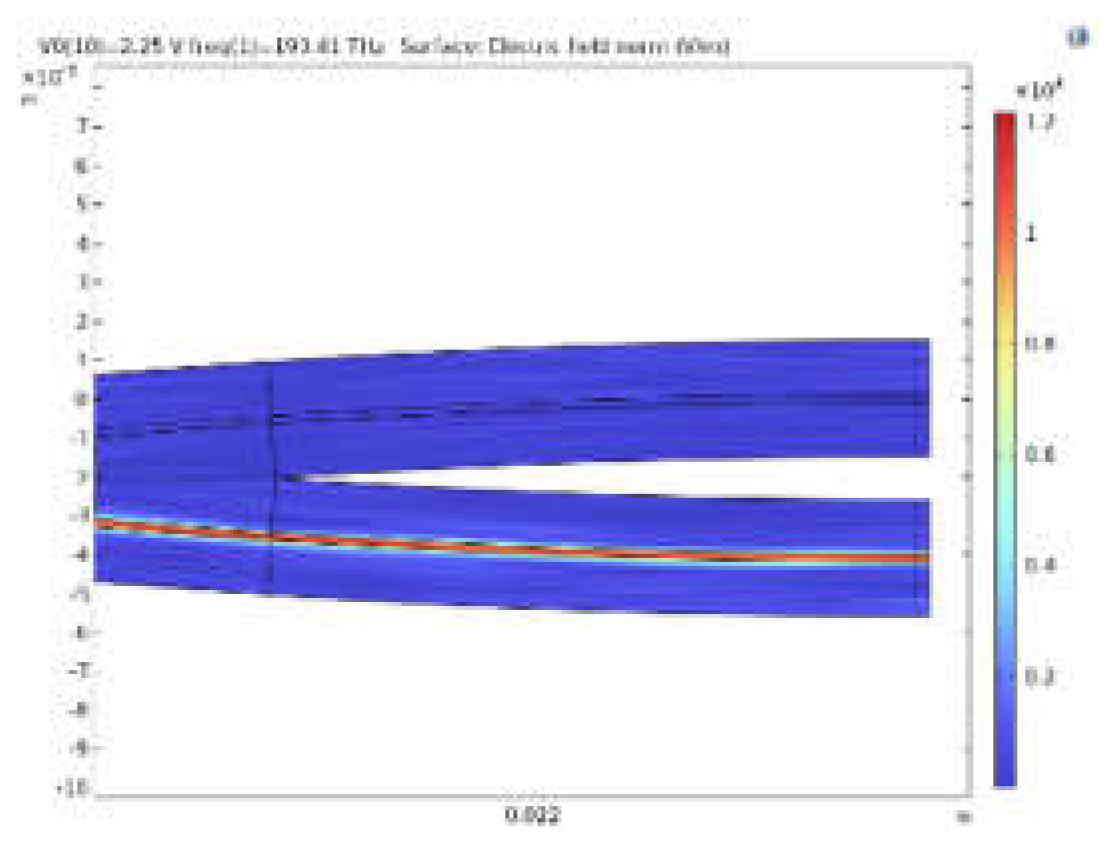
By optimizing the SiO2 layer (or the Si layer in the case of CdTe) thickness for every RF frequency, the propagation constant, the effective index, and the phase velocity of the RF wave at that frequency are calculated.
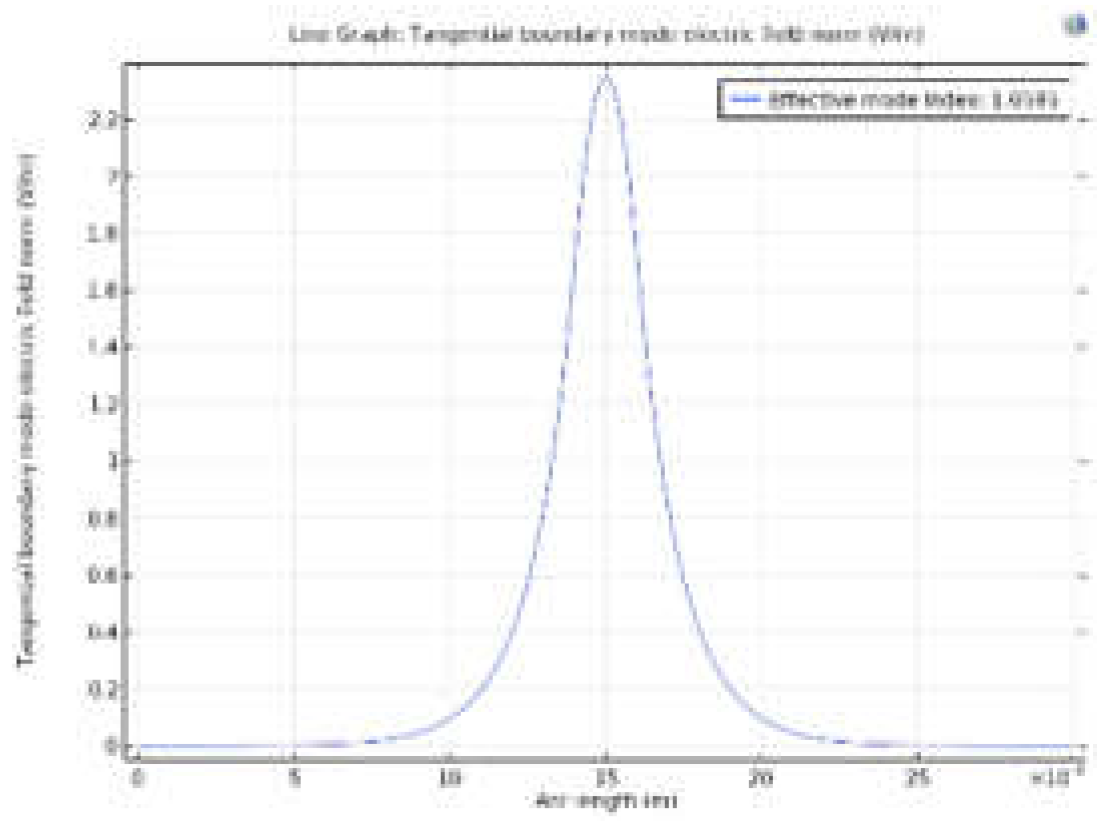
The RF field at every frequency is evaluated by optimizing the SiO2 layer (or Si layer in the case of CdTe) thickness for every RF frequency.
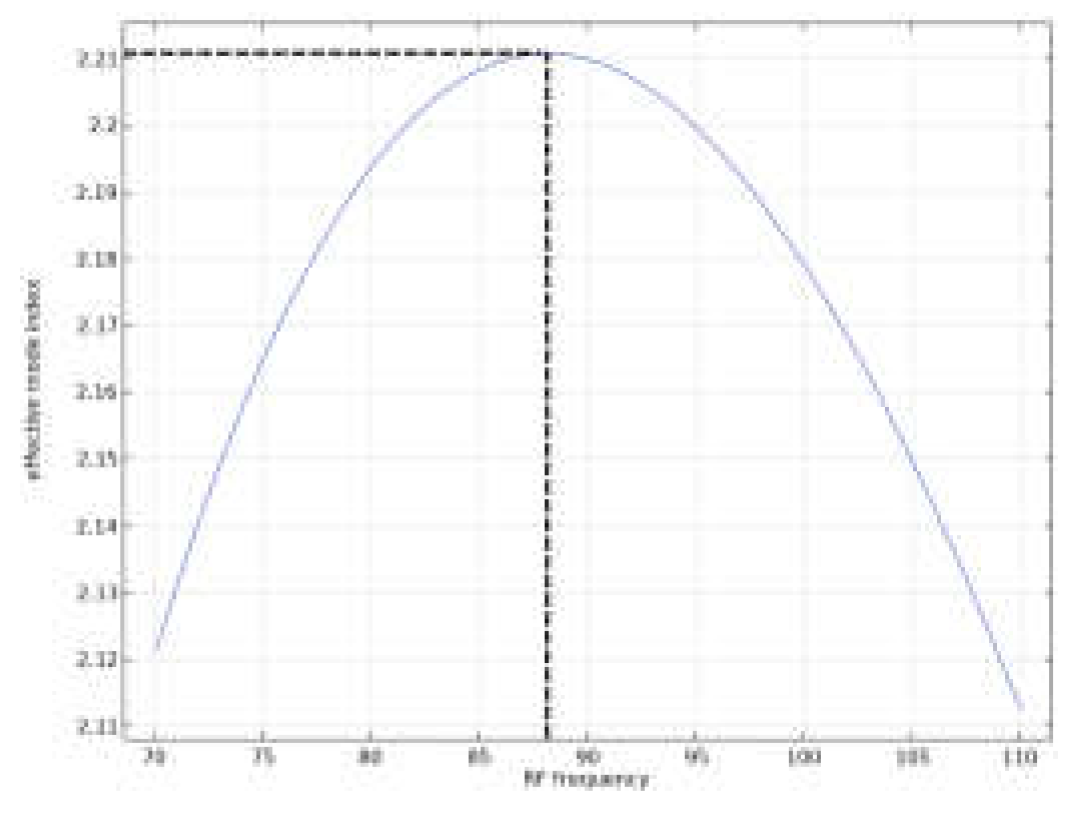
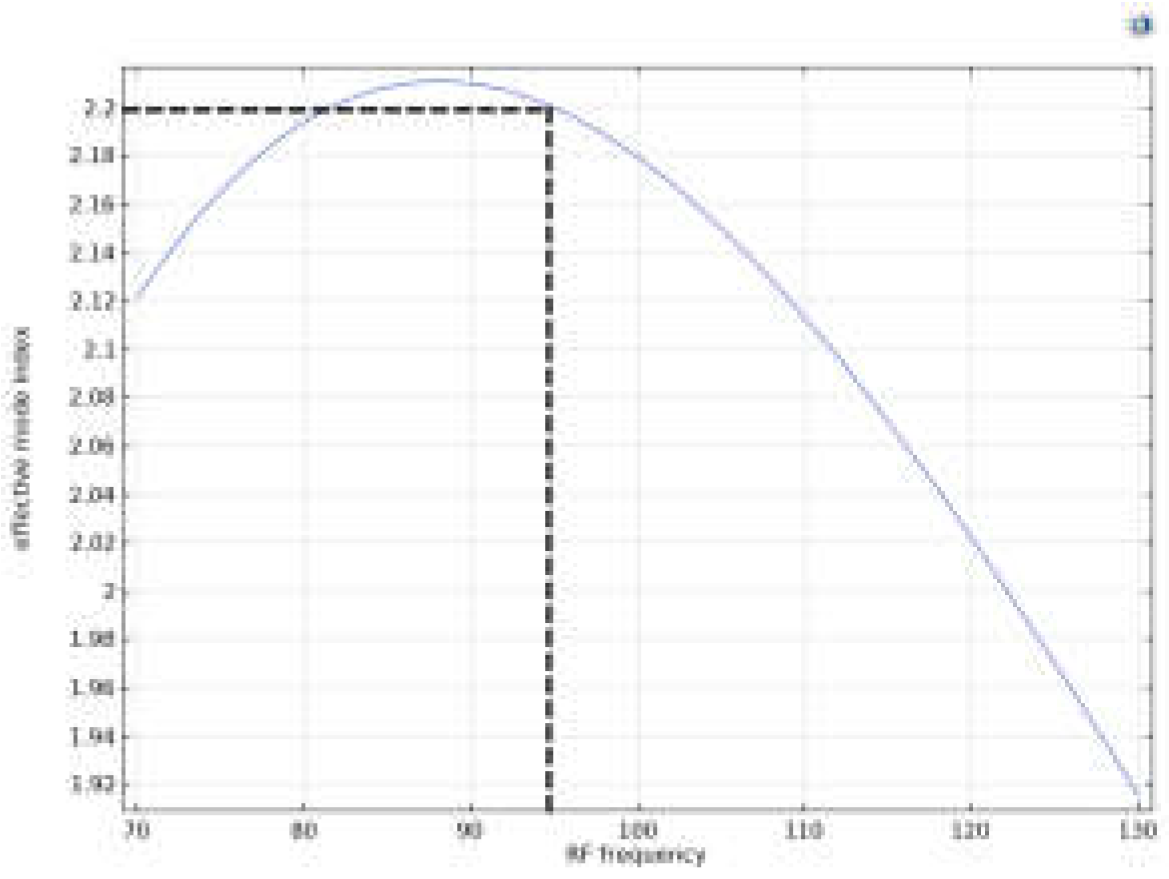
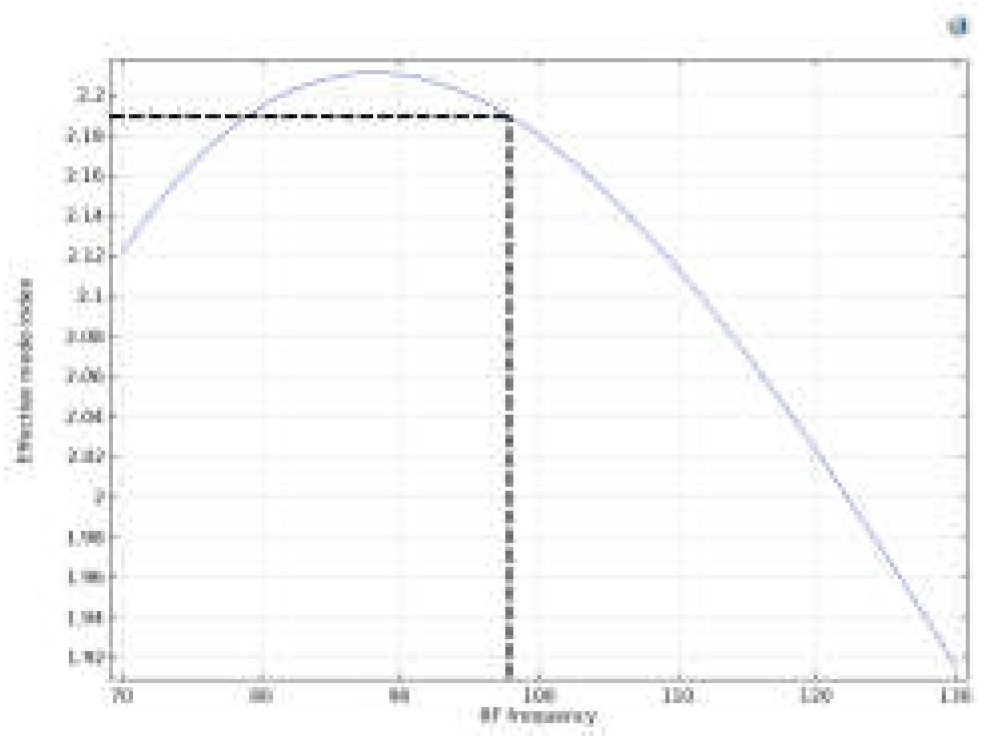
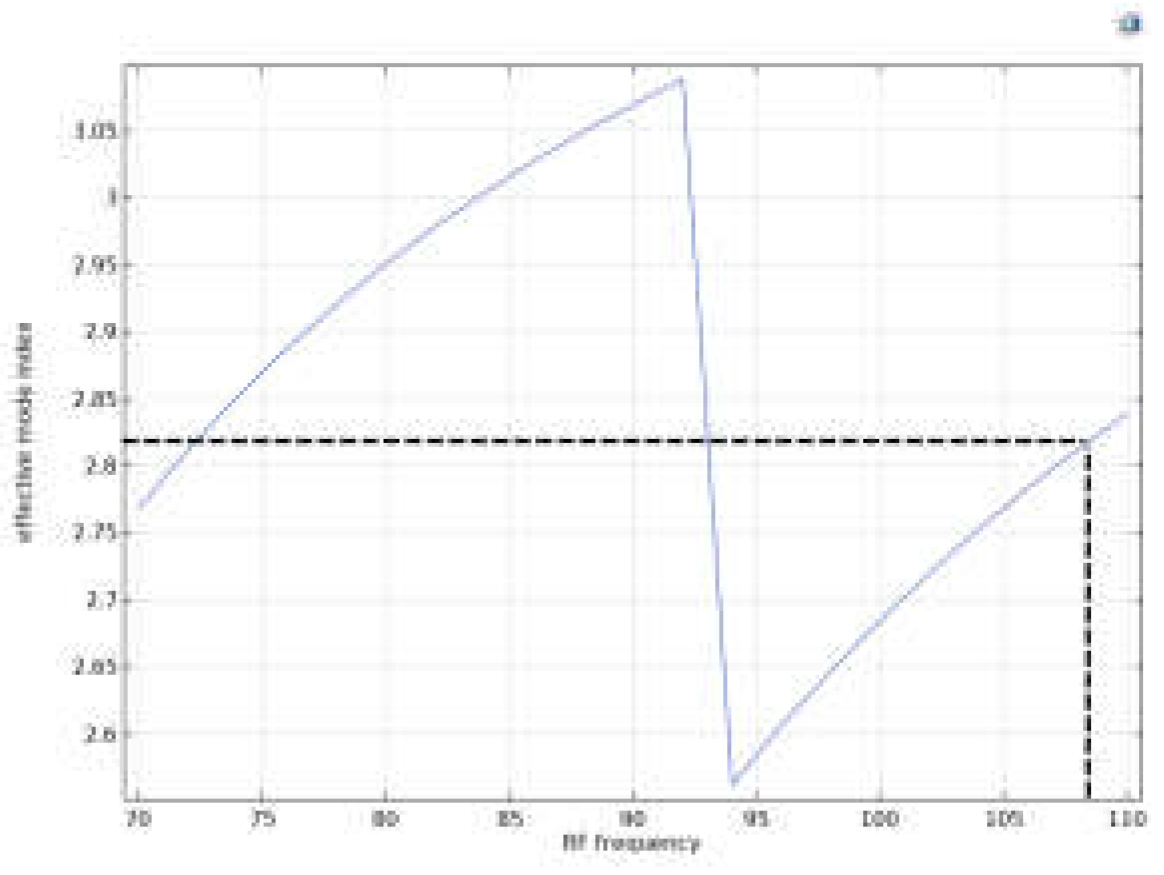
The effective index of the fundamental mode of the RF wave after optimizing the thickness of the SiO2 is plotted versus the frequency of the RF wave.
The maximum bandwidth of the modulation, as the frequency of the RF wave with the fundamental mode effective index matching to the optical wave’s fundamental mode effective index, is estimated.
The RF loss coefficient is calculated using the imaginary part of the RF propagation constant resulting from the velocity matching.

The TW-MZM’s performance and the maximum bandwidth depend on the type of EO material used for modulation and the modulator’s geometry and structure. This model was run for six different EO materials, and the performance results, including the loss and maximum bandwidth of modulation associated with each EO material after optimization of the selected geometry for velocity matching, were evaluated.

3. Results and Discussions

3.1. The Results of the Model for Using Lithium Niobate (LNB) as the EO Medium

Lithium Niobate (LNB), a ferroelectric crystal with uniaxial birefringence, is commonly utilized for waveguide fabrication. The waveguide structures can be created through two methods: indiffusion of titanium (Ti) into the core regions or annealed proton exchange. In the indiffusion process, titanium is diffused into specific areas of the crystal’s core. On the other hand, annealed proton exchange involves exchanging lithium ions with protons from an acid bath. Both approaches enable the formation of waveguides in lithium niobate.

Table 3 shows the model output for using LNB as the EO material in the TW-MZM. The optical field at the output port under the voltage of 1V is given in Figure 7. The transmission, reflection, and loss in all ports for all applied voltages within the voltage range are given in Figure 8. The fundamental mode of the optical wave and its effective index is shown in Figure 9. The RF field at the optimum frequency is given in Figure 10. The effective index of the fundamental mode of RF wave versus the RF frequency is given in Figure 11.

As shown in Figure 11, the effective index of the RF wave with 88GHz frequency is matched to the effective index of the optical wave. Therefore, the maximum modulation bandwidth for using LNB as the EO medium in this specific geometry after the optimization for velocity matching would be 88GHz.

3.2. The Results of the Model for Using BBO as the EO Medium

Table 4 shows the model output for using BBO as the EO material in the TW-MZM. The fundamental mode of the optical wave and its effective index are shown in Figure 12. The RF field at the optimum frequency is given in Figure 13. The effective index of the fundamental mode of the RF wave versus the RF frequency is given in Figure 14.

As shown in Figure 14, the effective index of the RF wave with 148GHz frequency is matched to the effective index of the optical wave. Therefore, the maximum modulation bandwidth for using BBO as the EO medium in this geometry would be 148GHz.

3.3. The Results of the Model for Using Potassium Niobate (KNB) as the EO Medium

Table 5 shows the model output for using KNB as the EO material in the TW-MZM. The transmission, reflection, and loss in all ports for all applied voltages within the voltage range are given in Figure 15. The fundamental mode of the optical wave and its effective index are shown in Figure 16. The RF field at the optimum frequency is given in Figure 17. The effective index of the fundamental mode of RF wave versus the RF frequency is given in Figure 18.

As shown in Figure 18, the effective index of the RF wave with 94GHz frequency is matched to the effective index of the optical wave. Therefore, the maximum modulation bandwidth for using KNB as the EO medium in this geometry would be 94GHz.

3.4. The Results of the Model for Using LiTiO3 as the EO Medium

Table 6 shows the model output for using LTO as the EO material in the TW-MZM. The transmission, reflection, and loss in all ports for all applied voltages within the voltage range are given in Figure 19. The fundamental mode of the optical wave and its effective index are shown in Figure 20. The RF field at the optimum frequency is given in Figure 21. The effective index of the fundamental mode of RF wave versus the RF frequency is given in Figure 22.

As shown in Figure 22, the effective index of the RF wave with 97GHz frequency is matched to the effective index of the optical wave. Therefore, the maximum modulation bandwidth for using LTO as the EO medium in this geometry would be 97GHz.

3.5. The Results of the Model for Using CdTe as the EO Medium

The assumed geometry in this model does not converge when employing CdTe as the EO medium. The reason for that is the CdTe is a high index semiconductor, and adjusting the thickness of the SiO2 layer will not make the phase velocity of the RF wave low enough to match the group velocity of the optical wave. Therefore, to examine the performance of CdTe as the EO material in this TW-MZM, we needed to replace the SiO2 layer with the Si layer and try to optimize the thickness of the Si layer to get a velocity match between the RF and optical wave to estimate the maximum modulation bandwidth of the TW-MZM in the case of using CdTe as the EO medium and Si as the substrate. The fundamental mode of the optical wave and its effective index are shown in Figure 23. The optical field under 2.25V is shown in Figure 24. The RF field at the optimum frequency after optimization of the thickness of the Si layer is given in Figure 25. The effective index of the fundamental mode of RF wave versus the RF frequency is given in Figure 26.

Again, using CdTe as the EO material in this TW-MZM was not straightforward. That is because the optimization model could not converge. This means that adjusting the thickness of the SiO2 layer did not lower the RF wave’s phase velocity enough to equal the optical wave’s group velocity. That is why we had to replace the SiO2 layer with the Si layer and adjust its thickness to match the velocity of the RF and optical waves. As shown in Figure 26, the effective index of the RF wave with 108 GHz frequency is matched to the effective index of the optical wave. Therefore, the maximum modulation bandwidth for using CdTe as the EO medium in this geometry would be 108 GHz.

3.6. The Results for Using InP as the EO Medium Calculated by Pascher et al.

The assumed geometry in this model (Figure 6) did not converge when utilizing Indium Phosphide (InP) as the EO medium. Consequently, to investigate the possibility of employing InP as the EO material in a TW-MZM and evaluate its performance, the results published by Pascher et al. (2003) [5] were referred to in this study.

Figure 27 presents the top and sectional views of the TW-MZM, as examined in the study conducted by Pascher et al. (2003) [5]. Figure 28 shows the RF attenuation (α) and the real part of the RF index for the TW-MZM optimized for InP by Pascher et al. (2003) [5].

As seen in Figure 28, which was presented by Pascher et al. (2003)[5], the real part of the effective index of the RF wave, at approximately 40 GHz frequency, aligns with the effective index of the fundamental mode of the optical wave. Accordingly, within the optimized geometry proposed by Pascher et al. (2003), the potential maximum modulation bandwidth achievable when employing InP as the EO medium would be 40 GHz [5].

3.7. Comparing the Bandwidth, Optical Loss, and RF Loss of the TW-MZM Optimized for Each of the Six EO Crystals

This study investigated the suitability of six different EO materials, including LNB, BBO, KNB, LTO, CdTe, and InP, to be used as an EO medium in a Traveling-Wave Mach-Zehnder intensity modulator. Considering an optical wavelength of 1.55 μm and utilizing the specific structure described in this report after optimization for velocity matching, we present the key performance results for each of the six EO materials in Table 7.

4. Conclusions

Besides the type of electro-optical (EO) crystal, the performance of a Traveling-Wave Mach-Zehnder intensity modulator (TW-MZM) is also greatly influenced by the selected geometry and materials employed in other layers. This study aimed to evaluate the effects of different EO materials on the performance of the TW-MZM, with specific optimizations carried out for each of the six EO materials. In the case of CdTe utilization, the SiO2 layer was substituted with a Si layer, and the thickness of the Si layer was optimized instead of the SiO2 layer thickness. The assumed geometry in this model didn’t converge for InP; therefore, the results calculated by Pascher et al. (2003) [5] were presented and compared to the other five EO materials.

The results indicated that KNB, LTO, BBO, and CdTe have the potential to surpass LNB in terms of higher modulation bandwidth. However, it should be noted that KNB and LTO demonstrate a comparable level of loss compared to LNB. The findings demonstrate that BBO and, specifically, CdTe exhibit modulation bandwidths exceeding 100 GHz while exhibiting the lowest loss among the considered crystals based on the adopted geometry. The results of Pascher et al. showed that although InP exhibits the lowest RF loss, the associated modulation bandwidth is much lower than what can be achieved with the other five crystals.

Future studies will explore alternative geometries and different materials for other layers, aiming to define an optimal configuration that maximizes modulation bandwidth and minimizes optical and RF loss.

Acknowledgments

This research was supported by the Ohio Federal Research Network (OFRN).

Conflicts of Interest

The authors declare no conflicts of interest.

References

Cong, G., et al., Silicon traveling-wave Mach–Zehnder modulator under distributed-bias driving. Optics Letters, 2018. 43(3): p. 403-406. [CrossRef]
Ackermann, M., et al., Resonantly enhanced lumped-element O-band Mach–Zehnder modulator with an ultra-wide operating wavelength range. Optics Letters, 2023. 48(21): p. 5623-5626. [CrossRef]
Sharif Azadeh, S., et al., Power-efficient lumped-element meandered silicon Mach-Zehnder modulators. SPIE OPTO. Vol. 11285. 2020: SPIE.
Xu, H., et al., Demonstration and Characterization of High-Speed Silicon Depletion-Mode Mach–Zehnder Modulators. IEEE Journal of Selected Topics in Quantum Electronics, 2014. 20(4): p. 23-32. [CrossRef]
Pascher, W., et al. Modeling and Design of a Velocity-Matched Traveling-Wave Electro-Optic Modulator on InP. in Integrated Photonics Research. 2003. Washington, D.C.: Optica Publishing Group.
Ataei, A., et al., Determining the Quadratic Electro-Optic Coefficients for Polycrystalline Pb(Mg1/3Nb2/3)O3-PbTiO3 (PMN-PT) Using a Polarization-Independent Electro-Optical Laser Beam Steerer. Applied Sciences, 2021. 11(8): p. 3313.
Steglich, P., et al., Silicon-organic hybrid photonics: an overview of recent advances, electro-optical effects and CMOS integration concepts. Journal of Physics: Photonics, 2021. 3(2): p. 022009.
Benea-Chelmus, I.-C., et al., Electro-optic spatial light modulator from an engineered organic layer. Nature Communications, 2021. 12(1): p. 5928. [CrossRef]
Rahim, A., et al., Taking silicon photonics modulators to a higher performance level: state-of-the-art and a review of new technologies. Advanced Photonics, 2021. 3(2): p. 024003. [CrossRef]
Zhang, M., et al., Integrated lithium niobate electro-optic modulators: when performance meets scalability. Optica, 2021. 8(5): p. 652-667. [CrossRef]
Wang, C., et al., Integrated lithium niobate electro-optic modulators operating at CMOS-compatible voltages. Nature, 2018. 562(7725): p. 101-104. [CrossRef]
COMSOL Multiphysics^® v. 6.2. www.comsol.com. COMSOL AB, Stockholm, Sweden.
Ataei, A., et al., An electro-optic continuous laser beam steering device based on an SBN75 crystal. Ferroelectrics, 2023. 603(1): p. 34-51. [CrossRef]
Baehr-Jones, T., et al., Ultralow drive voltage silicon traveling-wave modulator. Optics Express, 2012. 20(11): p. 12014-12020. [CrossRef]
Qi, N., et al., Co-Design and Demonstration of a 25-Gb/s Silicon-Photonic Mach–Zehnder Modulator With a CMOS-Based High-Swing Driver. IEEE Journal of Selected Topics in Quantum Electronics, 2016. 22(6): p. 131-140. [CrossRef]

Figure 1. The geometry of the MZM considered in this study (a) versus that of a conventional MZM (b).

Figure 2. The geometries of the light modulators based on a) BTO, b) PZT, c) Organic EO material, and d) LNB [9,10].

Figure 3. The architecture of the phase, intensity, and combined phase and intensity modulator.

Figure 4. The structure of an MZM pursued in this study.

Figure 5. Adjusting the SiO₂ layer thickness enables velocity matching between the RF and optical waves.

Figure 6. The top view (a) and the section view (b) of the TW-MZM considered in this model.

Figure 7. The optical field at the output port under the voltage of 1V.

Figure 8. The transmission, reflection, and loss in all ports for all applied voltages within the voltage range.

Figure 9. The fundamental mode of the optical wave and its effective index.

Figure 10. The RF field at the optimum frequency.

Figure 11. The effective index of the fundamental mode of RF wave versus the RF frequency.

Figure 12. The fundamental mode of the optical wave and its effective index.

Figure 13. The RF field at the optimum frequency.

Figure 14. The effective index of the fundamental mode of RF wave versus the RF frequency.

Figure 15. The transmission, reflection, and loss in all ports for all applied voltages within the voltage range.

Figure 16. The fundamental mode of the optical wave and its effective index.

Figure 17. The RF field at the optimum frequency.

Figure 18. The effective index of the fundamental mode of RF wave versus the RF frequency.

Figure 19. The transmission, reflection, and loss in all ports for all applied voltages within the voltage range.

Figure 20. The fundamental mode of the optical wave and its effective index.

Figure 21. The RF field at the optimum frequency.

Figure 22. The effective index of the fundamental mode of RF wave versus the RF frequency.

Figure 23. The fundamental mode of the optical wave and its effective index.

Figure 24. The optical field at the output port under 2.25V.

Figure 25. The RF field at the optimum frequency after optimization of the thickness of the Si layer.

Figure 26. The effective index of the fundamental mode of RF wave after optimization of the thickness of the Si layer for each frequency versus the RF frequency.

Figure 27. The top view (a) and the section view (b) of the TW-MZM considered by Pascher et al. (2003)[5].

Figure 28. The RF attenuation (α) and the real part of the RF index for the TW-MZM optimized for InP by Pascher et al. (2003) [5].

Table 1. The main properties of some traditional χ(2) materials [6].

Material	n	ɛ	r (pmV−1)	n3r/ɛ (pmV−1)
Ferroelectrics (room temperature)
LiNbO3	2.26	29	31	12.339
LiTaO3	2.23	43	31	7.995
KNbO3	2.23	55	64	12.904
BaTiO3	2.4	1800	1670	12.826
SBN75	2.3	1550	1340	10.519
SBN60	2.3	750	216	3.504
BBO	1.67	6.7	2.7	1.877
Semiconductors (room temperature)
GaAs	3.5	13.2	1.2	3.898
InP	3.29	12.6	1.45	4.098
CdTe	2.82	9.4	6.8	16.223
Bi12SiO20	2.54	56	5	1.463
Bi12GeO20	2.55	47	3.4	1.200
Cubic (varied by temperature and frequency)
KTN	2.3	14000	8500	7.387
PMN-PT	2.37	7000	3400	6.466

Table 2. The list of the inputs of the TW-MZM simulation and design model.

Table 3. The output of the model for LNB as the EO material in this TW-MZM.

Table 4. The output of the model for BBO as the EO material in this TW-MZM.

Table 5. The output of the model for KNB as the EO material in this TW-MZM.

Table 6. The output of the model for LTO as the EO material in this TW-MZM.

Table 7. Performance comparison of six EO materials in the TW-MZM after optimization for velocity matching*.

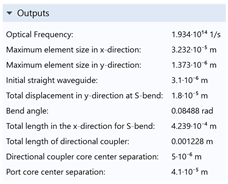
Parameters	LNB	BBO	KNB	LTO	CdTe	InP1
The effective index of the optical wave	2.2107	1.6595	2.2007	2.1907	2.8118	3.28
The operating voltage of the modulator (V)	1	11	0.5	1	2.25	NA
Maximum modulation bandwidth (GHz)	88	148	94	97	108	40
The optical intensity loss in the modulator (%)	6.14	5.82	6.76	6.66	7.48	NA
The RF loss in the modulator (dB/mm)	8.8	8.3	8.8	8.8	0.6	2.5

* The results obtained for utilizing Indium Phosphide (InP) as the electro-optical (EO) material are sourced from Pascher et al. (2003).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

110

Views

Comments

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Performance Analysis of Six Electro-Optical Crystals in a High-Bandwidth Traveling Wave Mach-Zehnder Light Modulator

Abstract

Keywords:

Subject:

1. Introduction

2. Materials and Methods

2.1. Selecting the Material and Geometry

2.2. Selecting the Type and Architecture of the Modulator

2.3. Selecting the Type of Electrodes

2.4. Velocity Matching between the RF and Optical Wave

2.5. The Loss Estimation Method for the RF and Optical Waves in the TW-MZM

2.6. Modeling in COMSOL Multiphysics

2.6.1. The Inputs of the Model

2.6.2. The Two Steps of the Model

3. Results and Discussions

3.1. The Results of the Model for Using Lithium Niobate (LNB) as the EO Medium

3.2. The Results of the Model for Using BBO as the EO Medium

3.3. The Results of the Model for Using Potassium Niobate (KNB) as the EO Medium

3.4. The Results of the Model for Using LiTiO3 as the EO Medium

3.5. The Results of the Model for Using CdTe as the EO Medium

3.6. The Results for Using InP as the EO Medium Calculated by Pascher et al.

3.7. Comparing the Bandwidth, Optical Loss, and RF Loss of the TW-MZM Optimized for Each of the Six EO Crystals

4. Conclusions

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe