Dynamic Simulation of the Leaf Mass Per Area (LMA) in Multilayer Crowns of young Larix principis-rupprechtii

1. Introduction

The Leaf economics spectrum (LES) is a set of interconnected and synergistic functional traits, which quantitatively represent a range of steadily shifting plant resource trade-off strategies [1,2]. At the heart of this complex and multifaceted trait network lies leaf mass per area (LMA) [3]. LMA is the ratio of dry leaf mass to the corresponding leaf area and is a combination of various leaf anatomical characteristics [4]. It is widely used to estimate leaf area indices [5,6] and simulate canopy photosynthesis [7,8]. LMA values vary among different tree species, different environmental conditions and different leaf developmental stages. Thus, the accurate and swift measurements of LMA and its dynamic changes are highly important for understanding the growth processes of trees, simulating canopy photosynthesis, and estimating forest productivity.

The crown is the primary organ responsible for photosynthesis in trees. Its intricate three-dimensional structure of branches and leaves affects the local microenvironment of the crown, resulting in spatial differences in leaf functional traits in different areas of the crown [9,10,11]. Studies have shown that the LMA of crowns in various forest types tends to increase from the bottom to the top of the crown [12,13,14]. This increasing pattern of LMA is usually associated with the light gradient through the crown and the water potential gradient from the root to the crown [15,16,17]. In addition to the vertical variation in the crown, LMA also varies significantly across the different developmental stages of trees. Nouvellon et al. [19] reported that LMA changes drastically over different months, which was also confirmed by Rossatto's research [20] on savanna grassland tree species and forest tree species in central Brazil. This variation in LMA can be attributed to differences in temperature, precipitation and solar radiation among the different periods.

The alteration of LMA typically depends on the leaf dry matter content (LDMC). Plants can acclimate to diverse circumstances through varied dry matter investments. Consequently, the correlation between traits is strongly associated with the resources and environment in which plants are located. Previous studies have demonstrated that there is a significant correlation between LMA and LDMC, and the association is significantly disparate under diverse environmental conditions [21,22]. For trees with a conspicuous canopy structure, the gradient discrepancy of the canopy microenvironment in the vertical direction [23] will cause a shift in the correlation between different canopy depths. Zhang [24] studied the vertical changes in the LMA and LDMC of Pinus yunnanensis with canopy height. The results showed that different LMA and LDMC values exhibited distinct changes with canopy height. Tian et al. [25] reached the same conclusion. Additionally, alterations in the temperature, precipitation and solar radiation of plants during different growing seasons will make the environment in which leaves are situated highly heterogeneous. This will lead to different changes in LMA and LDMC with canopy height at different growth stages.

Due to the limitations of leaf area measurement technology [26], it is very difficult to measure LMA. Currently, LMA is measured by retaining some leaves of the analysed tree and establishing a single tree leaf biomass model based on the leaf biomass of the analysed tree and its diameter at breast height [27] or by directly calculating LMA from the measured total leaf area and leaf dry mass. However, for coniferous plants, these methods require considerable manpower and material resources [28,29] because of their three-dimensional structure and large number of leaves. To address this issue, an increasing number of researchers are estimating LMA by establishing regression models between LMA and plant traits, leaf morphology, or environmental conditions such as leaf length, leaf width [30,31], branch height [32,33], and LDMC [34,35,36]. As the correlation between LMA and vertical direction in a tree crown is significant, variables related to vertical height, such as branch height, depth into crown and relative depth into crown, are often used as the main fitting factors. LDMC is also a common fitting factor, and many studies have discussed the relationship between these two parameters, and typical linear models or nonlinear models are used to fit LMA based on LDMC [37]. Peng's research [38] showed that the LMA of Chinese fir can be estimated by the LDMC and that the model meets the estimation requirements. Therefore, it is important to establish a simple and accurate LMA prediction model for the purpose of simplifying canopy models. Determining LDMC and RDINC is simpler than determining LMA, and both methods meet the estimation requirements of LMA. However, previous studies have taken only leaf samples at one particular point in time or at a specific canopy position. It is yet to be determined whether different leaf development stages and depths of the canopy have an effect on LMA prediction models. Few studies have examined which vertical factor or LDMC can most accurately predict LMA. Furthermore, whether leaf development time can be used as a single factor to predict LMA has not been tested.

Larix principis-rupprechtii is one of the most widely planted trees in North China; it is characterized by strong light tolerance, rapid growth, and longevity and is a valuable native species. This study used a 17-year-old L. principis-rupprechtii from the Saihanba Forest Farm in Chengde city, Hebei Province, as the object of study to compare the differences in the LMA of needles at various crown layers and various leaf development stages, analyse the changes in LMA, and compare the correlations between LMA and other indicators at various crown depths and various leaf development stages. Finally, the best prediction model of LMA for L. principis-rupprechtii plantations was established, which can be used to simulate crown photosynthesis and estimate regional primary productivity.

2. Results

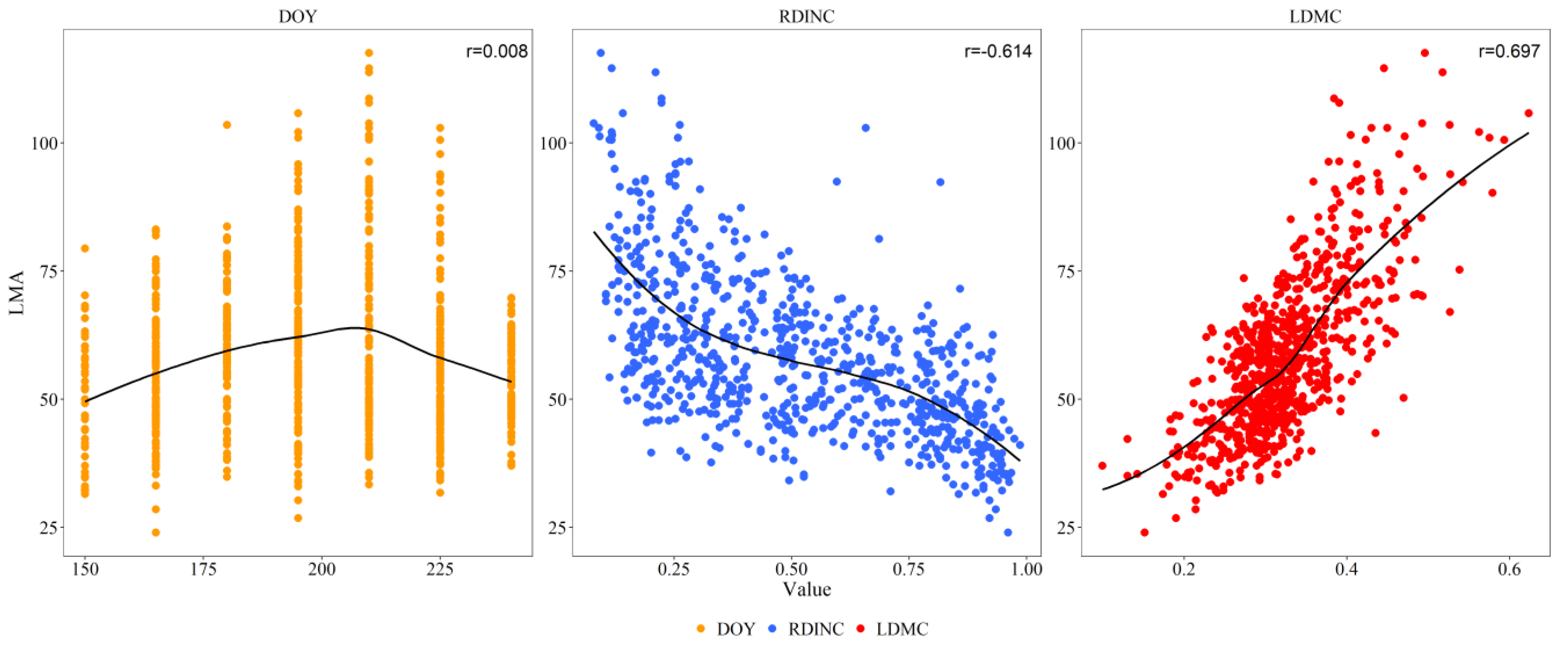
2.1. Correlations between LMA and DOY, RDINC and LDMC

It was evident from the results (Figure 1) that there was a significant negative correlation between LMA and RDINC, with a correlation coefficient of -0.614. However, LMA had a significant positive correlation with LDMC (r=0.697). LMA had no significant correlation with DOY but showed a unimodal trend with increasing DOY..

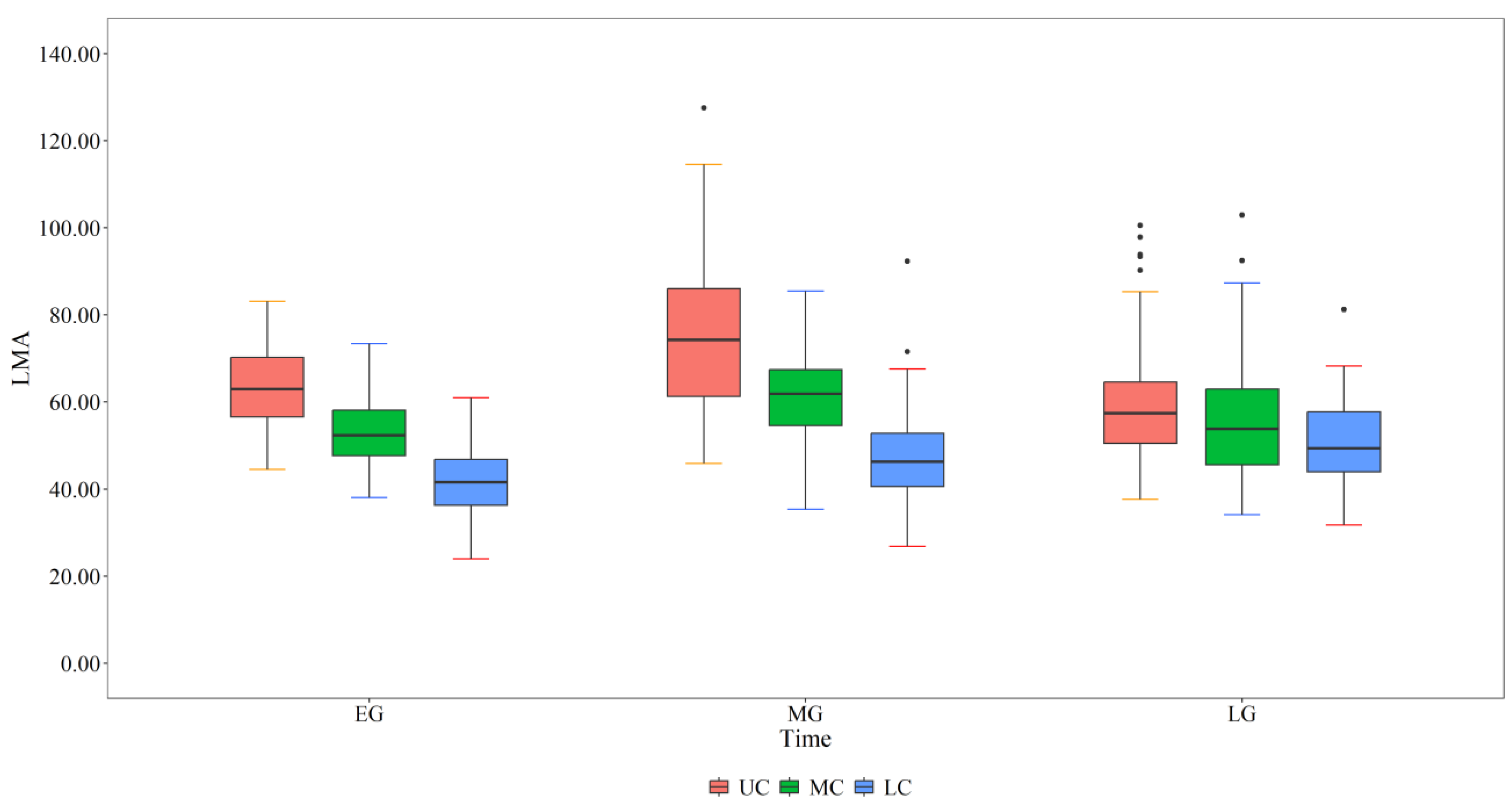
2.2. Variation in LMA at Different Crown Depths and Leaf Development Stages

The results of two-factor ANOVA (Table 1) revealed that the LMA of L. principis-rupprechtii significantly differed among leaf development stages and crown layers, and the interaction between the two factors had a significant effect on the LMA. There were significant differences between the upper, middle and lower layers of the crown at different stages of leaf development (Figure 2). At the start of leaf development, the LMA decreased from the upper crown (66.68 g·m^-2) to the lower crown (38.31 g·m^-2). At the middle stage of leaf development, the LMA ranged from 92.38 g·m^-2 at the top of the crown to 46.80 g·m^-2 at the bottom of the crown. At the end of leaf development, the LMA decreased from 68.24 g·m^-2 at the top of the crown to 47.17 g·m^-2 at the bottom of the crown.

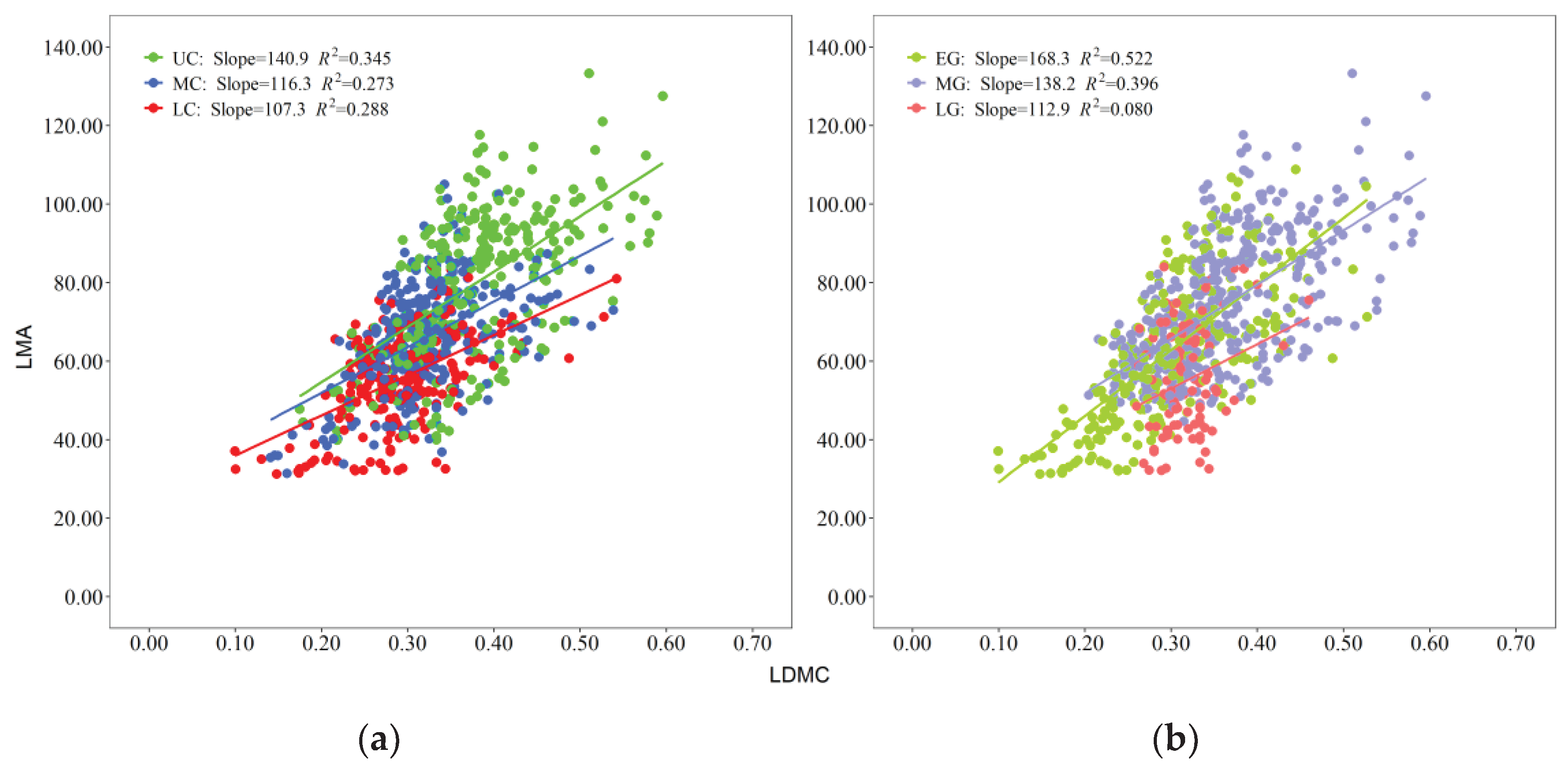
2.3. Standard Spindle Analysis Results

There was a significant positive correlation between LMA and LDMC across different crown layers and leaf growth phases (Figure 3). The slopes decreased from the upper crown to the lower crown (Figure 3a), and the slopes decreased from the early growth phase to the late growth phase (Figure 3b). On average, the correlations between LMA and LDMC were greater when grouped by leaf growth phase than when grouped by crown layer.

2.4. Model Fitting and Validation Results

Table 2 illustrates the goodness-of-fit results of the 7 basic models that were established with RDINC (Model 1~4), DOY (Model 5) and LDMC (Model 6~7). The models that were established based on DOY and LDMC showed better fitting performance than those that were established based on RDINC, with a high modified determination coefficient (R_a²), low root mean square error (RMSE) and akaike information criterion (AIC). Model 7 showed the best goodness-of-fit, with the highest R_a² value (0.447) and lowest RMSE value (9.38 g·m^-2).

The method of reparameterization was used to establish bivariate models based on the basic models (Table 2), resulting in Model 8~Model 13 (Table 3). The results showed that the fitting performances of the bivariate models were better than those of the univariate models (Table 2). Model 13 was the only model with a R_a² greater than 0.6 and a RMSE lower than 11 g·m^-2. The validation result of Model 13 also performed best, with the lowest value of MAE (MAE = 8.05) and the highest value of IF (0.682). The MEs of Model 8~Model 13 were all negative, indicating that those models were slightly overestimated.

3. Discussion

3.1. Temporal and Spatial Variation in LMA

Our results showed that LMA decreased gradually with increasing RDINC. Studies by Marshall and Monserud [32], Burgess and Dawson [33], Zhou et al. [34] and Tian et al. [25] on the vertical variation in crown LMA in Pinus monticola, Sequoiadendron giganteum, Betula platyphylla and Platycladus orientalis have shown that crown structure is the most direct and active interface between plants and their external environment. Complex crown structures usually exhibit different microenvironmental conditions, such as light, temperature and water vapour deficit pressure [8]. The upper leaves of the crown, which are exposed to strong light radiation and other conditions (e.g., temperature, wind speed, humidity), increase dry matter input to produce more protective tissues to resist the external environment [39,40]. Additionally, the upwards movement of water from roots to crowns inevitably leads to a decrease in the upper water potential [41]. Under water stress conditions, leaves increase investment in vascular tissues and promote water transport to compensate for the impact of lower leaf water potential, resulting in an increase in LMA [42,43]. Conversely, leaves face strong neighbourhood interference and fierce competition for light resources at the bottom of the crown, resulting in a lower LMA with a large and thin morphology.

During the leaf-spreading process, LMA showed a unimodal relationship with DOY (Figure 1) due to an increase in mesophyll cell numbers, inclusions, and cell wall thickness, as well as the maturation of mechanical tissue [15]. May and June are the periods of leaf spread and early leaf growth, and leaves spread quickly to enhance light-capturing abilities, resulting in a lower LMA. During this period, leaves grow rapidly with the division and expansion of leaf cells, which is consistent with the results of Meinzer et al. [44]. LMA significantly increased in the middle growth phase, particularly in the upper crown (Figure 2), which was similar to the finding that the LMA of leaves developing outside the tree crown was significantly greater than that of leaves developing inside the crown [45,46] because of light induction. In addition, LDMC in the form of nonstructural carbohydrates accumulates in cells [47] at the same time, and plants increase leaf thickness to improve leaf photosynthesis and stress resistance, which leads to an increase in LMA. Subsequently, the leaves enter the senescence stage, nutrients are translocated to the branches, the leaves lose water, and the LMA decreases [48]. Using time-integrated irradiance (PPFDINT), Colbe et al. [49] elucidated the seasonal increase in LMA in sugar maple leaves and demonstrated that the leaves are a long-term adaptation to light, with both seasonal accumulation and light intensity having significant impacts on LMA.

3.2. Changes in the Correlations between LMA and LDMC in Various Crown Layers (CLs) and Leaf Growth Phases (LGPs)

LMA and LDMC are interdependent leaf features. The distinct LMA and LDMC distributions revealed two plant resource allocation strategies, namely, accelerated expansion of the light absorption capacity and efficient storage of materials for leaf structure formation [50,51]. Leaf LMA and LDMC not only vary in a wide range of environments but also respond to different situations caused by alterations in crown depth or the leaf growth phase [52,53]. Our study revealed that there was a positive correlation between LMA and LDMC, but the patterns of their correlations differed among different CLs and LGPs (Figure 3). The increase rate of LMA with LDMC decreased from the upper crown layer to the lower crown layer (Figure 3a), implying that plants allocate more dry matter to the highest region of the crown for the same unit of fresh foliage area [54]. Leaves in the upper crown exposed to intense light may face an environment with increased investment in water transportation and relatively less availability of water [55,56]. Thus, leaves increase dry matter input and vascular tissue investment to improve their competitiveness and survival [13]. A denser cell structure and narrow air space could accelerate the exchange rate of leaf water, nutrients, etc., thus optimizing photosynthetic income and resulting in a greater LDMC. On the other hand, the light in the lower crown was weak, and the leaves should adapt to weak light and relatively low dry matter input, resulting in a larger leaf area [57]. This was in line with the research results of Tobias et al. [58].

As the development process of leaves increased, the slopes of the relationships between LMA and LDMC decreased (Figure 3b). The lowest LMA (31.25 g/m²) and LDMC (0.10 g) were observed in the early leaf growth phase (May-June). During this period, leaves tended to allocate less LMA and lower LDMC to enhance the capacity for capturing light, which was beneficial for competition [54]. During the middle leaf growth phase (July August), the leaves had the highest values of LDMC (0.60 g) and LMA (133.33 g/m²). During this period, the leaves were fully mature, displaying the strongest photosynthetic activity and dry matter production capability [14,59]. This finding was consistent with the research of Liu et al. [60], who showed that the crown of Larix olgensis had the greatest photosynthetic capacity in July and August. During the late leaf growth phase, the photosynthetic ability and carbon assimilation rate decrease to a certain extent with low temperature and nutrient depletion, leading to decreases in LDMC and LMA [61,62].

3.3. Optimal Model Selection

The vertical indices of crowns are the most commonly used leaf functional indicators [12,32]. Previous studies have shown that linear, power and exponential models, which were constructed based on RDINC, achieved good fitting performance. However, Peng et al. [38] demonstrated that the model using LDMC as a separate element performed well, which was consistent with our results (Table 2). The R_a² values for Models 6 and 7 exceeded 0.44, and the RMSEs were lower than 14.0 g·m^-2. Fewer previous studies have considered the influence of different leaf growth phases, especially in the early and later leaf growth phases, on the accuracy of the model. Coble et al. [63] demonstrated that disregarding seasonal factors would cause a biased estimation of LMA. Bivariate modelling could improve the goodness-of-fit (Table 3). After reparameterization, the accuracy of Model 8~Model 13 significantly improved, and the R_a² value increased by more than 0.2 compared to that of the univariate model. Model 13 was chosen as the optimal model with the highest R_a² (0.678) and lowest RMSE (10.25 g/m²). Interestingly, LDMC, which had the highest correlation with LMA, was not included in the optimal model (Model 13). Fortunately, model 13 had the ability to dynamically predict the DOY.

4. Materials and Methods

4.1. Site Description

The study site was located the Saihanba Forest Farm, Hebei Province, northern China (42°02′ ~ 42°36′N, 116°51′ ~ 117°39′E), with an altitude of 1010 ~ 1939.9 m. The main soil type is sand. The climate type is a typical temperate continental monsoon climate, with an annual average temperature of -1.3 °C, an extreme minimum temperature of -43.3 °C, an extreme maximum temperature of 33.4 °C, an annual average snow cover of 7 months, an annual average precipitation of 460 mm, an average annual frost-free period of 64 days, and an annual average windy day of 53 days. The main tree species are L. principis-rupprechtii, Picea asperata, Betula platyphylla, P. sylvestris var. Mongolica sylvestris, etc. The forest coverage rate is 82%, and the total forest stock is 5.025 million m³.

4.2. Sample Selection

In this research, five sample plots (20 m x 30 m) were established within a 17-year-old, pure L. principis-rupprechtii plantation of the same habitat. All trees with a diameter at breast height (DBH) larger than 5 cm in the sample plot were measured, and factors such as DBH, tree height (H), crown width (CW) and relative coordinates (X,Y) were included. Subsequently, five sample trees with a DBH similar to the quadratic mean diameter (Dg), representing the average state of each sample plot, were chosen. The basic information of the sample plots and sample trees is displayed in Table 1.

Table 1. The attributes of the sample plots and the photosynthetic sample trees were outlined.

Table 1. The attributes of the sample plots and the photosynthetic sample trees were outlined.

Sample plots					Sample trees
Plot number	Age (year)	Quadratic mean diameter (cm)	Mean tree height (m)	Stand density (trees·hm-2)	Tree number	Diameter at breast height (cm)	Tree height (m)
P1	17	12.0	11.95	2489	I	11.2	10.5
P2	15	10.0	9.95	2461	II	11.0	11.3
P3	16	13.5	13.80	2383	III	11.7	10.8
P4	16	12.7	12.81	2112	IV	11.2	11.5
P5	17	11.9	12.98	2049	V	11.9	10.9

4.3. Measurement of LMA

For a single tree, the crown was divided into various whorls by the whorls of branches from top to bottom. In each group, 3-4 healthy clusters were chosen as samples. The relative depth into the crown (the ratio of depth into the crown to crown length, RDINC) of every sample cluster was recorded, and then the samples were immediately removed and taken back to the laboratory for scanning. The scanned needle samples were dried to a constant weight of 85 °C and weighed (WD). The images were analysed using image analysis software (Image-Pro Plus 6.0, Media Cybernetics, Inc., Bethesda, MD, USA), resulting in a projected leaf area (LA, m²). The LMA and LDMC of each cluster of needle samples were then calculated. The data were collected every half month during the growing phases (approximately from June 1st to September 15th) in 2017.

The LMA and LDMC of each cluster of needle samples were calculated:

LMA_i,j=WD_i,j/LA_i,j (1)

LMA_i,j=WD_i,j/LA_i,j (2)

where _i represents the sample whorls, _j represents the date of the measurement, WD represents the dry weight, and FD represents the fresh weight.

Table 2. The attributes of LMA and LDMC.

Layer	Growth phase	LMA(g/m2)				LDMC(g)
		Mean	S.D.	Max.	Min.	Mean	S.D.	Max.	Min.
UC	EG	74.07	16.98	108.84	39.88	0.334	0.072	0.526	0.175
	MG	87.62	16.49	133.33	49.39	0.419	0.066	0.596	0.312
	LG	60.52	14.86	84.00	40.00	0.332	0.038	0.430	0.260
MC	EG	63.23	16.72	94.86	31.37	0.291	0.070	0.511	0.141
	MG	70.65	10.33	105.04	48.28	0.343	0.056	0.538	0.233
	LG	56.86	11.78	78.70	36.86	0.317	0.032	0.460	0.263
LC	EG	52.83	14.23	78.08	31.25	0.288	0.085	0.527	0.100
	MG	59.44	7.48	84.29	44.70	0.293	0.044	0.542	0.204
	LG	46.55	10.15	61.03	32.10	0.304	0.024	0.353	0.263
Pooled		67.75	18.12	133.33	31.25	0.333	0.077	0.596	0.099

Note: UC, MC and LC represent the upper, middle and lower canopies, respectively, while EG, MG and LG represent the early growth phase (June 1–July 15th), middle growth phase (July 16–August 31th) and late growth phase (September 1–defoliation), respectively. The same applies below.

4.4. Model Descriptions

4.4.1. Basic Model Selection

Based on previous research and the scatter plot distribution and correlation between LMA and LDMC, as well as spatial position and leaf growth phase (LGP) obtained in this study, a basic model was established with RDINC, date of year (DOY), and LDMC as independent variables (see Table 3).

Table 3. Model forms.

No.	Model form	Parameter
Model 1	LMA=a0×RDINC+a1	a0,a1
Model 2	LMA=b0×exp(b1×RDINC)	b0,b1
Model 3	LMA=c0×RDINC2+c1×RDINC+c2	c0,c1,c2
Model 4	LMA=d0×RDINCd1	d0,d1
Model 5	LMA=e0×(DOY-120)2+e1×(DOY-120)+e2	e0,e1,e2
Model 6	LMA=f0×LDMC+f1	f0,f1
Model 7	LMA=g0×exp(g1×LDMC)	g0,g1

Note: LMA represents leaf mass per area; RDINC represents relative depth into crown; DOY represents date of year. Leaves started to germinate when DOY=120; thus, DOY-120 represents the initial development time of the leaves.

4.4.2. Discrete Analysis and Reparameterization

According to prior research, the relationships between LMA and LDMC, leaf spatial position, and leaf growth phase are evident. Thus, to improve the accuracy of the model, it is necessary to further discretize the LMA data for feature analysis. Models 1-4 simulated the LMA in 9 groups, with intervals of 0.1, based on RDINC. Model 5 simulated the LMA in 6 groups, with groupings of 150, 165, 180, 195, 210, and 225, based on the DOY. Models 6-7 simulated the LMA on RDINC and DOY. Then, the reparameterization was conducted in Models 1-7 according to the correlations between the parameters and RDINC and DOY to form 6 new models with multiple independent variables (RDINC, DOY and LDMC). Finally, the optimal LMA model for L. principis-rupprechtii was selected based on its goodness-of-fit (Equations (1)–(3)) and validation performance (Equations (4)–(6)). The LMA prediction model was then established through parameterization.

4.4.3. Model Assessment and Validation

When fitting the model, 80% of the data are randomly chosen for model fitting, and 20% are used for model validation. The indicators chosen to assess the model's goodness-of-fit are the adjusted determination coefficient (R²), root mean square error (RMSE) and Akaike information criterion (AIC). The indicators for validation are the mean error (ME), absolute mean error (MAE) and fit index (FI). The formulas for computing each index are as follows:

$$R_a^2=1-\left(1-R^2\right)\left(\frac{n-1}{n-p}\right)\mathrm{a}=1,\mathrm{where}{R}^2=1-\frac{{\displaystyle {\sum }_{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2}}{{{\displaystyle {\sum }_{i=1}^n\left(y_i-{\overline{y}}_i\right)}}^2}$$

(1)

$$RMSE=\sqrt{\frac{{\displaystyle {\sum }_{i=1}^n{(y_i-{\widehat{y}}_i)}^2}}{n-p}}$$

(2)

$$AIC=nIn({(y_i-{\widehat{y}}_i)}^2)-nIn(n)+2p$$

(3)

$$ME={\displaystyle {\sum }_{i=1}^n\left(\frac{y_i-{\widehat{y}}_i}{n}\right)}$$

(4)

$$MAE={\displaystyle {\sum }_{i=1}^n\left|\frac{y_i-{\widehat{y}}_i}{n}\right|}$$

(5)

$$\mathrm{FI}=1-\frac{{\displaystyle {\sum }_{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2}}{{{\displaystyle {\sum }_{i=1}^n\left(y_i-{\overline{y}}_i\right)}}^2}$$

(6)

where yi is the observed value, ӯi is the average of the observed values,ŷi is the predicted value, n is the number of samples, and p is the number of parameters.

4.5. Data Analysis

Two-factor ANOVA was utilized to examine whether the LMA of L. principis-rupprechtii significantly differed between different trees and different ring whorls at various growth and developmental stages. Furthermore, Pearson correlation coefficients among LMA, LDMC, RDINC, and DOY were computed, and the correlations between LMA and other factors were analysed. The LMA and LDMC of different canopies and different growth periods were fitted by standardized principal axis analysis. Tests were conducted to determine whether there was a significant difference in slope among the different groups to ascertain whether different canopy depths and growth periods had a significant influence on the correlation between LMA and LDMC.

Microsoft Excel 2010 was used to collate the data of the study; descriptive statistical analysis was performed using SPSS 24; model fitting was completed by the nls package in R 4.0.5; standardized principal axis analysis was completed by the smatr package in R 4.0.5; and diagrams were drawn with the ggplot2 package in R 4.0.5 and Origin 2019.

5. Conclusions

Tree leaves (such as L. principis-rupprechtii) can adapt to complex crown structures by altering their own morphological characteristics, which results in significant spatial heterogeneity within the tree crown. In addition, the morphological characteristics of leaves from different crown layers exhibited different seasonal patterns (such as LMA and LDMC). The LMA prediction model using the reparameterization method (Model 13) had the best fitting performance (R²=0.68, RMSE=10.25 g/m²), and the best validation result was obtained (MAE=8.05 g/m², FI=0.682). Furthermore, Model 13 exhibited dynamic predictions that benefited from the incorporation of DOY.