Prerpints.org logo
Preprint
Article

Influence of New Parameterization Schemes on Arctic Sea Ice Simulation

Altmetrics

Downloads

100

Views

48

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

12 March 2024

Posted:

12 March 2024

You are already at the latest version

Alerts
Abstract
Two coupled climate models which participated the CMIP6 project (Coupled Model Intercomparison Project Phase 6), the Earth System Model of Chinese Academy of Sciences version 2 (CAS-ESM2-0) and the Nanjing University of Information Science and Technology Earth System Model version 3 (NESM3), were assessed in terms of the impact of four new sea ice parameterization schemes. These four new schemes are related to air-sea heat flux, radiation penetration and absorption, melt ponds, ice-ocean flux, respectively. To evaluate the effectiveness of these schemes, key sea ice variables with and without these new schemes, such as sea ice concentration (SIC) and sea ice thickness (SIT), were compared against observation and reanalysis product from 1980 to 2014. The simulations followed the design of historical experiments within the CMIP6 framework. The results revealed that both models demonstrated improvements in simulating Arctic SIC and SIT when the new parameterization schemes were implemented. The model bias of SIC in some marginal sea ice zones of Arctic was reduced, especially during March. The SIT was increased and the transpolar gradient of SIT was reproduced. The changes of spatial pattern of SIC and SIT after adding new schemes bear similarities between the two coupled models. This suggests that the new schemes have potential for broad application in climate models, especially for those with underestimated SIT.
Keywords: 
Subject: Environmental and Earth Sciences  -   Oceanography

1. Introduction

The Coupled Model Intercomparison Project Phase 6 (CMIP6) is ongoing under the leadership of the World Climate Research Program (WCRP) Working Group on Coupled Modelling (WGCM) [1]. The evaluation of sea ice simulation is an essential part of CMIP6 [2]. CMIP6 sea ice output has been widely analyzed, and it is found that coupled models involved in the comparison still have biases in the simulation of main sea ice variables such as sea ice concentration (SIC), sea ice extent (SIE), and sea ice thickness (SIT) [3,4,5,6,7,8,9,10]. CMIP6 coupled models from China have also been evaluated to identify common issues [4]. It was found that the Chinese CMIP6 models tends to overestimate the March SIC in marginal ice zones, especially in the Pacific region, and underestimate the September SIC in the central Arctic. These results indicate that the sea ice models in climate models from Chinese research institutions still need further improvement.
In the commonly used Los Alamos Sea Ice Model (CICE), the bulk formula [11] is used for calculating air-sea heat fluxes. Bulk flux formula uses the difference of temperature and humidity between ice surface and near surface air and surface winds, together with empirical transfer coefficients to calculate ice surface heat fluxes. However, the empirical coefficients could bring uncertainty in flux calculation. The delta-Eddington (dEdd) scheme [12] is used for shortwave radiation calculation in CICE. It uses the Inherent Optical Properties (IOP) to calculate the Apparent Optical Properties (AOP) such as albedo and transmittance, which directly links albedo and sea ice characteristics. However, ice microstructures (gas bubbles, brine pockets, and particulate matter) inside the sea ice are not considered. These ice microstructures could have significant effect on radiation transfer. Community Earth System Model (CESM) scheme [13], Topography (TOPO) scheme [14], and Level ice (LVL) scheme [15] are three melt pond schemes of CICE. Among them LVL scheme is commonly used. The LVL scheme assumes that the melt ponds can only exist on level ice, and uses the level ice variable in CICE to carry melt pond tracers. The change in melt pond area and melt pond depth is determined by an empirical parameter pond aspect ratio. The problem of this scheme is that few observations can be used to constrain the pond aspect ratio parameter. Furthermore, the horizontal sizes of melt ponds can have influences on melt pond depth and radiation transfer, but they are not considered in the LVL scheme. The default ice-ocean heat flux parametrization scheme in CICE is a two-equation (2EQ) scheme [16,17]. It consists of one equation describing the energy balance between the heat conduction and oceanic heat flux at the ice-ocean interface and another equation treating the ocean freezing point as a linear function of mixed layer salinity. However, the 2EQ scheme could simulate a lower freezing temperature and thinner SIT [18,19].
The Earth System Model of Chinese Academy of Sciences version 2 (CAS-ESM2-0) and the Nanjing University of Information Science and Technology Earth System Model version 3 (NESM3) are two of the nine Chinese models participating CMIP6 (Table 1, column 1 and column 3, hereafter referred as CAS-ESM2-0 old version and NESM3 old version). These two models both use CICE as sea ice component. Since CMIP6 [20,21], four new sea ice parameterization schemes (Table 2) have been developed and implemented in the above two Chinese models (Table 1, column 2 and column 4, hereafter referred as CAS-ESM2-0 new version and NESM3 new version). The four schemes are the maximum entropy production (MEP) scheme, the melt pond size distribution (MPSD) scheme, the Inherent Optical Properties (IOP) scheme, and the three-equation ice-ocean boundary layer (3EQ) scheme. The MEP scheme [22] is originally developed for land surface heat flux calculation and is adapted to use for air-ice heat flux calculation. It does not need temperature and moisture gradient, wind speed, and surface roughness as input. It just uses radiation heat flux and temperature to compute sensible and latent heat flux directly. The IOP scheme [23] is developed to describe the effects of ice microstructure on inherent optical properties and used with the dEdd scheme to calculate the apparent optical properties of sea ice. The MPSD scheme [24] is used to determine the sub-grid melt pond size distribution after melt pond fraction is calculated by melt pond schemes such as the LVL scheme. The three-equation (3EQ) scheme [25] uses the salinity of the ice-ocean interface to define the actual freezing temperature. An equation describing the salt flux balance at the ice-ocean interface is added. The summary of four new sea ice schemes can be found in Table 2.
The implementation of these four new schemes is expected to improve the sea ice component model and hence the coupled model. Therefore, it is necessary to make a complete evaluation of their influence on global coupled sea ice simulation. In this study, an assessment of the two coupled models with and without new schemes is presented. The remainder of this paper is structured as follows. In Section 2, the coupled climate models, datasets, and Taylor Score method are introduced. In Section 3, the simulations from the two coupled models with and without four new schemes are compared. In Section 4, the influence of new schemes is discussed. In Section 5, the conclusion of the present study is provided.

2. Materials and Methods

2.1. Model Description

2.1.1. The CAS-ESM2-0 Earth System Model

The Earth System Model (ESM) CAS-ESM2-0 used in the study was developed at IAP/CAS (Institute of Atmospheric Physics, Chinese Academy of Sciences), which includes IAP AGCM version 5 and the LASG/IAP Climate System Ocean Model (LICOM3), Beijing Normal University/IAP Common Land Model (CoLM), Los Alamos Sea Ice Model (CICE version 6). The infrastructure of CESM Coupler 7 [26] is adopted to ensure that the component models are coupled together. Additional components in CAS-ESM2-0 include the IAP Vegetation Dynamics Model and IAP fire model, which are embedded within the land model; the IAP ocean biogeochemistry model, which is embedded within the ocean model; an atmospheric aerosol and chemistry model. The Los Alamos Sea Ice Model uses the same grid as the oceanic model. It is based on an ice thickness distribution function with 5 thickness categories [27]. The vertical grid contains four ice layers and one snow layer on top of the ice. Elastic-Viscous-Plastic rheology [28] and incremental remapping advection scheme are used to describe the geophysical scale motion of sea ice. The horizontal grid spacing is nearly 1 degree. The mechanical redistribution scheme is used to describe the local scale ice motion [29]. Detailed model descriptions of the version participating CMIP6 can be found in [30,31]. The difference of the version of CAS-ESM2-0 used in present research and the version participating the CMIP6 project is the addition of four new parameterization schemes in the updated sea ice component model from v4 to v6 and a change in the ocean model mainly in terms of the tri-polar grid (Table 1 and Table 2).

2.1.2. The NESM3 Earth System Model

The Nanjing University of Information Science and Technology Earth System Model version 3 (NESM3) consists of three component models, which are coupled together by the OASIS_3.0-MCT3 coupler [32]. The atmospheric component model of NESM3 is ECHAM v6.3, which implicitly couples the JSBACH land surface model [33]. The ocean and sea ice component models are NEMO v3.4 [34] and CICE v4.1 [35], respectively. NESM3 includes two subversions—namely, standard resolution and lower resolution. The standard resolution NESM3 is used to perform all CMIP6 experiments. The resolution of the atmospheric component model is T63L47, which corresponds to ~1.9° × ~1.9°, and 47 vertical levels extending from the surface to 0.01 hPa. The ocean component model uses the ORCA1 configuration, which is a tri-polar grid system. The horizontal resolution is ~1° in both longitudinal and latitudinal direction, with meridional refinement to 1/3° near the equator. There are 46 vertical layers in the ocean model, with 10 layers in the uppermost 100 m. The sea ice component model is configured from CICE v4 which uses a displaced-polar grid system with the horizontal resolution of the sea-ice model being ~1° and ~0.5° in longitudinal and latitudinal direction, respectively. Detailed model descriptions and model development can be found in [36]. The revision of NESM3 model in present research is an update of sea ice component model from version 4 to version 6 and the addition of four new schemes (Table 1 and Table 2).

2.2. Observation Data Used for the Evaluation

2.2.1. NSIDC Sea Ice Concentration

NSIDC (National Snow and Ice Data Center, USA) passive microwave SIC data retrieved by the NASA (National Aeronautics and Space Administration, USA) bootstrap algorithm [37] was used in the assessment. This dataset has a spatial coverage of the entire Arctic and Antarctic region with a resolution of 25 km × 25 km. The time range is from 25 October 1978 to present, with a resolution of one day. It should be mentioned that the SIC may be underestimated due to melt ponds [38,39] or very low temperatures [40].

2.2.2. PIOMAS Sea Ice Thickness

SIT product from the Pan-Arctic Ice Ocean Modeling and Assimilation System (PIOMAS; [41]) was used as the reference data to assess the simulated SIT. PIOMAS was developed to assimilate the satellite-observed SIC and sea surface temperature (SST) in a global ice-ocean coupled model system. Leap years in PIOMAS are treated by integrating forward for 365 days. The PIOMAS thickness data is provided in the form of averaged thickness over the PIOMAS domain for areas with ice thicker than 0.15 m. This dataset is widely used for sea ice model validation and evaluation. The time range is from 1978 to present, with a resolution of one month. PIOMAS can capture the major features of sea ice motion, concentration, extent, and thickness in both polar oceans [41]. PIOMAS results are in reasonably good agreement with submarine SIT observations. The SIT biases are within 9% in Arctic [41].

2.3. Taylor Score

The Taylor Score (TS; [42]) was used here to assess the performance of the two models in simulating the spatial pattern of sea ice variable.
T S = 4 1 + R 4 σ m σ o + σ o σ m 2 1 + R 0 4
Here, R is the pattern correlation coefficient of the observations and model outputs, and R 0 is the maximum attainable value of R taken as 1 in our study. σ m is the standard deviation of the model field and σ 0 is the standard deviation of the observation field. A higher TS value indicates a greater similarity between the model field and the observation field.

2.4. Data Processing

SIC and SIT are two important physical variables of sea ice. The NSIDC and PIOMAS provides data since 1978. Both the runs with and without new parameterization schemes follow the CMIP6 historical run and spans from 1850 to 2014. The comparison conducted in this study is from 1980 to 2014. All data have been gridded into 1º × 1º before comparison for convenience. The SIC data have been scaled into 0–1 interval. Grid cells with climatological SIC less than 0.15 are not shown in the figures of climatological SIC and SIT spatial patterns. But all grid cells participate in the calculation of SIC and SIT differences and Taylor Score calculation. The SIT from NESM3 old version is provided in the form of actual sea ice thickness which is the ice thickness averaged over ice-covered area of a grid cell. This dataset is converted into equivalent sea ice thickness to match other SIT datasets by simply multiplying the SIT of each grid cell by its SIC.

3. Results

3.1. Spatial Patterns of SIC and SIT

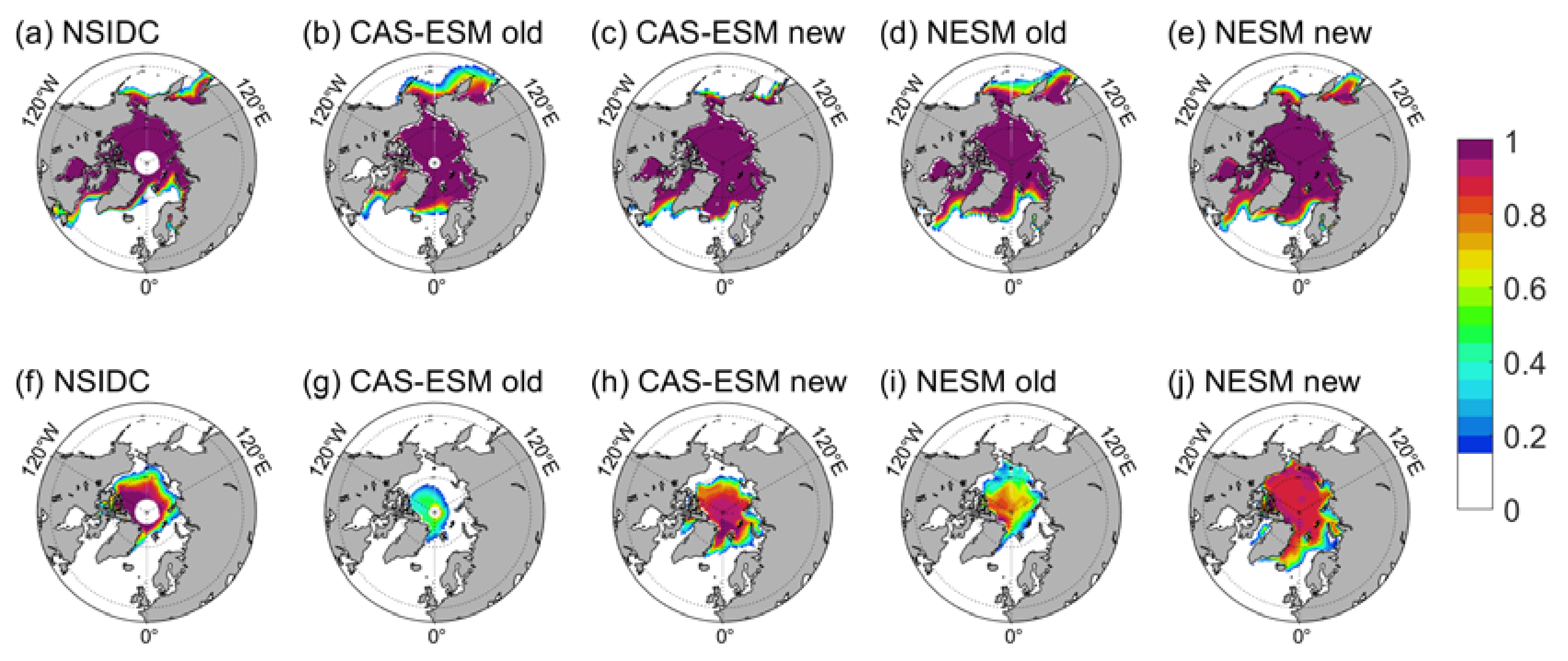
Figure 1 compares the climatological (1980–2014) spatial pattern of observed and simulated SIC with and without these four new schemes. After adopting the new parameterization schemes, the simulated March SIC is reduced and is closer to NSIDC data (Figure 1a,c,e) for both models, especially in the Pacific sector. In March, excessive marginal sea ice cover around the Bering Strait and Okhotsk Sea is corrected by applying the new schemes. However, there are still some unrealistic features when these new schemes are used, such as too much sea ice is generated in the Greenland Sea and Barents Sea. In September, the situation of the two models differs. For the CAS-ESM2-0 model, the new version has a more realistic spatial distribution compared with the observation than the old version (Figure 1f,g,h). For the NESM3 model, the new version has a higher SIC than the old version in the central Arctic which is more similar to the observation. However, the NESM3 new version has a much larger spatial coverage compared to the old version, and is further deviated from the observation (Figure 1f,i,j).
After applying the new parameterization schemes, the simulated March and September SIT is increased in both models. Figure 2 compares the climatological (1980–2014) spatial pattern of observed and simulated SIT with and without these four new schemes. The observed SIT reduces gradually from west to east. The thickest ice (thicker than 5 m) is in the west of the Arctic, north of the Canadian Arctic Archipelago. The central Arctic sea ice has a thickness of around 3 m. In the east of the Arctic, the sea ice is much thinner (less than 2 m). Therefore, the PIOMAS March and September SIT has a transpolar gradient (Figure 2a,f). This gradient has been reproduced in both models with the addition of four new schemes in both March and September (Figure 2c,e,h,j). However, the SIT has been adjusted too much in the Beaufort Sea, Chukchi Sea, and Baffin Bay.
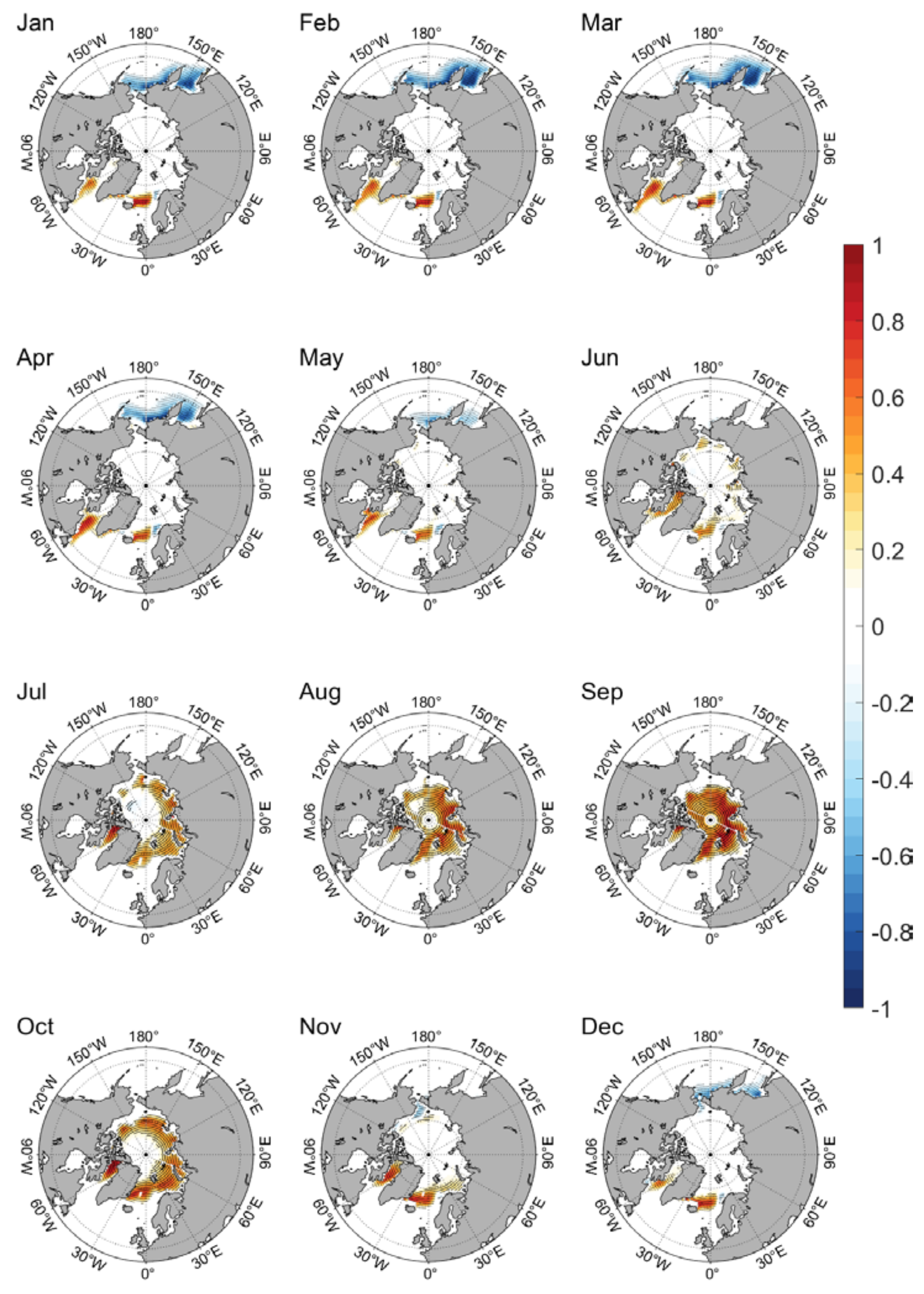
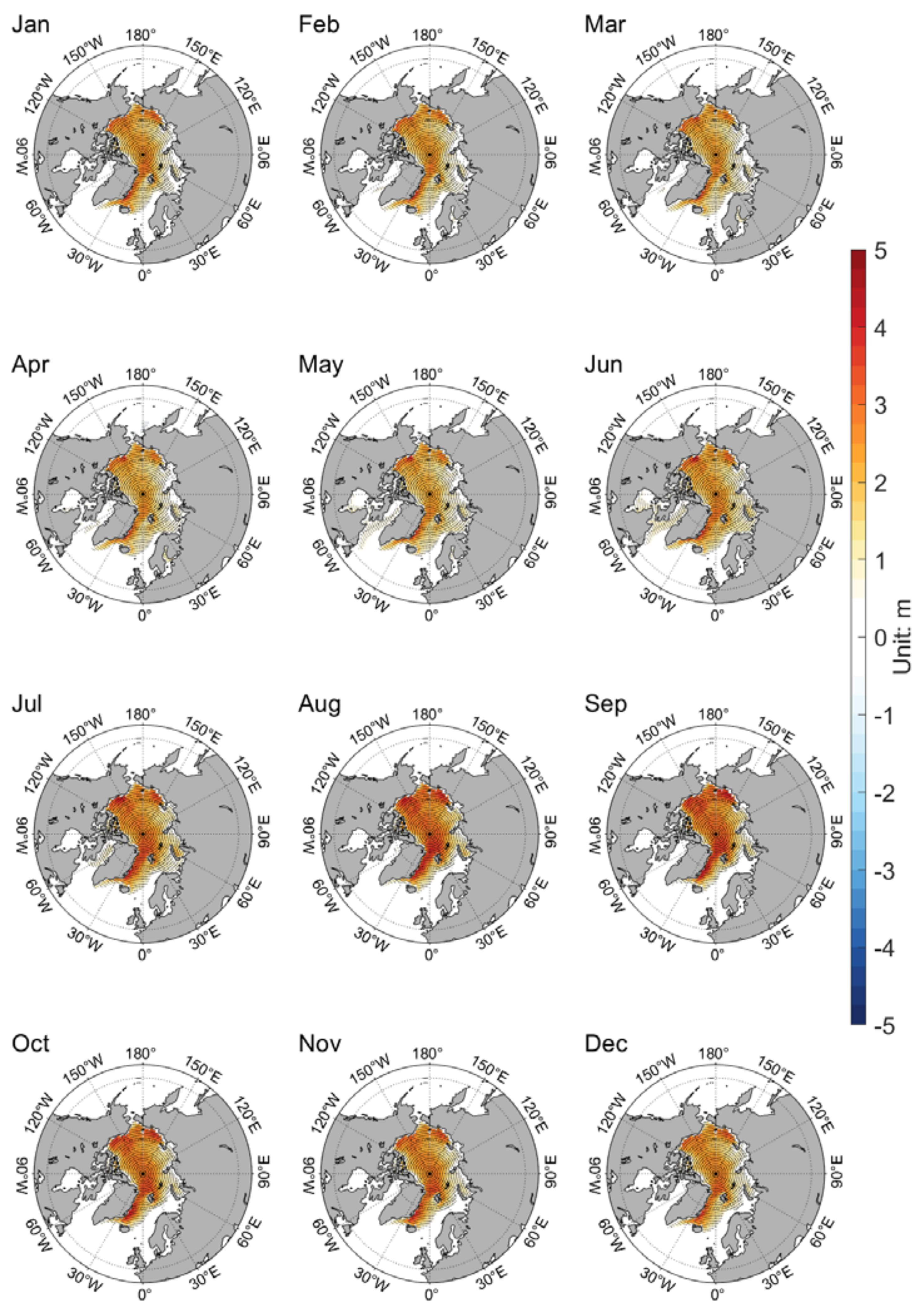
The difference of SIC with and without new schemes bears similarity between the two models (Figure 3 and Figure 4). Black dots on Figure 3 and Figure 4 represent points that are significant at 99% confidence level for Student’s t-test. Figure 3 shows the multi-year mean monthly SIC difference between the CAS-ESM2-0 new version and the old version from January to December (result of the new version minus that of the old version). It can be concluded that there are two types of spatial patterns in SIC difference of CAS-ESM2-0. From December to May, the SIC of the new version decreases in the Pacific and increases in the Atlantic. From June to November, the SIC of the new version increases in the central and marginal Arctic Ocean. 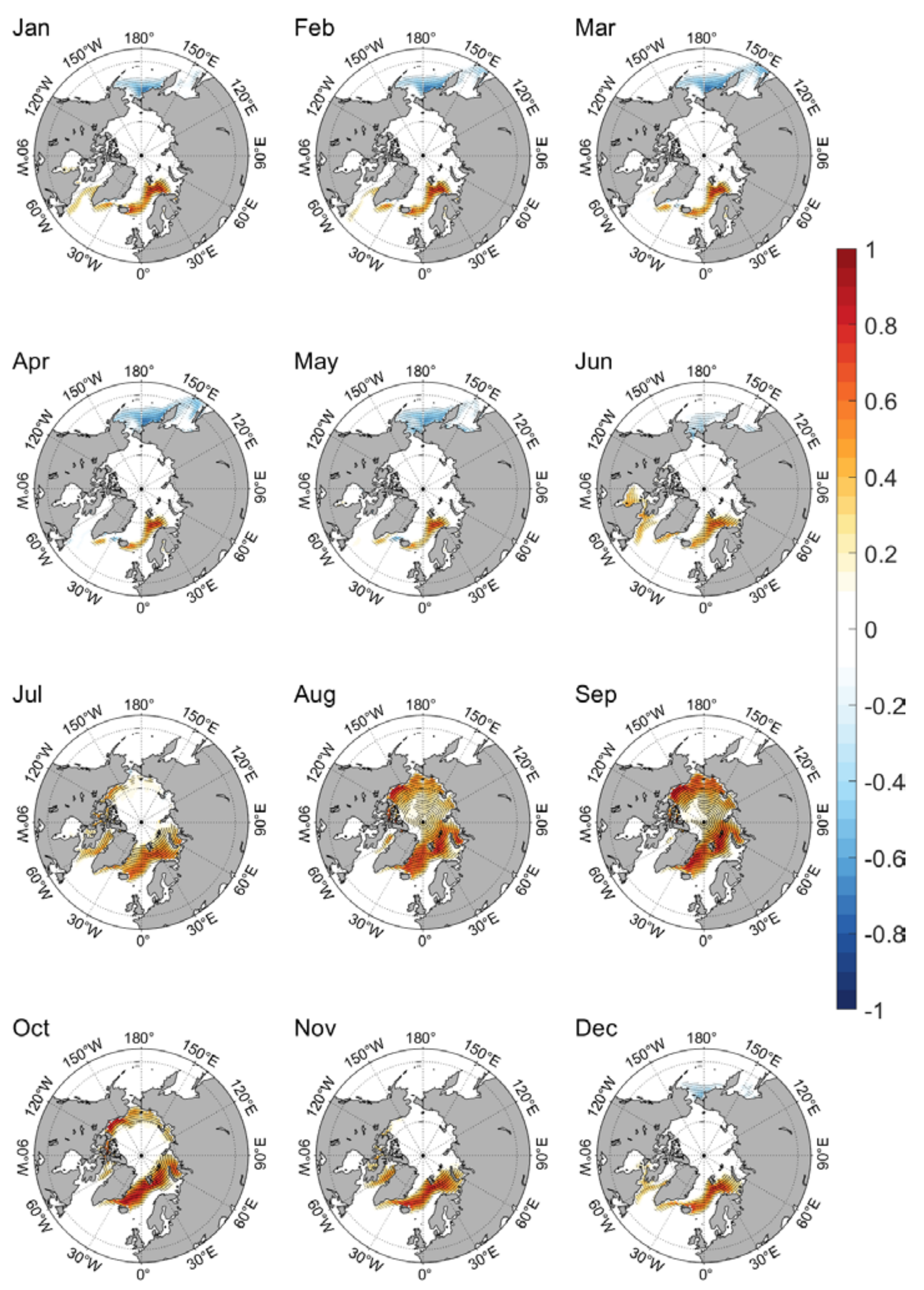Figure 4 shows the monthly SIC difference between the NESM3 new version and the old version from January to December (result of the new version minus that of the old version). Similar to the situation of CAS-ESM2-0, from December to May, the SIC of the new version decreases in the Pacific and increases in the Atlantic. From June to November, the SIC of the new version increases in the central and marginal Arctic Ocean. Comparing Figure 3 and Figure 4, the difference of SIC from two models with and without four parameterization schemes are very similar in their spatial patterns and temporal evolutions. The results of t-test show that the SIC changes associated with these four new schemes are significant in most regions mentioned above.
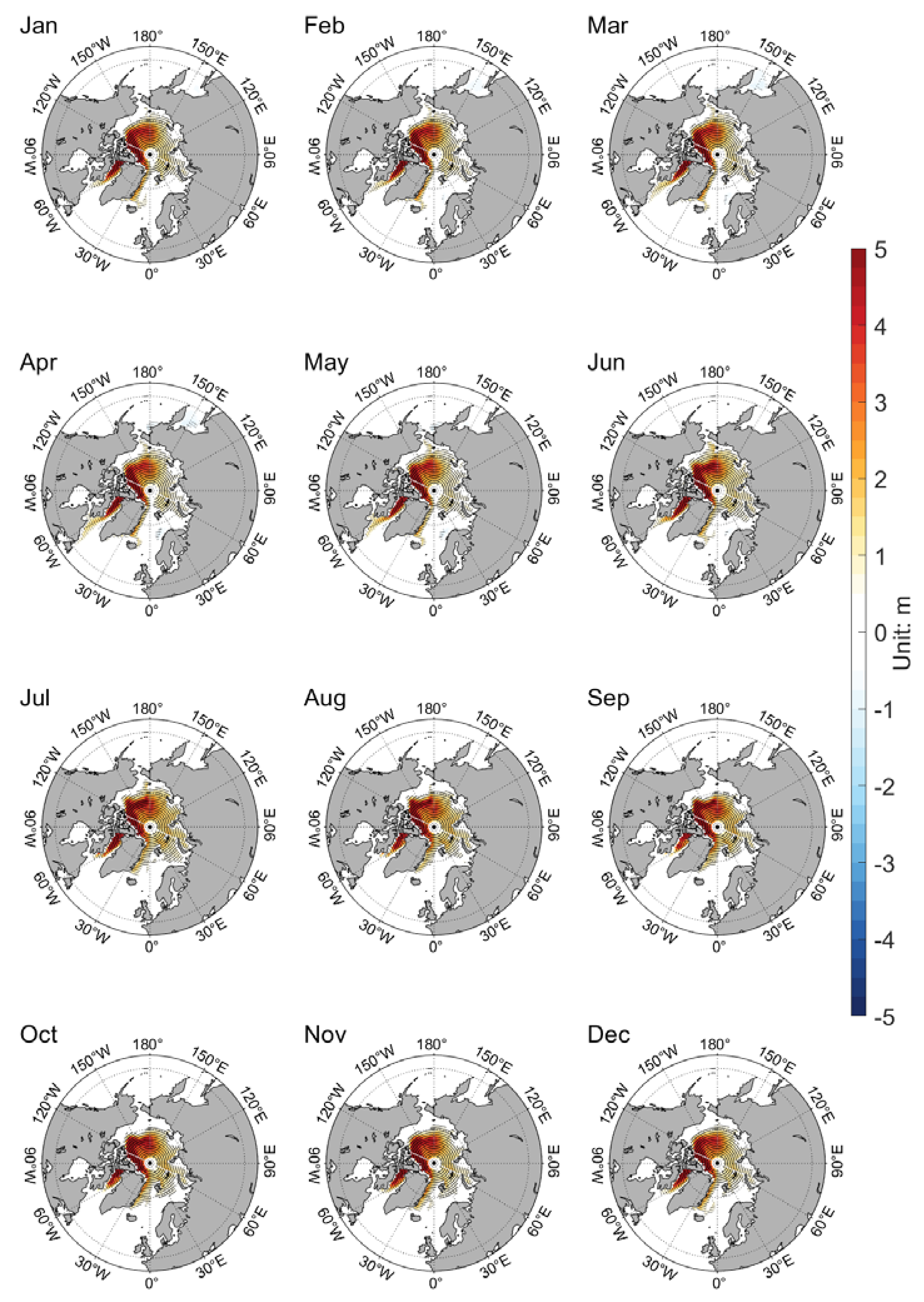
The SIT difference of these two coupled models with and without these four new schemes are also similar (Figure 5 and Figure 6). Black dots in Figure 5 and Figure 6 represent points that are significant at 99% confidence level for Student’s t-test. Figure 5 shows the difference of multi-year monthly mean SIT difference between the CAS-ESM2-0 new version and the CAS-ESM2-0 old version. From January to December, positive SIT difference exists in the western part of Arctic, including Baffin Bay, Beaufort Sea and Chukchi Sea. This spatial pattern of SIT difference shows minor seasonal variations. Figure 6 shows the difference of multi-year monthly mean SIT between the NESM3 new version and old version. Though similar to the spatial pattern of CAS-ESM2-0 SIT difference, positive SIT difference exists over the entire Arctic for the NESM3, the magnitude of SIT difference from the NESM3 is smaller than that of CAS-ESM2-0. Comparing Figure 5 and Figure 6, it could be concluded that the difference of SIT with and without new schemes from the two coupled models is similar in that the SIT increased over the entire Arctic throughout the whole year. The results of t-test show that the SIT differences associated with these four new schemes are significant in most regions.

3.2. Taylor Score of 1980–2014 Mean SIC and SIT

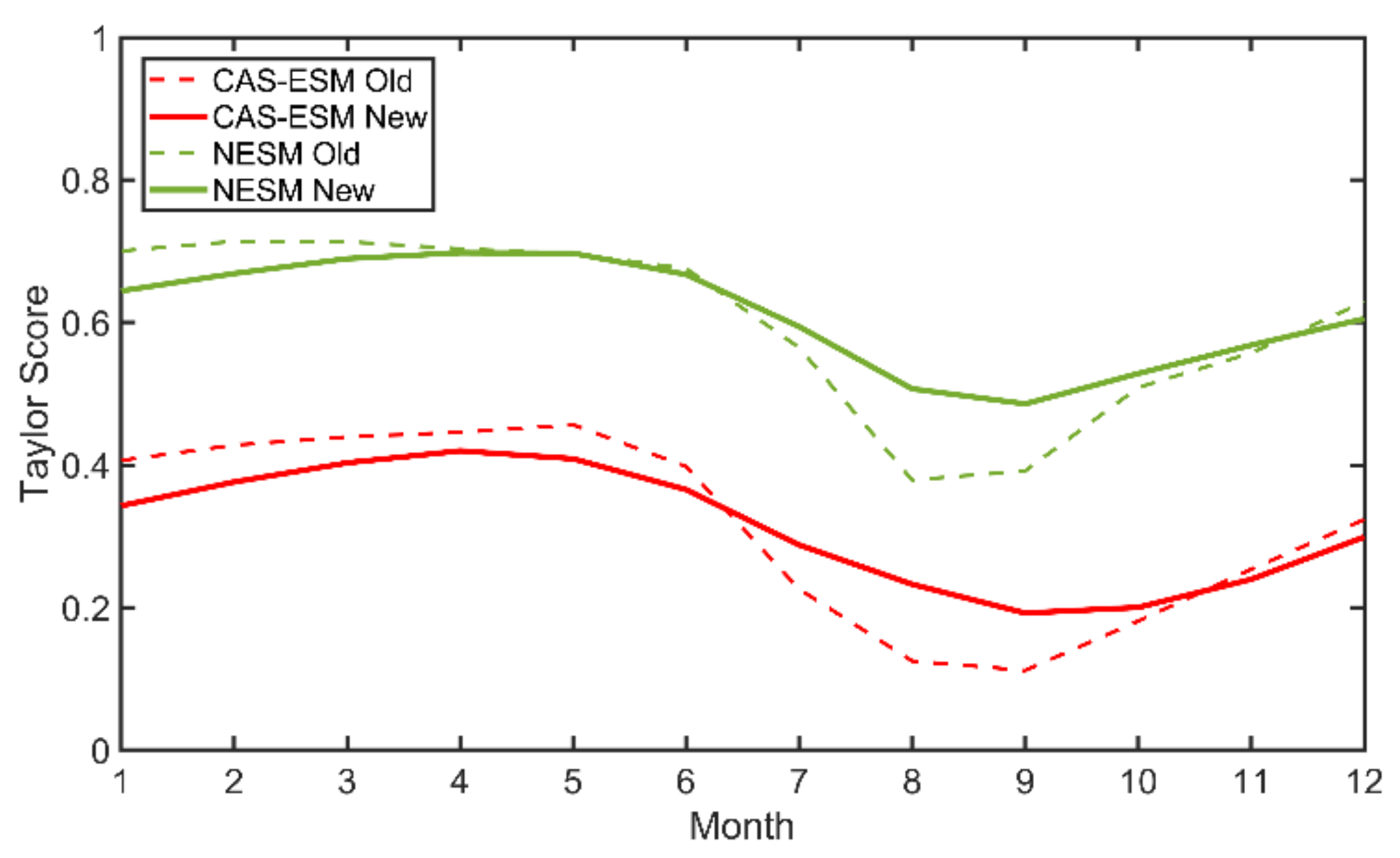
Model improvement mentioned above can also be found in Taylor Score (TS) by comparing model SIC with NSIDC observation. Figure 7 shows the TS value of 1980–2014 multi-year mean SIC of the old and new version of the two models from January to December. For the CAS-ESM2-0, the TS value of the old version has its minimum in September (red dashed line). The TS value of the new version (red solid line) is higher than that of the old version, especially in August and September. For the NESM3 model, the TS value of the old version is around 0.5 without significant seasonal variations (green dashed line), and the TS value of the new version (green solid line) with the addition of four new schemes is about 0.1 higher than that of the old version. With these new schemes, the SIC spatial distribution of the two models is improved over the whole year.
Figure 8 shows the TS value of 1980–2014 multi-year mean SIT of the old and new version of the two models by comparing model SIT with the PIOMAS product. For the CAS-ESM2-0 model, the TS value of the old version has its minimum in September (red dashed line). The TS value of the new version (red solid line) is higher than that of the old version in July, August, September, and October, but slightly lower in other months. For the NESM3 model, the TS value of the old version has its minimum in August (green dashed line). The TS value of the new version (green solid line) is higher than that of the old version in July, August, September, and October. With these new schemes, the SIT spatial distribution of the two models is improved in melting season.
Figure 7 and Figure 8 support the notion that SIC and SIT simulation have been improved in the two coupled models with the addition of four new schemes. The improvement is mainly in melting season.

4. Discussion

These four new sea ice parameterization schemes mainly influence sea ice thermodynamic processes. In a stand-alone CICE simulation, Zhang et al. has compared the MEP scheme with the bulk formula scheme [43]. Their simulation results show that, during sea ice growing season, in the central Arctic, the change of surface heat flux is positive (positive heat flux represents upward heat flux from the sea ice to the atmosphere, while negative heat flux represents downward heat flux from the atmosphere to the sea ice) and ocean tends to lose more heat, and this effect could increase local SIT. Their simulation results also show that, during melting season, the change of surface heat flux is negative in the central Arctic, but positive in the marginal seas. This could lead to an increase in heat loss of marginal sea ice during the melting season, hence increase SIT. Overall, in Zhang’s stand-alone CICE simulation, for the whole year, the simulated SIT using MEP scheme is thicker than that of bulk formula scheme. This is consistent with the coupled simulation in this paper, as is shown in Figure 2.
In stand-alone sea ice model simulations, compared to the 2EQ scheme, the 3EQ parameterization leads to thicker ice [25,44], especially in the marginal ice zone during summer. In these stand-alone simulations, the salinity of ice-ocean interface in the 3EQ scheme is much lower than the salinity of ocean mixed layer in the 2EQ scheme. Therefore, the freezing temperature at the ice-ocean interface is relatively higher than that of the 2EQ scheme, hence narrows the gap between sea water temperature and the freezing temperature at the ice-ocean interface. This reduces the upward temperature gradient towards the interface, leading to a decrease of oceanic turbulent heat flux. Meanwhile, the downward heat conduction in ice is also decreased due to reduced temperature gradient between ice bottom and ice-ocean interface. Finally, the decrease of upward oceanic heat flux and downward heat conduction could decrease basal melt of sea ice and increase SIT. In this paper, the application of 3EQ scheme in the two coupled models leads to thicker summer SIT in marginal ice zone, as is seen in Figure 2, which is consistent with the previous stand-alone simulations.
Though more numerical simulations and diagnostic analysis are needed to understand the effect of each individual parameterization scheme, the consistence between coupled and stand-alone simulation is reassuring.

5. Conclusions

Four new sea ice parameterization schemes, namely MEP scheme, IOP scheme, MPSD scheme and 3EQ scheme, were added into two different CMIP6 climate models, the CAS-ESM2-0 model and the NESM3 model. These four new schemes are related with the computation of air-sea heat flux, radiation penetration and absorption, melt ponds, ice-ocean heat and salt fluxes. In this work, an evaluation and comparison of the sea ice variables (sea ice concentration and sea ice thickness) of the two models were carried out based on numerical simulation with and without these four schemes following the CMIP6 historical experiment setup. The main conclusions are as following.
(1) New parameterization schemes improved SIC and SIT in the Arctic region. The SIC spatial pattern with the new schemes is closer to observation. The March SIC overestimation in the Bering Strait and Okhotsk Sea is reduced. The September SIC underestimation is also reduced. The spatial gradient of SIT from western Arctic to eastern Artic is reproduced in the new version of the two models.
(2) The improvement in modeling SIC and SIT is shown by the similarity of the spatial pattern of these two fields compared with observation and PIOMAS product, as shown by Taylor Scores. With new schemes, the TS values of SIC from two models have been improved by around 0.1 for all months. The TS values of SIT from two models have been improved by around 0.2 in melting season.
(3) The changes of spatial pattern of SIC and SIT after adding new schemes share certain common features between the two different coupled models. For the two models, the SIC decreases in the Pacific and increases in the Atlantic in winter and spring season (December to May), and increases over the entire Arctic in summer and autumn season (from June to November). For the two models, the SIT increases over the entire Arctic throughout the entire year.
There should be interactions among these four sea ice schemes and other sea ice parameterization schemes. This increases the difficulty in explaining the combined contribution of these four new schemes in a coupled model. Instead of analyzing their individual effects, the combined effects of these four schemes are investigated in the historical experiment setup of CMIP6. More numerical simulations and diagnostic analysis could be conducted to understand the effect of each individual scheme in the future.
Since CAS-ESM2-0 and NESM3 are very different climate models, and may represent the performance of other models in CMIP6, the similarity of model improvement after adding new parameterization schemes indicates that these schemes have the potential to be applied in other climate models. By adding these four new parameterization schemes, the sea ice simulation in other models might be improved as well, although the scope of improvements needs to be assessed individually.

Author Contributions

Conceptualization, X.W. and J.L.; Data curation, Y.L., J.J. and J.C.; Formal analysis, Y.L.; Funding acquisition, X.W., Y.H., J.L., J.H., Y.Y., X.G. and M.S.; Investigation, Y.L.; Methodology, Y.L. and X.W.; Project administration, X.W. and Y.H.; Resources, X.W. and Y.H.; Software, J.J. and J.C.; Supervision, X.W. and Y.H.; Validation, Y.L. and X.W.; Visualization, Y.L.; Writing—original draft, Y.L.; Writing—review & editing, X.W., Y.H., J.L., J.J., J.C., M.S. and Y.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This study is supported by the National Key R&D Program of China (No. 2018YFA0605900), the National Natural Science Foundation of China (No. 42376200; No. 42005123; No. 42130608).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data partly available in a publicly accessible repository. The NSIDC SIC data presented in this study are openly available in https://nsidc.org/data/G02202/versions/3 accessed on 14 February 2024. The PIOMAS SIT data presented in this study are openly available in https://psc.apl.uw.edu/data/ accessed on 14 February 2024. The old version of CAS-ESM2-0 and NESM3 coupled model data presented in this study are openly available in https://aims2.llnl.gov/ accessed on 14 February 2024.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Eyring, V.; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 2016, 9, 1937–1958. [Google Scholar] [CrossRef]
  2. Notz, D.; Jahn, A.; Holland, M.; Hunke, E.; Massonnet, F.; Stroeve, J.; Tremblay, B.; Vancoppenolle, M. The CMIP6 Sea-Ice Model Intercomparison Project (SIMIP): Understanding sea ice through climate-model simulations. Geosci. Model Dev. 2016, 9, 3427–3446. [Google Scholar] [CrossRef]
  3. Chen, L.; Wu, R.; Shu, Q.; Min, C.; Yang, Q.; Han, B. The Arctic Sea Ice Thickness Change in CMIP6′s Historical Simulations. Adv. Atmos. Sci. 2023, 40, 1–13. [Google Scholar] [CrossRef]
  4. Li, J.; WANG, X.; WANG, Z.; ZHAO, L.; WANG, J. Evaluation of Arctic sea ice simulation of CMIP6 models from China. Adv. Polar Sci. 2022, 33, 220–234. [Google Scholar] [CrossRef]
  5. Watts, M.; Maslowski, W.; Lee, Y.J.; Kinney, J.C.; Osinski, R. A Spatial Evaluation of Arctic Sea Ice and Regional Limitations in CMIP6 Historical Simulations. J. Clim. 2021, 34, 6399–6420. [Google Scholar] [CrossRef]
  6. Shen, Z.; Duan, A.; Li, D.; Li, J. Assessment and Ranking of Climate Models in Arctic Sea Ice Cover Simulation: From CMIP5 to CMIP6. J. Clim. 2021, 34, 3609–3627. [Google Scholar] [CrossRef]
  7. Long, M.; Zhang, L.; Hu, S.; Qian, S. Multi-Aspect Assessment of CMIP6 Models for Arctic Sea Ice Simulation. J. Clim. 2021, 34, 1515–1529. [Google Scholar] [CrossRef]
  8. Shu, Q.; Wang, Q.; Song, Z.; Qiao, F.; Zhao, J.; Chu, M.; Li, X. Assessment of Sea Ice Extent in CMIP6 With Comparison to Observations and CMIP5. Geophys. Res. Lett. 2020, 47, e87965. [Google Scholar] [CrossRef]
  9. Roach, L.A.; Dörr, J.; Holmes, C.R.; Massonnet, F.; Blockley, E.W.; Notz, D.; Rackow, T.; Raphael, M.N.; O’Farrell, S.P.; Bailey, D.A.; et al. Antarctic Sea Ice Area in CMIP6. Geophys. Res. Lett. 2020, 47, e2019GL086729. [Google Scholar] [CrossRef]
  10. Notz, D.; Community, S. Arctic Sea Ice in CMIP6. Geophys. Res. Lett. 2020, 47, e2019GL086749. [Google Scholar] [CrossRef]
  11. Kauffman, B.G.; Large, W.G. The CCSM coupler. version 5.0.1: Combined user’s guide, source code reference, and scientific description; National Center for Atmospheric Research: Boulder, Colorado, USA, 2002; pp. 1–46. [Google Scholar]
  12. Briegleb, B.P.; Light, B. A Delta-Eddington Multiple Scattering Parameterization for Solar Radiation in the Sea Ice Component of the Community Climate System Model (No. NCAR/TN-472+STR); University Corporation for Atmospheric Research: Boulder, Colorado, USA, 2007; 100p. [Google Scholar] [CrossRef]
  13. Holland, M.M.; Bailey, D.A.; Briegleb, B.P.; Light, B.; Hunke, E. Improved Sea Ice Shortwave Radiation Physics in CCSM4: The Impact of Melt Ponds and Aerosols on Arctic Sea Ice*. J. Clim. 2011, 25, 1413–1430. [Google Scholar] [CrossRef]
  14. Flocco, D.; Feltham, D.L.; Turner, A.K. Incorporation of a physically based melt pond scheme into the sea ice component of a climate model. J. Geophys. Res. Ocean. 2010, 115, C08012. [Google Scholar] [CrossRef]
  15. Hunke, E.C.; Hebert, D.A.; Lecomte, O. Level-ice melt ponds in the Los Alamos sea ice model, CICE. Ocean Model. 2013, 71, 26–42. [Google Scholar] [CrossRef]
  16. McPhee, M.G. Turbulent heat flux in the upper ocean under sea ice. J. Geophys. Res. Ocean. 1992, 97, 5365–5379. [Google Scholar] [CrossRef]
  17. Maykut, G.A.; McPhee, M.G. Solar heating of the Arctic mixed layer. J. Geophys. Res. Ocean. 1995, 100, 24691–24703. [Google Scholar] [CrossRef]
  18. Notz, D.; McPhee, M.G.; Worster, M.G.; Maykut, G.A.; Schlu¨nzen, K.H.; Eicken, H. Impact of underwater-ice evolution on Arctic summer sea ice. J. Geophys. Res. 2003, 108, 3223. [Google Scholar] [CrossRef]
  19. McPhee, M.G.; Morison, J.H.; Nilsen, F. Revisiting heat and salt exchange at the ice-ocean interface: Ocean flux and modeling considerations. J. Geophys. Res. Ocean. 2008, 113. [Google Scholar] [CrossRef]
  20. Zhang, H.; Zhang, M.; Jin, J.; Fei, K.; Ji, D.; Wu, C.; Zhu, J.; He, J.; Chai, Z.; Xie, J.; et al. Description and Climate Simulation Performance of CAS-ESM Version 2. J. Adv. Model. Earth. Syst. 2020, 12, e2020MS002210. [Google Scholar] [CrossRef]
  21. Jin, J.; Zhang, H.; Dong, X.; Liu, H.; Zhang, M.; Gao, X.; He, J.; Chai, Z.; Zeng, Q.; Zhou, G.; et al. CAS-ESM2.0 Model Datasets for the CMIP6 Flux-Anomaly-Forced Model Intercomparison Project (FAFMIP). Adv. Atmos. Sci. 2021, 38, 296–306. [Google Scholar] [CrossRef]
  22. Wang, J.; Bras, R.L.; Nieves, V.; Deng, Y. A model of energy budgets over water, snow, and ice surfaces. J. Geophys. Res. Atmos. 2014, 119, 6034–6051. [Google Scholar] [CrossRef]
  23. Yu, M.; Lu, P.; Cheng, B.; Leppäranta, M.; Li, Z. Impact of Microstructure on Solar Radiation Transfer Within Sea Ice During Summer in the Arctic: A Model Sensitivity Study. Front. Mar. Sci. 2022, 9, 861994. [Google Scholar] [CrossRef]
  24. Popović, P.; Cael, B.B.; Silber, M.; Abbot, D.S. Simple Rules Govern the Patterns of Arctic Sea Ice Melt Ponds. Phys. Rev. Lett. 2018, 120, 148701. [Google Scholar] [CrossRef]
  25. Shi, X.; Notz, D.; Liu, J.; Yang, H.; Lohmann, G. Sensitivity of Northern Hemisphere climate to ice–ocean interface heat flux parameterizations. Geosci. Model Dev. 2021, 14, 4891–4908. [Google Scholar] [CrossRef]
  26. Craig, A.P.; Vertenstein, M.; Jacob, R. A new flexible coupler for earth system modeling developed for CCSM4 and CESM1. Int. J. High. Perform. Comput. Appl. 2012, 26, 31–42. [Google Scholar] [CrossRef]
  27. Thorndike, A.S.; Rothrock, D.A.; Maykut, G.A.; Colony, R. The thickness distribution of sea ice. J. Geophys. Res. 1975, 80, 4501–4513. [Google Scholar] [CrossRef]
  28. Hunke, E.C.; Dukowicz, J.K. An Elastic Viscous Plastic Model for Sea Ice Dynamics. J. Phys. Oceanogr. 1997, 27, 1849–1867. [Google Scholar] [CrossRef]
  29. Lipscomb, W.H.; Hunke, E.C.; Maslowski, W.; Jakacki, J. Ridging, strength, and stability in high-resolution sea ice models. J. Geophys. Res. Ocean. 2007, 112. [Google Scholar] [CrossRef]
  30. Dong, X.; Jin, J.; Liu, H.; Zhang, H.; Zhang, M.; Lin, P.; Zeng, Q.; Zhou, G.; Yu, Y.; Song, M.; et al. CAS-ESM2.0 Model Datasets for the CMIP6 Ocean Model Intercomparison Project Phase 1 (OMIP1). Adv. Atmos. Sci. 2021, 38, 307–316. [Google Scholar] [CrossRef]
  31. Guo, Y.; Yu, Y.; Lin, P.; Liu, H.; He, B.; Bao, Q.; Zhao, S.; Wang, X. Overview of the CMIP6 Historical Experiment Datasets with the Climate System Model CAS FGOALS-f3-L. Adv. Atmos. Sci. 2020, 37, 1057–1066. [Google Scholar] [CrossRef]
  32. Valcke, S.; Craig, T.; Coquart, L. OASIS3-MCT User Guide, OASIS3-MCT 3.0; CERFACS Technical Report; CERFACS TR/CMGC/15/38: Toulouse, France, 2015. [Google Scholar]
  33. Giorgetta, M.A.; Roeckner, E.; Mauritsen, T.; Bader, J.; Crueger, T.; Esch, M.; Rast, S.; Kornblueh, L.; Schmidt, H.; Kinne, S.; et al. The atmospheric general circulation model ECHAM6: Model description; Max Planck Institute for Meteorology: Hamburg, Germany, 2013; 135p. [Google Scholar]
  34. Gurvan, M.; Bourdallé-Badie, R.; Bouttier, P.-A.; Bricaud, C.; Bruciaferri, D.; Calvert, D.; Chanut, J.; Clementi, E.; Coward, A.; Delrosso, D.; et al. NEMO ocean engine; Note du pole de modélisation de l’Institut Pierre-Simon Laplace. No 27; Institut Pierre-Simon Laplace (IPSL): Guyancourt, France, 2017. [Google Scholar] [CrossRef]
  35. Hunke, E.C.; Lipscomb, W.H. CICE: The Los Alamos Sea Ice Model Documentation and Software User’s Manual Version 4.0; Los Alamos National Laboratory: Los Alamos, NM, USA, 2010. [Google Scholar]
  36. Cao, J.; Wang, B.; Yang, Y.-M.; Ma, L.; Li, J.; Sun, B.; Bao, Y.; He, J.; Zhou, X.; Wu, L. The NUIST Earth System Model (NESM) version 3: Description and preliminary evaluation. Geosci. Model Dev. 2018, 11, 2975–2993. [Google Scholar] [CrossRef]
  37. Comiso, J.C.; Parkinson, C.L.; Gersten, R.; Stock, L. Accelerated decline in the Arctic sea ice cover. Geophys. Res. Lett. 2008, 35, L01703. [Google Scholar] [CrossRef]
  38. Ivanova, N.; Pedersen, L.T.; Tonboe, R.T.; Kern, S.; Heygster, G.; Lavergne, T.; Sørensen, A.; Saldo, R.; Dybkjær, G.; Brucker, L.; et al. Inter-comparison and evaluation of sea ice algorithms: Towards further identification of challenges and optimal approach using passive microwave observations. The Cryosphere 2015, 9, 1797–1817. [Google Scholar] [CrossRef]
  39. Kern, S.; Lavergne, T.; Notz, D.; Pedersen, L.T.; Tonboe, R. Satellite passive microwave sea-ice concentration data set inter-comparison for Arctic summer conditions. The Cryosphere 2020, 14, 2469–2493. [Google Scholar] [CrossRef]
  40. Comiso, J.C.; Cavalieri, D.J.; Parkinson, C.L.; Gloersen, P. Passive microwave algorithms for sea ice concentration: A comparison of two techniques. Remote Sens. Environ. 1997, 60, 357–384. [Google Scholar] [CrossRef]
  41. Zhang, J.; Rothrock, D.A. Modeling Global Sea Ice with a Thickness and Enthalpy Distribution Model in Generalized Curvilinear Coordinates. Mon. Weather Rev. 2003, 131, 845–861. [Google Scholar] [CrossRef]
  42. Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
  43. Zhang, Y.; Song, M.; Dong, C.; Liu, J. Modeling turbulent heat fluxes over Arctic sea ice using a maximum-entropy-production approach. Adv. Clim. Chang. Res. 2021, 12, 517–526. [Google Scholar] [CrossRef]
  44. Yu, L.; Liu, J.; Gao, Y.; Shu, Q. A Sensitivity Study of Arctic Ice-Ocean Heat Exchange to the Three-Equation Boundary Condition Parametrization in CICE6. Adv. Atmos. Sci. 2022, 39, 1398–1416. [Google Scholar] [CrossRef]
Preprints 101135 g001
Figure 1. Spatial distribution of climatological (1980–2014) March (upper) and September (lower) SIC from NSIDC observation (a,f), CAS-ESM2-0 old version (b,g), CAS-ESM2-0 new version (c,h), NESM3 old version (d,i) and NESM3 new version (e,j).
Figure 1. Spatial distribution of climatological (1980–2014) March (upper) and September (lower) SIC from NSIDC observation (a,f), CAS-ESM2-0 old version (b,g), CAS-ESM2-0 new version (c,h), NESM3 old version (d,i) and NESM3 new version (e,j).
Preprints 101135 g001
Preprints 101135 g002
Figure 2. Spatial distribution of climatological (1980–2014) March (upper) and September (lower) SIT from PIOMAS (a,f), CAS-ESM2-0 old version (b,g), CAS-ESM2-0 new version (c,h), NESM3 old version (d,i) and NESM3 new version (e,j).
Figure 2. Spatial distribution of climatological (1980–2014) March (upper) and September (lower) SIT from PIOMAS (a,f), CAS-ESM2-0 old version (b,g), CAS-ESM2-0 new version (c,h), NESM3 old version (d,i) and NESM3 new version (e,j).
Preprints 101135 g002
Preprints 101135 g003
Figure 3. Climatological (1980–2014) monthly evolution of SIC differences between CAS-ESM2-0 new version and old version (new version minus old version). Black dots represent points that are significant at 99% confidence level for Student’s t-test.
Figure 3. Climatological (1980–2014) monthly evolution of SIC differences between CAS-ESM2-0 new version and old version (new version minus old version). Black dots represent points that are significant at 99% confidence level for Student’s t-test.
Preprints 101135 g003
Preprints 101135 g004
Figure 4. Climatological (1980–2014) monthly evolution of SIC differences between NESM3 new version and old version (new version minus old version). Black dots represent points that are significant at 99% confidence level for Student’s t-test.
Figure 4. Climatological (1980–2014) monthly evolution of SIC differences between NESM3 new version and old version (new version minus old version). Black dots represent points that are significant at 99% confidence level for Student’s t-test.
Preprints 101135 g004
Preprints 101135 g005
Figure 5. Climatological (1980–2014) monthly of SIT differences between CAS-ESM2-0 new version and old version (new version minus old version). Black dots represent points that are significant at 99% confidence level for Student’s t-test.
Figure 5. Climatological (1980–2014) monthly of SIT differences between CAS-ESM2-0 new version and old version (new version minus old version). Black dots represent points that are significant at 99% confidence level for Student’s t-test.
Preprints 101135 g005
Preprints 101135 g006
Figure 6. Climatological (1980–2014) monthly of SIT differences between NESM3 new version and old version (new version minus old version). Black dots represent points that are significant for at 99% confidence level for Student’s t-test.
Figure 6. Climatological (1980–2014) monthly of SIT differences between NESM3 new version and old version (new version minus old version). Black dots represent points that are significant for at 99% confidence level for Student’s t-test.
Preprints 101135 g006
Preprints 101135 g007
Figure 7. The Taylor Score of 1980–2014 multi-year mean SIC field from CAS-ESM2-0 old version (red dash line), CAS-ESM2-0 new version (red solid line), NESM3 old version (green dash line), and NESM3 new version (green solid line). All the model SIC fields are compared against the NSIDC observation.
Figure 7. The Taylor Score of 1980–2014 multi-year mean SIC field from CAS-ESM2-0 old version (red dash line), CAS-ESM2-0 new version (red solid line), NESM3 old version (green dash line), and NESM3 new version (green solid line). All the model SIC fields are compared against the NSIDC observation.
Preprints 101135 g007
Preprints 101135 g008
Figure 8. The Taylor Score of 1980–2014 multi-year mean SIT field from CAS-ESM2-0 old version (red dash line), CAS-ESM2-0 new version (red solid line), NESM3 old version (green dash line), and NESM3 new version (green solid line). All model fields are compared against the PIOMAS product.
Figure 8. The Taylor Score of 1980–2014 multi-year mean SIT field from CAS-ESM2-0 old version (red dash line), CAS-ESM2-0 new version (red solid line), NESM3 old version (green dash line), and NESM3 new version (green solid line). All model fields are compared against the PIOMAS product.
Preprints 101135 g008
Table 1. Details of the CAS-EMS2-0 model and NESM3 model.
Table 1. Details of the CAS-EMS2-0 model and NESM3 model.
Component CAS-ESM2-0 Old Version CAS-ESM2-0 New Version NESM3 Old Version NESM3 New Version
Atmosphere IAP AGCM5 IAP AGCM5 ECHAM 6.3 ECHAM 6.3
Ocean LICOM2 LICOM3 NEMO3.4 NEMO3.4
Sea Ice CICE4 CICE6 CICE4 CICE6
Land CoLM CoLM JSBACH JSBACH
Coupler Coupler7 Coupler7 OASIS_3.0-MCT3 OASIS_3.0-MCT3
Table 2. Summary of four old and new sea ice schemes.
Table 2. Summary of four old and new sea ice schemes.
Scheme Air-Ice Heat Flux Exchanges Shortwave Radiation Melt Pond Ice-Ocean Heat Flux Exchanges
old version Bulk formula dEdd LVL 2EQ
new version MEP dEdd + IOP LVL + MPSD 3EQ
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated