Submitted:
09 March 2024
Posted:
12 March 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Method and Materials
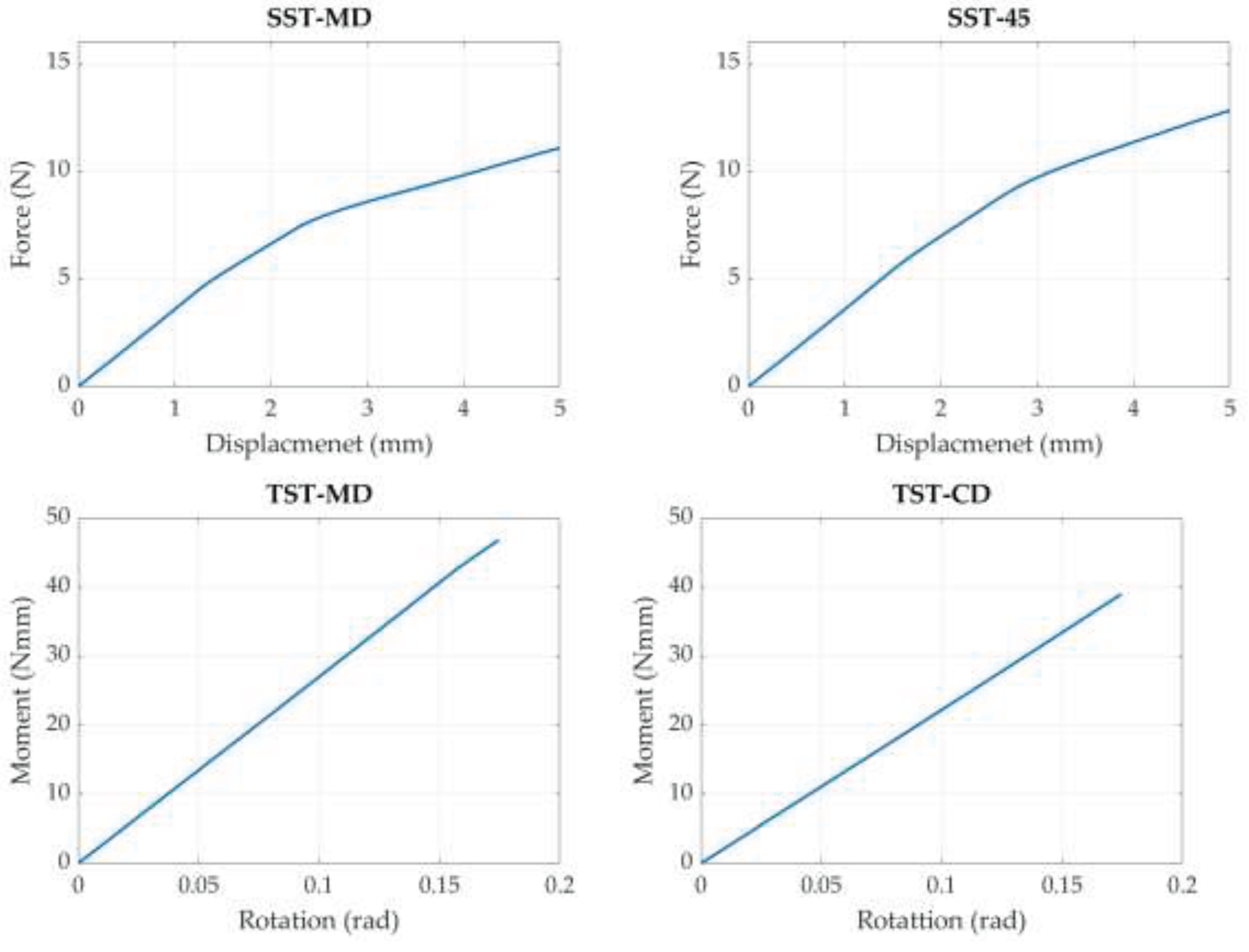
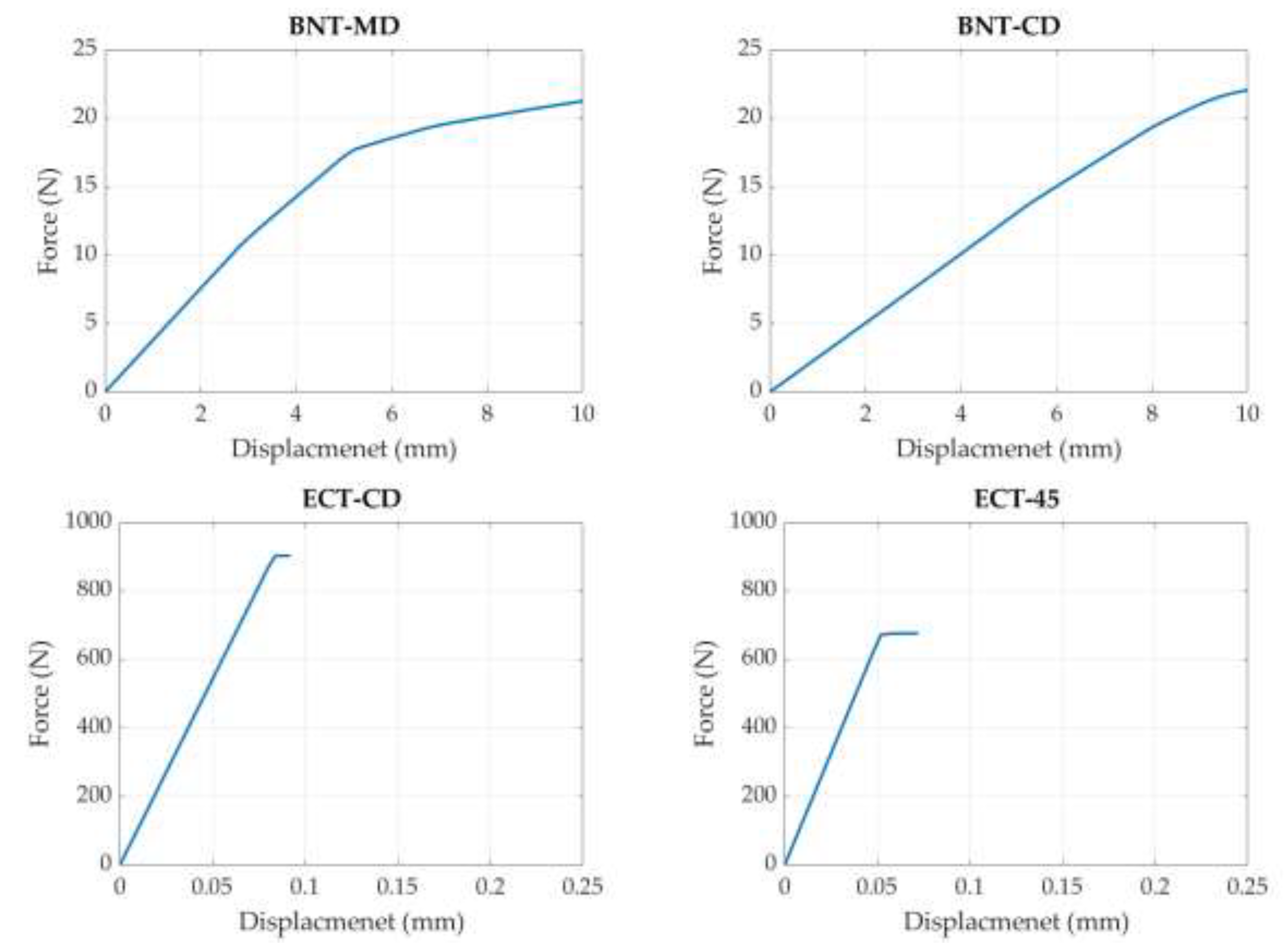
2.1. Selected Experimental Setup – Brief Presentation
2.2. Numerical Models
2.3. Constitutive Modelling of Corrugated Board
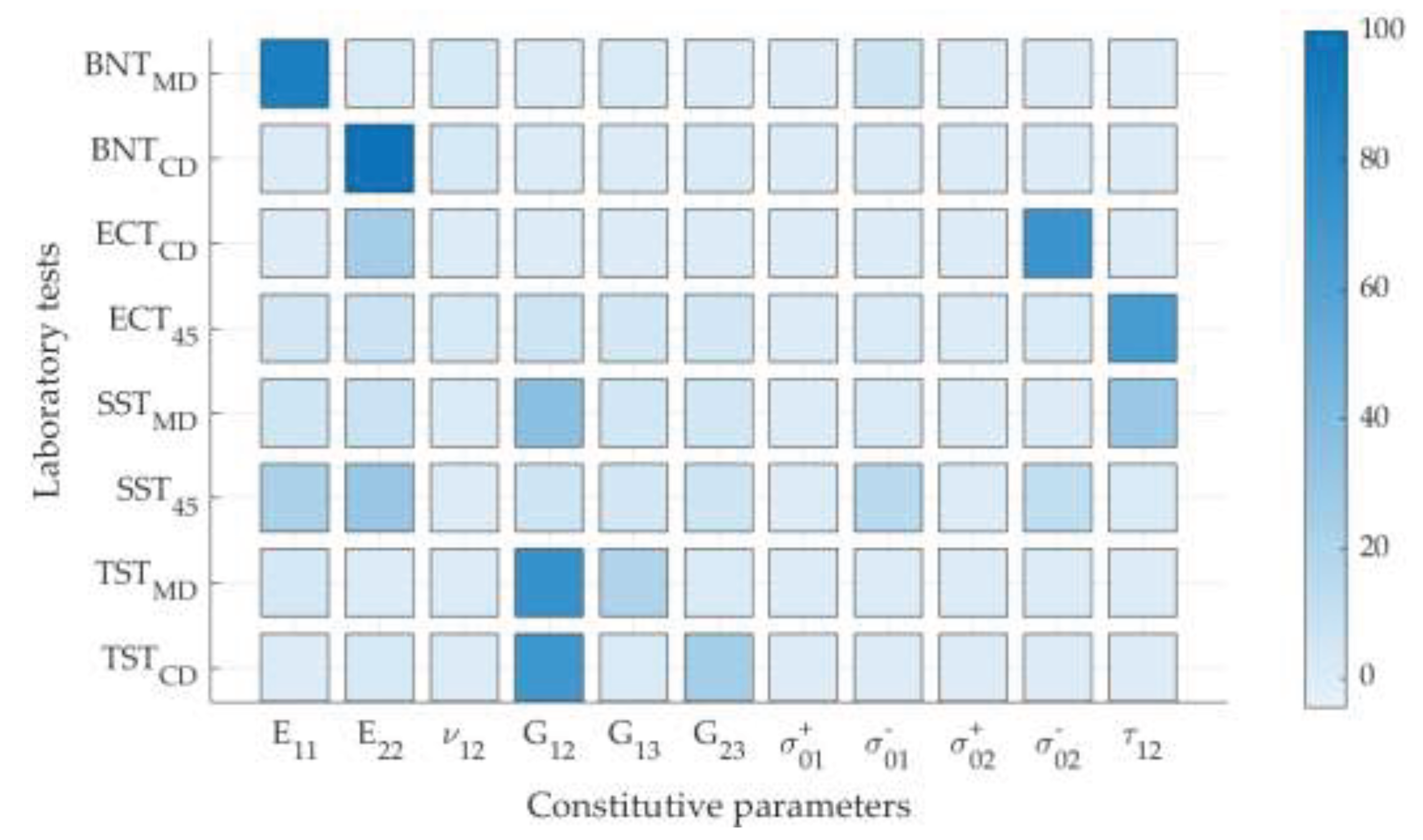
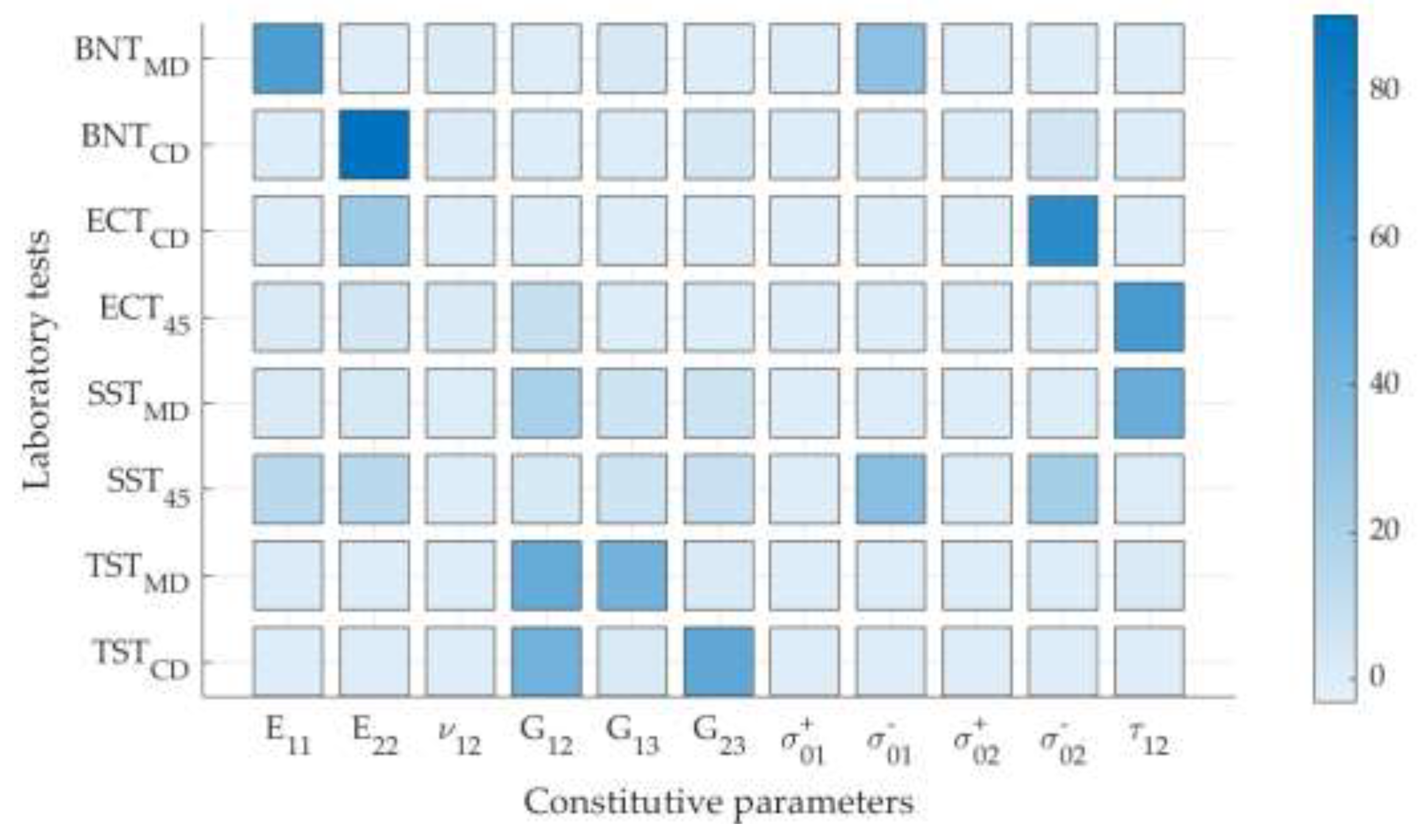
2.4. Sensitivity Analysis
3. Results and Discussion
4. Conclusions
References
- Putz, H.-J. & Schabel, S. The myth of limited fibre life cycles. Wochenblatt für Papierfabrikation 2018, 6, 350–356. [Google Scholar]
- Lorang, E. , Lobianco, A. & Delacote, P. Increasing paper and cardboard recycling: impacts on the forest sector and carbon emissions. Environ. Model. Assess. 2023, 28, 189–200. [Google Scholar]
- Sanchez-Salvador, J.L. , Balea, A., Monte, M.C. et al. Comparison Of Mechanical And Chemical Nanocellulose As Additives To Reinforce Recycled Cardboard. Sci Rep 2020, 10, 3778. [Google Scholar] [CrossRef]
- Wang, C.-C. , Chen, C.-H. & Jiang, B.C. Shock absorption characteristics and optimal design of corrugated fiberboard using drop testing. Appl. Sci. 2021, 11, 5815. [Google Scholar] [CrossRef]
- Fehér, L., Pidl, R. & Böröcz, P. Compression strength estimation of corrugated board boxes for a reduction in sidewall surface cutouts – experimental and numerical approaches. Materials 2023, 16, 597. [CrossRef]
- Hung, D. , Nakano, Y., Tanaka, F., Hamanaka, D. & Uchino, T. Preserving the strength of corrugated cardboard under high humidity condition using nano-sized mists. Compos. Sci. Technol. 2010, 70, 2123–2127. [Google Scholar]
- Allaoui, S. , Aboura, Z. & Benzeggagh, M. L. Effects of the environmental conditions on the mechanical behaviour of the corrugated cardboard. Compos. Sci. Technol. 2009, 69, 104–110. [Google Scholar]
- Berry, T. M. , Ambaw, A., Defraeye, T., Coetzee, C. J. & Opara, U. L. Moisture adsorption in palletised corrugated fibreboard cartons under shipping conditions: a CFD modelling approach. Food Bioprod. Process. 2018, 114, 43–59. [Google Scholar]
- Alam, I. , Sharma, C. Degradation of paper products due to volatile organic compounds. Sci Rep 2023, 13, 6426. [Google Scholar] [CrossRef]
- Urbanik, T. J. Effect of corrugated flute shape on fibreboard edgewise crush strength and bending stiffness. J. Pulp Pap. Sci. 2001, 27, 330–335. [Google Scholar]
- Ihwah, A. , Dewi, I. A., Sukardi, S. & Fitriani, Y. Proportion of raw material optimisation in handicraft paper making made of Pinang fibre (Areca catechu l.) and old corrugated cardboard (used cardboard). Int. J. Environ. Waste Manag. 2021, 28, 282–297. [Google Scholar]
- Twede, D., Selke, S. E. M. & Shires, D. Cartons, Crates and Corrugated Board: Handbook of Paper and Wood Packaging Technology, 41–42, 55–56 (DEStech Publications, Inc, 2005). 2005.
- Zhang, Z. , Qiu, T., Song, R. & Sun, Y. Nonlinear finite element analysis of the fluted corrugated sheet in the corrugated cardboard. Advan. in Mater. Sci. and Engin. 2014, 2014, 65401. [Google Scholar] [CrossRef]
- Mrówczyński, D. , Pozorska J. , Garbowski T. & Pozorski Z. Corrugated board stiffness of unsymmetrical multilayered corrugated board: influence of boundary conditions. BioResources, 2023, 18, 7611–7628. [Google Scholar] [CrossRef]
- Lin, C. , Nicaise, S.M., Lilley, D.E. et al. Nanocardboard as a nanoscale analog of hollow sandwich plates. Nat Commun 2018, 9, 4442. [Google Scholar] [CrossRef]
- Aboura, Z. , Talbi, N., Allaoui, S. & Benzeggagh, M. L. Elastic behaviour of corrugated cardboard: experiments and modelling. Compos. Struct. 2004, 63, 53–62. [Google Scholar]
- Buannic, N. , Cartraud, P. & Quesnel, T. Homogenization of corrugated core sandwich panels. Compos. Struct. 2003, 59, 299–312. [Google Scholar]
- Suarez, B. , Muneta, M. L. M, Sanz-Bobi, J. D. & Romero G. Application of homogenization approaches to the numerical analysis of seating made of multi-wall corrugated cardboard. Compos. Struct. 2021, 262, 113642. [Google Scholar] [CrossRef]
- Hill, R. A theory of the yielding and plastic flow of anisotropic metals. Proc. R. Soc. Lond. Ser. A 1948, 193, 281–297. [Google Scholar]
- Caddell, R. M. , Raghava, R. S. & Atkins, A. G. Yield criterion for anisotropic and pressure dependent solids such as oriented polymers. J. Mater. Sci. 1973, 8, 1641–1646. [Google Scholar]
- Deshpande, V. S. , Fleck, N. A. & Ashby, M. F. Effective properties of the octet-truss lattice material. J. Mech. Phys. Solid. 2001, 49, 1747–1769. [Google Scholar]
- Mäkelä, P. , Östlund, S. Orthotropic Elastic–Plastic Material Model for Paper Materials. International Journal of Solids and Structures, 2003, 40, 5599–5620. [Google Scholar] [CrossRef]
- Hoffman, O. The brittle strength of orthotropic materials. J. Compos. Mater. 1967, 1, 200–206. [Google Scholar] [CrossRef]
- Xia, Q. S. , Boyce, M. C. & Parks, D. M. A constitutive model for the anisotropic elastic–plastic deformation of paper and paperboard. Int. J. Solids Struct. 2002, 39, 4053–4071. [Google Scholar]
- Alzweighi, M. , Mansour, R., Tryding, J. & Kulachenko A. Evaluation of Hoffman and Xia plasticity models against bi-axial tension experiments of planar fiber network materials. Int. J. Solids Struct. 2022, 238, 111358. [Google Scholar] [CrossRef]
- Garbowski, T., Maier, G. & Novati, G. On Calibration of Orthotropic Elastic-Plastic Constitutive Models for Paper Foils by Biaxial Tests and Inverse Analyses. Structural and Multidisciplinary Optimization, 46, 111–128 (2011). [CrossRef]
- Schrampfer, K. E., Whitsitt, W. J. & Baum, G. A. Combined Board Edge Crush (ECT) Technology. Institute of Paper Chemistry, Appleton, WI, USA (1987).
- Jamsari, M. A. , Kueh, C., Gray-Stuart, E. M., Dahm, K. & Bronlund, J. E. Modelling the impact of crushing on the strength performance of corrugated fibreboard. Packag. Technol. Sci. 2020, 33, 159–170. [Google Scholar]
- Urbanik, T. J. Effect of paperboard stress-strain characteristics on strength of singlewall corrugated fiberboard: a theoretical approach. US Forest Products Laboratory Report. FPL 401 ( 1981.
- TAPPI T820. Flexural Stiffness of Corrugated Board. Pulp and Paper Association. Norcross, GA, USA, (2019).
- Mujika, F. , Arrese, A. , Adarraga, I. & Oses, U. New correction terms concerning three-point and four-point bending tests. Polym. Test. 2016, 55, 25–37. [Google Scholar]
- Garbowski, T. & Knitter-Piątkowska, A. Analytical determination of the bending stiffness of a five-layer corrugated cardboard with imperfections. Materials 2022, 15, 663. [Google Scholar] [CrossRef]
- Yoshihara, H. , Yoshinobu, M. & Maruta, M. Bending stiffness and moment capacity of cardboard obtained from three-point and elastic bending tests. Nord. Pulp Paper Res. J. 2023, 38, 73–85. [Google Scholar]
- Nordstrand, T. , Carlsson, L. A. & Allen, H. G. Transverse shear stiffness of structural core sandwich. Comp. Struct. 1994, 27, 317–329. [Google Scholar]
- Reissner, E. On torsion and transverse flexure of orthotropic elastic plates. J. Appl. Mech. 1980, 47, 855–860. [Google Scholar] [CrossRef]
- ASTM Standard D5379. Standard test method for shear properties of composite materials by the V-notched beam method. ASTM International, West Conshohocken, USA (2005).
- ASTM Standard D4255. Test method for in-plane shear properties of polymer matrix composite materials by the rail shear method. ASTM International, West Conshohocken, USA (2007).
- ASTM Standard D3518. Standard test method for in-plane shear response of polymer matrix composite materials by tensile test of a ±45° laminate. ASTM International, West Conshohocken, USA (2007).
- Avilés, F. , Couoh-Solis, F., Carlsson, L. A., Hernández-Pérez, A. & May-Pat, A. Experimental determination of torsion and shear properties of sandwich panels and laminated composites by the plate twist test. Comp. Struct. 2011, 93, 1923–1928. [Google Scholar]
- Hernandez-Perez, A. , Avilés, F. & Carlsson, L. A. First-order shear deformation analysis of the sandwich plate twist specimen. J. Sandw. Struct. Mater. 2012, 14, 229–245. [Google Scholar]
- Popil, R. E. , Coffin, D. W. & Habeger, C. C. Transverse shear measurement for corrugated board and its significance. Appita J. 2008, 61, 307–312. [Google Scholar]
- Chalmers I. R. A new method for determining the shear stiffness of corrugated board, Appita J. 2006, 59, 357-361.
- Li, M., Wu, L., Ma, L., Xiong, J. & Guan, Z. Torsion of carbon fiber composite pyramidal core sandwich plates. Comp. Struct. 93, Issue 9, 2358-2367 (2011).
- Pozorski, Z. , Wojciechowski, S. The influence of symmetrical boundary conditions on the structural behaviour of sandwich panels subjected to torsion. Symmetry 2020, 12, 2093. [Google Scholar] [CrossRef]
- Garbowski, T. , Grabski, J. K. & Marek, A. Full-field measurements in the edge crush test of a corrugated board—Analytical and numerical predictive models. Materials 2021, 14, 2840. [Google Scholar] [CrossRef] [PubMed]
- Fadiji, T. , Ambaw, A., Coetzee, C. J., Berry, T.M. & Opara, U. L. Application of finite element analysis to predict the mechanical strength of ventilated corrugated paperboard packaging for handling fresh produce. Biosyst. Eng. 2018, 174, 260–281. [Google Scholar]
- Suarez, B., Muneta, M. L. M., Sanz-Bobi, J. D. & Romero, G. Application of homogenization approaches to the numerical analysis of seating made of multi-wall corrugated cardboard. Compos. Struct. 262, 113642. [CrossRef]
- FEMat Systems. Available online: http://www.fematsystems.pl/en/systems/sst/ (accessed on 30 December 2023).
- Tsai, S. W. & Wu, E. M. A general theory of strength for anisotropic materials. J. Compos. Mater. 5(1), 58–80 (1971).
- Wu, Z.R. , Yang, Y. & Lei, H. Progressive failure analysis of perforated composite laminates considering nonlinear shear effect. Sci Rep 2023, 13, 22375. [Google Scholar] [CrossRef]
- Alzweighi, M.; Tryding, J.; Mansour, R.; Borgqvist, E.; Kulachenko, A. Anisotropic Damage Behavior in Fiber-Based Materials: Modeling and Experimental Validation. Journal of the Mechanics and Physics of Solids, 2023, 181, 105430. [Google Scholar] [CrossRef]
- Garbowski, T.; Garbowska, L. Computer aided estimation of corrugated board box compression strength. Part 2. The sensitivity analysis in selected laboratory tests of corrugated board. Przegląd papierniczy, 2018, 74, 435–440. [Google Scholar] [CrossRef]
- Garbowski, T.; Garbowska, L. Computer aided estimation of corrugated board box compression strength. Part 3. Laboratory-numerical procedure for an identification of elastic properties of corrugated board. Przegląd papierniczy,, 2018, 74, 577–585. [Google Scholar] [CrossRef]
- Baum, G.A.: The elastic properties of paper: A review. IPC technical paper series number, 145 (1984).



| 89,8 | -2,0 | 0,0 | 5,2 | 5,4 | 22,2 | 3,6 | 0,0 | |
| 1,2 | 100,8 | 25,0 | 8,8 | 8,2 | 30,8 | 0,0 | 2,4 | |
| 3,0 | 2,4 | 0,0 | 2,4 | 0,6 | -4,6 | 0,0 | 0,0 | |
| 0,2 | 0,2 | 0,0 | 7,2 | 36,6 | 6,4 | 74,0 | 69,8 | |
| 1,0 | 0,2 | 0,0 | 4,6 | 4,2 | 4,4 | 20,2 | 1,0 | |
| 0,2 | 1,2 | 0,0 | 4,6 | 4,8 | 6,2 | 0,8 | 25,2 | |
| 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | |
| 6,0 | 0,0 | 0,0 | 1,0 | 1,0 | 15,8 | 0,0 | 0,0 | |
| 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | |
| -0,4 | 0,0 | 72,6 | 1,4 | 0,2 | 12,6 | 0,0 | 0,0 | |
| 0,0 | 0,0 | 0,0 | 66,2 | 30,2 | 1,0 | 0,0 | 0,0 |
| 58,6 | -0,8 | 0,0 | 1,6 | 2,2 | 14,6 | 1,0 | 0,0 | |
| 0,6 | 90,4 | 26,0 | 4,6 | 3,2 | 14,4 | 0,0 | 0,6 | |
| 1,2 | 1,0 | 0,0 | 1,4 | 0,2 | -3,2 | 0,0 | 0,0 | |
| 0,2 | 0,0 | 0,0 | 9,4 | 21,4 | 2,8 | 49,4 | 43,6 | |
| 2,4 | 0,2 | 0,0 | 0,0 | 6,4 | 6,6 | 43,2 | 1,6 | |
| 0,2 | 3,6 | 0,0 | 0,0 | 7,4 | 9,2 | 1,6 | 51,8 | |
| 0,2 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | |
| 32,8 | -1,4 | 0,0 | 0,0 | 0,4 | 34,4 | 0,0 | 0,0 | |
| 0,0 | 0,1 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | |
| -1,8 | 5,4 | 72,8 | 0,0 | 0,2 | 23,8 | 0,0 | 0,0 | |
| 0,0 | 0,0 | 0,0 | 61,0 | 47,6 | 0,6 | 1,6 | 0,0 |
| 39,8 | 0,0 | 0,0 | 1,4 | 1,6 | 10,0 | 1,0 | 0,0 | |
| 0,4 | 69,6 | 25,0 | 4,0 | 2,2 | 9,8 | 0,0 | 1,4 | |
| 0,4 | 0,4 | 0,0 | 1,2 | 0,0 | -2,2 | 0,0 | 0,0 | |
| 0,0 | 0,0 | 0,0 | 8,2 | 14,8 | 2,0 | 34,2 | 28,4 | |
| 3,4 | 0,2 | 0,0 | 0,0 | 8,2 | 8,6 | 58,4 | 2,6 | |
| 0,2 | 6,2 | 0,0 | 0,0 | 9,8 | 12,0 | 2,4 | 65,8 | |
| 7,2 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | |
| 45,0 | -3,6 | 0,0 | 0,0 | 0,4 | 39,0 | 0,0 | 0,0 | |
| 0,0 | 3,1 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | |
| -2,6 | 19,2 | 72,6 | 0,0 | 0,0 | 26,4 | 0,0 | 0,0 | |
| 0,2 | 0,0 | 0,0 | 61,4 | 51,6 | 0,4 | 1,2 | 0,0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





