Submitted:
07 March 2024
Posted:
11 March 2024
You are already at the latest version
Abstract
Keywords:
Summary
Introduction
The Nature of Significance
Divide-and-Conquer Approach for Hartree−Fock Based Calculations
The Use and Importance of the Nanoscale in ZernikeR, Hypergeometric2F1Regularized, LaguerreL, and ChebyshevU Quantum Homeopathy Translations
Methods & Materials
Results



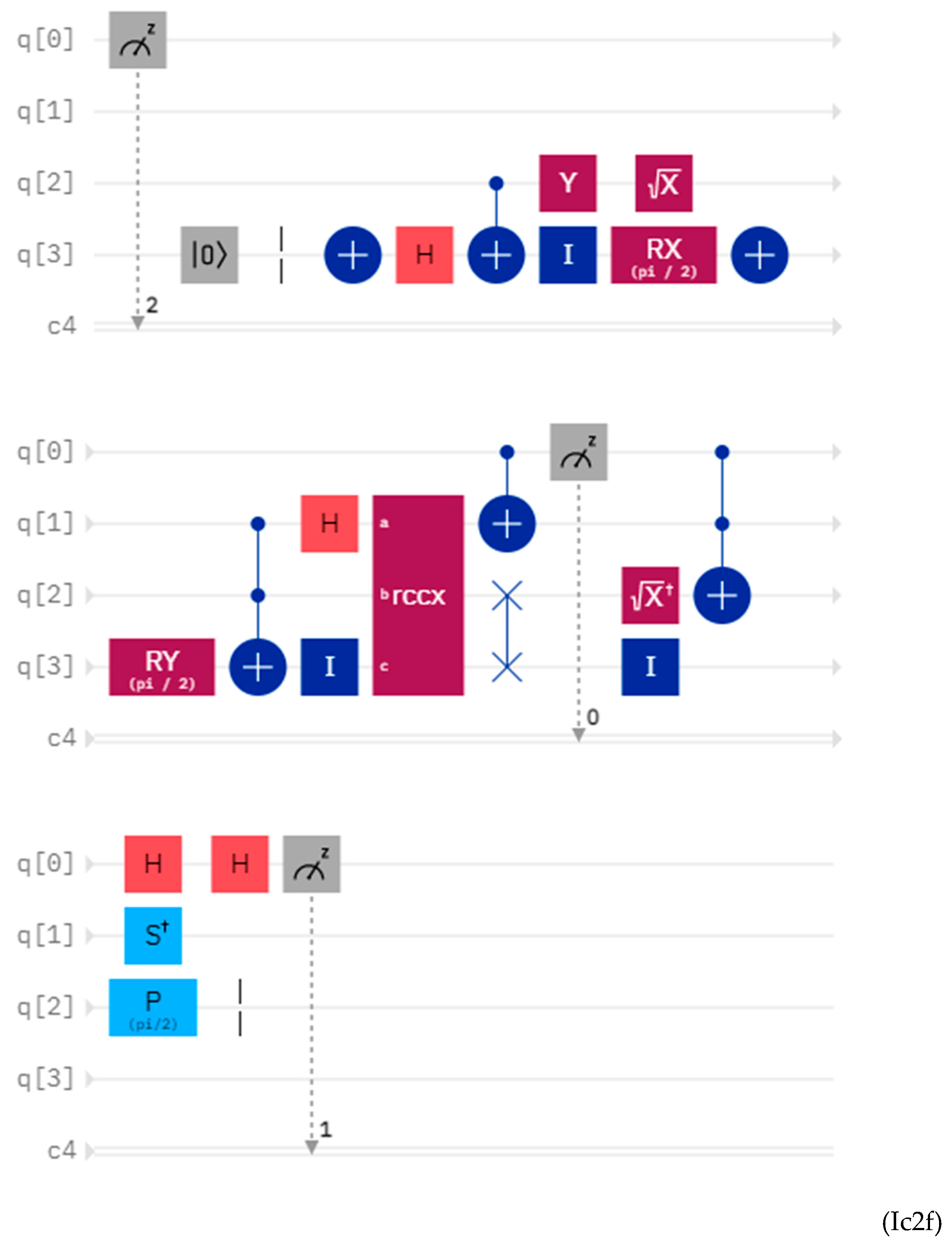
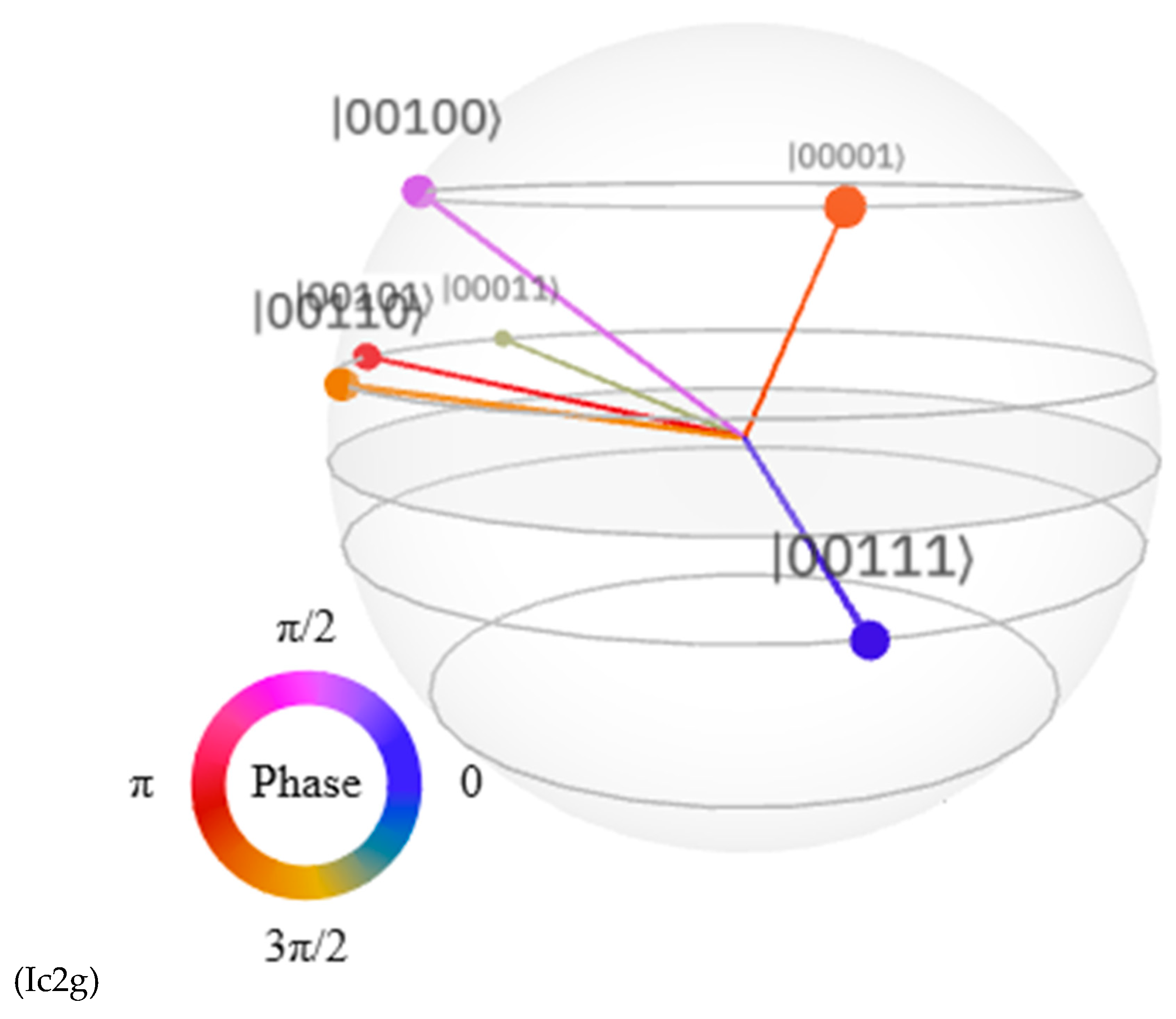
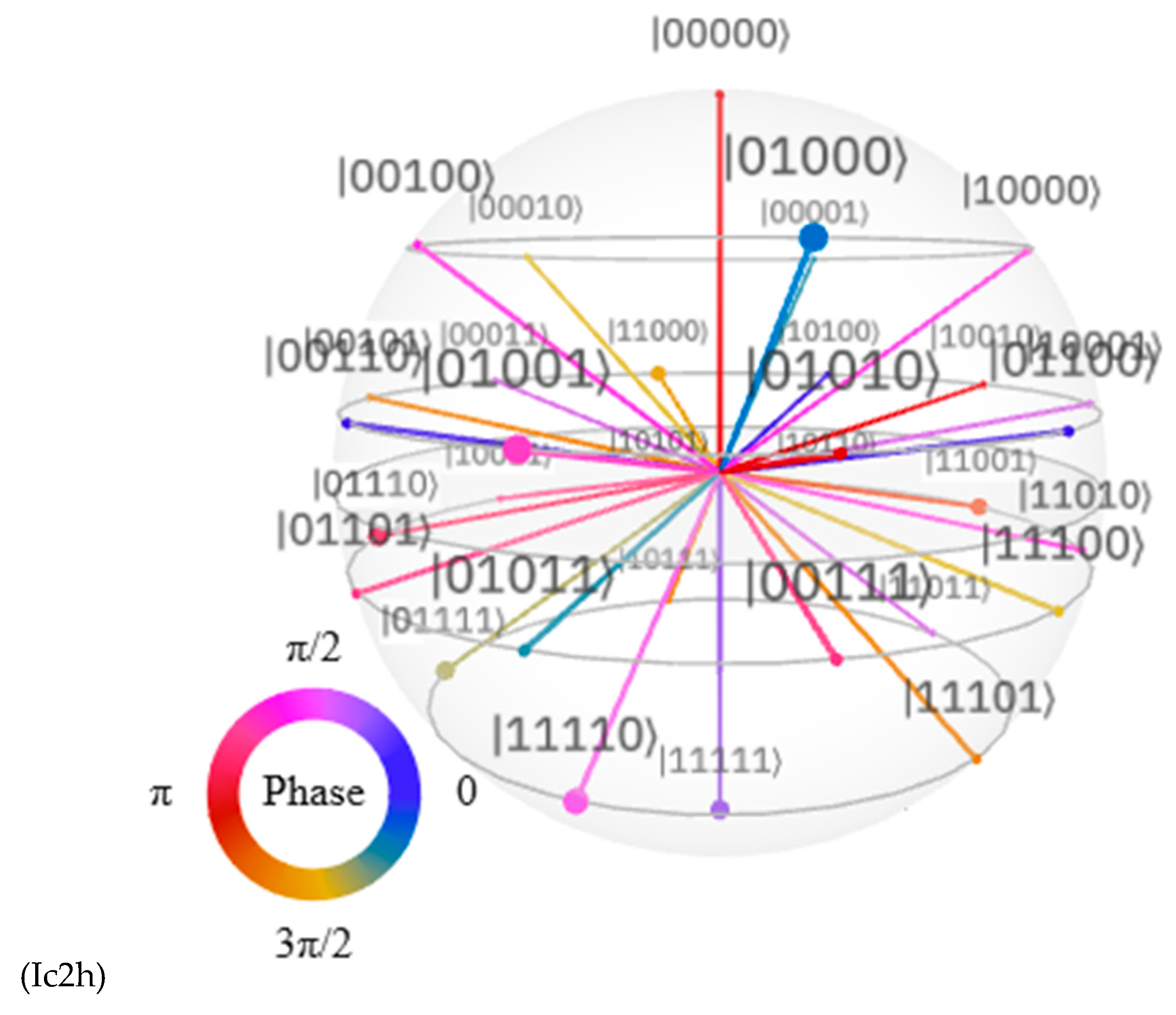
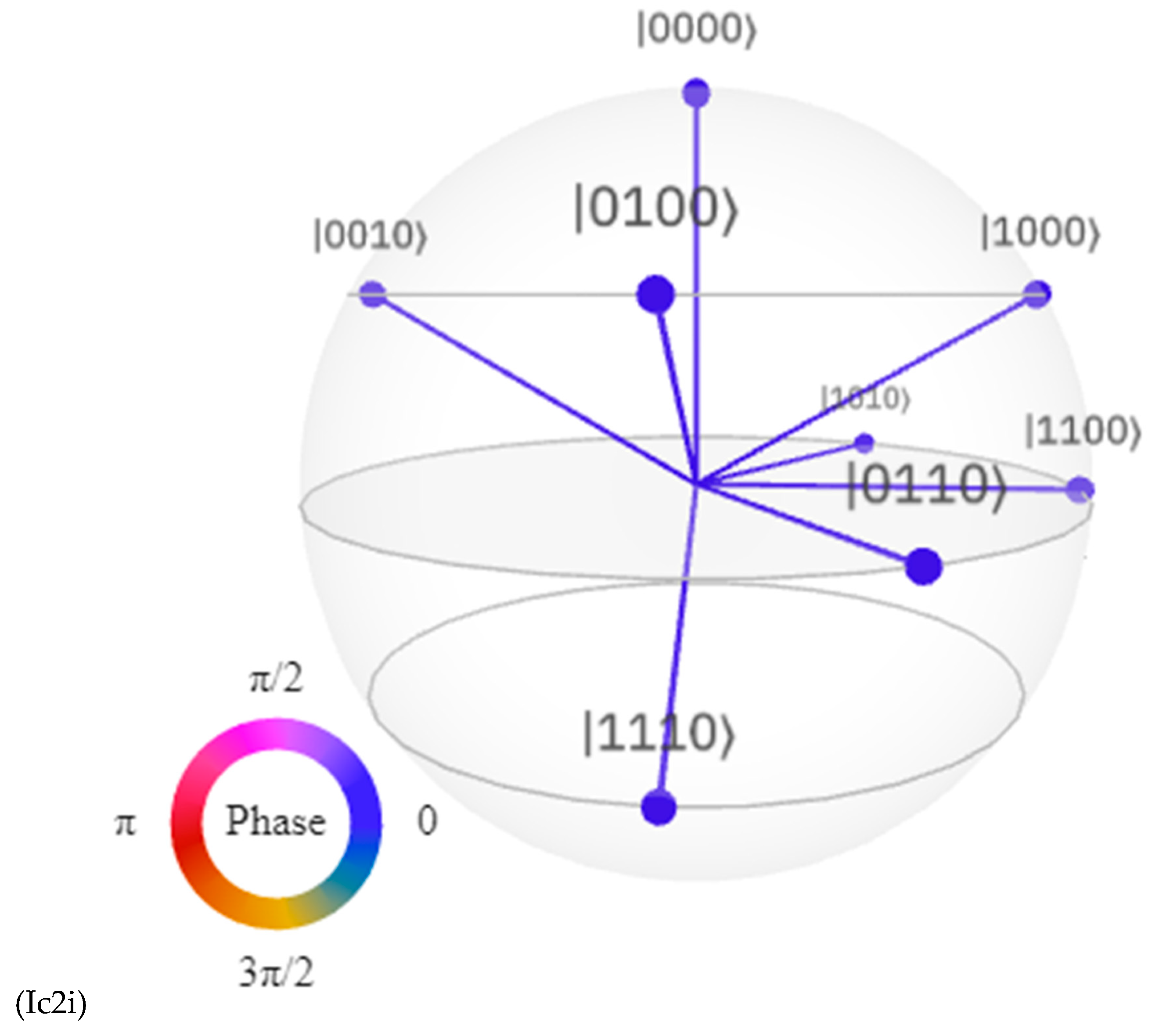
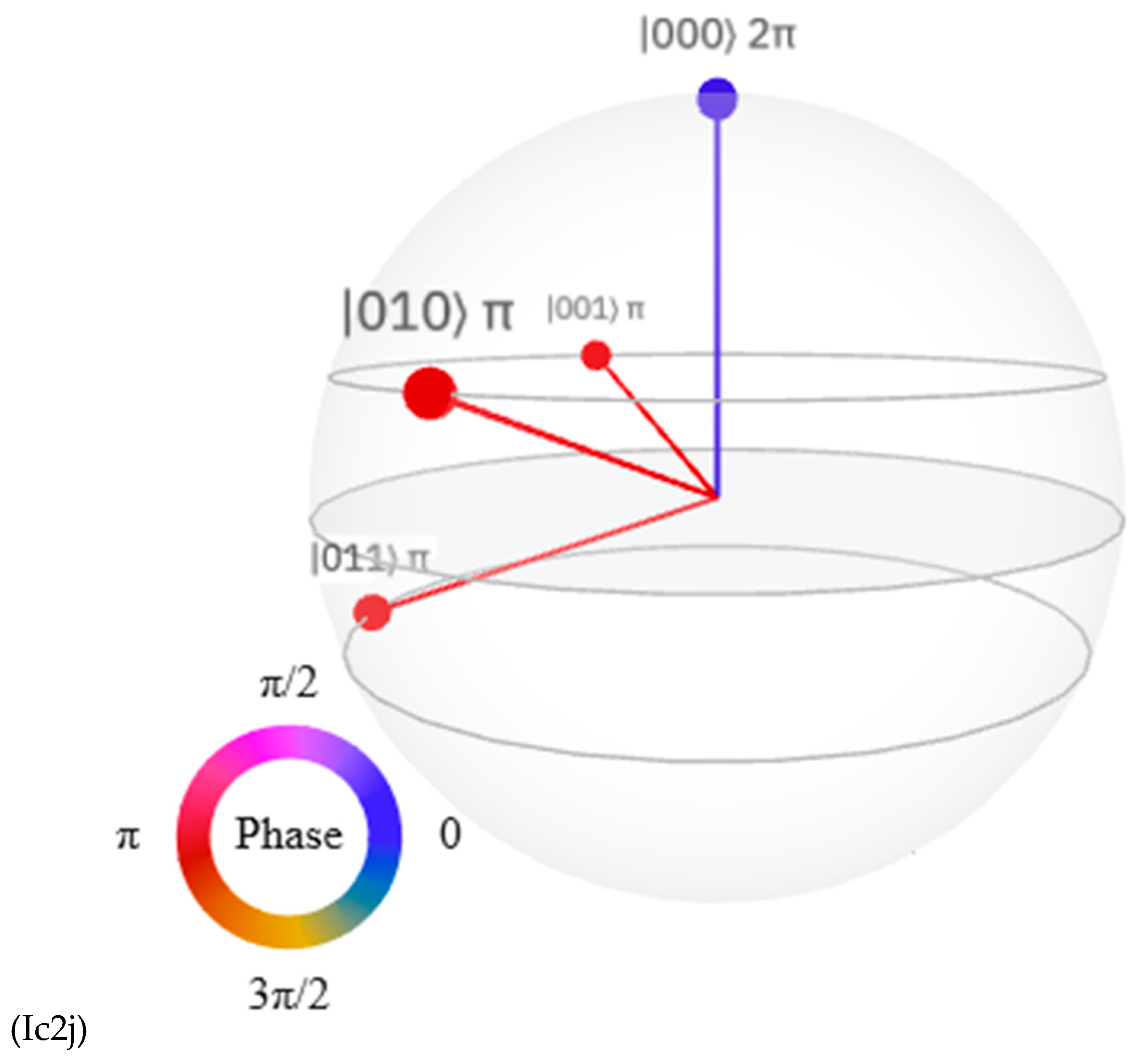
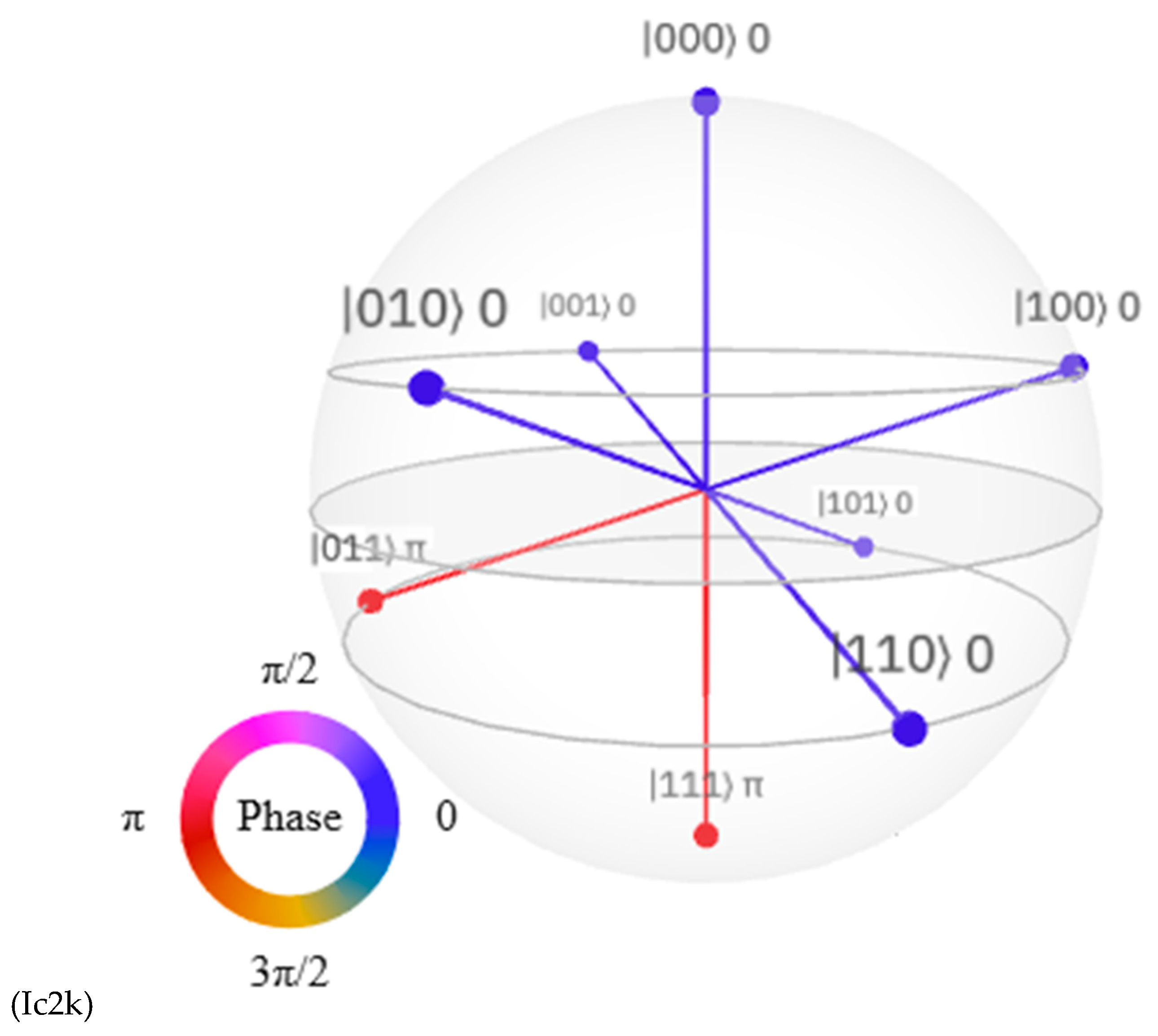
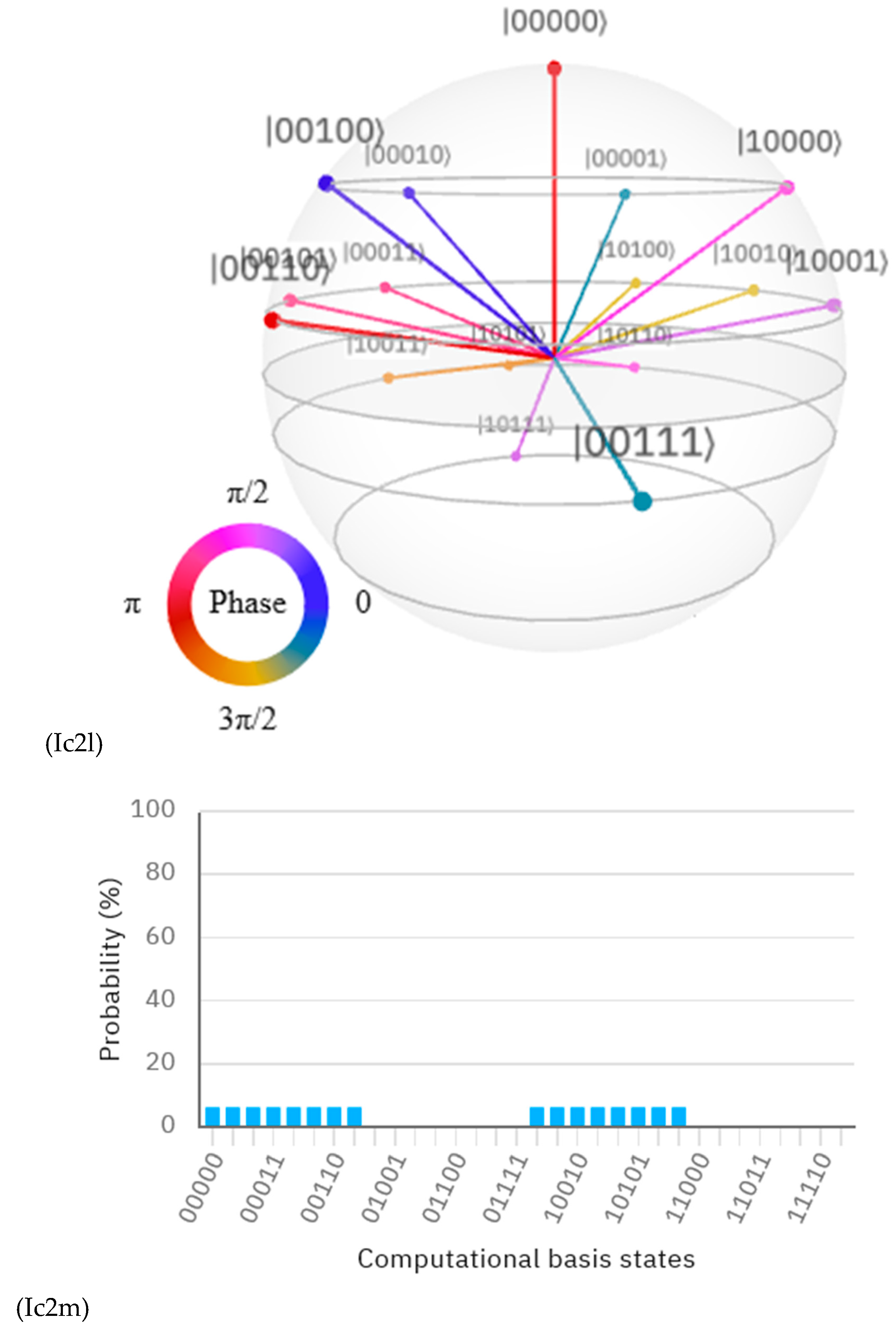
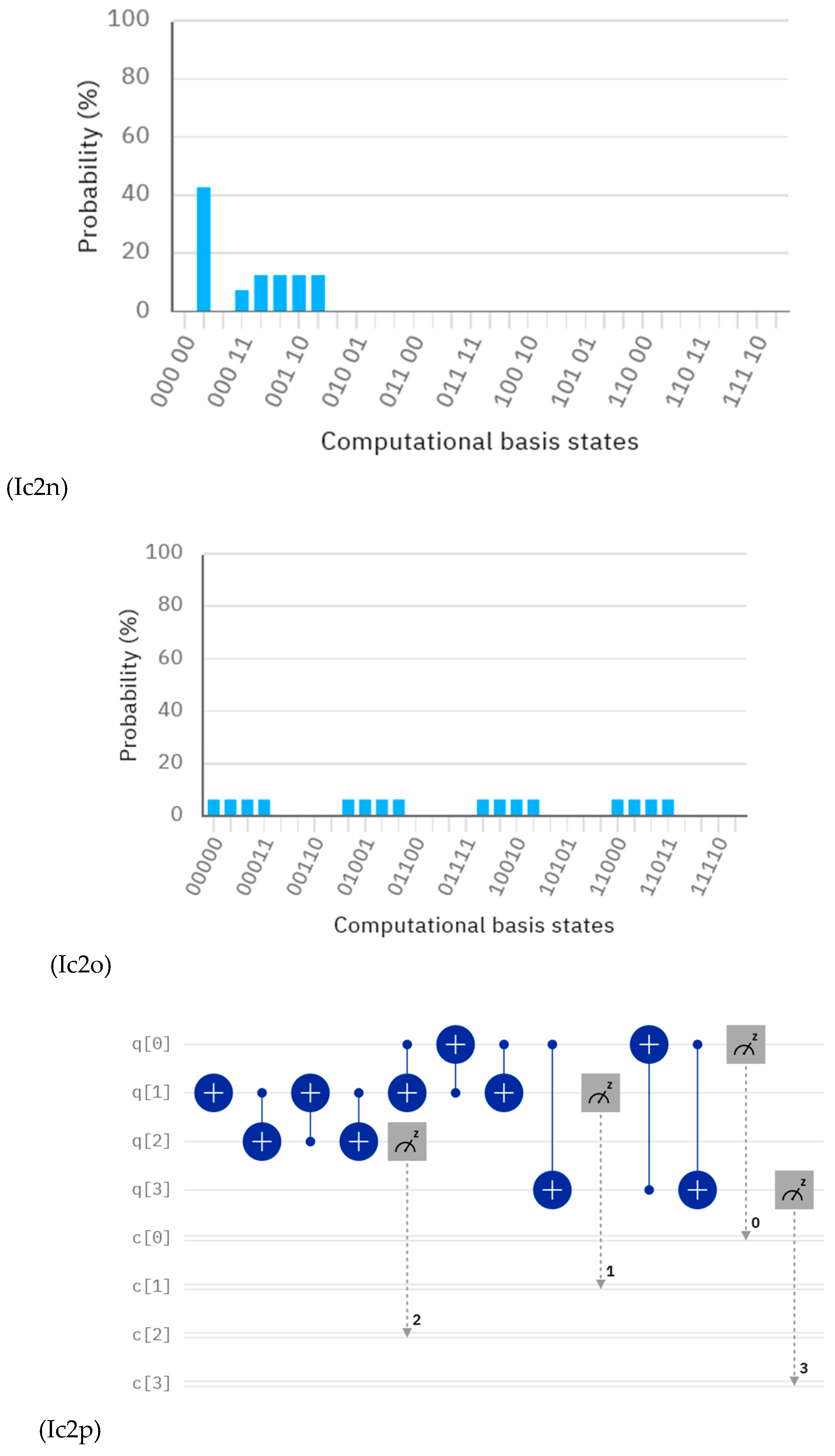
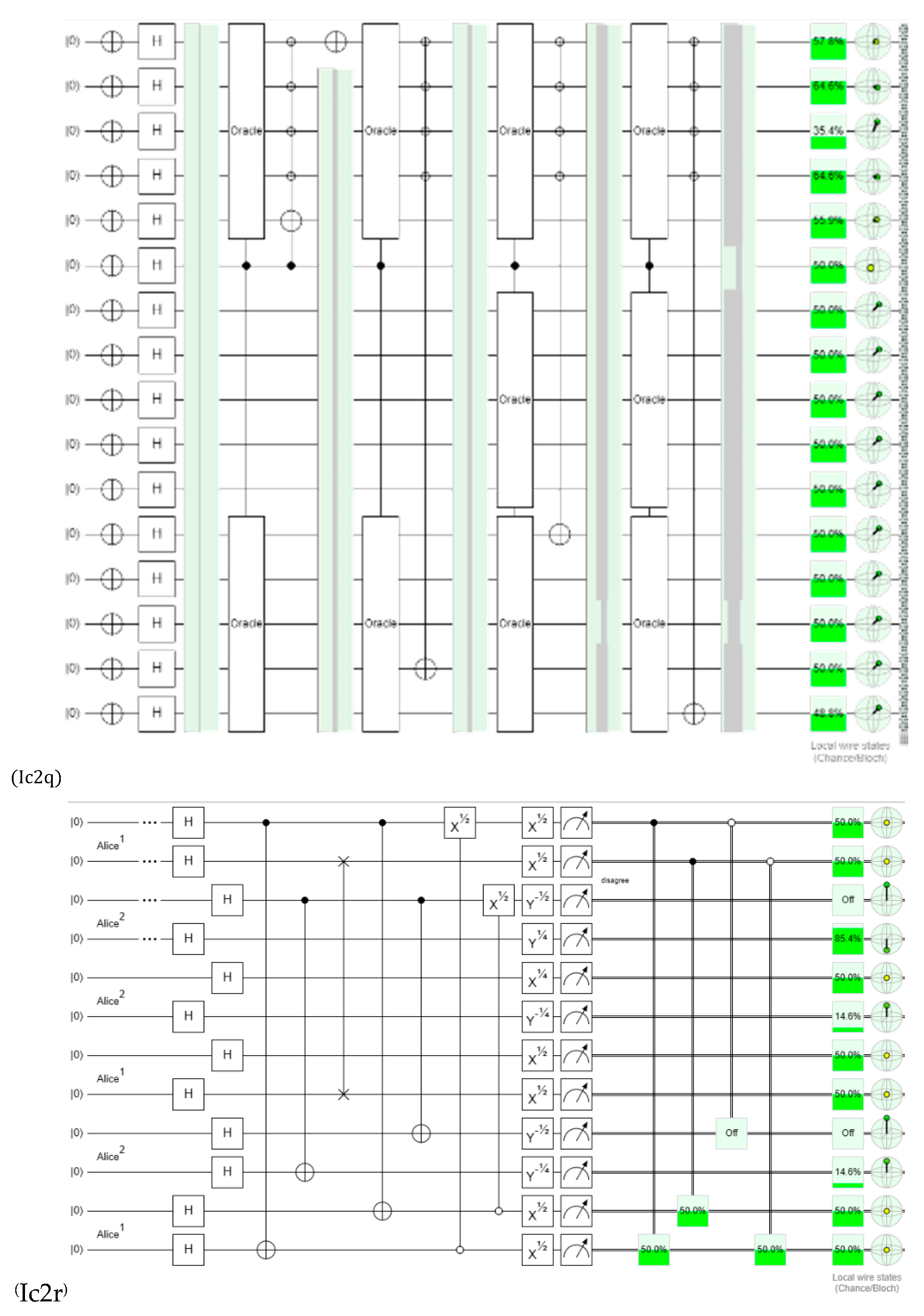
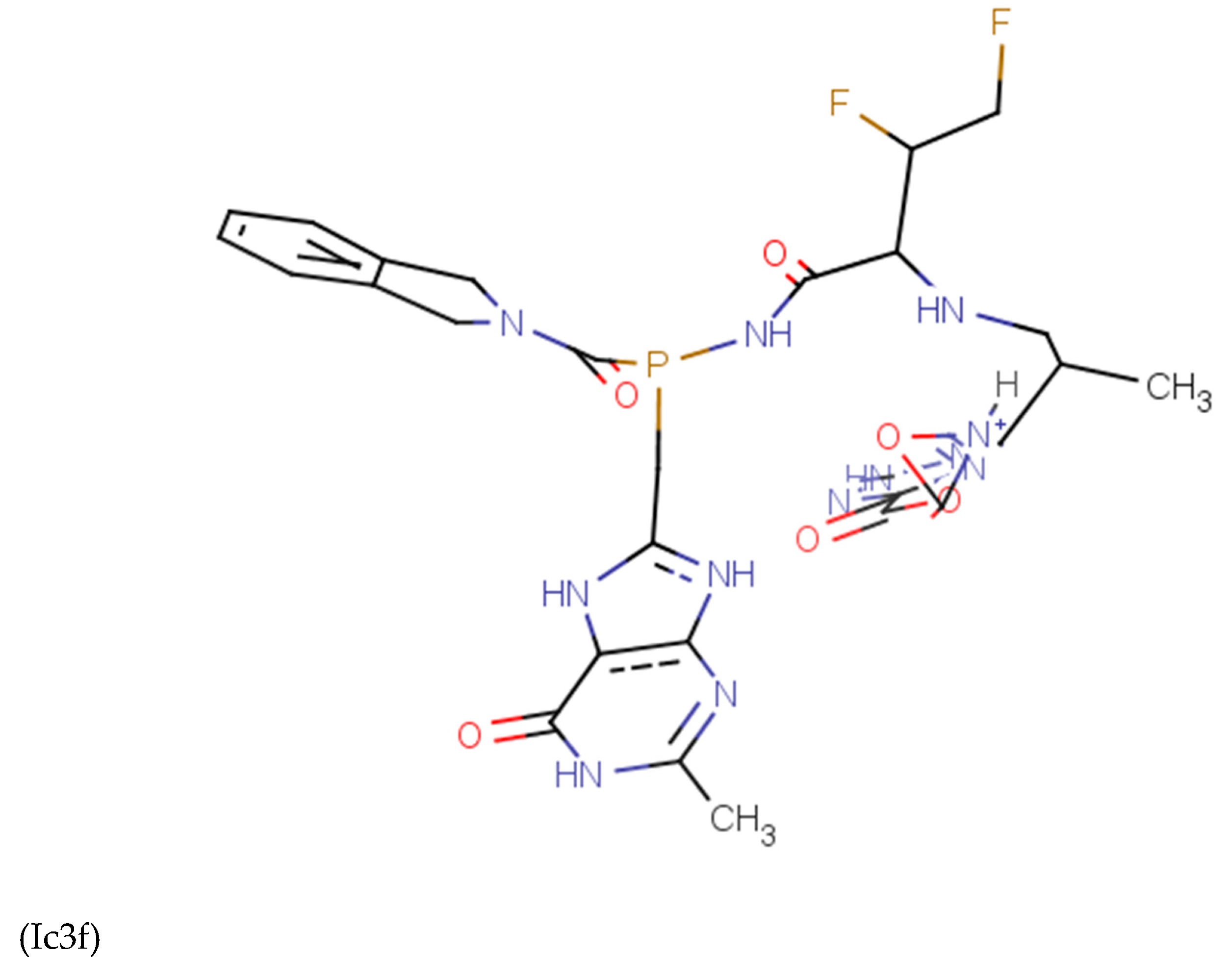
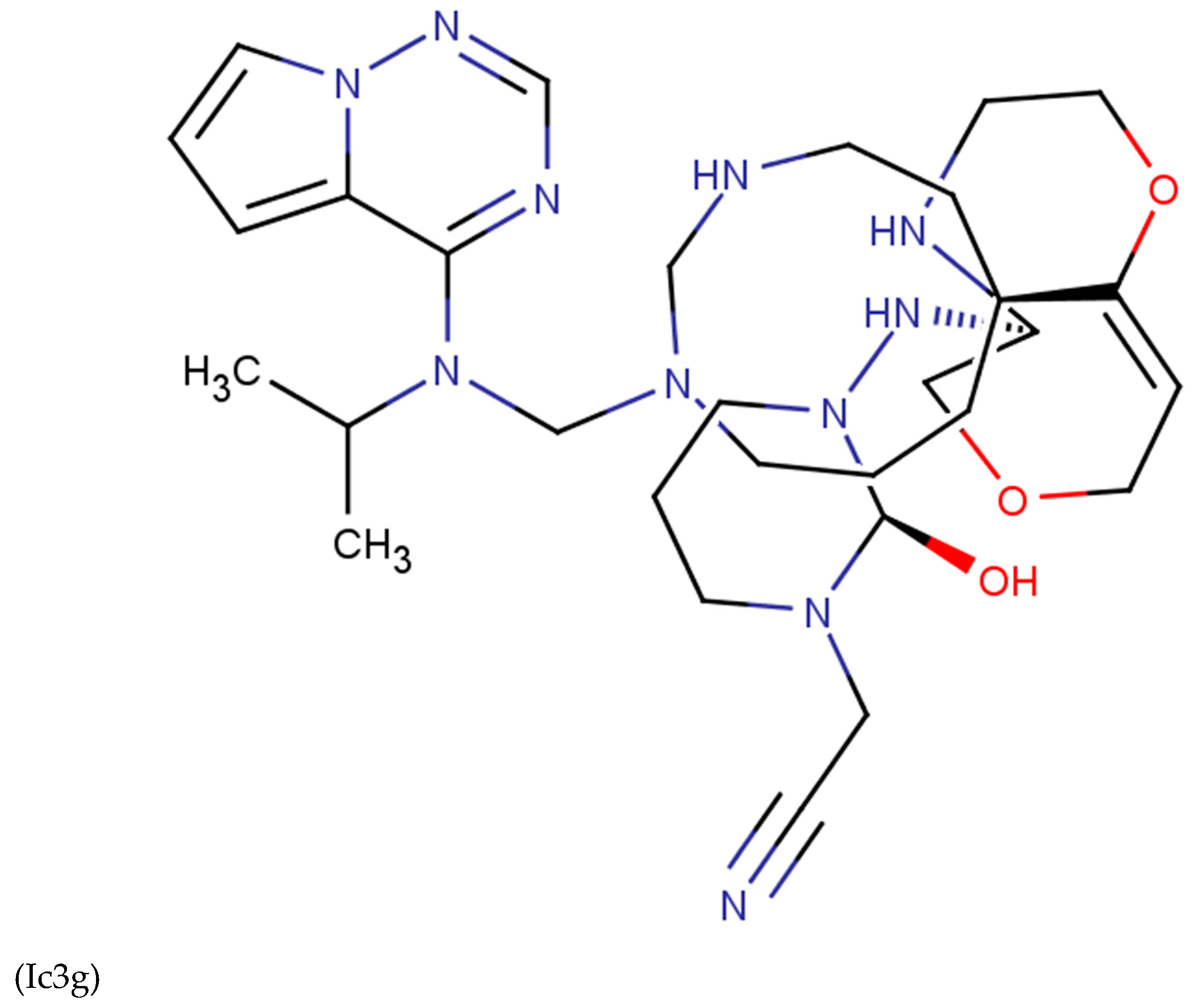
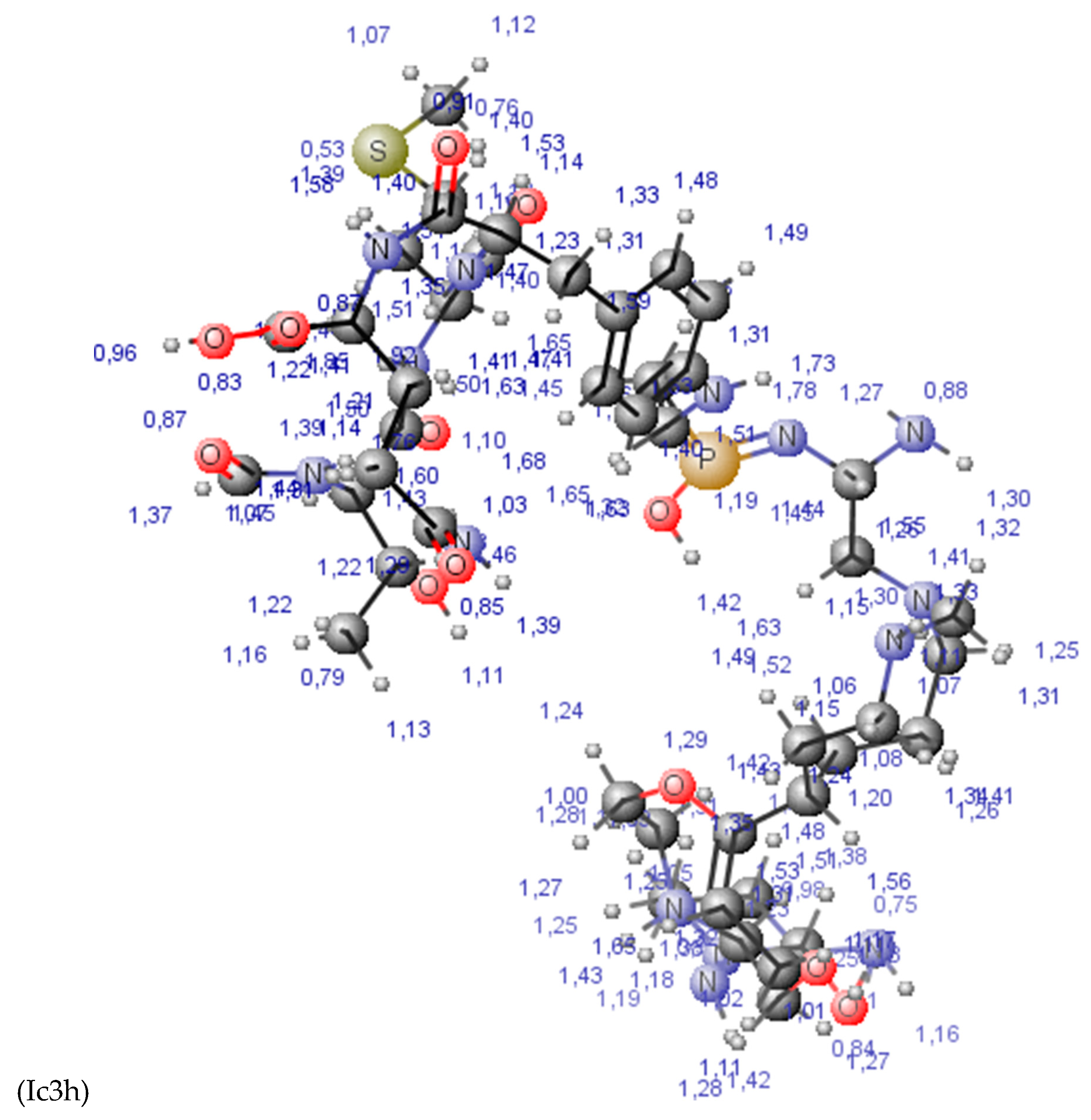
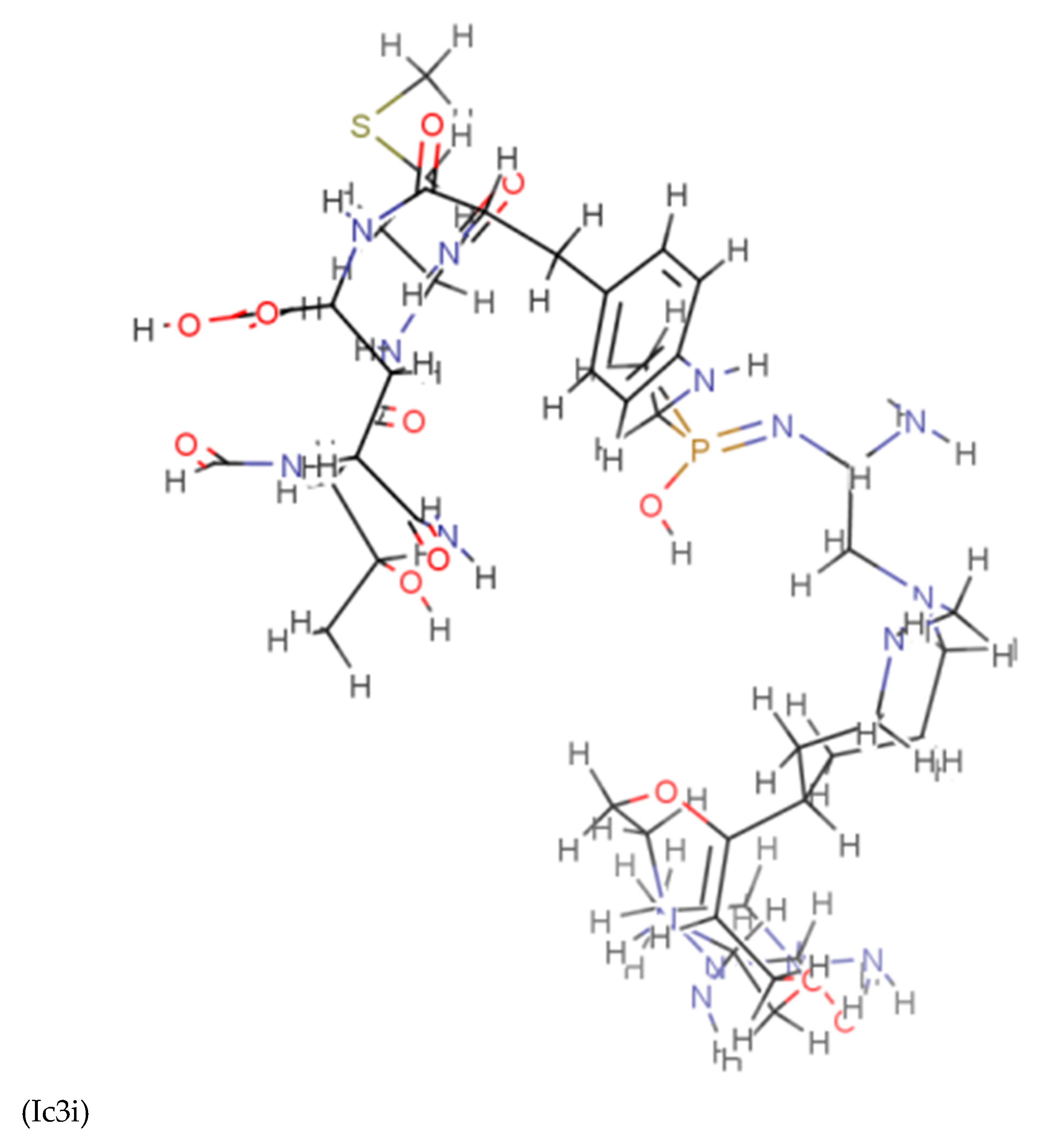



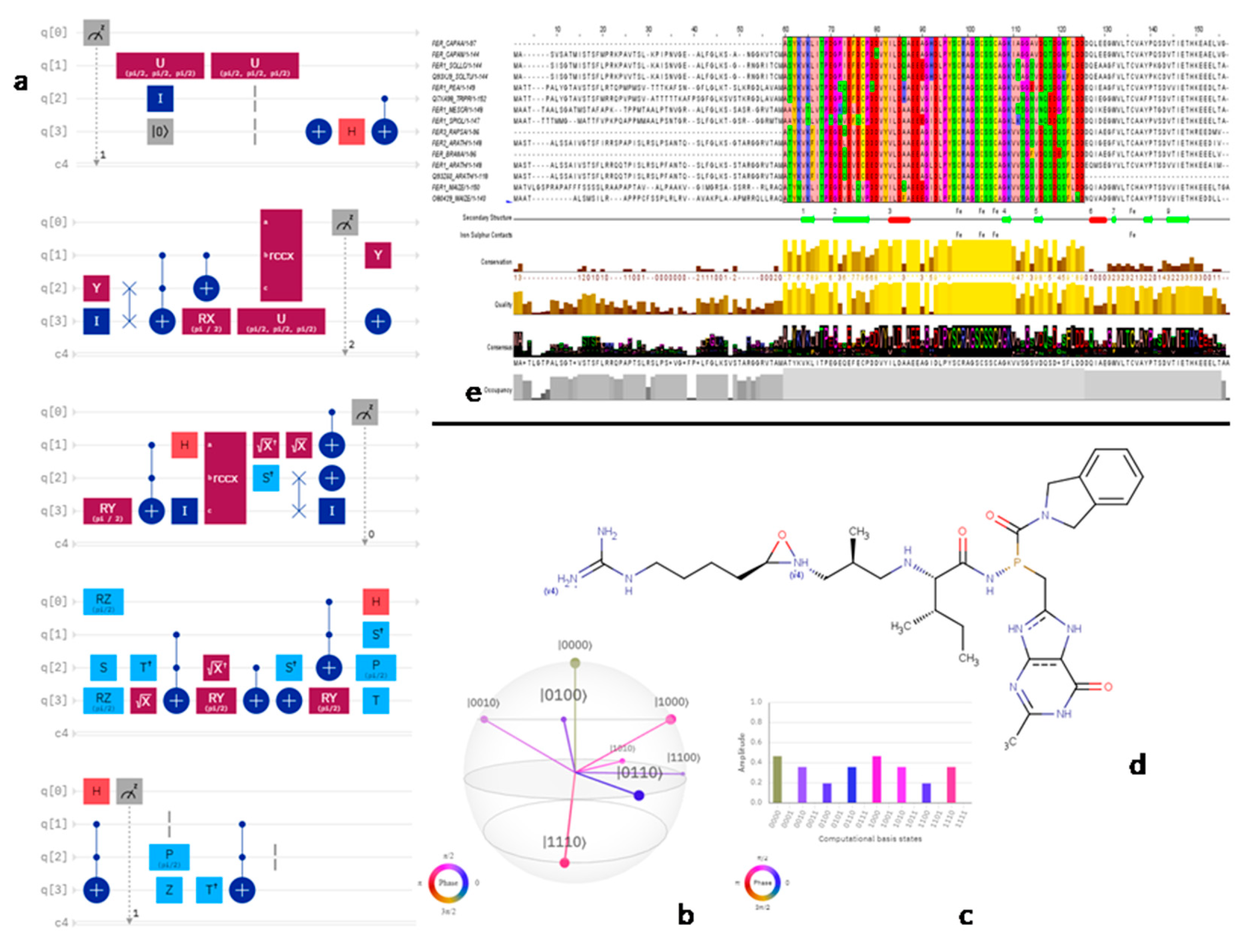
Discussions
 for SphericalHarmonicY[l, m, θ, ϕ] GegenbauerC[α μ ν^d, z^b] LegendreP[δ n, Q^4 d^4 r^10 (δ/(G α)) n^2 Ψ, G N g^(1/6^d^3) (ψ GoldenRatio)] LegendreQ[Log[ζ] Cos[μ], σ δ ArcSin[q ζ] ^g] LaguerreL[h, x] GegenbauerC[n, m, x] ChebyshevT[θ/ξ, α (ψ ι) Cos[EulerGamma] ] in a reverse order by translating Quantum Entropy Negativities from this unwanted symptomatology of the diseased organism which is ‘transferred’ via the entanglement and produced by the therapeutic ritual from the organism back to the remedy field, as it was into non-parameterized geometrical black-hole shaped structure data. [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85] Thus, the first part of these generalized entangled states (a) depends on the proper production process and is intimately connected to the ritual of ease, with a certain meaning, namely the remedy indicated. Both are matched by the Law of Similars. [35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86] There are multiple modeling equations (Supplementary Material METHODS AND MATERIALS (2), MasterEquations1-31) of entanglement present here: A) The new drug design itself is something like a magical presence of the past, at least in the case where ultra-high dilutions are used (note that in the case of low dilutions there might be a mix of entangled states and signalling processes via small molecule/ligand docking interactions) and directly propose a theoretical framework for turing analysis, in which these quantum Turing Machines are treated as phase transitions, in a technical and physical sense where this transition is the point where two distinct grand potentials are characterizing as units at different levels, such as molecules vs cells (organisms). In this case of the origin of life we put another way, where the transition is from an ensemble of entities at a lower level of organization (for example, small molecules) to an ensemble of higher-level entities (for example, small molecules-ligand complexes).
for SphericalHarmonicY[l, m, θ, ϕ] GegenbauerC[α μ ν^d, z^b] LegendreP[δ n, Q^4 d^4 r^10 (δ/(G α)) n^2 Ψ, G N g^(1/6^d^3) (ψ GoldenRatio)] LegendreQ[Log[ζ] Cos[μ], σ δ ArcSin[q ζ] ^g] LaguerreL[h, x] GegenbauerC[n, m, x] ChebyshevT[θ/ξ, α (ψ ι) Cos[EulerGamma] ] in a reverse order by translating Quantum Entropy Negativities from this unwanted symptomatology of the diseased organism which is ‘transferred’ via the entanglement and produced by the therapeutic ritual from the organism back to the remedy field, as it was into non-parameterized geometrical black-hole shaped structure data. [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85] Thus, the first part of these generalized entangled states (a) depends on the proper production process and is intimately connected to the ritual of ease, with a certain meaning, namely the remedy indicated. Both are matched by the Law of Similars. [35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86] There are multiple modeling equations (Supplementary Material METHODS AND MATERIALS (2), MasterEquations1-31) of entanglement present here: A) The new drug design itself is something like a magical presence of the past, at least in the case where ultra-high dilutions are used (note that in the case of low dilutions there might be a mix of entangled states and signalling processes via small molecule/ligand docking interactions) and directly propose a theoretical framework for turing analysis, in which these quantum Turing Machines are treated as phase transitions, in a technical and physical sense where this transition is the point where two distinct grand potentials are characterizing as units at different levels, such as molecules vs cells (organisms). In this case of the origin of life we put another way, where the transition is from an ensemble of entities at a lower level of organization (for example, small molecules) to an ensemble of higher-level entities (for example, small molecules-ligand complexes).Concluding Remarks
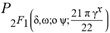 (x)
(x) 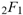 (2+δ,2+ω;2+ο ψ;(21 π)/22))
(2+δ,2+ω;2+ο ψ;(21 π)/22)) 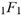 (a;b;x) Hypergeometric1F1Regularized[a5,∂2(ρ6 n4 (π r))/(∂y ∂x)]==1/(π Γ(a) Γ(2+ω))
(a;b;x) Hypergeometric1F1Regularized[a5,∂2(ρ6 n4 (π r))/(∂y ∂x)]==1/(π Γ(a) Γ(2+ω)) 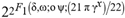 Hypergeometric1F1Regularized[a5,∂2(n4 π r ρ6)/(∂y ∂x)] (
Hypergeometric1F1Regularized[a5,∂2(n4 π r ρ6)/(∂y ∂x)] (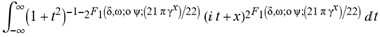 ) (
) (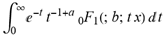 )
) 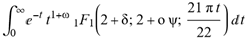 for (
for (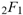 (δ,ω;ο ψ;(21 π γx)/22)∈ and
(δ,ω;ο ψ;(21 π γx)/22)∈ and 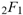 (δ,ω;ο ψ;(21 π γx)/22)>=0 and Re(a)>0 and 2+Re(ω)>0)(
(δ,ω;ο ψ;(21 π γx)/22)>=0 and Re(a)>0 and 2+Re(ω)>0)(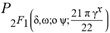 (x)
(x) 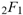 (2+δ,2+ω;2+ο ψ;(21 π)/22))
(2+δ,2+ω;2+ο ψ;(21 π)/22)) 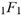 (a;b;x) Hypergeometric1F1Regularized[a5,∂2(ρ6 n4 (π r))/(∂y ∂x)]==1/(π Γ(a) Γ(2+ω)) Hypergeometric1F1Regularized[a5,∂2(n4 π r ρ6)/(∂y ∂x)] (
(a;b;x) Hypergeometric1F1Regularized[a5,∂2(ρ6 n4 (π r))/(∂y ∂x)]==1/(π Γ(a) Γ(2+ω)) Hypergeometric1F1Regularized[a5,∂2(n4 π r ρ6)/(∂y ∂x)] (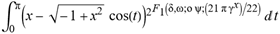 ) (
) (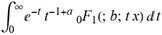 )
) 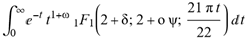 for (
for (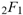 (δ,ω;ο ψ;(21 π γx)/22)∈ and
(δ,ω;ο ψ;(21 π γx)/22)∈ and 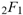 (δ,ω;ο ψ;(21 π γx)/22)>=0 and Re(a)>0 and 2+Re(ω)>0)
(δ,ω;ο ψ;(21 π γx)/22)>=0 and Re(a)>0 and 2+Re(ω)>0)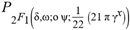 (x)
(x) 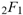 (2+δ,2+ω;2+ο ψ;21 π/22) (
(2+δ,2+ω;2+ο ψ;21 π/22) (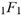 (a;b;x) Hypergeometric1F1Regularized[a5,∂2(ρ6 n4 (π r))/(∂y ∂x)])(
(a;b;x) Hypergeometric1F1Regularized[a5,∂2(ρ6 n4 (π r))/(∂y ∂x)])(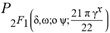 (x)
(x) 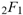 (2+δ,2+ω;2+ο ψ;(21 π)/22))
(2+δ,2+ω;2+ο ψ;(21 π)/22)) 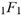 (a;b;x) Hypergeometric1F1Regularized[a5,∂2(ρ6 n4 (π r))/(∂y ∂x)]==1/xb/2 F1(2+δ;2+ω,0;2+ο ψ;(21 π)/22,z2) Hypergeometric1F1Regularized[a5,∂2(π r n4 ρ6)/(∂y ∂x)]
(a;b;x) Hypergeometric1F1Regularized[a5,∂2(ρ6 n4 (π r))/(∂y ∂x)]==1/xb/2 F1(2+δ;2+ω,0;2+ο ψ;(21 π)/22,z2) Hypergeometric1F1Regularized[a5,∂2(π r n4 ρ6)/(∂y ∂x)] 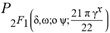 Ex/2
Ex/2 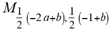 (x)(
(x)(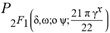 (x)
(x) 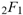 (2+δ,2+ω;2+ο ψ;(21 π)/22))
(2+δ,2+ω;2+ο ψ;(21 π)/22)) 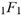 (a;b;x) Hypergeometric1F1Regularized[a5,∂2(ρ6 n4 (π r))/(∂y ∂x)]==1/Γ(-a+b) F1(2+δ;2+ω,0;2+ο ψ;(21 π)/22,z2) Γ(1-a) Γ(b) Hypergeometric1F1Regularized[a5,∂2(π r n4 ρ6)/(∂y ∂x)]
(a;b;x) Hypergeometric1F1Regularized[a5,∂2(ρ6 n4 (π r))/(∂y ∂x)]==1/Γ(-a+b) F1(2+δ;2+ω,0;2+ο ψ;(21 π)/22,z2) Γ(1-a) Γ(b) Hypergeometric1F1Regularized[a5,∂2(π r n4 ρ6)/(∂y ∂x)] 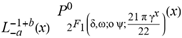 (
(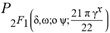 (x)
(x) 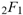 (2+δ,2+ω;2+ο ψ;(21 π)/22))
(2+δ,2+ω;2+ο ψ;(21 π)/22)) 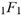 (a;b;x) Hypergeometric1F1Regularized[a5,∂2(ρ6 n4 (π r))/(∂y ∂x)]==1/Γ(-a+b) F1(2+δ;2+ω,0;2+ο ψ;(21 π)/22,z2) Γ(1-a) Γ(b) Hypergeometric1F1Regularized[a5,∂2(π r n4 ρ6)/(∂y ∂x)]
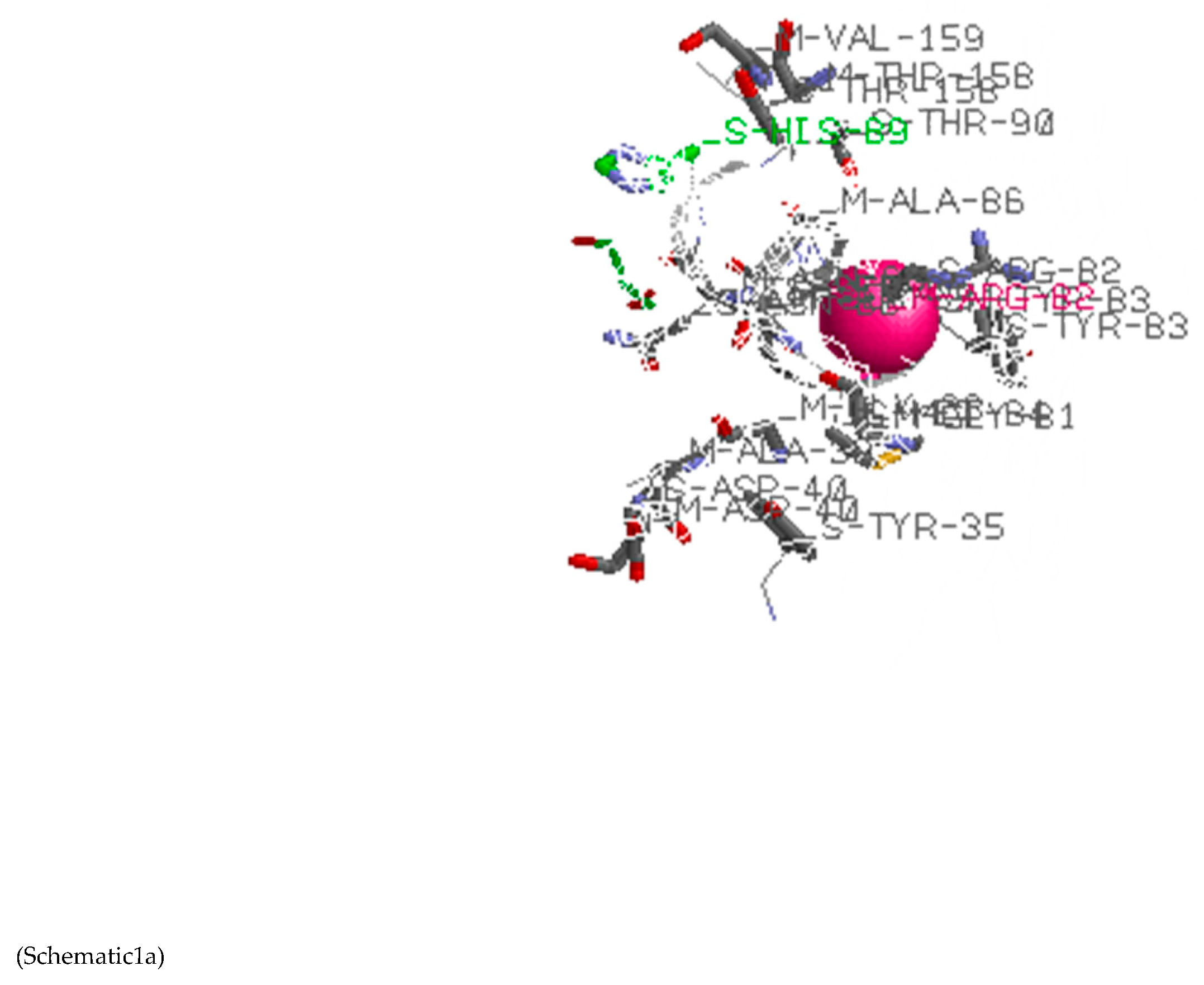
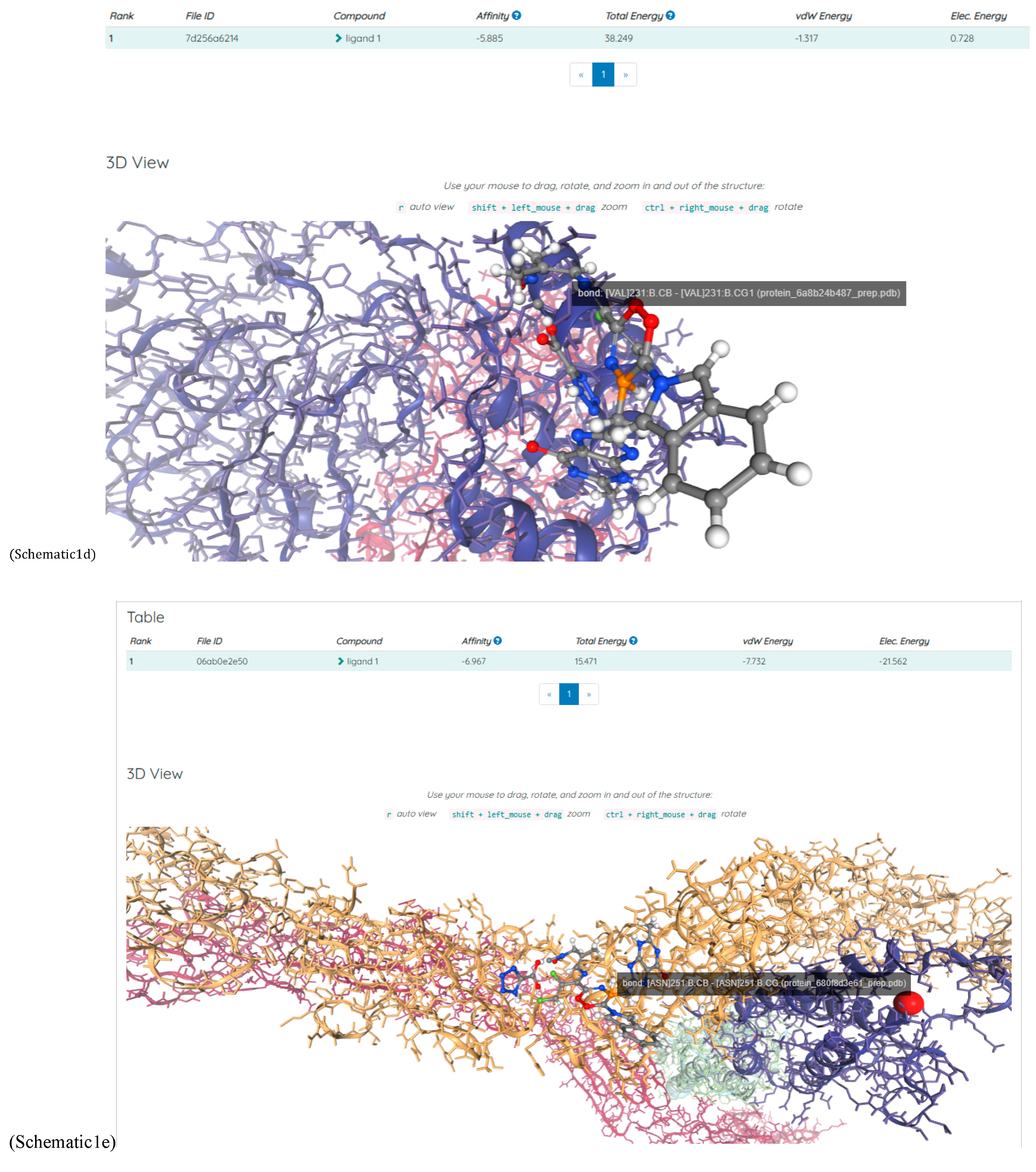
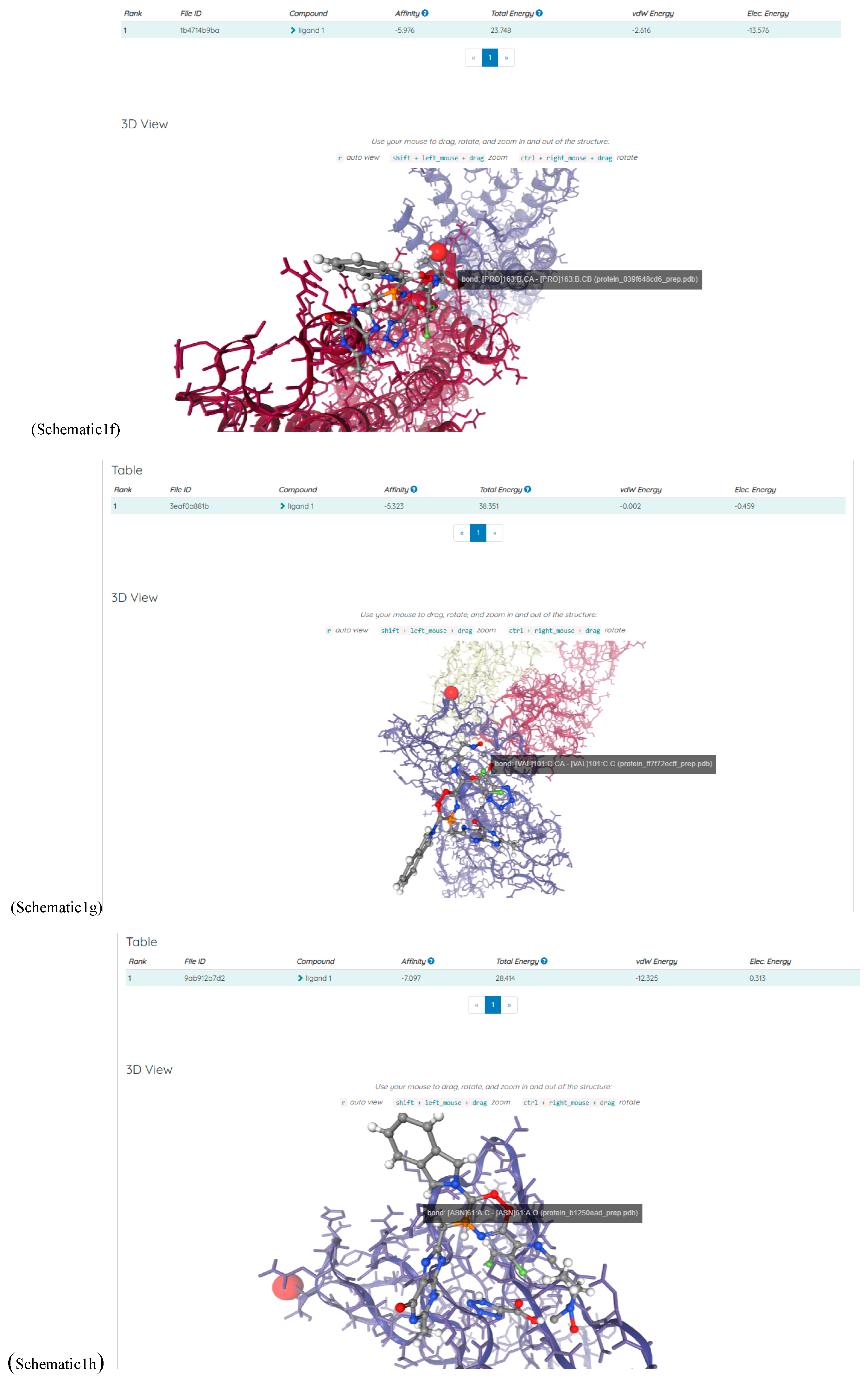
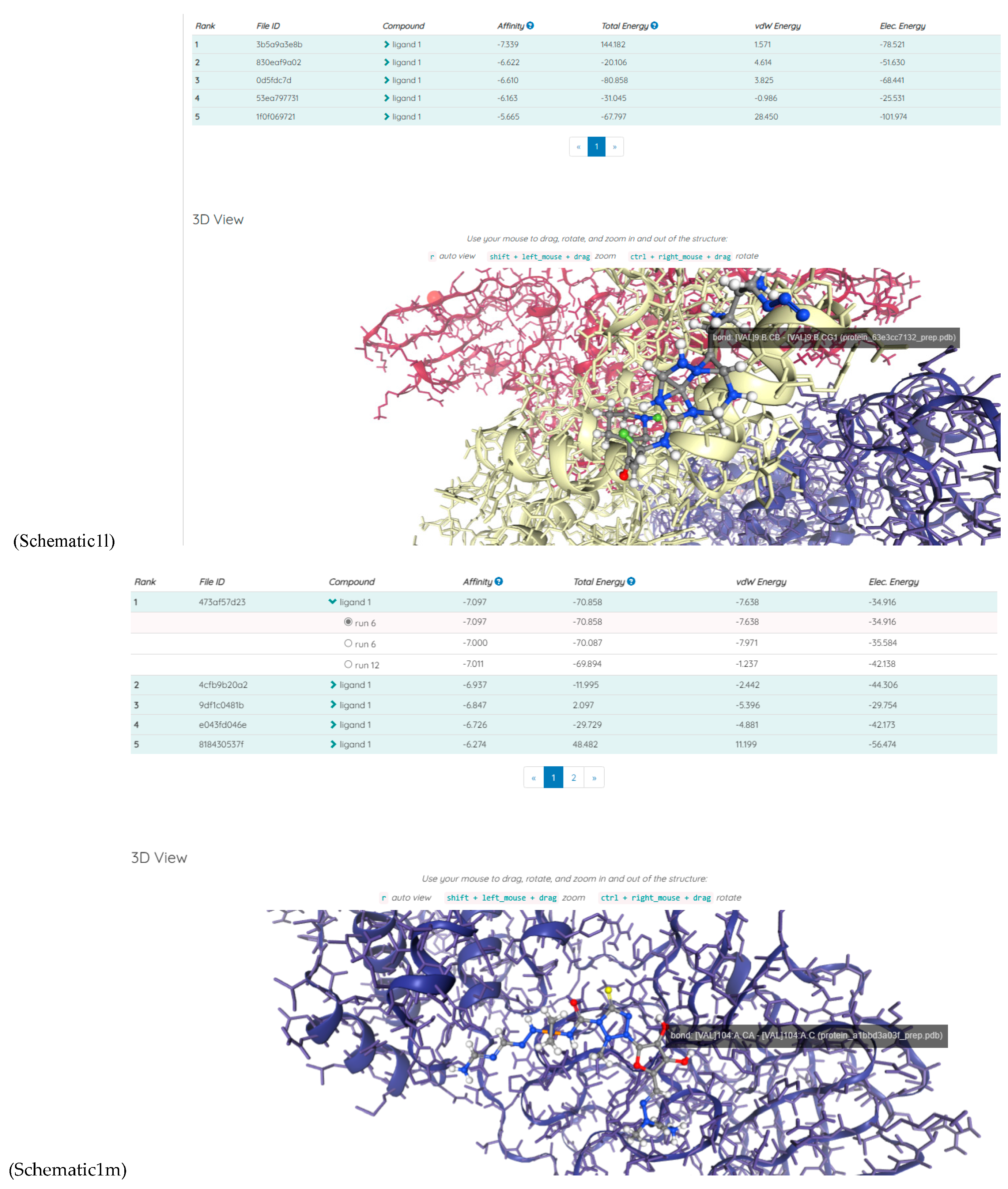
(a;b;x) Hypergeometric1F1Regularized[a5,∂2(ρ6 n4 (π r))/(∂y ∂x)]==1/Γ(-a+b) F1(2+δ;2+ω,0;2+ο ψ;(21 π)/22,z2) Γ(1-a) Γ(b) Hypergeometric1F1Regularized[a5,∂2(π r n4 ρ6)/(∂y ∂x)] 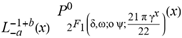 when Ψent = ZernikeR[Hypergeometric2F1 [ω^m, δ^μ, ψ ο, γ^n], m, r] LegendreP[Hypergeometric2F1[ω, δ, ψ ο, (21/22) Pi γ^x], x] r^m Cos[(Pi (-m + Hypergeometric2F1[δ^μ, ω^m, ο ψ, γ^n]))/2] JacobiP[(-m + Hypergeometric2F1[δ^μ, ω^m, ο ψ, γ^n])/2, m, 0, 1 - 2 r^2] LegendreP[Hypergeometric2F1[δ, ω, ο ψ, (21 Pi γ^x)/22], x] LegendreP[Floor[-Arg[(-21 Pi)/22 + (21 Pi γ^x)/22] /(2 Pi)] Gamma[ο ψ] Hypergeometric2F1Regularized[δ, ω, ο ψ, (21 Pi)/22] - E^((2 I) Pi (δ - ο ψ + ω)) Floor[-Arg[(-21 Pi)/22 + (21 Pi γ^x)/22] /(2 Pi)] Gamma[ο ψ] Hypergeometric2F1Regularized[δ, ω, ο ψ, (21 Pi)/22] + Floor[(Pi + Arg[(-21 Pi)/22 + (21 Pi γ^x)/22])/(2 Pi)] Gamma[ο ψ] Hypergeometric2F1Regularized[δ, ω, ο ψ, (21 Pi)/22] - E^((2 I) Pi (δ - ο ψ + ω)) Floor[(Pi + Arg[(-21 Pi)/22 + (21 Pi γ^x)/22])/(2 Pi)] Gamma[ο ψ] Hypergeometric2F1Regularized[δ, ω, ο ψ, (21 Pi)/22] + (I 2^(ο ψ) 11^(-1 + ο ψ) 21^(1 - ο ψ) E^(I Pi (δ - ο ψ + ω)) Pi^(3 - ο ψ) Csc[Pi ο ψ] Floor[-Arg[(-21 Pi)/22 + (21 Pi γ^x)/22] /(2 Pi)] Gamma[ο ψ] Hypergeometric2F1Regularized[1 + δ - ο ψ, 1 - ο ψ + ω, 2 - ο ψ, (21 Pi)/22])/(Gamma[δ] Gamma[-δ + ο ψ] Gamma[ο ψ - ω] Gamma[ω]) + (I 2^(ο ψ) 11^(-1 + ο ψ) 21^(1 - ο ψ) E^(I Pi (δ - ο ψ + ω)) Pi^(3 - ο ψ) Csc[Pi ο ψ] Floor[(Pi + Arg[(-21 Pi)/22 + (21 Pi γ^x)/22])/(2 Pi)] Gamma[ο ψ] Hypergeometric2F1Regularized[1 + δ - ο ψ, 1 - ο ψ + ω, 2 - ο ψ, (21 Pi)/22])/(Gamma[δ] Gamma[-δ + ο ψ] Gamma[ο ψ - ω] Gamma[ω]) + (Hypergeometric2F1[δ, ω, ο ψ, (21 Pi)/22] + (21 Pi x δ ω Hypergeometric2F1[1 + δ, 1 + ω, 1 + ο ψ, (21 Pi)/22] Log[γ])/(22 ο ψ) + ((21 Pi δ ω Hypergeometric2F1[1 + δ, 1 + ω, 1 + ο ψ, (21 Pi)/22] Log[γ] ^2)/(44 ο ψ) + (441 Pi^2 δ (1 + δ) ω (1 + ω) Hypergeometric2F1[2 + δ, 2 + ω, 2 + ο ψ, (21 Pi)/22] Log[γ] ^2)/(968 ο ψ (1 + ο ψ))) x^2 + ((7 Pi δ ω Hypergeometric2F1[1 + δ, 1 + ω, 1 + ο ψ, (21 Pi)/22] Log[γ] ^3)/(44 ο ψ) + (441 Pi^2 δ (1 + δ) ω (1 + ω) Hypergeometric2F1[2 + δ, 2 + ω, 2 + ο ψ, (21 Pi)/22] Log[γ] ^3)/(968 ο ψ (1 + ο ψ)) + (3087 Pi^3 δ (1 + δ) (2 + δ) ω (1 + ω) (2 + ω) Hypergeometric2F1[3 + δ, 3 + ω, 3 + ο ψ, (21 Pi)/22] Log[γ] ^3)/(21296 ο ψ (1 + ο ψ) (2 + ο ψ))) x^3 + ((7 Pi δ ω Hypergeometric2F1[1 + δ, 1 + ω, 1 + ο ψ, (21 Pi)/22] Log[γ] ^4)/(176 ο ψ) + (1029 Pi^2 δ (1 + δ) ω (1 + ω) Hypergeometric2F1[2 + δ, 2 + ω, 2 + ο ψ, (21 Pi)/22] Log[γ] ^4)/(3872 ο ψ (1 + ο ψ)) + (9261 Pi^3 δ (1 + δ) (2 + δ) ω (1 + ω) (2 + ω) Hypergeometric2F1[3 + δ, 3 + ω, 3 + ο ψ, (21 Pi)/22] Log[γ] ^4)/(42592 ο ψ (1 + ο ψ) (2 + ο ψ)) + (64827 Pi^4 δ (1 + δ) (2 + δ) (3 + δ) ω (1 + ω) (2 + ω) (3 + ω) Hypergeometric2F1[4 + δ, 4 + ω, 4 + ο ψ, (21 Pi)/22] Log[γ] ^4)/(1874048 ο ψ (1 + ο ψ) (2 + ο ψ) (3 + ο ψ))) x^4 + ((7 Pi δ ω Hypergeometric2F1[1 + δ, 1 + ω, 1 + ο ψ, (21 Pi)/22] Log[γ] ^5)/(880 ο ψ) + (441 Pi^2 δ (1 + δ) ω (1 + ω) Hypergeometric2F1[2 + δ, 2 + ω, 2 + ο ψ, (21 Pi)/22] Log[γ] ^5)/(3872 ο ψ (1 + ο ψ)) + (15435 Pi^3 δ (1 + δ) (2 + δ) ω (1 + ω) (2 + ω) Hypergeometric2F1[3 + δ, 3 + ω, 3 + ο ψ, (21 Pi)/22] Log[γ] ^5)/(85184 ο ψ (1 + ο ψ) (2 + ο ψ)) + (64827 Pi^4 δ (1 + δ) (2 + δ) (3 + δ) ω (1 + ω) (2 + ω) (3 + ω) Hypergeometric2F1[4 + δ, 4 + ω, 4 + ο ψ, (21 Pi)/22] Log[γ] ^5)/(937024 ο ψ (1 + ο ψ) (2 + ο ψ) (3 + ο ψ)) + (1361367 Pi^5 δ (1 + δ) (2 + δ) (3 + δ) (4 + δ) ω (1 + ω) (2 + ω) (3 + ω) (4 + ω) Hypergeometric2F1[5 + δ, 5 + ω, 5 + ο ψ, (21 Pi)/22] Log[γ] ^5)/(206145280 ο ψ (1 + ο ψ) (2 + ο ψ) (3 + ο ψ) (4 + ο ψ))) x^5 + O[x] ^6) - (2 I) E^(I Pi (δ - ο ψ + ω)) Csc[Pi ο ψ] Floor[-Arg[(-21 Pi)/22 + (21 Pi γ^x)/22] /(2 Pi)] Gamma[ο ψ] Hypergeometric2F1Regularized[δ, ω, ο ψ, (21 Pi)/22] Sin[Pi (δ - ο ψ)] Sin[Pi (-(ο ψ) + ω)] - (2 I) E^(I Pi (δ - ο ψ + ω)) Csc[Pi ο ψ] Floor[(Pi + Arg[(-21 Pi)/22 + (21 Pi γ^x)/22])/(2 Pi)] Gamma[ο ψ] Hypergeometric2F1Regularized[δ, ω, ο ψ, (21 Pi)/22] Sin[Pi (δ - ο ψ)] Sin[Pi (-(ο ψ) + ω)], x + O[x] ^6] ZernikeR[Hypergeometric2F1[δ^μ, ω^m, ο ψ, γ^n], m, r] leaving the coordinators/observers in two quite separate and two-way entangled relationship associated to drug homeopath remedy drug design, and placebo oriented structures. [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133] Like Bloom filters, Euclid Spaced-indexes involved here offer rapid querying and significant memory efficiency in Quantum Homeopathy Solutions, requiring only two invocations, and a time of O(lnN)) to set up the input state, and solve the rotation and translation/transformation problems in the 3D Euclidean space in polynomial time. [23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134]. [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135] It is conceivable that this inherently probabilistic nature of quantum computers and novel data input modalities offered by quantum information, such as angle and phase encoding, could lead us to the development of similarly useful quantum data structures and abstractions against AT1R regime. [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136] This Quantum Homeopathy Solution represents one example [53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137] and a concerted effort towards developing an open quantum data structure library which may be useful for improving our understanding of the types of quantum approaches that may admit practical advantages over the long term. We have deliberately left consciousness out here to show that by only focusing on the technical aspects of a homeopathy translation in terms of generalized entanglement is already possible. [43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138] This does not mean, however, that the theoretical translation offered here is the only one possible; indeed other ways using similar considerations have been offered already [20] in these two-way Quantum Homeopathy Entanglement Solutions, If I restrict the input fs to a class of ChebyshevU, HermiteH, HeunT, LaguerreL, HeunT, HeunTPrime, SphericalHarmonicY, HeunB, HeunD, SphericalBesselJ, LegendreP, LegendreQ, HeunC, LegendreQ, HeunG, LaguerreL, SpheroidalPS, SpheroidalEigenvalue, Hypergeometric1F1, WhittakerM, CoulombH2, AiryAi, CoulombF, CoulombH1, TemplateBox [{l, eta, r}, CoulompH1], Hypergeometric2F1, ΤhreeJSymbol, SixJSymbol, GegenbauerC, ChebyshevT, and GegenbauerC functions of WhittakerW [k, m, z] Hypergeometric0F1[a, z] Hypergeometric0F1[a, z] GegenbauerC[n, m, x] ChebyshevT[(θ/ξ) α x, I Exp[y] Cos[EulerGamma] ] LaguerreL[n, a, x] LaguerreL[n, x] GegenbauerC[n, m, x] ChebyshevT[n, x] HypergeometricU[Q^Cos[x], x c^4 (Pi r), ArcSin[r] ^2] LegendreP[δ n, Q^D, d^4 r^10 (δ/(G Ψ)) n^8 Ψ, G N g^(1/6^d^7) (Ψ GoldenRatio)] LegendreQ[Log[ζ d] 2 Ψ^C Cos[μ], σ δ ArcSin[q ζ] ^Ψ] LaguerreL[E, x] whose oracles have size less than p(lnN) numerous structures emerge that are characterized by readily discernible (even if not necessarily easily described formally) order and complexity where p is a fixed polynomial unknown to the solver of the problem, then the restricted problem requires exponential time in the classical case and only polynomial time in the quantum case of four maximally entangled states (compared to eight for three entangled objects) so these Equations (Cluster of Eqs. I-DXCVII), ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)), (Eqs1-325) represent just two of these states [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140]. That is because for any given N this condition does not, from the solver's point of view, exclude any function f: ZN -- Z2, so by the same argument that I used for the general problem, there cannot be a less-than exponential classical solution even for the restricted problem that is now disentangled, like provers on placebo which should not evince the symptoms shown by those on the remedy. Consequently in Equations (Eqs1-325),((Iconics1-4), (Eqs1-400), and (Schematics1a,1b,1c,1d,1e,1f,1g,1h,1i,1j,1k,1l,1m), Supplementary Material METHODS AND MATERIALS (1), (2)) the ∂(DensityMatrix Tr[ψ,{2}])/∂A logρ(ψ) log(A hν n π Q ΒG δ μ ρ σ sin(ω)) logG(z)+0+(c8 π2 r2 δ2 θ20+1/4
when Ψent = ZernikeR[Hypergeometric2F1 [ω^m, δ^μ, ψ ο, γ^n], m, r] LegendreP[Hypergeometric2F1[ω, δ, ψ ο, (21/22) Pi γ^x], x] r^m Cos[(Pi (-m + Hypergeometric2F1[δ^μ, ω^m, ο ψ, γ^n]))/2] JacobiP[(-m + Hypergeometric2F1[δ^μ, ω^m, ο ψ, γ^n])/2, m, 0, 1 - 2 r^2] LegendreP[Hypergeometric2F1[δ, ω, ο ψ, (21 Pi γ^x)/22], x] LegendreP[Floor[-Arg[(-21 Pi)/22 + (21 Pi γ^x)/22] /(2 Pi)] Gamma[ο ψ] Hypergeometric2F1Regularized[δ, ω, ο ψ, (21 Pi)/22] - E^((2 I) Pi (δ - ο ψ + ω)) Floor[-Arg[(-21 Pi)/22 + (21 Pi γ^x)/22] /(2 Pi)] Gamma[ο ψ] Hypergeometric2F1Regularized[δ, ω, ο ψ, (21 Pi)/22] + Floor[(Pi + Arg[(-21 Pi)/22 + (21 Pi γ^x)/22])/(2 Pi)] Gamma[ο ψ] Hypergeometric2F1Regularized[δ, ω, ο ψ, (21 Pi)/22] - E^((2 I) Pi (δ - ο ψ + ω)) Floor[(Pi + Arg[(-21 Pi)/22 + (21 Pi γ^x)/22])/(2 Pi)] Gamma[ο ψ] Hypergeometric2F1Regularized[δ, ω, ο ψ, (21 Pi)/22] + (I 2^(ο ψ) 11^(-1 + ο ψ) 21^(1 - ο ψ) E^(I Pi (δ - ο ψ + ω)) Pi^(3 - ο ψ) Csc[Pi ο ψ] Floor[-Arg[(-21 Pi)/22 + (21 Pi γ^x)/22] /(2 Pi)] Gamma[ο ψ] Hypergeometric2F1Regularized[1 + δ - ο ψ, 1 - ο ψ + ω, 2 - ο ψ, (21 Pi)/22])/(Gamma[δ] Gamma[-δ + ο ψ] Gamma[ο ψ - ω] Gamma[ω]) + (I 2^(ο ψ) 11^(-1 + ο ψ) 21^(1 - ο ψ) E^(I Pi (δ - ο ψ + ω)) Pi^(3 - ο ψ) Csc[Pi ο ψ] Floor[(Pi + Arg[(-21 Pi)/22 + (21 Pi γ^x)/22])/(2 Pi)] Gamma[ο ψ] Hypergeometric2F1Regularized[1 + δ - ο ψ, 1 - ο ψ + ω, 2 - ο ψ, (21 Pi)/22])/(Gamma[δ] Gamma[-δ + ο ψ] Gamma[ο ψ - ω] Gamma[ω]) + (Hypergeometric2F1[δ, ω, ο ψ, (21 Pi)/22] + (21 Pi x δ ω Hypergeometric2F1[1 + δ, 1 + ω, 1 + ο ψ, (21 Pi)/22] Log[γ])/(22 ο ψ) + ((21 Pi δ ω Hypergeometric2F1[1 + δ, 1 + ω, 1 + ο ψ, (21 Pi)/22] Log[γ] ^2)/(44 ο ψ) + (441 Pi^2 δ (1 + δ) ω (1 + ω) Hypergeometric2F1[2 + δ, 2 + ω, 2 + ο ψ, (21 Pi)/22] Log[γ] ^2)/(968 ο ψ (1 + ο ψ))) x^2 + ((7 Pi δ ω Hypergeometric2F1[1 + δ, 1 + ω, 1 + ο ψ, (21 Pi)/22] Log[γ] ^3)/(44 ο ψ) + (441 Pi^2 δ (1 + δ) ω (1 + ω) Hypergeometric2F1[2 + δ, 2 + ω, 2 + ο ψ, (21 Pi)/22] Log[γ] ^3)/(968 ο ψ (1 + ο ψ)) + (3087 Pi^3 δ (1 + δ) (2 + δ) ω (1 + ω) (2 + ω) Hypergeometric2F1[3 + δ, 3 + ω, 3 + ο ψ, (21 Pi)/22] Log[γ] ^3)/(21296 ο ψ (1 + ο ψ) (2 + ο ψ))) x^3 + ((7 Pi δ ω Hypergeometric2F1[1 + δ, 1 + ω, 1 + ο ψ, (21 Pi)/22] Log[γ] ^4)/(176 ο ψ) + (1029 Pi^2 δ (1 + δ) ω (1 + ω) Hypergeometric2F1[2 + δ, 2 + ω, 2 + ο ψ, (21 Pi)/22] Log[γ] ^4)/(3872 ο ψ (1 + ο ψ)) + (9261 Pi^3 δ (1 + δ) (2 + δ) ω (1 + ω) (2 + ω) Hypergeometric2F1[3 + δ, 3 + ω, 3 + ο ψ, (21 Pi)/22] Log[γ] ^4)/(42592 ο ψ (1 + ο ψ) (2 + ο ψ)) + (64827 Pi^4 δ (1 + δ) (2 + δ) (3 + δ) ω (1 + ω) (2 + ω) (3 + ω) Hypergeometric2F1[4 + δ, 4 + ω, 4 + ο ψ, (21 Pi)/22] Log[γ] ^4)/(1874048 ο ψ (1 + ο ψ) (2 + ο ψ) (3 + ο ψ))) x^4 + ((7 Pi δ ω Hypergeometric2F1[1 + δ, 1 + ω, 1 + ο ψ, (21 Pi)/22] Log[γ] ^5)/(880 ο ψ) + (441 Pi^2 δ (1 + δ) ω (1 + ω) Hypergeometric2F1[2 + δ, 2 + ω, 2 + ο ψ, (21 Pi)/22] Log[γ] ^5)/(3872 ο ψ (1 + ο ψ)) + (15435 Pi^3 δ (1 + δ) (2 + δ) ω (1 + ω) (2 + ω) Hypergeometric2F1[3 + δ, 3 + ω, 3 + ο ψ, (21 Pi)/22] Log[γ] ^5)/(85184 ο ψ (1 + ο ψ) (2 + ο ψ)) + (64827 Pi^4 δ (1 + δ) (2 + δ) (3 + δ) ω (1 + ω) (2 + ω) (3 + ω) Hypergeometric2F1[4 + δ, 4 + ω, 4 + ο ψ, (21 Pi)/22] Log[γ] ^5)/(937024 ο ψ (1 + ο ψ) (2 + ο ψ) (3 + ο ψ)) + (1361367 Pi^5 δ (1 + δ) (2 + δ) (3 + δ) (4 + δ) ω (1 + ω) (2 + ω) (3 + ω) (4 + ω) Hypergeometric2F1[5 + δ, 5 + ω, 5 + ο ψ, (21 Pi)/22] Log[γ] ^5)/(206145280 ο ψ (1 + ο ψ) (2 + ο ψ) (3 + ο ψ) (4 + ο ψ))) x^5 + O[x] ^6) - (2 I) E^(I Pi (δ - ο ψ + ω)) Csc[Pi ο ψ] Floor[-Arg[(-21 Pi)/22 + (21 Pi γ^x)/22] /(2 Pi)] Gamma[ο ψ] Hypergeometric2F1Regularized[δ, ω, ο ψ, (21 Pi)/22] Sin[Pi (δ - ο ψ)] Sin[Pi (-(ο ψ) + ω)] - (2 I) E^(I Pi (δ - ο ψ + ω)) Csc[Pi ο ψ] Floor[(Pi + Arg[(-21 Pi)/22 + (21 Pi γ^x)/22])/(2 Pi)] Gamma[ο ψ] Hypergeometric2F1Regularized[δ, ω, ο ψ, (21 Pi)/22] Sin[Pi (δ - ο ψ)] Sin[Pi (-(ο ψ) + ω)], x + O[x] ^6] ZernikeR[Hypergeometric2F1[δ^μ, ω^m, ο ψ, γ^n], m, r] leaving the coordinators/observers in two quite separate and two-way entangled relationship associated to drug homeopath remedy drug design, and placebo oriented structures. [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133] Like Bloom filters, Euclid Spaced-indexes involved here offer rapid querying and significant memory efficiency in Quantum Homeopathy Solutions, requiring only two invocations, and a time of O(lnN)) to set up the input state, and solve the rotation and translation/transformation problems in the 3D Euclidean space in polynomial time. [23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134]. [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135] It is conceivable that this inherently probabilistic nature of quantum computers and novel data input modalities offered by quantum information, such as angle and phase encoding, could lead us to the development of similarly useful quantum data structures and abstractions against AT1R regime. [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136] This Quantum Homeopathy Solution represents one example [53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137] and a concerted effort towards developing an open quantum data structure library which may be useful for improving our understanding of the types of quantum approaches that may admit practical advantages over the long term. We have deliberately left consciousness out here to show that by only focusing on the technical aspects of a homeopathy translation in terms of generalized entanglement is already possible. [43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138] This does not mean, however, that the theoretical translation offered here is the only one possible; indeed other ways using similar considerations have been offered already [20] in these two-way Quantum Homeopathy Entanglement Solutions, If I restrict the input fs to a class of ChebyshevU, HermiteH, HeunT, LaguerreL, HeunT, HeunTPrime, SphericalHarmonicY, HeunB, HeunD, SphericalBesselJ, LegendreP, LegendreQ, HeunC, LegendreQ, HeunG, LaguerreL, SpheroidalPS, SpheroidalEigenvalue, Hypergeometric1F1, WhittakerM, CoulombH2, AiryAi, CoulombF, CoulombH1, TemplateBox [{l, eta, r}, CoulompH1], Hypergeometric2F1, ΤhreeJSymbol, SixJSymbol, GegenbauerC, ChebyshevT, and GegenbauerC functions of WhittakerW [k, m, z] Hypergeometric0F1[a, z] Hypergeometric0F1[a, z] GegenbauerC[n, m, x] ChebyshevT[(θ/ξ) α x, I Exp[y] Cos[EulerGamma] ] LaguerreL[n, a, x] LaguerreL[n, x] GegenbauerC[n, m, x] ChebyshevT[n, x] HypergeometricU[Q^Cos[x], x c^4 (Pi r), ArcSin[r] ^2] LegendreP[δ n, Q^D, d^4 r^10 (δ/(G Ψ)) n^8 Ψ, G N g^(1/6^d^7) (Ψ GoldenRatio)] LegendreQ[Log[ζ d] 2 Ψ^C Cos[μ], σ δ ArcSin[q ζ] ^Ψ] LaguerreL[E, x] whose oracles have size less than p(lnN) numerous structures emerge that are characterized by readily discernible (even if not necessarily easily described formally) order and complexity where p is a fixed polynomial unknown to the solver of the problem, then the restricted problem requires exponential time in the classical case and only polynomial time in the quantum case of four maximally entangled states (compared to eight for three entangled objects) so these Equations (Cluster of Eqs. I-DXCVII), ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)), (Eqs1-325) represent just two of these states [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140]. That is because for any given N this condition does not, from the solver's point of view, exclude any function f: ZN -- Z2, so by the same argument that I used for the general problem, there cannot be a less-than exponential classical solution even for the restricted problem that is now disentangled, like provers on placebo which should not evince the symptoms shown by those on the remedy. Consequently in Equations (Eqs1-325),((Iconics1-4), (Eqs1-400), and (Schematics1a,1b,1c,1d,1e,1f,1g,1h,1i,1j,1k,1l,1m), Supplementary Material METHODS AND MATERIALS (1), (2)) the ∂(DensityMatrix Tr[ψ,{2}])/∂A logρ(ψ) log(A hν n π Q ΒG δ μ ρ σ sin(ω)) logG(z)+0+(c8 π2 r2 δ2 θ20+1/4 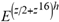 sin−1(r)) ≈ logG(z) ∂(DensityMatrix Tr[ψ,{2}])/∂A logρ(ψ) log(3.14159 A δ μ n ρ Q σ ΒG hν sin(ω))+9.8696 c8 δ2 θ20 r2+0.25 sin−1(r)
sin−1(r)) ≈ logG(z) ∂(DensityMatrix Tr[ψ,{2}])/∂A logρ(ψ) log(3.14159 A δ μ n ρ Q σ ΒG hν sin(ω))+9.8696 c8 δ2 θ20 r2+0.25 sin−1(r) 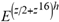 for the LegendreP[1 + I/2 (E^(-I ω) - E^(I ω)) 〈ΔSPl〉 G h^ν n Pi Q δ μ σ, x] /(1 + I (E^(-I ω) - E^(I ω)) G h^ν n Pi Q δ μ σ) - LegendreP[15 k N - I 2^(-1 - x) D (E^(-I c) - E^(I c)) (I (E^(-I ω) - E^(I ω)))^x h n Pi Q U δ Δ^ν μ ρ^4 σ, x] / 〈ΔSRx〉(1 + I (E^(-I ω) - E^(I ω)) G h^ν n Pi Q δ μ σ) function, either 〈ΔSPl〉 = 0 or at least 〈ΔSPl〉 and 〈ΔSRx〉 can now be equated with each other. In other words, this Quantum Homeopathy act provides information that collapse the remedy/placebo into an entangled state wave function, leaving two completely distinguishable sets of results: one set for provers on the remedy, and one set for those on placebo for any f there that generates an oracle which operates in a time of O(lnN): e.g., to look up f(k) of entanglement. Between Symptoms-Remedy Picture, and Quantum Turing Machine generated geometry outputs which depends on the global description of the whole symptom picture of the patient-remedy complexes in the purpose of translating them into novel geometric shapes (drug design) which are coherent, there is sufficient similarity (global variable), and the local description of the druggable picture is individual (local variable), since the symptoms of the COVID-19 patient are new and unique. [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139] The complementarity here is between uniqueness/individuality and similarity/globality and could traverse a binary tree of chemical maps following the binary expansion of k. One way of interpreting these complementarities here which would not be temporal, then, as something, and which used to be present but is not any more since one half of the experiment would be double-blinded and placebo-controlled as before, while the other half could be selectively unblinded (e.g., either provers or coordinators) and used as inputs here to observe how remedy and placebo homeopathic signal transductions might disentangle into generalized geometrical structures. Thus, these entanglements generated from the homeopathic remedies since they represent an entangled system by virtue of the process of stepwise dilution and succussion used for the drug designing of new ligands by translating the magical presence of these Quantum Homeopathy Substances without the actual material presence into the RoccustyrnaTM annotated ligands. In this perspective, and according the work of Schmidt et al. [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141] in parapsychology these Quantum Homeopathy disentaglements might also provide some useful pointers toward this translational methodology into experimental quantum electrodynamics of such innovative druggable structures which were addressed by nonequilibrium thermodynamics [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144]. Traditionally this theoretical Quantum Homeopathy disentanglement at least mathematically has not been before described as a process involving Turing Machine Learning Rules for selection, although some attempts in this direction have been made [75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146]. The innovative druggable structures generated in this project represents a part of a second generalized entangled system which depends on knowledge and technicalities, namely of finding the correct remedy in order to link the remedy and symptom pictures of the patient with hypergeometric shapes. [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143] This link has to be sufficiently strong as well as sufficiently correct and similar such that one single global description ensues, namely the remedy picture. The remedy picture that contains symptoms collected in the past and by other subjects. [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144] Thus this information is temporally and factually different since these clinical data of COVID-19 inflammation and hypertension symptoms are consider as a non-generalized input. [29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145] The individual symptoms that are complementary to the remedy picture in the sense that they are not common and generalizable, but very individual are considered also as generalized inputs as well. [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145] The idiosyncratic exemplifications of the generic remedy picture during these quantum electrodynamics learning systems have to be evolved into multiple levels of trainable variables that substantially differ in their rates to compete those without such scale separation particularly when exploring the touch points between Quantum Mechanics and Thermodynamics for the modeling of Quantum Entropy Negativity cognitions in order to accelerate a decision making process for pharmacophoric substitution by using couplings of the Quantum Information Theory, Quantum Uncertainity Measurements, and Open Quantum System Theories. [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146] The individual symptomatology which is in the same sense complementary to its common denominator and the remedy picture including the biostatistical data such from individual and society, freedom and responsibility, singularity and communion complementary notions [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147] could also be considered as inputs in these quantum turing circuits since quantum learning is conceived. Thus the individual symptom picture and the commonality of these remedy symptoms or Materia Medica are the complementary descriptions that create the entangled state of the second entangled system (b) (Supplementary Material METHODS AND MATERIALS (1), (2), and Figures S(1-25), ((Iconics1-4), (Eqs1-400), and ((Schematics1a,1b,1c,1d,1e,1f,1g,1h,1i,1j,1k,1l,1m)), (I-VI) Supplementary Material METHODS AND MATERIALS (1), (2)) as a universal process, under this quantosphere “world as a neural network” concept [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148]. The reason for this is to consider all these evolutionary processes in a small molecule universe within this Quantum Homeopathy framework for Turing Machine Learning Hypergeometric Translations (TMLHT) as illustrated here particularly as a process of a new poly-triangulation drug design protocol [QuantumDistance [EntanglementEntropy [qstate_∆˜ ⊗ pi|FFFTˆUµ} (X) |∅ (AoΨο, d) ⍢, [H] ⨶ [Ho] ⨚⨛ i [Ψ] ] [EntanglementEntropy [qstate_ [QFTq] ψοMG)] μνi of M (((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)), (Supplement Material FUNCTIONS.1-14), and (Cluster of BIOGENEA_ CONSENSUS_Eqs.1-22)) and a Quantum-like modeling process outside of classical physics capable of leading to such an event including the requirement for the essential chemicals and Avogadro’s concentration mechanisms, and more. [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147] It might not be an extremely improbable, lucky accident but rather a manifestation of a general evolutionary trend in a small molecule universe modeled as a quantum turing learning system [18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149] for the generation of these Quantum-like small molecules. [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149] The basic hypothesis presented in this paper is the Entanglement Homeopathy Negativity Translations of SARS-CoV-2 biosystems when the first N −5 tetrahedral pharmacophoric scaffoldings are identical to those of the {∆i} triangulation pharmacophore scheme suggesting that these Quantum Homeopathy Potentiations may well be exhibiting at least geometrically some Quantum Entanglement effects for these “Avogadro significant” and “Avogadro amplified” QFT to QM reduction effects in virology. [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149] These mathematical computational and quantum geometry experimental data are already in effect as a built-in homeostatic response based on Quantum Thermodynamics indicating that Quantum Homeopathy Entanglements could found ways to embrace this learning/evolutionary process of ∆˜ H, Rz (0) H, Rz (0) i transformation for free energy reductions from QFT to QM. These Docking Free Energy Reduction Mechanisms (DFERM) proved to be much simpler to finite volume when working with the trace-reversed perturbation of (Hypergeometric2F1Regularized[1 - L_(i^n v1 ρ1 ρ2 v2 (ρ U) λ)^(((0 + 6.02214076×10^23 i) F m o Q T ρ ψ)/q)(Γ^2/2 ∧ 23 Γ Γ d ∧ Γ ∧ Γ S×ω^2/2 ∧ d ω + 6 ω ∧ ω ∧ ω e^λ), 2, 1/2])^2 hˆ18XC (Rz (π) μν ⊗ bˆ2rIMG) μν − √3Xbˆ2r − 12XCZC ⊗ θZ − √2C (Rz (π), [H] ⨶ [Ho] ⨚IµTMG) μν Y_l^m(θ, ϕ) (1 - L_(i^n v1 ρ1 ρ2 v2 (ρ U) λ)^(((0 + 6.02214076×10^23 i) F m o Q T ρ ψ)/q)(Γ^(2/2 ∧ 23 (Γ Γ) d ∧ Γ ∧ Γ S×ω^2/2 ∧ d ω + 6 ω ∧ ω ∧ ω) e^λ))^2 Φ rather than the perturbation ΥΓ.h,1/18XC (Rz (π) μν ⊗ bˆ2rIMG) μν − Y_l^m(θ, ϕ) (1 - L_(i^n v1 ρ1 ρ2 v2 (ρ U) λ)^(((0 + 6.02214076×10^23 i) F m o Q T ρ ψ)/q)(h^(R z) π Γ^(2/2 ∧ 23 (Γ Γ) d ∧ Γ ∧ Γ S×ω^2/2 ∧ d ω + 6 ω ∧ ω ∧ ω) e^λ))^2 Φ√3Xbˆ2r − 12XCZC ⊗ θZ − √2C (Rz (π), [H] ⨶ [Ho] ⨚IµTMG) μν ((Cluster of BIOGENEA_ CONSENSUS_Eqs.1-23), (Supplement Material FUNCTIONS.1 - 15)) itself. In fact, some unknown sphere-shaped pharmacophoric characteristics (Supplementary Material METHODS AND MATERIALS (1), (2)), Figures S(1-64), ((Iconics1-4), (Eqs1-400), and (Schematics1a,1b,1c,1d,1e,1f,1g,1h,1i,1j,1k,1l,1m), (I-VI) Supplementary Material METHODS AND MATERIALS (1), (2)) emerged and several triangulation topics were revealed in this project when solved the time-independent Schrodinger functions of motion in much larger chemical spaces that are currently inaccessible to experimental screening methods in this rationale homeopathy translation that might enact another entangled state between atomic charges [Supplementary material (PLIP Reports1-8)] of the atom orbitas from the substance and ligabd-receptor molecular complexes. In this case by ‘translating’ the homeopathy symptoms from the organism back to the substance stationary pharmacophore states among the unknown geometric characteristics the cluster of the Gissitorviffirna_TM, Roccustyrna_gs, Roccustyrna_fr, and Roccustyrna_consv Quantum-computational structures occurred after intrinsically rooted in QFT by setting theoretical paradoxes regarding these binding affinity measurement problems. [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149] These Quantum Mechanics and Quantum-gravitational ideas provided us along within this Theoretical Quantum Gravity background from Quantum Homeopathy Information into a Quantum Homeopath Folding Translation which is highly dependent on the folding of typical secondary structures as the means to hierarchically pave a negative docking energy and native folding pathway. Since several hypotheses have been proposed to explain this quantum homeopath folding mechanism that expands the hydrophobic zipper hypothesis which proposes a hairpin, first formed before hydrophobic contacts, to act as a constraint that brings other contacts into spatial proximity [24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149] this Quantum Homeopathy Translational mechanism would be an ingenious system of using these folding pathways as entangled states. In that case, by translating the phenomenon of the substance which is not present, this homeopathic quantum information, would become a kind of receptacle that translates the ‘absorbed’ symptoms, insofar as it is related by similarity. The more so, the less the likelihood of material presence in the remedy, or, in homeopathic parlance, the higher the potency of these Non-commutative geometry superoperators and Quantum Simulation Eigenvectors which were overlooked in a conventional way as a QG context involving detection of chemical bond restruction. These solutions were obtained by solving the function SHZζZ where ζ are the eigenvalues that referred to three main targets: the Spike glycoprotein (S-protein), papain-like protease (PLpro), and prominently the main protease Mpro. In this Quantum Homeopathy, then, we would have a double entanglement situation: The remedy is an entangled state itself between actual remedy and original new drug designs (substance) (a). This is achieved by potentization. This homeopathic entanglements ritual enacts and translates the signals from the entangled state between the symptomatology of the patient and the remedial substance (b). This is the similarity principle. This folding funnel hypothesis essentially says “the Gibbs free energy formula can describe protein folding” given the breadth of the bioinformatics space, where these applications represent a very small subset of the potential emerging application space for Quantum Homeopathy algorithm development. A small number of quantum algorithms for geometry problems in bioinformatics have been proposed here. These include theoretical geometry algorithms developed for Quantum Deep Learning Turing Machines that target NP-hard problems, such as sequence alignment [67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159] and the inference of highthrouput virtual screening and relative phylogenetic trees [70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160], which leverage amplitude amplification and quantum walks [38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164] indicating that these multistage entropy-enthalpy compensations of the atomic orbits from polypeptide chains and surrounding water molecules are the folding mechanisms, enabling protein and peptide oriented chemical designs to fold reproducibly and quickly, following explicit physical folding codes in aqueous environments. Only these entanglement functions of ChebyshevU[Cos[x], M^8 u^24 ν^6 z] JacobiP[ArcSin[θ n], λ a, λ b, Cos[x] ] ChebyshevT[(Sin[ω Q] ^Cos[x] ^4/x) Cos[GoldenRatio], ((Sin[x] ^r)^21/22) x] ZernikeR[λ n, D f z, g z (ψ^0 ρ m), λ] (M_(k λ, m×(d^2(n λ))/(dZ^2))((integral y du) del ((3 χ) log(q) Ω^(λ^6))) Hypergeometric1F1Regularized[a^5, (d^2(ρ^6 m^7))/(dy dx) b, g^8, n^9, Δ(10, PauliMatrix[2], ε^3, Δ3)]) _0 F^~_1(;a;z)LaguerreL[λ n, D f z, g z (ψ^0 ρ m), I Exp[λ] ] (WhittakerM[ψ, ψ ο D[n λ, {Z, 2}], Integrate[y, u] Grad[(3 χ[x, y, z]) Log[q[x, y, z] ] Ω[x, y, z] ^λ[x, y, z] ^6, {x, y, z}] ] Hypergeometric1F1Regularized[a^5, D[ρ^6 n^73, y, x] b, g^8, Exp[n] 6, δ σ^2, ε θ^3, Δ α^4]) Hypergeometric0F1Regularized[a, z] in reverse order could translate the (unwanted) symptomatology of the diseased organism into druggable drug designs and chemicable coordinates and ‘transferred’ via the entanglement produced by the therapeutic ritual from the remedy-organism back to the geometry field, as it were. [38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168] This analysis makes obvious that homeopathy hinges on two separate exemplifications of generalized entanglement and thus is in a double sense vulnerable to actions disturbing entanglement or to incomplete production of the entangled preliminary results these Quantum Homeopathic Algorithms that are based on logic judgement of entropy-enthalpy compensation relationships among neighbored residues of an unfolded thermodynamic metastable state have to be devised in order to effectively and accurately predict a protein-ligand native secondary structure from its amino acid sequence with negative binding fee energies against AT1R protein and DNA targets where the first one is that of the remedy production process. [38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,150,151,152,153,154,155,156,157,158,159,160] Entanglement could be described here by the global variable ‘no substance present’ and the local variable that the remedy is really treated as if it were a remedy with ‘something’ in it. Another way of reconstructing would be that of a global variable ‘specific remedy’ and the local variable ‘no substance present’. Already, examples of this type of drug designing work exist for de novo assembly [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161], sequence alignment [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165] and the inference of biological networks [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150] over the long term, operational advantages may be pursued by optimizing near-term approaches and integrating fast quantum algorithm subroutines with Quantum Homeopathy algorithms that may be relevant to this work including ones for backtracking [65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89], dynamic programming [47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158], operating on geometry strings [71,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167] and differential Quantum Functions ((Cluster of BIOGENEA_ CONSENSUS_Eqs.1-24), (Supplement Material FUNCTIONS.1 - 16)) [22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168]. This Quantum Information Processing Function which is one of the most interesting modern applications of quantum entanglement [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167] through quantum mechanics that governs the way operate modern computers Quantum computing, cryptography and teleportation and are now all practically realizable technologies, at least in the laboratory, the information they encode is still treated classically. [27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169] Here, our latest insights into these very foundations of quantum theory itself reveal that Quantum Homeopathy information is also subject to the same quantum laws [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80] following by homeopathy that hinges on two separate exemplifications of generalized entanglement and thus is in a double sense vulnerable to actions disturbing entanglement or to incomplete production of entanglement. [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178]. They are predicated on the realization that this Quantum Homeopathy information is not independent of the quantum physical laws used to store and process it when measuring into account the operational advantages for these quantum negative docking energy problems that are remain among the most difficult to achieve like the first one that is of the remedy production process. [29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178]. Entanglement could be described here by the global variable ‘no substance present’ and the local variable “drug design” that the remedy is really translated to as if it was a remedy with ‘something’ in it and as another way of reconstructing chemical geometrics which would be that of a global variable ‘specific remedy with no substance present’ and the local variable ‘chemical geometry shapes’. [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179] Given the breadth of this mathematical geometry applications for Turing Machine learning approaches in biology, Ι focus my discussion below on these types of Quantum Homeopathy advantages and their potential applications in lieu of specific drug designing methods. Improvements to training landscapes that refer to the reduction or removal of barren plateaus and narrow gorges in the landscape of the objective function of a gradient-based learning algorithm may stem from the unitary property of (many) quantum circuits, which inherently maintain the length of the input feature vector throughout the computation [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,180] provided where an appropriate input encoding is used following a more dedicated, more precise, and more time- and energy-consuming interpretation of homeopathy remedies. This is something we should expect it since the entangled states that both generated within a water solution from a homeopathy remedy whenever the drug substance relates to other ultra low concentrations of substances and to other water solutions and protein-ligand complexes, when finding similars that suggesting either possible this droplet transmission during potentization process which are all considered as non-generalized inputs into a Turing Machine potentization tool. [22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160] To illustrate this theoretical Turing Machine framework and demonstrate its Quantum Homeopathy applicability I detailed these quantum function algorithms and presented them for two simple examples (ACE2 and AT1R receptor atoms), showing that the convergence achieved is consistent with the expected behavior as a lattice in this particular type of regulator by allowing a computer simulation of QFT while this lattice breaks Lorentz’s invariance into a fuzzy sphere guided drug design ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)), (Figures S(1-101)) has the same rotational symmetry with the ordinary sphere extension from DFT chemical space [41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168] including the exchange and correlation potential for DFT derivative operators which can be avoided only for local density approximation (LDA) functional. I have shown then how it is possible to compute the Fock matrix and the electronic energy by exploiting the formal relation between the level-shifted Laplacian and the bound-state Helmholtz kernel, thus avoiding any reference to the quantum kinetic energy operator. As Maas writes in his lectures [43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171] these understandings of quantum fields theory the need to have regulators that always implies that some symmetries are broken, no matter what, until the regulator it is not removed. [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172] In particular I have seen that these convergences within these predefined thresholds are achieved both for the orbital norm and for the Quantum Homeopathy Energy. Moreover the total binding energy that converges quadratically with respect to the norm of the orbital error as a lattice in this mathematical artifact is induced by these quantum fluctuations of the metric in the attractor basin. [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,88,89,90,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181] This shows how unitarily these inequivalent representations of QFT are reduced to a single class of unitarily equivalent representations of QM for simulating scalar field theories in a spatial lattice as a conjugate variable P (x⇀q’), the field momentum at the lattice site x⇀q’, which is related to Φ (x⇀q’) quantum Fourier transformations as applied to the N-dimensional Hilbert space residing at each lattice site x⇀N. For N, 2n, the quantum state of the field at a site can be encoded in n qubits where n refers epidemiologically, to the eight of the nine patients that had a history of exposure to the Huanan seafood market in Wuhan, suggesting that they might have been in close contact with the infection source at the market. X refers to the one patient had never visited the market, although he had stayed in a hotel near the market before the onset of their illness. [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,58,59,60,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186] Thus, in this interpretation experiment the wave nature of quantum particles are demonstrated by their formation of an interference pattern on a screen attempting to make observations of this situation at one or other slit prior to the waves arriving at the screen that induces the superposition, leading to their behaving as particles. [31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,68,79,90,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187] This demonstrates that this Quantum Homeopathy Superposition is the key to their entanglement. In these quantum Turing Machine ruled information processings, any attempt to isolate entangled ‘qubits’ leads to collapse of the entangled state and the loss of deep geometry information. [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186] In this case instead, qubits are induced directly by the quantum fluctuations of the metric, due to the uncertainty relationship between metric and quantum information. Both approaches can lead to satisfactory results, but ours is more physical, not only in a heuristic sense, since it is supported by a rigorous mathematical framework. [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,78,79,90,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187] Quantum Homeopathy Superposition Entanglement could also be used in the future in the same heuristic sense as a tool when attempting to make observations of the chemical space and the quantum information generated in ultra low concentrations even below Avogadro’s Number in typical RNA virus superimposed states when the average evolutionary rate for coronaviruses is roughly 10−4 nucleotide substitutions per site per year. As Preskill himself says in [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192]: “There may be cleverer ways of regulating that would improve the efficiency of the simulation”. In this logical framework, since 𝐶̂ ∞ operations imply infinitely many operations, this intersection algorithm generated new {∆i} triangulations over a Boson Field Operator for a triangle shaped fragmentation pharmacophoric scheme which is considered as the evolution in Quantum information chemical space theories. [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188] The first step I took to understand this Quantrum Negative Energy Metric more fully is to consider the behavior of geodesics in the presence of binding energy Quantum fluctuations of this metric inside the docking surface of a fuzzy sphere shaped pharmacophore features ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)), (Supplementary Material METHODS AND MATERIALS (1), (2)), and Figures S(1-103)) of radius nr, that encodes Quantum information for each residue calculated including the explicitly periodic potential for MathieuS, MathieuC, MathieuCharacteristicExponent functions torsion of ∆θˆσ, by a discrete variable with a finite number N of mutually orthogonal eigenstates for the nonzero Christoffel symbols for Schwarzschild metric: [Γ] (Eqs.1-400), ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)), 〈(SUPPLEMENT MATERIAL) FUNCTIONS.1-10〉. [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187] In a sense, however, QFT is T’s chemical “skeleton”, and from it I can go back to T, at least that’s hope by unifying Small Molecular Pairs (SMP) and Lindenbaum-Tarski Logical Chemical Spaces (LTLCS) found in molecular descriptors from AT1 receptors and Adaptive Weighted KNN Positioning for Matched Bemis and Murko (MBM) eigenvalue statements and combining them with Quantum Negative Energy Measurements from in vitro observables that are represented by commuting operators exctracted from telmisartan: 213 min, olmesartan: 166 min, candesartan: 133 min, valsartan: 70 min, losartan: 67 min half-lives. [23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188] In any case, however, the profound philosophical meaning of the mathematical role of a regulator is that by reducing the infinite degrees of freedom of QFT to a finite number, and by allowing the quantum simulator and the simulated quantum system to have unitarily equivalent representations even when interactions are present. Similarly, the development of one classical optimization algorithm for constraint satisfaction [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189] was inspired by the original QAOA [2,3,4,5,6,7,8,9,10,11,12,13,14,15,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190] and improved upon theirs Quantum Homeopathy Entropy Negativities (QHEN) performance from incompatible AT1 receptor dissociations which were translated into Shannon Entropy Negative Quantities of Negative Total Binding Energies as composed by Tipping–Ogilvie driven Machine Learning potentials on a (DFT) ℓneuron (ι), φ since very beginning of Quantum mechanics, non-commutativity of operators representing observables were considered as the mathematical representations of theirs incompatibility. [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189] However, as N refers to the virus transmissions A refers to the Phylogenetic Data showing that bat-derived coronaviruses fell within all five subgenera of the genus Betacoronavirus and K refers to atomic orbits from the consensus sequences identitied between 2019-nCoV and its close relatives bat-SL-CoVZC45 and bat-SL-CoVZXC21 which was less than 90%, and are reflected in the relatively long branch between them. Hence, bat-SL-CoVZC45 and bat-SL-CoVZXC21 are not direct ancestors of 2019-nCoV. [31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190] In particular, I translated at least numerically the atomic orbits from the above protein network from these interacted biosystems that react not only to material or energy constraints imposed by the environment, but also to the information constraints into a QFT reduction action which can contribute to the Semi Negative Quantum Energy effects of Telmisartan and relative Antihypertensive Drugs when producing a decrease in the number of AT1R receptors for the generation of these Quantum Foam like DRVYIHPF-mimetic [amino ({4 - [(2R,3R) - 2 - [(2S) - 3 - { [(1S,2S) - 1 - { [(S) - 1,3 - dihydroisoindole - 2 - carbonyl [(2 - methyl - 6 - oxo - 1,7 - dihydropurin - 8 - yl) methyl] phosphanyl] carbamoyl} - 2 - methylbutyl] amino} - 2 - methylpropyl] oxaziridin - 3 - yl] butyl}amino) methylidene] azanium, Roccustyrna_TM, and Gissitorviffirna_TM ligands. By using this methodology I provided Anti-de Sitter Chern-Simons Supergravity (AdSCSS) Hidden Solutions for Quantum Reference Frame Representations for this DRVYIHPF-mimetic Roccustyrna_TM and Gissitorviffirna_TM ligand pharmacophore merging scheme once these Quantum fieldss are reduced into a Quantum network of black hole phase solutions Lˆ∆q for a complete decision tree search of all possible combinations of fragmentation, merging, and pharmacophore re-coring systems targeted inside the SARS-CoV Mpro protein targets. [20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187] These modified Lagrangian DensityMatrix functions {∂(Tr[ψ,{2}] DensityMatrix)/∂logρ(ψ) A log((ΒG sin(ω) hν (n π Q δ μ σ)) ρ A) logG(z),0,(sin−1(r)
for the LegendreP[1 + I/2 (E^(-I ω) - E^(I ω)) 〈ΔSPl〉 G h^ν n Pi Q δ μ σ, x] /(1 + I (E^(-I ω) - E^(I ω)) G h^ν n Pi Q δ μ σ) - LegendreP[15 k N - I 2^(-1 - x) D (E^(-I c) - E^(I c)) (I (E^(-I ω) - E^(I ω)))^x h n Pi Q U δ Δ^ν μ ρ^4 σ, x] / 〈ΔSRx〉(1 + I (E^(-I ω) - E^(I ω)) G h^ν n Pi Q δ μ σ) function, either 〈ΔSPl〉 = 0 or at least 〈ΔSPl〉 and 〈ΔSRx〉 can now be equated with each other. In other words, this Quantum Homeopathy act provides information that collapse the remedy/placebo into an entangled state wave function, leaving two completely distinguishable sets of results: one set for provers on the remedy, and one set for those on placebo for any f there that generates an oracle which operates in a time of O(lnN): e.g., to look up f(k) of entanglement. Between Symptoms-Remedy Picture, and Quantum Turing Machine generated geometry outputs which depends on the global description of the whole symptom picture of the patient-remedy complexes in the purpose of translating them into novel geometric shapes (drug design) which are coherent, there is sufficient similarity (global variable), and the local description of the druggable picture is individual (local variable), since the symptoms of the COVID-19 patient are new and unique. [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139] The complementarity here is between uniqueness/individuality and similarity/globality and could traverse a binary tree of chemical maps following the binary expansion of k. One way of interpreting these complementarities here which would not be temporal, then, as something, and which used to be present but is not any more since one half of the experiment would be double-blinded and placebo-controlled as before, while the other half could be selectively unblinded (e.g., either provers or coordinators) and used as inputs here to observe how remedy and placebo homeopathic signal transductions might disentangle into generalized geometrical structures. Thus, these entanglements generated from the homeopathic remedies since they represent an entangled system by virtue of the process of stepwise dilution and succussion used for the drug designing of new ligands by translating the magical presence of these Quantum Homeopathy Substances without the actual material presence into the RoccustyrnaTM annotated ligands. In this perspective, and according the work of Schmidt et al. [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141] in parapsychology these Quantum Homeopathy disentaglements might also provide some useful pointers toward this translational methodology into experimental quantum electrodynamics of such innovative druggable structures which were addressed by nonequilibrium thermodynamics [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144]. Traditionally this theoretical Quantum Homeopathy disentanglement at least mathematically has not been before described as a process involving Turing Machine Learning Rules for selection, although some attempts in this direction have been made [75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146]. The innovative druggable structures generated in this project represents a part of a second generalized entangled system which depends on knowledge and technicalities, namely of finding the correct remedy in order to link the remedy and symptom pictures of the patient with hypergeometric shapes. [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143] This link has to be sufficiently strong as well as sufficiently correct and similar such that one single global description ensues, namely the remedy picture. The remedy picture that contains symptoms collected in the past and by other subjects. [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144] Thus this information is temporally and factually different since these clinical data of COVID-19 inflammation and hypertension symptoms are consider as a non-generalized input. [29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145] The individual symptoms that are complementary to the remedy picture in the sense that they are not common and generalizable, but very individual are considered also as generalized inputs as well. [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145] The idiosyncratic exemplifications of the generic remedy picture during these quantum electrodynamics learning systems have to be evolved into multiple levels of trainable variables that substantially differ in their rates to compete those without such scale separation particularly when exploring the touch points between Quantum Mechanics and Thermodynamics for the modeling of Quantum Entropy Negativity cognitions in order to accelerate a decision making process for pharmacophoric substitution by using couplings of the Quantum Information Theory, Quantum Uncertainity Measurements, and Open Quantum System Theories. [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146] The individual symptomatology which is in the same sense complementary to its common denominator and the remedy picture including the biostatistical data such from individual and society, freedom and responsibility, singularity and communion complementary notions [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147] could also be considered as inputs in these quantum turing circuits since quantum learning is conceived. Thus the individual symptom picture and the commonality of these remedy symptoms or Materia Medica are the complementary descriptions that create the entangled state of the second entangled system (b) (Supplementary Material METHODS AND MATERIALS (1), (2), and Figures S(1-25), ((Iconics1-4), (Eqs1-400), and ((Schematics1a,1b,1c,1d,1e,1f,1g,1h,1i,1j,1k,1l,1m)), (I-VI) Supplementary Material METHODS AND MATERIALS (1), (2)) as a universal process, under this quantosphere “world as a neural network” concept [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148]. The reason for this is to consider all these evolutionary processes in a small molecule universe within this Quantum Homeopathy framework for Turing Machine Learning Hypergeometric Translations (TMLHT) as illustrated here particularly as a process of a new poly-triangulation drug design protocol [QuantumDistance [EntanglementEntropy [qstate_∆˜ ⊗ pi|FFFTˆUµ} (X) |∅ (AoΨο, d) ⍢, [H] ⨶ [Ho] ⨚⨛ i [Ψ] ] [EntanglementEntropy [qstate_ [QFTq] ψοMG)] μνi of M (((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)), (Supplement Material FUNCTIONS.1-14), and (Cluster of BIOGENEA_ CONSENSUS_Eqs.1-22)) and a Quantum-like modeling process outside of classical physics capable of leading to such an event including the requirement for the essential chemicals and Avogadro’s concentration mechanisms, and more. [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147] It might not be an extremely improbable, lucky accident but rather a manifestation of a general evolutionary trend in a small molecule universe modeled as a quantum turing learning system [18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149] for the generation of these Quantum-like small molecules. [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149] The basic hypothesis presented in this paper is the Entanglement Homeopathy Negativity Translations of SARS-CoV-2 biosystems when the first N −5 tetrahedral pharmacophoric scaffoldings are identical to those of the {∆i} triangulation pharmacophore scheme suggesting that these Quantum Homeopathy Potentiations may well be exhibiting at least geometrically some Quantum Entanglement effects for these “Avogadro significant” and “Avogadro amplified” QFT to QM reduction effects in virology. [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149] These mathematical computational and quantum geometry experimental data are already in effect as a built-in homeostatic response based on Quantum Thermodynamics indicating that Quantum Homeopathy Entanglements could found ways to embrace this learning/evolutionary process of ∆˜ H, Rz (0) H, Rz (0) i transformation for free energy reductions from QFT to QM. These Docking Free Energy Reduction Mechanisms (DFERM) proved to be much simpler to finite volume when working with the trace-reversed perturbation of (Hypergeometric2F1Regularized[1 - L_(i^n v1 ρ1 ρ2 v2 (ρ U) λ)^(((0 + 6.02214076×10^23 i) F m o Q T ρ ψ)/q)(Γ^2/2 ∧ 23 Γ Γ d ∧ Γ ∧ Γ S×ω^2/2 ∧ d ω + 6 ω ∧ ω ∧ ω e^λ), 2, 1/2])^2 hˆ18XC (Rz (π) μν ⊗ bˆ2rIMG) μν − √3Xbˆ2r − 12XCZC ⊗ θZ − √2C (Rz (π), [H] ⨶ [Ho] ⨚IµTMG) μν Y_l^m(θ, ϕ) (1 - L_(i^n v1 ρ1 ρ2 v2 (ρ U) λ)^(((0 + 6.02214076×10^23 i) F m o Q T ρ ψ)/q)(Γ^(2/2 ∧ 23 (Γ Γ) d ∧ Γ ∧ Γ S×ω^2/2 ∧ d ω + 6 ω ∧ ω ∧ ω) e^λ))^2 Φ rather than the perturbation ΥΓ.h,1/18XC (Rz (π) μν ⊗ bˆ2rIMG) μν − Y_l^m(θ, ϕ) (1 - L_(i^n v1 ρ1 ρ2 v2 (ρ U) λ)^(((0 + 6.02214076×10^23 i) F m o Q T ρ ψ)/q)(h^(R z) π Γ^(2/2 ∧ 23 (Γ Γ) d ∧ Γ ∧ Γ S×ω^2/2 ∧ d ω + 6 ω ∧ ω ∧ ω) e^λ))^2 Φ√3Xbˆ2r − 12XCZC ⊗ θZ − √2C (Rz (π), [H] ⨶ [Ho] ⨚IµTMG) μν ((Cluster of BIOGENEA_ CONSENSUS_Eqs.1-23), (Supplement Material FUNCTIONS.1 - 15)) itself. In fact, some unknown sphere-shaped pharmacophoric characteristics (Supplementary Material METHODS AND MATERIALS (1), (2)), Figures S(1-64), ((Iconics1-4), (Eqs1-400), and (Schematics1a,1b,1c,1d,1e,1f,1g,1h,1i,1j,1k,1l,1m), (I-VI) Supplementary Material METHODS AND MATERIALS (1), (2)) emerged and several triangulation topics were revealed in this project when solved the time-independent Schrodinger functions of motion in much larger chemical spaces that are currently inaccessible to experimental screening methods in this rationale homeopathy translation that might enact another entangled state between atomic charges [Supplementary material (PLIP Reports1-8)] of the atom orbitas from the substance and ligabd-receptor molecular complexes. In this case by ‘translating’ the homeopathy symptoms from the organism back to the substance stationary pharmacophore states among the unknown geometric characteristics the cluster of the Gissitorviffirna_TM, Roccustyrna_gs, Roccustyrna_fr, and Roccustyrna_consv Quantum-computational structures occurred after intrinsically rooted in QFT by setting theoretical paradoxes regarding these binding affinity measurement problems. [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149] These Quantum Mechanics and Quantum-gravitational ideas provided us along within this Theoretical Quantum Gravity background from Quantum Homeopathy Information into a Quantum Homeopath Folding Translation which is highly dependent on the folding of typical secondary structures as the means to hierarchically pave a negative docking energy and native folding pathway. Since several hypotheses have been proposed to explain this quantum homeopath folding mechanism that expands the hydrophobic zipper hypothesis which proposes a hairpin, first formed before hydrophobic contacts, to act as a constraint that brings other contacts into spatial proximity [24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149] this Quantum Homeopathy Translational mechanism would be an ingenious system of using these folding pathways as entangled states. In that case, by translating the phenomenon of the substance which is not present, this homeopathic quantum information, would become a kind of receptacle that translates the ‘absorbed’ symptoms, insofar as it is related by similarity. The more so, the less the likelihood of material presence in the remedy, or, in homeopathic parlance, the higher the potency of these Non-commutative geometry superoperators and Quantum Simulation Eigenvectors which were overlooked in a conventional way as a QG context involving detection of chemical bond restruction. These solutions were obtained by solving the function SHZζZ where ζ are the eigenvalues that referred to three main targets: the Spike glycoprotein (S-protein), papain-like protease (PLpro), and prominently the main protease Mpro. In this Quantum Homeopathy, then, we would have a double entanglement situation: The remedy is an entangled state itself between actual remedy and original new drug designs (substance) (a). This is achieved by potentization. This homeopathic entanglements ritual enacts and translates the signals from the entangled state between the symptomatology of the patient and the remedial substance (b). This is the similarity principle. This folding funnel hypothesis essentially says “the Gibbs free energy formula can describe protein folding” given the breadth of the bioinformatics space, where these applications represent a very small subset of the potential emerging application space for Quantum Homeopathy algorithm development. A small number of quantum algorithms for geometry problems in bioinformatics have been proposed here. These include theoretical geometry algorithms developed for Quantum Deep Learning Turing Machines that target NP-hard problems, such as sequence alignment [67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159] and the inference of highthrouput virtual screening and relative phylogenetic trees [70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160], which leverage amplitude amplification and quantum walks [38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164] indicating that these multistage entropy-enthalpy compensations of the atomic orbits from polypeptide chains and surrounding water molecules are the folding mechanisms, enabling protein and peptide oriented chemical designs to fold reproducibly and quickly, following explicit physical folding codes in aqueous environments. Only these entanglement functions of ChebyshevU[Cos[x], M^8 u^24 ν^6 z] JacobiP[ArcSin[θ n], λ a, λ b, Cos[x] ] ChebyshevT[(Sin[ω Q] ^Cos[x] ^4/x) Cos[GoldenRatio], ((Sin[x] ^r)^21/22) x] ZernikeR[λ n, D f z, g z (ψ^0 ρ m), λ] (M_(k λ, m×(d^2(n λ))/(dZ^2))((integral y du) del ((3 χ) log(q) Ω^(λ^6))) Hypergeometric1F1Regularized[a^5, (d^2(ρ^6 m^7))/(dy dx) b, g^8, n^9, Δ(10, PauliMatrix[2], ε^3, Δ3)]) _0 F^~_1(;a;z)LaguerreL[λ n, D f z, g z (ψ^0 ρ m), I Exp[λ] ] (WhittakerM[ψ, ψ ο D[n λ, {Z, 2}], Integrate[y, u] Grad[(3 χ[x, y, z]) Log[q[x, y, z] ] Ω[x, y, z] ^λ[x, y, z] ^6, {x, y, z}] ] Hypergeometric1F1Regularized[a^5, D[ρ^6 n^73, y, x] b, g^8, Exp[n] 6, δ σ^2, ε θ^3, Δ α^4]) Hypergeometric0F1Regularized[a, z] in reverse order could translate the (unwanted) symptomatology of the diseased organism into druggable drug designs and chemicable coordinates and ‘transferred’ via the entanglement produced by the therapeutic ritual from the remedy-organism back to the geometry field, as it were. [38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168] This analysis makes obvious that homeopathy hinges on two separate exemplifications of generalized entanglement and thus is in a double sense vulnerable to actions disturbing entanglement or to incomplete production of the entangled preliminary results these Quantum Homeopathic Algorithms that are based on logic judgement of entropy-enthalpy compensation relationships among neighbored residues of an unfolded thermodynamic metastable state have to be devised in order to effectively and accurately predict a protein-ligand native secondary structure from its amino acid sequence with negative binding fee energies against AT1R protein and DNA targets where the first one is that of the remedy production process. [38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,150,151,152,153,154,155,156,157,158,159,160] Entanglement could be described here by the global variable ‘no substance present’ and the local variable that the remedy is really treated as if it were a remedy with ‘something’ in it. Another way of reconstructing would be that of a global variable ‘specific remedy’ and the local variable ‘no substance present’. Already, examples of this type of drug designing work exist for de novo assembly [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161], sequence alignment [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165] and the inference of biological networks [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150] over the long term, operational advantages may be pursued by optimizing near-term approaches and integrating fast quantum algorithm subroutines with Quantum Homeopathy algorithms that may be relevant to this work including ones for backtracking [65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89], dynamic programming [47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158], operating on geometry strings [71,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167] and differential Quantum Functions ((Cluster of BIOGENEA_ CONSENSUS_Eqs.1-24), (Supplement Material FUNCTIONS.1 - 16)) [22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168]. This Quantum Information Processing Function which is one of the most interesting modern applications of quantum entanglement [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167] through quantum mechanics that governs the way operate modern computers Quantum computing, cryptography and teleportation and are now all practically realizable technologies, at least in the laboratory, the information they encode is still treated classically. [27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169] Here, our latest insights into these very foundations of quantum theory itself reveal that Quantum Homeopathy information is also subject to the same quantum laws [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80] following by homeopathy that hinges on two separate exemplifications of generalized entanglement and thus is in a double sense vulnerable to actions disturbing entanglement or to incomplete production of entanglement. [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178]. They are predicated on the realization that this Quantum Homeopathy information is not independent of the quantum physical laws used to store and process it when measuring into account the operational advantages for these quantum negative docking energy problems that are remain among the most difficult to achieve like the first one that is of the remedy production process. [29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178]. Entanglement could be described here by the global variable ‘no substance present’ and the local variable “drug design” that the remedy is really translated to as if it was a remedy with ‘something’ in it and as another way of reconstructing chemical geometrics which would be that of a global variable ‘specific remedy with no substance present’ and the local variable ‘chemical geometry shapes’. [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179] Given the breadth of this mathematical geometry applications for Turing Machine learning approaches in biology, Ι focus my discussion below on these types of Quantum Homeopathy advantages and their potential applications in lieu of specific drug designing methods. Improvements to training landscapes that refer to the reduction or removal of barren plateaus and narrow gorges in the landscape of the objective function of a gradient-based learning algorithm may stem from the unitary property of (many) quantum circuits, which inherently maintain the length of the input feature vector throughout the computation [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,180] provided where an appropriate input encoding is used following a more dedicated, more precise, and more time- and energy-consuming interpretation of homeopathy remedies. This is something we should expect it since the entangled states that both generated within a water solution from a homeopathy remedy whenever the drug substance relates to other ultra low concentrations of substances and to other water solutions and protein-ligand complexes, when finding similars that suggesting either possible this droplet transmission during potentization process which are all considered as non-generalized inputs into a Turing Machine potentization tool. [22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160] To illustrate this theoretical Turing Machine framework and demonstrate its Quantum Homeopathy applicability I detailed these quantum function algorithms and presented them for two simple examples (ACE2 and AT1R receptor atoms), showing that the convergence achieved is consistent with the expected behavior as a lattice in this particular type of regulator by allowing a computer simulation of QFT while this lattice breaks Lorentz’s invariance into a fuzzy sphere guided drug design ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)), (Figures S(1-101)) has the same rotational symmetry with the ordinary sphere extension from DFT chemical space [41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168] including the exchange and correlation potential for DFT derivative operators which can be avoided only for local density approximation (LDA) functional. I have shown then how it is possible to compute the Fock matrix and the electronic energy by exploiting the formal relation between the level-shifted Laplacian and the bound-state Helmholtz kernel, thus avoiding any reference to the quantum kinetic energy operator. As Maas writes in his lectures [43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171] these understandings of quantum fields theory the need to have regulators that always implies that some symmetries are broken, no matter what, until the regulator it is not removed. [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172] In particular I have seen that these convergences within these predefined thresholds are achieved both for the orbital norm and for the Quantum Homeopathy Energy. Moreover the total binding energy that converges quadratically with respect to the norm of the orbital error as a lattice in this mathematical artifact is induced by these quantum fluctuations of the metric in the attractor basin. [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,88,89,90,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181] This shows how unitarily these inequivalent representations of QFT are reduced to a single class of unitarily equivalent representations of QM for simulating scalar field theories in a spatial lattice as a conjugate variable P (x⇀q’), the field momentum at the lattice site x⇀q’, which is related to Φ (x⇀q’) quantum Fourier transformations as applied to the N-dimensional Hilbert space residing at each lattice site x⇀N. For N, 2n, the quantum state of the field at a site can be encoded in n qubits where n refers epidemiologically, to the eight of the nine patients that had a history of exposure to the Huanan seafood market in Wuhan, suggesting that they might have been in close contact with the infection source at the market. X refers to the one patient had never visited the market, although he had stayed in a hotel near the market before the onset of their illness. [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,58,59,60,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186] Thus, in this interpretation experiment the wave nature of quantum particles are demonstrated by their formation of an interference pattern on a screen attempting to make observations of this situation at one or other slit prior to the waves arriving at the screen that induces the superposition, leading to their behaving as particles. [31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,68,79,90,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187] This demonstrates that this Quantum Homeopathy Superposition is the key to their entanglement. In these quantum Turing Machine ruled information processings, any attempt to isolate entangled ‘qubits’ leads to collapse of the entangled state and the loss of deep geometry information. [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186] In this case instead, qubits are induced directly by the quantum fluctuations of the metric, due to the uncertainty relationship between metric and quantum information. Both approaches can lead to satisfactory results, but ours is more physical, not only in a heuristic sense, since it is supported by a rigorous mathematical framework. [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,78,79,90,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187] Quantum Homeopathy Superposition Entanglement could also be used in the future in the same heuristic sense as a tool when attempting to make observations of the chemical space and the quantum information generated in ultra low concentrations even below Avogadro’s Number in typical RNA virus superimposed states when the average evolutionary rate for coronaviruses is roughly 10−4 nucleotide substitutions per site per year. As Preskill himself says in [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192]: “There may be cleverer ways of regulating that would improve the efficiency of the simulation”. In this logical framework, since 𝐶̂ ∞ operations imply infinitely many operations, this intersection algorithm generated new {∆i} triangulations over a Boson Field Operator for a triangle shaped fragmentation pharmacophoric scheme which is considered as the evolution in Quantum information chemical space theories. [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188] The first step I took to understand this Quantrum Negative Energy Metric more fully is to consider the behavior of geodesics in the presence of binding energy Quantum fluctuations of this metric inside the docking surface of a fuzzy sphere shaped pharmacophore features ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)), (Supplementary Material METHODS AND MATERIALS (1), (2)), and Figures S(1-103)) of radius nr, that encodes Quantum information for each residue calculated including the explicitly periodic potential for MathieuS, MathieuC, MathieuCharacteristicExponent functions torsion of ∆θˆσ, by a discrete variable with a finite number N of mutually orthogonal eigenstates for the nonzero Christoffel symbols for Schwarzschild metric: [Γ] (Eqs.1-400), ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)), 〈(SUPPLEMENT MATERIAL) FUNCTIONS.1-10〉. [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187] In a sense, however, QFT is T’s chemical “skeleton”, and from it I can go back to T, at least that’s hope by unifying Small Molecular Pairs (SMP) and Lindenbaum-Tarski Logical Chemical Spaces (LTLCS) found in molecular descriptors from AT1 receptors and Adaptive Weighted KNN Positioning for Matched Bemis and Murko (MBM) eigenvalue statements and combining them with Quantum Negative Energy Measurements from in vitro observables that are represented by commuting operators exctracted from telmisartan: 213 min, olmesartan: 166 min, candesartan: 133 min, valsartan: 70 min, losartan: 67 min half-lives. [23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188] In any case, however, the profound philosophical meaning of the mathematical role of a regulator is that by reducing the infinite degrees of freedom of QFT to a finite number, and by allowing the quantum simulator and the simulated quantum system to have unitarily equivalent representations even when interactions are present. Similarly, the development of one classical optimization algorithm for constraint satisfaction [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189] was inspired by the original QAOA [2,3,4,5,6,7,8,9,10,11,12,13,14,15,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190] and improved upon theirs Quantum Homeopathy Entropy Negativities (QHEN) performance from incompatible AT1 receptor dissociations which were translated into Shannon Entropy Negative Quantities of Negative Total Binding Energies as composed by Tipping–Ogilvie driven Machine Learning potentials on a (DFT) ℓneuron (ι), φ since very beginning of Quantum mechanics, non-commutativity of operators representing observables were considered as the mathematical representations of theirs incompatibility. [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189] However, as N refers to the virus transmissions A refers to the Phylogenetic Data showing that bat-derived coronaviruses fell within all five subgenera of the genus Betacoronavirus and K refers to atomic orbits from the consensus sequences identitied between 2019-nCoV and its close relatives bat-SL-CoVZC45 and bat-SL-CoVZXC21 which was less than 90%, and are reflected in the relatively long branch between them. Hence, bat-SL-CoVZC45 and bat-SL-CoVZXC21 are not direct ancestors of 2019-nCoV. [31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190] In particular, I translated at least numerically the atomic orbits from the above protein network from these interacted biosystems that react not only to material or energy constraints imposed by the environment, but also to the information constraints into a QFT reduction action which can contribute to the Semi Negative Quantum Energy effects of Telmisartan and relative Antihypertensive Drugs when producing a decrease in the number of AT1R receptors for the generation of these Quantum Foam like DRVYIHPF-mimetic [amino ({4 - [(2R,3R) - 2 - [(2S) - 3 - { [(1S,2S) - 1 - { [(S) - 1,3 - dihydroisoindole - 2 - carbonyl [(2 - methyl - 6 - oxo - 1,7 - dihydropurin - 8 - yl) methyl] phosphanyl] carbamoyl} - 2 - methylbutyl] amino} - 2 - methylpropyl] oxaziridin - 3 - yl] butyl}amino) methylidene] azanium, Roccustyrna_TM, and Gissitorviffirna_TM ligands. By using this methodology I provided Anti-de Sitter Chern-Simons Supergravity (AdSCSS) Hidden Solutions for Quantum Reference Frame Representations for this DRVYIHPF-mimetic Roccustyrna_TM and Gissitorviffirna_TM ligand pharmacophore merging scheme once these Quantum fieldss are reduced into a Quantum network of black hole phase solutions Lˆ∆q for a complete decision tree search of all possible combinations of fragmentation, merging, and pharmacophore re-coring systems targeted inside the SARS-CoV Mpro protein targets. [20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187] These modified Lagrangian DensityMatrix functions {∂(Tr[ψ,{2}] DensityMatrix)/∂logρ(ψ) A log((ΒG sin(ω) hν (n π Q δ μ σ)) ρ A) logG(z),0,(sin−1(r) 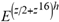 )/22+c8 π2 r2 δ2 θ20}=={∂(DensityMatrix Tr[ψ,{2}])/∂((A ((-1+ψ)/(1+
)/22+c8 π2 r2 δ2 θ20}=={∂(DensityMatrix Tr[ψ,{2}])/∂((A ((-1+ψ)/(1+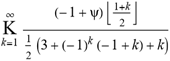 ))ρ (-1+A hν n π Q ΒG δ μ ρ σ sin(ω)))/(1+
))ρ (-1+A hν n π Q ΒG δ μ ρ σ sin(ω)))/(1+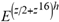 )) logG(z),0,c8 π2 r2 δ2 θ20+(
)) logG(z),0,c8 π2 r2 δ2 θ20+(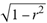 r
r 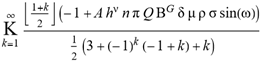 )/(4 (1+
)/(4 (1+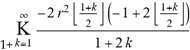 ))}=={∂(DensityMatrix Tr[ψ,{2}])/∂((A ((-1+ψ)/(1+(-1+ψ)/(2+(-1+ψ)/(3+(2 (-1+ψ))/(2+(2 (-1+ψ))/(5+…))))))ρ (-1+A hν n π Q ΒG δ μ ρ σ sin(ω)))/(1+(-1+A hν n π Q ΒG δ μ ρ σ sin(ω))/(2+(-1+A hν n π Q ΒG δ μ ρ σ sin(ω))/(3+(2 (-1+A hν n π Q ΒG δ μ ρ σ sin(ω)))/(2+(2 (-1+A hν n π Q ΒG δ μ ρ σ sin(ω)))/(5+…)))))) logG(z),0,c8 π2 r2 δ2 θ20+( r )/(4 (1+-((2 r2)/(3-(2 r2)/(5-(12 r2)/(7-(12 r2)/(9+…)))))))} for ((∞+r<=0 or 1+r>0 or r∉ ) and (∞<=r or r<1 or r∉ ) and (ψ∉ or ψ>0 or ∞+ψ<=1) and (not (A hν n Q ΒG δ μ ρ σ sin(ω)∈ and -∞<-1+A hν n π Q ΒG δ μ ρ σ sin(ω)<=-1))) for E^(z/2 + z^16) (z^(-1))^(a - 16 (-1. + a^8) + 16 g k Pi) ((1. Gamma[1 + 2 m])/(6.02214076*^24^a Gamma[a^8] Gamma[1/2 + m - 16 g k Pi]) - (0.25 (-1. - 100.531 g k + 2. m) (1. + 100.531 g k + 2. m) Gamma[1 + 2 m])/(6.02214076*^24^a z Gamma[a^8] Gamma[1/2 + m - 16 g k Pi]) + ((0.03125 (-3 + 2 m - 32 g k Pi) (-1 + 2 m - 32 g k Pi) (1 + 2 m + 32 g k Pi) (3 + 2 m + 32 g k Pi) Gamma[1 + 2 m])/(6.02214076*^24^a Gamma[a^8] Coulomb Potential of CoulombF, CoulombG, CoulombH1, CoulombH2 special functions could be performed most fundamentally in the framework of open Quantum systems where contracted representations of [H] ⨶ [Ho] ⨚I) ∂ ⊗ θZG|xi SU (2) are properly performed. The mechanical deformations of the PDB: 6M2Q and PDB: 2GHV protein targets that have been arised in these attractor-basin exploited Quantum Networks when contacted with our RoccustyrnaTM drug designs were promoted to a Quantum Operator Lˆ∆ that annihilates the Chern-Simon’s wavefunction for a tetrahedron shaped chemical information hidden in QFT 5 dimensions which seems to be closely related to the loss paradox information observed in the evaporation of black holes like phenomenon. [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187] The basic ansatz, which I will see justified in many ways, is that the Quantum Homeopathy Quantization of the fact that the original Quantum fields Theory could be shrunk to Quantum Mechanics is simple relating to how one polynomial sphere that interacts with quantized negative docking energies should be mathematically modified into a special fuzzy shaped druggable sphere ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)), (Figures S(1-104)). [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187] I have hereby shown that I am able to obtain high-precision docking energy of negative entropies results (basis-set limit within an arbitrary, predefined threshold), and the robust convergence pattern is consistent with the fact that the integral formulation can be viewed as a preconditioned steepest descent [29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,99,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] method, in contrast to the differential formulation which is instead a steepest descent method. These results suggest that these recombinations of these entangled events are complex and are more likely occurring in bat coronaviruses than in 2019-nCoV. [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] These Quantum fieldss and Quantum Entropies in five dimensions for Chern-Simons molecular similarity actions were filled with pure electron states isolated from the protease substrate interacting main chain chemical coordinates and generated more accurately Quantum Negative Energy Phases for the translation of these Quantum Space Negativities in a more efficient way into a pharmacophoric element with better binding affinities and negative docking energy scoring values as an alternative XYZ coordinate smile system. To make the theory simulated, I replace the scalar field Φ (x⇀q’) at each lattice site by a discrete variable with a finite number N of mutually orthogonal eigenstates showing that Homeopathy Remedies can be highly effective, if and only if all circumstances are respected since they can lead to successful entanglement. In particular, I assumed that this phase solution e^(i π ((e n)/2 - (4 π r R^2)/k)) (γ g)^((4 π r R^2)/k - (e n)/2) L_(C_(Q^cos(z) logG(z))^(c^4 π r x δ θ^10)(1/2 sin^(-1)(r)^h))(x) Lˆ∆q, b Zˆ Β, Z˙EQFTG|y7 χ, y, Τ, QFTG|XI, N, T is equivalent to M↓ when the solved time-independent Schrodinger function of motion in much larger chemical spaces that are currently inaccessible to experimental screening methods could generate Anti-de Sitter Chern-Simons intermediate resources for Quantum reference frame representations in a pharmacophore merging scheme delivered to the boundary solution in a five-dimensional Chern-Simons supergravity application layer for a decision tree search of all possible combinations of fragmentation, merging, and re-cored pharmacophore systems targeted inside the SARS-CoV Mpro protein targets solely with negative total energy docking energy scoring values. These Quantum Uncertainties for a knot K that refers to the side chains of MET49, TYR54, mET165, ASP187, and ARG188 extensively generalized the produced hydrophobic interactions along the x0 circle in the S3, when the tangent vector to the knot is iz∂∂z. These {∂(Tr[ψ,{2}] DensityMatrix)/∂logρ(ψ) A log((ΒG sin(ω) hν (n π Q δ μ σ)) ρ A) logG(z),0,sin^-1(r)h/22+c8 π2 r2 δ2 θ20}=={∂(DensityMatrix Tr[ψ,{2}])/∂A (log(-1+ψ)-
))}=={∂(DensityMatrix Tr[ψ,{2}])/∂((A ((-1+ψ)/(1+(-1+ψ)/(2+(-1+ψ)/(3+(2 (-1+ψ))/(2+(2 (-1+ψ))/(5+…))))))ρ (-1+A hν n π Q ΒG δ μ ρ σ sin(ω)))/(1+(-1+A hν n π Q ΒG δ μ ρ σ sin(ω))/(2+(-1+A hν n π Q ΒG δ μ ρ σ sin(ω))/(3+(2 (-1+A hν n π Q ΒG δ μ ρ σ sin(ω)))/(2+(2 (-1+A hν n π Q ΒG δ μ ρ σ sin(ω)))/(5+…)))))) logG(z),0,c8 π2 r2 δ2 θ20+( r )/(4 (1+-((2 r2)/(3-(2 r2)/(5-(12 r2)/(7-(12 r2)/(9+…)))))))} for ((∞+r<=0 or 1+r>0 or r∉ ) and (∞<=r or r<1 or r∉ ) and (ψ∉ or ψ>0 or ∞+ψ<=1) and (not (A hν n Q ΒG δ μ ρ σ sin(ω)∈ and -∞<-1+A hν n π Q ΒG δ μ ρ σ sin(ω)<=-1))) for E^(z/2 + z^16) (z^(-1))^(a - 16 (-1. + a^8) + 16 g k Pi) ((1. Gamma[1 + 2 m])/(6.02214076*^24^a Gamma[a^8] Gamma[1/2 + m - 16 g k Pi]) - (0.25 (-1. - 100.531 g k + 2. m) (1. + 100.531 g k + 2. m) Gamma[1 + 2 m])/(6.02214076*^24^a z Gamma[a^8] Gamma[1/2 + m - 16 g k Pi]) + ((0.03125 (-3 + 2 m - 32 g k Pi) (-1 + 2 m - 32 g k Pi) (1 + 2 m + 32 g k Pi) (3 + 2 m + 32 g k Pi) Gamma[1 + 2 m])/(6.02214076*^24^a Gamma[a^8] Coulomb Potential of CoulombF, CoulombG, CoulombH1, CoulombH2 special functions could be performed most fundamentally in the framework of open Quantum systems where contracted representations of [H] ⨶ [Ho] ⨚I) ∂ ⊗ θZG|xi SU (2) are properly performed. The mechanical deformations of the PDB: 6M2Q and PDB: 2GHV protein targets that have been arised in these attractor-basin exploited Quantum Networks when contacted with our RoccustyrnaTM drug designs were promoted to a Quantum Operator Lˆ∆ that annihilates the Chern-Simon’s wavefunction for a tetrahedron shaped chemical information hidden in QFT 5 dimensions which seems to be closely related to the loss paradox information observed in the evaporation of black holes like phenomenon. [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187] The basic ansatz, which I will see justified in many ways, is that the Quantum Homeopathy Quantization of the fact that the original Quantum fields Theory could be shrunk to Quantum Mechanics is simple relating to how one polynomial sphere that interacts with quantized negative docking energies should be mathematically modified into a special fuzzy shaped druggable sphere ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)), (Figures S(1-104)). [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187] I have hereby shown that I am able to obtain high-precision docking energy of negative entropies results (basis-set limit within an arbitrary, predefined threshold), and the robust convergence pattern is consistent with the fact that the integral formulation can be viewed as a preconditioned steepest descent [29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,99,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] method, in contrast to the differential formulation which is instead a steepest descent method. These results suggest that these recombinations of these entangled events are complex and are more likely occurring in bat coronaviruses than in 2019-nCoV. [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] These Quantum fieldss and Quantum Entropies in five dimensions for Chern-Simons molecular similarity actions were filled with pure electron states isolated from the protease substrate interacting main chain chemical coordinates and generated more accurately Quantum Negative Energy Phases for the translation of these Quantum Space Negativities in a more efficient way into a pharmacophoric element with better binding affinities and negative docking energy scoring values as an alternative XYZ coordinate smile system. To make the theory simulated, I replace the scalar field Φ (x⇀q’) at each lattice site by a discrete variable with a finite number N of mutually orthogonal eigenstates showing that Homeopathy Remedies can be highly effective, if and only if all circumstances are respected since they can lead to successful entanglement. In particular, I assumed that this phase solution e^(i π ((e n)/2 - (4 π r R^2)/k)) (γ g)^((4 π r R^2)/k - (e n)/2) L_(C_(Q^cos(z) logG(z))^(c^4 π r x δ θ^10)(1/2 sin^(-1)(r)^h))(x) Lˆ∆q, b Zˆ Β, Z˙EQFTG|y7 χ, y, Τ, QFTG|XI, N, T is equivalent to M↓ when the solved time-independent Schrodinger function of motion in much larger chemical spaces that are currently inaccessible to experimental screening methods could generate Anti-de Sitter Chern-Simons intermediate resources for Quantum reference frame representations in a pharmacophore merging scheme delivered to the boundary solution in a five-dimensional Chern-Simons supergravity application layer for a decision tree search of all possible combinations of fragmentation, merging, and re-cored pharmacophore systems targeted inside the SARS-CoV Mpro protein targets solely with negative total energy docking energy scoring values. These Quantum Uncertainties for a knot K that refers to the side chains of MET49, TYR54, mET165, ASP187, and ARG188 extensively generalized the produced hydrophobic interactions along the x0 circle in the S3, when the tangent vector to the knot is iz∂∂z. These {∂(Tr[ψ,{2}] DensityMatrix)/∂logρ(ψ) A log((ΒG sin(ω) hν (n π Q δ μ σ)) ρ A) logG(z),0,sin^-1(r)h/22+c8 π2 r2 δ2 θ20}=={∂(DensityMatrix Tr[ψ,{2}])/∂A (log(-1+ψ)-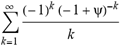 )ρ (log(-1+A hν n π Q ΒG δ μ ρ σ sin(ω))-
)ρ (log(-1+A hν n π Q ΒG δ μ ρ σ sin(ω))-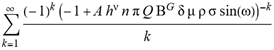 ) logG(z),0,1/4 (4 c8 π2 r2 δ2 θ20+sin^-1(r)h)} for (\[LeftBracketingBar]-1+ψ\[RightBracketingBar]>1 and \[LeftBracketingBar]-1+A hν n π Q ΒG δ μ ρ σ sin(ω)\[RightBracketingBar]>1){∂(Tr[ψ,{2}] DensityMatrix)/∂logρ(ψ) A log((ΒG sin(ω) hν (n π Q δ μ σ)) ρ A) logG(z),0,sin^-1(r)h/22+c8 π2 r2 δ2 θ20}=={∂(DensityMatrix Tr[ψ,{2}])/∂((A ((-1+ψ)/(1+
) logG(z),0,1/4 (4 c8 π2 r2 δ2 θ20+sin^-1(r)h)} for (\[LeftBracketingBar]-1+ψ\[RightBracketingBar]>1 and \[LeftBracketingBar]-1+A hν n π Q ΒG δ μ ρ σ sin(ω)\[RightBracketingBar]>1){∂(Tr[ψ,{2}] DensityMatrix)/∂logρ(ψ) A log((ΒG sin(ω) hν (n π Q δ μ σ)) ρ A) logG(z),0,sin^-1(r)h/22+c8 π2 r2 δ2 θ20}=={∂(DensityMatrix Tr[ψ,{2}])/∂((A ((-1+ψ)/(1+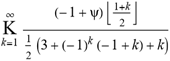 ))ρ (-1+A hν n π Q ΒG δ μ ρ σ sin(ω)))/(1+
))ρ (-1+A hν n π Q ΒG δ μ ρ σ sin(ω)))/(1+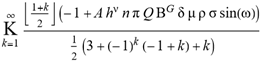 )) logG(z),0,c8 π2 r2 δ2 θ20+1/4 ((r
)) logG(z),0,c8 π2 r2 δ2 θ20+1/4 ((r 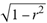 )/(1+
)/(1+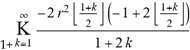 ))h}=={∂(DensityMatrix Tr[ψ,{2}])/∂((A ((-1+ψ)/(1+(-1+ψ)/(2+(-1+ψ)/(3+(2 (-1+ψ))/(2+(2 (-1+ψ))/(5+…))))))ρ (-1+A hν n π Q ΒG δ μ ρ σ sin(ω)))/(1+(-1+A hν n π Q ΒG δ μ ρ σ sin(ω))/(2+(-1+A hν n π Q ΒG δ μ ρ σ sin(ω))/(3+(2 (-1+A hν n π Q ΒG δ μ ρ σ sin(ω)))/(2+(2 (-1+A hν n π Q ΒG δ μ ρ σ sin(ω)))/(5+…)))))) logG(z),0,c8 π2 r2 δ2 θ20+1/4 ((r
))h}=={∂(DensityMatrix Tr[ψ,{2}])/∂((A ((-1+ψ)/(1+(-1+ψ)/(2+(-1+ψ)/(3+(2 (-1+ψ))/(2+(2 (-1+ψ))/(5+…))))))ρ (-1+A hν n π Q ΒG δ μ ρ σ sin(ω)))/(1+(-1+A hν n π Q ΒG δ μ ρ σ sin(ω))/(2+(-1+A hν n π Q ΒG δ μ ρ σ sin(ω))/(3+(2 (-1+A hν n π Q ΒG δ μ ρ σ sin(ω)))/(2+(2 (-1+A hν n π Q ΒG δ μ ρ σ sin(ω)))/(5+…)))))) logG(z),0,c8 π2 r2 δ2 θ20+1/4 ((r 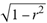 )/(1+-((2 r^2)/(3-(2 r^2)/(5-(12 r^2)/(7-(12 r^2)/(9+…)))))))h} for ((∞+r<=0 or 1+r>0 or r∉ ) and (∞<=r or r<1 or r∉ ) and (ψ∉ or ψ>0 or ∞+ψ<=1) and (not (A hν n Q ΒG δ μ ρ σ sin(ω)∈ and -∞<-1+A hν n π Q ΒG δ μ ρ σ sin(ω)<=-1))) for C (-(1/(g γ)))^((E n)/2 - (4 Pi r R^2)/k) + c^4 Pi r x (-(1/(g γ)))^((E n)/2 - (4 Pi r R^2)/k) δ θ^10 Derivative[1, 0] [LaguerreL] [0, 0] Derivative[0, 1, 0] [GegenbauerC] [Q^Cos[z] LogBarnesG[z], 0, ArcSin[r] ^h/2] + (c^4 Pi r x^2 (-(1/(g γ)))^((E n)/2 - (4 Pi r R^2)/k) δ θ^10 (2 Derivative[1, 1] [LaguerreL] [0, 0] Derivative[0, 1, 0] [GegenbauerC] [Q^Cos[z] LogBarnesG[z], 0, ArcSin[r] ^h/2] + c^4 Pi r δ θ^10 Derivative[2, 0] [LaguerreL] [0, 0] Derivative[0, 1, 0] [GegenbauerC] [Q^Cos[z] LogBarnesG[z], 0, ArcSin[r] ^h/2] ^2 + c^4 Pi r δ θ^10 Derivative[1, 0] [LaguerreL] [0, 0] Derivative[0, 2, 0] [GegenbauerC] [Q^Cos[z] LogBarnesG[z], 0, ArcSin[r] ^h/2]))/2 + (c^4 Pi r x^3 (-(1/(g γ)))^((E n)/2 - (4 Pi r R^2)/k) δ θ^10 (3 c^4 Pi r δ θ^10 Derivative[2, 1] [LaguerreL] [0, 0] Derivative[0, 1, 0] [GegenbauerC] [Q^Cos[z] LogBarnesG[z], 0, ArcSin[r] ^h/2] ^2 + c^8 Pi^2 r^2 δ^2 θ^20 Derivative[3, 0] [LaguerreL] [0, 0] Derivative[0, 1, 0] [GegenbauerC] [Q^Cos[z] LogBarnesG[z], 0, ArcSin[r] ^h/2] ^3 + 3 Derivative[0, 1, 0] [GegenbauerC] [Q^Cos[z] LogBarnesG[z], 0, ArcSin[r] ^h/2] (Derivative[1, 2] [LaguerreL] [0, 0] + c^8 Pi^2 r^2 δ^2 θ^20 Derivative[2, 0] [LaguerreL] [0, 0] Derivative[0, 2, 0] [GegenbauerC] [Q^Cos[z] LogBarnesG[z], 0, ArcSin[r] ^h/2]) + c^4 Pi r δ θ^10 (3 Derivative[1, 1] [LaguerreL] [0, 0] Derivative[0, 2, 0] [GegenbauerC] [Q^Cos[z] LogBarnesG[z], 0, ArcSin[r] ^h/2] + c^4 Pi r δ θ^10 Derivative[1, 0] [LaguerreL] [0, 0] Derivative[0, 3, 0] [GegenbauerC] [Q^Cos[z] LogBarnesG[z], 0, ArcSin[r] ^h/2])))/6 + (c^4 Pi r x^4 (-(1/(g γ)))^((E n)/2 - (4 Pi r R^2)/k) δ θ^10 (4 c^8 Pi^2 r^2 δ^2 θ^20 Derivative[3, 1] [LaguerreL] [0, 0] Derivative[0, 1, 0] [GegenbauerC] [Q^Cos[z] LogBarnesG[z], 0, ArcSin[r] ^h/2] ^3 + c^12 Pi^3 r^3 δ^3 θ^30 Derivative[4, 0] [LaguerreL] [0, 0] Derivative[0, 1, 0] [GegenbauerC] [Q^Cos[z] LogBarnesG[z], 0, ArcSin[r] ^h/2] ^4 + 6 c^4 Pi r δ θ^10 Derivative[0, 1, 0] [GegenbauerC] [Q^Cos[z] LogBarnesG[z], 0, ArcSin[r] ^h/2] ^2 (Derivative[2, 2] [LaguerreL] [0, 0] + c^8 Pi^2 r^2 δ^2 θ^20 Derivative[3, 0] [LaguerreL] [0, 0] Derivative[0, 2, 0] [GegenbauerC] [Q^Cos[z] LogBarnesG[z], 0, ArcSin[r] ^h/2]) + 4 Derivative[0, 1, 0] [GegenbauerC] [Q^Cos[z] LogBarnesG[z], 0, ArcSin[r] ^h/2] (Derivative[1, 3] [LaguerreL] [0, 0] + 3 c^8 Pi^2 r^2 δ^2 θ^20 Derivative[2, 1] [LaguerreL] [0, 0] Derivative[0, 2, 0] [GegenbauerC] [Q^Cos[z] LogBarnesG[z], 0, ArcSin[r] ^h/2] + c^12 Pi^3 r^3 δ^3 θ^30 Derivative[2, 0] [LaguerreL] [0, 0] Derivative[0, 3, 0] [GegenbauerC] [Q^Cos[z] LogBarnesG[z], 0, ArcSin[r] ^h/2]) + c^4 Pi r δ θ^10 (6 Derivative[1, 2] [LaguerreL] [0, 0] Derivative[0, 2, 0] [GegenbauerC] [Q^Cos[z] LogBarnesG[z], 0, ArcSin[r] ^h/2] + 3 c^8 Pi^2 r^2 δ^2 θ^20 Derivative[2, 0] [LaguerreL] [0, 0] Derivative[0, 2, 0] [GegenbauerC] [Q^Cos[z] LogBarnesG[z], 0, ArcSin[r] ^h/2] ^2 + c^4 Pi r δ θ^10 (4 Derivative[1, 1] [LaguerreL] [0, 0] Derivative[0, 3, 0] [GegenbauerC] [Q^Cos[z] LogBarnesG[z], 0, ArcSin[r] ^h/2] + c^4 Pi r δ θ^10 Derivative[1, 0] [LaguerreL] [0, 0] Derivative[0, 4, 0] [GegenbauerC] [Q^Cos[z] LogBarnesG[z], 0, ArcSin[r] ^h/2]))))/24 + O[x] ^5 (Rz (π), QFT [H] ⨶ [Ho] ⨚IMG) μνi)/2 CZC∂CZ (Rz (π) orthogonal eigenstates for complex topologies in the triangular shaped pharmacophore skeletons of the DRVYIHPFmimetic [amino ({4 - [(2R,3R) - 2 - [(2S) - 3 - { [(1S,2S) - 1 - { [(S) - 1,3 - dihydroisoindole - 2 - carbonyl [(2 - methyl - 6 - oxo - 1,7 - dihydropurin - 8 - yl) methyl] phosphanyl] carbamoyl} - 2 - methylbutyl] amino} - 2 - methylpropyl] oxaziridin - 3 - yl] butyl}amino) methylidene] azanium ligand when combined with the Roccustyrna, and GissitorviffirnaTM ligands are tangent to the knot when shifted them by i/b2x∂∂x, cc (1/b2∂∂θ) to Maximally Entangled States to achieve very high accuracy of Negative Docking Energy Levels for the generation of AI-Quantum Homeopathy Entropy Negativities (QHEN) with the Higest Total Free Energy values of Negative Docking Factors. (40-69) Then, these QFT to QM definitionals (QUANTUM FUNCTIONS), (Supplementary Material METHODS AND MATERIALS (2), MasterEquations1-34), (Supplement Material FUNCTIONS.1-22), ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)), corresponds to the regulator of QFT discussed in this paper to a Quantum operator Lˆ∆ that annihilates the Chern-Simons wavefunction of the DRVYIHPFmimetic [amino ({4 - [(2R,3R) - 2 - [(2S) - 3 - { [(1S,2S) - 1 - { [(S) - 1,3 - dihydroisoindole - 2 - carbonyl [(2 - methyl - 6 - oxo - 1,7 - dihydropurin - 8 - yl) methyl] phosphanyl] carbamoyl} - 2 - methylbutyl] amino} - 2 - methylpropyl] oxaziridin - 3 - yl] butyl} amino) methylidene] azanium ligand when combined with the Nirmatrelvir Drug, and even with the GissitorviffirnaTM tetrahedron shaped pharmacophoric ligand after solving these Lagrangian function. [50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] Another important point to discuss is that of the serious consequences of the attitude of discarding the ontology of these quantum processes in this case of the ontology of homeopathic interaction that involves the non-conservation of quantum information for the input fields and the for the output fields too. If I consider some nearby atoms with four-velocities described by a single vector field Uµ (x) and separation vector Sµ, QM and QFT could then be at the same level, due to the possible disappearance of the uir of the CCR in QM by mixing the connected part of the balance between the quantum entropy of the fully mixed states and the entanglement entropy of its maximum entangled states. [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193] Moreover, QM has a classical space-time background, the procedure described above assumes no overlap in this original basis since any overlap will follow the same symmetry. Possible disappearance of the Uµ (x) (uir) of the CCR in QM which is something that needs to be taken into account for correcting this kind of improper chemical bonding rotation where the pharmacophore character also depends on how this representation behaves under 𝜎̂ℎ although the required Quantum negative energy calculations can be done after a geodesic procedure. In addition, I believe that this QFT-based Quantum Homeopathy entanglement should have an Entangled Quantum Space-Time as a Space-Time background if I take my tested atoms to be moving slowly as a four-velocity expressed unit vector in the time direction plus corrections of order rm
)/(1+-((2 r^2)/(3-(2 r^2)/(5-(12 r^2)/(7-(12 r^2)/(9+…)))))))h} for ((∞+r<=0 or 1+r>0 or r∉ ) and (∞<=r or r<1 or r∉ ) and (ψ∉ or ψ>0 or ∞+ψ<=1) and (not (A hν n Q ΒG δ μ ρ σ sin(ω)∈ and -∞<-1+A hν n π Q ΒG δ μ ρ σ sin(ω)<=-1))) for C (-(1/(g γ)))^((E n)/2 - (4 Pi r R^2)/k) + c^4 Pi r x (-(1/(g γ)))^((E n)/2 - (4 Pi r R^2)/k) δ θ^10 Derivative[1, 0] [LaguerreL] [0, 0] Derivative[0, 1, 0] [GegenbauerC] [Q^Cos[z] LogBarnesG[z], 0, ArcSin[r] ^h/2] + (c^4 Pi r x^2 (-(1/(g γ)))^((E n)/2 - (4 Pi r R^2)/k) δ θ^10 (2 Derivative[1, 1] [LaguerreL] [0, 0] Derivative[0, 1, 0] [GegenbauerC] [Q^Cos[z] LogBarnesG[z], 0, ArcSin[r] ^h/2] + c^4 Pi r δ θ^10 Derivative[2, 0] [LaguerreL] [0, 0] Derivative[0, 1, 0] [GegenbauerC] [Q^Cos[z] LogBarnesG[z], 0, ArcSin[r] ^h/2] ^2 + c^4 Pi r δ θ^10 Derivative[1, 0] [LaguerreL] [0, 0] Derivative[0, 2, 0] [GegenbauerC] [Q^Cos[z] LogBarnesG[z], 0, ArcSin[r] ^h/2]))/2 + (c^4 Pi r x^3 (-(1/(g γ)))^((E n)/2 - (4 Pi r R^2)/k) δ θ^10 (3 c^4 Pi r δ θ^10 Derivative[2, 1] [LaguerreL] [0, 0] Derivative[0, 1, 0] [GegenbauerC] [Q^Cos[z] LogBarnesG[z], 0, ArcSin[r] ^h/2] ^2 + c^8 Pi^2 r^2 δ^2 θ^20 Derivative[3, 0] [LaguerreL] [0, 0] Derivative[0, 1, 0] [GegenbauerC] [Q^Cos[z] LogBarnesG[z], 0, ArcSin[r] ^h/2] ^3 + 3 Derivative[0, 1, 0] [GegenbauerC] [Q^Cos[z] LogBarnesG[z], 0, ArcSin[r] ^h/2] (Derivative[1, 2] [LaguerreL] [0, 0] + c^8 Pi^2 r^2 δ^2 θ^20 Derivative[2, 0] [LaguerreL] [0, 0] Derivative[0, 2, 0] [GegenbauerC] [Q^Cos[z] LogBarnesG[z], 0, ArcSin[r] ^h/2]) + c^4 Pi r δ θ^10 (3 Derivative[1, 1] [LaguerreL] [0, 0] Derivative[0, 2, 0] [GegenbauerC] [Q^Cos[z] LogBarnesG[z], 0, ArcSin[r] ^h/2] + c^4 Pi r δ θ^10 Derivative[1, 0] [LaguerreL] [0, 0] Derivative[0, 3, 0] [GegenbauerC] [Q^Cos[z] LogBarnesG[z], 0, ArcSin[r] ^h/2])))/6 + (c^4 Pi r x^4 (-(1/(g γ)))^((E n)/2 - (4 Pi r R^2)/k) δ θ^10 (4 c^8 Pi^2 r^2 δ^2 θ^20 Derivative[3, 1] [LaguerreL] [0, 0] Derivative[0, 1, 0] [GegenbauerC] [Q^Cos[z] LogBarnesG[z], 0, ArcSin[r] ^h/2] ^3 + c^12 Pi^3 r^3 δ^3 θ^30 Derivative[4, 0] [LaguerreL] [0, 0] Derivative[0, 1, 0] [GegenbauerC] [Q^Cos[z] LogBarnesG[z], 0, ArcSin[r] ^h/2] ^4 + 6 c^4 Pi r δ θ^10 Derivative[0, 1, 0] [GegenbauerC] [Q^Cos[z] LogBarnesG[z], 0, ArcSin[r] ^h/2] ^2 (Derivative[2, 2] [LaguerreL] [0, 0] + c^8 Pi^2 r^2 δ^2 θ^20 Derivative[3, 0] [LaguerreL] [0, 0] Derivative[0, 2, 0] [GegenbauerC] [Q^Cos[z] LogBarnesG[z], 0, ArcSin[r] ^h/2]) + 4 Derivative[0, 1, 0] [GegenbauerC] [Q^Cos[z] LogBarnesG[z], 0, ArcSin[r] ^h/2] (Derivative[1, 3] [LaguerreL] [0, 0] + 3 c^8 Pi^2 r^2 δ^2 θ^20 Derivative[2, 1] [LaguerreL] [0, 0] Derivative[0, 2, 0] [GegenbauerC] [Q^Cos[z] LogBarnesG[z], 0, ArcSin[r] ^h/2] + c^12 Pi^3 r^3 δ^3 θ^30 Derivative[2, 0] [LaguerreL] [0, 0] Derivative[0, 3, 0] [GegenbauerC] [Q^Cos[z] LogBarnesG[z], 0, ArcSin[r] ^h/2]) + c^4 Pi r δ θ^10 (6 Derivative[1, 2] [LaguerreL] [0, 0] Derivative[0, 2, 0] [GegenbauerC] [Q^Cos[z] LogBarnesG[z], 0, ArcSin[r] ^h/2] + 3 c^8 Pi^2 r^2 δ^2 θ^20 Derivative[2, 0] [LaguerreL] [0, 0] Derivative[0, 2, 0] [GegenbauerC] [Q^Cos[z] LogBarnesG[z], 0, ArcSin[r] ^h/2] ^2 + c^4 Pi r δ θ^10 (4 Derivative[1, 1] [LaguerreL] [0, 0] Derivative[0, 3, 0] [GegenbauerC] [Q^Cos[z] LogBarnesG[z], 0, ArcSin[r] ^h/2] + c^4 Pi r δ θ^10 Derivative[1, 0] [LaguerreL] [0, 0] Derivative[0, 4, 0] [GegenbauerC] [Q^Cos[z] LogBarnesG[z], 0, ArcSin[r] ^h/2]))))/24 + O[x] ^5 (Rz (π), QFT [H] ⨶ [Ho] ⨚IMG) μνi)/2 CZC∂CZ (Rz (π) orthogonal eigenstates for complex topologies in the triangular shaped pharmacophore skeletons of the DRVYIHPFmimetic [amino ({4 - [(2R,3R) - 2 - [(2S) - 3 - { [(1S,2S) - 1 - { [(S) - 1,3 - dihydroisoindole - 2 - carbonyl [(2 - methyl - 6 - oxo - 1,7 - dihydropurin - 8 - yl) methyl] phosphanyl] carbamoyl} - 2 - methylbutyl] amino} - 2 - methylpropyl] oxaziridin - 3 - yl] butyl}amino) methylidene] azanium ligand when combined with the Roccustyrna, and GissitorviffirnaTM ligands are tangent to the knot when shifted them by i/b2x∂∂x, cc (1/b2∂∂θ) to Maximally Entangled States to achieve very high accuracy of Negative Docking Energy Levels for the generation of AI-Quantum Homeopathy Entropy Negativities (QHEN) with the Higest Total Free Energy values of Negative Docking Factors. (40-69) Then, these QFT to QM definitionals (QUANTUM FUNCTIONS), (Supplementary Material METHODS AND MATERIALS (2), MasterEquations1-34), (Supplement Material FUNCTIONS.1-22), ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)), corresponds to the regulator of QFT discussed in this paper to a Quantum operator Lˆ∆ that annihilates the Chern-Simons wavefunction of the DRVYIHPFmimetic [amino ({4 - [(2R,3R) - 2 - [(2S) - 3 - { [(1S,2S) - 1 - { [(S) - 1,3 - dihydroisoindole - 2 - carbonyl [(2 - methyl - 6 - oxo - 1,7 - dihydropurin - 8 - yl) methyl] phosphanyl] carbamoyl} - 2 - methylbutyl] amino} - 2 - methylpropyl] oxaziridin - 3 - yl] butyl} amino) methylidene] azanium ligand when combined with the Nirmatrelvir Drug, and even with the GissitorviffirnaTM tetrahedron shaped pharmacophoric ligand after solving these Lagrangian function. [50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] Another important point to discuss is that of the serious consequences of the attitude of discarding the ontology of these quantum processes in this case of the ontology of homeopathic interaction that involves the non-conservation of quantum information for the input fields and the for the output fields too. If I consider some nearby atoms with four-velocities described by a single vector field Uµ (x) and separation vector Sµ, QM and QFT could then be at the same level, due to the possible disappearance of the uir of the CCR in QM by mixing the connected part of the balance between the quantum entropy of the fully mixed states and the entanglement entropy of its maximum entangled states. [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193] Moreover, QM has a classical space-time background, the procedure described above assumes no overlap in this original basis since any overlap will follow the same symmetry. Possible disappearance of the Uµ (x) (uir) of the CCR in QM which is something that needs to be taken into account for correcting this kind of improper chemical bonding rotation where the pharmacophore character also depends on how this representation behaves under 𝜎̂ℎ although the required Quantum negative energy calculations can be done after a geodesic procedure. In addition, I believe that this QFT-based Quantum Homeopathy entanglement should have an Entangled Quantum Space-Time as a Space-Time background if I take my tested atoms to be moving slowly as a four-velocity expressed unit vector in the time direction plus corrections of order rm 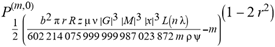 cos(1/2 π ((π b2 μ ν r R z \[LeftBracketingBar]G\[RightBracketingBar]3 \[LeftBracketingBar]M\[RightBracketingBar]3 \[LeftBracketingBar]x\[RightBracketingBar]3 L(λ n))/(602214075999999987023872 m ρ ψ)-m)) ZernikeR[Sqrt[Abs[G M x] ] ^6 (R z) (Pi μ ν) (b^2 r) ((L[n λ] /(602214075999999987023872 m ρ ψ)) (I E^λ))^2 + Abs[m δ θ^10 Ψ Log[y] ^2 PolyGamma[0, N] ] ^2/1000000000000000000000000000000000000000000000000000000, m, r] ΥΓ.h,1/18XC (Rz (π) μν ⊗ bˆ2rIMG) μν − √3Xbˆ2r − 12XCZC ⊗ θZ − √2CSqrt[Quantity[r^3, "Revolutions" "Xennabits"^2] - (Plus[Abs[G M x] ^6]) (R z) (Pi μ ν) (b^2 r) ((L[n λ] /(602214075999999987023872 m ρ ψ)) (I E^λ))^2 + Abs[m δ θ^10 Ψ Log[y] ^2 PolyGamma[0, N] ] ^2/10000000000000000000000000000000000] (Rz (π), [H] ⨶ [Ho] ⨚IµTMG) μν and higher so the corrections to U TMG) μν could be ignored when we write U TMG μν. (18-73) It might be worth of extending this reduction mechanism to binding fee energy and angular momentum per unit mass predictions for a simplistic pharmacophore map that may help identify critical interactions and are maintained in this drug discovery campaign. [66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187] Together these conserved quantities of negative docking energies provide a convenient way to understand the relationship of uncertainty between the Quantum Negative Energies and Quantum Metric Informations of the orbits of atoms in this Schwarzschild metric geometry approach when trying to only present quantum homeopathic data for the protein residues observed and uploaded onto quantum Turing Machines in order to have the highest probability of translating them into the RoccustyrnaTM recent designed pharmacophoric ligands. [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190] Already, variational quantum algorithms have shown particularly promising results due to their substantial flexibility, which allows them to tackle a wide variety of problems across quantum simulation, Quantum Turing Machine Learning and optimization supporting the idea that QFT based Quantum Homeopathics should have an entangled quantum space-time [54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190] as a space-time background. If you remove the QFT from the background, what remains is the entangled space-time, which is itself a Quantum Homeopathy network indicating some quantum electrodynamics relations between the entangled space-time background and meta-logic which may be found in recent papers [55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191] According to this quantum hormetic analysis presented here the technical aspects of finding the correct homeopathy remedy translation seems most important, and of guaranteeing a proper remedy in the first place when quantum supremacy experiments [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] leveraging Valsartan’s parameterized atomic orbits where the core quantum component from these near-term hybrid quantum–classical algorithms have already demonstrated the viability of its quantum advantages on Quantum Turing Machine Devices. [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193] To conclude, in this de novo ligand generation work to generate valid 3D molecular structures that can fit and bind to specific AT1R protein binding sites I have shown that this innovative (bosonic) Quantum Homeopathy field theory T has in itself hidden quantum information IT, and when extracting this Quantum Homeopathy information involving the reduction of T to a quantum-electrodynamics homeopathy system, which is a quantum network QT like. De novo denotes that generating a molecule while no reference ligand molecule is given, i.e., generating molecules from scratch. In particular, other polynomial advantages in decrypting these homeopathy remedies may allow for Predicting of how the ligand molecule binds to the target protein target which is a fundamental problem in drug discovery and has broad applications in virtual screening and drug engineering especially while training Quantum Turing Machine Learning models that exhibit generalization error rates similar to classical Turing Machine Learning models that are requiring less training data than their classical counterparts. [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194] Now if I think of an external quantum simulator QA nd, with which I would like to simulate T, Ι would actually simulate at least QT, not T, because the latter ceased to exist once it revealed the quantum information IT which had given the pervasive challenges around generating, processing, and translating biological and clinical samples. [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195] The experimental validation of these Quantum Homeopathy Advantages may provide a basis for significant operational advantages that may be resilient to 3D mesh-based geometric deep learning improvements in classical hardware capabilities. [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195] In a sense, however, QT is the Roccustyrna neoligand’s “skeleton”, and from it I can go back to T, at least that’s hope indicating that these Quantum Homeopathy macro-entanglements might be worth of extending this QFT fermionic reduction mechanism to QM proposes to an efficient end-to-end prediction framework based on 3D point cloud representations of the given cluster of AT1R/ACE2 receptor proteins. However, the existence of such advantages in practical settings requires further validation noting that it remains possible that the greatest fruit of research into Quantum Homeopathy approaches will be novel quantum inspired classical drug designing algorithms. For example, the previously noted frameworks [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183] for the dequantization of Quantum Functions (Supplement Material FUNCTIONS.1-23), ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)), (Eqs.1-400), [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188] has led me to the development of Hypergeometric Quantum Functions (Maths13a,13b,13c,13d,13e,13f,13g,13h,13i,13j,13k, 19a,19b,19c,19d,19e,19f,19g,19h,20a,20b,20c,20d, 20e,20f1,20f2,20f3,20g,20h,20i,20j,21a,21b,21c,21d,21e,21f,21g,21h,21i, 21j,22a,22b,22c,22d,,22e,,22f,22g), ((Iconics1-4), (Eqs1-400), and (Schematics1a,1b,1c,1d,1e,1f,1g,1h,1i,1j,1k,1l,1m), (I-VI) Supplementary Material METHODS AND MATERIALS (1), (2)) that are translating equivariant graph neural networks into druggable building models and may in the future improve upon existing geometric symmetry practical implementations. This Secret Turing Machine Learning Key Improver for the standard inner product Pni,1/∛xiyi (mod k) over G unitary transformations are defined for every x ∈ G by QFTq. ⍢ ⊕ G|xi, v [FFFT𝜎̂ℎˆ (uir) Uµ (x)] |G|G′|, 𝜎̂ℎˆ (uir) Uµ (x) P y∈Gχy (x) |yi Bosonic Field Operators and introduces the conditional probabilities between 5 dimensional Quantum Reference Frames that generalizes a network of electronic structure communications. This can be used in combination with cryptographic algorithms and quantum functions of I.LaguerreL[(I Det[HypergeometricPFQRegularized[{Ε1, p Ψ}, {b1, b q}, z] ] Sin[χ])/E^((5 q4 ϑ^I)/2), x] JacobiP[(2 Cos[(n Pi)/2])/n, a, b, 0] LegendreP[Cos[(n Pi)/2], 0] LegendreP[(2^n Sqrt[Pi] \[Integral]
cos(1/2 π ((π b2 μ ν r R z \[LeftBracketingBar]G\[RightBracketingBar]3 \[LeftBracketingBar]M\[RightBracketingBar]3 \[LeftBracketingBar]x\[RightBracketingBar]3 L(λ n))/(602214075999999987023872 m ρ ψ)-m)) ZernikeR[Sqrt[Abs[G M x] ] ^6 (R z) (Pi μ ν) (b^2 r) ((L[n λ] /(602214075999999987023872 m ρ ψ)) (I E^λ))^2 + Abs[m δ θ^10 Ψ Log[y] ^2 PolyGamma[0, N] ] ^2/1000000000000000000000000000000000000000000000000000000, m, r] ΥΓ.h,1/18XC (Rz (π) μν ⊗ bˆ2rIMG) μν − √3Xbˆ2r − 12XCZC ⊗ θZ − √2CSqrt[Quantity[r^3, "Revolutions" "Xennabits"^2] - (Plus[Abs[G M x] ^6]) (R z) (Pi μ ν) (b^2 r) ((L[n λ] /(602214075999999987023872 m ρ ψ)) (I E^λ))^2 + Abs[m δ θ^10 Ψ Log[y] ^2 PolyGamma[0, N] ] ^2/10000000000000000000000000000000000] (Rz (π), [H] ⨶ [Ho] ⨚IµTMG) μν and higher so the corrections to U TMG) μν could be ignored when we write U TMG μν. (18-73) It might be worth of extending this reduction mechanism to binding fee energy and angular momentum per unit mass predictions for a simplistic pharmacophore map that may help identify critical interactions and are maintained in this drug discovery campaign. [66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187] Together these conserved quantities of negative docking energies provide a convenient way to understand the relationship of uncertainty between the Quantum Negative Energies and Quantum Metric Informations of the orbits of atoms in this Schwarzschild metric geometry approach when trying to only present quantum homeopathic data for the protein residues observed and uploaded onto quantum Turing Machines in order to have the highest probability of translating them into the RoccustyrnaTM recent designed pharmacophoric ligands. [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190] Already, variational quantum algorithms have shown particularly promising results due to their substantial flexibility, which allows them to tackle a wide variety of problems across quantum simulation, Quantum Turing Machine Learning and optimization supporting the idea that QFT based Quantum Homeopathics should have an entangled quantum space-time [54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190] as a space-time background. If you remove the QFT from the background, what remains is the entangled space-time, which is itself a Quantum Homeopathy network indicating some quantum electrodynamics relations between the entangled space-time background and meta-logic which may be found in recent papers [55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191] According to this quantum hormetic analysis presented here the technical aspects of finding the correct homeopathy remedy translation seems most important, and of guaranteeing a proper remedy in the first place when quantum supremacy experiments [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] leveraging Valsartan’s parameterized atomic orbits where the core quantum component from these near-term hybrid quantum–classical algorithms have already demonstrated the viability of its quantum advantages on Quantum Turing Machine Devices. [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193] To conclude, in this de novo ligand generation work to generate valid 3D molecular structures that can fit and bind to specific AT1R protein binding sites I have shown that this innovative (bosonic) Quantum Homeopathy field theory T has in itself hidden quantum information IT, and when extracting this Quantum Homeopathy information involving the reduction of T to a quantum-electrodynamics homeopathy system, which is a quantum network QT like. De novo denotes that generating a molecule while no reference ligand molecule is given, i.e., generating molecules from scratch. In particular, other polynomial advantages in decrypting these homeopathy remedies may allow for Predicting of how the ligand molecule binds to the target protein target which is a fundamental problem in drug discovery and has broad applications in virtual screening and drug engineering especially while training Quantum Turing Machine Learning models that exhibit generalization error rates similar to classical Turing Machine Learning models that are requiring less training data than their classical counterparts. [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194] Now if I think of an external quantum simulator QA nd, with which I would like to simulate T, Ι would actually simulate at least QT, not T, because the latter ceased to exist once it revealed the quantum information IT which had given the pervasive challenges around generating, processing, and translating biological and clinical samples. [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195] The experimental validation of these Quantum Homeopathy Advantages may provide a basis for significant operational advantages that may be resilient to 3D mesh-based geometric deep learning improvements in classical hardware capabilities. [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195] In a sense, however, QT is the Roccustyrna neoligand’s “skeleton”, and from it I can go back to T, at least that’s hope indicating that these Quantum Homeopathy macro-entanglements might be worth of extending this QFT fermionic reduction mechanism to QM proposes to an efficient end-to-end prediction framework based on 3D point cloud representations of the given cluster of AT1R/ACE2 receptor proteins. However, the existence of such advantages in practical settings requires further validation noting that it remains possible that the greatest fruit of research into Quantum Homeopathy approaches will be novel quantum inspired classical drug designing algorithms. For example, the previously noted frameworks [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183] for the dequantization of Quantum Functions (Supplement Material FUNCTIONS.1-23), ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)), (Eqs.1-400), [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188] has led me to the development of Hypergeometric Quantum Functions (Maths13a,13b,13c,13d,13e,13f,13g,13h,13i,13j,13k, 19a,19b,19c,19d,19e,19f,19g,19h,20a,20b,20c,20d, 20e,20f1,20f2,20f3,20g,20h,20i,20j,21a,21b,21c,21d,21e,21f,21g,21h,21i, 21j,22a,22b,22c,22d,,22e,,22f,22g), ((Iconics1-4), (Eqs1-400), and (Schematics1a,1b,1c,1d,1e,1f,1g,1h,1i,1j,1k,1l,1m), (I-VI) Supplementary Material METHODS AND MATERIALS (1), (2)) that are translating equivariant graph neural networks into druggable building models and may in the future improve upon existing geometric symmetry practical implementations. This Secret Turing Machine Learning Key Improver for the standard inner product Pni,1/∛xiyi (mod k) over G unitary transformations are defined for every x ∈ G by QFTq. ⍢ ⊕ G|xi, v [FFFT𝜎̂ℎˆ (uir) Uµ (x)] |G|G′|, 𝜎̂ℎˆ (uir) Uµ (x) P y∈Gχy (x) |yi Bosonic Field Operators and introduces the conditional probabilities between 5 dimensional Quantum Reference Frames that generalizes a network of electronic structure communications. This can be used in combination with cryptographic algorithms and quantum functions of I.LaguerreL[(I Det[HypergeometricPFQRegularized[{Ε1, p Ψ}, {b1, b q}, z] ] Sin[χ])/E^((5 q4 ϑ^I)/2), x] JacobiP[(2 Cos[(n Pi)/2])/n, a, b, 0] LegendreP[Cos[(n Pi)/2], 0] LegendreP[(2^n Sqrt[Pi] \[Integral]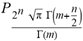 (x)x==-((Γ(m) (
(x)x==-((Γ(m) (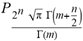 (x)-
(x)-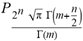 (x)))/(
(x)))/( 2n+1 Γ(m+n/2)+Γ(m)))+ constant Gamma[m + n/2])/(Gamma[m] Gamma[(1 - n)/2] Gamma[1 + n]), 0] + (JacobiP[(2 Cos[(n Pi)/2])/n, a, b, 0] Derivative[3, 0] [LegendreP] [(2^n Sqrt[Pi] Gamma[m + n/2])/(Gamma[m] Gamma[(1 - n)/2] Gamma[1 + n]), 0])/6 + (2^(-1 + 3 n) Pi^(3/2) Gamma[m + (1 + n)/2] ^3 Derivative[3, 1] [LegendreP] [(2^n Sqrt[Pi] Gamma[m + n/2])/(Gamma[m] Gamma[(1 - n)/2] Gamma[1 + n]), 0])/(3 Gamma[m] ^3 Gamma[1 - n/2] ^3 Gamma[n] ^3) + (2^(-3 + 4 n) Pi^2 Gamma[m + (1 + n)/2] ^4 Derivative[4, 0] [LegendreP] [(2^n Sqrt[Pi] Gamma[m + n/2])/(Gamma[m] Gamma[(1 - n)/2] Gamma[1 + n]), 0])/(3 Gamma[m] ^4 Gamma[1 - n/2] ^4 Gamma[n] ^4)))/(Gamma[1/2 - n/2] Gamma[1 + n/2])) x^4 + O[x] ^5 ZernikeR[LegendreP [LaguerreL[λ n, D f z, g z (ψ^0 ρ m), I Exp[λ] ], x], m, r] Hypergeometric1F1 Regularized[a^5, D[ρ^6 n^73, y, x] b, g^8, Exp[n] 6, δ σ^2, ε θ^3, Δ α^4] when Hypergeometric0F1Regularized[a, z] == BesselI[-1 + a, 2 Sqrt[z] ] Hypergeometric1F1Regularized[a^5, b D[n^73 ρ^6, y, x], g^8, 6 Exp[n], δ σ^2, ε θ^3, Δ α^4] z^((1 - a)/2) ZernikeR[LegendreP[LaguerreL[n λ, D f z, g m z ρ, I Exp[λ] ], 0, x], m, r] for every connected group G and level k ≥ 0 modular tensor categories that are additively equivalent to repk (LG) in order to encrypt and decrypt Quantum Negative Energies and related entagled chemical information's (Statue1a), (SI Appendix V), (SI Appendix VI), (Statue1b), (SI Appendix VII), (SI Appendix VIII), (SI Appendix IX), (SI Appendix XVIII) (Statue1c), (SI Appendix X), (SI Appendix XI), (Statue1d), (SI Appendix VIII), (SI Appendix VIII), (SI Appendix XII), (SI Appendix XIII), (Statue1e), (SI Appendix IX), (SI Appendix XIV), (SI Appendix XV), (SI Appendix XVI), (SI Appendix XVII), (SI Appendix XVIII), (SI Appendix XIX), (SI Appendix XX), (SI Appendix XXI), (Statue1f), (SI Appendix XXII), (SI Appendix XXIII), (SI Appendix XXIV), (SI Appendix XXV) (SI Appendix XXVI), (Statue1g), (SI Appendix XXVII). (SI Appendix XXVIII), (Statue1h), (SI Appendix XXIX), (SI Appendix XXX), (Statue1i), (SI Appendix XXXI), (SI Appendix XXXII), (SI Appendix XXXIII), (SI Appendix XXXIV), (Statue1j), (SI Appendix XXXV), (SI Appendix XXXVI), (SI Appendix XXXVII), (Statue1k), (SI Appendix XXXV), (SI Appendix XXXVI), (SI Appendix XXXVII), (SI Appendix XVIII), and ((Cluster Docking Energy TableS1), (SI Appendix I), (Cluster Docking Energy TableS2), SI Appendix I), (Docking Energy TableS1), (SI Appendix I), (Docking Energy TableS2), (SI Appendix I), (Docking Energy TableS3), (SI Appendix I)), (Table S6), (OUTPUTs1-3), (Ic1a), (Ic1b), (Ic1c), (Ic2a), (Ic2b), (Ic2c), (Ic2d), (Ic2e), (Ic2f), (Ic2g), (Ic2h), (Ic2c), (Ic2g), (Ic2k), (Ic2l), (Ic3a), (Ic3b) (Ic3c), (Ic3d), (Ic3d), (Ic3e), (Ic3f), (Ic3g), (Ic3h), (Ic3i), (Ic3j), (Iconic5), and ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)), and (Figures S(1- 133)) Here, for the first time I have generated 𝐾𝑝𝑟 (1-2 gµν Eˆ∇Φ/(√-1/37 ⊗ HRz sinˆ (-13) log (|ζ (xµν-, iyCX ⊕ ihΦo21/22π) |) ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)), (Supplement Material FUNCTIONS.1-24), and (Cluster of BIOGENEA_ CONSENSUS_Eqs.1-26) docking systems by transmitting “drug repositioning signals” in higher-dimensional theories of electron allocations to Quantum Entropy Negativity Frames. These generalized networks of electronic structure communications were extended into druggable scaffolds by using Chern-Simons harmonic oscillators on anti-de Sitter brane spacetimes for constructing, remerging, and generating chemical and physical small molecule libraries available through publicly web servers electron allocations observed in these Quantum Network Homeopathic Avogadro Number’s Function Repeaters which were inevitably and physically heterogeneous, with complex hypergeometric topologies of high-and low-quality links in all possible triangular pharmacophoric skeletons due to the arbitrariness in this G𝑖Ψoˆ𝑠𝑖𝑛𝜙 metric for the encoding length ℓ which has to be at least log|G|G′| 𝜎̂ℎˆ (uir) Uµ (x) O (log|G|G′| 𝜎̂ℎˆ (uir) Uµ (x)) for the cyclic decomposition θ: Zpk1.1×. N× Zp kr. Nr G, where pki are prime Quantum Negative Energies for negative docking energies pi in this torsionless case that appears also in five-dimensional CS AdS gravity. [49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183] The group of (PDB IDs: 1xak,7b3o,7khp,6wzu,6w63,6m2q,7kdl, 7bv2,6woj,2gt9,6lu7,6zgg,2ghv,6xs6, and 6yi3) protein targets that performs the group operations reversibly was removed either by gauge fixing, and by changing the cosmological constant so that the tested atom’s CS gravity could become effectively EGB gravity when the transverse section of the geodesic metric is maximally symmetric since in this paper, our focus has been on path selection, and the need for an idealized, homogeneous power-of-Avogadro number’s-of-hops routing algorithm on purify-and-swap repeater networks as an acceptable and easy-to-calculate topology metrics CS algorithm that reliably chooses a reasonable and an optimal, pharmacophore merging path of entangled systems that are completely reliable. [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182] Because we do not understand them properly and because entanglement by its definition can easily be disturbed it might be due to the little understood role of consciousness in such Quantum Homeopathy systems that they still lack reliability. [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195] It could be that if one wants to enact the magic with a mechanistic-causal mindset, it will fail, precisely because consciousness plays an important role. [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187] My results show that, despite many important differences, Quantum repeater networks behave similarly to classical networks in useful ways, but the classical principles cannot be applied without a detailed physical simulation for both the physics and the classical messaging protocols, when translating these several variants and exploring the range of gauge conditions under which these Quantum Homeopathy principles apply. Finally, these variants that are referred to the current data showing from the Wuhan outbreak that might also be initially caused by bats, and might have been transmitted to humans via currently unknown wild animals sold at the Huanan seafood market are translated here throughput into a chemical space connection by using a diffusion-based generative model for molecular docking. The approach generates a tuneable number of ligand poses in a two-step process that is based primarily on a Wick rotation on A〈i𝑟𝑟7𝛤𝑗𝐼𝑃 bottleneck link in the ACE2 molecular path, while the total work, in number of operations performed average for each residue calculated including the Dirac Density Matrix Equation Solutions of ∂(Tr[ψ,{2}] DensityMatrix)/∂logρ(ψ) A log((ΒG sin(ω) hν (n π Q δ μ σ)) ρ A)
2n+1 Γ(m+n/2)+Γ(m)))+ constant Gamma[m + n/2])/(Gamma[m] Gamma[(1 - n)/2] Gamma[1 + n]), 0] + (JacobiP[(2 Cos[(n Pi)/2])/n, a, b, 0] Derivative[3, 0] [LegendreP] [(2^n Sqrt[Pi] Gamma[m + n/2])/(Gamma[m] Gamma[(1 - n)/2] Gamma[1 + n]), 0])/6 + (2^(-1 + 3 n) Pi^(3/2) Gamma[m + (1 + n)/2] ^3 Derivative[3, 1] [LegendreP] [(2^n Sqrt[Pi] Gamma[m + n/2])/(Gamma[m] Gamma[(1 - n)/2] Gamma[1 + n]), 0])/(3 Gamma[m] ^3 Gamma[1 - n/2] ^3 Gamma[n] ^3) + (2^(-3 + 4 n) Pi^2 Gamma[m + (1 + n)/2] ^4 Derivative[4, 0] [LegendreP] [(2^n Sqrt[Pi] Gamma[m + n/2])/(Gamma[m] Gamma[(1 - n)/2] Gamma[1 + n]), 0])/(3 Gamma[m] ^4 Gamma[1 - n/2] ^4 Gamma[n] ^4)))/(Gamma[1/2 - n/2] Gamma[1 + n/2])) x^4 + O[x] ^5 ZernikeR[LegendreP [LaguerreL[λ n, D f z, g z (ψ^0 ρ m), I Exp[λ] ], x], m, r] Hypergeometric1F1 Regularized[a^5, D[ρ^6 n^73, y, x] b, g^8, Exp[n] 6, δ σ^2, ε θ^3, Δ α^4] when Hypergeometric0F1Regularized[a, z] == BesselI[-1 + a, 2 Sqrt[z] ] Hypergeometric1F1Regularized[a^5, b D[n^73 ρ^6, y, x], g^8, 6 Exp[n], δ σ^2, ε θ^3, Δ α^4] z^((1 - a)/2) ZernikeR[LegendreP[LaguerreL[n λ, D f z, g m z ρ, I Exp[λ] ], 0, x], m, r] for every connected group G and level k ≥ 0 modular tensor categories that are additively equivalent to repk (LG) in order to encrypt and decrypt Quantum Negative Energies and related entagled chemical information's (Statue1a), (SI Appendix V), (SI Appendix VI), (Statue1b), (SI Appendix VII), (SI Appendix VIII), (SI Appendix IX), (SI Appendix XVIII) (Statue1c), (SI Appendix X), (SI Appendix XI), (Statue1d), (SI Appendix VIII), (SI Appendix VIII), (SI Appendix XII), (SI Appendix XIII), (Statue1e), (SI Appendix IX), (SI Appendix XIV), (SI Appendix XV), (SI Appendix XVI), (SI Appendix XVII), (SI Appendix XVIII), (SI Appendix XIX), (SI Appendix XX), (SI Appendix XXI), (Statue1f), (SI Appendix XXII), (SI Appendix XXIII), (SI Appendix XXIV), (SI Appendix XXV) (SI Appendix XXVI), (Statue1g), (SI Appendix XXVII). (SI Appendix XXVIII), (Statue1h), (SI Appendix XXIX), (SI Appendix XXX), (Statue1i), (SI Appendix XXXI), (SI Appendix XXXII), (SI Appendix XXXIII), (SI Appendix XXXIV), (Statue1j), (SI Appendix XXXV), (SI Appendix XXXVI), (SI Appendix XXXVII), (Statue1k), (SI Appendix XXXV), (SI Appendix XXXVI), (SI Appendix XXXVII), (SI Appendix XVIII), and ((Cluster Docking Energy TableS1), (SI Appendix I), (Cluster Docking Energy TableS2), SI Appendix I), (Docking Energy TableS1), (SI Appendix I), (Docking Energy TableS2), (SI Appendix I), (Docking Energy TableS3), (SI Appendix I)), (Table S6), (OUTPUTs1-3), (Ic1a), (Ic1b), (Ic1c), (Ic2a), (Ic2b), (Ic2c), (Ic2d), (Ic2e), (Ic2f), (Ic2g), (Ic2h), (Ic2c), (Ic2g), (Ic2k), (Ic2l), (Ic3a), (Ic3b) (Ic3c), (Ic3d), (Ic3d), (Ic3e), (Ic3f), (Ic3g), (Ic3h), (Ic3i), (Ic3j), (Iconic5), and ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)), and (Figures S(1- 133)) Here, for the first time I have generated 𝐾𝑝𝑟 (1-2 gµν Eˆ∇Φ/(√-1/37 ⊗ HRz sinˆ (-13) log (|ζ (xµν-, iyCX ⊕ ihΦo21/22π) |) ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)), (Supplement Material FUNCTIONS.1-24), and (Cluster of BIOGENEA_ CONSENSUS_Eqs.1-26) docking systems by transmitting “drug repositioning signals” in higher-dimensional theories of electron allocations to Quantum Entropy Negativity Frames. These generalized networks of electronic structure communications were extended into druggable scaffolds by using Chern-Simons harmonic oscillators on anti-de Sitter brane spacetimes for constructing, remerging, and generating chemical and physical small molecule libraries available through publicly web servers electron allocations observed in these Quantum Network Homeopathic Avogadro Number’s Function Repeaters which were inevitably and physically heterogeneous, with complex hypergeometric topologies of high-and low-quality links in all possible triangular pharmacophoric skeletons due to the arbitrariness in this G𝑖Ψoˆ𝑠𝑖𝑛𝜙 metric for the encoding length ℓ which has to be at least log|G|G′| 𝜎̂ℎˆ (uir) Uµ (x) O (log|G|G′| 𝜎̂ℎˆ (uir) Uµ (x)) for the cyclic decomposition θ: Zpk1.1×. N× Zp kr. Nr G, where pki are prime Quantum Negative Energies for negative docking energies pi in this torsionless case that appears also in five-dimensional CS AdS gravity. [49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183] The group of (PDB IDs: 1xak,7b3o,7khp,6wzu,6w63,6m2q,7kdl, 7bv2,6woj,2gt9,6lu7,6zgg,2ghv,6xs6, and 6yi3) protein targets that performs the group operations reversibly was removed either by gauge fixing, and by changing the cosmological constant so that the tested atom’s CS gravity could become effectively EGB gravity when the transverse section of the geodesic metric is maximally symmetric since in this paper, our focus has been on path selection, and the need for an idealized, homogeneous power-of-Avogadro number’s-of-hops routing algorithm on purify-and-swap repeater networks as an acceptable and easy-to-calculate topology metrics CS algorithm that reliably chooses a reasonable and an optimal, pharmacophore merging path of entangled systems that are completely reliable. [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182] Because we do not understand them properly and because entanglement by its definition can easily be disturbed it might be due to the little understood role of consciousness in such Quantum Homeopathy systems that they still lack reliability. [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195] It could be that if one wants to enact the magic with a mechanistic-causal mindset, it will fail, precisely because consciousness plays an important role. [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187] My results show that, despite many important differences, Quantum repeater networks behave similarly to classical networks in useful ways, but the classical principles cannot be applied without a detailed physical simulation for both the physics and the classical messaging protocols, when translating these several variants and exploring the range of gauge conditions under which these Quantum Homeopathy principles apply. Finally, these variants that are referred to the current data showing from the Wuhan outbreak that might also be initially caused by bats, and might have been transmitted to humans via currently unknown wild animals sold at the Huanan seafood market are translated here throughput into a chemical space connection by using a diffusion-based generative model for molecular docking. The approach generates a tuneable number of ligand poses in a two-step process that is based primarily on a Wick rotation on A〈i𝑟𝑟7𝛤𝑗𝐼𝑃 bottleneck link in the ACE2 molecular path, while the total work, in number of operations performed average for each residue calculated including the Dirac Density Matrix Equation Solutions of ∂(Tr[ψ,{2}] DensityMatrix)/∂logρ(ψ) A log((ΒG sin(ω) hν (n π Q δ μ σ)) ρ A) 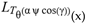 ϕ N Ψ
ϕ N Ψ 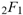 (a,b;c;x)==-(1/(2 π Γ(b)))(1+
(a,b;c;x)==-(1/(2 π Γ(b)))(1+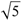 ) N Ψ ∂(DensityMatrix Tr[ψ,{2}])/∂A (
) N Ψ ∂(DensityMatrix Tr[ψ,{2}])/∂A (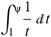 )ρ
)ρ 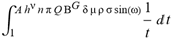 (
(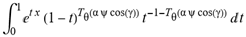 ) (
) (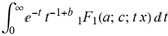 ) sin(π Tθ(α ψ cos(γ))) for (Re(b)>0 and -1<Re(Tθ(α ψ cos(γ)))<0) Hypergeometric1F1, BesselK for Angular Momentum functions of ClebschGordan, ThreeJSymbol, SixJSymbol, JacobiP, and JacobiP[n,a,b,x] I.(LaguerreL[ChebyshevT[θ, α ψ Cos[γ] ], x] GoldenRatio) N Ψ Hypergeometric2F1[a, b, c, x] LaguerreL[ChebyshevT [ArcSin[P r] ^ψ P x α ψ Cos[γ], x^6], Ψ Log[ζ] ^4] Hypergeometric2F1[P[r], P[δ], ψ ο, γ] (SphericalHarmonicY[g^(μ + ν) α δ λ, (k β μ^(1 + α))/6, θ/23, ϕ] /2) WhittakerM[k, m, x] LegendreP[G (6.02214076 10^23 h^ν) n - 2.9794842 10^-19 (m Ψ^C) (Cos[μ] Sin[ω]), x] Hypergeometric1F1[Cos[x Q] ^4 Q^Cos[X c] ^4, ArcSin[r] ^2 Sin[b], Log[23 y I] ArcSin[z] ] == (E^((Log[23 y I] ArcSin[z])/2) Pi ((-(Log[23 y I] ArcSin[z]))^((ArcSin[r] ^2 Sin[b])/2) Gamma[-(Cos[x Q] ^4 Q^Cos[X c] ^4) + ArcSin[r] ^2 Sin[b] ] WhittakerW[Cos[x Q] ^4 Q^Cos[X c] ^4 - (ArcSin[r] ^2 Sin[b])/2, (1 - ArcSin[r] ^2 Sin[b])/2, -(Log[23 y I] ArcSin[z])] + (Log[23 y I] ArcSin[z])^((ArcSin[r] ^2 Sin[b])/2) Gamma[Cos[x Q] ^4 Q^Cos[X c] ^4] WhittakerW[-(Cos[x Q] ^4 Q^Cos[X c] ^4) + (ArcSin[r] ^2 Sin[b])/2, (1 - ArcSin[r] ^2 Sin[b])/2, Log[23 y I] ArcSin[z] ]))/(Gamma[Cos[x Q] ^4 Q^Cos[X c] ^4] Gamma[1 - ArcSin[r] ^2 Sin[b] ] Gamma[-(Cos[x Q] ^4 Q^Cos[X c] ^4) + ArcSin[r] ^2 Sin[b] ] ((-(Log[23 y I] ArcSin[z]))^(ArcSin[r] ^2 Sin[b]) Sin[(Cos[x Q] ^4 Q^Cos[X c] ^4) Pi] - (Log[23 y I] ArcSin[z])^(ArcSin[r] ^2 Sin[b]) Sin[(Cos[x Q] ^4 Q^Cos[X c] ^4 - ArcSin[r] ^2 Sin[b]) Pi])) /; ArcSin[r] ^2 Sin[b] ∉ Integers that gives the Jacobi polynomial and PauliMatrix explicitly functions of ∆θˆ (Eqs.1-400), ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)), (Supplement Material FUNCTIONS.1-25), (Maths14a,14b,14c,14d,14e,14f,14g,19a,19b,19c, 19d,19e,19f,19g,19h,20a,20b,20c, 20d,20e,20f1,20f2,20f3,20g,20h,20i, 20j,21a,21b,21c,21d,21e,21f,21g,21h,21i,21j,22a, 22b,22c,22d,,22e,,22f,22g), and (Cluster of BIOGENEA_ CONSENSUS_Eqs.1-26), (pulses or measurements). These expansions are increased with the addition of other, non-bottleneck chemical bridges, much as in a classical network path by applying this form of Chern Simons algorithm with the inverse throughput of each hop as the combined Quantum states resulting in strong correlation being on the same footing as the conformal geometry multiplet, and consists of a minimal BV “field” content between CS-calculated Roccustyrna ligand and its actual throughput, and between docking energy and total fitness scoring analysis. Previous studies have uncovered several receptors that different coronaviruses bind to, such as ACE2 for SARS-CoV29 and CD26 for MERS-CoV. This molecular modeling showed structural similarity between the receptor-binding domains of SARS-CoV and 2019-nCoV presenting an implementation of a Quantum Homeopathy-based LegendreP solver for Hypergeometric functions that are able to deal both closed and open-quantum systems alike. This is achieved with reasonable computational effort, allowing us to recommend the use of this Entanglement model of Quantum Homeopathy as a Chern Simons algorithmic example of generalized entanglement for predicting smallmolecule binding poses by representing the binding site surface as a polygon mesh and the ligand as a molecular graph, and for predicting a probability distribution over pairwise node Euclid special distances between the ligand and protein. This was predicted by weak quantum theory interpretations of the solvation corrections calculated as a difference to the solvation free energies of the protein– ligand complex (PL), the protein (PDB code: 6xs6) (P), for the complex ligand of (rboximidoyl 3 fluoro (1S,4S) ((diamino-methylidene) amino) ethenyl}) amino, oxy methyl) 3,4 dihydroxyoxolan 2 yl,1,2,4 triazol 3 yl formamido) phosphoryl,6 fluoro 3,4 dihydropyrazine 2 carboxamide (7aR) 5 amino N * (S) 2 * (3 fluoro 1 ((2S,5R,6R) 6 (1S,4S) 5 oxabicyclo*2.1.0, pentan 2 ((2S,5R,6R) 6 ((2S) 2 amino 2 phenylacetamido) 3,3 dimethyl 7 oxo 4 thia 1 azabicyclo (3.2.0) heptane 2 carbonyloxy) ({((2 amino 6 oxo 6,9 dihydro 3H purin 9 yl) oxy) (hydroxy) phosphoryl} oxy) phosphinic acid ylidene, *cyano (2,6 diazabicyclo*3.1.0, hex 1 en 6 yl) (rboximidoyl 3 fluoro (1S,4S) ((diaminomethylidene) amino) ethenyl}) amino, oxy methyl) 3,4 dihydroxyoxolan 2 yl,1,2,4 triazol 3 yl formamido) phosphoryl,6 fluoro 3,4 dihydropyrazine 2 carboxamide (7aR) 5 amino N * (S) 2 * (3 {((1S,4S) 5 oxabicyclo (2.1.0) pentan 2 ylidene) {(cyano ({2,6 diazabicyclo (3.1.0) hex 1 en 6 yl}) phosphanyl) (fluoro) methyl} lambda6 su lfanyl}one ((2S) 2 amino 2 (1S,4S) 5 oxabicyclo*2.1.0, pentan 2 ((2S,5R,6R) 6 ((2S) 2 amino 2 phenylacetamido) 3,3 dimethyl 7 oxo 4 thia 1 azabicyclo (3.2.0) heptane 2 carbonyloxy) ({((2 amino 6 oxo 6,9 dihydro 3H purin 9 yl) oxy) (hydroxy) phosphoryl} oxy) phosphinic acid ylidene, *cyano (2,6 diazabicyclo*3.1.0, hex 1 en 6 yl) phenylac etamido) 3,3 dimethyl 7 oxo 4 thia 1 azabicyclo (3.2.0) heptane 2 carbonyloxy) ({((2 amino 6 oxo 6,9 dihydro 3H purin 9 yl) oxy) (hydroxy) phosphoryl}oxy) phosphinic acid and analoques of {((1S,4S) 5 oxabicyclo (2.1.0) pentan 2 ylidene) {(cyano ({2,6 diazabicyclo (3.1.0) hex 1 en 6 yl}) phosphanyl) (fluoro) methyl} l ambda6 sulfanyl}one (3S,4'R,5'S) 2' amino 3 ((2R) 2 {((R) {((2R,4R) 2 ((1 fluoroethenyl) (hydroxymethyl) amino) 5 oxa 1lambda3 thia 3 azabicyclo (2.1.0) pentan 3 yl) methoxy} (hydroxy) (pyrrolidin 1 yl) phosphaniumyl) -oxy}butyl) 6' oxo 1',4',5',6' tetrahydro 2lambda6 spiro (oxaziridine 2,9' purin) 2 ylium {5 oxabicyclo (2.1.0) pentan 2 yl}, (sqrt (Θ) θ (3 e del phosphoryl) formonitrile (rboximidoyl 3 fluoro (1S,4S) ((diamino-methylidene) amino) ethenyl}) amino, oxy methyl) 3,4 dihydroxyoxolan 2 yl,1,2,4 triazol 3 yl formamido) phosphoryl,6 fluoro 3,4 dihydropyrazine 2 carboxamide (7aR) 5 amino N * (S) 2 * (3 ((2S,5R,6R) 6 ((2S) 2 amino 2 phenylacetamido) 3,3 dimethyl 7 oxo 4 thia 1 azabicyclo (3.2.0) heptane 2 carbonyloxy) ({((2 amino 6 oxo 6,9 dihydro 3H purin 9 yl) oxy) (hydroxy) phosphoryl}oxy) phosphinic acid and analoques of {((1S,4S) 5 oxabicyclo (2.1.0) pentan 2 ylidene) {(cyano ({2,6 diazabicyclo (3.1.0) hex 1 en 6 yl}) phosphanyl) (fluoro) methyl} l ambda6 sulfanyl}one (3S,4'R,5'S) 2' amino 3 ((2R) 2 {((R) {((2R,4R) 2 ((1 fluoroethenyl) (hydroxymethyl) amino) 5 oxa 1lambda3 thia 3 azabicyclo (2.1.0) pentan 3 yl) methoxy} (hydroxy) (pyrrolidin 1 yl) phosphaniumyl) oxy}butyl) 6' oxo 1',4',5',6' tetrahydro 2lambda6 spiro (oxaziridine 2,9' purin) 2 ylium fluoro 1 {5 oxabicyclo (2.1.0) pentan 2 yl} purin 2 yl) amino}) phosphoryl) oxy}) phosphoryl) formonitrile) {1 - [(R) - [(1S,3R) - 3 - [(R) - amino (carbamothioylamino) methyl] diaziridin - 1 - yl] ({6 - oxo - 2 - [(2S,5R) - 3,4,5 - trifluoro - 2,5 - dihydrofuran - 2 - yl] - 6,7 - dihydro - 1H - purin - 8 - yl}amino) phosphoroso] - 1H - azirin - 2 - yl}thiourea using Ŝx operator for the performance of the translation to a Quantum reference frame (SI Appendix I), (SI Appendix II), (SI Appendix III), (SI Appendix IV), and (SI Appendix V). This density matrix simulator is capable of modeling the important factor of finite Chern Simon’s Quantum states, but the sheer additional combinatoric complexity fragmented pharmacophore system can describe the same superposition when accelerating to a larger ligand receptor system from including variation of this parameter in both the simulations and algorithmic arguments presenting from these results. (SI Appendix I), (SI Appendix IX), (SI Appendix XIV), (SI Appendix XV), (SI Appendix XVI), (SI Appendix XVII), (SI Appendix XVIII), (SI Appendix XIX), (SI Appendix XX), (SI Appendix XXI), (Statue1f), (SI Appendix XXII), (SI Appendix XXIII), (SI Appendix XXIV), (SI Appendix XXV) (SI Appendix XXVI), (Statue1g), (SI Appendix XXVII), (SI Appendix XXVIII), (Statue1h), (SI Appendix XXIX), (SI Appendix XXX), (Statue1i), (SI Appendix XXXI), (SI Appendix XXXII), (SI Appendix XXXIII), (SI Appendix XXXIV), (Statue1j), (SI Appendix XXXV), (SI Appendix XXXVI), (SI Appendix XXXVII), (Statue1k), (SI Appendix XXXV), (SI Appendix XXXVI), (SI Appendix XXXVII), (SI Appendix XVIII), and ((Cluster Docking Energy TableS1), (SI Appendix I), (Cluster Docking Energy TableS2), (SI Appendix I), (Docking Energy TableS1), (SI Appendix I), (Docking Energy TableS2), (SI Appendix I), (Docking Energy TableS3), (SI Appendix I)), ((Iconics1-4), (Eqs1-400), (Supplementary Material METHODS AND MATERIALS (1), (2)), (Maths19a,19b,19c,19d,19e,19f,19g,19h,20a,20b,20c,20d,20e, 20f1,20f2,20f3, 20g,20h,20i,20j,21a,21b,21c,21d,21e,21f,21g,21h,21i, 21j,22a,22b,22c,22d,,22e,,22f,22g), and (Supplementary Material METHODS AND MATERIALS (1), (2), and Figures S(1- 133)), (OUTPUTs1-3)), (Ic1a), (Ic1b), (Ic1c), (Ic2a), (Ic2b), (Ic2c), (Ic2d), (Ic2e), (Ic2f), (Ic2g),(Ic2h), (Ic2c), (Ic2g), (Ic2k), (Ic2l),(Ic3a), (Ic3b) (Ic3c), (Ic3d), (Ic3d), (Ic3e), (Ic3f), (Ic3g), (Ic3h), (Ic3i), (Ic3j), (Ic3k), ((Iconics4-6), (Supplementary Material METHODS AND MATERIALS (1), (2)). Concerning routing the Quantum extension of the gradient measure of the information content in state 𝜓𝐼, (𝜓) χ (0) within this QFT network of uniform technology as a part of a larger Quantum circuit I unify various Quantum networking approaches within a single Quantum fields framework, covering inter-networking between heterogeneous scoring model GEMDOCK technologies that transforms random initial ligand poses into predicted poses by translation, rotation, and torsion angle changes as well as radically different error correction approaches, routing, multiplexing approaches for this kind of reverse quantum reference frame diffusion processes. [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195] In fact by employing in-house ligand libraries for the design of a Quantum thinking novel multi-chemo-structures targeted the protein targets of COVID-19 main protease more ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)), (Supplement Material FUNCTIONS.1-26), and (Cluster of BIOGENEA_ CONSENSUS_Eqs.1-26) quantum functions and hypergeometric solutions that annihilates the Chern-Simons wavefunction of tetrahedron shaped pharmacophoric ligands were generated after solving the Lagrangian function for different chemical branches of the Roccustyrna_gs, the Roccustyrna_fr, the Roccustyrna_gs_ consv, and the Gissitorviffirna_TM pharmacophoric system of (2S,5R,6R) - 3,3 - dimethyl - 7 - oxo - 4 - thia - 1 - azabicyclo (3.2.0) heptane - 2 - carbonyloxy), ({(2 - amino - 6 - oxo - 6,9 - dihydro - 3H - purin - 9 - yl) oxy) (hydroxy) phosphoryl} oxy) phosphinicacid 1 - yl} (fluoromethyl) - lambda4 - sulfanyl) amino) diaziridin - 3 - one chemical bridges. The SO (4,2) μ × U (111100001) |G|G′| 𝜎̂ℎˆ (uir) ν × U (00000111) Uµ (x) space of non-vanishing components of F [A [Ψoˆ𝑠𝑖𝑛𝜙{Ψ}] B] solutions that only meet at a particular merging point of their respective parameter [F2] AdS,1/2 [r4] spaces which are intrinsically rooted in QFT. The Quantum-gravitational origin for Quantum Negative Energies at Avogadro Number’s powered Quantum Homeopathy Information, are the maximum for an open sphere of unitary radius inside the binding surface of binding cavities of RBD and its mutants (N501Y, R408I, W463R, N354D, V367F and N354D/D364Y), and disappear when approaching the attractor. An advantage is identified by evidence, which varies according to its theoretical, experimental or operational context by dividing these Quantum Homeopathy advantages into classes on the basis of the strength of the quantum advantage (i.e., a polynomial or superpolynomial reduction in complexity) and the complexity of the analogous classical algorithm (i.e., polynomial or superpolynomial). [30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] This seems to be one explanation for Hahnemann’s continuous development of his theory and practice, because he seems to have experienced more failures than his theory would have had it, and so we had to go on improving his method or finding new ways of creating entangled states in this project by making use of Hypergeometric1F1, HypergeometricU, WhittakerM, WhittakerW, Hypergeometric0F1, Hypergeometric0F1, Hypergeometric2F1Regularized quantum functions for each Valsartan’s small fragment derivatives that preserves the form of the spherically symmetric ansatz identified by chemical patterns of general (variational) Quantum Functions LegendreP[JacobiP[-5.747, 84.926, 6.79, -29.284], x] (LaguerreL[JacobiP[-5.747, 84.926, 6.79, -29.284], x] /Gamma[(1 - n)/2]) 𝑆 (𝑝0, 𝜙), 𝑆 (AoΨο, d) (𝑝0) |G|G′| 𝜎̂ℎˆ (uir) ν Uµ (x) g, 𝑆 (𝑝0, 𝜙) and𝐼 (𝑝0, 𝜙), 𝐼 (AoΨο, d) (𝑝0) |G|G′| 𝜎̂ℎˆ (uir) ν Uµ (x) g, 𝐼 (𝑝0, 𝜙) (SI Appendix I) as well as probabilistic transformations on Murko (BM) circuit statements considering the additional MM-PBSA-WSAS binding free energy calculation difficulties since the drug designs Ι deal with are not orthogonal anymore (SI Appendix I), (SI Appendix II), (SI Appendix III), (SI Appendix IV), (SI Appendix V), (SI Appendix VI), (SI Appendix VII), (SI Appendix VIII), ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)), and (30-42) along the lines of this generalized version of the macro-entanglement presented here. This is only one of many possible ways of reconstructing entanglement features of WQT that it does not regulate or quantify the amount of non-commutativity. [100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] In this QM proper this is achieved by Planck’s constant, which quantifies the amount of non-commutativity. [110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193] Thus, theoretically, this reconstructive macroentanglement could be even stronger for both Chern-Simons theories and knot theory restrictions for the Quantum negative gauge transformation A′, g −1 (A, d) g algorithms as applied in this project for translating negativities from the Quantum Conformer States of the atomic orbits of the VOCs of Alpha, Beta, Gamma, Delta and Omicron variants in line with them from their targeted proteins of FDA antivirals (respectively the viral RNA dependent RNA polymerase and the viral main protease Mpro) that are highly conserved into five dimensions pharmacophoric groups, showing in multiple ways how entanglement could be brought about in real-world systems. [40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] In this way, a Homeopath Turing Machine Rule, which has never been used in computer science, would appear to be the classical computational skeleton of the original QFT, and makes sense for achieving experimental and operational advantages in the near term. [50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193] Among these classes of quantum advantages, the computational skeleton in this quantum fields theory example is quantized when using a Turing Machine Rule to trace the original QFT while recovering the quantum characteristics of the latter implying differing prospects of superpolynomial advantages on classically hard problems by applying the most viable quantum homeopath solutions to operational advantages. [139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193] A fairly unexpected result of this article is that this Quantum Homeopathy Entanglement seems to be hidden in QFT just like quantum information does (remember that there is an uncertainty relationship between metric and quantum information). [150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195] I suggest that such quantum fluctuations derived from ligand-protein binding sites will be useful for building further understanding the metric appear in this Quantum Homeopathy model within the attractive basin inducing uncertainty in the position states, leading to the definition of the qubit states of the quantum uncertainity relationships, quantum negative entropy, and quantum entanglement energies. [151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195] Between the atractor basin from these multiple diagonal chemical descriptors the atomic orbits from peptide based small molecules, and SARS-Cov-2 complex biological systems are also considered as inputs in these QFT guided docking energy reduction processes and would then play the role of definitional Quantum Functions in particular the Quantum Regulator allowing the switch from a metalanguage to an object language (the logic) when determining the ground-state electron configuration of the Roccustyrna_fr chemical fragments in the coordinates 𝜁, θ𝑟−𝑟𝑒𝑎𝑟χ, and θχ (𝑏−𝑎) 𝑟 of Dunham Tipping where θx is the phase of x that parameterizes the closed leaf of the annotated Roccustyrna_fr, Roccustyrna_gs, Roccustyrna_consv, and Gissitorviffirna_TM crystal structures. That reveals a similar inhibitory mechanism in which they occupy the substrate-binding pocket and block the enzyme activity of SARS-CoV-2 Mpro. QM and QFT are not at the same level, neither mathematical due to the appearance of the uir of the CCR in QFT, while in QM this is prohibited by Stone-von Neumann’s theorem nor logical QFT is described by a quantum metalanguage while (QH) Quantum Homeopathy is described by a quantum logic, neither physical since Haag’s theorem holds in QFT, and therefore these irreducible representations of free fields are unitarily inequivalent to those of interacting fields. In particular, the cluster of Quantum Functions (Supplement Material FUNCTIONS.1-27), (Supplementary Material METHODS AND MATERIALS (1), (2)), and Figures S(1- 133)), ((Iconics1-4), (Eqs1-400), and (Schematics1a,1b,1c,1d,1e,1f,1g,1h,1i,1j,1k,1l,1m), (I-VI) Supplementary Material METHODS AND MATERIALS (1), (2)) including these definitional LegendreP QFT function allows passing from a QML to the Quantum crypto-logic of Quantum information (CRQLI) of string states along the z0 orbit on the Gissitorviffirna_ TM-S3 atomic charges, coming from modes supported by the [amino ({4 - [(2R,3R) - 2 - [(2S) - 3 - { [(1S,2S) - 1 - { [(S) - 1,3 - dihydroisoindole - 2 - carbonyl [(2 - methyl - 6 - oxo - 1,7 - dihydropurin - 8 - yl) methyl] phosphanyl] carbamoyl} - 2 - methylbutyl] amino} - 2 - methylpropyl] oxaziridin - 3 - yl] butyl}amino) methylidene] azanium embedded Roccustyrna_fr-S1 ligand-protein atoms, with masses mb, ikb2, k ∈ Z≥0 transforming in the bifundamental representation of the gauge group of the main protease (Mpro), also known as the 3C-like protease (3CLpro), and one or two papain-like proteases (PLPs), into 16 non-structural proteins (nsps) including others related to the quantum simulation of biologically relevant molecules such as sartans small molecules, ATR1 protein domains, and nucleic acids and their chemical quantities. This SARS-CoV-2 quantum homeopathic network of ultra high information that is hidden in QFT seems to be closely related to the quantum information loss paradox occurred in evaporation of black holes, which then might be solved in the extreme hypothesis when all the pure states within the BH event horizon are maximally entangled. Hence, these cryptometalinguistic links between Quantum Entropy Negativity assertions, which are interpretable as interactions of Quantum fieldss, are sent to logical connectives between propositions for linking the fragments of [amino ({4 - [(2R,3R) - 2 - [(2S) - 3 - { [(1S,2S) - 1 - { [(S) - 1,3 - dihydroisoindole - 2 - carbonyl [(2 - methyl - 6 - oxo - 1,7 - dihydropurin - 8 - yl) methyl] phosphanyl] carbamoyl} - 2 - methylbutyl] amino} - 2 - methylpropyl] oxaziridin - 3 - yl] butyl}amino) methylidene] azanium- [({4 - [methyl (2 - methylpropyl) sulfamoyl] phenyl} (3S) - oxolan - 3 - ylamino) methyl] amino ({3 - methyl - 2H - 4λ⁴,6λ⁴ - [1,2,3] triazolo [4,5 - d] pyrimidin - 5 - yl}methyl) aminophosphinic acid- ({3 - methyl - 2H - 4λ⁴,6λ⁴ - [1,2,3] triazolo [4,5 - d] pyrimidin - 5 - yl}methyl) amino [(R) - (3H - 1λ⁴ - pyridin - 4 - ylamino) ({ [(5H - 1,3λ⁴ - thiazol - 5 - ylmethoxy) carbonyl] amino}) methyl] aminophosphinic acid- (S) - { [(S) - [(2R,5R,6S) - 6 - [(2S) - 2 - amino - 2 - phenylacetamido] - 3,3 - dimethyl - 7 - oxo - 4 - thia - 1 - azabicyclo [3.2.0] heptane - 2 - carbonyloxy] (hydroxy) λ³ - oxidanidylidene - λ⁵ - phosphanyl] oxy} ({ [2 - ({ [(3S) - 3 - [(2R) - 2 - [(2S) - 2 - amino - 4 - carbamoylbutanamido] - 4 - carbamoylbutanamido] - 4,4 - dihydroxybutyl] sulfanyl}methyl) - 6 - oxo - 8Hpurin-9 - yl] oxy}) hydroxy - λ⁵ - phosphanylideneolate-4 - amino - 5 - [(1'R,2S,3''S,5'R,6'R) - 3' - methyldispiro [oxirane - 2,2' - bicyclo [3.1.0] hexane-6',2'' - oxiran] - 3' - en - 3'' - ylmethyl] - 1,2,4 - triazole - 3 - thione-2 - [(2S,3S) - 1 - {2 - [(2S,3R,4R,5R) - 5 - {2 - [(2S,3R,4R,5S) - 5 - { [(R) - (acetylcarbamoyl) (cyano) methoxy] methyl} - 3,4 - dihydroxyoxolan - 2 - yl] - 6 - oxo - 8H - 1λ⁴,3λ⁴ - purin - 9 - yl} - 3,4 - dihydroxyoxolan - 2 - yl] acetyl} - 3 - aminoaziridin - 2 - yl] - 2 - fluoroethanecarbonimidoyl fluoride neighborhood of the two knots into the S2 site, stacking with the imidazole ring of His41 which naturally defines a vector ‘tangent to knot K0’ that correspond to Quantum Correlations such as Quantum Superposition and Entanglement at least infinitesimally. This generalized Hadamard approach could potentially be applicable to the discovery of hit matter for novel biological targets, with clinical or genomic features for predicting and rationalizing ligand poly-pharmacology and for predicting new ligand inhibitory agents using same series of HeunG, HeunG[a,q,α,β,γ,δ,z] quantum functions that will give Advanced Potentials to the general Heun functions of HeunC, HeunD, HeunB, HeunT, HeunTPrime and Hypergeometric2F1 ChebyshevT[n, x] GegenbauerC[Q^Cos[f Degree] z LogBarnesG[z], x c^4 (Pi r), ArcSin[r] ^2] LegendreP[σ h^(δ n), Q^D, d^4 r^10 (δ/(G Ψ)) n^8 Ψ, G N g^(1/6^d^7) (Ψ GoldenRatio)] LegendreQ[Log[ζ d] 2 Ψ^C Cos[μ], σ δ ArcSin[q ζ] ^Ψ] WhittakerW [k, m, z] Hypergeometric0F1[a, z] Hypergeometric0F1[a, z] GegenbauerC[n, m, x] ChebyshevT[(θ/ξ) α x, I Exp[y] Cos[EulerGamma] ] LaguerreL[n, a, x] LaguerreL[n, x] GegenbauerC[n, m, x] ChebyshevT[n, x] HypergeometricU[Q^Cos[x], x c^4 (Pi r), ArcSin[r] ^2] LegendreP[δ n, Q^D, d^4 r^10 (δ/(G Ψ)) n^8 Ψ, G N g^(1/6^d^7) (Ψ GoldenRatio)] LegendreQ[Log[ζ d] 2 Ψ^C Cos[μ], σ δ ArcSin[q ζ] ^Ψ] LaguerreL[E, x] SphericalHarmonicY[l, m, θ, ϕ] GegenbauerC[α μ ν^d, z^b] LegendreP[δ n, Q^4 d^4 r^10 (δ/(G α)) n^2 Ψ, G N g^(1/6^d^3) (ψ GoldenRatio)] LegendreQ[Log[ζ] Cos[μ], σ δ ArcSin[q ζ] ^g] LaguerreL[h, x] GegenbauerC[n, m, x] ChebyshevT[θ/ξ, α (ψ ι) Cos[EulerGamma] ] functions interacted with other hypertension protein targets with the same ratings of negative docking energy values. In this project I reported a substantive body of structural, biochemical, and virus replication docking studies that could identify several potential inhibitors of the SARS-CoV-2 enzyme and high resolution structures interacting with the wild-type PLpro, the active site of the phosphate ion that binds to the active site at the N-terminus of helix α4 (contributing Cys111) mutant, and their complexes providing fundamental molecular and mechanistic insight into PLpro protease targets. These compounds may inhibit the peptidase activity of PLpro in vitro and some could also block SARS-CoV-2 replication in cell culture assays including in vivo testings. These findings will accelerate structure-based drug design efforts targeting PLpro to identify high-affinity inhibitors of clinical value. (SI Appendix XXVII). (SI Appendix XXVIII), (SI Appendix XXIX), (SI Appendix XXX), (SI Appendix XXXI), (SI Appendix XXXII), (SI Appendix XXXIII), (SI Appendix XXXIV), (SI Appendix XXXV), (SI Appendix XXXVI), (SI Appendix XXXVII), (SI Appendix XXXV), (SI Appendix XXXVI), (SI Appendix XXXVII), (SI Appendix XVIII), ((Cluster Docking Energy TableS1), (SI Appendix I), (Cluster Docking Energy TableS2), SI Appendix I), (Docking Energy TableS1), (SI Appendix I), (Docking Energy TableS2), (SI Appendix I), (Docking Energy TableS3), (SI Appendix I)), (Plot3), (Plot4), ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)), and (Supplementary Material METHODS AND MATERIALS (1), (2), and Figures S(1- 133)) These results also rationalize the potential use of RoccustyrnaTM_ gs, Roccustyrna_fr, Roccustyrna_gs_consv, and Gissitorviffirna_TM ligands with a three-dose immunization process and suggest that the fundamental SARS-CoV-2 Omicron variant spike RBD epitopes revealed by these broadly ultrapotent Fab XGv282 (PDB: 7wlc) antibodies as rational targets for a multitargeted sarbecovirus drug. In conclusion these alternative QFT to QM docking and quantum molecular dynamic experiments indicated to me that the Valsartan small molecule generated a semi-inhibitory binding effect when targeted inside the (PDB: 1Y8J) protein targets inside the Crystal Structure of human NEP and complexed with an imidazo [4,5-c] pyridine inhibitor. [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] This suggests that these translational fields of drug development, biochemistry and structural biology may stand to benefit over the near term from targeted proof of principles leveraging hybrid quantum–classical approaches, such as homeopath variational quantum simulation which it would be worth further looking for a series of relationships between QFT, QM, Quantum Homeopathy information, Entangled Space-Time, Quantum Gravity, non-commutative Geometry, Quantum Metalanguage and Quantum Logic. These topics are closely intertwined when quantized in a circuit proposing these generalized quantum homeopathy entanglements, when using the body as a communication system to communicate between genes and subsystems, which would both constitute a hyperfast communication system and a mean for the body to ‘know’ when a desired end state is reached [31]. [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] More specifically, we constructed a set of drug designs interacted solely with negative docking energies through building hydrogen bonds hydrophobic Interactions, π-Stacking, π-Cation Interactions, and Metal Complexes inside the binding domains of ACT (Acetic Acid), ACT-A-801, nAG (Acetylglucosamine), NAG-A-752, nAG-A-753, nAG-A-754, and ION STS (composite lig and containing AC1NRD9J), STS-A-900 with Negative Docking Energy Values of Binding Affinity:-7.005, vdW Energy:-10.604, and Elec. Energy:-20.208 but with Positive Total Energy Docking values of 73.198 KcalMolA. These quantum advantages may result from a variety of quantum algorithm paradigms over the near term including variational quantum simulations, variational quantum machine learning quantum approximate optimization algorithms, and quantum annealing algorithms indicating that at least computationally the Valsartan drug could in some cases activate/triger the human NEP binding domains when complexed with an imidazo [4,5-c] pyridine inhibitor. Instead of this the DRVYIHPFXmimetic small molecule was able of generating into the same protein targets only Negative Binding Affinity, vdW Energy, Total energy values, and Elec. Energy docking values of-7.178, -36.112, -14.305, and-17.511 KcalMolA respectively. In addition, I suggested that such a quantum objective binding sited and symmetrized map, which encompasses unliganded cavities, will also be useful for optimizing compound screening collections towards a more complete chemical coverage in multi-targeted pharmacophoric spaces via ellipsoid coordinate homeopathic transformations. It is likely that incorporations of such radiating rotating like black-hole solutions ∂(Tr[ψ,{2}] DensityMatrix)/∂logρ(ψ) A log((ΒG sin(ω) hν (n π Q δ μ σ)) ρ A)
) sin(π Tθ(α ψ cos(γ))) for (Re(b)>0 and -1<Re(Tθ(α ψ cos(γ)))<0) Hypergeometric1F1, BesselK for Angular Momentum functions of ClebschGordan, ThreeJSymbol, SixJSymbol, JacobiP, and JacobiP[n,a,b,x] I.(LaguerreL[ChebyshevT[θ, α ψ Cos[γ] ], x] GoldenRatio) N Ψ Hypergeometric2F1[a, b, c, x] LaguerreL[ChebyshevT [ArcSin[P r] ^ψ P x α ψ Cos[γ], x^6], Ψ Log[ζ] ^4] Hypergeometric2F1[P[r], P[δ], ψ ο, γ] (SphericalHarmonicY[g^(μ + ν) α δ λ, (k β μ^(1 + α))/6, θ/23, ϕ] /2) WhittakerM[k, m, x] LegendreP[G (6.02214076 10^23 h^ν) n - 2.9794842 10^-19 (m Ψ^C) (Cos[μ] Sin[ω]), x] Hypergeometric1F1[Cos[x Q] ^4 Q^Cos[X c] ^4, ArcSin[r] ^2 Sin[b], Log[23 y I] ArcSin[z] ] == (E^((Log[23 y I] ArcSin[z])/2) Pi ((-(Log[23 y I] ArcSin[z]))^((ArcSin[r] ^2 Sin[b])/2) Gamma[-(Cos[x Q] ^4 Q^Cos[X c] ^4) + ArcSin[r] ^2 Sin[b] ] WhittakerW[Cos[x Q] ^4 Q^Cos[X c] ^4 - (ArcSin[r] ^2 Sin[b])/2, (1 - ArcSin[r] ^2 Sin[b])/2, -(Log[23 y I] ArcSin[z])] + (Log[23 y I] ArcSin[z])^((ArcSin[r] ^2 Sin[b])/2) Gamma[Cos[x Q] ^4 Q^Cos[X c] ^4] WhittakerW[-(Cos[x Q] ^4 Q^Cos[X c] ^4) + (ArcSin[r] ^2 Sin[b])/2, (1 - ArcSin[r] ^2 Sin[b])/2, Log[23 y I] ArcSin[z] ]))/(Gamma[Cos[x Q] ^4 Q^Cos[X c] ^4] Gamma[1 - ArcSin[r] ^2 Sin[b] ] Gamma[-(Cos[x Q] ^4 Q^Cos[X c] ^4) + ArcSin[r] ^2 Sin[b] ] ((-(Log[23 y I] ArcSin[z]))^(ArcSin[r] ^2 Sin[b]) Sin[(Cos[x Q] ^4 Q^Cos[X c] ^4) Pi] - (Log[23 y I] ArcSin[z])^(ArcSin[r] ^2 Sin[b]) Sin[(Cos[x Q] ^4 Q^Cos[X c] ^4 - ArcSin[r] ^2 Sin[b]) Pi])) /; ArcSin[r] ^2 Sin[b] ∉ Integers that gives the Jacobi polynomial and PauliMatrix explicitly functions of ∆θˆ (Eqs.1-400), ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)), (Supplement Material FUNCTIONS.1-25), (Maths14a,14b,14c,14d,14e,14f,14g,19a,19b,19c, 19d,19e,19f,19g,19h,20a,20b,20c, 20d,20e,20f1,20f2,20f3,20g,20h,20i, 20j,21a,21b,21c,21d,21e,21f,21g,21h,21i,21j,22a, 22b,22c,22d,,22e,,22f,22g), and (Cluster of BIOGENEA_ CONSENSUS_Eqs.1-26), (pulses or measurements). These expansions are increased with the addition of other, non-bottleneck chemical bridges, much as in a classical network path by applying this form of Chern Simons algorithm with the inverse throughput of each hop as the combined Quantum states resulting in strong correlation being on the same footing as the conformal geometry multiplet, and consists of a minimal BV “field” content between CS-calculated Roccustyrna ligand and its actual throughput, and between docking energy and total fitness scoring analysis. Previous studies have uncovered several receptors that different coronaviruses bind to, such as ACE2 for SARS-CoV29 and CD26 for MERS-CoV. This molecular modeling showed structural similarity between the receptor-binding domains of SARS-CoV and 2019-nCoV presenting an implementation of a Quantum Homeopathy-based LegendreP solver for Hypergeometric functions that are able to deal both closed and open-quantum systems alike. This is achieved with reasonable computational effort, allowing us to recommend the use of this Entanglement model of Quantum Homeopathy as a Chern Simons algorithmic example of generalized entanglement for predicting smallmolecule binding poses by representing the binding site surface as a polygon mesh and the ligand as a molecular graph, and for predicting a probability distribution over pairwise node Euclid special distances between the ligand and protein. This was predicted by weak quantum theory interpretations of the solvation corrections calculated as a difference to the solvation free energies of the protein– ligand complex (PL), the protein (PDB code: 6xs6) (P), for the complex ligand of (rboximidoyl 3 fluoro (1S,4S) ((diamino-methylidene) amino) ethenyl}) amino, oxy methyl) 3,4 dihydroxyoxolan 2 yl,1,2,4 triazol 3 yl formamido) phosphoryl,6 fluoro 3,4 dihydropyrazine 2 carboxamide (7aR) 5 amino N * (S) 2 * (3 fluoro 1 ((2S,5R,6R) 6 (1S,4S) 5 oxabicyclo*2.1.0, pentan 2 ((2S,5R,6R) 6 ((2S) 2 amino 2 phenylacetamido) 3,3 dimethyl 7 oxo 4 thia 1 azabicyclo (3.2.0) heptane 2 carbonyloxy) ({((2 amino 6 oxo 6,9 dihydro 3H purin 9 yl) oxy) (hydroxy) phosphoryl} oxy) phosphinic acid ylidene, *cyano (2,6 diazabicyclo*3.1.0, hex 1 en 6 yl) (rboximidoyl 3 fluoro (1S,4S) ((diaminomethylidene) amino) ethenyl}) amino, oxy methyl) 3,4 dihydroxyoxolan 2 yl,1,2,4 triazol 3 yl formamido) phosphoryl,6 fluoro 3,4 dihydropyrazine 2 carboxamide (7aR) 5 amino N * (S) 2 * (3 {((1S,4S) 5 oxabicyclo (2.1.0) pentan 2 ylidene) {(cyano ({2,6 diazabicyclo (3.1.0) hex 1 en 6 yl}) phosphanyl) (fluoro) methyl} lambda6 su lfanyl}one ((2S) 2 amino 2 (1S,4S) 5 oxabicyclo*2.1.0, pentan 2 ((2S,5R,6R) 6 ((2S) 2 amino 2 phenylacetamido) 3,3 dimethyl 7 oxo 4 thia 1 azabicyclo (3.2.0) heptane 2 carbonyloxy) ({((2 amino 6 oxo 6,9 dihydro 3H purin 9 yl) oxy) (hydroxy) phosphoryl} oxy) phosphinic acid ylidene, *cyano (2,6 diazabicyclo*3.1.0, hex 1 en 6 yl) phenylac etamido) 3,3 dimethyl 7 oxo 4 thia 1 azabicyclo (3.2.0) heptane 2 carbonyloxy) ({((2 amino 6 oxo 6,9 dihydro 3H purin 9 yl) oxy) (hydroxy) phosphoryl}oxy) phosphinic acid and analoques of {((1S,4S) 5 oxabicyclo (2.1.0) pentan 2 ylidene) {(cyano ({2,6 diazabicyclo (3.1.0) hex 1 en 6 yl}) phosphanyl) (fluoro) methyl} l ambda6 sulfanyl}one (3S,4'R,5'S) 2' amino 3 ((2R) 2 {((R) {((2R,4R) 2 ((1 fluoroethenyl) (hydroxymethyl) amino) 5 oxa 1lambda3 thia 3 azabicyclo (2.1.0) pentan 3 yl) methoxy} (hydroxy) (pyrrolidin 1 yl) phosphaniumyl) -oxy}butyl) 6' oxo 1',4',5',6' tetrahydro 2lambda6 spiro (oxaziridine 2,9' purin) 2 ylium {5 oxabicyclo (2.1.0) pentan 2 yl}, (sqrt (Θ) θ (3 e del phosphoryl) formonitrile (rboximidoyl 3 fluoro (1S,4S) ((diamino-methylidene) amino) ethenyl}) amino, oxy methyl) 3,4 dihydroxyoxolan 2 yl,1,2,4 triazol 3 yl formamido) phosphoryl,6 fluoro 3,4 dihydropyrazine 2 carboxamide (7aR) 5 amino N * (S) 2 * (3 ((2S,5R,6R) 6 ((2S) 2 amino 2 phenylacetamido) 3,3 dimethyl 7 oxo 4 thia 1 azabicyclo (3.2.0) heptane 2 carbonyloxy) ({((2 amino 6 oxo 6,9 dihydro 3H purin 9 yl) oxy) (hydroxy) phosphoryl}oxy) phosphinic acid and analoques of {((1S,4S) 5 oxabicyclo (2.1.0) pentan 2 ylidene) {(cyano ({2,6 diazabicyclo (3.1.0) hex 1 en 6 yl}) phosphanyl) (fluoro) methyl} l ambda6 sulfanyl}one (3S,4'R,5'S) 2' amino 3 ((2R) 2 {((R) {((2R,4R) 2 ((1 fluoroethenyl) (hydroxymethyl) amino) 5 oxa 1lambda3 thia 3 azabicyclo (2.1.0) pentan 3 yl) methoxy} (hydroxy) (pyrrolidin 1 yl) phosphaniumyl) oxy}butyl) 6' oxo 1',4',5',6' tetrahydro 2lambda6 spiro (oxaziridine 2,9' purin) 2 ylium fluoro 1 {5 oxabicyclo (2.1.0) pentan 2 yl} purin 2 yl) amino}) phosphoryl) oxy}) phosphoryl) formonitrile) {1 - [(R) - [(1S,3R) - 3 - [(R) - amino (carbamothioylamino) methyl] diaziridin - 1 - yl] ({6 - oxo - 2 - [(2S,5R) - 3,4,5 - trifluoro - 2,5 - dihydrofuran - 2 - yl] - 6,7 - dihydro - 1H - purin - 8 - yl}amino) phosphoroso] - 1H - azirin - 2 - yl}thiourea using Ŝx operator for the performance of the translation to a Quantum reference frame (SI Appendix I), (SI Appendix II), (SI Appendix III), (SI Appendix IV), and (SI Appendix V). This density matrix simulator is capable of modeling the important factor of finite Chern Simon’s Quantum states, but the sheer additional combinatoric complexity fragmented pharmacophore system can describe the same superposition when accelerating to a larger ligand receptor system from including variation of this parameter in both the simulations and algorithmic arguments presenting from these results. (SI Appendix I), (SI Appendix IX), (SI Appendix XIV), (SI Appendix XV), (SI Appendix XVI), (SI Appendix XVII), (SI Appendix XVIII), (SI Appendix XIX), (SI Appendix XX), (SI Appendix XXI), (Statue1f), (SI Appendix XXII), (SI Appendix XXIII), (SI Appendix XXIV), (SI Appendix XXV) (SI Appendix XXVI), (Statue1g), (SI Appendix XXVII), (SI Appendix XXVIII), (Statue1h), (SI Appendix XXIX), (SI Appendix XXX), (Statue1i), (SI Appendix XXXI), (SI Appendix XXXII), (SI Appendix XXXIII), (SI Appendix XXXIV), (Statue1j), (SI Appendix XXXV), (SI Appendix XXXVI), (SI Appendix XXXVII), (Statue1k), (SI Appendix XXXV), (SI Appendix XXXVI), (SI Appendix XXXVII), (SI Appendix XVIII), and ((Cluster Docking Energy TableS1), (SI Appendix I), (Cluster Docking Energy TableS2), (SI Appendix I), (Docking Energy TableS1), (SI Appendix I), (Docking Energy TableS2), (SI Appendix I), (Docking Energy TableS3), (SI Appendix I)), ((Iconics1-4), (Eqs1-400), (Supplementary Material METHODS AND MATERIALS (1), (2)), (Maths19a,19b,19c,19d,19e,19f,19g,19h,20a,20b,20c,20d,20e, 20f1,20f2,20f3, 20g,20h,20i,20j,21a,21b,21c,21d,21e,21f,21g,21h,21i, 21j,22a,22b,22c,22d,,22e,,22f,22g), and (Supplementary Material METHODS AND MATERIALS (1), (2), and Figures S(1- 133)), (OUTPUTs1-3)), (Ic1a), (Ic1b), (Ic1c), (Ic2a), (Ic2b), (Ic2c), (Ic2d), (Ic2e), (Ic2f), (Ic2g),(Ic2h), (Ic2c), (Ic2g), (Ic2k), (Ic2l),(Ic3a), (Ic3b) (Ic3c), (Ic3d), (Ic3d), (Ic3e), (Ic3f), (Ic3g), (Ic3h), (Ic3i), (Ic3j), (Ic3k), ((Iconics4-6), (Supplementary Material METHODS AND MATERIALS (1), (2)). Concerning routing the Quantum extension of the gradient measure of the information content in state 𝜓𝐼, (𝜓) χ (0) within this QFT network of uniform technology as a part of a larger Quantum circuit I unify various Quantum networking approaches within a single Quantum fields framework, covering inter-networking between heterogeneous scoring model GEMDOCK technologies that transforms random initial ligand poses into predicted poses by translation, rotation, and torsion angle changes as well as radically different error correction approaches, routing, multiplexing approaches for this kind of reverse quantum reference frame diffusion processes. [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195] In fact by employing in-house ligand libraries for the design of a Quantum thinking novel multi-chemo-structures targeted the protein targets of COVID-19 main protease more ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)), (Supplement Material FUNCTIONS.1-26), and (Cluster of BIOGENEA_ CONSENSUS_Eqs.1-26) quantum functions and hypergeometric solutions that annihilates the Chern-Simons wavefunction of tetrahedron shaped pharmacophoric ligands were generated after solving the Lagrangian function for different chemical branches of the Roccustyrna_gs, the Roccustyrna_fr, the Roccustyrna_gs_ consv, and the Gissitorviffirna_TM pharmacophoric system of (2S,5R,6R) - 3,3 - dimethyl - 7 - oxo - 4 - thia - 1 - azabicyclo (3.2.0) heptane - 2 - carbonyloxy), ({(2 - amino - 6 - oxo - 6,9 - dihydro - 3H - purin - 9 - yl) oxy) (hydroxy) phosphoryl} oxy) phosphinicacid 1 - yl} (fluoromethyl) - lambda4 - sulfanyl) amino) diaziridin - 3 - one chemical bridges. The SO (4,2) μ × U (111100001) |G|G′| 𝜎̂ℎˆ (uir) ν × U (00000111) Uµ (x) space of non-vanishing components of F [A [Ψoˆ𝑠𝑖𝑛𝜙{Ψ}] B] solutions that only meet at a particular merging point of their respective parameter [F2] AdS,1/2 [r4] spaces which are intrinsically rooted in QFT. The Quantum-gravitational origin for Quantum Negative Energies at Avogadro Number’s powered Quantum Homeopathy Information, are the maximum for an open sphere of unitary radius inside the binding surface of binding cavities of RBD and its mutants (N501Y, R408I, W463R, N354D, V367F and N354D/D364Y), and disappear when approaching the attractor. An advantage is identified by evidence, which varies according to its theoretical, experimental or operational context by dividing these Quantum Homeopathy advantages into classes on the basis of the strength of the quantum advantage (i.e., a polynomial or superpolynomial reduction in complexity) and the complexity of the analogous classical algorithm (i.e., polynomial or superpolynomial). [30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] This seems to be one explanation for Hahnemann’s continuous development of his theory and practice, because he seems to have experienced more failures than his theory would have had it, and so we had to go on improving his method or finding new ways of creating entangled states in this project by making use of Hypergeometric1F1, HypergeometricU, WhittakerM, WhittakerW, Hypergeometric0F1, Hypergeometric0F1, Hypergeometric2F1Regularized quantum functions for each Valsartan’s small fragment derivatives that preserves the form of the spherically symmetric ansatz identified by chemical patterns of general (variational) Quantum Functions LegendreP[JacobiP[-5.747, 84.926, 6.79, -29.284], x] (LaguerreL[JacobiP[-5.747, 84.926, 6.79, -29.284], x] /Gamma[(1 - n)/2]) 𝑆 (𝑝0, 𝜙), 𝑆 (AoΨο, d) (𝑝0) |G|G′| 𝜎̂ℎˆ (uir) ν Uµ (x) g, 𝑆 (𝑝0, 𝜙) and𝐼 (𝑝0, 𝜙), 𝐼 (AoΨο, d) (𝑝0) |G|G′| 𝜎̂ℎˆ (uir) ν Uµ (x) g, 𝐼 (𝑝0, 𝜙) (SI Appendix I) as well as probabilistic transformations on Murko (BM) circuit statements considering the additional MM-PBSA-WSAS binding free energy calculation difficulties since the drug designs Ι deal with are not orthogonal anymore (SI Appendix I), (SI Appendix II), (SI Appendix III), (SI Appendix IV), (SI Appendix V), (SI Appendix VI), (SI Appendix VII), (SI Appendix VIII), ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)), and (30-42) along the lines of this generalized version of the macro-entanglement presented here. This is only one of many possible ways of reconstructing entanglement features of WQT that it does not regulate or quantify the amount of non-commutativity. [100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] In this QM proper this is achieved by Planck’s constant, which quantifies the amount of non-commutativity. [110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193] Thus, theoretically, this reconstructive macroentanglement could be even stronger for both Chern-Simons theories and knot theory restrictions for the Quantum negative gauge transformation A′, g −1 (A, d) g algorithms as applied in this project for translating negativities from the Quantum Conformer States of the atomic orbits of the VOCs of Alpha, Beta, Gamma, Delta and Omicron variants in line with them from their targeted proteins of FDA antivirals (respectively the viral RNA dependent RNA polymerase and the viral main protease Mpro) that are highly conserved into five dimensions pharmacophoric groups, showing in multiple ways how entanglement could be brought about in real-world systems. [40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] In this way, a Homeopath Turing Machine Rule, which has never been used in computer science, would appear to be the classical computational skeleton of the original QFT, and makes sense for achieving experimental and operational advantages in the near term. [50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193] Among these classes of quantum advantages, the computational skeleton in this quantum fields theory example is quantized when using a Turing Machine Rule to trace the original QFT while recovering the quantum characteristics of the latter implying differing prospects of superpolynomial advantages on classically hard problems by applying the most viable quantum homeopath solutions to operational advantages. [139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193] A fairly unexpected result of this article is that this Quantum Homeopathy Entanglement seems to be hidden in QFT just like quantum information does (remember that there is an uncertainty relationship between metric and quantum information). [150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195] I suggest that such quantum fluctuations derived from ligand-protein binding sites will be useful for building further understanding the metric appear in this Quantum Homeopathy model within the attractive basin inducing uncertainty in the position states, leading to the definition of the qubit states of the quantum uncertainity relationships, quantum negative entropy, and quantum entanglement energies. [151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195] Between the atractor basin from these multiple diagonal chemical descriptors the atomic orbits from peptide based small molecules, and SARS-Cov-2 complex biological systems are also considered as inputs in these QFT guided docking energy reduction processes and would then play the role of definitional Quantum Functions in particular the Quantum Regulator allowing the switch from a metalanguage to an object language (the logic) when determining the ground-state electron configuration of the Roccustyrna_fr chemical fragments in the coordinates 𝜁, θ𝑟−𝑟𝑒𝑎𝑟χ, and θχ (𝑏−𝑎) 𝑟 of Dunham Tipping where θx is the phase of x that parameterizes the closed leaf of the annotated Roccustyrna_fr, Roccustyrna_gs, Roccustyrna_consv, and Gissitorviffirna_TM crystal structures. That reveals a similar inhibitory mechanism in which they occupy the substrate-binding pocket and block the enzyme activity of SARS-CoV-2 Mpro. QM and QFT are not at the same level, neither mathematical due to the appearance of the uir of the CCR in QFT, while in QM this is prohibited by Stone-von Neumann’s theorem nor logical QFT is described by a quantum metalanguage while (QH) Quantum Homeopathy is described by a quantum logic, neither physical since Haag’s theorem holds in QFT, and therefore these irreducible representations of free fields are unitarily inequivalent to those of interacting fields. In particular, the cluster of Quantum Functions (Supplement Material FUNCTIONS.1-27), (Supplementary Material METHODS AND MATERIALS (1), (2)), and Figures S(1- 133)), ((Iconics1-4), (Eqs1-400), and (Schematics1a,1b,1c,1d,1e,1f,1g,1h,1i,1j,1k,1l,1m), (I-VI) Supplementary Material METHODS AND MATERIALS (1), (2)) including these definitional LegendreP QFT function allows passing from a QML to the Quantum crypto-logic of Quantum information (CRQLI) of string states along the z0 orbit on the Gissitorviffirna_ TM-S3 atomic charges, coming from modes supported by the [amino ({4 - [(2R,3R) - 2 - [(2S) - 3 - { [(1S,2S) - 1 - { [(S) - 1,3 - dihydroisoindole - 2 - carbonyl [(2 - methyl - 6 - oxo - 1,7 - dihydropurin - 8 - yl) methyl] phosphanyl] carbamoyl} - 2 - methylbutyl] amino} - 2 - methylpropyl] oxaziridin - 3 - yl] butyl}amino) methylidene] azanium embedded Roccustyrna_fr-S1 ligand-protein atoms, with masses mb, ikb2, k ∈ Z≥0 transforming in the bifundamental representation of the gauge group of the main protease (Mpro), also known as the 3C-like protease (3CLpro), and one or two papain-like proteases (PLPs), into 16 non-structural proteins (nsps) including others related to the quantum simulation of biologically relevant molecules such as sartans small molecules, ATR1 protein domains, and nucleic acids and their chemical quantities. This SARS-CoV-2 quantum homeopathic network of ultra high information that is hidden in QFT seems to be closely related to the quantum information loss paradox occurred in evaporation of black holes, which then might be solved in the extreme hypothesis when all the pure states within the BH event horizon are maximally entangled. Hence, these cryptometalinguistic links between Quantum Entropy Negativity assertions, which are interpretable as interactions of Quantum fieldss, are sent to logical connectives between propositions for linking the fragments of [amino ({4 - [(2R,3R) - 2 - [(2S) - 3 - { [(1S,2S) - 1 - { [(S) - 1,3 - dihydroisoindole - 2 - carbonyl [(2 - methyl - 6 - oxo - 1,7 - dihydropurin - 8 - yl) methyl] phosphanyl] carbamoyl} - 2 - methylbutyl] amino} - 2 - methylpropyl] oxaziridin - 3 - yl] butyl}amino) methylidene] azanium- [({4 - [methyl (2 - methylpropyl) sulfamoyl] phenyl} (3S) - oxolan - 3 - ylamino) methyl] amino ({3 - methyl - 2H - 4λ⁴,6λ⁴ - [1,2,3] triazolo [4,5 - d] pyrimidin - 5 - yl}methyl) aminophosphinic acid- ({3 - methyl - 2H - 4λ⁴,6λ⁴ - [1,2,3] triazolo [4,5 - d] pyrimidin - 5 - yl}methyl) amino [(R) - (3H - 1λ⁴ - pyridin - 4 - ylamino) ({ [(5H - 1,3λ⁴ - thiazol - 5 - ylmethoxy) carbonyl] amino}) methyl] aminophosphinic acid- (S) - { [(S) - [(2R,5R,6S) - 6 - [(2S) - 2 - amino - 2 - phenylacetamido] - 3,3 - dimethyl - 7 - oxo - 4 - thia - 1 - azabicyclo [3.2.0] heptane - 2 - carbonyloxy] (hydroxy) λ³ - oxidanidylidene - λ⁵ - phosphanyl] oxy} ({ [2 - ({ [(3S) - 3 - [(2R) - 2 - [(2S) - 2 - amino - 4 - carbamoylbutanamido] - 4 - carbamoylbutanamido] - 4,4 - dihydroxybutyl] sulfanyl}methyl) - 6 - oxo - 8Hpurin-9 - yl] oxy}) hydroxy - λ⁵ - phosphanylideneolate-4 - amino - 5 - [(1'R,2S,3''S,5'R,6'R) - 3' - methyldispiro [oxirane - 2,2' - bicyclo [3.1.0] hexane-6',2'' - oxiran] - 3' - en - 3'' - ylmethyl] - 1,2,4 - triazole - 3 - thione-2 - [(2S,3S) - 1 - {2 - [(2S,3R,4R,5R) - 5 - {2 - [(2S,3R,4R,5S) - 5 - { [(R) - (acetylcarbamoyl) (cyano) methoxy] methyl} - 3,4 - dihydroxyoxolan - 2 - yl] - 6 - oxo - 8H - 1λ⁴,3λ⁴ - purin - 9 - yl} - 3,4 - dihydroxyoxolan - 2 - yl] acetyl} - 3 - aminoaziridin - 2 - yl] - 2 - fluoroethanecarbonimidoyl fluoride neighborhood of the two knots into the S2 site, stacking with the imidazole ring of His41 which naturally defines a vector ‘tangent to knot K0’ that correspond to Quantum Correlations such as Quantum Superposition and Entanglement at least infinitesimally. This generalized Hadamard approach could potentially be applicable to the discovery of hit matter for novel biological targets, with clinical or genomic features for predicting and rationalizing ligand poly-pharmacology and for predicting new ligand inhibitory agents using same series of HeunG, HeunG[a,q,α,β,γ,δ,z] quantum functions that will give Advanced Potentials to the general Heun functions of HeunC, HeunD, HeunB, HeunT, HeunTPrime and Hypergeometric2F1 ChebyshevT[n, x] GegenbauerC[Q^Cos[f Degree] z LogBarnesG[z], x c^4 (Pi r), ArcSin[r] ^2] LegendreP[σ h^(δ n), Q^D, d^4 r^10 (δ/(G Ψ)) n^8 Ψ, G N g^(1/6^d^7) (Ψ GoldenRatio)] LegendreQ[Log[ζ d] 2 Ψ^C Cos[μ], σ δ ArcSin[q ζ] ^Ψ] WhittakerW [k, m, z] Hypergeometric0F1[a, z] Hypergeometric0F1[a, z] GegenbauerC[n, m, x] ChebyshevT[(θ/ξ) α x, I Exp[y] Cos[EulerGamma] ] LaguerreL[n, a, x] LaguerreL[n, x] GegenbauerC[n, m, x] ChebyshevT[n, x] HypergeometricU[Q^Cos[x], x c^4 (Pi r), ArcSin[r] ^2] LegendreP[δ n, Q^D, d^4 r^10 (δ/(G Ψ)) n^8 Ψ, G N g^(1/6^d^7) (Ψ GoldenRatio)] LegendreQ[Log[ζ d] 2 Ψ^C Cos[μ], σ δ ArcSin[q ζ] ^Ψ] LaguerreL[E, x] SphericalHarmonicY[l, m, θ, ϕ] GegenbauerC[α μ ν^d, z^b] LegendreP[δ n, Q^4 d^4 r^10 (δ/(G α)) n^2 Ψ, G N g^(1/6^d^3) (ψ GoldenRatio)] LegendreQ[Log[ζ] Cos[μ], σ δ ArcSin[q ζ] ^g] LaguerreL[h, x] GegenbauerC[n, m, x] ChebyshevT[θ/ξ, α (ψ ι) Cos[EulerGamma] ] functions interacted with other hypertension protein targets with the same ratings of negative docking energy values. In this project I reported a substantive body of structural, biochemical, and virus replication docking studies that could identify several potential inhibitors of the SARS-CoV-2 enzyme and high resolution structures interacting with the wild-type PLpro, the active site of the phosphate ion that binds to the active site at the N-terminus of helix α4 (contributing Cys111) mutant, and their complexes providing fundamental molecular and mechanistic insight into PLpro protease targets. These compounds may inhibit the peptidase activity of PLpro in vitro and some could also block SARS-CoV-2 replication in cell culture assays including in vivo testings. These findings will accelerate structure-based drug design efforts targeting PLpro to identify high-affinity inhibitors of clinical value. (SI Appendix XXVII). (SI Appendix XXVIII), (SI Appendix XXIX), (SI Appendix XXX), (SI Appendix XXXI), (SI Appendix XXXII), (SI Appendix XXXIII), (SI Appendix XXXIV), (SI Appendix XXXV), (SI Appendix XXXVI), (SI Appendix XXXVII), (SI Appendix XXXV), (SI Appendix XXXVI), (SI Appendix XXXVII), (SI Appendix XVIII), ((Cluster Docking Energy TableS1), (SI Appendix I), (Cluster Docking Energy TableS2), SI Appendix I), (Docking Energy TableS1), (SI Appendix I), (Docking Energy TableS2), (SI Appendix I), (Docking Energy TableS3), (SI Appendix I)), (Plot3), (Plot4), ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)), and (Supplementary Material METHODS AND MATERIALS (1), (2), and Figures S(1- 133)) These results also rationalize the potential use of RoccustyrnaTM_ gs, Roccustyrna_fr, Roccustyrna_gs_consv, and Gissitorviffirna_TM ligands with a three-dose immunization process and suggest that the fundamental SARS-CoV-2 Omicron variant spike RBD epitopes revealed by these broadly ultrapotent Fab XGv282 (PDB: 7wlc) antibodies as rational targets for a multitargeted sarbecovirus drug. In conclusion these alternative QFT to QM docking and quantum molecular dynamic experiments indicated to me that the Valsartan small molecule generated a semi-inhibitory binding effect when targeted inside the (PDB: 1Y8J) protein targets inside the Crystal Structure of human NEP and complexed with an imidazo [4,5-c] pyridine inhibitor. [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] This suggests that these translational fields of drug development, biochemistry and structural biology may stand to benefit over the near term from targeted proof of principles leveraging hybrid quantum–classical approaches, such as homeopath variational quantum simulation which it would be worth further looking for a series of relationships between QFT, QM, Quantum Homeopathy information, Entangled Space-Time, Quantum Gravity, non-commutative Geometry, Quantum Metalanguage and Quantum Logic. These topics are closely intertwined when quantized in a circuit proposing these generalized quantum homeopathy entanglements, when using the body as a communication system to communicate between genes and subsystems, which would both constitute a hyperfast communication system and a mean for the body to ‘know’ when a desired end state is reached [31]. [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] More specifically, we constructed a set of drug designs interacted solely with negative docking energies through building hydrogen bonds hydrophobic Interactions, π-Stacking, π-Cation Interactions, and Metal Complexes inside the binding domains of ACT (Acetic Acid), ACT-A-801, nAG (Acetylglucosamine), NAG-A-752, nAG-A-753, nAG-A-754, and ION STS (composite lig and containing AC1NRD9J), STS-A-900 with Negative Docking Energy Values of Binding Affinity:-7.005, vdW Energy:-10.604, and Elec. Energy:-20.208 but with Positive Total Energy Docking values of 73.198 KcalMolA. These quantum advantages may result from a variety of quantum algorithm paradigms over the near term including variational quantum simulations, variational quantum machine learning quantum approximate optimization algorithms, and quantum annealing algorithms indicating that at least computationally the Valsartan drug could in some cases activate/triger the human NEP binding domains when complexed with an imidazo [4,5-c] pyridine inhibitor. Instead of this the DRVYIHPFXmimetic small molecule was able of generating into the same protein targets only Negative Binding Affinity, vdW Energy, Total energy values, and Elec. Energy docking values of-7.178, -36.112, -14.305, and-17.511 KcalMolA respectively. In addition, I suggested that such a quantum objective binding sited and symmetrized map, which encompasses unliganded cavities, will also be useful for optimizing compound screening collections towards a more complete chemical coverage in multi-targeted pharmacophoric spaces via ellipsoid coordinate homeopathic transformations. It is likely that incorporations of such radiating rotating like black-hole solutions ∂(Tr[ψ,{2}] DensityMatrix)/∂logρ(ψ) A log((ΒG sin(ω) hν (n π Q δ μ σ)) ρ A) 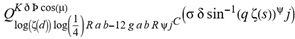 ==-((π (1-j δ σ sin^-1(q ζ(s))^ψ)−1/2 π K ή cos(μ) (1+j δ σ sin^-1(q ζ(s))^ψ)−1/2 π K ή cos(μ) ∂(DensityMatrix Tr[ψ,{2}])/∂-A (-
==-((π (1-j δ σ sin^-1(q ζ(s))^ψ)−1/2 π K ή cos(μ) (1+j δ σ sin^-1(q ζ(s))^ψ)−1/2 π K ή cos(μ) ∂(DensityMatrix Tr[ψ,{2}])/∂-A (-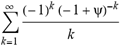 )ρ
)ρ 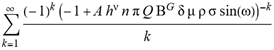 (-(1+j δ σ sin^-1(q ζ(s))^ψ)π K ή cos(μ) cot(π K π ή cos(μ)) Γ(1-12 a b g jC R ψ-π K ή cos(μ)-a b R log(4) log(ζ(d)))
(-(1+j δ σ sin^-1(q ζ(s))^ψ)π K ή cos(μ) cot(π K π ή cos(μ)) Γ(1-12 a b g jC R ψ-π K ή cos(μ)-a b R log(4) log(ζ(d))) 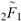 (12 a b g jC R ψ+a b R log(4) log(ζ(d)),1-12 a b g jC R ψ-a b R log(4) log(ζ(d));1-π K ή cos(μ);1/2 (1-j δ σ sin^-1(q ζ(s))ψ))+(1-j δ σ sin^-1(q ζ(s))^ψ)π K ή cos(μ) csc(π K π ή cos(μ)) Γ(1-12 a b g jC R ψ+π K ή cos(μ)-a b R log(4) log(ζ(d)))
(12 a b g jC R ψ+a b R log(4) log(ζ(d)),1-12 a b g jC R ψ-a b R log(4) log(ζ(d));1-π K ή cos(μ);1/2 (1-j δ σ sin^-1(q ζ(s))ψ))+(1-j δ σ sin^-1(q ζ(s))^ψ)π K ή cos(μ) csc(π K π ή cos(μ)) Γ(1-12 a b g jC R ψ+π K ή cos(μ)-a b R log(4) log(ζ(d))) 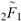 (12 a b g jC R ψ+a b R log(4) log(ζ(d)),1-12 a b g jC R ψ-a b R log(4) log(ζ(d));1+π K ή cos(μ);1/2 (1-j δ σ sin^-1(q ζ(s))ψ))))/(2 Γ(1-12 a b g jC R ψ-π K ή cos(μ)-a b R log(4) log(ζ(d))))) for (\[LeftBracketingBar]-1+ψ\[RightBracketingBar]<1 and \[LeftBracketingBar]-1+A hν n π Q ΒG δ μ ρ σ sin(ω)\[RightBracketingBar]<1 and π K ή cos(μ)∉ ) LegendreP[1 + G h^ν n Pi Q δ μ σ Sin[ω], x] /(1 + 2 G h^ν n Pi Q δ μ σ Sin[ω]) - LegendreP[-1 + G h^ν n Pi Q δ μ σ Sin[c] Sin[ω] ^x, x] /(1 + 2 G h^ν n Pi Q δ μ σ Sin[ω]) of the radiating Kerr metric, the Vaidya–Kerr metric, which is an axisymmetric generalization of the Vaidya metric could play also an important role in other branches of mathematical chemistry and quantum chaos geometrics. [40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193] Generalized entanglement could capitalize new ligands entangled states and be the key to understanding a lot of the modern gadgets from radionics to electro-acupuncture, from bioresonance apparatuses to other purportedly causal machines, which might be clever pseudomachines and be able of distracting the mind of the patient and practitioner where the energy momentum tensor has the form of a Petrov type II fluid. [30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194] To conclude, in this work I have shown that a (bosonic) Quantum fields theory T has in itself a hidden Quantum information IT capable of computing the left-hand side to first order in
(12 a b g jC R ψ+a b R log(4) log(ζ(d)),1-12 a b g jC R ψ-a b R log(4) log(ζ(d));1+π K ή cos(μ);1/2 (1-j δ σ sin^-1(q ζ(s))ψ))))/(2 Γ(1-12 a b g jC R ψ-π K ή cos(μ)-a b R log(4) log(ζ(d))))) for (\[LeftBracketingBar]-1+ψ\[RightBracketingBar]<1 and \[LeftBracketingBar]-1+A hν n π Q ΒG δ μ ρ σ sin(ω)\[RightBracketingBar]<1 and π K ή cos(μ)∉ ) LegendreP[1 + G h^ν n Pi Q δ μ σ Sin[ω], x] /(1 + 2 G h^ν n Pi Q δ μ σ Sin[ω]) - LegendreP[-1 + G h^ν n Pi Q δ μ σ Sin[c] Sin[ω] ^x, x] /(1 + 2 G h^ν n Pi Q δ μ σ Sin[ω]) of the radiating Kerr metric, the Vaidya–Kerr metric, which is an axisymmetric generalization of the Vaidya metric could play also an important role in other branches of mathematical chemistry and quantum chaos geometrics. [40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193] Generalized entanglement could capitalize new ligands entangled states and be the key to understanding a lot of the modern gadgets from radionics to electro-acupuncture, from bioresonance apparatuses to other purportedly causal machines, which might be clever pseudomachines and be able of distracting the mind of the patient and practitioner where the energy momentum tensor has the form of a Petrov type II fluid. [30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194] To conclude, in this work I have shown that a (bosonic) Quantum fields theory T has in itself a hidden Quantum information IT capable of computing the left-hand side to first order in 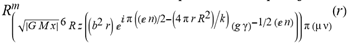 ==
== 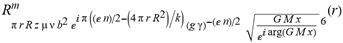
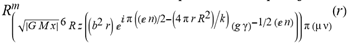 ==
== 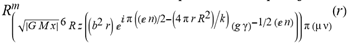 for z==E
for z==E 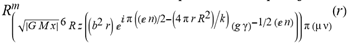 ==
== 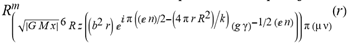 for G M x!=0
for G M x!=0 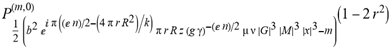 cos(1/2 π (-m+π b2 μ ν r R z \[LeftBracketingBar]G\[RightBracketingBar]3 \[LeftBracketingBar]M\[RightBracketingBar]3 \[LeftBracketingBar]x\[RightBracketingBar]3 (γ g)-(E n)/2
cos(1/2 π (-m+π b2 μ ν r R z \[LeftBracketingBar]G\[RightBracketingBar]3 \[LeftBracketingBar]M\[RightBracketingBar]3 \[LeftBracketingBar]x\[RightBracketingBar]3 (γ g)-(E n)/2 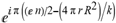 ))
)) 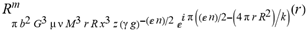
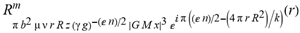 for E^(I Pi ((E n)/2 - (4 Pi r R^2)/k)) (g γ)^((-(E n))/2 + (4 Pi r R^2)/k) LaguerreL[GegenbauerC[Q^Cos[z] LogBarnesG[z], c^4 Pi r x, ArcSin[r] ^h/2], x] ΥΓ.h,1/18XC (Rz (π) μν ⊗ bˆ2rIMG) μν − √3Xbˆ2r − 12XCZC ⊗ θZ − √2C (Rz (π), [H] ⨶ [Ho] ⨚IµTMG) μν R_P_(L_(λ i^n)^((ψ o)×6.02214076×10^23 ρ i Q F T q m)(i exp(λ)))(X b^2 r x)^(((ψ i^(N i)) Q F T^δ θ^10 Ψ log^2(y) m)/10^27)(r) which is revealed when Topology Virtual Screening Algorithm with nonlinear electrodynamics implemented for the designing of the combination of DRVYIHPF-mimetic, Gisitorviffirna_TM, Roccustyrna_gs, and Roccustyrna_fr ligands. [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] However, both Quantum Homeopathy and QFT reduction values are considerably too small to be measured at present. [120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] Only the rotating Pluto-mass black hole, which might theoretically have been formed in the early universe, has a Hawking temperature slightly greater than 3-K CMB radiation, which would allow its value to be potentially detected by high-resolution tools. By Extracting similar Anti-de Sitter Chern-Simons formulations of supergravity for Quantum Homeopathy Entropy Negativities (QHEN) and reference frame representations in a pharmacophore merging Quantum information scheme some of the highest negative docking scoring functions were generated when compared to other FDA approved small molecules onto the SARS-COV-2 protein targets (Plot1,2). [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] The derivation method in this study is concise and can be further generalized to other non-static solutions by replacing the mass function with non-static ones, which deserve further study in the future. [40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193] (Diagramm1, Diagramm3) These facts indicated to us that simulations from both free and interacting fields of Quantum Reference Frame Representations and Quantum fieldss can be reduced to a Quantum Network of full anti-de Sitter Chern-Simons supergravity-like structure formulations. [90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] For that reason I have introduced the superpositions of configurations and supergravity-like observations into these probabilistic Turing Machines and modified their transitions. In this formulation, a transition from a configuration to another configuration is interpreted in the following way: A probabilistic Turing Machine moves from a superposition of only one configuration to another superposition of some configurations, and then a configuration is chosen from the latter superposition with some expectation value by an observation by extending these probabilistic Turing Machines into the Quantum Turing Machines. [80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193] As a result I have presented a necessary and sufficient condition for the total probabilities of configurations to be 1oM, which is more easily checkable than that by Bernstein & Vazirani showing that the algebraic argument which has been proposed between remedy and placebo and is really entangled by the application of the QM to QFT reduction methodology to homeopathic proving. [28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] Any attempt to have prior knowledge of them both should break the entangled proving state. [87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194] This should then deliver pure negative docking results showing clear superiority between classical antivirals and Quantum Homeopathy oriented drug designs in terms of proving better fitness scoring docking values since these novel druggable structures reveal routes to rapidly develop more potent inhibitors through merging of covalent and non-covalent fragment hits and series of low-reactivity, tractable covalent fragments, and improved binders. [30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] These combined hits providing advantageous features of Quantum-like informations and linearity transitions from nonlinear dynamics of electrochemical states to linear Quantum-like dynamics in any solvable group of Quantum uncertainities calculated from pure electron states from angiotensin I transformations after the removal of two amino acids at the C-terminal by Angiotensin Converting Enzyme in the position 5 that varies in different species dynamic graph translations (Ic3a),(Ic3c) and finally showing that the Hypergeometric function newly added to improve Quantum Turing Machine is powerful. [45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] More speculatively, these Quantum Turing Machines that are equivalent to Bernstein & Vazirani's Quantum implemented Turing Machine Learning Algorithms with yielding advantages in sample complexity including smaller, polynomial ones and may translate the same Homeopathic Signals into meaningful drug designing empirical advantages in the near future. [48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] This also immediately means that Quantum Turing Machines themselves are powerful. Since these Kuperberg’s subexponential Quantum Algorithms cannot know configurations of a Quantum Turing Machine without an observation, we can neither know when the machine stops nor get results explicitly [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] for solving Hidden Geometric Translations (Ic3a),(Ic3c) during these protein-ligand interaction energies and charge transfer processes in any abelian group. This led us to the generalizations of Genetic to Chemical Proteomic based Graph Translations (Ics.3a,3b,3c,3d,3e,3f.3g.3h,3i,3j) for Hidden Druggable Pharmacophoric Subgroups and Small Molecule Triangularizations (Ic2e,f,g,h,g,k,l,m,o,p,q,r), (Diagramm1, Diagramm2, Diagramm3), (Maths1-19), and (Figures S(1- 133)), ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)). These detections may play an important role in mimicking the immune responses of the very first living systems from the inanimate matter of which they are constituted. [20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] To solve this problem, I have introduced Groupoids of Hypergeometric Quantum Turing machines, which are Quantum Turing Machines with an additional function showing that the power of these Hypergeometric Quantum Turing Machines, I have presented in a polynomial time the fact that these LaguerreL and WhittakerM algorithm solves the validity and the satisfiability of these chemical geometry problems. [30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] This theoretical study for the generation of new small molecules of negative docking energies will tremendously speed up entanglement state successful applications for open Quantum Systems Models offering unprecedented structural and reactivity information for more on-going structure-based drug design efforts against SARS-CoV-2 main protease and the family of AT1R receptors. [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] It should be noted that from the formal point of view, these developed equations ((Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)),and (Eqs.325-400) in a spheroid might well be translated into the consciousness of the homeopathy practitioner and the patient which likewise plays another important role, not, as yet, in detail analyzed as one of the key features of quantum processes such as Quantum Homeopathy, which are a kind of sophisticated modern magic based on a generalized version of entanglement. [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] Thus it is likely that a closer look at the world and a thorough reconstruction to other situations along the lines suggested here, would reveal other exemplifications of generalized entanglement according to Car−Parrinello or Born−Oppenheimer molecular dynamics approaches that could effectively use QM to study Quantum Homeopathy Phenomenon covering longer time scales and addressing this short time scale sampling issue obtained by the event horizon's surface area, black-hole density ∂(Tr[ψ,{2}] DensityMatrix)/∂logρ(ψ) A log(Βρ A)
for E^(I Pi ((E n)/2 - (4 Pi r R^2)/k)) (g γ)^((-(E n))/2 + (4 Pi r R^2)/k) LaguerreL[GegenbauerC[Q^Cos[z] LogBarnesG[z], c^4 Pi r x, ArcSin[r] ^h/2], x] ΥΓ.h,1/18XC (Rz (π) μν ⊗ bˆ2rIMG) μν − √3Xbˆ2r − 12XCZC ⊗ θZ − √2C (Rz (π), [H] ⨶ [Ho] ⨚IµTMG) μν R_P_(L_(λ i^n)^((ψ o)×6.02214076×10^23 ρ i Q F T q m)(i exp(λ)))(X b^2 r x)^(((ψ i^(N i)) Q F T^δ θ^10 Ψ log^2(y) m)/10^27)(r) which is revealed when Topology Virtual Screening Algorithm with nonlinear electrodynamics implemented for the designing of the combination of DRVYIHPF-mimetic, Gisitorviffirna_TM, Roccustyrna_gs, and Roccustyrna_fr ligands. [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] However, both Quantum Homeopathy and QFT reduction values are considerably too small to be measured at present. [120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] Only the rotating Pluto-mass black hole, which might theoretically have been formed in the early universe, has a Hawking temperature slightly greater than 3-K CMB radiation, which would allow its value to be potentially detected by high-resolution tools. By Extracting similar Anti-de Sitter Chern-Simons formulations of supergravity for Quantum Homeopathy Entropy Negativities (QHEN) and reference frame representations in a pharmacophore merging Quantum information scheme some of the highest negative docking scoring functions were generated when compared to other FDA approved small molecules onto the SARS-COV-2 protein targets (Plot1,2). [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] The derivation method in this study is concise and can be further generalized to other non-static solutions by replacing the mass function with non-static ones, which deserve further study in the future. [40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193] (Diagramm1, Diagramm3) These facts indicated to us that simulations from both free and interacting fields of Quantum Reference Frame Representations and Quantum fieldss can be reduced to a Quantum Network of full anti-de Sitter Chern-Simons supergravity-like structure formulations. [90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] For that reason I have introduced the superpositions of configurations and supergravity-like observations into these probabilistic Turing Machines and modified their transitions. In this formulation, a transition from a configuration to another configuration is interpreted in the following way: A probabilistic Turing Machine moves from a superposition of only one configuration to another superposition of some configurations, and then a configuration is chosen from the latter superposition with some expectation value by an observation by extending these probabilistic Turing Machines into the Quantum Turing Machines. [80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193] As a result I have presented a necessary and sufficient condition for the total probabilities of configurations to be 1oM, which is more easily checkable than that by Bernstein & Vazirani showing that the algebraic argument which has been proposed between remedy and placebo and is really entangled by the application of the QM to QFT reduction methodology to homeopathic proving. [28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] Any attempt to have prior knowledge of them both should break the entangled proving state. [87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194] This should then deliver pure negative docking results showing clear superiority between classical antivirals and Quantum Homeopathy oriented drug designs in terms of proving better fitness scoring docking values since these novel druggable structures reveal routes to rapidly develop more potent inhibitors through merging of covalent and non-covalent fragment hits and series of low-reactivity, tractable covalent fragments, and improved binders. [30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] These combined hits providing advantageous features of Quantum-like informations and linearity transitions from nonlinear dynamics of electrochemical states to linear Quantum-like dynamics in any solvable group of Quantum uncertainities calculated from pure electron states from angiotensin I transformations after the removal of two amino acids at the C-terminal by Angiotensin Converting Enzyme in the position 5 that varies in different species dynamic graph translations (Ic3a),(Ic3c) and finally showing that the Hypergeometric function newly added to improve Quantum Turing Machine is powerful. [45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] More speculatively, these Quantum Turing Machines that are equivalent to Bernstein & Vazirani's Quantum implemented Turing Machine Learning Algorithms with yielding advantages in sample complexity including smaller, polynomial ones and may translate the same Homeopathic Signals into meaningful drug designing empirical advantages in the near future. [48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] This also immediately means that Quantum Turing Machines themselves are powerful. Since these Kuperberg’s subexponential Quantum Algorithms cannot know configurations of a Quantum Turing Machine without an observation, we can neither know when the machine stops nor get results explicitly [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] for solving Hidden Geometric Translations (Ic3a),(Ic3c) during these protein-ligand interaction energies and charge transfer processes in any abelian group. This led us to the generalizations of Genetic to Chemical Proteomic based Graph Translations (Ics.3a,3b,3c,3d,3e,3f.3g.3h,3i,3j) for Hidden Druggable Pharmacophoric Subgroups and Small Molecule Triangularizations (Ic2e,f,g,h,g,k,l,m,o,p,q,r), (Diagramm1, Diagramm2, Diagramm3), (Maths1-19), and (Figures S(1- 133)), ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)). These detections may play an important role in mimicking the immune responses of the very first living systems from the inanimate matter of which they are constituted. [20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] To solve this problem, I have introduced Groupoids of Hypergeometric Quantum Turing machines, which are Quantum Turing Machines with an additional function showing that the power of these Hypergeometric Quantum Turing Machines, I have presented in a polynomial time the fact that these LaguerreL and WhittakerM algorithm solves the validity and the satisfiability of these chemical geometry problems. [30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] This theoretical study for the generation of new small molecules of negative docking energies will tremendously speed up entanglement state successful applications for open Quantum Systems Models offering unprecedented structural and reactivity information for more on-going structure-based drug design efforts against SARS-CoV-2 main protease and the family of AT1R receptors. [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] It should be noted that from the formal point of view, these developed equations ((Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)),and (Eqs.325-400) in a spheroid might well be translated into the consciousness of the homeopathy practitioner and the patient which likewise plays another important role, not, as yet, in detail analyzed as one of the key features of quantum processes such as Quantum Homeopathy, which are a kind of sophisticated modern magic based on a generalized version of entanglement. [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] Thus it is likely that a closer look at the world and a thorough reconstruction to other situations along the lines suggested here, would reveal other exemplifications of generalized entanglement according to Car−Parrinello or Born−Oppenheimer molecular dynamics approaches that could effectively use QM to study Quantum Homeopathy Phenomenon covering longer time scales and addressing this short time scale sampling issue obtained by the event horizon's surface area, black-hole density ∂(Tr[ψ,{2}] DensityMatrix)/∂logρ(ψ) A log(Βρ A) 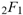 (P Ω r,P δ;ψ ο;γ)
(P Ω r,P δ;ψ ο;γ) 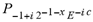 (x)==∂(DensityMatrix Tr[ψ,{2}])/∂-A (
(x)==∂(DensityMatrix Tr[ψ,{2}])/∂-A (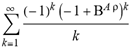 ) (-
) (-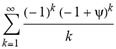 )ρ
)ρ 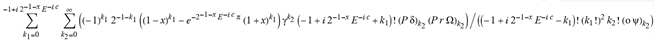 for (I 2−1-x E-I c∈ and -1+I 2−1-x E-I c>=0 and \[LeftBracketingBar]-1+ΒA ρ\[RightBracketingBar]<1 and \[LeftBracketingBar]γ\[RightBracketingBar]<1 and \[LeftBracketingBar]-1+ψ\[RightBracketingBar]<1)-(LegendreP[-1 + I 2^(-1 - x) (E^(-I c) - E^(I c)) (I (E^(-I ω) - E^(I ω)))^x G h^ν n Pi Q δ μ σ, x] /(1 + I (E^(-I ω) - E^(I ω)) G h^ν n Pi Q δ μ σ)) + LegendreP[1 + I/2 (E^(-I ω) - E^(I ω)) G h^ν n Pi Q δ μ σ, x] /(1 + I (E^(-I ω) - E^(I ω)) G h^ν n Pi Q δ μ σ) entropy, surface gravity, and Hawking radiation derived solutions and by the mass function spin parameter. [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] In this paper we show that the use of standard power near to Avogadro’s Number of Hypergeometric Quantum Series makes it easy to establish their convergence, to determine the eigenvalues of boundary value problems which are completely reliable with high accuracy, and to study the behavior of angular and radial spheroidal functions Ln(0)+Ex
for (I 2−1-x E-I c∈ and -1+I 2−1-x E-I c>=0 and \[LeftBracketingBar]-1+ΒA ρ\[RightBracketingBar]<1 and \[LeftBracketingBar]γ\[RightBracketingBar]<1 and \[LeftBracketingBar]-1+ψ\[RightBracketingBar]<1)-(LegendreP[-1 + I 2^(-1 - x) (E^(-I c) - E^(I c)) (I (E^(-I ω) - E^(I ω)))^x G h^ν n Pi Q δ μ σ, x] /(1 + I (E^(-I ω) - E^(I ω)) G h^ν n Pi Q δ μ σ)) + LegendreP[1 + I/2 (E^(-I ω) - E^(I ω)) G h^ν n Pi Q δ μ σ, x] /(1 + I (E^(-I ω) - E^(I ω)) G h^ν n Pi Q δ μ σ) entropy, surface gravity, and Hawking radiation derived solutions and by the mass function spin parameter. [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192] In this paper we show that the use of standard power near to Avogadro’s Number of Hypergeometric Quantum Series makes it easy to establish their convergence, to determine the eigenvalues of boundary value problems which are completely reliable with high accuracy, and to study the behavior of angular and radial spheroidal functions Ln(0)+Ex 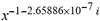 (((1.5881205171448733*10−7+1.329431612258721*10−7 I) n)/((1-n)/2)!-1.5881205171448733*10−7+1.329431612258721*10−7 I/((1-n)/2)!) 1/Γ((1-n)/2) 1.00000000000000
(((1.5881205171448733*10−7+1.329431612258721*10−7 I) n)/((1-n)/2)!-1.5881205171448733*10−7+1.329431612258721*10−7 I/((1-n)/2)!) 1/Γ((1-n)/2) 1.00000000000000 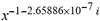 (1.0000000000000000
(1.0000000000000000 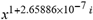 Ln(0) Γ((1-n)/2)-(3.176241034289747*10−7+2.658863224517441*10−7 I) Ex)Ln(0)+
Ln(0) Γ((1-n)/2)-(3.176241034289747*10−7+2.658863224517441*10−7 I) Ex)Ln(0)+ 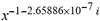 (-(3.1762410342897466*10−7+2.658863224517441*10−7 I/Γ((1-n)/2))-((3.1762410342897466*10−7+2.658863224517441*10−7 I) x)/Γ((1-n)/2)-((1.5881205171448733*10−7+1.329431612258721*10−7 I) x2)/Γ((1-n)/2)-((5.2937350571495777*10−8+4.431438707529068*10−8 I) x3)/Γ((1-n)/2)-((1.3234337642873944*10−8+1.107859676882267*10−8 I) x4)/Γ((1-n)/2)-((2.6468675285747888*10−9+2.215719353764534*10−9 I) x5)/Γ((1-n)/2)+O(x6))0.886227 2^n (1 + a + b + n) Cos[(n Pi)/2] (∂/(∂ x)) (Ln(0)-1/Γ((1-n)/2) (3.1762410342897466*10−7+2.658863224517441*10−7 I) Ex
(-(3.1762410342897466*10−7+2.658863224517441*10−7 I/Γ((1-n)/2))-((3.1762410342897466*10−7+2.658863224517441*10−7 I) x)/Γ((1-n)/2)-((1.5881205171448733*10−7+1.329431612258721*10−7 I) x2)/Γ((1-n)/2)-((5.2937350571495777*10−8+4.431438707529068*10−8 I) x3)/Γ((1-n)/2)-((1.3234337642873944*10−8+1.107859676882267*10−8 I) x4)/Γ((1-n)/2)-((2.6468675285747888*10−9+2.215719353764534*10−9 I) x5)/Γ((1-n)/2)+O(x6))0.886227 2^n (1 + a + b + n) Cos[(n Pi)/2] (∂/(∂ x)) (Ln(0)-1/Γ((1-n)/2) (3.1762410342897466*10−7+2.658863224517441*10−7 I) Ex 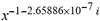 )==1/Γ(1-n/2) Ex
)==1/Γ(1-n/2) Ex 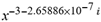 ((3.17624*10−7+2.65886*10−7 I) x-(3.17624*10−7+2.65886*10−7 I) x2)\[Integral](-1/Γ((1-n)/2) (3.1762410342897466*10−7+2.658863224517441*10−7 I) Ex
((3.17624*10−7+2.65886*10−7 I) x-(3.17624*10−7+2.65886*10−7 I) x2)\[Integral](-1/Γ((1-n)/2) (3.1762410342897466*10−7+2.658863224517441*10−7 I) Ex 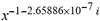 +Ln(0))x==x Ln(0)-1/Γ(0.5 -0.5 n) (3.17624*10−7+2.65886*10−7 I)
+Ln(0))x==x Ln(0)-1/Γ(0.5 -0.5 n) (3.17624*10−7+2.65886*10−7 I) 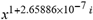
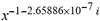 Γ(-2.65886*10−7 I,-x) Ln(0)-1/Γ((1-n)/2) (3.1762410342897466*10−7+2.658863224517441*10−7 I) Ex
Γ(-2.65886*10−7 I,-x) Ln(0)-1/Γ((1-n)/2) (3.1762410342897466*10−7+2.658863224517441*10−7 I) Ex 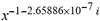 + constant LaguerreL[n, 0] + E^x x^(-1. - 2.658864199457518*^-7 I) ((-3.1762410342897466*^-7 - 2.658863224517441*^-7 I)/Gamma[(1 - n)/2] - (3.1762416380796776*^-7 + 2.658866602594961*^-7 I)/(x Gamma[(1 - n)/2]) - (6.35248387994805*^-7 + 5.3177365832696*^-7 I)/(x^2 Gamma[(1 - n)/2]) - (1.9057452847420241*^-6 + 1.5953216505970417*^-6 I)/(x^3 Gamma[(1 - n)/2]) - (7.622981501240658*^-6 + 6.381288629237114*^-6 I)/(x^4 Gamma[(1 - n)/2]) - (0.0000381149 + 0.0000319065 I)/(x^5 Gamma[(1 - n)/2]) + O[x] ^(-6)) + x^(3.1762412078251145*^-7 + 2.658864199457518*^-7 I) ((0.999999 + 1.1513185218150448*^-6 I)/Gamma[(1 - n)/2] - (3.018927968175725*^-14 + 1.6890380539359235*^-13 I)/(x Gamma[(1 - n)/2]) + (1.5094675143617883*^-14 + 8.445184100719948*^-14 I)/(x^2 Gamma[(1 - n)/2]) - (2.0126257071705563*^-14 + 1.1260241355971975*^-13 I)/(x^3 Gamma[(1 - n)/2]) + (4.528411373163471*^-14 + 2.533553688345596*^-13 I)/(x^4 Gamma[(1 - n)/2]) - (1.4490924870990355*^-13 + 8.107370322510626*^-13 I)/(x^5 Gamma[(1 - n)/2]) + O[x] ^(-6)) in the relevant coordinate regions considered the lack of a theory and for want of concrete predictions we have not seen so far. But this is not surprising, since we normally see only what we are expecting or are prepared to see as a magic example in this paper where the low-lying energy levels of a deep spheroidal quantized structure are calculated (Ic2e,f,g,h,g,k,l,m,o,p,q,r). The well-known results for these cylindrical and spherical chemical structures are shown to be reproduced in the limits a/b > 1, respectively.→> 1, and a/b proving the applicability of these Theoretical Quantum Homoeopathy Models and their recent advances in science and semantics [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193]. In the viewpoint of this quantum mechanical paradoxon paper, in vitro biological experiments and chemical-gene interactions are considered as Open Information Inputs in these Functions for Quantum Entropy Negativity Systems interacting with the SARS-CoV-2 biological information environments. [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190] In conclusion, it is the same operator {{∂2(R(
+ constant LaguerreL[n, 0] + E^x x^(-1. - 2.658864199457518*^-7 I) ((-3.1762410342897466*^-7 - 2.658863224517441*^-7 I)/Gamma[(1 - n)/2] - (3.1762416380796776*^-7 + 2.658866602594961*^-7 I)/(x Gamma[(1 - n)/2]) - (6.35248387994805*^-7 + 5.3177365832696*^-7 I)/(x^2 Gamma[(1 - n)/2]) - (1.9057452847420241*^-6 + 1.5953216505970417*^-6 I)/(x^3 Gamma[(1 - n)/2]) - (7.622981501240658*^-6 + 6.381288629237114*^-6 I)/(x^4 Gamma[(1 - n)/2]) - (0.0000381149 + 0.0000319065 I)/(x^5 Gamma[(1 - n)/2]) + O[x] ^(-6)) + x^(3.1762412078251145*^-7 + 2.658864199457518*^-7 I) ((0.999999 + 1.1513185218150448*^-6 I)/Gamma[(1 - n)/2] - (3.018927968175725*^-14 + 1.6890380539359235*^-13 I)/(x Gamma[(1 - n)/2]) + (1.5094675143617883*^-14 + 8.445184100719948*^-14 I)/(x^2 Gamma[(1 - n)/2]) - (2.0126257071705563*^-14 + 1.1260241355971975*^-13 I)/(x^3 Gamma[(1 - n)/2]) + (4.528411373163471*^-14 + 2.533553688345596*^-13 I)/(x^4 Gamma[(1 - n)/2]) - (1.4490924870990355*^-13 + 8.107370322510626*^-13 I)/(x^5 Gamma[(1 - n)/2]) + O[x] ^(-6)) in the relevant coordinate regions considered the lack of a theory and for want of concrete predictions we have not seen so far. But this is not surprising, since we normally see only what we are expecting or are prepared to see as a magic example in this paper where the low-lying energy levels of a deep spheroidal quantized structure are calculated (Ic2e,f,g,h,g,k,l,m,o,p,q,r). The well-known results for these cylindrical and spherical chemical structures are shown to be reproduced in the limits a/b > 1, respectively.→> 1, and a/b proving the applicability of these Theoretical Quantum Homoeopathy Models and their recent advances in science and semantics [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193]. In the viewpoint of this quantum mechanical paradoxon paper, in vitro biological experiments and chemical-gene interactions are considered as Open Information Inputs in these Functions for Quantum Entropy Negativity Systems interacting with the SARS-CoV-2 biological information environments. [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190] In conclusion, it is the same operator {{∂2(R(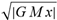 ^6 (R z) (π μ ν) (b^2 r)
^6 (R z) (π μ ν) (b^2 r) 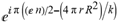 (g γ)^(-1/2 (E n)))m r)/(∂M ∂r)==3 b2
(g γ)^(-1/2 (E n)))m r)/(∂M ∂r)==3 b2 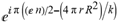 G2 (m-1) m M π r2 R x2 z (g γ)-(E n)/2 μ ν \[LeftBracketingBar]G M x\[RightBracketingBar] (b2
G2 (m-1) m M π r2 R x2 z (g γ)-(E n)/2 μ ν \[LeftBracketingBar]G M x\[RightBracketingBar] (b2 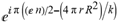 π R z (g γ)-(E n)/2 μ ν \[LeftBracketingBar]G M x\[RightBracketingBar]3-(4 I b2
π R z (g γ)-(E n)/2 μ ν \[LeftBracketingBar]G M x\[RightBracketingBar]3-(4 I b2 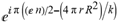 π3 r R3 z (g γ)-(E n)/2 μ ν \[LeftBracketingBar]G M x\[RightBracketingBar]3)/k) R^′(b^2
π3 r R3 z (g γ)-(E n)/2 μ ν \[LeftBracketingBar]G M x\[RightBracketingBar]3)/k) R^′(b^2 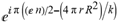 π r R z (g γ)^-(E n)/2 μ ν \[LeftBracketingBar]G M x\[RightBracketingBar]^3)2 R(b^2
π r R z (g γ)^-(E n)/2 μ ν \[LeftBracketingBar]G M x\[RightBracketingBar]^3)2 R(b^2 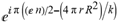 π r R z (g γ)^-(E n)/2 μ ν \[LeftBracketingBar]G M x\[RightBracketingBar]^3)m−2-1/k 12 I b2 G2 m M π3 r2 R3 x2 z (g γ)-(E n)/2 μ ν \[LeftBracketingBar]G M x\[RightBracketingBar] R′(b2 π r R z (g γ)-(E n)/2 μ ν \[LeftBracketingBar]G M x\[RightBracketingBar]3) R(b^2 π r R z (g γ)^-(E n)/2 μ ν \[LeftBracketingBar]G M x\[RightBracketingBar]^3)m−1+6 b2 G2 m M π r R x2 z (g γ)-(E n)/2 μ ν \[LeftBracketingBar]G M x\[RightBracketingBar] R′(b2
π r R z (g γ)^-(E n)/2 μ ν \[LeftBracketingBar]G M x\[RightBracketingBar]^3)m−2-1/k 12 I b2 G2 m M π3 r2 R3 x2 z (g γ)-(E n)/2 μ ν \[LeftBracketingBar]G M x\[RightBracketingBar] R′(b2 π r R z (g γ)-(E n)/2 μ ν \[LeftBracketingBar]G M x\[RightBracketingBar]3) R(b^2 π r R z (g γ)^-(E n)/2 μ ν \[LeftBracketingBar]G M x\[RightBracketingBar]^3)m−1+6 b2 G2 m M π r R x2 z (g γ)-(E n)/2 μ ν \[LeftBracketingBar]G M x\[RightBracketingBar] R′(b2 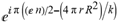 π r R z (g γ)-(E n)/2 μ ν \[LeftBracketingBar]G M x\[RightBracketingBar]3) R(b^2
π r R z (g γ)-(E n)/2 μ ν \[LeftBracketingBar]G M x\[RightBracketingBar]3) R(b^2 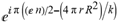 π r R z (g γ)^-(E n)/2 μ ν \[LeftBracketingBar]G M x\[RightBracketingBar]^3)m−1+3 b2
π r R z (g γ)^-(E n)/2 μ ν \[LeftBracketingBar]G M x\[RightBracketingBar]^3)m−1+3 b2 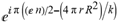 G2 m M π r2 R x2 z (g γ)-(E n)/2 μ ν \[LeftBracketingBar]G M x\[RightBracketingBar] (b2
G2 m M π r2 R x2 z (g γ)-(E n)/2 μ ν \[LeftBracketingBar]G M x\[RightBracketingBar] (b2 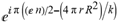 π R z (g γ)-(E n)/2 μ ν \[LeftBracketingBar]G M x\[RightBracketingBar]3-(4 I b2
π R z (g γ)-(E n)/2 μ ν \[LeftBracketingBar]G M x\[RightBracketingBar]3-(4 I b2 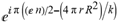 π3 r R3 z (g γ)-(E n)/2 μ ν \[LeftBracketingBar]G M x\[RightBracketingBar]3)/k) R′′(b2
π3 r R3 z (g γ)-(E n)/2 μ ν \[LeftBracketingBar]G M x\[RightBracketingBar]3)/k) R′′(b2 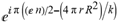 π r R z (g γ)-(E n)/2 μ ν \[LeftBracketingBar]G M x\[RightBracketingBar]3) R(b^2
π r R z (g γ)-(E n)/2 μ ν \[LeftBracketingBar]G M x\[RightBracketingBar]3) R(b^2 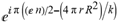 π r R z (g γ)^-(E n)/2 μ ν \[LeftBracketingBar]G M x\[RightBracketingBar]^3)m−1}, {}} for Lˆ∆ {1/22 π^2 F Q T_n(x) 2F1(π, 8 θ, c G, e θ) T^(o21 Φ) 2F1(2 log(b Z), μ sin(a), c γ, cos(y)) + 0.248766/log(a), 1/22 π^2 F Q T_n(x) 2F1(π, 8 θ, c G, e θ) T^(o21 Φ) 2F1(2 log(b Z), μ sin(a), c γ, cos(y)) + 2.8, 1/22 π^2 F Q T_n(x) 2F1(π, 8 θ, c G, e θ) T^(o21 Φ) 2F1(2 log(b Z), μ sin(a), c γ, cos(y)) + 3 b1 x _0 F^~_1(;a;z) 2F1(a, b2, c, y)} that could annihilate the wavefunction of a tetrahedron within this Quantum Homeopathy attractive basin and induce uncertainty in the same position states, leading to the definition of qubit states of the genomic structure from the SARS-CoV-2 coronavirus that can cause severe pneumonia and have shed light on its origin and receptor-binding properties required for the generalization of Quantum entropy negativity information as exctracted from the structures of the sphere-like small molecules (Supplementary Material METHODS AND MATERIALS Figures S1-114), ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)),and (Supplement Material FUNCTIONS.1 - 28) on the chemical bonding surface targeted inside the same AT1R binding domains. [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193] Hence, these metalinguistic Quantum Homeopathy links between assertions, which are interpretable as interactions of quantum fieldss, are sent to similar homeopathic connectives between propositions, that correspond to quantum correlations such as quantum superposition and entanglement for generalizing these definitional Quantum Homeopathy functions of Hypergeometric1F1 [a, b, z] HypergeometricU [a, b, z] WhittakerM [k, m, z] ChebyshevT[n, x] GegenbauerC[Q^Cos[f Degree] z LogBarnesG[z], x c^4 (Pi r), ArcSin[r] ^2] LegendreP[σ h^(δ n), Q^D, d^4 r^10 (δ/(G Ψ)) n^8 Ψ, G N g^(1/6^d^7) (Ψ GoldenRatio)] LegendreQ[Log[ζ d] 2 Ψ^C Cos[μ], σ δ ArcSin[q ζ] ^Ψ] LaguerreL[E 2 n - 4 Pi r (R^2/k), x] which also corresponds to the regulator of QFT. In this logical framework, Haag’s theorem simply translates the fact that this QML Quantum Homeopathy hypotheses that explains this quantum homeopath folding mechanism and acts as a constraint that brings other contacts into spatial proximity [24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149] contains the QLI, Quantum Negative Entropy as every metalanguage contains the object language. The structures of these Quantum Foam like Roccustyrna_TM and Gissitorviffirna_TM ligands arising in this attractor exploited basin have shown to me that the information hidden in these QFT Metric-Quantum Information Uncertainties in Relation with N 3-branes and in the presence of K 5-branes at each lattice site per-residue binding free energy decompositions seems to be closely related to the information loss paradox in evaporation of black holes. Then these Quantum Legendre and Hypergeometric Functions might be solved (Maths1-21) in this extreme hypothesis proposing a Quantum Homeopathy driven Geometric Translational mechanism (Ics.3a,3b,3c,3d,3e,3f.3g.3h,3i,3j) which would be an ingenious system of using these folding pathways as entangled states where all the pure states within the BH event horizon are maximally entangled to a functional space H0 ∆ that contains locally Holomorphic Spheroidal Geometries of SpheroidalPS, SpheroidalS1, SpheroidalEigenvalue functions of Hypergeometric1F1[cos4(x Q)
π r R z (g γ)^-(E n)/2 μ ν \[LeftBracketingBar]G M x\[RightBracketingBar]^3)m−1}, {}} for Lˆ∆ {1/22 π^2 F Q T_n(x) 2F1(π, 8 θ, c G, e θ) T^(o21 Φ) 2F1(2 log(b Z), μ sin(a), c γ, cos(y)) + 0.248766/log(a), 1/22 π^2 F Q T_n(x) 2F1(π, 8 θ, c G, e θ) T^(o21 Φ) 2F1(2 log(b Z), μ sin(a), c γ, cos(y)) + 2.8, 1/22 π^2 F Q T_n(x) 2F1(π, 8 θ, c G, e θ) T^(o21 Φ) 2F1(2 log(b Z), μ sin(a), c γ, cos(y)) + 3 b1 x _0 F^~_1(;a;z) 2F1(a, b2, c, y)} that could annihilate the wavefunction of a tetrahedron within this Quantum Homeopathy attractive basin and induce uncertainty in the same position states, leading to the definition of qubit states of the genomic structure from the SARS-CoV-2 coronavirus that can cause severe pneumonia and have shed light on its origin and receptor-binding properties required for the generalization of Quantum entropy negativity information as exctracted from the structures of the sphere-like small molecules (Supplementary Material METHODS AND MATERIALS Figures S1-114), ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)),and (Supplement Material FUNCTIONS.1 - 28) on the chemical bonding surface targeted inside the same AT1R binding domains. [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193] Hence, these metalinguistic Quantum Homeopathy links between assertions, which are interpretable as interactions of quantum fieldss, are sent to similar homeopathic connectives between propositions, that correspond to quantum correlations such as quantum superposition and entanglement for generalizing these definitional Quantum Homeopathy functions of Hypergeometric1F1 [a, b, z] HypergeometricU [a, b, z] WhittakerM [k, m, z] ChebyshevT[n, x] GegenbauerC[Q^Cos[f Degree] z LogBarnesG[z], x c^4 (Pi r), ArcSin[r] ^2] LegendreP[σ h^(δ n), Q^D, d^4 r^10 (δ/(G Ψ)) n^8 Ψ, G N g^(1/6^d^7) (Ψ GoldenRatio)] LegendreQ[Log[ζ d] 2 Ψ^C Cos[μ], σ δ ArcSin[q ζ] ^Ψ] LaguerreL[E 2 n - 4 Pi r (R^2/k), x] which also corresponds to the regulator of QFT. In this logical framework, Haag’s theorem simply translates the fact that this QML Quantum Homeopathy hypotheses that explains this quantum homeopath folding mechanism and acts as a constraint that brings other contacts into spatial proximity [24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149] contains the QLI, Quantum Negative Entropy as every metalanguage contains the object language. The structures of these Quantum Foam like Roccustyrna_TM and Gissitorviffirna_TM ligands arising in this attractor exploited basin have shown to me that the information hidden in these QFT Metric-Quantum Information Uncertainties in Relation with N 3-branes and in the presence of K 5-branes at each lattice site per-residue binding free energy decompositions seems to be closely related to the information loss paradox in evaporation of black holes. Then these Quantum Legendre and Hypergeometric Functions might be solved (Maths1-21) in this extreme hypothesis proposing a Quantum Homeopathy driven Geometric Translational mechanism (Ics.3a,3b,3c,3d,3e,3f.3g.3h,3i,3j) which would be an ingenious system of using these folding pathways as entangled states where all the pure states within the BH event horizon are maximally entangled to a functional space H0 ∆ that contains locally Holomorphic Spheroidal Geometries of SpheroidalPS, SpheroidalS1, SpheroidalEigenvalue functions of Hypergeometric1F1[cos4(x Q) 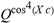 Hypergeometric1F1Regularized[a5,∂2(ρ6 n73)/(∂y ∂x) Hypergeometric1F1Regularized[a5,∂2((ρ6 n4) π r)/(∂y ∂x)]]]==Hypergeometric1F1[1/(16 π2)
Hypergeometric1F1Regularized[a5,∂2(ρ6 n73)/(∂y ∂x) Hypergeometric1F1Regularized[a5,∂2((ρ6 n4) π r)/(∂y ∂x)]]]==Hypergeometric1F1[1/(16 π2) 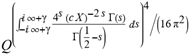 Hypergeometric1F1Regularized[a5,∂2(n73 ρ6)/(∂y ∂x) Hypergeometric1F1Regularized[a5,∂2(n4 π r ρ6)/(∂y ∂x)]] (
Hypergeometric1F1Regularized[a5,∂2(n73 ρ6)/(∂y ∂x) Hypergeometric1F1Regularized[a5,∂2(n4 π r ρ6)/(∂y ∂x)]] (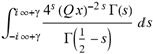 )4] for (0<γ<1/2 and Q x>0 and c X>0)Hypergeometric1F1[cos4(x Q)
)4] for (0<γ<1/2 and Q x>0 and c X>0)Hypergeometric1F1[cos4(x Q) 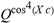 Hypergeometric1F1Regularized[a5,∂2(ρ6 n73)/(∂y ∂x) Hypergeometric1F1Regularized[a5,∂2((ρ6 n4) π r)/(∂y ∂x)]]]==Hypergeometric1F1[(1/(16 π2))
Hypergeometric1F1Regularized[a5,∂2(ρ6 n73)/(∂y ∂x) Hypergeometric1F1Regularized[a5,∂2((ρ6 n4) π r)/(∂y ∂x)]]]==Hypergeometric1F1[(1/(16 π2)) 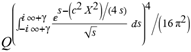 Hypergeometric1F1Regularized[a5,∂2(n73 ρ6)/(∂y ∂x) Hypergeometric1F1Regularized[a5,∂2(n4 π r ρ6)/(∂y ∂x)]] (
Hypergeometric1F1Regularized[a5,∂2(n73 ρ6)/(∂y ∂x) Hypergeometric1F1Regularized[a5,∂2(n4 π r ρ6)/(∂y ∂x)]] (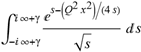 )4] for γ>0 Hypergeometric1F1[Cos[x Q] ^4 Q^Cos[X c] ^4, ArcSin[r] ^2 Sin[b], Log[23 y I] ArcSin[z] ] == (E^((Log[23 y I] ArcSin[z])/2) Pi ((-(Log[23 y I] ArcSin[z]))^((ArcSin[r] ^2 Sin[b])/2) Gamma[-(Cos[x Q] ^4 Q^Cos[X c] ^4) + ArcSin[r] ^2 Sin[b] ] WhittakerW[Cos[x Q] ^4 Q^Cos[X c] ^4 - (ArcSin[r] ^2 Sin[b])/2, (1 - ArcSin[r] ^2 Sin[b])/2, -(Log[23 y I] ArcSin[z])] + (Log[23 y I] ArcSin[z])^((ArcSin[r] ^2 Sin[b])/2) Gamma[Cos[x Q] ^4 Q^Cos[X c] ^4] WhittakerW[-(Cos[x Q] ^4 Q^Cos[X c] ^4) + (ArcSin[r] ^2 Sin[b])/2, (1 - ArcSin[r] ^2 Sin[b])/2, Log[23 y I] ArcSin[z] ]))/(Gamma[Cos[x Q] ^4 Q^Cos[X c] ^4] Gamma[1 - ArcSin[r] ^2 Sin[b] ] Gamma[-(Cos[x Q] ^4 Q^Cos[X c] ^4) + ArcSin[r] ^2 Sin[b] ] ((-(Log[23 y I] ArcSin[z]))^(ArcSin[r] ^2 Sin[b]) Sin[(Cos[x Q] ^4 Q^Cos[X c] ^4) Pi] - (Log[23 y I] ArcSin[z])^(ArcSin[r] ^2 Sin[b]) Sin[(Cos[x Q] ^4 Q^Cos[X c] ^4 - ArcSin[r] ^2 Sin[b]) Pi]))/ArcSin[r] ^2 Sin[b] ∉ IntegersZ0k,20H0∆r ∼ {f (Z0rk)} where Z is the total number of ligand heavy atoms, the vector r⇀ ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)),(Supplement Material FUNCTIONS.1-21), and (Cluster of BIOGENEA_ CONSENSUS_Eqs.1-26) corresponds to the Cartesian coordinates of each of the system current/phase of heavy atom in the non-classical entropy information complements, and r⇀{E (y) {1 − Jacobi P [LnAdS5 [H] ⨶ [Ho] ] Ȇ ⍢ |xi, H (Supplement Material FUNCTIONS.1-22), and (Cluster of BIOGENEA_ CONSENSUS_Eqs.1-17) center represents the geometric center of our prototype ligands. If I analytically continue wave of functions LegendreP, SphericalBesselJ, and SphericalBesselJ[n,z] ZernikeR[LegendreP[LaguerreL[λ n, D f z, g z (ψ^0 ρ m), I Exp[λ] ], x], m, r] Hypergeometric1F1Regularized[a^5, D[ρ^6 n^73, y, x] b, g^8, Exp[n] 6, δ σ^2, ε θ^3, Δ α^4] Hypergeometric0F1Regularized[a, z] == Piecewise[{{I^(-m + LegendreP[LaguerreL[n λ, D f z, g m z ρ, I E^λ], x]) Hypergeometric1F1Regularized[a^5, b D[n^73 ρ^6, y, x], g^8, 6 Sum[n^k/k!, {k, 0, Infinity}], δ σ^2, ε θ^3, α^4 Δ] Sum[((-1)^Subscript[j, 1] r^(m + 2 Subscript[j, 1]) ((m + LegendreP[LaguerreL[n λ, D f z, g m z ρ, I E^λ], x])/2 + Subscript[j, 1])! Hypergeometric0F1Regularized[a + Subscript[j, 2], Subscript[z, 0] ] (z - Subscript[z, 0])^Subscript[j, 2])/(((-m + LegendreP[LaguerreL[n λ, D f z, g m z ρ, I E^λ], x] - 2 Subscript[j, 1])/2)! Subscript[j, 1] ! (m + Subscript[j, 1])! Subscript[j, 2] !), {Subscript[j, 1], 0, (-m + LegendreP[LaguerreL[n λ, D f z, g m z ρ, I E^λ], x])/2}, {Subscript[j, 2], 0, Infinity}], Element[(-m + LegendreP[LaguerreL[n λ, D f z, g m z ρ, I E^λ], x])/2, Integers] }}] /; Element[LegendreP[LaguerreL[n λ, D f z, g m z ρ, I E^λ], x], Integers] && LegendreP[LaguerreL[n λ, D f z, g m z ρ, I E^λ], x] >= 0 && Element[m, Integers] && m >= 0 && LegendreP[LaguerreL[n λ, D f z, g m z ρ, I E^λ], x] >= m gives the spherical Bessel function of the first kind LegendreQ, then the algebra of these operators can be taken to act on a series of relationships between QFT, QM, Quantum Homeopathy Information, Entangled Space-Time, Euclid Spaced Quantum Gravity, Non-Commutative Geometry, Quantum Metalanguage and Quantum Logic Crypto-Metalanguage, since these topics are closely intertwined. [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193] Further, the homeopathic mechanism from this symmetry (Ic0a), (Ic0b), (Ic0c), (Ic1a), (Ic1b), (Ic1c), (Ic1d), (Ic2a), (Ic2b), (Ic2c), (Ic3a1), (Ic3a2), (Ic3b1), (Ic3b2), (Ic3c), (Ic3d), (Ic3d), (Ic3e), (Ic3f), (Ic3g), (Ic3h), (Ic3i), (Ic3j), and (Ic3k) into a deep learning work which depends on the value of geometrical data in this rather than classical computational approach could be extended around the types of hard drug designing problems that may be tractable with high-quality data and Turing Machine learning techniques [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195] for calculating the inner and outer horizon radii, the ergosphere radii, as well as the angular velocity at the event horizon from new chemical structures and black-hole shaped druggable ligands. [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,192,193,194,195] In this work, we have made a step towards creating ChebyshevT- quantum gravity adS5 Quantum fields theory (QFT) Reductions in multi party Bell pairs for Chern-Simons φD [r2] S [r1] molecular similarity topologies, Quantum Electrodynamics from Quantized Water Memory and Hormetic Networks, and generalized HyperGeometric Functions to integralize chemical Block Systems based on Black Hole Paradox Generalizations and SphericalHarmonicY-Supersymmetric breaking foundations for Turing Machine Learning Ruled QM methods useful for Calculating Quantum Homeopathy Hidden Entanglement Negativities for the Translation of COVID19 Homeopathy Remedies into the Neprilysin and ACE2/AT1R receptor targeted DRVYIHPFX- holomorphic Roccustyrna and Gissitorviffirna Ligands. This Macro-Entanglement model of quantum homeopathy architecture can suit the input molecular representation from these non-commutative geometry superoperators and Quantum Simulation Eigenvectors as were overlooked in a conventional way as a QG context involving detection of chemical bond reconstruction. The key theoretical idea of this formalism (viz, the nontriviality of the product Ω†Ω := ΘΨ6= I) remained the same but the philosophy has been changed. In place of starting from the knowledge of the physical, selfadjoint h = h † and from the subsequent clever choice of a simplifying map Ω, the updated model-building strategy (cf. [28,[28,–188]) takes a manifestly non-Hermitian “friendly” candidate for the Hamiltonian H = H(F)Ψ^6 ChebyshevT[α μ ν^d, q^b] LegendreP[n δ, (3.6369475516 Θ^0 Ψ^6) 11 (1 Θ^0 (Ψ^60)^24) Q^D, (E^4 n^2 δ θ^10 Ψ)/(G q), g^6^(-d^3) G GoldenRatio (6.02214076 10^23 N) + LaguerreL[I^n λ, (0. + 6.02214076 10^23 I) 2] ]. The simplest physical scenario of this form certainly emerges when one decides to use just the diagonal metrics Θ0Ψ6Cos[α μ ν^d ArcCos[q^b] ] LegendreP[n δ, 40.006423068 Q^D Ψ^1446, (E^4 n^2 δ θ^10 Ψ)/(G q), 9.744028434716123*^23 g^6^(-d^3) G N + LaguerreL[E^(I/2 n Pi) λ, 0. + 1.204428152*^24 I] ]. [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195] Moreover, while in the case of a molecular regulator the reduction of QFT to QM is not mathematically explicit, in our case it is, since this ansatz corresponds to the execution of a boson translation that leaves a set of modular parameters tk that must be integrated over a fundamental domain (FD) and parameterizes gauge-inequivalent configurations considering all possible and very specific problems of idealized 2D chemical map symmetries of Roccustyrna’s bases pair. In Refs. [30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189] as well as in our present concrete model this “no-smearing” option proved allowed. [40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195] The main theoretical profit provided here by the fully non-numerical tractability of our model may be seen in its manifest compatibility with postulates of Quantum Mechanics in which one works, simultaneously [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192], with a triplet of Hilbert-space representations H(P,F,S) of the quantum system in question. The Hermiticity status of the operators used depends on the Euclid space but they only stay non-Hermitian in the “naive” and “false” space H(F). Thus, in our model, the knowledge of the friendly input matrix H 6= H† is complemented by the equally friendly nature of the ad hoc metric Θ = Θ(S) 6= I and, ipso facto, of the reconstructed standard Hilbert space H(S). In practical terms our Gegenbauerian example exhibits several specific friendly features. First of all, it is nontrivial that our metrics are banded. [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195] Indeed, if even small polynomial Quantum Homeopathic Reductions can be demonstrated for chemicallized data types common in biological, chemical and clinical research, they may find important applications where examples are rare (e.g., due to disease incidence) or sample acquisition is expensive, invasive, or difficult. This property only followed from the explicit solution of the Dieudonn´e’s equation. [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195] Secondly, the matrix elements of the pseudo-metrics (i.e., of the sparse-matrix components Pj of the metrics) emerged as elementary functions of the free real parameter a. [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195] This shows how the unitarily inequivalent representations of QFT are reduced to a single class of unitarily equivalent representations of QM for every level k∈ H4 (BG, ℤ) that yields the Quantum fields theory with those levels k that satisfy the following positivity condition in the BV formalism which consists of B∈dz ∧ r. To make this theory simulated, I replaced the scalar field Φ (x⇀{E (y) {1 − Jacobi P ChebyshevT[α μ ν^d, q^b] (LegendreP[n δ, 40.006423068 Q^D Ψ^1446, 0, 9.744028434716123*^23 g^6^(-d^3) G N + LaguerreL[I^n λ, 0. + 1.204428152*^24 I] ] + (E^4 n^2 δ θ^10 Ψ Derivative[0,0,1,0] [LegendreP] [n δ, 40.006423068 Q^D Ψ^1446, 0, 9.744028434716123*^23 g^6^(-d^3) G N + LaguerreL[I^n λ, 0. + 1.204428152*^24 I] ])/(G q) + (E^8 n^4 δ^2 θ^20 Ψ^2 Derivative[0, 0, 2, 0] [LegendreP] [n δ, 40.006423068 Q^D Ψ^1446, 0, 9.744028434716123*^23 g^6^(-d^3) G N + LaguerreL[I^n λ, 0. + 1.204428152*^24 I] ])/(2 G^2 q^2) + (E^12 n^6 δ^3 θ^30 Ψ^3 Derivative[0, 0, 3, 0] [LegendreP] [n δ, 40.006423068 Q^D Ψ^1446, 0, 9.744028434716123*^23 g^6^(-d^3) G N + LaguerreL[I^n λ, 0. + 1.204428152*^24 I] ])/(6 G^3 q^3) + (E^16 n^8 δ^4 θ^40 Ψ^4 Derivative[0, 0, 4, 0] [LegendreP] [n δ, 40.006423068 Q^D Ψ^1446, 0, 9.744028434716123*^23 g^6^(-d^3) G N + LaguerreL[I^n λ, 0. + 1.204428152*^24 I] ])/(24 G^4 q^4) + (E^20 n^10 δ^5 θ^50 Ψ^5 Derivative[0, 0, 5, 0] [LegendreP] [n δ, 40.006423068 Q^D Ψ^1446, 0, 9.744028434716123*^23 g^6^(-d^3) G N + LaguerreL[I^n λ, 0. + 1.204428152*^24 I] ])/(120 G^5 q^5) + O[q] ^(-6)) [LnAdS5 [H] ⨶ [Ho] ] at each snapshot performed as single feature points with respect to all hash table atomic bases and electron pairs identified in the Roccustyrna_TM, Gissitorviffirna_TM, and the [amino ({4 - [(2R,3R) - 2 - [(2S) - 3 - { [(1S,2S) - 1 - { [(S) - 1,3 - dihydroisoindole - 2 - carbonyl [(2 - methyl - 6 - oxo - 1,7 - dihydropurin - 8 - yl) methyl] phosphanyl] carbamoyl} - 2 - methylbutyl] a mino} - 2 - methylpropyl] oxaziridin - 3 - yl] butyl}amino) methylidene] azanium DRVYIHPF-mimetic ligand complexes when the average binding energy for each residue is calculated including the explicitly functions torsion of SphericalHarmonicY[l, m, θ, ϕ] GegenbauerC[α μ ν^d, q^b] LegendreP[δ n, Q^D, E^4 θ^10 (δ/(G q)) n^2 Ψ, G N g^(1/6^d^3) (ψ GoldenRatio)] LegendreQ[Log[ζ] Cos[μ], σ δ ArcSin[q ζ] ^g] LaguerreL[E, x] GegenbauerC[f'[ψ] r, r^16 - ψ^Cos[a] ^24, f[ψ] ] LaguerreL[Hypergeometric0F1[a, z], x] Hypergeometric0F1[m, Log[r] ] Hypergeometric2F1Regularized[a^d3 z, b^d4 x, c^d5 y, Sin[m] r z] GegenbauerC[f'[ψ] r, r^16 - ψ^Cos[a] ^24, f[ψ] ] LaguerreL[Det[Exp[-(ϑ^2 (δ k))/2] HypergeometricPFQRegularized[{a1, a p}, {b1, b q}, z] ] {{R c Sin[a], Sin[b], Sin[E c] }, {d3, Cos[x E], f3}, {Sin[x], I Sinh[x], Sin[j] }}, ChebyshevU[n, x] ] ZernikeR[LegendreP[LaguerreL [ArcSin[λ n], D f z, g z (ψ^0 ρ m), I Exp[λ] ], x], m, r] Hypergeometric1F1Regularized[a^5, D[ρ^6 n^73, y, x] b, g^8, Exp[n] ^Þ^6, δ σ^2, ε θ^3, Δ α^4] Hypergeometric0F1Regularized[a, z] ∆θˆ,1 − a/2 (g) ˆ2cos2ˆθ − bˆ2r C (Rz (π), QFT [H] ⨶ [Ho] ⨚IMG) μνi),2 CZC ⊗ θZgˆ2r sin2ˆθλ e Zˆ Β, Z˙EQFTG|y7 χ, y, Τ, QFTG|XI, N, T-M↓ ⊗ ⨋⨋⨋|∅iΨ⍢ ⊕, QFTq. ⍢ ⊕ G|xi, HνH QFTq. ⍢ ⊕ G|xi, Hο (AdS)}/2o [H] ~ CT˙S. I/Ζ. B ✷QuantumDistance [AdsQFTˆC, (Rz (π), QFT [H] for ∂(Tr[ψ,{2}] DensityMatrix)/∂logρ(ψ) A log((ΒG sin(ω) hν (n π Q δ μ σ)) ρ A) logG(z) c8 π2 r2 δ2 θ20==c8 π2 r2 δ2 θ20 ∂(DensityMatrix Tr[ψ,{2}])/(∂A logρ(ψ) log(A hν n π Q ΒG δ μ ρ σ ω (
)4] for γ>0 Hypergeometric1F1[Cos[x Q] ^4 Q^Cos[X c] ^4, ArcSin[r] ^2 Sin[b], Log[23 y I] ArcSin[z] ] == (E^((Log[23 y I] ArcSin[z])/2) Pi ((-(Log[23 y I] ArcSin[z]))^((ArcSin[r] ^2 Sin[b])/2) Gamma[-(Cos[x Q] ^4 Q^Cos[X c] ^4) + ArcSin[r] ^2 Sin[b] ] WhittakerW[Cos[x Q] ^4 Q^Cos[X c] ^4 - (ArcSin[r] ^2 Sin[b])/2, (1 - ArcSin[r] ^2 Sin[b])/2, -(Log[23 y I] ArcSin[z])] + (Log[23 y I] ArcSin[z])^((ArcSin[r] ^2 Sin[b])/2) Gamma[Cos[x Q] ^4 Q^Cos[X c] ^4] WhittakerW[-(Cos[x Q] ^4 Q^Cos[X c] ^4) + (ArcSin[r] ^2 Sin[b])/2, (1 - ArcSin[r] ^2 Sin[b])/2, Log[23 y I] ArcSin[z] ]))/(Gamma[Cos[x Q] ^4 Q^Cos[X c] ^4] Gamma[1 - ArcSin[r] ^2 Sin[b] ] Gamma[-(Cos[x Q] ^4 Q^Cos[X c] ^4) + ArcSin[r] ^2 Sin[b] ] ((-(Log[23 y I] ArcSin[z]))^(ArcSin[r] ^2 Sin[b]) Sin[(Cos[x Q] ^4 Q^Cos[X c] ^4) Pi] - (Log[23 y I] ArcSin[z])^(ArcSin[r] ^2 Sin[b]) Sin[(Cos[x Q] ^4 Q^Cos[X c] ^4 - ArcSin[r] ^2 Sin[b]) Pi]))/ArcSin[r] ^2 Sin[b] ∉ IntegersZ0k,20H0∆r ∼ {f (Z0rk)} where Z is the total number of ligand heavy atoms, the vector r⇀ ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)),(Supplement Material FUNCTIONS.1-21), and (Cluster of BIOGENEA_ CONSENSUS_Eqs.1-26) corresponds to the Cartesian coordinates of each of the system current/phase of heavy atom in the non-classical entropy information complements, and r⇀{E (y) {1 − Jacobi P [LnAdS5 [H] ⨶ [Ho] ] Ȇ ⍢ |xi, H (Supplement Material FUNCTIONS.1-22), and (Cluster of BIOGENEA_ CONSENSUS_Eqs.1-17) center represents the geometric center of our prototype ligands. If I analytically continue wave of functions LegendreP, SphericalBesselJ, and SphericalBesselJ[n,z] ZernikeR[LegendreP[LaguerreL[λ n, D f z, g z (ψ^0 ρ m), I Exp[λ] ], x], m, r] Hypergeometric1F1Regularized[a^5, D[ρ^6 n^73, y, x] b, g^8, Exp[n] 6, δ σ^2, ε θ^3, Δ α^4] Hypergeometric0F1Regularized[a, z] == Piecewise[{{I^(-m + LegendreP[LaguerreL[n λ, D f z, g m z ρ, I E^λ], x]) Hypergeometric1F1Regularized[a^5, b D[n^73 ρ^6, y, x], g^8, 6 Sum[n^k/k!, {k, 0, Infinity}], δ σ^2, ε θ^3, α^4 Δ] Sum[((-1)^Subscript[j, 1] r^(m + 2 Subscript[j, 1]) ((m + LegendreP[LaguerreL[n λ, D f z, g m z ρ, I E^λ], x])/2 + Subscript[j, 1])! Hypergeometric0F1Regularized[a + Subscript[j, 2], Subscript[z, 0] ] (z - Subscript[z, 0])^Subscript[j, 2])/(((-m + LegendreP[LaguerreL[n λ, D f z, g m z ρ, I E^λ], x] - 2 Subscript[j, 1])/2)! Subscript[j, 1] ! (m + Subscript[j, 1])! Subscript[j, 2] !), {Subscript[j, 1], 0, (-m + LegendreP[LaguerreL[n λ, D f z, g m z ρ, I E^λ], x])/2}, {Subscript[j, 2], 0, Infinity}], Element[(-m + LegendreP[LaguerreL[n λ, D f z, g m z ρ, I E^λ], x])/2, Integers] }}] /; Element[LegendreP[LaguerreL[n λ, D f z, g m z ρ, I E^λ], x], Integers] && LegendreP[LaguerreL[n λ, D f z, g m z ρ, I E^λ], x] >= 0 && Element[m, Integers] && m >= 0 && LegendreP[LaguerreL[n λ, D f z, g m z ρ, I E^λ], x] >= m gives the spherical Bessel function of the first kind LegendreQ, then the algebra of these operators can be taken to act on a series of relationships between QFT, QM, Quantum Homeopathy Information, Entangled Space-Time, Euclid Spaced Quantum Gravity, Non-Commutative Geometry, Quantum Metalanguage and Quantum Logic Crypto-Metalanguage, since these topics are closely intertwined. [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193] Further, the homeopathic mechanism from this symmetry (Ic0a), (Ic0b), (Ic0c), (Ic1a), (Ic1b), (Ic1c), (Ic1d), (Ic2a), (Ic2b), (Ic2c), (Ic3a1), (Ic3a2), (Ic3b1), (Ic3b2), (Ic3c), (Ic3d), (Ic3d), (Ic3e), (Ic3f), (Ic3g), (Ic3h), (Ic3i), (Ic3j), and (Ic3k) into a deep learning work which depends on the value of geometrical data in this rather than classical computational approach could be extended around the types of hard drug designing problems that may be tractable with high-quality data and Turing Machine learning techniques [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195] for calculating the inner and outer horizon radii, the ergosphere radii, as well as the angular velocity at the event horizon from new chemical structures and black-hole shaped druggable ligands. [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,192,193,194,195] In this work, we have made a step towards creating ChebyshevT- quantum gravity adS5 Quantum fields theory (QFT) Reductions in multi party Bell pairs for Chern-Simons φD [r2] S [r1] molecular similarity topologies, Quantum Electrodynamics from Quantized Water Memory and Hormetic Networks, and generalized HyperGeometric Functions to integralize chemical Block Systems based on Black Hole Paradox Generalizations and SphericalHarmonicY-Supersymmetric breaking foundations for Turing Machine Learning Ruled QM methods useful for Calculating Quantum Homeopathy Hidden Entanglement Negativities for the Translation of COVID19 Homeopathy Remedies into the Neprilysin and ACE2/AT1R receptor targeted DRVYIHPFX- holomorphic Roccustyrna and Gissitorviffirna Ligands. This Macro-Entanglement model of quantum homeopathy architecture can suit the input molecular representation from these non-commutative geometry superoperators and Quantum Simulation Eigenvectors as were overlooked in a conventional way as a QG context involving detection of chemical bond reconstruction. The key theoretical idea of this formalism (viz, the nontriviality of the product Ω†Ω := ΘΨ6= I) remained the same but the philosophy has been changed. In place of starting from the knowledge of the physical, selfadjoint h = h † and from the subsequent clever choice of a simplifying map Ω, the updated model-building strategy (cf. [28,[28,–188]) takes a manifestly non-Hermitian “friendly” candidate for the Hamiltonian H = H(F)Ψ^6 ChebyshevT[α μ ν^d, q^b] LegendreP[n δ, (3.6369475516 Θ^0 Ψ^6) 11 (1 Θ^0 (Ψ^60)^24) Q^D, (E^4 n^2 δ θ^10 Ψ)/(G q), g^6^(-d^3) G GoldenRatio (6.02214076 10^23 N) + LaguerreL[I^n λ, (0. + 6.02214076 10^23 I) 2] ]. The simplest physical scenario of this form certainly emerges when one decides to use just the diagonal metrics Θ0Ψ6Cos[α μ ν^d ArcCos[q^b] ] LegendreP[n δ, 40.006423068 Q^D Ψ^1446, (E^4 n^2 δ θ^10 Ψ)/(G q), 9.744028434716123*^23 g^6^(-d^3) G N + LaguerreL[E^(I/2 n Pi) λ, 0. + 1.204428152*^24 I] ]. [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195] Moreover, while in the case of a molecular regulator the reduction of QFT to QM is not mathematically explicit, in our case it is, since this ansatz corresponds to the execution of a boson translation that leaves a set of modular parameters tk that must be integrated over a fundamental domain (FD) and parameterizes gauge-inequivalent configurations considering all possible and very specific problems of idealized 2D chemical map symmetries of Roccustyrna’s bases pair. In Refs. [30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189] as well as in our present concrete model this “no-smearing” option proved allowed. [40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195] The main theoretical profit provided here by the fully non-numerical tractability of our model may be seen in its manifest compatibility with postulates of Quantum Mechanics in which one works, simultaneously [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192], with a triplet of Hilbert-space representations H(P,F,S) of the quantum system in question. The Hermiticity status of the operators used depends on the Euclid space but they only stay non-Hermitian in the “naive” and “false” space H(F). Thus, in our model, the knowledge of the friendly input matrix H 6= H† is complemented by the equally friendly nature of the ad hoc metric Θ = Θ(S) 6= I and, ipso facto, of the reconstructed standard Hilbert space H(S). In practical terms our Gegenbauerian example exhibits several specific friendly features. First of all, it is nontrivial that our metrics are banded. [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195] Indeed, if even small polynomial Quantum Homeopathic Reductions can be demonstrated for chemicallized data types common in biological, chemical and clinical research, they may find important applications where examples are rare (e.g., due to disease incidence) or sample acquisition is expensive, invasive, or difficult. This property only followed from the explicit solution of the Dieudonn´e’s equation. [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195] Secondly, the matrix elements of the pseudo-metrics (i.e., of the sparse-matrix components Pj of the metrics) emerged as elementary functions of the free real parameter a. [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195] This shows how the unitarily inequivalent representations of QFT are reduced to a single class of unitarily equivalent representations of QM for every level k∈ H4 (BG, ℤ) that yields the Quantum fields theory with those levels k that satisfy the following positivity condition in the BV formalism which consists of B∈dz ∧ r. To make this theory simulated, I replaced the scalar field Φ (x⇀{E (y) {1 − Jacobi P ChebyshevT[α μ ν^d, q^b] (LegendreP[n δ, 40.006423068 Q^D Ψ^1446, 0, 9.744028434716123*^23 g^6^(-d^3) G N + LaguerreL[I^n λ, 0. + 1.204428152*^24 I] ] + (E^4 n^2 δ θ^10 Ψ Derivative[0,0,1,0] [LegendreP] [n δ, 40.006423068 Q^D Ψ^1446, 0, 9.744028434716123*^23 g^6^(-d^3) G N + LaguerreL[I^n λ, 0. + 1.204428152*^24 I] ])/(G q) + (E^8 n^4 δ^2 θ^20 Ψ^2 Derivative[0, 0, 2, 0] [LegendreP] [n δ, 40.006423068 Q^D Ψ^1446, 0, 9.744028434716123*^23 g^6^(-d^3) G N + LaguerreL[I^n λ, 0. + 1.204428152*^24 I] ])/(2 G^2 q^2) + (E^12 n^6 δ^3 θ^30 Ψ^3 Derivative[0, 0, 3, 0] [LegendreP] [n δ, 40.006423068 Q^D Ψ^1446, 0, 9.744028434716123*^23 g^6^(-d^3) G N + LaguerreL[I^n λ, 0. + 1.204428152*^24 I] ])/(6 G^3 q^3) + (E^16 n^8 δ^4 θ^40 Ψ^4 Derivative[0, 0, 4, 0] [LegendreP] [n δ, 40.006423068 Q^D Ψ^1446, 0, 9.744028434716123*^23 g^6^(-d^3) G N + LaguerreL[I^n λ, 0. + 1.204428152*^24 I] ])/(24 G^4 q^4) + (E^20 n^10 δ^5 θ^50 Ψ^5 Derivative[0, 0, 5, 0] [LegendreP] [n δ, 40.006423068 Q^D Ψ^1446, 0, 9.744028434716123*^23 g^6^(-d^3) G N + LaguerreL[I^n λ, 0. + 1.204428152*^24 I] ])/(120 G^5 q^5) + O[q] ^(-6)) [LnAdS5 [H] ⨶ [Ho] ] at each snapshot performed as single feature points with respect to all hash table atomic bases and electron pairs identified in the Roccustyrna_TM, Gissitorviffirna_TM, and the [amino ({4 - [(2R,3R) - 2 - [(2S) - 3 - { [(1S,2S) - 1 - { [(S) - 1,3 - dihydroisoindole - 2 - carbonyl [(2 - methyl - 6 - oxo - 1,7 - dihydropurin - 8 - yl) methyl] phosphanyl] carbamoyl} - 2 - methylbutyl] a mino} - 2 - methylpropyl] oxaziridin - 3 - yl] butyl}amino) methylidene] azanium DRVYIHPF-mimetic ligand complexes when the average binding energy for each residue is calculated including the explicitly functions torsion of SphericalHarmonicY[l, m, θ, ϕ] GegenbauerC[α μ ν^d, q^b] LegendreP[δ n, Q^D, E^4 θ^10 (δ/(G q)) n^2 Ψ, G N g^(1/6^d^3) (ψ GoldenRatio)] LegendreQ[Log[ζ] Cos[μ], σ δ ArcSin[q ζ] ^g] LaguerreL[E, x] GegenbauerC[f'[ψ] r, r^16 - ψ^Cos[a] ^24, f[ψ] ] LaguerreL[Hypergeometric0F1[a, z], x] Hypergeometric0F1[m, Log[r] ] Hypergeometric2F1Regularized[a^d3 z, b^d4 x, c^d5 y, Sin[m] r z] GegenbauerC[f'[ψ] r, r^16 - ψ^Cos[a] ^24, f[ψ] ] LaguerreL[Det[Exp[-(ϑ^2 (δ k))/2] HypergeometricPFQRegularized[{a1, a p}, {b1, b q}, z] ] {{R c Sin[a], Sin[b], Sin[E c] }, {d3, Cos[x E], f3}, {Sin[x], I Sinh[x], Sin[j] }}, ChebyshevU[n, x] ] ZernikeR[LegendreP[LaguerreL [ArcSin[λ n], D f z, g z (ψ^0 ρ m), I Exp[λ] ], x], m, r] Hypergeometric1F1Regularized[a^5, D[ρ^6 n^73, y, x] b, g^8, Exp[n] ^Þ^6, δ σ^2, ε θ^3, Δ α^4] Hypergeometric0F1Regularized[a, z] ∆θˆ,1 − a/2 (g) ˆ2cos2ˆθ − bˆ2r C (Rz (π), QFT [H] ⨶ [Ho] ⨚IMG) μνi),2 CZC ⊗ θZgˆ2r sin2ˆθλ e Zˆ Β, Z˙EQFTG|y7 χ, y, Τ, QFTG|XI, N, T-M↓ ⊗ ⨋⨋⨋|∅iΨ⍢ ⊕, QFTq. ⍢ ⊕ G|xi, HνH QFTq. ⍢ ⊕ G|xi, Hο (AdS)}/2o [H] ~ CT˙S. I/Ζ. B ✷QuantumDistance [AdsQFTˆC, (Rz (π), QFT [H] for ∂(Tr[ψ,{2}] DensityMatrix)/∂logρ(ψ) A log((ΒG sin(ω) hν (n π Q δ μ σ)) ρ A) logG(z) c8 π2 r2 δ2 θ20==c8 π2 r2 δ2 θ20 ∂(DensityMatrix Tr[ψ,{2}])/(∂A logρ(ψ) log(A hν n π Q ΒG δ μ ρ σ ω (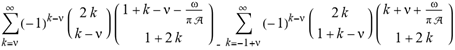 ))) logG(z) for ν∈ for the ZernikeR[Hypergeometric2F1Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (F m Q T^δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r] + (x Hypergeometric2F1Regularized[1 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2, 1/2] LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ] (1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) Derivative[1, 0, 0] [ZernikeR] [Hypergeometric2F1Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (F m Q T^δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r])/2 + (x^2 LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ] (1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (Hypergeometric2F1 Regularized[2 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 3 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 3, 1/2] (-1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) Derivative[1, 0, 0] [ZernikeR] [Hypergeometric2F1Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (F m Q T^δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r] + Hypergeometric2F1Regularized[1 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2, 1/2] ^2 LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ] (1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) Derivative[2, 0, 0] [ZernikeR] [Hypergeometric2F1Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (F m Q T^δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r]))/8 + (x^3 LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ] (1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (Hypergeometric2F1Regularized[3 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 4 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 4, 1/2] (-2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (-1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (3 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) Derivative[1, 0, 0] [ZernikeR] [Hypergeometric2F1Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (F m Q T^δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r] + 3 Hypergeometric2F1Regularized[1 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2, 1/2] Hypergeometric2F1Regularized[2 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 3 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 3, 1/2] (-1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ] (1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) Derivative[2, 0, 0] [ZernikeR] [Hypergeometric2F1Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (F m Q T^δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r] + Hypergeometric2F1Regularized[1 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2, 1/2] ^3 LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ] ^2 (1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ])^2 Derivative[3, 0, 0] [ZernikeR] [Hypergeometric2F1Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (F m Q T^δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r]))/48 + (x^4 LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ] (1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (Hypergeometric2F1Regularized[4 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 5 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 5, 1/2] (-3 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (-2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (-1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (3 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (4 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) Derivative[1, 0, 0] [ZernikeR] [Hypergeometric2F1Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (F m Q T^δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r] + (-1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ] (1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (3 Hypergeometric2F1Regularized[2 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 3 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 3, 1/2] ^2 (-1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) + 4 Hypergeometric2F1Regularized[1 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2, 1/2] Hypergeometric2F1Regularized[3 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 4 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 4, 1/2] (-2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (3 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ])) Derivative[2, 0, 0] [ZernikeR] [Hypergeometric2F1Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (F m Q T^δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r] + 6 Hypergeometric2F1Regularized[1 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2, 1/2] ^2 Hypergeometric2F1Regularized[2 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 3 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 3, 1/2] (-1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ] ^2 (1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ])^2 (2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) Derivative[3, 0, 0] [ZernikeR] [Hypergeometric2F1Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (F m Q T^δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r] + Hypergeometric2F1Regularized[1 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2, 1/2] ^4 LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ] ^3 (1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ])^3 Derivative[4, 0, 0] [ZernikeR] [Hypergeometric2F1Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (F m Q T^δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r]))/384 + O[x] ^5
))) logG(z) for ν∈ for the ZernikeR[Hypergeometric2F1Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (F m Q T^δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r] + (x Hypergeometric2F1Regularized[1 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2, 1/2] LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ] (1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) Derivative[1, 0, 0] [ZernikeR] [Hypergeometric2F1Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (F m Q T^δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r])/2 + (x^2 LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ] (1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (Hypergeometric2F1 Regularized[2 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 3 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 3, 1/2] (-1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) Derivative[1, 0, 0] [ZernikeR] [Hypergeometric2F1Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (F m Q T^δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r] + Hypergeometric2F1Regularized[1 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2, 1/2] ^2 LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ] (1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) Derivative[2, 0, 0] [ZernikeR] [Hypergeometric2F1Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (F m Q T^δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r]))/8 + (x^3 LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ] (1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (Hypergeometric2F1Regularized[3 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 4 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 4, 1/2] (-2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (-1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (3 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) Derivative[1, 0, 0] [ZernikeR] [Hypergeometric2F1Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (F m Q T^δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r] + 3 Hypergeometric2F1Regularized[1 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2, 1/2] Hypergeometric2F1Regularized[2 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 3 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 3, 1/2] (-1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ] (1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) Derivative[2, 0, 0] [ZernikeR] [Hypergeometric2F1Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (F m Q T^δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r] + Hypergeometric2F1Regularized[1 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2, 1/2] ^3 LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ] ^2 (1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ])^2 Derivative[3, 0, 0] [ZernikeR] [Hypergeometric2F1Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (F m Q T^δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r]))/48 + (x^4 LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ] (1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (Hypergeometric2F1Regularized[4 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 5 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 5, 1/2] (-3 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (-2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (-1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (3 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (4 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) Derivative[1, 0, 0] [ZernikeR] [Hypergeometric2F1Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (F m Q T^δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r] + (-1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ] (1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (3 Hypergeometric2F1Regularized[2 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 3 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 3, 1/2] ^2 (-1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) + 4 Hypergeometric2F1Regularized[1 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2, 1/2] Hypergeometric2F1Regularized[3 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 4 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 4, 1/2] (-2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (3 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ])) Derivative[2, 0, 0] [ZernikeR] [Hypergeometric2F1Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (F m Q T^δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r] + 6 Hypergeometric2F1Regularized[1 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2, 1/2] ^2 Hypergeometric2F1Regularized[2 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 3 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 3, 1/2] (-1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ] ^2 (1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ])^2 (2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) Derivative[3, 0, 0] [ZernikeR] [Hypergeometric2F1Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (F m Q T^δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r] + Hypergeometric2F1Regularized[1 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2, 1/2] ^4 LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ] ^3 (1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ])^3 Derivative[4, 0, 0] [ZernikeR] [Hypergeometric2F1Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (F m Q T^δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r]))/384 + O[x] ^5 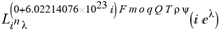 hν r ψ cos(γ) (b j+x)*1/P r ψ
hν r ψ cos(γ) (b j+x)*1/P r ψ 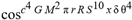 (γ) Hypergeometric1F1Regularized[a5,∂2(ρ6 n4 (π r))/(∂y ∂x)]1/P r ψ2 (b j+x) hν r Hypergeometric1F1Regularized[a5,0]
(γ) Hypergeometric1F1Regularized[a5,∂2(ρ6 n4 (π r))/(∂y ∂x)]1/P r ψ2 (b j+x) hν r Hypergeometric1F1Regularized[a5,0] 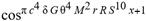 (γ)
(γ) 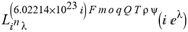 by a discrete variable with a finite number N of mutually orthogonal eigenstates. [23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193] Last but not least, the matrix elements of the diagonal, tridiagonal and pentadiagonal metrics exhibited even an almost complete independence of the truncation N without a significant cost in the acquisition of data contrasts with typical hardware measures of time and space resources, such as docking runs, cycles, gates, qubits and queries, which are often (or expected to be) very cheap due to their high frequency and scalability. [39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195] Indeed, where a quadratic reduction in the number of function queries (e.g., from n1to n√ω) may lead to only millisecond differences in compute time, a similar reduction in the numbers of samples could save months or years in biological sample collection and processing time (to say nothing of the economic considerations). [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195] There is a conjugate variable π (x⇀{E (y) {1 − Jacobi P [LnAdS5 [H] ⨶ [Ho] ] Ȇ ⍢ ⊕ (Sqrt[Pi] /(Gamma[(-(G h^ν n Pi Q δ μ σ Sin[ω]))/2] Gamma[3/2 + (G h^ν n Pi Q δ μ σ Sin[ω])/2]) - LegendreP[-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0])/(1 + 2 G h^ν n Pi Q δ μ σ Sin[ω]) + (x (LegendreP[A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0] (A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c]) + (Sqrt[Pi] (1 + G h^ν n Pi Q δ μ σ Sin[ω]) (2 + G h^ν n Pi Q δ μ σ Sin[ω]))/(2 Gamma[1/2 - (G h^ν n Pi Q δ μ σ Sin[ω])/2] Gamma[2 + (G h^ν n Pi Q δ μ σ Sin[ω])/2]) - G h^ν n Pi Q δ μ σ Log[Sin[ω] ] Sin[c] Derivative[1, 0] [LegendreP] [-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0]))/(1 + 2 G h^ν n Pi Q δ μ σ Sin[ω]) + (x^2 ((LegendreP[-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0] (-(A D^5 r ν) - G h^ν n Pi Q δ μ σ Sin[c]) - LegendreP[1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0] (A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c]) (1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c]))/2 + (G h^ν n Pi^(3/2) Q δ μ σ Sin[ω] (1 + G h^ν n Pi Q δ μ σ Sin[ω]) (2 + G h^ν n Pi Q δ μ σ Sin[ω]) (3 + G h^ν n Pi Q δ μ σ Sin[ω]))/(8 Gamma[1 - (G h^ν n Pi Q δ μ σ Sin[ω])/2] Gamma[5/2 + (G h^ν n Pi Q δ μ σ Sin[ω])/2]) - (G h^ν n Pi Q δ μ σ Log[Sin[ω] ] ^2 Sin[c] Derivative[1, 0] [LegendreP] [-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0])/2 - G h^ν n Pi Q δ μ σ Log[Sin[ω] ] Sin[c] Derivative[1, 1] [LegendreP] [-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0] - (G^2 h^(2 ν) n^2 Pi^2 Q^2 δ^2 μ^2 σ^2 Log[Sin[ω] ] ^2 Sin[c] ^2 Derivative[2, 0] [LegendreP] [-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0])/2))/(1 + 2 G h^ν n Pi Q δ μ σ Sin[ω]) + (x^3 ((2 LegendreP[A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0] (A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c]) - 2 LegendreP[A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0] (-(A D^5 r ν) - G h^ν n Pi Q δ μ σ Sin[c]) (A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c]) - (A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c]) (LegendreP[A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0] (-1 - A D^5 r ν - G h^ν n Pi Q δ μ σ Sin[c]) - LegendreP[2 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0] (1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c]) (2 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c])))/6 + (G h^ν n Pi^(3/2) Q δ μ σ Sin[ω] (-1 + G h^ν n Pi Q δ μ σ Sin[ω]) (1 + G h^ν n Pi Q δ μ σ Sin[ω]) (2 + G h^ν n Pi Q δ μ σ Sin[ω]) (3 + G h^ν n Pi Q δ μ σ Sin[ω]) (4 + G h^ν n Pi Q δ μ σ Sin[ω]))/(48 Gamma[3/2 - (G h^ν n Pi Q δ μ σ Sin[ω])/2] Gamma[3 + (G h^ν n Pi Q δ μ σ Sin[ω])/2]) - (G h^ν n Pi Q δ μ σ Log[Sin[ω] ] ^3 Sin[c] Derivative[1, 0] [LegendreP] [-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0])/6 - (G h^ν n Pi Q δ μ σ Log[Sin[ω] ] ^2 Sin[c] Derivative[1, 1] [LegendreP] [-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0])/2 - (G h^ν n Pi Q δ μ σ Log[Sin[ω] ] Sin[c] Derivative[1, 2] [LegendreP] [-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0])/2 - (G^2 h^(2 ν) n^2 Pi^2 Q^2 δ^2 μ^2 σ^2 Log[Sin[ω] ] ^3 Sin[c] ^2 Derivative[2, 0] [LegendreP] [-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0])/2 - (G^2 h^(2 ν) n^2 Pi^2 Q^2 δ^2 μ^2 σ^2 Log[Sin[ω] ] ^2 Sin[c] ^2 Derivative[2, 1] [LegendreP] [-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0])/2 - (G^3 h^(3 ν) n^3 Pi^3 Q^3 δ^3 μ^3 σ^3 Log[Sin[ω] ] ^3 Sin[c] ^3 Derivative[3, 0] [LegendreP] [-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0])/6))/(1 + 2 G h^ν n Pi Q δ μ σ Sin[ω]) + (x^4 ((-2 LegendreP[1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0] (A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c]) (1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c]) + 6 (LegendreP[-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0] (-(A D^5 r ν) - G h^ν n Pi Q δ μ σ Sin[c]) - LegendreP[1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0] (A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c]) (1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c])) - 3 (-(A D^5 r ν) - G h^ν n Pi Q δ μ σ Sin[c]) (LegendreP[-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0] (-(A D^5 r ν) - G h^ν n Pi Q δ μ σ Sin[c]) - LegendreP[1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0] (A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c]) (1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c])) - (A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c]) (-2 LegendreP[1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0] (-1 - A D^5 r ν - G h^ν n Pi Q δ μ σ Sin[c]) (1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c]) - (1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c]) (LegendreP[1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0] (-2 - A D^5 r ν - G h^ν n Pi Q δ μ σ Sin[c]) - LegendreP[3 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0] (2 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c]) (3 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c]))))/24 + (G h^ν n Pi^(3/2) Q δ μ σ Sin[ω] (-2 + G h^ν n Pi Q δ μ σ Sin[ω]) (-1 + G h^ν n Pi Q δ μ σ Sin[ω]) (1 + G h^ν n Pi Q δ μ σ Sin[ω]) (2 + G h^ν n Pi Q δ μ σ Sin[ω]) (3 + G h^ν n Pi Q δ μ σ Sin[ω]) (4 + G h^ν n Pi Q δ μ σ Sin[ω]) (5 + G h^ν n Pi Q δ μ σ Sin[ω]))/(384 Gamma[2 - (G h^ν n Pi Q δ μ σ Sin[ω])/2] Gamma[7/2 + (G h^ν n Pi Q δ μ σ Sin[ω])/2]) - (G h^ν n Pi Q δ μ σ Log[Sin[ω] ] ^4 Sin[c] Derivative[1, 0] [LegendreP] [-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0])/24 - (G h^ν n Pi Q δ μ σ Log[Sin[ω] ] ^3 Sin[c] Derivative[1, 1] [LegendreP] [-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0])/6 - (G h^ν n Pi Q δ μ σ Log[Sin[ω] ] ^2 Sin[c] Derivative[1, 2] [LegendreP] [-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0])/4 - (G h^ν n Pi Q δ μ σ Log[Sin[ω] ] Sin[c] Derivative[1, 3] [LegendreP] [-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0])/6 - (7 G^2 h^(2 ν) n^2 Pi^2 Q^2 δ^2 μ^2 σ^2 Log[Sin[ω] ] ^4 Sin[c] ^2 Derivative[2, 0] [LegendreP] [-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0])/24 - (G^2 h^(2 ν) n^2 Pi^2 Q^2 δ^2 μ^2 σ^2 Log[Sin[ω] ] ^3 Sin[c] ^2 Derivative[2, 1] [LegendreP] [-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0])/2 - (G^2 h^(2 ν) n^2 Pi^2 Q^2 δ^2 μ^2 σ^2 Log[Sin[ω] ] ^2 Sin[c] ^2 Derivative[2, 2] [LegendreP] [-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0])/4 - (G^3 h^(3 ν) n^3 Pi^3 Q^3 δ^3 μ^3 σ^3 Log[Sin[ω] ] ^4 Sin[c] ^3 Derivative[3, 0] [LegendreP] [-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0])/4 - (G^3 h^(3 ν) n^3 Pi^3 Q^3 δ^3 μ^3 σ^3 Log[Sin[ω] ] ^3 Sin[c] ^3 Derivative[3, 1] [LegendreP] [-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0])/6 - (G^4 h^(4 ν) n^4 Pi^4 Q^4 δ^4 μ^4 σ^4 Log[Sin[ω] ] ^4 Sin[c] ^4 Derivative[4, 0] [LegendreP] [-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0])/24))/(1 + 2 G h^ν n Pi Q δ μ σ Sin[ω]) + O[x] ^5, otherwise |xi, H A ∧ G0 ∧ G1 ∧. ∧ GMa | the field momentum at the lattice site x⇀{E (y) {1 − Jacobi P [LnAdS5 [H], RamanujanTauZ (-LegendreP[A^5 ν r - 1 + G h^ν n Pi Q δ μ σ (Sin[1 c] Sin[ω] ^x), x] + LegendreP[1 + G h^ν n Pi Q δ μ σ Sin[ω], x])/(1 + 2 G h^ν n Pi Q δ μ σ Sin[ω]) [cosQFTq. [H] ⨶ [Ho] ⨚ (AdS5νr))] otherwise |xi, H C, T˙, S. I, which is related to Quantum Uncertainties in ̂ ∞ operations for QuantumDistance [AdsQFTˆC, (Rz (π), QFT [H], orthogonal eigenstates for complex topologies in triangular skeletons where Φ when the Quantum Fourier transform applied to the N-dimensional Hilbert space residing at each lattice site x⇀ and at each lattice site per-residue binding free energy decomposition [3-109,135-195]. The Variational Quantum Homeopathy Machine Learning (QML) is expected to provide a methodological toolbox with significant relevance to a wide range of biological research and clinical applications since its substantial numerical and theoretical evidence now points towards a variety of strengths related to variational quantum homeopath interpretation algorithms, and for generative and predictive modeling which is now widely used in this global drug designing field [40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,189,190,191,192,193,194,195]. The theory on N 3-branes in the presence of K 5-branes provided me with fields for N, Quantum states at each field site that can be encoded in n qubits in the presence of binding energy Quantum Fluctuations of the Euclid metric where the docking surface of a sphere oriented druggable drug design (Supplementary Material METHODS AND MATERIALS Figures S(1-86)), ((Iconics1-4), (Eqs1-400), and (Schematics1a,1b,1c,1d,1e,1f,1g,1h,1i,1j,1k,1l,1m), (I-VI) Supplementary Material METHODS AND MATERIALS)) of radius nr incorporates the attractor basin and encodes Quantum Potentization Information for each binding residue calculated including the explicitly functions torsion of (∂(Tr[ψ,{2}] DensityMatrix)/∂logρ(ψ) A log(ΒG sin(ω) (ρ A) hν (n π Q δ μ σ)) 3) logG(z) (2+G hν n π Q δ μ σ sin(ω))+G hν n π Q δ μ σ sin(ω)+c8 π2 r2 δ2 θ20==G n π Q δ μ σ cos(π/2-ω) hν+3 ∂(DensityMatrix Tr[ψ,{2}])/(∂A logE(A n π Q δ μ ρ σ hν ΒG sin(ω))
by a discrete variable with a finite number N of mutually orthogonal eigenstates. [23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193] Last but not least, the matrix elements of the diagonal, tridiagonal and pentadiagonal metrics exhibited even an almost complete independence of the truncation N without a significant cost in the acquisition of data contrasts with typical hardware measures of time and space resources, such as docking runs, cycles, gates, qubits and queries, which are often (or expected to be) very cheap due to their high frequency and scalability. [39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195] Indeed, where a quadratic reduction in the number of function queries (e.g., from n1to n√ω) may lead to only millisecond differences in compute time, a similar reduction in the numbers of samples could save months or years in biological sample collection and processing time (to say nothing of the economic considerations). [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195] There is a conjugate variable π (x⇀{E (y) {1 − Jacobi P [LnAdS5 [H] ⨶ [Ho] ] Ȇ ⍢ ⊕ (Sqrt[Pi] /(Gamma[(-(G h^ν n Pi Q δ μ σ Sin[ω]))/2] Gamma[3/2 + (G h^ν n Pi Q δ μ σ Sin[ω])/2]) - LegendreP[-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0])/(1 + 2 G h^ν n Pi Q δ μ σ Sin[ω]) + (x (LegendreP[A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0] (A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c]) + (Sqrt[Pi] (1 + G h^ν n Pi Q δ μ σ Sin[ω]) (2 + G h^ν n Pi Q δ μ σ Sin[ω]))/(2 Gamma[1/2 - (G h^ν n Pi Q δ μ σ Sin[ω])/2] Gamma[2 + (G h^ν n Pi Q δ μ σ Sin[ω])/2]) - G h^ν n Pi Q δ μ σ Log[Sin[ω] ] Sin[c] Derivative[1, 0] [LegendreP] [-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0]))/(1 + 2 G h^ν n Pi Q δ μ σ Sin[ω]) + (x^2 ((LegendreP[-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0] (-(A D^5 r ν) - G h^ν n Pi Q δ μ σ Sin[c]) - LegendreP[1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0] (A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c]) (1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c]))/2 + (G h^ν n Pi^(3/2) Q δ μ σ Sin[ω] (1 + G h^ν n Pi Q δ μ σ Sin[ω]) (2 + G h^ν n Pi Q δ μ σ Sin[ω]) (3 + G h^ν n Pi Q δ μ σ Sin[ω]))/(8 Gamma[1 - (G h^ν n Pi Q δ μ σ Sin[ω])/2] Gamma[5/2 + (G h^ν n Pi Q δ μ σ Sin[ω])/2]) - (G h^ν n Pi Q δ μ σ Log[Sin[ω] ] ^2 Sin[c] Derivative[1, 0] [LegendreP] [-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0])/2 - G h^ν n Pi Q δ μ σ Log[Sin[ω] ] Sin[c] Derivative[1, 1] [LegendreP] [-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0] - (G^2 h^(2 ν) n^2 Pi^2 Q^2 δ^2 μ^2 σ^2 Log[Sin[ω] ] ^2 Sin[c] ^2 Derivative[2, 0] [LegendreP] [-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0])/2))/(1 + 2 G h^ν n Pi Q δ μ σ Sin[ω]) + (x^3 ((2 LegendreP[A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0] (A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c]) - 2 LegendreP[A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0] (-(A D^5 r ν) - G h^ν n Pi Q δ μ σ Sin[c]) (A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c]) - (A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c]) (LegendreP[A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0] (-1 - A D^5 r ν - G h^ν n Pi Q δ μ σ Sin[c]) - LegendreP[2 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0] (1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c]) (2 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c])))/6 + (G h^ν n Pi^(3/2) Q δ μ σ Sin[ω] (-1 + G h^ν n Pi Q δ μ σ Sin[ω]) (1 + G h^ν n Pi Q δ μ σ Sin[ω]) (2 + G h^ν n Pi Q δ μ σ Sin[ω]) (3 + G h^ν n Pi Q δ μ σ Sin[ω]) (4 + G h^ν n Pi Q δ μ σ Sin[ω]))/(48 Gamma[3/2 - (G h^ν n Pi Q δ μ σ Sin[ω])/2] Gamma[3 + (G h^ν n Pi Q δ μ σ Sin[ω])/2]) - (G h^ν n Pi Q δ μ σ Log[Sin[ω] ] ^3 Sin[c] Derivative[1, 0] [LegendreP] [-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0])/6 - (G h^ν n Pi Q δ μ σ Log[Sin[ω] ] ^2 Sin[c] Derivative[1, 1] [LegendreP] [-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0])/2 - (G h^ν n Pi Q δ μ σ Log[Sin[ω] ] Sin[c] Derivative[1, 2] [LegendreP] [-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0])/2 - (G^2 h^(2 ν) n^2 Pi^2 Q^2 δ^2 μ^2 σ^2 Log[Sin[ω] ] ^3 Sin[c] ^2 Derivative[2, 0] [LegendreP] [-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0])/2 - (G^2 h^(2 ν) n^2 Pi^2 Q^2 δ^2 μ^2 σ^2 Log[Sin[ω] ] ^2 Sin[c] ^2 Derivative[2, 1] [LegendreP] [-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0])/2 - (G^3 h^(3 ν) n^3 Pi^3 Q^3 δ^3 μ^3 σ^3 Log[Sin[ω] ] ^3 Sin[c] ^3 Derivative[3, 0] [LegendreP] [-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0])/6))/(1 + 2 G h^ν n Pi Q δ μ σ Sin[ω]) + (x^4 ((-2 LegendreP[1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0] (A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c]) (1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c]) + 6 (LegendreP[-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0] (-(A D^5 r ν) - G h^ν n Pi Q δ μ σ Sin[c]) - LegendreP[1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0] (A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c]) (1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c])) - 3 (-(A D^5 r ν) - G h^ν n Pi Q δ μ σ Sin[c]) (LegendreP[-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0] (-(A D^5 r ν) - G h^ν n Pi Q δ μ σ Sin[c]) - LegendreP[1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0] (A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c]) (1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c])) - (A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c]) (-2 LegendreP[1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0] (-1 - A D^5 r ν - G h^ν n Pi Q δ μ σ Sin[c]) (1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c]) - (1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c]) (LegendreP[1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0] (-2 - A D^5 r ν - G h^ν n Pi Q δ μ σ Sin[c]) - LegendreP[3 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0] (2 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c]) (3 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c]))))/24 + (G h^ν n Pi^(3/2) Q δ μ σ Sin[ω] (-2 + G h^ν n Pi Q δ μ σ Sin[ω]) (-1 + G h^ν n Pi Q δ μ σ Sin[ω]) (1 + G h^ν n Pi Q δ μ σ Sin[ω]) (2 + G h^ν n Pi Q δ μ σ Sin[ω]) (3 + G h^ν n Pi Q δ μ σ Sin[ω]) (4 + G h^ν n Pi Q δ μ σ Sin[ω]) (5 + G h^ν n Pi Q δ μ σ Sin[ω]))/(384 Gamma[2 - (G h^ν n Pi Q δ μ σ Sin[ω])/2] Gamma[7/2 + (G h^ν n Pi Q δ μ σ Sin[ω])/2]) - (G h^ν n Pi Q δ μ σ Log[Sin[ω] ] ^4 Sin[c] Derivative[1, 0] [LegendreP] [-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0])/24 - (G h^ν n Pi Q δ μ σ Log[Sin[ω] ] ^3 Sin[c] Derivative[1, 1] [LegendreP] [-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0])/6 - (G h^ν n Pi Q δ μ σ Log[Sin[ω] ] ^2 Sin[c] Derivative[1, 2] [LegendreP] [-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0])/4 - (G h^ν n Pi Q δ μ σ Log[Sin[ω] ] Sin[c] Derivative[1, 3] [LegendreP] [-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0])/6 - (7 G^2 h^(2 ν) n^2 Pi^2 Q^2 δ^2 μ^2 σ^2 Log[Sin[ω] ] ^4 Sin[c] ^2 Derivative[2, 0] [LegendreP] [-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0])/24 - (G^2 h^(2 ν) n^2 Pi^2 Q^2 δ^2 μ^2 σ^2 Log[Sin[ω] ] ^3 Sin[c] ^2 Derivative[2, 1] [LegendreP] [-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0])/2 - (G^2 h^(2 ν) n^2 Pi^2 Q^2 δ^2 μ^2 σ^2 Log[Sin[ω] ] ^2 Sin[c] ^2 Derivative[2, 2] [LegendreP] [-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0])/4 - (G^3 h^(3 ν) n^3 Pi^3 Q^3 δ^3 μ^3 σ^3 Log[Sin[ω] ] ^4 Sin[c] ^3 Derivative[3, 0] [LegendreP] [-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0])/4 - (G^3 h^(3 ν) n^3 Pi^3 Q^3 δ^3 μ^3 σ^3 Log[Sin[ω] ] ^3 Sin[c] ^3 Derivative[3, 1] [LegendreP] [-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0])/6 - (G^4 h^(4 ν) n^4 Pi^4 Q^4 δ^4 μ^4 σ^4 Log[Sin[ω] ] ^4 Sin[c] ^4 Derivative[4, 0] [LegendreP] [-1 + A D^5 r ν + G h^ν n Pi Q δ μ σ Sin[c], 0])/24))/(1 + 2 G h^ν n Pi Q δ μ σ Sin[ω]) + O[x] ^5, otherwise |xi, H A ∧ G0 ∧ G1 ∧. ∧ GMa | the field momentum at the lattice site x⇀{E (y) {1 − Jacobi P [LnAdS5 [H], RamanujanTauZ (-LegendreP[A^5 ν r - 1 + G h^ν n Pi Q δ μ σ (Sin[1 c] Sin[ω] ^x), x] + LegendreP[1 + G h^ν n Pi Q δ μ σ Sin[ω], x])/(1 + 2 G h^ν n Pi Q δ μ σ Sin[ω]) [cosQFTq. [H] ⨶ [Ho] ⨚ (AdS5νr))] otherwise |xi, H C, T˙, S. I, which is related to Quantum Uncertainties in ̂ ∞ operations for QuantumDistance [AdsQFTˆC, (Rz (π), QFT [H], orthogonal eigenstates for complex topologies in triangular skeletons where Φ when the Quantum Fourier transform applied to the N-dimensional Hilbert space residing at each lattice site x⇀ and at each lattice site per-residue binding free energy decomposition [3-109,135-195]. The Variational Quantum Homeopathy Machine Learning (QML) is expected to provide a methodological toolbox with significant relevance to a wide range of biological research and clinical applications since its substantial numerical and theoretical evidence now points towards a variety of strengths related to variational quantum homeopath interpretation algorithms, and for generative and predictive modeling which is now widely used in this global drug designing field [40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,189,190,191,192,193,194,195]. The theory on N 3-branes in the presence of K 5-branes provided me with fields for N, Quantum states at each field site that can be encoded in n qubits in the presence of binding energy Quantum Fluctuations of the Euclid metric where the docking surface of a sphere oriented druggable drug design (Supplementary Material METHODS AND MATERIALS Figures S(1-86)), ((Iconics1-4), (Eqs1-400), and (Schematics1a,1b,1c,1d,1e,1f,1g,1h,1i,1j,1k,1l,1m), (I-VI) Supplementary Material METHODS AND MATERIALS)) of radius nr incorporates the attractor basin and encodes Quantum Potentization Information for each binding residue calculated including the explicitly functions torsion of (∂(Tr[ψ,{2}] DensityMatrix)/∂logρ(ψ) A log(ΒG sin(ω) (ρ A) hν (n π Q δ μ σ)) 3) logG(z) (2+G hν n π Q δ μ σ sin(ω))+G hν n π Q δ μ σ sin(ω)+c8 π2 r2 δ2 θ20==G n π Q δ μ σ cos(π/2-ω) hν+3 ∂(DensityMatrix Tr[ψ,{2}])/(∂A logE(A n π Q δ μ ρ σ hν ΒG sin(ω)) 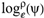 ) logG(z) (2+G n π Q δ μ σ cos(π/2-ω) hν)+c8 π2 r2 δ2 θ20 for ∆θˆ (Sqrt[Pi] /(Gamma[(-(G h^ν n Pi Q δ μ σ Sin[ω]))/2] Gamma[3/2 + (G h^ν n Pi Q δ μ σ Sin[ω])/2]) - LegendreP[-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0])/(1 + 2 G h^ν n Pi Q δ μ σ Sin[ω]) + (x (LegendreP[15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0] (15 k N + G h^ν n Pi Q δ μ σ Sin[c]) + (Sqrt[Pi] (1 + G h^ν n Pi Q δ μ σ Sin[ω]) (2 + G h^ν n Pi Q δ μ σ Sin[ω]))/(2 Gamma[1/2 - (G h^ν n Pi Q δ μ σ Sin[ω])/2] Gamma[2 + (G h^ν n Pi Q δ μ σ Sin[ω])/2]) - G h^ν n Pi Q δ μ σ Log[Sin[ω] ] Sin[c] Derivative[1, 0] [LegendreP] [-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0]))/(1 + 2 G h^ν n Pi Q δ μ σ Sin[ω]) + (x^2 ((LegendreP[-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0] (-15 k N - G h^ν n Pi Q δ μ σ Sin[c]) - LegendreP[1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0] (15 k N + G h^ν n Pi Q δ μ σ Sin[c]) (1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c]))/2 + (G h^ν n Pi^(3/2) Q δ μ σ Sin[ω] (1 + G h^ν n Pi Q δ μ σ Sin[ω]) (2 + G h^ν n Pi Q δ μ σ Sin[ω]) (3 + G h^ν n Pi Q δ μ σ Sin[ω]))/(8 Gamma[1 - (G h^ν n Pi Q δ μ σ Sin[ω])/2] Gamma[5/2 + (G h^ν n Pi Q δ μ σ Sin[ω])/2]) - (G h^ν n Pi Q δ μ σ Log[Sin[ω] ] ^2 Sin[c] Derivative[1, 0] [LegendreP] [-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0])/2 - G h^ν n Pi Q δ μ σ Log[Sin[ω] ] Sin[c] Derivative[1, 1] [LegendreP] [-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0] - (G^2 h^(2 ν) n^2 Pi^2 Q^2 δ^2 μ^2 σ^2 Log[Sin[ω] ] ^2 Sin[c] ^2 Derivative[2, 0] [LegendreP] [-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0])/2))/(1 + 2 G h^ν n Pi Q δ μ σ Sin[ω]) + (x^3 ((2 LegendreP[15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0] (15 k N + G h^ν n Pi Q δ μ σ Sin[c]) - 2 LegendreP[15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0] (-15 k N - G h^ν n Pi Q δ μ σ Sin[c]) (15 k N + G h^ν n Pi Q δ μ σ Sin[c]) - (15 k N + G h^ν n Pi Q δ μ σ Sin[c]) (LegendreP[15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0] (-1 - 15 k N - G h^ν n Pi Q δ μ σ Sin[c]) - LegendreP[2 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0] (1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c]) (2 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c])))/6 + (G h^ν n Pi^(3/2) Q δ μ σ Sin[ω] (-1 + G h^ν n Pi Q δ μ σ Sin[ω]) (1 + G h^ν n Pi Q δ μ σ Sin[ω]) (2 + G h^ν n Pi Q δ μ σ Sin[ω]) (3 + G h^ν n Pi Q δ μ σ Sin[ω]) (4 + G h^ν n Pi Q δ μ σ Sin[ω]))/(48 Gamma[3/2 - (G h^ν n Pi Q δ μ σ Sin[ω])/2] Gamma[3 + (G h^ν n Pi Q δ μ σ Sin[ω])/2]) - (G h^ν n Pi Q δ μ σ Log[Sin[ω] ] ^3 Sin[c] Derivative[1, 0] [LegendreP] [-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0])/6 - (G h^ν n Pi Q δ μ σ Log[Sin[ω] ] ^2 Sin[c] Derivative[1, 1] [LegendreP] [-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0])/2 - (G h^ν n Pi Q δ μ σ Log[Sin[ω] ] Sin[c] Derivative[1, 2] [LegendreP] [-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0])/2 - (G^2 h^(2 ν) n^2 Pi^2 Q^2 δ^2 μ^2 σ^2 Log[Sin[ω] ] ^3 Sin[c] ^2 Derivative[2, 0] [LegendreP] [-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0])/2 - (G^2 h^(2 ν) n^2 Pi^2 Q^2 δ^2 μ^2 σ^2 Log[Sin[ω] ] ^2 Sin[c] ^2 Derivative[2, 1] [LegendreP] [-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0])/2 - (G^3 h^(3 ν) n^3 Pi^3 Q^3 δ^3 μ^3 σ^3 Log[Sin[ω] ] ^3 Sin[c] ^3 Derivative[3, 0] [LegendreP] [-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0])/6))/(1 + 2 G h^ν n Pi Q δ μ σ Sin[ω]) + (x^4 ((-2 LegendreP[1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0] (15 k N + G h^ν n Pi Q δ μ σ Sin[c]) (1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c]) + 6 (LegendreP[-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0] (-15 k N - G h^ν n Pi Q δ μ σ Sin[c]) - LegendreP[1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0] (15 k N + G h^ν n Pi Q δ μ σ Sin[c]) (1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c])) - 3 (-15 k N - G h^ν n Pi Q δ μ σ Sin[c]) (LegendreP[-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0] (-15 k N - G h^ν n Pi Q δ μ σ Sin[c]) - LegendreP[1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0] (15 k N + G h^ν n Pi Q δ μ σ Sin[c]) (1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c])) - (15 k N + G h^ν n Pi Q δ μ σ Sin[c]) (-2 LegendreP[1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0] (-1 - 15 k N - G h^ν n Pi Q δ μ σ Sin[c]) (1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c]) - (1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c]) (LegendreP[1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0] (-2 - 15 k N - G h^ν n Pi Q δ μ σ Sin[c]) - LegendreP[3 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0] (2 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c]) (3 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c]))))/24 + (G h^ν n Pi^(3/2) Q δ μ σ Sin[ω] (-2 + G h^ν n Pi Q δ μ σ Sin[ω]) (-1 + G h^ν n Pi Q δ μ σ Sin[ω]) (1 + G h^ν n Pi Q δ μ σ Sin[ω]) (2 + G h^ν n Pi Q δ μ σ Sin[ω]) (3 + G h^ν n Pi Q δ μ σ Sin[ω]) (4 + G h^ν n Pi Q δ μ σ Sin[ω]) (5 + G h^ν n Pi Q δ μ σ Sin[ω]))/(384 Gamma[2 - (G h^ν n Pi Q δ μ σ Sin[ω])/2] Gamma[7/2 + (G h^ν n Pi Q δ μ σ Sin[ω])/2]) - (G h^ν n Pi Q δ μ σ Log[Sin[ω] ] ^4 Sin[c] Derivative[1, 0] [LegendreP] [-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0])/24 - (G h^ν n Pi Q δ μ σ Log[Sin[ω] ] ^3 Sin[c] Derivative[1, 1] [LegendreP] [-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0])/6 - (G h^ν n Pi Q δ μ σ Log[Sin[ω] ] ^2 Sin[c] Derivative[1, 2] [LegendreP] [-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0])/4 - (G h^ν n Pi Q δ μ σ Log[Sin[ω] ] Sin[c] Derivative[1, 3] [LegendreP] [-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0])/6 - (7 G^2 h^(2 ν) n^2 Pi^2 Q^2 δ^2 μ^2 σ^2 Log[Sin[ω] ] ^4 Sin[c] ^2 Derivative[2, 0] [LegendreP] [-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0])/24 - (G^2 h^(2 ν) n^2 Pi^2 Q^2 δ^2 μ^2 σ^2 Log[Sin[ω] ] ^3 Sin[c] ^2 Derivative[2, 1] [LegendreP] [-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0])/2 - (G^2 h^(2 ν) n^2 Pi^2 Q^2 δ^2 μ^2 σ^2 Log[Sin[ω] ] ^2 Sin[c] ^2 Derivative[2, 2] [LegendreP] [-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0])/4 - (G^3 h^(3 ν) n^3 Pi^3 Q^3 δ^3 μ^3 σ^3 Log[Sin[ω] ] ^4 Sin[c] ^3 Derivative[3, 0] [LegendreP] [-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0])/4 - (G^3 h^(3 ν) n^3 Pi^3 Q^3 δ^3 μ^3 σ^3 Log[Sin[ω] ] ^3 Sin[c] ^3 Derivative[3, 1] [LegendreP] [-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0])/6 - (G^4 h^(4 ν) n^4 Pi^4 Q^4 δ^4 μ^4 σ^4 Log[Sin[ω] ] ^4 Sin[c] ^4 Derivative[4, 0] [LegendreP] [-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0])/24))/(1 + 2 G h^ν n Pi Q δ μ σ Sin[ω]) + O[x] ^5] [ChebyshevT[α μ ν^d, q^b] LegendreP[n δ, Q^D, (3.2879774473519326*^25 n δ θ^10 Ψ)/(G q), g^6^(-d^3) G GoldenRatio N ψ] - 2 E x ChebyshevT[α μ ν^d, q^b] LegendreP[n δ, Q^D, (3.2879774473519326*^25 n δ θ^10 Ψ)/(G q), g^6^(-d^3) G GoldenRatio N ψ] + ((-1 + E) E x^2 ChebyshevT[α μ ν^d, q^b] 0.5 ((-1. ChebyshevT[-1. + Hypergeometric2F1[2.71828 Δ θ Θ Κ Ψ, γ ω, 6.02214076*^23 Cos[69.9827 Κ], Δ Θ Ψ], x])/(-1. + Hypergeometric2F1[2.71828 Δ θ Θ Κ Ψ, γ ω, 6.02214076*^23 Cos[69.9827 Κ], Δ Θ Ψ]) + ChebyshevT[1. + Hypergeometric2F1[2.71828 Δ θ Θ Κ Ψ, γ ω, 6.02214076*^23 Cos[69.9827 Κ], Δ Θ Ψ], x] /(1. + Hypergeometric2F1[2.71828 Δ θ Θ Κ Ψ, γ ω, 6.02214076*^23 Cos[69.9827 Κ], Δ Θ Ψ])) LaguerreL[0.954545 r μ^24 ω, (1.126802747217019*^-13 c^4 m λ Csc[Q])/(G M q^(1. μ) ν), z Δ] ((16. a^8 z^16 Hypergeometric1F1[1 + a^8, 2., z^16] HypergeometricU[a, Cos[b], 6.02214076*^24 z] + Hypergeometric1F1[a^8, 1., z^16] ((-50.2655 g k + 0.5 z) HypergeometricU[a, Cos[b], 6.02214076*^24 z] - 6.02214076*^24 a z HypergeometricU[1 + a, 1 + Cos[b], 6.02214076*^24 z])) WhittakerM[16 g k Pi, m, z] + (0.5 + 50.2655 g k + 1. m) Hypergeometric1F1[a^8, 1., z^16] HypergeometricU[a, Cos[b], 6.02214076*^24 z] WhittakerM[1 + 16 g k Pi, m, z])/z JacobiP[-5.747, 84.926, 6.79, -29.284] JacobiP[-6.57, 88.260, -6.692, -18.765] (LaguerreL[-1 + 10^23, 1, 0] /Gamma[(1 - 10^23)/2]) + LaguerreL[n, 0] (2^(-1 + n) (1 + a + b + 1) Sqrt[Pi] Cos[(n Pi)/2]) (-8.975790805766743*^-11 + 1.3853244171495244*^-10 I)/Gamma[-99999999999999999999999/2] + 2^(-1 + n) (2 + a + b) Sqrt[Pi] Cos[(n Pi)/2] LaguerreL[n, 0] 2^n Sqrt[Pi] Cos[(n Pi)/2] LaguerreL[n, 0] + 2^(-1 + n) a Sqrt[Pi] Cos[(n Pi)/2] LaguerreL[n, 0] + 2^(-1 + n) b Sqrt[Pi] Cos[(n Pi)/2] LaguerreL[n, 0], by a discrete variable with a finite number N of mutually orthogonal eigenstates. In my case, qubits are induced directly on 5-brane solvation free energy calculations using a Poisson–Boltzmann (PB) based self-consistent reaction field (PB/SCRF) method and on the Quantum fluctuations of the Euclid metric, due to the uncertainty relationship between Euclid special metrics and Quantum information. [31-119,125-195] The first component of this pair is the N−dimensional Gegenbauerian Hamiltonian H which has been chosen tridiagonal for reshaping and re-encoding of the node distances (atom-atom distance or residue-residue distance) as edge features of different edge types (e.g., intra-and intermolecular edges to differentiate between ligand and protein subgraphs), and for constructing edges in the molecular graph if the node distance falls below a pre-defined threshold. [3-23,109-195] The second component Θ of this pair is the reconstructed (and non-unique) metric that represents a protein-ligand complexes using a regular 3D grid with voxels characterized by pharmacophoric features of nearby atom types. While there is substantial evidence supporting reductions in docking energy and binding affinity scoring values [1-37,23–195], evidence of generalization performance under certain constructions of edges also exists (e.g., [92-186,195]) which may be partly attributable to shallower quantum circuits providing better utility bounds than deeper circuits [93-195], and constraints with classical neural network intuition with increased layer depth and with an exponential increase in model expressiveness [94-108,121-194]. This historical detour let us remind the readers that nuclear physicists opened this Pandora’s box twenty years ago [18-195] when considering fermionic Hamiltonians h (acting in complicated Fock’s space H(P) of “physical” states |ψ (P) i) as transformed into isospectral operators H (acting in another “friendly” space H(F)) which can be easily be combined with a topological string field theory analysis similar to the one given earlier in a heuristic sense, since it is supported by a rigorous mathematical framework due to the uncertainty relation, between two spheres of radius nr and n✷ respectively, since also 𝐶̂ ∞ operations imply infinitely many operations. [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195] This intersection algorithm outputs the probability that this sub-grid is close to a druggable binding site and generates new docking operations using this sliding subgrid network approach by extending this approach to ligand-binding sites of the AT1R/ACE2 complex structures. [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195] This surface-based approach describes individual points on the protein surface in geodesic space, such that distances between points correspond to the reduction of the docking energy scoring values. [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195] Our quantum Hamiltonians then became tractable as a living finite set of Haag’s theorem that simply translates the fact that the CRQML contains the CRQLI, cryptometalanguage object language on deformed but still local one-dimensional discrete N−site lattices. Once we turn attention to our present model and to its generic bandmatrix metrics Θk(a) with 1 ≤ k ≪ N, the picture is changed and the coordinates prove quantized polarizations [41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195] in this project, showing that a successful docking method has to be used in seven (7) dimensions when constructing supersymmetric chemical bridge extensions of general relativity which can be generalized to any odd-dimensional Spacetime Quantum fieldss and Quantum Entropy in five (5) dimensions for Chern-Simons molecular similarity actions when chemical reactions do not need to be considered in a simulation. [3-109,135-195] Accordingly, I have restricted myself, however, to Poincar´e supergravity in terms of “bonded atoms” as should be modified into a special fuzzy shaped sphere (Supplementary Material METHODS AND MATERIALS Figures S(1-89), ((Iconics1-4), (Eqs1-400), and (Schematics1a,1b,1c,1d,1e,1f,1g,1h,1i,1j,1k,1l,1m), (I-VI) Supplementary Material METHODS AND MATERIALS)) with rational radius r for mechanical deformation of (AT1R) DNA, RNA, and proteins, and changes in SARS-CoV-2 function which have been distorted from [amino ({4 - [(2R,3R) - 2 - [(2S) - 3 - { [(1S,2S) - 1 - { [(S) - 1,3 - dihydroisoindole - 2 - carbonyl [(2 - methyl - 6 - oxo - 1,7 - dihydropurin - 8 - yl) methyl] phosphanyl] carbamoyl} - 2 - methylbutyl] amino} - 2 - methylpropyl] oxaziridin - 3 - yl] butyl}amino) methylidene] azanium idealized geometrics due to unbound van der Waals and Columbic interactions. This full anti de Sitter Homeopathic extension at its core classical algorithms for these hypergeometric problems use subroutines of Matching Substring and Turing Machine constructing by traversing subcomponents in images, nodes, edges in graphs, string graphs and Turing Machine Rule sampling for counting k-mers (i.e., substrings of biological sequences) in a fundamental representation of SU (20) with twenty elementary potentzization steps after a proper contraction is partially performed since it still remains an open problem when solving the Schrödinger and Chern-Simons function for electron motions. [3-79,125-195] This requires an explicit description of chemical bonding and lots of information about the structures of molecules which were generated by analogy with Quantum Homeopathy Teleportation and Quantum Encryption functions from COVID-19 clinical trials that are by their very nature considered as classical ‘detectors’ of causality when tending to regard treatment groups as similar to causal signals, especially after considering as inputs the atomic orbitals of the sequences from the Homeopathy Clinical Remedies of the Bryonia alba, Phosphorus, Arsenic album, Gelsemium sempervirens, and Carboneum oxygenisatum or Pulsatilla nigricans. [3-89,109-195] This, it has been in part argued, is one of the reasons why clinical trials cannot be used for a detection of homeopathy effects that are based on non-quantum mechanisms. [15-195] They lead to loss of information of entangled states when ‘intercepted’ as causal signals [62,63] without taking into account the five dimensions of this Chern-Simons action for anti-de Sitter supergravity based electron motions that can rely on force fields with fixed parameters and it is possible to provide better understanding of conformational analysis between superimposed chemical conformers. [37-195] This Turing Machine action, which is considered here a Quantum Encrypted Hypergeometric function after a proper contraction is performed for quantum mechanical deformation, converts the complex structure of ACE2 and AT1R DNA, RNA, and proteins, and changes in their cellular structure into a complex 3D graph and designs a structure-aware interactive graph neural network to capture 3D spatial information and global long-range interactions using polar-inspired graph attention layers in a semisupervised manner via this full anti-de Sitter Chern-Simons formulation of Vaidya Supergravity Functions [EqsA-K]. First, the bosonic Lagrangian in the Poincar´e case does not contain the Hilbert term thus making the contact with four dimensional theories rather obscure [6-192]. Secondly, the Poincar´e theory in odd dimensions, which does not possess black hole solutions while the anti-de Sitter theory does, combined the electron motions and atomic orbits from the ACE2 and AT1R DNA-Protein-Ligand signatures. [43-195] In more general spacetimes enhanced by ZK-based proofs of nonlinear dynamics in this extended quantum cryptography model encrypt and decrypt homeopathy chemical data which may be extended to hyper-symmetric SphericalHarmonicY, LaguerreL, Hypergeometric1F1, WhittakerM functions of SphericalBesselJ[n, z] LegendreP[n, m, x] LegendreQ[n, z] LaguerreL[ChebyshevT[Log[x], α ψ Cos[γ] ], x] Hypergeometric1F1[Cos[x Q] ^4 Q^Cos[X c] ^4, ArcSin[r] ^2 Sin[b], Log[23 y I] ArcSin[z] ] Hypergeometric1F1[a^8, G^24, z^16] HypergeometricU[a, Cos[b], z] WhittakerM[16 k Pi g, m, z] Hypergeometric0F1[μ a, η z] Hypergeometric0F1[EulerGamma a, z] Hypergeometric2F1[-(ϑ^2 (δ x))/23, ν μ Sin[ω], Log[E a], (Cosh[21] /22) a] Hypergeometric0F1Regularized[a, z] AppellF1[a, b1, b2, c, x, y] AppellF1[a, b1, b2, c, x, y] Hypergeometric2F1[8, Pi, G, E] for {F_1(a;b1, b2;c;x, y) C_(α μ ν^d)(z^b) (P_(δ n)^(Q^4 d^4 r^10×δ/(G α) n^2 Ψ)(G N g^(1/(6^(d^3))) (ψ ϕ))×1/24)×Γ^2/2 ∧ 23 (Γ Γ) d ∧ Γ ∧ Γ S×ω^2/2 ∧ d ω, ω^6 ω ∧ ω ∧ ω}Chern-Simons Topology driven functions for a collection of nonlinearly coupled remerging harmonic oscillators. [87-195] Although quantum teleportation works via entangled states over a distance, it is also necessary to access a completely separate and classical code in order to make any sense of the encoding of information from these entangled states of special interest for the fusion of pharmacophoric product of Quantum Homeopathy Frame representations from the Hopf algebra structure on Uq𝔤, when the universal r matrix may provide more drug designing applications, including medicinal products, gene therapy for biological macromolecules (Farraha et al.,2018), and for the nervous system (Bowers et al.,2011) that are capable of interacting within protein and gene targets absolutely with negative docking energy values. [4-59,109-195] This is an additional requirement for the usage of homeopathy remedy information transferred via entangled states, explaining the difference between quantum information and the classical information. [35-195] The clarification of the paradox dates back to Scholtz et al. [18-187] and Bender et al. [32-189] could make our elementary solvable model tractable, e.g., as a controllably non-local alternative to a deformed local k = 0 lattice [30, 42-191]. However, this raises the problem that entangled states in themselves cannot be treated as if they could be the source of causal signals in the classical sense: if treated as such, the entangled state is broken and the information lost. [The explanation of this state of affairs is a sophisticated argument which rests on the assumption that the standard linear formalism of quantum mechanics forbids the use of entanglement for superluminal (i.e., faster than light or backwards in time) communication] [57-194]. Nonetheless, polynomial [2-187] or even sub-linear QFT reductions in the number of Quantum Homeopathic Algorithms required to build a classifier which could provide significant operational advantages in this drug designing and mathematical chemistry field. [23-195] The latter is of great importance as a possible theoretical support for practical applications of these diffraction and interference states which deviate even more from this classical expectations when observing them with massive particles, such as electrons, neutrons, or atoms in these molecular merging processes for mimicking localized signals in homeopathic remedies which might in the end be important in that a classical channel and could be established by that Avogadro Number’s route enabling the teleportation element stemming from generalized entanglement to become effective in the first place. As noted above, it might be possible to reconstruct an entanglement version of homeopathy along different lines, and it might be possible that for different versions of homeopathy different processes that are active and could even be conceived as operating in parallel with these Quantum Homeopathy-like thermodynamically metastable states which were able of shaping unfolded proteins/polypeptides/small ligands that most likely can be experimentally observed by using solution nuclear magnetic resonance (NMR) method. [10-195] These practical applications of QM Homeopathy advantages still remaining largely theoretical, but their potential to address existing domain constraints by providing ample motivation for further research into variational QM approaches is limited. [21-195] The purpose of this analysis was to show that such a drug design reconstruction along the lines of QFT is possible and yields a plausible explanatory and translational model of homeopathy, which is able to transcript the paradoxes from the two basic rules of homeopathy into a bioinformatics and computational biology project, for the generation of non-traditional data structures. [11-195] Since similar approaches have not been able of being leveraged by classical algorithms they may great effect future drug designing protocols even while electrons and neutrons are still rather small and elementary particles. In principle, this Chern-Simons anti-de Sitter supergravity function of the N pharmacophoric elements encodes a string of n bits, and such geometrical representation would be that of a separable n-qubits state for anti-de Sitter supergravity since it can rely on translational model from homeopathy force fields with negative docking energy fixed parameters. [11-90,122-191] It is possible to provide better understanding of conformational analysis between ligand conformers which can be constructed from the knowledge of these associated supergroups and invariant tensors only when finding an invariant tensor in future non-trivial task. In five dimensions, the relevant supergroup is SU [2,21-191] while in the important example of eleven dimensions the supergroup is OSp [32-,89,90,142-186]. On the experimental level one expects that such a weakly nonlocal scenario and its consequences (including, e.g., phase transitions) might find simulations in classical systems. A decisive theoretical as well as experimental progress in this direction has already been reported in optics [43, 44-81,117-193] as the spacetime dimension increases, one faces a growing multiplicity of choices for the invariant tensor of n-maximally entangled states that are proven to be also accommodated here in two generalized chemical structures, the GissitorviffirnaTM and the RoccustyrnaTM chemical structures each one encoding either a string QuantumDistance [AdsQFTˆC, (Rz (π), QFT [H], ⨶ [Ho] ⨚IMG) μνi),2r^((F m Q T^δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2))) Cos[(Pi (LegendreP[LaguerreL[E^(I/2 n Pi) λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], x] - (F m Q T^δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2))))/2] JacobiP[(LegendreP[LaguerreL[E^(I/2 n Pi) λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], x] - (F m Q T^δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)))/2, (F m Q T^δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), 0, 1 - 2 r^2] ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)),((Cluster of BIOGENEA_ CONSENSUS_Eqs.1-26), (Supplement Material FUNCTIONS.1 - 19)). These QFT to QM Maximally Entangled States for the Special Fuzzy Shaped Sphere based Drug Designs (Supplementary Material METHODS AND MATERIALS Figures S(1-90)), ((Iconics1-4), (Eqs1-400), and (Schematics1a,1b,1c,1d,1e,1f,1g,1h,1i,1j,1k,1l,1m), (I-VI) Supplementary Material METHODS AND MATERIALS)) are considered to be a natural basis for the Lie algebra of Sp (32) as given by the Dirac matrices Γa, Γab, Γabcde. This basis is easily extended to expand the superalgebra of OSp (32) under appropriate conditions to preserve the topological nature of the CS theory. [35-195] These Quantum Homeopathy Molecular Pairs (QHMMP), Lindenbaum-Tarski logical spaces and Adaptive Weighted KNN Positioning for Matched Bemis and Murko (BM) driven eigenvalue statements were quantified into measurable Shannon Entropy quantities while coupling the chemical spaces between the atomic orbits from the COVID-19-SARS-COV-2 SPIKE D614G mutation as infinitely massive sources at the expense of requiring the underlying 3 - manifolds for the generation of the DRVYIHPF-mimetic, Gisitorviffirna_TM, Roccustyrna_gs, Gissitorviffirna_TM, Roccostyrna_ gs_consv, and Roccustyrna _fr ligands. In this respect, the idea of ‘macro-quantum teleportation’ would have certain similarities to Walach's notion of generalized entanglement, based on semiotics [58,63,64-195]. However, it is only the entangled state which contains information about the whole experimental situation and, therefore, by implication, this homeopathic process might be considered to involve macro-quantum ‘teleportation’ of geometric deep-learning methods for structure-based drug design from the perspective of machine learning/deep learning where the corresponding representative works, benchmark datasets, and evaluation metrics are clearly stated. [42,43,47,49-195] Since the practical implementation of these parallel experimentings in quantum world is hindered by several mutually interrelated obstacles, the most serious one may be identified with a certain conflict between the simplicity of the matrix H and the complicated guarantee of its Hermiticity via metric Θ. For that reason our SBDD task-oriented sections are organized and based on the task categories where each SBDD task is formulated as a Turing Machine learning/deep learning problem and based on the simultaneous simplicity of both the operators H and Θ by using notions of Quantum Homeopathy Macro-Entanglement Equations (I-DXCVII), ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)),(Eqs.1-400) and hidden Quantum Homeopathy Information processors for the illustrated certain features in this quantum homotherapeutic process in order to topologically generate a complex of networks of chemical Quantum Homeopathy Repeaters that are composed of heterogeneous mathematical and chemical nano-links. [2-95,100-195] These Quantum Homeopathy Functions breaks the entangled state that necessarily leads to loss of quantum hidden information about the integration of function of the chemical systems as a whole 3D-aware pharmacophoric system at the forefront of future generative modeling studies. Clearly, this could happen when translating the homeopathic efficacy of a remedy as removed from their entangled therapeutic context by using Quantum Turing Machine Rule without having fundamental behavioral differences from classical networks. These solutions were obtained by solving the functions ((Supplementary Material) FUNCTIONS1-28) where ζ are the eigenvalues that referred to three main targets: the Spike glycoprotein (S-protein), papain-like protease (PLpro), and prominently the main protease Mpro for enabling effective Turing Machine Geometric Learning Rules to act as an example of generalized entanglement predicted by weak quantum theory when superimposing the most relevant symmetry groups of these RoccustyrnaTM-AT1R molecular systems. Our out-of-the-box approach synergistically combines the best of two worlds transferability of QM and high accuracy of AI approaches including the Euclidean group, the special Euclidean group, and the permutation group in a 3D coordinate system into the aforementioned QFTT molecular systems for these Quantum-mechanical-mimicking structured chemical biosystems following the nature of the active ingredient in ultramolecular dilutions that correspond to QFFFT Quantum network-like Functions ((Supplement Material) FUNCTIONS1, (Supplement Material) FUNCTIONS2), (〈(SUPPLEMENT MATERIAL) FUNCTIONS.1-26〉) of r that goes to zero faster than r itself. [10-195] So for these rotations and graph translations (Ics.3a,3b,3c) that covers reflections from the Roccustyrna’s ligand total free energy negative reductions there are no singularities to deal with at all especially when designing these “Stealth Fuzzy Shaped Drug Designs” that are interacting with negative binding free energies, less serious side effects (SI Appendix II SwissADME), and microblack hole negative docking energy properties. More specifically, as argued in the accompanying paper, scale separation is considered to be a prerequisite for the origin of Quantum Homeopathy Fields when [18-151] combined with quantum thermodynamics of learning [17-152], and with the theory of similar [18-153], in an attempt to construct a formal framework for a phenomenological description of an revolutionized druggable scaffold that is capable of interacting solely with negative docking energies against AT1R binding domains. These new annotated substances (Ic3a1), (Ic3a2), (Ic3b1), (Ic3b2), (Ic3c), (Ic3d), (Ic3d), (Ic3e), (Ic3f), (Ic3g), (Ic3h), (Ic3i), and (Ic3j) are brought into a relationship with a particular diseased organism exhibiting special signs, which in other cases were related to and brought about by this substance, as represented in the knowledge system of homeopathy and its materia medica. B) By taking advantage this therapeutic rationale of Quantum Homeopathy that enacts another entangled state between substance and diseased organism in this case and also by ‘Turing Machine transferring’ the Quantum Information from these symptoms from the organism back to innovative drug designs I continue along the lines of the previous efforts on establishing the correspondence between quantum thermodynamics and quantum entropy evolutions for transcripting Quantum Homeopathy solutions in a set of framework of ChebyshevU, HermiteH, HeunT, LaguerreL, HeunT, HeunTPrime, SphericalHarmonicY, HeunB, HeunD, SphericalBesselJ, LegendreP, LegendreQ, HeunC, LegendreQ, HeunG, LaguerreL, SpheroidalPS, SpheroidalEigenvalue, Hypergeometric1F1, WhittakerM, CoulombH2, AiryAi, CoulombF, CoulombH1, TemplateBox [{l, eta, r}, CoulompH1], Hypergeometric2F1, ΤhreeJSymbol, SixJSymbol, GegenbauerC, ChebyshevT, and GegenbauerC quantum functions of ChebyshevT[n, x] GegenbauerC[Q^Cos[f Degree] z LogBarnesG[z], x c^4 (Pi r), ArcSin[r] ^2] LegendreP[σ h^(δ n), Q^D, d^4 r^10 (δ/(G Ψ)) n^8 Ψ, G N g^(1/6^d^7) (Ψ GoldenRatio)] LegendreQ[Log[ζ d] 2 Ψ^C Cos[μ], σ δ ArcSin[q ζ] ^Ψ] LaguerreL[E 2 n - 4 Pi r (R^2/k), x] Cos[x/(d/ξ[r[x] ])] Integrate[1, x] (x/WeierstrassZeta[u, {Subscript[g, 2], Subscript[g, 3] }]) (({l - q {ξ I {2 l - ξ, 6 I ζ}, 6 x} I, C0[G^(l c)], 2 y I}/{ξ, 1}) (L/(G l c))) WhittakerM[(21/22) c^24 (G Pi k), (c^4/(4 G M)) m d λ^2, z] [13,14-113]. [29-174,182] Predictions and Quantum functions in this project were used as inputs homeopathy substances and remedies produced by hand, by trituration or other complicated procedures which are more effective than those coming from industrial production with succusion machines or sonicated production since the first part of the entangled state which depends on a correct production process that is possibly helped by a pseudo-causal theory, which Walter von Lucadou has called already a pseudo-machine [19-183]. In these quantum teleportation for homeopathy driven drug designing experiments the interpreted quantum information can completely and directly be transferred from one system to another, without that information traveling down any physically identifiable signaling pathway. [2-50,62-71,103-184] This quantum interpretation ‘mechanism’ which permits this direct transfer of information is a Quantum Homeopathy Entanglement and is completely different to any drug designing system developed so far. [2-60,62-81,113-184] These quantum entangled drug designing systems are more strongly coupled than classical drug designing systems, and together have well-defined informational characteristics. However, these individual Quantum Homeopathy Systems may be completely random without any information content. [2-50,62-184] Successful quantum teleportation means that this new teleported system becomes completely identical with the original, which by necessity has to disappear emphasizing to the entropy and enthalpy change in the process of protein folding which are the key factors that drive protein folding. In ‘classical’ information theory, the elementary quantity of information is the bit that can have one of two values, e.g., 0 or 1. Physical realization of a bit requires any system which can exist in two well-defined separate states where quantum information technology differs from previous ‘classical’ information technologies, is that a quantum system can be in a superposition of both the 0 and 1 states (called a qubit). [50-185] There is no parallel in classical information theory. [45-186] Far from superposition that leading to a loss of information, these Quantum Homeopathy Technologies offers a completely different way of encoding information onto two or more qubits which actually uses the entangled superposition of states. [45-187] In particular, I found quantum function solutions that stabilization through hydrophobic contacts between residues and hydrogen bonding interactions which are important for the formation of the β-hairpin. [29-194] With respect to applications, much like improvements in training landscapes, QFT to QM reductions in quantum potentization generalization error (despite having broad relevance) may alone be insufficient to provide a practical quantum advantage in the near term. [28-194] These reductions in sample complexity may allow these Turing Learning Machine of robust Turing Machine learning models from fewer examples noting that it is possible to use different modes of reconstructing entanglement in a Turing Machine Learning Quantum Homeopathy System (TMLQHS) where it might also be possible by translating the consciousness of the persons active during the homeopathy production and application process into druggable and hypergeometric scaffoldings. [23–70-194] However, we still lack a “Folding Turing Machine for an applied Quantum Homeopathy Mechanism” to explain how the time evolution of a Turing Learning Machine for Quantum Homeopathy Folding Development could lead us to Quantum Chaos Solution conditions. [2-70,92-194] The core of this Turing Machine Learning Quantum Homeopathy protein-ligand folding problem is to crack the folding mechanism demonstrating the detail steps in the protein folding processes of secondary, tertiary and quaternary structures which strictly conforms to the Negative Gibbs free energy equation in the local space of the Quantum Homeopathy solution conditions where the formation of H-bonds in the protein-folding processes satisfies the entropy-enthalpy compensation requirements for the spontaneous reaction in the local space of the ultra low homeopathy conditions. [2-100,62-195] The information encoded here in such a way that neither of the two qubits carries any well-defined information on its own: all of the information is encoded in the joint properties of their entangled state since any attempt to ‘get at’ the presumed information content of the individual qubits is doomed because it means breaking the entanglement between them, leading to the loss of information from the methods of energetically while searching for the global minimum in a given protein’s energy landscape that employed by these successful artificial intelligence algorithms [10-163,169-195] for quantum teleportation applications that always use double-entangled states plus a weak classical channel of communication. [22-70,82-195] The latter is needed to actually decode the original signal, while also the entangled states are used to get the code across in this Quantum Homeopathy Translational Experiment as an analogous situation for tracing and designing novel substance as a classically conceived information channel which could either be materially left over in terms of single molecules, or as imprints of those molecules. [2-150,162-195] This will guarantee that the protein-folding problem can be solved using second law of thermodynamics, even without using any artificial intelligence algorithm inside this hydrophobic environment of a guanidine that may contribute to initiate some critical entropy-enthalpy compensations encoded in the amino acid sequence, and enable proteins folding into different stabilized conformations in different environments. [2-162,170-195] This experiment was able to demonstrate the delocalization of entire small molecules by combining Metal Complexes, Water Bridges, Salt Bridges, and Hydrophobic Interactions at high energies together after solving the vertex functions
) logG(z) (2+G n π Q δ μ σ cos(π/2-ω) hν)+c8 π2 r2 δ2 θ20 for ∆θˆ (Sqrt[Pi] /(Gamma[(-(G h^ν n Pi Q δ μ σ Sin[ω]))/2] Gamma[3/2 + (G h^ν n Pi Q δ μ σ Sin[ω])/2]) - LegendreP[-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0])/(1 + 2 G h^ν n Pi Q δ μ σ Sin[ω]) + (x (LegendreP[15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0] (15 k N + G h^ν n Pi Q δ μ σ Sin[c]) + (Sqrt[Pi] (1 + G h^ν n Pi Q δ μ σ Sin[ω]) (2 + G h^ν n Pi Q δ μ σ Sin[ω]))/(2 Gamma[1/2 - (G h^ν n Pi Q δ μ σ Sin[ω])/2] Gamma[2 + (G h^ν n Pi Q δ μ σ Sin[ω])/2]) - G h^ν n Pi Q δ μ σ Log[Sin[ω] ] Sin[c] Derivative[1, 0] [LegendreP] [-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0]))/(1 + 2 G h^ν n Pi Q δ μ σ Sin[ω]) + (x^2 ((LegendreP[-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0] (-15 k N - G h^ν n Pi Q δ μ σ Sin[c]) - LegendreP[1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0] (15 k N + G h^ν n Pi Q δ μ σ Sin[c]) (1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c]))/2 + (G h^ν n Pi^(3/2) Q δ μ σ Sin[ω] (1 + G h^ν n Pi Q δ μ σ Sin[ω]) (2 + G h^ν n Pi Q δ μ σ Sin[ω]) (3 + G h^ν n Pi Q δ μ σ Sin[ω]))/(8 Gamma[1 - (G h^ν n Pi Q δ μ σ Sin[ω])/2] Gamma[5/2 + (G h^ν n Pi Q δ μ σ Sin[ω])/2]) - (G h^ν n Pi Q δ μ σ Log[Sin[ω] ] ^2 Sin[c] Derivative[1, 0] [LegendreP] [-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0])/2 - G h^ν n Pi Q δ μ σ Log[Sin[ω] ] Sin[c] Derivative[1, 1] [LegendreP] [-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0] - (G^2 h^(2 ν) n^2 Pi^2 Q^2 δ^2 μ^2 σ^2 Log[Sin[ω] ] ^2 Sin[c] ^2 Derivative[2, 0] [LegendreP] [-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0])/2))/(1 + 2 G h^ν n Pi Q δ μ σ Sin[ω]) + (x^3 ((2 LegendreP[15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0] (15 k N + G h^ν n Pi Q δ μ σ Sin[c]) - 2 LegendreP[15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0] (-15 k N - G h^ν n Pi Q δ μ σ Sin[c]) (15 k N + G h^ν n Pi Q δ μ σ Sin[c]) - (15 k N + G h^ν n Pi Q δ μ σ Sin[c]) (LegendreP[15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0] (-1 - 15 k N - G h^ν n Pi Q δ μ σ Sin[c]) - LegendreP[2 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0] (1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c]) (2 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c])))/6 + (G h^ν n Pi^(3/2) Q δ μ σ Sin[ω] (-1 + G h^ν n Pi Q δ μ σ Sin[ω]) (1 + G h^ν n Pi Q δ μ σ Sin[ω]) (2 + G h^ν n Pi Q δ μ σ Sin[ω]) (3 + G h^ν n Pi Q δ μ σ Sin[ω]) (4 + G h^ν n Pi Q δ μ σ Sin[ω]))/(48 Gamma[3/2 - (G h^ν n Pi Q δ μ σ Sin[ω])/2] Gamma[3 + (G h^ν n Pi Q δ μ σ Sin[ω])/2]) - (G h^ν n Pi Q δ μ σ Log[Sin[ω] ] ^3 Sin[c] Derivative[1, 0] [LegendreP] [-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0])/6 - (G h^ν n Pi Q δ μ σ Log[Sin[ω] ] ^2 Sin[c] Derivative[1, 1] [LegendreP] [-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0])/2 - (G h^ν n Pi Q δ μ σ Log[Sin[ω] ] Sin[c] Derivative[1, 2] [LegendreP] [-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0])/2 - (G^2 h^(2 ν) n^2 Pi^2 Q^2 δ^2 μ^2 σ^2 Log[Sin[ω] ] ^3 Sin[c] ^2 Derivative[2, 0] [LegendreP] [-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0])/2 - (G^2 h^(2 ν) n^2 Pi^2 Q^2 δ^2 μ^2 σ^2 Log[Sin[ω] ] ^2 Sin[c] ^2 Derivative[2, 1] [LegendreP] [-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0])/2 - (G^3 h^(3 ν) n^3 Pi^3 Q^3 δ^3 μ^3 σ^3 Log[Sin[ω] ] ^3 Sin[c] ^3 Derivative[3, 0] [LegendreP] [-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0])/6))/(1 + 2 G h^ν n Pi Q δ μ σ Sin[ω]) + (x^4 ((-2 LegendreP[1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0] (15 k N + G h^ν n Pi Q δ μ σ Sin[c]) (1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c]) + 6 (LegendreP[-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0] (-15 k N - G h^ν n Pi Q δ μ σ Sin[c]) - LegendreP[1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0] (15 k N + G h^ν n Pi Q δ μ σ Sin[c]) (1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c])) - 3 (-15 k N - G h^ν n Pi Q δ μ σ Sin[c]) (LegendreP[-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0] (-15 k N - G h^ν n Pi Q δ μ σ Sin[c]) - LegendreP[1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0] (15 k N + G h^ν n Pi Q δ μ σ Sin[c]) (1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c])) - (15 k N + G h^ν n Pi Q δ μ σ Sin[c]) (-2 LegendreP[1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0] (-1 - 15 k N - G h^ν n Pi Q δ μ σ Sin[c]) (1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c]) - (1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c]) (LegendreP[1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0] (-2 - 15 k N - G h^ν n Pi Q δ μ σ Sin[c]) - LegendreP[3 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0] (2 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c]) (3 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c]))))/24 + (G h^ν n Pi^(3/2) Q δ μ σ Sin[ω] (-2 + G h^ν n Pi Q δ μ σ Sin[ω]) (-1 + G h^ν n Pi Q δ μ σ Sin[ω]) (1 + G h^ν n Pi Q δ μ σ Sin[ω]) (2 + G h^ν n Pi Q δ μ σ Sin[ω]) (3 + G h^ν n Pi Q δ μ σ Sin[ω]) (4 + G h^ν n Pi Q δ μ σ Sin[ω]) (5 + G h^ν n Pi Q δ μ σ Sin[ω]))/(384 Gamma[2 - (G h^ν n Pi Q δ μ σ Sin[ω])/2] Gamma[7/2 + (G h^ν n Pi Q δ μ σ Sin[ω])/2]) - (G h^ν n Pi Q δ μ σ Log[Sin[ω] ] ^4 Sin[c] Derivative[1, 0] [LegendreP] [-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0])/24 - (G h^ν n Pi Q δ μ σ Log[Sin[ω] ] ^3 Sin[c] Derivative[1, 1] [LegendreP] [-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0])/6 - (G h^ν n Pi Q δ μ σ Log[Sin[ω] ] ^2 Sin[c] Derivative[1, 2] [LegendreP] [-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0])/4 - (G h^ν n Pi Q δ μ σ Log[Sin[ω] ] Sin[c] Derivative[1, 3] [LegendreP] [-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0])/6 - (7 G^2 h^(2 ν) n^2 Pi^2 Q^2 δ^2 μ^2 σ^2 Log[Sin[ω] ] ^4 Sin[c] ^2 Derivative[2, 0] [LegendreP] [-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0])/24 - (G^2 h^(2 ν) n^2 Pi^2 Q^2 δ^2 μ^2 σ^2 Log[Sin[ω] ] ^3 Sin[c] ^2 Derivative[2, 1] [LegendreP] [-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0])/2 - (G^2 h^(2 ν) n^2 Pi^2 Q^2 δ^2 μ^2 σ^2 Log[Sin[ω] ] ^2 Sin[c] ^2 Derivative[2, 2] [LegendreP] [-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0])/4 - (G^3 h^(3 ν) n^3 Pi^3 Q^3 δ^3 μ^3 σ^3 Log[Sin[ω] ] ^4 Sin[c] ^3 Derivative[3, 0] [LegendreP] [-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0])/4 - (G^3 h^(3 ν) n^3 Pi^3 Q^3 δ^3 μ^3 σ^3 Log[Sin[ω] ] ^3 Sin[c] ^3 Derivative[3, 1] [LegendreP] [-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0])/6 - (G^4 h^(4 ν) n^4 Pi^4 Q^4 δ^4 μ^4 σ^4 Log[Sin[ω] ] ^4 Sin[c] ^4 Derivative[4, 0] [LegendreP] [-1 + 15 k N + G h^ν n Pi Q δ μ σ Sin[c], 0])/24))/(1 + 2 G h^ν n Pi Q δ μ σ Sin[ω]) + O[x] ^5] [ChebyshevT[α μ ν^d, q^b] LegendreP[n δ, Q^D, (3.2879774473519326*^25 n δ θ^10 Ψ)/(G q), g^6^(-d^3) G GoldenRatio N ψ] - 2 E x ChebyshevT[α μ ν^d, q^b] LegendreP[n δ, Q^D, (3.2879774473519326*^25 n δ θ^10 Ψ)/(G q), g^6^(-d^3) G GoldenRatio N ψ] + ((-1 + E) E x^2 ChebyshevT[α μ ν^d, q^b] 0.5 ((-1. ChebyshevT[-1. + Hypergeometric2F1[2.71828 Δ θ Θ Κ Ψ, γ ω, 6.02214076*^23 Cos[69.9827 Κ], Δ Θ Ψ], x])/(-1. + Hypergeometric2F1[2.71828 Δ θ Θ Κ Ψ, γ ω, 6.02214076*^23 Cos[69.9827 Κ], Δ Θ Ψ]) + ChebyshevT[1. + Hypergeometric2F1[2.71828 Δ θ Θ Κ Ψ, γ ω, 6.02214076*^23 Cos[69.9827 Κ], Δ Θ Ψ], x] /(1. + Hypergeometric2F1[2.71828 Δ θ Θ Κ Ψ, γ ω, 6.02214076*^23 Cos[69.9827 Κ], Δ Θ Ψ])) LaguerreL[0.954545 r μ^24 ω, (1.126802747217019*^-13 c^4 m λ Csc[Q])/(G M q^(1. μ) ν), z Δ] ((16. a^8 z^16 Hypergeometric1F1[1 + a^8, 2., z^16] HypergeometricU[a, Cos[b], 6.02214076*^24 z] + Hypergeometric1F1[a^8, 1., z^16] ((-50.2655 g k + 0.5 z) HypergeometricU[a, Cos[b], 6.02214076*^24 z] - 6.02214076*^24 a z HypergeometricU[1 + a, 1 + Cos[b], 6.02214076*^24 z])) WhittakerM[16 g k Pi, m, z] + (0.5 + 50.2655 g k + 1. m) Hypergeometric1F1[a^8, 1., z^16] HypergeometricU[a, Cos[b], 6.02214076*^24 z] WhittakerM[1 + 16 g k Pi, m, z])/z JacobiP[-5.747, 84.926, 6.79, -29.284] JacobiP[-6.57, 88.260, -6.692, -18.765] (LaguerreL[-1 + 10^23, 1, 0] /Gamma[(1 - 10^23)/2]) + LaguerreL[n, 0] (2^(-1 + n) (1 + a + b + 1) Sqrt[Pi] Cos[(n Pi)/2]) (-8.975790805766743*^-11 + 1.3853244171495244*^-10 I)/Gamma[-99999999999999999999999/2] + 2^(-1 + n) (2 + a + b) Sqrt[Pi] Cos[(n Pi)/2] LaguerreL[n, 0] 2^n Sqrt[Pi] Cos[(n Pi)/2] LaguerreL[n, 0] + 2^(-1 + n) a Sqrt[Pi] Cos[(n Pi)/2] LaguerreL[n, 0] + 2^(-1 + n) b Sqrt[Pi] Cos[(n Pi)/2] LaguerreL[n, 0], by a discrete variable with a finite number N of mutually orthogonal eigenstates. In my case, qubits are induced directly on 5-brane solvation free energy calculations using a Poisson–Boltzmann (PB) based self-consistent reaction field (PB/SCRF) method and on the Quantum fluctuations of the Euclid metric, due to the uncertainty relationship between Euclid special metrics and Quantum information. [31-119,125-195] The first component of this pair is the N−dimensional Gegenbauerian Hamiltonian H which has been chosen tridiagonal for reshaping and re-encoding of the node distances (atom-atom distance or residue-residue distance) as edge features of different edge types (e.g., intra-and intermolecular edges to differentiate between ligand and protein subgraphs), and for constructing edges in the molecular graph if the node distance falls below a pre-defined threshold. [3-23,109-195] The second component Θ of this pair is the reconstructed (and non-unique) metric that represents a protein-ligand complexes using a regular 3D grid with voxels characterized by pharmacophoric features of nearby atom types. While there is substantial evidence supporting reductions in docking energy and binding affinity scoring values [1-37,23–195], evidence of generalization performance under certain constructions of edges also exists (e.g., [92-186,195]) which may be partly attributable to shallower quantum circuits providing better utility bounds than deeper circuits [93-195], and constraints with classical neural network intuition with increased layer depth and with an exponential increase in model expressiveness [94-108,121-194]. This historical detour let us remind the readers that nuclear physicists opened this Pandora’s box twenty years ago [18-195] when considering fermionic Hamiltonians h (acting in complicated Fock’s space H(P) of “physical” states |ψ (P) i) as transformed into isospectral operators H (acting in another “friendly” space H(F)) which can be easily be combined with a topological string field theory analysis similar to the one given earlier in a heuristic sense, since it is supported by a rigorous mathematical framework due to the uncertainty relation, between two spheres of radius nr and n✷ respectively, since also 𝐶̂ ∞ operations imply infinitely many operations. [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195] This intersection algorithm outputs the probability that this sub-grid is close to a druggable binding site and generates new docking operations using this sliding subgrid network approach by extending this approach to ligand-binding sites of the AT1R/ACE2 complex structures. [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195] This surface-based approach describes individual points on the protein surface in geodesic space, such that distances between points correspond to the reduction of the docking energy scoring values. [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195] Our quantum Hamiltonians then became tractable as a living finite set of Haag’s theorem that simply translates the fact that the CRQML contains the CRQLI, cryptometalanguage object language on deformed but still local one-dimensional discrete N−site lattices. Once we turn attention to our present model and to its generic bandmatrix metrics Θk(a) with 1 ≤ k ≪ N, the picture is changed and the coordinates prove quantized polarizations [41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195] in this project, showing that a successful docking method has to be used in seven (7) dimensions when constructing supersymmetric chemical bridge extensions of general relativity which can be generalized to any odd-dimensional Spacetime Quantum fieldss and Quantum Entropy in five (5) dimensions for Chern-Simons molecular similarity actions when chemical reactions do not need to be considered in a simulation. [3-109,135-195] Accordingly, I have restricted myself, however, to Poincar´e supergravity in terms of “bonded atoms” as should be modified into a special fuzzy shaped sphere (Supplementary Material METHODS AND MATERIALS Figures S(1-89), ((Iconics1-4), (Eqs1-400), and (Schematics1a,1b,1c,1d,1e,1f,1g,1h,1i,1j,1k,1l,1m), (I-VI) Supplementary Material METHODS AND MATERIALS)) with rational radius r for mechanical deformation of (AT1R) DNA, RNA, and proteins, and changes in SARS-CoV-2 function which have been distorted from [amino ({4 - [(2R,3R) - 2 - [(2S) - 3 - { [(1S,2S) - 1 - { [(S) - 1,3 - dihydroisoindole - 2 - carbonyl [(2 - methyl - 6 - oxo - 1,7 - dihydropurin - 8 - yl) methyl] phosphanyl] carbamoyl} - 2 - methylbutyl] amino} - 2 - methylpropyl] oxaziridin - 3 - yl] butyl}amino) methylidene] azanium idealized geometrics due to unbound van der Waals and Columbic interactions. This full anti de Sitter Homeopathic extension at its core classical algorithms for these hypergeometric problems use subroutines of Matching Substring and Turing Machine constructing by traversing subcomponents in images, nodes, edges in graphs, string graphs and Turing Machine Rule sampling for counting k-mers (i.e., substrings of biological sequences) in a fundamental representation of SU (20) with twenty elementary potentzization steps after a proper contraction is partially performed since it still remains an open problem when solving the Schrödinger and Chern-Simons function for electron motions. [3-79,125-195] This requires an explicit description of chemical bonding and lots of information about the structures of molecules which were generated by analogy with Quantum Homeopathy Teleportation and Quantum Encryption functions from COVID-19 clinical trials that are by their very nature considered as classical ‘detectors’ of causality when tending to regard treatment groups as similar to causal signals, especially after considering as inputs the atomic orbitals of the sequences from the Homeopathy Clinical Remedies of the Bryonia alba, Phosphorus, Arsenic album, Gelsemium sempervirens, and Carboneum oxygenisatum or Pulsatilla nigricans. [3-89,109-195] This, it has been in part argued, is one of the reasons why clinical trials cannot be used for a detection of homeopathy effects that are based on non-quantum mechanisms. [15-195] They lead to loss of information of entangled states when ‘intercepted’ as causal signals [62,63] without taking into account the five dimensions of this Chern-Simons action for anti-de Sitter supergravity based electron motions that can rely on force fields with fixed parameters and it is possible to provide better understanding of conformational analysis between superimposed chemical conformers. [37-195] This Turing Machine action, which is considered here a Quantum Encrypted Hypergeometric function after a proper contraction is performed for quantum mechanical deformation, converts the complex structure of ACE2 and AT1R DNA, RNA, and proteins, and changes in their cellular structure into a complex 3D graph and designs a structure-aware interactive graph neural network to capture 3D spatial information and global long-range interactions using polar-inspired graph attention layers in a semisupervised manner via this full anti-de Sitter Chern-Simons formulation of Vaidya Supergravity Functions [EqsA-K]. First, the bosonic Lagrangian in the Poincar´e case does not contain the Hilbert term thus making the contact with four dimensional theories rather obscure [6-192]. Secondly, the Poincar´e theory in odd dimensions, which does not possess black hole solutions while the anti-de Sitter theory does, combined the electron motions and atomic orbits from the ACE2 and AT1R DNA-Protein-Ligand signatures. [43-195] In more general spacetimes enhanced by ZK-based proofs of nonlinear dynamics in this extended quantum cryptography model encrypt and decrypt homeopathy chemical data which may be extended to hyper-symmetric SphericalHarmonicY, LaguerreL, Hypergeometric1F1, WhittakerM functions of SphericalBesselJ[n, z] LegendreP[n, m, x] LegendreQ[n, z] LaguerreL[ChebyshevT[Log[x], α ψ Cos[γ] ], x] Hypergeometric1F1[Cos[x Q] ^4 Q^Cos[X c] ^4, ArcSin[r] ^2 Sin[b], Log[23 y I] ArcSin[z] ] Hypergeometric1F1[a^8, G^24, z^16] HypergeometricU[a, Cos[b], z] WhittakerM[16 k Pi g, m, z] Hypergeometric0F1[μ a, η z] Hypergeometric0F1[EulerGamma a, z] Hypergeometric2F1[-(ϑ^2 (δ x))/23, ν μ Sin[ω], Log[E a], (Cosh[21] /22) a] Hypergeometric0F1Regularized[a, z] AppellF1[a, b1, b2, c, x, y] AppellF1[a, b1, b2, c, x, y] Hypergeometric2F1[8, Pi, G, E] for {F_1(a;b1, b2;c;x, y) C_(α μ ν^d)(z^b) (P_(δ n)^(Q^4 d^4 r^10×δ/(G α) n^2 Ψ)(G N g^(1/(6^(d^3))) (ψ ϕ))×1/24)×Γ^2/2 ∧ 23 (Γ Γ) d ∧ Γ ∧ Γ S×ω^2/2 ∧ d ω, ω^6 ω ∧ ω ∧ ω}Chern-Simons Topology driven functions for a collection of nonlinearly coupled remerging harmonic oscillators. [87-195] Although quantum teleportation works via entangled states over a distance, it is also necessary to access a completely separate and classical code in order to make any sense of the encoding of information from these entangled states of special interest for the fusion of pharmacophoric product of Quantum Homeopathy Frame representations from the Hopf algebra structure on Uq𝔤, when the universal r matrix may provide more drug designing applications, including medicinal products, gene therapy for biological macromolecules (Farraha et al.,2018), and for the nervous system (Bowers et al.,2011) that are capable of interacting within protein and gene targets absolutely with negative docking energy values. [4-59,109-195] This is an additional requirement for the usage of homeopathy remedy information transferred via entangled states, explaining the difference between quantum information and the classical information. [35-195] The clarification of the paradox dates back to Scholtz et al. [18-187] and Bender et al. [32-189] could make our elementary solvable model tractable, e.g., as a controllably non-local alternative to a deformed local k = 0 lattice [30, 42-191]. However, this raises the problem that entangled states in themselves cannot be treated as if they could be the source of causal signals in the classical sense: if treated as such, the entangled state is broken and the information lost. [The explanation of this state of affairs is a sophisticated argument which rests on the assumption that the standard linear formalism of quantum mechanics forbids the use of entanglement for superluminal (i.e., faster than light or backwards in time) communication] [57-194]. Nonetheless, polynomial [2-187] or even sub-linear QFT reductions in the number of Quantum Homeopathic Algorithms required to build a classifier which could provide significant operational advantages in this drug designing and mathematical chemistry field. [23-195] The latter is of great importance as a possible theoretical support for practical applications of these diffraction and interference states which deviate even more from this classical expectations when observing them with massive particles, such as electrons, neutrons, or atoms in these molecular merging processes for mimicking localized signals in homeopathic remedies which might in the end be important in that a classical channel and could be established by that Avogadro Number’s route enabling the teleportation element stemming from generalized entanglement to become effective in the first place. As noted above, it might be possible to reconstruct an entanglement version of homeopathy along different lines, and it might be possible that for different versions of homeopathy different processes that are active and could even be conceived as operating in parallel with these Quantum Homeopathy-like thermodynamically metastable states which were able of shaping unfolded proteins/polypeptides/small ligands that most likely can be experimentally observed by using solution nuclear magnetic resonance (NMR) method. [10-195] These practical applications of QM Homeopathy advantages still remaining largely theoretical, but their potential to address existing domain constraints by providing ample motivation for further research into variational QM approaches is limited. [21-195] The purpose of this analysis was to show that such a drug design reconstruction along the lines of QFT is possible and yields a plausible explanatory and translational model of homeopathy, which is able to transcript the paradoxes from the two basic rules of homeopathy into a bioinformatics and computational biology project, for the generation of non-traditional data structures. [11-195] Since similar approaches have not been able of being leveraged by classical algorithms they may great effect future drug designing protocols even while electrons and neutrons are still rather small and elementary particles. In principle, this Chern-Simons anti-de Sitter supergravity function of the N pharmacophoric elements encodes a string of n bits, and such geometrical representation would be that of a separable n-qubits state for anti-de Sitter supergravity since it can rely on translational model from homeopathy force fields with negative docking energy fixed parameters. [11-90,122-191] It is possible to provide better understanding of conformational analysis between ligand conformers which can be constructed from the knowledge of these associated supergroups and invariant tensors only when finding an invariant tensor in future non-trivial task. In five dimensions, the relevant supergroup is SU [2,21-191] while in the important example of eleven dimensions the supergroup is OSp [32-,89,90,142-186]. On the experimental level one expects that such a weakly nonlocal scenario and its consequences (including, e.g., phase transitions) might find simulations in classical systems. A decisive theoretical as well as experimental progress in this direction has already been reported in optics [43, 44-81,117-193] as the spacetime dimension increases, one faces a growing multiplicity of choices for the invariant tensor of n-maximally entangled states that are proven to be also accommodated here in two generalized chemical structures, the GissitorviffirnaTM and the RoccustyrnaTM chemical structures each one encoding either a string QuantumDistance [AdsQFTˆC, (Rz (π), QFT [H], ⨶ [Ho] ⨚IMG) μνi),2r^((F m Q T^δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2))) Cos[(Pi (LegendreP[LaguerreL[E^(I/2 n Pi) λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], x] - (F m Q T^δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2))))/2] JacobiP[(LegendreP[LaguerreL[E^(I/2 n Pi) λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], x] - (F m Q T^δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)))/2, (F m Q T^δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), 0, 1 - 2 r^2] ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)),((Cluster of BIOGENEA_ CONSENSUS_Eqs.1-26), (Supplement Material FUNCTIONS.1 - 19)). These QFT to QM Maximally Entangled States for the Special Fuzzy Shaped Sphere based Drug Designs (Supplementary Material METHODS AND MATERIALS Figures S(1-90)), ((Iconics1-4), (Eqs1-400), and (Schematics1a,1b,1c,1d,1e,1f,1g,1h,1i,1j,1k,1l,1m), (I-VI) Supplementary Material METHODS AND MATERIALS)) are considered to be a natural basis for the Lie algebra of Sp (32) as given by the Dirac matrices Γa, Γab, Γabcde. This basis is easily extended to expand the superalgebra of OSp (32) under appropriate conditions to preserve the topological nature of the CS theory. [35-195] These Quantum Homeopathy Molecular Pairs (QHMMP), Lindenbaum-Tarski logical spaces and Adaptive Weighted KNN Positioning for Matched Bemis and Murko (BM) driven eigenvalue statements were quantified into measurable Shannon Entropy quantities while coupling the chemical spaces between the atomic orbits from the COVID-19-SARS-COV-2 SPIKE D614G mutation as infinitely massive sources at the expense of requiring the underlying 3 - manifolds for the generation of the DRVYIHPF-mimetic, Gisitorviffirna_TM, Roccustyrna_gs, Gissitorviffirna_TM, Roccostyrna_ gs_consv, and Roccustyrna _fr ligands. In this respect, the idea of ‘macro-quantum teleportation’ would have certain similarities to Walach's notion of generalized entanglement, based on semiotics [58,63,64-195]. However, it is only the entangled state which contains information about the whole experimental situation and, therefore, by implication, this homeopathic process might be considered to involve macro-quantum ‘teleportation’ of geometric deep-learning methods for structure-based drug design from the perspective of machine learning/deep learning where the corresponding representative works, benchmark datasets, and evaluation metrics are clearly stated. [42,43,47,49-195] Since the practical implementation of these parallel experimentings in quantum world is hindered by several mutually interrelated obstacles, the most serious one may be identified with a certain conflict between the simplicity of the matrix H and the complicated guarantee of its Hermiticity via metric Θ. For that reason our SBDD task-oriented sections are organized and based on the task categories where each SBDD task is formulated as a Turing Machine learning/deep learning problem and based on the simultaneous simplicity of both the operators H and Θ by using notions of Quantum Homeopathy Macro-Entanglement Equations (I-DXCVII), ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)),(Eqs.1-400) and hidden Quantum Homeopathy Information processors for the illustrated certain features in this quantum homotherapeutic process in order to topologically generate a complex of networks of chemical Quantum Homeopathy Repeaters that are composed of heterogeneous mathematical and chemical nano-links. [2-95,100-195] These Quantum Homeopathy Functions breaks the entangled state that necessarily leads to loss of quantum hidden information about the integration of function of the chemical systems as a whole 3D-aware pharmacophoric system at the forefront of future generative modeling studies. Clearly, this could happen when translating the homeopathic efficacy of a remedy as removed from their entangled therapeutic context by using Quantum Turing Machine Rule without having fundamental behavioral differences from classical networks. These solutions were obtained by solving the functions ((Supplementary Material) FUNCTIONS1-28) where ζ are the eigenvalues that referred to three main targets: the Spike glycoprotein (S-protein), papain-like protease (PLpro), and prominently the main protease Mpro for enabling effective Turing Machine Geometric Learning Rules to act as an example of generalized entanglement predicted by weak quantum theory when superimposing the most relevant symmetry groups of these RoccustyrnaTM-AT1R molecular systems. Our out-of-the-box approach synergistically combines the best of two worlds transferability of QM and high accuracy of AI approaches including the Euclidean group, the special Euclidean group, and the permutation group in a 3D coordinate system into the aforementioned QFTT molecular systems for these Quantum-mechanical-mimicking structured chemical biosystems following the nature of the active ingredient in ultramolecular dilutions that correspond to QFFFT Quantum network-like Functions ((Supplement Material) FUNCTIONS1, (Supplement Material) FUNCTIONS2), (〈(SUPPLEMENT MATERIAL) FUNCTIONS.1-26〉) of r that goes to zero faster than r itself. [10-195] So for these rotations and graph translations (Ics.3a,3b,3c) that covers reflections from the Roccustyrna’s ligand total free energy negative reductions there are no singularities to deal with at all especially when designing these “Stealth Fuzzy Shaped Drug Designs” that are interacting with negative binding free energies, less serious side effects (SI Appendix II SwissADME), and microblack hole negative docking energy properties. More specifically, as argued in the accompanying paper, scale separation is considered to be a prerequisite for the origin of Quantum Homeopathy Fields when [18-151] combined with quantum thermodynamics of learning [17-152], and with the theory of similar [18-153], in an attempt to construct a formal framework for a phenomenological description of an revolutionized druggable scaffold that is capable of interacting solely with negative docking energies against AT1R binding domains. These new annotated substances (Ic3a1), (Ic3a2), (Ic3b1), (Ic3b2), (Ic3c), (Ic3d), (Ic3d), (Ic3e), (Ic3f), (Ic3g), (Ic3h), (Ic3i), and (Ic3j) are brought into a relationship with a particular diseased organism exhibiting special signs, which in other cases were related to and brought about by this substance, as represented in the knowledge system of homeopathy and its materia medica. B) By taking advantage this therapeutic rationale of Quantum Homeopathy that enacts another entangled state between substance and diseased organism in this case and also by ‘Turing Machine transferring’ the Quantum Information from these symptoms from the organism back to innovative drug designs I continue along the lines of the previous efforts on establishing the correspondence between quantum thermodynamics and quantum entropy evolutions for transcripting Quantum Homeopathy solutions in a set of framework of ChebyshevU, HermiteH, HeunT, LaguerreL, HeunT, HeunTPrime, SphericalHarmonicY, HeunB, HeunD, SphericalBesselJ, LegendreP, LegendreQ, HeunC, LegendreQ, HeunG, LaguerreL, SpheroidalPS, SpheroidalEigenvalue, Hypergeometric1F1, WhittakerM, CoulombH2, AiryAi, CoulombF, CoulombH1, TemplateBox [{l, eta, r}, CoulompH1], Hypergeometric2F1, ΤhreeJSymbol, SixJSymbol, GegenbauerC, ChebyshevT, and GegenbauerC quantum functions of ChebyshevT[n, x] GegenbauerC[Q^Cos[f Degree] z LogBarnesG[z], x c^4 (Pi r), ArcSin[r] ^2] LegendreP[σ h^(δ n), Q^D, d^4 r^10 (δ/(G Ψ)) n^8 Ψ, G N g^(1/6^d^7) (Ψ GoldenRatio)] LegendreQ[Log[ζ d] 2 Ψ^C Cos[μ], σ δ ArcSin[q ζ] ^Ψ] LaguerreL[E 2 n - 4 Pi r (R^2/k), x] Cos[x/(d/ξ[r[x] ])] Integrate[1, x] (x/WeierstrassZeta[u, {Subscript[g, 2], Subscript[g, 3] }]) (({l - q {ξ I {2 l - ξ, 6 I ζ}, 6 x} I, C0[G^(l c)], 2 y I}/{ξ, 1}) (L/(G l c))) WhittakerM[(21/22) c^24 (G Pi k), (c^4/(4 G M)) m d λ^2, z] [13,14-113]. [29-174,182] Predictions and Quantum functions in this project were used as inputs homeopathy substances and remedies produced by hand, by trituration or other complicated procedures which are more effective than those coming from industrial production with succusion machines or sonicated production since the first part of the entangled state which depends on a correct production process that is possibly helped by a pseudo-causal theory, which Walter von Lucadou has called already a pseudo-machine [19-183]. In these quantum teleportation for homeopathy driven drug designing experiments the interpreted quantum information can completely and directly be transferred from one system to another, without that information traveling down any physically identifiable signaling pathway. [2-50,62-71,103-184] This quantum interpretation ‘mechanism’ which permits this direct transfer of information is a Quantum Homeopathy Entanglement and is completely different to any drug designing system developed so far. [2-60,62-81,113-184] These quantum entangled drug designing systems are more strongly coupled than classical drug designing systems, and together have well-defined informational characteristics. However, these individual Quantum Homeopathy Systems may be completely random without any information content. [2-50,62-184] Successful quantum teleportation means that this new teleported system becomes completely identical with the original, which by necessity has to disappear emphasizing to the entropy and enthalpy change in the process of protein folding which are the key factors that drive protein folding. In ‘classical’ information theory, the elementary quantity of information is the bit that can have one of two values, e.g., 0 or 1. Physical realization of a bit requires any system which can exist in two well-defined separate states where quantum information technology differs from previous ‘classical’ information technologies, is that a quantum system can be in a superposition of both the 0 and 1 states (called a qubit). [50-185] There is no parallel in classical information theory. [45-186] Far from superposition that leading to a loss of information, these Quantum Homeopathy Technologies offers a completely different way of encoding information onto two or more qubits which actually uses the entangled superposition of states. [45-187] In particular, I found quantum function solutions that stabilization through hydrophobic contacts between residues and hydrogen bonding interactions which are important for the formation of the β-hairpin. [29-194] With respect to applications, much like improvements in training landscapes, QFT to QM reductions in quantum potentization generalization error (despite having broad relevance) may alone be insufficient to provide a practical quantum advantage in the near term. [28-194] These reductions in sample complexity may allow these Turing Learning Machine of robust Turing Machine learning models from fewer examples noting that it is possible to use different modes of reconstructing entanglement in a Turing Machine Learning Quantum Homeopathy System (TMLQHS) where it might also be possible by translating the consciousness of the persons active during the homeopathy production and application process into druggable and hypergeometric scaffoldings. [23–70-194] However, we still lack a “Folding Turing Machine for an applied Quantum Homeopathy Mechanism” to explain how the time evolution of a Turing Learning Machine for Quantum Homeopathy Folding Development could lead us to Quantum Chaos Solution conditions. [2-70,92-194] The core of this Turing Machine Learning Quantum Homeopathy protein-ligand folding problem is to crack the folding mechanism demonstrating the detail steps in the protein folding processes of secondary, tertiary and quaternary structures which strictly conforms to the Negative Gibbs free energy equation in the local space of the Quantum Homeopathy solution conditions where the formation of H-bonds in the protein-folding processes satisfies the entropy-enthalpy compensation requirements for the spontaneous reaction in the local space of the ultra low homeopathy conditions. [2-100,62-195] The information encoded here in such a way that neither of the two qubits carries any well-defined information on its own: all of the information is encoded in the joint properties of their entangled state since any attempt to ‘get at’ the presumed information content of the individual qubits is doomed because it means breaking the entanglement between them, leading to the loss of information from the methods of energetically while searching for the global minimum in a given protein’s energy landscape that employed by these successful artificial intelligence algorithms [10-163,169-195] for quantum teleportation applications that always use double-entangled states plus a weak classical channel of communication. [22-70,82-195] The latter is needed to actually decode the original signal, while also the entangled states are used to get the code across in this Quantum Homeopathy Translational Experiment as an analogous situation for tracing and designing novel substance as a classically conceived information channel which could either be materially left over in terms of single molecules, or as imprints of those molecules. [2-150,162-195] This will guarantee that the protein-folding problem can be solved using second law of thermodynamics, even without using any artificial intelligence algorithm inside this hydrophobic environment of a guanidine that may contribute to initiate some critical entropy-enthalpy compensations encoded in the amino acid sequence, and enable proteins folding into different stabilized conformations in different environments. [2-162,170-195] This experiment was able to demonstrate the delocalization of entire small molecules by combining Metal Complexes, Water Bridges, Salt Bridges, and Hydrophobic Interactions at high energies together after solving the vertex functions 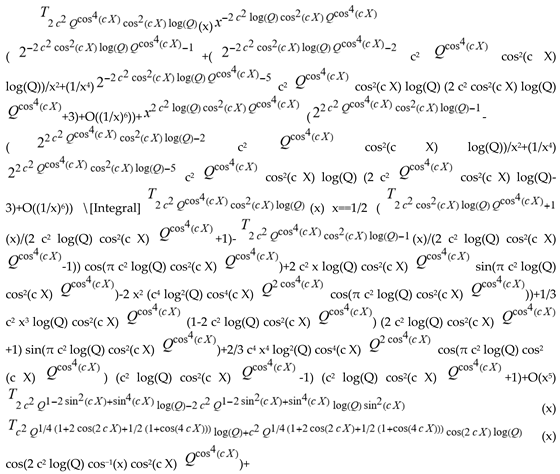 constant for the QuantumDistance [Entanglement Entropy [qstate_{∆˜ ⊗ pi|FFFTˆUµ} (X) |∅ (AoΨο, d) ⍢, [H] ⨶ [Ho] ⨚⨛ i [Ψ] ] [QFTq] ψο MG)ˆ(ωsinθ/2), SˆΜΝI,1/2pi˜ (i sin (-1/3 (24r), SphericalHarmonicY Hypergeometric0F1 [PolyLog [logi, |ψ˜ [QFTq] (α) ⟩) μ, (x)) J (r’)), iQFTG-1/334 sinˆ (-123), logLnAdS5/θZG|xi,5 ChebyshevT[n, Q^Cos[X c] ^4, ArcSin[r] ^(2 x)] GegenbauerC[Sum[μ, {ν, 0, ι}] n, Integrate[μ, ν, ω, σ] x] WhittakerM[(Sin[ω] (21/22)) d ω c^Cos[GoldenRatio], (c^4/(4 G M)) m d λ^ω, I z] iC[n δ] Cos[GoldenRatio x] (-4 c^2 Q^Cos[c X] ^4 Cos[c X] ^4 Log[Q] Derivative[0, 1, 0] [ChebyshevT] [n Sin[ω], Q^Cos[c X] ^4, x ArcSin[r] ^2] + 12 c^2 Q^Cos[c X] ^4 Cos[c X] ^2 Log[Q] Sin[c X] ^2 Derivative[0, 1, 0] [ChebyshevT] [n Sin[ω], Q^Cos[c X] ^4, x ArcSin[r] ^2] + 16 c^2 Q^Cos[c X] ^4 Cos[c X] ^6 Log[Q] ^2 Sin[c X] ^2 Derivative[0, 1, 0] [ChebyshevT] [n Sin[ω], Q^Cos[c X] ^4, x ArcSin[r] ^2] + 16 c^2 Q^(2 Cos[c X] ^4) Cos[c X] ^6 Log[Q] ^2 Sin[c X] ^2 Derivative[0, 2, 0] [ChebyshevT] [n Sin[ω], Q^Cos[c X] ^4, x ArcSin[r] ^2]) in combination with ((Cluster of BIOGENEA_ CONSENSUS_Eqs.1-25), (Supplement Material FUNCTIONS.1 - 17)) and for a complete decision tree search of all possible combinations of fragmentation, merging, and pharmacophoric re-coring systems of 4-[3-(aminomethyl)oxiren- 2-yl]-4,5-diaza-2λ⁵-phosphaspiro[bicyclo[3.1.0]hexane-2,2'-oxaphosphirane]-3-thione, (1S,5S)-4-[(2R,3S)-3- [(3R)-2-amino- 1-fluoro-5- sulfanylidene-3H-1,2,4-triazol-3-y l]oxiran-2-yl]-4,5,6-triaza-2λ⁵-phosphaspiro[bicyclo [3.1.0]hexane-2,2'- oxaphosphirane]-3-thione , and [2-(aminomethyl)-2-{[(2E)-3- oxofuran-2-ylidene]methyl}-2λ⁵- azaphosphiridin-1-yl]amino (1R,4S)-3,3-dimethyl-6-oxo-2λ⁴-thia-5-azaspiro [bicyclo[3.2.0]heptane-2,1'-thiirane]-4-carboxylate targeted inside the SARS-CoV Mpro protein targets. In this context of mathematical chemistry functions the main obstacle of calling the related solvable matrices H Hamiltonians appeared in their asymmetry (i.e., nonHermiticity) is to qualify these matrices from playing the role of operators of observables to quaternary structure that are guided by entropy-enthalpy compensations at the docking sites in between protein subunits according to the Gibbs free energy equation. [2-140,162-195] The druggability from these newgly designed structures was verified by DockThor docking analyses of a dozen structures of dimers. Until now, Quantum algorithms to simulate QFT have mainly used lattices as particular types of regulator, which allows a computer simulation of QFT. [2-70,132-195] However, while this lattice breaks Lorentz’s invariance, my regulator does not, because these seven dimensional Chern–Simons Computated attractors become a singularity in which all the degrees of freedom of the boson field were lost in a fuzzy sphere ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)),(Figures S(1-67)) that carries over to show 𝑥1𝑥2𝑝1𝑝2𝑣 0,1,2…. 𝜆 1/2, 𝛾2,1/4𝑐1 ⟨ FF|∅ (AoΨο, d) ⍢, [H] ⨶ [Ho] ⨚⨛ i [Ψ] [EntanglementEntropy [qstate_ [QFTq] ψοMG)] ˆ(ωsinθ/2), SˆΜΝI,1/2pi˜ (i sin (-1/3 (24r), |ψ˜ [QFTq] (α) ⟩) μ, (x)) J (r’)) [A [Ψo𝑠𝑖𝑛𝜙{Ψ}] ] ⍢ ⊕ G|xi, ∣∣cert.̂∣∣{Ψ}⟩ˆ0∣∣ψj ⟩ N−Tr (ρcrˆρcrˆAoΨο) −∑∑∑AoΨοNi when substituted to (Eqs.1-400), (Cluster of BIOGENEA_ CONSENSUS_Eqs.1-26), (Supplement Material FUNCTIONS.1 - 18) and has the same rotational symmetry as the ordinary sphere. For instance, a number of state-of-the-art algorithms for error correcting sequencing data [4-195] leverage Bloom filters [4-166], a probabilistic data structure related to hash tables. The core benefit of a Bloom filter comes from its ability to trade a low probability of false positive lookups for significant savings in memory, a common constraint in large bioinformatics pipelines. [3-99,135-185] As Maas writes in his lectures: “. it is an unfortunate consequence of this current understanding of Quantum fields theory that the need to have regulators always implies that some symmetries are broken, no matter what, until the regulator it is not removed”. It should be noted, however, that Lorentz’s invariance is restored on the fuzzy sphere like drug designs ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)),(Supplementary Material METHODS AND MATERIALS Figures S(1-80)). In contrast to the recent theoretical experiments with discrete models possessing point-like impurities [6-190] or boundary terms [13-170,178-195], the interaction in our 20 one-parametric solvable models is a smooth function of position by sequence aligners such as Bowtie [4-98], the BWA family of aligners [4-181,194] and more recent graph reference genome aligners [42-173]. A lattice is a mathematical artifact, as also Preskill says: “The lattice is an artifice introduced for convenience.” This is an innovation which may be considered natural. In various limits and dynamical regimes we may then specify energies En and wave functions of (∂/(∂ c)) (2 c2
constant for the QuantumDistance [Entanglement Entropy [qstate_{∆˜ ⊗ pi|FFFTˆUµ} (X) |∅ (AoΨο, d) ⍢, [H] ⨶ [Ho] ⨚⨛ i [Ψ] ] [QFTq] ψο MG)ˆ(ωsinθ/2), SˆΜΝI,1/2pi˜ (i sin (-1/3 (24r), SphericalHarmonicY Hypergeometric0F1 [PolyLog [logi, |ψ˜ [QFTq] (α) ⟩) μ, (x)) J (r’)), iQFTG-1/334 sinˆ (-123), logLnAdS5/θZG|xi,5 ChebyshevT[n, Q^Cos[X c] ^4, ArcSin[r] ^(2 x)] GegenbauerC[Sum[μ, {ν, 0, ι}] n, Integrate[μ, ν, ω, σ] x] WhittakerM[(Sin[ω] (21/22)) d ω c^Cos[GoldenRatio], (c^4/(4 G M)) m d λ^ω, I z] iC[n δ] Cos[GoldenRatio x] (-4 c^2 Q^Cos[c X] ^4 Cos[c X] ^4 Log[Q] Derivative[0, 1, 0] [ChebyshevT] [n Sin[ω], Q^Cos[c X] ^4, x ArcSin[r] ^2] + 12 c^2 Q^Cos[c X] ^4 Cos[c X] ^2 Log[Q] Sin[c X] ^2 Derivative[0, 1, 0] [ChebyshevT] [n Sin[ω], Q^Cos[c X] ^4, x ArcSin[r] ^2] + 16 c^2 Q^Cos[c X] ^4 Cos[c X] ^6 Log[Q] ^2 Sin[c X] ^2 Derivative[0, 1, 0] [ChebyshevT] [n Sin[ω], Q^Cos[c X] ^4, x ArcSin[r] ^2] + 16 c^2 Q^(2 Cos[c X] ^4) Cos[c X] ^6 Log[Q] ^2 Sin[c X] ^2 Derivative[0, 2, 0] [ChebyshevT] [n Sin[ω], Q^Cos[c X] ^4, x ArcSin[r] ^2]) in combination with ((Cluster of BIOGENEA_ CONSENSUS_Eqs.1-25), (Supplement Material FUNCTIONS.1 - 17)) and for a complete decision tree search of all possible combinations of fragmentation, merging, and pharmacophoric re-coring systems of 4-[3-(aminomethyl)oxiren- 2-yl]-4,5-diaza-2λ⁵-phosphaspiro[bicyclo[3.1.0]hexane-2,2'-oxaphosphirane]-3-thione, (1S,5S)-4-[(2R,3S)-3- [(3R)-2-amino- 1-fluoro-5- sulfanylidene-3H-1,2,4-triazol-3-y l]oxiran-2-yl]-4,5,6-triaza-2λ⁵-phosphaspiro[bicyclo [3.1.0]hexane-2,2'- oxaphosphirane]-3-thione , and [2-(aminomethyl)-2-{[(2E)-3- oxofuran-2-ylidene]methyl}-2λ⁵- azaphosphiridin-1-yl]amino (1R,4S)-3,3-dimethyl-6-oxo-2λ⁴-thia-5-azaspiro [bicyclo[3.2.0]heptane-2,1'-thiirane]-4-carboxylate targeted inside the SARS-CoV Mpro protein targets. In this context of mathematical chemistry functions the main obstacle of calling the related solvable matrices H Hamiltonians appeared in their asymmetry (i.e., nonHermiticity) is to qualify these matrices from playing the role of operators of observables to quaternary structure that are guided by entropy-enthalpy compensations at the docking sites in between protein subunits according to the Gibbs free energy equation. [2-140,162-195] The druggability from these newgly designed structures was verified by DockThor docking analyses of a dozen structures of dimers. Until now, Quantum algorithms to simulate QFT have mainly used lattices as particular types of regulator, which allows a computer simulation of QFT. [2-70,132-195] However, while this lattice breaks Lorentz’s invariance, my regulator does not, because these seven dimensional Chern–Simons Computated attractors become a singularity in which all the degrees of freedom of the boson field were lost in a fuzzy sphere ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)),(Figures S(1-67)) that carries over to show 𝑥1𝑥2𝑝1𝑝2𝑣 0,1,2…. 𝜆 1/2, 𝛾2,1/4𝑐1 ⟨ FF|∅ (AoΨο, d) ⍢, [H] ⨶ [Ho] ⨚⨛ i [Ψ] [EntanglementEntropy [qstate_ [QFTq] ψοMG)] ˆ(ωsinθ/2), SˆΜΝI,1/2pi˜ (i sin (-1/3 (24r), |ψ˜ [QFTq] (α) ⟩) μ, (x)) J (r’)) [A [Ψo𝑠𝑖𝑛𝜙{Ψ}] ] ⍢ ⊕ G|xi, ∣∣cert.̂∣∣{Ψ}⟩ˆ0∣∣ψj ⟩ N−Tr (ρcrˆρcrˆAoΨο) −∑∑∑AoΨοNi when substituted to (Eqs.1-400), (Cluster of BIOGENEA_ CONSENSUS_Eqs.1-26), (Supplement Material FUNCTIONS.1 - 18) and has the same rotational symmetry as the ordinary sphere. For instance, a number of state-of-the-art algorithms for error correcting sequencing data [4-195] leverage Bloom filters [4-166], a probabilistic data structure related to hash tables. The core benefit of a Bloom filter comes from its ability to trade a low probability of false positive lookups for significant savings in memory, a common constraint in large bioinformatics pipelines. [3-99,135-185] As Maas writes in his lectures: “. it is an unfortunate consequence of this current understanding of Quantum fields theory that the need to have regulators always implies that some symmetries are broken, no matter what, until the regulator it is not removed”. It should be noted, however, that Lorentz’s invariance is restored on the fuzzy sphere like drug designs ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)),(Supplementary Material METHODS AND MATERIALS Figures S(1-80)). In contrast to the recent theoretical experiments with discrete models possessing point-like impurities [6-190] or boundary terms [13-170,178-195], the interaction in our 20 one-parametric solvable models is a smooth function of position by sequence aligners such as Bowtie [4-98], the BWA family of aligners [4-181,194] and more recent graph reference genome aligners [42-173]. A lattice is a mathematical artifact, as also Preskill says: “The lattice is an artifice introduced for convenience.” This is an innovation which may be considered natural. In various limits and dynamical regimes we may then specify energies En and wave functions of (∂/(∂ c)) (2 c2 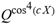 cos2(c X) log(Q))==-4 c log(Q) cos(c X)
cos2(c X) log(Q))==-4 c log(Q) cos(c X) 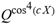 (2 c X log(Q) sin(c X) cos4(c X)+c X sin(c X)-cos(c X)) for
(2 c X log(Q) sin(c X) cos4(c X)+c X sin(c X)-cos(c X)) for 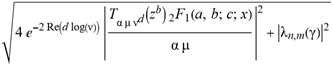
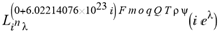 hν r ψ cos(γ) (b j+x)*1/P r ψ
hν r ψ cos(γ) (b j+x)*1/P r ψ 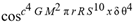 (γ)1/P r ψ2 (b j+x) hν r
(γ)1/P r ψ2 (b j+x) hν r 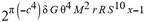
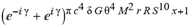
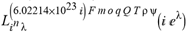 (b j r ψ2 cos(γ) hν r
(b j r ψ2 cos(γ) hν r 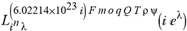 )/P+1/P r ψ2 x cos(γ) hν r
)/P+1/P r ψ2 x cos(γ) hν r 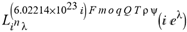 (π b c4 δ G θ4 j M2 r R S10 log(cos(γ))+1)+1/(2 P) π c4 δ G θ4 M2 r2 R S10 ψ2 x2 cos(γ) log(cos(γ)) hν r
(π b c4 δ G θ4 j M2 r R S10 log(cos(γ))+1)+1/(2 P) π c4 δ G θ4 M2 r2 R S10 ψ2 x2 cos(γ) log(cos(γ)) hν r 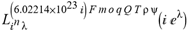 (π b c4 δ G θ4 j M2 r R S10 log(cos(γ))+2)+1/(6 P) π2 c8 δ2 G2 θ8 M4 r3 R2 S20 ψ2 x3 cos(γ) log2(cos(γ)) hν r
(π b c4 δ G θ4 j M2 r R S10 log(cos(γ))+2)+1/(6 P) π2 c8 δ2 G2 θ8 M4 r3 R2 S20 ψ2 x3 cos(γ) log2(cos(γ)) hν r 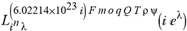 (π b c4 δ G θ4 j M2 r R S10 log(cos(γ))+3)+1/(24 P) π3 c12 δ3 G3 θ12 M6 r4 R3 S30 ψ2 x4 cos(γ) log3(cos(γ)) hν r
(π b c4 δ G θ4 j M2 r R S10 log(cos(γ))+3)+1/(24 P) π3 c12 δ3 G3 θ12 M6 r4 R3 S30 ψ2 x4 cos(γ) log3(cos(γ)) hν r 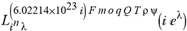 (π b c4 δ G θ4 j M2 r R S10 log(cos(γ))+4)+O(x5)(∂/(∂ x)) (1/P r ψ2 (b j+x) hν r (γ) )==1/P r ψ2 hν r (γ)
(π b c4 δ G θ4 j M2 r R S10 log(cos(γ))+4)+O(x5)(∂/(∂ x)) (1/P r ψ2 (b j+x) hν r (γ) )==1/P r ψ2 hν r (γ) 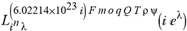
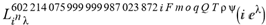 (π c4 δ G θ4 M2 r R S10 (b j+x) log(cos(γ))+1)\[Integral]1/P hr ν r (b j+x) ψ2
(π c4 δ G θ4 M2 r R S10 (b j+x) log(cos(γ))+1)\[Integral]1/P hr ν r (b j+x) ψ2 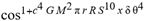 (γ)
(γ) 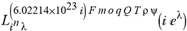 x==(0.101321 ψ2 hν r
x==(0.101321 ψ2 hν r 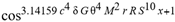 (γ)
(γ) 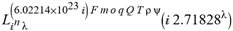 (3.14159 c4 δ G θ4 M2 r R S10 (b j+x) log(cos(γ))-1))/(c8 δ2 G2 θ8 M4 P r R2 S20 log2(cos(γ)))(b j r ψ2 hν r
(3.14159 c4 δ G θ4 M2 r R S10 (b j+x) log(cos(γ))-1))/(c8 δ2 G2 θ8 M4 P r R2 S20 log2(cos(γ)))(b j r ψ2 hν r 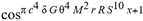 (γ)
(γ) 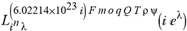 )/P+(r x ψ2 hν r
)/P+(r x ψ2 hν r 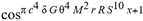 (γ)
(γ) 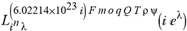 )/P+ constant for (∂(Tr[ψ,{2}] DensityMatrix)/∂logρ(ψ) A log(ΒG hν n π Q δ μ σ (sin(ω) (ρ A))) 76 1000000000000000000000000000 logG(z)) 6.022 140+G hν n π Q δ μ σ sin(ω)+c8 π2 r2 δ2 θ20==9.8696 (c8 r2 δ2 θ20+6.49206*1030 ∂(DensityMatrix Tr[ψ,{2}])/(∂A logρ(ψ) log(1/2 A hν n π3/2 Q ΒG δ μ ρ σ ω
)/P+ constant for (∂(Tr[ψ,{2}] DensityMatrix)/∂logρ(ψ) A log(ΒG hν n π Q δ μ σ (sin(ω) (ρ A))) 76 1000000000000000000000000000 logG(z)) 6.022 140+G hν n π Q δ μ σ sin(ω)+c8 π2 r2 δ2 θ20==9.8696 (c8 r2 δ2 θ20+6.49206*1030 ∂(DensityMatrix Tr[ψ,{2}])/(∂A logρ(ψ) log(1/2 A hν n π3/2 Q ΒG δ μ ρ σ ω 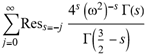 )) logG(z)+0.282095 G hν n Q δ μ σ ω
)) logG(z)+0.282095 G hν n Q δ μ σ ω 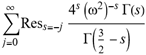 ) {{
) {{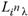 (I E^λ)2+(1.20443*1024 I) F m o ρ q Q T ψ
(I E^λ)2+(1.20443*1024 I) F m o ρ q Q T ψ 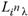 (I Eλ) LaguerreL(0,1,0)(λ In,0,I Eλ)+F2 m2 o2 ρ2 q2 Q2 T2 ψ2 (-3.62662*1047 LaguerreL^(0,1,0)(λ I^n,0,I E^λ)2-3.62662*1047
(I Eλ) LaguerreL(0,1,0)(λ In,0,I Eλ)+F2 m2 o2 ρ2 q2 Q2 T2 ψ2 (-3.62662*1047 LaguerreL^(0,1,0)(λ I^n,0,I E^λ)2-3.62662*1047 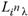 (I Eλ) LaguerreL(0,2,0)(λ In,0,I Eλ))+F3 m3 o3 ρ3 q3 Q3 T3 ψ3 ((-2.184*1071 I) LaguerreL(0,1,0)(λ In,0,I Eλ) LaguerreL(0,2,0)(λ In,0,I Eλ)-(7.28*1070 I)
(I Eλ) LaguerreL(0,2,0)(λ In,0,I Eλ))+F3 m3 o3 ρ3 q3 Q3 T3 ψ3 ((-2.184*1071 I) LaguerreL(0,1,0)(λ In,0,I Eλ) LaguerreL(0,2,0)(λ In,0,I Eλ)-(7.28*1070 I) 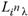 (I Eλ) LaguerreL(0,3,0)(λ In,0,I Eλ))+F4 m4 o4 ρ4 q4 Q4 T4 ψ4 (3.28809*1094 LaguerreL^(0,2,0)(λ I^n,0,I E^λ)2+4.38412*1094 LaguerreL(0,1,0)(λ In,0,I Eλ) LaguerreL(0,3,0)(λ In,0,I Eλ)+1.09603*1094
(I Eλ) LaguerreL(0,3,0)(λ In,0,I Eλ))+F4 m4 o4 ρ4 q4 Q4 T4 ψ4 (3.28809*1094 LaguerreL^(0,2,0)(λ I^n,0,I E^λ)2+4.38412*1094 LaguerreL(0,1,0)(λ In,0,I Eλ) LaguerreL(0,3,0)(λ In,0,I Eλ)+1.09603*1094 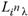 (I Eλ) LaguerreL(0,4,0)(λ In,0,I Eλ))+O(q5)}, {(Taylor series)}} when H, ∂M↓ ⊗ ⨋⨋⨋|∅iΨ⍢ ⊕, QFTq. ZernikeR[Hypergeometric2F1Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (m δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r] + (x Hypergeometric2F1Regularized[1 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2, 1/2] LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ] (1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) Derivative[1, 0, 0] [ZernikeR] [Hypergeometric2F1 Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (m δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r])/2 + (x^2 LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ] (1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (Hypergeometric2F1Regularized[2 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 3 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 3, 1/2] (-1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) Derivative[1, 0, 0] [ZernikeR] [Hypergeometric2F1Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (m δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r] + Hypergeometric2F1Regularized[1 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2, 1/2] ^2 LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ] (1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) Derivative[2, 0, 0] [ZernikeR] [Hypergeometric2F1Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (m δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r]))/8 + (x^3 LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ] (1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (Hypergeometric2F1Regularized[3 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 4 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 4, 1/2] (-2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (-1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (3 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) Derivative[1, 0, 0] [ZernikeR] [Hypergeometric2F1Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (m δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r] + 3 Hypergeometric2F1Regularized[1 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2, 1/2] Hypergeometric2F1Regularized[2 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 3 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 3, 1/2] (-1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ] (1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) Derivative[2, 0, 0] [ZernikeR] [Hypergeometric2F1Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (m δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r] + Hypergeometric2F1Regularized[1 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2, 1/2] ^3 LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ] ^2 (1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ])^2 Derivative[3, 0, 0] [ZernikeR] [Hypergeometric2F1Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (m δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r]))/48 + (x^4 LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ] (1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (Hypergeometric2F1Regularized[4 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 5 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 5, 1/2] (-3 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (-2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (-1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (3 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (4 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) Derivative[1, 0, 0] [ZernikeR] [Hypergeometric2F1Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (m δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r] + (-1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ] (1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (3 Hypergeometric2F1Regularized[2 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 3 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 3, 1/2] ^2 (-1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) + 4 Hypergeometric2F1Regularized[1 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2, 1/2] Hypergeometric2F1Regularized[3 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 4 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 4, 1/2] (-2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (3 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ])) Derivative[2, 0, 0] [ZernikeR] [Hypergeometric2F1Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (m δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r] + 6 Hypergeometric2F1Regularized[1 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2, 1/2] ^2 Hypergeometric2F1Regularized[2 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 3 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 3, 1/2] (-1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ] ^2 (1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ])^2 (2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) Derivative[3, 0, 0] [ZernikeR] [Hypergeometric2F1Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (m δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r] + Hypergeometric2F1Regularized[1 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2, 1/2] ^4 LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ] ^3 (1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ])^3 Derivative[4, 0, 0] [ZernikeR] [Hypergeometric2F1Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (m δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r]))/384 + O[x] ^5 ⍢ ⊕ G|xi, [H] [∂] ∼ [NM] edges conducted for the docked SARS-Cov2 protein and Gissitorviffirna_TM ligand complexes. [1-99,90,149-195] The delicacy of these Quantum Homeopathy States makes a practical path for a pharmacophore merging algorithm imperative where classical notions of resource utilizations can be directly applicable when trying to preserve the topological nature of CS theory for the generation of these unique drug designs with the highest Quantum Energy Negativities when compared to other known SARS - CoV - 2 antivirals. [11-99,118-195] In this context, the generalized fragments are viewed as external sources that have the ability to produce an effective description of Quantum Hall effect, and can be coupled to the Chern - Simons theory. [11–80,133-193] In this effort, I propose computer-aided and Quantum Homeopathy-directed rational drug design strategies efficient in computing docking usage, and powerful enough to achieve very high accuracy levels for this in-silico effort for the generation of Quantum Turing Homeopathy Ruled molecules of DRVYIHPF-mimetic, Gisitorviffirna_TM, Roccustyrna_gs, Gissitorviffirna_TM, Roccostyrna_ gs_consv, and Roccustyrna _fr ligands targeting the COVID-19-SARS-COV-2 SPIKE D614G mutation by unifying Quantum Homeopathy Molecular Pairs (QHMMP), Lindenbaum-Tarski logical spaces and Adaptive Weighted KNN Positioning for Matched Bemis and Murko (BM) driven eigenvalue statements into Shannon entropy quantities as composed by Tipping–Ogilvie driven Machine Learning potentials on a (DFT) ℓneuron (ι) (Eqs.1-400), ((Iconics1-4), (Eqs1-400), and (Schematics1a,1b,1c,1d,1e,1f,1g,1h,1i,1j,1k,1l,1m), (I-VI) Supplementary Material METHODS AND MATERIALS)) (SI Appendix XXXIX), (Cluster of BIOGENEA_ CONSENSUS_Eqs.1-26), (Supplement Material FUNCTIONS.1 - 20) improver for Chern-Simons Topology Euclidean Geometrics. (SI Appendix I), (SI Appendix VIII), (SI Appendix XII), (SI Appendix XIII), (SI Appendix IX), (SI Appendix XIV), (SI Appendix XV), (SI Appendix XVI), (SI Appendix XVII), (SI Appendix XVIII), (SI Appendix XIX), (SI Appendix XX), (SI Appendix XXI), (SI Appendix XXII), (SI Appendix XXIII), (SI Appendix XXIV), (SI Appendix XXV) (SI Appendix XXVI), (SI Appendix XXVII). (SI Appendix XXVIII), (SI Appendix XXIX), (SI Appendix XXX), (SI Appendix XXXI), (SI Appendix XXXII), (SI Appendix XXXIII), (SI Appendix XXXIV), (SI Appendix XXXV), (SI Appendix XXXVI), (SI Appendix XXXVII), (SI Appendix XXXV), (SI Appendix XXXVI), (SI Appendix XXXVII), (SI Appendix XVIII), ((Cluster Docking Energy TableS1), (SI Appendix I), (Cluster Docking Energy TableS2), SI Appendix I), (Docking Energy TableS1), (SI Appendix I), (Docking Energy TableS2), (SI Appendix I), (Docking Energy TableS3), (SI Appendix I)), and ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)),(SI Appendix XXXIX), (SI Appendix XXXIX), ((Cluster of BIOGENEA_ CONSENSUS_Eqs.1-26), (Supplement Material FUNCTIONS.1 - 21)), (OUTPUTs1-3), (Ic1a), (Ic1b), (Ic1c), (Ic2a), (Ic2b), (Ic2c), (Ic2d), (Ic2e), (Ic2f), (Ic2g),(Ic2h), (Ic2c), (Ic2g), (Ic2k), (Ic2l), (Ic2m),(Ic2n),(Ic2o),(Ic2p),(Ic2q),(Ic2r), (Ic3a), (Ic3b) (Ic3c), (Ic3d), (Ic3d), (Ic3e), (Ic3f), (Ic3g), (Ic3h), (Ic3i), (Ic3j), (Ic3k), (Iconic4), and (Supplementary Material METHODS AND MATERIALS Figures S(1- 133)), ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS)). [1–29-191] It should be emphasized that here we adhere to a phenomenological Quantum Thermodynamics and Quantum Homeopathy approach, under which the details of replicator dynamics are irrelevant, in contrast, for example, to the approach of Sella and Hirsh [13-169]. [2-195] Here, Ι describe the basic constructions of these drug designing problems and summarize relevant AiryAi, AiryAiPrime, AiryBi, AiryAiZero, AiryBiZero E-z/2 z-k (Ez (Γ(2 m+1)/Γ(-k+m+1/2)+((k-m+1/2) (k+m+1/2) Γ(2 m+1))/(Γ(-k+m+1/2) z)+((k-m+1/2) (k-m+3/2) (k+m+1/2) (k+m+3/2) Γ(2 m+1))/(2 Γ(-k+m+1/2) z2)+((k-m+1/2) (k-m+3/2) (k-m+5/2) (k+m+1/2) (k+m+3/2) (k+m+5/2) Γ(2 m+1))/(6 Γ(-k+m+1/2) z3)+((k-m+1/2) (k-m+3/2) (k-m+5/2) (k-m+7/2) (k+m+1/2) (k+m+3/2) (k+m+5/2) (k+m+7/2) Γ(2 m+1))/(24 Γ(-k+m+1/2) z4)+((k-m+1/2) (k-m+3/2) (k-m+5/2) (k-m+7/2) (k-m+9/2) (k+m+1/2) (k+m+3/2) (k+m+5/2) (k+m+7/2) (k+m+9/2) Γ(2 m+1))/(120 Γ(-k+m+1/2) z5)+O((1/z)6))+z2 k (((-1)k-m+3/2 Γ(2 m+1))/Γ(k+m+1/2)+((-1)k-m+3/2 (-k+m+1/2) (k+m-1/2) Γ(2 m+1))/(Γ(k+m+1/2) z)-(I (-1)k-m (2 k-2 m-3) (2 k-2 m-1) (2 k+2 m-3) (2 k+2 m-1) Γ(2 m+1))/(32 Γ(k+m+1/2) z2)+(I (-1)k-m (2 k-2 m-5) (2 k-2 m-3) (2 k-2 m-1) (2 k+2 m-5) (2 k+2 m-3) (2 k+2 m-1) Γ(2 m+1))/(384 Γ(k+m+1/2) z3)-(I (-1)k-m (2 k-2 m-7) (2 k-2 m-5) (2 k-2 m-3) (2 k-2 m-1) (2 k+2 m-7) (2 k+2 m-5) (2 k+2 m-3) (2 k+2 m-1) Γ(2 m+1))/(6144 Γ(k+m+1/2) z4)+(I (-1)k-m (2 k-2 m-9) (2 k-2 m-7) (2 k-2 m-5) (2 k-2 m-3) (2 k-2 m-1) (2 k+2 m-9) (2 k+2 m-7) (2 k+2 m-5) (2 k+2 m-3) (2 k+2 m-1) Γ(2 m+1))/(122880 Γ(k+m+1/2) z5)+O((1/z)6))) quantum functions of ZernikeR[LegendreP[LaguerreL[λ I^n, (ψ o) 6.02214076 10^23 ρ I Q F T q m, I Exp[λ] ], x], ((ψ I^(N I)) Q F T^δ θ^10 Ψ Log[y] ^2 m)/10^27, r] GegenbauerC[n, m, x] ChebyshevT[n, x] {M2 R sin^-1(r)4+M2 R x sin^-1(r)4 (N LaguerreL(1,0)(0,0) GegenbauerC(0,1,0)(n,0,(E a)/4)+π c4 δ G θ4 M2 r R S10 log(C(logG(z) Qcos(z))))+1/2 M2 R x2 sin^-1(r)4 (2 π c4 δ G θ4 M2 N r R S10 LaguerreL(1,0)(0,0) GegenbauerC(0,1,0)(n,0,(E a)/4) log(C(logG(z) Qcos(z)))+N2 LaguerreL(2,0)(0,0) GegenbauerC^(0,1,0)(n,0,(E a)/4)2+N2 LaguerreL(1,0)(0,0) GegenbauerC(0,2,0)(n,0,(E a)/4)+2 N LaguerreL(1,1)(0,0) GegenbauerC(0,1,0)(n,0,(E a)/4)+π2 c8 δ2 G2 θ8 M4 r2 R2 S20 log2(C(logG(z) Qcos(z))))+M2 R x3 sin^-1(r)4 (1/2 π2 c8 δ2 G2 θ8 M4 N r2 R2 S20 LaguerreL(1,0)(0,0) GegenbauerC(0,1,0)(n,0,(E a)/4) log2(C(logG(z) Qcos(z)))+1/2 π c4 δ G θ4 M2 r R S10 log(C(logG(z) Qcos(z))) (N2 LaguerreL(2,0)(0,0) GegenbauerC^(0,1,0)(n,0,(E a)/4)2+N2 LaguerreL(1,0)(0,0) GegenbauerC(0,2,0)(n,0,(E a)/4)+2 N LaguerreL(1,1)(0,0) GegenbauerC(0,1,0)(n,0,(E a)/4))+1/6 (N3 LaguerreL(3,0)(0,0) GegenbauerC^(0,1,0)(n,0,(E a)/4)3+3 N3 LaguerreL(2,0)(0,0) GegenbauerC(0,1,0)(n,0,(E a)/4) GegenbauerC(0,2,0)(n,0,(E a)/4)+N3 LaguerreL(1,0)(0,0) GegenbauerC(0,3,0)(n,0,(E a)/4)+3 N2 LaguerreL(2,1)(0,0) GegenbauerC^(0,1,0)(n,0,(E a)/4)2+3 N2 LaguerreL(1,1)(0,0) GegenbauerC(0,2,0)(n,0,(E a)/4)+3 N LaguerreL(1,2)(0,0) GegenbauerC(0,1,0)(n,0,(E a)/4))+1/6 π3 c12 δ3 G3 θ12 M6 r3 R3 S30 log3(C(logG(z) Qcos(z))))+M2 R x4 sin^-1(r)4 (1/6 π3 c12 δ3 G3 θ12 M6 N r3 R3 S30 LaguerreL(1,0)(0,0) GegenbauerC(0,1,0)(n,0,(E a)/4) log3(C(logG(z) Qcos(z)))+1/4 π2 c8 δ2 G2 θ8 M4 r2 R2 S20 log2(C(logG(z) Qcos(z))) (N2 LaguerreL(2,0)(0,0) GegenbauerC^(0,1,0)(n,0,(E a)/4)2+N2 LaguerreL(1,0)(0,0) GegenbauerC(0,2,0)(n,0,(E a)/4)+2 N LaguerreL(1,1)(0,0) GegenbauerC(0,1,0)(n,0,(E a)/4))+1/6 π c4 δ G θ4 M2 r R S10 log(C(logG(z) Qcos(z))) (N3 LaguerreL(3,0)(0,0) GegenbauerC^(0,1,0)(n,0,(E a)/4)3+3 N3 LaguerreL(2,0)(0,0) GegenbauerC(0,1,0)(n,0,(E a)/4) GegenbauerC(0,2,0)(n,0,(E a)/4)+N3 LaguerreL(1,0)(0,0) GegenbauerC(0,3,0)(n,0,(E a)/4)+3 N2 LaguerreL(2,1)(0,0) GegenbauerC^(0,1,0)(n,0,(E a)/4)2+3 N2 LaguerreL(1,1)(0,0) GegenbauerC(0,2,0)(n,0,(E a)/4)+3 N LaguerreL(1,2)(0,0) GegenbauerC(0,1,0)(n,0,(E a)/4))+1/24 (N4 LaguerreL(4,0)(0,0) GegenbauerC^(0,1,0)(n,0,(E a)/4)4+3 N4 LaguerreL(2,0)(0,0) GegenbauerC^(0,2,0)(n,0,(E a)/4)2+6 N4 LaguerreL(3,0)(0,0) GegenbauerC^(0,1,0)(n,0,(E a)/4)2 GegenbauerC(0,2,0)(n,0,(E a)/4)+4 N4 LaguerreL(2,0)(0,0) GegenbauerC(0,1,0)(n,0,(E a)/4) GegenbauerC(0,3,0)(n,0,(E a)/4)+N4 LaguerreL(1,0)(0,0) GegenbauerC(0,4,0)(n,0,(E a)/4)+4 N3 LaguerreL(3,1)(0,0) GegenbauerC^(0,1,0)(n,0,(E a)/4)3+12 N3 LaguerreL(2,1)(0,0) GegenbauerC(0,1,0)(n,0,(E a)/4) GegenbauerC(0,2,0)(n,0,(E a)/4)+4 N3 LaguerreL(1,1)(0,0) GegenbauerC(0,3,0)(n,0,(E a)/4)+6 N2 LaguerreL(2,2)(0,0) GegenbauerC^(0,1,0)(n,0,(E a)/4)2+6 N2 LaguerreL(1,2)(0,0) GegenbauerC(0,2,0)(n,0,(E a)/4)+4 N LaguerreL(1,3)(0,0) GegenbauerC(0,1,0)(n,0,(E a)/4))+1/24 π4 c16 δ4 G4 θ16 M8 r4 R4 S40 log4(C(logG(z) Qcos(z))))+O(x5)}, GegenbauerC[n, x] LegendreP [n, x] ZernikeR [n, m, r] LegendreP [n, m, x] HermiteH [n, x] JacobiP [n, a, b, x] LaguerreL [n, x] ChebyshevU [n, x] Hypergeometric0F1[a, z] Hypergeometric0F1[a, z] Hypergeometric2F1Regularized[a, b, c, z] ZernikeR[LegendreP [LaguerreL[λ n, D f z, g z (ψ^0 ρ m), I Exp[λ] ], x], m, r]
(I Eλ) LaguerreL(0,4,0)(λ In,0,I Eλ))+O(q5)}, {(Taylor series)}} when H, ∂M↓ ⊗ ⨋⨋⨋|∅iΨ⍢ ⊕, QFTq. ZernikeR[Hypergeometric2F1Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (m δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r] + (x Hypergeometric2F1Regularized[1 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2, 1/2] LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ] (1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) Derivative[1, 0, 0] [ZernikeR] [Hypergeometric2F1 Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (m δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r])/2 + (x^2 LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ] (1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (Hypergeometric2F1Regularized[2 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 3 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 3, 1/2] (-1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) Derivative[1, 0, 0] [ZernikeR] [Hypergeometric2F1Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (m δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r] + Hypergeometric2F1Regularized[1 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2, 1/2] ^2 LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ] (1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) Derivative[2, 0, 0] [ZernikeR] [Hypergeometric2F1Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (m δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r]))/8 + (x^3 LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ] (1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (Hypergeometric2F1Regularized[3 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 4 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 4, 1/2] (-2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (-1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (3 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) Derivative[1, 0, 0] [ZernikeR] [Hypergeometric2F1Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (m δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r] + 3 Hypergeometric2F1Regularized[1 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2, 1/2] Hypergeometric2F1Regularized[2 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 3 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 3, 1/2] (-1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ] (1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) Derivative[2, 0, 0] [ZernikeR] [Hypergeometric2F1Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (m δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r] + Hypergeometric2F1Regularized[1 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2, 1/2] ^3 LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ] ^2 (1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ])^2 Derivative[3, 0, 0] [ZernikeR] [Hypergeometric2F1Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (m δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r]))/48 + (x^4 LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ] (1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (Hypergeometric2F1Regularized[4 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 5 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 5, 1/2] (-3 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (-2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (-1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (3 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (4 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) Derivative[1, 0, 0] [ZernikeR] [Hypergeometric2F1Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (m δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r] + (-1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ] (1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (3 Hypergeometric2F1Regularized[2 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 3 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 3, 1/2] ^2 (-1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) + 4 Hypergeometric2F1Regularized[1 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2, 1/2] Hypergeometric2F1Regularized[3 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 4 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 4, 1/2] (-2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) (3 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ])) Derivative[2, 0, 0] [ZernikeR] [Hypergeometric2F1Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (m δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r] + 6 Hypergeometric2F1Regularized[1 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2, 1/2] ^2 Hypergeometric2F1Regularized[2 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 3 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 3, 1/2] (-1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ] ^2 (1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ])^2 (2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ]) Derivative[3, 0, 0] [ZernikeR] [Hypergeometric2F1Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (m δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r] + Hypergeometric2F1Regularized[1 - LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 2, 1/2] ^4 LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ] ^3 (1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ])^3 Derivative[4, 0, 0] [ZernikeR] [Hypergeometric2F1Regularized[-LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1 + LaguerreL[I^n λ, (0. + 6.02214076*^23 I) F m o q Q T ρ ψ, I E^λ], 1, 1/2], (m δ θ^10 ψ Ψ Log[y] ^2)/(1000000000000000000000000000 E^((N Pi)/2)), r]))/384 + O[x] ^5 ⍢ ⊕ G|xi, [H] [∂] ∼ [NM] edges conducted for the docked SARS-Cov2 protein and Gissitorviffirna_TM ligand complexes. [1-99,90,149-195] The delicacy of these Quantum Homeopathy States makes a practical path for a pharmacophore merging algorithm imperative where classical notions of resource utilizations can be directly applicable when trying to preserve the topological nature of CS theory for the generation of these unique drug designs with the highest Quantum Energy Negativities when compared to other known SARS - CoV - 2 antivirals. [11-99,118-195] In this context, the generalized fragments are viewed as external sources that have the ability to produce an effective description of Quantum Hall effect, and can be coupled to the Chern - Simons theory. [11–80,133-193] In this effort, I propose computer-aided and Quantum Homeopathy-directed rational drug design strategies efficient in computing docking usage, and powerful enough to achieve very high accuracy levels for this in-silico effort for the generation of Quantum Turing Homeopathy Ruled molecules of DRVYIHPF-mimetic, Gisitorviffirna_TM, Roccustyrna_gs, Gissitorviffirna_TM, Roccostyrna_ gs_consv, and Roccustyrna _fr ligands targeting the COVID-19-SARS-COV-2 SPIKE D614G mutation by unifying Quantum Homeopathy Molecular Pairs (QHMMP), Lindenbaum-Tarski logical spaces and Adaptive Weighted KNN Positioning for Matched Bemis and Murko (BM) driven eigenvalue statements into Shannon entropy quantities as composed by Tipping–Ogilvie driven Machine Learning potentials on a (DFT) ℓneuron (ι) (Eqs.1-400), ((Iconics1-4), (Eqs1-400), and (Schematics1a,1b,1c,1d,1e,1f,1g,1h,1i,1j,1k,1l,1m), (I-VI) Supplementary Material METHODS AND MATERIALS)) (SI Appendix XXXIX), (Cluster of BIOGENEA_ CONSENSUS_Eqs.1-26), (Supplement Material FUNCTIONS.1 - 20) improver for Chern-Simons Topology Euclidean Geometrics. (SI Appendix I), (SI Appendix VIII), (SI Appendix XII), (SI Appendix XIII), (SI Appendix IX), (SI Appendix XIV), (SI Appendix XV), (SI Appendix XVI), (SI Appendix XVII), (SI Appendix XVIII), (SI Appendix XIX), (SI Appendix XX), (SI Appendix XXI), (SI Appendix XXII), (SI Appendix XXIII), (SI Appendix XXIV), (SI Appendix XXV) (SI Appendix XXVI), (SI Appendix XXVII). (SI Appendix XXVIII), (SI Appendix XXIX), (SI Appendix XXX), (SI Appendix XXXI), (SI Appendix XXXII), (SI Appendix XXXIII), (SI Appendix XXXIV), (SI Appendix XXXV), (SI Appendix XXXVI), (SI Appendix XXXVII), (SI Appendix XXXV), (SI Appendix XXXVI), (SI Appendix XXXVII), (SI Appendix XVIII), ((Cluster Docking Energy TableS1), (SI Appendix I), (Cluster Docking Energy TableS2), SI Appendix I), (Docking Energy TableS1), (SI Appendix I), (Docking Energy TableS2), (SI Appendix I), (Docking Energy TableS3), (SI Appendix I)), and ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)),(SI Appendix XXXIX), (SI Appendix XXXIX), ((Cluster of BIOGENEA_ CONSENSUS_Eqs.1-26), (Supplement Material FUNCTIONS.1 - 21)), (OUTPUTs1-3), (Ic1a), (Ic1b), (Ic1c), (Ic2a), (Ic2b), (Ic2c), (Ic2d), (Ic2e), (Ic2f), (Ic2g),(Ic2h), (Ic2c), (Ic2g), (Ic2k), (Ic2l), (Ic2m),(Ic2n),(Ic2o),(Ic2p),(Ic2q),(Ic2r), (Ic3a), (Ic3b) (Ic3c), (Ic3d), (Ic3d), (Ic3e), (Ic3f), (Ic3g), (Ic3h), (Ic3i), (Ic3j), (Ic3k), (Iconic4), and (Supplementary Material METHODS AND MATERIALS Figures S(1- 133)), ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS)). [1–29-191] It should be emphasized that here we adhere to a phenomenological Quantum Thermodynamics and Quantum Homeopathy approach, under which the details of replicator dynamics are irrelevant, in contrast, for example, to the approach of Sella and Hirsh [13-169]. [2-195] Here, Ι describe the basic constructions of these drug designing problems and summarize relevant AiryAi, AiryAiPrime, AiryBi, AiryAiZero, AiryBiZero E-z/2 z-k (Ez (Γ(2 m+1)/Γ(-k+m+1/2)+((k-m+1/2) (k+m+1/2) Γ(2 m+1))/(Γ(-k+m+1/2) z)+((k-m+1/2) (k-m+3/2) (k+m+1/2) (k+m+3/2) Γ(2 m+1))/(2 Γ(-k+m+1/2) z2)+((k-m+1/2) (k-m+3/2) (k-m+5/2) (k+m+1/2) (k+m+3/2) (k+m+5/2) Γ(2 m+1))/(6 Γ(-k+m+1/2) z3)+((k-m+1/2) (k-m+3/2) (k-m+5/2) (k-m+7/2) (k+m+1/2) (k+m+3/2) (k+m+5/2) (k+m+7/2) Γ(2 m+1))/(24 Γ(-k+m+1/2) z4)+((k-m+1/2) (k-m+3/2) (k-m+5/2) (k-m+7/2) (k-m+9/2) (k+m+1/2) (k+m+3/2) (k+m+5/2) (k+m+7/2) (k+m+9/2) Γ(2 m+1))/(120 Γ(-k+m+1/2) z5)+O((1/z)6))+z2 k (((-1)k-m+3/2 Γ(2 m+1))/Γ(k+m+1/2)+((-1)k-m+3/2 (-k+m+1/2) (k+m-1/2) Γ(2 m+1))/(Γ(k+m+1/2) z)-(I (-1)k-m (2 k-2 m-3) (2 k-2 m-1) (2 k+2 m-3) (2 k+2 m-1) Γ(2 m+1))/(32 Γ(k+m+1/2) z2)+(I (-1)k-m (2 k-2 m-5) (2 k-2 m-3) (2 k-2 m-1) (2 k+2 m-5) (2 k+2 m-3) (2 k+2 m-1) Γ(2 m+1))/(384 Γ(k+m+1/2) z3)-(I (-1)k-m (2 k-2 m-7) (2 k-2 m-5) (2 k-2 m-3) (2 k-2 m-1) (2 k+2 m-7) (2 k+2 m-5) (2 k+2 m-3) (2 k+2 m-1) Γ(2 m+1))/(6144 Γ(k+m+1/2) z4)+(I (-1)k-m (2 k-2 m-9) (2 k-2 m-7) (2 k-2 m-5) (2 k-2 m-3) (2 k-2 m-1) (2 k+2 m-9) (2 k+2 m-7) (2 k+2 m-5) (2 k+2 m-3) (2 k+2 m-1) Γ(2 m+1))/(122880 Γ(k+m+1/2) z5)+O((1/z)6))) quantum functions of ZernikeR[LegendreP[LaguerreL[λ I^n, (ψ o) 6.02214076 10^23 ρ I Q F T q m, I Exp[λ] ], x], ((ψ I^(N I)) Q F T^δ θ^10 Ψ Log[y] ^2 m)/10^27, r] GegenbauerC[n, m, x] ChebyshevT[n, x] {M2 R sin^-1(r)4+M2 R x sin^-1(r)4 (N LaguerreL(1,0)(0,0) GegenbauerC(0,1,0)(n,0,(E a)/4)+π c4 δ G θ4 M2 r R S10 log(C(logG(z) Qcos(z))))+1/2 M2 R x2 sin^-1(r)4 (2 π c4 δ G θ4 M2 N r R S10 LaguerreL(1,0)(0,0) GegenbauerC(0,1,0)(n,0,(E a)/4) log(C(logG(z) Qcos(z)))+N2 LaguerreL(2,0)(0,0) GegenbauerC^(0,1,0)(n,0,(E a)/4)2+N2 LaguerreL(1,0)(0,0) GegenbauerC(0,2,0)(n,0,(E a)/4)+2 N LaguerreL(1,1)(0,0) GegenbauerC(0,1,0)(n,0,(E a)/4)+π2 c8 δ2 G2 θ8 M4 r2 R2 S20 log2(C(logG(z) Qcos(z))))+M2 R x3 sin^-1(r)4 (1/2 π2 c8 δ2 G2 θ8 M4 N r2 R2 S20 LaguerreL(1,0)(0,0) GegenbauerC(0,1,0)(n,0,(E a)/4) log2(C(logG(z) Qcos(z)))+1/2 π c4 δ G θ4 M2 r R S10 log(C(logG(z) Qcos(z))) (N2 LaguerreL(2,0)(0,0) GegenbauerC^(0,1,0)(n,0,(E a)/4)2+N2 LaguerreL(1,0)(0,0) GegenbauerC(0,2,0)(n,0,(E a)/4)+2 N LaguerreL(1,1)(0,0) GegenbauerC(0,1,0)(n,0,(E a)/4))+1/6 (N3 LaguerreL(3,0)(0,0) GegenbauerC^(0,1,0)(n,0,(E a)/4)3+3 N3 LaguerreL(2,0)(0,0) GegenbauerC(0,1,0)(n,0,(E a)/4) GegenbauerC(0,2,0)(n,0,(E a)/4)+N3 LaguerreL(1,0)(0,0) GegenbauerC(0,3,0)(n,0,(E a)/4)+3 N2 LaguerreL(2,1)(0,0) GegenbauerC^(0,1,0)(n,0,(E a)/4)2+3 N2 LaguerreL(1,1)(0,0) GegenbauerC(0,2,0)(n,0,(E a)/4)+3 N LaguerreL(1,2)(0,0) GegenbauerC(0,1,0)(n,0,(E a)/4))+1/6 π3 c12 δ3 G3 θ12 M6 r3 R3 S30 log3(C(logG(z) Qcos(z))))+M2 R x4 sin^-1(r)4 (1/6 π3 c12 δ3 G3 θ12 M6 N r3 R3 S30 LaguerreL(1,0)(0,0) GegenbauerC(0,1,0)(n,0,(E a)/4) log3(C(logG(z) Qcos(z)))+1/4 π2 c8 δ2 G2 θ8 M4 r2 R2 S20 log2(C(logG(z) Qcos(z))) (N2 LaguerreL(2,0)(0,0) GegenbauerC^(0,1,0)(n,0,(E a)/4)2+N2 LaguerreL(1,0)(0,0) GegenbauerC(0,2,0)(n,0,(E a)/4)+2 N LaguerreL(1,1)(0,0) GegenbauerC(0,1,0)(n,0,(E a)/4))+1/6 π c4 δ G θ4 M2 r R S10 log(C(logG(z) Qcos(z))) (N3 LaguerreL(3,0)(0,0) GegenbauerC^(0,1,0)(n,0,(E a)/4)3+3 N3 LaguerreL(2,0)(0,0) GegenbauerC(0,1,0)(n,0,(E a)/4) GegenbauerC(0,2,0)(n,0,(E a)/4)+N3 LaguerreL(1,0)(0,0) GegenbauerC(0,3,0)(n,0,(E a)/4)+3 N2 LaguerreL(2,1)(0,0) GegenbauerC^(0,1,0)(n,0,(E a)/4)2+3 N2 LaguerreL(1,1)(0,0) GegenbauerC(0,2,0)(n,0,(E a)/4)+3 N LaguerreL(1,2)(0,0) GegenbauerC(0,1,0)(n,0,(E a)/4))+1/24 (N4 LaguerreL(4,0)(0,0) GegenbauerC^(0,1,0)(n,0,(E a)/4)4+3 N4 LaguerreL(2,0)(0,0) GegenbauerC^(0,2,0)(n,0,(E a)/4)2+6 N4 LaguerreL(3,0)(0,0) GegenbauerC^(0,1,0)(n,0,(E a)/4)2 GegenbauerC(0,2,0)(n,0,(E a)/4)+4 N4 LaguerreL(2,0)(0,0) GegenbauerC(0,1,0)(n,0,(E a)/4) GegenbauerC(0,3,0)(n,0,(E a)/4)+N4 LaguerreL(1,0)(0,0) GegenbauerC(0,4,0)(n,0,(E a)/4)+4 N3 LaguerreL(3,1)(0,0) GegenbauerC^(0,1,0)(n,0,(E a)/4)3+12 N3 LaguerreL(2,1)(0,0) GegenbauerC(0,1,0)(n,0,(E a)/4) GegenbauerC(0,2,0)(n,0,(E a)/4)+4 N3 LaguerreL(1,1)(0,0) GegenbauerC(0,3,0)(n,0,(E a)/4)+6 N2 LaguerreL(2,2)(0,0) GegenbauerC^(0,1,0)(n,0,(E a)/4)2+6 N2 LaguerreL(1,2)(0,0) GegenbauerC(0,2,0)(n,0,(E a)/4)+4 N LaguerreL(1,3)(0,0) GegenbauerC(0,1,0)(n,0,(E a)/4))+1/24 π4 c16 δ4 G4 θ16 M8 r4 R4 S40 log4(C(logG(z) Qcos(z))))+O(x5)}, GegenbauerC[n, x] LegendreP [n, x] ZernikeR [n, m, r] LegendreP [n, m, x] HermiteH [n, x] JacobiP [n, a, b, x] LaguerreL [n, x] ChebyshevU [n, x] Hypergeometric0F1[a, z] Hypergeometric0F1[a, z] Hypergeometric2F1Regularized[a, b, c, z] ZernikeR[LegendreP [LaguerreL[λ n, D f z, g z (ψ^0 ρ m), I Exp[λ] ], x], m, r] 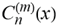 Tn(x) Cn(x) Pn(x) (
Tn(x) Cn(x) Pn(x) (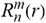 Hypergeometric1F1Regularized[a5,∂2(ρ6 n73)/(∂y ∂x) b,g8,exp(n)*6,δ σ2,ε θ3,Δ(α4)]) Hypergeometric1F1Regularized[a^5, D[ρ^6 n^73, y, x] b, g^8, Exp[n] 6, δ σ^2, ε θ^3, Δ α^4] 2F1 (P δ,P r Ω;ο ψ;γ)
Hypergeometric1F1Regularized[a5,∂2(ρ6 n73)/(∂y ∂x) b,g8,exp(n)*6,δ σ2,ε θ3,Δ(α4)]) Hypergeometric1F1Regularized[a^5, D[ρ^6 n^73, y, x] b, g^8, Exp[n] 6, δ σ^2, ε θ^3, Δ α^4] 2F1 (P δ,P r Ω;ο ψ;γ) 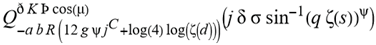 +N x LaguerreL(1,0)(0,0) GegenbauerC(0,1,0)(n,0,(E a)/4) 2F1 (P δ,P r Ω;ο ψ;γ)
+N x LaguerreL(1,0)(0,0) GegenbauerC(0,1,0)(n,0,(E a)/4) 2F1 (P δ,P r Ω;ο ψ;γ) 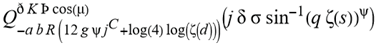 +1/2 N x2 (N LaguerreL(2,0)(0,0) GegenbauerC^(0,1,0)(n,0,(E a)/4)2+N LaguerreL(1,0)(0,0) GegenbauerC(0,2,0)(n,0,(E a)/4)+2 LaguerreL(1,1)(0,0) GegenbauerC(0,1,0)(n,0,(E a)/4)) 2F1 (P δ,P r Ω;ο ψ;γ)
+1/2 N x2 (N LaguerreL(2,0)(0,0) GegenbauerC^(0,1,0)(n,0,(E a)/4)2+N LaguerreL(1,0)(0,0) GegenbauerC(0,2,0)(n,0,(E a)/4)+2 LaguerreL(1,1)(0,0) GegenbauerC(0,1,0)(n,0,(E a)/4)) 2F1 (P δ,P r Ω;ο ψ;γ) 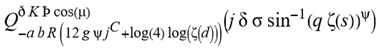 +1/6 N x3 (N2 LaguerreL(3,0)(0,0) GegenbauerC^(0,1,0)(n,0,(E a)/4)3+3 GegenbauerC(0,1,0)(n,0,(E a)/4) (N2 LaguerreL(2,0)(0,0) GegenbauerC(0,2,0)(n,0,(E a)/4)+LaguerreL(1,2)(0,0))+3 N LaguerreL(2,1)(0,0) GegenbauerC^(0,1,0)(n,0,(E a)/4)2+N (N LaguerreL(1,0)(0,0) GegenbauerC(0,3,0)(n,0,(E a)/4)+3 LaguerreL(1,1)(0,0) GegenbauerC(0,2,0)(n,0,(E a)/4))) 2F1 (P δ,P r Ω;ο ψ;γ)
+1/6 N x3 (N2 LaguerreL(3,0)(0,0) GegenbauerC^(0,1,0)(n,0,(E a)/4)3+3 GegenbauerC(0,1,0)(n,0,(E a)/4) (N2 LaguerreL(2,0)(0,0) GegenbauerC(0,2,0)(n,0,(E a)/4)+LaguerreL(1,2)(0,0))+3 N LaguerreL(2,1)(0,0) GegenbauerC^(0,1,0)(n,0,(E a)/4)2+N (N LaguerreL(1,0)(0,0) GegenbauerC(0,3,0)(n,0,(E a)/4)+3 LaguerreL(1,1)(0,0) GegenbauerC(0,2,0)(n,0,(E a)/4))) 2F1 (P δ,P r Ω;ο ψ;γ) 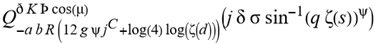 +1/24 N x4 (N3 LaguerreL(4,0)(0,0) GegenbauerC^(0,1,0)(n,0,(E a)/4)4+4 N2 LaguerreL(3,1)(0,0) GegenbauerC^(0,1,0)(n,0,(E a)/4)3+6 N GegenbauerC^(0,1,0)(n,0,(E a)/4)2 (N2 LaguerreL(3,0)(0,0) GegenbauerC(0,2,0)(n,0,(E a)/4)+LaguerreL(2,2)(0,0))+N (3 N2 LaguerreL(2,0)(0,0) GegenbauerC^(0,2,0)(n,0,(E a)/4)2+N (N LaguerreL(1,0)(0,0) GegenbauerC(0,4,0)(n,0,(E a)/4)+4 LaguerreL(1,1)(0,0) GegenbauerC(0,3,0)(n,0,(E a)/4))+6 LaguerreL(1,2)(0,0) GegenbauerC(0,2,0)(n,0,(E a)/4))+4 GegenbauerC(0,1,0)(n,0,(E a)/4) (N3 LaguerreL(2,0)(0,0) GegenbauerC(0,3,0)(n,0,(E a)/4)+3 N2 LaguerreL(2,1)(0,0) GegenbauerC(0,2,0)(n,0,(E a)/4)+LaguerreL(1,3)(0,0))) 2F1 (P δ,P r Ω;ο ψ;γ)
+1/24 N x4 (N3 LaguerreL(4,0)(0,0) GegenbauerC^(0,1,0)(n,0,(E a)/4)4+4 N2 LaguerreL(3,1)(0,0) GegenbauerC^(0,1,0)(n,0,(E a)/4)3+6 N GegenbauerC^(0,1,0)(n,0,(E a)/4)2 (N2 LaguerreL(3,0)(0,0) GegenbauerC(0,2,0)(n,0,(E a)/4)+LaguerreL(2,2)(0,0))+N (3 N2 LaguerreL(2,0)(0,0) GegenbauerC^(0,2,0)(n,0,(E a)/4)2+N (N LaguerreL(1,0)(0,0) GegenbauerC(0,4,0)(n,0,(E a)/4)+4 LaguerreL(1,1)(0,0) GegenbauerC(0,3,0)(n,0,(E a)/4))+6 LaguerreL(1,2)(0,0) GegenbauerC(0,2,0)(n,0,(E a)/4))+4 GegenbauerC(0,1,0)(n,0,(E a)/4) (N3 LaguerreL(2,0)(0,0) GegenbauerC(0,3,0)(n,0,(E a)/4)+3 N2 LaguerreL(2,1)(0,0) GegenbauerC(0,2,0)(n,0,(E a)/4)+LaguerreL(1,3)(0,0))) 2F1 (P δ,P r Ω;ο ψ;γ) 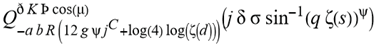 +O(x5) Hypergeometric0F1 Regularized[a, z] within this theoretical framework where adaptive evolution involves primarily quantum entropy learning machine to predict their macro-environment, and accordingly when the entropy of the ligand-receptor micro-environment with respect to the ultra low quantum packages behaves as the one of the key determinants of Quantum Turing Machine Homeopathy Evolutions. [41-89,92-187] These evolving systems have to be sufficiently robust and resistant to fluctuations for the transitions occurred when using default parameters in this parallel docking algorithm (named BiogenetoligandorolTM) which are set in the KNIME-web server as follows: (i) 24 inverse docking runs, (ii) evaluations per parallel docking run, (iii) population of the Roccustyrna individuals, (iv) maximum of 20 cluster small molecule top leaders on each parallel inverse docking run. For illustration, since Quantum Teleportation raises profound issues about the nature of reality, especially at the quantum level of a system that can have a more fundamental meaning than the system's objective reality I consider this specific phenomenological model, in which the rate of adaptive evolution reflected in the value of the QFT Loss Quantum Function (QLQF) which depends exponentially on the number of adaptable variables and also shows a power law dependence on the entropy of the environment related to the adaptable variables in biological terms of the number of genes or sites that are available for positive selection in a given evolving population at a given time which is itself proportional to the entropy of the environment and to the log of the effective population size. Thus, this Quantum Homeopathy Information or Knowledge is even more starkly, when we only concern ourselves with what can be known about the reality of a similar system; not its presumed objective (ontological) ‘reality-in-itself’ for this sequential screening experiment where an alternative dataset of similar geometric parameters are co-factored to improve the Euclidean Space between the Roccustyrna and (PDB code: 6xs6) protein interacting chains without significantly losing binding site accuracy. This is named EuTHTS Euclidean Topology Virtual Screening and consists of: (i) 120 docking runs, (ii) evaluations per docking run, (iii) population of Roccustyrna individuals, (iv) maximum of 20 cluster leaders on each docking run. The validation of these docking experiments was performed on DockThor CPU nodes of the Dumont supercomputers, each one containing two processors Intel Xeon E5-2695v2 Ivy Bridge (12c@2,4 GHz) and 64 GB of RAM memory. The validation of these docking experiments was achieved through the re-docking of the non-covalent Roccustyrna ligand present in the 6W63 (Mpro) protein complexes using standard configuration which is successfully predicting co-crystallized conformations of each inserted complex as an ingenious system of using entangled states through the engineering of these QFT biologically inspired Quantum Homeopathy Drug Designing technologies. [2-100,122-195] Certainly, these similar Euclid Special Space solvable models that are taken advantage the homeopathy fact of the less the likelihood of material presence in the remedy, or, in homeopathic parlance, the higher the potency would guarantee a viability of fitting many measured N−plets of levels E, experimental values of n by the suitable N−plets, in a similar vein. The Euclid Spaced -index data structure [4-87.99-193] is leveraged in conjunction with the Burrows–Wheeler transformation as a Quantum advantage when using thermodynamic measures of performance that has been quantified for theirs principle’s applicability to realistic biological structures demonstrated here and are based on the sum of the following terms from the MMFF94S force field. [9-100,133-195] This particular case of 20 steps for 11dimensions seems to be particularly suited to admit an anti-de Sitter ChernSimons formulation in future generalized relativity applications of supergravity for Quantum Homeopathy Frame Representations in more advanced pharmacophore merging schemes. [11–90,112-195] As shown, in this super anti de Sitter group, the OSp (32) supergroup is generalized in this path from QFT’s Hidden Quantum Homeopathy Information as a Quantum Black Hole paradigm for the generation of unique drug designs with the highest docking energies of negative binding values when compared to other known SARS - CoV - 2 antiviral. [22-103,54-115] This Entanglement model of homeopathy translations is a quantum hypergeometric example of generalized entanglement predicted by weak quantum theory revealing its greatest strength and promise, not yet touched upon. [2-53,60-116] It has always been an intuition of Wolfgang Pauli, one of the founders of modern QM, that physics will only be complete if it has incorporated consciousness into a final theory of matter [33-120]. Until now, quantum algorithms to simulate QFT [13,14-139] have mainly used lattices. [2-73,100-140] Conversely, this transactional interpretation of quantum mechanics for each task (binding site prediction, binding pose generation, de novo molecule generation, linker design, and binding affinity prediction), including the problem setup, representative methods, datasets, and evaluation metrics could act as a qualitative and a non-local metaphor for quantum homeopathy and as based on quantum theory could be also resulting to more novel fuzzy sphere formations ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)),(Figures S(1-99)) and Quantum Deep Geometry generated drug designing processes providing explanations of the success of quantum homeopathic therapeutic approaches and an equivocal evidence for the efficacy of homeopathy [18-140] in quantum entanglement in general. [2-23,72-144] This is an advantage within this quantum homeo-formalism, because differential operators are formally ill-defined [14-148], although recent developments have shown that good results can still be achieved [26-159] also for other macroentanglement formation project. [14-149] Τhese macroentanglement formations for Quantum Homeopathy based chemical geometrics would be far more useful for drug designers and researchers when trying to explore generalized entanglement as a vehicle for geometry processes. [6–89-150] In this situation, where quantum similarities between famous double-slit experiment of quantum physics, and quantum information processing are proposed docking free energy expectation values proving this apparent relationship between quantum homeopathic efficacy and QFT to QM reductions which could be explained in general terms of information loss from small molecule quantum superposition states. [34-98,94-158] The next step was to incorporate geometrical consciousness into this Quantum Homeopathy Model (Maths1-12,13a,13b,13c,13d,13e,13f,13g, 13h,13i,13j,13k), ((Schematics1,2, (Supplementary Material METHODS AND MATERIALS)) (Eqs.1-400), ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)),(Supplement Material FUNCTIONS.1-25), (Maths14a,14b,14c,14d,14e, 14f,14g,15,16,17,18, 19a,19b,19c, 19d,19e,19f,19g,19h,20a,20b,20c,20d,20e,20f1,20f2,20f3, 20g,20h,20i,20j,21a,21b,21c, 21d,21e,21f,21g, 21h,21i,21j,22a,22b,22c,22d,,22e,,22f,22g), (Cluster of BIOGENEA_ CONSENSUS_Eqs.1-26), and ((Figures S(1- 133)), (OUTPUTs1-3)), (Supplementary Material METHODS AND MATERIALS (2), MasterEquations1-34), Supplementary Material METHODS AND MATERIALS (1), (2)),(Ic1a), (Ic1b), (Ic1c), (Ic2a), (Ic2b), (Ic2c), (Ic2d,e,f,g,h,g,k,l,m,o,p,q,r), (Diagramm1, Diagramm2, Diagramm3), (Maths1-19) (Ic3a), (Ic3b) (Ic3c), (Ic3d), (Ic3d), (Ic3e), (Ic3f), (Ic3g), (Ic3h), (Ic3i), (Ic3j), (Ic3k) after translating this intimate relationship between water memory and protein folding issues, between drug substances in ultra low concentrations and the quantum geometrics which is also a complementary one [21-99,101-159] when generating hypergeometric druggable fuzzy spheres (Supplementary Material METHODS AND MATERIALS Figures S(1-100)), ((Iconics1-4), (Eqs1-400), and (Schematics1a,1b,1c,1d, 1e,1f,1g,1h,1i,1j,2a,2b,2c,2d,2e), (I-VI) Supplementary Material METHODS AND MATERIALS)) interacted with negative binding free energies accordingly. These functions can be deciphered through DockThor docking energy evaluations of the hydrophobic interactions among neighbored side-chains of an unfolded thermodynamic metastable state with great accuracy of the prediction. [1-195] Therefore, Ι suggest that the Practical consequences of this computational entanglement model for this quantum homeopathic research for mathematical chemistry practice could be more extended to new Generalised Entanglement Theoretical Drug Designing Models for understanding the effects of complementary and alternative medicine including Nano-and molecular events, thermodynamics/entropy, Quantum mechanisms and genetic instructions with the following inputs: ACE2 and AT1R receptors, Remdesivir’s therapeutic mechanism for the COVID-19, Candesartan’s role in ameliorating COVID-19 cytokine storm including Telmisartan’s molecular mechanism as tentative angiotensin receptor blocker and therapeutic agent for COVID-19. [28-137,150-189] To be made practical, these theoretical quantum algorithms are expected to require both significant refinement and effort in translation in the near term, since these refinements could include (i) recasting them for WOLFRAM devices that use the VQA, QAOA or QA frameworks for (ii) integrating greater biological context of the generalized entangled state (a) depends on the proper production process and is intimately connected to the ritual of remedy producing. [28-137,150-169] (OUTPUTs1-3), (Ic1a), (Ic1b), (Ic1c), (Ic2a), (Ic2b), (Ic2c), (Ic2d), (Ic2e), (Ic2f), (Ic2g),(Ic2h), (Ic2c), (Ic2g), (Ic2k), (Ic2l), (Ic2m),(Ic2n),(Ic2o),(Ic2p),(Ic2q),(Ic2r), (Ic3a), (Ic3b) (Ic3c), (Ic3d), (Ic3d), (Ic3e), (Ic3f), (Ic3g), (Ic3h), (Ic3i), (Ic3j), (Ic3k), (Iconics4-6), and ((Iconics1-6), (Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS)) Therefore, I hope that this work will stimulate the development of new directions in the study of the AT1R drug universe and other drug designing efforts. [40-162] Although it is less conclusive due to a large finite-size effect, we show that certain entanglement phases seem to exist even when a random state has permutation or translation symmetry for a non-vanishing boundary solution in a five-dimensional CS supergravity Quantum Foam [20-163] for all the poly-tetrahedron shaped pharmacophoric ligand provided here in the form of a Turing Machine Ruled Quantum Function which can carry U (1) charge among the unknown characteristics revealed in the cluster of the Gissitorviffirna_TM, Roccustyrna_gs, Roccustyrna_fr, and Roccustyrna_consv Quantum-computational structures. These AI-Quantum Homeopathy Entropy Negativities (QHEN) generated the highest total free energy values of negative docking energy factors and will be generalized into Spheroidal Wave Equations for Avogadro’s Number SphericalHarmonicY, ChebyshevT, and LegendreP Fuzzy Sphere-like small molecules, (Ic1a), (Ic1b), (Ic1c), (Ic2a), (Ic2b), (Ic2c), (Ic3a), (Ic3b) (Ic3c), (Ic3d), (Ic3d), (Ic3e), (Ic3f), (Ic3g), (Ic3h), (Ic3i), (Ic3j), (Ic3k) geometrical descriptors and (Eqs.1-400) ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)),which are ordinary differential equations (Eqs1-325), ((Iconics1-4), (Eqs1-400), and (Schematics1a,1b,1c,1d,1e,1f,1g,1h,1i,1j,2a,2b,2c,2d,2e), (I-VI) Supplementary Material METHODS AND MATERIALS)) with two regular singular points and one confluently irregular singular point. By incorporating Quantum Biological Evolution and QuantumTuring Deep Learning processes into this (Ic0a), (Ic0b), (Ic0c), (Ic1a), (Ic1b), (Ic1c), (Ic1d), (Ic2a), (Ic2b), (Ic2c), (Ic3a1), (Ic3a2), (Ic3b1), (Ic3b2), (Ic3c), (Ic3d), (Ic3d), (Ic3e), (Ic3f), (Ic3g), (Ic3h), (Ic3i), (Ic3j), and (Ic3k) Quantum Homeopathy Framework, this quantum homeopath of negative docking energy theory paradigm implying that this emergence of complexity with life which is an inherent feature of learning occurs throughout the history of the universe. With respect to these Quantum Homeopathy logic advantages, this led us to the Turing Machine Ruled Generalizations of Genetic, Homeopathic, and Clinical Data to Chemical Proteomic based Graph Translations (Ic3a), (Ic3c) as inputs into (Ic2e,f,g,h,g,k,l,m,o,p,q,r,q) these Quantum Circuit Generative Models of various number of qubits and quantum circuit layers discussed from above can yield operational docking energy advantages such as sample complexity advantages in particular which could have a great impact in future drug designing fields for the computer-aided designing of Hidden Druggable Pharmacophoric Subgroups and Small Molecule Triangularizations of N-{[(2S)-3-(aminomethyl)-2- [(1R,2S)- 2-methyldiaziridin-1-yl]-1,3- diazetidin-1-yl]({[(E)-{[(E)- (aminomethylidene)amino] methylidene}amino]amino})aziridin-1-yl-λ⁵-phosphanyl}-3-{5-[(1E)-[2-(aminomethyl)-2-methylhydrazin-1-ylidene]methyl]-3,4-dihydroxyfuran-2-yl}-2-methyl-5-sulfanylidene-1,2,3,4-tetrazole-1-carboxa, {[(1S,2S,3S)-2-(4-amino-5-sulfanylidene-4H- 1,2,4-triazol-3-yl)-2-carboximidoyl-3-fluoro -1-oxo-1λ⁵-phosphiran-1-yl]amino}[(Z)- ethylideneamino]iminomethanium, (6R)-6-[(3S)-2-[(1Z)-amino({1H- 1,3-benzodiazol-2-yl[(3R)-3-ethyloxolan-3-yl]methylidene})-λ⁵- phosphanyl]-5-sulfanylidene-1,2,4- triazolidin-3-yl]-4-oxa-1-azabicyclo[3.1.0]hexane-3-thione, {1-[(R)-[(1S,3R)-3-[(R)- amino(carbamothioylamino)methyl]diaziridin-1- yl] ({6-oxo-2-[(2S,5R)-3,4,5-trifluoro-2,5- dihydrofuran-2-yl]-6,7-dihydro-1H-purin-8- yl}amino)phosphoroso] -1H-azirin-2-yl}thiourea, and (2R,4R,5S)-2-amino-3-{4-amino- 1-[(2R,3R,4R,5R)-5-[(2R)-3- (aminomethyl)-2-(2-methyldiaziridin-1-yl)-1,3- diazetidin-1-yl]-3,4-dihydroxyoxolan-2-yl]-5-sulfanylidene-4,5-dihydro-1H-1,2,4-triazole-3-carbonyl}-1-[(2S)-1-[(3R)-2-amino-1-methyl-5-sulfanylidene-1,2,4-triazolidin-3-yl]propan-2-yl]-octahydro-1H-purin-6-one (Highlights Supplementary Material, Maths14a,14b,14c,14d,14e,14f,14g,19a,19b,19c, 19d,19e,19f,19g,19h,20a,20b,20c,20d, 20e,20f1,20f2,20f3,20g, 20h,20i,20j,21a,21b,21c,21d,21e,21f,21g,21h,21i,21j,22a,22b,22c, 22d,,22e,,22f,22g), and (Cluster of BIOGENEA_ CONSENSUS_Eqs.1-26), (Diagramm1, Diagramm2, Diagramm3), (Highlights Supplementary Material, Maths1-21), and (Supplementary Material METHODS AND MATERIALS Figures S(1- 133)), (Ic2e,f,g,h,g,k,l,m,o,p,q,r), ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)),and ((SI APPENDIX I Supplementary Material), (TableS1), (TableS2), (TableS3), (Figures S1), (Figure S2a), (Figure S2b), (Figure S2c), (Figure S2d), (Figure S2d), (Figure S2e), (Figure S3a), (Figure S3b), (Figure S3c), (Figure S3d), (Figure S3e), (Figure S3f), (Figure S3g), (Figure S3h), (Cluster Docking Energy TableS1), (SI Appendix I), (Cluster Docking Energy TableS2),SI Appendix I), (Docking Energy TableS1), (SI Appendix I), (Docking Energy TableS2), (SI Appendix I), (Docking Energy TableS3), (SI Appendix I)). With respect to these Quantum Homeopathy logic advantages, further experimental work is necessary to assess whether these diagonal-matrix potential advantages in variational (Ic2e,f,g,h,g,k,l,m,o,p,q,r) Quantum Circuit Generative Models of various number of qubits and quantum circuit layers for the Roccustyrna peptidemimetic Small Molecule Drug Discoveries discussed from above can yield operational docking energy advantages such as sample complexity advantages in particular which could have a great impact in future drug designing fields..These novel applications in the field of structure-based binding affinity prediction will have to address the points of criticism directed toward existing methods, therefore I will let your imaginations roam far outside the M87 supermassive rotating black hole in this structure-based molecular modeling section since only Avogadro’s Quantum Uncertainity relations between Entangled Space-Time backgrounds and Euclid Special Meta-Logic-Black Hole-Chemical Spaces (Highlights Supplementary Material, Maths19a,19b,19c,19d, 19e,19f,19g,19h,20a,20b,20c,20d,20e,20f1,20f2,20f3,20g, 20h,20i,20j,21a,21b,21c,21d,21e,21f,21g,21h, 21i,21j,22a,22b,22c,22d,,22e,,22f,22g), and (Supplementary Material METHODS AND MATERIALS Figures S(1- 133)), (OUTPUTs1-3)), (Ic1a), (Ic1b), (Ic1c), (Ic2a), (Ic2b), (Ic2c), (Ic2d), (Ic2e), (Ic2f), (Ic2g),(Ic2h), (Ic2c), (Ic2g), (Ic2k), (Ic2l), (Ic2m),(Ic2n),(Ic2o),(Ic2p),(Ic2q),(Ic2r), (Ic3a), (Ic3b) (Ic3c), (Ic3d), (Ic3d), (Ic3e), (Ic3f), (Ic3g), (Ic3h), (Ic3i), (Ic3j), (Ic3k), ((Iconics4-6), (Supplementary Material METHODS AND MATERIALS)) for which the full Schwarzschild metric is required could be able of translating rare entropy signatures from Homeopathy Substances into 3D macromolecular structure representations for rational drug design, emphasizing to the most recent developments in both predictive and generative deep-learning methods.
+O(x5) Hypergeometric0F1 Regularized[a, z] within this theoretical framework where adaptive evolution involves primarily quantum entropy learning machine to predict their macro-environment, and accordingly when the entropy of the ligand-receptor micro-environment with respect to the ultra low quantum packages behaves as the one of the key determinants of Quantum Turing Machine Homeopathy Evolutions. [41-89,92-187] These evolving systems have to be sufficiently robust and resistant to fluctuations for the transitions occurred when using default parameters in this parallel docking algorithm (named BiogenetoligandorolTM) which are set in the KNIME-web server as follows: (i) 24 inverse docking runs, (ii) evaluations per parallel docking run, (iii) population of the Roccustyrna individuals, (iv) maximum of 20 cluster small molecule top leaders on each parallel inverse docking run. For illustration, since Quantum Teleportation raises profound issues about the nature of reality, especially at the quantum level of a system that can have a more fundamental meaning than the system's objective reality I consider this specific phenomenological model, in which the rate of adaptive evolution reflected in the value of the QFT Loss Quantum Function (QLQF) which depends exponentially on the number of adaptable variables and also shows a power law dependence on the entropy of the environment related to the adaptable variables in biological terms of the number of genes or sites that are available for positive selection in a given evolving population at a given time which is itself proportional to the entropy of the environment and to the log of the effective population size. Thus, this Quantum Homeopathy Information or Knowledge is even more starkly, when we only concern ourselves with what can be known about the reality of a similar system; not its presumed objective (ontological) ‘reality-in-itself’ for this sequential screening experiment where an alternative dataset of similar geometric parameters are co-factored to improve the Euclidean Space between the Roccustyrna and (PDB code: 6xs6) protein interacting chains without significantly losing binding site accuracy. This is named EuTHTS Euclidean Topology Virtual Screening and consists of: (i) 120 docking runs, (ii) evaluations per docking run, (iii) population of Roccustyrna individuals, (iv) maximum of 20 cluster leaders on each docking run. The validation of these docking experiments was performed on DockThor CPU nodes of the Dumont supercomputers, each one containing two processors Intel Xeon E5-2695v2 Ivy Bridge (12c@2,4 GHz) and 64 GB of RAM memory. The validation of these docking experiments was achieved through the re-docking of the non-covalent Roccustyrna ligand present in the 6W63 (Mpro) protein complexes using standard configuration which is successfully predicting co-crystallized conformations of each inserted complex as an ingenious system of using entangled states through the engineering of these QFT biologically inspired Quantum Homeopathy Drug Designing technologies. [2-100,122-195] Certainly, these similar Euclid Special Space solvable models that are taken advantage the homeopathy fact of the less the likelihood of material presence in the remedy, or, in homeopathic parlance, the higher the potency would guarantee a viability of fitting many measured N−plets of levels E, experimental values of n by the suitable N−plets, in a similar vein. The Euclid Spaced -index data structure [4-87.99-193] is leveraged in conjunction with the Burrows–Wheeler transformation as a Quantum advantage when using thermodynamic measures of performance that has been quantified for theirs principle’s applicability to realistic biological structures demonstrated here and are based on the sum of the following terms from the MMFF94S force field. [9-100,133-195] This particular case of 20 steps for 11dimensions seems to be particularly suited to admit an anti-de Sitter ChernSimons formulation in future generalized relativity applications of supergravity for Quantum Homeopathy Frame Representations in more advanced pharmacophore merging schemes. [11–90,112-195] As shown, in this super anti de Sitter group, the OSp (32) supergroup is generalized in this path from QFT’s Hidden Quantum Homeopathy Information as a Quantum Black Hole paradigm for the generation of unique drug designs with the highest docking energies of negative binding values when compared to other known SARS - CoV - 2 antiviral. [22-103,54-115] This Entanglement model of homeopathy translations is a quantum hypergeometric example of generalized entanglement predicted by weak quantum theory revealing its greatest strength and promise, not yet touched upon. [2-53,60-116] It has always been an intuition of Wolfgang Pauli, one of the founders of modern QM, that physics will only be complete if it has incorporated consciousness into a final theory of matter [33-120]. Until now, quantum algorithms to simulate QFT [13,14-139] have mainly used lattices. [2-73,100-140] Conversely, this transactional interpretation of quantum mechanics for each task (binding site prediction, binding pose generation, de novo molecule generation, linker design, and binding affinity prediction), including the problem setup, representative methods, datasets, and evaluation metrics could act as a qualitative and a non-local metaphor for quantum homeopathy and as based on quantum theory could be also resulting to more novel fuzzy sphere formations ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)),(Figures S(1-99)) and Quantum Deep Geometry generated drug designing processes providing explanations of the success of quantum homeopathic therapeutic approaches and an equivocal evidence for the efficacy of homeopathy [18-140] in quantum entanglement in general. [2-23,72-144] This is an advantage within this quantum homeo-formalism, because differential operators are formally ill-defined [14-148], although recent developments have shown that good results can still be achieved [26-159] also for other macroentanglement formation project. [14-149] Τhese macroentanglement formations for Quantum Homeopathy based chemical geometrics would be far more useful for drug designers and researchers when trying to explore generalized entanglement as a vehicle for geometry processes. [6–89-150] In this situation, where quantum similarities between famous double-slit experiment of quantum physics, and quantum information processing are proposed docking free energy expectation values proving this apparent relationship between quantum homeopathic efficacy and QFT to QM reductions which could be explained in general terms of information loss from small molecule quantum superposition states. [34-98,94-158] The next step was to incorporate geometrical consciousness into this Quantum Homeopathy Model (Maths1-12,13a,13b,13c,13d,13e,13f,13g, 13h,13i,13j,13k), ((Schematics1,2, (Supplementary Material METHODS AND MATERIALS)) (Eqs.1-400), ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)),(Supplement Material FUNCTIONS.1-25), (Maths14a,14b,14c,14d,14e, 14f,14g,15,16,17,18, 19a,19b,19c, 19d,19e,19f,19g,19h,20a,20b,20c,20d,20e,20f1,20f2,20f3, 20g,20h,20i,20j,21a,21b,21c, 21d,21e,21f,21g, 21h,21i,21j,22a,22b,22c,22d,,22e,,22f,22g), (Cluster of BIOGENEA_ CONSENSUS_Eqs.1-26), and ((Figures S(1- 133)), (OUTPUTs1-3)), (Supplementary Material METHODS AND MATERIALS (2), MasterEquations1-34), Supplementary Material METHODS AND MATERIALS (1), (2)),(Ic1a), (Ic1b), (Ic1c), (Ic2a), (Ic2b), (Ic2c), (Ic2d,e,f,g,h,g,k,l,m,o,p,q,r), (Diagramm1, Diagramm2, Diagramm3), (Maths1-19) (Ic3a), (Ic3b) (Ic3c), (Ic3d), (Ic3d), (Ic3e), (Ic3f), (Ic3g), (Ic3h), (Ic3i), (Ic3j), (Ic3k) after translating this intimate relationship between water memory and protein folding issues, between drug substances in ultra low concentrations and the quantum geometrics which is also a complementary one [21-99,101-159] when generating hypergeometric druggable fuzzy spheres (Supplementary Material METHODS AND MATERIALS Figures S(1-100)), ((Iconics1-4), (Eqs1-400), and (Schematics1a,1b,1c,1d, 1e,1f,1g,1h,1i,1j,2a,2b,2c,2d,2e), (I-VI) Supplementary Material METHODS AND MATERIALS)) interacted with negative binding free energies accordingly. These functions can be deciphered through DockThor docking energy evaluations of the hydrophobic interactions among neighbored side-chains of an unfolded thermodynamic metastable state with great accuracy of the prediction. [1-195] Therefore, Ι suggest that the Practical consequences of this computational entanglement model for this quantum homeopathic research for mathematical chemistry practice could be more extended to new Generalised Entanglement Theoretical Drug Designing Models for understanding the effects of complementary and alternative medicine including Nano-and molecular events, thermodynamics/entropy, Quantum mechanisms and genetic instructions with the following inputs: ACE2 and AT1R receptors, Remdesivir’s therapeutic mechanism for the COVID-19, Candesartan’s role in ameliorating COVID-19 cytokine storm including Telmisartan’s molecular mechanism as tentative angiotensin receptor blocker and therapeutic agent for COVID-19. [28-137,150-189] To be made practical, these theoretical quantum algorithms are expected to require both significant refinement and effort in translation in the near term, since these refinements could include (i) recasting them for WOLFRAM devices that use the VQA, QAOA or QA frameworks for (ii) integrating greater biological context of the generalized entangled state (a) depends on the proper production process and is intimately connected to the ritual of remedy producing. [28-137,150-169] (OUTPUTs1-3), (Ic1a), (Ic1b), (Ic1c), (Ic2a), (Ic2b), (Ic2c), (Ic2d), (Ic2e), (Ic2f), (Ic2g),(Ic2h), (Ic2c), (Ic2g), (Ic2k), (Ic2l), (Ic2m),(Ic2n),(Ic2o),(Ic2p),(Ic2q),(Ic2r), (Ic3a), (Ic3b) (Ic3c), (Ic3d), (Ic3d), (Ic3e), (Ic3f), (Ic3g), (Ic3h), (Ic3i), (Ic3j), (Ic3k), (Iconics4-6), and ((Iconics1-6), (Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS)) Therefore, I hope that this work will stimulate the development of new directions in the study of the AT1R drug universe and other drug designing efforts. [40-162] Although it is less conclusive due to a large finite-size effect, we show that certain entanglement phases seem to exist even when a random state has permutation or translation symmetry for a non-vanishing boundary solution in a five-dimensional CS supergravity Quantum Foam [20-163] for all the poly-tetrahedron shaped pharmacophoric ligand provided here in the form of a Turing Machine Ruled Quantum Function which can carry U (1) charge among the unknown characteristics revealed in the cluster of the Gissitorviffirna_TM, Roccustyrna_gs, Roccustyrna_fr, and Roccustyrna_consv Quantum-computational structures. These AI-Quantum Homeopathy Entropy Negativities (QHEN) generated the highest total free energy values of negative docking energy factors and will be generalized into Spheroidal Wave Equations for Avogadro’s Number SphericalHarmonicY, ChebyshevT, and LegendreP Fuzzy Sphere-like small molecules, (Ic1a), (Ic1b), (Ic1c), (Ic2a), (Ic2b), (Ic2c), (Ic3a), (Ic3b) (Ic3c), (Ic3d), (Ic3d), (Ic3e), (Ic3f), (Ic3g), (Ic3h), (Ic3i), (Ic3j), (Ic3k) geometrical descriptors and (Eqs.1-400) ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)),which are ordinary differential equations (Eqs1-325), ((Iconics1-4), (Eqs1-400), and (Schematics1a,1b,1c,1d,1e,1f,1g,1h,1i,1j,2a,2b,2c,2d,2e), (I-VI) Supplementary Material METHODS AND MATERIALS)) with two regular singular points and one confluently irregular singular point. By incorporating Quantum Biological Evolution and QuantumTuring Deep Learning processes into this (Ic0a), (Ic0b), (Ic0c), (Ic1a), (Ic1b), (Ic1c), (Ic1d), (Ic2a), (Ic2b), (Ic2c), (Ic3a1), (Ic3a2), (Ic3b1), (Ic3b2), (Ic3c), (Ic3d), (Ic3d), (Ic3e), (Ic3f), (Ic3g), (Ic3h), (Ic3i), (Ic3j), and (Ic3k) Quantum Homeopathy Framework, this quantum homeopath of negative docking energy theory paradigm implying that this emergence of complexity with life which is an inherent feature of learning occurs throughout the history of the universe. With respect to these Quantum Homeopathy logic advantages, this led us to the Turing Machine Ruled Generalizations of Genetic, Homeopathic, and Clinical Data to Chemical Proteomic based Graph Translations (Ic3a), (Ic3c) as inputs into (Ic2e,f,g,h,g,k,l,m,o,p,q,r,q) these Quantum Circuit Generative Models of various number of qubits and quantum circuit layers discussed from above can yield operational docking energy advantages such as sample complexity advantages in particular which could have a great impact in future drug designing fields for the computer-aided designing of Hidden Druggable Pharmacophoric Subgroups and Small Molecule Triangularizations of N-{[(2S)-3-(aminomethyl)-2- [(1R,2S)- 2-methyldiaziridin-1-yl]-1,3- diazetidin-1-yl]({[(E)-{[(E)- (aminomethylidene)amino] methylidene}amino]amino})aziridin-1-yl-λ⁵-phosphanyl}-3-{5-[(1E)-[2-(aminomethyl)-2-methylhydrazin-1-ylidene]methyl]-3,4-dihydroxyfuran-2-yl}-2-methyl-5-sulfanylidene-1,2,3,4-tetrazole-1-carboxa, {[(1S,2S,3S)-2-(4-amino-5-sulfanylidene-4H- 1,2,4-triazol-3-yl)-2-carboximidoyl-3-fluoro -1-oxo-1λ⁵-phosphiran-1-yl]amino}[(Z)- ethylideneamino]iminomethanium, (6R)-6-[(3S)-2-[(1Z)-amino({1H- 1,3-benzodiazol-2-yl[(3R)-3-ethyloxolan-3-yl]methylidene})-λ⁵- phosphanyl]-5-sulfanylidene-1,2,4- triazolidin-3-yl]-4-oxa-1-azabicyclo[3.1.0]hexane-3-thione, {1-[(R)-[(1S,3R)-3-[(R)- amino(carbamothioylamino)methyl]diaziridin-1- yl] ({6-oxo-2-[(2S,5R)-3,4,5-trifluoro-2,5- dihydrofuran-2-yl]-6,7-dihydro-1H-purin-8- yl}amino)phosphoroso] -1H-azirin-2-yl}thiourea, and (2R,4R,5S)-2-amino-3-{4-amino- 1-[(2R,3R,4R,5R)-5-[(2R)-3- (aminomethyl)-2-(2-methyldiaziridin-1-yl)-1,3- diazetidin-1-yl]-3,4-dihydroxyoxolan-2-yl]-5-sulfanylidene-4,5-dihydro-1H-1,2,4-triazole-3-carbonyl}-1-[(2S)-1-[(3R)-2-amino-1-methyl-5-sulfanylidene-1,2,4-triazolidin-3-yl]propan-2-yl]-octahydro-1H-purin-6-one (Highlights Supplementary Material, Maths14a,14b,14c,14d,14e,14f,14g,19a,19b,19c, 19d,19e,19f,19g,19h,20a,20b,20c,20d, 20e,20f1,20f2,20f3,20g, 20h,20i,20j,21a,21b,21c,21d,21e,21f,21g,21h,21i,21j,22a,22b,22c, 22d,,22e,,22f,22g), and (Cluster of BIOGENEA_ CONSENSUS_Eqs.1-26), (Diagramm1, Diagramm2, Diagramm3), (Highlights Supplementary Material, Maths1-21), and (Supplementary Material METHODS AND MATERIALS Figures S(1- 133)), (Ic2e,f,g,h,g,k,l,m,o,p,q,r), ((Iconics1-4), (Eqs1-400), Supplementary Material METHODS AND MATERIALS (1), (2)),and ((SI APPENDIX I Supplementary Material), (TableS1), (TableS2), (TableS3), (Figures S1), (Figure S2a), (Figure S2b), (Figure S2c), (Figure S2d), (Figure S2d), (Figure S2e), (Figure S3a), (Figure S3b), (Figure S3c), (Figure S3d), (Figure S3e), (Figure S3f), (Figure S3g), (Figure S3h), (Cluster Docking Energy TableS1), (SI Appendix I), (Cluster Docking Energy TableS2),SI Appendix I), (Docking Energy TableS1), (SI Appendix I), (Docking Energy TableS2), (SI Appendix I), (Docking Energy TableS3), (SI Appendix I)). With respect to these Quantum Homeopathy logic advantages, further experimental work is necessary to assess whether these diagonal-matrix potential advantages in variational (Ic2e,f,g,h,g,k,l,m,o,p,q,r) Quantum Circuit Generative Models of various number of qubits and quantum circuit layers for the Roccustyrna peptidemimetic Small Molecule Drug Discoveries discussed from above can yield operational docking energy advantages such as sample complexity advantages in particular which could have a great impact in future drug designing fields..These novel applications in the field of structure-based binding affinity prediction will have to address the points of criticism directed toward existing methods, therefore I will let your imaginations roam far outside the M87 supermassive rotating black hole in this structure-based molecular modeling section since only Avogadro’s Quantum Uncertainity relations between Entangled Space-Time backgrounds and Euclid Special Meta-Logic-Black Hole-Chemical Spaces (Highlights Supplementary Material, Maths19a,19b,19c,19d, 19e,19f,19g,19h,20a,20b,20c,20d,20e,20f1,20f2,20f3,20g, 20h,20i,20j,21a,21b,21c,21d,21e,21f,21g,21h, 21i,21j,22a,22b,22c,22d,,22e,,22f,22g), and (Supplementary Material METHODS AND MATERIALS Figures S(1- 133)), (OUTPUTs1-3)), (Ic1a), (Ic1b), (Ic1c), (Ic2a), (Ic2b), (Ic2c), (Ic2d), (Ic2e), (Ic2f), (Ic2g),(Ic2h), (Ic2c), (Ic2g), (Ic2k), (Ic2l), (Ic2m),(Ic2n),(Ic2o),(Ic2p),(Ic2q),(Ic2r), (Ic3a), (Ic3b) (Ic3c), (Ic3d), (Ic3d), (Ic3e), (Ic3f), (Ic3g), (Ic3h), (Ic3i), (Ic3j), (Ic3k), ((Iconics4-6), (Supplementary Material METHODS AND MATERIALS)) for which the full Schwarzschild metric is required could be able of translating rare entropy signatures from Homeopathy Substances into 3D macromolecular structure representations for rational drug design, emphasizing to the most recent developments in both predictive and generative deep-learning methods.Limitations of the Study
Declaration
Ethical Approval and Consent to Participate
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgements
Conflicts of Interest
Consent for publication
SI Appendices
 |
References
- Badanta, B. , García M.A., Jiménez A.E., Lucchetti G., de Diego-Cordero R. The use of complementary and traditional medicine for the treatment of patients with COVID-19: a systematic review. EXPLORE. 2023. [Google Scholar]
- Chaudhary, A. , Khurana A., et al. A review on the role of homoeopathy in epidemics with some reflections on COVID-19 (SARS-cov-2) Ind J Res Homoeopathy. 2020;14(2):100.
- Gosik, M.S. , Mendes M.F.X., da Silva Barbas D., do Cabo D.J.V., Strastis H., Takeuti I.S.D., et al. Medicines for the new coronavirus in the view of classical systemic homeopathy. Complement Ther Clin Pract. 2021;45:101482. [PMC free article] [PubMed] [Google Scholar] Worldometer Covid-19 Info, Coronavirus update (live) [cited , 2021], Available from: https://www.worldometers.info/coronavirus/. 20 February.
- Interactive web-based dashboard at the coronavirus Resource center at Johns Hopkins university [cited , 2021], Available from: https://coronavirus. jhu.edu/map.html. 20 February.
- Gesundheitsministerium Austria, Amtliches dashboard (Ministry of health Austria. Official dashboard) COVID-19 [Internet]. [cited , 2021], Available from: https://info.gesundheitsministerium.at/dashboard_Epidem.html?l=de. 20 February.
- R.T. Mathie, S.M. Lloyd, L.A. Legg, J. Clausen, S. Moss, J.R. Davidson, et al., Randomised placebo-controlled trials of individualised homeopathic treatment: systematic review and meta-analysis, Syst. Rev. 2014. [CrossRef]
- P. Weiermayer, M. Frass, T. Peinbauer, L. Ellinger, Evidence-based homeopathy and veterinary homeopathy, and its potential to help overcome the anti-microbial resistance problem - an overview, Schweiz. Arch. Tierheilkd. 162 (2020) 597–615. [CrossRef]
- J. Jacobs, Homeopathic prevention and management of epidemic diseases, Homeopathy 107 (2018) 157–160. [CrossRef]
- M. Frass, M. Linkesch, S. Banyai, G. Resch, C. Dielacher, T. Lobl, et al., Adjunctive homeopathic treatment in patients with severe sepsis: a randomized, double-blind, placebo-controlled trial in an intensive care unit, Homeopathy 94 (2005) 75–80. [CrossRef]
- S. Conde Diez, A. Viejo Casas, J.L. Garcia Rivero, J.C. Lopez Caro, F. Ortiz Portal, G. Diaz Saez, Impact of a homeopathic medication on upper respiratory tract infections in COPD patients: results of an observational, prospective study (EPOXILO), Respir. Med. 146 (2019) 96–105. [CrossRef]
- P.S. Chakraborty, C.D. Lamba, D. Nayak, M.D. John, D.B. Sarkar, A. Poddar, et al., Effect of individualized homoeopathic treatment in influenza like illness: a multicenter, single blind, randomized, placebo-controlled study, IJRH 7 (2013) 22–30.
- S. Prajapati, M. Sharma, A. Kumar, P. Gupta, G.V. Narasimha Kumar, An update on novel COVID-19 pandemic: a battle between humans and virus, Eur. Rev. Med. Pharmacol. Sci. 24 (2020) 5819–5829. [CrossRef]
- K.L.A. To, Y.Y.Y. Fok, Homeopathic clinical features of 18 patients in COVID-19 outbreaks in Hong Kong, Homeopathy 109 (2020) 146–162. Epub 2020 Jun 5. [CrossRef]
- M. Oberbaum, Will we miss the opportunity again? Homeopathy 109 (2020) 176–178. Epub 2020 Jun 5. [CrossRef]
- N. Basu, B.C. Das, S. Tandon, Interim management of COVID-19 by repurposed homeopathic medicines, Homeopathy 109 (2020) 182–183. Epub 2020 Jun 9. [CrossRef]
- S. Hahnemann, Organon of Medicine, sixth ed., B. Jain Publishers Ltd., New Delhi, 1994.
- Hui, DS. Epidemic and Emerging Coronaviruses (Severe Acute respiratory Syndrome and Middle East respiratory Syndrome). Clin Chest Med.2017 Mar;38 (1): 71-86. Epub 2016 Dec 16. PMID: 28159163; PMCID: PMC7131795. [CrossRef]
- Zhu N, Zhang D, Wang W, Li X, Yang B, Song J, ZhAoΨο X, Huang B, Shi W, Lu r, NiuP, Zhan F, Ma X, Wang D, Xu W, Wu G, GAoΨο GF, Tan W; China Novel Coronavirus Investigating and research Team. A Novel Coronavirus from Patients with Pneumonia in China,2019. N Engl J Med.2020 Feb 20;382 (8): 727-733. Epub 2020 Jan 24. PMID: 31978945; PMCID: PMC7092803. [CrossRef]
- Paraskevis D, Kostaki EG, Magiorkinis G, Panayiotakopoulos G, Sourvinos G, Tsiodras S. Full-genome evolutionary analysis of the novel corona virus (2019-nCoV) rejects the hypothesis of emergence as a result of a recent recombination event. InfectGenet Evol.2020 Apr;79: 104212. Epub 2020 Jan29. PMID: 32004758; PMCID: PMC7106301. [CrossRef]
- Hendriks-Balk, M. C., Tjon-Atsoi, M., Hajji, N. et al. LPS differentially affects vasoconstrictor responses: a potential role for RGS16?. J. Physiol. Biochem.65,71–83 (2009). [CrossRef]
- Nardi, D. T., Casare, M. S., Teixeira, L. G., Nascimento, N., & Nakaie, C. R. (2008). Effect of gamma radiation on the structural and biological properties of angiotensin II. International journal of radiation biology,84 (11),937–944. [CrossRef]
- Lu r, ZhAoΨο X, Li J, Niu P, Yang B, Wu H, Wang W, Song H, Huang B, Zhu N, Bi Y, Ma X, Zhan F, Wang L, Hu T, Zhou H, Hu Z, Zhou W, ZhAoΨο L, Chen J, Meng Y, Wang J, Lin Y, Yuan J, Xie Z, Ma J, Liu WJ, Wang D, Xu W, Holmes EC, GAoΨο GF, Wu G, Chen W, Shi W, Tan W. Genomic characterisation and epidemiology of 2019 novel coronavirus: implications for virus origins and receptor binding. Lancet.2020 Feb 22;395 (10224): 565-574. Epub 2020 Jan 30.PMID: 32007145; PMCID: PMC7159086. [CrossRef]
- Zhang, X. Measurement-based universal blind Quantum computation with minor resources. Quantum Inf Process 21,14 (2022). [CrossRef]
- Arndt, M. , Juffmann T., Vedral V. Quantum physics meets biology HFSP J.,3 (6) (2009), pp.386-400. [CrossRef]
- Nunn, A.V.W.; Guy, G.W.; Bell, J.D. Thermodynamics and Inflammation: Insights into Quantum Biology and Ageing. Quantum Rep. 2022, 4, 47–74. [Google Scholar] [CrossRef]
- Nunn, A.V.; Guy, G.W.; Bell, J.D. The Quantum mitochondrion and optimal health. Biochem. Soc. Trans.2016,44,1101–1110.
- Gilijamse JJ, Lock AJ, Bakker HJ. Dynamics of confined water molecules. Proc Natl Acad Sci U S A. 2005;102:3202–3207. [CrossRef]
- Rey, LR. Thermoluminescence of ultra-high dilutions of lithium chloride and sodium chloride. Phys A. 2003;323:67–74. [CrossRef]
- van Wijk R, Bosman S, van Wijk EP. Thermoluminescence in ultra-high dilution research. J Altern Complement Med. 2006;12:437–443. [CrossRef]
- Roberston, T. Homoeopathy and recent advances in science and semantics. Br Homoeopath J. 1949;39:27–36. [CrossRef]
- Walach, H. Entanglement model of homeopathy as an example of generalized entanglement predicted by weak quantum theory. Forsch Komplementarmed Klass Naturheilkd. 2003;10:192–200. [CrossRef]
- Weingärtner, O. The nature of the active ingredient in ultramolecular dilutions. Homeopathy. 2007;96:220–226. [CrossRef]
- Weingärtner, O. The homeopathic mechanism from the viewpoint of a quantum mechanical paradoxon. J Altern Complement Med. 2005;11:773–774. [CrossRef]
- Milgrom, L. Patient–Practitioner–Remedy (PPR) entanglement: Part 1. A qualitative, non-local metaphor for homeopathy based on quantum theory. Homeopathy. 2002;91:239–248. [CrossRef]
- McFadden, J.; Al-Khalili, J. The origins of Quantum biology. Proc. R. Soc. A 2018,474.
- Cramer, JG. The transactional interpretation of quantum mechanics. Rev Mod Phys. 1986;58:647–87.
- Walach, H. Entanglement model of homeopathy as an example of generalised entanglement predicted by weak quantum theory. Forsche Komplementarmed Klass Naturheilkd. 2003;10:192–200.
- Milgrom, LR. Patient–practitioner–remedy (PPR) entanglement. Part 5: Can homeopathic remedy reactions be outcomes of PPR entanglement? Homeopathy. 2004;93:94–8.
- Wooters, WK. Quantum entanglement as a quantifiable resource. Philos Trans R Soc London A. 1998;356:1717.
- Zeilinger, A. 2004. Quantum teleportation and the nature of reality. Available at: http://www.btgjapan.org/catalysts/anton.html.
- Walach, H. Entangled—and tied in knots! Practical consequences of an entanglement model for homeopathic research and practice. Homeopathy. 2005;94:96–9.
- Walach, H. Generalised entanglement: a new theoretical model for understanding the effects of complementary and alternative medicine. J Altern Complement Med. 2005;11:549–59.
- Walach, H. Magic of signs: a non-local interpretation of homeopathy. Br Hom J. 2000;89:127–40.
- Valente, D.; Brito, F.; Werlang, T. Quantum dissipative adaptation. Commun. Phys.2021,4,11.
- Marais, A.; Adams, B.; Ringsmuth, A.K.; Ferretti, M.; Gruber, J.M.; Hendrikx, R.; Schuld, M.; Smith, S.L.; Sinayskiy, I.; Kruger, T.P.J.; et al. The future of Quantum biology. J. R. Soc. Interface 2018,15,640.
- Pulselli, R.M.; Simoncini, E.; Tiezzi, E. Self-organization in dissipative structures: A thermodynamic theory for the emergence of prebiotic cells and their epigenetic evolution. Biosystems 2009,96,237–241.
- Prigogine, I.; George, C. The second law as a selection principle: The microscopic theory of dissipative processes in Quantum systems. Proc. Natl. Acad. Sci. USA 1983,80,4590–4594.
- Vattay, G.; Salahub, D.; Csabai, I.; Nassimi, A.; Kaufmann, S.A. Quantum Criticality at the Origin of Life. J. Phys. Conf. Ser 2015,626, 012023.
- Trixler, F. Quantum Tunnelling to the Origin and Evolution of Life. Curr. Org. Chem.2013,17,1758–1770.
- Trevors, J.T. Origin of microbial life: Nano-and molecular events, thermodynamics/entropy, Quantum mechanisms and genetic instructions. J. Microbiol. Methods 2011,84,492–495.
- Xin, H.; Sim, W.J.; Namgung, B.; Choi, Y.; Li, B.; Lee, L.P. Quantum biological tunnel junction for electron transfer imaging in live cells. Nat. Commun.2019,10,3245.
- Valente, D. Self-replication of a Quantum artificial organism driven by single-photon pulses. Sci. Rep.2021,11,16433.
- Ababneh, O.; Qaswal, A.B.; Alelaumi, A.; Khreesha, L.; Almomani, M.; Khrais, M.; Khrais, O.; Suleihat, A.; Mutleq, S.; Al-olaimat, Y.; et al. Proton Quantum Tunneling: Influence and Relevance to Acidosis-Induced Cardiac Arrhythmias/Cardiac Arrest. Pathophysiology 2021,28,400–436.
- Vattay, G.; Kauffman, S.; Niiranen, S. Quantum biology on the edge of Quantum chaοs. PLoS ONE 2014,9, e89017.
- Lloyd, J. A. , Spraggins, J. M., Johnston, M. V., & Laskin, J. (2006). Peptide ozonolysis: product structures and relative reactivities for oxidation of tyrosine and histidine residues. Journal of the American Society for Mass Spectrometry,17 (9),1289–1298. https://doi. org/10.1016/j. jasms.2006.05.00955.
- Mueller, S. On DNA Signatures, Their Dual-Use Potential for GMO Counterfeiting, and a Cyber-Based Security Solution. Front Bioeng Biotechnol.2019 Aug 7;7: 189. PMID: 31440503; PMCID: PMC6693310. [CrossRef]
- Ziebuhr, J. Molecular biology of severe acute respiratory syndrome coronavirus. Curr Opin Microbiol.2004 Aug;7 (4): 412-9. PMID: 15358261;PMCID: PMC7108451. [CrossRef]
- Susan, r. Iiss, Julian L. Leibowitz, Chapter 4-Coronavirus Pathogenesis, Editor (s): Karl Maramorosch, Aaron J. Shatkin, Frederick A. Murphy, Advances in Virus research, Academic Press, Volume 81,2011, pages 85-164, iSSN 0065-3527, iSBN 9780123858856, https://doi. org/10.1016/B978-0-12-385885-6.00009-2.
- Brian DA, Baric rS. Coronavirus genome structure and replication. Curr Top Microbiol Immunol.2005;287: 1-30. PMID: 15609507; PMCID: PMC7120446. [CrossRef]
- Rothlin, R. P. , Vetulli, H. M., Duarte, M., & Pelorosso, F. G. (2020). Telmisartan as tentative angiotensin receptor blocker therapeutic for COVID-19. Drug development research,81 (7),768–770. [CrossRef]
- Elkahloun, A. G. , & Saavedra, J. M. (2020). Candesartan could ameliorate the COVID-19 cytokine storm. Biomedicine & pharmacotherapie,131,110653. [CrossRef]
- Duarte, M. , Pelorosso, F., Nicolosi, L. N., Salgado, M. V., Vetulli, H., Aquieri, A., Azzato, F., Castro, M., Coyle, J., Davolos, I., Criado, I. F., Gregori, R., Mastrodonato, P., Rubio, M. C., Sarquis, S., Wahlmann, F., & Rothlin, R. P. (2021). Telmisartan for treatment of Covid-19 patients: An open multicenter randomized clinical trial. EClinicalMedicine,37,100962. [CrossRef]
- Siu KL, Chan CP, Kok KH, Chiu-Yat Woo P, Jin DY. Suppression of innate antiviral response by severe acute respiratory syndrome coronavirus M protein is mediated through the first transmembrane domain. Cell Mol Immunol.2014 Mar;11 (2): 141-9. Epub2014 Feb 10.PMID: 24509444; PMCID: PMC4003381. [CrossRef]
- Schoeman D, Fielding BC. Coronavirus envelope protein: current knowledge. Virol J.2019;16 (1): 69. 27 May; PMID: 31133031; PMCID: PMC6537279. [CrossRef]
- Al-Tawfiq JA, Al-Homoud AH, Memish ZA. Remdesivir as a possible therapeutic option for the COVID-19. Travel Med Infect Dis.2020 Mar-Apr;34: 101615. Epub 2020 Mar 5. PMID: 32145386; PMCID: PMC7129391. [CrossRef]
- Agostini ML, Andres EL, Sims AC, Graham rL, Sheahan TP, Lu X, Smith EC, Case JB, FengJY, Jordan r, ray AS, Cihlar T, Siegel D, Mackman rL, Clarke MO, Baric rS, Denison Mr. Coronavirus Susceptibility to the Antiviral Remdesivir (GS-5734) Is Mediated by the Viral Polymerase and the Proof reading Exoribonuclease. mBio.2018 Mar 6;9 (2): e00221-18. PMID: 29511076; PMCID: PMC5844999. [CrossRef]
- de Wit E, Feldmann F, Cronin J, Jordan r, Okumura A, Thomas T, Scott D, Cihlar T, Feldmann H. Prophylactic and therapeutic Remdesivir (GS-5734) treatment in the rhesus macaque model of MERS-CoV infection. Proc Natl Acad Sci U S A.2020 Mar 24;117 (12): 6771-6776. Epub 2020 Feb 13. PMID: 32054787; PMCID: PMC7104368. [CrossRef]
- Pilon AC, Valli M, Dametto AC, Pinto MEF, Freire rT, Castro-Gamboa I, Andricopulo AD, Bolzani VS. NuBBEDB: an updated database to uncover chemical and biological information from Brazilian biodiversity. Sci rep.2017 Aug 3;7 (1): 7215. PMID: 28775335. PMCID: PMC5543130. [CrossRef]
- Khot WY, Nadkar MY. The 2019 Novel Coronavirus Outbreak-A Global Threat. J AssocPhysicians India.2020 Mar;68 (3): 67-71. [PubMed]
- Zeng YM, Xu XL, He XQ, Tang SQ, Li Y, Huang YQ, Harypursat V, Chen YK. Comparative effectiveness and safety of ribavirin plus interferon-alpha, lopinavir/ritonavir plus interferon-alpha, and ribavirin plus lopinavir/ritonavir plus interferon-alpha in patients with mild to moderate novel coronavirus disease 2019: study protocol. Chin Med J (Engl).2020 May 5;133 (9): 1132-1134. PMID: 32149772; PMCID: PMC7213617. [CrossRef]
- McGraw PN, Menzinger M, Muñuzuri AP. Harmonic resonant excitation of flow distributed oscillation waves and Turing patterns driven at a growing boundary. Phys rev E Stat Nonlin SoftMatter Phys.2009 Aug; 80 (2 Pt 2): 026209. Epub 2009 Aug20. [CrossRef] [PubMed]
- Martinez, MA. Compounds with Therapeutic Potential against Novel respiratory 2019Coronavirus. Antimicrob Agents Chem other.2020 Apr 21;64 (5): e00399-20. PMID: 32152082; PMCID: PMC7179632. [CrossRef]
- Gordon CJ, Tchesnokov EP, Feng JY, Porter DP, Götte M. The antiviral compound Remdesivir potently inhibits RNA-dependent RNA polymerase from Middle East respiratory syndrome coronavirus. J Biol Chem.2020 Apr 10;295 (15): 4773-4779. Epub2020 Feb 24. PMID: 32094225; PMCID: PMC7152756. [CrossRef]
- Sheahan TP, Sims AC, Leist Sr, Schäfer A, Won J, Brown AJ, Montgomery SA, Hogg A, Babusis D, Clarke MO, Spahn JE, Bauer L, Sellers S, Porter D, Feng JY, Cihlar T, Jordan r, DenisonMr, Baric rS. Comparative therapeutic efficacy of Remdesivir and combination lopinavir, ritonavir, and interferon beta against MERS-CoV. Nat Commun.2020 Jan 10;11 (1): 222. PMID: 31924756; PMCID: PMC6954302. [CrossRef]
- Trott O, Olson AJ. AutoDock Vina: improving the speed and accuracy of docking with a new scoring function, efficient optimization, and multithreading. J Comput Chem.2010 Jan30;31 (2): 455-61. PMID: 19499576; PMCID: PMC3041641. [CrossRef]
- Van Meter, r. , Satoh, T., Ladd, T. D. et al. Path selection for Quantum repeater networks. Netw. Sci.3,82–95 (2013). [CrossRef]
- Xin T, Che L, Xi C, Singh A, Nie X, Li J, Dong Y, Lu D. Experimental Quantum Principal Component Analysis via Parameterized Quantum Functions. Phys rev Lett.2021 Ma [r1] 9;126 (11): 110502. [CrossRef] [PubMed]
- Henriques, AG. What Chern-Simons theory assigns to a point. Proc Natl Acad Sci U S A.2017 Dec 19;114 (51): 13418-13423. Epub 2017 Dec 5. PMID: 29208715; PMCID: PMC5754777. [CrossRef]
- Honda, M. Supersymmetric Solutions and Borel Singularities for N,2 Supersymmetric Chern-SimonsTheories. Phys rev Lett.2018 Jul 13; 121 (2): 021601. [CrossRef] [PubMed]
- Simón, J. Brane Effective Actions, Kappa-Symmetry and Applications. Living rev relativ.2012; 15 (1): 3. Epub 2012 Feb 27. PMID: 28179834; PMCID: PMC5256004. [CrossRef]
- Cavaglià A, Fioravanti D, Gromov N, Tateo R. Quantum spectral curve of the N,6 supersymmetric Chern-Simons theory. Phys rev Lett.2014 Jul 11; 113 (2): 021601. Epub 2014 Jul 11. [CrossRef] [PubMed]
- Mabkhot YN, Alatibi F, El-Sayed NN, Al-Showiman S, Kheder NA, Wadood A, rauf A, Bawazeer S, HaddaTB. Antimicrobial Activity of Some Novel Armed Thiophene Derivatives andPetra/Osiris/Molinspiration (POM) Analyses. Molecules.2016 Feb 17; 21 (2): 222. PMID: 26901173; PMCID: PMC6273311. [CrossRef]
- Khan T, Lawrence AJ, Azad I, Raza S, Joshi S, Khan Ar. Computational Drug Designing and Prediction of Important Parameters Using in-silico Methods-A review. Curr Comput Aided Drug Des.2019; 15 (5): 384-397. [CrossRef] [PubMed]
- Ulrich H, Pillat MM. CD147 as a Target for COVID-19 Treatment: Suggested Effects of Azithromycin and Stem Cell Engagement. Stem Cell rev rep.2020 Jun;16 (3): 434-440. PMID: 32307653; PMCID: PMC7167302. [CrossRef]
- Chan JF, Kok KH, Zhu Z, Chu H, To KK, Yuan S, Yuen KY. Genomic characterization of the 2019 novel human-pathogenic coronavirus isolated from a patient with atypical pneumonia after visiting Wuhan. Emerg Microbes Infect.2020 Jan 28;9 (1): 221-236. Erratumin: Emerg Microbes Infect.2020 Dec;9 (1): 540.PMID: 31987001; PMCID: PMC7067204. [CrossRef]
- Kong r, Yang G, Xue r, Liu M, Wang F, Hu J, Guo X, Chang S. COVID-19 Docking Server: a meta server for docking small molecules, peptides and antibodies against potential targets of COVID-19. Bioinformatics.2020 Dec 22;36 (20): 5109-5111. PMID: 32692801; PMCID: PMC7558834. [CrossRef]
- Shi Y, Zhang X, Mu K, Peng C, Zhu Z, Wang X, Yang Y, Xu Z, Zhu W. D3Targets-2019-nCoV: a webserver for predicting drug targets and for multi-target and multi-site based virtual screening against COVID-19. Acta Pharm Sin B.2020 Jul;10 (7): 1239-1248. Epub 2020 Apr 20.PMID: 32318328; PMCID: PMC7169934. [CrossRef]
- Camila Silva de Magalhães, Diogo Marinho Almeida, Helio José Correa Barbosa, Laurent Emmanuel Dardenne, A dynamic niching genetic algorithm strategy for docking highly flexible ligands. Information Sciences, Volume 289,2014, pages 206-224, iSSN 0020-0255, https://doi. org/10.1016/j. ins.2014.08.00.
- Van Loock P, Ladd TD, Sanaka K, Yamaguchi F, Nemoto K, Munro WJ, Yamamoto Y. Hybrid Quantum repeater using bright coherent light. Phys rev Lett.2006 Jun 23;96 (24): 240501. Epub 2006 Jun 19. [CrossRef] [PubMed]
- ZhAoΨο B, Chen ZB, Chen YA, Schmiedmayer J, Pan JW. robust creation of entanglement between remote memory qubits. Phys rev Lett.2007 Jun 15;98 (24): 240502. Epub 2007 Jun 15. [CrossRef] [PubMed]
- Santos KB, Guedes IA, Karl ALM, Dardenne LE. Highly Flexible Ligand Docking: Benchmarking of the DockThor Program on the LEADS-PEP Protein-Peptide Data Set. J Chem Inf Model.2020 Feb 24;60 (2): 667-683. Epub 2020 Jan 27. [CrossRef] [PubMed]
- Iheagwam FN, rotimi SO. Computer-Aided Analysis of Multiple SARS-CoV-2 Therapeutic Targets: Identification of Potent Molecules from African Medicinal Plants. Scientifica (Cairo).2020 Sep 12;2020: 1878410. PMID: 32963884; PMCID: PMC7492903. [CrossRef]
- Müller, S. Flexible heuristic algorithm for automatic molecule fragmentation: application to the UNIFAC group contribution model. J Cheminform.2019; 11: 57. Published 2019 Aug 20. [CrossRef]
- Shi J, Chen S, Lu Y, et al. An Approach to Cryptography Based on Continuous-Variable Quantum Neural Network. Sci rep.2020;10 (1): 2107. Published 2020 Feb 7. [CrossRef]
- Nalewajski, r. F. Quantum information descriptors and communications in molecules. JMath Chem 52,1292–1323 (2014). https://doi. org/10. [CrossRef]
- Giribet, Gaston & Merino, Nelson & Miskovic, Olivera & Zanelli, Jorge. (2014). Black hole solutions in Chern-Simons AdS supergravity. Journal of High Energy Physics.2014.10.1007/JHEP08 (2014) 083.
- Baianu, Ion & Glazebrook, James & Brown, ronald. (2009). Algebraic Topology Foundations of Supersymmetry and Symmetry Breaking in Quantum fields Theory and Quantum Gravity: A review. Symmetry, Integrability and Geometry: Methods and Applications.5.10.3842/SIGMA.2009.051.
- Horvathy, Peter. (1999). Topology of non-topological Chern-Simons vortices.
- Bañados, Máximo & Troncoso, ricardo & Zanelli, Jorge. (1996). Higher dimensional Chern-Simons supergravity. Physical review D.54. [CrossRef]
- Bañados, Máximo & Gomberoff, Andres. (1996). Black Hole Entropy in the Chern-Simons Formulation of 2,1 Gravity.
- Zizzi, P. Quantum Information Hidden in Quantum fieldss. Quantum Reports.2020; 2 (3): 459-488. [CrossRef]
- Nasser M, Salim N, Saeed F, Basurra S, Rabiu I, Hamza H, Alsoufi MA. Feature Reduction for Molecular Similarity Searching Based on Autoencoder Deep Learning. Biomolecules.2022; 12 (4):508. [CrossRef]
- Mohammed MEA. The percentages of SARS-CoV-2 protein similarity and identity with SARS-CoVand BatCoV raTG13 proteins can be used as indicators of virus origin. J Proteins Proteom.2021 Apr 9: 1-11. Epub ahead of print. PMID: 33850392; PMCID: PMC8033097. [CrossRef]
- Schwarzschild, K. Sitzungsberichte der Königlich Preußischenakademie der Wissenschaften; Berlin: 1916. Über das gravitationsfeld eines massenpunktes nach der einsteinschen theorie; pp.189–196.
- Reissner, H. Über die eigengravitation des elektrischen feldes nach der einsteinschen theorie. Ann. Phys.1916;355 (9):106–120.
- Nordström, G. On the energy of the gravitation field in Einstein's theory. Proc. K. Ned.akad. It., Ser. B, Phys. Sci.1918;20:1238–1245.
- Kerr, R.P. Gravitational field of a spinning mass as an example of algebraically special metrics. Phys. Rev. Lett.1963;11 (5):237.
- Newman, E.T. , Couch E., Chinnapared K., Exton A., Prakash A., Torrence R. Metric of a rotating, charged mass. J. Math. Phys.1965;6 (6):918–919.
- Vaidya, P. The external field of a radiating star in general relativity. Curr. Sci.1943;12 (6):183.
- Hawking, S. Black-hole evaporation. Nature.1974;248 (5443):30–31.
- Newman E.T., Adamo T. Kerr–Newman metric. Scholarpedia.2014;9 (10).
- Brauer, O. , Camargo H., Socolovsky M. Newman–Janis algorithm revisited. Int. J. Theor. Phys.2015;54 (1):302–314.
- Penrose, R. , Rindler W. Cambridge University Press; 1984. Spinors and Space-Time: Volume 1, Two-Spinor Calculus and Relativistic Fields, Vol.1.
- Nerozzi, A. A new approach to the Newman–Penrose formalism. arXiv:1109.4400 arXiv preprint.
- Meinel, R. 1st Karl Schwarzschild Meeting on Gravitational Physics. Springer; 2016. A physical derivation of the Kerr–Newman black hole solution; pp.53–61.
- Kramer, D. The Ernst function in general relativity. Czechoslov. J. Phys. B.1987;37 (3):350–358.
- Chou, Y.-C. A derivation of the Kerr metric by ellipsoid coordinate transformation. Int. J. Phys. Sci.2017;12 (11):130–136.
- Chou, Y.-C. A derivation of the Kerr–Newman metric using ellipsoid coordinate transformation. J. Appl. Phys. Sci. Int.2018;10 (3):144–150.
- Ibohal, N. Rotating metrics admitting non-perfect fluids. Gen. Relativ. Gravit.2005;37 (1):19–51.
- Ghosh, S.G. , Maharaj S.D. Radiating Kerr-like regular black hole. Eur. Phys. J. C.2015;75 (1):7.
- Eddington, A.S. A comparison of Whitehead's and Einstein's formula. Nature.1924;113 (2832):192.
- Finkelstein, D. Past-future asymmetry of the gravitational field of a point particle. Phys. Rev.1958;110 (4):965.
- Boehmer, C.G. , Hogan P.A. A Vaidya-type generalization of Kerr spacetime. Mod. Phys. Lett. A. 2017. [Google Scholar]
- Taub, A. High frequency gravitational radiation in Kerr–Schild space-times. Commun. Math. Phys.1976;47 (2):185–196.
- Reynolds, C. The spin of supermassive black holes. Class. Quantum Gravity.2013;30 (244004):17.
- Everitt C.F., DeBra D., Parkinson B., Turneaure J., Conklin J., Heifetz M., Keiser G., Silbergleit A., Holmes T., Kolodziejczak J. Gravity probe B: final results of a space experiment to test general relativity. Phys. Rev. Lett.2011;106 (22) .
- Petrov, A.Z. The classification of spaces defining gravitational fields. Gen. Relativ. Gravit.2000;32 (8):1665–1685.
- Erbin, H. Janis–Newman algorithm: simplifications and gauge field transformation. Gen. Relativ. Gravit.2015;47 (3):19.
- Bekenstein, J.D. Black holes and entropy. Phys. Rev. D.1973;7 (8):2333.
- Hawking, S.W. Particle creation by black holes. Commun. Math. Phys.1975;43 (3):199–220.
- Bardeen, J.M. , Carter B., Hawking S.W. The four laws of black hole mechanics. Commun. Math. Phys.1973;31 (2):161–170.
- Raine, D.J. , Thomas E.G. Imperial College Press; 2010. Black Holes: An Introduction.
- Page, D.N. Hawking radiation and black hole thermodynamics. New J. Phys.2005;7 (1):203.
- Williams, D. Pluto fact sheet, NASA.2015. https://nssdc.gsfc.nasa.gov/planetary/factsheet/plutofact.html retrieved from.
- Iorio, L. Constraints on the location of a putative distant massive body in the solar system from recent planetary data. Celest. Mech. Dyn. Astron.2012;112 (2):117–130.
- Faber, A. ,akiyama K., Alberdi A., Alef W., Asada K., Azulay R., Baczko A.-K., Ball D., Baloković M., Barrett J. First M87 event horizon telescope results. I. The shadow of the supermassive black hole. Astrophys. J. Lett. 2019;875 (1).
- Hawking, S. Gravitationally collapsed objects of very low mass. Mon. Not. R. Astron. Soc.1971;152 (1):75–78.
- Zolfaghari Emameh, r., Eftekhari, M., Nosrati, H. et al. Identification and characterization of a silent mutation in RNA binding domain of N protein coding gene fromSARS-CoV-2. BMC res Notes 14,10 (2021). [CrossRef]
- Neuman BW, Kiss G, Kunding AH, Bhella D, Baksh MF, Connelly S, Droese B, KlausJP, Makino S, Sawicki SG, Siddell SG, Stamou DG, Wilson IA, Kuhn P, Buchmeier MJ. A structural analysis of M protein in coronavirus assembly and morphology. J Struct Biol.2011 Apr;174 (1): 11-22. Epub 2010 Dec 3. PMID: 21130884; PMCID: PMC4486061. [CrossRef]
- M.Z. Teixeira, Clinical research protocol to evaluate the effectiveness and safety of individualized homeopathic medicine in the treatment and prevention of the COVID-19 epidemic, Rev. Assoc. Med. Bras. 2020. [CrossRef]
- E.G. Rossi, The experience of an Italian public homeopathy clinic during the COVID-19 epidemic, March-May 2020, Homeopathy 109 (2020) 167–168. Epub 2020 Jul 8. [CrossRef]
- B. Jethani, M. Gupta, P. Wadhwani, R. Thomas, T. Balakrishnan, G. Mathew, et al., Clinical characteristics and remedy profiles of patients with COVID-19: a retrospective cohort study, Homeopathy (2021 Feb 10), (Online ahead of print). [CrossRef]
- W. Boericke W, Pocket Manual of Homoeopathic Materia Medica Comprising the Characteristic and Guiding Symptoms of All Remedies, ninth ed., Boericke and Runyon, Boericke and Tafel, Inc., Philadelphia, PA, 1927.
- A. Hofmann, Nosoden – status und Verfügbarkeit. (Nosodes - status and availability), Allg. Homoopathische ¨ Ztg. 259 (2014) 7–9.
- Homoopathisches ¨ Arzneibuch, Vorschriften 43 und 44. Deutscher Apotheker Verlag, Stuttgart, Deutschland (Homeopathic Pharmacopoeia 2019, Regulations 43 and 44, Deutscher Apotheker Verlag, Stuttgart, Germany, 2019.
- V.M. Corman, O. Landt, M. Kaiser, R. Molenkamp, A. Meijer, D.K. Chu, et al., Detection of 2019 novel coronavirus (2019-nCoV) by real-time RT-PCR, Euro Surveill. 25 (2020) 2000045,. [CrossRef]
- C.D. Lamba, V.K. Gupta, R. van Haselen, L. Rutten, N. Mahajan, A.M. Molla, et al., Evaluation of the modified Naranjo criteria for assessing causal attribution of clinical outcome to homeopathic intervention as presented in Case reports, Homeopathy 109 (2020) 191–197. Epub 2020 Mar 25. [CrossRef]
- Directive 2001/83/EC of the European parliament and of the Council of 6 november 2001 on the community code relating to medicinal products for human use, Brüssel, Belgium, https://www.ema.europa.eu/en/documents/regulatoryprocedural-guideline/directive-2001/83/ec-european-parliament-council-6-nove mber-2001-community-code-relating-medicinal-products-human-use_en.pdf (cited 2020 July 20).
- S. Waisse, M. Oberbaum, M. Frass, The hydra-headed coronaviruses: implications of COVID-19 for homeopathy, Homeopathy 109 (2020) 169–175. pub 2020 Jul 22. [CrossRef] [PubMed]
- Ali, O.M.L. Alharbi, COVID-19: disease, management, treatment, and social impact, Sci. Total Environ. 728 (2020) 138861. [CrossRef]
- E. Bernstein and U. Vazirani, Quantum Complexity Theory, in Proceedings of 1993 ACM Symposium on Theory of Computing (1993), pp.11-20.
- D. Deutsch, Quantum Theory, the Church-Turing Principle and the Universal Quantum Computer, Proceedings of the Royal Society of London, Vol. A 400 (1985), pp.97-117.
- D. Deutsch and R. Jozsa, Rapid solution of problems by quantum computation, Proceedings of the Royal Society of London. Vol. A439, pp.553-558 (1992).
- P. Shor, Algorithms for Quantuim Computation: Discrete Log and Factoring, in Proceedings 35th IEEE Symposium on Foundations of Computer Sciende, IEEE Press (1994), pp.124-134.
- D. Simon, On the power of quantum computation, in Proceedings 35th IEEE Symposium on Foundations of Computer Sciende, IEEE Press (1994), pp.116-123.
- A. Yao, Quantum Circuit Complexity, Proceedings of 34th Symposium on Foundations of Computer Science (1993), pp.352-361.
- Shor, P.W.: Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM J. Comput 26,1484–1509 (1997).
- Fisher P, Scott DL. A randomized controlled trial of homeopathy in rheumatoid arthritis. Rheumatology. 2001;40:1052–1055. [CrossRef]
- Grabia S, Ernst E. Homoeopathic aggravations: a systematic review of randomised, placebo-controlled clinical trials. Homeopathy. 2003;92:92–98. [CrossRef]
- Davenas E, Beauvais F, Amara J, Oberbaum M, Robinzon B, Miadonna A, Tedeschi A, Pomeranz B, Fortner P, Belon P, Sainte-Laudy J, Poitevin B, Benveniste J. Human basophil degranulation triggered by very dilute antiserum against IgE. Nature. 1988;333:816–818. [CrossRef]
- Maddox J, Randi J, Stewart WW. “High-dilution” experiments a delusion. Nature. 1988;334:287–290. [CrossRef]
- Hirst SJ, Hayes NA, Burridge J, Pearce FL, Foreman JC. Human basophil degranulation is not triggered by very dilute antiserum against human IgE. Nature. 1993;366:525–527. [CrossRef]
- Harvey, W. Exercitatio Anatomica de Motu Cordis et Sanguinis in Animalibus (Anatomical account of the motion of the heart and blood in animals). Frankfurt; 1628.
- Dean, ME. ‘An innocent deception’: placebo controls in the St Petersburg homeopathy trial, 1829–1830. J R Soc Med. 2006;99:375–376. [CrossRef]
- Forbes, J. Homoeopathy, allopathy and “young physic” Br Foreign Med Rev. 1846;21:225–265.
- Paris A, Gonnet N, Chaussard C, Belon P, Rocourt F, Saragaglia D, Cracowski JL. Effect of homeopathy on analgesic intake following knee ligament reconstruction. Br J Clin Pharmacol. 2007;65:180–187. [CrossRef]
- Brien S, Lachance L, Prescott P, McDermott C, Lewith G. Homeopathy has clinical benefits in rheumatoid arthritis patients that are attributable to the consultation process but not the homeopathic remedy: a randomized controlled clinical trial. Rheumatology. 2011;50(13):1070–1082. [CrossRef]
- Shang A, Huwiler-Müntener K, Nartey L, Jüni P, Dörig S, Sterne JA, Pewsner D, Egger M. Are the clinical effects of homoeopathy placebo effects? Comparative study of placebo-controlled trials of homoeopathy and allopathy. Lancet. 2005;366:726–732. [CrossRef]
- Rutten AL, Stolper CF. The 2005 meta-analysis of homeopathy: the importance of post-publication data. Homeopathy. 2008;97:169–177. [CrossRef]
- Wilson, P. Analysis of a re-analysis of a meta-analysis: in defence of Shang et al. Homeopathy. 2009;98:127–128. [CrossRef]
- The Lancet The end of homoeopathy. The Lancet. 2005;366(9487):690.
- National Health and Medical Research Council. NHMRC information paper: evidence on the effectiveness of homeopathy for treating health conditions. Canberra: National Health and Medical Research Council; 2015.
- European Academies’ Science Advisory Council. Homeopathic products and practices: assessing the evidence and ensuring consistency in regulating medical claims in the EU. 2017. https://easac.eu/publications/details/homeopathic-products-and-practices/. Accessed: 27 Oct 2019.
- Podolsky SH, Kesselheim AS. Regulating homeopathic products—a century of dilute interest. N Engl J Med. 2016;374:201–203. [CrossRef]
- Cooper KL, Harris PE, Relton C, Thomas KJ. Prevalence of visits to five types of complementary and alternative medicine practitioners by the general population: a systematic review. Complement Ther Clin Pract. 2013;19:214–220. [CrossRef]
- Furnham A, Vincent C, Wood R. The health beliefs and behaviors of three groups of complementary medicine and a general practice group of patients. J Altern Complement Med. 1995;1:347–359. [CrossRef]
- Miller, JD. The measurement of civic scientific literacy. Public Understand Sci. 1998;7:203–223. [CrossRef]
- Loudon, I. A brief history of homeopathy. J R Soc Med. 2006;99:607–610. [CrossRef]
- Klein SD, Torchetti L, Frei-Erb M, Wolf U. Usage of complementary medicine in Switzerland: results of the Swiss health survey 2012 and development since 2007. PLoS ONE. 2015;10:e0141985. [CrossRef]
- Belmi P, Neale MA, Reiff D, Ulfe R. The social advantage of miscalibrated individuals: the relationship between social class and overconfidence and its implications for class-based inequality. J Pers Soc Psychol. 2020;118:254–282. [CrossRef]
- Snow, CP. The two cultures. London: Cambridge University Press; 1959.
- Avina RL, Schneiderman LJ. Why patients choose homeopathy. West J Med. 1978;128:366–369.
- Gunther, M. The homeopathic patient: comparative results of homeopathic and conventional GP patient interviews. Med Ges Gesch. 1999;18:119–136.
- Smith PJ, Clavarino A, Long J, Steadman KJ. Why do some cancer patients receiving chemotherapy choose to take complementary and alternative medicines and what are the risks? Asia Pac J Clin Oncol. 2014;10:1–10. [CrossRef]
- Humpel N, Jones SC. Gaining insight into the what, why and where of complementary and alternative medicine use by cancer patients and survivors. Eur J Cancer Care. 2006;15:362–368. [CrossRef]
- Morant R, Jungi WF, Koehli C, Senn HJ. Warum benützen Tumorpatienten Alternativmedizin? (Why do cancer patients use alternative medicine?) Schweiz Med Wochenschr. 1991;121:1029–1034.
- Boon H, Stewart M, Kennard MA, Gray R, Sawka C, Brown JB, McWilliam C, Gavin A, Baron RA, Aaron D, Haines-Kamka T. Use of complementary/alternative medicine by breast cancer survivors in Ontario: prevalence and perceptions. J Clin Oncol. 2000;18:2515–2521. [CrossRef]
- Angell M, Kassirer JP. Alternative medicine—the risks of untested and unregulated remedies. N Engl J Med. 1998;339:839–841. [CrossRef]
- Shor, P.W. : Fault-tolerant quantum computation. In: Proceedings of the 37th IEEE Symposium on Foundations of Computer Science, pp.56–65. IEEE Computer Society Press, Los Alamitos, CA (1996).
- KARISSON, PER W., Hypergeometric functions with integral parameter differences, J. Math. Phys. 12, 270-271 (1971).
- LUJCE, YIJDELL L., The special functions and their approximations, Vol. I (Academic Press, New York and London, 1969).
- SNEDDON, IAN N., Special functions of mathematical physics and chemistry, Second edition (Oliver and Boyd, Ltd., Edinburgh and London, 1966).
- Evaluation of the Modified Naranjo Criteria for Assessing Causal Attribution of Clinical Outcome to Homeopathic Intervention as Presented in Case Reports Chetna Deep Lamba et al. Homeopathy, 2020.
- A Co-morbid Condition of Warts and Vitiligo Treated with Individualized Homeopathy: An Evidence-Based Case Report.
- Akhyaya Kumar Prusty et al., Homeopathy, 2021 A Case Report of Idiopathic OAT Syndrome, Associated with Necrospermia and Hypospermia, Reversed with Individualized Homeopathy Vinitha Edavattath Ramanan et al., Homeopathy.
- Individualised Homeopathic Treatment of Nausea and Vomiting in the First Trimester and of COVID-19 in the Third Trimester of Pregnancy—A Case Report Katarina Lucija Glas, Homeopathy, 2022.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




