Prerpints.org logo
Preprint
Article

Discussion and Demonstration of RF-MEMS Attenuators Design Concepts and Modules for Advanced Beamforming in the Beyond-5G and 6G scenario – Part 1

This version is not peer-reviewed.

Submitted:

06 March 2024

Posted:

07 March 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
This paper describes different variants of broadband and simple attenuator modules for beamforming applications, based on Radio Frequency Micro Electro-Mechanical Systems (RF-MEMS), framed within Coplanar Waveguide (CPW) structures. The modules proposed in the first part of this work differ in their actuation voltage, topology, and desired attenuation level. Fabricated samples of basic 1-bit attenuation modules, characterized by a moderate footprint of 690 x 1960 µm2 and aiming at attenuation levels of -2, -3 and -5 dB in the 24.25-27.5 GHz range, are presented in their variants featuring both low actuation voltages (5-7 V) as well as higher values (~ 45V), the latter ones ensuring larger mechanical restoring force (and robustness against stiction). Beyond the fabrication non-idealities that affected the described samples, the substantial agreement between simulations and measurement outcomes proved that the proposed designs could provide precise attenuation levels up to 40 GHz, ranging up to nearly -3 dB and -5 dB for the series and shunt variants, respectively. Moreover, they could be effective building blocks for future wideband and reconfigurable RF-MEMS attenuators. In fact, in the second part of this work, combinations of the discussed cells and other configurations meant for larger attenuation levels will be investigated.
Keywords: 
RF-MEMS
;  
Attenuators
;  
Low Actuation Voltage
;  
Beamforming
;  
5G
;  
B5G
Subject: 
Engineering  -   Electrical and Electronic Engineering

1. Introduction

Variable attenuators represent an indispensable component in modern Radio Frequency (RF) devices or systems. Maintaining signal integrity while exerting control over signal power is a fundamental requirement for attenuators. Their predominant usage lies in applications demanding high linearity, low power consumption, and minimal temperature dependency, attributes that are almost unattainable with variable amplifiers [1]. Additionally, these components must meet criteria such as high dynamic range, low insertion loss, wide attenuation range, and broad frequency bandwidth [2].
Their applications span across automatic gain control amplifiers (AGC), impedance matching networks and broadband vector modulators [3], and as a result, they are quite common in RF transceivers and front ends for full duplex wireless systems [4] and measurement devices [5]. In fact, attenuators are adopted in RF transceivers both at the transmitter and receiver side to correct variations in gain and signal strength [6], whereas they are meant to improve the isolation between ports in full duplex systems [7].
Concerning the current and future telecommunication scenario, variable attenuators play an important role in phased array antenna systems, a paradigm that characterizes the Multiple-Input-Multiple-Output (MIMO) antennas used in the base stations and in the small cells for the radio access the current 5G network [8,9].
In such phased-array systems, ensuring gain control in each element is crucial for compensating gain and suppressing sidelobes [10]. A uniform array with identical gain in each element tends to exhibit a relatively high sidelobe level (SLL). Introducing gain tapering to the array elements results in reduced SLL, thereby reducing the impact of interfering signals, which is vital at least on the receiver’s side [11]. A broad tuning range is generally necessary when aiming for significant sidelobe suppression. For instance, the Taylor method mandates a tapering range of about 21 dB for a linear array when targeting an SLL below -30 dB [12,13]. Additionally, as the number of elements increases, the required gain/amplitude tuning resolution must also rise to minimize quantitative errors during gain tapering. Passive and active gain control topologies are available, namely attenuators and variable gain amplifiers (VGA), and the key parameters governing their design include: the gain tuning range and resolution, the insertion loss (for attenuators) or power gain (for VGAs), the DC power consumption, the associated phase error, and the input and output matchings.
On one hand, the use of all-passive components in attenuators results in zero DC power consumption [14], which is generally preferable, especially in case of large antenna arrays. On the other hand, the allocation of spectrum for the current and future telecommunications scenario led to growing frequency carriers and to growing amount of their bandwidth. This leads to an increasing miniaturization of both the radiating elements and raises the need for highly miniaturized and wideband components in their radio front ends [15].
Traditionally, RF variable attenuators have been developed utilizing semiconductor device technologies, including RF complementary metal-oxide-semiconductor (CMOS) field-effect transistors [16], monolithic microwave integrated circuits (MMICs) [17], and PIN diodes [18]. Despite their effectiveness, these semiconductor-device-based variable attenuators, as active components, face inherent drawbacks such as elevated power consumption, limited power handling and the generation of harmonics. These factors render them less favorable for applications demanding high linearity performance, especially at high frequencies [19]. Power saving in both user terminal and base station adopting active antennas, for 5G and future mobile networks, is also a crucial objective. Devices based on materials like graphene, and vanadium oxide have been considered in recent times. However, in the case of graphene, the observed insertion loss does not exhibit sufficiently flat levels across the considered frequency band [20], whereas, a high voltage is demanded to tune the attenuation of the structure based on vanadium oxide [21].
The RF Micro Electro-Mechanical Systems (RF-MEMS) are becoming progressively more popular in the development of the devices that are commonly found in modern radio front ends, since their low power consumption, insertion loss, together with their superior isolation and wideband linearity, make them a favorable candidate for microwave and millimeter-wave (mmWave) applications [22]. For this reason, different RF components have been developed in the past years, ranging from switching matrixes [23], filters [24], and impedance matching networks [25], to phase shifters [26] and attenuators [27]. As compared to the other kind of devices, the field of RF-MEMS attenuators is the relatively less investigated to date. In fact, since the very first device presented in 2009 [28], less than two dozen devices of this kind have populated the scientific literature. Both digital and analog [2,3] implementations have been considered for the developed RF-MEMS attenuators, with the former representing the vast majority. Reconfigurability, broadband behavior, and good linearity represent the most sought after features of RF MEMS attenuators. Within this context, the research effort has been put into increasing the number of attenuation states, while maintaining a flat and stable impedance value across a broad spectrum of frequencies and a minimal error as compared to the desired attenuation level [29].
Generally, most of the existing RF-MEMS attenuators are based on a coplanar waveguide (CPW) transmission line and multiple metallic membranes, operated by electrostatic actuation and ohmic contact. They are meant to enable or disable the series or shunt resistors [30] (or both, combined in a Pi-shaped topology [27]) along the RF signal line, representing multiple and cascaded attenuation units. As an example, 8 units comprising series and shunt resistors are placed alternately along the signal line in [31] to form a 256-states device. In some cases [28,32], such units are placed along different branches, selectable by Single-Pole-Double-Throw (SPDT) switches, while in others, sections consisting of two selectable RF lines (one attenuated and the other not attenuated) are cascaded [27,33,34].
The analog and digital devices developed so far find application in multiple frequency bands, with some ranging from DC up to 20 GHz [33,34], and others reaching the 40 GHz [32] or 80 GHz [31]. Concerning the number of achievable attenuation states, most of the digital implementations consist in 3- or 4-bit architectures [27,33], while some reach the 8 bits [31]. The maximum attenuation levels of the general-purpose devices developed so far are quite broad: most of the implementations attain almost -20 dB [2,28], while others achieving -35 dB [34] or even -70 dB [33]. Regarding the attenuation steps, they are quite small in case of analog devices (0.2 dB in [2]) and ampler in digital implementations (e.g. 5 dB in [34] and 10 dB in [33]), with small Root-Mean-Square errors ranging from 0.2% [2] to 5% [34]. Despite such promising results, many of these general-purpose devices still present two limitations: on one hand, the pursue of an ever-growing number of attenuation states has led to devices with a substantial footprint or aspect ratio, while on the other hand, the use of electrostatic actuation often led to devices operated by a high bias voltage. In fact, if the 3.2 mm2 area reported in [34] is not alarming, footprints like 8.77 mm2, 2.15x7.5 mm2 or 8.28x2.37 mm2 of the devices, reported in [27,28,35] respectively, are not suitable for realistic mm-Wave MIMO systems. From a system level viewpoint, regardless the brick or tiling architecture of the array [36], it may be problematic to fit such bulky devices in the current RF front ends or dense beamforming architectures serving array of small radiating elements [37], each spaced by half-wavelength. Moreover, the integration of such attenuators with common CMOS-based electronic components (with driving voltages typically up to 6.5V) could be problematic because of their substantially higher driving voltage, which would imply the use of step-up DC converters in case of actuation voltages around 35 V [33], 45 V [31] or 51 V [35]. Such need could be harmful especially in case of large mm-Wave arrays, both in terms of space and costs. For this purpose, commercial variable attenuators based on RF-MEMS usually feature low driving voltages (3.3 V in [38]).
In this paper, we propose different variants of broadband and simple RF-MEMS attenuator modules featuring a reduced actuation voltage. The modules differ in their actuation voltage, topology, desired attenuation level and number of states. From the lowest (in the 5-9 V range) to the highest driving voltage (45 V), different topologies of resistors (series and shunt) have been optimized to attain different attenuation levels. Characterized by limited attenuation levels (-2, -3, -5 dB), the different modules have been assessed as building blocks to develop more complex attenuators for beamforming applications, operating in the 24.25-27.5 GHz range, the spectrum allocated to 5G communications in Europe. This paper is organized as follows: after the brief description regarding the fabrication technology adopted at our facilities of Section 2, the electromechanical features of the membranes employed in the cells characterized by low actuation voltage are described in Section 3. In Section 4 basic attenuation cells featuring series and shunt resistors are described and critically assessed, both in their variants with low and more marked actuation voltages. Finally, some conclusive remarks conclude this first part of the present paper.

2. Fabrication

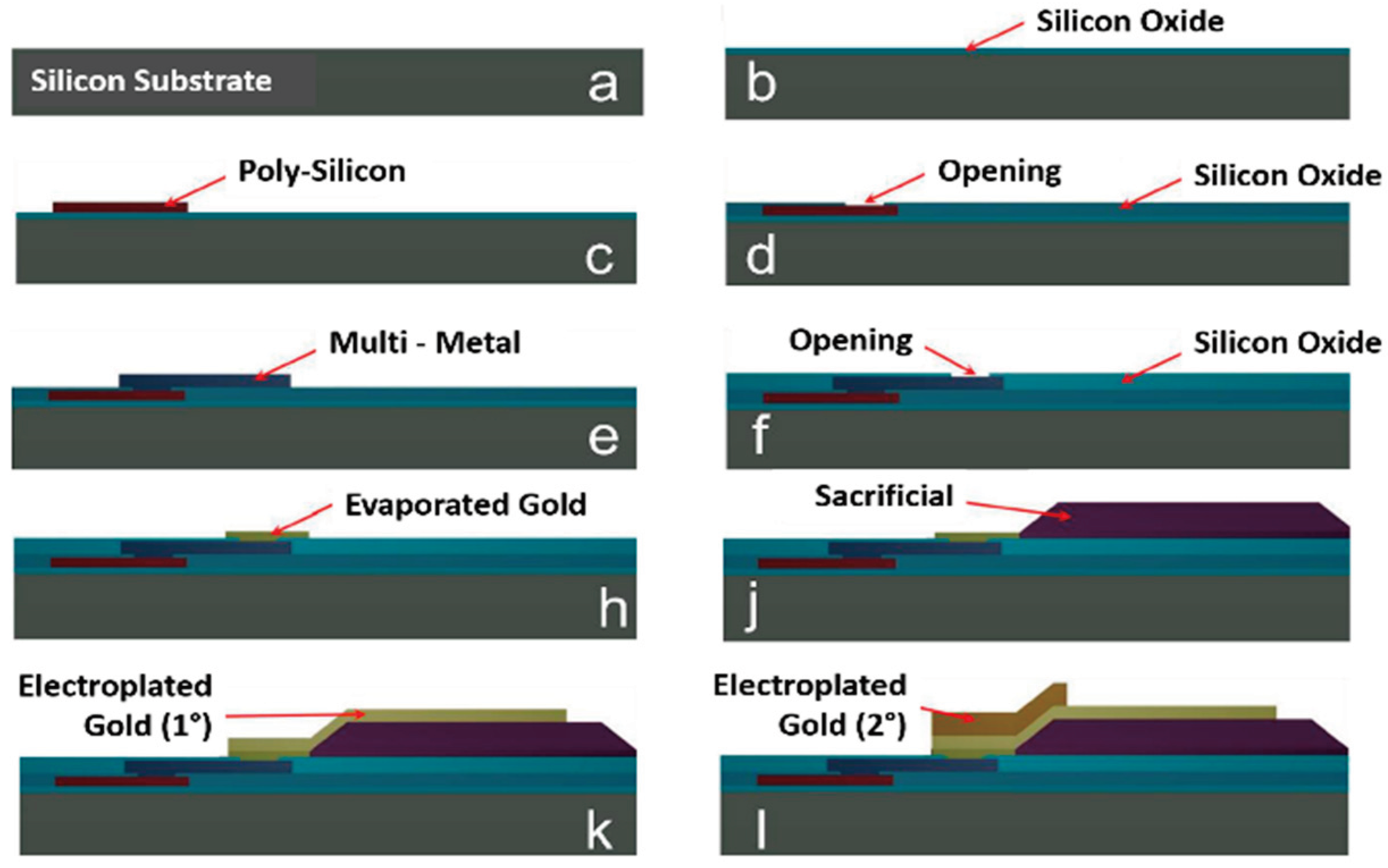
The manufacturing process at the FBK facility utilizes surface micromachining techniques and eight masks/layers [39], as depicted in Figure 1. The substrate is a 6-inch Silicon or Quartz wafer, onto which a layer of Silicon oxide is deposited. The initial layer is a 630 nm thick Poly-Silicon layer, deposited and patterned over areas designated for conductive paths or buried electrodes. The resistivity of this layer varies depending on the Boron dopant concentration, resulting in different possible resistivity values. The second layer consists of the subsequently deposited 300 nm Silicon oxide layer, and in the openings facilitating electrical connections to the underlying Poly-Silicon layer. These openings will be filled with the same material used in the third layer: a 630 nm thick Aluminum-based Multi-Metal layer. This Multi-Metal layer will be sputtered and patterned, and serve as either a buried conductive path for RF signals or an electrical connection with the first layer.
The openings etched into the subsequently deposited 100 nm Silicon oxide form the most important features of the fourth layer, necessary for establishing an electrical connection with the Multi-Metal. These openings will be filled with the material specified in the fifth layer. The fifth layer consists of 150 nm of Gold, evaporated onto the openings to serve as an electrical link between the Multi-Metal and the electroplated Gold layers composing the actual MEMS structure.
The sixth layer is characterized by a 3 μm photoresist sacrificial tier, patterned in areas where suspended MEMS structures will be located. The seventh mask involves a 2 μm thick electroplated Gold, positioned at RF signal lines, ground, various pads, and the suspended membrane, along with its anchoring points or surfaces. An additional and thicker (3 μm) layer of electroplated Gold constitutes the eighth and last layer, that is present on RF signal and ground surfaces enclosing the MEMS device, as well as on parts of the suspended membrane intended to be more rigid. In a subsequent phase, the sacrificial layer will be removed through Oxygen plasma etching, leading to the release of the RF-MEMS bridge.
The fabrication process described is slightly more intricate when compared to procedures outlined in recent studies [40,41]. However, it comes with substantial benefits, including an expanded range of design possibilities during the planning stage and the ability to maintain effective physical separation between the paths of the DC signal and the routed RF signals.

3. The Membranes

The adopted class of membranes rely on meandered supports to achieve a reduced spring constant along the vertical direction for the movable structure, and thus a reduced actuation voltage (or pull-in).
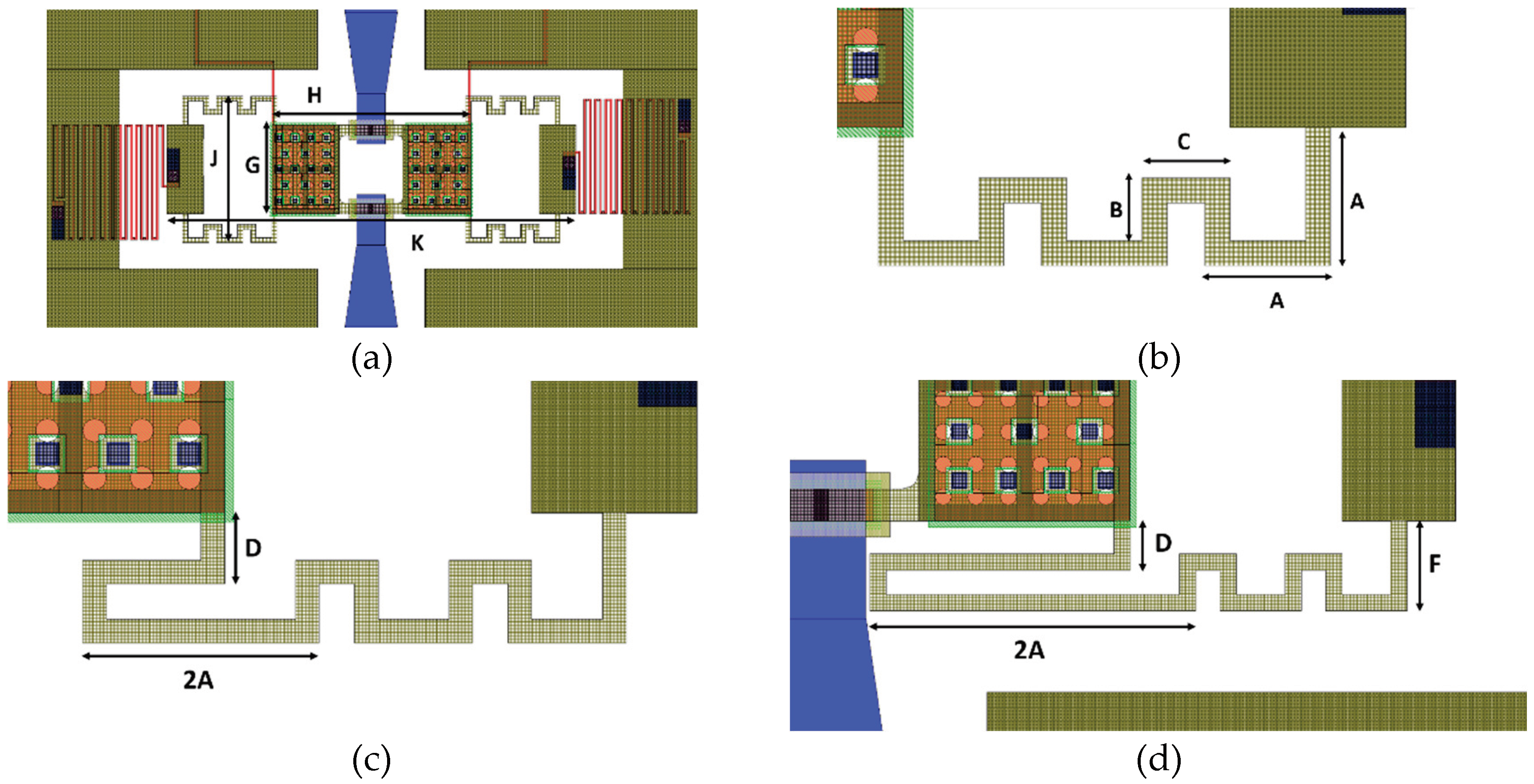
Commencing with the layout depicted in Figure 2a, various critical layers can be discerned, with the initial layer of the fabrication process being the polycrystalline silicon. This layer constitutes both the central buried electrodes and the lateral decoupling resistors. The central buried electrodes, positioned beneath the membrane's perforated sections, are designed to induce the membrane's collapse. Meanwhile, the lateral decoupling resistors prevent the diversion of RF signals toward the ground planes when the membrane is activated.
The multi-metal layer is utilized for implementing both the central and interrupted RF signal lines, featuring terminals enclosed by rectangular contact pads made of evaporated gold. These regions serve as the contact surfaces with the collapsed membrane, constructed using two layers of electroplated gold. The first layer forms the primary structure of the central membrane, while the second, thicker layer is positioned specifically over surfaces intended to provide greater stiffness, such as anchors and borders of the movable membrane.
As visible in the following figures, the class of membranes is characterized by beams with uniform meanders, except for the terminal one, which has been elongated to achieve a progressively lower pull-in voltage. Three devices (Dev 1, Dev 2 and Dev 3) have been studied with modifications described in Figure 2. In particular, Figure 2a reports the overall footprint of the membrane (780x270 μm²), consisting of a central rectangular plate measuring 380x170 μm² and beams formed by uniformly meandering segments measuring 50 μm by 25 μm (as indicated by A and B in Figure 2b) with a width of 10 μm. Such dimensions are the result of the desire to balance the elongation introduced by the meandered beams with size of the central plate, aiming at a movable structure characterized by a moderate footprint. The second device, partially shown in Figure 2c, features non-uniform meandered beams achieved by doubling the length of each terminal meander. In the third device, depicted by the beam in Figure 2d, the length of the terminal meander is increased to four times its original length, and the lateral dimension of the meanders (F in Figure 2b) has been slightly enlarged to maintain a minimum distance of 10 μm between the contact pads and the beams. As a result, the target pull-in voltage of the three membranes has been progressively lowered without a substantial increase of the footprint. All the parameters reported in the following figures are detailed in Table 1, while additional considerations concerning the discussed structures can be found in [42].
The devices were simulated by Finite Elements Method (FEM) in the Ansys Workbench software environment, while the measurements were conducted by a manual probe station and two digital multimeters. The initial multimeter supplied the DC bias voltage and established the ground reference for the device under test (DUT) pads. Simultaneously, the second multimeter maintained a restricted voltage drop between the input and output terminals of the central RF signal line. This was done to assess the resistance of the line and the level of DC current flowing. Specifically, when the DC bias attains the pull-in voltage, the membrane’s collapse induces a sudden decrease in resistance (accompanied by an increase in DC current) along the RF line.
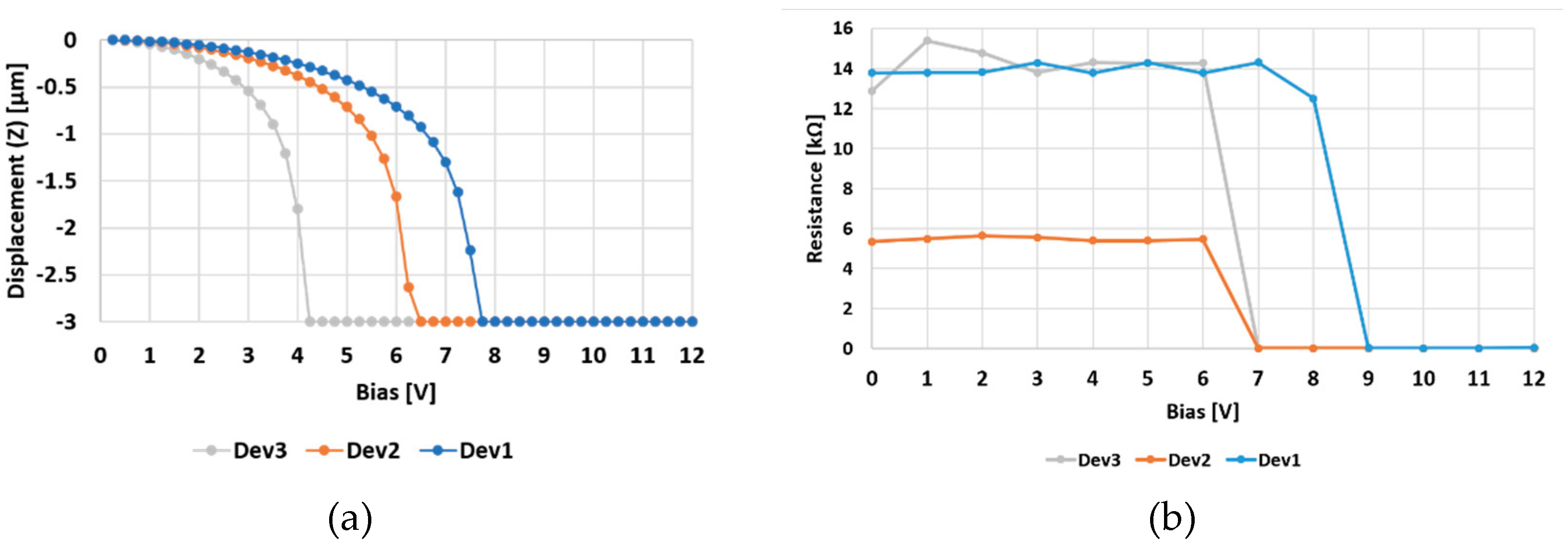
Since the DC bias was applied by increments of 1 V, the values presented in Figure 3 demonstrate a favorable agreement between the simulated and measured outcomes. Notably, while the measured pull-in voltages for Dev3 and Dev1 (9V and 7V) are slightly higher than the simulated values (8V and 5V, respectively), the measured actuation of Dev2 aligns with the anticipated performance.
The slight discrepancy observed in the Dev3 and Dev1 switches can be attributed to the heightened stiffness of their movable membranes, resulting from residual tensile stress introduced during the fabrication process. Initially, the measurements indicated pull-in voltages that exceeded those shown in Figure 3b by 10-15V. Subsequently, a re-baking thermal treatment was applied, involving the devices being maintained at 200 °C for a few hours and then slowly cooled, resulting in the release of most of the initial residual stress. The reported measurements were conducted thereafter. Additional considerations concerning the electromagnetic behavior of the considered membranes can be found in [42].

4. Series and Shunt Attenuation Cells

The discussed set of membranes has been adopted to develop the layout of different low-voltage attenuation cells. Concerning the topology of these cells, both series and shunt resistors has been considered, following the approach reported in [30]. In such work, single attenuation cells are presented, each featuring a series or a shunt resistor loading the RF signal line. As reported in the schematics of Figure 4, the resistors either load the line or are short-circuited based on the movement of clamped-clamped membranes. Depending on the architecture of the cell, the actuation of the membrane may short-circuit the series resistor or load the RF signal line with resistive shunt paths. Starting from the layout, 3D models of the two variants of cells have been developed and the width, length and sheet resistance of the resistors have been parametrized in order to optimize them.

4.1. Test Bench Cells

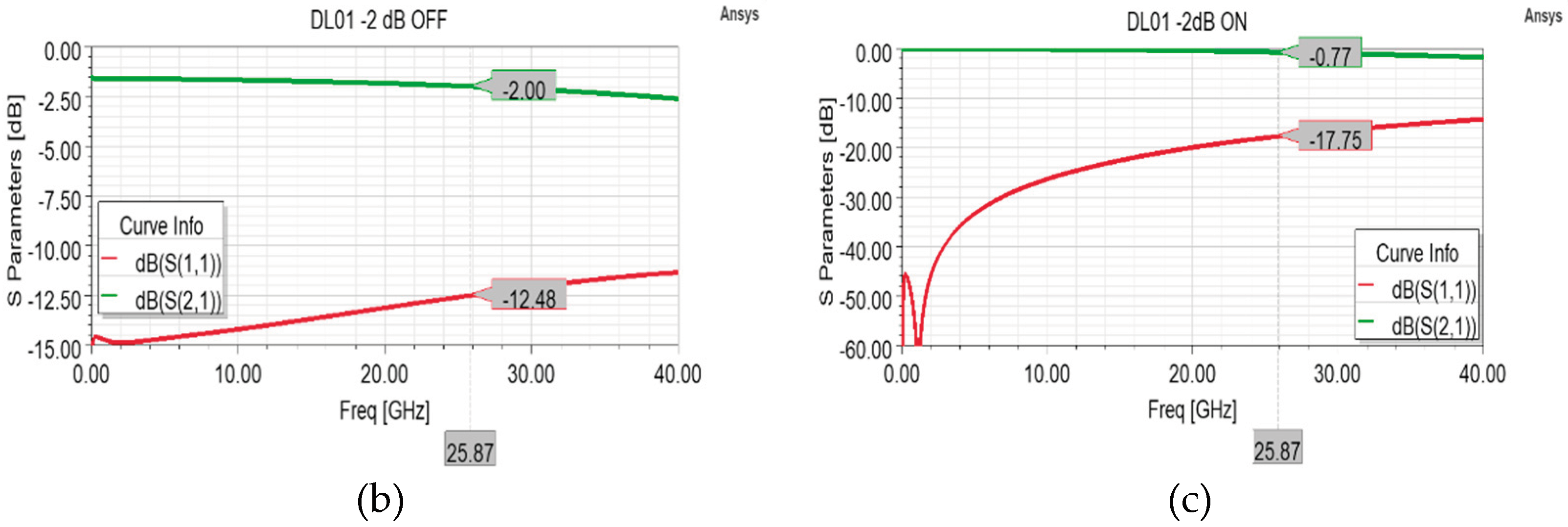
As starting point, the design of the abovementioned attenuation cells has been optimized to determine a specific values of attenuation (-2 dB, -3 dB and -5 dB) at the center frequency (25.87 GHz) of the 24.25-27-5 GHz band, which has been chosen as practical use case since it represents the higher frequency range allocated to 5G communications in Europe. As for the membranes reported in [30], also the membranes employed in the cells displayed in Figure 5, Figure 7 and Figure 8 are characterized by a substantial actuation voltage (~ 45V), since this topology has been used as initial test bench.
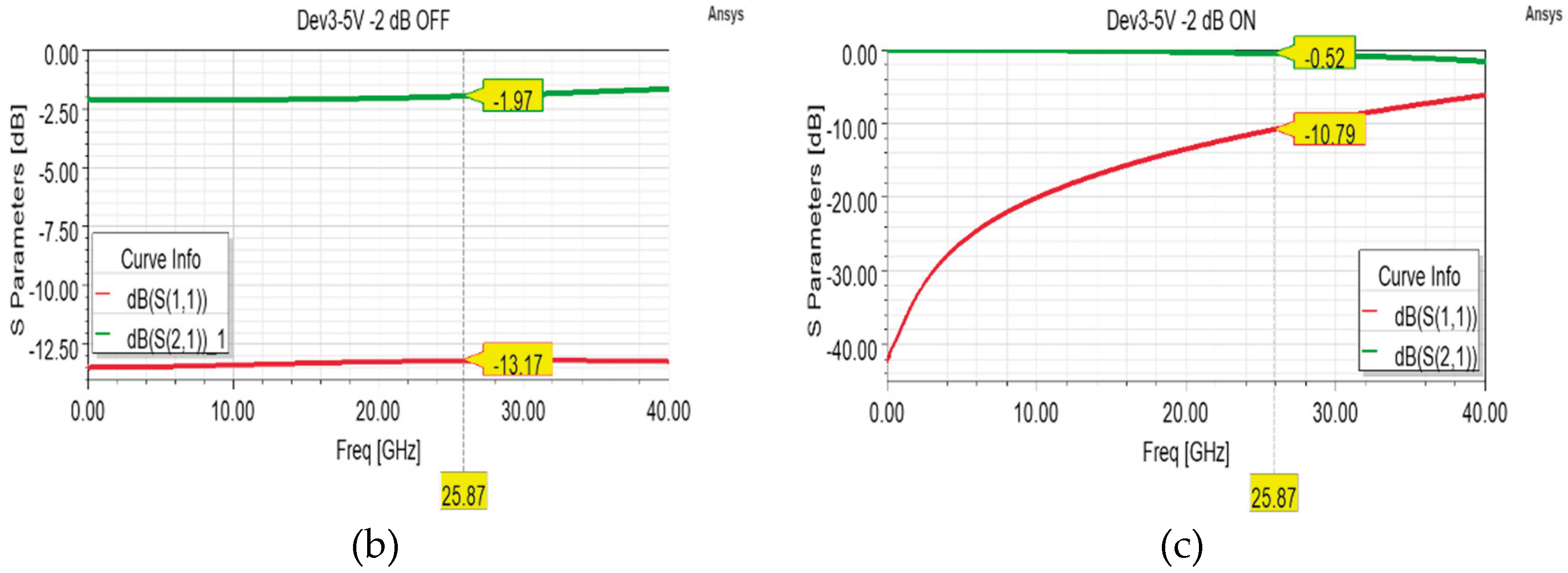
Among the most salient features of the layout reported in Figure 5a, it is possible to distinguish the central and buried Poly-Silicon resistor (in red) along the RF signal line, which extends along the Multi-Metal buried sections (in blue) and the sections of electroplated Gold (in dark green). The operation of the device involves a default attenuation state due to the series resistor along the RF line, which can be short-circuited by actuating the membrane. As visible in Figure 5b, in the default attenuation state this cell introduces an attenuation level of -2 dB thanks to its 63x113 µm2 (length x width) resistor and a sheet resistance of 100 Ohm/Sq of the Poly-Silicon composing the resistor. The return loss and insertion loss curves are quite flat, and the range of their values is satisfying along the entire 30 GHz range (Figure 5a,b).
Unfortunately, in order to fabricate this and other attenuation cells discussed in the following lines on the first available opportunity, they have been added to the wafer layout containing devices to be fabricated as part of another project. A proper doping of the Poly-Silicon layer was not important for the devices developed during that project, and delays during the fabrication process have caused the fact the Poly-Silicon layer of the devices contained in such wafer layouts underwent a coarse doping just to lower the basic sheet resistance of the basic Poly-Silicon. As a result, the sheet resistance of some of the following devices turned out to be in the 600-800 Ohm/Sq range, depending on the particular wafer, instead of the intended 100 Ohm/Sq, with a consequent alteration of the achieved performances.
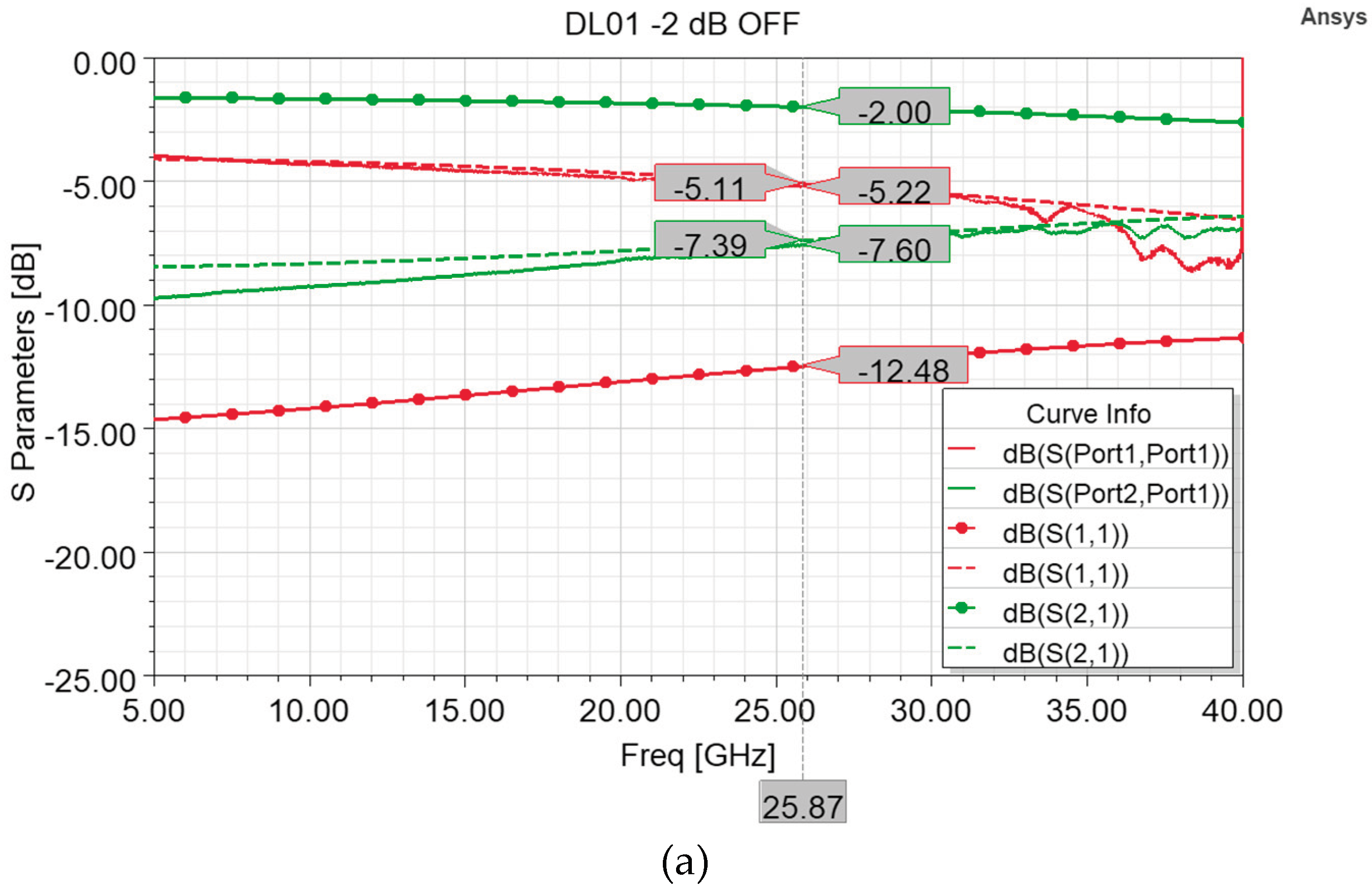
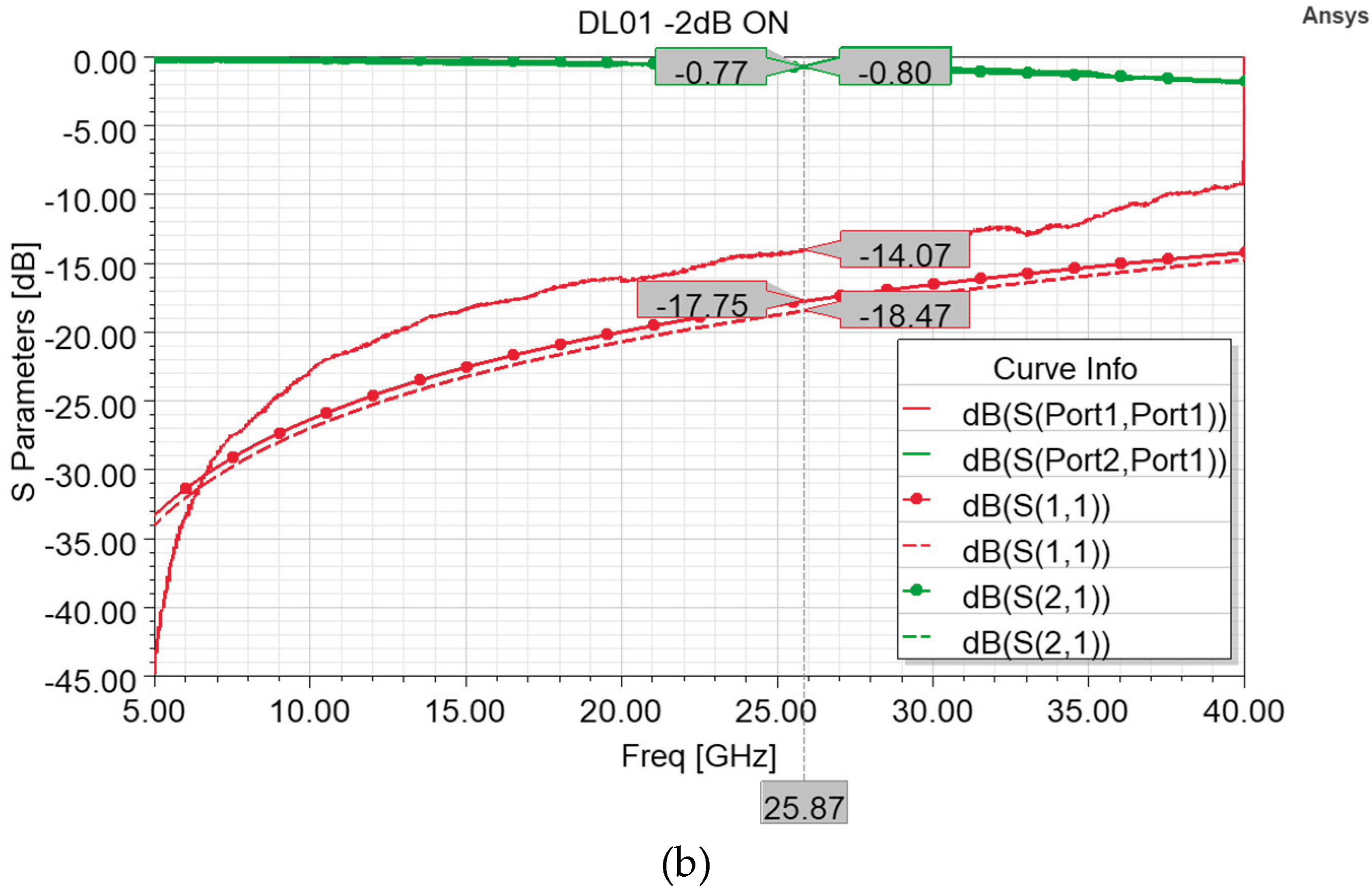
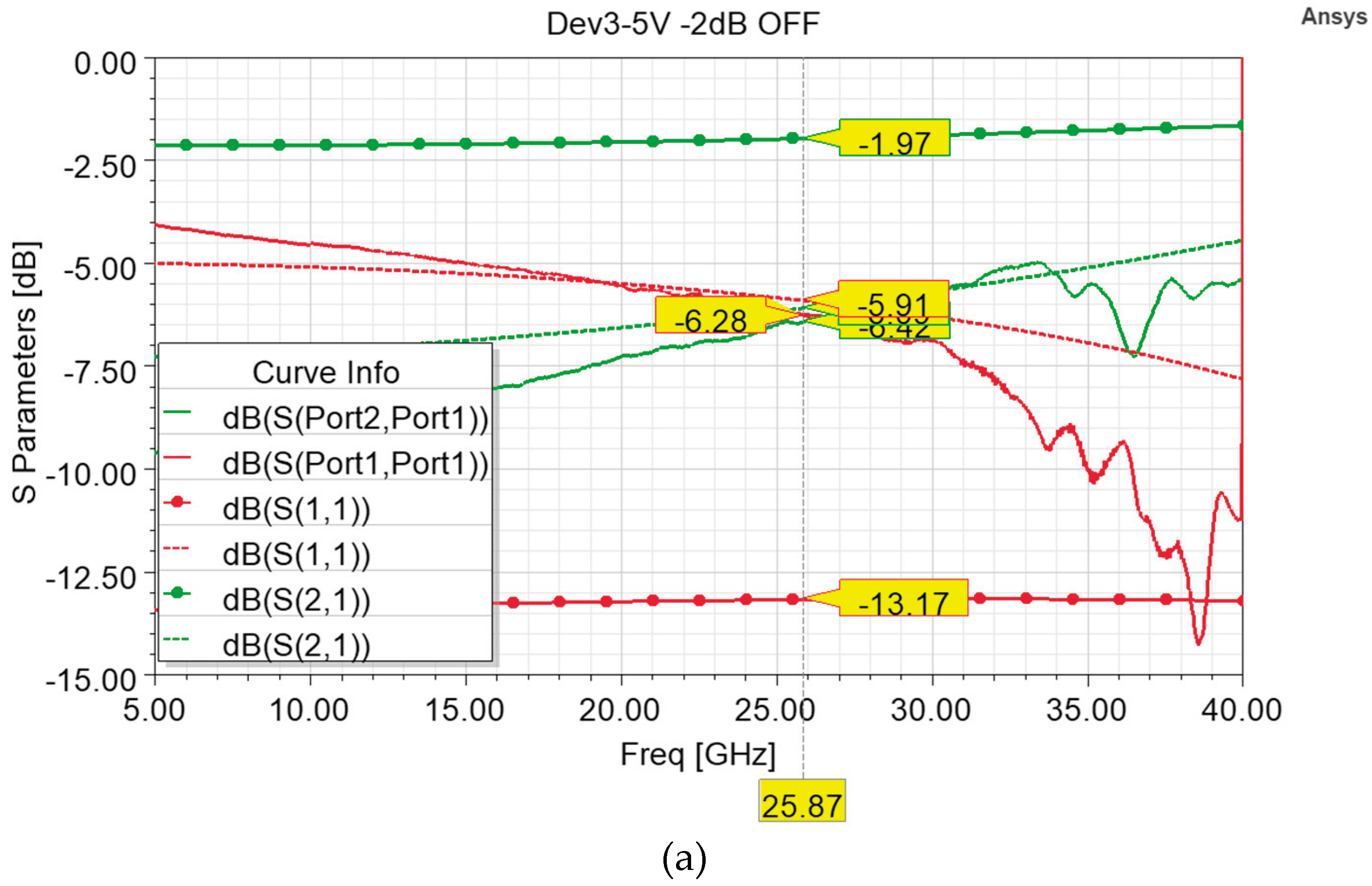
As visible in Figure 6, the measurement conducted along the 5-40 GHz interval in both the OFF (resting membrane, attenuation) state and ON (actuated membrane) state displayed insertion loss values that are far from the ones of the optimized model of Figure 5. In particular, the measured insertion loss in the OFF state (-7.6 dB) and the related excessive return loss curve (-5.22 dB) at 25.87 GHz are due to a sheet resistance of 800 Ohm/Sq of the Poly-Silicon composing the 63x113 µm2 resistor. In fact, as visible in Figure 6a, the attenuation cell simulated by taking into account a sheet resistance of 800 Ohm/Sq exhibits return loss and insertion loss curves that approximated the measured curves with a high degree of agreement. This proves that the measured performance is due to a different sheet resistance value characterizing the fabricated samples, and a doping of the Poly-Silicon layer in compliance with the intended value would have determined the desired performances. Beside such issue that affected the device behavior primarily in its attenuation state, it is possible to notice in Figure 6b that the measured insertion loss (-0.69 dB) is better than the simulated one, even in case of the intended simulated behavior (-0.77 dB). In the other hand, the measured return loss is slightly worse (-14.07 dB) than the simulated ones, in both the cases of 100 and 800 Ohm/Sq, -17.75 dB and -18.47 dB respectively.
A cell featuring shunt resistors has been adopted in order to achieve a -3 dB attenuation level at the center frequency of the desired frequency interval. In this topology, the signal experiences no attenuation when the membrane is in rest position (OFF state), while part of the signal power is dissipated along the shunt resistors connecting the membrane to the ground planes when the membrane is actuated (ON state). As a result, the desired attenuation level can be achieved by controlling the dimensions and the sheet resistance of the Poly-Silicon resistors. In the case of the cell depicted in Figure 7a, an attenuation level of -3 dB can be reached by 93x28 µm2 (length x width) resistors and a sheet resistance of 100 Ohm/Sq. Concerning the simulated scattering curves of Figure 7b,c, it is worth noticing the flatness of the return loss curve along the entire frequency interval and the precise attenuation level reached at the center frequency in the ON state. On the other hand, the return loss and insertion loss curves in the OFF state could be improved by a further optimization of the CPW structure.
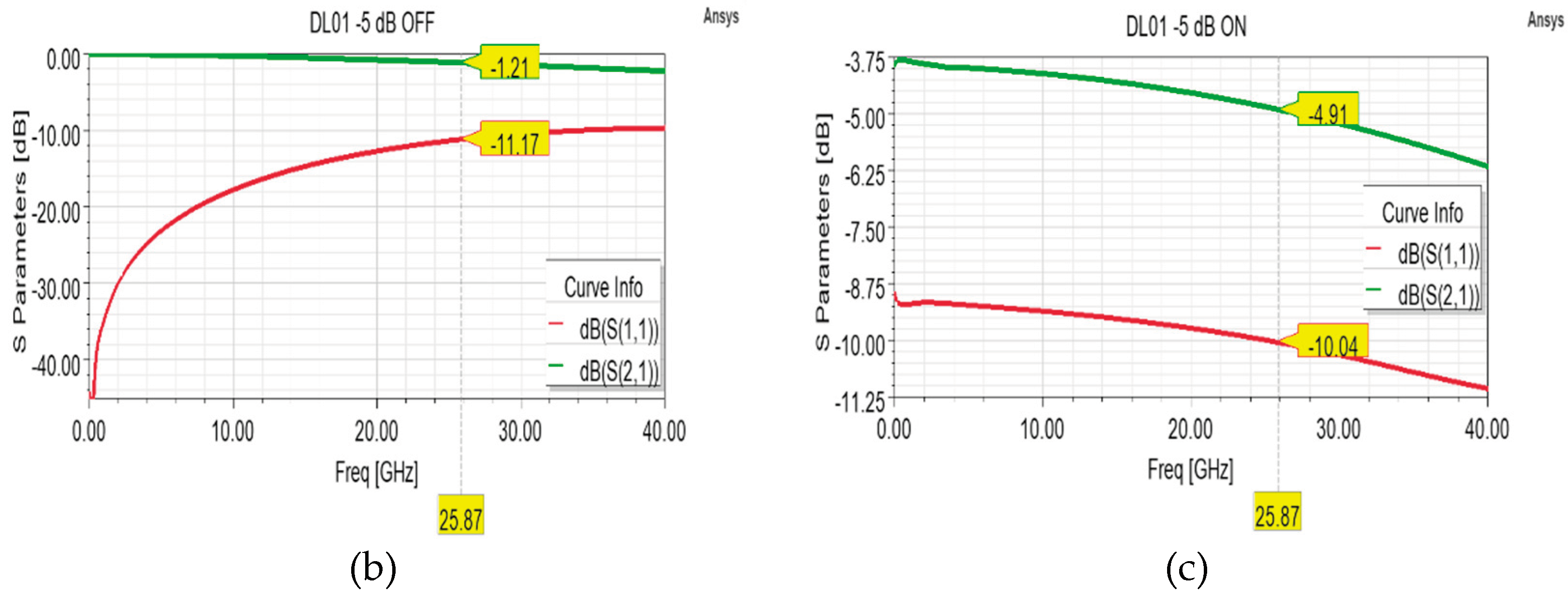
Another optimized version has been developed to verify the maximum attenuation level that can be achieved by means of this shunt topology used as test bench. The resulting layout is depicted in Figure 8a, whose main feature is represented by the 39x74 µm2 (length x width) shunt resistors, sized on the basis of a 100 Ohm/Sq sheet resistance. As visible in Figure 8c, a maximum attenuation level of almost -5 dB can be reached by this topology, without substantial degradation of the return loss curve, which lies between -9.94 and -10.14 dB within the 24.25-27.5 GHz interval. Also, in this case, the return loss and insertion loss curves of the OFF state could be improved by further optimization of the CPW parameters.
Fabricated samples of both the -3 dB and the -5 dB cell variants have been characterized, and the post-measurement simulations have shown that also the sheet resistance of the fabricated -3 dB and -5 dB cell variants corresponds to 800 Ohm/Sq. Thus, just the simulated S parameters of the -3 and -5 dB variants have been reported for sake of brevity.
Preprints 100727 g007
Figure 7. (a) Overall layout of the attenuation cell featuring shunt resistors for a desired attenuation level of -3 dB, (b) simulated S parameter curves in the OFF state, and (c) ON state.
Figure 7. (a) Overall layout of the attenuation cell featuring shunt resistors for a desired attenuation level of -3 dB, (b) simulated S parameter curves in the OFF state, and (c) ON state.
Preprints 100727 g007
Preprints 100727 g008aPreprints 100727 g008b
Figure 8. (a) Overall layout of the attenuation cell featuring shunt resistors for a desired attenuation level of -5 dB, (b) simulated S parameter curves in the OFF state, and (c) ON state.
Figure 8. (a) Overall layout of the attenuation cell featuring shunt resistors for a desired attenuation level of -5 dB, (b) simulated S parameter curves in the OFF state, and (c) ON state.
Preprints 100727 g008aPreprints 100727 g008b

4.2. Low Pull-in Cells

For each of the abovementioned attenuation levels, variants equipped with the 5V, 7V and 9V membranes of Figure 3 have been fabricated and characterized. The layout and the operation of the cell displayed in Figure 9a does not substantially differ from the one displayed in Figure 5, except for being a “dielectric-less” design. In fact, in this design the layers of silicon oxide covering the buried electrodes in correspondence of the squared areas of the movable membrane are meant to be removed in order to avoid the phenomenon of charge accumulation/trapping. In their place, quadrangular stopping pillars of Poly-Silicon, covered by the Multi-Metal and evaporated-Gold layers have been placed, to avoid the contact between the fixed electrodes and the movable membrane. The present attenuation cell has been optimized by maintaining the same dimensions of the series resistor (63x113 µm2) and varying the sheet resistance of the Poly-Silicon. In particular, by a 130 Ohm/Sq sheet resistance this design can achieve an attenuation level of nearly – 2 dB (Figure 9b), with rather flat curves of return loss and insertion loss along the whole considered interval. When the membrane is actuated and the resistor is short-circuited in its ON state (Figure 9c), this variant shows a quite limited insertion loss and a return loss ranging between -11.46 and -10.15dB along the 24.25-27.5 GHz.
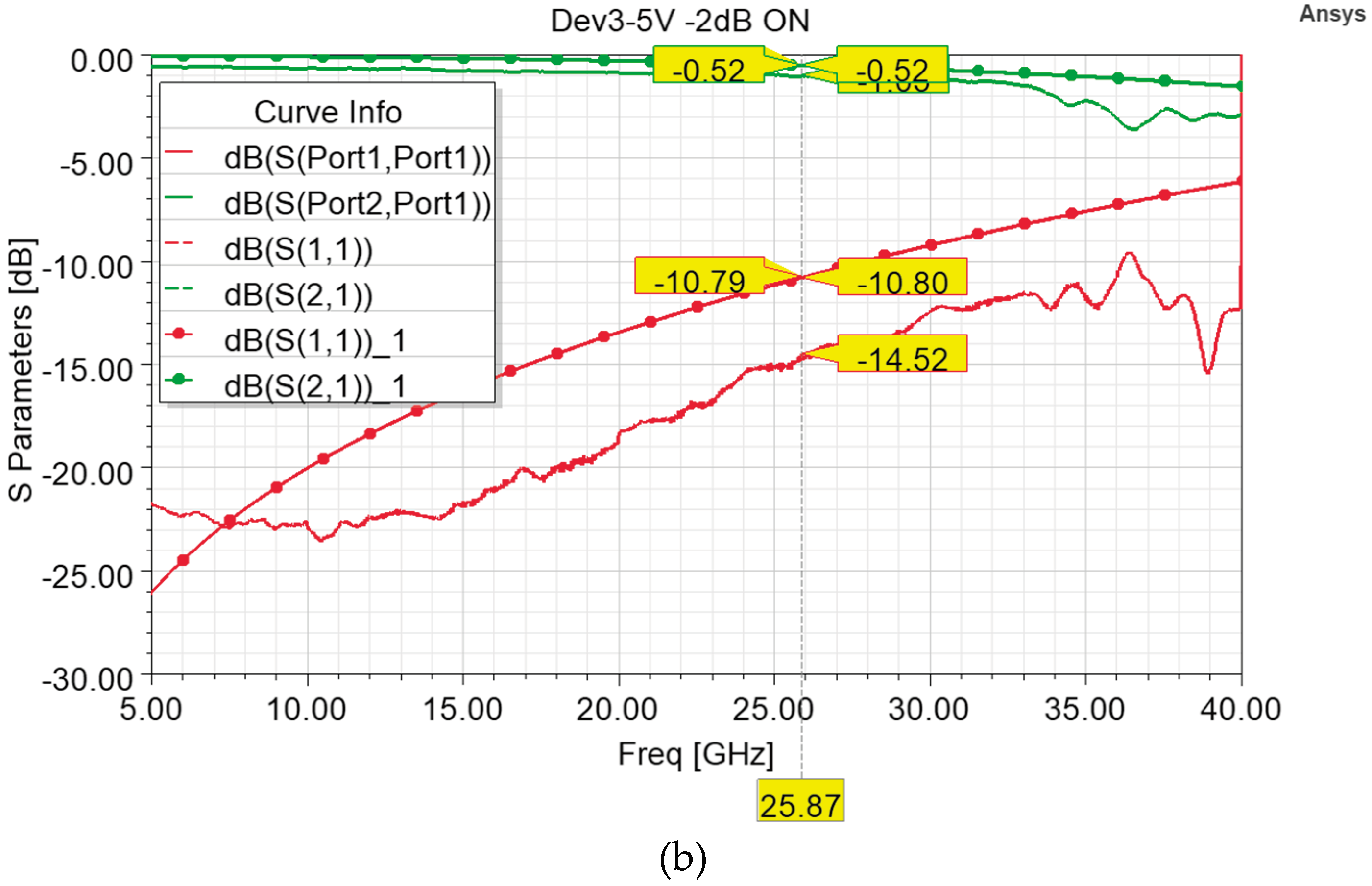
As for the previous cells, also the Poly-Silicon of the cells featuring the low pull-in membranes was subject to coarse doping. In particular, the Poly-Silicon on the wafer containing the fabricated samples that have been characterized is marked by a sheet resistance of 600 Ohm/Sq, instead of the planned 130 Ohm/Sq. Like for the abovementioned -2 dB variant, the measured performances inevitably differ from the planned ones and the outcomes of the model simulated by taking into account a 600 Ohm/Sq sheet resistance have a good agreement with the measurements. In particular, the simulated curves of the OFF state (Figure 10a) qualitatively match the measurements up to 31 GHz, after which the measurements become noisier, and growing ripples appear. Unlike the previous -2 dB variant, when the series resistor is short-circuited in the ON state, the measured return loss is generally better the simulated ones (both the intended 100 Ohm/Sq, -10.79 dB, and the unplanned 600 Ohm/Sq, -10.80 dB) along the majority of the frequency interval. On the other hand, the measured insertion loss (-1.05 dB) is worse than the simulated ones.
Concerning the variants aiming at a -3 dB attenuation level, a cell equipped with the membrane with a 7 V pull-in voltage is reported in Figure 11a. Also in this case, during the design phase the dimension of the shunt resistors has been kept the same as the ones of the -3 dB test bench model and the sheet resistance has been varied to reach the attenuation of -3 dB at the desired frequency. As a result, 93x28 µm2 (length x width) shunt resistors marked by 80 Ohm/Sq sheet resistance characterize this cell. Like the previous cell, when no attenuation is imposed to the signal (OFF state) the measured return loss is definitely better than the simulated one, while the measured insertion loss is generally greater than the simulated one (~ 0.7 dB), and a good qualitative agreement between the two curves can be noticed in Figure 11b. The same trend marks the curves displayed in Figure 11c: a discrepancy of ~ 0.7 dB can be seen among the attenuations, while the return loss of the fabricated sample is definitely better than the simulated one along the entire frequency interval.
Concerning such discrepancies, as a general remark, it is worth noticing that in case of electromagnetic full-wave simulations of devices meant for high frequencies, some simplifications are necessarily introduced to the 3D model to ease the meshing process and the convergence of solution. Starting from the emulation of the fabrication process, it is not always possible to faithfully replicate some operations (e. g. isotropic deposition), so that slight modifications to the thickness of some layers is performed to achieve an overall correct stacking. For the same reason, the deformation of the membrane due to the sacrificial layer cannot be easily reproduced, therefore flat membranes are adopted in the 3D model and moved to model the actuation and its rest position, which slightly alter the amount of capacitive coupling between the membrane and signal line during both states. In addition, bodies which are not strictly necessary to the functioning of the device (in its operations in the AC regime), such as the DC decoupling resistors, are suppressed to ease the meshing process and the convergence of the solution. All those simplifications can be cast as a set of distributed complex impedances that globally play a role as I/O mismatches (referring to the return loss) and/or adjunctive losses (referring to the insertion loss). Those effects, combined with possible non-idealities in the multi-step manufacturing process, motivate the differences between simulation and measurements, and can be investigated and mitigated in further steps of optimizations.
The abovementioned cells featuring low pull-in membranes display an interesting behavior, for which the return losses of the fabricated samples are significantly limited as compared to the simulation outcomes, despite a minimal discrepancy between the simulated and the measured insertion loss curves. However, the substantial agreement between the displayed performances of the different cells proves that the expected performance can be achieved for the considered designs, providing a faithful fabrication process.
From a critical perspective, the simulations and the measurement outcomes showed that by such basic design, maximum attenuation levels of about -3 dB and -5 dB can be achieved, by series and shunt design, respectively. For larger amounts, the other topologies and combinations described in the second part of the present paper should be considered.

7. Conclusions

In this paper, different variants of basic and compact attenuator modules for beamforming applications are described and critically assessed. Starting from the 1-bit modules targeting attenuation values of -2, -3 and -5 dB, they are presented in different variants, featuring movable membranes characterized by substantial actuation voltage (~ 45V) or low actuation (5-7V). Beyond the fabrication non-idealities that affected the discussed samples, a substantial agreement marked the simulated and the measured performances of the attenuation cells up to 40 GHz. The behavior of the proposed cells based on series and shunt resistors proved that they could be adopted to achieve fine attenuation levels up to nearly -3 dB and -5 dB, respectively. In addition, the overall compactness of their design suggests that they could be effectively employed as basic building blocks for more complex networks aiming at a wider attenuation range.

Author Contributions

Conceptualization, G.T. and J.I.; methodology, J.I., R.M. and G.M.S.; software, G.T. and M.M.; validation, G.T., M.M. and F.G.; formal analysis, G.T.; investigation, M.M.; resources, F.G.; data curation, G.T.; writing—original draft preparation, G.T.; writing—review and editing, J.I., F.G., G.M.S., R.M.; visualization, M.M. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Min, B.-W.; Rebeiz, G.M. A 10–50-GHz CMOS Distributed Step Attenuator With Low Loss and Low Phase Imbalance. IEEE J. Solid-State Circuits 2007, 42, 2547–2554. [Google Scholar] [CrossRef]
  2. Raeesi, A.; Al-Saedi, H.; Palizban, A.; Taeb, A.; Abdel-Wahab, W.M.; Gigoyan, S.; Safavi-Naeini, S. Low-Cost Planar RF MEMS-Based Attenuator. In Proceedings of the 2019 IEEE MTT-S International Microwave Symposium (IMS); 2019; pp. 869–872. [Google Scholar]
  3. Khaira, N.K.; Singh, T.; Mansour, R.R. Monolithically Integrated RF MEMS-Based Variable Attenuator for Millimeter-Wave Applications. IEEE Trans. Microw. Theory Tech. 2019, 67, 3251–3259. [Google Scholar] [CrossRef]
  4. Destino, G.; Kursu, O.; Tammelin, S.; Haukipuro, J.; Sonkki, M.; Rahkonen, T.; Pärssinen, A.; Latva-aho, M.; Korvala, A.; Pettissalo, M. System Analysis and Design of MmW Mobile Backhaul Transceiver at 28 GHz. In Proceedings of the 2017 European Conference on Networks and Communications (EuCNC); 2017; pp. 1–5. [Google Scholar]
  5. Kumar, D.; Siju, V.; Pathak, S.K. Design of RF AGC Scheme for Improving Dynamic Range of Multichannel Heterodyne ECE Radiometer in SST-1 Tokamak. Fusion Eng. Des. 2019, 142, 80–84. [Google Scholar] [CrossRef]
  6. Levinger, R.; Yishay, R. Ben; Katz, O.; Sheinman, B.; Mazor, N.; Carmon, R.; Elad, D. High-Performance E-Band Transceiver Chipset for Point-to-Point Communication in SiGe BiCMOS Technology. IEEE Trans. Microw. Theory Tech. 2016, 64, 1078–1087. [Google Scholar] [CrossRef]
  7. Kolodziej, K.E.; McMichael, J.G.; Perry, B.T. Multitap RF Canceller for In-Band Full-Duplex Wireless Communications. IEEE Trans. Wirel. Commun. 2016, 15, 4321–4334. [Google Scholar] [CrossRef]
  8. Fernandez-Martinez, P.; Martin-Anton, S.; Segovia-Vargas, D. Design of a Wideband Vivaldi Antenna for 5G Base Stations. In Proceedings of the 2019 IEEE International Symposium on Antennas and Propagation and USNC-URSI Radio Science Meeting; 2019; pp. 149–150. [Google Scholar]
  9. Chang, C.-C.; Lin, Y.-F.; Nguyen, M.-T.; Liu, Y.-X.; Chen, H.-T.; Chen, H.-M. Design of MIMO Antennas for WiFi/5G Small Cell Applications. In Proceedings of the 2021 International Symposium on Antennas and Propagation (ISAP); 2021; pp. 1–2. [Google Scholar]
  10. Sadhu, B.; Bulzacchelli, J.F.; Valdes-Garcia, A. A 28GHz SiGe BiCMOS Phase Invariant VGA. In Proceedings of the 2016 IEEE Radio Frequency Integrated Circuits Symposium (RFIC); 2016; pp. 150–153. [Google Scholar]
  11. Harris, M. Transmit Receive Modules for Radar and Communication Systems; 2015. [Google Scholar]
  12. Gu, P.; Zhao, D.; You, X. A DC-50 GHz CMOS Switched-Type Attenuator With Capacitive Compensation Technique. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 3389–3399. [Google Scholar] [CrossRef]
  13. Hansen, R.C. Linear Array Pattern Synthesis. In Phased Array Antennas; John Wiley & Sons, Ltd, 2009; pp. 49–107. ISBN 9780470529188. [Google Scholar]
  14. Zhao, D.; Gu, P.; Zhong, J.; Peng, N.; Yang, M.; Yi, Y.; Zhang, J.; He, P.; Chai, Y.; Chen, Z.; et al. Millimeter-Wave Integrated Phased Arrays. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 3977–3990. [Google Scholar] [CrossRef]
  15. Gao, H.; Wang, W.; Fan, W.; Zhang, F.; Wang, Z.; Wu, Y.; Liu, Y.; Pedersen, G.F. Design and Experimental Validation of Automated Millimeter-Wave Phased Array Antenna-in-Package (AiP) Experimental Platform. IEEE Trans. Instrum. Meas. 2021, 70, 1–11. [Google Scholar] [CrossRef]
  16. Huang, Y.-Y.; Woo, W.; Yoon, Y.; Lee, C.-H. Highly Linear RF CMOS Variable Attenuators With Adaptive Body Biasing. IEEE J. Solid-State Circuits 2011, 46, 1023–1033. [Google Scholar] [CrossRef]
  17. Wang, K.; Wang, Z.; Wang, G.; Chen, H.; Zheng, Q.; Yu, F. Design of a Low-Insertion-Phase-Shift MMIC Attenuator Integrated with a Serial-to-Parallel Converter. IEICE Electron. Express 2017, 14, 20170924. [Google Scholar] [CrossRef]
  18. Sun, K.-O.; Choi, M.K.; van der Weide, D. A PIN Diode Controlled Variable Attenuator Using a 0-DB Branch-Line Coupler. IEEE Microw. Wirel. Components Lett. 2005, 15, 440–442. [Google Scholar] [CrossRef]
  19. Dogan, H.; Meyer, R.G.; Niknejad, A.M. Analysis and Design of RF CMOS Attenuators. IEEE J. Solid-State Circuits 2008, 43, 2269–2283. [Google Scholar] [CrossRef]
  20. Pierantoni, L.; Mencarelli, D.; Bozzi, M.; Moro, R.; Moscato, S.; Perregrini, L.; Micciulla, F.; Cataldo, A.; Bellucci, S. Broadband Microwave Attenuator Based on Few Layer Graphene Flakes. IEEE Trans. Microw. Theory Tech. 2015, 63, 2491–2497. [Google Scholar] [CrossRef]
  21. Jiang, J.; Wong, K.W.; Mansour, R.R. A VO2-Based 30 GHz Variable Attenuator. In Proceedings of the 2017 IEEE MTT-S International Microwave Symposium (IMS); 2017; pp. 911–913. [Google Scholar]
  22. Singh, T.; Khaira, N.K.; Mansour, R.R. Thermally Actuated SOI RF MEMS-Based Fully Integrated Passive Reflective-Type Analog Phase Shifter for MmWave Applications. IEEE Trans. Microw. Theory Tech. 2021, 69, 119–131. [Google Scholar] [CrossRef]
  23. Daneshmand, M.; Mansour, R.R. Redundancy RF MEMS Multiport Switches and Switch Matrices. J. Microelectromechanical Syst. 2007, 16, 296–303. [Google Scholar] [CrossRef]
  24. Pelliccia, L.; Cacciamani, F.; Farinelli, P.; Sorrentino, R. High-Q Tunable Waveguide Filters Using Ohmic RF MEMS Switches. IEEE Trans. Microw. Theory Tech. 2015, 63, 3381–3390. [Google Scholar] [CrossRef]
  25. Kandala, S.K.; Sohn, S.-M. Design of Standalone Wireless Impedance Matching (SWIM) System for RF Coils in MRI. Sci. Rep. 2022, 12, 21604. [Google Scholar] [CrossRef] [PubMed]
  26. Dey, S.; Koul, S.K. Reliability Analysis of Ku-Band 5-Bit Phase Shifters Using MEMS SP4T and SPDT Switches. IEEE Trans. Microw. Theory Tech. 2015, 63, 3997–4012. [Google Scholar] [CrossRef]
  27. Li, M.; Zhang, Y.; Zhao, Y.; Xue, P.; Wu, Q. Design and Fabrication of a 4-Bit RF MEMS Attenuator with a High Attenuation Accuracy. Analog Integr. Circuits Signal Process. 2020, 102, 617–624. [Google Scholar] [CrossRef]
  28. Iannacci, J.; Giacomozzi, F.; Colpo, S.; Margesin, B.; Bartek, M. A General Purpose Reconfigurable MEMS-Based Attenuator for Radio Frequency and Microwave Applications. In Proceedings of the IEEE EUROCON 2009; 2009; pp. 1197–1205. [Google Scholar]
  29. Hah, D. RF MEMS Variable Attenuators with Improved DB-Linearity. Microsyst. Technol. 2023, 29, 311–320. [Google Scholar] [CrossRef]
  30. Iannacci, J.; Huhn, M.; Tschoban, C.; Pötter, H. RF-MEMS Technology for 5G: Series and Shunt Attenuator Modules Demonstrated up to 110 GHz. IEEE Electron Device Lett. 2016, 37, 1336–1339. [Google Scholar] [CrossRef]
  31. Iannacci, J.; Huhn, M.; Tschoban, C.; Pötter, H. RF-MEMS Technology for Future Mobile and High-Frequency Applications: Reconfigurable 8-Bit Power Attenuator Tested up to 110 GHz. IEEE Electron Device Lett. 2016, 37, 1646–1649. [Google Scholar] [CrossRef]
  32. Faes, A.; Iannacci, J.; Masotti, D.; Mastri, F.; Rizzoli, V. A MEMS-Based Wide-Band Multi-State Power Attenuator for Radio Frequency and Microwave Applications.; 2010.
  33. Guo, X.; Gong, Z.; Zhong, Q.; Liang, X.; Liu, Z. A Miniaturized Reconfigurable Broadband Attenuator Based on RF MEMS Switches. J. Micromechanics Microengineering 2016, 26, 74002. [Google Scholar] [CrossRef]
  34. Sun, J.; Zhu, J.; Jiang, L.; Yu, Y.; Li, Z. A Broadband DC to 20 GHz 3-Bit MEMS Digital Attenuator. J. Micromechanics Microengineering 2016, 26, 55005. [Google Scholar] [CrossRef]
  35. Zhong, Q.; Guo, X.; Liu, Z. A DC-20GHz Attenuator Design with RF MEMS Technologies and Distributed Attenuation Networks. In Proceedings of the 2016 8th IEEE International Conference on Communication Software and Networks (ICCSN); 2016; pp. 352–355. [Google Scholar]
  36. Chaloun, T.; Boccia, L.; Arnieri, E.; Fischer, M.; Valenta, V.; Fonseca, N.J.G.; Waldschmidt, C. Electronically Steerable Antennas for Future Heterogeneous Communication Networks: Review and Perspectives. IEEE J. Microwaves 2022, 2, 545–581. [Google Scholar] [CrossRef]
  37. Novak, M.H.; Miranda, F.A.; Volakis, J.L. Ultra-Wideband Phased Array for Millimeter-Wave ISM and 5G Bands, Realized in PCB. IEEE Trans. Antennas Propag. 2018, 66, 6930–6938. [Google Scholar] [CrossRef]
  38. Analog Devices, I. CN0377 - DC to 2.5 GHz Switchable RF Attenuator Implemented with RF MEMS Switches. Available online: https://www.analog.com/en/resources/reference-designs/circuits-from-the-lab/cn0377.html (accessed on 14 February 2024).
  39. Iannacci, J. Design. In Practical Guide to RF-MEMS; John Wiley & Sons, Ltd, 2013; pp. 57–83. ISBN 9783527680856. [Google Scholar]
  40. Dey, S.; Koul, S.K.; Poddar, A.K.; Rohde, U.L. COMPACT, BROADBAND AND RELIABLE LATERAL MEMS SWITCHING NETWORKS FOR 5G COMMUNICATIONS. Prog. Electromagn. Res. M 2019. [Google Scholar] [CrossRef]
  41. Bansal, D.; Bajpai, A.; Mehta, K.; Kumar, P.; Kumar, A. Improved Design of Ohmic RF MEMS Switch for Reduced Fabrication Steps. IEEE Trans. Electron Devices 2019, 66, 4361–4366. [Google Scholar] [CrossRef]
  42. Tagliapietra, G.; Iannacci, J. Design and Analysis of RF - MEMS Switches with Meandered Beams for Reduced Actuation Voltage. In Proceedings of the 2021 IEEE 32nd International Conference on Microelectronics (MIEL); 2021; pp. 181–184. [Google Scholar]
Preprints 100727 g001
Figure 1. Surface micromachining process used for the fabrication of the reported devices.
Figure 1. Surface micromachining process used for the fabrication of the reported devices.
Preprints 100727 g001
Preprints 100727 g002
Figure 2. Main design parameters of the employed class of membranes, including the (a) overall view, and the detail of the beams characterizing the membranes of (b) Dev1, (c) Dev2, and (d) Dev3.
Figure 2. Main design parameters of the employed class of membranes, including the (a) overall view, and the detail of the beams characterizing the membranes of (b) Dev1, (c) Dev2, and (d) Dev3.
Preprints 100727 g002
Preprints 100727 g003
Figure 3. (a) Simulated vertical displacement and (b) measured pull-in voltage of the three considered membranes.
Figure 3. (a) Simulated vertical displacement and (b) measured pull-in voltage of the three considered membranes.
Preprints 100727 g003
Preprints 100727 g004
Figure 4. Equivalent circuit of the following (a) series and (b) shunt attenuation cells.
Figure 4. Equivalent circuit of the following (a) series and (b) shunt attenuation cells.
Preprints 100727 g004
Preprints 100727 g005aPreprints 100727 g005b
Figure 5. (a) Overall layout of the attenuation cell featuring a single series resistor for a desired attenuation level of -2 dB, (b) simulated S parameter curves in the OFF state, and (c) ON state.
Figure 5. (a) Overall layout of the attenuation cell featuring a single series resistor for a desired attenuation level of -2 dB, (b) simulated S parameter curves in the OFF state, and (c) ON state.
Preprints 100727 g005aPreprints 100727 g005b
Preprints 100727 g006aPreprints 100727 g006b
Figure 6. Comparison between different insertion loss (green) and return loss (red) curves. In particular, measured curves (solid lines), simulated curves taking into account a proper 100 Ohm/Sq sheet resistance (circle marks) and simulated curves taking into account the actual 800 Ohm/Sq sheet resistance of the fabricated devices (dashed lines) in both the default attenuation state (a) and non-attenuation state (b).
Figure 6. Comparison between different insertion loss (green) and return loss (red) curves. In particular, measured curves (solid lines), simulated curves taking into account a proper 100 Ohm/Sq sheet resistance (circle marks) and simulated curves taking into account the actual 800 Ohm/Sq sheet resistance of the fabricated devices (dashed lines) in both the default attenuation state (a) and non-attenuation state (b).
Preprints 100727 g006aPreprints 100727 g006b
Preprints 100727 g009aPreprints 100727 g009b
Figure 9. (a) Overall layout of the attenuation cell featuring a single series resistor for a desired attenuation level of -2 dB, (b) simulated S parameter curves in the OFF state, and (c) ON state.
Figure 9. (a) Overall layout of the attenuation cell featuring a single series resistor for a desired attenuation level of -2 dB, (b) simulated S parameter curves in the OFF state, and (c) ON state.
Preprints 100727 g009aPreprints 100727 g009b
Preprints 100727 g010aPreprints 100727 g010b
Figure 10. Comparison between different insertion loss (green) and return loss (red) curves. In particular, measured curves (solid lines), simulated curves taking into account the planned 130 Ohm/Sq sheet resistance (circle marks) and simulated curves taking into account the actual 600 Ohm/Sq sheet resistance of the fabricated devices (dashed lines) in both the default attenuation state (a) and non-attenuation state (b).
Figure 10. Comparison between different insertion loss (green) and return loss (red) curves. In particular, measured curves (solid lines), simulated curves taking into account the planned 130 Ohm/Sq sheet resistance (circle marks) and simulated curves taking into account the actual 600 Ohm/Sq sheet resistance of the fabricated devices (dashed lines) in both the default attenuation state (a) and non-attenuation state (b).
Preprints 100727 g010aPreprints 100727 g010b
Preprints 100727 g011
Figure 11. (a) Overall layout of the attenuation cell featuring shunt resistors for a desired attenuation level of -3 dB, (b) simulated S parameter curves in the OFF state, and (c) ON state.
Figure 11. (a) Overall layout of the attenuation cell featuring shunt resistors for a desired attenuation level of -3 dB, (b) simulated S parameter curves in the OFF state, and (c) ON state.
Preprints 100727 g011
Table 1. Design parameters of the represented devices.
Table 1. Design parameters of the represented devices.
Parameter Value [µm] Parameter Value [µm]
A 50 B 25
C 35 D 25
E 30 F 55
G 170 H 380
J 270 K 780
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

82

Views

32

Comments

0

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

Email

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated