Prerpints.org logo
Preprint
Review

What is the “Hydrogen Bond”? A QFT-QED Perspective

Altmetrics

Downloads

130

Views

78

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

06 March 2024

Posted:

08 March 2024

You are already at the latest version

Alerts
Abstract
By this contribution we would like to briefly highlight the problems in conceiving the “Hydrogen Bond” (HB) as a real short-range, directional, electrostatic, attractive interaction and to reframe its nature through the non-approximated view of condensed matter offered by a Quantum Electro-Dynamic (QED) perspective. We focus our attention on water, as the paramount case to show the effectiveness of this 40-years’ old theoretical background, which depicts water as a two-fluid system (where one of the two phases is coherent). The HB emerge to be the result of the electromagnetic field gradient in the coherent phase of water, whose vacuum level is lower than the non-coherent (gas-like) fraction. Thus, the HB can be properly looked at, i.e. no more as a “dipolar force” among molecules, but as the phenomenological effect of their collective thermodynamic tendency to occupy a lower ground-state, compatibly with temperature and pressure. This perspective allows to account for many “anomalous” behaviours of water and to understand why the calculated energy associated to HB should change when considering two molecules (water-dimer), or the liquid state, or the several kinds of ice. The emergence of a condensed, liquid, phase at room temperature is indeed the consequence of the boson condensation as described in the framework of spontaneous symmetry breakings (SSB). The switch from a still semi-classical Quantum Mechanical (QM) in the 1st quantization to a Quantum Field Theory (QFT) view embedded in the 2nd quantization is advocated for a more realistic and authentic description of water, condensed matter and living systems.
Keywords: 
Subject: Biology and Life Sciences  -   Biophysics

1. Introduction

The existence of “forces” deemed responsible for cohesion among molecules such as H2O, HF, NH3 or many other compounds such as carboxylic acids, amino acids, etc. has been firstly conceived and worked out in the early decades of the last century, when it was not clear why the melting points and latent heats of water, ammonia, or hydrogen fluoride were higher than those of other hydrides of heavier elements (such as H2S, HCl, PH3, SiH4, …). The studies, at that time, suggested that the higher the molecular weight is the higher the boiling or melting point and latent heat of vaporization should be (Simons, 1931) (Nernst, 1891) (Moore & Winmill, 1912). Moreover, after the discovery of X-ray diffraction, it became clear that, in ice, water molecules are strongly arranged in a tetrahedral crystalline structure, characterized by large hexagonal channels in which various gases can be trapped (Bragg, 1922).
When Huggins first introduced the HB in 1921 (Huggins, 1971) it was a concept that fitted into the prevailing paradigm. However, it was not foreseeable that this concept shall became a pivotal pillar in biochemistry, ignoring the fact that contemporary physics was about to offer a more elegant and better fitting concept. Carl Linus Pauling eventually gave some “chemical respectability” to the HB passing from an earlier static conception (Pauling L., 1928), (Pauling L., 1931) to a more dynamic picture, based on resonance hybrids of molecules where the delocalization of electrons provides thermodynamical stability to the HBs (or H-bridges) (Pauling & Brockway, 1934). Similarly, the seminal paper by (Bernal & Fowler, 1933) promoted that the liquid nature of water is the result of HB-ing network and therefore proposed a large-scale adaptation of the HB-model in physical and chemical applications. Eventually, by using electrically neutral molecular formulas for the water molecule, he published a paper in which he claimed that the structure and residual entropy of hexagonal ice is linked to the intrinsic asymmetry of the HB itself (Pauling L., 1935). It was William H. Zachariasen, in his 1935 study of the structure of liquid methyl alcohol, to suggest for the first time the dipolar nature of the HB (Zachariasen, 1935).
To justify the strong attraction which raises the boiling point of water from -150°C (in absence of the postulated HB) to +100°C (based on experimental value), most scientists prefer to focus on the average number of electrons around the nuclei. Quantum analysis shows a slight excess of electrons around the oxygen atom (note δ-) combined with a slight deficit around the hydrogen atom (note δ+), which is all in line with Zachariasens’s interpretation. But as we shall see later on, this does not solve the problem as quantum-calculated polarity of such a constellation yields a relative dielectric constant of liquid water that differ substantially from experimental values. Nonetheless, the studies of the early days have been used so broadly to establish the arbitrary concept of the HB, that nowadays it’s so widely used in chemistry and foremost in biological sciences. Thus, in 2011, the International Union of Pure and Applied Chemistry (IUPAC) gave an “official definition” of the HB (quoted below) which is accompanied by twelve “emendations” listed therein (Elangannan & al., 2011):
Most of the 12 criteria are purely empirical (see E3 to E6 and C1 to C6 in the reference quoted above). These tell us absolutely nothing about the causes behind the observed closeness/attraction between atoms X and Y as they are purely technical criteria based on a variety of independent observations. Moreover, the remaining statements provided by the IUPAC (El and E2, see the Appendix A below) claim (i) the existence of “forces” based on a purely electrostatic nature of the interaction among electric charges and (ii) the “covalence” of such bonds that is confuted by refined experimental evidence, quoted in the following. The fact that it takes such a long definition to define a single concept clearly underlines its weak foundations. This model as it stands is just capable to explain how alpha-helices or beta-sheets formation in proteins are stabilized by the HB as originally proclaimed by Pauling (Pauling, Corey, & Branson, 1951) These inconsistencies prompted Marc Henry to state that the HB per definition remains «a guest without a face» (Henry M. , 2015, p. 5).

2. Theoretical Background and Comments on Experimental Data

2.1. Resuming Some of the Problems within the Corpuscular QM View (1st Quantization)

As a matter of fact, the whole picture on which Pauling, the IUPAC, and the most of chemists, based their stances, counts just for describing matter through a corpuscular approach (both classical and Quantum Mechanical, QM) which is not able to explain the tricky features of condensed systems like liquid water. Indeed, the problem is that, according to Maxwell’s equations (Langevin’s theory), liquid water should have a relative dielectric constant given by:
ε r = 1 + N A · ρ · p 0 2 3 k B T · ε 0 = 1 + 18500 · [ ρ / g · c m − 3 ] · [ p 0 / D ] 2 [ T / K ] · [ M / g · m o l − 1 ]
A first problem is that, with NA the Avogadro number, p0 = 1.85498 D (D: Debye, such as 1 D = 3.336·10−30 C·m), ρ = 1 g·cm-3 and M = 18 g·mol-1, we predict εr (T = 300 K) ≈ 13 instead of the experimental value of εr = 80 for bulk water. Moreover, this approach is not able to explain why the solvent power of water for ionic salt increases with temperature while at the same time the dielectric permittivity diminishes (Del Giudice & Preparata, 2000). In order to yield the electrical rigidity of water molecules (with polarizability volume α’ = 1.47 Å3, ionization potential, or ionization threshold, Ith = 12.6 eV, molecular radius R =v2.4 Å), Maxwell equations suggest dipolar interaction energies (Matcha & King, 1976) equal to:
  • 0.05 eV for direct dipole-dipole Keesom interactions (Equation (2))
U d d = − 2 p 0 4 3 ( 4 π ε 0 ) 2 · k B T · R 6 ⇒ U d d = − 3013.81 ( p 0 / D ) 4 ( T / K ) · ( R / Å ) 6 ≈ 0.05   e V
  • 0.03 eV for Debye interactions between permanent and induced dipoles (Equation (3))
U i n d = − 2 α · p 0 2 ( 4 π ε 0 ) 2 · R 6 ⇒ U i n d = − 1.2483 ( α / Å 3 ) · ( p 0 / D ) 2 ( R / Å ) 6 ≈ 0.03   e V
  • 0.12 eV for dispersive London interactions between two induced dipoles (Equation (4))
U d i s p l = − 3 α 2 · I 4 ( 4 π ε 0 ) 2 · R 6 ⇒ U d i s p l = − 0.75 ( α / Å 3 ) 2 ( R / Å ) 6 · ( I / e V ) ≈ 0.12   e V
These calculations assume an oxygen-oxygen distance of 3.65 Å, corresponding to the O-H covalent bond length (0.95 Å), augmented by the sum of van der Waals radii of hydrogen (1.2 Å) and oxygen (1.5 Å). Such values cannot explain the abnormally high boiling point of liquid water, or the HB energy of about 0.2 eV. Moreover, not even summing these classical-theory values does help, since the HBs’ energy depends on the molecular environment of the water molecules. Indeed HB energy is said, for instance, to be 0.15 eV in the “water dimer”, 0.24 eV in liquid water and 0.29 eV in hexagonal ice (Ghanty, Staroverov, Koren, & Davidson, 2000) and its apparent covalency puts in doubt its electrostatic nature (Isaacs, et al., 1999). The problem is that it’s impossible to measure each classical/QM interaction (Keesom, Debye and London) separately, they can only be evaluated by using a theoretical model and these interactions would remain exactly the same whatever the aggregation state of the water molecules is. So, from an energetic viewpoint, HBs behave quite differently from van der Waals forces (Keesom, Debye, London) (Henry M. , 2014).
Especially for liquid water, the agreement of theoretical models – based on the QM picture of matter – to the experimental results and the well-known water anomalies is not satisfying at all. In this regard we quote Marc Henry (Henry M. , 2015):
«The claim that chemistry has been completely explained in terms of quantum theory is now received wisdom among physicists and chemists. Yet quantum physics is able neither to predict nor explain the strong association of water molecules in liquid or ice. Quantum chemistry algorithms either exclude hydrogen bonded (H-bonded) systems, or treat them by modelling a water molecule as an asymmetric tetrahedron having two positive and two negative electrical charges at its vertices. Recent calculations of the potential energy surface of the simple water dimer {H2O}2 yield 30,000 ab initio energies at the coupled clustering techniques (CCT) level (Shank, Wang, Kaledin, Braams, & Bowman, 2009). But free OH-stretches [deviate from] experimental values by 30-40 cm-1 and their dissociation energy 1.1 kJ·mol-1 [are likewise] below benchmark experimental values. To obtain satisfactory agreement with experiment, it is necessary to replace ab initio potentials with spectroscopically accurate measurements. This is hardly a ringing endorsement of the underlying theory» (despite Dirac’s 1929 claims (Dirac, 1929)).
Indeed, Molecular Orbital (MO) Theory (basically an application of a QM-first quantisation theory to the molecular orbital approximations) studies molecular bonding by approximating the positions of bonded electrons through a Linear Combination of their Atomic Orbitals (LCAO). This is achieved, for example, by applying the Hartree-Fock model to Schrödinger’s equation (Matcha & King, 1976). But in the LCAO picture there are big problems about the topology and overlap of orbitals of the water molecule. If we consider the basic C2v-symmetry of H2O (according to the Schönflies classification (Flurry, 1980)), water has four irreducible representations named a1, a2, b1 and b2, where “a” (“b”) indicates symmetric (anti-symmetric) representation with respect to a rotation around the main symmetry axis, in this case the z-axis, the same one along which the pz oxygen orbital is oriented. The subscripts “1” and “2”, respectively, indicate symmetric and antisymmetric representations with respect to the rotation around a C2 axis, perpendicular to the main symmetry axis, or with respect to a plane σv, if C2 is missing.
In a single water molecule, we have ten electrons (their occupation number for each orbital is given by the superscript out of the brackets in the following expression) that must be distributed among five energy levels according to the electronic configuration: (1a1)2(2a1)2(1b2)2(3a1)2(1b1)2(4a1)0(2b2)0 (see Figure 1).
Accordingly, this does not allow the establishment of the partial covalence involving the Highest Occupied Molecular Orbital (HOMO), displaying b1-symmetry (non-symmetric with respect to the z axis, the same along which is oriented the pz oxygen orbital) and the Lowest Unoccupied Molecular Orbital (LUMO), displaying a1-symmetry (symmetric with respect to the z axis). Thus, no HOMO-LUMO interaction overlap can possibly occur.
Even by arguing that, during hydrogen bonding, the symmetry is lowered, thus leading to a possible non-zero overlap, is still unsatisfying because prior to the HB, both partners display their full C2v-symmetry with zero overlap, while, from the experiments, we know that the final symmetry of water dimers, or more numerous aggregates, is Cs (reflection with respect to a σ-plane). So, at what distance would the symmetry change from C2v to Cs? The assumption that Cs-symmetry would be held at every distance is useless because the HOMO level would still represent one symmetry, and the LUMO another: the overlapping integral would be again zero. Someone could think that overlaps may occur through other molecular orbitals, describing the covalent O-H as σ-bonds, leaving two outer non-equivalent “lone-pairs” (3a1, 1b1) available for making HB with other water molecules, but at both 2.75 Å (the distance reached by 3a1) and 2.98 Å (the distance reached by 1b1), the overlap between the acceptor oxygen and the hydrogen-bonding proton is negative, because the 3a1 (HOMO-1)1 and the 1b1 (HOMO) have two very different topologies and energies, pointing to a net anti-bonding covalent interaction in the quantum sense (Ghanty, Staroverov, Koren, & Davidson, 2000). Furthermore, X-ray emission spectroscopy (XES) reveals that in a water molecule the 1b1 HOMO-level is not affected by the HB [23], while, on the contrary, a strong perturbation of the 3a1 (HOMO-1) level is observed. This is evidence for a rather unconventional (within the LCAO QM picture) HOMO-1/LUMO interaction (see Figure 2). In addition, Compton scattering experiments which revealed a strong anisotropy of the momentum density of valence electrons) in hexagonal ice (Ih-type), is evidence of a neat anti-bonding, repulsive, interaction between neighbouring water molecules despite the multicentred character of the QM wave functions (Romero, Silvestrelli, & Parrinello, 2001). Eventually, topological analysis of electronic density revealed that it’s not possible to distinguish between HBs and mere van der Waals interactions (Bader, 1990).
Given the experimental photoelectron spectrum of the water molecule (Figure 3), its most faithful representation should display three kinds of orbitals (two σ-bonds, one 2s-type lone pair and one 2p-type lone pair), and not two types (two σ-bonds and two equivalent lone pairs), as suggested by MO theory (Becke & Edgecombe, 1990). The only way to retrieve a physical picture involving two lone pairs and two σ-bonds approximately oriented towards the vertices of a tetrahedron, is to look at the positions of the largest eigenvalues and corresponding eigenvectors of the Hessian minima in their molecular electrostatic potential (Kumar, Gadre, Mohan, & Suresh, 2014). But, again, this means reverting to a purely electrostatic view of HBs with all the annexed issues we’re listing out.
The situation is so confusing that the scientific community today is divided into two opposing camps, one promoting water as a random tetrahedral network with flickering HBs (Bukowski, Szalewicz, Groenenboom, & van der Avoird, 2007), and the other promoting water in terms of a two-state model, one being tetrahedral, the other not (Wernet, et al., 2004) [23], despite a very different picture is obtained if X-rays are absorbed by water, as the water appears not arranged in a local tetrahedral geometry but rather formed of entangled chains (Wernet P. e., 2004). However, this two-state model is closer to the truth, but the underlying idea on which it is based – still corpuscular QM – implies a physically unmotivated “cut-off energy” at which the two populations of molecules should be separated (this point will be elaborated further below). By picturing liquid water as a flickering network of HBs, the problem lays in how this interaction is commonly conceived and treated in the theoretical models: electrostatically or electrodynamically but still in a perturbative way and in a first quantisation only. This is not satisfying, indeed, neutron scattering experiments2, as well as molecular dynamic simulations, have shown that the average residence-time of a hydrogen atom around a water molecule is, in average, about 2 ps at T = 300 K, and increases to 20 ps at T = 250 K (Teixeira, Bellissent-Funel, Chen, & Dianoux, 1985). Electrical charges moving on the picosecond timescale, may be expected to generate an electromagnetic field with at least a frequency of the order of 1012 Hz. However, the electromagnetic fields should not be treated classically, instead the interaction of molecules with the ubiquitous vacuum electromagnetic fluctuations must be considered to properly understand the condensation (Preparata G. , 1995).
  • 1HOMO-1, HOMO-2, HOMO-3, …, HOMO-N or LUMO+1, LUMO+2, LUMO+3, …, LUMO+N denote electronic levels, among the several molecular orbitals, placed at the Nth level below (-) the HOMO or at the Nth level above (+) the LUMO.
  • 2The problem with X-ray scattering, indeed, is that it tends to give a static image of water, whereas it is a dynamic medium. Neutron scattering, on the contrary, has revealed the existence of two relaxation times in liquid water (Teixeira, Bellissent-Funel, Chen, & Dianoux, 1985). Thus, the first time close to 1-2 ps at room temperature corresponds to the fluctuation of the network of hydrogen bonds following the rotations of the water molecules. This relaxation time follows an Arrhenius law τLH= τ0 ∙ exp(U#/kBT) with τ0=0.0485 ps and an activation energy U# = 7.7 kJ/mol. As for the second relaxation time, it varies very strongly with temperature, from 1.25 ps at 20 °C to 22.7 ps at −20 °C. This indicates that two fraction exists, and one of the two has intrinsic dynamics independent on temperature (the one which is coherent, as it will be discussed deeply in the following).

2.1. Synthesis of the Theoretical Background in QFT-QED for Liquid Water

By adopting a QFT-QED description of liquid water (and condensed matter in general) where a complementarity relationship between phase of oscillation and number of oscillating quanta emerges, the HB is consistently countable for as an emergent property of boson condensation at a new (lower) ground level (vacuum) of water molecules. Under these circumstances their dipolar oscillations are kept in phase by a coupled and self-trapped electromagnetic (em) vector potential (A), as it has been shown by relevant literature (Arani, Bono, Del Giudice, & Preparata, 1995), (Bono, Del Giudice, Gamberale, & Henry, 2012), (Del Giudice, Galimberti, Gamberale, & Preparata, 1995), (Preparata G. , 1995).
By letting decay some approximations in the matter-em-field interaction, (like the SVE,3 valid for a system of isolated particles and displaying a finite number of degrees of freedom), and by moving to the “2nd quantisation” of QFT (having an infinite number of degrees of freedom), new profound insights about liquid water and the nature of HB emerge. In the QFT-QED picture the cohesive energy emerges to come from the coherence energy gap (denoted as Δg or Ecoh) associated to millions of water molecules being phase-locked and packed together by a self-trapped em-field and not from the sum of individual incoherent, directional, interactions as it’s usually deemed within the framework of the 1st quantization.
In doing so we briefly summarize the two-fluid picture for water as it emerges from the QED theory, firstly developed in the ‘80s, (Preparata, Del Giudice, & Vitiello, 1988) (Arani, Bono, Del Giudice, & Preparata, 1995) (Preparata G. , 1995) (Bono, Del Giudice, Gamberale, & Henry, 2012) and show some crucial experimental data which endorse this theoretical approach.
Despite the thermodynamics of water liquefaction from vapour has been precisely tackled in classical physical-chemistry (enabling quantifying the amounts of entropy variation and latent heat) (Franks, 1972-1982), within a purely QM corpuscular picture (which relies, for the condensation to a liquid state, on the establishment of a flickering network of local, directional, intermolecular forces, such as the deemed “HBs”), the real physical origin of such high values of entropy variation, boiling temperature and latent heat of vaporisation are not fully derivable.
The main limits in the framework of corpuscular QM consist mainly in two points interwoven with each other: (i) the inability to consider systems with large amounts of, or infinite, degrees of freedom (where the number operator N ^ , is left undefined) (Preparata G. , 2002), and (ii) the inability to describe symmetry breakings (i.e.,: phase transitions), being a theory which obeys the von Neumann’s theorem (von Neumann, 1955). According to this theorem, only one ground state, vacuum level, is considered, thus rendering unfeasible the description of symmetry breakings and phase transitions (Blasone, Jizba, & Vitiello, 2011). The main problem associated to such limitations is the impossibility to predict non-trivial solutions for the equations of motion starting from the perturbative ground state of the system (like vapour being cooled down). Therein, the vacuum fluctuations (able to excite the electron of water molecule) are counted for, but – being of the other of δ ≈ 1 ppm (i.e.,: the Lamb shift (Lamb & Retherford, 1947)) – are deemed as negligible. Actually, when the number of matter quanta (molecules) overcomes a critical threshold, this coupling (between vacuum virtual excitations and matter), becomes so meaningful as to change dramatically the system layout because it is not proportional just to N but to N√N (Arani, Bono, Del Giudice, & Preparata, 1995) (Bono, Del Giudice, Gamberale, & Henry, 2012). Moreover, in a QM picture, beyond the investigated transition, excitations over other levels in the spectrum of the molecule are not taken into account for the evolution of the system (Teixeira & Luzar, Physics of liquid water: Structure and dynamics, 1999). Thus, when several billions of molecules are coupled with em-quanta of the vacuum, they are back-reformed by this new emergent condition and a purely bottom-up description (based on the mere summation of the interaction calculated over few quanta) does not deliver a truthful picture (Henry M. , 2014).
In a QFT-QED perspective, when water vapour is at the liquefaction threshold (for instance, pressure P = 1 atm and temperature T = 373.15 K), water molecules are in constant dialogue with virtual quanta popping out of vacuum. Based on their energetic content (ΔE), these quanta can excite the electrons of water molecule at several levels. Of course, this process isolated molecules do not produce any permanent energetic gain and the excitation lasts – in accordance with the Heisenberg relationship – just a short time ∆ τ ≤ h / 4 π ∆ E . The interesting aspect, looking at water photoemission spectrum (see Figure 3), is that the first possible transition has an energy of about 7.5 eV, and the other energetic levels are placed at >10 eV. This means that the spatial range of such excitations (the wavelength, λ, of virtual photons) is at least in the order of 100 nm (i.e.,: about one thousand times bigger than the water molecule itself!).
The numerical density of water vapour, at its boiling point (T = 373.15 K at P=1 atm), is around 2∙1019 molecules⋅cm-3, it means that an em-excitation, able to set a water molecule on a different electron configuration, includes within its own volume (V~λ3) about 20’000 molecules. The more the density increases (by lowering T, for instance) and the more the probability grows that the photon released by a previously excited molecule – originally adsorbed from the vacuum – could then be re-absorbed by another one. At a critical density the photons of other molecules in the volume get involved in the same dynamics, until a sizeable em-field is established and self-trapped in an ensemble of water molecules which steadily grows. In doing so it keeps sucking in millions of molecules until the volume is filled. This saturation level is determined by short-range forces at which molecules are closely packed (intermolecular distance >3.1 Å, which is larger than the molecular radius >1 Å) resulting in an increase of the molecular size (Arani, Bono, Del Giudice, & Preparata, 1995). All photons set in phase among each other and with the molecules oscillating between the two electron levels. This new ordered state occurs because it is thermodynamically more favourable, provided that the system is open and could dissipate excess energy as heat (entropy). For liquid water, it has been computed that the energy difference, the energy gap, Δg, is 0.16 ±0.05 eV (Bono, Del Giudice, Gamberale, & Henry, 2012). This is the origin of the high latent heat of liquefaction, where an excess energy with respect to the one received by the original vacuum, is given back to the environment. In water, QED calculations, using several possible candidate levels of its spectrum (as depicted in Figure 3), showed that this probability becomes 100 % for the 5d level (at 12.07 eV above the ground state), above the density threshold ρc ≥ 0.32 g/cm3. In the election of this level as the favourite one to settle a coherent excitation supporting the formation of the liquid phase there are also other parameters like: excitation energy or frequency (ωq), coupling constant between em-field and oscillating charges (g), photon mass renormalization term (µr), oscillator strength (fq), renormalized frequency (ωr), energy gap (Δg), mixing angle (α) (see Tables 1 and 2 in ref. (Bono, Del Giudice, Gamberale, & Henry, 2012) for details).
The original frequency, ωq, of the exciting em-field, which now spends part of its lifetime as excited molecules (and no more as a free field) become renormalized to a lower value, ωr, which is associated to the phase variation and locking between em- and matter-field. This renormalization implies that the field is made of quasi-particles – according of the Anderson-Higgs-Kibble mechanism have imaginary mass (negative squared mass) (Anderson, 1958) – and thus unable to propagate outside the region where the coupling with the matter-field is in force (Anderson, 1984). Such a region is named coherence domain (CD) and constitutes a self-generated sub-radiant cavity of the trapped fields (Del Giudice & Vitiello, 2006). It’s appropriate to speak of “matter-field” since the CD is an open system where a permanent crossover of molecules in and out of the CD occurs and the number (N) of matter quanta is undefined, allowing the phase ( φ ) to be well-defined. This complies with the QFT complementarity relationship holding for phase and number operators, such that the higher the uncertainty ( ∂ ) in terms of number, the better defined is the phase. Thus the “fundamental uncertainty relationship” is expressed as: ∂ φ · ∂ N ≥ 1 2 (in natural units, where ℏ = c = kB = 1) (Preparata G. , 1995).
The expulsion of a large amount of entropic energy per molecule (which tells us a lot about the physical origin of latent heat of liquid water condensation) sets the coherent ensemble of molecules (namely, about 6 millions per CD) on a lower, desirable, ground state (vacuum level) whose energy difference with respect of the isolated molecules’ is denoted as the energy gap, Δg. This energy difference represents a crucial quantity of the system and expresses its thermodynamical stability, defining how much energy must be spent to liberate a molecule from a CD:
∆ g = ω q A 0 2 1 + 2 μ r + s i n 2 α − 3 2 g A 0 s i n 2 α
where g is the coupling constant between em-field and matter, µr the photon mass renormalization term, and A0 the maximum amplitude of the em-field (i.e., the em-vector potential). The renormalized frequency, ωr is defined as a function of the energy (i.e., frequency) of the exciting virtual photon (equal of the energy difference existing between sp3 and 5d orbitals):
ω r = ω q 1 − ϕ ˙ ⇒     ω r = ω q 1 − g s i n 2 α A 0 < ω q
whereby the phase variation of the em-field, ϕ ˙ is defined by the phase-factors time derivatives of the ground ( θ ˙ 0 ) and excited ( θ ˙ q ) states of the matter-field. The em-field is characterized by:
ϕ ˙ = θ ˙ q − θ ˙ 0 = g A 0 tan ⁡ α − g A 0 tan ⁡ α
where α is the mixing angle between the two (fundamental, “0”, and excited, “q”) levels, so that 0<α<π/2. In these calculations the Natural Units system is used (where ℏ = c = kB = 1, and the elementary electrical charge e = 0.302814). As shown in Figure 4, the coherent state results to be a time-weighted average of the new ground state (at 90 %) and the excited one (10 %) where molecules assume an expanded shape (due to the larger 5d volume). This comes with two major implications: (i) the coherent fraction is less denser than the interstitial vapour-like incoherent one, and (ii) the re-arranged shape of the water molecules produces a physical explanation of the electron-cloud protrusions necessary for some tetrahedral arrangements observed in some water systems through suitable techniques (Tokushima, et al., 2008) (Huang, et al., 2009) (Taschin, Bartolini, Eramo, Righini, & Torre, 2013).
Of course, if the temperature were to approach 0 K, the whole system would become fully coherent: this occurs only at T <220 K (Garbelli, 2000). At higher temperatures the system is made up of two populations of molecules (those gathered in CDs, Fcoh(T) and those incoherent, constituting the vapour-like phase, placed interstitially among the CDs, Finc(T)) whose relative quantities obey a sum-rule: Fcoh(T) + Finc(T) = 1. The higher the temperature is, the lower the coherent fraction becomes, enabling thermal agitation being able to gradually erode more molecules from the CDs’ periphery, reducing their diameter. At room conditions (T = 300 K), Fcoh ~40 % the effective size of the CDs is about 60 nm (Figure 5).
Furthermore, it’s noteworthy to mention that the coherent oscillations implies that 10 % of electrons in each CD stay very close to the ionisation threshold (placed at 12.62 eV, about 0.5 eV above the 5d orbital). Thus, with about six million molecules per CD, there are about 0.6∙106 quasi-free electrons per CD. These electrons circulate on the periphery of the CD, being subjected to a repulsive ponderomotive force (see Equation (10) in the following) and are coherent, therefore they cannot dissipate energy by thermal relaxation, nor friction (yielding closed supercurrents, said cold vortexes). The implications of these aspect are huge, but out of the scope of this work, for which we refer to (Del Giudice & Tedeschi, 2009) (Del Giudice, Spinetti, & Tedeschi, 2012) (Del Giudice, Voeikov, Tedeschi, & Vitiello, 2015) (Renati P. , 2020), (Madl & Renati, 2023).
The existence of incoherent fraction, above 273.15 K allows water to be a liquid, whereas below that temperature the mobility is too low, thus inducing crystallization. However, the global density, ρ(T), is lower, right because Fcoh(T) is increased with respect to 277.14 K (4 °C), at which water shows its maximum density (Figure 5), more than how much the incoherent fraction increased its density by lowering T from 277.15 to 273.15 K. Only by applying such a two-fluid model is it possible to predict form first principles the peculiar density trend of liquid water (Arani, Bono, Del Giudice, & Preparata, 1995) (Preparata G. , 1995) (Garbelli, 2000):
ρ T = 0.92 · F c o h T + 1 − F c o h T · ρ n ( T )
The density of coherent fraction does not depend on the temperature and has been calculated to be 0.92 g/cm3 on the basis of the wider shape given by the mixing angle weights over the coherent oscillation, ρn(T) is the density of the normal (incoherent) fraction (Finc(T) = 1 – Fcoh(T)). See (Arani, Bono, Del Giudice, & Preparata, 1995) and (Henry M. , 2014) for further details.
Recently some important experimental data showed both (i) the impossibility to explain some features within the corpuscular-QM picture and (ii) the necessity to contemplate, within the models, coherence as a key property to correctly fit the experimental data.
  • The first case refers to infrared (IR) and near IR (NIR) analysis of water or water solutions spectra (of O-H stretch mode range, IR, or of its first harmonic, NIR) taken at different temperatures (De Ninno, Del Giudice, Gamberale, & Castellano, 2014), (Renati, Kovacs, De Ninno, & Tsenkova, 2019) whose trends showed the clear existence of an isosbestic points that expresses the existence of two populations of molecules which depend reciprocally on T. This, of course, is not a novelty, but what it’s worth to look at are the resulting van’t Hoff plots (i.e.,: the Log (equilibrium constant of the passage from one population to the other) vs 1/T) is linear, revealing that (i) the energy difference between the two states does not depend on T and (ii) that its slope is in good agreement with the energy gap predicted by QED theory. Moreover, in (Renati, Kovacs, De Ninno, & Tsenkova, 2019) it has been shown how the plot of the logarithm of the ratios between the spectral intensity of one population (distinguished from the other one by the isosbestic point) with respect to the total, taken at each temperature, plotted as a function of log T yields a straight line. This accounts for a scale-free behaviour, revealing the underlying coherent dynamics for the demonstrated isomorphism existing between self-similar (fractal) topologies and squeezed quantum coherent states (Celeghini, De Martino, De Siena, Rasetti, & Vitiello, 1995) (Celeghini, Rasetti, & Vitiello, 1992) (Vitiello, 2009).
  • The second case deals with the fit of dielectric permittivity of pure water and electrolytes water solutions in the range 0.2-1.5 THz (De Ninno, Nikollari, Missori, & Frezza, 2020), (Nikollari, De Ninno, & Frezza, 2023). The fit to the experimental data requires a two-fluid Debye model that mimics the electrical permittivity (both for the real and the imaginary part). However, in order to be effective over the whole spectral range, it requires an additional linear term (ξω, where ξ ≈ 0.47 ps) to the imaginary part of the dielectric function. This fact has a profound physical meaning because implies the violation of Kramers-Kronig (KK) relations (Toll, 1956) within the time span ξ. The KK relations express the causal relation between the forcing field and the charge displacement. This tiny violation, within a time scale right of the order of magnitude of the renormalized oscillation period of the coherent field within the CDs (which excite and relax in a few hundreds of femtoseconds, τr ≈ 1/ωr ~ 300-500 fs) witnesses temporally non-local correlations in the medium (i.e., phase correlations), possible if the system is in an entangled coherent state (a phase eigenstate). As Ke-Hsueh Li pointed out (Li, 1994) (Li, 1992a), the concept of coherence is strictly linked to Heisenberg’s uncertainty principle, i.e., coherence space-time being actually equivalent to the uncertainty space-time. This is the range of space and time within which particles lose their classical features as individuality and countability (the N ^ operator become undefined). The particles and fields within coherence space-time range must be considered as an indivisible whole where phase is well-defined: thus, what occurs to “a part” of a CD, within its coherent space-time range, is occurring to the whole CD (Li, 1994). This is a noteworthy point also for overcoming the prevailing naïve picture of the HBs (Del Giudice, Galimberti, Gamberale, & Preparata, 1995) conceived still as forces among “particles”. As described, this classic idea originated from the 1st quantization can be fruitfully replaced by the QFT perspective (2nd quantization) where the apparent (non-directional) force is the emergent property deriving from an energy gradient which is NOT primarily tied to the bonding among molecules, but established is routed on the ground energy level (vacuum) (Preparata G. , 1995) as a consequence of the “em-field + matter-field” coupling over the whole high-numbered system, (Bono, Del Giudice, Gamberale, & Henry, 2012).
  • Another crucial topic is the one concerning ions and their solvation in water. Within an electrostatic conception of dissolution of electrolytes in water, the initial dynamics has no physical consistency, since few layers of water molecules should be able to keep some Na+ and Cl- ions apart from their crystal lattice when the energy barrier to be overcome in order to brake ion bonds is in the order of 5 eV and a single water layer could produce at most a dielectric drop of the Coulomb force equal to 13 ( εr = 13 and not εr = 80 which holds for the bulk). Again, only by abandoning an ingenuous “stics’n’balls” interpretation of condensed matter, and by taking into account the quantum electrodynamic nature of objects like ions and their coupling with vacuum, it is possible to describe consistently the spontaneous process of solvation showing that ions establish in the incoherent fraction of water their own coherence domains, with their energy gaps (bigger than the ion-bond energy), dissolving in the liquid phase of the solvent without collisions (Del Giudice & Preparata, 2000). This explains (i) why by increasing temperature the solvent power of water increases (despite the net value of bulk dielectric permittivity decreases), (ii) why there is no emission of bremsstrahlung radiation from an electrolyte solution and (iii) why the phenomenon of ion-cyclotron resonance occurs (Del Giudice, Fleischmann, Preparata, & Talpo, 2002).
  • There are numerous other cases, which we will only briefly mention here, as they go beyond the scope of this topic and will therefore be dealt with in future papers. These regard the morphogenic role of water in biological matter (Henry M. , 2020), interfacial water (Pollack, 2013), dispersion properties of biologically bound water upon exposure in the 10 Hz to 100 GHz range (Schwan, 1977), burning salt water upon RF-exposure (Roy, Rao, & Kanzius, 2008), branching chain reaction of water (Voeikov, 2010), coherent water and cellular information processing (Henry M. , 2015) as well as stable water mixtures of both hydrophobic/hydrophilic liquids (Germany Patent No. DE 1.557.213, 1966) by Viktor Schauberger.
  • 3According to the slowly varying envelope (SVE) approximation the frequency spectrum of the “envelope amplitudes” of the em-field is concentrated only on one mode, |ω| ≪ ωk = |k| (in natural units). Doing so means to neglect the third order time-derivative term in the equations of motion, which shows an instability of the perturbative ground state (PGS) in the matter-em field coupling, and is responsible for a departure from it towards a non-trivial solution of the equation of motion: a coherent state (see (Bono, Del Giudice, Gamberale, & Henry, 2012) for further details).

3. Discussion

The picture of liquid water, the paramount “HB-based” liquid within the commonly shared vision, now assumes a quite different portrait which, including electrodynamic coherence, is able to account for many non-trivial properties and their dependence on temperature.
For a better understanding of this new paradigm as a result of the 2nd quantization, it is necessary to focus on the nature of cohesive forces within the coherent system and to deepen some details about the em-field dynamics within the CD. Molecules resonating inside a CD are forced to stack among each other, as much as their repulsive short-range forces allow it, because (i) from a thermodynamic perspective they are driven to settle on a ground state lower than what is experienced outside a CD, when uncoupled from the coherent em-field; and because (ii) from a electrodynamic perspective the more quanta are oscillating in phase, the better the phase is defined and, again, the more stable coherence is. That is to say that the energy gap is deepened (Preparata G. , 2002). This second aspect is also responsible for the cohesion among CDs, yielding a macroscopically condensed system, like a liquid at room conditions, and not a gas (Arani, Bono, Del Giudice, & Preparata, 1995), (Bono, Del Giudice, Gamberale, & Henry, 2012). The other important term underlying CDs’ cohesion concerns the emergence of long-range dispersive forces from the self-trapped em-field gradient along the radial distance centre-to-periphery in the CD (Bono, Del Giudice, Gamberale, & Henry, 2012). These forces are developed into two contributions: one frequency-independent electrostatic (Equation (9)), the other frequency-dependent electro-dynamic (Equation (10)):
F = − q 2 M ∇ A 2 ≈ q V   ( V ≅ 0.1 V o l t )
F i − C D = C ω C D 2 − ω i 2 ω C D 2 − ω i 2 2 − Γ 2 ∇ A 2
The upper (Equation (9)) expresses the ponderomotive term showing that any electrical charge (independently of its sign) at the surface of a CD is repulsed outwards by a force proportional to the ratio q2/m. This is what can be observed with quasi-free electrons of the cold vortexes which are confined at the external surface. Electrons, being about 2000 times lighter than protons, are forced outwards much more intensely than protons. This means that any molecule able to reach the surface of the CD is set in a polarized, thus unstable state becoming promptly a more available species for possible chemical reactions (Del Giudice, Spinetti, & Tedeschi, 2012). On the other hand, (Equation (10)) expresses how an i-th system (made of electrical charges, but not necessarily displaying a net charge), is able to oscillate at a frequency ωi, very close to the one of the CD (ωCD ≈ ωi), is selectively attracted to the surface of the CD by a diverging attractive force (if positive) ore repelled (if the difference ω2CD – ω2i is negative). In other words: if a species (like ions or any molecule, even without a net electrical charge) has one mode of oscillation whose frequency is very close to the frequency of the CD, it is selectively subjected to a diverging force (typically interesting when it is attractive) which vanishes with the drop of the squared-frequency difference. In ordinary settings, the CDs experience the same boundary conditions, thus they oscillate at the same frequency. This leads to the cohesion of the liquid on the macroscopic scale (Arani, Bono, Del Giudice, & Preparata, 1995) (Bono, Del Giudice, Gamberale, & Henry, 2012).
By understanding what has been said so far, it clearly emerges that:
  • water is necessarily a two-fluid system, like already Röntgen proposed over a century ago (Röntgen, 1892);
  • the two phases in liquid water differentiate from one another for much deeper physical reasons than “different arrangements” (furthermore unjustifiable) of the classical “HB-networks”;
  • the short-range (electrostatic or perturbatively electrodynamic) forces – such van der Waals interactions – act mainly in the non-coherent fraction and do not change their typicality in dependence on the aggregation state (clusters, normal liquid, supercooled liquid, kinds of ice, etc.) and together with the long-range forces, they determine the maximum reachable close-packing level in coherent fraction;
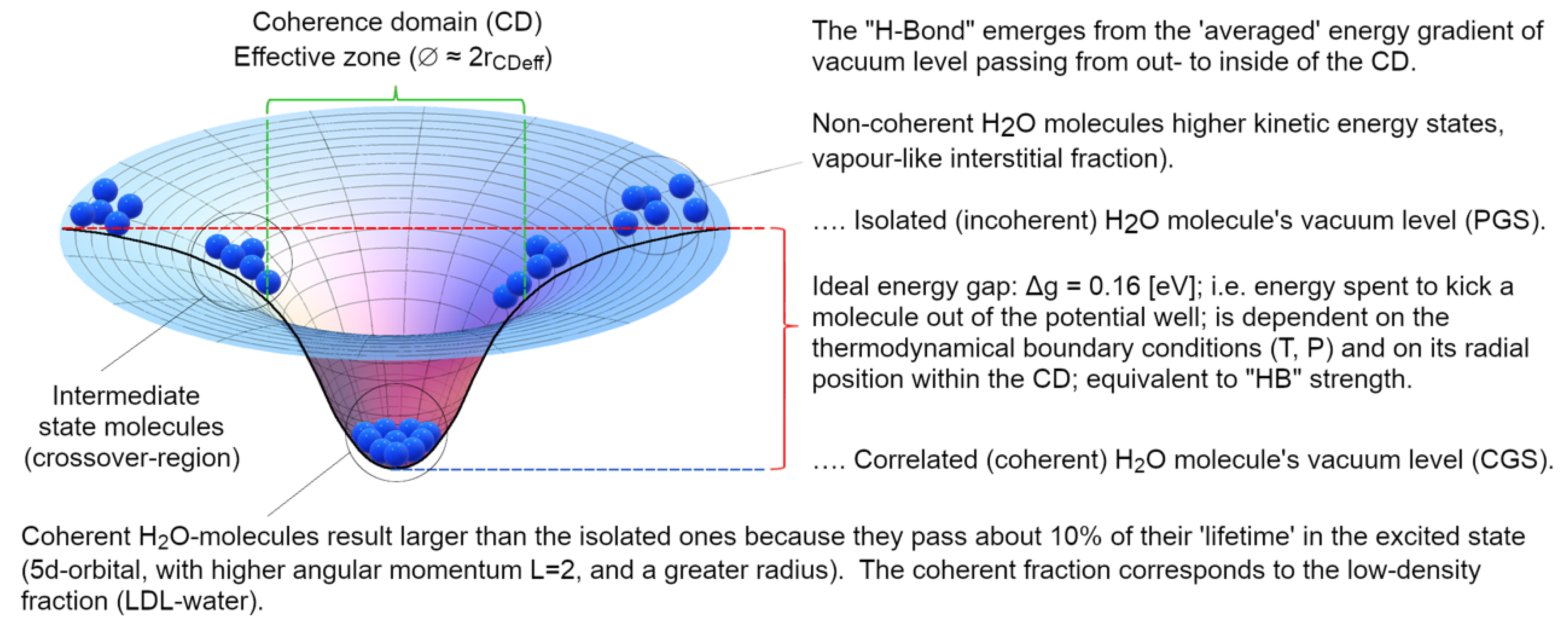
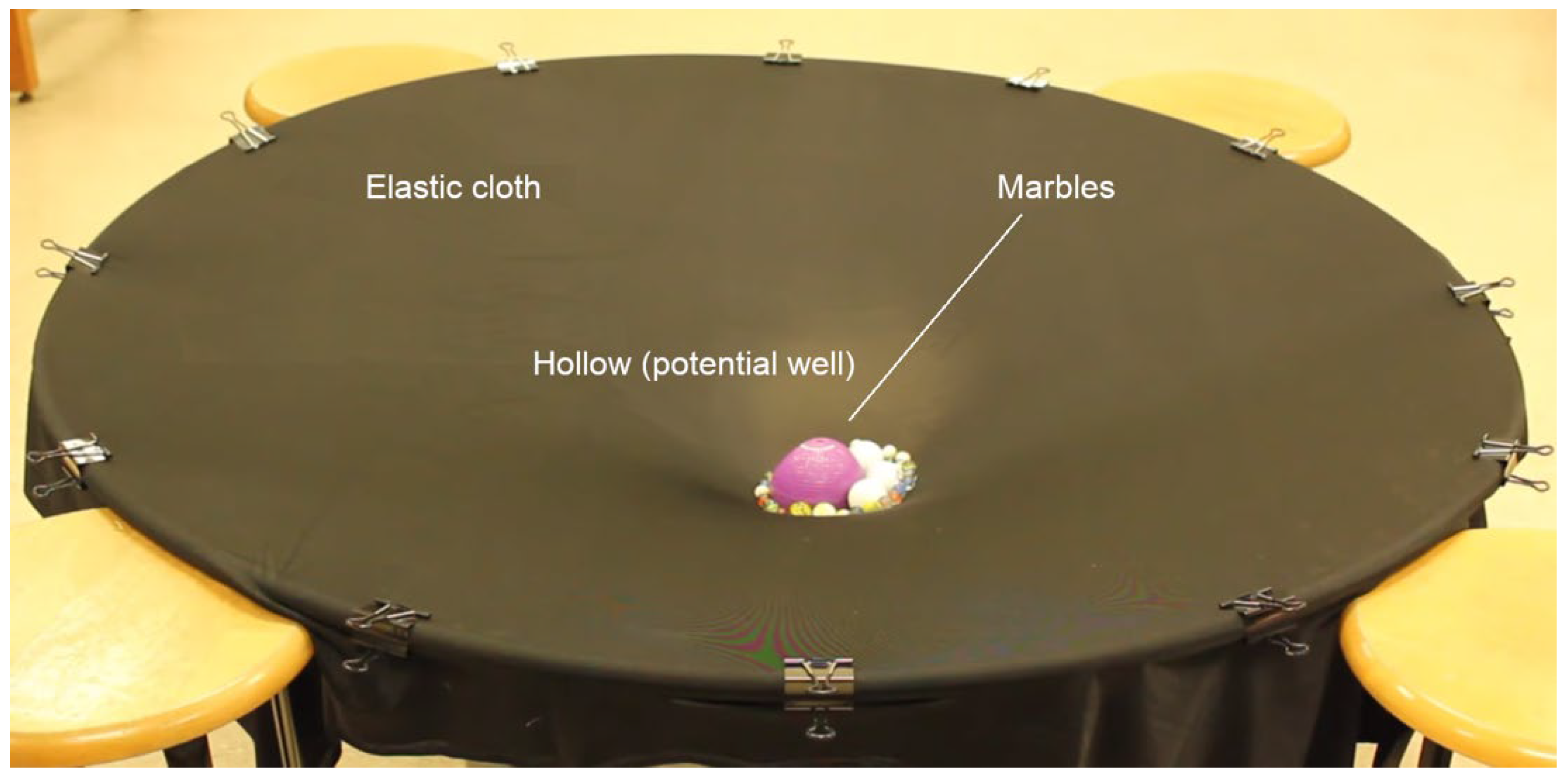
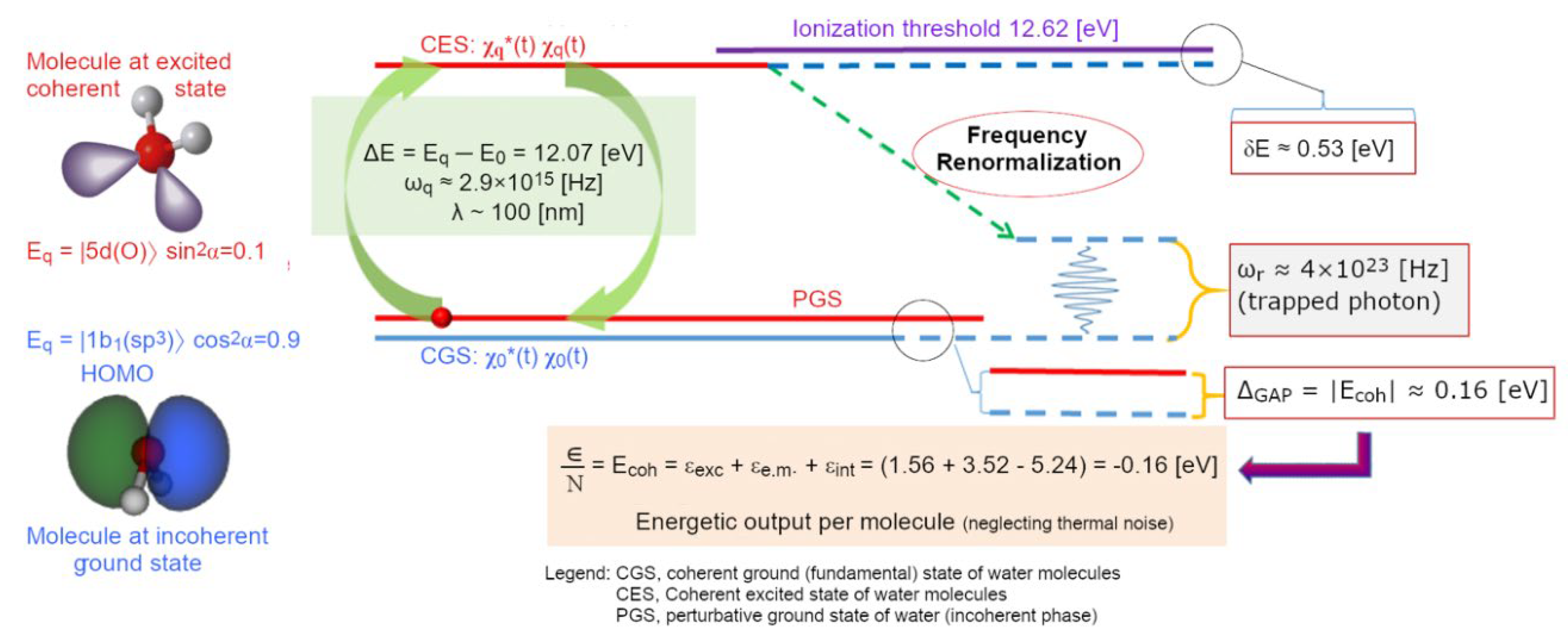
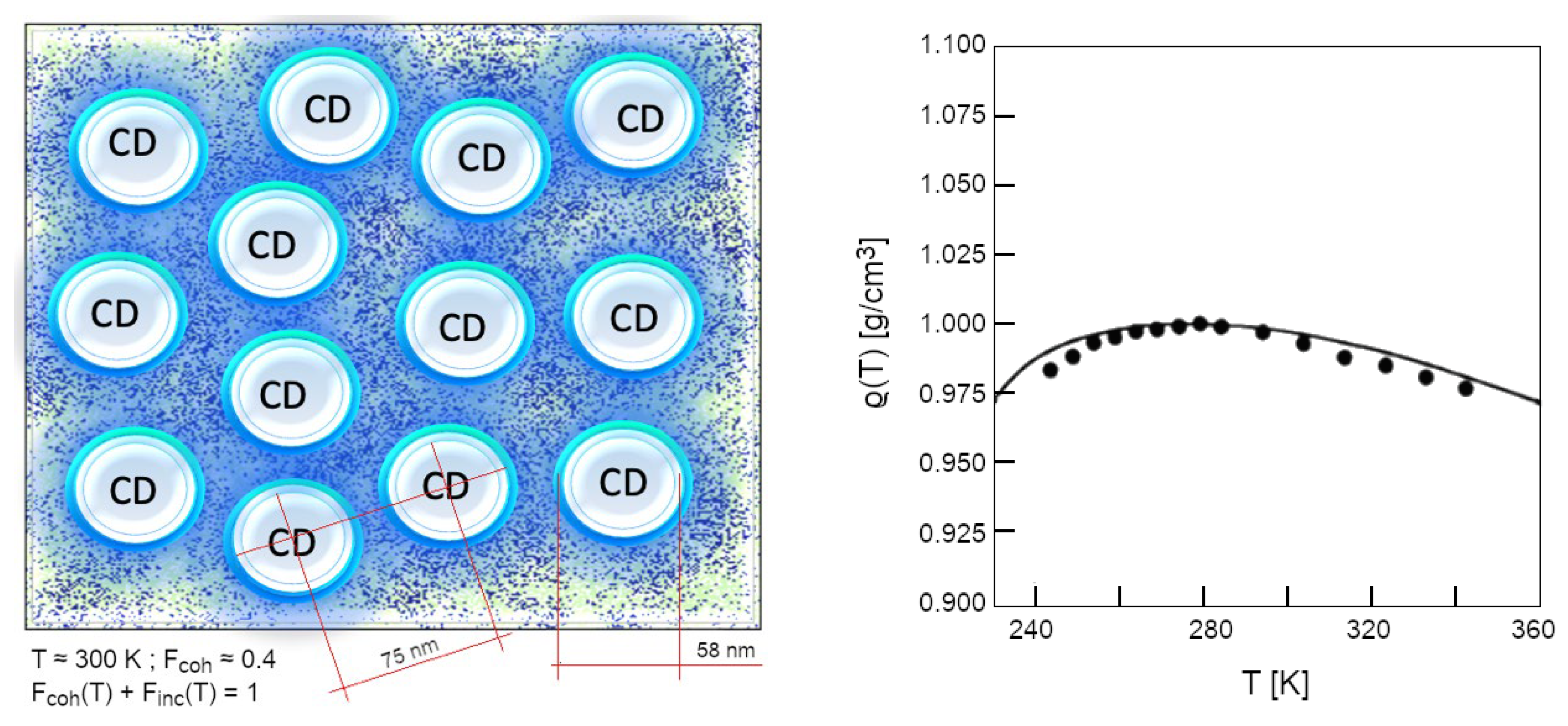
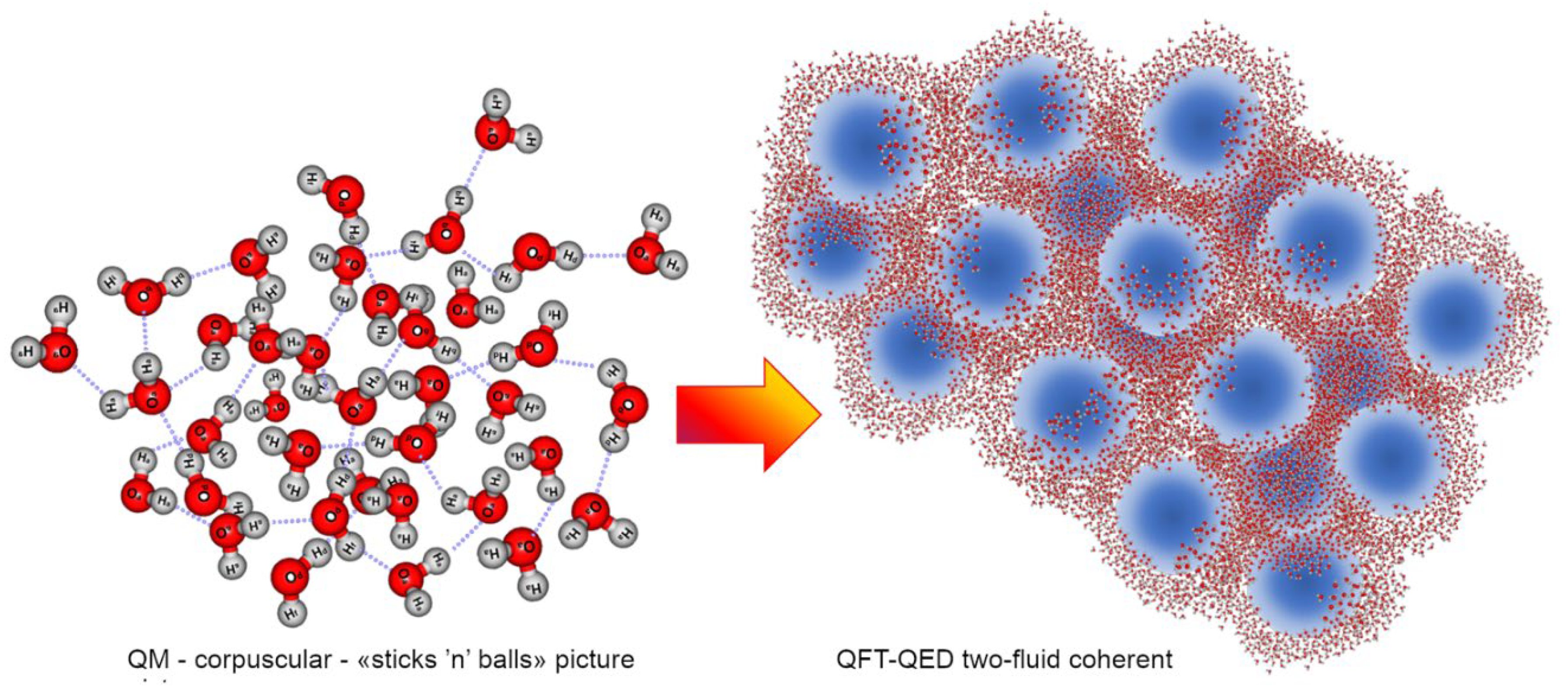
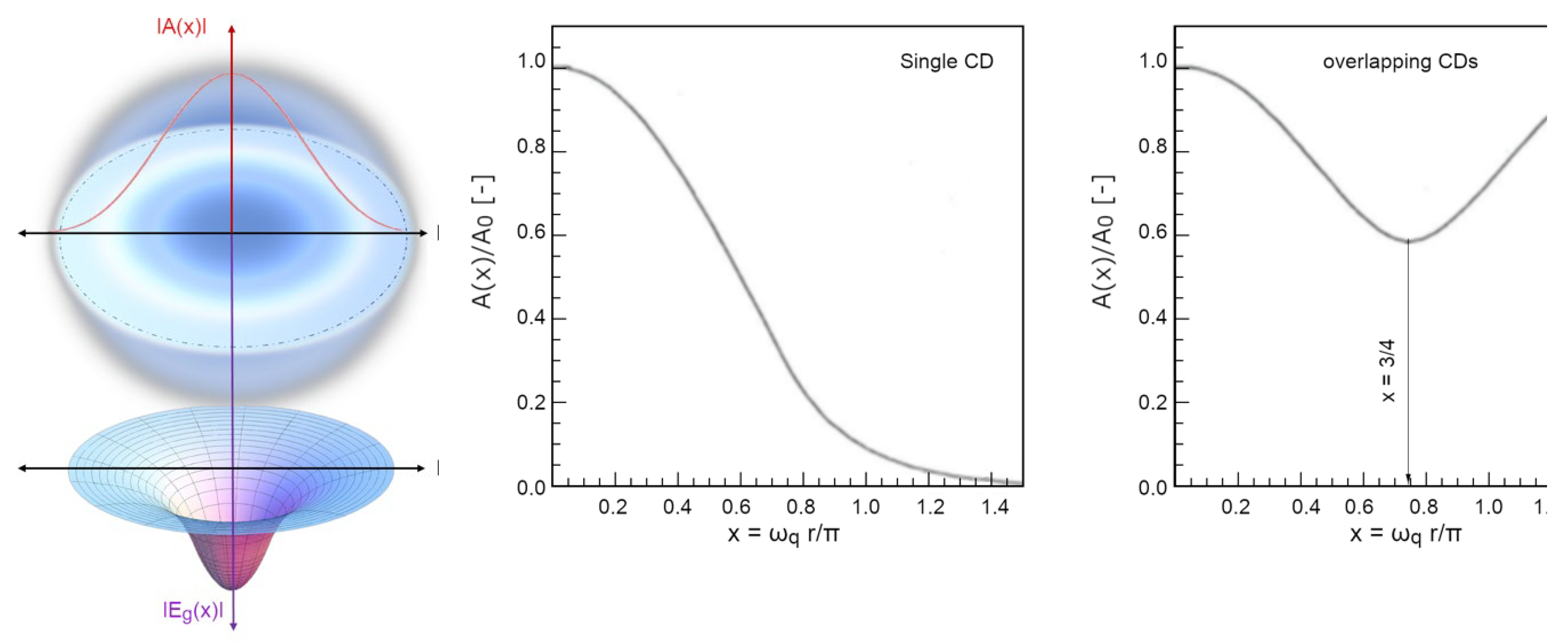
  • the main agent for the cohesion of the system cannot be primarily assigned to local, directional, short-range forces among molecules (which, if attractive, would not be sufficient at room temperature (Del Giudice, Galimberti, Gamberale, & Preparata, 1995), (Bono, Del Giudice, Gamberale, & Henry, 2012), (Henry M. , 2015)). Instead, the emergence of a coherent field matter constituted of in-phase oscillating electric charges and photons, produces potential wells (namely as large as the volume of the photons) at the ground level (vacuum) that is experienced by nearby molecules. An analogy can be made with marbles placed on an elastic cloth that cluster next to one another in the hollow produced by their own weight (if they’re sufficiently close to one another, i.e.,: enough dense), and not because of the existence of a net attractive force between them. Due to coherence, water molecules flip into such a minimum potential energy well, see Figure 7;
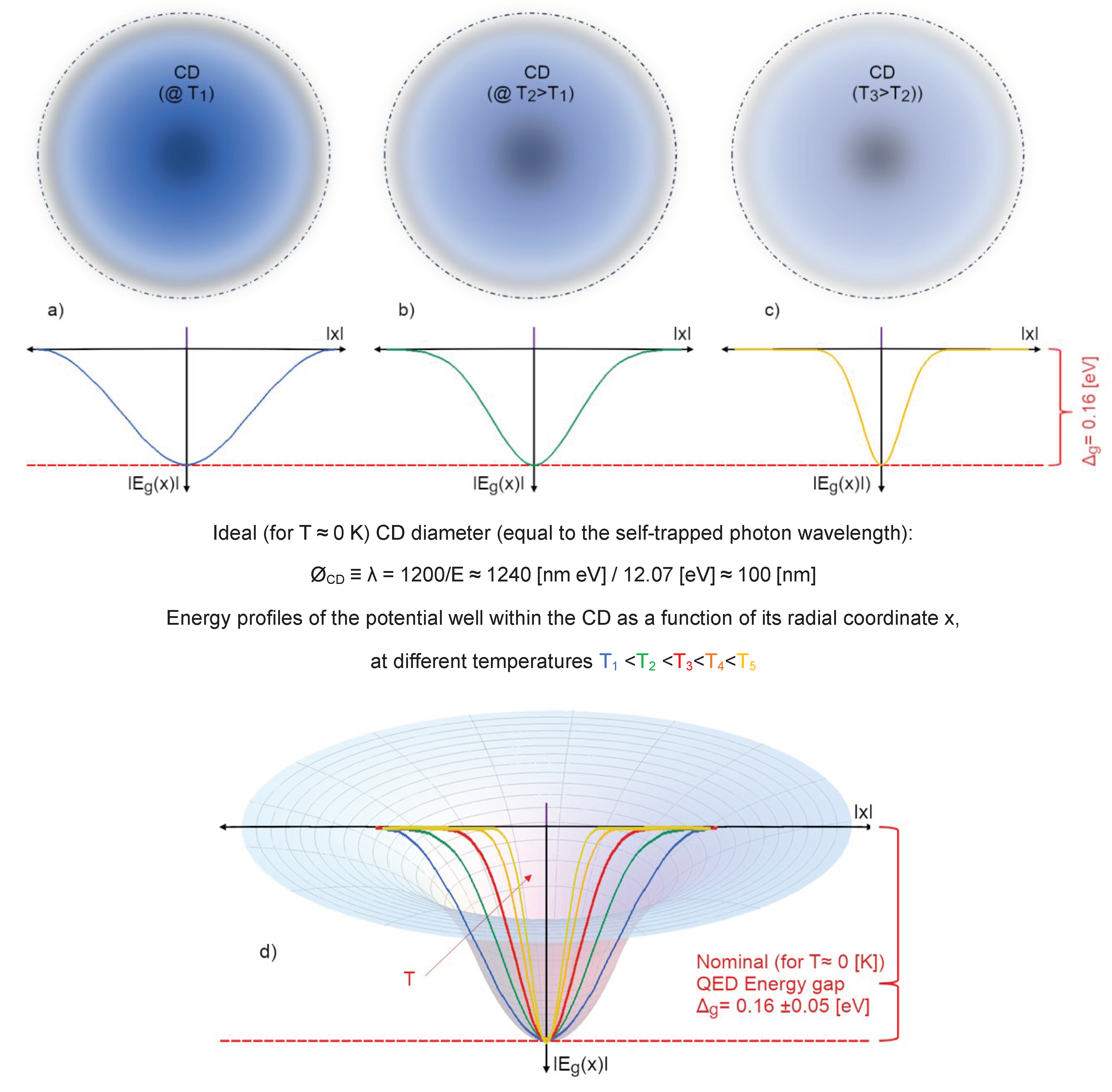
  • the differences retrieved experimentally in the emergent intermolecular “attraction”, called in a QM-corpuscular perspective “Hydrogen Bonds” derive from the dependence on the energy-well profile within the CD, thus we can understand why this apparent “intermolecular” force depends on the thermodynamic boundary conditions and on the kind of aggregation experienced by the molecules (see Figure 8).
Preprints 100724 g008aPreprints 100724 g008b
Figure 8. The top panel represents the different ground states (vacua) experienced by water molecules (schematized as blue spheres) within and outside of the CD. Due to the em-field confinement a potential gradient becomes established across the CD interface: the scheme serves to help figuring out how the effective thermodynamic stability enjoyed by molecules belonging to the CD depends also on the radial position within the CD. Thus, thermodynamical stability of coherence, which is usually interpreted through experimental data as different kinds/strengths/arrangements of “HB” is the averaged resultant out of many potential depths experienced by molecules in dependence on their radial position and on the width of the CD. What is deemed as a force existing among molecules, once close enough to a critical density, becomes macroscopically manifest as condensation (as is generally conceived within the QM view of the 1st quantization), is now understood through a metaphor to be just the same “apparent force” that we face if we try to separate some marbles from others resting at the bottom of the pit. This “force” is not something which exists intrinsically among marbles. It’s an emergent property, which manifests itself by the coupling between marbles and their vacuum (ground) level, of the deformed cloth (2nd quantization). See the text for further details.
Figure 8. The top panel represents the different ground states (vacua) experienced by water molecules (schematized as blue spheres) within and outside of the CD. Due to the em-field confinement a potential gradient becomes established across the CD interface: the scheme serves to help figuring out how the effective thermodynamic stability enjoyed by molecules belonging to the CD depends also on the radial position within the CD. Thus, thermodynamical stability of coherence, which is usually interpreted through experimental data as different kinds/strengths/arrangements of “HB” is the averaged resultant out of many potential depths experienced by molecules in dependence on their radial position and on the width of the CD. What is deemed as a force existing among molecules, once close enough to a critical density, becomes macroscopically manifest as condensation (as is generally conceived within the QM view of the 1st quantization), is now understood through a metaphor to be just the same “apparent force” that we face if we try to separate some marbles from others resting at the bottom of the pit. This “force” is not something which exists intrinsically among marbles. It’s an emergent property, which manifests itself by the coupling between marbles and their vacuum (ground) level, of the deformed cloth (2nd quantization). See the text for further details.
Preprints 100724 g008aPreprints 100724 g008b
Now let us explain better these last two points.
The energy gap, namely, is independent of temperature and of external conditions since it depends just on intrinsic physical quantities of the system and on the field amplitude which is described spatially in two regimes (inside and outside the CD, whose radius is rCD) as follows (Bono, Del Giudice, Gamberale, & Henry, 2012):
For   r < r C D ⇒ A r , t = A 0 · sin ⁡ ω q r ω q r · exp ⁡ ( − i ω r t ) r > r C D ⇒ d 2 ( r A ) d 2 r − ( ω q 2 − ω r 2 ) / r A ) = 0 ⇒
⇒ r C D − e f f = 3 4 π 1 ω q A r ≈ A 0 2 · e x p − ω q 2 − ω r 2 ( r − r C D − e f f ) r ω q
By using a dimensionless spatial parameter, 0 < x = r ωq/π < ¾ (scaled to the CD radius, in natural units π/ωq = λq ≈ 2rCD), the decay of the self-trapped em-field, from the centre to the periphery of the CD, is modulated by an envelope function F(x), which expresses its exponential damping:
A x = A 0 · F x = A 0 · − s i n π x π x + 2 π · e x p ⁡ − π ( 3 4 − x ) 3 − 2 x
The energy gain Eg(x), as a function of the radial distance x, follows an envelope analogous to the self-trapped field (as the former being built upon the latter, see Figure 7):
E g x = ∆ g · g ( x )
with
g x = F ( x 2 = − s i n π x π x + 2 π · e x p ⁡ − π ( 3 4 − x ) 3 − 2 x 2
We can now draw our final considerations. The usual misunderstanding around the generally accepted view of condensed matter (Preparata G. , 1995) is embedded in the limited perspective from which the problem is examined, as it neglects the coupling terms between matter- and em-field. To explain how in QFT the apparent intermolecular forces and bonds emerge we use a toy-system (as shown in lower part of Figure 8.
If we look at the condensed state of matter (e.g., liquid water) and try to separate one molecule from another, we expect to detect a force, a «bond», opposing our distancing action. The erroneous interpretation within the corpuscular view is rooted in the believe that this «bond» is a real force acting ‘among’ molecules: it is assumed that molecules are the same as when they are in their isolated state, with the same structure and individual features, and that such a “force” becomes relevant when their relative distance is sufficiently small. Actually, it is right the funnel-like deformation of the elastic cloth (metaphor of a gradient in vacuum level) created by the same weight of the sufficiently many marbles (Figure 8) cause them to cluster together at the bottom. Water molecules within the CD just tend to occupy the same minimal potential state (i.e.,: a lower ground state achieved thanks to the coupling between matter and em-field (unpredictable in a merely perturbative regime as the corpuscular view of the QM pair-potential (Henry M. , 2015)). Thus, the apparent “force” which we would experience while trying to separate a few marbles from some others, is the result of the potential gradient, their thermodynamic tendency, to remain in the minimal available energy state, as outlined by the deformed cloth (which is the alter ego of the vacuum, the ground state). This gradient, represented as an “invisible” elastic cloth, transduces itself into a «force», into a «bond strength». Yet, the marbles do not attract to one another if placed on a rigid floor (except for perturbative regimes, which are ridiculously small and thus negligible - of the order of 1/√N for molecules (Bono, Del Giudice, Gamberale, & Henry, 2012)).
The elastic cloth is the allegory of vacuum, ground state; while the fact that it can be deformed (and change its level) is a metaphor of the violation of von Neuman’s theorem, i.e.,: many vacua are possible in the framework of the 2nd quantization (QFT), but not within the 1st quantization (QM). The fact that the marbles, when numerous, cause the elastic cloth to bend is a figurative representation of the coupling between matter and em-field which becomes relevant as soon as a density threshold is reached. The resulting deformation, just like a black hole, attracts further marbles until the pit is densely populated, and corresponds to the sub-radiant lasing cavity called coherence domain. In terms of water, this self-sustained dynamics is produced by the numerical density of molecules which, once they overcome a critical threshold, cannot do anything but to further attract other molecules (Arani, Bono, Del Giudice, & Preparata, 1995). A characteristic feature of this ensemble is that they start to oscillate all in phase (tuned by the now trapped em-field) shifting into the so-called runaway escalation yielding into liquid condensation (Arani, Bono, Del Giudice, & Preparata, 1995)).
Of course, in phenomenological terms, we could say that a “bonding force” among molecules exists and that this force changes in dependence on the system. However, having this electrodynamic image at hand we are able to understand the physical meaning of that and we can consistently account for the fact that in ice the resulting calculated “bonding force” is dramatically bigger than in a cluster of supercooled confined liquid water or in a pretended “water dimer” (Ghanty, Staroverov, Koren, & Davidson, 2000) (Del Giudice, Galimberti, Gamberale, & Preparata, 1995).
The degree of coherence, and the establishment of other possible coherences (associated to other available levels in the water electronic spectrum, see Table 3 in (Bono, Del Giudice, Gamberale, & Henry, 2012)), determines the overall strength of the cohesion (manifesting as “strength of the bonds”). The degree of coherence (for each) is expressed by the electrodynamic functions of the field amplitude and the energy profile in dependence of the radial distance from the centre of the CD and these functions depends also on temperature (Garbelli, 2000). And on the macroscopic level their percentage is expressed by the sum rule: Fcoh(T) + Finc(T) = 1. This makes it possible to qualitatively deduce that the strength of any kind of coherence experienced by matter quanta (molecules) is not uniform across the whole CD volume but is rather dependent on their radial position within the CD and thus is affected by the shape of the energy gradient of the ground state (see, Figure 9). The overall resulting “bond strength” thus results from all the contributions acting on the system, like the possibility that coherence is undertaken also for other modes as it has been outlined for ice and low temperature states of water in (Bono, Del Giudice, Gamberale, & Henry, 2012) and (Buzzacchi, Del Giudice, & Preparata, 2002)). This explains why in hexagonal Ih-type ice the estimated “HB-strength” is higher than in the amorphous state (Buzzacchi, Del Giudice, & Preparata, 1999).
With this contemporary interpretation at hand, it is also easier to account for the 75 known water anomalies (Chaplin, 2023) and that would remain still a mystery when addressed within 1st quantization. Within 2nd quantization however, these various peculiar properties of water suddenly will lose their mysterious veil once each of those anomalies undergoes vigorous testing within the QFT-QED framework – as was shown with the classical HB concept.

4. Conclusions

In this review we wanted to address the problematic HB concept that still relies on the corpuscular “sticks-and-balls” view describing numerous condensed matter systems (from liquid water to biological molecules). We showed that, within the generally QM-theoretical approach (1st quantization), it is not possible to return a consistent physically-based description of the underlying dynamics that such a supposed “bond” should have. The usual picture of condensed matter to interpret the experimental data retrieved in physical-chemistry and spectroscopy, for instance, continue to emphasize this paradigm. The result of such a view is a conceptual dichotomy: the QM-corpuscular description of matter, where the interaction matter-em field is described by considering the interaction with vacuum just at perturbative order, on the one hand delivers a picture where molecules (like H2O) exist in physical states (electron cloud shapes) unable to satisfy the same conditions that would be necessary to originate those cohesive forces (like HBs). While, on the other hand, the HB cannot be justified any longer in its peculiar dependence on the thermodynamic boundary conditions of the systems, since, within the same purely QM picture, it would remain always the same (like van der Waals forces!).
We focused our attention on liquid water, but the general ideas can be applied to all condensed systems (Blasone, Jizba, & Vitiello, 2011) (Del Giudice & Vitiello, 2006) (Preparata G. , 1995). Having addressed the main problems created by the QM-corpuscular view, we rewrapped key aspects of the HB-concept by applying CD-structures as these emerge by the QFT-QED theoretical description developed since 1988. In the case of liquid water, it is sufficient to reframe challenges of condensed phases of matter along with the concept of the “HB”, as well as spectroscopic data within a “field view”. The two-fluid model of water within 2nd quantisation not only accounts for the shift in boiling point from -150 to +100 °C but also the density anomaly observed at +4 °C as well as for the strong cohesion of crystalline hexagonal (Ih) ice, where also coherence among molecule positions is established (Preparata G. , 1995), and for the supercooled liquid state (Henry M. , 2020). In fact, using the QED approach, quite a number of anomalous behaviours of water no longer need to be classified “anomalous” but are a logical consequence of the applied principles within the QED interpretation. Finally, once clarified that liquid water is not just a two-fluid system – as postulated by (Nilsson & Petterson, 2015) but one with a coherent and an incoherent phase, we delineated a QED interpretation for HBs by supporting it by calculations, and graphical intercomparison, in order to let this powerful, eye-opening view to be seized, discussed and the potential consequences it implies with as many scientists as possible.

Author Contributions

Both the authors contributed equally to the compilation of this article. All authors have read and agreed to the published version of the manuscript.

Institutional Review Board Statement

Not applicable as this study did not involve experimental trials with humans or animals.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

We want deeply to thank Marc Henry for the precious conversations held during these last years about the problem of H-bond, about water properties and their implications for life and biology. We are grateful for his precious efforts in challenging the mainstream mindset in chemistry and physical chemistry about condensed matter and water science. He’s been one of the very few chemists able to do that so profoundly, being courageous and persistent study of the heritage left to us by Giuliano Preparata and Emilio Del Giudice.

Conflicts of Interest

The authors declare no conflicts of interest.

Appendix A. Definition of the Hydrogen Bond within 1st Quantization

An excerpt of the Hydrogen bond, as introduced more than 100 years ago (Huggins, 1971), which was refined and officially adapted a decade ago by the IUAPC chemists (Elangannan & al., 2011). Therein, the hydrogen bond is [regarded] as an attractive interaction between a hydrogen atom from a molecule or a molecular fragment X–H (in which X is more electronegative than H), and an atom or a group of atoms in the same or a different molecule, in which there is evidence of bond formation. A typical hydrogen bond may be depicted as X–H∙∙∙Y–Z, where the three dots denote the bond. X–H represents the hydrogen bond donor. The acceptor may be an atom or an anion Y, or a fragment or a molecule Y–Z, where Y is bonded to Z …. The evidence for hydrogen bond formation may be experimental or theoretical, or ideally, a combination of both ….
The 12 criteria listed are divided into two groups – the first group (E) feature the HB itself (X–H∙∙∙Y–Z), whereas the second group (C) list some characteristics of HB:
(E1) The forces involved in the formation of a hydrogen bond include those of an electrostatic origin, those arising from charge transfer between the donor and acceptor leading to partial covalent bond formation between H and Y, and those originating from dispersion.
(E2) The atoms X and H are covalently bonded to one another and the X–H bond is polarized, the H∙∙∙Y bond strength increasing with the increase in electronegativity of X.
(E3 The X–H∙∙∙Y angle is usually linear (180°) and the closer the angle is to 180°, the stronger is the hydrogen bond and the shorter is the H∙∙∙Y distance.
(E4) The length of the X–H bond usually increases on hydrogen bond formation leading to a red shift in the infrared X–H stretching frequency and an increase in the infrared absorption cross-section for the X–H stretching vibration. The greater the lengthening of the X–H bond in X–H∙∙∙Y, the stronger is the H∙∙∙Y bond. Simultaneously, new vibrational modes associated with the formation of the H∙∙∙Y bond are generated.
(E5) The X–H∙∙∙Y–Z hydrogen bond leads to characteristic NMR signatures that typically include pronounced proton deshielding for H in X–H, through hydrogen bond spin–spin couplings between X and Y, and nuclear Overhauser enhancements.
(E6) The Gibbs energy of formation for the HB should be greater than the thermal energy of the system for the hydrogen bond to be detected experimentally.
(C1) The pKa of X–H and pKb of Y–Z in a given solvent correlate strongly with the energy of the hydrogen bond formed between them.
(C2) Hydrogen bonds are involved in proton-transfer reactions (X–H∙∙∙Y →X∙∙∙H–Y) and may be considered the partially activated precursors to such reactions.
(C3) Networks of hydrogen bonds can show the phenomenon of co-operativity, leading to deviations from pair-wise additivity in hydrogen bond properties.
(C4) Hydrogen bonds show directional preferences and influence packing modes in crystal structures.
(C5) Estimates of charge transfer in hydrogen bonds show that the interaction energy correlates well with the extent of charge transfer between the donor and the acceptor.
(C6) Analysis of the electron density topology of hydrogen-bonded systems usually shows a bond path connecting H and Y and a (3,–1) bond critical point between H and Y.
Most of these criteria (E3 to E6) and (C1 to C6) are purely empirical, and provide absolutely no information about the physical origin of the HB. The only criteria that provide clues about the physics behind HB-formation are criteria E1 and E2. While (E1) says only that whatever the nature of the HB, it is not entirely covalent, a point that doesn’t need to be questioned; and (E2) refers to a presumed bond strength instead of referring to its more physical and measurable stabilization energy. However, both criteria rely on the classical notion force, which however can only be defined for macroscopic systems moving at very low speeds compared with the speed of light (Henry, 2016). The fact that the definition of the HB requires an extensive list of criteria is a clear indication that it is based on incomplete assumptions.

References

  1. Anderson, P. Coherent Excited States in the Theory of Superconductivity: Gauge Invariance and the Meissner Effect. Phys Rev, 1958 110(4), 827–835. [CrossRef]
  2. Anderson, P. Basic Notions Of Condensed Matter Physics. Basic Books. XXXX, 1984. [CrossRef]
  3. Arani, R.; Bono, I.; Del Giudice, E.; Preparata, G. QED coherence and the thermodynamics of water. International Journal of Modern Physics B, 1995, 9, 1813–1841. [CrossRef]
  4. Bader, v.R. Atoms in Molecules. A Quantum Theory (Vol. 22). Clanderson Press. Oxford, 1990. [CrossRef]
  5. Becke, A.; Edgecombe, K. A simple measure of electron localization in atomic and molecular systems. JOurnal of Chemical Physics, 1990, 92(9), 5397. [CrossRef]
  6. Blasone, M.; Jizba, J.; Vitiello, G. Quantum field theory and its macroscopic manifestations. Imperial College Press. London, 2011. [CrossRef]
  7. Bono, I., Del Giudice, E., Gamberale, L., & Henry, M. (2012). Emergence of the Coherent Structure of Liquid Water. Water, 4, 510–532. [CrossRef]
  8. Bragg, W. The Crystal Structure of Ice. Proc Phys Soc London, 1922, 34(1), 98–103. [CrossRef]
  9. Bukowski, R.; Szalewicz, K.; Groenenboom, G. C.; van der Avoird, A. Predictions of the Properties of Water from First Principles. Science, 2007, 315(5816), 1249–1252. [CrossRef]
  10. Buzzacchi, M.; Del Giudice, E.; Preparata, G. Glasses: a new view from QED. MITH, 1999, 1-15. arXiv:cond-mat/9906395.
  11. Buzzacchi, M.; Del Giudice, E.; Preparata, G. Coherence of the Glassy State. Int J Mod Phys B, 2002, 16(25), 3771-3786. [CrossRef]
  12. Celeghini, E.; De Martino, S.; De Siena, S.; Rasetti, M.; Vitiello, G. Quantum Groups, Coherent States, Squeezing and Lattice Quantum Mechanics. Annals of Physics, 1995, 241, 50-67. [CrossRef]
  13. Celeghini, E.; Rasetti, M.; Vitiello, G. Quantum dissipation. Ann Phys, 1992, 215, 156–170. [Google Scholar] [CrossRef]
  14. De Ninno, A.; Del Giudice, E.; Gamberale, L.; Castellano, C. The structure of liquid water emerging from the vibrational spectroscopy interpretation with QED theory. Water, 2014, 6, 13–25. [Google Scholar] [CrossRef]
  15. De Ninno, A.; Nikollari, E.; Missori, M.; Frezza, F. Dielectric permittivity of aqueous solutions of electrolytes probed by THz time-domain and FTIR spectroscopy. Phys Lett A, 2020, 384(34), 126865. [CrossRef]
  16. Del Giudice, E.; Preparata, G. QED coherence and electrolyte solutions. J Electroanal Chem, 2000, 482(2), 110–116. [CrossRef]
  17. Del Giudice, E.; Tedeschi, A. Water and Autocatalysis in Living Matter. Electromag Biol Med, 2009, 28, 46–52. [Google Scholar] [CrossRef] [PubMed]
  18. Del Giudice, E.; Vitiello, G. The Role of the electromagnetic field in the formation of domains in the process of symmetry-breaking phase transitions. Phys Rev A, 2006, 74, 022105. [CrossRef]
  19. Del Giudice, E.; Galimberti, U.; Gamberale, L.; Preparata, G. Electrodynamic Coherence in water: a possible origin of the tetrahedral coordination. Mod Phys Lett B, 1995, 9(15), 953-961. [CrossRef]
  20. Del Giudice, E.; Spinetti, P. R.; Tedeschi, A. Water Dynamics at the Root of Metamorphosis in Living Organisms. Water, 2012, 566-586. [CrossRef]
  21. Del Giudice, E.; Voeikov, V.; Tedeschi, A.; Vitiello, G. The origin and the special role of coherent water in living systems. In M. C. D. Fels, Fields of the Cell (pp. 95-111). Research Signpost, Kerala, 2015. [CrossRef]
  22. Elangannan, A.; Desiraju, G.R.; Klein, R.A.; Sadlej, J.; Scheiner, S.; Alkorta, I.; Clary, D.C.; Crabtree, R.H.; Dannenberg, J.J.; Hobza, P.; Kjaergaard, H.G.; Legon, A.C. ; Mennucci, B;. Nesbitt, D.J. Definition of the hydrogen bond, Pure Applied Chemistry, 2011, 83(8), 1637–1641. [CrossRef]
  23. Flurry, R.L. Symmetry Groups: Theory and Chemical Applications. Prentice-Hall, XXXX, 1980. ISBN 0-13-880013-8.
  24. Franks, F. Water a comprehensive treatise (7 volumes). Plenum Press. New York:.
  25. Vol.1 (1974, 2nd ed. [CrossRef]
  26. Vol 2 (1973):. [CrossRef]
  27. Vol 3 (1977), 2nd ed.):. [CrossRef]
  28. Vol 4 (1975):. [CrossRef]
  29. Vol 5 (1975):. [CrossRef]
  30. Vol.6 (1979):. [CrossRef]
  31. Vol 7 (1982):. [CrossRef]
  32. Garbelli, A. Proprietà termodinamiche e dielettriche dell’acqua alla luce della teoria complessa delle interazioni molecolari rlettrodinamiche ed elettrostatiche (Thermodynamic and Dielectric Properties of Water in the Light of the Complex Theory of Electrodinamic and Electrostatic Molecular Interactions). Ph.D. Thesis, University of Milan, Italy, 2000. Tesi Laurea 2000, 1–89. [Google Scholar]
  33. Ghanty, T.K.; Staroverov, V.N.; Koren, P.R.; Davidson, E.R. Is the Hydrogen Bond in Water Dimer and Ice Covalent? J Am Cheml Soc, 2000, 122(6), 1210. [CrossRef]
  34. Guo, J.H.; Luo, Y.; Augustsson, A.; Rubensson, J.E.; Såthe, C.; Ågren, H.; Siegbahn, H.; Nordgren, J. X-Ray Emission Spectroscopy of Hydrogen Bonding and Electronic Structure of Liquid Water. Phys Rev Lett, 2002, 89(13), 137402. [CrossRef]
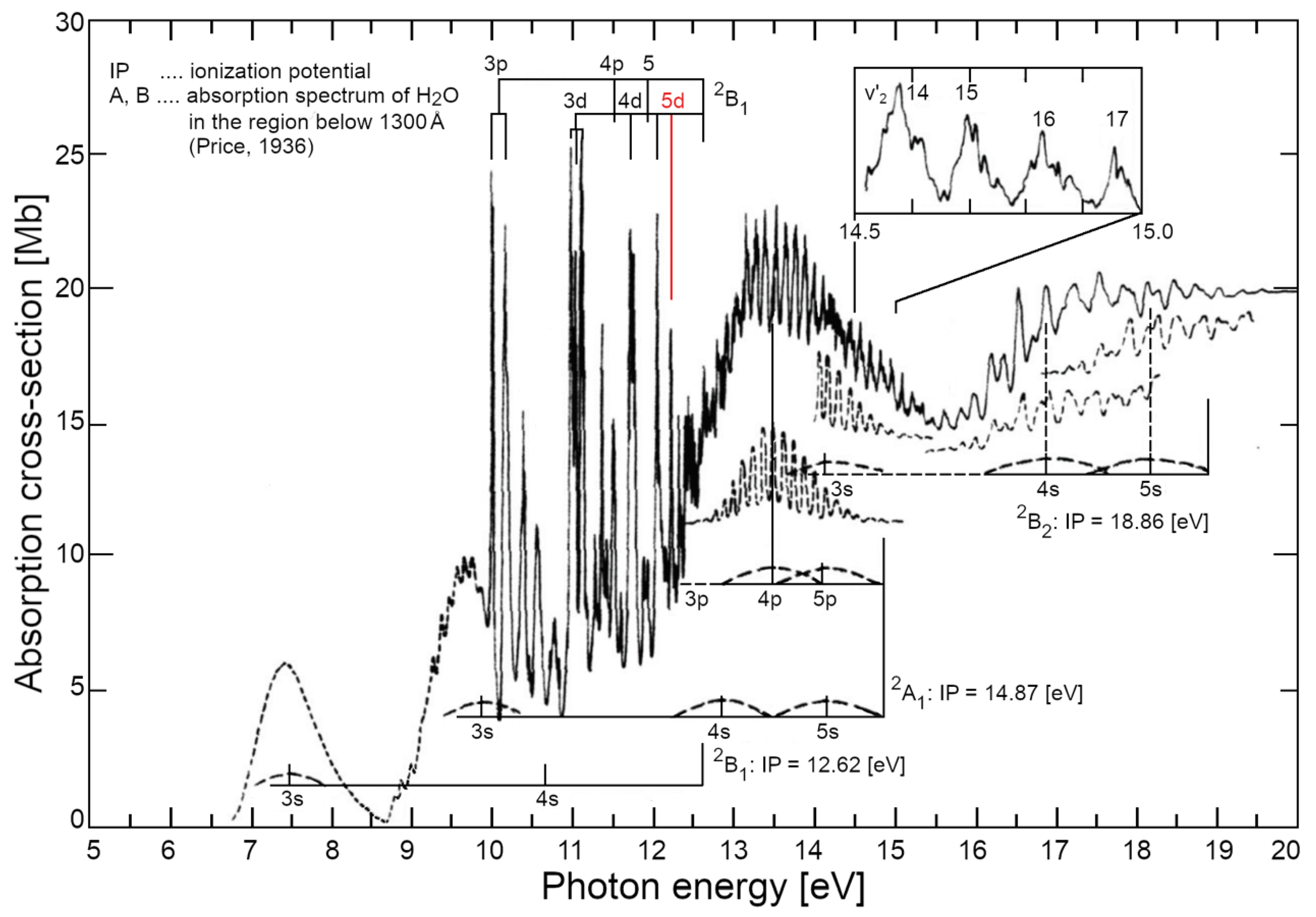
  35. Gürtler, P.; Saile, V.; Koch, E. Rydberg series in the absorption spectra of H2O and D2O in the vacuum ultraviolet. Chem Phys Lett, 1977, 51(2), 386-391. [CrossRef]
  36. Henry, M. The topological and quantum structure of zoemorphic water. In: Aqua Incognita: Why Ice Floats on Water and Galileo 400 Years on. (P. N. LoNostro, Ed.) Connor Court Publisher, Ballarat, 2014. ISBN 978-1-925138-21-4.
  37. Henry, M. The Hydrogen Bond. Inference Review, 2015, 1(2). [CrossRef]
  38. Henry, M. L’eau Morphogenique—Sante, Information Et Champs de Coscience, Escalquens; Éditions Dangles, 2020. ISBN: 978-2-7033-1269-7.
  39. Henry, M. The topological and quantum structure of zoemorphic water. In Aqua Incognita: Why Ice Floats on Water and Galileo 400 Years on; LoNostro, P.N.B.E., Ed.; Connor Court Publisher: Ballarat, Australia, 2014; pp. 197–239. ISBN 978-1925138214. [Google Scholar]
  40. Henry, M. L’Eau et la physique quantique, Dangles Editions. Escalquens, 2016. ISBN 978-2703311478.
  41. Henry, M. De l’information a l’exformation - une historie de vide, d’eau ou d’AND? (From Information to Exformation – a story of vacuum, water or DNA?). Ed. NAQ Strassbourg, ISBN 10-95620-03-7.
  42. Huang, C.; Wikfeldt, K.; Tokushima, T.; Nordlund, D.; Harada, Y.; Bergmann, U.; Niebuhr, M.; Weiss, T.M.; Horikawa, Y.; Leetmaa, M.; Ljungberg, M.P.; Takahashi, O.; Lenz, A.; Ojamäe, L.; Lyubartsev, A.P.; Shin, S.; Pettersson, L.G.; Nilsson, A. The inhomogeneous structure of water at ambient conditions. PNAS, 2009, 106, 15214-15218. [CrossRef]
  43. Huggins, M.L. 50 Years of Hydrogen Bond Theory. Ang Chem Int Ed, 1971, 10(3), 147–152. [CrossRef]
  44. Isaacs, E. D.; Shukla, A.; Platzman, P. M.; Hamann, D.R.; Barbiellini, B.; Tulk, C. Covalency of the Hydrogen Bond in Ice: A Direct X-Ray Measurement. Phys Rev Lett, 1999, 82(3), 600-603. [CrossRef]
  45. Kumar, A.; Gadre, S.R.; Mohan, N.; Suresh, C.H. Lone Pairs: An Electrostatic Viewpoint. J Phys Chem, 2014, 118(2), 526-532. [CrossRef]
  46. Li, K. Coherence in physics and biology. In Popp, F.; Li, K.; Gu, Q (eds), Recent Advances in Biophoton Research and its Applications. World Scientific Publishing. Sinngapore, 1992. [CrossRef]
  47. Li, K. Uncertainty Principle, Coherence and Structures. Springer Series in Synergetics, 1994, 61, 113-155. [CrossRef]
  48. Madl, P.; Renati, P. Quantum Electrodynamics Coherence and Hormesis: Foundations of Quantum Biology. Int J Molec Scie, 2023, 24(18), 14003. [CrossRef]
  49. Matcha, R.L. : King, S.C. Theory of the chemical bond. 1. Implicit perturbation theory and dipole moment model for diatomic molecules. J Am Chem Soc, 1976, 98(12), 3415-3420. [CrossRef]
  50. Moore, T.; Winmill, T. The States of Amines in Aqueous Solutions. J Chem Soc Trans, 1912, 101, 1635. [CrossRef]
  51. Nernst, W. Verteilung eines Stoffes zwischen zwei Lösungsmitteln und zwischen Lösungsmittel und Dampfraum. Zeitschr Physik Chem, 1891, 8(1), 110-139. [CrossRef]
  52. Nilsson, A.; Ogasawara, H.; Cavalleri, M.; Nordlund, D.; Nyberg, M.; Wernet, P.; Pettersson, L.G.M. The hydrogen bond in ice probed by soft x-ray spectroscopy and density functional theory. J Chem Phys, 2005, 122(15), 154505. [CrossRef]
  53. Pauling, L. The Shared-Electron Chemical Bond. PNAS, 1928, 14(4), 359-362. [CrossRef]
  54. Pauling, L. The Nature of the Chemical Bond. Application of Results Obtained from the Quantum Mechanics and from a Theory of Paramagnetic Susceptibility to the Structure of Molecules. J Am Chem Soc, 1931, 53(4), 1367-1400. [CrossRef]
  55. Pauling, L. The Structure and Entropy of Ice and of Other Crystals with Some Randomness of Atomic Arrangement. J Am Chem Soc, 1935, 57(12), 2680-2684. [CrossRef]
  56. Pauling, L.; Brockway, L. The Structure of the Carboxyl Group: I. The Investigation of Formic Acid by the Diffraction of Electrons. PNAS, 1934, 20(6), 336-340. [CrossRef]
  57. Pollack, G.H. The Fourth Phase of Water - Beyond Solid, Liquid, and Vapor. Ebner & Sons, Seatle), 2013. ISBN 978-0962-6895-4-3.
  58. Preparata, G. QED Coherence in Matter; World Scientific. Singapore, 1995. [CrossRef]
  59. Preparata, G. An Introduction to a Realistic Quantum Physics; World Scientific: Singapore, 2002. [Google Scholar] [CrossRef]
  60. Preparata, G.; Del Giudice, E.; Vitiello, G. Water as a Free Electric Dipole Laser. Phys Rev Lett, 1988, 61(9), 1085-1088. [CrossRef]
  61. Price, W.C. The Far Ultraviolet Absorption Spectra and Ionization Potentials of H2O and H2S. Journal of Chem Phys 4(3), 1936, 147-153. [CrossRef]
  62. Renati, P. Electrodynamic Coherence as a Physical Basis for Emergence of Perception, Semantics, and Adaptation in Living Systems. J. Genet. Mol. Cell. Biol. 2020, 7, 1–34. [Google Scholar] [CrossRef]
  63. Renati, P.; Kovacs, Z.; De Ninno, A.; Tsenkova, R. Temperature dependence analysis of the NIR spectra of liquid water confirms the existence of two phases, one of which is in a coherent state. J Mol Liq, 019, 292, 111449. [CrossRef]
  64. Robinson, G.W.; Cho, C.H.; Urquidi, J. Isosbestic points in liquid water: Further strong evidence for the two-state mixture model. J Chem Phys, 1999, 111(2), 698. [CrossRef]
  65. Romero, A.; Silvestrelli, P.; Parrinello, M. Compton scattering and the character of the hydrogen bond in ice Ih. J Chem Phys, 2001, 115(1), 115. [CrossRef]
  66. Röntgen, W. Über die Constitution des flüssigen Wassers. Ann Phys, 1892, 281(1), 91-97. [CrossRef]
  67. Roy, R.; Rao, M.L.; Kanzius, J. Observations of polarised RF radiation catalysis of dissociation of H2O–NaCl solutions, Mat Res Innov, 2008, 12(1): 3-6. [CrossRef]
  68. Shank, A.; Wang, Y.M.; Kaledin, A.; Braams, B.J.; Bowman, J.M. Accurate ab initio and “hybrid” potential energy surfaces, intramolecular vibrational energies, and classical ir spectrum of the water dimer. J Chem Phys, 2009, 130(14), 144314. [CrossRef]
  69. Schauberger W (1966) Verfahren und Vorrichtung zur Herstellung von Gemischen, Lösungen, Emulsionen, Suspensionen u. dgl. sowie zur biologischen Reinigung von freien Gewässern (Process and apparatus for the preparation of mixtures, solutions, emulsions, suspensions and the like and for the biological purification of open waters) Patent AT00000025991B; https://depatisnet.dpma.de/DepatisNet/depatisnet?action=pdf&docid=AT000000265991B&xxxfull=1 (accessed:Jan.
  70. Schwan, H.P. Field interaction with biological matter. Ann N Y Acad Sci, 1977, 303: 198-216. [CrossRef]
  71. Simons, J. Hydrogen Fluoride and its Solutions. Chem Rev, 1931, 8(2), 213-235. [CrossRef]
  72. Taschin, A.; Bartolini, P.; Eramo, R.; Righini, R.; Torre, R. Evidence of two distinct local structures of water from ambient to supercooled conditions. Nature Comm, 2013, 4, 2401. [CrossRef]
  73. Teixeira, J. Experimental determination of the nature of diffusive motions of water molecules at low temperatures. Phys Rev A, 1985, 31(3), 1913–1917. [CrossRef]
  74. Teixeira, J.; Luzar, A. Physics of liquid water: Structure and dynamics. In M. Bellissent-Funel (ed), Hydration Processes in Biology: Theoretical and Experimental Approaches. IOS Press, Amsterdam, 1999. ISBN 9-051-9943-9-7.
  75. Tokushima, T.; Harada, Y.; Takahashi, O.; Senba, Y.; Ohashi, H.; Pettersson, Nilsson, A.; L.; Shin, S. High resolution X-ray emission spectroscopy of liquid water: The observation of two structural motifs. Chem Physcs Lett, 2008, 460. [CrossRef]
  76. Toll, J.S. Causality and the Dispersion Relation: Logical Foundations. Phys Rev J Arch, 1956, 104(6), 1760–1770. [CrossRef]
  77. Vitiello, G. Coherent states, fractals and brain waves. New Math Nat Comp, 2009, 5(1), 245-264. [CrossRef]
  78. von Neumann, J. Mathematical Foundations of Quantum Theory. Princeton University Press, Princeton, 1955. ISBN XXXX.
  79. Wernet, P.; Nordlund, D.; Bergmann, U.; Cavalleri, M.; Odelius, M.; Ogasawara, H.; Näslund, L.A.; Hirsch, T.K.; Ojamäe, L.; Glatzel, P.; Pettersson, L.G.M.; Nilsson, A. The Structure of the First Coordination Shell in Liquid Water. Science, 2004, 304(5673), 995-999. [CrossRef]
  80. Voeikov, V. Reactive oxygen species, water, photons and life. Riv Biol. 2010, 103(2-3): 321-342. PMID: 21384328. [PubMed]
  81. Anderson, P. (1958). Coherent Excited States in the Theory of Superconductivity: Gauge Invariance and the Meissner Effect. Physical Review, 110(4), 827-835. [CrossRef]
  82. Anderson, P. (1984). Basic Notions Of Condensed Matter Physics. Basic Books.
  83. Arani, R., Bono, I., Del Giudice, E., & Preparata, G. (1995). QED coherence and the thermodynamics of water. International Journal of Modern Physics B, 9, 1813-1841.
  84. Bader, v. R. (1990). Atoms in Molecules. A Quantum Theory, (Vol. 22). Oxford: Clanderson Press. [CrossRef]
  85. Becke, A., & Edgecombe, K. (1990). A simple measure of electron localization in atomic and molecular systems. Journal of Chemical Physics, 92(9), 5397. [CrossRef]
  86. Bernal, J., & Fowler, R. (1933). A Theory of Water and Ionic Solution, with Particular Reference to Hydrogen and Hydroxyl Ions. Journal of Chemical Physics, 1(8), 515. [CrossRef]
  87. Blasone, M. , Jizba, J., & Vitiello, G. (2011). Quantum field theory and its macroscopic manifestations. London: Imperial College Press.
  88. Bono, I., Del Giudice, E., Gamberale, L., & Henry, M. (2012). Emergence of the Coherent Structure of Liquid Water. Water, 4, 510-532. [CrossRef]
  89. Bragg, W. (1922). The Crystal Structure of Ice. Proceedings of the Physical Society of London, 34(1), 98-103. Retrieved from https://iopscience.iop.org/article/10.1088/1478-7814/34/1/322.
  90. Bukowski, R. , Szalewicz, K., Groenenboom, G. C., & van der Avoird, A. (2007, March). Predictions of the Properties of Water from First Principles. Science, 315(5816), 1249-1252. [CrossRef]
  91. Buzzacchi, M. , Del Giudice, E., & Preparata, G. (1999, June). Glasses: a new view from QED. MITH-98/9, 1-15. arXiv:cond-mat/9906395.
  92. Buzzacchi, M. , Del Giudice, E., & Preparata, G. (2002). COHERENCE OF THE GLASSY STATE. International Journal of Modern Physics B, 16(25), 3771–3786. [CrossRef]
  93. Celeghini, E., De Martino, S., De Siena, S., Rasetti, M., & Vitiello, G. (1995). Quantum Groups, Coherent States, Squeezing and Lattice Quantum Mechanics. Annals of Physics, 241, 50-67.
  94. Celeghini, E., Rasetti, M., & Vitiello, G. (1992). Quantum dissipation. Annals of Physics, 215, 156–170.
  95. Chaplin, M. (2023, January 18). Water Absorption Spectrum. Retrieved from Water structure and science:. http://www1.lsbu.ac.uk/water/water_anomalies.html.
  96. De Ninno, A., Del Giudice, E., Gamberale, L., & Castellano, C. (2014). The structure of liquid water emerging from the vibrational spectroscopy interpretation with QED theory. Water, 6, 13-25. [CrossRef]
  97. De Ninno, A. , Nikollari, E., Missori, M., & Frezza, F. (2020). Dielectric permittivity of aqueous solutions of electrolytes probed by THz time-domain and FTIR spectroscopy. Physics Letters A, 384(34), 126865. [CrossRef]
  98. Del Giudice, E., & Preparata, G. a. (2000, January). QED coherence and electrolyte solutions. Journal of Electroanalytical Chemistry, 482(2), 110-116. [CrossRef]
  99. Del Giudice, E., & Tedeschi, A. (2009). Water and Autocatalysis in Living Matter. Electromagnetic Biology and Medicine, 28, 46–52. [CrossRef]
  100. Del Giudice, E. , & Vitiello, G. (2006). The Role of the electromagnetic field in the formation of domains in the process of symmetry-breaking phase transitions. Physical Review A, 74, 022105.
  101. Del Giudice, E. , Fleischmann, M., Preparata, G., & Talpo, G. (2002, October). On the “unreasonable” effects of ELF magnetic fields upon a system of ions. Bioelectromagnetics, 23(7), 522-530. [CrossRef]
  102. Del Giudice, E. , Galimberti, U., Gamberale, L., & Preparata, G. (1995). Electrodynamic Coherence in water: a possible origin of the tetrahedral coordination. Modern Physics Letters B, 9(15), 953-961. [CrossRef]
  103. Del Giudice, E., Spinetti, P. R., & Tedeschi, A. (2012). Water Dynamics at the Root of Metamorphosis in Living Organisms. Water, 566-586.
  104. Del Giudice, E. , Voeikov, V., Tedeschi, A., & Vitiello, G. (2015). The origin and the special role of coherent water in living systems. In M. C. D. Fels, Fields of the Cell (pp. 95-111). Kerala, India: Research Signpost. Retrieved from https://www.emmind.net/openpapers_repos/Endogenous_Fields-Mind/Water_EMF/Exclusion_Zones/2014_The_origin_and_the_special_role_of_coherent_water_in_living_systems.pdf.
  105. Dirac, P. (1929). Quantum Mechanics of Many-Electron Systems. Proceedings of the Royal Society of London. Containing Papers of a Mathematical and Physical Character 123. Series A, p. 714. London: Royal Society of London.
  106. Elangannan, A., & al., e. (2011, July). Pure Applied Chemistry, 83(8), 1637–1641. [CrossRef]
  107. Flurry, R. L. (1980). Symmetry Groups: Theory and Chemical Applications. Prentice-Hall.
  108. Franks, F. (1972-1982). Water a comprehensive treatise (7 volumes). New York: Plenum Press. Retrieved from https://www.springer.com/gp/book/9781468429602.
  109. Garbelli, A. (2000, May). Proprietà termodinamiche e dielettriche dell’acqua alla luce della teoria complessa delle interazioni molecolari rlettrodinamiche ed elettrostatiche. (G. Preparata, & E. Del Giudice, Eds.) Tesi di Laurea, 1-89.
  110. Ghanty, T. K. , Staroverov, V. N., Koren, P. R., & Davidson, E. R. (2000). Is the Hydrogen Bond in Water Dimer and Ice Covalent? Journal of American Chemical Society, 122(6), 1210. [CrossRef]
  111. Guo, J.-H. , Luo, Y., Augustsson, A., Rubensson, J.-E., Såthe, C., Ågren, H., … Nordgren, J. (2002, September). X-Ray Emission Spectroscopy of Hydrogen Bonding and Electronic Structure of Liquid Water. Physical Review Letters, 89(13), 137402. [CrossRef]
  112. Gürtler, P., Saile, V., & Koch, E. (1977, October). Rydberg series in the absorption spectra of H2O and D2O in the vacuum ultraviolet. Chemical Physics Letters, 51(2), 386-391. [CrossRef]
  113. Henry, M. (2014). The topological and quantum structure of zoemorphic water. In: Aqua Incognita: Why Ice Floats on Water and Galileo 400 Years on. (P. N. LoNostro, Ed.) Ballarat, Australia: Connor Court Publisher.
  114. Henry, M. (2015). De l’information a l’exformation - une historie de vide, d’eau ou d’ADN” (From Information to Exformation – a story of vacuum, water or DNA?). Strassbourg, France: NAQ Strassbourg.
  115. Henry, M. (2015, March). The Hydrogen Bond. Inference Review, 1(2). Retrieved from https://inferencereview.com/article/the-hydrogen-bond.
  116. Henry, M. (2016). L’Eau et La Physique Quantique – Vers une révolution de la médecine (Water and Quantum Physics – progres-sing towards a medical revolution, in French). Escalquens, France: Éditions Dangles.
  117. Henry, M. (2020). L’eau Morphogenique – Sante, Information Et Champs de Coscience. Escalquens, France: Éditions Dangles.
  118. Huang, C., Wikfeldt, K., Tokushima, T., Nordlund, D., Harada, Y., Bergmann, U., … Nilsson, A. (2009). The inhomogeneous structure of water at ambient conditions. PNAS, 106, 15214-15218. [CrossRef]
  119. Huggins, M. (1971). 50 Years of Hydrogen Bond Theory. Angewandte Chemie International (Edition in English), 10(3), 147-152. [CrossRef]
  120. Isaacs, E. D. , Shukla, A., Platzman, P. M., Hamann, D. R., Barbiellini, B., & Tulk, C. (1999, November). Covalency of the Hydrogen Bond in Ice: A Direct X-Ray Measurement. Phyical Review Letters, 82(3), 600-603. [CrossRef]
  121. Kumar, A. , Gadre, S. R., Mohan, N., & Suresh, C. H. (2014). Lone Pairs: An Electrostatic Viewpoint. Journal of Physical Chemistry, 118(2), 526-532. [CrossRef]
  122. Lamb, W. E., & Retherford, R. C. (1947). Fine structure of the hydrogen atom by a microwave method. Physical Review Letter(72), 241-243.
  123. Li, K. (1992a). Coherence in physics and biology. In F. Popp, K. Li, & Q. Gu, Recent Advances in Biophoton Research and its Applications (pp. 113-155). Singapore: World Scientific Publishing.
  124. Li, K. (1994). Uncertainty Principle, Coherence and Structures. Springer Series in Synergetics, 61, 113-155.
  125. Madl, P. , & Renati, P. (2023). Quantum Electrodynamics Coherence and Hormesis: Foundations of Quantum Biology. International Journal of Molecular Sciences, 24(18), 14003. [CrossRef]
  126. Matcha, R. L., & King, S. C. (1976). Theory of the chemical bond. 1. Implicit perturbation theory and dipole moment model for diatomic molecules. Journal of the American Chemical Society, 98(12), 3415-3420. [CrossRef]
  127. Moore, T. , & Winmill, T. (1912). The States of Amines in Aqueous Solutions. Journal of the Chemical Society Transactions, 101, 1635. Retrieved from https://pubs.rsc.org/en/content/articlelanding/1912/ct/ct9120101635#!divAbstract.
  128. Nernst, W. (1891, January). Verteilung eines Stoffes zwischen zwei Lösungsmitteln und zwischen Lösungsmittel und Dampfraum. Zeitschrift für Physikalische Chemie, 8(1), 110-139. [CrossRef]
  129. Nikollari, E. , De Ninno, A., & Frezza, A. (2023). Dielectric response of liquid water and aqueous solutions: Two-fluid behaviour. 3rd European Aquaphotomics Conference (02-04 September 2023). Rome, Italy.
  130. Nilsson, A. , & al., e. (2005). The hydrogen bond in ice probed by soft x-ray spectroscopy and density functional theory. The Journal of Chemical physics, 122(15), 154505. [CrossRef]
  131. Nilsson, A., & Petterson, L. (2015). The structural origin of anomalous properties of liquid water. Nature Communications, 6, 8998. [CrossRef]
  132. Pauling, L. (1928, Aprile). The Shared-Electron Chemical Bond. Proceedings of the National Academi of Sciences of the United Sates of America (PNAS), 14(4), 359-362. [CrossRef]
  133. Pauling, L. (1931). The Nature of the Chemical Bond. Application of Results Obtained from the Quantum Mechanics and from a Theory of Paramagnetic Susceptibility to the Structure of Molecules. Journal of the American Chemical Society, 53(4), 1367-1400. [CrossRef]
  134. Pauling, L. (1935). The Structure and Entropy of Ice and of Other Crystals with Some Randomness of Atomic Arrangement. Journal of the American Chemical Society, 57(12), 2680-2684. [CrossRef]
  135. Pauling, L., & Brockway, L. (1934). THE STRUCTURE OF THE CARBOXYL GROUP. I. THE INVESTIGATION OF FORMIC ACID BY THE DIFFRACTION OF ELECTRONS. Proceedings of The National Academy of Sciences of The uNited Sates of America (PNAS), 20(6), 336-340. [CrossRef]
  136. Pauling, L. , Corey, R., & Branson, H. (1951). The structure of proteins; two hydrogen-bonded helical configurations of the polypeptide chain. Proceedings of the National Academy of Sciences (PNAS), 37(4), 205-211. [CrossRef]
  137. Pollack, G. H. (2013). The Fourth Phase of Water. Seattle: Ebner and Sons.
  138. Preparata, G. (1995). QED Coherence in Matter, World Scientific.
  139. Preparata, G. (2002). An Introduction to a Realistic Quantum Physics. World Scientific.
  140. Preparata, G., Del Giudice, E., & Vitiello, G. (1988, August). Water as a Free Electric Dipole Laser. Physical Review Letters, 61(9), 1085-1088.
  141. Price, W. (1936). he Far Ultraviolet Absorption Spectra and Ionization Potentials of H2O and H2S. Journal of Chemical Physics, 4(3), 147-153. [CrossRef]
  142. Quane, D. (1990). The Reception of Hydrogen Bonding by the Chemical Community: 1920-1937. Bulletin for the History of Chemistry, 7, 3-13. Retrieved from http://acshist.scs.illinois.edu/bulletin_open_access/num7/num7%20p3-13.pdf.
  143. Renati, P. (2020). Electrodynamic Coherence as a Physical Basis for Emergence of Perception, Semantics, and Adaptation in Living Systems. Journal of Genetic, Molecular and Cellular Biology, 7(2), 1-34. [CrossRef]
  144. Renati, P., Kovacs, Z., De Ninno, A., & Tsenkova, R. (2019). Temperature dependence analysis of the NIR spectra of liquid water confirms the existence of two phases, one of which is in a coherent state. Journal of Molecular Liquids, 292, 111449. [CrossRef]
  145. Robinson, G. W. , Cho, C. H., & Urquidi, J. (1999, April). Isosbestic points in liquid water: Further strong evidence for the two-state mixture model. The Journal of Chemical Physics, 111(2), 698. [CrossRef]
  146. Romero, A. , Silvestrelli, P., & Parrinello, M. (2001). Compton scattering and the character of the hydrogen bond in ice Ih. The Journal of Chemical Physics, 115(1), 115. [CrossRef]
  147. Röntgen, W. (1892). Ueber die Constitution des flüssigen Wassers Annalen der Physik. Annalen der Physik, 281 (1), 91-97. [CrossRef]
  148. Roy, R. , Rao, M., & Kanzius, J. (2008). Observations of polarised RF radiation catalysis of dissociation of H2O–NaCl solutions. Materials Research Innovations, 12(1), 3-6. [CrossRef]
  149. Schauberger, V. (1966). Germany Patent No. DE 1.557.213. Retrieved January 29, 2024, from http://pks.or.at/wp-content/uploads/PAT_265_991_DE.pdf.
  150. Schwan, H. (1977). Field interaction with biological matter. Annals of New York Academy of Sciences, 198-216. [CrossRef]
  151. 151. Shank, Wang, Kaledin, Braams, & Bowman. (2009). Accurate ab initio and “hybrid” potential energy surfaces, intramolecular vibrational energies, and classical ir spectrum of the water dimer. Journal of Chemical Physics, 130(14), 144314. [CrossRef]
  152. Simons, J. (1931, April). Hydrogen Fluoride and its Solutions. Chemical Reviews, 8(2), 213-235. [CrossRef]
  153. Taschin, A., Bartolini, P., Eramo, R., Righini, R., & Torre, R. (2013). Evidence of two distinct local structures of water from ambient to supercooled conditions. Nature Communications, 4, 2401. [CrossRef]
  154. Teixeira, J. , & Luzar, A. (1999). Physics of liquid water: Structure and dynamics. In M. Bellissent-Funel, Hydration Processes in Biology: Theoretical and Experimental Approaches (pp. 35-65). Amsterdam: IOS Press.
  155. Teixeira, J. , Bellissent-Funel, M., Chen, S. H., & Dianoux, A. J. (1985, March). Experimental determination of the nature of diffusive motions of water molecules at low temperatures. Physical Review A, 31(3), 1913-1917. [CrossRef]
  156. Tokushima, T. , Harada, Y., Takahashi, O., Senba, Y., Ohashi, H., Pettersson, L., … Shin, S. (2008). High resolution X-ray emission spectroscopy of liquid water: The observation of two structural motifs. Chemical Physics Letters, 460. [CrossRef]
  157. Toll, J. S. (1956, December). Causality and the Dispersion Relation: Logical Foundations. Physical Review Journals Archive, 104(6), 1760-1770. [CrossRef]
  158. Vitiello, G. (2009). Coherent states, fractals and brain waves. New Mathematics and Natural Computing, 5(1), 245-264. [CrossRef]
  159. Voeikov, V. (2010). Reactive oxygen species, water, photons and life. Biology Forum, 321-342. Retrieved from https://www.researchgate.net/publication/50305420_Reactive_Oxygen_Species_Water_Photons_and_Life.
  160. von Neumann, J. (1955). Mathematical Foundations of Quantum Theory. Princeton: Princeton University Press.
  161. Wernet, P. e. (2004). The Structure of the First Coordination Shell in Liquid Water. Science, 304(5673), 995-999. [CrossRef]
  162. Wernet, P., Nordlund, D., Bergmann, U., Cavalleri, M., Odelius, M., Ogasawara, H., … Nilsson, A. (2004, May). The Structure of the First Coordination Shell in Liquid Water. Science, 304(5673), 995-999. [CrossRef]
  163. Zachariasen, W. H. (1935). The Liquid “Structure” of Methyl Alcohol. The Journal of Chemical Physics, 3(3), 158–161. [CrossRef]
Preprints 100724 g001
Figure 1. Molecular orbitals of water molecule in LCAO theory of the isolated molecule. Note: inner 1s orbital not shown; σ denotes bonding constellation; σ* denotes anti-bonding constellation, leading to molecular instability and thus splitting of the constituting atoms. [Source: Adapted after: Chaplin M (2022) Water Structure and Science – Molecular Orbitals for Water (H2O). (Chaplin, 2022). https://water.lsbu.ac.uk/water/h2o_orbitals.html (accessed Jan.’24) and Locke W (1996) Introduction to molecular Orbital Theory. ICSTM Department of Chemistry. Imperial College, London (UK) https://www.ch.ic.ac.uk/vchemlib/course/mo_theory/].
Figure 1. Molecular orbitals of water molecule in LCAO theory of the isolated molecule. Note: inner 1s orbital not shown; σ denotes bonding constellation; σ* denotes anti-bonding constellation, leading to molecular instability and thus splitting of the constituting atoms. [Source: Adapted after: Chaplin M (2022) Water Structure and Science – Molecular Orbitals for Water (H2O). (Chaplin, 2022). https://water.lsbu.ac.uk/water/h2o_orbitals.html (accessed Jan.’24) and Locke W (1996) Introduction to molecular Orbital Theory. ICSTM Department of Chemistry. Imperial College, London (UK) https://www.ch.ic.ac.uk/vchemlib/course/mo_theory/].
Preprints 100724 g001
Preprints 100724 g002
Figure 2. Schematic Left: Gas phase PES spectrum of water measured at a photon energy of 100 eV and PES spectra of ice at photon energies of 100 eV and 530 eV. XAS spectra of gas phase water and ice together with a Density Functional Theory (DFT) calculation of hexagonal ice described with a 44-molecule cluster [23]. Right: Scheme showing that the 3a1(HOMO-1) molecular orbital lies in the molecular plane, whereas the 1b1-(HOMO) orbital lies in a plane perpendicular to σ-bonds (O–H). Yellow-blue pairing denotes anti-bonding, yellow-green paring denotes bonding orbitals. The overlapping is expressed by the exchange-integral S. Partial HB’s covalence is thus possible only when the in-plane fully occupied 3a1-(HOMO-1) level overlaps with an empty 4a1-(LUMO) of a neighbouring molecule, the overlapping being zero with the other out-of-plane 1b1-(HOMO). Strong HBs are then expected by interacting with the 3a1-level while van der Waals interactions are expected for the 1b1-level. But the changes in the 3a1 orbital revealed by XES [23] are not experimental evidence for electron sharing (covalence) in HBs (Guo, et al., 2002) because in (HOMO-LUMO) frontier-orbitals theory the assumed covalence would primarily affect the HOMO outmost 1b1 orbital and definitively not the 3a1-(HOMO-1). Covalence in a QM sense, i.e., HOMO-LUMO interaction, is thus not supported by experimental data. In other words, a valid CP or QM picture of HB seems impossible.
Figure 2. Schematic Left: Gas phase PES spectrum of water measured at a photon energy of 100 eV and PES spectra of ice at photon energies of 100 eV and 530 eV. XAS spectra of gas phase water and ice together with a Density Functional Theory (DFT) calculation of hexagonal ice described with a 44-molecule cluster [23]. Right: Scheme showing that the 3a1(HOMO-1) molecular orbital lies in the molecular plane, whereas the 1b1-(HOMO) orbital lies in a plane perpendicular to σ-bonds (O–H). Yellow-blue pairing denotes anti-bonding, yellow-green paring denotes bonding orbitals. The overlapping is expressed by the exchange-integral S. Partial HB’s covalence is thus possible only when the in-plane fully occupied 3a1-(HOMO-1) level overlaps with an empty 4a1-(LUMO) of a neighbouring molecule, the overlapping being zero with the other out-of-plane 1b1-(HOMO). Strong HBs are then expected by interacting with the 3a1-level while van der Waals interactions are expected for the 1b1-level. But the changes in the 3a1 orbital revealed by XES [23] are not experimental evidence for electron sharing (covalence) in HBs (Guo, et al., 2002) because in (HOMO-LUMO) frontier-orbitals theory the assumed covalence would primarily affect the HOMO outmost 1b1 orbital and definitively not the 3a1-(HOMO-1). Covalence in a QM sense, i.e., HOMO-LUMO interaction, is thus not supported by experimental data. In other words, a valid CP or QM picture of HB seems impossible.
Preprints 100724 g002
Preprints 100724 g003
Figure 3. The excitation spectrum (Gürtler, Saile, & Koch, 1977) and (Price, 1936) of water vapour (isolated molecules) in the visible and near UV range (up to 20 eV); the red line indicates (by considering the final density of the liquid at room P and T) the predicted excited level (5d orbital) that satisfies several favourable conditions at once, such as not too high critical density, sufficient oscillator strength, relevant coupling constants gc, μr and energy gap.
Figure 3. The excitation spectrum (Gürtler, Saile, & Koch, 1977) and (Price, 1936) of water vapour (isolated molecules) in the visible and near UV range (up to 20 eV); the red line indicates (by considering the final density of the liquid at room P and T) the predicted excited level (5d orbital) that satisfies several favourable conditions at once, such as not too high critical density, sufficient oscillator strength, relevant coupling constants gc, μr and energy gap.
Preprints 100724 g003
Preprints 100724 g004
Figure 4. A scheme of the energetics of the coherent state of water molecules showing that such a state is the outcome of an unceasing collective oscillation of the molecules between two states mediated by the self-trapped em-field whose phase (and renormalized frequency) are locked to the phase of the matter-field. Considering the coherent oscillation, water molecules assume two limit-shapes (excited and relaxed) during the oscillation cycle with different time-weights. The value of the energy gap, (Δg≈0.16 eV) in this scheme refers to the last calculation done for liquid water neglecting the temperature contribution (Bono, Del Giudice, Gamberale, & Henry, 2012). However, as will be discussed in the following, the energy stability is not independent of the radial position within the CD (see Equations (13a) and (13b) in the text), thus the energetic profile of the coherent ground state within CDs is dependent on the aggregation state and on thermodynamic conditions. As expressed in (Bono, Del Giudice, Gamberale, & Henry, 2012), the thermodynamic parameters (like pressure and temperature) are able to affect the establishment of other types of coherence, by yielding favourable the election of other excited levels among the others available in the electron spectrum of water (to which other field amplitude, oscillator strength, energy gap, coupling constant, critical density, renormalization frequency are associated). This is a key aspect to understand why the classical concept of “HB” depends on the aggregation state (water dimer, liquid, ice, supercooled clusters, etc.) (Henry M. , 2014). A mixing angle α, giving sin2(α) = 0.1 indicates that electrons in water molecules spend 10 % of their time on the excited level (Eq, the 5d oxygen orbital), thus coherent water molecules are larger than incoherent water molecules. Such a fact can count for (i) the flickering landscape of intermolecular interactions (among which the called “HBs”), as well as for (ii) the evidence of somehow tetrahedral structures in some regions of the liquid (or as in hexagonal ice and in confined water). Indeed, two of the five d-orbitals (z2, x2-y2) transform into the totally symmetric a1-representation of the C2v group and can mix themselves with the two other molecular orbitals (2a1, 3a1) giving rise to a set of four a1-type levels arranged in a more or less tetrahedral configuration to minimize electronic repulsions (Del Giudice, Galimberti, Gamberale, & Preparata, 1995).
Figure 4. A scheme of the energetics of the coherent state of water molecules showing that such a state is the outcome of an unceasing collective oscillation of the molecules between two states mediated by the self-trapped em-field whose phase (and renormalized frequency) are locked to the phase of the matter-field. Considering the coherent oscillation, water molecules assume two limit-shapes (excited and relaxed) during the oscillation cycle with different time-weights. The value of the energy gap, (Δg≈0.16 eV) in this scheme refers to the last calculation done for liquid water neglecting the temperature contribution (Bono, Del Giudice, Gamberale, & Henry, 2012). However, as will be discussed in the following, the energy stability is not independent of the radial position within the CD (see Equations (13a) and (13b) in the text), thus the energetic profile of the coherent ground state within CDs is dependent on the aggregation state and on thermodynamic conditions. As expressed in (Bono, Del Giudice, Gamberale, & Henry, 2012), the thermodynamic parameters (like pressure and temperature) are able to affect the establishment of other types of coherence, by yielding favourable the election of other excited levels among the others available in the electron spectrum of water (to which other field amplitude, oscillator strength, energy gap, coupling constant, critical density, renormalization frequency are associated). This is a key aspect to understand why the classical concept of “HB” depends on the aggregation state (water dimer, liquid, ice, supercooled clusters, etc.) (Henry M. , 2014). A mixing angle α, giving sin2(α) = 0.1 indicates that electrons in water molecules spend 10 % of their time on the excited level (Eq, the 5d oxygen orbital), thus coherent water molecules are larger than incoherent water molecules. Such a fact can count for (i) the flickering landscape of intermolecular interactions (among which the called “HBs”), as well as for (ii) the evidence of somehow tetrahedral structures in some regions of the liquid (or as in hexagonal ice and in confined water). Indeed, two of the five d-orbitals (z2, x2-y2) transform into the totally symmetric a1-representation of the C2v group and can mix themselves with the two other molecular orbitals (2a1, 3a1) giving rise to a set of four a1-type levels arranged in a more or less tetrahedral configuration to minimize electronic repulsions (Del Giudice, Galimberti, Gamberale, & Preparata, 1995).
Preprints 100724 g004
Preprints 100724 g005
Figure 5. On the left, an artistic sketch to give an idea of the biphasic picture of liquid water: at room conditions the coherent fraction, Fcoh(T), involves about 40 % of the total molecules and its density (0.92 g/cm3) is independent of temperature, while the density of the incoherent interstitial fraction depends on T. This requires, as shown in the right panel, modelling water density as a function of T, ρ(T). This can be done via the sum of two contributions (one for each fluid, coherent and normal), like it has been shown to be successful also for predicting the trends of other properties in water systems (as isobar specific heat (Arani, Bono, Del Giudice, & Preparata, 1995), (Garbelli, 2000) viscosity (Buzzacchi, Del Giudice, & Preparata, 2002) and electric susceptivity (De Ninno, Nikollari, Missori, & Frezza, 2020)).
Figure 5. On the left, an artistic sketch to give an idea of the biphasic picture of liquid water: at room conditions the coherent fraction, Fcoh(T), involves about 40 % of the total molecules and its density (0.92 g/cm3) is independent of temperature, while the density of the incoherent interstitial fraction depends on T. This requires, as shown in the right panel, modelling water density as a function of T, ρ(T). This can be done via the sum of two contributions (one for each fluid, coherent and normal), like it has been shown to be successful also for predicting the trends of other properties in water systems (as isobar specific heat (Arani, Bono, Del Giudice, & Preparata, 1995), (Garbelli, 2000) viscosity (Buzzacchi, Del Giudice, & Preparata, 2002) and electric susceptivity (De Ninno, Nikollari, Missori, & Frezza, 2020)).
Preprints 100724 g005
Preprints 100724 g006
Figure 6. Artistic sketch to graphically yield an intuitive idea of the two different pictures emerging from corpuscular QM (left) and QFT-QED (right) views: within the former approach – where electrodynamic interactions are counted for just perturbatively – liquid water cohesion and condensed state is supposed to lay on a flickering network of local directional forces. This picture suffers from the inability to physically justify how water molecules could express a topology of their electron cloud enough protruded as to give directional electrostatic oriented pair-potentials and how (i.e., for which physical reason) this flickering network in such “mixture model” (Robinson, Cho, & Urquidi, 1999) should be divided into two populations (as required in order to fit the nowadays shared experimental evidence by which liquid water is a two-phase system) (Nilsson & al., The hydrogen bond in ice probed by soft x-ray spectroscopy and density functional theory, 2005). On the right side, an “instantaneous frame” representing liquid water at ordinary temperatures, where CDs (in blue), that appear and disappear every few hundreds of femtoseconds, are immersed within a stochastic, vapor-like, incoherent (denser) fraction, becoming more and more abundant with raising temperature. In the latter case two kinds of dynamics, time-relaxations, kinetics, orderings, and geometries coexist (Del Giudice, Galimberti, Gamberale, & Preparata, 1995).
Figure 6. Artistic sketch to graphically yield an intuitive idea of the two different pictures emerging from corpuscular QM (left) and QFT-QED (right) views: within the former approach – where electrodynamic interactions are counted for just perturbatively – liquid water cohesion and condensed state is supposed to lay on a flickering network of local directional forces. This picture suffers from the inability to physically justify how water molecules could express a topology of their electron cloud enough protruded as to give directional electrostatic oriented pair-potentials and how (i.e., for which physical reason) this flickering network in such “mixture model” (Robinson, Cho, & Urquidi, 1999) should be divided into two populations (as required in order to fit the nowadays shared experimental evidence by which liquid water is a two-phase system) (Nilsson & al., The hydrogen bond in ice probed by soft x-ray spectroscopy and density functional theory, 2005). On the right side, an “instantaneous frame” representing liquid water at ordinary temperatures, where CDs (in blue), that appear and disappear every few hundreds of femtoseconds, are immersed within a stochastic, vapor-like, incoherent (denser) fraction, becoming more and more abundant with raising temperature. In the latter case two kinds of dynamics, time-relaxations, kinetics, orderings, and geometries coexist (Del Giudice, Galimberti, Gamberale, & Preparata, 1995).
Preprints 100724 g006
Preprints 100724 g007
Figure 7. on the left panel, an intuitive sketch to describe the CD like a space region where, the confined decaying em-field (top scheme) couples with matter quanta engendering a new, energetically lower, vacuum level (where phase correlations are acted thanks to the condensation of bosonic quasi-particles. In SSB, these quasi-particles are also called phasons (Del Giudice & Vitiello, 2006) and constitute, under an energetic profile, a potential well (bottom scheme). This potential well is populated with coherent molecules that experience a potential energy at the fundamental state that is lower than in the isolated, vapour state. The right panel depicts the profiles of the reduced field amplitude, A(x)/A0, as a function of radial parameter x, within the CD (reported from (Arani, Bono, Del Giudice, & Preparata, 1995)). The centremost panel depicts a single-CD decaying profile, whereas the right panel shows the overlapping field amplitude between two neighbouring CDs.
Figure 7. on the left panel, an intuitive sketch to describe the CD like a space region where, the confined decaying em-field (top scheme) couples with matter quanta engendering a new, energetically lower, vacuum level (where phase correlations are acted thanks to the condensation of bosonic quasi-particles. In SSB, these quasi-particles are also called phasons (Del Giudice & Vitiello, 2006) and constitute, under an energetic profile, a potential well (bottom scheme). This potential well is populated with coherent molecules that experience a potential energy at the fundamental state that is lower than in the isolated, vapour state. The right panel depicts the profiles of the reduced field amplitude, A(x)/A0, as a function of radial parameter x, within the CD (reported from (Arani, Bono, Del Giudice, & Preparata, 1995)). The centremost panel depicts a single-CD decaying profile, whereas the right panel shows the overlapping field amplitude between two neighbouring CDs.
Preprints 100724 g007
Preprints 100724 g009
Figure 9. Scheme of qualitative change of the profile gradient in the ground level for three different temperature values T1<T2<T3 (grouped together in the top panels a to c). The maximum depth of the well, represented as a gradation of blue colours (where darker means deeper), within the framework of theoretical QED, is predicted to be independent of temperature, Δg≈0.16 eV, but the higher the thermal erosion is and the narrower the CD’s energy cone becomes (thermodynamically less stabilized), the more molecules (primarily at CD boundaries) experience weaker coherence. Increasing the temperature is comparable to reducing the available peripheral CD volume (rendering it narrower) where coherence is strong (good potential depth). Panel d shows a sketch for 5 temperatures). There something peculiar can be observed in that the profile of the energy-well becomes steeper and steeper as T rises, making it more difficult for molecules to “jump” out of the narrowing pit: such dynamics prevents an avalanche process that may otherwise result in the destruction of the coherent phase during evaporation. In fact, many CDs persist, with a reduced size, even in the gas phase, and to dissolve them completely one needs to reach temperatures quite above the thermodynamic boiling point, of around 600 K (Garbelli, 2000, p. 71-73).
Figure 9. Scheme of qualitative change of the profile gradient in the ground level for three different temperature values T1<T2<T3 (grouped together in the top panels a to c). The maximum depth of the well, represented as a gradation of blue colours (where darker means deeper), within the framework of theoretical QED, is predicted to be independent of temperature, Δg≈0.16 eV, but the higher the thermal erosion is and the narrower the CD’s energy cone becomes (thermodynamically less stabilized), the more molecules (primarily at CD boundaries) experience weaker coherence. Increasing the temperature is comparable to reducing the available peripheral CD volume (rendering it narrower) where coherence is strong (good potential depth). Panel d shows a sketch for 5 temperatures). There something peculiar can be observed in that the profile of the energy-well becomes steeper and steeper as T rises, making it more difficult for molecules to “jump” out of the narrowing pit: such dynamics prevents an avalanche process that may otherwise result in the destruction of the coherent phase during evaporation. In fact, many CDs persist, with a reduced size, even in the gas phase, and to dissolve them completely one needs to reach temperatures quite above the thermodynamic boiling point, of around 600 K (Garbelli, 2000, p. 71-73).
Preprints 100724 g009
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated