Analytical Theory of Fractional Vibrations

1. Introduction

Conventionally, vibration elements, say, mass m, damping c, and stiffness k, are commonly assumed to be constants. However, in vibration engineering, people pay attention to the phenomena of frequency dependent elements (mass or damping or stiffness), see e.g., Harris [1], Korotkin [2], Palley et al. [3], Kristiansen and Egeland [4], Zou et al. [5], Wu and Hsie [6], Qiao et al. [7], Jaberzadeh et al. [8], Xu et al. [9], Ghaemmaghami and Kwon [10], Hamdaoui et al. [11]. Since the analytical theory of fractional vibrations established by Li [12,13,14] adopts frequency dependent elements in the equivalent sense, we feel the usefulness of showing several realistic cases of frequency dependent mass, damping, and stiffness respectively in Section 2, Section 3 and Section 4, so as to purposely write a general form of a vibration system with frequency dependent mass, damping, and stiffness and discuss its vibration theory in Section 5, Section 6, Section 7, Section 8 and Section 9. The intention of writing Section 5, Section 6, Section 7, Section 8 and Section 9 is in two aspects. One is for the pavement of seven classes of fractional vibrators addressed in Section 10, Section 11, Section 12 and Section 13. The other is to facilitate smoothing away possible hesitations why m and or c and or k may be frequency dependent. As an application, we discuss the closed form expression of the forced response to the multi-fractional Euler-Bernoulli beam in Section 13. The nonlinearity of fractional vibrations is discussed in Section 14, which is followed by conclusions.

2. Cases of Frequency Dependent Mass

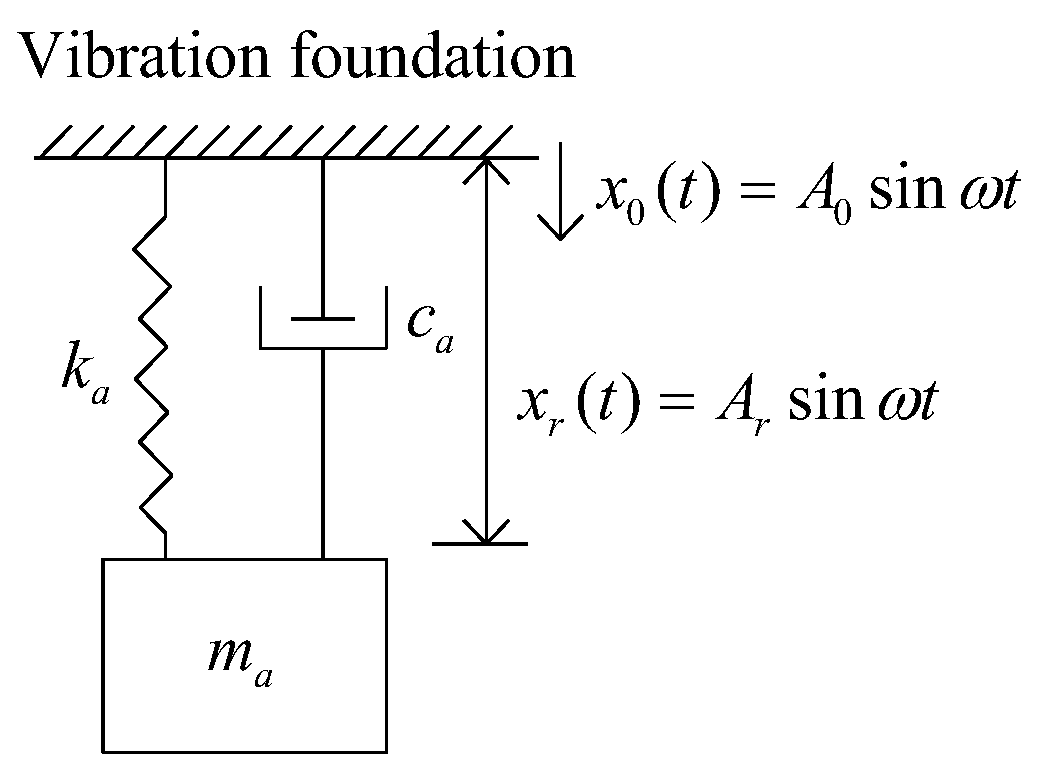
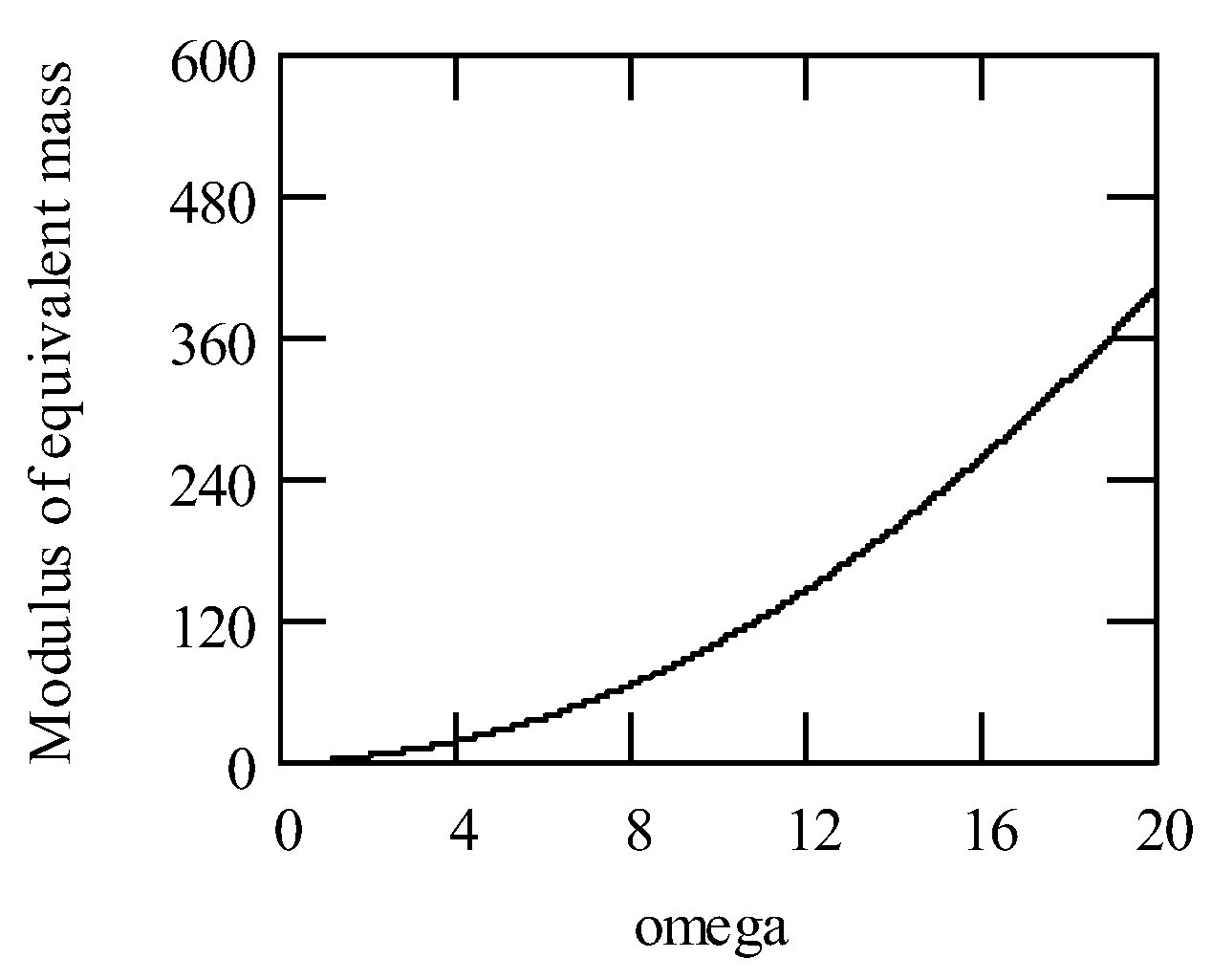
2.1. Frequency Dependent Mass in Auxiliary Mass Damper System

Consider a simple auxiliary mass damper indicated in Figure 1 (Harris [1]). The system consists of a mass m_a, spring k_a, and viscous damper c_a.

The motion equation of the auxiliary mass damper system is given by

$$-k_a{x}_r(t)-c_a\frac{d{x}_r(t)}{dt}=m_a\frac{d^2[x_0(t)+x_r(t)]}{d{t}^2}.$$

(2.1)

Let X_r and X₀ be the phasors of x_r(t) and x₀(t), respectively. The phasor equation of the above is in the form

$$\left(-k_a-i\omega c_a\right)X_r=-m_a{\omega }^2(X_r+X_0).$$

(2.2)

Therefore,

$$X_r=\frac{m_a{\omega }^2}{-m_a{\omega }^2+k_a+i\omega c_a}.$$

(2.3)

Denote by F the phasor of the force exerting on the foundation. Then,

$$F=\frac{m_a{\omega }^2\left(k_a+i\omega c_a\right)}{-m_a{\omega }^2+k_a+i\omega c_a}{X}_0.$$

(2.4)

As the force acted by an equivalent mass m_eq is rigidly attached to the foundation, we have

$$F=m_{\mathrm{eq}}{\omega }^2{X}_0,$$

(2.5)

where

$$m_{\mathrm{eq}}=\frac{k_a+i\omega c_a}{-m_a{\omega }^2+k_a+i\omega c_a}{m}_a.$$

(2.6)

Rewriting the above yields

$$m_{\mathrm{eq}}=\frac{\left(k_a+i\omega c_a\right)\left(k_a-m_a{\omega }^2-i\omega c_a\right)}{{\left(k_a-m_a{\omega }^2\right)}^2+{\left(\omega c_a\right)}^2}{m}_a=\frac{k_a\left(k_a-m_a{\omega }^2\right)+{\left(\omega c_a\right)}^2-i{m}_a{c}_a{\omega }^3}{{\left(k_a-m_a{\omega }^2\right)}^2+{\left(\omega c_a\right)}^2}{m}_a.$$

(2.7)

In the polar system,

$$m_{\mathrm{eq}}=\left|m_{\mathrm{eq}}\right|\mathrm{Arg}{m}_{\mathrm{eq}},$$

(2.8)

where

$$\left|m_{\mathrm{eq}}\right|=\frac{{\left[k_a\left(k_a-m_a{\omega }^2\right)+{\left(\omega c_a\right)}^2\right]}^2+{\left(m_a{c}_a{\omega }^3\right)}^2}{{\left(k_a-m_a{\omega }^2\right)}^2+{\left(\omega c_a\right)}^2}{m}_a,$$

(2.9)

and

$$\mathrm{Arg}{m}_{\mathrm{eq}}={\tan }^{-1}\frac{-i{m}_a{c}_a{\omega }^3}{k_a\left(k_a-m_a{\omega }^2\right)+{\left(\omega c_a\right)}^2}.$$

(2.10)

The above exhibits that both the modulus and argument of m_eq are the functions of ω. When ω = 0, m_eq reduces to the primary mass m_a. In general, 0 ≤ |m_eq| < ∞. When c_a = 0, m_eq is real. Figure 2 illustrates a curve of |m_eq|.

2.2. Added Mass

The frequency dependence of added mass is well known in the field of ship mechanics (Korotkin [2]). In general, a ship motion is with six degrees of freedom (Palley et al. [3]). We adopt the following symbols for discussions.

• q_n (n = 1, …, 6): generalized coordinates.
• f_n: generalized forces.
• m_jn: dry mass of the ship in direction j.
• c_jn: dry damping of the ship in direction j.
• k_jn: dry stiffness of the ship in direction j.
• m_{add, jn}: added mass of the ship in direction j.
• h_jn(t): impulse response function in direction j to an impulse in velocity in direction n.

When q_n(t) = q_n cos(ωt), according to Kristiansen and Egeland [4], one has

$${\displaystyle \sum _{n=1}^6\left[m_{jn}+m_{\mathrm{add},jn}(\omega )\right]q_n^{″}}+{\displaystyle \sum _{n=1}^6{c}_{\mathrm{eq},jn}(\omega )q_n^{\prime }}+{\displaystyle \sum _{n=1}^6{k}_{jn}{q}_n}=f_j(t),$$

(2.11)

where f_j(t) is a sinusoidal force at ω,

$$m_{\mathrm{add},jn}(\omega )=m_{jn}-\frac{1}{\omega }{\displaystyle \underset{0}{\overset{\infty }{\int }}{h}_{jn}(t)\sin \omega tdt}$$

(2.12)

and

$$c_{\mathrm{eq},jn}(\omega )=c_{jn}+{\displaystyle \underset{0}{\overset{\infty }{\int }}{h}_{jn}(t)\cos \omega tdt}.$$

(2.13)

Considering the equivalent mass m_eq, we have

m_eq = m_jn + m_{add, jn}(ω).

(2.14)

Therefore, the equivalent mass m_eq of a ship in general is frequency dependent. Consequently, m_eq = m_eq(ω).

There are other types of expressions with respect to frequency dependent mass, see e.g., Zou et al. [5], Wu and Hsieh [6], Qiao et al. [7], Jaberzadeh et al. [8], Xu et al. [9], Ghaemmaghami, and Kwon [10], Hamdaoui et al. [11], Li [12,13,14], Banerjee [15], White et al. [16], Dumont and Oliveira [17], Zhang et al. [18], Sun et al. [19].

3. Cases of Frequency Dependent Damping

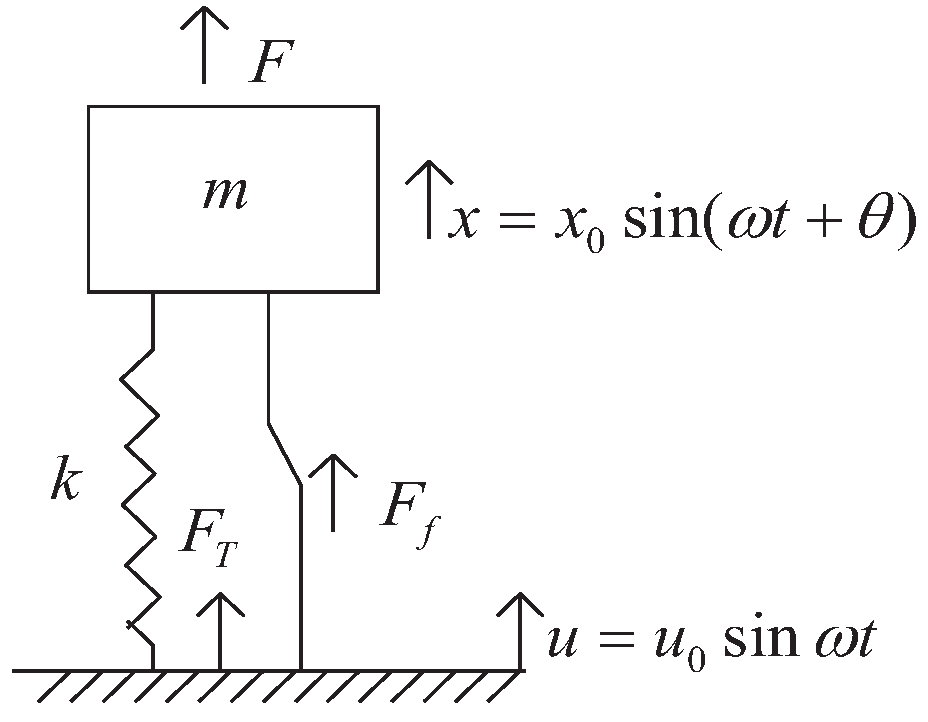
3.1. Rigidly Connected Coulomb Damper

Have a look at Figure 3 that indicates a rigidly connected Coulomb damper.

The motion equation is given by

$$m{x}^{″}+k(x-u)\pm F_f=F_0+\sin \omega t.$$

(3.1)

Since there is discontinuity in the damping force that occurs as the sign of the velocity changes at each half cycle, a step-by-step solution of the above is required (Harris [1], Den Hartog [20]). Let δ = x − u. Using the equivalence of energy dissipation for equating the energy dissipation per cycle for viscous-damped and Coulomb damped systems produces (Harris [1], Jacobsen [21])

$$\pi c_{\mathrm{eq}}\omega {\delta }_0^2=4F_f{\delta }_0.$$

(3.2)

In the above, the left side refers to the viscous-damped system and the right side to the Coulomb-damped system. The symbol δ₀ is the amplitude of relative displacement across the damper.

From the above, one has the equivalent viscous damping coefficient for a Coulomb-damped system that has equivalent energy dissipation in the form

$$c_{\mathrm{eq}}=\frac{4F_f}{\pi \omega {\delta }_0}.$$

(3.3)

One thing worth noting is that c_eq is frequency dependent. Hence,

c_eq = c_eq(ω).

(3.4)

3.2. Rayleigh Damping

The Rayleigh damping introduced by Rayleigh [22] is widely adopted in the field, see e.g., Harris [1], Palley et al. [3], Li [12,13,14], Jin and Xia [23], Trombetti and Silvestri [24,25], Mohammad et al. [26], Kim and Wiebe [27]. Rayleigh assumed his damping in the form

c_Raylegh = am + bk,

(3.5)

where a is proportional to ω while b is inversely proportional to ω. Thus, we may write

c_Raylegh = c_Raylegh(ω).

(3.6)

The above exhibits that the frequency dependence is a radical property of the damping Rayleigh assumed.

3.3. Remarks

Other types of frequency dependent dampers, refer to Kuo et al. [28], Stollwitzer et al. [29], Jith and Sarkar [30], Zhou et al. [31], Zarraga et al. [32], Xie et al. [33,34], Hu et al. [35], Rouleau et al. [36], Hamdaoui et al. [37], Deng et al. [38], Dai et al. [39], Adessina et al. [40], Chang et al. [41], Lin et al. [42], Dai et al. [43], Catania and Sorrentino [44,45], Zhang and Turner [46], Yoshida et al. [47], Assimaki and Kausel [48], Pan et al. [49], Ghosh and Viswanath [50], Mcdaniel et al. [51], Zhang et al. [52], Wang et al. [53], Lundén and Dahlberg [54], Figueroa et al. [55], Lázaro [56], and Crandall [57], simply citing a few.

4. Cases of Frequency Dependent Stiffness

4.1. Frequency Dependent Stiffness in a Shaft Driven by a Periodic Force

Consider a shaft driven by a periodic force as shown in Figure 4. The mass m is supported by two springs with the primary stiffness k. Under the excitation of a force in axis direction, there is a force produced by displacement in the form$\frac{x}{l}F\cos \omega t.$

Thus, the motion equation is given by

$$m{x}^{″}+kx-\frac{x}{l}F\cos \omega t=0.$$

(4.1)

Denote by k_eq the equivalent stiffness of the system. Then,

$$m{x}^{″}+k_{\mathrm{eq}}x=0,$$

(4.2)

where

$$k_{\mathrm{eq}}=k-\frac{F\cos \omega t}{l}.$$

(4.3)

The above designates that the equivalent stiffness k_eq is frequency dependent. Hence, k_eq = k_eq(ω).

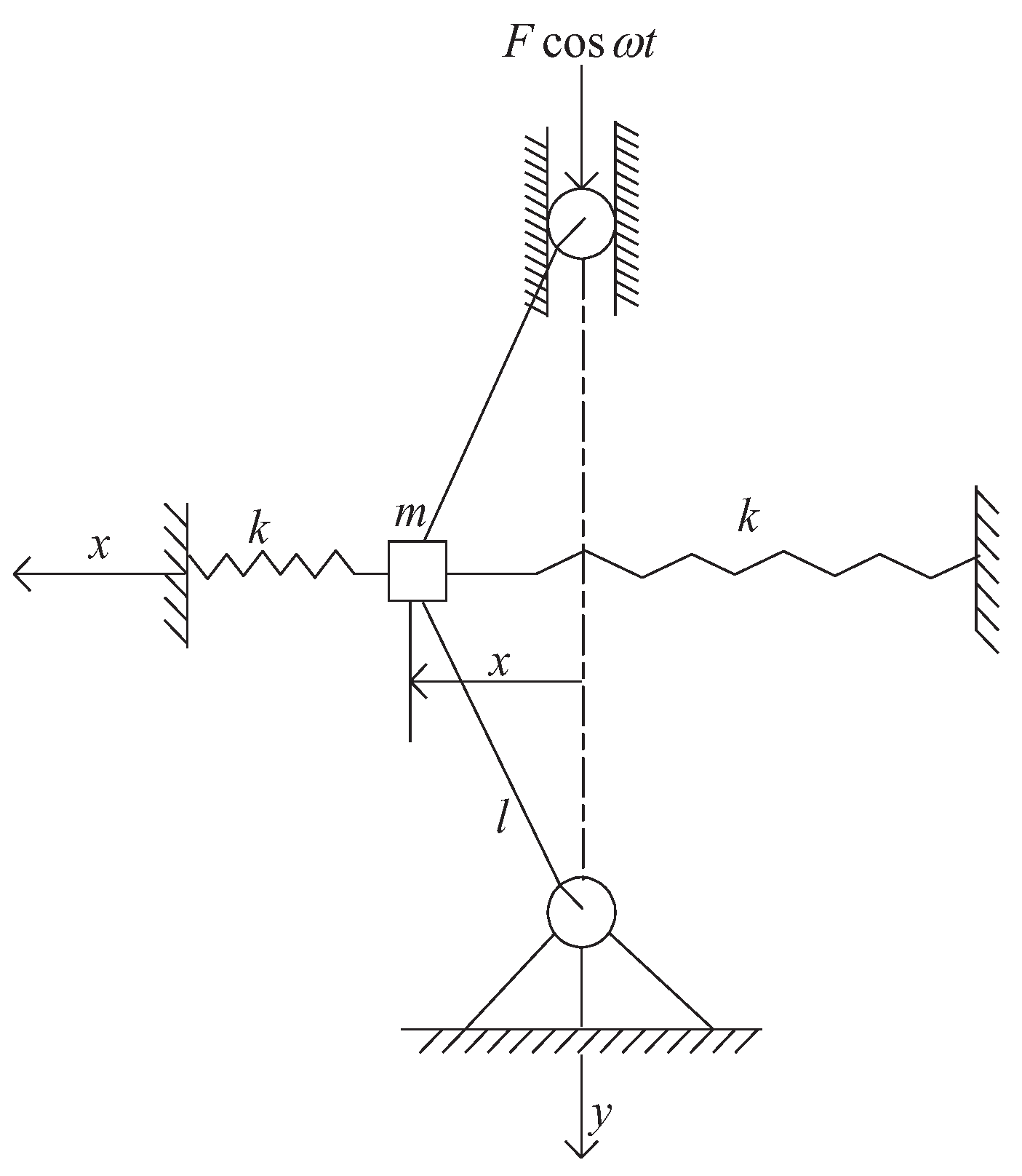
4.2. Frequency Dependent Stiffness in Simple Pendulum

Let l be the length of a simple pendulum. Denote by m the mass of the simple pendulum. Suppose that the fulcrum position of the pendulum moves periodically as A₀cosxl, see Figure 5.

The motion equation of the simple pendulum is given by

$$ml{\theta }^{″}+m\left(g-{\omega }^2{A}_0\cos \omega t\right)\sin \theta =0.$$

(4.4)

When θ is small such that sinθ ≈ θ, we have

$$ml{\theta }^{″}+m\left(g-{\omega }^2{A}_0\cos \omega t\right)\theta =0.$$

(4.5)

Replacing θ by x yields

$$m{x}^{″}+\frac{m}{l}\left(g-{\omega }^2{A}_0\cos \omega t\right)x=0.$$

(4.6)

Let k_eq be the equivalent stiffness. Then,

$$k_{\mathrm{eq}}=\frac{m}{l}\left(g-{\omega }^2{A}_0\cos \omega t\right).$$

(4.7)

Therefore, the motion equation is expressed by

$$m{x}^{″}+k_{\mathrm{eq}}x=0.$$

(4.8)

The above exhibits that the stiffness k_eq is frequency dependent.

The topic of frequency dependent stiffness attracts the interests of researchers. The other references regarding frequency dependent stiffness refer to Li [12,13,14], Banerjee [15], White et al. [16], Dumont and de Oliveira [17], Zhang et al. [18], Sun et al. [19], Yoshida et al. [47], Wu et al. [58], Blom and Kari [59], Gao et al. [60], Song et al. [61], Liu et al. [62], Zhang et al. [63], Banerjee et al. [64,65], Lu et al. [66], Sung et al. [67], Mezghani et al. [68], Liu et al. [69], Kong et al. [70], Ege et al. [71], Mukhopadhyay et al. [72], Sainz-AjaIsidro et al. [73], Bozyigit [74], Varghese et al. [75], Failla et al. [76], Fan et al. [77], Roozen et al. [78], Mochida and Ilanko [79], just citing a few.

5. General Vibration System with Frequency Dependent Elements

5.1. Motion Equation of General Vibration System

Based on the previous discussions, we write the motion equation with frequency dependent elements by

$$m_{\mathrm{eq}}(\omega )x^{″}+c_{\mathrm{eq}}(\omega )x^{\prime }+k_{\mathrm{eq}}(\omega )x=f(t),$$

(5.1)

where f(t) is an excitation force.

Let X(ω) and F(ω) be the Fourier transform of x(t) and f(t), respectively. Then, the motion equation in the frequency domain is expressed by

$$\left[-{\omega }^2{m}_{\mathrm{eq}}(\omega )+i\omega c_{\mathrm{eq}}(\omega )+k_{\mathrm{eq}}(\omega )\right]X(\omega )=F(\omega ).$$

(5.2)

5.2. Vibration Parameters of General Vibration System

Denote by ω_eqn the equivalent natural angular frequency with damping free. It is given by

$${\omega }_{\mathrm{eqn}}=\sqrt{\frac{k_{\mathrm{eq}}(\omega )}{m_{\mathrm{eq}}(\omega )}}.$$

(5.3)

Since either m_eq or k_eq is a function of ω, ω_eqn is a function of ω. Thus,

$${\omega }_{\mathrm{eqn}}={\omega }_{\mathrm{eqn}}(\omega ).$$

(5.4)

Let ζ_eq(ω) be the equivalent damping ratio in the form

$${\varsigma }_{\mathrm{eq}}(\omega )=\frac{1}{2}\frac{c_{\mathrm{eq}}}{\sqrt{m_{\mathrm{eq}}{k}_{\mathrm{eq}}}}.$$

(5.5)

Then, we rewrite (5.1) by

$$x^{″}+2{\varsigma }_{\mathrm{eq}}(\omega ){\omega }_{\mathrm{eqn}}(\omega )x^{\prime }+{\omega }_{\mathrm{eqn}}^2(\omega )x=\frac{f(t)}{m_{\mathrm{eq}}(\omega )}.$$

(5.6)

Denote by ω_eqd(ω) the equivalent damped natural angular frequency. Since |ζ_eq(ω)| > 1 does not make sense in vibrations (Harris [1], Palley et al. [2], Li [13], Nakagawa and Ringo [80]), we restrict ζ_eq by |ζ_eq(ω)| ≤ 1. Thus,

$${\omega }_{\mathrm{eqd}}(\omega )={\omega }_{\mathrm{eqn}}(\omega )\sqrt{1-{\varsigma }_{\mathrm{eq}}^2(\omega )}.$$

(5.7)

The equivalent frequency ratio is given by

$${\gamma }_{\mathrm{eq}}=\frac{\omega }{{\omega }_{\mathrm{eqn}}(\omega )}.$$

(5.8)

5.3. Free Response of General Vibration System with Frequency Dependent Elements

When considering the free response to a general vibration system with frequency dependent elements, we have

$$\{\begin{array}{c}{m}_{\mathrm{eq}}(\omega )x^{″}(t)+c_{\mathrm{eq}}(\omega )x^{\prime }(t)+k_{\mathrm{eq}}(\omega )x(t)=0,\\ x(0)=x_0,x^{\prime }(0)=v_0.\end{array}$$

(5.9)

The above equation can be rewritten by

$$\{\begin{array}{c}{x}^{″}+2{\varsigma }_{\mathrm{eq}}(\omega ){\omega }_{\mathrm{eqn}}(\omega )x^{\prime }+{\omega }_{\mathrm{eqn}}^2(\omega )x=0,\\ x(0)=x_0,x^{\prime }(0)=v_0.\end{array}$$

(5.10)

Then, the free response is

$$x(t)=e^{-{\varsigma }_{\mathrm{eq}}{\omega }_{\mathrm{eqn}}t}\left(x_0\cos {\omega }_{\mathrm{eqd}}t+\frac{v_0+{\varsigma }_{\mathrm{eq}}{\omega }_{\mathrm{eqn}}{x}_0}{{\omega }_{\mathrm{eqd}}}\sin {\omega }_{\mathrm{eqd}}t\right),t\ge 0.$$

(5.11)

5.4. Impulse Response of General Vibration System with Frequency Dependent Elements

When investigating the impulse response to a general vibration system with frequency dependent elements, we use the following equation

$$\{\begin{array}{c}{h}^{″}(t)+2{\varsigma }_{\mathrm{eq}}(\omega ){\omega }_{\mathrm{eqn}}(\omega )h^{\prime }(t)+{\omega }_{\mathrm{eqn}}^2(\omega )h(t)=\frac{\delta (t)}{m_{\mathrm{eq}}(\omega )},\\ h(0)=0,h^{\prime }(0)=0.\end{array}$$

(5.12)

Thus,

$$h(t)=e^{-{\varsigma }_{\mathrm{eq}}{\omega }_{\mathrm{eqn}}t}\frac{1}{m_{\mathrm{eq}}{\omega }_{\mathrm{eqd}}}\sin {\omega }_{\mathrm{eqd}}t,t\ge 0.$$

(5.13)

5.5. Step Response of General Vibration System with Frequency Dependent Elements

Denote by g(t) the unit step response (step response for short) to a general vibration system with frequency dependent elements. Consider the following equation

$$\{\begin{array}{c}{g}^{″}(t)+2{\varsigma }_{\mathrm{eq}}(\omega ){\omega }_{\mathrm{eqn}}(\omega )g^{\prime }(t)+{\omega }_{\mathrm{eqn}}^2(\omega )g(t)=\frac{u(t)}{m_{\mathrm{eq}}(\omega )},\\ g(0)=0,g^{\prime }(0)=0.\end{array}$$

(5.14)

Then,

$$g(t)=\frac{1}{k_{\mathrm{eq}}(\omega )}\left[1-\frac{e^{-{\varsigma }_{\mathrm{eq}}{\omega }_{\mathrm{eqn}}t}}{\sqrt{1-{\varsigma }_{\mathrm{eq}}^2}}\cos \left({\omega }_{\mathrm{eqd}}t-\varphi \right)\right],t\ge 0,$$

(5.15)

where

$$\varphi ={\tan }^{-1}\frac{{\varsigma }_{\mathrm{eq}}}{\sqrt{1-{\varsigma }_{\mathrm{eq}}^2}}.$$

(5.16)

6. Frequency Transfer Function of General Vibration System with Frequency Dependent Elements

Let H(ω) be the Fourier transform of h(t). From (5.12), we have

$$\left[{\omega }_{\mathrm{eqn}}^2(\omega )-{\omega }^2+i2{\varsigma }_{\mathrm{eq}}(\omega ){\omega }_{\mathrm{eqn}}(\omega )\omega \right]H(\omega )=\frac{1}{m_{\mathrm{eq}}(\omega )}.$$

(6.1)

Therefore,

$$\begin{array}{l}H(\omega )=\frac{1}{m_{\mathrm{eq}}(\omega )\left[{\omega }_{\mathrm{eqn}}^2(\omega )-{\omega }^2+i2{\varsigma }_{\mathrm{eq}}(\omega ){\omega }_{\mathrm{eqn}}(\omega )\omega \right]}\\ =\frac{1}{k_{\mathrm{eq}}(\omega )\left[1-{\gamma }_{\mathrm{eq}}^2+i2{\varsigma }_{\mathrm{eq}}(\omega ){\gamma }_{\mathrm{eq}}\right]}.\end{array}$$

(6.2)

The amplitude |H(ω)| is given by

$$\left|H(\omega )\right|=\frac{1/k_{\mathrm{eq}}}{\sqrt{{\left(1-{\gamma }_{\mathrm{eq}}^2\right)}^2+{\left(2{\varsigma }_{\mathrm{eq}}{\gamma }_{\mathrm{eq}}\right)}^2}}.$$

(6.3)

The phase is expressed by

$$\phi (\omega )=-{\tan }^{-1}\frac{2{\varsigma }_{\mathrm{eq}}(\omega ){\gamma }_{\mathrm{eq}}}{1-{\gamma }_{\mathrm{eq}}^2}.$$

(6.4)

When computing ϕ(ω) using digital computers,

$$\phi (\omega )={\cos }^{-1}\frac{1-{\gamma }_{\mathrm{eq}}^2}{\sqrt{{\left(1-{\gamma }_{\mathrm{eq}}^2\right)}^2+{\left(2{\varsigma }_{\mathrm{eq}}{\gamma }_{\mathrm{eq}}\right)}^2}}.$$

(6.5)

7. Logarithmic Decrement and Q Factor of General Vibration System with Frequency Dependent Elements

Let t_i and t_{i + 1} be two time points of the free response x(t), where x(t_i) and x(t_{i + 1}) are successive peak values at t_i and t_{i + 1}. Let Δ_eq be the logarithmic decrement of x(t). Then,

$${\Delta }_{\mathrm{eq}}={\Delta }_{\mathrm{eq}}(\omega )=\ln \frac{x(t_i)}{x(t_{i+1})}=\frac{2\pi {\varsigma }_{\mathrm{eq}}(\omega )}{\sqrt{1-{\varsigma }_{\mathrm{eq}}^2(\omega )}}.$$

(7.1)

Let Q_eq be the Q factor of a general vibration system with frequency dependent elements. Then,

$$Q_{\mathrm{eq}}=Q_{\mathrm{eq}}(\omega )=\frac{1}{2{\varsigma }_{\mathrm{eq}}(\omega )}.$$

(7.2)

8. Li's Vibration System with Frequency Dependent Elements

8.1. Motion Equation of Li's Vibration System

Recently, Li introduced a class of vibration systems with frequency dependent elements. Its motion equation is in the form

$$\begin{array}{l}-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)\frac{d^2{x}_6(t)}{d{t}^2}\\ +\left(m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}+k{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}\right)\frac{d{x}_6(t)}{dt}\\ +k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}{x}_6(t)=f(t),1<\alpha <3,0<\beta <2,0\le \lambda <1,\end{array}$$

(8.1)

where f(t) is driven force and x₆(t) is the response. For facilitating discussions, we call the above Li's vibration system with frequency dependent elements or Li's vibration system in short.

8.2. Vibration Parameters of Li's Vibration System

When writing (8.1) by

$$m_{\mathrm{eq}6}\frac{d^2{x}_6(t)}{d{t}^2}+c_{\mathrm{eq}6}\frac{d{x}_6(t)}{dt}+k_{\mathrm{eq}6}{x}_6(t)=f(t),1<\alpha <3,0<\beta <2,0\le \lambda <1,$$

(8.2)

we have the equivalent mass of (8.1) in the form

$$m_{\mathrm{eq}6}=m_{\mathrm{eq}6}(\omega )=-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right),$$

(8.3)

the equivalent damping expressed by

$$c_{\mathrm{eq}6}=c_{\mathrm{eq}6}(\omega )=c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}+k{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2},$$

(8.4)

and the equivalent stiffness given by

$$k_{\mathrm{eq}6}=k_{\mathrm{eq}6}(\omega )=k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}.$$

(8.5)

Let ζ_eq6 be the equivalent damping ratio for the system (8.1). Define it by

$${\varsigma }_{\mathrm{eq}6}=\frac{c_{\mathrm{eq}6}}{2\sqrt{m_{\mathrm{eq}6}{k}_{\mathrm{eq}6}}}.$$

(8.6)

Then,

$${\varsigma }_{\mathrm{eq}6}={\varsigma }_{\mathrm{eq}6}(\omega )=\frac{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}+k{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}}{2\sqrt{-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}.$$

(8.7)

Denote by ω_eqn6 the equivalent natural angular frequency with damping free with respect to the system (8.1). Define it by

$${\omega }_{\mathrm{eqn}6}=\sqrt{\frac{k_{\mathrm{eq}6}(\omega )}{m_{\mathrm{eq}6}(\omega )}}.$$

(8.8)

Then,

$${\omega }_{\mathrm{eqn}6}=\sqrt{\frac{k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}{-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}.$$

(8.9)

Let ω_eqd6 be the equivalent damped natural angular frequency for the system (8.1). In vibrations, small damping |ζ_eq6| ≤ 1 is assumed in what follows. Define ω_eqd6 by

$${\omega }_{\mathrm{eqd}6}={\omega }_{\mathrm{eqn}6}\sqrt{1-{\varsigma }_{\mathrm{eq}6}^2},\left|{\varsigma }_{\mathrm{eq}6}\right|\le 1.$$

(8.10)

Then,

$$\begin{array}{l}{\omega }_{\mathrm{eqd}6}=\sqrt{\frac{k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}{-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}}\\ \sqrt{1-{\left(\frac{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}sin\frac{\beta \pi }{2}+k{\omega }^{\lambda -1}sin\frac{\lambda \pi }{2}}{2\sqrt{-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}\right)}^2}.\end{array}$$

(8.11)

Denote the equivalent frequency ratio for the system (8.1) by γ_eq6 and define it by

$${\gamma }_{\mathrm{eq}6}=\frac{\omega }{{\omega }_{\mathrm{eqn}6}}.$$

(8.12)

Then,

$${\gamma }_{\mathrm{eq}6}=\gamma \sqrt{\frac{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}{{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}},$$

(8.13)

where $\gamma =\frac{\omega }{{\omega }_n}$ and ${\omega }_n=\sqrt{\frac{k}{m}}.$

8.3. Free Response of Li's Vibration System

Consider

$$\{\begin{array}{c}{m}_{\mathrm{eq}6}\frac{d^2{x}_6(t)}{d{t}^2}+c_{\mathrm{eq}6}\frac{d{x}_6(t)}{dt}+k_{\mathrm{eq}6}{x}_6(t)=0,\\ x_6(0)=x_{60},{x^{\prime }}_6(0)=v_{60}.\end{array}$$

(8.14)

Then, the free response x₆(t) is expressed by

$$x_6(t)=e^{-{\varsigma }_{\mathrm{eq}6}{\omega }_{\mathrm{eqn}6}t}\left(x_{60}\cos {\omega }_{\mathrm{eqd}6}t+\frac{v_{60}+{\varsigma }_{\mathrm{eq}6}{\omega }_{\mathrm{eqn}6}{x}_{60}}{{\omega }_{\mathrm{eqd}6}}\sin {\omega }_{\mathrm{eqd}6}t\right),t\ge 0.$$

(8.15)

8.4. Impulse Response of Li's Vibration System

Let h₆(t) be the impulse response of the system (8.1). Then,

$$h_6(t)=e^{-{\varsigma }_{\mathrm{eq}6}{\omega }_{\mathrm{eqn}6}t}\frac{1}{m_{\mathrm{eq}6}{\omega }_{\mathrm{eqd}6}}\sin {\omega }_{\mathrm{eqd}6}t,t\ge 0.$$

(8.16)

8.5. Step Response of Li's Vibration System

Denote by g₆(t) the unit step response of the system (8.1). Then,

$$g_6(t)=\frac{1}{k_{\mathrm{eq}6}}\left[1-\frac{e^{-{\varsigma }_{\mathrm{eq}6}{\omega }_{\mathrm{eqn}6}t}}{\sqrt{1-{\varsigma }_{\mathrm{eq}6}^2}}\cos \left({\omega }_{\mathrm{eqd}6}t-{\varphi }_6\right)\right],t\ge 0,$$

(8.17)

where

$${\varphi }_6={\tan }^{-1}\frac{{\varsigma }_{\mathrm{eq}6}}{\sqrt{1-{\zeta }_{\mathrm{eq}6}^2}}.$$

(8.18)

8.6. Frequency Transfer Function of Li's Vibration System

Let H₆(ω) be the frequency transfer function of the system (8.1). Then,

$$\begin{array}{l}{H}_6(\omega )=\frac{1}{k_{\mathrm{eq}6}\left(1-{\gamma }_{\mathrm{eq}6}^2+i2{\varsigma }_{\mathrm{eq}6}{\gamma }_{\mathrm{eq}6}\right)}\\ =\frac{1}{k\left[\begin{array}{l}{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}+{\gamma }^2\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)\\ +i\gamma \left({\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+2\zeta {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}+{\omega }_n^2{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}\right)\end{array}\right]}.\end{array}$$

(8.19)

8.7. Logarithmic Decrement and Q Factor of Li's Vibration System

Let t_i and t_{i + 1} be two time points of the fractional free response x₆(t), where x₆(t_i) and x₆(t_{i + 1}) are its successive peak values at t_i and t_{i + 1}. Let Δ_eq6 be the equivalent logarithmic decrement of x₆(t). Then,

$${\Delta }_{\mathrm{eq}6}=\ln \frac{x_6(t_i)}{x_6(t_{i+1})}=\frac{\pi \frac{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}+k{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}}{\sqrt{-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}}{\sqrt{1-\frac{{\left(m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}sin\frac{\beta \pi }{2}+k{\omega }^{\lambda -1}sin\frac{\lambda \pi }{2}\right)}^2}{4\left[-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}\right]}}}.$$

(8.20)

Denote by Q_eq6 the equivalent Q factor of the system (8.1). Then,

$$Q_{\mathrm{eq}6}=\frac{\sqrt{-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}+k{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}}.$$

(8.21)

8.8. Equivalent Fractional System of Li's Vibration System

Theorem 1.

An equivalent fractional system of Li's vibration system is expressed by

$$m\frac{d^{\alpha }{x}_6(t)}{d{t}^{\alpha }}+c\frac{d^{\beta }{x}_6(t)}{d{t}^{\beta }}+k\frac{d^{\lambda }{x}_6(t)}{d{t}^{\lambda }}=f(t).$$

(8.22)

roof. 

Let F be the operator of Fourier transform. Let

$$\begin{array}{l}{A}_6(t)=-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)\frac{d^2{x}_6(t)}{d{t}^2}\\ +\left(m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}+k{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}\right)\frac{d{x}_6(t)}{dt}+k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}{x}_6(t).\end{array}$$

(8.23)

Let

$$B_6(t)=m\frac{d^{\alpha }{x}_6(t)}{d{t}^{\alpha }}+c\frac{d^{\beta }{x}_6(t)}{d{t}^{\beta }}+k\frac{d^{\lambda }{x}_6(t)}{d{t}^{\lambda }}.$$

(8.24)

Because F[A₆(t)] = F[B₆(t)], we have

A₆(t) = B₆(t)

(8.25)

in the sense of F[A₆(t) − B₆(t)] = 0. The proof is finished.

9. Seven Classes of Li's Vibration Systems with Frequency Dependent Elements and Their Fractional Equivalences

The system (8.1) contains other six classes of vibration systems with frequency dependent elements. Meanwhile, the system (8.22) includes six other classes of fractional vibration systems. We address them in this subsection.

9.1. Li's Vibration System of Class I and its Fractional Equivalence

When c = 0 and λ = 0 in (8.1), we have the motion equation in the form

$$-m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}\frac{d^2{x}_1(t)}{d{t}^2}+m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}\frac{d{x}_1(t)}{dt}+k{x}_1(t)\triangleq A_1(t),\hspace{1em}1<\alpha <3.$$

(9.1)

The above is called the class I Li's vibration system with frequency dependent elements. Letting c = 0 and λ = 0 in (8.22) produces the motion equation

$$m\frac{d^{\alpha }{x}_1(t)}{d{t}^{\alpha }}+k{x}_1(t)\triangleq B_1(t),\hspace{1em}1<\alpha <3.$$

(9.2)

We call the above the class I fractional vibration system. That is the fractional equivalence of the class I Li's vibration system. In face, F[A₁(t) − B₁(t)] = 0.

9.2. Li's Vibration System of Class II and its Fractional Equivalence

Let α = 2 and λ = 0 in (8.1). Then, (8.1) reduces to

$$\left(m-c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)\frac{d^2{x}_2(t)}{d{t}^2}+\left(c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}\right)\frac{d{x}_2(t)}{dt}+k{x}_2(t)\triangleq A_2(t),0<\beta <2.$$

(9.3)

We call the above the class II Li's vibration system with frequency dependent elements. If α = 2 and λ = 0 in (8.22), (8.22) becomes

$$m\frac{d^2{x}_2(t)}{d{t}^2}+c\frac{d^{\beta }{x}_2(t)}{d{t}^{\beta }}+k{x}_2(t)\triangleq B_2(t),$$

(9.4)

which we call the class II fractional vibrator. That is the fractional equivalence of the class II Li's vibration system. Obviously, F[A₂(t) − B₂(t)] = 0.

9.3. Li's Vibration System of Class III and its Fractional Equivalence

Let λ = 0 in (8.1). Then, (8.1) turns to be

$$\begin{array}{l}-\left(m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)\frac{d^2{x}_3(t)}{d{t}^2}\\ +\left(m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}\right)\frac{d{x}_3(t)}{dt}+k{x}_3(t)\triangleq A_3(t),1<\alpha <3,0<\beta <2.\end{array}$$

(9.5)

The above is called the class III Li's vibration system. Letting λ = 0 in (8.22) yields the class III fractional vibrator in the form

$$m\frac{d^{\alpha }{x}_3(t)}{d{t}^{\alpha }}+c\frac{d^{\beta }{x}_3(t)}{d{t}^{\beta }}+kx(t)\triangleq B_3(t).$$

(9.6)

That is the fractional equivalence of the class III Li's vibration system. Clearly, F[A₃(t) − B₃(t)] = 0.

9.4. Li's Vibration System of Class IV and its Fractional Equivalence

By letting c = 0 in (8.1), we have the class IV Li's vibration system in the form

$$\begin{array}{l}-m{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}\frac{d^2{x}_4(t)}{d{t}^2}+\left(m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+k{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}\right)\frac{d{x}_4(t)}{dt}\\ +k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}{x}_4(t)\triangleq A_4(t),\hspace{1em}1<\alpha <3,0\le \lambda <1.\end{array}$$

(9.7)

Similarly, letting c = 0 in (8.22) results in the class IV fractional vibrator given by

$$m\frac{d^{\alpha }{x}_4(t)}{d{t}^{\alpha }}+k\frac{d^{\lambda }{x}_4(t)}{d{t}^{\lambda }}\triangleq B_4(t),\hspace{1em}1<\alpha <3,0\le \lambda <1.$$

(9.8)

The above is the fractional equivalence of the class IV Li's vibration system. It is easily seen that F[A₄(t) − B₄(t)] = 0.

9.5. Li's Vibration System of Class V and its Fractional Equivalence

When α = 2 and c = 0 in (8.1), we have the class V Li's vibration system in the form

$$m\frac{d^2{x}_5(t)}{d{t}^2}+k{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}\frac{d{x}_5(t)}{dt}+k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}{x}_5(t)\triangleq A_5(t),\hspace{1em}0\le \lambda <1.$$

(9.9)

Letting α = 2 and c = 0 in (8.22) produces the class V fractional vibrator given by

$$m\frac{d^2{x}_5(t)}{d{t}^2}+k\frac{d^{\lambda }{x}_5(t)}{d{t}^{\lambda }}\triangleq B_5(t),\hspace{1em}0\le \lambda <1.$$

(9.10)

The above is the fractional equivalence of the class V Li's vibration system. As a matter of fact, F[A₅(t) − B₅(t)] = 0.

9.6. Li's Vibration System of Class VI and its Fractional Equivalence

The expression (8.1) stands for the class VI Li' vibration system. Its fractional equivalence, that is, (8.22), designates the class VI fractional vibrator.

9.7. Li's Vibration System of Class VII and its Fractional Equivalence

If α = 2 in (8.1), we have the class VII Li's vibration system expressed by

$$\begin{array}{l}\left(m-c{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)\frac{d^2{x}_7(t)}{d{t}^2}+\left(c{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}+k{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}\right)\frac{d{x}_7(t)}{dt}\\ +k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}{x}_7(t)\triangleq A_7(t),0<\beta <2,0\le \lambda <1.\end{array}$$

(9.11)

When α = 2 in (8.22), we have the class VII fractional vibrator in the form

$$m\frac{d^2{x}_7(t)}{d{t}^2}+c\frac{d^{\beta }{x}_7(t)}{d{t}^{\beta }}+k\frac{d^{\lambda }{x}_7(t)}{d{t}^{\lambda }}\triangleq B_7(t),\hspace{1em}0<\beta <2,0\le \lambda <1.$$

(9.12)

The above is the fractional equivalence of the class VII Li's vibration system. Obviously, F[A₇(t) − B₇(t)] = 0.

10. Vibration Parameters of Seven Classes of Fractional Vibrators

Consider

$$A_j(t)=m_{\mathrm{eq}j}\frac{d^2{x}_j(t)}{d{t}^2}+c_{\mathrm{eq}j}\frac{d{x}_j(t)}{dt}+k_{\mathrm{eq}j}\frac{d{x}_j(t)}{dt},$$

(10.1)

where m_eqj is the equivalent mass of the jth class fractional vibrator (j = 1, ..., 7). Let c_eqj be the equivalent damping of the jth class fractional vibrator. Then, from Section 9, we list m_eqj and c_eqj in Table 1.

Denote by k_eqj be the equivalent stiffness of the jth class fractional vibrator. Let

$${\varsigma }_{\mathrm{eq}j}=\frac{c_{\mathrm{eq}j}}{2\sqrt{m_{\mathrm{eq}j}{k}_{\mathrm{eq}j}}}.$$

(10.2)

We list k_eqj and ζ_eqj in Table 2.

Let ω_eqnj be the equivalent damping free natural angular frequency of the jth class fractional vibrator. Define it by

$${\omega }_{\mathrm{eqn}j}=\sqrt{\frac{k_{\mathrm{eq}j}}{m_{\mathrm{eq}j}}}.$$

(10.3)

Denote by ω_eqdj the equivalent damped natural angular frequency for the jth class fractional vibrator. Suppose small damping of |ζ_eqj| ≤ 1 from a view of engineering.

Define ω_eqdj by

$${\omega }_{\mathrm{eqd}j}={\omega }_{\mathrm{eqn}j}\sqrt{1-{\varsigma }_{\mathrm{eq}j}^2}.$$

(10.4)

We list ω_eqnj and ω_eqdj in Table 3.

Let γ_eqj be the equivalent frequency ratio of the jth class fractional vibrator. It is defined by

$${\gamma }_{\mathrm{eq}j}=\frac{\omega }{{\omega }_{\mathrm{eqn}j}}.$$

(10.5)

Then,

$$\begin{gathered} {\gamma }_{\mathrm{eq}1}=\frac{\omega \sqrt{-{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}}}{{\omega }_n},{\gamma }_{\mathrm{eq}2}=\gamma \sqrt{1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}, \\ {\gamma }_{\mathrm{eq}3}=\gamma \sqrt{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)},{\gamma }_{\mathrm{eq}4}=\gamma \sqrt{\frac{-{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}}{{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}, \\ {\gamma }_{\mathrm{eq}5}=\gamma \sqrt{\frac{1}{{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}},{\gamma }_{\mathrm{eq}6}=\gamma \sqrt{\frac{-\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}{{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}, \\ {\gamma }_{\mathrm{eq}7}=\gamma \sqrt{\frac{1-2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}}{{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}, \end{gathered}$$

(10.6)

where $\gamma =\frac{\omega }{{\omega }_n}.$

11. Responses of Seven Classes of Fractional Vibrators

Let x_j(t) be the free response of the jth class fractional vibrator. It is the solution to the following fractional differential equation

$$\{\begin{array}{c}{B}_j(t)=0,\\ x_j(0)=x_{j0},x_j^{\prime }(0)=v_{j0},\end{array}$$

(11.1)

where x_j0 and v_j0 are initial conditions. Due to F[B_j(t) − A_j(t)] = 0, the above can be equivalently expressed by

$$\{\begin{array}{c}{A}_j(t)=0,\\ x_j(0)=x_{j0},x_j^{\prime }(0)=v_{j0}.\end{array}$$

(11.2)

Thus,

$$x_j(t)=e^{-{\varsigma }_{\mathrm{eq}j}{\omega }_{\mathrm{eqn}j}t}\left(x_{j0}\cos {\omega }_{\mathrm{eqd}j}t+\frac{v_{j0}+{\varsigma }_{\mathrm{eq}j}{\omega }_{\mathrm{eqn}j}{x}_{j0}}{{\omega }_{\mathrm{eqd}j}}\sin {\omega }_{\mathrm{eqd}j}t\right),t\ge 0.$$

(11.3)

Let h_j(t) be the impulse response of the jth class fractional vibrator. It is the solution to

B_j(t) = δ(t).

(11.4)

Owing to F[B_j(t) − A_j(t)] = 0, the above is equivalent to

A_j(t) = δ(t).

(11.5)

Thus,

$$h_j(t)=\frac{e^{-{\varsigma }_{\mathrm{eq}j}{\omega }_{\mathrm{eqn}j}t}}{m_{\mathrm{eq}j}{\omega }_{\mathrm{eqd}j}}\sin {\omega }_{\mathrm{eqd}j}t,\hspace{1em}t\ge 0.$$

(11.6)

Denote by g_j(t) the unit step response of the jth class fractional vibrator. Then,

$$g_j(t)=\frac{1}{k_{\mathrm{eq}j}}\left[1-\frac{e^{-{\varsigma }_{\mathrm{eq}j}{\omega }_{\mathrm{eqn}j}t}}{\sqrt{1-{\varsigma }_{\mathrm{eq}j}^2}}\cos \left({\omega }_{\mathrm{eqd}j}t-{\varphi }_j\right)\right],\hspace{1em}t\ge 0,$$

(11.7)

where

$${\varphi }_j={\tan }^{-1}\frac{{\varsigma }_{\mathrm{eq}j}}{\sqrt{1-{\zeta }_{\mathrm{eq}j}^2}}.$$

(11.8)

12. Frequency Transfer Funcitons of Seven Classes of Fractional Vibrators

Denote by H_j(ω) the frequency transfer function of the jth class fractional vibrator. Doing the Fourier transform on both sides of (11.4) yields

$$H_j(\omega )=\frac{1}{k_{\mathrm{eq}j}\left(1-{\gamma }_{\mathrm{eq}j}^2+i2{\varsigma }_{\mathrm{eq}j}{\gamma }_{\mathrm{eq}j}\right)}.$$

(11.9)

Table 4. lists the frequency transfer functions of seven classes of fractional vibrators.

Table 4. Frequency transfer functions of seven classes of fractional vibrators.

Fractional vibrators	Frequency transfer functions
Class I	$H_1(\omega )=\frac{1}{k\left(1-\frac{{\omega }^{\alpha }}{{\omega }_n^2}\left|\cos \frac{\alpha \pi }{2}\right|+i\frac{{\omega }^{\alpha }}{{\omega }_n^2}\sin \frac{\alpha \pi }{2}\right)}$
Class II	$H_2(\omega )=\frac{1/k}{1-{\gamma }^2\left(1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)+i\frac{2\varsigma {\omega }^{\beta }\sin \frac{\beta \pi }{2}}{{\omega }_n}}$
Class III	$H_3(\omega )=\frac{1/k}{\begin{array}{l}1-{\gamma }^2\left({\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|-2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)\\ +i\frac{\gamma \left({\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}\right)}{{\omega }_n\left({\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|-2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}\end{array}}$
Class IV	$H_4(\omega )=\frac{1}{k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}\left(\begin{array}{l}1-{\gamma }^2\frac{-{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}}{{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}\\ +i2\gamma \frac{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+k{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}}{2\sqrt{mk{\omega }^{\alpha +\lambda -2}\left|\cos \frac{\alpha \pi }{2}\right|\cos \frac{\lambda \pi }{2}}}\sqrt{\frac{-{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}}{{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}\end{array}\right)},$
Class V	$H_5(\omega )=\frac{1}{k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}\left(1-\frac{{\gamma }^2}{{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}+i2\gamma \frac{k{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}}{2\sqrt{mk{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}\sqrt{\frac{1}{{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}\right)}$
Class VI	$H_6(\omega )=\frac{1}{k\left[\begin{array}{l}{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}+{\gamma }^2\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)\\ +i\gamma \left({\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+2\zeta {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}+{\omega }_n^2{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}\right)\end{array}\right]}$
Class VII	$H_7(\omega )=\frac{1}{k\left[\begin{array}{l}{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}-\gamma \left(1-2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)\\ +i\gamma \left(2\varsigma {\omega }^{\beta -1}\sin \frac{\beta \pi }{2}+{\omega }_n{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}\right)\end{array}\right]}$

Table 4. Frequency transfer functions of seven classes of fractional vibrators.

Fractional vibrators	Frequency transfer functions
Class I	$H_1(\omega )=\frac{1}{k\left(1-\frac{{\omega }^{\alpha }}{{\omega }_n^2}\left|\cos \frac{\alpha \pi }{2}\right|+i\frac{{\omega }^{\alpha }}{{\omega }_n^2}\sin \frac{\alpha \pi }{2}\right)}$
Class II	$H_2(\omega )=\frac{1/k}{1-{\gamma }^2\left(1-\frac{c}{m}{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)+i\frac{2\varsigma {\omega }^{\beta }\sin \frac{\beta \pi }{2}}{{\omega }_n}}$
Class III	$H_3(\omega )=\frac{1/k}{\begin{array}{l}1-{\gamma }^2\left({\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|-2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)\\ +i\frac{\gamma \left({\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}\right)}{{\omega }_n\left({\omega }^{\alpha -2}\left|\cos \frac{\alpha \pi }{2}\right|-2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)}\end{array}}$
Class IV	$H_4(\omega )=\frac{1}{k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}\left(\begin{array}{l}1-{\gamma }^2\frac{-{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}}{{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}\\ +i2\gamma \frac{m{\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+k{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}}{2\sqrt{mk{\omega }^{\alpha +\lambda -2}\left|\cos \frac{\alpha \pi }{2}\right|\cos \frac{\lambda \pi }{2}}}\sqrt{\frac{-{\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}}{{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}\end{array}\right)},$
Class V	$H_5(\omega )=\frac{1}{k{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}\left(1-\frac{{\gamma }^2}{{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}+i2\gamma \frac{k{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}}{2\sqrt{mk{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}\sqrt{\frac{1}{{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}}}\right)}$
Class VI	$H_6(\omega )=\frac{1}{k\left[\begin{array}{l}{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}+{\gamma }^2\left({\omega }^{\alpha -2}\cos \frac{\alpha \pi }{2}+2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)\\ +i\gamma \left({\omega }^{\alpha -1}\sin \frac{\alpha \pi }{2}+2\zeta {\omega }_n{\omega }^{\beta -1}\sin \frac{\beta \pi }{2}+{\omega }_n^2{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}\right)\end{array}\right]}$
Class VII	$H_7(\omega )=\frac{1}{k\left[\begin{array}{l}{\omega }^{\lambda }\cos \frac{\lambda \pi }{2}-\gamma \left(1-2\varsigma {\omega }_n{\omega }^{\beta -2}\cos \frac{\beta \pi }{2}\right)\\ +i\gamma \left(2\varsigma {\omega }^{\beta -1}\sin \frac{\beta \pi }{2}+{\omega }_n{\omega }^{\lambda -1}\sin \frac{\lambda \pi }{2}\right)\end{array}\right]}$

Let Δ_eqj be the equivalent logarithmic decrement of the free response of the jth class fractional vibrator. Let Q_eqj be the equivalent Q factor of the jth class fractional vibrator. They are listed in Table 5.

13. Application: Multi-Fractional Damped Euler-Bernoulli Beam

We address the forced response to a multi-fractional damped Euler-Bernoulli beam as an application of the analytical theory of fractional vibrations previously discussed. By multi-fractional, we mean that inertia force, internal and external damping forces are of fractional orders.

13.1. Multi-Fractional Damped Euler-Bernoulli Beam

The following is the motion equation of the conventional damped Euler-Bernoulli beam

$$\frac{{\partial }^2}{\partial x^2}\left(EI\frac{{\partial }^{2}w}{\partial x^2}+c_{s}I\frac{{\partial }^{3}w}{\partial x^2\partial t}\right)+\rho A\frac{{\partial }^{2}w}{\partial t^2}+c\frac{\partial w}{\partial t}=q(x,t),$$

(13.1)

where c_s is internal damping and c is external one, $c\frac{\partial w}{\partial t}$ is external damping force, $c_{s}I\frac{{\partial }^{3}w}{\partial x^2\partial t}$is internal damping force, and $\rho A\frac{{\partial }^{2}w}{\partial t^2}$is inertia force (Palley et al. [3]). The forced response to (13.1) under the Rayleigh damping assumption is known (Palley et al. [3], Jin and Xia [23]).

The above equation takes into account the Voigt assumption on materials about internal damping. In this research, following Li [13], we describe the closed form of the forced response to the multi-fractional damped Euler-Bernoulli beam in the form

$$\frac{{\partial }^2}{\partial x^2}\left(EI\frac{{\partial }^{2}w}{\partial x^2}+c_{s}I\frac{{\partial }^{2+\lambda }w}{\partial x^2\partial t^{\lambda }}\right)+\rho A\frac{{\partial }^{\alpha }w}{\partial t^{\alpha }}+c\frac{{\partial }^{\beta }w}{\partial t^{\beta }}=q(x,t),1\text{<}\alpha <3,0<\beta <2,0<\lambda <2.$$

(13.2)

Precisely, the above stands for a beam with the fractional inertia force$\rho A\frac{{\partial }^{\alpha }w}{\partial t^{\alpha }},$fractional internal damping force $c_{s}I\frac{{\partial }^{2+\lambda }w}{\partial x^2\partial t^{\lambda }},$ and fractional external damping one $c\frac{{\partial }^{\beta }w}{\partial t^{\beta }}.$

13.2. Closed Form Forced Response

Using separation of variables, we write the response by w(x, t) = ϕ(x)p(t). Substituting it into (13.2) produces

$$\begin{array}{l}{\displaystyle \sum _{j=1}^{\infty }\rho A{\phi }_j(x)\frac{d^{\alpha }{p}_j(t)}{d{t}^{\alpha }}}+{\displaystyle \sum _{j=1}^{\infty }c{\phi }_j(x)\frac{d^{\beta }{p}_j(t)}{d{t}^{\beta }}}+{\displaystyle \sum _{j=1}^{\infty }\frac{d^2}{d{x}^2}\left[c_{s}I\frac{d^2{\phi }_j(x)}{d{x}^2}\right]\frac{d^{\lambda }{p}_j(t)}{d{t}^{\lambda }}}\\ +{\displaystyle \sum _{j=1}^{\infty }\frac{d^2}{d{x}^2}\left[EI\frac{d^2{\phi }_j(x)}{d{x}^2}\right]p_j(t)}=q(x,t).\end{array}$$

(13.3)

Using the orthogonality of vibration modes ϕ_m(x) on both sides of the above equation produces

$$\begin{array}{l}{M}_j\frac{d^{\alpha }{p}_j(t)}{d{t}^{\alpha }}+\frac{M_{j}c}{\rho A}\frac{d^{\beta }{p}_j(t)}{d{t}^{\beta }}+{\displaystyle \sum _{j=1}^{\infty }{\displaystyle \underset{0}{\overset{l}{\int }}{\phi }_m(x)\frac{d^2}{d{x}^2}\left[c_{s}I\frac{d^2{\phi }_j(x)}{d{x}^2}\right]}dx\frac{d^{\lambda }{p}_j(t)}{d{t}^{\lambda }}}\\ +{\displaystyle \sum _{j=1}^{\infty }{\displaystyle \underset{0}{\overset{l}{\int }}{\phi }_m(x)\frac{d^2}{d{x}^2}\left[EI\frac{d^2{\phi }_j(x)}{d{x}^2}\right]}dx{p}_j(t)}=Q_j(t),\end{array}$$

(13.4)

where $M_j=\rho A{\displaystyle \underset{0}{\overset{l}{\int }}{\phi }_j^2(x)}dx.$

Using

$$\frac{d^2}{d{x}^2}\left[EI\frac{d^2{\phi }_j(x)}{d{x}^2}\right]=\rho A{\omega }_{\mathrm{n}j}^2{\phi }_j(x),$$

(13.5)

we rewrite (13.4) by

$$\begin{array}{l}{M}_j\frac{d^{\alpha }{p}_j(t)}{d{t}^{\alpha }}+\frac{M_{j}c}{\rho A}\frac{d^{\beta }{p}_j(t)}{d{t}^{\beta }}+{\displaystyle \sum _{j=1}^{\infty }{\displaystyle \underset{0}{\overset{l}{\int }}{\phi }_m(x)\frac{d^2}{d{x}^2}\left[c_{s}I\frac{d^2{\phi }_j(x)}{d{x}^2}\right]}dx\frac{d^{\lambda }{p}_j(t)}{d{t}^{\lambda }}}\\ +M_j{\omega }_{\mathrm{n}j}^2{p}_j(t)=Q_j(t).\end{array}$$

(13.6)

According to the Rayleigh damping assumption,

c = ρAa,

(13.7)

where a is a coefficient with the unit of time since ρA is with the unit of mass and

c_s = Eb,

(13.8)

where b is a coefficient with the unit of frequency as E is with the unit [N/m].

Substituting (13.7) and (13.8) into (13.6) and taking into account the orthogonality of vibration modes, we have

$$M_j\frac{d^{\alpha }{p}_j(t)}{d{t}^{\alpha }}+M_{j}a\frac{d^{\beta }{p}_j(t)}{d{t}^{\beta }}+M_j{\omega }_{\mathrm{n}j}^{2}b\frac{d^{\lambda }{p}_j(t)}{d{t}^{\lambda }}+M_j{\omega }_{\mathrm{n}j}^2{p}_j(t)=Q_j(t).$$

(13.9)

Therefore, the jth order coordinate function is of multi-fractional in the form

$$\frac{d^{\alpha }{p}_j(t)}{d{t}^{\alpha }}+\left(a\frac{d^{\beta }{p}_j(t)}{d{t}^{\beta }}+{\omega }_{\mathrm{n}j}^{2}b\frac{d^{\lambda }{p}_j(t)}{d{t}^{\lambda }}\right)+{\omega }_{\mathrm{n}j}^2{p}_j(t)=f_j(t),$$

(13.10)

where

$$f_j(t)=\frac{Q_j(t)}{M_j}.$$

(13.11)

According to the theory of Li's vibration systems previously explained, the above is simply the equivalence of the following equation

$$\begin{array}{l}-\left(\cos \frac{\alpha \pi }{2}{\omega }^{\alpha -2}+a\cos \frac{\beta \pi }{2}{\omega }^{\beta -2}+{\omega }_{\mathrm{n}j}^{2}b\cos \frac{\lambda \pi }{2}{\omega }^{\lambda -2}\right)\frac{d^2{p}_j(t)}{d{t}^2}\\ +\left(\sin \frac{\alpha \pi }{2}{\omega }^{\alpha -1}+a\sin \frac{\beta \pi }{2}{\omega }^{\beta -1}+{\omega }_{\mathrm{n}j}^{2}b\sin \frac{\lambda \pi }{2}{\omega }^{\lambda -1}\right)\frac{d{p}_j(t)}{dt}+{\omega }_{\mathrm{n}j}^2{p}_j(t)=f_j(t).\end{array}$$

(13.12)

As a matter of fact, let

$$\begin{array}{l}{C}_j(t)\triangleq -\left(\cos \frac{\alpha \pi }{2}{\omega }^{\alpha -2}+a\cos \frac{\beta \pi }{2}{\omega }^{\beta -2}+{\omega }_{\mathrm{n}j}^{2}b\cos \frac{\lambda \pi }{2}{\omega }^{\lambda -2}\right)\frac{d^2{p}_j(t)}{d{t}^2}\\ +\left(\sin \frac{\alpha \pi }{2}{\omega }^{\alpha -1}+a\sin \frac{\beta \pi }{2}{\omega }^{\beta -1}+{\omega }_{\mathrm{n}j}^{2}b\sin \frac{\lambda \pi }{2}{\omega }^{\lambda -1}\right)\frac{d{p}_j(t)}{dt}+{\omega }_{\mathrm{n}j}^2{p}_j(t).\end{array}$$

(13.13)

Let

$$D_j(t)\triangleq \frac{d^{\alpha }{p}_j(t)}{d{t}^{\alpha }}+\left(a\frac{d^{\beta }{p}_j(t)}{d{t}^{\beta }}+{\omega }_{\mathrm{n}j}^{2}b\frac{d^{\lambda }{p}_j(t)}{d{t}^{\lambda }}\right)+{\omega }_{\mathrm{n}j}^2{p}_j(t).$$

(13.14)

Then, F[C_j(t) − D_j(t)] = 0.

Denote by m_e-EBj the jth equivalent mass in the system (13.10) in the form

$$m_{\mathrm{e}\text{-}\mathrm{EB}j}=-\left(\cos \frac{\alpha \pi }{2}{\omega }^{\alpha -2}+a\cos \frac{\beta \pi }{2}{\omega }^{\beta -2}+{\omega }_{\mathrm{n}j}^{2}b\cos \frac{\lambda \pi }{2}{\omega }^{\lambda -2}\right).$$

(13.15)

Let c_e-EBj the jth equivalent damping in the system (13.10). It is given by

$$c_{\mathrm{e}\text{-}\mathrm{EB}j}=\sin \frac{\alpha \pi }{2}{\omega }^{\alpha -1}+a\sin \frac{\beta \pi }{2}{\omega }^{\beta -1}+{\omega }_{\mathrm{n}j}^{2}b\sin \frac{\lambda \pi }{2}{\omega }^{\lambda -1}.$$

(13.16)

Using m_e-EBj and c_e-EBj, we have

$$m_{\mathrm{e}\text{-}\mathrm{EB}j}\frac{d^2{p}_j(t)}{d{t}^2}+c_{\mathrm{e}\text{-}\mathrm{EB}j}\frac{d{p}_j(t)}{dt}+{\omega }_{\mathrm{n}j}^2{p}_j(t)=f_j(t).$$

(13.17)

Denote by ζ_e-EBj the jth equivalent damping ratio in the system (13.10). Define it by ${\varsigma }_{\mathrm{e}\text{-}\mathrm{EB}j}=\frac{c_{\mathrm{e}\text{-}\mathrm{EB}j}}{2\sqrt{m_{\mathrm{e}\text{-}\mathrm{EB}j}}}.$Then,

$${\varsigma }_{\mathrm{e}\text{-}\mathrm{EB}j}=\frac{\sin \frac{\alpha \pi }{2}{\omega }^{\alpha -1}+a\sin \frac{\beta \pi }{2}{\omega }^{\beta -1}+{\omega }_{\mathrm{n}j}^{2}b\sin \frac{\lambda \pi }{2}{\omega }^{\lambda -1}}{2\sqrt{-\left(\cos \frac{\alpha \pi }{2}{\omega }^{\alpha -2}+a\cos \frac{\beta \pi }{2}{\omega }^{\beta -2}+{\omega }_{\mathrm{n}j}^{2}b\cos \frac{\lambda \pi }{2}{\omega }^{\lambda -2}\right)}}.$$

(13.18)

Let ω_en-EBj be the jth equivalent damping free natural frequency regarding the system (13.10). It is given by

$${\omega }_{\mathrm{en}\text{-}\mathrm{EB}j}^2=\frac{{\omega }_{\mathrm{n}j}^2}{m_{\mathrm{e}\text{-}\mathrm{EB}j}}.$$

(13.19)

From a view of vibration engineering, we are interested in

$$\left|{\varsigma }_{\mathrm{e}\text{-}\mathrm{EB}j}\right|\le 1.$$

(13.20)

Let ω_end-EBj be the jth equivalent damped natural frequency regarding the system (13.10). Then,

$${\omega }_{\mathrm{end}\text{-}\mathrm{EB}j}={\omega }_{\mathrm{en}\text{-}\mathrm{EB}j}\sqrt{1-{\varsigma }_{\mathrm{eEB}j}^2}.$$

(13.21)

Therefore, we rewrite (13.17) by

$$\frac{d^2{p}_j(t)}{d{t}^2}+2{\varsigma }_{\mathrm{e}\text{-}\mathrm{EB}j}{\omega }_{\mathrm{en}\text{-}\mathrm{EB}j}\frac{d{p}_j(t)}{dt}+{\omega }_{\mathrm{en}\text{-}\mathrm{EB}j}^2{p}_j(t)=\frac{f_j(t)}{m_{\mathrm{e}\text{-}\mathrm{EB}j}}.$$

(13.22)

Let h_j(t) be the jth impulse response function of the system (13.22). Then,

$$h_j(t)=\frac{1}{m_{\mathrm{e}\text{-}\mathrm{EB}j}{\omega }_{\mathrm{end}\text{-}\mathrm{EB}j}}{e}^{-{\varsigma }_{\mathrm{e}\text{-}\mathrm{EB}j}{\omega }_{\mathrm{en}\text{-}\mathrm{EB}j}t}\sin {\omega }_{\mathrm{end}\text{-}\mathrm{EB}j}t,\hspace{1em}t>0.$$

(13.23)

Because

$$p_j(t)=f_j(t)\ast h_j(t),$$

(13.24)

the zero-state forced response to a multi-fractional damped Euler-Bernoulli beam is expressed by

$$w(x,t)={\displaystyle \sum _{j=1}^{\infty }\frac{{\phi }_j(x)}{m_{\mathrm{e}\text{-}\mathrm{EB}j}{\omega }_{\mathrm{end}\text{-}\mathrm{EB}j}}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{e}^{-{\varsigma }_{\mathrm{e}\text{-}\mathrm{EB}j}{\omega }_{\mathrm{en}\text{-}\mathrm{EB}j}\tau }\sin {\omega }_{\mathrm{end}\text{-}\mathrm{EB}j}\tau f_j(t-\tau )}d\tau }.$$

(13.25)

14. Nonlinearity of Fractional Vibraitons

Seven classes of fractional vibration systems satisfy the superposition. However, they are nonlinear in general. The nonlinearity of fractional vibrations can be explained as follows. The fractional inertia force$m\frac{d^{\alpha }{x}_6(t)}{d{t}^{\alpha }}$ is non-Newtonian unless α = 2. Besides, the fractional damping force $c\frac{d^{\beta }{x}_6(t)}{d{t}^{\beta }}$is non-Newtonian if β ≠ 1. Moreover, the fractional restoration force$k\frac{d^{\lambda }{x}_6(t)}{d{t}^{\lambda }}$is non-Newtonian for λ ≠ 0. Those reflect the nonlinearity of fractional vibrations. By linearization using Li's systems, the nonlinearity of a fractional vibrator is reflected in the aspect of frequency dependent mass or frequency dependent damping or frequency dependent stiffness.

15. Conclusions

We have shown the cases of structures with frequency dependent elements (mass or damping or stiffness) in Section 2, Section 3 and Section 4. Then, we have introduced the general form of a vibration system with frequency dependent elements and its vibrations in Section 5, Section 6, Section 7 and Section 8. In Section 9, we have addressed the fractional equivalences of seven classes of Li's systems with frequency dependent elements. After that, we have proposed the analytical theory of seven classes of fractional vibrations in Section 10, Section 11 and Section 12. The closed form of the forced response to multi-fractional Euler-Bernoulli beam has been presented in Section 13. The nonlinearity of fractional vibrations has been explained in Section 14.