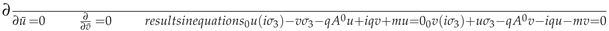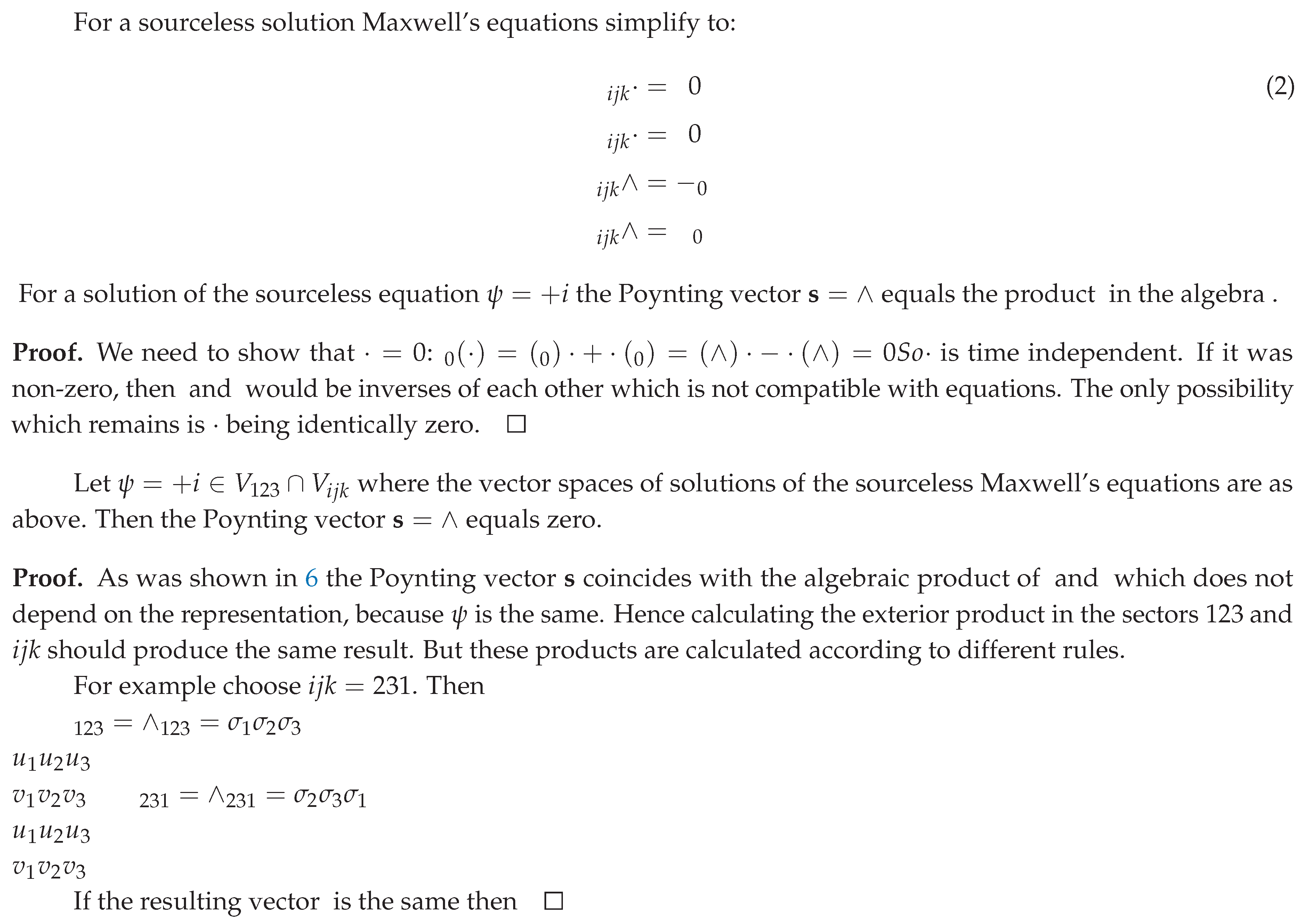Six-fold discrete symmetry of the QED Lagrangian

1. Introduction

The main difference between the standard QED Lagrangian [1,2,3] : L_QED = $\overline{\Psi }\left(i{\gamma }^{\mu }{\partial }^{\mu }-m\right)\Psi -q{A}_{\mu }\overline{\Psi }{\gamma }^{\mu }\Psi -F^{\mu v}{F}_{\mu v}$

and the Pauli algebra Lagrangian used here is use of the multiplicative structure of the algebra.

The other difference is that unlike the usual procedure for recovering the equations of motion from the Lagrangian, using the Euler-Lagrange equations, a different procedure is used, namely equating to zero the formal derivatives. This results in equations equivalent to Dirac equation and its complex conjugate ([4]), and to the inhomogeneous wave equations.

Here is the Pauli algebra version of the QED Lagrangian:

$$\begin{array}{c}=\psi \partial \psi \left(i{\sigma }_3\right)-q\psi \overline{A}\psi +m\psi \psi +\left(\overline{\partial A}\right)\partial A+\hfill \\ +\overline{\psi }\overline{\partial }\psi \left(i{\sigma }_3\right)-q\overline{\psi }A\psi +m\overline{\psi }\psi +\left(\overline{\overline{\partial }\overline{A}}\right)\overline{\partial }\overline{A}\hfill \end{array}$$

The Lagrangian is intentionally written in two lines because these lines are transformed one into the other by the bar-star automorphism of the Pauli algebra (see [4]).

The notation is explained in the next section. The Lagrangian can equivalently be written as:

$=\psi \partial \psi \left(i{\sigma }_3\right)-(\overline{A}J+\overline{J}A)+m\psi \psi +\overline{A}A$

$+\overline{\psi }\overline{\partial }\psi \left(i{\sigma }_3\right)-(A\overline{J}+J\overline{A})+m\overline{\psi }\psi +A\overline{A}\mathit{Thereasonforthisisthat}A=\partial \overline{\partial }A=A$ and also (see 3) $\mathrm{q}\psi \overline{A}\psi +q\overline{\psi }A\psi =(\overline{A}J+A\overline{J}+\overline{J}A+J\overline{A})$

Recovering the equations of motion is done by equating to zero the formal derivatives of the Lagrangian with respect to $\psi$, $\overline{\psi }$, $\overline{A}$, A:

This results in four equations $\partial \psi \left(i{\sigma }_3\right)-q\overline{A}\psi +m\psi =0$

$$\begin{array}{c}\overline{\partial }\psi \left(i{\sigma }_3\right)-qA\psi +m\psi =0\hfill \\ -J+A=0\hfill \\ -\overline{J}+\overline{A}=0\hfill \end{array}$$

(1)

The first two equations are equivalent to the and its complex conjugate, [4] and the last two are the inhomogeneous wave equations [5].

The sign of the d’Alembertian used here is the opposite of the sign used in [5].

2. Notation and preliminaries

For any $a\in$ the "bar" anti-isomorphism operation $\overline{a}$ inverts the sign of ${\sigma }_k$ leaving ${\sigma }_0$ without change. All elements of the Pauli algebra can be split into their scalar and vector components as follows: a₀=(a+$\overline{a}$), =(a-), a=a₀+, =a₀-

Elements of Pauli algebra whose zeroeth component is real and the other three are imaginary are called real quaternionic. They are fixed by the bar-star automorphism. Elements whose zeroeth component is imaginary and the other three are real are called imaginary quaternionic. They change sign under the bar-star automorphism.

A product of any two vectors splits as a sum of inner and outer products:   =· + ∧   · =(+)   ∧=(-)

The first summand is scalar, the second is vector as it changes sign under the bar anti-isomorphism. A product of any two elements splits as a sum of scalar and vector summands: ab=(a₀+)(b₀+)= $a_0{b}_0+·+a_0+b_0+\wedge$

where the first two terms are scalar.

The Pauli algebra spinor $\psi$ is constructed out of the four-component spinor $\Psi$ by first completing it with a second column and then splitting it as the sum of real quaternionic and imaginary quaternionic components: $\psi =u+iv\psi =u-iv$

where $u,v\in$ are real quaternionic functions of spacetime, so $iv\in$ is an imaginary quaternionic function. This procedure is described in [4].

The differential, the four-potential and the four-current are represented as elements of the Pauli algebra split into scalar and vector parts as follows:

$$\begin{array}{cc}\partial ={\partial }_{\mu }{\sigma }_{\mu }={\partial }_0+\hfill & \overline{\partial }={\partial }_0-\\ A=A^{\mu }{\sigma }_{\mu }=A^0+\hfill & \overline{A}=A^0-\\ J=J^{\mu }{\sigma }_{\mu }=J^0+\hfill & \overline{J}=J^0-\end{array}$$

If $u\in$ then $u=\overline{u}$, $u=u$. For $iv$ the opposite holds $\left(iv\right)=-i\overline{v}$.

For any $\psi \in$$\overline{\psi }\psi =\det \left(\psi \right)I_2$

Both compositions of the differential and its bar are the d’Alembertian: $\partial \overline{\partial }=\overline{\partial }\partial$=

Hence

$$\begin{array}{c}\overline{(\partial A)}\partial A=\overline{A}\overline{\partial }\partial A=\overline{A}A\\ \overline{\left(\overline{\partial }\overline{A}\right)}\overline{\partial }\overline{A}=A\partial \overline{\partial }\overline{A}=A\overline{A}\end{array}$$

The Lagrangian is rewritten separating the elements into their scalar and vector parts. This will be used when writing the representation independent form of the Lagrangian.

$$\begin{array}{c}=\psi \left({\partial }_0+\right)\psi \left(i{\sigma }_3\right)-\hfill \\ -\left[\left(A^0-\right)\left(J^0+\right)+\left(J^0-\right)\left(A^0+\right)\right]+m\psi \psi +\left(A^0-\right)\left(A^0+\right)+\hfill \\ +\overline{\psi }\left({\partial }_0-\right)\psi \left(i{\sigma }_3\right)-\hfill \\ -\left[\left(A^0+\right)\left(J^0-\right)+\left(J^0+\right)\left(A^0-\right)\right]+m\overline{\psi }\psi +\left(A^0+\right)\left(A^0-\right)\mathit{Takingintoaccountthat}\psi =\overline{u}-i\overline{v}\overline{\psi }=\hfill \\ \overline{u}+i\overline{v}\psi =u-iv\psi =u+iv\hfill \end{array}$$

and the expressions for the current 3 which imply: ${\mathrm{J}}^0=q(\overline{u}u+\overline{v}v){\sigma }_0=J^k{\sigma }_k=iq\left(\overline{u}{\sigma }_{k}v-\right.\left.\overline{v}{\sigma }_{k}u\right){\sigma }_k$

the Lagrangian is rewritten in quaternionic functions u and v as follows:

$$\begin{array}{c}=\left({ }_{0}u+{ }_{0}v\right)\left(i{\sigma }_3\right)-(v-u){\sigma }_3-\hfill \\ -q{A}^0(\overline{u}u+\overline{v}v)+iq{A}^k\left(\overline{u}{\sigma }_{k}v-\overline{v}{\sigma }_{k}u\right)+\hfill \\ +A^0{A}^0-+m(u-v)\hfill \end{array}$$

Equating to zero the derivatives

which are equivalent to the first two equations of 1.

In order to have a representation-independent form of the Lagrangian, the quaternionic functions u and $iv$ need to be rewritten in terms of sigma matrices:

$$\begin{array}{c}\mathrm{u}=\mathrm{c}-\mathrm{d}\hfill \\ \mathrm{dc}={\mathrm{c}}_0+i{c}_1-d_0+i{d}_1\hfill \\ d_0+i{d}_1{c}_0-i{c}_1=c_0{\sigma }_0+i{d}_1{\sigma }_1-i{d}_0{\sigma }_2+i{c}_1{\sigma }_3\hfill \\ \mathrm{iv}=\mathrm{ab}\hfill \\ \mathrm{b}-\mathrm{a}={\mathrm{a}}_0+i{a}_1{b}_0-i{b}_1\hfill \\ b_0+i{b}_1-a_0+i{a}_1=i{a}_1{\sigma }_0+b_0{\sigma }_1+b_1{\sigma }_2+a_0{\sigma }_3\hfill \end{array}$$

3. Proof that the the two forms of the interaction term are equal

The two sums forming the interaction terms in 1 are equal:

$$q\psi \overline{A}\psi +q\overline{\psi }A\overline{\psi }=(\overline{A}J+A\overline{J}+\overline{J}A+J\overline{A})$$

Proof. 

The probability current $J^{\mu }$ is calculated out of the real quaternionic and imaginary quaternionic components of the Pauli algebra spinor $\psi$ as follows:

$$J^{\mu }=u{\sigma }_{\mu }\left(iv\right)+\left(iv\right){\sigma }_{\mu }u$$

(the equality needs to be understood as between complex numbers to the left of the equal sign and scalar matrices to the right of the equal sign).

This formula can be checked by using the two-column completion of the four-component spinor $\Psi$ as described in [4] and then rewriting the usual formula for the probability current [3] with $2\times 2$ blocks $iv$ and u.

We need to calculate separately the scalar and the vector components of the current:

$$J^0=q[uu+\left(iv\right)\left(iv\right)]{\sigma }_0=J^k{\sigma }_k=q[u{\sigma }_k\left(iv\right)+\left(iv\right){\sigma }_{k}u]{\sigma }_k$$

(Note that both $uu+\left(iv\right)\left(iv\right)$ and $u{\sigma }_k\left(iv\right)+\left(iv\right){\sigma }_{k}u$ are real scalars)

To prove 3 we calculate separately the left side and the right side. The spinor $\psi =u+iv$ is decomposed as sum of a real quaternionic and an imaginary quaternionic function. We begin with the left side:

$$\begin{array}{c}L.S.=q\psi \overline{A}\psi +q\overline{\psi }A\psi =\hfill \\ q[u+\left(iv\right)](A^0-)(u+iv)+q[u-\left(iv\right)](A^0+)(u-iv)=\hfill \\ =q(\overline{u}-i\overline{v})(A^0-)(u+iv)+q(\overline{u}+i\overline{v})(A^0+)(u-iv)=\hfill \\ =2q{A}^0(\overline{u}u+\overline{v}v){\sigma }_0-2iq{A}^k(\overline{u}{\sigma }_{k}v-\overline{v}{\sigma }_{k}u){\sigma }_k=\hfill \\ =2q{A}^0[uu+\left(iv\right)\left(iv\right)]{\sigma }_0-2q{A}^k[u{\sigma }_k\left(iv\right)+\left(iv\right){\sigma }_{k}u]{\sigma }_k\hfill \end{array}$$

(Note that the expressions in square brackets are real scalars)

Now calculate the right side:

$$\begin{array}{c}R.S.=(\overline{A}J+A\overline{J}+\overline{J}A+J\overline{A})=\hfill \\ =[(A^0-)(J^0+)+(A^0+)(J^0-)+\hfill \\ +(J^0-)(A^0+)+(J^0+)(A^0-)]=\hfill \\ =2(A^0{J}^0-2·-2\wedge -2\wedge )=\hfill \\ =2(A^0{J}^0-2·)\hfill \end{array}$$

(the last equality because the outer product is anticommutative)

Now use the expressions for the current in (3):

$$R.S.=2q{A}^0[uu+\left(iv\right)\left(iv\right)]{\sigma }_0-2q{A}^k[u{\sigma }_k\left(iv\right)+\left(iv\right){\sigma }_{k}u]{\sigma }_k$$

$L.S.=R.S.$□

4. The representation-independent form of the QED Lagrangian

The Pauli algebra is isomorphic to the Clifford algebra so that every element can be expressed in its three generators:  ²=1,  ²=-1,  ²=-1

The table below defines six matrix representations of into , of which the first is chosen to be the standard one.

The automorphisms of are labelled by their action on the three cyclic subgroups of order 4 of the finite quaternion group . These automorphisms form a group isomorphic to the group of permutations of three letters, see [6,7].

Here the finite quaternion group is (and their opposite signs):

$$=\{{\sigma }_0,-i{\sigma }_1,-i{\sigma }_2,-i{\sigma }_3\}\leftrightarrow \{1,,,\}$$

This action can be seen in the columns corresponding to the generators

$$,,$$

The subscripts $ijk$ in the following table show the isomorphism between the outer automorphisms of and the group of permutations of three letters.

The morphisms between the representations are obtained by combining the inverse of one representation with another. The automorphism of converting the $D{E}_{123}$ into $D{E}_{231}$ for example will be

$${\phi }_{231}\circ {\phi }_{123}^{-1}$$

Here is the table for ${\phi }_{ijk}:\to$:

$$\begin{array}{cccccccc}\hfill {\phi }_{ijk}& \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \\ \\ \hfill {\phi }_{123}& {\sigma }_3\hfill & \hfill -i{\sigma }_1& -i{\sigma }_2\hfill & \hfill -i{\sigma }_3& {\sigma }_2\hfill & \hfill -{\sigma }_1& -i{\sigma }_0\hfill \\ \\ \hfill {\phi }_{231}& {\sigma }_1\hfill & \hfill -i{\sigma }_2& -i{\sigma }_3\hfill & \hfill -i{\sigma }_1& {\sigma }_3\hfill & \hfill -{\sigma }_2& -i{\sigma }_0\hfill \\ \\ \hfill {\phi }_{312}& {\sigma }_2\hfill & \hfill -i{\sigma }_3& -i{\sigma }_1\hfill & \hfill -i{\sigma }_2& {\sigma }_1\hfill & \hfill -{\sigma }_3& -i{\sigma }_0\hfill \\ \\ \hfill {\phi }_{213}& {\sigma }_3\hfill & \hfill -i{\sigma }_2& -i{\sigma }_1\hfill & \hfill i{\sigma }_3& -{\sigma }_1\hfill & \hfill {\sigma }_2& i{\sigma }_0\hfill \\ \\ \hfill {\phi }_{132}& {\sigma }_2\hfill & \hfill -i{\sigma }_1& -i{\sigma }_3\hfill & \hfill i{\sigma }_2& -{\sigma }_3\hfill & \hfill {\sigma }_1& i{\sigma }_0\hfill \\ \\ \hfill {\phi }_{321}& {\sigma }_1\hfill & \hfill -i{\sigma }_3& -i{\sigma }_2\hfill & \hfill i{\sigma }_1& -{\sigma }_2\hfill & \hfill {\sigma }_3& i{\sigma }_0\hfill \end{array}$$

The action of the bar-star automorphism and of the bar and of "star" (Hermitian conjugate) anti-automorphisms on the generators of the Clifford algebra can be seen in the following table:

operation
bar-star	-1	1	1	1	-1	-1	-1
bar	-1	-1	-1	-1	-1	-1	1
star	1	-1	-1	-1	1	1	-1

Now use ${\phi }_{123}^{-1}$ to rewrite all the vector expressions in terms of generators of the Clifford algebra, according to the first line in the table. The ${\sigma }_0$ being identity is omitted. = - ∂₁+ ∂₂ + ∂₃

= - A₁+ A₂+ A₃

= - J₁+ J₂+ J₃ The other elements of the Lagrangian that depends on the representation are $i{\sigma }_3$ and ${\sigma }_3$, and according to the first line of the table, they should be replaced with − and with .

Now one can write the representation-independent Lagrangian, by substituting 4 into 2. In this article the substitution is done only for the case of the free .

If the six representations are applied to all the expressions in the Lagrangian and in the resulting equations, then the morphisms between representations will transform solutions into solutions. Both the new Pauli algebra spinors and the corresponding new equations will be different but the underlying eight equations of the and its Hermitian conjugate will be exactly the same.

This raises the question, will the solutions to the transformed equations be the same as before, or will they be genuinely different? This question is answered in 5. Only the free is needed there, so here is its representation-independent form:

$$(0-{\partial }_1+{\partial }_2+{\partial }_3)\psi +\psi =0$$

5. The six sectors of fermion fields are distinct

The method used to show this is the mass inversion symmetry, described in [4]. For convenience this short argument is reproduced here. Given a solution $\psi$ of the free Dirac equation define $\psi =\psi {\sigma }_3$. Then multiply this equation, which appears first, on the right by ${\sigma }_3$, and recall that $\overline{{\sigma }_3}=-{\sigma }_3$:

$$\partial \psi =i\psi {\sigma }_3\partial \psi {\sigma }_3=i\psi {\sigma }_3{\sigma }_3\partial \psi {\sigma }_3=-i\left(\psi {\sigma }_3\right){\sigma }_3\partial \psi =-i\psi {\sigma }_3$$

So ${\psi }^{\prime }$ is also a solution of the but with the mass of opposite sign. Only massless spinors can be solutions to two versions of the free belonging to two different sectors.

Proof. 

These are the six versions of the free obtained by applying the six representations to the representation-independent free:

$$\begin{array}{ccc}\hfill 123({\partial }_0+{\sigma }_1{\partial }_1+{\sigma }_2{\partial }_2+{\sigma }_3{\partial }_3)\psi -i\psi {\sigma }_3& =& 0\hfill \\ \hfill 231({\partial }_0+{\sigma }_2{\partial }_1+{\sigma }_3{\partial }_2+{\sigma }_1{\partial }_3)\psi -i\psi {\sigma }_2& =& 0\hfill \\ \hfill 312({\partial }_0+{\sigma }_3{\partial }_1+{\sigma }_1{\partial }_2+{\sigma }_2{\partial }_3)\psi -i\psi {\sigma }_1& =& 0\hfill \\ \hfill 213({\partial }_0-{\sigma }_2{\partial }_1-{\sigma }_1{\partial }_2+{\sigma }_3{\partial }_3)\psi +i\psi {\sigma }_3& =& 0\hfill \\ \hfill 132({\partial }_0-{\sigma }_1{\partial }_1-{\sigma }_3{\partial }_2+{\sigma }_2{\partial }_3)\psi +i\psi {\sigma }_1& =& 0\hfill \\ \hfill 321({\partial }_0-{\sigma }_3{\partial }_1-{\sigma }_2{\partial }_2+{\sigma }_1{\partial }_3)\psi +i\psi {\sigma }_2& =& 0\hfill \end{array}$$

Suppose that the spinor $\psi$ is a solution of two different equations, with the same mass. We can always use the morphisms between representation to make the first of two equations the top line 123. Now let the second equation be any other except 213 (this case will be dealt with separately). For example suppose the second equation is 231. Multiply both equations on the right by ${\sigma }_3$:

$$\begin{array}{ccc}\hfill 123(0+{\sigma }_1{\partial }_1+{\sigma }_2{\partial }_2+{\sigma }_3{\partial }_3)\psi +i\psi {\sigma }_3& =& 0\hfill \\ \hfill 231(0+{\sigma }_2{\partial }_1+{\sigma }_3{\partial }_2+{\sigma }_1{\partial }_3){\psi }^{\prime }-i\psi {\sigma }_2& =& 0\hfill \end{array}$$

So $\psi$ is a solution for the first equation with mass − and for the second with mass , which is only possible if the mass is zero. This argument applies to all lines except 213 where we do not have the anticommutation.

For the lines 123 and 213 suppose that $\ne 0$ and consider also their bar-star equations:

$$\begin{array}{ccc}\hfill (0+{\sigma }_1{\partial }_1+{\sigma }_2{\partial }_2+{\sigma }_3{\partial }_3)\psi -i\psi {\sigma }_3& =& 0\hfill \\ \hfill (0-{\sigma }_2{\partial }_1-{\sigma }_1{\partial }_2+{\sigma }_3{\partial }_3)\psi +i\psi {\sigma }_3& =& 0\hfill \\ \hfill (0-{\sigma }_1{\partial }_1-{\sigma }_2{\partial }_2-{\sigma }_3{\partial }_3)\psi -i\psi {\sigma }_3& =& 0\hfill \\ \hfill (0+{\sigma }_2{\partial }_1+{\sigma }_1{\partial }_2-{\sigma }_3{\partial }_3)\psi +i\psi {\sigma }_3& =& 0\hfill \end{array}$$

Subtracting the first two lines and the last two lines we get

$$({\sigma }_1+{\sigma }_2)(+)\psi =i\psi {\sigma }_3({\sigma }_1+{\sigma }_2)(+)\psi =-i\psi {\sigma }_3$$

Combining we get $\frac{1}{2^2{(+)}^2\psi =\psi }$ and with a change of coordinates we have an ODE

$$\frac{1}{2^{2}2\psi s-\psi =0}$$

with real roots of its characteristic equation. So $\psi$ is an exponential function and this is incompatible with it being normalizable. □

6. Absence of EM interaction between different sectors

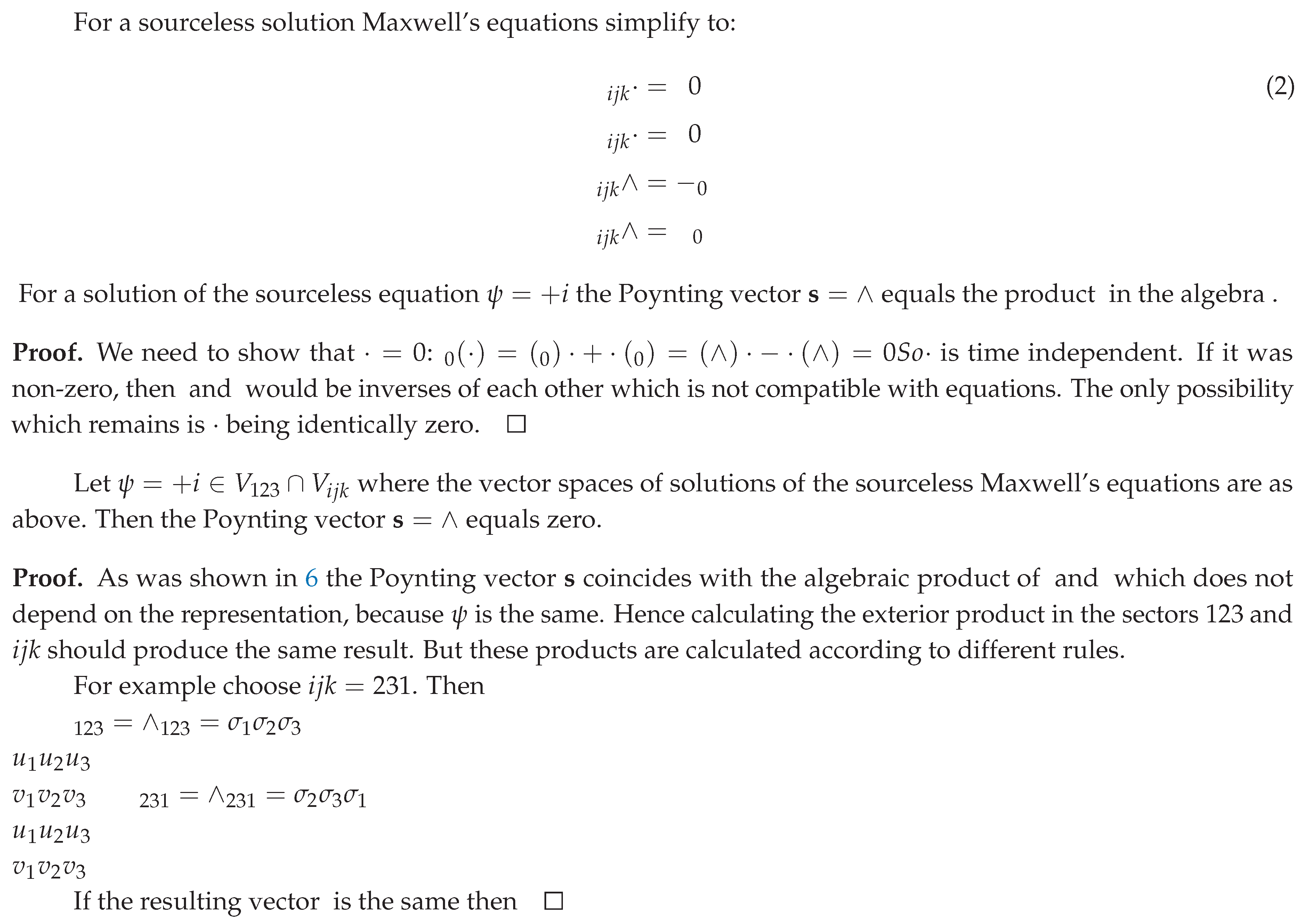
7. Conclusions

For the six-fold discrete symmetry to be a candidate to explain dark matter, two issues need to be addressed: first, show that the six sectors of free fermion fields are genuinely distinct from each other; and second, show the absence of electromagnetic interaction between different sectors. Only the first issue of the two is addressed in this article.

To properly address the second issue one would need to show the existence of six symmetric types of photons. It is possible to construct the six symmetric Maxwell’s equations and show that their solutions are distinct, but this would not be a sufficient treatment of the issue.

Also, the six-fold symmetry must be extended to weak and strong interactions to be a reasonable explanation.

According to [8] the universe consists of approximately $5\%$ ordinary baryonic matter, $\sim 26\%$ dark matter, and $\sim 61\%$ dark energy. This gives the ratio of dark matter to ordinary matter of $5.2:1$ which is close to $5:1$, as predicted by the six-fold symmetry.