ISM: A New Space-Learning Model for Heterogenous Multi-view Data Reduction, Visualization and Clustering

1. Introduction

2. Materials and Methods

2.2. Methods

Outline of ISM and comparison with other Latent Space approaches

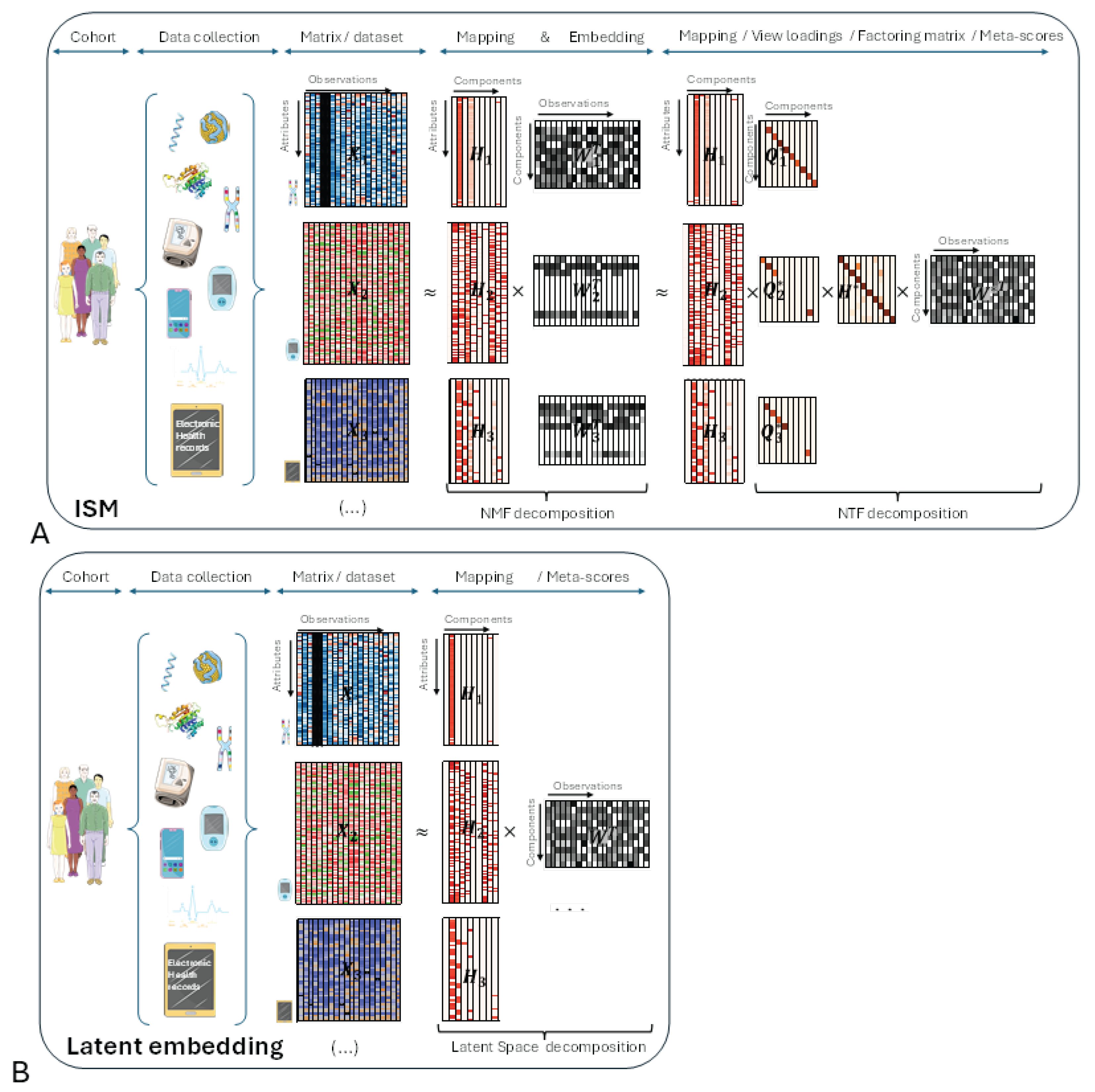
Before delving into the details of the ISM workflow, let’s introduce the main underlying ideas with an illustrative figure (Figure 1, panel A) and try to compare with other Latent Space approaches (Figure 2, panel B). The different views are represented by heatmaps on the left side of both panels, with attributes on the vertical axis and observations on the horizontal axis, respectively.

ISM (Figure 1A):

In the central part of the figure, each non-negative view ${\mathit{X}}_v$ has been decomposed into the product of two non-negative matrices ${\mathit{H}}_v$ and ${\mathit{W}}_v$ using NMF. Each ${\mathit{W}}_v$ matrix corresponds to the transformation of a particular view $v$ to a latent space that is common to all transformed views. ISM ensures that the transformed views ${\mathit{W}}_v$ share the same number and type of latent attributes, called components, as explained in the detailed description. This transforming process, which we call embedding, results in a three-dimensional array, or tensor. The corresponding ${\mathit{H}}_v$ matrices contain the loadings of the original attributes on each component. We call these matrices the mapping between the original and transformed views.

In the right part of the figure, the three-dimensional array is decomposed into the tensor product of three matrices: ${\mathit{W}}^{\mathit{*}}{,\mathit{H}}^{\mathit{*}},{\mathit{Q}}^{\mathit{*}}$using NTF. ${\mathit{W}}^{\mathit{*}}$contains the meta-scores – the single transformation to the latent space common to all views. ${\mathit{H}}^{\mathit{*}}$ and ${\mathit{Q}}^{\mathit{*}}$ contain the loadings of NMF latent attributes and views, respectively, on each NTF component. Each row of ${\mathit{Q}}^{\mathit{*}}$ is represented by a diagonal matrix, where the diagonal contains the loadings for a particular view. This allows, for each view of the tensor, to translate in the figure the tensor product into a simple matrix product ${\mathit{W}}^{*}{{(\mathit{H}}^{*}{\mathit{Q}}_v^{*})}^{\mathit{T}}$

Other Latent Space approaches (Figure 1B):

In the right part of the figure, each view $v$ has been decomposed into the product of two matrices ${\mathit{H}}_v$ and $\mathit{W}$ using the latent space method algorithm. As with ISM, $\mathit{W}$ contains the meta-scores – the single transformation in the latent space common to all views.

Figure 1. Comparison between ISM, (panel A) and other Latent Space approaches (panel B).

Figure 1. Comparison between ISM, (panel A) and other Latent Space approaches (panel B).

Comparison between ISM and other Latent Space approaches:

If we multiply in Figure 1A each mapping matrix ${\mathit{H}}_v$ by ${{\mathit{H}}^{\mathit{*}}\mathit{Q}}^{\mathit{*}}$, we obtain a representation that is similar to Figure 1B. This shows that ISM belongs to the family of Latent Space decomposition methods. However, view loadings are a constitutive part of ISM, whereas they are derived in other models, e.g., using variance decomposition by factor as in the MOFA article [3].

Important implications of ISM’s preliminary embedding:

As will be seen in the detailed description of the workflow, ISM begins by applying NMF to the concatenated views. Importantly, NMF can be applied to each view ${\mathit{X}}_v$ independently, leading to view-specific decompositions ${\mathit{X}}_v={\mathit{W}}_v^{nmf}{{\mathit{H}}_v^{nmf}}^{\mathit{T}}$before ISM itself is applied to the $m$ NMF transformed views ${\mathit{W}}_v^{nmf}$. In this case, the view mapping returned by ISM, ${\mathit{H}}_v^{ism}$, refers to the NMF components of each ${\mathit{W}}_v^{nmf}$. However, by embedding the ${\mathit{W}}_v^{nmf}$ in a 3-dimensional array, ISM allows ${\mathit{H}}_v^{ism}$ to be mapped back to the original views by simple chained matrix multiplication so that: ${\mathit{X}}_v={\mathit{W}}^{\mathit{*}}{{\mathit{H}}_{\mathit{v}}}^{\mathit{T}}$ with ${\mathit{H}}_v={\mathit{H}}_v^{nmf}{\mathit{H}}_v^{ism}{\mathit{H}}^{*}{\mathit{Q}}_v^{*}$ . This “meta-ISM” approach has important consequences in several respects, which will be presented in the Discussion.

Detailed workflows

In this section, we present three workflows. The first workflow consists of training the ISM model to generate a latent space representation and view-mapping. The second workflow enables the projection of new observations obtained in multiple views into the latent space. The third workflow contains the detailed analysis steps for each example.

Workflow 1: Latent space representation and view-mapping

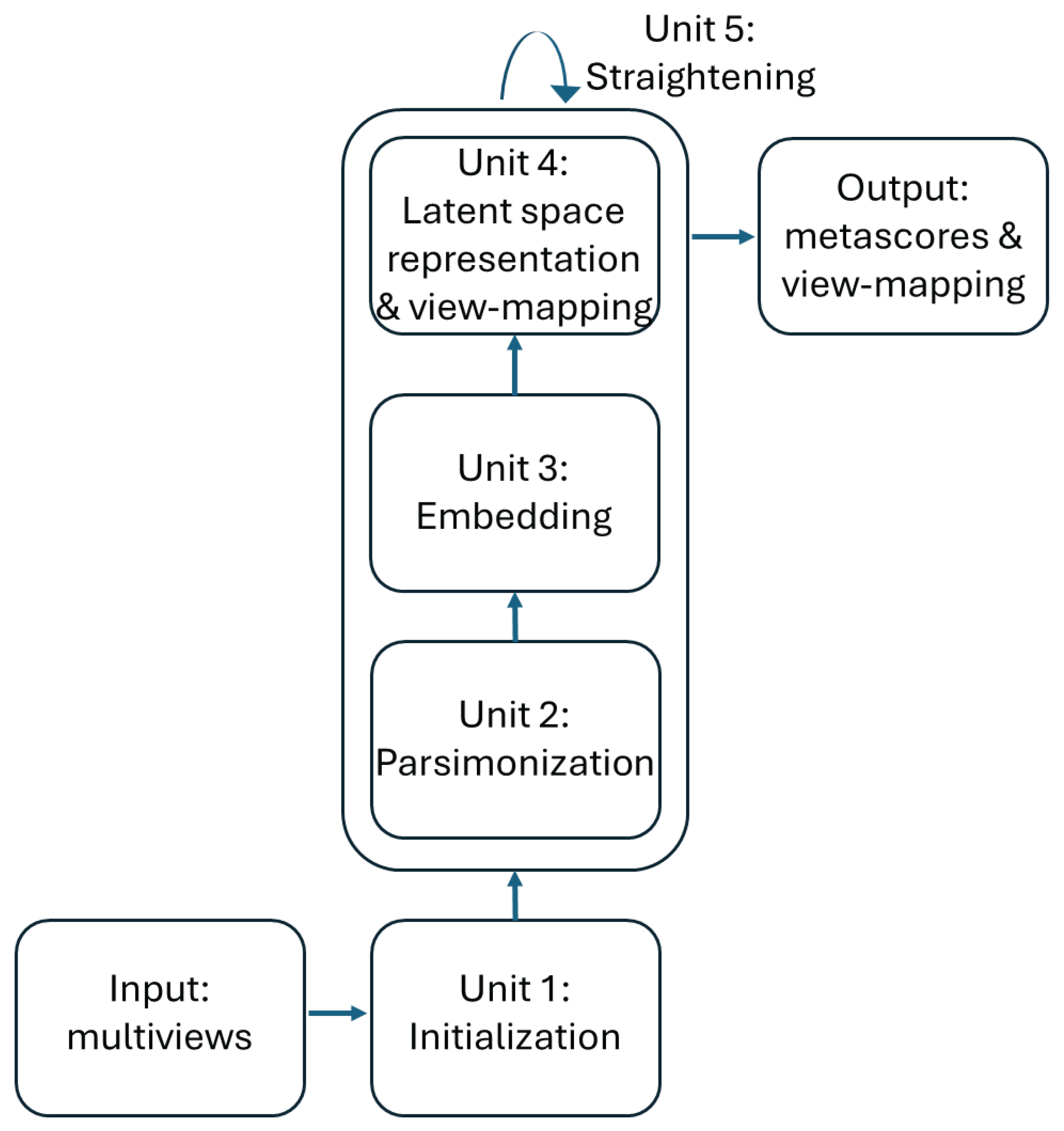
The training of the ISM model can be divided into 5 units as described in Figure 2. The first 4 process units enable the discovery of the latent space in an “embedding” space. Once the latent space has been found, it is assimilated with the embedding space. During the fifth “straightening” unit, the latent space remains fixed, while the sequence of units 3, 4 and 2 is repeated to further parsimonize the view-mapping until the degree of sparsity remains unchanged. The sizes of the embedding space and the latent space are discussed in the section describing the third workflow.

Figure 2. Training of the ISM model.

Figure 2. Training of the ISM model.

Unit 1: Initialization

A non-negative matrix factorization is first performed on the matrix $\mathit{X}$ of the $m$ concatenated views ${\mathit{X}}_v, 1\le v\le m$, resulting in the decomposition: $\mathit{X}=\mathit{W}{\mathit{H}}^{\mathit{T}}+\mathit{E},\mathit{W}\in {\mathbb{R}}_{+}^{n\times d_e} , \mathit{H}\in {\mathbb{R}}_{+}^{d\times d_e},\mathit{E}\in {\mathbb{R}}^{n\times }$where $\mathit{W}$ represents the transformed data, the columns of $\mathit{H}$ contain the loadings of the $d=\sum _{v\le m}{d}_v$ attributes across all views on each component, $d_e$ is the embedding size and $n$ is the total number of observations.

Unit 1 Initialization
	Input: $m$ views $\left\{{\mathit{X}}_1,\cdots ,{\mathit{X}}_m\right\},{\mathit{X}}_v\in {\mathbb{R}}_{+}^{n\times d_v}$ where $n$ is the number of rows common to all views and $d_v$ is the number of columns in the $v^{th}$ view (it is assumed for each column that its values lie between 0 and 1 after normalization by the maximum row value).
	Output: Factoring matrices $\mathit{W}\in {\mathbb{R}}_{+}^{n\times d_e} , \mathit{H}\in {\mathbb{R}}_{+}^{d\times d_e}$ where $d_e$ is the embedding dimension and $d=\sum _{v\le m}{d}_v$ is the sum of the number of columns in all views, and the matrix of concatenated views $\mathit{X}$.
	1: Concatenate the $m$ views: $\mathit{X}=\left[{\mathit{X}}_1,\cdots ,{\mathit{X}}_m\right],\mathit{X}\in {\mathbb{R}}_{+}^{n\times d}$;
	2: Factorize $\mathit{X}$ using NMF with $d_e$ components:
		$\mathit{X}=\mathit{W}{\mathit{H}}^{\mathit{T}}+\mathit{E},\mathit{W}\in {\mathbb{R}}_{+}^{n\times d_e} , \mathit{H}\in {\mathbb{R}}_{+}^{d\times d_e},\mathit{E}\in {\mathbb{R}}^{n\times d}$

Unit 2: Parsimonization

The initial degree of sparsity in $\mathit{H}$ is crucial to the embedding dimensions from being overly distorted between the different views during the embedding process, as will be seen in the next section. This is achieved by applying a hard-threshold to each column of the $\mathit{H}$ matrix. The threshold is based on the reciprocal of the Herfindhal-Hirschman index [16], which provides an estimate of the number of non-negligible values in a non-negative vector. For columns with strongly positively skewed values, the use of the L2 norm for the estimate’s denominator can lead to excessively sparse factors, which in turn can lead to an overly large approximation error during embedding. Therefore, the estimate is multiplied by a coefficient whose default value was set at 0.8 after extensive testing with various data sets.

Unit 2 Parsimonization
	Input: Factoring matrix $\mathit{H}\in {\mathbb{R}}_{+}^{d\times d_e}$
	Output: Parsimonized factoring matrix $\mathit{H}\in {\mathbb{R}}_{+}^{d\times d_e}$ (since the initial $\mathit{H}$ is not used outside parsimonization, we use the same symbol for the sake of simplicity)
	1: for each component ${\mathit{h}}_k$ of $\mathit{H}$ do
	2:	Calculate Herfindahl-Hirschman Inverse Index to estimate the number of non-negligible entries in ${\mathit{h}}_k$ : ${\tau }_k=\frac{{\left(\sum _{i\le d}h\left[i,k\right]\right)}^2}{\sum _{i\le d}{h\left[i,k\right]}^2}=\frac{{‖{\mathit{h}}_k‖}_1^2}{{‖{\mathit{h}}_k‖}_2^2}$;
	3:	Enforce sparsity on ${\mathit{h}}_k$ using hard-thresholding: $if \mathit{rank}\left(h\left[i,k\right]\right)<{\tau }_k\times \lambda then set h\left[i,k\right]=$ 0 where $\lambda$ is a sparsity parameter (0$<\lambda <$1, the default value $\lambda =.$ 8 was chosen as it led in many trials to better results than the original index ${\tau }_k$, which may be a too strict filter);
	4: end for

Unit 3: Embedding

$\mathit{W}$ and $\mathit{H}$ are further updated along each view, yielding matrices ${\mathit{W}}_v\in {\mathbb{R}}_{+}^{n\times d_e}$ of common shape (number of observations $n$ $\times$ factorization rank $d_e$) corresponding to the transformed views.

NMF multiplicative updates are used during view matching to leave the zeros in the primary $\mathit{H}$ matrix unchanged. Further optimizations of the simplicial cones ${\mathit{H}}_v\in {\mathbb{R}}_{+}^{d_v\times d_e}$ for each view $v$ are therefore limited to the non-zero loadings so that they remain tightly connected. This ensures that the transformed views ${\mathit{W}}_v,v\le m$ form a tensor. Multiplicative updates usually start with a linear rate of convergence, which becomes sublinear after a few hundred iterations [17]. By default, the number of iterations is set to 200 to ensure a reasonable approximation to each view, as required for the latent space representation described in the next section.

Unit 3 Embedding
	Input: $m$ views $\left\{{\mathit{X}}^1,\cdots ,{\mathit{X}}^m\right\}$ and factoring matrices $\mathit{W}\in {\mathbb{R}}_{+}^{n\times d_e} , \mathit{H}\in {\mathbb{R}}_{+}^{d\times d_e}$
	Output: view-specific factoring matrices ${\mathit{W}}_v\in {\mathbb{R}}_{+}^{n\times d_e}, {\mathit{H}}_v\in {\mathbb{R}}_{+}^{d_v\times d_e}$and tensor $\mathcal{A}$.
	1: for each view $v$ do
	2:	Define ${\mathit{H}}_v\in {\mathbb{R}}_{+}^{d_v\times d_e}$ as the part of $\mathit{H}$ corresponding to view $v$;
	3:	Factorize ${\mathit{X}}^v$ into view-specific ${\mathit{W}}_v\in {\mathbb{R}}_{+}^{n\times d_e} and$ ${\mathit{H}}_v\in {\mathbb{R}}_{+}^{d_v\times d_e}$ using NMF multiplicative updating rules and initialization matrices $\mathit{W}\in {\mathbb{R}}_{+}^{n\times d_e} , {\mathit{H}}_v\in {\mathbb{R}}_{+}^{d_v\times d_e}$: ${\mathit{X}}_v={\mathit{W}}_v{{\mathit{H}}_v}^{\mathit{T}}+{\mathit{E}}_v,{\mathit{W}}_v\in {\mathbb{R}}_{+}^{n\times d_e}, {\mathit{H}}_v\in {\mathbb{R}}_{+}^{d_v\times d_e},{\mathit{E}}_v\in {\mathbb{R}}^{n\times d_v}$
	4:	Normalize each component of ${\mathit{W}}_v$ by its maximum value and update ${\mathit{H}}_v$ accordingly;
	5:	Define tensor slice: $\mathcal{A}\left(:,:,v\right)={\mathit{W}}_v;$
	6: end for

Unit 4: Latent space representation and view-mapping

The resulting tensor $\mathcal{A}$ is analyzed using NTF, which leads to the decomposition: $\mathcal{A}={\mathit{W}}^{\mathit{*}}\otimes {\mathit{H}}^{\mathit{*}}\otimes {\mathit{Q}}^{\mathit{*}}+\mathit{\epsilon }$ where ${\mathit{W}}^{\mathit{*}}\in {\mathbb{R}}_{+}^{n\times d_l} , {\mathit{H}}^{\mathit{*}}\in {\mathbb{R}}_{+}^{d_e\times d_l},{\mathit{Q}}^{\mathit{*}}\in {\mathbb{R}}_{+}^{m\times d_l}, \mathcal{E}\in {\mathbb{R}}_{+}^{n\times d_e\times m}$and $d_l$ is the dimension of the latent space. The components ${\mathit{W}}^{\mathit{*}}$, ${\mathit{H}}^{\mathit{*}}$ and ${\mathit{Q}}^{\mathit{*}}$ enable the reconstruction of the horizontal, lateral and frontal slices of the embedding tensor: the loadings of the views on each component are contained in the matrix ${\mathit{Q}}^{\mathit{*}}$; the integrated multiple views, or meta-scores, are contained in the matrix ${\mathit{W}}^{\mathit{*}}$; and the matrix ${\mathit{H}}^{\mathit{*}}$ represents the latent space in the form of a simplicial cone contained in the embedding space. Finally, the view-mapping matrix $\mathit{H}$ is updated by applying steps 3-8 of unit 4. Its sparsity is ensured by further applying the parsimonization unit 2.

Unit 4 Latent space representation & View-mapping
	Input: view-specific factoring matrices ${\mathit{H}}_v\in {\mathbb{R}}_{+}^{d_v\times d_e}$and tensor $\mathcal{A}$
	Output: NTF factors ${\mathit{W}}^{\mathit{*}}\in {\mathbb{R}}_{+}^{n\times d_l},{\mathit{H}}^{\mathit{*}}{\in \mathbb{R}}_{+}^{d_e\times d_l},{\mathit{Q}}^{\mathit{*}}\in {\mathbb{R}}_{+}^{m\times d_l}$ and view-mapping matrix $\mathit{H}\in {\mathbb{R}}_{+}^{d\times d_l}$.
	1: Define view-mapping matrix $\mathit{H}\in {\mathbb{R}}_{+}^{d\times d_e}$ as the concatenation of ${\mathit{H}}_v\in {\mathbb{R}}_{+}^{d_v\times d_e}$
	2: Factorize $\mathcal{A}$ using NTF with $d_l$ components: $\mathcal{A}={\mathit{W}}^{\mathit{*}}⨂{\mathit{H}}^{\mathit{*}}⨂{\mathit{Q}}^{\mathit{*}}+\mathcal{E}$ where ${\mathit{W}}^{\mathit{*}}\in {\mathbb{R}}_{+}^{n\times d_l} , {\mathit{H}}^{\mathit{*}}\in {\mathbb{R}}_{+}^{d_e\times d_l},{\mathit{Q}}^{\mathit{*}}\in {\mathbb{R}}_{+}^{m\times d_l}, \mathcal{E}\in {\mathbb{R}}_{+}^{n\times d_e\times m};$
	3: Update view-mapping matrix $\mathit{H}\in {\mathbb{R}}_{+}^{d\times d_l}$: $\mathit{H}\leftarrow \mathit{H}{\mathit{H}}^{\mathit{*}}$;
	4: for each view $v$ do
	5:	Update ${\mathit{H}}_v$: ${\mathit{H}}_v\leftarrow {\mathit{H}}_v\circ {\mathit{Q}}^{\mathit{*}}\left[v,:\right]$;
	6 end for
	7: Update view-mapping matrix $\mathit{H}\in {\mathbb{R}}_{+}^{d\times d_l}$as the concatenation of updated ${\mathit{H}}_v$;
	8: Parsimonize view-mapping matrix $\mathit{H}\in {\mathbb{R}}_{+}^{d\times d_l}$ by applying Unit 2;

Unit 5: Straightening

The sparsity of the view-mapping matrix $\mathit{H}$ can be further optimized together with the meta-scores ${\mathit{W}}^{\mathit{*}}$ and the view-loadings ${\mathit{Q}}^{\mathit{*}}$ by repeating units 3, 4 and 2 until the number of 0-entries in $\mathit{H}$ remains unchanged. To achieve this, the embedding is restricted to the latent space defined by the simplicial cone formed by ${\mathit{H}}^{\mathit{*}}$. In this simplified embedding space, ${\mathit{H}}^{\mathit{*}}$ becomes the Identity matrix ${\mathit{I}}_{d_l}$ when the updating process of ${\mathit{W}}^{\mathit{*}},{\mathit{H}}^{\mathit{*}}$ and ${\mathit{Q}}^{\mathit{*}}$ starts. In other words, embedding and latent spaces are being assimilated during the straightening process. Optionally, for faster convergence, ${\mathit{H}}^{\mathit{*}}$ can be fixed to ${\mathit{I}}_{d_l}$, at the cost of a slightly higher approximation error, as observed in numerous experiments, due to only small deviations from ${\mathit{I}}_{d_l}$.

Unit 5 Straightening
	Input: $\mathit{X},\mathcal{A},\mathit{H},{\mathit{W}}^{\mathit{*}},{\mathit{H}}^{\mathit{*}},{\mathit{Q}}^{\mathit{*}}$.
	Output: NTF factors ${\mathit{W}}^{\mathit{*}},{\mathit{H}}^{\mathit{*}},{\mathit{Q}}^{\mathit{*}}$and updated view-mapping matrix $\mathit{H}$.
	1: Set ${\mathit{H}}^{\mathit{*}}={\mathit{I}}_{d_l}$ where $d_l$ is the size of the latent space;
	2: do until number of zero entries in $\mathit{H}$ remains unchanged
	3:	Apply Unit 3 to embed $\mathit{X}$using embedding size ${d_e=d}_l$, initialization matrices ${\mathit{W}}^{\mathit{*}}\in {\mathbb{R}}_{+}^{n\times d_l}$ and view-mapping matrix $\mathit{H}\in {\mathbb{R}}_{+}^{d\times d_l}$ found in previous iteration;
	4:	Apply Unit 4 to factorize $\mathcal{A}$ and update view-mapping matrix $\mathit{H}\in {\mathbb{R}}_{+}^{d\times d_l}$, using embedding size ${d_e=d}_l,$ initialization matrices ${\mathit{W}}^{\mathit{*}},{{\mathit{H}}^{\mathit{*}},\mathit{Q}}^{\mathit{*}}$obtained in previous iteration, and fixed ${\mathit{H}}^{\mathit{*}}={\mathit{I}}_{d_l}$;
	5: end for

Workflow 2: Projection of new observations

For new observations $\mathit{Y}$ comprising $k$ views, $k\le m$, ISM parameters ${\mathit{H}}^{\mathit{*}}$, ${\mathit{Q}}^{\mathit{*}}$ and view-mapping matrix $\mathit{H}$ can be used to project $\mathit{Y}$ on the latent ISM components, as described in workflow 2.

Workflow 2 Projection of new observations
	Input: New observations $\mathit{Y}$ ($k$ views, $k\le m$),
		NTF factors ${\mathit{H}}^{\mathit{*}},{\mathit{Q}}^{\mathit{*}}$and mapping matrix $\mathit{H}$.
	Output: Estimation ${\mathit{Y}}^{\mathit{*}}$.
	1: Disregard any views in ${\mathit{Q}}^{\mathit{*}},\mathit{H}$ that are absent in $\mathit{Y}$;
	2: Apply Unit 3 of workflow 1 to embed $\mathit{Y}$ with $\mathit{W}$ initialized with ones and with fixed mapping matrix $\mathit{H}$;
	3: Apply step 2 of Unit 4 of workflow 1 to calculate ${\mathit{W}}^{\mathit{*}}$ with fixed NTF factors ${\mathit{H}}^{\mathit{*}},{\mathit{Q}}^{\mathit{*}}$and define the projection of $\mathit{Y}$ on the latent space as ${\mathit{Y}}^{\mathit{*}}={\mathit{W}}^{\mathit{*}}$;

Workflow 3: Data analysis

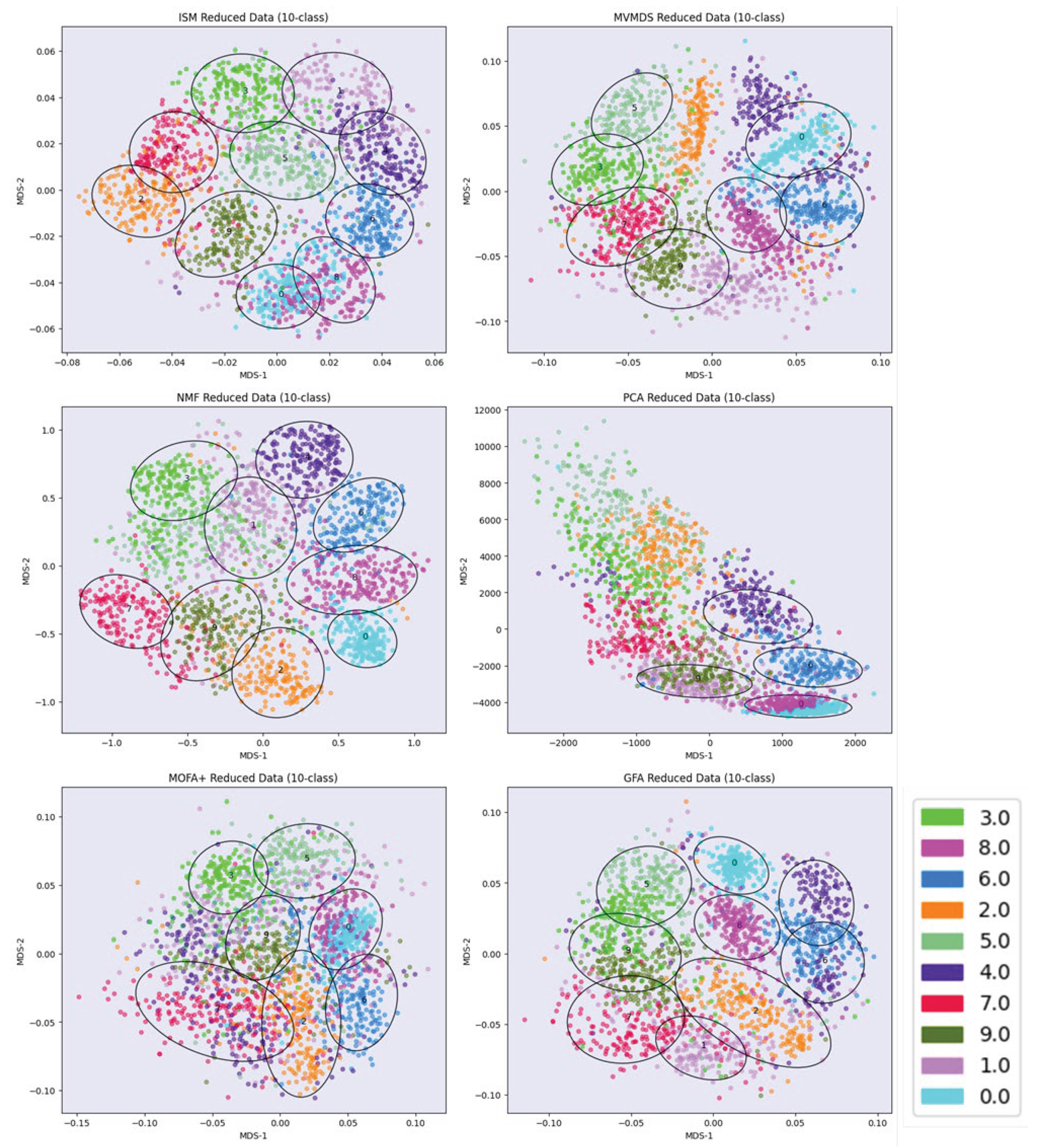
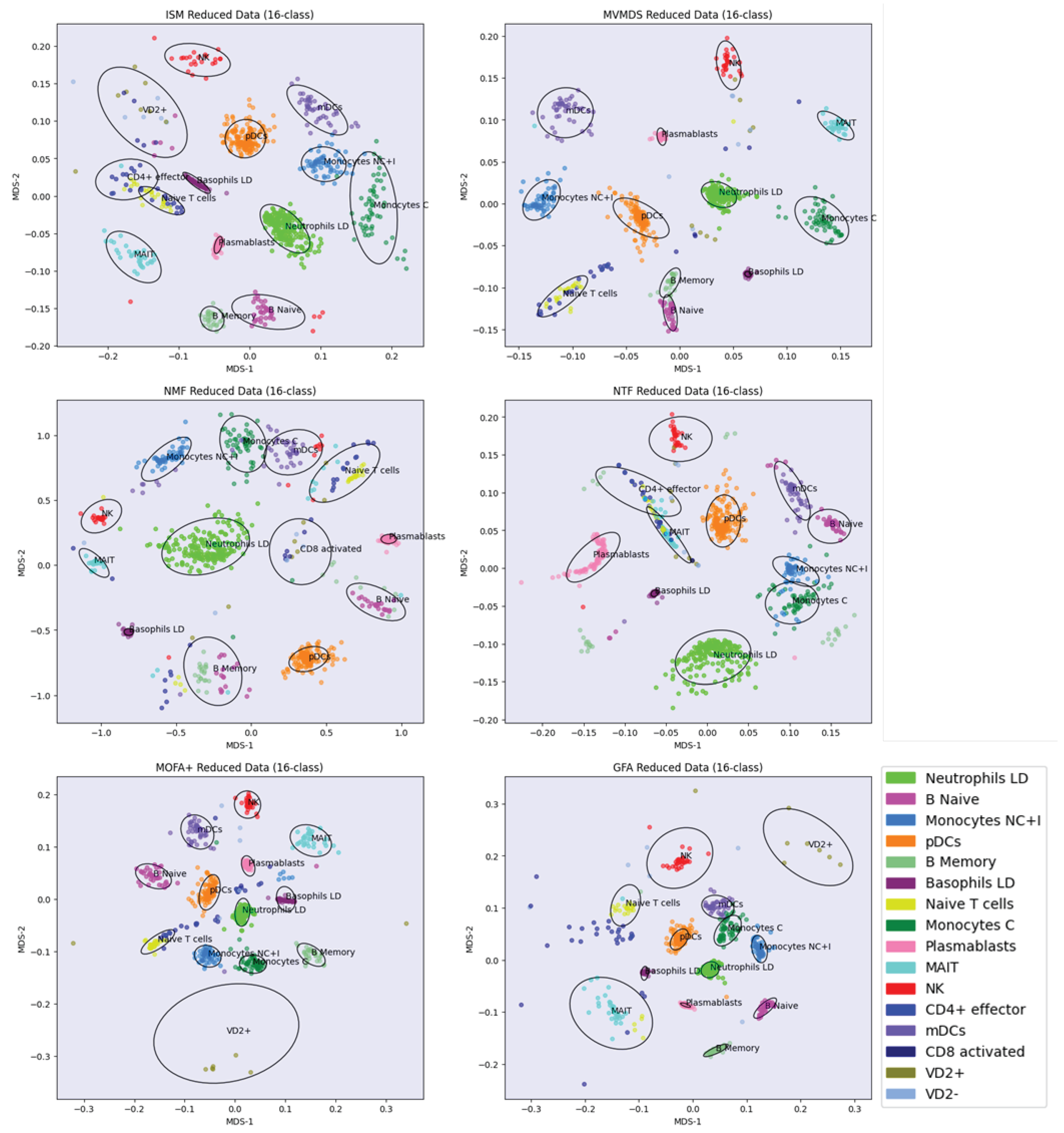
The data from the UCI Digits and Signature 915 datasets are analyzed using several alternative approaches: ISM, Multi-View Multi-Dimensional Scaling (MVMDS), NMF, NTF, Principal Components Analysis (PCA), Group Factor Analysis (GFA), and Multi-Omic Factor Analysis (MOFA+). Because PCA and NMF are not multi-view approaches, they are applied to the concatenated views. To facilitate interpretation, the transformed data is projected onto a 2D map before being subjected to k-means clustering, where k is the known number of classes (k-means clustering was chosen for its versatility and simplicity, as it only requires the number of clusters to be found, and this number is known in both our example datasets). Within each cluster, the class that contains the majority of the points, i.e., the main class, is identified. If two clusters share the same main class, they are merged, unless they are not contiguous (ratio of the distance between the centroids to the intra-cluster distance between points > 1). In this case, the non-contiguous clusters are excluded because they are assigned to the same class, which should appear homogeneous in the representation. Similarly, any cluster that does not contain an absolute majority is not considered clearly representative of the class to which it is assigned and is excluded. A global purity index is then calculated for the remaining clusters. To enhance clarity, the clusters are visualized using 95% confidence ellipses, while the classes are represented using as distinct colors as possible. In addition to the global purity index defined above, the adjusted Rand index [18] is also included.

Multidimensional scaling (MDS) is applied to the 2D map projection. MDS uses a simple metric objective to find a low-dimensional embedding that accurately represents the distances between points in the latent space [19]. MDS is therefore agnostic to the intrinsic clustering performances of the methods that we want to evaluate. Effective embedding methods, e.g., UMAP or t-SNE, are not as optimal for preserving the global geometric structure in the latent space [20]. For example, a resolution parameter needs to be defined for the UMAP embedding of single-cell data, whereby a higher resolution leads to a higher number of clusters. In addition, the subtle differences between some cell types from one family can be smoothed out if the dataset contains transcriptionally distinct cell types from multiple families, as is the case with immune cells (second dataset in the article).

Latent Space methods require that the rank of the factorization is determined in advance. ISM benefits from the advantages of the NMF and NTF workflow components, i.e., the choice of the correct rank is less critical than with other methods (we will come back to this point in the Results and Discussion). This allows, even if we expect some redundancy in the latent factors due to the proximity of certain digits or cell types, to set the rank to the number of known classes. However, the dimension of the ISM embedding space must also be determined during the discovery step. The choice of close dimensions for the embedding and latent spaces is consistent with the fact that both spaces are merged at the end of the ISM workflow. Thus, we examine the approximation error for an embedding dimension in the neighborhood of the chosen rank. The rank for PCA, MVMDS, GFA and MOFA+ is set by inspecting the screeplot of the variance ratio.

The analysis of the Signature 915 data also examines the biological relevance of the distance between clusters in each latent multi-view space.

Detailed analysis steps are provided in workflow 3.

Workflow 3 Analysis steps
	Input: 2D map projection of the data transformation in the latent space.
	Output: Cluster purity index.
	1: Perform k-means with k equal to the number of known classes;
	2: For each cluster, identify the main class related to the cluster, i.e., the class corresponding to the majority of observations in the cluster;
	3: Merge contiguous clusters that refer to the same class or ignore them if not contiguous;
	4: for each cluster do
	5:	$p_1=$ proportion of the main class in relation to all elements in the cluster; $p_2=$ proportion of the main class in cluster c in relation to all elements of the same class;
	6:	If  $p_2<0.5$ then
	7:		Disregard cluster as the main class does not constitute an absolute majority in relation to all elements of the same class;
	8:	else
	9:		${p=p}_1\times p_2=$ purity corrected for cluster representativity for the main class;
	10: end for
	11: Calculate the global purity = sum of corrected purities over all retained clusters;

3. Results

4. Discussion

a)

Performance:

i

Independent view factorizations can be achieved using parallel computing.

ii

The number of attributes in each transformed view is reduced to its factorization rank so ISM is performed on a much smaller data set.

b)

GDPR (General Data Protection Regulation) compliance: ISM makes it possible to collect the transformed data for the different views without knowledge of the original data. ISM’s meta-scores and view mappings can be provided to the data owner, who can then perform the mapping to the original views using the NMF factorization view maps that are computed at their end.

c)

Versatility: ISM can be applied to compute NMF on big data in a federated or distributed way. To this end, smaller slices are constructed at random, where each slide is considered a particular view that is submitted to ISM, thereby ensuring performance and GDPR compliance as described above (see workflow S2 in the Supplementary Materials).

5. Conclusion

6. Implementation

7. Patents

References

1. Cichocki, A.; Zdunek, R.; Phan, A.; Amari, S. Nonnegative Matrix and Tensor Factorizations - Applications to Exploratory Multi-way Data Analysis and Blind Source Separation. IEEE Signal Processing Magazine 2009, 25, 142–145. [Google Scholar] [CrossRef]
2. Perry, R.; Mischler, G.; Guo, R.; Lee, T.V.; Chang, A.; Koul, A.; Franz, C.; Vogelstein, J.T. mvlearn: Multiview Machine Learning in Python. ArXiv 2020, arXiv:abs/2005.11890. [Google Scholar]
3. Argelaguet, R.; Velten, B.; Arnol, D.; Dietrich, S.; Zenz, T.; Marioni, J.C.; Buettner, F.; Huber, W.; Stegle, O. Multi-Omics Factor Analysis—a framework for unsupervised integration of multi-omics data sets. Molecular Systems Biology 2018, 14. [Google Scholar] [CrossRef] [PubMed]
4. Argelaguet, R.; Arnol, D.; Bredikhin, D.; Deloro, Y.; Velten, B.; Marioni, J.C.; Stegle, O. MOFA+: a statistical framework for comprehensive integration of multi-modal single-cell data. Genome Biol. 2020, 21, 1–17. [Google Scholar] [CrossRef] [PubMed]
5. Wu, J.; Lin, Z.; Zha, H. Essential Tensor Learning for Multi-View Spectral Clustering. IEEE Trans. Image Process. 2018, 28, 5910–5922. [Google Scholar] [CrossRef] [PubMed]
6. Li, J.; Gao, Q.; Wang, Q.; Xia, W.; Gao, X. Multi-View Clustering via Semi-non-negative Tensor Factorization. ArXiv 2023, arXiv:abs/2303.16748. [Google Scholar]
7. Smilde, A.K.; Westerhuis, J.A.; de Jong, S. A framework for sequential multiblock component methods. J. Chemom. 2003, 17, 323–337. [Google Scholar] [CrossRef]
8. Trendafilov, N.T. Stepwise estimation of common principal components. Comput. Stat. Data Anal. 2010, 54, 3446–3457. [Google Scholar] [CrossRef]
9. Tenenhaus, A.; Tenenhaus, M. Regularized generalized canonical correlation analysis for multiblock or multigroup data analysis. Eur. J. Oper. Res. 2013, 238, 391–403. [Google Scholar] [CrossRef]
10. Zhang, C.; Hu, Q.; Fu, H.; Zhu, P.F.; Cao, X. (2017) Latent Multi-view Subspace Clustering. 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 4333-4341.
11. Chen, M., Huang, L., Wang, C., & Huang, D. (2020). Multi-View Clustering in Latent Embedding Space. AAAI Conference on Artificial Intelligence.
12. Leppäaho, E.; Ammad-ud-din, M.; Kaski, S. GFA: Exploratory Analysis of Multiple Data Sources with Group Factor Analysis. J. Mach. Learn. Res. 2016, 18, 1–5. [Google Scholar]
13. Zhao, S.; Gao, C.; Mukherjee, S.; Engelhardt, B.E. Bayesian group factor analysis with structured sparsity. J. Mach. Learn. Res. 2016, 17, 1–47. [Google Scholar]
14. Zhang, X.; Zhao, L.; Zong, L.; Liu, X.; Yu, H. Multi-view Clustering via Multi-manifold Regularized Nonnegative Matrix Factorization. 2014 IEEE International Conference on Data Mining (ICDM). LOCATION OF CONFERENCE, ChinaDATE OF CONFERENCE; pp. 1103–1108.
15. Fu, L.; Lin, P.; Vasilakos, A.V.; Wang, S. An overview of recent multi-view clustering. Neurocomputing 2020, 402, 148–161. [Google Scholar] [CrossRef]
16. Hirschman, A.O. The Paternity of an Index. The American Economic Review 1964, 54, 761–762. [Google Scholar]
17. Badeau, R.; Bertin, N.; Vincent, E. Stability Analysis of Multiplicative Update Algorithms and Application to Nonnegative Matrix Factorization. IEEE Trans. Neural Networks 2010, 21, 1869–1881. [Google Scholar] [CrossRef] [PubMed]
18. Hubert, L.; Arabie, P. Comparing partitions. J. Classif. 1985, 2, 193–208. [Google Scholar] [CrossRef]
19. Demaine, E.D., Hesterberg, A., Koehler, F., Lynch, J., & Urschel, J.C. (2021). Multidimensional Scaling: Approximation and Complexity. International Conference on Machine Learning.
20. Zhai, Z.; Lei, Y.L.; Wang, R.; Xie, Y. Supervised capacity preserving mapping: a clustering guided visualization method for scRNA-seq data. Bioinformatics 2022, 38, 2496–2503. [Google Scholar] [CrossRef]
21. Fogel, P.; Hawkins, D.M.; Beecher, C.; Luta, G.; Young, S.S. A Tale of Two Matrix Factorizations. Am. Stat. 2013, 67, 207–218. [Google Scholar] [CrossRef]
22. Brunet, J.; Tamayo, P.; Golub, T.R.; Mesirov, J.P. Metagenes and molecular pattern discovery using matrix factorization. Proc. Natl. Acad. Sci. USA 2004, 101, 4164–4169. [Google Scholar] [CrossRef]
23. Fogel, P.; Geissler, C.; Morizet, N.; Luta, G. On Rank Selection in Non-Negative Matrix Factorization Using Concordance. Mathematics 2023, 11, 4611. [Google Scholar] [CrossRef]
24. Donoho, D.L., & Stodden, V. (2003). When Does Non-Negative Matrix Factorization Give a Correct Decomposition into Parts? Neural Information Processing Systems.
25. Hoyer, P.O. Non-negative matrix factorization with sparseness constraints. J. Mach. Learn. Res. 2004, 5, 1457–1469. [Google Scholar]
26. Potluru, V.K., Plis, S., Le Roux, J., Pearlmutter, B.A., Calhoun, V.D., & Hayes, T.P. (2013). Block Coordinate Descent for Sparse NMF. CoRR, abs/1301.3527.
27. Boutsidis, C.; Gallopoulos, E. SVD based initialization: A head start for nonnegative matrix factorization. Pattern Recognit. 2008, 41, 1350–1362. [Google Scholar] [CrossRef]
28. Ma, A.; Wang, X.; Li, J.; Wang, C.; Xiao, T.; Liu, Y.; Cheng, H.; Wang, J.; Li, Y.; Chang, Y.; et al. Single-cell biological network inference using a heterogeneous graph transformer. Nat. Commun. 2023, 14, 1–18. [Google Scholar] [CrossRef] [PubMed]
29. Vaswani, Ashish, Noam M. Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Lukasz Kaiser and Illia Polosukhin. “Attention is All you Need.” Neural Information Processing Systems (2017).
30. Park, J.; Jin, I.H.; Jeon, M. How Social Networks Influence Human Behavior: An Integrated Latent Space Approach for Differential Social Influence. Psychometrika 2021, 88, 1–27. [Google Scholar] [CrossRef] [PubMed]
31. Pinel, P.; Guichaoua, G.; Najm, M.; Labouille, S.; Drizard, N.; Gaston-Mathé, Y.; Hoffmann, B.; Stoven, V. Exploring isofunctional molecules: Design of a benchmark and evaluation of prediction performance. Mol. Informatics 2023, 42, e2200216. [Google Scholar] [CrossRef]
32. Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Louppe, G.; Prettenhofer, P.; Weiss, R.; Weiss, R.J.; Vanderplas, J.; Passos, A.; Cournapeau, D.; Brucher, M.; Perrot, M.; Duchesnay, E. Scikit-learn: Machine Learning in Python. ArXiv 2011, arXiv:abs/1201.0490. [Google Scholar]