Submitted:
02 February 2024
Posted:
07 February 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Two-channel systems
2.1. Problem Setting
- (i)
- the first layer
- (ii)
- -layer ()
2.2. About TCS structural aspects
2.3. TCS Adaptive identification
3. Interconnected systems
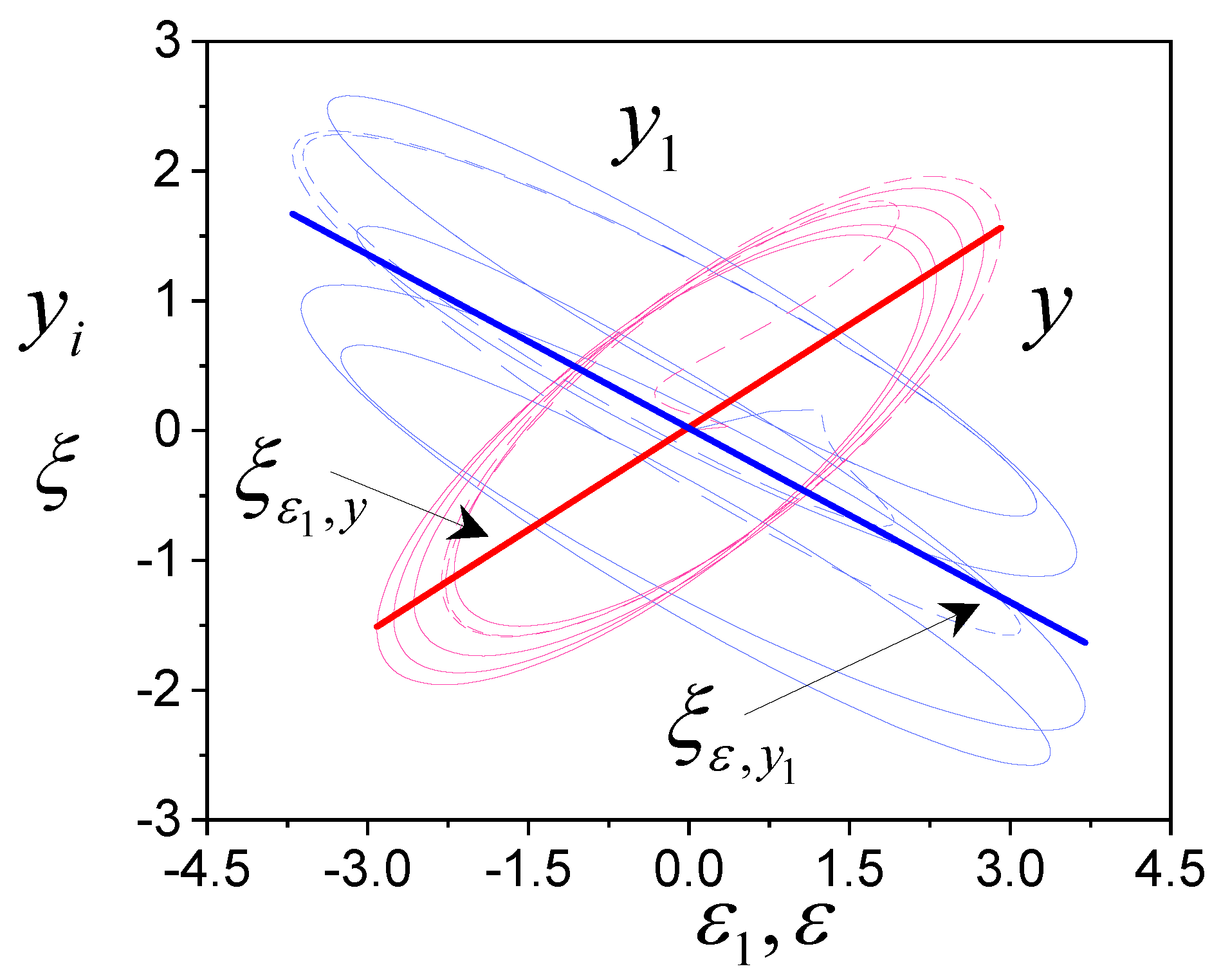
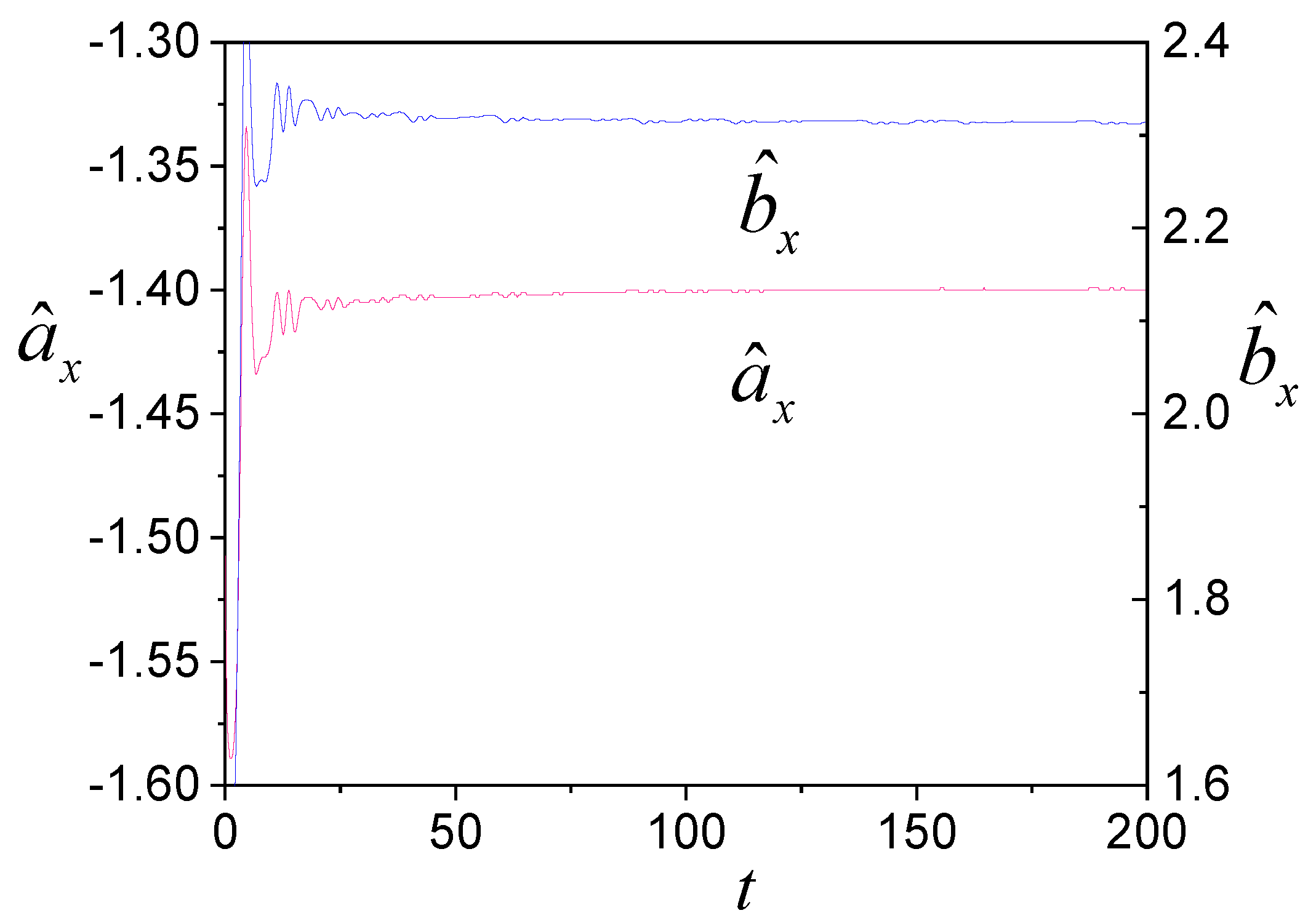
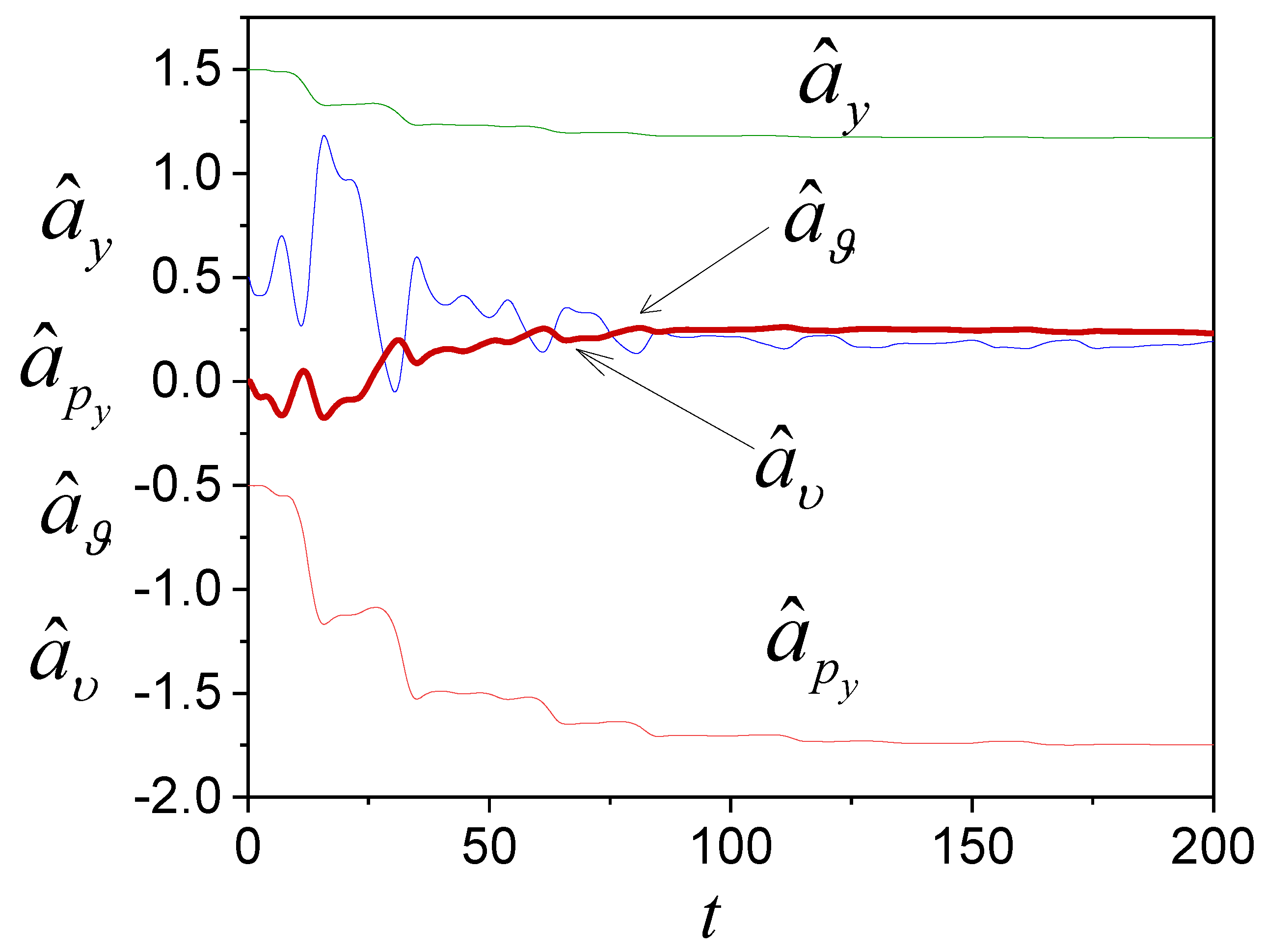
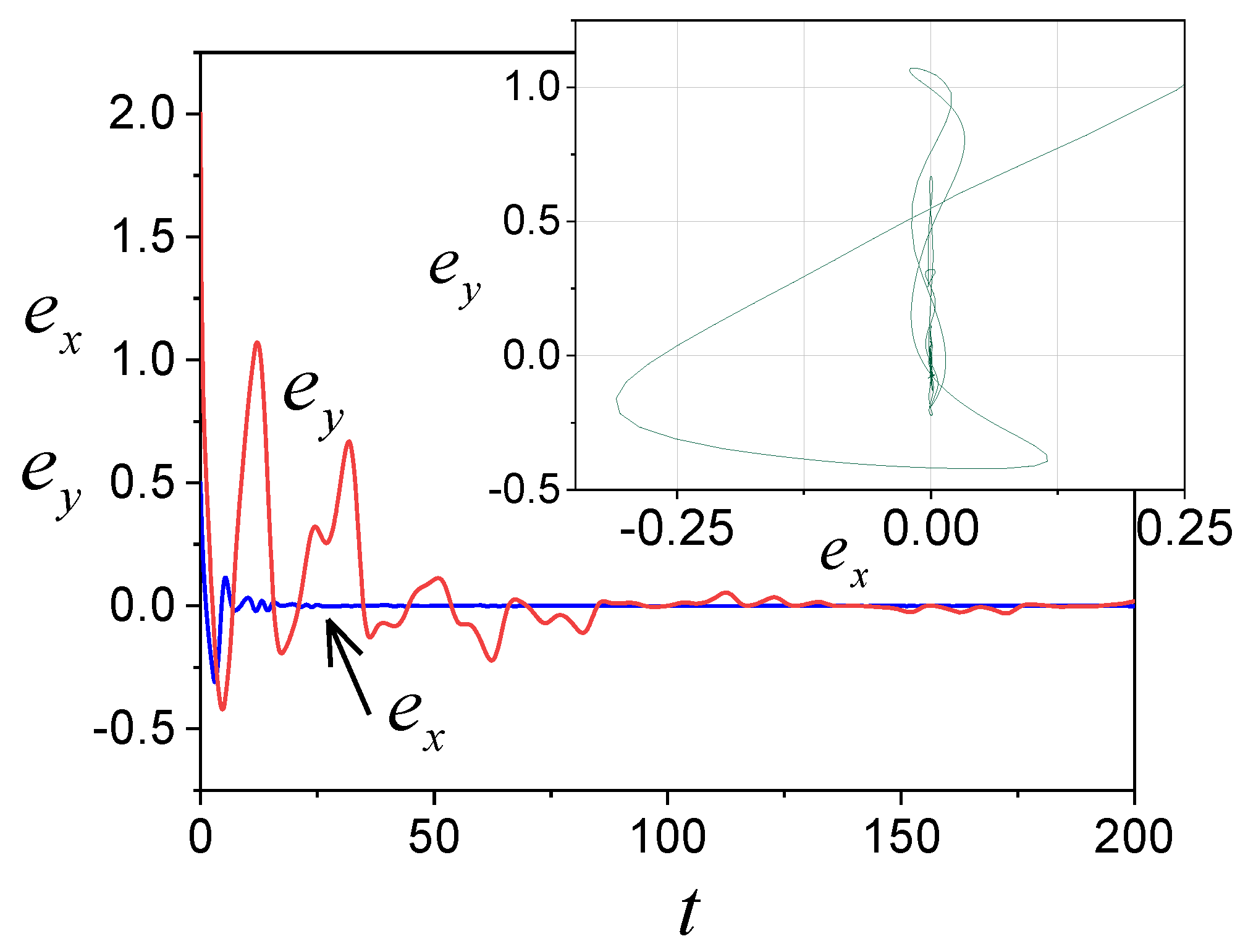
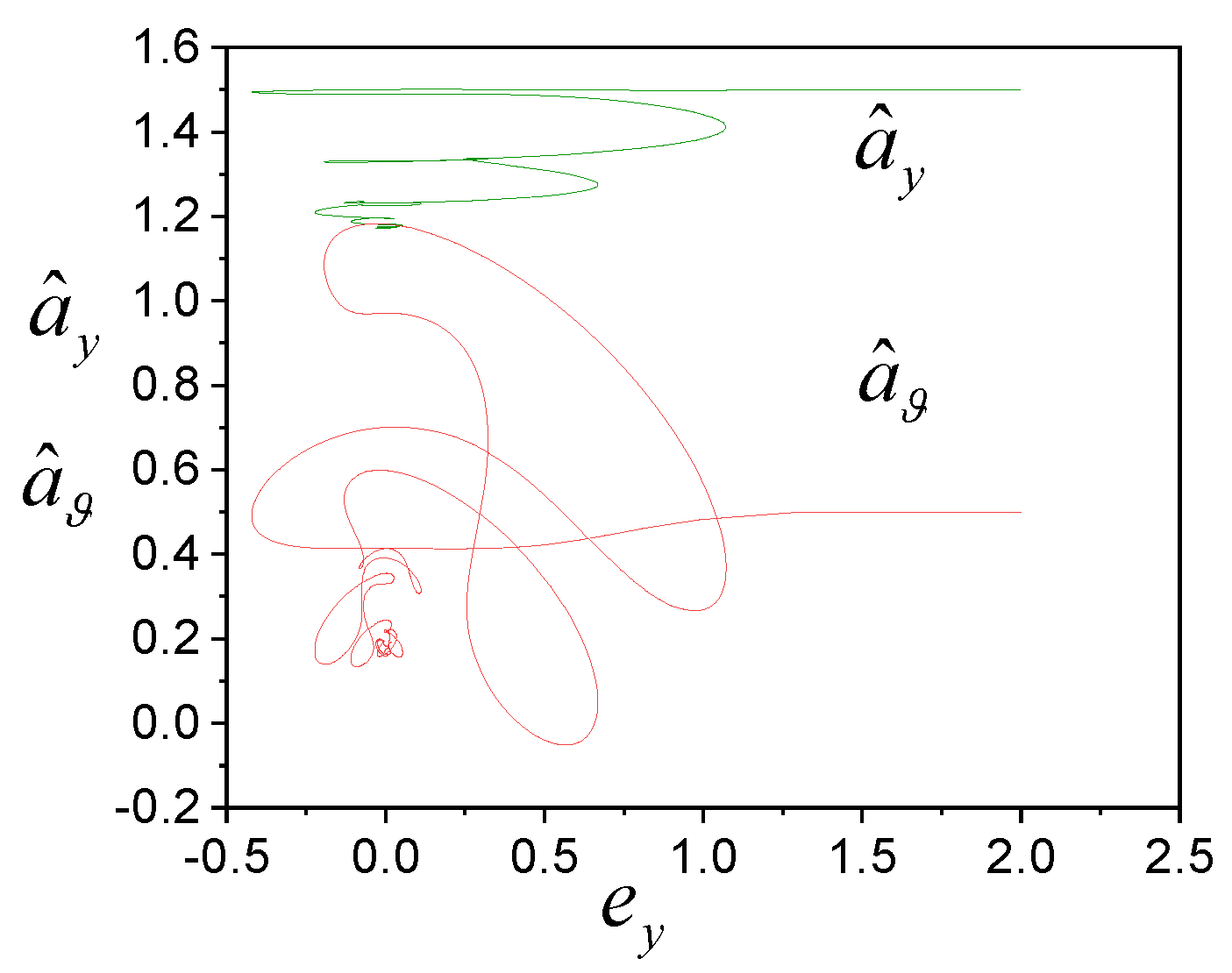
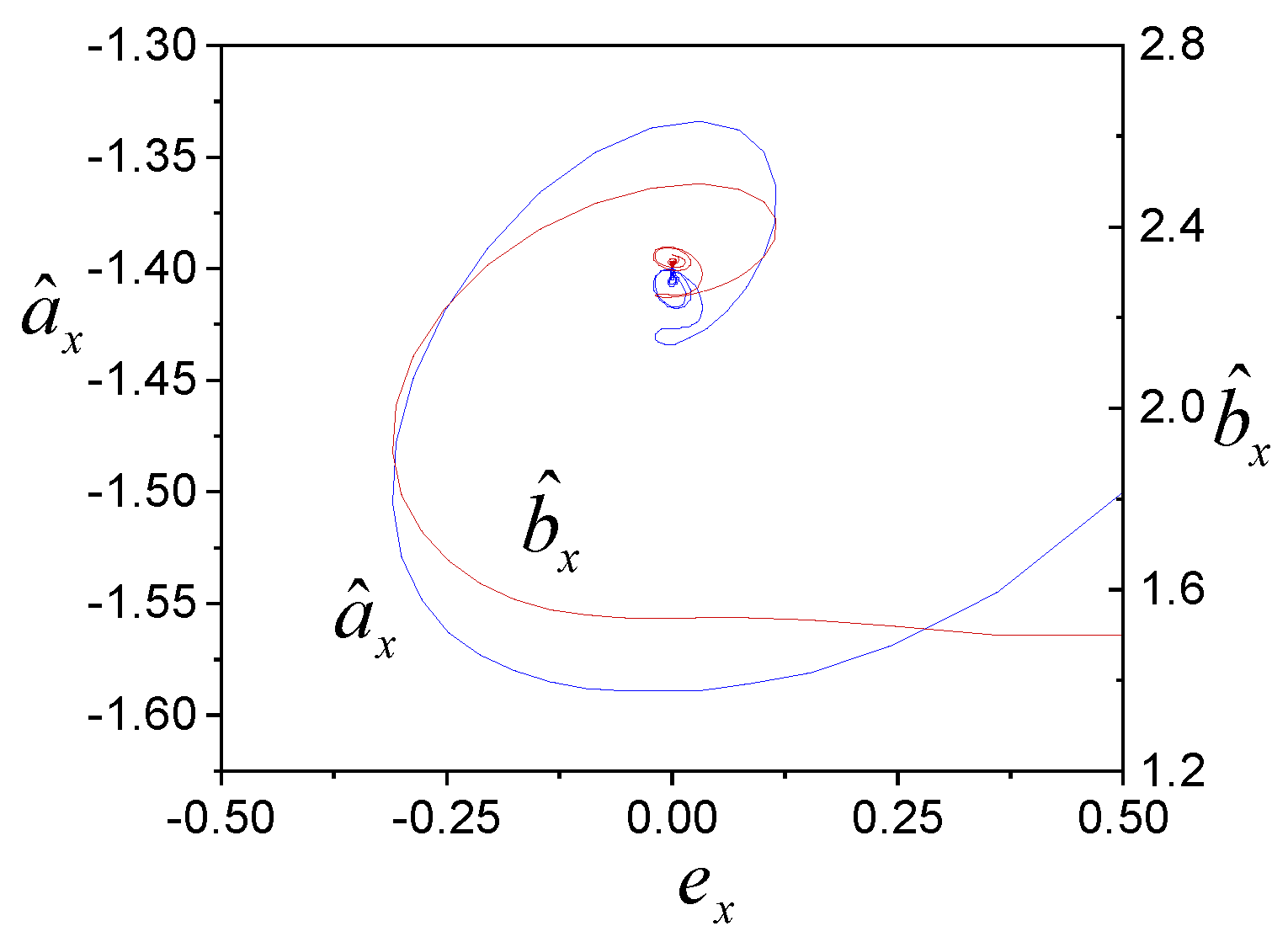
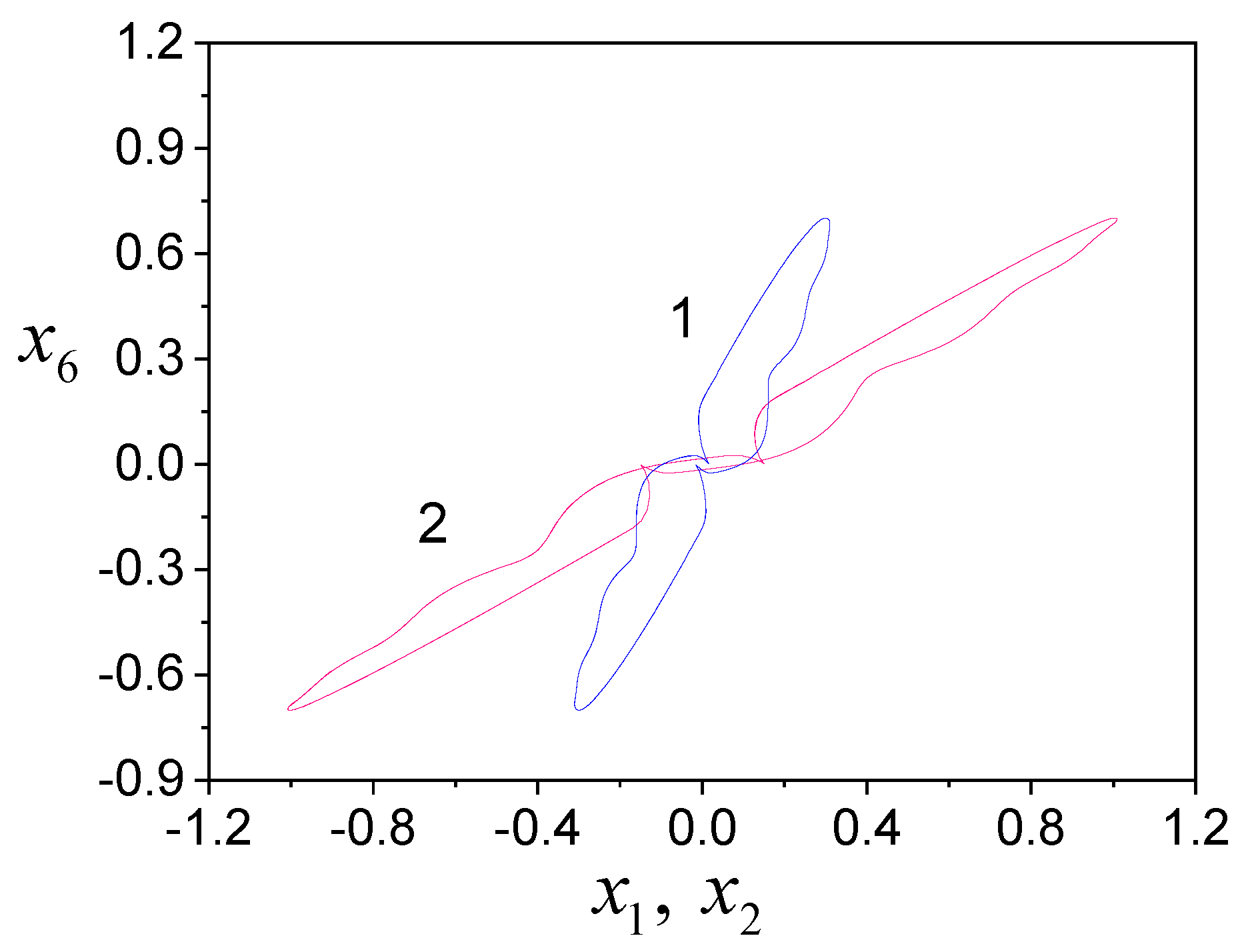
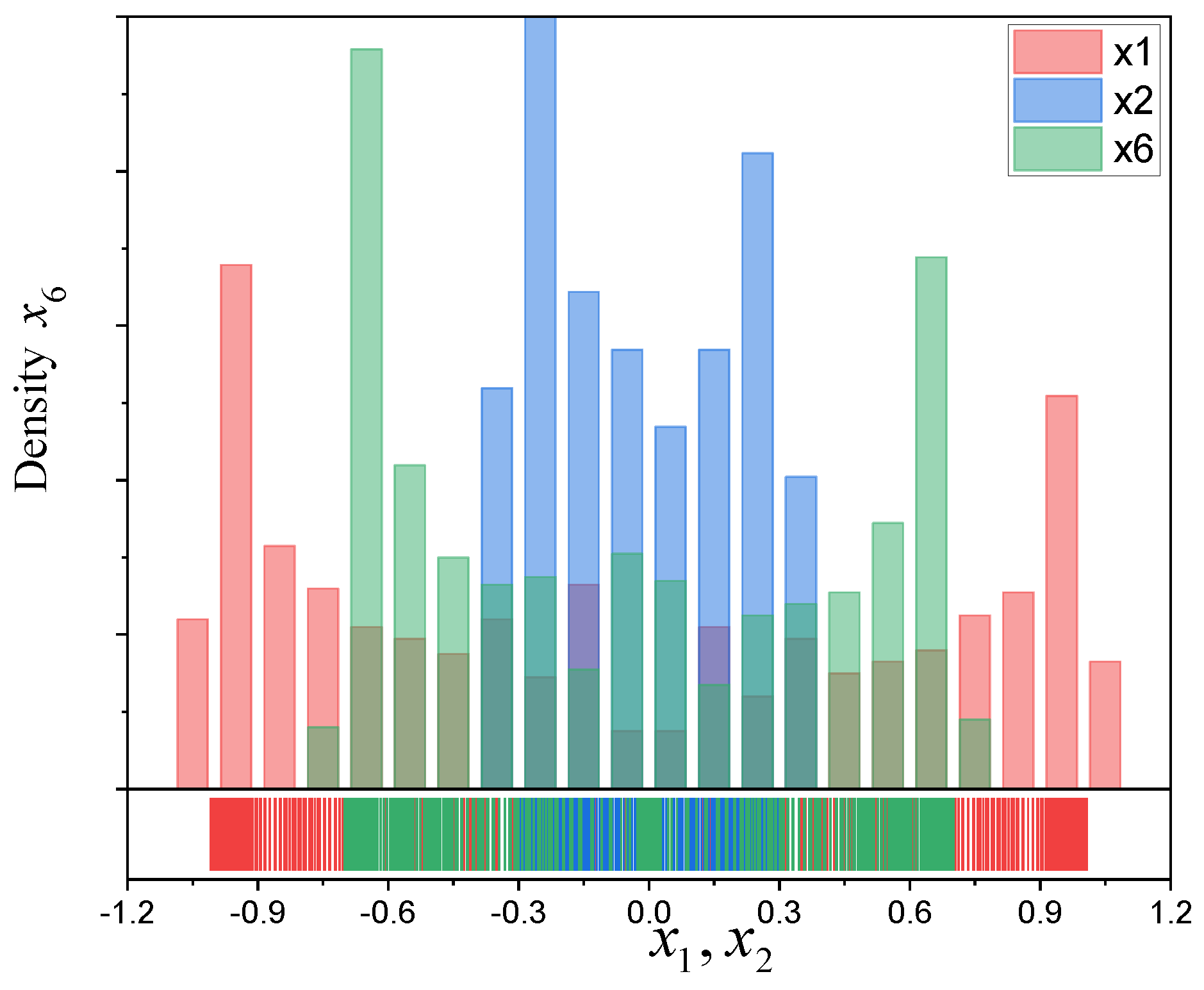
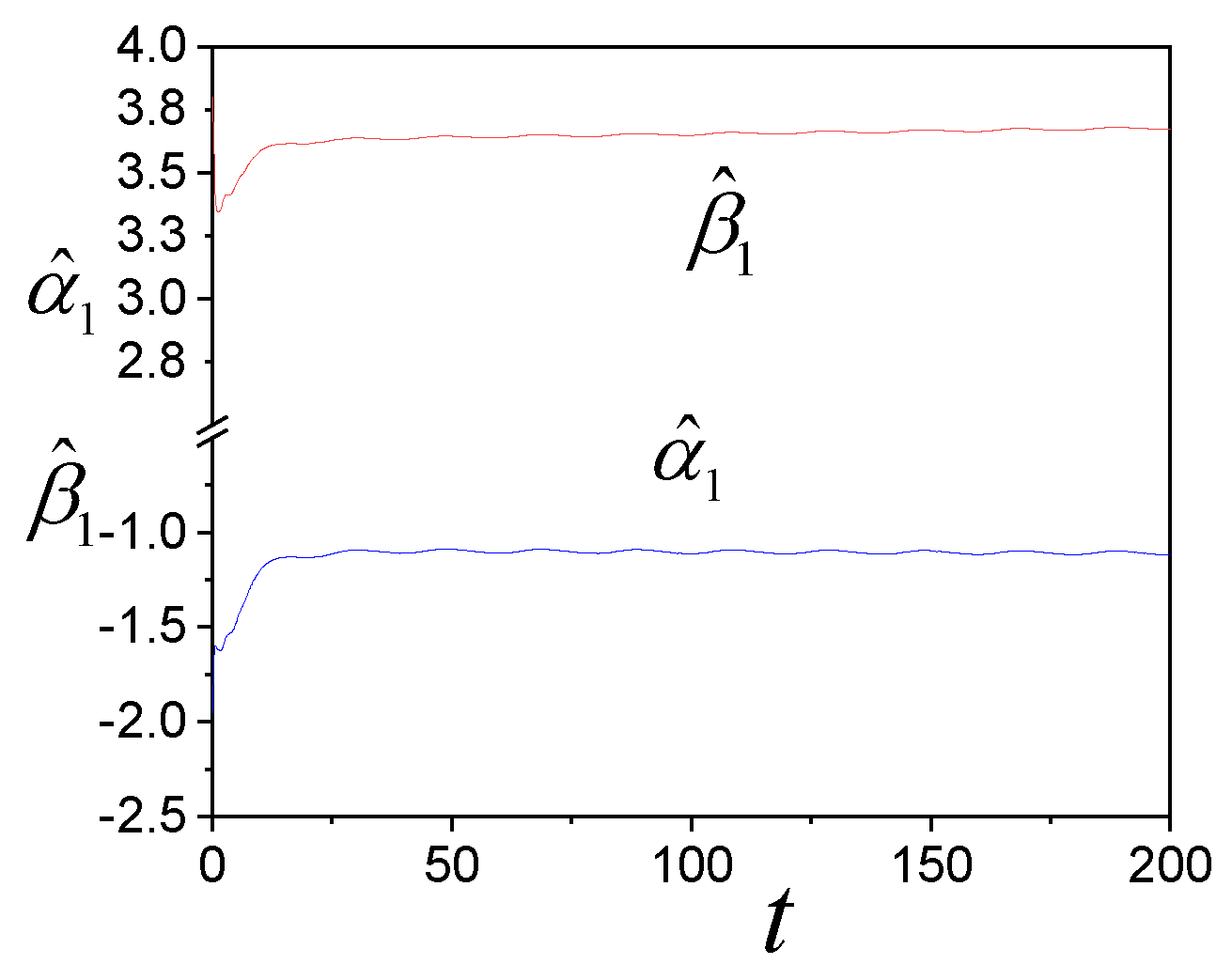
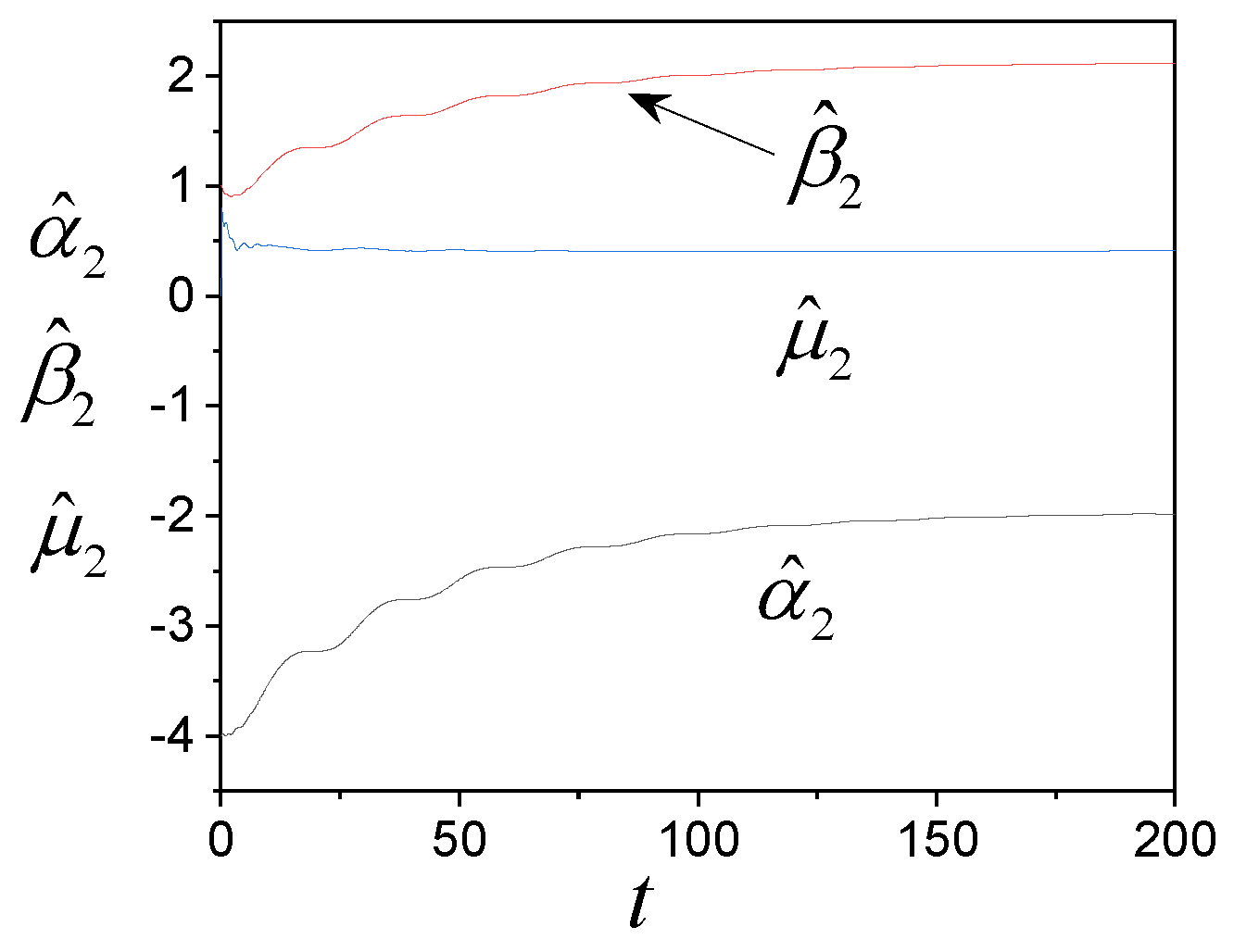
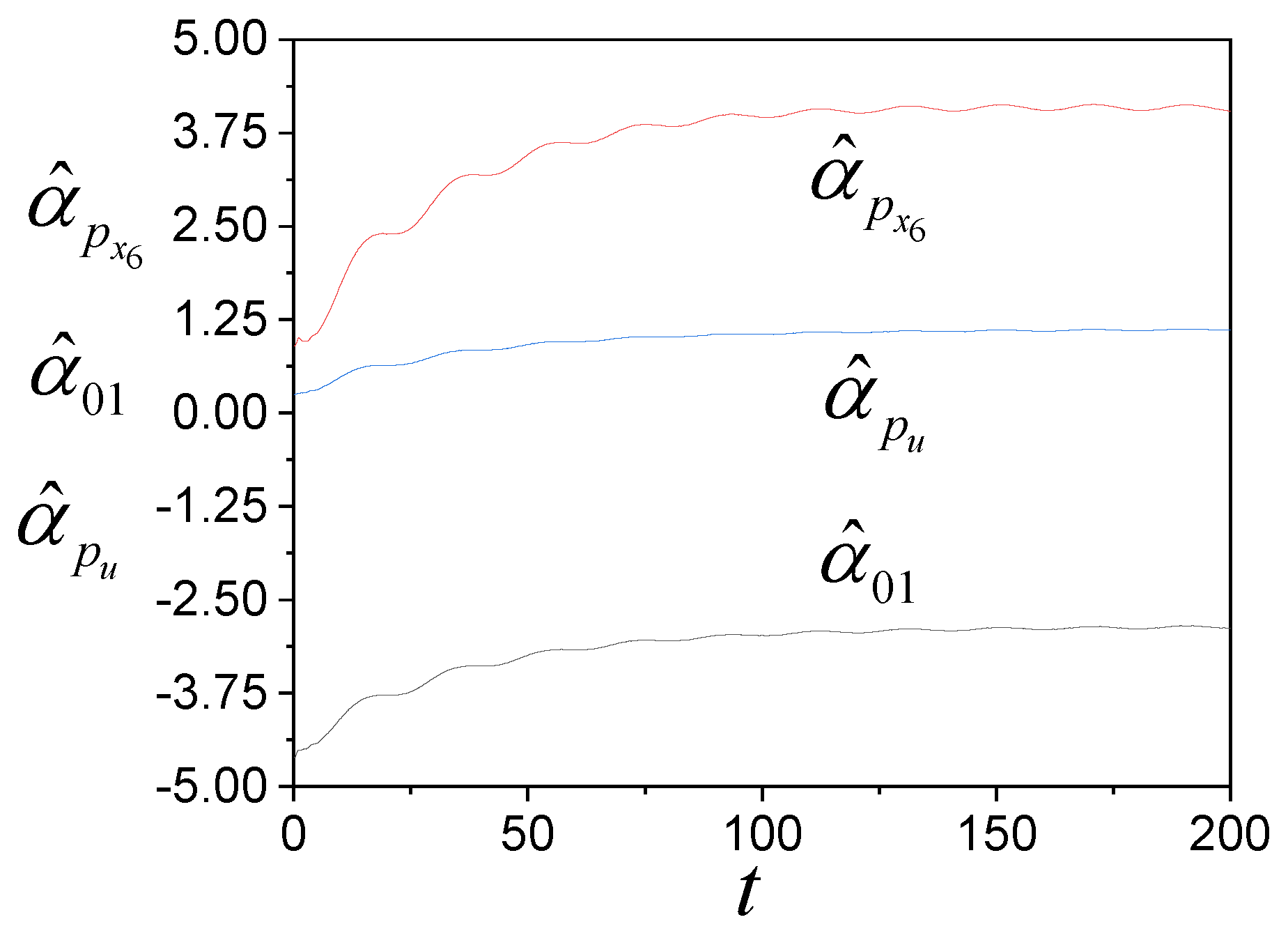
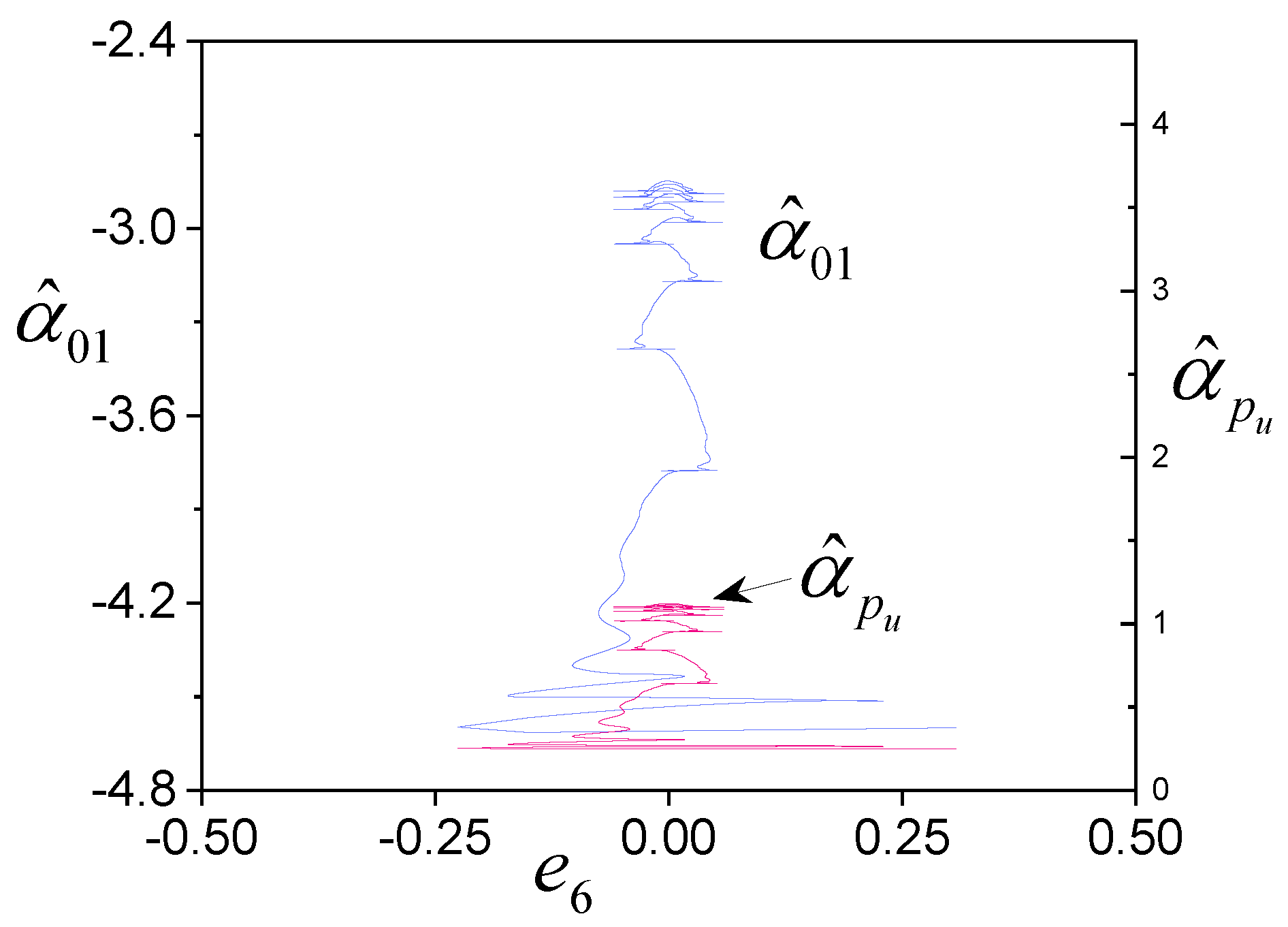
4. Examples
5. Conclusion
Appendix A
Theorem 1 proof.
Appendix B
Theorem 2 proof.
Appendix C
Theorem 3 proof.
Appendix D
Getting representation (13).
Appendix E
Theorem 4 proof.
Appendix F
Theorem 5 proof.
References
- Morozovsky, V.E. Multi-connected automatic control systems. Moscow: Energiya, 1970.
- Zyryanov, G.V. Control systems for multi-connected objects: a textbook. Chelyabinsk: SUSU Publishing Center, 2010.
- Meerov M.V., Litvak B.L. Optimization of multicommunicated control systems. Moscow: Nauka, 1972.
- Bukov V.N., Maksimenko I.M., Ryabchenko V.N. Control of multivariable systems. Autom. Remote Control; 1998; 6; 97–110.
- Voronov, A.A. Introduction in dynamics of complex controlled systems. Moscow: Nauka, 1985.
- Egorov I.N., Umnov V.P. Control systems for electric drives of technological robots and manipulators: textbook. Vladimir: Publishing house of Vladimir State University, 2022.
- Egorov, I.N. Positional force control of robotic and mechatronic devices. Vladimir: Publishing House of Vladimir State University, 2010.
- Gupta N., Chopra N. Stability analysis of a two-channel feedback networked control system. Conference: 2016 Indian Control Conference (ICC), 2016;8.
- Pawlak А., Hasiewicz Z. Non-parametric identification of multi-channel systems by multiscale expansions. 2002 IEEE International Conference on Acoustics, Speech, and Signal Processing, 2011.
- Kholmatov U. The possibility of applying the theory of adaptive identification to automate multi-connected objects. The American journal of engineering and technology, 2023, 31-38.
- Aliyeva A.S. Identification of multiconnected dynamic objects with uncertainty based on neural technology and reference converters. Informatics and Control Problems, 2019;39(2);93-102.
- Hua C., Guan X., Shi P. Decentralized robust model reference adaptive control for interconnected time-delay systems. Proceeding of the 2004 American Control Conference Boston, Massachusetts June 30 - July 2, 2004;4285-4289. [CrossRef]
- Gupta N., Chopra N. Stability analysis of a two-channel feedback networked control system. Conference: 2016 Indian Control Conference (ICC), 2016.
- Glentis G.-O. and Slump C. H. A highly modular normalized adaptive lattice algorithm for multichannel least squares filtering. International Conference on Acoustics, Speech, and Signal Processing, 1995.
- Ali M., Abbas H., Chughtai S. S. and Werner H. Identification of spatially interconnected systems using neural network. 49th IEEE Conference on decision and control (CDC), 2011.
- Yang Q., Zhu M., Jiang T. He J., Yuan J., and Han J. Decentralized robust adaptive output feedback stabilization for interconnected nonlinear systems with uncertainties, Journal of control science and engineering, 2016;2016;3656578;12. [CrossRef]
- Wu H. Decentralized adaptive robust control of uncertain large-scale non-linear dynamical systems with time-varying delays. IET Control Theory and Applications, 2012;6(5);629–640. [CrossRef]
- Fan H., Han L., Wen C., and Xu L. Decentralized adaptive output-feedback controller design for stochastic nonlinear interconnected systems. Automatica, 2012;48;11. [CrossRef]
- Ali M., Chughtai S.S, Werner H. Identification of spatially interconnected systems. Proceedings of the 48h IEEE Conference on Decision and Control (CDC) held jointly with 2009 28th Chinese Control Conference, 2010.
- Ioannou P. A. Decentralized adaptive control of interconnected systems. IEEE Transactions on automatic control, 1986;ac-31(4);291-298. [CrossRef]
- Sanandaji B.M., Vincent T.L., Wakin M.B. A review of sufficient conditions for structure identification in interconnected systems. IFAC proceedings volumes, 2012;45(16);1623-1628. [CrossRef]
- Soverini U., Söderström T. Blind identification of two-channel FIR systems: a frequency domain approach, IFAC PapersOnLine 53-2, 2020;914–920. [CrossRef]
- Huang Y., Benesty J., Chen J. Adaptive blind multichannel identification. In: Benesty, J., Sondhi, M.M., Huang, Y.A. (eds) Springer Handbook of Speech Processing. Springer Handbooks. Springer, Berlin, Heidelberg. 2008.
- Benesty J., Paleologu C., Dogariu L.-M., and Ciochină S. Identification of linear and bilinear systems: a unified study. Electronics, 2021;10(1790);33. [CrossRef]
- Bretthauer G., Gamaleja T., Wilfert H.-H. Identification of parametric and nonparametric models for MIMO closed loop systems by the correlation method. IFAC Proceedings Volumes, 1984;17(2);753-758. [CrossRef]
- Lomov A.A. On quantitative a priori measures of identifiability of coefficients of linear dynamic systems. Journal of computer and systems sciences international, 2011;50;1–13.
- Krasovsky A. A. On two-channel automatic control systems with antisymmetric connections. Automation and telemechanics. 1957,18(2),126–136.
- Karabutov N.N. On adaptive identification of systems having multiple nonlinearities. Russ. Technol. J. 2023;11(5);94−105. [CrossRef]
- Karabutov N.N. Adaptive identification of systems. Moscow: URSS, 2007.
- Gantmacher F. R. The theory of matrices. AMS Chelsea Publishing, 2000.
- Karabutov N. Structural identifiability of systems with multiple nonlinearities. Contemporary Mathematics, 2021;2(2); 140-161. [CrossRef]
- Barsky A.G. On the theory of two-dimensional and three-dimensional automatic control systems. Moscow: Logos, 2015.
- Skorospeshkin M.V. Adaptive two-channel correction device for automatic control systems. Bulletin of the Tomsk Polytechnic University, 2008;312(5):52-57.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).



