Prerpints.org logo
Preprint
Article

Turbulent Channel Flow: Direct Numerical Simulation-Data-Driven Modeling

Altmetrics

Downloads

138

Views

211

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

06 February 2024

Posted:

07 February 2024

You are already at the latest version

Alerts
Abstract
Data obtained by Direct Numerical Simulations (DNS) of pressure-driven turbulent channel flow are studied in the range 180 ≤ Reτ≤ 10,000. Reynolds number effects on the Mean Velocity Profile (MVP) and second order statistics are analyzed with a view of finding logarithmic behavior in the overlap region or even further from the wall, well in the boundary layer’s outer region. Values of Kármán constant for the MVPs and the Townsend-Perry constants for the streamwise and spanwise fluctuation variances are determined for the Reynolds numbers considered. A data-driven model of the MVP, proposed and validated for zero pressure gradient flow over a flat plate, is employed for pressure-driven channel flow by appropriately adjusting Coles’ strength of the wake function parameter, Π. There is excellent agreement between the analytic model predictions of MVP and the DNS-computed MVP as well as of the Reynolds shear stress profile. The skin friction coefficient Cf is calculated analytically. The agreement between the analytical model predictions and the DNS-based computed discrete values of Cf is excellent.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

The study of wall turbulence is one of the most challenging topics in turbulence research. Theoretical, experimental, and computational approaches encounter insurmountable difficulties especially in the high-Reynolds-number regime. However, the great importance of wall turbulence in engineering applications and the challenging nature of the physics involved have maintained a continuous string of efforts to understand, model, and compute such flows.
Fundamental research has focused on several turbulent flows in simple geometries usually referred as canonical flows. Canonical turbulent flows include turbulent Couette and Poiseuille flows between parallel plates, flows in straight pipes of constant circular cross section, liquid flows of uniform depth in wide open channels and zero pressure gradient external flow over a flat plate. The mean flow field in wall-bounded cases (such as flow in channels and pipes) is parallel and the thickness of the boundary layers formed is constant. Furthermore, in planar and axisymmetric Poiseuille flows the gradient of the wall pressure in the streamwise direction is a negative constant. In contradistinction, in the canonical flat plate boundary layer, the mean flow is not parallel, it is developing under zero pressure gradient (ZPG) and the boundary layer thickness, δ, is a weak function of the streamwise coordinate.
Canonical flows have been studied extensively by experimental methods. Important improvements in experimental techniques have been made over the years. However, the complexity of the turbulent flows is such that accuracy is still below the desired level especially very close to solid walls. On the other hand, Direct Numerical Simulations (DNS) provide us with high-quality, high-resolution data for turbulent flows in simple geometries. Although Direct Numerical Simulations are currently limited to relatively low Reynolds numbers their accuracy, especially close to a rigid wall boundary, makes them invaluable in studying wall turbulence. Nowadays various authors have reported DNS studies of canonical turbulent flows (see [1,2,3,4,5] and references cited therein).
Despite the plethora of relevant publications in scientific literature, there are still many open questions related to wall turbulence. In this work we have compiled a number of DNS datasets in the range of friction Reynolds number R e τ [180 to 10,000]. We have treated the datasets as having roughly the same accuracy level and proceeded in their analysis. Reynolds number effects on the Mean Velocity Profile (MVP) and second order statistics have been analyzed with a view of finding logarithmic behavior in the overlap region or even further from the wall, well into the boundary layer’s outer region. Values of Kármán constant for the MVPs and the Townsend-Perry constants for the streamwise and spanwise fluctuation variances were determined for the Reynolds numbers considered. A mathematical model of the MVP, thereinafter referred to as AL84, is presented together with its direct consequences. AL84 was developed for Zero Pressure Gradient Turbulent Boundary Layers (ZPG-TBL) [6] and recently validated with DNS data for ZPG-TBLs [7]. A number of analytical results are derived.
The paper is structured as follows. In section 2 we summarize some aspects of the pressure-driven channel flow which are needed for the discussion of the results in the remainder of the paper. In section 3 we present the findings based on the DNS datasets with a view to compare them with the mathematical model predictions presented in section 4. Conclusions are summarized in section 5.

2. Pressure-Driven Channel Flow

We consider pressure-driven turbulent flow in a channel formed by two parallel, large, motionless plates. The channel is sufficiently long so that after a developing length near the channel entrance, the turbulent flow field becomes homogenous in the streamwise (x) and spanwise (z) directions. Taking into account the symmetry of the flow about the channel midplane we denote the distance between the two plates as 2h. In the equations that follow overbars denote averages-in-time (equivalent to ensemble averages) and primes denote fluctuations-in-time.
Preprints 98331 g001
Figure 1. Channel geometry and coordinate system.
Figure 1. Channel geometry and coordinate system.
Preprints 98331 g001
In this paper ( u ¯ , v ¯ , w ¯ ) denote the streamwise, wall-normal, and spanwise averaged-in-time velocity components at a point, ( u ′ , v ′ , w ′ ) the corresponding velocity fluctuations, and p ¯ the time-----averaged pressure. The time-averaged flow is parallel i.e., the mean velocity field is ( u ¯ , 0, 0), and the mean streamwise velocity component u ¯ is a function of the distance from the lower wall.
Simplifying the Reynolds-Averaged Navier-Stokes (RANS) equations for fully developed incompressible turbulent flow, one obtains
( x − − − − − c o m p o n e n t ) − ∂ p ¯ ∂ x + μ ∂ 2 u ¯ ∂ y 2 − ρ ∂ u ′ v ′ ¯ ∂ y = 0
( y − − − − − c o m p o n e n t ) − ∂ p ¯ ∂ y − ρ ∂ v ′ 2 ¯ ∂ y = 0
We note that the Reynolds shear stress term in Equation (1) cannot be neglected and that the mean pressure p ¯ at a cross section x = const. is a function of y due to Equation (2).
After some mathematical manipulations of Equations (1) and (2) one finds that
ν d u ¯ d y + − u ′ v ′ ¯ = u * 2 1 − y h
where u * = τ w / ρ is the friction velocity, τ w   is the mean shear stress at the wall, ν the kinematic viscosity and ρ the fluid density. The wall pressure gradient in the streamwise direction d p w / d x is related to the mean shear stress at the wall, τ w , by the relation
τ w = − h d p w d x
Equation (3), expressed in terms of the inner-law variables y + = y u * / ν , u + = u ¯ / u * , is put in the dimensionless form
d u + d y + + ( − u ′ v ′ ¯ ) + = 1 − y + R e τ
where R e τ = u * h / ν is the friction Reynolds number formed using the channel half height as characteristic length and the friction velocity as characteristic velocity. The term ( − u ′ v ′ ¯ ) + = − u ′ v ′ ¯ / u * 2 which corresponds to the normalized Reynolds shear stress − ρ u ′ v ′ ¯ / u * 2 .

3. Analysis of DNS datasets

In this work we consider DNS data published by Lee and Moser [1], Bernardini, Pirozzoli and Orlandi [2], Lozano-Durán and Jimenez [3], Yamamoto and Tsuji [4], Hoyas, Oberlack et al. [5] and discuss their salient features. The specific DNS datasets analyzed in the present work are listed in Table 1 together with the friction Reynolds number corresponding to each dataset.

3.1. Mean Velocity Profiles (MVPs) and Integration-Based Quantities

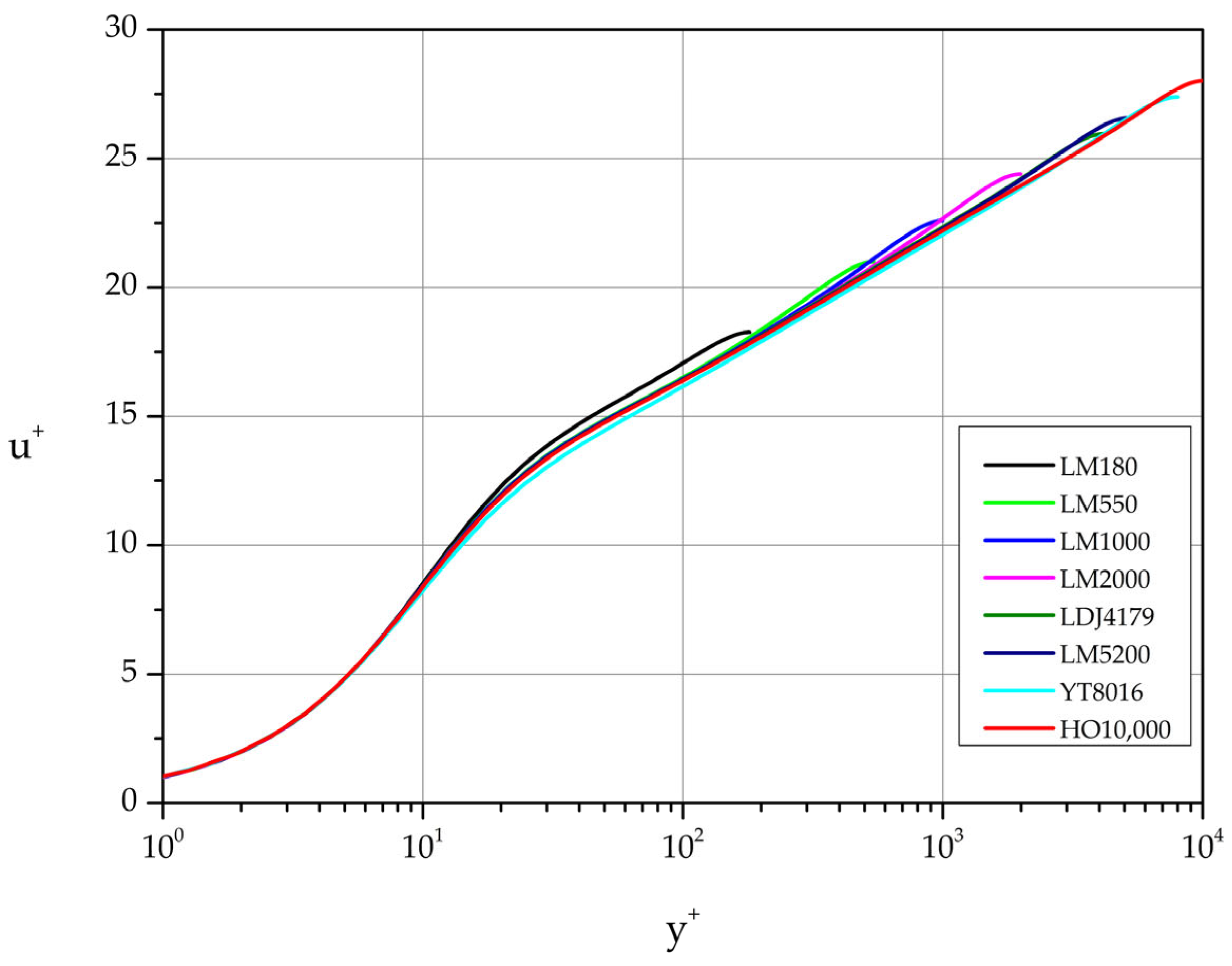
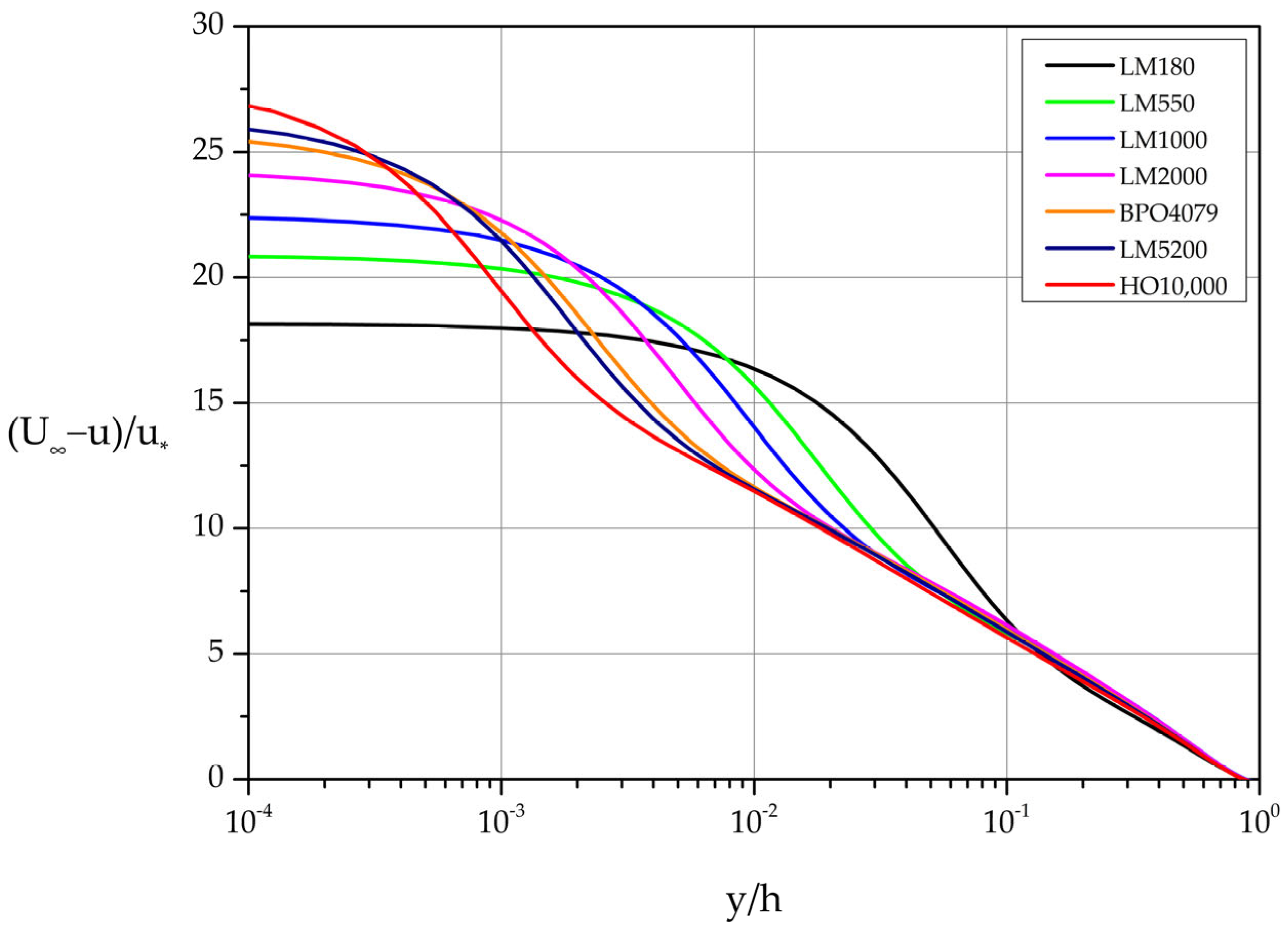
Figure 2 shows the velocity profiles in law of the wall variables (u+, y+) while Figure 3 presents the same data in the standard velocity-defect form. The Reynolds number independence of u+(y+) near the wall is captured with perfect accuracy for all Reynolds numbers listed in Table 1. On the other hand, the Reynolds number independence far from the wall in velocity-defect variables shows small deviations (especially for the smaller Reynolds number cases) from the theoretical collapse to a single curve demanded by similarity considerations.
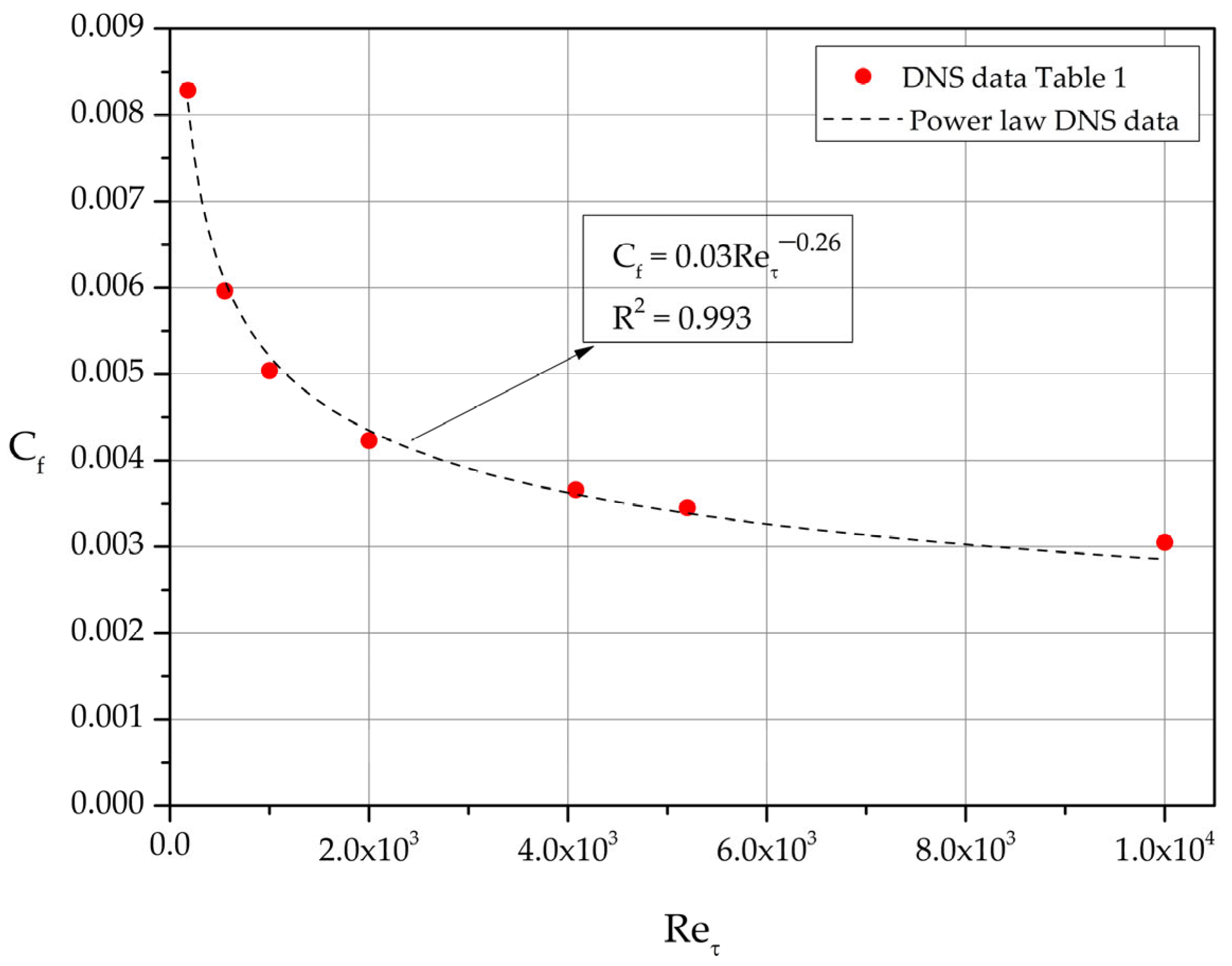
Based on the DNS mean velocity profiles, one can calculate the cross-sectional average velocity, V ¯ , and the dimensionless ratio V ¯ / u * . As it is customary, in canonical wall-bounded flows (straight pipes and channels of constant cross section) we calculate the resistance law in the form of the friction factor f, or equivalently the skin friction coefficient, C f . In the case of channel flow, the Darcy-Weisbach equation [8] takes the form
Δ p = f L D h ρ V ¯ 2 2 o r − ∂ p w ∂ x = f 1 D h ρ V ¯ 2 2
where D h is the hydraulic diameter of the channel cross-section and V ¯ denotes the bulk (cross sectional average) velocity. For the 2-D channel shown in Figure 1 (cross section of “infinite” aspect ratio), the hydraulic diameter D h = 4 h and consequently considering Equation (4)
f = − 4 h ∂ p w ∂ x 1 2 ρ V ¯ 2 = 8 τ w ρ V ¯ 2 = 8 u * 2 V ¯ 2
Alternatively, we can work with the skin friction coefficient defined as
C f = 2 u * 2 V ¯ 2
The calculated values of C f   for each dataset of Table 1 are shown as filled circles in Figure 4. Least squares fit reveal the power-law relation
C f = 0.03 R e τ − 0.26
valid in the range 180 ≤   R e τ ≤ 10,000.
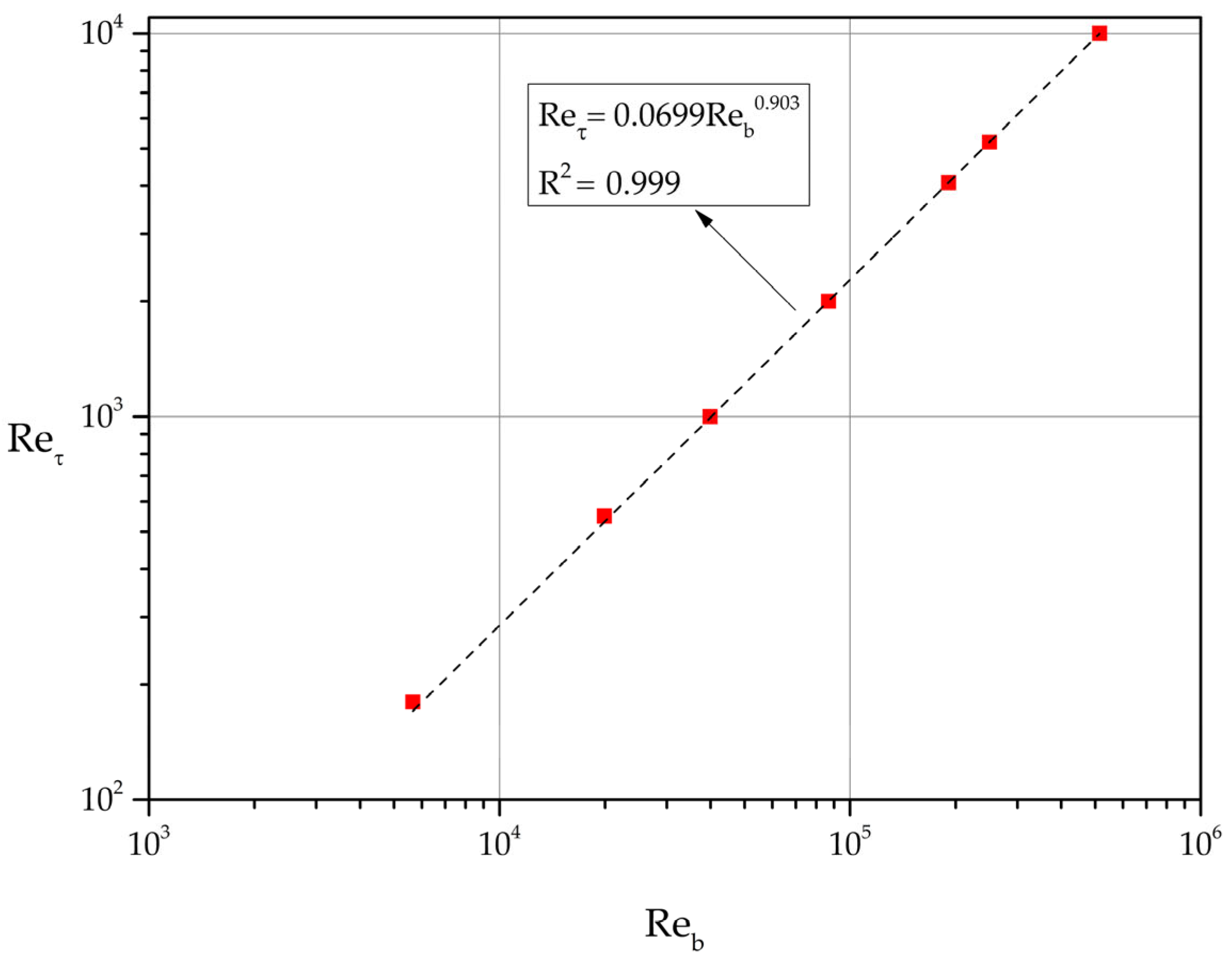
The relation between the bulk Reynolds number as R e b = V ¯ ( 2 h ) / ν and R e τ is found to be R e τ = 0.07 R e b 0.9 with excellent accuracy (see Figure 5). It follows that
C f = 0.06 R e b − 0.23
based on least squares fit.
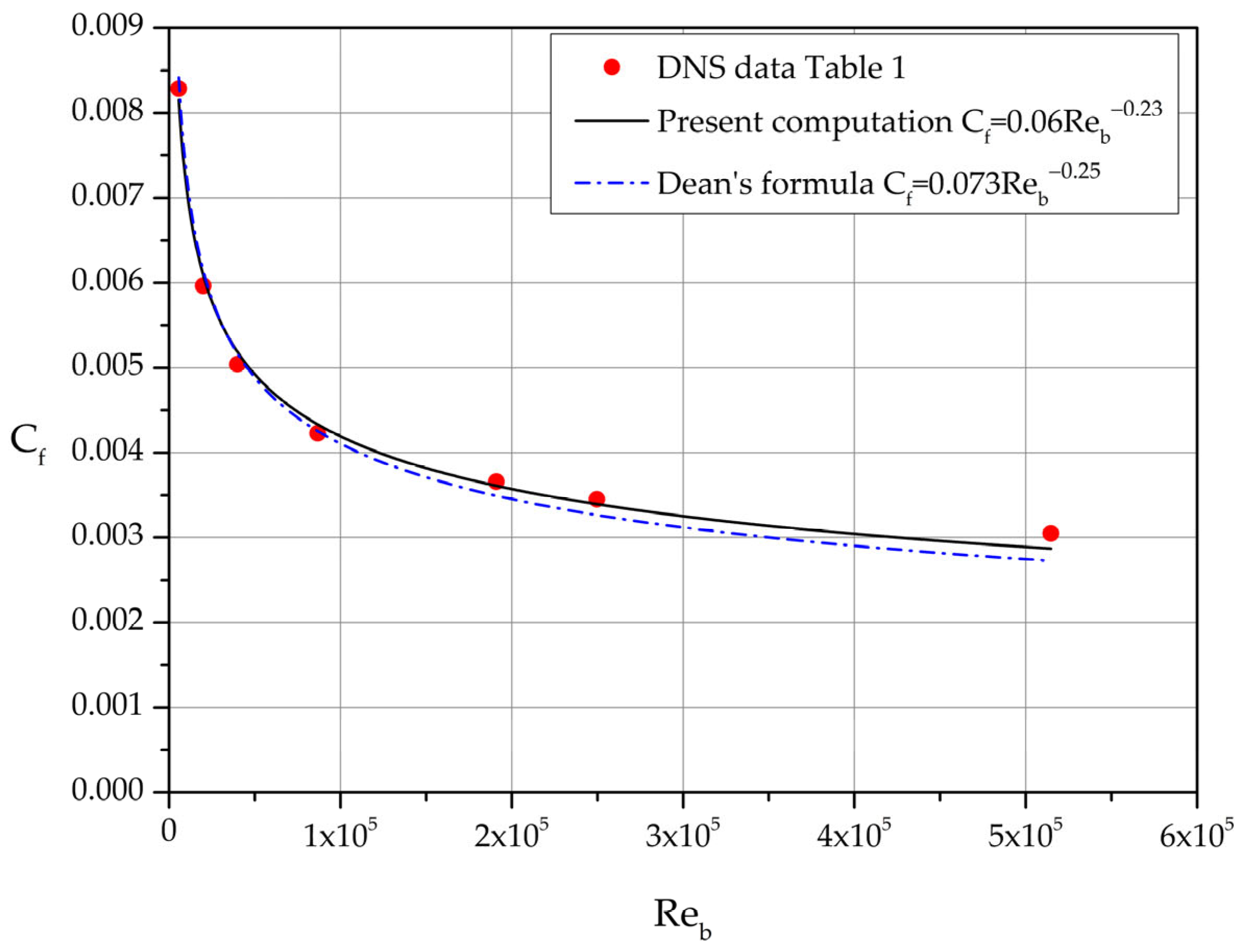
The skin friction coefficient expressed as function of R e b differs slightly from Dean’s formula [9]
C f = 0.073 R e b − 0.25
Dean based his formula on selected experimental measurements of high Reynolds number flows in channels with cross section aspect ratio greater than 1:12 [9,10]. The comparison is shown in graphical form in Figure 6.
In a recently published work, Nucci & Absi [11] analyzed DNS data for low Reynolds numbers in the range 110 ≤   R e τ   ≤ 2000. Their computed values for C f differ slightly from the skin friction Equation (9).
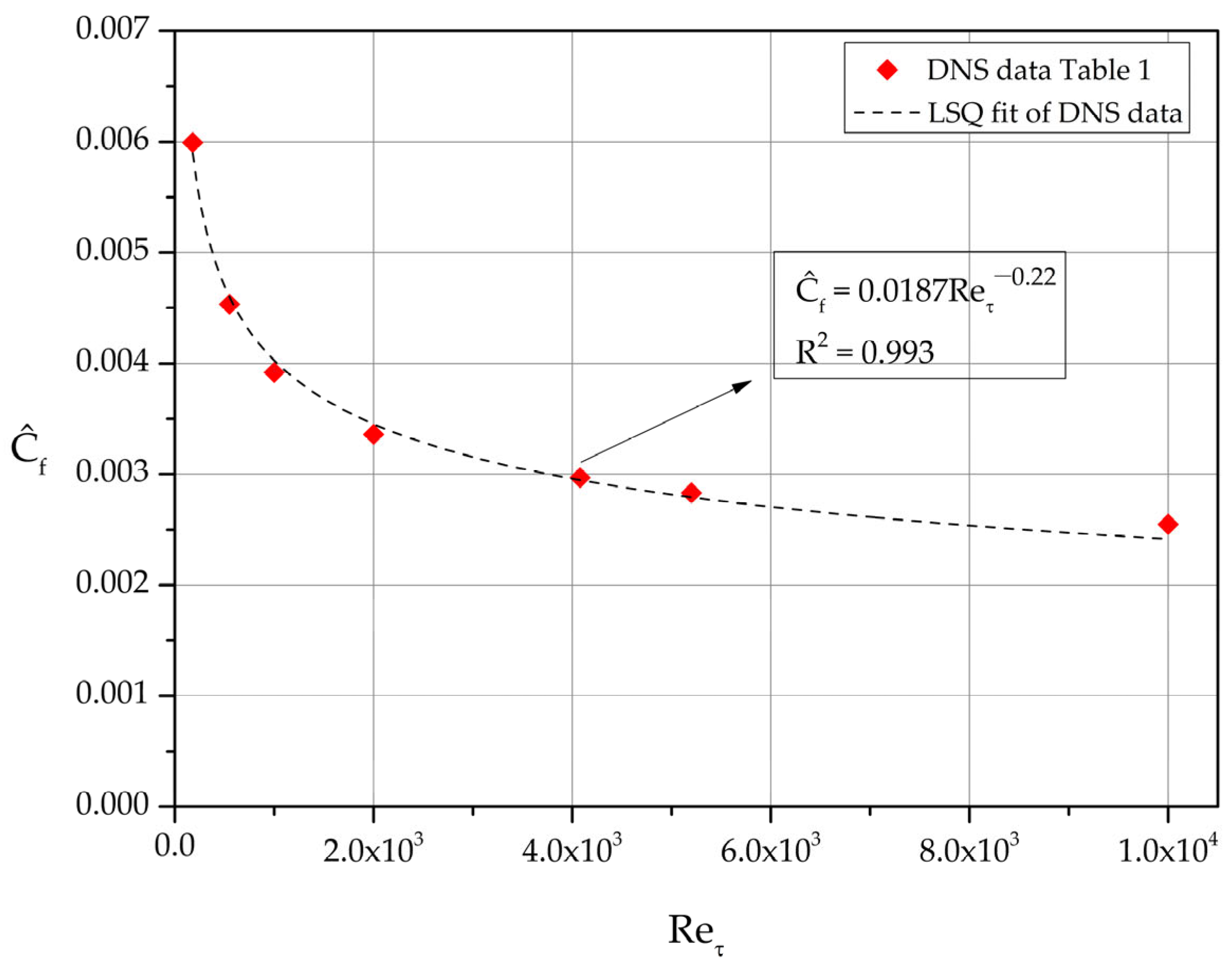
Next, we consider the lower half of the channel flow as a boundary layer of thickness δ = h and introduce the skin friction coefficient C f ^ = τ w / 1 2 ρ U 2 where U =   u ¯ ( y = h ) = u m a x . Introducing the friction velocity, u * , in the local skin friction coefficient definition we obtain
C f ^ = 2 u * 2 u m a x 2 = > C f ^ = 2 u m a x + 2
Least squares fit of the C f ^ values, computed based on the DNS datasets of Table 1, is shown in Figure 7.
It is worth commenting on the mean velocity profile in the central region of the channel flow. We define
ξ = u m a x − V ¯ u * = u m a x + − V ¯ +
and list the computed values in Table 2.
A least square fit of the values ξ( R e τ ), calculated for the DNS datasets of Table 1, is shown in Figure 8.
The linear relation ξ = 2.71 − 3.25 * 10 − 5 ( R e τ ) gives a fair approximation of the function ξ( R e τ ) in the range of the R e τ values considered in this work. It clearly shows the correct trend since in the limit of infinite Reynolds number ξ should tend to zero.

3.2 Diag@nostic Functions Ξ and Γ for the MVP

A great deal of research has been conducted and lively discussions appeared in the scientific literature on whether a logarithmic or a power function describes better the overlap region of the MVP. To decipher where these approximations fit better the data, two diagnostic functions may be used.
The first function, defined as Ξ = y + ( d u + / d y + ) , serves to detect intervals where u+ is a logarithmic function of y+. It is easy to prove that when Ξ attains a constant value, u+ exhibits a logarithmic behavior of the form
u + = A l n y + + B = A l n y + y o = 1 κ l n y + + B
The second diagnostic function, defined as Γ = ( y + / u + ) ( d u + / d y + ) , is useful in detecting intervals where u+ is approximated well by a power function of the form
u + = α y + λ
In the interval where Γ = const., u+ is approximated by a function of the form (15) with λ = Γ.
Both diagnostic functions require the computation of the derivative d u + / d y + . Since numerical differentiation acts as an error amplifier, analyzing the DNS data in terms of the two diagnostic functions help us to indicate the interval of the appropriate approximation with greater confidence and accuracy.
To avoid misunderstandings in the remainder of this section it should be stressed that the logarithmic law, Equation (14), is theoretically valid only asymptotically for Re →   ∞ . The logarithmic law has been derived based on various sets of assumptions. The well-known Millikan’s [12] argument is based on the notion that, in the intermediate region (layer), both the wall law and the velocity-defect laws should be valid. In the limit of infinite Reynolds number this leads to the existence of a logarithmic layer in the overlap (inertial) region. Landau’s [13] treatment of the infinite flat plate in terms of the notion of “logarithmic accuracy” also provides a firm ground for the existence of logarithmic behavior. There are two schools of thought with respect to the constant A = 1 / κ (κ is the Kármán constant) in Equation (14). One insists that κ is a universal constant while the other maintains that the value of κ depends on the type (geometry) of the flow [14,15,16,17,18,19,20,21,22].
For finite Reynolds number turbulent flows, a number of researchers [23,24,25,26,27] have argued that a power law (with Reynolds number dependent coefficients) fits better experimental and DNS results.
In this work the numerical evaluation of the derivative is performed using the following formula for unequally spaced data
d u + d y + = u + y i − 1 + 2 y + − y i + − y i + 1 + y i − 1 + − y i + y i − 1 + − y i + 1 + + u + y i + 2 y + − y i − 1 + − y i + 1 + y i + − y i − 1 + y i + − y i + 1 + + u + y i + 1 + 2 y + − y i − 1 + − y i + y i + 1 + − y i − 1 + y i + 1 + − y i +

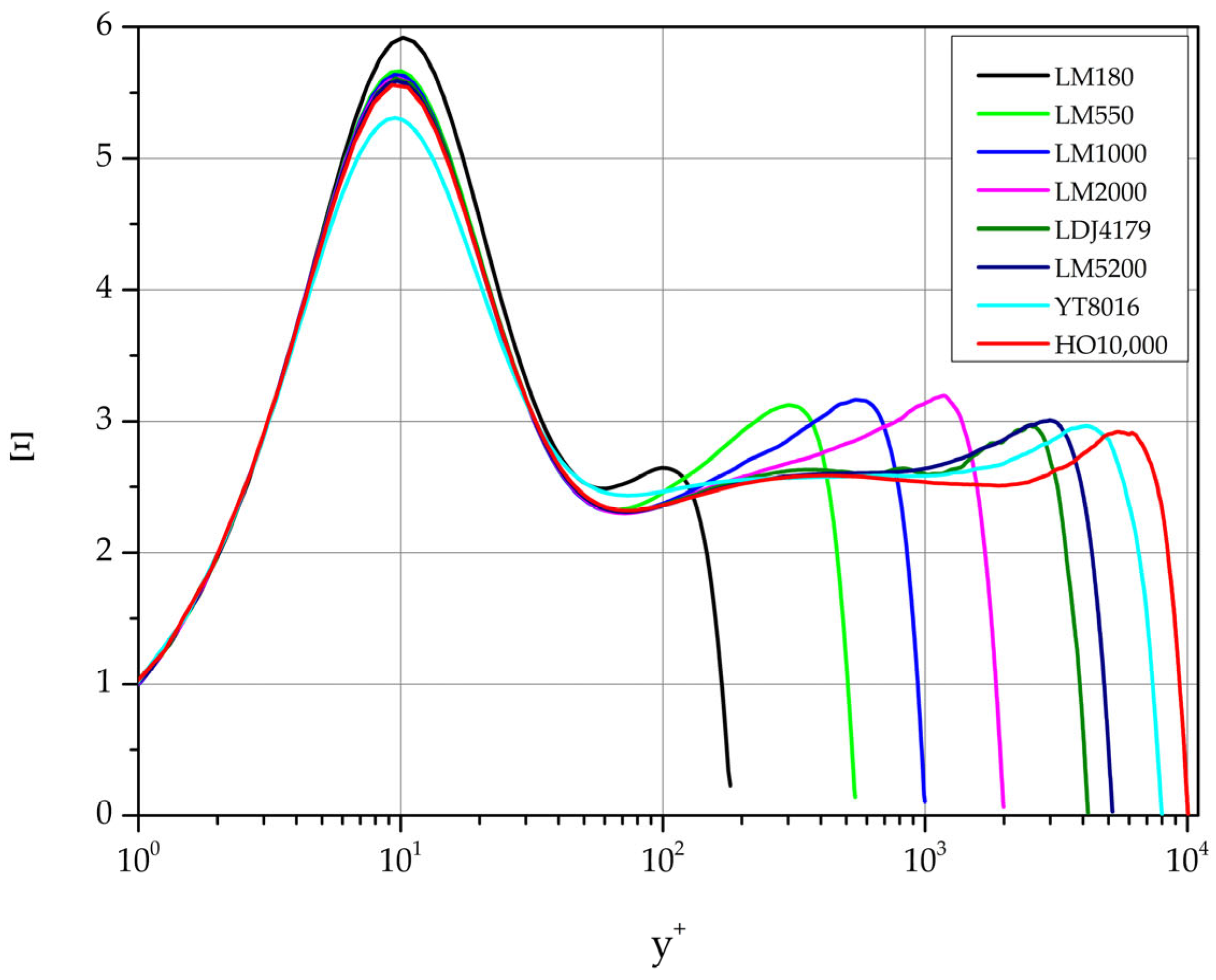
3.2.1. Diagnostic Function Ξ

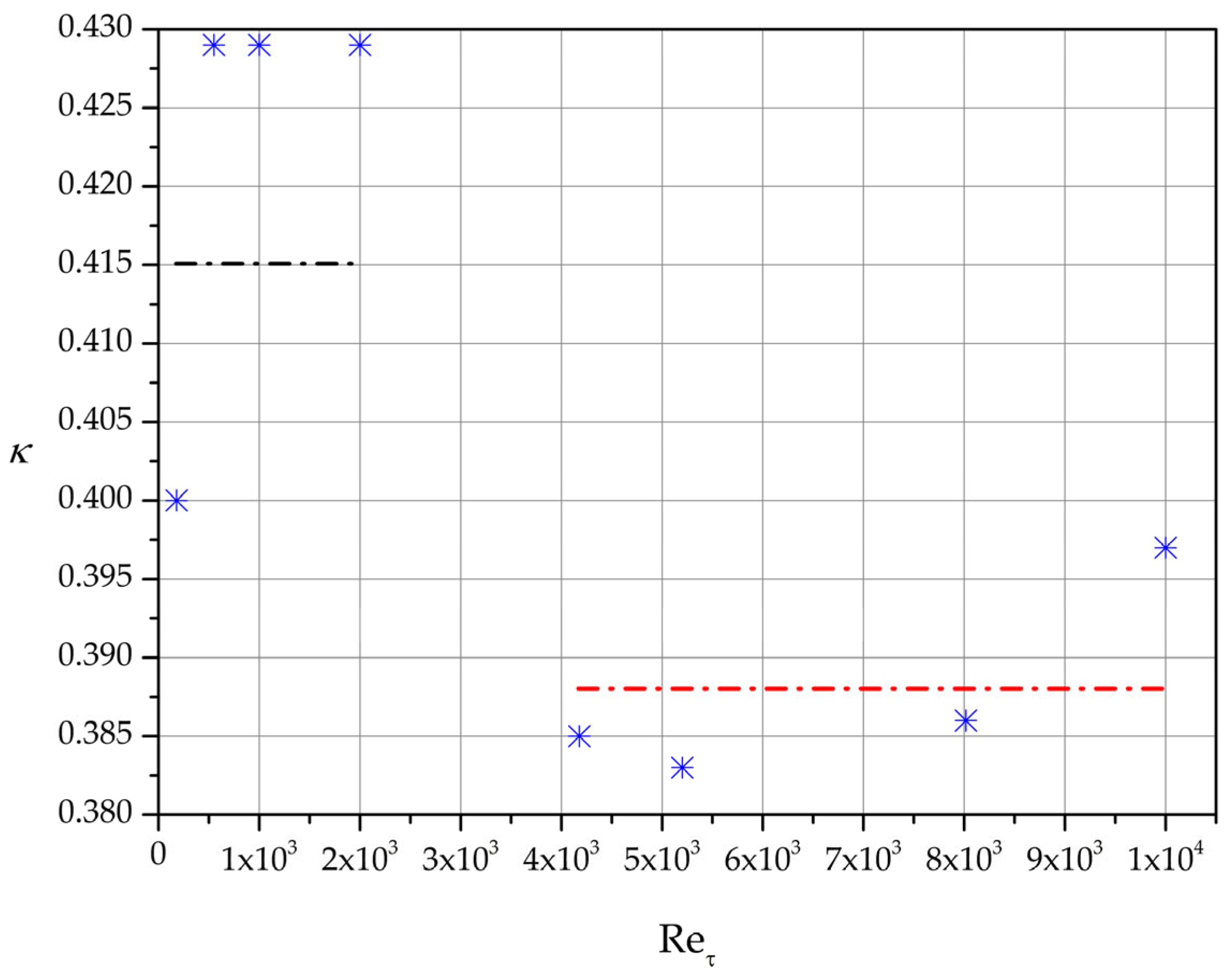
Figure 9 depicts the calculated Ξ(y+ ; Reτ) curves for the cases listed in Table 1. As R e τ   increases the y+ intervals where Ξ is approximately constant become longer, which implies an increase of the log-law region. In Table 3 our estimates of κ are listed together with the intervals where Ξ = const. =   1 / κ .
For R e τ = 180 our estimate of the Kármán constant is κ  = 0.40 while for R e τ   = 550, 1000, 2000 κ  = 0.429. For higher values of friction Reynolds number in the range [4000 ----- 10,000], a good representative value for κ is 0.388. Finally, a good overall approximation of κ in the R e τ range [180 ----- 10,000] is found to be 0.405 (see Figure 10).

3.2.2. Diagnostic Function Γ

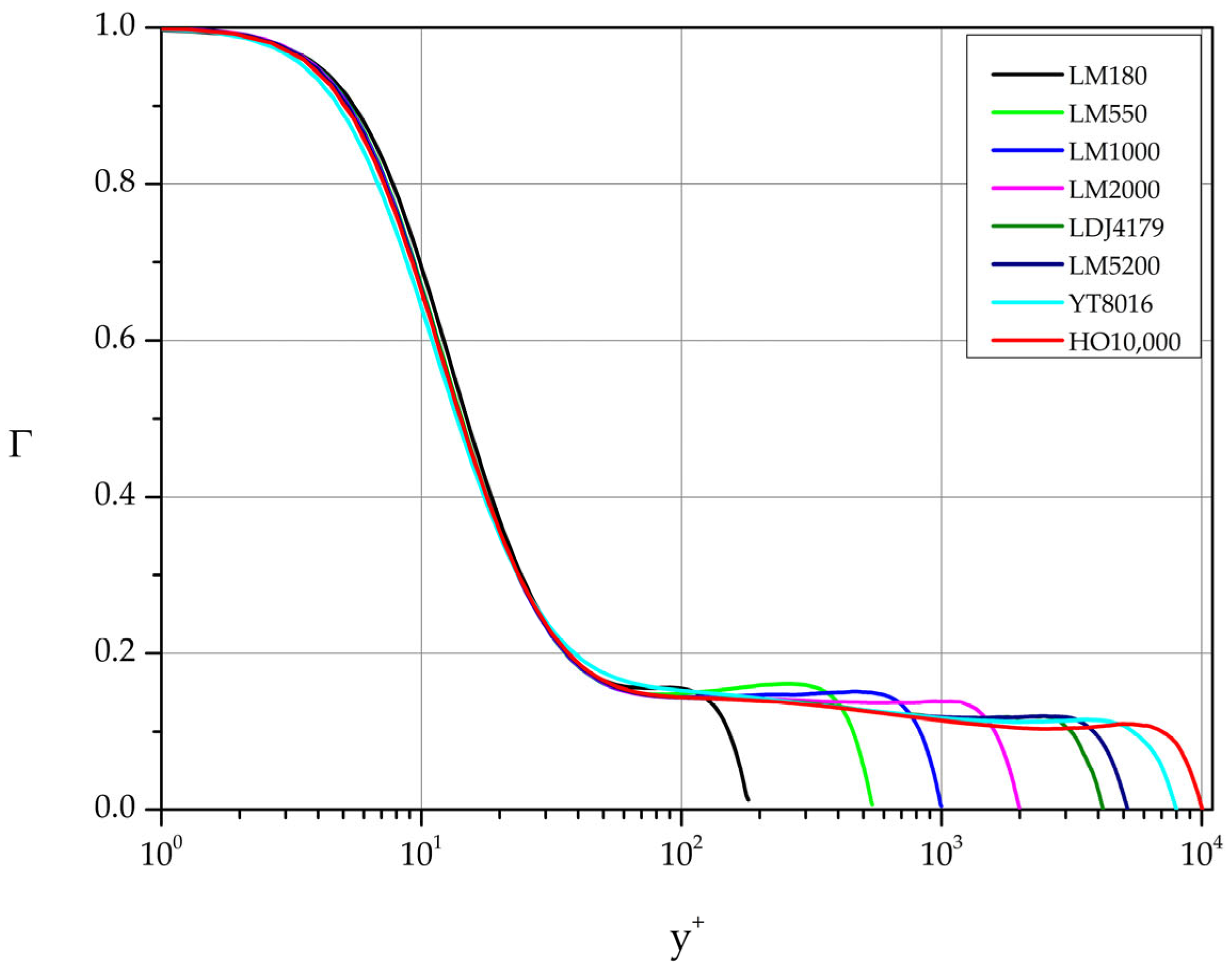
Figure 11 depicts the variation of Γ function for each dataset listed in Table 1. Analyzing the behavior of these curves we identify intervals [ y l o w + , y h i g h + ]   where Γ attains a constant value. These intervals together with the implied values of the exponent λ in Equation (15) are listed in Table 4.

3.3. Second Order Statistics

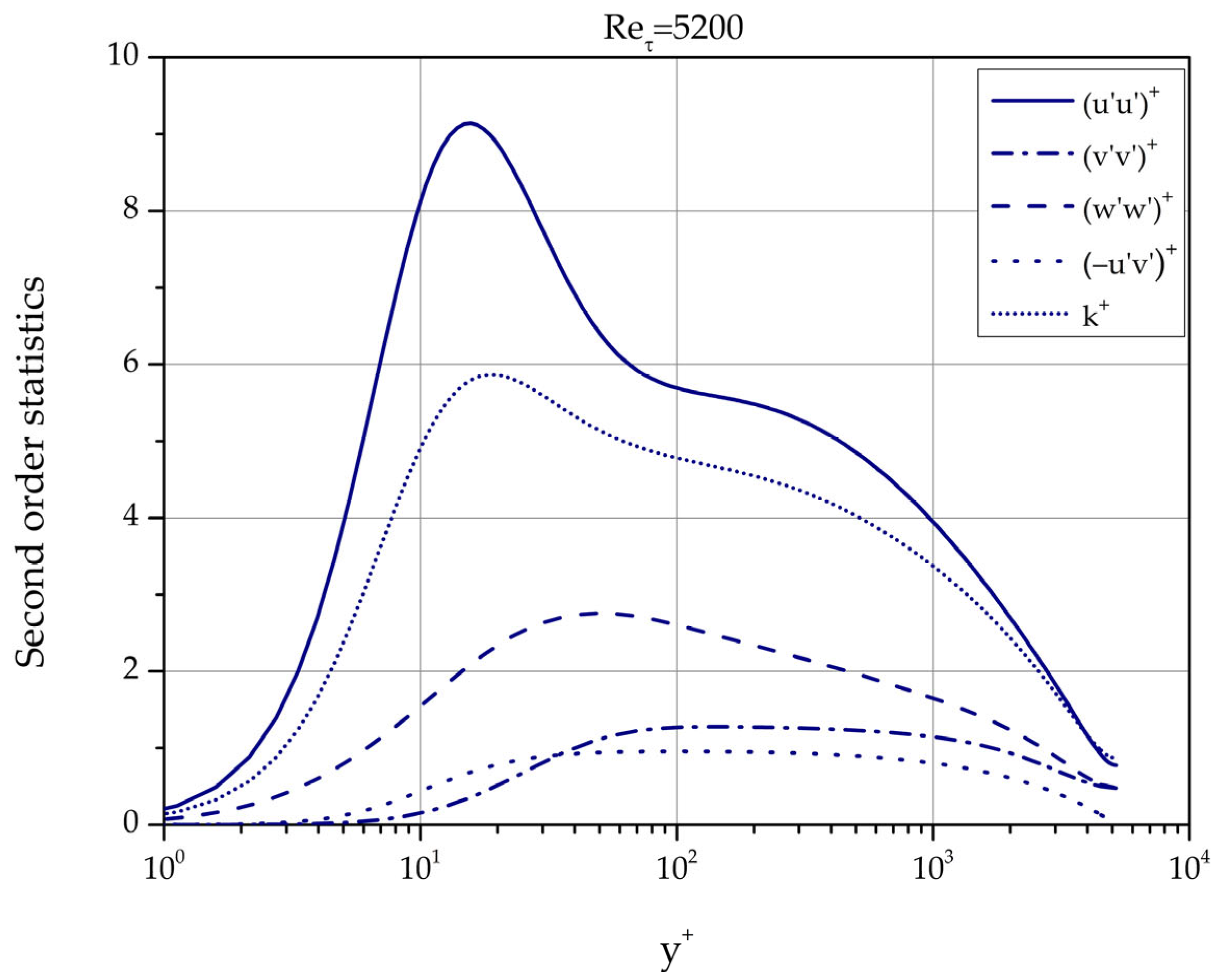
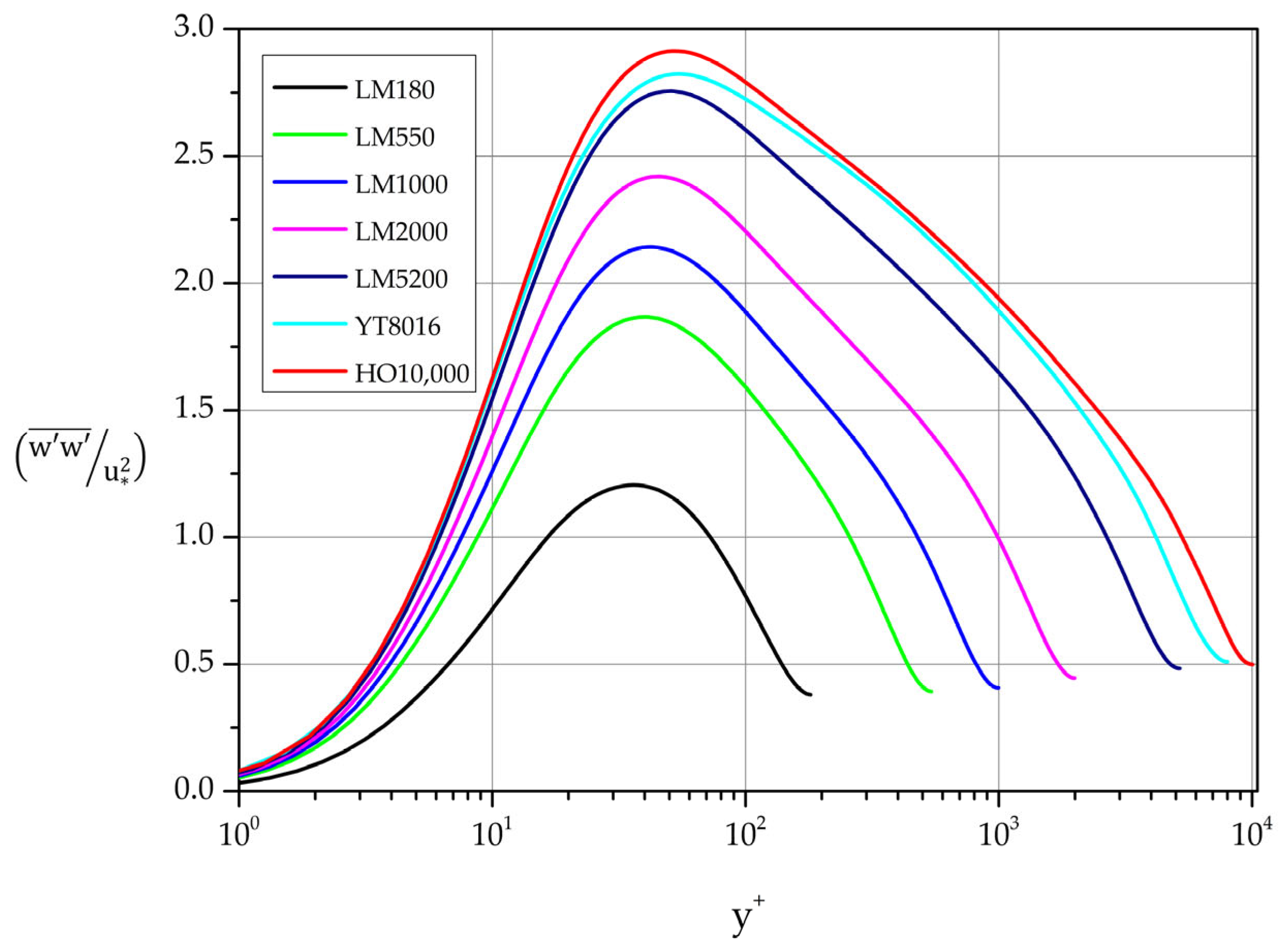
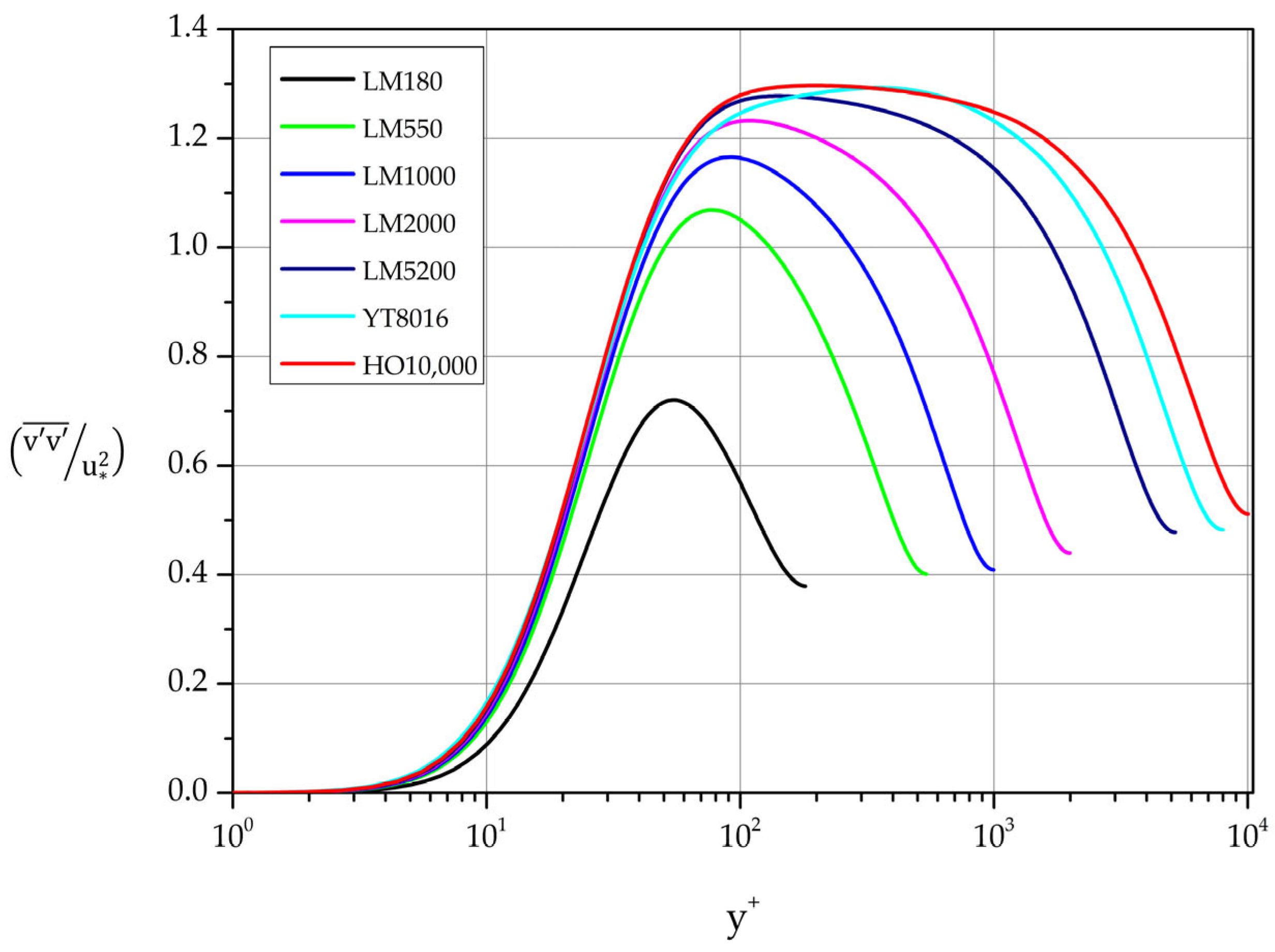
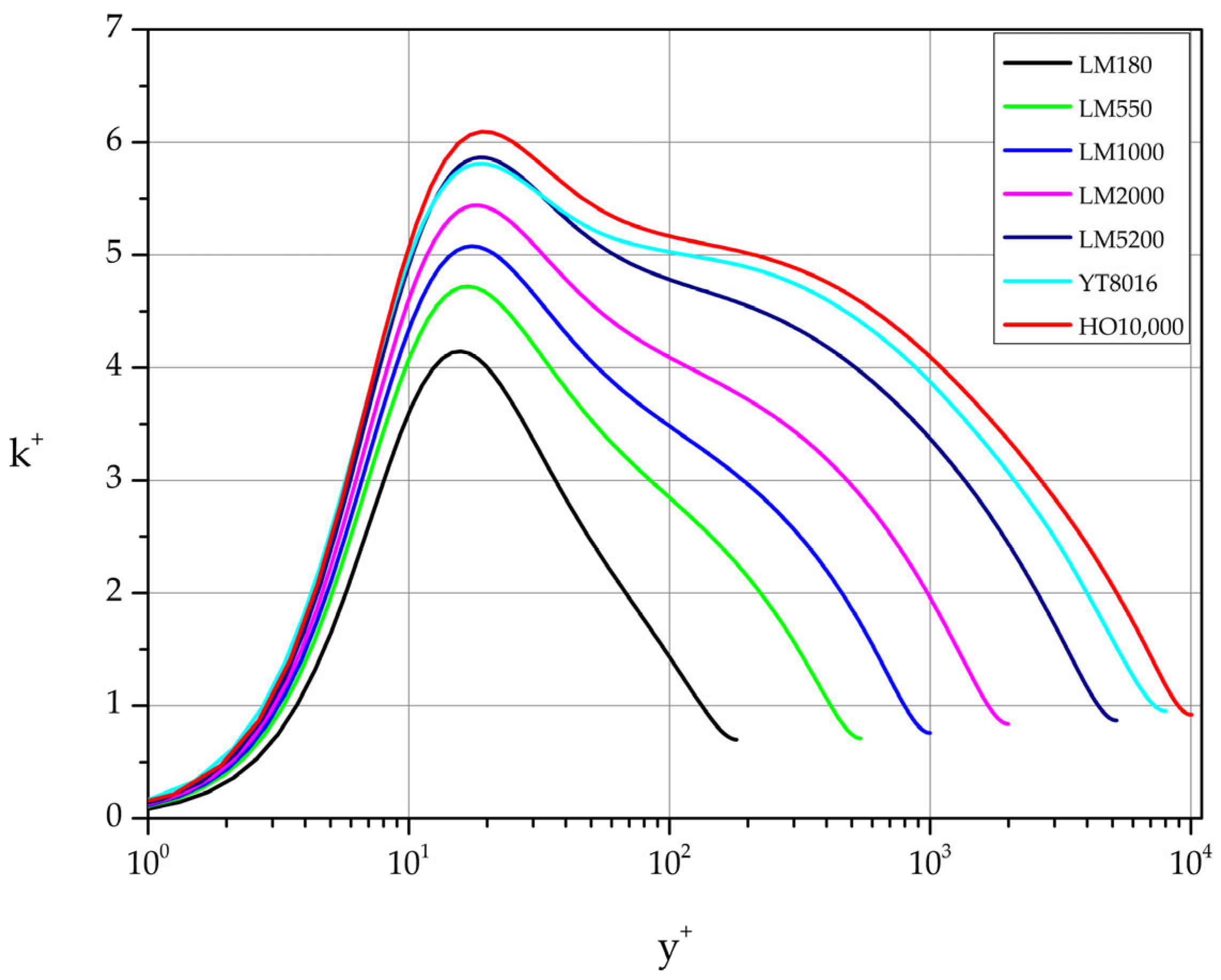
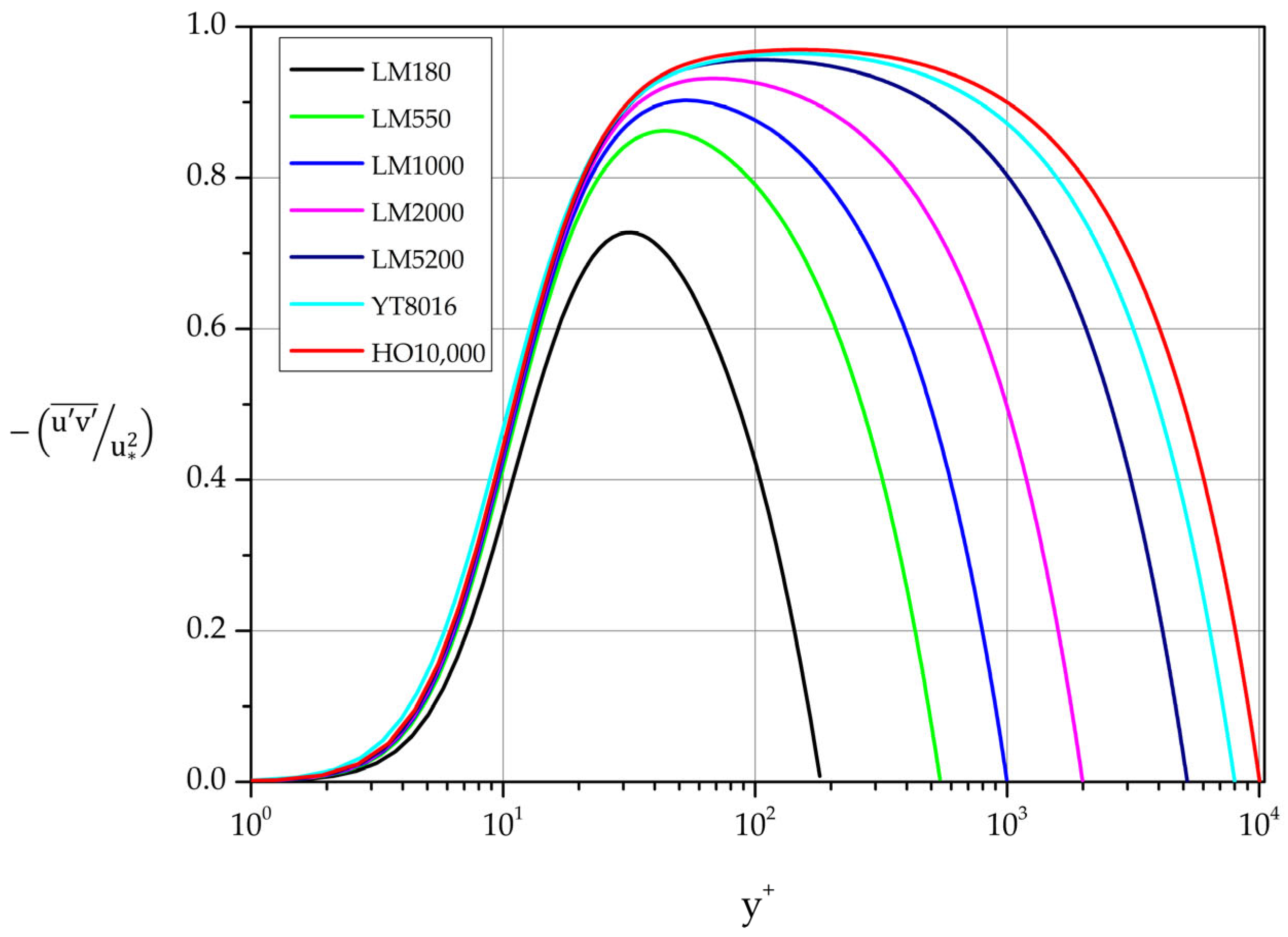
Typical profiles of the normal and shear Reynolds stresses as well as of the turbulence kinetic energy are shown in Figure 12 for R e τ = 5200.
In the remainder of section 3 we explore the Reynolds number effects on second order statistics of turbulence fluctuations. A logarithmic region is expected in the streamwise and spanwise normal Reynolds stresses at sufficiently high Reynolds number [28,29,30,31,32,33]. We also discuss below the Reynolds number dependence (or independence) of the Reynolds stresses and turbulence kinetic energy [34,35,36].

3.3.1. u ' 2 ¯

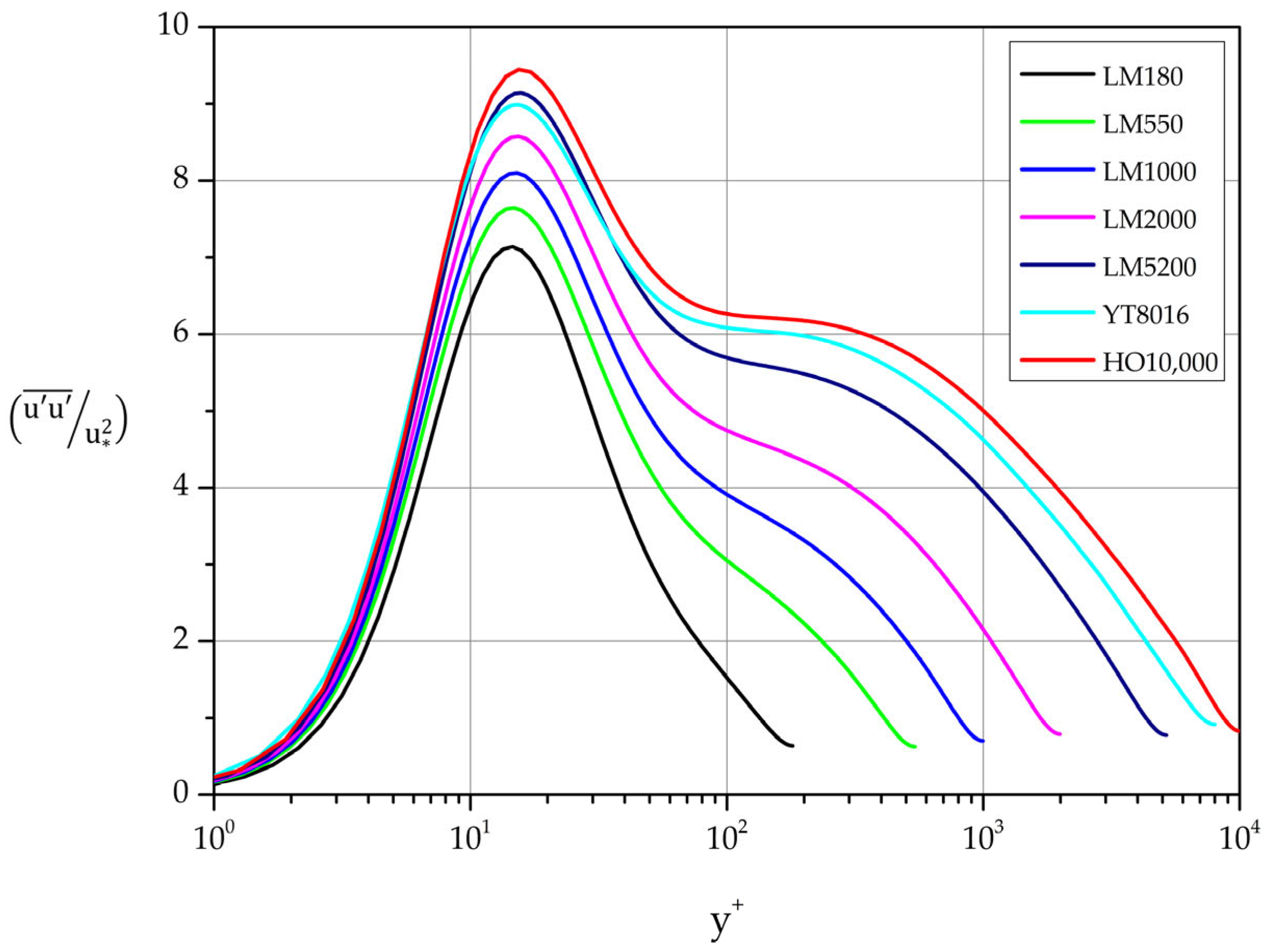
The normalized variance profiles of the streamwise fluctuations are shown in Figure 13. A clear maximum characterizes each curve. Least squares fit gives the following expression for the near wall maxima of the normalized variance profiles of streamwise fluctuations
u ′ u ′ ¯ m a x + = 0.56 l n ( R e τ ) + 4.2
Turning now to the search for logarithmic behavior in u ′ u ′ ¯ + , we search for a relation of the form
u ′ 2 ¯ u * 2 = B 1 − A 1 l n y h
where A 1 is the Townsend-Perry constant and B 1   an additive parameter that depends on Reynolds number [31]. The term “sufficiently high Reynolds number” in this case means R e τ > 7000 [4]. Calculating and plotting the indicator function
T = y + d u ′ 2 ¯ + d y +
we have identified regions of logarithmic variation in the cases YT8016 and HO10,000 (see Figure 13 and Table 5).
The values on the top 2 lines compare quite well with the values given in the literature for A 1 R e τ and Β 1 R e τ [4,28,29,30]. However, we have opted to list additional intervals at larger distances from the wall where behavior of the form (18) can be identified.

3.3.2. w ′ 2 ¯

The variance profiles of the spanwise fluctuations are shown in Figure 14. A near wall maximum characterizes each profile. Least squares fit gives the following dependence on R e τ
w ′ w ′ ¯ m a x + = 0.41 l n ( R e τ ) − 0.78
Next, we search for regions of logarithmic behavior of the form
w ′ 2 ¯ u * 2 = C 1 − D 1 l n y h
With the help of the appropriate indicator function we estimate the constant D 1   and the additive parameter C 1 as shown in Table 6.
Obviously, some regions can be merged by relaxing the tolerance allowed on deviations from the requirement of constancy of the diagnostic function. We also note that in w ′ w ′ ¯ + we observe logarithmic behavior for R e τ as low as 2000. As in Table 5 we have opted to list additional intervals where behavior of the form (21) can be identified.

3.3.3. v ′ 2 ¯

The variance profiles of wall-normal fluctuations (Figure 15) exhibit a different behavior for high Reynolds number. Specifically,
v ′ 2 ¯ u * 2 = B ν ≈ 1.30
in the interval 150 ≲ y+ ≲ 550 for R e τ = 8016 and R e τ = 10,000. In particularly, case YT8016 displays a constant B v = 1.29 in the region 250 ≤   y + ≤ 550 while in case HO10,000 B v = 1.30 in the interval 150 ≤ y + ≤ 450.
In the lower Reynolds number cases a plateau is not formed. Instead, clear maxima are formed for 180 ≤   R e τ ≤ 5200. A least square fit approximates the v ′ v ′ ¯ m a x + dependence on R e τ by
v ′ v ′ ¯ m a x + = 0.07 l n R e τ + 0.642
in the range 550 ≤   R e τ ≤ 10,000.

3.3.4. Turbulence Kinetic Energy, k

Each nondimensional turbulence kinetic energy profile is characterized by a maximum at approximately y + ≈ 18. The exact location of the maximum is weakly influenced by R e τ (see Table 7). The normalized k m a x + value is strongly influenced by R e τ in the range of the Reynolds number values considered (see Figure 16 and Table 7).
Least squares fit of the ( k m a x + , R e τ ) pairs of values gives the relation
k m a x + = 0.46 l n ( R e τ ) + 1.8
and describes the function k m a x + = f ( R e τ ) with very good approximation.
Turning to the question of existence or not of logarithmic behavior in the turbulence kinetic energy profiles of the form
k + = k u * 2 = E 1 − F 1 ln ⁡ y h
we have identified the regions listed in Table 8.

3.3.5. Reynolds Shear Stress

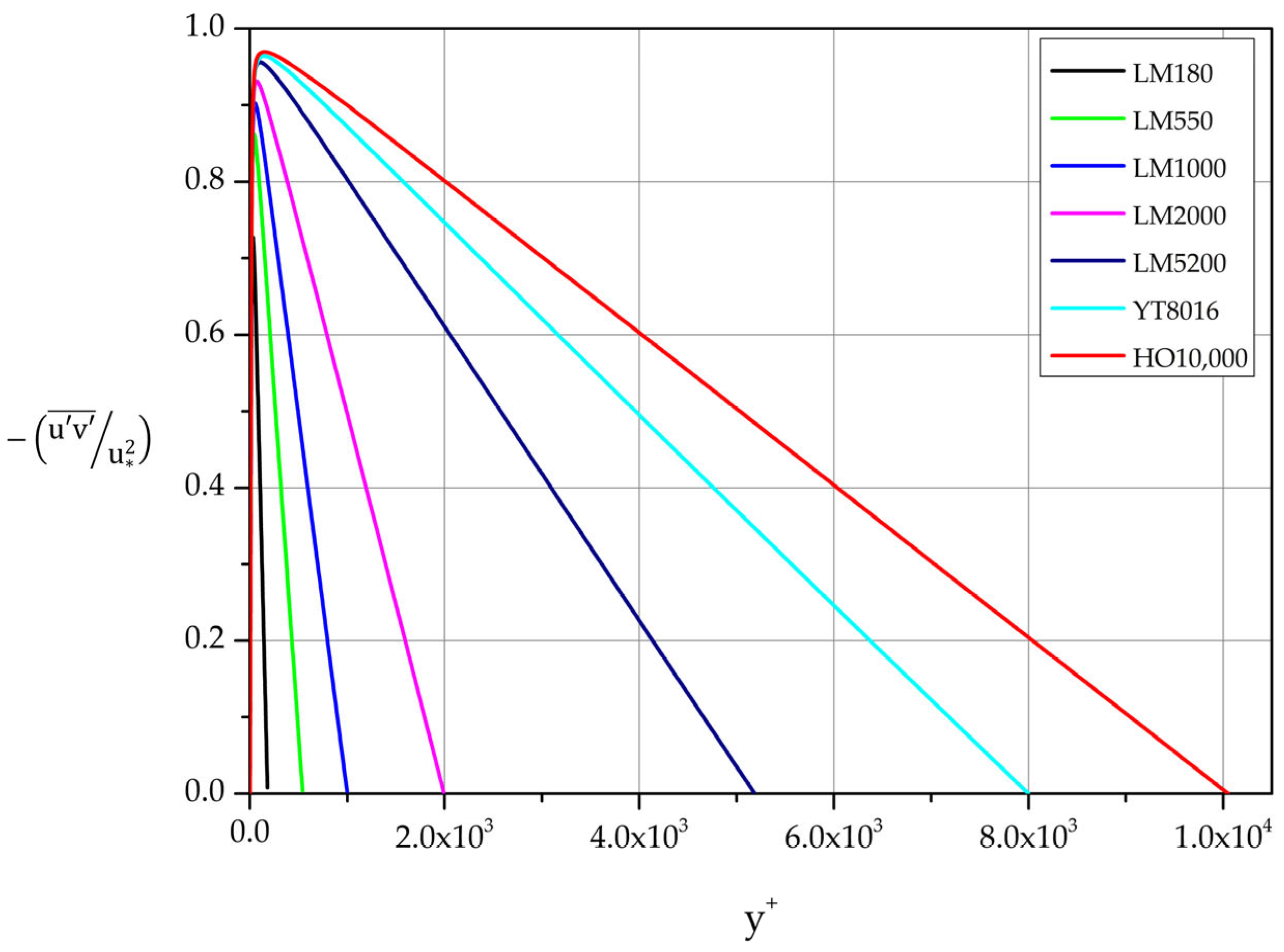
Profiles of the normalized covariance of streamwise and wall-normal fluctuations are shown in Figure 17 and Figure 18. They are strongly influenced by Reynolds number. For R e τ   equal to 8016 and 10,000 a clear plateau is formed. Specifically
at R e τ = 8016: − u ′ v ′ ¯ / u * 2 = 0.963 in the interval y + = [100 - 200]
at R e τ = 10,000: − u ′ v ′ ¯ / u * 2 = 0.969 in the interval y + = [100 - 250]
The maxima of the curves in the range 550 ≤   R e τ ≤ 10,000 follow the relation
− u ′ v ′ ¯ m a x + = 0.03 l n R e τ + 0.66
obtained by least squares fit, while the location of the − u ′ v ′ ¯ m a x + varies with R e τ according to relation
y w h e r e max ⁡ a p p e a r s + = 0.01 l n R e τ + 41.21
for the same range of R e τ .
For large values of y + / R e τ = y + / δ + the derivative of the mean velocity is small compared to the Reynolds stress term in Equation (5). Consequently, we expect
( − u ′ v ′ ¯ ) + ≈ 1 − y + R e τ
i.e., the Reynolds shear stress varies linearly with distance from the wall in the region further than the layer closest to the wall [37]. This behavior is captured very accurately by the DNS data as shown in Figure 18.

4. The AL84 Model

In this section the most important aspects of AL84 model are outlined. The reader is referred to [6] for detailed description of the model construction and to reference [7] for a discussion on the accuracy of the AL84 model predictions for ZPG-TBL flows over a flat plate.
In the AL84 model the nondimensionalized mean velocity profile (MVP) is approximated by superposing two functions f and g, i.e.,
u ¯ + = f y + + g Π , y δ
where
f ( y + ) = l n ( y + + 11 ) 4.02 ( y + 2 − 7.37 y + + 83.3 ) 0.79 + 5.63 tan − 1 ⁡ ( 0.12 y + − 0.441 ) − 3.81
g Π , y δ = 1 κ 1 + 6 Π y δ 2 − 1 κ 1 + 4 Π y δ 3
κ is the von Kármán constant and Π Coles’ [38] parameter.
Considering the channel cross section as a whole, the flow rate per unit width of the channel is given by q = ∫ 0 2 h u d y or, in terms of inner law variables, q = 2 ν q a + where q a + = ∫ 0 h + u + d y + . This integral is calculated as the sum of two terms i.e., q a + = q 1 / ν + q 2 / ν where
q 1 ν = ∫ 0 h + f y + d y +   a n d   q 2 ν = ∫ 0 1 g d η
In the case of fully developed channel flow the boundary layer thickness δ is equal to the half channel “height” ( δ = h ) and in wall-law variables δ + = h + = u * h / ν = R e τ . Analytical evaluation of the two integrals leads to the expressions
q 1 ν = ( 33.91 − 5.63 R e τ ) tan − 1 ⁡ 0.441 − 0.12 R e τ        − 20.55 + 0.79 R e τ ln ⁡ R e τ 2 − 7.37 R e τ + 83.3                     + 44.22 + 4.02 R e τ ln ⁡ R e τ + 11 − ( 6.25 R e τ + 29.26 )
and
q 2 ν = R e τ κ Π + 1 12
The average velocity at a channel cross section is then given as V ¯ = q / 2 h and, taking again into account the symmetry of the channel flow,
V ¯ u * = q a + δ + = q a + R e τ
In turn, the Darcy-Weisbach friction factor defined as f = 8 u * 2 / V ¯ 2 can be calculated analytically based on Equation (35). The same information can be expressed in terms of the skin-friction coefficient C f = 2 u * 2 / V ¯ 2 .
We note that for pressure-driven channel flow, Equation (5) allows us to evaluate the Reynolds shear stress based on the AL84 model by inserting the derivative of the mean velocity with respect to y + (evaluated analytically based on Equation (30) and (31)) into Equation (5). This topic is discussed further in Section 4.3.

4.1. Global Absolute Error and Local Relative Error in AL84 Predictions

As explained in Reference [6], the values κ  =  0.41 and the additive constant in the MVP logarithmic law Β = 5.0 (see Equation 14) are incorporated in Equations (30) and (31) while the third parameter in AL84, Π, is free to vary with Reynolds number. Estimates of Π obtained from the DNS datasets analyzed are listed in Table 9.
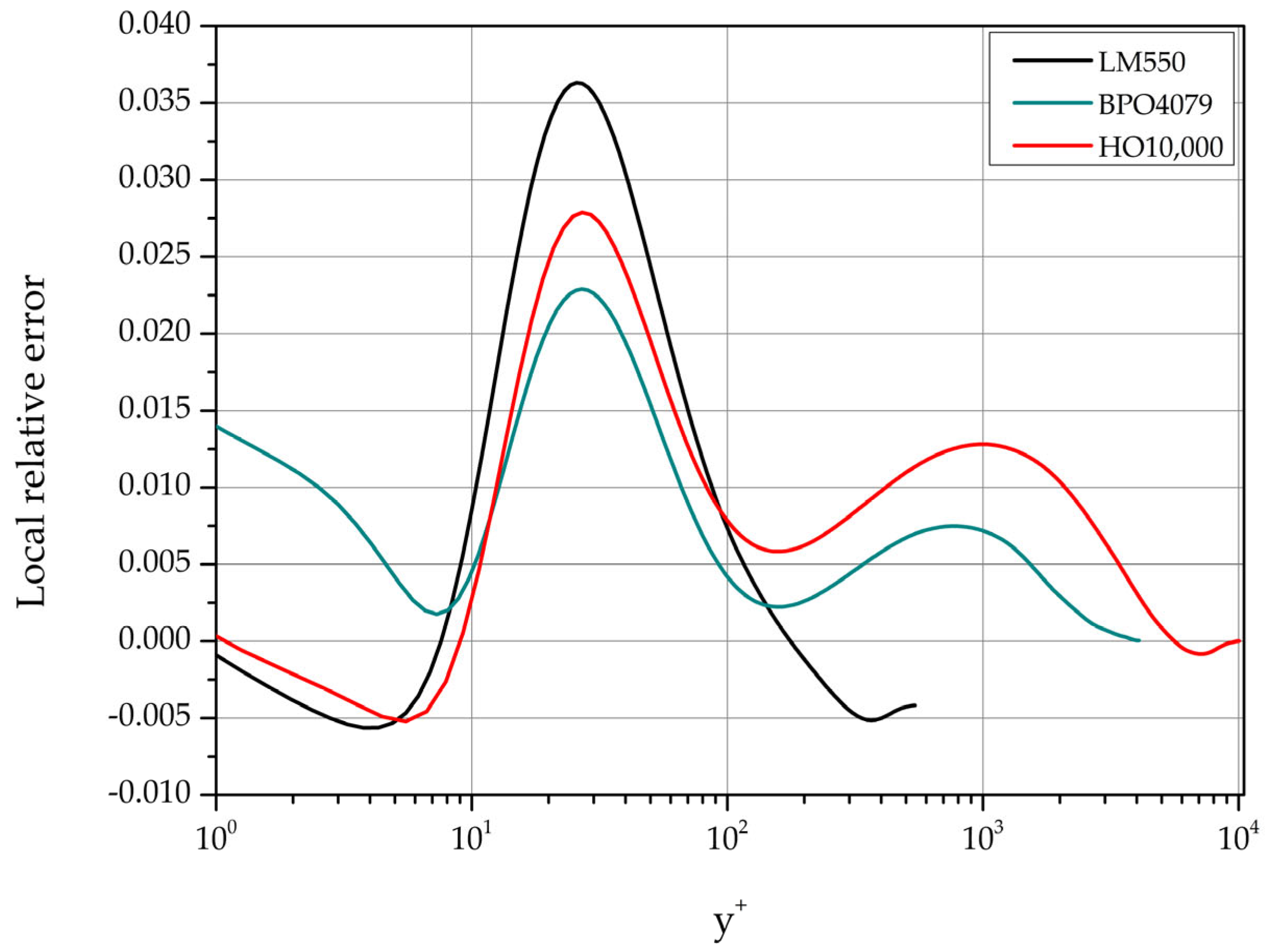
The AL84 model performance is evaluated with these parameter values. The error at a distance y + from the lower channel wall is defined as e ( y + )   =   u + ( y + ) − [f(y+) + g( y / h , Π)].
Representative local relative error profiles are shown in Figure 19 for three cases (low, moderate, and high) R e τ = 550, 4079 and 10,000.
The maximum local relative error is located approximately at y+  ≅ 26 as shown in Table 10. In the range 2000 ≤   R e τ ≤ 10,000 it is less than 3‰.
The global statistics of the absolute error in the MVP approximation are summarized in Table 11.

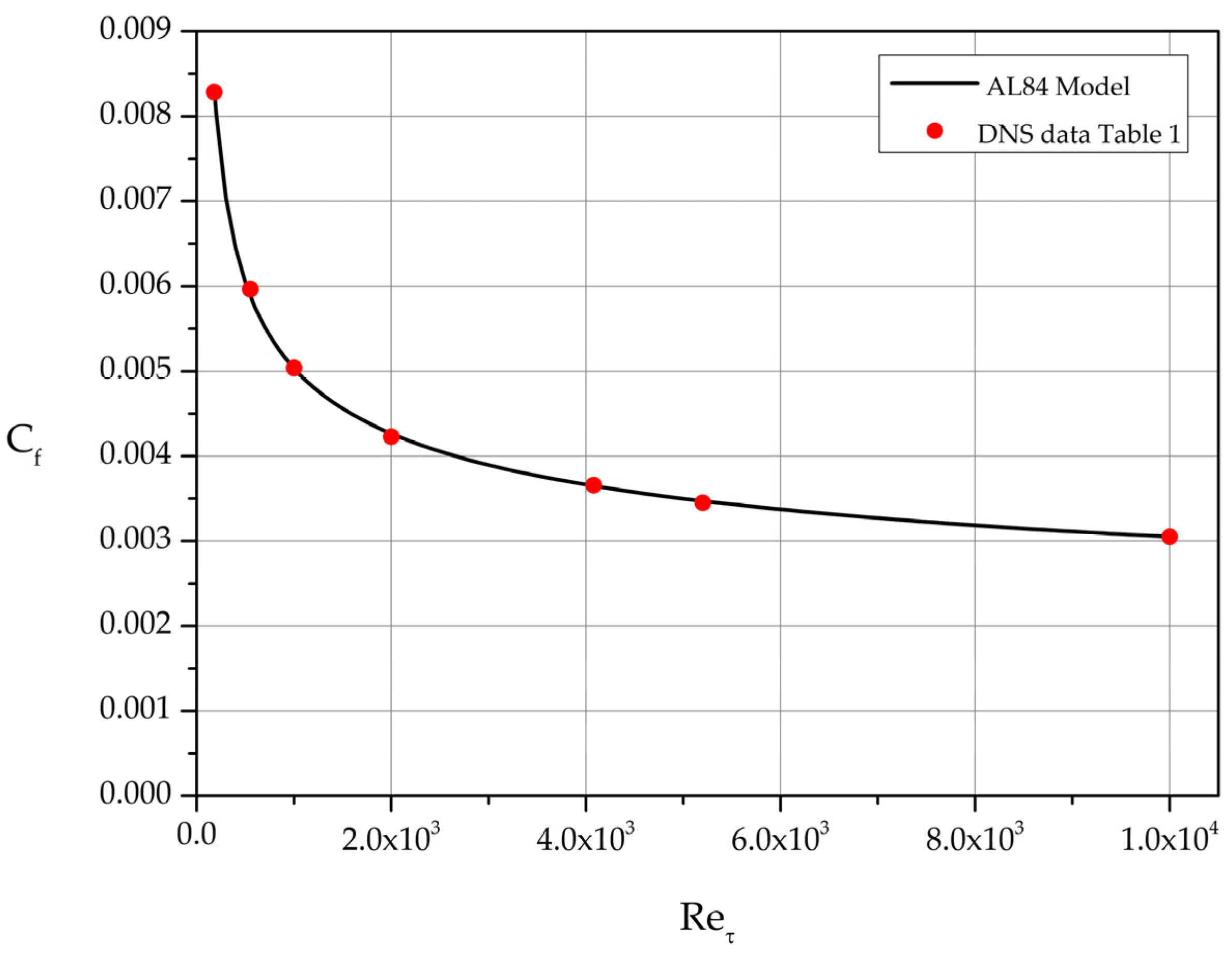
4.2. Cf based on AL84

Comparing AL84-based results with those based solely on DNS we find that the agreement is excellent. The analytically computed C f curve passes exactly through the filled circles representing the C f values calculated directly from the datasets of Table 1 (see Figure 20).

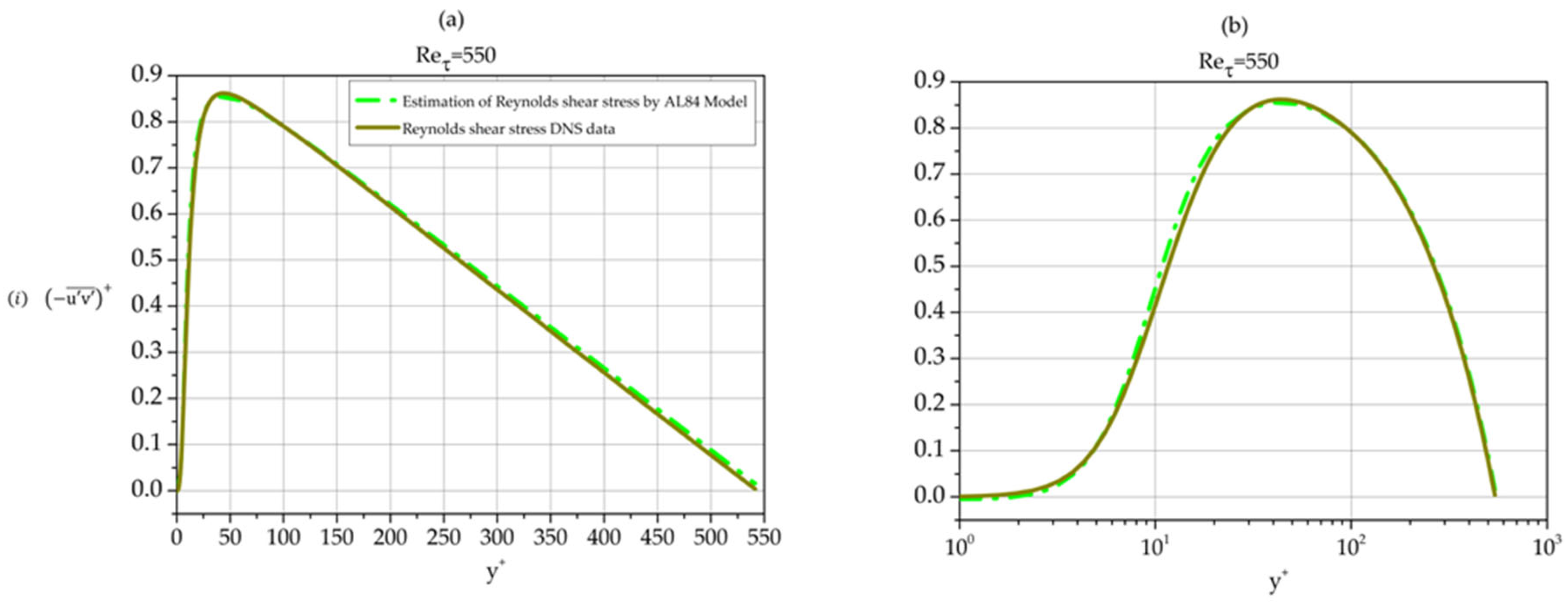
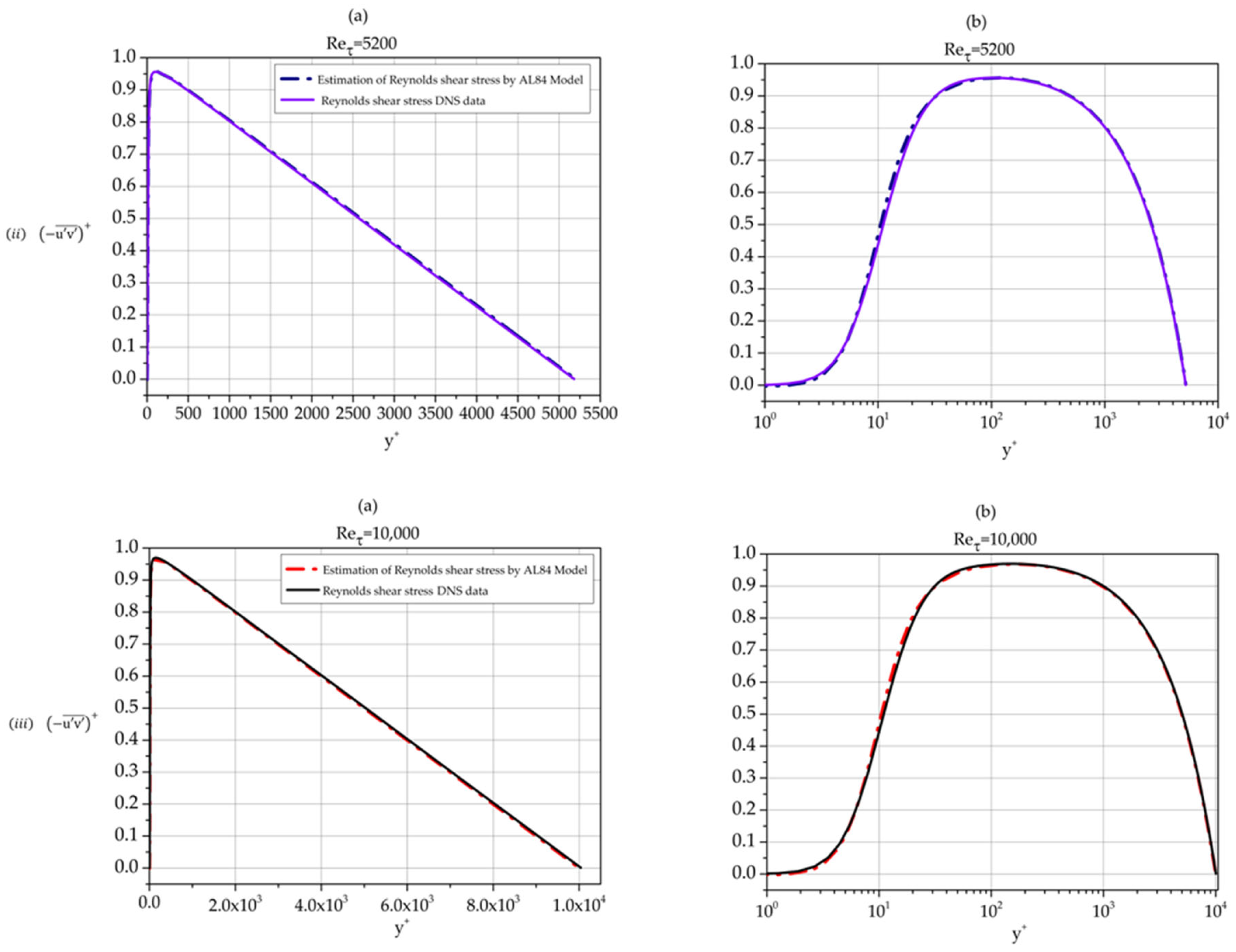
4.3. Reynolds Shear Stress ( − u ' v ' ¯ )

Using Equation (5), the covariance of fluctuations u ′ and v ′ as function of the distance from the wall can be calculated providing us with an AL84-based analytic approximation of the Reynolds shear stress profile. Such profiles are shown in Figure 21 together with DNS Reynolds shear stress data per se for three Reynolds numbers.
The approximation is excellent in all three cases. We note that the approximation is best for the moderate Reynolds number R e τ = 5200 while the agreement between AL84 prediction and DNS data for R e τ = 10,000 is better than the one for the low Reynolds number case R e τ = 550.

5. Conclusions

In the first part of the paper, we concentrated on high accuracy DNS datasets in the range 180 ≤   R e τ   ≤ 10,000. We have identified logarithmic regions in the mean velocity profiles and the corresponding values of the von Kármán constant for each Reynolds number based on the diagnostic function Ξ. Kármán constant estimates based on the DNS data range from κ  = 0.429 for 550 ≤   R e τ   ≤ 2000 to κ  = 0.388 for 4179 ≤   R e τ   ≤ 10,000. Similarly, based on the diagnostic function Γ, we identified the intervals where the power law approximates well the MVP and determined the corresponding exponent as function of the Reynolds number which ranges from 1/6 to 1/9. The calculated skin friction coefficient differs slightly from Dean’s least squares fit of selected measurements of high Reynolds number flows in channels with cross section aspect ratio greater than 1:12.
For the higher order statistics, we have determined the logarithmic regions in the variance profiles of streamwise u ′ u ′ ¯ + and spanwise w ′ w ′ ¯ + fluctuations and the corresponding values of the Townsend-Perry constants. We have listed logarithmic regions beyond the one expected by the Townsend’s attached eddy hypothesis. In the region 150 ≲ y + ≲   450 the variance of the wall-normal fluctuations v ′ v ′ ¯ + takes the value B v = 1.30 for R e τ = 8016 and 10,000. The peak values of the u ′ u ′ ¯ + , w ′ w ′ ¯ + , v ′ v ′ ¯ + , k m a x + have been approximated as functions of R e τ with logarithmic dependence. In contradistinction, the normalized Reynolds shear stress attains a constant value (approximately ≈ 0.96) in the interval 100 ≲ y +   ≲   250 for R e τ higher than 8000.
In the second part of the paper, a data-driven model (AL84), developed for ZPG-TBL, is calibrated for pressure-driven channel flow. It is shown that AL84 describes very accurately the mean velocity profile as well as the Reynolds shear stress profile for pressure-driven channel flow. In the framework of AL84 the skin friction coefficient is expressed analytically as function of R e τ and in various comparisons is in excellent agreement with the DNS data least squared fits.
The AL84-Model accuracy can be further improved, and its range of applicability can be extended as higher Reynolds number DNS data become available. We expect that the accuracy of the AL84 model will be further enhanced since it incorporates the logarithmic law in the overlap region of the boundary layer which is expected to be approached asymptotically as Re → ∞ . We conclude that, in addition to its pertinence to theoretical developments and in providing guidance in searching for the asymptotic structure of turbulent boundary layers, AL84 is useful in developing and calibrating turbulence models of the flow very near to the wall [39].

Acknowledgments

This research project was supported by the Hellenic Foundation for Research and Innovation (H.F.R.I.) under the “2nd Call for H.F.R.I. Research Projects to support Faculty Members & Researchers” (Project Number: 4584).

References

  1. Lee, M.; Moser, R. D. Direct numerical simulation of turbulent channel flow up to Reτ = 5200. Journal of fluid mechanics 2015, 774, 395–415. [Google Scholar] [CrossRef]
  2. Bernardini, M.; Pirozzoli, S.; Orlandi, P. Velocity statistics in turbulent channel flow up to Reτ = 4000. Journal of Fluid Mechanics 2014, 742, 171–191. [Google Scholar] [CrossRef]
  3. Lozano-Durán, A.; Jiménez, J. Effect of the computational domain on direct simulations of turbulent channels up to Reτ = 4200. Physics of Fluids 2014, 26, 26. [Google Scholar] [CrossRef]
  4. Yamamoto, Y.; Tsuji, Y. Numerical evidence of logarithmic regions in channel flow at Reτ = 8000. Physical Review Fluids 2018, 3, 012602. [Google Scholar] [CrossRef]
  5. Hoyas, S.; Oberlack, M.; Alcántara-Ávila, F.; Kraheberger, S. V.; Laux, J. Wall turbulence at high friction Reynolds numbers. Physical Review Fluids 2022, 7, 014602. [Google Scholar] [CrossRef]
  6. Liakopoulos, A. Explicit representations of the complete velocity profile in a turbulent boundary layer. AIAA Journal 1984, 22, 844–846. [Google Scholar] [CrossRef]
  7. Liakopoulos, A.; Palasis, A. On the Composite Velocity Profile in Zero Pressure Gradient Turbulent Boundary Layer: Comparison with DNS Datasets. Fluids 2023, 8, 260. [Google Scholar] [CrossRef]
  8. Liakopoulos, A. Fluid Mechanics., 2nd ed.; Tziolas Publications: Thessaloniki, Greece, 2019; ISBN 978-960-418-774-4. (in Greek) [Google Scholar]
  9. Dean, R. B. Reynolds number dependence of skin friction and other bulk flow variables in two-dimensional rectangular duct flow. J. Fluids Eng. 1978, 100, 215–223. [Google Scholar] [CrossRef]
  10. Zanoun, E. S.; Nagib, H.; Durst, F. Refined Cf relation for turbulent channels and consequences for high-Re experiments. Fluid dynamics research 2009, 41, 021405–10. [Google Scholar] [CrossRef]
  11. Di Nucci, C.; Absi, R. Comparison of Mean Properties of Turbulent Pipe and Channel Flows at Low-to-Moderate Reynolds Numbers. Fluids 2023, 8, 97. [Google Scholar] [CrossRef]
  12. Millikan, C. B. A Critical discussion of turbulent flows in channels and circular tubes. Proc. Fifth Intern. Congr. Appl. Mech., Cambridge, Massachusetts, 12-16 September 1938.
  13. Landau, L.D.; Lifshitz, E.M. Fluid Mechanics: Course of Theoretical Physics, Volume 6, 2nd ed.; Pergamon Press: Oxford, United Kingdom, 1987; ISBN 0-08-033933-6. [Google Scholar]
  14. Zagarola, M. V.; Smits, A. J. Mean-flow scaling of turbulent pipe flow. Journal of Fluid Mechanics 1998, 373, 33–79. [Google Scholar] [CrossRef]
  15. McKeon, B. J.; Zagarola, M. V.; Smits, A. J. A new friction factor relationship for fully developed pipe flow. Journal of fluid mechanics 2005, 538, 429–443. [Google Scholar] [CrossRef]
  16. Fiorini, T. Turbulent pipe flow-high resolution measurements in CICLoPE. Dissertation Thesis, Alma Mater Studiorum Università di Bologna, 4 May 2017. Available online: http://amsdottorato.unibo.it/8158/1/Fiorini_Tommaso_tesi.pdf.
  17. Marusic, I.; Monty, J. P.; Hultmark, M.; Smits, A. J. On the logarithmic region in wall turbulence. Journal of Fluid Mechanics 2013, 716, R3. [Google Scholar] [CrossRef]
  18. Smits, A. J.; McKeon, B. J.; Marusic, I. High-Reynolds number wall turbulence. Annu. Rev. Fluid Mech 2011, 43, 353–375. [Google Scholar] [CrossRef]
  19. Oberlack, M. Asymptotic Expansion, Symmetry Groups, and Invariant Solutions of Laminar and Turbulent Wall ----- Bounded Flows. ZAMM ----- Zeitschrift für Angewandte Mathematik und Mechanik. Journal of Applied Mathematics and Mechanics 2000, 80, 791–800. [Google Scholar] [CrossRef]
  20. Hultmark, M.; Vallikivi, M.; Bailey, S. C. C.; Smits, A. J. Turbulent pipe flow at extreme Reynolds numbers. Physical review letters 2012, 108, 094501. [Google Scholar] [CrossRef]
  21. Schultz, M. P.; Flack, K. A. Reynolds-number scaling of turbulent channel flow. Physics of Fluids 2013, 25. [Google Scholar] [CrossRef]
  22. Palasis, A. Turbulent Boundary Layers: Analysis of DNS Data. Diploma Thesis, Department of Civil Engineering, University of Thessaly, 31 August 2021. (in Greek). [Google Scholar]
  23. Barenblatt, G. I.; Chorin, A. J.; Prostokishin, V. M. Scaling laws for fully developed turbulent flow in pipes. Applied Mechanics Reviews 1997, 50, 413–429. [Google Scholar] [CrossRef]
  24. Barenblatt, G. I.; Chorin, A. J.; Hald, O. H.; Prostokishin, V. M. Structure of the zero-pressure-gradient turbulent boundary layer. Proceedings of the National Academy of Sciences 1997, 94, 7817–7819. [Google Scholar] [CrossRef]
  25. Barenblatt, G. I.; Chorin, A. J.; Prostokishin, V. M. On the problem of turbulent flows in pipes at very large Reynolds numbers. Physics-Uspekhi 2015, 58, 199–10. [Google Scholar] [CrossRef]
  26. Zanoun, E. S.; Durst, F.; Nagib, H. Evaluating the law of the wall in two-dimensional fully developed turbulent channel flows. Physics of fluids 2003, 15, 3079–3089. [Google Scholar] [CrossRef]
  27. Afzal, N.; Seena, A.; Bushra, A. Friction factor power law with equivalent log law, of a turbulent fully developed flow, in a fully smooth pipe. Zeitschrift für angewandte Mathematik und Physik 2023, 74, 144. [Google Scholar] [CrossRef]
  28. Marusic, I.; Monty, J. P. Attached eddy model of wall turbulence. Annual Review of Fluid Mechanics 2019, 51, 49–74. [Google Scholar] [CrossRef]
  29. Laval, J. P.; Vassilicos, J. C.; Foucaut, J. M.; Stanislas, M. Comparison of turbulence profiles in high-Reynolds-number turbulent boundary layers and validation of a predictive model. Journal of Fluid Mechanics 2017, 814, R2. [Google Scholar] [CrossRef]
  30. Vassilicos, J. C.; Laval, J. P.; Foucaut, J. M.; Stanislas, M. The streamwise turbulence intensity in the intermediate layer of turbulent pipe flow. Journal of Fluid Mechanics 2015, 774, 324–341. [Google Scholar] [CrossRef]
  31. Meneveau, C.; Marusic, I. Generalized logarithmic law for high-order moments in turbulent boundary layers. Journal of Fluid Mechanics 2013, 719, R1. [Google Scholar] [CrossRef]
  32. Monty, J. P.; Chong, M. S. Turbulent channel flow: comparison of streamwise velocity data from experiments and direct numerical simulation. Journal of Fluid Mechanics 2009, 633, 461–474. [Google Scholar] [CrossRef]
  33. Townsend, A.A.R. The structure of turbulent shear flow., 2nd ed.; Cambridge University Press: Cambridge, United Kingdom, 1976; ISBN 9780521298193. [Google Scholar]
  34. Chesnokov, Y. G. Influence of the reynolds number on the plane-channel turbulent flow of a fluid. Technical Physics 2010, 55, 1741–1747. [Google Scholar] [CrossRef]
  35. Chesnokov, Y. G. Influence of the Reynolds Number on the Distribution of Turbulent Pulsation Kinetic Energy over a Channel’s Cross Section. Technical Physics 2019, 64, 790–795. [Google Scholar] [CrossRef]
  36. Hoyas, S.; Jiménez, J. Reynolds number effects on the Reynolds-stress budgets in turbulent channels. Physics of Fluids 2008, 20. [Google Scholar] [CrossRef]
  37. Landahl, M. T.; Mollo-Christensen, E. Turbulence and random processes in fluid mechanics, 2nd ed.; Cambridge University Press: Cambridge, New York, 1992; ISBN 978-0521422130. [Google Scholar]
  38. Coles, D. The law of the wake in the turbulent boundary layer. Journal of Fluid Mechanics 1956, 1, 191–226. [Google Scholar] [CrossRef]
  39. Liakopoulos, A. Computation of high speed turbulent boundary-layer flows using the k–ϵ turbulence model. International Journal for Numerical Methods in Fluids 1985, 5, 81–97. [Google Scholar] [CrossRef]
Preprints 98331 g002
Figure 2. Mean velocity profiles expressed in law of the wall variables.
Figure 2. Mean velocity profiles expressed in law of the wall variables.
Preprints 98331 g002
Preprints 98331 g003
Figure 3. Mean velocity profiles expressed in velocity-defect law variables.
Figure 3. Mean velocity profiles expressed in velocity-defect law variables.
Preprints 98331 g003
Preprints 98331 g004
Figure 4. Skin friction coefficient as function of R e τ .
Figure 4. Skin friction coefficient as function of R e τ .
Preprints 98331 g004
Preprints 98331 g005
Figure 5. Relation between R e τ and R e b .
Figure 5. Relation between R e τ and R e b .
Preprints 98331 g005
Preprints 98331 g006
Figure 6. Comparison of DNS-based Equation (10) with Dean’s formula, Equation (11).
Figure 6. Comparison of DNS-based Equation (10) with Dean’s formula, Equation (11).
Preprints 98331 g006
Preprints 98331 g007
Figure 7. Dependence of the alternate skin friction coefficient C f ^ on Reτ.
Figure 7. Dependence of the alternate skin friction coefficient C f ^ on Reτ.
Preprints 98331 g007
Preprints 98331 g008
Figure 8. Least squares fit of ξ versus R e τ .
Figure 8. Least squares fit of ξ versus R e τ .
Preprints 98331 g008
Preprints 98331 g009
Figure 9. Diagnostic function Ξ based on DNS datasets of Table 1.
Figure 9. Diagnostic function Ξ based on DNS datasets of Table 1.
Preprints 98331 g009
Preprints 98331 g010
Figure 10. Kármán constant estimates.
Figure 10. Kármán constant estimates.
Preprints 98331 g010
Preprints 98331 g011
Figure 11. Diagnostic function Γ based on the DNS datasets of Table 1.
Figure 11. Diagnostic function Γ based on the DNS datasets of Table 1.
Preprints 98331 g011
Preprints 98331 g012
Figure 12. Second order statistics of turbulence fluctuations for Reτ = 5200. All data are normalized with u * 2 . Case: LM5200.
Figure 12. Second order statistics of turbulence fluctuations for Reτ = 5200. All data are normalized with u * 2 . Case: LM5200.
Preprints 98331 g012
Preprints 98331 g013
Figure 13. Streamwise fluctuations. Normalized variance profiles.
Figure 13. Streamwise fluctuations. Normalized variance profiles.
Preprints 98331 g013
Preprints 98331 g014
Figure 14. Normalized spanwise fluctuations. Variance profiles.
Figure 14. Normalized spanwise fluctuations. Variance profiles.
Preprints 98331 g014
Preprints 98331 g015
Figure 15. Normalized wall-normal fluctuations. Variance profiles.
Figure 15. Normalized wall-normal fluctuations. Variance profiles.
Preprints 98331 g015
Preprints 98331 g016
Figure 16. Normalized turbulence kinetic energy profiles.
Figure 16. Normalized turbulence kinetic energy profiles.
Preprints 98331 g016
Preprints 98331 g017
Figure 17. Normalized covariance profiles of streamwise and wall-normal fluctuations in law of the wall variables.
Figure 17. Normalized covariance profiles of streamwise and wall-normal fluctuations in law of the wall variables.
Preprints 98331 g017
Preprints 98331 g018
Figure 18. Normalized covariance profiles of the streamwise and wall-normal fluctuations in law of the wall variables.
Figure 18. Normalized covariance profiles of the streamwise and wall-normal fluctuations in law of the wall variables.
Preprints 98331 g018
Preprints 98331 g019
Figure 19. Profiles of relative error in u+ computed with AL84.
Figure 19. Profiles of relative error in u+ computed with AL84.
Preprints 98331 g019
Preprints 98331 g020
Figure 20. Skin friction coefficient Cf. Comparison of AL84 model predictions with Cf computed for the DNS datasets of Table 1.
Figure 20. Skin friction coefficient Cf. Comparison of AL84 model predictions with Cf computed for the DNS datasets of Table 1.
Preprints 98331 g020
Preprints 98331 g021aPreprints 98331 g021b
Figure 21. Normalized Reynolds shear stress profiles. Comparison of AL84-based calculation with DNS data per se. (i) Reτ = 550 (ii) Reτ = 5200 and (iii) Reτ = 10,000. (a) linear-linear plots (b) semi log plots.
Figure 21. Normalized Reynolds shear stress profiles. Comparison of AL84-based calculation with DNS data per se. (i) Reτ = 550 (ii) Reτ = 5200 and (iii) Reτ = 10,000. (a) linear-linear plots (b) semi log plots.
Preprints 98331 g021aPreprints 98331 g021b
Table 1. Datasets analyzed in the present study. R e τ = u * h / ν .
Table 1. Datasets analyzed in the present study. R e τ = u * h / ν .
Case Datasets Reτ
LM180 Lee and Moser, 2015 [1] 180
LM550 Lee and Moser, 2015 [1] 550
LM1000 Lee and Moser, 2015 [1] 1000
LM2000 Lee and Moser, 2015 [1] 2000
BPO4079 Bernardini, Pirozzoli and Orlandi, 2014 [2] 4079
LDJ4179 Lozano-Durán and Jiménez, 2014 [3] 4179
LM5200 Lee and Moser, 2015 [1] 5200
YT8016 Yamamoto and Tsuji, 2018 [4] 8016
HO10,000 Hoyas, Oberlack et al., 2022 [5] 10,000
Table 2. Reynolds number dependence of ξ = u m a x + − V ¯ + .
Table 2. Reynolds number dependence of ξ = u m a x + − V ¯ + .
Case Reτ ξ
LM180 180 2.73
LM550 550 2.69
LM1000 1000 2.67
LM2000 2000 2.65
BPO4079 4079 2.57
LM5200 5200 2.50
HO10,000 10,000 2.41
Table 3. Estimation of Kármán constant.
Table 3. Estimation of Kármán constant.
Case Reτ κ [ y l o w + , y h i g h + ] [(y/h)low , (y/h)high]
LM180 180 0.40 [52 , 72] [0.29 , 0.40]
LM550 550 0.429 [65 , 75] [0.12 , 0.14]
LM1000 1000 0.429 [70 , 95] [0.07 , 0.095]
LM2000 2000 0.429 [75 , 100] [0.0375 , 0.05]
LDJ4179 4179 0.385 [550 , 750] [0.13 , 0.18]
LM5200 5200 0.383 [400 , 800] [0.08 , 0.15]
YT8016 8016 0.386 [500 , 1100] [0.06 , 0.14]
HO10,000 10,000 0.397 [1000 , 2400] [0.1 , 0.24]
Table 4. Estimates of the λ exponent in the power-law Equation (15).
Table 4. Estimates of the λ exponent in the power-law Equation (15).
Case Reτ λ [ y l o w + , y h i g h + ] [(y/h)low , (y/h)high]
LM180 180 0.156 (≈1/6) [60 , 110] [0.33 , 0.61]
LM550 550 0.153 (≈1/7) [80 , 200] [0.15 , 0.37]
LM1000 1000 0.148 (≈1/7) [100 , 550] [0.10 , 0.55]
LM2000 2000 0.139 (≈1/7) [100 , 1000] [0.05 , 0.50]
LDJ4179 4179 0.115 (≈1/9) [1000 , 1500] [0.24 , 0.36]
LM5200 5200 0.117 (≈1/9) [800 , 3200] [0.15 , 0.62]
YT8016 8016 0.114 (≈1/9) [1200 , 4500] [0.15 , 0.56]
HO10,000 10,000 0.11 (≈1/9) [2000 , 6500] [0.20 , 0.65]
Table 5. u ′ u ′ ¯ + . Estimates of Townsend-Perry parameters.
Table 5. u ′ u ′ ¯ + . Estimates of Townsend-Perry parameters.
Case A1 B1 “Region” (y+) “Region” (y/h)
HO10,000 1.56 1.45 [1200 ----- 2000] [0.119 ----- 0.199]
YT8016 1.65 1.24 [1200 ----- 2000] [0.149 ----- 0.249]
HO10,000 1.76 1.13 [2000 ----- 3000] [0.199 ----- 0.299]
YT8016 1.83 0.98 [2000 ----- 2800] [0.249 ----- 0.349]
HO10,000 1.91 0.93 [3400 ----- 4000] [0.339 ----- 0.398]
HO10,000 2.01 0.85 [4000 ----- 5400] [0.398 ----- 0.538]
YT8016 2.07 0.72 [4000 ----- 4800] [0.499 ----- 0.599]
HO10,000 2.42 0.63 [6400 ----- 7000] [0.637 ----- 0.697]
Table 6. w ′ w ′ ¯ + . Estimates of Townsend-Perry parameters.
Table 6. w ′ w ′ ¯ + . Estimates of Townsend-Perry parameters.
Case D1 C1 “Region” (y+) “Region” (y/h)
YT8016 0.31 1.37 [140 ----- 260] [0.0175 ----- 0.032]
HO10,000 0.35 2 [150 ----- 400] [0.015 ----- 0.04]
LM5200 0.41 1.04 [200 ----- 500] [0.04 ----- 0.096]
LM2000 0.47 0.82 [180 ----- 400] [0.09 ----- 0.20]
YT8016 0.50 0.85 [1100 ----- 1500] [0.137 ----- 0.187]
HO10,000 0.50 0.80 [1400 ----- 2000] [0.139 ----- 0.199]
HO10,000 0.90 0.42 [5400 ----- 6200] [0.538 ----- 0.617]
LM5200 0.99 0.35 [3100 ----- 3500] [0.598 ----- 0.676]
LM2000 0.99 0.32 [1270 ----- 1400] [0.635 ----- 0.70]
YT8016 1.01 0.34 [4600 ----- 4900] [0.574 ----- 0.611]
Table 7. Reynolds number effect on k m a x + .
Table 7. Reynolds number effect on k m a x + .
Case Reτ k m a x + y + location   of   k m a x +
LM180 180 4.15 15.84
LM550 550 4.72 15.87
LM1000 1000 5.08 17.45
LM2000 2000 5.44 17.45
LM5200 5200 5.87 18.66
YT8016 8016 5.81 18.96
HO10,000 10,000 6.09 18.98
Table 8. Logarithmic behavior regions in k + = k / u * 2 .
Table 8. Logarithmic behavior regions in k + = k / u * 2 .
Case F1 E1 “Region” (y+) “Region” (y/h)
HO10,000 1.03 1.73 [1200 ----- 1300] [0.119 ----- 0.129]
YT8016 1.18 1.45 [1400 ----- 1600] [0.175 ----- 0.20]
HO10,000 1.35 1.21 [2850 ----- 3000] [0.284 – 0.299]
YT8016 1.40 1.13 [2350 ----- 2450] [0.293 ----- 0.306]
HO10,000 1.74 0.86 [5100 ----- 5350] [0.508 ----- 0.532]
YT8016 1.79 0.76 [3600 ----- 4200] [0.449 ----- 0.524]
HO10,000 1.99 0.72 [6500 ----- 7300] [0.647 ----- 0.727]
Table 9. Estimates of Coles’ parameter Π for channel flow.
Table 9. Estimates of Coles’ parameter Π for channel flow.
Case Reτ Π (Coles’ parameter)
LM180 180 0.10
LM550 550 0.14
LM1000 1000 0.14
LM2000 2000 0.14
BPO4079 4179 0.13
LM5200 5200 0.13
HO10,000 10,000 0.10
Table 10. Maximum local relative error in AL84-based u+.
Table 10. Maximum local relative error in AL84-based u+.
Reτ 180 550 1000 2000 4079 5200 10,000
Max relative error 0.057 0.036 0.035 0.032 0.023 0.031 0.028
Position y+, where max appears 25.69 25.70 26.46 27.20 26.97 27.33 27.02
Table 11. Statistics of absolute error in the lower half of the channel 0 ≤ y ≤ h.
Table 11. Statistics of absolute error in the lower half of the channel 0 ≤ y ≤ h.
Statistics Reτ = 180 Reτ = 550 Reτ = 1000
Mean 0.2708 0.0535 0.0861
Standard Error 0.0277 0.0127 0.0078
Root Mean Square Error 0.3827 0.1834 0.1518
Mean Square Deviation 0.2719 0.1759 0.1253
Variance 0.0739 0.0309 0.0157
Range 0.8101 0.5841 0.4792
Min −0.0397 −0.1040 −0.0220
Max 0.7704 0.4801 0.4572
Number of data points 96 192 256
Statistics Reτ = 2000 Reτ = 4079 Reτ = 5200 Reτ = 10,000
Mean 0.1522 0.0873 0.1530 0.1049
Standard Error 0.0040 0.0030 0.0034 0.0036
Root Mean Square Error 0.1714 0.1105 0.1792 0.1561
Mean Square Deviation 0.0789 0.0679 0.0935 0.1156
Variance 0.0062 0.0046 0.0087 0.0134
Range 0.4498 0.2998 0.4316 0.3968
Min −0.0222 0.0009 −0.0237 −0.0283
Max 0.4276 0.3007 0.4079 0.3686
Number of data points 384 512 768 1051
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated