Prerpints.org logo
Preprint
Communication

Mean Adjusted Exponent (MADEX): A Novel Metric for the Evaluation of Blood Glucose Prediction Machine Learning Models

Altmetrics

Downloads

135

Views

58

Comments

0

Submitted:

25 January 2024

Posted:

26 January 2024

You are already at the latest version

Alerts
Abstract
A crucial aspect in developing machine learning algorithms (or any type of predictive models) is the comparison of different algorithmic candidates based on evaluation criteria that measure their accuracy and practical value in terms of successfully capturing the complexity of the underlying problem and generalizing in a wide range of real-world scenarios. In the domain of diabetes mellitus machine learning techniques are widely employed in the prediction of future values of glucose concentration in the blood in order to assist the patient in avoiding deviations from the normo-glycemic value range and the consequences of hyper- and hypoglycemia. In the relative literature there is an apparent lack of a uniformly adopted evaluation metric which could combine the clarity and direct comparative nature of statistical mathematical formulas dealing with prediction error residuals (e.g., the RMSE) with the clinical insights and the visual-qualitative approach of clinical evaluation tools (e.g., Clarke's EGA). Mean Adjusted Exponent (MADEX) error metric, proposed in this paper, attempts to address this need by providing a validation tool based on an easy to implement mathematical formula, that incorporates adjustable parameters of clinical significance.
Keywords: 
Subject: Public Health and Healthcare  -   Other

1. Introduction

Due to various reasons, Diabetes Mellitus (DM) worldwide prevalence has been on a constant and alarming rise during the past decades. This trend is expected to continue unhindered for the years to come. Recent data [1,2,3] show that almost one in ten adults (~537 million) are living with the disease, and this number is expected to increase to 643 and 783 million by the years 2030 and 2045, respectively. In addition, another 541 million adults are affected by Impaired Glucose Tolerance (IGT), being at high risk of developing diabetes in the following years.
The hypothesis that there is an excess risk link between diabetes and cancer is not new in the literature [4], for both Type 1 and Type 2 DM patients [5] and it remains an active field of scientific investigation [6]. Cancer is one of the most common mortality causes for Type 1 DM [7] and its death risk has been shown to be increased in the presence of DM comorbidity [8,9]. This highly probable link arguably adds grave importance to the enrichment of the arsenal available to tackle the challenges of DM prevention, timely diagnosis and management.
In response to this situation and mainly fueled by data and computational resources availability and the rising adoption of medical Internet-of-Things in the last years, there has been a momentous production in machine learning/deep learning research, aspiring to address several aspects of the disease (onset and adverse events prediction/prevention, blood glucose levels regulation, etc.) [10,11,12] .
Often overlooked, the common denominator of every relative research effort is the need for reliable metrics that facilitate the absolute and relative/comparative assessment of the models under consideration and play a crucial role in the algorithms' training-evaluation workflow. After all, the applicability and success of a trained model in real world conditions is directly analogous to the proper assessment of its accuracy during the development and validation phase.
In the relevant literature, one observes various combinations of mathematical/statistical and clinical evaluation criteria, and the lack of uniformity is apparent. This can be mainly attributed to the fact that widely used mathematical evaluation metrics, generic by nature, do not give due consideration to the clinical implications of the results. In contrast, clinical evaluation tools like error grid analyses and expert comparisons do not promote easy comparison between the examined methods.

2. State of the Art

Woldaregay et al. [13] conducted a comprehensive literature review regarding the machine learning modelling strategies/techniques and reported that the most commonly used prediction/modelling performance evaluation tools, accounting for 80% of the included studies were the Root Mean Squared Error (36%), the Clarke Error Grid Analysis (19%), the Correlation Coefficient (12%), the Temporal Gain (8%) and the Mean Absolute Error (5%) [13].

2.1. Mathematical/Statistical Tools

2.1.1. Root Mean Squared Error (RMSE)

The Root Mean Squared Error – RMSE (1.2) measures the average error performed by the model in predicting the outcome for an observation. Mathematically, the RMSE is the square root of the Mean Squared Error – MSE (Eq. 1.1), which is the average squared difference between the observed actual outcome values and the values predicted by the model. The lower the RMSE, the better the model.
M S E = 1 N ∑ i = 1 N y i − y ^ 2
R M S E = M S E

2.1.2. Correlation Coefficient

The Correlation Coefficient (Pearson's r) measures the linear correlation (2) between the prediction ( Y ^ ) and the actual values (Y) datasets (cov: covariation, σ: standard deviation).
ρ Y , Y ^ = c o v ( Y , Y ^ ) σ Y σ Y ^
cov: covariation, σ: standard deviation

2.1.3. Mean Absolute Error

The Mean Absolute Error -MAE (3) is an arithmetic average of the absolute errors e i = y i − y ^ where y ^ is the prediction and y i the true value.
M A E = 1 N ∑ i = 1 N y i − y ^ 2

2.2. Clinical Tools

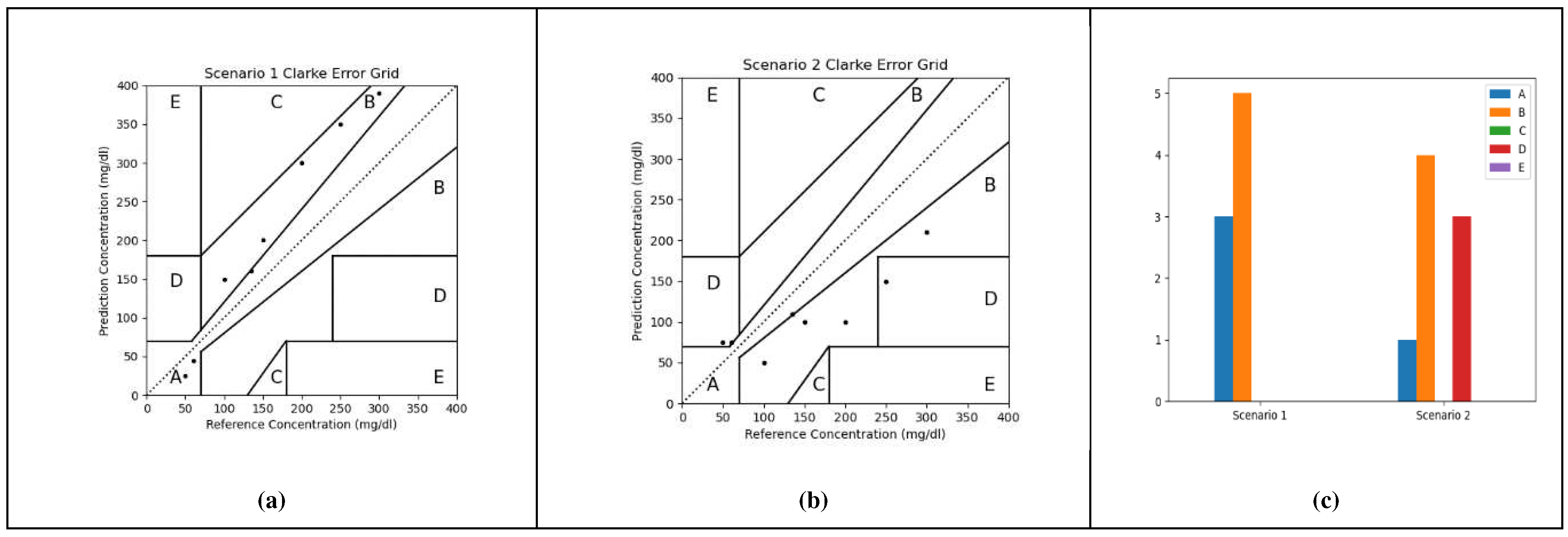
2.2.1. Clarke’s Error Grid Analysis (C-EGA)

The Clarke Error Grid Analysis (EGA) was developed in 1987 to quantify the clinical accuracy of patient estimates of their current blood glucose as compared to the blood glucose value obtained in their meter [14]. It was then used to quantify the clinical accuracy of blood glucose estimates generated by meters as compared to a reference value. A description of the EGA appeared in Diabetes Care in 1987. Eventually, the EGA became accepted as one of the “gold standards” for determining the accuracy of blood glucose meters.
The grid breaks down a scatterplot of a reference glucose meter and an evaluated glucose meter into five regions:
  • Region A: points within 20% deviation from of the reference value.
  • Region B: points outside 20% deviation but would not lead to inappropriate treatment.
  • Region C: points leading to unnecessary treatment.
  • Region D: points indicating a potentially dangerous failure to detect hypoglycemia or hyperglycemia.
  • Region E: points that would confuse the treatment of hypoglycemia for hyperglycemia and vice versa.

2.2.2. Parkes’ Error Grid Analysis

The consensus error grid (also known as the Parkes error grid) was developed as a new tool for evaluating the accuracy of a blood glucose meter. In recent times, the consensus error grid has been used increasingly by blood glucose meter manufacturers in their clinical studies. It was published in August 2000 [15].

3. Methods

3.1. Derivation of the Metric Equation

Adding clinical significance to the mathematical representation of the error function can be achieved by applying different weights on the residuals based on the clinical importance of the error in different situations. To achieve this, we defined the desirable behaviour as follows:
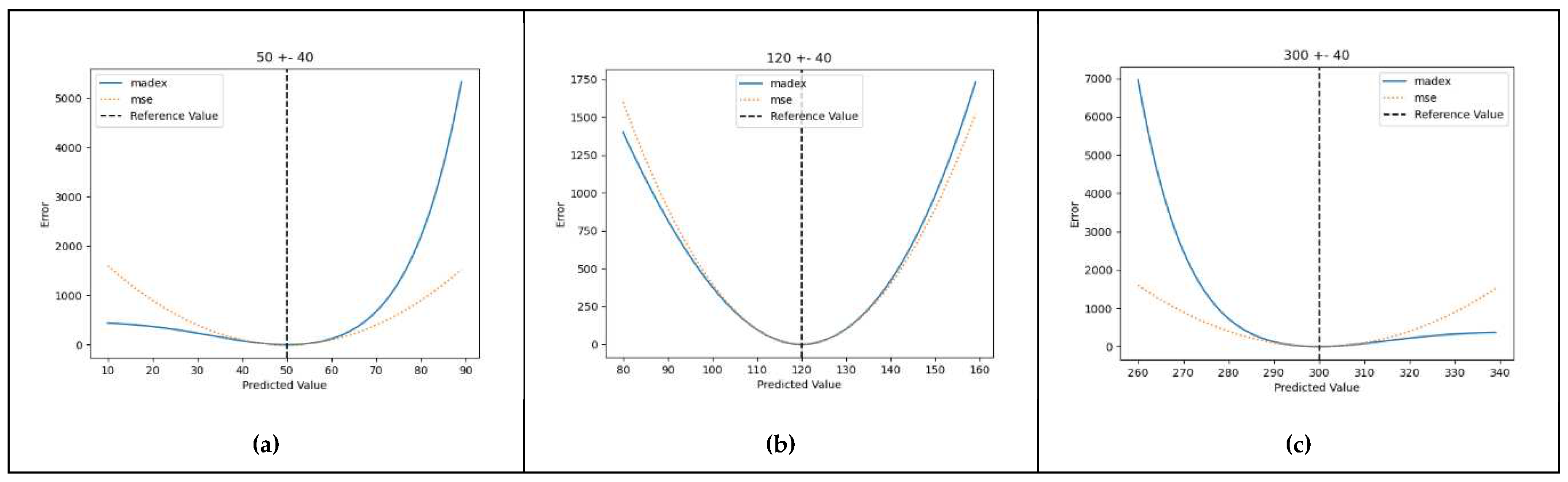
  • The penalizing power applied to the residuals should vary, getting bigger in proportion to the distance of the reference value from a certain point on the reference axis (the arithmetical center of the normal range). In this manner, the calculated error gets more prominent as the reference value moves away from the normal levels (euglycaemia).
  • The penalizing factor should be specific and behave differently based on the direction of the error. More specifically it should penalize more heavily values that provide a distorted evaluation of the reference glycaemic status, that is high predicted values when the true value is in the hypoglycaemic range, as well as low values when the true value is in the hyperglycaemic range.
Based on these preconditions, finding a suitable mathematical function with such behaviour suggests a member of the “S” shaped function family [16]. After testing several candidate functions, using as criteria i) the mathematical behavior and ii) the convenience of factoring in relevant clinical parameters, we derived the following metric (4):
M e a n A D j u s t e d E X p o n e n t E r r o r = 1 N ∑ i = 1 n y i ^ − y i e x p e x p = 2 − t a n h y i − a b × y i ^ − y i c , a :   c e n t e r ,   b : c r i t i c a l   r a n g e ,   c : s l o p e
Figure 1 shows the behaviour of the equation in three characteristic circumstances. We observe that when the reference value lies in the normal range (e.g., 120 mg/dL) the error calculation for both sides of the predicted value difference is almost identical with the respective MSE value. However, in the abnormal ranges the asymmetry and the difference from the MSE calculation is apparent: “deceptive” predicted values (lower than reference in the hyperglycemic range and higher than reference in the hypoglycemic range) are highly penalized.

3.2. Proof-Of-Concept Marginal Test

Checking the usefulness of the proposed approach requires considering mathematically marginal but clinically plausible scenarios in which MADEX metric performs better than existing “golden standard” alternatives, in terms of assessing successfully both mathematically and clinically a set of measures or modelling predictions. Table 2 shows the scenarios used for our testing purposes. Both scenarios’ scores are identical in terms of the MSE and RMSE metrics, 4321.88 and 65.74 respectively. However, their clinical evaluation is critically different, as shown in Figure 2. All the values in scenario 1 fall within ranges A and B (considered not to lead to inappropriate treatment), whilst a considerable proportion of the second scenario’s values (3 out of 7, ~43%) falls into range D (potentially dangerous).

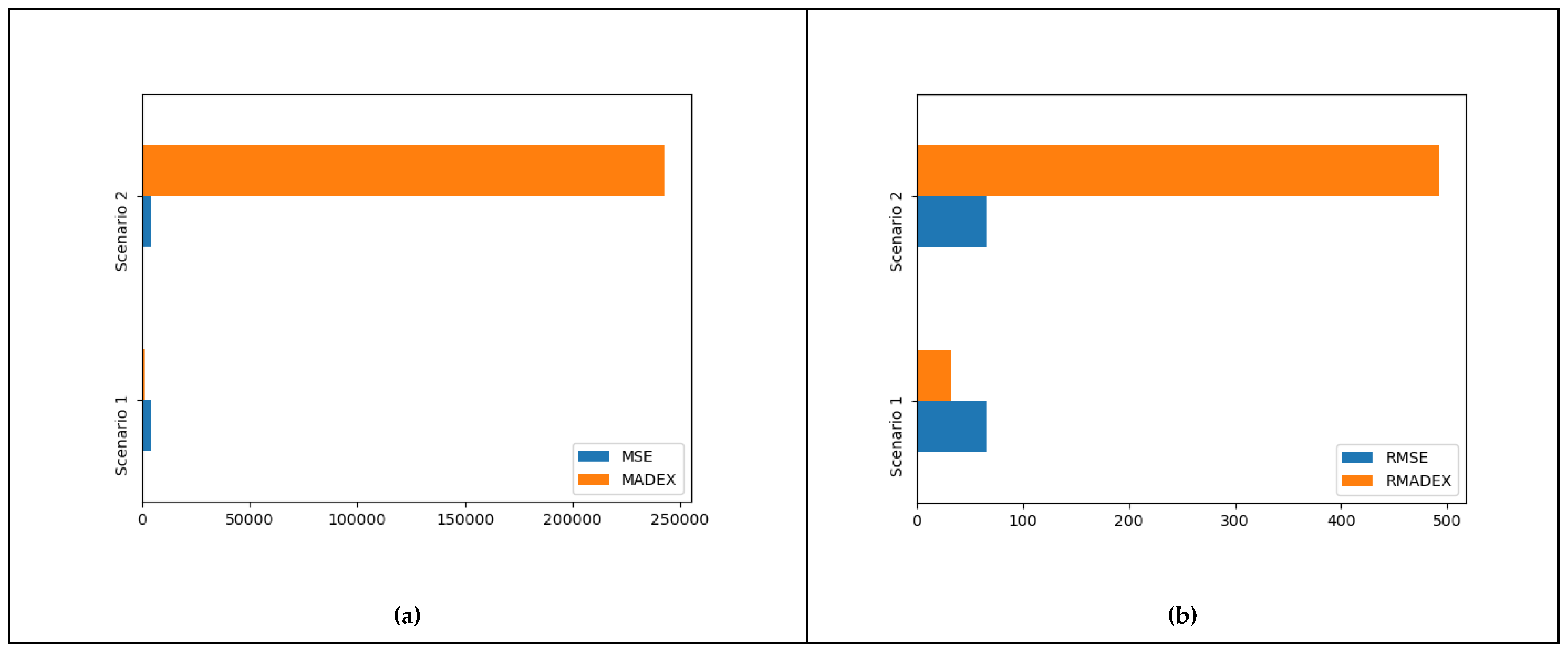
3.3. Preliminary Application on Real-World Data

In the context of author’s SP doctoral thesis [17] personalized blood glycose concentration prediction models were developed using real-world data from the OHIO-T1DM dataset [18], which contains data collected from six people with type 1 diabetes over eight weeks. All subjects were between 40 and 60 years old at the time of data collection. Two were men and four women.
For each combination of subject, time-window, and prediction horizon, a trial training takes place using a multitude of Regression Machine Learning algorithms and an ordered list is obtained on the axis of the performance dimension, as calculated based on a series of metrics. The PyCaret library [19], an open source library that facilitates machine learning workflows, manages the end-to-end process, significantly speeds up the experimental cycle, and ensures mistakes and/or omissions are avoided, was used to automate this process. In the table below (Table 3), there is a list of the Machine Learning algorithms, which are available in the model training and verification processes and were used in the experimental investigation and software development of the platform.
The main metric used for model assessment, to the extent that the desired estimate should take into account both the mathematical and clinical dimensions of the efficacy of the models under consideration, is that introduced in the context of this work, MADEX, and its square root (RMADEX).

4. Results

The values of the Proof-Of-Concept Test scenarios were explicitly chosen to depict a situation in which two models with the same performance based on the (R)MSE metrics could have very different clinical significance. Table 4 and Figure 3 show that in scenarios like this, the (R)MADEX metrics can capture the clinical context and penalize the model with the worse predictions clinical-wise accordingly.
As far as the application to real-world data is concerned, the following table (Table 5) gives an example of an “algorithm leaderboard” for one of the investigated patient cases:
The best and worst performing algorithms (LGBM and Dummy Regressors, respectively) in this example are the same for RMADEX and RMSE which is chosen as the “golden standard” comparison metric. However, there are evident differences in the ranking, as well as indicators of RMADEX’s clinical value. For example, the Linear Regression algorithm which is usually considered clinically underperforming, ranks 2nd (25.6) in the RMSE list, while only 9th (1860) in the RMADEX list.

5. Discussion

This approach, compared with the alternative of defining specific penalties to clinically defined regions of the reference-prediction value space, has apparent advantages, as follows:
  • It is a continuous function assuring smooth value progression and avoiding stepping phenomena
  • It is not dependent on clinical interpretations (a center of euglycemia is easier to agree upon)
  • It is computationally more efficient compared to algorithms with conditional (if_then_else, switch case) arguments
One of MADEX's interesting features is that it could, in theory, apply to medical domains totally different from diabetes, as it could be parametrized to handle, instead of blood glucose concentration, any quantity (e.g., biomarkers or in-vitro biochemical tests) whose value lies in a continuum with a centre and a range of "normality".
The main limitation of this work is that choosing the scenario data conveniently to facilitate the proof-of-concept of the MADEX metric does not guarantee its comparable performance in a real-data setting; thus, extended experimentation with real-world data and application in actual machine learning research workflows is warranted in order for MADEX to become established as a valuable tool in the arsenal of researchers, data scientists and machine learning practitioners.

6. Conclusions

This paper proposes a mathematical formula (MADEX) that can be used to assess machine learning predictive models for the future concentration of glucose in a patient's blood. This formula combines numerical error/residual calculation with clinical context, a property which, to the best of our knowledge, has not yet been proposed in the relevant literature. This work holds promise for modelling and prediction efforts in the domain of diabetes, as well as other medical domains with quantities that share common characteristics with blood glucose concentration. However, extensive testing by application in real-world data is warranted if MADEX should be promoted from its current proof-of-concept status to an actual item in the practitioner's toolset.

Author Contributions

Conceptualization, S.P.; methodology, software, S.P.; validation, A.A.; writing—original draft preparation, S.P.; writing—review and editing, A.A.; supervision, D.-D.K. All authors have read and agreed to the published version of the manuscript.

Funding

N/A.

Institutional Review Board Statement

N/A.

Informed Consent Statement

N/A.

Data Availability Statement

N/A.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. D. J. Magliano, E. J. Boyko, and I. D. A. 10th edition scientific committee, “IDF DIABETES ATLAS,” pp. 54–55, 2021.
  2. P. Saeedi et al., “Global and regional diabetes prevalence estimates for 2019 and projections for 2030 and 2045: Results from the International Diabetes Federation Diabetes Atlas, 9th edition,” Diabetes Res. Clin. Pract., vol. 157, p. 107843, Nov. 2019, doi: 10.1016/J.DIABRES.2019.107843.
  3. X. Lin et al., “Global, regional, and national burden and trend of diabetes in 195 countries and territories: an analysis from 1990 to 2025,” Sci. Rep. 2020 101, vol. 10, no. 1, pp. 1–11, Sep. 2020. [CrossRef]
  4. M. Greenwood and F. Wood, “The Relation between the Cancer and Diabetes Death-rates,” J. Hyg. (Lond.), vol. 14, no. 1, pp. 83–118, Apr. 1914. [CrossRef]
  5. Cignarelli et al., “Diabetes and cancer: Pathophysiological fundamentals of a ‘dangerous affair,’” Diabetes Res. Clin. Pract., vol. 143, pp. 378–388, Sep. 2018. [CrossRef]
  6. Zhu and S. Qu, “The Relationship Between Diabetes Mellitus and Cancers and Its Underlying Mechanisms,” Front. Endocrinol., vol. 13, 2022, Accessed: Dec. 04, 2023. [Online]. Available: https://www.frontiersin.org/articles/10.3389/fendo.2022.800995.
  7. S. J. Livingstone et al., “Estimated life expectancy in a Scottish cohort with type 1 diabetes, 2008-2010,” JAMA, vol. 313, no. 1, pp. 37–44, Jan. 2015. [CrossRef]
  8. K. K. Tsilidis, J. C. Kasimis, D. S. Lopez, E. E. Ntzani, and J. P. A. Ioannidis, “Type 2 diabetes and cancer: umbrella review of meta-analyses of observational studies,” BMJ, vol. 350, p. g7607, Jan. 2015. [CrossRef]
  9. Y. Chen et al., “Association between type 2 diabetes and risk of cancer mortality: a pooled analysis of over 771,000 individuals in the Asia Cohort Consortium,” Diabetologia, vol. 60, no. 6, pp. 1022–1032, Jun. 2017. [CrossRef]
  10. S. Ellahham, “Artificial Intelligence: The Future for Diabetes Care,” Am. J. Med., vol. 133, no. 8, pp. 895–900, Aug. 2020. [CrossRef]
  11. Dankwa-Mullan, M. Rivo, M. Sepulveda, Y. Park, J. Snowdon, and K. Rhee, “Transforming Diabetes Care Through Artificial Intelligence: The Future Is Here,” Popul. Health Manag., vol. 22, no. 3, pp. 229–242, Jun. 2019. [CrossRef]
  12. Nomura, M. Noguchi, M. Kometani, K. Furukawa, and T. Yoneda, “Artificial Intelligence in Current Diabetes Management and Prediction,” Curr. Diab. Rep., vol. 21, no. 12, Dec. 2021. [CrossRef]
  13. Z. Woldaregay et al., “Data-driven modeling and prediction of blood glucose dynamics: Machine learning applications in type 1 diabetes,” Artif. Intell. Med., vol. 98, pp. 109–134, Jul. 2019. [CrossRef]
  14. W. L. Clarke, D. Cox, L. A. Gonder-Frederick, W. Carter, and S. L. Pohl, “Evaluating clinical accuracy of systems for self-monitoring of blood glucose,” Diabetes Care, vol. 10, no. 5, pp. 622–628, 1987. [CrossRef]
  15. L. Parkes, S. L. Slatin, S. Pardo, and B. H. Ginsberg, “A new consensus error grid to evaluate the clinical significance of inaccuracies in the measurement of blood glucose,” Diabetes Care, vol. 23, no. 8, pp. 1143–1148, 2000. [CrossRef]
  16. “Sigmoid Function Definition | DeepAI.” Accessed: Apr. 18, 2022. [Online]. Available: https://deepai.org/machine-learning-glossary-and-terms/sigmoid-function.
  17. S. Pitoglou, PhD thesis 2023. Accessed: Dec. 23, 2023. [Online]. Available: http://artemis.cslab.ece.ntua.gr:8080/jspui/handle/123456789/18960.
  18. Marling and R. Bunescu, “The OhioT1DM dataset for blood glucose level prediction,” in CEUR Workshop Proceedings, 2018.
  19. “PyCaret 3.0.” Accessed: Dec. 01, 2023. [Online]. Available: https://pycaret.gitbook.io/docs/.
  20. “Linear regression,” Wikipedia. Oct. 23, 2023. Accessed: Oct. 24, 2023. [Online]. Available: https://en.wikipedia.org/w/index.php?title=Linear_regression&oldid=1181530004.
  21. “Linear regression | Definition, Formula, & Facts | Britannica.” Accessed: Oct. 24, 2023. [Online]. Available: https://www.britannica.com/topic/linear-regression.
  22. Zach, “Introduction to Lasso Regression,” Statology. Accessed: Oct. 24, 2023. [Online]. Available: https://www.statology.org/lasso-regression/.
  23. G. L. Team, “A Complete understanding of LASSO Regression,” Great Learning Blog: Free Resources what Matters to shape your Career! Accessed: Oct. 24, 2023. [Online]. Available: https://www.mygreatlearning.com/blog/understanding-of-lasso-regression/.
  24. “Ridge regression,” Wikipedia. Aug. 29, 2023. Accessed: Oct. 24, 2023. [Online]. Available: https://en.wikipedia.org/w/index.php?title=Ridge_regression&oldid=1172832572.
  25. “Tikhonov Regularization - an overview | ScienceDirect Topics.” Accessed: Oct. 24, 2023. [Online]. Available: https://www.sciencedirect.com/topics/computer-science/tikhonov-regularization.
  26. Friedman, T. Hastie, and R. Tibshirani, “Regularization Paths for Generalized Linear Models via Coordinate Descent,” J. Stat. Softw., vol. 33, no. 1, pp. 1–22, 2010.
  27. S.-J. Kim, K. Koh, M. Lustig, S. Boyd, and D. Gorinevsky, “An Interior-Point Method for Large-Scale \ell_1-Regularized Least Squares,” IEEE J. Sel. Top. Signal Process., vol. 1, no. 4, pp. 606–617, Dec. 2007. [CrossRef]
  28. Efron, T. Hastie, I. Johnstone, and R. Tibshirani, “Least angle regression,” Ann. Stat., vol. 32, no. 2, Apr. 2004. [CrossRef]
  29. S. G. Mallat and Z. Zhang, “Matching pursuits with time-frequency dictionaries,” IEEE Trans. Signal Process., vol. 41, no. 12, pp. 3397–3415, Dec. 1993. [CrossRef]
  30. R. Rubinstein, M. Zibulevsky, and M. Elad, “Efficient Implementation of the K-SVD Algorithm using Batch Orthogonal Matching Pursuit,” 2008. Accessed: Oct. 24, 2023. [Online]. Available: https://www.semanticscholar.org/paper/Efficient-Implementation-of-the-K-SVD-Algorithm-Rubinstein-Zibulevsky/7f98bd398a6b422e140b9cd83f0d64444f8dbca5.
  31. H. Zhu, W. Chen, and Y. Wu, “Efficient Implementations for Orthogonal Matching Pursuit,” Electronics, vol. 9, no. 9, Art. no. 9, Sep. 2020. [CrossRef]
  32. Pattern Recognition and Machine Learning. Accessed: Oct. 24, 2023. [Online]. Available: https://link.springer.com/book/9780387310732.
  33. J. C. MacKay, “Bayesian Interpolation,” Neural Comput., vol. 4, no. 3, pp. 415–447, 1992. [CrossRef]
  34. E. Tipping, “Sparse bayesian learning and the relevance vector machine,” J. Mach. Learn. Res., vol. 1, pp. 211–244, Sep. 2001. [CrossRef]
  35. Wipf and S. Nagarajan, “A new view of automatic relevance determination,” in Proceedings of the 20th International Conference on Neural Information Processing Systems, in NIPS’07. Red Hook, NY, USA: Curran Associates Inc., Dec. 2007, pp. 1625–1632.
  36. K. Crammer, O. Dekel, J. Keshet, S. Shalev-Shwartz, and Y. Singer, “Online Passive-Aggressive Algorithms,” J. Mach. Learn. Res., vol. 7, pp. 551–585, Dec. 2006.
  37. S. Choi, T. Kim, and W. Yu, “Performance Evaluation of RANSAC Family,” in Procedings of the British Machine Vision Conference 2009, London: British Machine Vision Association, 2009, p. 81.1-81.12. doi: 10.5244/C.23.81.
  38. A. Fischler and R. C. Bolles, “Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography,” Commun. ACM, vol. 24, no. 6, pp. 381–395, Jun. 1981. [CrossRef]
  39. “Random sample consensus,” Wikipedia. Oct. 11, 2023. Accessed: Oct. 24, 2023. [Online]. Available: https://en.wikipedia.org/w/index.php?title=Random_sample_consensus&oldid=1179652738.
  40. “Theil–Sen estimator,” Wikipedia. Sep. 20, 2023. Accessed: Oct. 24, 2023. [Online]. Available: https://en.wikipedia.org/w/index.php?title=Theil%E2%80%93Sen_estimator&oldid=1176301934.
  41. X. Wang, X. Dang, H. Peng, and H. Zhang, “THE THEIL-SEN ESTIMATORS IN A MULTIPLE LINEAR REGRESSION MODEL,” 2009. Accessed: Oct. 24, 2023. [Online]. Available: https://www.semanticscholar.org/paper/THE-THEIL-SEN-ESTIMATORS-IN-A-MULTIPLE-LINEAR-MODEL-Wang-Dang/63167c5dbb9bae6f0a269237a9b6a28fa7e1ac20.
  42. T. Kärkkäinen and S. Äyrämö, “ON COMPUTATION OF SPATIAL MEDIAN FOR ROBUST DATA MINING,” Accessed: Oct. 24, 2023. [Online]. Available: https://www.semanticscholar.org/paper/ON-COMPUTATION-OF-SPATIAL-MEDIAN-FOR-ROBUST-DATA-K%C3%A4rkk%C3%A4inen-%C3%84yr%C3%A4m%C3%B6/4db73e6aac3c7b7390a912ec0a6bbd9344622586.
  43. P. J. Huber and E. M. Ronchetti, Robust Statistics. John Wiley & Sons, 2011.
  44. K. P. Murphy, Machine Learning: A Probabilistic Perspective, Illustrated edition. Cambridge, MA: The MIT Press, 2012.
  45. J. Platt and N. Karampatziakis, “Probabilistic Outputs for SVMs and Comparisons to Regularized Likelihood Methods,” 2007. Accessed: Oct. 24, 2023. [Online]. Available: https://www.semanticscholar.org/paper/Probabilistic-Outputs-for-SVMs-and-Comparisons-to-Platt-Karampatziakis/18a72c64859a700c16685386514c30d70765a63e.
  46. “A tutorial on support vector regression | Statistics and Computing.” Accessed: Oct. 24, 2023. [Online]. Available: https://dl.acm.org/doi/10.1023/B%3ASTCO.0000035301.49549.88.
  47. “k-nearest neighbors algorithm,” Wikipedia. Sep. 27, 2023. Accessed: Oct. 24, 2023. [Online]. Available: https://en.wikipedia.org/w/index.php?title=K-nearest_neighbors_algorithm&oldid=1177452500.
  48. L. Breiman, J. H. Friedman, R. A. Olshen, and C. J. Stone, Classification and Regression Trees, vol. 19. 1984. doi: 10.1371/journal.pone.0015807.
  49. L. Breiman, “Random forests,” Mach. Learn., vol. 45, no. 1, pp. 5–32, 2001. [CrossRef]
  50. P. Geurts, D. Ernst, and L. Wehenkel, “Extremely randomized trees,” Mach. Learn., vol. 63, no. 1, pp. 3–42, Apr. 2006. [CrossRef]
  51. Y. Freund and R. E. Schapire, “A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting,” J. Comput. Syst. Sci., vol. 55, no. 1, pp. 119–139, Aug. 1997. [CrossRef]
  52. H. Drucker, “Improving Regressors using Boosting Techniques,” presented at the International Conference on Machine Learning, Jul. 1997. Accessed: Oct. 24, 2023. [Online]. Available: https://www.semanticscholar.org/paper/Improving-Regressors-using-Boosting-Techniques-Drucker/6d8226a52ebc70c8d97ccae10a74e1b0a3908ec1.
  53. J. H. Friedman, “Greedy function approximation: A gradient boosting machine.,” Ann. Stat., vol. 29, no. 5, pp. 1189–1232, Oct. 2001. [CrossRef]
  54. J. H. Friedman, “Stochastic gradient boosting,” Comput. Stat. Data Anal., vol. 38, no. 4, pp. 367–378, Feb. 2002. [CrossRef]
  55. T. Hastie, R. Tibshirani, and J. Friedman, The Elements of Statistical Learning. in Springer Series in Statistics. New York, NY: Springer, 2009. doi: 10.1007/978-0-387-84858-7.
  56. E. Hinton, “Connectionist learning procedures,” Artif. Intell., vol. 40, no. 1–3, pp. 185–234, Sep. 1989. [CrossRef]
  57. “Extreme Gradient Boosting - an overview | ScienceDirect Topics.” Accessed: Oct. 24, 2023. [Online]. Available: https://www.sciencedirect.com/topics/computer-science/extreme-gradient-boosting.
  58. Ke et al., “LightGBM: A Highly Efficient Gradient Boosting Decision Tree,” in Advances in Neural Information Processing Systems, Curran Associates, Inc., 2017. Accessed: Aug. 30, 2023. [Online]. Available: https://proceedings.neurips.cc/paper_files/paper/2017/hash/6449f44a102fde848669bdd9eb6b76fa-Abstract.html.
  59. L. Ostroumova, G. Gusev, A. Vorobev, A. V. Dorogush, and A. Gulin, “CatBoost: unbiased boosting with categorical features,” presented at the Neural Information Processing Systems, Jun. 2017. Accessed: Oct. 26, 2023. [Online]. Available: https://www.semanticscholar.org/paper/CatBoost%3A-unbiased-boosting-with-categorical-Ostroumova-Gusev/ee0a0f04d45f86bf50b24d7258e884725fcaa621.
  60. “CatBoost.” Accessed: Oct. 26, 2023. [Online]. Available: https://catboost.ai/en/docs/.
Preprints 97291 g001
Figure 1. The behavior of the MADEX equation compared to the MSE in three different regions of the Blood Glucose concentration continuum: (a) hypoglycemia, (b) euglycemia, (c) hyperglycemia.
Figure 1. The behavior of the MADEX equation compared to the MSE in three different regions of the Blood Glucose concentration continuum: (a) hypoglycemia, (b) euglycemia, (c) hyperglycemia.
Preprints 97291 g001
Preprints 97291 g002
Figure 2. (a), (b) Clarke’s EGAs for scenarios 1 and 2, (c) CEGA’s regions where points are located in scenarios 1 and 2.
Figure 2. (a), (b) Clarke’s EGAs for scenarios 1 and 2, (c) CEGA’s regions where points are located in scenarios 1 and 2.
Preprints 97291 g002
Preprints 97291 g003
Figure 3. Graphical comparison of MSE vs MADEX (a) and their squared counterparts RMSE vs RMADEX (b) for the Proof-Of-Concept Test.
Figure 3. Graphical comparison of MSE vs MADEX (a) and their squared counterparts RMSE vs RMADEX (b) for the Proof-Of-Concept Test.
Preprints 97291 g003
Table 1. Key for the symbols used in Eq. 1-3.
Table 1. Key for the symbols used in Eq. 1-3.
Symbol Explanation
y i Reference("real"/expected) value
y ¯ Mean value of y
y ^ Predicted value of y
N Number of observations/measurements
Table 2. Testing Scenarios.
Table 2. Testing Scenarios.
Reference Values Scenario 1 predictions Scenario 2 predictions
50 25 75
60 45 75
100 150 50
135 160 110
150 200 100
200 300 100
250 350 150
300 390 210
Table 3. Reference to utilized machine learning algorithms.
Table 3. Reference to utilized machine learning algorithms.
Algorithm Reference
Linear Regression [20,21]
Lasso Regression [22,23]
Ridge Regression [24,25]
Elastic Net [26,27]
Least Angle Regression [28]
Lasso Least Angle Regression [28]
Orthogonal Matching Pursuit [29,30,31]
Bayesian Ridge [32,33,34]
Automatic Relevance Determination [32,34,35]
Passive Aggressive Regressor [36]
Random Sample Consensus [37,38,39]
TheilSen Regressor [40,41,42]
Huber Regressor [43]
Kernel Ridge [44]
Support Vector Regression [32,45,46]
K Neighbors Regressor [47]
Decision Tree Regressor [48]
Random Forest Regressor [49]
Extra Trees Regressor [50]
AdaBoost Regressor [51,52]
Gradient Boosting Regressor [53,54,55]
MLP Regressor [56]
Extreme Gradient Boosting [57]
Light Gradient Boosting Machine [58]
CatBoost Regressor [59,60]
Table 4. Results of the Proof-Of-Concept Test.
Table 4. Results of the Proof-Of-Concept Test.
A B C D E MSE RMSE MADEX RMADEX
Scenario 1 3 5 0 0 0 4321.88 65.74 1034.32 32.16
Scenario 2 1 4 0 3 0 4321.88 65.74 242936.4 492.89
Table 5. Example Algorithm Leaderboard (Subject No: 559, time-window: 30 min, prediction-horizon 30 min).
Table 5. Example Algorithm Leaderboard (Subject No: 559, time-window: 30 min, prediction-horizon 30 min).
Model Name MAE MSE RMSE MAPE MADEX RMADEX
Light Gradient Boosting Machine 1.70E+01 5.72E+02 2.39E+01 1.14E-01 6.39E+04 1.60E+02
Decision Tree Regressor 2.35E+01 1.15E+03 3.39E+01 1.57E-01 7.97E+05 7.37E+02
Lasso Least Angle Regression 1.79E+01 6.58E+02 2.56E+01 1.21E-01 1.41E+06 8.48E+02
Elastic Net 1.79E+01 6.59E+02 2.57E+01 1.21E-01 1.51E+06 8.74E+02
Lasso Regression 1.80E+01 6.59E+02 2.56E+01 1.21E-01 1.66E+06 9.08E+02
Bayesian Ridge 1.79E+01 6.64E+02 2.57E+01 1.20E-01 2.01E+06 9.59E+02
Orthogonal Matching Pursuit 1.92E+01 7.19E+02 2.68E+01 1.29E-01 2.38E+06 9.88E+02
K Neighbors Regressor 2.36E+01 1.16E+03 3.24E+01 1.58E-01 4.00E+06 1.07E+03
Linear Regression 1.77E+01 6.59E+02 2.56E+01 1.19E-01 1.92E+07 1.86E+03
Ridge Regression 1.78E+01 6.60E+02 2.57E+01 1.19E-01 1.70E+07 1.87E+03
Dummy Regressor 5.76E+01 4.92E+03 7.02E+01 4.32E-01 7.41E+07 8.33E+03
Huber Regressor 1.82E+01 7.59E+02 2.74E+01 1.17E-01 8.80E+08 1.04E+04
Passive Aggressive Regressor 3.94E+01 5.88E+03 6.44E+01 2.40E-01 3.10E+57 1.76E+28
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated