1. Introduction
The prediction of Remaining Useful Life (RUL) for lithium-ion batteries is a critical task for ensuring the safe and optimal operation of battery packs, especially in applications like electric vehicles (EVs) [
1]. This literature delves into two primary approaches for RUL prediction: Physics-based Models (PBM) and Data-driven Models (DDM). PBMs leverage the fundamental principles of electrochemistry and battery physics to simulate battery behaviour over time [
2]. These models consider factors such as ion diffusion, electrode reactions [
3], discharge capacity [
4,
5], cycles, capacity fade [
6], and thermal effects [
7]. While PBMs provide valuable insights into degradation mechanisms, they are computationally intensive, require detailed knowledge of electrochemical processes [
2,
8], and may struggle to capture real-world complexities. DDMs, on the other hand, use machine learning algorithms to learn patterns and relationships directly from available data [
9,
10]. They have gained prominence due to their ability to capture complex and nonlinear relationships that exist in the data, making them more adaptable and flexible compared to PBMs.
DDMs can be further categorised into statistical machine learning and deep learning methods, which provide valuable insights into their respective strengths and applications. Shallow learning, a subset of statistical machine learning, employs neural networks with a single layer, as exemplified by Support Vector Machines (SVMs). On the other hand, deep learning methods utilize neural networks with multiple hidden layers.
Statistical learning methods, including SVMs [
10], Gaussian Process Regression (GPR) [
11,
12,
13], Random Forest [
14,
15], and Bayesian approaches [
16,
17,
18], are well-suited for modeling small datasets with prior knowledge of the generative process. However, they may face challenges in capturing complex battery characteristics and long-term dependencies in the data [
2,
19].
In contrast, deep learning methods, represented by Recurrent Neural Networks (RNNs) [
20,
21], Convolutional Neural Networks (CNNs) [
22,
23], and hybrid models [
24,
25], excel in handling extensive datasets with limited knowledge about the underlying process or suitable features. They demonstrate remarkable capabilities in capturing intricate patterns from raw battery data, particularly in dealing with multi-variate time-series information.
Recent advancements in sequence-to-sequence learning in the domain of further contribute to the discourse on multi-horizon time series forecasting (MTSF). Sutskever et al. introduced a powerful end-to-end approach employing multilayered Long Short-Term Memory (LSTM) networks for sequence learning, showcasing impressive results in translation tasks [
26]. Similarly Yang et al. explored incorporating cross-entity attention mechanism in MTFS in [
27]. These method minimizes assumptions on sequence structures and proves effective, particularly in tasks where large labeled training sets are available.
However in the context of RUL prediction, improvements in robustness, generalizability, and addressing challenges like variable sampling rates and incomplete data remain areas of focus [
28]. Hence, despite the progress in RUL prediction, current research has several knowledge gaps and limitations. These include the 1) need for more robust and accurate models, enhanced generalizability, 2) exploration of various deep learning architectures, 3) utilisation of complete datasets with varying sampling rates, and consideration of factors like battery ageing and non-stationary signals.
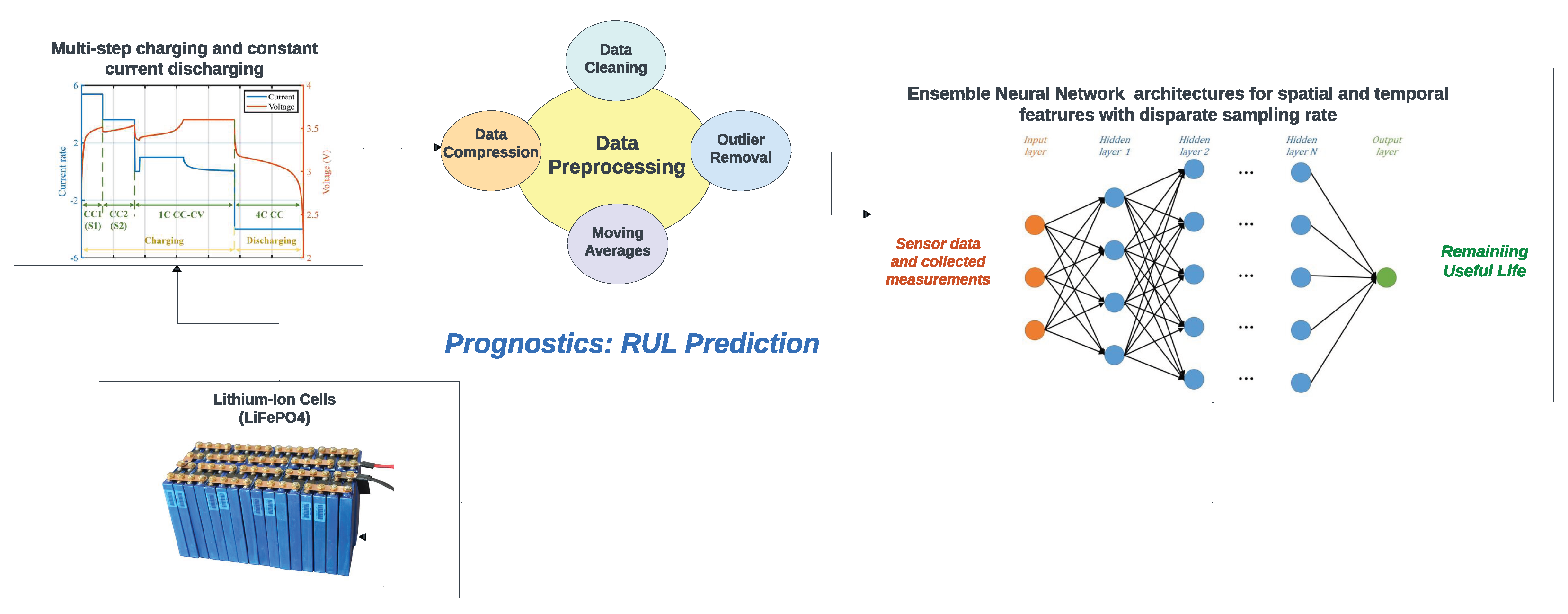
Considering the limitations of previous research and methods, our study takes a comprehensive approach to address data-driven methods for RUL prediction of LIB. We recognise that the key to successful prediction lies in harnessing the potential of a diverse dataset. Our dataset comprises 124 commercial lithium-ion batteries [
29], each subjected to extensive cycling until failure under specific operational conditions (an overview can be seen in
Figure 1). It encompasses crucial parameters such as discharge capacity, temperature, internal resistance, and discharge time.
To effectively address the heterogeneity within our dataset, we adopted a hybrid approach known as CLDNN proposed by Sainath et. al. [
30], which stands for Convolutional, Long Short-Term Memory, and Dense Neural Networks. CLDNN harnesses the collective power of these neural network architectures, providing a solution to the multifaceted nature of LIB RUL prediction. In addition, we repurposed the hybrid model called the Temporal Transformer (TT) proposed by Chadha et. al. [
31] to enhance prediction accuracy and robustness in LIB RUL. The TT model combines the strengths of Transformer self-attention layers and LSTM architectures, presenting a unique approach to sequential modelling that effectively addresses the challenge of capturing long-term dependencies [
32]. While the Temporal Transformer shares a name with the Temporal Fusion Transformer (TFT) introduced by Lim et al. [
33], it is important to note their architectural differences. The TFT is designed for handling multi-modal data, allowing it to incorporate various relevant features for forecasting tasks. In contrast, our dataset did not require such multi-modal capabilities, leading to divergent architectural choices in our models.
It is worth emphasising that our experimentation phase encompassed the exploration of multiple temporal hybrid models, however, we only detail the most effective models. The remainder of this article is structured as follows: In
Section 2, we delve into the related works within the field of Lithium-Ion Battery RUL prediction focusing on Deep-learning approaches.
Section 3 provides a comprehensive overview of our proposed methodology, followed by a detailed account of the experimental procedure.
Section 4 is dedicated to discussions regarding the outcomes of our experiments. Lastly,
Section 5 concludes this article with our conclusion and future work.
3. Methodology
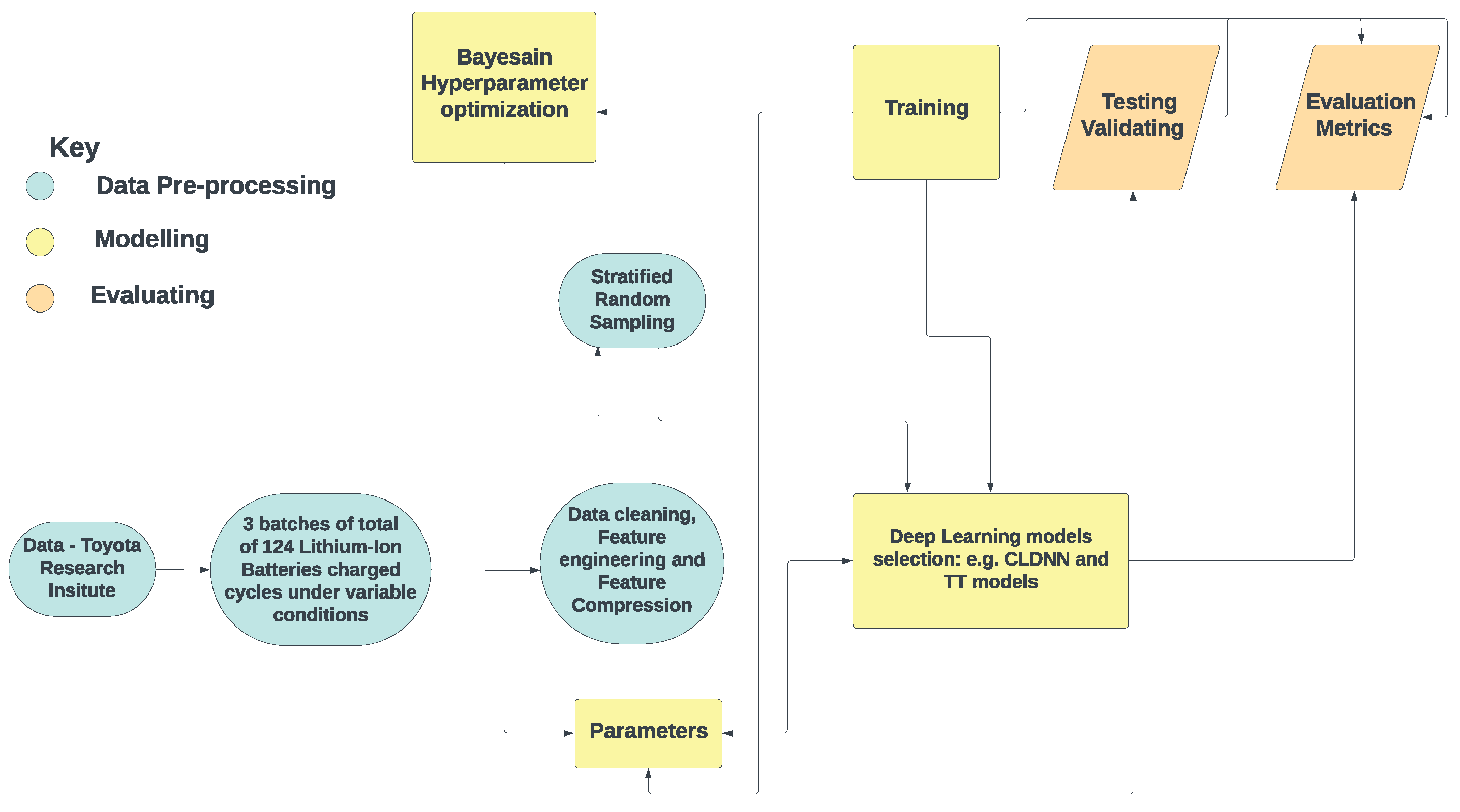
This section presents the framework (
Figure 2) of the proposed LIB RUL prediction method. An important part of this research was the optimisation of model hyperparameters using Bayesian optimization techniques aimed at maximising the models’ predictive accuracy. The primary objective was to develop a robust predictive model for estimating the RULs of LIB, accounting for intricate temporal dynamics and feature variations across different battery batches.
3.1. Dataset Description
This project employed a dataset comprising 124 lithium-ion batteries of the lithium iron phosphate (LFP)/graphite type, each with a nominal capacity of 1.1 Ah and a nominal voltage of 3.3 V. These batteries underwent cycling until failure under fast-charging conditions within a convection temperature chamber set to 30°C. The dataset, sourced from the Toyota Research Institution [
64], included information on various parameters, such as voltage, capacity, and current, continuously measured during cycling, spanning from a single cycle to the End Of Life. Charging involved an initial phase with current C1 until a state-of-charge (SOC) of S1 was reached, followed by charging with current C2 until reaching SOC S2, consistently set at 80% for all cells. Subsequently, the cells underwent an 80% to 100% SOC transition using a 1 C-rate constant current-constant voltage (CC-CV) charging approach, up to a 3.6 V cut-off voltage [
65]. The batteries’ lifetimes were determined based on the cycle number at which their capacity declined to 80% of the original value, with observed lifetimes ranging from 1350 to 2300 cycles.
3.2. Stratified Random Sampling
Stratified random sampling was employed to create a representative dataset for the model’s training and testing. This approach ensured that cells from different battery batches, characterised by varying quality control protocols, were proportionally included in the dataset. By preventing models from overfitting to specific batch attributes, this method improved model robustness and generalisation across different LIB batches.
3.3. Feature Selection
The dataset, divided into three batches of approximately 48 cells each, was prepared for analysis. Essential features for RUL prediction were identified, including linearly interpolated Discharge Capacity (Qdlin), Linearly Interpolated Temperature (Tdlin), Internal Resistance (IR), discharge data, discharge time, and remaining cycles. Qdlin and Tdlin were interpolated to maintain a consistent sampling rate for all cells.
3.4. Data Preprocessing
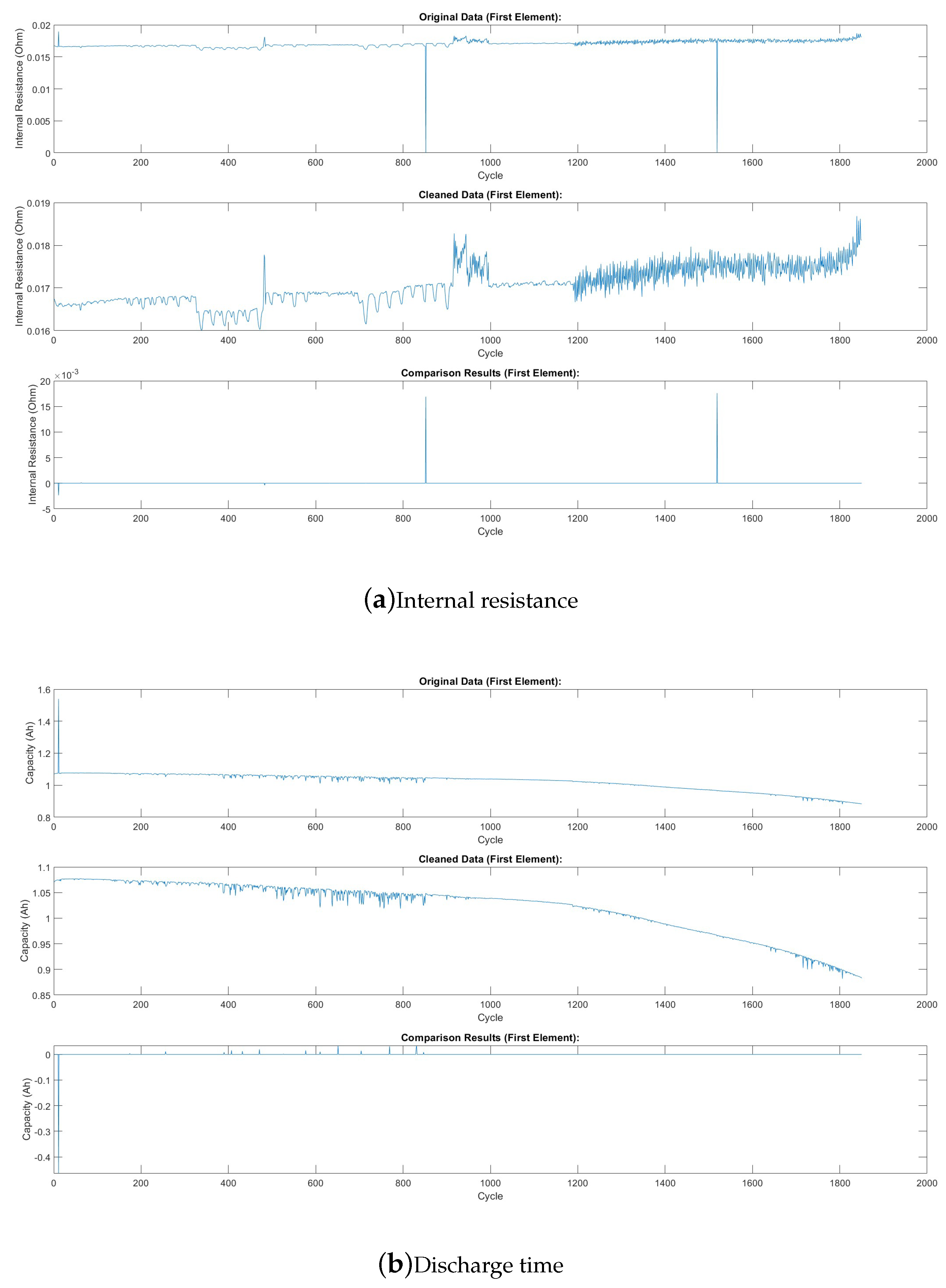
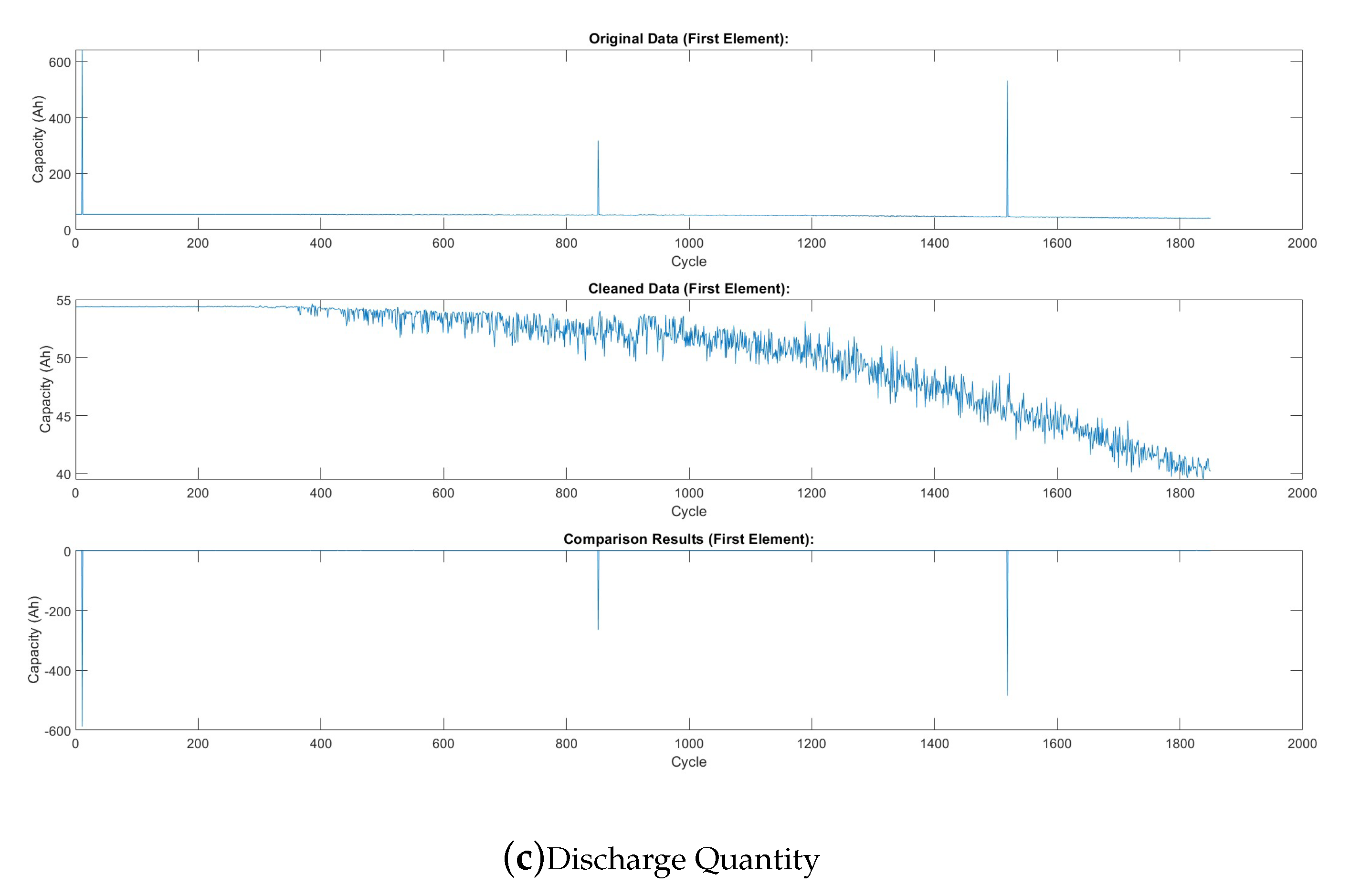
To prepare the data for deep neural networks, we implemented a comprehensive preprocessing pipeline. Outliers in internal resistance, discharge time, and discharge quantity were removed using the fill outliers function with the cubic spline method and a moving average window of 100 (Figure a–c, respectively). These figures show the features before and after preprocessing (Note: these plots depict the first cell in the first batch). Smoothing techniques, such as moving average filters with a window size of 15, were applied to discharge data. To capture temporal dynamics in Qdlin and Tdlin, the sampling rate was standardized to 1000 entries per cycle. Finally, PCA was employed to reduce the dimensionality of Qdlin and Tdlin while preserving their essential features.
Figure 3.
Comparison of Data Features Before and After Preprocessing.
Figure 3.
Comparison of Data Features Before and After Preprocessing.
3.5. RUL estimation
Traditional supervised learning approaches rely on the existence of labelled training data, where each data point is associated with a known target value. However, in the context of prognostics, this assumption often does not hold. The remaining useful life (RUL) of individual components is typically not known a priori, making it challenging to train predictive models using standard regression techniques. To overcome this hurdle, researchers have explored alternative approaches, such as employing physics-based models or utilizing machine learning algorithms to estimate the RUL of training data. While assigning a constant RUL value to all training points may seem like a straightforward solution, this can lead to inaccurate representations of the actual degradation patterns and hinder the model’s ability to generalize effectively. A more sophisticated approach involves estimating the RUL based on a suitable model, as demonstrated by the use of a Deep Convolution Neural Network [
66]. This approach offers a more realistic representation of the degradation process and can potentially enhance the model’s predictive performance.
3.6. Metrics
A variety of metrics were used in this study. The success of the model was calculated based on the deviation (
) of the predicted number (model prediction
) of cycles from the actual number (ground truth
) of cycles remaining after every 100 cycle count as shown in Equation (
1). The choice of loss function significantly impacts the outcome of RUL prediction. Along with Mean Absolute Error (MAE) shown in Equation (
3) and Mean Absolute Percentage Error (MAPE) shown in Equation (
4), which simply average the absolute errors, and calculate the percentage respectively, we also tracked the Root Mean Squared Error (RMSE) shown in Equation (
2) which squares the errors before averaging, placing greater emphasis on larger deviations. This sensitivity to larger errors makes RMSE a more suitable metric for prognostics, where accurately predicting RUL is crucial and substantial errors can lead to poor performance. Additionally, the rationale behind tracking these specific metrics is that they allow for meaningful comparisons against state-of-the-art approaches.
3.7. Proposed Architectures
The most successful architectures in our study were the Convolutional Long Short-Term Memory Deep Neural Network (CLDNN), originally proposed by Sainath et al. [
30] for Natural Language Processing specifically used for Large Vocabulary Continuous Speech Recognition (LVCSR) tasks [
30]. In their work, CLDNN outperformed Gaussian Mixture Model (GMM) and Hidden Markov Model (HMM) systems [
67]. We repurposed the CLDNN architecture for the specific task of Remaining Useful Life (RUL) estimation.
Another noteworthy model in our investigation was the Temporal-Transformer (TT), initially introduced by Chadha et al.[
31] for RUL estimation using the Commercial Modular Aero-Propulsion System Simulation (C-MAPSS) dataset. The TT model demonstrated effectiveness in predicting the Remaining Useful Life of aircraft engines. Ma et al. [
68] presented a similar use case where their model utilized multi-head attention to capture global features from various representation sub-spaces. Although originally designed for predicting the Remaining Useful Life of aerospace engines, we adapted these models for estimating the Remaining Useful Life of Lithium-Ion Batteries (LIB). This adaptation involved specific architectural deviations and adjustments to hyperparameters.
3.7.1. CLDNN
Adapting a Convolutional Long Short-Term Memory Deep Neural Network (CLDNN), initially developed for Natural Language Processing (NLP) tasks with tokenized sentences, to predict Remaining Useful Life (RUL) in Lithium-Ion Batteries (LIB) necessitates several architectural and algorithmic modifications.
Input Representation: In NLP tasks, CLDNN takes tokenized sentences as input. For RUL prediction, the input representation needs to be tailored to the characteristics of battery data. Time-series data from sensors measuring various parameters (voltage, current, temperature, etc.) were used as input. The input data was reshaped into a format suitable for time series analysis.
Sequence Length and Padding: LIB data has variable lengths of sequences as the cycle count for each battery differs, unlike fixed-length sentences in NLP. Padding or trimming sequences to a uniform length was not necessary. The network architecture was able to handle variable-length input sequences.
Temporal Features: LIB data is inherently temporal, reflecting the degradation of the battery over time. The CLDNN architecture incorporates mechanisms to capture temporal dependencies effectively. Long-Short-Term Memory (LSTM) layers allow us to model temporal patterns.
Feature Extraction: The features relevant to RUL prediction in LIB differ from those important for NLP tasks. Modifications to the convolutional layers had to be made to extract features that are indicative of the battery’s health and degradation.
Hyperparameter Tuning: The hyperparameters, such as learning rate (), filter size (), kernel parameters (), activation functions (a), and dropout rates () needed adjustment for the new task. Bayesian hyperparameter tuning was used to optimize the model for RUL prediction.
Fine-tuning: The model is fine-tuned with different optimizer choices to minimize loss functions.
The final optimized CLDNN architecture excelled at predicting the remaining useful cycles (RUL) for lithium-ion batteries. It comprises a total of
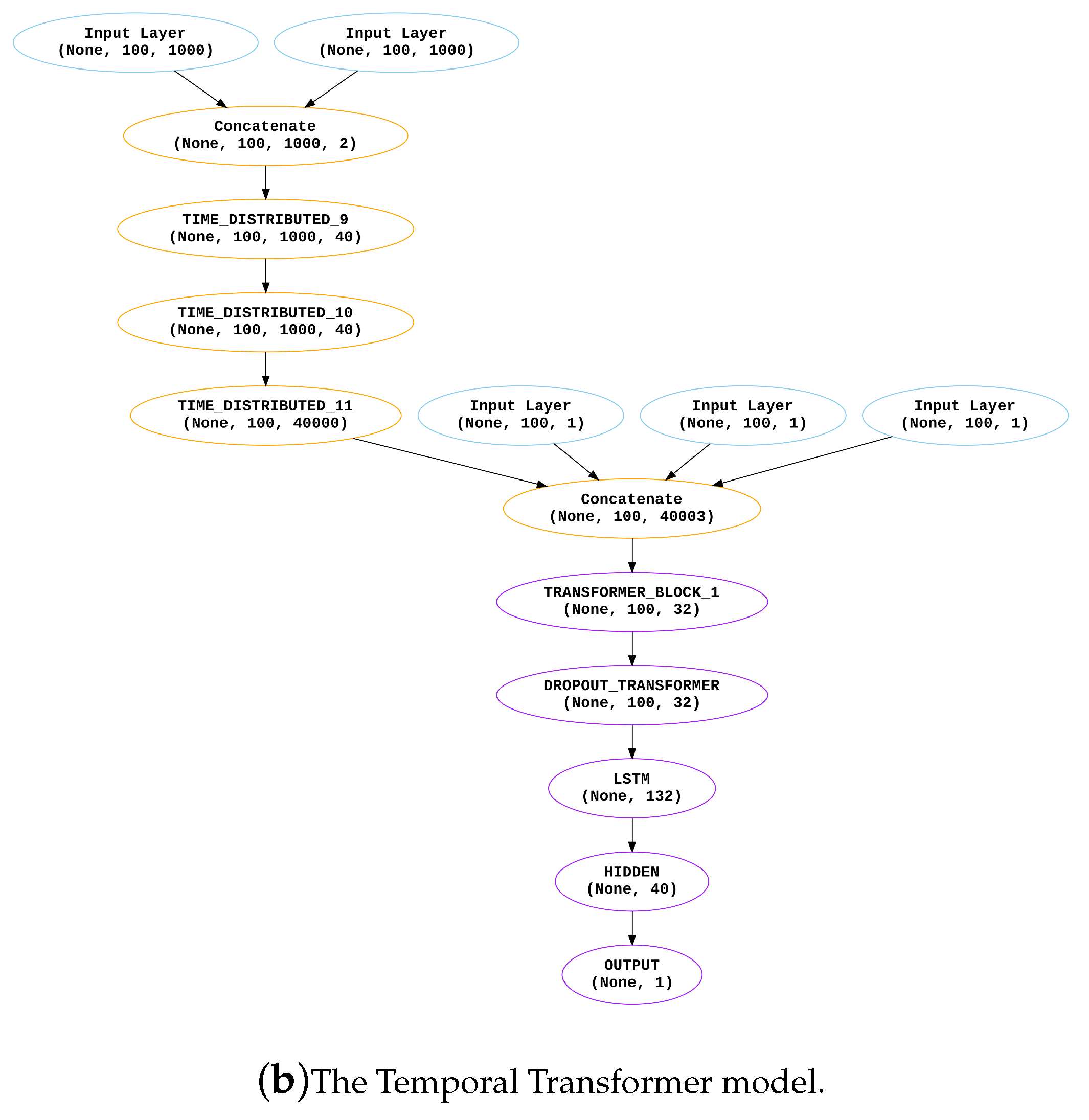
1,518,665 trainable parameters and integrates Convolutional Neural Networks (CNN), Long Short-Term Memory (LSTM), and Dense Neural Networks (DNN) to leverage the unique strengths of each component. The CNN layers capture intricate spatial patterns within features, while the LSTM layers facilitate the capture of temporal dependencies. Dropout layers and dense layers contribute to the model’s regularization and refined prediction capabilities. The CLDNN Architecture for our task is shown in Algorithm 1 and Figure a this model demonstrates a strong efficiency in handling the heterogeneity of the dataset.
Figure 4.
Comparison of the CLDNN and Temporal Transformer architecture
Figure 4.
Comparison of the CLDNN and Temporal Transformer architecture
3.7.2. Temporal-Transformer
Adapting the Temporal-Transformer (TT) model, originally designed for the Remaining Useful Life (RUL) estimation of aircraft engines, for the estimation of RUL in Lithium-Ion Batteries (LIB), involves several architectural differences and adjustments. Here are some modifications that might be considered.
Input Representation: Adjustment to the input representation to accommodate the characteristics of LIB data. The original model took input sequences related to engine parameters. LIB data consists of time series measurements of capacity, temperature, resistance, and discharge time.
Attention Mechanisms: Multi-head attention mechanisms were used in the original model by Ma et al. [
68] needed adjustments for LIB data. Tailoring attention mechanisms to focus on features relevant to battery degradation patterns about the linearly interpolated feature.
Model Size and Complexity: The overall size and complexity of the LIB dataset required an increase in the size and complexity of the TT model. This involved adding layers, adjusting attention mechanisms, and increasing the model depth, which led to 3,936,281 trainable parameters.
Hyperparameter Tuning: Fine-tune hyperparameters using Bayesian optimization specific to LIB data. This includes learning rates, the number of attention heads, embedding dimensions, layer sizes, and dropout rates.
The temporal Transformer (TT) architecture, combines two potent neural network paradigms: the Transformer and Long Short-Term Memory (LSTM). The Transformer’s multi-head self-attention mechanism empowers the model to decipher complex temporal dependencies within the dataset. By parallel processing different parts of the input sequence, it extracts a rich contextual understanding of each data point. Meanwhile, LSTM units adeptly capture long-term relationships between features, enhancing the model’s predictive capabilities. The architecture employs feed-forward neural networks (FFN) for further refinement, facilitating the modelling of non-linear data relationships. Regularisation techniques namely dropout and layer normalisation are employed to ensure training stability and generalisation. The TT algorithm is outlined in the provided Algorithm 2 and Figure b (Note: : Input data with dimensions , where B is the batch size, T is the time dimension, and D is the feature dimension).
The
SelfAttention function in Algorithm 2, computes weighted representations of input data by considering inter-dependencies across multiple dimensions, employing a scaled dot-product attention mechanism. The
TransformerBlock further refines these representations through layer normalization and feed-forward networks, enhancing their expressiveness while retaining sequential relationships. This modular and hierarchical structure allows the LSTM-Transformer to capture patterns in sequential data, making it versatile for offering a robust solution for accurate RUL predictions in lithium-ion batteries.
|
Algorithm 2:Temporal-Transformer |
|
3.8. Hyperparameter Optimization
The hyperparameter tuning for the proposed LIB RUL prediction models was achieved using Bayesian Optimization. Hyperparameter tuning is a critical step in the development of machine learning models, involving the search for optimal configurations to enhance predictive accuracy [
69]. In this study, Bayesian Optimization was chosen due to its effectiveness in handling non-linear and complex search spaces. Unlike traditional grid search or cross-validation methods, Bayesian Optimization uses probabilistic models to predict the performance of different hyperparameter configurations, guiding the search toward promising regions [
70]. This is particularly beneficial in high-dimensional spaces, where an exhaustive search becomes computationally expensive. The implementation of Bayesian Optimization can be seen in Algorithm 3, which was developed using the Keras Tuner library [
71]. The tuning process involved defining a hypermodel class (
MyHyperModel) that inherits from the Keras Tuner
HyperModel class. This class encapsulates the structure of the LIB RUL prediction models (CLDNN or TT), as well as the search space of hyperparameters. Additionally, a custom Bayesian Optimization tuner class (
MyBayesianOptimizationTuner) was defined, extending the
BayesianOptimization class from Keras Tuner. The tuner was configured to minimize, which was set as the validation mean absolute error (MAE) of the LIB RUL prediction models. The search was conducted over a specified number of trials (100 in this case) on the training dataset for a given number of epochs (10 in this case), and the models’ performance was evaluated on the validation dataset.
|
Algorithm 3:Hyperparameter Optimization with Keras Tuner |
|
After completing the search, the optimal hyperparameter set was retrieved, and a new model was built using these parameters. This process ensured that the final CLDNN and TT model was fine-tuned for optimal performance, leveraging the power of Bayesian Optimization to navigate the hyperparameter space efficiently.
5. Conclusions and Future Work
This study addresses the critical challenge of accurately estimating the RUL of LIBs within the context of electric vehicles. By leveraging deep learning techniques and utilizing a rich dataset from the Toyota Research Institute, we have developed and evaluated two hybrid models: CLDNN and TT. Our contributions encompass the creation of a pre-processed high-quality dataset through stratified random sampling, by implementation of a comprehensive data preprocessing pipeline, and the development of two hybrid models. This pipeline ensures feature consistency and captures temporal dynamics, thereby laying the foundation for precise RUL predictions.
Both the CLDNN and TT models exhibited commendable performance, surpassing existing approaches with Mean Absolute Errors (MAEs) of 84.012 and 85.134, respectively. Furthermore, they demonstrated improvements in Mean Absolute Percentage Error (MAPE) ranging from 4.01% to 7.12%. These models prove to be well-suited for LIB RUL prediction, making substantial contributions to battery recycling and sustainability within the electric vehicle industry.
Despite these achievements, several areas for future improvement have been identified. Real-world implementation and validation on a broader dataset are crucial for bolstering confidence in the models’ applicability. Exploring complex augmentation methods, alternative ensemble solutions, and liquid neural networks (LNNs) [
73,
74,
75] could further refine model performance and introduce more efficient, adaptable, and robust approaches to battery health estimation. There is also potential for the use of explaining the LIB RUL using graph neural networks which have also been shown to significantly reduce parameter count and perform better than their traditional physics-based model’s counterparts [
76,
77]. Future research may leverage LNNs or GNNs, known for their dynamic adaptability, to potentially enhance RUL prediction for LIBs. With reduced computational intensity, these networks may offer superior generalization and efficiency for large-scale applications like electric vehicle battery management systems.
Reducing parameter counts to enhance model efficiency, measuring processing times in Online scenarios, and investigating the alignment between hyperparameter optimization and a comparison between physics-based models are promising avenues for future research. In conclusion, while this study represents a significant step forward in battery health estimation, ongoing research should focus on diversifying data sources, simplifying model complexities, and exploring emerging technologies, such as LNNs, to further advance this field.