The Cephalometric Relationship between the Facial Height Ratio and the Growth Pattern in a Group of Patients from Timis County, Romania

Any malocclusion can be associated with various face development patterns, including hyper, neutral and hypodivergent growth patterns. We measured face height ratios, angle formed by Y axis to SN and growth patterns in various malocclusions in a group of patients from Timis county. The pretreatment digital cephalograms of 350 participants were split into three groups based on Angle's classification of dentoalveolar malocclusion. Every cephalogram was digitally traced and analyzed using a composite cephalometric method analysis utilizing the WebCeph imaging cephalometric program, which included two linear and one angular. In general, patients from Timis county have a hypodivergent development pattern. Hypodivergent development pattern predominated in group I, II, and III. Group I hyperdivergent 5.14%, normodivergent 16.01%, hypodivergent 78.85%. Group II hyperdivergent 2.78%, normodivergent 14.44%, hypodivergent 82.78%. Group III hyperdivergent 10.53%, normodivergent 10.53%, hypodivergent 78.94%. In all three groups, the value of the angle formed by Y axis to SN is within normal limits group I 65.4 ±4.34°, group II 63.87± 3.86° and group III 64.66 ±5.28°. A strong negative correlation was found between angle: Y axis to SN and facial height ratio (r= -0,766; p <0.001). In all kinds of malocclusion, patients from Timis county show primarily a hypodivergent development pattern.

Keywords:

Subject: Medicine and Pharmacology - Other

1. Introduction

The relationship between the skeletal, dental and soft tissue of the face can be determined using cephalometry, a crucial diagnostic technique. The anteroposterior and vertical dimensions are also susceptible to malocclusion. The severity of malocclusion in the anterior-posterior direction is analyzed using cephalometric analysis to determine the impact of vertical alterations [1].

In relation to the cranial base line, facial growth moves in a direction that is made up of varying amounts of horizontal forward development and vertical downward growth. Mandibular growth is crucial to the growth and development of the face. The terms hypodivergent and hyperdivergent were introduced by Schudy to describe the vertical development patterns of the face. Short faces have hypodivergent patterns, while long faces have hyperdivergent patterns. Other variables affect craniofacial development and change the resulting facial morphology [2].

One crucial factor considered during orthodontic diagnosis is the anterioposterior connection between the maxillary and mandibular apical bases. The saggital mismatch in the connection of the jaws is frequently associated with the vertical disharmonies. An aberrant growth pattern can be identified practically by carefully analyzing linear and angular measurements, which also aids in determining the case’s prognosis [3].

To achieve appropriate vertical proportions during orthodontic treatment, Sassouni claims that the vertical facial forms are divided into long, average and short faces and reported a clear association between facial patterns and anterior vertical facial proportions. Anterior facial height (AFH) and posterior face height (PFH) are included in the vertical dimension. The phrases "hyperdivergent" and "hypodivergent" were first used by Schudy to describe extremes along the vertical spectrum. To evaluate a person’s facial vertical growth, linear measures like Jarabak’s ratio and the facial height ratio (LAFH/TAFH) are also used [4].

In the field of orthodontics, accuracy in diagnosis and evaluation of developing patients is important because it enables planning orthopedic, orthodontic or surgical therapy with the goal of a satisfactory outcome by predicting and assessing the amount of development [5]. The great variability in the direction and amount of craniofacial growth implies great importance for the success of orthodontic treatment, which has sparked intense interest in the search for methods to predict the direction and magnitude of individual facial growth, since it would allow to estimate future changes in the vertical or horizontal relationship [6,7]. However, evidence would show that there are changes in the growth pattern over time in both direction and quantity, which would support the search for some system to predict craniofacial growth in the future. In the past, the theory made popular by Brodie and Brodie et al. suggested that growth patterns were established at an early age [8].

The intricacy of their growth prediction is heightened by the interaction of all parts of the craniofacial system, including genetic and environmental influences [9].

In order to create predictive models that have recently been constructed and have enabled us to infer the progression of the dentoalveolar imbalance in accordance with biological principles of growth and development, the integration of the components should be formed [10].

Variable growth vectors along horizontal forward and vertical downward growth are present in the development of facial structures in relation to the cranial base.

For each person, the proportions of growth in both the horizontal and vertical axes are essentially constant. The amount and timing of the increments of growth in the anterior and posterior facial skeletons should be comparable; otherwise, imbalances will cause the mandible and maxilla to rotate, resulting in unbalanced face types.

Extreme facial forms, such as long faces and short faces, are mostly caused by the disproportionate vertical development of the posterior dentoalveolar area. Long face syndrome is characterized by increased heights of the posterior molars. Based on the percentage and severity of dental overbite, the ratio of the upper and lower anterior facial heights, the angle between the mandibular plane and the Frankfort horizontal plane and the visual perception of the change in the lower anterior facial height, the classification of vertical facial heights has been done. However, these selection criteria are arbitrary [11].

For a precise diagnosis, the importance of the sagittal jaw base relationship, assessed by a broad view of the patient’s profile, has been emphasized. Based on the first permanent molar relationship, Angle published the first clinical evaluations of jaw-based relationships in 1899. It did not, however, take into account the face skeleton, which was highlighted by later investigations. Studies using cephalometry in the 19th century came to the conclusion that many malocclusions were caused by flawed jaw relationships rather than improperly positioned teeth. Anteroposterior alignment between the dental arch and the jaw base was found to be off in at least one out of every three people by Zhou et al. [12].

More accurately reflecting the relationship between the dental arch and the jaw than angular measurements is the linear measurement of the sagittal jaw-base relationship. In order to diagnose anteroposterior discrepancies and determine a treatment strategy, both linear and angular measures had been incorporated into various cephalometric assessments. The soft tissue paradigm was presented in the twenty-first century. It argues that "the soft tissue of the face, not the teeth and bones, determines both the goals and limitations of modern orthodontics and orthognathic treatment." According to face features, Schudy divided facial patterns into three categories: hyperdivergent, neutral and hypodivergent.

In the Caucasian population, Jarabak discovered many vertical inter-maxillary correlations. Certain cephalometric tests can provide information on facial growth patterns that can be very helpful in determining an accurate diagnosis, treatment strategy and prognosis [13].

Hence, in diverse malocclusions, we looked at the face height ratios and growth patterns, the correlation between FHR with Y axis to SN angle, total anterior facial height (TAFH) and total posterior facial height (TPFH) in a group of patients from Timis county, Romania.

2. Materials and Methods

The preparatory procedure data from the Department of Orthodontics and Dentofacial Orthopedics of Timisoara were used in this retrospective analysis. A total of 350 patient records (140 men and 210 females) were included, with consultations taking place between March 2021 and December 2022. All of the patients were of Timis county, aged 9 to 48 (female 9-48 and male 10-41). The 350 individuals were separated in three groups based on Angle’s dentoalveolar malocclusion, which was assessed using pre-treatment study models, pictures and a clinical questionnaire record. Edward H. Angle proposed the Angle classification in 1899, based on the relative AP position of the first molars. Angle believed that the first molars erupted in a fixed position within the arches, allowing the AP skeletal connection to be determined.

All the 350 subjects were divided into three groups based on the Angle’s dento-alveolar malocclusion, evaluated from the pre-treatment study models in confirmation with photographs and clinical questionnaire record (Table 1).

Procedure methodology: The lateral cephalograms were all obtained with a PLANMECA (PROMAX) in the normal head position. The procedure described by Beni Solow was used to determine optimal natural head posture [14].

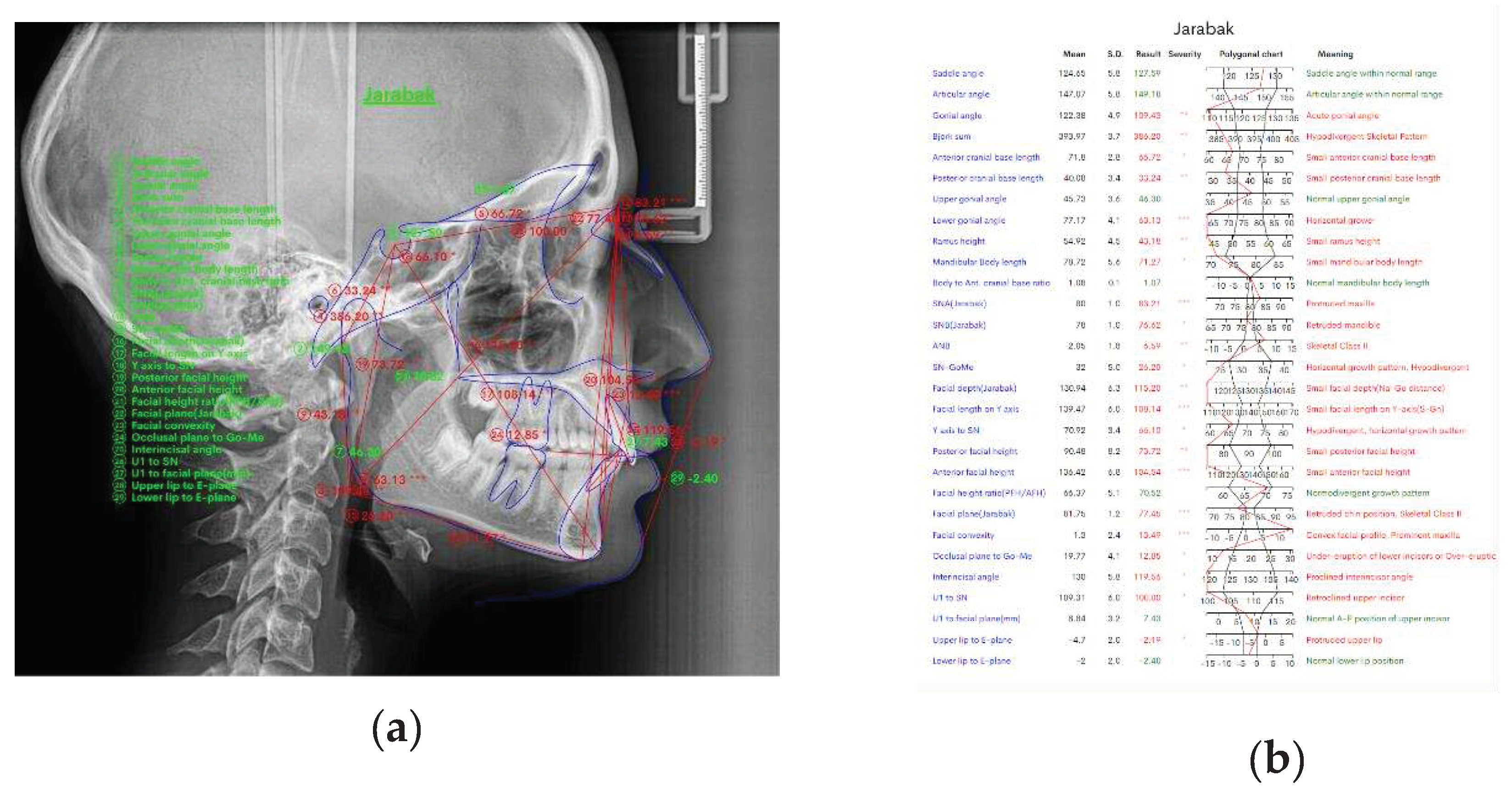
Using the WebCeph (version 1.00.00) imaging cephalometric program, pretreatment digital cephalograms were digitally traced and evaluated using a composite cephalometric analysis consisting of two linear measures and one angular measurement.

The cephalometric landmarks and planes used in this experiment were as follows (Figure 1):

Landmarks:

S- Sella turcica– mid-point of the hypophyseal fossa.
N- Nasion -most anterior point on the Naso-Frontal suture in the medial plane.
Go- Gonion - meeting point of posterior ramal plane and the MP angle.
Me- Menton - the lowest point in the median plane of the chin.

Planes that have been built include the following:

N-Me (Nasion-Menton) line
S-Go (Sella-Gonion) line.

According to Angle, the first permanent molar relationship served as the basis for the first clinical evaluations of jaw-based relationships in 1899. The facial skeleton, which was highlighted by subsequent investigations, was not taken into account. [11]

Angle’s classification of malocclusion in the 1890s was a significant step in the history of orthodontics since it featured the first concise and understandable explanation of normal occlusion in the natural dentition in addition to subdividing the main categories of malocclusion. According to Angle’s theory, the upper first molars are essential for occlusion and the upper and lower molars should be connected so that the top molar’s mesiobucal cusp occludes in the lower molar’s buccal groove. This molar relationship and normal occlusion would arise from the teeth being positioned on a line of occlusion that was smoothly curved. This marvelously simple explanation of normal occlusion, which 100 years of experience has shown to be true except in cases where there are aberrations in tooth size.

Angle proposed a classification system that is still in use today, based on the relationship between the first permanent molars. This classification allows for the division of occlusion into three groups:

Class I: The molar relationships are normal, but the line of occlusion is wrong due to rotated teeth, malpositioned teeth, or other factors.
Class II: Distally positioned lower molar in relation to upper molar; unclear occlusion line.
Class III: Mesially positioned lower molar in relation to upper molar; unclear occlusion line. [12].

Figure 2(a) above shows the measurements made in the WebCeph program that we used in this study. Figure 2(b) shows the results of the measurements we performed in this study using the WebCeph digital program.

Using the aforesaid planes, the following measurements were made:

Total anterior facial height (TAFH): N-Me line
Total posterior facial height (TPFH): S-Go line
Facial height ratio (FHR): It is the ratio of TPFH to TAFH multiplied by 100, Jarabak ratio is another name. Based on the face height ratio, Jarabak classified facial morphology into three unique patterns [15]

The following are some examples of these patterns:

Hyperdivergent growth pattern: FHR <59%, predominantly vertical growth pattern.
Neutral or normodivergent growth pattern: FHR between 59-63%.
Hypodivergent growth pattern: FHR >63%, predominantly horizontal growth pattern.

Nahidh et al. in their study reported that the vertical relation is better measured by the sum of posterior angles and the Jarabak ratio [16].

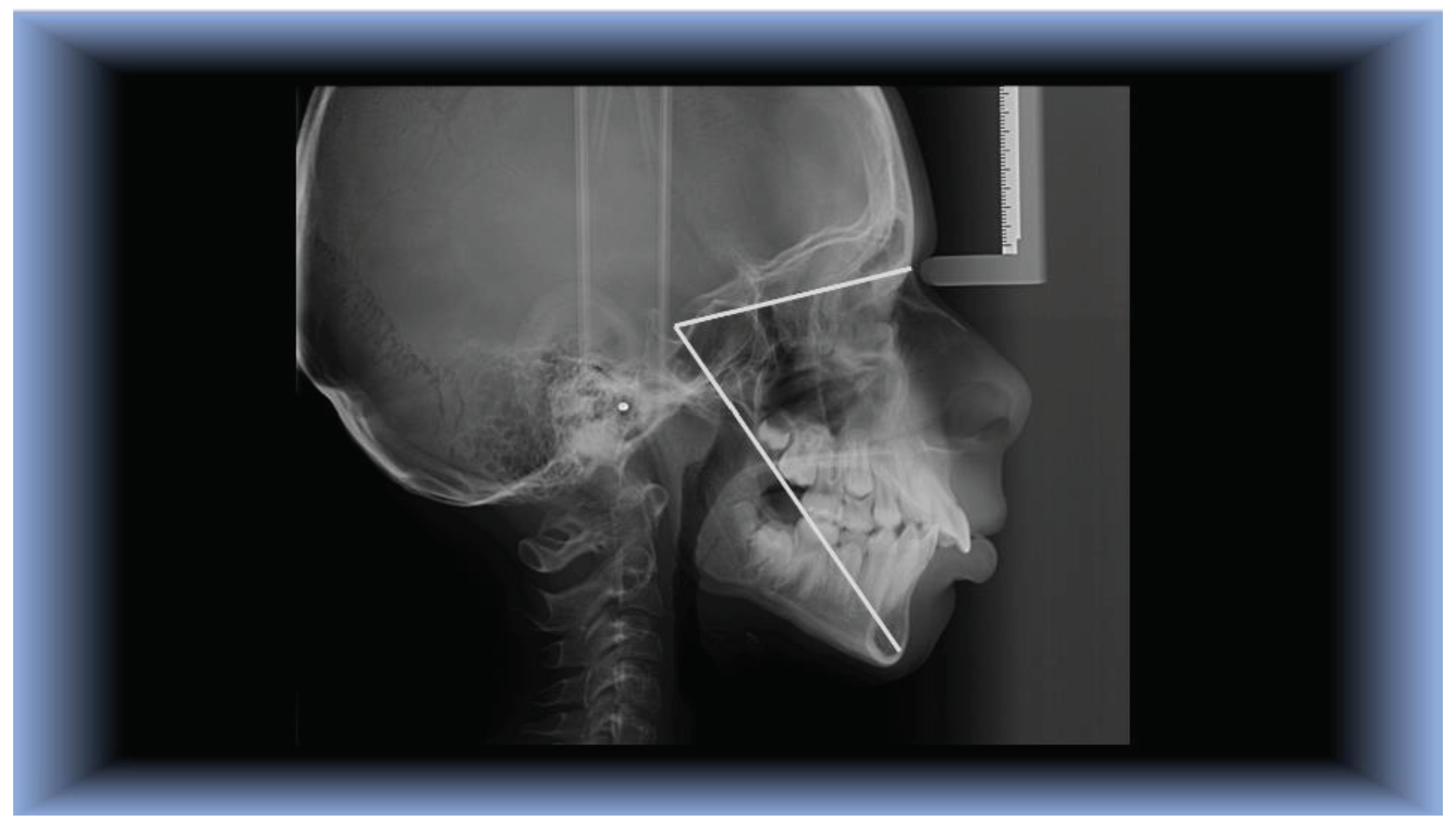
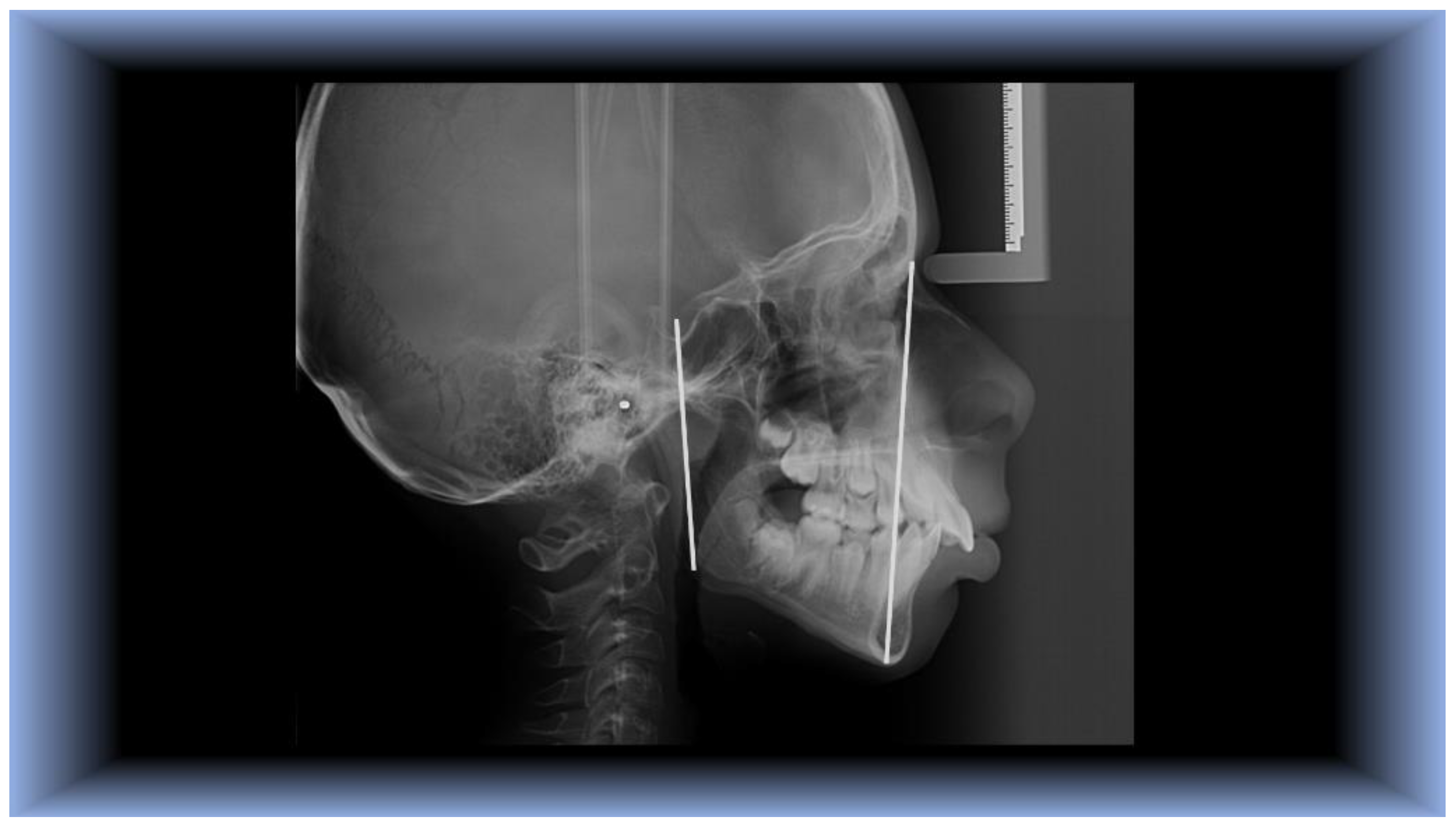
S-Gn (Y-Axis): As an extra check, this angle defines the location of the mandible in relation to the cranial base. It has a mean value of 66°; if it is higher, the mandible is in a posterior position, with vertical growth dominating, if the angle is less than 66°, the mandible is in front of the cranial base and growth is mostly anterior [17].

Y SN angle: The SN plane and the Y axis create an angle. At Frankfort Horizontal, this shows the downward and forward posture of the chin with reference to the upper face [18]. The quality of the treatment process, the compatibility of the soft tissues and the patient’s expectations all affect the postoperative aesthetic outcome [19,20,21].

Figure 3. Y axis to SN, made up of Sella-Nasion and Sella-Gnation (N-S-Gn).

Statistical analysis: To eliminate inter-observer error, all radiographs were traced and measured by the same investigator and each measurement was repeated after 2 weeks to decrease intra-observer error. The parameters listed above were measured and tabulated SPSS version 20.0 was used to conduct statistical analysis. Version 20.0 of the Statistical Package for Social Service. To establish the connection between the specified variables, the Pearson correlation test was used to determine the relationship between the two variables. A 0.05 p-value was used as the level of significance.

3. Results

The findings of this investigation were collected and statistically examined.

The mean values of total anterior facial height, total posterior facial height and Y axis to SN among the three groups is given in Table 2.

Table 3 shows mean facial height ratios of 350 patients.

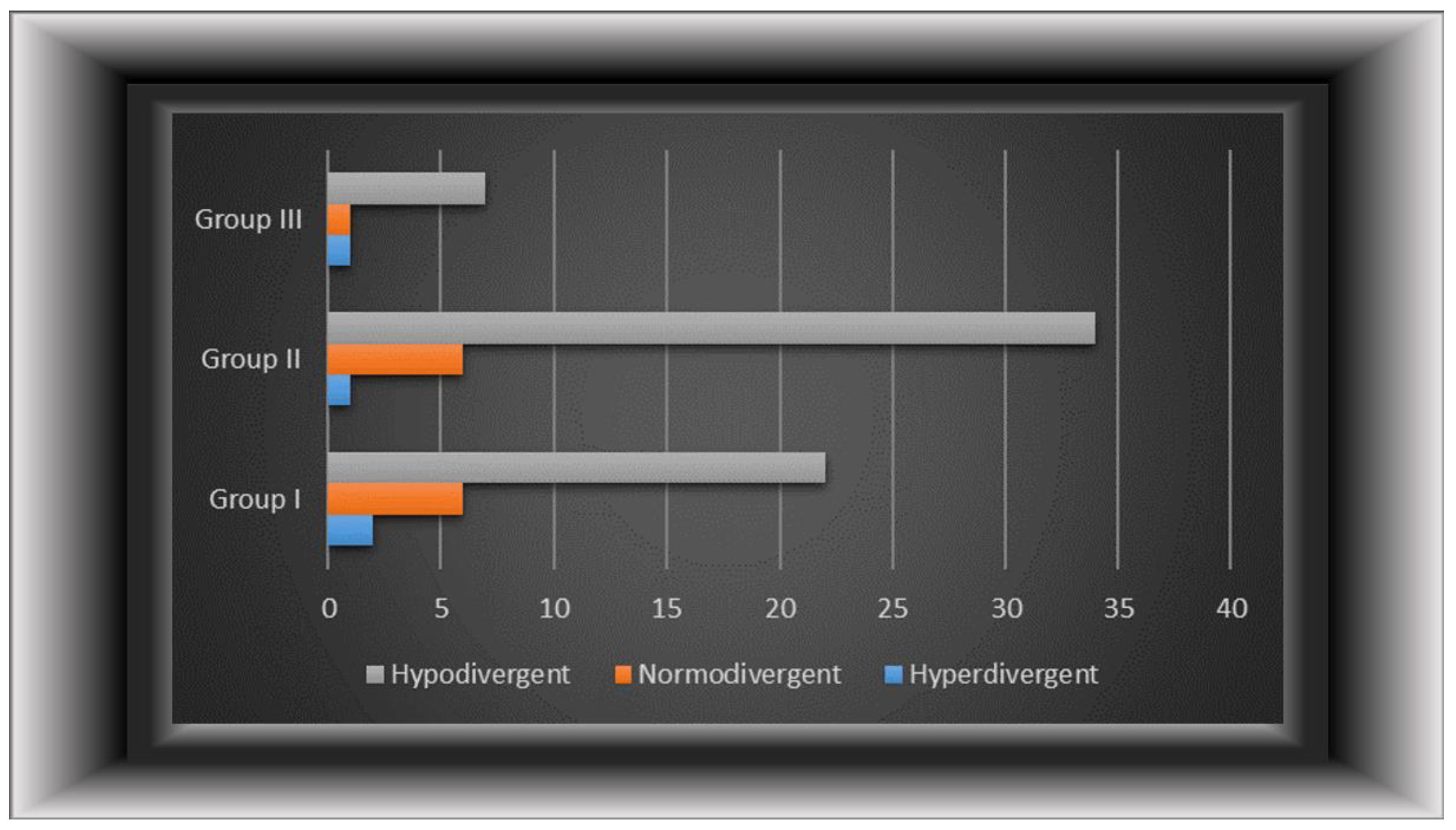
Figure 4 depicts the various development trends across various groupings in both genders.

In the entire sample, hypodivergent growth patterns were most common in all groups, followed by normodivergent and hyperdivergent development patterns (p<0.05).

Different growth patterns of males and females in each group are displayed in Table 4. Among males, in group I (75.47%) and group II (83.54%) majority of the subjects had hypodivergent growth pattern followed by normodivergent and hyperdivergent growth patterns. In group III most of the subjects had hypodivergent growth pattern (100%) followed by hyperdivergent (13.33%) and normodivergent (13.33%) growth patterns. The majority of the female and males patients had hypodivergent growth pattern in first three groups (p<0.01).

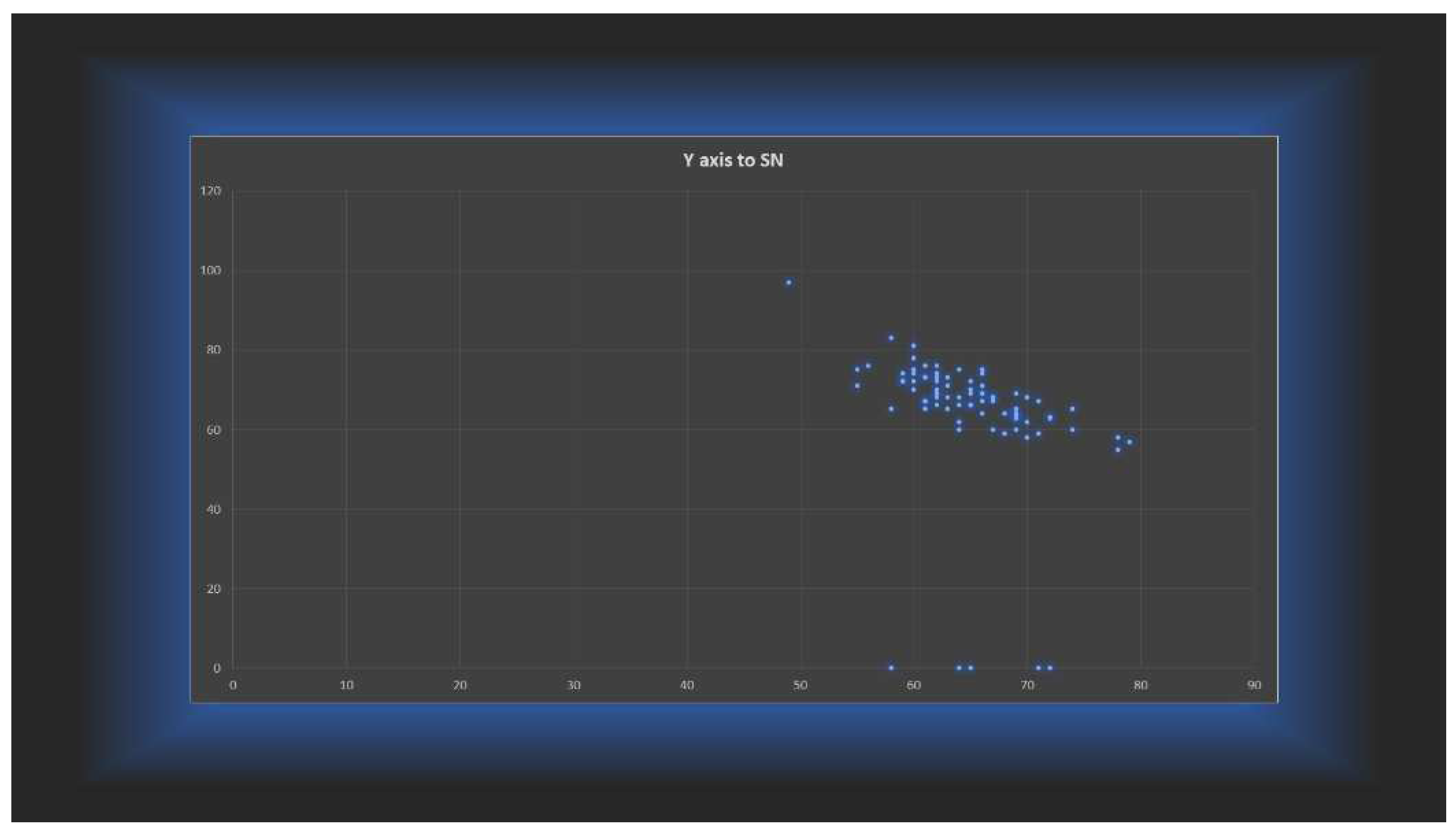
Correlation coefficient of FHR with Y axis to SN, TAFH and TPFH in different groups were evaluated (Table 5). A strong negative correlation was found between FHR and Y axis to SN in all groups, group I of males (r=-0,709**), II of females (r=-0,890**) and positive in group I (r=0,791**), III at females (r=0,76**) shown in Figure 5. A moderate negative relationship in group II of males (r=-0,531*). In group II (r=-0,549*), III (r=-0,646 *) of females FHR and TAFH exhibited a moderate negative and group I (r=-0,687**) a strong negative correlation. A strong positive correlation found between FHR and TPFH in group II males (r=0,707**) and group III females (r=0,807**). A moderate positive correlation between FHR and TPFH was seen in group I of males (r=0,65*) and females and group II of females(r=0,64*). Where we have perfect values of -1 at group III males, the correlation it is no relevant because only eight subjects were there.

Correlation coefficient between Y axis to SN angle and FHR = -0,76685.

4. Discussion

The mandible’s vertical development is what mainly determines facial harmony. The mandibular rotation causes noticeable changes to the face pattern [22]. To evaluate the growth patterns of various malocclusions in various populations, numerous researches have been carried out [23]. Due to the substantial differences in facial morphology, these findings cannot be directly transferred to individuals of various racial and ethnic groups. Therefore, the current study’s objective was to assess the relationships between facial height and growth patterns in population of Timis county heritage. The degree of the dentofacial deformity cannot be fully revealed by Angle’s classification of malocclusion alone, according to an evaluation of the relationship between the anteroposterior dental arch and jaw-base relationships [24].

According to Milacic et al., there is a strong association between sagittal skeletal relationship and molar relation. The direction of jaw growth will be strongly influenced by the vertical growth pattern, which has a substantial impact on an individual’s facial heights.

The mandible’s rotation determines whether the facial pattern is hypo or hyper-divergent. As a result, for the purposes of the current study, we divided the participants into three main groups in accordance with Angle’s classification and assessed the parameters of the vertical growth pattern [11].

Jarabak’s ratio determines the percentage of the anterior and posterior facial proportions. In the present study, Class I malocclusion demonstrated 5,14% hyperdivergent, 16,01% normodivergent and 78,85% hypodivergent growth pattern. This was similar to the study done by Lall et al [25] in which angle Class I malocclusion demonstrated 11.1% hyperdivergent, 16.7% normodivergent and 72.2% hypodivergent growth pattern. Similar results were also obtained in the study done by Padarthi et al. [11].

The findings in this study differs from the study done by by Siriwat and Jarabak, [26] they found normodivergent growth pattern dominant in Class I whereas, in the present study hypodivergent growth pattern was more dominant in skeletal Class I subjects. These discrepancies might be due to racial variation.

According to Maskey and Shrestha [27] Taner [28] et al., Wang et al., [29] the mean posterior facial height of females was lower than that of males discovered that PFH and not AFH is important in the vertical face structure type. This was also true in the current investigation, but only in the hypodivergent group, since PFH and Jarabak ratio were only connected in the hypodivergent group. In terms of AFP, PFH and Jarabak ratio’s gender dimorphism was also seen in the hypodivergent group. The gender dimorphism was lowest in Class I malocclusion, according to Siriwat and Jarabak [15].

Siriwat PP, Jaraback JR. found in class I malocclusion PFH sample total 70.9±4.7, AFH 112.2±6.5, FHR 63.3±4.1, class II/1 malocclusion PFH 71.4±4.9, AFH 111.7±5.8, FHR 63.9±3.9 and II/2 malocclusion PFH 71.7±4.9, AFH 109.2±5.3, FHR 65.7±4.1 and in class III malocclusion PFH 72.4±4.8, AFH 114.0±6.6, FHR 63.6±4.2 and we found in class I malocclusion TAFH 113.06±8.96, TPFH 76.74±5.73, FHR 68,03±5.11, class II malocclusion TAFH 107.53±9.08, TPFH 75.34±6.48, FHR 70.57±6.52 and class III malocclusion TAFH 110.44±6.84, TPH 73.44±4.39, FHR 66.67±4.02.

We found distribution malocclusions among growth patterns female class I hyperdivergent 9(11.39%), class II 5(4.95%), class III 4(13.33%). Normodivergent class I 13(16.46%), class II 13(14.85%), class III 4(13.33%), hypodivergent class I 57(72.15%), class II 83(80,2%), class III 22(73.34%) and males class I hyperdivergent 0, class II 0, class III 0. Normodivergent class I 13(24.53%), class II 13(16.46%), class III 0. And hypodivergent class I 40(75.47%), class II 66(83.54%), class III 8(100%). Again Siriwat PP, Jarabak JR. found distribution malocclusions amoung growth patterns: females class I hyperdivergent 16(11.9%), class II/1 10(8.8%), class II/2 1(3.8%), neutral class I 68 (50.8%), class II/1 55(48.7%), II/2 12(46.2% ), class III 10(52.6%), class III 145(49.7%) and hypodivergent class I 50(37.3%), class II/1 48(42.5%), class II/2 13(50.0%), class III 6(31.6%). Males hyperdivergent class I 15(14.7%), class II/1 2(2.6%) and class III 3(23.1%), neutral class I 46( 45.1%), class II/1 36(46.8%), class II 3(18.8%), class III 85(40.9%) and hyperdivergent class I 41(40.2%), class II/1 39(50.6%), class II/2 13(81.2%) and Class III 10(76.9%) [26].

According to Manish Valiathan et al., found : Y axis to SN in class I males 63.67± 3.39° and females 64.74±3.61° [18], we found females 66.5±4.44° and males 63.66 ±3.16°. Vertical development of the mandible is most often the determining factor in facial harmony. The mandibular rotation causes significant alterations in facial pattern [22].

Changes in the mandibular and maxillary jaw base, according to Holdaway, can have a considerable impact on the soft tissue drape [30]. Several research have been carried out to evaluate the development trends of various malocclusions in different populations [26]. As a result, the current study attempted to assess the face height ratios and growth patterns at people of Timis county with various malocclusions.

With increasing age, the cranio-facial characteristics of patients in the normal and malocclusion groups grew more defined, hence differences are more likely to be observed in the adult sample groups grew more defined, hence differences are more likely to be observed in the adult sample [31].

Because face traits vary often during growing, the respondents in this study were chosen from the age 9 to 48 to prevent bias in interpreting facial patterns. Angle’s classification of malocclusion alone cannot show the whole degree of the dentofacial deformity, according to a study that looked at the link between the anteroposterior dental arch and the jaw-base relationships [24,32]. Milacic et al [33] had found a high correlation between molar relation and sagittal skeletal relationship. Vertical development pattern has a substantial influence on the direction of jaw growth, which has a significant impact on an individual’s face heights [40]. The facial pattern is classified as hypodivergent or hyperdivergent based on the rotation of the jaw [34]. As a result, for this investigation, we used Angle’s classification to divide the participants into three primary groups and examined the vertical development pattern characteristics.

A growth projection is a estimation of how much growth may be expected in the future and the amount and direction of development of teeth in orthodontics, the skeletal bones of the craniofacial region and the soft tissue. To make a good forecast, you need to know both the situation and the outcome in terms of the volume and direction of growth as point of reference [35].

Both hypodivergent and hyperdivergent face forms are deemed unattractive and are thus recorded in the orthodontic problem data base [36].

If there are several variables that contribute to malocclusion, the orthodontist should favor and consider using fixed and functional appliances in tandem during a certain growth stage, as this can generate greater outcomes than using fixed and functional appliances separately [37,38].

As muscles, bones and teeth confidently collide throughout the growing process, there is a greater risk of face abnormalities [39].

Lateral cephalograms of patients from Timis county were used in the investigation. This does not reflect the entire population. A research that takes into account all skeletal malocclusions is more accurate and would provide details on how different skeletal malocclusions affect growth patterns. A balanced face is necessary for perfect esthetics.

A detailed assessment of the dentofacial complex in the anterior and posterior is necessary for optimal esthetics. The goal of orthodontic treatment is to achieve normal vertical proportion [4].

5. Conclusions

As a result, treatment planning should begin with a visual representation of the eventual result, including both hard and soft tissue alteration. The majority of participants had a hypo divergent growth pattern. Group I hyperdivergent 5.14%, normodivergent 16.01%, hypodivergent 78.85%. Group II hyperdivergent 2.78%, normodivergent 14.44%, hypodi-vergent 82.78%. Group III hyperdivergent 10.53%, normodivergent 10.53%, hypodivergent 78.94%. FHR and Y axis to SN angle have a strong negative correlation.

Author Contributions

Conceptualization: A.A.S.; Data curation: A.A.S.; Formal analysis: A.A.S.; Investigation: A.A.S.; Project administration: C.A.S.; Resources: C.A.S., F.V.; Supervision: C.A.S., R.N., A.P.; Visualization: C.A.S., F.V., R.N., A.P.; Writing: A.A.S, C.A.S.; All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

All data regarding this manuscript can be checked with the corresponding author at andra.stancioiu@umft.ro

Conflicts of Interest

The authors declare that they have no conflict of interest regarding this manuscript.

References

Amatya, S.; Shrestha, R.M.; Napit, S. Growth pattern in skeletal Class I malocclusion: A Cephalometric Study. Orthod. J. Nepal 2021, 11, 49–54. [Google Scholar] [CrossRef]
Gowda, R.S.; Raghunath, N.; Sahoo, K.C.; & Shivlinga, B.M. Comparative study of mandibular morphology in patients with hypodivergent and hyperdivergent growth patterns: a cephalometric study. J. Indian Orthod. Soc. 2013, 47(4_suppl3), 377-381.
Vashisht, L.; Negi, S.; Aggarwal, M.; Sandhu, G.P.S.; Kaushal, B. TO check the reliability of various cephalometric parameters used for predicting the types of malocclusion and growth pattern. J. Adv. Med. Dent. Sci. Res. 2016, 4, 15. [Google Scholar]
Yadav, R.; Dutta, K.; Gosain, N.; Yadav, A.K.; Yadav, N.; Singh, K.K. Vertical Proportion of the Face: A Cephalometric study. Orthod. J. Nepal 2021, 11, 24–28. [Google Scholar] [CrossRef]
Alhaija, E.S.A.; Richardson, A. Growth prediction in Class III patients using cluster and discriminant function analysis. Eur. J. Orthod. 2003, 25, 599–608. [Google Scholar] [CrossRef]
Wins, S.M.; Antonarakis, G.S.; Kiliaridis, S. Predictive factors of sagittal stability after treatment of Class II malocclusions. Angle Orthod. 2016, 86, 1033–1041. [Google Scholar] [CrossRef] [PubMed]
Cruz, C. V.; Mattos, C. T.; Maia, J. C.; Granjeiro, J. M.; Reis, M. F.; Mucha, J. N.; ... & Vieira, A. R. Genetic polymorphisms underlying the skeletal Class III phenotype. American journal of orthodontics and dentofacial orthopedics. 2017, 151(4), 700-707.
Auconi, P.; Scazzocchio, M.; Defraia, E.; McNamara, J.A.; Franchi, L. Forecasting craniofacial growth in individuals with class III malocclusion by computational modelling. Eur. J. Orthod. 2014, 36, 207–216. [Google Scholar] [CrossRef] [PubMed]
Jiménez-Silva, A.; Carnevali-Arellano, R.; Vivanco-Coke, S.; Tobar-Reyes, J.; Araya-Díaz, P.; Palomino-Montenegro, H. Craniofacial growth predictors for class II and III malocclusions: A systematic review. Clin. Exp. Dent. Res. 2021, 7, 242–262. [Google Scholar] [CrossRef]
Hakeem, U.U.H.; Sidhu, M.S.; Prabhakar, M. A Cephalometric evaluation of dentoskeletal variables and ratios in three different facial types. J. Adv. Med. Dent. Sci. Res. 2021, 9, 51–63. [Google Scholar]
Padarthi, S.C.; Vijayalakshmi, D.; Apparao, H. Evaluation of Facial Height Ratios and Growth Patterns in Different Malocclusions in a Population of Dravidian Origin–A Cephalometric study. IOSR J. Dent. Med. Sci. 2019, 18, 59–66. [Google Scholar]
Proffit, W.R.; Fields, H.; Msd, D.M.; Larson, B.; & Sarver, D.M. Contemporary Orthodontics, 6e: South Asia Edition-E-Book, 2019. Elsevier India.
Nadim, K.A.R.; Rizwan, S. Prevalence of angles malocclusion according to age groups and gender. Pak. Oral Dent. J. 2014, 34. [Google Scholar]
Solow, B.; Tallgren, A. Head posture and craniofacial morphology. Am. J. Phys. Anthropol. 1976, 44, 417–435. [Google Scholar] [CrossRef] [PubMed]
Siriwat, P.P.; Jarabak, J.R. Malocclusion and facial morphology is there a relationship? An epidemiologic study. Angle Orthod. 1985, 55, 127–138. [Google Scholar] [PubMed]
Ahmed, H.M.; Mahmoud, A.B.; & Al-Shaham, S.A. The relation among different methods for assessing the vertical jaws relation 2016.
Rakosi, T. An atlas and manual of cephalometric radiography, 1982.
Valiathan, M.; Valiathan, A.; Ravinder, V. Jarabak cephalometric analysis reborn. J. Indian Orthod. Soc. 2001, 35, 66–76. [Google Scholar] [CrossRef]
Alizadeh, V.S.; Nucci, L.; Farahmand, M.; Aghdam, H.M.; Fateh, A.; Jamilian, A.; & d’Apuzzo, F, 2020. Science Repository.
Mucedero, M.; Coviello, A.; Baccetti, T.; Franchi, L.; Cozza, P. Stability factors after double-jaw surgery in Class III malocclusion: a systematic review. Angle Orthod. 2008, 78, 1141–1152. [Google Scholar] [CrossRef] [PubMed]
Abeltins, A.; Jakobsone, G.; Urtane, I.; Bigestans, A. The stability of bilateral sagittal ramus osteotomy and vertical ramus osteotomy after bimaxillary correction of class III malocclusion. J. Cranio-Maxillofac. Surg. 2011, 39, 583–587. [Google Scholar] [CrossRef] [PubMed]
Mangla, R.; Singh, N.; Dua, V.; Padmanabhan, P.; Khanna, M. Evaluation of mandibular morphology in different facial types. Contemp. Clin. Dent. 2011, 2, 200. [Google Scholar] [CrossRef]
Vieira, F.P.; Pinzan, A.; Janson, G.; Fernandes, T.M.F.; Sathler, R.C.; Henriques, R.P. Facial height in Japanese-Brazilian descendants with normal occlusion. Dent. Press J. Orthod. 2014, 19, 54–66. [Google Scholar] [CrossRef]
Al-Jabaa, A.H.; Aldrees, A.M. ANB, Wits and Molar Relationship, Do they correlate in Orthodontic Patients? Dentistry 2014, 4, 1. [Google Scholar]
Sahu, A.; Kumar, V.; Thakur, S.; Rai, S.; Bharti, P. Facial Morphology and Malocclusion Is there any Relation? A Cephalometric Analysis in Hazaribag Population. J. Contemp. Orthod. 2018, 2, 64–9. [Google Scholar]
Steiner, C.C. Cephalometrics in clinical practice. Angle Orthod. 1959, 29, 8–29. [Google Scholar]
Maskey, S.; Shrestha, R. Cephalometric approach to vertical facial height. Orthod. J. Nepal 2019, 9, 54–58. [Google Scholar] [CrossRef]
Taner, L.; Gürsoy, G.M.; Uzuner, F.D. Does Gender Have an Effect on Craniofacial Measurements? Turk. J. Orthod. 2019, 32, 59. [Google Scholar] [CrossRef] [PubMed]
Wang, M.F.; Otsuka, T.; Akimoto, S.; Sato, S. Vertical facial height and its correlation with facial width and depth: Three dimensional cone beam computed tomography evaluation based on dry skulls. Int. J. Stomatol. Occlusion Med. 2013, 6, 120–129. [Google Scholar] [CrossRef] [PubMed]
Holdaway, R.A. A Soft Tissue Cephalometric Analysis And Its Use In Orthodontic Treatment Planning Part II. Am. J. Orthod. 1984, 84, 1–28. [Google Scholar] [CrossRef] [PubMed]
Kerr, W.J.S.; Hirst, D. Craniofacial characteristics of subjects with normal and postnormal occlusions—a longitudinal study. Am. J. Orthod. Dentofac. Orthop. 1987, 92, 207–212. [Google Scholar] [CrossRef] [PubMed]
Zhou, L.; Mok, C.W.; Hägg, U.; McGrath, C.; Bendeus, M.; Wu, J. Anteroposterior dental arch and jaw-base relationships in a population sample. Angle Orthod. 2008, 78, 1023–1029. [Google Scholar] [CrossRef] [PubMed]
Milacic, M.; Markovic, M. A comparative occlusal and cephalometric study of dental and skeletal anteroposterior relationships. Br. J. Orthod. 1983, 10, 53–54. [Google Scholar] [CrossRef]
Schudy, F.F. Vertical growth versus anteroposterior growth as related to function and treatment. Angle Orthod. 1964, 34, 75–93. [Google Scholar]
Johnston, L.E. A simplified approach to prediction. Am. J. Orthod. 1975, 67, 253–257. [Google Scholar] [CrossRef]
Opdebeeck, H.; Bell, W.H. The short face syndrome. Am. J. Orthod. 1978, 73, 499–511. [Google Scholar] [CrossRef]
Francisconi, M.F.; Henriques, J.F.C.; Janson, G.; Freitas, K.M.S.D.; Santos, P.B.D.D. Stability of Class II treatment with the Bionator followed by fixed appliances. J. Appl. Oral Sci. 2013, 21, 547–553. [Google Scholar] [CrossRef]
Miguel, J.A.M.; Cunha, D.L.; Calheiros, A.D.A.; Koo, D. Rationale for referring class II patients for early orthodontic treatment. J. Appl. Oral Sci. 2005, 13, 312–317. [Google Scholar] [CrossRef]
Michele, C.; Federica, A.; Alessandro, S. Two-dimensional and three-dimensional cephalometry using cone beam computed tomography scans. J. Craniofacial Surg. 2015, 26, e311–e315. [Google Scholar] [CrossRef]
Björk, A. The nature of facial prognathism and its relation to normal occlusion of the teeth. Am. J. Orthod. 1951, 37, 106–124. [Google Scholar] [CrossRef]

Figure 1. Constructed planes and cephalometric markers were used in this investigation, Nasion-Menton and Sella-Gonion.

Figure 2. (a) WebCeph-Line analysis; (b) WebCeph-Chart.

Figure 4. In various groups, the distribution of growth patterns is varied, the gray color represents the hypodivergent growth pattern, the orange color represents the normodivergent pattern and the blue color represents the hyperdivergent growth pattern.

Figure 5. In total subjects, the Y axis has a correlation with the SN and FHR.

Table 1. Subjects are divided into three categories using Angle’s classification.

Group	Angle’s class	N
I	Class I molar relation	151 (60 M and 91 F)
II III	Class II molar relation Class III molar relation	179 (79 M and 100 F) 20 (4 M and 16 F)

*M: Male; F: Female; N: No. of cases.

Table 2. The three groups mean values for total anterior face height and total posterior facial height.

Group TAFH TPFH Y axis
to SN angle

Mean±SD(mm) Mean±SD(mm)
Mean±SD

Group I (n=151) 113,06±8,96 76,74±5,73
65,4°±4,34°

Group II (n=179) 107,53±9,08 75,34±6,48
63,87°±3,86°

Group III (n=20) 110,44±6,84 73,44±4,39
64,66°±5,28°

* n: No. of cases; TAFH: total anterior facial height; TPFH: total posterior facial height; SD: standard deviation.

Table 3. The mean face height ratios of 350 patients with sexual dimorphism were computed. The subjects were split into three groups.

Group M F T

Mean±SD Mean±SD Mean±SD

Group I (n=151) 69,93±4,74 66,77±5,11 68,03±5,11

Group II (n=179) 69,86±6,12 66,57±6,17 70,57±6,52

Group III (n=20) 68,58±2,41 66,31±4,50 66,77±4,02

* P value 0.001*, p< 0.05 statistically significant, n: No. of cases; SD: standard deviation; M: male; F: female; T: total.

Table 4. Male (n=140) and female (n=210) participants’ growth patterns were distributed.

Group	Hyperdivergent	Normodivergent		Hypodivergent		P value
M	F	M	F	M	F	M	F
Group I 0	9(11,39%)	13(24,53%)	13(16,46%)	40(75,47%)	57(72,15%)	< 0.003*	<0.001*
Group II 0	5(4,95%)	13(16,46%)	13(14,85%)	66(83,54%)	83(80,2%)
Group III 0	4(13,33%)	0	4(13,33%)	8(100%)	22(73,34%)

*p< 0. 05 statistically significant, M: male; F: female; n: No. of cases.

Table 5. Correlation Coefficients of FHR with Y axis to SN, TAFH and TPFH.

FHR

M F T

Group I Group II Group III Group I Group II Group III Group I
Group II Group III

Y axis to SN -0,709** -0,531* -1 0,791** -0,890** 0,76** -0,772** -
0,802* -0,785**

TAFH 0,002 -0,061* -1 -0,687** -0,549* -0,646* -0,364* -
0,446* -0,559*

TPFH 0,65* 0,707** -1 0,463* 0,64* 0,807** 0,556*
0,532* 0,387*

* At the 0.05 level, there is a correlation ** At the 0.01 level, there is a correlation, FHR: Facial Height Ratio, M: male; F: female, T: total, TAFH: total anterior facial height; TPFH: total posterior facial height.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer