Submitted:
24 January 2024
Posted:
25 January 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
1.1. Notation
2. Background
2.1. PID Based of Channel Orders
2.2. PID Based on Redundancy Measures
- Measures that are not concerned with information content, only information size, which makes them easy to compute even for distributions with many variables, but at the cost that the resulting decompositions may not give realistic insights into the system, precisely because they are not sensitive to informational content. Examples are [1] or [22], and applications of these can be found in [27,28,29,30].
- Measures that satisfy the Blackwell property - which arguably do measure information content - but are insensitive to changes in the sources’ distribution (as long as remain the same). Examples are [21] (see Equation (2)) or [14]. It should be noted that is only defined for the bivariate case, that is, for distributions with at most two sources, described by . Applications of these can be found in [31,32,33].
-
Case 1: there is an ordering between the channels, that is, w.l.o.g., . This means that and the decomposition (as in (1)) is given by and . Moreover, if , then .As an example, consider the leftmost distribution in Table 1, which satisfies . In this case,yielding and , as expected, because .
| t | |||
|---|---|---|---|
| 0 | 0 | 0 | 0.25 |
| 0 | 0 | 1 | 0.25 |
| 1 | 1 | 0 | 0.25 |
| 1 | 1 | 1 | 0.25 |
| t | |||
|---|---|---|---|
| (0,0) | 0 | 0 | 0.25 |
| (0,1) | 0 | 1 | 0.25 |
| (1,0) | 1 | 0 | 0.25 |
| (1,1) | 1 | 1 | 0.25 |
| t | |||
|---|---|---|---|
| 0 | 0 | 2 | 1/6 |
| 1 | 0 | 0 | 1/6 |
| 1 | 1 | 2 | 1/6 |
| 2 | 0 | 0 | 1/6 |
| 2 | 2 | 0 | 1/6 |
| 2 | 2 | 1 | 1/6 |
-
Case 2: there is no ordering between the channels and the solution of is a trivial channel, in the sense that it has no information about T. The decomposition is given by and , which may lead to a negative value of synergy.As an example, consider the COPY distribution with and i.i.d. Bernoulli variables with parameter 0.5, shown in the center of Table 1. In this case, channels and have the formwith no degradation order between them. This yields and .
-
Case 3: there is no ordering between the channels and is achieved by a nontrivial channel . The decomposition is given by and .
3. A New Measure of Union Information
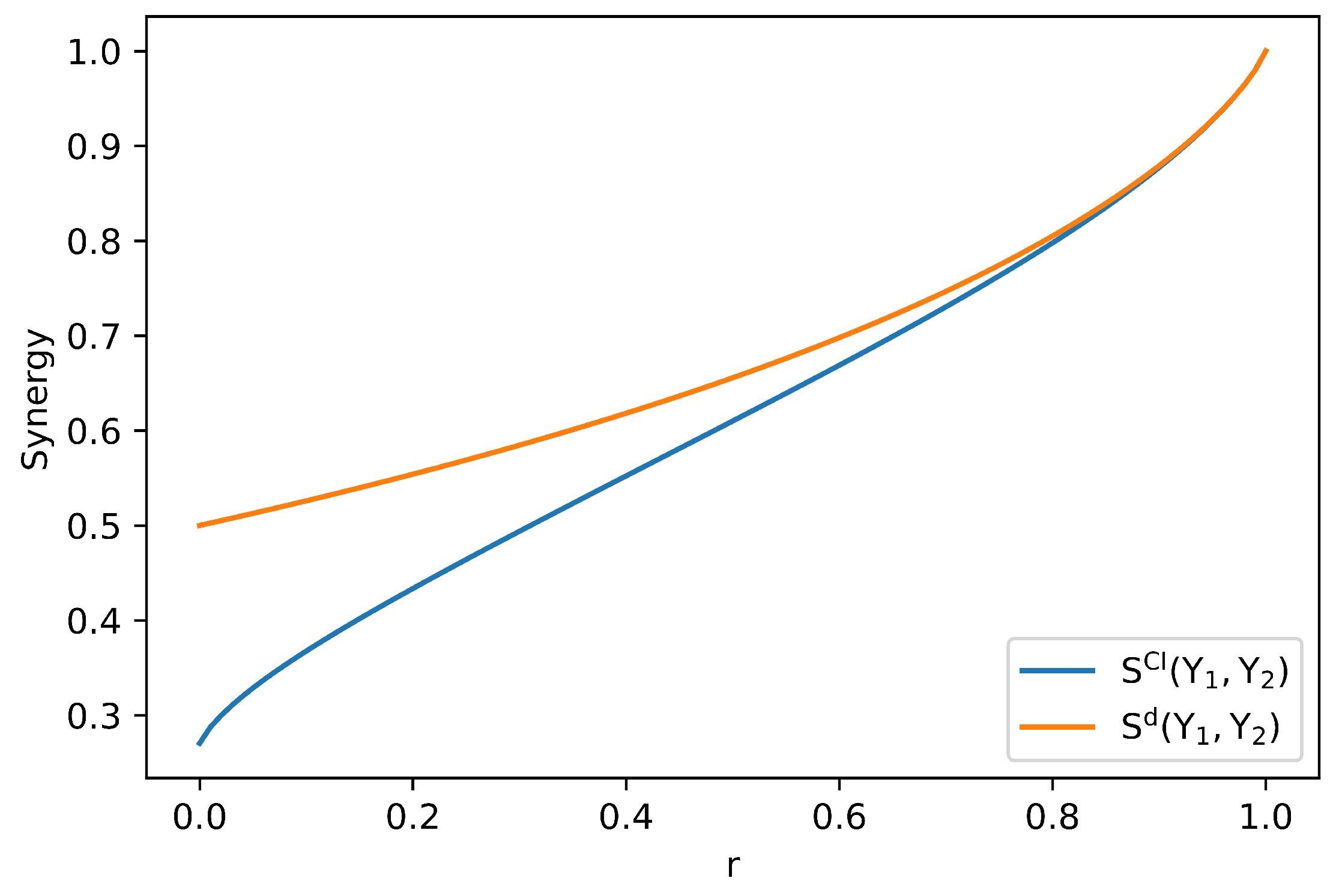
3.1. Motivation and Bivariate Definition
| t | |||
|---|---|---|---|
| 0 | 0 | 0 | 0.5 |
| 1 | 0 | 0 | r/4 |
| 1 | 1 | 0 | (1-r)/4 |
| 1 | 0 | 1 | (1-r)/4 |
| 1 | 1 | 1 | r/4 |
| t | |||
|---|---|---|---|
| 0 | 0 | 0 | 0.5 |
| 1 | 0 | 0 | 1/8 |
| 1 | 1 | 0 | 1/8 |
| 1 | 0 | 1 | 1/8 |
| 1 | 1 | 1 | 1/8 |
3.2. Operational Interpretation
3.3. General (Multivariate) Definition
- The condition that no source is a subset of another source (which also excludes the case where two sources are the same) implies no loss of generality: if one source is a subset of another, say , then may be removed without affecting either A or , thus yielding the same value for . The removal of source is also done for measures of intersection information, but under the opposite condition: whenever .
- The condition that no source is a deterministic function of other sources is slightly more nuanced. In our perspective, an intuitive and desired property of measures of both union and synergistic information is that their value should not change whenever one adds a source that is a deterministic function of sources that are already considered. We provide arguments in favor of this property in Section 4.2.1. This property may not be satisfied by computing without previously excluding such sources. For instance, consider , where and are two i.i.d. random variables following a Bernoulli distribution with parameter 0.5, (that is, is deterministic function of ), and . Computing without excluding (or ) yields and . This issue is resolved by removing deterministic sources before computing .
4. Properties of Measures of Union Information and Synergy
4.1. Extension of the Williams-Beer Axioms for Measures of Union Information
- 1.
- Symmetry: is symmetric in the ’s.
- 2.
- Self-redundancy: .
- 3.
- Monotonicity: .
- 4.
- Equality for monotonicity: .
- Symmetry follows from the symmetry of mutual information, which in turn is a consequence of the well-known symmetry of joint entropy.
- Self-redundancy follows from the fact that agent i has access to and , which means that is one of the distributions in the set , which implies that .
- To show that monotonicity holds, begin by noting thatdue to the monotonicity of mutual information. Let be the set of distributions that the sources can construct and that which the sources can construct. Since , it is clear thatConsequently,which means monotonicity holds.
- Finally, the proof that equality for monotonicity is the same that was used above to show that the assumption that no source is a subset of another source entails no loss of generality. If , then the presence of is irrelevant: and , which implies that .
4.2. Review of Suggested Properties: Griffith and Koch [15]
- Duplicating a predictor does not change synergistic information; formally,where , for some . Griffith and Koch [15] show that this property holds if the equality for monotonicity property holds for the “corresponding" measure of union information (“corresponding" in the sense of equation (7)). As shown in the previous subsection, satisfies this property, and so does the corresponding synergy .
- Adding a new predictor can decrease synergy, which is a weak statement. We suggest a stronger property: adding a new predictor cannot increase synergy, which is formally written asThis property simply follows from monotonicity for the corresponding measure of union information, which we proved above holds for .
- Global positivity: .
- Self-redundancy: .
- Symmetry: is invariant under permutations of .
- Stronger monotonicity: , with equality if there is some such that .
- Target monotonicity: for any (discrete) random variables T and Z, .
- Weak local positivity: for the derived partial informations are nonnegative. This is equivalent to
- Strong identity: .
4.2.1. Stronger Monotonicity
4.2.2. Target Monotonicity
| T | Z | |||
|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0.419 |
| 1 | 1 | 2 | 1 | 0.203 |
| 2 | 1 | 3 | 0 | 0.007 |
| 0 | 0 | 3 | 1 | 0.346 |
| 2 | 2 | 4 | 4 | 0.025 |
4.3. Review of Suggested Properties: Quax et al. [35]
- Nonnegativity: .
- Upper-Bounded by Mutual Information: .
- Weak Symmetry: is invariant under any reordering of .
- Zero synergy about a single variable: for any .
- Zero synergy in a single variable: for any .
4.4. Relationship with the extended Williams-Beer axioms
4.5. Review of Suggested Properties: Rosas et al. [36]
- Target data processing inequality: if is a Markov chain, then .
- Channel convexity: is a convex function of for a given .
| T | |||
|---|---|---|---|
| 0 | 0 | 0 | |
| 1 | 0 | 0 | |
| 1 | 1 | 0 | 0.25 |
| 1 | 0 | 1 | 0.25 |
| 0 | 1 | 1 | 0.25 |
5. Previous Measures of Union Information and Synergy
5.1. Qualitative comparison
- , derived from , the original redundancy measure proposed by Williams and Beer [1], using the IEP;
- the whole-minus-sum (WMS) synergy, ;
- the correlational importance synergy, .
5.2. Quantitative comparison
- XOR yields . The XOR distribution is the hallmark of synergy. Indeed, the only solution of (1) is , and all of the above measures yield 1 bit of synergy.
- AND yields . Unlike XOR, there are multiple solutions for (1), and none is universally agreed upon, since different information measures capture different concepts of information.
- COPY yields . Most PID measures argue one of two different possibilities for this distribution. They suggest that the solution is either or . Our measure suggests that all information flows uniquely from each source.
- RDNXOR yields . In words, this distribution is the concatenation of two XOR ‘blocks’, each of which with its own symbols, and not allowing the two blocks to mix. That is, both and can determine in which XOR block the resulting value T will be - which intuitively means that they both have this information, meaning it is redundant - but neither nor have information about the outcome of the XOR operation - as is expected in the XOR distribution - which intuitively means that such information must be synergistic. All measures except agree with this.
- RDNUNQXOR yields . According to Griffith and Koch [15], it was constructed to carry 1 bit of each information type. Although the solution is not unique, it must satisfy . Indeed our measure yields the solution , like most measures except and . This confirms the intuition by Griffith and Koch [15] that and overestimate and underestimate synergy, respectively. In fact, in the decomposition resulting from , there are 2 bits of synergy and 2 bits of redundancy, which we argue cannot be the case, as this would imply that , and given the construction of this distribution, it is clear that there is some unique information since, unlike in RDNXOR, the XOR blocks are allowed to mix, thus is a possible outcome, but so is . That is not the case with RDNXOR. On the other hand, yields zero synergy and redundancy, with and each evaluating to 2 bits. Since this distribution is a mix of blocks satisfying a relation of the form , we argue that there must be some non-null amount of synergy, which is why we claim that is not valid.
- XORDUPLICATE yields . All measures correctly identify that the duplication of a source shouldn’t change synergy, at least for this particular distribution.
- ANDDUPLICATE yields . Unlike in the previous example, both and yield a change in their synergy value. This is a shortcoming since duplicating a source should not increase either synergy or union information. The other measures are not affected by the duplication of a source.
- XORLOSES yields . Its distribution is the same as XOR but with a new source satisfying . As such, since uniquely determines T, we expect no synergy. All measures agree with this.
- XORMULTICOAL yields . Its distribution is such that any pair , is able to determine T with no uncertainty. All measures agree that the information present in this distribution is purely synergistic.
5.3. Relation to other PID measures
6. Conclusion and future work
- We introduced new measures of union information and synergy for the PID framework, which thus far was mainly developed based on measures of redundant or unique information. We provided its operational interpretation and defined it for an arbitrary number of sources.
- We proposed an extension of the Williams-Beer axioms for measures of union information and showed our proposed measure satisfies them.
- We reviewed, commented on and rejected some of the previously proposed properties for measures of union information and synergy in the literature.
- We showed that measures of union information that satisfy the extension of the Williams-Beer axioms necessarily satisfy a few other appealing properties, as well as the derived measures of synergy.
- We reviewed previous measures of union information and synergy, critiqued them and compared them with our proposed measure.
- The new measure is easy to compute. For example in the bivariate case, if the supports of , and T have size , and , respectively, the computation time of our measure grows like .
- We provide code for the computation of our measure for the bivariate case and for source in the trivariate case.
- We saw that the synergy yielded by the measure of James et al. [16] is given by . Given its analytical expression, one could start by defining a measure of union information as , possibly tweak it so it satisfies the WB axioms, study its properties and possibly extend it to the multivariate case.
- Our proposed measure may ignore conditional dependencies that are present in p in favor of maximizing mutual information, as we commented in Section 3.3. This is a compromise so that the measure satisfies monotonicity. We believe this is a potential drawback of our measure, and we suggest the investigation of a measure similar to ours, but that doesn’t ignore conditional dependencies that it has access to.
- Implementing our measure in the dit package [38].
- This paper reviewed measures of union information and synergy, as well as properties that were suggested throughout the literature. Sometimes we did so by providing examples where the suggested properties fail, and other times simply by commenting. We suggest something similar be done for measures of redundant information.
7. Code availability
Funding
Conflicts of Interest
Appendix A
| T | ||
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| 0 | 1 | 1 |
| 2 | 2 | 2 |
| 3 | 2 | 3 |
| 3 | 3 | 2 |
| 2 | 3 | 3 |
| T | |||
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| T | |||
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 0 | 2 | 2 | 2 |
| 0 | 3 | 3 | 3 |
| 1 | 2 | 1 | 0 |
| 1 | 3 | 0 | 1 |
| 1 | 0 | 3 | 2 |
| 1 | 1 | 2 | 3 |
References
- Williams, P.; Beer, R. Nonnegative decomposition of multivariate information. arXiv preprint arXiv:1004.2515 2010. [CrossRef]
- Lizier, J.; Flecker, B.; Williams, P. Towards a synergy-based approach to measuring information modification. 2013 IEEE Symposium on Artificial Life (ALIFE). IEEE, 2013, pp. 43–51. [CrossRef]
- Wibral, M.; Finn, C.; Wollstadt, P.; Lizier, J.T.; Priesemann, V. Quantifying information modification in developing neural networks via partial information decomposition. Entropy 2017, 19, 494. [Google Scholar] [CrossRef]
- Rauh, J. Secret sharing and shared information. Entropy 2017, 19, 601. [Google Scholar] [CrossRef]
- Vicente, R.; Wibral, M.; Lindner, M.; Pipa, G. Transfer entropy—a model-free measure of effective connectivity for the neurosciences. Journal of computational neuroscience 2011, 30, 45–67. [Google Scholar] [CrossRef] [PubMed]
- Ince, R.; Van Rijsbergen, N.; Thut, G.; Rousselet, G.; Gross, J.; Panzeri, S.; Schyns, P. Tracing the flow of perceptual features in an algorithmic brain network. Scientific reports 2015, 5, 1–17. [Google Scholar] [CrossRef]
- Gates, A.; Rocha, L. Control of complex networks requires both structure and dynamics. Scientific reports 2016, 6, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Faber, S.; Timme, N.; Beggs, J.; Newman, E. Computation is concentrated in rich clubs of local cortical networks. Network Neuroscience 2019, 3, 384–404. [Google Scholar] [CrossRef]
- James, R.; Ayala, B.; Zakirov, B.; Crutchfield, J. Modes of information flow. arXiv preprint arXiv:1808.06723, 2018. [Google Scholar] [CrossRef]
- Arellano-Valle, R.; Contreras-Reyes, J.; Genton, M. Shannon Entropy and Mutual Information for Multivariate Skew-Elliptical Distributions. Scandinavian Journal of Statistics 2013, 40, 42–62. [Google Scholar] [CrossRef]
- Cover, T. Elements of information theory; John Wiley & Sons, 1999. [CrossRef]
- Harder, M.; Salge, C.; Polani, D. Bivariate measure of redundant information. Physical Review E 2013, 87, 012130. [Google Scholar] [CrossRef]
- Gutknecht, A.; Wibral, M.; Makkeh, A. Bits and pieces: Understanding information decomposition from part-whole relationships and formal logic. Proceedings of the Royal Society A 2021, 477, 20210110. [Google Scholar] [CrossRef]
- Bertschinger, N.; Rauh, J.; Olbrich, E.; Jost, J.; Ay, N. Quantifying unique information. Entropy 2014, 16, 2161–2183. [Google Scholar] [CrossRef]
- Griffith, V.; Koch, C. Quantifying synergistic mutual information. In Guided self-organization: inception; Springer, 2014; pp. 159–190. [CrossRef]
- James, R.; Emenheiser, J.; Crutchfield, J. Unique information via dependency constraints. Journal of Physics A: Mathematical and Theoretical 2018, 52, 014002. [Google Scholar] [CrossRef]
- Chicharro, D.; Panzeri, S. Synergy and redundancy in dual decompositions of mutual information gain and information loss. Entropy 2017, 19, 71. [Google Scholar] [CrossRef]
- Bertschinger, N.; Rauh, J.; Olbrich, E.; Jost, J. Shared information—New insights and problems in decomposing information in complex systems. Proceedings of the European conference on complex systems 2012. Springer, 2013, pp. 251–269. [CrossRef]
- Rauh, J.; Banerjee, P.; Olbrich, E.; Jost, J.; Bertschinger, N.; Wolpert, D. Coarse-graining and the Blackwell order. Entropy 2017, 19, 527. [Google Scholar] [CrossRef]
- Ince, R. Measuring multivariate redundant information with pointwise common change in surprisal. Entropy 2017, 19, 318. [Google Scholar] [CrossRef]
- Kolchinsky, A. A Novel Approach to the Partial Information Decomposition. Entropy 2022, 24, 403. [Google Scholar] [CrossRef] [PubMed]
- Barrett, A. Exploration of synergistic and redundant information sharing in static and dynamical Gaussian systems. Physical Review E 2015, 91, 052802. [Google Scholar] [CrossRef] [PubMed]
- Griffith, V.; Chong, E.; James, R.; Ellison, C.; Crutchfield, J. Intersection information based on common randomness. Entropy 2014, 16, 1985–2000. [Google Scholar] [CrossRef]
- Griffith, V.; Ho, T. Quantifying redundant information in predicting a target random variable. Entropy 2015, 17, 4644–4653. [Google Scholar] [CrossRef]
- Gomes, A.F.; Figueiredo, M.A. Orders between Channels and Implications for Partial Information Decomposition. Entropy 2023, 25, 975. [Google Scholar] [CrossRef]
- Pearl, J. Causality; Cambridge university press, 2009. [CrossRef]
- Colenbier, N.; Van de Steen, F.; Uddin, L.Q.; Poldrack, R.A.; Calhoun, V.D.; Marinazzo, D. Disambiguating the role of blood flow and global signal with partial information decomposition. NeuroImage 2020, 213, 116699. [Google Scholar] [CrossRef]
- Sherrill, S.P.; Timme, N.M.; Beggs, J.M.; Newman, E.L. Partial information decomposition reveals that synergistic neural integration is greater downstream of recurrent information flow in organotypic cortical cultures. PLoS computational biology 2021, 17, e1009196. [Google Scholar] [CrossRef]
- Sherrill, S.P.; Timme, N.M.; Beggs, J.M.; Newman, E.L. Correlated activity favors synergistic processing in local cortical networks in vitro at synaptically relevant timescales. Network Neuroscience 2020, 4, 678–697. [Google Scholar] [CrossRef] [PubMed]
- Proca, A.M.; Rosas, F.E.; Luppi, A.I.; Bor, D.; Crosby, M.; Mediano, P.A. Synergistic information supports modality integration and flexible learning in neural networks solving multiple tasks. arXiv preprint arXiv:2210.02996, 2022. [Google Scholar] [CrossRef]
- Kay, J.W.; Schulz, J.M.; Phillips, W.A. A comparison of partial information decompositions using data from real and simulated layer 5b pyramidal cells. Entropy 2022, 24, 1021. [Google Scholar] [CrossRef] [PubMed]
- Liang, P.P.; Cheng, Y.; Fan, X.; Ling, C.K.; Nie, S.; Chen, R.; Deng, Z.; Mahmood, F.; Salakhutdinov, R.; Morency, L.P. Quantifying & modeling feature interactions: An information decomposition framework. arXiv preprint arXiv:2302.12247, 2023. [Google Scholar] [CrossRef]
- Hamman, F.; Dutta, S. Demystifying Local and Global Fairness Trade-offs in Federated Learning Using Partial Information Decomposition. arXiv preprint arXiv:2307.11333, 2023. [Google Scholar] [CrossRef]
- Gutknecht, A.J.; Makkeh, A.; Wibral, M. From Babel to Boole: The Logical Organization of Information Decompositions. arXiv preprint arXiv:2306.00734, 2023. [Google Scholar] [CrossRef]
- Quax, R.; Har-Shemesh, O.; Sloot, P.M. Quantifying synergistic information using intermediate stochastic variables. Entropy 2017, 19, 85. [Google Scholar] [CrossRef]
- Rosas, F.E.; Mediano, P.A.; Rassouli, B.; Barrett, A.B. An operational information decomposition via synergistic disclosure. Journal of Physics A: Mathematical and Theoretical 2020, 53, 485001. [Google Scholar] [CrossRef]
- Krippendorff, K. Ross Ashby’s information theory: a bit of history, some solutions to problems, and what we face today. International journal of general systems 2009, 38, 189–212. [Google Scholar] [CrossRef]
- James, R.; Ellison, C.; Crutchfield, J. “dit“: a Python package for discrete information theory. Journal of Open Source Software 2018, 3, 738. [Google Scholar] [CrossRef]
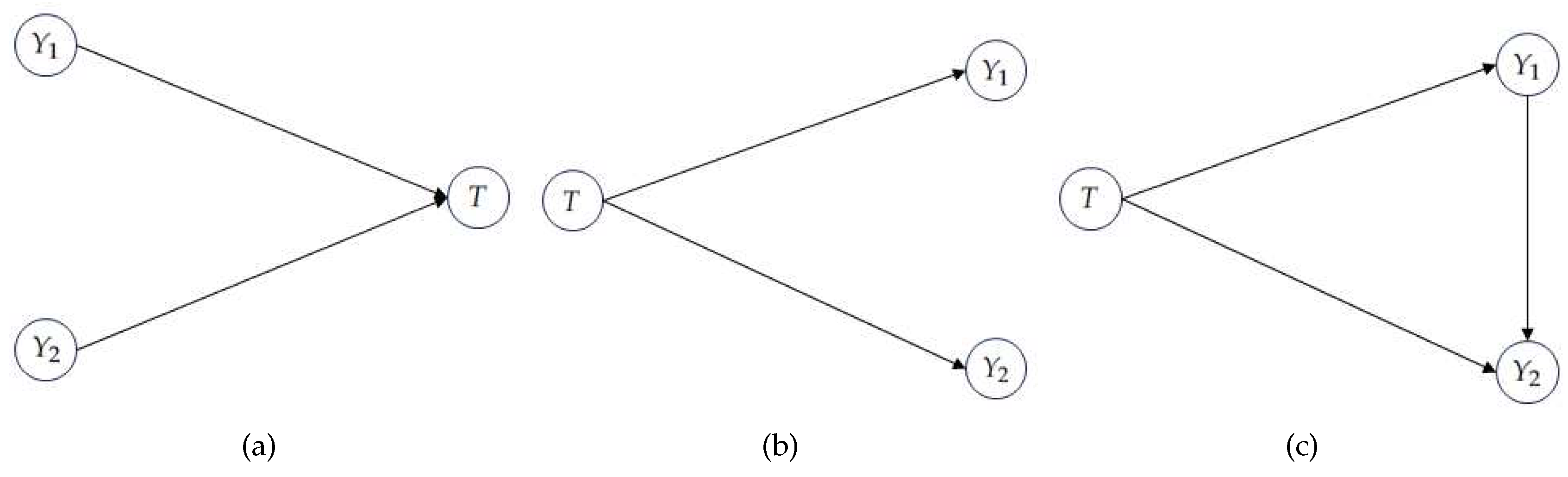
| T | |||
|---|---|---|---|
| (0,0) | 0 | 0 | 1/3 |
| (0,1) | 0 | 1 | 1/3 |
| (1,0) | 1 | 0 | 1/3 |
| T | Z | |||
|---|---|---|---|---|
| 0 | (0,0) | 0 | 0 | 0.25 |
| 0 | (0,1) | 0 | 1 | 0.25 |
| 0 | (1,0) | 1 | 0 | 0.25 |
| 1 | (1,1) | 1 | 1 | 0.25 |
| 0 | 0 | 0 | 0 | 0.25 |
| 1 | 1 | 0 | 1 | 0.25 |
| 1 | 2 | 1 | 0 | 0.25 |
| 0 | 3 | 1 | 1 | 0.25 |
| T | |||
|---|---|---|---|
| 0 | 0 | 0 | |
| 1 | 0 | 0 | |
| 1 | 1 | 0 | 0.4 |
| 1 | 0 | 1 | 0.4 |
| 0 | 1 | 1 | 0.1 |
| Example | ||||||
|---|---|---|---|---|---|---|
| XOR | 1 | 1 | 1 | 1 | 1 | 1 |
| AND | 0.5 | 0.189 | 0.104 | 0.5 | 0.311 | 0.270 |
| COPY | 1 | 0 | 0 | 0 | 1 | 0 |
| RDNXOR | 1 | 0 | 1 | 1 | 1 | 1 |
| RDNUNQXOR | 2 | 0 | 1 | 1 | DNF | 1 |
| XORDUPLICATE | 1 | 1 | 1 | 1 | 1 | 1 |
| ANDDUPLICATE | 0.5 | -0.123 | 0.038 | 0.5 | 0.311 | 0.270 |
| XORLOSES | 0 | 0 | 0 | 0 | 0 | 0 |
| XORMULTICOAL | 1 | 1 | 1 | 1 | DNF | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





