Submitted:
16 January 2024
Posted:
17 January 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Formalism
The fitting procedure of SEI
3. Symmetric and Asymmetric Nuclear Matter Properties
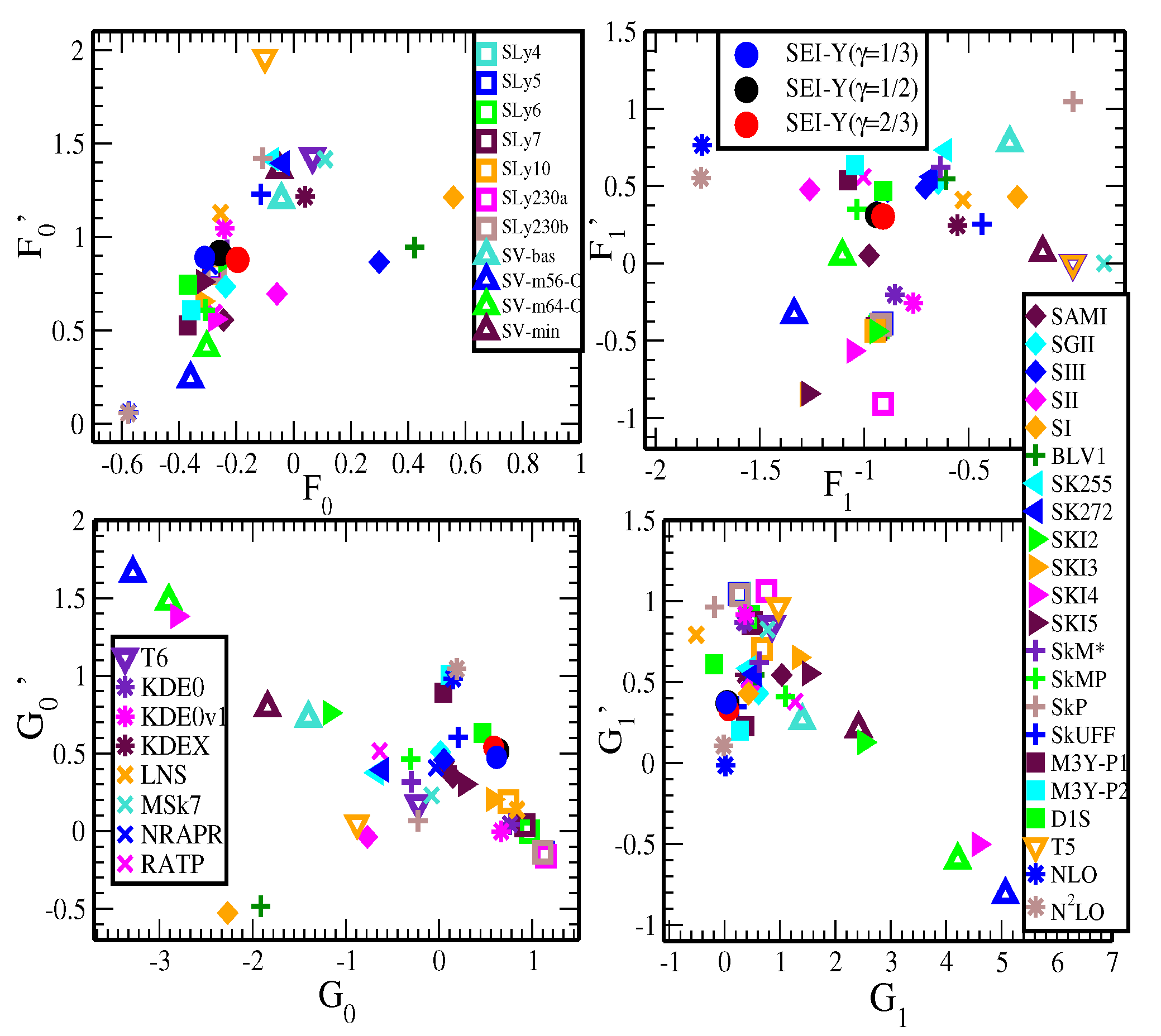
Landau parameters
High-order Derivatives of the Energy per Particle in Asymmetric Nuclear Matter
4. Neutron Star Phenomenology
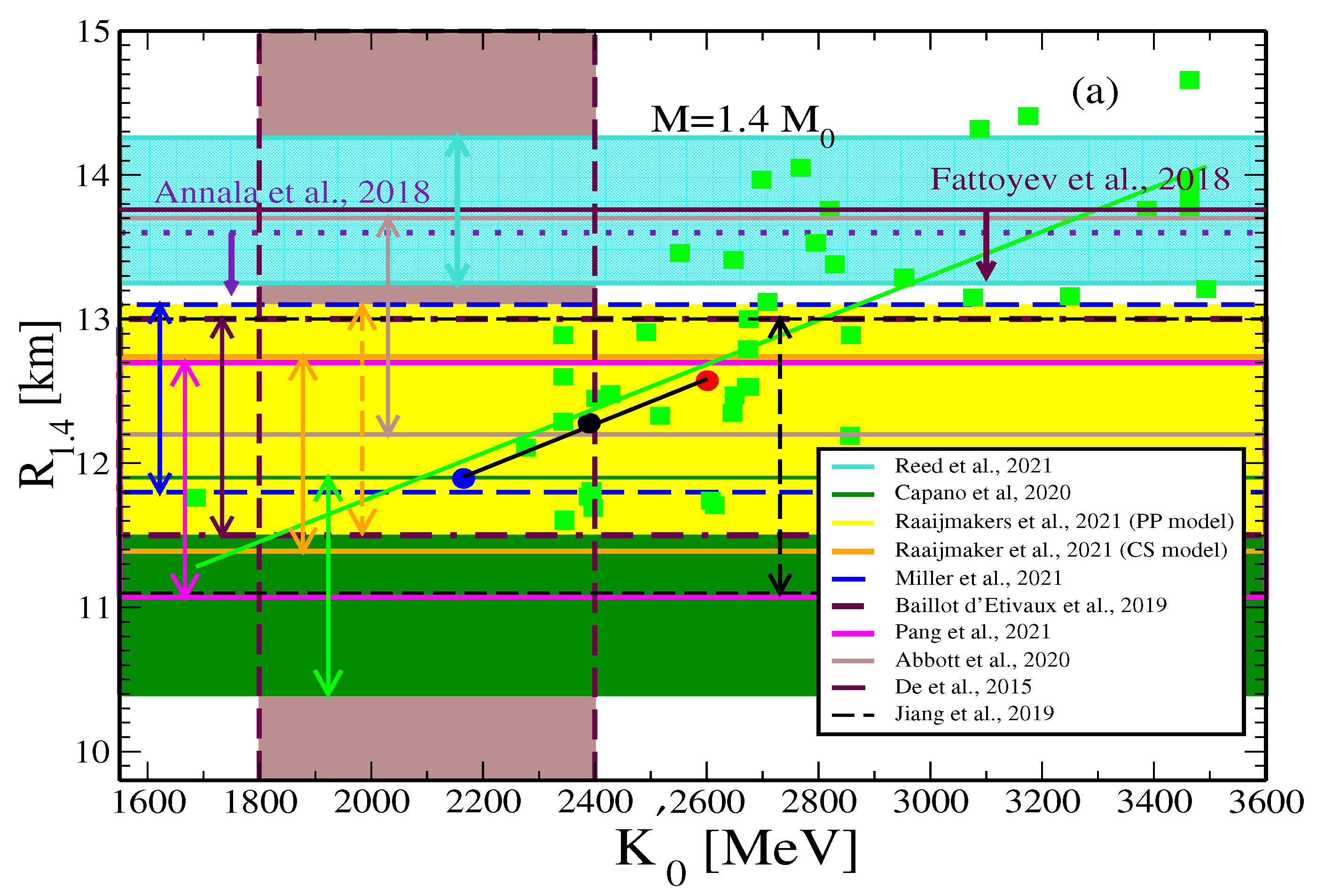
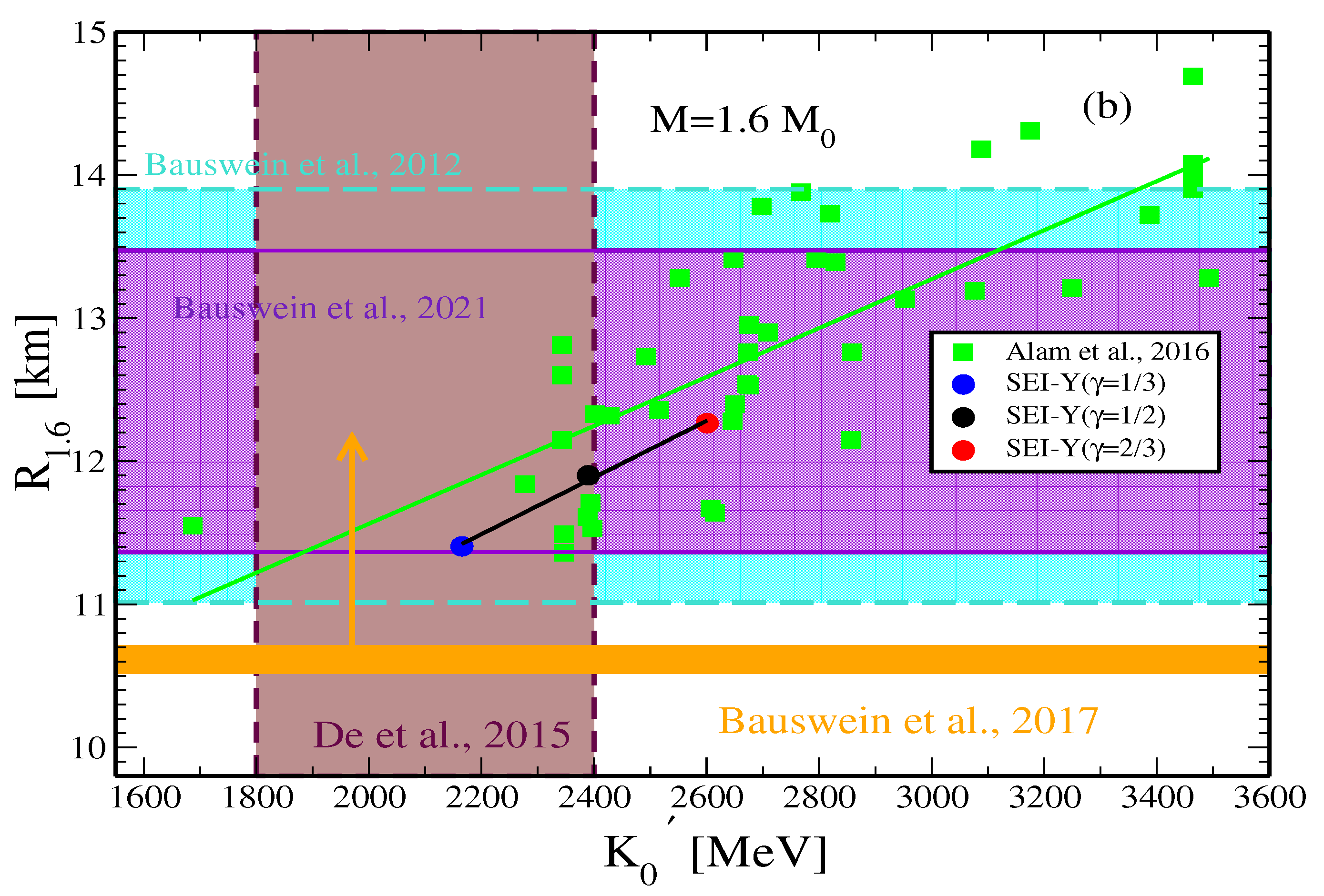
The Radius of Neutron Stars and the Slope of the Isoscalar Incompressibility
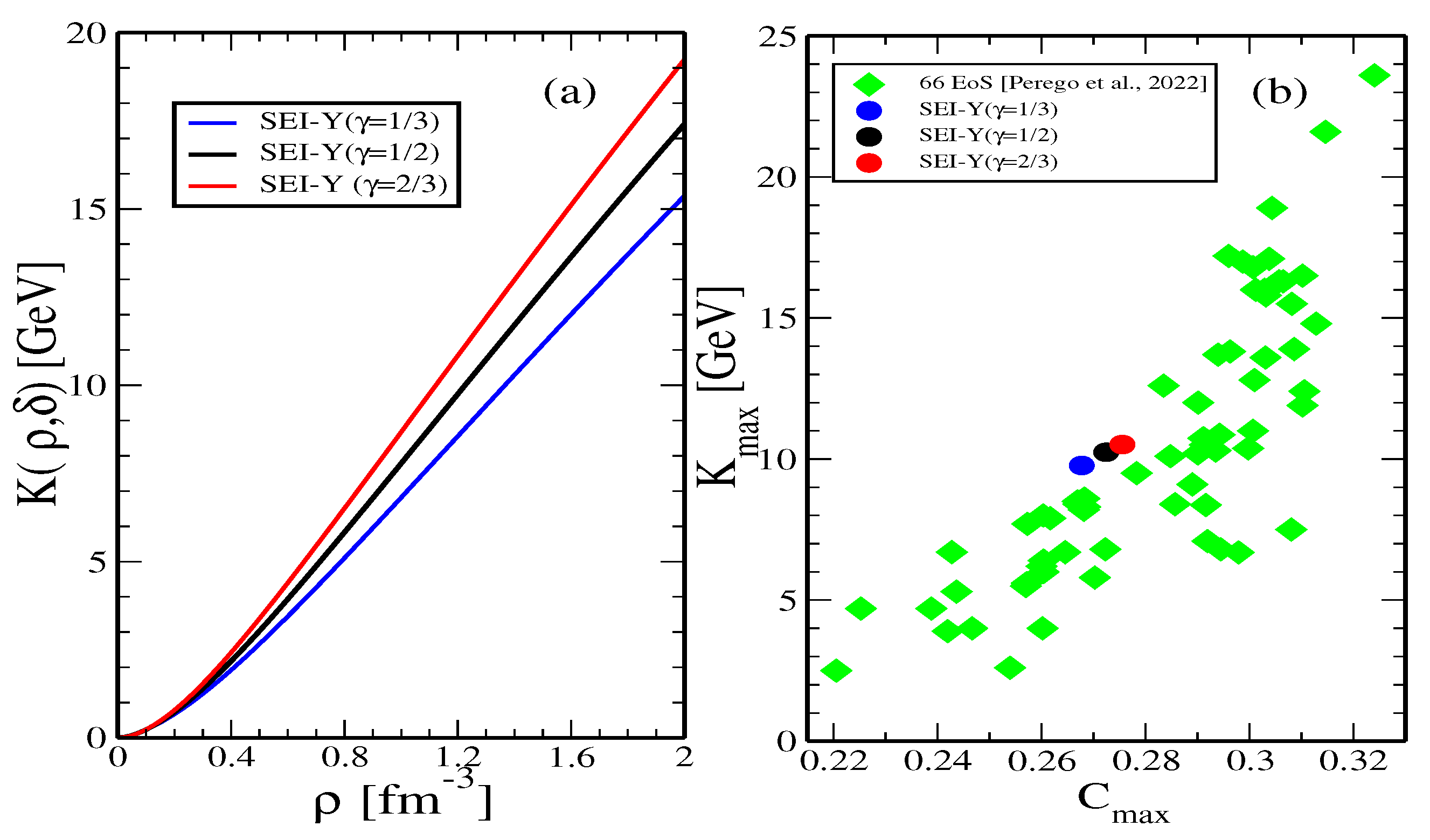
Neutron Star Merger and Incompressibility of Asymmetric Nuclear Matter
Sound Speed in Neutron Star Matter
Gravitational redshift
Neutron star mass, radius and gravitational redshift at different central densities
5. Summary and Outlook
Acknowledgments
Appendix A. Relations between the six strength parameters and the interaction parameters
| b [] | [fm] | [MeVfm3(γ+1)] | W [MeV] | ||
|---|---|---|---|---|---|
| 1/3 | 0.4161 | 0.4232 | -0.0630 | 9536.129 | -1380.539 |
| 1/2 | 0.5880 | 0.4242 | -0.112 | 9277.281 | -1321.847 |
| 2/3 | 0.7796 | 0.4250 | -0.153 | 10228.257 | -1214.475 |
| B [MeV] | H [MeV] | M [MeV] | [MeV] | ||
| 128.0918 | -630.968 | -808.871 | 333.5 | 1.151 | 119.3 |
| 100.950 | -575.215 | -832.339 | 566.7 | 0.664 | 118.4 |
| 49.094 | -470.284 | -881.144 | 647.4 | 0.520 | 118.2 |
Appendix B. Landau Parameters
References
- Haar, B. T.; and Malfliet, R. Nucleons, mesons and deltas in nuclear matter a relativistic Dirac-Brueckner approach. Phys. Rep. 1987, 149, 207. [https://doi.org/10.1016/0370-1573(87)90085-8]; Van Dalen, E. N. E.; Fuchs, C.; and Faessler, A. The relativistic Dirac–Brueckner approach to asymmetric nuclear matter. Nucl. Phys. A 2004, 744, 227-248. [https://doi.org/10.1016/j.nuclphysa.2004.08.019]; Jong, F. de.; and Lenske, H. Asymmetric nuclear matter in the relativistic Brueckner-Hartree-Fock approach. Phys. Rev. C 1998, 57, 3099. [https://doi.org/10.1103/PhysRevC.57.3099]. [CrossRef]
- Cugnon, J.; Deneye, P.; and Lejeune, A. Z. Neutron matter properties in an extended Brueckner approach Physik A - Atomic Nuclei 1987 328, 409-415. [https://doi.org/10.1007/BF01289626] ; Zuo, W.; Lejeune A.; Lombardo, U.; and Mathiot, J. F. Microscopic three-body force for asymmetric nuclear matter. Eur. Phys. J. A 2002, 14, 469-475. [https://doi.org/10.1140/epja/i2002-10031-y]; Bombaci, I.; and Lombardo, U.; Asymmetric nuclear matter equation of state. Phys. Rev. C 1991, 44, 1892. [https://doi.org/10.1103/PhysRevC.44.1892]; Day, B. D.; and Wiringa, R. B. Brueckner-Bethe and variational calculations of nuclear matter. Phys. Rev. C 1985, 32, 1057. [https://doi.org/10.1103/PhysRevC.32.1057]; Baldo, M.; Burgio, G. F.; and Schulze, H.-J. Hyperon stars in the Brueckner-Bethe-Goldstone theory. Phys. Rev. C 2000, 61, 055801 [https://doi.org/10.1103/PhysRevC.61.055801]; Vidaña, I.; Polls, A.; Ramos, A.; Engvik, L.; and Hjorth-Jensen, M. Hyperon-hyperon interactions and properties of neutron star matter. Phys. Rev. C 2000, 62, 035801. [https://doi.org/10.1103/PhysRevC.62.035801]. [CrossRef]
- Akmal, A.; Pandharipande, V. R.; and Ravenhall, D. G. Equation of state of nucleon matter and neutron star structure. Phys. Rev. C 1998, 58, 1804. [CrossRef]
- Mukherjee, A.; and Pandharipande, V. R. Variational theory of hot nucleon matter. Phys. Rev. C 2007, 75, 035802. [CrossRef]
- Hebeler, K.; and Schwenk, A. Chiral three-nucleon forces and neutron matter. Phys. Rev. C 2010, 82, 014314. [CrossRef]
- Hebeler, K.; Lattimer, J. M.; Pethick, C. J.; and Schwenk, A. Constraints on Neutron Star Radii Based on Chiral Effective Field Theory Interactions. Phys. Rev. Lett. 2010, 105, 161102. [CrossRef]
- Haensel, P.; Kutschera, M.; and Prószyński, M. Uncertainty in the saturation density of nuclear matter and neutron star models. Astron. Astrophys. 1981, 102, 299-302. [http://adsabs.harvard.edu/abs/1981A%26A...102..299H].
- Skyrme, T. H. R. CVII. The Nuclear Surface. Phil. Mag. (1956) 1, 1043. [CrossRef]
- Decharge, J; and Gogny, D. Hartree-Fock-Bogolyubov calculations with the D1 effective interaction on spherical nuclei. Phys. Rev. C 1980, 21, 1568. [CrossRef]
- Bertsch, G.; Borysowicz, J.; McManus, H.; and Love, W.G. Interactions for inelastic scattering derived from realistic potentials. Nucl. Phys. A 1977, 284, 399-419. [CrossRef]
- Behera, B; Routray, T R; and Satpathy, R K . Momentum and density dependence of the mean field in nuclear matter. J. Phys. G: Nucl. Part. Phys. 1998, 24, 2073. [CrossRef]
- Behera, B.; Routray, T. R.; et al. Momentum and density dependence of the isospin part of nuclear mean field and equation of state of asymmetric nuclear matter. Nuclear Physics A 2005, 753, 367-386. [CrossRef]
- Behera, B; Vin˜as, X.; Routray, T. R.; Centelles, M.. Study of spin polarized nuclear matter and finite nuclei with finite range simple effective interaction. J. Phys G: Nucl. Part. Phys. 2015, 42, 045103. http://iopscience.iop.org/0954-3899/42/4/045103.
- Behera, B; Vi n˜as, X; Bhuyan, M; Routray, T. R.; Sharma, B. K.; and Patra, S. K. Simple effective interaction: infinite nuclear matter and finite nuclei. J. Phys G: Nucl. Part. Phys. 2013, 40, 095105. [http://iopscience.iop.org/0954-3899/40/9/095105].
- Bertsch, G. F.; and Das Gupta, S. A guide to microscopic models for intermediate energy heavy ion collisions. Phys. Rep. 1988, 160 189. [CrossRef]
- Gale, C; Bertsch, G. F.; and Das Gupta, S. Heavy-ion collision theory with momentum-dependent interactions. Phys. Rev. C, 1987, 35, 1666. [CrossRef]
- Gale, C; Welke, G. M.; Prakash, M; Lee, S. J.; and Das Gupta, S. Transverse momenta, nuclear equation of state, and momentum-dependent interactions in heavy-ion collisions. Phys. Rev. C 1990, 41, 1545. [CrossRef]
- Csernai, L. P.; Fai, G; Gale, C; and Osnes, E. Nuclear equation of state with momentum-dependent interactions. Phys. Rev. C 1992, 46, 736. [CrossRef]
- Behera, B; Routray, T. R.; and Satpathy, R. K. Causal violation of the speed of sound and the equation of state of nuclear matter. J. Phys. G 1997, 23, 445. [http://iopscience.iop.org/0954-3899/23/4/005].
- Danielewicz, P.; Lacey, R.; and Lynch, W. G. Determination of the Equation of State of Dense Matter. Science 2002, 298, 1592. [CrossRef]
- Behera, B.; Routray, T. R.; and Tripathy, S. K. Neutron–proton effective mass splitting and thermal evolution in neutron-rich matter. J. Phys. G: Nucl. Part. Phys. 2011, 38, 115104. [http://iopscience.iop.org/0954-3899/38/11/115104)].
- Dutra, M.; Lourenço, O.; et al. Skyrme interaction and nuclear matter constraints. Phys. Rev. C 2012, 85, 035201. [CrossRef]
- Behera, B.; Routray, T. R.; Pradhan, A.; Patra, S. K.; and Sahu, P. K.; Nuclear mean field and equation of state of asymmetric nuclear matterNucl. Phys. A 2007, 794, 132-148. [CrossRef]
- Wiringa, R. B. Single-particle potential in dense nuclear matter. Phys. Rev. C 1988, 38, 2967. [CrossRef]
- Sammarruca, F. The Microscopic Approach to Nuclear Matter and Neutron Star Matter. Int. J. Mod. Phys. E 2010, 19, 1259-1313. [CrossRef]
- Behera, B.; Routray, T. R.; and Tripathy, S. K. Temperature dependence of the nuclear symmetry energy and equation of state of charge neutral n + p + e + μ matter in beta equilibrium. J. Phys. G: Nucl. Part. Phys. 2009, 36, 125105. [CrossRef]
- Behera, B.; Viñas, X.; Routray, T. R.; Robledo, L. M.; Centelles, M.; and Pattnaik, S. P. Deformation properties with a finite-range simple effective interaction. J. Phys. G: Nucl. Part. Phys. 2016, 43, 045115. [http://iopscience.iop.org/0954-3899/43/4/045115].
- Bano, P; Pattnaik, S. P.; Centelles, M.; Viñas X.; and Routray, T. R. Correlations between charge radii differences of mirror nuclei and stellar observables. Phys. Rev. C 2023, 108, 015802. [CrossRef]
- Sammarruca, F.; and Krastev, P. G. Spin polarized neutron matter within the Dirac-Brueckner-Hartree-Fock approach. Phys. Rev. C 2007, 75, 034315. [CrossRef]
- Bombaci, I.; and Lombardo, U.; Asymmetric nuclear matter equation of state. Phys. Rev. C 1991, 44, 1892. [CrossRef]
- Li, B. A.; Ramos, À.; Verde, G.; Vidaña I. Eur. Phys. J. A 2014, 50, 9. [CrossRef]
- Chen, L.W.; Cai, B.J.; Ko, C.M.; Li, B. A.; Shen, C.; and Xu, J. Higher-order effects on the incompressibility of isospin asymmetric nuclear matter. Phys. Rev. C 2009, 80, 014322. [CrossRef]
- Prakash, M.; and Bedell, K. S. Incompressibility of neutron-rich nuclear matter. Phys. Rev. C 1985, 32, 1118(R). [CrossRef]
- Shlomo, S.; Kolomietz, V.M.; and G, Colò. Deducing the nuclear-matter incompressibility coefficient from data on isoscalar compression modes. Eur. Phys. J. A 2006, 30, 23-30. [CrossRef]
- Garg, U and G, Colò. The compression-mode giant resonances and nuclear incompressibility. Prog. Part. Nucl. Phys. 2018, 101, 55. [CrossRef]
- Stone, J. R.; Stone, N. J.; and Moszkowski, S. A. Incompressibility in finite nuclei and nuclear matter. Phys. Rev. C, 2014, 89, 044316. [CrossRef]
- Avogadro, P.; and Bertulani, C. A.; Role of pairing in the description of giant monopole resonances. Phys. Rev. C, 2013, 88, 044319. [CrossRef]
- Khan, E.; Margueron, J.; and Vidaña, I. Constraining the Nuclear Equation of State at Subsaturation Densities . Phys. Rev. Lett. 2012, 109, 092501. [CrossRef]
- Vretenar, D.; Nikšić, T. and Ring, P. A microscopic estimate of the nuclear matter compressibility and symmetry energy in relativistic mean-field models. Phys. Rev. C 2003, 68, 024310. [CrossRef]
- Dutra, M.; Lourenço, O.; et al. Relativistic mean-field hadronic models under nuclear matter constraints. Phys. Rev. C 2014, 90, 055203. [CrossRef]
- Tagami, S.; Wakasa, T.; and Yahiro, M. Slope parameters determined from CREX and PREX2. Results in Physics 2022, 43, 106037. [CrossRef]
- Landau, L. D. The Theory of a Fermi Liquid. JETP 1957 3, 920. [http://jetp.ras.ru/cgi-bin/e/index/e/3/6/p920?a=list]; Landau, L. D. Oscillations in a Fermi Liquid. JETP 1957, 5, 101. [http://jetp.ras.ru/cgi-bin/e/index/e/5/1/p101?a=list]; Landau, L. D. On the theory of the Fermi liquid. JETP 1959, 8, 70. [http://jetp.ras.ru/cgi-bin/dn/e_008_01_0070.pdf].
- Vautherin, D.; and Brink, D. M. Hartree-Fock calculations with Skyrme’s interaction. I. Spherical nuclei. Phys. Rev. C 1972, 5, 626. [CrossRef]
- Bäckman, S. O.; Källman, C. G.; and Sjöberg, O. Calculation of Landau’s fermi-liquid parameters in pure neutron matter. Phys. Lett. B 1973, 43, 263-266. [CrossRef]
- Bäckman, S. O.; Jackson, A. D.; and Speth, J. Landau parameters for nuclear matter using the Skyrme interaction. Phys. Lett. B 1975, 56, 209-211. [CrossRef]
- Cao, Li-Gang.; G Colò; and Sagawa, H. Spin and spin-isospin instabilities and Landau parameters of Skyrme interactions with tensor correlations. Phys. Rev. C 2010, 81, 044302. [CrossRef]
- Chabanat, E.; Bonche, P.; et al. A Skyrme parametrization from subnuclear to neutron star densities Part II. Nuclei far from stabilities. Nuclear Physics A 1998, 635 231-256. [CrossRef]
- Chabanat, E.; Bonche, P.; et al. A Skyrme parametrization from subnuclear to neutron star densities. Nuclear Physics A 1997, 627, 710-746. [CrossRef]
- Taqi, A. H.; and Khidher, E. G. Nuclear multipole excitations in the framework of self-consistent Hartree–Fock random phase approximation for Skyrme forces. Pramana -J. Phys., 2019, 93, 60. [CrossRef]
- Goriely, S.; Tondeur, F.; and Pearson, J. M. A Hartree-Fock nuclear mass table. Atomic Data and Nuclear Data Tables 2001, 77, 311-381. [CrossRef]
- Tselyaev, V.; Lyutorovich, N.; et al. Low-energy M1 excitations in 208Pb and the spin channel of the Skyrme energy-density functional. Phys. Rev. C 2019, 99, 064329. [CrossRef]
- Agrawal, B. K.; Shlomo, S.; and Kim Au, V. Determination of the parameters of a Skyrme type effective interaction using the simulated annealing approach. Phys. Rev. C, 2005, 72, 014310. [CrossRef]
- Lahiri, J.; Atta, D.; and Basu, D. N. Properties of glitching pulsars in the Skyrme-Hartree-Fock framework. arXiv:2207.13384v3 [nucl-th]. [CrossRef]
- Keh-Fei. L.; Hongde, L.; Ma, Z.; Shen, Q; and Moszkowski S. A. Skyrme-Landau parameterization of effective interactions (I). Hartree-Fock ground states. Nuclear Physics A 1991, 534, 1-24. [CrossRef]
- Vuong, Au Kim. New Skyrme nucleon-nucleon interaction for the mean-field approximation. Doctoral Dissertation, Texas A & M University, 2003. [http://hdl.handle.net/1969.1/5996].
- Dutra, M.; Lourenço O.; and Delfino, A. Consistent Skyrme parametrization and its critical parameter values. J. Phys.: Conf. Ser. 2019, 1291, 012040. [https://iopscience.iop.org/article/10.1088/1742-6596/1291/1/012040/meta].
- Nakada, H. Hartree-Fock approach to nuclear matter and finite nuclei with M3Y-type nucleon-nucleon interactions. Phys. Rev. C 2003, 68, 014316. [CrossRef]
- Idini, A.; Bennaceur, K.; and Dobaczewski, J. Landau parameters for energy density functionals generated by local finite-range pseudopotentials. J. Phys. G: Nucl. Part. Phys. 2017, 44, 064004 (10pp). [CrossRef]
- Margueron, J.; Navarro, J.; and Van Giai N. Phys. Rev. C 2002, 66, 014303. [CrossRef]
- Goriely, S.; Chamel, N.; and Pearson, J. M. Further explorations of Skyrme-Hartree-Fock-Bogoliubov mass formulas. XII. Stiffness and stability of neutron-star matter. Phys. Rev. C 2010, 82, 035804. [CrossRef]
- Li, B. A.; and Han, X.; Constraining the neutron–proton effective mass splitting using empirical constraints on the density dependence of nuclear symmetry energy around normal density. Physics Letters B 2013, 727, 276-281. [CrossRef]
- Oertel, M.; Hempel, M.; Klähn, T.; and Typel, S. Equations of state for supernovae and compact stars. Rev. Mod. Phys., 2017, 89, 1. [CrossRef]
- Reed, B. T.; Fattoyev, F. J.; Horowitz C. J.; and Piekarewicz, J. Phys. Rev. Lett. 2021, 126, 172503. [CrossRef]
- Estee, J.; Lynch, W. G.; et al. Probing the Symmetry Energy with the Spectral Pion Ratio. Phys. Rev. Lett. 2021, 126, 162701. [CrossRef]
- Danielewicz, P.; Singh, P.; and Lee, J. Symmetry energy III: Isovector skins. Nucl. Phys. A 2017, 958, 147. [CrossRef]
- Russotto P.; et al.; Results of the ASY-EOS experiment at GSI: The symmetry energy at suprasaturation density. Phys. Rev. C 2016, 94, 034608. [CrossRef]
- Senger, P. Probing Dense Nuclear Matter in the Laboratory: Experiments at FAIR and NICA. Universe 2021, 7, 171. [CrossRef]
- Zhang, Y.; Liu, M.; Xia C. J.; Li, Z.; and Biswal, S. K.; Constraints on the symmetry energy and its associated parameters from nuclei to neutron stars. Phys. Rev. C 2020, 101, 034303. [CrossRef]
- Zhang, N. B.; and Li, B. A. Extracting nuclear symmetry energies at high densities from observations of neutron stars and gravitational waves. Eur. Phys. J. A 2019, 55, 39. [CrossRef]
- Xie, W.-J.; and Li, B.-A. Bayesian Inference of High-density Nuclear Symmetry Energy from Radii of Canonical Neutron Stars. The Astrophysical Journal 2019, 883:174 (21pp). [CrossRef]
- Tong, H.;, Zhao, P.; and Meng J. Symmetry energy at supra-saturation densities via the gravitational waves from GW170817. Phys. Rev C 2020, 101, 035802. [CrossRef]
- Drischler, C.; Furnstahl, R. J.; Melendez, J. A.; & Phillips, D. R. How Well Do We Know the Neutron-Matter Equation of State at the Densities Inside Neutron Stars? A Bayesian Approach with Correlated Uncertainties. Phys. rev. Lett. 2020, 125, 202702. [CrossRef]
- Lonardoni, D.; Tews, I.; Gandolfi, S.; & Carlson, J. Nuclear and neutron-star matter from local chiral interactions. Phys. Rev. Research, 2020, 2, 022033(R). [CrossRef]
- Li, B.-A.; Cai, B.-J.; Xie, W.-J.; Zhang, N.-B. Progress in Constraining Nuclear Symmetry Energy Using Neutron Star Observables Since GW170817 Universe 2021, 7, 182. [CrossRef]
- Nakazato, K.;and Suzuki H. Cooling Timescale for Protoneutron Stars and Properties of Nuclear Matter: Effective Mass and Symmetry Energy at High Densities. The Astrophysical Journal 2019, 878:25 (11pp). [CrossRef]
- Yue T.-G.; Chen L.-W.;, Zhang, Z.; and Zhou, Y. Constraints on the symmetry energy from PREX-II in the multimessenger era. Phys. Rev. Research 2022, 4, L022054. [CrossRef]
- Xie, W. J.; and Li, B. A. Bayesian Inference of the Symmetry Energy of Superdense Neutron-rich Matter from Future Radius Measurements of Massive Neutron Stars. Astrophys. J. 2020, 899, 4. [CrossRef]
- Zhou, Y.; Chen, L.-W.; and Zhang, Z. Equation of state of dense matter in the multimessenger era. Phys. Rev. D 2019, 99, 121301(R). [CrossRef]
- Chen, L.-W. Symmetry energy systematics and its high density behavior. EPJ Web of Conferences 2015, 88, 00017. [CrossRef]
- Lattimer, J. M.; & Lim, Y. Constraining the symmetry parameters of the nuclear interaction. The Astrophysical Journal 2013, 771:51, 14pp. [CrossRef]
- Lynch, W. G.; & Tsang, M. B. Decoding the density dependence of the nuclear symmetry energy. Physics Letters B 2022, 830, 137098. [CrossRef]
- Chen, L. W.; Ko, C. M.; and Li, B. A. Nuclear matter symmetry energy and the neutron skin thickness of heavy nuclei. Phys. Rev. C 2005, 72, 064309. [CrossRef]
- Li B.-A.; and Magno, M. Curvature-slope correlation of nuclear symmetry energy and its imprints on the crust-core transition, radius, and tidal deformability of canonical neutron stars. Phy. Rev. C 2020, 102, 045807. [CrossRef]
- d’Etivaux, N. B.; Guillot, S.; Margueron, J.; et al.New Constraints on the Nuclear Equation of State from the Thermal Emission of Neutron Stars in Quiescent Low-mass X-Ray Binaries. The Astrophysical Journal 2019, 887:48, 16pp. [CrossRef]
- Carson, Z.; Steiner, A. W.; and Yagi, K. Constraining nuclear matter parameters with GW170817. [CrossRef]
- Choi, S.; Miyatsu, T.; Cheoun, M.; and Saito, K. Constraints on Nuclear Saturation Properties from Terrestrial Experiments and Astrophysical Observations of Neutron Stars The Astrophysical Journal 2021, 909:156, 9pp. [CrossRef]
- Drischler, C.; Hebeler, K.; & Schwenk, A. Asymmetric nuclear matter based on chiral two- and three-nucleon interactions. Phys. Rev. C 2016, 93, 054314. [CrossRef]
- Newton, W. G.; & Crocombe, G. Nuclear symmetry energy from neutron skins and pure neutron matter in a Bayesian framework. Phy Rev C 2021, 103, 064323. [CrossRef]
- Grams, G.; Somasundaram, R.; Margueron, J.; and Khan, E. Nuclear incompressibility and speed of sound in uniform matter and finite nuclei. Phys. Rev. C 2022, 106, 044305. [CrossRef]
- Sagawa, H.; Yoshida, S.; and Cao, L.-G. Sagawa H, Yoshida S and Cao Li-Gang, EoS from terrestrial experiments: Static and dynamic polarizations of nuclear density .AIP Conference Proceedings 2019, 2127, 020002. [CrossRef]
- Tews, I.; Lattimer, J. M.; Ohnishi, A.; & Kolomeitsev, E. E. Symmetry Parameter Constraints from a Lower Bound on Neutron-matter Energy. The Astrophysical Journal 2017, 848, 105. [CrossRef]
- Zhang, N. B.; Cai, B. J.; Li, B. A.; Newton, W. G.; & Xu, J. How tightly is the nuclear symmetry energy constrained by a unitary Fermi gas?. Nucl. Sci. Tech. 2017, 28, 181. [CrossRef]
- Mondal, C.; Agrawal, B. K.; De, J. N., et al. Interdependence of different symmetry energy elements. Phy. Rev C 2017, 96, 021302(R). [CrossRef]
- Sagawa, H.; Yoshida, S.; et al. Isospin dependence of incompressibility in relativistic and nonrelativistic mean field calculations. Phys. Rev. C 2007, 76, 034327; 2008 77, 049902(E). [CrossRef]
- Li, T.; et al. Isotopic Dependence of the Giant Monopole Resonance in the Even-A 112-124Sn Isotopes and the Asymmetry Term in Nuclear Incompressibility. 2007 99, 162503. [https://doi.org/10.1103/PhysRevLett.99.162503]; Li, T.; et al. Isoscalar giant resonances in the Sn nuclei and implications for the asymmetry term in the nuclear-matter incompressibility. Phys. Rev. Lett. Phys. Rev. C 2010, 81, 034309. [https://doi.org/10.1103/PhysRevC.81.034309]. [CrossRef]
- Cozma, M. D. Feasibility of constraining the curvature parameter of the symmetry energy using elliptic flow data. Eur. Phys. J. A 2018, 54, 40. [CrossRef]
- Centelles, M.; Roca-Maza, X.; Viñas, X.; Warda, M. Nuclear Symmetry Energy Probed by Neutron Skin Thickness of Nuclei. Phys. Rev. Lett. 2009, 102, 122502. [CrossRef]
- Cai, B. J.; & Chen, L. W. Constraints on the skewness coefficient of symmetric nuclear matter within the nonlinear relativistic mean field model. Nucl Sci Tech 2017, 28, 185. [CrossRef]
- Farine, M.; Pearson, J. M.; & Tondeur, F. Nuclear-matter incompressibility from fits of generalized Skyrme force to breathing-mode energies. Nucl. Phy A 1997, 615, 135. [CrossRef]
- Xie, W-J.; and Li B-A. Bayesian inference of the incompressibility, skewness and kurtosis of nuclear matter from empirical pressures in relativistic heavy-ion collisions. J. Phys. G: Nucl. Part. Phys. 2021, 48, 025110. [CrossRef]
- Steiner, A. W.; Lattimer; J. M.; Brown, E. F. The Equation of State from Observed Masses and Radii of Neutron Stars. Astrophys. J. 2010, 722, 33-54. [CrossRef]
- Alam, N.; Agrawal, B. K.; De, J. N.; Samaddar, S. K. and Colò G. Phys. Rev. C 2014, 90, 054317. [CrossRef]
- Alam, N.; Agrawal, B. K.; et al. Strong correlations of neutron star radii with the slopes of nuclear matter incompressibility and symmetry energy at saturation. Phys. Rev. C 2016, 94, 052801(R). [CrossRef]
- Baym. G.; Bethe, H. A. and Pethick, C. J. Neutron star matter. Nucl. Phys. A 1971, 175, 225-271. [CrossRef]
- Baym, G.; Pethick, C. J.; and Sutherland P. The Ground State of Matter at High Densities: Equation of State and Stellar Models . Astrophys. J 1971, 170, 299-317. [CrossRef]
- De, J. N.; Samaddar, S. K.; and Agrawal, B. K. Reassessing nuclear matter incompressibility and its density dependence. Phys. Rev. C 2015, 92, 014304. [CrossRef]
- Capano, C.; Tews, I.; et al. Stringent constraints on neutron-star radii from multimessenger observations and nuclear theory. Nat Astron 2020, 4, 625-632. [CrossRef]
- Raaijmakers, G.; Greif, S. K.; et al. Constraints on the Dense Matter Equation of State and Neutron Star Properties from NICER’s Mass–Radius Estimate of PSR J0740 + 6620 and Multimessenger Observations The Astrophysical Journal Letters 2021, 918:L29, 13pp. [CrossRef]
- Miller, M. C.; Lamb, F. K.; et al. The Radius of PSR J0740+6620 from NICER and XMM-Newton Data. The Astrophysical Journal Letters, 918:L28 (31pp), 2021. [CrossRef]
- Pang P. T. H.; Tews. I. et al. Nuclear Physics Multimessenger Astrophysics Constraints on the Neutron Star Equation of State: Adding NICER’s PSR J0740 + 6620 Measurement. The Astrophysical Journal, 2021, 922:14, 9pp. [CrossRef]
- Jiang J.-L.; Tang S.-P.; et al. The Equation of State and Some Key Parameters of Neutron Stars: Constraints from GW170817, the Nuclear Data, and the Low-mass X-Ray Binary Data. The Astrophysical Journal 2019, 885:39, 10pp. [CrossRef]
- Abbott, R.; Abbott, T. D. et al. GW190814: Gravitational Waves from the Coalescence of a 23 Solar Mass Black Hole with a 2.6 Solar Mass Compact Object. (LIGO Scientific Collaboration and Virgo Collaboration), Astrophys. J. 2020, 896, L44. [CrossRef]
- Bauswein, A.; Blacker, S. et al. Systematics of prompt black-hole formation in neutron star mergers. Phys. Rev. D 2021, 103, 123004. [CrossRef]
- Bauswein, A.; Janka, H.-T. Hebeler, K.; and Schwenk A.; Equation-of-state dependence of the gravitational-wave signal from the ring-down phase of neutron-star mergers. Phys. Rev. D 2012, 86, 063001. [CrossRef]
- Annala, E.; Gorda, T.; Kurkela, A.; & Vuorinen, A.; Phys. Rev. Lett. 2018, 120, 172703. [CrossRef]
- Fattoyev, F. J.; Piekarewicz, J.; and Horowitz, C. J. Neutron Skins and Neutron Stars in the Multimessenger Era. Phys. Rev. Lett. 2018, 120, 172702. [CrossRef]
- Bauswein, A.; Just, O.; et al. Neutron-star Radius Constraints from GW170817 and Future Detections. The Astrophysical Journal Letters, 2017, 850:L34 (5pp). [CrossRef]
- Bauswein, A.; Baumgarte, T. W,; and Janka, H. T.; Prompt Merger Collapse and the Maximum Mass of Neutron Stars. Phys. Rev. Lett. 2013, 111, 131101. [CrossRef]
- Perego, A.; Logoteta, D.; et al. Probing the Incompressibility of Nuclear Matter at Ultrahigh Density through the Prompt Collapse of Asymmetric Neutron Star Binaries. Phys. Rev. Lett. 2022, 129, 032701. [CrossRef]
- Shibata, M.; Taniguchi, K; and Uryū, K. Merger of binary neutron stars with realistic equations of state in full general relativity. Phys. Rev. D 2005, 71, 084021. [CrossRef]
- Hotokezaka, k.;, Kyutoku K., Okawa, H.; Shibata M.; and Kiuchi K. Binary neutron star mergers: Dependence on the nuclear equation of state. Phys. Rev. D 2011, 83, 124008. [CrossRef]
- Köppel, S.; Bovard, L.; and Rezzolla, L. A General-relativistic Determination of the Threshold Mass to Prompt Collapse in Binary Neutron Star Mergers. The Astrophysical Journal Letters, 2019 872:L16, 5pp. [CrossRef]
- Kashyap, R.; Das, A.; et al. Numerical relativity simulations of prompt collapse mergers: Threshold mass and phenomenological constraints on neutron star properties after GW170817. Phys. Rev. D 2022, 105, 103022. [CrossRef]
- Glendenning, N. K.; Compact Stars: Nuclear Physics, Particle Physics, and General Relativity (Springer, Berlin, 2000). [CrossRef]
- Margaritis, Ch.; Koliogiannis, P. S.; and Moustakidis, Ch. C. Speed of sound constraints on maximally rotating neutron stars. Phys. Rev. D 2020, 101, 043023. [CrossRef]
- Koliogiannis, P. S.; and Moustakidis, C. C. Constraints on the equation of state from the stability condition of neutron stars. Astrophys. Space Sci. 2019, 364, 52. [CrossRef]
- Blaizot, J. P. Nuclear compressibilities Phys. Rep. 1980, 64, 171-248. [CrossRef]
- Zhang, N. B.; and Li, B. A. Impact of symmetry energy on sound speed and spinodal decomposition in dense neutron-rich matter. Eur. Phys. J. A 2023, 59, 86. [CrossRef]
- Hartle, J. B. Bounds on the mass and moment of inertia of non-rotating neutron stars. Phys. Rep. 1978, 46, 201-247. [CrossRef]
- Margaritis, C.; Koliogiannis, P. S.; and Moustakidis, C. C. Speed of sound constraints on maximally rotating neutron stars. Phys. Rev. D 2020, 101, 043023. [CrossRef]
- Reed, B. and Horowitz, C. J. Large sound speed in dense matter and the deformability of neutron stars. Phys. Rev. C 2020, 101, 045803.
- Cottam, J.; Paerels, F. & Mendez, M. Gravitationally redshifted absorption lines in the X-ray burst spectra of a neutron star. Nature 2002, 420, 51-54. [CrossRef]
- Hambaryan, V.; Neuhäuser, R.; Suleimanov, V.; and Werner, K. J. Phys.: Conf. Ser. 2014, 496, 012015. [CrossRef]
- Hambaryan, V.; Suleimanov, V.; Haberl, F. et al., The compactness of the isolated neutron star RXJ0720.4-3125. Astronomy & Astrophysics 2017, 601, A108. [CrossRef]
- Tang, S. P.; Jiang, J. L.; et al. The Masses of Isolated Neutron Stars Inferred from the Gravitational Redshift Measurements. The Astrophysical Journal 2020, 888, 45. [CrossRef]
- Sotani, H.; Iida, K.; Oyamatsu, K.; and Ohnishi, A. Mass and radius formulas for low-mass neutron stars. Prog. Theor. Exp. Phys. 2014, 5, 051E01. [CrossRef]
- Sotani, H.; Nishimura, N.; and Naito, T. New constraints on the neutron-star mass and radius relation from terrestrial nuclear experiments. Prog. Theor. Exp. Phys. 2022, 4, 041D01. [CrossRef]
- Carlson, B. V.; Dutra, M; Lourenço, O.; and Margueron, J. Low-energy nuclear physics and global neutron star properties. Phys. Rev. C 2023, 107, 035805. [CrossRef]

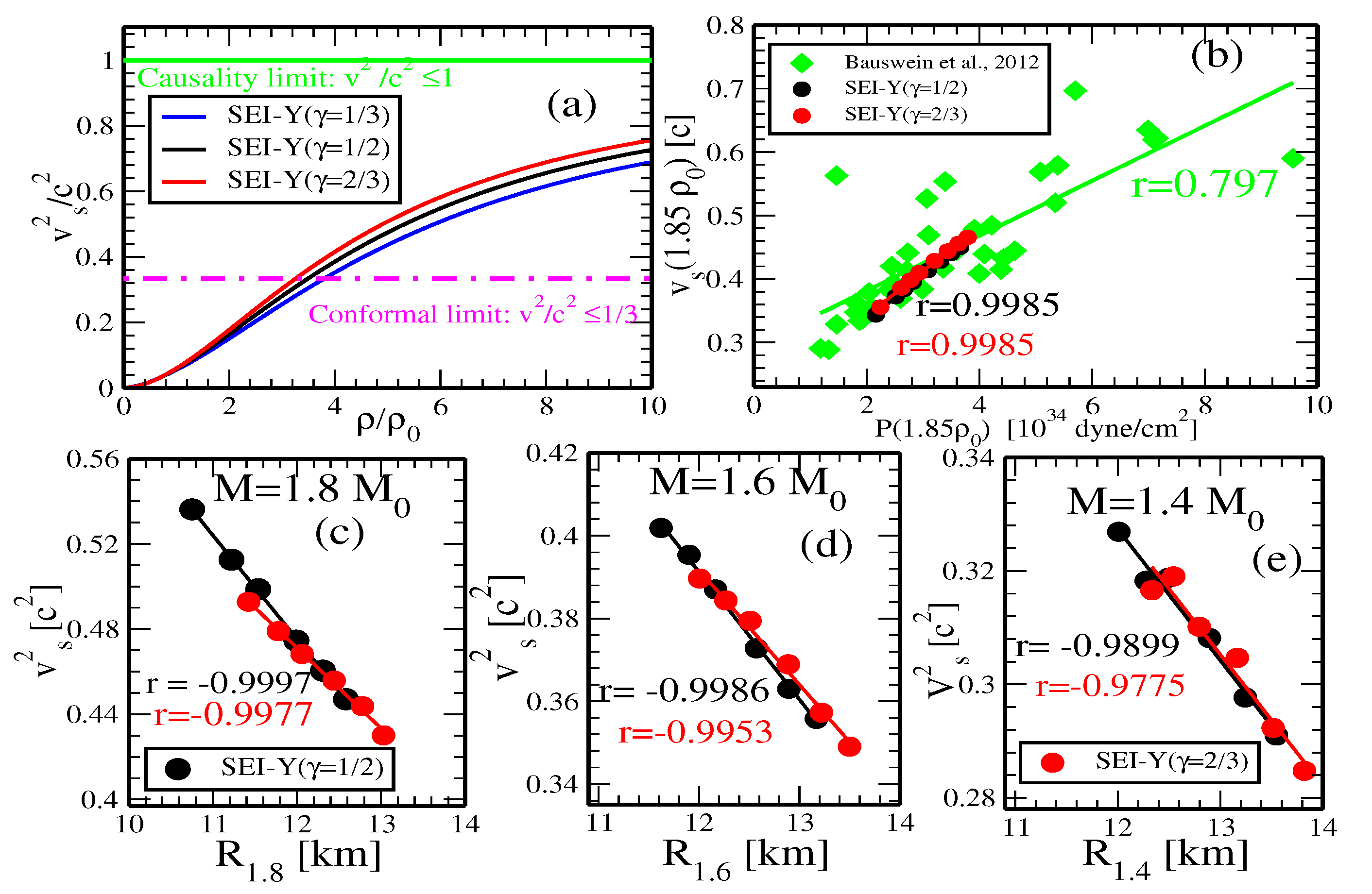
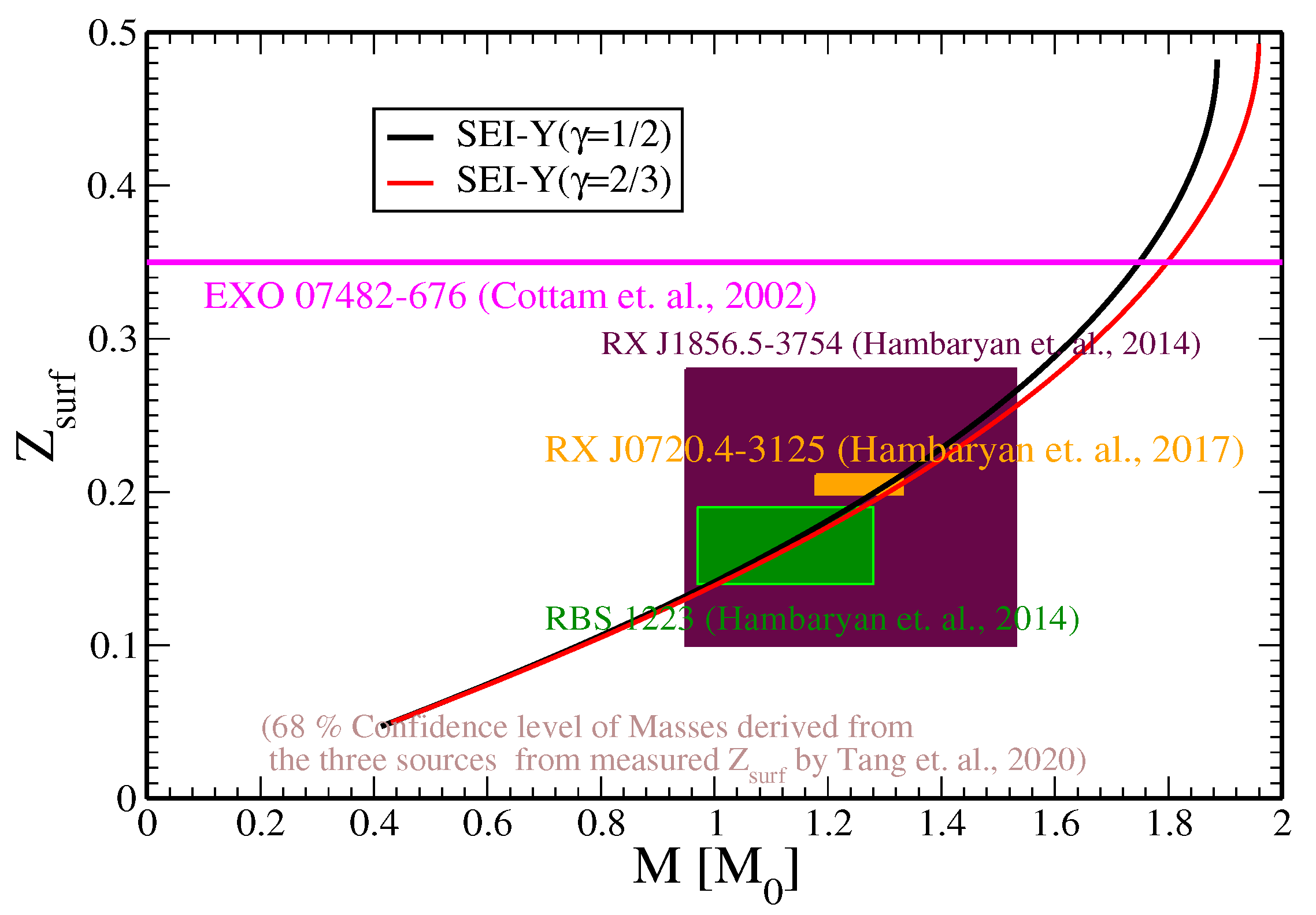
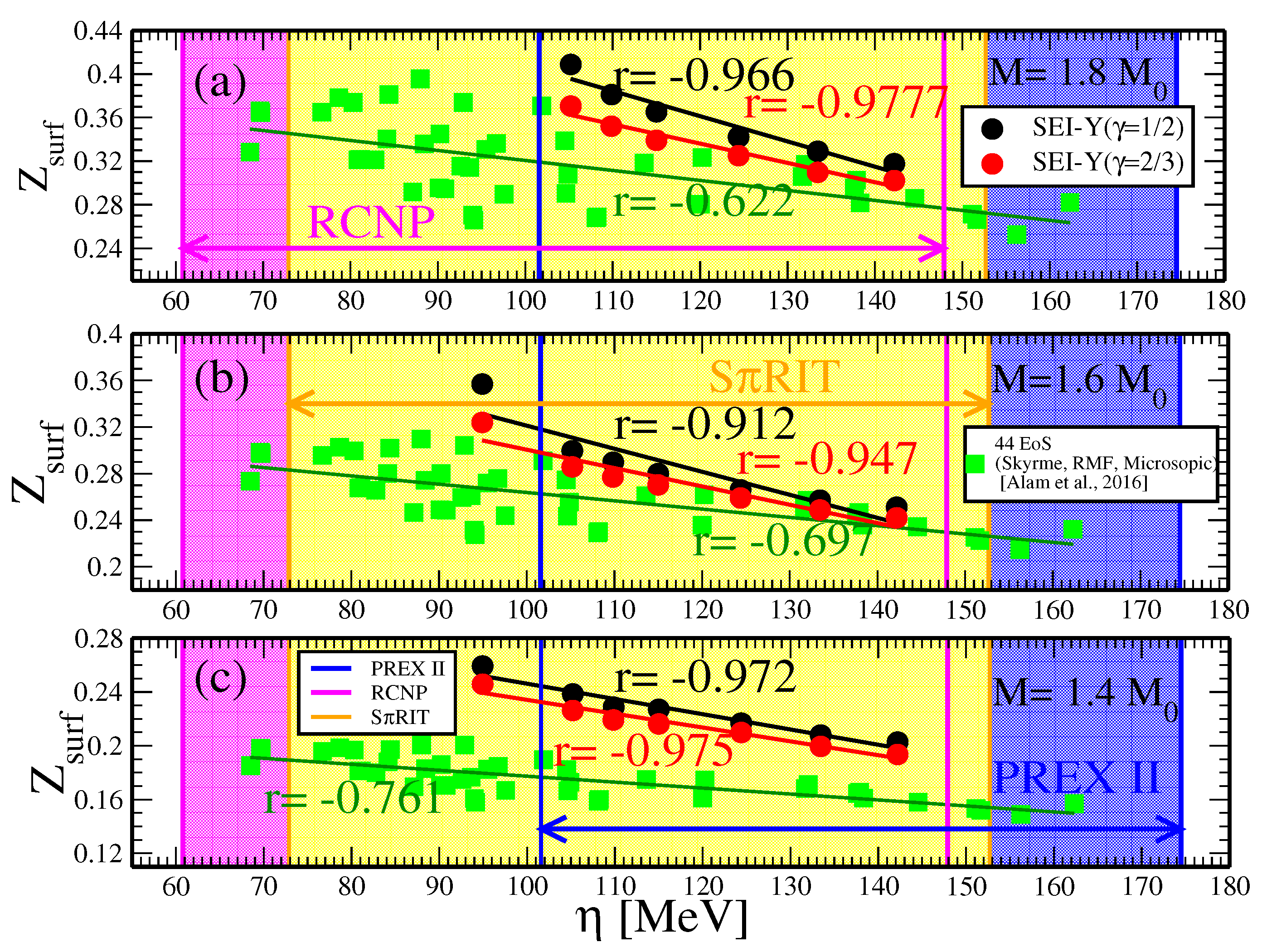
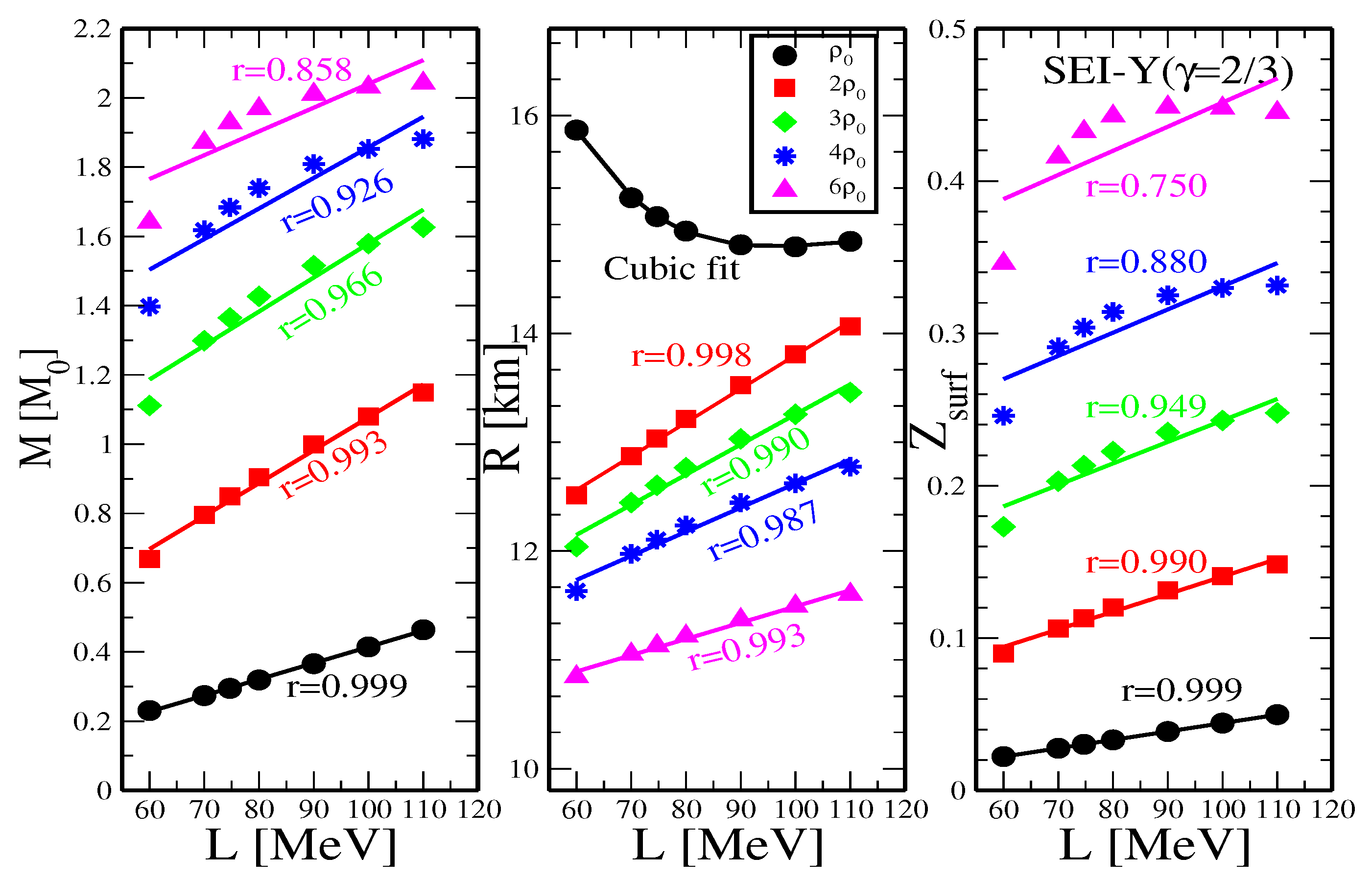
| b [] | [fm] | [MeV] | [MeV] | [MeV] | |
|---|---|---|---|---|---|
| 1/3 | 0.4161 | 0.4232 | -129.344 | -86.229 | -82.245 |
| 1/2 | 0.5880 | 0.4242 | -127.707 | -85.138 | -50.600 |
| 2/3 | 0.7796 | 0.4250 | -126.390 | -84.260 | -34.904 |
| [MeV] | [MeV] | [MeV] | |||
| -47.189 | 104.428 | 74.006 | 333.5 | 1.151 | 119.3 |
| -27.509 | 73.124 | 54.250 | 566.7 | 0.664 | 118.4 |
| -17.859 | 58.095 | 44.690 | 647.4 | 0.520 | 118.2 |
| SEI-Y() | SEI-Y() | SEI-Y() | |
|---|---|---|---|
| 0.161 | 0.158 | 0.156 | |
| [MeV] | -16.04 | -16 | -16 |
| 0.664 | 0.686 | 0.666 | |
| 0.685 | 0.621 | 0.622 | |
| [MeV] | 220.346 | 237.643 | 253.219 |
| [MeV] | -478.763 | -461.807 | -437.529 |
| -0.163 | -0.149 | -0.138 | |
| [MeV] | 35.5 | 35 | 34.5 |
| L [MeV] | 74.4 | 74.7 | 74.7 |
| [MeV] | -103.487 | -101.471 | -99.252 |
| [MeV] | 273.008 | 252.462 | 234.0525 |
| [MeV] | -388.232 | -404.509 | -418.381 |
| [MeV] | 19.46 | 19 | 18.5 |
| [MeV] | 116.858 | 136.172 | 153.966 |
| [MeV] | -205.754 | -209.345 | -203.476 |
| Expt./Theory | [MeV] |
|---|---|
| Analysis of experimental data of the GMR | |
| S. Shlomo et al., (2006) [34] | |
| U. Garg et al., (2018) [35] | |
| J.R. Stone et al., 2014 [36] | 250-315 |
| P. Avogadro & C.A. Bertulani, 2013 [37] | 200 |
| Relativistic and non-relativistic mean-field calculations of the GMR | |
| E. Khan et al., 2012 [38] | |
| D. Vretenar et al.,2003 [39] | 250-270 |
| M. Dutra et al., 2012 [22] | 246±41 |
| M. Dutra et al., 2014 [40] | 271±86 |
| Analysis of PREX-II and CREX data | |
| S. Tagami et al., 2022 [41] | 210-275 |
| EoS | ||||||
|---|---|---|---|---|---|---|
| SEI-Y() | -0.31 | -0.913 | -0.247 | 0.89 | 0.304 | 0.0826 |
| SEI-Y() | -0.257 | -0.939 | -0.253 | 0.914 | 0.313 | 0.0845 |
| SEI-Y() | -0.195 | -0.9091 | -0.2447 | 0.8771 | 0.303 | 0.0816 |
| EoS | ||||||
| SEI-Y() | 0.617 | 0.0321 | 0.0087 | 0.474 | 0.3739 | 0.1013 |
| SEI-Y() | 0.627 | 0.0479 | 0.0129 | 0.514 | 0.3690 | 0.0998 |
| SEI-Y() | 0.584 | 0.0744 | 0.02001 | 0.5401 | 0.3297 | 0.0887 |
| SEI-Y() | ||||||||
|---|---|---|---|---|---|---|---|---|
| () | [MeV] | [MeV] | [MeV] | [MeV] | [MeV] | |||
| () | 0.161 | 230.59 | 0.695 | 1.101 | 35.10 | 30.02 | 27.38 | 24.47 |
| () | 0.158 | 237.74 | 0.686 | 1.104 | 34.048 | 28.95 | 26.94 | 26.38 |
| () | 0.156 | 263.14 | 0.696 | 1.101 | 34.10 | 28.79 | 27.97 | 27.94 |
| Expt/Observation/Theory | [MeV] |
|---|---|
| Mean-field calculations and Astrophysical Observations | |
| Dutra et al.,2012 [22] | 27-36 |
| B A Li and Han, 2013 [61] | 31.6±0.92 |
| Oertel et al., 2017 [62] | 31.7 ± 3.2 |
| PREX II Experiment Reed et al., 2021 [63] | 38.1±4.7 |
| Charged Pion Spectra at high momenta Estee et al., 2021 [64] | 32.5-38.1 |
| Charge exchange and elastic scattering data Danielewicz et al., 2017 [65] | 33.5-36.4 |
| Expt/Observation/Theory | [MeV] |
| SEI-Y() | 55.74 |
| SEI-Y() | 55.38 |
| SEI-Y() | 54.93 |
| HIC and Transport Calculations | |
| ASY-EoS experiment at GSI [66] | 46-54 |
| UrQMD transport calculation [67] | 55±5 |
| Zhang et al., 2020 [68] | 35-55 |
| Gravitational Waves Zhang & Li (2019) [69] | |
| Xie & Li (2019) [70] | 39.2 − 8.2 + 12.1 |
| Tong et al., 2020[71] | 60.7±10.9 |
| Chiral Effective Field Theory | |
| Drischler et al., 2020 [72] | 45±3 |
| Lonardoni et al.,2020 [73] | 45±5 |
| Neutron Star Observables B A Li et al., 2021 [74] | 51±13 |
| Nakazato & Suzuki 2019 [75] | 40-60 |
| Yue et al., 2022 [76] | 62.8±15.9 |
| Xie and Li 2020 [77] | |
| Zhou et al., 2019[78] | [] |
| Mean-Field Calculations Chen et al., 2015 [79] | 40.2±12.8 |
| Expt/Observation/Theory | L[MeV] |
|---|---|
| Terrestrial Experiments and Astrophysical Observations | |
| Li and Han, 2013 [61] | 58.9 ± 16.5 |
| Oertel et al., 2017 [62] | 58.7 ± 28.1 |
| Lattimer and Lim, 2013 [80] | 40.5-61.9 |
| Xie et al. 2019, 2020 [70,77] | |
| PREX-II Experiment | |
| Reed et al., 2021 [63] | 106±37 |
| Charge exchange and elastic scattering data Danielewicz et al., 2017 [65] | 70-101 |
| Charged Pion Spectra at high momenta Estee et al., 2021 [64] | 42-117 |
| Isospin Diffusion Data Chen et al., 2005 [82] | 63-113 |
| Charge radii difference in mirror pairs | |
| Bano et al. 2023, [28] | 70-100 |
| Expt./Observation/Theory | [MeV] |
| Analysis of Different Neutron Star Observables Li et al., 2020 [83] | |
| d’Etivaux et al., 2019 [84] | |
| Carson et al., 2019 [85] | 32 |
| Choi et al., 2021 [86] | -128 to -33 |
| Chiral Effective Field Theory | |
| Drischler et al., 2016 [87] | -240 to -70 |
| Newton & Crocombe, 2021[88] | |
| Grams et. al., 2022 [89] | 50 |
| Terrestrial Nuclear Experiments and Mean-Field Predictions | |
| Sagawa et al., 2019 [90] | |
| Tews et al., 2017 [91], Zhang et al., 2017 [92] | -400 to -100 |
| Mondal et al., 2017 [93] | |
| Expt./Theory | [MeV] |
| Experimental data of Isoscalar Giant Monopole Resonances | |
| Sagawa et al., 2008 [94] | |
| Li et al., 2010 [95] | |
| Stone et al., 2014 [36] | -840 to -350 |
| Theoretical calculations of GMR with MDI interactions Chen et al., 2009 [32] | |
| Cozma, 2018 [96] | |
| Neutron skin sizes across the mass table | |
| Centelles et al., 2009 [97] |
| SEI-Y() | ||||||
|---|---|---|---|---|---|---|
| Ref | a | b | k | |||
| [118] | -3.342 | 2.42 | 10.523 | 0.275 | 1.499 | 2.937 |
| [117] | -3.38 | 2.43 | 10.523 | 0.275 | 1.498 | 2.936 |
| [123] | 10.523 | 0.275 | ||||
| SEI-Y() | ||||||
| Ref | a | b | k | |||
| [118] | -3.342 | 2.42 | 10.243 | 0.272 | 1.5095 | 2.846 |
| [117] | -3.38 | 2.43 | 10.243 | 0.272 | 1.5091 | 2.845 |
| [123] | 10.243 | 0.272 | ||||
| SEI-Y() | ||||||
| Ref | a | b | k | |||
| [118] | -3.342 | 2.42 | 9.943 | 0.267 | 1.5252 | 2.7437 |
| [117] | -3.38 | 2.43 | 9.943 | 0.267 | 1.5250 | 2.7434 |
| [123] | 9.943 | 0.267 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





