The Intermittency of Turbulence in Magneto-Hydodynamical Simulations and in the Cosmos

1. Introduction

1.1. The Abyss between Cosmic Turbulence and Theory and Laboratory Experiments ...

Theoretical approaches and experiments on isotropic, homogeneous, incompressible turbulence remain a powerful source of inspiration and guidance to the studies of the complex turbulence pervading space from the terrestrial atmosphere and solar wind to galaxies and galaxy clusters. To name a few in the scope of this paper: Chandrasekhar and Fermi [1] for the expression of the turbulent pressure and viscosity, Meneveau and Sreenivasan [2] and She and Leveque [3] on intermittency, Alexakis et al. [4,5] on non-local interactions in MHD turbulence, Moffatt et al. [6] for qualifying the coherent structures of vorticity as the sinews of turbulence, Kimura et al. [7] for the formation of strong temperature fronts in stratified turbulence, Cadot et al. [8] for imaging intense small scale vortices in turbulent water seeded with gas bubbles, Tabeling et al. [9] for experiments in superfluid Helium, Politano and Pouquet [10] for their predictions of scaling laws in incompressible magnetised turbulence and Schekochihin [11] for opening bridges between MHD and kinetic turbulence.

The applicability to cosmic turbulence of theoretical results obtained in idealised conditions is unexpected because cosmic turbulence is highly compressible, magnetized and multi-phasic with Reynolds numbers $Re=L{u}_{\mathrm{r}.\mathrm{m}.\mathrm{s}.}/\nu$ larger than ${10}^8$ where $L>100$ pc1 and $u_{\mathrm{r}.\mathrm{m}.\mathrm{s}.}>10$ km ${\mathrm{s}}^{-1}$ are the characteristic length and velocity of the integral scales of turbulence in galaxies and $\nu =\frac{1}{3}\lambda v_{\mathrm{th}}\sim {10}^{18}$ ${\mathrm{cm}}^2$ ${\mathrm{s}}^{-1}$, with $v_{\mathrm{th}}$ the thermal velocity, is the molecular viscosity. The colossal range of densities and temperatures experienced by the gas along its cycle between stars and the interstellar medium (ISM) is illustrated in Figure 1.

The CNM and WNM (Figure 1) are two thermally stable phases [15] that build up the so-called "cold" ISM, with respect to the hot space-filling phase. They are in thermal pressure equilibrium but their densities (and temperatures) differ by about 2 orders of magnitude. The ISM therefore harbours gas structures about 100 × denser than their environment [16]. The mass fraction in the dense phase depends on the ambient thermal pressure, therefore on the distance from the stellar disks in galaxies. The ISM is fully or partially ionised depending on the ambient density of ionising UV photons and relativistic particles (the cosmic rays, CR). The gas is therefore more or less coupled to the magnetic fields. The ISM also comprises sub-micron size dust particles that contribute only 1% of the gas mass but play a key role in the gas coupling to the magnetic fields because these dust particles are charged and have a large collisional cross-section with the gas. They bear predominantly positive charges, except the smallest that are predominantly negative [17] but their charge varies with time and place depending on their environment (UV radiation and gas density) .

Turbulence is ubiquitous throughout this cycle. Its origins are multiple, including the differential rotation of galaxies, the gravitational energy in gas accretion processes and the stellar feedback in the form of supernovae explosions but also jets and winds all along the stellar lifetime that spans several ${10}^9$ years for solar-type stars. The role of turbulence in star formation, in particular its link with the observed very low efficiency of star formation, is a highly debated issue because turbulence can both trigger and hamper star formation (see the review of Hennebelle and Falgarone [18]).

Large scales in cosmic turbulence are rotating, shearing, stratified by the gravitation field, with an additional anisotropy due to the ubiquitous magnetic fields. The associated dynamical timescales are all different and span a broad range from hundreds of Myr to $\sim {10}^3$yr. The latter are shorter than collisional times, providing the ISM with facets of collisionless plasma (see the review of Ferriere [19]). A fraction of the cold medium lies in the thermally unstable phase because turbulence continuously drives the phase transition from the WNM to CNM [20]: the hydrodynamic pressure fluctuations of the turbulence destabilise the WNM and cause its fragmentation into CNM droplets. Buoyancy in the galactic gravitational field is also inevitable given the gas equation of state and the multiplicity of energy and ionisation sources.

Finally, the weakly ionised ISM phases are not fully coupled to the magnetic fields. There is a whole range of high frequencies of magnetic waves which are not perceived by the plasma because collisions of neutrals with ions and charged dust grains, closely coupled to the magnetic fields, are too rare. There is also a domain, at low frequency, where the waves no longer propagate because all their energy is dissipated in ion-neutral collisions. The frequencies that limit these regimes depend on the collision cross sections between the ions and the neutrals and their respective densities [21]. Between these two extremes, the magnetic fields drift through the medium. This is an important phenomenon in the diffuse ISM because it is a major source of energy dissipation but it is also the reason why C-shocks (i.e. continuous shocks) exist because, unlike J-shocks, they develop magnetic precursors [22,23,24,25,26]. This is also why they are so rich in molecules [27].

1.2. And Yet...

In spite of all the above, the electron density of the ISM and interplanetary ionised medium exhibits a Kolmogorov power spectrum spanning more than 10 orders of magnitude in scales down to $\sim {10}^8$ cm (known as "The big power law in the sky") [28]. The slope of this spectrum suggests a link with turbulence.

Cold atomic gas too exhibits structure down to very small scales of 10 to ${10}^4$ au, [16]. A few power spectra have been observed in the CNM: that of the continuum emission of dust in a high galactic latitude cloud extending from 20 pc down to 2000 au [29], that of light scattered by dust in a similar field extending over 3 orders of magnitude down to 10 mpc [30]. Both are consistent with the Kolmogorov spectrum, given the projection effects in the observations.

The molecular component of the CNM (hereafter molecular clouds) also exhibits power law scalings between the velocity dispersion and sizescale, the well-known linewidth-size relations of Larson [31], and now observed in many environments including external galaxies (e.g. [18,32]) with a range of slope values close, but not equal, to the Kolmogorov spectrum. An extension of the Kolmogorov cascade, taking into account compressibility, has been proposed by Kritsuk et al. [33] using a density-weighted velocity $\mathbf{v}={\rho }^{1/3}\mathbf{u}$ with $\rho$ the mass density: it preserves the Kolmogorov scaling of the power spectra and the third order structure function behavior. But the respective roles of self-gravity and turbulence in these size-linewidth scalings remain an outstanding issue (e.g. [34]).

Diffuse molecular gas (Figure 1) harbors the very first steps of chemistry in space with the formation of light hydrides, such as CH, OH, ${\mathrm{CH}}^{+}$, ${\mathrm{OH}}^{+}$, ..., the most simple molecules that are the building blocks of the complex species found in dense proto-stellar cores or proto-planetary discs. It is in that diffuse medium of density $n_{\mathrm{H}}\sim 10-100$ ${\mathrm{cm}}^{-3}$ that the turbulent dissipation scale, estimated as $l_{\mathrm{diss}}={({\nu }^3/ϵ)}^{1/4}$ with the spatially averaged kinetic energy transfer rate $ϵ\approx 2\times {10}^{-25}$ $\mathrm{erg}{\mathrm{cm}}^{-3}{\mathrm{s}}^{-1}$ inferred from observations [18,35] is of the same order as the mean free path of atoms, or $\lambda \sim l_{\mathrm{diss}}\sim 2-10$ au. It is therefore predictable that turbulent dissipation plays a key role in the very first steps of chemistry in space.

1.3. Specific Molecules, as Tracers of Turbulent Dissipation

The emergence of molecules in the diffuse ISM raises outstanding issues: the observed abundances of the CO molecule in the diffuse molecular gas are an order of magnitude larger than what the chemistry driven by the UV photons and cosmic rays is able to produce [36,37]. This problem emerged in fact in the 1940’s with the discovery of the first molecules in the diffuse medium, CH, ${\mathrm{CH}}^{+}$ and CN, the formation of ${\mathrm{CH}}^{+}$ being extremely endothermic. Energy inputs from stellar UV-photons and cosmic rays are not sufficient to reproduce the observed column densities of these species. The same problem appeared later for ${\mathrm{HCO}}^{+}$ (e.g. [38]) and for CO. Another major power source was needed. Several processes have been proposed, such as thermal conduction at WNM/CNM interfaces [39], turbulent transport at the CNM/WNM interface [40] or extreme dissipative events in interstellar turbulence, such as C-shocks [22,23,27,41,42], magnetised Burgers vortices [36,43], and velocity shear layers [44,45]. The two former inject the thermal energy of the WNM into the CNM, while the latter feeds the chemistry with the turbulent energy of the CNM which is an order of magnitude larger than its thermal energy, but comparable to the thermal energy of the WNM. Ion-neutral drift in Alfvén waves have also been considered [46]. It is likely that they all contribute exemplifying the tight coupling between the thermal and turbulent facets of ISM physics.

In situ measurements in the ISM are impossible and the measured quantities suffer projection effects. Velocities are measured via the Doppler effect of spectral lines so that only line-of-sight (los) velocities are accessible. Displacements are inferred from distances projected in the plane of the sky (pos), so that only the pos variations of the los velocity are accessible, providing a proxy of the pos vorticity projection. Kinetic helicity cannot be directly measured. Only the intensity of the magnetic fields los projection is accessible via the Zeeman effect [47,48] and the fields direction, pos projected, is provided by polarisation measurements in different wavelength ranges (see the review of Ferriere [19]).

This is why, alike luminescent plankton that shines in the spots of intense velocity shear in the breaking waves of tropical seas, molecules with highly endothermic formation rates are used as the tracers of dissipation bursts in cosmic turbulence. These specific molecules in diffuse molecular gas are therefore not only the tracers of extreme dissipation events in cosmic turbulence but also of the small-scale coherent structures that may be the seeds of more massive structures in molecular clouds, grown through braiding and coalescing [49].

This paper reports on numerical simulations of compressible MHD turbulence, dedicated to dissipation scales, performed to characterise the nature of the coherent structures in ISM turbulence where dissipation is concentrated [50] and to illustrate the statistics performed on synthetic observations to disclose such coherent structures of dissipation extrema in diffuse molecular gas. Then, the first example of such a statistical study in a nearby diffuse molecular cloud is presented. A long and thin parsec-scale coherent structure of intense velocity shear is identified [51,52]. High-angular resolution observations disclose an even more intense velocity shear within it, on linear scales of only a few mpc. Last, the power of the so-called "warm chemistry" triggered by turbulent dissipation [36,43] is illustrated by observations in the circum-galactic medium of a starburst galaxy group at redshift $z=2.8$ [53].

2. Intermittency in Simulations of Magnetised Turbulence

2.1. Numerical Dissipation

Coherent structures that are the signposts of intermittency [6,8,11] are hard to characterise in controlled laboratory experiments, because measurements can only be made at a small finite number of points. On the contrary, a numerical simulation allows its user to access every state variable at every position. Unfortunately, that advantage comes with distortion from the unavoidable discretisation artefacts.

Simulations of incompressible gases allow to compute gradients in Fourier space. Such techniques ("pseudo-spectral") can obtain exponentially good accuracy with respect to the number of resolution elements. This greatly helps trusting the dissipation terms when the resolution is large enough (i.e. when a bottleneck effect is absent)2. The results of such incompressible simulations for HD turbulence [54] show that dissipation is localised around vortices or current sheets, while for MHD turbulence [14,55] they show that viscous and resistive dissipation are well separated on sheets which can therefore easily be identified as shearing or current sheets.

Compressible simulations are much more difficult to interpret. The finite size of the zoning and the necessary reconstruction of variables from the center to the edges of each pixel introduces a spurious diffusion length scale for every conservation equation (including mass conservation). To this effect, we built a method to estimate locally the total dissipation including the one inherent to the numerical scheme [14,50]. The method consists in replaying a simulation step while integrating a redundant conservation equation for a variant of the energy (total mechanical energy, for example). In isothermal simulations, that quantity is best taken as the generalised isothermal total mechanical energy $E=\frac{1}{2}\rho u^2+\frac{1}{8\pi }B+plog\rho$ where $\rho$,u, B and $p=\rho c_{\mathrm{s}}^2$ are respectively the mass density, the velocity, the magnetic fields intensity and the thermal pressure (with $c_{\mathrm{s}}$ the isothermal sound speed). An estimation of the flux ${\mathcal{F}}_E$ of this quantity and its time-derivative then allows to recover the local total dissipation of energy as $\epsilon ={\partial }_{t}E+\nabla .{\mathcal{F}}_E$.

Once the dissipation rate is known everywhere, we can study the regions of strongest dissipation. For instance, we can plot the line of sight integrated dissipation as on Figure 2, which displays ridges of intense integrated dissipation. These ridges appear as a caustic effect from the projection of sheets where dissipation is strong and where the plane of the sheets contains the line of sight (see [50]).

2.2. The Nature of Coherent Structures in MHD Turbulence

Strong dissipation in MHD turbulence is seen to lie on thin sheets whether it is incompressible [14,55] or compressible [50].

In incompressible MHD turbulence, viscous and ohmic dissipation always appear disconnected (e.g. [14,55]), and the same probably holds for reduced MHD as in [56]. In these works, it makes it easy to differentiate shearing sheets and current sheets as connected sets of strong viscous dissipation or resistive dissipation. In compressible MHD, this is much less obvious, as hinted at by Figure 2 where different natures of dissipation heating can be intermixed. Lehmann et al. [57] with the SHOCKFIND algorithm and Richard et al. [50] designed several criteria which allow to carefully select strong dissipation regions and characterise their physical nature as fast shocks, slow shocks, rotational discontinuities or Parker sheets. Some of these criteria are based on Rankine-Hugoniot relations [58], which seem to hold strikingly well far from their domain of application (i.e. in a non stationary medium, inhomogeneous, with curved working surfaces etc...). Some of these criteria are based on a decomposition along free traveling waves, which characterise suprisingly well most of these structures 3.

A systematic investigation of these coherent structures was performed by Richard et al. [50] for 3-dimensional (3D) MHD and in Lesaffre et al. [59] for 2-dimensional (2D) HD turbulence. For 2D HD, we were able to show that almost 80% of the dissipation was accounted for near the shock fronts, with the remainder as diffuse viscous shear in the wakes of these shocks [59]. For 3D MHD [50], we could not clearly prove whether there was a significant contribution from dissipation outside the detected strongest dissipation regions, given the technical difficulties introduced by the 3D geometry. However, we were surprised as most of the dissipation was accounted for by weakly compressive structures. This is illustrated by the distribution of the dissipation rate according to velocity convergence in Figure 3. Another surprise we found in Richard et al. [50] is that the entrance parameters in the Rankine-Hugoniot fronts we extract from the simulations are not spanning the whole parameter space available to them. Indeed, geometry and symmetries alone allow to reduce to three the number of free parameters characterising a Rankine-Hugoniot discontinuity [58]. However, the dynamics of these coherent structures seem to constrain them to lie on a 2-dimensional parameter space. To be more precise: slow shocks and Alfvénic discontinuities have entrance magnetic fields nearly orthogonal to the discontinuity while fast shocks have their entrance magnetic fields nearly transverse. It will be the object of future investigations to understand the underlying reasons why this is.

2.3. Synthetic Observables and the Regions of Strong Dissipation

Laboratory measurements or in situ probes such as the CLUSTER satellites in the solar wind allow to probe only a small fraction of the volume of interest. In experiments, the progress of particle image velocimetry (PIV) techniques now authorise somewhat more widespread measurements, and Cadot et al. [8] cleverly used cavitation bubbles to reveal the strongest coherent structures in their experiments. On the other hand, astrophysical images of the nearby interstellar medium offer a global view. However, this means the data are projected on the plane of sky: we loose one dimension of interest. Nevertheless some distinctive features survive the projection. Figure 2 suggests that when viewed sideways, dissipation sheets can still be seen as prominent features in the integrated image.

Here, we compute some proxies for line of sight integrated observable variables in our isothermal simulations of decaying MHD turbulence (see [50] for a detailed presentation of the simulations), and we investigate where they vary strongly. The first obvious quantity we can have access to is the column-density $I={\int }_0^L\rho dz$ (where L is the box length and z is the line of sight coordinate), often probed indirectly by the total dust continuum intensity. Thanks to line profiles measurements (see section 4), one could hope to have access to the average line of sight velocity $v_z={\int }_0^L\rho u_{z}dz/I$, provided one finds a trustable tracer with emission proportional to density. In practice, temperature and chemical effects due to local heating as well as radiative transfer effects strongly hinder this measurement (see sections 3 and 4). Finally, in a magnetised medium, dust and synchrotron emissions are polarised. Modern astronomical instruments are able to measure the polarisation state of these emissions, which they characterise through the Stokes parameters Q and U. The observed Stokes parameters are thus probes, however rather convoluted, of the integrated magnetic fields direction along the line of sight. For instance, the polarisation of the dust thermal emission is due to the fact that dust grains are elongated and spin with their longer axis perpendicular to the magnetic fields direction, thus orienting their thermal emission’s polarisation vector orthogonal to the magnetic fields direction. The resulting Stokes parameters of dust emission are therefore $Q+iU={\int }_0^{L}dz\rho {\widehat{B}}_{\perp }^2{e}^{2i\varphi }$ where $\varphi$ is the position angle of the magnetic fields on the plane of sky and ${\widehat{B}}_{\perp }$ is its relative norm compared to the local total fields.

In order to emphasise the places where these observables change abruptly, we compute their one-pixel increments on the plane of sky: i.e. around each pixel, we compute the standard deviation of the difference with its nearest neighbours. We then overlay 2-$\sigma$ contours of these increments onto our integrated dissipation map (see Figure 4). In most cases such contours delimit a region of strong dissipation. Indeed, whenever a physical quantity varies strongly, it is most often associated to dissipation. However, not all dissipation regions are detected, and various observables highlight different parts of the regions, depending on which component of the velocity or the magnetic fields is probed by the observable considered. Indeed, some dissipation regions can involve a jump in magnetic fields or velocity components which cannot be probed by astrophysical observables because of the projections discussed in Sect. 1. Unfortunately, we are not yet in a capacity to link the nature of the observable jumps to the nature of the underlying coherent structure, except for the simple fact that strongly compressive shocks (slow shocks) should appear as a ridge of strong $\delta I$ when their working surface contains the line of sight.

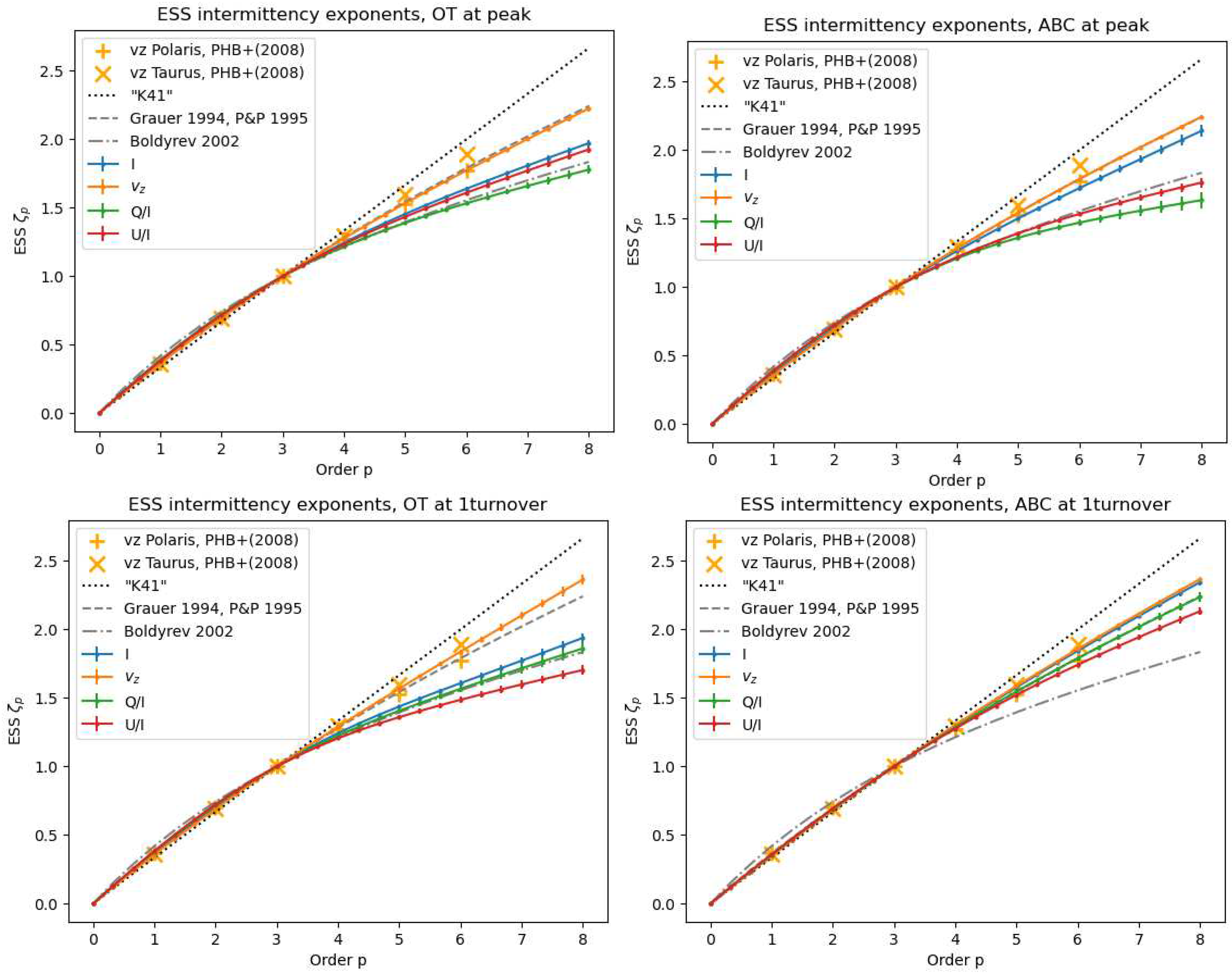
2.4. Intermittency Statistics from Increments of Observables.

Since the early works of Kolmogorov [60] (K41), who predicted it in the case of incompressible hydrodynamics, one of the first characteristics of turbulence that researchers have strived to predict is the power-law slope of the velocity power spectrum. In the case of incompressible MHD turbulence, the exact scaling laws of the velocity and magnetic fields are still a matter of debate [11,61,62,63]. In compressible turbulence, theoretical discussions are scarce, but suggest that one could obtain the K41 scaling for ${\rho }^{1/3}u$ in isothermal turbulence [64], while numerical simulations [65] display different scalings for subsonic (K41) and supersonic scales (Burgers). Banerjee and Galtier [66] also managed to derive exact expressions for convoluted transfer functions in isothermal MHD, from which it is however hard to derive scaling laws for any simply defined quantity. The power spectrum of the density and the column-density have also been discussed and either proven to be K41 in the Gaussian case [67], or shown to to be close to K41 thanks to numerical simulations [68,69,70].

Twenty years after K41, Kolmogorov [71] realised that the spatial intermittency of the dissipation rate would introduce corrections to the structure function power-law scalings with lag (the so-called anomalous scalings, characterised by intermittency exponents or multifractal spectra [72]). These anomalous scalings were linked to the fractal dimension of the dissipative structures, and generic models such as that of She and Leveque [3] were put in place, with shape parameters for the fractal geometry of the dissipative structures. Based on the observation that these were sheets in the case of MHD turbulence, this led to independent predictions from Grauer et al. [73] and Politano and Pouquet [74] for the Iroshnikov-Kraichnan scaling and later from Boldyrev et al. [75] for the Goldreich-Sridhar scaling (similar to K41).

Note that the causal link between the geometry of the coherent structures and the form of the intermittency exponents goes only one way. For instance, Chevillard et al. [76], Durrive et al. [77] were able to build random fields with controlled anomalous scalings close to those of hydrodynamics [76] or MHD [77] while these fields do not display any coherent structures. It is only in the case where a statistical collection of well defined structures of strong dissipation is presupposed that the anomalous scaling coefficients can constrain the fractal dimension and geometry of these structures.

In the previous section, we demonstrated a spatial link between the increments of the synthetic observables and the coherent structures of dissipation extrema. We now investigate these increments at various lags, and look at classical structure functions built from these increments. Even though these indicators are very indirect and probably have not much to do with the underlying physics of the above intermittent theoretical models, we proceed to compute them as they will presumably still be good probes of the relative orientation and size of the salient features in the astrophysical images (they will be sensitive to their fractal structure, for example). As such, they provide a quantitative estimate to link the texture of the simulated images to the observed ones. In addition, the link to physics is blurred by the projections, and this analysis should rather be regarded as a quantitative characterisation of the evolution of the observable increments statistics with scale.

We now define ${\delta }_{\ell }X\left(\mathbf{r}\right)=X(\mathbf{r}+\ell )-X\left(\mathbf{r}\right)$ as the increment of an integrated observable X over a lag ℓ at position $\mathbf{r}$ in the plane of sky and we investigate the statistics of these increments for lags where the norm is comprised between ℓ and $\ell +1$ pixels (hence, we compute all increments in a corona of width 1 pixel around each pixel).

Figure 5, for example, shows how the PDF of the increment of the line of sight integrated velocity ($v_z$) varies from having strong non-Gaussian wings at small scales to nearly Gaussian at large scales. As an illustration, the interior of the green contours of Figure 4 corresponds to the wings of the PDF for the smallest lag (dark blue on Figure 3), where the normalised increment $\delta v_z/\sigma \left(\delta v_z\right)$ exceeds 2 in absolute value.

We then define “structure functions” in a natural way similarly to three dimensional dynamically relevant structure functions: $S(p,\ell )=<|{\delta }_{\ell }{X|}^p{>}_{\ell \le |\ell |<\ell +1}$ where the average is done over the image. These are displayed in Figure 6, left panel. We now measure scaling exponents ${\zeta }_p$ by adjusting a power law $S(p,\ell )\sim {\ell }^{{\zeta }_p}$ in a range of scales ${\ell }_{min}\le \ell \le {\ell }_{max}$. We adopt here the range of scales for the lags between 12 and 48 pixels (over a periodic computational domain of 1024 pixels aside) as this seemed to minimise the dispersion (see Figure 6 left panel).

The values of the scalings, displayed on the left panel of Figure 7, usually fall way above K41: even if we would fit a slope to the values of ${\zeta }_p$ vs p, we would find slopes much bigger than K41 or Iroshnikov-Kraichnan: we are clearly not in the domain of application of these theories. Furthermore, all exponents measured on different variables (column density, projected velocity, U and Q Stokes parameters) display anomalous scalings in the sense that ${\zeta }_p$ is not proportional to p (see Figure 7). The uncertainty of the fit is displayed as error bars of one standard deviation around these intermittency exponents. It is a quantitative measurement of whether the scaling is indeed good or not, i.e. whether intermittency exponents are a good representation of the data. Note that these error bars do not reflect the temporal variation in the simulation, as they are displayed here only for one selected snapshot (at a time close to the dissipation peak, about a third of the non-linear initial turnover time). The temporal variability of these coefficients is in fact a few times larger than the displayed error bars.

Figure 6 demonstrates that when we plot the structure functions against $S(3,\ell )$ instead of the lag (right panel vs left panel), they behave much more like power laws. This was first discovered by Benzi et al. [78] for 3-dimensional velocity field increments in hydrodynamics experiments. Because it allowed to significantly extend the range of the scaling, this property was named “Extended Self-Similarity” (ESS). Similarly, we define ESS exponents as the exponents in the power-law scalings $S(p,\ell )\sim S{(3,\ell )}^{\mathrm{ESS}{\zeta }_p}$. This significantly improves the quality of the fit, hence our error bars (see right panel of Figure 7), even though we now use the full range of scales instead of the small restricted range of scales used in the left panel. This ESS property has been tested and verified in many independent data but has yet to find an underlying physical interpretation or proof. In addition, in our astrophysical case, for the observables integrated on the line of sight, the notion of an inertial range is hard to characterise. Indeed, projection brings larger scales onto smaller ones, and in doing so mixes dissipation, injection and inertial scales: this ESS property comes even more as a surprise.

We have investigated two types of initial conditions (an ABC flow, with large magnetic helicity and small cross helicity and an Orzag-Tang vortex, with zero magnetic helicity and large cross helicity, see [50]) and we selected two different snapshots for each of these initial conditions. The earliest time is around peak dissipation, when stationarity is most likely to be realised (the second derivative in time of the total energy is zero), which also corresponds to when the coherent structures have just been born. The later time is after one turnover time, as a compromise between a time when turbulence has been well established and initial conditions washed out, but nevertheless turbulence has not yet decayed too much and remains strong.

We summarise the results of our intermittency exponents measurements for all four cases on Figure 8. There is clear anomalous scaling (i.e. departure from the linearity of ${\zeta }_p$) in all four cases we investigated. However, the intermittency exponents are highly variable depending on the type of variable, the time and the initial conditions. Although the intermittency exponents differ slightly between the different observables, the use of ESS brings them closer to one another (see Figure 7 for example), spanning values between Grauer et al. [73] or Politano and Pouquet [74] and Boldyrev et al. [75]. In all cases, magnetic fields appear more intermittent than the velocity or column density, as already discussed in Schekochihin [11]. As in Figure 7, the error bars in Figure 8 characterise the goodness of the ESS fit for the whole lag range between 1 and 256 pixels. The exponents for the line of sight integrated velocity, $v_z$, are always close to the models of Grauer et al. [73] and Politano and Pouquet [74] and also close to the observed values measured in Polaris and Taurus by Hily-Blant et al. [51]. Although the variability of the anomalous scalings is strong, ESS${\zeta }_p$ for the column-density scalings stays within one error bar of the scaling by Boldyrev et al. [75], except for the ABC flow at one turnover time. Provided we could neglect projection effects, and if we accept that dissipation is mainly occurring in sheets, this could mean that the correct ESS scaling for the velocity is closer to the Iroshnikov-Kraichnan scaling, while that of the mass density is closer to the Goldreich-Sridhar scaling.

3. Intermittency in Cosmic Turbulence

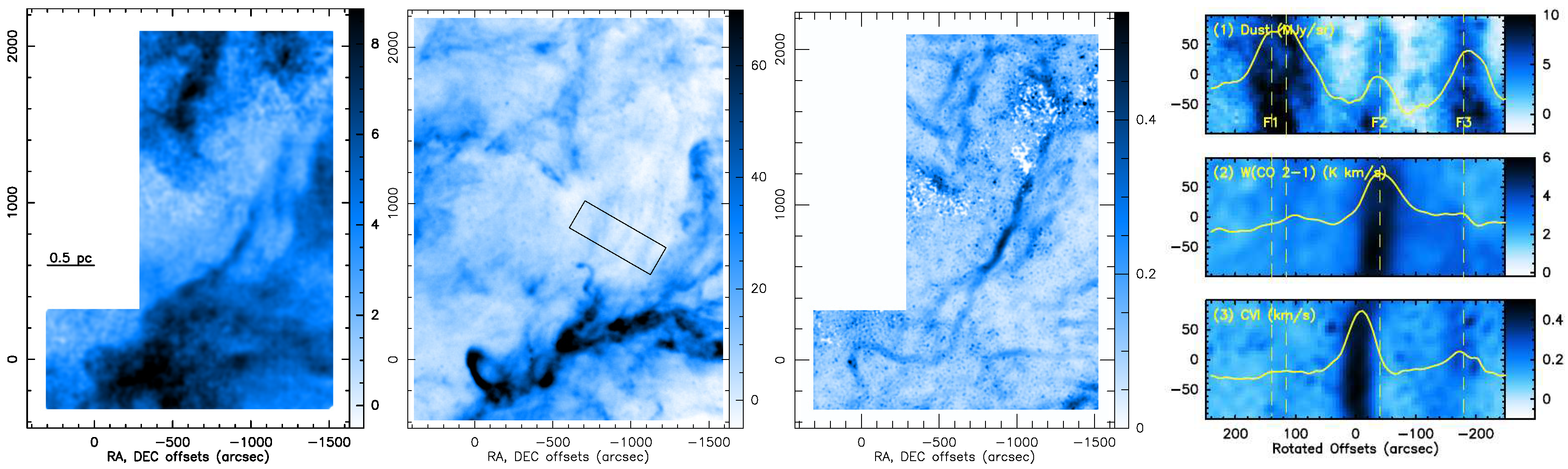
3.1. Extrema of Turbulent Dissipation in a Nearby Diffuse Molecular Cloud: A Source of CO Molecules

A statistical analysis similar to that conducted on the simulations described in the previous section was performed in a nearby diffuse molecular cloud in the Polaris Flare, on the centroid velocities of ${ }^{12}\mathrm{CO}$(J=2-1) lines, defined as $\int vT\left(v\right)\mathrm{d}v/\int T\left(v\right)\mathrm{d}v$ with $T\left(v\right)$ the line intensity as a function of velocity. The map of ${ }^{12}\mathrm{CO}$(2-1) emission shown in Figure 9 (left) comprises almost ${10}^5$ independent spectra obtained with the IRAM-30m telescope at an angular resolution of 11arcsec corresponding to $\sim 20$ mpc at the distance of the cloud ($d=350$pc). The map of the thermal dust emission of the same field, Figure 9 (2nd panel), obtained at 250$\mu$m with the Herschel satellite, displays the projected distribution of matter in the field, including bright and dense regions in the bottom of the map that harbour pre-stellar dense cores. The rectangular box encompasses three very faint dust filaments connected to the main massive structure.

The probability distribution functions of the CO(2-1) line centroid velocity increments (CVI) between two positions separated by a lag ℓ, develop non-Gaussian wings, the wing intensity increasing with decreasing lag [51,52]. The locus of the positions contributing to these non-Gaussian wings (hereafter, the ECVI structure for extreme-CVI structure) is shown in Figure 9 (3rd panel); as is evident, these large gradients are not randomly distributed but form coherent structures, the most prominent of which is a parsec-long, thin filament (in projection) that resembles coherent structures found in incompressible and compressible turbulence [33,79,80,81]. The velocity gradient reaches 40 km s${ }^{-1}$ pc${ }^{-1}$, about 40 × larger than the average velocity shear in molecular gas [52]. Furthermore, the coherent structures are themselves not random and seem to cluster around the most prominent one [54].

Interestingly, the behavior of the high-order structure functions of the CO centroid velocities with order p, measured in that Polaris field and in the Taurus molecular cloud, closely follows that found for the velocity in the numerical simulations of compressible MHD turbulence of Richard et al. [50] (Figure 8).

It is clear on Figure 9 (right) that the ECVI structure is bright in CO line emission, but almost undetected in the dust continuum. This ECVI structure is 10× more CO-rich, given its total gas column density inferred from its dust sub-mm brightness, than the two other nearby filaments that have the properties of diffuse molecular gas with an ${\mathrm{H}}_2$ fraction of 0.3, inferred from the CO line width a standard CO-to-${\mathrm{H}}_2$ ratio.

High-angular resolution observations with the IRAM-NOEMA interferometer unveil similarly straight and elongated structures at the mpc-scale, embedded within the ECVI structure and parallel to its parsec-scale orientation (Hily-Blant et al., in prep.). Not only the orientation of the large- and small-scale structures is preserved over three-orders of magnitude in scale, but also the magnitude of the velocity differences. The remarkable coincidence at the 3 arcsec NOEMA resolution (in projection) of two elongated structures separated by 3 km s${ }^{-1}$ reveals a local velocity shear larger than 600 km s${ }^{-1}$ pc${ }^{-1}$, or a dynamical timescale shorter than 1000 yr. Sharp variations across the ECVI structure of both the CO abundance and excitation are also derived from the ${ }^{13}\mathrm{CO}$/${ }^{12}\mathrm{CO}$ and CO(2-1)/CO(1-0) line ratios.

The emergent scenario of CO-enriched gas produced by the intense velocity shear is inspired by the models of warm chemistry in turbulent dissipation regions of Godard et al. [43] and the numerical results of Richard et al. [50]. This CO-rich filament, associated with a velocity shear 600 × larger than the average value in local molecular clouds, may be the first direct detection of the outcome of warm chemistry locally driven by a turbulent dissipation burst. The mpc-scale is still far larger than the viscous dissipation scale, but these results unveil the possible role of intermittent turbulent dissipation in seeding the growth of molecular structures in diffuse gas, as suggested in Falgarone et al. [49].

The detailed modellings of the chemical outcome of turbulent dissipation are hard to reconcile with a coherent description of the energy cascade from the large scales of turbulence down to the dissipation scales, including intermittency. It has been attempted in 2-dimensions by Lesaffre et al. [42] and by chemical post-processing of state-of-the-art numerical simulations of MHD turbulence, including ion-neutral drift (e.g. Moseley et al. [82]). These results are promising, but nevertheless, the former simulations are not magnetised, and the latter simulations are far from resolving the dissipation scales.

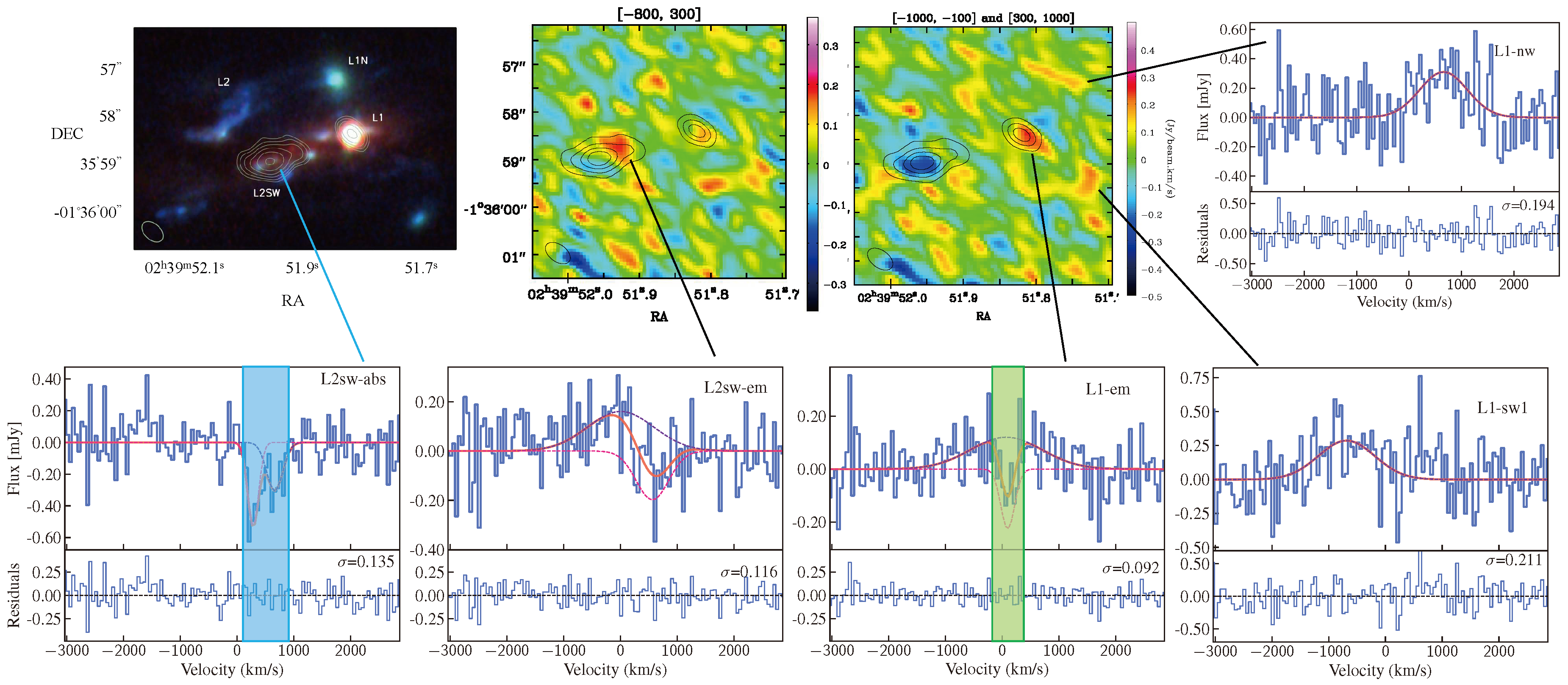
3.2. Turbulent Dissipation in the Circum-Galactic Medium of a Galaxy Group at Redshift $z=$2.8

Another illustration of the power of chemistry fed by turbulent dissipation bursts is the analysis of the dynamics of kpc-scale highly turbulent environments of starburst galaxies at redshift $z=2$ to 6 (Vidal-García et al. [53], Falgarone et al. [83]).

In numerical simulations, galaxies grow by accreting cold streams, modulo ejection of matter by stars and Active Galactic Nuclei (AGN) (Madau and Dickinson [84]). While the feedback from AGNs and star formation is observed through powerful outflows [85], cold stream accretion is still elusive. The momentum exchange between the streams and a growing galaxy is so violent that a large turbulent region is generated around the galaxy. An indirect way of detecting cold stream accretion is therefore the detection of large turbulent reservoirs around galaxies. It is what has been achieved with the detection of the CH${ }^{+}$(1-0) line in emission and/or in absorption in all the gravitationally lensed starburst galaxies observed so far with ALMA at redshifts $z\sim$2 to 4 [83]. The unique spectroscopic and chemical properties of CH${ }^{+}$ allow its $J=$1-0 transition to highlight the sites of dissipation of mechanical energy. Moreover, it is such a fragile species that it cannot be transported and is observed where it forms. Absorption lines reveal massive (a few ${10}^{10}$ ${\mathrm{M}}_{\odot }$), highly turbulent reservoirs of low-density extending far out of the galaxies. Broad emission lines, with widths up to a few thousands of km s${ }^{-1}$, arise in myriad low-velocity molecular shocks (Lehmann et al. [26]) powered by the feedback of star formation and AGNs.

4. Conclusions and Perspectives

We have used numerical simulations to build synthetic observables projected on the plane of sky. From these synthetic maps, we have computed the plane of sky increments of these variables and measured their structure functions at various scales (or lags). We have shown that the large deviations of the smallest lags correlate spatially with the line-of-sight integrated dissipation: the shortest increments may be a way to detect the regions of strong dissipation on the sky plane.

Very suprisingly, we find that ESS applies to these structure functions. The "E" in "ESS" originally stands for "extended". This meant that, when scales are remapped onto the third order structure function, the range of scales where the self-similar scalings of the structure functions applies is considerably extended outside the inertial range. In this work, we have shown that this ESS property can be furthermore extended. Indeed, it seems to apply:

• in a situation outside stationary driven turbulence (we are in a case of decaying turbulence).
• for other variables than the proper transfer functions predicted by theory (such as Galtier and Banerjee [64] or Banerjee and Galtier [66] who nail the scaling for the order $p=3$, in the inertial range and for very specific transfer functions).
• for projected variables and plane of sky increments instead of the actual 3D increments.

For all these reasons, we feel that there might be something more fundamental behind the ESS, with a lot still to be understood in the statistics of turbulence which may explain such behaviour of the structure functions.

Because ESS applies to our data, it makes sense to measure intermittency exponents. These exponents vary in time and according to the initial conditions. The velocity exponents lie close to the models of Grauer et al. [73] and Politano and Pouquet [74], designed for incompressible MHD and increments of Elsasser functions assuming an Iroshnikov-Kraichnan scaling. The exponents for the column-density lie rather close to the model of Boldyrev et al. [75], a similar model based on the K41 scaling. Nevertheless, since we are far from the domain of application of both these theories, it is still premature to interpret these results as good matches. Meanwhile, we prefer to use the measurements of these intermittency exponents as a way to constrain quantitatively the geometry of the structures as they are observed on the plane of sky.

The mere existence of large-scale and thin coherent structures in observations of cosmic turbulence provide unique informations on their stability. Thorough investigations of the predicted anisotropy of magnetised turbulence (i.e. structures linked to the intermittency of turbulence develop in the non-linear cascade perpendicular to the magnetic fields while coherence is driven by waves propagating along the fields [11]), its balanced or imbalanced characteristics and the corresponding scaling laws (see the review of Schekochihin [11]) are a challenging opening for future observations.

Last, isothermal simulations are still very idealised compared to the complexity of the interstellar medium. Cooling, heating, chemistry, time-dependent excitation of molecules have to be included in order to bridge the gap between the simulations and observations. This has been done only in 2D without magnetic fields [59]: there is yet a lot more to be achieved in order to interpret observations. However, detailed computations in 1D for a well chosen statistical collection of dissipative structures may be used to access the complexity of ISM turbulence. Simplified simulations in a multi-dimensional framework can help us pinpoint these statistics and hopefully understand what the interstellar medium has to tell us on magnetised turbulence.