Prerpints.org logo
Preprint
Article

Improving Genomic Predictions in Multi-Breed Cattle Populations: A Comparative Analysis of BayesR and GBLUP Models

Altmetrics

Downloads

130

Views

61

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

15 January 2024

Posted:

15 January 2024

You are already at the latest version

Alerts
Abstract
Abstract Background: Numerous studies have demonstrated that the amalgamation of populations belonging to the same breed or closely related breeds leads to enhanced accuracies in genomic predictions (GP). Extensive experimentation with diverse Bayesian and Genome-enabled best linear unbiased prediction (GBLUP) models has been conducted to explore multi-breed genomic selection (GS) in livestock, ultimately establishing they as successful approaches for predicting genomic estimated breeding value (GEBV). This study aimed to examine the efficacy of BayesR and GBLUP model with different weighted genomic relationship matrices (GRM) in making genomic predictions for three distinct beef cattle breeds. Subsequently, we conducted a comparative analysis of the predictive accuracy pertaining to various marker densities and genetic correlations across three distinct beef cattle breeds. This investigation aimed to identify the optimal approach for enhancing the predictive accuracy of multi-breed genomic selection in beef cattle. Results：Genetic relationship matrices revealed moderate similarities between YL and the other breeds, with a striking genetic similarity of 0.87 between WG and HX. In HX cattle, BayesR demonstrated an enhancement in prediction accuracy, achieving 0.52 with HD and 0.46 with WGS, a marked improvement over 0.41 with HD and 0.42 with WGS in GBLUP. In WG and YL breeds, both methods showed comparable accuracies with HD, but BayesR slightly outperformed GBLUP with WGS. Further, multi-breed GS analysis indicated that BayesR consistently surpassed GBLUP in prediction accuracy, particularly with WGS data. For instance, in a combined HX and WG reference population, BayesR achieved a superior accuracy of 0.53 with WGS in HX cattle, a significant enhancement over GBLUP models. The study also underscores the advantage of incorporating multiple breeds in the reference population, which improved prediction accuracy, underscoring the value of broad-based genomic selection strategies. Conclusion: The results show that accuracy of multi-breed genomic predictions was higher with BayesR than with GBLUP, especially for the distantly genetic relationship between reference and validation breeds. Further improvements of multi-breed accuracy of genomic predictions could be achieved by increasing the density of the SNP marker. These findings underscore that BayesR providing a substantial improvement in genomic prediction and the importance of considering genetic relationships in the development of GS strategies for multi-breed cattle populations. Further research is warranted to optimize GRM construction and to explore alternative models for genomic prediction across breeds.
Keywords: 
Subject: Biology and Life Sciences  -   Animal Science, Veterinary Science and Zoology

1. Introduction

Genomic Selection (GS) is currently widely used in plant, animal breeding and polygenic disease risk prediction(Brondum et al. 2012). The accuracy of genomic estimated breeding values (GEBV) is primarily contingent upon the magnitude of the reference population, thus rendering genomic evaluations predominantly applicable to breeds of substantial size (Hayes et al. 2009). In China, GS were introduced in Simmental beef cattle breeding in 2007. However, in numerous local cattle populations with a small numeric size and a larger effective population size, it can be difficult or impossible to assemble a large enough training population to sufficiently predict GEBV. Pooling animals from related breeds has been proposed as an option to overcome the small size of reference populations but has not been very successful due to non-persistent associations between Single Nucleotide Polymorphism (SNP) and quantitative trait loci (QTL) across breeds (populations), or inconsistent linkage disequilibrium (LD) between SNPs and QTL across more distantly genetic related populations(Hayes et al. 2009; Brondum et al. 2011; Lund et al. 2011; Pryce et al. 2011; Iheshiulor et al. 2016).
Previous studies based on SNP markers from the Illumina 50K SNP chip have reported that distances between markers would be too large for high persistence of LD phase across breeds, and accuracies of across breed prediction were zero (Erbe et al. 2012a; Vanraden et al. 2013; Kemper et al. 2015). According to the literature, the BovineHD BeadChip (HD chip; Illumina Inc., San Diego, CA), a high-density genotyping array comprising 777,609 single nucleotide polymorphisms (SNPs), was developed in 2010. This chip is known for its short-range linkage disequilibrium, which is anticipated to persist across different breeds of cattle(Hozé et al. 2014). Meanwhile, whole-genome sequence (WGS), a recently developed method, has been used to incorporate more genetic variants than SNP arrays. WGS data differ fundamentally from the current data obtained with dense SNP chips because all variants, such as SNPs, indels, copy number variants (CNV), etc., are included. Since all variants, both rare and common, are captured for a population, WGS data could provide more precise signals for causative mutations, both within and across breeds; hence predictions would no longer have to completely rely on LD between SNPs and QTL. Consequently, WGS data could lead to more accurate genomic predictions. In the case of multi-breed predictions, the use of WGS data could reduce or remove the need to rely on associations between SNPs and QTL which may not persist across the breeds being evaluated(Kemper et al. 2015). Although Meuwissen and Goddard (Meuwissen and Goddard 2010)[9] reported an advantage of WGS data over dense SNP data using simulated data, their results were restricted to within-population predictions and to a small number of QTL/Morgan. Therefore, the advantages of WGS data for multi-breed predictions and divergent small populations remain largely unknown.
Multi-breed genomic prediction methods have been developed using both BLUP (Olson et al. 2012; Calus et al. 2018a; van den Berg et al. 2020) and Bayesian methods (Kemper et al. 2015; van den Berg et al. 2017; Calus et al. 2018b). The primary focus of research in mulit-breed GBLUP models lies in the innovation of construction methods for the G-matrix. Zhou et al used different sources of information, such as consistencies of LD phase and marker effects, to construct the genomic relationship matrices (GRM) by using 50k SNP chip across these two breeds(Zhou et al. 2014; Mohammad Rahimi et al. 2020). Their research show that weighting the two-breed GRM by LD phase consistencies, marker effects or both did not further improve accuracies of the two-breed predictions. When comparing methods, these researchers confirmed the advantage of Bayesian approaches compared with genomic BLUP for EBV estimation(Hayes et al. 2009; Erbe et al. 2012a; Hozé et al. 2014); they stated that setting a large proportion of SNP effects to zero is necessary to take advantage of the density of the HD chip(Erbe et al. 2012a). This conclusion is in agreement with conserved QTL-marker association at small distances only. Furthermore, adding a polygenic component avoids spurious SNP-QTL associations due to pedigree relationship (Solberg et al. 2009) and helps to select QTL with rare alleles, small effects, or both(Calus and Veerkamp 2007; Goddard 2009). Inclusion of a polygenic component also increases the accuracy of GEBV prediction and allows for regression slopes closer to 1 (Erbe et al. 2012b; Hozé et al. 2014).
The objective of this study was 1) to compare the prediction performance using Unweight G-Matrix GBLUP( G U N W -GBLUP), LD Weight G-Matrix GBLUP ( G L D -GBLUP) and BayesR for within-population and multi-breed reference populations. 2) to assess how much predictive accuracy is gained by using WGS compared to HD chip SNP data, with emphasis on divergent cattle breeds with different genetic correlations.

2. Material and Methods

2.1. Ethics Statement

We followed guidelines advanced by the China Council on Animal Care. All steps and activities were authorized by the Institute of Animal Science (IAS) and the Chinese Academy of Agricultural Science (CAAS), Beijing, China. Animal examinations followed rules of the China’s Animal Welfare council.

2.2. Animals and Phenotype

The real data set included 1478 HUAXI cattle (HX), which derived from Chinese Simmental beef cattle, 600 Chinese Wagyu cattle (WG) and 400 Yunling Cattle (YL). The HX cattle, originating from five farms in Ulgai Grassland, Xilingole League, Inner Mongolia of China, were born between 2008 and 2020. Following the weaning stage, the animals were relocated to Beijing for the purpose of fattening, where they were consistently raised under identical feeding conditions. The WG cattle originated from Dalian and Haikou cities in China, with birthdates ranging from 2012 to 2022. In contrast, the YL cattle were born between 2020 and 2023, hailing from Kunming cities in China. The age at which the animals were slaughtered varied between 18 and 32 months. In this research, slaughter weight (SWT; kg) were analyzed. The SWT was measured prior to slaughter following a 24-hour fasting period.

2.3. Genotyping Data

The DNA was extracted from blood samples obtained from three cattle breeds. Genotyping was performed using the Illumina BovineHD BeadChips, which consist of 777,962 SNPs. We conducted SNP quality control for each breed using PLINK v1.9 (Purcell et al. 2007) Individual SNP genotypes were excluded if the sample call rates (CR) were below 90%, if the minor allele frequencies (MAF) were less than 0.01, or if the SNP genotype frequency deviated significantly from the Hardy-Weinberg Equilibrium (p < 1.0×10-6). Only autosomal SNPs were included in the subsequent analyses. Subsequently, a total of 1478 individuals and 672,060 SNPs were retained and further phased using BEAGLE (v4.1) with default parameters, as outlined by Browning (Browning et al. 2018).
A total of 44 unrelated HX, 20 WG, and 20 YL cattle specimens were selected for the purpose of conducting genetic resequencing of the whole genome. Each animal was subjected to library preparation using the Illumina Hiseq 2500 genome sequencing system (Illumina Inc., San Diego, CA, USA). The average sequencing depth for each sample was about 20X with a range of 17X to 25X (X represents a number of times which each base is sequenced) (Bordbar et al. 2020).
We obtained a total of 9,621,765,847 reads, which were subsequently subjected to our quality control procedures. Reads that exhibited low quality, defined as containing more than 10% unknown bases, more than 10% mismatches, or more than 50% low-quality bases, were excluded from further analysis. Additionally, putative PCR duplicates resulting from the PCR amplification during library construction were removed. SNP with a MAF greater than 0.05 underwent imputation. Utilizing the 21,043,398 sequence variants identified in the genetically sequenced cattle, imputation was performed separated by breed using BEAGLE v4.1 with its default parameter settings. The genotypes for imputed sequence variants were coded as 0 (representing homozygotes), 1 (representing heterozygotes), or 2 (representing alternative homozygotes). Only R-sq. data exceeding a threshold of 0.1 were considered for association studies. Subsequent to the imputation process, a total of 12,468,401 markers were obtained for Chromosomes 1–29 among breeds (Bordbar et al. 2020).

2.4. Genetic Correlations

We utilized the persistence of the LD phase between populations to determine the genetic relationship among breeds. In this method, we calculated the correlation of linkage disequilibrium (r2) of adjacent marker pairs on each autosome and used average correlation to represent the genetic relationship (de Roos et al. 2008; Ma et al. 2018). The calculated of r was proposed by Hill and Robertson (Hill and Robertson 1968), and the r2 was calculated as:
r 2 = D 2 f ( A ) f ( a ) f ( B ) f ( b )
where D = f A B − f A f ( B ) , and f A B , f A , f a , f B , and f b are observed frequencies of haplotype AB and alleles A, a, B, and b, respectively.

2.5. Statistical Models

Three prediction models were analyzed and compared in this study.

2.5.1. GBLUP Model

The GBLUP method was used in this study to predict breeding values (Vanraden 2008). The model was:
y = X b + Z g + e
where y is a vector of phenotypes, X is a design matrix relating the fixed effects to each animal, b is a vector of fixed effects, Z is a design matrix allocating records to genetic values, g is a vector of additive genetic effects for an individual, and e is a vector of random normal deviates with variance σ e 2 . In addition, v a r ( g ) = G σ g 2 where G is the genomic relationship matrix, and σ g 2 is the genetic variance for this model. The vector g contains animals with phenotypic data but can be extended to animals without phenotypes.

2.5.2. Multi-Breed GBLUP Model

A two-trait GBLUP model was used for genomic predictions across breeds. the same trait from different cattle breeds was regarded as two different traits (Zhou et al. 2014). The model was:
y 1 y 2 = 1 μ 1 1 μ 2 + Z 1 0 0 Z 2 a 1 a 2 + e 1 e 2
where y 1 was the vector of the phenotype of breed 1 and y 2 was the vector of the phenotype of breed 2. μ 1 and μ 2 were means of the two breeds, a 1 and a 2 were the vectors of genomic breeding values, e 1 and e 2 were the vectors of residual effects, and Z 1 and Z 2 were incidence matrices associating genomic breeding values with y 1 and y 2 , respectively. It was assumed that:
V a r a 1 a 2 e 1 e 2 = σ 11 2 G σ 12 G 0 0 σ 12 G σ 22 2 G 0 0 0 0 R 1 0 0 0 0 R 2
where G was the two-breed genomic relationship matrix, σ 11 2 and σ 22 2 were the additive genetic variance of breed 1 and breed 2, and σ 12 was the genetic covariance between breed 1 and breed 2. R 1 and R 2 were covariance matrices of residual effects for breed 1 and breed 2. Totally three different strategies to construct the two-breed genomic relationship matrix were shown below.

2.5.3. Unweight G-Matrix ( G U N W )

Unlike GMIX, the G matrix was built with four parts alone (Wientjes et al. 2017), and named this matrix as GUNW. Two within-breed blocks were built identically for the G-Matrix of a single breed, but allele frequencies were calculated for each breed separately. The between-breed blocks were constructed by multiplying the genotypes of two breeds and dividing by the geometric mean of the sum of 2 p ( 1 − p ) of two breeds. Thus, the genomic relationship coefficient ( g i j ) between individual i in breed 1 and individual j in breed 2 was calculated as:
g i j = ∑ k = 1 m M 1 ( i , k ) M 2 ( j , k ) ∑ 2 p 1 , k ( 1 − p 1 , k ) ∑ 2 p 2 , k ( 1 − p 2 , k )
where M 1 and M 2 were genotype matrices of breed 1 and breed 2, m is the number of markers, and p 1 , k and p 2 , k was the observed allele frequencies of A 2 at locus k for breed 1 and breed 2, respectively.

2.5.4. LD Weight G-Matrix ( G L D )

Since the concordance of LD phases between markers and QTL of different breeds may vary across the genome, it is inappropriate to assume that the covariance of SNP effects on two breeds is the same for all SNPs in the genome (Zhou et al. 2014). Therefore, we accounted for LD phase consistencies in constructing the two-breed GRM. As the phase consistency was defined as 1 for two animals of the same breed, within-breed blocks of the GLD matrices were constructed without weighting or weighting all markers by one (the same as the GUNW matrix). Therefore, differential marker weighting was only applied on the between-breed blocks. For example, g i j of individual i in breed 1 and individual j in breed 2 was calculated as:
g i j = ∑ k = 1 m M 1 ( i , k ) M 2 ( j , k ) w k ∑ 2 p 1 , k ( 1 − p 1 , k ) ∑ 2 p 2 , k ( 1 − p 2 , k )
where M 1 , M 2 , m, p 1 , k and p 2 , k were defined as above, w k was the weight on marker k. The weights (w) were LD phase consistencies, measured as correlations of all pairwise r L D 2 between two breeds (indicated as c o r L D ). The r L D 2 was the measurement of LD between any pair of markers within a marker interval, described as before. We divided all SNPs (common to both breeds) into three intervals of different sizes, which contained 10 SNPs in each interval. We used these makers in each interval to calculate the LD phase consistencies ( c o r L D ) and took r L D 2 as the weight for all the SNPs in the corresponding interval. For each locus, we calculated the r L D 2 of the ten nearest loci to it and calculated the correlation of r L D 2 between two breeds as weights. If there is only one shared pair, we used the mean of all SNPs pairs instead.

2.5.5. BayesR Model

We used the hybrid variant of the BayesR model (Wang et al. 2016) that first uses an expectation-maximization (EM) module, followed by a Monte Carlo Markov chain (MCMC) model for 10,000 iterations, fitting the following model:
y i = X b + ∑ j = 1 p m i j α j + W v + e i
where y i is a vector of phenotypes, m i j is the genotype covariate at locus j for individual i (coded as 0, 1,2), p is the number of genotyped loci, α j is a vector of allele substitution effects for locus j, W is a design matrix of genotypes and v a vector of variant effects, drawn from 4 normal distributions with N (0,0* σ g 2 ), N (0,0.0001* σ g 2 ), N (0,0.001* σ g 2 ), and N (0,0.01* σ g 2 ), where σ g 2 is the additive genetic variance and prior distribution of the proportion of variants per distribution P ~ Dirichlet(α), with α = [1,1,1,1], and e i is a vector of random residuals for individual i. Fixed effects or general mean, in this case, are assigned flat priors (Brondum et al. 2012; van den Berg et al. 2019). Fix effects and covariates including gender, farm, breed, birth year and individual age of slaughter (day) were considered in the model.
The results of each model were evaluated using the accuracy of predictions. The prediction accuracy ( r G E B V , y ^ ) was measured with Pearson's correlation coefficient, that calculated as   r G E B V , y ^ = C o r ( G B E V , y ^ ) , where y ^   is the residual value after correcting the fixed effect. Each dataset was randomly divided into five groups, four groups of them were used as a training dataset and the remain groups were used for validation, 10 replicates of 5-fold cross-validation for each trait. Accuracy was determined as the mean of results for five-fold cross-validation procedures. we sampled 100 random individuals to compose the training population, and the remaining individuals compose the reference population (Wang et al. 2023).

3. Results

3.1. Descriptive Statistics of the Analyzed Traits

Table 1 presents a comprehensive summary of the statistical attributes of slaughter weights across three distinct cattle breeds: Huaxi cattle ( S W T H X ), Chinese Wagyu ( S W T W G ), and Yunling cattle ( S W T Y L ). The mean slaughter weights are 544.05kg, 605.10kg and 372kg with standard deviations of 80.95kg, 72.05kg, and 36.01kg for HX, WG and YL cattle, respectively. The coefficient of variation for each breed are 14.88%, 11.91%, and 9.68%, indicating a relative dispersion of data points. The small phenotypic variation in each population shows that the quality of phenotype data for the three breeds were relatively high. Heritability estimates are 0.40 for S W T H X , 0.53 for S W T W G , and 0.49 for S W T Y L , suggesting a moderate to high genetic influence on these traits.

3.2. Genomic Relationship of Two Breeds

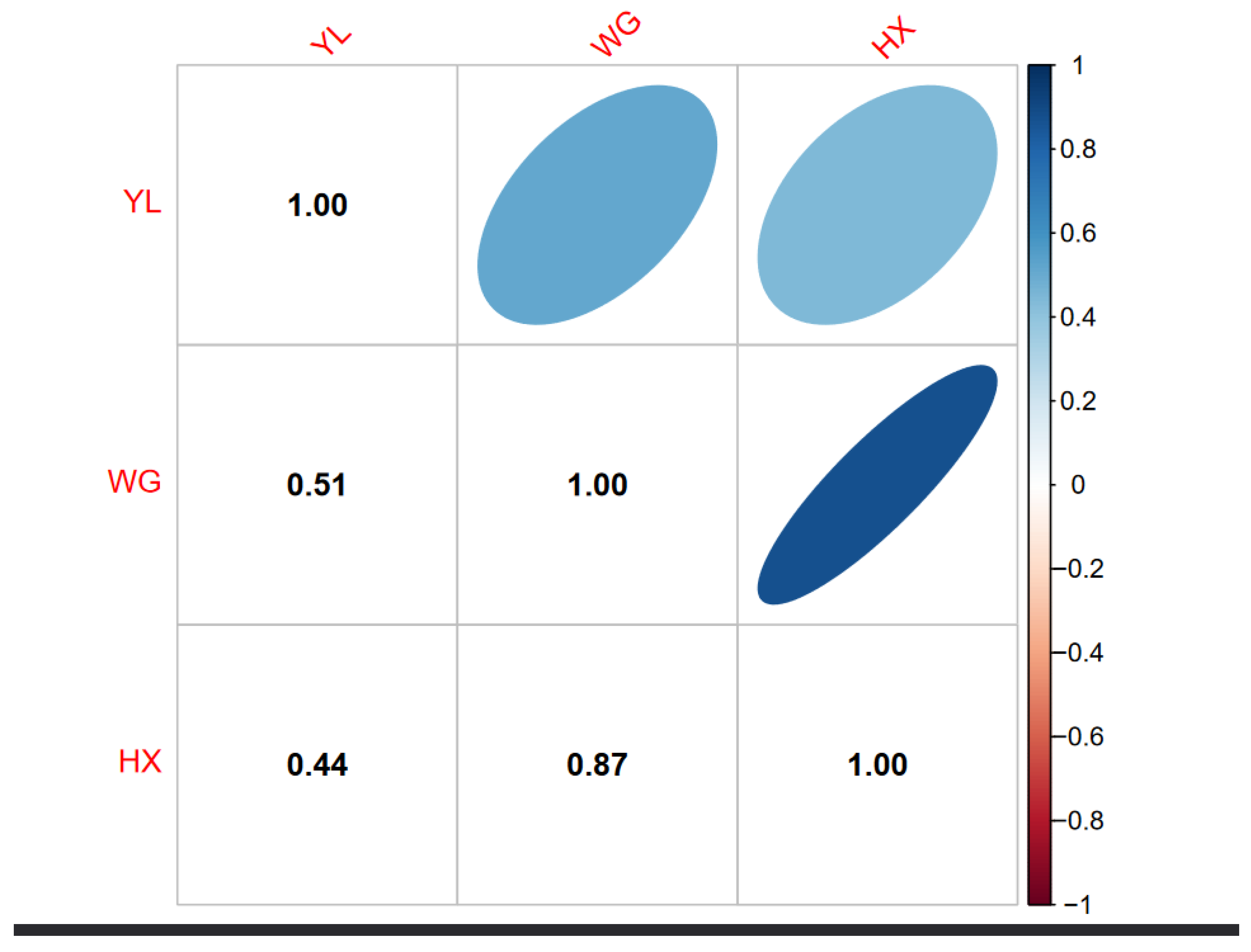
Figure 1 illustrates the genetic relationship among three cattle breeds: YL, WG, and HX. The off-diagonal elements represent the genetic relationships between breeds. The genetic similarity between YL and WG is represented as 0.51, between YL and HXN as 0.44, and between WG and HX as 0.87. These values suggest a moderate genetic relationship between YL and the other two breeds, and a high genetic similarity between WG and HX.

3.3. Prediction Accuracy of Within-Breed GS

The Table 2 compares the prediction accuracy of two genomic selection methods, GBLUP and BayesR, using high-density chip data (HD) and whole-genome sequence data (WGS) across three cattle breeds: Huaxi (HX), Chinese Wagyu (WG), and Yunling (YL).
In Huaxi cattle, the prediction accuracy of GBLUP is 0.41 (±0.013) with HD and 0.42 (±0.010) with WGS. BayesR outperforms GBLUP, showing accuracies of 0.52 (±0.010) for HD and 0.46 (±0.008) for WGS.For Chinese Wagyu cattle, both GBLUP and BayesR show equal accuracies of 0.34 (±0.017 and ±0.012, respectively) with HD. Similarly, with WGS, both methods yield an accuracy of 0.38, but with slightly different standard errors (GBLUP: ±0.012, BayesR: ±0.011).In Yunling cattle, GBLUP’s accuracy is 0.28 (±0.021) with HD and 0.28 (±0.019) with WGS. BayesR shows a slightly better performance with accuracies of 0.30 (±0.016) for HD and 0.32 (±0.011) for WGS.
The table demonstrates that BayesR generally provides higher prediction accuracies compared to GBLUP, especially in the Huaxi cattle breed. The impact of SNP density (HD vs. WGS) varies depending on the breed and the method, with notable differences in Huaxi cattle but less so in the other breeds.

3.4. Accuracy of Multi-Breed GS

Table 3 presents the prediction accuracies of GUNW-GBLUP, GLD-GBLUP and BayesR models using high-density chip data (HD) and whole-genome sequence data (WGS) in various combinations of reference populations (refPop) for HX, WG, and YL cattle breeds.
The results highlight significant differences in prediction accuracies between GBLUP and BayesR models across different breeds and genomic data types. Notably, BayesR generally exhibits higher prediction accuracies than GBLUP models. For instance, in the HX+WG refPop, BayesR achieves a prediction accuracy of 0.48±0.014 with HD and 0.53±0.012 with WGS in HX cattle, outperforming the GBLUP models. Similarly, across different refPop combinations, BayesR consistently demonstrates superior performance in capturing the genetic architecture of the traits, particularly with WGS data. Meanwhile, the average prediction accuracy of G U N W -GBLUP in multi-breed strategy were similar with the within-breed strategy, and the prediction accuracy of G L D -GBLUP usually higher than that of G U N W -GBLUP in multi-breed and within-breed strategies.
Furthermore, the table also underscores the impact of different reference populations on prediction accuracy. The inclusion of multiple breeds in the reference population generally enhances prediction accuracy for each breed, indicating the benefit of multi-breed genomic selection approaches in capturing broader genetic variation.

4. Discussion

4.1. Impact of BayesR and GBLUP on GEBV in Single and Multiple Breed Genomic Selection

The results from the study indicate an advantage of BayesR over GBLUP in GS, especially in multi-breed contexts like HX, WG and YL cattle breeds. BayesR with its ability to handle polygenic traits and complex genetic architectures, provides higher prediction accuracies compared to GBLUP. This is particularly evident in Huaxi cattle, where BayesR achieves a prediction accuracy of 0.52 with HD chip data and 0.46 with whole-genome sequence WGS data, significantly outperforming GBLUP. This is in agreement with Wang et al.(Wang et al. 2016) and Irene et al.(van den Berg et al. 2017) who show that the accuracy with the hybrid model was equal to that with Bayes R, which confirms that the hybrid model is an efficient alternative to Bayes R. This superiority is particularly evident in multi-breed genomic selection scenarios, highlighting potential of BayesR in handling the complex genetic architecture of diverse cattle populations.
The efficacy of genomic predictions utilizing GBLUP is contingent upon the magnitude of the reference population (Goddard 2009; Daetwyler et al. 2010). Consequently, when a substantial reference population is accessible for a singular breed of HX, GBLUP attains a significant portion of the prospective accuracy for genomic predictions, thereby rendering the utilization of nonlinear BayesR techniques for prediction or WGS genomic markers seemingly inconsequential (Vanraden et al. 2013). However, Habier et al. (Habier et al. 2010) have indicated that the efficacy of genomic prediction using GBLUP with medium density SNPs diminishes when more robust predictions are required, particularly for predicting the genetic merit of distantly-related animals, such as those in future generations or from different breeds. They further reported inferior predictive performance of GBLUP over successive generations in comparison to BayesB (Habier et al. 2010). Nevertheless, our findings demonstrate the merits of employing nonlinear genomic prediction methods for multi-breed predictions.

4.2. Effect of Using LD Information Weighted GRM on GEBV Accuracy

In our findings, it was observed that the prediction accuracy of G L D -GBLUP generally slightly surpasses that of G U N W -GBLUP when employing both multi-breed and within-breed strategies. The use of LD information in weighting GRMs can impact the accuracy of GEBV(Steyn et al. 2019). LD-weighted matrices capture the non-uniform distribution of informative markers across the genome, which is crucial for traits influenced by regions with high LD. Such weighting schemes can enhance the prediction ability to capture the genetic architecture of traits, thereby improving prediction accuracy. This approach is particularly beneficial in populations with varying marker density and LD patterns, enabling more precise estimation of genetic similarities and differences.
However, concurrently, certain articles present an alternative perspective. The study conducted by Zhou et al. revealed that the inclusion of LD phase consistencies, marker effects, or a combination of both, in the weighting of the G-matrices in Nordic Holstein and Nordic Red cattle, did not result in any notable improvement in the accuracies of the two-breed predictions (Zhou et al. 2014).

4.3. Influence of Genetic Correlation between Different Breeds on GEBV Accuracy

Variations in complex traits across populations can be attributed to disparities in genetic and environmental factors(Wientjes et al. 2017). In current study, the application of LD phase persistence in determining relationships among breeds demonstrates the impact of LD-weighted GRMs on GEBV accuracy. This underscores the importance of considering LD information in GRM construction, especially in multi-breed genomic selection scenarios (Ma et al. 2018).
The examination of genetic correlation among populations offers valuable insights into the variations in genetic architecture of traits across different populations (Brown et al. 2016). This is pivotal for genomic prediction strategies, as evidenced by Lund et al. and Brøndum et al., who showed improved prediction accuracy using closely related breeds in reference groups(Brondum et al. 2011; Brown et al. 2016). The study reiterates the necessity of considering genetic correlation and relatedness between populations when transferring genomic information across breeds. A diminished genetic correlation between populations suggests that causal loci exhibit distinct effects and/or that diverse causal loci underlie the trait(Wientjes et al. 2017).
Furthermore, the genetic correlation offers valuable insights into the feasibility of utilizing data from multiple populations for the purpose of genomic prediction. In cases where the genetic correlation is low, the efficacy of merging populations into a single training population or incorporating information regarding the distribution of causal variants across populations, as practiced in multi-task Bayesian models (Chen et al. 2014; Technow and Totir 2015), is unlikely to enhance the accuracy of estimated genetic values. This is primarily due to the expected dissimilarities in effects and locations of causal loci.
For implementing multi-population genomic prediction, explicit and accurate knowledge of genetic (co)variances and correlations is not required. Therefore, accuracy of estimated genetic values is quite consistent across methods for calculating GRM (Makgahlela et al. 2013, 2014; Lourenco et al. 2016). For predicting the accuracy in those scenarios, however, an accurate estimation of genetic correlations is essential (Wientjes et al. 2015). In academic contexts, the amalgamation of populations is advantageous when the training population for one of the groups is limited in size, and there exists a substantial degree of genetic relatedness and correlation between the populations. This circumstance is particularly evident in the scenario of subpopulations originating from the same breed but residing in disparate environments.

4.4. Impact of Marker Density on the Accuracy of Genomic Estimated Breeding Values

The study also addresses the influence of marker density on the accuracy of genomic predictions, highlighting that increased marker density enhances GEBV accuracy both in within- and multi-breed GS. This aligns with the understanding that higher marker density captures more genetic variation, providing a more detailed genetic profile for selection. This is particularly significant in multi-breed genomic selection contexts.
Irene et al. (van den Berg et al. 2017) demonstrated that the utilization of simulated data revealed a superior accuracy in the analysis of sequence data compared to the analysis of HD SNP genotypes. Specifically, the employment of WGS data conferred a significant advantage over the HD dataset, thereby leading to higher accuracy in all scenarios involving sequence data as opposed to the HD dataset. The authors utilized authentic data to demonstrate that the superiority of WGS over HD genotyping was significantly less pronounced in the Red Holstein validation population compared to the Australian Red validation population. This discrepancy can be attributed to the conservation of LD over shorter distances across breeds compared to within breeds. Consequently, the utilization of sequence data is believed to offer particular advantages in multi-breed and across-breed prediction scenarios (Lund et al. 2016).
There are two factors contributing to the enhanced accuracy achieved through the utilization of sequence data: firstly, it has the potential to encompass a greater extent of genetic variability, and secondly, it can encompass QTL with substantial effects in cases where there is an absence of high-density SNPs in complete LD with said QTL. Irene et al. have suggested that predictive models based on sequence data should prioritize variants that are in closer proximity to the QTL, or even coincide with the QTL itself, as this LD is more effectively preserved in the validation population. Furthermore, the adoption of sequence data serves to mitigate the issue of missing heritability (van den Berg et al. 2017).

5. Conclusions

The results of the study suggest that BayesR outperforms GBLUP in terms of multi-breed genomic prediction accuracy, particularly in situations involving breeds with distant genetic relationships. This improved performance of BayesR is crucial in genomic predictions where breed diversity plays a significant role. Additionally, increasing the density of SNP markers is observed to enhance the precision of multi-breed genomic predictions. The findings underscore the efficacy of BayesR in enhancing genomic prediction capabilities and underscore the pivotal role of genetic relationship consideration in devising tailored GS strategies for diverse cattle populations. The study advocates for further investigation into optimizing GRM construction and exploring alternative models to broaden the scope of genomic prediction across different cattle breeds. Such endeavors have the potential to yield more refined and efficient breeding strategies, thereby advancing the field.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org. Figure S1. Plot of Linkage disequilibrium (LD, r 2 ) against distance between SNPs in Huaxi cattle(HX), Chinese Wagyu cattle (WG) and Yunling (YL) genome. Solid curves show the expected decay of LD in the genome-wide data, as well as within and outside the divergence regions, respectively, estimated by nonlinear regression of r 2 . Figure S2. A principal component analysis with first and second components (PCs) with the three different breeds.

Author Contributions

WZZ and LJY conceived and designed the study. MHR and LHW performed statistical analyses. WZZ and MHR wrote the paper. GF, ZB, ZLP, XLY and GHJ participated in data analyses. HYL and ZLP contributed to the acquisition of data. All authors read and approved the final manuscript.

Funding

This study was supported by the Central-level public welfare research institutes basic research business expenses special funds projects (2022-YWF-ZYSQ-02 and 2023-YWF-ZX-04).

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

The data and computing programs used in this manuscript are available from the corresponding author on request.

Acknowledgments

The authors would like to thank all staff at the cattle experimental unit in Beijing for animal care and sample collection.

Conflicts of Interest

The authors declare that they have no competing interests.

Consent to publish

Not applicable.

Abbreviations

CNV copy number variants
CR call rates
EM expectation-maximization
GBLUP Genome-enabled best linear unbiased prediction
GEBV Genomic estimated breeding value
GP Genomic prediction
GRM Genomic relationship matrices
GS Genomic selection
HD High density
HX Huaxi cattle
HW Hardy-Weinberg Equilibrium
LD linkage disequilibrium
MAF Minor allele frequencies
MCMC Markov chain Monte Carlo
PCV Phenotypic coefficient of variation
QTL Quantitative trait loci
SNP Single nucleotide polymorphism
SWT slaughter weight
WG Chinese Wagyu cattle
WGS whole-genome sequence
YL Yunling Cattle

References

  1. Bordbar F, Jensen J, Du M, Abied A, Guo W, Xu L, Gao H, Zhang L, Li J. 2020. Identification and validation of a novel candidate gene regulating net meat weight in simmental beef cattle based on imputed next-generation sequencing. Cell Proliferation, 53, e12870. [CrossRef]
  2. Brondum R F, Rius-Vilarrasa E, Stranden I, Su G, Guldbrandtsen B, Fikse W F, Lund M S. 2011. Reliabilities of genomic prediction using combined reference data of the nordic red dairy cattle populations. Journal of Dairy Science, 94, 4700-4707. [CrossRef]
  3. Brondum R F, Su G, Lund M S, Bowman P J, Goddard M E, Hayes B J. 2012. Genome position specific priors for genomic prediction. Bmc Genomics, 13, 543. [CrossRef]
  4. Brown B C, Ye C J, Price A L, Zaitlen N. 2016. Transethnic genetic-correlation estimates from summary statistics. The American Journal of Human Genetics, 99, 76-88. [CrossRef]
  5. Browning B L, Zhou Y, Browning S R. 2018. A one-penny imputed genome from next-generation reference panels. The American Journal of Human Genetics, 103, 338-348. [CrossRef]
  6. Calus M P L, Goddard M E, Wientjes Y C J, Bowman P J, Hayes B J. 2018a. Multibreed genomic prediction using multitrait genomic residual maximum likelihood and multitask bayesian variable selection. Journal of Dairy Science. [CrossRef]
  7. Calus M P L, Goddard M E, Wientjes Y C J, Bowman P J, Hayes B J. 2018b. Multibreed genomic prediction using multitrait genomic residual maximum likelihood and multitask bayesian variable selection. Journal of Dairy Science, 101, 4279-4294. [CrossRef]
  8. Calus M P, Veerkamp R F. 2007. Accuracy of breeding values when using and ignoring the polygenic effect in genomic breeding value estimation with a marker density of one snp per cm. Journal of Animal Breeding and Genetics, 124, 362-368. [CrossRef]
  9. Chen L, Li C, Miller S, Schenkel F. 2014. Multi-population genomic prediction using a multi-task bayesian learning model. Bmc Genetics, 15, 53. [CrossRef]
  10. Daetwyler H D, Pong-Wong R, Villanueva B, Woolliams J A. 2010. The impact of genetic architecture on genome-wide evaluation methods. Genetics, 185, 1021-1031. [CrossRef]
  11. de Roos A P W, Hayes B J, Spelman R J, Goddard M E. 2008. Linkage disequilibrium and persistence of phase in holstein–friesian, jersey and angus cattle. Genetics, 179, 1503-1512. [CrossRef]
  12. Erbe M, Hayes B J, Matukumalli L K, Goswami S, Bowman P J, Reich C M, Mason B A, Goddard M E. 2012a. Improving accuracy of genomic predictions within and between dairy cattle breeds with imputed high-density single nucleotide polymorphism panels. Journal of Dairy Science, 95, 4114-4129. [CrossRef]
  13. Erbe M, Hayes B J, Matukumalli L K, Goswami S, Bowman P J, Reich C M, Mason B A, Goddard M E. 2012b. Improving accuracy of genomic predictions within and between dairy cattle breeds with imputed high-density single nucleotide polymorphism panels. Journal of Dairy Science, 95, 4114-4129. [CrossRef]
  14. Goddard M. 2009. Genomic selection: prediction of accuracy and maximisation of long term response. Genetica, 136, 245-257. [CrossRef]
  15. Habier D, Tetens J, Seefried F R, Lichtner P, Thaller G. 2010. The impact of genetic relationship information on genomic breeding values in german holstein cattle. Genetics Selection Evolution, 42, 5. [CrossRef]
  16. Hayes B J, Bowman P J, Chamberlain A C, Verbyla K, Goddard M E. 2009. Accuracy of genomic breeding values in multi-breed dairy cattle populations. Genetics Selection Evolution, 41, 51. [CrossRef]
  17. Hill W G, Robertson A. 1968. Linkage disequilibrium in finite populations. Theoretical and Applied Genetics, 38, 226-231. [CrossRef]
  18. Hozé C, Fritz S, Phocas F, Boichard D, Ducrocq V, Croiseau P. 2014. Efficiency of multi-breed genomic selection for dairy cattle breeds with different sizes of reference population. Journal of Dairy Science, 97, 3918-3929. [CrossRef]
  19. Iheshiulor O O, Woolliams J A, Yu X, Wellmann R, Meuwissen T H. 2016. Within- and across-breed genomic prediction using whole-genome sequence and single nucleotide polymorphism panels. Genetics Selection Evolution, 48, 15. [CrossRef]
  20. Kemper K E, Reich C M, Bowman P J, Vander Jagt C J, Chamberlain A J, Mason B A, Hayes B J, Goddard M E. 2015. Improved precision of qtl mapping using a nonlinear bayesian method in a multi-breed population leads to greater accuracy of across-breed genomic predictions. Genetics Selection Evolution (Paris), 47, 29. [CrossRef]
  21. Lourenco D A, Tsuruta S, Fragomeni B O, Chen C Y, Herring W O, Misztal I. 2016. Crossbreed evaluations in single-step genomic best linear unbiased predictor using adjusted realized relationship matrices. Journal of Animal Science, 94, 909-919. [CrossRef]
  22. Lund M S, de Roos A P, de Vries A G, Druet T, Ducrocq V, Fritz S, Guillaume F, Guldbrandtsen B, Liu Z, Reents R, Schrooten C, Seefried F, Su G. 2011. A common reference population from four european holstein populations increases reliability of genomic predictions. Genetics Selection Evolution, 43, 43. [CrossRef]
  23. Lund M S, van den Berg I, Ma P, Brondum R F, Su G. 2016. Review: how to improve genomic predictions in small dairy cattle populations. Animal, 10, 1042-1049. [CrossRef]
  24. Ma P, Huang J, Gong W, Li X, Gao H, Zhang Q, Ding X, Wang C. 2018. The impact of genomic relatedness between populations on the genomic estimated breeding values. Journal of Animal Science and Biotechnology, 9. [CrossRef]
  25. Ma P, Huang J, Gong W, Li X, Gao H, Zhang Q, Ding X, Wang C. 2018. The impact of genomic relatedness between populations on the genomic estimated breeding values. Journal of Animal Science and Biotechnology, 9, 64. [CrossRef]
  26. Makgahlela M L, Stranden I, Nielsen U S, Sillanpaa M J, Mantysaari E A. 2013. The estimation of genomic relationships using breedwise allele frequencies among animals in multibreed populations. Journal of Dairy Science, 96, 5364-5375. [CrossRef]
  27. Makgahlela M L, Stranden I, Nielsen U S, Sillanpaa M J, Mantysaari E A. 2014. Using the unified relationship matrix adjusted by breed-wise allele frequencies in genomic evaluation of a multibreed population. Journal of Dairy Science, 97, 1117-1127. [CrossRef]
  28. Meuwissen T, Goddard M. 2010. Accurate prediction of genetic values for complex traits by whole-genome resequencing. Genetics, 185, 623-631. [CrossRef]
  29. Mohammad Rahimi S, Rashidi A, Esfandyari H. 2020. Accounting for differences in linkage disequilibrium in multi-breed genomic prediction. Livestock Science, 240, 104165. [CrossRef]
  30. Olson K M, Vanraden P M, Tooker M E. 2012. Multibreed genomic evaluations using purebred holsteins, jerseys, and brown swiss. Journal of Dairy Science, 95, 5378-5383. [CrossRef]
  31. Pryce J E, Gredler B, Bolormaa S, Bowman P J, Egger-Danner C, Fuerst C, Emmerling R, Sölkner J, Goddard M E, Hayes B J. 2011. Short communication: genomic selection using a multi-breed, across-country reference population. Journal of Dairy Science, 94, 2625-2630. [CrossRef]
  32. Purcell S, Neale B, Todd-Brown K, Thomas L, Ferreira M A R, Bender D, Maller J, Sklar P, de Bakker P I W, Daly M J, Sham P C. 2007. Plink: a tool set for whole-genome association and population-based linkage analyses. The American Journal of Human Genetics, 81, 559-575. [CrossRef]
  33. Solberg T R, Sonesson A K, Woolliams J A, Odegard J, Meuwissen T H. 2009. Persistence of accuracy of genome-wide breeding values over generations when including a polygenic effect. Genetics Selection Evolution, 41, 53. [CrossRef]
  34. Steyn Y, Lourenco D, Misztal I. 2019. Genomic predictions in purebreds with a multibreed genomic relationship matrix. Journal of Animal Science, 97, 4418-4427. [CrossRef]
  35. Technow F, Totir L R. 2015. Using bayesian multilevel whole genome regression models for partial pooling of training sets in genomic prediction. G3-Genes Genomes Genetics, 5, 1603-1612. [CrossRef]
  36. van den Berg I, Bowman P J, Macleod I M, Hayes B J, Wang T, Bolormaa S, Goddard M E. 2017. Multi-breed genomic prediction using bayes r with sequence data and dropping variants with a small effect. Genetics Selection Evolution (Paris), 49, 70. [CrossRef]
  37. van den Berg I, Macleod I M, Reich C M, Breen E J, Pryce J E. 2020. Optimizing genomic prediction for australian red dairy cattle. Journal of Dairy Science, 103, 6276-6298. [CrossRef]
  38. van den Berg I, Meuwissen T H E, Macleod I M, Goddard M E. 2019. Predicting the effect of reference population on the accuracy of within, across, and multibreed genomic prediction. Journal of Dairy Science, 102, 3155-3174. [CrossRef]
  39. Vanraden P M. 2008. Efficient methods to compute genomic predictions. Journal of Dairy Science, 91, 4414-4423. [CrossRef]
  40. Vanraden P M, Null D J, Sargolzaei M, Wiggans G R, Tooker M E, Cole J B, Sonstegard T S, Connor E E, Winters M, van Kaam J B C H, Valentini A, Van Doormaal B J, Faust M A, Doak G A. 2013. Genomic imputation and evaluation using high-density holstein genotypes. Journal of Dairy Science, 96, 668-678. [CrossRef]
  41. Wang T, Chen Y P, Bowman P J, Goddard M E, Hayes B J. 2016. A hybrid expectation maximisation and mcmc sampling algorithm to implement bayesian mixture model based genomic prediction and qtl mapping. Bmc Genomics, 17, 744. [CrossRef]
  42. Wang Z, Ma H, Li H, Xu L, Li H, Zhu B, Hay E H, Xu L, Li J. 2023. Multi-trait genomic predictions using gblup and bayesian mixture prior model in beef cattle. Animal Research and One Health, 1, 17-29. [CrossRef]
  43. Wientjes Y C J, Bijma P, Vandenplas J, Calus M P L. 2017. Multi-population genomic relationships for estimating current genetic variances within and genetic correlations between populations. Genetics (Austin), 207, 503-515. [CrossRef]
  44. Wientjes Y C, Veerkamp R F, Bijma P, Bovenhuis H, Schrooten C, Calus M P. 2015. Empirical and deterministic accuracies of across-population genomic prediction. Genetics Selection Evolution, 47, 5. [CrossRef]
  45. Zhou L, Lund M S, Wang Y, Su G. 2014. Genomic predictions across nordic holstein and nordic red using the genomic best linear unbiased prediction model with different genomic relationship matrices. Journal of Animal Breeding and Genetics, 131, 249-257. [CrossRef]
Preprints 96372 g001
Figure 1. Genomic relationship coefficients of Huaxi cattle(HX), Chinese Wagyu cattle (WG) and Yunling (YL). It was calculated based on the persistence of the LD phase between populations to determine the genetic relationship among breeds. The values range from -1 to 1, where 1 indicates identical genetic makeup and values approaching, 0 indicate lower genetic similarity.
Figure 1. Genomic relationship coefficients of Huaxi cattle(HX), Chinese Wagyu cattle (WG) and Yunling (YL). It was calculated based on the persistence of the LD phase between populations to determine the genetic relationship among breeds. The values range from -1 to 1, where 1 indicates identical genetic makeup and values approaching, 0 indicate lower genetic similarity.
Preprints 96372 g001
Table 1. Summary statistics of the analyzed traits.
Table 1. Summary statistics of the analyzed traits.
Trait Number Mean SD C.V Minimum Maximum Heritability
S W T H X 1302 544.05 80.95 14.88 318 790 0.40(0.04)
S W T W G 600 605.10 72.05 11.91 594 1001 0.53(0.06)
S W T Y L 400 372 36.01 9.68 295 420 0.49(0.07)
Note: S W T H X , Slaughter weight for Huaxi cattle, kg; S W T W G , Slaughter weight for Chinese Wagyu cattle, kg; S W T Y L , Slaughter weight for Yunling cattle, kg; C.V: coefficient of variation, %.
Table 2. Prediction accuracies of difference methods for within-breed genomic selection.
Table 2. Prediction accuracies of difference methods for within-breed genomic selection.
refPop Method SNP density
HD WGS
HX GBLUP 0.41(0.013) 0.42(0.010)
BayesR 0.52(0.010) 0.46(0.008)
WG GBLUP 0.34(0.017) 0.34(0.012)
BayesR 0.38(0.010) 0.38(0.011)
YL GBLUP 0.28(0.021) 0.28(0.019)
BayesR 0.30(0.016) 0.32(0.011)
Table 3. Prediction accuracies of difference methods for multi-breed genomic selection.
Table 3. Prediction accuracies of difference methods for multi-breed genomic selection.
refPop Method HX WG YL
HD WGS HD WGS HD WGS
HX+WG G U N W -GBLUP 0.41(0.014) 0.44(0.013) 0.34(0.014) 0.35(0.015) 0.10(0.014) 0.11(0.013)
G L D -GBLUP 0.42(0.015) 0.46(0.016) 0.35(0.013) 0.38(0.013) 0.10(0.014) 0.12(0.012)
BayesR 0.48(0.014) 0.53(0.012) 0.4(0.016) 0.44(0.014) 0.13(0.019) 0.17(0.016)
HX+YL G U N W -GBLUP 0.41(0.015) 0.44(0.017) 0.13(0.015) 0.15(0.013) 0.3(0.011) 0.31(0.015)
G L D -GBLUP 0.41(0.019) 0.45(0.018) 0.13(0.019) 0.16(0.015) 0.32(0.015) 0.34(0.019)
BayesR 0.43(0.016) 0.48(0.013) 0.15(0.014) 0.19(0.012) 0.33(0.016) 0.38(0.011)
WG+YL G U N W -GBLUP 0.11(0.018) 0.12(0.017) 0.34(0.015) 0.35(0.018) 0.31(0.017) 0.32(0.017)
G L D -GBLUP 0.13(0.017) 0.15(0.015) 0.35(0.015) 0.37(0.017) 0.33(0.013) 0.35(0.011)
BayesR 0.18(0.016) 0.2(0.013) 0.41(0.018) 0.44(0.018) 0.34(0.016) 0.38(0.014)
HX+WG+YL G U N W -GBLUP 0.42(0.013) 0.44(0.017) 0.35(0.014) 0.36(0.016) 0.31(0.012) 0.32(0.018)
G L D -GBLUP 0.42(0.019) 0.45(0.017) 0.36(0.016) 0.4(0.013) 0.32(0.017) 0.34(0.016)
BayesR 0.45(0.012) 0.49(0.012) 0.43(0.018) 0.48(0.015) 0.34(0.018) 0.39(0.013)
Note: refPop, Reference population; HD, high density chip data; WGS, whole-genome sequence data; HX, Huaxi cattle; WG, Chinese Wagyu cattle; YL, Yunling Cattle; The standard error of prediction accuracy in parentheses.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated