Prerpints.org logo
Preprint
Review

Measurement Uncertainty Analysis of Optical Current Sensors Used in Power Systems

Altmetrics

Downloads

84

Views

25

Comments

0

Submitted:

11 January 2024

Posted:

12 January 2024

You are already at the latest version

Alerts
Abstract
Optical current sensors have been developed and improved in recent decades, and their use has been widespread in power systems, including smart grids. Like any measuring instrument or system, the result of its measurements is associated with a measurement uncertainty, which quantifies its precision. This article presents a review of the main uncertainty contributions that affect the quality and performance of optical current sensors.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

Electromagnetic induction current transformers (CTs) are measuring equipment of significant importance in power systems, being used for the most diverse purposes, through the measurement of high voltage electric current. Optical current sensors (OCSs) have many advantages over conventional CTs, such as: reduced weight and dimensions, facilitating installation, maintenance and use in remote or difficult-to-access areas; operational safety, as they constructed with dielectric materials and potential catastrophic events will not cause explosions as in the case of conventional oil-filled transformers - in addition to that there will be no critical situations of opening the secondary of the current transformers; linearity throughout its dynamic range; relative lower prices; wide bandwidth; absence of magnetic saturation effects; electromagnetic immunity (as they are non-electric sensors); AC and DC measurements; and low power consumption [1,2,3].
However, despite the extensive list of advantages of optical current sensors over conventional sensors, current transformers are still known to be reliable in terms of accuracy and long-term stability. OCSs evaluations regarding these characteristics have not yet yielded conclusive or definitive results. This is one of the reasons why their use has not yet been disseminated, and it is the current challenge for the development of OCSs [4,5,6,7].
Optical current sensors have several components, each of which has behavior and performance that contribute to the measurement uncertainty of these sensors, some of which are insignificant and others more significant, depending on the situation and characteristics of the measurement process where the sensor it is inserted. There is still little literature available on discussions about the modeling and quantification of each of the OCS uncertainty sources, and their combination to obtain sensor measurement uncertainty.
In this paper, the main sources of uncertainty that affect the performance of optical current sensors based on the Faraday effect are presented. Some proposals for modeling, classifying and quantifying these sources of uncertainty are also presented, with the aim of obtaining the measurement uncertainty of these sensors. This paper is divided as follows: section 2 presents the operating principle and the main characteristics of optical current sensors that are relevant for estimating their measurement uncertainty; Section 3 presents the main uncertainty contributions that affect the performance of OCSs. Section 4 analyzes possible statistical modeling of uncertainty contributions to enable the estimation of measurement uncertainty of the OCSs. Finally, section 5 presents some conclusions.

2. Optical Current Sensors

Currently, optical current sensors are used for the most diverse purposes in electrical power systems, such as control, protection, revenue metering, power quality monitoring, measurement of the arbitrary form of primary current, and measurement of current transients and impulses [8,9]. Rose et al. [10] presented the use and performance of optical current sensor with inline-Sagnac interferometer, using a spun polarization maintaining fiber as sensing element, in measurement and protection applications in high voltage alternating current systems, and in control, measurement and protection applications in power systems in high voltage direct current (HVDC) systems. In the area of protection of power systems, Azad et al. [11] present a data-based primary fault detection and identification algorithm for HVDC grids where current measurements are performed by OCSs. The algorithm benefits from the wide bandwidth of OCSs. Lei et al. [12] proposed a method for measurement of transformer inrush current using an OCS, taking advantage of its immunity to the effects of magnetic saturation. Ivanov et al. [13] provided a comparison between CTs and OCSs measurements of a 250 MVA auto-transformer re-energizing inrush current, obtained during a field test at a 500 kV substation.
Applications of OCSs in high voltage substations usually require accuracies down to 0.2%, often over a temperature range of tens of degrees Celsius. However, research has shown that ensuring this accuracy is challenging. Several influence factors, such as mechanical disturbances, temperature variation effects on the optical elements, vibration, residual linear birefringence inside the sensing coil and others deteriorate the performance of OCSs [14,15].
Regarding smart grids, they have been disseminated in recent years, and their monitoring is increasingly crucial for their reliable and safe operation, which is carried out through sensors that measure generation and consumption of energy, characterize operating states and detect the current topology of the network. In electrical systems, the most important electrical parameters to be measured are voltage and current. Considering that optical current sensors have the advantages of reduced weight and dimensions, facilitating their installation and maintenance, even allowing the measurement of electrical current without contact with the primary circuit, and still have relatively low prices, they become promising alternatives for use in smart grids [1,16].
The optical sensors discussed in this paper have their operating principle based on the Faraday Effect. The Faraday effect describes the relation between light and magnetic field. Also called the magnetic-optical effect, and first observed by the English physicist Michael Faraday in 1845, this phenomenon consists of the rotation of the polarization direction of a linearly polarized (LP) light wave when subjected to the action of a magnetic field throughout its propagation in a transparent medium. The Faraday rotation angle θF resulting from propagation along a path L under the action of a magnetic field B is given by:
θ F = ∫ L   V λ , T . B . d L
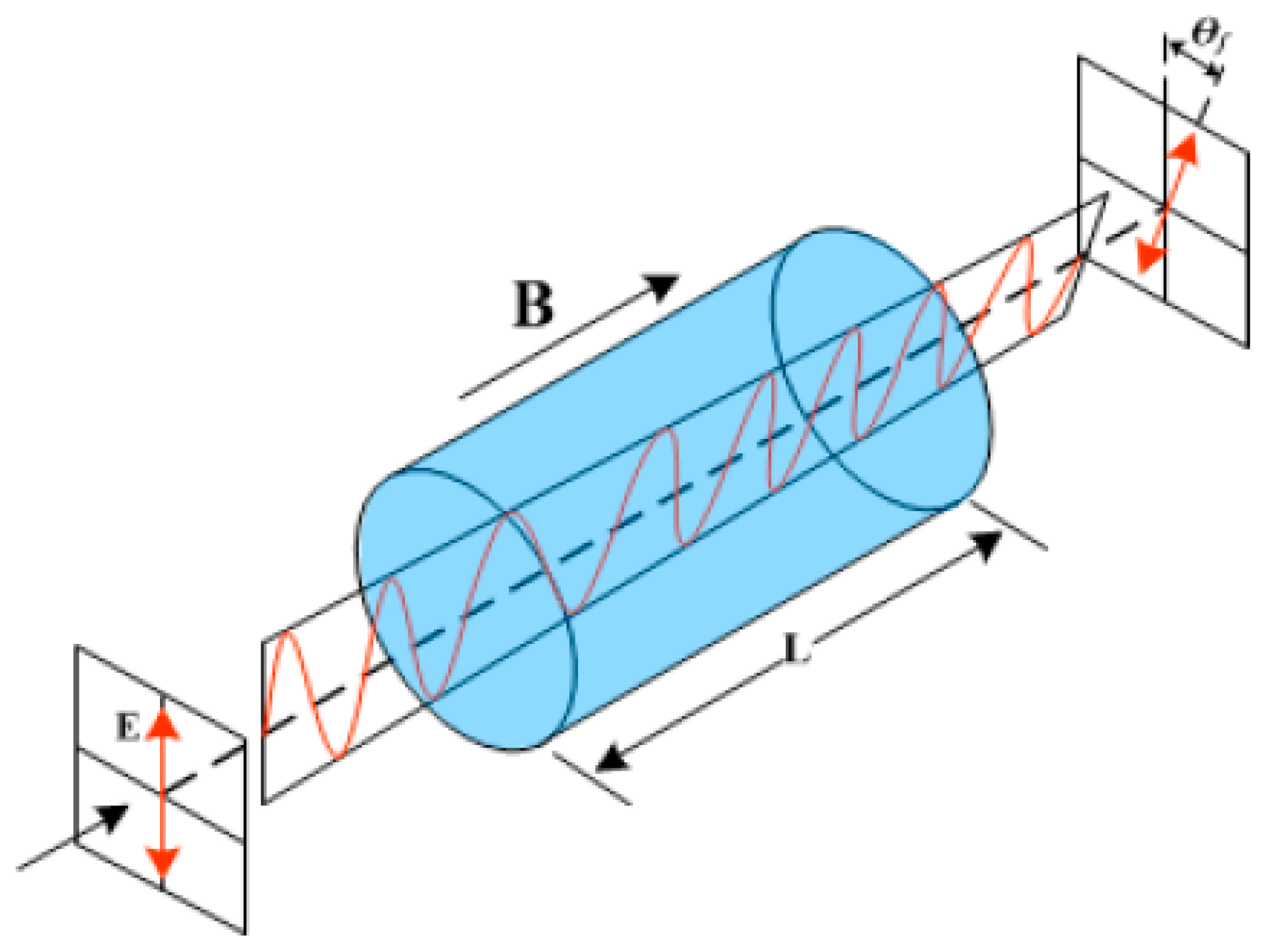
Preprints 96147 g001
Figure 1. Faraday effect in linearly polarized light [17].
Figure 1. Faraday effect in linearly polarized light [17].
Preprints 96147 g001
The measurement of the Faraday rotation angle can be performed using two methods: polarimetric and interferometric detection. In the polarimetric method, the intensity change due to polarization rotation from the induced magnetic field generated by current is detected. A LP light wave is injected into the optical sensor that will measure the electric current. The light wave is then analyzed at the output of the sensor using a second polarizer and a photodetector. The analyzer and photodetector combination converts and modulates polarized light into an electrical signal, which in turn corresponds to electric current to be measured [18,19]. The bandwidth of the polarimetric detection scheme is only affected by the response speed of the detector, and its upper measurement frequency can be up to 100 MHz, so it can be used for transient current measurements. Polarimetric devices are severely susceptible to the effect of linear and circular birefringence, which can cause distortion of the polarization rotation, as well as reducing sensor accuracy and sensitivity. This results in false current readings from these perturbations [20].
In the interferometric method, the linear polarization of light is divided into two orthogonal circular polarizations light waves: one with circular polarization on the left and one on the right. When light waves pass through the sensor, the magnetic field that is created by the current being measure slows down one component and speeds up the other, due to the Faraday effect. The change between the two circular polarized light waves can be used as detection signal [21,22].
OCSs can have two types of structure, regarding the enclosure of the conductor of the electrical current to be measured by the sensing element: closed-core sensors completely surround the current conductor, and for this reason they are less susceptible to certain types of influences, such as vibration and that from stray magnetic fields. Open-core sensors do not completely surround the conductor and are therefore more susceptible to vibration and stray magnetic fields but are easy to install and use [23].
According to their sensing element, OCSs can be classified into two main groups: bulk sensors and fiber sensors. The first group uses a magneto-optical glass structure as a sensor element, with a high Verdet constant. The sensor can be used involving the entire conductor of the current to be measured or only part of it. The problem with using this type of sensor is the influence of external magnetic fields, like those generated by other adjacent current conductors. For example, in three-phase transmission lines, adjacent conductors are in parallel directions, so that the external magnetic field is orthogonal to the current to be measured. Bulk sensors have some advantages over fiber sensors: in addition to having a higher Verdet constant, they are smaller and more mechanically rigid, in such a way that mechanical gradients, thermal variations, vibrations and external noise do not significantly alter performance. Furthermore, due to its low photoelastic coefficient, birefringence linear is very small, which allows to obtain sensors with high sensitivity [17,23,24].
In fiber optic current sensors, the sensing element is the fiber itself. The main advantage of these sensors is the possibility of involving the entire conductor of the electrical current to be measured. The sensitivity of this sensor can be adjusted by increasing or decreasing the number of fiber turns around the conductor. This way, the sensor can use several meters of fiber, which will make it more sensitive to environmental variables, such as temperature and vibration, when compared to bulk sensors. However, as the fiber optic sensor forms a closed path along the electrical current conductor, it becomes insensitive to external magnetic fields [17].
Figure 2 shows an OCS block diagram. This is useful to identify and classify uncertainty sources. In an OCS, a light wave is launched from an optical source, passes through a linear polarizer, and becomes LP light. This LP light propagates through a magneto-optical material along the external magnetic field produced by the electric current to be measured (the sensor itself). The detector part of an OCS converts the measurement of the rotation angle to an electric signal and digitizes it through an analog-to-digital (A/D) card. A software then processes the digital signals and presents to the user the measured current.

3. Uncertainty Sources

This section presents and discusses the most important contributions to OCS measurement uncertainty. Some of the most important uncertainty contributions are those due to the influence of temperature, vibration, birefringence and the aging of optical devices and signal processing on the sensors [10,25,26].

3.1. Temperature

Temperature contributes to OCS measurement uncertainty due to the main following mechanisms: (a) temperature fluctuations change the wavelength of light generated by the light source, thus modifying the Verdet constant of the optic material and the Faraday rotation measured by the OCS; (b) As the Verdet constant of the optical material depends on the temperature, it will fluctuate with temperature variations; (c) temperature fluctuations change metrological properties of optoelectronics components used in the OCS, such as photodiodes and data acquisition units; (d) birefringence of the optic material varies with temperature variations. When modeling uncertainty contributions arising from temperature, two main situations can be established: one in which temperature fluctuations during measurement modify the performance of the sensor and its components and another where the sensor is used at a temperature different from that at which it and its components have been calibrated.
Many temperature compensation schemes have been proposed and can be found in the literature [27,28,29,30]. Despite this, the residual temperature needs to be quantified and have its influence on the uncertainty of the measurement evaluated.
Hoffman [31] presented the variation of the Verdet Constant of different optical glasses according to the wavelength in the visible spectral range. It was observed that glasses with a higher concentration of PbO presented higher Verdet constants. Müller et al. [32] demonstrated a method for self-compensation of the change in the response of an interferometric fiber optic current sensor, caused by deviations in the wavelength of the light emitted by the light source caused by temperature variations. This variation of sensor response with respect to wavelength variation is reduced from more than 1% to <0.2%, in wavelength ranges of at least 10 nm around 1305 nm. Chen et al. [33] measured the average wavelength variation of a superluminescent diode (SLD), in the temperature range of 15 °C to 45 °C. When the temperature varies, the variation in the average wavelength has a linear trend. A variation in wavelength of about +0.6 nm/K was measured, in the wavelength region of 1310 nm.
Williams et al. [34] measured the temperature dependence of the Verdet constant of SiO2, SF-57 and BK-7. The Verdet constant variation per K was about (1.3 ± 0.08) x 10-4 for SF-57, about (0.7 ± 0.03) x 10-4 for SiO2 and (0.6 ± 0.06) x 10-4 for BK-7. When the optical material has a high Verdet constant, and its linear thermal expansion coefficient is much lower than its coefficient of relative variation of Verdet constant as a function of temperature, its length temperature-induced variation becomes non-significant. For example, for the SF-57 glass, linear thermal expansion coefficient is 8.3 x 10-6 per K in the range of -30 °C to 70 °C, about 16 times lower than relative change of Verdet constant due to temperature [35].
Temkina et al. [15,36] proposed a method for compensating the response variation of a fiber optic current sensor with an interferometric detection scheme, due to the dependence on the temperature of the fiber quarter-wave plate. The maximum deviation using the proposed method was ±0.2% on the temperature range of 10°C to 50°C. It was also presented that the errors due to dependence of the temperature of the circulator and electro-optical modulator were non-significant, but errors of the fiber delay line and the spun fiber used as sensing element due to temperature variation were significant.

3.2. Vibration and impact

For OCSs with an open core, the conductor of the electrical current to be measured is not surrounded by the optical material of the sensor, meaning that the line integral of the magnetic field along the optical path is not equal to the total current. However, a linear relationship between sensor measurement and electrical current can be determined based on the geometry and distribution of the field. Vibration causes variations in the relative position between the sensor and conductor, which in turn cause variations in the distribution of the magnetic field across the sensor, introducing changes in the sensor response. Samimi et al. [37] showed that vibration causes large error in open-core OCSs. This error becomes smaller with the increase of distance between the sensor and conductor, the conductor radius or the sensor length. Deviations on OCS accuracy were about ±0.5 % for a vertical displacement of ±0.5 mm when sensor head and the conductor were 7.5 cm apart.
Short et al. [18] showed that OCSs with a polarimetric detection method cannot differentiate an acoustic vibration disturbance detected in the sensing element from the electrical current to be measured. They also showed that the OCSs with in-line Sagnac interferometer are immune to acoustic vibrations in the sensing element, however they are more sensitive to vibrations that occur further away from this sensing element.
Xueming et al. [38] presented an analysis of errors caused by linear stress on inline- Sagnac fiber OCSs under impact. A bias error, which is mainly caused by the stress acting on the delay coil leading to a non-reciprocity birefringence, was found.

3.3. Stability

The detector module of an OCS uses optoelectronic devices, such as photodiodes, photodetectors, and A/D boards. These devices, together with the light source and other components or the sensor as polarizers, couplers, etc. contribute to the measurement uncertainty of an OCS due to their metrological characteristics and their stability – short-term and long-term stability. The metrological data of these devices comes from their technical sheets or manuals. The long-term stability refers to the drift since last calibration.
Aging of the light source device will change the central wavelength of the emitted light, and as the Verdet constant depends on the wavelength, sensor response will change. Wang and Guan [25] analyzed some OCSs used in 110 kV voltage substations. The results showed that OCSs long-term stability was strongly affected by the aging and the performance reduction of the main optical devices of the sensors. Lenner et al. [3] investigated the long-term stability of an interferometric fiber OCS on both component and system perspective. Some components, as the SLD used as the light source, the phase modulator and other passive components were submitted to accelerated ageing by extended temperature cycling. Investigation results showed that the long-term drift of the center wavelength of the SLDs from two manufacturers varied from ±0.19 nm to ±0.38 nm.

3.4. Linear Birefringence

Linear birefringence is the difference between the refraction index of two LP lights. In a linearly birefringent glass, horizontally and vertically polarized light propagates at different speeds, and thus accumulate phase difference. However, the phase difference changes the polarization from linear to elliptical state. Linear birefringence disturbs the sensor behavior, decreasing its sensitivity to Faraday rotation and accuracy. Thus, to improve Faraday Effect measurement quality in OCSs, the linear birefringence must be reduced [39,40].
The optical fiber birefringence can come from several sources. One of the possibilities is that it is intrinsic to the fiber, generated due to imperfections in the manufacturing process. As multimode fibers disrupt the polarization state of light, single-mode optical fibers are the only option for the sensor head. Unfortunately, single-mode fibers suffer from this inherent birefringence. In general, each type of optical fiber has an intrinsic birefringence characteristic, so several types of optical fibers can be evaluated, and the choice of appropriate fibers can reduce it. [39]. Another source of birefringence arises when the fiber is bent to wrap it around the conductor. Curving the fiber breaks the symmetry of its structure because the outer part of the fiber supports stress tension and, on the contrary, the inner part supports compressive stress. The linear birefringence effect is more significant when the fiber is wrapped in many turns around the conductor for higher sensitivity [41]. If the state of polarization (SOP) of the propagating light remains perfectly linear or circular, the sensor response is not affected. But, if the SOP of the propagating light becomes elliptical, due to linear birefringence, the polarization evolution depends not only on the Faraday effect at each position along the fiber, but also on the SOP at the position. Thus, sensor performance is degraded, as its response is affected by the polarization evolution due to the linear birefringence [42].
Temperature and vibration effects also induce birefringence in fiber optic sensors. When temperature fluctuates, the different coefficients of thermal expansion between fiber core and cladding would lead to axial deformation, thus inducing linear birefringence [43]. Zhang et al. [44] presented the results of experiments on the influence of temperature and vibration on sensor performance using three different reflection schemes and three distinct types of fiber. The 90° Faraday rotating mirror showed the best results, regardless of the sensor fiber type. Sima et al. [45] proposed a fiber optic current transformer with improved temperature and vibration robustness. In the temperature influence tests, the ratio error variation was less than ±2% in the temperature range from -20°C to 80°C, while the maximum type A uncertainty was 0.12%. In the vibration tests, the maximum ratio error variation was less than ±0.4%, with the type A uncertainty of 0.029%. Tantaswadi et al. [46] analyzed the effects of the induced linear birefringence due to vibration on the performance of a reciprocal fiber optic current sensor with polarimetric detection. The deviation due to this effect was within ±0.1%

3.5. Other contributions

Resolution uncertainty is important because it considers the limitations of measurement equipment. The accuracy, precision, and capability of your measurements are limited by the resolution of the measurement instruments. Depending on certain conditions of a given measurement process, the contribution of uncertainty associated with resolution is significant in relation to the other contributions. Similar situations can occur in the analog-to-digital conversion process, where electronics resolution impacts the repeated sampling of a signal, leading to digital samples that can differ by just one or two bits. Usually, for a digital indication instrument, its resolution is divided by two to calculate the resolution uncertainty [47,48]. This is the case of sensors that present their measurements in the format of digital indications, as on a computer or display.
Measurement repeatability is the precision of a measurement taken under repeatability conditions. The repeatability conditions include same operating conditions, same location, same operator, same measuring systems and replicated measurements for a measurement of the same measurand (the quantity intended to be measured) [49,50]. In the case of OCSs, perform measurements under these repeatability conditions can be useful to estimate the uncertainty contributions due to the influence of temperature fluctuations and due to the short-term stability of the sensor components.

4. Uncertainty Analysis

Reference [51] sets out general rules for evaluating and expressing the measurement uncertainty that are intended to be applicable to a wide range of measurements. The measurement uncertainty is a qualitative parameter and represents the doubt about the result of that measurement and the incompleteness of the knowledge of the measurand. The terms error and uncertainty are often confused - they are complementary but distinct. It is assumed that the result of a measurement has been corrected for all recognized significant systematic effects and that every effort has been made to identify such effects. The corrections are considered imperfect, due to the lack of knowledge about them. Sometimes it may be impractical to correct for a systematic effect, so it is necessary to model this effect as a source of uncertainty. However, the best option to improve measurement uncertainty is to perform the correction and estimate an uncertainty contribution due to this correction, as it is considered imperfect. In addition to the uncertainty of imperfect corrections, the measurement result is also affected by uncertainty due to random effects and is therefore only an estimate [52].
According to Reference [51], there are two types of uncertainties, categorized respectively as Type A and Type B. A Type A uncertainty is based on the statistical analysis of a series of measurements (for example, statistical data obtained from quality control results). A Type B uncertainty has been obtained by non-statistical procedures and may include: information associated with the numerical quantity of a certified reference material; previous measurements; data obtained from a calibration certificate; information obtained from limits deduced through personal experience; information published in datasheets or manuals; scientific judgment [53]. In some cases, uncertainty contributions that could be assessed as type B are included in a type A assessment, when a reasonable number of observations are able to be performed in the measurement process.
When classifying the uncertainty contributions of optical current sensors, uncertainties arising from short-term effects that are difficult to correct are best quantified through a series of observations, and are therefore defined as type A. This is the case, for example, of uncertainty contributions due to the effects of temperature fluctuation on the light source and other components, as well as the short-term stability of these same components. The combined effect of these uncertainties will be observed if the measurement procedure provides a reasonable number of readings that cover all conditions related to these uncertainty contributions.
On the other hand, effects that allow corrections to be applied to the mathematical model, such as the effect of performing measurements at a temperature different from that at which the sensor components were calibrated, give rise to uncertainty contributions that can be classified as type B. In this case of temperature difference, after applying the correction to the model, the uncertainty due to this correction must be quantified. Other uncertainty contributions that can be classified as type B are those whose assessment using a statistical method is difficult, impractical, or economically unfeasible. This is the case for uncertainties due to the long-term stability of the sensor components and the resolution of the A/D board. Table 1 shows the identified relevant uncertainty contributions to the measurement uncertainty of optical current sensors and their classification.

5. Conclusions

This article presented a review of the main factors that affect the performance of optical current sensors, and how they can be classified and quantified in order to estimate the measurement uncertainty of these sensors. Factors such as temperature, birefringence and component aging can be the biggest contributors to uncertainty. Many schemes have been proposed to compensate or correct the effects of some of these factors, such as temperature. However, it is considered that these compensations or corrections are imperfect, and that there is always an associated uncertainty contribution.

References

  1. Pong, P. W. T.; Annaswamy, A. M.; Kroposki, B.; Zhang, Y.; Rajagopal, R.; Zussman, G.; Poor, H. V. Cyber-enabled grids: Shaping future energy systems. Advances in Applied Energy 2021, 1, 100003. [Google Scholar] [CrossRef]
  2. Larruskain, M.; Valverde, V.; Torres, E.; Buigues, G.; Santos-Mugica, M. Protection Systems for Multi-Terminal HVDC Grids. Renewable Energy and Power Quality Journal 2018, 1, 310–315. [Google Scholar] [CrossRef]
  3. Lenner, M.; Frank, A.; Yang, L.; Roininen, T. M.; Bohnert, K. Long-Term Reliability of Fiber-Optic Current Sensors. IEEE Sensors Journal 2020, 20, 823–832. [Google Scholar] [CrossRef]
  4. Schon, K. High Voltage Measurement Techniques, Fundamentals, Measuring Instruments, and Measuring Methods, 1st ed.; Springer International Publishing: Basel, Switzerland, 2019. [Google Scholar]
  5. Wu, J.; Zhang, X. Recent Progress of All Fiber Optic Current Transformers. In Proceedings of the 7th International Forum on Electrical Engineering and Automation (IFEEA), Hefei, China, 25–27 September 2020. [Google Scholar]
  6. Laurano, C.; Toscani, S.; Zanoni, M. A Simple Method for Compensating Harmonic Distortion in Current Transformers: Experimental Validation. Sensors 2021, 21, 2907. [Google Scholar] [CrossRef]
  7. N’cho, J.S.; Fofana, I. Review of Fiber Optic Diagnostic Techniques for Power Transformers. Energies 2020, 13, 1789. [Google Scholar] [CrossRef]
  8. FOCS - Fiber Optic Current Sensors Enabling smart grids and digital substations. Available online: https://library.e.abb.com/public/a0c2264f26b94c748f7ef2d54bd0bea2/ABB_FOCS%20Kit%20Flyer_20190723.pdf?x-sign=LYr+kJPJwQ5xVj5qzJbKZJh4FzKJcbujknH4FAtts1Vn3ZBMi2r3CYgbxrCrjws8 (accessed on 1 December 2023).
  9. Rahmatian, F.; Ortega, A. Applications of Optical Current and Voltage Sensors in High-Voltage Systems. Proceedings of IEEE/PES Transmission & Distribution Conference and Exposition, Latin America, Caracas, Venezuela, 15–18 August 2006; 18 August 2006. [Google Scholar] [CrossRef]
  10. Rose, A. H.; Hudson, M. C.; Hadley, E.; Perkins, P. Optical Inline-Sagnac Current Sensor, Part II: Performance and Applications. IEEE Transactions on Power Delivery 2022, 6, 6–5401. [Google Scholar] [CrossRef]
  11. Azad, S. P.; Leterme, W.; Van Hertem, D. A DC grid primary protection algorithm based on current measurements. In Proceedings of the 17th European Conference on Power Electronics and Applications (EPE’15 ECCE-Europe), Geneva, Switzerland, 8–10 September 2015. [Google Scholar] [CrossRef]
  12. Lei, C.; Zhizhong, G.; Yue, C.; Guizhong, W. Measurement of inrush current in transformer based on optical current transducer. J. Phys.: Conf. Ser. 2019, 1187, 022004. [Google Scholar] [CrossRef]
  13. Ivanov, N.; Vorobev, P.; Bialek, J.; Kanafeev, R.; Yanin, M. Fiber Optic Current Transformers for Transformer Differential Protection during Inrush Current: a Field Study. Proceedings of IEEE Madrid PowerTech, Madrid, Spain, 28 June-02 July 2021. [Google Scholar] [CrossRef]
  14. Bohnert, K.; Gabus, P.; Nehring, J.; Brandle, H. Temperature and vibration insensitive fiber-optic current sensor. Journal of Lightwave Technology 2002, 20, 267–276. [Google Scholar] [CrossRef]
  15. Temkina, V.; Medvedev, A.; Mayzel, A.; Sivolenko, E.; Poletaeva, E.; Dudnik, I. Experimental Study of Temperature Impact on Fiber Optic Current Sensor Elements. Internet of Things, Smart Spaces, and Next Generation Networks and Systems 2022, 13158. [Google Scholar] [CrossRef]
  16. Oppegård, A.; Katoulaei, M. K.; Oleinikova, I. Complete FEM-based model of a bulk-glass optical current transformer. Proceedings of International Conference on Smart Energy Systems and Technologies (SEST), Eindhoven, Netherlands, 5–7 September 2022. [Google Scholar] [CrossRef]
  17. Silva, R. M.; Martins, H.; Nascimento, I.; Baptista, J. M.; Ribeiro, A. L.; Santos, J. L.; Jorge, P.; Frazão, O. Optical Current Sensors for High Power Systems: A Review. Appl. Sci. 2012, 3, 602–628. [Google Scholar] [CrossRef]
  18. Short, S. X.; Tantaswadi, P.; Carvalho, R. T.; Russell, B. D.; Blake, J. An experimental study of acoustic vibration effects in optical fiber current sensors. IEEE Transactions on Power Delivery 1996, 11, 4–1702. [Google Scholar] [CrossRef]
  19. Tantaswadi, P.; Tangtrongbenchasil, C. Numerical analysis of localized vibration effects and its compensation technique on reciprocal fiber-optic polarimetric current sensor. Proceedings of IEEE International Conference on Industrial Technology, Bangkok, Thailand, 11–14 December 2002. [Google Scholar] [CrossRef]
  20. Leung, F. Y. C.; Chiu, W. C. K.; Demokan, M. S. Fiber-optic current sensor developed for power system measurement. Proceedings of International Conference on Advances in Power System Control, Operation and Management, APSCOM-91., Hong Kong, 5–8 November 1991. [Google Scholar]
  21. Morello, R.; Mukhopadhyay, S. C.; Liu, Z.; Slomovitz, D.; Samantaray, S. R. Advances on Sensing Technologies for Smart Cities and Power Grids: A Review. IEEE Sensors Journal 2017, 17, 7596–7610. [Google Scholar] [CrossRef]
  22. Tzelepis, D. et al. Voltage and Current Measuring Technologies for High Voltage Direct Current Supergrids: A Technology Review Identifying the Options for Protection, Fault Location and Automation Applications. IEEE Access 2020, 8, 203398–203428. [CrossRef]
  23. Samimi, M. H.; Akmal, A. A. S.; Mohseni, H.; Jadidian, J. Open-Core Optical Current Transducer: Modeling and Experiment. IEEE Trans Power Delivery 2016, 31, 5–2028. [Google Scholar] [CrossRef]
  24. Shao, J.; Liu, W.; Liu, C.; Xu, D. A passive optical fiber current sensor based on YIG. In Proceedings of the 1st Asia-Pacific Optical Fiber Sensors Conference, Chengdu, China, 7–9 November 2008; pp. 1–4. [Google Scholar] [CrossRef]
  25. Wang, H.; Guan, Y. Study on Long-Term Operation Stability of Fiber Optical Current Transformer Based on Faraday Effect. Proceedings of International Conference on Intelligent Transportation, Big Data and Smart City, Halong Bay, Vietnam, 19–20 December 2015. [Google Scholar] [CrossRef]
  26. Xu, Z.; Yue, C.; Yan, X.; Fan, J.; Pang, F. Multi-Scale Anomaly Detection in Fiber Optic Current Transformers. Proceedings of IEEE 6th International Electrical and Energy Conference (CIEEC), Hefei, China, 12–14 May 2023. [Google Scholar] [CrossRef]
  27. Müller, G. M.; Gu, X.; Yang, L.; Frank, A.; Bohnert, K. Inherent temperature compensation of fiber-optic current sensors employing spun highly birefringent fiber. Opt. Express 2016, 24, 10–11164. [Google Scholar] [CrossRef]
  28. Liu, C.; Wang, D.; Li, C.; Su, K. Li, D. Yu, D.; Wang, L.; Si, L.; Jin, J. Fiber optic current sensor temperature compensation through RBF neural network. In Proceedings of the Applied Optics and Photonics China, Beijing, China, 30 November–2 December 2020. [CrossRef]
  29. Petricevic, S.J.; Mihailovic, P.M. Compensation of Verdet Constant Temperature Dependence by Crystal Core Temperature Measurement. Sensors 2016, 16, 1627. [Google Scholar] [CrossRef]
  30. Müller, G. M.; Frank, A.; Yang, L.; Gu, X.; Bohnert, K. Temperature Compensation of Interferometric and Polarimetric Fiber-Optic Current Sensors with Spun Highly Birefringent Fiber. Journal of Lightwave Technology 2019, 37, 18–4507. [Google Scholar] [CrossRef]
  31. Hoffmann, H. J. A survey of isotropic and anisotropic modifications of the refractive index. J. Phys. IV France 1992, 02, C2-21–C2-30. [Google Scholar] [CrossRef]
  32. Müller, G. M.; Quan, W.; Lenner, M.; Yang, L.; Frank, A.; Bohnert, K. Fiber-optic current sensor with self-compensation of source wavelength changes. Opt. Lett. 2016, 41, 2867–2870. [Google Scholar] [CrossRef]
  33. Chen, X.; Jiang, L.; Yang, M.; Yang, J.; Shu, X. Research on the mean-wavelength drift mechanism of SLD light source in FOG. J. Phys.: Conf. Ser. 2019, 1300, 012047. [Google Scholar] [CrossRef]
  34. Williams, P. A.; Rose, A. H.; Day, G. W.; Milner, T. E.; Deeter, M. N. Temperature dependence of the Verdet constant in several diamagnetic glasses. Appl. Opt. 1991, 30, 1176–1178. [Google Scholar] [CrossRef]
  35. Schott Optical glass - datasheets. Available online: https://refractiveindex.info/download/data/2017/schott_2017-01-20.pdf (accessed on 18 November 2023).
  36. Temkina, V.; Medvedev, A.; Mayzel, A.; Mokeev, A. Compensation of Fiber Quarter-Wave Plate Temperature Deviation in Fiber Optic Current Sensor. Proceedings of IEEE International Conference on Electrical Engineering and Photonics, St. Petersburg, Russia, 17–18 October 2019. [Google Scholar] [CrossRef]
  37. Samimi, M. H.; Bahrami, S.; Akmal, A. A. S.; Mohseni, H. Effect of Nonideal Linear Polarizers, Stray Magnetic Field, and Vibration on the Accuracy of Open-Core Optical Current Transducers. IEEE Sensors Journal 2014, 14, 10–3508. [Google Scholar] [CrossRef]
  38. He, X.; Wang, G.; Gao, W.; Wang, Y.; Gao, H. The effect analysis of impact on a fiber optic current sensor. Optik 2021, 238, 166724. [Google Scholar] [CrossRef]
  39. Samimi, M. H.; Akmal, A. A. S.; Mohseni, H. Optical Current Transducers and Error Sources in Them: A Review. IEEE Sensors Journal 2015, 9, 9–4728. [Google Scholar] [CrossRef]
  40. Sawale, B. A. Effect of induced linear birefringence on Faraday current sensor using Ultra-low birefringence Optical Fiber. In Proceeding of International Conference on Electrical Power and Energy Systems (ICEPES), Bhopal, India, 14–16 December 2016. [Google Scholar] [CrossRef]
  41. Madaschi, A.; Brunero, M.; Ferrario, M.; Martelli, P.; Boffi, P.; Martinelli, M. Experimental Evaluation of the Birefringence Effect on Faraday-Based Fiber-Optic Current Sensors. IEEE Sensors Letters 2022, 6, 1–4. [Google Scholar] [CrossRef]
  42. Hotate, K.; Konishi, Y. Formulas describing error induced by fiber linear-birefringence in fiber-optic current sensors. Proceedings of 15th Optical Fiber Sensors Conference Technical Digest, Portland, USA, 10 May 2002. [Google Scholar] [CrossRef]
  43. Song, C.; Zhizhong, G.; Guoqing, Z.; Wenbin, Y.; Yan, S.; Shixin, J. The Analysis on Temperature Characteristic of Fiber Optic Current Sensor Ratio Error. In Proceedings of the Fifth International Conference on Instrumentation and Measurement, Computer, Communication and Control (IMCCC), Qinhuangdao, China, 18–20 September 2015. [Google Scholar] [CrossRef]
  44. Zhang, H. Temperature and Vibration Robustness of Reflecting All-Fiber Current Sensor Using Common Single-Mode Fiber. Journal of Lightwave Technology 2014, 32, 4311–4317. [Google Scholar] [CrossRef]
  45. Sima, W.; Zeng, L.; Yang, M.; Yuan, T.; Sun, P. Improving the Temperature and Vibration Robustness of Fiber Optic Current Transformer Using Fiber Polarization Rotator. IEEE Transactions on Instrumentation and Measurement 2022, 71, 1–12. [Google Scholar] [CrossRef]
  46. Tantaswadi, P.; Tangtrongbenchasil, C.; Maheshwari, S. Study of current measurement error due to vibration in reciprocal fiber-optic polarimetric current sensor. Proceedings of 4th IEEE International Conference on Power Electronics and Drive Systems, Denpasar, Indonesia, 25 October 2001. [Google Scholar] [CrossRef]
  47. Hogan, R. How to Determine Resolution Uncertainty. Cal Lab Magazine 2017, 24, 1–20. [Google Scholar]
  48. Phillips, S. D.; Toman, B.; Estler, W. T. Uncertainty Due to Finite Resolution Measurements. Journal of Research of the National Institute of Standards and Technology 2008, 113, 3–143. [Google Scholar] [CrossRef]
  49. De Bièvre, P. Measurement uncertainty is not synonym of measurement repeatability or measurement reproducibility. Accred Qual Assur 2008, 13, 61–62. [Google Scholar] [CrossRef]
  50. Alvarez-Prieto, M.; Jiménez-Chacón, J.; Montero-Curbelo, Á. Do we need to consider metrological meanings of different measurement uncertainty estimations? Accred Qual Assur 2009, 14, 623–634. [Google Scholar] [CrossRef]
  51. Evaluation of measurement data — Guide to the expression of uncertainty in measurement - JCGM 100:2008 - GUM 1995 with minor corrections. Available online: https://www.bipm.org/documents/20126/2071204/JCGM_100_2008_E.pdf/cb0ef43f-baa5-11cf-3f85-4dcd86f77bd6 (accessed on 19 December 2023).
  52. Cohen, E. R. Error and Uncertainty in Physical Measurements. In Modeling Complex Data for Creating Information. Data and Knowledge in a Changing World; Dubois, J. E., Gershon, N., Eds.; Springer: Berlin/Heidelberg, Germany. [CrossRef]
  53. Farrance, I.; Frenkel, R. Uncertainty of Measurement: A Review of the Rules for Calculating Uncertainty Components through Functional Relationships. The Clinical Biochemist Reviews 2012, 33, 49–75. [Google Scholar] [PubMed]
Preprints 96147 g002
Figure 2. OCS basic block diagram.
Figure 2. OCS basic block diagram.
Preprints 96147 g002
Table 1. Classification of OCSs uncertainty sources.
Table 1. Classification of OCSs uncertainty sources.
Uncertainty source Type
Light source wavelength short-term stability A
Correction due to light source wavelength long-term stability B
Light source wavelength variation due to temperature fluctuations A
Correction of the light source wavelength drift due to using the sensor at a temperature far from that at which it was calibrated B
Verdet constant variation due to temperature fluctuations A
Correction of the Verdet constant drift due to using the sensor at a temperature far from that at which it was calibrated B
Vibration A
Correction due to the drift since the last photodetector calibration B
Photodetector short-term stability A
Photodetector performance variation due to temperature fluctuations A
Correction of the photodetector performance drift due to using the sensor at a temperature far from that at which it was calibrated B
Correction of the drift since the last A/D card calibration B
A/D card short-term stability A
A/D card performance variation due to temperature fluctuations B
Correction of the A/D card performance drift due to using the sensor at a temperature far from that at which it was calibrated B
Finite resolution in indicating the measured current to the user B
Repeatability of current measurements A
Correction due to birefringence B
Calibration of the OCS 1 B
1 Calibration can be of the entire sensor or of each of its components.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated